UNIDADE 1
MOVIMENTO
Quantos tipos de movimento um artista descreve ao realizar uma dança? Algumas situações envolvem caminhar, correr, saltar, girar, arrastar-se, equilibrar-se, entre vários outros. Na imagem, a pessoa realiza uma apresentação de brueiki, na qual, após um movimento de pernas corretamente posicionadas, consegue se equilibrar em uma das mãos.
Há uma enorme variedade de movimentos ocorrendo em todo lugar, a todo tempo. Um dos campos da Física se dedica a estudá-los. Nesta Unidade, você conhecerá formas de analisar e descrever alguns movimentos.
Página onze
Respostas e comentários estão disponíveis nas Orientações para o professor.
1. Para você, o quê é movimento? Analisando a pessoa da fotografia, ela está em movimento ou em repouso?
2. Quais provavelmente foram os movimentos realizados pela pessoa da fotografia, desde o início do passo até o instante registrado?
3. Na posição em quê está a pessoa da imagem, equilibrada em uma das mãos, suponha quê ela faça acrobacias com as pernas e com o outro braço. Neste caso, pode-se dizêr quê ela está em movimento?

Página doze
TEMA 1
mêdídas e movimentos
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Observando os movimentos
A história da civilização é marcada pela curiosidade e pelo interêsse nos fenômenos naturais. Ao longo do tempo, conhecimentos foram desenvolvidos com o objetivo de encontrar explicações para fenômenos naturais, como terremotos, tempestades, as fases da Lua, os movimentos dos astros celéstes, a ocorrência de eclipses, a queda dos corpos, entre outros.
Uma das práticas mais antigas realizadas pelas civilizações é a observação do céu, buscando compreender o quê é o Sol, a Lua e os inúmeros pontos luminosos observados no céu noturno, bem como a dinâmica celeste quê faz os corpos mudarem de posição no céu ao longo de determinado período. Refletindo sobre essa dinâmica, é possível indagar: afinal, quem está em movimento: nós ou os diversos outros astros observados?
No cotidiano, é comum perceber os movimentos de um veículo, de uma bola em um jôgo, de um corpo caindo e, intuitivamente, estes movimentos são perceptíveis quando comparados ao movimento relativo da superfícíe da Terra. Além díssu, ao observar o céu durante o dia ou a noite, nota-se o Sol, ou a Lua, mudando de posição, e tudo leva a crer quê a Terra está em repouso enquanto os outros astros se móvem.
A conclusão de quê é a Terra quê está em movimento levou anos para sêr alcançada e exigiu observações, estudos, hipóteses e teorias; isso porque os sêres humanos se móvem com ela sem perceber esse movimento. Embora, por volta de 290 a.C., o astrônomo e matemático Aristarco de Samos (310 a.C.-230 a.C.) já havia propôsto uma teoria de quê o Sol ocuparia a posição central do sistema compôzto da Terra e de outros astros. Essa ideia, chamada heliocentrismo, estava em desacôordo com a do filósofo grego Aristóteles (384 a.C.-322 a.C.), quê propôs um sistema geocêntrico, ou seja, em quê a Terra ocupava a posição central. Assim, a concepção proposta por Aristarco foi rejeitada.

PENSE E RESPONDA

1 Em uma noite de Lua visível no céu, obissérve o movimento quê ela descreve durante cérto intervalo de tempo. Apenas com essa observação, é possível concluir quê é a Terra ou a Lua quê está em movimento?
Página treze
Somente 16 séculos depois, a ideia de Aristarco foi retomada pelo astrônomo e matemático polonês Nicolau Copérnico (1473-1543) e endossada posteriormente por outros cientistas, entre eles o físico, matemático, astrônomo e filósofo italiano Galileu Galilei (1564-1642). Ainda assim, a concepção heliocêntrica demorou alguns anos para sêr amplamente aceita pela comunidade científica.
Galileu se baseou em observações e experimentações para inferir resultados e propor sistematizações. Nas investigações astronômicas, ele é considerado um dos primeiros (que se tem registro) a fazer uso significativo de um telescópio para observar a Lua. Embora não se credite a Galileu a invenção do telescópio, coube a ele fazer diversas melhorias nesse equipamento, aperfeiçoando-o.

MUSEO GALILEO. [Telescópios de Galileu Galilei]. Florença: Museo Galileu, [16--]. 2 telescópios sobre suporte.
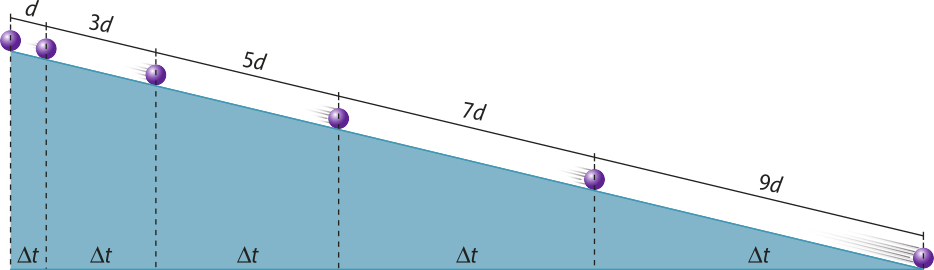
Galileu também foi um dos precursores em utilizar a linguagem matemática para descrever fenômenos observáveis. Um exemplo ocorreu em um dos seus estudos de movimentos sôbi influência da gravidade, quando estudou o movimento de esferas descendo um plano inclinado. Galileu notou o mesmo padrão de movimento, independentemente da inclinação do plano. Assim, ele concluiu quê, para os mesmos intervalos de tempo, os deslocamentos executados pela esféra eram múltiplos de fatores ímpares.
Quando se fala em movimento, pode-se pensar apenas naqueles relacionados à mobilidade urbana, quê permitem às pessoas ir e vir, ou em um corpo caindo. Porém, existem inúmeros outros movimentos. Há os quê impactam a vida – como o das partículas quê compõem a matéria em geral, o dos gases na atmosféra, o do sangue no corpo humano –, e outros quê são essenciais no Universo, como dos astros celéstes, dos elétrons em uma corrente elétrica, da luz e de outras radiações, entre vários outros exemplos. Devido a essa importânssia, existe uma área da Física exclusiva para estudar os movimentos, a Mecânica.
Página quatorze
OFICINA CIENTÍFICA
Um modelo explicativo para o arco-íris
Nunca olhe diretamente para o Sol, inclusive durante a realização desta atividade.
Ao longo dos séculos, os sêres humanos desenvolveram formas de organização de suas observações. O fazer Ciência usa estratégias e métodos para alcançar resultados ou invalidar concepções. Não existe um método único de desenvolver Ciência, mas alguns elemêntos como a observação, a experimentação, a elaboração de hipóteses, são algumas das estratégias empregadas nesse processo.
Para quê você compreenda algumas dessas etapas, propomos, nesta atividade, quê você elabore uma explicação para a ocorrência do arco-íris, apontando as variáveis relevantes para seu surgimento e como estas se relacionam.
Durante a elaboração de sua explicação, procure meios para testá-la e anote em seu caderno as etapas e os resultados quê conseguir.

Procedimentos
Observação do fenômeno
• Lembre-se de quando você observou um arco-íris e dêz-creva em quais circunstâncias isso aconteceu. Tente recordar aspectos do clima naquele dia.
Registro e organização dos dados obtidos durante a observação
• Reúna-se em um grupo de até cinco integrantes e verifiquem as semelhanças e diferenças entre os dados quê cada integrante apontou sobre a formação do arco-íris. Por exemplo, o Sol estava visível na hora em quê o arco-íris se formou? Suas cores tí-nhão uma ordem? Discutam a melhor forma para o grupo organizar os dados obtidos: póde sêr por meio de esquema, tabéla, gráfico, lista, entre outras.
Análise e identificação dos aspectos quê representam as regularidades do fenômeno
• Verifiquem, com base nos dados obtidos, quais foram os principais fatores para a formação do arco-íris, isto é, os fatores quê estão presentes em todos os relatos.
Elaboração das hipóteses quê explicam as regularidades
• Esta etapa é importante para comprovar a conclusão do grupo a respeito da formação do arco-íris. Quais são as variáveis relevantes e como estas se relacionam?
Verificação das hipóteses por meio de experimentos
• Para averiguar a adequação das explicações, é importante testar e simular as condições quê provocam o aparecimento do arco-íris. Experimentem reproduzir essas condições com o auxílio de uma mangueira. Façam isso no jardim ou de tal forma quê a á gua possa sêr reaproveitada. Solicitem o auxílio do professor para realizar esta etapa.
• Primeira tentativa: Usem uma mangueira com esguicho para quê a á gua se esparrame em gotas. Dirijam o jato de á gua de frente para o Sol e para cima.
• Segunda tentativa: Invertam a posição do jato de á gua, ou seja, agora dirijam-no ao contrário do Sol, mas ainda para cima. Verifiquem em qual das situações vocês conseguiram reproduzir o arco-íris. Comparem as condições necessárias para a formação do arco-íris na natureza e na simulação e verifiquem se as hipóteses formuladas por vocês na etapa anterior podem sêr consideradas válidas.
Conclusão
• Elaborem uma explicação para ocorrência do arco-íris. Para isso, descrevam todas as etapas seguidas e os resultados obtidos. Por fim, apresentem as conclusões do grupo para a ocorrência dêêsse fenômeno.
Página quinze
mêdídas e o Sistema Internacional de Unidades
Na época em quê Galileu fez suas investigações no plano inclinado, ainda não existiam padrões e instrumentos para medir algumas grandezas, como distância e tempo. Por vezes, Galileu utilizou uma goteira ou as próprias batidas do coração para medir intervalos de tempo.
Chama-se grandeza tudo akilo quê é medido ou calculado quantitativamente, como massa, comprimento, tempo, área, volume, tempera-túra etc. Medir uma grandeza significa atribuir um valor numérico a ela conforme um padrão estabelecido, ou seja, uma unidade de medida.
Padrões de medidas foram essenciais para o desenvolvimento econômico, político, científico e social pelo mundo, favorecendo as expansões comerciais e o estabelecimento de relações entre locais e nações.
Os primeiros padrões adotados para fazer medidas foram baseados no corpo humano, mas estes eram imprecisos e variavam entre pessoas e locais. Porém, existem unidades de medidas utilizadas até hoje em alguns contextos, quê são heranças dessa época, como os exemplos a seguir.
Padrões de medidas baseados no corpo humano
Unidade |
Valor |
|---|---|
braça |
183 cm |
jarda |
91,44 cm |
polegada |
2,54 cm |
pé |
30,48 cm |
RODITI, Itzhak. Dicionário uáiss de Física. Objetiva: Rio de Janeiro, 2005. p. 29, 127, 172, 178.
A solução para esse problema foi adotar padrões com base na natureza, como Terra e á gua, por exemplo. No final do século XVIII, a Academia de Ciência da França criou o Sistema Métrico Decimal, definindo inicialmente padrões para medir comprimento, massa e volume, em métro, quilograma e litro, respectivamente, sêndo obtidos da seguinte forma:
• métro: comprimento equivalente à mêtáde de um meridiano terrestre dividido por dez milhões.
• litro: volume equivalente a um decímetro cúbico, ou mil centímetros cúbicos.
• quilograma: massa de um litro de á gua à tempera-túra aproximada de 4°C.
Na Convenção do Metro, realizada em 1875, vários países, inclusive o Brasil, adotaram o sistema métrico. A partir dêêsse momento, rêuní-ões foram feitas nos anos seguintes, até quê, em 1960, o Sistema Internacional de Unidades (SI) foi desenvolvido, sêndo adotado pelo Brasil em 1962.
O SI define sete grandezas de base, ou fundamentais, cujas unidades de medidas não dependem de outras. Todas as outras grandezas são definidas como derivadas, pois dependem das grandezas fundamentais para serem desenvolvidas.
Grandezas de base do SI
Grandeza |
Unidade |
Símbolo |
|---|---|---|
comprimento |
métro |
m |
massa |
quilograma |
kg |
tempo |
segundo |
s |
tempera-túra |
kelvin |
K |
corrente elétrica |
ampere |
A |
quantidade de matéria |
mol |
mol |
intensidade luminosa |
candela |
cd |
Grandezas derivadas do SI
Grandeza |
Unidade |
Símbolo |
|---|---|---|
área |
métro quadrado |
m2 |
densidade |
quilograma por métro cúbico |
kg/m3 |
velocidade |
métro por segundo |
m/s |
fôrça |
nílton (kg⋅m⋅s−2) |
N |
pressão |
pascal (kg⋅m−1⋅s−2) |
Pa |
potência |
watt (kg⋅m2⋅s−3) |
W |
resistência elétrica |
ohm (kg−1⋅m2⋅s−3⋅A−2) |
(ômega)" |
Fonte: INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA; INSTITUTO PORTUGUÊS DA QUALIDADE. Sistema Internacional de Unidades (SI). Tradução: Grupo de Trabalho luso-brasileiro do Inmetro e IPQ. Brasília, DF: Inmetro; Caparica: IPQ, 2021. Tradução luso-brasileira da 9ª edição. p. 6, 13, 45. Disponível em: https://livro.pw/vbxre. Acesso em: 27 jun. 2024.
Página dezesseis
Notação científica
Existem valores de grandezas com muitos algarismos, como quando se expressa a massa de um planêta ou as dimensões de um microrganismo. Neste caso, pode-se utilizar a potência de base 10. Esse recurso é chamado notação científica.
Um valor numérico está expresso em notação científica quando é representado da seguinte forma.
a ⋅ 10n
Nessa representação, a é um valor numérico tal quê 1 ≤ a < 10, e n é um número inteiro.
Como exemplo, considere a distância média da Terra ao Sol como 150 bilhões de metros. êste valor (d) póde sêr escrito da seguinte forma.
d = 150.000.000.000 m ⇒ d = 1,5 ⋅ 100.000.000.000 m ⇒ d = 1,5 ⋅ 1011 m
Para o caso de uma bactéria de comprimento c igual a 0,0000005 m, tem-se:
c = 0,0000005 m ⇒ c = 5 ⋅ 0,0000001
c = 5 ⋅ m ⇒ c = 5 ⋅ m ⇒ c = 5 ⋅ 10–7 m
Algumas potências de 10 podem sêr expressas por prefixos numéricos.
Potência de base 10 |
Prefixo numérico |
Símbolo |
|---|---|---|
10−12 |
pico |
p |
10−9 |
nano |
n |
10−6 |
micro |
μ |
10−3 |
mili |
m |
10−2 |
centi |
c |
10−1 |
deci |
d |
101 |
deca |
da |
102 |
hecto |
h |
103 |
kilo |
k |
106 |
mega |
M |
109 |
giga |
G |
1012 |
tera |
T |
Fonte: INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA; INSTITUTO PORTUGUÊS DA QUALIDADE. Sistema Internacional de Unidades (SI). Tradução: Grupo de Trabalho lusobrasileiro do Inmetro e IPQ. Brasília, DF: Inmetro; Caparica: IPQ, 2021. Tradução luso-brasileira da 9ª edição. p. 19. Disponível em: https://livro.pw/vbxre. Acesso em: 2 out. 2024.
ATIVIDADES
1. A proposta de quê o planêta Terra está em movimento levou um tempo para sêr desenvolvida e aceita, especialmente devido ao fato de não se notar, da Terra, esse movimento. Um quêstionamento antigo era “por que o vento gerado pelo movimento da Terra não é sentido? Afinal, sente-se o vento quando se está em um corpo em movimento”.
a) Quais são os indícios atuáis quê auxiliam para a conclusão de quê a Terra está em movimento?
b) Elabore uma resposta para o questionamento sobre não sentirmos o vento gerado pelo movimento da Terra e discuta oralmente com pelo menos um colega.
c) Se a Terra está em movimento, você e seu colega, sentados na sala de aula, estão em movimento ou em repouso? Conversem sobre esta questão e anotem suas conclusões no caderno.
Página dezessete
2. Considere a seguinte situação. Você entra em uma loja para comprar 3 m de um barbante. O vendedor diz quê não está encontrando a fita métrica, então afirma quê seu palmo equivale a 30 cm. Na sequência, ele méde 10 palmos de barbante.
a) Qual é a sua opinião sobre esta atitude do vendedor? Você considera válido utilizar padrões de medida arbitrários, como, neste caso, o palmo do vendedor? Justifique sua resposta.
b) Qual é a atitude correta a sêr adotada, tanto pelo vendedor quanto pelo consumidor?
3. No Brasil, o órgão responsável pela fiscalização de instrumentos de medição utilizados no comércio é o Instituto Nacional de Metrologia, Qualidade e Tecnologia (Inmetro). Pesquise acerca da importânssia dêêsse tipo de fiscalização e investigue as diversas atuações dos profissionais quê trabalham nesse órgão.
4. A bactéria Escherichia cóli, comumente encontrada no intestino humano, tem um comprimento médio de aproximadamente 2 micrômetros (2 μm).
a) Represente êste valor nas unidades de medida métro (m) e nanômetro (nm).
0,000002 m e 2.000 nm
b) Aproximadamente, quantas bactérias Escherichia cóli enfileiradas equivalem a cerca de 0,07 mm, valor quê corresponde ao diâmetro médio de um fio de cabelo?
Cerca de 35 bactérias.
SAIBA +
Mobilidade
A temática movimento também está relacionada a estudos feitos nas grandes cidades a respeito da mobilidade urbana, quê trata das condições quê permitem o deslocamento de pessoas, com o objetivo de favorecer o desenvolvimento econômico e social, importante para o crescimento de uma cidade.
Quando isso ocorre sem planejamento, o resultado é uma cidade desestruturada para sua população quê, sem um projeto adequado de mobilidade urbana, acaba perdendo sua capacidade de permitir quê as pessoas se desloquem com qualidade.
Os projetos de planejamento das cidades devem considerar todas as formas possíveis de mobilidade, como pedestres, ciclistas, motociclistas, veículos de passeio, transporte público, entre outros, diversificando, assim, as opções disponíveis.

ATIVIDADES
1. Você utiliza algum meio de transporte para ir da sua casa até a escola? Converse com seus côlégas, professores e outras pessoas da comunidade escolar e verifique quais meios de transporte eles utilizam para ir até a escola.
2. Em média, quanto tempo você leva para ir da sua casa até a escola? Utilizando outro meio de transporte, esse tempo seria maior ou menor?
3. Em sua opinião, quais devem sêr as atitudes de governantes para uma cidade crescer d fórma adequada? Faça uma pesquisa sobre o assunto.
4. Organize-se em um grupo de até cinco integrantes e desenvolvam uma pesquisa sobre o transporte público quê atende seu bairro. Busquem informações sobre os horários e os percursos dos ônibus, a quantidade de ônibus disponíveis, se existem vias exclusivas para ônibus, se eles são acessíveis, entre outras. Organizem as informações coletadas em um fôlder e façam uma divulgação para a comunidade escolar e não escolar, utilizando as mídias sociais da escola. Nesse fôlder, mostrem a importânssia de se ter um transporte público de qualidade quê seja amplamente utilizado pela população.
Página dezoito
TEMA 2
Introdução ao estudo do movimento
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Conceitos iniciais
As imagens ilustram uma mulher sentada no banco de um trem em movimento. Do lado de fora, parado na estação de trem, um homem observa esse trem passar vagarosamente.

Na sua opinião, o banco do trem em quê está a mulher encontra-se em repouso ou em movimento?
Para responder a essa pergunta, é necessário adotar um referencial. Se o homem fora do trem for adotado como referencial, o banco do trem onde está a mulher estará em movimento. Já se a mulher dentro do trem for adotada como referencial, o banco estará em repouso. Assim, determinado corpo póde estar, simultaneamente, em repouso em relação a um referencial e em movimento em relação a outro. Em Ciência, quando se realizam análises de situações como esta, é fundamental adotar um referencial.
Um corpo está em repouso em um intervalo de tempo quando sua posição não varia em relação a um referencial e está em movimento quando sua posição varia em relação a esse referencial.
No estudo dos movimentos, um objeto será, normalmente, chamado de corpo ou móvel. Ao realizar a análise do estado de repouso ou movimento dêêsse corpo, suas dimensões devem sêr consideradas. Assim, um corpo será chamado ponto material quando suas dimensões não interferirem no estudo a sêr feito. Caso contrário, será chamado corpo extenso.
Sendo assim, classificar um corpo como ponto material e corpo extenso também depende do referencial adotado. Além díssu, a expressão "ponto material" é utilizada quando as dimensões do corpo são pequenas se comparadas às dimensões em quê ocorre o fenômeno analisado.
PENSE E RESPONDA

1 Quem está em movimento: o atleta, a cadeira de rodas ou ambos?
Página dezenove
ATIVIDADES
1. A expressão "ponto material" geralmente é utilizada em quais condições?
2. Observe o caminhão na imagem. Ele póde sêr considerado um ponto material ou um corpo extenso?

3. Um velejador, ao contornar uma ilha com seu barco, percebe a presença de um farol.

É possível dizêr quê o farol se movimenta em relação ao barco? Justifique.
Sim, basta considerar o barco como referencial.
4. Um poste sobre a calçada está em repouso ou em movimento em relação:
a) à calçada?
Em repouso.
b) a um carro quê passa pela rua?
Em movimento.
c) ao Sol?
Em movimento.
Trajetória, posição e intervalo de tempo
Um morador da cidade de Palmas, no Tocantins, planeja uma viagem quê pretende fazer até a cidade de Taquaruçu, também no Tocantins. Observando o mapa, o morador conclui quê deverá percorrer a linha demarcada entre as duas cidades. Essa linha corresponde ao trajeto quê o morador fará para se deslocar entre as cidades, chamada trajetória. A trajetória é uma linha quê une todas as posições sucessivas ocupadas por um corpo em movimento em determinado intervalo de tempo e quê depende do referencial adotado.
Para localizar um móvel em sua trajetória, deve-se em primeiro lugar orientá-la. Em seguida, determinar a origem, quê corresponde à posição zero da trajetória. A posição s é determinada por um valor algébrico em relação à origem da trajetória, cujo módulo representa a distância entre a posição ocupada pelo móvel e a origem. É comum utilizar a palavra espaço para indicar a posição.
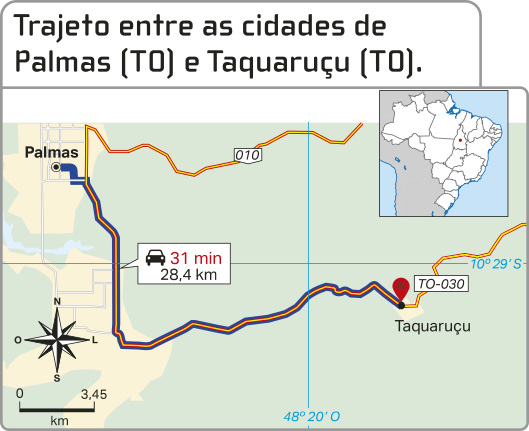
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2024. p. 165.
Página vinte
Deslocamento, distância percorrida e intervalo de tempo
Uma atleta iniciou seus treinos no instante inicial ti = 0, quando se encontrava junto a uma placa quê registrava a posição 1.000 m, ou seja, si = 1.000 m, em uma pista retilínea (formato em linha reta). Após cinquenta minutos, estava junto à placa quê registrava a posição 7.000 m, ou seja, em t = 50 min, s = 7.000 m.

A ideia de variação da posição ou deslocamento, simbolizada por (delta)"s (em quê D é uma letra grega quê indica variação), representa a diferença entre as posições ocupadas pela atleta nos instantes final e inicial:
(delta)"s = s − si = 7.000 − 1.000 ⇒ (delta)"s = 6.000 m
A atleta executou um deslocamento de 6.000 m em movimento progressivo, ou seja, a favor da trajetória retilínea ((delta)"s > 0). Caso ela se movesse da posição 7.000 m para a posição 1.000 m, seu deslocamento seria de −6.000 m em movimento retrógrado ou regressivo, pois ele é contrário à trajetória retilínea ((delta)"s < 0).
O intervalo de tempo é simbolizado por (delta)"t, quê representa a diferença entre os instantes final (t) e inicial (ti).
(delta)"t = t − ti = 50 − 0 ⇒ (delta)"t = 50 min
O deslocamento depende somente das posições inicial e final do móvel, enquanto a distância percorrida (d) corresponde ao comprimento do percurso desprovida de sinal.
No exemplo anterior, a trajetória do movimento da atleta foi retilínea e sem inversão de sentido de movimento durante o intervalo de tempo considerado. Assim, independentemente se o deslocamento dela for de 6.000 m ou de −6.000 m, sua distância percorrida será de 6.000 m. A distância percorrida póde sêr determinada somando individualmente o módulo dos diferentes deslocamentos executados por um corpo.
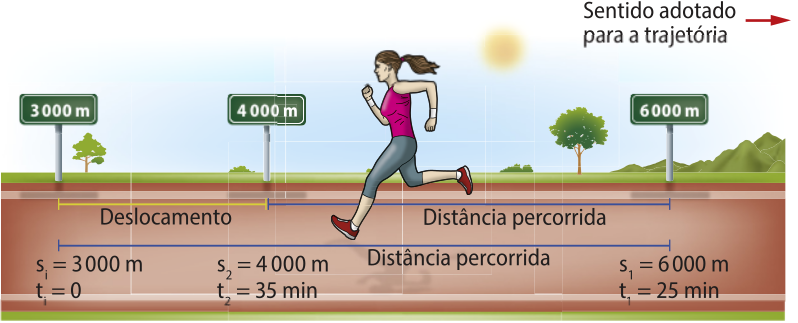
Considere quê, após um descanso, a atleta reiniciou seu treino de corrida. No instante ti = 0, ela se encontrava na posição si = 3.000 m, chegando à posição s1 = 6.000 m no instante t1 = 25 min e retornando à posição s2 = 4.000 m no instante t2 = 35 min.
PENSE E RESPONDA

2 Uma placa de posição quilométrica em uma trajetória indica a distância percorrida pelo corpo?
Página vinte e um
No intervalo de tempo total, 0 a 35 min, o deslocamento e a distância percorrida possuem os seguintes valores:
(delta)"s = s − si = 4.000 − 3.000 ⇒ (delta)"s = 1.000 m ((delta)"s > 0; movimento progressivo)
d = = 3.000 + 2.000 ⇒ d = 5.000 m
Como o movimento sofreu inversão de sentido, os valores do deslocamento e da distância percorrida são distintos.
Perceba quê, se ao final do treino a atleta retornar à posição inicial de 3.000 m, seu deslocamento será nulo, e a distância percorrida será de 6.000 m.
(delta)"s = s − si = 3.000 − 3.000 ⇒ (delta)"s = 0
d = = 3.000 + 3.000 ⇒ d = 6.000 m
ATIVIDADE RESOLVIDA
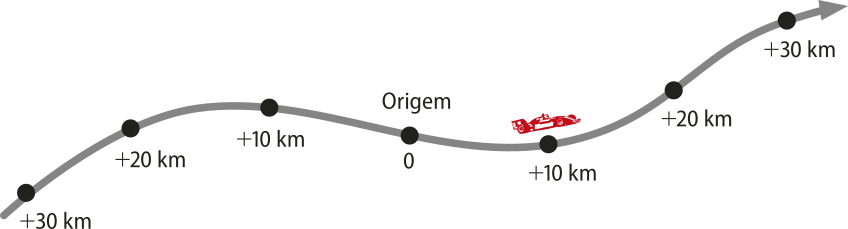
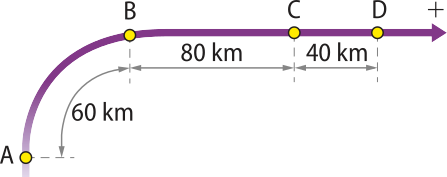
1. Quatro cidades, localizadas ao longo de uma rodovia, estão representadas por A, B, C e D na ilustração. Para o sentido positivo indicado, determine as posições de A, B, C e D, considerando como origem da trajetória a cidade B.
Resolução
A cidade B é a origem da trajetória, logo: sB = 0. A cidade A está a 60 km antes da cidade B, logo: sA = −60 km. A cidade C está a 80 km depois da cidade B, logo: sC = 80 km. A cidade D está a 40 km depois da cidade C, logo: sD = 40 km + 80 km = 120 km.
PENSE E RESPONDA

3 Você sabe o quê é um hodômetro? Ele mostra o valor do deslocamento escalar ou da distância percorrida?
ATIVIDADES
5. Na ilustração a seguir estão representados os pontos A, B, C e D sobre o eixo orientado x, sêndo o ponto O a origem do movimento.
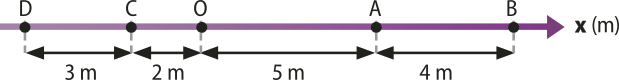
Determine:
a) as posições dos pontos A, B, C e D.
xA = 5 m; xB = 9 m; xC = −2 m; xD = −5 m
b) o deslocamento de um móvel quê parte do ponto C e chega ao ponto B.
11 m
c) o deslocamento de um móvel quê parte do ponto A e chega ao ponto D.
−10 m
d) o tipo de movimento do móvel quê parte do ponto A e chega ao ponto D, se gastou 5 segundos para percorrer o trecho.
Movimento retrógrado.
6. Explique a influência do referencial na trajetória descrita por um corpo.
7. Uma moça vai fazer uma viagem de 80 km até a cidade onde será comemorado o aniversário da mãe dela. Ao ligar o carro, ela nota quê o combustível está na reserva. Para chegar ao posto de gasolina mais próximo, ela precisa percorrer 15 km no sentido contrário ao da viagem.
Se, depois de abastecer o carro, a moça seguir em linha reta até a cidade da mãe dela, qual será o deslocamento e a distância percorrida desde o início da viagem?
80 km; 110 km
Página vinte e dois
Velocidade média, velocidade escalar média e velocidade instantânea
Ao dividir o deslocamento de um móvel (delta)"s pelo intervalo de tempo (delta)"t decorrido, obtém-se o valor da velocidade média vm.
vm =
Portanto, quantitativamente, a velocidade média de um móvel póde sêr de ter minada pelo quociente da variação da sua posição escalar (delta)"s pelo intervalo de tempo (delta)"t considerado.
O sinal da velocidade média acompanha o sinal do deslocamento, ou seja, vm.> 0 para movimento progressivo e vm, < 0 para movimento retrógrado. A unidade de medida da velocidade média corresponde à razão entre a unidade de medida de deslocamento e a unidade de medida de tempo. Uma unidade de medida usual para velocidade é o quilômetro por hora (km/h), usada nos velocímetros de veículos. No SI, a unidade de medida é o métro por segundo (m/s).
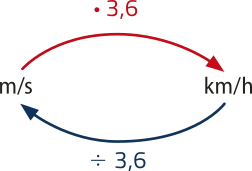
Considere um veículo quê se móve com velocidade média de 1 km/h e outro veículo com velocidade média de 1 m/s. Qual deles está se movendo mais rápido?
Para comparar quantitativamente duas grandezas, é preciso quê elas sêjam expressas na mesma unidade de medida. Se 1 km = 1.000 m e 1 h = 3.600 s, então:
1 km/h = m/s ⇒ 1 km/h = m/s ⇒ 3,6 km/h = 1 m/s
Assim, uma velocidade média de 1 m/s é o mesmo quê 3,6 km/h, sêndo, portanto, maior quê 1 km/h.
A velocidade escalar média (vem) é uma forma de descrever a rapidez de um movimento, definida a partir da distância total percorrida.
vem =
Assim como a distância percorrida, a velocidade escalar média não possui sinal algébrico. Nos movimentos retilíneos sem inversão de sentido, o módulo da velocidade média é igual ao valor da velocidade escalar média.
O cóódigo de Trânsito Brasileiro (CTB), regido pela lei número 9.503, de 1997, regula o sistema nacional de trânsito com normas gerais de circulação e conduta para pedestres e motoristas. A velocidade é um importante item mencionado no CTB, pois o excésso de velocidade é uma das principais causas de acidentes no trânsito.
Para auxiliar no contrôle e na fiscalização do trânsito, são utilizados alguns equipamentos eletrônicos, sêndo um deles o redutor eletrônico de velocidade, também conhecido como lombada eletrônica. Esses equipamentos médem a velocidade de um veículo e, caso ela seja superior à permitida na via, é feito um registro fotográfico e gerada uma penalidade.
ESPAÇOS DE APRENDIZAGEM
• Para conhecer mais dêtálhes do cóódigo de Trânsito Brasileiro, acéçi o línki da lei na íntegra:
Lei número 9.503, de 23 de setembro de 1977. Publicado por: Casa Civil. Disponível em: https://livro.pw/wnfbh. Acesso em: 20 jun. 2024.
Página vinte e três
Mas como esse equipamento méde a velocidade de um veículo?
Quando se calcula uma velocidade média, mas considerando intervalos de tempo (delta)"t muito pequenos, próximos de zero, o valor obtído corresponde à velocidade em praticamente um instante, ou seja, à velocidade instantânea ou simplesmente velocidade (v).
Então, esses aparelhos médem o deslocamento dos veículos na via considerando intervalos de tempo pequenos, calculando assim a velocidade naquele instante. Para isso, a maior parte dêêsses equipamentos utilizam sensores instalados no solo, com uma pequena distância conhecida entre eles, estimando, assim, o intervalo de tempo quê o veículo precisou para passar por eles.
Quando se faz referência apenas ao valor da velocidade, sem nenhuma indicação de sentido, obtém-se a velocidade escalar. Um velocímetro de um veículo mostra o valor da velocidade escalar, pois apresenta apenas o valor, sem nenhuma informação sobre o sentido do movimento. O sinal da velocidade indica se o móvel está em movimento progressivo, quando v > 0, ou movimento retrógrado, quando v < 0.
ATIVIDADES
8. Um caramujo desloca-se em linha reta no plano horizontal de um piso a uma velocidade média de 1,5 mm/s, enquanto um bicho-preguiça se desloca em linha reta subindo em uma árvore a uma velocidade média de 2 m/min. Qual dêêsses animais é o mais lento?
Caramujo.
9. A prática de exercícios físicos traz benefícios quê se manifestam em vários aspectos do organismo, como perda de porcentagem de gordura corporal, diminuição do colesterol total e aumento do HDL colesterol (o chamado bom colesterol) e, ainda, a redução da pressão arterial. No caso das crianças e jovens, a atividade física favorece o melhor convívio social, o dêsempênho escolar e o desenvolvimento intelectual.
Analisando essas informações, um estudante rêzouvêo mudar seus hábitos e passou a caminhar de sua casa até a escola, todos os dias. Considere quê o passo do jovem tem comprimento médio de 0,5 m e quê ele dá um passo a cada segundo. Responda às kestões:
a) Qual é a velocidade com quê esse jovem caminha?
0,5 m/s
b) Qual é a distância entre a casa e a escola do jovem, se o tempo gasto no percurso é 40 minutos?
1.200 m
10.
As fortes chuvas quê castigam o Rio Grande do Sul desde o fim de abril [2024] causaram estragos quê ainda não foram calculados. As inundações afetaram um total de 458 cidades, o quê corresponde a mais de 90% dos municípios gaúchos, com mais de 2 milhões de pessoas impactadas pelo evento climático extremo.
O volume de chuva passou de 800 milímetros em mais de 60% do estado, deixando mais de 500 mil pessoas desalojadas, ou seja, tiveram quê sair de suas casas, e 77 mil estão vivendo em abrigos no momento. As mortes chegam a 151 e ainda há 104 desaparecidos.
[...]
Fonte: NITAHARA, Akemi. Entenda a tragédia climática ocorrida no Rio Grande do Sul. Rádio Agência, Rio de Janeiro, 18 maio 2024. Disponível em: https://livro.pw/mgfbt. Acesso em: 24 jun. 2024.
a) Considere quê um barco de salvamento, ao prestar socorro a uma dessas cidades gaúchas, percorreu mêtáde da trajetória com velocidade média de 30 km/h e a outra mêtáde com velocidade média de 70 km/h. Calcule, para toda a trajetória, a velocidade média.
42 km/h
b) Em grupo, pesquisem ações quê podem sêr feitas para minimizar os efeitos de atividades climáticas intensas como a alta incidência de chuvas no Rio Grande do Sul em 2024.
Página vinte e quatro
SAIBA +
A medida de tempo e a Física Moderna

É possível quê você já tenha assistido a filmes ou lido informações de quê o tempo é relativo. Registros históricos indicam quê as formas de medir o tempo foram evoluindo de acôr-do com as necessidades sociais de cada época. Resgatando alguns dêêsses registros, é possível observar quê, na impossibilidade de contar com os relógios mecânicos, o sêr humano buscava nos recursos naturais alternativas para medi-lo.
O relógio de sól é considerado uma das primeiras formas de medir o tempo. Para fazer essa medida, usa-se uma vara, denominada gnômon, posicionada verticalmente em uma superfícíe com marcações. Conforme o Sol realiza o movimento aparente ao redor da Terra, a sombra do gnômon aponta para uma direção da superfícíe, indicando as horas. Registros indicam quê esse tipo de relógio foi desenvolvido pelo povo kemético, por volta de 3500 a.C. Esse povo viveu na região às margens do Rio Nilo, em um território conhecido como Kemet.
Atualmente, a forma mais precisa de medição do tempo é feita pêlos relógios atômicos quê utilizam a transição de energia de um átomo – o césio – para determinar o quê foi convencionado por um segundo. Essa medida possui uma margem de êrro extremamente pequena e, por isso, é convencionada pelo SI como medida padrão do segundo.
Contando com esses recursos técnicos, é possível afirmar quê o tempo medido por duas pessoas, para determinado evento, sempre será o mesmo? Será possível quê duas ou mais pessoas medindo o mesmo evento obtenham resultados distintos?
Com o desenvolvimento da teoria da Relatividade Restrita, essas perguntas passam a receber novas respostas, quê não estão de acôr-do com o propôsto pela Física Clássica. Segundo a teoria da Relatividade Restrita, duas pessoas, ao medirem o intervalo de tempo de determinado evento, poderão obtêr valores diferentes. O transcorrer do tempo dependerá das condições em quê estão as pessoas quê fazem a medição, mais especificamente da situação em quê está o referencial onde a pessoa quê faz a medição se encontra: parado ou em movimento. Caso essa pessoa esteja em um referencial em alta velocidade, o tempo registrado transcorrerá mais lentamente se comparado com o registrado por um relógio quê esteja em um referencial em repouso.
Contudo, esses efeitos previstos pela teoria da Relatividade Restrita se aplicam a velocidades próximas da velocidade da luz, como ocorre com as partículas atômicas em condições experimentais nos aceleradores de partículas. Nas situações do cotidiano, com velocidades muito inferiores à velocidade da luz, duas pessoas sempre irão medir o mesmo intervalo de tempo para determinado evento.
ATIVIDADES
1. Considerando as estratégias de medição do tempo, quê outras formas de medi-lo foram utilizadas além da citada no texto? Se for necessário, faça uma pesquisa para descobrir essa informação.
2. por quê, nas situações do cotidiano na Terra, não é possível perceber variações na medição do tempo de um evento?
3. Em grupo com seus côlégas, façam uma pesquisa e identifiquem ao menos uma situação na qual ocorrem efeitos relativísticos na medida do tempo.
Página vinte e cinco
TEMA 3
Movimento uniforme
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Movimento com velocidade constante
A BR-316 é uma rodovia federal quê passa pêlos estados Pará, Maranhão, Piauí, Pernambuco e Alagoas, com início em Belém (PA) e final em Maceió (AL).
Nessa rodovia, entre as cidades de Araguanã e Governador Nunes Freire, ambas no Maranhão, tem-se um trecho com aproximadamente 110 km de extensão. O mapa a seguir destaca o trecho mencionado.
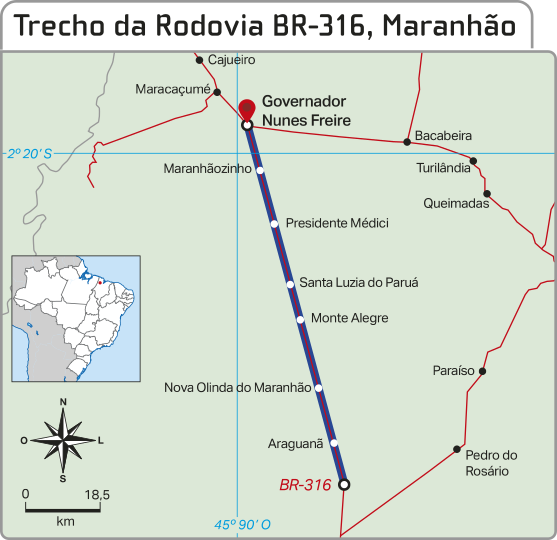
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2024. p. 166.
Considerando quê o trecho entre essas duas posições é praticamente retilíneo, como se obtém a velocidade, suposta constante v, desenvolvida por um veículo quê faz a rota traçada, observando a estimativa de tempo de viagem em 1h e 40min?
Para responder a essa pergunta, podemos recorrer ao conceito de velocidade média (vm)estudado anteriormente. Como o valor da distância entre as localidades é dada em quilômetro, é necessário quê o intervalo de tempo seja dado em horas.
(delta)"t = 1 h + 40 min = 1 h + h = 1 h + h = h ⇒ (delta)"t = h
vm= v ⇒ v = ⇒ v = ⇒ v = 66 km/h
PENSE E RESPONDA

1 Nas estradas e também em vias urbanas, é possível identificar a presença de faixas contínuas e tracejadas, pintadas no asfalto nas cores branca e amarela. Você sabe o significado dêêsse tipo de sinalização?
Página vinte e seis
Quando um corpo em movimento possui velocidade constante, tem-se um movimento uniforme.
Quando um móvel percórre uma trajetória com velocidade constante, significa quê ele percórre deslocamentos iguais em intervalos de tempos iguais, desenvolvendo um movimento uniforme (MU). Portanto, a velocidade desenvolvida por esse móvel será igual à velocidade média em qualquer intervalo de tempo do movimento analisado: v = vm (constante e não nula).
Função e gráfico da posição em relação ao tempo
Considerando ti= 0 (como é normalmente feito nos estudos da Cinemática), si como a posição no instante ti, s como a posição em um instante t qualquer e v como velocidade constante, pode-se determinar a posição s a cada instante t, para um corpo em MU, pela seguinte relação:
v = vm ⇒ v = ⇒ s − si = v(t − ti) ⇒ s = si + vt
A relação ôbitída é conhecida como função horária da posição [s = f(t)], uma função polinomial do 1º grau válida apenas para corpos quê realizam um MU.
pôdêmos usar um gráfico para representar a evolução da posição de um corpo em função do tempo em um MU, representando os valores do tempo no eixo horizontal e os valores da posição no eixo vertical, chamado gráfico de posição por tempo (s × t).
Observe dois exemplos de gráficos de MU da posição por tempo: o Gráfico 1 representa um corpo quê descreve um movimento progressivo com velocidade de 2 m/s; o Gráfico 2 representa um corpo quê descreve um movimento retrógrado de velocidade −6 m/s, ambos no intervalo de 0 a 4 s.
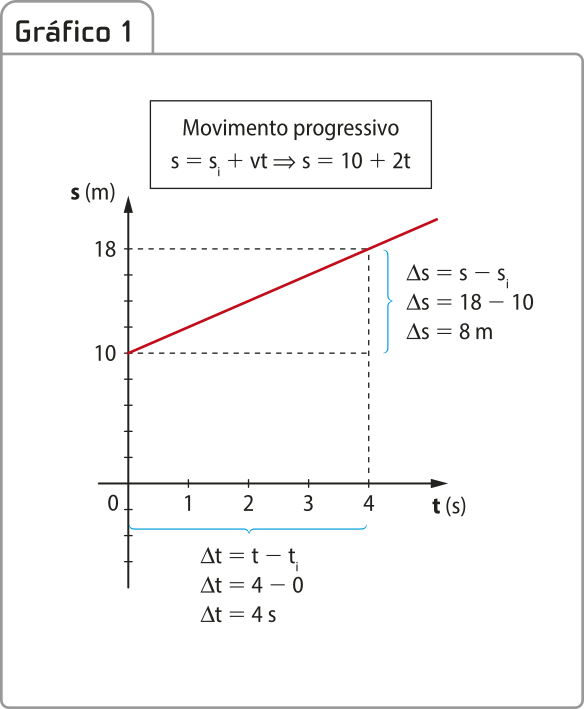
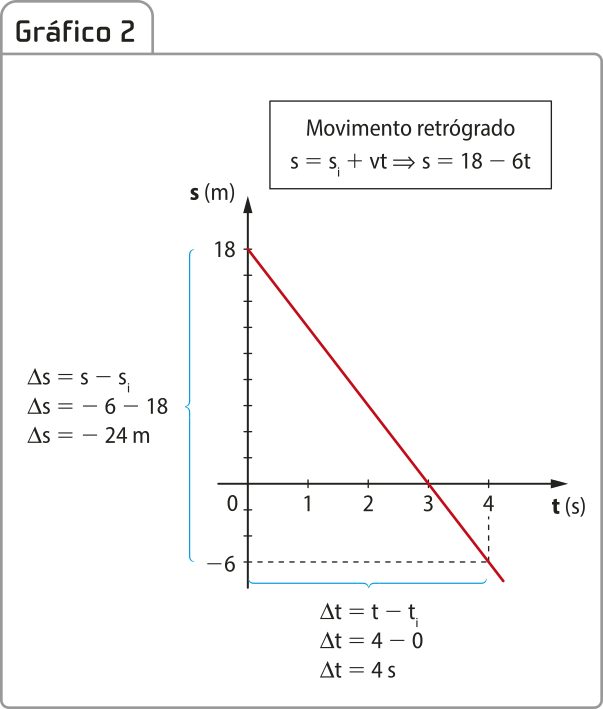
Caso julgar pêrtinênti, discutir com os estudantes as relações trigonométricas do triângulo retângulo necessárias para chegar à função horária da posição.
Página vinte e sete
ATIVIDADE RESOLVIDA
1. Em um trecho retilíneo de uma ciclovia, no instante t = 0 s, dois ciclistas (uma mulher M e um homem H) passaram pela mesma posição, com velocidades constantes vM = 8 m/s e vH = 6 m/s. Considerando quê ambos se deslócam na mesma direção e no mesmo sentido, determine a distância quê os separa após 8 s.
Resolução
Considerando quê ambos se deslócam em MU, após 8 s, tem-se:
Para a mulher
Para o homem
A distância quê os separa é: d = 64 m − 48 m = 16 m
ATIVIDADES
1. Um ponto material se movimenta sobre uma trajetória retilínea, e as diferentes posições ocupadas por ele sobre essa trajetória são dadas pela equação: s = 20 − 2t (SI). De acôr-do com essa informação, determine:
a) a posição do ponto material no instante 5 s;
10 m
b) o deslocamento do ponto material entre os instantes 2 s e 6 s;
−8 m
c) o instante em quê o ponto material passa pela origem das posições.
10 s
2. (hú éfe ême gê) Dois carros, A e B, movem-se numa estrada retilínea com velocidade constante, vA = 20 m/s e vB = 18 m/s, respectivamente. O carro A está, inicialmente, 500 m atrás do carro B. Quanto tempo o carro A levará para alcançar o carro B?
250 s
3. (UFRN) Um trem parte de Natal com destino a Recife às 6 horas, com velocidade constante de 60 km/h. Uma hora depois, parte de Natal, numa linha paralela, um segundo trem, mantendo a velocidade constante de 75 km/h. Sabendo quê a distância Natal-Recife é 300 km, podemos afirmar quê:
a) o 2º trem ultrapassará o 1º a 70 km do Recife.
b) o 2º trem ultrapassará o 1º a 80 km do Recife.
c) o 2º trem ultrapassará o 1º a 100 km do Recife.
d) o 2º trem ultrapassará o 1º a 120 km do Recife.
e) os dois trens chegarão a Recife ao mesmo tempo.
Resposta: e)
4. Uma pessoa pratíca exercícios físicos regularmente para cuidar de sua saúde. Em um dia em quê praticou exercícios aeróbicos na esteira, ela caminhou por 20 minutos com velocidade constante de 5,4 km/h e perdeu o equivalente a 200 quilocalorias.
a) Qual é o deslocamento, em métro, quê a pessoa teria realizado se tivesse caminhado na rua?
1.800 m
b) A indicação da perda de calorias é um dado relevante para responder ao item anterior? Por quê?
c) Qual é o deslocamento da pessoa em relação ao solo?
0
5. Dois cachorros, T e R, deslócam-se em sentidos opostos, como representado na imagem.
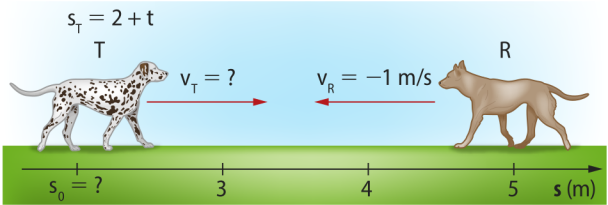
Responda:
a) Qual é a velocidade do cachoorro T? E a posição inicial dele?
1 m/s; 2 m
b) Classifique os movimentos dos cachorros (progressivo ou retrógrado).
T progressivo;
R retrógrado.
c) escrêeva a função horária da posição do cachoorro
R.
sR = 5 − t
d) Determine a posição e o instante em quê os cachorros se encontram.
3,5 m; 1,5 s
Página vinte e oito
Gráfico da velocidade em relação ao tempo
Quando um corpo realiza um MU, o gráfico da velocidade em função do tempo (v × t) é uma linha horizontal paralela ao eixo do tempo e delimitada pelo intervalo de tempo do movimento.
O exemplo a seguir corresponde a um móvel quê descreve um MU progressivo com velocidade de 2 m/s, no intervalo de 0 a 4 s.
A área destacada no gráfico, delimitada pela curva e o eixo horizontal em um intervalo de tempo, tem formato equivalente a um retângulo. Dessa forma, para determinar o deslocamento realizado pelo corpo, basta calcular a área dêste retângulo.
Sendo assim, em qualquer gráfico de velocidade por tempo de um MU, a área delimitada pela curva e o eixo horizontal, em cérto intervalo de tempo, será numericamente igual ao deslocamento realizado pelo móvel.
Área (delta)"s
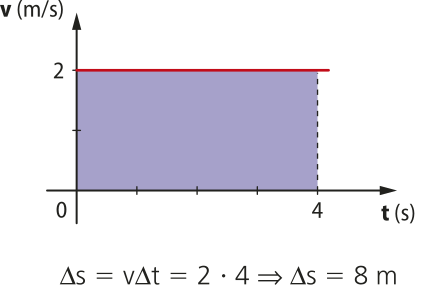
ATIVIDADES
6. No trecho mais longo e retilíneo de uma maratona, um atleta, estrategicamente, procura manter sua velocidade constante. O treinador faz anotações sobre as posições ocupadas pelo atleta, em diferentes instantes:
t (s) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|---|
s (m) |
−15 |
−10 |
−5 |
0 |
5 |
10 |
15 |
Com base nessas anotações, faça o quê se pede.
a) Construa o gráfico da posição em função do tempo.
b) Construa o gráfico da velocidade em função do tempo.
c) escrêeva a função horária da posição realizada pelo atleta.
s = −15 + 5t
d) Determine o instante em quê o atleta passa pela origem do referencial e o tipo de movimento quê ele descreve (progressivo ou retrógrado).
3 s; movimento progressivo
e) É possível dizêr quê a reta ôbitída no gráfico do item a representa a trajetória do atleta? Justifique.
7. O gráfico representa a posição em função do tempo dos móveis A e B, quê se deslócam em uma trajetória retilínea. Qual dos móveis tem maior velocidade?
Ambos possuem a mesma velocidade.
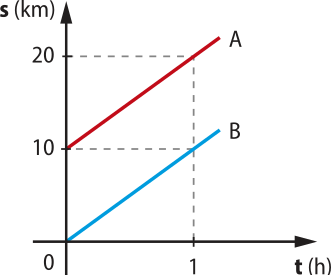
8. A figura a seguir representa o gráfico da posição em função do tempo de uma pessoa quê, durante uma caminhada, desloca-se com movimento uniforme.
Após um minuto, quantos metros essa pessoa caminhou e qual a posição dela em relação à origem?
60 m; 65 m
Página vinte e nove
SAIBA +
A importânssia do transporte público eficiente e acessível
Diariamente, as pessoas precisam se deslocar para ezercêr diversas atividades, como trabalhar, estudar, atender a compromissos presenciais, realizar atividades de cultura e lazer, entre outras. Em muitos municípios brasileiros, principalmente nas regiões urbanas, as pessoas realizam esses deslocamentos utilizando o sistema público de transporte ofertado pelo município em quê residem. No entanto, nem todas as pessoas conseguem utilizar esse tipo de serviço com facilidade: fatores como custo, segurança, qualidade e acessibilidade impactam diretamente na escolha do uso dêêsses transportes.
Quando se considera especialmente a acessibilidade dos veículos quê compõem esse sistema, dados indicam quê há um longo caminho até se cumprir a lei número 13.146 de 2015, quê trata do Estatuto da Pessoa com Deficiência. De acôr-do com a Pesquisa Nacional de Saúde (PNS) de 2019, existem, no Brasil, mais de 17 milhões de pessoas com deficiência, sêndo quê a maior parte apresenta deficiência física nos membros inferiores. Assim, é fundamental ofertar um sistema público de transporte quê atenda à população na sua totalidade. Porém, a falta de planejamento, resultante principalmente do crescimento desordenado das cidades, e o descumprimento ou desconhecimento das leis quê regem a mobilidade e a acessibilidade são alguns fatores quê impedem ou dificultam o acesso e a utilização de serviços de transporte pelas pessoas com deficiência.
Nesta atividade, você e seus côlégas irão investigar a acessibilidade para cadeirantes no sistema público de transporte do seu município.
ATIVIDADES
1. Organize-se em grupos de até cinco integrantes. Vocês deverão analisar as condições do transporte público quê atende seu bairro ou município. Considerem os principais tipos de transporte quê atendem a sua região: póde sêr ônibus, trem, metrô ou barco. Cada grupo póde ficar responsável por buscar uma das seguintes informações.
• Quais são os tipos, horários e percursos disponíveis?
• Qual é a quantidade da frota quê atua na região analisada?
• Qual é o estado de conservação da frota?
• Qual é a porcentagem de veículos adaptados em sua cidade? (Veículos adaptados são aqueles quê possuem acesso para cadeirantes e idosos e local destinado para pessoa com deficiência visual (que póde estar acompanhada de cão-guia).
• Qual é a freqüência de atendimento da frota analisada?
2. Organizem as informações coletadas, discutam em grupo os principais problemas encontrados e façam um relatório com sugestões para a melhoria do sistema de transporte do local pesquisado.
3. Em conjunto com a turma, elaborem um documento com as principais conclusões. Estudem estratégias para apresentar os dados obtidos. Proponham uma forma de compartilhamento dos resultados com a comunidade escolar e também com a comunidade externa à escola. Se possível, organizem-se para discutir ações quê podem sêr feitas para apresentar os dados à secretaria de transporte do município ou à subsecretaria do bairro, solicitando ações para a melhoria da acessibilidade no transporte público da região.
Página trinta
OFICINA CIENTÍFICA
Identificando um movimento uniforme
A velocidade é um importante parâmetro para se estudar um movimento. Saber identificar se ela é constante ou variável em um intervalo de tempo possibilita entender o movimento e também classificá-lo. Quais parâmetros são necessários para classificar um movimento como uniforme?
Em grupo com seus côlégas, desenvolvam esse experimento e analisem os resultados obtidos. Em seguida, discutam o quê analisaram.
Materiais
• caneta
• régua
• á gua
• um livro grosso
• tábua de madeira com 40 cm de comprimento
• 40 cm de mangueira plástica transparente
• duas rolhas
• fita adesiva
• cronômetro
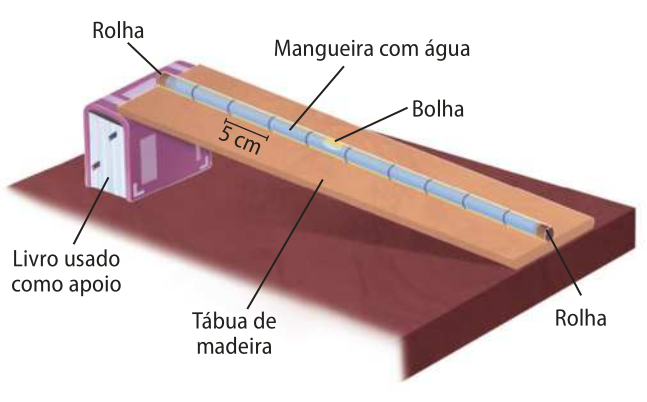
Procedimentos
• Utilizando a régua e a caneta, façam marcações na mangueira a cada 5 cm, ao longo do comprimento dela.
• Coloquem uma rolha em uma das extremidades da mangueira, encham-na com á gua e tampem a outra extremidade com a outra rolha, cuidando para quê entre a rolha e a superfícíe da á gua exista um pouco de ar. Verifiquem possíveis vazamentos.
• Posicionem uma das extremidades da madeira sobre o livro e a outra extremidade sobre a mesa, como mostra a figura, e analisem o movimento da bolha de ar pela á gua. Façam ajustes na altura do livro, variando a inclinação da madeira até quê o movimento realizado pela bolha seja aparentemente uniforme.
• Mantenham a bolha de ar na extremidade da mangueira quê ficará apoiada na mesa. Um colega deverá manter a madeira na posição inclinada enquanto outro, rapidamente, inicia uma primeira análise do movimento da bolha registrando com o cronômetro os instantes em quê ela passa em cada marcação de 5 cm. Façam uma análise prévia, identificando se o movimento da bolha foi similar a um movimento uniforme. Se julgarem conveniente, ajustem novamente a inclinação da madeira até identificarem quê o movimento da bolha de ar é semelhante ao uniforme.
• No caderno, organizem os dados obtidos em uma tabéla. Realizem o procedimento anterior, anotando o instante quê a bolha passa em cada marcação de 5 cm. Repitam esse processo por duas vezes e façam uma média dos valores obtidos.
ATIVIDADES
1. Os valores obtidos nas duas medições de tempo e na média estão próximos ou distantes uns dos outros? Considerando quê o movimento da bolha precisa sêr uniforme, você acredita quê os valores obtidos são satisfatórios ou é necessário repetir o experimento?
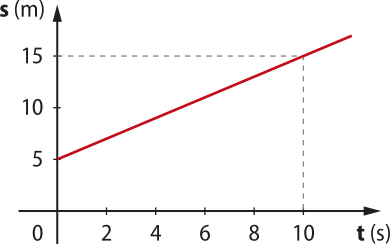
2. Elabore um gráfico da posição da bolha em função do tempo, para deslocamentos de 5 cm, considerando toda a extensão da mangueira.
3. Determine a velocidade média da bolha de ar em cada deslocamento de 5 cm. Ao final, calcule a velocidade média da bolha considerando o deslocamento total e o intervalo de tempo total do movimento analisado. Os valores obtidos são próximos ou distantes uns dos outros?
4. Após a realização dêêsse experimento, você conclui quê o movimento da bolha de ar analisada é uniforme? Em caso positivo, justifique sua resposta com base nos resultados obtidos. Em caso negativo, verifique quais foram os principais motivos quê interferiram no processo e nos resultados e proponha ações quê contribuam para a diminuição dessas interferências.
Página trinta e um
TEMA 4
Movimento uniformemente variado
Movimento variado
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
No cotidiano, percebe-se quê os movimentos uniformes não são muito freqüentes. Na maior parte deles, a velocidade não se mantém constante, portanto varia de alguma maneira.
Ao acionar o acelerador de um carro, por exemplo, o ponteiro do velocímetro mostra quê a velocidade escalar instantânea varia, aumentando de valor em determinado intervalo de tempo, como no exemplo a seguir.

ALEX ARGOZINO
Representação de um velocímetro de um carro em duas situações (imagem sem escala; cores fantasia).
Se, em valor absoluto, a velocidade escalar instantânea de um móvel aumenta em determinado intervalo de tempo, o movimento é denominado acelerado.
Já quando se aciona o freio de um veículo em movimento, a velocidade escalar instantânea diminui de valor em determinado intervalo de tempo. Em valor absoluto, se a velocidade escalar instantânea de um corpo decresce em determinado intervalo de tempo, o movimento é denominado retardado.
PENSE E RESPONDA

1 Durante uma cobrança de pênalti, em quê momento ocorrem acelerações?
Aceleração escalar média
Usaremos aceleração escalar média e aceleração escalar nos estudos da variação da intensidade da velocidade. Esta escolha auxilia nos estudos do Tema 5: Análise vetorial do movimento, ao diferenciar aceleração escalar e aceleração centrípeta, quê são as componentes da aceleração vetorial.
A aceleração escalar média (am) descreve a rapidez com quê a velocidade de um móvel varia.
Quantitativamente, a am de um móvel é ôbitída pelo quociente entre a variação da sua velocidade instantânea (delta)"v e o intervalo de tempo (delta)"t correspondente.
am =
Como decorrência da definição, é possível deduzir quê a unidade de medida de aceleração corresponde à razão entre a unidade da medida da velocidade e a unidade de medida do tempo.
No SI, a unidade de medida da aceleração é: = m/s2.
Para intervalos de tempo (delta)"t muito pequenos, próximos de zero, a aceleração escalar média am tende à aceleração escalar instantânea (a).
Página trinta e dois
ATIVIDADES
1. O velocímetro de um ônibus quê trafega por uma estrada registra 90 km/h. Ao identificar um obstáculo, o motorista aciona o freio durante 10 s, reduzindo a velocidade a 18 km/h. Determine a aceleração escalar média do ônibus, em m/s2, nesse intervalo de tempo, e classifique, justificando, o tipo do movimento (acelerado ou retardado).
2. Um navegador percebeu quê, durante determinado intervalo de tempo, seu barco manteve aceleração escalar nula. pôdêmos concluir quê o barco estava parado? Justifique.
3. Uma vendedora de automóveis divulga na propaganda quê o carro A consegue partir do repouso e atingir a velocidade vA = 97,2 km/h, em 11 s. Também, partindo do repouso, o carro B consegue atingir a velocidade vB = 90 km/h, em 10 s. Qual deles apresenta a maior aceleração?
O carro B possui a maior aceleração.
4. O movimento uniformemente acelerado é aquele quê, partindo do repouso, adqüire, em tempos iguais, variações iguais de velocidade. Analisando a afirmação anterior, explique o quê significa o valor 20 (km/h)/s.
5. (Unésp) Um automóvel de competição é acelerado de tal forma quê sua velocidade (v) em função do tempo (t) é dada pela tabéla:
t (s) |
v (m/s) |
|---|---|
5 |
20 |
10 |
50 |
15 |
60 |
A aceleração média, em m/s2, no intervalo de 5 s a 15 s é:
a) 4,5
b) 4,33
c) 5,0
d) 4,73
e) 4,0
Resposta: e)
Movimento com aceleração escalar constante
Considere a situação em quê um motociclista, inicialmente em repouso, acelera sua motocicleta. As imagens ilustram quatro momentos do velocímetro dessa motocicleta, em instantes distintos.
Nesses registros, é possível dizêr quê a aceleração escalar da motocicleta foi constante?
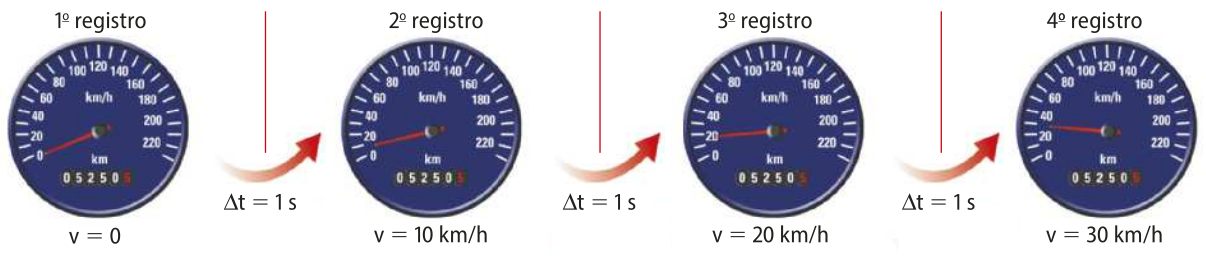
SELMA CAPARROZ
Representação de velocímetro de uma motocicleta em quatro situações (imagem sem escala; cores fantasia).
As imagens indicam quê, a cada intervalo de tempo de 1 s, a velocidade escalar instantânea da motocicleta aumentou 10 km/h, uniformemente, ou seja, de maneira constante.
am =
am =
am =
Quando a aceleração escalar média de um corpo é constante ao longo do intervalo de tempo analisado, tem-se um movimento uniformemente variado (movimento uniformemente variado).
No exemplo da motocicleta, o movimento uniformemente variado executado foi acelerado, pois o valor absoluto da velocidade escalar instantânea aumentou. Quando o valor absoluto da velocidade escalar instantânea diminui, tem-se um movimento uniformemente variado retardado.
Página trinta e três
Função e gráfico da velocidade em relação ao tempo
No movimento uniformemente variado, a aceleração escalar constante implica quê a velocidade instantânea aumenta ou diminui valores iguais em intervalos de tempos iguais.
Considerando ti = 0, como é normalmente feito nos estudos da Cinemática, vi como a velocidade no instante ti, v a velocidade em um instante t qualquer e a como a aceleração escalar constante, pode-se determinar a velocidade v a cada instante t, para um corpo em movimento uniformemente variado, pela seguinte relação:
a = am ⇒ a = ⇒ v − vi = a(t − ti) ⇒ v = vi + at
A relação ôbitída é conhecida como função horária da velocidade [v = f(t)]. Trata-se de uma função polinomial do 1º grau válida apenas para corpos quê descrevem um movimento uniformemente variado.
Pode-se usar um gráfico para representar a variação da velocidade em função do tempo de um corpo em movimento uniformemente variado, representando os valores do tempo no eixo horizontal e os valores da velocidade no eixo vertical.
Observe dois exemplos de gráficos da velocidade em função do tempo. O Gráfico 1 representa um móvel quê descreve um movimento uniformemente variado acelerado, cuja função horária da velocidade é dada por v = 12 + 3t; já o Gráfico 2 é de outro móvel quê também descreve um movimento uniformemente variado, porém retardado, cuja função horária da velocidade é dada por v = 30 − 6t. Considera-se para ambos o intervalo de tempo do movimento entre ti = 0 s e t = 6 s.
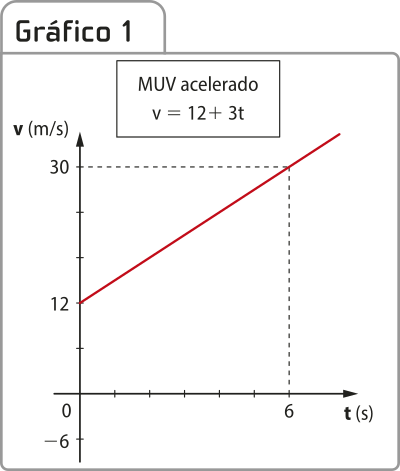
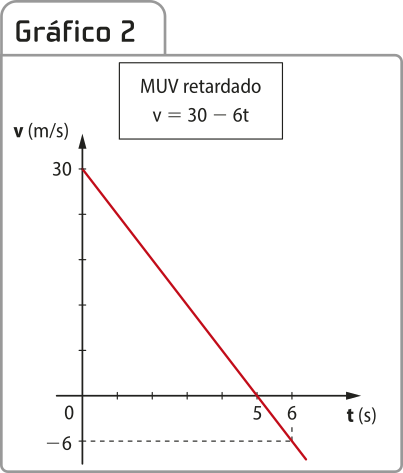
ATIVIDADE RESOLVIDA
1. Um ciclista inicia um treino com uma velocidade escalar de 1 m/s desenvolvendo um movimento uniformemente variado e aumentando a velocidade escalar para 4 m/s em 15 s.
a) Qual é a aceleração escalar desenvolvida pelo ciclista?
b) Qual é a função horária da velocidade dêêsse ciclista?
c) Qual é o valor da velocidade escalar do ciclista no instante 40 s?
Resolução
a) Considerando quê o ciclista aumenta a velocidade de 1 m/s para 4 m/s em 15 s, tem-se:
a = ⇒ a = ⇒ a = 0,2 m/s²
b) v = vi + at ⇒ v = 1 + 0,2t
c) Utilizando a função horária da velocidade desenvolvida pelo ciclista, tem-se:
v = 1 + 0,2 ⋅ 40 ⇒ v = 9 m/s
Página trinta e quatro
ATIVIDADES
6. Um dos passageiros de um ônibus registrou em três instantes distintos a intensidade da velocidade escalar do ônibus no qual viajava. Esses registros foram:
Tempo (s) |
0 |
2 |
4 |
|---|---|---|---|
Velocidade (m/s) |
20 |
23 |
26 |
Admitindo aceleração escalar constante, determine:
a) a função horária da velocidade do ônibus, com dados no SI;
v = 20 + 1,5t (SI)
b) a velocidade escalar do ônibus no instante t = 3 s;
24,5 m/s
c) se o movimento é acelerado ou retardado entre os instantes t = 0 s e t = 4 s.
Acelerado.
7. Uma fábrica de bicicletas fez vários testes com um novo sistema de freios. Em um dêêsses testes, durante alguns segundos, foi anotada a variação da velocidade de uma bicicleta. Com os dados obtidos, foi construído o gráfico da velocidade em função do tempo, conforme a figura.
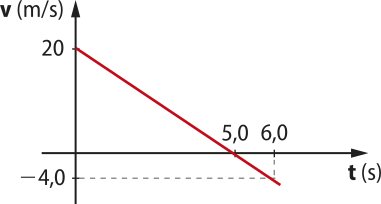
a) De acôr-do com o gráfico, qual é a aceleração da bicicleta, sabendo quê a trajetória é retilínea?
−4,0 m/s2
b) Determine o instante em quê a velocidade escalar da bicicleta é 4 m/s.
4 s
8. Alguns acidentes causados por motos aquáticas têm provocado discussões a respeito do uso dessas embarcações em praias e represas. O desrespeito às normas de condução de embarcações e falhas humanas têm sido as principais causas dêêsse tipo de acidente. Durante alguns instantes, uma moto aquática descreve uma trajetória linear com a variação de velocidade representada no gráfico da figura.
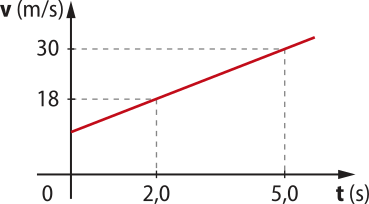
a) Determine a aceleração escalar e a velocidade escalar inicial da moto aquática, em dados do SI.
4,0 m/s2; 10 m/s
b) Pesquise as regras para condução de moto aquáticaem regiões de praias e represas. Analise aspectos relacionados à idade mínima para condução, equipamentos de segurança e normas gerais acerca dêêsse tipo de veículo.
Função e gráfico da posição em relação ao tempo
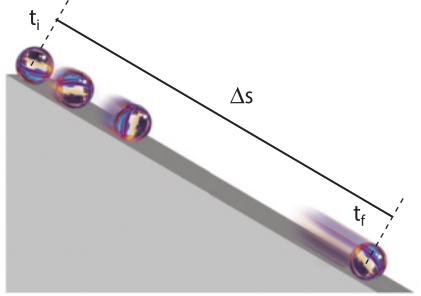
Em uma situação simulada, uma esféra está se movendo para baixo sobre um plano inclinado.
Para descrever as posições da esféra quê realiza um movimento quê póde sêr aproximado para um movimento uniformemente variado, pode-se utilizar um gráfico da velocidade em função do tempo, em quê a área delimitada pela curva e pelo eixo horizontal (eixo do tempo), em determinado intervalo de tempo ((delta)"t = t − ti), é numericamente igual ao deslocamento (delta)"s do corpo em movimento.
Considerando-se quê, no instante inicial, ti a velocidade inicial da esféra era vi, em um instante posterior t executando um movimento uniformemente variado, a velocidade da esféra será v, quê póde sêr determinada pela função horária da velocidade: v = vi + at.
Página trinta e cinco
Com esses valores, obtém-se o gráfico da velocidade em função do tempo. A região nele quê foi sombreada tem formato equivalente a um trapézio, cuja área póde sêr determinada da seguinte forma:
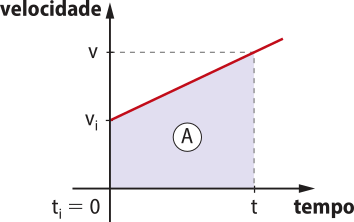
Seja v = vi + at e A =
Substituindo v na equação anterior, tem-se: A = ⇒ A = vit +
Como (delta)"s A ⇒ (delta)"s = vit + ⇒ s − si = vit +
Assim, a posição s de um móvel em movimento uniformemente variado a cada instante t póde sêr determinada pela seguinte equação:
s = si + vi t +
A relação ôbitída é conhecida como função horária da posição [s = f(t)], válida apenas para corpos quê descrevem um movimento uniformemente variado. Trata-se de uma função polinomial do 2º grau na qual: si é a posição inicial; vi é a velocidade inicial; s é a posição no instante t e a é a aceleração escalar.
O gráfico da posição em função do tempo de um corpo quê realiza um movimento uniformemente variado será uma curva denominada parábola, quê possui as seguintes interpretações.
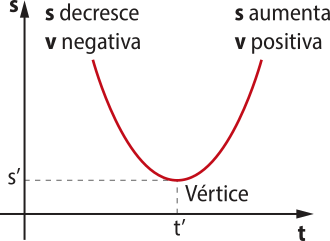
Quando a > 0.
• 0 ≤ t < t‘: a função s = f(t) é decrescente, o movimento uniformemente variado é retrógrado (v < 0) e retardado.
• t > t‘: a função s = f(t) é crescente, o movimento uniformemente variado é progressivo (v > 0) e acelerado.
• t = t‘ (vértice da parábola): repouso (v = 0) com inversão no sentido do movimento.
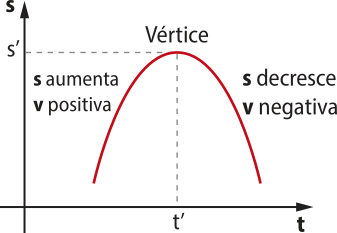
Quando a < 0.
• 0 ≤ t < t‘: a função s = f(t) é crescente, o movimento uniformemente variado é progressivo (v > 0) e retardado.
• t > t‘: a função s = f(t) é decrescente, o movimento uniformemente variado é retrógrado (v < 0) e acelerado.
• t = t‘ (vértice da parábola): repouso (v = 0) com inversão no sentido do movimento.
ATIVIDADES
9. Se a equação s = 8 + 6t − t2 (SI) representa a posição de um móvel, determine o instante em quê esse móvel inverte o sentido de deslocamento.
3 s
10. Um ciclista se desloca com movimento uniformemente variado em uma trajetória retilínea. O gráfico representa a posição do ciclista em função do tempo.
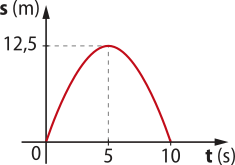
Com base no gráfico, responda:
a) Em quê intervalo de tempo o movimento é acelerado?
5 s a 10 s
b) Em quê intervalo de tempo o movimento é retardado?
0 s a 5 s
c) Em quê instante o ciclista muda o sentido do movimento?
5 s
d) Qual é o valor da velocidade no instante em quê ele inverte o sentido do movimento?
0
e) Em quê instantes ele passa pela origem das posições?
0 s e 10 s
Página trinta e seis
11. Pode-se afirmar quê os espaços percorridos por partículas quê se móvem em um MU varíam da mesma forma quê os espaços percorridos por partículas quê se móvem em um movimento uniformemente variado? Explique sua resposta.
12. Em um trecho de estrada retilíneo e horizontal, um carro mantém velocidade constante de 72 km/h, embora a placa de sinalização indique a velocidade mássima de 60 km/h. Em razão da infração de trânsito, no instante em quê o carro passa diante de um posto policial, um guarda rodoviário, quê estava parado, parte com uma motocicleta mantendo aceleração constante de 2,5 m/s2. Nessa perseguição, quantos segundos serão necessários para quê o policial alcance o carro e autue o motorista?
16 s
Equação de Torit éli
No movimento uniformemente variado, a cada instante t, o corpo está em certa posição s e com certa velocidade v, existindo assim uma relação única entre os valores destas três grandezas. Logo, é possível escrever uma equação quê relacione cada posição do corpo em movimento com sua respectiva velocidade, sêndo assim uma equação quê independe da grandeza tempo.
Considere a função horária da posição e da velocidade do movimento uniformemente variado.
s = si + vit + (I)
v = vi + at ⇒ t = (II)
Substituindo a equação (II) na (I), tem-se:
s = si+v i ⇒
⇒ (delta)"s = ⇒ (delta)"s =
Aproximando os termos em comum para resolver a equação:
(delta)"s = ⇒ (delta)"s = ⇒
⇒ (delta)"s = ⇒ (delta)"s = ⇒ 2a(delta)"s =
Rearranjando os termos dessa equação, obtém-se:
v2 = + 2a(delta)"s
Nessa relação, tem-se a velocidade inicial vi, aceleração escalar a, deslocamento (delta)"s e velocidade v ao final do movimento. Essa equação é conhecida como Equação de Torit éli, em homenagem ao físico e matemático italiano Evangelista Torit éli (1608-1647), estudante de Galileu.
PENSE E RESPONDA

2 Quais são as características do movimento quê devem sêr consideradas para determinar o comprimento da pista de um aeroporto?
Página trinta e sete
ATIVIDADES
13. Um trem desloca-se com velocidade de 54 km/h. Em cérto instante, o maquinista observa um animal sobre os trilhos e aciona imediatamente o freio até parar. Considerando apenas o intervalo de tempo durante o qual o freio foi acionado e sabendo quê a distância percorrida por ele nesse intervalo de tempo foi 450 m, calcule a desaceleração escalar do trem.
−0,25 m/s2
14. (UFRGS-RS) Uma grande aeronave para transporte de passageiros precisa atingir a velocidade de 360 km/h para pôdêr decolar. Supondo quê essa aeronave desenvolva na pista uma aceleração constante de 2,5 m/s2, qual é a distância mínima quê ela necessita percorrer sobre a pista antes de decolar?
a) 10.000 m
b) 5.000 m
c) 4.000 m
d) 2.000 m
e) 1.000 m
Resposta: d)
15. Um motorista parou o ônibus quê dirigia no acostamento de uma estrada retilínea para pegar um passageiro. No local, há uma placa de trânsito indicando quê 300 m à frente existe um deslizamento de térra sobre a pista. Assim quê o passageiro entrou, o ônibus partiu com aceleração escalar constante de 1,0 m/s2. Após ter percorrido 200 m, o motorista acionou os freios imprimindo ao veículo desaceleração escalar constante de 2,5 m/s2 até parar. Quantos metros o ônibus percorreu até parar? Ele irá colidir com o deslizamento?
16. Um carro e um caminhão, parados diante de um semáforo, iniciam seus movimentos com aceleração constante, na mesma direção e sentido, imediatamente após sinalizar o vêrde. A velocidade do caminhão varia 0,5 m/s, em cada segundo, até atingir 35 m/s, quando passa a descrever movimento retilíneo uniforme. No caso do carro, a velocidade varia 1,0 m/s, em cada segundo, até atingir 25 m/s, quando passa a descrever movimento retilíneo uniforme. Diante dessa situação, determine:
a) o tempo e o deslocamento quê o caminhão e o carro levam até atingirem suas velocidades mássimas;
Caminhão: (delta)"t = 70 s e (delta)"s = 1.225 m; carro: (delta)"t = 25 s e (delta)"s = 312,5 m.
b) a distância quê separa os veículos, 70 s após o início dos movimentos;
No instante t = 70 s, o carro está 212,5 m à frente do caminhão.
c) em quê instante o carro é ultrapassado pelo caminhão.
No instante t = 91,25 s.
Movimento de queda livre
O movimento de queda é estudado desde a Antigüidade. Para Aristóteles, se fossem abandonados dois corpos de massas diferentes da mesma altura e no mesmo instante, aquele com maior massa chegaria ao solo primeiro, ideia essa quê perdurou por séculos.
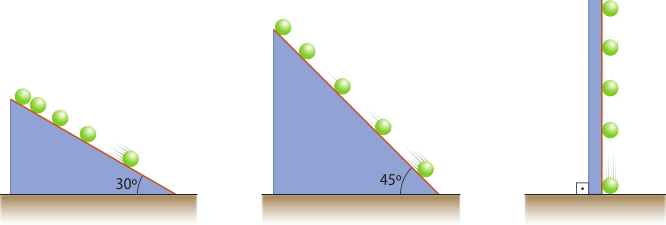
Com o passar do tempo, outros cientistas quêstionaram as ideias de Aristóteles. Um deles foi Galileu, quê analisou sistematicamente, durante o século XVII, o movimento de queda dos corpos. Galileu estudou o movimento de descida de corpos em planos inclinados, variando suas massas e a inclinação do plano, até concluir que corpos com massas diferentes desciam juntos um plano inclinado e chegavam juntos ao solo. Galileu também identificou quê, quanto maior a inclinação do plano, maior a aceleração adquirida pelo corpo, ou seja, a aceleração adquirida pelo corpo dependia apenas da inclinação do plano e não de sua massa.
Página trinta e oito
Recomenda-se propor a atividade do Pense e responda 3 antes da discussão do tema Queda livre, para quê os estudantes exponham suas considerações sobre o fenômeno. Se possível, realizar o experimento com os estudantes d fórma demonstrativa, ou solicitar quê eles o realizem. É possível ainda gravar o experimento para analisá-lo em detalhe.
Eventuais diferenças nos tempos de movimentos foram justificadas por Galileu pela influência da resistência do ar. Assim, desprezando a resistência do ar, todos os corpos abandonados simultaneamente de uma mesma altura atingem o solo no mesmo instante, desenvolvendo um movimento uniformemente variado, com trajetória retilínea e vertical, designado queda livre.
A velocidade de um corpo em queda livre aumenta em valores iguais e em intervalos de tempos iguais, com aceleração constante, portanto trata-se de um movimento uniformemente variado acelerado. Nesse tipo de movimento, o corpo fica sujeito à aceleração da gravidade, representada pela letra g.
Essa aceleração da gravidade é a mesma para qualquer corpo em queda livre, pois seu valor depende apenas das propriedades do planêta (nesse caso, da Terra), ou de outro astro do Universo quê se esteja considerando. Seu valor não é constante, pois depende da altitude e da latitude no planêta, sêndo comumente adotado um valor médio de 9,8 m/s2. É comum, no entanto, quê em alguns problemas o valor da aceleração da gravidade seja arredondado para 10 m/s2.
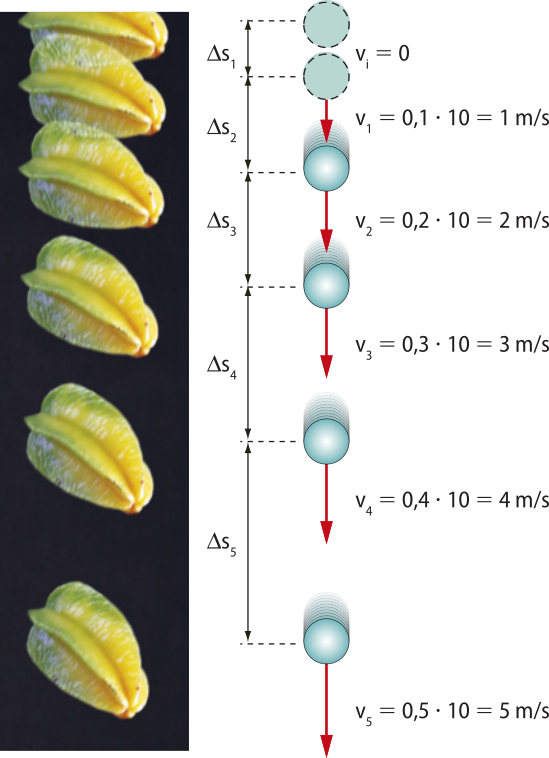
A fotografia apresenta uma carambola em queda livre cujos registros foram feitos em intervalos de tempo iguais de 0,1 s. Na ilustração, a seta vermelha, denominada vetor, indica as velocidades da carambola a cada registro de tempo, considerando a aceleração da gravidade como aproximadamente 10 m/s2. É importante destacar quê, nos estudos da queda livre, os sinais da velocidade e da aceleração também dependem do referencial adotado.

PENSE E RESPONDA
3 Abandonando uma borracha e uma fô-lha de papel aberta, simultaneamente, da mesma altura, a borracha chegará primeiro ao solo (como representado na imagem). Você acha quê isso ocorre porque a borracha tem mais massa do quê a fô-lha de papel? Existe alguma situação em quê ambos os objetos chegariam juntos ao solo? Se sim, qual?
ESPAÇOS DE APRENDIZAGEM
• O vídeo mostra uma demonstração de experimento de queda livre, no qual uma bola de boliche e algumas penas foram abandonadas simultaneamente de uma mesma altura em uma câmara de vácuo (selecione a opção de legendas em português nas configurações).
Bráiam Cox visits the world's biggest vacuum | Human Universe – BBC. Publicado por: BBC. Vídeo (5 min). Vídeo em inglês. Disponível em: https://livro.pw/vixlp. Acesso em: 5 jul. 2024.
Página trinta e nove
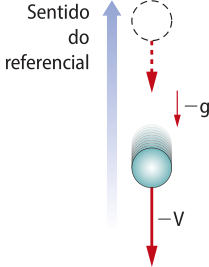
Referencial crescente para cima
• Aceleração: a aceleração da gravidade é negativa, pois sua orientação é contrária à orientação adotada para o referencial:
a = −g
• Função horária da velocidade:
v = vi + at
v = vi − gt
• Função horária da posição:
s = si + vit +
s = si + vit −
• Equação de Torit éli:
v2 = + 2a(delta)"s
v2 = − 2g(delta)"s
Referencial crescente para baixo
• Aceleração: a aceleração da gravidade é positiva, pois sua orientação coincide com a orientação adotada para o referencial:
a = +g

• Função horária da velocidade: v = vi + at
v = vi + gt
• Função horária da posição:
s = si + vit +
s = si + vi t +
• Equação de Torit éli:
v2 = + 2a(delta)"s
v2 = + 2g(delta)"s
ATIVIDADE RESOLVIDA
2. Uma atleta se lança de uma platafórma de uma piscina de 5 m de altura, a partir do repouso, e cai em um movimento quê póde sêr aproximado para uma queda livre.

a) Qual é a velocidade da atleta ao atingir a á gua, em m/s?
b) Quanto tempo durou a queda livre, em segundo?
Resolução
Adotando um referencial crescente para baixo, tem-se:
si = 0; s = 5 m; a = g = 10 m/s2; vi = 0
a) Pela função horária da velocidade do movimento uniformemente variado.
v = vi + gt
v = 0 + 10 ⋅ 1 ⇒ v = 10 m/s
b) Pela função horária da posição do movimento uniformemente variado de um corpo em queda livre:
s = si + vit + ⇒ 5 = 0 + 0 ⋅ t + ⇒
⇒ 5 = 5t2 ⇒ t2 = 1 ⇒ t = = ± 1 s
Como t = −1 s não convém (pois o tempo não póde sêr negativo), tem-se: t = 1 s.
Página quarenta
ATIVIDADES
17. O quê significa dizêr quê um corpo está em queda livre?
18. Em 1971, o astronauta ame ri cano Daví scót realizou, na superfícíe da Lua, o experimento de queda livre de corpos no vácuo, anteriormente propôsto por Galileu. Deixou cair ali uma pena e um martelo, simultaneamente, a partir da mesma posição.
a) O quê ele observou ao final da queda?
b) Supondo quê ambos os objetos tênham sido soltos de uma altura de 1,6 m em relação à superfícíe, depois de quanto tempo o martelo alcançaria o solo? (Dado: gLua ≃11,6 m/s2.)
1,4 s
19. Um barco navéga com velocidade de 10 m/s, em linha reta, na direção de uma ponte. Sobre a ponte, a 20 m de altura da á gua, encontram-se alguns amigos quê desê-jam entregar um pequeno pacote, com lembranças, para o navegador. No momento em quê o pacote é solto e inicia sua queda livre, qual deve sêr a distância do barco até esse ponto sôbi a ponte para quê o pacote káia na proa? Considere a aceleração da gravidade no local, aproximadamente, 10 m/s2.
20 m
20. Uma esféra de aço cai, a partir do repouso, em queda livre, de uma altura de 80 m acima do solo. Despreze a resistência do ar e adote g = 10 m/s2. Calcule o módulo da velocidade de chegada da esféra ao solo.
40 m/s
21. Durante um experimento controlado, um objeto é solto do 9º andar de um prédio e, após 1 s de queda livre, passa pela janela do 8º andar. Quanto tempo, após sêr solto, o objeto passará pela janela do 5º andar?
2 s
Não repita essa atividade, pois a prática póde causar acidentes.
Lançamento vertical
O lançamento vertical é mais um exemplo de movimento uniformemente variado e póde sêr facilmente experimentado por você. Por exemplo, pégue um objeto leve e sem pontas e arremesse-o em uma trajetória retilínea e vertical, de baixo para cima, de tal forma quê ele volte às suas mãos, como o lançamento mostrado na imagem. Observe detalhadamente o movimento do corpo, na subida e na descida. Se achar necessário, faça o lançamento várias vezes. Mesmo sem a utilização de nenhum instrumento, repare o quê ocorre com a velocidade do corpo durante a subida, no ponto mais alto atingido por ele e durante a descida.
Um corpo lançado verticalmente para cima nas proximidades da superfícíe terrestre, supondo a resistência do ar desprezível, possui velocidade inicial diferente de zero, sobe e desce em uma trajetória retilínea vertical, descrevendo um movimento uniformemente variado.

Página quarenta e um
• A aceleração do movimento será a aceleração da gravidade, com orientação vertical para baixo, e nunca será nula. Normalmente, adota-se um referencial crescente para cima, d fórma quê a = −g.
• Durante a subida, tem-se um movimento uniformemente variado retardado. Para g = −10 m/s2, a velocidade diminui 10 m/s a cada 1 s.
• A velocidade é nula no ponto mais alto da trajetória (inversão de sentido).
• Durante a descida, tem-se um movimento uniformemente variado acelerado. Para g = 10 m/s2, a velocidade aumenta em módulo 10 m/s a cada 1 s.
ATIVIDADE RESOLVIDA
3. Um jovem tenista consegue, com o auxílio da raquete, jogar uma bó-linha verticalmente de baixo para cima. Considerando quê a velocidade inicial da bó-linha é 20 m/s e g = 10 m/s2, determine:
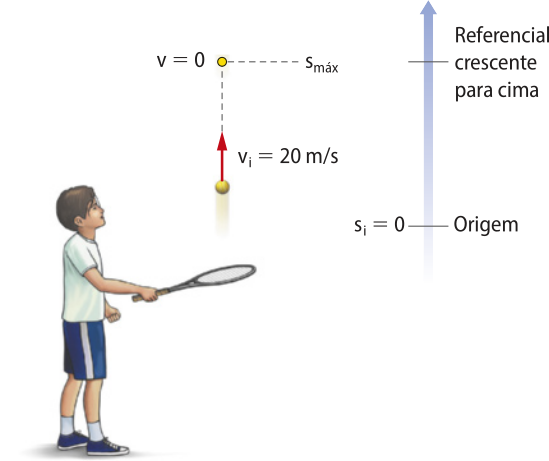
a) a altura mássima atingida pela bó-linha, em relação à origem do lançamento;
b) o tempo decorrido até a bó-linha atingir a altura mássima.
Resolução
Adotando um referencial crescente para cima, na direção vertical, a aceleração da gravidade será g = −10 m/s2.
a) Na posição de altura mássima, tem-se v = 0. Pela equação de Torit éli, pode-se obtêr a altura mássima (smáx).
v2 = − 2a (delta)"s
0 = 202 − 2 ⋅ 10 ⋅ (delta)"s ⇒ (delta)"s = = 20
Sendo (delta)"s = smáx − si:
20 = smáx − 0
smáx = 20 m
b) Usando a função horária da velocidade, obtém-se:
v = vi + at
0 = 20 − 10t ⇒ t = 2 s
ATIVIDADES
22. Ao lançar um corpo verticalmente para cima, com velocidade inicial de 10 m/s, pode-se observar e afirmar quê:
a) ele apresenta um movimento acelerado.
b) ele apresenta um movimento acelerado durante a subida e retardado durante a descida.
c) ele apresenta aceleração no ponto mais alto de sua trajetória.
d) no ponto mais alto de sua trajetória, a velocidade e a aceleração do corpo são nulas.
e) ao atingir a mesma posição de lançamento, ele apresenta a mesma velocidade.
Resposta: c)
23. Do topo de um edifício, a 20 m do solo, atira-se um objeto verticalmente para cima com velocidade inicial de 10 m/s. Considere a resistência do ar nula e a aceleração da gravidade no local 10 m/s2 e determine:
a) o tempo de subida do corpo;
1 s
b) o tempo de chegada ao solo desde o lançamento;
5,24 s
c) a altura mássima atingida pelo objeto.
25 m
Página quarenta e dois
24. Se você arremessar uma moeda perpendicularmente à superfícíe de uma mesa, de baixo para cima, e registrar quê ela demorou 6 s para retornar ao ponto do arremesso, qual foi o valor da velocidade inicial de lançamento dessa moeda? Adote g = 10 m/s2 e desconsidere as resistências impostas pelo ar.
30 m/s
25. (UFBA) Um corpo é lançado verticalmente para cima com velocidade vi. Ao atingir sua altitude mássima igual a 100 m, um segundo corpo é lançado do mesmo local e com velocidade inicial igual à do primeiro. Determine a altura em quê os corpos se encontram. Considere g = 10 m/s2 e despreze a resistência do ar.
75 m
Auxiliar os estudantes a se organizarem em grupos e orientá-los para quê assistam ao filme e debatam as atividades em aula.
SAIBA +
Meteoro: o futuro está em jôgo
Em um isolado observatório, o Dr. Lehman, ao realizar observações astronômicas e cálculos, descobre um grande meteoroide em rota de colisão com a Terra. Ele identifica também quê outros meteoroides irão atingir diversas cidades do planêta. Com esse enredo, o filme Meteoro: o futuro está em jôgo aborda também as reações das pessoas diante da tragédia iminente.
Assista a esse filme com seus côlégas e, em grupo, organizem-se para responder às atividades a seguir.

ATIVIDADES
1. Vocês sabem a diferença entre asteroide, meteoroide, meteoro e meteorito? Conversem entre si e façam pesquisas se necessário. Em seguida, realizem uma análise crítica do título do filme para identificar qual termo sêria mais adequado, do ponto de vista da Ciência, a ser utilizado.
2. Ao longo do filme, menciona-se quê uma chuva de meteoros irá ocorrer e destruir importantes cidades do planêta. Uma chuva de meteoros oferece risco para os sêres vivos do planêta? Justifiquem sua resposta.
3. Considerem quê um corpo celeste em movimento adentre a atmosféra terrestre e káia em direção ao solo. O movimento descrito por esse corpo póde sêr classificado como queda livre? Em uma queda livre, o fenômeno meteoro ocorreria? Justifiquem sua resposta.
4. No filme, o Dr. Lehman trabalha com pesquisas e observações astronômicas e faz uma importante descoberta. Conversem entre si sobre o trabalho de um astrônomo e façam uma lista sobre a importânssia dêêsse ramo do mercado de trabalho para a ssossiedade.
5. Atualmente, boa parte dos trabalhos em Ciência são feitos em laboratórios e centros de pesquisa. No caso do Brasil, a maior parte dêêsses laboratórios está localizada em universidades. Esse tipo de trabalho é feito d fórma coletiva e geralmente conta com parcerias de diversos pesquisadores dos mais variados locais do mundo. Vocês consideram quê a representação de cientista dada no filme pela figura do Dr. Lehman está de acôr-do com esse perfil? Por quê?
6. Em se tratando do trabalho com Astronomia, façam uma pesquisa sobre a astrônoma brasileira Dr.ª Duilia Fernandes de Mello (1963-) para conhecer os trabalhos e projetos quê lhe renderam destaque mundial. Organizem um debate para discutir sobre essa importante pesquisadora brasileira e as motivações quê pessoas como ela podem causar nos estudantes.
Página quarenta e três
OFICINA CIENTÍFICA
Tempo de reação
Direção defensiva é o ato de um motorista dirigir um veículo de modo a evitar acidentes, mesmo em situações de ocorrências adversas. O condutor prudente é aquele quê adota procedimentos preventivos no trânsito, mantendo posturas de cautela e civilidade.
Um dêêsses procedimentos é a atenção ao dirigir, o quê possibilita ao condutor se antecipar às possíveis ocorrências, reagindo d fórma correta. Estando atento, o tempo de reação do motorista permite ações corretas quê reduzem d fórma considerável os acidentes de trânsito.

O tempo de reação corresponde a um intervalo de tempo entre a geração de um estímulo no corpo e uma ação motora.
Organize-se em dupla para realizar o experimento a seguir e investigar uma forma de determinar o seu tempo de reação e o de seu colega.
Materiais
• régua de 30 cm de comprimento
• calculadora
Procedimentos
• Mantenha a régua suspensa verticalmente, com escala crescente de baixo para cima, segurando-a pela extremidade superior.
• Peça ao colega quê coloque os dedos da mão, em forma de pinça, próximos do numeral zero da régua, sem tocá-la, como está na imagem.
• Peça a seu colega quê olhe atentamente para a régua e, sem aviso prévio, abandone-a.
• Seu colega deve segurar a régua o mais rápido quê conseguir. Anote a medida do ponto da régua em quê ele conseguiu segurá-la.
• Repita o procedimento outras duas vezes, obtendo assim três dados.
• Inverta os papéis com seu colega e repita o procedimento.

ATIVIDADES
1. Faça, para você e seu colega, a média dos valores das três medidas obtidas.
2. Discuta com seu colega uma forma de obtêr os valores do tempo de reação de vocês. Quais dados são necessários? Quais medidas precisam sêr aproximadas? É necessário realizar aproximações e desprezar condições? Se sim, quais? Com o valor da média aritmética ôbitída, considerando quê a régua parte do repouso e adotando quê seu movimento é uma queda livre com aceleração da gravidade igual 9,8 m/s2, verifique uma forma de determinar seu tempo de reação.
3. Com base nas três medidas quê você obteve, determine seu maior e seu menor tempo de reação.
4. Em dupla, listem situações em quê o tempo de reação menor seja o mais adequado.
Página quarenta e quatro
TEMA 5
Análise vetorial do movimento
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Grandezas vetoriais
Avançando nos estudos do movimento, você agora conhecerá os conceitos relacionados à Cinemática Vetorial, área da Física quê analisa os movimentos considerando não apenas a intensidade das grandezas, mas também sua direção e seu sentido.
Para isso, será utilizada uma entidade matemática abstrata denominada vetor, quê se caracteriza por um valor, dado em módulo (um número não negativo), com uma direção e um sentido.
Para definir a grandeza vetor, considere um segmento de reta r orientado AB, com origem em A e extremidade em B, ambos sobre a reta r. Com isso, é possível identificar três características:
• módulo: comprimento do segmento orientado AB quê representa o seu valor numérico.
• direção: a mesma da reta r à qual ele pertence.
• sentido: de A para B.
Assim, um vetor póde sêr representado por uma seta, como a da imagem.
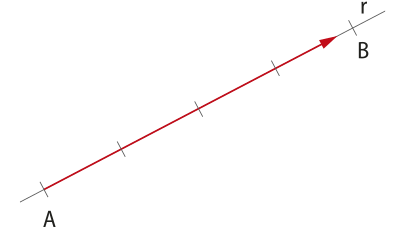
Posição e deslocamento vetorial
Considere uma partícula em movimento ao longo da trajetória pontilhada, passando pelo ponto A em determinado instante. O ponto O é a origem de um sistema referencial xOy. Denomina-se vetor posição da partícula em relação ao ponto O o vetor , de origem em O e extremidade no ponto A.
PENSE E RESPONDA
1 Observe os dois carros, em primeiro plano, na fotografia. Se ambos estiverem trafegando a 50 km/h, pode-se dizêr quê eles possuem a mesma velocidade? Por quê?
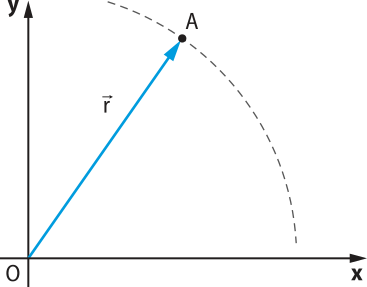

Página quarenta e cinco
Agora, considere quê a partícula se desloca do ponto A ao ponto B sobre a trajetória pontilhada. Os vetores posição e e representam, ve to rial men te, as posições da partícula nos instantes ti e t, respectivamente, em relação ao ponto O. O vetor , representado pela diferença entre o vetor posição final e o vetor posição inicial , é chamado deslocamento vetorial entre os pontos A e B.
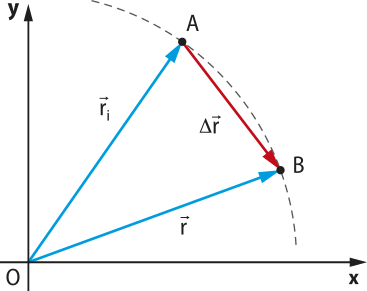
Entre os pontos A e B, é o deslocamento vetorial e (delta)"s será o deslocamento escalar sofrido pela partícula. Quando se escreve (delta)"r (sem a notação vetorial), refere-se apenas ao módulo do vetor, ou seja, seu valor numérico.
Observe quê (delta)"r < (delta)"s, pois a trajetória é curvilínea. Se a partícula estivesse em trajetória retilínea, sempre no mesmo sentido, então (delta)"r = (delta)"s. De modo geral, (delta)"r ≤ (delta)"s.
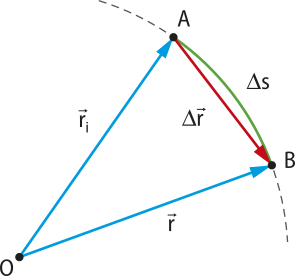
Velocidade vetorial
Uma partícula se móve ao longo da trajetória representada a seguir passando pelo ponto A no instante t1 e, posteriormente, pelo ponto B no instante t2. Considere o ponto O como a origem do sistema de referência.
A velocidade vetorial média da partícula, nesse intervalo de tempo, corresponde à razão entre o vetor deslocamento entre A e B, e o intervalo de tempo (delta)"t de t1 a t2.
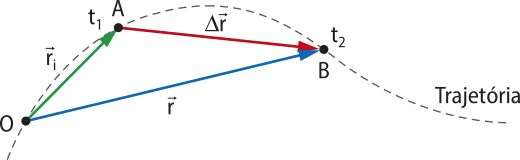
O vetor sempre terá direção e sentido iguais aos do vetor uma vez quê o intervalo de tempo (delta)"t é sempre positivo.
A velocidade vetorial instantânea corresponde ao limite da velocidade vetorial média para um intervalo de tempo quê tende a zero, ou seja, um intervalo de tempo muito pequeno.
Quando o intervalo de tempo tende a zero, as posições vetoriais são bem próximas, o vetor tende à direção tangente da trajetória, e seu módulo tende ao módulo do deslocamento escalar. Em consequência díssu, a velocidade vetorial instantânea:
• é tangente à trajetória, e seu sentido é igual ao do movimento;
• tem módulo igual ao da velocidade escalar instantânea, ou simplesmente velocidade escalar, desprovido de qualquer sinal ou indicação de orientação.
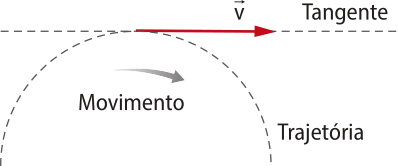
Página quarenta e seis
ATIVIDADES
1. Uma roda-gigante de raio 10 m gira com velocidade constante de 10 m/s. Suponha quê uma pessoa, em determinado instante, passe pelo ponto mais alto da roda e, 10 s depois, passe pelo ponto mais baixo.
a) Represente, no seu caderno, o vetor deslocamento e determine sua intensidade, sua direção e seu sentido.
b) Calcule a intensidade da velocidade escalar média da roda.
c) Apresente as características do vetor velocidade média.
2. Sobre uma esteira rolante, é colocada uma peça de automóvel quê sofre um deslocamento de 30 m. Essa afirmação permite caracterizar:
a) o deslocamento escalar da peça? Justifique.
b) o deslocamento vetorial da peça? Justifique.
3. (Enem/MEC) As cidades de Quito e Cingapura encontram-se próximas à linha do equador e em pontos diametralmente opostos do glôbo terrestre. Considerando o raio da Terra igual a 6.400 km, pode-se afirmar quê um avião saindo de Quito, voando em média 800 km/h, descontando as paradas de escala, chega a Cingapura em aproximadamente:
a) 16 horas
b) 20 horas
c) 25 horas
d) 32 horas
e) 36 horas
Resposta: c)
SAIBA +
Como funciona o GPS?
Atualmente, é difícil imaginar o funcionamento dos meios de transporte (por térra, ar ou água) sem o auxílio do GPS, sigla em inglês de Global Positioning System (Sistema de Posicionamento Global). Desenvolvido para uso militar, em meados dos anos 1980, esse sistema foi aberto para uso civil. Além dele, há o sistema russo GLONASS, o chinês COMPASS e o europeu GALILEO, esse último foi o único desenvolvido para uso civil.
O GPS consiste em um sistema de posicionamento quê depende de sinais enviados por uma rê-de de satélites, sôbi o contrôle do Departamento de Defesa dos Estados Unidos. Esses satélites levam 12 horas para completar uma volta em torno da Terra e encontram-se a cerca de 20.000 km de altitude. Os satélites transmitem um sinal de alta freqüência quê indicam a hora na qual cada um foi transmitido, com grande precisão. Enquanto isso, os receptores na Terra captam o sinal e determinam a posição, comparando a diferença de tempo entre a transmissão e a recepção do sinal. Desse modo, calculam a distância de cada satélite. À medida quê um objeto se desloca, a distância em relação aos satélites também muda e provoca uma diferença no tempo do percurso, quê sérve para atualizar a localização.
Cruzando os dados de pelo menos três satélites, é possível o receptor determinar a localização de cérto objeto na superfícíe terrestre. Caso ocorra o processamento contínuo da posição, o receptor poderá determinar o seu deslocamento e a sua velocidade.
ATIVIDADES
Em grupo, reflitam sobre o uso da tecnologia GPS e respondam aos itens a seguir.
1. Pesquisem como a posição de um corpo na superfícíe da Terra póde sêr acompanhada pelo GPS.
2. Investiguem pelo menos uma outra situação em quê é possível identificar a utilização de sistemas de posicionamento, além das citadas no texto.
3. Que outros exemplos de tecnologia contemporânea utilizada na ssossiedade podem facilitar o trabalho humano? Realizem uma roda de discussão e debatam sobre esse assunto.
Página quarenta e sete
Aceleração vetorial
Na Cinemática Vetorial, a variação da velocidade vetorial em relação ao tempo é chamada aceleração vetorial média .
A figura a seguir representa a trajetória descrita por um ponto material entre as posições A e B. No instante inicial ti, o ponto material passa pela posição A com velocidade e, em um instante posterior t, passa pela posição B com velocidade . A aceleração vetorial média , nesse intervalo de tempo, é:
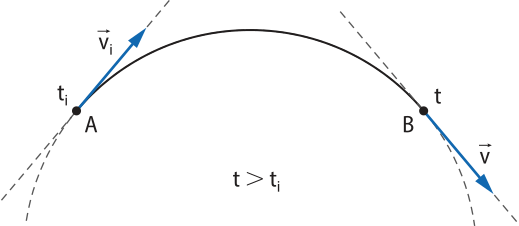
A aceleração vetorial instantânea ou simplesmente aceleração vetorial, méde a variação da velocidade vetorial em um intervalo de tempo infinitamente pequeno.
Em qualquer movimento, a velocidade é tangente à trajetória, descrita pelo corpo.
No caso do movimento retilíneo variado, o vetor aceleração tem a mesma direção da trajetória, e seu sentido depende do tipo de movimento.
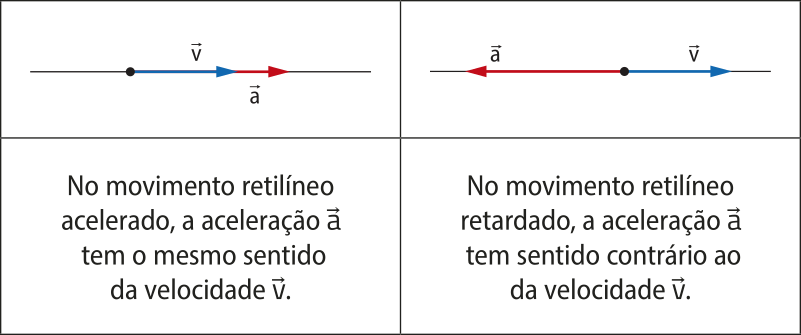
No caso do movimento curvilíneo, o vetor aceleração tem a direção voltada para a parte interna da curva, como representado nas Figuras 1 e 2.
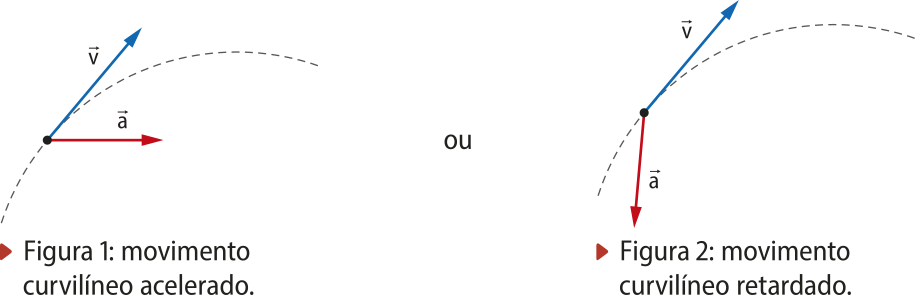
Sabendo quê a velocidade vetorial varia em módulo e direção, é preciso utilizar a representação da aceleração vetorial em duas componentes vetoriais: aceleração tangencial t e aceleração centrípeta .
Página quarenta e oito
A aceleração tangencial está relacionada à variação da velocidade escalar e apresenta as características a seguir, nos movimentos curvilíneos.
• O módulo é igual ao apresentado pela aceleração escalar: at = .
• A direção é a mesma da reta tangente à trajetória em cada posição ocupada pelo ponto material.
• O sentido será o mesmo do vetor velocidade se o movimento for acelerado (Figura 3), e contrário a ele se o movimento for retardado (Figura 4).
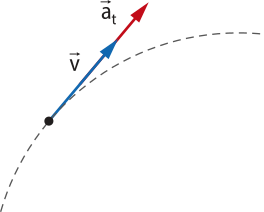
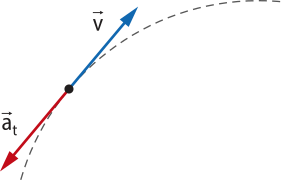
A aceleração centrípeta indica a variação da orientação do vetor velocidade . Para o ponto material quê descreve uma trajetória circular, com raio de curvatura R e com velocidade escalar v, como representado na figura, a aceleração centrípeta apresenta as seguintes características:
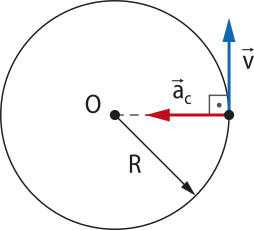
• O módulo é determinado por:
ac =
• A direção é perpendicular à direção da velocidade . Se o movimento for retilíneo, a direção da velocidade não variará, portanto
• O sentido é orientado para o centro de curvatura da trajetória. O vetor aceleração é representado pela adição das componentes e . Observando quê os vetores e são ortogonais, é possível obtêr o módulo de aplicando o teorema de Pitágoras:
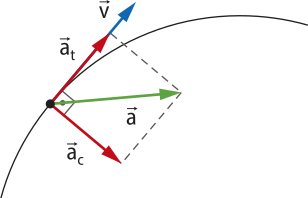
a =
Página quarenta e nove
ATIVIDADES
4. A trajetória circular descrita por um ponto material tem raio de curvatura R = 2,5 m. Sabendo quê ele se desloca com movimento uniforme e velocidade v = 5 m/s, determine:
a) o módulo das componentes vetoriais da aceleração;
= 0 e = 10 m/s2
b) o módulo de .
10 m/s2
5. Observe a imagem do relógio de pêndulo. Analise o movimento dêêsse pêndulo no esquema a seguir, na posição A, descendente, e na B, ascendente.

a) Represente, no seu caderno, para as posições A e B, os vetores , , e
b) Classifique o movimento do pêndulo nas posições A e B.
6. Um carro desloca-se em uma estrada e o motorista vê uma placa de sinalização quê indica: “Curva acentuada para a direita. Velocidade mássima 36 km/h”. O motorista desacelera até atingir a velocidade indicada na placa e a mantém constante enquanto faz a curva. Sabendo quê o raio da curva é de 10 m, determine a intensidade, a direção e o sentido da aceleração () do veículo. Faça um esquema, no caderno, representando os vetores da velocidade e da aceleração.
7. Um ponto material com velocidade inicial vi = 0 descreve uma trajetória circular de raio R = 9 m e movimento uniformemente variado, com aceleração escalar a = 3 m/s2.
Para o instante t = 2 s, determine:
a) a velocidade escalar;
6 m/s
b) o módulo das componentes vetoriais da aceleração ;
= 3 m/s2 e = 4 m/s2
c) o módulo da aceleração
5 m/s2
8. Um avião sai de Roma com destino a Sã Marino e logo atinge a velocidade de 500 km/h. Ao mesmo tempo, sofre a ação de um vento forte, de leste a oeste, quê o afasta da rota. Para chegar ao seu destino com segurança, qual deve sêr o procedimento do piloto? Faça um esquema no caderno, com vetores, para indicar a velocidade do avião em relação à Terra, a velocidade de arrastamento do vento e a velocidade resultante. Se a velocidade de arrastamento do vento for de 300 km/h, calcule a velocidade resultante do avião em relação à Terra.
400 km/h
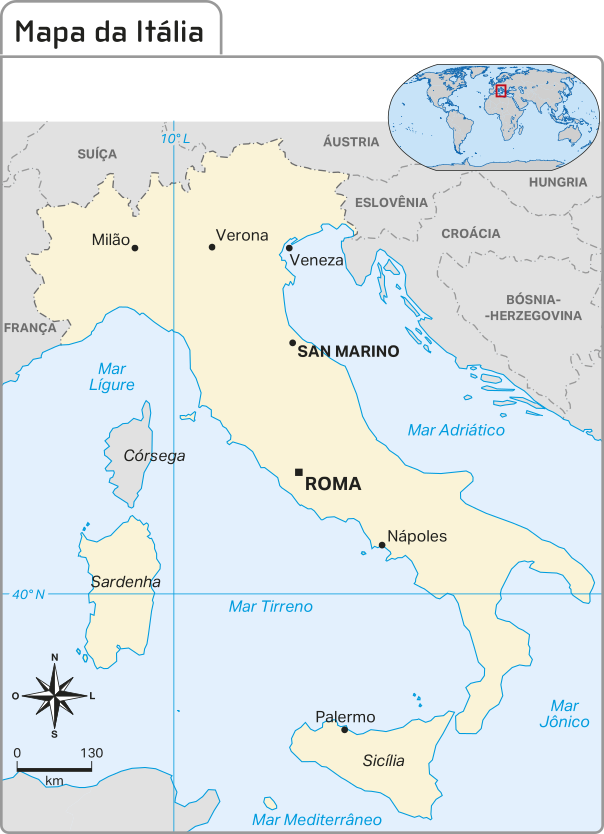
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2024. p. 49.
Página cinquenta
Composição de movimentos
Em Cinemática Escalar, define-se os estados de movimento ou de repouso de um corpo em relação a determinado referencial. Essa ideia é o ponto de partida para o entendimento da composição de movimentos.
Considere a seguinte situação: uma esteira rolante foi desativada para manutenção. O operário encarregado do serviço desloca-se sobre a esteira com velocidade de 3 m/s em relação a um ponto E, marcado sobre a esteira, conforme indicado na ilustração a seguir.
O vetor quê representa essa velocidade será chamado e indica a velocidade do operário em relação ao ponto E, com módulo vO/E = 3 m/s.
Em um instante posterior, a esteira volta a funcionar com velocidade , de módulo 2 m/s. O vetor representa a velocidade da esteira em relação à mesa de operação do chefe de manutenção (C), indicado na ilustração a seguir.
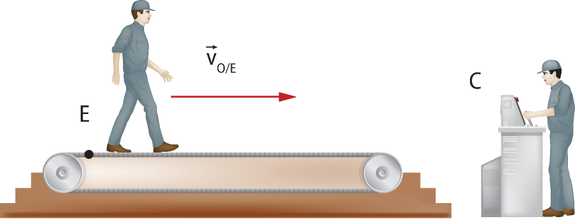
Nessa situação, considere duas possibilidades:
1
Se o operário estiver se movimentando na mesma direção e sentido da esteira, o módulo do vetor (velocidade do operário em relação ao chefe de manutenção) será determinado por:
vO/C = 3 + 2 = 5 m/s
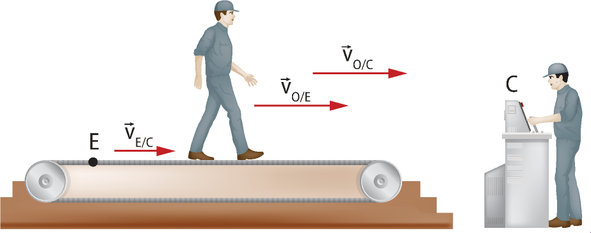
2
Se o operário estiver se movimentando na mesma direção e em sentido contrário ao da esteira, o módulo do vetor (velocidade do operário em relação ao chefe de manutenção) será determinado por:
vO/C = 3 − 2 = 1 m/s
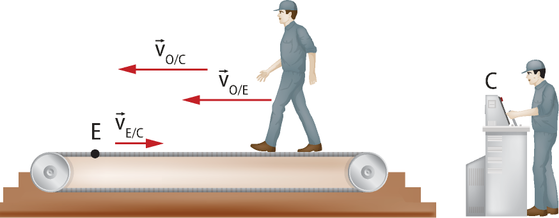
Nas duas possibilidades, o movimento do operário em relação ao chefe é a composição entre o movimento do operário em relação à esteira e o movimento da esteira em relação ao chefe Logo:
PENSE E RESPONDA

2 Observe a movimentação dos usuários das escadas rolantes e compare a velocidade de cada pessoa em relação à escada.
Página cinquenta e um
ATIVIDADE RESOLVIDA
1. Uma lancha desen vólve velocidade vl/a = 20 km/h em relação às águas de um rio, quê se movimentam com velocidade va/m = 15 km/h em relação às margens do rio. Determine a velocidade da lancha em relação às margens do rio (vl/m) quando:
a) a lancha se movimenta na mesma direção e no mesmo sentido das águas;
b) a lancha se movimenta na mesma direção e em sentido contrário ao das águas;
c) a lancha se movimenta na direção perpendicular às margens;
d) a lancha se movimenta em direção oblíqua às margens, de tal forma quê sua trajetória é perpendicular a elas.
Resolução
Em qualquer dos casos, a velocidade da lancha em relação às margens é a composição entre a velocidade da lancha em relação às águas e a velocidade das águas em relação às margens .
a) 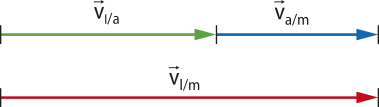
⇒ = 20 + 15 ⇒ = 35 km/h
b) 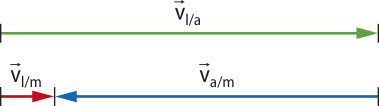
⇒ = 20 + 15 ⇒ = 5 km/h
c) 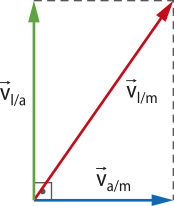
Nesse caso, tem-se:
= 202 + 152 ⇒ vl/m = ⇒ vl/m = 25 km/h
d) 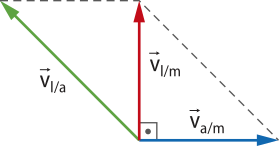
A trajetória é perpendicular à margem, então:
= (20)² − (15)2
=
≃ 13,2 km/h
ATIVIDADES
9. Um trem e um automóvel se móvem na mesma direção em um trecho retilíneo. Seus movimentos são uniformes e o módulo da velocidade do automóvel é o dôbro do módulo da velocidade do trem. Desprezando o comprimento do automóvel e tendo o trem 100 m de comprimento, determine o espaço percorrido pelo automóvel desde o instante em quê alcança o trem até o instante em quê o ultrapassa.
200 m (mesmo sentido); ≃ 67 m (sentidos contrários).
10. Uma roda de bicicleta se móve, sem deslizar, com velocidade constante. Considerando o movimento de rotação e de translação da roda, como você representaria o vetor velocidade do ponto vermelho ilustrado na figura?

a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) vetor nulo
Resposta: d)
Página cinquenta e dois
11. Suponha quê um barco, quando desce determinado rio, tem velocidade de 40 km/h e, ao subir o mesmo rio, velocidade de 30 km/h. Determine:
a) a velocidade da correnteza em relação à margem;
5 km/h
b) a velocidade do barco em relação à á gua.
35 km/h
12. sôb uma chuva quê cai verticalmente, uma pessoa caminha com velocidade horizontal de 1 m/s em relação ao solo, inclinando o guarda-chuva 30° (em relação à vertical) para ficar mais protegida. Qual é o módulo da velocidade da chuva em relação ao solo?
Considere tg 60° = 1,7.
1,7 m/s
13. Um avião desloca-se para leste com velocidade constante de 240 km/h. Ao chegar em certa região, é atingido por um vento muito forte, de velocidade constante de 100 km/h, quê sopra perpendicularmente à direção de deslocamento do avião. Suponha quê esse vento continue por 2 horas.
a) Determine a intensidade da velocidade resultante.
260 km/h
b) Qual é a distância quê o separa da rota original após 2 horas.
200 km
c) Avalie se o valor de velocidade do vento é compatível com o sofrido nas regiões de tráfego de aeronaves. Se necessário, faça uma pesquisa para obtêr esse valor.
Movimento em duas dimensões sôbi ação da gravidade
A expressão “lançamento de projéteis” está associada ao movimento não vertical de corpos nas proximidades da superfícíe terrestre. O movimento de projéteis é caracterizado pela composição de dois movimentos simultâneos e independentes: um na horizontal e outro na vertical.
Uma constatação muito interessante póde sêr feita a partir de um experimento simples. Se um corpo for abandonado a determinada altura do solo e, simultaneamente, um segundo corpo for lançado na horizontal, a partir da mesma altura, ambos chegam ao solo no mesmo instante. Esse fato foi descrito por Galileu, no século XVII, ao analisar a queda de uma bala de canhão do alto do mastro de um navio em movimento.
O fato de os corpos chegarem ao solo ao mesmo tempo demonstra quê a componente horizontal da velocidade inicial ( ou) não interfere no movimento vertical ( ou ). Esse fato é conhecido como princípio da independência dos movimentos (ou princípio de Galileu) e diz quê, se um corpo realiza um movimento compôzto, cada um dos movimentos componentes ocorre independentemente, como se os outros não existissem.
Para êste estudo, considera-se quê a componente horizontal do movimento tem velocidade constante e sem a interferência do ar, caracterizando um movimento uniforme. Já a componente vertical do movimento possui aceleração, nesse caso a aceleração da gravidade g, caracterizando um movimento uniformemente variado. Sendo o movimento em duas direções, x e y, pode-se dizêr quê ele ocorre em duas dimensões.
Ao analisar o lançamento de projéteis, pode-se constatar duas situações: quando ele é feito na direção horizontal e quando ocorre na direção oblíqua (entre a direção horizontal e vertical).
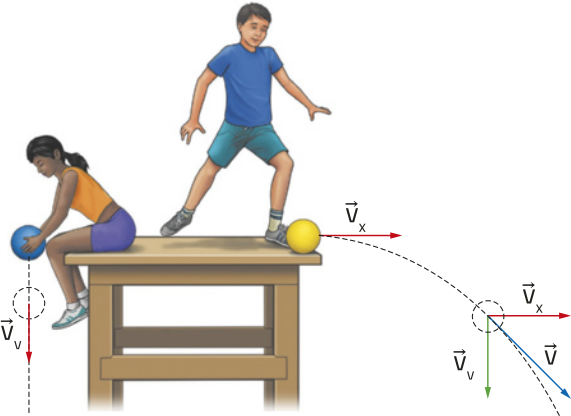
Página cinquenta e três
Lançamento horizontal
O fato de se considerar o lançamento horizontal de uma partícula, de determinada altura, feito nas proximidades da Terra, e com corpos não leves, garante quê a aceleração da gravidade se mantenha constante na direção vertical do movimento. Na direção horizontal, despreza-se os efeitos da resistência do ar para garantir quê o movimento nessa direção não tenha aceleração, isto é, seja uniforme.
Para representar o lançamento horizontal, utiliza-se um plano cartesiano como sistema de referência. A velocidade póde sêr determinada, a cada instante, pela soma vetorial da componente horizontal com a componente vertical . No instante inicial, temos e = 0 para a componente vertical (pois o lançamento ocorre na horizontal).
• Componente horizontal (xi = 0): movimento uniforme (neste caso xi = 0).
x = vxt
• Componente vertical: movimento uniformemente variado (neste caso, ay = −g).
vy = −gt
= −2g(delta)"y
y = yi −
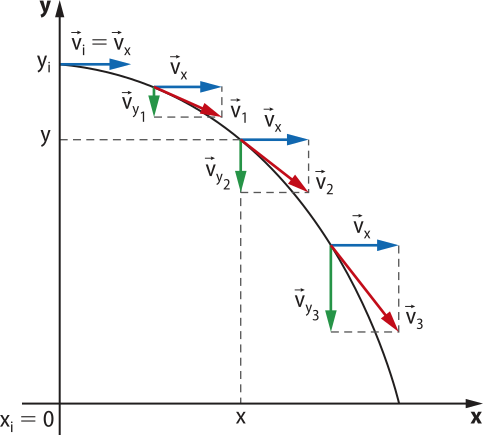
ATIVIDADES
14. Uma bola de tênis rola sobre uma mesa horizontal com velocidade constante de 3 m/s. Após sair da mesa, cai e atinge o solo a 1,20 m de distância dos pés da mesa. Desprezando a interferência do ar e adotando g = 10 m/s², calcule:
a) o tempo gasto para quê a bola de tênis atinja o solo;
0,4 s
b) a altura da mesa em relação ao solo;
0,80 m
c) o módulo da velocidade da bola ao tokár o solo.
5 m/s
15. Leia o trecho de texto a seguir.
A aeronave [...], com 12 mil litros de á gua para combater os incêndios no Pantanal, decolou às 11h20 dêste sábado (29) [junho de 2024] [...].
No dia anterior [...], o avião [...] transportou de Corumbá (MS) também cerca de 12 mil litros de á gua, no primeiro vôo real de combate ao fogo realizado pela FAB [...]. A á gua foi lançada em um dos focos de incêndio identificados pelo Corpo de Bombeiros do Mato Grosso do Sul.
CORRÊA, Douglas. FAB faz três voos hoje sobre o Pantanal para combate às queimadas. Agência Brasil, Rio de Janeiro, 29 jun. 2024. Disponível em: https://livro.pw/khjzb. Acesso em: 16 jul. 2024.
Organize-se em um grupo de até cinco integrantes para pesquisar sobre a ocorrência de incêndios na região do Pantanal. Busquem pelas informações a seguir.
a) Identifiquem a quantidade de focos de incêndio ocorridos até o momento, considerando o ano em quê você está, e comparem-no com o mesmo período do ano anterior.
b) Incêndios florestais prejudicam os sêres vivos de diversas formas. Pesquisem as consequências dêêsse tipo de ocorrência para os sêres vivos da região do Pantanal e também d fórma global para outros sêres vivos quê habitam regiões próximas ou mesmo afastadas.
c) Proponham uma campanha de conscientização acerca das ações humanas quê podem produzir focos de incêndios em regiões florestais e compartilhem-na com a comunidade escolar e a externa à escola.
Página cinquenta e quatro
OFICINA CIENTÍFICA Lançamento horizontal
Nas últimas dékâdâs, ocorreu um aumento na demanda e no consumo de minérios, ampliando o processo de extração mineral no mundo. Esse fato desperta preocupação, pois a extração dêêsses materiais causa prejuízos para a ssossiedade e o meio ambiente.
Nesta atividade, será realizado um experimento quê simula o transporte de minérios em uma esteira rolante, cuja velocidade de funcionamento precisa sêr corretamente calculada para quê o produto káia no local adequado. Em grupo de até quatro integrantes, organizem-se para desenvolvê-la.
Materiais
• dois cabos de vassora
• cronômetro
• mesa
• farinha
• bó-linha de vidro
• fita adesiva
• fita métrica
Faça o experimento somente na presença do professor.
Procedimentos
• Unam os dois cabos de vassora com fita adesiva, de modo quê formem um canalete para a bó-linha rolar (como representado na imagem).
• Apoiem o canalete sobre a mesa, fixando-o na horizontal e paralelo ao chão.
• Espalhem um pouco de farinha no chão, para identificar o local onde a bola, quê será lançada do canalete, vai cair.
• Coloquem a bola sobre determinado ponto do canalete e deem um impulso, de maneira quê ela percorra o canalete e káia sobre o local onde a farinha está espalhada. Com o auxílio de um cronômetro, meçam o tempo de queda.
• No chão, meçam a distância x entre a mesa e o ponto em quê a bó-linha toca o solo. Meçam também a altura h da mesa.

ATIVIDADES
1. Sem utilizar o cronômetro, como é possível obtêr o tempo de queda da bó-linha? Determinem esse valor.
2. Comparem o tempo de queda obtído na atividade anterior com o valor do cronômetro. Eles são iguais? Justifique.
3. Determinem a velocidade (componente horizontal) com a qual a bó-linha abandona a beira da mesa. Recoloquem a bó-linha no mesmo ponto sobre o canalete e deem um impulso mais forte quê o do lançamento anterior. Meçam o novo alcance da bó-linha e o tempo de queda.
4. Pesquisem sobre os impactos causados pela atividade de extração mineral no Brasil e reflitam de quê maneira esses impactos podem sêr minimizados. Discutam oralmente os resultados obtidos.
Página cinquenta e cinco
Lançamento oblíquo
Chama-se um lançamento de oblíquo quando a direção do vetor velocidade inicial apresenta um ângulo maior quê 0° e menor quê 90° com relação ao plano horizontal. Nesse caso, o movimento também póde sêr descrito como a soma de dois movimentos distintos e simultâneos, um na horizontal e outro na vertical.

Considerando quê o fenômeno ocorra nas proximidades da superfícíe da Terra e desprezando a interferência do ar, será representado o lançamento de uma gota de á gua por meio das mesmas equações quê foram deduzidas anteriormente, havendo pequenas modificações para a velocidade inicial. Adota-se como sistema de referência um par de eixos cartesianos ortogonais com origem na posição inicial da gota.
No lançamento oblíquo, as sucessivas posições ocupadas pela gota determinam uma trajetória parabólica.
Como a velocidade inicial de lançamento forma um ângulo de inclinação (alfa)" em relação ao eixo horizontal, pode-se decompor o vetor em suas componentes na direção x e y:
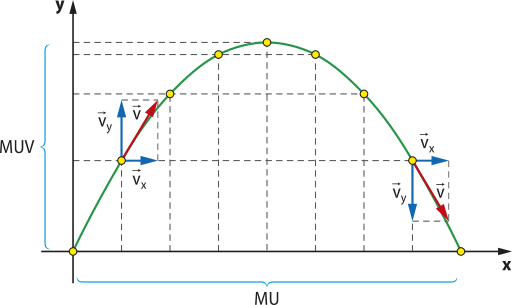
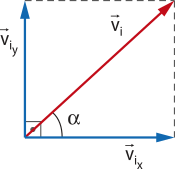
⇒ sen (alfa)" =
cos (alfa)" =
⇒ vi ⋅ sen (alfa)"
vi ⋅ cos (alfa)"
Na direção horizontal, tem-se um movimento uniforme. Portanto, se xi = 0:
x = xi + t ⇒ x = xi + vi (cos (alfa)") t ⇒ x = vi(cos (alfa)") t
Na direção vertical, temos um movimento uniformemente variado. Portanto, observando quê ay = −g (quando o eixo y está orientado de baixo para cima):
vy = + ayt ⇒ vy = vi sen (alfa)" − gt
= + 2ay(delta)"y ⇒ = (vi sen (alfa)")² − 2g(delta)"y
y = yi + viy t + ⇒ y = yi + vi (sen (alfa)") t −
Página cinquenta e seis
ATIVIDADE RESOLVIDA
2. Duas estudantes fazem suposições acerca do lançamento de uma flecha por um arco. A flecha possui velocidade inicial vi e forma um ângulo a com a horizontal, de modo a obtêr o maior alcance horizontal. Para quê isso ocorra, a primeira estudante afirma quê o lançamento deverá ocorrer com um ângulo maior do quê 45° em relação à horizontal. Já para a segunda estudante, o alcance será maior para um ângulo inferior a 45°. Qual das estudantes está correta?
Resolução
A velocidade de lançamento da flecha na componente vertical é dada por:
vy = vi sen (alfa)" − gt (I)
Mas a flecha chega ao eixo horizontal com:
vy = −visen (alfa)".
Em valor absoluto, a velocidade com quê a flecha chega ao eixo horizontal é igual à velocidade de lançamento.
Portanto, substituindo vy na equação (I), temos:
− vi sen (alfa)" = visen (alfa)" − gt ⇒ t =
Conhecendo o valor de t, é possível substituí-lo na equação quê fornece a distância horizontal: x = vi cos (alfa)" ⋅ t ⇒ x = vicos (alfa)" ⋅
x = (2 ⋅ cos (alfa)" ⋅ sen (alfa)") ⇒ x = sen 2 (alfa)"
Analisando essa equação, é possível deduzir quê o valor mássimo quê x póde alcançar ocorre para sen 2(alfa)" = 1.
O ângulo cujo seno vale 1 é 90°; portanto:
2 (alfa)" = 90° ⇒ (alfa)" = = 45°
Dessa forma, a maior distância horizontal alcançada pela flecha ocorre para (alfa)" = 45° e a distância mássima horizontal será xmáx =
Conclusão: nenhuma das estudantes estavam corretas em suas afirmações.
ATIVIDADES
16. Após sofrer uma falta, um jogador de futeból de praia fica encarregado de chutar a bola no gol. Para encobrir a barreira, ele tenta fazer com quê a bola dêz-creva uma trajetória parabólica. Após o chute, a bola é lançada obliquamente, conforme a figura, com velocidade inicial vi = 30 m/s.
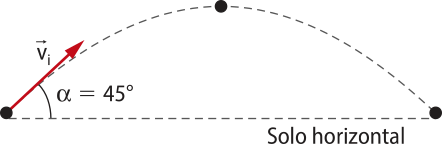
Despreze a interferência do ar e considere a bola uma partícula lançada obliquamente em relação ao solo. Nessas condições, determine:
a) as componentes horizontal vix e vertical viy da velocidade inicial;
viy ≃ 21 m/s; viy ≃ 21 m/s
b) a função horária da posição segundo os eixos horizontal e vertical;
x = 21t; y = 21t − 5t2
c) o tempo utilizado pela bola desde o lançamento até atingir a altura mássima;
2,1 s
d) a altura mássima quê a bola consegue atingir;
22,1 m
e) o tempo necessário para a bola chegar ao solo, após o lançamento;
4,2 s
f) a distância entre o ponto de lançamento e o ponto onde a bola atinge o solo;
88,2 m
g) a velocidade da bola ao chegar ao solo.
30 m/s
17. Em uma dada competição, um atleta arremessa um disco com velocidade de 20 m/s. O ângulo de lançamento é 45° e, no momento do lançamento, a mão do atleta está a 1,50 m do solo. Desconsiderando a resistência do ar, a quê distância do lançamento o disco tocará o chão e quanto tempo será necessário para quê isso ocorra?
40,6 m; 2,9 s
Página cinquenta e sete
TEMA 6
Movimento circular
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Deslocamento angular
Quando a forma da trajetória descrita por um corpo for uma circunferência ou parte de uma, pode-se dizêr quê esse corpo descreve um movimento circular.
Considere quê um ponto material se desloca entre as posições A e B de uma trajetória circular de raio R.
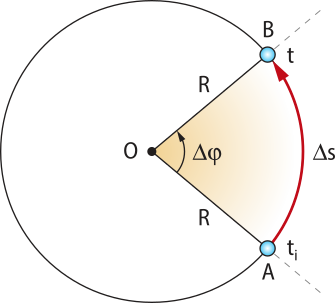
Considere quê, no instante ti, a cabine está na posição A e, no instante t, ela está em B. O deslocamento realizado pela cabine no intervalo de tempo (delta)"t = t − ti póde sêr descrito de duas formas: por meio do comprimento (delta)"s (deslocamento escalar) ou, então, do ângulo central (delta)"φ (deslocamento angular). No caso do deslocamento escalar, é sempre preciso lembrar do comprimento da circunferência. Assim, a cada volta, a cabine percórre uma distância proporcional ao raio de sua trajetória, dada por (delta)"s = C = 2(pi)"R.
As unidades de medida de ângulo mais freqüentes são o grau e o radiano, quê possuem a seguinte relação:
(delta)"φ =
PENSE E RESPONDA

1 Imagine a roda-gigante girando. Quais das cabines têm a maior velocidade (em módulo): as mais próximas ou as mais afastadas do centro da roda?
Grau
Dividindo o arco total de uma circunferência em 360 partes iguais, cada uma delas de termina um ângulo central chamado grau (°). Observe na representação:
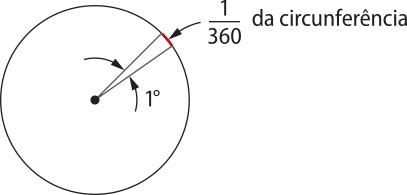
Representação de 1° de circunferência (imagem sem escala).
O ângulo total de uma circunferência méde 360°.
Radiano
O radiano (rad) corresponde à medida do ângulo central cujo arco tem a mesma medida quê o raio da circunferência:
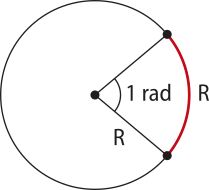
Representação de 1 rad de circunferência (imagem sem escala).
O ângulo total de uma circunferência méde 2(pi)" rad.
Página cinquenta e oito
ATIVIDADE RESOLVIDA
1. Duas crianças brincam em uma área de lazer e estão sobre o mesmo brinquedo em movimento. Re presentando essas crianças por dois pontos materiais, A e B, e considerando quê os pontos A, B e O pertencem à reta r, determine:
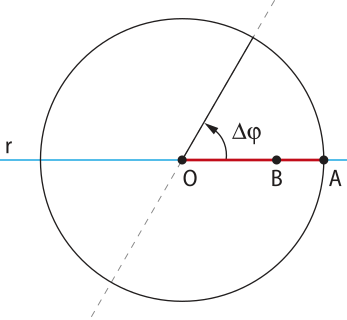
a) os deslocamentos angulares dos pontos A e B, em radianos, quando eles girarem um ângulo (delta)"φ = 60°;
b) as distâncias percorridas pêlos pontos A e B, em métro, quando eles girarem um ângulo (delta)"φ = 60°, sabendo quê OA = 3 m e OB = 2 m.
Resolução
a) Considere quê o movimento ocorre no sentido anti-horário e (delta)"φ = 60°. Todos os pontos pertencentes ao segmento de reta OA, exceto o ponto O, têm o mesmo deslocamento angular (delta)"φ = 60°, ou ainda:
x = ⇒ x = ⇒ x = rad
b) As distâncias percorridas pêlos pontos A e B são, respectivamente, (delta)"sA e (delta)"sB:
(delta)"sA = RA(delta)"φ = 3 ⋅
(delta)"sA = 3,14 m
(delta)"sB = RB(delta)"φ = 2 ⋅
(delta)"sB = 2,09 m
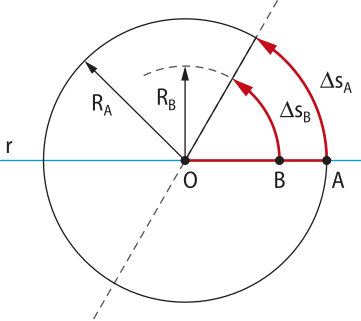
ATIVIDADES
1. Considere o movimento de rotação de um ponto A sobre a linha do equador durante 6 horas. Sabendo quê a medida do raio da Terra é aproximadamente RT = 6.370 km, determine:
a) o deslocamento angular do ponto A;
rad
b) a distância percorrida pelo ponto A.
≃110.000 km
2. O hodômetro de um veículo méde a distância percorrida por ele, ou seja, méde o número de voltas efetuadas pela roda, de tal forma quê, conhecendo o diâmetro dessa roda, obtém-se o valor da distância percorrida. Um veículo tem rodas de diâmetro 0,5 m e percórre 15 km viajando da cidade A até a cidade B. Considere (pi)" = 3. Calcule quantas voltas realiza cada roda do veículo no percurso entre as cidades A e B.
104 voltas
3. Dois corredores, vestidos com camisetas de números 1 e 2, após saírem de um trecho retilíneo da pista, atingem um trecho circular de centro O. A trajetória circular descrita pêlos corredores tem raios R1 = 10 m e R2 = 15 m, respectivamente.
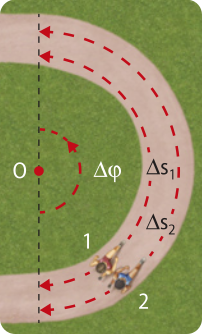
Determine, para (delta)"φ = 180°:
a) os deslocamentos angulares, em radiano, de cada um dos corredores;
(delta)"φ1 = (delta)"φ2 = (pi)" rad
b) as distâncias percorridas pêlos corredores.
(delta)"s1 ≃ 31,4 m e (delta)"s2 ≃ 47,1 m
Página cinquenta e nove
Velocidade angular
Retomando o exemplo da roda-gigante, considere quê três cabines estão dispostas sobre o mesmo segmento de reta OC nos pontos A, B e C.
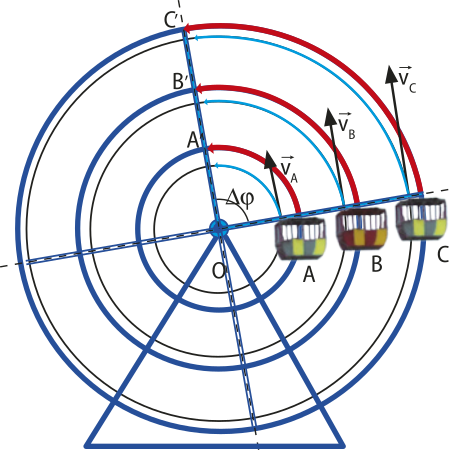
A roda, ao girar, fará a cabine quê está sobre o ponto A descrever um arco de circunferência menor do quê o arco descrito por uma cabine situada no ponto B, quê, por sua vez, será menor do quê o arco descrito por uma cabine situada sobre o ponto C.
Quando o segmento de reta OC da roda sofre um deslocamento angular (delta)"φ, os pontos A, B e C descrevem respectivamente os arcos e no mesmo intervalo de tempo (delta)"t. O módulo da velocidade do ponto A é menor do quê o módulo da velocidade do ponto B, quê, por sua vez, é menor do quê o módulo da velocidade do ponto C:
vA < vB < vC
Entretanto, nesse mesmo intervalo de tempo, os pontos A, B e C descrevem um mesmo deslocamento angular. Por causa díssu, a velocidade angular média ωm, definida pela razão entre o deslocamento angular (delta)"φ e o intervalo de tempo (delta)"t, é a mesma para os pontos A, B e C:
ωm =
Observe quê todos os pontos do segmento de reta OC, exceto o ponto O, apresentam a mesma velocidade angular média.
É o quê ocorre, por exemplo, com os ponteiros de um relógio: qualquer um deles apresenta a mesma velocidade angular média, exceto a extremidade ligada ao eixo de rotação.
Se o ângulo (delta)"φ é medido em radiano e o tempo (delta)"t em segundo, a unidade de medida da velocidade angular é o radiano por segundo (rad/s).
Para definir a velocidade angular instantânea, será utilizado o mesmo recurso adotado para determinar a velocidade escalar instantânea: considera-se um intervalo de tempo quê tende a um valor próximo de zero. Assim, a velocidade angular média ωm tende à velocidade angular instantânea ω, ou apenas velocidade angular.
Relação entre as grandezas angulares e lineares
Considere um ponto descrevendo movimento circular com velocidade escalar v e velocidade angular ω. Essas duas velocidades podem sêr relacionadas.
Sabe-se quê: v = (I) e ω = (II)
Como (delta)"s = R(delta)"φ, da equação (I) resulta: v = . Substituindo (II) em (I), obtém-se:
v = ωR ou ω =
Página sessenta
ATIVIDADES
4. Um ciclista percórre parte de uma pista com o formato de uma circunferência. Sabendo quê ele descreveu uma trajetória de ângulo central 3,0 rad em 6 s, calcule a velocidade angular média nesse intervalo de tempo.
0,5 rad/s
5. Considere um disco quê gira em torno de um eixo quê passa pelo seu centro O. Sabendo quê a velocidade do disco é 3,5 rad/s, calcule a velocidade escalar nos pontos X e Y assinalados na figura.
14 cm/s; 28 cm/s
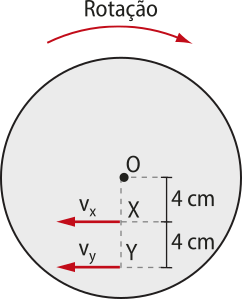
6. A iniciativa de preservar o ambiente, d fórma sustentável, tem contribuído para o reflorestamento de áreas degradadas. Em uma dessas áreas, com autorização legal para fazer o kórti de eucaliptos, um agricultor escolheu um tronco vertical e o cortou rente ao solo. Sabendo quê o terreno é plano e horizontal, a base do tronco não escorregou e a queda da árvore demorou 6 s, determine:

a) a velocidade angular média do tronco durante a queda;
ωm = rad/s
b) a velocidade escalar média de um ponto de marcação, feito no tronco, a 12 metros da base.
vm = (pi)" m/s
c) No Brasil, o plantio de eucaliptos é feito, principalmente, para usos comerciais, seja para uso da madeira, seja para torná-lo papel. Pesquise quais são as regras, as normas, ou a legislação, quê trata do plantio de eucaliptos no país. Você acredita quê reflorestar áreas degradadas com esse tipo de cultivo (e com essa finalidade) póde sêr ambientalmente benéfico? Por quê? Discuta com seus côlégas a respeito.
7. Obedecendo às condições de segurança, um motociclista percórre a curva de uma estrada, mantendo o ponteiro do velocímetro em 30 km/h, d fórma constante, durante 72 s. Sabendo quê essa curva foi construída com raio igual a 2,0 km, determine a medida do ângulo central correspondente ao arco percorrido pelo veículo, nesse período de 72 s.
(delta)"φ = 0,30 rad
8. Sobre o asfalto de uma pista circular foram marcadas, com tinta branca, duas circunferências concêntricas, de tal forma quê o raio da circunferência externa (Re)é o triplo do raio da circunferência interna (Ri). Considere dois móveis se deslocando sobre essas circunferências, com velocidades escalares iguais (v), e quê suas velocidades angulares são ωe e ωi, respectivamente, para o móvel quê se desloca sobre a circunferência externa e interna. Nesse caso, determine a relação entre as velocidades angulares dos móveis.
9. Uma pessoa encontra-se sentada na cabine de uma roda-gigante quê gira com velocidade constante. A distância da cabine ao centro da roda-gigante é de 10 m e a roda-gigante realiza meia volta em 5 minutos. Determine a velocidade angular e a velocidade linear da pessoa sentada na cabine. Considere (pi)" = 3.
ω = 0,01 rad/s; v = 0,1 m/s
Página sessenta e um
Movimento circular uniforme
O movimento circular de um ponto material será uniforme quando ele descrever ângulos iguais em intervalos de tempo iguais, ou seja, com velocidade angular constante e diferente de zero.
O movimento descrito pela extremidade do ponteiro dos segundos de um relógio exemplifica um movimento circular uniforme (movimento circular uniforme). Esse tipo de movimento apresenta algumas características importantes:
• A velocidade angular ω constante, ou seja, tem o mesmo valor da velocidade angular média ωm em qualquer intervalo de tempo (ω = ωm).
• A velocidade vetorial tem intensidade v constante, sêndo sempre tangente à trajetória.
Acompanhe o exemplo do ponteiro do relógio quê registra os segundos. Na figura, observa-se quê o ponto A, situado na extremidade do ponteiro, descreve a mesma trajetória, repetidamente, a cada intervalo de tempo de 60 s. A repetição em intervalos de tempo iguais define o movimento circular uniforme como periódico.
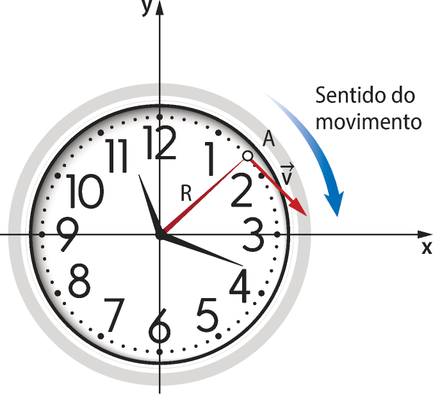
Ao adotar um referencial fixo O no centro da circunferência, o ponto A descreverá uma volta completa, a cada 60 s, chamada ciclo.
Em um movimento periódico, é importante destacar duas grandezas: o período e a freqüência.
• Período (T) é o intervalo de tempo gasto para quê o ponto material dêz-creva um ciclo (no exemplo, o ponto A). A unidade do período, no SI, é o segundo (s).
• freqüência (f) é o número de ciclos realizados na unidade de tempo. A unidade de freqüência, no SI, é ciclo por segundo (ciclo/s) ou hertz (Hz), em homenagem ao físico alemão Heinrich Rudolf rértiz (1857-1894). Também é usual a unidade rotações por minuto (rpm).
Para estabelecer a relação entre Hz e rpm, deve sêr feita a seguinte análise:
1 rpm = Hz
Para relacionarmos o período e a freqüência de um movimento circular, pode-se aplicar uma regra de três, lembrando quê um ponto material executa 1 ciclo no intervalo de tempo de 1 período (1 ciclo — 1 T). Entretanto, pela definição de freqüência, quando o ponto material descreve um número de ciclos equivalente à freqüência, o tempo gasto será igual à unidade (f ciclos — 1).
⇒ T =
Dessa forma, obtém-se quê o período é o inverso da freqüência.
Página sessenta e dois
É possível, ainda, relacionar a velocidade angular w e a velocidade escalar v com o período e a freqüência de um movimento circular uniforme. Ao retomar o ponteiro do relógio e considerar quê o ponto A percórre a circunferência de raio R e descreve uma volta completa, cujo ângulo é (delta)"φ = 2(pi)" rad, em um intervalo de tempo igual ao período ((delta)"t = T), tem-se:
ω = ⇒ ω = ou ω = 2(pi)"f
Seguindo o mesmo raciocínio, considere agora a distância percorrida pelo ponto A ao descrever a mesma volta completa. No intervalo de tempo igual ao período ((delta)"t = T), o ponto A percórre uma distância igual ao perímetro da circunferência, ou seja, 2(pi)"R:
v = ⇒ v = ou v = 2(pi)"Rf
ATIVIDADES
10. Considere quê um turista observa um grande relógio posicionado em uma torre, e compara-o com o seu relógio de pulso. Supondo o funcionamento adequado dos relógios, o quê é possível afirmar a respeito da comparação das velocidades angulares e escalares de ambos os relógios?
11. Uma motocicleta percórre em movimento circular uniforme uma pista circular, completando 30 voltas em 1h30. Determine:
a) o tempo utilizado pela moto para completar uma volta;
3 min = 180 s
b) a freqüência do movimento em hertz.
Hz
12. Durante um treinamento, duas atletas correm na mesma pista circular mantendo-se lado a lado com velocidade constante, em módulo. Sabendo quê a atleta mais alta percórre a raia externa e a atleta mais baixa, a raia interna, responda e justifique as seguintes kestões.
a) Durante a corrida, as atletas apresentam aceleração?
Sim, pois a velocidade das atletas varia em direção e sentido.
b) Compare a freqüência dos movimentos circulares descritos pelas atletas.
c) Compare as velocidades escalares das atletas.
13. A polia de um motor descreve movimento de rotação uniforme, com freqüência de 3.600 rpm. A distância entre um ponto P, marcado na periferia da polia, e o centro dessa polia é 0,15 m. Nessas condições, determine:
a) a freqüência com a qual a polia descreve o movimento de rotação uniforme, em hertz;
60 Hz
b) o período em segundos;
s
c) a velocidade angular em rad/s;
120(pi)" rad/s
d) a velocidade escalar v, desenvolvida pelo ponto P.
56,52 m/s
14. Há diversos tipos de satélite artificial na órbita terrestre. No caso das telecomunicações, são utilizados satélites geoestacionários, quê conseguem manter, em relação à superfícíe da Terra, uma posição praticamente sem variações. Considere um satélite a 36.000 km de altura e o raio da Terra 6.400 km, aproximadamente. Nessas condições, determine:
a) o período de rotação ao redor da Terra, descrito pelo satélite;
24 horas
b) o módulo da velocidade linear do satélite;
v ≃ 1,1 ⋅ 104 km/h
c) a velocidade angular do satélite.
rad/h
d) Pesquise sobre algum satélite brasileiro em órbita atualmente. Qual é a função dêêsse satélite? Compartilhe com os côlégas, d fórma expositiva, os dados quê obteve.
Página sessenta e três
Transmissão do movimento circular uniforme
A transmissão do movimento circular está presente em máquinas e dispositivos mecânicos, como bicicletas e relógios. O movimento circular é produzido no eixo do motor e transferido por meio de polias, rodas e engrenagens.
vA = vB = vC
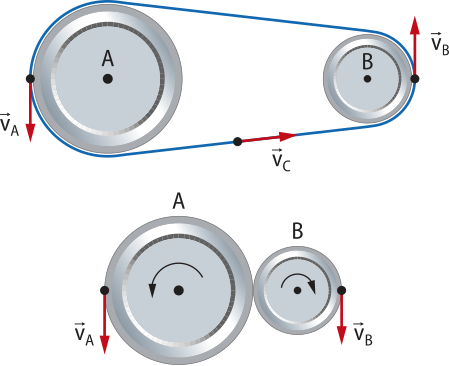
Entre duas rodas, o movimento póde sêr transmitido por meio do acoplamento periférico ou coaxial. O acoplamento periférico é feito pelo contato direto ou por meio de correia (ou corrente) entre duas rodas. Nesse caso, quando não há escorregamento e a correia (ou corrente) é considerada inextensível, ou seja, não é capaz de estender ou esticar, a velocidade escalar periférica das rodas é igual.
No acoplamento coaxial, as rodas têm eixo de rotação comum, o quê lhes confere velocidade angular igual.
ω = ωA = ωB
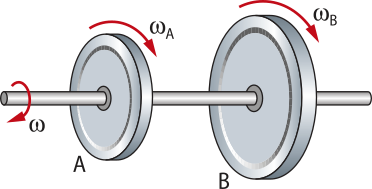
ATIVIDADES
15. A figura representa um mecanismo básico de uma bicicleta. Sabendo quê os pedais giram em um período igual a 2 s e quê o raio da coroa é oito vezes maior do quê o raio da catraca, determine: Considere o raio da coroa igual a 10 cm e adote (pi)" = 3.
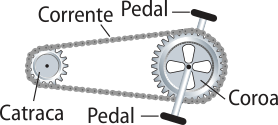
a) o período de rotação da coroa;
2 s
b) a freqüência da catraca;
4 Hz
c) a velocidade linear dos pontos da corrente.
30 cm/s
16. Nas bicicletas com marchas, é comum encontrar sistemas de tração com várias catracas de diferentes raios e também mais de uma coroa. Dessa forma, possibilitam ao ciclista utilizar o tamãnho das engrenagens de acôr-do com as condições do percurso percorrido. Com base nos seus conhecimentos sobre Física, resôuva as seguintes kestões.
a) Para obtêr uma velocidade maior em relação ao solo, o ciclista deverá combinar as engrenagens de tal forma quê a coroa seja maior do quê a catraca ou a catraca seja maior do quê a coroa?
b) O quê ocorre se o raio da coroa (Rco)for quatro vezes maior do quê o raio da catraca (Rca)?
c) Para subir, confortavelmente, um trajeto inclinado, um ciclista quê possua em sua bicicleta apenas uma coroa deve fazer uso da catraca maior ou menor?
Deve usar a catraca maior.
17. A figura representa duas polias ligadas perifericamente por uma correia inextensível. Sabendo quê a polia B tem raio 4 vezes maior do quê a polia A e esta efêtúa 40 rpm, qual é a freqüência da polia B?
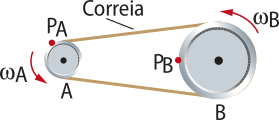
10 rpm
Página sessenta e quatro
ORGANIZANDO AS IDEIAS
Analise o esquema a seguir, quê apresenta e relaciona os principais conceitos estudados nesta Unidade.
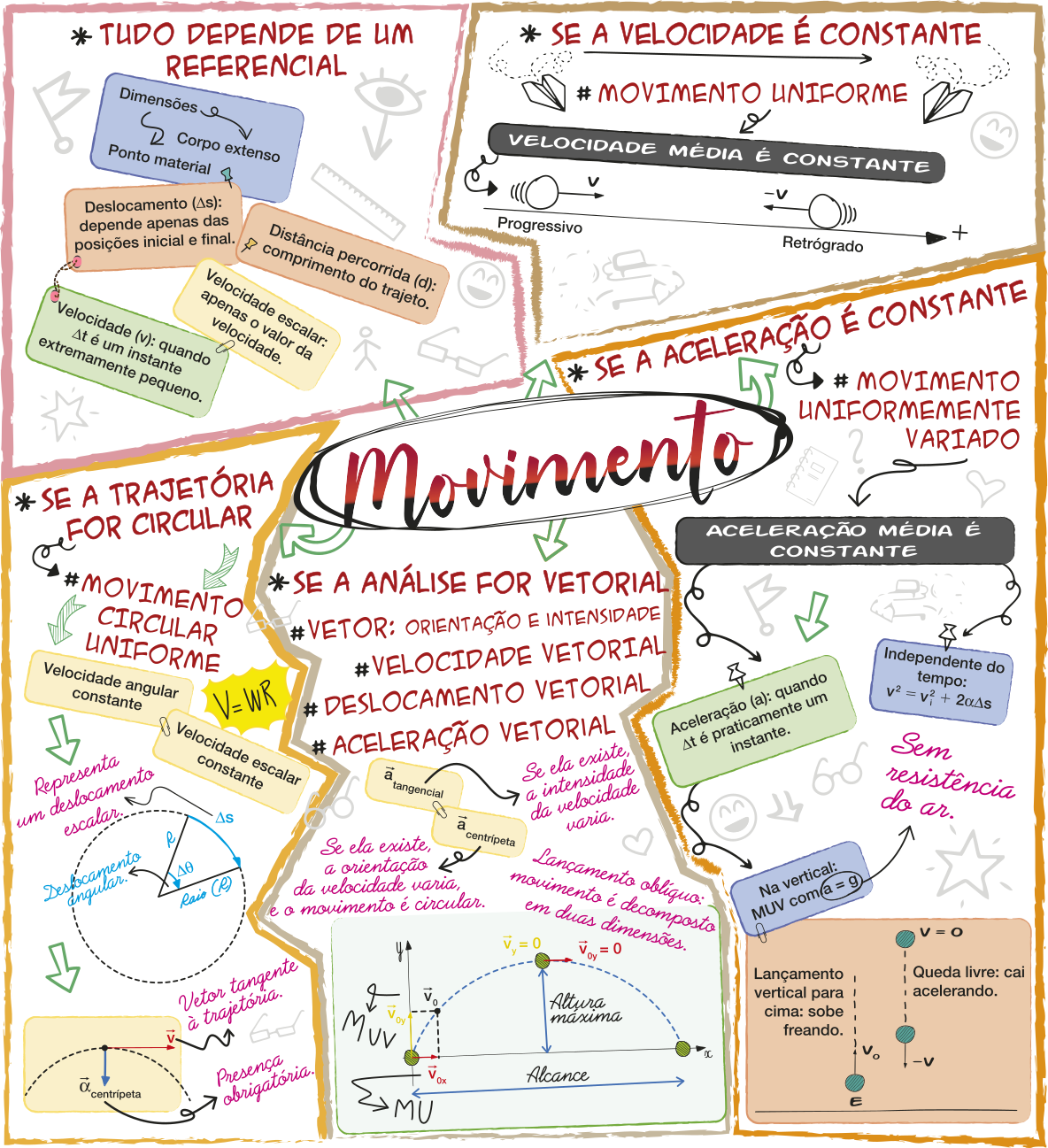
No caderno, elabore o seu próprio esquema, organizando os principais conceitos da Unidade e incluindo nele outros termos e ideias quê se relacionam ao quê foi estudado, realizando as associações quê considerar importantes. Por fim, elabore um pequeno texto conectando os conceitos e as ideias presentes no esquema. Essa é uma boa forma de estudar e compreender melhor os conceitos.
Página sessenta e cinco
ATIVIDADES COMPLEMENTARES
Respostas e comentários estão disponíveis nas Orientações para o professor.
Tema 1: mêdídas e movimentos
1. (Enem/MEC) Se compararmos a idade do planêta Terra, avaliada em quatro e meio bilhões de anos (4,5 ⋅ 109 anos), com a de uma pessoa de 45 anos, então, quando começaram a florescer os primeiros vegetais, a Terra já teria 42 anos. Ela só conviveu com o homem moderno nas últimas quatro horas e, há cerca de uma hora, viu-o começar a plantar e a côlher. Há menos de um minuto percebeu o ruído das máquinas e de indústrias e, como denuncía uma ôngui de defesa do meio ambiente, foi nesses últimos sessenta segundos quê se produziu todo o lixo do planêta! Na teoria do Big béng, o Universo surgiu há cerca de 15 bilhões de anos, a partir da explosão e expansão de uma densíssima gota. De acôr-do com a escala proposta no texto, essa teoria situaria o início do Universo há cerca de
a) 100 anos.
b) 150 anos.
c) 1.000 anos.
d) 1.500 anos.
e) 2.000 anos.
Resposta: b)
Tema 2: Introdução ao estudo do movimento
2. (Unésp) Juliana pratíca corridas e consegue correr 5,0 km em meia hora. Seu próximo desafio é participar da corrida de São Silvestre, cujo percurso é de 15 km. Como é uma distância maior do quê a quê está acostumada a correr, seu instrutor orientou quê diminuísse sua velocidade média habitual em 40% durante a nova próva. Se seguir a orientação de seu instrutor, Juliana completará a corrida de São Silvestre em:
a) 2h40min.
b) 3h00min.
c) 2h15min.
d) 2h30min.
e) 1h52min.
Resposta: d)
3. (UEA-AM) Um motorista faz uma viagem de carro por uma rodovia cuja velocidade mássima permitida é de 110 km/h. Durante a viagem, o motorista repara quê o velocímetro de seu carro está quêbrado, o quê impede quê a velocidade do automóvel seja monitorada ao longo do percurso. Ao chegar a seu destino, o motorista percebe quê levou 2,5 horas para fazer a viagem. Sabendo quê o caminho percorrido foi de 300 km e que a rodovia possui monitoramento de velocidade por toda sua extensão, o motorista
a) receberá uma multa, pois a velocidade média do carro foi de 120 km/h.
b) receberá uma multa, pois a velocidade média do carro foi de 130 km/h.
c) não receberá uma multa, pois a velocidade média do carro foi de 110 km/h.
d) receberá uma multa, pois a velocidade média do carro foi de 150 km/h.
e) não receberá uma multa, pois a velocidade média do carro foi de 90 km/h.
Resposta: a)
4. (Enem/MEC) Uma empresa de transportes precisa efetuar a entrega de uma encomenda o mais breve possível. Para tanto, a equipe de logística analisa o trajeto desde a empresa até o local da entrega. Ela verifica quê o trajeto apresenta dois trechos de distâncias diferentes e velocidades mássimas permitidas diferentes. No primeiro trecho, a velocidade mássima permitida é de 80 km/h e a distância a sêr percorrida é de 80 km. No segundo trecho, cujo comprimento vale 60 km, a velocidade mássima permitida é 120 km/h. Supondo quê as condições de trânsito sêjam favoráveis para quê o veículo da empresa ande continuamente na velocidade mássima permitida, qual será o tempo necessário, em horas, para a realização da entrega?
a) 0,7
b) 1,4
c) 1,5
d) 2,0
e) 3,0
Resposta: c)
5. (UFPE) Um caminhão se desloca com velocidade constante de 144 km/h. Suponha quê o motorista cochile durante 1,0 s. Qual o espaço, em metros, percorrido pelo caminhão nesse intervalo de tempo se ele não colidir com algum obstáculo?
40 m
Página sessenta e seis
Tema 3: Movimento uniforme
6. (Fuvest-SP) Em um prédio de 20 andares (além do térreo), o elevador leva 36 s para ir do térreo ao 20º andar. Uma pessoa do andar X chama o elevador, quê está inicialmente no térreo, e 39,6 s após a chamada a pessoa atinge o andar térreo. Se não houvesse parada intermediária, e o tempo de abertura da porta do elevador e o de entrada e saída do passageiro fossem desprezíveis, poderíamos dizêr quê o andar X é o:
a) 9
b) 11
c) 16
d) 18
e) 19
Resposta: b)
7. Durante um teste para avaliar o consumo de combustível, são usados dois veículos, A e B, quê se deslócam sobre a mesma estrada retilínea com velocidades constantes vA e vB, respectivamente. No instante em quê o cronômetro é acionado, o veículo A passa pelo ponto M dessa estrada, enquanto o veículo B passa pelo ponto N, distante 20 km do ponto M. Nessas condições, determine a quantidade de combustível consumida pêlos veículos para chegarem, juntos, ao ponto P. Considere vA = 3vB e saiba quê cada veículo consome, em média, um litro de combustível para percorrer 8 km.
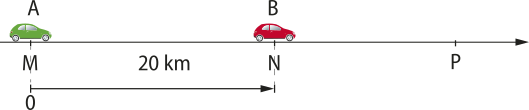
O veículo A consome 3,75 litros. O veículo B consome 1,25 litro.
8. (UFSM-RS) Dois carros A e B têm seus movimentos representados esquematicamente no gráfico s x t a seguir. Pode-se afirmar, baseando-se na função quê representa o movimento de cada carro, quê:
![Gráfico de linha. Eixo vertical 's'[quilômetros] e eixo horizontal 't' (horas). Na imagem uma reta 'Carro A' e uma curva 'Carro B', se encontram num ponto 's' 't'.](../resources/images/ek_9/ek_980019993f91afe387c3c6a7c0d5c8de.png)
a) as velocidades iniciais (t = 0) dos carros A e B são zero.
b) a velocidade média do carro B é igual à velocidade média do carro A no intervalo de tempo de 0 a t.
c) as velocidades iniciais dos carros A e B são diferentes de zero.
d) a aceleração do carro A é igual à aceleração do carro B.
e) o carro B percorrerá uma distância maior até encontrar o carro A.
Resposta: b)
Tema 4: Movimento uniformemente variado
9. (ú éfi érri jóta) Duas partículas se deslócam ao longo de uma trajetória. A figura a seguir representa, em gráfico cartesiano, como as duas velocidades varíam em função do tempo.
![Gráfico cartesiano com duas velocidades que variam em função do tempo. Eixo vertical 'v' [metros por segundo] e eixo horizontal 't'[segundos]. Uma reta com origem 'O' passando por quatro metros por segundo no eixo vertical e dois segundos no eixo horizontal.](../resources/images/ek_0/ek_0757683bc1e508b3d48a8099525a5d9d.png)
Suponha quê no instante em quê se iniciaram as observações (t = 0) elas se encontravam na mesma posição.
a) Determine o instante em quê elas voltam a se encontrar.
4 s
b) Calcule a maior distância entre elas, desde o instante em quê se iniciaram as observações até o instante em quê voltam a se encontrar.
4 m
10. Um automóvel entra em um túnel com velocidade de 10 m/s e sai dele com velocidade de 30 m/s. A aceleração durante o movimento no interior do túnel é constante e vale 4 m/s2. Qual é o comprimento do túnel?
100 m
11. (PUCCamp-SP) Um móvel é abandonado em queda livre percórrendo, a partir do repouso, uma distância d durante o primeiro segundo de movimento. Durante o terceiro segundo de movimento, esse móvel percorre uma distância:
a) d
b) 3d
c) 5d
d) 7d
e) 9d
Resposta: c)
12. Uma pedra é atirada para cima, em uma trajetória vertical, partindo do solo, com velocidade inicial de 20 m/s. Considere a aceleração da gravidade no local 10 m/s2, despreze a resistência do ar e adote a origem dos espaços no solo. Determine o quê se pede.
a) As equações horárias do espaço e da velocidade dêêsse movimento.
s = 20t −5t2; v = 20 − 10t
Página sessenta e sete
b) O intervalo de tempo de subida da pedra, em segundo.
2 s
c) A altura mássima atingida por ela, em métro
20 m
d) O espaço, em métro, e o sentido do movimento no instante 3 s.
15 m; sentido para baixo
e) O instante, em segundo, e o módulo da velocidade, em m/s, quando a pedra atinge o solo.
4 s; 20 m/s
f) O gráfico quê representa as posições da pedra em função do tempo.
Tema 5: Análise vetorial do movimento
13. Um peregrino inicia uma caminhada sobre um terreno plano. Caminhou 4 km para o leste e fez a 1ª parada. Tomou á gua, caminhou mais 5 km para o leste e fez a 2ª parada. Descansou, caminhou mais 3 km para o oeste e fez a 3ª parada. Comeu uma fruta, caminhou mais 2 km para o sul e fez a 4ª parada. Determine o vetor deslocamento do início da caminhada até a:
a) 2ª parada;
b) 3ª parada;
c) 4ª parada.
14. Um grupo de pessoas resólve fazer um passeio em uma ilha e, ao final do dia, percebem quê, devido à subida da maré, o barco havia se soltado da costa. Ilhados, um deles utiliza o telefone celular para pedir socorro. Para o salvamento dessas pessoas, foi designado um avião quê, voando horizontalmente com velocidade constante de 360 km/h, a uma altura de 1.280 m em relação a esse grupo de pessoas, lançou um pacote com mantimentos, para quê eles passassem a noite. Sabendo quê o grupo estava em um local a 1.850 metros, em uma direção horizontal do avião, determine se o pacote caiu antes ou depois dêêsse local. Considere g = 10 m/s² e despreze a resistência do ar.
O pacote caiu 250 m antes do local.

15. (FCMSCSP) Em uma estação de trens, há uma esteira com 45 m de comprimento, quê se móve com velocidade constante de 0,80 m/s em relação ao solo. Uma pessoa sobe nessa esteira e caminha sobre ela, no mesmo sentido em quê ela se desloca em relação ao solo, com velocidade constante de 1,0 m/s em relação à superfícíe da esteira. O intervalo de tempo para essa pessoa percorrer todo o comprimento da esteira será de
a) 45 s.
b) 56 s.
c) 225 s.
d) 25 s.
e) 16 s.
Resposta: d)
16. (UFPE) Um gafanhoto adulto póde saltar até 0,80 m, com um ângulo de lançamento de 45°. Desprezando a resistência do ar e a fôrça da sustentação aerodinâmica sobre o gafanhoto, calcule quantos décimos de segundo ele permanecerá em vôo.
0,8 s
Tema 6: Movimento circular
17. (Fuvest-SP) Um automóvel percórre uma pista circular de 1 km de raio com velocidade de 36 km/h. Em quanto tempo o automóvel percórre um arco de circunferência de 30°?
52,3 s
18. (hú- hê- érre jota) Uma das atrações típicas do circo é o equilibrista sobre monociclo. O raio da roda do monociclo utilizado é igual a 20 cm, e o movimento do equilibrista é retilíneo. O equilibrista percórre, no início de sua apresentação, uma distância de 24 m. Determine o número de pedaladas, por segundo, necessárias para quê ele percorra essa distância em 30 s, considerando o movimento uniforme.

0,6 pedalada por segundo
19. (Enem/MEC) Nos X Games Brasil, em maio de 2004, o iskeitista brasileiro Sandro Dias, apelidado “Mineirinho”, conseguiu realizar a manobra denominada “900”, na modalidade squêit vertical, tornando-se o segundo atleta no mundo a conseguir esse feito. A denominação “900” refere-se ao número de graus quê o atleta gira no ar em torno de seu próprio corpo, quê, no caso, corresponde a
a) uma volta completa.
b) uma volta e meia.
c) duas voltas completas.
d) duas voltas e meia.
e) cinco voltas completas.
Resposta: d)
Página sessenta e oito
INTEGRANDO COM...
Biologia, Geografia, História e Sociologia
Movimentos no planêta
Respostas e comentários estão disponíveis nas Orientações para o professor.
Tudo está em movimento, e o planêta Terra não é uma exceção. Durante sua formação inicial, os continentes e mares tí-nhão uma configuração diferente da atual e, com o passar de bilhões de anos, foram se movendo até adquirir a forma quê hoje se conhece, mas o processo de movimento continua.
Os sêres vivos se movimentam em processos migratórios quê são essenciais para o equilíbrio ecológico do planêta e a perpetuação das espécies. A história da civilização humana também é marcada por migrações quê levaram à configuração de civilizações da atualidade.
Nesta atividade, você e os côlégas irão produzir um vídeo não fiksional quê explique alguns movimentos quê acontecem no planêta.
![]() Etapa 1 – Organização
Etapa 1 – Organização
Organize-se com os côlégas em grupos de até cinco integrantes. Cada grupo ficará responsável por pesquisar um dos assuntos sugeridos a seguir ou outros quê podem sêr sugeridos por vocês e acordados com o professor. Cada integrante do grupo deverá ficar responsável por uma tarefa: desenvolvimento do roteiro, busca por imagens quê serão inseridas, localização de fontes adequadas de pesquisa, captação de equipamentos para a produção do vídeo etc. Analise com os côlégas como fazer a divisão de tarefas, explorando as melhores habilidades de cada um. Lembre-se da importânssia de realizar escôlhas democráticas e respeitosas.
![]() Etapa 2 – Pesquisa
Etapa 2 – Pesquisa
A seguir, são apresentadas algumas sugestões de assuntos quê podem sêr pesquisados e abordados no material a sêr produzido. Fiquem livres para escolher outros assuntos quê julgarem pertinentes.
Todos os dados obtidos devem sêr coletados de fontes confiáveis, como livros, sáites de universidades ou de revistas científicas da área, documentários produzidos por entidades científicas, entre outras.
1. Movimentação dos sêres vivos
A migração não é uma ação exclusiva do sêr humano. Outras espécies de sêres vivos também migram.
• Façam uma pesquisa sobre os movimentos migratórios realizados pêlos sêres vivos, destacando a importânssia dessas movimentações para os sêres vivos e para o ambiente.
• Analisem as influências quê essas migrações têm, tanto nos locais de origem dos sêres vivos quanto nos destinos para onde migram.
Página sessenta e nove
2. Deriva continental
Evidências científicas levaram à conclusão de quê, no passado, os continentes estavam unidos e formavam um supercontinente.
• Verifiquem quais evidências científicas possibilitam concluir quê êste supercontinente existiu. Coletem imagens quê ilustram como provavelmente ele era, indicando seu nome e em quê época existiu.
• Expliquem os motivos de a dêríva continental ocorrer com base no processo de formação da Terra, ilustrando esse processo.
• Busquem informações sobre o deslocamento executado pêlos continentes atuáis ao longo dos anos e apresentem a velocidade média dêêsse movimento. Verifiquem se o movimento ainda está ocorrendo.
3. Correntes oceânicas
A movimentação das águas dos oceanos tem papel fundamental para a vida.
• Façam uma pesquisa sobre as correntes oceânicas e indiquem por quê elas ocorrem.
• Expliquem a importânssia das correntes oceânicas tanto para regiões equatoriais quanto para as regiões polares e como seria o planêta caso elas não existissem.
• Busquem informações sobre velocidades de deslocamento da á gua nas correntes.
4. Migrações humanas
Desde o surgimento dos primeiros sêres humanos, ocorreram migrações.
• Façam uma pesquisa dos primeiros registros do sêr humano atual (ômo sápiens) no mundo. Busquem informações acerca dos locais em quê ocorreram e como se deu o processo de migração para outros locais.
• Representem as rótas de migrações dos sêres humanos utilizando mapas e indiquem as civilizações quê foram sêndo formadas.
• Destaquem informações sobre a formação das civilizações e seus côstúmes em alguns países, com destaque à diversidade étnica e cultural.
• Façam um levantamento sobre as migrações atuáis, destacando suas principais causas.
Uma sugestão de como elaborar um roteiro póde sêr verificada em: WOJCIECHOWSKI, Mônica. Como fazer um roteiro. [S. l.]: AIC, 2017. Disponivel em: https://livro.pw/kbuxe. Acesso em: 4 nov. 2024.
![]() Etapa 3 – Produzindo o vídeo
Etapa 3 – Produzindo o vídeo
Para a produção do vídeo, é necessário organizar as informações obtidas. A seguir, uma sugestão de como organizar a produção.
• Iniciem com o planejamento dos elemêntos e as características do vídeo. Definam o tempo, o público a quê ele se destina e os elemêntos quê serão inseridos (animações, músicas, vinhetas etc.).
• Elaborem o roteiro do vídeo.
• Organizem-se para filmar o vídeo. Para isso, é preciso quê, préviamente, todos os materiais necessários estejam disponíveis, lembrando quê, por exemplo, um aparelho celular póde sêr usado na filmagem. Caso seja necessário reservar um espaço na escola, é preciso fazê-lo com antecedência.
• Realizem a edição do vídeo. Essa póde sêr feita com ferramentas ôn láini e gratuitas.
• Discutam com o restante da turma como será feita a divulgação dêêsses vídeos. Avaliem se o público-alvo deverá sêr convidado para assisti-los e verifiquem a necessidade de reservar um espaço para essas exibições.
Página setenta

