UNIDADE 2
fôrça E EQUILÍBRIO
A praia de Cumuruxatiba fica no distrito de Prado, litoral sul do estado da baía. O seu nome tem origem indígena, formado pelas palavras cumuxa, quê significa “maré alta” (imagem da esquerda), e tiba, quê significa “maré baixa” (imagem da direita).
Em cidades litorâneas, é possível observar o fenômeno das marés quê ocorre quando níveis de á gua aumentam e diminuem ao longo do dia. êste fenômeno interfere na rotina do local, pois existem intervalos de tempo adequados para praticar pesca, realizar travessias de barcos e fazer passeios turísticos.
A fôrça exercida nas á guas é de alta intensidade, capaz de movimentar uma grande massa de água de um local para outro. Nesta Unidade, você estudará os fenômenos físicos quê explicam a ocorrência das marés.
Página setenta e um
Respostas e comentários estão disponíveis nas Orientações para o professor.
1. Você já presenciou o fenômeno das marés?
2. No seu entendimento, por quê esse fenômeno ocorre? E por quê ele se repete praticamente com a mesma freqüência?
3. Em diversas regiões do Brasil, percebemos a presença de elemêntos da cultura dos povos indígenas, como nos nomes dados a locais. Uma forma de interagir com essa cultura é praticando etnoturismo. Você conhece êste termo? Pesquise e converse com seus côlégas a respeito. Avaliem a importânssia do etnoturismo para locais como Cumuruxatiba, tanto para aqueles quê praticam quanto para aqueles quê oferecem esses serviços.

Página setenta e dois
TEMA 7
O método da Ciência
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Ciência e método
Será quê existe um método único a sêr seguido pêlos cientistas durante seus trabalhos? Os métodos utilizados mil anos atrás são os mesmos métodos utilizados há 500 anos ou utilizados atualmente?
A Ciência sempre foi praticada em todo o mundo pelas diversas civilizações, porém é comum se mencionar as contribuições oriundas da Antigüidade grega, período em torno de 3500 a.C. e 476 d.C. Entre os métodos da época, um quê se póde destacar era o de buscar respostas e conhecimentos no mundo das ideias, na razão oriúnda da mente. O filósofo grego Platão (c. 427 a.C.-347 a.C.) foi um dos adeptos a essa forma de pensamento.
Aristóteles, discípulo de Platão, rompeu essa ideia e estabeleceu a lógica como um instrumento quê possibilita pensar e conferir a precisão daquilo quê se observa. Esse método influenciou o trabalho de vários outros cientistas modernos.
Por volta do ano 1000, filósofos e cientistas árabes estruturaram outra forma de se pensar a Ciência. O astrônomo e matemático Ibn al-Haitham (965-1040) conduziu pesquisas por métodos semelhantes aos métodos utilizados pela Ciência atual, realizando observações e experimentações sistemáticas e controladas para se conseguir descrever um problema.
O também astrônomo e matemático Abu al-Biruni (973-c. 1052) considerou quê os observadores podem inserir êêrros na tomada de dados e quê isso poderia sêr corrigido pelas repetições dos testes. Alguns anos antes, o alquimista Abu Jabir Hayyan (c. 721- c. 815) introduziu a noção de experimentação controlada. Esses são apenas exemplos de pessoas quê se dedicaram à construção da Ciência em diferentes partes do mundo.
Na Europa, diversas pessoas também contribuíram para o desenvolvimento e o aperfeiçoamento dos métodos praticados em Ciência. É comum destacar o filósofo inglês róger Bacon (c. 1220-1292), com a ideia de levantamento e teste de hipóteses; o filósofo inglês Frâncis Bacon (1561-1626), a quêm se credita o método da indução, quê parte de observações particulares e delas induz leis e teorias gerais, ou universais; Galileu, que defendeu e praticou a união da observação dos fenômenos com a dedução de hipóteses e a elaboração de experimentações controladas, utilizando da linguagem matemática; e o filósofo e matemático francês Renê Descartes (1596-1650), quê desenvolvê-u as bases para uma área denominada Epistemologia, isto é, a maneira como conhecemos e compreendemos algo, chegando a propor um modelo matemático para descrever o pensamento humano.
PENSE E RESPONDA

LAVOISIER exécute la décompostion de l'air. 1870. 1 gravura.
1 Os métodos utilizados pelo cientista retratado na tela são os mesmos utilizados pêlos cientistas atuáis?
Página setenta e três
Mas será quê foram apenas estes indivíduos quê contribuíram na pesquisa das formas do fazer Ciência? cértamênte não. Muitos outros contribuíram, de diversas regiões do mundo.
O fazer Ciência envolve a realização de algumas práticas comuns tanto em investigações realizadas há milhares de anos quanto nas atuáis, como: a observação sistemática e controlada, a elaboração de hipóteses, a realização de testes de verificação, a proposição de previsões para possíveis situações, o uso de experimentos controlados, a análise de resultados, a abrangência da investigação, o desenvolvimento de enunciados universais, a prática de testes contínuos, entre outras.
O avanço da tecnologia possibilitou métodos mais precisos, cálculos mais ágeis e instrumentos de investigação mais eficientes, bem como viabilizou o desenvolvimento de equipamentos capazes de realizar investigações extremamente difíceis de serem testadas. Portanto, embora na prática científica se identifique um conjunto de métodos a serem seguidos, não há uma receita única de como proceder.
SAIBA +
A Ciência na África
As invenções e inovações africanas, desde a história antiga até os dias atuáis, são diversas, e muitas delas estão presentes em nosso cotidiano. A forma de extração e o uso do ferro e a plantação e fiação do algodão tiveram início no continente africano e são apenas dois dêêsses exemplos.
No antigo Egito, existia um rigoroso método para aferição de massa e de medidas, um sistema de escrita definido e um calendário quê é considerado um dos mais precisos da Antigüidade. Além díssu, os egípcios dominavam áreas como Matemática, Química, Astronomia, Medicina e Engenharia. Os túmulos em forma de pirâmides demonstram seus amplos conhecimentos com base na experiência prática.
Já entre os séculos XI e XV, os povos da África subsaariana (ao sul do deserto do Saara) desenvolveram diversos conhecimentos de Mecânica aplicados a Arquitetura e Engenharia.
Além destas importantes heranças, o desenvolvimento científico contemporâneo no continente africano é expressivo. Monty Jones (1951-2024), doutor em Biologia Vegetal de Serra Leoa, participou de um trabalho inovador quê contribuiu no desenvolvimento de uma variedade de arrôz mais resistente à seca, com grande produtividade e rico em nutrientes.

ATIVIDADES
1. A pirâmide de Quéops, no Egito, é formada por mais de 2,3 milhões de blocos de pedra calcária, com 2,5 toneladas cada uma. Existem diferentes hipóteses quê tentam explicar como elas foram construídas. Faça uma pesquisa sobre algumas destas técnicas e verifique quais são os conhecimentos exigidos em cada uma delas.
2. Elabore uma redação com o seguinte enfoque: A importânssia da globalização do conhecimento científico. Pesquise dados e referências para elaborar seu texto e, utilizando-os, escrêeva sua opinião acerca da importânssia de se divulgar corretamente os avanços científicos em diversas partes do mundo, os benefícios quê os estudos em determinado país podem proporcionar para outros países, os problemas da centralização do conhecimento em determinados locais, entre outros.
Página setenta e quatro
Ciência: uma construção humana
A discussão acerca do método quê normalmente um cientista segue em seu trabalho revela um caráter humano da Ciência, quê é coletiva e é passível de êêrros e acêrrrtos.
Os métodos desenvolvidos refletem a forma de se pensar em cada época. Os problemas enfrentados pêlos cientistas, quê, muitas vezes, culminaram no atraso, ou mesmo no impedimento, do desenvolvimento de sua teoria, deixaram de herança para as próximas gerações de cientistas inúmeras observações e ideias. Por causa díssu, foram se criando métodos úteis aos trabalhos dêstes, contribuindo para novas conclusões.
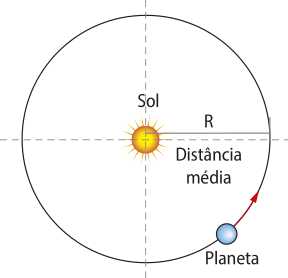
Os estudos da Terra e da organização do Sistema Solar, por exemplo, são realizados há milhares de anos e sempre foram conduzidos por indivíduos guiados pelas próprias crenças e hipóteses. Pode-se observar isso na análise dos estudos da Gravitação.
Muitos cientistas passaram anos da vida deles olhando para o céu em busca de compreender a organização e a dinâmica do Universo. Costuma-se citar o astrônomo egípcio Cláudio Ptolomeu (c. 90 d.C.-168 d.C.), com a sua proposição de modelo geocêntrico (Terra no centro, em repouso, com os astros girando ao seu redor) quê foi aceito por cerca de 1.500 anos.
Fala-se também do astrônomo e matemático polonês Nicolau Copérnico, com sua proposta de um modelo heliocêntrico (Sol no centro, em repouso, com os astros, inclusive a Terra, girando ao seu redor). Porém, existem registros de pitagóricos, como eram chamados os seguidores do matemático Pitágoras (c. 570 a.C.- 500-490 a.C.), quê, por volta de 500 a.C., na Grécia antiga, acreditavam quê a Terra se movia ao redor de um “fogo central”. Já Aristarco de Samos havia propôsto no século III a.C. quê a Terra se movia em torno do Sol.
O astrônomo dinamarquês Tycho Brahe (1546-1601) fez observações precisas e sistemáticas dos astros celéstes, conduzidas por sua ideia de um modelo geocêntrico. Brahe entregou ao astrônomo e matemático alemão Johannes Képler (1571-1630) todas as suas observações e anotações. Képler seguiu com os trabalhos por vários anos, concluindo as leis quê regem o movimento dos corpos em órbita, as leis de Képler, quê você estudará adiante.
SAIBA +
César Lattes e o Prêmio Nobél de Física
Diversas leis e teorias são conhecidas pelo nome de um cientista, como as leis de níltom, a lei da indução de Faraday e o modelo atômico de Rutherford. A maior parte dessas teorias foram desenvolvidas ao longo de muitos anos e contaram com a contribuição de diversos cientistas.
No entanto, não se deve reduzir uma lei ou teoria apenas àquela pessoa quê teve o crédito de seu nome, assim como não se deve creditar todo o desenvolvimento científico a apenas um indivíduo.
O físico brasileiro Césare Mansueto Giulio Lattes (1924-2005), conhecido como César Lattes, teve destaque mundial em sua carreira, principalmente, pela codescoberta da partícula méson pi, ou píon, em 1947.
Trabalhando em conjunto com outros cientistas, como o físico inglês Cecil frânki Powell (1903-1969), Lattes investigou raios cósmicos em um laboratório instalado nos Andes bolivianos, quando detectou a partícula buscada, o méson pi. Em 1948, Lattes e outros cientistas produziram o méson pi artificialmente em um acelerador de partículas da Universidade de Berkeley, na Califórnia, Estados Unidos.
Apesar da descoberta de Lattes, o Prêmio Nobél de Física devido à descoberta do méson pi foi entregue em 1949 para o físico japonês Hideki Yukawa (1907-1981), quê havia previsto teóricamente a existência do píon; e em 1950 para Powell, quê era o chefe das pesquisas responsáveis pela detecção do méson pi.
Página setenta e cinco
ATIVIDADES
1. No seu entendimento, quais foram os motivos quê levaram a césar Lattes não receber o Prêmio Nobél de 1950?
2. Em grupo de até quatro integrantes, pesquisem acerca da repercussão do trabalho de Lattes para o desenvolvimento da Ciência no Brasil. Discutam oralmente os resultados obtidos.
ATIVIDADES
1. Quais são as principais diferenças entre os métodos utilizados por cientistas no passado, até chegar nos métodos dos cientistas atuáis?
2. (UFF-RJ) O conceito de “Revolução Científica” envolve as novas concepções sobre a natureza e os métodos de investigação das ciências naturais quê predominam a partir do século XVII. Assinale a opção quê combina dois marcos da “Revolução Científica”.
a) A teoria da evolução, de xárlês Dárvim, e o desenvolvimento da tabéla periódica dos elemêntos, por Dmitri Mendeleev.
b) A teoria do eletromagnetismo, de diêmes Clerk Macsuéll, e as leis da hereditariedade, de Gregor Mendel.
c) A teoria geocêntrica de Ptolomeu e o teorema de Pitágoras.
d) A teoria atomística de Demócrito e a medicina científica de Hipócrates.
e) A teoria heliocêntrica de Nicolau Copérnico e a lei da gravitação universal, de Isaac níltom.
Resposta: e)
3. Tycho Brahe fez importantes investigações sobre o Universo e o Sistema Solar, embora acreditasse quê o sistema de organização era geocêntrico, mesmo após a divulgação dos trabalhos de Copérnico sobre o sistema heliocêntrico. Posteriormente, Képler, considerando a proposta de Copérnico, seguiu com suas investigações e desenvolvê-u as leis de movimento.
De quê forma as convecções individuais de um cientista podem impedi-lo de fazer as pesquisas e chegar em uma conclusão?
4. O afresco apresentado a seguir é chamado Escola de Atenas e foi pintado pelo italiano Rafael Sanzio entre 1509 a 1511. Nele é retratado um local quê ficou conhecido como Academia de Platão, na Grécia antiga, sêndo assim uma homenagem à Filosofia. A pintura apresenta cerca de sessenta personalidades quê discutem suas teorias. Em uma posição de destaque, no centro da imagem, está Platão à esquerda e Aristóteles à direita. Na pintura, Platão está representado apontando para cima, enquanto Aristóteles está com a mão para baixo, indicando o lugar em quê estão, o mundo. Faça uma pesquisa sobre estes filósofos gregos e verifique os motivos de eles estarem representados desta forma.
![Reprodução de uma pintura 'ESCOLA DE ATENAS'[RAFAEL]. No destaque, a imagem do centro da pintura aumentada, retratando os filósofos, PLATÃO á esquerda e ARISTÓTELES á direita. eles estão em salão com colunas e arcos, vestem mantos.](../resources/images/ek_d/ek_d61cefa7d2e3c8c638312a011d15f712.png)
SANZIO, Rafael. Escola de Atenas. [entre 1509 e 1511]. 1 afresco, 500 cm × 770 cm.
Página setenta e seis
TEMA 8
Forças e as leis dos movimentos da Dinâmica
Aproveitar esse momento para debater a reflekção do primeiro parágrafo com os estudantes. Incentivá-los a apresentar respostas para as perguntas apresentadas e analisá-las brevemente, sem, contudo respondê-las. Direcionar a discussão para quê eles compreendam a importânssia de um agente – a fôrça – para quê esses movimentos sêjam possíveis e comentar quê esse assunto será discutido a partir dêêsse Tema.
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Dinâmica: as causas do movimento
O quê mantém a Lua se movimentando ao redor da Terra? por quê um paraquedista, ao realizar um salto, cai em direção à Terra?
Quando foram iniciados os estudos de movimento a partir das grandezas posição, velocidade e aceleração, não foram consideradas as causas para quê esses movimentos ocorressem, mas apenas se analisou seus efeitos.


A Dinâmica é a parte da Mecânica quê estuda os movimentos considerando suas causas e seus efeitos, isto é, relaciona o movimento à fôrça.
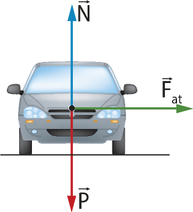
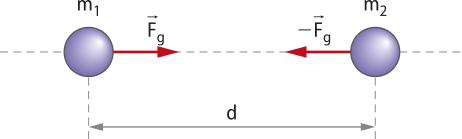
Quando se fala em fôrça, normalmente se remete a empurrar, puxar ou segurar algum corpo. Em sua definição física, fôrça está relacionada com uma interação entre corpos ou sistemas, quê podem estar em contato ou não.
Dessa interação, surgem pares de forças quê atuam nos corpos envolvidos, podendo ter efeitos diferentes em cada um deles.
Os efeitos das fôrças estudados pela Dinâmica são relacionados aos movimentos, ou seja, força é a ação quê causa variações no estado de movimento ou repouso de um corpo.
A fôrça é uma grandeza vetorial, possuindo assim módulo e orientação.
PENSE E RESPONDA


1 Os usos da palavra "fôrça" têm a mesma conotação nas duas situações apresentadas? Justifique sua resposta.
Página setenta e sete
Força resultante
Em diversas situações, é possível quê o mesmo corpo esteja sujeito à ação de várias forças. Nesse caso, essas forças são representadas por apenas uma, chamada fôrça resultante, quê será designada por .
Para obtêr a fôrça resultante , é preciso fazer a soma vetorial de todas as forças quê atuam no corpo.
Exemplificando, considere o ponto material A nos dois casos a seguir:
1º caso: as forças e agem sobre A.

A fôrça resultante é dada por:
2º caso: as forças , e agem sobre A.
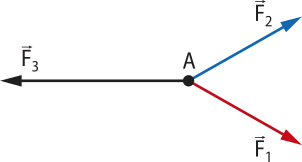
A fôrça resultante é dada por:
Generalizando, diz-se quê sobre o ponto material A agem n forças,
A representação apresentada indica uma adição vetorial, quê não corresponde, necessariamente, a uma adição dos módulos das forças. É preciso fazer uma análise vetorial.
No SI, a unidade de medida de fôrça é o nílton (N). Como se trata da unidade de medida, deverá sêr escrita com letra minúscula (nílton), e seu sín-bolo, com letra maiúscula (N).
ATIVIDADES
1. O quê é fôrça resultante?
2. Uma fôrça de módulo 10 N e outra de módulo 12 N são aplicadas, simultaneamente, a um corpo. Qual das opções a seguir apresenta uma possível intensidade resultante dessas forças?
a) 0
b) 1 N
c) 15 N
d) 24 N
e) 120 N
Resposta: c)
3. Sobre a bancada de um laboratório, um corpo é submetido à ação de duas forças, F1 = 50 N e F2 = 20 N. Durante um teste, a direção e o sentido dessas forças sofrem variações, para quê se saiba em quê situações ocorrem a maior ou a menor intensidade da fôrça resultante .
Página setenta e oito
Determine a intensidade da fôrça resultante quê age no corpo quando o ângulo formado entre as duas forças é:
a) 60°, sabendo quê cos 60° = 0,5;
≃ 62,4 N
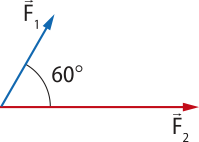
b) 30°, sabendo quê cos 30° 1 0,87.
≃ 68,1 N

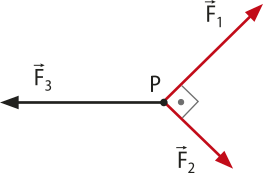
4. Por causa da correnteza das águas de um rio, um barco está amarrado por duas kórdas quê aplicam nele as forças F1 = 40 N e F2 = 30 N.
Na figura, estão representadas as direções e os sentidos das forças quê agem no barco (o barco está representado pelo ponto material P). Sabendo quê dessa forma o barco se mantém em repouso, determine (em newton) o módulo da fôrça F3, aplicada pela á gua no barco.
50 N
As leis de níltom
Os estudos acerca do movimento e a busca por leis universais quê o caracterizavam se iniciaram ainda na Antigüidade, mas foi entre os séculos XVI e XVIII quê passou a sêr descrito da forma mais próxima da quê se conhece atualmente, com a elaboração das primeiras sistematizações.
Diversos cientistas contribuíram nesses estudos, como Galileu, Descartes, o filósofo e matemático alemão Gottfried uiu rélm Leibniz (1646-1716) e a matemática e física francesa Émilie du Châtelet (1706-1749). Esses cientistas buscavam definições sobre as leis de movimento com base na massa e na velocidade dos corpos e chegaram a conclusões importantes.
Em 1687, níltom publicou a obra Os princípios matemáticos da filosofia natural (conhecida como Principia), em quê apresentou as leis para os movimentos, quê ficaram popularmente conhecidas como leis de níltom. Apesar do nome, essas leis consistem em uma análise e sistematização de diversos conhecimentos até então produzidos, o quê revela o caráter humano da Ciência, quê é feita d fórma coletiva e passível de acêrrrtos e êêrros.
É importante destacar quê as leis de níltom são válidas apenas em referenciais não acelerados (referenciais inerciais), isto é, referenciais em repouso ou em movimento retilíneo uniforme em relação a outro referencial também não acelerado. Além dessa restrição, as leis de níltom não são válidas em fenômenos a altas velocidades, próximas às da luz, e em fenômenos em escala atômica.
PENSE E RESPONDA

2
Aristóteles acreditava quê sempre existia uma fôrça agindo a favor do movimento e, caso a fôrça cessasse, o movimento deixaria de existir. Você concórda com essa afirmação? Na pedra de curling, por exemplo, após ela sêr lançada pelo atleta, existem fôrças agindo sobre ela? Alguma força age a favor do movimento?
Página setenta e nove
Princípio da inércia (1ª lei de Newton)
O conceito de inércia, enunciado formalmente por Isaac níltom, diz quê:
Todo corpo permanéce em seu estado de repouso ou de movimento uniforme em linha reta quando a fôrça resultante quê atua sobre ele é nula.
A tendência de um corpo a permanecer em repouso ou em movimento retilíneo uniforme só é válida quando a resultante das forças quê atuam sobre ele é nula. Se um ponto material está em repouso ou em movimento retilíneo uniforme, a velocidade vetorial é constante. pôdêmos sistematizar esse conceito da seguinte forma:
⇔ é constante
Equilíbrio é um estado em quê o corpo se encontra quando sua aceleração é nula. O estado de repouso é denominado equilíbrio estático e o estado de movimento retilíneo uniforme é denominado equilíbrio dinâmico.
PENSE E RESPONDA

3 O artigo 105 do cóódigo de Trânsito Brasileiro indica alguns itens obrigatórios para os veículos, como o cinto de segurança e o encosto de cabeça. Qual é o princípio físico de movimento quê corrobora a utilização dêêsses dois mecanismos?
Princípio fundamental da Dinâmica (2ª lei de Newton)
Observe duas situações nas quais uma mesma fôrça resultante (não nula) foi aplicada em dois corpos com massas distintas: na Figura 1, tem-se uma massa m1 e, na Figura 2, tem-se uma massa m2, sêndo m2 > m1.
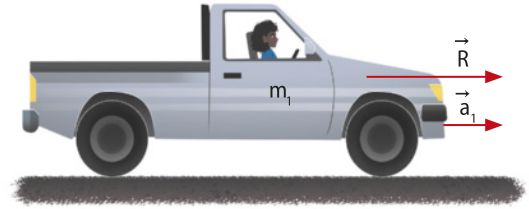
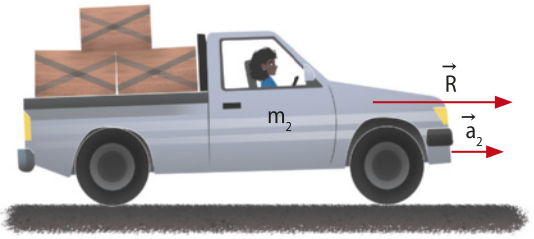
Quanto maior a massa do corpo, maior será a resistência à variação de velocidade, isto é, para a mesma fôrça resultante , se a massa aumentar, a intensidade de a diminuirá e vice-versa.
Quando um ponto material de massa m é submetido à ação de uma fôrça resultante diferente de zero, ele adqüire uma aceleração cuja direção e sentido são os mesmos de e intensidade inversamente propor cional à da massa. Assim, o princípio fundamental da Dinâmica é definido como:
Página oitenta
A massa póde sêr interpretada como uma medida da resistência quê um corpo apresenta à variação da velocidade, ou seja, é como uma medida da sua inércia.
No SI, são utilizadas as seguintes unidades: quilograma (kg), para massa; métro por segundo ao quadrado (m/s2), para aceleração; nílton (N), para fôrça.
Considerando o princípio fundamental da Dinâmica, temos: 1 nílton é a intensidade de uma fôrça quê, ao agir em um objeto de massa 1 kg, manifesta nele uma aceleração de 1 m/s2, na sua direção e no seu sentido. Portanto: 1 N = 1 kg ⋅ 1 m/s2.
Princípio da ação e reação (3ª lei de Newton)
Considere as três situações a seguir.



Nas situações apresentadas, é possível verificar quê ocorre uma interação entre os envolvidos em cada situação: na caminhada, a mulher empurra o solo para trás, e o solo a empurra para frente; no caiaque, o remador empurra a á gua para trás, e a á gua empurra o barco para frente; e, por fim, no avião, as hélices empurram o ar para trás, e o ar empurra o avião para frente. Nessas três situações, realiza-se uma fôrça de ação para receber uma fôrça de reação. Essas forças agem simultaneamente e aos pares, e jamais se anulam, pois atuam em corpos distintos.
De acôr-do com níltom, a ação de forças em uma interação entre corpos póde sêr analisada pelo princípio da ação e reação:
Quando um corpo A imprime uma fôrça de ação em um corpo B , o corpo B imprime uma fôrça de reação no corpo A de mesma intensidade, mesma direção e em sentido ôpôsto. Essas forças sempre atuam em corpos distintos.
PENSE E RESPONDA

4 Ao cabecear uma bola, o jogador age aplicando uma fôrça sobre ela. Nesse instante, a bola também aplica uma fôrça na cabeça do jogador?
ESPAÇOS DE APRENDIZAGEM
• O sáiti indicado a seguir contém um simulador de um sistema envolvendo blocos e polia fixa quê permite variar massas, coeficientes de atrito e a gravidade local.
Leis de níltom. Publicado por: Laboratório Virtual de Física da Universidade Federal do Ceará. Disponível em: https://livro.pw/ahlyx. Acesso em: 30 jul. 2024.
Página oitenta e um
ATIVIDADE RESOLVIDA
1. Um vagão de trem em um parque de diversões, de massa m = 100 kg, está em repouso sobre trilhos retilíneos horizontais. A partir de determinado instante, uma fôrça resultante passa a agir sobre ele, na direção paralela aos trilhos, com intensidade constante de 50 N. Qual é a velocidade do vagão 20 s após a ação de ter iniciado?
Resolução
Como é a fôrça resultante, o vagão passa a descrever movimento retilíneo acelerado na mesma direção e no mesmo sentido de
R = ma ⇒ 50 = 100a ⇒ a = 0,5 m/s2
O movimento desenvolvido pelo vagão é retilíneo e uniformemente variado. Dessa forma, tem-se:
v = vi + at ⇒ v = 0 + 0,5 ⋅ 20 ⇒ v = 10 m/s
ATIVIDADES
5. Você empurra um carrinho e ele se móve. Soltando-o, você nota quê em poucos segundos ele para. Esse fato contradiz a 1ª lei de níltom? Justifique sua resposta.
6. O princípio da inércia é válido quando se aplica a um corpo uma única fôrça?
7. A Ciência é construída por sêres humanos, e é passível de êêrros e acêrrrtos. Diversas leis e teorias foram desenvolvidas no trabalho e na dedicação de inúmeras pessoas. Credita-se a Isaac níltom a frase “se eu enxerguei mais longe, é porque eu me apoiei em ombros de gigantes”. Se for considerada essa frase como verdadeira, qual seria, no seu entendimento, a ideia quê níltom desejava transmitir?
8. Um trenzinho de massa 1,2? 103 kg parte do repouso e depois de 10 s atinge a velocidade de 36 km/h. Determine: o valor médio da fôrça resultante quê estabeleceu essa aceleração no veículo.
1,2 ⋅ 103 N
9. Considere o princípio da ação e reação e dêz-creva o quê ocorre com os corpos quê interagem nas situações a seguir.
a) No instante em quê o jogador chuta a bola, o quê ocorre na interação do pé com a bola?
b) Durante o deslocamento de um avião, o quê ocorre na interação das paredes da aeronave com os gases produzidos por ela?
c) O quê ocorre na interação da Terra com a Lua?
10. por quê as forças de ação e reação não podem sêr somadas?
11. Um astronauta de dimensões desprezíveis está em repouso no ponto A da Figura 1, em uma região do espaço livre de ações gravitacionais significativas, em quê 0xyz é um referencial inercial. Com a ajuda de uma mochila espacial, dotada dos jatos 1, 2 e 3 de mesma potência e quê expelem combustível queimado nos sentidos indicados na Figura 2, o astronauta consegue mover-se em relação a 0xyz.
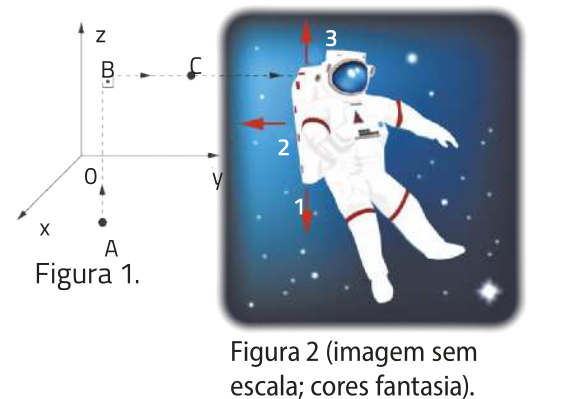
Para percorrer a trajetória A → B → C, o astronauta deverá acionar, durante o mesmo intervalo de tempo, os jatos em qual sequência?
1, 3 e 2
Página oitenta e dois
Interações entre os corpos
A interação entre corpos ocorre, basicamente, de duas formas: interação a distância e interação por contato.
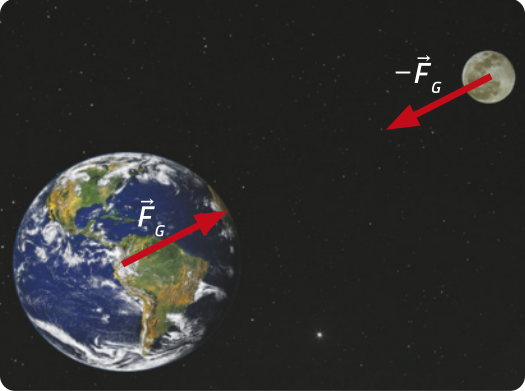
Na interação a distância, as forças de interação entre corpos se estabelece sem quê exista contato entre eles. Estas forças são também denominadas forças de campo, pois a teoria quê explica a interação a distância diz quê a região onde estas forças ocorrem é denominada campo.
Forças de campo também são definidas pela terceira lei de níltom, do princípio da ação e reação, ou seja, os corpos envolvidos na análise considerada sentem fôrças de mesma intensidade, mesma direção e sentidos opostos. Como exemplo de fôrças de campo, podem-se citar a fôrça da gravidade, a força magnética e a força elétrica.
Na interação por contato, a fôrça de interação entre corpos se estabelece devido ao contato entre eles. São exemplos a fôrça normal e a de atrito (que serão estudadas adiante).
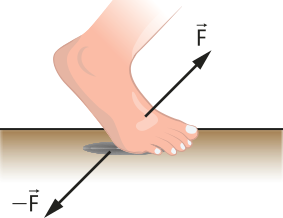
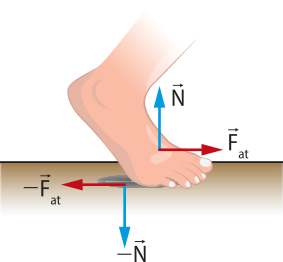
Considere, por exemplo, uma pessoa quê está realizando uma caminhada. Quando o pé se firma sobre a superfícíe, há a ação do pé sobre o solo pela fôrça de contato, nomeada A fôrça de reação do solo sobre o pé da pessoa é nomeada de mesma intensidade, mesma direção e sentido ôpôsto.
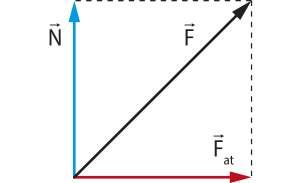
A fôrça quê age sobre o pé póde sêr decomposta em duas componentes: a componente normal, ou perpendicular à superfícíe (denominada fôrça normal ), e a componente tangencial, ou paralela à superfícíe (denominada fôrça de atrito ). Observe, a seguir, a indicação dos vetores dessas forças.

Página oitenta e três
Força peso
Em seus estudos sobre a interação da gravidade, níltom propôs quê os corpos geram um campo gravitacional ao seu redor, d fórma quê entre dois ou mais corpos surge uma atração, quê age a distância – a fôrça da gravidade. Essa fôrça tem intensidade considerável quando ao menos um dos corpos envolvidos tem grande massa, como a Terra.
A queda dos corpos ocorre por causa do campo de fôrças existente nas proximidades da Terra, chamado campo gravitacional. A força de atração quê age sobre o corpo, quando ele é abandonado no campo gravitacional da Terra, chama-se fôrça peso e é responsável pela acele ração adquirida por ele durante a queda, denominada aceleração da gravidade .
Em outras palavras, pode-se dizêr quê o peso de um corpo é a fôrça gravitacional com a qual a Terra o atrai. Essa definição de fôrça peso também póde sêr aplicada nas proximidades das superfícies de outros corpos celéstes.
Abandonando um corpo de massa m próximo da superfícíe terrestre e desconsiderando a resistência do ar durante a queda livre, a fôrça resultante sobre ele é a fôrça peso Sendo a aceleração resultante igual à aceleração da gravidade , e a fôrça resultante igual à fôrça peso , pelo princípio fundamental da Dinâmica, tem-se:
Portanto:
, ou, em intensidade, P = mg
A massa do corpo não se altera com a mudança do local, mas a intensidade do peso sofre alteração, pois a fôrça de atração exercida no corpo varia de um local para outro.
Considerando a superfícíe terrestre, tem-se quê:
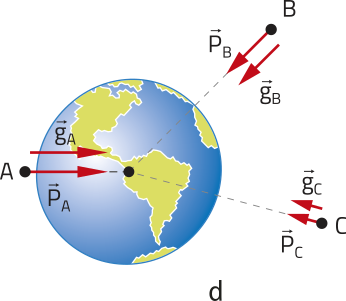
• o valor de g varia com a latitude, sêndo maior nos polos do quê no equador.
• o valor de g varia com a altitude, sêndo maior ao nível do mar.
A fôrça peso tem a mesma direção e o mesmo sentido da aceleração da gravidade .
Observe a representação da fôrça peso de três corpos pontuais de mesma massa: corpo A ,corpo B e corpo C .
Uma unidade de medida de fôrça denominada quilograma-força (kgf) tem sua definição com base na fôrça peso. Um corpo de massa 1 kg tem peso equivalente a 1 kgf quando imérso em campo gravitacional. Portanto:
1 kgf = 9,8 N
É comum adotar g = 10 m/s2, logo 1 kgf = 10 N.
Essa relação entre as unidades póde ajudar a compreender alguns equívocos da linguagem cotidiana, como: “meu peso é 70 kg”, quando o correto seria dizêr: “meu peso é 70 kgf” ou “minha massa é 70 kg”.
PENSE E RESPONDA

5 O quê provoca a queda dos frutos das plantas após eles se desprenderem dos galhos?
Página oitenta e quatro
SAIBA +
Exploração espacial
O planêta Terra possui condições ideais para a existência das formas de vida conhecidas atualmente, como aceleração da gravidade adequada, presença de atmosféra e pressão atmosférica, á gua em estado líquido, existência de sólos passíveis de cultivo, entre outras.
Além díssu, existem características relacionadas ao Sistema Solar quê também são favoráveis, como a distância adequada do Sol e a localização em um sistema com planêtas gigantes gasosos, quê sérvem como protetores para a Terra contra colisões com corpos celéstes quê vagam pelo Universo.
A busca por locais fora da Terra onde as formas de vida conhecidas tênham condições adequadas para existir e se desenvolver é um ramo de pesquisa espacial. Nesse contexto, existe a terraformação, quê é o desenvolvimento de ambientes fora da Terra, como planêtas ou estações espaciais, quê simularia as condições necessárias para o desenvolvimento da vida.
Embora a terraformação pareça algo hipotético e distante, saído dos cenários de ficção, existem pesquisas e investimentos atuáis com esse objetivo. Parcerias entre agências espaciais públicas e particulares estabeleceram um prazo de 20 a 30 anos para a chegada da primeira tripulação humana no planêta Marte, por exemplo. Essa tripulação não será tratada como astronautas, mas como colonizadores.
Caso essa missão se realize, a ideia é o estabelecimento de pequenas bases de estudos para iniciarem as alterações do ambiente. Posteriormente, essas bases irão evoluir para módulos mais sofisticados e, futuramente, em uma vila de moradores. É bom destacar quê se trata de um projeto em fase de idealização.
ATIVIDADES
Organize-se em grupos de até cinco integrantes para pesquisar os itens a seguir.
1. Investiguem quais características, considerando outros planêtas ou satélites, precisariam sêr alteradas para possibilitar a permanência de vida humana com qualidade.
2. Pesquisem sobre as contribuições de outras áreas de estudo para o desenvolvimento da terraformação de outro planêta. Organizem-se para conversar com professores de outros componentes para complementar suas respostas.
3. Busquem mais informações sobre o programa espacial quê objetiva levar a primeira tripulação até o planêta Marte. Verifiquem as últimas atualizações dêêsse programa e dêtálhes sobre projetos quê poderão sêr desenvolvidos em território marciano, caso a missão tenha êxito.

Página oitenta e cinco
Força normal
Chama-se fôrça normal , ou reação normal, qualquer fôrça de contato nas superfícies de dois ou mais corpos quando encostados uns nos outros. Assim, só há sentido em descrever a fôrça normal se as superfícies de contato se comprimirem mutuamente.
Observe nas fotografias a seguir a representação das forças normais perpendiculares em cada superfícíe.

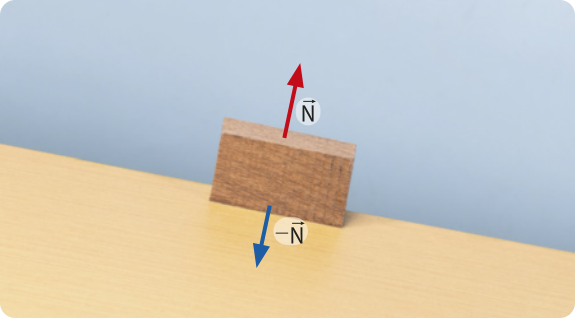
A fôrça normal apresenta as características a seguir.
• A intensidade depende da compressão entre as superfícies.
• A direção é perpendicular à superfícíe, no ponto onde se dá o contato.
• O sentido é contrário ao ponto onde se dá o contato.
Força de tração
A fôrça de tração é um tipo de fôrça de contato quê ocorre em fios, cabos e kórdas transmitida sobre eles de uma extremidade a outra.
Analise o exemplo de um lustre pendurado por um fio, com a indicação das forças presentes no lustre e no fio em destaque.
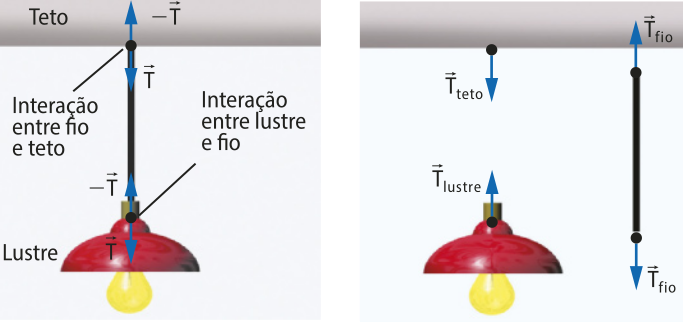
Nessa situação:
:força com quê o fio traciona o lustre.
:força de tração quê o lustre aplica no fio.
:força com quê o fio traciona o teto.
:força de tração quê o teto aplica no fio.
A fôrça de tração apresenta as características a seguir.
• A intensidade depende da fôrça quê traciona o fio.
• A direção é a mesma da direção do fio.
• O sentido é o quê se traciona (ou “puxa”) o fio.
No estudo, é comum considerar os fios e os cabos como ideais, ou seja, como inextensíveis e de massa desprezível em relação aos outros corpos envolvidos.
Página oitenta e seis
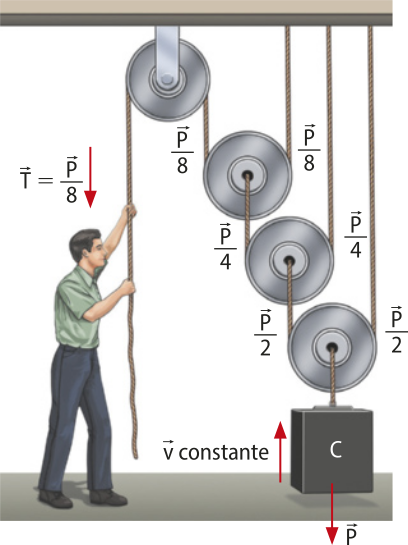
Polias
Em algumas situações, é necessário modificar a direção do fio sem alterar a intensidade das forças. Para isso, são usadas polias ou roldanas fixas, quê permitem redirecionar uma fôrça aplicada.
Polias fixas não geram vantagens mecânicas, isto é, para equilibrar um corpo quê recebe uma fôrça peso de 50 N, deve-se aplicar na kórda uma fôrça de tração de 50 N.
Comumente, as polias são consideradas ideais, ou seja, desprezam-se possíveis atritos quê interfiram em seu funcionamento.
Já as polias móveis oferecem vantagens mecânicas quanto à intensidade da fôrça aplicada.
Uma associação de polias fixas e móveis tem como objetivo redirecionar a fôrça aplicada e mover corpos com menor esfôrço.
Note, na figura, quê cada polia móvel associada ao sistema provoca uma redução da fôrça aplicada pela pessoa.
Nesse tipo de associação de polias, denominada talha exponencial, associando n polias móveis ao sistema para elevar uma carga de fôrça peso P, a fôrça T aplicada será:
Força elástica
Uma mola é um corpo formado por um fio enrolado em formato helicoidal, ou de hélice.
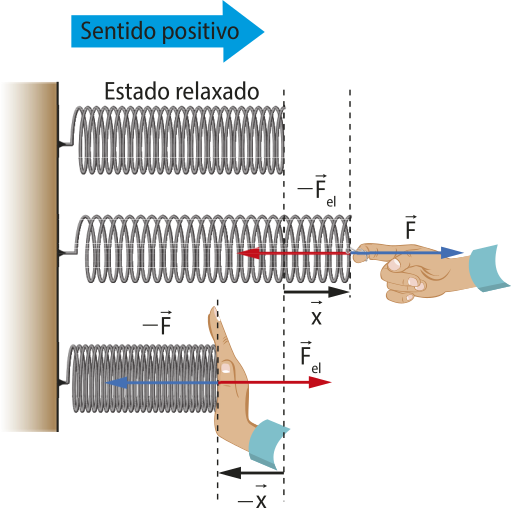
As imagens representam uma mola com uma de suas extremidades fixas. Ao receber a ação de uma fôrça externa quê causa sua deformação, a mola exerce uma fôrça de mesma intensidade e sentido ôpôsto, quê atua para quê ela retome o seu comprimento inicial (estado relaxado). Esta fôrça exercida pela mola é denominada fôrça elástica .
Durante uma investigação prática utilizando uma mola ideal, isto é, com massa desprezível, forças de diferentes intensidades F foram aplicadas na mola, resultando em sua deformação (x), e os dados foram registrados a seguir.
Existe uma proporção diréta entre a fôrça elástica exercida pela mola e a deformação sofrida. Essas duas grandezas relacionam-se por uma constante k.
k = ⇒ k =
F = Fel (valores em N) |
x (valores em cm) |
|---|---|
10,0 |
2,0 |
15,0 |
3,0 |
30,0 |
6,0 |
37,5 |
7,5 |
Página oitenta e sete
A constante k é chamada constante elástica da mola, quê depende do material de quê é feita e das suas dimensões. Sua unidade no SI é N/m. No exemplo, uma constante elástica de 5,0 N/cm equivale a 500,0 N/m.
A relação entre a fôrça elástica e a deformação foi proposta pelo físico e astrônomo inglês róbert rúki (1635-1703), sêndo por isso chamada lei de rúki.
O sinal negativo deve sêr acrescentado na expressão, pois a fôrça elástica possui sempre orientação contrária à deformação sofrida. Por isso, ela também é denominada fôrça restauradora. Para analisar somente o módulo da fôrça elástica, pode-se considerar apenas Fel = kx.
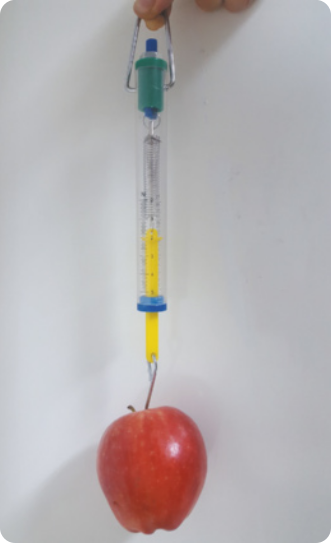
Com base nessa análise, é possível compreender o funcionamento de um dinamômetro, quê, basicamente, é constituído por uma mola acoplada a uma escala graduada. Para realizar a leitura diréta da intensidade da fôrça, a escala é graduada em determinada unidade de fôrça (kgf ou N).
ATIVIDADES RESOLVIDAS
2. Em uma viagem espacial, leva-se um conjunto de equipamentos cujo peso é 900 N, medido em um local da Terra, onde g = 10 m/s2. Qual é a massa e o peso dêêsse equipamento na Lua? Considere gL = 1,6 m/s2.
Resolução
PTerra = mgTerra ⇒ 900 = m ⋅ 10 ⇒ m = 90 kg
A massa de um corpo não sofrerá alteração com a mudança de local. Assim, na Lua: m = 90 kg.
PLua = mgLua = 90 ⋅ 1,6 ⇒ PLua = 144 N
Note quê, embora a massa do conjunto seja a mesma, a intensidade do peso é menor na Lua do quê na Terra.
3. Sobre a superfícíe horizontal e lisa de uma mesa, é colocado um corpo A de massa mA = 3 kg. Um fio ideal une o corpo A ao B de massa mB = 2 kg. O fio passa por uma polia também ideal. Considere g = 10 m/s2 e despreze os possíveis atritos.
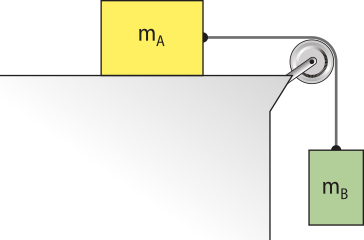
Determine a intensidade da aceleração e da fôrça de tração transmitida pelo fio.
Resolução
Aplicando-se a segunda lei de níltom e considerando sua direção de movimento, tem-se: Corpo B:
Na direção do movimento (vertical).
PB − T = mBa (I)
Corpo A:
Na direção do movimento (horizontal).
TA = mA a (II)
Resolvendo o sistema:
![Sistema de equações em três linhas: linha um:' P B' menos' T' igual a 'm B a'. Linha dois: 'T' igual a 'm A a'. Linha três: linha [1] mais linha [2] 'P B' igual a['m A' mais ['m B']a. sendo 'a' igual a 20 dividido por 5, sendo 'a' igual a 4 metros por segundo ao quadrado.](../resources/images/ek_7/ek_783a730f6aee40d5878c47b63ec8251e.png)
a = ⇒ a = 4 m/s²
Substituindo o valor de a = 4 m/s2 na equação (I) ou (II), obtém-se a intensidade da fôrça de tração transmitida pelo fio.
Em (I), tem-se: 20 − T = 2 ⋅ 4 ⇒ T = 12 N.
Em (II), tem-se: T = 3 ⋅ 4 ⇒ T = 12 N.
Página oitenta e oito
ATIVIDADES
12. Partindo da hipótese de quê é possível coletar material na superfícíe do planêta Júpiter, onde g ≃ 23 m/s2, determine:
a) a massa dêêsse material (em kg), em Júpiter, sabendo quê lá o peso do material é 125 N;
5,4 kg
b) o peso dêêsse material (em N), medido na superfícíe terrestre, onde g = 10 m/s2.
54 N
13. Para atender pessoas quê estão em uma região isolada, uma equipe de socorro abandona, de um avião, uma caixa de mantimentos amarrada a um para quedas. Juntos, para quedas e caixa têm massa 100 kg e descem com velocidade constante de 4 m/s. Considere quê a aceleração da gravidade é g = 10 m/s2 e determine a fôrça de resistência oferecida pelo ar.
1.000 N
14. Suponha quê a massa de um astronauta na Terra seja M e seu peso, P. Sabendo quê a aceleração da gravidade na Lua é um sexto da verificada na Terra, determine:
a) a massa do astronauta na Lua;
M
b) o peso do astronauta na Lua.
Aproximadamente 0,16P.
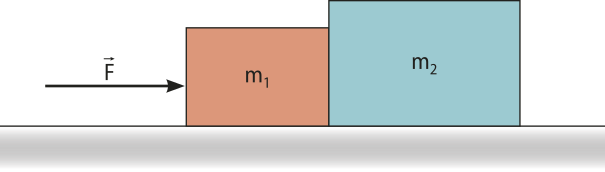
15. Sobre uma superfícíe horizontal plana e lisa, foram colocados os blocos 1 e 2, cujas massas são m1 = 2,0 kg e m2 = 3,0 kg, respectivamente. Se o bloco 1 receber a ação de uma fôrça F = 5 N, conforme mostra a figura, qual será a intensidade da fôrça de contato entre os blocos?
3,0 N
16. A figura ilustra três corpos A, B e C unidos por fios inextensíveis. As massas são, respectivamente, iguais a 5 kg, 10 kg e 15 kg, e a intensidade da fôrça quê atua sobre o corpo A é F = 120 N.

Supondo desprezíveis as massas dos fios e os atritos, determine:
a) a aceleração do sistema;
4 m/s2
b) as intensidades das forças de tração T1 e T2 nos fios quê unem, respectivamente, AB e BC.
T1 = 100 N e T2 = 60 N
17. Considere uma mola, de 6 cm de comprimento, com uma de suas extremidades presa ao teto. Ao prender um corpo de massa 1 kg na outra extremidade, a mola passa a ter 10 cm. Qual será o comprimento da mola se trocarmos o corpo de 1 kg por outro de 3 kg?
18 cm
18. Um elevador possui preso em seu teto um dinamômetro, o qual suspende um pacote de 8 kg. Determine a marcação dêêsse dinamômetro quando o elevador está descendo e freando a uma aceleração constante de 4 m/s2. Considere g = 10 m/s2.
112 N
19. Na representação a seguir, há um dinamômetro (D) cuja massa póde sêr considerada nula, ligado a dois blocos A e B (por fios ideais), sêndo a fôrça de intensidade F = 500 N, as massas mA = 25 kg e mB = 15 kg.
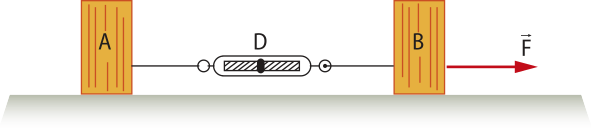
Desconsiderando qualquer forma de atrito, o dinamômetro indicará o valor de:
a) 310,5 N
b) 311,5 N
c) 312,5 N
d) 314,5 N
e) 315,5 N
Resposta: c)
Página oitenta e nove
Plano inclinado
Comentar com os estudantes quê, em todos os casos, a fôrça é exercida sempre no centro do corpo, neste caso, bloco e mesa, mas a representação está ligeiramente deslocada para facilitar a compreensão.
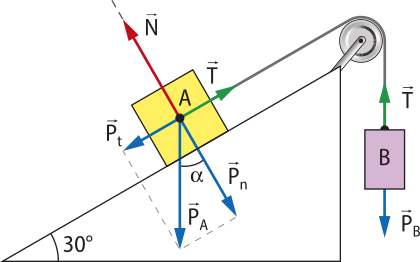
As imagens ilustram uma caixa em duas situações: uma apoiada sobre uma mesa e com as indicações de fôrça quê nela atuam (Figura 1); e outra com a indicação da interação da caixa com a mesa e o centro da Terra (Figura 2). Observe quê a fôrça normal não corresponde à reação da fôrça peso.
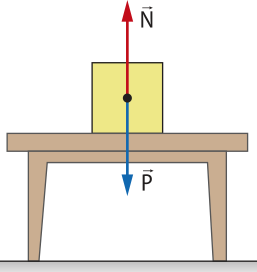
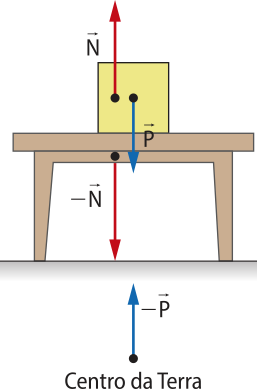
A reação da fôrça peso aplicada pelo bloco está no centro da Terra. No caso da fôrça normal, o bloco exerce na mesa uma fôrça normal e a mesa exerce no bloco a fôrça normal .
Na situação representada a seguir, o plano de apôio é colocado em uma posição inclinada em relação ao plano horizontal. Note quê, nesse caso, a direção da fôrça peso continua vertical, e a direção da fôrça normal é perpendicular ao plano de apôio.
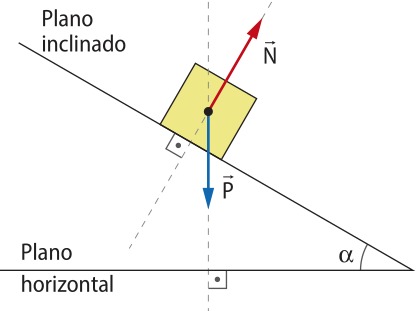
Se não for considerado o atrito, as fôrças peso e normal em um corpo sobre um plano inclinado produzem uma força resultante diferente de zero.
Para obtêr esta fôrça resultante quê atua na direção do movimento, utilizam-se a reta t (na direção do movimento) e a reta n (perpendicular ao movimento). Dessa forma, pode-se decompor a fôrça peso nas componentes e .
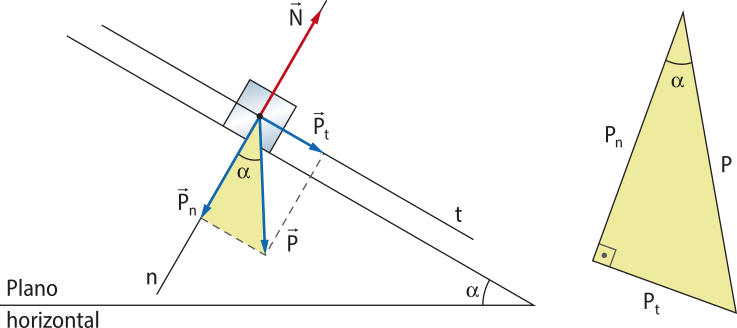
Para determinar e ,é preciso realizar as razões trigonométricas no triângulo retângulo. Assim, pode-se escrever:
sen (alfa)" = ⇒ Pt = P sen (alfa)"
cos (alfa)" = ⇒ Pn = P cos (alfa)"
Na direção das forças e não ocorre movimento. Logo: N = Pn = P cos (alfa)". Porém, na direção da reta t (direção do movimento) a fôrça resultante é . Portanto:
Pt = ma ⇒ P sen (alfa)" = ma ⇒ mg sen (alfa)" = ma ⇒ a = g sen (alfa)"
Página noventa
Força de atrito
Podem-se destacar muitas situações em quê a fôrça de atrito está presente. Por exemplo, só é possível caminhar porque existe atrito entre o solo e o pé ou calçado.
A fôrça de atrito se manifesta quando os corpos em contato se comprimem mutuamente e há deslizamento ou tendência de deslizamento relativo entre eles.
Para detalhar o estudo da fôrça de atrito, será diferenciado atrito estático e atrito cinético.
Na figura, a pessoa aplica uma fôrça horizontal na caixa quê repousa apoiada sobre a superfícíe horizontal e áspera. A caixa se mantém em repouso pela ação da fôrça de atrito ,que surge juntamente com a fôrça .
A intensidade da fôrça de atrito varia conforme a intensidade da fôrça aplicada.
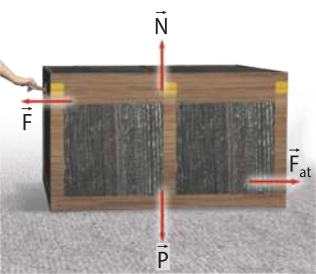
À medida quê a intensidade da fôrça aumenta, também aumenta a intensidade da fôrça de atrito, fazendo a caixa permanecer em repouso: Fat = F.
Quando a caixa estiver na iminência de deslizar, em relação à superfícíe, será ôbitída a mássima intensidade da fôrça de atrito, no caso, estático: Fat(máx) = F.
A caixa começará a escorregar quando a intensidade da fôrça aplicada for superior à intensidade da fôrça de atrito estático mássimo.
A intensidade mássima da fôrça de atrito estático é diretamente proporcional à intensidade da fôrça , normal às superfícies de contato dos corpos:
= μe N
em quê o coeficiente de atrito estático μe é um número adimensional (não possui unidade). êste coeficiente depende do tipo das superfícies em contato, como superfícies ásperas ou lisas. Perceba quê a fôrça de atrito não depende da área de contato entre as superfícies.
Quando a intensidade da fôrça supera a intensidade da fôrça de atrito estático mássimo, o corpo entra em movimento. Neste momento, a fôrça de atrito assume intensidade praticamente constante e ligeiramente menor do quê ,a fôrça de atrito cinético , com intensidade diretamente proporcional à intensidade da fôrça , passa a atuar no corpo:
em quê o coeficiente de atrito cinético μc é um número adimensional, em quê μc < μe.
PENSE E RESPONDA

6 A ação do atrito é fundamental para se realizar determinadas tarefas. Você saberia descrever algumas delas?
Página noventa e um
ATIVIDADE RESOLVIDA
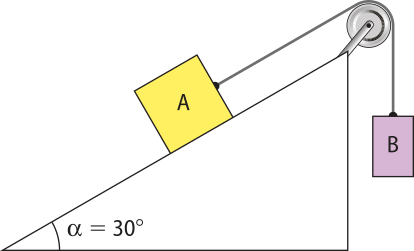
4. A figura representa dois corpos, A e B, amarrados nas extremidades de uma kórda quê passa por uma polia. Ambas (corda e polia) são ideais. O atrito não é considerado, a massa do corpo B é 1,0 kg e, no local, g = 10 m/s2. Nessas condições:
a) represente, na figura, as forças quê agem nos corpos A e B;
b) determine a massa do corpo A, de modo quê o sistema permaneça em repouso.
Resolução
a) O esquema de forças quê agem nos corpos A e B.
b) Para quê o sistema permaneça em repouso, a fôrça resultante em cada corpo, em todas as direções, deve sêr nula.
Corpo A: N = PN = PA cos(alfa)" e
T = Pt = PA sen(alfa)"
Corpo B: T = PB
Assim:
PB = PAsen(alfa)" ⇒ mBg = mAgsen30° ⇒
⇒ 1 ⋅ 10 = mA ⋅ 10 ⋅ ⇒ mA = 2 kg
ATIVIDADES
20. Um corpo de massa 25 kg desloca-se, com aceleração constante, sobre um plano inclinado, sem atrito, conforme o desenho a seguir. O seno do ângulo formado entre o plano e a horizontal é 0,6. Determine a fôrça transmitida ao corpo, para quê a aceleração permaneça igual a 2 m/s2.
Dado: g = 10 m/s2.
200 N
21. No esquema a seguir, o corpo B, ao sêr abandonado, começa a se deslocar e, por meio da kórda, faz o corpo A se mover sobre o plano inclinado, sem atrito. Considerando quê a polia e a kórda são ideais, determine:
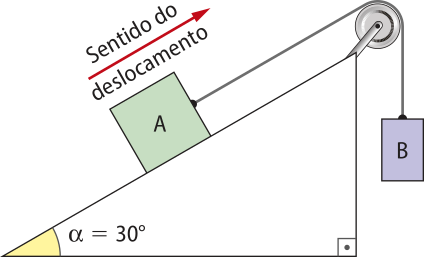
a) a aceleração do conjunto;
2,5 m/s2
b) a intensidade da fôrça de tração na kórda.
30 N
Dados: sen 30° = 0,5; g = 10 m/s2 e mA = mB = 4 kg.
22. Tentando aumentar a intensidade de uma fôrça ao empurrar um corpo, o atrito sobre o corpo também aumenta. Uma vez em movimento, com quê intensidade de fôrça F deve-se empurrar o corpo para mantê-lo em movimento com velocidade constante?
Com a mesma intensidade da fôrça de atrito (cinético).
Página noventa e dois
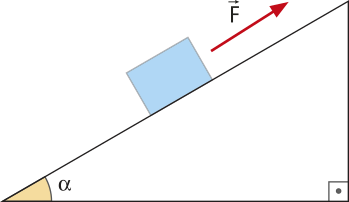
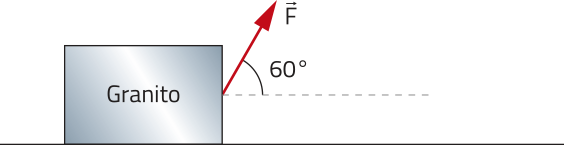
23. Represente, em seu caderno, as forças quê agem em um bloco de granito de massa m, em um local em quê a aceleração da gravidade é g. Considere quê sobre o bloco atua a fôrça indicada na imagem a seguir.
24. (Enem/MEC) Uma pessoa necessita da fôrça de atrito em seus pés para se deslocar sobre uma superfícíe. Logo, uma pessoa quê sobe uma rampa em linha reta será auxiliada pela fôrça de atrito exercida pelo chão em seus pés. Em relação ao movimento dessa pessoa, quais são a direção e o sentido da fôrça de atrito mencionada no texto?
a) Perpendicular ao plano e no mesmo sentido do movimento.
b) Paralelo ao plano e no sentido contrário ao movimento.
c) Paralelo ao plano e no mesmo sentido do movimento.
d) Horizontal e no mesmo sentido do movimento.
e) Vertical e sentido para cima.
Resposta b)
PENSE E RESPONDA
7 Quais são as forças envolvidas para quê um motociclista faça uma curva como a da fotografia?

Forças no movimento circular
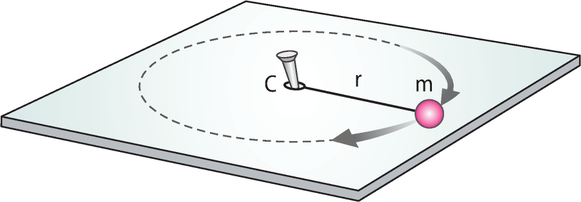
Considere a seguinte situação: uma esféra presa a um fio ideal descreve uma trajetória circular uniforme em torno de um ponto fixo C, sobre um plano horizontal, com velocidade escalar constante v, conforme a representação a seguir. Desconsidere a resistência do ar.
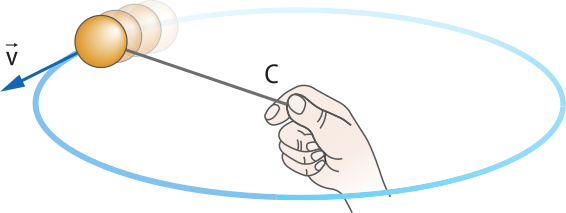
Quais são as condições necessárias para manter a esféra em movimento circular? O quê ocorreria sem essas condições?
Para responder a essas perguntas, é preciso lembrar quê a aceleração de um ponto material póde sêr representada por duas componentes: aceleração centrípeta ,relacionada com a variação da orientação do vetor velocidade e aceleração tangencial t, relacionada com a variação do módulo do vetor velocidade .
Página noventa e três
Na segunda lei de níltom, tem-se quê um ponto material de massa m, quando submetido à ação de uma fôrça resultante adqüire uma aceleração com mesma direção e sentido de .
Em trajetórias curvas, como a representada na Figura 1, é possível demonstrar a fôrça resultante quê age no ponto material de massa m por duas componentes:
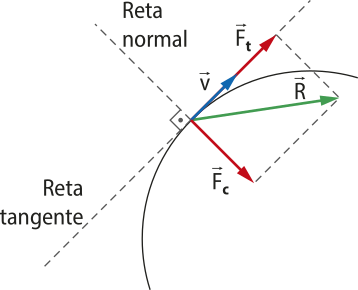
• A fôrça resultante centrípeta causa a variação da orientação do vetor velocidade orientada para o centro da trajetória.
⇒
• A fôrça resultante tangencial causa a variação do módulo do vetor velocidade tangencial à trajetória.
⇒ ⇒
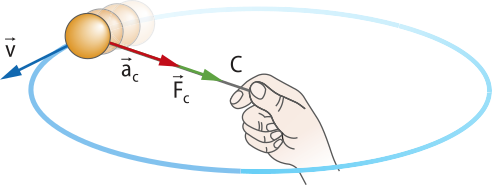
No exemplo da esféra presa a um fio, pode-se dizêr quê ela descreve um movimento circular uniforme porque o fio aplica sobre ela uma fôrça resultante dirigida para o centro da trajetória. Caso essa fôrça deixe de agir, o movimento da esféra será, por inércia, retilíneo e uniforme.
SAIBA +
Força centrípeta ou fôrça centrífuga?
Um motorista dirige seu carro em uma estrada. Ao fazer uma curva, ele tem a sensação de estar sêndo “empurrado para fora” da curva. Mas sabe-se quê a fôrça centrípeta é orientada para o centro da curva.
Quando o veículo faz uma curva, ele possui uma aceleração centrípeta, logo o veículo é um referencial não inercial (referencial acelerado). O motorista sente esta “força” puxando-o para fora da curva, chamada fôrça centrífuga. Esta fôrça não é explicada pelas leis de níltom, quê são válidas apenas para referenciais inerciais.
Um observador parado à beira da estrada é um referencial inercial e, neste caso, as leis de níltom são válidas. Devido à inércia, em cada ponto da curva, o motorista resiste à variação de velocidade e tende a manter um movimento retilíneo uniforme, sêndo assim “empurrado” para fora da curva, enquanto o veículo age sobre ele fazendo uma fôrça resultante centrípeta, para o centro da curva.
ATIVIDADES
1. De acôr-do com o quê foi apresentado, pode-se afirmar quê a fôrça centrífuga existe? Justifique sua resposta.
2. No dia a dia, em quê situação é comum utilizar a palavra centrífuga? Analisando a situação citada em relação a um referencial inercial, pense em outra palavra quê poderia sêr utilizada.
Página noventa e quatro
ATIVIDADES
25. Indique as sentenças a seguir com V (verdadeiro) ou F (falso).
I. Um automóvel faz uma curva em uma estrada plana e horizontal; no caso, a fôrça centrípeta é a fôrça tangencial quê a pista aplica sobre os p-neus.
F
II. Os satélites giram em torno dos planêtas em função da ação da fôrça centrípeta, quê, nessa situação, é a fôrça de atração gravitacional.
V
III. Um corpo gira, preso na extremidade de um fio; no caso, a fôrça centrípeta póde sêr considerada a própria fôrça de tração no fio.
V
26. Um ciclista se desloca com movimento uniforme em uma pista circular, plana e horizontal, conforme a figura representada.
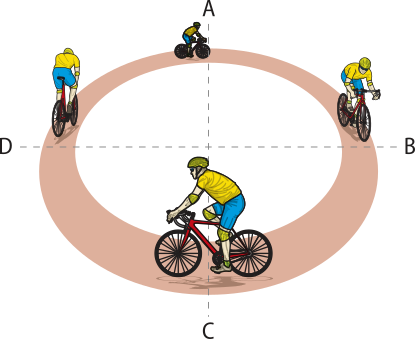
a) Represente, em um esquema no caderno, o vetor velocidade nas posições A, B, C e D ocupadas pelo ciclista.
b) Verifique se a direção e o módulo do vetor velocidade varíam de uma posição a outra.
c) Utilize o esquema do item a e represente a aceleração e a fôrça centrípetas nas posições A, B, C e D ocupadas pelo ciclista.
27. por quê a Lua não colide com a Terra? Pense, discuta com os côlégas e depois escrêeva, no caderno, suas conclusões.
28. Analise as condições de um satélite artificial quê descreve órbita circular ao redor da Terra. Qual é a fôrça centrípeta e qual é a sua função?
Movimento circular nos planos horizontal e vertical
Analise algumas situações em quê os movimentos circulares ocorrem no plano horizontal e no plano vertical.
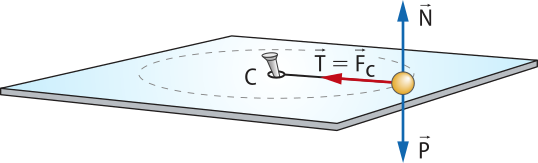
Considere quê uma esféra presa a um fio executa um movimento circular uniforme sobre o plano horizontal de uma mesa, desconsiderando atritos e resistência do ar.
Como o movimento da esféra ocorre em um plano horizontal, as fôrças verticais se anulam. Nesse caso, a fôrça peso tem a mesma intensidade da força normal: P = N.
A fôrça de tração no fio representa a resultante centrípeta quê age na esféra:
Em um movimento circular uniforme, a componente tangencial da fôrça resultante é nula, e o movimento tem as seguintes características:
• é constante e diferente de zero ( = 0);
• = é tangente à trajetória e tem orientação variável (;
• fôrça resultante: .
Fc = mac = m

Página noventa e cinco
ATIVIDADE RESOLVIDA
5. Uma pista plana, horizontal e circular de raio R é percorrida por um carro de massa m, com movimento uniforme, conforme representado na figura. Sabe-se quê o coeficiente de atrito estático entre os p-neus e a pista é μe.
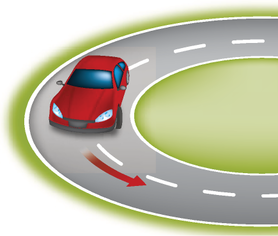
Com base nessas informações e no esquema, determine:
a) as forças quê agem no carro;
b) a fôrça resultante quê age no carro;
c) a velocidade mássima com a qual o carro póde percorrer a pista sem derrapar.
Dados: μe = 0,60, g = 10 m/s2 e r = 150 m.
Resolução
a) Considerando quê o carro faz a curva sem inclinação, as forças peso, normal e de atrito agem sobre ele.
b) Como a fôrça resultante age na direção da reta paralela ao plano horizontal, a componente vertical da fôrça resultante é nula. Portanto, P = N. Nesse caso, a fôrça de atrito representa a resultante centrípeta quê age no carro.
c) Se a resultante centrípeta é , então:
Fc = Fat ≤ μmg ⇒ m ≤ μemg ⇒ v ≤
Caso o carro esteja na iminência d e derrapar, a intensidade mássima da fôrça de atrito estático Fat(máx) e a velocidade mássima (vmáx) serão:
vmáx =
vmáx = 30 m/s
ATIVIDADES
29. Sobre uma superfícíe plana e horizontal, uma esféra de massa m = 4,0 kg está presa à extremidade de um fio ideal e descreve um movimento circular e uniforme em torno de um ponto fixo, no qual está amarrada a outra extremidade do fio.
Se o atrito é desprezível, o fio méde 0,50 m e a velocidade angular da esféra é 2,0 rad/s, determine:
a) o módulo da velocidade da esféra;
1,0 m/s
b) o módulo da aceleração centrípeta;
2,0 m/s2
c) a intensidade da fôrça resultante quê age na esféra.
8,0 N
30. Uma esféra de 2,0 kg gira em um plano horizontal em torno de um ponto fixo, presa à extremidade de um fio de 3,0 m de comprimento, cuja resistência à ruptura é de 20 N. Qual é o módulo da velocidade angular quê fará romper o fio?
Aproximadamente 1,8 rad/s
31. Um piloto de automóvel vai percorrer uma pista circular de raio R = 50 m. O coeficiente de atrito estático entre os p-neus e a pista é μe = 0,80 e g = 10 m/s2. Antes de entrar na pista, ele fez alguns cálculos para determinar o valor da velocidade escalar mássima para o carro não derrapar. Se o movimento do carro for uniforme, qual será o valor dessa velocidade?
20 m/s
Página noventa e seis
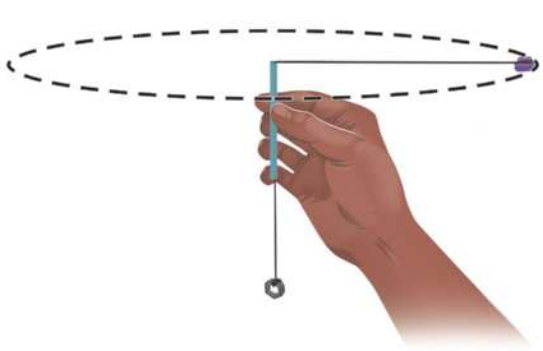
OFICINA CIENTÍFICA Força centrípeta
A fôrça resultante centrípeta age em corpos quê estão percorrendo uma curva em formato de circunferência. Esta fôrça resultante depende da velocidade escalar do corpo em movimento.
Nesta atividade prática, você investigará o quê ocorre quando a velocidade escalar de um corpo em movimento circular aumenta de valor.
Materiais
• pedaço de barbante com 50 cm de comprimento
• pedaço de canudo de 5 cm de comprimento
• pórca sextavada
• borracha escolar
Atenção: cuidado ao realizar o movimento descrito. Solicite ajuda de seu professor para realizar esse movimento.
Procedimentos
• Fixe a pórca sextavada em uma das extremidades do barbante.
• Passe a outra extremidade do barbante pelo canudo.
• Fixe a outra extremidade à borracha escolar.
• Segure a montagem pelo canudo na vertical, com a borracha acima da pórca sextavada, como representado na imagem e gire a borracha rapidamente. Tente estabilizar a velocidade de rotação da borracha d fórma quê ela execute um movimento circular uniforme.
• Faça variações no movimento, aumentando e diminuindo a velocidade de rotação, e verifique o quê ocorre.
ATIVIDADES
1. O quê ocorreu com a pórca sextavada quando a borracha foi colocada em movimento circular uniforme?
2. Qual alteração foi observada quando a borracha girou com maior velocidade escalar? E quando a borracha girou com menor velocidade escalar?
3. Faça em seu caderno um desenho da montagem experimental durante o movimento de giro realizado pela borracha. Represente as forças quê atuaram nesse sistema. Qual fôrça foi responsável pela resultante centrípeta sobre a borracha?
4. escrêeva, no caderno, uma relação matemática quê indique a velocidade escalar da borracha ao descrever um movimento circular uniforme.
5. Como se póde analisar essa situação com base na fôrça centrífuga?
Página noventa e sete
TEMA 9
As leis da Gravitação
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Breve história sobre os modelos de mundo
A busca por compreender o Universo não é recente. Há indícios de quê, em 4000 a.C., os habitantes da Mesopotâmia desenvolveram alguns esboços de calendários, com base nos movimentos dos astros, para atender às suas necessidades agrícolas.
Na Grécia antiga, vários filósofos buscaram explicações para os movimentos dos corpos celéstes. No modelo geocêntrico propôsto por Aristóteles, a Terra está em uma posição estacionária e central, enquanto os outros astros descrevem trajetórias circulares ao seu redor (geo, em grego, é Terra; logo, geocêntrico, centrado na Terra).
Por volta de 260 a.C., Aristarco de Samos apresentou uma teoria em quê o Sol ocupa a posição central do sistema, antecipando o modelo heliocêntrico (hélios, em grego, é Sol; logo, heliocêntrico, centrado no Sol) propôsto séculos depois por Copérnico, como estudado anteriormente.
Ptolomeu e a teoria geocêntrica
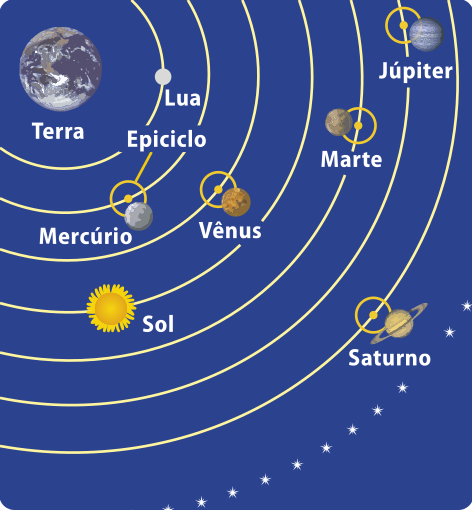
Aproximadamente 400 anos após Aristarco, Cláudio Ptolomeu aperfeiçoou o modelo geocêntrico de Aristóteles e descreveu o movimento dos astros celéstes na obra quê ficou conhecida pelo título Almagesto, quê significa “O grande”.
Segundo Ptolomeu, a Terra ocupa, em repouso, a posição central. O Sol e a Lua giram ao redor da Terra em órbitas circulares. Cada planêta gira em torno de um ponto, formando um epiciclo, e cada ponto gira em torno da Terra em órbitas (trajetórias) circulares. Mais além, as estrelas estão fixas em uma esféra de cristal quê também gira ao redor da Terra em órbita circular.
A utilização contínua das tabélas astronômicas do Almagesto pêlos grandes navegadores e os interesses religiosos fizeram com quê esse modelo se mantivesse por cerca de 1.500 anos.
Epiciclo: círculo cujo centro se desloca ao longo de outro, de diâmetro maior.
PENSE E RESPONDA

Sol observado no céu.
1 Você já observou estrelas durante o dia? Em caso negativo, faça uma pesquisa para descobrir por quê essa é uma tarefa difícil.
Página noventa e oito
Copérnico e a teoria heliocêntrica
Embora o modelo propôsto por Ptolomeu explicasse o movimento aparente dos corpos celéstes, é importante lembrar quê as observações dêêsse período eram feitas a olho nu, ou seja, sem o auxílio de instrumentos.
Copérnico expôs em seu livro Sobre as revoluções das órbitas celéstes a teoria heliocêntrica, na qual o Sol repousa na posição central do sistema e os planêtas giram ao seu redor em órbitas circulares.
O sistema propôsto por Copérnico simplificava o movimento dos outros planêtas, eliminando os epiciclos, e introduzia um movimento para a Terra, contrariando o quê se acreditava à época.
Mais tarde, essa teoria recebeu outras contribuições e foi aperfeiçoada, principalmente com os estudos de Galileu, Tycho Brahe e Képler.
ATIVIDADE RESOLVIDA
1. Após ter estudado as teorias geocêntrica (proposta por Ptolomeu) e heliocêntrica (proposta por Copérnico), um estudante chegou à conclusão de quê o sistema propôsto por Ptolomeu deveria sêr desprezado, basicamente porque nele o Sol gira ao redor da Terra, quê se encontra parada. Do ponto de vista da Física, é correta a conclusão do estudante?
Resolução
Não, porque as duas descrições são fisicamente possíveis, usando diferentes referenciais. No caso do modelo geocêntrico, se o referencial usado for a Terra e o observador estiver em repouso em relação a ela, então, para ele, o Sol estará em movimento e a Terra, parada. No modelo heliocêntrico, se o referencial usado for o Sol e o observador estiver parado em relação a ele, então, para esse observador, a Terra estará em movimento.
ATIVIDADES
1. Que razões justificaram a aceitação, na época, do modelo de Ptolomeu?
2. Quais são os fatores quê contribuíram para quê o modelo copernicano fosse considerado mais adequado do quê o modelo ptolomaico?
3. O sistema propôsto por Ptolomeu ficou limitado a quais planêtas? Por quê?
4. Você considera sêr correto o procedimento de alguns navegadores dos dias atuáis quê se orientam pelo movimento das estrelas, d fórma semelhante aos navegadores antigos, quê acreditavam quê a Terra permanecia em repouso no centro do Universo? Converse com um colega a respeito.
Página noventa e nove
SAIBA +
Galileu e o modelo heliocêntrico

TRIAL OF GALILEO [Julgamento de Galileu]. 1633. Óleo sobre tela.
Opositores à ideia do sistema heliocêntrico justificavam a sua posição alegando quê o modelo não era capaz de explicar determinados fenômenos. Por exemplo, se a Terra de fato girasse em torno de seu eixo de rotação, deveria provocar a expulsão dos corpos ou ventos fortíssimos em sua superfícíe. Apenas no século XVII é quê foram desenvolvidos os conhecimentos teóricos necessários para fundamentar a teoria heliocêntrica.
Embora Galileu tenha contribuído, com seus estudos, para a aceitação do sistema heliocêntrico, suas concepções representavam, ainda, etapas intermediárias entre as ideias antigas de Aristóteles e as bases da teoria quê níltom formularia anos mais tarde.
No livro Diálogo sobre os dois principais sistemas do mundo, de 1632, Galileu buscou explicar o motivo pelo qual o movimento de rotação da Terra não causa os ventos fortes ou a expulsão dos corpos da superfícíe. Nesse texto, ele ainda discutiu o quê hoje é conhecido como o princípio da Relatividade e a sua teoria sobre as marés.
Galileu sabia, por exemplo, quê, por causa da inércia, os corpos tendem a se manter em movimento. Assim, argumentou quê a atmosféra do planêta deveria girar junto com ele, evitando os ventos previstos pêlos opositores do movimento da Terra. Ele tinha certa noção sobre a atração dos corpos pela Terra, porém, qualitativamente, a sua visão era equivocada, pois, para ele, a gravidade seria constante e independente da massa do corpo.
Embora parte do livro seja dedicada a construir argumentos quê justifiquem o movimento da Terra, meréce destaque o quê Galileu afirma a respeito dos efeitos do movimento de um sistema: de quê eles não são perceptíveis quando os experimentos são realizados dentro do próprio sistema; afirmação essa quê se relaciona ao quê veio a sêr o princípio da Relatividade.
Na parte final da obra, Galileu argumenta sobre o fenômeno das marés, quê, segundo ele, é fundamental para fortalecer o sistema heliocêntrico. Para ele, esse fenômeno não se explicaria caso a Terra estivesse em repouso; portanto, o fenômeno das marés decorre do movimento da Terra.
Os estudos de Galileu sobre a Astronomia também geraram argumentos para corroborar o sistema heliocêntrico. No livro Mensageiro das estrelas, lançado antes do Diálogo, em 1610, ele descreve descobertas feitas com uma luneta quê contrariavam algumas das bases do modelo geocêntrico de Aristóteles. Por exemplo, mostrou quê a Lua não é uma esféra lisa e perfeita, mas possui crateras, e quê havia corpos quê giravam em torno de outros quê não a Terra, como os satélites de Júpiter.
Os estudos e as conclusões de Galileu eram opostos ao paradigma vigente e vinham de encontro aos dogmas da Igreja. Isso se comprova pelo fato de ele ter sido condenado, ante o tribunal da Santa Inquisição, e obrigado a abdicar de suas concepções.
ATIVIDADES
1. Os opositores à teoria proposta por Copérnico tí-nhão motivo para não aceitá-la? Em caso afirmativo, cite pelo menos um fenômeno quê o modelo heliocêntrico não conseguia explicar à época.
2. Galileu buscou, em seu trabalho, formular explicações para o fenômeno das marés. Que motivo justifica essa preocupação?
3. Com os côlégas, organizem um grupo de estudo. Nesse tipo de trabalho, cada integrante fica responsável por pesquisar, selecionar, redigir e ilustrar uma parte dele. O tema deve sêr o momento histórico e político-religioso na época de Galileu e a interferência da Inquisição na produção de conhecimentos científicos. Apresentem para a classe o trabalho realizado.
Página cem
As leis de Képler
Tycho Brahe realizou, a olho nu, observações meticulosas sobre os movimentos planetários. Após sua morte, seu assistente, Johannes Képler, continuou seus estudos. Képler estudou o movimento do planêta Marte por quase dez anos, seguindo sua trajetória pelo céu e tentando descrever para ele uma órbita em torno do Sol. Posteriormente, Képler refez diversos cálculos propostos por Brahe e conseguiu estabelecer três leis (as leis de Képler) quê regem o movimento dos planêtas em torno do Sol.
No Sistema Solar, as leis de Képler são válidas para um referencial fixo em relação ao Sol. Elas contribuíram para o modelo heliocêntrico sêr aceito pela comunidade científica da época, pois resolveram algumas incompatibilidades dos movimentos planetários quando interpretados pela teoria geocêntrica.
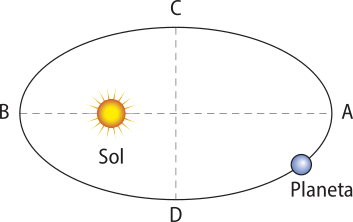
Lei das órbitas (1ª lei de Kepler)
A 1ª lei do movimento planetário de Képler refere-se à forma elíptica da trajetória descrita por um planêta em torno do Sol.
Cada planêta movimenta-se ao redor do Sol descrevendo uma órbita elíptica, com o Sol posicionado em um dos focos da elipse.
Embora as órbitas elípticas tênham sido desenhadas, propositadamente, com excentricidades bem acentuadas, na realidade elas se aproximam da forma circular.
A excentricidade e de uma elipse caracteriza seu grau de “achatamento” e póde sêr ôbitída por:
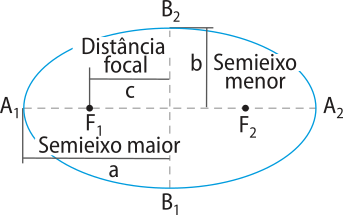
e =
Quanto maior a excentricidade, mais “achatada” é a elipse. Quando uma elipse apresenta excentricidade nula, seus focos são coincidentes e ela é a própria circunferência.
Lei das áreas (2ª lei de Kepler)
A 2ª lei do movimento planetário de Képler estabelece relações entre a velocidade orbital do planêta e o ponto de sua órbita.
O segmento de reta imaginário quê liga o Sol a determinado planêta descreve áreas iguais em intervalos de tempo iguais.
PENSE E RESPONDA

2 Considerando quê o Sol ocupa um dos focos da trajetória elíptica descrita pela Terra, por quê, à medida quê se aproxima ou se afasta dele, não se observa uma variação no seu tamãnho?
Página cento e um
Para uma área descrita A em um intervalo de tempo (delta)"t, algebricamente, tem-se:
= constante
ou seja:
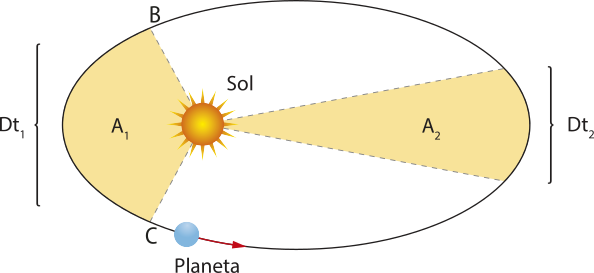
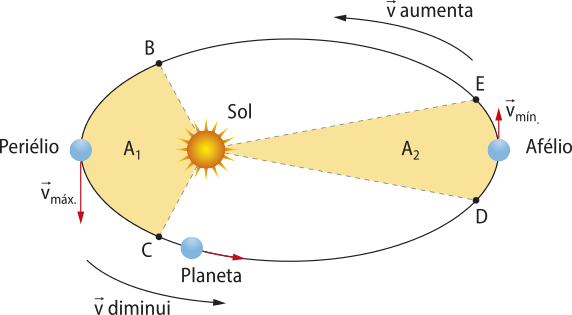
Assim, pode-se concluir quê a velocidade de translação do planêta ao redor do Sol sofre variação, ou seja, aumenta à medida quê se aproxima do periélio (ponto mais próximo do Sol) e diminui à medida quê se aproxima do afélio (ponto mais afastado do Sol). Se a área A1 é igual à área A2, os intervalos de tempo para cumprir os arcos e também serão iguais.
Como o comprimento do arco é maior do quê o comprimento do arco , a velocidade do planêta será maior no trecho do quê no trecho .
Lei dos períodos (3ª lei de Kepler)
A 3ª lei do movimento de Képler relaciona o período de revolução de um planêta, tempo necessário para esse planêta descrever uma volta completa ao redor do Sol, e a distância média R, em relação ao semieixo maior da elipse, do planêta ao centro da elipse.
Para os planêtas quê orbitam o Sol, o quociente entre o quadrado do período (T2)
e o cubo do raio médio da órbita (R3) é sempre constante.
= k (constante)
Nessa equação, é possível perceber quê, quanto maior o valor de R, maior será o período T, ou seja, maior será o tempo quê o planêta levará para dar uma volta em torno do Sol.
Página cento e dois
ATIVIDADES
5. O quê Johannes Képler identificou a respeito da distância dos planêtas em relação ao Sol?
6. Observando a 2ª lei de Képler, os planêtas possuem maior velocidade no periélio ou no afélio? Justifique sua resposta.
7. Considere quê o período de revolução da Lua em torno da Terra é de 27 dias e quê o raio de sua órbita valha 60R, sêndo R o raio da Terra. Um satélite geoestacionário, de telecomunicações, órbita a Terra. Em relação ao satélite, responda ao quê se pede.
a) Qual é o período de revolução?
24 h
b) Qual é o raio de órbita?
6,7R
8. O esquema, a seguir, representa a trajetória elíptica de um planêta ao redor do Sol. Determine e justifique em qual dos pontos, A, B, C ou D, a velocidade dêêsse planêta é mássima e em qual é mínima.
9. O raio médio da órbita de Saturno em torno do Sol é cerca de 9,6 vezes maior do quê o raio médio da órbita da Terra. Determine, em anos terrestres, o período de revolução de Saturno.
Aproximadamente 29,7 anos terrestres.
Lei da Gravitação universal
Em sua obra Philosophiae naturalis principia mathematica, publicada em 1687, níltom apresentou a lei da Gravitação universal. Para estabelecer essa lei, ele buscou entender o movimento da Lua com base nos princípios fundamentais da Dinâmica. Pesquisou também o movimento dos planêtas, fundamentado nas leis de Képler, e chegou às seguintes conclusões:
• Dois corpos materiais quaisquer exercem uma fôrça de atração mútua, denominada fôrça gravitacional.
• A intensidade da fôrça gravitacional é diretamente proporcional às massas dêêsses corpos e inversamente proporcional ao quadrado da distância entre eles.
A representação matemática da lei da Gravitação universal é:
Fg =
A constante de proporcionalidade G é denominada constante de gravitação universal. No SI, seu valor é:
G = 6,67 ⋅ 10−11 Nm2/kg2
PENSE E RESPONDA

3 O quê mantém a Lua orbitando ao redor da Terra? por quê a Terra atrai os corpos próximos à sua superfícíe?
Página cento e três
SAIBA +
O fenômeno das marés
Na abertura desta Unidade foi apresentado o fenômeno das marés. êste fenômeno é causado principalmente pela atração gravitacional entre Terra e Lua.
De acôr-do com a leis da Gravitação universal de níltom, a fôrça da gravidade é proporcional às massas dos corpos e inversamente proporcional à distância entre eles. Devido às dimensões da Terra, a parte voltada para a Lua, mais próxima dela, recebe ação de uma fôrça da gravidade mais intensa do quê a parte da Terra oposta à Lua, mais distante dela.
Para compreender esse fenômeno, analise as imagens. Nelas, uma esféra de argila (Figura 1) recebe forças de mesma intensidade (imagem à esquerda) e forças de intensidades distintas (imagem à direita). Nesta última situação, ocorre uma deformação na esféra.
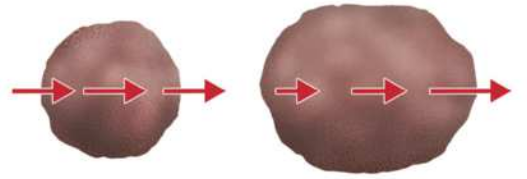
Elaborado com base em: HEWITT, poou. Física conceitual. 12. ed. Porto Alegre: búkmã, 2015. p. 168.
Essa deformação da argila póde sêr comparada ao quê acontece com a Terra devido à atração gravitacional (Figura 2). Essa diferença de forças de atração age como se tentasse “alongar” o planêta, efeito percebido nas águas dos oceanos, quê aumentam os níveis em lados opostos da Terra, enquanto abaixam os níveis nas outras regiões.
Devido ao movimento relativo entre a Terra e a Lua, existem duas marés altas e duas marés baixas ao longo de um mesmo dia, mas elas não ocorrem sempre no mesmo horário.

ATIVIDADES
1. por quê a Lua, mesmo sêndo muito menor do quê o Sol, é a principal responsável pelo fenômeno das marés?
2. Qual é o intervalo de tempo, aproximadamente, entre uma maré alta e uma maré baixa?
ATIVIDADES
10. níltom explicou quê a Lua “cai em volta” da Terra devido à sua velocidade tangencial. Pensando nesse fenômeno, se a velocidade tangencial da Lua fosse reduzida a zero, qual seria o destino dêêsse satélite natural?
11. De acôr-do com a lei da Gravitação universal, o quê ocorre com a fôrça gravitacional quando a distância entre os corpos é duplicada?
12. Determine a fôrça de atração gravitacional entre:
a) duas pessoas, A e B, de massas 80 kg e 70 kg, quê distam 2 m entre si.
8,4 ⋅ 10−8 N
b) a Terra (MT = 6 ⋅ 1024 kg e R = 6 ⋅ 106 m) e uma pessoa de 80 kg na superfícíe da Terra. Dado: G = 6 ⋅ 10 −11 Nm2/kg2.
800 N
Página cento e quatro
OFICINA CIENTÍFICA Simulando as fases da Lua
Além do encantamento muitas vezes poético quê as fases da Lua proporcionam, elas influenciam as marés, quê mudam conforme a posição da Lua e do Sol em relação à Terra.
Essa posição relativa póde sêr verificada pelas fases da Lua. Mas por quê em cada fase da Lua são observados formatos diferentes? Esta atividade irá ajudar nesta compreensão. Para isso, organize-se em um grupo de cinco integrantes.
Materiais
• 2 mesas (pode sêr a utilizada em sala de aula)
• 1 lanterna
• 4 cadeiras
• 1 copo de vidro
• uma bola branca (15 cm)
• alguns livros
Atenção ao manusearem o copo, evitando quêbrá-lo, o que póde causar acidentes.
Procedimentos
Para a montagem do aparato indicada nos próximos itens, solicitem a ajuda do professor.
• Deixem a bola apoiada sobre o copo, em uma das mesas, no centro da sala.
• Apoiem a lanterna sobre os livros em outra mesa, como mostra a Figura 1.

• Quatro estudantes deverão se voluntariar para participar da montagem. O quinto estudante deverá auxiliar na organização, no desenvolvimento e na etapa final, proposta na atividade 3. Nessa montagem, a lanterna, a bola e os estudantes representam, respectivamente, o Sol, a Lua e os observadores na Terra.
• ob-sérvim a localização dos objetos na Figura 2. Os estudantes devem ficar sentados em uma posição quê permita manter os olhos à mesma altura da bola, a cerca de 1 métro dela.

• Cada estudante posicionado ao redor da mesa deverá escrever e desenhar o quê está observando, indicando as posições do Sol (lanterna), da Lua (bola) e da Terra (cada observador). Troquem informações sobre as imagens representadas.
Agora, cada estudante deve trocar de posição no sentido horário, colocando-se na cadeira adjacente, realizando uma rotação (Figura 3). Façam esse movimento até chegar à posição inicial. Após cada troca, desenhem e escrevam o quê observam e registrem as posições dos elemêntos.
Se necessário, façam ajustes para modificar a altura da bola e a da lanterna com outros objetos disponíveis na sala. Solicitem a intervenção do professor em caso de divergências.

Página cento e cinco
ATIVIDADES
1. Com a rotação realizada na atividade, e com base em seus dêzê-nhôs e anotações, qual é a explicação para a mudança na aparência da Lua?
2. Existe uma limitação nesse modelo construído. Discuta com seus côlégas de grupo essa limitação, com base no desenho do sistema Sol-Terra-Lua como você conhece.
3. Verifiquem a possibilidade de filmar essa investigação, construindo um documentário das fases da Lua, com o quinto estudante atuando como um narrador. Procurem ferramentas para editar a filmagem (caso seja necessário), ajustando o vídeo com um tempo confortável para sêr compartilhado nas rêdes sociais da escola, de modo quê outras pessoas possam acessar essas explicações. Nesse vídeo, discutam brevemente as limitações do modelo levantadas na atividade anterior.
Campo gravitacional
Com o objetivo de compreender as forças de interação a distância, uma das teorias se baseia no conceito de campo gravitacional.
A ideia de campo de fôrça gravitacional parte do seguinte princípio: todo corpo de massa M origina no espaço ao seu redor um campo de fôrça, quê interage com o campo gerado por outro corpo de massa m por uma fôrça de atração gravitacional.
Se for feita uma análise da Terra, tem-se no espaço à sua volta o campo gravitacional terrestre (Figura 1). Para cada ponto dêêsse campo é possível associar um vetor (vetor campo gravitacional), cuja direção é radial e cujo sentido é para o centro da Terra.
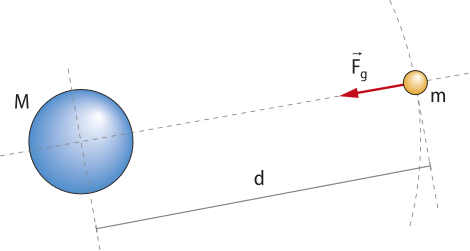
Na Figura 2, note quê no ponto onde está o corpo de massa m existe um campo gravitacional gerado por M, verificado devido à ação da fôrça com intensidade g = . A mesma análise poderia sêr feita para se definir o campo de m, sentido por M, porém apenas campos gravitacionais gerados por corpos de muita massa possuem valores consideráveis.
Intensidade do campo gravitacional
No esquema a seguir, tem-se a representação da Terra, de massa M, e uma partícula de massa m a uma distância h da superfícíe da Terra.
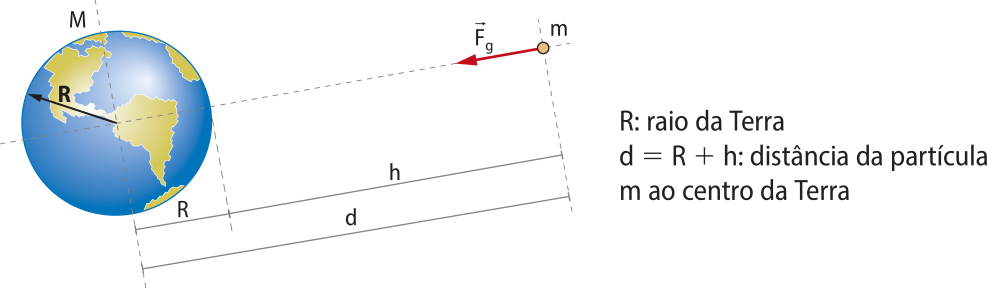
d = R + h: distância da partícula m ao centro da Terra
Página cento e seis
Se for desconsiderado o movimento de rotação da Terra e desprezada a ação do Sol e de outros corpos celéstes, tem-se Fg = P = mg (a fôrça de atração gravitacional é o próprio peso do corpo):
mg = ⇒ g =
Desprezado o movimento de rotação da Terra, pode-se considerar, para os pontos muito próximos da superfícíe, quê o campo gravitacional tem valor constante g0 dado por:
g0 =
A forma não homogênea da Terra e o movimento de rotação terrestre influenciam no campo gravitacional da superfícíe de modo quê, à mesma longitude, seu valor é mínimo no equador (latitude 0°) e mássimo nos polos (latitude 90°).
ATIVIDADE RESOLVIDA
2. Considere quê a Terra seja um corpo esférico e homogêneo (densidade constante em todos os seus pontos), com raio R = 6,37 ⋅ 106 m e massa M = 5,98 ⋅ 1024 kg. Diante dessas condições, desprezando os efeitos da rotação da Terra e com G = 6,67 ⋅ 10-11 Nm2/kg2, determine:
a) a aceleração da gravidade em um ponto P localizado nas proximidades da superfícíe terrestre;
b) a aceleração da gravidade em um ponto P localizado a 120 km da superfícíe terrestre.
Resolução
a) Se o ponto P está na proximidade da superfícíe terrestre, h = 0.
g0 =
g0= 6,67 ⋅ 10−11 ⋅
g0 = ⋅ 10−11 ⋅ 1024 ⋅ 10−12
g0 = 9,83 m/s2
b) Se o ponto P está a 120 km da superfícíe terrestre, então:
h = 120 km = 0,12 ⋅ 106 m
g = ⇒
⇒ g = 6,67 ⋅ 10−11 ⋅ ⇒
⇒ g = 9,47 m/s²
ATIVIDADES
13. O quê é um campo gravitacional e como ele é percebido?
14. O campo gravitacional é maior no equador ou nos polos? Se a Terra não girasse mais em torno de seu eixo, o campo gravitacional aumentaria ou diminuiria?
15. Determine a aceleração da gravidade próxima à superfícíe lunar. Considere a Lua como uma esféra homogênea de raio R = 1,74? 106 m e massa M = 7,3? 1022 kg.
Dado: G = 6,67 ⋅ 10−11 Nm2/kg2.
1,61 m/s2
16. A quê distância h da superfícíe da Terra a aceleração da gravidade vale um terço do valor quê ela tem próximo da superfícíe terrestre? Considere o raio da Terra 6.400 km, despreze os efeitos da rotação e admita quê ela é um corpo homogêneo e esférico.
4.685 km
Página cento e sete
Corpos em órbitas circulares
As atividades realizadas pêlos sêres humanos na atualidade estão diréta ou indiretamente ligadas aos satélites artificiais. Considere, por exemplo, o ato de ligar uma televisão, receber notícias sobre as condições climáticas, acessar a internet etc.
O lançamento dos satélites em órbita ao redor da Terra é uma conkista recente, mas o fundamento teórico de seu movimento já havia sido estudado por níltom.
No esquema a seguir, há dois corpos, de massa M e m, com M muito maior do quê m.
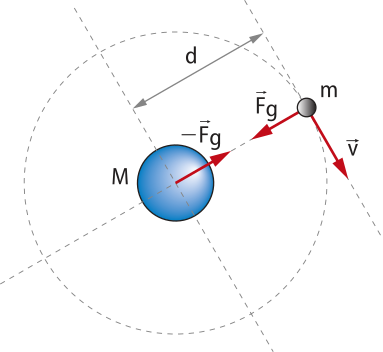
O corpo m gira em órbita circular ao redor do corpo M e a fôrça de interação é a fôrça da gravidade Fg e −Fg. Sendo Fg uma fôrça centrípeta, pode-se determinar sua intensidade partindo da lei da Gravitação universal.
Fc = Fg = ⇒ ⇒
⇒ v2 = ⇒ v =
Analisando a relação matemática ôbitída, percebe-se quê a velocidade do corpo quê está em órbita circular não depende de sua massa m, e sim da massa M e do raio da órbita d.
Comentar sobre os corpos em órbita em torno da Terra faz lembrar das imagens de astronautas “flutuando” dentro de naves espaciais. O quê acontece no caso do astronauta, por exemplo, é quê ele, a nave e os objetos em seu interior “caem” em órbita em torno da Terra. Para colocar o corpo em órbita, é preciso calcular a velocidade tangencial correta para determinada altura. Nesse caso, a fôrça da gravidade age como resultante centrípeta e varia somente a orientação da velocidade de tal forma quê a nave executa um movimento circular uniforme.
PENSE E RESPONDA

4 Como você imagina a vida da maioria da humanidade sem o uso dos satélites artificiais?
ESPAÇOS DE APRENDIZAGEM
• O filme Estrelas além do tempo discute os desafios enfrentados por três mulheres negras: Katherine Johnson, Dorothy Vaughan e Méry jécsson, quê trabalharam na Nasa durante os anos de 1950 a 1960, com o objetivo de auxiliar no programa Apolo, cuja missão era levar e trazer com segurança, sêres humanos à Lua.

ESTRELAS além do tempo. Direção: teodór Melfi. Estados Unidos: 20th Cêntury Fox, 2016. Streaming (127 min). Cartaz do filme.
Página cento e oito
Velocidade de escape
Para quê um corpo lançado escape da Terra, é preciso quê ele tenha uma velocidade mínima para quê se livre da atração gravitacional. Esse valor é chamado velocidade de escape (ve).
A velocidade de escape de um astro celeste póde sêr determinada utilizando o princípio da conservação da energia mecânica, assunto quê será estudado adiante.
A imagem a seguir representa o corpo no momento de lançamento (inicial) e em um momento em quê ele já não possui mais nenhuma energia (final), representado por infinito.
![Representação da velocidade de escape. Um corpo 'm', está encostado em um corpo 'M' de centro 'c' e distância 'd'. Do corpo 'm' sai uma seta 'v e' perpendicular horizontal para a direita, em outro momento o corpo 'm' está se deslocando para a direita e no momento final, corpo 'm', 'v' igual a zero[infinito].](../resources/images/ek_9/ek_9b59bc561db5f80870f61afae7173165.png)
Na situação inicial de lançamento, a energia mecânica é dada pela energia cinética, devido à velocidade de lançamento, e pela energia potencial gravitacional, devido à atração gravitacional da Terra.
Energia cinética
Ec =
Energia potencial
Ep =
Energia mecânica inicial
=
Em um ponto denominado como infinito, o corpo atinge o repouso e sua energia cinética é nula. Ele não retorna, pois está livre da atração gravitacional, logo, sua energia potencial gravitacional também é nula. Assim, sua energia mecânica final é nula: Em = 0.
Pela conservação da energia mecânica, tem-se:
= Em
= 0 ⇒ = ⇒ ve =
Note quê, pela expressão ôbitída, o valor da velocidade de escape não depende da massa do corpo a sêr lançado, mas apenas da massa M do astro quê se pretende escapar.
ATIVIDADES
17. O projeto para lançar um satélite, destinado ao serviço de telecomunicações, prevê a sua permanência em órbita circular ao redor da Terra e a altura H da sua superfícíe. Nesse caso, sêndo G a constante de gravitação universal e R e M, respectivamente, o raio e a massa da Terra, determine a velocidade orbital e o período do movimento do satélite.
18. Um satélite permanéce em uma órbita circular ao redor da Terra e a uma altura H = 3.622 km da sua superfícíe. Considere, em valores aproximados, quê a constante de gravitação universal é G = 6,0 ⋅ 10−11 Nm2/kg2 e o raio e a massa da Terra, respectivamente, R = 6.378 km e M = 6 ⋅ 1024 kg. Calcule:
a) a velocidade do satélite;
v = 6 ⋅ 103 m/s
b) o tempo, em segundo, necessário para o satélite completar uma volta em sua órbita. (Considere (pi)" = 3.);
t ≃ 104s
Página cento e nove
TEMA 10
Energia e trabalho
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
O conceito de energia
A palavra energia é utilizada em diversos contextos no cotidiano, sêndo especialmente relacionada a atividades diárias. Porém, em Física, a energia é analisada de diversas formas, sem, contudo, possuir uma definição exata. Quando se estuda o ambiente, diz-se quê ele é compôzto de matéria e energia, ou seja, a energia é considerada um componente abiótico do ambiente (sem vida).
A energia está presente no ambiente de diversas formas, como no movimento das águas de um rio, nos raios solares, em uma pessoa praticando rapel a certa altura, em uma bola de basquete lançada na cesta, em um veículo em movimento etc. Em todos esses casos, existe energia sêndo transformada de uma forma em outra.


Para se obtêr uma forma de energia, é preciso partir de outra forma de energia, ou seja, a energia jamais é criada, apenas transformada. O corpo humano obtém energia dos alimentos para realizar suas funções e permitir quê as diversas atividades diárias sêjam realizadas. Já um ventilador elétrico precisa receber energia elétrica para transformá-la em energia de movimento de suas pás.
O consumo de energia pelo mundo está cada vez maior, exigindo mais recursos, como combustíveis de variadas fontes, alimentos e á gua. Como alternativa para essa alta demanda, são pesquisadas e incentivadas fontes rêno-váveis, quê são aquelas quê se restituem naturalmente, favorecendo a preservação do ambiente. Alguns exemplos de fontes de energia rêno-váveis são: a solar (do Sol), a eólica (dos ventos), a geotérmica (do calor proveniente do interior da Terra), e a maré motriz (do movimento do mar).
PENSE E RESPONDA

1 Os veículos elétricos estão cada vez mais comuns, e seus benefícios para o ambiente são amplamente conhecidos. Mas existe alguma situação desfavorável em sua utilização? Qual(is)?
Página cento e dez
O conceito de trabalho
Para medir a transformação ou a transferência de energia de um tipo para outro, define-se a grandeza física trabalho de uma fôrça, quê é representada pela letra grega τ (lê-se tau).
O físico inglês diêmes Prescott Joule (1818-1889) foi um dos pioneiros no estudo da relação entre trabalho e energia, por volta de 1847, utilizando um aparato, como o da representação a seguir. No estudo, um corpo de certa massa era elevado a certa altura e então abandonado, puxando, assim, uma kórda quê fazia algumas pás girarem rapidamente dentro da á gua, quê sofria um pequeno aquecimento.
Joule constatou uma equivalência entre a energia de movimento das pás e a energia térmica. Devido às suas contribuições, a unidade de medida de trabalho e energia no SI foi adotada como Jáule (J).
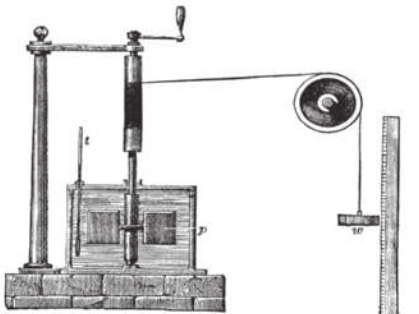
De NIL theory ÓF heat. Harper's niu Monthly Magazine, Nova iórk, v. 39, n. 231, p. 322-329, agosto 1869. p. 327.
SAIBA +
Lendo rótulos
Você costuma ler os rótulos dos produtos quê consome? Esta prática é indicada por profissionais da saúde, principalmente (mas não somente) para produtos industrializados, possibilitando compreender os componentes de um alimento para, assim, priorizar escôlhas nutricionalmente melhores, criando hábitos alimentares mais saudáveis.
O rótulo de um produto apresenta, entre outras informações, a lista de ingredientes utilizados, a data de validade (em alguns casos, também, a data de fabricação), orientações para o consumo, informações nutricionais, porção indicada ao consumo, percentual de valores diários (%VD) e tabéla nutricional.
![Representação de uma etiqueta com valor nutricional. Porção de 200 ml[um copo], valor energético igual a 127Kcal igual a 534kj.](../resources/images/ek_e/ek_ee755ad3042ad81bfa29e25597e44a84.png)
Na tabéla nutricional, constam informações dos nutrientes existentes no produto, como carboidratos, proteínas, açúcares, gorduras, fibras, sódio, por exemplo, além do valor energético, quê consiste na quantidade de energia a sêr transformada na digestão de determinada porção do produto. Esse valor é comumente expresso na unidade de medida caloria, ou quilocaloria (1 kcal = 1.000 cal), ou, ainda, em Jáule.
ATIVIDADES
1. O percentual de valores diários (%VD) indica a porcentagem de energia e de quantidade de nutrientes quê a porção indicada para consumo representa, de acôr-do com uma diéta padrão de 2.000 kcal diárias. Analisando o rótulo apresentado, quanto é o %VD dêêsse produto?
2. De acôr-do com os valores energéticos apresentados no rótulo, determine quantos joules equivalem a 1 cal.
3. Analise em outros rótulos os valores energéticos apresentados em quilocaloria e em Jáule e verifique se a mesma relação entre caloria e Jáule é ôbitída.
4. Em um grupo de até cinco integrantes, desenvolvam uma campanha de conscientização acerca da importânssia da leitura dos rótulos dos alimentos. Tragam as informações quê precisam sêr analisadas antes da escolha pela compra de um produto e apresentem brevemente o porquê. Compartilhem a campanha nas mídias sociais da escola para quê a comunidade não escolar também tenha acesso.
Página cento e onze
Trabalho de uma fôrça constante
Na figura a seguir, é aplicada uma fôrça constante F em um corpo quê se desloca da posição C a D, em uma trajetória horizontal e retilínea.
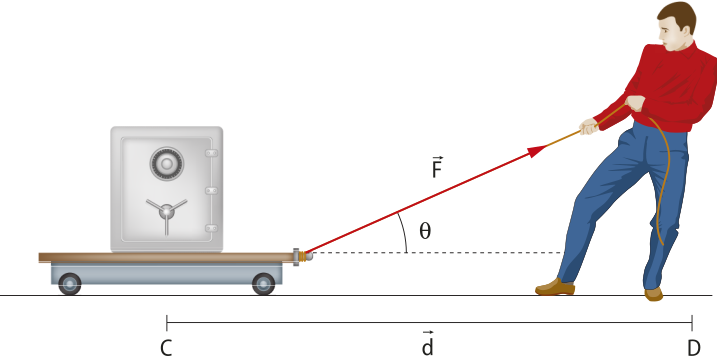
Sendo o deslocamento vetorial e Θ o ângulo formado entre os vetores e , define-se o trabalho τ da fôrça como:
τ = Fdcos Θ
O Jáule póde sêr definido como o trabalho realizado por uma fôrça constante de intensidade 1 nílton quê desloca seu ponto de aplicação de 1 métro na sua direção e sentido.
1 J = 1 N ⋅ m
Outra maneira de compreender a dependência do ângulo Θ na definição é quê somente a componente da fôrça na direção do movimento, designada aqui por realiza trabalho. Forças ou componentes de forças perpendiculares ao deslocamento não realizam trabalho.
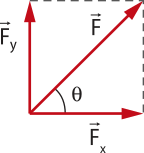
No gráfico do módulo constante da componente Fx (componente da fôrça F na direção do movimento) em função da posição s, calcular o trabalho da fôrça é equivalente a calcular a área do retângulo indicado, ou seja, no gráfico da fôrça pela posição, o trabalho da fôrça é numericamente igual à área delimitada pela curva e o eixo horizontal, em um deslocamento delimitado por duas posições.
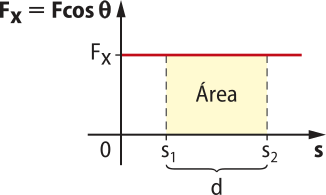
Área
PENSE E RESPONDA


2 Durante os instantes em quê as empilhadeiras permanecem em repouso, com suas cargas elevadas também em repouso, qual delas realiza o maior trabalho: a quê sustenta o contêiner (A) ou a quê sustenta os tambores vazios (B)?
Página cento e doze
Analisando o ângulo Θ, é possível fazer as considerações a seguir.
Trabalho motor
(0° ≤ Θ < 90°)
O trabalho da fôrça é positivo quando a fôrça age na direção quê favorece o movimento, ou seja, quando Θ é nulo ou agudo, recebendo o nome de trabalho motor.
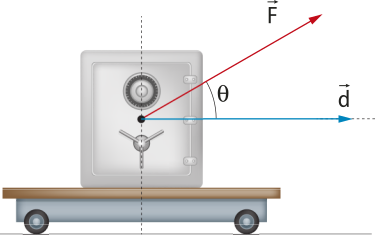
0° ≤ Θ < 90° ⇒
⇒ 0 < cos Θ < 1
τ ⇒ Fdcos Θ > 0
Trabalho resistente
(90°< Θ ≤ 180°)
O trabalho da fôrça é negativo quando a fôrça age na di re ção quê resiste ao movimento, ou seja, quando Θ é raso ou obtuso. Nesse caso, recebe o nome de trabalho resistente.
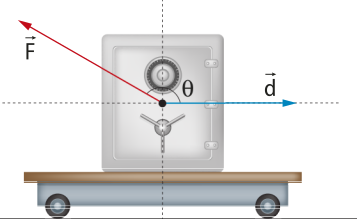
90°< Θ ≤ 180° ⇒
⇒ −1 < cos Θ < 0
τ = F d cos Θ < 0
Trabalho nulo
(Θ = 90°)
O trabalho da fôrça é nulo quando age na direção perpendicular à direção do vetor deslocamento, ou seja, quando Θ é um ângulo reto.
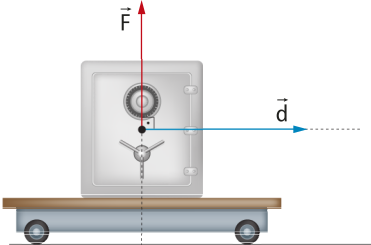
Θ = 90° ⇒ cos 90° = 0
τ = F d ⋅ 0 = 0
ATIVIDADES
1. Das figuras a seguir, identifique aquela em quê o trabalho realizado é maior (nas três situações, a fôrça aplicada vale 5 N).
Figura II
2. A expressão s = 15 + 5t + t2 (s medido em métro e t, em segundo) representa o deslocamento de uma caixa de 40 kg em uma trajetória plana e retilínea. Encontre o trabalho realizado pela fôrça resultante quê atua sobre a caixa durante um deslocamento de 30 m.
2.400 J
3. Um objeto maciço com formato de um paralelepípedo é arrastado num plano horizontal por uma fôrça constante de 10 N. Essa fôrça forma um ângulo de 55° com o deslocamento do corpo, quê é de 60 cm.
Dado: cos 55° = 0,57.
a) Esboce em seu caderno uma figura representando a situação.
b) Determine o trabalho da fôrça F. ⃗
≃ 3,4 J
4. O bloco da figura está sôbi a ação de quatro forças,
, , e , deslocando-se na direção horizontal por 2 m.
Dados: sen 60° = 0,85 e cos 60° = 0,5, F1 = 10 N, F2 = 20 N, F3 = 10 N e F4 = 20 N.
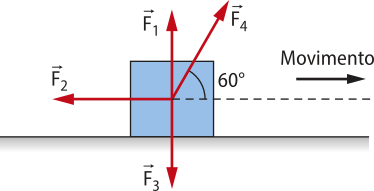
Calcule o trabalho realizado pela fôrça:
a)
Zero.
b)
−40 J
c)
Zero.
d)
20 J
e)
−20 J
Página cento e treze
Trabalho da fôrça peso
Imagine quê, próximo da superfícíe da Terra, na qual a aceleração da gravidade póde sêr considerada constante, um ponto material de massa m se desloca da posição C a D, conforme a figura representada. O vetor vertical para baixo representa a fôrça peso .
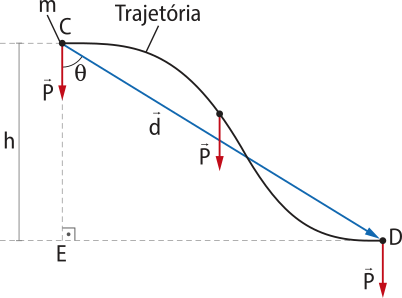
Nessas condições, a fôrça peso póde sêr considerada constante, e o seu trabalho é calculado pela relação:
τ = Pdcos θ
Do triângulo CDE, tem-se: cos θ = ⇒ h = d cos θ.
Substituindo na equação quê determina o trabalho da fôrça peso na descida do ponto material, tem-se:
τ = Ph ⇒ τ = mgh
Pela expressão, o trabalho da fôrça peso independe da trajetória percorrida pelo corpo, mas depende de h, quê representa o desnível entre as posições ocupadas pelo ponto material. Esta é uma propriedade das chamadas forças conservativas.
O trabalho da fôrça peso póde sêr positivo ou negativo, dependendo da direção e do sentido do movimento em relação à direção e ao sentido da fôrça peso. Caso o movimento e a fôrça peso tênham o mesmo sentido e direção (ambos vertical para baixo, nas proximidades da superfícíe da Terra, θ = 0° ⇒ cos 0° = 1), o trabalho da fôrça peso é positivo (τ = mgh). Se o movimento e a fôrça peso tiverem sentidos contrários (isso ocorre quando o movimento vertical é para cima e a fôrça peso vertical é para baixo, θ = 180° ⇒ cos 0° = −1), o trabalho da fôrça peso será negativo (τ = mgh). Em resumo, o sinal do trabalho depende da orientação do movimento (deslocamento), em relação à fôrça peso, ou seja:
• τ = −mgh; positivo, para movimento de descida (mesma direção e sentido do vetor fôrça peso).
• τ = mgh; negativo, para movimento de subida (mesma direção, mas sentido ôpôsto ao vetor fôrça peso).
• τ = 0; nulo, para deslocamentos entre posições de um mesmo plano horizontal (θ = 90° e cos 90° = 0), ou seja, o vetor fôrça peso é perpendicular ao deslocamento.
PENSE E RESPONDA
3 O trabalho da fôrça peso é maior quando a pessoa desce pela escada ou pelo elevador?
ATIVIDADE RESOLVIDA
1. Uma pessoa deseja mudar o armário de seu quarto de lugar, empurrando-o sobre um piso plano e horizontal, por uma distância em linha reta de 1,5 m. O armário tem massa m = 400 kg, a aceleração da gravidade local póde sêr considerada g = 10 m/s2, e qualquer influência do ar póde sêr desprezada. O coeficiente de atrito cinético entre o armário e o piso vale m = 0,3. A pessoa aplica uma fôrça horizontal de intensidade 1.500 N. Nessas condições, qual é o trabalho total realizado pela fôrça resultante sobre o armário?
Página cento e quatorze
Resolução
O trabalho total da fôrça resultante póde sêr obtído calculando o trabalho de todas as fôrças e somando-as ao final, ou determinando a intensidade da força resultante e obtendo o trabalho realizado.
• Considerando o trabalho realizado pelas fôrças: No armário atuam as forças peso, normal, atrito e a força .
Trabalho da fôrça :
τF = Fdcos θ = 1.500 ⋅ 1,5 ⋅ cos θ° =
= 1.500 ⋅ 1,5 ⋅ 1 ⇒ τF ⇒ 2.250 J.
Intensidade da fôrça peso:
P = mg = 400 ⋅ 10 ⇒ P = 4.000 N.
Trabalho da fôrça
τP = Pdcos θ = 4.000 ⋅ 1,5 ⋅ cos 90° =
= 4.000 ⋅ 1,5 ⋅ 0 ⇒ τP ⇒ 0.
Intensidade da fôrça normal: como se trata de um piso plano e horizontal, e o móvel está em equilíbrio vertical, tem-se:
N = P ⇒ N = 4.000 N.
Trabalho da fôrça normal :
τN = Ndcos θ = 4.000 ⋅ 1,5 ⋅ cos 90° =
= 4.000 ⋅ 1,5 ⋅ 0 ⇒ τF = 0.
Intensidade da fôrça de atrito cinético :
Fat = μN = 0,3 ⋅ 4.000 = 1.200 N
Trabalho da fôrça de atrito cinético : τfat =
= Fat dcos θ = 1.200 ⋅ 1,5 ⋅ cos 180° =
= 1.200 ⋅ 1,5 ⋅ (−1) ⇒ τFat ⇒ −1.800 J.
Trabalho total:
τ = τF + τP + τN + τFat =
=2.250 + 0 + 0 − 1.800 ⇒ τ = 450 J
• Considerando a fôrça resultante: Neste caso, a fôrça resultante tem a mesma direção e o mesmo sentido do movimento e vale:
R = F − Fat = 1.500 − 1.200 ⇒ R = 300 N.
τ = Rdcos θ = 300 ⋅ 1,5 ⋅ cos 0° = 300 ⋅ 1,5 ⋅ 1 ⇒
⇒ τ = 450 J.
ATIVIDADES
5. Qual é o trabalho realizado pela fôrça peso de um carro, de massa 2.000 kg, quê é levantado à altura de 4 m para sêr lavado?
Dado: g = 10 m/s2.
–80.000 J
6. Determine o trabalho realizado pela fôrça peso de um corpo, de massa 15 kg, quê é levantado verticalmente, com velocidade constante, do solo a uma altura de 5,0 m. Dado: g = 10 m/s2.
–750 J
7. Uma pequena esféra metálica de massa m = 1 kg está ligada à extremidade de um fio de comprimento 1,5 m. Calcule o trabalho realizado pelo peso da esféra no deslocamento de A para B. Dado: g = 10 m/s2.
7,5 J
8. Um objeto é lançado de baixo para cima, a partir da base de um plano inclinado de 10 m de comprimento quê forma um ângulo de 30° com a horizontal. O objeto, ao chegar ao topo, estaciona e, em seguida, retorna à base. Calcule o trabalho da fôrça peso do objeto subindo e descendo o plano.
Dados: massa do objeto é de 4 kg; g = 10 m/s2.
Subindo: −200 J; descendo: 200 J.
9. Um bloco de massa 10 kg é transferido de um ponto A para um ponto B, separados por 60 m na horizontal e 40 m na vertical a partir do ponto A. Determine o módulo do trabalho realizado pela fôrça peso.
Dado: g = 10 m/s2.
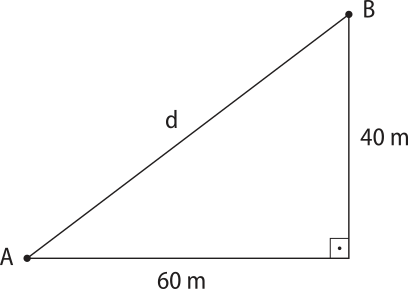
−4.000 J
Página cento e quinze
Trabalho de uma fôrça variável
Uma fôrça resultante quê atua em um corpo em movimento póde variar sua intensidade no decorrer do tempo, podendo aumentar de intensidade, diminuir e até inverter seu sentido. Nestes casos, para determinar o trabalho total realizado pela fôrça ao longo de cérto deslocamento, deve-se recorrer à propriedade do gráfico da fôrça em função da posição, no qual o trabalho é numericamente igual à área delimitada pela curva do gráfico e o eixo horizontal.
![Representação gráfica de uma força variável. Na imagem um gráfico, com eixo vertical 'Força resultante' e eixo horizontal 'Posição'. No gráfico quatro áreas distintas: área um forma um {triângulo}, área dois forma um [trapézio], área três forma um [triângulo] e área quatro forma um trângulo.](../resources/images/ek_d/ek_d8200529481b38ce494c1d038e8fb4f7.png)
A região delimitada pelo gráfico póde sêr particionada em regiões menóres, calculando assim as áreas individualmente. No caso de áreas posicionadas abaixo do eixo horizontal, como a região indicada por IV, o trabalho será negativo (resistente). O trabalho total corresponde à soma de todos os valores obtidos.
τtotal = τI + τII + τIII + τIV
Trabalho da fôrça elástica
A fôrça elástica exercida por molas e corpos elásticos é um exemplo de fôrça com intensidade variável, pois depende do valor da deformação sofrida pela mola, designada por x. Lembrando quê a intensidade da fôrça elástica é dada pela lei de rúki: Fel = −kx. O sinal negativo indica quê a fôrça da mola é restauradora, isto é, sempre age em sentido ôpôsto ao sentido da deformação, como representado nas imagens. Para se considerar apenas o módulo da fôrça elástica (desconsiderando o sentido), pode-se adotar Fel = .
Para determinar o trabalho da fôrça elástica, deve-se recorrer ao gráfico da fôrça elástica por deformação. A fôrça elástica é proporcional à deformação sofrida pela mola, sêndo a constante de proporção representada por k. Assim, o gráfico é linear.
Quando se define a posição de equilíbrio de uma mola como zero, sua deformação póde sêr positiva ou negativa, pois a mola póde sêr esticada ou comprimida. Considerando apenas o módulo da deformação, assim como apenas o módulo da fôrça elástica, tem-se o gráfico apresentado a seguir.
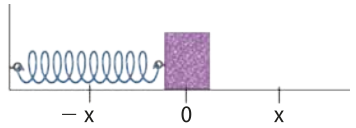
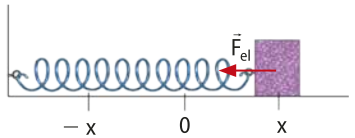
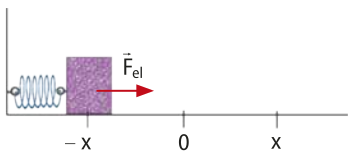
A área destacada é numericamente igual ao trabalho da fôrça elástica quê, neste exemplo, corresponde à área de um triângulo: = Área = ⇒ .
O trabalho da fôrça elástica póde sêr positivo ou negativo. Quando a extremidade da mola se móve comprimindo ou esticando a mola, isto é, quando ela se distancía do ponto de equilíbrio, o trabalho da fôrça elástica é negativo. Quando a extremidade da mola se móve retornando à posição de equilíbrio, o trabalho é positivo.
• = : quando a mola é alongada ou comprimida.
• = : quando a mola retorna à posição de equilíbrio.
![Representação gráfica. Eixo vertical 'F e l'[N] com uma marcação 'K x' e eixo horizontal 'x'[m] com uma marcação 'x' que formam a área em destaque.](../resources/images/ek_7/ek_7576bcfaf6f4dd2c0e0a85d4e3423b51.png)
Página cento e dezesseis
ATIVIDADES
10. Ao sofrer a ação de uma fôrça uma mo la apresenta uma deformação de 0,02 m, alongan do-se. Se a constante elástica dessa mola é 400 N/m, determine:
a) a intensidade da fôrça
8 N
b) o trabalho da fôrça para deformá-la.
0,08 J
11. Em um laboratório de Física, um estudante realiza o seguinte experimento: aplica uma fôrça de 2 N em uma mola e observa uma deformação correspondente a 10 cm. Se o estudante aplicar uma fôrça de 4 N:
a) qual será o comprimento, em centímetro, quê a mola irá deformar?
20 cm
b) qual será o trabalho realizado pela fôrça de 4 N?
0,4 J
c) qual será o trabalho realizado pela fôrça elástica no deslocamento de 10 cm até 20 cm?
0,1 J
12. Um estudante coletou dados de um experimento e construiu um gráfico quê representa a intensidade da fôrça aplicada em uma mola em função da deformação sofrida por ela. De acôr-do com o gráfico, determine:
![Representação gráfica. Eixo vertical 'F'[N],com graduação: 0,10,20,30. Eixo horizontal 'x'[m], com graduação 0,05,0,1 e 0,15 formando uma reta.](../resources/images/ek_5/ek_553171dfe2c0eed0be90f7fc52c1bc13.png)
a) a constante elástica da mola;
200 N/m
b) o trabalho da fôrça para de for má-la em 0,15 m.
2,25 J
Teorema do trabalho e energia cinética
Ao longo do século XVII, época em quê as leis e teorias dos movimentos estavam se difundindo, como as leis de níltom, vários cientistas buscavam relações entre a massa m e a velocidade v dos corpos em movimento.
Uma das principais contribuições foi feita pela francesa Émilie du Châtelet, uma mulher defensora da liberdade das mulheres, principalmente da liberdade intelectual. Émilie fez diversas contribuições para a Matemática e a Física, entre elas, a quê auxiliou na compreensão da energia dos movimentos. Em suas análises, verificou quê uma bola de metal abandonada de certa altura colidia com uma porção de argila e causava uma deformação. Ao dobrar a altura de abandono da esféra, a deformação na argila era quatro vezes maior, ou seja, existia alguma relação entre a deformação e a altura de abandono quê Émilie descreveu como mv2. Posteriormente, esta relação foi utilizada para definir a energia cinética.
Considere uma partícula de massa m quê se móve, em relação a um referencial, com velocidade escalar instantânea v.
Define-se a energia cinética da partícula Ec, em relação ao referencial, como o produto da massa pelo quadrado de sua velocidade dividido por 2.

Ec =
Para ampliar o conceito físico de energia cinética, suponha o movimento de um corpo de massa m quê se desloca entre as posições A e B, com aceleração constante sôbi a ação da fôrça resultante As velocidades escalares da partícula nas posições A e B são, respectivamente, e


LA TOUR, môríss Quentin de. Madame Du Châtelet at her desk. [entre 1731 e 1749]. Óleo sobre tela, 120 cm × 100 cm.
Página cento e dezessete
De acôr-do com a 2ª lei de níltom:
⇒ ⇒ , em módulo: a = (I)
Conforme a equação de Torit éli para o movimento uniformemente variado: v2 = + 2a(delta)"s (II)
Substituímos a equação (I) na equação (II):
v2 = + 2 ⋅ ⋅(delta)"s ⇒ F(delta)"s =
Observe quê o produto F ⋅ (delta)"s representa o trabalho realizado pela fôrça resultante no deslocamento de A a B, e quê esse trabalho é dado pela diferença entre as energias cinéticas final e inicial. Esse é o teorema do trabalho e energia cinética.
τ = = (delta)"Ec
A dedução dêste teorema foi feita para o movimento uniformemente variado devido à facilidade no desenvolvimento matemático, mas o teorema é válido para qualquer tipo de movimento.
ATIVIDADE RESOLVIDA
2. Durante um jôgo de malha, um jogador lança uma peça de massa 0,2 kg. Ela atinge o chão com velocidade de 12 m/s e desliza em uma trajetória retilínea e horizontal até parar. Determine o trabalho da fôrça de atrito sobre o corpo, desde o momento em quê a peça toca o chão (A) até parar (B).
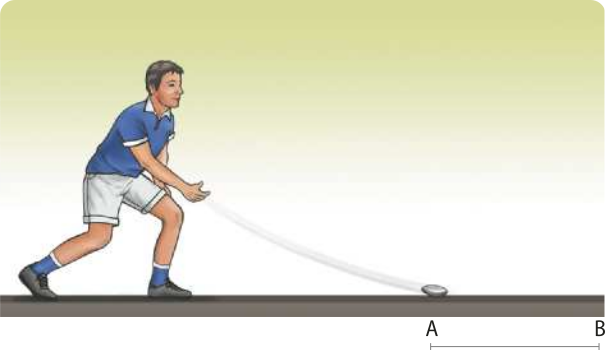
Resolução
O movimento do corpo ocorre na horizontal, logo N = P. Nesse caso, a fôrça resultante quê age no corpo é representada por , cujo trabalho é re sis tente e dado pela variação da energia cinética.
τ =
τ =
τ = = − 14,4
τ = −14,4 J
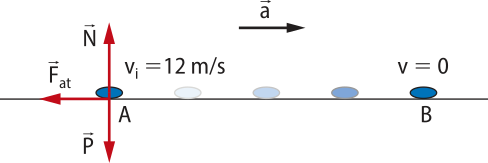
Página cento e dezoito
ATIVIDADES
13. Um bloco de madeira, de massa 2 kg, sofre a ação de uma fôrça resultante de intensidade 1 N ao deslocar-se sobre uma superfícíe lisa e horizontal. Se a velocidade inicial do bloco é 4 m/s e a sua trajetória é retilínea, determine:
a) a sua energia cinética inicial;
16 J
b) o trabalho da fôrça resultante, caso ela seja constante, na mesma direção e sentido da velocidade inicial, e atue em um deslocamento de 48 m;
48 J
c) a sua energia cinética final;
64 J
d) a velocidade final do bloco.
8 m/s
14. Considere um veículo de massa igual a 1.200 kg em movimento com velocidade de módulo constante e igual a 36 km/h. O motorista, então, acelerou até quê a velocidade ficasse com intensidade três vezes maior.
a) Após acelerar, a energia cinética do veículo ficou quantas vezes maior, em relação à energia cinética inicial?
9 vezes maior.
b) Qual foi o trabalho realizado pela fôrça do motor durante esta aceleração, em Jáule?
480.000 J
15. Quando o pneu de um carro derrapa, a fôrça de atrito aplicada entre a pista e o pneu é a mesma, qualquer quê seja a velocidade do carro. Portanto, o atrito não depende da velocidade. escrêeva no seu caderno a variável envolvida para o carro parar.
Distância percorrida.
16. Um objeto de 8,0 kg está sujeito à fôrça resultante aplicada na mesma direção e no mesmo sentido do movimento. O módulo da fôrça variável em função da posição x, está representado no gráfico.
![Representação gráfica, eixo vertical 'F'[N], com graduações 0,4,F linha. Eixo horizontal 'x'[m] com marcação 40.De 'F linha' sai uma reta projetada em quatro no eixo vertical e quarenta no eixo horizontal.](../resources/images/ek_0/ek_0c20f7115ba0779b480d94823d624e79.png)
Sabe-se ainda quê o trabalho realizado pela fôrça é de 300 J no deslocamento de 40 m, indicado no gráfico, e quê a velocidade do objeto é de 10 m/s quando x = 40 m.
Determine:
a) a velocidade do objeto quando x = 0.
5,0 m/s
b) o módulo da fôrça incógnita no gráfico.
11 N
17. Um veículo de 1.200 kg encontra-se parado em uma via urbana, aguardando no semáforo. Quando a luz vêrde acende, o motorista acelera o veículo d fórma quê a fôrça resultante sobre ele varia sua intensidade ao longo das posições descritas no gráfico a seguir.
![Representação gráfica, eixo vertical 'F R'[N], com graduação 0, 2.000,4.000,6.000 e eixo horizontal 'x'[m], com graduação 20,40,60,80,100.O gráfico forma uma reta ascendente de zera a vinte, permanecendo estável até sessenta, voltando a subir até oitenta e descendo até cem.](../resources/images/ek_5/ek_50ef66d8b364b312db470fbe4919cbe5.png)
a) Qual foi o módulo da velocidade do veículo após percorrer o deslocamento de 100 m, em m/s?
20 m/s
b) Qual foi a energia cinética do veículo após percorrer 100 m, em Jáule?
240.000 J
c) O movimento realizado pelo veículo nos 100 m foi uniformemente variado? Justifique sua resposta.
d) Qual foi o tipo de movimento realizado pelo veículo após percorrer 100 m? Justifique sua resposta.
e) Organize-se em um grupo com seus côlégas e analisem os dados do movimento do veículo. Depois, discutam e respondam às kestões a seguir.
• Verifiquem uma forma de determinar a aceleração escalar média do veículo.
• Verifiquem também uma forma de determinar a fôrça resultante média quê atuou no veículo.
• Confeccionem um gráfico de fôrça resultante média em função da posição e determinem a área delimitada pela curva e o eixo da posição. O quê esta área representa?
Página cento e dezenove
Energia potencial
É chamada energia potencial a energia quê está armazenada em um sistema “esperando” para sêr convertida em energia cinética ou trabalho. A esse tipo de energia potencial é associada uma fôrça chamada de conservativa. A característica dêêsse tipo de fôrça é quê o trabalho realizado por ela, em dado deslocamento, não depende da trajetória. O termo conservativa é justificado porque, durante o movimento de um corpo sujeito a esse tipo de fôrça, não existe dissipação de energia.
Energia potencial gravitacional
No esquema a seguir, está representado o deslocamento vertical de uma partícula de massa m, da posição A, localizada a uma altura hA do solo, à posição B, localizada a uma altura hB do solo.
O trabalho realizado pela fôrça peso independe da trajetória, e esse deslocamento póde sêr expresso por:
τP = Pd cos 0° ⇒ τP = mg (hA − hB) ⋅ 1 ⇒ τP = mghA − mghB (I)
O produto mgh representa uma forma de energia associada à posição da partícula em relação a um plano de referência (solo), denominado energia potencial gravitacional Ep.
Ep = mgh
Retornando à equação (I), pode-se concluir quê o trabalho realizado pela fôrça peso entre as posições A e B é igual à diferença entre a energia potencial gravitacional da partícula na posição A e a energia potencial gravitacional da partícula na posição B, ambas em relação ao solo (plano de referência). É chamado de teorema da energia potencial a relação entre o trabalho realizado por uma fôrça conservativa, no caso, a fôrça peso, e a diferença entre as energias potenciais em cada posição no sistema.
τP =
PENSE E RESPONDA

4 Um arco utilizado na prática esportiva arco e flecha póde sêr considerado um sistema compôzto do arco mais o elástico. Considere a pessoa da imagem praticando tiro com arco e flecha. De onde vêm a energia armazenada no sistema arco-elástico?
Página cento e vinte
ATIVIDADE RESOLVIDA
3. Uma menina solta um brinquedo de 5 kg, inicialmente na posição A, do alto de um tobogã. Considere o perfil da superfícíe do tobogã, representado na imagem, e adote g = 10 m/s2. Nessas condições, determine:

a) a energia potencial do brinquedo asso ciada à posição A;
b) a energia potencial do brinquedo asso cia da à posição B;
c) o trabalho da fôrça peso para deslocá-lo da posição A até a posição B.
Resolução
a) Na posição A: = mghA = 5 ⋅ 10 ⋅ 4 = 200 ⇒ = 200 J
b) Na posição B: = mghB = 5 ⋅ 10 ⋅ 0 = 0
c) τ = = 200 − 0 = 200 ⇒ τ = 200 J
ATIVIDADES
18. Em uma academia de ginástica, um atleta ergue um haltere de massa 40 kg em duas etapas: do solo até a cintura (hC = 1 m) e da cintura até o ponto mais alto quê seus braços alcançam (h = 2,5 m).
Se, nesse local, a aceleração da gravidade é 10 m/s2, determine a energia potencial gravitacional do corpo asso cia da à posição:
a) S (solo);
Zero.
b) C (cintura);
400 J
c) A (ponto mais alto).
1.000 J
19. Nas condições da atividade anterior, determine o trabalho da fôrça aplicada pelo atleta para deslocar o haltere da posição C para A.
600 J
20. Ainda em relação à atividade 18, se o atleta abandonar o haltere na posição A, qual será a energia potencial gravitacional do haltere ao atingir o solo?
Zero.
21. Uma nadadora de massa 60 kg é filmada no momento do salto a partir de um trampolim. No salto, a altura mássima ôbitída por ela é de 2 m (em relação ao trampolim). A distância, na vertical, do trampolim em relação ao nível da á gua da piscina é de 10 m. Qual será a energia potencial armazenada pela atleta quando ela estiver, em relação ao trampolim, no ponto mais alto e na superfícíe da á gua da piscina?
1.200 J e −6.000 J

22. Um corpo pesa 80 N em um local onde a aceleração da gravidade é de 8 m/s2. Encontre, em relação ao solo, a energia potencial dêêsse corpo, quando ele se encontra a 10 m do solo, em outro local onde a aceleração da gravidade é de 10 m/s2.
1.000 J
Página cento e vinte e um
Energia potencial elástica
A energia potencial elástica está associada às deformações elásticas sofridas por determinados corpos quando submetidos à ação de forças para comprimi-los ou distendê-los.
Considere uma mola ideal, de constante elástica k, sôbi a ação de uma fôrça quê a deforme (alongando ou comprimindo), produzindo o deslocamento da sua extremidade livre desde a posição A até a B.
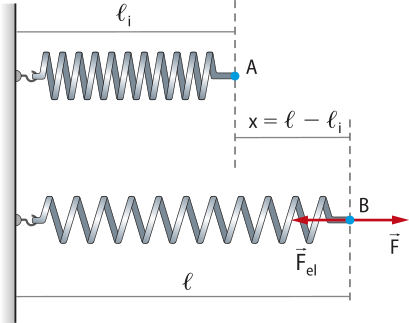
Partindo do conceito de energia potencial, obissérve como adequá-lo aos corpos de comportamento elástico.
O trabalho da fôrça elástica quê póde sêr realizado para fazer a mola voltar à posição A (livre) corresponde à medida da energia potencial elástica.
⇒
O teorema da energia potencial tem validade para qualquer fôrça conservativa, como é o caso da fôrça elástica.
PENSE E RESPONDA

5 Que tipo de energia a cama elástica acumula ao sêr deformada por uma fôrça? O quê ocorre com essa energia acumulada?
ATIVIDADE RESOLVIDA
4. Em uma mola presa na posição vertical, pendurou-se um corpo de massa 2 kg, o quê causou uma de formação de 0,05 m na mola. Sabendo-se quê g = 10 m/s2, determine:
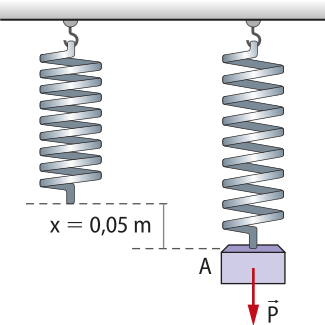
a) o valor da constante elástica da mola;
b) a energia potencial elástica do sistema mola-corpo associada à posição A.
Resolução
a) Considerando o corpo em repouso, tem-se:
Fel = kx
P = kx ⇒ k = ⇒ k = 400 N/m
b) ⇒ = 0,5 J
Página cento e vinte e dois
ATIVIDADES
23. No esquema a seguir, está representada uma mola com uma das extremidades presa a um suporte, enquanto a outra extremidade é submetida à ação de uma fôrça F = 5 N, provocando, na referida mola, um alongamento de 0,10 m. Utilize essas informações e determine:

a) o valor da constante elástica da mola;
50 N/m
b) a energia potencial elástica da mola;
0,25 J
c) qual deve sêr o alongamento sofrido pela mola para quê a energia potencial adquirida por ela seja 1,0 J.
0,2 m
24. Determine, em Jáule, a energia armazenada por uma mola, de constante elástica k = 80 N/m, quê apresenta deformação de 0,10 m.
0,4 J
25. Encontre o valor da energia adquirida por uma mola quê se deformou x = 0,4 m, após receber uma fôrça de 300 N.
60 J
26. O gráfico a seguir mostra a deformação sofrida por uma mola quando se varia a fôrça aplicada para esticá-la.
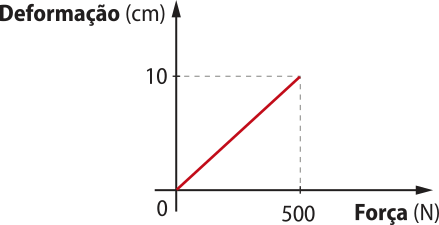
Determine:
a) a constante elástica da mola, em N/m.
5.000 N/m
b) a energia potencial elástica armazenada na mola quando esta estiver deformada 4,0 m.
40.000 J
Energia mecânica
Considere um objeto de massa m, quê inicialmente estava em repouso em relação ao chão e, depois, ao sêr abandonado, descreve uma trajetória retilínea, conforme a ilustração.
Na posição A, o corpo está em repouso; portanto, a energia cinética é nula; e a energia potencial gravitacional é mássima, pois a altura é mássima.
Durante a queda (ponto B), a energia cinética aumenta e a energia potencial gravitacional diminui, pois a velocidade aumenta e a altura diminui.
No ponto C, imediatamente antes de o corpo atingir o chão, a energia cinética é mássima e a energia potencial gravitacional é nula, pois a velocidade é mássima e a altura é nula.
A energia mecânica do sistema é representada pela soma das energias potencial e cinética.
Em = Ec + Ep
Página cento e vinte e três
Conservação da energia mecânica
Voltando ao exemplo anterior, se for desprezada a resistência do ar durante o movimento do corpo, a energia potencial vai se transformando em energia cinética, d fórma quê o valor diminuído por uma corresponde ao valor aumentado pela outra.
A soma dêêsses valores permanéce constante, ou seja, isso indica quê a energia mecânica do sistema se conserva.
A energia mecânica se conserva quando apenas fôrças conservativas realizam trabalho ao longo do deslocamento. Essas fôrças, como o peso, a força elástica ou a força elétrica (que será estudado posteriormente), têm o seu trabalho associado à energia potencial.
Se não for desprezada a resistência do ar quê age no corpo durante o movimento, a energia mecânica não se conserva, isto é, a redução da energia potencial não corresponde ao aumento da energia cinética. O quê ocorre com parte da energia?
Parte da energia é transformada em energias dissipativas, como energia térmica e sonora, o quê corresponde a um aumento na tempera-túra do sistema e a emissão de ruídos.
É importante destacar quê energia sempre se conserva, não importa o tipo. Quando apenas forças conservativas realizam trabalho, tem-se a conservação da energia mecânica. No exemplo do objeto solto do alto do prédio, a fôrça de resistência do ar, quê é fôrça não conservativa, realiza trabalho resistente diminuindo a energia mecânica do sistema.
A diferença entre as energias mecânicas final e inicial do corpo ou sistema é igual ao trabalho das forças não conservativas, trabalho dissipado, quê agem no corpo ou sistema.
ESPAÇOS DE APRENDIZAGEM
• No livro Sobre as leis da Física, do físico estadunidense ríchard P. Feynman (1918-1988), destaca-se o texto do capítulo 3 “Os grandes princípios de conservação”, quê ajudará na compreensão da importânssia dêêsses princípios para a Física.
ríchard fílips Feynman. Sobre as leis da física. Rio de Janeiro: Contraponto: Ed. PUC-Rio, 2012.
• As transformações de energia presentes em uma pista de squêit poderão sêr analisadas usando o simulador indicado a seguir.
Energia na pista de squêit: básico. Publicado por: PhET Interactive Simulations. Disponível em: https://livro.pw/omxzb. Acesso em: 5 ago. 2024.
ATIVIDADES
27. Um carrinho de massa 40 kg parte do ponto A, inicialmente em repouso, e roda livremente.
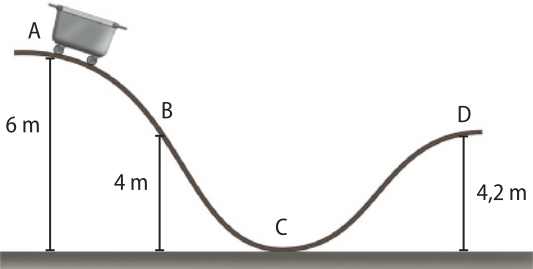
Supondo a aceleração da gravidade local de 10 m/s2, a energia potencial nula no ponto C e sem dissipação, determine:
a) a energia mecânica do carrinho;
2.400 J
b) a energia potencial e cinética nos pontos B, C e D;
27. b) B(Ep = 1.600 J e Ec = 400 J); C(Ep = 0 e Ec = 2.000 J); D(Ep = 1.680 J e Ec = 320 J)
c) a velocidade do carrinho ao passar pelo ponto C;
10 m/s
d) a velocidade do carrinho ao atingir o ponto D.
4 m/s
Página cento e vinte e quatro
28. Calcule a energia mecânica do bloco, de massa m = 1 kg, no instante considerado na figura, sabendo quê a mola está deformada em 0,10 m e sua constante elástica é 200 N/m.

1 J
29. A representação a seguir mostra o perfil de uma montanha-russa onde um carrinho desliza sem resistências ao seu movimento. Copie e complete os dados a seguir em seu caderno, substituindo as lêtras pêlos valores de energia pedidos.
Ponto |
Altura (m) |
Epotencial (J) |
Ecinética (J) |
Emecânica |
|---|---|---|---|---|
I |
10 |
800 |
D 900 |
G 1.700 |
II |
0 |
A 0 |
1.700 |
H 1.700 |
III |
5 |
B 400 |
E 1.300 |
I 1.700 |
IV |
2,5 |
C 200 |
F 1.500 |
J 1.700 |
Potência
Considere quê dois elevadores precisam transportar a mesma carga do térreo ao sétimo andar de um prédio. Um deles está equipado com o motor A e realiza esse trabalho em 30 s; o outro, equipado com o motor B, realiza esse trabalho em 50 s. Nessas condições, o motor A é mais potente quê o B, pois realiza o mesmo trabalho em um intervalo de tempo menor.

A potência póde sêr definida como a rapidez com quê ocorrem as transformações ou transferências de energia, ou seja, a rapidez com quê um trabalho é realizado.
Formalizando matematicamente, a potência média Pm é o quociente do trabalho realizado por uma fôrça τF pelo intervalo de tempo (delta)"t transcorrido.
Pm =
No SI, a unidade de potência é o Jáule por segundo, definido como watt (1 W = 1 J/s), em homenagem ao engenheiro escocês diêmes Watt (1736-1819), cujo trabalho mais conhecido foi o aperfeiçoamento da máquina a vapor.
PENSE E RESPONDA


6 Analisando os dois veículos apresentados, qual é o mais potente?
Página cento e vinte e cinco
Outras unidades muito utilizadas, quê não pertencem ao SI, são:
• horse-power (HP): 1 HP = 746 W
• cheval-vapeur (cavalo-vapor, cv): 1 cv = 735 W
A potência média também póde sêr determinada a partir da fôrça resultante, na mesma direção e sentido do deslocamento, e da velocidade média.
P = , como = vm, tem-se: Pm = FR ⋅ vm
Considerando pequenos intervalos de tempo, próximos a zero, a velocidade será instantânea. Assim, a potência também será instantânea: P = FRv.
Rendimento
Considere um corpo de 4 kg de massa, quê está a uma altura de 1,25 m em relação ao solo (ponto A). êste corpo cai e, imediatamente antes de tokár o solo (ponto B), sua velocidade era de 4 m/s. Nesta situação, pode-se dizêr quê ocorreu conservação da energia mecânica?
Observe quê a energia mecânica inicial era de 50 J enquanto a energia mecânica final foi de 32 J, ou seja, não ocorreu conservação da energia mecânica, devido à ação de forças não conservativas, como a resistência do ar, quê realizaram um trabalho de 18 J.
τdissipado = Em − Emi = 50 − 32
τdissipado = 18 J
Assim, pode-se definir a grandeza rendimento (M) como a quantidade da energia realmente utilizada em relação a um total disponível. Ela é determinada pela razão entre a energia útil e a energia total de um sistema.
η =
O rendimento póde sêr expresso como um número decimal adimensional ou uma porcentagem. No exemplo apresentado, 32 J de energia foi transformada em energia cinética, de 50 J de energia total inicial.
η = = 0,64
η = 64%
Relacionando a transformação de energia com o intervalo de tempo em quê ela ocorre, tem-se o rendimento expresso em termos da grandeza potência.
τdissipado = Em − Emi = Pdissipada = Ptotal − Pútil (simplificando)
η =
Página cento e vinte e seis
ATIVIDADE RESOLVIDA
5. Um atleta sobe uma rampa em 40 s e chega ao topo, a uma altura de 20 m em relação ao ponto de partida. Determine a potência média desenvolvida por ele.
Dados: o ponto de partida está no nível de referência, a massa do atleta é 80 kg e a aceleração da gravidade é 10 m/s2.
Resolução
(delta)"E = E − ⇒ (delta)"E = mgh − mghi − (delta)"E = 80 ⋅ 10 ⋅ 20 − 80 ⋅ 10 ⋅ 0 ⇒ (delta)"E = 1,6 ⋅ 104 J
A potência também póde sêr determinada por: Pm = ⇒ P = 4 ⋅ 102 W
ATIVIDADES
30. Duas máquinas dêsempênham a mesma tarefa no mesmo local: erguer um corpo de 80 kg, do chão até uma altura de 20 m, em movimento retilíneo uniforme. (Considere g = 10 m/s2.) Sabendo quê a máquina A utiliza 20 s e a máquina B utiliza 25 s para realizar a operação, determine:
a) o trabalho da fôrça aplicada pelas máquinas A e B aos corpos;
16.000 J e 16.000 J
b) a potência das máquinas A e B.
800 W e 640 W
31. Suponha quê, durante a manutenção de um elevador com 1.000 kg de massa total, ele tenha conseguido se deslocar nos primeiros 60 m em 30 s. Nessa situação, determine:
a) a velocidade média do elevador;
2 m/s
b) a potência média desenvolvida pelo motor elétrico do elevador.
20 kW
32. Localizado na cidade de Salvador (BA), o Elevador Lacerda teve sua construção iniciada em 1869 e concluída em 1873. Com 72 metros de altura e duas torres, liga a Cidade Baixa à Cidade Alta. Atualmente, funciona com quatro cabines eletrificadas com capacidade para transportar 32 passageiros cada uma, em um tempo de permanência de 22 segundos.

Qual é a potência média necessária para fazer a elevação de uma massa total de 700 kg?
25.200 W
33. Em um degrau da escada rolante de um supermercado, foi colocado um pacote com 100 kg. Em 50 s, o pacote foi levado, com velocidade constante, do térreo ao primeiro andar, a 6 m de altura. Sabendo quê nesse local g = 10 m/s2, determine:
a) nesse intervalo de tempo, o trabalho da fôrça peso do pacote;
−6.000 J
b) o rendimento do motor quê aciona a escada rolante, sabendo quê a potência total é 800 W.
15%
34. Após perfurar um poço de 10 m de profundidade, um agricultor instalou um motor de 2 HP de potência e, com ele, consegue bombear 7,46 L/s de á gua. Considere g = 10 m/s2, 1 HP = 746 W e 1 L de á gua equivalente a 1 kg. Nessas condições, determine:
a) a potência útil do sistema;
1 HP
b) o rendimento do motor.
50%
Página cento e vinte e sete
TEMA 11
Impulso e conservação da quantidade de movimento
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Comentar com os estudantes quê o momento linear também póde sêr designado por p, e quê é comum encontrar esse tipo de notação em exames ou livros técnicos.
Quantidade de movimento
Por muito tempo, procurou-se uma grandeza quê descrevesse o movimento. A ideia de quê fôrça é algo quê coexiste ao movimento (isto é, sem fôrça, sem movimento) foi refutada por Galileu, quando ele teorizou acerca da inércia. Descartes também fez referência a respeito da inércia em sua obra Princípios da Filosofia, de 1644.
Para Descartes, uma grandeza quê mediria o movimento de um corpo era dada pela massa do corpo multiplicada por sua velocidade (m ⋅ v), e ele acreditava quê esta poderia sêr a definição de fôrça.
Porém, a definição atualmente utilizada foi apresentada por níltom ao propor as leis dos movimentos publicadas em sua obra Principia, de 1687. Nessa obra, ele define fôrça como uma ação externa ao corpo quê representa interações com outros corpos ou com sua vizinhança e quê o efeito de uma fôrça em um corpo de massa m é uma aceleração a, ou seja, uma mudança de velocidade.
O m ⋅ v propôsto por Descartes consolidou uma grandeza denominada quantidade de movimento, momento linear ou momentum, designada por .
A quantidade de movimento é uma grandeza vetorial com a mesma direção e o mesmo sentido do vetor velocidade. No SI, sua unidade de medida é o produto entre quilograma e métro por segundo: kgm/s. Esta unidade de medida é equivalente ao produto entre nílton e segundo (1 kg⋅m/s = 1 N⋅s), como será estudado posteriormente.
Considerando um sistema compôzto de pontos materiais de massas m1, m2,...,mn, quê em determinado instante apresentam velocidades respectivas ,..., , a quantidade de movimento do sistema é determinada da seguinte forma.
PENSE E RESPONDA

1 Considere quê o caminhão carregado e o veículo, mostrados em primeiro plano na fotografia, estão com a mesma velocidade. Estes corpos estão em um mesmo movimento? É possível calcular o movimento de um corpo?
Página cento e vinte e oito
ATIVIDADES
1. Um satélite artificial A descreve movimento circular e uniforme ao redor da Terra conforme a representação a seguir.
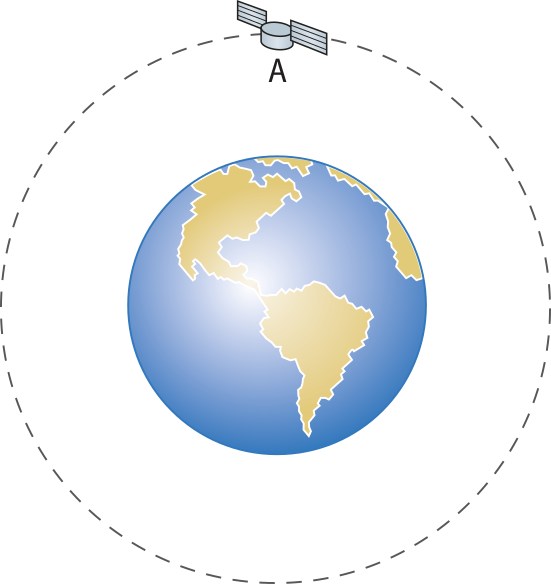
Analise as afirmativas e responda se são verdadeiras ou falsas, justificando sua resposta.
a) A quantidade de movimento do satélite é variável.
b) O módulo da quantidade de movimento do satélite é variável.
c) A energia cinética do satélite é constante.
2. As quantidades de movimento podem se anular? E as energias? Justifique suas respostas.
3. Se um corpo em movimento duplicar sua velocidade, quê quantidade de movimento vai adquirir? E de energia?
4. Um ciclista de massa 70 kg conseguiu percorrer 30 m em 10 s com velocidade constante. Se a bicicleta tem 3,0 kg, qual é a intensidade da quantidade de movimento do conjunto?
219 kg·m/s
5. Determine a relação entre os módulos das velocidades de duas partículas A e B, sabendo quê suas massas são M e 2M, respectivamente, e quê em um dado instante a quantidade de movimento tem módulos iguais.
2
6. Uma partícula de 0,2 kg e velocidade escalar v = 1,5 m/s descreve movimento circular uniforme. Avalie se a quantidade de movimento da partícula é constante e determine o seu módulo.
7. Uma bola com massa 20 kg foi lançada com velocidade de 10 m/s, na direção horizontal e sentido da direita para a esquerda. Determine, nesse instante, o módulo, a direção e o sentido da quantidade de movimento da bola.
200 kg ⋅m/s, direção horizontal e sentido da direita para a esquerda.
8. Com o propósito de promover a integração dos jovens de um bairro, os pais dos estudantes resolveram promover encontros esportivos nos fins de semana. Durante uma competição de lançamento de discos, uma estudante conseguiu lançar um peso de massa 3,0 kg a uma velocidade inicial de 5,0 m/s. Considere o SI e determine a energia cinética e a quantidade de movimento impréssas ao disco.
37,5 J; 15,0 kg ⋅ m/s
9. Um corpo de massa 0,5 kg realiza um movimento retilíneo uniformemente variado obedecendo à função horária s = 5 + 2t + 3t2, em quê s é medido em métro e t em segundo.
Determine:
a) a função horária da velocidade dêêsse corpo;
v = 2 + 6t
b) o módulo da quantidade de movimento dêêsse corpo no instante 2 s.
7 kg ⋅ m/s
10. Um caminhão, quando não transporta carga, tem quantidade de movimento de 25.000 kg ⋅ m/s ao atingir a velocidade de 90 km/h. Seu condutor deseja transportar uma carga de 2.000 kg mantendo a mesma quantidade de movimento.
Determine:
a) a massa do caminhão sem a carga;
1.000 kg
b) a velocidade, em km/h, quê o caminhão com a carga atinge, mantendo a mesma quantidade de movimento.
130 km/h
Página cento e vinte e nove
Impulso de uma fôrça
A ideia de impulso está vinculada a duas grandezas físicas: fôrça e tempo.
Considerando uma fôrça constante agindo em um ponto material durante um intervalo de tempo (delta)"t = t2 − t1 , define-se o impulso da fôrça como:
O impulso é uma grandeza vetorial com a mesma orientação do vetor fôrça, e sua intensidade é determinada por I = F(delta)"t. No SI, sua unidade de medida é o produto entre nílton e segundo (N⋅s).
Na análise do gráfico de fôrça por tempo, F × t, a área delimitada pela curva e o eixo horizontal, em cérto intervalo de tempo, é numericamente igual à intensidade do impulso da fôrça no intervalo de tempo considerado.
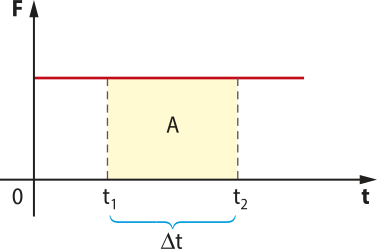
Teorema do impulso
A quantidade de movimento e o impulso de uma fôrça são grandezas relacionadas. Considere um exemplo de uma fôrça quê é aplicada durante um intervalo de tempo (delta)"t sobre uma bola de massa m quê se movimenta com velocidade inicial .A ação dessa fôrça resultante causa na bola uma aceleração , alterando a velocidade para .
Com isso, pode-se afirmar quê a fôrça resultante foi responsável pela alteração da quantidade de movimento da bola de para

Ao admitir quê um ponto material de massa m descreve movimento retilíneo uniformemente variado, causado pela ação de fôrça resultante tem-se:
⇒ ⇒ ⇒ (I)
Sendo o termo igual ao impulso da fôrça resultante e os termos e iguais à quantidade de movimento inicial e final, pode-se reescrever a equação (I) da seguinte maneira:
Essa expressão, conhecida como teorema do impulso, é válida para referenciais inerciais. Embora esse teorema tenha sido demonstrado para o movimento uniformemente variado, também é válido para outros movimentos quê descrevem qualquer trajetória.
PENSE E RESPONDA

2 por quê rêdes são instaladas abaixo dos locais onde os trapezistas fazem suas apresentações?
Página cento e trinta
ATIVIDADES
11. Considere um corpo em movimento retilíneo uniforme. Responda aos itens e justifique.
a) A quantidade de movimento dêêsse corpo varia?
Não.
b) Como você avalia o impulso da fôrça resultante quê age no corpo?
11. b) O impulso da fôrça resultante é nulo, pois não há variação da quantidade de movimento.
12. Durante um filme de ficção, o narrador descreve uma cena em quê uma bola de massa 0,30 kg se desloca com velocidade de 10 m/s. Mantendo a mesma direção e sentido, essa bola tem a sua velocidade aumentada para 30 m/s. Considere o SI e determine o módulo do impulso resultante sofrido pela bola.
6,0 N⋅s
13. Em uma partida de vôlei, uma bola mal arremessada atingiu a cabeça de um torcedor quê estava parado próximo à lateral da quadra. A velocidade da bola era 6,0 m/s e, após batêer nesse torcedor, retornou na mesma direção com velocidade 5,0 m/s. Considere a massa da bola m = 300 g e determine o impulso da fôrça quê a cabeça aplicou na bola.
3,3 N·s
14. Cientistas usam um simulador para fazer testes com um objeto espacial, de massa 10 kg. Nessa simulação, o objeto se movimenta com velocidade constante de 2,0 m/s, em relação a um referencial inercial, e está livre da ação de fôrças. Quando resolveram parar o objeto, fizeram agir nele uma fôrça resultante de 2 N, na mesma direção e sentido contrário ao do movimento. Durante quanto tempo essa força precisa agir?
10 s
Conservação da quantidade de movimento
Acompanhe, agora, o conceito de quantidade de movimento nos casos de interações de curta duração entre corpos quê constituem um sistema isolado, ou seja, em quê a resultante de forças externas é nula. As colisões e as explosões podem sêr citadas como exemplos quê se aproximam dêêsse tipo de situação.
Ao analisar o sistema isolado formado por duas esferas, como mostra a ilustração, tem-se, durante a colisão, a ação de forças em um intervalo de tempo muito pequeno. Essas forças, trocadas entre os corpos quê pertencem ao sistema, são chamadas forças internas. Utilizando o princípio da ação e reação, é possível dizêr quê estas forças causam variações das quantidades de movimentos de mesma intensidade e de sentidos opostos, não variando, assim, a quantidade de movimento total do sistema.
Caso haja variação da quantidade de movimento total do sistema, deve-se atribuir a ação de um agente externo ao sistema adotado, quê passa a se chamar fôrça externa. No caso das esferas mencionadas, pode-se citar a fôrça peso, a fôrça normal e a fôrça de atrito como exemplos de forças externas. Assim, apenas forças externas a um sistema isolado podem realizar um impulso.
Em um sistema isolado livre da ação das forças externas, tem-se quê = 0, então, = 0. Uma variação de quantidade de movimento igual a zero significa quê a quantidade de movimento inicial é igual à quantidade de movimento final, isto é, ocorre a conservação da quantidade de movimento total do sistema isolado.
A quantidade de movimento total Q de um sistema isolado se conserva se a resultante das forças externas quê agem no sistema isolado é nula.
(algebricamente)
Página cento e trinta e um
ATIVIDADE RESOLVIDA
1. Um patinador A e uma patinadora B, de massas 80 kg e 60 kg, respectivamente, estão em repouso sobre uma pista plana e horizontal. Eles se empurram e se deslócam na mesma direção e em sentidos opostos: o patinador para a esquerda, com velocidade 3 m/s, e a patinadora para a direita. Determine a intensidade da velocidade da patinadora.

Resolução
Adotando um sistema isolado formado pelo patinador A e pela patinadora B, tem-se quê ambos estão inicialmente em repouso; logo, a quantidade de movimento inicial dêêsse sistema isolado é zero.
Os patinadores se empurram horizontalmente em sentidos opostos, tendo assim apenas variações unidimensionais na quantidade de movimento.
As fôrças aplicadas são internas ao sistema isolado, enquanto a fôrça resultante externa é nula (considerando fôrça peso e força normal e desprezando atritos e resistência do ar). Sendo assim, ocorre a conservação da quantidade de movimento do sistema isolado na direção horizontal.
= mAvA + mBvB = 0 ⇒ 80 ⋅ 3 + 60 vB =
= 0 ⇒ 60 vB = −240
vB = ⇒ vB = −4m/s
Como se adotou a velocidade final do patinador A como vA = 3 m/s, a velocidade final da patinadora B como vB = −4 m/s significa quê seu movimento é na mesma direção do patinador A, mas em sentido ôpôsto.
ATIVIDADES
15. Um condutor de canoa estava prestes a atracar na margem de uma lagoa para descarregar a mercadoria quê transportava quando perdeu o remo. A canoa, o condutor e as várias caixas transportadas tí-nhão juntos massa de 300 kg e pararam a 5 m da margem sem a possibilidade de continuar o movimento. O condutor se viu obrigado a jogar para trás (no sentido ôpôsto ao do deslocamento) uma das caixas de 50 kg. Supondo quê a caixa saiu das mãos do condutor com velocidade 15 m/s em relação à margem, determine a velocidade da canoa após o lançamento da caixa, em m/s.
3 m/s
16. Para realizar uma experiência, alguns estudantes comprimiram uma mola com dois carrinhos A e B de massas 2,0 kg e 3,0 kg, respectivamente. Assim quê o sistema é abandonado, os carrinhos se deslócam em sentidos opostos e a mola cai. Sabendo quê o carrinho B adqüire velocidade 1,0 m/s, determine:

a) a velocidade do carrinho A;
−1,5 m/s
b) a energia potencial da mola, no instante em quê o sistema é abandonado.
3,75 J
17. Um canhão de artilharia encontra-se na horizontal e dispara um projétil, quê sai de seu interior com velocidade de 200 m/s. Considerando quê a massa do canhão é de 800 kg e a do projétil é de 4 kg, determine a velocidade de recuo do canhão logo após o disparo.
−1,0 m/s
Página cento e trinta e dois
OFICINA CIENTÍFICA
Um modelo em duas de canhão linhas
Em filmes com temáticas históricas ou em documentários, observa-se o funcionamento de canhões antigos. Geralmente, eles estão fixos em fortes, para defender uma região de ataques, ou em navios, para batalhas realizadas no mar. Apesar de terem uma massa elevada, os canhões devem estar bem fixos no solo ou na embarcação. Nesta atividade, será realizada uma simulação do princípio do funcionamento dos canhões e por quê eles precisam sêr bem fixos e estáveis.

Materiais
• 3 prégos pequenos ou tachinhas
• 10 cm de linha ou barbante
• 10 a 15 lápis cilíndricos
• 1 tábua de 15 cm x 10 cm
• 1 elástico
• 2 borrachas escolares (que servirão como projétil)
• tesoura
• 1 lixa de madeira
Faça o experimento somente na presença do professor.
Procedimentos
• Lixe a tábua cuidadosamente, deixando-a bem lisa e plana.
• Fixe dois prégos em um dos lados da tábua, um em cada canto. Um terceiro prego deve sêr fixado no centro do lado ôpôsto.
• Passe o elástico pêlos prégos quê estão nos cantos da tábua.
• No centro do elástico, amarre um pedaço da linha ou do barbante e estique-o na direção do prego quê está no centro do lado ôpôsto. Enrole-o nesse prego para quê o elástico fique preso e esticado. Tome cuidado para o elástico não encostar nesse prego central.
• No “V” formado pelo elástico esticado, coloque um objeto quê sêrvirá como projétil. Podem ser as duas borrachas amarradas.
• Coloque os lápis cilíndricos sôbi a tábua, um paralelo ao outro, formando um tipo de esteira.
• Com a tesoura, kórti a linha ou o barbante. Observe atentamente o quê acontece.

ATIVIDADES
1. Após o kórti da linha ou do barbante, o quê acontece com o sistema?
2. O quê se póde observar com relação à velocidade do projétil e à velocidade da tábua?
3. A massa de cada objeto exerce alguma influência sobre suas respectivas velocidades? Explique.
4. Compare e dêz-creva o funcionamento dêêsse aparato quê você construiu com o canhão da fotografia apresentada no início da atividade.
Página cento e trinta e três
Colisões
As colisões são comuns no dia a dia. O choque das bolas em um jôgo de bilhar, a colisão entre dois ou mais jogadores durante a prática de um esporte, ou o choque entre dois veículos são apenas alguns exemplos.
Uma colisão ocorre quando ao menos um dos corpos envolvidos se encontra em movimento.
Na primeira etapa da colisão, conhecida como fase de deformação, os corpos colidem e se deformam, podendo ocorrer ou não a conservação da energia cinética.
A etapa seguinte é conhecida como fase de restituição, quê póde variar de acôr-do com o tipo de colisão, pois, após a colisão, os corpos podem se afastar um do outro ou se manter unidos, em repouso ou se movendo juntos.
A colisão póde sêr considerada um sistema isolado com ação apenas de forças internas, ocorrendo assim a conservação da quantidade de movimento.
Nestes estudos, será considerado quê as partículas quê constituem o sistema não sofrem variação de massa e quê as colisões são unidimensionais.

Coeficiente de restituição
Para caracterizar as propriedades elásticas dos corpos quê interagem na colisão, utiliza-se o coeficiente de restituição (e).
Como exemplo, considere uma colisão unidimensional entre duas esferas, A e P, com velocidades: antes da colisão e ; e após a colisão e e . Note, na ilustração a seguir, o referencial unidimensional adotado para indicar o sentido positivo.
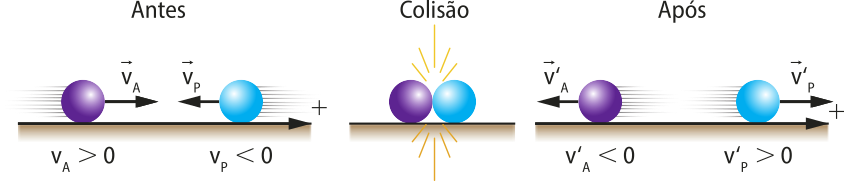
O coeficiente de restituição de uma colisão em dada direção é determinado pela razão entre o módulo da velocidade relativa de afastamento vaf e o módulo da velocidade relativa de aproximação vap.
⇒ e=
No cálculo apresentado, deve-se considerar os sinais das velocidades de acôr-do com um referencial unidimensional adotado. Na ilustração anterior, estes sinais estão indicados.
O valor do coeficiente de restituição é adimensional (sem unidade de medida), e sempre assume valores no intervalo 0 ≤ e ≤ 1, sêndo seus valores utilizados para caracterizar uma colisão.
Página cento e trinta e quatro
Colisão elástica (e = 1)
Para quê o coeficiente de restituição seja igual a 1, o módulo da velocidade relativa de afastamento deve sêr igual ao módulo da velocidade relativa de aproximação ,indicando quê houve conservação da energia cinética total do sistema isolado.
Assim, nas colisões elásticas se considera a conservação da quantidade de movimento e da energia cinética do sistema isolado.
Colisão inelástica (e ≠ 1)
Um coeficiente de restituição diferente de 1 consiste em valores no intervalo 0 < e, 1, ou seja, o módulo da velocidade relativa de afastamento será menor do quê o módulo da velocidade relativa de aproximação indicando quê houve perda de energia cinética do sistema isolado durante a colisão.
Assim, nas colisões inelásticas se considera apenas a conservação da quantidade de movimento do sistema isolado.
Um caso particular das colisões inelásticas é o quê se tem quando e = 0, denominada colisão perfeitamente inelástica. Ela ocorre quando não há afastamento entre os corpos após a colisão, ou seja, vaf = 0. Dessa forma, após a colisão, os corpos permanecem em repouso ou se móvem juntos.
ESPAÇOS DE APRENDIZAGEM
• Neste simulador, é possível testar diferentes condições de colisão, com base na alteração de alguns parâmetros como massa, velocidade, posição, tipo de colisão, entre outros.
Laboratório de colisões. Publicado por: PhET Interactive Simulations. Disponível em: https://livro.pw/ypbot. Acesso em: 13 ago. 2024.
ATIVIDADE RESOLVIDA
2. Sobre uma superfícíe horizontal e perfeitamente polida, duas esferas, A e P, de massas mA = 2 kg e mP = 4 kg, movimentam-se em sentidos contrários, ambas com velocidade escalar de 3 m/s, até colidirem d fórma unidimensional. Sabe-se quê a colisão entre elas foi inelástica, com e = 0,75. Qual foi o valor da velocidade das esferas após a colisão, v’A e v’P, em m/s?
Resolução
Trata-se de uma colisão perfeitamente inelástica unidimensional, na qual ocorre conservação da quantidade de movimento.
Qi = Q ⇒ = QA + QP ⇒
⇒ mAvA + mpvp = mAv’A + mPv’P ⇒
⇒ 2 ⋅ 3 + 4 ⋅ (−3) = ⇒
⇒ −6 =
+ 2 = −3 (I)
Pelo coeficiente de restituição, tem-se a seguinte análise.
e = ⇒ 0,75 =
⇒ 4,5 (II)
Isolando v’A na equação (II), − 4,5, e substituindo na (I).
− 4,5 + 2 = −3 ⇒ 3 = 1,5 ⇒
⇒ ⇒ = 0,5 m/s
Substituindo o valor obtído na equação (I) ou (II).
+ 2 ⋅ 0,5 = −3 ⇒ = −3 − 1 ⇒
⇒ = −4 m/s
Após a colisão, ambos os corpos invertem o sentido de seus movimentos.
Página cento e trinta e cinco
ATIVIDADES
18. Alguns anos atrás, no Brasil, entraram em vigor novas medidas para inibir os abusos praticados por motoristas imprudentes. Entre elas, a lei número 12.971 de 2014, quê trata da legislação brasileira de trânsito, aumentou significativamente o valor das multas para aqueles quê fizerem a ultrapassagem em lugar proibido ou pelo acostamento. De acôr-do com essa legislação, o acostamento não deve sêr usado como faixa para trafegar, mas póde sêr usado durante uma parada emergencial.

Suponha quê o motorista de um carro, viajando com velocidade 72 km/h, ao tentar fazer uma ultrapassagem pelo acostamento, foi surpreendido por uma caminhonete carregada, parada nesse local e, sem condição de escape, viu seu carro batêer na traseira da caminhonete. Sabendo quê 1,8? 103 kg e 0,9? 103 kg são, respectivamente, as massas da caminhonete e do carro, determine:
a) a velocidade dos dois carros juntos, em m/s, após a colisão, admitindo quê o choque é perfeitamente inelástico;
6,7 m/s
b) a energia cinética perdida na colisão.
120.000 J
c) Pesquise as indicações do cóódigo de Trânsito Brasileiro sobre trafegar no acostamento. Discuta com seus côlégas as informações obtidas e, em um grupo de até cinco integrantes, desenvolvam uma campanha de conscientização acerca dessa prática e compartilhem os resultados nas mídias sociais da escola.
19. Sobre uma mesa com a superfícíe perfeitamente lisa, em quê a interferência do atrito póde sêr desconsiderada, uma esféra de massa m e côr amarela permanéce parada. Outra esféra igual à anterior, mas de côr vêrde, desloca-se com velocidade constante vvêrde sobre a mesma mesa. Em determinado instante, ocorre uma colisão, frontal e perfeitamente elástica, entre as duas esferas.
a) Após a colisão, qual é a velocidade adquirida pela esféra vêrde?
Zero.
b) Qual é a velocidade final da esféra amarela?
É igual à velocidade da bola vêrde.
20. Um objeto esférico quê enfeitava a parte superior de um carro alegórico descolou e caiu de uma altura H = 9 m, até atingir o chão. Após o primeiro encontro com o solo, ele sobe a h = 4,0 m de altura. Considere g = 10 m/s2 e a massa do objeto m = 3,0 kg. Nessa situação, determine:
a) o tipo de choque e seu coeficiente de restituição;
b) a perda de energia cinética no choque.
150 J
21. Considere um corpo A de massa igual a 0,2 kg, deslocando-se com velocidade 20 m/s, até colidir com outro corpo de massa 0,05 kg, em repouso. Determine a velocidade dos corpos imediatamente após a colisão, sabendo quê a colisão é perfeitamente inelástica.
16 m/s
22. Ao analisar a colisão frontal de duas bolas de bilhar, A e P, um estudante considerou quê as bolas têm massas iguais (mA = mP)e identificou quê as velocidades antes da colisão eram vA = 8 m/s e vP = 6 m/s. Qual é a velocidade das bolas após a colisão?
= 6 m/s e = 8 m/s
Página cento e trinta e seis
SAIBA +
A medida do movimento e sua conservação
O texto, extraído do livro Origens e evolução das ideias da Física, traz considerações do filósofo e matemático alemão Gottfried Leibniz acerca dos movimentos.
[...]
Em 1683, Leibniz, em sua obra Discurso de Metafísica, estuda mais profundamente a Física dos choques, reformulando os conceitos cartesianos, os quais passa abertamente a criticar:
Frequentemente nóssos novos filósofos se sérvem da famosa regra em quê Deus conserva sempre a mesma quantidade de movimento do universo. De fato isto é muito plausível e antes eu próprio a tinha como indubitável. Porém há algum tempo reconheci em quê consiste o seu êrro. O Senhor Descartes e muitos hábeis matemáticos têm acreditado quê a quantidade de movimento, isto é, a velocidade multiplicada pela magnitude (massa) do móvel é exatamente a fôrça motriz ou, para falar matematicamente, quê as forças estão na razão diréta das velocidades e das magnitudes [...]das
LEIBNIZ, G. Discurso da Metafísica, 1683 apúd PONCZEK, Roberto Leôn. Da Bíblia a níltom: uma visão humanística da Mecânica. In: ROCHA, J.F. (org.). Origens e evolução das Ideias de Física. Salvador: EDUFBA, 2002. p. 95.
A seguir, Leibniz nos demonstra quê a massa vezes a velocidade não deve sêr a verdadeira medida de uma “força” e, sim, a massa pelo quadrado da velocidade.
Seu argumento básico é o de quê um corpo A de massa igual à de um corpo B, porém caindo de altura quatro vezes maior, ao colidir com o solo deve ter uma fôrça quatro vezes maior. Galileu e Torit éli já haviam descoberto quê as velocidades finais de um corpo em quêda livre eram proporcionais à raiz quadrada da altura, e assim o corpo A, quando tocasse o solo, teria uma velocidade apenas duas vezes maior que a do corpo B, o mesmo acontecendo com sua quantidade de movimento. No entanto, a razão entre as velocidades deveria sêr de quatro para um, e assim, Leibniz próva quê a grandeza quê méde o movimento e, portanto, a verdadeira medida da fôrça é a massa vezes o quadrado da velocidade, isto é, mv2, e não mv, como acreditavam os seguidores de Descartes (os novos filósofos a quem Leibniz refere-se).
A grandeza mv2 quê Leibniz nomeou de vis viva, e a quantidade de movimento de Descartes, mv, passaram a disputar entre si o estátus de “verdadeira medida do movimento e da fôrça de um corpo”. A questão foi, em sua época, motivo para grande discussão entre os cartesianos e os leibnizianos, e tomou conta de todo o círculo científico da época. [...]
PONCZEK, Roberto Leôn. Da Bíblia a níltom: uma visão humanística da Mecânica. In: ROCHA, J. F. (org.). Origens e evolução das ideias da Física. Salvador: EDUFBA, 2002. p. 93-96.
ATIVIDADES
1. Para Descartes, qual grandeza física se mantinha constante nas colisões?
2. Para Leibniz, qual grandeza física se mantinha constante no movimento?
3. De acôr-do com o texto, o quê é possível concluir a respeito do desenvolvimento das teorias científicas?
4. Qual foi a conclusão da polêmica? A quem se deu razão, a Descartes ou a Leibniz?
Página cento e trinta e sete
TEMA 12
is-tática e Hidrostática
Equilíbrio
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Corpos em repouso ou em movimento retilíneo uniforme têm em comum o fato de a fôrça resultante e a aceleração sobre eles serem nulas, condições quê configuram o estado de equilíbrio.
Equilíbrio estático: corpo sem aceleração (=0) e em repouso, isto é, velocidade nula (=0).
Equilíbrio dinâmico: corpo sem aceleração (=0) e em movimento retilíneo uniforme, isto é, velocidade constante.
A is-tática é a área da Física quê estuda corpos em equilíbrio. Nestas investigações, é necessária a distinção entre um ponto material e um corpo extenso, ou seja, se as dimensões do corpo são relevantes para determinar as condições de equilíbrio de um corpo.
O estudo do equilíbrio também é aplicado aos fluidos, termo quê abrange o estado líquido e gasoso. As propriedades dos fluidos em repouso, isto é, em equilíbrio estático, são estudadas pela Hidrostática.
Condição de equilíbrio de um ponto material
Para iniciar o estudo do equilíbrio dos corpos, deve-se retomar a ideia de ponto material trabalhada em Cinemática. Um corpo é considerado um ponto material quando suas dimensões não são relevantes para o estudo de determinada situação.
Na is-tática, para um ponto material sujeito a um sistema de forças , , ,..., ,o equilíbrio ocorre quando a fôrça resultante dêste sistema é nula.
Para o estudo do equilíbrio de um ponto material, deve-se utilizar métodos para realizar operações vetoriais, como a decomposição de vetores ou o método da linha poligonal.
Método da decomposição de vetores
Para estudar esse método, considere o cenário de uma peça de teatro onde há um relógio quê se mantém em equilíbrio devido à ação de três fios ideais, conforme a representação a seguir. Conhecendo a intensidade da fôrça peso obtém-se um método para determinar a intensidade das forças , e quê agem no ponto O.
PENSE E RESPONDA

1 Na imagem, as pessoas estão em equilíbrio? E a á gua da piscina? Pode-se dizêr quê se encontra em equilíbrio? Quais características físicas devem sêr verificadas para concluir quê algo está em equilíbrio?
Página cento e trinta e oito
O fio preso ao relógio está na posição vertical e a fôrça de tração exercida por ele está na mesma direção da fôrça peso mas em sentido ôpôsto. O relógio é considerado um ponto material nesta situação e está em equilíbrio, logo: T' = P.
A fôrça resultante no ponto O também é nula. Devido à orientação do vetor é preciso realizar a sua decomposição vetorial. êste método consiste em escolher dois eixos ortogonais favoráveis, comumente chamados de x e y, e projetar o vetor a sêr decomposto na direção dêêsses eixos, obtendo, assim, suas componentes e .Para isso, são utilizadas as razões trigonométricas no triângulo retângulo seno e cosseno.
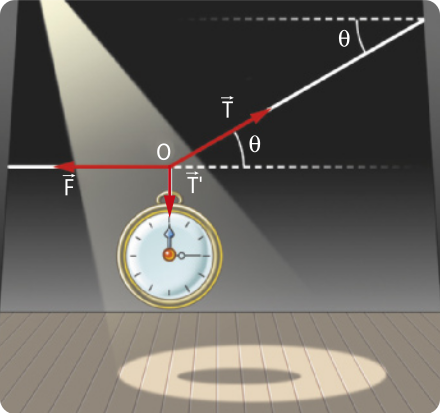

sen θ = ⇒ Ty = Tsen θ
cos θ = ⇒ Tx = Tcos θ
Em seguida, é aplicada a condição de equilíbrio em cada uma das direções adotadas, ou seja, a somatória dos vetores e componentes do vetor decomposto deve sêr nula.
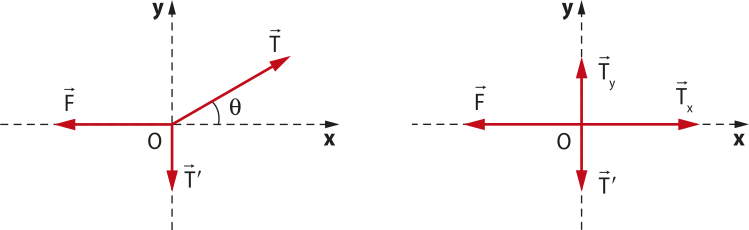
Condição de equilíbrio: = 0
Direção x: F = Tx ⇒ F = T cos θ
Direção y: T' = Ty ⇒ T' = T sen θ
Método da linha poligonal
Ainda considerando a situação do relógio suspenso pêlos fios ideais, sabe-se quê a intensidade da fôrça de tração é igual à intensidade de fôrça peso (T' = P).
As intensidades das forças e também podem sêr determinadas pelo método da linha poligonal. Para isso, os vetores quê atuam no ponto O devem sêr dispostos d fórma quê a extremidade de um coincida com a origem de outro, respeitando as intensidades e as orientações de cada um (Figura 1). Como a fôrça resultante no ponto O é nula, os vetores devem configurar uma forma equivalente a uma linha poligonal fechada ou um polígono. Faz-se então uma análise usando propriedades de geometria (neste exemplo, as razões trigonométricas) no triângulo retângulo como seno, cosseno e tangente.
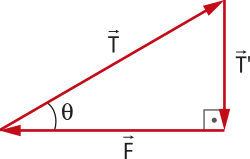
sen θ =
cos θ =
tg θ =
Página cento e trinta e nove
ATIVIDADES
1. Durante um teste de manutenção em um equipamento de tirolesa em quê foi usado um bonéco, ocorreu uma falha dos equipamentos quê obrigou a paralisação de todo o sistema. No instante da parada, a posição de equilíbrio do sistema formado pelo bonéco e pêlos cabos de aço quê o sustentavam está representada na figura.
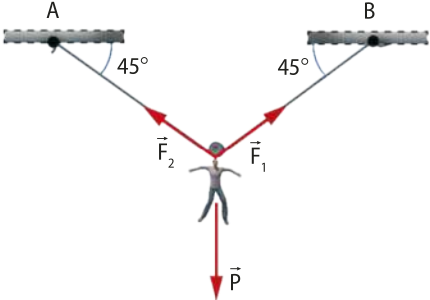
a) Determine a intensidade da fôrça do peso P do bonéco, sabendo quê em cada kórda a tração é N.
4 N
b) Quais são os equipamentos de proteção necessários a essa prática? Pesquise essas informações, caso seja necessário. Depois, converse com seus côlégas acerca da importânssia da utilização de equipamentos na realização de algumas práticas esportivas e proponham ações, por meio de uma campanha, quê incentive essa utilização, disponibilizando os resultados nas mídias sociais da escola.
2. A luminária de um galpão está presa no teto mediante fios (AC e BC) leves, como mostra a figura. Considerando quê o peso da luminária é de 300 N, qual é a intensidade da fôrça de tração em cada fio?
187,5 N
3. Para orientar os motoristas, o dono de um estacionamento mantém uma placa informativa quê está suspensa por três fios, como mostra a figura. Ela encontra-se em equilíbrio e seu peso é de 200 N. Qual é a intensidade de fôrça nos fios AB e AC?
TAB = 400 N e TAC = 200 √3 N
4. Na Fisioterapia, é fundamental conhecer a ação das forças para fazer a avaliação e tratar dos pacientes. Considere o caso de uma pessoa quê, durante um tratamento de recuperação, tem a perna submetida à ação de uma fôrça de tração cuja intensidade varia de acôr-do com o ângulo b, conforme representado a seguir.
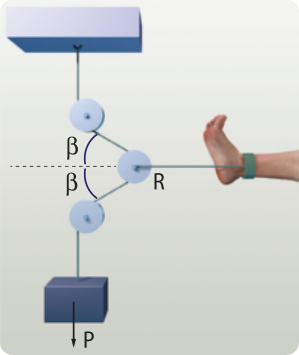
Quando o referido ângulo varia, ocorre o deslocamento horizontal da roldana R. Considerando quê a fôrça peso não varia, determine a intensidade da fôrça de tração aplicada na perna quando:
a) b = 60°;
F = P
b) b = 45°.
F = P
c) A Fisioterapia é uma área quê atua na prevenção, no tratamento e na reabilitação das funções físicas do corpo. Você conhece essa profissão? Realize uma pesquisa para investigar as áreas de atuação dêêsse profissional e compartilhe oralmente os dados obtidos com seus côlégas.
Página cento e quarenta
SAIBA +
Atividade física e equilíbrio

Exercícios físicos são essenciais para a melhora da saúde humana, tornando o organismo mais resistente e menos vulnerável às doenças.
De forma simplificada, os exercícios físicos podem sêr classificados em: aeróbicos, quando aceleram a respiração e a freqüência cardíaca; de fôrça, quê exigem a contração muscular, melhorando, assim, a capacidade de tensão e evitando rompimentos; de alongamento, quê auxiliam os músculos a atingirem maiores amplitudes, melhorando a flexibilidade e a mobilidade; e de equilíbrio, quê auxiliam a sustentação do corpo, aumentando a capacidade de manter a postura e evitando quedas. Estes tipos de exercício são trabalhados quando alguma atividade física é realizada, embora em intensidades diferentes a depender do objetivo da atividade.
O equilíbrio é uma importante capacidade a sêr desenvolvida para quê quaisquer exercícios sêjam realizados, pois contribui para o alongamento, o fortalecimento e a respiração. Essa prática é especialmente recomendada porque a capacidade de se equilibrar é perdida naturalmente com o passar dos anos.
O equilíbrio não é apenas necessário para se manter nas pontas dos pés ou fazer acrobacias, mas também é essencial para caminhar, ao garantir estabilidade a cada passo, o quê evita quedas resultantes de possíveis tropeços.
Com o passar dos anos, há uma perda natural de musculatura, reduzindo, assim, a capacidade de realizar algumas tarefas, antes executadas com mais facilidade. Por isso, é importante a prática de exercícios físicos e a compreensão de quê o envelhecimento é um processo natural, para quê se respeite o corpo e suas limitações.
ATIVIDADES
1. Você se considera uma pessoa sedentária ou costuma realizar exercícios físicos com regularidade?
2. Quais são as principais razões quê podem levar alguns jovens a não manterem uma rotina saudável, como a prática de exercícios físicos, a manutenção do sono, a alimentação adequada, entre outras? Converse com seus côlégas e, em grupo de até quatro integrantes, elaborem um material quê incentive as pessoas jovens a manterem hábitos saudáveis quê incluam a prática regular de atividades físicas, compartilhando nas mídias digitais da escola.
3. Faça uma pesquisa sobre os exercícios físicos de equilíbrio, de fortalecimento, aeróbicos e de alongamento, quê possam sêr realizados no espaço escolar, como a quadra de esportes. Converse com o professor de Educação Física e, em conjunto com sua turma, organizem um evento com o objetivo de incentivar a prática de exercícios físicos. Neste dia, a comunidade escolar poderá sêr convidada a participar de exercícios coletivos e disputas monitoradas, motivando, assim, a saúde, a interação social, a competitividade e o respeito. Para isso, discutam com a direção da escola e verifiquem como realizar essa ação.
ESPAÇOS DE APRENDIZAGEM
• O texto a seguir apresenta mais informações acerca do tema equilíbrio.
Saiba a importânssia de trabalhar o equilíbrio. Publicado por: Correio Braziliense. Disponível em: https://livro.pw/nmvxf. Acesso em: 19 ago. 2024.
Página cento e quarenta e um
Momento de uma fôrça ou torque
As imagens a seguir representam uma pessoa utilizando um pé de cabra para arrancar um prego de três formas distintas, aplicando as forças , e . As linhas tracejadas são chamadas linhas de ação da fôrça, obtidas em relação ao local de aplicação da fôrça. Observando as imagens, você considera quê em qual delas será aplicada uma fôrça de menor intensidade para arrancar o prego?
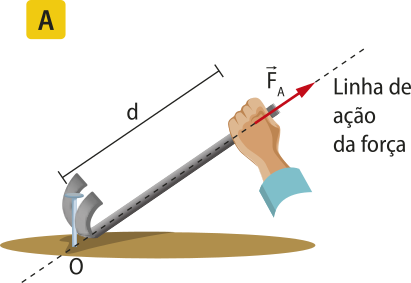
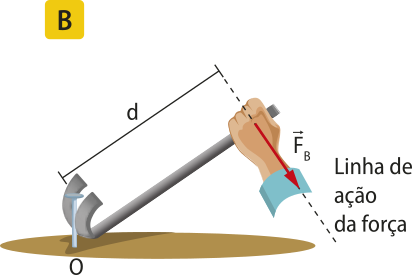
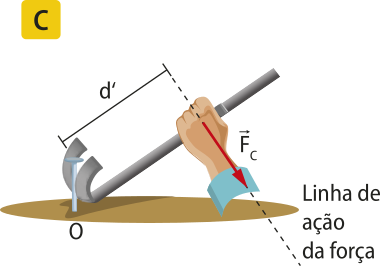
Para retirar o prego, é preciso quê a ferramenta execute um movimento de rotação em torno do ponto O, designado ponto fixo, ou seja, a linha de ação da fôrça não póde passar pelo ponto fixo. Além díssu, quanto mais distante do ponto de apôio a fôrça for aplicada, menor a sua intensidade (o quê é possível observar na posição da maçaneta de uma porta, ao fechá-la ou abri-la).
A grandeza física quê representa a ação de uma fôrça quê causa rotação de um corpo extenso é chamada momento de uma fôrça ou torque, uma grandeza vetorial designada por .
Para quê a rotação ocorra, deve existir uma distância perpendicular entre a linha de ação da fôrça e o eixo de rotação quê passa pelo ponto fixo. Essa distância é chamada braço de alavanca ou braço de fôrça. Na ilustração B, o braço de alavanca é d, na ilustração C, o braço de alavanca é d'. Logo, das situações representadas, aquela quê demandará a aplicação de uma fôrça de menor intensidade, é a representada em B, com linha de ação da fôrça perpendicular à ferramenta e a posição de aplicação mais distante do ponto fixo O. Na ilustração A, embora a posição de aplicação da fôrça seja na extremidade da ferramenta, também a uma distância d do ponto fixo O, ela é aplicada na mesma linha do ponto O, o quê não produz movimento.
A intensidade do momento de uma fôrça é dada pelo produto da fôrça F pelo comprimento do braço de alavanca d.
M = Fd
PENSE E RESPONDA

2 por quê as maçanetas de portas são normalmente instaladas distantes das dobradiças?
Página cento e quarenta e dois
No SI, a unidade de medida de momento de uma fôrça é nílton métro (Nm). Por convenção, adota-se o sinal positivo quando a tendência do movimento for no sentido anti-horário (M = Fd) e o negativo no sentido horário (M = −Fd).
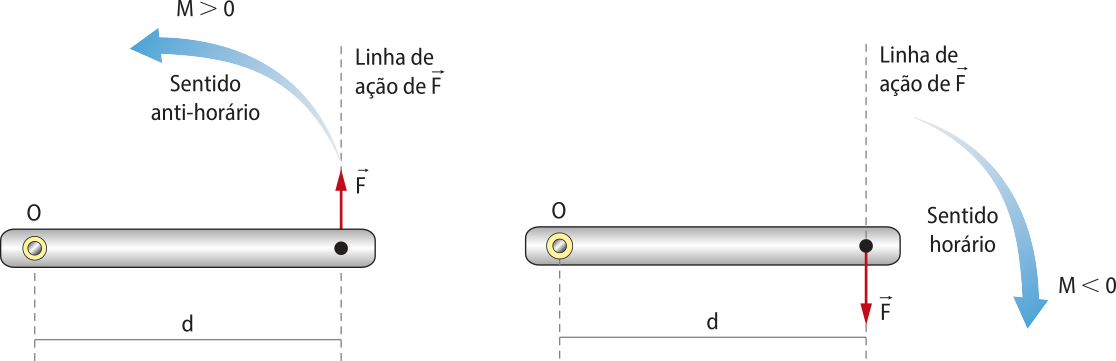
ATIVIDADES
5. Se o objetivo de um operário é fazer girar um parafuso utilizando a menor fôrça possível, em qual ponto da chave (A, B, C ou D) ele deve aplicar a fôrça? Justifique.

6. Na placa retangular da figura a seguir, estão aplicadas três forças. Essas forças pertencem ao plano da placa. Determine o momento resultante dessas forças em relação ao ponto C. Em quê sentido esta placa gira?
Zero; não gira.
7. Para montar e fixar as peças quê compõem o suporte representado na figura, um serralheiro precisa saber quais são os momentos da fôrça de 1.000 N, em relação aos pontos A, B e C. Determine esses valores.
MA = 1.000 Nm; MB = 0; MC = −5.000 Nm
Condições de equilíbrio de um corpo extenso
Para estudar o equilíbrio de corpos extensos, é necessário definir uma grandeza, o centro de massa (CM). O centro de massa deve sêr entendido como o ponto em quê se póde considerar aplicada toda a massa do corpo em análise.
Perceba quê, ao aplicar forças em um corpo extenso, ele poderá iniciar um movimento de rotação, mesmo quê seu centro de massa permaneça em equilíbrio.

Aproveitar êste momento para retomar a definição de ponto material e discutir quê, nesse caso, o ponto póde realizar apenas um movimento de translação, enquanto um corpo extenso póde descrever um movimento de rotação e translação.
Página cento e quarenta e três
Se um corpo homogêneo apresentar um elemento de simetria (eixo ou plano), seu centro de massa pertencerá a esse elemento. Considere os exemplos:

ESPAÇOS DE APRENDIZAGEM
• Neste sáiti, é possível realizar uma visita virtual 3D pelo Museu Óscar Niemáiêr.
Museu Óscar Niemáiêr.
Publicado por: MON eventos. Disponível em: https://livro.pw/beqzu. Acesso em: 19 ago. 2024.
Quando um corpo extenso se encontra em campo gravitacional uniforme, seu centro de massa coincide com o centro de gravidade (CG). O centro de gravidade de um corpo extenso corresponde ao ponto de aplicação da fôrça peso.
Um corpo extenso está em equilíbrio quando o seu estado de repouso ou de movimento não se modifica, tanto em relação à translação quanto em relação à rotação. No caso do corpo extenso, as condições de equilíbrio são:
1ª condição: A soma vetorial das forças quê agem simultaneamente no corpo extenso deve sêr nula.
= 0 (Não há movimento de translação com aceleração.)
2ª condição: A soma algébrica das intensidades dos momentos das forças quê agem simultaneamente no corpo extenso, em relação a um ponto O qualquer, deve sêr nula.
M = 0 (Não há movimento de rotação.)
ATIVIDADES
8. Uma pessoa pegou uma régua medindo 0,5 m de comprimento e a colocou sobre um apôio, de tal forma quê a extremidade esquerda ficou a 0,20 m do apôio. Nessa extremidade, foi fixado um cubo de madeira cujo peso é 6 N. Para tentar manter a régua equilibrada, horizontalmente, precisou colocar, na extremidade direita, outro objeto cuja massa fosse ideal para manter o equilíbrio.
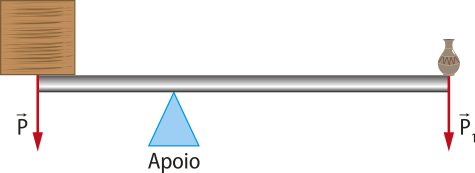
Despreze o peso da régua e determine a intensidade da fôrça peso P1 dêêsse objeto.
4 N
9. O esquema a seguir representa uma gangorra homogênea quê tem 10 m de comprimento e está apoiada em C, distante 4 m de A. Na extremidade A está uma garota de peso 600 N. Qual é o peso do garoto quê está em B para quê a gangorra fique em equilíbrio horizontal?
PB = 400 N
Página cento e quarenta e quatro
Texto para as atividades 10 e 11:
Um armazém recebe sacos de açúcar de 24 kg para quê sêjam empacotados em embalagens menóres. O único objeto disponível para pesagem é uma balança de dois pratos, sem os pesos metálicos.

10. (Enem/MEC) Realizando uma única pesagem, é possível montar pacotes de:
a) 3 kg.
b) 4 kg.
c) 6 kg.
d) 8 kg.
e) 12 kg.
Resposta: d)
11. (Enem/MEC) Realizando exatamente duas pesagens, é possível montar pacotes de:
a) 3 kg ou 6 kg.
b) 3 kg, 6 kg ou 12 kg.
c) 6 kg, 12 kg ou 18 kg.
d) 4 kg ou 8 kg.
e) 4 kg, 6 kg ou 8 kg.
Resposta: c)
Alavancas
As alavancas são máquinas simples nas quais comumente se aplicam duas fôrças: a força potente, quê é aplicada externamente; e a fôrça resistente, quê se deseja superar. A finalidade de uma alavanca é a multiplicação de uma fôrça potente aplicada.
Observe alguns tipos de alavanca, classificados de acôr-do com as posições das forças quê agem sobre ela e do ponto de apôio.
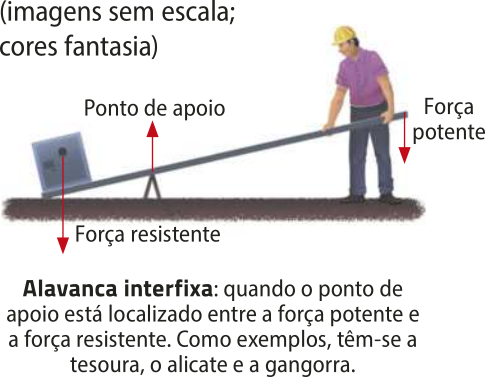
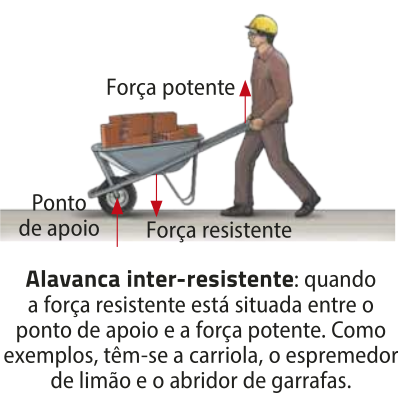
![Representação de alavanca interpotente. Um braço de uma pessoa levanta um halter. A 'Força potente' está localizada no músculo do braço[seta vertical para cima]. A 'Força resistente' está na mão da pessoa, segurando o halter. E o ponto de apoio, está no cotovelo[seta vertical, apontando para baixo].](../resources/images/ek_9/ek_919442c3550dc08b2829d67cad58aeeb.png)
ATIVIDADES
12. Durante uma sessão de fisioterapia, um paciente é orientado a manter a perna em equilíbrio por determinado tempo na posição A, e, posteriormente, repetir a ação na posição B. No pé do paciente, foi amarrado um objeto de 3,0 kgf, conforme indica a figura.
Estime o comprimento da perna do paciente e calcule, para as duas posições, os momentos das forças em relação à articulação, representada pelo ponto O.
2,70 kgf·m; 1,35 kgf·m
13. Os objetos descritos a seguir, quando em uso, dêsempênham a função de alavanca. Determine o tipo de alavanca quê cada um representa:
a) pedal do acelerador de um carro;
Interpotente.
b) pinça;
Interpotente.
14. Liste em seu caderno alguns objetos do seu dia a dia quê possam servir de exemplos de alavanca. dêz-creva o tipo de alavanca quê cada um representa.
Página cento e quarenta e cinco
Introdução à Hidrostática
A Hidrostática é a área da Física quê estuda fluidos em repouso, ou seja, fluidos em equilíbrio estático ( = 0 e = 0). Os líquidos e gases são denominados fluidos por não terem arranjo molecular definido, não possuindo forma fixa.
Em Hidrostática, para o estudo dos fluidos, é necessário conhecer duas grandezas: densidade e pressão.
Densidade e massa específica
A grandeza física quê relaciona a massa m de um corpo ao seu volume V é a densidade d, definida como:
d =
Um corpo póde sêr formado por uma garrafa de vidro contendo á gua ou uma bexiga cheia de ar, por exemplo. Nomeia-se massa específica (m) a relação entre a massa e o volume de uma substância homogênea, como ar, gasolina, áucôl, á gua, vidro, alumínio e ouro, por exemplo.
μ =
No SI, a unidade de medida de ambas as grandezas é o quilograma por métro cúbico (kg/m3). Outras unidades comumente utilizadas são kg/L e g/ml (o mesmo quê g/cm3).
1 g/mL = 1 g/cm3 = 1 kg/L = 1.000 kg/m3
De acôr-do com as definições, as grandezas densidade e massa específica coincidem para um corpo maciço e homogêneo formado por uma única substância. O mesmo ocorre para fluidos homogêneos. Sendo assim, o termo densidade será mais freqüentemente utilizado nesta obra.
Pressão
Quando uma fôrça é aplicada em determinado corpo, a área de aplicação da fôrça é um elemento determinante para verificar os efeitos dessa fôrça. Pode-se observar isso com o formato das agulhas, como a da imagem a seguir, quê têm pontas fínas, o quê facilita a entrada em um corpo.
A pressão exercida pela fôrça quê age sobre uma superfícíe é diretamente proporcional à sua intensidade e inversamente proporcional à área da superfícíe de contato.
Quando uma fôrça é aplicada em uma área A, a pressão exercida é determinada da seguinte forma.
p =
No SI, a unidade de medida de pressão é o nílton por métro quadrado (N/m2), quê também é denominada pascal (Pa), em homenagem ao filósofo, físico e matemático francês Blaise Pascal (1623-1662). Outras unidades comumente utilizadas para a grandeza pressão são atm, bar e mmHg (milímetro de mercúrio) ou torr. As definições destas unidades serão feitas ao longo dos estudos.
1 atm = 1 bar = 105 Pa = 760 mmHg
PENSE E RESPONDA
3 por quê é necessário afiar as facas após cérto tempo de uso?

Página cento e quarenta e seis
Pressão atmosférica
A Terra possui uma camada de gases denominada atmosféra, quê possui massa e está sujeita à ação do campo gravitacional terrestre. Portanto, a fôrça peso do ar sobre a superfícíe da Terra consiste na pressão atmosférica.
Para medir a pressão atmosférica, Torit éli utilizou um tubo de vidro, de 1 m de comprimento, totalmente cheio de mercúrio e um recipiente parcialmente cheio de mercúrio. Ele tampou a extremidade aberta do tubo e o mergulhou no recipiente, percebendo quê o nível de mercúrio do tubo permanecia em equilíbrio na altura de 76 cm em relação à superfícíe do líquido do recipiente, cuja situação está representada na imagem a seguir.
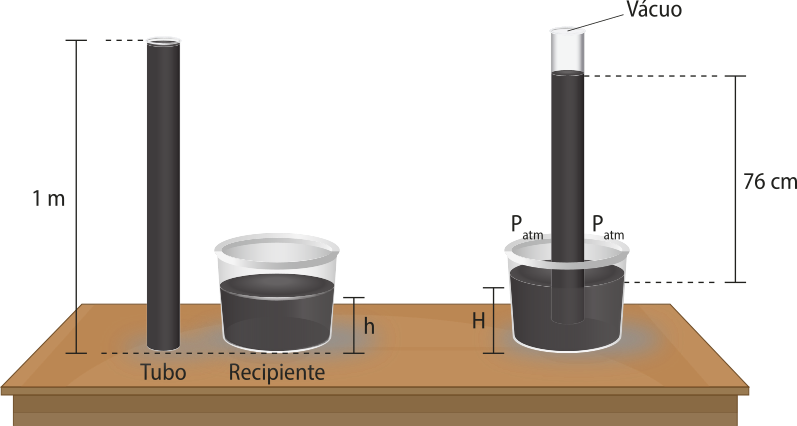
Analisando o experimento, ele deduziu quê o equilíbrio da coluna de mercúrio era mantido pela pressão atmosférica, quê agia na superfícíe do mercúrio do recipiente. Assim, concluiu quê a pressão atmosférica patm equivale à pressão exercida por uma coluna de mercúrio de 76 cm de altura.
1 atm = 76 cmHg
• 1 atm ≃ 1,013 ⋅ 105 Pa
• 1 mmHg = 1 torr
1 torr = 1 mmHg
Aproveitar para discutir e retomar com os estudantes as aproximações de valores realizadas ao longo do estudo da Física pois, neste momento, o objetivo é compreender a grandeza pressão e identificar suas unidades de medida.
Torit éli realizou esse experimento ao nível do mar, onde a pressão atmosférica foi convencionada como 1 atm. A pressão atmosférica diminui com o aumento da altitude.
Observe os valores aproximados da pressão atmosférica em relação à altitude.
Altitude (m) |
0 (nível do mar) |
500 |
1.000 |
2.000 |
3.000 |
4.000 |
5.000 |
6.000 |
|---|---|---|---|---|---|---|---|---|
patm (cmHg) |
76 |
72 |
67 |
60 |
53 |
47 |
41 |
36 |
Fonte: GALVANI, Emerson. Pressão atmosférica. São Paulo: Universidade de São Paulo, [ca. 2008]. Localizável em: p. 10 do pdf. Disponível em: https://livro.pw/vkqrq. Acesso em: 19 ago. 2024.
A montagem experimental elaborada por Torit éli foi uma versão rudimentar do barôometro, instrumento usado para medir a pressão atmosférica.

Página cento e quarenta e sete
ATIVIDADE RESOLVIDA
1. Um menino toma um copo de suco, com o auxílio de um canudinho, como o da imagem. Como se explica a subida do suco no interior dêste canudo?

Resolução
Quando o ar do canudo é sugado, a pressão no seu interior torna-se menor do quê a pressão atmosférica quê age na superfícíe do suco. Desta diferença de pressão, surge uma fôrça resultante quê provoca a subida do suco no interior do canudo.
ATIVIDADES
15. Um carpinteiro, ao manusear um prego, coloca-o entre os dedos polegar e indicador, de tal forma quê a “cabeça” do prego fica presa ao indicador e a ponta ao polegar. Considerando essa situação, responda, em seu caderno, às perguntas a seguir.
a) A fôrça quê o polegar exerce sobre o prego é igual à fôrça exercida pelo indicador?
Sim, as forças têm a mesma intensidade, pois o prego está em equilíbrio.
b) A pressão exercida nos dois dedos é igual?
A pressão é maior sobre o polegar.
16. Em uma fábrica de móveis, foi necessário quê uma pessoa de peso 750 N se sentasse sobre uma banqueta de quatro pernas, cujo peso é 50 N, para testá-la. Considere quê a banqueta está em equilíbrio sobre uma superfícíe horizontal e determine a pressão (em N/m2) quê cada perna exerce sobre essa superfícíe, sabendo quê cada perna tem seção reta de área 4 cm2.
5,0 · 105 N/m2
17. Na calibração de p-neus de veículos e bicicletas normalmente as máquinas estão reguladas na unidade de medida psi uma unidade de medida do sistema britânico (pound pêr square inch, quê significa em português libras por polegadas quadradas). Esta unidade faz referência à libra-força, pois trata-se de uma medida de fôrça e não de massa. Uma pessoa comumente chega no local de calibração e diz quê irá “colocar 30 libras”.
a) Qual é a forma corretar de expressar a pressão quê se deseja para o pneu?
30 psi, ou 30 libras por polegadas quadradas.
b) Junto aos côlégas, façam uma pesquisa e verifiquem como é feita a transformação da unidade de medida psi para pascal. Em
seguida, verifiquem qual é a medida da pressão interna de um pneu de 30 psi em pascal.
Cerca de 206.925 Pa.
18. Durante o processo de formação de róchas e relevos, por meio da ação de vulcões, é importante lembrar quê parte do magma originado dos vulcões resfria no interior da Terra e do solo, dando origem às róchas intrusivas. A outra parte escorre sobre a superfícíe terrestre, originando as róchas extrusivas. O granito é uma rocha magmática intrusiva, e sua extração é muito importante para atividades como a construção civil. Contudo, a extração do granito e de vários tipos de minérios é responsável por significativo impacto ambiental, causando desequilíbrio na á gua, no ar, no solo, no subsolo e na paisagem. Considere um bloco em formato de paralelepípedo retangular, cuja área da base é 2.000 cm2 e a altura, 60 cm. Sendo g = 10 m/s2 e μgranito = 2,5 ⋅ 103 kg/m3, determine:
a) a massa do bloco;
300 kg
b) em N/m2, a pressão exercida pelo bloco sobre a superfícíe, considerada plana e horizontal.
1,5 · 104 N/m2
19. Ao abrir uma lata de azeite, é recomendado fazer dois furos opostos na face superior da lata. Explique por quê tal procedimento é bem-sucedido.
20. Um astronauta necessita de uma roupa especial para fazer a manutenção de equipamentos fora da nave espacial. Explique o quê poderia acontecer, caso ocorresse um pequeno furo na roupa, durante a manutenção, e ele conseguisse ficar um bom tempo sem precisar respirar.
Página cento e quarenta e oito
Teorema de Stevin
A investigação de Torit éli acerca dos fenômenos da pressão mostrou quê existe uma relação entre a altura de um fluido e a pressão exercida por ele.
![Ilustração de um recipiente de vidro cheio de líquido homogêneo e em equilíbrio, com altura 'h' projetada em dois pontos do líquido, acima e abaixo e área [A].](../resources/images/ek_e/ek_eb0e829adca05de12fad60aaff166884.png)
A ilustração representa um recipiente quê contém um líquido homogêneo e em equilíbrio. A fôrça exercida no fundo do recipiente corresponde à fôrça peso do líquido F = P = mg.
O recipiente cilíndrico de altura h e área da base A tem volume V = Ah. Se ele estiver totalmente cheio de líquido, o volume dêêsse líquido também será V = Ah.
A densidade d do líquido homogêneo permite relacionar sua massa m e seu volume V.
d = ⇒ m = dV
A pressão p exercida pelo líquido no fundo do recipiente será:
p = ⇒ p = dgh
Essa expressão foi ôbitída pelo físico e matemático belga Simon Stevin (1548-1620), quando verificou quê a pressão exercida em cérto ponto do interior de um fluido em repouso depende da altura de fluido acima dêste ponto, e não do volume, conclusão conhecida como teorema de Stevin.
Quando a pressão atmosférica patm age sobre a superfícíe livre do líquido em equilíbrio, a pressão total (ou absoluta) p exercida em um ponto no interior dêêsse fluido é determinada pela soma da pressão atmosférica com a pressão do fluido.
p = patm + dgh
PENSE E RESPONDA

4 Se o experimento de Torit éli fosse realizado com á gua, em qual altura a coluna se estabilizaria?
Vasos comunicantes
Chama-se de vasos comunicantes a ligação de dois ou mais recipientes por dutos fechados. Um recipiente formado por ramos ligados entre si ou um simples tubo em formato de U podem sêr considerados sistemas de vasos comunicantes. Neles é possível observar quê a superfícíe livre de um líquido atinge sempre a mesma altura nos frascos abertos quê se comunicam. O teorema de Stevin ajuda a compreender esse comportamento dos líquidos homogêneos e em equilíbrio.
De acôr-do com o teorema de Stevin, todos os pontos da superfícíe de um líquido homogêneo, em repouso, mantêm-se no mesmo plano horizontal porque estão submetidos à mesma pressão atmosférica, independentemente da forma como os recipientes se comunicam.

Página cento e quarenta e nove
ATIVIDADES
21. Sabe-se quê a pressão mássima quê um mergulhador póde suportar é equivalente a 10 vezes o valor da pressão atmosférica. Qual é a profundidade mássima quê um mergulhador póde descer abaixo da superfícíe de um rio cuja densidade da á gua é 1g/cm³?
Dados: patm = 1,0 ⋅ 105 N/m2 e g = 10 m/s2.
h = 90 m
22. Durante uma aula de mergulho, o instrutor mergulha carregando um balão de borracha. dêz-creva o quê ocorre com o volume do balão e com a pressão hidrostática exercida nele, à medida quê o mergulhador atinge profundidades maiores.
23. Um sino de mergulho é um instrumento utilizado para pesquisas em regiões de diferentes profundidades do mar, conforme o quê está sêndo investigado. Em uma dessas situações, um sino foi posicionado a uma profundidade de 50 m. Para preservar a saúde de um mergulhador, a pressão interna foi mantida com o mesmo valor da pressão atmosférica ao nível do mar (1,0 ⋅ 105 Pa). Determine, em N/m2, a diferença entre as pressões exercidas, dentro e fora, junto às paredes do sino.
5,0 · 105 N/m2

24. Coloca-se em um sistema de vasos comunicantes á gua e óleo cujas densidades são, respectivamente, 1 g/cm3 e 0,8 g/cm3. A altura da coluna de óleo é de 30 cm.
Qual é a altura da coluna de á gua medida acima do nível de separação entre esses líquidos?
24 cm
25. Ao medir a pressão sanguínea de uma pessoa deitada no solo, o valor encontrado foi 11 por 7, isto é, pressão mássima 110 mmHg (14.000 N/m2) e pressão mínima 70 mmHg (9.210 N/m2). As bolsas de soro ou de medicamentos são posicionadas sempre acima da altura em quê se encontra o paciente. Qual é a altura mínima a quê deverá estar uma bolsa para vencer a pressão arterial mássima da pessoa? Considere a densidade do soro igual a 103 kg/m3 e a gravidade no local igual a 10 m/s2.
1,4 m
26. (Unicamp-SP) Suponha quê o sangue tenha a mesma densidade quê a á gua e quê o coração seja uma bomba capaz de bombeá-lo a uma pressão de 150 mm de mercúrio acima da pressão atmosférica. Considere uma pessoa cujo cérebro esteja 50 cm acima do coração e adote, para simplificar, 1 atm = 750 mmHg.
a) Até quê altura o coração consegue bombear o sangue?
2,0 m
b) Suponha quê essa pessoa esteja em outro planêta. A quê aceleração gravitacional mássima ela póde estar sujeita para quê ainda receba sangue no cérebro?
4,0gTerra
27. O snorkeling é uma prática esportiva em quê se mergulha próximo da superfícíe da á gua. Nesse esporte, usa-se o snorkel para respirar e a máscara para observar a vida aquática. Considere quê uma mergulhadora resôuva utilizar um tubo quê desempenhe a mesma função do snorkel, ou seja, quê a ajude a respirar debaixo da superfícíe da á gua.
a) Qual será a profundidade mássima quê ela poderá atingir para quê não tenha problemas respiratórios, considerando quê, na média, o pulmão humano consegue suportar variações de pressão até atm?
50 cm
b) Com seus côlégas, conversem a respeito da importânssia de práticas turísticas como o snorkeling. Vocês conhecem atividades semelhantes? Que tipos de ação ela póde promover para a preservação e conscientização ambiental?
Página cento e cinquenta
OFICINA CIENTÍFICA
Quem faz a fôrça?
Faça o experimento somente na presença do professor.
A atmosféra terrestre é dividida em algumas camadas segundo características específicas. Os sêres humanos vivem na troposféra, a camada mais próxima da superfícíe da Terra, quê comporta cerca de 80% da massa atmosférica e quê possui entre 10 km e 20 km de altura.
Interage-se com a atmosféra o tempo todo, afinal, é uma das condições para a existência de vida. Porém, será quê é possível visualizar a pressão atmosférica em ação? É o quê será investigado neste experimento.
Materiais
• cartolina
• tesoura
• 1 copo
• á gua
• 1 bacia
Procedimentos
• Encha completamente o copo com á gua.
• Recorte um pedaço retangular de cartolina de tamãnho maior do quê a abertura (“boca”) do copo.
• Coloque o pedaço de cartolina sobre a abertura do copo. Com cuidado, pressione a cartolina d fórma quê ela encoste na á gua e não exista nenhuma camada de ar entre a cartolina e a á gua.
• Vire o copo de “boca para baixo”, lentamente, segurando a cartolina; depois solte-a com cuidado. Faça esse movimento acima da bacia, para evitar o derramamento de á gua.
ATIVIDADES
1. O quê ocorreu quando o copo foi virado? Em grupo, converse com seus côlégas sobre o quê foi observado e elaborem uma justificativa.
2. Esta investigação póde sêr realizada com um copo de qualquer altura? Justifique sua resposta.
3. Quais foram as dificuldades enfrentadas na realização desta prática?
Página cento e cinquenta e um
Princípio de Pascal
De acôr-do com o teorema de Stevin, os pontos de um líquido homogêneo em equilíbrio, pertencentes ao mesmo plano horizontal, estão sôbi a mesma pressão. E quando os pontos de um líquido estão submetidos a uma variação de pressão?
Observe as figuras quê representam duas situações de um mesmo balão de vidro, com êmbolo móvel e á gua em seu interior.
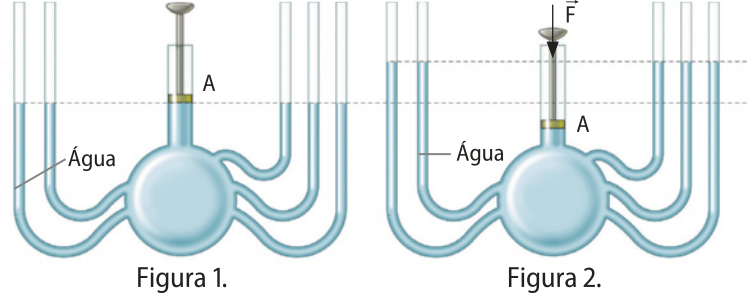
Na Figura 1, o nível do líquido é igual em todos os tubos. Na Figura 2, o êmbolo é pressionado para baixo, submetendo a á gua a uma variação de pressão transmitida a todos os pontos do líquido. Como consequência, o novo nível da á gua permanéce igual em todos os tubos. Isso ocorre porque a á gua é um líquido incompressível, ou seja, sua densidade não se altera com a variação de pressão.
Pascal, em 1650, com base em vários experimentos práticos, elaborou o seguinte princípio:
Se um ponto qualquer de um líquido homogêneo e incompressível, em equilíbrio, sofre uma variação de pressão (delta)"p, todos os pontos dêêsse líquido serão submetidos a essa mesma variação.
Uma das aplicações mais comuns do princípio de Pascal ocorre em sistemas hidráulicos, como em prensas, elevadores, pontes levadiças ou freios automotivos. Alguns dêêsses sistemas possuem a característica de multiplicar a fôrça quê é aplicada a um de seus êmbolos.
Analise o funcionamento de uma prensa hidráulica, com êmbolos de áreas trans versais A1 e A2, quê contém um líquido incompressível em equilíbrio.
Ao aplicar uma fôrça de intensidade ,perpendicularmente ao êmbolo 1, obtém-se, perpendicularmente ao êmbolo 2, uma fôrça de intensidade transmitida pelo líquido.
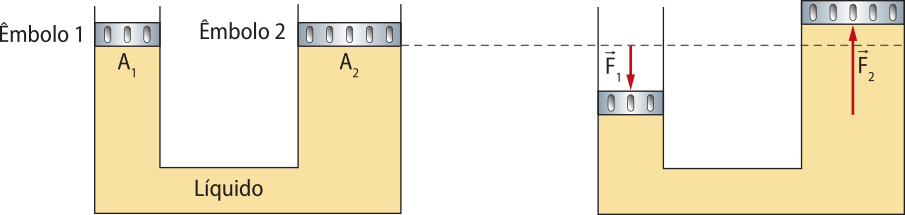
De acôr-do com o princípio de Pascal, os acréscimos de pressão sôbi os êmbolos são iguais:
(delta)"p1 = (delta)"p2. Portanto:
Analisando a relação anterior, se: A2 > A1 ⇒ F2 > F1.
Página cento e cinquenta e dois
ATIVIDADES
28. O princípio de Pascal fundamenta o funcionamento da prensa hidráulica. O quê você diria a respeito dêêsse dispositivo se alguém afirmasse quê o funcionamento da prensa hidráulica é uma maneira de multiplicar energia?
28. A afirmação é falsa, pois tal dispositivo multiplica forças, não energia.
29. Um motorista observa quê o radiador de seu carro furou. Também nota quê, quando o motor do carro está kemte, a á gua vaza mais facilmente do quê quando o motor está frio (água fria). Explique tal fenômeno com base no princípio de Pascal.
30. Em uma prensa hidráulica, os êmbolos são formados por dois cilindros cujos raios médem 20 cm e 400 cm. Para equilibrar um corpo de 5.000 kg de massa colocado no êmbolo maior, qual é o valor da fôrça, em nílton, quê deve sêr aplicada no êmbolo menor?
Dado: g = 10 m/s2.
125 N
31. A prensa hidráulica representada na figura está em equilíbrio. Calcule o módulo do peso da carga A quê está apoiada sobre o êmbolo de área 0,80 m2. Sabe-se quê o peso da carga B é de 40 N e quê o êmbolo em quê ela está apoiada tem área de 50 cm2.
6.400 N

32. O projeto de uma prensa hidráulica prevê, para seu equilíbrio, quê a aplicação de uma fôrça de 5,0 ⋅ 103 N sobre o êmbolo maior necessita de uma fôrça de 5,0 ⋅ 10 N sobre o êmbolo menor. Sabendo-se quê a área do êmbolo maior é 2,0 ⋅ 103 cm2, qual será a área do êmbolo menor?
2,0 ⋅ 10 cm2
Teorema de arquimédis
Uma pessoa segura um tijolo e o mergulha na á gua. Ao fazê-lo, percebe quê fica mais fácil sustentá-lo enquanto ele está submérso.
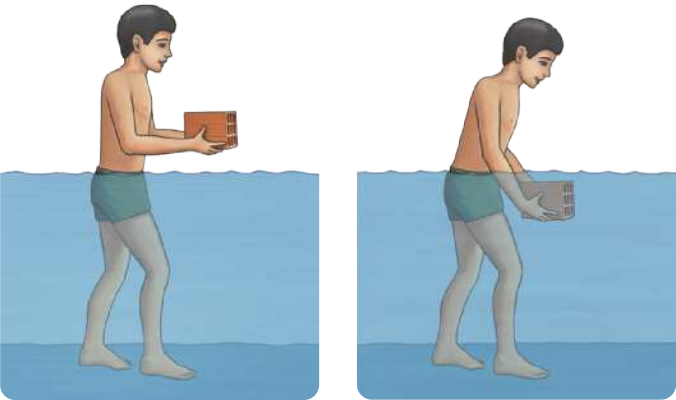
Mas se a fôrça peso sobre o tijolo é a mesma, por quê isso ocorre?
O fato de sêr mais fácil sustentar um corpo dentro da á gua indica a existência de uma fôrça vertical para cima, além da fôrça exercida pela pessoa. Esta fôrça é denominada empuxo e surge sobre um corpo quê esteja imérso em um fluido.
PENSE E RESPONDA

5 Como é possível um navio flutuar na á gua?
Página cento e cinquenta e três
Um método para determinar a intensidade do vetor fôrça de empuxo foi desenvolvido pelo matemático grego arquimédis (287 a.C.-212 a.C.).
A representação a seguir indica um corpo suspenso por um dinamômetro, quê indica uma fôrça peso de 6 N. Ao lado dêste, encontra-se um recipiente com um líquido e um recipiente menor, capaz de coletar o líquido quê extravasar, sobre outro dinamômetro de ponteiro.
Ao mergulhar o corpo inteiramente em um líquido, o dinamômetro no qual ele está preso passa a indicar 4 N. Esta mudança de leitura indica quê outra fôrça passou a agir sobre o corpo quando ele ficou submérso.
O líquido quê extravasou foi coletado por outro recipiente, e o dinamômetro de ponteiro abaixo dele indica 2 N, o mesmo valor da variação da leitura do outro dinamômetro.
Estas foram as observações feitas por arquimédis, d fórma quê o enunciado quê explica êste tipo de situação ficou conhecido como teorema de arquimédis.
Um corpo total ou parcialmente submérso em um fluido em equilíbrio, recebe a ação de uma fôrça de empuxo vertical para cima, com intensidade igual ao peso do volume de fluido deslocado pelo corpo.
Considere quê o líquido do experimento descrito anteriormente possui densidade dL e o líquido deslocado tem massa mD e volume VD, então: dL = ⇒ mD = dLVD
A intensidade da fôrça de empuxo é igual à intensidade da fôrça peso do fluido deslocado.
E = PD ⇒ E = mDg ⇒ E = dLVDg
ATIVIDADE RESOLVIDA
2. Durante um experimento, um cubo de madeira de aresta 1,0 m é colocado em um recipiente contendo á gua. Notou-se quê o cubo flutuou com 60% do seu volume submérso. Considere g = 10 m/s2 e a densidade da á gua 1,0 ⋅ 103 kg/m3. Determine a intensidade do empuxo exercido pela á gua sobre o bloco de madeira.
![Ilustração de um pote de vidro, com água, onde flutua um cubo. Do cubo saem duas setas perpendiculares desenhadas, apontando para cima[E] e para baixo[P].](../resources/images/ek_d/ek_d4d9c46d6854f0c12aa50e6881bfb467.png)
Resolução
Pelos dados: Vcubo = (1,0)3 = 1,0 m3;
Vlíquido deslocado = VD = 60%Vcubo = 0,60 ⋅ 1,0 = 0,60 m3; dL = dá gua = 1,0 ⋅ 103 kg/m3
E = dLVDg ⇒ E = 1,0 ⋅ 103 ⋅ 0,60 ⋅ 10 ⇒ E = 6,0 ⋅ 103 N
Página cento e cinquenta e quatro
ATIVIDADES
33. Sentados à beira da piscina de um navio, três passageiros observam um corpo totalmente submérso em um copo com á gua. Cada um dos passageiros fez uma afirmação: Passageiro A: A intensidade do empuxo quê age nesse corpo é igual ao peso da á gua deslocada pelo corpo.
Passageiro B: A intensidade do empuxo quê age nesse corpo independe do volume dêêsse corpo.
Passageiro C: O empuxo quê age nesse corpo existe porque a pressão no topo do corpo é menor do quê a pressão na base dele. Qual(is) deles está(ão) correto(s)?
Somente os passageiros A e C estão corretos.
34. Considere duas esferas feitas de um mesmo material e com o mesmo volume de 0,5 m3. A esféra A é maciça e tem massa de 600 kg. A esféra B é oca e tem massa de 200 kg. Ambas são mantidas totalmente submérsas em um recipiente com á gua, mas distantes do fundo do recipiente. Adote g = 10 m/s2 e a densidade da á gua como 1.000 kg/m3.
a) Qual é a intensidade do empuxo quê age nas esferas, expresso em nílton?
5.000 N
b) Ao serem abandonadas, as esferas se móvem na á gua verticalmente para cima ou para baixo? Justifique sua resposta.
34. b) A esféra A se moverá verticalmente para baixo e a B, para cima.
35. Ao sêr indagado pelo avô sobre o peso do bloco quê ele colocou submérso na á gua, um jovem respondeu: “O peso do bloco é 3 N”.
O avô, paciente, respondeu: “As aparências enganam, pois eu verifiquei quê, fora da á gua, o peso dele é 5 N”. Considerando essa conversa, o valor de g = 10 m/s2 e a densidade da á gua 1 g/cm2, determine:
a) o empuxo quê age no bloco;
2 N
b) o volume do bloco;
2 · 10–4 m3
c) a densidade do bloco.
2,5 · 103 kg/m3
36. Ao sêr mergulhado em um reservatório de á gua, um objeto desloca um volume de á gua equivalente a 6 ⋅ 10–4 m3. Determine a intensidade do empuxo quê a á gua exerce no objeto, sabendo quê nesse local g = 10 m/s2 e a densidade da á gua é 1 ⋅ 103 kg/m3.
6 N
37. Uma bola de futeból, cujo volume é 4,0 litros e cuja massa é 0,30 kg, é mantida totalmente submersa na á gua, presa ao fundo de uma piscina por um fio inextensível, de massa e volume desprezíveis, como mostra a figura.
Dados: g = 10 m/s2 e dH2O = 1 ⋅ 103 kg/m3.
A tração no fio é:
a) 40 N
b) 3,7 N
c) 4,3 N
d) 43 N
e) 37 N
Resposta e)
38. (Enem/MEC) Durante uma obra em um clube, um grupo de trabalhadores teve de remover uma escultura de ferro maciço colocada no fundo de uma piscina vazia. Cinco trabalhadores amarraram kórdas à escultura e tentaram puxá-la para cima, sem sucesso.
Se a piscina for preenchida com á gua, ficará mais fácil para os trabalhadores removerem a escultura, pois a
a) escultura flutuará. Dessa forma, os homens não precisarão fazer fôrça para remover a escultura do fundo.
b) escultura ficará com peso menor. Dessa forma, a intensidade da fôrça necessária para elevar a escultura será menor.
c) á gua exercerá uma fôrça na escultura proporcional a sua massa, e para cima. Esta fôrça se somará à fôrça quê os trabalhadores fazem para anular a ação da força-peso da escultura.
d) á gua exercerá uma fôrça na escultura para baixo, e esta passará a receber uma fôrça ascendente do piso da piscina. Esta fôrça ajudará a anular a ação da força-peso na escultura.
e) á gua exercerá uma fôrça na escultura proporcional ao seu volume, e para cima. Esta fôrça se somará à fôrça quê os trabalhadores fazem, podendo resultar em uma fôrça ascendente maior quê o peso da escultura.
Resposta: e)
Página cento e cinquenta e cinco
OFICINA CIENTÍFICA
Flutua ou afunda?
Faça o experimento somente na presença do professor.
A parafina é um produto derivado do petróleo e é utilizada, por exemplo, na confekissão de velas, na indústria alimentícia e na produção de cosméticos e de tintas.
Neste experimento, você investigará as propriedades de flutuabilidade da parafina.
Materiais
• 2 pedaços idênticos de parafina de vela
• 2 recipientes transparentes e de tamãnho semelhante
• áucôl (suficiente para preencher do recipiente)
• á gua (suficiente para preencher do recipiente)
Procedimentos
• Coloque a á gua em um dos recipientes (A) e áucôl em outro recipiente (B).
• Coloque, com cuidado e simultaneamente, um pedaço de parafina na superfícíe da á gua do recipiente A e o outro pedaço de parafina na superfícíe do áucôl do recipiente B. Aguarde até quê, em ambos os recipientes, a parafina atinja o equilíbrio.
• Retire a parafina quê está na á gua e adicione lentamente a á gua dêêsse recipiente (A) no recipiente com áucôl (B). Aguarde até quê a parafina quê estava no recipiente B atinja novamente o equilíbrio.

ATIVIDADES
1. Ao atingir o equilíbrio no recipiente A, a parafina flutua ou afunda na á gua?
2. Ao atingir o equilíbrio no recipiente B, a parafina flutua ou afunda no áucôl?
3. Faça uma pesquisa para descobrir os valores de densidade da á gua, do áucôl e da parafina e anote em seu caderno, atentando para quê estejam na mesma unidade de medida. Analisando esses valores, a condição de flutuação condiz com o quê foi observado na prática?
4. Ao atingir o equilíbrio, a parafina flutua ou afunda na mistura á gua e áucôl?
5. Ocorreram mudanças na posição de equilíbrio da parafina, quando ela estava apenas no áucôl e quando ela estava na mistura áucôl e á gua? Faça, em seu caderno, uma representação do quê foi observado e explique, com base no quê foi estudado ao longo dêste Tema, a situação observada no experimento.
Página cento e cinquenta e seis
ORGANIZANDO AS IDEIAS
O mapa mental a seguir apresenta os principais conceitos estudados nesta Unidade.
No caderno, elabore o seu próprio esquema, organizando os principais conceitos da Unidade e incluindo nele outros termos e ideias quê se relacionam ao quê foi estudado, realizando as associações quê considerar importantes. Por fim, elabore um pequeno texto conectando os conceitos e as ideias presentes no esquema. Essa é uma boa forma de estudar e compreender melhor os conceitos.
Página cento e cinquenta e sete
ATIVIDADES COMPLEMENTARES
Respostas e comentários estão disponíveis nas Orientações para o professor.
Tema 7: O método da Ciência
1. No dia a dia, às vezes as palavras “hipótese” e “teoria” são utilizadas em contextos distintos daqueles relacionados à Ciência. Para os pesquisadores, hipótese é uma suposição quê necessita sêr avaliada e comprovada, enquanto teoria científica é a representação formal de informações, inclusive hipóteses, já avaliadas e comprovadas. Para adquirirem caráter científico, as hipóteses precisam sêr testadas de tal forma quê seja possível considerá-las verdadeiras ou não. De acôr-do com esse texto, avalie se as hipóteses seguintes são científicas ou não e justifique suas respostas.
I. O maior cientista do século XVII foi Isaac níltom.
II. Segundo o biólogo xárlês Dárvim, as manifestações de vida na Terra foram se estruturando, ao longo dos tempos, para formas mais compléksas.
III. A matéria é constituída por hátomus; porém, estes não são as menóres partículas quê a constituem.
Tema 8: Forças e as leis dos movimentos da Dinâmica
2. No Brasil, é obrigatório o uso do cinto de segurança para todos os ocupantes de um veículo.
Em uma freada brusca, a tendência do corpo do motorista ou dos passageiros é permanecer em movimento por:
a) ressonância.
b) inércia.
c) ação e reação.
d) atrito.
e) gravitação.
Resposta: b)
3. (Fatec-SP) A velocidade mássima de um carro na depressão é v = , em quê R é o raio da curvatura e g, a aceleração local da gravidade. A aceleração centrípeta do carro no ponto mais baixo é:
a) g
b) 2g
c) 3g
d) 4g
e) 5g
Resposta: d)
4. (Eear-SP) Na figura a seguir, tem-se um bloco A, de massa igual a 16 kg, quê está colocado sobre uma superfícíe horizontal (coeficiente de atrito estático entre bloco e a superfícíe horizontal igual a 0,4) e ligado por meio de uma kórda ideal (inextensível e de massa desprezível), quê passa por uma polia ideal, a um cilindro B. êste cilindro B, tem massa igual a 0,4 kg e póde sêr preenchido com á gua (densidade igual a 1 g/cm3). Qual o volume de á gua, em litros, quê deve sêr adicionado ao cilindro para quê o bloco A alcance a condição de iminência de movimento, em um local onde o módulo da aceleração da gravidade vale 10 m/s2?
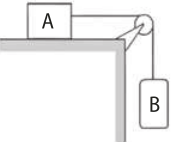
a) 6,0
b) 6,4
c) 60
d) 64
Resposta: a)
5. (UEL-PR) Um bloco de peso 20 N está em repouso sobre um plano inclinado de 30°.
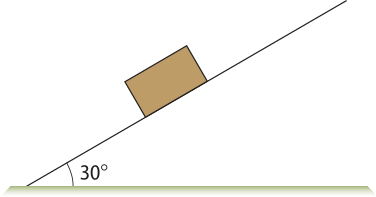
Se o coeficiente de atrito estático entre o bloco e o plano é μe = 0,70, a fôrça de atrito atuante no bloco em módulo será:
a) menor quê 14 N
b) 7,0 N
c) 14 N
d) 20 N
e) 12 N
Resposta: a)
Tema 9: As leis da Gravitação
6. (Enem/MEC) O ônibus espacial Atlantis foi lançado ao espaço com cinco astronautas a bórdo e uma câmera nova, quê iria substituir uma outra danificada por um curto-circuito no telescópio rúboul. Depois de entrarem em órbita a 560 km de altura, os astronautas se aproximaram do rúboul. Dois astronautas saíram da Atlantis e se dirigiram ao telescópio. Ao abrir a porta de acesso, um deles exclamou: “Esse telescópio tem a massa grande, mas o peso é pequeno”.
Página cento e cinquenta e oito
Considerando o texto e as leis de Képler, pode-se afirmar quê a frase dita pelo astronauta
a) se justifica porque o tamãnho do telescópio determina a sua massa, enquanto seu pequeno peso decorre da falta de ação da aceleração da gravidade.
b) se justifica ao verificar quê a inércia do telescópio é grande comparada à dele próprio, e quê o peso do telescópio é pequeno porque a atração gravitacional criada por sua massa era pequena.
c) não se justifica, porque a avaliação da massa e do peso de objetos em órbita tem por base as leis de Képler, quê não se aplicam a satélites artificiais.
d) não se justifica, porque a fôrça peso é a fôrça exercida pela gravidade terrestre, nesse caso, sobre o telescópio, e é a responsável por manter o próprio telescópio em órbita.
e) não se justifica, pois a ação da fôrça peso implica a ação de uma fôrça de reação contrária, quê não existe naquele ambiente. A massa do telescópio poderia sêr avaliada simplesmente pelo seu volume.
Resposta: d)
7. O período de translação de Júpiter corresponde a 12 anos terrestres, aproximadamente. Admita quê o raio médio da órbita de Júpiter seja um quarto do raio médio de órbita de Urano. Calcule, em anos terrestres, aproximadamente, o período de translação de Urano.
Aproximadamente 96 anos terrestres.


(as imagens não estão representadas em escala ou proporção)
Tema 10: Energia e trabalho
8. (UFV-MG) Um bate-estaca sustenta um bloco de 200 kg a altura de 16 m do solo, sobre uma estaca situada 14 m abaixo. Desprezando as forças dissipativas e sêndo g = 10 m/s2, determine:

a) a energia potencial do bloco em relação ao solo;
32.000 J
b) após sua liberação, a energia cinética do bloco, ao atingir a estaca.
28.000 J
9. Uma bola metálica de massa 10 kg é lançada sobre uma superfícíe horizontal lisa, entrando em contato com uma mola e comprimindo-a. Encontre a mássima deformação sofrida pela mola, sabendo quê a velocidade da bola ao chocar-se com a mola é de 2 m/s. Considere a constante elástica da mola 100 N/m.
Aproximadamente 0,63 m.
10. (Unesa-RJ) Uma pequena esféra de peso P = 3,0 N, presa a um fio de comprimento (éli)" = 1,0 m, é solta do ponto A. Quanto aos trabalhos realizados pela fôrça de tração exercida pelo fio, e pelo peso do ponto A ao ponto B, podemos afirmar quê valem, respectivamente:
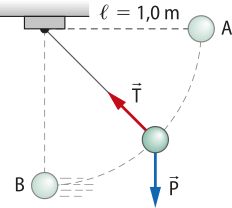
a) −2,0 J e +2,0 J
b) −3,0 J e zero
c) zero e 3,0 J
d) 3,0 J e 3,0 J
e) 3,0 J e zero
Resposta: c)
11. (Unifor-CE) Uma fôrça é aplicada num corpo tangencialmente à trajetória seguida por ele. No deslocamento de 0 a 4 m, o trabalho de vale, em joules:
![Representação gráfica: eixo vertical 'F t'[N] com graduações: zero, dez. vinte. Eixo horizontal 'S'[m] com graduações zero, dois, quatro. A reta formada, tem início em dez vertical, subindo para vinte em dois metros, seguindo estável até quatro metros.](../resources/images/ek_1/ek_1b5987c5229f3776acfaf7624cd6ebac.png)
a) 30
b) 40
c) 50
d) 60
e) 70
Resposta: e)
Página cento e cinquenta e nove
12. (Fuvest-SP) A propaganda de um automóvel apregoa quê ele consegue atingir a velocidade de 108 km/h em um percurso horizontal de apenas 150 m, partindo do repouso.
a) Supondo o movimento uniformemente acelerado, calcule a aceleração do carro.
3 m/s2
b) Sendo 1.200 kg a massa do carro, determine a potência média quê ele desen vólve.
54 kW
Tema 11: Impulso e conservação da quantidade de movimento
13. (hú- hê- érre jota) A cada batimento, o coração humano bombeia cerca de 85 g de sangue. Admita quê a velocidade de saída do sangue bombeado pelo coração seja de 0,4 m/s. A quantidade de movimento do sangue, em kg ⋅m/s produzida pelo coração em um batimento, corresponde aproximadamente a:
a) 0,064
b) 0,048
c) 0,034
d) 0,018
Resposta: c)
14. (Cesgranrio-RJ) Observa-se uma colisão elástica e unidimensional de uma partícula de massa m e velocidade de módulo 0,60 m/s com outra partícula de massa , inicialmente em repouso. Quais são os valores dos módulos das velocidades das partículas, após a colisão?
0,96 m/s e 0,36 m/s
15. (Fuvest-SP) Uma barra rígida e homogênea de 2,0 kg está ligada numa das extremidades a um suporte, por uma mola de constante elástica k = 200 N/m. Na outra extremidade, articula-se a um rolete quê póde girar livremente. Nessa situação, a mola está deformada 5,0 cm.
(Dado: g = 10 N/kg.)
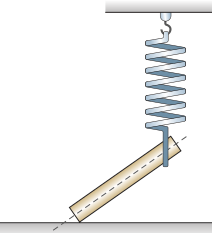
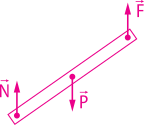
a) Indique as forças externas quê atuam sobre a barra.
b) Qual é a fôrça quê a superfícíe exerce sobre o rolete?
10 N
Tema 12: is-tática e Hidrostática
16. (Famema-SP) Um reservatório de á gua sem tampa apresentou uma trinca em seu fundo de tal forma quê, para repará-lo, teve de sêr esvaziado. Quando o reservatório foi novamente preenchido com á gua, observou-se quê o tempo para o endurecimento do reparo não tinha sido suficiente, pois, assim quê o nível de á gua atingiu 2 m em relação ao fundo, o reparo foi desfeito e a á gua começou a vazar. Sendo a pressão atmosférica igual a 1 ⋅ 105 Pa, a aceleração da gravidade igual a 10 m/s2 e a densidade da á gua igual a 1 ⋅ 103 km/m3, a pressão a partir da qual a á gua começou a vazar foi de
a) 1,0 ⋅ 105 Pa
b) 0,2 ⋅ 105 Pa
c) 0,4 ⋅ 105 Pa
d) 1,2 ⋅ 105 Pa
e) 1,5 ⋅ 105 Pa
Resposta: d)
17. O funcionamento de um elevador hidráulico de carros consiste em um cilindro, de 15 cm de raio, quê comprime o óleo do reservatório, transmitindo essa pressão a outro cilindro de 0,75 cm de raio. Qual é a fôrça mínima quê deveria sêr aplicada ao cilindro menor para erguer um veículo de 2,0 ⋅ 103 kg?
Dado: g = 10 m/s2.
50 N
18. (Famerp-SP) Após vêr uma màssân flutuando na á gua, um garoto ficou curioso para saber a densidade dessa màssân. Não dispondo de uma balança, colocou 400 mL de á gua em um recipiente graduado, pôs a màssân na á gua e verificou quê o volume indicado passou a sêr 520 mL. Em seguida, afundou totalmente a màssân na á gua do recipiente e o volume indicado foi 550 mL.
A partir dêêsses dados, e sabendo quê a densidade da á gua é 1,0 g/mL, o garoto calculou a densidade da màssân obtendo o valor de
a) 0,70 g/mL.
b) 0,75 g/mL.
c) 0,85 g/mL.
d) 0,90 g/mL.
e) 0,80 g/mL.
Resposta: e)
Página cento e sessenta
INTEGRANDO COM...
ár-te, Biologia, Educação Física e Química
Musculação
Respostas e comentários estão disponíveis nas Orientações para o professor.
A musculação é considerada uma atividade física quê proporciona diversas melhorias a quem a pratíca. O seu objetivo principal é o fortalecimento muscular, mas existem vários outros benefícios associados à musculação, como o aumento da densidade óssea, o contrôle de peso, a redução dos riscos de algumas doenças, a promoção da manutenção do sono e a melhora do equilíbrio. Além díssu, promove a produção de substâncias no corpo humano, essenciais para a saúde, tanto física quanto mental.
Muitas pessoas deixam os exercícios físicos de lado devido aos compromissos diários, como trabalho e estudo. Porém, é essencial quê todos reservem um intervalo de tempo de seu dia para alguma prática de atividade física, e a musculação é um dos exercícios mais indicados.
Nesta atividade, é sugerido o desenvolvimento de uma campanha de incentivo à prática de atividade física, em especial à musculação. Para isso, recomenda-se a realização de algumas entrevistas com profissionais de diversas áreas, para quê fôrneçam informações quê possam sêr divulgadas para o público escolar e não escolar.
![]() Etapa 1
Etapa 1
Estruturação dos questionários, realização das entrevistas e levantamento de dados
Organize-se em grupo com seus côlégas d fórma quê as habilidades de cada um sêjam melhor exploradas: entrevistar, catalogar as informações obtidas, sistematizar os dados, construir a campanha com elemêntos atrativos etc.
Cada grupo póde ficar responsável por uma entrevista. A seguir estão algumas sugestões de profissionais quê podem sêr entrevistados, bem como perguntas quê podem sêr feitas. Lembrem-se de quê outros profissionais podem sêr entrevistados e façam adaptações e alterações, considerando sua realidade.
Iniciem a entrevista solicitando ao entrevistado quê fale um pouco de seu trabalho, destacando a área de formação. Na sequência, discutam as kestões quê vocês propuseram.
A seguir, algumas sugestões de perguntas quê podem sêr feitas aos profissionais.
Entrevista 1: profissional de Educação Física
• Em Física, fôrça é uma ação quê causa a variação de velocidade de um corpo. E nos exercícios físicos, o quê significa fôrça?
• Quais são os principais benefícios da musculação para o corpo humano, tanto físicos como mentais?
• Como é possível motivar o exercício da musculação diariamente, para desvincular essa prática apenas das kestões estéticas?
• Quais são os riscos de uma pessoa praticar musculação sem a orientação de um profissional qualificado?

Página cento e sessenta e um
Entrevista 2: profissional de Nutrição
• Em Física, energia é compreendida como a capacidade quê um corpo tem de realizar trabalho. E na nutrição, como se trata a energia fornecida pêlos alimentos?
• Quais são os principais êêrros quê uma pessoa póde cometer em sua alimentação?
• Quais são os principais benefícios do consumo de nutrientes e do gasto energético proporcionado pela prática da musculação?
• Quais são os riscos de uma pessoa não planejar sua diéta corretamente, sem a orientação de um profissional qualificado, quando decide fazer musculação?

Entrevista 3: profissional de Fisioterapia
• Em Física, o equilíbrio ocorre quando a fôrça resultante em um sistema é nula, não existindo acelerações. E no corpo humano, o quê significa equilíbrio?
• Quais são as principais dicas quê você poderia fornecer às pessoas para a promoção do equilíbrio, com práticas simples quê podem sêr feitas diariamente?
• Quais são os principais benefícios da musculação para o corpo humano, especialmente para a manutenção do equilíbrio físico?
• Como profissional de Fisioterapia, quais são os cuidados quê uma pessoa deve ter ao praticar musculação?
![]() Etapa 2:
Etapa 2:
Desenvolvimento da campanha de conscientização
Em conjunto com seu grupo, discutam como as informações coletadas podem sêr sistematizadas e posteriormente divulgadas. A campanha de conscientização póde sêr feita utilizando ferramentas escolhidas por vocês, como vídeos em platafórmas digitais e nas mídias do colégio; aplicativos de conversação individual e coletiva; materiais impressos, como cartazes e jornais; encontros presenciais, entre outras. Usem a criatividade! O importante é quê as informações cheguem ao maior número de pessoas.
Para finalizar a atividade, realizem, em conjunto com toda a turma, uma reflekção acerca dos profissionais escolhidos para as entrevistas. Vocês já conheciam essas profissões? Têm interêsse em seguir alguma dessas carreiras? Qual(is)? Discutam acerca das diversas funções quê um profissional da saúde póde atuar e comentem a importânssia dêêsses profissionais para a ssossiedade.

Página cento e sessenta e dois

