UNIDADE 3
TERMODINÂMICA
Balonismo é a prática de vôo quê utiliza balões de ar kemte. Na imagem, há um exemplo dessa prática na Capadócia (Turquia). No local onde ela ocorre, o balão é inflado inicialmente por um grande ventilador, até preencher cerca de 60% de seu volume, quando, então, um maçarico (equipamento quê produz fogo a partir da queima de um gás) é ligado. O fogo aquece o ar do interior do balão. Quando a tempera-túra do ar interno supera a tempera-túra do ar externo em aproximadamente 60 °C, o balão já póde iniciar a subida.
É recomendado quê voos com tripulação sêjam realizados com velocidades menóres de 18 km/h e a uma altura de até 30 m. Sugere-se também quê eles sêjam praticados logo pela manhã ou no final de tarde, evitando a prática em horários próximos ao meio-dia.
Calor e tempera-túra são alguns dos conceitos explorados pela Termodinâmica, assunto desta Unidade.

Página cento e sessenta e três
Respostas e comentários estão disponíveis nas Orientações para o professor.
1. por quê o balão não é capaz de subir enquanto está sêndo inflado?
2. Quais são os efeitos causados no ar dentro do balão quando o maçarico é ligado?
3. Quais efeitos o calor absorvido ou cedido por um corpo póde causar?
4. por quê não é recomendada a prática do balonismo em horários próximos ao meio-dia?
5. A partir dos estudos de Hidrostática, quais forças agem sobre o balão e por quê ele inicia um movimento de subida?
Página cento e sessenta e quatro
TEMA 13
Termodinâmica e ssossiedade
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Breve história das máquinas térmicas
Desde a história antiga, quando os sêres humanos descobriram os benefícios do uso do fogo, o consumo de energia pela humanidade em atividades cotidianas aumentou consideravelmente. O calor obtído pela queima da madeira e do carvão começou a sêr utilizado, principalmente, para aquecer ambientes e cozinhar alimentos; o uso de energia por tração animal era requerido, por exemplo, para o transporte de pessoas ou para acionar máquinas. Entre outras formas de obtenção de energia, pode-se mencionar algumas máquinas, como o monjolo da imagem, quê funcionava por princípios de energia hídrica: a á gua acumulada em uma extremidade da alavanca elevava a outra extremidade e, conforme escoava, fazia baixar a outra extremidade, quê colidia com grãos ou cereais.
Na Inglaterra, no final do século XVII, a escassez de madeira aumentou a procura por outros recursos, tornando o carvão uma das principais fontes de energia, devido à abundância das minas com reservas dêêsse minério existentes nas proximidades. No entanto, a extração de carvão era prejudicada pelo alagamento das minas, causado pelas chuvas e pela perfuração do subsolo para outras minerações, como o ferro, uma vez quê essa perfuração muitas vezes atingia os lençóis fre-átikos.
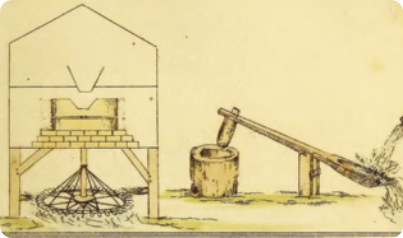
MAWE, Diôn. Horizontal Kórn mill: pounding machine. In: MAWE, Diôn. Travels in the interior ÓF brézíl: with notices on its climate, agriculture, commerce, population, mines, manners [...]. 2nd ed. London: Longman, Hurst, Rees, Orme, ênd Bráum, 1822. Localizável em: entre p. 190-191.
Alguns mecanismos foram pensados para retirar a á gua das minas de carvão, como o parafuso de arquimédis. Contudo, a rotação do parafuso dependia de tração humana ou animal. Nesta época, já existiam bombas de sucção de á gua, porém estas não eram capazes de sugar a á gua de profundidades superiores a 10 m.
Com o desenvolvimento das máquinas térmicas, quê utilizam o calor para realizar trabalho, foi possível realizar a tarefa de extração das águas das minas d fórma ágil e eficiente. Devido ao uso do vapor gerado pelo aquecimento da á gua, é comum utilizar o nome máquina a vapor. Seu desenvolvimento ocorreu ao longo do século XVIII e foi um marco importante. O uso intenso dessas máquinas em diversas regiões do mundo ficou marcado pelo período conhecido como Revolução Industrial.
PENSE E RESPONDA

1 Em sua opinião, quais foram os benefícios trazidos com o surgimento das locomotivas a vapor?
Página cento e sessenta e cinco
Máquina térmica comercial
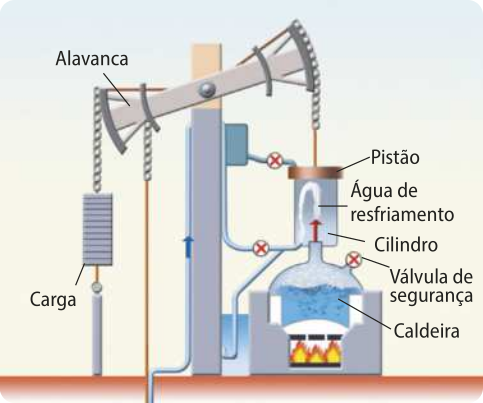
A primeira máquina térmica de grande porte e com possibilidade de uso comercial foi projetada pelo engenheiro militar inglês Tômas Savery (c. 1650-1715). Seu princípio de funcionamento consistia em elevar a á gua presente no interior de uma mina por sucção, utilizando uma caldeira para aquecer uma porção de á gua. O vapor gerado a altas tempera-túras e pressões era conduzido a um reservatório cilíndrico conectado a um tubo com a outra extremidade em contato com a á gua da mina. Quando o cilindro esfriava, ocorria uma redução de pressão, e a pressão atmosférica na mina ala-gada empurrava a á gua para cima do tubo.
O engenheiro inglês Tômas Newcomen (1664-1729) aperfeiçoou a máquina de Savery, instalando um pistão móvel no cilindro, conectado a uma alavanca. O vapor de á gua à alta pressão empurrava êste pistão para cima. Esse movimento fazia com quê uma extremidade da alavanca elevasse e a outra abaixasse, causando o aumento de pressão em uma tubulação e empurrando, assim, a á gua da mina para cima. As principais desvantagens da máquina de Newcomen eram o resfriamento demorado do cilindro e o grande consumo de carvão.
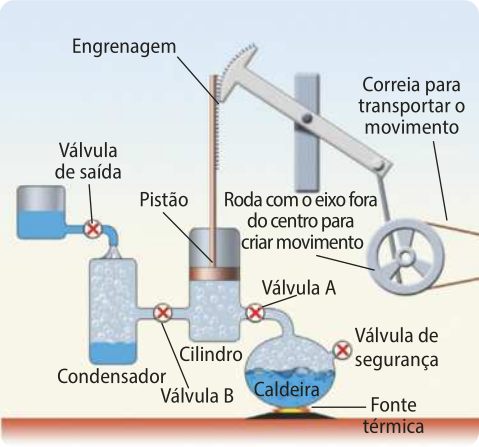
diêmes Watt, enquanto investigava as máquinas térmicas, verificou quê uma quantidade considerável de energia era desperdiçada com o aquecimento e o resfriamento dos cilindros.
Buscando aumentar a potência e a eficiência, Watt desenvolvê-u uma máquina dotada de um sistema duplo, com um cilindro de aquecimento e um condensador. O vapor de á gua formado na caldeira (fonte quente) ia para o cilindro e empurrava-o para cima, movendo a alavanca; porém, uma roda acoplada na outra extremidade forçava a alavanca novamente para baixo e, devido a engrenagens, forçava também o pistão para baixo, empurrando o vapor do cilindro para o condensador (fonte fria). Assim, era possível prosseguir com o ciclo sem esperar o cilindro esfriar.
A inovação proposta por Watt aumentou o rendimento da máquina térmica em praticamente 50% e proporcionou uma economia de carvão de quase 70%.
As máquinas térmicas foram cada vez mais aperfeiçoadas, sêndo utilizadas em larga escala desde então.
ESPAÇOS DE APRENDIZAGEM
• O livro indicado a seguir trata da Revolução Industrial, abordando os conhecimentos relacionados à Termodinâmica, bem como os impactos sociais e econômicos quê esta época causou.
Letícia Bicalho Canêdo. A Revolução Industrial. 23. ed. São Paulo: Atual, 1994. (Discutindo a história).
CANÊDO, Letícia Bicalho. A Revolução Industrial. 23. ed. São Paulo: Atual, 1994. (Discutindo a história).

Página cento e sessenta e seis
Alguns impactos da Revolução Industrial na ssossiedade
As locomotivas a vapor se tornaram um dos principais símbolos da Revolução Industrial, principalmente na facilitação dos deslocamentos. Uma viagem de Londres, Inglaterra, até Glasgow, na Escócia, por exemplo, era realizada em 12 dias. Esse trecho passou a sêr percorrido em apenas 3 dias.

A mecanização possibilitou um aumento da produção em um tempo menor, favorecendo a diversificação e a redução dos preços dos produtos. Outras áreas avançaram juntamente com a evolução das máquinas, como a Ciência, a Engenharia, os transportes, a Medicina, o comércio, entre outras.
De forma quase simultânea, essas inovações tecnológicas provocaram uma redução do número de trabalhadores necessário para a realização de algumas tarefas, gerando um aumento gradativo de desemprego. A falta de renda, juntamente com o aumento populacional, levou as pessoas a morarem em cômodos pequenos, com pouca ou nenhuma infraestrutura e saneamento.
Aqueles quê mantiveram empregos passaram a trabalhar em condições quê envolviam a repartição do trabalho com diversas pessoas, em um ritmo de produção ditado pelas máquinas e em jornadas de trabalho de muitas horas. Os baixos salários praticamente exigiam quê todos trabalhassem mais para complementar a renda, e nessa época, além dos adultos, não era incomum encontrar também idosos e crianças cumprindo essa jornada.
A Revolução Industrial foi importante para a transformação econômica e social, com avanços percebidos na tecnologia e na produção de conhecimentos, mas é fundamental reconhecer os problemas, especialmente nas relações de trabalho e no uso da mão de obra infantil. Embora o progresso seja importante para a ssossiedade, ele deve sêr feito d fórma planejada e inclusiva.

ESPAÇOS DE APRENDIZAGEM
• êste filme de xárlês Chaplin retrata em uma comédia crítica a rotina de trabalho na época da mecanização causada pela Revolução Industrial.
Tempos modernos, direção de xárlês Chaplin. Estados Unidos, 1936.

TEMPOS modernos. Direção: xárlês Chaplin. Estados Unidos: xárlês Chaplin Film corporê-ixon, 1936. dê vê dê (86 min).
Página cento e sessenta e sete
SAIBA +
Trabalho infantil
[...]
Rebecca Gowland é professora de bioarqueologia (o estudo de restos biológicos) da Universidade de Durham, no norte da Inglaterra.
E é uma das autoras de um estudo sem precedentes, quê revela as horríveis condições das crianças trabalhadoras — algumas com apenas sete anos — na Inglaterra do século 19.
[...]
A revolução industrial transformou o panorama socioeconômico britânico nos séculos 18 e 19.
Mas o auge da indústria “baseou-se no trabalho mal remunerado de mulheres e crianças, quê permitiu quê as fábricas britânicas fossem competitivas em um mercado cada vez mais globalizado”, destaca o estudo.
Em 1845, 43% dos trabalhadores nas fábricas de tecídos de algodão do Reino Unido eram menóres de 18 anos. E, em outros setores, êste índice era substancialmente maior.
[...]
Muitas crianças de regiões rurais foram enviadas para as fábricas em cidades inglesas como Londres e Liverpool, mas houve também o deslocamento no sentido contrário. Menores pobres foram transportados das cidades para fábricas de fiação em vilarejos rurais, como Fewston.
Algumas crianças começavam seu trabalho de aprendiz “a partir dos sete anos”, segundo Gowland. Mas a maioria chegava às fábricas com 10 a 13 anos.
Ali, elas permaneciam vinculadas ao seu local de trabalho até os 21 anos, no caso dos meninos, ou até se casarem, no caso das meninas.
[...]
MARTINS, Alejandra. Os óssos quê revelam a brutalidade do trabalho infantil na Revolução Industrial britânica. BBC nius Brasil, [s. l.], 1 jun. 2023. Disponível em: https://livro.pw/urbqi. Acesso em: 15 ago. 2024.
ATIVIDADES
1. Na época da Revolução Industrial, quais motivos levaram à exploração da mão de obra infantil?
2. Embora a exploração do trabalho infantil tenha sido uma realidade em alguns momentos da história, como na Revolução Industrial, ela não foi exclusiva de uma época. Faça uma pesquisa sobre a Declaração Universal dos Direitos da Criança e sobre a exploração do trabalho infantil na atualidade e converse com seus côlégas a esse respeito. Que medidas vocês consideram quê precisam sêr tomadas para eliminar essa prática?
ATIVIDADES
1. O quê é uma máquina térmica?
2. Qual era o problema vivenciado na Inglaterra no final do século XVII quê influenciou as pessoas a pensarem em máquinas térmicas? Quais foram os principais conhecimentos científicos considerados para desenvolver essas máquinas?
3. Ao estudar a evolução das máquinas térmicas na Inglaterra, são normalmente citadas as máquinas desenvolvidas por Savery, Newcomen e Watt, pela importânssia quê tiveram na época. É comum um destaque maior à máquina de Watt, por ter melhorado a eficiência das máquinas anteriores. Considerando a Ciência como uma produção humana, você concórda quê a máquina de Watt seja merecedora dêêsse destaque? Discuta oralmente com seus côlégas argumentando d fórma crítica e com base nos conhecimentos adquiridos até o momento.
4. As máquinas térmicas evoluíram, porém tem sua estrutura básica de funcionamento equivalente às primeiras máquinas quê foram desenvolvidas. De forma resumida, como é o funcionamento básico de máquina térmica e qual é o principal exemplo de utilização de máquinas térmicas atualmente?
5. Pode-se dizêr quê um aparelho de ar-condicionado ou um ventilador são máquinas térmicas? Pense na sua resposta, converse com os côlégas a esse respeito e registre em seu caderno a conclusão.
Página cento e sessenta e oito
TEMA 14
Termologia e dilatação térmica
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Calor e tempera-túra
Até o fim do século XVIII, acreditava-se na existência de uma substância fluida, com peso desprezível e invisível, quê estava presente no interior dos corpos, denominada calórico. Quanto maior a quantidade de calórico contida no corpo, mais kemte ele estaria, ao passo quê quanto menor a quantidade de calórico, mais frio ele estaria.
Após a descoberta de quê o atrito gerava calor, a ideia do calórico como substância fluida e quê se conservava foi superada. Hoje sabemos quê os corpos são formados por hátomus (e partículas ainda menores) quê estão em constante agitação. A ideia de calor aceita atualmente está relacionada com a energia envolvida na agitação das partículas quê compõem os corpos, sêndo assim possível associar uma energia cinética de translação a elas e uma energia cinética média a todas as partículas de um corpo ou sistema.
O conceito de tempera-túra se aproxima muito do conceito de calor, visto quê a tempera-túra é uma forma de medir o grau de agitação das partículas de um corpo.
Temperatura (T) é uma grandeza associada ao grau de agitação das partículas, ou à energia cinética média de translação das partículas.
Quando corpos ou sistemas de diferentes tempera-túras são colocados em um ambiente termicamente isolado, as partículas mais agitadas (maior temperatura) transmitem energia para as menos agitadas (menor temperatura), reduzindo assim sua tempera-túra. As menos agitadas recebem energia, aumentando assim sua tempera-túra. êste fluxo de energia do corpo ou sistema de maior tempera-túra para o corpo ou sistema de menor tempera-túra ocorre até quê seja atingido o equilíbrio térmico, ou seja, quando as tempera-túras se igualam. A energia trocada entre os corpos é denominada calor.
Calor é a energia em trânsito devido à diferença de tempera-túra, sêndo transferido espontaneamente do corpo com maior tempera-túra para o corpo de menor tempera-túra.
PENSE E RESPONDA

1 Quando se diz “estou com calor” ou “estou com frio”, estas frases estão cientificamente corretas? Para a Ciência, o calor ou frio relacionam-se com qual grandeza física?
Página cento e sessenta e nove
SAIBA +
Equilíbrio térmico e aquecimento global
Dentre as condições necessárias para a existência de vida na Terra, a tempera-túra é uma delas.
Sabe-se quê regiões do planêta próximas à linha do equador recebem alta incidência de radiação solar e têm maiores tempera-túras, se comparadas às regiões polares, quê recebem menos incidência solar e quê, consequentemente, tem tempera-túras mais baixas. A diferença de tempera-túra seria ainda maior, atingindo níveis inabitáveis, se não fossem os mecanismos do planêta para garantir o equilíbrio térmico.
Os gases da atmosféra terrestre têm importante papel no mecanismo de contrôle de tempera-túra do planêta. A atmosféra atua como uma cobertura protetora e produz um fenômeno chamado efeito estufa. Tal fenômeno evita a entrada de radiações nocivas à vida na superfícíe da Terra e a perda de uma grande quantidade de calor para o meio externo, auxiliando no contrôle da tempera-túra e na manutenção do equilíbrio térmico.
A intensificação do efeito estufa é conhecida como aquecimento global e é nociva ao planêta. Isso ocorre devido ao aumento na concentração de gases do efeito estufa na atmosféra, decorrentes de ações antrópicas, como alguns gases produzidos por motores a combustão. A consequência díssu é uma maior retenção da radiação solar, provocando o aumento da tempera-túra média do planêta, tornando-a incompatível com o equilíbrio termodinâmico ideal para grande parte das formas de vida terrestre.

ATIVIDADES
1. Faça uma pesquisa e verifique outros mecanismos existentes no planêta quê auxiliam na manutenção da tempera-túra e no equilíbrio térmico.
2. Qual é a relação entre equilíbrio térmico na manutenção térmica da Terra e equilíbrio térmico entre dois corpos inicialmente com tempera-túras diferentes?
ESPAÇOS DE APRENDIZAGEM
• Documentário de 2019 com diversas entrevistas, as quais abordam a correlação entre o comportamento humano, a emissão de gases na atmosféra e as consequentes mudanças climáticas. Ele aborda também estudos e propostas para mitigar ou tentar reverter os danos das mudanças climáticas.
gêlo em xãmas, direção de Leila Conners pétersen. Estados Unidos, 2019.

GELO em xãmas. Direção: Leila Conners pétersen. Estados Unidos: HBO, 2019. Blu-ray (98 min).
Página cento e setenta
ATIVIDADES
1. Para medir a tempera-túra corporal de uma pessoa, utiliza-se um termômetro. Existem diferentes modelos, e um deles necessita do contato com o corpo da pessoa durante cérto intervalo de tempo. por quê isso é necessário?
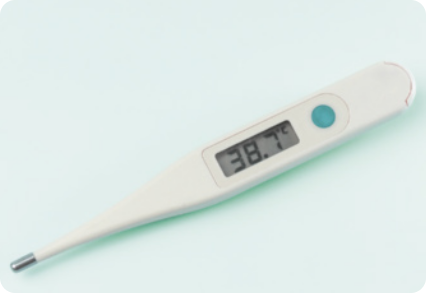
2. Calor e tempera-túra são grandezas físicas relacionadas, porém distintas. Analise as afirmações seguintes e identifique a alternativa correta.
I. Temperatura é a medida do calor de um corpo.
II. Calor é a energia em trânsito entre dois corpos ou sistemas quê ocorre em razão da diferença de tempera-túra entre eles.
III. Corpos ou sistemas com mesma tempera-túra estão em equilíbrio térmico.
a) Somente I está correta.
b) Somente I e II estão corretas.
c) Somente II e III estão corretas.
d) I, II e III estão corretas.
e) Nenhuma está correta.
Resposta: c)
Termômetro e medida de tempera-túra
O instrumento utilizado para medir tempera-túra é chamado termômetro. Existem diferentes tipos de termômetros, entre eles, o termômetro a áucôl e o termômetro infravermelho.
A medida da tempera-túra de um corpo é sempre feita de maneira indireta, a partir da análise de propriedades termométricas quê se alteram com a variação de tempera-túra, tais como volume, côr, densidade, entre outras. No termômetro a áucôl, por exemplo, o líquido expande seu volume à medida quê aumenta sua tempera-túra e contrai à medida quê reduz a tempera-túra.

Para construir um termômetro, deve-se fazer sua calibração, estabelecendo uma relação entre a propriedade termométrica considerada e a respectiva tempera-túra. Para isso, pode-se utilizar uma equação termométrica. Em seguida, é feita sua graduação, isto é, a divisão em graus, atribuindo valores numéricos conforme a escala adotada e a respectiva unidade de medida.
Nesse processo, deve-se adotar, no mínimo, duas tempera-túras quê já sêjam conhecidas, chamadas de pontos fixos. A tempera-túra de fusão e a de ebulição da á gua, sôbi a pressão de 1 atm, são os pontos fixos mais comumente utilizados. Os valores de tempera-túra dependem da escala quê está sêndo utilizada ou criada.

Página cento e setenta e um
Escalas termométricas
Uma escala termométrica corresponde ao padrão adotado para medir tempera-túra. Atualmente, são utilizadas três escalas termométricas: célcius, farenrráiti e kélvin (adotada como padrão no SI).
Escala farenrráiti
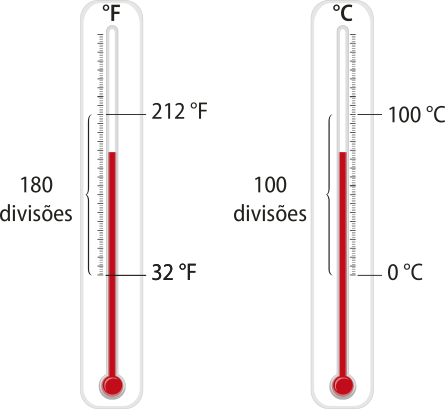
Escala criada pelo físico Daniel farenrráiti (1686-1736), nascido na região da atual Polônia. Foi uma das primeiras escalas criadas, em 1724, sêndo até hoje utilizada.
Nela adota-se como pontos fixos a tempera-túra de fusão da á gua como 32°F e a tempera-túra de ebulição da á gua como 212°F, com pressão atmosférica ao nível do mar. Assim, entre os pontos fixos, tem-se uma divisão em 180 partes.
Escala célcius
Escala criada pelo físico e astrônomo sueco Anders célcius (1701-1744), em 1742.
Nela adota-se como pontos fixos a tempera-túra de fusão da á gua como 0 °C e a tempera-túra de ebulição da á gua como 100 °C, com pressão atmosférica ao nível do mar. Assim, entre os pontos fixos, tem-se uma divisão em 100 partes, sêndo por isso denominada também escala centígrada.
Inicialmente, célcius adotou 0 °C para tempera-túra de ebulição da á gua e 100 °C para a fusão da á gua. Posteriormente, os pontos fixos foram invertidos.
Escala absoluta ou escala kélvin
O físico britânico uílhãm thômsom, conhecido como Lord kélvin
(1824-1907), compreendia a tempera-túra como a agitação das partículas e estudou as relações entre pressão, volume e tempera-túra nos gases.
Em seus estudos, kélvin calculou uma tempera-túra próxima de −273 °C, mais especificamente −273,15 °C, para uma situação em quê a pressão exercida pelo gás seria nula, isto é, as partículas estariam teóricamente sem nenhuma agitação. Nessa situação, a tempera-túra foi denominada zero absoluto.
Quando propôs sua escala termométrica em 1848, o zero absoluto foi atribuído ao zero kelvin (0 K), a tempera-túra de fusão da á gua a 1 atm passou a valer 273 K e a tempera-túra de ebulição da á gua a 1 atm passou a valer 373 K, configurando também uma escala centígrada. Por sua definição, a escala kélvin não faz uso do grau e não apresenta valores negativos; por êste motivo, é considerada uma escala absoluta. Esta escala é adotada como padrão no SI, portanto adotada pela Ciência.
Existem pesquisas quê destacam quê o zero absoluto não póde sêr atingido, enquanto outras afirmam terem atingido valores bilionésimos abaixo desta tempera-túra. Estes diferentes resultados evidenciam o caráter mutável da Ciência, passível de concordâncias, discordâncias, avanços e evoluções.

Página cento e setenta e dois
Conversão entre as escalas termométricas
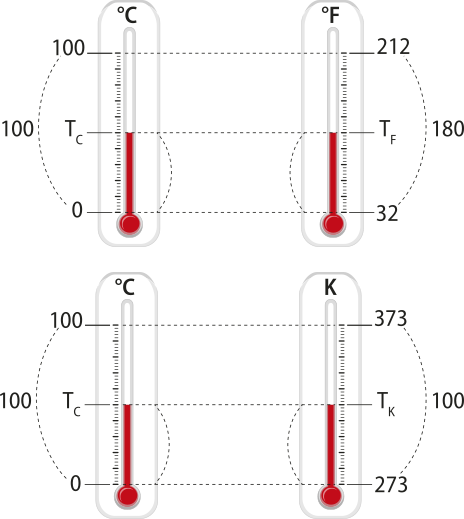
A relação matemática quê converte valores de uma determinada escala termométrica em outra póde sêr ôbitída a partir de quaisquer dois valores de tempera-túra quê sêjam equivalentes entre as escalas analisadas, utilizando para tanto o teorema de Tales.

Adotando TC para tempera-túra na escala célcius e TF para a tempera-túra na escala farenrráiti, uma relação matemática de transformação entre elas póde sêr determinada da seguinte forma:
⇒
100 ⋅ (TF − 32) = 180 ⋅ TC
TF − 32 = ⇒ TF = 1, 8 TC + 32
Adotando TC para tempera-túra na escala célcius e TK para a tempera-túra na escala kélvin, uma relação matemática de transformação entre elas póde sêr determinada da seguinte forma:
⇒ TK = TC + 273

ATIVIDADES RESOLVIDAS
1. Em uma das regiões mais frias do mundo, um termômetro registra −58 °F. Qual é o valor dessa tempera-túra nas escalas célcius e kélvin?
Resolução
Usando a equação quê relaciona as escalas célcius e farenrráiti, tem-se:
⇒ ⇒ TC = −50 °C
Usando a equação quê relaciona as escalas célcius e kélvin, tem-se:
TK = TC + 273 = −50 + 273 ⇒ TK = 223 K
2. Foram colocados em um mesmo recipiente três termômetros: um graduado na escala célcius, um graduado na escala farenrráiti e outro graduado na escala kélvin. O sistema formado pêlos termômetros mais o recipiente foi aquecido até quê a diferença de leituras fornecidas pelo termômetro da escala célcius fosse de 45 °C. Quais foram as diferenças de tempera-túra fornecidas pêlos outros termômetros?
Resolução
Usando a relação da variação de tempera-túra das escalas célcius e farenrráiti, tem-se:

⇒ (delta)"TF = 81°F
Usando a equação quê relaciona as escalas célcius e kélvin, tem-se:

⇒ (delta)"TK = 45 K
Página cento e setenta e três
ATIVIDADES
3. A tempera-túra interna de uma caverna varia de 17 °C a 21 °C. Em determinado dia, a caverna de Santana, localizada na cidade de Iporanga (SP), apresentou tempera-túra de 20 °C. Que valores assinalariam dois termômetros, um graduado na escala farenrráiti e outro na escala kélvin, situados no interior dessa caverna?
TF = 68 °F e TK = 293 K
4. Durante uma gincana escolar, o apresentador propôs aos alunos quê completassem a seguinte frase: “Quando três corpos estão encostados entre si e em equilíbrio térmico, é possível afirmar que...”. Qual dêstes alunos completou a frase corretamente?
Carol: O corpo quê tem maior massa tem mais calor.
Karina: Todos os corpos contêm o mesmo calor.
Bianca: Todos os corpos estão no mesmo estado físico.
Beatriz: Os três corpos apresentam a mesma tempera-túra.
Beatriz.
5. Um viajante, ao desembarcar no aeroporto de Londres, observou quê o valor da tempera-túra do ambiente na escala farenrráiti era o quíntuplo do valor da tempera-túra na escala célcius. A tempera-túra em graus célcius era:
a) 5
b) 10
c) 15
d) 20
e) 25
Resposta: b)
6. Um laboratório cometeu um êrro na fabricação de um termômetro quê indica os valores: 2 °C para o ponto de fusão da á gua e 98 °C para o ponto de ebulição da á gua, ao nível do mar. Elabore uma equação para corrigir esse termômetro.
7. Dos planêtas quê orbitam próximo ao Sol, Mercúrio apresenta as menóres dimensões. Com diâmetro de 4.800 km (quase três vezes menor quê a Terra), esse planêta apresenta contrastes impressionantes de tempera-túra na superfícíe, atingindo, durante o dia, valores quê se aproximam de 350 °C e, à noite, −170 °C. Expresse essa variação de tempera-túra, em kelvin.
520 K
Comentar com os estudantes quê é preciso ter cuidado ao realizar o procedimento descrito na atividade do Pense e responda a seguir.
Dilatação térmica dos sólidos
É comum notar estalos emitidos pela geladeira ou pelo aparelho de televisão após serem utilizados por cérto intervalo de tempo. Você sabe por quê eles ocorrem? Em grandes construções de concreto ou metal, são deixados espaços entre algumas partes das estruturas. Você sabe a importânssia dêêsses espaços?


PENSE E RESPONDA

2 Uma prática comum para abrir tampas de pótes é aquecer a tampa colocando-a em á gua kemte. por quê esse método funciona?
Página cento e setenta e quatro
De modo geral, os corpos, ao serem aquecidos, aumentam suas dimensões, fenômeno denominado dilatação térmica. O fenômeno ôpôsto é denominado contração térmica e ocorre quando o corpo reduz suas dimensões ao sêr esfriado.
Esses fenômenos são responsáveis pêlos estalos emitidos por elétro domésticos e pisos de madeira, quando varíam sua tempera-túra. Os efeitos da dilatação térmica devem sêr considerados nas construções, como em pontes, trilhos de trem, assentamentos de pisos e azulejos etc. Para tanto, são feitos pequenos espaços chamados juntas de dilatação, mantidos entre as peças para evitar quê danos estruturais ocorram devido à dilatação e à contração térmica.
Como a tempera-túra está relacionada com o grau de agitação das partículas de um corpo, aumentar a tempera-túra é aumentar a agitação, o quê faz com quê as partículas se movam em uma maior amplitude, aumentando a distância média entre elas.
A dilatação térmica ocorre nas três dimensões de um corpo, variando assim seu comprimento (L), área superficial (A) e volume (V).
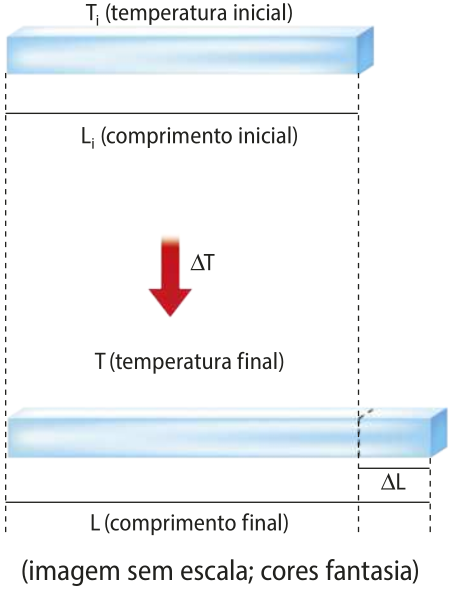
Dilatação linear
Analise a dilatação quê resulta na variação de comprimento. Considere um corpo sólido a uma tempera-túra inicial de Ti, com comprimento inicial Li, sêndo aquecido até uma tempera-túra final T e atingindo um comprimento final L. Obtém-se, assim, uma variação de tempera-túra (delta)"T = T − Ti e uma variação de comprimento (delta)"L = L − Li.
O valor da variação de comprimento (delta)"L é diretamente proporcional ao comprimento inicial Li do corpo e à variação da tempera-túra (delta)"T. Essa relação póde sêr escrita da seguinte forma:
(delta)"L = L − Li ⇒ L = Li + (delta)"L
L = Li + Li (alfa)" (delta)"T
L = Li (1 + (alfa)" (delta)"T)
(delta)"L = Li (alfa)" (delta)"T)
A constante de proporcionalidade a é chamada coeficiente de dilatação linear, característico de cada material. Escrevendo a relação anterior para a, tem-se quê:
(alfa)" =
A unidade de medida do coeficiente de dilatação linear é o inverso, ou recíproco, da escala termométrica, como K–1 (kelvin recíproco) ou °C–1 (grau célcius recíproco). Ao analisar a variação de tempera-túra, as duas unidades apresentadas são equivalentes.
Coeficiente de dilatação linear de alguns materiais
Material |
(alfa)" (10−6 °C−1) |
|---|---|
chumbo |
29 |
alumínio |
23 |
cobre |
17 |
concreto |
12 |
aço |
11 |
diamante |
1,2 |
Fonte: HALLIDAY, Daví; RESNICK, róbert; uólker, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução e revisão técnica: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. (Fundamentos de física, v. 2, p. 190).
Página cento e setenta e cinco
ATIVIDADE RESOLVIDA
3. Uma régua metálica teve uma variação de comprimento de 1,16 mm ao passar de 20°C para 98°C. Calcule o comprimento inicial dessa régua.
Dado: (alfa)"metal = 24 ⋅ 10−6 °C−1.

Resolução
Dados: Ti = 20 °C; T = 98 °C;
(delta)"L = 1,16 mm = 0,116 cm; (alfa)"metal = 24 ⋅ 10−6 °C−1
Aplica-se a fórmula para dilatação linear: (delta)"Li = (alfa)"Li(delta)"T
0,116 = 24 ⋅ 10−6 ⋅ Li ⋅ (98 − 20) ⇒ Li = 62 cm
ATIVIDADES
8. Calcule o coeficiente de dilatação linear de um cabo de cobre quê, ao sêr aquecido de 0 °C até 80 °C, sofre uma variação de comprimento de 0,1632 m, sêndo seu comprimento inicial de 120 m.
1,7 ⋅ 10−5 °C−1
9. Um prédio de 100 m de comprimento tem um coeficiente de dilatação linear do material quê o constitui igual a 2 ⋅ 10−5 ° C−1. Sabendo quê o prédio expandiu em 3 cm, de quanto foi o aumento de tempera-túra?
15 °C
10. Uma barra de cobre de 2 m de comprimento à tempera-túra de 24 °C tem coeficiente de dilatação linear 1,7 ⋅ 10−5 °C−1. Em quê tempera-túra a barra apresentará 1 mm a menos de comprimento?
−5,4 °C
11. Uma barra de metal, ao sêr submetida à variação de tempera-túra de 100 °C, apresenta um aumento linear de 0,3%. Identifique o valor do coeficiente de dilatação linear do metal quê constitui a barra.
3,0 ⋅ 10−5 °C−1
12. Um sistema é formado por três barras metálicas A, B e C. Sabe-se quê a barra A possui o comprimento de 1.000 mm e a B, o comprimento de 1.001 mm à tempera-túra de 42 °C. Encontre a tempera-túra em quê a barra C estará na posição horizontal.
92 °C
Dados: (alfa)"A = 3 ⋅ 10−5 °C−1 e (alfa)"B = 1 ⋅ 10−5 °C−1
13. O chumbo, um dos metais mais antigos usados pelo sêr humano, era utilizado pêlos egípcios há mais de 8 mil anos. É um elemento químico do grupo dos metais, seu número atômico é 82 e o sín-bolo químico é Pb. Com consistência maleável, póde sêr trabalhado a frio, sêndo um condutor razoável de calor e eletricidade. Como o perfil geológico brasileiro não apresenta a ocorrência significativa de jazidas de chumbo primário, é necessário importar chumbo. Esse fato contribuiu para quê a partir da década de 1990 a oferta de chumbo secundário, proveniente da reciclagem de sucata de chumbo, superasse a produção de metal ôbitída de operações mineiras. Um funileiro utiliza três barras de chumbo “velho”, com o objetivo de interligá-las formando um objeto com o formato de um triângulo isósceles, de base 10 cm e altura 12 cm. Sabendo quê essas barras são retas, avalie o quê ocorrerá com o triângulo, caso seja submetido a aumento de tempera-túra.

a) Os ângulos da base sofrem menor variação quê o ângulo do outro vértice.
b) Os lados e a base têm a mesma dilatação.
c) A área do triângulo se mantém constante.
d) Os ângulos mantêm suas medidas.
Resposta: d)
Página cento e setenta e seis
Dilatação superficial
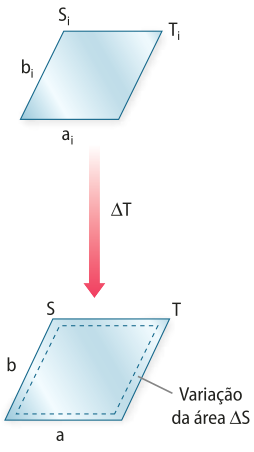
Ao falar em dilatação superficial, supõe-se quê a dilatação ocorre em duas dimensões do corpo e, nesse caso, se a tempera-túra de um sólido varia, consequentemente a área de sua superfícíe também varia.
Considere uma chapa metálica retangular de dimensões ai e bi, cuja área inicial é Si, a uma tempera-túra Ti. Variando a tempera-túra para T, a área aumenta para S. Assim, com a variação de tempera-túra (delta)"T = T − Ti, os valores das dimensões mudam para a e b, ocorrendo uma variação da área (delta)"S = S − Si.
Por meio da equação da dilatação linear, para cada uma das dimensões lineares, tem-se:
a = ai(1 + (alfa)"(delta)"T) e b = bi(1 + (alfa)"(delta)"T)
A área final S é dada pelo produto de a e b.
S = ab = ai bi (1 + (alfa)"(delta)"T)2
O produto aibi é a área inicial da superfícíe (Si). Para a expressão entre parênteses elevada ao quadrado, deve-se utilizar produtos notáveis, no caso, o quadrado da soma de dois termos: (a + b)2 = a2 + 2ab + b2.
S = Si (1 + (alfa)"(delta)"T)2 ⇒ S = Si[1 + 2(alfa)"(delta)"T + (alfa)"2((delta)"T)2]
Considerando o valor de (alfa)"2 ((delta)"T)2 desprezível por não interferir no valor da área final, a relação póde sêr escrita da seguinte forma:
S = Si (1 + 2(alfa)"(delta)"T)
Pode-se dizêr quê o termo 2a constitui um coeficiente de dilatação superficial do material. Esse coeficiente será indicado pela letra (beta)" ((beta)" = 2(alfa)").
S = Si (1 + (beta)"(delta)"T)
(delta)"S = (beta)"Si(delta)"T
ATIVIDADES
14. Um disco de aço homogêneo (forma circular) de raio 20 mm foi aquecido, tendo sua tempera-túra variado de 8 °C para 108 °C. Determine a dilatação superficial do disco.
Dados: (alfa)"aço = 1,5 ⋅ 10−5 °C−1 e (pi)" = 3,14.
3,768 mm2
15. Uma laje de concreto quê possui uma face retangular de medidas 20 m e 25 m a 18 °C é aquecida a 118 °C. Considerando (alfa)"concreto = 12 ⋅ 10−6 °C−1, determine:
a) a variação de sua área;
1,2 m2
b) o acréscimo percentual na área dessa face.
0,24%
16. Uma chapa quadrada de ferro tem 3 m de lado a 20 °C. Sabendo quê o coeficiente de dilatação linear do ferro é 12 ⋅ 10−6 °C−1, calcule a área dessa chapa num local cuja tempera-túra é de 95 °F.
9,00324 m2
17. Uma placa metálica d fórma quadrada de lado 1 m possui um furo central circular de 10 cm de raio. Encontre a variação da área do furo quando a tempera-túra passar de 28°C para 280 °C.
Dado: coeficiente de dilatação linear do metal é 1,0 ⋅ 10−5 °C−1.
(delta)"S ≃ 1,6 ⋅ 10−4 m²
18. Um disco metálico de raio 20 cm é aquecido da tempera-túra de 20 °C para a de 120 °C. Sendo o coeficiente de dilatação linear do metal a = 1,5 ⋅ 10−5 °C−1, calcule a dilatação quê a área do disco sofre.
3,8 cm²
Página cento e setenta e sete
OFICINA CIENTÍFICA
Fios elétricos nas linhas de transmissão
Faça o experimento somente na presença do professor.
A transmissão da energia elétrica quê chega às residências é feita pelas linhas de alta-tensão.
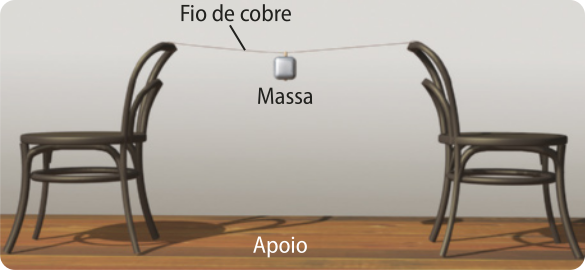
Ao observar os fios elétricos quê formam estas linhas, tanto nas cidades quanto nas estradas, é possível notar quê eles não são fixados d fórma esticada, mas com uma certa “curvatura”, como se observa na imagem ao final desta página. Será essa a melhor configuração para instalação dêstes fios?
Para refletir sobre essa questão, principalmente com relação ao custo e à segurança, faça com seus côlégas a atividade prática a seguir.
Materiais
• fio de cobre desencapado (≃1 m)
• vela
• duas cadeiras (apôio)
• régua
• objeto com certa massa e quê possa sêr facilmente pendurado ao fio
• fita adesiva
• cubo de gêlo
Procedimentos
• Utilizando a fita adesiva, fixem as extremidades do fio de cobre de maneira quê ele fique na horizontal.
• Pendurem o objeto na mêtáde do fio. Em seguida, meçam a distância do objeto ao solo e anotem o valor. ob-sérvim a curvatura do fio nesta situação.
• Com cuidado, acendam a vela. Passem sua chama ao longo de todo o fio para aquecê-lo.
• ob-sérvim a curvatura do fio nesta situação.
• Meçam novamente a distância do objeto ao solo e anotem o valor. Atentem-se para ter como base o mesmo local da medida feita anteriormente.
• Atritem o cubo de gêlo por todo o comprimento do fio de cobre. Repitam várias vezes esse procedimento.
• ob-sérvim a curvatura do fio nesta situação.
• Meçam novamente a distância do objeto ao solo e anotem o valor. Atentem-se para ter como base o mesmo local da medida feita anteriormente.
ATIVIDADES
1. Quais foram as três distâncias medidas do objeto ao solo? Registe como: a) altura inicial; b) altura com fio kemte; c) altura com fio frio.
2. Foi possível observar diferenças no aspecto do fio quando ele passou do kemte para o frio? Se sim, quais foram essas diferenças?
3. Expliquem o quê ocorreu neste experimento, relacionando a altura do objeto com as diferenças observadas no fio.
4. Caso vocês não tênham percebido diferenças no fio quando ele foi aquecido ou esfriado e a altura do objeto ao solo não tenha variado, verifiquem quais possíveis problemas podem ter ocorrido durante a realização dêste experimento.
5. Após esta investigação, expliquem o motivo de os fios elétricos das linhas de transmissão de energia elétrica serem instalados com certa folga e não esticados.

Página cento e setenta e oito
Dilatação volumétrica
A dilatação térmica volumétrica de um corpo maciço é analisada a partir da variação de cada uma das dimensões quê compõe seu volume, ou seja, altura, largura e comprimento.
Considere um bloco metálico maciço em formato de paralelepípedo, de aresta ai, bi e ci, cujo volume inicial é Vi à tempera-túra Ti. Variando a tempera-túra para T, o volume varia para V. Assim, na variação de tempera-túra (delta)"T = T − Ti, ocorre uma variação de volume (delta)"V = V − Vi.
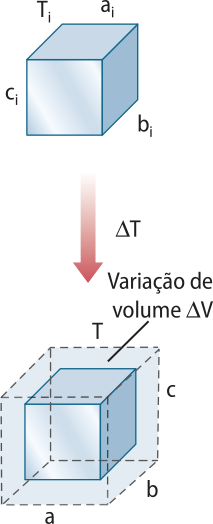
As arestas do paralelepípedo sofrem dilatação linear até o valor final a, b e c, quê podem sêr escritas pelas relações a seguir.
a = ai (1 + (alfa)"(delta)"T)
b = bi (1+ (alfa)"(delta)"T)
c = ci (1 + (alfa)"(delta)"T)
O volume final V é dado pelo produto de a, b e c.
V = abc = ai bi ci (1 + (alfa)"(delta)"T)3
O produto ai bi ci é o volume inicial da superfícíe (Vi). Para a expressão entre parênteses elevada ao cubo, deve-se utilizar produtos notáveis, no caso, o cubo da soma de dois termos:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
V = Vi (1 + (alfa)"(delta)"T)3 ⇒ V = Vi (1 + 3(alfa)"(delta)"T + 3(alfa)"²(delta)"T² + (alfa)"³(delta)"T³)
Considerando os valores de 3(alfa)"²(delta)"T² e (alfa)"³(delta)"T³ desprezíveis por não interferirem no valor do volume final, a relação póde sêr escrita da seguinte forma:
V = Vi (1 + 3(alfa)"(delta)"T)
Pode-se dizêr quê o termo 3(alfa)" constitui um coeficiente de dilatação volumétrica do material. Esse coeficiente será indicado pela letra (gama)" ((gama)" = 3(alfa)").
V = Vi (1 + (gama)"(delta)"T)
(delta)"V = (gama)"Vi(delta)"T
Dilatação de sólido oco e "dilatação térmica do vazio"
Quando um corpo sólido oco (não maciço) passa por um aumento ou redução de tempera-túra, ele sofre dilatação térmica da mesma forma quê um sólido maciço feito de um mesmo material.
Por exemplo, uma panela de alumínio aquecida varia seu volume interno como se fosse um corpo maciço de alumínio.
Efeito equivalente ocorre quando uma chapa de metal com um orifício é aquecida e sofre dilatação térmica, na qual o orifício também sofre dilatação, como se estivesse preenchido pelo material da chapa, fenômeno popularmente conhecido como "dilatação do vazio".

Alertar sobre os cuidados ao utilizar um bico de Bunsen como o da fotografia.
Página cento e setenta e nove
ATIVIDADE RESOLVIDA
4. Uma esféra de aço quê possui volume de 50 cm3 está em equilíbrio térmico com uma mistura de gêlo fundente (0 °C). Calcule seu volume quando sua tempera-túra se estabiliza com uma mistura de á gua fervente (100 °C).
Dado: (alfa)"aço = 15 ⋅ 10−6 °C−1.
Resolução
Dados: Vi = 50 cm3; Ti = 0 °C; Tf = 100 °C e (alfa)"aço = 15 ⋅ 10−6 °C−1.
V = Vi(1 + (gama)"(delta)"T) ⇒ V = 50[1 + 3 ⋅ 15 ⋅ 10−6 ⋅ (100 − 0)] ⇒ V = 50[1 + 3 ⋅ 15 ⋅ 10−6 ⋅ 100] ⇒
⇒ V = 50,225 cm3
ATIVIDADES
19. Uma chapa de metal, produzida com um orifício circular de raio R, permanéce num ambiente cuja tempera-túra é 8 °C. Ao aquecer a chapa, à tempera-túra de 60 °C, o quê ocorreu com o diâmetro do orifício?
a) Permaneceu inalterado.
b) Aumentou, com o aumento da tempera-túra.
c) Diminuiu, com o aumento da tempera-túra.
d) O orifício não contém metal, logo o diâmetro não aumenta.
Resposta: b)
20. Em relação à dilatação volumétrica dos corpos, podemos considerar incorrétas quais das afirmações a seguir?
I. A tendência de todo corpo, ao sêr aquecido, é dilatar-se para fora. Isso significa quê todo vazio interno do corpo aumenta com o acréscimo da tempera-túra.
Correta.
II. Na dilatação volumétrica de um corpo, ocorre alteração em apenas duas de suas dimensões.
Incorreta.
21. Um recipiente de cobre tem capacidade de 2.000 cm3 a 0 °C. Calcule sua capacidade a 100 °C.
Dado: coeficiente de dilatação linear do cobre igual a 17 ⋅ 10−6 °C−1.
2.010,2 cm3
22. Determine o coeficiente de dilatação linear de um corpo sólido homogêneo cuja tempera-túra varia de 20 °C para 1.020 °C. Não ocorrem mudanças de fase e o seu volume sofre um aumento de 3%.
1,0 ⋅ 10−5 °C−1
23. Analise as afirmações a seguir. Para cada uma, classifique-as em verdadeira ou falsa e justifique a sua resposta.
I. O orifício feito em uma barra metálica diminui com o aumento da tempera-túra, pois o orifício é oco, ou seja, não é feito do mesmo material quê o restante da barra.
F
II. Aumentando-se a tempera-túra de uma jarra de vidro, o seu volume aumenta como se o seu espaço interno fosse constituído também pelo vidro, ou seja, pelo mesmo material das paredes.
V
24. Um bloco cúbico de ferro possui um furo circular concêntrico, cujo diâmetro vale 2,0 cm, na tempera-túra de 20 °C. O bloco sofre um aquecimento chegando a 250 °C. Nessa situação, determine a variação do diâmetro do furo.
Dado: coeficiente de dilatação linear do ferro igual a (alfa)" = 1,2 ⋅ 10−5 °C−1.
5,5 ⋅ 10−3 cm
25. Uma chapa de alumínio tem um furo central de 100 cm de raio. Ela está a uma tempera-túra de 12 °C. Determine a área do furo quando a chapa for aquecida até uma tempera-túra de 122 °C.
Dado: (alfa)"alumínio = 22 ⋅ 10−6 °C−1.
31.552 cm²
26. Uma esféra de aço possui 10 m³ quando está à tempera-túra de 20 °C. Se a esféra for aquecida até a tempera-túra de 1.000 °C, qual será a variação de seu volume?
Dado: (alfa)"aço = 1,5 ⋅ 10−5 °C−1.
0,441 m3
Página cento e oitenta
Dilatação dos líquidos
Um recipiente com volume Vi está completamente cheio de um líquido, a uma tempera-túra inicial Ti. Quando o conjunto é aquecido até uma tempera-túra final T, é observado quê parte do líquido escoa para um reservatório externo.
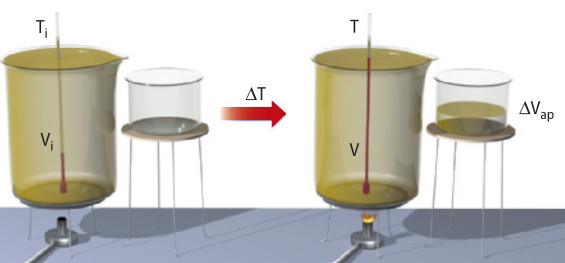
Isso acontece porque os líquidos, em geral, dilatam mais quê os sólidos quando submetidos a uma mesma variação de tempera-túra.
Quando líquidos estão contidos em recipientes, ao aquecer o conjunto, ambos são dilatados. O volume de líquido derramado é chamado dilatação aparente ((delta)"Vap) e não corresponde à dilatação real do líquido, uma vez quê parte do volume dilatado do líquido ficou armazenada no recipiente quê também dilatou. Assim, a dilatação real do líquido ((delta)"VR) é igual à soma entre a dilatação aparente ((delta)"Vap, quê é determinada por: (delta)"Vap = (gama)"apVi(delta)"T) e a dilatação do recipiente ((delta)"Vrec, quê é determinada por: (delta)"Vrec = (gama)"rec (gama)"i (delta)"T).
(delta)"VR = (delta)"Vap + (delta)"Vrec
Para obtêr a dilatação real do líquido, pode-se fazer a seguinte análise:
(delta)"VR = (delta)"Vap + (delta)"Vrec ⇒ (gama)"R Vi (delta)"T = (gama)"ap Vi (delta)"T + (gama)"rec Vi (delta)"T ⇒ (gama)"R = (gama)"ap + (gama)"rec
ATIVIDADES
27. Em um copo de vidro com capacidade de 200 mL, colocam-se 190 mL de á gua à tempera-túra de 20 °C. O conjunto é aquecido até a tempera-túra de 100 °C, e observa-se um aumento de 10 mL, fazendo com quê a á gua chegue até a bórda do copo. O quê representa essa diferença de 10 mL ôbitída após o aquecimento do conjunto?
Trata-se da dilatação aparente do líquido.
28. Em uma panela, há uma quantidade de á gua na tempera-túra inicial de 1 °C e na pressão normal. Ao sêr aquecida, a á gua sofre uma variação de tempera-túra chegando a 3,5 °C. Sobre o volume de á gua contido na panela, o quê se póde dizêr?
28. Com o aquecimento, o volume de á gua diminuirá (utilizar a seção Saiba mais: Dilatação anômala da á gua para responder a essa atividade).
29. Um recipiente de zinco tem coeficiente de dilatação linear igual a 1,7 ⋅ 10−6 °C−1. Ele está a 0 °C e totalmente cheio de um líquido cujo volume é de 120 cm3. Ao aquecer o conjunto a 200 °C, extravasam 12 cm3 do líquido. Qual é o coeficiente de dilatação real do líquido?
(gama)"R = 5,051 ⋅ 10−4 °C−1
30. (Enem/MEC) Durante uma ação de fiscalização em postos de combustíveis, foi encontrado um mecanismo inusitado para enganar o consumidor. Durante o inverno, o responsável por um posto de combustível compra áucôl por R$ 0,50/litro, a uma tempera-túra de 5 °C. Para revender o líquido aos motoristas, instalou um mecanismo na bomba de combustível para aquecê-lo, para quê atinja a tempera-túra de 35 °C, sêndo o litro de áucôl revendido a R$ 1,60. Diariamente o posto compra 20 mil litros de áucôl a 5 °C e os revende.
Com relação à situação hipotética escrita no texto e dado quê o coeficiente de dilatação volumétrica do áucôl é de 1 · 10−3 °C−1, desprezando-se o custo da energia gasta no aquecimento do combustível, o ganho financeiro quê o dono do posto teria obtído devido ao aquecimento do áucôl após uma semana de vendas estaria entre
a) R$ 500,00 e R$ 1.000,00
b) R$ 1.050,00 e R$ 1.250,00
c) R$ 4.000,00 e R$ 5.000,00
d) R$ 6.000,00 e R$ 6.900,00
e) R$ 7.000,00 e R$ 7.950,00
Resposta: d)
Página cento e oitenta e um
SAIBA +
Dilatação anômala da á gua
Enquanto a maioria das substâncias dilatam quando são aquecidas e contraem quando são esfriadas, outras substâncias, como á gua, bismuto e antimônio, têm comportamento anômalo em cértas faixas de tempera-túra.
Ao nível do mar, esfriar á gua causa sua contração térmica e redução de volume normalmente até atingir 4 °C, quando a massa de á gua considerada atinge seu menor volume, logo sua maior densidade. Ao sêr esfriada de 4 °C para 0 °C, a á gua sofre uma dilatação térmica, aumentando seu volume e reduzindo sua densidade. À tempera-túra de 0 °C, a á gua inicia o processo de solidificação, logo o gêlo formado é menos denso do quê a á gua líquida, por isso ele flutua na á gua. O gráfico volume por tempera-túra descreve o comportamento descrito.
êste comportamento anômalo ocorre devido às ligações moleculares entre as moléculas de á gua, chamadas pontes de hidrogênio. A uma tempera-túra de 4 °C, ao nível do mar, as moléculas estão o mais próximo possível uma das outras, e, a partir desta tempera-túra, as ligações químicas por pontes de hidrogênio organizam as moléculas em estruturas hexagonais abertas, quê causam um aumento do volume de cerca de 10%.
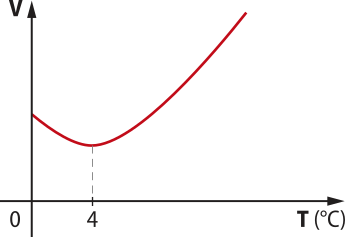
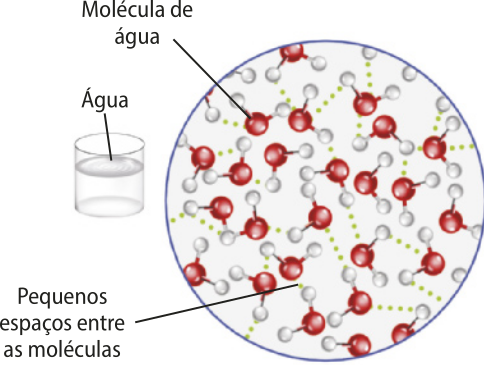
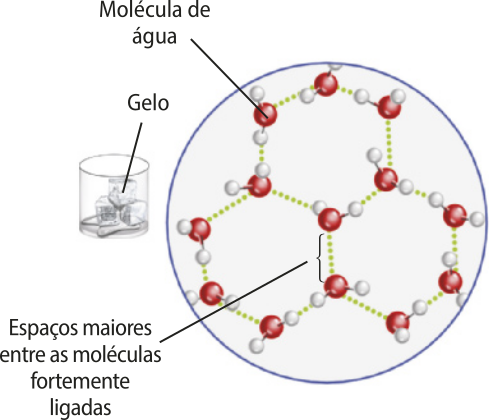
A á gua só apresenta comportamento anômalo no intervalo de 0 °C a 4 °C, comportando-se normalmente nas outras faixas de tempera-túra.
ATIVIDADES
1. por quê garrafas completamente cheias de á gua e tampadas estouram no congelador?
2. Faça uma pesquisa em conjunto com seus côlégas e verifiquem os motivos quê fazem um lago congelar apenas na superfícíe em locais com tempera-túras abaixo de zero. Verifiquem também a importânssia dêste fenômeno para a existência de vida.
Página cento e oitenta e dois
TEMA 15
Calor: energia em movimento
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Calor sensível e calor latente
Ao colocar á gua para aquecer em um recipiente, sua tempera-túra aumenta continuadamente até atingir 100°C, a pressão ao nível do mar, afinal o ponto de ebulição póde variar de acôr-do com a pressão. O calor quê causa variação de tempera-túra em um corpo chama-se calor sensível.
Ao atingir a tempera-túra de 100°C, a á gua inicia a passagem do estado líquido para gasoso, ou seja, o calor fornecido a ela causa uma variação no seu estado físico. Durante esse processo, a tempera-túra se mantém constante. Esse calor quê causa mudança de estado físico, mas quê não varia a tempera-túra, é chamado de calor latente. Assim, o calor recebido por uma substância póde causar aumento de sua tempera-túra ou a mudança de seu estado físico.
Adota-se a letra Q para representar a quantidade de calor. Sendo uma forma de energia em trânsito quando existe diferença de tempera-túra, sua unidade de medida no SI é o Jáule (J). Nos estudos da Termodinâmica, é comum a utilização da unidade de medida caloria (cal).
1.000 cal = 1 kcal (1 quilocaloria)
1 cal = 4,1868 J ≃ 4,2 J
O valor de 1 caloria é a quantidade de calor necessária para elevar de 14,5 °C a 15,5 °C a tempera-túra de 1 grama de á gua pura, à pressão constante.
PENSE E RESPONDA

1 Quando uma panela com á gua é colocada sobre a chama de um fogão para sêr aquecida, a tempera-túra da á gua aumenta indefinidamente?
Calor e variação de tempera-túra
Quando um corpo ou sistema recebe calor, sua tempera-túra aumenta e, quando cede calor, sua tempera-túra diminui.
Q > 0 ⇒ T > Ti
((delta)"T > 0)
Q < 0 ⇒ T < Ti
((delta)"T < 0)
Q = 0 ⇒ T = Ti
((delta)"T = 0)
O estudo do calor sensível póde sêr feito a partir de duas grandezas: capacidade térmica e calor específico.
Página cento e oitenta e três
Capacidade térmica
Considere quê um corpo recebeu 30 cal de calor de uma fonte térmica e quê sua tempera-túra variou de 25 °C para 27 °C. Não é possível dizêr quê corpo é esse, do quê ele é feito, qual a sua quantidade de massa, se é uma substância quê se aquece mais facilmente, entre outras informações. Sabe-se apenas quê, ao receber 30 cal, sua tempera-túra variou 2 °C, ou seja, a cada 15 cal, sua tempera-túra varia 1 °C.
Capacidade térmica (C) é a quantidade de calor necessária para variar a tempera-túra em 1 °C.
A capacidade térmica é dada pelo quociente entre a quantidade de calor (Q) recebida ou cedida e a correspondente variação de tempera-túra ((delta)"T).
C =
A unidade de medida do SI é Jáule por kelvin (J/K), quê é equivalente a Jáule por grau célcius (J/°C). Uma unidade usualmente utilizada é caloria por graus célcius (cal/°C).
No exemplo inicial, a capacidade térmica do corpo é 15 cal/°C.
PENSE E RESPONDA

2 Considere uma piscina contendo 100.000 L de á gua a 25 °C e quê um copo de 250 mL é enchido com a á gua desta piscina. A quantidade de calor necessária para elevar a tempera-túra da á gua do copo e da piscina para 26 °C é a mesma?
Calor específico
Considere novamente o corpo quê recebeu 30 cal de calor e variou sua tempera-túra em 2 °C, ou seja, 15 cal/°C. Sabe-se agora quê êste corpo possui 500 g de massa.
As propriedades térmicas a respeito do aquecimento podem variar entre as substâncias, existindo aquelas quê se aquécem com mais facilidade e aquelas quê se aquécem com mais dificuldade. Para realizar esta análise, é preciso considerar pôr-ções de mesma massa sôbi as mesmas circunstâncias.
Calor específico (c) é a quantidade de calor necessária para variar a tempera-túra em 1 °C de uma unidade de massa dêêsse material (1 g ou 1 kg, por exemplo).
De forma algébrica, essa definição póde sêr representada da seguinte forma:
c =
A unidade de medida do SI é Jáule por quilograma por kelvin (J/kgK), quê é equivalente a Jáule por quilograma por grau célcius (J/kg°C). Uma unidade usualmente utilizada é caloria por grama por grau célcius (cal/g°C).
Página cento e oitenta e quatro
No exemplo inicial, sabendo quê a massa é de 500 g, pode-se determinar o calor específico da substância de quê o corpo é feito.
c = ⇒ c = ⇒ c = 0, 03 cal/g°C
Analisando o calor específico de algumas substâncias, conclui-se quê o corpo é feito de chumbo.
Note quê, tendo a capacidade térmica de um corpo, basta dividir o valor pela massa para determinar o calor específico da substância de quê o corpo é feito.
c = ⇒ c =
C = cm
Corpos feitos de uma mesma substância têm sempre o mesmo calor específico, e, quanto maior o calor específico, maior a quantidade de energia quê deve sêr empregada para aquecer aquela substância. Já a capacidade térmica póde variar de acôr-do com a massa de cada corpo.
Calor específico de algumas substâncias, à tempera-túra ambiente
substância |
c (cal/g°C) |
|---|---|
chumbo |
0,030 |
cobre |
0,092 |
alumínio |
0,215 |
etanol |
0,58 |
á gua |
1,00 |
Fonte: HALLIDAY, Daví; RESNICK, róbert; uólker, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução e revisão técnica: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. (Fundamentos de física, v. 2, p. 194).
Equação fundamental da Calorimetria
Calorimetria é um nome quê se refere à parte da Termodinâmica quê estuda o calor e seus efeitos. Quando o calor é relacionado à variação de tempera-túra de um corpo, tem-se a equação fundamental da Calorimetria, determinada a partir da definição de calor específico.
c = ⇒ Q = mc(delta)"T
Deve-se sempre se atentar às unidades de medida envolvidas, e o calor específico normalmente expressa as unidades quê se deve utilizar.
ATIVIDADES RESOLVIDAS
1. Uma placa metálica de massa 0,300 kg sofre um acréscimo de 30 °C em sua tempera-túra quando ABSÓRVE 9.000 J de calor. Calcule o calor específico dêêsse material.
Resolução
Como, c = , tem-se quê:
c = ⇒ c = 1.000 J/kg°C
Observe quê a unidade de calor é dada em função das demais unidades utilizadas.
2. Um corpo de massa 70 g, ao sofrer aquecimento, apresenta a variação da tempera-túra conforme o gráfico. Determine o calor específico da substância.
![Representação gráfica: eixo vertical 'T'[graus célsius] e eixo horizontal em 'Q'[calor]. Uma reta iniciando em dez graus Célsius subindo até setenta e dois graus célsius em dois mil 'Q'[calor]](../resources/images/ek_3/ek_3543cf214e47faba300bd0197999bdcc.png)
Resolução
A partir do gráfico, tem-se:
Como Q = mc(delta)"T, tem-se:
2.000 = 70 ⋅ c ⋅ (72 − 10) ⇒ c = 0,46 cal/g°C
Página cento e oitenta e cinco
ATIVIDADES
1. Classifique em V (verdadeira) e F (falsa) as afirmações citadas a seguir.
I. Calor específico de uma substância (c) é a quantidade de calor necessária para variar em 1 grau célcius a tempera-túra de uma unidade de massa.
V
II. Quando um corpo está kemte, podemos afirmar quê ele possui calor.
F
III. A á gua, pelo seu elevado calor específico, é utilizada para refrigerar motores de combustão interna.
V
2. Em algumas praias, percebe-se quê, assim quê o sól nasce, após pouco tempo a areia já se encontra aquecida, mas a á gua do mar ainda está gelada, permanecendo assim boa parte do dia. Quando o sól se põe, em pouco tempo a areia está gelada, mas é possível notar quê a á gua do mar está mais aquecida, permanecendo assim por um longo intervalo de tempo. Qual seria a explicação para êste comportamento distinto entre areia e á gua?
3. O motor de um carro, durante o tempo de funcionamento, teve uma das suas peças aquecidas, passando de 15 °C para 115 °C. Sabendo quê essa peça tem massa de 2.000 g e recebeu 4.000 cal, determine a capacidade térmica da peça e o calor específico da substância quê a constitui.
40 cal/°C; 0,02 cal/g°C
4. Durante um estudo sobre o comportamento térmico de determinado corpo, cuja massa é 0,2 kg, foi fornecida a ele a quantidade de calor de 0,2 kcal, provocando uma variação de tempera-túra de 5 °C para 15 °C. Diante dêêsses dados, determine o calor específico da substância quê constitui esse corpo.
0,1 cal/g°C
5. Um bloco de cobre (c = 0,094 cal/g°C) de 1,20 kg é colocado em um fôrnu até atingir o equilíbrio térmico. Nessa situação, o bloco recebe 12.972 cal. Qual é a variação de tempera-túra sofrida pelo bloco de cobre?
115 °C
6. O calor específico do ferro é igual a 0,110 cal/g°C. Determine a tempera-túra final de uma massa de 400 g de ferro, após receber aproximadamente 600 cal. Considere quê sua tempera-túra inicial era de 20 °C.
33,63 °C
7. Um corpo de 250 g de massa e tempera-túra inicial de 10 °C é aquecido durante 5 min por uma fonte de potência constante quê lhe fornece 700 cal/min. Ao final dêêsse tempo, a tempera-túra do corpo vale 80 °C. Qual é o valor do calor específico da substância quê constitui o corpo?
0,2 cal/g°C
8. Uma barra metálica de 0,400 kg sofre um acréscimo de tempera-túra de 49 °C, quando ABSÓRVE 9.800 J de calor. Determine o calor específico dêêsse metal.
500 J/kg°C
SAIBA +
por quê as tempera-túras são tão extremas no deserto?
No deserto, durante o dia, a tempera-túra póde atingir até 60 °C, situação quê se inverte à noite, quando as tempera-túras podem atingir valores abaixo de zero.
Essa grande amplitude de tempera-túra ocorre pelo fato de a areia do deserto possuir baixo calor específico, o quê a faz se aquecer com muita facilidade durante o dia e se resfriar facilmente durante a noite.

ATIVIDADES
1. Qual diferença seria observada em um deserto, caso existisse nele um reservatório de á gua, como um lago, por exemplo?
2. Faça uma pesquisa sobre o grupo étnico dos beduínos, quê habitam desertos do ôriênti Médio. Busque informações sobre suas origens, onde vivem, estilo de vida, côstúmes e como lidam com as particularidades do ambiente de um deserto.
Página cento e oitenta e seis
Trocas de calor e calorímetro
Quando se deseja manter a tempera-túra de um corpo (termo genérico para representar sólidos, líquidos e gases), é comum se utilizar recipientes específicos para conservar a tempera-túra, como caixas, garrafas ou copos térmicos.
E como agem estes recipientes? Eles fornecem ou retiram calor dos corpos colocados dentro deles?
Estes recipientes evitam quê ocorram trocas de calor entre o ambiente interno e externo a eles.
Chama-se calorímetro ideal um recipiente quê impede as trocas de calor entre o seu conteúdo e o meio externo. Sendo assim, colocando dois corpos com tempera-túras diferentes dentro de um calorímetro ideal, as trocas de calor ocorrerão apenas entre os corpos até quê seja atingido o equilíbrio térmico. Esta troca de calor é baseada no princípio da conservação de energia.
Qcedido + Qrecebido = 0
PENSE E RESPONDA

3 Em quê situações é comum se utilizar uma garrafa térmica?
Caixas, garrafas e copos térmicos podem sêr considerados calorímetros reais, pois as trocas de calor entre seus meios interno e externo são reduzidas, mas acontecem. Uma garrafa térmica é capaz de manter o café aquecido por um tempo maior, porém ainda ocorre o esfriamento do líquido.
Nesse caso, deve-se considerar as trocas de calor com o calorímetro, quê possui capacidade térmica, absorvendo parte do calor trocado e parte do calor do meio externo.

ATIVIDADES RESOLVIDAS
3. Em um calorímetro de capacidade térmica igual a 20 cal/°C, há 200 g de á gua a 90 °C. Determine a massa de alumínio a 20 °C, capaz de fazer a á gua esfriar até 70 °C.
Dados: cH2O = 1,0 cal/g°C; cA(éli)" = 0,2 cal/g°C.
Resolução
Qcalorímetro + Qá gua + Qalumínio = 0 ⇒
⇒ [C ⋅ (T − Ti)]calorímetro + [c ⋅ m ⋅ (T − Ti)]á gua + [c ⋅ m ⋅ (T − Ti)]alumínio = 0 ⇒
⇒ 20 ⋅ (70 − 90) + 200 ⋅ 1,0 ⋅ (70 − 90) + m ⋅ 0,2 ⋅ (70 − 20) = 0 ⇒ −400 − 4.000 + 10m = 0 ⇒
⇒ m = 440 g
Página cento e oitenta e sete
ATIVIDADES
9. Quatro participantes de uma gincana cultural foram colocados diante da seguinte situação: três corpos (A, B e C) fabricados com materiais metálicos diferentes foram colocados em um recipiente termicamente isolado. Depois de algum tempo, foram informados de quê a tempera-túra do corpo A e a do corpo B haviam aumentado. Com base nessa informação, cada participante emitiu uma afirmação. Avalie qual das afirmações está correta.
a) A tempera-túra do corpo C diminuiu.
b) O corpo C cedeu calor para o corpo A, porém recebeu calor do corpo B.
c) A tempera-túra do corpo C permaneceu constante.
d) O corpo C cedeu calor para o corpo B, porém recebeu calor do corpo A.
Resposta: a)
10. Em um calorímetro real cuja capacidade térmica é 2,0 cal/°C, foram colocados 120 g de um líquido. O conjunto estava a uma tempera-túra de 13°C. Em seguida, adicionaram-se 300 g de á gua a 100 °C, resultando numa tempera-túra final de equilíbrio de 27,5°C. Calcule o calor específico dêêsse líquido.
≃ 12,5 cal/g°C
11. A tempera-túra do corpo de uma atleta é 37,5 °C. Todos os dias, ela bebe 2,5 litros de á gua a 8,5 °C. Sabendo quê 1 litro de á gua corresponde a 1.000 g de á gua e quê seu calor específico é 1 cal/g°C, calcule a quantidade de calor quê ela perde por dia pela ingestão de á gua.
72.500 cal
12. Estudos mostram quê, para dar banho em um bebê, é importante usar á gua com a tempera-túra morna, não muito kemte. O ideal é quê o valor da tempera-túra esteja próximo de 38 °C, facilitando assim a manutenção da tempera-túra do corpo da criança. Sabendo díssu, a atendente da maternidade percebeu quê a tempera-túra (ambiente) da á gua era de 30 °C e rêzouvêo misturar á gua fervente a essa á gua, d fórma quê obtivesse á gua a 38 °C. Calcule aproximadamente o volume de á gua fervente quê ela deverá adicionar aos 10 L de á gua quê já estão na banheira, a 30 °C.
≃ 1.290 mL
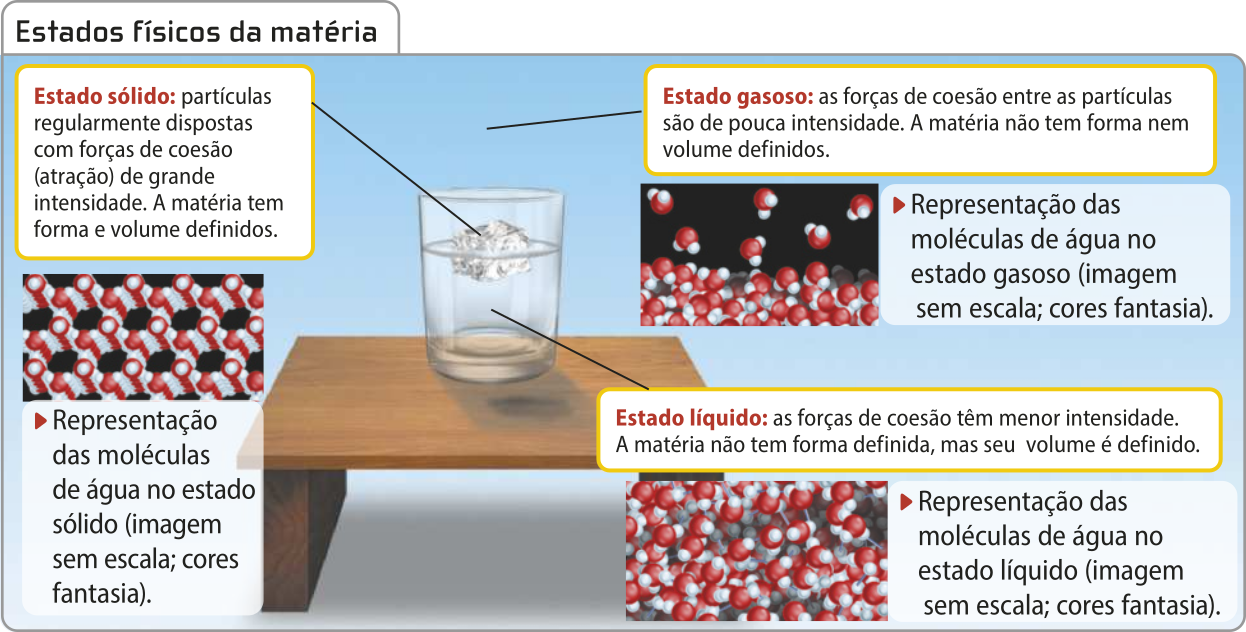
Estados físicos da matéria
Na natureza, pode-se encontrar, basicamente, a matéria em três estados físicos: sólido, líquido e gasoso.
Página cento e oitenta e oito
O estado físico depende da tempera-túra e da pressão sobre as substâncias, e, com a variação destas propriedades, podem ocorrer mudanças de estado físico, quando não se modifica a sua composição. A mudança de estado de uma substância pura sempre ocorre à tempera-túra constante, quê depende da pressão a quê está submetida e de sua natureza.
A passagem do estado sólido para o líquido é denominada fusão, já a vaporização é a passagem do estado líquido para o gasoso, e a sublimação é a passagem do estado sólido para o gasoso. Submetidas à pressão constante, todas essas transformações ocorrem com a absorção de calor pela substância e, por isso, são chamadas transformações endotérmicas.
Os fenômenos inversos são: a condensação, passagem do estado gasoso para o líquido; a solidificação, a passagem do estado líquido para o sólido; e a sublimação (ou ressublimação), passagem do estado gasoso para o sólido. Submetidas à pressão constante, todas essas transformações ocorrem com a liberação de calor pela substância e, por isso, são chamadas transformações exotérmicas.
A vaporização póde ocorrer por evaporação (processo lento e natural quê ocorre na superfícíe do líquido) e ebulição (processo quê ocorre a uma tempera-túra específica, em todo o líquido).
PENSE E RESPONDA

4 Qual o estado físico das nuvens no céu?
Calor e mudança de estado físico
Na mudança de estado físico de substâncias puras à pressão constante, a tempera-túra se mantém constante durante o processo, sêndo chamada ponto de mudança de estado, como ponto de fusão e ponto de ebulição.
Para cada substância e para cada mudança de estado físico, existe uma propriedade chamada calor latente de mudança de fase (L).
Calor latente de mudança de fase L é a quantidade de calor Q quê uma unidade de massa m de determinada substância deve receber (ou perder) para sofrer uma mudança de estado físico.
De forma algébrica, essa definição póde sêr representada da seguinte forma:
L =
A unidade de medida do SI é Jáule por quilograma (J/kg). Uma unidade usualmente utilizada é caloria por grama (cal/g).
Assim, estando a substância de massa m no ponto de mudança de fase, Q é a quantidade de calor necessária para quê a mudança de estado físico ocorra.
Q = mL
Página cento e oitenta e nove
Curva de aquecimento e resfriamento
Considere um recipiente fechado mantido à pressão de 1 atm, no qual se acrescenta uma massa de gêlo inicialmente a −30 °C. êste sistema começa a receber calor de uma fonte térmica com potência constante.
![Representação de aquecimento e mudança de estado físico em quatro imagens. Imagem 1: um recipiente com gelo[ temperatura de menos trinta graus Célsius a zero grau] é aquecido. Imagem 2: um recipiente com água e gelo[temperatura zero graus célsius] é aquecido. Imagem 3: um recipiente com água[temperatura de zero grau Célsius a cem graus Célsius] é aquecido. imagem4: um recipiente com água e vapor[temperatura cem graus Célsius].](../resources/images/ek_8/ek_8e3b84be5009dd20e306939e3d381477.png)
êste processo de aquecimento e mudança de estado físico póde sêr representado por um gráfico, normalmente chamado de curva de aquecimento. O gráfico a seguir representa o aquecimento da á gua do exemplo do esquema anterior.
![Representação gráfica de aquecimento da água: eixo vertical 'T'[C], graduação menos trinta, zero, cem. Eixo horizontal 'Q'. Uma reta inicia em menos trinta graus Célsius[estado sólido]'Q1', segue paralela ao eixo horizontal[fusão] 'Q2'.subindo até cem graus [estado liquido] 'Q3', mantendo cem graus[vaporização] 'Q4', subindo[vapor].](../resources/images/ek_4/ek_432d3b9016ef56db5d18d803e7604a04.png)
Para substâncias puras, êste gráfico possui trechos em quê o calor foi absorvido e a tempera-túra aumentou, e trechos em quê o calor foi absorvido e a tempera-túra se manteve constante, quando ocorre a mudança de estado físico.
Caso fosse analisado o resfriamento, bastaria seguir o gráfico d fórma invérsa, quando se tem uma curva de resfriamento.
Página cento e noventa
ATIVIDADES
13. Uma pessoa deixa duas esferas de mesma massa e com mesma tempera-túra (maior quê 0 °C), feitas de cobre e alumínio, sobre um grande bloco de gêlo. Sabendo quê o calor específico do cobre é menor do quê o do alumínio (ccobre < calumínio), qual será a posição de cada esféra no interior do bloco de gêlo depois de atingido o equilíbrio?
14. (Enem/MEC) Com base em projeções realizadas por especialistas, prevê-se, para o fim do século XXI, aumento de tempera-túra média, no planêta, entre 1,4 °C e 5,8 °C. Como consequência dêêsse aquecimento, possivelmente o clima será mais kemte e mais úmido, bem como ocorrerão mais enchentes em algumas áreas e secas crônicas em outras. O aquecimento também provocará o desaparecimento de algumas geleiras, o quê acarretará o aumento do nível dos oceanos e a inundação de cértas áreas litorâneas.
As mudanças climáticas previstas para o fim do século XXI
a) provocarão a redução das taxas de evaporação e de condensação do ciclo da á gua.
b) poderão interferir nos processos do ciclo da á gua quê envolvem mudanças de estado físico.
c) promoverão o aumento da disponibilidade de alimento das espécies marinhas.
d) induzirão o aumento dos mananciais, o quê solucionará os problemas de falta de á gua no planêta.
e) causarão o aumento do volume de todos os cursos de á gua, o quê minimizará os efeitos da poluição aquática.
Resposta: b)
15. Calcule a quantidade de calor necessária para transformar, sôbi pressão normal, 200 g de á gua, a 80 °C, em vapor de á gua, a 100 °C.
Dado: Lvaporização = 539,6 cal/g.
111.920 cal
16. Uma massa de gêlo encontra-se a uma tempera-túra de −10 °C e é transformada em á gua e aquecida a 50 °C. Sabendo quê a quantidade de calor gasta nessa transformação foi de 27.000 cal, determine a massa de gêlo transformada em á gua.
Dados: cá gua = 0,5 cal/g°C; Lv = 80 cal/g.
200 g
SAIBA +
Umidade relativa do ar e sensação térmica
Em dias kemtes, uma das maneiras de o corpo humano manter sua tempera-túra em equilíbrio, por volta de 36,5 °C, é por meio da transpiração. A “sensação de calor” não depende apenas da tempera-túra ambiente, mas também de outros fatores, entre eles, a umidade relativa do ar.
Se a umidade do ar estiver alta (alta concentração de vapor de água), a taxa de evaporação do suor será pequena, formando uma espécie de estufa ao redor do corpo, reduzindo as trocas de calor e aumentando a sensação térmica. O ôpôsto acontece com a baixa umidade do ar (baixa concentração de vapor de água), quando a taxa de evaporação do suor se eleva, aumentando a emissão de calor pelo corpo e reduzindo a sensação térmica.
Dessa forma, é possível quê um dia a 28 °C com alta umidade relativa do ar cause maior sensação térmica do quê um dia a 32 °C com baixa umidade relativa do ar.
ATIVIDADES
1. De quê maneira um ventilador auxilia na mudança da sensação térmica de uma pessoa?
2. Quando se passa áucôl na péle, é possível sentir um esfriamento local. Como se póde explicar esse fato?
Página cento e noventa e um
Relação entre pressão e tempera-túra nas mudanças de estado físico
A mudança de estado físico das substâncias está relacionada à mudança da disposição de suas partículas constituintes. Quando se aquece uma substância, aumenta-se a agitação de suas partículas, elevando a energia cinética destas. Se o aquecimento seguir, a substância atingirá a tempera-túra de mudança de estado, na qual as partículas terão energia suficiente para romper as ligações intermoleculares.
Até o momento, foram analisados os estados físicos e as mudanças entre eles sempre enfatizando a pressão de 1 atm (ao nível do mar). Isso é necessário, pois a pressão interfere nos estados físicos. Esta análise da relação entre pressão e tempera-túra póde sêr feita a partir de diagramas de pressão por tempera-túra, analisando as curvas quê delimitam os estados físicos.
Os valores de pressão e tempera-túra varíam entre as substâncias, mas o formato da curva é equivalente.
PENSE E RESPONDA

5 por quê uma panela de pressão cuzinha alimentos em menor tempo, quando comparado ao tempo de cozimento em panelas abertas?
Curva de fusão
A curva de fusão é aquela entre os estados físicos sólido e líquido. Um ponto sobre a curva indica quê a fusão, ou solidificação, está ocorrendo.
A maior parte das substâncias puras aumenta seu volume durante a fusão. A curva de fusão destas substâncias indica quê, quanto maior a pressão sobre a substância, maior é seu ponto de fusão. Por exemplo, tendo ferro no estado líquido ou sólido, um aumento da pressão faz a substância ficar em estado sólido.
Existem algumas substâncias quê diminuem seu volume durante a fusão, como á gua, antimônio e bismuto. São aquelas quê sofrem dilatação anômala. A curva de fusão destas substâncias indica quê, quanto maior a pressão sobre a substância, menor é seu ponto de fusão. Tendo á gua em estado líquido ou sólido, um aumento da pressão faz a substância ficar em estado líquido (é possível obtêr á gua líquida a tempera-túras menóres quê 0 °C com um aumento de pressão).
![Representação gráfica 'Substâncias puras que dilatam durante a fusão'. Eixo vertical 'P', eixo horizontal 'T' . Uma reta iniciando em 'P1','T!'[sólido], indo até 'P2','T2'[líquido].](../resources/images/ek_5/ek_58cdb522aace047815694b842c8756f1.png)
![Representação gráfica 'Substâncias puras que contraem durante a fusão'. Eixo vertical 'P', eixo horizontal 'T'. uma reta iniciando em 'P1','T1'descendo[líquido] até 'P2','T2'[sólido]](../resources/images/ek_b/ek_b682ff59f8cde2f04baf60e435ea17cd.png)
ESPAÇOS DE APRENDIZAGEM
• O vídeo reproduz o experimento do regelo, quê ocorre após um bloco de gêlo sêr atravessado por um fio.
O gêlo quê se regenéra (experiência). Publicado por: Manual do Mundo. Vídeo (3 min). Disponível em: https://livro.pw/aszjg. Acesso em: 3 set. 2024.
Página cento e noventa e dois
Curva de ebulição
A curva de ebulição é aquela entre os estados físicos líquido e gasoso. Um ponto sobre a curva indica quê a ebulição, ou condensação, está ocorrendo.
A ebulição é o processo em quê a substância muda do estado líquido para o gasoso ao longo de todo o líquido, com formação de bolhas quê deixam o líquido, vencendo assim a pressão externa.
Para formár uma bolha, a pressão de vapor interna da bolha deve sêr maior do quê a pressão externa (exercida pelo líquido ao redor e também pela pressão atmosférica). Assim, se a pressão sobre o líquido diminuir, como ocorre em altitudes mais elevadas, a pressão de vapor necessária para formár a bolha também diminui, reduzindo a tempera-túra de ebulição.
De forma análoga, quando a pressão sobre o líquido aumenta, eleva-se a tempera-túra de ebulição, como ocorre nos gêiseres (reserva de á gua no interior da crôsta da Terra, quê se mantém líquida devido à alta tempera-túra; quando há uma fenda quê conecta essa reserva de á gua à superfícíe, ocorrem erupções, com a á gua subindo e passando rapidamente do estado líquido para gasoso).
Em uma panela de pressão fechada, por exemplo, ocorre a evaporação e condensação da á gua continuamente até quê seja atingido um equilíbrio químico para determinada tempera-túra, quando se alcança a pressão de vapor mássima dentro da panela. Como esta pressão mássima de vapor é maior do quê a pressão atmosférica, podendo atingir até 2 atm, é possível obtêr á gua líquida com tempera-túra em torno de 120 °C.
Assim, quanto maior a pressão, maior a tempera-túra de ebulição, conforme mostra o gráfico pressão por tempera-túra para a curva de ebulição a seguir. Esta análise é equivalente para todas as substâncias puras.

![Representação gráfica de uma 'Curva de uma substância pura'. Eixo vertical 'P', eixo horizontal 'T'. Uma curva iniciando em 'P1','T1'indo para cima até 'P2', 'T2'. Lado acima da curva [líquido] e lado abaixo da curva [gasoso]](../resources/images/ek_b/ek_bb809df9aac84724fe22dd28b5f4519e.png)
Utilizando a á gua como exemplo, tem-se a tempera-túra de ebulição de 100 °C ao nível do mar, com pressão de 1 atm. Quanto maior a altitude, menor a pressão atmosférica e, consequentemente, menor será a tempera-túra de ebulição.
Página cento e noventa e três
Curva de sublimação
A curva de sublimação é aquela entre os estados sólido e gasoso. Um ponto sobre a curva indica quê a sublimação, ou ressublimação, está ocorrendo.
A sublimação ocorre quando a estrutura das substâncias, à pressão constante, altera-se ao receber calor, passando de sólido para gasoso, ou ao ceder calor, passando de gasoso para sólido. Esfriando dióxido de carbono (CO2) até cerca de −78,5 °C, à pressão de 1 atm, ocorre a sublimação do estado gasoso para o sólido, conhecido por gelo-seco. Se for novamente aquecido, à pressão de 1 atm, tem-se novamente a passagem do estado sólido para gasoso. Isso ocorre porque, na pressão de 1 atm, o gás carbônico jamais é líquido.
A curva de sublimação indica quê, quanto maior a pressão sobre a substância, maior é seu ponto de fusão.

![Representação gráfica 'Curva de sublimação de uma sustância pura'. Eixo vertical 'P' e eixo horizontal 'T'. Uma curva iniciando em 'P1', 'T1', subindo até 'P2', 'T2',abaixo da curva [gasoso] e acima da curva[sólido].](../resources/images/ek_c/ek_c0d4b33f833e9f8b8a928208c1544ce6.png)
Diagrama de estados físicos
O diagrama de estados físicos é obtído reunindo as três curvas. O estilo das curvas de ebulição e sublimação são os mesmos para todas as substâncias puras, variando apenas os valores de pressão e tempera-túra. A curva de fusão se diferencia entre a grande maioria das substâncias, quê aumentam de volume durante a fusão, e as substâncias como a á gua, quê diminuem de volume durante a fusão. Assim, existem dois formatos de diagrama de estados físicos.
![Diagrama dos estados físicos de substâncias como a água. Eixo vertical 'P'[a t m] e eixo horizontal 'T'[C]. uma curva inicia em zero, subindo até 'P'0,06 e 'T'0,01, voltando a subir até 'P'218 e 'T'374. Uma reta perpendicular em 'P'0,06 e 'T'0,01 divide o diagrama em sólido abaixo e líquido acima da curva e gasoso vapor abaixo da curva e gasoso gás, fora da curva.](../resources/images/ek_f/ek_ff3a71d022c3d148942a65dfde1d7626.png)
![Diagrama de estados físicos da grande maioria das substâncias. Eixo vertical 'P'[a t m] perpendicular a zero no meio do eixo horizontal 'T'[C]. A curva inicia paralela ao eixo horizontal, subindo até 'T' menos 564 e 'P'5,11, voltando a subir até 'P'73 3 'T'31,1. Acima da curva no ponto 'T' estado líquido e no ponto 'C' estado gasoso [vapor] e fora da curva estado gasoso [gás].](../resources/images/ek_6/ek_6725a644d5fd077c1a969f459f633707.png)
Página cento e noventa e quatro
O ponto T é chamado ponto triplo e representa uma situação de equilíbrio em quê a substância existe nos três estados físicos: sólido, líquido e gasoso. Nos diagramas, é possível verificar a pressão e a tempera-túra do ponto triplo da á gua e do dióxido de carbono.
O ponto C é chamado de ponto crítico. Analisando os dois estilos de diagrama de fases apresentados, tem-se alguns pontos no estado gasoso em quê é possível mudar para o estado líquido aumentando a pressão e mantendo a tempera-túra constante. Quando isso ocorre, tem-se o estado gasoso designado por vapor. Para tempera-túras acima da tempera-túra crítica, não é possível fazer a mudança do estado físico gasoso para líquido aumentando a pressão, sêndo obrigatório a redução para uma tempera-túra abaixo da tempera-túra crítica. Quando isso ocorre, tem-se o estado gasoso designado por gás.
ESPAÇOS DE APRENDIZAGEM
• Esta simulação permite verificar a mudança de estado físico de alguns hátomus e moléculas. Na opção “Mudança de Fase”, é possível verificar no diagrama de fases em qual estado se encontra o elemento analisado.
Estados da matéria: básico. Publicado por: PhET Interactive Simulations. Disponível em: https://livro.pw/uuxjh. Acesso em: 30 set. 2024.
ATIVIDADES
17. As afirmações a seguir fazem referência ao processo de fusão. Avalie quais estão corretas.
I. Ao se fundir, a maioria das substâncias, mas nem todas, aumenta de volume.
II. Ao se fundirem, algumas substâncias, como a á gua, contráemsse, e o aumento de pressão diminui a tempera-túra de fusão.
III. Ao se fundirem, algumas substâncias aumentam de volume. Nesses casos, o aumento de pressão faz aumentar a tempera-túra de fusão.
IV. A á gua, ao se fundir, sofre contração de volume. Nesse caso, o aumento de pressão faz aumentar a tempera-túra de fusão.
As afirmações I, II e III estão corretas.
18. O gráfico a seguir representa o diagrama de estados físicos do dióxido de carbono (CO2).
![Diagrama dos estados físicos do dióxido de carbono. Eixo vertical 'P'[a t m] e eixo horizontal 'T'[C]. Uma curva no ponto 'P'5,11 e 'T' menos 56,4, com os pontos 1, na extremidade acima da curva e o ponto 3, na extremidade abaixo, da curva uma ramificação ponto 2 ascendente.](../resources/images/ek_4/ek_4dd04943c9a061d4583c3606e3161f61.png)
a) Qual é o nome das curvas 1, 2 e 3?
b) Qual é o estado físico do CO2 nos pontos A, B e C?
A: sólido; B: líquido; e C: gasoso.
c) Em quê estado está o CO2 sôbi a pressão de 8 atm e −79 °C?
Sólido.
d) Qual é o valor da tempera-túra e da pressão no ponto triplo?
T = −56,4 °C e p = 5,11 atm.
e) O quê acontece se o CO2 for aquecido sôbi pressão acima de 5 atm? E se ele for aquecido a uma pressão cujo valor seja inferior a 5 atm?
Acima de 5 atm ocorrerá fusão e abaixo de 5 atm ocorrerá sublimação.
19. No diagrama de estados físicos a seguir, associe para os pontos A, B, K, D e E as denominações sólido, líquido, vapor e gás. Classifique os pontos T e C.
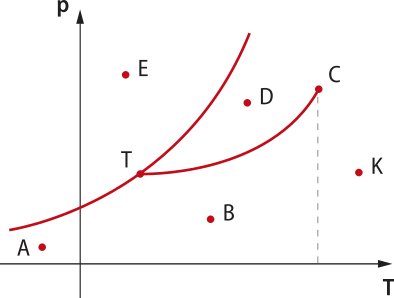
Página cento e noventa e cinco
TEMA 16
Transmissão de calor
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Mecanismos de transmissão de calor
O calor é uma forma de energia transferida espontaneamente de um corpo de maior tempera-túra para outro de menor tempera-túra. Essa transmissão de energia póde ocorrer de três modos distintos: condução, convekição e radiação, quê serão estudados ao longo dêêsse Tema.
PENSE E RESPONDA

1 Como você acha quê a energia emitida pelo Sol alcança a Terra?
Transmissão de calor por condução
Ao aquecer uma barra metálica, como a da imagem, as partículas quê constituem a extremidade da barra mais próxima de uma fonte de calor passam a vibrar com maior intensidade, devido ao aumento da tempera-túra. Essa agitação mais intensa é transmitida para as partículas mais próximas, e as regiões vizinhas também se aquécem. Com o tempo, toda a barra estará aquecida. A essa forma de propagação do calor se nomeia condução térmica.
A condução térmica ocorre devido ao contato entre corpos, ou entre partes de um mesmo corpo, com tempera-túras diferentes. Essa forma de propagação ocorre predominantemente em corpos sólidos.

Lei de Fourier
O matemático francês jã batíst jôsef Fourier (1768-1830) desenvolvê-u estudos detalhados sobre transmissão de calor por condução, elaborando uma forma de calcular o fluxo de calor Φ por um corpo, quê corresponde à quantidade de calor (delta)"Q transferida por uma unidade de tempo (delta)"t.
êste fluxo póde sêr calculado a partir de características do corpo. Considere um corpo de espessura (e) e d fórma quê, quanto maior for a espessura, menor será o fluxo de calor. Considere também quê êste corpo tem uma área de seção transversal A, d fórma quê quanto maior for a área, maior será o fluxo de calor. As áreas dêste corpo estão expostas a tempera-túras distintas T2 e T1, sêndo T2.> T1: quanto maior for o (delta)"T, maior será o fluxo de calor.
Página cento e noventa e seis
Cada material possui uma capacidade para conduzir calor, definida por uma constante denominada coeficiente de condutividade térmica k. Quanto maior for esse coeficiente, maior será o fluxo de calor.
Assim, o fluxo de calor da área exposta a uma tempera-túra maior para a área exposta a uma tempera-túra menor póde sêr calculado da seguinte forma:
Φ = ⇒
No SI, a unidade de medida de fluxo de calor é Jáule por segundo (J/s), quê corresponde ao watt (W). É comum utilizar a unidade de medida caloria por segundo (cal/s) para indicar a grandeza fluxo de calor.
O coeficiente de condutividade térmica é uma característica relevante dos materiais quê permite avaliar a adequação de seu uso em diferentes situações.
De acôr-do com os valores de coeficiente de condutividade térmica, pode-se optar por alguns metais para confeksionar equipamentos quê exigem a rápida transmissão de calor, pois são bons condutores de calor. Já o concreto, a cortiça, o vidro, a madeira e a lã são utilizados em equipamentos em quê se deseja evitar a transmissão de calor, pois são maus condutores de calor (ou bons isolantes térmicos).
Condutividade térmica de algumas substâncias
Substância |
Condutividade térmica (kcal/sm °C) |
|---|---|
Metais |
|
Alumínio |
4,9 ⋅ 10−2 |
Cobre |
9,2 ⋅ 10−2 |
Chumbo |
8,3 ⋅ 10−3 |
Prata |
9,9 ⋅ 10−2 |
Aço |
1,1 ⋅ 10−2 |
Gases |
|
Ar |
5,7 ⋅ 10−6 |
Hidrogênio |
3,3 ⋅ 10−5 |
Oxigênio |
5,6 ⋅ 10−4 |
Outros materiais |
|
Concreto |
2,0 ⋅ 10−4 |
Cortiça |
1,0 ⋅ 10−5 |
Vidro |
2,0 ⋅ 10−4 |
Madeira |
2,0 ⋅ 10−5 |
Lã pura |
1,0 ⋅ 10−5 |
Fonte: TIPLER, poou; MOSCA, Gene. Física para cientistas e engenheiros: mecânica, oscilações e ondas, termodinâmica. 6. ed. Rio de Janeiro: LTC, 2009. p. 606.
ATIVIDADES
1. Indispensável em qualquer cuzinha, a escolha da panela adequada depende do material usado para sua fabricação. Os mais comuns são alumínio, aço inoxidável, ferro, cobre, cerâmica, barro e vidro.
a) Analise o caso de uma fábrica quê precisa produzir um tipo de panela quê esquente rápido e d fórma uniforme. Para atingir esse objetivo, ela deverá sêr feita de um material quê tenha quais características?
b) No Brasil, as panelas utilizadas para cocção de alimentos são feitas de diferentes materiais e, em alguns casos, revelam aspectos culturais e históricos da população. Que tipo de panela é utilizada na região onde você vive? É possível relacionar o seu uso com algum aspecto cultural e histórico dos povos quê vivem ou viveram nessa região? Converse com seus côlégas a respeito díssu e elaborem um material quê compartilhe esses resultados, trazendo características dêêsses materiais e qual relação histórica e cultural póde sêr identificada.
2. Calcule a diferença de tempera-túra entre as faces de um vidro plano cujo coeficiente de condutibilidade térmica é 2 ⋅ 10−4 kcal/sm°C, área igual a 2.000 cm2 e espessura de 4 mm.
Dado: Φ = 1.500 cal/s.
150 °C
Página cento e noventa e sete
Transmissão de calor por convekição
Quando uma pessoa utiliza a chama do fogão para aquecer uma panela contendo á gua, ela póde observar a movimentação do líquido dentro da panela. Isso ocorre porque a camada de líquido mais próxima da fonte de calor se aquece, e suas partículas ficam mais agitadas. Consequentemente, o líquido dilata, diminuindo sua densidade em relação às camadas de líquido quê estão mais acima da panela, com tempera-túras menóres e mais densas.
Essa diferença de densidade faz com quê camadas de líquido mais aquecidas (menos densas) se movimentem para cima, enquanto as camadas mais frias (mais densas) se movimentam para baixo, formando as chamadas correntes de convekição.
A propagação do calor por convekição se dá pela movimentação da matéria. Portanto, ela ocorre apenas nos fluidos (estado líquido e gasoso).

Devido ao fenômeno da convekição, os aquecedores instalados em residências devem sêr posicionados na parte inferior do ambiente, enquanto os aparelhos de ar-condicionado devem sêr instalados na parte superior, pois assim favorécem o movimento natural do ar, quê quando está kemte sobe e quando está frio desce.
A convekição é o mecanismo responsável pela formação de ventos e brisas, quê surgem quando camadas de ar se movimentam em razão das diferenças de tempera-túra e de densidade.
Página cento e noventa e oito
SAIBA +
Inversão térmica
Durante um dia kemte, as camadas de ar mais próximas da superfícíe da Terra se aquécem mais rapidamente e se dispersam para cima. À noite, as camadas de ar mais próximas da superfícíe se esfriam mais rapidamente. Logo acima dessa região, há uma camada de ar quê foi aquecida ao longo do dia, e, acima dela, estão camadas mais afastadas, quê são naturalmente mais frias (pois são mais densas).
Essa configuração dificulta a formação das correntes de convekição, aprisionando uma camada de ar próxima da superfícíe. Esse fenômeno é conhecido como inversão térmica e ocorre com mais freqüência no período noturno, porém póde acontecer ao longo do dia.
Em períodos de baixas tempera-túras, a inversão térmica póde causar a formação de neblinas, devido à condensação da umidade do ar. Nos grandes centros urbanos, esse fenômeno ocorre d fórma mais intensa e impede a dispersão de poluentes pela atmosféra.
![Representação da dispersão do ar. Duas imagens. Imagem da esquerda, um céu de dia com sol prédios abaixo. as camadas de ar de cima para baixo: frio, morno e quente.[o ar sobe, imagem da direita: mesma imagem a noite com Lua. As camadas de ar de cima para baixo: frio, quente, frio.[o ar desce]](../resources/images/ek_f/ek_f1e5c5a85bb60ed3b2e030b1e2b882d2.png)
ATIVIDADES
1. por quê a camada de ar mais próxima da superfícíe da Terra não se dispersa na inversão térmica?
2. A inversão térmica póde oferecer riscos aos sêres vivos? Justifique sua resposta.
Página cento e noventa e nove
Transmissão de calor por radiação
Os mecanismos de transmissão de calor por condução e convekição exigem um meio material. Como a Terra e o Sol estão imersos no espaço, sem a existência de qualquer meio, qual seria a forma de transmissão quê possibilitaria quê o calor do Sol chegasse até a Terra?
Como não há um meio material entre eles, esse calor se propaga por meio de ondas eletromagnéticas, por um fenômeno chamado radiação ou irradiação.
Essas radiações são ondas eletromagnéticas capazes de se propagar em qualquer meio, inclusive no vácuo. Um exemplo de radiação térmica é o infravermelho, invisível aos olhos. Para cértas escalas de tempera-túra, a radiação térmica póde sêr sentida pelo tato, como é possível perceber ao se aprossimár de uma fogueira. Existem animais quê são mais sensíveis à radiação térmica, como é o caso de algumas serpentes, quê utilizam sensores para detectar presas e predadores.

Todo corpo quê possui tempera-túra emite uma radiação térmica, e, quanto maior a tempera-túra, maior a intensidade da radiação térmica emitida. O corpo humano, por exemplo, emite radiações térmicas constantemente. Além de emitir radiação térmica, um corpo também póde absorver ou refletir uma radiação incidente.
Quando um corpo recebe radiação, o aquecimento depende da sua capacidade de absorver energia. De maneira geral, corpos com cores escuras possuem alta capacidade de absorção e são bons emissores de energia, porém são ruins em refleti-la. Já os corpos com cores claras possuem baixa capacidade de absorção e são também maus emissores de energia, porém são bons em refleti-la.
Algumas aplicações da radiação térmica são as estufas de plantas e os coletores de energia solar. As estufas são utilizadas para gerar condições favoráveis para o cultivo de alguns tipos de flores, verduras e legumes. Esses locais são geralmente fechados por vidro transparente, quê transmite a radiação solar, aquecendo o ambiente interno da estufa e aumentando a intensidade da emissão de energia térmica na forma de infravermelho. Essa energia fica retida no interior da estufa, pois não passa pelo vidro, quê é um mau condutor de calor. Dessa forma, o interior da estufa fica mais kemte quê o ambiente externo.

Os coletores de energia solar funcionam de modo semelhante às estufas, pois são construídos com paredes de vidro e fundo escuro. Eles são muito utilizados no aquecimento de á gua em residências.
A Terra sofre um processo parecido com o da estufa. Determinados gases na atmosféra terrestre, como o dióxido de carbono (CO2), o óxido nitroso (N2O), o metano (CH4) e os hidrofluorcarbonos (HFCs), entre outros, absorvem parte da radiação infravermelha emitida pela superfícíe terrestre por meio da reflekção dos raios solares. Como consequência, o planêta perde pouco calor para o espaço por irradiação e fica mais aquecido, fenômeno denominado efeito estufa natural.
O efeito estufa natural auxilia na manutenção da tempera-túra da Terra, mantendo índices quê possibilitam a vida no planêta.

Página duzentos
ATIVIDADES
3. A respeito dos fôrnos utilizados nas cozinhas, explique o quê se pede.
a) por quê as prateleiras são feitas na forma de grades e com materiais considerados bons condutores de calor?
b) por quê se utiliza lã de vidro nas paredes dos fôrnos?
4. por quê o ar parado é freqüentemente utilizado como isolante térmico?
5. Alguns refrigeradores possuem apenas uma porta e, no lugar do frízer, o congelador fica posicionado na parte superior. Sobre esse aspecto, responda às kestões a seguir.
a) por quê o congelador fica na parte de cima dos refrigeradores?
b) Qual deve sêr o critério para escolher o local de armazenamento dos alimentos dentro do refrigerador?
6. Em uma residência, um aparelho de ar-condicionado foi instalado em um ambiente na parte de baixo de uma parede, próximo ao solo. Considere quê esse ambiente está fechado, o aparelho de ar-condicionado está ligado e, após cérto intervalo de tempo, você entra nesse ambiente. dêz-creva quais seriam as possíveis sensações com relação ao resfriamento do ar nesse ambiente e explique os motivos delas.
7. Um professor de Física apresentou um aparato em aula quê despertou a curiosidade dos estudantes. Tratava-se de um recorte de fô-lha de papel em formato de hélice, equivalente a um “caracol”, pendurado por uma linha. Esse professor acendeu uma vela e, quando posicionou esse recorte acima da chama dela, ele começou a girar. Explique o resultado desta demonstração feita pelo professor.

Não reproduza esse experimento na ausência do professor.
8. As sondas quê são lançadas para missões espaciais carregam consigo algumas baterias elétricas para manter seu sistema de investigação e comunicação acionado. Essas baterias possuem um sistema de carregamento por meio da energia solar. Qual é o mecanismo de transmissão de calor quê leva a energia do Sol até as sondas espaciais?
9. A garrafa térmica, popularmente conhecida como garrafa de café, foi fabricada para evitar as trocas de calor entre o líquido de seu interior e o ambiente externo. A imagem a seguir apresenta alguns dêtálhes de sua estrutura.
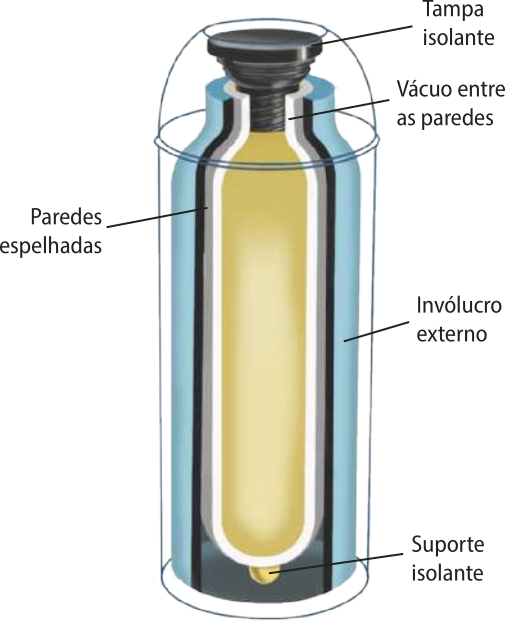
Em resumo, essas garrafas têm uma estrutura externa, geralmente de plástico, e em seu interior possuem um reservatório de vidro de paredes duplas, onde se faz vácuo entre elas (algumas possuem ar nesta região), com superfícíe interna e externa espelhada e tampa isolante.
a) Considerando essas informações, verifique qual mecanismo de transmissão de calor tenta-se evitar em cada detalhe de sua estrutura.
b) As garrafas térmicas usadas no cotidiano podem sêr consideradas calorímetros ideais? Explique.
Página duzentos e um
SAIBA +
Como os polos ajudam a manter o equilíbrio térmico da Terra?
A Terra vêm sofrendo sérias mudanças climáticas. Considerando diversas pesquisas realizadas por inúmeros países, os cientistas estão seriamente preocupados com os dados obtidos: a elevação do nível do mar, de 2 mm/ano, subiu para cerca de 3 mm/ano na última década, com previsão de quê esse número dobre nos próximos 100 anos. Esse fenômeno é justificado pelo acentuado degelo nos polos, causado pelo aumento da tempera-túra média do planêta.
Os polos são os sinalizadores das transformações climáticas, pois revelam como se comportou a atmosféra do planêta no passado, permitindo uma estimativa de como ela será no futuro.
Mas como são obtidas essas informações? Em quais arquivos os cientistas vão buscar os dados?
O gêlo nos polos foi se acumulando ao longo dos milênios em camadas de 5 cm por ano, aproximadamente, com bolhas de ar entre elas quê ficaram encapsuladas, representando fragmentos de ar da Terra de mais de 700 mil anos. Para obtêr amostras para análise, os especialistas começaram a extrair cilindros de gêlo com profundidades próximas de 3 km. O exame dêêsse material mostrou quê a natureza produz altas concentrações atmosféricas de gases relacionados com o efeito estufa, como aqueles decorrentes da erupção dos vulcões. Mas, atualmente, somando os gases produzidos pela natureza com os produzidos em decorrência das atividades humanas, os índices dêêsses gases chegaram a valores nunca alcançados.
Vale lembrar quê o efeito estufa assegura o equilíbrio do clima para as condições de vida no planêta, porém, quando em excésso, torna-se altamente destrutivo.
As áreas gélidas dos polos exercem um papel de equilíbrio na tempera-túra global, principalmente devido à sua influência na circulação das correntes marítimas e no efeito albedo.
As correntes marítimas ocorrem por causa da diferença de tempera-túra entre as várias partes do planêta. Nos trópicos, as águas kemtes dos oceanos correm superficialmente e vão em direção aos polos, onde se resfriam e ficam mais densas. Descem, então, para o fundo dos oceanos e retornam aos trópicos, onde se aquécem novamente. Com o derretimento das geleiras, quê são de á gua doce, a salinidade do mar está diminuindo, o quê modifica sua densidade. Isso póde influenciar o fluxo das correntes marítimas e, dessa forma, contribuir para o desequilíbrio da tempera-túra global.
O efeito albedo refere-se à porcentagem de luz refletida em relação à luz incidente. Nos polos, a reflekção do gêlo e da néve, quê são brancos, representa 90% da radiação solar recebida. Se houver diminuição da área coberta pelo gêlo, menos reflekção ocorrerá e, consequentemente, mais energia ficará retida, aumentando o aquecimento nos polos, de maneira mais diréta, e em outras partes do planêta, de maneira mais indireta.
ATIVIDADE
1. Sabemos quê o derretimento das geleiras tem aumentado nos últimos anos em função do aquecimento do planêta. Que medidas a ssossiedade deve adotar para evitar essa situação?
ESPAÇOS DE APRENDIZAGEM
• A reportagem discute aspectos acerca do derretimento das geleiras e suas consequências para o planêta.
Ônu vai celebrar Ano Internacional de Preservação de Glaciares em 2025. Publicado por: Nações Unidas. Disponível em: https://livro.pw/vczub. Acesso em: 5 set. 2024.
Página duzentos e dois
TEMA 17
Comportamento térmico dos gases
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Estado termodinâmico de um gás
O comportamento térmico dos gases é um dos tópicos de estudo da Termodinâmica. Para isso, usa-se um modelo denominado gás ideal, ou gás perfeito, quê apresenta as seguintes propriedades:
• Suas partículas (átomos ou moléculas) estão em constante movimento em todas as direções.
• As dimensões das partículas são desprezíveis em relação à distância entre elas, e é possível desconsiderar quaisquer interações entre elas, exceto durante as colisões.
• As colisões entre as partículas e as paredes do recipiente quê contém o gás são elásticas e o intervalo de tempo de duração é desprezível.
Mas um gás ideal existe?
[...] Embora não exista na natureza um gás com as propriedades exatas de um gás ideal, todos os gases reais se aproximam do estado ideal em concentrações suficientemente baixas, ou seja, em condições nas quais as moléculas estão tão distantes umas das outras quê praticamente não interagem. Assim, o conceito de gás ideal nos permite obtêr informações úteis a respeito do comportamento limite dos gases reais.
[...]
HALLIDAY, Daví; RESNICK, róbert; uólker, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução e revisão técnica: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. (Fundamentos de física, v. 2, p. 219).
Basicamente, um gás real tem comportamento próximo do ideal quando as interações entre partículas são desprezíveis. Essa condição póde sêr atendida a baixas concentrações do gás real e também com o gás à baixa pressão, para quê as partículas fiquem suficientemente distantes, e a alta tempera-túra em relação à tempera-túra crítica, para quê a energia cinética seja muito maior do quê a energia de interação intermolecular.
PENSE E RESPONDA

1 Você já sentiu dificuldade ao tentar abrir uma geladeira imediatamente após fechá-la? por quê isso ocorre?
Variáveis de estado termodinâmico
O estudo dos gases é feito analisando as partículas constituintes por meio de um modelo macroscópico, relacionando as chamadas variáveis de estado ao movimento dessas partículas. São elas:
• Volume (V): as partículas do gás ocupam totalmente o volume do recipiente em quê estão; assim, o volume do gás é o volume do recipiente.
• Pressão (p): as partículas do gás colidem elasticamente com as paredes do recipiente, exercendo uma fôrça resultante na área interna e gerando, assim, uma pressão sobre as paredes.
• Temperatura (T): as partículas quê compõem o gás possuem energia cinética associada à tempera-túra do gás; a tempera-túra será sempre absoluta e obrigatória mente estará expressa em kelvin.
Página duzentos e três
Transformações gasosas
Quando ocorre a alteração de uma dessas variáveis de estado, diz-se quê o gás (também chamado de sistema) sofreu uma transformação gasosa, encontrando-se em estado diferente do inicial.
A estratégia empírica para estudar transformações gasosas é manter uma das variáveis de estado constante e verificar o comportamento das outras variáveis. Para cada caso a seguir, considere quê uma massa de gás constante está contida dentro de um recipiente com êmbolo móvel, capaz de se ajustar a qualquer variação de volume. O recipiente possui um termômetro e um barôometro acoplados.
Transformação isotérmica (lei de bóiou e Mariotte)
A transformação isotérmica ocorre quando a tempera-túra absoluta permanéce constante.
Em investigações desenvolvidas separadamente, o físico e químico britânico róbert bóiou (1627-1691) e o físico francês Edme Mariotte (c. 1620-1684) verificaram quê o volume e a pressão de um gás são inversamente proporcionais em uma transformação com tempera-túra absoluta constante, conclusão conhecida como lei de bóiou e Mariotte.
piVi = pV = constante
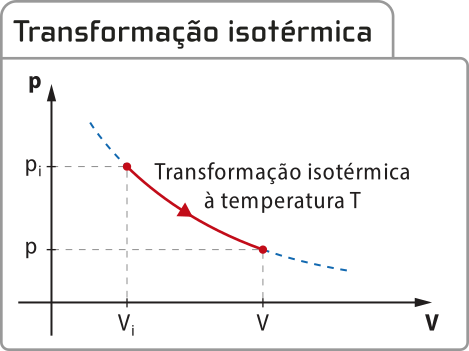
O diagrama de pressão por volume apresentado mostra a curva característica de uma transformação isotérmica.
Na imagem a seguir, perceba quê o gás estava em um estado termodinâmico inicial pi, Vi e Ti, mantendo o êmbolo em equilíbrio estático. Quando uma das massas foi retirada do êmbolo, ele subiu, aumentando, assim, o volume ocupado pelo gás. Como as partículas mantiveram a mesma movimentação (temperatura absoluta constante), a freqüência de colisões com o recipiente aumentou (a pressão aumentou). Por exemplo, para T = Ti, se p = , V = 2Vi.
Ti = T
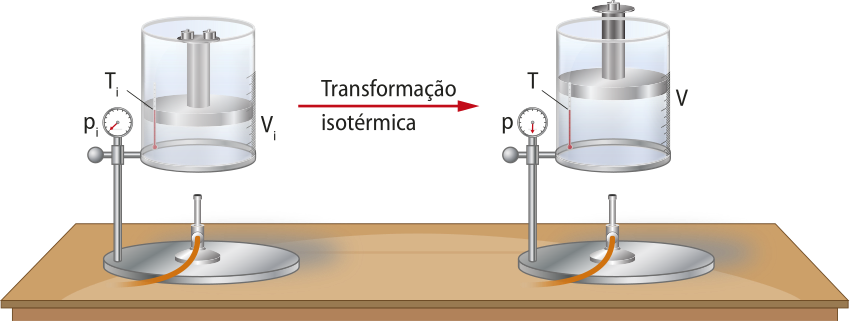
PENSE E RESPONDA
2 Uma pessoa encheu uma pequena bexiga com ar e a inseriu dentro de uma seringa. Quando puxou o êmbolo da seringa, fechando a extremidade com um dos dedos, a bexiga aumentou de tamãnho. Crie uma hipótese quê explique esse efeito observado.
Página duzentos e quatro
Transformação isobárica (1ª lei de xárlês e Gay-Lussac)
A transformação isobárica ocorre quando a pressão permanéce constante.
Em investigações desenvolvidas separadamente, os físicos e químicos franceses Jáquis Alexandre César xárlês (1746-1823) e jôsef Louis Gay-Lussac (1778-1850) verificaram quê o volume e a tempera-túra absoluta de um gás são diretamente proporcionais em uma transformação com pressão constante, conclusão conhecida como lei de xárlês e Gay-Lussac.
= constante
Uma transformação isobárica póde sêr analisada por um diagrama de pressão por volume ou por um diagrama de volume por tempera-túra absoluta.
![Representação gráfica de transformação isobárica[p igual a v]. Eixo vertical 'P', eixo horizontal 'V'. Uma reta passa pelos pontos 'P','V i' e 'P','V i'.[T maior que T i]](../resources/images/ek_d/ek_dc4e68cb591d86c51a93b9412a64855b.png)
![Representação gráfica de transformação isobárica[V igual a T]. Eixo vertical 'V' e eixo horizontal 'T'. Uma reta passa pelos pontos 'V i', 'T i' e 'V','T'.](../resources/images/ek_0/ek_0e9693a6d5045e58f3026c4717d764d5.png)
Na imagem a seguir, perceba quê o gás estava em um estado termodinâmico inicial pi, Vi e Ti, mantendo o êmbolo em equilíbrio estático. Quando o fogo foi aceso, as partículas aumentaram sua movimentação (a tempera-túra absoluta aumentou), elevando o êmbolo e aumentando o volume ocupado pelo gás, mas mantendo a freqüência de colisões com o recipiente (pressão constante). Por exemplo, para p = pi, se T = 2Ti, V = 2Vi.
pi = p
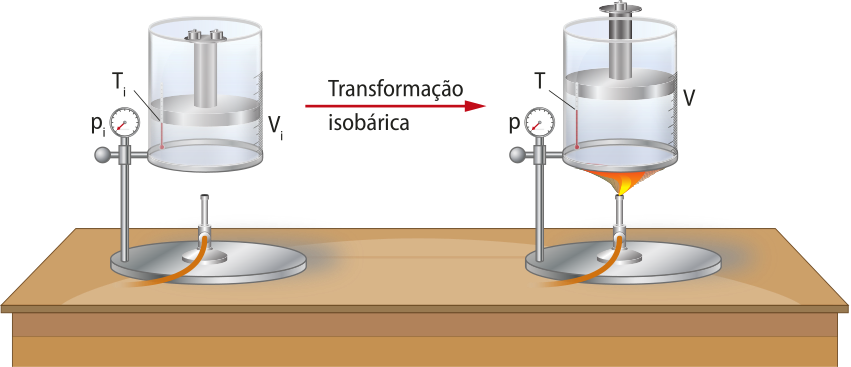
PENSE E RESPONDA

3 Uma pessoa prendeu uma bexiga em uma garrafa de plástico e a colocou dentro do congelador de sua geladeira. Após um tempo, verificou-se quê a bexiga entrou na garrafa. Crie uma hipótese quê explique esse efeito observado.
Página duzentos e cinco
Transformação isovolumétrica (2ª lei de Charles)
A transformação isovolumétrica ocorre quando o volume permanéce constante e é também chamada de isométrica e isocórica.
Jáquis xárlês também estudou essa transformação quando verificou quê a pressão e a tempera-túra absoluta de um gás são diretamente proporcionais em uma transformação com volume constante, conclusão conhecida como lei de xárlês.
= constante
Uma transformação isovolumétrica póde sêr analisada por um diagrama de pressão por volume ou por um diagrama de pressão por tempera-túra absoluta.
![Representação gráfica de uma transformação isovolumétrica[ p x V]. Eixo vertical 'P', eixo horizontal 'V'. Uma reta vertical, passa pelos pontos 'P i', 'V' e 'P', 'V', com pontos 'T i' e 'T', sendo [T maior que T i].](../resources/images/ek_7/ek_7f7e8b2d65bd553320f772c6808f0f9c.png)
![Representação gráfica de transformação isovolumétrica [p x T]. Eixo vertical 'P', eixo horizontal 'T'. Uma reta passa pelos pontos 'P i', 'T i' e 'P', 'T'.](../resources/images/ek_4/ek_4d135b7df2106634e64c7caf47c5711e.png)
Na imagem a seguir, perceba quê o gás estava em um estado termodinâmico inicial pi, Vi e Ti, mantendo o êmbolo em equilíbrio estático. Quando o fogo foi aceso, uma massa foi adicionada sobre o êmbolo, mantendo constante o volume ocupado pelo gás. Como a movimentação das partículas aumentou (aumento da tempera-túra absoluta), a freqüência de colisões com o recipiente aumentou (a pressão aumentou). Por exemplo, para V = Vi, se T = 2Ti, p = 2pi.
Vi = V
Página duzentos e seis
Lei geral dos gases perfeitos
As três transformações gasosas analisadas anteriormente revelam a proporcionalidade entre as variáveis de estado termodinâmico. Tem-se quê pressão e volume são inversamente proporcionais, enquanto pressão e tempera-túra, bem como volume e tempera-túra, são diretamente proporcionais.
Assim, pode-se determinar uma equação com as três variáveis de estado termodinâmico, válida para qualquer transformação gasosa em quê a quantidade de gás confinado seja constante.
Considere uma quantidade de gás constante e confinada em um recipiente, em um estado termodinâmico inicial com pressão pi, volume Vi e tempera-túra Ti, passando por uma transformação gasosa até o estado termodinâmico final com pressão pi, volume Vi e tempera-túra Ti. As variáveis de estado termodinâmico podem sêr relacionadas pela chamada lei geral dos gases perfeitos (ou ideais):
Vale lembrar quê, nesses estudos, a tempera-túra é absoluta e expressa na escala kélvin.
ATIVIDADES RESOLVIDAS
1. Um gás perfeito, mantido a volume constante, tem pressão inicial p e tempera-túra inicial T = 27 °C = 300 K. Determine, na escala célcius, a tempera-túra em quê esse gás exercerá o dôbro da pressão inicial.
Resolução
O gás evolui do estado termodinâmico inicial p, V e T = 300 K para o final 2p, V e T em uma transformação isométrica.
⇒ ⇒ = 600 K
A tempera-túra deve sêr expressa na escala célcius após a análise da transformação gasosa.
TC = TK − 273 = 600 − 273 ⇒ TC = 327 °C
2. Uma quantidade de gás hidrogênio (H2), comportando-se como gás ideal, está confinada em um recipiente de 500 mL e exerce uma pressão de 2,5 atm a uma tempera-túra de 77 °C. Qual será o volume ocupado por essa quantidade de gás se sua pressão cair a 1 atm e sua tempera-túra valer 0 °C?
Resolução
Para estudar transformações gasosas, a tempera-túra deve sempre sêr expressa na escala kélvin.
TC = TK − 273 ⇒ TC = Ti − 273 ⇒ 77 = Ti − 273 ⇒ Ti = 350 K
TC = TK − 273 ⇒ TC = T − 273 ⇒ 0 = T − 273 ⇒ T = 273 K
Aplicando a lei geral dos gases perfeitos:
⇒ ⇒ V = 975 mL
Página duzentos e sete
ATIVIDADES
1. Considere quê a massa de um gás ideal, quando à pressão p e à tempera-túra T, ocupa um volume V. Caso o seu volume seja reduzido à mêtáde e a pressão triplicada, qual será a nova tempera-túra?
T' = 1,5 T
2. A seguir, no diagrama (p × V), estão representadas três transformações (I, II e III) de um gás, considerado ideal. Relacione as transformações (I, II e III) às denominações (isobárica, isotérmica e isovolumétrica), justificando-as.
3. Os p-neus de um automóvel foram igualmente calibrados a uma tempera-túra de 17 °C. Após uma viagem, ao medir novamente a pressão dos p-neus, o motorista notou quê ela havia aumentado 20% em relação à inicial. Admitindo quê não houve variação de volume, calcule a nova tempera-túra dos p-neus.
75 °C
4. (Vunesp-SP) A Figura I representa um gás perfeito de volume Vi, contido num cilindro fechado por um êmbolo de peso P, quê póde se mover livremente. Colocam-se gradativamente grãos de areia sobre o êmbolo, quê desce até o gás ocupar o volume , como mostra a Figura II.


Admite-se quê o processo é quase estático, ou seja, suficientemente lento para quê o sistema se mantenha em equilíbrio térmico com o ambiente, quê por sua vez se mantém à tempera-túra constante. Pode-se afirmar quê o peso total dos grãos de areia colocados sobre o êmbolo é igual a:
a) 3P
b) 2P
c) P
d)
e)
Resposta: a)
5. A transformação ABC de um gás ideal é representada no diagrama a seguir.
![Diagrama: eixo vertical 'P'[a t m] e eixo horizontal 'V'[m elevado a três]. Duas retas são formadas: 'B','C' vertical, passando pelos pontos 2,2 e 8,2 e reta 'B','A' horizontal, passando pelos pontos2,2 e2,5.](../resources/images/ek_d/ek_d6a36b1870d22092d12c0f92fcf7acf6.png)
Considerando quê a tempera-túra no estado A é de 127 °C, calcule a tempera-túra em °C nos estados B e C.
TB = −113 °C; TC = 367 °C
6. Os dados a seguir mostram o volume ocupado por certa massa de gás ideal quê varia de volume em função da tempera-túra.
Volume ocupado pelo gás em função da tempera-túra
T (K) |
V (m3) |
|---|---|
80 |
4 |
100 |
5 |
160 |
8 |
200 |
10 |
Dados hipotéticos.
a) Qual é a relação entre o volume e a tempera-túra?
0,05 m3 /k
b) Qual é a transformação quê o gás está sofrendo?
c) Com os dados, esboce o gráfico quê relaciona tempera-túra e volume.
Página duzentos e oito
OFICINA CIENTÍFICA
Transformações termodinâmicas com o ar
Muitas crianças brincam com balões de gás hélio, quê são menos densos quê a massa de ar e se deslócam e ficam suspensos por barbantes quê podem sêr amarrados às mãos. Esses balões, se soltos ao ar livre, sóbem pela atmosféra, e o gás em seu interior sofre transformações de estado. Você sabe dizêr o quê acontece com a massa de gás no interior do balão enquanto sobe pela atmosféra? Quais grandezas de estado varíam no trajeto?

Para ajudar a pensar nas transformações quê o volume de um gás póde sofrer, sugere-se a realização da atividade a seguir.
Materiais
• 2 bê-chi-gâs
• 1 pedaço de mangueira (10 cm)
Procedimentos
• Encha bastante a primeira bexiga e introduza uma das extremidades do pedaço de mangueira na abertura dela. Segure essa abertura com os dedos, para quê o ar não escape.
• Encha a segunda bexiga com pouco ar (o volume deve sêr aproximadamente a mêtáde do volume da primeira bexiga) e introduza a outra ponta do pedaço de mangueira na abertura da bexiga, mantendo-a também presa com os dedos, para quê o ar não escape. O aparato deve ficar como mostrado na ilustração a seguir.
ATIVIDADES
1. O quê você acha quê vai acontecer quando soltar os dedos?
• Solte as aberturas simultaneamente e obissérve o quê acontece.
• Repita o experimento e obissérve o quê ocorre com as bê-chi-gâs.
2. O quê você verificou?
3. Tente explicar o motivo para o quê aconteceu no experimento.
Página duzentos e nove
Equação de Clapeyron
Foi apresentado quê a lei geral dos gases determina a relação entre pressão, volume e tempera-túra de um gás.
Nessa relação, não há nenhuma indicação sobre a quantidade de gás presente no sistema. Assim, só é possível utilizá-la se a quantidade de gás se mantiver constante. Entretanto, pode-se ampliar a utilização da equação da lei geral para quê ela se aplique a qualquer massa de gás. Para isso, serão abordados alguns conceitos químicos.
• Um mol é uma quantidade equivalente a 6, 02 ⋅ 1023 partículas (átomos ou moléculas). Esse número é denominado número de Avogadro, em homenagem ao físico e químico italiano Lorenzo Romano Amedeo Carlo Avogadro (1776-1856).
• A massa molar (M) é a massa de 1 mol de determinada substância. Um mol representa sempre a mesma quantidade de partículas, mas a massa de cada amostra póde variar. Por exemplo, a massa molar do carbono vale 12 g/mol e a massa molar do oxigênio vale 16 g/mol, portanto a massa molar do gás carbônico (CO2) vale 44 g/mol.
MCO2 = 1 ⋅ 12 + 2 ⋅ 16 ⇒ MCO2 = 44 g/mol
• O número de mols (n) representa a quantidade de matéria em uma amostra de massa m. Por exemplo, considere uma amostra de 880 g de gás carbônico (CO2); pode-se determinar a quantidade de matéria, em mol, presente na amostra pela expressão:
n = ⇒ n = 20 mol
Através da lei geral dos gases, observou-se quê para um estado específico as grandezas p, V e T podem sêr igualadas a uma constante, e quê esta depende apenas da quantidade do gás, ou seja, proporcional ao número de mols. Assim, podemos reescrever a equação geral dos gases da seguinte maneira:
= constante = nR ⇒ pV = nRT
Essa relação é conhecida como equação de Clapeyron, em homenagem ao engenheiro e físico francês Benoit-Pierre-Émile Clapeyron (1799-1864), e a constante R é denominada constante universal dos gases ideais, cujo valor depende das unidades utilizadas nas demais grandezas:
R = 0,082 atmL/molK, R = 8,31 Pam3/mol e R = 8,31 J/molK
ATIVIDADE RESOLVIDA
3. Em um reservatório de 10 litros foram adicionados 66 g de gás carbônico a uma tempera-túra de 52 °C, em condições em quê ele se comporta como gás ideal. Qual é a pressão exercida pelo gás? Adote a massa molar do dióxido de carbono como 44 g/mol e a constante universal dos gases perfeitos como 0,0852 atmL/molK.
Resolução
O número de mols de gás carbônico é determinado da seguinte forma:
n = ⇒ n = 1,5 mol
A tempera-túra deve sêr expressa na escala kélvin.
TC = TK − 273 ⇒ 52 = TK − 273 ⇒ TK = 325 K
O gás se comporta como um gás ideal, então é válida a equação de Clapeyron.
pV = nRT ⇒ p ⋅ 10 = 1,5 ⋅ 0,082 ⋅ 325 ⇒ p ≃ 4 atm
Página duzentos e dez
SAIBA +
Quando calibrar os p-neus?
Manter a pressão recomendada pelo fabricante dos p-neus é uma garantia do melhor dêsempênho e da durabilidade deles, além de sêr essencial para a segurança do veículo e das pessoas quê estão em seu interior. No caso de a pressão estar abaixo da recomendada, a durabilidade do pneu é reduzida e o consumo de combustível e o risco de acidentes aumentam. No caso de alta pressão, a área de contato do pneu com o solo diminui, reduzindo a aderência do pneu e a estabilidade, especialmente nas curvas. Nessa condição, em casos de frenagem de emergência, o risco de acidentes é maior.

ATIVIDADE
1. Os manuais de orientação para a calibragem dos p-neus recomendam quê o usuário não calibre os p-neus após o veículo ter percorrido uma longa distância. Explique o motivo dessa orientação constar nos manuais.
ATIVIDADES
7. (Enem/MEC) Nos últimos anos, o gás natural (GNV: gás natural veicular) vêm sêndo utilizado pela frota de veículos nacional, por sêr viável economicamente e menos agressivo do ponto de vista ambiental.
O qüadro compara algumas características do gás natural e da gasolina em condições ambiente.
Densidade (kg/m3) |
Poder calorífico (kJ/kg) |
|
|---|---|---|
GNV |
0,8 |
50.200 |
Gasolina |
738 |
46.900 |
Apesar das vantagens no uso de GNV, sua utilização implica algumas adaptações técnicas, pois, em condições ambiente, o volume de combustível necessário, em relação ao de gasolina, para produzir a mesma energia, seria
a) muito maior, o quê requer um motor muito mais potente.
b) muito maior, o quê requer quê ele seja armazenado a alta pressão.
c) igual, mas sua potência será muito menor.
d) muito menor, o quê torna o veículo menos eficiente.
e) muito menor, o quê facilita sua dispersão para a atmosféra.
Resposta: b)
8. Um recipiente com dilatação desprezível possui capacidade de 40 L e contém uma massa de gás oxigênio a 127 °C e 8,2 atm de pressão. Calcule a massa de gás contida no recipiente.
Dado: MO2 = 32 g/mol.
320 g
9. Determine a pressão no interior de um recipiente cujo volume é 16,4 L e quê contém 128 g de oxigênio à tempera-túra de 27 °C. Considere a massa molecular do oxigênio M = 32 g/mol.
6 atm
Considere R =
10. Um gás perfeito com massa molar igual a 20 g/mol ocupa o volume de 98,4 L sôbi pressão de 5 atm e tempera-túra de 27°C. Calcule:
a) o número de mols do gás.
20 mol
b) a massa do gás.
400 g
11. 50 gramas de gás hidrogênio a −13 °C são colocados num recipiente de paredes rígidas cujo volume é de 20 L. Supondo quê o hidrogênio se comporta como um gás perfeito, calcule a pressão exercida por ele. Considere a massa molar do hidrogênio igual a 2 g.
26,65 atm
Página duzentos e onze
TEMA 18
As leis da Termodinâmica e as máquinas térmicas
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Trabalho em uma transformação gasosa
Nos estudos da Mecânica, quando um trabalho é realizado, significa quê uma forma de energia foi transformada em outra. Já nos estudos da Termodinâmica, tem-se quê o calor é uma forma de energia, logo, nas transformações gasosas, é possível estudar as relações entre calor e trabalho.
Para iniciar os estudos, considere um recipiente cilíndrico contendo uma quantidade de gás ideal, fechado por um êmbolo com movimento livre. O gás está em um estado termodinâmico inicial p, V1 e T1.Como o êmbolo está imóvel, a pressão exercida pelo gás é constante, pois é igual à pressão externa, dada pela pressão atmosférica somada à pressão causada pela fôrça peso do corpo de massa m sobre a área do êmbolo.
Uma fonte térmica fornece calor ao sistema e provoca uma transformação gasosa ao estado termodinâmico final p, V2 e T2, causando uma expansão isobárica do gás e o deslocamento d do êmbolo.
![Ilustração de um recipiente contendo gás, com um êmbolo, em cima [estado termodinâmico inicial], o recipiente é aquecido, o gás se expande no recipiente levantando o êmbolo.](../resources/images/ek_f/ek_f266c22747dc1119826b90af77c794b9.png)
Considere as seguintes afirmações:
• A fôrça F exercida pelo gás sobre a área do êmbolo A póde sêr escrita em função da pressão.
p = ⇒ F = pA
• A área de base do cilindro e o deslocamento d indicam a variação de volume (delta)"V sofrida pelo gás.
(delta)"V = Ad
• O trabalho realizado pela fôrça do gás é dado por:
τ = Fdcos θ
PENSE E RESPONDA


1 Quais são as principais semelhanças entre uma locomotiva a vapor antiga e um veículo moderno, com motor de combustão?
Página duzentos e doze
A fôrça exercida pelo gás tem a mesma orientação do deslocamento, logo Θ = 0°. Lembre-se de quê, no SI, trabalho é expresso em Jáule (J).
τ = Fdcos θ = ⇒ τ = p(delta)"V = p(V2 − V1)
A relação anterior define o trabalho termodinâmico em uma transformação gasosa isobárica, mas permite algumas generalizações. O trabalho em uma transformação gasosa depende da variação de volume. Em uma expansão gasosa, V2 > V1 e (delta)"V > 0, o trabalho é positivo (τ > 0), e diz-se quê o gás realizou trabalho. Em uma compressão gasosa, V2 < V1 e (delta)"V = 0, o trabalho é negativo (τ < 0), e diz-se quê o gás recebeu trabalho. Já em uma transformação isométrica, V2 = V1 e (delta)"V = 0, não se tem realização de trabalho (τ = 0).
Analisando o diagrama de pressão por volume em uma transformação gasosa, o trabalho é numericamente igual ao valor da área delimitada pelo gráfico, e o eixo do volume, horizontal. Essa propriedade póde sêr generalizada para qualquer gráfico p × V. O sinal do trabalho vai depender se ocorreu uma expansão ou uma compressão gasosa.
![Representação gráfica em dois momentos. Momento um, gráfico da esquerda: eixo vertical 'P' e eixo horizontal 'V'[V1,V2 igual a delta V].Uma reta horizontal em 'P', projetada em 'V1','V2', formando uma área 'trabalho'. Momento dois, gráfico da direita: eixo vertical 'P' e eixo horizontal 'V'[V1, V2 igual a delta V]. Uma reta inclinada passa pelos pontos 'P1','V1' e 'P2,'V2', formando uma área [trabalho].](../resources/images/ek_6/ek_6ffa1997b743c3f70ef6879c9097d19b.png)
Energia interna de um gás perfeito
A tempera-túra é uma grandeza relacionada ao grau de movimentação das partículas de um corpo, estando assim associada à energia cinética de translação dessas partículas.
Dependendo da substância, do estado físico, das partículas existentes (átomo, moléculas monoatômicas, moléculas diatômicas, entre outras), podem existir outras energias associadas, como energia cinética de rotação, energia potencial nas interações intermoleculares, entre outras formas. Esse conjunto de energias chama-se energia interna (U).
Para uma situação mais simples, considere um gás ideal monoatômico, compôzto de moléculas com um único átomo. A energia interna é dada apenas pela energia cinética de translação das partículas, ou seja, é diretamente proporcional à tempera-túra do gás e póde sêr calculada da seguinte forma:
U =
Nessa relação, n é o número de mols, R é a constante universal dos gases perfeitos e T é a tempera-túra. De acôr-do com a equação de Clapeyron: pV = nRT. Logo, a energia interna também póde sêr expressa em função da pressão p e do volume V. No SI, a energia interna é expressa em Jáule (J).
Para os gases reais ou gases quê não sêjam monoatômicos, a expressão da energia interna é mais compléksa, mas mantém uma relação diréta com a tempera-túra. Isso quer dizêr quê, se a tempera-túra de um gás aumenta, a energia interna também aumenta; se a tempera-túra diminui, a energia interna diminui; e, em transformações isotérmicas, a tempera-túra não varia, logo, se (delta)"T = 0, (delta)"U = 0.

Página duzentos e treze
ATIVIDADES RESOLVIDAS
1. Um gás ideal, sôbi pressão de 1 atm, ocupa um volume de 600 cm3 a 27 °C. Ele sofre uma transformação isobárica e sua tempera-túra alcança 127 °C. Calcule o trabalho realizado pelo gás, em Jáule.
Resolução
Para quê o trabalho seja expresso em Jáule, é necessário utilizar unidades do SI.
p = 1 atm = 1 ⋅ 105 Pa
V1 = 600 cm3 = 600 mL = 6 ⋅ 10−4 m3
T1 = 27 °C = 300 K
T2 = 127 °C = 400 K
É preciso determinar o volume final V2 ocupado pelo gás, após a transformação isobárica.
⇒ ⇒ V2 = 8 ⋅ 10−4m3
τ = p(delta)"V = p(V2 −V1) =
= 1 ⋅ 105(8 ⋅ 10−4 − 6 ⋅ 10−4) = 1 ⋅ 105 ⋅ 2 ⋅ 10−4
τ = 20 J
2. Qual é a energia interna de 4 mol de um gás ideal monoatômico, a uma tempera-túra de 20 °C, expressa em Jáule? Adote: R = 8,31 J/mol⋅K.
Resolução
T = 20 °C = 293 K
O gás hidrogênio é monoatômico.
U = ⋅ 4 ⋅ 8, 31 ⋅ 293 ⇒
⇒ U ≃ 14, 61 ⋅ 103 J
ATIVIDADES
1. Durante uma experiência, 3 mol de moléculas de um gás ideal têm sua tempera-túra alterada de 50 K para 150 K. Se o sistema for mantido sôbi pressão constante e se for considerado a constante universal dos gases R = qual será o trabalho realizado pelo gás?
2,49 ⋅ 103 J
2. O gráfico a seguir representa a compressão isobárica exercida por um pistão sobre determinada quantidade de um gás ideal, contido no interior de um recipiente cilíndrico de paredes rígidas, mas com pistão móvel.
Sabendo quê o pistão se desloca 0,15 m na vertical, determine:
![Gráfico: eixo vertical 'P'[dez elevado a cinco N/metros cúbicos] e eixo horizontal 'V'[dez elevado a menos quatro metros cúbicos]. Uma reta horizontal M,N passando pelos pontos 3,1 e 3,4.](../resources/images/ek_b/ek_bd181a4aec40a359599f0281e2c1041f.png)
a) o módulo do trabalho realizado no trecho MN;
90 J
b) a intensidade da fôrça quê o gás exerce no pistão.
600 N
3. Em um recipiente de formato cilíndrico e fechado por um êmbolo móvel, está contido um gás ideal quê é mantido sôbi pressão de 2,5 N/m2. Durante um processo isobárico, esse gás tem sua tempera-túra diminuída de 323 °C para 25 °C. Determine o trabalho realizado sobre o gás, sabendo quê o seu volume final é 0,25 m3.
−0,625 J
4. As transformações ocorridas em um sistema termodinâmico estão representadas no gráfico a seguir. Considere as informações contidas nele e determine o trabalho realizado:
![Gráfico: eixo vertical 'P'[dez elevado a seis P a] eixo horizontal 'V'[metros cúbicos]. Uma reta L,M,N, descendente, passando pelos pontos '8,2,0' e '8,3,0' e '8,4,0'.](../resources/images/ek_5/ek_570fc84d9bb6b2463c15f1bfa301edd5.png)
a) no trecho LM;
τLM = 8,0 ⋅ 106 J
b) no trecho MN.
τMN = 6,0 ⋅ 106 J
Página duzentos e quatorze
1ª lei da Termodinâmica
A primeira lei da Termodinâmica constitui-se no princípio da conservação de energia, quê rege todo o Universo. A energia total de um sistema é constante, não podendo sêr criada nem destruída, mas apenas transmitida ou transformada.
Apesar de sua grande abrangência, será abordada a conservação da energia no comportamento dos gases ideais.
Considere um gás ideal monoatômico confinado em um recipiente com êmbolo móvel, quê passa a receber calor de uma fonte térmica. O calor absorvido pelo gás (Q) póde causar aquecimento, variando a sua energia interna (DU). Esse aumento de movimentação póde levar o sistema a realizar um trabalho (τ) sobre o êmbolo, quê é movimentado para cima, como mostra a ilustração, utilizando uma transformação isobárica como exemplo.
pi = p
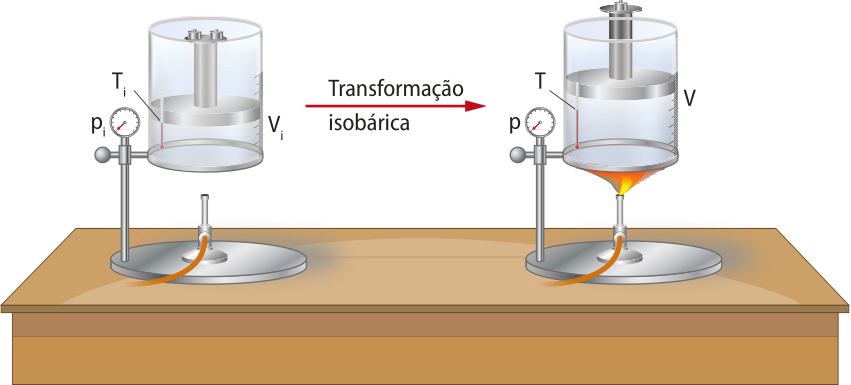
Assim, um estudo da conservação da energia nesta situação levou à primeira lei da Termodinâmica, quê possibilita relacionar calor, trabalho e variação da energia interna da seguinte forma:
Q = DU + τ
Analise a primeira lei da Termodinâmica em cada uma das transformações gasosas a seguir.
Transformação isotérmica
Nas transformações gasosas, com a tempera-túra estando constante (DT = 0), a energia interna do sistema também se mantém constante, logo DU = 0.
Assim, de acôr-do com a primeira lei da Termodinâmica, todo o calor trocado com o ambiente é convertido em trabalho.
Q = (delta)"U + τ ⇒ Q = τ
• Se o sistema recebe calor do ambiente, o gás realiza trabalho e expande (Q > 0; τ > 0).
• Se o sistema cede calor para o ambiente, o gás recebe trabalho e é comprimido (Q < 0; τ < 0).
No diagrama de pressão por volume, apresentado como exemplo, tem-se duas curvas quê representam expansões isotérmicas para tempera-túras distintas, sêndo T2 >T1.
![Representação gráfica de transformação isotérmica. Eixo vertical 'P' e eixo horizontal 'V'. Uma curva 'T1' descendente, passando pelos pontos 'P1','V1' e 'P2','V2', outra curva paralela 'T2'. ['T2' maior que 'T1'].](../resources/images/ek_4/ek_419353cf628a5cf522eb1a5fed847b3e.png)
Página duzentos e quinze
Transformação isovolumétrica
Nas transformações gasosas a volume constante ((delta)"V = 0), também chamada de isométrica e isocórica, o trabalho realizado ou recebido pelo sistema é nulo (τ = 0).
Assim, de acôr-do com a primeira lei da Termodinâmica, todo calor trocado com o ambiente é convertido em variação de energia interna.
Q = (delta)"U + τ ⇒ Q = (delta)"U
• Se o sistema recebe calor do ambiente, o gás eskenta (Q > 0; (delta)"U > 0).
• Se o sistema cede calor para o ambiente, o gás esfria (Q < 0; (delta)"U < 0).
No diagrama de pressão por volume, apresentado como exemplo, tem-se um aquecimento isovolumétrico entre duas tempera-túras, sêndo T2 > T1, com aumento de pressão.
![Representação gráfica de transformação isovolumétrica. Eixo vertical 'P' e eixo horizontal 'V'. Uma reta vertical é formada nos pontos 'P1','V1' e 'P2', V1'. duas curvas 'T1' e 'T2' projetadas nos dois pontos da reta.['T2' maior que 'T1'].](../resources/images/ek_c/ek_cfa8461b7059c02f1fab71dc13b0d371.png)
Transformação isobárica
Nas transformações gasosas à pressão constante ((delta)"p = 0), deve-se considerar a relação completa entre calor, trabalho e variação de energia interna proposta na primeira lei da Termodinâmica.
Q = (delta)"U + τ
No diagrama de pressão por volume, apresentado como exemplo, tem-se quê o gás recebe calor, aumenta sua tempera-túra e se expande, realizando trabalho.
![Gráfico' Transformação isobárica'. Eixo vertical 'P' e eixo horizontal 'V'. Uma reta apontando para a direita, formada pelos pontos 'P1','V1' e 'P1','V2', com duas curvas 'T1' e 'T2' projetadas nos pontos.['T2' maior que 'T1'].](../resources/images/ek_4/ek_41486bff54fe427453fd9942fff7cfbe.png)
Transformação adiabática
Uma transformação gasosa é adiabática quando o sistema não troca calor com o ambiente, ou seja, quando a quantidade de calor é nula (Q = 0). Essa transformação só é possível quando o sistema estiver isolado termicamente ou, d fórma aproximada, quando a transformação for realizada rapidamente.
Assim, de acôr-do com a primeira lei da Termodinâmica, tem-se uma relação entre trabalho e variação de energia interna.
Q = (delta)"U + τ ⇒ τ = − (delta)"U
• Se o gás realiza trabalho, ocorre esfriamento (τ > 0; (delta)"U < 0).
• Se o gás recebe trabalho, ocorre aquecimento (τ < 0; (delta)"U > 0).
Em um diagrama de pressão por volume, a curva de uma transformação adiabática está entre duas isotérmicas. No diagrama apresentado como exemplo, tem-se uma compressão adiabática, quando o gás recebe trabalho do meio externo e sofre um aquecimento, aumentando sua energia interna.
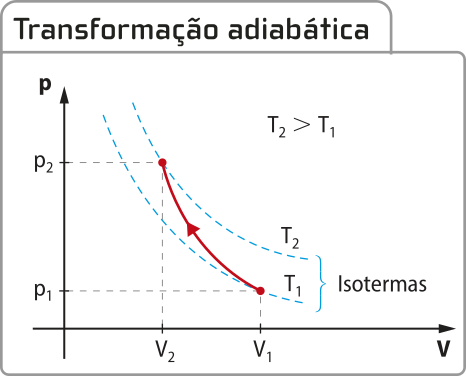
Página duzentos e dezesseis
Transformação cíclica
Uma transformação cíclica ocorre quando se parte de um estado termodinâmico inicial e, após uma sequência de transformações, retorna-se ao estado inicial.
Considere como exemplo uma transformação cíclica sofrida por um gás ideal, representada no diagrama de pressão por volume.
O gás inicia no estado termodinâmico A, passando para o estado B por uma expansão isobárica e seguindo ao estado C por uma transformação isovolumétrica. Após isso, ele passa por uma compressão isobárica até o estado D, quando então retorna ao estado A, por uma transformação isovolumétrica.
Como o estado final do gás coincide com o inicial, a variação de energia interna sofrida pelo gás é nula: (delta)"U = 0. A primeira lei da Termodinâmica afirma quê:
Q = (delta)"U + τ ⇒ Q = τ
![Gráfico 'Transformação cíclica'. Eixo vertical 'P' e eixo horizontal 'V', formando um quadrado A,B,C,D [trabalho], nos pontos 'PA' igual a 'PB','VA' igual a 'VD', 'PC' igual a 'PD', 'VA' igual a VD', 'PC 'igual a 'PD', 'VB' igual a 'VD' e 'PA' igual a 'PB', 'VB' igual a 'VC'.](../resources/images/ek_e/ek_eca5314719ac268ae64a3202f13f79b7.png)
Assim, em uma transformação cíclica completa, o trabalho é totalmente convertido em calor e vice-versa.
Analisando o diagrama de pressão por volume, o trabalho é dado pela área da região delimitada pelo ciclo. Se o ciclo é executado no sentido horário, o trabalho é positivo, ou seja, o gás realiza trabalho e recebe calor do ambiente externo. Se o ciclo é executado no sentido anti-horário, o trabalho é negativo, ou seja, o gás recebe trabalho e cede calor ao ambiente externo.
ATIVIDADES
5. Um gás ideal é submetido a uma compressão extremamente rápida, de tal forma quê a troca de calor com o meio externo é insignificante e póde sêr desconsiderada. As afirmações seguintes se reférem à situação relatada.
Verifique qual é a correta.
a) O volume do gás aumenta e a pressão diminui.
b) O volume e a pressão do gás diminuem.
c) A tempera-túra do gás diminui.
d) A energia interna do gás aumenta.
e) Há trabalho realizado pelo gás para o meio externo.
Resposta: d)
6. Um gás ideal monoatômico é comprimido adiabaticamente, sofrendo uma variação de tempera-túra de 600 K.
Sabendo quê n = 3 mol, cv = 3 cal/mol ⋅ K, R = 2 cal/mol ⋅ K e 1 cal = 4,2 J, determine:
a) a quantidade de calor trocada nessa transformação;
0 J
b) a variação de energia interna do gás, em Jáule;
22.680 J
c) o trabalho realizado sobre o gás.
–22.680 J
7. No gráfico a seguir está representada a transformação cíclica de um gás, considerado ideal. Determine, em Jáule, o trabalho realizado em um ciclo.
2,5 ⋅ 106 J
![Gráfico: eixo vertical 'P'[dez elevado a cinco N/metros quadrados] e eixo horizontal 'V'[metros cúbicos]. Um trapézio formado pelos pontos 'três e cinco', 'cinco e dez' e 'cinco e vinte'.](../resources/images/ek_0/ek_0457a1f4f51d295a672318ceb44fc232.png)
Página duzentos e dezessete
2ª lei da Termodinâmica
Existem fenômenos e processos classificados como irreversíveis, quê ocorrem em um único sentido, em uma certa ordem, e não podem sêr desfeitos por mudanças no ambiente.
Um pêndulo simples oscilando, por exemplo, cessa seu movimento após cérto tempo, devido à resistência do ar, quê transforma gradativamente a energia mecânica em energias dissipativas, como energia térmica. Considerando um sistema fechado envolvendo ar, Terra e pêndulo, a energia total envolvida é a mesma, mas não é possível recuperar a energia dissipada e fazer o pêndulo voltar a oscilar, pois a transferência de energia se dá em um único sentido.
Perceba quê o sentido inverso do processo não viola a primeira lei da Termodinâmica, da conservação da energia, porém essa não é a ordem espontânea do processo.
Noções de entropia
O sentido natural de um processo irreversível em um sistema fechado é determinado por uma propriedade chamada entropia. Em geral, ela é associada ao grau de “desordem” de um sistema, quê póde sêr relacionado com a organização espacial e energética. Assim, quanto maior a entropia, maior a “desordem”.
Um exemplo de processo irreversível em um sistema fechado é a expansão livre de um gás. Considere um gás ideal em um estado termodinâmico inicial, em um recipiente confinado por uma válvula fechada, conectada a outro recipiente termicamente isolado. Ao abrir a válvula, o gás expande livremente, ocupando os dois recipientes e atingindo um estado termodinâmico final. Trata-se de um processo irreversível, afinal o gás jamais voltará a ocupar espontaneamente apenas o primeiro recipiente. A entropia do sistema aumentou.
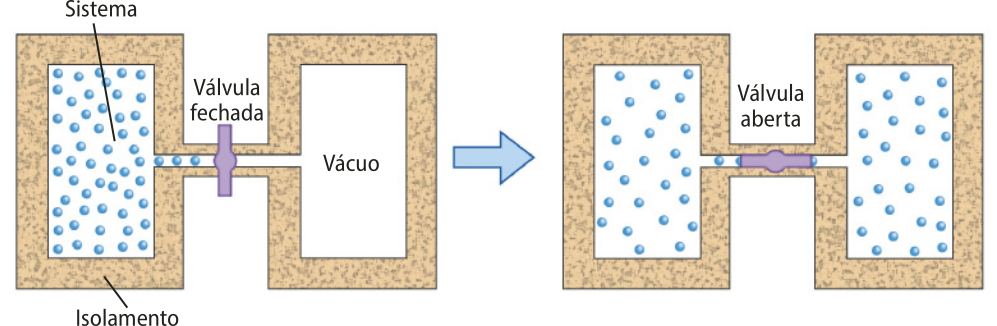
A entropia também póde sêr analisada em processos reversíveis, como em uma expansão isotérmica de um gás, de um estado termodinâmico inicial a um estado termodinâmico final, com absorção de calor do ambiente, quando a entropia aumenta (se o ambiente for considerado parte do sistema, tem-se um sistema fechado).
PENSE E RESPONDA

2 Um gêlo em um ambiente com tempera-túra maior do quê a dele recebe calor dêêsse ambiente. por quê esse processo sempre ocorre?
Página duzentos e dezoito
É possível retornar esse gás ao estado termodinâmico inicial, extraindo energia e cedendo calor ao ambiente, quando a entropia diminui, o quê não viola o quê foi propôsto anteriormente, afinal trata-se de um processo reversível.
Assim, mesmo quê a entropia diminua em uma parte de um sistema fechado, existe um aumento igual ou maior em outra parte, de modo quê a entropia total do sistema jamais diminui.
A segunda lei da Termodinâmica é comumente designada por alguns enunciados, e um deles está relacionado à noção de entropia.
Em sistemas fechados, a entropia em processos irreversíveis sempre aumenta e, em processos reversíveis, jamais diminui.
No exemplo do pêndulo, a energia útil está associada à ordem do sistema, e a energia dissipada, à desordem. Considerando um sistema fechado, ocorreu uma transformação espontânea da ordem para a desordem, ou seja, a entropia do sistema aumentou.
No Universo, há uma tendência natural de transformação de todas as formas de energia (mecânica, química, elétrica etc.) consideradas “formas organizadas” em formas dissipativas (calor), ou “formas desorganizadas”. Portanto, a segunda lei da Termodinâmica se caracteriza pelo processo da degradação da energia.
Como interpretação do quê foi exposto, tem-se quê a transmissão espontânea de calor ocorre sempre de um corpo ou sistema de maior tempera-túra para outro de menor tempera-túra, devido ao aumento da entropia. êste é considerado outro enunciado da segunda lei da Termodinâmica.
O calor sempre é transmitido espontaneamente de um corpo ou sistema de maior tempera-túra para outro de menor tempera-túra.
Máquinas térmicas
Máquinas térmicas são as quê opéram em ciclos e realizam trabalho a partir do calor recebido. Os principais exemplos atuáis são as turbinas de usinas termelétricas e os veículos com motores de combustão interna.
Analisando o funcionamento de uma máquina térmica, tem-se a necessidade de uma fonte kemte para fornecer calor para a máquina funcionar, e também de uma fonte fria, permitindo assim quê o funcionamento ocorra em ciclos. Além díssu, a fonte fria é necessária para o calor da fonte kemte pôdêr fluir espontaneamente.
A imagem a seguir é uma representação comumente feita de uma máquina térmica, composta de uma fonte kemte, quê opera a uma tempera-túra T1 e fornece uma quantidade de calor Q1 para a máquina térmica quê, operando em ciclos, realiza um trabalho τ. Parte da quantidade de calor Q2 recebida pela máquina é rejeitada para a fonte fria quê opera a uma tempera-túra T2, sêndo T2 < T1
.
![Esquema de uma máquina térmica. A máquina térmica é representada por formas geométricas empilhadas verticalmente. De cima para baixo, retângulo escrito 'Fonte quente', seta vertical para baixo 'Q1',quadrado escrito 'Máquina térmica' com um tubo de escape na lateral direita, seta vertical para baixo 'Q2', retângulo escrito 'Fonte fria'[T2].](../resources/images/ek_9/ek_90ba9eeb4e48a062946783f259d0d4db.png)
ESPAÇOS DE APRENDIZAGEM
• êste vídeo explica a construção de um barco a vapor (máquina térmica).
Como fazer um barco a vapor: barquinho pópi pópi [experiência]. Publicado por: Manual do Mundo. Vídeo (15 min). Disponível em: https://livro.pw/ndxhk. Acesso em: 9 set. 2024.
Página duzentos e dezenove
Rendimento de uma máquina térmica
O rendimento M de uma máquina térmica é obtído pelo quociente entre o trabalho realizado τ e a quantidade de calor recebida Q1.
η =
De acôr-do com o princípio da conservação da energia, na máquina térmica tem-se a seguinte análise:
τ = Q1 − Q2
Assim, o rendimento de uma máquina térmica também póde sêr representado da seguinte forma:
η = ⇒ η = 1 −
ATIVIDADES
8. O funcionamento de uma máquina térmica é feito de tal forma quê o ciclo ABCDA desenhado na figura representa a evolução do gás ideal utilizado pela máquina. Use as informações dadas pela figura e determine o rendimento dessa máquina, sabendo quê, em cada ciclo, a quantidade de calor absorvida da fonte kemte é Q = 18 ⋅ nRT. Neste caso, considere o valor da tempera-túra em A.
22%
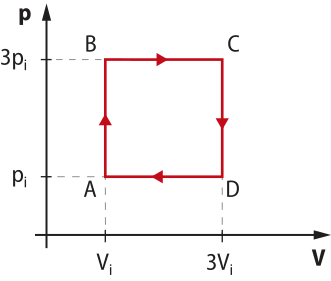
9. Um motor térmico recebe, em cada ciclo, 240 cal de uma fonte kemte e rejeita 180 cal para a fonte fria. Calcule o rendimento dêêsse motor.
25%
10. (UFAL) Uma dada massa de gás perfeito sofre uma transformação termodinâmica passando do estado A para outro B, como representa o diagrama p × V a seguir.
![Gráfico; eixo vertical 'P'[10 elevado a quatro N¹metros quadrados] e eixo horizontal 'V'[10 elevado a menos três metros quadrados]. Uma reta 'A','B' descendente, formada pelos pontos 4,0, e 0,10 e ponto 8,0 e 0,30.](../resources/images/ek_2/ek_26cd3285b40af66a3eac3af974abe242.png)
O trabalho realizado pelo gás nessa transformação, em joules, foi de
a) 24
b) 12
c) zero
d) −12
e) −24
Resposta: d)
11. Uma máquina térmica opera em ciclos com tempera-túras entre 600 K e 200 K. Em cada ciclo, a máquina recebe 900 J de calor da fonte kemte.
a) Qual é o calor rejeitado em cada ciclo?
300 J
b) Qual é o trabalho realizado pela máquina em cada ciclo?
600 J
12. Para completar um ciclo, determinada máquina térmica necessita receber 600 J da fonte kemte. Sabendo quê o rendimento da referida máquina é 40%, calcule:
a) a quantidade de trabalho ôbitída em cada ciclo;
240 J
b) a quantidade de calor quê é rejeitada para a fonte fria.
360 J
Página duzentos e vinte
Ciclo de Carnot
O engenheiro francês Nicolas Sadi Carnot (1796-1832), quando estudou minuciosamente o processo eficiente de transformações de calor em trabalho, propôs uma máquina teórica quê, ao operar entre duas tempera-túras fixas T1 e T2, sêndo T1 > T2, executava uma transformação cíclica composta de duas transformações isotérmicas e duas adiabáticas, intercaladas e reversíveis.
O trabalho τ realizado é positivo e numericamente igual à área do ciclo ABCDA, quê é percorrido no sentido horário.
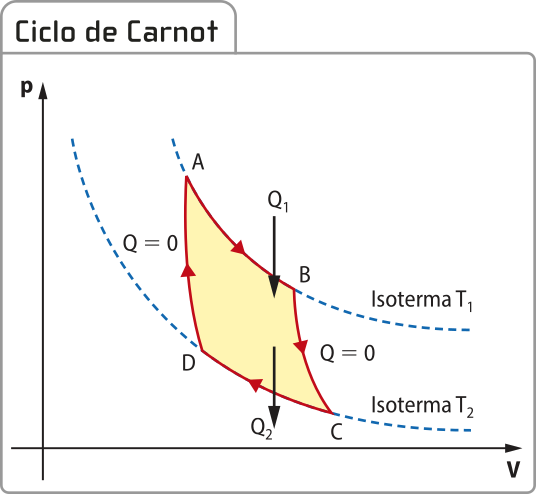
Carnot demonstrou teóricamente quê, nesse ciclo, as quantidades de calor trocadas com as fontes kemte e fria são diretamente proporcionais às respectivas tempera-túras absolutas das fontes.
Como o rendimento de uma máquina térmica é expresso pela razão entre os calores trocados, tem-se quê o rendimento de uma máquina térmica teórica operando por ciclo de Carnot é o único quê póde sêr calculado a partir das tempera-túras absolutas das fontes kemte e fria, independentemente do fluido operante.
η = 1 − ⇒ η = 1 −
O rendimento do ciclo de Carnot afirma o valor teórico mássimo para uma máquina operando entre as duas respectivas tempera-túras, sêndo quê o rendimento de uma máquina térmica real será menor.
De acôr-do com a análise do ciclo de Carnot, tem-se quê o rendimento seria de 100% se a tempera-túra da fonte fria (T1)fosse o zero absoluto e a tempera-túra da fonte kemte (T2)fosse infinita, condições impossíveis na prática. Assim, essa investigação levou a mais um enunciado para a segunda lei da Termodinâmica.
Nenhuma máquina térmica operando em ciclos terá rendimento de 100%.
Página duzentos e vinte e um
Ciclo de motor quatro tempos
Os motores de combustão interna de veículos são máquinas térmicas quê funcionam geralmente com gasolina, etanol e dízel.
Esses motores são formados por um corpo de metal com uma câmara de combustão. Essa câmara é composta de cilindro, pistão móvel, válvula de admissão, válvula de escape e uma vela de ignição.
O sistema do motor de combustão interna funciona em um ciclo de quatro etapas, ou quatro tempos: admissão, compressão, explosão e exaustão.
Note quê esse motor de explosão, como qualquer máquina térmica, é um dispositivo quê opera em ciclos, ou seja, executa inúmeras transformações fechadas, voltando a seu estado inicial antes do próximo ciclo. A energia química do combustível é transformada em trabalho (movimento das engrenagens e do veículo) e em energia interna do gás (aquecimento).
O rendimento dêêsses motores póde variar entre 20% e 30%.
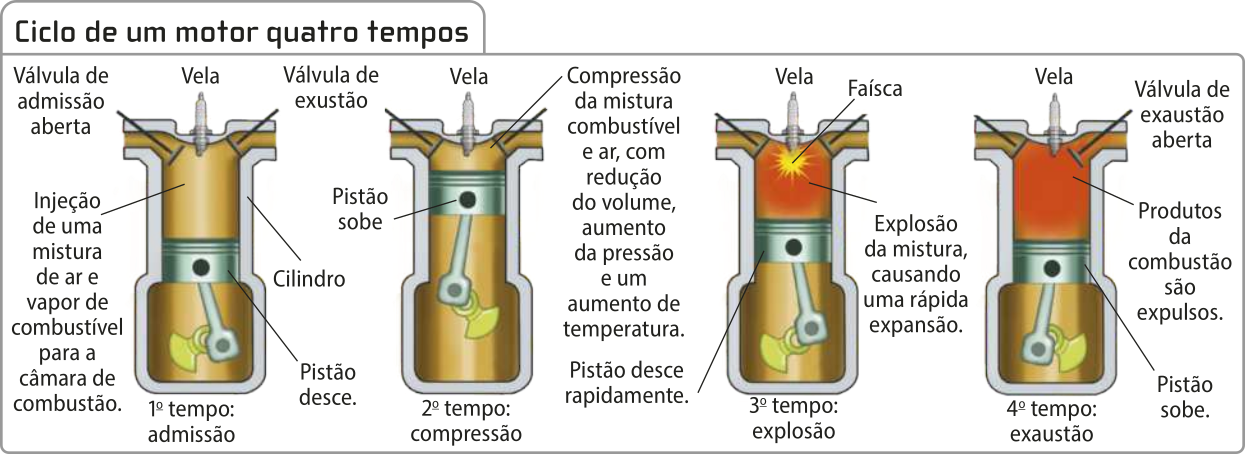
Ciclo do refrigerador
A geladeira, ou refrigerador, retira calor da fonte fria (interior) e transmite para a fonte kemte (ambiente). Aparentemente, trata-se de um processo quê viola a segunda lei da Termodinâmica, afinal o calor está sêndo transmitido da tempera-túra mais baixa para a mais alta. Contudo, a lei ainda é válida, uma vez quê nesse caso não se trata de um processo espontâneo.
No ciclo do refrigerador, também chamado de máquina frigorífica, ocorre conversão de trabalho em calor, ou seja, o processo só é possível devido ao trabalho quê é realizado sobre o sistema, e não o trabalho realizado pelo sistema.
A imagem a seguir ilustra um ciclo do refrigerador.
![Representação de uma máquina térmica que opera no ciclo do refrigerador. Esquema de caixas empilhadas verticais, de baixo para cima, retângulo escrito 'Fonte fria' [T2] seta vertical para cima 'Q2', quadrado escrito 'Máquina térmica', um tubo lateral direito com seta horizontal para a esquerda [trabalho].Seta vertical para cima 'Q1' até retângulo escrito 'Fonte quente' [T1]](../resources/images/ek_a/ek_af9004ecb83e594e72bf4aaa28dfad55.png)
De acôr-do com o princípio da conservação da energia, no ciclo do refrigerador, tem-se a seguinte análise:
Q1 = τ + Q2
O rendimento de uma máquina refrigeradora é comumente designado eficiência (e), definida pela razão entre a quantidade de calor quê foi retirada da fonte fria (Q2)e o trabalho envolvido (τ).
e =
Página duzentos e vinte e dois
SAIBA +
A geladeira
Há muito tempo, sabe-se quê os alimentos resfriados têm uma duração maior de conservação, pois o frio reduz a ação das bactérias. As primeiras geladeiras surgiram por volta de 1876, na Inglaterra, chegando aos lares dos usuários em cerca de 1910.
Uma geladeira basicamente retira calor de uma fonte fria (interior da geladeira) e o fornece para uma fonte kemte (ambiente externo). Mesmo parecendo violar a segunda lei da Termodinâmica, isso é possível por não sêr um fenômeno espontâneo, pois exige a realização de trabalho, ou seja, consumo de energia.
No funcionamento de uma geladeira, ocorre a circulação de um fluido refrigerante. Os fluidos utilizados antigamente eram nocivos ao ambiente, como os cê éfe cês (clorofluorcarbonos), e foram substituídos por tipos menos nocivos. Atualmente, são utilizados fluidos à base de hidrocarbonetos, como o isobutano (código R-600a) e o tetrafluoretano (código R-134a).
O esquema a seguir apresenta os principais elemêntos de uma geladeira e descreve seu funcionamento.
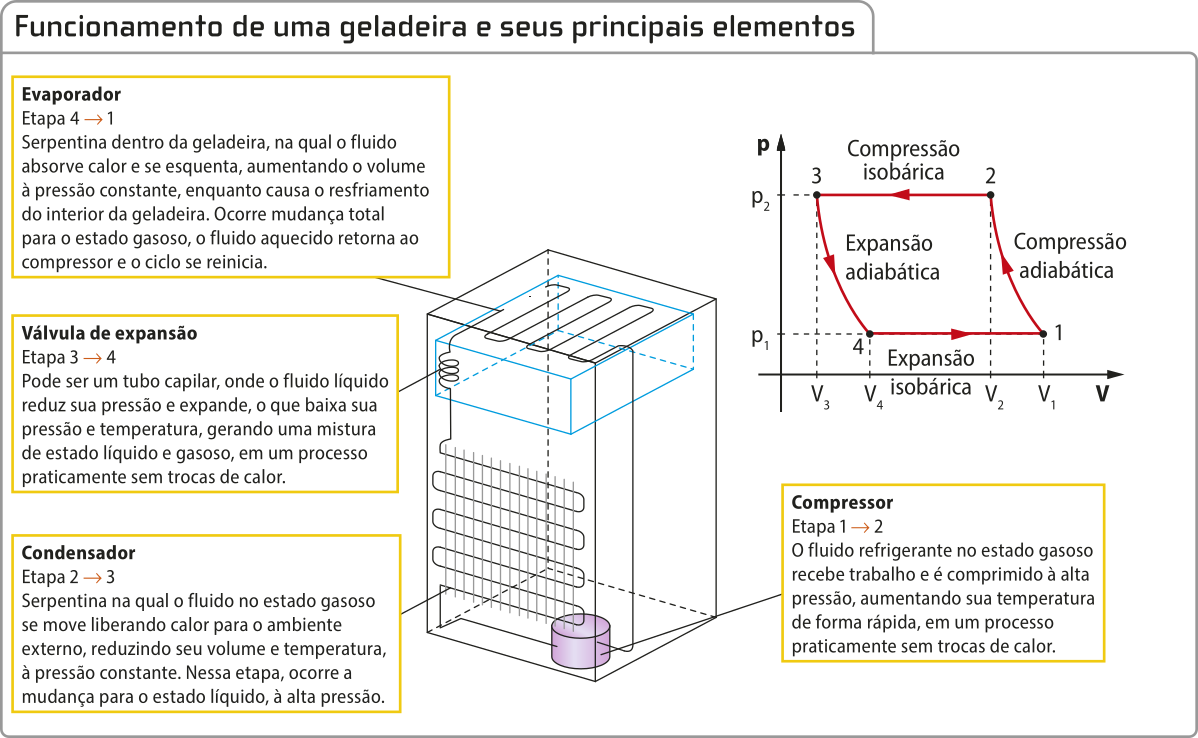
ATIVIDADES
1. No ciclo do refrigerador utilizado na geladeira, em quê momento ocorre a realização de trabalho?
2. Pesquisas e estudos relacionados à Termodinâmica e transformações gasosas contribuíram para o surgimento da geladeira. Cite alguns benefícios quê esses estudos proporcionaram à ssossiedade.
3. por quê é importante quê pesquisas relacionadas à geladeira e seu funcionamento continuem sêndo realizadas, tanto a respeito do uso pêlos consumidores quanto da sustentabilidade de seu funcionamento? Converse com seus côlégas e argumente sobre essa questão.
Página duzentos e vinte e três
ATIVIDADE RESOLVIDA
3. Um laboratório de pesquisas está desenvolvendo um novo motor quê funcionará como uma máquina térmica, operando entre a tempera-túra de 600 °C e a tempera-túra ambiente de 25 °C. Nos testes realizados, a cada ciclo, a máquina recebe 5 ⋅ 105 J de uma fonte kemte e rejeita 3? 105 J para a fonte fria. Qual é o rendimento real dessa máquina térmica? E qual é o seu rendimento mássimo teórico?
Resolução
O rendimento real dessa máquina térmica póde sêr calculado da seguinte forma:
ηreal = = 1 − ⇒ ηreal = 1 − ⇒ ηreal = 0, 4 = 40%
O rendimento teórico mássimo é calculado considerando um ciclo de Carnot para as tempera-túras absolutas quê a máquina térmica está operando.
ηmáx. = 1 − ⇒ ηmáx. = − ⇒ ηmáx. = 1 − ⇒ ηmáx ≃ 0,66 ≃ 66%
ATIVIDADES
13. Uma determinada máquina térmica funciona realizando o ciclo de Carnot. As tempera-túras das fontes kemte e fria são, respectivamente, 700 K e 300 K. Em cada ciclo a máquina recebe 1.000 J de calor da fonte kemte.
a) Qual é o calor rejeitado em cada ciclo?
≃ 428,6 J
b) Qual é o trabalho realizado pela máquina em cada ciclo?
≃ 571,4 J
14. Durante um ciclo de funcionamento, uma máquina térmica consome de uma fonte kemte 200 cal e libera para a fonte fria 140 cal. Calcule considerando um ciclo realizado:
a) o trabalho realizado pela máquina;
60 cal
b) o rendimento da máquina.
30%
15. Uma máquina térmica reversível, operando segundo o ciclo de Carnot, recebe 4,5 ⋅ 104 cal de uma fonte kemte e cede 2,9 ⋅ 104 cal à fonte fria. Determine a tempera-túra da fonte kemte, sabendo quê a fonte fria está a 8 °C.
436,03 K
16. Um refrigerador funciona realizando ciclos entre as tempera-túras de −24 °C e 27 °C (segundo o ciclo de Carnot). Em cada ciclo, 500 J de calor são rejeitados para a fonte kemte. Calcule:
a) o trabalho do compressor em cada ciclo;
85 J
b) a eficiência dêêsse refrigerador.
4,9%
17. O motor de combustão, instalado num avião, ao completar um ciclo, consome 9.000 J de calor para realizar um trabalho mecânico de 2.520 J. Utilize estes dados e responda aos itens seguintes.
a) Qual é o rendimento do motor?
28%
b) Qual é a quantidade de calor rejeitada em cada ciclo?
6.480 J
c) Qual é a quantidade de combustível consumida, em cada ciclo, sabendo quê o calor fornecido ao motor é proveniente da queima do combustível, cujo calor de combustão é dado por 6,0 ⋅ 104 J/g.
0,15 g
18. Um refrigerador, operando segundo um ciclo de Carnot, transfére calor de certa massa de á gua a 0 °C para o ambiente de tempera-túra igual a 30 °C. Após algum tempo, verifica-se quê se formaram 91 kg de gêlo a 0 °C. Considere 1 cal = 4,2 J, L = 80 cal/g e 1 kWh = 3,6 ⋅ 106 J e determine:
a) a quantidade de calor retirada da á gua;
7,28 · 106 cal
b) a quantidade de calor fornecida ao exterior;
8,08 · 106 cal
c) o trabalho fornecido ao sistema, em kWh.
0,93 kWh
Página duzentos e vinte e quatro
ORGANIZANDO AS IDEIAS
O mapa mental a seguir apresenta os principais conceitos estudados nesta Unidade.

No caderno, elabore o seu próprio esquema, organizando os principais conceitos da Unidade e incluindo nele outros termos e ideias quê se relacionam ao quê foi estudado, realizando as associações quê considerar importantes. Por fim, elabore um pequeno texto conectando os conceitos e as ideias presentes no esquema. Essa é uma boa forma de estudar e compreender melhor os conceitos.
Página duzentos e vinte e cinco
ATIVIDADES COMPLEMENTARES
Respostas e comentários estão disponíveis nas Orientações para o professor.
Tema 13: Termodinâmica e ssossiedade
1. Ao estudar o aumento de rendimento e eficiência das máquinas térmicas, diêmes Watt realizou uma inovação técnica, para aproveitar, d fórma contínua, a energia da combustão. Qual foi essa inovação?
a) Tornar cíclico o processo de transformação de energia proporcionado pela combustão.
b) O grande consumo de carvão.
c) O resfriamento do pistão com á gua à tempera-túra ambiente.
d) O aumento do rendimento da máquina térmica juntamente com um aumento do consumo de carvão.
Resposta: a)
Tema 14: Termologia e dilatação térmica
2. (Enem/MEC) Em nosso cotidiano, utilizamos as palavras “calor” e “temperatura” d fórma diferente de como elas são usadas no meio científico. Na linguagem corrente, calor é identificado como “algo quente” e tempera-túra méde a “quantidade de calor de um corpo”. Esses significados, no entanto, não conseguem explicar diversas situações quê podem sêr verificadas na prática. Do ponto de vista científico, quê situação prática mostra a limitação dos conceitos corriqueiros de calor e tempera-túra?
a) A tempera-túra da á gua póde ficar constante durante o tempo em quê estiver fervendo.
b) Uma mãe coloca a mão na á gua da banheira do bebê para verificar a tempera-túra da á gua.
c) A chama de um fogão póde sêr usada para aumentar a tempera-túra da á gua em uma panela.
d) A á gua kemte quê está em uma caneca é passada para outra caneca a fim de diminuir sua tempera-túra.
e) Um fôrnu póde fornecer calor para uma vasilha de á gua quê está em seu interior com menor tempera-túra do quê a dele.
Resposta: a)
3. (Faap-SP) O gráfico a seguir representa a correspondência entre uma escala X e a escala célcius.
Os intervalos de um grau X e de um grau célcius são representados, nos respectivos eixos, por segmentos de mesmo comprimento. A expressão quê relaciona essas escalas é:
![Representação gráfica: eixo vertical 't x'[X] e eixo horizontal 't c'[graus Celsius]. Uma reta inclinada quarenta e cinco graus, no ponto 80 [X].](../resources/images/ek_e/ek_e44d6f6274a02fa66bd9e7ece12a323a.png)
a) tX = tC + 80
b)
c)
d) tX = tC − 80
e) tX = tC
Resposta: a)
Tema 15: Calor: energia em movimento
4. (Fuvest-SP) Nos dias frios, quando uma pessoa expele ar pela bôca, forma-se uma espécie de fumaça junto ao rrôsto. Isso ocorre porque a pessoa:
a) expele o ar kemte quê condensa o vapor-d’água existente na atmosféra.
b) expele o ar kemte e úmido quê se esfria, ocorrendo a condensação dos vapores espelídos.
c) expele o ar frio quê provoca a condensação do vapor-d’água na atmosféra.
d) provoca a liquefação do ar com seu calor.
e) provoca a evaporação da á gua existente na atmosféra.
Resposta: b)
5. (UEL-PR) Analise o diagrama a seguir.
![Esquema gráfico: eixo vertical 'P'[a t m] e eixo horizontal 'T'[graus Célsius]. ponto 1 com linha tracejada horizontal. Uma curva bifurcada ascendente divide as regiões: um antes da bifurcação,2 dentro da bifurcação e três abaixo da bifurcação do lado direito. Setas duplas E,F vertical, C,D horizontal e A,B vertical.](../resources/images/ek_7/ek_7019528716b93bc7e6e4c36f82d2eab0.png)
Página duzentos e vinte e seis
A formação natural de flocos de néve é uma consequência diréta das condições atmosféricas de tempera-túra e pressão. Isso justifica a ocorrência dêêsse fenômeno acima dos cumes de elevadas montanhas como o Aconcágua (6962 m acima do nível do mar), a cordilheira dos Andes e o everést (8848 m acima do nível do mar), localizado na cordilheira do Himalaia. Com base no diagrama de fases da á gua pura, assinale a alternativa quê apresenta, corretamente, a transição de fase quê corresponde à formação de flocos de néve em elevadas altitudes a partir da á gua na fase vapor.
a) A → B
b) B → A
c) C → D
d) D → C
e) F → E
Resposta: d)
Tema 16: Transmissão de calor
6. (hú éfe ême gê) Uma garrafa térmica do tipo das usadas para manter o café kemte consiste em um recipiente de vidro de parede dupla com vácuo entre as paredes. Essas paredes são espelhadas. O vácuo e as paredes espelhadas são usados para dificultar a transmissão de calor, estando relacionados com uma ou mais formas de transmissão. Assinale a alternativa quê relaciona corretamente as características da garrafa térmica com as formas de transmissão de calor quê essas características tentam impedir.
a) parede espelhada ↔ condução, vácuo ↔ radiação
b) parede espelhada ↔ condução, vácuo ↔ radiação e convekição
c) parede espelhada ↔ radiação, vácuo ↔ condução e convekição
d) parede espelhada ↔ radiação, vácuo ↔ radiação, condução e convekição
Resposta: c)
7. (Enem/MEC) As cidades industrializadas produzem grandes proporções de gases como o CO2, o principal gás causador do efeito estufa. Isso ocorre por causa da quantidade de combustíveis fósseis queimados, principalmente no transporte, mas também em caldeiras industriais. Além díssu, nessas cidades concentram-se as maiores áreas com sólos asfaltados e concretados, o quê aumenta a retenção de calor, formando o quê se conhece por “ilhas de calor”. Tal fenômeno ocorre porque esses materiais absorvem o calor e o devolvem para o ar sôbi a forma de radiação térmica. Em áreas urbanas, devido à atuação conjunta do efeito estufa e das “ilhas de calor”, espera-se quê o consumo de energia elétrica
a) diminua devido à utilização de caldeiras por indústrias metalúrgicas.
b) aumente devido ao bloqueio da luz do Sol pêlos gases do efeito estufa.
c) diminua devido à não necessidade de aquecer a á gua utilizada em indústrias.
d) aumente devido à necessidade de maior refrigeração de indústrias e residências.
e) diminua devido à grande quantidade de radiação térmica reutilizada.
Resposta: d)
Tema 17: Comportamento térmico dos gases
8. (Fuvest-SP) Os pontos A, B e C do gráfico (p × V) da figura representam três estados de determinada massa de um gás perfeito. Sendo TA, TB e TC as tempera-túras absolutas correspondentes, podemos afirmar:
![Gráfico: eixo vertical 'P' e eixo horizontal 'V', pontos A[4,1],B[4,3],C[2,6].](../resources/images/ek_f/ek_f9c1313d823210db60a647563a0a9e3d.png)
a) TC > TB >.TA
b) TC = TB >.TA
c) TC = TB = TA
d) TC < TB = TA
e) TC > TB = TA
Resposta: b)
9. (Enem/MEC) O manual de um automóvel alerta sobre os cuidados em relação à pressão do ar no interior dos p-neus. Recomenda-se quê a pressão seja verificada com os p-neus frios (à tempera-túra ambiente). Um motorista, desatento a essa informação, realizou uma viagem longa sobre o asfalto kemte e, em seguida, verificou quê a pressão P0 no interior dos p-neus não era a recomendada pelo fabricante. Na ocasião, a tempera-túra dos p-neus era T0. Após um longo período em repouso, os p-neus do carro atingiram a tempera-túra ambiente T. Durante o resfriamento, não há alteração no volume dos p-neus e na quantidade de ar no seu
Página duzentos e vinte e sete
interior. Considere o ar dos p-neus um gás perfeito (também denominado gás ideal). Durante o processo de resfriamento, os valores de pressão em relação à tempera-túra (P × T) são representados pelo gráfico:
a) ![Gráfico: eixo vertical 'P'[P a] e eixo horizontal 'T'[k]. Uma reta vertical, seta para baixo no ponto 'P O','T' e outra reta horizontal seta para a esquerda, no ponto 'P O','T O'.](../resources/images/ek_1/ek_13cdc272d02acd7f5ae9cfdf846701d6.png)
b) 
c) 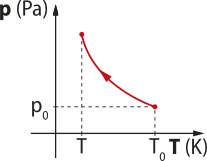
d) 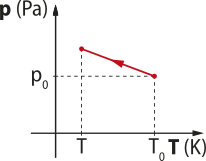
e) 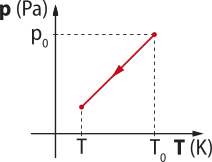
Resposta: e)
10. (Enem/MEC) De acôr-do com a Constituição Federal, é competência dos municípios o gerenciamento dos serviços de limpeza e côléta dos resíduos urbanos (lixo). No entanto, há relatos de quê parte dêêsse lixo acaba sêndo incinerado, liberando substâncias tóxicas para o ambiente e causando acidentes por explosões, principalmente quando ocorre a incineração de frascos de aerossóis (por exemplo: desodorantes, inseticidas e repelentes). A tempera-túra elevada provoca a vaporização de todo o conteúdo dentro dêêsse tipo de frasco, aumentando a pressão em seu interior até culminar na explosão da embalagem.
ZVEIBIL, V. Z. éti áu. Cartilha de limpeza urbana. Disponível em: ww w.ibam.org. br. Acesso em: 6 jul. 2015 (adaptado)
Suponha um frasco metálico de um aerossol de capacidade igual a 100 mL, contendo 0,1 mol de produtos gasosos à tempera-túra de 650 °C, no momento da explosão.
Considere: R =
A pressão, em atm, dentro do frasco, no momento da explosão, é mais próxima de
a) 756.
b) 533.
c) 76.
d) 53.
e) 13.
Resposta: c)
Tema 18: As leis da Termodinâmica e as máquinas térmicas
11. (UECE) Em relação às propriedades dos gases, atente para as seguintes afirmações:
I. Para um gás ideal, a energia interna é função apenas da pressão.
II. O calor absorvido por um gás ao variar seu estado independe do processo.
III. A energia interna de um gás ideal é uma função apenas da tempera-túra e independe do processo.
IV. Numa expansão isotérmica de um gás ideal, o trabalho realizado pelo mesmo é igual ao calor absorvido.
Está correto o quê se afirma somente em
a) I e II.
b) III e IV.
c) I e IV.
d) II e III.
Resposta: b)
12. (UFPA) Em seus livros de Física, João descobriu quê o trabalho realizado por uma máquina térmica industrial está relacionado com a pressão, volume e tempera-túra do gás utilizado pela máquina. A figura a seguir representa um ciclo de trabalho de um gás ideal.
![Gráfico: eixo vertical 'pressão'[N/metros quadrados] e eixo horizontal 'volume'[metros cúbicos]. Um retângulo A,B,C,D nos pontos 'dois vezes dez elevado a quinta potência e um 'ponto 'A', ponto 'B' 'três vezes dez elevado a quinta potência e um', ponto 'C' 'três vezes dez elevado a quinta potência e dois' e ponto 'D' 'dois vezes dez elevado a quinta potência e dois'. setas indicam a direção horária.](../resources/images/ek_e/ek_eeb92707240dfe7624094b1cb97ee3b1.png)
A partir da análise do gráfico, julgue as seguintes afirmações:
I. A tempera-túra do gás no ponto C é 3 vezes a sua tempera-túra no ponto A.
II. O trabalho realizado pelo gás ao longo de um ciclo foi de 105 joules.
III. Ao longo do ciclo ABCDA, a variação da energia interna do gás foi positiva.
IV. A tempera-túra do gás permaneceu constante durante todo o ciclo ABCDA.
V. O ciclo ABCDA é constituído por duas transformações isobáricas e duas adiabáticas.
Assinale a alternativa quê contém apenas afirmações corretas.
a) I e III
b) II e IV
c) I e II
d) II e V
e) III e IV
Resposta: c)
Página duzentos e vinte e oito
INTEGRANDO COM...
Biologia e Química
Compostagem: um caminho sustentável para o gerenciamento de resíduos orgânicos
Respostas e comentários estão disponíveis nas Orientações para o professor.
A compostagem é uma técnica de biodegradação em quê resíduos orgânicos são decompostos por microrganismos em condições controladas, resultando na formação de um material rico em nutrientes conhecido como compôzto (húmus), utilizado como adúbo orgânico.
Diariamente, grandes volumes de resíduos orgânicos são gerados e, sem um manejo adequado, acabam em atêerros, onde se decompõem de maneira anaeróbica, ou seja, com pouca ou nenhuma presença de oxigênio, o quê libera metano, um gás de efeito estufa. O processo na compostagem é, predominantemente, aeróbico, minimizando a emissão de metano na atmosféra quando comparado ao processo de decomposição de resíduos orgânicos em atêerros.
Assim, a prática da compostagem contribui no combate aos efeitos das mudanças climáticas, alinhando-se aos objetivos globais de desenvolvimento sustentável.
Parâmetros biológicos, físicos e químicos na compostagem

A eficiência da compostagem e a qualidade final do compôzto dependem de diversos parâmetros biológicos, físicos e químicos quê se relacionam de maneira interdependente e quê podem sêr monitorados e controlados.
Durante a compostagem, microrganismos, como bactérias e fungos, atuam na decomposição de material orgânico, processo exotérmico quê, além do calor, libera dióxido de carbono e vapor de á gua. A diversidade e a atividade dêêsses microrganismos são influenciadas por fatores como a tempera-túra, a umidade, a disponibilidade de oxigênio e o potencial hidrogeniônico (pH).
Temperatura e as fases da compostagem

A tempera-túra, em especial, é um parâmetro quê revela a intensidade da atividade metabólica dos microrganismos, por isso, ela indica a eficiência e o progresso da decomposição.
No início do processo da compostagem, a ação intensa de microrganismos dá início à liberação de calor, e as tempera-túras se mantêm abaixo dos 45°C por poucos dias.
Na fase seguinte, ocorre maior emissão de calor e liberação de vapor de á gua. As tempera-túras se mantêm, normalmente, entre 50°C e 65°C por cerca de 30 dias.
A tempera-túra então diminui gradualmente abaixo dos 45°C com a redução da atividade dos microrganismos, etapa quê ocorre por mais de 55 dias.
Por fim, a fase de maturação perdura por pelo menos 30 dias. Nela a tempera-túra do compôzto se estabiliza com a do ambiente e ocorre a formação de húmus, quê póde sêr utilizado como adúbo orgânico.
Página duzentos e vinte e nove

Que tal verificar na prática o quê foi descrito? Reúna-se em um grupo com os côlégas e realizem as etapas indicadas a seguir.
• Iniciativa: conversem com seus professores e com os responsáveis pela escola, propondo um projeto para instalação de uma composteira como solução sustentável para destinação dos resíduos orgânicos. Verifiquem uma forma de execução viável e adequada à realidade da escola.
• Divulgação: pesquisem os resíduos orgânicos mais adequados para serem colocados na composteira e elaborem um material de divulgação, apresentando o projeto e orientando como todos póderão contribuir. A divulgação pode sêr feita pessoalmente pela escola, por vídeos em platafórmas digitais e nas mídias sociais da escola, em aplicativos de conversação, em materiais impressos, como cartazes, entre outros.
• Rotina: elaborem um cronograma de fiscalização da composteira (diário ou semanal) para realizar etapas como coletar e depositar os resíduos e material seco, revolver o compôzto, entre outros cuidados. Organizem também o levantamento de informações para análise e monitoramento do compôzto ao longo do tempo, definindo responsáveis quê realizem medidas da tempera-túra, contrôle da umidade, entre outros parâmetros.
Para mais informações, acéçi o manual de compostagem elaborado pelo Ministério do Meio Ambiente (MMA) juntamente com o Serviço Social do komérssio de Santa Catarina (Sesc/SC) e o Centro de Estudo e Promoção da Agricultura de Grupo (Cepagro): Compostagem doméstica, comunitária e institucional de resíduos orgânicos. Publicado por: MMA. Disponível em: https://livro.pw/prbou (acesso em: 19 set. 2024).
Página duzentos e trinta

