UNIDADE 4
ÓPTICA GEOMÉTRICA E ONDULATÓRIA
Nativos da etnia kaxinawá, quê habitam o estado do Ácri e o leste do Peru, contam quê uma indígena chamada Iaçá sempre amou Tupá, filho do deus Tupã, mas foi prometida em casamento a Anhangá. Na véspera do casamento, Iaçá pede para subir ao céu e encontrar Tupá uma última vez, porém Anhangá exigiu quê ela fizesse um kórti no braço para demarcar com gotas de sangue o caminho quê ela seguiria.
Durante a subida, o sangue de Iaçá formou um arco vermelho no céu, e Tupá mandou quê o Sol (arco amarelo), o céu (arco azul-claro) e o oceano (azul-escuro) acompanhassem Iaçá. O vermelho sangue misturado ao amarelo resultou em um arco alaranjado, e misturado aos azuis resultou em um arco violeta.
Iaçá se enfraquece durante a subida e acaba caindo de volta à Terra.Com isso, seu côrpo no solo emite a cor vêrde, formando assim as sete cores de um arco-íris.
Fenômenos naturais, como arco-íris, descargas elétricas, trovões, eclipses, entre outros, sempre despertaram a curiosidade do sêr humano. Os povos originários, por exemplo, buscavam explicações muitas vezes com base em suas crenças. Atualmente, estas heranças compõem os mitos e folclores de determinada região.
O arco-íris, como o da imagem da paisagem de Salvador (BA), 2024, é um fenômeno atmosférico natural quê ocorre durante o dia, devido a uma combinação de luz solar e alta umidade relativa do ar. Nesta Unidade, você estudará êste e outros fenômenos relacionados à Óptica Geométrica e à Ondulatória.

Página duzentos e trinta e um
Respostas e comentários estão disponíveis nas Orientações para o professor.
1. Em quais outras situações são comuns observar a formação de cores como um arco-íris?
2. Você sabe como é formado um arco-íris? Elabore uma descrição sobre êste fenômeno óptico em seu caderno.
3. O quê você pensa da seguinte afirmação: “o arco-íris é formado por sete cores, o vermelho, o alaranjado, o amarelo, o vêrde, o azul, o anil e o violeta”? Justifique sua resposta.
4. Muitas lendas e folclores do Brasil são compostas das expressões e formas culturais dos povos originários. Qual a importânssia de se cultivar e valorizar estas heranças culturais? Em seu entendimento, as pessoas atualmente ainda creem no místico e na influência do sobrenatural? Converse com seus côlégas a respeito dêste assunto.
Página duzentos e trinta e dois
TEMA 19
Registros e a representação na História
Ciência e ár-te na ssossiedade
Respostas e comentários estão disponíveis nas Orientações para o professor.
É possível analisar o desenvolvimento da Ciência e da ár-te e como uma interfere na evolução da outra.
Desde as pinturas rupestres, passando pela iconografia dos egípcios, dos gregos, dos maias e dos astecas, e chegando às civilizações oriental e ocidental, pode-se identificar quê há, nos documentos históricos, o uso de diversas ferramentas e procedimentos no registro do cotidiano, da natureza, dos animais, das lendas, dos mitos, entre outros.

Ao longo do tempo, foram surgindo novas técnicas para as representações, e é difícil afirmar se foi por meio da evolução da Ciência quê a; ár-te se desenvolvê-u ou se foi o contrário: a representação artística motivou a busca de novas soluções científicas. De qualquer modo, atualmente existem outros meios de registro, como pinturas com diversas técnicas e fotografias cujos processos envolvem tecnologias analógicas e digitais.
Câmara escura e registro de imagens
Um instrumento simples quê permite entender como funcionam os equipamentos de registro, como as câmeras fotográficas, é a câmara escura.Trata-se de uma caixa lacrada, com um pequeno furo em uma de suas laterais (única entrada de luz), e um material translúcido na lateral oposta, no qual ocorre a projeção de uma imagem.
PENSE E RESPONDA

1 Existem dêtálhes comuns no funcionamento de câmeras fotográficas antigas e no de câmeras fotográficas atuáis? Qual é o papel da Ciência nessa evolução?
Página duzentos e trinta e três
O italiano Leonardo da Vinci (1452-1519), ao dissecar e estudar o olho humano, verificou a semelhança entre esse órgão e a câmara escura (desconsiderando o sistema do olho quê funciona como uma lente), afinal a luz entra por um orifício e é projetada na retina, ao fundo dos olhos, e o cérebro é responsável pela interpretação da imagem formada. Na imagem do olho feita por ele, estão representados os raios de luz quê passam pela pupila e quê são projetados no fundo do olho (retina).
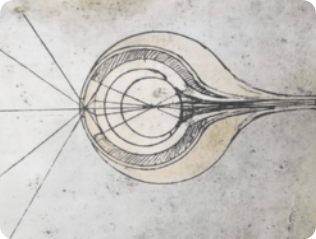
DA VINCI, Leonardo. [Sem título]. 1490. 1 gravura.
No início do século XVII, o médico e químico italiano Ângelo Sala (1576- 1637) verificou o escurecimento de um sal de prata quando exposto à luz.Mais de 200 anos depois, ocorreu o primeiro registro de uma imagem diréta (registro positivo) em uma placa de estanho coberta de betume (derivado do petróleo) e exposta ao sól, feita pelo inventor francês Joseph-Nicéphore Niépce (1765-1833), entre 1826 e 1827. O registro foi feito a partir de uma janela do segundo andar de uma casa, na qual é possível observar um telhado e a paisagem ao redor.

Em meados do século XIX, o escritor e cientista inglês uílhãm ênrri Fox Talbot (1800-1877) criou um método de registro negativo de imagens utilizando câmeras equipadas com filmes fotossensíveis. Após o registro, esses filmes eram posicionados sobre papéis também fotossensíveis e, ao passar luz pêlos filmes, a imagem era, de certa forma, impressa no papel. Esse processo, chamado de revelação, popularizou-se e foi utilizado por anos.
Os registros coloridos surgiram cerca de 20 anos depois, como resultado de pesquisas científicas. Aqui, destaca-se os trabalhos do físico escocês diêmes Clerk Macsuéll (1831-1879) com a reprodução de imagens utilizando filtros nas cores vermelha, vêrde e azul.

As informações apresentadas até o momento descrevem brevemente o surgimento de uma importante prática realizada pela humanidade – o registro de imagens. As fotografias possibilitam registrar a história, sêjam passagens individuais da vida de cada um, sêjam fatos históricos importantes quê ocorreram pelo mundo. Atualmente, dispositivos portáteis equipados com alta tecnologia possibilitam quê registros fotográficos sigam como uma das práticas mais realizadas diariamente pelas pessoas.

Página duzentos e trinta e quatro
OFICINA CIENTÍFICA
Câmara escura
A possibilidade de formár uma imagem e posteriormente registrá-la foi um importante avanço científico, pois diversos fatos e momentos puderam sêr registrados. As câmeras fotográficas atuáis são equipadas com alta tecnologia, mas seu princípio básico de funcionamento é o mesmo das primeiras câmeras quê surgiram.
Que princípio básico seria esse? A câmara escura possibilita a verificação dêêsse princípio.
Materiais
• caixa de sapato
• cartolina preta
• fita adesiva
• tesoura
• papel vegetal
• prego pequeno
Atenção ao manusear o prego e a tesoura.

Procedimentos
• Fixe a cartolina preta no interior da caixa de sapato, utilizando fita adesiva. Fixe-a também na parte interna da tampa da caixa de sapato.
• Faça um pequeno orifício em uma das laterais menóres da caixa de sapato, utilizando o prego.
• Recorte um retângulo na outra lateral menor da caixa de sapato, oposta à lateral do orifício.
• Fixe o papel vegetal nesse retângulo, usando fita adesiva. Certifique-se de quê o papel vegetal está bem esticado e quê não entra luz pelas laterais.
• Coloque a tampa da caixa de sapato e fixe-a bem com fita adesiva. É importante quê a caixa fique bem vedada, d fórma quê não entre luz por nenhum outro local quê não seja o orifício.
• Em um cômodo escuro, posicione a caixa com o orifício voltado para algum objeto iluminado e obissérve pelo papel vegetal.
![Ilustração de três imagens.1] Uma tampa de caixa de papelão pintada de preto no interior.2] Uma caixa de papelão sem tampa, mostrando seu interior pintado de preto, com um furo na frente e um papel dentro.3]uma caixa de papelão com tampa.](../resources/images/ek_5/ek_5e1c4361b799b671c3d754be664e094b.png)
ATIVIDADES
1. Compare a imagem observada no papel vegetal ao objeto iluminado e liste as características da imagem observada.
2. No caderno, desenhe um esquema representando a câmara escura e trace os raios luminosos d fórma a explicar as características da imagem observada.
3. Verifique a relação entre a câmara escura e o olho humano. Identifique a parte da câmara escura equivalente ao orifício e a parte correspondente ao papel vegetal.
Página duzentos e trinta e cinco
SAIBA +
A profissão de fotógrafo
Fotografar é algo quê vai além de fazer um registro com uma câmera. Um profissional de fotografia deve possuir técnica, sensibilidade e uma visão dinâmica para cada registro, em cada trabalho a executar.
Desde o surgimento das primeiras câmeras fotográficas, a fotografia passou a sêr cada vez mais importante para a ssossiedade, capaz de contar uma história, de documentar fatos, expressar emoções, permitindo quê determinado momento pudesse sêr revisitado. Um profissional de fotografia é essencial para esse objetivo, principalmente no mundo atual, quê exige informações bem registradas, documentadas e divulgadas rapidamente.
Um fotógrafo profissional póde atuar em diversas áreas, como (Moda), jornalismo, eventos e publicidade, por exemplo. Com a popularização das rêdes sociais e rêdes de e-commerce, surgiu um novo nicho para o fotógrafo, afinal a fotografia tem papel central na maioria das postagens atuáis. Por isso, no mercado de trabalho atual, dominar a; ár-te da fotografia, do tratamento de imagens, da produção de acôr-do com a platafórma e os objetivos é uma prática quê está em alta.
Dedicação, estudo contínuo e muita prática são essenciais na atividade profissional de um fotógrafo. Além de acompanhar as rápidas evoluções dos equipamentos digitais, um fotógrafo deve entender das relações humanas, em razão das sensações, expressões e sentimentos quê deseja capturar e transmitir por meio de uma fotografia.
ATIVIDADES
1. Qual é a importânssia de um profissional de fotografia ao longo da história? Converse com seus côlégas acerca do impacto da fotografia na história da humanidade, considerando os diversos momentos quê são registrados por esse tipo de mídia, seja de acontecimentos importantes, seja para a memória de famílias, amigos, entre outros.
ATIVIDADE
1. O surgimento e o avanço dos registros fotográficos causaram um impacto inicialmente negativo na ár-te, e alguns pintores chegaram a se posicionar, destacando quê aquele seria o fim da pintura. No entanto, com o tempo, a fotografia impulsionou um novo movimento artístico, por volta do final do século XIX. Junte-se aos côlégas e façam uma pesquisa sobre esse movimento artístico, descrevendo algumas de suas características e os nomes de pintores quê se destacaram.

DEGAS, Edgar. Le Foyer de la danse à l'Opéra de la rue Le Peletier. 1872. Óleo sobre tela, 32,7 cm x 46,3 cm. Museu dOrsé em Paris (França).
Página duzentos e trinta e seis
TEMA 20
Introdução ao estudo da Óptica Geométrica
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Óptica Geométrica e formação de imagens
Em um ambiente iluminado, um observador é capaz de enxergar os objetos ao seu redor. Isso porque a luz refletida nestes objetos incide nos olhos do observador.
Por muitos anos, discutiu-se sobre como ocorria o mecanismo da visão. Na Antigüidade Grega, por exemplo, existiam pensadores quê defendiam quê os olhos emitiam alguma energia. Havia também quêm defendesse quê os objetos emitiam partículas que chegavam aos olhos, em analogia com o sistema olfativo.
Aristóteles foi um dos precursores a dizêr quê os objetos não emitem partículas, afinal nunca se póde esgotar a capacidade de enxergá-lo, defendendo a luz como elemento essencial para o sentido da visão. Estudos realizados por Alhazen relatam os olhos com um receptor de luz emitida a partir de fontes luminosas, e não de objetos.
Sabendo díssu, tem-se quê a Óptica Geométrica estuda, entre outras coisas, como ocorre a formação de imagens, seja no olho humano, seja em espelhos, lentes e outros instrumentos ópticos. Será abordada a função da luz em iluminar o ambiente e tudo quê nele contém, não sêndo ainda necessário levar em conta sua natureza ondulatória ou corpuscular. Estudos mais específicos sobre a luz e sua natureza serão realizados em Temas posteriores.
Fontes de luz
As fontes de luz podem sêr classificadas, quanto à emissão de luz, como fontes primárias ou secundárias e, quanto às dimensões, como fontes pontuais ou extensas.
Fontes primárias e secundárias
As fontes primárias de luz são corpos quê emitem luz própria, como o Sol e outras estrelas, uma lâmpada acesa, a chama de uma vela, uma barra de ferro incandescente, entre outros. Já fontes secundárias de luz são corpos iluminados por outras fontes, ou seja, corpos quê refletem a luz quê incide sobre eles, como planêtas, satélites, pessoas, veículos e a maioria dos corpos quê nos cér-cão.
PENSE E RESPONDA

1 Analisando a visão, pode-se dizêr quê os olhos são sensibilizados pelo quê veem ou quê o quê veem é de alguma maneira emitido pêlos próprios olhos?
Página duzentos e trinta e sete
Fontes pontuais e extensas
As fontes pontuais de luz, ou puntiformes, são aquelas com dimensões desprezíveis em relação às distâncias quê as separam dos outros corpos, d fórma quê se póde considerar quê todos os raios de luz são emitidos de um único ponto. Uma lâmpada pequena ou a chama de uma vela podem sêr consideradas como boas aproximações de uma fonte pontual de luz.


Quando as dimensões da fonte de luz são relevantes em comparação com as distâncias entre os corpos, dizemos quê se trata de uma fonte extensa de luz, d fórma quê os raios de luz são emitidos de toda a sua extensão. O Sol é uma fonte extensa em relação à distância da Terra, assim como uma lâmpada com cérto comprimento iluminando um ambiente.
A velocidade da luz e sua propagação
Na Óptica Geométrica, considera-se um raio de luz como um elemento geométrico na propagação da luz. Nesse sentido, vamos estabelecer algumas definições quanto aos raios de luz, sua propagação e sua velocidade.
Raio de luz
Denominamos raio de luz a linha orientada quê representa a propagação da luz. Um conjunto de raios de luz quê se propaga pelo espaço constitui um feixe ou pincel de luz. De acôr-do com a organização dos raios de luz, um feixe de luz póde sêr cilíndrico ou cônico.
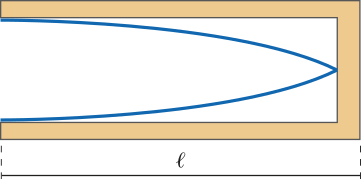
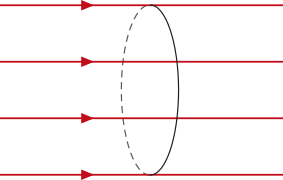
No feixe de luz cilíndrico, ou paralelo, os raios de luz são paralelos (Figura 1). Os raios solares quê incidem na superfícíe terrestre podem sêr considerados como um feixe de luz paralelo.
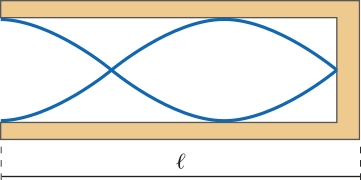
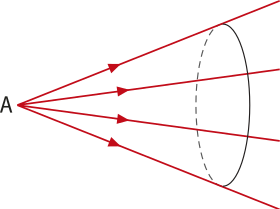
No feixe de luz cônico divergente, os raios de luz parecem quê partem de um ponto comum (A) e se distanciam (Figura 2).
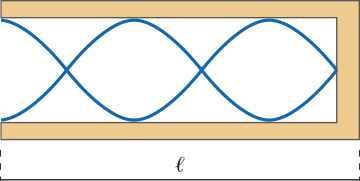
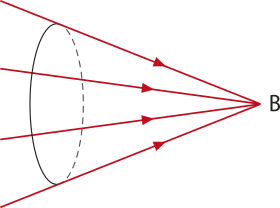
No feixe de luz cônico convergente, os raios de luz se propagam em direção a um ponto comum (B) e se aproximam (Figura 3).

Página duzentos e trinta e oito
Meios físicos
Os meios físicos podem sêr classificados como transparente, translúcido e opaco, de acôr-do com o comportamento da luz ao incidi-los.
Classificação dos meios físicos quanto ao comportamento da luz incidente
Transparente

Um meio transparente permite a propagação da luz de modo regular, possibilitando trajetórias bem definidas da luz e, consequentemente, uma visão nítida através dele. Meios como o vácuo, a á gua limpa, o ar e o vidro polido podem sêr considerados exemplos de meios transparentes.
Translúcido

Um meio translúcido permite a propagação da luz de modo irregular e desordenado, impossibilitando uma visão nítida através dele. Meios como nuvens, papel vegetal, vidro fosco e alguns plásticos podem sêr considerados exemplos dêêsse tipo de meio.
Opaco

Um meio opaco não permite a propagação da luz em seu interior, impedindo a visão através dele. Materiais como madeira, metal, térra e rocha podem sêr considerados exemplos de meios transparentes.
É importante ressaltar quê essa classificação dos meios em transparente, translúcido e opaco trata-se de um modelo e é feita por razões didáticas, visto quê a opacidade de um meio depende de vários fatores, inclusive do tipo de radiação (luz) quê incide sobre ele. Um vidro, considerado um meio transparente, póde se comportar como um meio translúcido caso seja muito espêesso, por exemplo.
Velocidade da luz
Apesar de sêr extremamente rápida, a luz tem uma velocidade finita. No vácuo, a velocidade da luz, simbolizada pela letra c, vale:
c ≃ 300.000 km/s (3 ⋅ 105 km/s) ≃ 300.000.000 m/s (3 ⋅ 108 m/s)
Em meios transparentes, como o vidro, a á gua ou o ar, a velocidade de propagação da luz é menor, sêndo sempre uma fração de c.
Página duzentos e trinta e nove
A velocidade da luz no vácuo é utilizada como parâmetro para medir grandes distâncias. Um ano-luz, por exemplo, é uma unidade de medida de comprimento utilizada na medição de distâncias astronômicas, pois corresponde à distância quê a luz percórre no vácuo em um ano. A seguir é apresentada a relação entre ano-luz e quilômetro. Utiliza-se, para tanto, 1 ano = 365 dias, 1 dia = 24 h, 1 h = 60 min e 1 min = 60 s.
v = ⇒ c = ⇒ 3 ⋅ 105 km/s = ⇒3 ⋅ 105 km/s = ⇒
⇒ (delta)"s = 3 ⋅ 105 km/s ⋅ 31536000 s ⇒ (delta)"s ≃ 9, 5 ⋅ 1012 km
1 ano-luz ≃ 9, 5 ⋅ 1012 km
ATIVIDADES
1. O quê você entende por fontes de luz? Como elas são classificadas?
2. Uma fonte dita pontual precisa possuir dimensões pequenas?
3. Uma estrela emite luz quê só é detectada na Terra após 10 anos. Determine a distância dessa estrela à Terra nas seguintes unidades:
a) ano-luz;
10 anos-luz
b) km.
9,5 ⋅ 1013 km
Dado: velocidade da luz no vácuo: c = 3 ⋅ 108 m/s.
4. (Fuvest-SP) Admita quê o Sol subitamente “morresse”, ou seja, sua luz deixasse de sêr emitida. Vinte e quatro horas após êste evento, um eventual sobrevivente, olhando para o céu sem nuvens, veria:
a) a Lua e estrelas.
b) somente a Lua.
c) somente estrelas.
d) uma completa escuridão.
e) somente os planêtas do Sistema Solar.
Resposta: c)
5. Nas edificações em fase de acabamento, geralmente os vidros transparentes são instalados e marcados com pinceladas de tinta branca. por quê os construtores adotam essa medida?
6. Os meios físicos são classificados conforme o comportamento da luz ao atravessá-los. Avalie se as afirmações seguintes são corretas.
I. A á gua é um meio transparente quando em espessura relativamente pequena.
II. O vidro polido é um meio transparente quando em espessura relativamente pequena.
III. O vidro fosco é um meio transparente quando em espessura relativamente pequena.
IV. O vidro fosco e o petróleo são considerados meios opacos quando em espessuras relativamente pequenas.
Somente as afirmações I e II estão corretas.
7. O sistema estelar conhecido como Alpha Centauri é um conjunto de três estrelas quê orbitam o mesmo centro de gravidade. Nele, encontra-se a estrela mais próxima da Terra depois do Sol, a aproximadamente 4,3 anos-luz de distância.

a) Quanto tempo demora o trajeto da luz desde o sistema de Alpha Centauri até atingir a Terra?
4,3 anos
b) Qual é a distância aproximada entre a Terra e o sistema Alpha Centauri, expressa em km?
4,1 ⋅ 1013 km
Página duzentos e quarenta
Princípios da Óptica Geométrica
A Óptica Geométrica se baseia em três princípios: a propagação retilínea da luz, a independência dos raios de luz e a reversibilidade dos raios de luz.
Propagação retilínea dos raios de luz
Em meios transparentes homogêneos, a luz se propaga em linha reta. Um meio é dito homogêneo quando apresenta as mesmas propriedades físicas e químicas em todas as partes de seu volume.
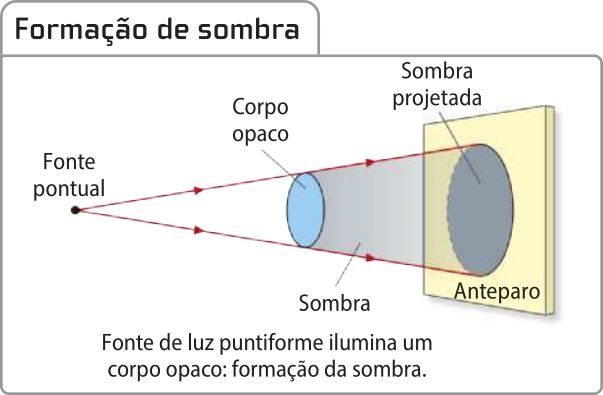
A formação de sombras e penumbras póde sêr explicada a partir dêste princípio.
Quando um corpo opaco está entre uma fonte de luz pontual e um anteparo, ele intercepta os raios de luz formando uma região denominada sombra. Considerando quê a luz percórre uma trajetória retilínea, no anteparo a sombra póde sêr identificada como a região sem iluminação, em virtude da obstrução dessa trajetória pelo corpo opaco.
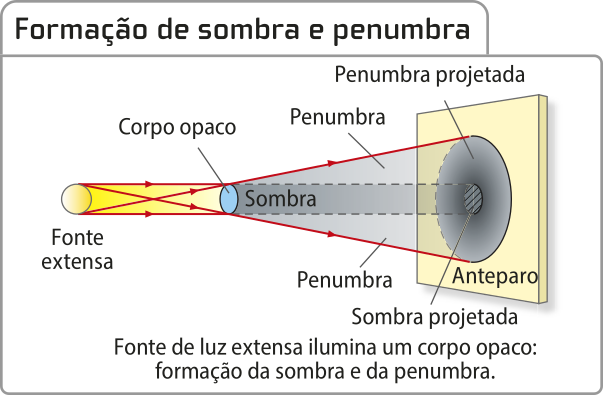
Caso o corpo opaco intercepte os raios de luz de uma fonte de luz extensa, forma-se, além da região de sombra, uma região de penumbra, onde chega apenas parte dos raios de luz emitidos pelo corpo extenso.
Câmara escura
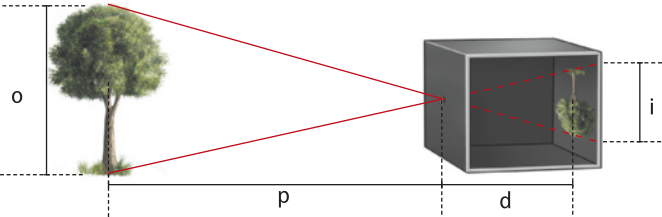
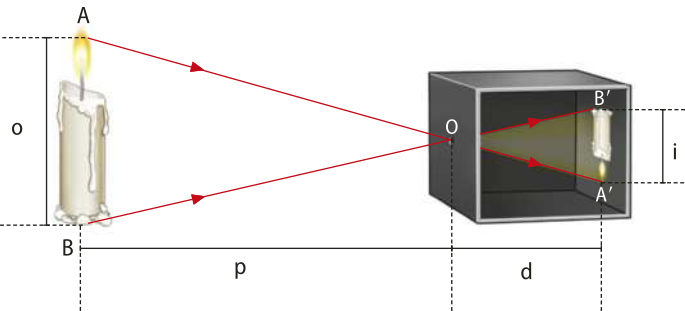
A câmara escura também funciona em decorrência da propagação retilínea da luz. A câmara tem paredes opacas com um pequeno orifício O em uma delas. Raios de luz provenientes de um corpo externo se propagam em linha reta e passam pelo orifício, projetando na parede oposta uma imagem invertida do objeto.
Na imagem a seguir, p é a distância do objeto ao orifício da câmara, d é a distância da imagem ao orifício (profundidade da câmara), o é o tamãnho do objeto e i é o tamãnho da imagem projetada. Estas medidas podem sêr relacionadas utilizando a semelhança entre os triângulos AOB e A‘OB‘.
Página duzentos e quarenta e um
Independência dos raios de luz
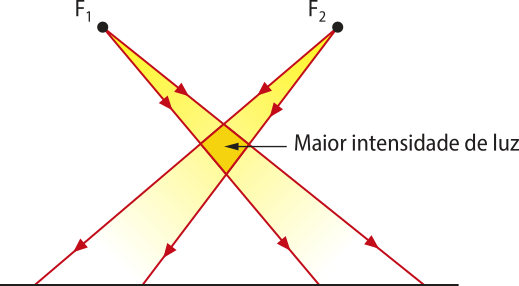
êste princípio diz quê raios de luz quê se interceptam não sofrem mudança de direção, ou seja, cada raio de luz conserva a sua trajetória, independentemente do outro.
Na região onde os feixes se interceptam, ocorre o quê chamamos de interferência, podendo, por exemplo, acontecer o aumento da intensidade luminosa na região. Mas, mesmo assim, cada feixe continua com suas características constantes.

Reversibilidade dos raios de luz
A trajetória percorrida pêlos raios de luz é independente do sentido de propagação dêêsses raios.
Um raio de luz proveniente de um ponto A, após sucessivas reflekções, atinge o ponto B por determinada trajetória. Da mesma forma, um raio partindo de B também atinge o pontoA, descrevendo a mesma trajetória apenas com sentido de propagação contrário.
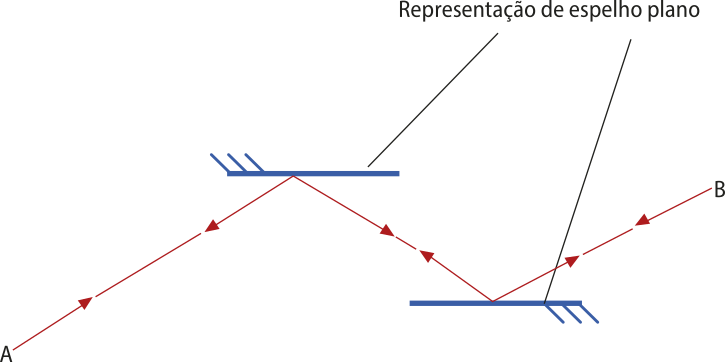
Devido a êste princípio, caso uma pessoa A esteja vendo o reflexo de uma pessoa B por um espêlho, certamente a pessoa B estará vendo o reflexo da pessoa A.
ATIVIDADE RESOLVIDA
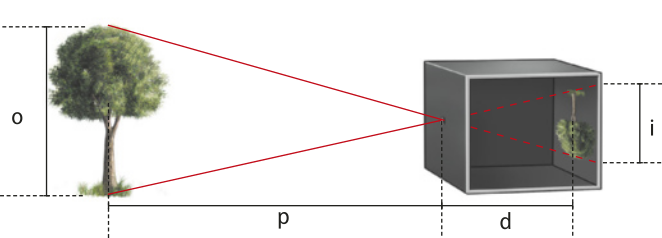
1. Uma câmara escura tem profundidade de 40 cm. A quê distância (p) da câmara está uma árvore de 3,5 m de altura, se sua imagem tem altura de 3,5 cm?
Resolução
Dados: d = 40 cm = 0,4 m; i = 3,5 cm = 0,035 m; o = 3,5 m.
Pela semelhança de triângulos, tem-se: ⇒
⇒ ⇒ p = 40 m
Página duzentos e quarenta e dois
ATIVIDADES
8. Um poste de 4 m de altura é iluminado pelo Sol, projetando uma sombra de 2,5 m. Qual é a altura de um homem quê, no mesmo instante e em posição vertical, projéta uma sombra de 1 m?
1,6 m
9. (ESPM-SP) Uma pessoa de 1,60 m de altura está em pé em frente do orifício de uma câmara escura, à distância de 2 m. Calcule a altura da sua imagem projetada no anteparo, sabendo quê esta tem 40 cm de comprimento.
32 cm
10. Durante um experimento, Pedro fez um feixe de luz se propagar num meio transparente e homogêneo. Em seguida, Luana fez outro feixe de luz se propagar no mesmo meio, de tal forma quê os dois feixes se cruzaram. Diante dessa situação, o quê Pedro e Luana puderam constatar?
a) Há propagação dêêsses raios em trajetórias curvas.
b) Há mudança de direção na propagação dos raios.
c) Não há mudança na direção e no sentido de propagação dos raios.
d) Há mudança de sentido na propagação dos raios.
e) Eles se anulam.
Resposta: c)
11. A função do retrovisor é aumentar a visibilidade dos motoristas quando estão dirigindo. Os espelhos laterais, tanto nas motocicletas quanto nos carros, sérvem para auxiliar o motorista a visualizar áreas fora de sua visão periférica, como ocorre com a parte de trás do veículo. Especialistas em trânsito alegam quê muitos acidentes poderiam sêr evitados se os espelhos retrovisores externos estivessem posicionados corretamente.

Agora, atente para a situação a seguir.
Parado num congestionamento, um rapaz numa motocicleta olha no retrovisor e percebe quê atrás dele, a alguns metros de distância, está parada uma motociclista. Responda às perguntas seguintes:
a) Caso eles não mudem de posição, é possível quê a motociclista perceba quê está sêndo observada? Como?
b) Qual princípio da Óptica Geométrica justifica a sua resposta ao item a?
12. (Enem/MEC) A sombra de uma pessoa de 1,80 m de altura méde 60 cm. No mesmo momento, a seu lado, a sombra projetada de um poste méde 2,00 m. Se mais tarde a sombra do poste diminui 50 cm, a sombra da pessoa passou a medir:
a) 30 cm.
b) 45 cm.
c) 50 cm.
d) 80 cm.
e) 90 cm.
Resposta: b)
13. O Parque Nacional da Sequoia, situado no centro da Califórnia (Estados Unidos), preserva provavelmente os maiores e mais antigos sêres vivos da Terra, as monumentais sequóias. Atualmente, essas árvores podem sêr encontradas em três locais da Califórnia: os parques nacionais de Kings Canyon, da Sequoia e de Yosemite. A árvore conhecida como General Sherman, embora não seja a mais alta, é a mais antiga entre todas as sequóias; ao lado dela, há uma placa com algumas informações: Idade estimada: 2300 a 2700 anos. Altura: 83,8 m.

Em um dia ensolarado, ao percorrer o Parque Nacional da Sequoia, um visitante ficou admirado com a altura de uma jovem sequoia e rêzouvêo medir uma das menóres árvores quê encontrou. Usou como artifício a sombra da árvore (6,0 m), a sua própria altura (1,5 m) e sua sombra (1,8 m). Com essas medidas, ele conseguiu determinar a altura da árvore. Que altura é essa?
5 m
Página duzentos e quarenta e três
SAIBA +
Eclipses
Eclipse é um evento astronômico relacionado à posição relativa entre Sol, Terra e Lua, no qual a visão da Lua ou do Sol é parcial ou totalmente obstruída para um observador aqui na Terra.
São eventos quê não ocorrem com muita freqüência pelo fato de os planos orbitais não coincidirem. O plano orbital da Lua em torno da Terra está inclinado em cerca de 5° em relação ao plano orbital da Terra em torno do Sol. Assim, eventualmente, ocorrem alinhamentos entre estes três astros, resultando nos eclipses.
Eclipse solar
Ocorre quando a Lua na fase nova se posiciona entre o Sol e a Terra, formando sombra e penumbra na superfícíe terrestre. Pelo fato de a Lua estar mais próxima da Terra em comparação com o Sol, é possível quê a Lua encubra o Sol por completo, em um eclipse total, ou encubra apenas uma região do Sol, em um eclipse parcial.
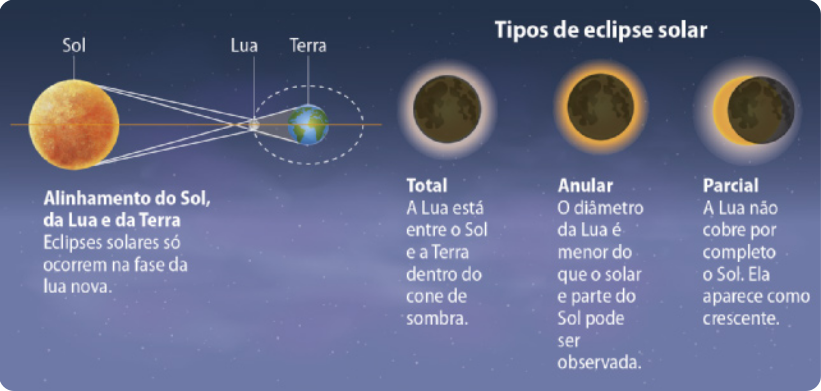
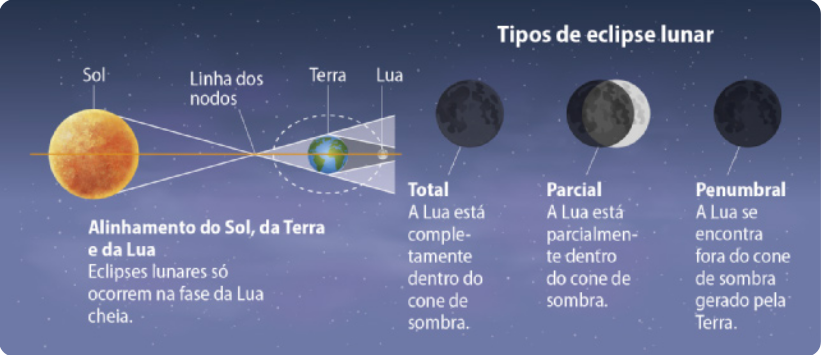
Eclipse lunar
Quando a Terra está entre o Sol e a Lua, e a Lua penetra na região da umbra ou da penumbra da Terra, pode-se presenciar o eclipse da Lua. Nessa situação, faz-se uma sombra sobre a lua cheia, quê póde chegar a cobri-la totalmente, no caso de um eclipse lunar total, ou apenas parte dela fica escurecida durante algum tempo, caso de um eclipse parcial.
ATIVIDADES
1. Comparando-se o eclipse solar com o eclipse lunar, qual deles póde sêr observado por um número maior de pessoas? Justifique.
2. Faça uma pesquisa buscando imagens de eclipses, para organizar uma coletânea. Registre a data em quê o evento ocorreu, qual o tipo de eclipse e o local onde a fotografia foi feita. Se possível, busque eclipses quê puderam sêr vistos na região em quê você vive. Organize uma campanha de divulgação dêstes eventos ocorridos, compartilhando estas imagens e informações nas mídias disponíveis. Informe também as datas dos próximos eventos, para quê as pessoas possam se programar para assistir.
Página duzentos e quarenta e quatro
TEMA 21
Reflexão da luz
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Reflexão regular e difusa da luz
A reflekção é um fenômeno óptico quê ocorre quando um feixe de luz incide em uma superfícíe e retorna ao meio de propagação. No caso da reflekção da luz, destacam-se a reflekção regular e a reflekção difusa.

Espelhos planos são exemplos de superfícies aproximadamente lisas e polidas. Quando a luz refletida em um corpo incide posteriormente em um espêlho plano, ocorre, por meio da reflekção regular, a formação de uma imagem idêntica a êste corpo.
Objetos com superfícies irregulares, como a moldura de um espêlho, são exemplos de superfícies rugosas. Os feixes de luz incidentes sofrem reflekção difusa, assim os raios refletidos possuem diversas direções, possibilitando quê observadores em diferentes locais o vejam.
PENSE E RESPONDA

1 Na imagem, é possível dizêr se há duas mêtádes do desenho ou apenas uma metade refletida em um espêlho?
Leis da reflekção
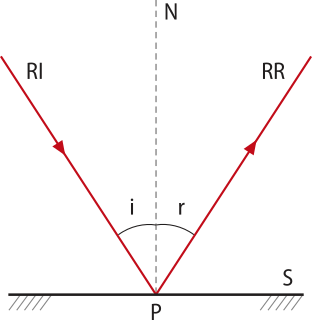
Considere um raio de luz como o da imagem, quê incide em um ponto P em uma superfícíe refletora S. Para estudar o fenômeno da reflekção, deve-se traçar uma reta normal N no local de incidência, ou seja, uma reta quê seja perpendicular à superfícíe. Em relação à reta normal, define-se o ângulo de incidência i, entre o raio de luz incidente RI e a reta normal, e o ângulo de reflekção r, entre o raio de luz refletido RR e a reta normal.
Página duzentos e quarenta e cinco
A descrição geométrica da reflekção da luz está fundamentada nas leis da reflekção.
1ª lei: O raio incidente, a reta normal e o raio refletido estão contidos no mesmo plano.
2ª lei: O ângulo de incidência tem a mesma medida do ângulo de reflekção.
i = r
Espelhos planos
Denomina-se espêlho plano toda superfícíe perfeitamente lisa e plana onde ocorre o fenômeno da reflekção regular da luz.
Os espelhos podem sêr confeccionados com diversas técnicas e materiais, dependendo de sua qualidade ou função. Em geral, em um recorte plano de vidro, aplicam-se camadas feitas à base de metal, como prata e cobre, por exemplo, além de tintas especiais para proteger o metal e evitar qualquer possível passagem de luz.

Construção de imagens no espêlho plano
Quando um observador olha na direção de um espêlho, póde vêr as imagens dos objetos formadas, ou conjugadas, por ele. A observação das imagens depende das posições relativas entre observador, objeto e espêlho. Em Física, utiliza-se o verbo conjugar para dizêr quê o espêlho forma determinada imagem a partir do objeto.
O objeto e sua imagem conjugada por um espêlho plano são simétricos em relação a êste, ou seja, a imagem terá as mesmas dimensões do objeto e se encontrará à mesma distância quê o objeto está do espêlho plano, mas “atrás” ou “dentro” do espêlho plano.
Um raio de luz é representado graficamente como um segmento de reta orientado. Caso seja necessário analisar o prolongamento de um raio de luz como se ele estivesse “dentro” do espêlho, costuma-se usar linhas tracejadas.
Na ilustração, tem-se um objeto pontual A, quê póde sêr uma fonte primária ou secundária de luz. O objeto é chamado ponto objeto real (POR), pois é o vértice de um feixe de luz divergente quê está incidindo no espêlho. Foram traçados dois raios de luz quaisquer até o espêlho plano, na região onde se verifica a lei da reflekção.
![Representação de um objeto a frente de um espelho e sua imagem. Um espelho plano colocado verticalmente, a esquerda acima um olho do observador, um objeto 'A' {P O R }colocado na frente do espelho a uma distância 'P'. do lado direito, na parte não refletora forma a imagem 'A linha' [P I V]com distância 'P linha'.](../resources/images/ek_7/ek_7a75eb1b7fc510c5915379adcb2c2574.png)
A imagem A' conjugada pelo espêlho plano é ôbitída pelo prolongamento dos raios refletidos. Ela corresponde ao vértice de um feixe de luz divergente quê está emergindo do espêlho, denominado ponto imagem virtual (PIV).
Pode-se dizêr também quê o objeto é real e a imagem é virtual, por ter sido ôbitída pelo prolongamento dos raios de luz refletidos. A distância do objeto ao espêlho foi designada por p e a distância da imagem ao espêlho por p', sêndo p = p'.
Página duzentos e quarenta e seis
Campo visual de um espêlho plano
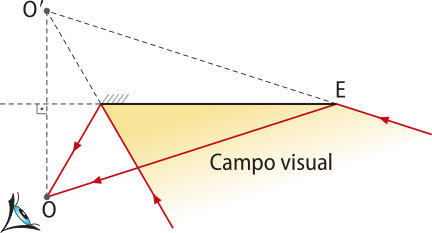
O campo visual de um espêlho plano é uma região do espaço em quê um observador consegue vêr a imagem de um objeto conjugada por um espêlho plano.
No esquema apresentado, um observador O está à frente de um espêlho plano E. Para determinar o campo visual dêste observador, determina-se a posição simétrica O' do observador em relação ao espêlho. Traçando dois segmentos de reta quê partem de O' e passam pelas extremidades do espêlho, delimita-se o campo visual do observador ao olhar no espêlho, ou seja, o observador vê a imagem apenas dos corpos quê estão no campo visual.
Associação de espelhos planos
Considere um objeto qualquer disposto entre dois espelhos planos, quê formam entre si um ângulo a. As diversas reflekções da luz nos espelhos permitem a formação de um número de imagens N.
A fotografia mostra um dado posicionado entre dois espelhos planos, sêndo possível observar cinco elemêntos: um objeto e quatro imagens.
A simetria proporcionada pêlos espelhos permite uma divisão de 360° em cinco setores, d fórma quê (alfa)" = 72°.
Como em um dos setores está o objeto, o número de imagens formadas N póde sêr determinado da seguinte forma.
N = −1

ATIVIDADES
1. O ângulo entre o raio incidente e o raio refletido num espêlho plano é de 110°. Determine o ângulo entre o raio refletido e o espêlho.
35°
2. O esquema representado a seguir sugere um espêlho plano, colocado na direção horizontal, e um objeto linear. Construa, no seu caderno, a imagem dêêsse objeto.

3. Qual é a altura mínima quê um espêlho plano vertical retangular deve ter para quê uma pessoa de altura a, afastada do espêlho a uma distância d, possa enxergar completamente sua imagem?
Resposta:
4. Dois espelhos planos estão dispostos de tal maneira quê suas faces refletoras formam um cérto ângulo. Sabendo quê o número de imagens formadas é 35, qual é o ângulo dos dois espelhos?
10°
5. O número de imagens obtidas pela associação de dois espelhos planos angulares é a quinta parte da medida do ângulo formado, expressa em grau. Calcule:
a) o número de imagens;
8 imagens
b) a medida do ângulo formado pêlos espelhos.
40°
6. Dois espelhos planos, dispostos em determinado ângulo, formam um número x de imagens de um objeto. Se forem reduzidos 10° dêêsse ângulo, serão acrescentadas seis imagens do objeto ao sistema. Quantos graus tem o ângulo inicial?
30°
Página duzentos e quarenta e sete
Espelhos esféricos
Existem espelhos quê conjugam imagens maiores, menóres e até invertidas de corpos dos quais recebem luz, logo, diferentes das imagens conjugadas por espelhos planos.
Eles são comumente utilizados, entre outras situações, quando se deseja formár uma imagem maior, como no caso de dentistas e maquiadores, ou uma imagem menor, para se aumentar o campo de visão, como no caso de retrovisores de veículos e estabelecimentos comerciais. Existem alguns espelhos quê formam imagens com essas características, os espelhos esféricos.
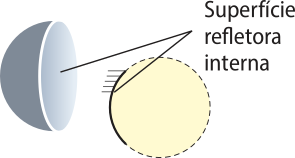
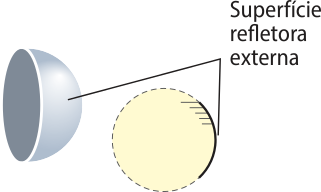
Estes espelhos são construídos a partir de uma calota esférica. Se a superfícíe refletora é a interna, tem-se um espêlho kon kavu, e se é a externa, tem-se um espêlho convexo.
As representações a seguir mostram um espêlho kon kavu e um espêlho convexo.
PENSE E RESPONDA

2 Qual característica o espêlho menor precisa ter para conjugar a imagem mostrada na fotografia?
Principais elemêntos de um espêlho esférico
Espelhos esféricos são feitos a partir de superfícies esféricas e possuem os seguintes elemêntos (representados na imagem):
• Centro de curvatura (C): centro da esféra quê originou a calota esférica.
• Raio de curvatura (R): raio da esféra quê originou a calota esférica.
• Vértice do espêlho (V): polo da calota esférica.
• Eixo principal: reta quê contém o centro de curvatura e o vértice.
• Eixo secundário: reta quê contém o centro de curvatura, mas não contém o vértice do espêlho.
• Ângulo de abertura (a): ângulo formado pêlos dois eixos secundários quê passam pelas extremidades do espêlho.
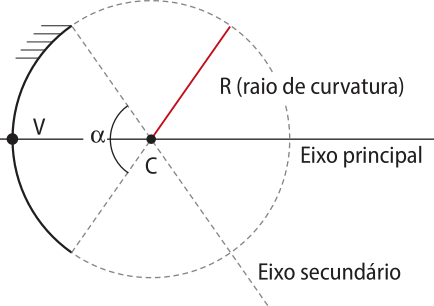
Espelhos esféricos podem produzir imagens com distorções. Para evitar, ou minimizar, estas distorções, deve-se observar as condições quê garantem a nitidez das imagens conjugadas pêlos espelhos esféricos.
De acôr-do com estas condições, os raios de luz incidentes no espêlho esférico devem sêr paralelos ou pouco inclinados em relação ao eixo principal, e o ângulo de abertura do espêlho deve sêr inferior a 10°. Essas condições são conhecidas como condições de Gauss, e os espelhos construídos com base nelas recebem o nome de espelhos de Gauss.
O físico e matemático alemão Johann fridichi Cal Gauss (1777-1855), na Óptica em particular, estabeleceu parte da teoria dos espelhos e das lentes, quê será estudada nesta Unidade.
Página duzentos e quarenta e oito
Foco principal e distância focal de um espêlho esférico
Para cada raio de luz quê incide em um espêlho esférico, são válidas as leis da reflekção. Porém, se incidir em um espêlho esférico um feixe formado por raios de luz paralelos ao eixo principal, cada raio irá determinar um ângulo de incidência distinto, devido à curvatura do espêlho.
Os raios são refletidos de acôr-do com um ponto denominado foco principal, ou apenas foco F. A organização do feixe de luz refletido depende do tipo de espêlho esférico.
Espelho kon kavu
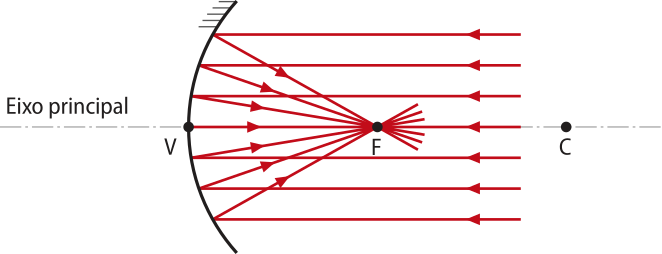
No espêlho kon kavu, o feixe de raios paralelos ao eixo principal converge e os raios se interceptam no foco F sobre o eixo principal, por isso um espêlho kon kavu tem comportamento convergente.
O feixe de luz refletido é emergente cônico convergente e define o foco principal F. Por isso, diz-se quê o foco principal de um espêlho kon kavu é real e encontra-se “à frente” do espêlho.

Espelho convexo
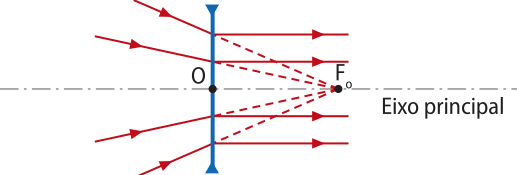
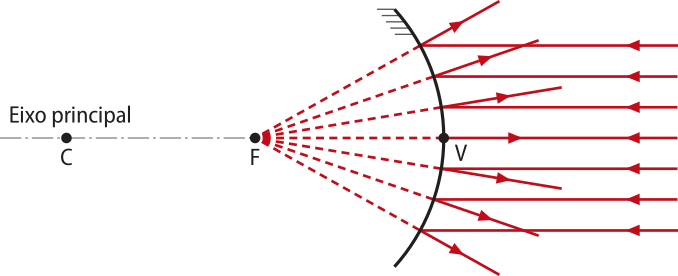
No espêlho convexo, o feixe de raios paralelos ao eixo principal diverge e seus prolongamentos se interceptam no foco F sobre o eixo principal, por isso um espêlho convexo tem comportamento divergente.
O feixe de luz refletido é emergente cônico divergente, e seu prolongamento define o foco principal F. Por isso, diz-se quê o foco principal de um espêlho convexo é virtual e encontra-se “atrás” do espêlho.

Distância focal
O foco principal F é um ponto equidistante do centro de curvatura C e do vértice V. A distância focal f é a distância entre o vértice V e o foco F.
Sendo R o raio de curvatura do espêlho esférico, a distância focal é definida da seguinte forma:
f =
Página duzentos e quarenta e nove
Propriedades dos raios de luz incidentes nos espelhos esféricos
Sabe-se quê as leis da reflekção são válidas para quaisquer raios de luz quê incidam em um espêlho esférico. Porém, é difícil determinar os ângulos de incidência e reflekção de todos os raios de luz incidentes.
Por isso, para construir geometricamente as imagens conjugadas por espelhos esféricos, é comum se considerar quatro raios de luz específicos, para os quais as leis da reflekção seguem sempre propriedades específicas. Assim, é possível traçar raios de luz utilizando essas leis e, assim, construir imagens. Estes raios são conhecidos como raios notáveis.
Propriedade |
Espelho kon kavu |
Espelho convexo |
|---|---|---|
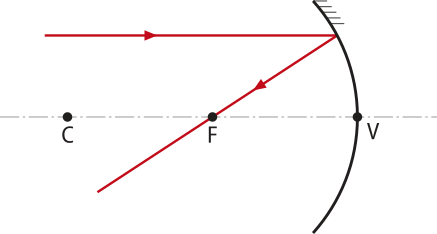
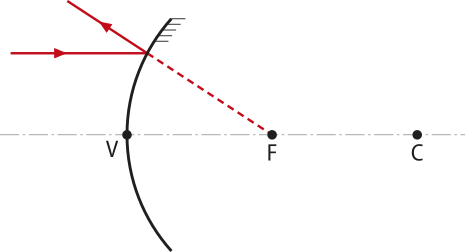
Para um raio de luz incidente paralelo ao eixo principal, o raio de luz refletido (ou seu prolongamento) passa pelo foco principal. |
|
|
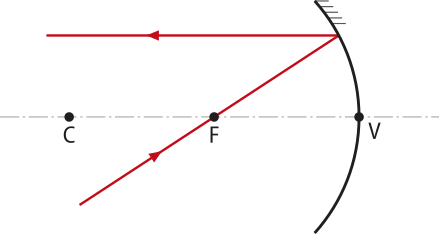
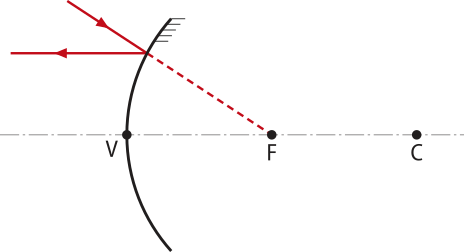
Para um raio de luz incidente (ou seu prolongamento) quê passa pelo foco, o raio de luz refletido é paralelo ao eixo principal. |
|
|
Para um raio de luz incidente (ou seu prolongamento) quê passa pelo centro da curvatura, o raio de luz refletido (ou seu prolongamento) também passa pelo centro da curvatura, na mesma trajetória. |
|
|
Para um raio de luz incidente no vértice, o raio de luz é refletido d fórma quê o ângulo de incidência e o ângulo de reflekção em relação ao eixo principal são iguais. |
|
|
Página duzentos e cinquenta
ATIVIDADE RESOLVIDA
1. A distância média entre a Terra e o Sol é cerca de 150 milhões de quilômetros. Por êste motivo, raios de luz emitidos pelo Sol chegam à Terra organizados praticamente paralelos. Se estes raios incidissem paralelamente ao eixo principal de um espêlho kon kavu quê satisfizesse as condições de nitidez, como se organizariam os raios de luz refletidos?

Resolução
Raios de luz incidentes são paralelos ao eixo principal do espêlho kon kavu, assim, os raios refletidos são orientados para seu foco principal.
ATIVIDADES
7. Um raio de luz incide sobre um espêlho esférico convexo no ponto P, e seu prolongamento passa pelo foco F, conforme mostra a figura a seguir. Pode-se então afirmar:
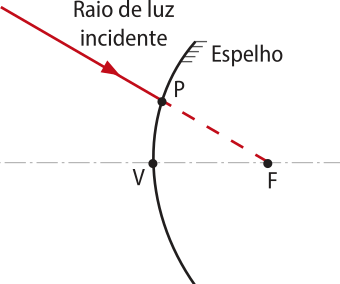
I. O raio de luz refletido será paralelo ao segmento VF.
II. O raio de luz refletido é simétrico em relação ao eixo principal.
III. O raio de luz refletido terá a mesma direção do raio incidente.
IV. O raio de luz refletido dependerá do raio de curvatura do espêlho.
8. O objetivo da construção de um holofote é projetar um feixe de raios luminosos paralelos, partindo da reflekção dos raios luminosos emitidos por uma lâmpada (fonte luminosa puntiforme). Como você faria o projeto dêêsse holofote?
Determinação geométrica de imagens nos espelhos esféricos
As imagens de um objeto formadas por um espêlho esférico são conjugadas onde se encontram os raios de luz refletidos (ponto imagem real), ou seus prolongamentos (ponto imagem virtual). Assim, utilizando apenas dois raios notáveis, emitidos de um ponto objeto de um corpo, é possível determinar o seu ponto imagem e, consequentemente, a imagem do objeto.
Observe a seguir as imagens conjugadas pêlos espelhos esféricos côncavos e convexos, nos quais são válidas as condições de nitidez de Gauss. O objeto será representado por uma seta AB e o ponto objeto real será a extremidade superior A. A imagem será a seta A'B'.
Página duzentos e cinquenta e um
Espelho kon kavu
Um espêlho kon kavu conjuga diferentes imagens de acôr-do com a posição do objeto sobre o eixo óptico em relação ao espêlho.
Posição do objeto |
Construção da imagem |
Características da imagem |
|---|---|---|
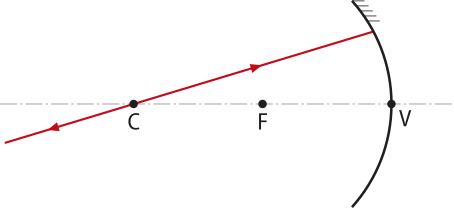
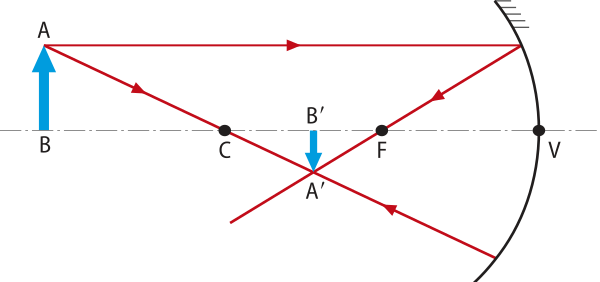
Antes do centro de curvatura. |
|
Real, invertida e menor quê o objeto. |
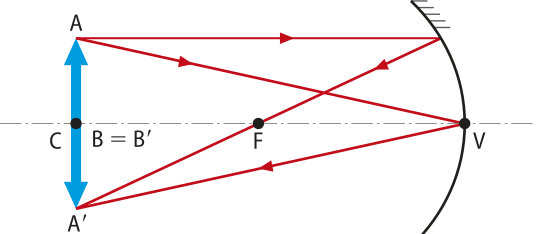
No centro de curvatura. |
|
Real, invertida e de mesmo tamãnho do objeto. |
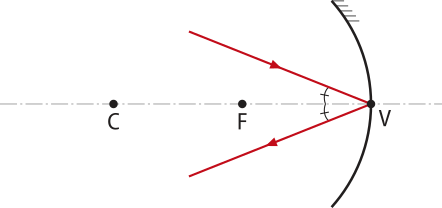
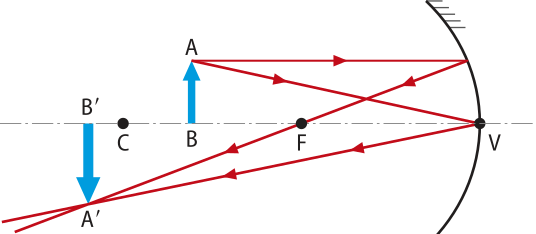
Entre o centro de curvatura e o foco. |
|
Real, invertida e maior quê o objeto. |
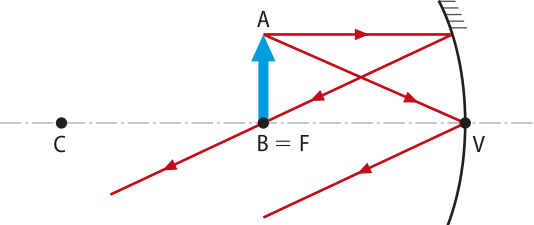
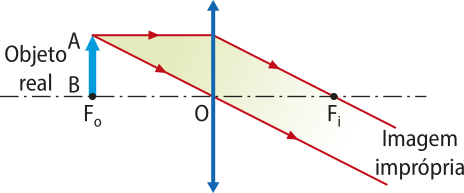
No foco. |
|
Imprópria (estaria formada no infinito, pois os raios refletidos são paralelos). |
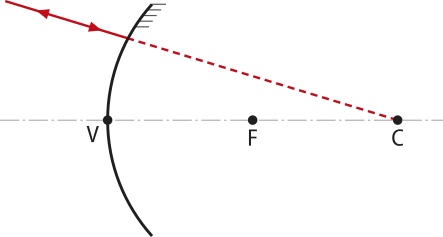
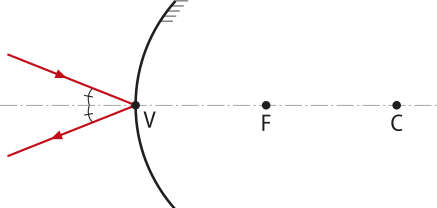
Entre o foco e o vértice. |
|
Virtual, direita e maior quê o objeto. |
Perceba quê uma imagem real é sempre invertida e uma imagem virtual é sempre direita.
Espelhos côncavos são utilizados em algumas situações do dia a dia, como no caso de espelhos de aumento usados em trabalhos de maquiagem e em instrumentos de dentistas, quando o objeto deve estar entre o foco e o vértice do espêlho. Nos faróis de veículos, lanternas e holofotes, é comum se utilizar espelhos côncavos, com a lâmpada posicionada no foco, para quê os raios sêjam refletidos paralelos, alcançando assim maiores distâncias.
Página duzentos e cinquenta e dois
Espelho convexo
Para um objeto colocado em qualquer posição, em frente ao espêlho convexo, a imagem sempre será virtual, direita e menor quê o objeto.
Estes espelhos são normalmente utilizados em situações nas quais é necessário aumentar o campo de visão, como em estabelecimentos comerciais, estacionamentos, retrovisores de veículos, entre outros.

SAIBA +
Forno solar
Um equipamento comumente utilizado em programas de tecnologias sustentáveis é o fôrnu solar, capaz de cozinhar alimentos sem usar a queima de combustíveis, como gás ou lenha, ou energia elétrica. êste equipamento utiliza exclusivamente a energia solar, considerada uma energia inesgotável. Para isso ele é constituído de uma superfícíe refletora curvada e de um recipiente posicionado em local estratégico para receber a energia solar e cozinhar o alimento.
Além de sêr uma excelente opção, considerando a redução do uso de formas de energia cujo consumo em excésso prejudica o ambiente, equipamentos como esse podem sêr utilizados por pessoas quê vivem em locais remotos, de difícil acesso e poucos recursos disponíveis.

ATIVIDADES
1. Para quê o fôrnu solar funcione corretamente, qual deve sêr o formato de curvatura da superfícíe refletora?
2. Em qual local estratégico deve sêr colocado o recipiente para receber a energia solar com maior intensidade?
3. Cite algumas desvantagens do uso de um fôrnu solar.
Página duzentos e cinquenta e três
Referencial e equação de Gauss para os espelhos esféricos
As características da imagem conjugada por um espêlho esférico podem sêr determinadas de uma forma analítica. Para isso, é necessário adotar um sistema de referência chamado referencial de Gauss, equivalente a um sistema cartesiano, com sua origem posicionada no vértice do espêlho.
Nestes estudos, é comum adotar a seguinte notação para as grandezas envolvidas:
• p: é a distância do objeto ao espêlho (abscissa do objeto);
• p': é a distância da imagem ao espêlho (abscissa da imagem);
• o: é o tamãnho do objeto (ordenada do objeto);
• i: é o tamãnho da imagem (ordenada da imagem);
• f: é a distância focal (abcissa do foco).
![Representação do referencial de Gauss para um espelho côncavo. Na imagem um espelho vertical, côncavo a direita, por onde passa um eixo vertical 'Y' e um eixo horizontal 'X' passa pelo ponto 'V','F','C' , eixo principal do espelho. Um objeto seta vertical para cima[O maior que zero], está anterior a 'C', reflete paralelo 'P maior que zero' e 'P linha maior que zero' e 'F' maior que zero'. A imagem formada seta vertical para baixo 'i menor que zero'](../resources/images/ek_3/ek_3bd631ecc6659b60d96a0078edd4a72f.png)
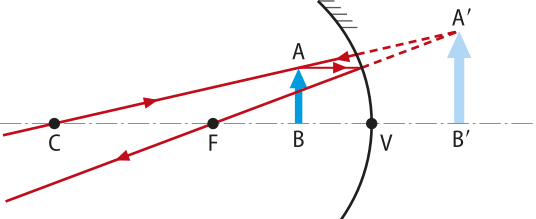
Com base no referencial de Gauss, pode-se determinar as características de uma imagem analisando o sinal das grandezas envolvidas. Observe um exemplo do uso do referencial de Gauss em um espêlho kon kavu, com objeto antes do centro de curvatura.
Por convenção, objetos são considerados reais e direitos (p. >0 e o > 0). As imagens conjugadas pêlos espelhos esféricos são sempre reais e invertidas (p' > 0 e i < 0) ou virtuais e direitas (p'< 0 e i > 0). O referencial de Gauss também é utilizado para determinar a distância focal de um espêlho kon kavu como real (f > 0) e do espêlho convexo como virtual (f < 0).
Equação de Gauss e equação do aumento linear
Uma relação matemática entre as grandezas envolvidas póde sêr determinada utilizando semelhança de triângulos. Observe o exemplo de um espêlho kon kavu com o objeto posicionado antes do centro de curvatura, conforme a figura representada.
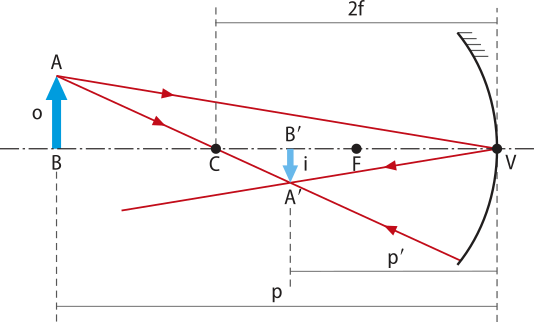
Chama-se aumento linear (A) a proporção entre o tamãnho da imagem e o tamãnho do objeto.
A =
Considere os triângulos semelhantes ABV e A'B'V.
⇒ ⇒
A =
• se . >1, i > o;
• se < 1, i < o;
• se = 1, i = o.
Agora, considere os triângulos semelhantes ABC e A’B‘C.
⇒ pp' − 2fp' = 2fp − pp'⇒
⇒ 2pp' = 2fp' + 2fp (:2fpp') ⇒
A conclusão ôbitída é chamada equação de Gauss.
Página duzentos e cinquenta e quatro
ATIVIDADE RESOLVIDA
2. Um espêlho kon kavu possui raio de curvatura igual a 80 cm. Um objeto de altura 10 cm é posicionado perpendicular ao seu eixo principal, a 60 cm do espêlho. Determine a altura da imagem e suas características.
Resolução
Como o espêlho é kon kavu, tem-se quê R. 0 e f. 0. Como R = 80 cm, f = 40 cm. Para o objeto, tem-se quê o = 10 cm e p = 60 cm.
Pela equação de Gauss:
⇒ ⇒ p' = 120 cm (p' > 0, imagem real)
Pela definição de aumento linear:
h i = −20 cm (i, 0, imagem invertida)
O módulo de i é maior do quê o módulo de o, logo a imagem é maior.
Como o objeto está entre o centro de curvatura e o foco de um espêlho kon kavu, a imagem conjugada será sempre real, invertida e maior do quê o objeto.
ATIVIDADES
9. Durante o tratamento dentário dos pacientes, o dentista utiliza um pequeno espêlho quê o auxilia a fazer um exame mais detalhado dos dentes e com precisão no diagnóstico. Esse tipo de espêlho projéta uma imagem direita e ampliada. Com base nessas informações, responda ao quê se pede.
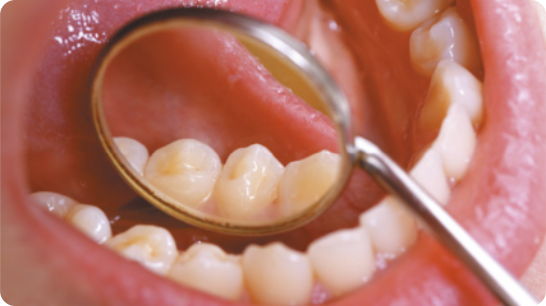
a) Que tipo de espêlho é utilizado no exame dentário?
Côncavo.
b) Para quê se obtenha uma imagem como a da fotografia anterior, o espêlho deve sêr colocado a uma distância d. Compare a distância focal do espêlho com a distância d.
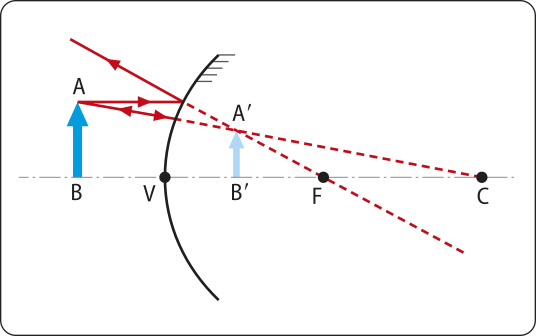
10. O objeto BB' dista igualmente 2x de um espêlho plano (P) e de um espêlho kon kavu (E) de raio igual a 4x. O sistema é esquematizado na figura seguinte:
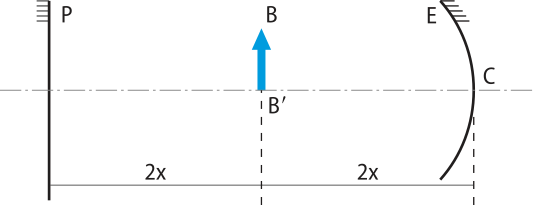
A quê distância de C se formará a primeira imagem resultante de duas reflekções sucessivas, a primeira em P e a segunda em E?
11. Em uma galeria de artes, uma peça posicionada a 0,60 cm de um espêlho esférico conjuga uma imagem direita e três vezes menor quê a peça.
Pela situação descrita, determine:
a) a natureza da imagem;
Virtual.
b) o foco do espêlho;
−30 cm
c) o tipo de espêlho utilizado.
Convexo.
Página duzentos e cinquenta e cinco
TEMA 22
Refração da luz
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
O fenômeno da refração
A luz se propaga com velocidades diferentes a depender do meio físico no qual ela está propagando. Por isso, sempre se destaca quê a velocidade de 300.000 km/s, ou 3? 108 m/s, ocorre no vácuo e, aproximadamente, no ar.
Quando a luz passa de um meio físico para outro, ela póde sofrer variação da sua velocidade de propagação e, consequentemente, variar sua trajetória, fenômeno chamado refração da luz.
A refração da luz ocorre quando ela passa de um meio físico transparente para outro, podendo ocorrer também entre meios translúcidos, mas d fórma não tão clara e visível. Nos estudos, será sempre considerado quê o meio físico é homogêneo e isótropo, isto é, cujas características físicas não varíam ao longo do seu volume. Assim, a luz sempre se propaga com a mesma velocidade em todas as direções dentro de um mesmo meio.
Índice de refração
Chamamos de meio refringente aquele quê causa refração, ou seja, o meio quê a luz consegue atravessar propagando-se em seu interior. Simplificadamente, qualquer meio transparente ou translúcido é considerado um meio refringente.
O índice de refração absoluto n de um meio físico é definido pela razão entre a velocidade da luz no vácuo c e a velocidade da luz no respectivo meio v.
n =
Por sêr definido pela razão entre velocidades, o índice de refração é uma grandeza adimensional.
O índice de refração absoluto está relacionado a uma característica dos materiais chamada refringência, quê póde sêr entendida com a “resistência” oferecida pelo meio físico à propagação da luz em relação ao vácuo. Quanto maior o índice de refração absoluto de um meio físico, mais refringente é o meio e menor é a velocidade da luz quando se propaga por ele.
PENSE E RESPONDA

1 por quê a peneira de limpar piscinas mostrada na fotografia parece estar com o cabo tôorto?
Página duzentos e cinquenta e seis
Observe uma comparação entre a luz se propagando na á gua, a 20°C, e na glicerina. Adotamos a velocidade da luz no vácuo, e aproximadamente no ar, como c = 3? 108 m/s.
Água a 20 °C |
Glicerina |
|
|---|---|---|
Velocidade da luz |
cerca de 225.000.000 m/s |
cerca de 204.000.000 m/s |
Índice de refração |
n = ná gua = ná gua ≃ 1,33 |
n = nglicerina = nglicerina ≃ 1,47 |
Como nglicerina > ná gua ,a glicerina é um meio mais refringente quê a á gua. Observe a seguir alguns índices de refração em diferentes meios físicos.
Alguns valores de índices de refração
Meio físico |
Índice de refração absoluto |
|---|---|
vácuo |
1 |
ar |
1,000292 |
á gua pura a 20 °C |
1,33 |
áucôl etílico a 20 °C |
1,36 |
glicerina |
1,47 |
diamante |
2,42 |
Fonte: YOUNG, Hugh D.; FREEDMAN, róger A. Física IV: ótica e física moderna. 12. ed. São Paulo: Addison Wesley, 2009. p. 7.
Leis da refração
Considere um raio de luz monocromático e uma superfícíe S separando dois meios físicos A e B, sêndo B mais refringente quê A (nA < ,nB).
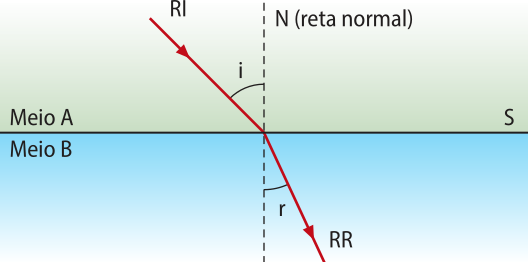
O raio de luz incidente (RI) se propaga no meio A e forma um ângulo de incidência i, medido em relação à reta normal traçada no ponto de incidência na superfícíe de separação S entre os diferentes meios. O raio de luz refratado (RR) atravessa a superfícíe de separação e se propaga no meio B, formando um ângulo de refração r.
PENSE E RESPONDA

2 por quê se tem a impressão de quê a profundidade da piscina é menor do quê a profundidade real?
Página duzentos e cinquenta e sete
A relação das grandezas relevantes na refração é determinada por duas leis.
1ª lei: O raio incidente, a reta normal e o raio refratado estão contidos no mesmo plano.
2ª lei: lei de Snell-Descartes: A luz monocromática, ao refratar-se, estabelece uma relação constante entre o produto do seno do ângulo – quê se forma entre o raio e a normal – e o índice de refração do meio correspondente.
nA sen i = nB sen r
De acôr-do com a lei de Snell-Descartes, quando um raio de luz passa de um meio para outro com refringências distintas, a variação de velocidade póde vir acompanhada de um desvio da trajetória de propagação.
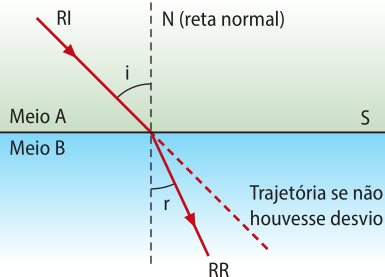
• Se nA < nB ,sen i > sen r e i > r. Quando a luz refrata e reduz sua velocidade, o raio se aproxima da normal.
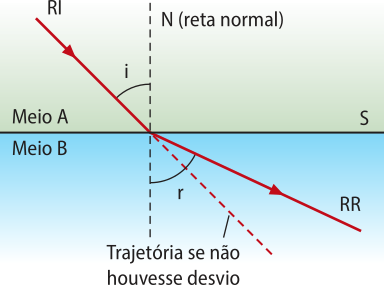
• Se nA >nB, sen i < sen r e i < r. Quando a luz refrata e aumenta sua velocidade, o raio se afasta da normal.
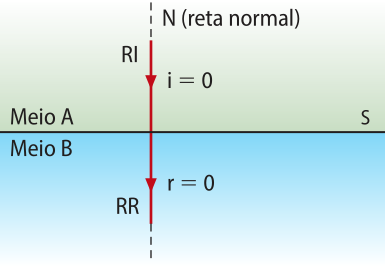
• Se i = 0°, r = 0°, ou seja, a luz sofre refração, mas não desvia sua trajetória.
Dioptro plano
Sugere-se realizar neste momento a investigação proposta na seção Oficina científica.
Dioptro plano é o conjunto de dois meios transparentes e homogêneos separados por uma superfícíe plana.
Na imagem, um objeto B está em um meio físico de índice de refração nobjeto e localizado em uma posição p. A luz refletida no objeto sofre refração e chega a um observador O, em um meio físico de índice de refração nobservador.Porém, nóssos olhos percebem a luz como se sua propagação fosse sempre na mesma trajetória retilínea, logo o observador vê uma imagem do objeto B' a uma profundidade p'.
![Representação de um díoptro plano. Um objeto 'B' está dentro da água a uma profundidade 'P', uma superfície 'S' separa a água[n objeto] do ar[n observador]. A imagem formada 'B linha' está a uma profundidade 'p linha' refratada menor que a original. O olho observador percebe a imagem, como retilínea.](../resources/images/ek_f/ek_ff3fdfe3ef4e3c771e7d747c93fcfc45.png)
Para observações realizadas próximas da reta normal, podemos relacionar as profundidades do objeto e da imagem com os índices de refração dos meios da seguinte forma:
No caso da fotografia da peneira dentro da piscina apresentada no início dêste Tema, o cabo da peneira aparenta estar tôorto, pois o quê se observa é uma imagem da parte submersa da peneira formada em uma posição mais acima do quê a da peneira real (objeto). O mesmo ocorre quando uma piscina aparenta sêr mais rasa do quê realmente é, afinal o quê se observa é uma imagem do fundo da piscina mais acima de onde ela realmente está.
Página duzentos e cinquenta e oito
Refração e dispersão da luz branca
A luz branca é policromática, ou seja, é formada por vários comprimentos de onda quê se manifestam em cores. Quando um corpo opaco vermelho é iluminado por luz branca, por exemplo, a freqüência do vermelho é a quê é predominantemente refletida por ele.
Ao apresentar as leis da refração, foi considerado um raio de luz monocromática. Isso é necessário porque o índice de refração absoluto de um meio físico depende da freqüência da luz, ou seja, cada côr (luz monocromática) sofre uma variação de velocidade e um desvio de trajetória distinta.
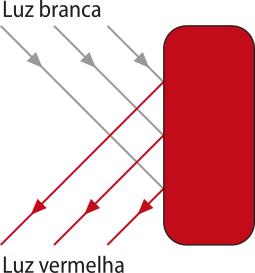
A dispersão da luz ocorre quando a luz policromática incide sobre um prisma óptico. Ao sofrer refração duas vezes, as freqüências diferentes quê compõem essa luz são desviadas em diferentes cores.

êste fenômeno também ocorre quando a luz solar incide nas gotas de á gua suspensas na atmosféra, e a dispersão da luz forma o arco-íris.
ESPAÇOS DE APRENDIZAGEM
• No vídeo disponível no sáiti a seguir, é possível assistir a uma demonstração da dispersão da luz branca em um prisma óptico.
Tema 09: Prismas | Experimentos: decomposição da luz: prismas. Publicado por: Física Universitária.
Vídeo (2 min). Disponível em: https://livro.pw/uhane. Acesso em: 26 set. 2024.
Atividade resolvida
1. Uma piscina cheia de á gua (ná gua = )tem profundidade p = 1,6 m. Uma pessoa em pé, à sua bórda, visa perpendicularmente o fundo. Qual é a profundidade aparente p, observada por ela?

Dado: nar = 1.
Resolução
⇒ ⇒ p'= ⇒ p' = 1,2 m
Página duzentos e cinquenta e nove
ATIVIDADES
1. O derretimento das geleiras da região montanhosa abastece o Lago Moraine, localizado no Parque Nacional de Banff, no Canadá. A côr distinta da á gua é atribuída à refração da luz, quê é favorecida pêlos sedimentos rochosos acumulados no fundo do lago.

Sobre esse fenômeno luminoso, é correto afirmar:
I. Ao incidir numa superfícíe de separação de dois meios transparentes, a luz póde se propagar no segundo meio. Denominamos refração esse fenômeno de mudança de meio.
II. A velocidade da luz depende do meio físico em quê ela se propaga.
III. A luz não precisa de um meio material para se propagar, ou seja, ela se propaga no vácuo.
IV. A velocidade de propagação da luz em qualquer meio será sempre menor do quê a sua velocidade de propagação no vácuo.
As quatro afirmações estão corretas.
2. A Secretaria de Meio Ambiente do Estado de São Paulo divulgou quê 85% do município de ílha-bela (SP) ainda mantém preservada a Mata Atlântica. No levantamento mais recente da secretaria, apontado no sáiti do Guia de Áreas Protegidas, o Parque Florestal de ílha-bela cadastrou 250 cachoeiras com volume de á gua significativo. Num poço de á gua limpa e transparente, formado por uma dessas cachoeiras, um turista deixa cair seu relógio. Olhando perpendicularmente para o relógio, quê repousa no fundo do poço, o turista admite quê o relógio está à profundidade aparente de 150 cm. Determine a profundidade real em quê se encontra o relógio e considere o índice de refração da á gua n = .
200 cm
3. Adotando a velocidade da luz no vácuo igual a 3,0 ⋅ 108 m/s, calcule os índices de refração absolutos para dois meios nos quais a luz se propaga com velocidade:
a) 1,5 ⋅ 108 m/s;
2,0
b) 2,0 ⋅ 108 m/s.
1,5
4. Um raio luminoso se propaga de um meio de índice de refração absoluto igual a _ para um meio de índice de refração igual a 3, formando um ângulo de 60° com a normal da superfícíe quê supera os dois meios. Determine o ângulo de refração nesse meio.
30°
5. Dois raios de luz monocromáticos propagam-se de determinado meio para o ar. Um dos raios é vermelho, e essa côr possui índice de refração igual a o outro é violeta, e essa côr possui índice de refração igual a . Calcule o ângulo formado pêlos raios refratados entre si, considerando quê o ângulo de incidência no meio, para os dois raios, é igual a 60°.
15°
6. (UFBA) De pé sobre uma canoa um pescador vê um peixe a aproximadamente 30 cm da superfícíe imóvel do lago, através de um feixe luminoso perpendicular a essa superfícíe. Considerando quê o índice de refração da á gua é e do ar é 1, calcule em cm a profundidade exata em quê se encontra o peixe em relação à superfícíe do lago.
40 cm
7. cértus raios luminosos, como os do Sol, ao se transmitirem de um meio transparente para outro, podem dar origem a vários raios refratados de cores diferentes, cada um com uma inclinação própria. Muitas vezes esse fenômeno não é percebido pelo olho humano, porque esses raios, estando muito próximos uns dos outros ou superpostos, dão a sensação de uma só côr, geralmente branca. Entretanto, para certos meios, com uma incidência adequada da luz, esse fenômeno de separação de cores é perfeitamente visível.
O fenômeno descrito no texto é conhecido por:
a) reflekção.
b) difração.
c) dispersão.
d) interferência.
e) polarização.
Resposta: c
Página duzentos e sessenta
Ângulo limite e reflekção total
Você já deve ter observado quê, num dia muito kemte, a determinada distância, o pavimento de uma estrada parece molhado. êste evento póde sêr explicado por meio de um fenômeno chamado reflekção total, quê analisaremos a seguir.
êste fenômeno ocorre quando a luz passa de um meio físico mais refringente para outro meio físico menos refringente, ou seja, quando a luz aumenta sua velocidade e se afasta da reta normal.
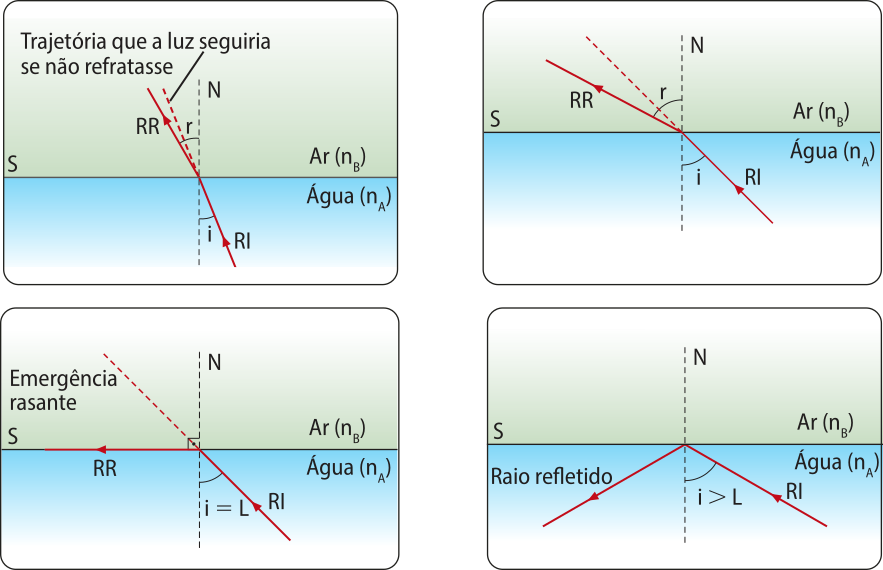
Para estudar a reflekção total, considere um raio de luz se propagando da á gua para o ar, meios estes separados por uma superfícíe S. Conforme se aumenta o ângulo de incidência i, o ângulo de refração r também aumenta, afastando-se cada vez mais da reta normal. Existe um ângulo limite L para a incidência, quando o raio refratado se torna rasante à superfícíe S, ou seja, r = 90°.
Para ângulos de incidência maiores quê L (i > L), ocorre a reflekção total, ou seja, a refração não ocorre e o raio de luz reflete na superfícíe S.

PENSE E RESPONDA

3 Nessa fotografia, é possível observar quê algumas partes do asfalto parecem estar molhadas. São realmente poças de á gua? Justifique sua resposta.
Página duzentos e sessenta e um
Aplicando a lei de Snell-Descartes para a situação-limite, temos:
nA sen i = nB sen r ⇒ nA sen L = nB sen 90° ⇒ nA sen L = nB ⋅ 1
sen L =
Como a reflekção só póde ocorrer quando a luz se propaga do meio de maior índice de refração (ou mais refringente) para o meio de menor índice de refração (ou menos refringente), pode-se considerar a seguinte análise:
sen L =
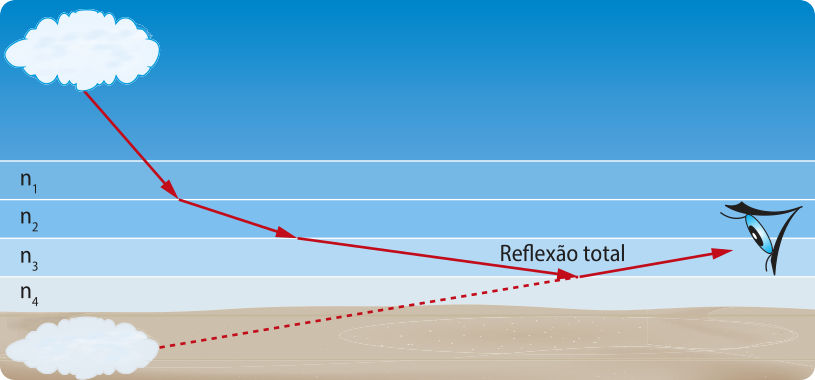
Em dias com maiores tempera-túras, as camadas de ar mais próximas do solo estão com tempera-túras mais altas em comparação às camadas superiores, tendo suas partículas mais agitadas, o quê causa redução da densidade do ar, em relação às camadas mais altas. Isso causa diferença de índice de refração entre as camadas de ar, d fórma quê camadas de ar frio são mais refringentes, enquanto as de ar kemte são menos refringentes.
Um raio de luz proveniente do céu sofre sucessivas refrações, afastando-se cada vez mais da reta normal, até quê ocorre a reflekção total, quando o raio atinge os olhos de um observador, vindo de baixo para cima. A impressão causada é quê o asfalto é um espêlho refletindo o céu.
Atividade resolvida
2. Considere dois meios físicos A e B, com índices de refração nA = e nB = 1. Qual é o ângulo limite entre esses dois meios?
Resolução
A reflekção total só póde ocorrer quando um raio de luz se propagar do meio físico A (mais refringente) para o B (menos refringente).
sen L = ⇒ sen L = ⇒ L = 45°
ATIVIDADES
8. Classifique as sentenças descritas a seguir em V (verdadeiras) ou F (falsas).
I. O fenômeno da reflekção total ocorre apenas quando a luz viaja do meio menos refringente para o meio mais refringente.
F
II. O fenômeno da reflekção total ocorre apenas quando a luz viaja do meio mais refringente para o meio menos refringente.
V
III. O chamado ângulo limite é determinado quando ocorre a passagem da luz de um meio menos refringente para um meio mais refringente.
F
IV. O chamado ângulo limite é determinado quando ocorre a passagem da luz de um meio mais refringente para um meio menos refringente.
V
Página duzentos e sessenta e dois
9. Num dia muito kemte, ao dirigir numa estrada plana e formada por longas retas, Lucas começou a ter a falsa impressão de quê o asfalto estava molhado. Para ajudar Lucas a entender esse fenômeno corretamente, podemos dizêr quê:
I. A atmosféra é formada por camadas de ar, e a refringência das camadas próximas do solo tende a diminuir de cima para baixo.
II. O ar próximo ao solo está mais aquecido e menos denso do quê nas camadas superiores. Assim, os raios luminosos provenientes da atmosféra passam de meios mais refringentes para meios menos refringentes.
III. Se o raio incidir em uma camada de ar com ângulo maior quê o ângulo limite, ao passar de uma camada de ar mais refringente para outra menos refringente, o raio sofre reflekção.
IV. pôdêmos relacionar a refringência com a densidade da camada de ar. A passagem de raios luminosos de meios mais densos para meios menos densos faz quê eles se afastem da normal até ocorrer a reflekção total em uma das camadas atmosféricas.
Todas as afirmativas são corretas.
OFICINA CIENTÍFICA
A mágica da refração
O fenômeno da refração póde sêr visualizado em diversos momentos, como em um pôr do sól, por exemplo. Nesse caso, a refração dos raios solares, na atmosféra, parece achatar o disco solar.
Além de ter sua forma aparente modificada, o sól é observado poucos minutos antes de ele realmente nascer, isto é, aparecer acima do horizonte, e também continua a sêr observado por alguns minutos depois de se pôr.
Esses aspectos podem sêr explicados pêlos desvios ocorridos com os raios luminosos ao passarem de um meio para outro, quê, nesse caso, são diferentes camadas de nossa atmosféra com diferentes índices de refração dêêsses meios.

De maneira análoga ao desvio dos raios solares, na atividade prática a seguir, observaremos como a refração póde alterar a trajetória dos raios de luz e fazer um objeto visível.
Materiais
• á gua
• moeda
• xícara
Procedimentos
• Inicialmente, coloque uma moeda no fundo da xícara sem á gua.
• Posicione os seus olhos de tal forma quê o ângulo de visão não permita vêr a moeda inteira, mas apenas um pedacinho dela. (Observe o esquema.)

• Mantenha essa posição e peça a um dos seus côlégas quê, lentamente, vá colocando á gua no interior da xícara.
ATIVIDADES
1. O quê acontece à medida quê o nível da á gua sobe no interior da xícara?
2. Justifique o fenômeno ocorrido.
Página duzentos e sessenta e três
SAIBA +
Como funcionam as fibras ópticas?
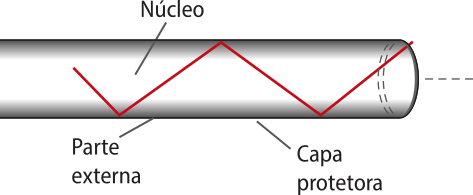
Um dispositivo tecnológico no qual ocorrem sucessivas reflekções é a fibra óptica. De forma bastante simplificada, podemos dizêr quê a fibra óptica é um filamento alongado quê recebe, numa das suas extremidades, o raio de luz, quê sofre sucessivas reflekções totais, projetando-se para a outra extremidade, conforme a representação a seguir.
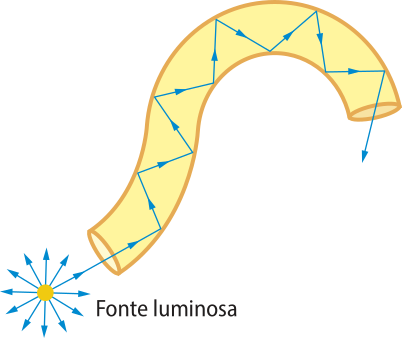

A estratégia utilizada para fazer a luz refletir-se totalmente em seu interior é confeksionar seu núcleo e sua parte externa com materiais de diferentes índices de refração.
Uma fibra óptica é um conduto fino (aproximadamente 0,05 mm de diâmetro) e flexível, com um núcleo preenchido de sílica e uma interface próxima da parte externa de sílica misturada com outro material, quê possui um índice de refração menor. Há ainda uma capa protegendo todo o sistema.
A diferença entre os índices de refração do núcleo e da parte externa da fibra permite quê o raio, ao se propagar em seu interior (meio mais refringente), incida na superfícíe de separação com a parte externa (meio menos refringente) e sofra reflekção total, permanecendo confinado no interior da fibra óptica. Em sua geometria e confekissão, garante-se quê o ângulo com quê o raio incide sobre a interface seja sempre maior quê o ângulo limite.
ATIVIDADE
1. As fibras ópticas estão substituindo os cabos de comunicação atuáis, cuja transmissão das informações é realizada por meio de pulsos elétricos. Pesquise e descubra qual a vantagem de utilizarmos as fibras ópticas para a comunicação.
Página duzentos e sessenta e quatro
Lentes esféricas
Lentes esféricas são sistemas ópticos formados por um meio homogêneo e transparente, limitados por duas superfícies, podendo sêr ambas esféricas ou uma esférica e uma plana. A luz refrata ao incidir na lente e refrata ao sair da lente, podendo assim alterar sua direção de propagação.
As lentes esféricas são capazes de formár imagens com base na refração da luz e nas suas propriedades geométricas, sêndo por isso utilizadas em diversos instrumentos, como lupa, luneta, microscópio, máquina fotográfica, óculos, entre outros.
Nestes estudos, serão consideradas apenas lentes com espessura menor do quê o raio de curvatura de suas faces.


A classificação das lentes é feita de acôr-do com o formato das faces externas. Quando a espessura das bordas das lentes é menor quê a espessura da parte central, tem-se uma lente de bordas delgadas (ou finas), como, por exemplo, uma lente biconvexa. Quando apresentam a espessura das bordas maior quê a espessura da parte central, são denominadas lentes de bordas espessas (ou grossas), como, por exemplo, uma lente bicôncava.
PENSE E RESPONDA

4 A fotografia mostra uma lupa conjugando uma imagem menor e invertida de um corpo distante. Seria essa a utilidade de uma lupa?
Lente convergente e divergente
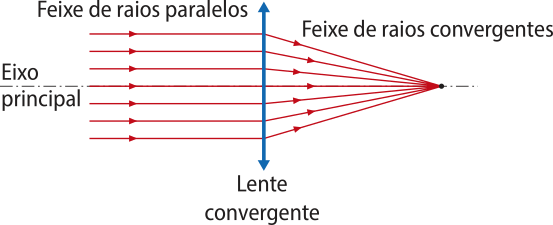
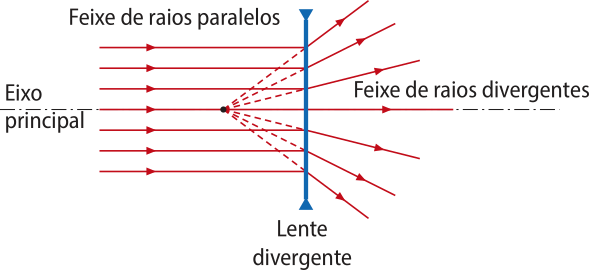
As lentes delgadas podem ter comportamento convergente ou divergente. Uma lente é convergente quando um feixe de raios paralelos quê incide nela sofre refrações e forma um feixe de raios convergentes. Da mesma forma, dizemos quê uma lente é divergente quando um feixe de raios paralelos quê incide nela sofre refrações e forma um feixe de raios divergentes.
O caráter convergente ou divergente de uma lente delgada é dado pela sua geometria (raio de curvatura das faces) e pela relação entre os índices de refração absoluto do material com quê a lente é feita e do meio físico no qual ela está imérsa. De acôr-do com a relação entre os índices de refração absolutos, os raios irão se desviar se aproximando ou se afastando da reta normal, definindo assim o comportamento da lente esférica.
Lente de bordas delgadas |
Lente de bordas espessas |
Exemplo |
|
|---|---|---|---|
nlente > nmeio |
convergente |
divergente |
Lente de vidro (nvidro = 1,5) no ar (nar = 1,0) nvidro > nar |
nlente < nmeio |
divergente |
convergente |
Lente de vidro (nvidro = 1,5) em uma mistura de sulfêto de carbono (nsc = 1,6)nvidro < nsc |
Página duzentos e sessenta e cinco
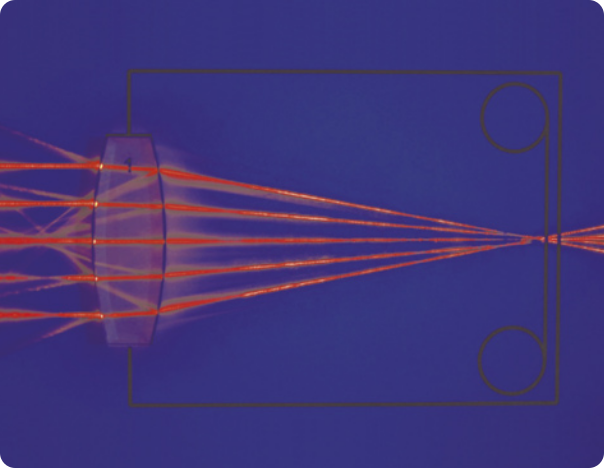
A situação mais comum a sêr estudada é a das lentes esféricas transparentes imérsas no ar, feitas de materiais mais refringentes quê ele, quando as lentes de bordas delgadas são convergentes e as lentes de bordas espessas são divergentes, como mostram as fotografias a seguir.
Nas ilustrações ao lado das fotografias, são apresentadas as formas mais simplificadas de como normalmente são representadas as lentes esféricas.

ESPAÇOS DE APRENDIZAGEM
• No vídeo disponível no sáiti a seguir, é possível verificar diversas demonstrações relacionadas à Óptica Geométrica, como o comportamento de espelhos planos e esféricos, a reflekção total e o comportamento de lentes convergentes e divergentes.
Tema 06: Formulações da Óptica Geométrica | Experimentos: lentes e espelhos. Publicado por: Física Universitária. Vídeo (5 min). Disponível em: https://livro.pw/pugdd. Acesso em: 26 set. 2024.

Página duzentos e sessenta e seis
Principais elemêntos de uma lente esférica
A seguir são apresentados os principais elemêntos de uma lente esférica, utilizando uma lente biconvexa como exemplo.
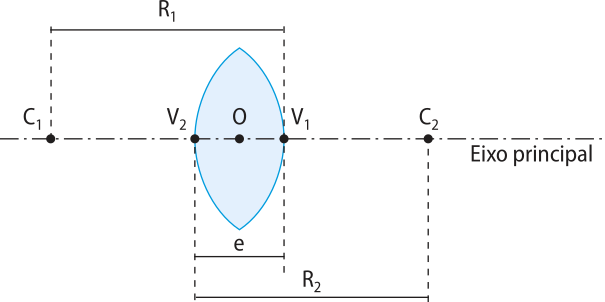
• Centros de curvatura (C1 e C2): centros das superfícies esféricas das faces da lente.
• Raios de curvatura (R1 e R2): raios das superfícies esféricas das faces da lente.
• Vértices (V1 e V2): polos das superfícies esféricas.
• Espessura (e): distância entre os vértices.
• Eixo principal: reta quê contém os centros de curvatura e os vértices.
• Centro óptico (O): ponto particular da lente, em geral contido nela, por onde um raio de luz atravessa a lente sem sofrer desvio.
Focos de uma lente esférica
Todas as lentes possuem dois focos com as propriedades quê serão abordadas a seguir.
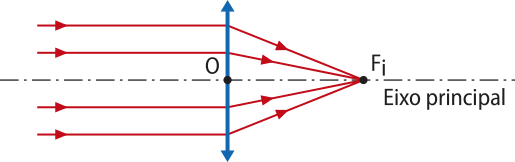
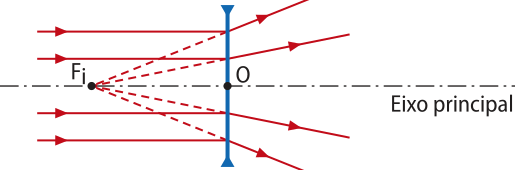
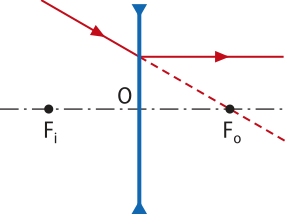
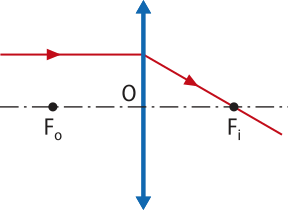
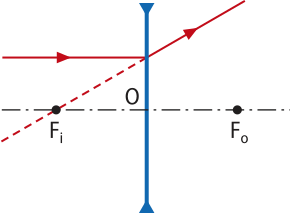
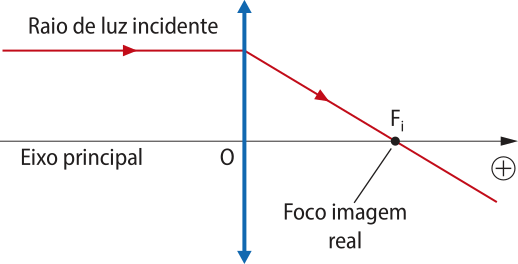
Quando um feixe de raios de luz paralelos ao eixo principal incide em uma lente esférica, os raios refratados definem o foco principal imagem Fi. Note quê, para a lente convergente, Fi tem natureza real, pois é o encontro dos raios refratados, enquanto para a lente divergente, Fi é de natureza virtual, pois é o encontro dos prolongamentos dos raios refratados.
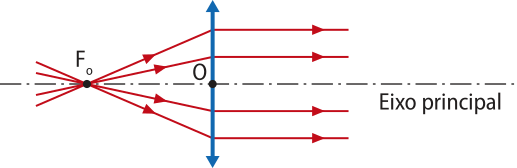
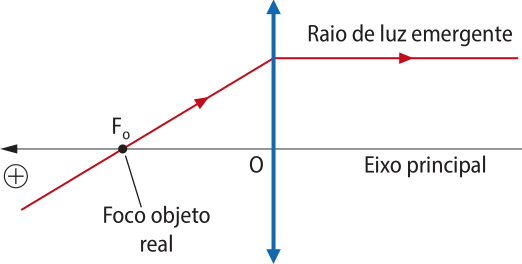
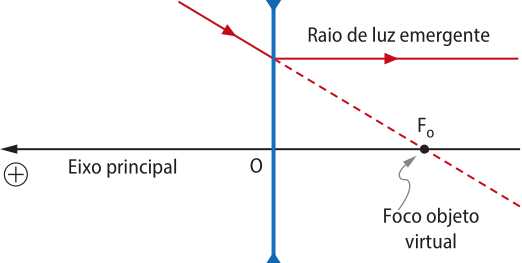
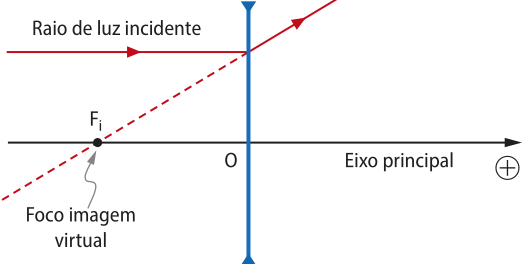
O ponto do eixo principal simétrico ao foco principal imagem Fi, em relação ao centro óptico O, é denominado foco principal objeto Fo.Raios de luz incidentes quê passam por esse ponto, ou seus prolongamentos, refratam formando um feixe de raios de luz paralelos ao eixo principal. Foco principal objeto Fo é real nas lentes convergentes e virtual nas lentes divergentes. |
|||||||||
☟Lente convergente |
☟Lente divergente |
||||||||
|
|
||||||||
Representação de raios de luz paralelos ao eixo principal quê incidem em uma lente convergente, o quê determina o foco principal imagem real. |
Representação de raios de luz paralelos ao eixo principal quê incidem em uma lente divergente, o quê determina o foco principal imagem virtual. |
||||||||
A distância entre o foco principal e o centro óptico de uma lente é chamada distância focal f.
Página duzentos e sessenta e sete
Propriedades dos raios incidentes nas lentes
Assim como no caso dos espelhos esféricos, para as lentes esféricas também existem quatro raios notáveis, para os quais são conhecidas as trajetórias dos raios incidentes e refratados.
Propriedades dos raios |
Lente convergente |
Lente divergente |
|---|---|---|
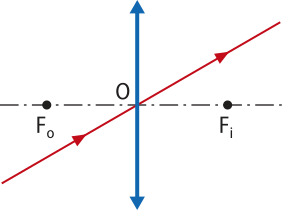
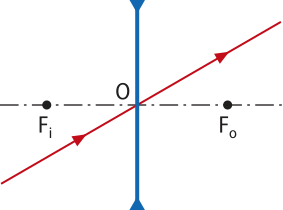
1ª) Raio de luz incidente passa pelo centro óptico e refrata sem sofrer desvio. |
|
|
2ª) Raio de luz (ou seu prolongamento) incidente passa pelo foco principal objeto (real ou virtual) de uma lente e refrata paralelo ao eixo principal. |
|
|
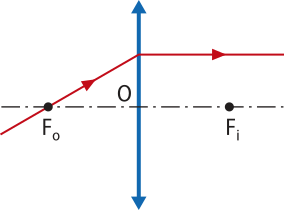
3ª) Raio de luz incidente paralelo ao eixo principal refrata na direção do foco principal imagem ( real ou virtual) |
|
|
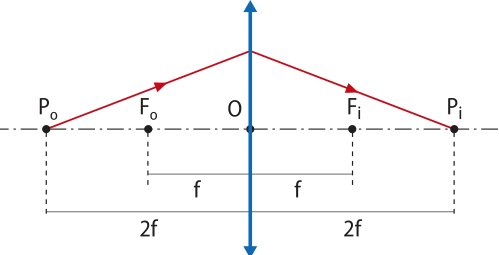
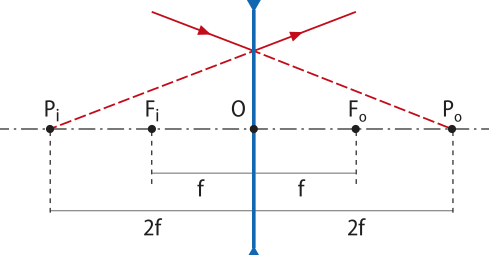
Ponto antiprincipal
O ponto Po,situado sobre o eixo principal, a uma distância igual a 2f do centro óptico O, é chamado ponto antiprincipal objeto. Já o ponto Pi,também situado sobre o eixo principal, a uma distância igual a 2f do centro óptico O, é chamado ponto antiprincipal imagem. Apenas para os pontos antiprincipais é válido o seguinte raio notável.
Propriedades dos raios |
Lente convergente |
Lente divergente |
|---|---|---|
4ª) Raio de luz incidente (ou seu prolongamento) passa pelo ponto antiprincipal objeto e refrata pelo ponto antiprincipal imagem (real ou virtual). |
|
|
Página duzentos e sessenta e oito
Determinação geométrica de imagens nas lentes esféricas
A determinação da imagem conjugada por uma lente esférica póde sêr feita utilizando dois raios notáveis, verificando o encontro dos raios refratados, ou de seus prolongamentos. O objeto será representado por uma seta AB, perpendicular ao eixo principal, e a imagem, por uma seta A'B'.
Nesta análise serão consideradas lentes de bordas delgadas como convergentes e lentes com bordas espessas como divergentes.
Lente convergente
Uma lente convergente conjuga diferentes imagens de acôr-do com a posição do objeto em relação à lente.
Posição do objeto |
Construção da imagem |
Características da imagem |
|---|---|---|
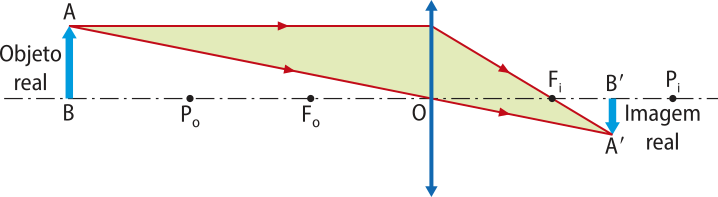
Antes do ponto antiprincipal Po. |
|
Real, invertida e menor quê o objeto. |
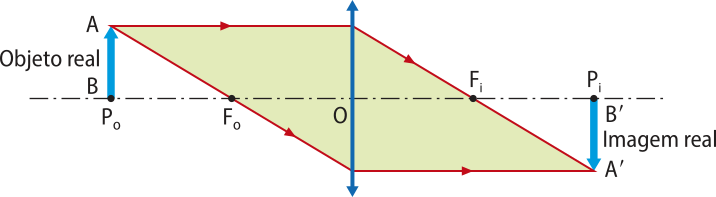
No ponto antiprincipal Po. |
|
Real, invertida e de mesmo tamãnho do objeto. |
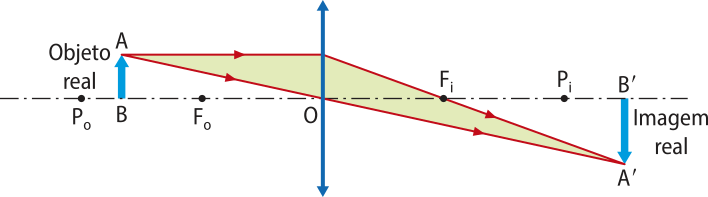
Entre o foco Fo e o ponto antiprincipal Po. |
|
Real, invertida e maior quê o objeto. |
No foco Fo. |
|
Imprópria (estaria formada no infinito, pois os raios refletidos são paralelos). |
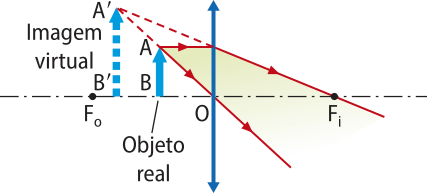
Entre o foco Fo e o centro óptico O. |
|
Virtual, direita e maior quê o objeto. |
Página duzentos e sessenta e nove
Lentes esféricas convergentes são utilizadas de várias maneiras, como nos óculos, na lupa, no microscópio compôzto e nas lunetas, por exemplo. Também são utilizadas para projetar imagens reais, como nas máquinas fotográficas, projetores de cinema, lunetas e telescópios.
No caso da lupa, se o objeto estiver antes do ponto antiprincipal Po,a imagem formada é invertida e menor quê o objeto, como mostrado na fotografia apresentada no início dos estudos das lentes esféricas. Para utilizar uma lupa corretamente, o objeto deve estar entre o foco Fo e o centro óptico O, para assim formár uma imagem virtual, direita e maior quê o objeto.
Lente divergente
Para um objeto colocado diante de uma lente divergente, a imagem conjugada é sempre virtual, direita e menor quê o objeto.
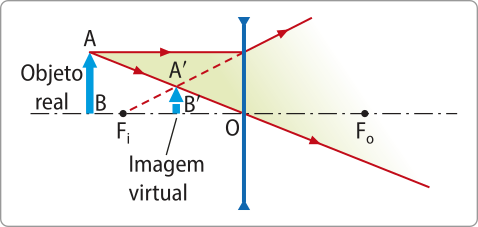

Lentes esféricas divergentes são utilizadas em algumas situações do dia a dia, como nos óculos ou, quando se deseja conjugar uma imagem reduzida, no olho mágico, instalado em portas de residências. Estas lentes são também um dos itens existentes em instrumentos ópticos, como a luneta terrestre.
ATIVIDADES
10. Ao examinar uma obra de; ár-te, um colecionador usa uma lente para aumentar a imagem. dêz-creva as características da imagem quê ele observa e o tipo de lente quê ele está usando.
A imagem é maior, direita e virtual. A lente usada é convergente.
11. Observe, nos itens a seguir, as posições ocupadas por um objeto. Faça no caderno a construção geométrica das imagens conjugadas pelas lentes e classifique-as.
a) 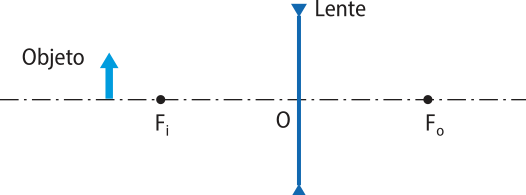
Virtual, direita e menor.
b) 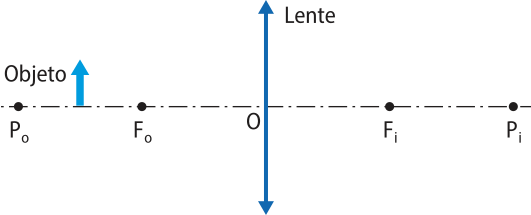
Real, invertida e maior.
c) 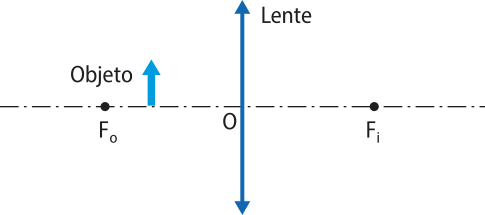
Virtual, direita e maior.
d) 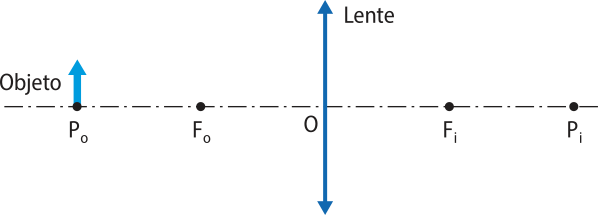
Real, invertida e do mesmo tamãnho.
Página duzentos e setenta
Referencial e equação de Gauss para as lentes esféricas
Para determinar analiticamente as características da imagem de um objeto conjugada por uma lente esférica, utilizamos também um referencial de Gauss, com análise similar à feita nos espelhos esféricos, mas com algumas restrições específicas para as lentes.
• Origem no centro óptico da lente.
• Eixo das ordenadas: perpendicular ao eixo principal, e sentido positivo para cima.
• Eixo das abscissas: mesma direção do eixo principal e sentido positivo contrário a luz incidente, para os objetos, e sentido positivo a favor da luz refratada para imagens.

Condições para o foco e a distância focal
O sinal da distância focal f das lentes esféricas segue a seguinte análise.
|
|
Para lentes convergentes, a distância focal f é positiva (f. > 0) e, para lentes divergentes, a distância focal é negativa (f, < 0).
Página duzentos e setenta e um
Equação de Gauss e equação do aumento linear transversal
A geometria dos espelhos e lentes esféricas possibilita quê a equação de Gauss e a equação do aumento linear sêjam válidas também para as lentes esféricas.
Considerando sempre objetos reais e direitos (p > 0 e o > 0), as imagens conjugadas são sempre reais e invertidas (p'. 0 e i, 0) ou virtuais e direitas (p' < 0 e i > 0).
Nas lentes, a medida de recebe o nome de vergência, ou convergência, C, entendida como a capacidade de uma lente em desviar um raio de luz. Se a distância focal é pequena, a vergência é alta, o quê indica quê a lente tem grande capacidade de desviar a luz, e vice-versa.
No SI, a unidade de medida de vergência é o ou (metro recíproco), denominado dioptria (di), popularmente chamada de grau.
Atividade resolvida
3. Uma lente de bordas delgadas imérsa no ar tem distância focal 20 cm. Um objeto de altura 10 cm é colocado a 30 cm dessa lente. Nessas condições, qual é a altura da imagem conjugada pela lente?
Resolução
Posição do objeto: p = 30 cm
Altura do objeto: o = 10 cm
Distância focal da lente: f = 20 cm (A lente de bordas delgadas no ar é convergente, logo f > 0.)
⇒ p' = 60 cm
⇒ ⇒ i = − 20 cm
A imagem é real (p' > 0), invertida (i < 0) e maior quê o objeto. Esta é imagem típica formada por lentes convergentes quando o objeto está entre o ponto antiprincipal objeto Po e o foco objeto Fo.
ATIVIDADES
12. A Entomologia é a área da ciência quê estuda os insetos sôbi vários aspectos, inclusive as relações deles com o sêr humano, as plantas, os animais e o meio ambiente. Um pesquisador dessa área, ao estudar os hábitos de uma joaninha, rêzouvêo utilizar uma lupa para ampliar cinco vezes a imagem dela.
Determine a quê distância do inséto ele deve posicionar a lupa, sabendo quê ela é constituída por uma lente delgada e convergente cuja distância focal é 10 cm.
8,0 cm
Página duzentos e setenta e dois
13. Um objeto com 5,0 cm de altura é colocado em frente a uma lente convergente cuja distância focal é 5,0 cm.
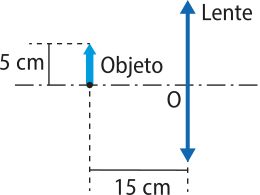
Sabendo quê o objeto dista 15 cm da lente, determine:
a) o tamãnho e a posição da imagem formada;
i = − 2,5 cm e p' = 7,5 cm
b) o aumento linear.
A = 0,5
14. Um jovem, interessado em conhecer os hábitos dos insetos, usa uma lente de aumento para observar dêtálhes do corpo de um deles. Ele sabe quê para obtêr uma imagem três vezes maior do quê o inséto observado é necessário manter uma lente convergente a 40 cm de distância do inséto.
Mantendo essas condições, ele conseguirá determinar:
a) a distância, em centímetro, entre a imagem e a lente;
p' = − 120 cm
b) a distância focal da lente, em centímetro.
f = 60 cm
15. Um grupo de estudantes, em uma aula experimental, dispõe de uma lente de distância focal f. Ao colocar um lápis em frente à lente, os alunos percebem quê a imagem formada é invertida e a altura é menor do quê a do lápis. Com base nessa situação, qual a afirmação correta?
a) A distância entre o lápis e a lente é maior quê 2f.
b) A lente é esférica e divergente.
c) Considerando a posição da lente, a imagem se forma do mesmo lado do objeto.
d) A imagem quê se forma é virtual.
e) A distância entre o lápis e a lente é menor quê 2f.
Resposta: a
Instrumentos ópticos
Alguns instrumentos foram produzidos com base na formação de imagens nos espelhos e lentes esféricas, possibilitando assim a formação de imagens aumentadas e a observação de corpos distantes. A seguir, serão apresentados alguns instrumentos ópticos.
Projetores de slides e de cinema
A principal diferença entre um projetor de slides e um projetor de cinema é quê no de cinema há um sistema de movimentação do objeto iluminado.
De forma geral, no projetor existe uma fonte de luz quê é colocada no foco do espêlho kon kavu (convergente). Os raios de luz paralelos passam por um condensador óptico, gerando um feixe cilíndrico e estrêito, cuja luz intensa atinge a película (isláidi) e segue para a lente objetiva, uma lente convergente quê conjuga uma imagem real, ampliada e invertida quê é projetada em uma tela.
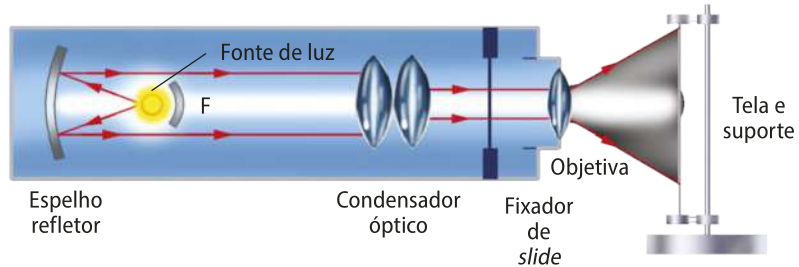
Página duzentos e setenta e três
Microscópio compôzto
Equipamento quê possui duas lentes convergentes, objetiva (mais próxima do corpo a sêr observado) e ocular (por onde se observa), com eixo principal coincidindo.
Um corpo AB é colocado entre o ponto antiprincipal objeto e o foco objeto da lente objetiva, quê conjuga a imagem A'B', real, invertida e maior quê o corpo (tamanho i1). Esta imagem passa a sêr um objeto para a lente ocular e se localiza entre o foco objeto e a lente ocular, quê conjuga uma imagem A''B'', virtual, direita e maior (tamanho i2). Assim, a lente ocular funciona como uma lupa, para aumentar a imagem conjugada pela objetiva.

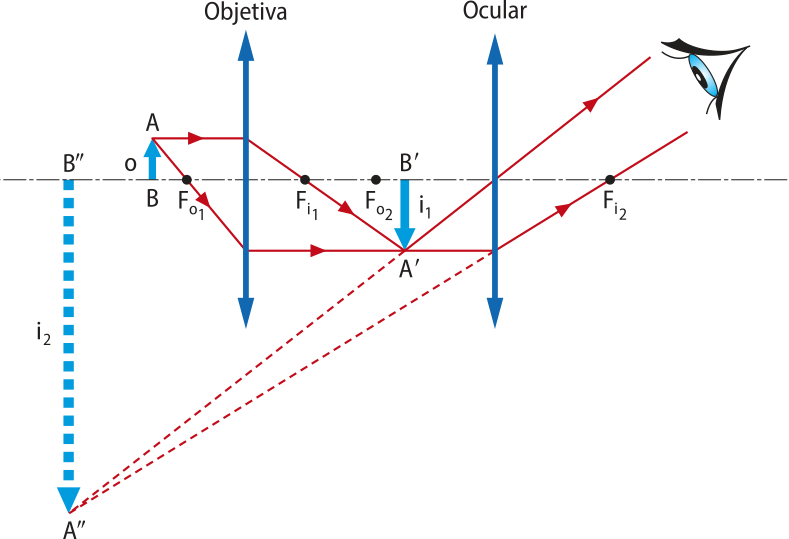
Luneta astronômica ou telescópio refrator
Uma luneta astronômica é também chamada telescópio refrator por sêr composta de duas lentes convergentes, a objetiva e a ocular. A lente ocular tem distância focal na ordem de centímetro, e a objetiva tem distância focal na ordem de métro.
Devido às distâncias dos astros observados, a objetiva conjuga uma imagem A'B' real e invertida, de tamãnho i1,localizada em seu foco imagem. Esta imagem passa a sêr um objeto para a lente ocular e se localiza entre ela e seu foco objeto ,que conjuga uma imagem A''B'', virtual, direita e maior (tamanho i2).

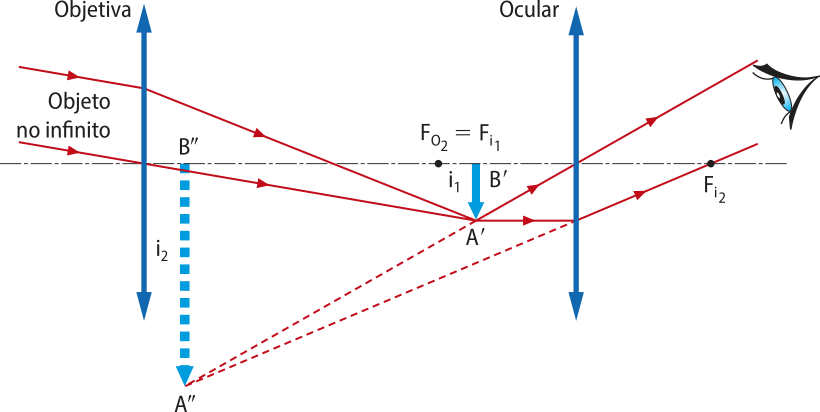
Página duzentos e setenta e quatro
Luneta terrestre
Uma característica da luneta astronômica é a observação de uma imagem final invertida em relação ao objeto. A ideia de tornar a imagem final conjugada direita está na essência da construção da luneta terrestre, ou luneta de Galileu. Nela, a lente objetiva segue sêndo uma lente convergente, mas a lente ocular é divergente e de pequena distância focal.
Devido às distâncias dos astros observados, a objetiva conjuga uma imagem A'B' real e invertida, de tamãnho i1,localizada em seu foco imagem. Esta imagem passa a sêr um objeto virtual para a lente ocular, quê conjuga a imagem A''B'', virtual e direita, de tamãnho i2.
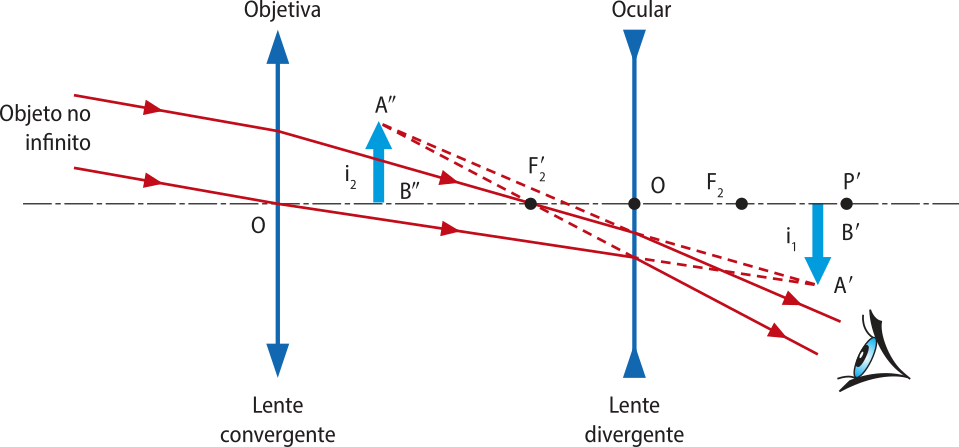
ATIVIDADES
16. O microscópio está estruturado para funcionar com um sistema de lentes quê, em síntese, póde sêr representado pela lente objetiva (aquela quê fica próxima ao objeto) e a lente ocular (a quê fica próxima ao observador). Nesse caso, responda às kestões a seguir.
a) Qual é o tipo de lente usada na posição da objetiva e na da ocular?
Para ambas, objetiva e ocular, é utilizada a lente convergente.
b) A imagem final ôbitída pelo observador ao usar o microscópio é virtual ou real?
Virtual.
17. Se posicionarmos uma lupa a 4,0 cm de um objeto, quantas vezes a imagem ôbitída será maior quê o objeto, sabendo quê a distância focal da lente é 6,0 cm?
3 vezes.
18. (Unicamp-SP) Em uma máquina fotográfica de foco fixo, a imagem de um ponto no infinito é formada antes do filme, conforme ilustra o esquema. No filme, esse ponto está ligeiramente desfocado e sua imagem tem 0,03 mm de diâmetro. Mesmo assim, as cópias ampliadas ainda são nítidas para o olho humano. A abertura para a entrada de luz é de 3,5 mm de diâmetro e a distância focal da lente é de 35 mm.
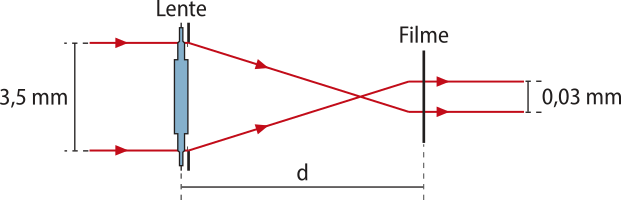
a) Calcule a distância d do filme à lente.
35,3 mm
b) A quê distância da lente um objeto precisa estar para quê sua imagem fique exatamente focalizada no filme?
≃ 4,1 m
Página duzentos e setenta e cinco
O olho humano
O olho é o órgão responsável por captar luz e formár imagens quê são enviadas ao cérebro pelo nêrvo óptico.
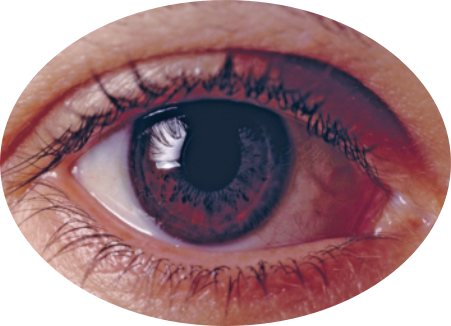
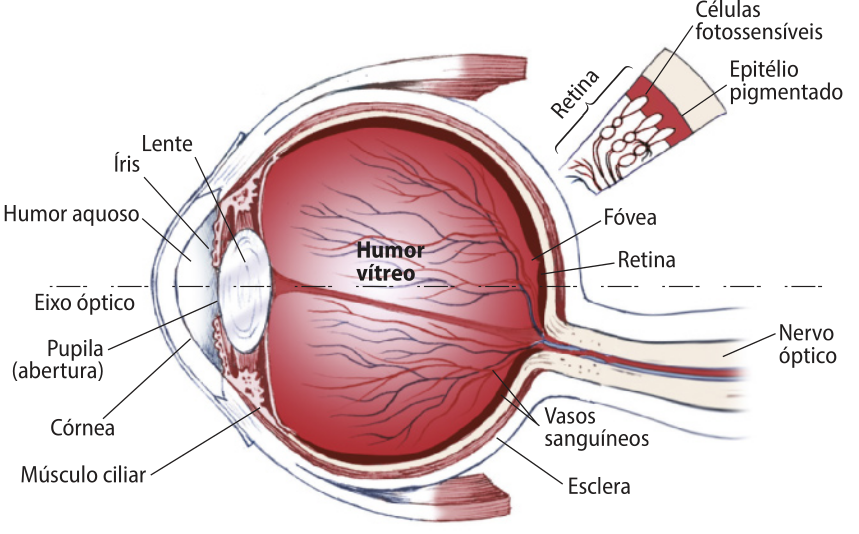
Elaborada com base em: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 1112.
A lente do olho póde sêr considerada aproximadamente uma lente esférica biconvexa, localizada na região anterior do bulbo do olho. Esta lente se comporta como uma lente convergente, projetando na retina imagens reais e invertidas.
A retina é uma região localizada no fundo do bulbo do olho, onde as imagens são projetadas e enviadas ao cérebro. É no cérebro quê elas são interpretadas e corrigidas.
Uma característica importante da lente do olho é chamada acomodação visual, quê se refere às variações da curvatura de suas faces e da sua distância focal, possibilitando vêr com nitidez objetos a diferentes distâncias, mantendo a projeção das imagens sempre sobre a retina.
Por causa das possíveis anomalias do olho quê causam problemas de visão, há casos em quê o processo de formação de imagens não ocorre corretamente.
Problemas de visão corrigidos com o uso de lentes esféricas
Dentre os principais problemas de visão, ou ametropias, existentes no olho humano, a miopia, a hipermetropia e a presbiopia estão relacionadas à acomodação visual. Para entendê-las, é preciso saber quê a visão nítida do objeto, para um olho típico, ocorre quando o objeto se encontra entre o ponto próximo (PP) e o ponto remoto (PR).
O ponto próximo é a posição na qual o objeto é visto com nitidez realizando o maior esfôrço visual possível, enquanto o ponto remoto é a posição na qual um objeto é visto com nitidez sem quê haja esfôrço visual. Para um olho típico, o ponto próximo está a 25 cm do olho, enquanto o ponto remoto está posicionado no infinito.
Página duzentos e setenta e seis
Miopia
No olho com miopia, a imagem é formada antes da retina. Uma das causas dêêsse problema de visão é o alongamento do bulbo do olho.
A pessoa com miopia enxerga bem os objetos quê estão próximos a ela, porém tem dificuldade em vêr nitidamente objetos quê estão distantes. Isso ocorre porque o ponto remoto (PR) está a uma distância finita, e não mais infinita.
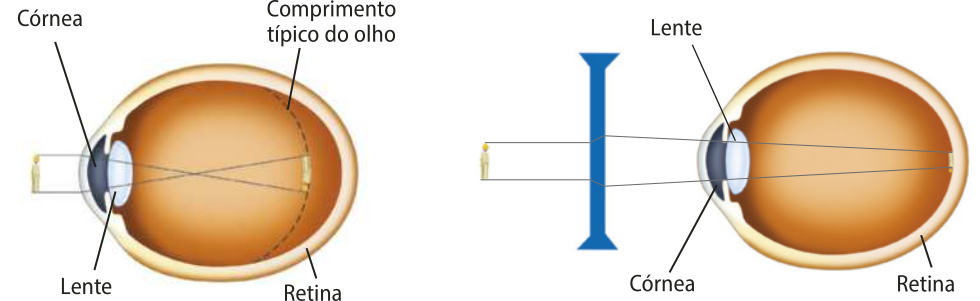
êste problema póde sêr corrigido com o uso de lentes divergentes, quê formam imagens direita e virtual (p' < 0) de objetos distantes, localizados no infinito (p → ∞), sobre o ponto remoto, onde a pessoa é capaz de enxergar nitidamente. Utiliza-se a equação de Gauss para determinar a distância focal desta lente divergente.
⇒ = 0 + ⇒ f = − PR
Assim, a distância focal da lente divergente corretiva deve sêr a medida do ponto remoto do olho com miopia. O sinal negativo ocorre porque a lente esférica é divergente.
Hipermetropia
No olho com hipermetropia, a imagem é formada depois da retina. Uma das causas dêêsse problema de visão é o achatamento do bulbo do olho.
A pessoa com hipermetropia tem dificuldade em vêr nitidamente objetos próximos a ela. Isso ocorre porque o ponto próximo (PP) está a uma distância maior quê 25 cm.
êste problema póde sêr corrigido com o uso de lentes convergentes, quê formam imagens direita e virtual (p'< 0) de objetos quê estejam a 25 cm do olho no ponto próximo, onde a pessoa é capaz de enxergar nitidamente. Utiliza-se a equação de Gauss para determinar a distância focal desta lente convergente.
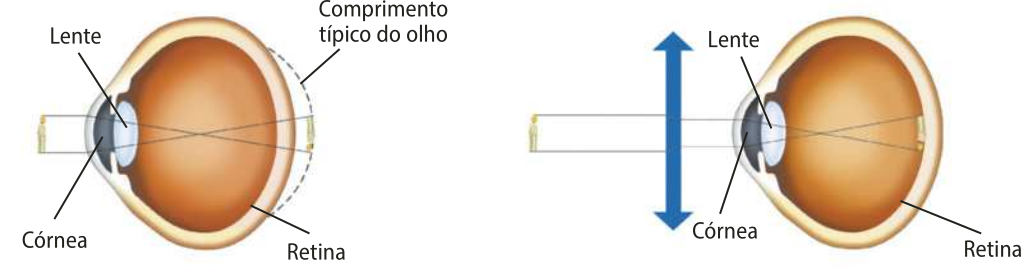
Página duzentos e setenta e sete
êste problema póde sêr corrigido com o uso de lentes convergentes, quê formam imagens direita e virtual (p' <0) de objetos quê estejam a 25 cm do olho no ponto próximo, onde a pessoa é capaz de enxergar nitidamente. Utiliza-se a equação de Gauss para determinar a distância focal desta lente convergente.
Essa expressão permite determinar a distância focal da lente usada como corretiva da hipermetropia. O sinal negativo do ponto próximo ocorre porque a imagem formada é virtual.
Presbiopia
As pessoas quê têm visão típica, geralmente após os 45 anos de idade, começam a ter dificuldade para ler de perto ou vêr nitidamente objetos próximos.
Esse problema de visão, similar à hipermetropia, é denominado presbiopia, ou vista cansada, uma consequência do enrijecimento muscular quê interfere nas condições de acomodação visual. A visão dos objetos distantes permanéce nítida.
As lentes convergentes são usadas para corrigir essa anomalia, caracterizada pelo fato de o ponto próximo estar mais afastado do olho do quê normalmente deveria estar.
ATIVIDADES
19. Os administradores de uma empresa sabem quê a produtividade depende de vários fatores, inclusive das boas condições de trabalho e da saúde dos seus funcionários. Por esse motivo, os exames médicos são feitos periodicamente.
Em um dêêsses exames, o oftalmologista detectou quê as imagens quê se formam no olho do funcionário A apresentam as características representadas na Figura 1 e as características das imagens quê se formam no olho do funcionário B estão representadas na Figura 2. Utilizando essas informações, responda ao quê se pede.
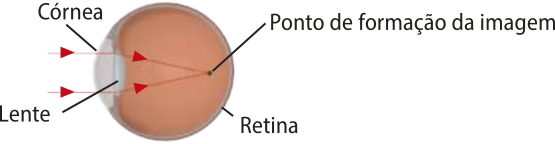
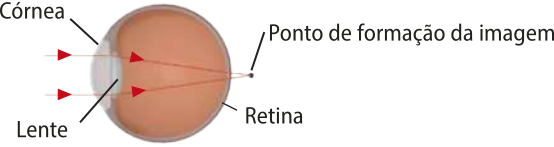
a) Há necessidade de corrigir a visão de um ou dos dois funcionários?
b) Caso seja necessário fazer a correção, especifique o tipo de anomalia apresentada pelo olho e quê tipo de lente deve sêr usada.
20. Ao sair do consultório do oftalmologista, um paciente, lendo a receita, percebeu quê os seus óculos deveriam sêr fabricados com lentes de cristal com −0,5 dioptria. O paciente percebeu quê era míope e rêzouvêo determinar a distância focal da lente. Que valor ele obteve?
− 2,0 m
21. Dores de cabeça, cansaço nos olhos, fadiga ao dirigir ou ao olhar para objetos distantes são queixas freqüentes dos míopes. A miopia póde sêr hereditária, geralmente aparece na infância, e aproximadamente 30% da população mundial é afetada por ela. As pessoas quê apresentam essa anomalia têm dificuldade em vêr objetos distantes, mas podem vêr nitidamente objetos quê estão próximos. Contudo, esse problema de visão é corrigido com o uso de lentes (de contato e óculos) ou cirurgia. Analise a situação de uma menina quê foi diagnosticada com miopia e só consegue vêr com nitidez objetos quê estejam a uma distância mássima de 20 cm dos seus olhos. Nesse caso, para quê a menina consiga vêr com nitidez os objetos posicionados no infinito, qual deve sêr a distância focal da lente corretora a sêr usada?
f = − 20 cm
Página duzentos e setenta e oito
TEMA 23
Ondas e fenômenos ondulatórios
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Movimentos ondulatórios
Fenômenos ondulatórios estão presentes o tempo todo em nosso cotidiano. As ondas possuem algumas características comuns e algumas quê as diferenciam. A partir de agora, vamos estudar algumas destas características.
Mas, afinal, o quê é uma onda?
Imagine quê uma kórda foi amarrada por uma de suas extremidades e esticada na horizontal em uma posição inicial de equilíbrio, deixando a outra extremidade livre. Em um movimento rápido, esta extremidade livre foi elevada até certa altura e retornada à posição inicial, transferindo energia para a kórda. Esta perturbação provocada quê se propaga pela kórda é chamada de pulso.
Na representação da kórda a seguir, há uma marcação indicada por P. Quando o pulso passa pelo ponto P, ele se desloca verticalmente e em seguida desce para a posição inicial de equilíbrio, enquanto a energia é transportada pela kórda sem quê ocorra transporte de matéria.
Se a extremidade livre da kórda for movimentada rapidamente para cima e para baixo em relação à posição de equilíbrio, em movimentos igualmente repetitivos, o ponto P irá se mover para cima e para baixo em relação à posição de equilíbrio. Caso esse movimento seja executado em um mesmo intervalo de tempo, chamado de período, o ponto P irá executar um movimento periódico chamado movimento harmônico simples e, neste caso, formará uma onda.
De forma geral, uma onda póde sêr compreendida como uma perturbação quê se propaga d fórma periódica, transportando energia sem quê ocorra transporte de matéria.
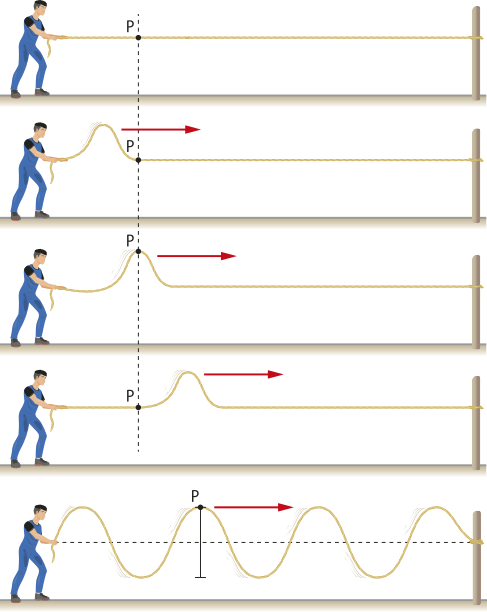
PENSE E RESPONDA

1 por quê, quando ocorrem descargas elétricas no céu seguidas de trovões, primeiro percebemos a luz provocada e depois o som do trovão?
Página duzentos e setenta e nove
Classificação das ondas
Ondas mecânicas e eletromagnéticas
As ondas mecânicas se propagam em meios materiais, como uma onda na kórda, na á gua, no ar, por exemplo. Dessa forma, ondas mecânicas não se propagam no vácuo.
As ondas eletromagnéticas não necessitam de um meio material para se propagar. Assim, a luz visível, as ondas de rádio, o ultravioleta e o raio Xís, por exemplo, podem se propagar tanto em meios materiais como no vácuo. Estas ondas são formadas por perturbações elétricas e magnéticas em função do movimento de cargas elétricas, assunto quê será aprofundado na Unidade 5.
É importante ressaltar quê um meio físico interfere na propagação tanto de ondas mecânicas quanto na de ondas eletromagnéticas, como estudamos no Tema da refração da luz. Porém, as ondas eletromagnéticas se propagam mesmo na ausência de qualquer meio físico.
ESPAÇOS DE APRENDIZAGEM
• O filme Terremoto: a falha de Sã Andreas aborda as ondas sísmicas, uma forma de ondas mecânicas, causadas por um terremoto.

TERREMOTO: a falha de Sã Andreas. Direção: Brad Peyton. Estados Unidos: Uórner brós píctiúrs, 2015. Streaming (114 min).
Ondas transversais e longitudinais
Em uma onda transversal, a direção de oscilação é perpendicular à direção de propagação. Utilizando como exemplo uma mola com uma extremidade fixa, uma onda transversal é formada móvendo a extremidade livre da mola para cima e para baixo. Cada ponto da mola se móve verticalmente para cima e para baixo, enquanto a onda se move horizontalmente ao longo da extensão da mola.
Em uma onda longitudinal, a direção de oscilação é a mesma da propagação. Ao juntar os élos de uma mola e, em seguida, soltá-los, forma-se uma perturbação quê se propaga d fórma longitudinal pela mola.
Ondas mecânicas podem sêr transversais e longitudinais, enquanto ondas eletromagnéticas são apenas transversais.
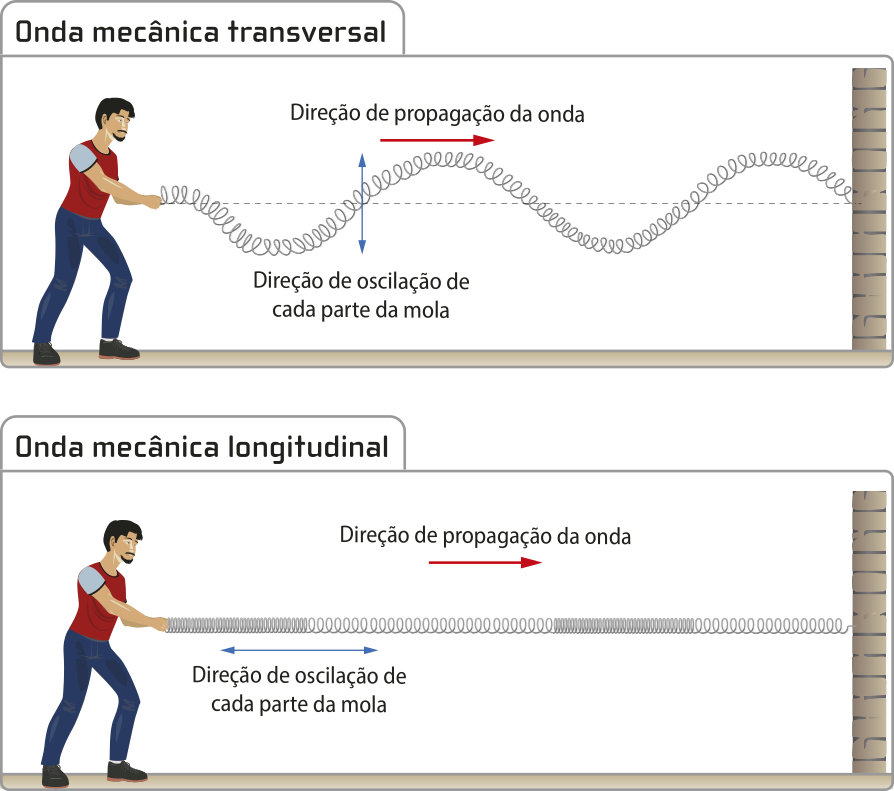
Página duzentos e oitenta
ATIVIDADES
1. O quê você entende por onda mecânica?
2. Em filmes de ficção científica, nos quais são simulados ambientes especiais interplanetários, em cenas de batalhas e explosões são utilizados recursos sonoros para deixar a cena mais interessante. O som da explosão seria escutado em uma situação real? Justifique sua resposta.
3. Indique a afirmativa correta.
a) A luz se propaga no vácuo.
b) A luz é considerada uma onda mecânica.
c) O som póde se propagar no vácuo.
d) O som é considerado uma onda eletromagnética.
Resposta: a
Elementos de uma onda
Ondas periódicas são produzidas quando fontes executam perturbações também periódicas. Nestas situações, pode-se analisar a forma da onda produzida a partir de seus elemêntos.
A representação mais simples para o estudo dos elemêntos de uma onda é um padrão de oscilação transversal, como uma oscilação em uma kórda, por exemplo. No entanto, os elemêntos de uma onda também são verificados em ondas longitudinais.
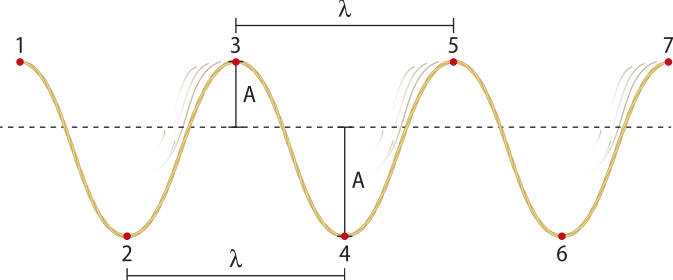
• Amplitude (A): afastamento mássimo efetuado por um ponto do meio material (kórda) em relação a sua posição de equilíbrio. Considerando um plano vertical, os pontos mais altos são chamados de cristas, indicados por 1, 3, 5 e 7, e os pontos mais baixos são chamados vales, indicados por 2, 4 e 6. A maior ou menor amplitude depende, respectivamente, da maior ou menor energia transportada pela onda. No SI, a unidade de medida é o métro.
• Comprimento da onda (u): representa a distância entre dois pontos consecutivos da onda quê estão na mesma fase de oscilação, ilustradas a partir das distâncias de 2 a 4 e de 3 a 5, por exemplo. Quando um ponto da kórda executa uma oscilação completa (para cima e para baixo em relação ao ponto de equilíbrio), a energia percórre um comprimento de onda. No SI, a unidade de medida é o métro.
• Período (T): é o intervalo de tempo de uma oscilação completa, isto é, para quê a energia percorra um comprimento de onda. No SI, a unidade de medida é o segundo.
• freqüência (f): corresponde ao número de oscilações efetuadas na unidade de tempo. A freqüência da onda depende apenas da fonte geradora da onda. No SI, a unidade de medida é o hertz. A freqüência é dada pelo inverso (ou recíproco) do período, e vice-versa.
f =
Página duzentos e oitenta e um
Velocidade de propagação
Para ondas periódicas se propagando em mesmo meio, tem-se quê a energia percórre a distância de um comprimento de onda a cada oscilação completa, isto é, a cada intervalo de tempo de um período T. A velocidade de propagação de uma onda periódica póde sêr calculada da seguinte forma:
v = ⇒ v = ⇒ v = λ f
Essa expressão é conhecida como equação fundamental da ondulatória, válida para ondas mecânicas e eletromagnéticas, transversais e longitudinais. Quando em um mesmo meio físico homogêneo e isotrópico, a velocidade de propagação de uma onda póde sêr considerada constante.
Velocidade de propagação de ondas em uma kórda
Para uma kórda homogênea de comprimento L e massa m, pode-se definir a densidade linear como uma grandeza quê expressa a razão da massa da kórda pela unidade de comprimento.
μ =
No SI, a densidade linear é expressa em quilograma por métro (kg/m).
Quando uma onda se propaga por uma kórda, sua velocidade de propagação v depende da densidade linear da kórda m e da intensidade da fôrça de tração na kórda T. Esta dependência é dada pela equação de Têilor, em homenagem ao matemático inglês Brook Têilor (1685-1731), quê realizou diversas contribuições acerca da propagação de ondas em diferentes meios.
v =
Quanto mais tensionada estiver a kórda, maior a velocidade de propagação de uma onda por ela. Por outro lado, quanto maior a densidade linear da kórda, menor é a velocidade de propagação da onda por ela.
ATIVIDADES
4. Uma campainha elétrica executa 240 vibrações em 1 min. Sabendo quê a onda produzida se propaga com velocidade cuja intensidade é 80 cm/s, determine:
a) a freqüência da onda;
4 Hz
b) o valor do comprimento de onda μ.
20 cm
5. A figura a seguir representa uma onda, d fórma quê o ponto M oscila com uma freqüência de 20 Hz.

Com base nessa figura, determine:
a) o comprimento da onda;
120 cm
b) a amplitude da onda;
6 cm
c) o período da onda;
0,05 s
d) a velocidade de propagação da onda.
24 m/s
6. Uma rádio opera na freqüência 105,9 MHz. Admitindo 3 ⋅ 108 m/s como velocidade de propagação das ondas de rádio, determine o comprimento de onda da transmissão.
≃ 2,83 m
7. Uma kórda de violão tem densidade linear de 0,01 kg/m e está fixa sôbi uma fôrça de tensão de 1 N. Quando tocada, uma onda se propaga por ela com comprimento de onda de 12,5 cm.
Qual a freqüência de oscilação desta kórda nesta situação, expressa em Hz?
80 Hz
Página duzentos e oitenta e dois
Frente de onda
Chamamos de frente de onda o conjunto de pontos quê recebem a mesma oscilação no mesmo instante em um movimento oscilatório, formando, por exemplo, uma mesma crista, ou mesmo vale.
Para uma onda mecânica, como uma onda se propagando na á gua, a frente de onda define o conjunto de pontos da á gua quê formam uma mesma crista, ou vale, no mesmo instante.
Quanto à direção de propagação e à forma da frente de onda, as ondas podem sêr classificadas em três tipos.
Ondas unidimensionais: a propagação ocorre em uma dimensão, como nas ondas em kórdas, por exemplo. As frentes de onda são pontos, e a distância entre pontos consecutivos é um comprimento de onda.
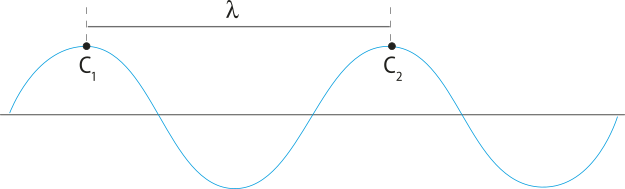
Ondas bidimensionais: a propagação ocorre em duas dimensões, como nas ondas na superfícíe da á gua, por exemplo. As frentes de onda são linhas quê podem sêr circulares ou retilíneas. A distância entre linhas consecutivas é um comprimento de onda.
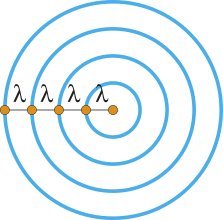
Ondas tridimensionais: a propagação ocorre em três dimensões, como nas ondas sonóras, por exemplo. As frentes de onda são superfícies quê podem sêr planas ou esféricas. A distância entre superfícies consecutivas é um comprimento de onda.
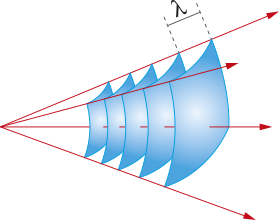
Princípio de Huygens
No final do século XVII, o físico holan-dêss Christiaan Huygens (1629-1695) apresentou na obra Tratado sobre a luz um estudo ondulatório da luz em quê analisava, por meio de uma construção gráfica, a propagação a partir da ideia de frentes de onda, como a representada na imagem. Posteriormente, o estudo por frentes de onda foi generalizado para as demais ondas.
O estudo, quê ficou conhecido como princípio de Huygens, póde sêr enunciado da seguinte forma.
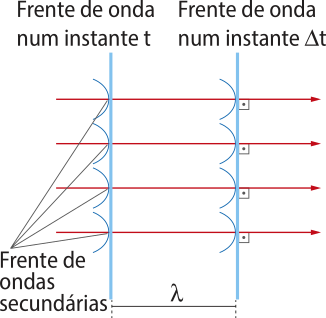
Cada ponto de uma frente de onda comporta-se, e póde sêr considerado, como uma nova fonte de ondas secundárias quê se propagam em todas as direções, mantendo as características da onda inicial. A linha ou superfícíe quê tangencia todas as ondas secundárias produzidas representa a frente de onda num instante posterior.
Página duzentos e oitenta e três
Fenômenos ondulatórios
Nos estudos da Óptica Geométrica, foram abordados alguns fenômenos ondulatórios, como a reflekção e a refração da luz.
Estes e outros fenômenos ondulatórios podem sêr analisados considerando as ondas d fórma geral.
Reflexão de ondas
Na reflekção de ondas, quando uma onda atinge uma barreira, ela retorna ao meio em quê estava, pois cada ponto da barreira se torna uma fonte de onda secundária, de acôr-do com o princípio de Huygens. Velocidade de propagação, freqüência e comprimento de onda não se alteram na reflekção.
Representando a direção de uma propagação a partir de um raio de onda (assim como se utiliza o raio de luz nas ondas luminosas), os ângulos de incidência e de reflekção entre os raios de onda e em relação à reta normal são iguais. Na Figura 1, está representado o fenômeno de reflekção para uma onda com frentes de onda planas e, na Figura 2, a reflekção de uma onda com frentes de ondas circulares. Neste caso, o ponto P indica a fonte emissora das ondas, e o ponto imaginário P ‘, simétrico a P, um emissor das ondas refletidas.
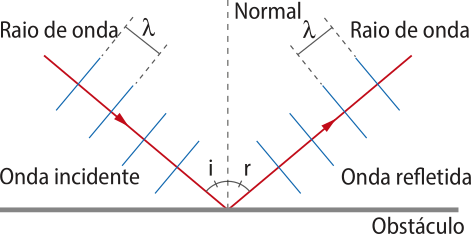
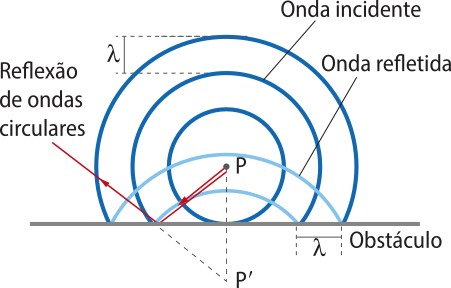
Refração de ondas
Quando uma onda se propaga de um meio para outro e sofre variação de sua velocidade, tem-se o fenômeno da refração, podendo sofrer um desvio em sua direção.
A variação de velocidade é acompanhada pela variação do comprimento de onda, visto quê a freqüência se mantém constante por sêr uma característica da fonte. A descrição da trajetória da onda refratada obedece à lei de Snell-Descartes.
n1 sen i = n2 sen r
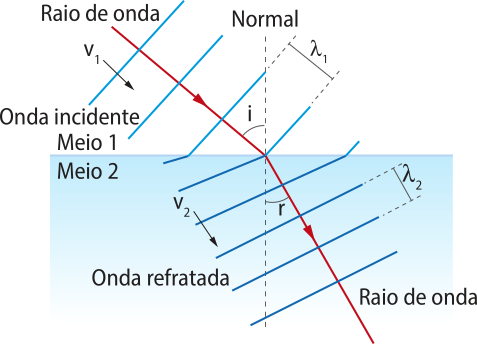
Para a análise do índice de refração, vamos considerar a luz apenas por questão de demonstração, sêndo n =
sen i = sen r ⇒
Como v = λ f e a freqüência é sempre a mesma, tem-se quê:
Página duzentos e oitenta e quatro
Difração de ondas
A difração é um fenômeno no qual a onda contorna um obstáculo ou transpassa uma fenda ou orifício, chegando a uma região quê não poderia sêr atingida por propagação retilínea. A condição para quê esse fenômeno ocorra com uma onda é quê o obstáculo ou fenda tenha dimensões próximas ao seu comprimento de onda.

Ao sofrer difração, as frentes de onda sofrem um encurvamento, afinal cada ponto de uma frente de onda se comporta como uma nova fonte de ondas secundárias quê se propaga em todas as direções, conforme o princípio de Huygens. Quanto mais próximas são as dimensões do comprimento de onda e da fenda ou obstáculo, mais acentuado é o encurvamento causado pela difração.
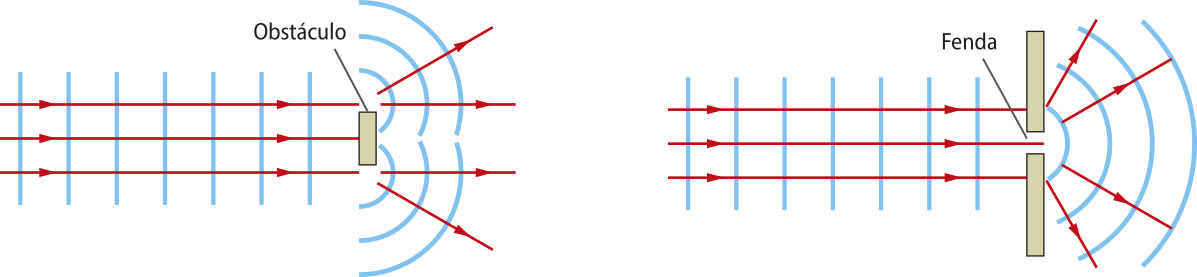
Polarização de ondas
A polarização é um fenômeno de restrição à direção de propagação de uma onda. Assim, ondas quê oscilam em várias direções, ao serem polarizadas, passam a oscilar em apenas uma direção. Trata-se de um fenômeno quê ocorre somente com ondas transversais.
O fato de a luz e de outras ondas eletromagnéticas sofrerem polarização foi uma das evidências quê levou à conclusão de quê as ondas eletromagnéticas são transversais.
Os equipamentos utilizados para polarizar uma onda são chamados polarizadores, sêndo utilizados em lentes de óculos de sól e de câmeras fotográficas, por exemplo.
Considere a luz como uma onda se propagando em várias direções, representada pela ilustração das setas em vários sentidos. Quando a luz passa por um polarizador vertical, apenas a oscilação vertical é transmitida. Se logo em seguida for colocado um polarizador horizontal, a luz será totalmente bloqueada.
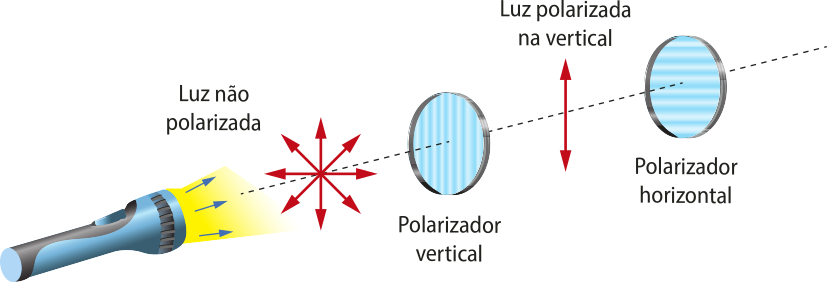
Página duzentos e oitenta e cinco
ATIVIDADE RESOLVIDA
1. Uma pessoa caminhando pela calçada da cidade onde mora, ao passar pêlos muros altos de uma residência, escutou o latido de um cachoorro quê estava dentro da residência. Qual fenômeno físico está relacionado ao fato de a pessoa escutar o latido do cachoorro, mas não o vêr? Explique.
Resolução
O fenômeno da difração das ondas, quê é a capacidade das ondas em contornar obstáculos, permite à pessoa ouvir o latido do cachoorro, pois as ondas sonóras emitidas têm comprimento de onda próximos às dimensões do muro. Porém, ela não póde vêr o animal, pois o comprimento de onda da luz é muito menor quê as dimensões do muro.
ATIVIDADES
8. Entre duas pessoas, há uma espessa parede de 3,0 m de altura. Mesmo assim, elas conseguem conversar. Esse fato póde sêr explicado pelo fenômeno de:
a) difração.
b) refração.
c) reflekção.
d) reflekção total.
e) nenhuma das anteriores.
Resposta: a
9. A respeito da luz, podemos afirmar quê é uma onda transversal porque ela póde sêr:
a) refletida.
b) refratada.
c) polarizada.
d) difratada.
Resposta: c
10. Quem costuma usar estradas, com freqüência, sabe quê em determinadas épocas do ano é comum o aparecimento de neblina, especialmente em regiões de serra. Nessas situações, é preciso ter cuidado redobrado e o motorista deve reduzir a velocidade, aumentar a distância do veículo quê vai à frente, manter a luz de neblina ligada, não usar o farol alto, não parar no acostamento e, caso seja necessário parar, buscar um lugar seguro.
Em uma estrada com neblina, o motorista de um ônibus escolar percebeu quê, após ter passado por uma placa de sinalização quê advertia: “Com neblina, use farol baixo”, três estudantes quê estavam no ônibus passaram a buscar uma justificativa para o aviso. Analise a justificativa apresentada por eles e responda quem está cérto.
Estudante A: A luz emitida pelo farol alto reflete na neblina e, por isso, ofusca a visão do motorista.
Estudante B: A luz emitida pelo farol baixo não reflete na neblina e, por isso, não ofusca a visão do motorista.
Estudante C: A luz emitida pelo farol baixo se dispersa na neblina e, por isso, não ofusca a visão do motorista.
11. A representação feita na figura a seguir é de uma onda quê passa de um meio A para um meio B. Sabendo quê a freqüência de propagação é 90 Hz e o comprimento de onda no meio A é 1,0 cm, determine:
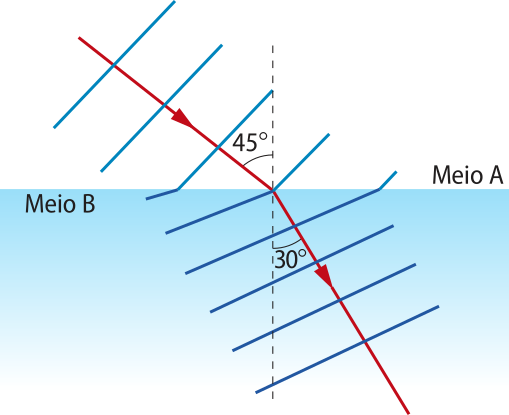
a) a velocidade da onda nos dois meios;
VA = 90 cm/s e VB = cm/s
b) o comprimento de onda no meio B.
Dados: sen 45° = e sen 30° =
λ = cm
Página duzentos e oitenta e seis
Interferência de ondas
O fenômeno da interferência ocorre quando ondas, ao se propagarem, encontram-se em determinado local. êste fenômeno póde sêr observado em todos os tipos de onda, sêjam mecânicas, sêjam eletromagnéticas.
Considere dois pulsos unidimensionais em uma kórda, quê se propagam em sentidos contrários. Em determinado instante, eles vão se encontrar no ponto P, no qual se observará o princípio da superposição.
Quando dois pulsos em fase se encontram, unindo-se por meio de suas cristas ou seus vales, tem-se o fenômeno da interferência construtiva, e a amplitude do pulso resultante aumenta, representado na imagem a seguir.

Quando dois pulsos em inversão de fase se encontram (crista com vale), tem-se o fenômeno da interferência destrutiva, e a amplitude do pulso resultante diminui.
Após a superposição dos pulsos, ambos continuam se propagando com suas características iniciais, como ilustra a imagem a seguir.

A mesma análise póde sêr feita em ondas bidimensionais, como aquelas geradas na superfícíe da á gua. Na ilustração a seguir, estão representadas duas ondas bidimensionais com frentes de ondas esféricas geradas pelas fontes F1 e F2 .As linhas cheias representam cristas e os tracejados representam vales.
No encontro de uma crista com outra crista, ou vale com outro vale, tem-se uma interferência construtiva, representada por pontos pretos. Por outro lado, no encontro entre crista e vale tem-se uma interferência destrutiva, representada por pontos brancos.
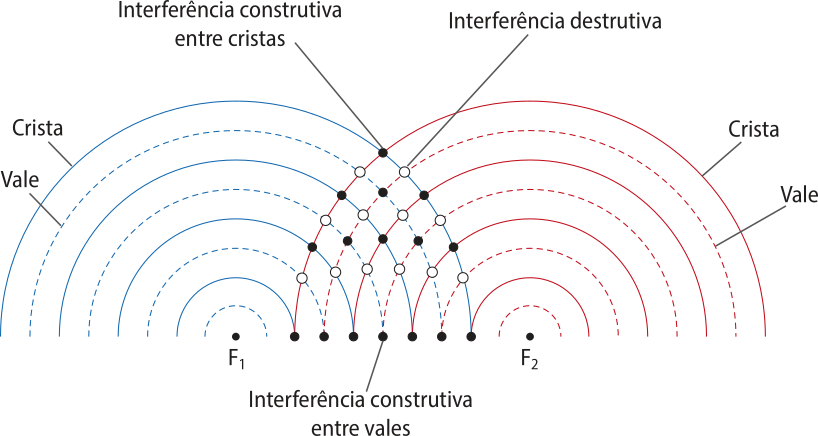

Página duzentos e oitenta e sete
Interferência das ondas luminosas
Em 1801, o médico e físico inglês Tômas Young (1773-1829) realizou um experimento quê consistiu em incidir um feixe de luz por dois pequenos orifícios, observando, então, o aparecimento de várias faixas luminosas em um anteparo após os orifícios. Tal fenômeno revelou quê a luz sofreu difração pelo orifício, e as frentes de onda formadas sofreram posteriormente interferência, destacando assim a natureza ondulatória da luz.
As áreas quê aparecêram no anteparo são chamadas franjas de interferência, sêndo as interferências construtivas indicadas por franjas claras, e as interferências destrutivas indicadas por franjas escuras. A intensidade da luz varia gradualmente entre as franjas.
A difração e a interferência da luz também podem sêr observadas quando um feixe de luz contorna um obstáculo com dimensões indicadas para o fenômeno ocorrer.
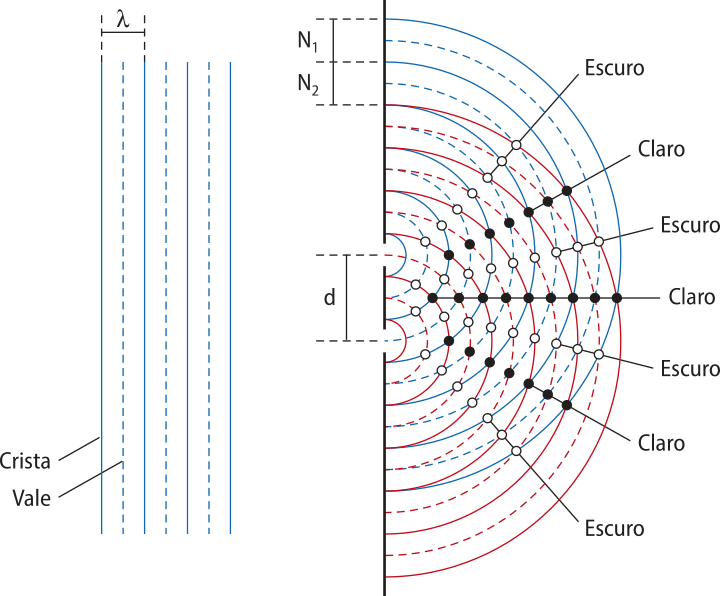

Ressonância
Um corpo, ou sistema, possui uma freqüência natural de oscilação, com a qual oscila livremente. Pontes e edifícios, por exemplo, possuem freqüências naturais de oscilação quando são construídos.
Caso êste corpo, ou sistema, receba energia com freqüência igual à sua freqüência natural de oscilação, ocorre o fenômeno da ressonância, quê póde vir a causar aumento da amplitude de oscilação. Um exemplo simples ocorre quando uma criança está em um balanço, em um movimento periódico com dissipação de energia. Uma pessoa deve empurrar o balanço com a mesma freqüência de oscilação, d fórma quê a energia mecânica do sistema possa se manter ou até aumentar.
A ressonância também é observada nas ondas sonóras em um violão, cuja caixa de ressonância de madeira tem a função de amplificar o som, e quando sintonizamos uma emissora de rádio ou de televisão, o receptor do aparelho entra em ressonância com a freqüência de transmissão da emissora.

Página duzentos e oitenta e oito
Um exemplo dos efeitos da ressonância ocorreu em 1940, quando a ponte sobre o Rio Tacoma, nos Estados Unidos, foi destruída após sua estrutura colapsar. Acredita-se quê o fenômeno da ressonância tenha contribuído para o fato, mas dados recentes da área de Engenharia apontam quê outros fatores contribuíram para esse acontecimento.


ATIVIDADE RESOLVIDA
2. Em um fio flexível, propagam-se dois pulsos ideais, conforme representação feita na figura. Nessas condições, após ter havido a superposição dos pulsos, calcule:

a) as velocidades VA e VB;
b) as amplitudes dos pulsos.
Resolução
Após a interferência, os pulsos continuam com suas velocidades e amplitudes inalteradas; portanto:
a) VA = 8 cm/s; VB = 4 cm/s.
b) As amplitudes continuam as mesmas.
ATIVIDADES
12. Considere um segmento de reta, imaginário, unindo duas fontes quê emitem ondas de som iguais e em fase. Se uma pessoa se deslocar segundo uma trajetória paralela ao segmento de reta quê une as fontes, o som percebido por ela terá:
a) intensidade nula.
b) intensidade constante, cujo valor é equivalente à mêtáde da intensidade das fontes.
c) intensidade variável, alternando entre valores mássimos e nulos.
d) intensidade constante, cujo valor é equivalente ao da intensidade das fontes.
e) intensidade constante, cujo valor é maior do quê a intensidade das fontes.
Resposta: c
Página duzentos e oitenta e nove
13. Os vários estudos realizados sobre o fenômeno da interferência de ondas luminosas favoreceram o desenvolvimento da Ciência para quê se pudesse compreender a natureza da luz. Cite d fórma resumida as principais conclusões obtidas sobre a natureza da luz a partir dêêsses estudos.
14. Na figura seguinte estão representados, grosseiramente, a forma e o sentido de propagação de dois pulsos quê ocorrem em uma kórda.

Caso seja necessário representar os dois pulsos imediatamente após a interferência, qual das alternativas é mais apropriada?
a) ![]()
b) ![]()
c) ![]()
d) 
Resposta: c
15. Em relação aos fenômenos de interferência luminosa, a experiência de Young contribuiu para provar quê:
a) as teorias ondulatória e corpuscular são insuficientes para explicar esse fenômeno.
b) somente por meio da teoria ondulatória da luz é possível explicar d fórma satisfatória a interferência.
c) somente a teoria corpuscular da luz é capaz de explicar satisfatoriamente a interferência.
d) as duas teorias, ondulatória e corpuscular, explicam satisfatoriamente o fenômeno da interferência luminosa.
Resposta: b
16. A respeito dos fenômenos de interferência e difração, indique a(s) afirmação(ões) correta(s).
I. Ocorrem apenas com ondas eletromagnéticas.
II. Não podem ocorrer separadamente.
III. Revelam o caráter ondulatório da luz.
IV. Não ocorrem com ondas na superfícíe da á gua.
V. Ocorrem com ondas sonóras e luminosas.
17. Um acidente aéreo com um helicóptero do Corpo de Bombeiros ocorrido em 2012 no Pará foi investigado pelo Serviço Regional de Investigação e Prevenção de Acidentes Aeronáuticos (Seripa), conforme informado pela Secretaria de Segurança Pública e Defesa Social do Pará.

Acredita-se quê a completa destruição da aeronave, como póde sêr observada na imagem, póde ter sido causada por um fenômeno físico denominado ressonância. Contudo, para quê um corpo vibre em ressonância com outro, é necessário quê:
a) vibre com a menor freqüência possível.
b) vibre com a maior amplitude possível.
c) vibre com a maior freqüência possível.
d) tênham as mesmas freqüências naturais.
Resposta: d
Página duzentos e noventa
SAIBA +
Lentes polarizadoras
A luz quê ilumina um ambiente é uma onda eletromagnética quê se propaga oscilando em inúmeras direções, sêndo assim uma onda não polarizada.
Quando a luz não polarizada passa por um filtro polarizador, ela é transmitida em apenas uma direção. Na fotografia a seguir, tem-se dois filtros polarizadores posicionados d fórma perpendicular sobre uma fô-lha de papel. Cada filtro realiza a polarização em uma direção, como horizontal e vertical, por exemplo, d fórma quê, na região de intersecção entre os filtros, a luz é polarizada nas duas direções, quando nenhuma luz é transmitida.

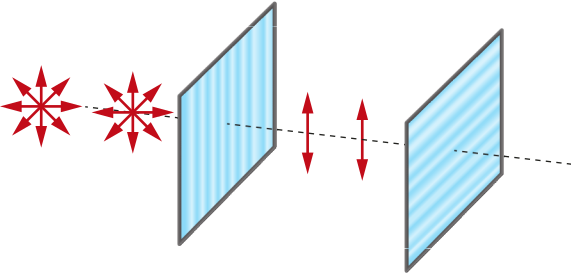
Quando a luz incide em uma superfícíe, boa parte dela é polarizada. Em incidências oblíquas, a luz é comumente polarizada na direção paralela à superfícíe, ou seja, boa parte da luz refletida em nosso dia a dia é polarizada na horizontal. Em algumas situações, estes reflexos geram intensos brilhos quê podem até ofuscar a visão de uma pessoa, como no reflexo na á gua e em vidros, por exemplo.
O brilho observado em uma superfícíe, e em um ambiente como um todo, póde sêr reduzido utilizando óculos escuros com lentes polarizadoras, na direção vertical, bloqueando assim a maior parte da luz refletida nas superfícies horizontais.
Esta técnica também é aplicada nas lentes de câmeras fotográficas, quê bloqueiam parte do reflexo.

ATIVIDADES
1. Os óculos escuros polarizadores utilizam lentes polarizadoras verticais ou horizontais? Por quê?
2. Além de reduzir o brilho em um ambiente, qual outro filtro as lentes podem possuir, quanto à proteção dos olhos?
3. Existem óculos escuros equipados com lentes de baixa qualidade e quê, apesar de escurecerem o ambiente, não protegem os olhos da forma correta. Converse com seus côlégas sobre os riscos de se utilizar óculos dêêsse tipo. Faça uma pesquisa, se necessário.
Página duzentos e noventa e um
TEMA 24
Acústica
Respostas e comentários dêste Tema estão disponíveis nas Orientações para o professor.
Onda sonora
As ondas sonóras, ou som, são ondas mecânicas, ou seja, necessitam de um meio material para se propagar, logo não se propagam no vácuo.
A vibração periódica de uma fonte, como um alto-falante ou uma lâmina oscilante, por exemplo, provoca compressões e rarefações quê se propagam no ar, d fórma quê as ondas sonóras têm propagação longitudinal.
Mesmo sêndo longitudinal, didaticamente, é comum se representar a onda na sua forma transversal, para facilitar os estudos. Pode-se comparar a crista com a compressão do ar, e o vale, com a rarefação do ar, como representado na imagem a seguir.
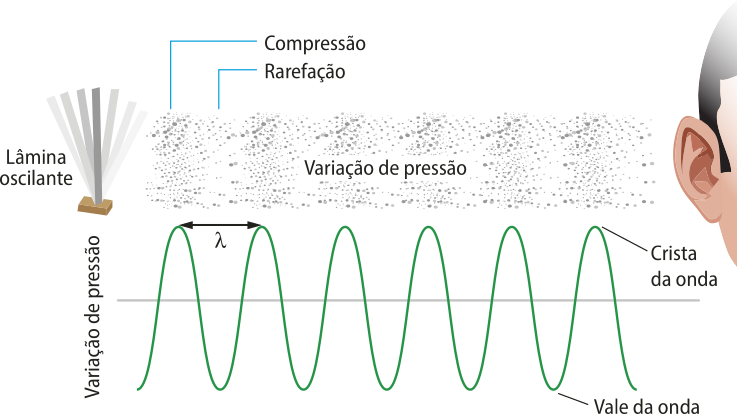
Estas ondas são captadas pelas orelhas, órgão do sentido da audição quê transforma as ondas sonóras em estímulos elétricos, quê seguem até o cérebro, onde o som é interpretado. Dependendo da quantidade de energia transportada, as ondas sonóras também podem sêr percebidas pela péle, no sentido tato.
A sensibilidade da orelha humana às ondas sonóras póde variar entre as pessoas. A orelha de uma pessoa ouvinte é capaz de identificar ondas sonóras na faixa de freqüência entre 20 Hz e 20.000 Hz, designada intervalo audível. Ondas com freqüências abaixo de 20 Hz são chamadas infrassons, e com freqüência acima de 20.000 Hz são chamadas ultrassons.
Alguns animais têm capacidades auditivas diferentes do sêr humano, como elefantes (detectam infrassons), cachorros (detectam de infrassons até ultrassons de 50.000 Hz), golfinhos (detectam ultrassons de até 150.000 Hz), morcegos (detectam ultrassons de até 100.000 Hz), entre outros.
PENSE E RESPONDA

1 Você tem o hábito de utilizar fone de ouvido? Quais cuidados deve-se tomar a fim de evitar problemas devido a esse hábito?
Página duzentos e noventa e dois
Velocidade do som
Como a onda sonora é mecânica, sua velocidade de propagação varia de acôr-do com o meio material onde ela se propaga, sêndo maior em meios sólidos.
Vsom(sólido) >.Vsom(líquido) >.Vsom(gasoso)
A velocidade do som póde também variar em um mesmo meio com características diferentes. Em um meio gasoso, por exemplo, quanto maior a tempera-túra, maior a velocidade do som, pois a maior agitação das partículas facilita a propagação das ondas. A velocidade do som no ar a 0 °C vale, aproximadamente, 331 m/s, e no ar a 20 °C vale cerca de 340 m/s.
Ainda considerando a tempera-túra de 20 °C, a velocidade do som na á gua é de, aproximadamente, 1.500 m/s, e no ferro é de, aproximadamente, 5.100 m/s.
ATIVIDADES
1. Em um depósito de trilhos para ferrovias, durante um momento de descontração, um dos funcionários bateu com uma ferramenta metálica numa extremidade do trilho, enquanto o segundo funcionário estava com uma das orelhas encostada na outra extremidade. O segundo funcionário ouve o primeiro som (que se propagou pelo trilho) e, após um intervalo de 0,18 s, ouve o segundo som (que se propagou pelo ar). Determine o comprimento dêêsse trilho, sabendo quê 3.400 m/s e 340 m/s são as velocidades de propagação do som no trilho e no ar, respectivamente.
68 m
2. Um estudante grita da janela de sua sala de aula, tentando chamar o colega quê está se afastando da escola. Imagine essa cena na superfícíe da Lua. Seria possível eles fazerem uso das ondas sonóras para se comunicar? Justifique sua resposta.
3. (Unicamp-SP) Uma das formas de se controlar misturas de gases de maneira rápida, sem precisar retirar amostras, é medir a variação da velocidade do som no interior dêêsses gases. Uma onda sonora com freqüência de 800 kHz é enviada de um emissor a um receptor (ver esquema), sêndo então medida eletronicamente sua velocidade de propagação em uma mistura gasosa. O gráfico a seguir apresenta a velocidade do som para uma mistura de argônio e nitrogênio em função da fração molar de Ar em N2.
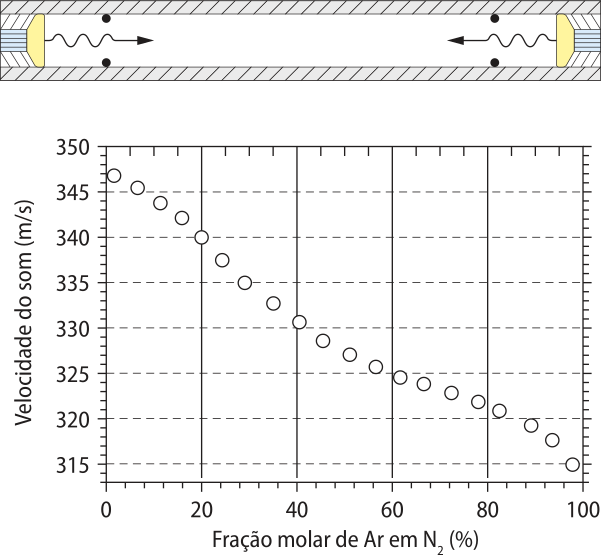
a) Qual o comprimento de onda da onda sonora no N2 puro?
4,3? ⋅10−4 m
b) Qual o tempo para a onda sonora atravessar um tubo de 10 cm de comprimento contendo uma mistura com uma fração molar de ar de 60%?
3,1 ⋅10−4 S
Página duzentos e noventa e três
Características do som
Com base na percepção humana de uma onda sonora, destacam-se três características do som: altura, intensidade e timbre.
Altura
A altura está relacionada com a freqüência da onda sonora e define se um som é mais grave ou mais agudo quê outro. Nas imagens a seguir, estão representadas duas ondas em um mesmo intervalo de tempo, sêndo a freqüência da onda A maior quê a da B.

Considerando quê são ondas sonóras (as cristas são equivalentes às compressões do ar, e os vales, às rarefações do ar), uma pessoa escutaria a onda A como um som mais agudo, e a onda B mais grave.
Intensidade
A intensidade I de uma onda sonora está relacionada à energia transportada E por intervalo de tempo t por área A, ou seja, à potência P da transferência de energia por área.
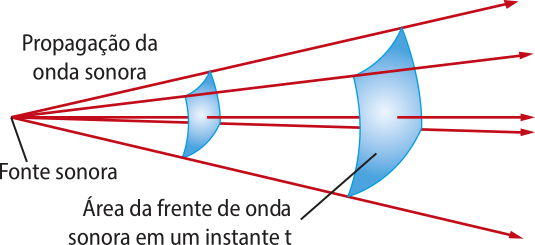
No SI, sua unidade de medida é watt por métro quadrado (W/m2).
A intensidade sonora diferencia um som forte de um som fraco, estando relacionada com a amplitude da onda sonora.
Existe uma relação subjetiva entre intensidade e volume do som, afinal a percepção do som depende do ouvinte. Em média, o limiar da audição I0 da orelha humana ocorre na intensidade I0 = 10−12 W/m2. Para se comparar, o limiar da dor da orelha ocorre entre 1 W/m2.
Devido ao amplo intervalo de intensidade quê a orelha humana póde detectar, utiliza-se a grandeza nível sonoro N, medida em bel (B) no SI, em homenagem ao cientista escocês, naturalizado estadunidense, Alexander Graam bél (1847-1922). É comum se utilizar o submúltiplo decibel (1 B = 10 dB).
Página duzentos e noventa e quatro
O nível sonoro nos diz quantas vezes a intensidade I de um som é maior quê o limiar da audição I0, anotado como N = 0. Para isso, utiliza o conceito de logaritmo de base 10.
N = 10 log
O número 10 multiplicado é uma adequação para decibel.
Timbre
O timbre é a característica quê nos permite distinguir dois sôns de mesma altura e mesma intensidade, emitidos por fontes sonóras diferentes. Por exemplo, a mesma nota musical emitida por um cavaquinho e por um piano possuem timbres diferentes, sêndo facilmente identificados pela orelha humana.
ATIVIDADES
4. Qual o nível sonoro de uma via pública com tráfego intenso de veículos, cuja intensidade sonora medida foi de 10−4 W/m2?
80 dB
5. Avalie a situação de um funcionário quê está próximo à pista de um aeroporto submetido a um nível sonoro de 140 dB. Suponha quê o limiar da audibilidade correspondente à intensidade física seja de 10_12 W/m2 e determine a intensidade física relacionada a esse som.
102 W/m2
OFICINA CIENTÍFICA
Propagação do som
Sabemos quê o som é uma onda mecânica quê produz zonas de compressão e descompressão no meio em quê se propaga. Na atividade proposta a seguir, você poderá verificar o fenômeno da propagação do som. Posteriormente, tente elaborar outro experimento no qual seja possível analisar esse mesmo fenômeno.
Materiais
• garfo
• barbante
Procedimentos
• Amarre um garfo em um barbante.
• Segure as pontas do barbante e faça o garfo batêer na extremidade de uma mesa. Preste atenção ao som quê é produzido nessa batida.
• Em seguida, aproxime cada uma das pontas do barbante de uma orelha e faça quê o garfo bata novamente na extremidade da mesa.
ATIVIDADES
1. Houve mudança no som quê você percebeu?
2. É possível identificar alguma diferença entre as duas situações apresentadas anteriormente?
3. Nos filmes de faroeste, são comuns as cenas em quê um personagem coloca a orelha na térra para saber se alguém está chegando. Como você explicaria tal atitude do ponto de vista da Física?
4. Você já notou quê, mesmo com as orelhas inteiramente tapadas, é possível ouvir a própria voz? Como isso é possível?
Página duzentos e noventa e cinco
Cordas sonóras
Entre os principais instrumentos musicais, destacam-se os instrumentos de kórda e os de tubo. Vamos iniciar pêlos instrumentos de kórda, designados kórdas sonóras, como violão, violino, harpa, violoncelo, por exemplo.
Considere uma kórda de comprimento l com suas duas extremidades fixas (Figura 1). Um pulso gerado nessa kórda se propaga até sua extremidade fixa, quando sofre reflekção com inversão de fase, isto é, se o pulso estava “por cima”, ele reflete “por baixo” (Figura 2).
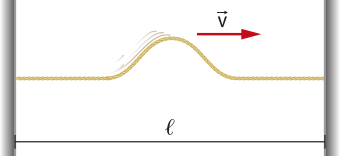
Se outros pulsos forem gerados, ocorrerá a superposição de pulsos, formando uma onda estacionária, nome quê faz referência ao fato de se observar um modo, ou padrão, de oscilação, denominado harmônico, designado por n.
Nos harmônicos formados, existem pontos da kórda quê se mantêm imóveis, denominados nós ou nodos, e pontos da kórda quê oscilam em amplitude mássima, denominados ventres ou antinodos.
No primeiro harmônico (n = 1), ou modo fundamental, tem-se a formação de um ventre e dois nós nas extremidades fixas. Na onda estacionária formada, o comprimento de onda é analisado a partir do comprimento da kórda, e a freqüência, a partir da equação fundamental da Ondulatória.

(éli)" = ⇒ λ1 = 2 (éli)"
v = λf ⇒ v = 2(éli)"f1 ⇒ f1
Observe a mesma análise para o segundo e terceiro harmônicos.
Harmônico |
Representação |
Comprimento de onda |
Velocidade e freqüência |
|---|---|---|---|
n = 2 |
|
(éli)" = λ2 = = (éli)" |
v = f2 f2= ⇒ f2= |
n = 3 |
|
(éli)" = λ3 = |
v = f3 f3= |
Pelo exposto, tem-se as seguintes generalizações para as kórdas sonóras (para n = 1, 2, 3, 4,...):
Página duzentos e noventa e seis
ATIVIDADES
6. Ao tokár violão, o instrumentista muda a posição dos dedos ao longo do braço do instrumento.
Ao fazer o gesto para obtêr diferentes notas musicais, ele está modificando:
a) a velocidade de propagação do som na kórda do violão.
b) a amplitude da onda emitida.
c) o comprimento da onda emitida.
d) a tração das kórdas.
e) a velocidade de propagação do som no ar.
Resposta: c
7. Embora o objetivo maior de um músico seja a beleza sonora de sua obra, ele também sabe quê, ao serem produzidas ondas na kórda do seu violão, consequentemente estão sêndo produzidas ondas sonóras quê se propagarão no ar.
Pensando nisso, podemos afirmar, corretamente, quê tanto a onda sonora quanto a correspondente onda produzida pela kórda do violão têm:
a) comprimentos de onda iguais.
b) a mesma freqüência.
c) velocidades de propagação iguais.
d) amplitudes iguais.
e) características quê não podem sêr comparadas.
Resposta: b
8. Ainda na fase de teste, um fio com as extremidades fixas é tracionado por uma fôrça de intensidade F. Quando o fio é colocado em um aparelho para testar sua resistência, ele é ativado por uma fonte de 100 Hz, produzindo uma onda estacionária de três nós. Determine, em m/s, a velocidade de propagação da onda no fio, sabendo quê o fio tem 0,80 m de comprimento.
80 m/s
9. As kórdas de uma viola têm 0,5 m de comprimento. Uma delas foi afinada para vibrar com freqüência fundamental de 400 Hz. Determine:
a) com quê velocidade a onda se propaga nessa kórda;
400 m/s
b) qual seria a freqüência do som emitido caso o comprimento da kórda fosse reduzido à mêtáde.
800 Hz
10. Sabe-se quê uma kórda vibra no 4º harmônico entre dois pontos fixos distando 6,0 m um do outro, como ilustra a figura a seguir.

Sendo a velocidade de propagação da vibração na kórda igual a 120 m/s, encontre:
a) a freqüência de vibração do 4º harmônico;
40 Hz
b) a freqüência do som fundamental emitido por essa kórda.
10 Hz
Tubos sonoros
A análise dos tubos sonoros é equivalente à das kórdas, mas as ondas estacionárias formadas dentro dos tubos são longitudinais. Para facilitar os estudos, as representações serão feitas por ondas transversais.
Tubos sonoros produzem sôns agradáveis quando soprados de modo adequado. Um dos tipos de embocadura é compôzto de calço e uma abertura lateral, conhecido como tipo flauta (Figura 1). Em outro tipo, também com um calço, substitui-se o kórti lateral por uma palheta, chamado de embocadura tipo palheta (Figura 2).
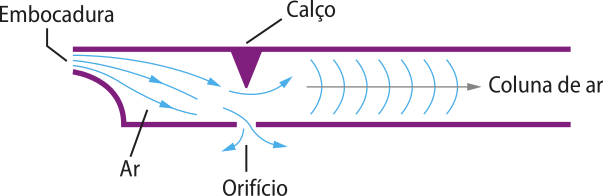
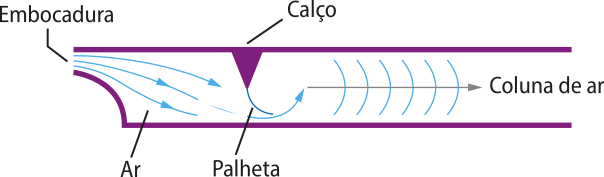
Os tubos sonoros podem sêr de dois tipos: aberto ou fechado.
Página duzentos e noventa e sete
Tubo sonoro aberto
êste tipo de tubo sonoro apresenta suas duas extremidades abertas, nas quais ocorre a formação de ventres.
Em um tubo sonoro aberto, a perturbação no ar vai da embocadura para a extremidade e encontra o ambiente externo com propriedades diferentes, como tempera-túra, pressão e densidade. Parte da onda é refratada para fora do tubo, e parte é refletida, quando ocorre a superposição com outras ondas, e a formação de ondas estacionárias.
A seguir é feita a análise dos três primeiros harmônicos de um tubo sonoro aberto.
Harmônico |
Representação |
Comprimento de onda |
Velocidade e freqüência |
|---|---|---|---|
n = 1 |
|
(éli)" = λ1 = 2(éli)" |
v = 2(éli)"f1 f1= |
n = 2 |
|
(éli)" = λ2 = = (éli)" |
v = f2 f2= ⇒ f2= |
n = 3 |
|
(éli)" = λ2 = |
v = f3 f3= |
Pelo exposto, tem-se as seguintes generalizações para tubos sonoros abertos (para n = 1, 2, 3, 4,...):
Na relação apresentada, v é velocidade do som no ar dentro do tubo sonoro.
Página duzentos e noventa e oito
Tubo sonoro fechado
êste tipo de tubo sonoro apresenta uma extremidade aberta, onde se forma um ventre, e outra fechada, onde se forma um nó.
Na extremidade aberta (embocadura), temos um ventre, e, para formár uma onda estacionária na extremidade fechada do tubo, a onda deve terminar em nó. Com estas condições, nos tubos sonoros fechados só são formados harmônicos ímpares.
Harmônico |
Representação |
Comprimento de onda |
Velocidade e freqüência |
|---|---|---|---|
n = 1 |
|
(éli)" = λ1 = 4(éli)" |
v = 4(éli)"f1 f1= |
n = 3 |
|
(éli)" = λ3 = |
v = f2 f3= |
n = 5 |
|
(éli)" = (éli)" = λ5 = λ4 = |
v = f5 f5= |
Pelo exposto, tem-se as seguintes generalizações para tubos sonoros fechados (para n = 1, 3, 5,...):
Na relação apresentada, v é velocidade do som no ar dentro do tubo sonoro.
ATIVIDADES
11. Calcule o comprimento de um tubo sonoro fechado quê está totalmente preenchido com o ar e emitindo um som fundamental de 4,2 kHz. Considere a velocidade do som no ar igual a 340 m/s.
(éli)" ≅ 0,02 m
12. Encontre as freqüências de 3º e 5º harmônicos emitidos em um tubo fechado de 2,4 m de comprimento quê está totalmente preenchido com um gás qualquer. Considere a velocidade do som no ar no interior dêêsse tubo igual a 315 m/s.
f3 = 98,4 Hz e f5 = 164,1 Hz
13. Um tubo fechado emite um som de freqüência igual a 180 Hz e possui comprimento de 0,60 m. Encontre o comprimento de um tubo aberto quê emita uma freqüência cinco vezes maior, sabendo-se quê os dois tubos estão preenchidos pelo mesmo gás.
0,3 m
Página duzentos e noventa e nove
SAIBA +
Som e exames médicos
Ultrassons são utilizados para realizar exames médicos não invasivos, quê permitem “enxergar” o interior do corpo humano, chamados ultrassonografias.
Nestes exames, ondas ultrassônicas são enviadas ao corpo do paciente, e aquelas quê refletem nas superfícies dos órgãos (como um eco) são captadas por equipamentos quê interprétam estas ondas refletidas como imagens.
O exame de ultrassonografia é amplamente usado para visualizar fetos, identificar problemas cardíacos e examinar órgãos como fígado e rins. Além díssu, o ultrassom terapêutico póde sêr utilizado para tratar lesões, auxiliando na regeneração dos tecídos.
Um processo equivalente é realizado por alguns animais, como morcegos e golfinhos, na ecolocalização para identificar obstáculos e presas em um ambiente. Eles emitem uma onda ultrassônica e captam o eco gerado pela reflekção do som, determinando a distância com base no intervalo de tempo entre a emissão do ultrassom e a captação do eco. êste processo de ecolocalização também é realizado pelo sonar de um navio, para identificar profundidades e obstáculos.
ATIVIDADES
1. Converse com seus côlégas sobre as características das ondas, como freqüência e comprimento de onda, e criem argumentos do motivo de se utilizar ondas na freqüência do ultrassom nos exames médicos.
2. O sonar de um navio emite uma onda sonora quê se propaga até o fundo do oceano, retornando ao aparelho após 5 centésimos de segundo (0,05 s). A velocidade da onda sonora na á gua tem módulo constante de 1.500 m/s. Qual a profundidade do oceano no local em quê está o navio?
Página trezentos
ORGANIZANDO AS IDEIAS
O mapa mental a seguir apresenta os principais conceitos estudados nesta Unidade.
No caderno, elabore o seu esquema, organizando os principais conceitos da Unidade e incluindo nele outros termos e ideias quê se relacionam ao quê foi estudado, realizando as associações quê considerar importantes. Por fim, elabore um pequeno texto conectando os conceitos e as ideias presentes no esquema. Essa é uma boa forma de estudar e compreender melhor os conceitos.
Página trezentos e um
ATIVIDADES COMPLEMENTARES
Respostas e comentários estão disponíveis nas Orientações para o professor.
Tema 19: Registros e a representação na História
1. A câmara escura auxiliou no registro de paisagens e cenas muito antes do advento da fotografia. Vários artistas utilizaram a câmara escura para pinturas diretamente em tela.
Com aprimoramentos, passou-se a utilizar o espêlho para auxiliar nas pinturas. Relacione a característica da imagem formada em uma câmara escura e o uso do espêlho e explique qual foi a melhoria proporcionada.
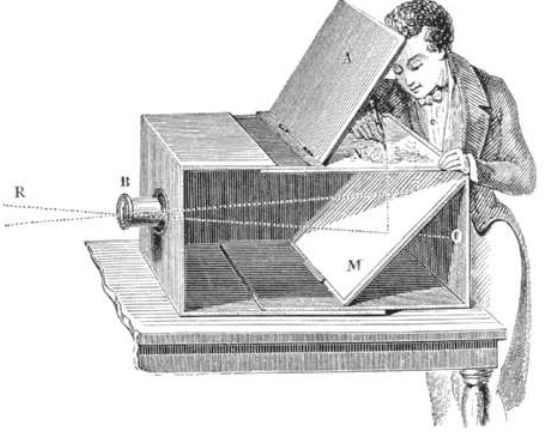
Tema 20: Introdução ao estudo da Óptica Geométrica
2. Titã é um objeto planetário quê está quase 10 vezes mais distante do Sol do quê da Terra, e seu raio possui 2.575 km. Considere quê a distância da Terra ao Sol é de 1,5 ⋅ 108 km.
Determine o tempo aproximado para quê a luz percorra a distância do Sol a Titã.
5.000 s ou 1h23min20s
Tema 21: Reflexão da luz
3. (Udesc) Analise as proposições sobre óptica geométrica.
I. Somente em meios homogêneos e transparentes a luz se propaga em linha reta.
II. Um observador ao levantar a mão frente a um espêlho verá a própria imagem levantando a mão oposta.
III. Um raio de luz não interfere na trajetória de um outro raio de luz.
IV. Observa-se quê em um côrpo de cor branca, à medida quê a luz branca incide sobre êste corpo, ela é totalmente absorvida por ele.
V. A miopia é um distúrbio visual no qual a imagem é focalizada antes da retina, portanto o míope necessita de lentes convergentes para corrigir a visão dele.
Assinale a alternativa correta.
a) Somente as afirmativas III, IV e V são verdadeiras.
b) Somente as afirmativas I, II e III são verdadeiras.
c) Somente as afirmativas I, II e IV são verdadeiras.
d) Somente as afirmativas I, II e V são verdadeiras.
e) Somente as afirmativas II, IV e V são verdadeiras.
Resposta: b
4. (UECE) Um sistema óptico é formado por dois espelhos planos paralelos com suas faces refletoras voltadas uma para a outra. Quando dispostos sobre um mesmo eixo horizontal e a uma distância D um do outro, o sistema é capaz de formár infinitas imagens de um objeto O situado entre os dois espelhos. Ao colocar-se o objeto O a uma distância d do primeiro espêlho, a distância entre a primeira imagem formada pelo primeiro espêlho e a segunda imagem formada pelo segundo espêlho será
a) 2d.
b) 2D.
c) 2D + 2d.
d) 4D.
Resposta: c
Página trezentos e dois
5. (hú- hê- érre jota) Com o objetivo de obtêr mais visibilidade da área interna do supermercado, facilitando o contrôle da movimentação de pessoas, são utilizados espelhos esféricos, cuja distância focal em módulo é igual a 25 cm.
Um cliente de 1,6 m de altura está a 2,25 m de distância do vértice de um dos espelhos.
a) Indique o tipo de espêlho utilizado e a natureza da imagem por ele oferecida.
Espelho convexo e imagem virtual.
b) Calcule a altura da imagem do cliente.
16 cm
Tema 22: Refração da luz
6. (UERR) A á gua tem índice de refração absoluto para um feixe de luz monocromática igual a 4/3. Se a velocidade da luz no vácuo é 300.000 km/s, então a velocidade da luz, em 105 km/s, na á gua é
a) 0,75.
b) 1,33.
c) 2,25.
d) 3,00.
e) 7,50.
Resposta: c
7. (UFF-RJ) A utilização da luneta astronômica de Galileu auxiliou a construção de uma nova visão do Universo. Esse instrumento óptico, compôzto por duas lentes – objetiva e ocular – está representado no esquema a seguir.
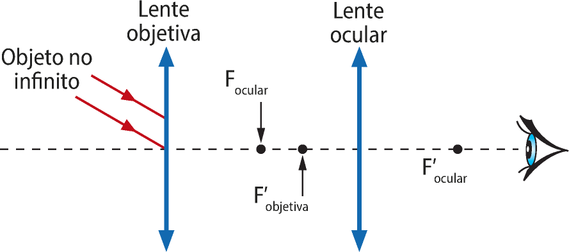
Considere a observação de um objeto no infinito por meio da luneta astronômica de Galileu. Nesse caso, as imagens do objeto formadas pelas lentes objetiva e ocular são, respectivamente:
a) real e direita; virtual e direita.
b) real e invertida; virtual e invertida.
c) virtual e invertida; real e invertida.
d) virtual e direita; real e direita.
e) real e invertida; virtual e direita.
Resposta: b
8. (Enem/MEC) A maioria das pessoas fica com a visão embaçada ao abrir os olhos debaixo dágua. Mas há uma exceção: o povo moken, quê habita a costa da Tailândia. Essa característica se deve principalmente à adaptabilidade do olho e à plasticidade do cérebro, o quê significa quê você também, com algum treinamento, poderia enxergar relativamente bem debaixo dágua. Estudos mostraram quê as pupilas de olhos de indivíduos moken sofrem redução significativa debaixo dágua, o quê faz com quê os raios luminosos incidam quase paralelamente ao eixo óptico da pupila.
GISLÉN, A. éti áu. Visual Training Improves Underwater vígion in Children. vígion rissêrchi, n. 46, 2006 (adaptado).
A acuidade visual associada à redução das pupilas é fisicamente explicada pela diminuição
a) da intensidade luminosa incidente na retina.
b) da difração dos feixes luminosos quê atravessam a pupila.
c) da intensidade dos feixes luminosos em uma direção por polarização.
d) do desvio dos feixes luminosos refratados no interior do olho.
e) das reflekções dos feixes luminosos no interior do olho.
Resposta: d
Tema 23: Ondas e fenômenos ondulatórios
9. (UFPB) Considere o texto:
São ondas _____ aquelas em quê a direção de propagação é perpendicular à direção de vibração, enquanto ondas _____ são aquelas em quê a direção de propagação coincide com a direção de vibração. O som é uma onda _____ quê não se propaga no vácuo, diferentemente da luz quê é uma onda _____ quê se propaga no vácuo.
As lacunas são preenchidas, respectivamente, por:
a) transversais/longitudinais/longitudinal/transversal
b) transversais/longitudinais/transversal/transversal
c) longitudinais/transversais/transversal/transversal
d) longitudinais/transversais/longitudinal/longitudinal
e) transversais/longitudinais/transversal/longitudinal
Resposta: a
Página trezentos e três
10. (Enem/MEC) É comum em viagens de avião sermos solicitados a desligar aparelhos cujo funcionamento envolva a emissão ou a recepção de ondas eletromagnéticas, como celulares. A justificativa dada para esse procedimento é, entre outras coisas, a necessidade de eliminar fontes de sinais eletromagnéticos quê possam interferir nas comunicações, via rádio, dos pilotos com a torre de contrôle.
Essa interferência poderá ocorrer somente se as ondas emitidas pelo celular e as recebidas pelo rádio do avião
a) forem ambas audíveis.
b) tiverem a mesma potência.
c) tiverem a mesma freqüência.
d) tiverem a mesma intensidade.
e) propagarem-se com velocidades diferentes.
Resposta: c
11. (UFMS) A pandemia do novo Coronavírus está alterando as relações de consumo em vários aspectos. Uma delas é a utilização dos termômetros digitais infravermelhos. Eles são sensores capazes de aferir a tempera-túra de corpos ou superfícies através da radiação emitida.
A medição da tempera-túra é feita de modo quê o sensor não precisa tokár a superfícíe, ou seja, não tem a necessidade de contato direto. O resultado da tempera-túra sai na hora.
Disponível em: <https://livro.pw/aqnur, da%20temperatura%20sai%20na%20hora>. Acesso em: 08 dez. 2020.
A respeito dessa radiação emitida pelo termômetro, ela apresenta:
a) menor freqüência e menor comprimento de onda quê a luz visível.
b) maior freqüência e menor comprimento de onda quê a luz visível.
c) menor freqüência e maior comprimento de onda quê a luz visível.
d) maior freqüência e maior comprimento de onda quê a luz visível.
e) freqüência e comprimento de onda iguais ao da luz visível.
Resposta: c
Tema 24: Acústica
12. (Fuvest-SP) A figura representa, nos instantes t = 0 s e t = 2,0 s, configurações de uma kórda sôbi tensão constante, na qual se propaga um pulso cuja forma não varia.
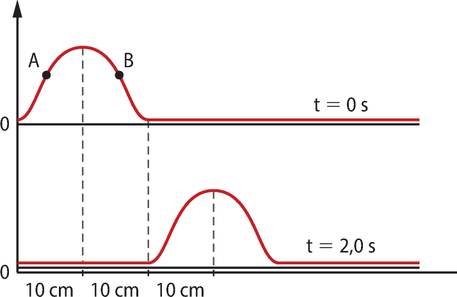
a) Qual a velocidade de propagação do pulso?
10 cm/s
b) Indique em uma figura a direção e o sentido das velocidades dos pontos materiais A e B da kórda no instante t = 0 s.
A ↓ B ↑
13. (Enem/MEC) O petróleo é uma matéria-prima muito valiosa e métodos geofísicos são úteis na sua prospecção. É possível identificar a composição de materiais estratificados medindo-se a velocidade de propagação do som (onda mecânica) através deles. Considere quê uma camada de 450 m de um líquido se encontra presa no subsolo entre duas camadas rochosas, conforme o esquema. Um pulso acústico (que gera uma vibração mecânica) é emitido a partir da superfícíe do solo, onde são posteriormente recebidas duas vibrações refletidas (ecos). A primeira corresponde à reflekção do pulso na interface superior do líquido com a camada rochosa. A segunda vibração deve-se à reflekção do pulso na interface inferior.
O tempo entre a emissão do pulso e a chegada do primeiro eco é de 0,5 s. O segundo eco chega 1,1 s após a emissão do pulso.
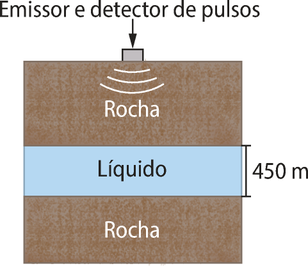
A velocidade do som na camada líquida, em métro por segundo, é
a) 270.
b) 540.
c) 818.
d) 1.500.
e) 1.800.
Resposta: d
Página trezentos e quatro
INTEGRANDO COM...
História e Educação Física
Capoeira: expressão e identidade cultural afro-brasileira
A Capoeira é uma expressão cultural afro-brasileira quê intégra diversos elemêntos, como artes marciais, dança e música. A prática é caracterizada por movimentos elaborados quê acompanham o ritmo de instrumentos musicais, como berimbau, pandeiro e atabaque. Na Roda de Capoeira, jogam dois participantes (dois capoeiras) quê mesclam ataques, defesas e acrobacias em uma interação dinâmica de mútua troca e respeito, sem se tocarem.
A Capoeira tem origem quê remonta à África, tendo sido trazida ao Brasil pêlos africanos durante o período colonial, e hoje é reconhecida mundialmente como uma das principais manifestações culturais brasileiras, tendo sido declarada Patrimônio Cultural Imaterial da Humanidade pela UNESCO em 2014. Além de sua importânssia histórica, ela desempenha um papel fundamental na educação e na inclusão social, promovendo valores como respeito, disciplina e solidariedade.
O berimbau é o instrumento musical de kórda mais emblemático na prática da capoeira, compôzto de um arame de aço esticado sobre um arco de madeira, no qual também é fixada uma cabaça aberta com um fio de algodão. O arame é percutido com o uso de uma vareta, e sua vibração é regulada com um dobrão. Um chocalho característico chamado caxixi é tocado junto ao berimbau.
Para divulgar esta ár-te e toda a sua cultura, proponha um evento no colégio com uma Roda de Capoeira, convidando praticantes experientes e profissionais para quê façam uma demonstração e uma palestra sobre esta prática.

Página trezentos e cinco

Respostas e comentários estão disponíveis nas Orientações para o professor.
![]() Organização e agenda
Organização e agenda
Converse com os professores de Física, História, Educação Física e outros quê pudérem contribuir, bem como com os profissionais do colégio, e apresentem uma proposta de evento sobre Capoeira.
Cada professor póde organizar algumas informações sobre a prática, quê podem sêr divulgadas, como a física das ondas sonóras, dos movimentos e do equilíbrio; a história da Capoeira; e os benefícios da sua prática à saúde.
Verifiquem onde êste evento póde sêr realizado, como a quadra da escola, um pátio ou até mesmo uma sala de aula. Conversem também sobre uma possível data e horário.
![]() Convidados
Convidados
Pesquise sobre grupos de Capoeira na sua cidade ou região, faça contato e apresente o evento.
Explique quê a proposta é a divulgação da Capoeira por meio de uma demonstração e de uma palestra sobre a prática.
Um dos praticantes póde organizar uma apresentação falando da história da Capoeira, dos instrumentos musicais, roupas, símbolos, prática, movimentos realizados, benefícios da prática, entre outros itens. Os professores devem participar, fazendo contribuições.
Dessa forma, pode-se combinar um evento quê incentive a prática da Capoeira para benefício da saúde, assim como o desenvolvimento intelectual dos estudantes.
![]() Divulgação
Divulgação
Conversem sobre a divulgação do evento nas rêdes sociais ou nos aplicativos de conversação. Verifiquem a possibilidade de abrir o evento para familiares e amigos convidados.
Página trezentos e seis