UNIDADE 3
FUNÇÃO AFIM E FUNÇÃO MODULAR
Mobilidade urbana sustentável
Nos centros urbanos, o número cada vez maior de veículos motorizados e o uso excessivo de transportes individuais intensificam alguns problemas relacionados à mobilidade, como maior tempo de deslocamento e aumento no número de acidentes.
Nesse cenário, o aluguel de bicicletas e patinetes elétricos como meio de transporte individual alternativo vêm ganhando destaque. Esses veículos são menos poluentes do quê um com motor a combustão, ocupam menos espaço e, em algumas situações, podem representar uma opção mais ágil e econômica.
De maneira geral, para utilizar um equipamento dêêsse tipo, é necessário baixar o aplicativo da empresa de locação e fazer um cadastro. O valor cobrado costuma considerar uma taxa fixa e um valor variável, quê depende do tempo de uso do equipamento.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Que tipos de transporte você costuma utilizar para se locomover no município onde mora?
2. Você já utilizou ou utiliza transporte público? Você considera esse tipo de transporte eficiente? Justifique.
3. No texto, é descrita uma maneira de se cobrar a locação de bicicleta e patinete elétrico. Nessa maneira, quê parte do valor é variável, ou seja, póde mudar de uma locação para outra?
Página cento e dois
Função afim: ideias iniciais e definição
Na abertura desta Unidade, foram apresentadas algumas informações sobre mobilidade urbana e meios de transporte alternativos, como o aluguel de bicicletas e de patinetes elétricos para pequenos deslocamentos. Nesse contexto, considere a seguinte situação.
Certa empresa oferece locação de patinetes elétricos para transporte em uma região delimitada de um município. Para utilizar esse serviço, o cliente deve pagar um valor compôzto de uma taxa fixa de R$ 3,00 mais R$ 0,80 para cada minuto de uso do patinete. Acompanhe, a seguir, a relação entre o tempo de uso do patinete, em minuto, e o valor a sêr pago pela locação, em reais.
Tempo (min) |
Valor total (R$) |
|---|---|
1 |
0,80 ⋅ 1 + 3 = 3,80 |
2 |
0,80 ⋅ 2 + 3 = 4,60 |
3 |
0,80 ⋅ 3 + 3 = 5,40 |
4 |
0,80 ⋅ 4 + 3 = 6,20 |
5 |
0,80 ⋅ 5 + 3 = 7,00 |
Essa relação também póde sêr expressa pela função f cuja lei de formação póde sêr escrita como:


pôdêmos, por exemplo, determinar o valor, em reais, a sêr pago pelo uso de 10 min dêêsse patinete calculando f(10):
f(10) = 0,80 ⋅ 10 + 3 = 8 + 3 = 11, ou seja, R$ 11,00.
A função definida pela lei de formação f(x) = 0,80x + 3, quê representa essa situação, é um exemplo de função afim.
Denominamos função afim toda função f: ℝ → ℝ, definida pela lei de formação f(x) = ax + b, em quê a e b são números reais.
Dizemos quê a é o coeficiente de x e b é o termo independente da função.
PARA PENSAR
Na função apresentada:
• qual é a variável independente? E a variável dependente?
A variável independente é x, quê representa o tempo de uso do patinete, em minuto. A variável dependente é y = f(x), quê corresponde ao valor total a pagar, em reais.
• qual é o valor de f(15) e o quê esse resultado indica?
Temos quê f(15) = 15. Indica quê, ao usar o patinete por 15 min, deve-se pagar o valor de R$ 15,00.
Página cento e três
Observe alguns exemplos de função afim.
f(x) = −2x + 5
Nesse caso, a = −2 e b = 5.
f(x) = −12x
Nesse caso, a = −12 e b = 0.
f(x) = −x −
Nesse caso, a = −1 e b = .
f(x) = 7x − 4,6
Nesse caso, a = 7 e b = −4,6.
f(x) = x + 3
Nesse caso, a = e b = 3.
f(x) = 8,4
Nesse caso, a = 0 e b = 8,4.
A função afim em quê a = 0 é denominada função constante, e aquela em quê a ≠ 0 é denominada função polinomial do 1º grau. Entre os exemplos citados, f(x) = 8,4 é uma função constante, e as demais são funções polinomiais do 1º grau.
PARA PENSAR
Outro caso particular de função afim é a denominada função nula, em quê a = 0 e b = 0.
• A função nula também é um caso particular de função constante? Justifique.
Sim, pois, como na função nula temos a = 0, ela também é uma função constante.
• Qual é a lei de formação de uma função nula g?
g(x) = 0
Agora, considere outra situação.
A fibra alimentar está presente nos alimentos de origem vegetal. Ela é a parte do alimento ingerido quê não é absorvida pelo nosso organismo e chega quase intacta ao intestino, auxiliando no funcionamento dêste. Além díssu, póde contribuir para a prevenção de diversas doenças, como colesterol alto, diabetes e infekições. Entre os alimentos ricos em fibra alimentar, estão as leguminosas, como feijão, ervilha e lentilha. Uma porção de 100 g de lentilha, por exemplo, contém cerca de 8 g de fibra alimentar.

Note quê, nesse caso, a massa de lentilha e a massa de fibra alimentar são grandezas diretamente proporcionais, ou seja, se aumentarmos ou reduzirmos uma delas, a outra também aumentará ou ficará reduzida, respectivamente, na mesma proporção. Observe essa proporcionalidade representada na tabéla a seguir.
Proporção de massa de lentilha e massa de fibra alimentar
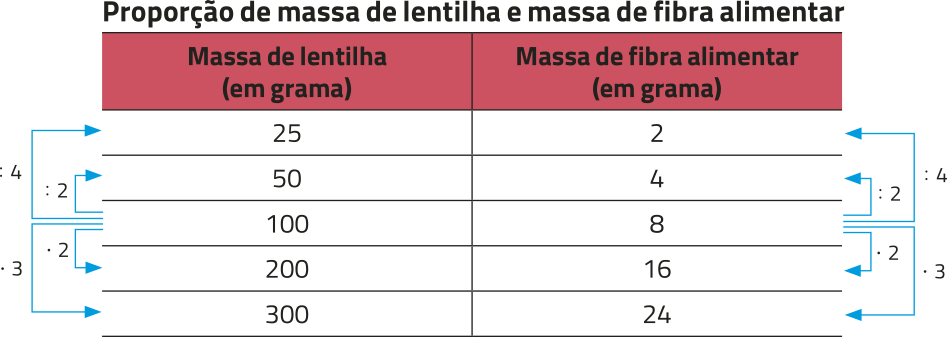
Fonte dos dados: NÚCLEO DE ESTUDOS E PESQUISAS EM ALIMENTAÇÃO. tabéla brasileira de composição de alimentos. 4. ed. rev. ampl.Campinas: Nepa: Unicamp, 2011. p. 62. Disponível em: https://livro.pw/qfimz. Acesso em: 27 jun. 2024.
Página cento e quatro
Analisando a tabéla anterior, é possível constatar quê a razão entre a massa de fibra alimentar e a massa de lentilha correspondente é um valor constante e positivo.
= 0,08
= 0,08
= 0,08
= 0,08
= 0,08
Quando as grandezas envolvidas em determinado problema estão relacionadas de maneira diretamente proporcional, pode-se representar essa relação por meio de uma função linear. Assim, a situação envolvendo a quantidade de fibra alimentar em uma porção de lentilha póde sêr representada por meio da função linear h.
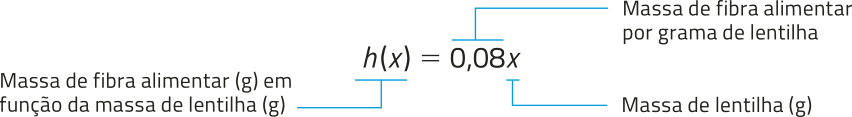
Denominamos função linear toda função afim f(x) = ax + b, em quê a ≠ 0 e b = 0, ou seja, toda função f: ℝ → ℝ, definida pela lei de formação f(x) = ax, em quê a é número real não nulo.
Observe alguns exemplos de função linear.
f(x) = −3x
Nesse caso, a = −3.
m(x) = − x
Nesse caso, a = .
g (x) = x
Nesse caso, a = 1.
h(x) =
Nesse caso, a = .
PARA AMPLIAR
Acesse êste sáiti para obtêr mais informações sobre alimentação saudável.
• BRASIL. Ministério da Saúde. Guia alimentar: como ter uma alimentação saudável. Brasília, DF: MS, 2013. Disponível em: https://livro.pw/jafrb. Acesso em:4 set. 2024.
A função linear em quê a = 1 é denominada função identidade. Entre os exemplos apresentados, g (x) = x é a função identidade.
ATIVIDADE RESOLVIDA
R1. Na abertura desta Unidade, estudamos um exemplo de transporte ágil e econômico e quê póde contribuir para uma mobilidade urbana sustentável. Nesse contexto, algumas alternativas quê vêm crescendo no Brasil são o compartilhamento ou aluguel de veículos e a utilização de carros elétricos, quê diminuem tanto a poluição atmosférica como a sonora. De olho nesse nicho, algumas empresas estão disponibilizando veículos elétricos para locação por períodos de apenas alguns minutos até algumas horas, geralmente para deslocamentos curtos em centros urbanos. Observe, a seguir, dois planos de locação de carros elétricos oferecidos por certa locadora.
• Plano A: R$ 10,00 mais R$ 0,25 por minuto.
• Plano B: R$ 30,00 mais R$ 0,09 por minuto.
Calcule o tempo t de locação de um carro elétrico dessa locadora de maneira quê o valor final seja o mesmo, independentemente do plano escolhido.
Página cento e cinco
Resolução
Inicialmente, podemos escrever a lei de formação de uma função afim para cada plano de locação.
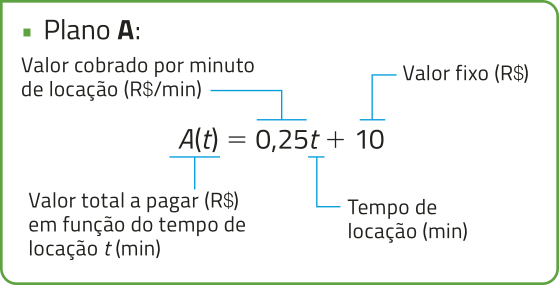
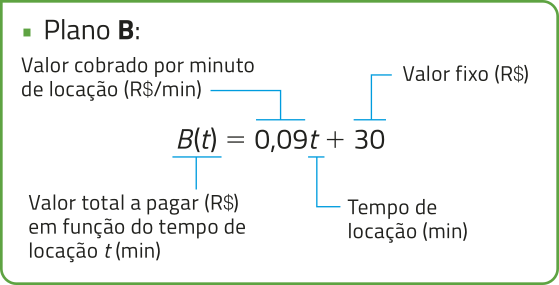
Consideramos k um número real tal quê A(k) = B(k), ou seja, o valor total a sêr pago pela locação em ambos os planos é o mesmo para o tempo k, em minuto. Assim, temos:
A(k) = B(k) ⇒ 0,25k + 10 = 0,09k + 30 ⇒ 0,16k = 20 ⇒ k = ⇒ k = 125, ou seja, 125 min.
Portanto, para quê o valor pago seja o mesmo, independentemente do plano escolhido, o tempo de locação do carro elétrico deve sêr de 125 min.
Determinação de uma função afim
Leia a situação a seguir.
Paulo trabalha como vendedor em uma loja de vestuário. Sua remuneração mensal, em reais, póde sêr expressa por uma função afim f composta de uma parte fixa e outra variável, correspondente à comissão, ou seja, um porcentual do valor de suas vendas no mês.
Observe as informações sobre a remuneração de Paulo em dois meses.
Valor mensal das vendas |
Remuneração mensal (R$) |
|---|---|
R$ 30.000,00 |
R$ 3.000,00 |
R$ 40.000,00 |
R$ 3.500,00 |
Com base nessas informações, temos:
• f(30.000) = 3.000;
• f(40.000) = 3.500.
pôdêmos determinar a lei de formação de f, representada por f(x) = ax + b, da maneira a seguir.
Substituindo os valores de x e de f(x) fornecidos na lei de formação de f, temos:
• f(30.000) = 3.000 ⇒ 30.000a + b = 3.000;
• f(40.000) = 3.500 ⇒ 40.000a + b = 3.500.

Vendedor de uma loja de roupas e calçados.
DICA
A igualdade f(30.000) = 3.000 indica quê, para x1 = 30.000, se tem, f(x1) = 3.000.
Página cento e seis
Com isso, podemos obtêr os valores de a e b resolvendo o seguinte sistema de equações.
⇒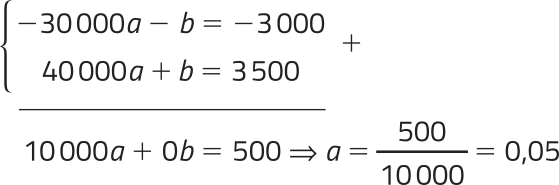
Substituindo a = 0,05 na primeira equação dêêsse sistema, temos:
30.000 ⋅ 0,05 + b = 3.000 ⇒ b = 3.000 − 1.500 = 1.500
Portanto, f(x) = 0,05x + 1.500.
ATIVIDADE RESOLVIDA
R2. A escala de tempera-túra kélvin, quê é a unidade de medida de tempera-túra termodinâmica do Sistema Internacional de mêdídas (SI), costuma sêr utilizada para fins científicos. Observe, na figura, a relação entre as escalas de tempera-túra kélvin e célcius. Sabendo quê essa relação póde sêr representada por uma função afim, calcule a quantos kelvin corresponde uma tempera-túra de −54 °C.

Resolução
Para resolver esta atividade, podemos fazer a decomposição dela em etapas, o quê auxilia na compreensão e na resolução.
Nesse caso, as kestões podem sêr as seguintes.
1ª) A qual tempera-túra, em grau célcius, corresponde 273 K? E 373 K?
2ª) Qual é a lei de formação de uma função afim f(x) = ax + b quê converte uma tempera-túra x em grau célcius para kelvin?
3ª) Qual é o valor de f(−54)?
1ª) Observando a figura apresentada, temos:
• 273 K corresponde a 0 °C;
• 373 K corresponde a 100 °C.
2ª) Da resposta à questão anterior, segue quê:
• f(0) = 273 ⇒ a ⋅ 0 + b = 273 ⇒ b = 273
• f(100) = 373 ⇒ a ⋅ 100 + b = 373 ⇒ 100a + b = 373
Substituindo b = 273 em 100a + b = 373, temos:
100a + 273 = 373 ⇒ 100a = 100 ⇒ a = 1
Portanto, f(x) = x + 273.
3ª) Considerando a função ôbitída na 2ª questão, temos:
f(−54) = −54 + 273 = 219
Logo, a tempera-túra −54 °C corresponde a 219 K.
Página cento e sete
ATIVIDADES
1. Em relação a cada função afim indicada a seguir, escrêeva os valores do coeficiente a (de x) e do termo independente b. Depois, identifique as funções lineares e a função identidade.
a) f(x) = 8x + 10
a = 8;
b = 10
b) f(x) = −2x − 8,4
1. b) a = −2; b = −8,4
c) f(x) = 4 − 6x
a = −6;
b = 4
d) f(x) = x
1. d) a = 1; b = 0; função linear e função identidade
e) f(x) =
1. e) a = ; b = 0; função linear
f) f(x) = −37
1. f) a = 0; b = −37
g) f(x) =
1. g) a = _; b =
h) f(x) = −x
a = −1; b = 0; função linear
2. Dadas as funções afins f(x) = 6x + 84 e g (x) = −4x − 6, calcule:
a) f(−7)
42
b) g (5)
−26
c) g (0)
−6
d) f
94
e) f(2) + g (−10)
130
f) g (4) − f(−3)
−88
g)
−3
3. Em cérto condomínio residencial, o consumo médio de á gua é de 2.000 L por hora. Para abastecer os moradores por determinado período, em casos de falta de fornecimento pela companhia de á gua, foi construída uma caixa-d’água com capacidade para 100.000 L.
a) Qual das alternativas a seguir corresponde à lei de formação de uma função v quê relaciona o volume v(t) de á gua nessa caixa, em litro, com o tempo t, em hora, quê esse condomínio fica sem fornecimento de á gua, considerando a caixa-d’água inicialmente cheia?
• v(t) = 2.000 − 100.000t
• v(t) = 100.000 − 2.000t
• v(t) = 100.000 + 2.000t
v(t) = 100.000 − 2.000t
b) Qual é o volume de á gua nessa caixa-d’água após um período de 15 h de suspensão do fornecimento de á gua?
70.000 L
c) Durante quantas horas o volume de á gua dessa caixa-d’água é capaz de abastecer os moradores dêêsse condomínio durante a suspensão de fornecimento de á gua?
50 h
4. Antes de sêr ligado, um fôrnu elétrico registra uma tempera-túra interna de 25 °C. Após sêr ligado, a tempera-túra interna dêêsse fôrnu aumenta 15 °C por minuto até atingir a tempera-túra selecionada.
a) Construa uma tabéla para relacionar a tempera-túra interna dêêsse fôrnu, em grau célcius, com os tempos de 0, 1, 2, 3, 4 e 5 minutos após o fôrnu ter sido ligado.
4. a) Resposta nas Orientações para o professor.
b) Qual dos itens a seguir indica a lei de formação de uma função afim f quê determina a tempera-túra interna do fôrnu, em grau célcius, de acôr-do com o tempo x, em minuto, em quê o fôrnu permanéce ligado? Explique com suas palavras como você chegou à conclusão.
I) f(x) = 25x + 15
II) f(x) = −15x + 25
III) f(x) = 5x + 3
IV) f(x) = 15x + 25
IV. Elaboração do estudante.
c) Leia a informação a seguir e responda às kestões.
Ao ligar o fôrnu, a tempera-túra selecionada foi de 280°C.
• Qual é a tempera-túra interna do fôrnu, após permanecer ligado por 10 min?
175°C
• Quantos minutos foram necessários para o fôrnu atingir a tempera-túra selecionada?
17 min
5. Para realizar o transporte rodoviário de leite, uma indústria de laticínios utiliza um caminhão-tanque com capacidade para 18.000 L. Esse caminhão é equipado com uma bomba de transferência de leite cuja vazão é de 160 L por minuto.
a) escrêeva a lei de formação de uma função L quê relaciona o volume L(t) de leite nesse caminhão, em litro, com o tempo t, em minuto, após a bomba sêr acionada para esvaziar o tanque, considerando-o inicialmente cheio.
L(t) = 18.000 − 160t
b) Qual é o tempo necessário para esvaziar completamente o tanque de leite dêêsse caminhão, considerando-o inicialmente cheio?
1h52min30s
Página cento e oito
6. ![]() Observe a cotação, em reais, para a compra de um dólar e de um euro ao final do dia 8 de janeiro de 2024.
Observe a cotação, em reais, para a compra de um dólar e de um euro ao final do dia 8 de janeiro de 2024.
Cotação de fechamento do dólar e do euro, para compra, 8/1/2024
Moeda |
preêço de compra (R$) |
|---|---|
Dólar |
4,8844 |
Euro |
5,3577 |
Fonte dos dados: BRASIL. Banco Central do Brasil. Cotações e boletins. Brasília, DF: BCB, 2024. Disponível em: https://livro.pw/xywwj. Acesso em: 9 jan. 2024.



Agora, responda.
a) Quantos reais eram necessários para comprar 70 dólares? E para comprar 200 euros?
6. a) aproximadamente R$ 341,91; R$ 1.071,54
b) Com R$ 1.465,32, era possível comprar quantos dólares? E quantos euros?
6. b) 300 dólares; aproximadamente 273,50 euros
c) As grandezas real e dólar e as grandezas real e euro estão relacionadas de maneira diretamente proporcional? Explique.
6. c) Sim, pois, se aumentarmos ou reduzirmos uma das grandezas, a outra também aumentará ou ficará reduzida, respectivamente, na mesma proporção.
d) escrêeva a lei de formação de uma função:
• f quê represente a quantia, em reais, necessária para comprar x dólares;
6. d) • f(x) = 4,8844x
• g quê represente a quantia, em reais, necessária para comprar p euros.
• g (p) = 5,3577p
e) Com base nas funções indicadas no item d, calcule f(40) e g (100). Depois, dêz-creva o quê esses resultados indicam.
6. e) f(40) = 195,376. Para comprar 40 dólares, eram necessários aproximadamente R$ 195,38. g (100) = 535,77. Para comprar 100 euros, eram necessários R$ 535,77.
![]() f) As funções f e g indicadas no item d podem sêr classificadas como funções lineares? Justifique.
f) As funções f e g indicadas no item d podem sêr classificadas como funções lineares? Justifique.
6. f) Sim, pois as funções f e g são funções afins em quê o termo independente é igual a zero.
g) Pesquise a cotação, em reais, para a compra de um dólar e de um euro em uma data recente. Depois, compare as cotações dessas moedas quê você obteve com as do final do dia 8 de janeiro de 2024.
Resposta pessoal.
7. ![]() Pense em um contexto quê envolva duas variáveis cuja relação entre elas possa sêr expressa por uma função afim. Depois, escrêeva a lei de formação dessa função e identifique as variáveis independente e dependente. Por fim, explique a um colega as características dessa função, por exemplo, se as grandezas envolvidas estão relacionadas de maneira proporcional.
Pense em um contexto quê envolva duas variáveis cuja relação entre elas possa sêr expressa por uma função afim. Depois, escrêeva a lei de formação dessa função e identifique as variáveis independente e dependente. Por fim, explique a um colega as características dessa função, por exemplo, se as grandezas envolvidas estão relacionadas de maneira proporcional.
Elaboração do estudante.
8. César é vendedor em uma loja de calçados. Seu salário é compôzto de uma parte fixa, de R$ 3.500,00, e de uma parte variável, quê corresponde a 3% do valor das vendas quê ele realizou durante o mês.
a) Qual foi o salário de César no mês em quê ele vendeu R$ 26.840,00 em calçados?
R$ 4.305,20
b) escrêeva a lei de formação de uma função afim s quê relaciona o salário s(v) de César com o valor v das vendas.
s(v) = 0,03v + 3.500
c) No mês cujo salário de César foi de R$ 4.541,84, qual foi a quantia total das vendas de calçados quê ele realizou?
R$ 34.728,00
9. Para esvaziar uma piscina, é utilizada uma bomba-d’água com vazão de 8 m3/h. Considerando a piscina inicialmente cheia, a variação do volume de á gua V de acôr-do com o tempo t decorrido após a bomba sêr ligada póde sêr expressa pela função V(t) = 100 − 8t, com V em métro cúbico e t em hora.

a) Qual é a capacidade mássima dessa piscina?
9. a) 100 m3
b) Qual é o volume de á gua nessa piscina, 4 horas após a bomba-d’água sêr ligada, considerando quê inicialmente a piscina está cheia?
68 m3
c) Qual é o tempo necessário para esvaziar completamente essa piscina?
12,5 h ou 12h30min
Página cento e nove
10. Um encanador cobra dos clientes uma quantia fixa, correspondente à visita, mais um valor variável de acôr-do com o tempo, em hora, necessário para realizar o serviço. Observe, a seguir, o preêço quê esse encanador cobrou em alguns atendimentos.
Tempo (h) |
preêço (R$) |
|---|---|
1 |
47 |
2 |
62 |
3 |
77 |
4 |
92 |
a) Nessa situação, as grandezas tempo (em hora) e preêço (em reais) são diretamente proporcionais? Justifique.
10. a) Não, pois, analisando cada linha do qüadro, é possível constatar quê a razão entre o preêço e o tempo não corresponde a uma constante.
b) escrêeva a lei de formação de uma função p quê determina o preêço cobrado pelo atendimento dêêsse encanador de acôr-do com o tempo t necessário para realizar o serviço.
10. b) p (t) = 15t + 32
c) Calcule quantos reais esse encanador cobra por um atendimento no qual foram necessárias:
• 5 horas de serviço;
R$ 107,00
• 10 horas de serviço.
R$ 182,00
d) Em cérto atendimento, esse encanador cobrou R$ 84,50 do cliente. Em quanto tempo esse serviço foi realizado?
3,5 h ou 3h30min
11. Para um trabalho de Geografia, Rafael imprimiu um mapa da região de Rio Grande (RS), município em quê mora. Depois, ele construiu a tabéla a seguir com distâncias reais, em linha reta, e medidas no mapa, entre Rio Grande e outros municípios da região.
Distâncias, em linha reta, entre Rio Grande (RS) e alguns municípios
Distância |
Município |
||
|---|---|---|---|
A |
B |
C |
|
Distância real (km) |
7,5 |
20 |
50 |
Medida no mapa (cm) |
3 |
8 |
20 |
Fonte: Pesquisas de Rafael.
a) escrêeva a lei de formação de uma função quê determine a distância real R entre os municípios, em quilômetro, de acôr-do com a distância d medida no mapa, em centímetro.
R(d) = 2,5d
b) Qual é a distância, em linha reta, em centímetro, indicada no mapa de Rafael, entre dois municípios cuja distância real entre eles é de 45 km?
18 cm
c) Qual é a escala do mapa de Rafael?
1: 250.000
![]() 12. Com base nas informações do cartaz a seguir, elabore um problema envolvendo função afim. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
12. Com base nas informações do cartaz a seguir, elabore um problema envolvendo função afim. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.

Elaboração do estudante.
NO MUNDO DO TRABALHO
Profissionais autônomos ou freelancer
Os profissionais autônomos, também chamados de freelancer (termo em inglês), são aqueles trabalhadores quê prestam serviços a empresas ou pessoas por um período determinado, sem vínculo empregatício. Alguns exemplos de profissionais autônomos são: encanador, eletricista, auxiliar de limpeza, vendedor ambulante, técnico em manutenção de computadores etc.
Para garantir seus direitos previdenciários, como auxílio-doença e salário-maternidade, é importante quê o profissional autônomo seja formalizado de acôr-do com a legislação trabalhista, por exemplo, cadastrando-se como um microempreendedor individual (MEI).
Em razão das particularidades inerêntes ao profissional autônomo, algumas habilidades comportamentais são necessárias para o bom desenvolvimento de sua carreira, como planejamento, organização, comunicação e relacionamento com o cliente.
Página cento e dez
13. Leia o trecho a seguir.
A mobilidade nas cidades brasileiras de médio e grande porte tem se caracterizado pela utilização cada vez mais ineficiente do espaço público em decorrência do aumento do uso do transporte individual motorizado – os automóveis e as motocicletas – e da redução da participação do transporte público coletivo (TPC). Como resultado, ocorrem o aumento do congestionamento do tráfego, da emissão de gases poluentes e do efeito estufa, do número de acidentes de trânsito, dos custos dos transportes e a incapacidade de atender satisfatoriamente as necessidades de locomoção da população.
BRASIL. Banco Nacional de Desenvolvimento Econômico e Social. Transporte público coletivo (TPC): os diferentes sistemas e suas características. Brasília, DF: BNDES, 2018. Disponível em: https://livro.pw/qwhek. Acesso em: 28 jun. 2024.
Um dos principais efeitos negativos da utilização de transporte individual motorizado é a poluição proveniente da emissão de gases do efeito estufa (GEE), como o CO2 (dióxido de carbono). Observe, a seguir, dados obtidos em um estudo realizado pelo Instituto de Pesquisa Econômica Aplicada (Ipea) sobre a estimativa da emissão de CO2 por categoria de veículo.

Fonte dos dados: CARVALHO, Carlos Henrique Ribeiro de. Emissões relativas de poluentes do transporte urbano. Boletim Regional, Urbano e Ambiental, Brasília, DF, n. 5, p. 123-139, jun. 2011. p. 127. Disponível em: https://livro.pw/umffy. Acesso em: 27 jun. 2024.
Com base nas informações apresentadas, resôuva os itens a seguir.
a) Quais são as consequências do aumento do uso de transportes individuais e da redução dos transportes coletivos?
Resposta esperada: Aumentam-se os congestionamentos, a emissão de gases poluentes e o efeito estufa, a quantidade de acidentes de trânsito, entre outras consequências.
b) Qual categoria de veículo emite mais CO2 por passageiro transportado no deslocamento de 1 km?
automóvel individual
c) Para cada categoria de veículo, escrêeva a lei de formação de uma função afim quê dêz-creva a emissão de CO2, em grama, no deslocamento de um passageiro por x quilômetros.
13. c) motocicleta: m(x) =71x; automóvel individual: a(x) = 127x; ônibus: o(x) = 16x
d) Considere uma pessoa quê se desloque diariamente 50 km para realizar suas atividades, como trabalhar e estudar. Calcule a emissão de CO2, em grama, no deslocamento diário dessa pessoa, considerando cada uma das categorias de veículo apresentadas.
13. d) motocicleta: 3.550 g; automóvel individual: 6.350 g; ônibus: 800 g
e) Pesquise ações, individuais e coletivas, quê podem minimizar os impactos ambientais causados pela emissão de CO2. Em seguida, com base nessas informações e nos itens anteriores, elabore um texto argumentativo quê apresente as ações pesquisadas e compare a emissão de gases poluentes de acôr-do com cada tipo de veículo.
Pesquisa e elaboração do estudante.
Página cento e onze
Taxa de variação média de uma função
Considere a situação descrita a seguir.
Uma bola de borracha quica em um piso plano e, a partir dêêsse momento até tokár no piso novamente, realiza uma trajetória quê póde sêr descrita pela função f: [0, 6] → ℝ, definida por f(x) = −x2 + 6x, em quê y = f(x) corresponde à altura da bola, em métro, após x segundos do momento em quê ela quicou. Observe o gráfico dessa função com três pontos destacados.
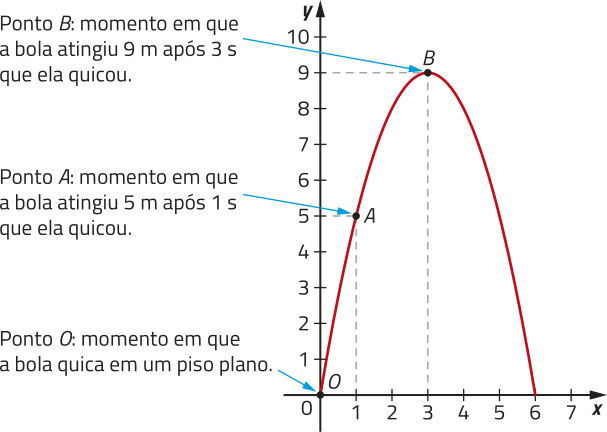

PARA PENSAR
Com suas palavras, explique como é possível verificar quê os pontos de coordenadas (0, 0), (1, 5) e (3, 9) pertencem ao gráfico da função f.
Resposta esperada: Calculando, de acôr-do com a lei de formação da função f, os valores de f(0) = 0, f(1) = 5 e f(3) = 9.
Na situação dêêsse exemplo, podemos estudar quanto variou, em média, a altura da bola no intervalo de tempo de 1 s até 3 s. Esse estudo está relacionado à determinação da taxa de variação média dessa função.
Dada uma função f: ℝ → ℝ e x1, x2 ∈ D(f), com x1 ≠ x2, temos quê a taxa de variação média de f, para x variando de x1 até x2, é dada por:
Em relação à situação apresentada, a taxa de variação média de f, para x variando de 1 até 3, é dada por:
= = 2
Portanto, podemos dizêr quê, no intervalo de tempo de 1 s até 3 s após o momento em quê a bola quicou no piso, a altura da bola de borracha variou, em média, 2 metros por segundo.
PARA PENSAR
Na situação apresentada, qual é a taxa de variação média da função f quando x varia de 0 até 2? intêrpréte esse resultado.
Resposta esperada: A taxa de variação média de f quando x varia de 0 até 2 é igual a 4. Esse resultado indica quê, no intervalo de tempo de 0 s até 2 s após o momento em quê a bola quicou no piso, a altura da bola de borracha variou, em média, 4 metros por segundo.
Página cento e doze
Taxa de variação média de uma função afim
Considere a situação descrita a seguir.
Um açude foi construído para disponibilizar á gua a uma comunidade quê vive em certa região árida do país. Na sua inauguração, verificou-se quê o açude tinha um volume de á gua estimado em 13 mil metros cúbicos. No entanto, um monitoramento identificou quê, a cada ano, o volume de á gua diminuía, de acôr-do com a função definida por f(x) = −2x + 13, em quê y = f(x) indicava o volume estimado de á gua no açude, em milhares de metros cúbicos, x anos após sua inauguração.

Com base nessa situação, podemos analisar quanto variou o volume de á gua do açude nos intervalos de tempo de 0 ano até 1 ano, de 1 ano até 2 anos e de 1 ano até 3 anos, por exemplo. Para isso, vamos calcular a taxa de variação média da função afim f para x variando de:
• 0 até 1: = −2
• 1 até 2: = −2
• 1 até 3: = −2
Note quê as taxas de variação média obtidas são todas iguais a −2, independentemente de x variar 1 ano ou mais.
Em uma função afim f: ℝ → ℝ, definida por f(x) = ax + b, chamamos a taxa de variação média de f, para x variando de x1 até x2, com x1 ≠ x2, apenas de taxa de variação de f, quê, nesse caso, é sempre igual ao coeficiente a.
pôdêmos estabelecer as propriedades a seguir para uma função afim f: ℝ → ℝ, definida por f(x) = a x + b, com a ≠ 0.
• f é crescente se, e somente se, a taxa de variação de f for positiva (a > 0), pois:
x2 > x1 ⇔ ax2 > ax1 ⇔ ax2 + b > ax1 + b ⇔ f(x2) > f(x1)
• f é decrescente se, e somente se, a taxa de variação de f for negativa (a < 0), pois:
x2 > x1 ⇔ ax2 < ax1 ⇔ ax2 + b < ax1 + b ⇔ f(x2) < f(x1)
PARA PENSAR
Em relação à função constante, o quê podemos afirmar sobre sua taxa de variação?
Resposta esperada: Em uma função constante, a taxa de variação é nula, ou seja, a = 0.
Página cento e treze
ATIVIDADE RESOLVIDA
R3. Considerando as informações apresentadas a seguir, classifique as funções afins f: ℝ→ ℝ e g: ℝ → ℝ em crescente ou decrescente.
a) f(0) = 3 e f(2) = −5
b) g (−2) = 4 e g (6) = 8
Resolução
Para determinar se uma função afim é crescente ou decrescente, podemos calcular e analisar sua taxa de variação.
a) = −4
Como −4 < 0, a função f é decrescente.
b)
Como > 0, a função g é crescente.
ATIVIDADES
14. Determine a taxa de variação média da função f: ℝ → ℝ em cada caso a seguir.
a) f(x) = 2x2 + 6, para x variando de −1 até 2.
2
b) f(x) = 4x − 1, para x variando de −4 até 0.
4
c) f(x) = 3x3, para x variando de 1 até 2.
21
d) f(x) = + 7, para x variando de −2 até 6.
15. Mostre quê, em uma função afim f: ℝ → ℝ, definida por f(x) = ax + b, o coeficiente a de x é igual à taxa de variação de f para x variando de x1 até x2, com x1 ≠ x2.
Resposta nas Orientações para o professor.
16. Sem realizar cálculos, determine a taxa de variação de cada função afim a seguir. Depois, classifique cada uma em crescente ou decrescente.
a) f(x) = 5x + 10
5; crescente
b) g(x) = − 8x +
−8; decrescente
c) h (x) = 2 − x
−1; decrescente
d) p(x) = − 1
; crescente
17. Em cada item a seguir, são apresentadas informações sobre uma função afim. Classifique cada função afim em crescente ou decrescente.
a) f(1) = 6 e f(5) = −2
decrescente
b) g (1) = −1 e g (−2) = −13
crescente
c) h (−3) = 0 e h (−6) = 3
decrescente
d) p (−3) = 1 e p (6) = 4
crescente
18. Um laboratório químico tem uma câmara fria com tempera-túra interna constante de −4 °C. Em um experimento, para avaliar as reações de uma solução líquida submetida a aquecimento, essa câmara foi programada para quê, em cérto momento, a tempera-túra começasse a aumentar gradativamente.
Sabendo quê a tempera-túra interna dessa câmara registrou 1°C após 1 h do experimento e 16 °C após 4 h do experimento e quê, no intervalo de tempo da realização do experimento, a tempera-túra interna dessa câmara pôde sêr expressa por uma função afim f, resôuva os itens a seguir.
a) As grandezas tempera-túra interna da câmara fria e tempo do experimento são grandezas diretamente proporcionais? Justifique.
18. a) Não, pois, por exemplo, ao quadruplicar o tempo do experimento, a tempera-túra interna da câmara fria não quadruplica, uma vez quê, em 1 h do experimento, a tempera-túra era de 1°C e, em 4 h, era de 16°C.
b) Qual é a taxa de variação da função f? O quê ela indica?
18. b) 5. Indica quê, a cada hora, a tempera-túra interna da câmara fria aumentou 5 °C.
c) escrêeva a lei de formação de f, representando o tempo, em hora, por t.
c) f: [0, 4] → ℝ, definida por f(t) = 5t − 4
d) Quanto tempo após o início dêêsse experimento a tempera-túra interna da câmara atingiu 6 °C?
2 h
Página cento e quatorze
Gráfico da função afim
Vamos retomar o contexto apresentado no início desta Unidade, em quê determinamos a função f(x) = 0,80x + 3, quê expressa o preêço a pagar y = f(x) pela locação de um patinete elétrico por um tempo x, em minuto.
DICA
Lembre-se de quê, nesta situação, o cliente deveria pagar um valor compôzto de uma taxa fixa de R$ 3,00 mais R$ 0,80 para cada minuto de uso do patinete elétrico.

Estudamos, na Unidade 2, quê uma função póde sêr representada por meio de um gráfico no plano cartesiano.
Em relação à situação quê envolve a locação de patinetes, para esboçarmos o gráfico de f, podemos obtêr pares ordenados (x, y) e representá-los no plano cartesiano.
x |
y |
(x, y) |
|---|---|---|
1 |
0,80 ⋅ 1 + 3 = 3,8 |
(1; 3,8) |
2 |
0,80 ⋅ 2 + 3 = 4,6 |
(2; 4,6) |
3 |
0,80 ⋅ 3 + 3 = 5,4 |
(3; 5,4) |
4 |
0,80 ⋅ 4 + 3 = 6,2 |
(4; 6,2) |
5 |
0,80 ⋅ 5 + 3 = 7 |
(5, 7) |
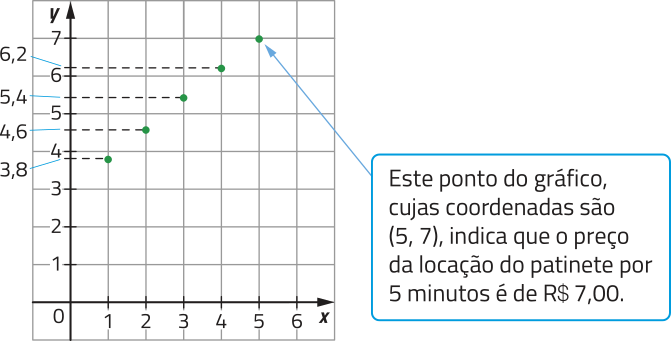
Note quê os pontos do gráfico da função f sugérem a construção de uma reta passando por eles. De fato, podemos conjecturar quê o gráfico de qualquer função afim, com domínio ℝ, é uma reta. Para garantir a validade dessa conjectura, precisamos demonstrar quê ela é verdadeira. Acompanhe.
Inicialmente, consideramos a função afim f: ℝ → ℝ, definida por f(x) = ax + b, com a ≠ 0 e b ∈ ℝ, e os pontos P (xP, yP) e Q (xQ, yQ) do gráfico dessa função. Vamos mostrar quê qualquer outro ponto M (x, y) dêêsse gráfico pertence à reta .
Como P, Q e M pertencem ao gráfico de f, temos quê:
Assim, podemos representar esses pontos no plano cartesiano da seguinte maneira.
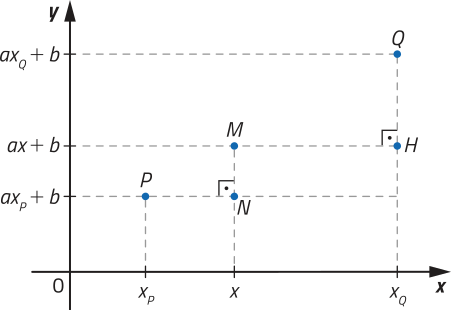
DICA
Na imagem, é possível notar quê a função afim representada é crescente, uma vez quê xQ > xP e yQ > yP. No entanto, a demonstração póde sêr realizada de maneira análoga para o caso da função afim decrescente.
Página cento e quinze
Note quê os pontos auxiliares H e N foram escolhidos de modo quê PMN e MQH sêjam triângulos retângulos. As coordenadas dêêsses pontos são H(xQ, ax + b) e N(x, axP + b). Assim, temos:
• QH = (axQ + b) − (ax + b) = axQ + b − ax − b = a (xQ − x)
• MN = (ax + b) − (axP + b) = ax + b − axP − b = a (x − xP)
• HM = xQ − x
• NP = x − xP
Logo, podemos escrever a seguinte relação entre as medidas dos catetos.
Como e med( ) = med( ) = 90°, temos pelo caso LAL (lado, ângulo, lado) quê os triângulos PMN e MQH são semelhantes. Logo, todos os demais pares de ângulos internos correspondentes têm medidas iguais.
med( ) = med( ) e
med( ) = med( ).
Como e med( ) = med( ), podemos afirmar quê os pontos P, Q e M são colineares, ou seja, pertencem a uma mesma reta. Logo, M pertence à reta .
Em relação à função constante f: ℝ → ℝ, ou seja, quando a = 0, a lei de formação é f(x) = b. Nesse caso, todos os pontos do gráfico de f são do tipo (x, b), quê resultam em uma reta paralela ou coincidente ao eixo x e quê cruza o eixo y na ordenada b.
Portanto, o gráfico de qualquer função afim, com domínio ℝ, é uma reta.
Como dois pontos distintos determinam uma única reta, podemos esboçar o gráfico de uma função afim com domínio ℝ determinando as coordenadas de apenas dois de seus pontos.
Em relação à situação do preêço de locação do patinete, é importante considerar quê o domínio da função é , uma vez quê o tempo de locação não póde sêr negativo ou nulo. Nesse caso, temos quê o gráfico de f é dado por:
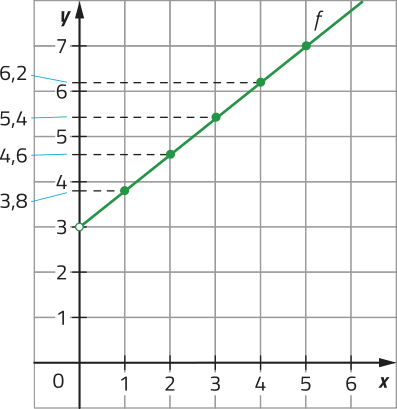
DICA
Indicamos a medida de um ângulo como med().
Indicamos quê as retas e são paralelas utilizando a notação // .
Página cento e dezesseis
Acompanhe os exemplos a seguir de construção de gráficos de algumas funções afins.
Exemplo 1
Função afim f: ℝ → ℝ, definida por f(x) = − 1.
x |
f(x) = −1 |
(x, y) |
|---|---|---|
−2 |
f(−2) = −1 = −2 |
(−2, −2) |
4 |
f(4) = −1 = 1 |
(4, 1) |
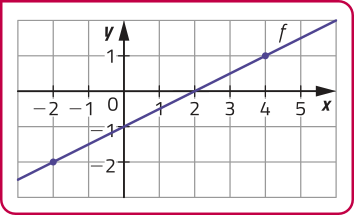
DICA
Note quê a taxa de variação de f é positiva ,ou seja, f é uma função crescente.
Nesse caso, o gráfico de f é uma reta ascendente da esquerda para a direita.
Exemplo 2
Função afim g: ℝ → ℝ, definida por g (x) = 3 − x.
x |
g(x) = 3 − x |
(x, y) |
|---|---|---|
−1 |
g(−1) = 3 − (−1) = 4 |
(−1, 4) |
5 |
g(5) = 3 − 5 = −2 |
(5, −2) |
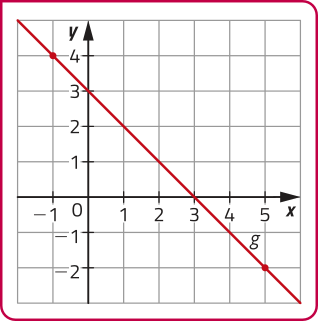
DICA
Note quê a taxa de variação de g é negativa (a = −1), ou seja, g é uma função decrescente. Nesse caso, o gráfico de g é uma reta descendente da esquerda para a direita.
Exemplo 3
Função afim h: ℝ → ℝ, definida por h (x) = 2x.
x |
h(x) = 2x |
(x, y) |
|---|---|---|
−1 |
h(−1) = 2 ⋅ (−1) = −2 |
(−1, −2) |
2 |
h(2) = 2 ⋅ 2 = 4 |
(2, 4) |
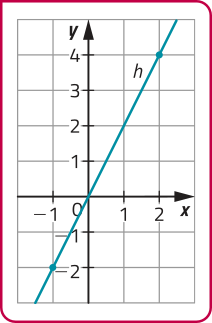
DICA
Note quê h é uma função linear. Nesse caso, o gráfico de h passa pela origem do plano cartesiano.
Página cento e dezessete
Exemplo 4
Função m: ℝ → ℝ, definida por m (x) = 3.
x |
m(x) = 3 |
(x, y) |
|---|---|---|
−1 |
m(−1) = 3 |
(−1, 3) |
2 |
m(2) = 3 |
(2, 3) |
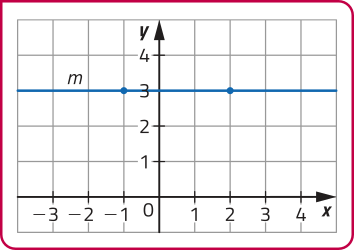
DICA
Note quê a taxa de variação de m é nula (a = 0), ou seja, m é uma função constante. O gráfico de uma função constante é uma reta paralela ao eixo das abscissas.
ATIVIDADES RESOLVIDAS
R4. Observe o gráfico de uma função afim f no plano cartesiano a seguir e resôuva as kestões.
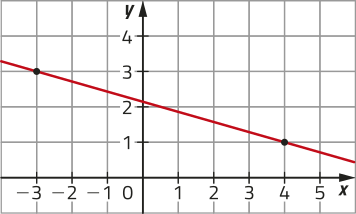
a) Qual é o valor de f(4)?
b) Para qual valor de x ∈ D(f) têm-se f(x) = 3?
c) A função f é crescente ou decrescente?
d) Determine a taxa de variação da função afim f.
Resolução
a) Para determinar f(4), analisando o gráfico podemos identificar a ordenada y do ponto dêêsse gráfico cuja abscissa é 4. Como o ponto de coordenadas (4, 1) pertence ao gráfico de f, temos f(4) = 1.
b) Para determinar o valor x do domínio de f para o qual f(x) = 3, analisando o gráfico podemos identificar a abscissa x do ponto dêêsse gráfico cuja ordenada é 3. Como o ponto de coordenadas (−3, 3) pertence ao gráfico de f, temos f(x) = 3 para x = −3.
c) Dos itens anteriores, temos f(4) = 1 e f(−3) = 3. Assim, dados os números reais −3 e 4 pertencentes ao domínio de f, sêndo −3 < 4, temos .
Portanto, a função f é decrescente.
d) Calculando a taxa de variação da função afim f, temos:
Portanto, a taxa de variação da função f é .
Página cento e dezoito
R5. (Enem/MEC) Um dos grandes desafios do Brasil é o gerenciamento dos seus recursos naturais, sobretudo os recursos hídricos. Existe uma demanda crescente por á gua e o risco de racionamento não póde sêr descartado. O nível de á gua de um reservatório foi monitorado por um período, sêndo o resultado mostrado no gráfico. Suponha quê essa tendência linear observada no monitoramento se prolongue pêlos próximos meses.
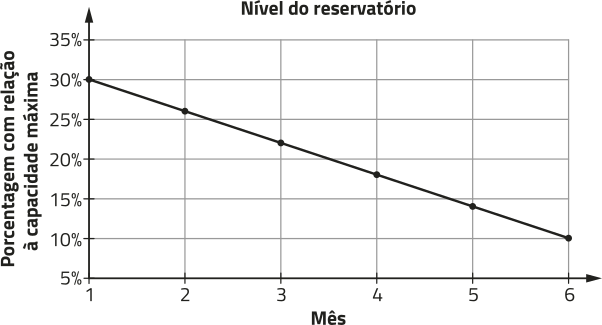
Nas condições dadas, qual o tempo mínimo, após o sexto mês, para quê o reservatório atinja o nível zero de sua capacidade?
a) 2 meses e meio.
b) 3 meses e meio.
c) 1 mês e meio.
d) 4 meses.
e) 1 mês.
Resolução
Para resolver esta atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• o nível de á gua de um reservatório foi monitorado por um período de tempo e o resultado é mostrado pelo gráfico, quê descreve uma tendência linear;
• os pontos de coordenadas (1, 30) e (6, 10) pertencem ao gráfico.
Temos de identificar qual é o tempo mínimo, após o sexto mês, para quê o reservatório atinja o nível zero de sua capacidade.
2ª ELABORAR UM PLANO
O gráfico “Nível do reservatório” representa a função afim f quê corresponde ao nível de á gua do reservatório, em porcentagem, no mês x. Analisando os pontos do gráfico, podemos determinar a lei de formação de f, expressa na forma f(x) = ax + b, e, então, calcular para qual valor de x temos f(x) = 0, isto é, o zero da função. Por fim, podemos subtrair 6 dêêsse resultado para obtêr a quantidade mínima de meses, após o sexto mês, para quê o nível de á gua do reservatório seja zero.
3ª EXECUTAR O PLANO
Como os pontos de coordenadas (1, 30) e (6, 10) pertencem ao gráfico de f, podemos determinar a taxa de variação de f e o valor de b:
• a = = −4;
• f(1) = 30 ⇒ −4 ⋅ 1 + b = 30 ⇒ b = 30 + 4 = 34.
Assim, temos quê f(x) = −4x + 34 e podemos calcular o zero de f:
0 = −4x + 34 ⇒ 4x = 34 ⇒ x = 8,5
Logo, em 8,5 meses, o nível de á gua do reservatório será zero, ou seja, 2,5 meses após o sexto mês (8,5 − 6).
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado obtído, podemos realizar os seguintes cálculos:
• f(1) = −4 ⋅ 1 + 34 = 30; • f(6) = −4 ⋅ 6 + 34 = 10; • f(8,5) = −4 ⋅ 8,5 + 34 = 0.
Note quê esses cálculos indicam quê os pontos de coordenadas (1, 30) e (6, 10) pertencem ao gráfico da função f e quê 8,5 é o zero dessa função.
Portanto, a alternativa a é a correta.
Página cento e dezenove
Interseção do gráfico de uma função afim com os eixos cartesianos
O gráfico de toda função afim, não constante, cruza cada um dos eixos cartesianos em um único ponto. Observe, por exemplo, o gráfico da função afim f: ℝ → ℝ, definida por f(x) = x + 2.
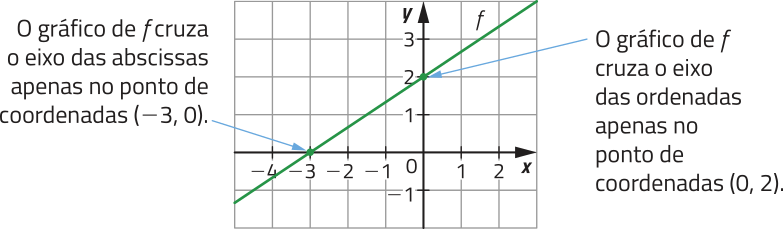
PARA PENSAR
Em quantos pontos o gráfico de uma função constante, não nula, cruza os eixos cartesianos? Justifique.
Resposta esperada: Cruza o eixo das ordenadas em um único ponto e não cruza o eixo das abscissas, pois é uma reta paralela e não coincidente ao eixo das abscissas.
Agora, obissérve como podemos determinar as coordenadas dos pontos em quê o gráfico de uma função afim cruza os eixos cartesianos.
Seja uma função afim f: ℝ → ℝ, definida por f(x) = ax + b, com a ≠ 0, sêndo P (xP, yP) e Q (xQ, yQ) os pontos em quê o gráfico de f cruza os eixos das abscissas e das ordenadas, respectivamente. pôdêmos estudar as coordenadas dêêsses pontos da seguinte maneira.
• P (xP, yP)
Como P pertence ao eixo das abscissas, temos quê yP = 0. Assim, segue quê:
yP = f(xP) = 0 ⇒ axP + b = 0 ⇒ xP =
Portanto, o gráfico da função afim f cruza o eixo das abscissas em xP = , ou seja, no ponto P ( 0).
O zero da função afim f: ℝ → ℝ, definida por f(x) = ax + b, com a ≠ 0 é dado por x =
• Q (xQ, yQ)
Como Q pertence ao eixo das ordenadas, temos quê xQ = 0. Assim, segue quê:
yQ = f(xQ) = f(0) = a ⋅ 0 + b ⇒ yQ = b
Portanto, o gráfico da função f cruza o eixo das ordenadas em yQ = b, ou seja, no ponto Q (0, b).
Em relação ao gráfico da função f(x) = + 2, apresentado anteriormente, as coordenadas dos pontos P e Q, em quê ele cruza os eixos das abscissas e das ordenadas, respectivamente, são dadas por:
• xP = = = −3, ou seja, P (−3, 0);
• yQ = b = 2, ou seja, Q (0, 2).
PARA PENSAR
Existe função afim cujo gráfico cruza os eixos das abscissas e das ordenadas em um mesmo ponto? Justifique.
Sim, as funções lineares cruzam os eixos das abscissas e das ordenadas no ponto O(0, 0).
Página cento e vinte
Translação do gráfico de uma função afim
Observe, em um mesmo plano cartesiano, o gráfico das funções f(x) = 2x, g (x) = 2x − 3 e m (x) = 2x + 4, quê têm a mesma taxa de variação, mas com diferentes termos independentes.
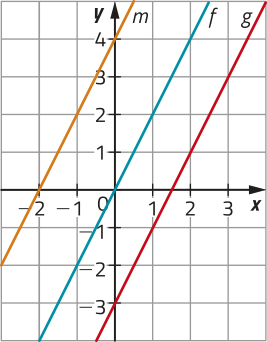
Note quê esses gráficos correspondem a retas paralelas. Além díssu, em relação ao gráfico da função f(x) = 2x, cujo termo independente é b = 0, temos quê o gráfico da função:
• g (x) = 2x − 3, cujo termo independente é b = −3, corresponde ao gráfico de f transladado 3 unidades para baixo, pois dado um ponto de coordenadas (x1, y1) do gráfico de f, então o ponto de coordenadas (x1, y1 − 3) pertence ao gráfico de g;
• m (x) = 2x + 4, cujo termo independente é b = 4, corresponde ao gráfico de f transladado 4 unidades para cima, pois, dado um ponto de coordenadas (x1, y1) do gráfico de f, então o ponto de coordenadas (x1, y1 + 4) pertence ao gráfico de m.
Considerando uma função afim f dada por f(x) = ax + b, com b ≠ 0, dizemos quê o gráfico de f corresponde ao gráfico de uma função g dada por g (x) = ax transladado |b | unidades:
• para cima, se b > 0; • para baixo, se b < 0.
PARA PENSAR
Quais são as coordenadas dos pontos em quê o gráfico de cada função indicada cruza o eixo das ordenadas?
f: (0, 0); g: (0, −3); m: (0, 4)
ATIVIDADES RESOLVIDAS
R6. Em um programa de computador, foi representado o gráfico da função afim definida por f(x) = 5x + 2. Em seguida, utilizando uma opção dêêsse programa, foram construídas duas retas, r e s, de maneira quê correspondessem a translações do gráfico de f 3 unidades para cima e 4 unidades para baixo, respectivamente. Determine a lei de formação das funções cujos gráficos correspondem às retas r e s.
Resolução
Sejam g e h as funções cujos gráficos correspondem, respectivamente, às retas r e s. Note quê o gráfico de f corresponde ao gráfico de uma função j dada por j (x) = 5x transladado duas unidades para cima. Sendo a reta quê corresponde ao gráfico de f e as retas r e s paralelas entre si, podemos escrever quê g (x) = 5x + b1 e h (x) = 5x + b2, com b1, b2 ∈ ℝ.
Assim, como o gráfico de g (reta r) corresponde ao de f transladado 3 unidades para cima, temos:
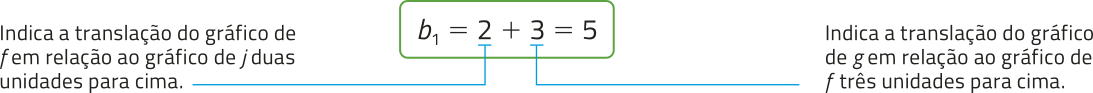
De maneira análoga, como o gráfico de h (reta s) corresponde ao de f transladado 4 unidades para baixo, temos:
b2 = 2 − 4 = −2
Portanto, as retas r e s correspondem, respectivamente, aos gráficos das funções cujas leis de formação são g (x) = 5x + 5 e h (x) = 5x − 2.
Página cento e vinte e um
R7. Leia, no trecho a seguir, as informações sobre a aorta, considerada a maior e mais importante artéria do corpo humano.
Durante a vida, a aorta ABSÓRVE o impacto de 2 a 3 bilhões de batimentos cardíacos enquanto distribui aproximadamente 2 milhões de litros de sangue pelo corpo.
[...]
O conhecimento dos valores dos diâmetros normais dos diversos segmentos aórticos é importante para avaliação e conduta das doenças da aorta. Os diâmetros da aorta aumentam com a idade [...].
DIAS, Ricardo Ribeiro; STOLF, Noedir Antônio Groppo. Doenças da aorta torácica. São Paulo: ABRECCV: SBCCV, c2023-2024. p. 1-2. Disponível em: https://livro.pw/fovla. Acesso em: 27 jun. 2024.
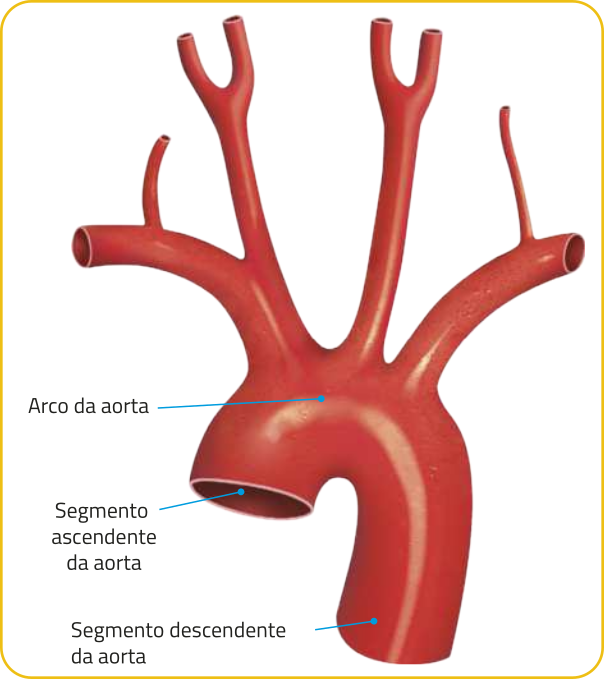
O diâmetro D do segmento ascendente da aorta, em milímetro, póde sêr modelado, de acôr-do com a idade i de uma pessoa (em ano), pela função dada por D (i) = 0,16i + 31.
Conforme esse modelo, resôuva as kestões.
a) Calcule D (50) e interpréte o resultado.
b) Considere d (i) = ai + b, a lei de formação da função quê modela o diâmetro d do segmento descendente da aorta, em milímetro, de acôr-do com a idade i de uma pessoa (em ano), sêndo a e b números reais. Sabendo quê os gráficos de d e D são paralelos, sêndo o gráfico de d correspondente ao de D transladado 10 unidades para baixo, determine os números reais a e b.
Resolução
a) Calculando D (50), temos:
D (50) = 0,16 ⋅ 50 + 31 = 8 + 31 = 39
Portanto, como D (50) = 39, temos quê, de acôr-do com o modelo apresentado, o diâmetro do segmento ascendente da aorta de uma pessoa de 50 anos de idade é de 39 mm.
b) Como os gráficos de d e D são paralelos, essas funções têm a mesma taxa de variação, ou seja, a = 0,16.
Como o gráfico de d corresponde ao gráfico de D transladado 10 unidades para baixo, temos quê:
b = 31 − 10 = 21
Assim, a = 0,16 e b = 21, ou seja, d (i) = 0,16i + 21.
PARA PENSAR
Com base na função ôbitída no item b, determine para quê idade de uma pessoa a medida de 33 mm para o diâmetro do segmento descendente da aorta é considerado adequado.
Para uma pessoa de 75 anos de idade.
Página cento e vinte e dois
R8. Construa o gráfico da função indicada em cada item e marque os pontos em quê ele cruza os eixos cartesianos.
a) f(x) = 2x − 8
b) g (x) = −3x + 6
Resolução
a) Calculando o zero de f, temos:
f(x) = 0 ⇒ 2x − 8 = 0 ⇒
⇒ 2x = 8 ⇒ x = = 4
Portanto, 4 é o zero da função e (4, 0) são as coordenadas do ponto em quê o gráfico de f cruza o eixo das abscissas. Como b = −8, o gráfico de f cruza o eixo das ordenadas no ponto de coordenadas (0, −8).
Para representar o gráfico de f, podemos marcar os pontos de coordenadas (4, 0) e (0, −8) e traçar a reta quê passar por eles.
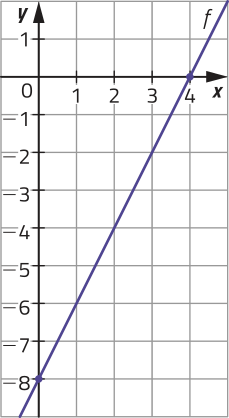
b) Calculando o zero de g, temos:
g (x) = 0 ⇒ −3x + 6 = 0 ⇒
⇒ −3x = −6 ⇒ x =
= 2
Portanto, 2 é o zero da função e (2, 0) são as coordenadas do ponto em quê o gráfico de g cruza o eixo das abscissas. Como b = 6, o gráfico de g cruza o eixo das ordenadas no ponto de coordenadas (0, 6).
Para representar o gráfico de g, podemos marcar os pontos de coordenadas (2, 0) e
(0, 6) e traçar a reta quê passar por eles.
ATIVIDADES
19. Em uma malha quadriculada, esboce o gráfico da função f: ℝ → ℝ, definida por:
19. Respostas nas Orientações para o professor.
a) f(x) = 3x − 1;
b) f(x)= x + 4;
c) f(x) = 5 − 2x;
d) f(x) = − 6.
20. Dada a função afim f: ℝ → ℝ, definida por f(x) = −2x + 5, responda às kestões.
a) Essa função é crescente ou decrescente?
decrescente
b) Qual é o zero dessa função?
x =
c) Quais são as coordenadas dos pontos em quê o gráfico dessa função cruza os eixos cartesianos?
20. c) eixo x: ; eixo y: (0, 5)
• Agora, esboce o gráfico de f e, com suas palavras, explique como rêzouvêo cada item anterior.
Resposta pessoal.
21. Em uma malha quadriculada, esboce o gráfico da função afim f quê passa pêlos pontos P(7, 5) e Q(−3, −1). Em seguida, determine se essa função é crescente ou decrescente.
Resposta nas Orientações para o professor. f é crescente.
Página cento e vinte e três
22. Observe os gráficos I, II e III de funções afins representados em um mesmo plano cartesiano e resôuva as kestões, justificando o procedimento de construção de cada um.
22. Resposta nas Orientações para o professor.
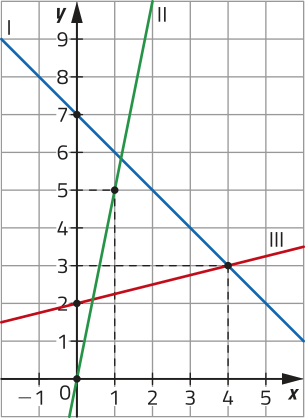
a) Classifique as funções representadas pêlos gráficos em crescente ou decrescente.
22. a) crescente: II e III; decrescente: I
b) A lei de formação da função correspondente a cada um dêêsses gráficos está indicada no qüadro a seguir. Relacione cada gráfico à lei de formação da função correspondente.
g (x) = 4x + 1
m (x) = + 2
n (x) = −x + 7
f(x) = x + 7 h
(x) = 5x
22. b) I: n(x) = −x + 7; II: h(x) = 5x; III: m(x) = + 2
![]() 23. Leia o texto a seguir e faça o quê se pede.
23. Leia o texto a seguir e faça o quê se pede.
Na safra 2022/2023, o Brasil se consolidou como o maior produtor de soja do mundo. Naquela safra, foram produzidos no país cerca de 155 milhões de toneladas de soja, com uma produtividade média de 3,5 t/ha, ou seja, a cada hectare de soja plantada, foram colhidos, em média, 3,5 t.
Fonte dos dados: BRASIL. Ministério da Agricultura e Pecuária. Empresa Brasileira de Pesquisa Agropecuária. Soja em números: safra 2022/23. Brasília, DF: Mapa: Embrapa, 2024. Disponível em: https://livro.pw/yztjk. Acesso em: 28 jun. 2024.
Considere q a função quê relaciona as grandezas quantidade de soja produzida, em tonelada, e a área x de plantio, em hectare.
a) As grandezas relacionadas pela função q são grandezas diretamente proporcionais? Justifique.
23. a) Sim, pois, se considerarmos, por exemplo, o dôbro da área de plantio, a quantidade de soja produzida também será o dôbro.
b) A função q é linear ou não linear? escrêeva a lei de formação dessa função e verifique a sua resposta.
função linear; q (x) = 3,5x
c) Qual dos gráficos a seguir representa a função q?
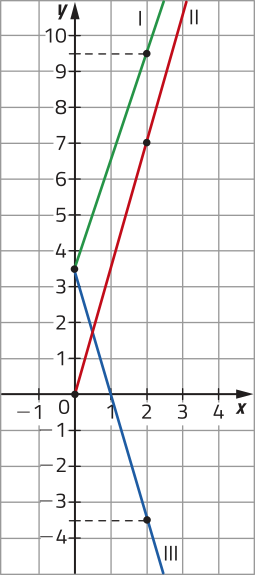
gráfico II
d) Sabendo quê 1 ha corresponde a 0,01 km2, responda: na safra 2022/2023, o plantio de soja no Brasil foi realizado em quantos quilômetros quadrados de térra? Utilize uma calculadora para efetuar o cálculo.
aproximadamente 443.000 km²
e) Sabendo quê a área territorial do Brasil é de aproximadamente 8,5 milhões de km2, calcule, com o auxílio de uma calculadora, a razão entre a área destinada ao plantio de soja na safra 2022/2023 e a área total do país. O quê esse valor representa?
23. e) Aproximadamente 0,052. Resposta esperada: Representa quê cerca de 5,2% da área territorial do Brasil foi utilizada no plantio de soja na safra 2022/2023.
24. Considere o gráfico da função afim f: ℝ → ℝ quê cruza o eixo das abscissas no ponto P(6, 0) e o eixo das ordenadas no ponto Q(0, 4) e responda às kestões a seguir.
a) A função f é crescente ou decrescente?
24. a) decrescente
b) Qual é a taxa de variação a da função f?
24. b) a =
c) Qual é a lei de formação da função f?
24. c) f(x) = + 4
25. Sejam f e g funções definidas por f(x)= + m + 5 e g(x) = 5x − 10, em quê m corresponde a um número inteiro. Determine o valor de m para quê o gráfico de f cruze o eixo:
a) das abscissas no ponto A(9, 0);
m = −2
b) das ordenadas no ponto B(0, 6);
m = 1
c) das abscissas e das ordenadas no ponto O(0, 0).
m = −5
DICA
Para resolver esta atividade, você póde, inicialmente, selecionar apenas os dados necessários indicados no enunciado.
Página cento e vinte e quatro
26. No plano cartesiano, estão representados os gráficos das funções afins definidas por f(x) = −kx + 6 e g (x) = 2kx + 3, em quê k corresponde a um número real.
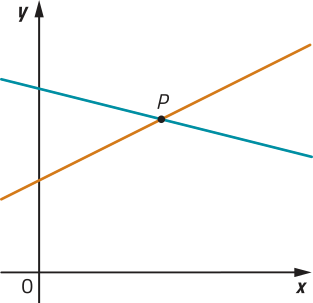
a) Sabendo quê P, de abscissa 4, é o ponto de interseção entre os gráficos dessas funções, calcule o valor de k e escrêeva a lei de formação das funções f e g.
26. a) k = ; f(x) = + 6e g(x) = +3
b) Quais são as coordenadas dos pontos em quê os gráficos dessas funções cruzam o:
• eixo das abscissas?
f: (24, 0); g: (−6, 0)
• eixo das ordenadas?
f: (0, 6); g: (0, 3)
27. O valor da fatura de energia elétrica cobrado nas residências em cérto município é determinado pelo produto da quantidade de energia consumida (em kWh) pela tarifa correspondente (em R$/kWh), acrescido de R$ 10,00 de iluminação pública. A seguir, estão representadas as tarifas cobradas pela companhia de energia elétrica de acôr-do com a faixa de consumo.
Faixa de consumo (kWh) |
Tarifa (R$/kWh) |
|---|---|
Até 50 |
0,50 |
Maior quê 50 até 200 |
0,70 |
Maior quê 200 até 500 |
0,80 |
Maior quê 500 |
0,90 |
a) pôdêmos definir uma função v, expressa por mais de uma sentença, para relacionar o valor cobrado na fatura de energia elétrica (em R$), de acôr-do com o consumo c (em kWh), nas residências dêêsse município. Por exemplo, para um consumo de até 50 kWh, temos:
v (c) = 0,50c + 10, para 0 ≤ c ≤ 50
Determine as sentenças quê expressam a função v para:
• 50 < c ≤ 200;
v (c) = 0,70c + 10
• 200 < c ≤ 500;
v (c) = 0,80c + 10
• c > 500.
v (c) = 0,90c + 10
b) Com base no item a, escrêeva a lei de formação da função v.
27. b) e d) Respostas nas Orientações para o professor.
c) Qual é o domínio da função v? E qual é o conjunto imagem dessa função? Justifique sua resposta.
D(v) = [0, +∞[; Im(v) = [10, +∞[
d) No caderno, esboce o gráfico da função v.
e) pôdêmos afirmar quê v é uma função crescente em todo o seu domínio? Justifique.
27. e) Sim, pois, ao escolhermos quaisquer valores c1, c2 ∈ D(v), com c 2 > c 1, temos quê v(c 2) > v(c 1).
f) Calcule o valor da fatura de energia elétrica em uma residência dêêsse município cujo consumo no mês foi de:
• 600 kWh;
R$ 550,00
• 400 kWh;
R$ 330,00
• 30 kWh;
R$ 25,00
• 120 kWh.
R$ 94,00
28. (hú- hê- érre jota) Os veículos para transporte de passageiros em determinado município têm vida útil quê varia entre 4 e 6 anos, dependendo do tipo de veículo. Nos gráficos, está representada a desvalorização de quatro dêêsses veículos ao longo dos anos, a partir de sua compra na fábrica.
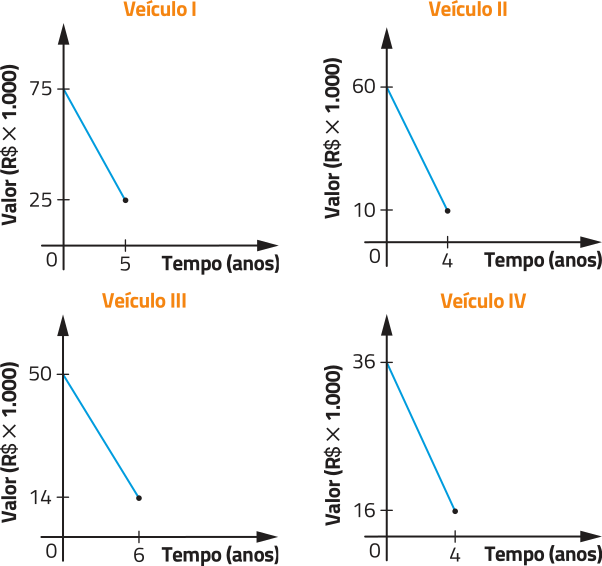
Com base nos gráficos, o veículo quê mais desvalorizou por ano foi:
a) I
b) II
c) III
d) IV
alternativa b
29. Identifique, entre as fichas, aquelas quê apresentam as leis de formação de cada gráfico apresentado na atividade anterior.
f(x) = −5x + 36
h (x) = −10x + 75
g (x) = −5x + 75
m (x) = −6x + 50
n (x) = −12,5x + 60
p (x) = 6x + 50
29. f: veículo IV; h: veículo I; m: veículo III; n: veículo II
Página cento e vinte e cinco
30. Rafael compra produtos no atacado para revender. Observe, a seguir, a cotação do preêço de um produto quê ele realizou em duas lojas virtuais.
Cotação, em reais, do preêço de cérto produto por quantidade comprada e valor do frete incluso
Loja |
Quantidade |
||||
|---|---|---|---|---|---|
50 |
80 |
120 |
200 |
300 |
|
A |
375 |
480 |
620 |
900 |
1.250 |
B |
305 |
440 |
620 |
980 |
1.430 |
Fonte: Dados fictícios
Sabendo quê o preêço da unidade dêêsse produto e o valor do frete, em cada loja, não varíam de acôr-do com a quantidade comprada, resôuva as kestões.
a) Qual é o valor do frete de cada loja citada?
loja A: R$ 200,00; loja B: R$ 80,00
b) Em qual das lojas o preêço unitário do produto é maior? Quanto custa, em reais, a unidade do produto nessa loja?
loja B; R$ 4,50
c) Represente, em um plano cartesiano, as informações apresentadas na tabéla anterior.
30. c) Resposta nas Orientações para o professor.
d) escrêeva a lei de formação de uma função quê expresse o preêço P, em reais, cobrado pela compra e entrega de uma quantidade x dêêsse produto em cada uma dessas lojas. Essas são funções afins?
30. d) loja A: PA (x) = 3,5x + 200; loja B: PB (x) = 4,50x + 80. Ambas são funções afins.
e) A partir de quantas unidades dêêsse produto é financeiramente mais vantajoso realizar a compra na loja A?
para quantidades maiores quê 120 unidades
31. Em um centro de recuperação de animais silvestres, um dos animais resgatados em condições físicas precárias foi submetido a uma suplementação alimentar por um período de 7 meses. A cada mês, sua massa foi aferida e registrada em uma planilha eletrônica.
Mês |
Massa (kg) |
|---|---|
Janeiro |
18 |
Fevereiro |
22 |
Março |
22 |
Abril |
26 |
Maio |
29 |
Junho |
30 |
Julho |
33 |
Nessa planilha eletrônica, os dados coletados foram representados por pontos em um plano cartesiano, utilizando os recursos: Gráfico... → XY (Dispersão). Em seguida, utilizando o recurso Linha de tendência para a série de dados ‘Massa (kg)’, esses pontos foram modelados por uma reta correspondente à função f(x) = 2,43x + 16, quê determina a massa do animal resgatado (em quilograma) no mês x, conforme indicado a seguir.
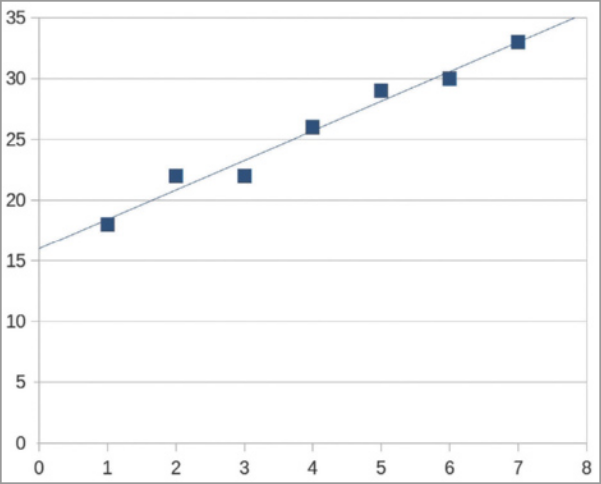
a) Olhando apenas para a planilha de dados coletados, quantos quilogramas o animal em recuperação ganhou em 7 meses?
15 kg
b) Calcule a diferença, em quilograma, entre os valores registrados na planilha de dados coletados e os determinados pela função f para cada um dos meses apresentados.
31. b) janeiro: 0,43 kg; fevereiro: 1,14 kg; março: 1,29 kg; abril: 0,28 kg; maio: 0,85 kg; junho: 0,58 kg; julho: 0,01 kg
c) Pela função f, qual teria sido o ganho estimado de massa do animal no período de recuperação?
14,58 kg
d) Você considera quê a função f indica, de maneira aproximada, os dados aferidos pelo centro de recuperação? Justifique sua resposta.
Resposta pessoal.
32. Considere o gráfico de uma função f: ℝ → ℝ, definida por f(x) = ax + b.
a) Que alterações ocorrerão no gráfico de f ao modificar o valor do coeficiente a?
32. a) A inclinação da reta correspondente ao gráfico da função f será alterada.
b) O quê você acredita quê vai ocorrer com o gráfico da função f ao modificar o valor do coeficiente b?
32. b) Resposta esperada: O gráfico da função f será transladado verticalmente.
Página cento e vinte e seis
Equação da reta
A Geometria Analítica é um campo da Matemática quê estuda, entre outros conceitos, a representação de figuras geométricas por meio de equações. A seguir, estudaremos uma importante relação entre função afim e Geometria Analítica, partindo do fato matemático demonstrado de quê o gráfico de qualquer função afim de domínio ℝ é uma reta.
Seja f: ℝ → ℝ uma função afim, definida por f(x) = ax + b, cujo gráfico é uma reta r. Dizemos quê y = ax + b é a equação da reta r.

Estudamos anteriormente quê, na função afim, o coeficiente a corresponde à taxa de variação e b ao termo independente. No estudo da equação da reta, denominamos a de coeficiente angular da reta e b de coeficiente linear da reta.
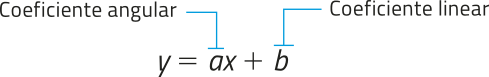
pôdêmos determinar a equação de uma reta r não paralela ao eixo y representada em um plano cartesiano com base nas coordenadas de um de seus pontos e do seu coeficiente angular a. Para isso, consideramos dois pontos de r: um ponto arbitrário P (x, y) e um ponto dado A (x0, y0). Observe.
a = ⇒
⇒ y − y0 = a(x − x0) ⇒
⇒ y = y0 + a(x − x0)
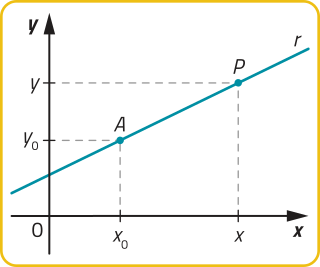
A equação de uma reta póde sêr expressa na forma reduzida (y = ax + b) ou na forma geral (mx + ny + c = 0). Por exemplo, em relação à reta representada no plano cartesiano da figura, temos quê a:
• equação reduzida da reta é y = 2x + 1;
• equação geral da reta é 2x − y + 1 = 0.

DICA
Toda reta não paralela ou não coincidente ao eixo y corresponde ao gráfico de uma função afim. Já as retas paralelas ou coincidentes ao eixo y não correspondem ao gráfico de função afim, mas também podem sêr expressas por uma equação.
Página cento e vinte e sete
ATIVIDADES RESOLVIDAS
R9. Observe a reta r representada a seguir.
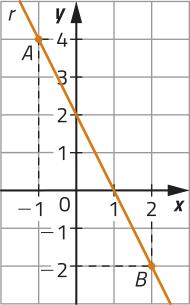
a) Determine a equação da reta r e expresse-a na forma reduzida e na forma geral.
b) Verifique se o ponto C (5, −8) pertence à reta r.
Resolução
a) Com base nas coordenadas dos pontos A (−1, 4) e B (2, −2) de r, calculamos seu coeficiente angular a.
a = = −2
Assim, a equação reduzida da reta r é dada por:
y = y0 + a (x − x0) ⇒ y = 4 + (−2)[x − (−1)] ⇒ y = −2x + 2
Com base na equação reduzida, determinamos a equação geral da reta r:
y = −2x + 2 ⇒ 2x + y − 2 = 0
Portanto, a equação reduzida da reta r é y = −2x + 2, e a equação geral é 2x + y − 2 = 0.
DICA
Note quê utilizamos as coordenadas do ponto A na determinação da equação reduzida da reta r. Porém poderíamos utilizar qualquer outro ponto de r, como o ponto B.
b) Para verificar se o ponto C (5, −8) pertence à reta r, podemos substituir x = 5 na equação da reta r (reduzida ou geral) e verificar se o resultado obtído é y = −8. Em relação à equação reduzida, temos:
y = −2 ⋅ 5 + 2 = −10 + 2 = −8
Portanto, temos quê o ponto C (5, −8) pertence à reta r.
R10. Considere, em um plano cartesiano, a reta r de equação 3y + 2x = 15 e uma reta s determinada pêlos pontos A (−1, 2) e B (7, 4). Quais são as coordenadas do ponto C, em quê as retas r e s se intersectam?
Resolução
Como s passa pêlos pontos A e B, temos:
as =
Assim, a equação da reta s é dada por:
y − 2 = [x − (−1)] ⇒ 4y − x = 9
Para determinar as coordenadas do ponto C, em quê as retas r e s se intersectam, podemos resolver o seguinte sistema de equações:
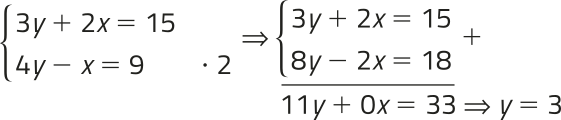
Substituindo y = 3 na equação 3y + 2x = 15, temos:
3 ⋅ 3 + 2x = 15 ⇒ x = 3
Portanto, as retas r e s se intersectam no ponto C (3, 3).
Página cento e vinte e oito
ATIVIDADES
33. Determine a equação de cada reta a seguir e expresse-a na forma reduzida.
a) 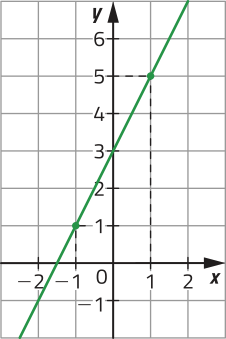
y = 2x + 3
b) 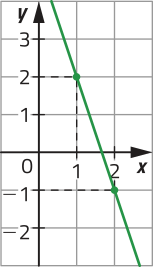
y = −3x + 5
c) 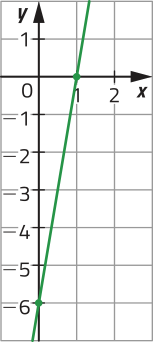
y = 6x − 6
d) 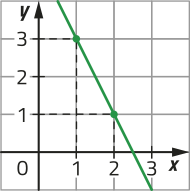
y = −2x + 5
34. Observe as retas r e s em um mesmo plano cartesiano e determine as coordenadas do ponto P em quê elas se cruzam.
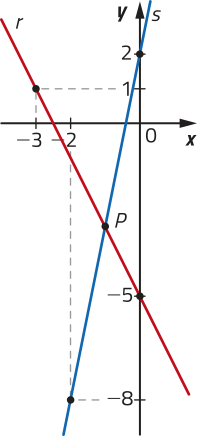
P (−1, −3)
35. Jorge tem uma loja e, para realizar entregas de produtos em domicílio, ele utiliza o serviço de uma empresa terceirizada. Sabe-se quê o preêço p cobrado por essa empresa para cada entrega, em reais, póde sêr descrito por uma função do tipo p(x) = ax + b, sêndo a e b números reais e x, a distância percorrida, em quilômetro. Observe, em uma planilha eletrônica, registros de entregas quê Jorge já contratou.

Nessas condições, determine:
a) o preêço cobrado pela empresa terceirizada para uma entrega com 25,5 km de distância percorrida;
R$ 40,00
b) a distância percorrida em certa entrega, sabendo quê o preêço cobrado pela empresa terceirizada foi de R$ 50,00;
34,5 km
c) a equação geral da reta r correspondente ao gráfico da função p.
−10x + 9y − 105 = 0
36. Considere as retas r e s representadas em um mesmo plano cartesiano, dado quê a reta r passa pêlos pontos A(6, 5) e B(−2, −1), e a reta s passa pêlos pontos C(−1, 6) e D(5, −2).
a) escrêeva a equação de cada uma dessas retas.
r: 3x − 4y = −2; s: 4x + 3y = 14
b) Quais são as coordenadas do ponto em quê as retas r e s se cruzam?
(2, 2)
37. escrêeva a equação da reta quê:
a) passa pelo ponto A (1, 4) e tem coeficiente angular a = 3;
y = 3x + 1
b) passa pelo ponto B (2, 1) e tem coeficiente angular a = .
y = 2 −
38. Determine a equação da reta quê passa pêlos pontos:
a) (1, 3) e (−2, 0).
y = x + 2
b) (2, −5) e (−1, 7).
y = −4x + 3
c) (−3, 5) e (3, 7).
y = +6
d) (−1, −2) e (3, 2).
y = x − 1
39. Para cada item, escrêeva a equação da reta quê passa pêlos pontos indicados.
a) A(5, 2) e B(7, 2)
y = 2
b) C(−3, 5) e D(0, 5)
y = 5
c) E(1, −3) e F(6, −3)
y = −3
d) G(−7, −1) e H(4, −1)
y = −1
• Que padrões você póde observar em relação às coordenadas dos pontos indicados em cada item? E quê padrão há entre as equações das retas quê você escreveu?
Resposta esperada: Em cada item, as ordenadas dos dois pontos indicados são iguais. Em cada item, a equação ôbitída tem o coeficiente angular igual a zero, o quê implica quê a reta é paralela ao eixo das abscissas e póde sêr expressa na forma y = c, sêndo c a ordenada dos dois pontos indicados.
Página cento e vinte e nove
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Movimento retilíneo uniforme
Entre as ciências quê se relacionam com a Matemática, a Física provavelmente é a mais lembrada, uma vez quê, para demonstrar, expressar e generalizar algumas de suas teorias, se faz uso da linguagem e de conceitos matemáticos. Para exemplificar isso, podemos citar o movimento retilíneo uniforme. Nesse tipo de movimento, o móvel se desloca sempre no mesmo sentido, em linha reta, e a sua velocidade se mantém constante no espaço percorrido em determinado tempo. Observe, a seguir, a denominada equação horária do movimento retilíneo uniforme, quê relaciona a posição do móvel com um instante de tempo.
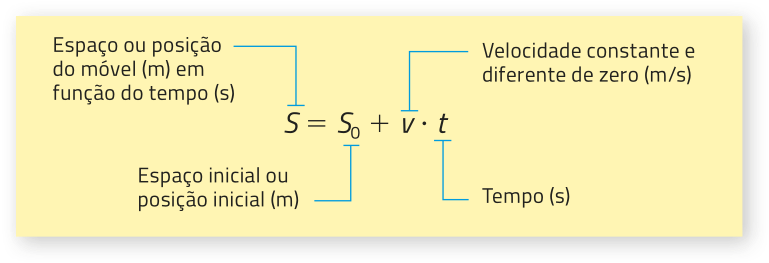
Nessa equação, a velocidade v é uma constante. Dessa maneira, tal equação póde sêr associada a uma função afim definida por S (t) = S0 + v ⋅ t, quê corresponde a um modelo matemático para o movimento retilíneo uniforme. Nesse caso, o espaço S corresponde à variável dependente; o tempo t, à variável independente; a velocidade constante v, à taxa de variação da função; e o espaço inicial S0, ao termo independente.
Fonte dos dados: KNIGHT, Randall D. Física: uma abordagem estratégica: mecânica newtoniana, gravitação, oscilações e ondas. Tradução: Trieste Freire Ricci. 2. ed. Porto Alegre: búkmã, 2009. v. 1, p. 34-37.
O exemplo do automóvel em movimento
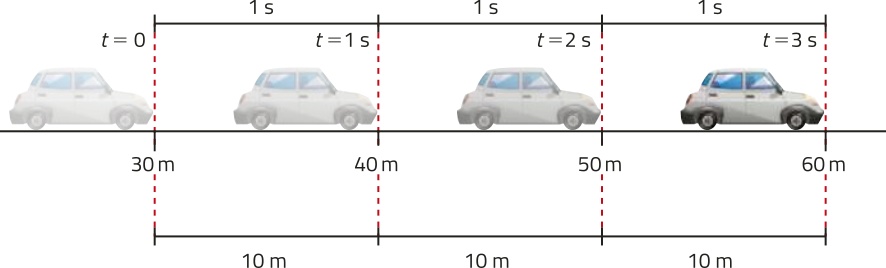
Na figura a seguir, estão representadas informações sobre a posição e o tempo de deslocamento de um automóvel em um movimento retilíneo uniforme, com velocidade constante de 10 m/s.
DICA
Nesta situação, consideramos D(S) = {t ∈ ℝ | t ≥ 0}, ou seja, a função descreve o movimento a partir da posição inicial do automóvel.
pôdêmos determinar a posição dêêsse automóvel, em métro, no tempo t, em segundo, por meio da função afim definida por:
S (t) = 30 + 10t
PARA PENSAR
Qual é o espaço percorrido pelo automóvel no intervalo de tempo entre t = 0 e t = 1? Justifique.
10 m, pois S (1) − S (0) = 10
Página cento e trinta
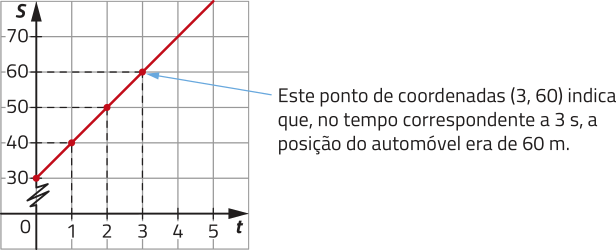
Também é possível expressar essa função, graficamente, no plano cartesiano. Observe.
DICA
Neste gráfico, as escalas dos eixos são diferentes e parte do eixo das ordenadas foi suprimido, indicado pelo sín-bolo ![]() .
.
PENSANDO NO ASSUNTO
1. Em relação ao movimento retilíneo uniforme, identifique as afirmativas verdadeiras.
a) A velocidade do móvel é sempre constante.
b) A velocidade do móvel varia de acôr-do com o intervalo de tempo.
c) O móvel póde percorrer uma mesma distância em intervalos de tempo diferentes.
d) Em dois intervalos de tempo iguais, o móvel percórre distâncias também iguais.
alternativas a e d
2. Analise as informações apresentadas nas páginas 129 e 130 para resolver as kestões.
a) No gráfico apresentado, o quê o ponto de coordenadas (2,50) representa?
2. a) O ponto de coordenadas (2, 50) representa quê, no tempo correspondente a 2 s, a posição do automóvel era de 50 m.
b) Calcule a posição do automóvel no tempo t = 12.
150 m
c) Em quê instante o automóvel ocupará a posição 200 m?
17 s
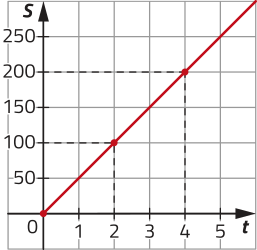
3. O gráfico a seguir representa o deslocamento S (em metro) de um móvel por meio de um movimento retilíneo uniforme, de acôr-do com o tempo t (em segundo). Observe.
DICA
Neste gráfico, as escalas dos eixos são diferentes.
a) Qual é a posição inicial dêêsse móvel? E no instante 4 s?
0 m; 200 m
b) Qual é a velocidade dêêsse móvel?
v = 50 m/s
c) Quantos metros esse móvel percórre em intervalos de tempo iguais a 2 s?
100 m
d) escrêeva a lei de formação dessa função.
S (t) = 50t
4. Um automóvel se desloca em uma rodovia retilínea com velocidade constante. A seguir, estão indicadas as posições dêêsse automóvel em alguns instantes. Determine a lei de formação da função quê descreve a posição S dêêsse automóvel (em quilômetro) no tempo t (em hora).
Tempo (h) |
0 |
1 |
2 |
3 |
|---|---|---|---|---|
Posição (km) |
10 |
60 |
110 |
160 |
S(t) = 10 + 50t
5. Dois móveis, A e B, ao percorrerem simultaneamente a mesma trajetória e no mesmo sentido, tiveram sua posição S, em métro, variando com o tempo t, em segundo, conforme a representação no gráfico a seguir.
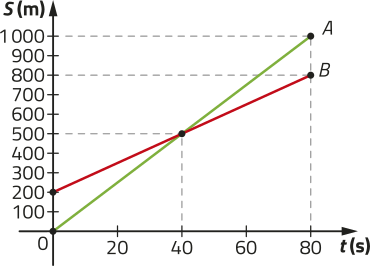
DICA
Neste gráfico, as escalas dos eixos são diferentes.
Com base nessas informações, determine:
a) a posição inicial S0, em métro, de cada móvel;
móvel A: 0 m; móvel B: 200 m
b) o instante t, em segundo, quê os móveis se encontram;
40 s
c) a distância quê cada móvel percorreu nessa trajetória, em métro;
móvel A: 1.000 m; móvel B: 800 m
d) para cada móvel, a lei de formação da função quê descreve a posição S (em metro) no tempo t (em segundo) nessa trajetória.
móvel A: SA (t) = 12,5t; móvel B: SB (t) = 200 + 7,5t
Página cento e trinta e um
![]() 6. Reúnam-se em grupos de três integrantes para realizar um experimento quê simula um movimento retilíneo uniforme. Para isso, providenciem os seguintes materiais:
6. Reúnam-se em grupos de três integrantes para realizar um experimento quê simula um movimento retilíneo uniforme. Para isso, providenciem os seguintes materiais:
Resposta pessoal.
• uma fita adesiva;
• uma fita métrica;
• á gua;
• uma mangueira ou um tubo transparente com 50 cm de comprimento;
• um pedaço de madeira de superfícíe plana com 50 cm de comprimento;
• cronômetro (pode sêr usado um aplicativo de smartphone);
• duas rolhas (para tampar as extremidades da mangueira ou do tubo).
Depois, realizem as etapas a seguir e, se possível, façam os registros em vídeo.
1ª) Utilizando fita adesiva, fixem, sobre o pedaço de madeira, a mangueira e a fita métrica paralelamente entre si. É importante quê a marcação 0 (zero) da fita métrica esteja alinhada com uma extremidade da mangueira (ver Figura A e Figura B).


2ª) Tampem uma das extremidades da mangueira com uma rolha (ou outro objeto capaz de vedar as extremidades da mangueira ou do tubo) e encham-na com á gua. Tampem a outra extremidade da mangueira com a outra rolha, deixando um pouco de ar entre a rolha e a á gua, formando uma pequena bolha de ar.
3ª) Em uma mesa, apoiem uma das extremidades da madeira sobre um livro e a outra extremidade na superfícíe dessa mesa, de modo quê o pedaço de madeira fique inclinado e a bolha de ar se desloque dentro da mangueira (Figura A). Quanto menor for essa inclinação, mais lento será o deslocamento da bolha de ar.
4ª) Aguardem até quê a bolha de ar chegue a uma extremidade da mangueira e alternem a posição da extremidade do pedaço de madeira sobre o livro para iniciar um novo deslocamento da bolha de ar. Após a bolha de ar começar a se deslocar, com auxílio de um cronômetro, obissérvem quanto tempo ela demora para realizar cada deslocamento de 5 cm e registrem os resultados (Figura B).
5ª) Organizem os resultados obtidos na etapa anterior em uma tabéla ou um gráfico. Depois, identifiquem a variação dos dados obtidos por vocês e comparem-nos com aqueles obtidos por outros grupos. Em seguida, considerem os eventuais êêrros das medidas aferidas no experimento e verifiquem se o deslocamento da bolha de ar corresponde a um movimento retilíneo uniforme, destacando as características dêêsse tipo de movimento. Por fim, elaborem um relatório dêêsse experimento e o compartilhem com os côlégas.
Página cento e trinta e dois
Estudo do sinal de uma função afim
Leia a situação a seguir.
A agricultura familiar é uma atividade econômica desenvolvida em pequenas propriedades rurais e costuma representar a principal fonte de renda das famílias quê nelas residem. Nicole é uma agricultora familiar quê cultiva uva. Para participar de uma feira e ter um espaço para vender o quê cultivou e colheu, ela tem de pagar uma taxa fixa de R$ 180,00. Descontados os custos de produção, sabe-se quê cada quilograma de uva vendida na feira rende R$ 4,50 para Nicole. Quantos quilogramas de uva, no mínimo, Nicole tem de vender para obtêr lucro nessa feira?

Para responder a essa questão, podemos determinar a lei de formação de uma função afim m quê descreve o lucro (ou o prejuízo) de Nicole de acôr-do com x quilogramas de uva vendidas, considerando a taxa fixa a sêr paga.
m (x) = 4,5x − 180
Note quê Nicole terá lucro quando a função m for positiva. Assim, vamos determinar para quais pontos do domínio a função é positiva, para quais é nula e para quais é negativa. Ao fazer isso, dizemos quê vamos estudar o sinal dessa função afim. Para isso, inicialmente, calculamos o zero de m, ou seja, o valor de x para o qual m (x) = 0, e identificamos se essa é uma função crescente ou decrescente.
• Zero de m: 4,5x − 180 = 0 ⇒ 4,5x = 180 ⇒ x = = 40
• a > 0, pois a = 4,5. Logo, m é uma função crescente.
Com base nessas informações, construímos um esboço do gráfico da função m com as informações relevantes para o estudo desejado. Essas informações são: o zero da função e o traçado da reta, ascendente ou descendente, dependendo do crescimento da função.
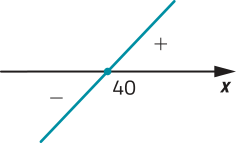
A partir do esboço do gráfico, concluímos quê:
• m é nula para x = 40, ou seja, se x = 40 ⇒ m (x) = 0;
• m é negativa para x < 40, ou seja, se x < 40 ⇒ m (x) < 0;
• m é positiva para x > 40, ou seja, se x > 40 ⇒ m (x) > 0.
Portanto, Nicole terá lucro nessa feira se vender mais quê 40 kg de uva.
PARA PENSAR
Na lei de formação da função m, o quê indica a taxa de variação? E o termo independente?
A taxa de variação a = 4,5 indica o rendimento, em reais, quê Nicole recebe a cada quilograma de uva vendida. O termo independente b = −180 indica o valor, em reais, a sêr descontado pela participação na feira.
DICA
pôdêmos, também, utilizar uma inequação para resolver a situação apresentada.
m (x) > 0 ⇒
⇒ 4,5x − 180 > 0 ⇒
⇒ 4,5x > 180 ⇒
⇒ x > ⇒ x >40
S = {x ∈ ℝ | x > 40}
Página cento e trinta e três
De maneira geral, para estudar o sinal de uma função afim, determinamos o zero e o crescimento dessa função e, em seguida, analisamos para quais valores do domínio a função é positiva, negativa ou nula. Como o zero de uma função afim é dado por x = podemos definir o seguinte.
Dada uma função afim f: ℝ → ℝ, definida por f(x) = ax + b com a ≠ 0.
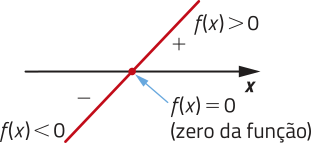
• Se f é uma função crescente (a > 0), temos:
• f(x) > 0 para x > ;
• f(x) < 0 para x < ;
• f(x) = 0 para x =
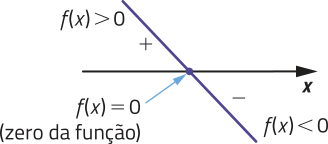
• Se f é uma função decrescente (a < 0), temos:
• f(x) > 0 para x < ;
• f(x) < 0 para x > ;
• f(x) = 0 para x = .
ATIVIDADE RESOLVIDA
R11. Realize o estudo do sinal das funções a seguir.
a) f(x) = − 1
b) g (x) = −2x + 4
Resolução
a) Vamos calcular o zero de f e identificar se ela é uma função crescente ou decrescente.
• Zero de f: − 1 = 0 ⇒ x = 2.
• a > 0, pois a = . Logo, f é uma função crescente.
Assim, segue quê:
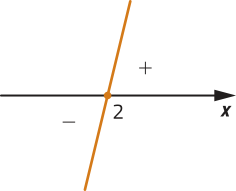
• Para x = 2, temos f(x) = 0.
• Para x < 2, temos f(x) < 0.
• Para x > 2, temos f(x) > 0.
b) Vamos calcular o zero de g e identificar se ela é uma função crescente ou decrescente.
• Zero de g: −2x + 4 = 0 ⇒ x = 2.
• a < 0, pois a = −2. Logo, g é uma função decrescente.
Assim, segue quê:
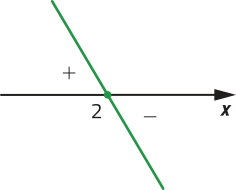
• Para x = 2, temos g (x) = 0.
• Para x < 2, temos g (x) > 0.
• Para x > 2, temos g (x) < 0.
Página cento e trinta e quatro
ATIVIDADES
40. Realize o estudo do sinal das funções a seguir.
40. Respostas nas Orientações para o professor.
a) f(x) = 6x − 2
b) g (x) = −7x + 1
c) h (x) = 9x − 3
d) m (x) = −5x − 4
e) n (x) = 3x + 12
f) p (x) = 10x
41. Determine para quais valores de x as funções representadas a seguir são positivas.
a) 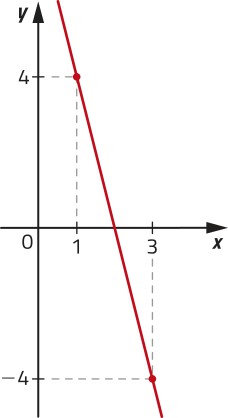
f(x) > 0 para x < 2
b) 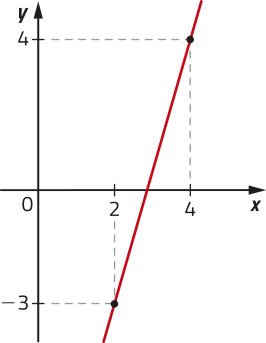
f(x) > 0 para x >
42. Considere as funções f(x) = −3x − 12 e g (x) = −4x − 4. Determine os valores reais de x para os quais ambas as funções são positivas. Explique, com suas palavras, como você realizou esta atividade.
x ∈]−∞, −4[; resposta pessoal
43. Em um experimento realizado em laboratório, cérto líquido foi submetido a um resfriamento por 10 min e sua tempera-túra foi registrada em um termômetro em dois momentos. Observe.
43. positiva: 0 ≤ t < 6; igual a zero: t = 6; negativa: 6 < t ≤ 10
DICA
O tempo registrado abaixo dos termômetros representa o período contabilizado após o início do experimento, em minuto.
Considerando quê a variação da tempera-túra durante o período de realização do experimento póde sêr modelada por uma função afim, dêz-creva em quais momentos essa tempera-túra, em grau célcius, foi negativa, positiva e igual a zero.
44. Mostre quê, em uma função afim decrescente f: ℝ → ℝ, definida por f(x) = ax + b, temos f(x) > 0 para x < .
Resposta nas Orientações para o professor.
45. Em uma rua movimentada de certa cidade, há dois estacionamentos para carros quê apresentam maneiras distintas de cobrança. Observe.
• Estacionamento A: R$ 12,00 por hora.
• Estacionamento B: R$ 20,00 fixos, mais R$ 6,00 por hora.
a) Qual dos estacionamentos é financeiramente mais vantajoso para um motorista deixar o carro estacionado por 2 horas? Nesse caso, quê quantia ele vai pagar?
45. a) estacionamento A; R$ 24,00
b) Para cada estacionamento, determine uma função quê expresse o valor V a pagar, em reais, de acôr-do com o tempo t, em hora, quê um carro fica estacionado.
45. b) estacionamento A: V(t) = 12t; estacionamento B: V(t) = 6t + 20
c) Qual dêêsses estacionamentos é mais vantajoso financeiramente para um motorista de acôr-do com o tempo em quê o carro fica estacionado? Explique.
45. c) Para períodos de até 3 horas de uso, o estacionamento A é mais vantajoso financeiramente para o motorista. Para períodos a partir de 3 horas, o estacionamento B é mais vantajoso.
DICA
Para resolver esta atividade, considere as frações de hora de permanência do carro no estacionamento como a hora exata seguinte. Por exemplo, se um carro ficar estacionado por 2h15min, é cobrada a permanência de 3 h.
46. (UEA-AM) Ana e Beatriz caminham em uma pista retilínea, na mesma direção e sentido, e com as respectivas velocidades constantes. Sabe-se quê a posição de Ana, PA, é dada por PA (t) = 200 + 25t, quê a posição de Beatriz, PB, é dada por PB (t) = 500 + 20t e quê o tempo t é dado em minutos. Nessas condições, o tempo quê Ana precisa para alcançar Beatriz é:
a) 60 minutos.
b) 45 minutos.
c) 25 minutos.
d) 20 minutos.
e) 40 minutos.
alternativa a
Página cento e trinta e cinco
Algumas aplicações
Estudaremos, a seguir, diferentes situações nas quais a compreensão do conceito e das características de uma função afim são importantes para a interpretação e a análise delas.
Função afim e perímetro de polígonos regulares
Você provavelmente estudou quê os polígonos regulares são aqueles cujas medidas de todos os seus lados são iguais e as medidas de todos os seus ângulos internos também são iguais. Observe alguns exemplos de polígonos regulares.
É possível representar por uma função afim o perímetro de um polígono regular de acôr-do com a medida de seus lados. No caso de um pentágono regular, por exemplo, a função afim f, quê determina seu perímetro de acôr-do com a medida x de um de seus lados, póde sêr definida pela seguinte lei de formação.

Nesse caso, note quê x póde assumir apenas valores reais positivos, ou seja, D(f) = {x ∈ ℝ | x > 0}, uma vez quê representa a medida de um lado do pentágono regular.
Observe o gráfico da função f.
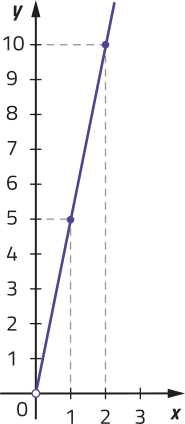
DICA
Nesta situação, é necessário estabelecer uma unidade de medida de comprimento para x. Por exemplo, considerando x = 1,5 e o centímetro como a unidade de medida de comprimento, temos:
f(1,5) = 5 ⋅ 1,5 = 7,5; ou seja, 7,5 cm
Um pentágono regular com 1,5 cm de lado tem 7,5 cm de perímetro.
PARA PENSAR
A medida do lado de um pentágono regular e seu perímetro são grandezas diretamente proporcionais? Justifique.
Resposta esperada: Sim, pois, se aumentarmos ou reduzirmos a medida de cada lado do pentágono regular, seu perímetro também aumenta ou reduz, respectivamente, na mesma proporção. Assim, se multiplicarmos a medida de cada lado do pentágono regular por um número real positivo k, seu perímetro também será multiplicado por esse mesmo número (5 ⋅ k x = k ⋅ 5x = k ⋅ f(x)).
Página cento e trinta e seis
Função afim e juro simples
O juro simples é uma modalidade de aplicação financeira quê envolve os elemêntos descritos a seguir.
• Juro (j): rendimento obtído.
• Capital (c): quantia investida ou correspondente à dívida inicial.
• Taxa de juro (i): porcentual de rendimento em cérto período de tempo.
• Tempo (t): período em quê o capital fica investido ou em dívida.
Na modalidade de juro simples, a relação entre esses elemêntos póde sêr expressa da maneira a seguir.
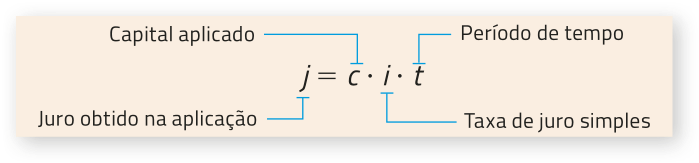
Agora, considere a situação descrita a seguir.
Sérgio fez uma aplicação financeira de R$ 500,00 a uma taxa de juro simples de 2% ao mês.
pôdêmos calcular, por exemplo, o juro obtído nessa aplicação após um período de 10 meses da seguinte maneira:
j = 500 ⋅ 0,02 ⋅ 10 = 100
DICA
Note quê i = 2% = = 0,02.
Assim, Sérgio obterá R$ 100,00 de juro ao final de 10 meses dessa aplicação.
Também podemos analisar o comportamento do juro nessa aplicação de acôr-do com o tempo. Para isso, substituímos os valores correspondentes ao capital e à taxa de juro na expressão: j = 500 ⋅ 0,02 ⋅ t ⇒ j = 10t.
Assim, podemos definir a lei de formação de uma função f(t) = 10t, em quê t é um número natural, para expressar o juro obtído nessa aplicação de acôr-do com o tempo t, em mês. Observe o gráfico dessa função.
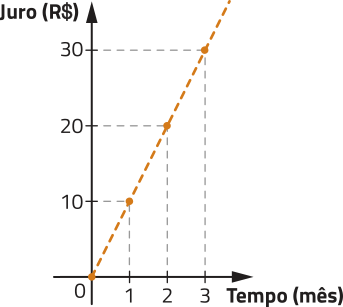
t |
f(t) |
|---|---|
0 |
0 |
1 |
10 |
2 |
20 |
3 |
30 |
DICA
Neste gráfico, as escalas dos eixos estão diferentes.
PARA PENSAR
Em quanto tempo o capital aplicado por Sérgio será dobrado?
após 50 meses da aplicação
Página cento e trinta e sete
ATIVIDADE RESOLVIDA
R12. O gráfico da figura representa o juro obtído em uma aplicação de R$ 1.500,00 no sistema de juro simples de acôr-do com o tempo. Determine a taxa mensal de juro dessa aplicação e escrêeva uma função f para expressar o juro obtído de acôr-do com o tempo t, em mês.
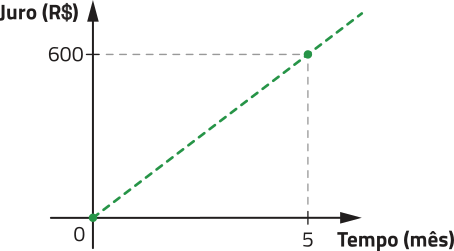
DICA
Neste gráfico, as escalas dos eixos estão diferentes.
Resolução
De acôr-do com o gráfico, ao fim de 5 meses da aplicação, o juro obtído é igual a R$ 600,00. Como o capital aplicado foi de R$ 1.500,00, temos quê:
j = c ⋅ i ⋅ t ⇒ 600 = 1.500 ⋅ i ⋅ 5 ⇒ i = 0,08 = 8%
Portanto, a taxa de juro dessa aplicação é de 8% ao mês.
Agora, devemos determinar uma função f quê expresse o juro obtído nessa aplicação de acôr-do com o tempo t, em mês.
Substituindo os valores de c e i na expressão, segue quê:
j = c ⋅ i ⋅ t ⇒ j = 1.500 ⋅ 0,08 ⋅ t ⇒ j = 120t
Assim, podemos escrever a função f: ℕ → ℝ, definida por f(t) = 120t.
PARA PENSAR
Explique por quê o domínio da função f deve sêr ℕ.
Porque os valores de t do domínio correspondem à quantidade de meses de uma aplicação financeira.
Função afim e progressão aritmética
Considere a função f: ℕ → ℝ, definida por f(x) = 2x + 3. Agora, vamos calcular o valor numérico dessa função fazendo x variar de acôr-do com a sequência dos números naturais, a partir de x = 0. Acompanhe.
• x = 0 → f(0) = 2 ⋅ 0 + 3 = 3
• x = 1 → f(1) = 2 ⋅ 1 + 3 = 5
• x = 2 → f(2) = 2 ⋅ 2 + 3 = 7
• x = 3 → f(3) = 2 ⋅ 3 + 3 = 9
• x = 4 → f(4) = 2 ⋅ 4 + 3 = 11
• x = 5 → f(5) = 2 ⋅ 5 + 3 = 13
⋮⋮
Note quê os valores obtidos, na ordem em quê foram calculados, correspondem a termos de uma sequência numérica em quê, a partir do 2º termo, cada termo corresponde ao anterior adicionado de duas unidades.

Essa sequência ôbitída é um exemplo de progressão aritmética.
Denominamos progressão aritmética (PA) toda sequência numérica em quê, a partir do 2º termo, a diferença entre um termo qualquer e seu antecessor é igual a uma constante. Essa constante, quê póde sêr indicada por r, é a razão da PA.
pôdêmos determinar os termos de uma PA a partir de uma função f: ℕ → ℝ, definida por f(x) = ax + b.
Página cento e trinta e oito
ATIVIDADE RESOLVIDA
R13. Considere uma função f: ℕ → ℝ, definida por f(x) = −3x + 2, e a PA dada por (f(0), f(1), f(2), f(3),..., f(n),...).
a) escrêeva os cinco primeiros termos dessa PA.
b) Qual é a razão dessa PA?
c) Construa o gráfico de f.
Resolução
a) Os cinco primeiros termos dessa PA são dados por f(0), f(1), f(2), f(3) e f(4).
• f(0) = −3 ⋅ 0 + 2 = 2
• f(1) = −3 ⋅ 1 + 2 = −1
• f(2) = −3 ⋅ 2 + 2 = −4
• f(3) = −3 ⋅ 3 + 2 = −7
• f(4) = −3 ⋅ 4 + 2 = −10
Portanto, os cinco primeiros termos dessa PA são 2, −1, −4, −7 e −10.
b) Como a razão r de uma PA corresponde, a partir do segundo termo, à diferença entre um termo qualquer e seu antecessor, temos:
r = −1 − 2 = −3
Portanto, a razão dessa PA é −3.
c) Construindo o gráfico de f, temos:
x |
y |
(x, y) |
|---|---|---|
0 |
2 |
(0, 2) |
1 |
−1 |
(1, −1) |
2 |
−4 |
(2, −4) |
3 |
−7 |
(3, −7) |
4 |
−10 |
(4, −10) |

ATIVIDADES
47. Observe a figura de um polígono regular.

a) Como é nomeado esse polígono em relação ao número de lados?
heptágono regular
b) escrêeva uma função f quê expresse o perímetro dêêsse polígono de acôr-do com a medida x de cada um de seus lados.
47. b) f:]0, +∞[ → ℝ, definida por f(x) = 7x
c) Em relação à função f quê você escreveu no item b, calcule f(4) e explique o quê esse cálculo indica.
47. c) f(4) = 28. Resposta esperada: Esse cálculo indica quê um heptágono regular tem perímetro com 28 unidades de comprimento quando cada um de seus lados méde 4 unidades de comprimento.
48. êste gráfico representa uma função g quê expressa o perímetro de um polígono regular em quê cada lado méde x. Qual é esse polígono?
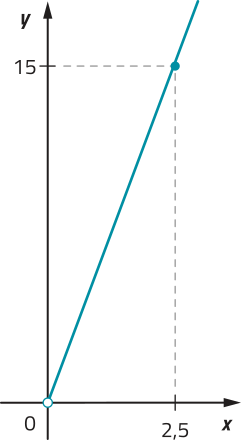
hekzágono regular
DICA
Neste gráfico, as escalas dos eixos são diferentes.
Página cento e trinta e nove
49. Em uma aplicação financeira, o montante (M) é a soma do capital aplicado e do juro obtído após cérto tempo. Esse montante póde sêr calculado por meio da expressão a seguir.
M = c + j ⇒ M = c + (c ⋅ i ⋅ t) ⇒
⇒ M = c (1 + i ⋅ t)
Considere um capital de R$ 600,00 aplicado a uma taxa de juro simples de 5% ao mês e resôuva os itens a seguir.
a) Qual é o montante obtído nessa aplicação após 1 mês? E após 5 meses?
R$ 630,00;
R$ 750,00
b) escrêeva uma função f quê expresse o montante dessa aplicação de acôr-do com o tempo t, em mês.
f: ℕ → ℝ, definida por f(t) = 30t + 600
c) Represente o gráfico da função quê você escreveu no item b.
Resposta nas Orientações para o professor.
50. O qüadro a seguir expressa a relação entre medidas do lado de um quadrado e os respectivos valores do perímetro e da área dele.
Lado (cm) |
Perímetro (cm) |
Área (cm2) |
|---|---|---|
1 |
4 |
1 |
2 |
8 |
4 |
3 |
12 |
9 |
4 |
16 |
16 |
a) Que regularidades há entre os números indicados nas colunas correspondentes às medidas do lado e ao perímetro do quadrado? E entre os números correspondentes às medidas do lado e à área do quadrado?
Resposta nas Orientações para o professor.
b) De acôr-do com a resposta ao item anterior, expresse o perímetro e a área de um quadrado cujo lado méde x, considerando certa unidade de medida de comprimento.
50. b) perímetro: 4x; área: x2
c) Se dobrarmos a medida do lado de um quadrado qualquer, a área dele também dobra? Justifique sua resposta.
Resposta nas Orientações para o professor.
d) Se dobrarmos a medida do lado de um quadrado, o perímetro dele também dobra? Justifique sua resposta.
Resposta nas Orientações para o professor.
e) escrêeva a lei de formação das funções p e s quê expressam, respectivamente, o perímetro e a área de um quadrado cujo lado méde x, considerando certa unidade de medida de comprimento.
p(x) = 4x; s(x) = x2.
51. Uma instituição oferece as opções A e B de investimentos sôbi sistema de juro simples. Observe, no gráfico, o montante quê um cliente póde obtêr aplicando capitais distintos nessas duas opções.
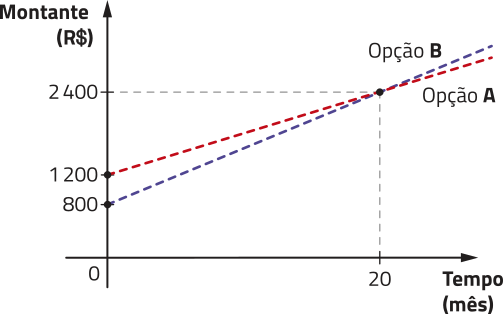
DICA
Neste gráfico, as escalas dos eixos são diferentes.
a) Que capital o cliente pretende aplicar em cada opção de investimento?
A: R$ 1.200,00;
B: R$ 800,00
b) Determine a taxa mensal de juro em cada opção de investimento.
A: 5%; B: 10%
c) escrêeva uma função quê expresse o montante obtído (em reais) ao final de t meses para cada um dêêsses investimentos.
51. c) A: f: ℕ → ℝ, definida por f(t) = 60t + 1.200; B: g: ℕ → ℝ, definida por g (t) = 80t + 800
d) Em qual investimento o montante obtído é o maior após 1 ano? E após 2 anos?
investimento A; investimento B
52. Antônio trabalha com vendas em certa loja de materiais esportivos. Seu salário mensal varia de acôr-do com a quantia, em reais, ôbitída nas vendas quê ele realizou no mês. Observe.
• Vendas de até R$ 5.000,00: salário de R$ 2.000,00.
• Vendas maiores quê R$ 5.000,00 até R$ 10.000,00: salário de R$ 2.000,00 mais 10% do valor das vendas quê ultrapassar R$ 5.000,00.
• Vendas maiores quê R$ 10.000,00: salário de R$ 2.500,00 mais 15% do valor das vendas quê ultrapassar R$ 10.000,00.
a) escrêeva a lei de formação de uma função definida por mais de uma sentença quê relacione o salário mensal S de Antônio com a quantia v, em reais, ôbitída nas vendas quê ele realizou no mês.
Resposta nas Orientações para o professor.
b) Em uma malha quadriculada, construa o gráfico da função S.
52. a) S(v) =
Página cento e quarenta
53. O gráfico a seguir representa a função V quê expressa o valor a pagar na fatura de gás de um condomínio de cérto município, em reais, de acôr-do com a quantidade x de métro cúbico de gás consumido.
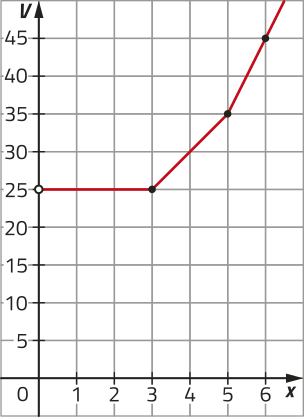
DICA
Neste gráfico, as escalas dos eixos são diferentes.
a) escrêeva a lei de formação da função V, apresentada no gráfico. as resoluções.
53. a) V(x) =
b) Elabore três kestões quê envolvam as informações apresentadas nesta atividade e trabalhe o conceito de função. Depois, troque-as com um colega para quê um resôuva as kestões do outro. Ao final, confiram juntos
Elaboração do estudante.
54. Considere uma função afim f: ℕ → ℝ, definida por f(x) = 5x − 20, e a PA dada por: (f(0), f(1), f(2),..., f(n),...).
a) escrêeva os cinco primeiros termos dessa PA.
20, −15, −10, −5 e 0
b) Qual é a razão dessa PA?
5
c) Construa o gráfico de f.
Resposta nas Orientações para o professor.
55. Observe o gráfico de uma função f: ℕ → ℝ.
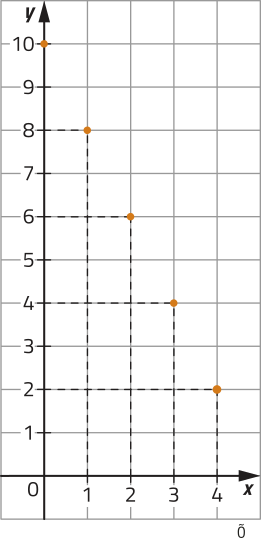
a) escrêeva a lei de formação da função f.
f(x) = −2x + 10
b) A partir da função f, podemos determinar uma PA de termos (f(0), f(1), f(2),..., f(n),...). Nessa PA, qual é o valor do:
• 10º termo?
−8
• 20º termo?
−28
• 100º termo?
−188
56. Ao aplicar um capital de R$ 900,00 a uma taxa de juro simples mensal de 7%, obteve-se R$ 252,00 de juro. Por quantos meses esse capital ficou aplicado?
4 meses
57. Observe a sequência figural a seguir, em quê cada figura é formada por quadrados e circunferências.
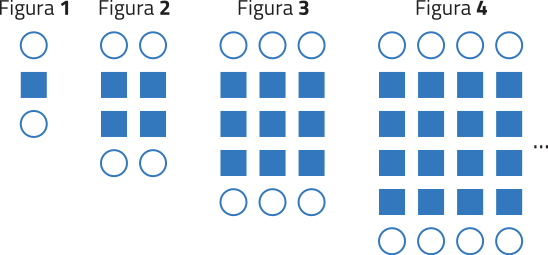
![]() a) Nessa sequência, quê regularidade você percebe na variação da quantidade de quadrados e de circunferências de uma figura para a seguinte? Explique com suas palavras.
a) Nessa sequência, quê regularidade você percebe na variação da quantidade de quadrados e de circunferências de uma figura para a seguinte? Explique com suas palavras.
Resposta pessoal.
b) Desenhe como você imagina sêr a figura 5 dessa sequência. Depois, compare com os dêzê-nhôs feitos pêlos côlégas.
Construção do estudante.
c) escrêeva uma sequência numérica para expressar a quantidade de:
• quadrados nas figuras dessa sequência figural.
(1, 4, 9, 16, 25,..., n2,...)
• circunferências nas figuras dessa sequência figural.
(2, 4, 6, 8, 10,..., 2n,...)
d) Qual das sequências numéricas quê você escreveu no item anterior é uma PA?
Justifique sua resposta.
57. d) A sequência numérica (2, 4, 6, 8, 10,..., 2n,...) é uma PA, pois, a partir do segundo termo, a diferença entre cada termo e o anterior é igual a 2, quê corresponde à razão da PA.
![]() 58. Pesquise uma situação quê envolva uma progressão aritmética. póde sêr uma situação do seu dia a dia ou de alguma área do conhecimento. Depois, dêz-creva como a progressão aritmética se relaciona com essa situação. Indique também os primeiros termos dessa sequência e defina uma função quê possa sêr relacionada a ela. Ao final, troque a situação quê você analisou com a de um colega para quê um avalie a produção do outro.
58. Pesquise uma situação quê envolva uma progressão aritmética. póde sêr uma situação do seu dia a dia ou de alguma área do conhecimento. Depois, dêz-creva como a progressão aritmética se relaciona com essa situação. Indique também os primeiros termos dessa sequência e defina uma função quê possa sêr relacionada a ela. Ao final, troque a situação quê você analisou com a de um colega para quê um avalie a produção do outro.
Pesquisa e elaboração do estudante.
![]() 59. Elabore um problema envolvendo uma função f: ℕ → ℝ, definida por f(x) = ax + b, e uma progressão aritmética. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
59. Elabore um problema envolvendo uma função f: ℕ → ℝ, definida por f(x) = ax + b, e uma progressão aritmética. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página cento e quarenta e um
Função modular
Estudamos na Unidade 1 quê o módulo de um número real x, indicado por |x |, é dado por x, se x ≥ 0, e por −x, se x < 0. Observe alguns exemplos.
• |3,7| = 3,7
• |−6| = 6
• |− | =
•
• |−100| = 100
A partir da definição de módulo de um número real, podemos determinar uma função f: ℝ → ℝ, definida por f(x) = |x |. Esse tipo de função é denominado função modular e póde sêr expresso da maneira a seguir.
f(x) =
Acompanhe as etapas quê podemos realizar para esboçar o gráfico de uma função modular.
1ª) Atribuir valores arbitrários para x < 0, determinar os pares ordenados (x, y) correspondentes e esboçar o gráfico para x < 0.
x |
f(x) = −x |
(x, y) |
|---|---|---|
−3 |
f(−3) = −(−3) = 3 |
(−3, 3) |
−2 |
f(−2) = −(−2) = 2 |
(−2, 2) |
−1 |
f(−1) = −(−1) = 1 |
(−1, 1) |
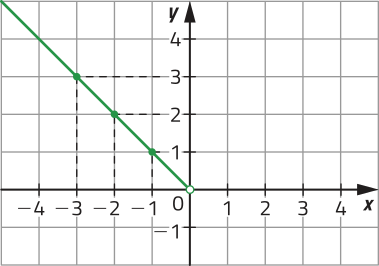
2ª) Em seguida, de maneira análoga à primeira etapa, atribuímos valores arbitrários para x ≥ 0 e esboçamos o gráfico para x ≥ 0. Assim, obtemos o gráfico da função modular f(x) = |x|.
x |
f(x) = x |
(x, y) |
|---|---|---|
0 |
f(0) = 0 |
(0, 0) |
1 |
f(1) = 1 |
(1, 1) |
2 |
f(2) = 2 |
(2, 2) |
3 |
f(3) = 3 |
(3, 3) |
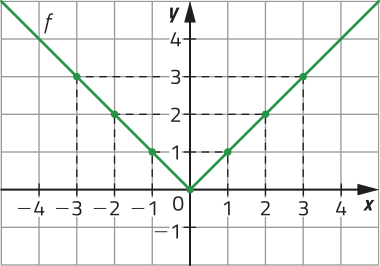
DICA
Note quê, para construir o gráfico da função modular f: ℝ → ℝ, definida por f(x) = |x|, podemos representar o gráfico de g(x) = −x, para x < 0, e de h(x) = x, para x ≥ 0.
PARA PENSAR
Para quais valores reais de x uma função modular do tipo f(x) = |x| é negativa? Justifique.
Não há valor real de x para o qual f(x) < 0, pois |x | ≥ 0 para todo x real.
Página cento e quarenta e dois
Também podemos obtêr o gráfico da função modular f(x) = |x| considerando o gráfico da função identidade g (x) = x e refletindo seus pontos em relação ao eixo das abscissas para x < 0. Observe.
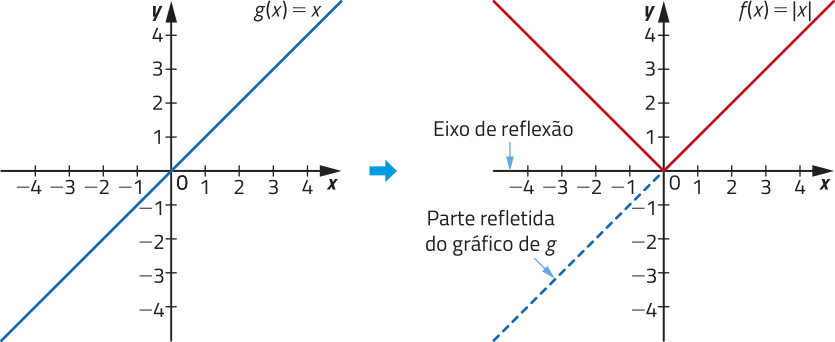
PARA PENSAR
Estabeleça as coordenadas de um ponto P pertencente ao gráfico de g, para x < 0. Depois, determine as coordenadas do ponto P’, simétrico a P por reflekção em relação ao eixo das abscissas. Por fim, mostre quê P ’ é um ponto do gráfico da função modular f. Explique a um colega os procedimentos realizados.
Resposta pessoal.
Translação do gráfico de uma função modular
O gráfico da função modular f(x) = |x | foi construído no GeoGebra e transladado diversas vezes, obtendo-se gráficos de diferentes funções.
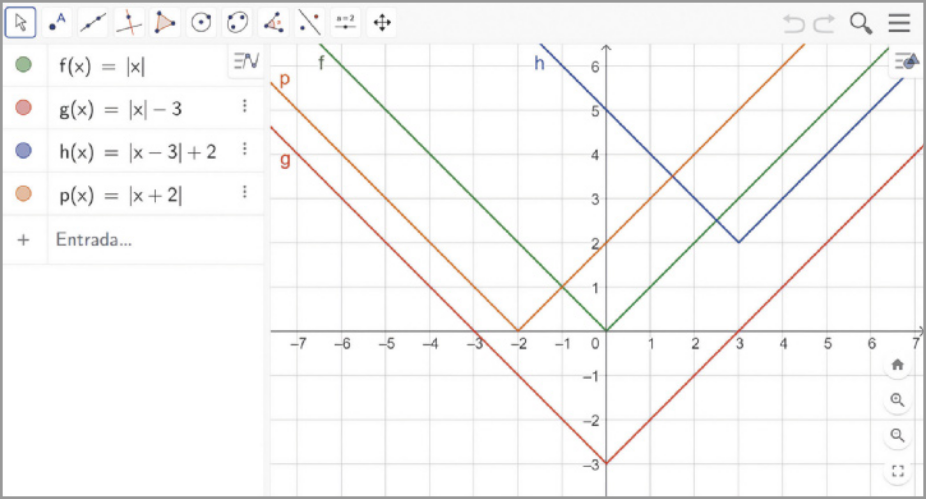
DICA
• Para escrever o módulo de um número real no campo Entrada do GeoGebra, utilizamos | (barra vertical do teclado).
• Utilizando as opções ![]() (Mover janela de visualização),
(Mover janela de visualização), ![]() (Ampliar) e
(Ampliar) e ![]() (Reduzir), é possível visualizar os gráficos dessas funções em diferentes intervalos do domínio real.
(Reduzir), é possível visualizar os gráficos dessas funções em diferentes intervalos do domínio real.
PARA PENSAR
Que regularidade você póde perceber entre cada translação do gráfico de f e a lei de formação da função correspondente ao gráfico obtído?
Resposta pessoal.
Dada uma função g: ℝ → ℝ, definida por g (x) = |x + a | + b, sêndo a e b números reais, podemos obtêr o gráfico de g transladando o gráfico da função modular f(x) = |x| da seguinte maneira:
• |a| unidades para a esquerda, se a > 0;
• |a| unidades para a direita, se a < 0;
• |b| unidades para cima, se b > 0;
• |b| unidades para baixo, se b < 0.
DICA
Quando a = 0, o gráfico não é transladado horizontalmente. Quando b = 0, o gráfico não é transladado verticalmente.
Página cento e quarenta e três
ATIVIDADES RESOLVIDAS
R14. Esboce os gráficos das funções indicadas a seguir com base no gráfico da função modular f(x) = |x |.
a) g: ℝ → ℝ, definida por g (x) = |x + 3|.
b) h: ℝ → ℝ, definida por h (x) = |x | − 2.
c) m: ℝ → ℝ, definida por m (x) = |x + 4| + 3.
d) n: ℝ → ℝ, definida por n (x) = |x − 5| − 1.
Resolução
a) 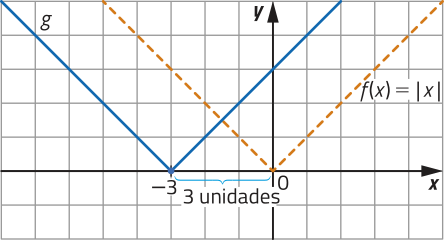
b) 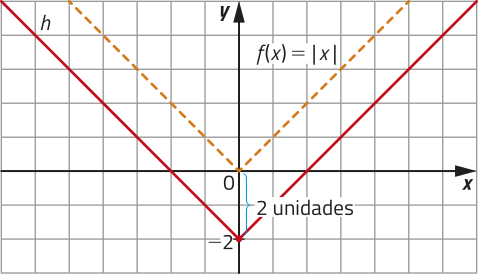
c) 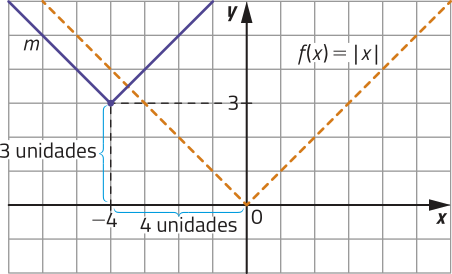
d) 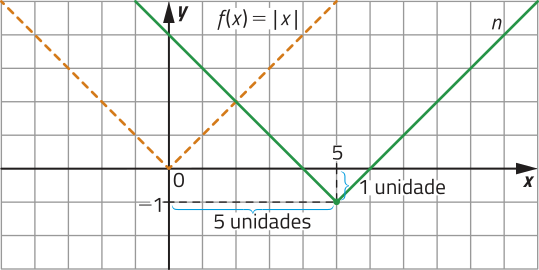
R15. O gráfico de uma função modular f(x) = |x | foi transladado em 7 unidades para a esquerda e em 3 unidades para baixo, determinando o gráfico de uma função g. Calcule g (−8).
Resolução
Como o gráfico de g foi obtído por translações horizontal e vertical do gráfico de uma função modular f(x) = |x |, temos quê sua lei de formação é dada por g (x) = |x + a | + b, sêndo a e b números reais.
Assim, segue quê:
• a = 7, pois a translação horizontal foi de 7 unidades para a esquerda;
• b = −3, pois a translação vertical foi de 3 unidades para baixo.
Logo, determinamos quê g (x) = |x + 7| − 3. Calculando g (−8), temos:
g (−8) = |−8 + 7| − 3 = |−1| −3 = 1 − 3 = −2
Portanto, g (−8) = −2.
PARA PENSAR
No caderno, esboce o gráfico da função g e destaque o ponto de coordenadas (−8, −2), correspondente a g (−8) = −2.
Construção do estudante.
ATIVIDADES
60. Dadas as funções f(x) = |x + 5| − 6 e g (x) = |x − 1| + 4, calcule:
a) f(−3);
−4
b) f(4);
3
c) g (6);
9
d) g (−1);
6
e) f(0) + g (3);
5
f) g (−2) − f(2).
6
61. Esboce o gráfico de cada função indicada a seguir.
a) f(x) = |x |
b) g (x) = |x − 2|
c) h (x) = |x| + 5
d) m (x) = |x + 1| − 4
Respostas nas Orientações para o professor.
Página cento e quarenta e quatro
62. Em um mesmo plano cartesiano, esboce os gráficos das funções g (x) = |x − 3| e h (x) = |x | − 3. Depois, com suas palavras, analise e compare esses gráficos.
Resposta nas Orientações para o professor.
63. Em cada item a seguir, obtenha a lei de formação da função correspondente, sabendo quê cada um dos gráficos representados corresponde a uma translação horizontal ou vertical do gráfico da função modular f(x) = |x |.
a) 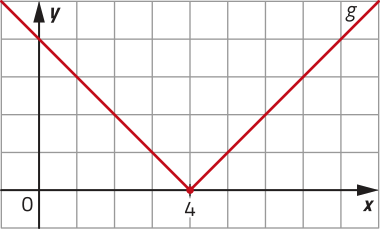
g(x) = |x − 4|
b) 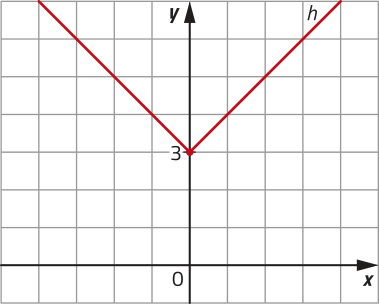
h (x) = |x | + 3
c) 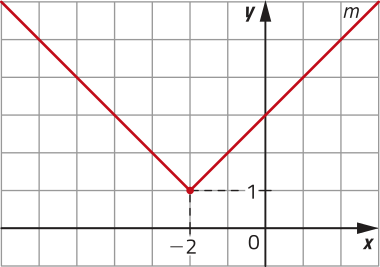
m (x) = |x + 2| + 1
![]() • Agora, explique a um colega os procedimentos quê você realizou para resolver os itens desta atividade.
• Agora, explique a um colega os procedimentos quê você realizou para resolver os itens desta atividade.
Resposta pessoal.
64. Com um programa de computador, Felipe construiu o gráfico da função modular f(x) = |x|. Depois, utilizando ferramentas dêêsse programa, Felipe transladou o gráfico de f em 5 unidades para cima e em duas unidades para a direita.
a) escrêeva a lei de formação da função g correspondente ao gráfico obtído por Felipe após as translações.
g (x) = |x − 2| + 5
b) Quais são as coordenadas do ponto em quê o gráfico de g cruza o eixo das ordenadas?
(0, 7)
65. Raquel faz um curso de programação em quê aprende a desenvolver aplicativos e jogos digitais. Em um de seus projetos, ela desenvolvê-u um jôgo chamado “Caminho da bola”, quê consiste em um tabuleiro disposto em um plano cartesiano, no qual uma bola é lançada a partir de um ponto descrevendo uma trajetória sobre o gráfico de uma função g (x) = |x + a| + b, com a e b reais. Tal bola deve atingir alvos definidos sobre pontos destacados. Ao atingir um ponto qualquer P (x, y), o jogador recebe x − y pontos. Observe uma jogada nesse tabuleiro, em quê estão destacados parte da trajetória da bola, quê estava sobre o ponto I, e os alvos disponíveis.
Alvo |
Coordenadas do ponto |
|---|---|
A |
(11, 6) |
B |
(11, 5) |
C |
(12, 5) |
D |
(12, 4) |
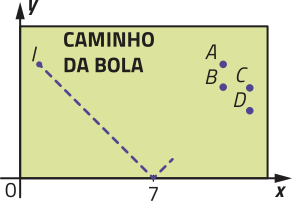
a) Qual é a lei de formação da função sobre a qual está a trajetória da bola nessa jogada?
65. a) g (x) = |x − 7|
b) Nessa jogada, quais alvos serão atingidos? Justifique.
65. b) O alvo C, pois é o único cujo ponto correspondente pertence ao gráfico da função g, pois g (12) = |12 − 7| = |5| = 5.
c) Nessa jogada, qual será a pontuação ôbitída?
Justifique.
7 pontos, pois x − y = 12 − 5 = 7.
66. O fluxograma a seguir representa um algoritmo por meio do qual é possível determinar os valores da função y = f(x) dado o número real x do domínio de f.
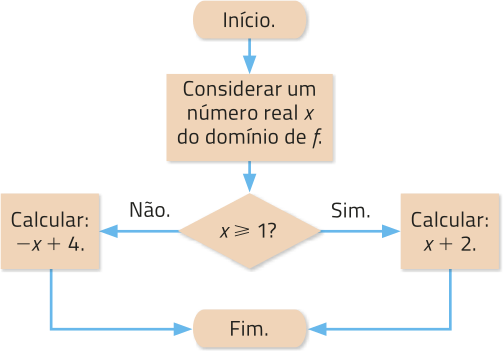
Qual é a lei de formação da função f?
a) f(x) = x + 2
b) f(x) = −x + 4
c) f(x) = |x + 2| + 4
d) f(x) = |x − 1| + 3
e) f(x) = |x − 4| + 5
alternativa d
Página cento e quarenta e cinco
VOCÊ CONECTADO
Construindo e analisando o gráfico da função afim
Observe como podemos construir e analisar o gráfico de uma função afim de acôr-do com sua lei de formação utilizando o software de geometria dinâmica GeoGebra.
Exemplo 1:
Vamos construir o gráfico da função f: ℝ → ℝ definida por f(x) = 2x − 4. Para isso, clicamos no campo Entrada, digitamos f(x) = 2x − 4 e pressionamos a tecla Enter.
Exemplo 2:
Utilizando a opção (Controle deslizante), podemos realizar uma construção no GeoGebra quê possibilita analisar a relação entre os coeficientes de uma função afim f: ℝ → ℝ, definida por f(x) = ax + b, e seu respectivo gráfico.
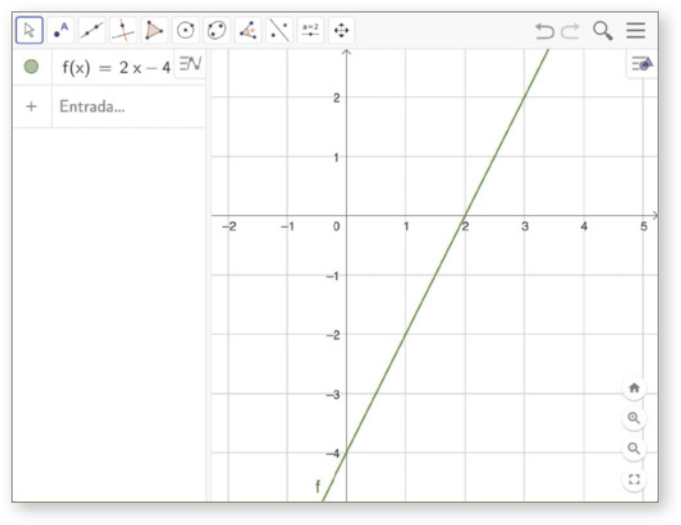

Para isso, siga estes passos.
A Vamos criar os controles deslizantes para os coeficientes a e b. Para o coeficiente a (com a ∈ [−5, 5]), selecionamos a opção ![]() (Controle deslizante) e clicamos em qualquer ponto na Janela de visualização. Em seguida, na caixa de texto quê vai abrir, digitamos a na opção Nome; na aba Intervalo, digitamos −5 na opção min e 5 na opção max; depois, clicamos em OK. De maneira análoga, criamos o contrôle deslizante para o coeficiente b (com b ∈ [−10, 10]).
(Controle deslizante) e clicamos em qualquer ponto na Janela de visualização. Em seguida, na caixa de texto quê vai abrir, digitamos a na opção Nome; na aba Intervalo, digitamos −5 na opção min e 5 na opção max; depois, clicamos em OK. De maneira análoga, criamos o contrôle deslizante para o coeficiente b (com b ∈ [−10, 10]).
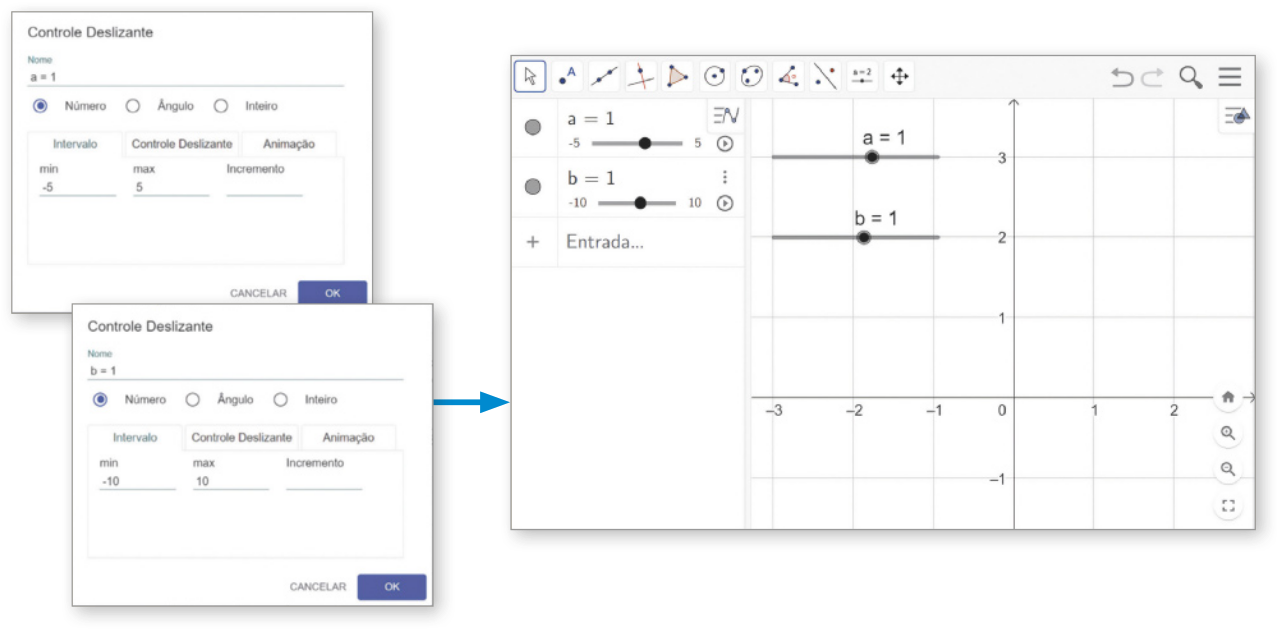
Página cento e quarenta e seis
B No campo Entrada, digitamos f(x) = ax + b e pressionamos a tecla Enter. Ao movimentar os controles deslizantes, variamos os valores dos coeficientes da função e o gráfico se ajusta automaticamente. Observe.
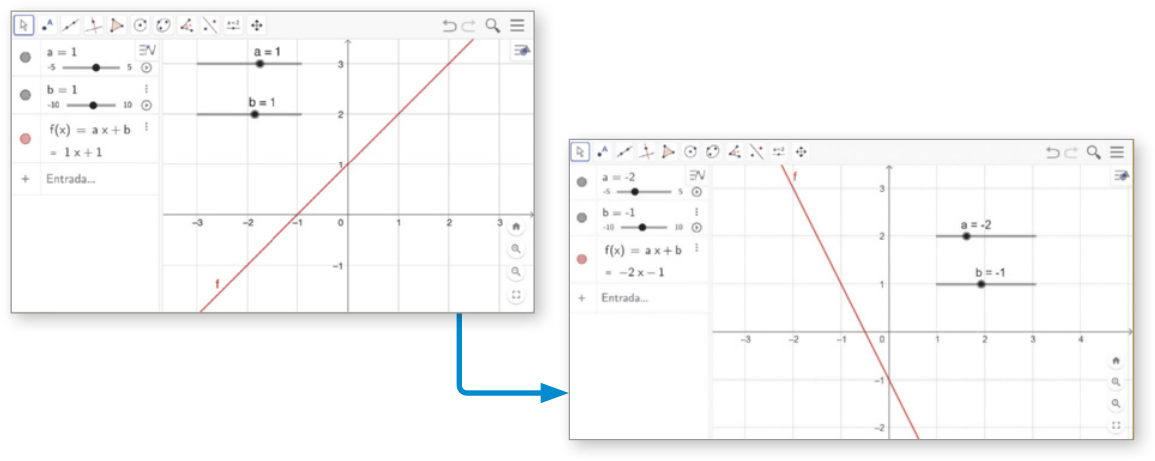
MÃOS À OBRA
1. No GeoGebra, reproduza a construção apresentada no exemplo 1 e, em relação à função f definida por f(x) = 2x − 4, resôuva as kestões.
a) Essa função é crescente ou decrescente?
crescente
b) Com a opção ![]() (Interseção de dois objetos), indique os pontos em quê o gráfico cruza os eixos cartesianos. Qual é o zero dessa função?
(Interseção de dois objetos), indique os pontos em quê o gráfico cruza os eixos cartesianos. Qual é o zero dessa função?
Cruza o eixo x no ponto de coordenadas (2, 0) e o eixo y no ponto de coordenadas (0, −4). O zero da função é x = 2.
c) Faça o estudo do sinal dessa função afim.
f(x) > 0 para x > 2, f(x) = 0 para x = 2 e f(x) < 0 para x < 2
2. Utilizando procedimentos análogos aos do exemplo 1, construa os gráficos das funções indicadas em cada item.
Construção do estudante.
a) f(x) = 3x − 1
b) g (x) = x + 4
c) h (x) = 5 − 2x
d) m (x) = −6
3. Com a opção ![]() (Reta), represente no GeoGebra as retas quê passam pêlos pontos indicados em cada item.
(Reta), represente no GeoGebra as retas quê passam pêlos pontos indicados em cada item.
Construção do estudante.
a) A (−2, 3) e B (3, 1)
b) C (5, 2) e D (−1, −1)
c) E (4, −1) e F(2, −3)
• Agora, obissérve a Janela de Álgebra e escrêeva as equações dessas retas.
a) 2x + 5y = 11;
b) x − 2y = 1;
c) x − y = 5
4. No GeoGebra, reproduza a construção apresentada no exemplo 2 e resôuva as kestões.
a) Movimente os controles deslizantes a e b. Em cada caso, quais alterações você póde observar no gráfico?
4. a) Resposta esperada: Ao movimentar o contrôle deslizante a, a inclinação da reta quê representa o gráfico da função é alterada e, ao movimentar o contrôle deslizante b, o gráfico da função é transladado verticalmente.
b) O quê você acredita quê vai ocorrer com o gráfico ao movimentar o contrôle deslizante b de −6 para 4?
Resposta pessoal.
c) Faça o ajuste indicado no item anterior e verifique sua resposta.
Resposta esperada: O gráfico da função foi transladado em 10 unidades para cima.
5. No GeoGebra, utilizando a opção ![]() (Controle deslizante), construa os controles deslizantes a e b, variando de −10 a 10, e o gráfico da função f: ℝ → ℝ, definida por f(x) = |x + a | + b. Em seguida, movimente os controles deslizantes e dêz-creva as alterações quê cada um deles ocasionou no gráfico de f.
(Controle deslizante), construa os controles deslizantes a e b, variando de −10 a 10, e o gráfico da função f: ℝ → ℝ, definida por f(x) = |x + a | + b. Em seguida, movimente os controles deslizantes e dêz-creva as alterações quê cada um deles ocasionou no gráfico de f.
Construção do estudante. Resposta esperada: O contrôle deslizante a transladou o gráfico para a direita ao diminuir seu valor e para a esquerda ao aumentar seu valor. O contrôle deslizante b transladou o gráfico para baixo ao diminuir seu valor e para cima ao aumentar seu valor.
Página cento e quarenta e sete
Construindo um modelo para representar relações entre grandezas
A planilha eletrônica LibreOffice Calc póde sêr usada para estudar o comportamento de duas grandezas quê se relacionam, construindo modelos correspondentes a funções afins e representações de retas no plano cartesiano. Para isso, considere a seguinte situação.
Uma empresa de desenvolvimento de aplicativos mobile lançou, há uma semana, um jôgo digital. No qüadro, está representada a quantidade de downloads dêêsse jôgo até o momento.
Dia |
Quantidade de downloads (milhares) |
|---|---|
1 |
2,2 |
2 |
2,4 |
3 |
2,8 |
4 |
3,6 |
5 |
3,8 |
6 |
4 |
7 |
4,3 |
A fim de estimar a quantidade de downloads dêêsse jôgo para os próximos dias, sabendo quê a situação póde sêr modelada por uma função afim, vamos obtêr, na planilha eletrônica LibreOffice Calc, a representação da reta e a função quê modela a relação entre a quantidade diária de downloads e a quantidade de dias após o lançamento do jôgo.
Para isso, siga estes passos.
A Organizamos os dados do qüadro na planilha eletrônica.
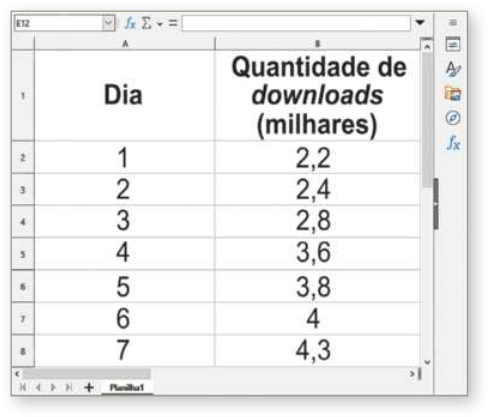
B Selecionamos as células A2:B8 e clicamos na opção Inserir gráfico do menú. Em seguida, ao abrir a caixa de diálogo Assistente de gráficos, na opção 1. Tipo de gráfico, selecionamos as opções XY (Dispersão) e Somente pontos. Por fim, clicamos em Finalizar e obtemos os pontos de coordenadas (x, y), quê indicam a quantidade x de dias após o lançamento do jôgo e a quantidade y de downloads diários, em milhar.
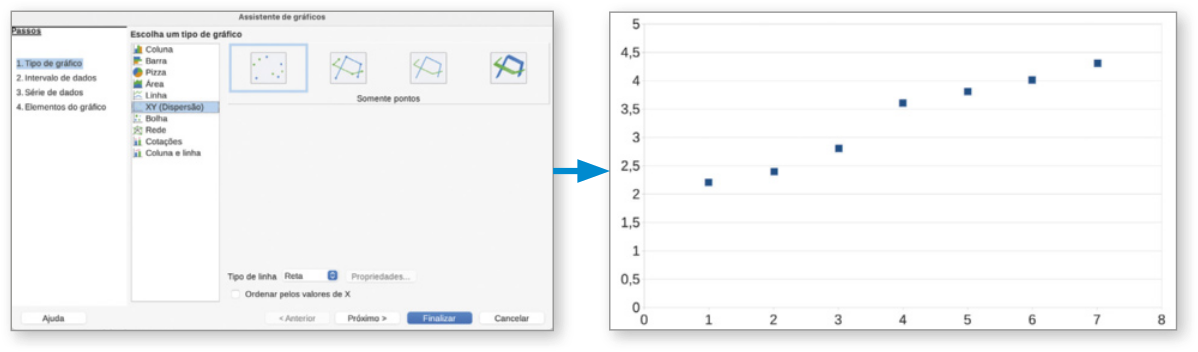
Página cento e quarenta e oito
C Para determinar a reta e a função afim quê modela a relação entre essas grandezas, clicamos sobre um dos pontos plotados para selecioná-lo. Em seguida, clicamos nas opções Inserir e Linha de tendência... do menú. Ao abrir a caixa de diálogo Linha de tendência para a série de dados ‘Coluna B’, na opção Tipo de regressão, selecionamos a opção Linear e, em Opções, marcamos Mostrar equação. Por fim, clicamos em OK.
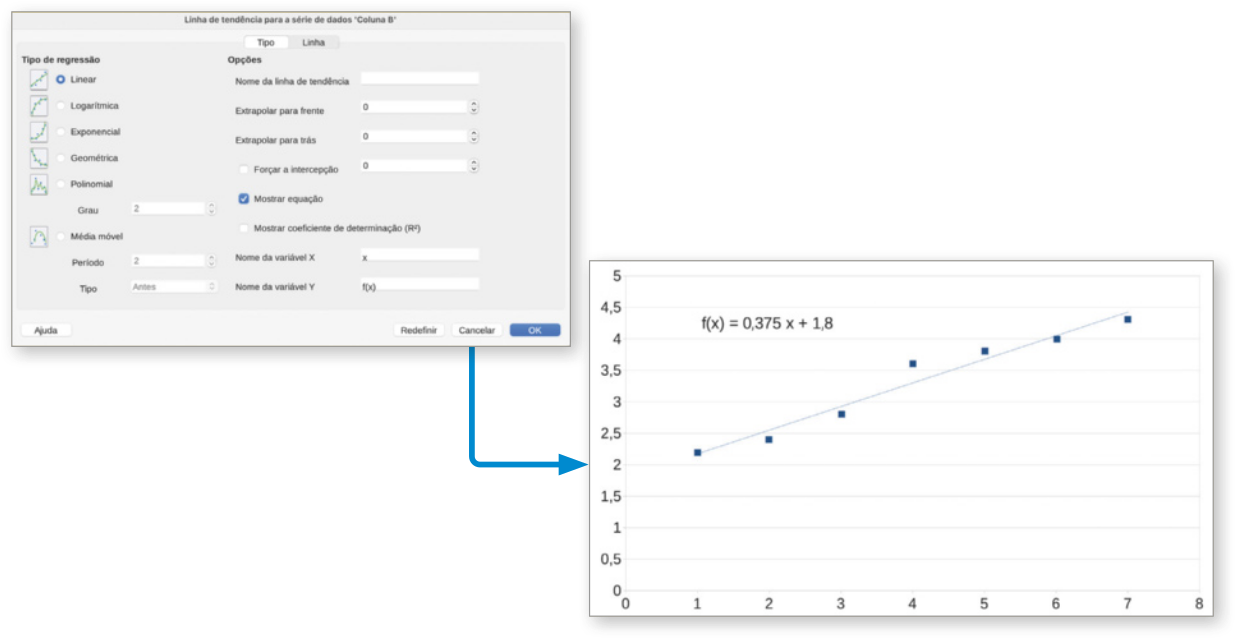
MÃOS À OBRA
1. De acôr-do com a situação apresentada no exemplo, faça o quê se pede.
a) Calcule a diferença entre a quantidade de downloads indicada no qüadro e a quantidade correspondente determinada pela função f para cada um dos dias apresentados.
1. a) dia 1: 25 downloads;
dia 2: 150 downloads;
dia 3: 125 downloads;
dia 4: 300 downloads;
dia 5: 125 downloads;
dia 6: 50 downloads;
dia 7: 125 downloads
b) Considerando a aproximação dos dados obtidos pela função f, estime a quantidade de downloads do jôgo para os próximos três dias.
1. b) dia 8: 4,8 mil downloads;
dia 9: 5,175 mil downloads;
dia 10: 5,55 mil downloads
2. Utilizando os mesmos procedimentos apresentados no exemplo, represente os dados a seguir em uma planilha eletrônica e obtenha a representação da reta e da função afim quê melhor descrevem a relação entre o faturamento de uma empresa de confecções e os 6 primeiros meses do ano.
Mês |
Faturamento (em milhares de reais) |
|---|---|
1 |
7 |
2 |
8 |
3 |
9,5 |
4 |
11 |
5 |
14 |
6 |
15 |
Construção do estudante.
![]() • Com base nas informações fornecidas e na construção quê você realizou, elabore um problema relacionado a função afim. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
• Com base nas informações fornecidas e na construção quê você realizou, elabore um problema relacionado a função afim. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
Página cento e quarenta e nove
O QUE ESTUDEI
![]() 1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Função afim
Função constante
Função linear
Função identidade
Taxa de variação média de uma função
Determinação de uma função afim
Gráfico da função afim
Função afim e progressão aritmética
Função afim e perímetro de polígonos regulares
Função afim e juro simples
Estudo do sinal de uma função afim
Função modular
![]() 3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações.
Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página cento e cinquenta
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre mobilidade urbana sustentável. Observe na figura mais informações sobre a cobrança de um serviço de aluguel de bicicletas.

O nome do estabelecimento quê aparece nesta página é fictício.
a) escrêeva a lei de formação de uma função f quê determine o preêço a sêr pago, nesse serviço de aluguel, por x minutos de uso da bicicleta.
f(x) = 0,5 x + 2,50
b) Calcule f(5) e f(10). Depois, explique o quê esses resultados indicam no contexto apresentado.
4. b) f(5) = 5 e f(10) = 7,50. Esses resultados indicam quê o aluguel da bicicleta por 5 min e por 10 min custam, respectivamente, R$ 5,00 e R$ 7,50.
c) Classifique f como uma função afim, linear, identidade, constante ou modular.
função afim
d) A função f é crescente ou decrescente? O quê isso indica no contexto apresentado?
4. d) Função crescente. Indica quê, ao aumentarmos o tempo de locação da bicicleta, o valor a pagar por esse serviço também aumenta.
e) Determine a taxa de variação da função f, para x variando de 2 min até 20 min.
0,5
f) Esboce o gráfico da função f.
4. f) Resposta nas Orientações para o professor.
g) Os gráficos a seguir foram obtidos ao se deslocar verticalmente o gráfico da função f. Determine a lei de formação da função correspondente a cada gráfico apresentado.
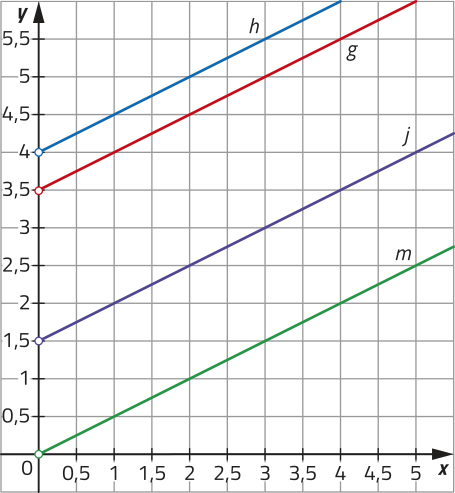
4. g) g (x) = 0,5 x + 3,5; h (x) = 0,5 x + 4;
j (x) = 0,5 x + 1,5; m (x) = 0,5 x
h) Pesquise na internet o preêço cobrado em algum serviço de mobilidade urbana sustentável, como a locação de bicicleta ou de patinete elétrico. Em seguida, dêz-creva a lei de formação de uma função quê possa expressar o valor a pagar por esse serviço de acôr-do com o tempo de uso ou da distância percorrida.
Pesquisa e elaboração do estudante.
![]() i) Em grupo com dois côlégas, investiguem e analisem dados sobre os principais meios de transporte utilizados na região onde vivem. Depois, com base nessa pesquisa, elaborem um texto quê contemple as seguintes kestões: A população, em geral, utiliza veículos automotores a combustão ou meios de transporte alternativos e menos poluentes? O transporte público oferecido no município onde vivem atende às necessidades e demandas da população por um preêço acessível? Por fim, compartilhem as produções com os côlégas e discutam o tema em uma roda de conversa.
i) Em grupo com dois côlégas, investiguem e analisem dados sobre os principais meios de transporte utilizados na região onde vivem. Depois, com base nessa pesquisa, elaborem um texto quê contemple as seguintes kestões: A população, em geral, utiliza veículos automotores a combustão ou meios de transporte alternativos e menos poluentes? O transporte público oferecido no município onde vivem atende às necessidades e demandas da população por um preêço acessível? Por fim, compartilhem as produções com os côlégas e discutam o tema em uma roda de conversa.
Pesquisa e elaboração do estudante.
Página cento e cinquenta e um
PRATICANDO: enêm E VESTIBUlARES
1. (hú éfe pê érre) Uma fábrica de calçados possui um custo fixo mensal de R$ 20.000,00 relacionado a pagamentos de salários, aluguel e outras despesas fixas. Sabendo quê, a cada par de calçados produzido, essa fábrica fatura R$ 28,00, a expressão quê descreve o lucro mensal, em reais, em função do número x de calçados produzidos é:
a) 20.000x − 28.
b) 28x − 20.000.
c) 28x + 20.000.
d) −28x + 20.000.
e) −20.000x + 28.
alternativa b
2. (Enem/MEC) Dirigir após ingerir bebidas alcoólicas é uma atitude extremamente perigosa, uma vez quê, a partir da primeira dose, a pessoa já começa a ter perda de sensibilidade de movimentos e de reflexos. Apesar de a eliminação e absorção do áucôl depender de cada pessoa e de como o organismo consegue mêtabolizar a substância, ao final da primeira hora após a ingestão, a concentração de áucôl (C) no sangue corresponde a aproximadamente 90% da quantidade (q) de áucôl ingerida, e a eliminação total dessa concentração póde demorar até 12 horas.
Disponível em: https://livro.pw/klwpy. Acesso em: 1 dez. 2018 (adaptado).
Nessas condições, ao final da primeira hora após a ingestão da quantidade q de áucôl, a concentração C dessa substância no sangue é expressa algebricamente por
a) C = 0,9q
b) C = 0,1q
c) C = 1 − 0,1q
d) C = 1 − 0,9q
e) C = q − 10
alternativa a
3. (Enem/MEC) Uma casa de dois andares está sêndo projetada. É necessário incluir no projeto a construção de uma escada para o acesso ao segundo andar. Para o cálculo das dimensões dos degraus utilizam-se as regras:
|2h + b − 63,5| ≤ 1,5 e 16 ≤ h < 19,
nas quais h é a altura do degrau (denominada espelho) e b é a profundidade da pisada, como mostra a figura. Por conveniência, escolheu-se a altura do degrau como sêndo h = 16. As unidades de h e b estão em centímetro.
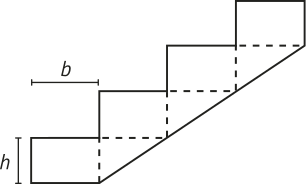
Nesse caso, o mais amplo intervalo numérico ao qual a profundidade da pisada (b) deve pertencer, para quê as regras sêjam satisfeitas é:
a) 30 ≤ b
b) 30 ≤ b ≤ 31,5
c) 30 ≤ b ≤ 33
d) 31,5 ≤ b ≤ 33
e) b ≤ 33
alternativa c
4. (Enem/MEC) Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sêndo construídos para serem lançados. O planejamento é quê eles sêjam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura mássima. Para quê isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.
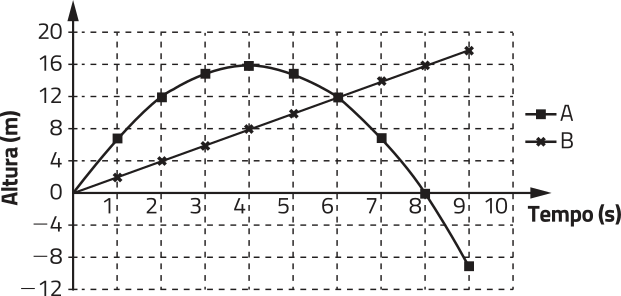
Com base nessas simulações, observou-se quê a trajetória do projétil B deveria sêr alterada para quê o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta quê representa a trajetória de B deverá
a) diminuir em duas unidades.
b) diminuir em 4 unidades.
c) aumentar em duas unidades.
d) aumentar em 4 unidades.
e) aumentar em 8 unidades.
alternativa c
Página cento e cinquenta e dois
5. (UECE) Ao representarmos a equação |x| − |y| = 1, no plano, com o sistema usual de coordenadas cartesianas, teremos:
a) quatro semirretas.
b) quatro segmentos de retas.
c) duas retas.
d) duas semirretas.
alternativa a
6. (Enem/MEC) Uma empresa tem diversos funcionários. Um deles é o gerente, quê recebe R$ 1.000,00 por semana. Os outros funcionários são diaristas. Cada um deles trabalha 2 dias por semana, recebendo R$ 80,00 por dia trabalhado.
Chamando de X a quantidade total de funcionários da empresa, a quantia Y, em reais, quê esta empresa gasta semanalmente para pagar seus funcionários é expressa por
a) Y = 80X + 920.
b) Y = 80X + 1.000.
c) Y = 80X + 1.080.
d) Y = 160X + 840.
e) Y = 160X + 1.000.
alternativa d
7. (Enem/MEC) A quantidade x de peças, em milhar, produzidas e o faturamento y, em milhar de real, de uma empresa estão representados nos gráficos, ambos em função do número t de horas trabalhadas por seus funcionários.
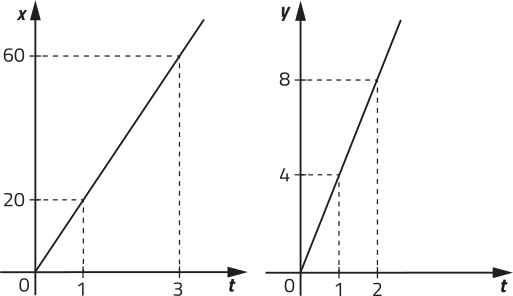
O número de peças quê devem sêr produzidas para se obtêr um faturamento de R$ 10.000,00 é
a) 2.000.
b) 2.500.
c) 40.000.
d) 50.000.
e) 200.000.
alternativa d
8. (UFMS) O Sr. Flávio é um apaixonado pela mobilidade e deseja pegar um transporte coletivo cuja função de custo é dada pela equação C(x) = 6,00 + 0,50 ⋅ x, em quê x representa a distância percorrida pelo transporte em km e C(x) o valor a sêr pago em reais. Esse custo póde sofrer modificação caso a viagem seja alterada. Se a viagem aconteceu conforme o previsto pelo aplicativo utilizado, e o Sr. Flávio percorreu uma distância de 48 km, o total a sêr pago para o motorista é:
a) R$ 6,00.
b) R$ 24,00.
c) R$ 30,00.
d) R$ 48,00.
e) R$ 54,00.
alternativa c
9. (hú- hê- érre jota) Observe o plano cartesiano, no qual estão representadas as funções f e g:
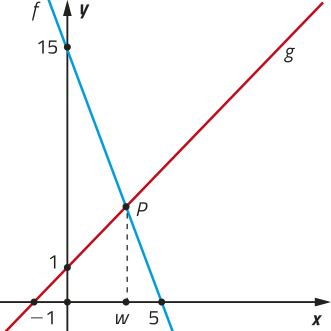
O ponto P de interseção entre os gráficos dessas funções possui abscissa w, cujo valor é:
a)
b) 3
c)
c) 4
alternativa c
10. (Famerp-SP) Um animal, submetido à ação de uma droga experimental, teve sua massa corporal registrada nos sete primeiros meses de vida. Os sete pontos destacados no gráfico mostram esses registros e a reta indica a tendência de evolução da massa corporal em animais quê não tênham sido submetidos à ação da droga experimental. Sabe-se quê houve correlação perfeita entre os registros coletados no experimento e a reta apenas no 1º e no 3º mês.
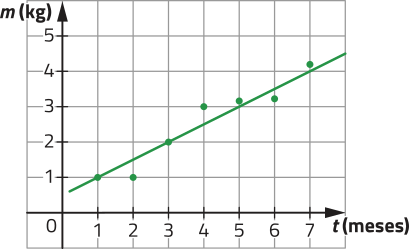
Se a massa registrada no 6º mês do experimento foi 210 gramas inferior à tendência de evolução da massa em animais não submetidos à droga experimental, o valor dessa massa registrada é igual a
a) 3,47 kg.
b) 3,27kg.
c) 3,31 kg.
d) 3,35 kg.
e) 3,29 kg.
alternativa e
Página cento e cinquenta e três


