Orientações gerais

Conhecendo a coleção

Esta coleção é composta de três livros da área de Matemática e suas Tecnologias destinados ao Ensino Médio. Nas Orientações gerais para o professor, estão presentes informações sobre o Ensino Médio, a Base Nacional Comum Curricular (BNCC), os fundamentos teóricos e metodológicos da coleção, orientações para avaliação, o papel do professor de Matemática, os estudantes no Ensino Médio, gestão da sala de aula, referências bibliográficas comentadas e indicações para o professor, comuns aos três livros da coleção, e são apresentadas, para cada volume, as orientações específicas e as resoluções das atividades propostas no Livro do estudante.

Na parte comum aos três volumes, é apresentada uma visão detalhada da estrutura do Livro do estudante e das orientações específicas, assim como os pressupostos teórico-metodológicos quê fundamentam a coleção e trazem reflekções acerca do ensino e da aprendizagem na área de Matemática e suas Tecnologias, explorando algumas tendências em educação matemática e metodologias ativas. A Base Nacional Comum Curricular (BNCC) Nota 1 é um dos documentos quê nortearam as reflekções e a elaboração desta coleção.

Nas orientações específicas, são apresentados comentários, complementos e orientações didáticas correspondentes às atividades propostas e aos conteúdos disponíveis nas páginas do Livro do estudante. Além díssu, são apresentadas informações gerais sobre o Volume da coleção, com sugestões de cronograma bimestral, trimestral e semestral e comentários referentes a cada uma de suas seis Unidades.

Estrutura do Livro do estudante

Cada um dos três Livros do estudante desta coleção é organizado em seis Unidades quê contêm abertura, atividades, seções e bókses. A seguir, serão apresentadas informações sobre alguns dêêsses elemêntos.

Seções

Na Abertura de cada Unidade, são apresentados recursos, como imagens, textos e infografias. Além díssu, são propostas kestões com o objetivo de identificar a compreensão dos estudantes em relação ao tema da Unidade e a aspectos de seu conhecimento prévio sobre algum conceito quê será estudado. É importante propor o trabalho com a abertura da Unidade de acôr-do com as características próprias da turma ou com os objetivos específicos para a aula, como a realização de leitura individual ou coletiva e discussão acerca das kestões. Sempre quê julgar oportuno, retomar com os estudantes a abertura no decorrer do estudo da Unidade.

A seção Integrando com... propõe o estudo de temas quê relacionam a área de Matemática e suas Tecnologias às outras áreas do conhecimento, em especial à área de Ciências da Natureza e suas Tecnologias, o quê possibilita a integração de conceitos de diferentes perspectivas. Sugere-se dialogar com professores das áreas relacionadas para planejar as aulas em quê a seção será realizada.

Na seção Você conectado, são propostas atividades quê envolvem o estudo de conceitos matemáticos com o apôio do software de geometria dinâmica GeoGebra ou da planilha eletrônica LibreOffice Calc, ambos de livre acesso na internet. As atividades propostas devem sêr realizadas de acôr-do com a realidade na qual a escola está inserida, ou seja, podem sêr desenvolvidas em um laboratório de informática ou coletivamente em um computador portátil, quê o professor póde levar para a sala de aula, acompanhado de um projetor ou, ainda, como uma atividade extraclasse.

A seção O quê estudei, apresentada ao final de cada Unidade, propõe um momento de reflekção e de autoavaliação tanto para os estudantes como para o professor. Em relação aos estudantes, são consideradas suas atitudes comportamentais e sua compreensão dos conceitos estudados na Unidade. Em relação ao professor, sua autoavaliação é condicionada às respostas dadas pêlos estudantes, as quais podem sêr objetos de reflekção a respeito de sua prática docente. Essa reflekção, por sua vez, póde propiciar ajustes nos planejamentos de aula das Unidades seguintes.

Na questão um, os estudantes devem fazer um retrospecto de seu comportamento nas aulas de Matemática. As respostas aos itens dessa questão devem sêr individuais, de maneira a evidenciar, da melhor maneira possível, suas atitudes comportamentais. Os estudantes podem eleger alguns itens para os quais responderam “concorda parcialmente” ou “não concorda” como pontos de atenção, de modo quê devam mudar a sua atitude para quê, no estudo das próximas Unidades, a resposta a tais itens seja “concorda”. No decorrer do ano, sugere-se reservar momentos para quê os estudantes possam comparar suas respostas a essa quêstão e verificar como seu comportamento evoluiu. Do ponto de vista do professor, além das análises individuais, cabe uma análise do todo para identificar ações que poderão sêr desenvolvidas para uma correção de rota coletiva.

A questão dois póde sêr, em um primeiro momento, trabalhada de maneira individual, de modo quê os estudantes identifiquem, entre os conteúdos apresentados, quais eles não compreenderam satisfatoriamente. A partir das respostas dos estudantes, em um segundo momento, o professor, ao identificar conteúdos quê uma parte significativa da turma póde não ter compreendido, tem a possibilidade de estabelecer um plano de ação para a turma, no qual podem sêr propostas monitorias, grupos de estudo, aulas de reforço, entre outras ações.

A quêstão 3 possibilita aos estudantes, de maneira coletiva, produzir materiais quê contribuam com a retomada de conteúdos estudados na Unidade. Nessa proposta, que utiliza elemêntos da metodologia ativa “sala de aula invertida”, o objetivo é quê os estudantes se preparem e estudem para ministrar um conteúdo escolhido a prióri. Sugere-se distribuir os conteúdos entre os grupos para quê sêjam contemplados todos aqueles indicados nas fichas da questão dois. A metodologia ativa mencionada será tratada mais adiante, no tópico Metodologias ativas e algumas tendências em educação matemática.

A questão 4 tem como objetivo obtêr indícios em relação à compreensão dos conceitos matemáticos estudados na Unidade, com base na retomada do tema abordado na página de abertura. Espera-se, nessa quêstão, que os estudantes resolvam os itens propostos usando os conceitos matemáticos estudados na Unidade. No entanto, caso os estudantes empreguem procedimentos e estratégias nos quais sêjam utilizados conceitos diferentes dos estudados, é importante quê o professor os valorize e, se possível, compartilhe com a turma.

Na seção Praticando: enêm e vestibulares, apresentada ao final de cada Unidade, são propostas kestões do enêm e de vestibulares aplicadas nas diferentes regiões do Brasil e quê tratam de conceitos estudados em cada Unidade. Sugere-se propor as kestões dessa seção ao final do trabalho com cada Unidade a fim de verificar se os estudantes compreenderam os conceitos abordados,

Página trezentos e oito

o quê póde constituir um momento de avaliação somativa. Para isso, propor a eles quê realizem as kestões em um tempo predeterminado durante a aula e individualmente, uma vez quê kestões de avaliações de larga escala são propostas nesse formato. A correção das kestões póde sêr realizada com toda a turma, constituindo, assim, momentos de aprendizagem.

Boxes

Os bókses estão distribuídos no decorrer das Unidades e cada um tem uma finalidade. O boxe Dica apresenta informações complementares ao texto principal ou fornece informações quê auxiliem os estudantes na resolução de alguma atividade. No boxe Para ampliar, são indicados materiais complementares, como sáites, vídeos, livros, documentos, quê visam enriquecer a abordagem apresentada no Livro do estudante. No boxe Para Pensar, são apresentadas kestões cujo objetivo é desencadear reflekções acerca da teoria ou de algum exemplo apresentado. O boxe Matemática na história tem como objetivo apresentar fatos quê mostrem a Matemática como uma ciência construída socialmente, por diversos membros da comunidade científica, no decorrer da história. O boxe No mundo do trabalho explora as profissões e suas características, destacando as soft skills – habilidades comportamentais essenciais para os profissionais atuáis. Além díssu, oferece informações sobre o mercado de trabalho.

Estrutura das Orientações específicas

Orientações Unidade a Unidade

Em cada Unidade, é apresentado um Quadro-síntese contendo as competências gerais, competências específicas e habilidades da área de Matemática e suas Tecnologias, os Temas Contemporâneos Transversais e os conteúdos abordados. Quando pêrtinênti, também são citadas competências específicas de outras áreas do conhecimento, em especial, da área Ciências da Natureza e suas Tecnologias. Na sequência, são apresentados os Objetivos da Unidade e as Orientações didáticas.

Nas Orientações didáticas, são apresentados comentários referentes à Abertura da Unidade e aos tópicos trabalhados no Livro do estudante. Nesses comentários, são abordadas orientações sobre os conteúdos propostos, bem como maneiras de articular a abordagem dêêsses conteúdos ao desenvolvimento das competências e habilidades da BNCC e sugestões de momentos em quê o professor póde avaliar os estudantes. Ainda, são apresentados comentários específicos em relação a cada uma das seções trabalhadas no Livro do estudante.

No decorrer das Orientações didáticas, também são propostas sugestões de atividades extras, como complemento de conteúdo ou de atividade, e são apresentadas, no boxe Conexões, indicação de materiais complementares para pesquisa ou consulta (sáites, vídeos, livros, documentos etc.), diferentes daqueles quê estão disponíveis no Livro do estudante no boxe Para ampliar.

O Ensino Médio

A Educação Básica brasileira é dividida em três etapas: Educação Infantil, Ensino Fundamental e Ensino Médio. A última etapa, à qual esta coleção se destina, vêm passando por várias mudanças nos últimos anos e é regulamentada, atualmente, pela resolução número 3, de 21 de novembro de 2018 Nota 2, e pela lei número 14.945, de 31 de julho de 2024, quê trazem um conjunto de alterações na legislação Nota 3.

Essa legislação e a BNCC propõem uma renovação curricular das instituições públicas e privadas quê oferecem vagas para esse segmento de ensino. A proposta constitui uma renovação resultante de um longo debate educacional. A seguir, são relembrados alguns momentos históricos quê fizeram parte dêêsse debate e quê contribuíram para a estruturação do atual Ensino Médio.

• 1988: Fica estabelecido pela Constituição da República Federativa do Brasil de 1988, em seu artigo 205, quê a educação é um direito de todos, “visando ao pleno desenvolvimento da pessoa, seu preparo para o exercício da cidadania e sua qualificação para o trabalho” Nota 4.

• 1996: A lei número 9.394 estabelece as Leis de Diretrizes e Bases da Educação Nacional (LDB) Nota 5, na qual se define o Ensino Médio com duração mínima de três anos, cujas finalidades são consolidar e aprofundar conhecimentos adquiridos no Ensino Fundamental; preparar para o trabalho e a cidadania do educando; aprimorar o educando como pessoa humana; e tornar o educando capaz de compreender os fundamentos científico-tecnológicos dos processos produtivos.

• 1998: A resolução da Câmara de Educação Básica (CEB) número 3 institui as Diretrizes Curriculares Nacionais (DCN) Nota 6 para o Ensino Médio, contendo definições quê dizem respeito à organização pedagógica e curricular das unidades escolares dos sistemas de ensino.

• 2000: Publicam-se os Parâmetros Curriculares Nacionais – Ensino Médio, com a finalidade de “difundir os princípios da reforma curricular e orientar o professor, na busca de novas abordagens e metodologias” Nota 7.

• 2014: O Ministério da Educação lança o Plano Nacional da Educação, lei número 13.005 Nota 8, para o período de 2014 a 2024, cujas metas 3 e 6 preveem, respectivamente, universalizar o atendimento escolar de jovens de 15 a 17 anos e ampliar a oferta de educação em tempo integral.

• 2017: A lei número 13.415 apresenta alterações para até a atual legislação vigente Nota 9, estabelecendo a ampliação da carga horária mínima, e propõe um currículo compôzto da BNCC e dos itinerários formativos.

• 2018: A publicação da resolução número 3 Nota 10 atualiza as Diretrizes Curriculares Nacionais para o Ensino Médio, de 1998. Entre as alterações na organização curricular, estão quê os currículos serão compostos de uma formação geral básica, com carga horária mássima de 1.800 horas, e por itinerários formativos, com carga horária de 1.200 horas. A formação geral básica será composta de competências e habilidades previstas na BNCC. A partir dessa resolução e da lei de 2017, fica estabelecido o chamado Novo Ensino Médio.

• 2023: O Novo Ensino Médio é suspenso, e são abertas consultas públicas para estabelecer a nova estrutura do Ensino Médio.

Página trezentos e nove

• 2024: Pela lei número 14.945 Nota 11, fica estabelecido quê o Ensino Médio será compôzto de uma formação geral básica, com carga horária de 2.400 horas, e pêlos itinerários formativos, com carga horária prevista de 600 horas.

Na atual estrutura do Ensino Médio, os componentes curriculares Língua Portuguesa, Matemática, Língua Inglesa, ár-te, Educação Física, Biologia, Física, Química, História, Geografia, Filosofia e Sociologia deverão sêr obrigatórios nos três anos, e os itinerários formativos vão se restringir às áreas previstas na BNCC.

A Base Nacional Comum Curricular (BNCC)

A BNCC define um conjunto de aprendizagens essenciais quê os estudantes brasileiros devem desenvolver durante a Educação Básica, independentemente da região onde vivem. Com isso, busca-se reduzir as desigualdades históricas estabelecidas, além de orientar a elaboração de um currículo específico de cada escola ou rê-de escolar, pública ou privada, e instruir as matrizes de referência das avaliações e dos exames externos. O principal objetivo é garantir quê todos os estudantes brasileiros tênham a mesma oportunidade de aprender o quê é considerado essencial. O documento é exclusivo à educação escolar e está orientado por princípios quê visam a uma formação humana integral e a uma ssossiedade mais justa, democrática e inclusiva.

Uma das características dêêsse documento é quê ele não define o modo como ensinar nem impede quê sêjam contempladas, no dia a dia escolar, as especificidades regionais. Assim, a BNCC estabelece um conjunto de conhecimentos básicos quê devem sêr assegurados, sem interferir na diversidade cultural e regional e na autonomia dos educadores.

Essas aprendizagens essenciais devem coexistir para assegurar aos estudantes o desenvolvimento de dez competências gerais no decorrer da Educação Básica.

Em articulação com as competências gerais e com as áreas do conhecimento em quê o Ensino Médio está organizado, nomeadamente, Linguagens e suas Tecnologias, Matemática e suas Tecnologias, Ciências da Natureza e suas Tecnologias e Ciências Humanas e Sociais Aplicadas, a BNCC define competências específicas para cada uma dessas áreas e habilidades quê lhes correspondem.

Nesta coleção, buscou-se articular, em diversos momentos, abordagens quê integrassem o desenvolvimento de competências gerais e competências específicas e habilidades da área de Matemática e suas Tecnologias. Nas Orientações específicas, serão apresentadas essas articulações e como elas estão sêndo contempladas no Livro do estudante.

As competências gerais

A seguir, estão listadas as dez competências gerais da Educação Básica definidas pela BNCC.

1 Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma ssossiedade justa, democrática e inclusiva.

2 Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflekção, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3 Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4 Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos quê lévem ao entendimento mútuo.

5 Compreender, utilizar e criar tecnologias digitais de informação e comunicação d fórma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e ezercêr protagonismo e altoría na vida pessoal e coletiva.

6 Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências quê lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escôlhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7 Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns quê respeitem e promovam os direitos humanos, a consciência sócio-ambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planêta.

8 Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com auto crítica e capacidade para lidar com elas.

9 Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10 Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários Nota 12.

A BNCC e os currículos

Considerando os múltiplos conhecimentos desenvolvidos pela humanidade ao longo do tempo, o currículo escolar é aquele quê seleciona e organiza o quê os estudantes devem aprender, regulando as práticas didáticas quê se dêsênvólvem na sala de aula Nota 13. Nesse sentido, existem diversos fatores quê contribuem para a elaboração do currículo escolar, como as políticas educativas nacionais, as secretarias de Educação de estados e municípios, as escolas e os professores. Embora cada um dêêsses fatores assuma a responsabilidade de concretizar o currículo nos diversos níveis, todos eles deveriam trabalhar para atingir as mesmas metas educacionais.

Considerada uma das principais políticas curriculares nacionais, a BNCC é o documento quê define as aprendizagens essenciais quê todos os estudantes devem desenvolver ao longo da Educação Básica Nota 14. Com base nesse documento, são as rêdes de ensino e as escolas as encarregadas de definir seu currículo escolar. Para isso, devem adequar as orientações da BNCC às realidades de cada localidade e contexto escolar, assim como às características dos estudantes. Cada estado, por exemplo, tem autonomia para elaborar o próprio currículo, desde quê siga as orientações propostas pela BNCC.

Nesse processo, as rêdes e as instituições escolares podem tomar decisões relativas a como vão contextualizar os conteúdos, definir as diversas formas de organização dos componentes curriculares, elaborar procedimentos de avaliação formativa, selecionar e produzir materiais e recursos para apoiar o processo de ensino-aprendizagem, entre outras ações. Assim, a BNCC e os currículos escolares dêsempênham papéis diferentes, mas complementares, e ambos reconhecem o compromisso da educação na formação e no desenvolvimento global do sêr humano.

Página trezentos e dez

Considerando as especificidades e os desafios do Ensino Médio, a BNCC organiza as aprendizagens essenciais para esse nível em áreas do conhecimento, definindo, para cada uma delas, competências específicas e habilidades a sêr desenvolvidas. Esse modo de organização, quê privilegia a integração dos componentes curriculares, tem impacto na formulação do currículo sem excluir, necessariamente, componentes curriculares; o objetivo é fortalecer as relações e a integração entre eles para quê os estudantes possam melhor compreender a complexidade da realidade e nela intervir. Tal organização impacta no trabalho dos professores, quê são chamados a desenvolver atividades de planejamento e implementação de maneira cooperativa e conjunta com os de outros componentes curriculares.

A área de Matemática e suas Tecnologias

Na BNCC, a Matemática é destacada como uma área do conhecimento essencial para os estudantes da Educação Básica tanto por suas aplicações como por suas potencialidades na formação de cidadãos críticos e engajados. Para o Ensino Médio, a proposta é a de quê as aprendizagens desenvolvidas na etapa anterior sêjam consolidadas, ampliadas e aprofundadas Nota 15, com foco na construção de uma visão integrada da Matemática e de sua aplicação à realidade, bem como com outras áreas do conhecimento.

O documento também apresenta o compromisso quê se deve ter no Ensino Médio com a ampliação do letramento matemático, definido como: “[…] as competências e habilidades de raciocinar, representar, comunicar e argumentar matematicamente, de modo a favorecer o estabelecimento de conjecturas, a formulação e a resolução de problemas em uma variedade de contextos, utilizando conceitos, procedimentos, fatos e ferramentas matemáticas” Nota 16.

Dessa maneira, a proposta é a de quê sêjam desenvolvidas as habilidades mencionadas, visando à ampliação dos conhecimentos matemáticos e maior reflekção e abstração dos estudantes para resolver problemas mais compléksos a fim de quê sêjam capazes de compreender o mundo e nele atuar.

Para isso, a BNCC cita os processos matemáticos de resolução de problemas, de investigação, de desenvolvimento de projetos e de modelagem. Esses processos podem sêr tomados como formas de organização da aprendizagem matemática e consideram a análise de situações do cotidiano, de outras áreas do conhecimento e da própria Matemática.

Com base no quê foi apresentado, a BNCC delimita competências específicas e habilidades relacionadas a cada uma delas para a área de Matemática e suas Tecnologias. Diferentemente do quê é apresentado para o Ensino Fundamental, as competências específicas e habilidades para o Ensino Médio não focam conteúdos específicos, mas a formação geral dos estudantes para a cidadania e o protagonismo no mundo em quê vivem. Essas competências não têm uma ordem preestabelecida, e a mobilização de uma ou mais delas póde ocorrer em determinadas situações. As habilidades podem contribuir para o desenvolvimento de uma ou mais competências específicas.

Competências específicas e habilidades da área de Matemática e suas Tecnologias para o Ensino Médio

Competência específica 1

Utilizar estratégias, conceitos e procedimentos matemáticos para interpretar situações em diversos contextos, sêjam atividades cotidianas, sêjam fatos das Ciências da Natureza e Humanas, das kestões socioeconômicas ou tecnológicas, divulgados por diferentes meios, de modo a contribuir para uma formação geral Nota 17.

Essa competência propõe aos estudantes quê utilizem seus conhecimentos matemáticos como ferramenta para interpretar e compreender as mais diversas situações e analisar criticamente e refletir acerca das informações relacionadas a elas.

Habilidades

(EM13MAT101) Interpretar criticamente situações econômicas, sociais e fatos relativos às Ciências da Natureza quê envolvam a variação de grandezas, pela análise dos gráficos das funções representadas e das taxas de variação, com ou sem apôio de tecnologias digitais.

(EM13MAT102) Analisar tabélas, gráficos e amostras de pesquisas estatísticas apresentadas em relatórios divulgados por diferentes meios de comunicação, identificando, quando for o caso, inadequações quê possam induzir a êêrros de interpretação, como escalas e amostras não apropriadas.

(EM13MAT103) Interpretar e compreender textos científicos ou divulgados pelas mídias, quê empregam unidades de medida de diferentes grandezas e as conversões possíveis entre elas, adotadas ou não pelo Sistema Internacional (SI), como as de armazenamento e velocidade de transferência de dados, ligadas aos avanços tecnológicos.

(EM13MAT104) Interpretar taxas e índices de natureza socioeconômica (índice de desenvolvimento humano, taxas de inflação, entre outros), investigando os processos de cálculo dêêsses números, para analisar criticamente a realidade e produzir argumentos.

(EM13MAT105) Utilizar as noções de transformações isométricas (translação, reflekção, rotação e composições destas) e transformações homotéticas para construir figuras e analisar elemêntos da natureza e diferentes produções humanas (fractais, construções civis, obras de; ár-te, entre outras).

(EM13MAT106) Identificar situações da vida cotidiana nas quais seja necessário fazer escôlhas levando-se em conta os riscos probabilísticos (usar êste ou aquele método contraceptivo, optar por um tratamento médico em detrimento de outro etc.) Nota 18.

Competência específica 2

Propor ou participar de ações para investigar desafios do mundo contemporâneo e tomar decisões éticas e socialmente responsáveis, com base na análise de problemas sociais, como os voltados a situações de saúde, sustentabilidade, das implicações da tecnologia no mundo do trabalho, entre outros, mobilizando e articulando conceitos, procedimentos e linguagens próprios da Matemática Nota 19.

O desenvolvimento dessa competência visa contribuir para quê os estudantes sêjam atuantes na ssossiedade e possam identificar e investigar eventuais problemas na comunidade em quê vivem, buscando e propondo ações para solucioná-los individual ou coletivamente.

Habilidades

(EM13MAT201) Propor ou participar de ações adequadas às demandas da região, preferencialmente para sua comunidade, envolvendo medições e cálculos de perímetro, de área, de volume, de capacidade ou de massa.

(EM13MAT202) Planejar e executar pesquisa amostral sobre kestões relevantes, usando dados coletados diretamente ou em diferentes fontes, e comunicar os resultados por meio de relatório contendo gráficos e interpretação das medidas de tendência

Página trezentos e onze

central e das medidas de dispersão (amplitude e desvio padrão), utilizando ou não recursos tecnológicos.

(EM13MAT203) Aplicar conceitos matemáticos no planejamento, na execução e na análise de ações envolvendo a utilização de aplicativos e a criação de planilhas (para o contrôle de orçamento familiar, simuladores de cálculos de juros simples e compostos, entre outros), para tomar decisões Nota 20.

Competência específica 3

Utilizar estratégias, conceitos, definições e procedimentos matemáticos para interpretar, construir modelos e resolver problemas em diversos contextos, analisando a plausibilidade dos resultados e a adequação das soluções propostas, de modo a construir argumentação consistente Nota 21.

Essa competência está relacionada à ação de resolver situações-problema, contemplando tanto contextos próprios da Matemática como de outras áreas do conhecimento e do cotidiano dos estudantes. Além da resolução, é propôsto aos estudantes quê elaborem problemas a fim de mobilizar os conceitos estudados e refletir sobre eles.

Habilidades

(EM13MAT301) Resolver e elaborar problemas do cotidiano, da Matemática e de outras áreas do conhecimento, quê envolvem equações lineares simultâneas, usando técnicas algébricas e gráficas, com ou sem apôio de tecnologias digitais.

(EM13MAT302) Construir modelos empregando as funções polinomiais de 1º ou 2º graus, para resolver problemas em contextos diversos, com ou sem apôio de tecnologias digitais.

(EM13MAT303) Interpretar e comparar situações quê envolvam juros simples com as quê envolvem juros compostos, por meio de representações gráficas ou análise de planilhas, destacando o crescimento linear ou exponencial de cada caso.

(EM13MAT304) Resolver e elaborar problemas com funções exponenciais nos quais seja necessário compreender e interpretar a variação das grandezas envolvidas, em contextos como o da Matemática Financeira, entre outros.

(EM13MAT305) Resolver e elaborar problemas com funções logarítmicas nos quais seja necessário compreender e interpretar a variação das grandezas envolvidas, em contextos como os de abalos sísmicos, pH, radioatividade, Matemática Financeira, entre outros.

(EM13MAT306) Resolver e elaborar problemas em contextos quê envolvem fenômenos periódicos reais (ondas sonóras, fases da lua, movimentos cíclicos, entre outros) e comparar suas representações com as funções seno e cosseno, no plano cartesiano, com ou sem apôio de aplicativos de álgebra e geometria.

(EM13MAT307) Empregar diferentes métodos para a obtenção da medida da área de uma superfícíe (reconfigurações, aproximação por cortes etc.) e deduzir expressões de cálculo para aplicá-las em situações reais (como o remanejamento e a distribuição de plantações, entre outros), com ou sem apôio de tecnologias digitais.

(EM13MAT308) Aplicar as relações métricas, incluindo as leis do seno e do cosseno ou as noções de congruência e semelhança, para resolver e elaborar problemas quê envolvem triângulos, em variados contextos.

(EM13MAT309) Resolver e elaborar problemas quê envolvem o cálculo de áreas totais e de volumes de prismas, pirâmides e corpos redondos em situações reais (como o cálculo do gasto de material para revestimento ou pinturas de objetos cujos formatos sêjam composições dos sólidos estudados), com ou sem apôio de tecnologias digitais.

(EM13MAT310) Resolver e elaborar problemas de contagem envolvendo agrupamentos ordenáveis ou não de elemêntos, por meio dos princípios multiplicativo e aditivo, recorrendo a estratégias diversas, como o diagrama de árvore.

(EM13MAT311) Identificar e descrever o espaço amostral de eventos aleatórios, realizando contagem das possibilidades, para resolver e elaborar problemas quê envolvem o cálculo da probabilidade.

(EM13MAT312) Resolver e elaborar problemas quê envolvem o cálculo de probabilidade de eventos em experimentos aleatórios sucessivos.

(EM13MAT313) Utilizar, quando necessário, a notação científica para expressar uma medida, compreendendo as noções de algarismos significativos e algarismos duvidosos, e reconhecendo quê toda medida é inevitavelmente acompanhada de êrro.

(EM13MAT314) Resolver e elaborar problemas quê envolvem grandezas determinadas pela razão ou pelo produto de outras (velocidade, densidade demográfica, energia elétrica etc.).

(EM13MAT315) Investigar e registrar, por meio de um fluxograma, quando possível, um algoritmo quê resólve um problema.

(EM13MAT316) Resolver e elaborar problemas, em diferentes contextos, quê envolvem cálculo e interpretação das medidas de tendência central (média, (Moda), mediana) e das medidas de dispersão (amplitude, variância e desvio padrão) Nota 22.

Competência específica 4

Compreender e utilizar, com flexibilidade e precisão, diferentes registros de representação matemáticos (algébrico, geométrico, estatístico, computacional etc.), na busca de solução e comunicação de resultados de problemas Nota 23.

Essa competência trata da utilização e da compreensão de diferentes tipos de registro na resolução de situações-problema, buscando expressar ideias matemáticas relacionadas e possibilitando a ampliação da capacidade dos estudantes de pensar matematicamente.

Habilidades

(EM13MAT401) Converter representações algébricas de funções polinomiais de 1º grau em representações geométricas no plano cartesiano, distinguindo os casos nos quais o comportamento é proporcional, recorrendo ou não a -softwares ou aplicativos de álgebra e geometria dinâmica.

(EM13MAT402) Converter representações algébricas de funções polinomiais de 2º grau em representações geométricas no plano cartesiano, distinguindo os casos nos quais uma variável for diretamente proporcional ao quadrado da outra, recorrendo ou não a softwares ou aplicativos de álgebra e geometria dinâmica, entre outros materiais.

(EM13MAT403) Analisar e estabelecer relações, com ou sem apôio de tecnologias digitais, entre as representações de funções exponencial e logarítmica expressas em tabélas e em plano cartesiano, para identificar as características fundamentais (domínio, imagem, crescimento) de cada função.

(EM13MAT404) Analisar funções definidas por uma ou mais sentenças (tabela do Imposto de Renda, contas de luz, á gua, gás etc.), em suas representações algébrica e gráfica, identificando domínios de validade, imagem, crescimento e decrescimento, e convertendo essas representações de uma para outra, com ou sem apôio de tecnologias digitais.

(EM13MAT405) Utilizar conceitos iniciais de uma linguagem de programação na implementação de algoritmos escritos em linguagem corrente e/ou matemática.

(EM13MAT406) Construir e interpretar tabélas e gráficos de freqüências com base em dados obtidos em pesquisas por amostras estatísticas, incluindo ou não o uso de softwares quê inter-relacionem estatística, geometria e álgebra.

Página trezentos e doze

(EM13MAT407) Interpretar e comparar conjuntos de dados estatísticos por meio de diferentes diagramas e gráficos (histograma, de caixa (box-plot), de ramos e fô-lhas, entre outros), reconhecendo os mais eficientes para sua análise Nota 24.

Competência específica 5

Investigar e estabelecer conjecturas a respeito de diferentes conceitos e propriedades matemáticas, empregando estratégias e recursos, como observação de padrões, experimentações e diferentes tecnologias, identificando a necessidade, ou não, de uma demonstração cada vez mais formal na validação das referidas conjecturas Nota 25.

O desenvolvimento dessa competência possibilita aos estudantes perceberem a natureza do raciocínio hipotético-dedutivo da Matemática e se apropriarem dessa ideia para raciocinar logicamente e validar proposições. Ao investigar, formular hipóteses e realizar tentativas de validá-las ou refutá-las, os estudantes buscam utilizar os conceitos matemáticos estudados em suas argumentações e, dessa maneira, estabelecer relações entre eles.

Habilidades

(EM13MAT501) Investigar relações entre números expressos em tabélas para representá-los no plano cartesiano, identificando padrões e criando conjecturas para generalizar e expressar algebricamente essa generalização, reconhecendo quando essa representação é de função polinomial de 1º grau.

(EM13MAT502) Investigar relações entre números expressos em tabélas para representá-los no plano cartesiano, identificando padrões e criando conjecturas para generalizar e expressar algebricamente essa generalização, reconhecendo quando essa representação é de função polinomial de 2º grau do tipo y = ax².

(EM13MAT503) Investigar pontos de mássimo ou de mínimo de funções quadráticas em contextos envolvendo superfícies, Matemática Financeira ou Cinemática, entre outros, com apôio de tecnologias digitais.

(EM13MAT504) Investigar processos de obtenção da medida do volume de prismas, pirâmides, cilindros e cones, incluindo o princípio de Cavalieri, para a obtenção das fórmulas de cálculo da medida do volume dessas figuras.

(EM13MAT505) Resolver problemas sobre ladrilhamento do plano, com ou sem apôio de aplicativos de geometria dinâmica, para conjecturar a respeito dos tipos ou composição de polígonos quê podem sêr utilizados em ladrilhamento, generalizando padrões observados.

(EM13MAT506) Representar graficamente a variação da área e do perímetro de um polígono regular quando os comprimentos de seus lados varíam, analisando e classificando as funções envolvidas.

(EM13MAT507) Identificar e associar progressões aritméticas (PA) a funções afins de domínios discrétos, para análise de propriedades, dedução de algumas fórmulas e resolução de problemas.

(EM13MAT508) Identificar e associar progressões geométricas (PG) a funções exponenciais de domínios discrétos, para análise de propriedades, dedução de algumas fórmulas e resolução de problemas.

(EM13MAT509) Investigar a deformação de ângulos e áreas provocada pelas diferentes projeções usadas em cartografia (como a cilíndrica e a cônica), com ou sem suporte de tecnologia digital.

(EM13MAT510) Investigar conjuntos de dados relativos ao comportamento de duas variáveis numéricas, usando ou não tecnologias da informação, e, quando apropriado, levar em conta a variação e utilizar uma reta para descrever a relação observada.

(EM13MAT511) Reconhecer a existência de diferentes tipos de espaços amostrais, discrétos ou não, e de eventos, equiprováveis ou não, e investigar implicações no cálculo de probabilidades Nota 26.

Os Temas Contemporâneos Transversais (TCTs)

De acôr-do com o documento Temas Contemporâneos Transversais na BNCC Nota 27, os TCTs têm como objetivo contextualizar o quê é ensinado, contribuindo com temas quê sêjam interessantes e relevantes para a formação dos cidadãos. Ao todo, são 15 temas distribuídos em seis macroáreas: Cidadania e Civismo (Vida Familiar e Social; Educação para o Trânsito; Educação em Direitos Humanos; Direitos da Criança e do Adolescente; Processo de envelhecimento, respeito e valorização do Idoso); Meio Ambiente (Educação Ambiental; Educação para o Consumo); Saúde (Saúde; Educação Alimentar e Nutricional); Multiculturalismo (Diversidade Cultural; Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras); Economia (Trabalho; Educação Financeira; Educação Fiscal); Ciência e Tecnologia (Ciência e Tecnologia).

Nas aulas de Matemática, as abordagens de kestões sociais, por meio de conhecimentos matemáticos, ao mesmo tempo quê possibilitam estabelecer relações com outras áreas do conhecimento, permitem contextualizações e reflekções críticas, além de conferir ao trabalho do professor a possibilidade de contribuir para a formação cidadã dos estudantes.

De acôr-do com a BNCC,

[…] cabe aos sistemas e rêdes de ensino, assim como às escolas, em suas respectivas esferas de autonomia e competência, incorporar aos currículos e às propostas pedagógicas a abordagem de temas contemporâneos quê afetam a vida humana em escala local, regional e global, preferencialmente d fórma transversal e integradora Nota 28.

Nessa perspectiva, busca-se romper com a ideia de quê a Matemática é uma ciência restrita à sala de aula e quê não está relacionada à realidade dos estudantes. Assim, espera-se quê os estudantes percêbam a Matemática presente nos mais diferentes contextos de vida deles.

Nesta coleção, os TCTs são discutidos em diversos momentos, sempre conectando-os aos conceitos matemáticos em estudo e, por vezes, estabelecendo relações com outras áreas do conhecimento. Por exemplo, em uma proposta de estudo de conceitos estatísticos, envolvendo a situação de búlin, em especial no ambiente escolar, tratou-se também dos TCTs Direitos da Criança e do Adolescente e Saúde.

Fundamentos teóricos e metodológicos da coleção

Em uma ssossiedade globalizada, o ensino de Matemática tem papel fundamental na formação de cidadãos conscientes, críticos e participativos. O incentivo a práticas reflexivas no estudo da Matemática escolar póde favorecer o desenvolvimento de estratégias para a resolução de problemas do dia a dia e a quebra de paradigmas.

A proposta didático-pedagógica desta coleção tem por objetivo contribuir para uma formação ampla dos estudantes, não apenas em aspectos cognitivos mas também em sua formação cidadã e na observância no mundo do trabalho. Nela, procurou-se articular, sempre quê possível, temas contemporâneos e interdisciplinares a conceitos matemáticos, oferecendo ao professor diferentes estratégias metodológicas e o aprimoramento de sua prática pedagógica. O tratamento dado aos conteúdos matemáticos, em sala de aula, deve considerar os recursos disponíveis para quê o trabalho seja efetuado.

A fim de sinalizar a proposta didático-pedagógica quê fundamentou a elaboração desta coleção, apresentam-se abordagens relacionadas à concepção de ensino e de aprendizagem de Matemática no Ensino Médio.

Página trezentos e treze

O ensino de Matemática

O ensino de Matemática precisa privilegiar a exploração de uma variedade de noções matemáticas quê contribuam para quê os estudantes construam e desenvolvam seu conhecimento matemático, sem perder o prazer, o interêsse e a curiosidade. Por isso, é importante quê esse trabalho seja realizado com abordagens quê valorizem a integração entre a Matemática e outras áreas do conhecimento, a proposição de temáticas sociais nas atividades a sêr desenvolvidas e o incentivo ao uso adequado das novas tecnologias da informação e comunicação no estudo.

De acôr-do com a BNCC, deve-se ter o compromisso de promover ações quê ampliem o letramento matemático, o qual, segundo o prôgrâmê for International istúdent ecésment (Pisa), conforme definição publicada pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep) no Relatório Nacional do PISA 2012, consiste na

[…] capacidade do indivíduo de formular, aplicar e interpretar a matemática em diferentes contextos, o quê inclui o raciocínio matemático e a aplicação de conceitos, procedimentos, ferramentas e fatos matemáticos para descrever, explicar e prever fenômenos. Além díssu, o letramento em matemática ajuda os indivíduos a reconhecer a importânssia da matemática do mundo, e agir de maneira consciente ao ponderar e tomar decisões necessárias a todos os cidadãos construtivos, engajados e reflexivos Nota 29.

Para isso, é necessário criar um ambiente propício em sala de aula quê tenha como base o diálogo e a comunicação. Assim, o professor deve incentivar os estudantes a se comunicar (oralmente, por exemplo) ou a registrar (por meio de textos, esquemas ou outras formas de registro) suas ideias matemáticas. O hábito de expressá-las póde sêr desenvolvido questionando os estudantes sobre como pensaram para realizar determinada atividade ou para resolver algum problema ou desafio.

Em relação às características das intervenções por parte do professor, elas devem sêr construtivas, dando oportunidade aos estudantes de reverem suas posições e perceberem as incoerências, quando existirem, contribuindo, assim, para a construção de seus conhecimentos. O professor póde fazer algumas intervenções por meio de perguntas, por exemplo: Como você obteve esse valor? Que estratégias você utilizou? É possível obtêr esse mesmo resultado por meio de outra estratégia? A estratégia quê você utilizou nessa situação póde sêr empregada em quê outros casos?

É importante quê os estudantes sêjam incentivados a buscar diferentes maneiras de pensar, ampliando sua capacidade cognitiva e sua atitude diante de novas situações. Aliado a isso, ressalta-se a realização de atividades coletivas e cooperativas, o quê favorece a socialização, a troca de ideias, a observação de outros pontos de vista, o reconhecimento de outras maneiras de pensar e de realizar as atividades.

Aprendizagem matemática

A Matemática no contexto escolar é, muitas vezes, temida e considerada pouco importante para uma parte de estudantes quê não percebem a conexão entre o quê aprende na sala de aula e o mundo além dos muros da escola. Por isso, é essencial despertar nos estudantes o prazer de aprender Matemática, mostrando quê os conceitos matemáticos devem sêr compreendidos como elemêntos quê contribuirão para sua vida social.

Quando a abordagem é feita exclusivamente de maneira expositiva, a Matemática escolar tende a afastar os estudantes e precisa sêr “reinventada” a fim de propiciar ensino e aprendizagem significativos, criativos, práticos e contextualizados de acôr-do com a realidade social e cultural dos estudantes.

Os autores Ausubel, nôvâki e Hanesian Nota 30 distinguem a aprendizagem significativa de outras aprendizagens ao proporem quê, para a ocorrência de aprendizagem significativa, por exemplo, além de considerar os conhecimentos prévios dos estudantes, é necessária a existência de uma predisposição positiva deles para aprender e materiais de ensino potencialmente significativos.

[…] a aprendizagem significativa ocorre quando a tarefa de aprendizagem implica relacionar, d fórma não arbitrária e substantiva (não literal), uma nova informação a outras com as quais o aluno já esteja familiarizado, e quando o aluno adota uma estratégia correspondente para assim proceder. Aprendizagem automática, por sua vez, ocorre se a tarefa consistir de associações puramente arbitrárias, como na associação de pares, quebra-cabeça, labirinto, ou aprendizagem de séries e quando falta ao aluno o conhecimento prévio relevante necessário para tornar a tarefa potencialmente significativa, e também (independentemente do potencial significativo contido na tarefa) se o aluno adota uma estratégia apenas para internalizá-la de uma forma arbitrária, literal (por exemplo, como uma série arbitrária de palavras) Nota 31.

A disposição dos estudantes para aprender não depende somente de sua estrutura cognitiva mas também de motivassão e materiais disponíveis no ambiente educacional. Os recursos materiais correspondem ao espaço físico quê circunda os estudantes e aos materiais dos quais fazem uso durante a realização das atividades. Os recursos de caráter afetivo dizem respeito às relações estabelecidas entre os estudantes e entre os estudantes e o professor.

Situações quê envolvem o cotidiano dos estudantes tendem a motivá-los para o estudo dos conteúdos matemáticos e podem constituir elemêntos motivacionais em sua predisposição para aprender. Ambientes educacionais diferenciados, bem como o uso de computadores, telefones celulares e tablets com fins pedagógicos também podem motivar os estudantes. Esses recursos tendem a promover a interação entre os pares e possibilitar a elaboração de estratégias e de modos de representação por meio de expressões textual, gráfica e oral. No entanto, é preciso destacar quê a ausência dêêsses recursos não póde limitar o trabalho do professor nem inviabilizar o processo de aprendizagem.

A argumentação e a inferência

Assim como em outras áreas do conhecimento, a área de Matemática e suas Tecnologias apresenta características próprias quê definem o tipo de conhecimento por ela desenvolvida. O modo de desenvolver raciocínios matemáticos é uma dessas características. Nesse tipo particular de raciocínio, a argumentação matemática, a produção de inferências e o pensamento computacional têm um papel central.

A argumentação matemática é indispensável para quê os estudantes possam assimilar significados dos objetos matemáticos e desenvolver a racionalidade matemática. Para envolver os estudantes em atividades de argumentação matemática, é necessário quê o professor ôfereça oportunidades para explorar os porquês de determinados resultados ou situações; resolver desacordos por meio de explicações e justificativas válidas de um ponto de vista matemático; formular conjecturas, investigar sua plausibilidade e refutá-las ou validá-las por meio da procura de contraexemplos ou a avaliação de demonstrações matemáticas, respectivamente Nota 32.

Página trezentos e quatorze

Fica evidente quê, para desenvolver as capacidades argumentativas dos estudantes, é necessário propor tarefas quê devem ir além da simples manipulação de símbolos ou procedimentos matemáticos. É necessário desafiá-los com atividades investigativas quê tênham potencial de originar discussões matemáticas, confrontar ideias e resoluções e justificar suas soluções. Nessa direção, a BNCC propõe, também, o uso de diferentes tecnologias para quê os estudantes do Ensino Médio investiguem e explorem conjecturas vinculadas a conceitos e propriedades matemáticas, obissérvem padrões, analisem dados e informações de maneira crítica, modelem e solucionem problemas da vida cotidiana. Nesse processo, é importante propor uma trajetória quê leve os estudantes a compreender como se originam e se formulam as argumentações matemáticas. É fundamental quê eles aprendam a distinguir uma conjectura de uma afirmação demonstrada; compreendam quê a apresentação de vários exemplos não garante a validade de uma conjectura; e vivenciem a elaboração de demonstrações matemáticas como um modo de explorar o motivo da validade de uma conjectura.

A reflekção a respeito da maneira como se estruturam as argumentações matemáticas leva a outro ponto central dos raciocínios matemáticos: a produção de inferências. Inferir é o processo por meio do qual se derivam conclusões a partir de cértas premissas. Em Lógica, podem-se distinguir três tipos de inferência: as deduções, quê partem de uma regra geral e uma premissa para inferir um caso particular; as induções, quê partem de premissas menóres e buscam sua generalização mediante a experimentação e a comprovação; e as abduções, quê partem de dados quê descrevem uma situação e colocam uma hipótese quê melhor explique ou esclareça esses dados. Embora a Matemática, quando considerada disciplina formal, muitas vezes se apoie em inferências dedutivas, os três tipos de inferência têm um papel relevante quando se consideram os processos de produção dos conhecimentos matemáticos.

Pensamento computacional

Atualmente, para quê os estudantes possam ezercêr sua plena cidadania, de modo a contribuir com um mundo mais justo e menos desigual, é necessário desenvolver competências e habilidades relacionadas ao pensamento computacional. Diferentemente do quê se possa presumir, o pensamento computacional não diz respeito a navegar pela internet na busca de informações. Brackmann propõe em sua tese quê

[…] O Pensamento Computacional é uma distinta capacidade criativa, crítica e estratégica humana de saber utilizar os fundamentos da Computação, nas mais diversas áreas do conhecimento, com a finalidade de identificar e resolver problemas, de maneira individual ou colaborativa, através de passos claros, de tal forma quê uma pessoa ou uma máquina possam executá-los eficazmente […] Nota 33.

O pensamento computacional é um dos eixos quê deve sêr trabalhado na Educação Básica, além do mundo digital e da cultura digital. O parecer número 2, de 12 de fevereiro de 2022, referente às normas sobre computação na Educação Básica, define quê o pensamento computacional

[…] refere-se à habilidade de compreender, analisar definir, modelar, resolver, comparar e automatizar problemas e suas soluções d fórma metódica e sistemática, através do desenvolvimento da capacidade de criar e adaptar algoritmos, aplicando fundamentos da computação para alavancar e aprimorar a aprendizagem e o pensamento criativo e crítico nas diversas áreas do conhecimento Nota 34.

Mobilizar o pensamento computacional contribui para o desenvolvimento do pensamento abstrato, distinguindo níveis de abstração nos problemas para pôdêr solucioná-los; do pensamento algorítmico, quê requer encontrar uma série de passos eficazes para resolver o problema; do pensamento lógico, formulando e excluindo hipóteses; e do pensamento dimensionável, vinculado à decomposição de um problema em pequenas partes.

Promover o desenvolvimento do pensamento computacional é uma oportunidade rica de os estudantes desenvolverem o raciocínio matemático. Para isso, o professor póde utilizar diferentes tecnologias, como planilhas eletrônicas, softwares de geometria dinâmica, calculadoras e aplicativos quê permítam investigar situações matemáticas, auxiliando na elaboração e na interpretação de algoritmos, além de propor a utilização de alguma linguagem de programação e o uso de registros por meio de fluxograma. Nesta coleção há momentos quê possibilitam ao professor incentivar os estudantes no desenvolvimento do pensamento computacional, como na realização de atividades em quê o pensamento computacional é trabalhado de maneira desplugada (sem o uso de computador), ou no estudo de noções de linguagem de programação, em quê se propõe, por exemplo, o trabalho com a linguagem Scratch.

Metodologias ativas e algumas tendências em educação matemática

As profundas modificações quê vêm ocorrendo em nossa ssossiedade, principalmente aquelas vinculadas ao desenvolvimento tecnológico, desafiam os professores a adotar novas metodologias. Para Moran,

[…] as metodologias precisam acompanhar os objetivos pretendidos. Se quêremos que os alunos sêjam proativos, precisamos adotar metodologias em quê os alunos se envolvam em atividades cada vez mais compléksas, em quê tênham quê tomar decisões e avaliar os resultados, com apôio de materiais relevantes. Se quêremos que sêjam criativos, eles precisam experimentar inúmeras novas possibilidades de mostrar sua iniciativa Nota 35.

Assim, as chamadas metodologias ativas podem se tornar um meio de alcançar tais objetivos. Nessas metodologias, são empregadas estratégias de ensino em quê os estudantes assumem uma postura ativa na problematização e na análise de situações compléksas, enquanto o professor assume o papel de mediador de discussões e de orientador dos estudantes. A seguir, são apresentadas brevemente algumas dessas metodologias.

A sala de aula invertida consiste em uma metodologia ativa de ensino em quê o professor, de antemão, disponibiliza o conteúdo quê será abordado na sala de aula, por meio de vídeos, textos, áudios, entre outros materiais. Aos estudantes, cabe a responsabilidade de estudar em casa o material propôsto, anotando dúvidas quê possam surgir nesse momento. Durante a aula, o professor assume o papel de mediador, ao esclarecer as dúvidas quê os estudantes tiveram, e propõe atividades relacionadas ao conteúdo. Após a aula, os estudantes devem revisar o conteúdo trabalhado, e o professor deve preparar novos materiais a sêr propostos.

Na aprendizagem baseada em projetos (Project-Based lãrnin – ABP), o objetivo é trabalhar problemas e/ou kestões da realidade, principalmente, associados ao cotidiano dos estudantes. Nessa abordagem, os estudantes se envolvem em um trabalho colaborativo, no qual buscam respostas a partir de seus conhecimentos prévios, enquanto constroem novos conhecimentos, com a mediação do professor. Outro ponto importante é o desenvolvimento do pensamento crítico e da comunicação, por meio do trabalho com essa

Página trezentos e quinze

metodologia, uma vez quê os estudantes têm de pesquisar e selecionar informações, propor soluções com base no quê foi encontrado e discutido e, por fim, comunicar os resultados.

Na aprendizagem baseada em problemas (Problem-Based lãrnin – PBL), os estudantes têm como ponto de partida um problema quê precisam solucionar com os conhecimentos quê têm a prióri. Em grupos, eles exploram o problema, levantam hipóteses, identificam o quê sabem e o quê não sabem e delegam responsabilidades a cada um dos integrantes do grupo, na busca pelas respostas quê faltam. Em um segundo momento, após o estudo autônomo, os estudantes compartilham o quê encontraram, ensinando uns aos outros. O professor, nessa metodologia, tem o papel de propor os problemas aos estudantes e mediar a interação entre eles.

A rotação por estações consiste em tornar a sala de aula uma espécie de circuito de aprendizagem, em quê os estudantes, organizados em pequenos grupos, passam por todas as estações, realizando as atividades quê são propostas. As atividades devem sêr independentes umas das outras; no entanto, devem atender a um objetivo principal. Geralmente, uma das atividades da estação envolve o uso de tecnologia. O papel do professor nessa metodologia é escolher as atividades, quê podem trabalhar diferentes competências e habilidades, e mediar as discussões quê acontecem nos pequenos grupos. Os estudantes devem se envolver com a atividade proposta e resolvê-la, e cada grupo tem um tempo predeterminado para permanecer em cada uma das estações.

Além díssu, no campo da educação matemática, são propostas práticas de ensino e de aprendizagem, comumente denominadas tendências em educação matemática, em quê os estudantes também são levados a assumir uma postura de protagonistas dos processos de ensino-aprendizagem. A seguir, são apresentadas algumas dessas tendências.

Resolução de problemas

Nessa perspectiva, a proposição de um problema, quê, para Onuchic e Allevato “é tudo akilo quê não se sabe fazer, mas quê se está interessado em fazer” Nota 36, póde sêr o ponto de partida para a construção de um novo conceito matemático. Para isso, é necessária uma prática na qual o conhecimento é construído por meio de interações sociais entre os próprios estudantes e entre os estudantes e o professor.

As autoras Onuchic e Allevato Nota 37 elaboraram, com base nos resultados de suas pesquisas, um roteiro para auxiliar o professor no trabalho com a resolução de problemas. Esse roteiro considera nove etapas para a organização da aula.

1ª) Seleção do problema, denominado problema gerador.

2ª) Leitura individual dos estudantes.

3ª) Leitura em conjunto.

4ª) Resolução do problema pêlos estudantes de modo cooperativo e colaborativo.

5ª) Observação e incentivo por parte do professor.

6ª) Registro das resoluções na lousa.

7ª) Plenária, com discussão das diferentes resoluções registradas na lousa.

8ª) Busca de consenso em relação ao resultado correto.

9ª) Formalização do conteúdo, com apresentação formal dos conceitos, princípios ou procedimentos construídos no decorrer da resolução do problema.

Espera-se quê os estudantes, ao resolverem os problemas, se tornem participantes ativos de sua aprendizagem, inserindo-se em um contexto no qual o estudo da Matemática ocorre em um movimento quê possibilita fazer análises, discussões, conjecturas, construção de conceitos e formulação de ideias. E o professor, nessa perspectiva, deve proporcionar aos estudantes a oportunidade de mobilizar seus conhecimentos prévios e gerenciar as informações disponíveis. Esse processo, além de contribuir para o desenvolvimento da autonomia dos estudantes, conduz à construção de conhecimentos. O professor deixa de sêr o transmissor do conhecimento para sêr o mediador, quê guia os estudantes.

Modelagem matemática

Entre as diferentes perspectivas de modelagem matemática, optou-se, neste texto, pela apresentada por Almeida e Ferruzzi Nota 38, uma alternativa pedagógica na qual, com base em situações oriundas da realidade, os conteúdos matemáticos se dêsênvólvem. De acôr-do com Almeida, Silva e Vertuan Nota 39, trata-se de criar possibilidades para enxergar situações do cotidiano por lentes matemáticas, ou seja, de interpretar e analisar situações do cotidiano por meio de linguagem matemática, e, assim, tomar decisões acerca delas.

De modo geral, no desenvolvimento de uma atividade de modelagem, estão presentes ações como buscar informações sobre a situação inicial, identificar e selecionar variáveis, elaborar hipóteses, realizar simplificações, obtêr um modelo matemático, validar e solucionar problemas. Essas ações podem sêr subsidiadas por orientações do professor.

Durante o processo de interpretação matemática da situação inicial, é necessário transformar a linguagem natural em linguagem matemática. Nessa direção, Almeida e Silva destacam quê

[…] um aspecto importante numa atividade de modelagem matemática é a necessidade de os próprios alunos, a partir de uma situação-problema não matemática, fazerem a associação com conceitos e/ou procedimentos matemáticos capazes de conduzir a uma solução para o problema e possibilitar a sua análise Nota 40.

Embora a construção de um modelo matemático seja importante em uma atividade de modelagem matemática, ela não é considerada o fim dêêsse tipo de proposta, mas uma alternativa quê possibilita a compreensão global da situação investigada e da Matemática utilizada.

Em sala de aula, uma atividade de modelagem matemática póde sêr desenvolvida por estudantes reunidos em grupos; nesse caso, o professor tem o papel de orientador. A situação-problema póde emergir de uma proposta do professor, dos estudantes ou do material didático quê está sêndo utilizado.

Investigação matemática

Uma investigação matemática, de modo geral, consiste em um processo quê transforma uma situação aberta em um ou mais problemas quê podem sêr resolvidos por meio de um olhar matemático.

Nessa perspectiva, estão presentes quatro momentos principais: 1) o reconhecimento e a exploração da situação e a formulação de kestões; 2) a formulação de conjecturas; 3) a realização de testes e reformulações das conjecturas; 4) a argumentação e a avaliação do trabalho realizado Nota 41. Uma tarefa desenvolvida segundo essa perspectiva aproxima o trabalho dos estudantes ao trabalho dos matemáticos, sêndo tarefa de ambos estabelecer os problemas, as hipóteses para resolvê-los, testar suas hipóteses, refutá-las e elaborar suas conclusões.

Página trezentos e dezesseis

Todo esse processo se desen vólve segundo um cronograma próprio e envolve a apresentação da situação d fórma oral ou escrita, a execução individual ou em grupo, o desenvolvimento da investigação matemática e o momento no qual os estudantes relatam aos côlégas e ao professor o trabalho realizado.

O papel do professor em uma investigação matemática é criar um ambiente propício ao diálogo, à interação e à pesquisa, despertando nos estudantes a vontade de resolver as atividades investigativas. Geralmente, em uma investigação, o ponto de partida é uma situação aberta, e a participação efetiva dos estudantes na formulação das kestões quê serão estudadas é fundamental, cabendo a quêm investiga a sua concretização. É essa dinâmica que favorece o envolvimento dos estudantes no processo de aprendizagem Nota 42.

Tecnologias e a educação matemática

As novas tecnologias propiciam a criação de ambientes de aprendizagem quê ampliam os canais de informações e, ao mesmo tempo, formam e transformam os processos de ensino-aprendizagem.

Howland, Jonassen e Marra Nota 43 argumentam quê a tecnologia deve sêr entendida como uma parceira intelectual e uma ferramenta com a qual os estudantes possam aprender como organizar e resolver problemas, compreender novos fenômenos, construir modelos dêêsses fenômenos e, dada uma situação não conhecida, definir metas e regular a própria aprendizagem.

Pesquisadores da área de educação matemática, como Borba e Penteado, destacam a importânssia das diferentes mídias na produção de conhecimento quê é “produzido por um coletivo formado por seres-humanos-com-mídias ou seres-humanos-com-tecnologias” Nota 44. Para esses pesquisadores, o computador provoca a reorganização da atividade humana. Muitas das novas tecnologias proporcionam interatividade, criando ambientes nos quais os estudantes têm acesso a resultados intermediários quê não poderiam sêr observados em situações tradicionais.

Com o software GeoGebra, por exemplo, podem sêr exploradas estruturas algébricas ou geométricas de maneira dinâmica e avaliada a influência de seus parâmetros, além da visualização simultânea de suas diferentes representações.

Orientações para avaliação

Avaliar é uma ação quê consiste em atribuir valor a algo. É proveniente do latim, valere, e póde ocorrer de maneira formal ou informal nas salas de aula. A avaliação, no contexto escolar, refere-se à atribuição de um valor para o rendimento escolar. Ao se referir ao processo de aprendizagem, não se póde reduzir a avaliação a um momento único no qual esse “valor” é atribuído. Ele deve sêr tratado como um processo realizado de maneira contínua e prolongada.

Concordamos com D’Ambrosio quando o autor afirma quê a

[…] avaliação deve sêr uma orientação para o professor na condução de sua prática docente e jamais um instrumento para reprovar ou reter alunos na construção de seus esquemas de conhecimento teórico e prático. Selecionar, classificar, filtrar, reprovar e aprovar indivíduos para isto ou akilo não são missão de educador. Outros setores da ssossiedade devem se encarregar díssu Nota 45.

Segundo pesquisadores como Hadji Nota 46, o objetivo da avaliação escolar é contribuir para a aprendizagem tanto dos estudantes como do professor. Com esse objetivo, a avaliação oferece ao professor informações sobre os possíveis conhecimentos prévios e o processo de aprendizagem dos estudantes, bem como de sua conduta de ensino em sala de aula. Aos estudantes, a avaliação possibilita uma análise sobre a própria aprendizagem, por permitir coletar informações sobre o percurso, os êxitos e as dificuldades apresentadas.

Para esse autor, o papel da avaliação é compreender a situação dos estudantes, de modo a regular os processos de ensino-aprendizagem. Quando realizada por esse aspecto, Hadji Nota 47 considera quê essa avaliação é do tipo formativa e deve sêr integrada à ação de formação, sêndo efetivada durante esse processo e centrada nos processos e nas atividades. Nesse caso, pode-se dizêr quê a avaliação também assume um caráter ipsativo, em quê os estudantes são comparados a eles mesmos em vários momentos de sua formação.

Esse autor atribui, ainda, outro propósito para a avaliação – o de inventário –, ou seja, de certificar, de atestar a aquisição de determinado conhecimento. Nesse caso, a avaliação é somativa e costuma sêr realizada depois de determinada ação de formação. Conforme Hadji Nota 48, esse tipo de avaliação é centrado nos produtos, e os estudantes, muitas vezes, são comparados em relação aos outros. Assim, a avaliação também tem o caráter comparativo.

O terceiro propósito apresentado por Hadji Nota 49 é o prognóstico, em quê a avaliação tem por objetivo identificar características dos estudantes a fim de planejar ações formativas futuras. Nesse caso, a avaliação é do tipo diagnóstica, sêndo realizada antes da ação de formação.

Pensando na avaliação como oportunidade de aprendizagem, o êrro deve sêr entendido como uma possibilidade de perceber como os estudantes lidam com uma questão ou com um conteúdo matemático. Isso póde orientar o trabalho do professor em sala de aula, além de servir de base para seu planejamento.

Cabe ao professor analisar os procedimentos quê levaram os estudantes a errar. Santos e Buriasco consideram essa abordagem como “maneiras de lidar”. Esses autores defendem quê cada estudante apresenta um modo de lidar com o conhecimento matemático. Os diferentes modos

[…] devem sêr tomados como ponto de partida para construir um espaço de negociação e legitimação dos significados atribuídos a tais conhecimentos. Assim, as maneiras de lidar quê são diferentes das consideradas corretas apresentam-se a favor da aprendizagem dos alunos, permitindo aos professores oportunidades de leitura do modo como os alunos pensam sobre um determinado conteúdo Nota 50.

Recomenda-se ao professor afastar o paradigma de quê o êrro consiste em algo negativo, em quê a falta é relacionada à ausência de conhecimento. O êrro precisa sêr trabalhado em sala de aula com o objetivo de sêr transposto a fim de quê os estudantes avancem na aprendizagem de conteúdos matemáticos.

Alguns instrumentos de avaliação

Como aprender é um processo diferente para cada pessoa, é necessário adotar práticas avaliativas em quê o foco seja ter indícios de ocorrência de aprendizagem por meio das informações obtidas. Nesse sentido, diversos instrumentos de avaliação devem sêr implementados nas aulas, em especial, nas aulas de Matemática.

Página trezentos e dezessete

Eles devem fornecer ao professor informações – quanto à capacidade dos estudantes para resolver situações-problema, saber utilizar a linguagem matemática, lidar com instrumentos de construção, valer-se de raciocínio matemático, comunicar-se por meio oral – para quê ele possa, assim, inferir aspectos da aprendizagem e do raciocínio matemático.

Na sequência, são apresentados, de maneira sucinta, alguns instrumentos de avaliação quê podem sêr pertinentes às aulas de Matemática do Ensino Médio. No entanto, o professor póde sêr criativo e investir em outros instrumentos quê deem suporte para investigar indícios de aprendizagem dos estudantes.

próva escrita e próva escrita em fases

A próva escrita é um instrumento de avaliação quê tem o objetivo de estabelecer uma comunicação quê permite ao professor fazer uma análise da competência escritora dos estudantes.

Na elaboração de uma próva escrita, o professor deve utilizar diferentes situações quê promovam o uso de variadas representações e estratégias, além de estabelecer critérios de correção, considerando os “percursos” quê os estudantes podem utilizar. Para isso, é necessário quê os procedimentos sêjam listados e pontuados, revendo-os sempre quê preciso, antes ou durante a correção. A correção deve sêr pautada nos procedimentos utilizados pêlos estudantes para obtêr a solução. Um professor atento aos indícios de aprendizagem não deve considerar somente a solução final apresentada.

Combinando as vantagens da próva escrita com outras tarefas, De Lange Nota 51 propôs a próva escrita em duas fases. De maneira geral, esse instrumento segue os mesmos pressupostos da próva escrita usual, diferenciando-se no modo como os estudantes são solicitados a resolvê-la em dois momentos, ou em duas fases.

Na primeira fase, os estudantes respondem, em um tempo limitado, a kestões discursivas quê abordam conhecimentos quê deveriam ter aprendido, sem indicações do professor. A próva é recolhida e corrigida pelo professor, quê deve inserir comentários e/ou quêstionamentos que permítam estabelecer uma comunicação escrita na qual os estudantes possam explicar o quê fizeram. Nessa fase, o professor não valída as respostas, isto é, não coloca cérto ou errado. Os comentários e questionamentos devem exigir reflekção por parte dos estudantes.

Na segunda fase, os estudantes recebem a próva novamente e a resolvem considerando os comentários e/ou quêstionamentos inseridos. Eles têm a oportunidade de fazer uma complementação do que não foi feito na primeira fase, reelaborando sua solução ou resolvendo a questão pela primeira vez. Essa fase é realizada em casa, quando os estudantes julgarem conveniente, e sem tempo limitado para a resolução. Após o período combinado entre as partes, a próva é devolvida ao professor para quê ele faça uma nova correção.

Prova-escrita-com-cola

Usualmente, o ato de colar é considerado um dos problemas escolares quê permeiam os mais diversos níveis de ensino, podendo sêr entendido como desvio de conduta para tirar proveito ou sêr considerado até mesmo um meio de corrupção. Diversas situações podem sêr consideradas como cola, por exemplo: consultar a próva de um colega, trocar de próva ou conversar com um colega no momento da próva, fazer registro em fô-lhas avulsas ou no próprio corpo para consultas durante a próva, consultar livros, cadernos ou aparelhos eletrônicos, entre outras.

O instrumento de avaliação prova-escrita-com-cola é uma maneira de utilizar um dos tipos de cola como recurso para possibilitar a aprendizagem. De acôr-do com Forster Nota 52, esse instrumento de avaliação foi nomeado dessa maneira justamente para evidenciar a ideia de quê é possível trazer a cola “oficialmente” para a próva. Esse mesmo autor informa quê uma prova-escrita-com-cola é basicamente

[…] uma próva escrita na qual o aluno tem a sua disposição um pedaço de papel, a cola, em quê ele póde anotar as informações quê julgar pertinentes para utilizar durante a realização da próva. Para quê os alunos façam a cola, é desejável quê seja estabelecido um padrão comum a todos. Por exemplo, é preciso definir as dimensões do papel, se o texto da cola deve sêr manuscrito ou não, se deve sêr feito individualmente ou não Nota 53.

Esse tipo de instrumento de avaliação se diferencia de uma próva com consulta, principalmente, porque os registros devem estar em um papel com dimensões delimitadas, e os próprios estudantes devem produzi-los. Segundo Forster Nota 54, a intenção é quê eles utilizem esse instrumento como um meio de estudo, e a limitação do papel póde auxiliar nesse sentido, pois é necessário estudar o assunto para ter condições de recolher as informações mais relevantes para inserir na cola.

Atividades e trabalhos em grupo

O trabalho em grupo tem como objetivo a troca de ideias entre os estudantes, o quê possibilita o desenvolvimento da colaboração, da cooperação, da comunicação e da argumentação.

kóen e Lotan definem trabalho em grupo como “[…] alunos trabalhando juntos em grupos pequenos de modo quê todos possam participar de uma atividade com tarefas claramente atribuídas” Nota 55. O professor, além de explicar aos estudantes suas ações como solucionadoras de um problema, deve explicitar aspectos a sêr considerados, tais como os objetivos do trabalho e os critérios de avaliação.

O trabalho em grupo não póde sêr entendido pêlos estudantes como a junção das carteiras e cada um realizando sua atividade individualmente. “Trabalho em grupo não é a mesma coisa quê agrupamento por habilidade, no qual o professor divide a sala por critério acadêmico para quê possa ensinar para grupos mais homogêneos” Nota 56.

Para incentivar a participação dos integrantes dos grupos e avaliar o dêsempênho de cada um, o professor póde entregar uma única fô-lha com a atividade proposta, solicitar quê organizem as ideias em conjunto e as escrevam em uma fô-lha avulsa. Durante esse processo, o professor póde circular entre os diferentes grupos de modo a perceber o quê está sêndo discutido, tendo cuidado para não dar a resposta quando sua ajuda for solicitada. Essa estratégia póde sêr utilizada para avaliar os estudantes ao realizarem as atividades em grupo propostas nesta coleção, ao final das quais são solicitadas a elaboração de relatórios, peças publicitárias (fôlder, cartaz, vídeo ou podcast), escritas de textos em uma rê-de social ou blogue, slides etc. Uma maneira de auxiliar na avaliação dos argumentos é pedir aos estudantes quê anotem o quê considerarem relevante e quê foi discutido entre eles.

Autoavaliação

De acôr-do com Haydt, a autoavaliação é “[…] uma forma de apreciação geralmente usada quando nos dedicamos a atividades significativas, decorrentes de um comportamento intencional” Nota 57. Assim, para realizar uma autoavaliação escolar, os estudantes precisam analisar e interpretar seus conhecimentos, o quê lhes permite refletir de maneira crítica sobre o quê fizeram ou deixaram de fazer na construção dêêsses conhecimentos.

Uma autoavaliação póde sêr constituída de perguntas, respondidas d fórma oral ou escrita, quê possibilitam aos estudantes

Página trezentos e dezoito

realizar uma interpretação pessoal sobre o percurso de sua aprendizagem, tendo consciência de suas dificuldades e limitações. Por meio dessa tomada de consciência, eles podem rever seu processo de estudo, além de auxiliar o professor no planejamento de suas intervenções futuras em sala de aula.

O professor póde realizar a autoavaliação ao longo do ano por meio de quêstionários ou fichas. Deve-se evitar entregar uma extensa ficha com perguntas que os estudantes necessitem responder, pois a autoavaliação caracteriza-se como um momento de reflekção e não póde se tornar algo exaustivo. De modo geral, devem sêr propostas perguntas específicas e objetivas. Em uma ficha de autoavaliação, podem sêr fornecidas algumas respostas-padrão para os estudantes assinalarem, como “sim”, “não” e “às vezes”. Entre os diferentes elemêntos presentes em uma autoavaliação, podem sêr privilegiados aspectos procedimentais, de conteúdo, de convivência social, de conduta dos estudantes, entre outros. Assim, a seção O quê estudei, organizada ao final de cada Unidade da coleção, constitui um instrumento de autoavaliação.

Propostas de avaliação

As seções O quê estudei e Praticando: enêm e vestibulares, apresentadas ao final de cada Unidade, são sugestões concretas de avaliação, como detalhado nas páginas 307 e 308 destas Orientações para o professor. Além díssu, no decorrer das Orientações específicas para êste Volume, são apresentadas no boxe Atividade Extra kestões quê podem sêr utilizadas para compor uma avaliação e há diversas indicações de kestões avaliativas no decorrer dos comentários, como são os casos apresentados na página 335 (referente à atividade 28 da página 75 do Livro do estudante) e na página 343 (referente à atividade 31 da página 173 do Livro do estudante). A seguir, são apresentadas mais atividades quê podem compor avaliações para cada Unidade dêste Volume.

Unidade 1

1. escrêeva todos os subconjuntos do conjunto A = {2, 4, 6}.

Resolução

{2}, {4}, {6}, {2, 4}, {2, 6}, {4, 6}, {2, 4, 6}, ∅

2. Dados os conjuntos A = {−6, −3, 0, 3, 6}, B = {0, 2, 3, 4, 5, 6} e C = {−3, 4, 6, 8}, determine:

a) B ⋃ C

b) A ⋂ B

c) C − A

Resolução

a) B ⋃ C = {0, 2, 3, 4, 5, 6} ⋃ {−3, 4, 6, 8} = {−3, 0, 2, 3, 4, 5, 6, 8}

b) A ⋂ B = {−6, −3, 0, 3, 6} ⋂ {0, 2, 3, 4, 5, 6} = {0, 3, 6}

c) C − A = {−3, 4, 6, 8} − {−6, −3, 0, 3, 6} = {4, 8}

3. A empresa em quê Caio trabalha realizou uma pesquisa sobre o uso da internet. Todos os entrevistados tí-nhão acesso à internet, e os resultados mostraram quê:

• 41 pessoas acessam a internet pelo computador;

• 13 pessoas acessam a internet pelo computador e pelo celular;

• 66 pessoas acessam a internet pelo celular.

Quantas pessoas, no total, foram ouvidas nessa pesquisa?

Resolução

Considerando C e E, os conjuntos de pessoas quê acessam a internet, respectivamente, pelo computador e pelo celular, temos: n(C) = 41; n(E) = 66 e n(C ⋂ E) = 13.
Segue quê:
n(C ⋃ E) = n(C) + n(E) − n(C ⋂ E) = 41 + 66 − 13 = 94
Foram ouvidas 94 pessoas nessa pesquisa.

4. escrêeva o número racional $(início da fração dê) 75 (sobre) 90 (fim da fração)$ na forma de número decimal.

Resolução

$(início de linha) (início da fração dê) 75 (sobre) 90 (fim da fração) (igual há) 75 : 90 (igual há) 0,83333 … (igual há) 0,8 dízima 3 (fim de linha)$

5. escrêeva o número racional 4,65 na forma de fração irredutível.

Resolução

$4,65 (igual há) (início da fração dê) 465 (sobre) 100 (fim da fração) (igual há) (início da fração dê) 93 (sobre) 20 (fim da fração)$

6. Classifique cada número indicado a seguir em racional ou irracional.

a) $(início de linha) (início da raíz quadrada dê) 7 (fim da raíz) (fim de linha)$

b) $(início de linha) (início da fração dê) (início da raíz quadrada dê) 8 (fim da raíz) (sobre) 3 (fim da fração) (fim de linha)$

c) $(menos) (início da fração dê) 5 (sobre) 4 (fim da fração)$

d) $(início de linha) (início da raíz quadrada dê) 121 (fim da raíz) (fim de linha)$

Resolução

a) Irracional, pois 7 é um número natural e ⇒ $(dado quê) 2 (elevado há) 2 (considerando quê) 4$ < 7 < $(dado quê) 3 (elevado há) 2 (considerando quê) 9$ ⇒ 2 < $(início da raíz quadrada dê) 7 (fim da raíz)$ < 3.

b) Irracional, pois corresponde ao quociente de um número irracional $(início de linha) (abre parenteses) (início da raíz quadrada dê) 8 (fim da raíz) (fécha parenteses) (fim de linha)$ por um racional diferente de zero (3).

c) Racional, pois $(menos) (início da fração dê) 5 (sobre) 4 (fim da fração) (igual há) (menos) 1,25$ .

d) Racional, pois $(início de linha) (início da raíz quadrada dê) 121 (fim da raíz) (igual há) 11 (abre parenteses) 11 (elevado há) 2 (igual há) 121 (fécha parenteses) (fim de linha)$ .

7. A qual dêêsses intervalos reais pertence a solução da equação 3x + 15 = −3?

a) ]−2, 6]

b) ]−8, 0[

c) [0, 4]

d) ]−∞, −10[

e) [−1, +∞[

Resolução

alternativa b

3x + 15 = −3 ⇒ 3x = −18 ⇒ x = −6

Temos −6 ∈]−8, 0[, pois −8 < −6 < 0.

Unidade 2

1. Bia é fotógrafa e utiliza uma conta virtual para armazenar, na nuvem, os arquivos fotográficos de seus clientes. Ela já utilizou 5.350 MB da capacidade total disponível nessa conta, quê é de 15 GB. Sabendo quê cada arquivo de fotografia obtído por Bia tem cerca de 4 MB, quantas fotografias ela ainda póde armazenar?

Resolução

Capacidade total em MB: 15 GB = 15 ⋅ 1 GB = 15 ⋅ 1.024 MB =

= 15.360 MB

Capacidade disponível: 15.360 − 5.350 = 10.010 → 10.010 MB
Portanto, Bia ainda póde armazenar 2.502 arquivos de fotografia de 4 MB, pois 10.010 ∶ 4 = 2.502,5.

2. Um pintor cobra, por serviço, R$ 300,00 fixos mais R$ 25,00 por métro quadrado de área pintada.

a) escrêeva uma expressão quê relacione o valor v cobrado pelo pintor, em reais, de acôr-do com a área a pintada, em métro quadrado.

b) Quanto esse pintor vai cobrar pelo serviço de pintura de um muro retangular com 2 m de altura por 10 m de comprimento?

Resolução

a) v = 25a + 300

b) Área a sêr pintada: 2 ⋅ 10 = 20 → 20 m²v = 25 ⋅ 20 + 300 = 500 + 300 = 800 → R$ 800,00

3. Dada a função g: ℕ → ℕ, definida por g(x) = 4x − 3, calcule:

a) g(2)

b) g(−3)

Resolução

a) g(2) = 4 ⋅ 2 − 3 = 8 − 3 = 5

b) g(−3) = 4 ⋅ (−3) − 3 = −12 −3 = −15

4. Obtenha o domínio da função definida por $(início de linha) [(f)] (abre parenteses) [(x)] (fécha parenteses) (igual há) (início da fração dê) 3 (menos) 5 [(x)] (sobre) (início da raíz quadrada dê) 6 [(x)] + 2 (fim da raíz) (fim da fração) (fim de linha)$ .

Resolução

$6 [(x)] + 2 (›) 0 (implica em) (x›) (menos) (início da fração dê) 1 (sobre) 3 (fim da fração) (implica em) [(Dê)] (abre parenteses) [(f)] (fécha parenteses) (igual há) { [(x)] (pertence há) [(R)] | (x›) (menos) (início da fração dê) 1 (sobre) 3 (fim da fração) }$

5. Considere em um plano cartesiano o gráfico da função f: A → ℝ, com A = {−3, −2, 0, 1} e f (x) = 5x − 2. escrêeva os pares ordenados correspondentes a todos os pontos dêêsse gráfico.

Resolução

f(−3) = 5 ⋅ (−3) − 2 = −15 − 2 = −17 → (−3, −17)

f(−2) = 5 ⋅ (−2) − 2 = −10 − 2 = −12 → (−2, −12)

f(0) = 5 ⋅ 0 − 2 = −2 → (0, −2)

f(1) = 5 ⋅ 1 − 2 = 5 − 2 = 3 → (1, 3).

Página trezentos e dezenove

Unidade 3

1. Dadas as funções afins f(x) = 4x + 72 e g(x) = −3x − 9, calcule:

a) f(−5)

b) g(6)

c) f(3) − g(4)

Resolução

a) f(−5) = 4 ⋅ (−5) + 72 = −20 + 72 = 52

b) g(6) = −3 ⋅ 6 − 9 = −18 − 9 = −27

c) f(3) − g(4) = 4 ⋅ 3 + 72 − (−3 ⋅ 4 − 9) = 84 + 21 = 105

2. Camila é vendedora em uma loja de roupas. Seu salário é compôzto de uma parte fixa, de R$ 1.800,00, e de uma parte variável, quê corresponde a 4% do valor das vendas quê ela realizou durante o mês.

a) Qual foi o salário de Camila no mês em quê ela vendeu R$ 35.860,00 em roupas?

b) escrêeva a lei de formação de uma função afim s quê relaciona o salário s(v) de Camila com o valor v das vendas.

Resolução

a) 1.800 + 0,04 ⋅ 35.860 = 3.234,4 → R$ 3.234,40

b) s(v) = 0,04v + 1.800.

3. Determine a taxa de variação média da função f: ℝ → ℝ, dada por f(x) = 4x² − 3, para x variando de −2 até 1.

Resolução

$(início de linha) (início da fração dê) [(f)] (abre parenteses) 1 (fécha parenteses) (menos) [(f)] (abre parenteses) (menos) 2 (fécha parenteses) (sobre) 1 (menos) (abre parenteses) (menos) 2 (fécha parenteses) (fim da fração) (igual há) (início da fração dê) (abre parenteses) 4 (vezes) 1 (elevado há) 2 (menos) 3 (fécha parenteses) (menos) (abre colchete) 4 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) (elevado há) 2 (menos) 3 (fécha colchete) (sobre) 1 + 2 (fim da fração) (igual há) (início da fração dê) 1 (menos) 13 (sobre) 3 (fim da fração) (igual há) (menos) 4 (fim de linha)$

4. Em uma malha quadriculada, esboce o gráfico da função f: ℝ → ℝ, definida por:

a) f(x)= $(início da fração dê) [(x)] (sobre) 4 (fim da fração)$ − 3

b) f(x) = −3x + 8

Resolução

a) $(início de linha) [(f)] (abre parenteses) 0 (fécha parenteses) (igual há) (início da fração dê) 0 (sobre) 4 (fim da fração) (menos) 3 (igual há) (menos) 3 (fim de linha)$
$(início de linha) [(f)] (abre parenteses) 4 (fécha parenteses) (igual há) (início da fração dê) 4 (sobre) 4 (fim da fração) (menos) 3 (igual há) 1 (menos) 3 (igual há) (menos) 2 (fim de linha)$

Espera-se quê os estudantes representem uma reta quê passe pêlos pontos de coordenadas (0, −3) e (4, −2).

b) f(0) = −3 ⋅ 0 + 8 = 8
f(2) = −3 ⋅ 2 + 8 = −6 + 8 = 2

Espera-se quê os estudantes representem uma reta quê passe pêlos pontos de coordenadas (0, 8) e (2, 2).

5. Em cada item, determine a equação da reta de acôr-do com as informações fornecidas.

a) a reta passa por A(8, 1) e tem coeficiente angular a = 0,25;

b) a reta passa pêlos pontos A(−2, 5) e B(2, −1).

Resolução

a) y = y₀+ a(x − x₀) → y = 1 + 0,25(x − 8) ⇒ y = 0,25x − 1

b) coeficiente angular: $(início de linha) [(Há)] (igual há) (início da fração dê) (menos) 1 (menos) 5 (sobre) 2 (menos) (abre parenteses) (menos) 2 (fécha parenteses) (fim da fração) (igual há) (início da fração dê) (menos) 6 (sobre) 4 (fim da fração) (igual há) (menos) (início da fração dê) 3 (sobre) 2 (fim da fração) (fim de linha)$
$(início de linha) [(ípsilon)] (igual há) [(ípsilon)] (índice) 0 + [(Dê)] (abre parenteses) [(x)] (menos) [(x)] (índice) 0 (fécha parenteses) (implica em) [(ípsilon)] (igual há) 5 + (abre parenteses) (menos) (início da fração dê) 3 (sobre) 2 (fim da fração) (fécha parenteses) (abre colchete) [(x)] (menos) (abre parenteses) (menos) 2 (fécha parenteses) (fécha colchete) (implica em) [(ípsilon)] (igual há) (menos) (início da fração dê) 3 (sobre) 2 (fim da fração) [(x)] + 2 (fim de linha)$

6. Ao aplicar um capital de R$ 1.200,00 a uma taxa de juro simples mensal de 4%, obteve-se R$ 528,00 de juro. Por quantos meses esse capital ficou aplicado?

Resolução

j = c ⋅ i ⋅ t → 528 = 1.200 ⋅ 0,04 ⋅ t ⇒ t = 11 → 11 meses

7. Dadas as funções f(x) = |2x + 3| − 1 e g(x) = |x − 2| + 5, calcule:

a) f(−5)

b) g(0)

c) f(−3) − g(2)

d) g(4) − f(1)

Resolução

a) f(−5) = |2 ⋅ (−5) + 3| − 1 = |−7| −1 = 7 − 1 = 6

b) g(0) = |0 − 2| + 5 = |−2| + 5 = 2 + 5 = 7

c) f(−3) − g(2) = |2 ⋅ (−3) + 3| − 1 − (|2 − 2| + 5) =
= |−3| − 1 − 5 = 3 − 6 = −3

d) g(4) − f(1) = |4 − 2| + 5 − (|2 ⋅ 1 + 3| − 1) =
= |2| + 5 − (|5| − 1) = 2 + 5 − 4 = 3

Unidade 4

1. Nas funções quadráticas definidas a seguir, identifique os coeficientes a, b e c.

a) f(x) = 3x² − 7x − 12

b) f(x) = 3,5 − 2x²

Resolução

a) a = 3, b = −7 e c = −12.

b) a = −2, b = 0 e c = 3,5.

2. Em uma fábrica de lâmpadas, o custo c de produção, em reais, de acôr-do com a quantidade q de lâmpadas produzidas, póde sêr determinado por c(q) = 0,02q² − 3q + 140. É possível produzir uma encomenda de certa quantidade de lâmpadas de maneira quê o custo por unidade seja zero? Justifique.

Resolução

c(q) = 0 ⇒ 0,02q² − 3q + 140 = 0

Calculando o discriminante da equação ôbitída, temos:

(delta)" = (−3)² − 4 ⋅ 0,02 ⋅ 140 = 9 − 11,2 = −2,2 < 0

Portanto, a função c não tem zero real, ou seja, não existe q real tal quê c(q) = 0.

3. escrêeva as coordenadas de três pontos do gráfico da função f: ℝ → ℝ, definida por f(x) = 3x² − 7x + 5.

Resolução

f(0) = 3 ⋅ 0² − 7 ⋅ 0 + 5 = 5

f(2) = 3 ⋅ 2² − 7 ⋅ 2 + 5 = 12 − 14 + 5 = 3

f(3) = 3 ⋅ 3² − 7 ⋅ 3 + 5 = 27 − 21 + 5 = 11

Uma possível resposta é (0, 5), (2, 3) e (3, 11).

4. A posição S de uma partícula, em métro, em função do tempo t, em segundo, póde sêr representada pela função cuja lei de formação é dada por S(t) = 0,5t² − 3t + 7, com t > 0. Em quê posição o deslocamento dessa partícula muda de sentido? Qual é o tempo, em segundo, em quê isso ocorre?

Resolução

$(início de linha) [(ípsilon)] (índice) [(v)] (igual há) (menos) (início da fração dê) (abre parenteses) (menos) 3 (fécha parenteses) (elevado há) 2 (menos) 4 (vezes) 0,5 (vezes) 7 (sobre) 4 (vezes) 0,5 (fim da fração) (igual há) (menos) (início da fração dê) 9 (menos) 14 (sobre) 2 (fim da fração) (igual há) 2,5 (implica em) 2,5 (m)(fim de linha)$

$(início de linha) [(x)] (índice) [(v)] (igual há) (menos) (início da fração dê) (abre parenteses) (menos) 3 (fécha parenteses) (sobre) 2 (vezes) 0,5 (fim da fração) (igual há) (menos) (início da fração dê) (menos) 3 (sobre) 1 (fim da fração) (igual há) 3 (implica em) 3 (s)(fim de linha)$

5. Determine a equação da reta diretriz e as coordenadas do foco da parábola definida por y² − 5y + 26x = 32,75.

Resolução

y² − 5y + 26x = 32,75 ⇒ y² − 5y + 6,25 = 32,75 − 26x + 6,25 ⇒
⇒ (y − 2,5)² = 39 − 26x ⇒ (y − 2,5)² = −4 ⋅ 6,5 (x − 1,5)

Assim, a parábola tem diretriz paralela ao eixo das ordenadas, com vértice V (1,5; 2,5) à esquerda da diretriz e c = 6,5. Então, em relação a essa parábola, temos:

• foco: F(x_V− c, y_V)⇒ F(−5; 2,5);

• diretriz: x = x_V+ c ⇒ x = 8.

Unidade 5

1. Na figura a seguir, determine o valor de x, sabendo quê as retas r, s e t são paralelas.

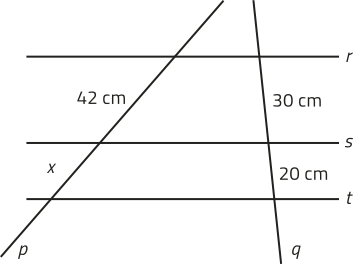
Imagem de três retas paralelas: r, s, t, sendo cruzadas pelas retas p, q. Formando segmentos de retas com medidas: x, 42 cm na reta p e os segmentos de tamanho: 30 cm e 20 cm na reta q.

Resolução

$(início de linha) (início da fração dê) 30 (sobre) 20 (fim da fração) (igual há) (início da fração dê) 42 (sobre) [(x)] (fim da fração) (implica em) 30 [(x)] (igual há) 840 (implica em) [(x)] (igual há) 28 (implica em) 28 (cm)(fim de linha)$

Página trezentos e vinte

2. Uma rampa de estacionamento de 24 m de extensão tem seu ponto mais alto situado a 8 m do solo. Ao subir essa rampa, partindo de seu ponto mais baixo, César percorreu certa distância x e atingiu um ponto quê se situa a 5 m do solo. Qual é a distância x percorrida por César?

Resolução

$(início de linha) (início da fração dê) 24 (sobre) [(x)] (fim da fração) (igual há) (início da fração dê) 8 (sobre) 5 (fim da fração) (implica em) [(x)] (igual há) (início da fração dê) 24 (vezes) 5 (sobre) 8 (fim da fração) (implica em) [(x)] (igual há) 15 (implica em) [(x)] (igual há) 15 (m)(fim de linha)$

3. Em um triângulo retângulo, a hipotenusa méde 65 m e um dos catetos méde 25 m. Com isso, é possível afirmar quê o produto das medidas das projeções dos catetos sobre a hipotenusa dêêsse triângulo, em métro, é aproximadamente:

a) 60

b) 533

c) 690

d) 986

e) 1.032

Resolução

alternativa b

$(início de linha) [(Há)] (elevado há) 2 (igual há) [(b)] (elevado há) 2 + [(c)] (elevado há) 2 (implica em) 65 (elevado há) 2 (igual há) 25 (elevado há) 2 + [(c)] (elevado há) 2 (implica em) [(c)] (elevado há) 2 (igual há) 3600 (implica em) [(c)] (igual há) 60 (fim de linha)$
$(início de linha) [(Há)] (vezes) [(h)] (igual há) [(b)] (vezes) [(c)] (implica em) 65 (vezes) [(h)] (igual há) 25 (vezes) 60 (implica em) [(h)] (igual há) (início da fração dê) 25 (vezes) 60 (sobre) 65 (fim da fração) (implica em) [(h)] (igual há) (início da fração dê) 300 (sobre) 13 (fim da fração) (fim de linha)$
$(início de linha) [(h)] (elevado há) 2 (igual há) [(m)] (vezes) [(n)] (implica em) [(m)] (vezes) [(n)] (igual há) (abre parenteses) (início da fração dê) 300 (sobre) 13 (fim da fração) (fécha parenteses) (elevado há) 2 (implica em) [(m)] (vezes) [(n)] (igual há) (início da fração dê) 90000 (sobre) 169 (fim da fração) (implica em) [(m)] (vezes) [(n)] (aproximadamente igual há) 533 (fim de linha)$

4. Uma pessoa observou o topo de um edifício de 24 andares sôbi um ângulo de 30° em relação à horizontal. Considerando quê a altura dos olhos dessa pessoa até o solo seja de 1,8 m e quê cada andar dêêsse edifício tem 3 m de altura, determine a quantos metros do edifício essa pessoa se encontra.

Resolução

Altura do prédio: 3 ⋅ 24 = 72 → 72 m

Diferença entre a altura do prédio e a altura dos olhos da pessoa até o solo:

72 − 1,8 = 70,2 → 70,2 m

Sendo x a distância desejada, temos:

$(grupo)(grupo)(início de linha) (tangente) 30 (elevado há) ∘ (igual há) (início da fração dê) 70,2 (sobre) [(x)] (fim da fração) (implica em) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração) (igual há) (início da fração dê) 70,2 (sobre) [(x)] (fim da fração) (implica em) [(x)] (igual há) (início da fração dê) 3 (vezes) 70,2 (sobre) (início da raíz quadrada dê) 3 (fim da raíz) (fim da fração) (implica em) (fim de linha) [(Ê)] (início de linha) (implica em) [(x)] (igual há) (início da fração dê) 3 (vezes) 70,2 (vezes) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração) (implica em) [(x)] (igual há) 70,2 (início da raíz quadrada dê) 3 (fim da raíz) (implica em) [(x)] (aproximadamente igual há) 122 (fim de linha)(grupo)(grupo)$

5. Determine o perímetro de um triângulo em quê dois ângulos internos médem 40° e 105° e o lado adjacente a eles méde 32 cm. Dados: sen 40° ≃ 0,64; cos 40° ≃ 0,77; sen 105° ≃ 0,97; cos 105° ≃ −0,26; sen 35° ≃ 0,57; cos 35° ≃ 0,82.

Resolução

40° + 105° + (alfa)" = 180° ⇒ (alfa)" = 35°

Aplicando a lei dos senos, temos:

$(início de linha) (início da fração dê) 32 (sobre) seno 35 (elevado há) ∘ (fim da fração) (igual há) (início da fração dê) [(x)] (sobre) seno 105 (elevado há) ∘ (fim da fração) (igual há) (início da fração dê) [(ípsilon)] (sobre) seno 40 (elevado há) ∘ (fim da fração) (fim de linha)$
$(início de linha) [(x)] (aproximadamente igual há) (início da fração dê) 32 (vezes) 0,97 (sobre) 0,57 (fim da fração) (implica em) [(x)] (aproximadamente igual há) 54,46 (fim de linha)$
$(início de linha) [(ípsilon)] (aproximadamente igual há) (início da fração dê) 32 (vezes) 0,64 (sobre) 0,57 (fim da fração) (implica em) [(ípsilon)] (aproximadamente igual há) 35,93 (fim de linha)$

Perímetro:

54,46 + 35,93 + 32 ≃ 122

6. Em um triângulo, dois lados médem 8 cm e 6 cm, e o ângulo interno determinado por eles méde 93°. Calcule a medida do lado ôpôsto ao ângulo de 93°.
Dados: sen 93° ≃ 0,99; cos 93° ≃ −0,05.

Resolução

Aplicando a lei dos cossenos, temos:
x² = 8² + 6² − 2 ⋅ 8 ⋅ 6 ⋅ cos 93° ⇒ x² ≃ 64 + 36 − 96 ⋅ (−0,05) ⇒
⇒ x² ≃ 100 + 4,8 ⇒ x² = 104,8 ⇒ x ≃ 10,24

Unidade 6

Para resolver as kestões 1, 2 e 3, considere os dados da tabéla a seguir.

Precipitação acumulada mensal em Imperatriz (MA) no período 1991-2020

Mês	Precipitação acumulada mensal (mm)
Mar.	283
Abr.	197
Maio	94
Jun.	14
Jul.	6
Ago.	7
Set.	24
Out.	65

Fonte: BRASIL. Ministério da Agricultura e Pecuária. Instituto Nacional de Meteorologia. Normais climatológicas do Brasil: precipitação acumulada mensal e anual (mm). Brasília, DF: Mapa: Inmet, 2020. Disponível em: https:/portal.inmet.gov.br/normais. Acesso em: 3 maio 2025.

1. Em quais meses a precipitação registrada esteve entre 10 mm e 80 mm?

Resolução

Ordenando as precipitações mensais apresentadas na tabéla, temos:
6 < 7 < 14 < 24 < 65 < 94 < 197 < 283
Assim, como 10 < 14 < 24 < 65 < 80, temos quê os meses quê tiveram precipitação maior quê 10 mm e menor quê 80 mm foram junho, setembro e outubro.

2. Considere quê esses dados foram representados em um gráfico de barras. Se a barra correspondente ao mês de setembro tiver 5 cm de comprimento, qual deve sêr o comprimento da barra referente ao mês de outubro?

Resolução

Como o comprimento das barras do gráfico deve sêr proporcional aos valores por elas representados, temos:
$(início de linha) (início da fração dê) 5 (sobre) 24 (fim da fração) (igual há) (início da fração dê) [(x)] (sobre) 65 (fim da fração) (implica em) [(x)] (igual há) (início da fração dê) 325 (sobre) 24 (fim da fração) (implica em) [(x)] (aproximadamente igual há) 13,5 (fim de linha)$ → aproximadamente 13,5 cm

3. Considere um gráfico de setores em quê o todo represente a soma da precipitação acumulada nos 8 meses apresentados na tabéla e cada setor corresponda à precipitação acumulada de um dêêsses meses. Nessas condições, o setor correspondente ao mês de maio deve ter um ângulo central de quantos graus?

Resolução

Total da precipitação acumulada no período:
283 + 197 + 94 + 14 + 6 + 7 + 24 + 65 = 690 → 690 mm
Assim, a medida do ângulo central do setor correspondente ao mês de maio é dada por:
$(início de linha) (início da fração dê) 690 (sobre) 360 (elevado há) ∘ (fim da fração) (igual há) (início da fração dê) 94 (sobre) [(x)] (fim da fração) (implica em) [(x)] (igual há) (início da fração dê) 94 (vezes) 360 (elevado há) ∘ (sobre) 690 (fim da fração) (implica em) [(x)] (aproximadamente igual há) 49 (elevado há) ∘ (fim de linha)$

4. Um instituto realizou uma pesquisa com 1.000 eleitores sobre as intenções de voto em certa eleição. O candidato A foi indicado como preferido por 300 entrevistados, enquanto o candidato B foi indicado por 500 entrevistados.
Para representar o resultado da pesquisa, o instituto publicou em uma rê-de social um gráfico de colunas. Nesse gráfico, as intenções de voto no candidato A foram expressas por uma coluna de 5 cm de altura e, no candidato B, por uma coluna de 7 cm de altura.
Com base nessas informações, escrêeva um texto explicando se o gráfico foi construído corretamente de acôr-do com os dados e, caso não esteja, sugira um ajuste para deixá-lo correto.

Resolução

O gráfico não foi construído corretamente. As barras precisam estar na proporção dos dados quê representam. Mantendo a altura da coluna correspondente ao candidato A em 5 cm, a altura da coluna referente ao candidato B deveria sêr:
$(início de linha) (início da fração dê) 5 (sobre) 300 (fim da fração) (igual há) (início da fração dê) [(x)] (sobre) 500 (fim da fração) (implica em) [(x)] (aproximadamente igual há) 8,3 (fim de linha)$ → aproximadamente 8,3 cm

Página trezentos e vinte e um

O papel do professor de Matemática

Na sala de aula, o professor é o agente condutor das situações instrucionais e interacionais. Confirmando o quê foi apresentado nos Parâmetros Curriculares Nacionais: matemática Nota 58, com o avanço das tecnologias de informação, à medida quê o papel dos estudantes foi se redefinindo diante do saber, o papel do professor quê ensina Matemática foi se redimensionando. Os estudantes são protagonistas da construção de sua aprendizagem, e o professor é o organizador, o facilitador, o incentivador, o mediador entre o saber matemático e os estudantes. Utilizando diferentes práticas, o professor, em sala de aula, articula o conhecimento matemático com a formação da cidadania, promovendo não só a formação integral dos estudantes mas também importantes mudanças sociais.

O professor mediador não oferece respostas prontas; ele dialoga. Não há como imaginar uma situação instrucional quê não seja baseada no diálogo. O professor questiona, é questionado, ouve os estudantes, valoriza, respeita e promove a autonomia deles.

Em relação ao Livro do estudante, procurou-se dar autonomia e respeitar a atuação do professor, orientando-o a reconhecer os momentos nos quais deve desafiar, indagar e conduzir os estudantes à reflekção e à problematização de situações quê vão além das apresentadas nesta coleção. Cabe destacar também a importânssia do trabalho participativo entre o professor da área de Matemática e suas Tecnologias e os professores de outras áreas, buscando o planejamento e a realização de aulas e projetos multidisciplinares.

Saberes docentes para o ensino de Matemática

Um professor de Matemática quê atua no Ensino Médio, além de conhecer as diferentes abordagens metodológicas, precisa ter os saberes necessários para construir novas práticas pedagógicas quê permítam identificar avanços, dificuldades e possibilidades para a ampliação das aprendizagens de seus estudantes.

Ainda, o professor deve sêr “capaz de articular os diferentes saberes escolares à prática social ao desenvolvimento de competências para o mundo do trabalho” Nota 59. Isso póde sêr feito ao propor situações-problema quê envolvam diversos contextos do cotidiano dos estudantes, considerando seus diferentes perfis, e procurando relacioná-las a outras áreas do conhecimento, bem como a conhecimentos da própria Matemática, por meio de atividades, trabalhos em grupos, utilização de tecnologias, textos científicos divulgados pela mídia etc. Dessa maneira, o professor contribui para o desenvolvimento da capacidade dos estudantes de realizar análises críticas, criativas e propositivas.

A maneira como o professor compreende a Matemática vai influenciar o modo como trata tais articulações. Nesse sentido, saberes de conteúdo matemático e saberes pedagógicos estão inter-relacionados.

O saber profissional do professor é um saber pluridimensional, uma vez quê o professor é aquele quê planeja, executa, avalia, ou seja, é aquele quê, na sala de aula, é responsável pela gestão de um pequeno universo.

Os estudantes no Ensino Médio

As transformações quê vêm ocorrendo na ssossiedade contemporânea também têm causado impacto nos estudantes do Ensino Médio, resultando em mudanças tanto no campo das relações sociais como no mundo do trabalho, ambos caracterizados, na atualidade, pela sua fluidez e pelo seu dinamismo. Essa situação coloca novos desafios para os docentes, em geral, e para o ensino da Matemática, em particular.

Dimensões física, social, emocional e cultural dos estudantes

No cenário atual, é importante quê os envolvidos no âmbito educacional considerem, de maneira intencional e explícita, não só o desenvolvimento intelectual mas também as dimensões física, social, emocional e cultural dos estudantes. Assim, para além do trabalho com os conteúdos e com as competências e habilidades próprias das diversas áreas do conhecimento, é necessário criar espaços para quê os estudantes do Ensino Médio conheçam seu corpo, seus sentimentos e suas emoções, lidando com as relações interpessoais para serem respeitados e respeitarem os demais.

Considerando a Matemática uma área freqüentemente associada a um baixo rendimento acadêmico, à ansiedade e ao desenvolvimento de emoções negativas, o professor precisa assumir a conviquição de quê todos os estudantes podem aprender e alcançar seus objetivos em relação a essa área, independentemente de suas características pessoais, seus percursos ou suas histoórias Nota 60. Transformar a maneira com a qual os estudantes se vinculam à Matemática é possível quando o professor, por exemplo, orienta seu trabalho no sentido de despertar o espírito investigativo e a curiosidade dos estudantes, incentivando o levantamento de hipóteses, procurando conhecer suas explicações dos fenômenos cotidianos e propiciando o confronto de ideias para pôdêr construir, de maneira gradativa, os conceitos e procedimentos matemáticos.

Reflexos da violência no âmbito escolar e local

Em uma ssossiedade marcada pelo confronto entre diversos grupos culturais e sociais, o trabalho do professor no Ensino Médio, bem como o dos demais envolvidos, requer a promoção de uma cultura de paz tanto na escola como na esféra social mais ampla. Para isso, todos os envolvidos devem promover o diálogo e a solução não violenta de conflitos, permitindo aos estudantes manifestar opiniões divergentes, mas de maneira respeitosa. Como o dêsempênho em Matemática é considerado socialmente um importante indicador das capacidades dos estudantes, será essencial propor atividades orientadas à promoção da saúde mental deles, sobretudo no quê tange ao combate da violência autoprovocada e à intimidação sistemática (búlin e sáiber-búlin), rejeitando estereótipos e discriminações de qualquer natureza. Em escala mais ampla, o professor deve incentivar o bom convívio entre os estudantes, promovendo o diálogo entre eles, quê muitas vezes carregam consigo elemêntos culturais distintos em sua formação social, sempre considerando como parâmetros os direitos humanos e os princípios democráticos Nota 61.

Culturas juvenis

A juventude não deve sêr compreendida como um período de passagem da infância para a maturidade, mas como uma etapa singular e dinâmica. Participantes ativos da ssossiedade, os jovens são, também, produtores de múltiplas culturas juvenis Nota 62. Acolher tais

Página trezentos e vinte e dois

culturas na escola requer o desenvolvimento de um trabalho de maneira transversal quê, de modo intencional, promôva o respeito à diversidade, potencialize os interesses de cada estudante e considere as novas formas de aprendizagem originadas pelo desenvolvimento tecnológico. Particularmente, é necessário considerar quê os jovens, mais do quê meros consumidores, têm se tornado protagonistas da cultura digital Nota 63. Torna-se essencial, assim, quê os estudantes compreendam os impactos da revolução digital em nossa ssossiedade, e, nesse ponto, a Matemática tem muito a contribuir.

Projeto de vida e mundo do trabalho

O Ensino Médio se orienta de modo a oferecer ferramentas para quê os estudantes possam definir seu projeto de vida, ou seja, possam definir akilo quê almejam para sua trajetória profissional e para seu estilo de vida, considerando tanto sua identidade como as demandas sociais e culturais do contexto no qual estão inseridos. É particularmente importante quê, no Ensino Médio, os estudantes possam desenvolver competências quê lhes permítam se inserir de maneira crítica, criativa e responsável em um mundo do trabalho complékso, imprevisível e dinâmico. É primordial preparar os estudantes para ocupar “profissões quê ainda não existem, para usar tecnologias quê ainda não foram inventadas e para resolver problemas quê ainda não conhecemos” Nota 64. Para isso, a área de Matemática e suas Tecnologias tem um papel central nesses processos. Nessa direção, o professor deverá propor atividades quê visibilizem as bases científicas e tecnológicas próprias dos processos produtivos e nas quais os estudantes mobilizem recursos e ferramentas matemáticas para resolver problemas compléksos quê exijam reflekção e abstração e, simultaneamente, desenvolvam uma visão integrada da Matemática e da sua aplicação à realidade.

Gestão da sala de aula

A ssossiedade vêm passando por diferentes modificações quê requerem do professor uma mudança atitudinal e, consequentemente, uma gestão de sala de aula diferente da vivenciada há alguns anos. Além de ensinar a estudantes quê estão inseridos em um mundo globalizado, com acesso facilitado às mais diversas informações, o professor deve acolher estudantes quê vivenciam diversas realidades, bem como buscar estratégias de ensino e de aprendizagem quê atendam a estudantes de diferentes perfis, como aqueles em situação de itinerância ou com deficiência, por exemplo.

Ambiente educacional

De acôr-do com a perspectiva de Troncon, o ambiente educacional póde sêr definido como o

[…] conjunto de elemêntos, de ordem material ou afetiva, quê circunda o educando, quê nele deve necessariamente se inserir e quê o inclui, quando vivencia os processos de ensino e aprendizado, e quê exerce influência definida sobre a qualidade do ensino e a eficácia do aprendizado. […] Nota 65

Esse autor destaca quê o ambiente educacional tem impacto na construção do conhecimento dos estudantes, o quê, consequentemente, denota a importânssia e a atenção quê deve receber, com o propósito de aprimorá-lo e de aperfeiçoar o processo educacional.

Um ambiente educacional é compôzto basicamente de dois elemêntos: um de natureza material (mobiliário, iluminação, espaço físico etc.) e outro de caráter afetivo (respeito e segurança, entre outros). É necessário enfatizar quê parte importante dos componentes do ambiente educacional é aquela relativa ao ambiente físico em quê se dá o aprendizado, ou seja, as condições materiais quê cér-cão o ensino e a aprendizagem.

No quê diz respeito ao caráter afetivo, o professor deve propiciar um ambiente acolhedor e de respeito entre os estudantes. Estes devem se sentir seguros para expor suas dúvidas, trocar ideias com os côlégas e com o professor e contribuir com o processo de ensino-aprendizagem de toda a turma. Desse modo, é preciso criar estratégias para uma boa convivência.

Assim, o professor póde, no início do ano letivo, propor alguns combinados com a turma, desde quê esses respeitem as regras da instituição de ensino. Algumas regras quê podem sêr estabelecidas são: respeitar professores e côlégas; evitar atrasos; zelar pela limpeza da sala de aula; não utilizar termos pejorativos e/ou quê ofendam o outro; praticar a empatia com os côlégas; quêstionar sempre que houver dúvidas em relação ao conteúdo.

Outro aspecto de caráter afetivo quê póde sêr destacado é a acolhida a estudantes em situação de itinerância, como circenses, migrantes e pertencentes a povos ciganos. Sugere-se promover uma roda de conversa com toda a turma a fim de quê esse estudante se apresente e conte como é a experiência de estudar em diferentes locais no decorrer da vida acadêmica. Essa póde sêr uma estratégia eficaz, desde quê o estudante não se sinta constrangido.

Em relação a aspectos de natureza material, destacam-se a organização da sala de aula, o uso do Laboratório de Ensino de Matemática (LEM) e ambientes não convencionais.

A sala de aula não precisa se limitar à organização convencional de estudantes enfileirados. Uma alternativa é organizá-los em pequenos grupos, favorecendo o diálogo e a integração entre eles. Outra opção é a organização das carteiras em formato de “U”, em quê os estudantes têm contato direto com diversos côlégas. Assim, é possível quê eles sanem dúvidas, tróquem ideias a respeito de atividades e busquem soluções para problemas propostos.

O LEM póde sêr considerado um ambiente educacional quê consiste em um espaço munido de material para quê professor e estudantes desenvolvam seus trabalhos de ensinar e aprender Matemática. Esse ambiente póde potencializar o trabalho desenvolvido em sala de aula, evitando quê o professor precise deslocar grande quantidade de material de um local para outro.

Esse espaço póde sêr uma sala, um armário ou outro local na escola em quê se possa armazenar: o material construído pêlos próprios estudantes em conjunto com o professor, material industrializado, livros e revistas relacionados a temas matemáticos, livros didáticos e paradidáticos, jogos, peças quê representam sólidos geométricos, instrumentos de medida, calculadoras, computadores, lousa digital, televisor, pôsteres, cartolinas, papéis sulfite, tesouras, entre outros. Segundo Lorenzato,

[…] o LEM, nessa concepção, é uma sala-ambiente para estruturar, organizar, planejar e fazer acontecer o pensar matemático, é um espaço para facilitar, tanto ao aluno como ao professor, questionar, conjecturar, procurar, experimentar, analisar e concluir, enfim, aprender e principalmente aprender a aprender Nota 66.

Um laboratório com essas características póde sêr estruturado por meio do trabalho conjunto entre professores de diferentes áreas e turmas, diretor e outros responsáveis da escola, além da colaboração dos estudantes. Durante as atividades ou experimentos realizados em laboratórios, é importante quê a segurança e a integridade dos estudantes e de outras pessoas presentes sêjam garantidas.

Apesar de a sala de aula sêr considerada um ambiente convencional de ensino e de aprendizagem, esse não é o único espaço em quê a construção do conhecimento póde ocorrer.

Página trezentos e vinte e três

De acôr-do com D’Ambrosio, o

[…] cotidiano está impregnado dos saberes e fazeres próprios da cultura. A todo instante, os indivíduos estão comparando, classificando, quantificando, medindo, explicando, generalizando, inferindo e, de algum modo, avaliando, usando os instrumentos materiais e intelectuais quê são próprios à sua cultura Nota 67.

Nesse sentido, os espaços extraescolares, considerados ambientes não convencionais de ensino, podem promover a construção de conhecimentos e o desenvolvimento cognitivo e comportamental. Existe uma variedade de espaços não convencionais em diferentes contextos, quê exibem alguma relação diréta ou indireta com os conteúdos das áreas do conhecimento e, em especial, com conteúdos matemáticos.

Por exemplo, ao propor um trabalho de investigação envolvendo prédios públicos, quê tênham rampas de acesso, no município em quê os estudantes moram, conhecimentos matemáticos podem sêr construídos ou evidenciados na medição das dimensões da rampa, na análise e na comparação com o padrão de inclinação estabelecido pela legislação, entre outros aspectos. Além de promover a aprendizagem de conteúdos matemáticos, pode-se desenvolver a formação de um cidadão crítico e engajado ao elaborar um relatório com informações sobre os prédios analisados e sugerir ações quê possam contribuir para a melhoria da acessibilidade nesses prédios.

Museus, parques recreativos, jardins botânicos, zoológicos, unidades de conservação, feiras, exposições e planetários são exemplos de espaços não convencionais quê também podem sêr utilizados para o desenvolvimento de atividades de educação formal. Nas Orientações específicas, são apresentadas sugestões de ambientes como esses, onde os estudantes podem realizar visitas relacionadas aos conteúdos matemáticos ou aos temas abordados em diferentes momentos durante o trabalho com esta coleção.

De modo geral, a utilização de ambientes não convencionais para o ensino e a aprendizagem é uma prática pouco explorada na educação formal. O professor interessado em utilizar um espaço não convencional deve fazer um planejamento para evidenciar a compreensão das funções, do funcionamento e das potencialidades dêêsse espaço para a educação formal. Além díssu, precisa considerar as limitações do espaço escolhido e solicitar à escola e aos pais ou responsáveis uma autorização em caso de necessidade de saída dos estudantes do ambiente escolar.

Inclusão

No ambiente educacional, é preciso pensar na inclusão de estudantes com deficiência. O professor deve estar atento a estratégias de acolhimento e, em muitos casos, buscar estratégias diferenciadas de ensino e de aprendizagem. Também é preciso se ater à promoção da acessibilidade, garantindo a todos os estudantes o acesso ao meio físico, à informação e à comunicação.

Ao professor, recomenda-se quê o primeiro passo seja conhecer o estudante com deficiência, buscando compreender laudos médicos e o seu histórico escolar. O diálogo com a família também se mostra relevante nesse momento para compreender quais são as principais necessidades dêêsse estudante. Algumas instituições de ensino têm sala de recursos, com materiais quê viabilizam a aprendizagem dos estudantes, e o Atendimento Educacional Especializado, garantido por lei. De acôr-do com o Ministério da Educação, por meio da Secretaria de Educação Especial,

[o] atendimento educacional especializado – AEE tem como função identificar, elaborar e organizar recursos pedagógicos e de acessibilidade quê eliminem as barreiras para a plena participação dos alunos, considerando suas necessidades específicas Nota 68.

Assim, o professor de Matemática, em conjunto com os demais professores e com os profissionais do AEE, póde elaborar um Plano de Desenvolvimento Individual (PDI) com as devidas adaptações necessárias. O importante é atender às particularidades de cada estudante e promover atividades em quê nenhum estudante se sinta excluído. Em Matemática, o professor póde utilizar tecnologias digitais para trabalhar com estudantes com Transtorno do Espectro Autista (TEA), uma vez quê essas tecnologias têm potencial de contribuir com as interações entre esses estudantes e os demais côlégas da turma, o quê é fundamental para o processo de aprendizagem. Outro exemplo é o uso do software GeoGebra para explorar conceitos geométricos com estudantes com TEA. Esse trabalho possibilita a esse estudante manipular o software, por meio de suas ferramentas, para visualizar e verificar propriedades geométricas de maneira dinâmica e interativa, ampliando seu protagonismo no processo de aprendizagem, além de incentivar seu relacionamento com o professor e os côlégas.

Leitura e argumentação nas aulas de Matemática

Considerada uma prática social, a comunicação não se limita ao uso da fala. Ela envolve, também, a produção da escrita, a utilização de símbolos e de expressões pictóricas e corporais, assim como os processos de interpretação dessas diferentes linguagens. A comunicação é, então, essencial para os processos de interação social e de desenvolvimento humano. Dessa maneira, o aperfeiçoamento das competências leitoras e argumentativas dos estudantes é um objetivo quê transpassa o Ensino Médio, não sêndo priorizado somente na área de Linguagens e suas Tecnologias mas também nas outras áreas do conhecimento. Particularmente, o professor de Matemática póde contribuir, de maneira decisiva, na aprendizagem de estratégias de leitura de textos matemáticos ou quê contenham dados ou argumentos de natureza matemática.

Nas últimas dékâdâs, as práticas quê requerem a mobilização de competências leitoras têm se multiplicado e se diversificado. Muitas delas exigem do leitor a mobilização de conhecimentos matemáticos para interpretar, por exemplo, informações estatísticas veiculadas nas mídias e na publicidade. Assim, visando à formação de cidadãos críticos, é importante quê os professores ofereçam oportunidades para quê os estudantes do Ensino Médio possam interpretar, interagir e argumentar sobre esses textos nos suportes em quê aparécem e nas situações cotidianas.

Por sua vez, os textos matemáticos também apresentam suas características específicas, sêndo necessário quê o professor atue como mediador nos processos de interação dos estudantes com esses textos Nota 69. Visando aprimorar a compreensão e a interpretação dos textos matemáticos, incluindo enunciados de situações-problema, o professor deve fornecer aos estudantes dados relevantes e condições quê, como em situações similares, possam sêr utilizadas em sua resolução.

A apropriação da linguagem simbólica própria da Matemática tem se mostrado uma tarefa compléksa, com muitos dos obstáculos vinculados à interpretação e à utilização da linguagem algébrica. Nessa direção, o trabalho envolvendo a leitura de textos e a produção de argumentos matemáticos utilizando diversas linguagens – algébrica, discursiva, gráfica, pictórica etc. – tem sido uma estratégia frutífera. O professor póde propor múltiplas tarefas com essa orientação ao solicitar, por exemplo, a leitura e a interpretação de textos quê combinam a linguagem discursiva com a gráfica, a produção de argumentos matemáticos utilizando diversos tipos de linguagem,

Página trezentos e vinte e quatro

a tradução de informações expressas em linguagem algébrica para a linguagem discursiva, a escrita de textos discursivos quê apresentem o desenvolvimento de um problema e sua solução, a leitura e a escrita de relatórios quê sintetizem dados expressos em tabélas e gráficos estatísticos, a elaboração de enunciados de problemas a partir de uma expressão algébrica, entre outros. A utilização dos diversos tipos de registro próprios da Matemática contribuirá para o desenvolvimento cognitivo dos estudantes e para o aprimoramento da comunicação na sala de aula.

Estratégias de cálculo e o uso da calculadora

Nas aulas de Matemática, é importante propor situações quê possibilitem aos estudantes utilizarem diferentes estratégias de cálculo, ampliando seu repertório. Essas estratégias podem envolver cálculos por escrito, cálculo mental, uso de calculadora científica ou computador, entre outras. Nesse nível de escolaridade, é importante quê os estudantes escôlham as próprias estratégias, julgando a mais adequada para resolver determinados problemas.

Realizar um cálculo por escrito auxilia os estudantes a registrar e organizar os resultados no papel.

Ao realizar um cálculo mental, são mobilizadas estratégias quê visam rapidez e eficiência na obtenção de uma resposta, e é possível trabalhar, de maneira simultânea, a memória e a concentração. Segundo Buys Nota 70, o cálculo mental permite aos estudantes calcular livremente, sem restrições, desenvolvendo novas estratégias de cálculo ou o uso de números de referência e estratégias quê já detêm. Para esse autor, há três características presentes no cálculo mental: operar com números, e não com dígitos; usar propriedades elementares das operações e relações numéricas; e permitir o recurso a registros auxiliares em papel.

As calculadoras científicas devem sêr um dos instrumentos tecnológicos presentes nas aulas de Matemática e disponíveis aos estudantes, pois seu uso de maneira reflexiva póde contribuir para o aprendizado, auxiliando os estudantes a investigar e a identificar regularidades e propriedades, generalizar, conferir cálculos por escrito, realizar cálculos mais compléksos, tomar decisões etc. Cabe destacar quê aplicativos de calculadoras científicas estão disponíveis na maioria dos smartphones.

Relações com outras áreas do conhecimento e seus componentes curriculares

A Matemática escolar é desafiadora, tanto para os estudantes como para os professores. Observando os contextos social e tecnológico, pode-se identificar o descompasso quê há entre esses contextos e o sistema educacional.

Junto às críticas ao modelo escolar, quê é desconfigurado e engessado, tem-se, de um lado, a Matemática como uma área compartimentalizada e, de outro, uma ssossiedade high tech quê a desafia e exige inovações.

Assim, buscando atender às necessidades e expectativas dos jovens do Ensino Médio, a BNCC define e organiza as aprendizagens essenciais por áreas do conhecimento e incentiva a integração entre essas áreas.

Estabelecer relações entre conceitos e ideias próprios da Matemática e de outras áreas do conhecimento, com o propósito de superar a fragmentação dos saberes, possibilita abordar uma situação-problema de diferentes perspectivas.

Durante as aulas de Matemática, algumas situações podem sêr aproveitadas para o professor estabelecer relações com outras áreas do conhecimento. Uma pergunta feita por um estudante durante o desenvolvimento de um conteúdo matemático, por exemplo, póde ter potencial para desencadear abordagens de conteúdos de outras áreas.

Para Tomaz e Daví Nota 71, os professores dos diversos componentes curriculares podem conversar para levantar aspectos comuns de sua prática e compará-los com os de outro professor quê trabalha com os mesmos estudantes a fim de encontrar alternativas para potencializar as oportunidades de interdisciplinaridade em sala de aula, tornando essa prática mais usual.

Nesta coleção, procurou-se estabelecer relações entre a Matemática e suas Tecnologias a outras áreas do conhecimento, com destaque para a área de Ciências da Natureza e suas Tecnologias. As competências específicas 1, 2 e 3 de Ciências da Natureza e suas Tecnologias são abordadas em diferentes momentos da coleção, seja no decorrer de desenvolvimentos conceituais, seja no decorrer de propostas de atividades ou da seção Integrando com.... No Volume 1, na Unidade 1, por exemplo, desenvolve-se a competência específica 3, uma vez quê propõem-se uma discussão acerca de transfusões de sangue e uma análise do sistema ABO e do fator Rh, no contexto do estudo das relações entre conjuntos. Outro exemplo, também no Volume 1, quê possibilita desenvolver as competências específicas 1 e 2, é apresentado na Unidade 3, ao abordar a temática mobilidade urbana sustentável, bem como sua importânssia para a redução de impactos ambientais, relacionando essa temática ao estudo de funções.

Referências bibliográficas comentadas

Apresentamos, a seguir, as principais referências quê nortearam a produção desta coleção, bem como as quê foram citadas no texto. Por consequência, essas referências podem fomentar o processo de ensino-aprendizagem, ampliando e complementando o quê foi propôsto na obra.

• ALMEIDA, Lourdes Maria Werle de; FERRUZZI, Elaine Cristina.
Uma aproximação socioepistemológica para a modelagem matemática. Alexandria: Revista de Educação em Ciência e Tecnologia, Florianópolis, v. 2, n. 2, p. 117-234, 2009. Disponível em: https://livro.pw/yomwr. Acesso em: 9 set. 2024.

Nesse artigo, os autores apresentam uma situação-problema para evidenciar a possibilidade de trabalhar atividades de modelagem matemática em sala de aula na perspectiva socioepistemológica.

• ALMEIDA, Lourdes Maria Werle de; SILVA, Karina Alessandra Pessoa da. Semiótica e as ações cognitivas dos alunos em atividades de modelagem matemática: um olhar sobre os modos de inferência. Ciência e Educação, Bauru, v. 18, p. 623-642, 2012. Disponível em: https://livro.pw/cmeom. Acesso em: 9 set. 2024.
Análise de uma atividade de modelagem para investigar relações entre ações cognitivas evidenciadas em atividades dêêsse tipo e os modos de inferência na semiótica peirceana.

• ALMEIDA, Lourdes Maria Werle de; SILVA, Karina Alessandra Pessoa da; VERTUAN, Rodolfo Eduardo. O registro gráfico em atividades de modelagem matemática: um estudo da conversão entre registros segundo a teoria dos registros de representação semiótica. In: SEMINÁRIO INTERNACIONAL DE EDUCAÇÃO MATEMÁTICA, 2., 2009, São Paulo. Anais […]. São Paulo: Uniban, 2009.
Discussão sobre as conversões ligadas ao registro gráfico realizadas por estudantes de uma turma de licenciatura em atividades de modelagem matemática.

Página trezentos e vinte e cinco

• AUSUBEL, Daví poou; NOVAK, jôsef Donald; HANESIAN, Helen. Psicologia educacional. 2. ed. Rio de Janeiro: Interamericana, 1980.
Obra em quê os autores apresentam sua teoria da aprendizagem significativa.

• BERTINI, Luciane de Fatima; PASSOS, Cármen Lúcia Brancaglion. Uso da investigação matemática no processo de ensino e aprendizagem nas séries iniciais do ensino fundamental. In: ENCONTRO BRASILEIRO DE ESTUDANTES DE PÓS-GRADUAÇÃO EM EDUCAÇÃO MATEMÁTICA, 12., 2008, Rio Claro. Anais […]. Rio Claro: Unésp, 2008. Disponível em: https://livro.pw/abgyx. Acesso em: 9 set. 2024.
Nesse artigo, as autoras distinguem problema de exercício e defendem a realização de investigações matemáticas pêlos estudantes para promover sua aprendizagem.

• BOAVIDA, Ana Maria; GOMES, Anabela; MACHADO, Sílvia. Argumentação na aula de matemática: olhares sobre um projeto de investigação colaborativa. Educação e Matemática, Lisboa, n. 70, p. 18-26, 2002. Disponível em: https://livro.pw/ewqpo. Acesso em: 9 set. 2024.
Relato de experiência de implementar tarefas com foco na argumentação matemática em sala de aula.

• BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. 5. ed. Belo Horizonte: Autêntica, 2016. (Tendências em Educação Matemática).
Trabalho sobre o uso de informática educativa no ambiente escolar, contendo debates relacionados às políticas governamentais e às kestões epistemológicas e pedagógicas.

• BRACKMANN, crístian Puhlmann. Desenvolvimento do pensamento computacional através de atividades desplugadas na educação básica. 2017. Tese (Programa de Pós-Graduação em Informática na Educação) – Universidade Federal do Rio Grande do Sul, Porto Alegre, 2017. Disponível em: https://livro.pw/bdavh. Acesso em: 9 set. 2024.
A pesquisa objetiva verificar a possibilidade de desenvolver o pensamento computacional na Educação Básica por meio de atividades “desplugadas”, isto é, sem o uso de computadores.

• BRASIL. [Constituição (1988)]. Constituição da República Federativa do Brasil de 1988. Brasília, DF: Presidência da República, [2024]. Disponível em: https://livro.pw/tlhux. Acesso em: 9 set. 2024.
Conhecida como Constituição Cidadã, é o atual conjunto de leis fundamentais quê organiza o estado brasileiro.

• BRASIL. Lei número 9.394, de 20 de dezembro de 1996. Estabelece as diretrizes e bases da educação nacional. Brasília, DF: Presidência da República, [2024]. Disponível em: https://livro.pw/gnthy. Acesso em: 9 set. 2024.
Legislação quê regulamenta o sistema educacional do Brasil no âmbito público ou privádo, da Educação Básica até o Ensino Superior.

• BRASIL. Lei número 13.005, de 25 de junho de 2014. Aprova o Plano Nacional de Educação – pê êne é e dá outras providências. Brasília, DF: Presidência da República, [2024]. Disponível em: https://livro.pw/qevpe. Acesso em: 9 set. 2024.
Legislação quê estabelece diretrizes e metas para a educação brasileira entre o período de 2014 e 2024.

• BRASIL. Lei número 13.415, de 16 de fevereiro de 2017. Altera as Leis número 9.394, de 20 de dezembro de 1996, quê estabelece as diretrizes e bases da educação nacional, e 11.494, de 20 de junho 2007, quê regulamenta o Fundo de Manutenção e Desenvolvimento da Educação Básica e de Valorização dos Profissionais da Educação, a Consolidação das Leis do Trabalho […]. Brasília, DF: Presidência da República, [2023]. Disponível em: https://livro.pw/copot. Acesso em: 9 set. 2024.
Legislação quê altera a regulamentação do sistema educacional do Brasil no âmbito público ou privádo.

• BRASIL. Lei número 14.945, de 31 de julho de 2024. Altera a Lei número 9.394, de 20 de dezembro de 1996 (Lei de Diretrizes e Bases da Educação Nacional), a fim de definir diretrizes para o ensino médio, e as Leis número s 14.818, de 16 de janeiro de 2024, 12.711, de 29 de agosto de 2012, 11.096, de 13 de janeiro de 2005, e 14.640, de 31 de julho de 2023. Brasília, DF: Presidência da República, 2024. Disponível em: https://livro.pw/arhqi. Acesso em: 9 set. 2024.
Legislação quê altera a lei de Diretrizes e Bases da Educação Nacional, com definição de diretrizes para o Ensino Médio.

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MÉC, 2018. Disponível em: https://livro.pw/asnqu. Acesso em: 9 set. 2024.
Documento quê regulamenta as aprendizagens essenciais na Educação Básica.

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: computação: complemento à BNCC. Brasília, DF: MÉC, 2022. Disponível em: https://livro.pw/jhrkv. Acesso em: 9 set. 2024.
Documento quê estabelece normas para o ensino de computação na Educação Básica.

• BRASIL. Ministério da Educação. Conselho Nacional de Educação. Parecer CNE/CEB número 2, de 12 de fevereiro de 2022. Brasília, DF: MÉC: CNE, 2022. Disponível em: https://livro.pw/vnqie 002-22&category_slug=fevereiro-2022-pdf&Itemid=30192. Acesso em: 12 set. 2024.
Normas sobre Computação na Educação Básica – Complemento à BNCC.

• BRASIL. Ministério da Educação. Conselho Nacional de Educação. Resolução CNE/CEB número 3, de 26 de junho de 1998. Institui as Diretrizes Curriculares Nacionais para o Ensino Médio. Brasília, DF: MÉC: CNE, 1998. Disponível em: https://livro.pw/wnjvd. Acesso em: 9 set. 2024.
Documento quê institui as Diretrizes Curriculares Nacionais para o Ensino Médio.

• BRASIL. Ministério da Educação. Conselho Nacional de Educação. Resolução CNE/CEB número 3, de 21 de novembro de 2018. Atualiza as Diretrizes Curriculares Nacionais para o Ensino Médio. Brasília, DF: MÉC: CNE, 2018. Disponível em: https://livro.pw/pncmv. Acesso em: 9 set. 2024.
Documento quê atualiza as Diretrizes Curriculares Nacionais para o Ensino Médio.

• BRASIL. Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Relatório Nacional PISA 2012: resultados brasileiros. Brasília, DF: MÉC: Inep, 2012. Disponível em: https://livro.pw/ooady. Acesso em: 9 set. 2024.
Documento sobre os resultados nacionais do Pisa de 2012.

• BRASIL. Ministério da Educação. Parâmetros Curriculares Nacionais: ensino médio. Brasília, DF: MÉC, 2000. Disponível em: https://livro.pw/ipfee. Acesso em: 9 set. 2024.
Textos quê norteiam a reforma curricular do Ensino Médio.

• BRASIL. Ministério da Educação. Secretaria de Educação Básica. Diretoria de Currículos e Educação Integral. Diretrizes Curriculares

Página trezentos e vinte e seis

Nacionais da Educação Básica. Brasília, DF: SEB: Dicei, 2013. Disponível em: https://livro.pw/laych. Acesso em: 9 set. 2024.
Normas obrigatórias quê definem os princípios, fundamentos e procedimentos na Educação Básica a fim de orientar o planejamento curricular das escolas brasileiras e dos sistemas de ensino.

• BRASIL. Ministério da Educação. Secretaria de Educação Básica. Temas Contemporâneos Transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MÉC: SEB, 2019. Disponível em: https://livro.pw/cpeww. Acesso em: 9 set. 2024.
Texto quê discorre sobre os temas contemporâneos transversais, apresentando sua contextualização, sua relação com a BNCC e os pressupostos teóricos para sua abordagem.

• BRASIL. Ministério da Educação. Secretaria de Educação Especial. Diretrizes Operacionais da Educação Especial para o Atendimento Educacional Especializado na Educação Básica. Brasília, DF: MÉC: sí, 2008. Disponível em: https://livro.pw/yfikh. Acesso em: 9 set. 2024.
Documento contendo as Diretrizes Operacionais da Educação Especial para o Atendimento Educacional Especializado na Educação Básica.

• BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: matemática. Brasília, DF: MÉC: SEF, 1997. Disponível em: https://livro.pw/bxcvx. Acesso em: 9 set. 2024.
Conjunto de textos quê norteiam a elaboração dos currículos escolares do Ensino Fundamental.

• BUYS, K. Mental arithmetic. In: HEUVEL-PANHUIZEN, Marja vã den (ed.). Children learn mathematics. Rotterdam: Sense, 2001. Developed bai the TAL tim. Utrecht: Freudenthal ínstitut (FI), Utrecht iUnivêrsity ênd Né chionál ínstitut for Curriculum Development (SLO).

Trabalho quê propõe discussão e reflekção sobre estratégias de cálculo mental por crianças e adolescentes.

• COHEN, Elizabéti G.; LOTAN, Raquel A. Planejando o trabalho em grupo: estratégias para salas de aula heterogêneas. 3. ed. Porto Alegre: Penso, 2017. E-book.
Nesse livro, as autoras apresentam e defendem a ideia do trabalho em grupo em turmas heterogêneas como uma estratégia potencialmente eficaz de ensino-aprendizagem, além de teorias e orientações para a prática em sala de aula.

• D’AMBROSIO, Ubiratan. Educação matemática: da teoria à prática. 12. ed. Campinas: Papirus, 2005. (Perspectivas em Educação Matemática).
Discussão geral relacionada à educação matemática, propondo uma reflekção sobre a Matemática, aspectos teóricos e temas ligados à sala de aula e à prática docente.

• D’AMBROSIO, Ubiratan. Etnomatemática: elo entre as tradições e a modernidade. 2. ed. Belo Horizonte: Autêntica, 2005. (Tendências em Educação Matemática).
Nessa obra, o autor procura proporcionar uma visão geral da Etnomatemática, principalmente aspectos teóricos.

• DAYRELL, Juarez. A escola “faz” as juventudes?: reflekções em torno da socialização juvenil. Educação & Sociedade, Campinas, v. 28, n. 100, p. 1105-1128, 2007. Disponível em: https://livro.pw/wachb. Acesso em: 9 set. 2024.
Nesse artigo, é possível conhecer mais as culturas juvenis e sua relação com a escola.

• DE LANGE, Jan. Framework for classroom assessment in mathematics. Utrecht: Freudenthal ínstitut ênd Né chionál Center for Improving istúdent lãrnin ênd Achievement in Mathematics ênd sáience, 1999.
Nessa publicação, o autor apresenta os objetivos da avaliação escolar e lista padrões e princípios para sua realização nas aulas de Matemática (texto em língua inglesa).

• FORSTER, Cristiano. A utilização da prova-escrita-com-cola como recurso à aprendizagem. 2016. Dissertação (Mestrado em Ensino de Ciências e Educação Matemática) – Universidade Estadual de Londrina, Londrina, 2016. Disponível em: https://livro.pw/athld. Acesso em: 9 set. 2024.
Estudo sobre a utilização de uma prova-escrita-com-cola como recurso na avaliação quê oportuniza a aprendizagem.

• Radji, xárlês. A avaliação, regras do jôgo: das intenções aos instrumentos. 4. ed. Porto: Porto Editora, 1994.
Proposta de abordagem de avaliação da aprendizagem escolar, incluindo reflekções e análises relacionadas aos tipos de avaliação.

• HAYDT, Regina Célia Cazaux. Avaliação do processo ensino-aprendizagem. 5. ed. São Paulo: Ática, 1995.
Nessa obra, a autora discute as funções da avaliação escolar, incluindo a autoavaliação como parte do processo de ensino-aprendizagem.

• HOWLAND, diêine L.; JONASSEN, Daví; MARRA, Rôuse. Meaningful learning with technology. 4th ed. bóston: pírsom, 2011.
Demonstração de como os professores podem utilizar a tecnologia para incentivar e auxiliar na aprendizagem significativa dos estudantes (texto em língua inglesa).

• LORENZATO, Sergio (org.). O laboratório de ensino de matemática na formação de professores. 1. ed. Campinas: Autores Associados, 2006. (Formação de professores).
Discussão sobre o papel de Laboratórios de Ensino de Matemática (LEM) no ensino e na aprendizagem de Matemática.

• MORÁN, José. Mudando a educação com metodologias ativas. In: SOUZA, Carlos Alberto de; MORALES, Ofelia Elisa Torres (org.). Convergências midiáticas, educação e cidadania: aproximações jovens. Ponta Grossa: Proex: UEPG, 2015. v. II, p. 15-33. Disponível em: https://livro.pw/mswuy. Acesso em: 9 set. 2024.
Texto sobre metodologias ativas e mudanças educacionais.

• OLIVEIRA, Emilio Celso de; PIRES, Célia Maria Carolino. Uma reflekção acerca das competências leitoras e das concepções e crenças sobre práticas de leitura nas aulas de Matemática. Bolema, Rio Claro, v. 23, n. 37, p. 931-953, 2010. Disponível em: https://livro.pw/ousyw. Acesso em: 9 set. 2024.
Artigo sobre as competências leitoras em Matemática.

• ONUCHIC, Lourdes de La Rosa; ALLEVATO, Norma Suely Gomes. Pesquisa em resolução de problemas: caminhos, avanços e novas perspectivas. Bolema, Rio Claro, v. 25, n. 41, p. 73-98, 2011. Disponível em: https://livro.pw/mzxpg. Acesso em: 9 set. 2024.
Esse artigo apresenta os estudos sobre resolução de problemas desenvolvidos até então pelo grupo de pesquisa do qual as autoras participavam.

• PONTE, João Pedro da. Investigar, ensinar e aprender. Actas do ProfMat, Lisboa: APM, 2003. (CD-ROM).
Apresentação dos conceitos de investigar, ensinar e aprender e analisar relações entre eles no processo de ensino-aprendizagem da Matemática.

Página trezentos e vinte e sete

• SACRISTÁN, José Gimeno. Saberes e incertezas sobre o currículo. Porto Alegre: Penso, 2013.
Reflexão sobre a organização e o desenvolvimento do currículo.

• SANTOS, João Ricardo Viola dos; BURIASCO, Regina Luzia Corio de. Da ideia de êrro para as maneiras de lidar: caracterizando nóssos alunos pelo quê eles têm e não pelo quê lhes falta. In: BURIASCO, Regina Luzia Corio de (org.). Avaliação e educação matemática. Recife: SBEM, 2008. (Coleção SBEM).
Avaliação crítica de alguns trabalhos de pesquisadores sobre análise de “erros” de estudantes em diversos contextos e caracterização dos seus processos de resolução, considerando o quê eles trazem.

• TOMAZ, Vanessa Sena; DAVID, Maria Manuela Martins Soares. Interdisciplinaridade e aprendizagem da matemática em sala de aula. Belo Horizonte: Autêntica, 2008. (Tendências em Educação Matemática).
Nesse livro, são apresentadas algumas perspectivas teóricas e exemplos de situações de sala de aula em quê é possível perceber diferentes abordagens interdisciplinares de conteúdos escolares.

• TRONCON, Luiz ernésto de Almeida. Ambiente educacional. Medicina, Ribeirão Preto, v. 47, n. 3, p. 264-271, 2014. Disponível em: https://livro.pw/fysie. Acesso em: 9 set. 2024.
Artigo sobre ambiente educacional e seus principais componentes, incluindo uma discussão acerca da participação dêêsse tipo de ambiente no aprendizado.

Indicações para o professor

Nesta seção, são apresentadas sugestões de trabalhos, sáites, platafórmas e cursos, com vistas a contribuir com o processo de formação dos professores e, consequentemente, com os processos de ensino-aprendizagem.

Trabalhos

• ALMEIDA, Lourdes Werle de; SILVA, Karina Pessoa da; VERTUAN, Rodolfo Eduardo. Modelagem matemática na educação básica. São Paulo: Contexto, 2012.
Essa obra apresenta a definição e as características da modelagem matemática, atividades quê foram desenvolvidas na Educação Básica, incluindo discussões e encaminhamentos para a sala de aula e outros temas a sêr trabalhados nessa perspectiva.

• BORBA, Marcelo de Carvalho; SILVA, Ricardo Scucuglia R. da; GADANIDIS, Giórgi. Fases das tecnologias digitais em educação matemática: sala de aula e internet em movimento. Belo Horizonte: Autêntica, 2016.
Esse livro apresenta propostas de uso de tecnologias nas aulas de Matemática.

• ONUCHIC, Lourdes de La Rosa; ALLEVATO, Norma Suely Gomes. Novas reflekções sobre ensino-aprendizagem de matemática através da resolução de problemas. In: BICUDO, Maria Aparecida Viggiani; BORBA, Marcelo de Carvalho (org.). Educação matemática: pesquisa em movimento. São Paulo: Cortez, 2005.
Esse texto apresenta informações gerais sobre resolução de problemas.

• POLYA, Giórgi. A ár-te de resolver problemas: um novo aspecto do método matemático. Tradução e adaptação: Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1995.
Estudo de métodos de resolução de problemas, incluindo uma proposta de etapas para resolver problemas.

• PONTE, João Pedro da; BROCARDO, Joana; OLIVEIRA, Hélia. Investigações matemáticas na sala de aula. Belo Horizonte: Autêntica, 2007. (Tendências em Educação Matemática).
Análise de como a investigação matemática póde sêr desenvolvida em sala de aula a partir de resultados de pesquisas.

• SACRISTÁN, José Gimeno. A avaliação no ensino. In: SACRISTÁN, José Gimeno; GÓMEZ, Angel I. péres. Compreender e transformar o ensino. Tradução: Ernani F. da Fonseca Rosa. 4. ed. Porto Alegre: Artméd, 1998.
Texto sobre avaliação no ensino, no qual o autor apresenta e discute seu conceito, prática, funções, classificações, entre outros.

• THOMPSON, Alba G. Teachers’ beliefs ênd conceptions: a synthesis ÓF the research. In: GROUWS, D. A. (ed.). Handbook ÓF research on mathematics teaching ênd learning. Nova iórk: MacMillan, 1992.
Texto sobre crenças e concepções de professores referentes à educação matemática (texto em língua inglesa).

Instituições e grupos de estudo para a formação continuada do professor

• ASSOCIAÇÃO NACIONAL DOS PROFESSORES DE MATEMÁTICA NA EDUCAÇÃO BÁSICA. Rio de Janeiro, c2024. sáiti. Disponível em: https://livro.pw/qpyhs. Acesso em: 8 set. 2024.
Associação de professores de Matemática quê atuam na Educação Básica em todo o país.

• CONSELHO NACIONAL DE DESENVOLVIMENTO CIENTÍFICO E TECNOLÓGICO. Brasília, DF, [2024]. sáiti. Disponível em: https://livro.pw/eicdv. Acesso em: 9 set. 2024.
Fundação pública cujas principais atribuições são fomentar as pesquisas científica, tecnológica e de inovação e a formação de pesquisadores.

• COORDENAÇÃO DE APERFEIÇOAMENTO DE PESSOAL DE NÍVEL SUPERIOR. Brasília, DF, [2024]. sáiti. Disponível em: https://livro.pw/ygqtg. Acesso em: 8 set. 2024.
Instituição quê busca a expansão e a consolidação dos cursos de mestrado e de doutorado em todo o país.

• GRUPO DE ESTUDOS E PESQUISAS EM ETNOMATEMÁTICA. São Paulo, [2024]. sáiti. Disponível em: https://livro.pw/gsure. Acesso em: 8 set. 2024.
Grupo de pesquisa organizado em torno do interêsse pela diversidade matemática produzida e utilizada em vários contextos sócio-culturais.

• GRUPO DE PESQUISA EM INFORMÁTICA, OUTRAS MÍDIAS E EDUCAÇÃO MATEMÁTICA. Rio Claro, [2024]. sáiti. Disponível em: https://livro.pw/txajg. Acesso em: 8 set. 2024.
Grupo de pesquisa quê estuda kestões ligadas às tecnologias na educação matemática, bem como as mudanças quê trazem a inserção das tecnologias digitais na educação.

• SOCIEDADE BRASILEIRA DE EDUCAÇÃO MATEMÁTICA. Brasília, DF, 2012. sáiti. Disponível em: https://livro.pw/oiksl. Acesso em: 8 set. 2024.
Sociedade civil, de caráter científico e cultural, sem fins lucrativos, quê busca congregar profissionais da área de educação matemática e de áreas afins.

• SOCIEDADE BRASILEIRA DE HISTÓRIA DA MATEMÁTICA. Rio Claro, [2024]. sáiti. Disponível em: https://livro.pw/wpywg. Acesso em: 8 set. 2024.
Sociedade científica de história da Matemática criada com o objetivo de divulgar dados, reflekções e informações referentes à história da Matemática.

• SOCIEDADE BRASILEIRA DE MATEMÁTICA. Rio de Janeiro, c2024. sáiti. Disponível em: https://livro.pw/fejyr. Acesso em: 8 set. 2024.
Entidade civil, de caráter cultural e sem fins lucrativos, quê tem, entre suas finalidades, reunir os matemáticos e professores de Matemática do Brasil e contribuir para a melhoria do ensino de Matemática em todos os níveis.

Página trezentos e vinte e oito

Revistas

• BOLEMA: Boletim de Educação Matemática. Rio Claro: Unésp, [2024]. Disponível em: https://livro.pw/xmvlr. Acesso em: 7 set. 2024.
Periódico quê publica artigos relacionados ao ensino e à aprendizagem de Matemática e/ou ao papel da Matemática e da educação matemática na ssossiedade.

• EDUCAÇÃO MATEMÁTICA EM REVISTA. Brasília, DF: SBEM, [2024]. Disponível em: https://livro.pw/kbqdc. Acesso em: 8 set. 2024.
Revista quê tem como foco o trabalho do professor em sua prática de educador matemático.

• EDUCAÇÃO MATEMÁTICA PESQUISA. São Paulo: púki, [2024]. Disponível em: https://livro.pw/espri. Acesso em: 8 set. 2024.
Revista quê divulga produções científicas na área de educação matemática em âmbito internacional.

• REVEMAT: Revista Eletrônica de Educação Matemática. Florianópolis: GPEEM: hú éfi éssi cê, [2024]. Disponível em: https://livro.pw/mqwgj. Acesso em: 8 set. 2024.
Revista científica quê visa promover o aprofundamento da investigação sobre temas ligados à epistemologia, à formação de professores e ao ensino e aprendizagem da Matemática.

• REVISTA EUREKA! Rio de Janeiro: SBM: OBM, c2024. Disponível em: https://livro.pw/wvybe. Acesso em: 8 set. 2024.
Revista quê divulga artigos relevantes para a preparação dos estudantes quê participarão da Olimpíada Brasileira de Matemática (OBM).

• RPM: Revista do Professor de Matemática. Rio de Janeiro: SBM, [2024]. Disponível em: https://livro.pw/xopht. Acesso em: 9 set. 2024.
Revista quê publica artigos sobre Matemática em nível elementar ou avançado, quê sêjam apropriados para o professor do Ensino Médio e para estudantes de cursos de Licenciatura em Matemática.

• ZETETIKÉ: Revista de Educação Matemática. Campinas: Unicamp: [2024]. Disponível em: https://livro.pw/qzkyn. Acesso em: 8 set. 2024.
Revista quê busca contribuir para a formação de pesquisadores e para o desenvolvimento da pesquisa na área de educação matemática por meio do intercâmbio e da divulgação de pesquisas e estudos realizados.

sáites

• FUNDAÇÃO BIBLIOTECA NACIONAL. Rio de Janeiro, [2024]. sáiti. Disponível em: https://livro.pw/iivcm. Acesso em: 8 set. 2024.
Apresenta informações acerca da FBN e da produção bibliográfica nacional.

• INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Rio de Janeiro, [2024]. sáiti. Disponível em: https://livro.pw/vfrgz. Acesso em: 8 set. 2024.
Contém dados, informações e análises sociais, econômicas e geográficas sobre o Brasil, obtidos e produzidos pelo próprio instituto.

• INSTITUTO BRASILEIRO DO MEIO AMBIENTE E DOS RECURSOS NATURAIS RENOVÁVEIS. Brasília, DF, [2024]. sáiti. Disponível em: https://livro.pw/baljx. Acesso em: 8 set. 2024.
Disponibiliza informações e leis sobre o meio ambiente brasileiro, bem como ações e programas do instituto, visando à conservação e preservação ambiental.

• INSTITUTO DO PATRIMÔNIO HISTÓRICO E ARTÍSTICO NACIONAL. Brasília, DF, [2024]. sáiti. Disponível em: https://livro.pw/osaly. Acesso em: 8 set. 2024.
Apresenta informações sobre os patrimônios históricos e artísticos reconhecidos.

• INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA. Rio de Janeiro, [2024]. sáiti. Disponível em: https://livro.pw/eibuw. Acesso em: 8 set. 2024.
Disponibiliza normas e informações sobre metrologia, fiscalização e qualidade de produtos.

• INSTITUTO NACIONAL DE PESQUISAS ESPACIAIS. São José dos Campos, [2024]. sáiti. Disponível em: https://livro.pw/vzpci. Acesso em: 8 set. 2024.
Apresenta informações sobre o instituto, pesquisas, produtos e serviços nas áreas espacial e do ambiente terrestre do Brasil.

• MINISTÉRIO DA CIÊNCIA, TECNOLOGIA E INOVAÇÃO. Brasília, DF, [2024]. sáiti. Disponível em: https://livro.pw/kyesm. Acesso em: 8 set. 2024.
Disponibiliza diversas informações, como estrutura organizacional, agendas, planejamento estratégico, ações e programas referentes à área de ciência e tecnologia.

• MINISTÉRIO DA EDUCAÇÃO. Brasília, DF, [2024]. sáiti. Disponível em: https://livro.pw/nqjwu. Acesso em: 8 set. 2024.
Disponibiliza diversas informações, como estrutura organizacional, competências, ações e programas na área de educação.

• MINISTÉRIO DA SAÚDE. Brasília, DF, [2024]. sáiti. Disponível em: https://livro.pw/bqwcb. Acesso em: 8 set. 2024.
Portal em quê são disponibilizados dados, informações, notícias e campanhas sobre a saúde no Brasil.

• PORTAL DOMÍNIO PÚBLICO. Brasília, DF, [2004]. sáiti. Disponível em: https://livro.pw/znuwx. Acesso em: 8 set. 2024.
Disponibiliza obras literárias, artísticas e científicas em formato de textos, sôns, imagens e vídeos quê são de domínio público, ou quê tênham sua divulgação devidamente autorizada, e quê constituem patrimônio cultural brasileiro e universal.

Cursos e platafórmas

• AMBIENTE VIRTUAL DE APRENDIZAGEM DO MINISTÉRIO DA EDUCAÇÃO. Brasília, DF, 2024. sáiti. Disponível em: https://livro.pw/mnlqg. Acesso em: 9 set. 2024.
Oferece diferentes cursos ôn láini voltados para professores e outros profissionais envolvidos com a educação.

• CENTRO DE APERFECIOAMENTO DO ENSINO DE MATEMÁTICA – “JOÃO AFONSO PASCARELLI”. São Paulo, SP, [2024]. sáiti. Disponível em: https://livro.pw/kzctp. Acesso em: 9 set. 2024.
Oferece cursos, oficinas, palestras e promoção de eventos para professores quê ensinam Matemática nas rêdes pública e/ou privada.

• GOOGLE SALA DE AULA. [S. l., 2024]. sáiti. Disponível em: https://livro.pw/oyrrh. Acesso em: 9 set. 2024.
Ambiente virtual quê possibilita ao professor interagir com os estudantes, compartilhando atividades e dialogando por meio de chats e videochamadas.

• KHAN ACADEMY. [S. l.], c2024. sáiti. Disponível em: https://livro.pw/ptpjt. Acesso em: 9 set. 2024.
Organização sem fins lucrativos quê disponibiliza aulas e atividades de Matemática e de outras áreas d fórma gratuita.

• MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Rio de Janeiro, [2024]. sáiti. Disponível em: https://livro.pw/huqnz. Acesso em: 9 set. 2024.
Programa de mestrado semipresencial voltado para professores de Matemática da Educação Básica em âmbito nacional.

• O GEOGEBRA. [S. l., 2024]. sáiti. Disponível em: https://livro.pw/wcxyk. Acesso em: 9 set. 2024.
Curso do software de geometria dinâmica GeoGebra para professores de todos os estados brasileiros.

Página trezentos e vinte e nove

Orientações gerais

Conhecendo a coleção

Estrutura do Livro do estudante

Estrutura das Orientações específicas

O Ensino Médio

A Base Nacional Comum Curricular (BNCC)

As competências gerais

A área de Matemática e suas Tecnologias

Os Temas Contemporâneos Transversais (TCTs)

Fundamentos teóricos e metodológicos da coleção

O ensino de Matemática

Aprendizagem matemática

Metodologias ativas e algumas tendências em educação matemática

Orientações para avaliação

Alguns instrumentos de avaliação

O papel do professor de Matemática

Saberes docentes para o ensino de Matemática

Os estudantes no Ensino Médio

Dimensões física, social, emocional e cultural dos estudantes

Reflexos da violência no âmbito escolar e local

Culturas juvenis

Projeto de vida e mundo do trabalho

Gestão da sala de aula

Ambiente educacional

Leitura e argumentação nas aulas de Matemática

Estratégias de cálculo e o uso da calculadora

Relações com outras áreas do conhecimento e seus componentes curriculares

Referências bibliográficas comentadas

Indicações para o professor

Trabalhos

Instituições e grupos de estudo para a formação continuada do professor

Cursos e platafórmasplataformas

Cursos e platafórmas