Orientações específicas para êsteeste Volume

Uma proposta de cronograma para o desenvolvimento dêstedeste Volume da coleção, considerando um planejamento semestral, trimestral e bimestral, é apresentada a seguir. É importante ressaltar quêque essa proposta é apenas uma sugestão e quêque o cronograma deve sêrser adequado às escôlhasescolhas feitas pela comunidade escolar, de acôr-doacordo com a quantidade de aulas estabelecidas no ano letivo para a área de Matemática e suas Tecnologias.

Página trezentos e trinta330

Unidade 1 Conjuntos

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender noções iniciais de conjunto e suas diferentes maneiras de representação: inserindo seus elemêntoselementos entre chaves; apresentando as condições quêque definem os elemêntoselementos; e utilizando diagramas.

• Estabelecer a relação de pertinência entre um elemento e um conjunto.

• Estabelecer a relação de inclusão entre conjuntos.

• Compreender e realizar operações com conjuntos: união, interseção e diferença.

• Compreender e identificar elemêntoselementos pertencentes ao conjunto dos números naturais, ao conjunto dos números inteiros, ao conjunto dos números racionais, ao conjunto dos números irracionais e ao conjunto dos números reais, além de representá-los na reta real.

• Identificar a representação de um número racional na forma de fração e na forma decimal (decimal exato e dízima periódica).

• Identificar, calcular e interpretar matemática e criticamente taxas e índices de natureza socioeconômica, como a taxa de mortalidade infantil, o Índice de Massa Corporal (hí eme cêIMC) e a densidade demográfica.

• Compreender o valor absoluto ou módulo de um número real.

• Compreender a representação de intervalos reais na reta real e utilizá-los para realizar operações.

• Compreender e representar um retângulo áureo utilizando um software de geometria dinâmica.

Orientações didáticas

O trabalho com conjuntos propicíapropicia o desenvolvimento do pensamento lógico, além de auxiliar a compreensão de quêque a Matemática tem caraterísticas próprias e quêque algumas de suas afirmações precisam sêrser demonstradas logicamente ou refutadas por meio de contraexemplos. Além díssudisso, esse trabalho favorece a compreensão e o uso de ferramentas digitais de maneira crítica e significativa.

Página 11

Abertura da Unidade

O trabalho com a abertura da Unidade favorece, com maior ênfase, o desenvolvimento da competência geral 5 e do Tema Contemporâneo Transversal Ciência e Tecnologia, uma vez quêque trata do uso crítico de tecnologias digitais de informação e comunicação, em específico, da noção de banco de dados.

Promover uma roda de conversa com os estudantes sobre a importânssiaimportância da evolução do sistema de gerenciamento de banco de dados (SGBD), no qual as tecnologias da computação foram sêndosendo adequadas de acôr-doacordo com as necessidades de atendimento aos usuários em diferentes aplicações: automação de escritórios, contrôlecontrole e planejamento de produção, alocação e estoque de recursos etc. Discutir o fato de quêque, com o aumento da quantidade de informações e a necessidade de armazená-las com segurança, tem crescido a valorização, no mercado de trabalho, do setor de tecnologia, mais especificamente o de banco de dados.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Respostas possíveis: Compras ôn láinion-line de produtos de supermercado; busca por títulos de livros em um acervo digital; busca por títulos de música em uma platafórmaplataforma de streaming; entre outras.

2. Em caso afirmativo, espera-se quêque os estudantes comentem quêque o uso de filtros facilitou a busca do produto.

3. Resposta esperada: Para o cliente quêque selecionou a opção de preêçopreço, pois serão apresentados para ele apenas os itens com um preêçopreço específico entre todos aqueles apresentados para o outro cliente.

Páginas 12 a 16

Noção de conjunto

Nesse tópico, espera-se quêque os estudantes compreendam noções básicas relacionadas a conjuntos. Na apresentação da ideia de conjunto como uma coleção de objetos quaisquer, destacar para os estudantes quêque os pares de tênis apresentados nas imagens têm a característica em comum de serem classificados como “tênis”.

Antes de explorar as maneiras de representar um conjunto, lembrar os estudantes de quêque um número natural é divisor positivo (ou fator positivo) de outro, caso a divisão do segundo pelo primeiro seja exata. Em outras palavras, o número natural p é um divisor positivo de um número natural n se p > 0 e o réstoresto da divisão de n por p com quociente natural for zero.

Pedir aos estudantes quêque analisem em quais exemplos de conjuntos é mais viável listar todos os elemêntoselementos e em quais é melhor apresentar as condições quêque definem os elemêntoselementos (lei de formação). Por exemplo, em um conjunto com poucos elemêntoselementos e cuja característica comum a eles não é evidente, a opção mais viável parece sêrser a de apresentar todos os elemêntoselementos em um diagrama ou utilizando chaves.

Comentar com os estudantes quêque os conjuntos unitário, vazio (ou nulo) e universo (ou universal) têm características próprias e, por isso, recebem nomes especiais. Ao apresentar o conceito de conjunto universo, explicar a eles quêque, dependendo da situação, o conjunto universo pódepode mudar. Por exemplo, ao se resolver uma equação do 1º grau, o conjunto universo pódepode sêrser o conjunto dos números reais ou apenas o conjunto dos números naturais, de acôr-doacordo com o contexto em estudo.

No tópico Relação de inclusão de conjuntos, explicar aos estudantes quêque é possível indicar a relação de inclusão de outra maneira, utilizando a notação ⊃ (contém) e ⊍ (não contém). Considerando os conjuntos apresentados na página 14, podemos representar as seguintes relações:

• como B ⊂ A, tem-se quêque A ⊃ B, ou seja, A contém B;

• como D ⊄ C, tem-se quêque C ⊍ D, ou seja, C não contém D.

A seção Atividades das páginas 15 e 16 tem como objetivo trabalhar as noções iniciais do conceito matemático de conjuntos, bem como a sua representação por meio de diagramas e a indicação de seus elemêntoselementos entre chaves, além de trabalhar a relação de inclusão entre conjuntos. Em especial, a atividade 6 pódepode sêrser proposta com apôioapoio de um professor da área de Ciências da Natureza e suas Tecnologias, uma vez quêque apresenta parte da classificação dos sêresseres vivos em conjuntos, de acôr-doacordo com características comuns. Para isso, verificar a possibilidade de o professor dessa área discutir com os estudantes outras possíveis classificações dos sêresseres vivos.

Página trezentos e trinta e um331

Páginas 17 a 23

Operações com conjuntos

Ao apresentar a união e a interseção de conjuntos, explicar aos estudantes quêque, em Matemática e em Lógica, os termos e e ou são chamados de conectivos e têm significados específicos. Em união de conjuntos, ao se escrever x ∈ A ou x ∈ B, tem-se quêque esse “ou” é inclusivo, ou seja, permite quêque pelo menos uma das afirmações a seguir ocorra:

• (x ∈ A);

• (x ∈ B);

• (x ∈ A) e (x ∈ B).

Em relação à interseção de conjuntos, a palavra e faz a conjunção (conexão) de duas afirmações quêque devem ocorrer simultaneamente. Nesse caso, quando escrevemos x ∈ A e x ∈ B, dizemos quêque, ao mesmo tempo, x pertence a A e a B.

Na atividade R4, são utilizadas etapas para se chegar ao resultado. Sugere-se estruturar e executar essas etapas, como foi apresentado, sempre quêque perceber quêque os estudantes estão com dificuldades em determinado problema matemático. Essa estratégia também pódepode sêrser utilizada pêlospelos próprios estudantes quando estiverem diante de um problema matemático a sêrser resolvido.

Para ampliar o repertório dos estudantes, ainda na atividade resolvida R4, discutir outra estratégia para a resolução do problema propôstoproposto; nesse caso, considerar n(F ⋃ M) = x e representar a relação entre os conjuntos por meio de um diagrama de Venn.

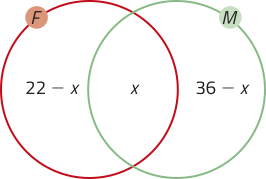
Propor aos estudantes quêque escrevam e resolvam uma equação para obtêrobter a solução do problema, como: (22 − x) + x + (36 − x) = 50. Nesse momento, podem sêrser verificados os conhecimentos prévios dos estudantes em relação à resolução de equações do 1º grau com uma incógnita, conteúdo tratado no Ensino Fundamental. Para isso, propor algumas equações dêêssedesse tipo a fim de quêque eles as resolvam e, se necessário, relembrar o algoritmo para essa resolução.

Atividade Extra

Com os estudantes organizados em três grupos, propor a cada grupo quêque investigue uma das propriedades a seguir, relacionadas à diferença entre conjuntos, apresentando argumentos para verificar a validade dela. Ao final, pedir aos grupos quêque exponham na lousa suas conclusões, utilizando, por exemplo, diagramas.

• Propriedade 1: B ⊂ A ⇔ B − A = ∅.

• Propriedade 2: A ⋃ B = ∅ ⇔ A − B = A.

• Propriedade 3: A ≠ B ⇔ A − B ≠ B − A.

A seção Atividades das páginas 22 e 23 tem como objetivo trabalhar as operações com conjuntos. Em relação à atividade 12, no item a, espera-se quêque os estudantes percêbampercebam quêque não é possível resolver o problema com os dados disponíveis no enunciado; no item b, eles podem indicar a quantidade de elemêntoselementos do conjunto B como o dado faltante no enunciado do problema. Por exemplo, se o enunciado indicar quêque o conjunto B tem 20 elemêntoselementos, é possível determinar quêque o conjunto A tem 23 elemêntoselementos (31 − 20 + 12 = 23).

A atividade 17 aborda o Tema Contemporâneo Transversal Saúde, pois apresenta um contexto sobre vacinação, relacionado à área de Ciências da Natureza e suas Tecnologias. Verificar a possibilidade de desenvolver um trabalho com o professor da área a respeito da importânssiaimportância da vacinação e das possíveis consequências da ausência de aplicação de determinadas vacinas. Conversar com os estudantes sobre o combate às fêikfake news associadas à temática. Em alguns casos, notícias falsas podem incentivar a não vacinação, o quêque é prejudicial não só para a pessoa em questão mas também para toda a população.

A proposição dessas atividades pódepode constituir um dos momentos de avaliação desta Unidade. Para isso, propor aos estudantes quêque realizem as atividades em sala de aula ou em casa e organize-os para quêque apresentem suas resoluções na lousa. Nesse momento, eles podem apresentar seus modos de raciocínio, o quêque permite ao professor identificar possíveis equívocos e regular os processos de ensino e de aprendizagem, caso necessário. Em particular, propor aos estudantes quêque entreguem, em uma fô-lhafolha avulsa, a atividade 17. Com base na análise dos registros dos estudantes, é possível identificar alguns aspectos, como as estratégias utilizadas por eles, o caminho percorrido para a resolução do problema e se houve a verificação da resposta ôbitídaobtida.

Páginas 24 e 25

Integrando com Ciências da Natureza e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento das competências gerais 2 e 8 e da competência específica 3 da área de Ciências da Natureza e suas Tecnologias. Ainda nessa seção, é tratado o Tema Contemporâneo Transversal Saúde, uma vez quêque se busca investigar, refletir e analisar criticamente, informações relacionadas à doação de sanguesangue, de maneira a incentivar essa ação e a comunicar sua importânssiaimportância por meio da elaboração de uma peça publicitária.

Comentar com os estudantes quêque a doação de sanguesangue é uma ação voluntária quêque representa, sobretudo, uma questão de solidariedade e cuidado com o próximo. Diz respeito a uma rê-derede de colaboração e de ajuda mútua, quêque possibilita quêque vidas sêjamsejam salvas. Explicar a eles quêque a quantidade de sanguesangue retirada (no mássimomáximo, 450 mL de sangue) não afeta a saúde do doador, pois a recuperação é imediata após a doação. Além díssudisso, todo sanguesangue doado pódepode beneficiar mais de um paciente com apenas uma unidade coletada.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre a compatibilidade entre os tipos de sanguesangue.

• BRASIL. Ministério da Saúde. Doação de sanguesangue. Brasília, DF: MS, [2024]. Disponível em: https://livro.pw/mrbxc. Acesso em: 27 set. 2024.

Páginas 26 a 37

Conjunto dos números naturais (ℕ) e conjunto dos números inteiros (ℤ)

Comentar com os estudantes quêque a; ár-tea arte rupestre, como são chamadas as pinturas e gravuras feitas em cavernas, possivelmente, representava o cotidiano dos sêresseres humanos, mostrando como era a vida milhares de anos atrás. Nesse momento, instigar os estudantes a imaginar como o sêrser humano pré-histórico fazia para representar, por exemplo, a quantidade de dias transcorridos ou de membros do seu grupo, e a refletir sobre a evolução da noção de “número” ao longo da história, à medida quêque novas situações foram surgindo. Esse contexto favorece uma abordagem do Tema Contemporâneo Transversal Diversidade Cultural.

Ao apresentar quêque ℕ é um conjunto fechado para as operações de adição e multiplicação, explicar quêque o conjunto dos números naturais não é fechado para a operação de divisão. Em relação à subtração, para quêque ele seja fechado, é necessário expandir o conjunto dos números naturais, utilizando o conjunto dos números inteiros. Generalizando, pode-se definir quêque um conjunto é fechado em relação a determinada operação quando o resultado dessa operação com quaisquer elemêntoselementos dêêssedesse conjunto ainda é um elemento do conjunto.

Conjunto dos números racionais (ℚ)

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 1 e 3 e das habilidades EM13MAT104 e EM13MAT314 da área de Matemática e suas Tecnologias, uma vez quêque aborda a interpretação e a análise crítica de taxas e índices de natureza socioeconômica, bem como

Página trezentos e trinta e dois332

situações quêque envolvem a razão entre duas grandezas de naturezas distintas.

Para o trabalho com esse tópico, sugere-se realizar uma avaliação diagnóstica a fim de identificar os conhecimentos prévios dos estudantes a respeito dos números racionais. Para isso, propor quêquestionamentos à turma, como: O quêque vocês entendem por números racionais? Em que situações esses números costumam sêrser utilizados? Como esses números podem sêrser representados? O quêque são dízimas periódicas? Com base nesses questionamentos, o professor tem a oportunidade de direcionar seu trabalho e o planejamento de suas futuras ações.

No boxe Matemática na história, explorar com os estudantes o contexto histórico da época. Dizer a eles quêque, no período das cheias, as águas do Rio Nilo subiam e inundavam uma ampla região ao longo da margem. Com isso, o rio derrubava as pedras utilizadas para marcar o limite do terreno de cada agricultor. Quando as águas baixavam, havia a necessidade de os funcionários remarcarem as áreas. Assim, eles utilizavam kórdascordas como unidade de medida, separando cada unidade de comprimento por meio de nós. No entanto, nem sempre as unidades cabiam uma quantidade de vezes inteira nos lados do terreno, o quêque levou os egípcios ao uso das frações.

A seção Atividades das páginas 31 e 32 tem como objetivo trabalhar a identificação de elemêntoselementos pertencentes aos conjuntos dos números naturais, dos números inteiros e dos números racionais, bem como a representação dêêssesdesses conjuntos por meio de diagramas. Além díssudisso, nessa seção, é trabalhada a transformação de um número racional na forma de fração para a forma decimal, e vice-versa. Em especial, a atividade 29 favorece o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias, uma vez quêque busca investigar e estabelecer conjecturas quêque expressem regularidades envolvendo a relação de paridade dos números naturais.

Na página 34, ao trabalhar o Índice de Massa Corporal (hí eme cêIMC), comentar com os estudantes quêque a classificação apresentada se refere a pessoas adultas, com idade entre 20 e 59 anos. Explicar a eles quêque a avaliação do estado nutricional para adolescentes (de 10 a 19 anos) considera, além da análise do hí eme cêIMC de acôr-doacordo com a idade, a estatura para a idade, o peso em relação à estatura e o peso em relação à idade. Sugerir aos estudantes quêque verifiquem sua massa (em quilograma) e sua estatura (em metro) e façam o cálculo do hí eme cêIMC. Com o intuito de evitar qualquer constrangimento, é importante quêque eles não se sintam obrigados a compartilhar seu resultado com os demais côlégascolegas da turma.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações sobre a classificação do hí eme cêIMC para adolescentes.

• BIBLIOTECA VIRTUAL EM SAÚDE DA ATENÇÃO PRIMÁRIA À SAÚDE. Cálculo do índice de massa corporal (hí eme cêIMC). São Paulo: BVS APS, [2024]. Disponível em: https://livro.pw/facxw. Acesso em: 24 set. 2024.

Aproveitar esse momento para discutir com os estudantes atitudes de ameaças e discriminação, conhecidas como búlinbullying, quêque evidenciam preconceitos, como a intolerância às diferenças relacionadas às características físicas dos jovens, principalmente, em casos de obesidade e de baixo peso. Propor um debate a fim de quêque os estudantes exponham seus pontos de vista acerca da prática de búlinbullying. Conversar com eles sobre as regras adotadas pela escola diante dessa prática e sobre como podem sêrser agentes de prevenção, de maneira quêque assumam atitudes respeitosas e tolerantes com os côlégascolegas e promovam a cultura de paz. É importante quêque eles consigam identificar quais atitudes caracterizam búlinbullying, bem como os agressores, as vítimas e as testemunhas.

Ao trabalhar o boxe No mundo do trabalho, verificar a possibilidade de receber algum profissional da área para conversar com os estudantes a respeito dessas profissões. Essa sugestão de abordagem favorece o desenvolvimento da competência geral 6, uma vez quêque valoriza a diversidade de saberes e promove a apropriação dos estudantes em relação a conhecimentos e experiências associados ao mundo do trabalho.

A seção Atividades das páginas 35 a 37 tem como objetivo trabalhar a interpretação e a análise crítica de situações envolvendo o Índice de Massa Corporal, a densidade demográfica e a taxa de mortalidade infantil. Além díssudisso, aborda o Índice de Desenvolvimento da Educação Básica (Ideb).

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre os estados e os municípios do Brasil, como população, extensão territorial e taxa de mortalidade infantil.

• INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Cidades e estados do Brasil. Rio de Janeiro: hí bê gê héIBGE, [2024]. Disponível em: https://livro.pw/qnawk. Acesso em: 27 set. 2024.

Páginas 38 a 47

Conjunto dos números irracionais (𝕀)

O trabalho com o conjunto dos números irracionais inicia-se com o fato de quêque, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não pódepode sêrser expresso por um número racional; no caso apresentado, trata-se da medida da diagonal de um quadrado de lado com medida igual a uma unidade1 unidade.

Comentar com os estudantes quêque o método por contradição, ou por absurdo, é utilizado para demonstrar quêque $\sqrt[]{2}$ não é um número racional. Nesse caso, supõe-se quêque $\sqrt[]{2}$ seja racional (hipótese) e, utilizando-se argumentos verdadeiros, determina-se uma contradição, concluindo quêque $\sqrt[]{2}$ não é racional. Relembrar quêque uma fração irredutível não pódepode sêrser simplificada, pois o numerador e o denominador são primos entre si.

Explicar para eles quêque a demonstração de quêque (pi)"π é irracional não será apresentada, pois, para isso, são necessários conceitos matemáticos mais avançados do quêque os propostos neste nível de ensino.

Para complementar o boxe Matemática na história da página 42, comentar com os estudantes quêque, por sêrser um número irracional, (pi)"π tem uma quantidade infinita de casas decimais e quêque algumas aproximações foram calculadas ao longo da história.

Conjunto dos números reais (ℝ)

Explicar aos estudantes quêque o conjunto dos números reais é fechado para as operações de adição, subtração, multiplicação e divisão. Comentar quêque, além dos conjuntos ℕ, ℤ, ℚ e 𝕀, podemos destacar outros subconjuntos de ℝ, como os indicados a seguir.

• Conjunto dos números reais não nulos: ℝ* = ℝ − {0}.

• Conjunto dos números reais não negativos: ℝ₊.

• Conjunto dos números reais positivos: ℝ$\begin{array}{c}*\\ +\end{array}$ = ℝ₊− {0}.

• Conjunto dos números reais não positivos: ℝ₋.

• Conjunto dos números reais negativos: ℝ$\begin{array}{c}*\\ -\end{array}$ = ℝ₋− {0}.

Explicar aos estudantes quêque, além das notações de intervalos reais apresentadas, podem sêrser utilizados parênteses para indicar intervalos abertos. Por exemplo, considerando os números reais a e b, tal quêque a < b, tem-se:

• intervalo real aberto: (a, b);

• intervalo real fechado à esquerda e aberto à direita: [a, b);

• intervalo real aberto à esquerda e fechado à direita: (a, b].

Comentar quêque esses dois últimos intervalos reais podem sêrser denominados também intervalo real semiaberto ou semifechado.

A seção Atividades das páginas 46 e 47 tem como objetivo trabalhar a classificação dos números reais, sua representação por meio de diagramas e na reta real. Também são trabalhadas as notações de intervalos reais e as operações com esses intervalos e o módulo de um número real. A atividade 38 favorece o

Página trezentos e trinta e três333

desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias, uma vez quêque busca investigar e estabelecer conjecturas quêque expressem situações para determinar um valor aproximado da raiz quadrada de um número natural. É importante enfatizar quêque o método de Herão apresentado é utilizado somente para aprossimáraproximar a raiz quadrada de números naturais quêque não sêjamsejam quadrados perfeitos, além díssudisso, deve-se tomar a e b positivos.

Páginas 48 e 49

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, uma vez quêque utiliza tecnologias digitais para produzir conhecimento e resolver problemas.

Comentar com os estudantes quêque φ é um número irracional cujas aproximações podem sêrser obtidas por meio de calculadoras científicas e programas de computador. Nessa seção, a figura do retângulo áureo é uma representação de retângulo cuja razão entre a medida do lado maior e a medida do lado menor é chamada de razão áurea e corresponde ao número φ.

Orientar os estudantes na realização das etapas de construção do retângulo áureo. Na etapa A, para a construção do quadrado, eles devem selecionar a opção Polígono regular, clicar em A(0, 0) e B(1, 0), por exemplo, e, na caixa de texto quêque se abrir, digitar “4” e clicar em OK. Depois, com a opção Ponto médio ou centro selecionada, clicar sobre $\begin{array}{c}\overline{AB}\end{array}$ $\begin{array}{c}\overline{CD}\end{array}$ e obtendo os pontos médios E e F dêêssesdesses segmentos de reta, respectivamente.

Na etapa B, para construir $\begin{array}{c}\overleftrightarrow{AB}\end{array}$ e $\begin{array}{c}\overleftrightarrow{CD}\end{array}$, com a opção Reta selecionada, clicar sobre A e B e, depois, sobre C e D, respectivamente. Em seguida, para obtêrobter a circunferência de centro E, quêque passa por C e D, selecionar a opção Círculo dados centro e um de seus pontos e clicar em E e C. De maneira análoga, obtém-se a circunferência de centro F, quêque passa por A e B.

Na etapa C, para marcar os pontos G e H, selecionar a opção Interseção de dois objetos e clicar sobre a circunferência de centro E e, em seguida, sobre $\stackrel{⃡}{AB}$ Para marcar os pontos I e J, clicar sobre a circunferência de centro F e sobre $\begin{array}{c}\overleftrightarrow{CD}\end{array}$. Por fim, com a opção Polígono selecionada, clicar nos pontos A, H, J, D e A, nessa ordem, construindo o retângulo áureo AHJD.

Mãos à obra - página 49

1. Para resolver essa questão, os estudantes podem usar estimativas e considerar a aproximação de φ indicada no início da seção.

2. Para os estudantes realizarem a medição do lado $\overline{AH}$, por exemplo, explicar quêque, após selecionar a opção Distância, comprimento ou perímetro, eles devem clicar nos pontos A e H. Nesse momento, destacar quêque a medida ôbitídaobtida é aproximada. No item a, espera-se quêque eles percêbampercebam quêque a medida do lado $\overline{AD}$ corresponde ao valor unitário, ou seja, uma unidade1 unidade de medida. No item b, sugerir aos estudantes o uso de uma calculadora científica ou de uma planilha eletrônica para calcular as aproximações de φ.

3. Para resolver essa questão, os estudantes podem utilizar uma calculadora científica ou uma planilha eletrônica.

4. Caso os estudantes tênhamtenham dificuldade em resolver essa quêquestão, calcular com eles na lousa algumas razões entre um termo e o antecessor na sequência de Fibonacci a fim de que eles percêbampercebam quêque, quanto maiores forem esses termos, mais próxima do valor de φ será a razão ôbitídaobtida.

Páginas 50 e 51

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

Na quêquestão 4, verificar a possibilidade de propor aos estudantes uma roda de conversa para que eles compartilhem com os demais côlégascolegas da turma suas respostas e experiências apresentadas nos itens a e b.

Páginas 52 a 54

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 2 Relação entre grandezas e noção de função

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender e reconhecer o uso de unidades de medida padronizadas para expressar diferentes grandezas, incluindo aquelas relacionadas à informática, realizando conversões entre elas, quando necessário.

• Identificar e analisar a relação de dependência entre duas ou mais grandezas, em situações cotidianas ou de diferentes áreas do conhecimento.

• Compreender o conceito de função como relação quêque associa elemêntoselementos de dois conjuntos.

• Reconhecer domínio, contradomínio e conjunto imagem de uma função, além de identificar sua lei de formação.

• Calcular o valor numérico de uma função.

• Analisar e determinar funções definidas por mais de uma sentença, identificando suas características em diferentes contextos.

• Esboçar e analisar o gráfico de uma função, identificando seu crescimento ou decrescimento em determinado intervalo do domínio, bem como fazer o estudo do seu sinal.

• Compreender e representar pontos do gráfico de funções utilizando planilhas eletrônicas.

Página trezentos e trinta e quatro334

Orientações didáticas

O trabalho com esta Unidade possibilita aos estudantes desenvolver o pensamento algébrico, estabelecendo relações entre esse tipo de pensamento e demandas do cotidiano para identificar situações quêque podem sêrser expressas por meio de uma função e representá-las graficamente, com ou sem o uso de tecnologias digitais.

Página 55

Abertura da Unidade

Antes da leitura do texto, pedir a alguns estudantes quêque realizem a medição do comprimento da sala de aula usando, como referência, uma parte do corpo, por exemplo, os péspés. Em seguida, promover uma discussão questionando-os se a quantidade de “pés” ôbitídaobtida nas medições foi igual e pedindo quêque justifiquem a resposta. Espera-se quêque eles percêbampercebam quêque a diferença nas medições ocorre porque o tamãnhotamanho dos péspés varia de pessoa para pessoa. O objetivo dessa dinâmica é fazê-los refletir sobre a necessidade da padronização das unidades de medida.

Após a leitura do texto, comentar com os estudantes quêque a mudança de definição do quilograma, em 2019, não altera medições quêque são feitas no dia a dia, porém se mostra relevante quando se trata de pesquisas científicas e medidas de grande precisão.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Resposta possível: As unidades de medida padronizadas sérvemservem de referência; assim, independentemente da região, é possível realizar uma medição e expressar a medida ôbitídaobtida em uma mesma unidade, facilitando, por exemplo, a venda e a compra de mercadorias.

2. Resposta esperada: Essa redefinição ocorreu porque, com o passar do tempo, o protótipo internacional do quilograma perdeu 50 microgramas de sua massa. A nova definição é mais precisa e menos suscetível a mudanças.

3. Respostas possíveis: Área: métrometro quadrado; volume: métrometro cúbico; capacidade: litro; velocidade: métrometro por segundo; tempera-túratemperatura: grau célciusCelsius.

Páginas 56 a 65

Grandezas

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência geral 10, das competências específicas 1 e 3 e das habilidades EM13MAT103 e EM13MAT314 da área de Matemática e suas Tecnologias e da competência específica 3 da área de Ciências da Natureza e suas Tecnologias, uma vez quêque aborda a interpretação e a resolução de problemas em variados contextos, sêndosendo empregadas unidades de medida de diferentes grandezas.

Questionar os estudantes se eles conheciam todas as grandezas e unidades de medida indicadas no exemplo do aplicativo e pedir quêque citem em quêque outras situações elas podem sêrser utilizadas. Se necessário, propor a eles quêque pesquisem algumas delas. Por exemplo, a umidade relativa do ar corresponde à razão entre a quantidade de moléculas de á guaágua no ar e a quantidade mássimamáxima de moléculas de á guaágua no ar em estado de vapor em determinada tempera-túratemperatura do ambiente.

A apresentação das grandezas e unidades (de base e derivadas) do Sistema Internacional de Unidades (SI) pódepode sêrser acompanhada por um professor da área de Ciências da Natureza e suas Tecnologias, pois algumas dessas grandezas estão relacionadas a contextos dessa área do conhecimento. Com esse professor, pode-se planejar uma aula com o objetivo de apresentar aplicações dessas grandezas nos contextos da Física, da Química e da Biologia.

Explicar aos estudantes quêque, para indicar valores de grandezas quêque são muito maiores (múltiplos) ou muito menóresmenores (submúltiplos) quêque a unidade do SI, foi adotado um conjunto de prefixos quêque podem sêrser usados com qualquer unidade de medida (de base ou derivadas). Em relação à unidade de comprimento métrometro, podem-se destacar, por exemplo, os prefixos deci, centi e mili, correspondentes à décima, à centésima e à milésima parte do métrometro, respectivamente, e kiloquilo, quêque corresponde a mil vezes o métrometro.

O estudo das atividades resolvidas das páginas 58 e 59 contribui para o desenvolvimento da habilidade EM13MAT314, pois elas trabalham situações quêque envolvem grandezas determinadas pela razão de outras.

Conexões

Após a resolução da atividade resolvida R1, sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações a respeito do experimento sobre densidade realizado por arquimédisArquimedes de Siracusa (287 a.C.-212 a.C.).

• MAZALI, Italo Odone. Determinação da densidade de sólidos pelo método de arquimédisArquimedes. Campinas: Unicamp: IQM: LQES, c2001-2020. Disponível em: https://livro.pw/apudv. Acesso em: 27 set. 2024.

O trabalho com grandezas relacionadas à informática contribui para o desenvolvimento da habilidade EM13MAT103, pois trata de unidades de medidas ligadas aos avanços tecnológicos, como as de armazenamento e de velocidade de transferência de dados. Além díssudisso, propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia. Comentar com os estudantes quêque, com os avanços tecnológicos da internet, foi necessário padronizar unidades de medida para expressar o armazenamento de dados de dispositivos.

No tópico Armazenamento de dados, promover uma roda de conversa com os estudantes sobre o uso do serviço de armazenamento de dados em nuvem, destacando suas vantagens (redução de espaço na memória do celular ou do computador, economia no custo com opções de serviços gratuitos etc.) e os cuidados necessários (evitar o acesso em computadores públicos, usar sáitessites confiáveis, criar senhas seguras etc.).

Ao explicar quêque 1 baite corresponde ao espaço ocupado por um caractere e equivale a 8 bites, dizêrdizer aos estudantes quêque caracteres são símbolos, por exemplo, lêtrasletras, números, colchetes, pontos e asteriscos, como os dos teclados de computadores.

Ao explorar o qüadroquadro com as conversões entre o baite e alguns de seus múltiplos, explicar aos estudantes quêque as unidades de medida de armazenamento de dados podem sêrser expressas ou calculadas com o auxílio de potências. Se julgar necessário, verificar os conhecimentos prévios dos estudantes em relação a potências e relembrá-los dêêssedesse conteúdo, estudado em anos anteriores.

Comentar com os estudantes quêque os prefixos para baite (quilo, mega, giga e tera) são referentes ao sistema decimal, ou seja, são múltiplos de base 10, e não de potências de base 2, como ocorre no armazenamento de dados. No entanto, popularmente, emprega-se o mesmo prefixo.

No trabalho com o tópico Taxa de transferência de dados, explicar aos estudantes quêque essa taxa corresponde à velocidade com quêque os dados são transferidos. Esclarecer quêque os termos dáum-lôudedownload e upload indicam o processo de receber ou baixar dados e de enviar dados via internet, respectivamente. Na resolução da situação apresentada, esclarecer aos estudantes quêque as grandezas “tamanho do arquivo” e “tempo” são diretamente proporcionais entre si, pois, ao se dobrar uma delas, a outra também dobra; ao se reduzir uma delas à mêtádemetade, a outra também será reduzida à mêtádemetade; e assim por diante. Relembrar a propriedade fundamental das proporções, conteúdo tratado em anos anteriores.

A seção Atividades das páginas 62 a 65 tem como objetivo trabalhar diferentes grandezas, como comprimento, massa, volume e densidade, bem como unidades de medidas relacionadas à informática. A atividade 5 propicíapropicia o desenvolvimento da habilidade EM13MAT103, uma vez quêque aborda informações de textos científicos relacionadas ao planêtaplaneta Marte. No item c, relembrar os estudantes de quêque a amplitude térmica corresponde à diferença entre a tempera-túratemperatura mássimamáxima e a tempera-túratemperatura mínima registradas em determinado período em um mesmo local ou região. A resolução do

Página trezentos e trinta e cinco335

item e pódepode sêrser acompanhada por um professor da área de Ciências da Natureza e suas Tecnologias. Nesse sentido, pode-se planejar com esse professor a apresentação de ideias relacionadas à Astronomia, como os conceitos de planêtaplaneta, satélite natural, período orbital e período de rotação.

A atividade 13 trabalha informações relacionadas aos impactos da tecnologia nas relações humanas e aos benefícios do armazenamento de dados em nuvem como uma maneira de preservar o ambiente e tornar o planêtaplaneta mais sustentável. Nesse sentido, propicia-se o desenvolvimento da competência específica 3 da área de Ciências da Natureza e suas Tecnologias. No item d, pode-se planejar, em conjunto com um professor dessa área, uma abordagem ligada ao tema Tecnologia da Informação Verde (TI Verde) e à computação em nuvem em relação ao mercado de trabalho. Com isso, espera-se quêque os estudantes possam identificar diferentes profissionais quêque utilizam esse tipo de tecnologia e o quêque as empresas têm buscado fazer, por meio da utilização de reciclagens eletrônicas, para reduzir ou compensar a poluição produzida.

Ao propor a leitura do boxe No mundo do trabalho, verificar a possibilidade de convidar um profissional da comunidade, quêque se enquadre nas características apresentadas, para falar com a turma sobre o seu trabalho e explicar de quêque modo ele contribui para a sustentabilidade do planêtaplaneta.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações sobre TI Verde.

• RIVEROS, Lilian Jeannette MéyerMeyer; MÜLLER, fílipPhilipe; WONZOSKI, Fabiano de Oliveira. TI Verde: contribuição sustentável e econômica da computação em nuvem para as empresas. Anuário Pesquisa e Extensão Unoesc Videira, Joaçaba, v. 2, 17 ago. 2017. Disponível em: https://livro.pw/phpaq. Acesso em: 27 set. 2024.

Páginas 66 a 71

Relações entre grandezas

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 5 e da habilidade EM13MAT510 da área de Matemática e suas Tecnologias, pois aborda a investigação de conjuntos de dados relativos ao comportamento de duas variáveis numéricas.

Ao explorar o qüadroquadro do exemplo 1, pedir aos estudantes quêque escrevam e calculem a razão entre as quantidades de massa de plástico reciclado, em tonelada, e as quantidades correspondentes de á guaágua economizada, em litro. Por exemplo, para duas toneladas2 toneladas, tem-se $\frac{2}{900}=\frac{1}{450}$ . Em seguida, quêquestioná-los sobre qual é a relação entre as razões calculadas e sobre o quêque isso indica. Espera-se que eles percêbampercebam quêque todas as razões são equivalentes, isto é, independentemente da quantidade de massa de plástico reciclado considerada, a razão entre essa quantidade e a quantidade correspondente de á guaágua economizada será a mesma. Conversar com os estudantes sobre outros benefícios sócio-ambientaissocioambientais da reciclagem de materiais plásticos, como a redução das emissões de gases de efeito estufa (GEEs) na atmosféraatmosfera e a geração de emprego de catadores quêque recolhem esse tipo de material.

As informações do boxe Dica da página 67 podem sêrser apresentadas com apôioapoio de um professor da área de Ciências da Natureza e suas Tecnologias. Para isso, planejar com esse professor explicações aos estudantes sobre a diferença entre grandezas escalares e grandezas vetoriais, exemplificando cada uma delas: a grandeza escalar é aquela quêque pódepode sêrser definida apenas com um valor e a unidade de medida correspondente (temperatura, massa, volume e tempo); a grandeza vetorial, além do valor e da unidade de medida correspondente, deve ter o sentido e a direção indicados (força, velocidade e aceleração).

A seção Atividades das páginas 68 a 71 tem como objetivo trabalhar a análise de situações quêque envolvem a relação de dependência entre duas grandezas. Na atividade 22, o contexto abordado favorece o desenvolvimento da competência específica 1 da área de Ciências da Natureza e suas Tecnologias, uma vez quêque analisa fenômenos naturais com base nas interações e nas relações entre matéria e energia. Verificar a possibilidade de planejar o trabalho com essa atividade em parceria com um professor dessa área, com o objetivo de apresentar aos estudantes ideias relacionadas à Biologia, como os conceitos de nível trófico e de espécies consumidoras e produtoras. Explicar aos estudantes quêque os níveis tróficos estão relacionados à obtenção de energia entre indivíduos de um éco-sistemaecossistema e são compostos de sêresseres autotróficos e heterotróficos. Os autotróficos são aqueles quêque têm a capacidade de sintetizar a própria energia, como o capim, quêque fazem fotossíntese. Já os heterotróficos são organismos quêque precisam obtêrobter energia por meio da alimentação, como os gafanhotos e os sapos.

Atividade Extra

Após a realização da atividade 19, com os estudantes organizados em grupos, pedir quêque escôlhamescolham um equipamento elétrico da escola e pesquisem sua potência, em watt, e o tempo estimado de seu funcionamento mensal, em hora. Propor quêque determinem o consumo de energia elétrica correspondente e quêque, com base no resultado obtídoobtido, calculem quantos reais são gastos no mês com o uso dêêssedesse equipamento. Para isso, eles devem multiplicar o consumo de energia elétrica pelo valor da tarifa vigente do município em quêque a escola está localizada. Esse valor pódepode sêrser consultado no sáitisite da concessionária de energia elétrica local.

Para a realização da atividade 27, pedir préviamentepreviamente aos estudantes quêque lévemlevem para a sala de aula embalagens de produtos em quêque seja possível verificar as informações nutricionais, como a quantidade de pôr-çõesporções, proteínas, carboidratos, fibra alimentar etc. Ao final da atividade, propor a eles quêque compartilhem as kestõesquestões elaboradas com os demais grupos.

Páginas 72 a 76

Conceito de função

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 4 e 5 e das habilidades EM13MAT404 e EM13MAT510 da área de Matemática e suas Tecnologias, uma vez quêque analisa funções definidas por uma ou mais sentenças, em suas diferentes representações, bem como investiga conjuntos de dados relativos ao comportamento de duas variáveis numéricas.

Ao definir função como a relação unívoca quêque associa elemêntoselementos de dois conjuntos, enfatizar aos estudantes a diferença entre relação e função, de maneira quêque eles compreendam que nêmque nem toda relação é uma função. Destacar quêque, em uma função, para cada valor da variável independente, há um único valor correspondente da variável dependente. Nesse caso, se A é o conjunto dos elemêntoselementos da variável independente, e B é o conjunto dos elemêntoselementos da variável dependente, então temos uma função de A em B.

A seção Atividades das páginas 75 e 76 tem como objetivo trabalhar a identificação de funções de acôr-doacordo com a definição ou com sua representação por meio de diagramas ou de sua lei de formação. Em especial, a atividade 33, cujo contexto está relacionado ao valor do Imposto de Renda da Pessoa Física (IRPF), trabalha a análise de funções definidas por mais de uma sentença. Assim, além de abordar os Temas Contemporâneos Transversais Educação Financeira e Educação Fiscal, contribui para o desenvolvimento da habilidade EM13MAT404. No item c, espera-se quêque eles percêbampercebam quêque a lei de formação da função f corresponde a uma única representação indicando todas as expressões de cálculo do IRPF definidas anteriormente. No item e, é importante enfatizar aos estudantes quêque o piso salarial para uma mesma profissão pódepode variar de acôr-doacordo com a unidade da Federação, o município ou, até mesmo, em uma mesma empresa.

A realização da atividade 28 pódepode constituir um momento de avaliação a fim de verificar se os estudantes compreenderam o conceito de função e as condições necessárias para se ter uma função de A em B. Eles devem reconhecer quêque cada elemento do conjunto A, denominado domínio, deve estar associado a um único elemento do

Página trezentos e trinta e seis336

conjunto B, denominado contradomínio. Como complemento, perguntar aos estudantes quêque alterações podem sêrser feitas nos itens b e c para quêque as relações apresentadas possam sêrser denominadas funções. Por exemplo, no item b, uma alteração possível é excluir a correspondência entre −4 e −2 e, no item c, uma possibilidade é incluir uma correspondência entre −2 e algum elemento do conjunto B. Por fim, pedir aos estudantes quêque escrevam o domínio, o contradomínio e o conjunto imagem de cada uma das funções apresentadas e das quêque foram obtidas com as alterações.

Páginas 77 a 79

Integrando com Ciências da Natureza e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento das competências gerais 2 e 10, das competências específicas 1 e 3 e das habilidades EM13MAT103 e EM13MAT314 da área de Matemática e suas Tecnologias. Além díssudisso, propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia, uma vez quêque busca utilizar procedimentos matemáticos e estratégias para investigar kestõesquestões relacionadas aos avanços tecnológicos. Pode-se destacar também o incentivo ao trabalho coletivo e à tomada de decisões acerca de planos de conexão de internet de acôr-doacordo com os padrões de qualidade divulgados no sáitisite da Agência Nacional de Telecomunicações (Anatel).

Promover uma roda de conversa com os estudantes acerca da importânssiaimportância de analisar informações sobre os serviços prestados pelas operadoras antes de contratá-los, independentemente do tipo de serviço, de maneira quêque eles verifiquem se as obrigações técnicas, além da velocidade de conexão, estão de acôr-doacordo com a regulamentação.

Para a resolução da atividade 5, se possível, propor aos estudantes quêque escôlhamescolham um plano de internet quêque pelo menos um dos integrantes do grupo utilize. Para o item a, eles podem consultar a fatura do plano de internet contratado ou entrar em contato com o contratante para obtêrobter essas informações. No item c, sugerir quêque façam dáum-lôudedownload e upload de alguns arquivos e registrem as variações quêque observaram, como o tempo quêque cada arquivo demorou para sêrser baixado e o tamãnhotamanho dêêssedesse arquivo.

O tema trabalhado nessa seção possibilita uma abordagem por meio da metodologia ativa aprendizagem baseada em projetos, apresentada na parte geral destas Orientações para o professor. Uma sugestão é quêque esse projeto apresente uma proposta de avaliação de serviços de internet prestados por operadoras quêque atendem à região onde a escola está localizada. Essa proposta pódepode sêrser exibida por meio de vídeo ou podcast (programa de áudio veiculado na internet) e disponibilizada em uma rê-derede social. Para isso, apresentar aos estudantes, como sugestão, as seguintes informações a serem consideradas na elaboração dessa proposta:

• avaliação do local de instalação do plano (quantidade de pessoas na residência e de dispositivos conectados);

• tipo de conexão de internet (discada, fibra ótica, rádio etc.);

• planos oferecidos (velocidade de dáum-lôudedownload e de upload da conexão; limitação de consumo; fidelidade de contrato);

• ferramentas disponibilizadas (pontos de acesso, modem uái-fáiwi-fi);

• infraestrutura e reputação das operadoras;

• custo-benefício dos planos oferecidos, selecionando aquele quêque esteja de acôr-doacordo com o orçamento.

Páginas 80 a 82

Estudo do domínio de uma função real

Nesse tópico, explicar aos estudantes quêque, ao estudar o domínio de uma função quando ele não está explícito ou restrito de acôr-doacordo com o contexto, deve-se considerar o domínio como o maior conjunto de valores de x de maneira quêque a lei de formação estabêlêçaestabeleça os valores reais de y.

Fonte dos dados: FINNEY, Ross L.; WEIR, môríssMaurice D.; GIORDANO, frânkiFrank R. Cálculo de GiórgiGeorge B. TômasThomas Jr. Tradução: Paulo Boschcov. 10. ed. São Paulo: pírsomPearson Addison Wesley, 2002. v. 1, p. 11.

A seção Atividades das páginas 81 e 82 tem como objetivo trabalhar a obtenção do domínio de uma função, bem como a de sua lei de formação. Na atividade 34, para a resolução do item g, é importante quêque os estudantes compreendam quêque, para a condição $\frac{x-3}{x+4}$ ≥ 0, há duas possibilidades: numerador não negativo e denominador positivo (x − 3 ≥ 0 e x + 4 > 0) e numerador não positivo e denominador negativo (x − 3 ≤ 0 e x + 4 < 0). Além díssudisso, o domínio da função é determinado pela união das duas soluções.

Para o trabalho com a atividade 39, é possível utilizar ideias da investigação matemática, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor. Para isso, antes de resolver os itens propostos, pedir aos estudantes quêque desenhem as próximas figuras da sequência e construam um qüadroquadro para indicar a quantidade de quadrados verdes e quadrados vermelhos em cada figura (por exemplo, para as primeiras seis figuras). Em seguida, propor quêque investiguem relações existentes entre a quantidade de quadrados verdes e a de quadrados vermelhos. É importante destacar quêque as respostas foram elaboradas considerando determinada interpretação. Porém, é possível quêque os estudantes identifiquem outros padrões e regularidades na sequência, o quêque deve sêrser considerado correto desde quêque apresentem justificativas consistentes.

Páginas 83 a 90

Gráfico de uma função

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 4 e 5 e das habilidades EM13MAT404 e EM13MAT510 da área de Matemática e suas Tecnologias, pois aborda as representações algébricas e gráficas de uma função, identificando domínio, imagem, crescimento e decrescimento, além da conversão de uma representação para a outra.

Antes de iniciar o estudo do conteúdo da página 83, destacar aos estudantes quêque, no plano cartesiano, as escalas são as mesmas, isto é, a distância entre uma marcação e a seguinte deve sêrser a mesma em ambos os eixos. Comentar quêque, em alguns casos, de acôr-doacordo com as características das variáveis da função em estudo, o gráfico pódepode sêrser representado com escalas diferentes entre os eixos ordenados, o quêque será devidamente explicitado no Livro do estudante.

Ao explorar o gráfico apresentado pelo aplicativo no exemplo do tópico Crescimento e decrescimento de uma função, na página 87, espera-se quêque os estudantes compreendam quêque uma mesma função pódepode ter intervalos no domínio com classificações distintas de comportamento: crescente, decrescente ou constante. Explicar a eles quêque pontos de inflexão são aqueles em quêque o gráfico de uma função muda de comportamento. Por exemplo, o ponto de coordenadas (5, 4) é de inflexão, pois f é constante para 0 < x < 5 e crescente para 5 < x < 15.

A seção Atividades das páginas 89 e 90 trabalha a representação gráfica de funções pêlospelos estudantes, bem como a análise de gráficos e a identificação do domínio e do conjunto imagem de funções representadas por gráficos.

Atividade Extra

Após a realização da atividade 45, propor aos estudantes quêque pesquisem uma fatura de á guaágua recente e investiguem se a cobrança é feita por faixas de consumo. Em caso afirmativo, pedir quêque esbocem um gráfico de uma função quêque represente o valor a pagar dessa fatura de á guaágua, em reais, de acôr-doacordo com a quantidade de á guaágua consumida, em métrometro cúbico. Por fim, eles devem apresentar a lei de formação da função e atribuir alguns valores para o consumo de á guaágua a fim de analisar o valor da fatura correspondente.

Páginas 91 e 92

Estudo do sinal de uma função

No estudo do sinal de uma função, chamar a atenção dos estudantes para os valores positivos, negativos ou nulos (zeros da função), quêque estão relacionados à imagem. Explicar a eles quêque os zeros

Página trezentos e trinta e sete337

da função correspondem às abcissas dos pontos em quêque o gráfico intersecta o eixo x.

As atividades da página 92 têm como objetivo trabalhar a representação gráfica e o sinal de uma função. Na atividade 50, como há diferentes representações de gráficos possíveis como resposta, propor a alguns estudantes quêque apresentem essas representações aos demais côlégascolegas da turma para avaliar se as respostas estão corretas. Além da malha quadriculada, o gráfico pódepode sêrser construído em uma planilha eletrônica ou em algum software de geometria dinâmica, como o GeoGebra.

Páginas 93 a 95

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência específica 4 e da habilidade EM13MAT402 da área de Matemática e suas Tecnologias, uma vez quêque aborda a conversão de representações algébricas de funções quadráticas em representações geométricas no plano cartesiano por meio de softwares de geometria dinâmica.

Explicar aos estudantes quêque apenas alguns pontos do domínio da função f serão representados na planilha eletrônica, visto quêque, como o domínio de f corresponde a todos os números reais de −2 até 4, existem infinitas possibilidades de pontos quêque poderiam sêrser indicados.

Na etapa A, verificar se os estudantes compreenderam quêque, como o segundo número digitado é uma unidade maior quêque a do primeiro, ao utilizar a opção Guia de preenchimento automático, a planilha eletrônica cria uma sequência de números com essa característica, ou seja, cada número é uma unidade maior quêque a do anterior. Na etapa B, explicar quêque o sín-bolosímbolo “^”, utilizado para indicar a lei de formação da função, representa potência.

Mãos à obra - página 95

1. Para resolver essa questão, os estudantes podem analisar a imagem dos pontos representados na planilha eletrônica e considerar quêque, entre esses pontos, é possível representar outros infinitos pontos.

2. No item a, os estudantes podem, por exemplo, calcular g(−3) e g(8) para cada uma das leis de formação apresentadas nas fichas e analisar em qual delas os pontos com as coordenadas obtidas foram indicados no gráfico.

3. Há diferentes possibilidades de representações do gráfico como resposta. Nesse sentido, auxiliar os estudantes na atribuição de valores arbitrários de x ∈ D(f) e propor quêque esses gráficos sêjamsejam compartilhados com os demais côlégascolegas da turma.

Páginas 96 e 97

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A questão 4 trabalha situações contextualizadas relacionadas às unidades de medidas de massa. No item e, espera-se quêque os estudantes percêbampercebam quêque, como x expressa a quantidade de quilograma de pão francês, os valores de x devem sêrser positivos. Pedir a eles quêque determinem o preêçopreço a pagar para diferentes medidas de massa de pão francês, em quilograma, e registrem os resultados em uma tabélatabela.

Páginas 98 a 100

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 3 Função afim e função modular

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender quêque o gráfico de qualquer função afim com domínio real, representado em um plano cartesiano, corresponde a uma reta e identificar quando as grandezas relacionadas por meio dessa função são diretamente proporcionais entre si.

• Analisar e calcular a taxa de variação média de funções, em especial, da função afim.

• Compreender, analisar e determinar as coordenadas dos pontos em quêque o gráfico de uma função afim intersecta os eixos cartesianos.

• Compreender a translação de gráficos de função afim e de função modular.

• Compreender e determinar a equação de reta e representá-la em um plano cartesiano.

• Analisar e investigar aplicações de função afim, estabelecendo associações com o cálculo de perímetro de polígono regular, de juro simples e de progressão aritmética.

• Investigar o comportamento entre duas variáveis numéricas de um conjunto de dados e, com auxílio de um software, construir um modelo matemático correspondente a uma função afim para representar relações entre grandezas e resolver problemas.

• Resolver e elaborar problemas, individualmente ou em grupo, envolvendo conjuntos, produtos ou razões entre grandezas e funções, relacionadas ou não a situações do cotidiano.

Orientações didáticas

O trabalho com esta Unidade possibilita desenvolver nos estudantes o pensamento algébrico, bem como estabelecer relações entre esse pensamento e o pensamento geométrico, a fim de quêque eles obtenham uma representação algébrica a partir de um dado gráfico, e vice-versa. Além díssudisso, na Unidade, são trabalhadas situações dos mais variados contextos quêque podem sêrser modeladas por uma função afim, o quêque propicíapropicia aos estudantes uma visão da Matemática integrada à ssossiedadesociedade e a outras áreas do conhecimento.

Página trezentos e trinta e oito338

Página 101

Abertura da Unidade

O trabalho com a abertura da Unidade propicíapropicia uma abordagem do Tema Contemporâneo Transversal Educação Ambiental, uma vez quêque trata dos impactos do deslocamento das pessoas ao optarem por transportes alternativos e menos poluentes. Nesse sentido, é possível explorar as informações dessa página em parceria com um professor da área de Ciências Humanas e Sociais Aplicadas, quêque pódepode auxiliar na discussão envolvendo conceitos como mobilidade urbana e poluição, buscando, sempre quêque possível, exemplificar com kestõesquestões locais.

Propor aos estudantes quêque reflitam sobre as dificuldades de locomoção quêque podem existir nos municípios brasileiros (congestionamentos, meios de transporte e infraestrutura de baixa qualidade etc.) e as atitudes quêque podem colaborar para atenuar os problemas de mobilidade, como realizar atividades do dia a dia a pé ou de bicicleta. Ao explorar o sistema de locação por meio de bicicletas e patinetes elétricos, conversar sobre as medidas de segurança necessárias para evitar acidentes, como respeitar as leis de trânsito e o limite de velocidade para tráfego na calçada e nas ciclovias; usar capacete; e ligar os faróis ou usar lâmpada portátil à noite.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Algumas respostas possíveis: Bicicleta, automóvel, motocicleta, ônibus e metrô.

2. Resposta pessoal.

3. O tempo de uso do equipamento.

Páginas 102 a 110

Função afim: ideias iniciais e definição

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência geral 7, das competências específicas 3 e 5 e das habilidades EM13MAT302 e EM13MAT501 da área de Matemática e suas Tecnologias, pois trabalha a investigação da relação entre números expressos em um qüadroquadro e a construção de um modelo empregando função afim. Além díssudisso, esse tópico favorece o desenvolvimento das competências específicas 1 e 2 da área de Ciências da Natureza e suas Tecnologias, pois propõe ações individuais e coletivas quêque visam minimizar impactos sócio-ambientaissocioambientais, com base em decisões responsáveis.

Na página 103, ao estabelecer a relação entre a massa de lentilha e a massa de fibra alimentar, relembrar com os estudantes a propriedade fundamental das proporções, conteúdo tratado em anos anteriores. Explicar quêque o valor constante correspondente à razão entre as duas massas é chamado de constante de proporcionalidade. No caso da função definida por h(x) = 0,08x, a constante de proporcionalidade é 0,08.

Na definição de função linear, destacar quêque ela é um caso particular de função afim, ou seja, toda função linear é afim, mas nem toda função afim é linear. Enfatizar também quêque, nas funções lineares, ou seja, do tipo y = ax, as variáveis se relacionam de maneira quêque $\frac{y}{x}=\frac{\mathrm{ax}}{x}$ = a(com x ≠ 0). Nesse caso, tem-se quêque a é a constante de proporcionalidade da função linear.

Para determinar a lei de formação da função, no tópico Determinação de uma função afim, verificar os conhecimentos prévios dos estudantes em relação à resolução de sistemas de duas equações do 1º grau com duas incógnitas. Caso necessário, retomar com eles esse conteúdo. Ao explorar a resolução do sistema, explicar quêque foi utilizado o método da adição. Para complementar, pode-se apresentar aos estudantes a resolução do sistema utilizando o método da substituição, como indicado a seguir.

• Escolher uma das equações e, nela, isolar uma incógnita.

30.000a + b = 3.000 ⇒ b = 3.000 − 30.000a

• Na outra equação, substituir a expressão equivalente à incógnita isolada anteriormente.

40.000a + (3.000 − 30.000a) = 3.500 ⇒ 10.000a = 500 ⇒

⇒ a = 0,05

• Substituir a incógnita calculada anteriormente em uma das equações do sistema.

30.000 ⋅ 0,05 + b = 3.000 ⇒ b = 3.000 − 1.500 = 1.500

A seção Atividades das páginas 107 a 110 tem como objetivo trabalhar a determinação dos coeficientes e do valor numérico de uma função afim, bem como explorar situações quêque envolvem variáveis quêque podem sêrser relacionadas por meio de uma função afim.

Atividade Extra

Após a realização da atividade 6, propor aos estudantes quêque realizem uma pesquisa sobre como é calculado o valor total de compra ou de venda de moeda estrangeira, quêque considera a taxa de câmbio, o Imposto sobre Operações Financeiras (IOF) e as eventuais tarifas cobradas. Em seguida, pedir quêque acessem o sáitisite do Banco Central do Brasil (disponível em: https://livro.pw/uzhdi; acesso em: 27 set. 2024) e explorem os custos de operações de câmbio praticados por uma das instituições apresentadas, analisando os tipos de operação, de moeda, de país etc. Ao final, eles devem elaborar um relatório com essas informações e escrever uma função afim quêque represente a quantia, em dólares, necessária para comprar ou vender x reais, por exemplo.

A atividade 12 trabalha a elaboração de um problema envolvendo função afim. Para essa elaboração, é importante quêque os estudantes analisem se as informações apresentadas são suficientes. Para isso, eles podem, inicialmente, listar possíveis perguntas para o problema, como: Qual será o valor de locação da sala para utilizá-la por 5 horas? E por 10 horas? (A lei de formação da função p quêque determina o preêçopreço da locação da sala, em reais, de acôr-doacordo com o tempo de uso t, em hora, é: p(t) = 8t + 10).

Ao abordar o boxe No mundo do trabalho, propor aos estudantes quêque pesquisem mais informações relacionadas aos direitos dos trabalhadores autônomos e apresentem-nas para toda a turma. Sugere-se também convidar um profissional quêque se enquadre nessa modalidade para conversar com os estudantes a respeito das vantagens e desvantagens de sêrser autônomo. Uma vantagem, por exemplo, é conseguir adaptar o horário de serviço conforme a necessidade.

A atividade 13 trabalha informações relacionadas aos impactos ambientais causados pelo aumento do uso de transportes motorizados. Nesse sentido, propicíapropicia o desenvolvimento das competências específicas 1 e 2 da área de Ciências da Natureza e suas Tecnologias. Uma possibilidade é desenvolver o trabalho com essa atividade em parceria com um professor dessa área quêque pódepode auxiliar na discussão envolvendo conceitos próprios da Química, como a composição de gases de efeito estufa.

Essa atividade também pódepode sêrser utilizada como um momento de avaliação formativa a fim de verificar se os estudantes reconhecem uma situação quêque pódepode sêrser modelada por uma função afim e se determinam o valor numérico de funções afins a partir de sua lei de formação. O professor pódepode identificar se os estudantes conseguem obtêrobter a lei de formação, para cada categoria de veículo, apenas analisando as informações apresentadas ou se é preciso quêque construam um qüadroquadro atribuindo possíveis valores para a variável independente para observar a regularidade e obtêrobter, assim, a lei de formação.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações sobre como reduzir os impactos ambientais causados pela mobilidade urbana.

• SÃO PAULO (Estado). Companhia Ambiental do Estado de São Paulo. Emissão veicular: transporte sustentável. São Paulo: cetésbiCetesb, [2024]. Disponível em: https://livro.pw/igwpu. Acesso em: 27 set. 2024.

Páginas 111 a 113

Taxa de variação média de uma função

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 1 e da habilidade

Página trezentos e trinta e nove339

EM13MAT101 da área de Matemática e suas Tecnologias, pois aborda situações relativas às Ciências da Natureza quêque envolvem a variação de grandezas e taxas de variação.

Na página 112, ao explorar as propriedades da função afim f, apresentar a demonstração de quêque, se o coeficiente a > 0, então f será crescente, conforme indicado a seguir.

Considerando dois números reais x₁ e x₂ tal quêque x₂ > x₁, tem-se quêque f(x₂)− f(x₁) = ax₂ + b − (ax₁ + b) = a (x₂ − x₁). Como a > 0 e x₂ > x₁, o quêque significa quêque x₂ − x₁ > 0, temos quêque f(x₂) − f(x₁)> 0, ou seja, f(x₂) > f(x₁). Logo, se a > 0 e x₂ > x₁, tem-se quêque f(x₂)> f(x₁), o quêque garante quêque f é crescente.

De maneira análoga, pode-se demonstrar quêque a função afim f é decrescente quando a < 0.

As atividades da página 113 trabalham a taxa de variação média de funções, incluindo a de funções afins, bem como abordam a classificação de uma função afim em crescente ou decrescente.

Páginas 114 a 125

Gráfico da função afim

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 1, 3, 4 e 5 e das habilidades EM13MAT101, EM13MAT302, EM13MAT401, EM13MAT404, EM13MAT501 e EM13MAT510 da área de Matemática e suas Tecnologias, já quêque usa representações algébricas, bem como as representações geométricas de registros algébricos, para resolver problemas ou tomar decisões.

No início da página 115, é importante quêque os estudantes percêbampercebam quêque a medida do segmento de reta $\overline{QH}$ corresponde à diferença entre a ordenada do ponto Q e a ordenada do ponto H. De maneira análoga, fazer essa análise para o segmento de reta $\overline{MN}$ e, considerando a diferença entre as abscissas, para os segmentos de reta $\overline{HM}$ e $\overline{NP}$. Se necessário, apresentar exemplos numéricos para as coordenadas dêêssesdesses pontos.

Na relação entre as medidas dos catetos dos triângulos PMN e MQH, relembrar com os estudantes quêque dois triângulos são semelhantes quando têm os ângulos internos correspondentes congruentes e os lados correspondentes proporcionais entre si. Para garantir a semelhança de triângulos, há alguns casos particulares. No caso LAL (lado, ângulo, lado), apresentado na demonstração, tem-se quêque dois lados correspondentes são proporcionais entre si e os ângulos internos formados por eles são congruentes.

Ao explorar quêque os pontos P, Q e M são colineares, relembrar quêque, quando uma reta transversal cruza um par de retas paralelas, podem-se classificar alguns pares de ângulos formados de acôr-doacordo com a posição quêque ocupam em relação às retas. Nesse caso, têm-se quêque $H\widehat{M}Q$ e $N\widehat{P}M\mathrm{}$são ângulos correspondentes entre si.

No tópico Translação do gráfico de uma função afim, conversar com os estudantes sobre o quêque eles compreendem do termo “translação”. Espera-se quêque eles percêbampercebam quêque a translação representa uma transformação em relação a todos os pontos de um gráfico, quêque se deslócamdeslocam em uma mesma direção, em um mesmo sentido e por uma mesma distância. A direção pódepode sêrser vertical, horizontal ou a combinação de ambas.

Ao formalizar a translação do gráfico de uma função afim, relembrar aos estudantes quêque, geometricamente, se pódepode interpretar o módulo de um número real b como a distância do ponto correspondente a b até a origem na reta real.

As atividades das páginas 122 a 125 têm como objetivo trabalhar a representação gráfica de uma função afim, sua classificação em crescente ou decrescente, bem como a determinação da taxa de variação e da lei de formação de uma função afim e as coordenadas dos pontos onde seu gráfico cruza os eixos cartesianos.

A atividade 23 trabalha, em uma situação contextualizada, a construção de um modelo empregando função afim, o quêque propicíapropicia o desenvolvimento da habilidade EM13MAT302. A atividade 27 trabalha, em uma situação contextualizada, a análise de função afim definida por mais de uma sentença, o quêque contribui para o desenvolvimento da habilidade EM13MAT404.

A atividade 30 trabalha, em uma situação contextualizada, a investigação da relação entre números expressos em tabélastabelas e a representação dessa relação no plano cartesiano, utilizando uma reta para descrevê-la. Além díssudisso, propõe a construção de um modelo empregando função afim, o quêque propicíapropicia o desenvolvimento das habilidades EM13MAT302, EM13MAT501 e EM13MAT510.

A atividade 31 trabalha a investigação do comportamento entre duas variáveis de um conjunto de dados expressos em uma planilha eletrônica, o quêque contribui para o desenvolvimento da habilidade EM13MAT510. Explicar aos estudantes quêque a linha de tendência representa o comportamento dos dados. Nesse caso, para apresentar a relação de dependência entre as duas variáveis, o melhor modelo quêque explica essa relação é representado por uma reta. Esse tipo de representação é utilizado para projetar ou estimar uma das variáveis em função da outra. Por exemplo, em análises técnicas no mercado de ações, essas linhas auxiliam na identificação das tendências nesse mercado e na tomada de decisões.

Páginas 126 a 128

Equação da reta

Nesse tópico, explicar aos estudantes quêque o coeficiente angular representa a inclinação da reta em relação ao eixo x e quêque o coeficiente linear representa a ordenada do ponto dessa reta onde ela intersecta o eixo y.

As atividades da página 128 trabalham a determinação da equação da reta com base nas coordenadas de um de seus pontos e nas do seu coeficiente angular ou nas coordenadas de dois de seus pontos. A atividade 35 trabalha a análise do comportamento de duas variáveis numéricas de um conjunto de dados expressos em uma planilha eletrônica e a construção de um modelo empregando função afim, o quêque contribui para o desenvolvimento das habilidades EM13MAT302 e EM13MAT510.

Páginas 129 a 131

Integrando com Ciências da Natureza e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento das competências específicas 1, 3, 4 e 5 e das habilidades EM13MAT101, EM13MAT302, EM13MAT401 e EM13MAT510 da área de Matemática e suas Tecnologias, uma vez quêque trata de aplicações de função afim para interpretar contextos das Ciências da Natureza, no caso, o movimento retilíneo uniforme (movimento retilíneo uniformeMRU). Assim, uma sugestão de condução para essa seção é trabalhar em parceria com um professor dessa área.

Explicar aos estudantes os conceitos relacionados à trajetória de um objeto sôbisob a ação dos diversos tipos de movimento e de aceleração, além de apresentar os gráficos das funções quêque descrevem esses movimentos. Por exemplo, pode-se citar a trajetória de um trem cujo movimento é retilíneo uniforme ou uniformemente variado.

A questão 6 trabalha a realização de um experimento pêlospelos estudantes sobre o movimento retilíneo uniformeMRU, além da análise dos resultados obtidos. Na 5ª etapa, os eventuais êêrroserros das medidas aferidas podem ocorrer durante a observação do movimento da bolha e na cronometragem. Assim, propor aos estudantes quêque repitam os procedimentos e comparem os resultados obtidos. Além díssudisso, uma sugestão é gravar em vídeo o experimento com o objetivo de pôdêrpoder rever a movimentação da bolha e realizar anotações mais detalhadas.

Na elaboração do relatório, por exemplo, os estudantes podem apresentar os conceitos abordados e os respectivos objetivos; os materiais utilizados e a condução do experimento; a comparação dos resultados obtidos com os de outros côlégascolegas; e a descrição do quêque foi aprendido com o experimento. Ainda, é possível propor quêque pesquisem mais informações sobre o movimento retilíneo uniformeMRU em livros, artigos e sáitessites confiáveis, com o objetivo de incentivar o interêsseinteresse pelo estudo científico.

Página trezentos e quarenta340

Conexões

Sugerir aos estudantes quêque assistam ao vídeo indicado a seguir, quêque pódepode auxiliá-los na realização do experimento.

• MOVIMENTO retilíneo uniforme. São Paulo: úspiUSP, 2019. 1 vídeo (1 min). Publicado por Plataforma Anísio Teixeira. Disponível em: https://livro.pw/xvocc. Acesso em: 27 set. 2024.

Páginas 132 a 134

Estudo do sinal de uma função afim

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT302 da área de Matemática e suas Tecnologias, uma vez quêque emprega modelos de funções afins para resolver problemas de variados contextos.

O estudo do sinal de uma função foi tratado na Unidade 2 dêstedeste Volume. Por isso, verificar os conhecimentos prévios dos estudantes referentes ao conteúdo e, se necessário, retomá-lo.

Explicar aos estudantes quêque o estudo do sinal da função afim, de maneira prática, pódepode sêrser feito por meio da representação de uma figura contendo inicialmente apenas o eixo x e, nele, indicar um ponto correspondente ao zero da função $\left(-\frac{b}{a}\right)$. Em seguida, de acôr-doacordo com a taxa de variação da função, deve-se traçar uma reta não horizontal quêque cruza o eixo x no ponto indicado.

As atividades da página 134 têm como objetivo trabalhar o estudo do sinal de funções afins. A atividade 43 trabalha, em uma situação contextualizada, a construção de um modelo empregando função afim e o estudo do sinal dessa função, o quêque propicíapropicia o desenvolvimento da habilidade EM13MAT302.

A atividade 44 trabalha a demonstração do estudo do sinal de uma função afim decrescente a partir do zero dessa função. Nesse sentido, contribui para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias. Na resolução, verificar se os estudantes compreenderam quêque, como f é decrescente, a < 0. Como complemento, propor a eles quêque mostrem quêque, em uma função crescente g: ℝ → ℝ, definida por g(x) = ax + b, tem-se g(x) > 0 para x > $-\frac{b}{a}$. Nesse caso, para g(x) > 0, tem-se ax + b > 0 ⇒ ax > −b. Como g é crescente, tem-se a > 0. Assim, divide-se a desigualdade ax > −b por a, obtendo x > $-\frac{b}{a}$

A atividade 45 trabalha, em uma situação contextualizada, o estudo do sinal de uma função afim. Além díssudisso, propõe a interpretação da situação de maneira crítica, o quêque propicíapropicia o desenvolvimento da habilidade EM13MAT101.

Páginas 135 a 140

Algumas aplicações

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 3, 4 e 5 e das habilidades EM13MAT303, EM13MAT401, EM13MAT506 e EM13MAT507 da área de Matemática e suas Tecnologias, uma vez quêque estabelece associações entre juro simples, progressão aritmética e cálculo do perímetro de polígonos regulares e função afim.

Antes de apresentar os conteúdos dessas páginas, propor aos estudantes quêque citem situações quêque podem envolver o conceito e as características de uma função afim, por exemplo, o número do sapato em função do tamãnhotamanho do pé. Esse pódepode constituir um momento de avaliação, de modo quêque o professor identifique se os estudantes são capazes de reconhecer situações de seu cotidiano quêque podem sêrser expressas por meio de uma função afim.

No tópico Função afim e perímetro de polígonos regulares, é importante quêque os estudantes compreendam quêque, quando as grandezas envolvidas em determinado problema estão relacionadas de maneira diretamente proporcional, pódepode-se representar tal relação por meio de uma função linear. Assim, a relação entre o perímetro de um polígono regular e a medida de um dos seus lados pode sêrser representada por meio de uma função linear.

O estudo do tópico Função afim e juro simples contribui para o desenvolvimento da habilidade EM13MAT303, propiciando, além díssudisso, uma abordagem dos Temas Contemporâneos Transversais Educação Financeira e Educação Fiscal.

Ao explorar a definição de PA, no tópico Função afim e progressão aritmética, explicar aos estudantes quêque uma PA pódepode sêrser classificada, de acôr-doacordo com sua razão decrescente, quando r < 0; constante, quando r = 0; ou crescente, quando r > 0. Comentar quêque o estudo de PA e de outros tipos de sequência será retomado e ampliado no Volume 2 desta coleção.

A seção Atividades das páginas 138 a 140 tem como objetivo trabalhar aplicações de funções afins relacionadas à variação do perímetro de um polígono regular, de acôr-doacordo com a medida de seu lado; ao juro simples; e à progressão aritmética.

Para o trabalho com a atividade 50, sugere-se organizar os estudantes em duplas e propor o uso de um software de geometria dinâmica, como o GeoGebra, para realizar uma atividade utilizando ideias da investigação matemática, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor. Para isso, pedir aos estudantes quêque representem quadrados de diferentes medidas de lados e quêque determinem o perímetro e a área correspondentes. Por fim, quêquestioná-los sobre o que ocorre com o perímetro e a área dos quadrados ao se dobrar, triplicar ou reduzir pela mêtádemetade a medida de seus lados. Nesse momento, é importante quêque eles levantem hipóteses com os côlégascolegas e registrem suas conclusões.

Na atividade 59, destacar aos estudantes quêque eles podem propor algum problema quêque, por falta de dados no enunciado, não possa sêrser resolvido. Por exemplo:

• Em uma PA infinita, temos quêque o 1º termo é −4 e quêque o número 31 também é um de seus termos. Defina uma função afim f tal quêque (f(0), f(1), f(2), …, f(n), …) corresponda a essa PA.

É importante, nesse caso, quêque o estudante, ao receber a quêquestão, identifique a falta de dados do enunciado e quêque faça sugestões de ajustes, de maneira a tornar possível sua resolução. Em relação a esse exemplo, pode-se propor a inclusão do valor da razão ou a posição do número 31 na PA, que podem sêrser, respectivamente, 7º e 6º termo. Com algum dêêssesdesses ajustes no enunciado, obtém-se f: ℕ → ℝ, definida por f(n) = 7n − 4.

Páginas 141 a 144

Função modular

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 4 e da habilidade EM13MAT404 da área de Matemática e suas Tecnologias, pois aborda a análise de funções definidas por uma ou mais sentenças, em suas representações algébrica e geométrica.

Discutir com os estudantes o conjunto imagem de uma função modular. Para isso, relembrar como é possível fazer uma análise do conjunto imagem de uma função por meio de seu gráfico, conforme apresentado na Unidade 2 dêstedeste Volume. Assim, o conjunto imagem da função f(x) = |x | corresponde ao conjunto dos números reais não negativos, ou seja, Im(f) = [0, +∞[.

Ao explorar os gráficos e o primeiro boxe Para pensar da página 142, é possível estabelecer relação com o estudo da simetria de reflekçãoreflexão: quando uma reta divide uma figura de maneira quêque, ao sêrser dobrada sobre essa reta, as partes obtidas são idênticas por sobreposição, essa figura apresenta simetria de reflekçãoreflexão em relação à reta. Essa reta corresponde ao eixo de simetria. Assim, os pontos correspondentes em cada uma das partes da figura são equidistantes ao eixo de simetria.

No tópico Translação do gráfico de uma função modular, explicar aos estudantes quêque também é possível escrever o módulo de um número real x no campo Entrada do GeoGebra utilizando o comando “abs(x)”.

Página trezentos e quarenta e um341

Reforçar quêque a translação do gráfico para a esquerda corresponde ao sentido negativo do eixo das abscissas e quêque a translação para a direita, ao sentido positivo. De maneira análoga, a translação do gráfico para baixo corresponde ao sentido negativo do eixo das ordenadas, e a translação para cima, ao sentido positivo.

As atividades das páginas 143 e 144 têm como objetivo trabalhar o valor numérico de uma função modular, a representação gráfica de funções modulares, bem como a determinação da lei de formação de uma função modular a partir de sua representação gráfica. Além díssudisso, na atividade 66, é trabalhado o pensamento computacional, ao sêrser explorado um algoritmo representado por um fluxograma.

Páginas 145 a 148

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, das competências específicas 3, 4 e 5 e das habilidades EM13MAT302, EM13MAT401, EM13MAT501 e EM13MAT510 da área de Matemática e suas Tecnologias.

Na proposta Construindo e analisando o gráfico da função afim, na etapa B, orientar os estudantes na movimentação dos contrôlecontroles deslizantes: basta clicar sobre o controle desejado e, com o botão do máuzimouse pressionado, arrastá-lo até a posição almejada.

Mãos à obra - página 146

1. No item b, orientar os estudantes a clicar sobre o gráfico de f e sobre o eixo x para obtêrobter o ponto em quêque o gráfico cruza o eixo das abscissas. Eles devem proceder de maneira análoga para obtêrobter o ponto de interseção do gráfico com o eixo y.

2. Orientar os estudantes na indicação das leis de formação das funções no campo Entrada.

3. Explicar aos estudantes quêque eles podem, inicialmente, indicar os pontos. Para isso, é possível clicar no ponto de acôr-doacordo com suas coordenadas ou utilizar o campo Entrada. Por exemplo, para A(−2, 3), digita-se: “A=(−2, 3)”.

Na proposta Construindo um modelo para representar relações entre grandezas, explicar aos estudantes quêque há outros tipos de gráfico quêque podem representar os dados apresentados, como funções polinomiais de maior grau. Porém a função afim é a quêque melhor representa a relação entre esses dados específicos.

Mãos à obra - página 148

2. Orientar os estudantes na representação dos dados na planilha eletrônica.

Páginas 149 e 150

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A quêquestão 4 trabalha uma situação quêque envolve variáveis que podem sêrser relacionadas por meio de função afim. Além díssudisso, propõe a discussão sobre a mobilidade urbana na região onde os estudantes vivem, retomando o tema da abertura da Unidade. No item f, o gráfico pódepode sêrser construído em uma planilha eletrônica ou em um software de geometria dinâmica, como o GeoGebra. No item i, sugerir aos estudantes quêque compartilhem as informações pesquisadas e o texto quêque produzirem com a comunidade local por meio de uma publicação em um blogue ou em uma rê-derede social ou por meio de um vídeo informativo.

Páginas 151 e 152

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 4 Função quadrática

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender a parábola como lugar geométrico e, a partir de sua representação no plano cartesiano, identificar alguns elemêntoselementos quêque a compõem.

• Reconhecer quêque toda parábola tem um eixo de simetria, o qual a intersecta em seu vértice.

• Compreender o conceito de função quadrática e utilizá-la para construir modelos matemáticos em diferentes contextos.

• Identificar os coeficientes e calcular o valor numérico de uma função quadrática.

• Determinar e interpretar, quando existirem, os zeros reais de uma função quadrática.

• Determinar a quantidade de zeros reais de uma função quadrática.

• Reconhecer quêque o gráfico de uma função quadrática é uma parábola.

• Esboçar e analisar o gráfico de uma função quadrática, identificando suas características e realizando o estudo de seu sinal.

• Associar a abscissa do vértice de uma parábola à média aritmética das abscissas de dois pontos simétricos pertencentes a ela.

• Determinar as coordenadas dos pontos de interseção do gráfico de uma função quadrática com os eixos cartesianos.

• Estabelecer relações entre os coeficientes de uma função quadrática e sua representação gráfica.

• Determinar as coordenadas do vértice de uma parábola a partir dos coeficientes da função quadrática representada por ela.

• Determinar o valor mássimomáximo ou mínimo e o conjunto imagem de uma função quadrática.

• Compreender e determinar a equação de uma parábola.

Página trezentos e quarenta e dois342

Orientações didáticas

O trabalho com a função quadrática, a partir de diferentes situações, possibilita aos estudantes interpretar e analisar criticamente a realidade, além de desenvolver conhecimentos e habilidades relacionados a outras áreas do conhecimento. Esse trabalho pódepode sêrser feito com o emprego de tecnologias digitais para construir modelos matemáticos quêque os auxiliem a refletir sobre problemas e a estabelecer soluções para eles.

Página 153

Abertura da Unidade

Ao abordar a abertura da Unidade, verificar a possibilidade de realizar um trabalho em parceria com um professor da área de Ciências da Natureza e suas Tecnologias, com o objetivo de discutir e analisar com os estudantes aspectos conceituais do lançamento oblíquo ou de um projétil (força, inclinação, deslocamento etc.). Nesse trabalho, pode-se, por exemplo, considerar a abordagem do alcance vertical de um projétil, quêque pódepode sêrser expresso por R = $\begin{array}{c}\frac{2v_0^2}{g}\end{array}$ sen 2θ, em quêque R é o alcance vertical, v₀ é a velocidade inicial, g é a aceleração da gravidade e θ, o ângulo de lançamento dêêssedesse projétil. Propor aos estudantes quêque, de acôr-doacordo com essa expressão e fixando v₀ e g, determinem para qual valor do sen 2θ o projétil teria alcance mássimomáximo e, de acôr-doacordo com esse valor, qual seria a medida de θ. Espera-se quêque eles percêbampercebam quêque, como −1 ≤ sen 2θ ≤ 1, R terá valor mássimomáximo quando sen 2θ = 1 e, ainda, quêque, para 0° ≤ θ ≤ 90°, temos sen 2θ = 1 = sen 90° ⇒ 2θ = 90° ⇒ θ = 45°. Assim, o alcance mássimomáximo em um lançamento é obtídoobtido quando o ângulo dêstedeste for de 45°.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Trajetória parabólica. Resposta pessoal.

2. Resposta esperada: Porque a aplicação dêêssesdesses conceitos da Física contribui para a análise e a melhoria do dêsempênhodesempenho dos atletas, pois permite conhecer diversos parâmetros, como distância percorrida e velocidade.

3. Construção do estudante.

Páginas 154 a 159

A parábola

Durante o trabalho com esse tópico, explorar os conhecimentos prévios dos estudantes em relação aos conceitos de simetria, tratados em anos anteriores. Perguntar-lhes qual é o tipo de simetria quêque pódepode sêrser observado em uma parábola e, considerando essa simetria, qual é a relação entre os pontos da parábola e o eixo de simetria. Espera-se quêque eles obissérvemobservem a simetria de reflekçãoreflexão em relação a um eixo e indiquem os pontos simétricos da parábola quêque são equidistantes a esse eixo.

Função quadrática: características e definição

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT302 da área de Matemática e suas Tecnologias, uma vez quêque trata da construção de modelos utilizando função quadrática para resolver problemas.

Nesse trabalho, espera-se quêque os estudantes compreendam a definição de função quadrática e algumas de suas características. Para isso, apresenta-se inicialmente uma situação quêque envolve o cálculo da área de um campo de futebólfutebol, com o objetivo de modelar tal situação por meio de uma função quadrática.

Dizer aos estudantes quêque, de acôr-doacordo com a Federação Internacional de Futebol (Fifa), entidade quêque regulamenta as regras do futebólfutebol, os campos oficiais devem sêrser retangulares, com comprimento variando de 90 m até 120 m e largura variando de 45 m até 90 m.

Fonte dos dados: DeTHE INTERNÉTIONALINTERNATIONAL FOOTBALL ASSOCIATION BOARD. Laws ÓFof the guêimegame: 2018/19. Zurich: Ifab, 2018. p. 34. Disponível em: https://livro.pw/ozird. Acesso em: 27 set. 2024.

Ao trabalhar os exemplos de função quadrática da página 156, pode-se propor aos estudantes quêque as classifiquem em funções quadráticas completas ou incompletas. Explicar a eles quêque as funções quadráticas em quêque b = 0 e c = 0, b = 0 e c ≠ 0 ou b ≠ 0 e c = 0 são denominadas incompletas. E as funções quadráticas completas são aquelas em quêque b ≠ 0 e c ≠ 0.

As atividades das páginas 157 a 159 têm como objetivo trabalhar a definição de funções quadráticas, a indicação de seus coeficientes e o cálculo de valores numéricos para algumas funções. Além díssudisso, é abordada a construção de modelos empregando uma função quadrática para descrever diferentes situações, o quêque possibilita desenvolver a habilidade EM13MAT302 da área de Matemática e suas Tecnologias.

A atividade 10 pódepode sêrser proposta e discutida com apôioapoio de um professor da área de Ciências da Natureza e suas Tecnologias, em particular, para explorar conceitos relacionados à Física. Assim, sugerir aos estudantes uma investigação sobre o estudo quêque Galileu Galilei (1564-1642) realizou e quêque fundamentou a lei dos corpos em queda.

O contexto da atividade 11 propicíapropicia uma abordagem do Tema Contemporâneo Transversal Educação em Direitos Humanos, pois apresenta informações sobre a acessibilidade. Caso seja possível, planejar o trabalho com essa atividade em conjunto com um professor da área de Ciências Humanas e Sociais Aplicadas, com o objetivo de discutir com os estudantes temáticas relacionadas à acessibilidade, em especial, na própria escola e no município em quêque moram.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre a norma brasileira de acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos.

• ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 9050: acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos. 4. ed. Rio de Janeiro: ABNT, 2020. Disponível em: https://livro.pw/gxslr. Acesso em: 27 set. 2024.

No boxe Matemática na história da atividade 12, comentar com os estudantes quêque o desenvolvimento dos conceitos matemáticos ao longo da história não ocorreu d fórmade forma linear, uma vez quêque situações inesperadas foram pontos de partida para estudos quêque originaram grandes descobertas matemáticas.

Páginas 160 a 165

Zeros de uma função quadrática

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT302 da área de Matemática e suas Tecnologias, pois trata da representação algébrica de uma função quadrática.

Em relação à conceituação de zero de uma função quadrática, comentar com os estudantes quêque ax² + bx + c = 0 representa uma equação do 2º grau, conteúdo estudado em anos anteriores. Sugere-se fazer, nesse momento, uma avaliação diagnóstica a fim de identificar se os estudantes determinam a solução de uma equação do 2º grau. Para isso, podem sêrser propostas algumas equações dêêssedesse tipo para quêque eles resolvam em uma fô-lhafolha avulsa. Depois da avaliação diagnóstica, se necessário, retomar esse conteúdo com a turma.

É importante quêque os estudantes saibam interpretar algebricamente o significado dos zeros de uma função quadrática: eles correspondem aos números reais x tais quêque f(x) = 0. Um pouco mais adiante, nessa Unidade, será estudada a interpretação geométrica dos zeros de uma função quadrática.

Página trezentos e quarenta e três343

Ao abordar o boxe No mundo do trabalho da página 160, comentar com os estudantes quêque o setor veterinário tem crescido nos últimos anos, o quêque pódepode constituir uma oportunidade para futuros profissionais. Comentar quêque a atuação do médico-veterinário não se restringe aos cuidados com animais de estimação, como cães e gatos; esse profissional também é habilitado para lidar com animais de grande porte, silvestres ou exóticos, por exemplo.

As atividades da página 165 têm como objetivo trabalhar a determinação dos zeros de uma função afim, bem como abordar a análise de funções quadráticas quêque descrevem diferentes situações. Na atividade 18, é apresentado um fluxograma quêque envolve o pensamento algorítmico, uma vez quêque mostra uma sequência de passos para determinar a quantidade de raízes reais de uma função quadrática. O pensamento algorítmico é associado ao pensamento computacional, tema abordado na parte geral destas Orientações para o professor.

A atividade 19 trabalha a demonstração de uma propriedade relacionada ao estudo dos zeros de uma função quadrática. Tal atividade pódepode não sêrser rotineira para os estudantes, de modo quêque poderão sêrser necessárias a intervenção e a condução do professor para quêque eles possam realizá-la. Ao final, propor quêque ao menos um dos estudantes apresente na lousa a demonstração para quêque os côlégascolegas possam avaliar se a estratégia utilizada está correta.

Página 166 a 177

Gráfico de uma função quadrática

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 1, 3, 4 e 5 e das habilidades EM13MAT101, EM13MAT302, EM13MAT402 e EM13MAT502 da área de Matemática e suas Tecnologias, pois trata da relação entre as representações algébricas e geométricas de uma função quadrática e suas diversas aplicações.

Inicialmente, destacar aos estudantes quêque o gráfico de uma função quadrática é uma parábola, assunto tratado anteriormente nesta Unidade e quêque será retomado. Em relação aos exemplos apresentados na página 166, sugerir aos estudantes quêque construam os gráficos das funções quadráticas utilizando um software de geometria dinâmica. No GeoGebra, por exemplo, basta os estudantes digitarem a lei de formação da função no campo Entrada. Para obtêrobter o gráfico da função f, digita-se “f(x)=x^2” e, para obtêrobter o gráfico da função g, digita-se “g(x)=x^2−4x+3”. Nesse momento, explicar a eles quêque o sín-bolosímbolo “^” representa potência.

Ainda na página 166, explicar aos estudantes quêque dois pontos de uma parábola são simétricos por reflekçãoreflexão em relação a um eixo quando a distância dêêssesdesses pontos ao eixo é igual e a reta quêque passa por esses pontos é perpendicular ao eixo.

No tópico Interseção do gráfico de uma função quadrática com os eixos cartesianos, é importante quêque os estudantes compreendam quêque a identificação dos pontos em quêque o gráfico de uma função quadrática intersecta os eixos cartesianos contribui para o esboço dêêssedesse gráfico. Verificar se eles perceberam quêque o gráfico de qualquer função quadrática necessariamente intersecta o eixo das ordenadas, porém os gráficos das funções quadráticas quêque não têm zero real não intersectam o eixo das abscissas.

Antes de apresentar as relações entre os coeficientes de uma função quadrática e as características da parábola correspondente ao seu gráfico, na página 169, uma sugestão é propor inicialmente a realização de um trabalho em grupo a fim de quêque os estudantes investiguem essas relações, o quêque pódepode sêrser feito utilizando um software de geometria dinâmica, como o GeoGebra. Para isso, pode-se propor um trabalho utilizando ideias da investigação matemática, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor.

As atividades das páginas 170 a 173 têm como objetivo trabalhar a determinação de pontos do gráfico de uma função quadrática quêque intersectam os eixos cartesianos, bem como abordar a análise dos coeficientes de funções quadráticas a partir de características do gráfico dessas funções. Também têm como objetivo trabalhar a determinação da lei de formação de uma função quadrática e da taxa de variação de funções dêêssedesse tipo.

A atividade 25 trabalha a representação gráfica de modelos, dados por uma função afim e uma função quadrática, para expressar, respectivamente, o perímetro e a área de um hekzágonohexágono regular, de acôr-doacordo com a medida de seu lado, o quêque contribui para o desenvolvimento da habilidade EM13MAT506.

Nas atividades 26 e 31, os estudantes devem determinar a lei de formação de funções quadráticas do tipo y = ax² a partir de alguns pontos de seus gráficos cujas coordenadas estão indicadas em quadros, o quêque contribui para o desenvolvimento da habilidade EM13MAT502. Além díssudisso, a atividade 31 pódepode sêrser utilizada para avaliação a fim de identificar se os estudantes esboçam o gráfico de uma função quadrática a partir da apresentação de um conjunto de dados, se eles determinam a lei de formação da função quadrática quêque descreve a situação e, por fim, se determinam o valor numérico de alguns dados a partir da função quadrática ôbitídaobtida. Os estudantes podem entregar a atividade resolvida em uma fô-lhafolha avulsa, e alguns deles podem sêrser selecionados para ir à lousa explicar o modo como pensaram para resolver cada um dos itens.

A atividade 30 trabalha a análise e a determinação de um modelo, dado por uma função quadrática, quêque descreve a distância de frenagem de um automóvel. Aproveitar o contexto dessa atividade, quêque propicíapropicia uma abordagem do Tema Contemporâneo Transversal Educação para o Trânsito, para promover uma roda de conversa com os estudantes sobre os riscos de utilizar o celular ao dirigir. Destacar quêque, além dos riscos de acidentes, há multas de trânsito quêque podem sêrser aplicadas nesses casos. Comentar quêque os pedestres também devem estar atentos ao trânsito e evitar a distração do uso dêêssesdesses aparelhos enquanto caminham pela cidade.

No tópico Vértice da parábola, explicar aos estudantes quêque, nas parábolas com eixo de simetria paralelo ao eixo das ordenadas, os pontos da parábola quêque têm a mesma ordenada são simétricos, pois o eixo de simetria corresponde à mediatriz do segmento com extremidades nesses pontos e, portanto, a distância deles ao eixo de simetria é a mesma. Explicar quêque, em razão díssudisso, a abscissa dos pontos pertencentes ao eixo de simetria é dada pela média aritmética das abscissas dos pontos simétricos e, portanto, a abscissa do vértice dessa parábola também é dada por essa média.

No boxe Para pensar da página 175, caso os estudantes apresentem dificuldade, orientá-los a escrever, utilizando as expressões para o cálculo das coordenadas do vértice de uma parábola e as coordenadas do vértice dadas, um sistema linear de duas equações e três incógnitas. Explicar a eles quêque se trata de um sistema possível e indeterminado e, para obtêrobter uma solução, podem-se atribuir valores para a, por exemplo, e determinar os valores de b e c pelo sistema.

No trabalho com o conjunto imagem de uma função quadrática, propor aos estudantes quêque, em duplas, realizem a atividade a seguir.

Atividade Extra

Propor aos estudantes quêque mostrem a validade das afirmações a seguir.

I) Dada uma função quadrática f(x) = ax² + bx + c, com a > 0 e gráfico de vértice V(x_v,y_v), então f é decrescente para x < x_v e crescente para x > x_v.

II) Dada uma função quadrática f(x) = ax² + bx + c, com a < 0 e gráfico de vértice V(x_v, y_v), então f é crescente para x < x_v e decrescente para x > x_v.

Resposta: Em relação à afirmação I, tem-se quêque, como a > 0, então o gráfico de f tem concavidade voltada para cima e, consequentemente, f(x₁)> f(x_v) para x₁ < x_v. Assim, tomando-se x₁< x₂< x_v^, segue-se quêque f(x₁) > f(x₂). Logo, f é decrescente para x < x_v. De maneira análoga, tem-se quêque f(x₁) > f(x_v)para x₁> x_v. Assim, tomando-se x₁> x₂> x_v, segue-se quêque f(x₁)> f(x₂). Logo, f é crescente para x > x_v. A afirmação II pódepode sêrser verificada de maneira análoga.

As atividades da página 177 abordam a determinação dos intervalos de crescimento e decrescimento, do conjunto imagem e das coordenadas do vértice de gráficos de funções quadráticas, além

Página trezentos e quarenta e quatro344

do estabelecimento da lei de formação de uma função quadrática a partir do seu gráfico.

Páginas 178 a 183

Valor mássimomáximo ou valor mínimo da função quadrática

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 5 e das habilidades EM13MAT404 e EM13MAT503 da área de Matemática e suas Tecnologias, ao abordar funções definidas por mais de uma sentença e os valores de mássimomáximo ou de mínimo de funções quadráticas.

As situações apresentadas na página 178 remetem à ideia de otimização, quêque, de modo geral, consiste em realizar procedimentos quêque buscam obtêrobter a solução mais adequada para um problema. Em Matemática, há áreas de estudo dedicadas ao trabalho com otimização, como é o caso da Programação Matemática.

Ao abordar o boxe No mundo do trabalho da página 179, promover uma roda de conversa com os estudantes, quêquestionando que outras características eles julgam importantes para a resolução de problemas e, consequentemente, para o mercado de trabalho. Sobre a sugestão de vídeo apresentada no boxe, questionar também se eles conheciam a expressão e o conceito de disáinidesign thinking e quais foram as informações do vídeo quêque chamaram a atenção deles.

Na atividade R15, são utilizadas etapas para se chegar ao resultado. Sugere-se estruturar e executar essas etapas, como foi apresentado, sempre quêque perceber quêque os estudantes estão com dificuldades em determinado problema matemático. Essa estratégia também pódepode sêrser utilizada pêlospelos próprios estudantes quando estiverem diante de um problema matemático a sêrser resolvido.

A seção Atividades das páginas 181 a 183 tem como objetivo trabalhar a determinação do valor mássimomáximo ou do valor mínimo de funções quadráticas. A atividade 42 trabalha a análise do valor mássimomáximo de uma função quadrática quêque descreve o número de batimentos cardíacos de uma pessoa de acôr-doacordo com o tempo de treino realizado. Além díssudisso, o contexto propicíapropicia uma abordagem do Tema Contemporâneo Transversal Saúde. Para complementar o trabalho com o item c, propor aos estudantes quêque, em grupos de três ou quatro integrantes, pesquisem os perigos de se ultrapassar, constantemente, a freqüênciafrequência cardíaca mássimamáxima recomendada. Essa proposta pódepode sêrser realizada em conjunto com um professor da área de Ciências da Natureza e suas Tecnologias e um professor de Educação Física (área de Linguagens e suas Tecnologias).

Na atividade 43, se for possível e houver a disponibilidade de um laboratório de Ciências na escola, realizar um trabalho em conjunto com um professor da área de Ciências da Natureza e suas Tecnologias para investigar, na prática, o comportamento de uma cultura de bactérias ao se variar a tempera-túratemperatura à qual ela está submetida. As observações realizadas pêlospelos estudantes podem sêrser organizadas em um relatório.

A atividade 47 aborda a habilidade EM13MAT404, uma vez quêque é propôstoproposto aos estudantes analisar uma função definida por mais de uma sentença.

Páginas 184 a 187

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, das competências específicas 3, 4 e 5 e das habilidades EM13MAT302, EM13MAT402 e EM13MAT503 da área de Matemática e suas Tecnologias, pois propõe o uso de ferramentas digitais para trabalhar as relações entre as representações algébricas e geométricas das funções.

Seguem os comentários sobre as kestõesquestões referentes à proposta Determinando as coordenadas do vértice de uma função quadrática.

Mãos à obra - página 185

3. Verificar se os estudantes perceberam quêque os pontos P₁ e P₂ correspondem aos zeros das funções f e g; quêque, como as duas funções têm os mesmos zeros, a reta de simetria é a mesma para ambas; e quêque, consequentemente, a abscissa do vértice também é a mesma para ambas as funções. Conversar com os estudantes sobre o fato de terem de representar os gráficos das duas funções no mesmo plano cartesiano para resolver a questão. Após obtêrobter as coordenadas do vértice de cada parábola, eles podem utilizar a opção Distância, comprimento ou perímetro para obtêrobter a distância entre os vértices dessas parábolas ou, ainda, calcular a diferença entre as ordenadas dêêssesdesses vértices.

Seguem os comentários sobre as kestõesquestões referentes à proposta Estudando relações entre grandezas por meio de modelos correspondentes a funções quadráticas.

Mãos à obra - página 187

1. Dizer aos estudantes quêque o artifício de determinar uma função para representar cértocerto conjunto de dados é denominado regressão. No exemplo apresentado, foi realizada uma regressão polinomial de grau 2. Se julgar conveniente, propor aos estudantes quêque pesquisem e apresentem exemplos de diferentes tipos de regressão.

2. Em relação à elaboração de um problema envolvendo função quadrática, é importante quêque os estudantes reflitam se os dados apresentados são suficientes para quêque o colega possa resolvê-lo. Para isso, eles podem inicialmente listar algumas perguntas para o problema, por exemplo: Qual é a lei de formação da função ôbitídaobtida na planilha eletrônica? Compare os valores obtidos pela função com os apresentados no qüadroquadro. Em seu entendimento, a função descreve de maneira satisfatória esses dados? Qual é, aproximadamente, a altura mássimamáxima atingida pelo disco? Quanto tempo após o lançamento o disco toca o solo?

Páginas 188 a 191

Estudo do sinal de uma função quadrática

O trabalho com esse tópico aborda diversos conceitos até então estudados na Unidade. Por isso, sugere-se propor uma avaliação formativa para quêque, caso necessário, seja realizada uma retomada de conteúdo. Para a avaliação, pode-se propor aos estudantes quêque façam um resumo de todo o conteúdo quêque estudaram até o momento nesta Unidade. Poderão sêrser direcionados alguns tópicos quêque deverão sêrser abordados no resumo, por exemplo, a posição da concavidade da parábola de acôr-doacordo com o coeficiente a, a determinação dos zeros reais de uma função quadrática, quando existirem, e a interpretação gráfica dêêssesdesses zeros da função. Os estudantes podem elaborar o resumo no próprio caderno, porém sem consulta a material didático. Ao final, o professor poderá selecionar alguns estudantes para apresentar seus resumos.

A seção Atividades das páginas 190 e 191 tem como objetivo trabalhar o estudo do sinal de funções quadráticas. A atividade 55 trabalha o estudo do sinal de uma função quadrática quêque modela uma situação relacionada à análise do comportamento de bactérias de acôr-doacordo com a variação da tempera-túratemperatura. Pode-se sugerir a parceria com um professor da área de Ciências da Natureza e suas Tecnologias para discutir como são realizadas essas análises nos laboratórios.

Páginas 192 a 196

Equação da parábola

Nesse tópico, destacar aos estudantes quêque a abscissa c do foco F não corresponde ao coeficiente c da lei de formação da função quadrática, ou seja, são elemêntoselementos distintos.

Após trabalhar com os estudantes a dedução da equação da parábola cuja diretriz é paralela ao eixo das ordenadas e cujo vértice corresponde à origem do sistema de eixos cartesianos e está localizado à direita da diretriz, propor a eles quêque deduzam a equação de cada um dos demais casos apresentados. Por exemplo, acompanhe, a seguir, essa dedução para o caso da diretriz paralela ao eixo das ordenadas e vértice V (x_v, y_v) qualquer à direita da diretriz.

Página trezentos e quarenta e cinco345

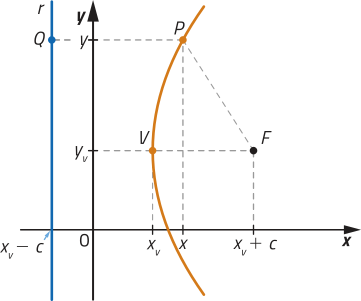
Como a distância de P a F é igual à distância de P a r, segue-se quêque:

PF = PQ ⇒ $\begin{array}{c}\sqrt[]{{\left(x-\left(x_v+c\right)\right)}^2+{\left(y-y_v\right)}^2}=\sqrt[]{{\left(x-\left(x_v-c\right)\right)}^2+{\left(y-y\right)}^2}\end{array}$ ⇒

⇒ (x − (x_v + c))² + (y − y_v)² = (x − (x_v − c))² + (y − y)² ⇒

⇒ y² − 2y y_v + y $\begin{array}{c}2\\ v\end{array}$ = 4cx − 4cx_v ⇒ (y − y_v)² = 4c(x − x_v)

A seção Atividades da página 196 tem como objetivo trabalhar a determinação da equação de uma parábola, bem como das coordenadas de pontos pertencentes a uma parábola a partir de sua representação no plano cartesiano. Também é trabalhada a determinação da equação de uma parábola a partir das coordenadas de três de seus pontos e sua posição em relação ao eixo das ordenadas. A atividade 60 explora a representação de um esboço de uma parábola utilizando um pedaço de barbante, régua e esquadro. Ao final, propor aos estudantes quêque compartilhem entre si as produções.

Páginas 197 a 199

Integrando com Ciências da Natureza e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 2 e da competência específica 3 da área de Ciências da Natureza e suas Tecnologias. Além díssudisso, propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia, uma vez quêque apresenta informações relacionadas à antena parabólica e uma reflekçãoreflexão sobre a importânssiaimportância do acesso às tecnologias de informação e da comunicação por pessoas quêque vivem em áreas remotas.

Verificar a possibilidade de explorar as informações dessas páginas em parceria com um professor da área de Ciências da Natureza e suas Tecnologias, elencando elemêntoselementos próprios da Física, como as transmissões de sinais de som e de vídeo por satélite.

Ao trabalhar o texto sobre a escolha do formato da antena, comentar com os estudantes quêque LNB é a sigla inglesa para a expressão Low-noise block converter (“conversor de baixo ruído”, em tradução livre).

A questão 4 do Pensando no assunto está relacionada ao Tema Contemporâneo Transversal Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras. Comentar com os estudantes quêque, no Brasil, existem diversos povos indígenas, cada um com sua cultura própria. Os textos podem sêrser produzidos pêlospelos grupos de estudantes em formato digital e disponibilizados no sáitisite da escola ou em alguma rê-derede social.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações acerca dos povos indígenas brasileiros.

• POVOS INDÍGENAS NO BRASIL MIRIM. [S. l., 2024]. sáitiSite. Disponível em: https://livro.pw/sopkk. Acesso em: 27 set. 2024.

Páginas 200 e 201

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A quêquestão 4 trabalha a análise de uma parábola que representa um lançamento oblíquo. No item c, verificar quais estratégias os estudantes utilizaram para obtêrobter a lei de formação da função g.

Páginas 202 a 204

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 5 Relações métricas e trigonometria no triângulo

Quadro-síntese da Unidade

Objetivos da Unidade

• Reconhecer a necessidade e a utilização de métodos científicos para obtêrobter e validar resultados, bem como identificar diferenças entre o método científico indutivo e dedutivo.

• Compreender e utilizar o teorema de Tales, o conceito de semelhança de figuras geométricas planas e as relações métricas no triângulo retângulo para resolver problemas em diversos contextos.

• Identificar figuras semelhantes e determinar a razão de semelhança entre elas.

• Compreender os casos de semelhança de triângulos e o teorema fundamental da semelhança.

• Obter e compreender relações quêque envolvem as medidas dos lados e as projeções dos catetos sobre a hipotenusa de um triângulo retângulo, incluindo o teorema de Pitágoras.

• Compreender razões trigonométricas no triângulo retângulo e reconhecer a importânssiaimportância delas na história da humanidade ao contribuírem para a resolução de problemas envolvendo, por exemplo, a determinação de distâncias inacessíveis.

Página trezentos e quarenta e seis346

• Utilizar a tabélatabela trigonométrica para consultar os valores do seno, do cosseno e da tangente de um ângulo agudo.

• Estabelecer razões trigonométricas em um triângulo qualquer: lei dos senos e lei dos cossenos.

Orientações didáticas

Abordar, com os estudantes, as contribuições históricas das relações métricas e das razões trigonométricas em triângulos para a ssossiedadesociedade pódepode ajudá-los no estudo de outros conceitos matemáticos, como as funções trigonométricas, além de possibilitar resolver e elaborar problemas, com ou sem auxílio de recursos tecnológicos, e na compreensão de aplicações em diferentes contextos ou áreas do conhecimento.

Página 205

Abertura da Unidade

O trabalho com a abertura da Unidade favorece, com maior ênfase, o desenvolvimento da competência geral 2 e propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia, pois possibilita um trabalho caracterizado pela análise de métodos científicos, promovendo o desenvolvimento de reflekçõesreflexões associadas ao processo de construção do conhecimento científico.

Promover uma roda de conversa com os estudantes, quêquestionando-os se já pensaram a respeito dos diferentes métodos que podem sêrser utilizados na Ciência. Destacar a responsabilidade dos cientistas ao utilizarem métodos científicos em suas pesquisas por meio da realização de algumas etapas, de modo quêque o conhecimento a sêrser compartilhado seja bem fundamentado. Ressaltar quêque compartilhar as descobertas e os conhecimentos com a ssossiedadesociedade é um dos principais objetivos da Ciência.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Determinar a validade de cértocerto fato.

2. Resposta esperada: No método indutivo, a conclusão é ôbitídaobtida a partir de um caso particular. No método dedutivo, a conclusão é ôbitídaobtida a partir de premissas mais gerais, tidas como verdadeiras e amplamente aceitas.

3. Resposta pessoal. Os estudantes podem citar a demonstração de algum teorema matemático ou a dedução de alguma expressão ou fórmula.

Páginas 206 a 210

Teorema de Tales

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT308 da área de Matemática e suas Tecnologias, pois são realizados estudos envolvendo ideias de congruência e de semelhança de figuras.

Caso seja necessário, para quêque os estudantes compreendam a verificação da validade do teorema de Tales, retomar os conceitos de congruência de triângulos e de proporcionalidade, estudados em anos anteriores.

No trabalho com as demonstrações nas páginas 207 e 208, explicar aos estudantes quêque:

• $\overline{AB}$ se refere a um segmento de reta com extremidades em A e em B;

• AB se refere à medida do segmento de reta com extremidades em A e em B.

Na demonstração do caso 1 da validade do teorema de Tales, relembrar os estudantes de quêque um paralelogramo é um quadrilátero com dois pares de lados opostos paralelos; por isso, pode-se afirmar quêque $\begin{array}{c}\overline{AB}\equiv \overline{DG}\end{array}$ e $\begin{array}{c}\overline{BC}\equiv \overline{EH}\end{array}$. Como foi definido quêque $\begin{array}{c}\overline{AB}\equiv \overline{BC}\end{array}$, segue-se quêque $\begin{array}{c}\overline{DG}\equiv \overline{AB}\equiv \overline{BC}\equiv \overline{EH}\end{array}$. Logo, por transitividade $\begin{array}{c}\overline{DG}\equiv \overline{EH}\end{array}$.

Ao apresentar aos estudantes quêque os ângulos $\begin{array}{c}D\widehat{G}E\equiv E\widehat{H}{F}_{,}\end{array}$ detalhar a demonstração a partir da imagem a seguir.

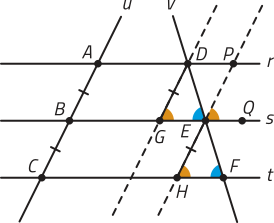
Dadas as retas paralelas s e t e os pontos auxiliares P e Q, contidos nas retas r e s, respectivamente, segue-se quêque os ângulos $\begin{array}{c}E\widehat{H}F\equiv P\widehat{E}Q\end{array}$, pois são correspondentes.

De modo análogo, dadas as retas paralelas quêque contêm os segmentos de reta $\overline{DG}$ e $\overline{EH}$ e os pontos auxiliares P e Q, segue-se quêque os ângulos $\begin{array}{c}P\widehat{E}Q\equiv D\widehat{G}E\end{array}$, pois também são correspondentes.

Como $\begin{array}{c}E\widehat{H}F\equiv P\widehat{E}Q\equiv D\widehat{G}E\end{array}$, segue-se, por transitividade, quêque $\begin{array}{c}D\widehat{G}E\equiv E\widehat{H}F\end{array}$.

As atividades da página 210 têm como objetivo trabalhar situações envolvendo o teorema de Tales. Na atividade 6, é importante avaliar se os problemas elaborados pêlospelos estudantes contemplam as ideias relacionadas ao conceito propôstoproposto. Ao final, alguns dêêssesdesses problemas elaborados podem sêrser reproduzidos na lousa e discutidos com a turma.

Páginas 211 a 215

Semelhança de polígonos

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT308 da área de Matemática e suas Tecnologias, ao abordar as ideias de congruência e semelhança de figuras. Além díssudisso, propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia ao serem explorados os diferentes formatos de vídeo (tela).

Ao trabalhar as informações sobre os formatos de vídeo, argumentar com os estudantes quêque esses formatos também podem sêrser chamados de aspect ratio.

Existem calculadoras ôn láinion-line quêque podem sêrser utilizadas para determinar proporções específicas ao redimensionar fotografias ou vídeos de acôr-doacordo com os formatos de tela de equipamentos quêque utilizamos no dia a dia, como a disponível em https://livro.pw/sxhfr (acesso em: 13 out. 2024).

Propor aos estudantes quêque pesquisem a tradução do termo widescreen (“panorâmico”).

Ao definir semelhança de polígonos, discutir com os estudantes quêque a mesma ideia pódepode sêrser utilizada para semelhança de figuras planas quaisquer. Intuitivamente, duas figuras planas são semelhantes quando têm o mesmo formato, independentemente do tamãnhotamanho. Argumentar quêque o significado da palavra semelhante na Língua Portuguesa é diferente do significado matemático. Na Língua Portuguesa, semelhante pódepode sêrser considerado sinônimo de “parecido”. Em Matemática, duas figuras parecidas não são necessariamente semelhantes.

No tópico Semelhança de triângulos, comentar com os estudantes quêque o pantógrafo, criado no início do século XVII pelo astrônomo Christoph Scheiner (1573-1650), tem como principal função ampliar ou reduzir figuras, mantendo seu formato.

O estudo da semelhança de triângulos possivelmente foi propôstoproposto em anos anteriores. Portanto, é importante quêque sêjamsejam resgatados os conhecimentos prévios dos estudantes e valorizadas as experiências de cada um deles. Destinar um tempo para quêque eles comentem esse conceito, manifestando suas impressões e possíveis dificuldades. É importante quêque os estudantes compreendam a necessidade de estabelecer casos de semelhança de triângulos, por exemplo, quando não é possível obtêrobter a medida de todos os lados de um triângulo.

Página trezentos e quarenta e sete347

Atividade Extra

Os três casos de semelhança de triângulos enunciados nas páginas 212 e 213 podem sêrser demonstrados. Com dois côlégascolegas, escôlhamescolham um dêêssesdesses casos, pesquisem e analisem uma demonstração da validade do caso de semelhança de triângulos escolhido. Depois, apresentem essa demonstração aos côlégascolegas. Vocês podem utilizar slides para isso.

Após a realização da atividade ésstraextra proposta, ressaltar para os estudantes quêque as demonstrações têm grande importânssiaimportância na Matemática. Por meio delas, as proposições matemáticas são consideradas socialmente verdadeiras. Aproveitar essa discussão para associá-la ao tema da abertura da Unidade, argumentando quêque grande parte das demonstrações matemáticas utiliza o método dedutivo.

Na atividade R3, trabalha-se semelhança de polígonos em uma situação quêque envolve um jôgojogo. As etapas apresentadas estão associadas à resolução de problemas. Sugere-se estruturar e executar essas etapas, como foi apresentado, sempre quêque perceber quêque os estudantes estão com dificuldades em determinado problema matemático. Para complementar, conversar com os estudantes sobre o tema dessa atividade em conjunto com um professor da área de Ciências da Natureza e suas Tecnologias, quêque poderá auxiliar com a proposta de experimentos e a utilização de argumentos, próprios de sua área, a respeito dos ângulos de incidência e rebatimento obtidos do ponto de vista da óptica.

As atividades da página 215 têm como objetivos principais trabalhar a semelhança de polígonos e o cálculo da razão de semelhança entre eles e explorar a semelhança de triângulos e o teorema fundamental da semelhança.

Páginas 216 a 220

Relações métricas no triângulo retângulo

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT308 da área de Matemática e suas Tecnologias, ao abordar as relações métricas no triângulo retângulo para elaborar e resolver problemas.

O estudo das relações métricas no triângulo retângulo foi abordado em anos anteriores; por isso, propor uma avaliação diagnóstica a fim de identificar possíveis dificuldades dos estudantes. Sugere-se desenhar na lousa um triângulo retângulo, indicando sua altura em relação à hipotenusa e demais elemêntoselementos, conforme apresentado na página 216. A partir díssudisso, quêquestionar os estudantes acerca das relações que podem sêrser estabelecidas considerando os elemêntoselementos dados.

Ao demonstrar quêque o triângulo DBA é semelhante ao triângulo DAC, na página 217, argumentar com os estudantes quêque essa conclusão somente pódepode sêrser considerada por causa da propriedade transitiva, quêque é válida para semelhança de triângulos.

Conexões

Ao abordar o boxe Matemática na história da página 218, sugerir aos estudantes a leitura do livro a seguir, quêque apresenta textos a respeito da vida e da obra do filósofo e matemático grego Pitágoras de Samos.

• STRATHERN, poouPaul. Pitágoras e seu teorema em 90 minutos. Tradução: Marcus Penchel. 2. ed. Rio de Janeiro: Jorge ZarrárZahar Editor, 1998. (Coleção Cientistas em 90 minutos).

A seção Atividades das páginas 219 e 220 tem como objetivo explorar as relações métricas em um triângulo retângulo. A atividade 18 trabalha uma exploração geométrica do teorema de Pitágoras. Antes de os estudantes resolverem os itens propostos, apresentar outros exemplos de ternos pitagóricos, como os indicados a seguir.

• 9, 12 e 15. • 5, 12 e 13. • 8, 15 e 17.

Perguntar à turma por quêpor que esses exemplos podem sêrser considerados ternos pitagóricos. Espera-se quêque os estudantes digam quêque são números naturais quêque podem representar as medidas dos catetos e da hipotenusa de um triângulo retângulo.

Páginas 221 a 230

Razões trigonométricas no triângulo retângulo

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência geral 1, da competência específica 3 e da habilidade EM13MAT308 da área de Matemática e suas Tecnologias, pois trata de relações entre as medidas de lados e ângulos internos de triângulos. No tópico, são abordadas situações com o objetivo de promover ações coletivas quêque melhorem as condições de vida em âmbito local e regional, o quêque propicíapropicia um trabalho com a competência específica 1 da área de Ciências da Natureza e suas Tecnologias e do Tema Contemporâneo Transversal Educação em Direitos Humanos.

Antes de iniciar a discussão sobre as normas da Associação Brasileira de Normas Técnicas (ABNT), realizar uma roda de conversa com os estudantes a fim de problematizar a importânssiaimportância de diretrizes gerais a sêrser estabelecidas para garantir ao maior número de pessoas a utilização dos espaços de maneira autônoma. Dizer quêque a criação dessas diretrizes possibilita promover a equidade, a valorização dos direitos humanos e a garantia da acessibilidade. Possibilitar aos estudantes quêque reconheçam quêque esse tipo de iniciativa promove o respeito a diferentes pessoas, a acessibilidade, o combate à violência e a valorização da saúde mental.

Explicar aos estudantes quêque a norma NBR 9050 da ABNT estabelece critérios e parâmetros voltados à acessibilidade em edificações, mobiliário, espaços e equipamentos urbanos.

Ao abordar a página 222, sugere-se trabalhar com ideias da investigação matemática, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor. Para isso, propor aos estudantes quêque, em uma malha quadriculada ou em um software de geometria dinâmica, como o GeoGebra, esbocem um triângulo retângulo ABC, destacando o ângulo reto e um ângulo interno agudo (alfa)"α. Em seguida, solicitar quêque construam segmentos de reta paralelos ao cateto ôpôstooposto a (alfa)"α, de maneira a obtêrobter triângulos semelhantes ao triângulo ABC, assim como apresentado na página 221. Por fim, considerando os diferentes triângulos retângulos obtidos, pedir a eles quêque determinem a razão entre as medidas:

• do cateto ôpôstooposto a (alfa)"α e da hipotenusa;

• do cateto adjacente a (alfa)"α e da hipotenusa;

• do cateto ôpôstooposto a (alfa)"α e do cateto adjacente a (alfa)"α.

O objetivo é quêque os estudantes percêbampercebam quêque cada uma dessas razões é sempre igual nos diferentes triângulos retângulos e quêque atribuam significados a essas razões, reconhecendo, com o trabalho dêêssedesse tópico, a necessidade do desenvolvimento da trigonometria.

As atividades da página 224 têm como objetivo trabalhar as razões trigonométricas no triângulo retângulo. A atividade 25 trabalha a representação de um triângulo retângulo pêlospelos estudantes com o uso de instrumentos de desenho e relações trigonométricas. Verificar os procedimentos utilizados pêlospelos estudantes na representação do triângulo retângulo e solicitar a um deles quêque apresente o modo como fez a construção para o restante da turma.

As atividades das páginas 227 a 230 abordam as razões trigonométricas no triângulo retângulo em variados contextos, incluindo a consulta à tabélatabela trigonométrica. Na atividade 35, destacar para os estudantes quêque o comprimento de uma sombra e a medida do ângulo formado pêlospelos raios solares com o solo não são grandezas diretamente proporcionais, ou seja, se dobrarmos o comprimento da sombra, as medidas dos ângulos não serão necessariamente dobradas também.

Página trezentos e quarenta e oito348

A atividade 37 trabalha a investigação de conjecturas por meio de uma tabélatabela trigonométrica. Para complementar, apresentar aos estudantes a demonstração de pelo menos uma das conjecturas quêque podem sêrser exploradas, por exemplo, sen (alfa)"α = cos (90° − (alfa)"α), com 0° < (alfa)"α < 90°.

Demonstração: Considere um triângulo ABC, com lados medindo a, b e c, com a, b, c ∈ $\begin{array}{c}{\mathrm{R}}_{+}^{*}\end{array}$ e ângulos internos medindo 90°, (alfa)"α e (beta)"β, conforme representado a seguir.

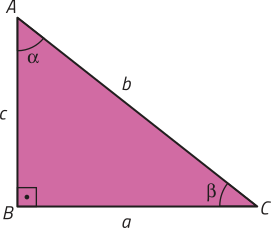
Assim, segue-se quêque sen (alfa)"α = $\frac{a}{b}$ e cos (beta)"β = $\frac{a}{b}$^. Portanto, sen (alfa)"α = cos (beta)"β.

Como (beta)"β = 90° − (alfa)"α, segue-se quêque: sen (alfa)"α = cos (90° − (alfa)"α), para 0° < (alfa)"α < 90°.

Aproveitar a temática da atividade 39 para desenvolver com os estudantes, se for conveniente, um projeto em parceria com um professor da área de Ciências da Natureza e suas Tecnologias sobre o tema sustentabilidade no uso da energia solar. Explorar kestõesquestões sociais, geográficas, físicas, biológicas e matemáticas associadas a esse tema. Desenvolver o projeto de modo quêque, ao final, os estudantes produzam fôlderes de divulgação para conscientizar os demais côlégascolegas da escola e a comunidade local a respeito dos benefícios do uso da energia solar.

No boxe No mundo do trabalho da página 230, perguntar aos estudantes se eles conhecem algum profissional quêque trabalhe nessa área. Em caso afirmativo, propor quêque, se possível, conversem com esse profissional, quêquestionando o que o atraiu nessa profissão e quais são os principais desafios enfrentados. Os estudantes também podem realizar uma pesquisa detalhada a respeito das profissões mencionadas e apresentar aos côlégascolegas por meio de exposição oral ou de cartazes.

Páginas 231 a 233

Integrando com Ciências Humanas e Sociais Aplicadas

O trabalho com essa seção, ao abordar a resolução de problemas por meio do uso de conhecimentos sobre as razões trigonométricas no triângulo retângulo, favorece, com maior ênfase, o desenvolvimento das competências gerais 1, 2 e 7, da competência específica 3 e da habilidade EM13MAT308 da área de Matemática e suas Tecnologias.

Inicialmente, questionar os estudantes sobre o termo acessibilidade e sua importânssiaimportância para quêque manifestem suas impressões e opiniões relacionadas ao tema. É relevante quêque, neste momento, seja discutido o fato de quêque a acessibilidade procura promover o respeito e a equidade entre as pessoas, de maneira quêque seus direitos e suas necessidades específicas sêjamsejam considerados.

No boxe No mundo do trabalho, promover uma roda de conversa com os estudantes a respeito do quêque eles entendem pelo termo empatia. Destacar quêque, independentemente de essa sêrser uma habilidade buscada no mercado de trabalho, a empatia deve sêrser praticada em qualquer relação humana e em todos os lugares, como na sala de aula, com os côlégascolegas de turma, com os professores e funcionários da escola.

Sugere-se quêque a questão 6 do Pensando no assunto seja desenvolvida, em grupos, de acôr-doacordo com etapas da modelagem matemática, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor, quêque pódepode sêrser organizada, para essa situação, em cinco etapas.

1ª) Reconhecimento/definição da situação-problema: Os estudantes reconhecem a situação-problema, quêque se associa ao cumprimento da norma NBR 9050 nas rampas no município em quêque moram.

2ª) Elaboração de hipóteses: Os estudantes elaboram hipóteses, considerando as experiências e os conhecimentos quêque têm a respeito das rampas no município em quêque moram. É importante quêque eles considerem quais rampas possibilitam uma análise mais aprofundada e quêque antecipem resultados quêque possam surgir.

3ª) Exploração da situação-problema: A partir das hipóteses elaboradas na 2ª etapa, os estudantes investigam informações relacionadas às rampas consideradas, buscando resolver a situação-problema.

4ª) Determinação do modelo matemático: Os estudantes buscam organizar as informações obtidas na 3ª etapa por meio de tabélatabela, gráfico, esquema etc. A ideia é organizar as informações para quêque sêjamsejam apresentadas ou divulgadas a outras pessoas a fim de quêque sêjamsejam compreendidas com facilidade.

5ª) Discussão dos resultados: Os grupos apresentam aos côlégascolegas os resultados quêque obtiveram.

No item b da quêquestão 6, comentar a determinação de quêque a altura de desnível seja de até 0,8 m, pois, para alturas maiores que essa, é necessário havêerhaver mais de um lance de rampa ou reduzir-se o ângulo de inclinação mássimamáxima. Verificar cada rampa escolhida pêlospelos grupos, orientando-os a não avaliar uma mesma rampa, de maneira quêque seja analisado o maior número de rampas possível.

Páginas 234 a 241

Razões trigonométricas em um triângulo qualquer

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT308 da área de Matemática e suas Tecnologias, uma vez quêque aborda, entre outros aspectos, as leis dos senos e dos cossenos na elaboração e na resolução de problemas.

Discutir com os estudantes quêque, anteriormente, o estudo do seno, do cosseno e da tangente era associado a ângulos de triângulos retângulos. Por esse motivo, os ângulos considerados, além do ângulo reto, eram agudos.

Na demonstração da lei dos senos, se necessário, retomar alguns conceitos, como os apresentados a seguir.

• Chama-se ângulo inscrito em uma circunferência todo ângulo cujo vértice está sobre a circunferência e cujos lados passam por outros pontos distintos dela.

• Um ângulo inscrito em uma circunferência tem vértice em V, lados quêque passam pêlospelos pontos A e B e medida (alfa)"α, sêndosendo V, A e B pontos sobre essa circunferência. Se outro ângulo inscrito nessa mesma circunferência tem vértice em U, distinto de V, e lados quêque passam pêlospelos mesmos pontos A e B, então esse ângulo também tem medida (alfa)"α.

As atividades das páginas 236 e 237 têm como objetivo trabalhar a lei dos senos em diferentes contextos. Na atividade 44, quêque propõe a elaboração de um problema envolvendo a lei dos senos, destacar aos estudantes quêque eles podem propor um problema quêque, por falta de dados no enunciado, não seja possível resolver. Por exemplo, de acôr-doacordo com o contexto escolhido, pode-se descrever uma região modelada por um triângulo em quêque sêjamsejam identificadas apenas as medidas de dois lados, apenas as medidas de um lado e de um ângulo interno ou apenas as medidas de dois ângulos internos. É importante, nesse caso, quêque os estudantes quêque receberem

Página trezentos e quarenta e nove349

o problema identifiquem a falta de dados do enunciado e façam sugestões de ajustes, de maneira a tornar possível sua resolução.

No tópico Lei dos cossenos, após a realização da demonstração da lei dos cossenos para triângulos acutângulos, apresentar aos estudantes as demonstrações da lei dos cossenos para triângulos obtusângulos e triângulos retângulos.

Triângulo obtusângulo

Considerar o triângulo ABC, cujos lados médemmedem a, b e c, e o ângulo _obtuso (alfa)"α em A. Traçando a altura do triângulo relativa ao lado $\overline{AB}$, são obtidas as medidas m e h, conforme representado a seguir.

Como os triângulos BCH e ACH são retângulos, pode-se utilizar o teorema de Pitágoras e obtêrobter as equações a seguir.

• h² + (c + m)² = a²

• h² + m² = b²

Subtraindo, membro a membro, essas duas equações, tem-se:

(c + m)² − m² = a² − b² ⇒ c² + 2cm + m² − m² = a² − b² ⇒

⇒ a² = b² + c² + 2cm (I)

Tem-se, ainda, quêque o ângulo $H\widehat{A}$ C é suplementar ao ângulo (alfa)"α, ou seja, tem medida igual a (180° − (alfa)"α). Assim:

cos (180° − (alfa)"α) = $\frac{m}{b}$

Como cos (180° − (alfa)"α) = −cos (alfa)"α, segue-se quêque cos (alfa)"α = − $\frac{m}{b}$ ⇒ ⇒ m = −b ⋅ cos (alfa)"α.

Substituindo m na equação I, tem-se quêque:

a² = b² + c² − 2 ⋅ b ⋅ c ⋅ cos (alfa)"α

De maneira análoga, pode-se verificar quêque:

• b² = a² + c² − 2 ⋅ a ⋅ c ⋅ cos $\widehat{B}$

• c² = a² + b² − 2 ⋅ a ⋅ b ⋅ cos $\widehat{C}$

Triângulo retângulo

Considerar um triângulo retângulo ABC, com lados de medidas a, b e c e ângulo reto em A.

Como o triângulo ABC é retângulo, pode-se utilizar o teorema de Pitágoras:

a² = b² + c²

Como −2 ⋅ b ⋅ c ⋅ cos 90° = 0, pode-se escrever a equação:

a² = b² + c² − 2 ⋅ b ⋅ c ⋅ cos 90°

As atividades das páginas 240 e 241 têm como objetivo trabalhar a lei dos cossenos, seja em situações contextualizadas, seja em situações estritamente matemáticas. Ao trabalhar a atividade 52, verificar a possibilidade de desenvolvê-la em parceria com um professor da área de Ciências da Natureza e suas Tecnologias. Pode-se planejar, por exemplo, uma proposta para quêque os estudantes realizem pesquisas em pequenos grupos sobre diferentes grandezas vetoriais e escalares. Explicar a eles quêque grandezas escalares são aquelas representadas apenas por um valor numérico (módulo) e uma unidade, como massa, tempera-túratemperatura e energia. No item a, discutir com os estudantes a diferença entre módulo, direção e sentido. Dizer quêque módulo é o valor numérico do vetor, cuja unidade é definida pela natureza da grandeza vetorial. A direção associa-se à posição em quêque se encontra o vetor, isto é, se está na diagonal, na vertical ou na horizontal. O sentido, por sua vez, refere-se à orientação do vetor, ou seja, se está orientado para norte, sul, leste, oeste, direita, esquerda, para cima, para baixo etc.

Com a finalidade de verificar se os estudantes compreenderam as razões trigonométricas, bem como a sua importânssiaimportância para a resolução de problemas, sugere-se propor uma prova-escrita-com-cola, conforme apresentado na parte geral destas Orientações para o professor. Para isso, propor aos estudantes quêque elaborem um resumo das razões trigonométricas estudadas, contendo os principais pontos, na mêtádemetade de uma fô-lhafolha avulsa. É importante quêque os estudantes elaborem suas “colas” individualmente e quêque esta seja entregue com a próvaprova resolvida. A próvaprova aplicada pódepode sêrser composta, também, de algumas kestõesquestões da seção Praticando: enêmEnem e vestibulares, disponível no final dessa Unidade.

Páginas 242 e 243

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, na medida em quêque utiliza tecnologias digitais d fórmade forma significativa para produzir conhecimentos e resolver problemas. Além díssudisso, possibilita o desenvolvimento da competência específica 3 e da habilidade EM13MAT308 da área de Matemática e suas Tecnologias.

Nessa seção, é importante quêque os estudantes consigam investigar a lei dos senos utilizando o GeoGebra. Por meio dessa tecnologia digital, eles podem produzir significado para essa relação trigonométrica, quêque foi sistematizada no decorrer do estudo desta Unidade.

Na etapa B, explicar aos estudantes quêque, na fórmula, (alfa)"α e a correspondem, respectivamente, às medidas do ângulo e do lado ôpôstooposto a esse ângulo no triângulo construído na etapa A. Ressaltar para os estudantes quêque, ao construírem essas representações no GeoGebra, é importante quêque mantenham as nomenclaturas correspondentes na fórmula inserida. Dizer quêque eles podem modificar os rótulos dêêssesdesses objetos de acôr-doacordo com o lado e o ângulo ôpôstooposto tomados como referência. Para isso, basta quêque selecionem o objeto, cliquem com o botão direito do máuzimouse e, em seguida, escôlhamescolham a opção Renomear.

Mãos à obra - página 243

1. Para complementar essa quêquestão, comparar com os estudantes a demonstração da lei dos senos realizada anteriormente nesta Unidade e sua verificação para o triângulo construído no GeoGebra nessa seção. Explicar que uma demonstração valídavalida um resultado de maneira generalizada, enquanto uma verificação valídavalida esse resultado apenas para um caso específico.

3. Essa quêquestão trabalha a verificação da lei dos cossenos para um triângulo qualquer no GeoGebra. Para complementar, escolher uma dupla de estudantes para apresentar a verificação que realizaram aos demais côlégascolegas.