RESOLUÇÕES DAS ATIVIDADES PROPOSTAS NO LIVRO DO ESTUDANTE
Unidade 1 • Conjuntos
1. A = {c, h, i, k}, B = {b, c, e, f, g, j, k} e C = {a, c, d, e, f, h}
2. a) A = {2, 4, 6}, B = {1, 2, 3, 4, 6, 12} e C = {1, 4, 9, 16, 25}
b) Sim, A é subconjunto de B, pois todo elemento de A também é elemento de B.
3. Respostas possíveis: ∅, {3, 6, 9}, {3, 6}, {3, 9}, {6, 9}, {3}, {6}, {9}.
4. 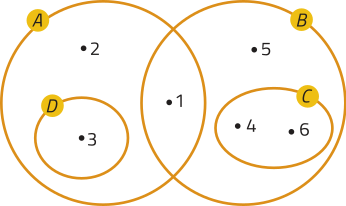
a) D ⊂ A
b) B ⊄ C
c) A ⊄ B
d) C ⊂ B
e) ∅ ⊂ D
f) B ⊄ D
5. Resposta possível: ∅ ⊂ A; B ⊄ A.
6. a) 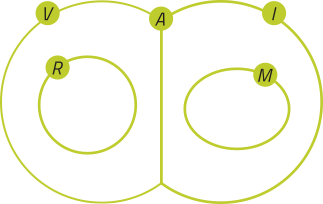
b) I ⊂ V
• V ⊂ A é verdadeiro, pois todo vertebrado é animal.
• I ⊂ V é falso, pois nenhum invertebrado é vertebrado.
• M ⊂ A é verdadeiro, pois todo molusco é invertebrado e todo invertebrado é animal; logo, todo molusco é animal.
• R ⊂ V é verdadeiro, pois todo réptil é vertebrado.
c) Uma tartaruga é um réptil (R), todo réptil é vertebrado (V) e todo vertebrado é animal (A). Portanto, a tartaruga é elemento de A, V e R.
7. a) Analisando as informações apresentadas na planilha, temos quê: 3 funcionários são do setor de produção (Antônio, Keila e Rosana) e 2 funcionários têm idade inferior a 30 anos (Bruna e Rosana).
b) Resposta esperada: Não, pois existe um funcionário nessa faixa etária quê é do setor de produção; no caso, Antônio, com 36 anos de idade.
c) Keila
d) Resposta possível: Selecionar apenas funcionários com idade inferior a 30 anos.
8. Resposta pessoal.
9. Considerando os conjuntos A = {−4, −2, 0, 2, 4}, B = {0, 1, 2, 3, 4} e C = {−2, 5, 7, 9}, temos:
a) A ∪ C = {−4, −2, 0, 2, 4, 5, 7, 9}
b) C ∩ A = {−2}
c) B ∩ C = ∅
d) A ∩ B = {0, 2, 4} C ∪ (A ∩ B) = {−2, 0, 2, 4, 5, 7, 9}
e) B − A = {1, 3}
f) B ∪ C = {−2, 0, 1, 2, 3, 4, 5, 7, 9} A − (B ∪ C) = {−4}
g) A − C = {−4, 0, 2, 4} B ∩ (A − C) = {0, 2, 4}
h) A ∪ B = {−4, −2, 0, 1, 2, 3, 4} A ∩ B = {0, 2, 4} (A ∪ B) − (A ∩ B) = {−4, −2, 1, 3}
10. Alternativa b, pois a parte destacada em vêrde no diagrama corresponde aos elemêntos quê pertencem aos conjuntos A ou B e não pertencem ao conjunto C, expressa por (A ∪ B) − C.
a: C − (A ∪ B); c: (A ∪ B); d: C
11. a) F, pois B ∪ C = {d, e, f, g, h}
b) V, pois B ⊂ A
c) V, pois A = {a, b, c, d, e}
d) F, pois C ∪ A = {a, b, c, d, e, f, g, h}, ou seja, n(C ∪ A) = 8
e) V, pois, como B ⊂ A, temos = A − B = {a, b, c, e}
f) F, pois B − A = ∅
12. a) Resposta esperada: Não é possível resolver o problema, pois, considerando a relação n(A ⋂ B) = n(A) + n(B) − n(A ∩ B), para determinar n(A), além das informações apresentadas sobre n(A ∪ B) e n(A ⋂ B), ainda é necessário saber o valor de n(B).
b) Resposta esperada: Para resolver o problema, é necessário conhecer, além dos dados apresentados, a quantidade de elemêntos do conjunto B. Assim, se considerarmos n(B) = 21, temos: n(A ∪ B) = n(A) + n(B) − n(A ∩ B) ⇒ 31 = n(A) + 21 − 12 ⇒ n(A) = 22; ou seja, se indicarmos no enunciado quê o conjunto B tem 21 elemêntos, podemos determinar quê o conjunto A tem 22 elemêntos.
13. a) Cinco regiões: Centro-Oeste, Nordeste, Norte, sudéste e Sul. Resposta pessoal.
b) 27 unidades da Federação, sêndo 26 estados e um Distrito Federal. Resposta pessoal.
c) As respostas dependem da região em quê os estudantes moram.
d) Conjunto formado pelas unidades da Federação localizadas nas regiões do Brasil em quê os estudantes não moram. A quantidade de elemêntos dêêsse conjunto depende da região em quê os estudantes moram.
14. a) Uma possível resposta:
• Identificar os elemêntos de A ∪ B, A − B e B − A.
• Determinar B = (A ∪ B) − (A − B) = {−5, 2, 3, 4, 8}.
• Determinar A = (A ∪ B) − (B − A) = {−5, −1, 2, 6}.
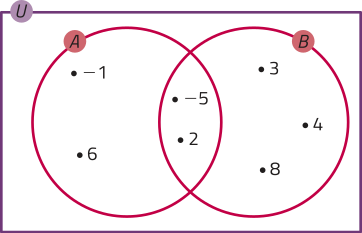
b) Resposta pessoal.
15. Considerando F, T e V os conjuntos de pessoas quê estudam, respectivamente, flauta, teclado e violão, temos o seguinte diagrama de Venn:
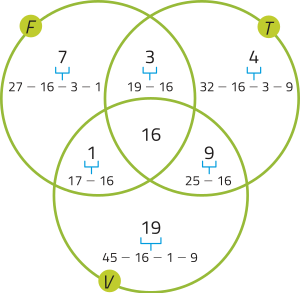
Assim, o total de pessoas quê estudam nessa escola é: 7 + 4 + 19 + 3 + 1 + 9 + 16 = 59 → 59 pessoas
16. Considere os conjuntos:
P: conjunto dos sócios quê usaram a piscina
A: conjunto dos sócios quê usaram a academia
No diagrama de Venn, temos:
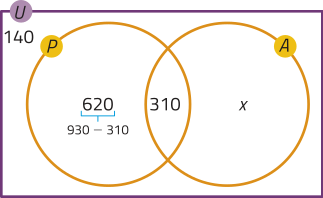
No diagrama, x é a quantidade de sócios quê utilizaram apenas a academia. Como há um total de 1 450 sócios, temos:
620 + 310 + x + 140 = 1 450 ⇒ x = 380
Portanto, 380 sócios.
b) Resposta pessoal.
17. a) 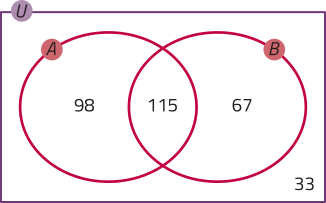
b) 98 + 115 + 67 + 33 = 313 → 313 estudantes
c) • Dupla Adulto (dT): 98 + 115 = 213 → 213 estudantes
Página trezentos e cinquenta e sete
• HPV: 67 + 115 = 182 → 182 estudantes
• Ambas as vacinas: 115 estudantes
d) 98 + 115 + 67 = 280 → 280 estudantes
e) A quantidade de doses de vacína Dupla Adulto (dT) e de HPV corresponde, respectivamente, a n( )e n ( ), ou seja:
• Dupla Adulto (dT): 67 + 33 = 100 → 100 vacinas
• HPV: 98 + 33 = 131 → 131 vacinas
18. n(A ∪ B) = n(A) + n(B) − n(A ⋂ B) ⇒ n(A ∪ B) = 35 + 49 − 23 ⇒ n(A ∪ B) = 61
Logo, 100 − 61 = 39 → 39 pessoas.
19. Elaboração do estudante. Resposta possível: Analisando os dados da tabéla, determine o porcentual de domicílios brasileiros quê não tí-nhão automóvel nem motocicleta em 2022. Resolução: O porcentual de domicílios brasileiros quê tí-nhão automóvel ou motocicleta em 2022 é dado por 49,8% + 25,0% − 13,1% = 61,7%. Assim, o porcentual de domicílios brasileiros quê não tí-nhão automóvel nem motocicleta em 2022 é dado por 100% − 61,7% = 38,3%.
Integrando com...
1. Respostas pessoais.
2. A − B: É o tipo sangüíneo de indivíduos cujas hemácias apresentam apenas o antígeno A, ou seja, sangue tipo A.
A ∩ B: É o tipo sangüíneo de indivíduos cujas hemácias apresentam o antígeno A e o antígeno B, ou seja, sangue tipo AB.
B − A: É o tipo sangüíneo de indivíduos cujas hemácias apresentam apenas o antígeno B, ou seja, sangue tipo B.
U − (A ∪ B): É o tipo sangüíneo de indivíduos cujas hemácias não apresentam o antígeno A nem o antígeno B, ou seja, sangue tipo O.
3. a) Resposta esperada: Apesar de o doador apresentar em suas hemácias o mesmo antígeno B do receptor, ele também apresenta em suas hemácias o antígeno Rh (Rh+), o quê o torna incompatível com o receptor, quê não tem o antígeno Rh (Rh−).
b) Resposta esperada: Como o doador apresenta o mesmo antígeno A do receptor e tem ausência de antígeno Rh (Rh−) em suas hemácias, ele é compatível com o receptor.
4. a) É doador para: A+, A−, AB+ e AB−. É receptor de: A− e O−.
b)
O− |
RECEBE DE |
O− |
|---|---|---|
DOA PARA |
O− O+ A− A+ B− B+ AB− AB+ |
O+ |
RECEBE DE |
O− O+ |
|---|---|---|
DOA PARA |
O+ A+ B+ AB+ |
A− |
RECEBE DE |
O− A− |
|---|---|---|
DOA PARA |
A− A+ AB− AB+ |
A+ |
RECEBE DE |
O− O+ A− A+ |
|---|---|---|
DOA PARA |
A+ AB+ |
B− |
RECEBE DE |
O− B− |
|---|---|---|
DOA PARA |
B− B+ AB− AB+ |
B+ |
RECEBE DE |
O− O+ B− B+ |
|---|---|---|
DOA PARA |
B+ AB+ |
AB− |
RECEBE DE |
O− A− B− AB− |
|---|---|---|
DOA PARA |
AB− AB+ |
AB+ |
RECEBE DE |
O− O+ A− A+ B− B+ AB− AB+ |
|---|---|---|
DOA PARA |
AB+ |
c) Resposta esperada: O doador universal corresponde ao tipo O−, pois ele póde doar sangue a todos os tipos sangüíneos; e o receptor universal corresponde ao tipo AB+, pois ele póde receber sangue de todos os tipos sangüíneos.
5. Respostas pessoais.
20. a) 2,5 ∉ ℤ
b) −3 ∉ ℕ
c) 0 ∈ ℤ
d) ∈ ℚ
e) 54 ∈ ℕ
f) −5,8 ∉ ℤ
g) 9 ∈ ℚ
h) −7,6 ∈ ℚ
21. a) A = {1, 2, 3, 4, 6, 12}
b) B = {−1, 0, 1, 2, 3}
c) A ∪ B = {−1, 0, 1, 2, 3, 4, 6, 12}
d) A ∩ B = {1, 2, 3}
22. a) = 7 ∶ 9 = 0,777... = 0,
b) = 26 ∶ 5 = 5,2
c) = 83 ∶ 90 = 0,9222... = 0,9
d) = 17 ∶ 250 = 0,068
23. a) 0,65 =
b) 8,024 =
c) = 2,777...
x = 2,777...
10x = 27,777...
10x = 25 +
10x = 25 + x
9x = 25
x =
d) 3,9 = 3,9555...
x = 3,9555...
10x = 39,555...
100x = 395,555...
100x = 356 +
100x = 356 + 10x
90x = 356
x =
24. 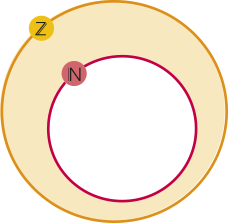
Resposta: Os números inteiros negativos.
25. Respostas pessoais. Nos itens a e b, espera-se quê os estudantes determinem dois números racionais e, posteriormente, outros contidos no intervalo por eles determinado.
No item c, espera-se quê os estudantes percêbam quê sempre é possível determinar um número racional compreendido entre outros dois números racionais dados.
No item d, uma estratégia é determinar o número racional c como a média aritmética dos números racionais a e b.
26. a)
b)
c)
27. alternativa c
= 3 ∶ 4 = 0,75
0,75 ⋅ 2,54 = 1,905 → 1,905 cm
Logo, a medida está, em centímetros, entre 1,5 e 2.
• Resposta esperada: Não, o comprimento do cano, por exemplo, é um dado desnecessário para a resolução desta atividade.
28. a) • Para n = 0: x = 2 ⋅ 0 + 1 = 1
• Para n = 1: x = 2 ⋅ 1 + 1 = 3
• Para n = 2: x = 2 ⋅ 2 + 1 = 5
• Para n = 3: x = 2 ⋅ 3 + 1 = 7
• Para n = 4: x = 2 ⋅ 4 + 1 = 9
• Para n = 5: x = 2 ⋅ 5 + 1 = 11
⋮
Página trezentos e cinquenta e oito
Algumas respostas possíveis: 1; 3; 5; 7; 9; 11.
b) II
c) Os números naturais pares são os números da forma 2n, com n ∈ ℕ.
Assim, B = {x | x = 2n, com n ∈ ℕ}.
d) Resposta esperada: Nenhum elemento, pois A ∩ B = ∅, uma vez quê não há número quê seja simultaneamente par e ímpar.
29. 12 = 1; 22 = 4; 32 = 9; 42 = 16;
52 = 25; 62 = 36; 72 = 49;
82 = 64; 92 = 81; 102 = 100;
112 = 121; 122 = 144
a) Resposta pessoal.
b) número par: 3422 e 2.7782; número ímpar: 1.6552 e 812
• Resposta pessoal.
c) Resposta esperada: Se um número natural é par, então seu quadrado também é par. Se um número natural é ímpar, então seu quadrado também é ímpar.
30. a) hí eme cê (fev.) = ≃ 31,6
obesidade, pois 31,6 > 30
b) 64,8 − 83,9 = −19,1 → redução de 19,1 kg
c) hí eme cê (nov.) = ≃ 24,4
Resposta esperada: Sim, pois, para sêr classificado como "peso adequado", o hí eme cê deve estar entre 18,5 kg/m2 e 25 kg/m2, e o hí eme cê de Sueli, no mês de novembro, foi de aproximadamente 24,4 kg/m2.
d) Resposta pessoal.
31. a) Amazonas: 13,9; Ceará: 11,6;
Goiás: 11,4; Santa Catarina: 9,3;
Rio de Janeiro: 12,6
b) Respostas possíveis: Sim, ao compararmos, por exemplo, a maior taxa de mortalidade calculada com a menor taxa de mortalidade calculada, há uma diferença de 4,6 óbitos de menóres de 1 ano de idade, valor significativo quando expresso em números absolutos. Não, ao compararmos, por exemplo, a taxa de mortalidade do estado do Ceará com a de Goiás, com a diferença de apenas 0,2 óbito de menóres de 1 ano por 1.000 nascidos vivos.
c) Resposta pessoal.
d) Resposta pessoal.
32. a) Veículo 1: ≃ 8,97 km/L;
veículo 2: ≃ 7,5 km/L;
veículo 3: ≃ 8,5 km/L;
veículo 4: ≃ 6,97 km/L;
veículo 5: ≃ 9,3 km/L.
b) Calculando 85% de 8,5 km/L, temos: 0,85 ⋅ 8,5 = 7,225 → 7,255 km/L
Comparando os resultados obtidos no item a, apenas o veículo 4 está com consumo inferior a 7,255 km/L (6,97 < 7,255).
33. a) Ensino Fundamental – Anos Iniciais, pois 0,98 > 0,96 > 0,90.
b) Ensino Fundamental – Anos Iniciais: I = 0,98 ⋅ ⇒ I = 0,98 ⋅ 5,8 ⇒ I = 5,684
Ensino Fundamental – Anos Finais: I = 0, 98 ⋅ ⇒ I = 0,96 ⋅ 5,45 ⇒ I = 5,232
Ensino Médio: I = 0, 90 ⋅ ⇒ I = 0,90 ⋅ 4,1 ⇒ I = 3,690
• Resposta pessoal.
34. a) • Norte: ≃ 4,51 → aproximadamente 4,51 hab./km2
• Nordeste: ≃ 35,21 → aproximadamente 35,21 hab./km2
• sudéste: ≃ 91,76 → aproximadamente 91,76 hab./km2
• Sul: ≃ 51,91 → aproximadamente 51,91 hab./km2
Centro-Oeste: ≃ 10,14 → aproximadamente 10,14 hab./km2
b) Resposta esperada: Sim, pois a densidade demográfica varia consideravelmente de uma região para outra do Brasil.
c) Resposta pessoal.
35. a) Irracional, pois
b) Racional, pois 2 = .
c) Racional, pois = −2.
d) Irracional, pois
e) Racional.
f) Irracional, pois é o quociente de um número irracional ((pi)") com um racional diferente de zero (3).
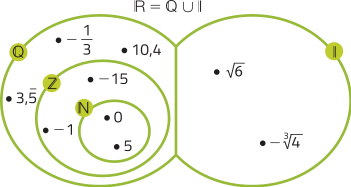
36. 
37. Resposta esperada: Considerando um triângulo equilátero ABC de lado 2 cm e D o ponto médio de , quê determina o triângulo retângulo ABD, com AB = 2, BD = 1 e correspondente a h. Utilizando o teorema de Pitágoras no triângulo retângulo ABD, temos: (AB)2 = h2 + (BD)2 ⇒ 22 = h2 + 12 ⇒ h2 = 3 ⇒ h = . Como 3 é um número natural, mas não é um número quadrado perfeito, temos quê , quê corresponde à medida h da altura do triângulo ABC, em centímetro, é um número irracional.
38. a) • ≃ 12,5
• ≃ 7
• ≃ 5,5
• ≃ 5
b) ≃ 4,898979. Resposta esperada: Sendo n = a ⋅ b um número natural quê não seja quadrado perfeito, quanto mais próximos entre si são a e b, melhor é a aproximação de pelo método de Herão.
c) Respostas pessoais.
39. a) ; = 2; = 3; = 4.
Como os números 1, 4, 9 e 16 são quadrados perfeitos, temos quê , , e são classificados como racionais. De modo análogo, temos quê as demais raízes correspondem a números irracionais.
b) Respostas pessoais.
c) Resposta esperada: Porque nessa espiral são formados triângulos retângulos, cujas medidas dos lados (catetos e hipotenusa) podem sêr relacionadas por meio do teorema de Pitágoras.
40. a) ![]()
b) ![]()
c) ![]()
d) ![]()
41. a) ]−∞, −7[ ou {x ∈ ℝ | x < −7}
b) [−3, ] ou { x ∈ ℝ | −3 ≤ x ≤ }
c) {x ∈ ℝ | x > }
d) ]−(pi)", 0] ou {x ∈ ℝ | −(pi)" < x ≤ 0}
42. a) 
A ⋃ B =]−20, 25[; A ⋂ B =]−10, 15[
Página trezentos e cinquenta e nove
b) 
A ∪ B = ℝ; A ⋂ B =]5, 10]
c) 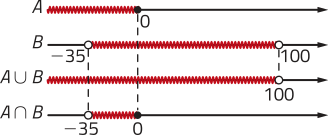
A ∪ B =]−∞, 100[; A ⋂ B =]−35, 0]
d) 
A ⋃ B = ℝ; A ⋂ B =]−150, 300[
43. a) −3 ⋅ |−10| = −3 ⋅ 10 = −30
b) |−4| ⋅ |−7| = 4 ⋅ 7 = 28
c) |6 − 18| = |−12| = 12
d) | |−10| − 15| = |10 − 15| = |−5| = 5
e) |3 − 8| − |−13 + 5| = |−5| − |−8| = 5 − 8 = −3
f) |2 ⋅ (−8)| = |−16| = 16
44. ≃ 2,3; ≃ −4,8; = −2,2;
≃ −3,3; ≃ 1; ≃ 5,2;
≃ 8,7; − ≃ −0,3
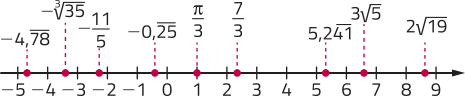
45. alternativa b
4x + 10 = 2 ⇒ 4x = −8 ⇒ x = −2
Temos −2 ∈]−4, 0[, pois −4 < −2 < 0.
46. Resposta pessoal. Sugestão de resposta: A alternativa c é correta apenas se z < y. Mas, de acôr-do com o enunciado, podemos ter tanto z < y como z > y.
47. a) O ponto correspondente a x póde estar à direita ou à esquerda do ponto correspondente a −7.
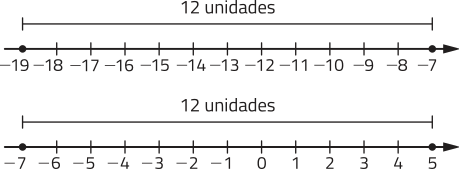
Respostas possíveis: −19 ou 5.
b) Respostas possíveis: |−7 − (−19)| = 12; |−19 − (−7)| = 12; |5 − (−7)| = 12; |−7 − 5| = 12.
48. a) entre dois números racionais
b) Resposta esperada: Temos quê ≃ 3,140845, (pi)" ≃ 3,141593e ≃ 3,142857.
Como 3,140845 < 3,141593 < 3,142857, a conclusão de arquimédis está correta, ou seja, .
49. Elaboração do estudante. Resposta possível: Quais números podem estar sêndo presentados pelas lêtras a, b, c e d no diagrama?
Resposta: 1, −2, ; .
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) Respostas pessoais. Espera-se quê os estudantes discutam a respeito do gerenciamento de bancos de dados e expressem seus conhecimentos sobre a temática, estabelecendo relações com as ideias de conjunto mobilizadas ao longo da Unidade.
b) Respostas pessoais. Espera-se quê os estudantes relacionem o conteúdo com suas vivências e discutam a respeito de diferentes tipos de estrutura de bancos de dados. Caso eles não tênham tido contanto com algum tipo de banco de dados, apresente características das principais estruturas, como o banco de dados hierárquico, considerado defasado em razão da sua estrutura do tipo árvore, e o relacional, muito utilizado atualmente e quê contempla relações existentes entre os dados.
c) • Comparando as alturas das colunas do gráfico, podemos identificar quê a categoria com a maior quantidade de livros é “aventura”.
•
livros
• ; 0,36. Número racional.
d) Sendo A e M os conjuntos formados pêlos motoristas habilitados para conduzir automóveis e motocicletas, respectivamente, temos n (A − M) = 13 e n (M − A) = 14. Considerando quê os 45 motoristas têm habilitação para ao menos um tipo de veículo, temos n(A ∪ B) = 45.
Assim, segue quê: n(AM) = n(A ∪ B) − n(A − M) − n(M − A) ⇒ n(A ∩ B) = 45 − 13 − 14 = 18.
Portanto, 18 motoristas são habilitados para os dois tipos de veículo.
e) Considere os conjuntos:
A: pessoas quê foram vacinadas contra febre amarela;
B: pessoas quê foram vacinadas contra sarampo. Temos:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B) = 200 + 153 − 23 = 330
Como havia 400 pessoas registradas, então o número de pessoas quê não haviam sido vacinadas contra sarampo nem febre amarela é:
400 − 330 = 70 → 70 pessoas
Praticando: enêm e Vestibulares
1. alternativa b
F1: = 3 mg/dia
F2: = 5 mg/dia
F3: = 4,5 mg/dia
F4: =2 mg/dia
F5: = 1,5 mg/dia
1,5 < 2 < 3 < 4,5 < 5
2. alternativa b
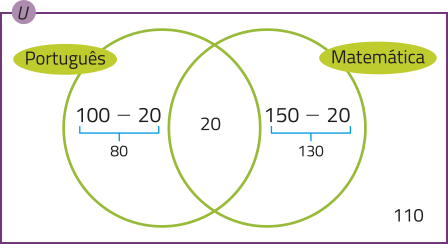
80 + 20 + 130 + 110 = 340
Página trezentos e sessenta
3. alternativa d
AC é o conjunto dos números maiores ou iguais a 250.
BC é o conjunto dos números naturais quê não são múltiplos de 4.
CC é o conjunto dos números ímpares.
Logo, 33 ∉ AC, 33 ∈ BC e 33 ∈ CC.
Assim, 33 ∈ (BC ∪ CC), e do mesmo modo 33 ∈ (AC ∩ BC) ⋂ (BC ∩ CC).
4. alternativa e
1,35 bilhão = 1.350 milhão = 1.350.000 mil = 1.350.000.000
5. alternativa c
Do enunciado, temos quê x ∈ A, x ∈ C e x ∉ B. Assim, x ∈ A ∩ C.
6. alternativa e
Multiplicando-se os elemêntos de A pêlos elemêntos de B e excluindo-se as repetições, temos: C = {−1, −2, −3, −4, −5, −6, −8, −9, −10, −12, −15, −16, −20, −25}, ou seja, 14 elemêntos.
7. alternativa e
Não obtiveram nota mínima em Matemática e Português: 5 − 3 = 2.
Não obtiveram nota mínima em Matemática e Inglês: 3 − 2 = 1.
Não obtiveram nota mínima em Inglês e Português: 7 − 2 = 5.
Não obtiveram nota mínima em Matemática: 14 − (3 + 2 + 1) = 8.
Não obtiveram nota mínima em Português: 16 − (3 + 2 + 5) = 6.
Não obtiveram nota mínima em Inglês: 12 − (1 + 2 + 5) = 4.
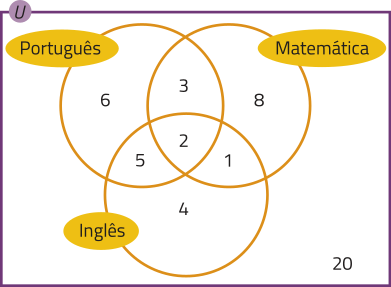
Participaram do concurso: 6 + 3 + 5 + 2 + 1 + 8 + 4 + 20 = 49 → 49.
8. alternativa b
12 pessoas escolherem números primos. Todos são ímpares e maiores quê 3, pelo enunciado, e nenhum deles é múltiplo de 3, por sêr primo.
30 pessoas escolherem um número par e 14 escolheram múltiplo de 3. Os múltiplos de 6 são também múltiplos de 3.
Assim, na interseção entre números pares e múltiplos de 3, estão os múltiplos de 6, como no diagrama a seguir.
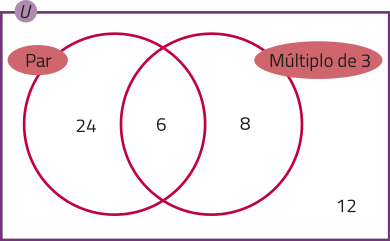
Pares ou múltiplos de 3:
24 + 6 + 8 = 38
Ímpares não múltiplo de 3:
64 − 38 = 26
9. alternativa b
Como 1 m = 10 dm, temos:
843 dm = 84,3 m.
Como 1 km = 1.000 m, temos:
35 km = 35.000 m.
10. alternativa c
Praticam apenas atletismo e esgrima: 105 − 40 = 65.
Praticam apenas natação e esgrima: 65 − 40 = 25.
Praticam apenas natação e atletismo: 70 − 40 = 30.
Praticam apenas esgrima: 200 − (65 + 25 + 40) = 70.
Praticam apenas atletismo: 250 − (30 + 65 + 40) = 115.
Praticam apenas natação: 300 − (25 + 30 + 40) = 205.
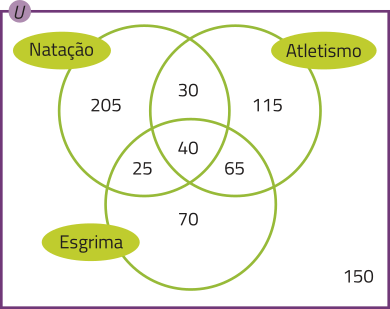
Entrevistados: 65 + 30 + 40 + 25 + 70 + 115 + 205 + 150 = 700
11. alternativa e
Sendo x a quantidade de alunos quê cursam as três disciplinas, temos:
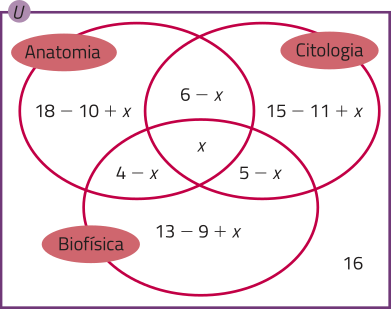
16 + 18 − 10 + x + 13 − 9 + x + 15 − 11 + x + 4 − x + x + 5 − x + 6 − x = 50 ⇒ x = 3
Alunos quê cursam exatamente duas disciplinas:
4 − 3 = 1; 6 − 3 = 3; 5 − 3 = 2.
Total: 1 + 3 + 2 = 6.
12. alternativa a
Distrito Federal: ≃ 4,08
Minas Gerais: ≃ 2,03
São Paulo: ≃ 2,64
Sergipe: ≃ 1,42
Piauí: ≃ 1,05
13. alternativa e
Considerando quê todos os melhores amigos de Eduardo estão entre seus amigos, temos quê M ⊂ E. Além díssu, como nem todos os melhores amigos de Eduardo foram à festa, temos quê M ⊄ F. O único diagrama quê apresenta simultaneamente essas relações é o do item e.
14. alternativa e
Área ocupada às 10 horas, em m2: 500 ⋅ 500 = 250.000
Quantidade de pessoas às 10 horas da manhã: 250.000 ⋅ 4 = 1.000.000
Quantidade de pessoas às 4 horas da tarde: 1.000.000 + 6 ⋅ 120.000 = 1.720.000
Assim, a quantidade necessária de policiais é: = 860 → 860 policiais
15. Considerando C, A e J os conjuntos dos funcionários quê ingerem algum tipo de proteína animal, respectivamente, no café da manhã, no almôço e no jantar, temos o seguinte diagrama de Venn:
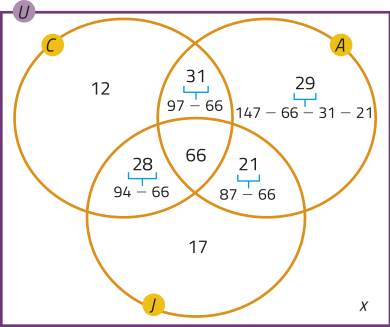
Assim, o número x de funcionários quê não se alimentam com proteína animal em nenhuma das refeições é dado por:
12 + 29 + 17 + 31 + 28 + 21 + 66 + x = 260 ⇒ x = 56 → 56 funcionários
16. alternativa b
200 + 150 − 70 = 280
500 − 280 = 220
= 0,44 → 44%
Unidade 2 • Relações entre grandezas e noção de função
1. a) massa; 8.500
• Toneladas (t) e quilogramas (kg) correspondem a medidas de massa.
• 8,5 t = 8,5 ⋅ 1.000 kg = 8.500 kg
Página trezentos e sessenta e um
b) comprimento; 90.000
• Metros (m) e quilômetros (km) correspondem a medidas de comprimento.
• 90 km = 90 ⋅ = 90 ⋅ 1.000 m =
= 90.000 m
c) tempo; 3
• Segundos (s) e horas (h) correspondem a medidas de tempo.
• 10.800 s =
= 10800 ⋅ =
= 180 ⋅ h = 3 h
d) comprimento; 0,07
• Decimetros (dm) e milímetros (mm) correspondem a medidas de comprimento.
• 7 mm = 7 ⋅ =
= 7 ⋅ 0,01 dm = 0,07 dm
e) massa; 1,65
• Quilogramas (kg) e gramas (g) correspondem a medidas de massa.
• 1.650 g = 1.650 ⋅ kg = 1,65 kg
f) tempo; 252
• Minutos (min) e segundos (s) correspondem a medidas de tempo.
4,2 min = 4,2 ⋅ =
= 4,2 ⋅ 60 s = 252 s
2. a) 4 TB = = 4 ⋅ 1.024 GB = 4.096 GB
b) 512 B =
= 512 ⋅ kB = 0,5 kB
c) 3.072 kB =
3.072 ⋅ MB = 3 MB
d) 0,5 GB =
0,5 ⋅
512 ⋅ 1.024 kB = 524.288 kB
3. Capacidade total em MB: 2 GB =
= 2048 MB
Total não utilizado: 2.048 − 1.460 = 588 → 588 MB
Portanto, jã ainda póde armazenar 147 arquivos de fotografia de 4 MB, pois 588 ∶ 4 = 147.
4. • A: d = ⇒ d = ⇒ d = 2, 4 → 2, 4 g/cm3
• B: d = ⇒ 7, 9 = ⇒ v = ⇒ v ≃ 0,35 → aproximadamente 0,35 cm3
• C: d = ⇒ 8,4 = ⇒ m = 42 → 42 g
5. a) comprimento: diâmetro e distância média do Sol; tempo: período orbital e período de rotação; tempera-túra: tempera-túra de superfícíe
b) • hectômetro: 6.792 km =
= 6.792 ⋅ = 6.792 ⋅ 10 hm =
= 67.920 hm
• métro: 6.792 km = 6.792 ⋅ 1.000 m = 6.792.000 m
• centímetro: 6.792 km = 6.792.000 m = 6.792.000 ⋅ 100 = 679.200.000 cm
c) 25 − (−125) = 25 + 125 = 150 → 150°C
d) • 0,62 h = 0,62 ⋅ 60 min = 37,2 min
• 0,2 min = 0,2 ⋅ = 0,2 ⋅ 60 s = 12 s
Assim: 24,62 h = 24h37,2min = 24h37min12s
e) Respostas pessoais. Espera-se quê os estudantes pesquisem informações como diâmetro, distância média do Sol, período de rotação, tempera-túra da superfícíe, número de satélites e outras referentes ao planêta escolhido. É importante quê, nas anotações, estejam indicadas as unidades de medidas de cada uma dessas informações e quê eles registrem as fontes das pesquisas.
6. a) rotação e translação
b) Grandeza: velocidade; Unidade de medida: quilômetro por hora (km/h).
c) Resposta esperada: Como o movimento de rotação da Terra tem duração aproximada de 24 h, podemos multiplicar esse valor pela medida da velocidade de rotação da Terra, quê é de aproximadamente 1.675 km/h, para estimar a medida do comprimento da linha do equador em 40.200 km (1.675 ⋅ 24 = 40.200).
7. A densidade da mistura homogênea (dT) é dada pela média aritmética ponderada das densidades de cada líquido (dA e dB), considerando o volume correspondente deles (VA e VB, com VA + VB = VT).
Assim, temos: dT = = dT = =
Calculando a densidade do objeto (dO), temos: dO = = 1,8 → 1,8 g/cm3
Como o objeto sólido flutuou na mistura homogênea, a densidade do objeto é menor ou igual a da mistura. Assim, segue quê: ≥ 1,8 ⇒ 0,9 + dB ≥ 3,6 ⇒ dB ≥ 3,6 − 0,9 ⇒ dB ≥ 2,7
Resposta: 2,7 g/cm3.
8. a) Como 1 mm = 106 nm, temos:
• dimensão mínima: = 10−5 mm ou 0,00001 mm
• dimensão mássima: = 3 ⋅ 10−4 mm ou 0,0003 mm
De 0,00001 mm ou 10−5 mm até 0,0003 mm ou 3 ⋅ 10−4 mm.
b) 4,8 ⋅ 0,000025 = 0,00012 → 0,00012 mm 0,00012 ⋅ 106 = 120 → 120 nm
c) • menor tamãnho médio de uma bactéria:
10 ⋅ 10 nm = 100 nm Convertendo essa medida para milímetro, temos: = 1 ⋅ 10−4 mm
ou 0,0001 mm Convertendo essa medida para métro, temos: = 1 ⋅ 10−7 m ou 0,0000001 m
• maior tamãnho médio de uma bactéria: 15 ⋅ 300 nm = 4.500 nm
Convertendo essa medida para milímetro, temos: = 4,5 ⋅ 10−3 mm ou 0,0045 mm
Convertendo essa medida para métro, temos: = 4,5 ⋅ 10−6 m ou 0,0000045 m
Página trezentos e sessenta e dois
De 0,0000001 m (10−7 m) até 0,0000045 m (4,5 ⋅ 10−6 m).
9. 275 MB = 275 ⋅ = 275 ⋅ 8 Mb = 2.200 Mb
Tamanho do arquivo (Mb) |
Tempo (s) |
|---|---|
50 |
1 |
2.200 |
x |
⇒ 50x = 2.200 ⇒ x = 44 → 44 s
10. Total de espaço ocupado pêlos arquivos em GB:
+ 9 + 12 = + 21 ≃ 22 → aproximadamente 22 GB
Vamos analisar cada item e verificar se o espaço é suficiente para fazer o backup.
a) Insuficiente, pois é necessário quase 22 GB.
b) Suficiente, pois 1 TB equivale a 1.024 GB.
c) Suficiente, pois os 5 dê vê dêz comportam GB.
d) Suficiente, pois 32 GB > 22 GB.
e) Insuficiente, pois cada cê dê tem menos de 1 GB de capacidade; assim, 10 cê(Dêss) comportam menos de 10 GB.
Portanto, ela poderá escolher os dispositivos das alternativas b, c ou d.
11. a) Resposta pessoal. Espera-se quê os estudantes concluam quê existem algumas possibilidades, como armazenar os dados em nuvem e excluir do smartphone ou táblêti e desinstalar aplicativos quê não são utilizados com freqüência.
b) Atividade de elaboração do estudante. Espera-se quê as kestões abordem medidas de capacidade de armazenamento de dados e conversões entre elas. Por exemplo, pode-se compor uma atividade em quê um smartphone tenha certa capacidade de armazenamento e esteja com parte dela ocupada; deseja-se baixar um aplicativo cujo tamãnho está dado em outra unidade; pode-se propor quê se verifique a viabilidade dêêsse dáum-lôude.
12. a)
Tamanho do arquivo (Mb) |
Tempo (s) |
|---|---|
x |
49 |
24 |
1 |
⇒ x = 24 ⋅ 49 = 1.176 → 1.176 Mb ⇒ 1.176 Mb = MB = 147 MB
Portanto, 1.176 Mb ou 147 MB.
b)
Tamanho do arquivo (Mb) |
Tempo (s) |
|---|---|
40 |
1 |
1.176 |
x |
⇒ 40x = 1.176 ⇒ x = 29,4 → 29,4 s
Portanto, o tempo estimado seria 29,4 s.
13. a) • Resposta esperada: O desenvolvimento de tecnologias e recursos voltados à preservação do meio ambiente, especialmente o armazenamento de dados em nuvem.
• Respostas esperadas: Permite quê arquivos digitais sêjam armazenados em sêrvidores especializados e possam ser acessados a qualquer momento. Possibilita reduzir a geração de resíduos eletrônicos, diminuir as emissões de CO2 e poupar o uso de papel para impressão de documentos.
b) Convertendo 10 GB em kB, temos:
10 GB = 10 ⋅ 1.024 MB = 10.240 MB = 10.240 ⋅ 1.024 kB = 10.485.760 kB
Assim, a quantidade de papel correspondente a 10 GB é: = 131.072 → 131.072 páginas de papel
c) 15 GB = 15 ⋅ 1.024 MB = 15.360 MB = 15.360 ⋅ 8 Mb = 122.880 Mb
4 min = 4 ⋅ 60 s = 240 s
Como foram transferidos 122.880 Mb em 240 s, temos quê a taxa de transferência foi:
= 512 → 512 Mbps
d) Resposta pessoal. Espera-se quê os estudantes compreendam a importânssia do armazenamento de dados em nuvem para a agilidade do compartilhamento de dados no dia a dia das empresas, para a facilidade de acesso e produção conjunta de documentos entre diferentes pessoas, para a diminuição do risco de perda de arquivos importantes e para a preservação do meio ambiente num futuro mais sustentável.
14. Como a cada 1 t economiza-se 450 L de á gua, temos:
1.000.000 ⋅ 450 = 450.000.000 L.
15. • 3,8 km: d = 3,8 ⇒ t = 5,50 + 0,25 ⋅ 3,8 = 6,45 → R$ 6,45
• 5 km: d = 5 ⇒ t = 5,50 + 0,25 ⋅ 5 = 6,75 → R$ 6,75
• 6,5 km: d = 6,5 ⇒ t = 5,50 + 0,25 ⋅ 6,5 = 7,125 → R$ 7,12
• 10 km: d = 10 ⇒ t = 5,50 + 0,25 ⋅ 10 = 8 → R$ 8,00
• 12 km: d = 12 ⇒ t = 5,50 + 0,25 ⋅ 12 = 8,5 → R$ 8,50
Deslocamento (km) |
Taxa de entrega (em reais) |
|---|---|
3,8 |
6,45 |
5 |
6,75 |
6,5 |
7,12 |
10 |
8 |
12 |
8,5 |
16. a) x = 12 ⇒ v = 3,90 ⋅ 2 ⋅ 122 = 1.123,2 → R$ 1.123,20
b) v = 1.755 ⇒ 3,90 ⋅ 2x2 = 1.755 ⇒ 7,8x2 = 1.755 ⇒ x2 = 225
A largura x deve sêr um número positivo; logo:
• x = = 15 → 15 m (largura)
• 2x = 2 ⋅ 15 = 30 → 30 m (comprimento)
17. a) • perímetro: p = 4x
• área: a = x2
b) • perímetro: x = 5 ⇒ p = 4 ⋅ 5 = 20 → 20 cm
• área: x = 5 ⇒ a = 52 = 25 → 25 cm2
c) • p = 56 ⇒ 4x = 56 ⇒ x = 14
• a = 144 ⇒ x2 = 144
A medida x deve sêr um número positivo; então, x = = 12.
18. preêço, em reais, por grama de comida servida: = 0,063
Sendo p a quantia paga e m a massa, em grama, temos: p = 0,063m.
19. a) Sim. Algumas respostas possíveis:
c = ; c = ; c = .
b) t = 8 ⇒ c = ⋅ 8 = 9,6 → 9,6 kWh
c) c ≤ 7,2 ⇒ ⋅ t ≤ 7,2 ⇒ t ≤ 6
Logo, póde sêr usado por, no mássimo, 6 h.
d) televisor: c = ; computador: c = ; aspirador de pó: c = ; condicionador de ar: c = ; micro-ondas: c =
• Resposta pessoal. Espera-se quê os estudantes identifiquem as potências de alguns aparelhos eletrônicos de suas
Página trezentos e sessenta e três
residências e utilizem a mesma estratégia dos itens a e b para definir as funções quê relacionam o consumo de energia e o tempo de uso.
20. alternativa b
Custo, em reais, por aluno no laboratório
A: = 4.200
Custo, em reais, por aluno no laboratório
B: = 2.300
Diferença: 4.200 − 2.300 = 1.900 → 1,90 mil reais
21. Tipo A:
c = ⇒ c = 1.800 + 600t
Tipo B:
c = ⇒ c = 1.500 + 200t
22. a) Resposta esperada:
• Sapos e gafanhotos:
Quantidade de gafanhotos |
Quantidade de sapos |
|---|---|
800 |
30 |
g |
s |
⇒ 800s = 30g ⇒ s = g
• Gafanhotos e plantas de capim:
Quantidade de plantas de capim |
Quantidade de gafanhotos |
|---|---|
5.000 |
800 |
c |
g |
⇒ 5.000g = 800c ⇒ g = c
b) Utilizando a relação s = g entre sapos e gafanhotos, temos: g = 560 ⇒ s = ⋅ 560 = 21 → 21 sapos
c) Utilizando a relação g = c entre gafanhotos e plantas de capim, temos: g = 1.000 ⇒ c = 1.000 ⇒ c = 6.250 → 6.250 plantas de capim
d) Resposta pessoal. Espera-se quê os estudantes identifiquem uma ação do homem quê causa desequilíbrio ambiental, como a realização de quêimadas, e promovam discussões que visem identificar meios de atenuar ou eliminar tais práticas e contribuir para a preservação do meio ambiente. Os estudantes podem trazer informações, por exemplo, sobre o aumento no número de queimadas em diversas áreas do território brasileiro nos últimos anos e as consequências dessa ação para o futuro do meio ambiente.
23. alternativa b
35 − 25 = 10
= 2 → R$ 2,00 por métro quadrado pintado
25 + 2 ⋅ 150 = 25 + 300 = 325 → R$ 325,00
24. Como são cobrados R$ 2,00 por métro quadrado, mais R$ 25,00 de taxa fixa, temos:
v = 2a + 25
25. a) 150 ⋅ 7 + 110 = 1.050 + 110 = 1.160 → R$ 1.160,00
b) Como são cobrados R$ 150,00 por diária mais R$ 110,00 de taxas, temos:
v = 150d + 110
c) 860 = 150d + 110 ⇒ 860 − 110 = 150d ⇒ 750 = 150d ⇒ d = = 5 → 5 dias
26. a) De acôr-do com a 2ª coluna e a 2ª linha da anotação, 216 mL.
b) De acôr-do com as anotações, a á gua enche o recipiente a uma velocidade de 18 mL por minuto, pois = … = = 18; logo, a expressão quê relaciona q e t é dada por q = 18t.
c) t = 60 ⇒ q = 18 ⋅ 60 ⇒ q = 1.080
Indica quê após 60 min de gotejamento havia 1.080 mL de á gua no recipiente.
d) q = 4.320 ⇒ 18t = 4.320 ⇒ t = 240
240 min = h =4 h
Portanto, o reparo foi feito após 4 h.
27. Respostas pessoais. Espera-se quê os estudantes estabeleçam relações algébricas entre os elemêntos das tabélas nutricionais e a quantidade de alimento a sêr ingerida. Eles podem elaborar, por exemplo, uma atividade relacionando a quantidade de determinado elemento da tabéla nutricional a cada grama de alimento ingerida.
28. alternativas a e d
a) É função, pois para cada elemento de A corresponde um único elemento de B.
b) Não é função, pois o elemento −4 ∈ A está associado a dois elemêntos em B: −3 e −2.
c) Não é função, pois o elemento −2 ∈ A não está associado a nenhum elemento em B.
d) É função, pois para cada elemento de A corresponde um único elemento de B.
29. • f(−3) = 2 ⋅ (−3) + 1 = −5
• f(−2) = 2 ⋅ (−2) + 1 = −3
• f(0) = 2 ⋅ 0 + 1 = 1
• f(1) = 2 ⋅ 1 + 1 = 3
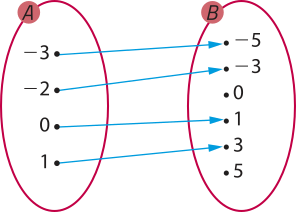
D(f) = {−3, −2, 0, 1};
CD(f) = {−5, −3, 0, 1, 3, 5};
Im(f) = {−5, −3, 1, 3}.
30.
a) g(3) = 3 ⋅ 3 + 5 = 14
b) g(0) = 3 ⋅ 0 + 5 = 5
c) g(10) = 3 ⋅ 10 + 5 = 35
d) g(5) = 3 ⋅ 5 + 5 = 20
• Resposta pessoal. Espera-se quê os estudantes sêjam capazes de apresentar uma função indicando seu domínio, contradomínio e lei de formação e quê possam determinar valores da imagem a partir da atribuição dos valores do domínio, a lei de formação.
31. alternativas b e c
a) Não corresponde, pois h(0) = 22 + 0 = 22 → 22 ∉ B.
b) Corresponde, pois f(x) = 5 − x associa para cada elemento em A um único elemento em B:
• f(−15) = 5 − (−15) = 20
• f(−8) = 5 − (−8) = 13
• f(−2) = 5 − (−2) = 7
• f(0) = 5 − 0 = 5
• f(4) = 5 − 4 = 1
• f(5) = 5 − 5 = 0
c) Corresponde, pois m(x) = x + 15 associa para cada elemento em A um único elemento em B:
• m(−15) = (−15) + 15 = 0
• m(−8) = (−8) + 15 = 7
• m(−2) = (−2) + 15 = 13
• m(0) = 0 + 15 = 15
• m(4) = 4 + 15 = 19
• m(5) = 5 + 15 = 20
d) Não corresponde, pois g (0) = −1 − 0 = −1 ∉ B.
e) Não corresponde, pois p(−8) = −(−8) = 8 ∉ B.
Página trezentos e sessenta e quatro
32. Uma resposta possível:
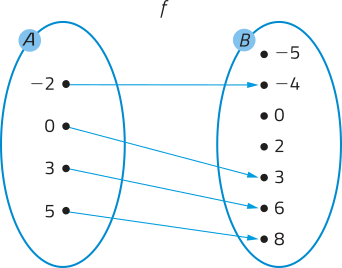
33. a) • Como 2.000,00 ≤ 2.112,00, esse contribuinte é isento de cobrança do IRPF.
• Como 2.112,01 ≤ 2.500,00 < 2.826,65, a alíquota dêêsse contribuinte será de 7,5% com dedução de R$ 158,40:
0,075 ⋅ 2.500,00 − 158,40 = 29,10 → R$ 29,10.
• Como 2.826,66 ≤ 3.200,00 < 3.751,05, a alíquota dêêsse contribuinte será de 15% com dedução de R$ 370,40:
0,15 ⋅ 3.200,00 − 370,40 = 109,60 → R$ 109,60.
b) Sendo r o salário e f(r) o valor a sêr pago, temos:
• Para R$ 2.826,66 ≤ r ≤ R$ 3.751,05, temos alíquota de 15% e R$ 370,40 de dedução:
f(r) = 0,15r − 370,40
• Para R$ 3.751,06 ≤ r ≤ R$ 4.664,68, temos alíquota de 22,5% e R$ 651,73 de dedução:
f(r) = 0,225r − 651,73
• Para r ≥ R$ 4.664,68, temos alíquota de 27,5% e R$ 884,96 de dedução:
f(r) = 0,275r − 884,96
c) f(r) =
d) Como f(r) = 0,275r − 884,96, se r > 4.664,68, segue quê: f(5.000,00) = 0,275 ⋅ 5.000,00 − 884,96 = 490,04 → f(5.000) = 490,04.
Esse cálculo indica quê um contribuinte, cuja renda mensal é R$ 5.000,00, paga R$ 490,04 de IRPF.
e) Resposta pessoal. Espera-se quê os estudantes identifiquem algumas profissões quê têm piso salarial, como as de professor, enfermeiro, metalúrgico, médico anestesiologista, advogado, arquiteto, contador, dentista e jornalista, e, a partir díssu, sêjam capazes de calcular o IRPF referente ao piso da profissão escolhida. Para isso, eles podem utilizar a função cuja lei de formação foi determinada no item c.
Integrando com...
1. a) Upload, quê significa “subir” em tradução simples, é a ação de transferir dados de um terminal local para um sistema remoto. E dáum-lôude, quê significa “baixar” em tradução simples, corresponde ao ato de transferir dados de um sistema remoto para um terminal local.
b) Resposta pessoal. Espera-se quê os estudantes apliquem os significados de upload e dáum-lôude na composição da frase. Por exemplo, eles podem escrever sobre o dáum-lôude de um aplicativo e sobre o upload de fotografias do celular para a nuvem.
2. Temos as seguintes equivalências:
4 MB = 32 Mb = 32.768 kb
• Em uma velocidade de 56 kbps:
Tamanho do arquivo (kb) |
Tempo (s) |
|---|---|
56 |
1 |
32.768 |
x |
⇒ 56x = 32.768 ⇒ x ≃ 585 → aproximadamente 585 s
• Em uma velocidade de 10 Mbps:
Tamanho do arquivo (Mb) |
Tempo (s) |
|---|---|
10 |
1 |
32 |
x |
⇒ 10x = 32 ⇒ x = 3,2 → 3,2 s
3. Resposta esperada: A medição 1 está de acôr-do com a regulamentação estabelecida pela Anatel, uma vez quê a velocidade aferida de dáum-lôude e upload é maior quê a velocidade da conexão contratada. A medição 2 não está de acôr-do com a regulamentação, pois a velocidade aferida de dáum-lôude e upload é inferior a 80% da velocidade da conexão contratada (80% de 500 Mbps = 400 Mbps, 185 Mbps < 400 Mbps; 80% de 35 Mbps = 28 Mbps; 12,95 Mbps < 35 Mbps). A medição 3 está de acôr-do com a regulamentação, pois a velocidade aferida de dáum-lôude e upload corresponde a um porcentual maior quê 80% da velocidade da conexão contratada (410 Mbps > 400 Mbps e 28,7 Mbps > 28 Mbps).
4. Resposta pessoal. Espera-se quê os estudantes possam aplicar funções no contexto da velocidade de conexão. Eles podem, por exemplo, utilizar a regulamentação estabelecida pela Anatel para criar um problema com a própria velocidade de conexão de suas residências. Outra possibilidade é estabelecer relação entre o custo e a velocidade de conexão de uma empresa de telefonia. Se necessário, orientar os estudantes a pesquisar em fontes confiáveis para utilização de dados reais.
5. Respostas pessoais. Espera-se quê os estudantes coletem dados reais sobre um plano de telefonia oferecido na região e investiguem se a norma relativa à velocidade de dáum-lôude e upload está sêndo cumprida. Os dados e as conclusões devem sêr expostos no relatório. Caso a conclusão seja negativa, orientar os estudantes a debater as medidas quê podem sêr tomadas para quê a empresa regularize a situação.
34. a) Temos a seguinte condição:
2x − 6 ≠ 0 ⇒ 2x ≠ 6 ⇒ x ≠ 3
Assim, D(f) = {x ∈ ℝ | x ≠ 3}.
b) Temos a seguinte condição:
9x + 3 > 0 ⇒ 9x > −3 ⇒ x >
Assim, D(f) = {x ∈ ℝ | x > − }
c) Temos a seguinte condição:
x2 − 81 ≠ 0 ⇒ x2 ≠ 81 ⇒ x ≠ −9 e x ≠ 9
Assim, D(f) = {x ∈ ℝ | x ≠ −9 e x ≠ 9}.
d) Temos as seguintes condições:
• 7x + 5 ≥ 0 ⇒ 7x ≥ −5 ⇒ x ≥ ≃ −0,7
• 6x + 1 > 0 ⇒ 6x > −1 ⇒ x > ≃ −0,2
Página trezentos e sessenta e cinco
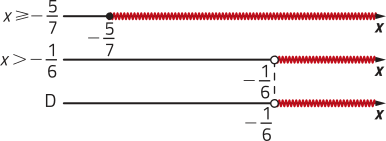
Assim, D(f) = {x ∈ ℝ | x > −}.
e) Temos as seguintes condições:
• 2x2 − 800 ≠ 0 ⇒ 2x2 ≠ 800 ⇒ x2 ≠ 400 ⇒ x ≠ 20 e x ≠ −20
• 3x − 5 ≥ 0 ⇒ 3x ≥ 5 ⇒ x ≥
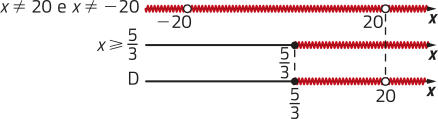
Assim, D(f) = { x ∈ ℝ | x ≥ e x ≠ 20}
f) Temos a seguinte condição:
≠ 0 ⇒ x ≠ 0
Assim, D(f) = {x ∈ ℝ | x ≠ 0}.
g) Temos a seguinte condição:
≥ 0
Essa condição será satisfeita se x − 3 ≥ 0 e x + 4 > 0, ou se x − 3 ≤ 0 e x + 4 < 0.
• x − 3 ≥ 0 e x + 4 > 0:

• x − 3 ≤ 0 e x + 4 < 0:

Assim, D(f) = D1 ∪ D2 = {x ∈ ℝ | x < −4 ou x ≥ 3}.
35. alternativa d
a) Não tem, pois:
f(9) = = 0
Ou seja, o número 9 pertence a D(f), mas não pertence ao intervalo dado.
b) Não tem, pois:
f(0) = = 4 ⋅ 3 = 12
Ou seja, o número 0 pertence a D(f), mas não pertence ao intervalo dado.
c) Não tem, pois:
f() =
A fração ôbitída não está definida, então não pertence a D(f), mas pertence ao intervalo dado.
d) Vamos obtêr o domínio de f. Temos as seguintes condições:
• 7x − 4 ≥ 0 ⇒ 7x ≥ 4 ⇒ x ≥
• 9 − x > 0 ⇒ −x > −9 ⇒ x < 9

Ou seja, o intervalo dado corresponde ao domínio de f.
e) Não tem, pois:
f(0) =
Ou seja, o número 0 pertence a D(f), mas não pertence ao intervalo dado.
36. a) A = = 40 → 40 cm2
b) A(h) = = 10h
A(h) = ou A(h) = 10h
c) Como o triângulo está inscrito na semicircunferência de raio 10 cm, sua altura mássima será 10 cm. Assim, temos:
D(A) = {h ∈ ℝ | 0 < h ≤ 10}
37. a) Sendo y a medida do outro par de lados, temos:
2x + 2y = 48 ⇒ 2y = 48 − 2x ⇒ y = 24 − x
Assim, a quadra de jôgo póde sêr representada por um retângulo de lados x e 24 − x.
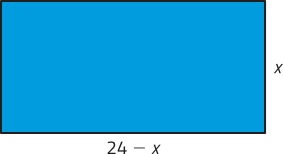
b) Como as medidas são x e 24 − x, conforme o item a, sua área póde sêr expressa por:
f(x) = x ⋅ (24 − x) ⇒ f(x) = 24x − x2
c) As medidas do retângulo quê representa a quadra devem sêr positivas, ou seja:
• x > 0
• 24 − x > 0 ⇒ −x > −24 ⇒ x < 24
Assim, D(f) = {x ∈ ℝ | 0 < x < 24}.
d) dimensões:
• x = 8 → 8 m
• 24 − x = 24 − 8 = 16 → 16 m área: 8 ⋅ 16 = 128 → 128 m2
38. x + 90 = 150 ⇒ x = 150 − 90 ⇒ 3x = 60 ⋅ 5 ⇒ 3x = 300 ⇒ x = 100
D(V) = {x ∈ ℝ | 0 ≤ x ≤ 100}
39. a) Considerando quê o número de quadrados vermelhos aumenta uma unidade de uma figura para a seguinte e o número de quadrados verdes aumenta três unidades de uma figura para a seguinte, temos quê a figura 4 terá 4 quadrados vermelhos e 12 verdes.
b) Resposta esperada: As figuras dessa sequência são formadas por quadrados vermelhos (fileira horizontal superior) e verdes (fileira horizontal inferior) cujas quantidades correspondem, respectivamente, às sequências dos números naturais positivos e à sequência dos múltiplos positivos de 3.
c) Resposta esperada: Como em cada figura os quadrados verdes correspondem ao triplo dos vermelhos, temos:
• 133 quadrados vermelhos;
• 133 ⋅ 3 = 399 → 399 quadrados verdes.
Página trezentos e sessenta e seis
d) Resposta esperada: A figura da posição n tem 3n quadrados verdes.
Assim:
3n = 900 ⇒ n = 300 → Figura 300
Essa figura é formada por 300 quadrados vermelhos.
e) Não, pois 31 não é múltiplo positivo de 3.
f) Resposta esperada: Conforme observado no item d, a figura da posição n tem 3n quadrados verdes. Então, a lei de formação é dada por:
f(n) = 3n
Essa função só tem sentido para valores naturais positivos de n. Assim, D(f) = {n ∈ ℕ | n > 0}.
g) Resposta esperada: Se x é a quantidade de quadrados verdes e n, a posição da figura correspondente, temos: 3n = x ⇒ n =
Assim, a lei de formação é dada por g(x) = , sêndo x um múltiplo positivo de 3, ou seja, D(g) = {x ∈ ℕ | x é múltiplo de 3 e x > 0}.
40. a)
x |
f(x) = 3x − 1 |
(x, y) |
|---|---|---|
−2 |
f(−2) = = 3 ⋅ (−2) − 1 = −7 |
(−2, −7) |
0 |
f(0) = 3 ⋅ 0 − 1 = −1 |
(0, −1) |
1 |
f(1) = 3 ⋅ 1 − 1 = 2 |
(1, 2) |
3 |
f(3) = 3 ⋅ 3 − 1 = 8 |
(3, 8) |
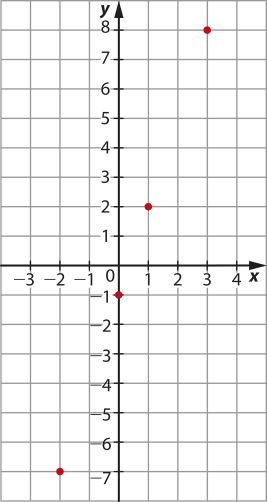
b)
x |
g(x) = x2 − 4 |
(x, y) |
|---|---|---|
−1 |
g(−1) = = (−1)2 − 4 = −3 |
(−1, −3) |
1 |
g(1) = 12 − 4 = −3 |
(1, −3) |
2 |
g(2) = 22 − 4 = 0 |
(2, 0) |
3 |
g(3) = 32 − 4 = 5 |
(3, 5) |
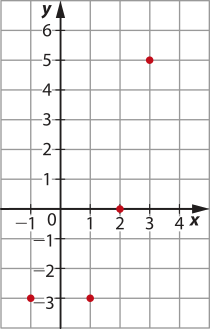
c)
x |
h(x) = 6 − 2x |
(x, y) |
|---|---|---|
−2 |
h(−2) = 6 − 2 ⋅ (−2) = 10 |
(−2, 10) |
0 |
h(0) = 6 − 2 ⋅ 0 = 6 |
(0, 6) |
1 |
h(1) = 6 − 2 ⋅ 1 = 4 |
(1, 4) |
2 |
h(2) = 6 − 2 ⋅ 2 = 2 |
(2, 2) |
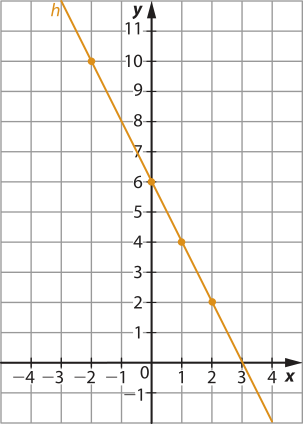
d) • Para x < 2:
x |
m(x) = 2 − x |
(x, y) |
|---|---|---|
−1 |
m(−1) = 2 − (−1) = 3 |
(−1, 3) |
0 |
m(0) = 2 − 0 = 2 |
(0, 2) |
1 |
m(1) = 2 − 1 = 1 |
(1, 1) |
• Para x ≥ 2:
x |
m(x) = x − 2 |
(x, y) |
|---|---|---|
2 |
m(2) = 2 − 2 = 0 |
(2, 0) |
3 |
m(3) = 3 − 2 = 1 |
(3, 1) |
4 |
m(4) = 4 − 2 = 2 |
(4, 2) |
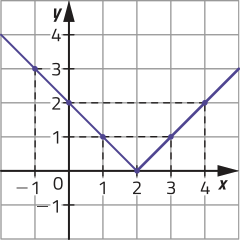
41. Respostas possíveis:
a) 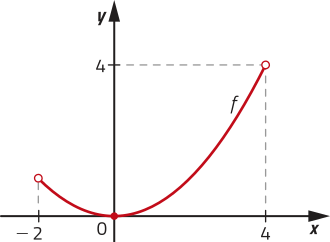
b) 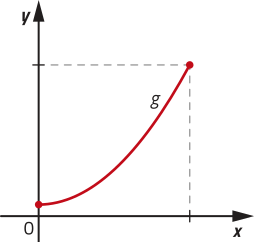
c) 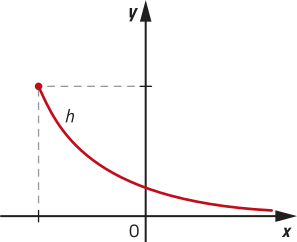
d) 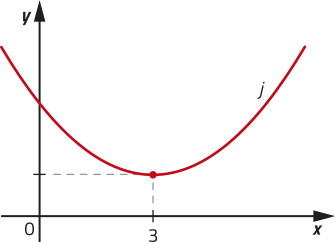
e) 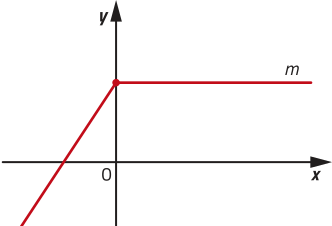
42. alternativas a e c
a) Representa uma função, pois cada abscissa está associada a uma única ordenada.
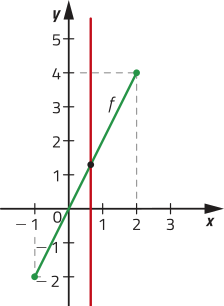
Página trezentos e sessenta e sete
b) Não representa uma função, pois existe pelo menos uma abscissa associada a mais de uma ordenada.
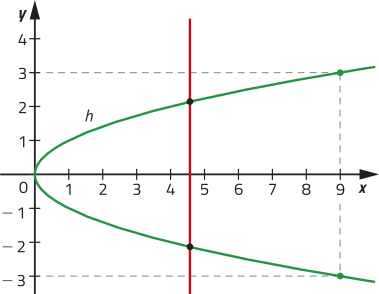
c) Representa uma função, pois cada abscissa está associada a uma única ordenada.
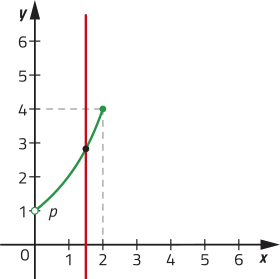
d) Não representa uma função, pois existe pelo menos uma abscissa associada a mais de uma ordenada.
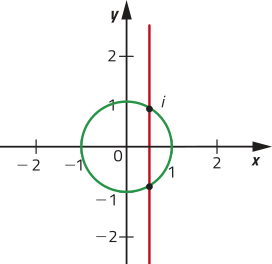
43. Com base nos gráficos apresentados, para determinar o domínio da função, observa-se o intervalo no eixo das abscissas em quê a função está definida. Para determinar o conjunto imagem, observa-se o intervalo no eixo das ordenadas em quê a função está definida. Assim, temos:
a) D(f) =]−4, 5]; Im(f) = [−1, 2]
b) D(g) = [−1, 1]; Im(g) = [2, 4]
c) D(h) =]−2, 2[; Im(h) = [1, 5[
44. a) Observando o intervalo em quê a função está definida no eixo das abscissas, temos:
D(f) = [−4, 4]
b) Observando o intervalo em quê a função está definida no eixo das ordenadas, temos:
Im(f) = [−4, 1]
c) Analisando os intervalos do domínio cuja função é crescente, temos: [−4, 0] e [3, 4]
d) Analisando os intervalos do domínio cuja função é decrescente, temos: [0, 1].
e) No gráfico, analisa-se o intervalo do domínio em quê a imagem da função não varia, ou seja, [1, 3].
45. a) Resposta esperada: O consumo foi entre 10 m3 e 25 m3 de á gua, pois, para consumo inferior a 10 m3, o valor da fatura é de R$ 26,90, enquanto para o consumo superior a 25 m3, o valor da fatura é maior quê R$ 101,90.
b) III
O item I não apresenta a lei de formação de f, pois, por essa lei, temos:
f(10) = 36,9 ≠ 26,9
A do item II também não é, pois a taxa de crescimento da função é alterada no ponto de abscissa x = 25, e não em x = 20.
Portanto, o item III é o correto.
c) • 9 m3: Observando o gráfico, o valor da fatura será R$ 26,90.
• 30 m3: Usando a lei de formação determinada no item b, temos:
f(30) = 8,7 ⋅ 30 − 115,6 = 145,4 → R$ 145,40
• 25 m3: Observando o gráfico, o valor da fatura será R$ 101,90.
d) Usando a lei de formação determinada no item b e sabendo quê o consumo x está entre 10 m3 e 25 m3, temos:
f(x) = 50 ⇒ 5x − 23,1 = 50 ⇒ 5x = 73,1 ⇒x = 14,62 → 14,62 m3
46. alternativa b
O gráfico contém os pontos de coordenadas (0, 50) e (500, 0).
Substituindo x = 0 nas expressões indicadas nas alternativas, temos:
a) y = −10 ⋅ 0 + 500 = 500
b) y = + 50 = 50
c) y = + 500 = 500
d) y = + 50 = 50
e) y = + 500 = 500
Assim, eliminamos as alternativas a, c e e, pois, de acôr-do com o gráfico, quando x = 0, tem-se y = 50.
Substituindo x = 500 nas expressões apresentadas nas alternativas b e d, temos:
b) y = + 50 = −50 + 50 = 0
d) y = + 50 = 50 + 50 = 100
Logo, a expressão quê contém o ponto de coordenadas (500, 0) é a da alternativa b.
47. a) Como o ponto de coordenadas (500, 0) pertence ao gráfico, o automóvel tem o tanque vazio após 500 km, distância quê corresponde à autonomia do automóvel.
b) Analisando a distância percorrida em quilômetro com um tanque de combustível, temos quê D(c) = [0, 500]; analisando a variação da quantidade de litros de combustível no tanque, temos quê Im(c) = [0, 50].
48. Resposta pessoal. Espera-se quê os estudantes reconheçam gráficos de função e de relações quê não representam uma função. Eles podem construir, por exemplo, gráficos correspondentes a retas não paralelas ao eixo y para representar funções e de curvas cujo mesmo elemento do domínio tenha duas imagens para um gráfico quê não represente uma função. A atividade póde sêr utilizada para retomar as características estudadas sobre gráfico de uma função.
49. Resposta pessoal. Espera-se quê os estudantes reconheçam funções crescentes, decrescentes e constantes. Verificar se eles compreenderam quê, para as funções crescentes, devem sêr consideradas situações em quê as duas grandezas aumentam ou diminuem simultaneamente; para as funções decrescentes, as situações consideradas devem apresentar grandezas em quê uma diminui ao passo quê a outra aumenta; por fim, para as funções constantes, nas situações consideradas, uma das grandezas deve permanecer invariável, com a variação da outra.
50. Resposta pessoal. Espera-se quê os estudantes construam um gráfico de função com três raízes reais no domínio dado, ou seja, quê cruze o eixo das abscissas em tal intervalo.
51. alternativa c
a) Não é o gráfico de f, pois a função é positiva para 4 < x < 6.
b) Não é o gráfico de f, pois a função não é nula para x = −3.
c) A função satisfaz a todas as condições dadas.
52. a) Analisando o gráfico, temos: f(−6) = 1; f(1) = 1; f(−2) = −2.
b) Observando os valores em quê o gráfico da função intersecta o eixo x, os zeros da função são: −4, −1 e 3.
c) • positiva: −8 ≤ x < −4 ou −1 < x < 3
• negativa: −4 < x < −1 ou 3 < x < 5
• nula: x = −4 ou x = −1 ou x = 3
53. a) pôdêmos observar quê −4 e 4 são zeros de f, pois −(−4)2 + 16 =−42 + 16 = 0, e 10 é um zero de g, pois 10 − 10 = 0. Assim, o gráfico de f foi representado em vermelho e o de g, em azul.
b) Função f positiva para −4 < x < 4, negativa para x < −4 ou x > 4 e nula para x = −4 ou x = 4; função g positiva para x < 10, negativa para x > 10 e nula para x = 10.
Página trezentos e sessenta e oito
c) 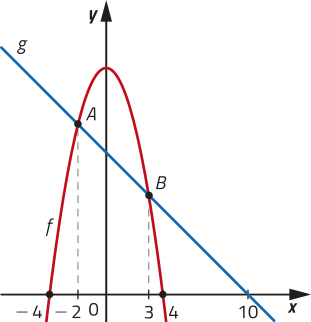
pôdêmos observar no gráfico quê:
• f(x) < g(x) para x < −2 e x > 3, ou seja, f < g em]−∞, −2[ ou]3, +∞[
• g(x) < f(x) para −2 < x < 3, ou seja, g < f em]−2, 3[
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) Resposta pessoal. Espera-se quê os estudantes construam argumentos a respeito das vantagens e desvantagens da venda sêr por unidade ou por quilograma. Para isso, podem utilizar funções quê determinem o preêço em função da quantidade ou da massa.
b) Como cada pão era vendido por
R$ 0,35, temos: c(p) = 0,35p.
c) 10,80 ∶ 15,00 = 0,72 → 0,72 kg ou 720 g
d) Gráfico III, pois f(0) = 0 e f(1) = 15,00.
e) • f(x) = 15x
• D(f) = ℝ+; CD(f) = ℝ; Im(f) = ℝ+
• Crescente, pois dados a ∈ D(f) e b ∈ D(f), com a < b, temos:
a < b ⇒ 15 ⋅ a < 15 ⋅ b ⇒ f(a) < f(b)
• f(x) = 0 ⇒ 15x = 0 ⇒ x = 0
• Como D(f) = ℝ+, f é crescente e x = 0 é zero de f, temos quê não existe x ∈ D(f) tal quê f(x) < 0.
• Como D(f) = ℝ+, f é crescente e x = 0 é zero de f, temos quê f(x) > 0 para x > 0.
f) Respostas pessoais. Espera-se quê os estudantes obtenham funções quê relacionem o preêço e a massa dos alimentos, ou o preêço e a quantidade adquirida. A comparação entre os resultados póde sêr feita utilizando a lei de formação da função e também a representação gráfica dela.
Praticando: enêm e vestibulares
1. alternativa c
A primeira bomba ligada foi responsável por escoar 1.000 L de á gua (6.000 − 5.000 = 1.000) na primeira hora. Considerando a mesma vazão de 1.000 L/h, nas duas horas seguintes ela escoou 2.000 L (2 ⋅ 1.000 = 2.000).
Como juntas as bombas escoaram 5.000 L na segunda hora, temos quê a segunda bomba quê foi ligada escoou 3.000 L (5.000 − 2.000 = 3.000) em duas horas. Assim, a vazão dessa bomba é dada por: 3.000 ∶ 2 = 1.500 → 1.500 L/h
2. alternativa c
50 ⋅ 1.610 = 80.500 → 80.500 m ou 80,5 km
3. alternativa b
Observando o gráfico, temos quê os valores de x e y varíam de 0 a 10, ou seja, 0 ≤ x ≤ 10 e 0 ≤ y ≤ 10.
Além díssu, para qualquer ponto do gráfico, temos quê y ≤ x. Assim, temos 0 ≤ y ≤ x ≤ 10.
4. alternativa d
I) Correta. Em uma fração, o denominador precisa sêr diferente de zero.
II) Correta. No conjunto dos números reais não estão definidas raízes de índice par para radicandos negativos.
III) Correta. No conjunto dos números reais não estão definidas raízes de índice par para radicandos negativos e, em uma fração, o denominador precisa sêr diferente de zero.
IV) Incorreta. No conjunto dos números reais, não estão definidas raízes de índice par para radicandos negativos, ou seja, para r(x) < 0. A função não estará definida.
5. alternativa b
1.008 − 252 = 756
Temos quê:
999 ⋅ 0,45 = 449,55
2.499 ⋅ 0,40 = 999,60
Logo, a quantidade de cê(Dêss) comprada foi maior quê 1.000 e menor quê 2.500.
Assim, o total de cê(Dêss) comprados é dado por:
6. alternativa b
Total de minutos em 60 dias:
60 ⋅ 24 ⋅ 60 = 86.400
Total de acionamentos do borrifador:
Quantidade de inseticida por borrifada:
= 0,2 → 0,200 mL
7. alternativa b
Sendo x a quantidade de quilômetros rodados, temos:
220,00 + 2,90x ≤ 2.300,00
2,90x ≤ 2.300,00 − 220,00
2,90x ≤ 2.080,00
x ≤
x ≤ 717,24
8. alternativa c
32,74 + 5 ⋅ 3,00 + 32,74 = 80,48 → R$ 80,48
9. alternativa b
Como o cojunto A é dados pêlos valores inteiros de S1, temos:
A = {0, 1, 2, 3}
Dos valores pertecentes ao conjunto A, temos:
x − 1 ≠ 0 → x ≠ 1
Se x = 0, então f(0) = 0.
Se x = 2, então
f(2) =
Se x = 3, então
f(3) = = 0.
Logo, apenas os números 0, 2 e 3 pertencem ao domínio da função e ao conjunto
A. Portanto, A ∩ B = {0, 2, 3}.
10. alternativa c
S = 5 ⋅ 0 + 4 ⋅ 1 + 3 ⋅ 0 + 2 ⋅ 0 = 4
= 0 com résto 4 → R = 4
N5 = 11 − R = 11 − 4 = 7
11. alternativa a
Analisando o gráfico, constatamos quê o veículo quê chegou em último lugar é representado pela linha reta mais escura.
Acompanhando a variação dessa linha, notamos quê o veículo representado por ela não realizou ultrapassagem alguma.
12. alternativa a
I) 120,00 ⋅ 8 = 960,00
II) 180,00 ⋅ 6 = 1.080,00
III) 170,00 ⋅ 6 + 20,00 = 1.020,00 + 20,00 = 1.040,00
IV) 110,00 ⋅ 9 + 10,00 = 990,00 + 10,00 = 1.000,00
V) 110,00 ⋅ 10 = 1.100,00
13. alternativa c
Tempo, em hora, quê a torneira ficou aberta: t = 18 − 10 = 8
Da expressão V (t) = 5.000 − kt, temos:
2.000 = 5.000 − k ⋅ 8 ⇒ 2.000 − 5.000 = −8k ⇒ −3.000 = −8k ⇒ k = = 375
2.750 = 5.000 − 375 ⋅ t ⇒ 2.750 − 5.000 = −375t ⇒ −2.250 = −375t ⇒ t = = 6
10 h + 6 h = 16 h
14. alternativa b
Plano A:
25,00 + (75 − 20) ⋅ 1,50 + 50 ⋅ 2,00 = 207,50
Plano B:
60,00 + (75 − 65) ⋅ 1,00 + 50 ⋅ 1,20 = 130,00
Página trezentos e sessenta e nove
Plano C:
60,00 + (75 − 75) ⋅ 1,00 + 50 ⋅ 1,50 = 135,00
Plano D:
120,00 + 50 ⋅ 0,90 = 165,00
Plano E:
120,00 + 50 ⋅ 1,20 = 180,00
Unidade 3 • Função afim e função modular
1. A função afim em cada item é da forma f(x) = ax + b. Nos casos em quê b = 0, temos uma função linear. Para além díssu, se b = 0 e a = 1, a função é também chamada de identidade. Dessa forma, temos:
a) a = 8; b = 10
b) a = −2; b = −8,4
c) a = −6; b = 4
d) a = 1; b = 0; função linear e função identidade
e) a = ; b = 0; função linear
f) a = 0; b = −37
g) a = ; b =
h) a = −1; b = 0; função linear
2. a) f(−7) = 6 ⋅ (−7) + 84 = 42
b) g(5) = −4 ⋅ 5 − 6 = −26
c) g(0) = −4 ⋅ 0 − 6 = −6
d) f( ) =6 ⋅ + 84 = 94
e) f(2) + g(−10) = (6 ⋅ 2 + 84) + [−4 ⋅ (−10) − 6] = 96 + 34 = 130
f) g(4) − f(−3) = (−4 ⋅ 4 − 6) − [6 ⋅ (−3) + 84] = −22 − 66 = −88
g) = −3
3. a) Como a caixa-d’água tem capacidade de 100.000 L e o consumo é de 2.000 L por hora, sêndo v(t) o volume de á gua na caixa em função do tempo t, em hora, temos: v(t) = 100.000 − 2.000t.
b) v(15) = 100.000 − 2.000 ⋅ 15 = 100.000 − 30.000 = 70.000 → 70.000 L
c) v(t) = 0 ⇒ 100.000 − 2.000t = 0 ⇒ t = ⇒ t = 50 → 50 h
4. a) • 0 minuto: 25 + 15 ⋅ 0 = 25 → 25°C
• 1 minuto: 25 + 15 ⋅ 1 = 40 → 40°C
• 2 minutos: 25 + 15 ⋅ 2 = 55 → 55°C
• 3 minutos: 25 + 15 ⋅ 3 = 70 → 70°C
• 4 minutos: 25 + 15 ⋅ 4 = 85 → 85°C
• 5 minutos: 25 + 15 ⋅ 5 = 100 → 100°C
Tempo (min) |
Temperatura (°C) |
|---|---|
0 |
25 |
1 |
40 |
2 |
55 |
3 |
70 |
4 |
85 |
5 |
100 |
b) Item IV, pois a tempera-túra interna do fôrnu é 25 °C quando ele é ligado e, a partir dêêsse momento, aumenta 15 °C por minuto.
c) • f(10) = 15 ⋅ 10 + 25 = 175 → 175 °C
• f(x) = 280 ⇒ 15x + 25 = 280 ⇒
⇒ 15x = 255 ⇒ x = 17 → 17 min
5. a) Considerando quê o tanque está cheio com 18.000 L e quê a bomba transfére 160 L por minuto, e sêndo L(t) o volume de leite, em litro, e t o tempo, em minuto, temos: L(t) = 18.000 − 160t.
b) L(t) = 0 ⇒ 18.000 − 160t = 0 ⇒ t = = 112,5 → 112,5 h
Como 1 h = 60 min e 0,5 min = 30 s, temos: 112,5 − 60 = 52,5 → 1h52min30s.
6. a) • 70 dólares:
Dólares |
Reais |
|---|---|
1 |
4,8844 |
70 |
y |
= ⇒ y = 70 ⋅ 4,8844 ≃ 341,91 → aproximadamente R$ 341,91
• 200 euros:
Euros |
Reais |
|---|---|
1 |
5,3577 |
200 |
y |
= ⇒ y = 200 ⋅ 5,3577 = 1.071,54 → R$ 1.071,54
b) • Dólares:
Dólares |
Reais |
|---|---|
1 |
4,8844 |
x |
1.465,32 |
= ⇒ 4,8844x = 1.465,32 ⇒ x = 300 → 300 dólares
• Euros:
Euros |
Reais |
|---|---|
1 |
5,3577 |
x |
1.465,32 |
= ⇒5,3577x = 1.465,32 ⇒ x ≃ 273,50 → aproximadamente 273,50 euros
c) Sim, pois, se aumentarmos ou reduzirmos uma das grandezas, a outra também aumentará ou será reduzida, respectivamente, na mesma proporção.
d)
Dólares |
Reais |
|---|---|
1 |
4,8844 |
x |
f(x) |
= ⇒ f(x) = 4,8844x
Euros |
Reais |
|---|---|
1 |
5,3577 |
p |
g(p) |
⇒ g(p) = 5,3577p
e) • f(40) = 4,8844 ⋅ 40 = 195,376
Para comprar 40 dólares, eram necessários aproximadamente R$ 195,38.
• g(100) = 5,3577 ⋅ 100 = 535,77
Para comprar 100 euros, eram necessários R$ 535,77.
f) Resposta esperada: Sim, pois as funções f e g são funções afins, em quê o termo independente é igual a zero.
g) Resposta pessoal. Espera-se quê os estudantes pesquisem em sáites confiáveis e verifiquem o quê aconteceu com o dólar e o euro de janeiro de 2024 até a data pesquisada. A atividade póde sêr ampliada quêstionando o que acontece com os valores encontrados nos itens a, b e e a partir das novas cotações do dólar e do euro a fim de quê os estudantes identifiquem a proporcionalidade envolvida na situação.
7. Resposta pessoal. Espera-se quê os estudantes identifiquem situações quê podem sêr descritas por uma função afim, como aquelas em quê há proporcionalidade diréta entre as grandezas. Verificar se as respostas contêm características como linearidade, proporcionalidade entre as grandezas e a presença das variáveis dependente e independente.
8. a) 3.500 + 0,03 ⋅ 26.840 = 3.500 + 805,2 = 4.305,2 → R$ 4.305,20
b) Como César recebe 3% do valor v das vendas adicionado a um valor fixo de R$ 3.500,00, temos:
s (v) = 0,03v + 3.500
c) 4.541,84 = 0,03v + 3.500 ⇒ v = = 34.728 → R$ 34.728,00
9. a) v(0) = 100 − 8 ⋅ 0 = 100 → 100 m3
b) v(4) = 100 − 8 ⋅ 4 = 100 − 32 = 68 → 68 m3
c) 0 = 100 − 8t ⇒ t = ⇒ t = 12,5 → 12,5 h ou 12h30min
10. a) Resposta esperada: Não, pois, analisando cada linha do qüadro, é possível constatar quê a razão entre o preêço e o tempo não corresponde a uma constante.
b) Sendo p(t) = at + b, com a, b ∈ ℝ, temos:
Página trezentos e setenta
Subtraindo (I) de (II), obtemos a = 15.
Assim, de (I), temos:
15 + b = 47 ⇒ b = 32
Portanto, p(t) = 15t + 32.
c) • p(5) = 15 ⋅ 5 + 32 = 107 → R$ 107,00
• p(10) = 15 ⋅ 10 + 32 = 182 → R$ 182,00
d) p(t) = 84,5 ⇒ 15t + 32 = 84,5 ⇒ 15t = 52,5 ⇒ t = 3,5 → 3,5 h ou 3h30min
11. a) No mapa, a distância real, em quilômetro correspondente a cada centímetro, é dada por: = 2,5.
Assim, sêndo d a distância medida no mapa (em cm) e R (d) a distância real (em km), temos: R(d) = 2,5d.
b) 45 = 2,5d ⇒ d = ⇒ d = 18 → 18 cm
c) Como 1 km = 100.000 cm e no mapa cada 2,5 cm representa uma distância real de 1 km, temos:
2,5 ⋅ 100.000 = 250.000
Portanto, a escala do mapa é 1 ∶ 250.000.
12. Atividade de elaboração do estudante. Espera-se quê os estudantes elaborem um problema tendo como base o cartaz do enunciado. Por exemplo, o problema póde envolver a função cuja lei de formação seja f(x) = 8x + 10, em quê f(x) indica a quantia a pagar pela locação da estação de trabalho por um período de x horas.
13. a) Resposta esperada: Aumentam-se os congestionamentos, a emissão de gases poluentes e o efeito estufa, a quantidade de acidentes de trânsito, entre outras consequências.
b) Automóvel individual, pois 127 g > 71 g > 16 g.
c) Como, por passageiro transportado no deslocamento de 1 km, a emissão de CO2 por motocicleta, automóvel individual e ônibus é de 71 g, 127 g e 16 g, respectivamente, temos:
• motocicleta: m(x) = 71x
• automóvel individual: a(x) = 127x
• ônibus: o(x) = 16x
d) • motocicleta:
m(50) = 71 ⋅ 50 = 3.550 → 3.550 g
• automóvel individual:
a(50) = 127 ⋅ 50 = 6.350 → 6.350 g
• ônibus:
o(50) = 16 ⋅ 50 = 800 → 800 g
e) Resposta pessoal. Espera-se quê os estudantes citem atitudes como trocar o transporte particular pelo coletivo, dar carona para côlégas de trabalho e utilizar mais meios de transporte sustentáveis, como as bicicletas. Eles podem, por exemplo, comparar a quantidade de CO2 emitida por passageiro a cada quilômetro percorrido ao longo de um ano com a quantidade não emitida ao tomarem atitudes como as descritas anteriormente.
14. a)
b)
c) = = 24 − 3 = 21
d)
15.
16. Como a taxa de variação é igual ao coeficiente a, podemos analisá-lo em cada item e verificar quê, se a < 0, então a função é decrescente e, se a > 0, então a função é crescente. Assim, temos:
a) 5; crescente
b) −8; decrescente
c) −1; decrescente
d) ; crescente
17. a) Taxa de variação:
a = = −2
Como a < 0, a função é decrescente.
b) Taxa de variação:
a = = 4
Como a > 0, a função é crescente.
c) Taxa de variação:
a = = −1
Como a < 0, a função é decrescente.
d) Taxa de variação:
a = =
Como a > 0, a função é crescente.
18. a) Não, pois, por exemplo, ao quadruplicarmos o tempo do experimento, a tempera-túra interna da câmara fria não quadruplica, uma vez quê, em 1 h do experimento, a tempera-túra era de 1 °C e, em 4 h, era de 16 °C.
b) Taxa de variação: = = 5
Indica quê, a cada hora, a tempera-túra interna da câmara fria aumenta 5°C.
c) Considere quê f(t) = at + b, com a, b ∈ ℝ. Pelo item b, temos a = 5 e, como a tempera-túra inicial era −4°C, temos:
f(0) = −4 ⇒ 5 ⋅ 0 + b = −4 ⇒ b = −4
Portanto, temos f: [0, 4] → ℝ, definida por f(t) = 5t − 4.
d) f(t) = 6 ⇒ 5t − 4 = 6 ⇒ 5t = 10 ⇒ t = 2 → 2 h
19. a)
x |
f(x) = 3x − 1 |
(x, y) |
|---|---|---|
−1 |
f(−1) = 3 ⋅ (−1) − 1 = −4 |
(−1, −4) |
1 |
f(1) = 3 ⋅ 1 − 1 = 2 |
(1, 2) |
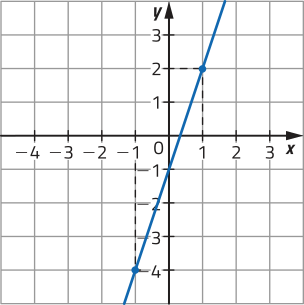
b)
x |
f(x) = x + 4 |
(x, y) |
|---|---|---|
−3 |
f(−3) = −3 + 4 = 1 |
(−3, 1) |
0 |
f(0) = 0 + 4 = 4 |
(0, 4) |
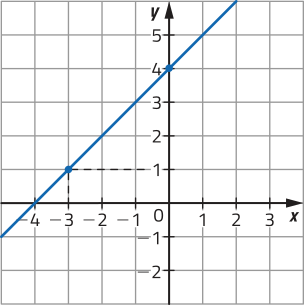
c)
x |
f(x) = 5 − 2x |
(x, y) |
|---|---|---|
0 |
f(0) = 5 − 2 ⋅ 0 = 5 |
(0, 5) |
3 |
f(3) = 5 − 2 ⋅ 3 = −1 |
(3, −1) |
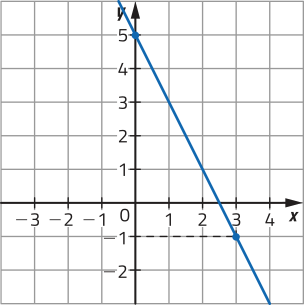
Página trezentos e setenta e um
d)
x |
f(x) = − 6 |
(x, y) |
|---|---|---|
−6 |
f(−6) = − 6 = −4 |
(−6, −4) |
0 |
f(0) = − 6 = −6 |
(0, −6) |
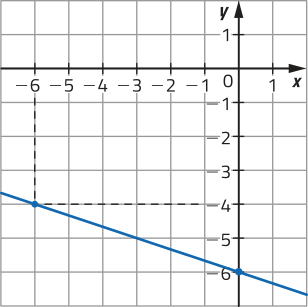
20. a) Decrescente, pois a taxa de variação é negativa (a = −2 < 0).
b) f(x) = 0 ⇒ −2x + 5 = 0 ⇒ −2x = −5 ⇒ x =
c) Pelo item b, é o zero da função; logo, o gráfico cruza o eixo x no ponto ( , 0) .
Temos f(0) = −2 ⋅ 0 + 5 = 5; logo, o gráfico cruza o eixo y no ponto (0, 5).
• Resposta pessoal. Os estudantes podem, por exemplo, construir uma tabéla e determinar alguns pares ordenados correspondentes a pontos do gráfico. Além díssu, podem utilizar os pontos conhecidos em quê a função cruza os eixos ordenados, considerando também a informação de quê a função é decrescente.
21. 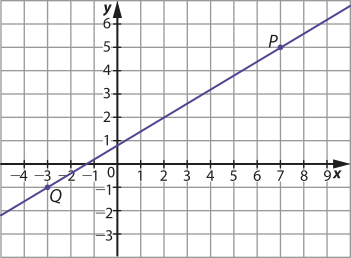
Observando o comportamento do gráfico, podemos concluir quê f é uma função crescente. Também podemos chegar a essa conclusão pelo fato de quê 7 > −3 e f(7) > f(−3).
22. a) Analisando o comportamento do gráfico de cada função, temos quê os gráficos II e III são de funções crescentes e o gráfico I é de função decrescente.
b) Observando os gráficos, podemos determinar a taxa de variação e o termo independente de cada função.
• I: taxa de variação: a = = = −1; termo independente: b = 7.
Portanto, o gráfico I corresponde à lei de formação n(x) = −x + 7.
• II: taxa de variação: a = = 5; termo independente: b = 0.
Portanto, o gráfico II corresponde à lei de formação h(x) = 5x.
• III: taxa de variação: a = ; termo independente: b = 2.
Portanto, o gráfico III corresponde à lei de formação m(x) = + 2.
23. a) Resposta esperada: Sim, pois, se considerarmos, por exemplo, o dôbro da área de plantio, a quantidade de soja produzida também será o dôbro.
b) Considerando quê a produtividade seja a mesma em qualquer área de plantio, a função q é linear e sua lei de formação é dada por q(x) = 3,5x.
c) A função q é crescente e passa pela origem (0, 0), pois é linear e a = 3,5 > 0.
Logo, o gráfico II é o quê representa essa função.
d) q(x) = 155 ⋅ 106 ⇒ 3,5x = 155 ⋅ 106 ⇒ x ≃ 44,3 ⋅ 106 → aproximadamente 44.300.000 ha
Convertendo para km2, temos:
44.300.000 ha = 44.300.000 ⋅ 0,01 km2 = 443.000 km2
Portanto, aproximadamente 443.000 km2.
e) ≃ 0,052 → aproximadamente 0,052
Resposta esperada: Representa quê cerca de 5,2% da área territorial do Brasil foi utilizada no plantio de soja na safra 2022/2023.
24. a) Considerando os pontos dados, é possível observar quê, à medida quê x cresce, o valor de f(x) decresce. Assim, f é decrescente.
b) a = = −
c) Como a função passa por (0, 4), temos quê b = 4. Considerando a = − , temos: f(x) = − + 4.
25. a) 0 = + m + 5 ⇒ m = −2
b) 6 = + m + 5 ⇒ m = 1
c) 0 = + m + 5 ⇒ m = −5
26. a) Tanto f(4) como g(4) são iguais à ordenada de P; logo:
f(4) = g(4) ⇒ −4k + 6 = 8k + 3 ⇒ −12k = −3 ⇒ k =
Segue quê:
• f(x) = x +6 ⇒ f(x) = + 6
• g(x) = 2 ⋅ x + 3 ⇒ g(x) = + 3
b) • eixo das abscissas:
f(x) = 0 ⇒ + 6 = 0 ⇒ = 6 ⇒ x =24
g(x) = 0 ⇒ + 3 = 0 ⇒ = −3 ⇒ x = −6
Logo, f cruza o eixo das abscissas em (24, 0) e g, em (−6, 0).
• eixo das ordenadas:
f(0) = + 6 =6
g(0) = + 3 = 3
Logo, f cruza o eixo das ordenadas em (0, 6) e g, em (0, 3).
27. a) Analisando, no qüadro, a tarifa por faixa de consumo, temos:
• 50 < c ≤ 200: v(c) = 0,70c + 10
• 200 < c ≤ 500: v(c) = 0,80c + 10
• c > 500: v(c) = 0,90c + 10
b) Com base nas respostas ao item a, para determinar a lei de formação da função, basta reunir as expressões determinadas para cada faixa de consumo, ou seja:
v(c) =
c) Resposta esperada: O consumo deve corresponder a um número não negativo, ou seja, D(v) = [0, +∞[. Ao considerar D(v) e a lei de formação da função v, tem-se quê Im(v) = [10, +∞[.
d) 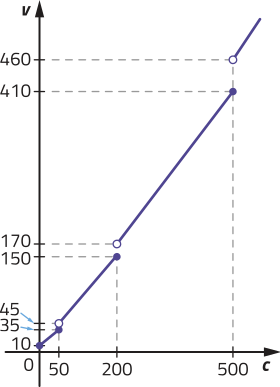
e) Resposta esperada: Sim, pois, ao escolhermos quaisquer valores c1, c2 ∈ D(v), com c2 > c1, temos quê v(c2) > v(c1).
f) • v(600) = 0,90 ⋅ 600 + 10 = 550 → R$ 550,00
• v(30) = 0,50 ⋅ 30 + 10 = 25 → R$ 25,00
• v(400) = 0,80 ⋅ 400 + 10 = 330 → R$ 330,00
• v(120) = 0,70 ⋅ 120 + 10 = 94 → R$ 94,00
Página trezentos e setenta e dois
28. alternativa b
A desvalorização por ano corresponde à taxa de variação de cada função.
• Veículo I: = −10 → desvalorização de R$ 10.000,00 por ano
• Veículo II: = −12,5 → desvalorização de R$ 12.500,00 por ano
• Veículo III: = −6 → desvalorização de R$ 6.000,00 por ano
• Veículo IV: = −5 → desvalorização de R$ 5.000,00 por ano
Logo, a maior desvalorização por ano é a do veículo II.
29. • Veículo I:
taxa de variação: a = −10; termo independente: b = 75
Logo, a lei de formação é h(x) = −10x + 75.
• Veículo II:
taxa de variação: a = −12,5; termo independente: b = 60
Logo, a lei de formação é n(x) = −12,5x + 60.
• Veículo III:
taxa de variação: a = −6; termo independente: b = 50
Logo, a lei de formação é m(x) = −6x + 50.
• Veículo IV:
taxa de variação: a = −5; termo independente: b = 36
Logo, a lei de formação é f(x) = −5x + 36.
30. a) Como o valor do frete é o mesmo para 80 ou 200 unidades, então a diferença entre as cotações de 200 e 80 unidades corresponde ao preêço de 120 unidades sem incluir o frete. Temos:
• preêço de 120 unidades na loja A:
900 − 480 = 420 → R$ 420,00
• preêço de 120 unidades na loja B:
980 − 440 = 540 → R$ 540,00
Logo, o preêço do frete na loja A é e, na loja B,
b) Conforme a resolução do item a, 120 unidades do produto custam R$ 420,00 na loja A e R$ 540,00 na loja B. Então, o preêço unitário em cada loja é:
• loja A: = 3,5 → R$ 3,50
• loja B: = 4,5 → R$ 4,50
Portanto, na loja B é mais caro, sêndo R$ 4,50 cada unidade.
c) 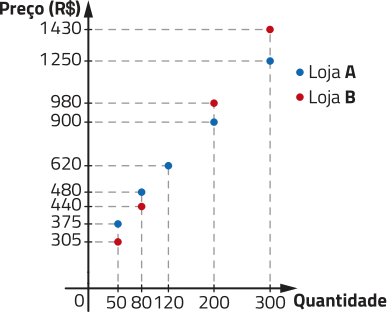
d) Para cada loja, podemos representar o preêço y em função da quantidade comprada x por uma função com lei de formação y = ax + b, em quê a é o preêço unitário do produto e b é o valor do frete.
Pelas resoluções dos itens a e b, temos:
• loja A: PA (x) = 3,5x + 200
• loja B: PB (x) = 4,50x + 80
Ambas são funções afins.
e) É financeiramente mais vantajoso na loja A se a quantidade x é tal quê PA (x) < PB (x), ou seja:
3,5x + 200 < 4,5x + 80 ⇒ −x < −120 ⇒ x > 120
Portanto, é mais vantajoso para quantidades maiores quê 120 unidades.
31. a) 33 − 18 = 15 → 15 kg
b) • janeiro: |18 − f(1)| = |18 − (2,43 ⋅ 1 + 16)| = 0,43 → 0,43 kg
• fevereiro: |22 − f(2)| = |22 − (2,43 ⋅ 2 + 16)| = 1,14 → 1,14 kg
• março: |22 − f(3)| = |22 − (2,43 ⋅ 3 + 16)| = 1,29 → 1,29 kg
• abril: |26 − f(4)| = |26 − (2,43 ⋅ 4 + 16)| = 0,28 → 0,28 kg
• maio: |29 − f(5)| = |29 − (2,43 ⋅ 5 + 16)| = 0,85 → 0,85 kg
• junho: |30 − f(6)| = |30 − (2,43 ⋅ 6 + 16)| = 0,58 → 0,58 kg
• julho: |33 − f(7)| = |33 − (2,43 ⋅ 7 + 16)| = 0,01 → 0,01 kg
c) f(7) − f(1) = (2,43 ⋅ 7 + 16) − (2,43 ⋅ 1 + 16) = 33,01 − 18,43 = 14,58 → 14,58 kg
d) Resposta pessoal. Espera-se quê os estudantes reconheçam quê a função determina uma aproximação razoável para os dados aferidos pelo centro de recuperação (diferença quase sempre abaixo de 1 kg em cada mês).
32. a) Como o coeficiente a corresponde à taxa de variação da função, ao alterá-lo, a inclinação da reta correspondente ao gráfico da função f se altera.
b) Como o coeficiente b corresponde à ordenada do ponto onde a reta cruza o eixo y, ao alterá-lo, o gráfico da função f é transladado verticalmente.
33. a) Seja y = ax + b. Temos o seguinte.
• Para x = −1, tem-se y = 1.
Logo, −a + b = 1.
• Para x = 1, tem-se y = 5.
Logo, a + b = 5.
⇒ ![]()
Substituindo a = 2 na primeira equação, temos:
−2 + b = 1 ⇒ b = 3
Portanto, y = 2x + 3.
b) Seja y = ax + b. Temos quê:
a = = −1 − 2 = −3
Segue quê:
para x = 1, tem-se y = 2.
Logo, −3 ⋅ 1 + b = 2 ⇒ b = 5
Portanto, y = −3x + 5.
c) Seja y = ax + b. Temos b = −6, pois o gráfico cruza o eixo y no ponto de ordenada −6. Segue quê:
para x = 1, tem-se y = 0.
Logo, a ⋅ 1 − 6 = 0 ⇒ a = 6
Portanto, y = 6x − 6.
d) Seja y = ax + b, como a reta passa pêlos pontos de coordenadas (1, 3), (2, 1), temos: a = =−2.
Segue quê:
3 = −2 ⋅ 1 + b ⇒ b = 5
Portanto, y = −2x + 5.
34. Inicialmente, vamos determinar a equação de cada reta.
• O coeficiente angular da reta s é = 5, e seu coeficiente linear é 2, pois a reta cruza o eixo y no ponto de ordenada 2. Logo, y = 5x + 2.
• O coeficiente angular de r é = −2, e seu coeficiente linear é −5, pois a reta cruza o eixo y no ponto de ordenada −5. Logo, y = −2x − 5.
Assim, segue quê:
5x + 2 = −2x − 5 ⇒ 7x = −7 ⇒ x = −1
Para x = −1, temos:
y = 5 ⋅ (−1) + 2 = −3
Portanto, P (−1, −3).
35. Para resolver os itens a, b e c, vamos determinar a lei de formação da função p. Temos:
a = =
p(3) = 15 ⇒ ⋅ 3 + b = 15 ⇒ b = 15
Página trezentos e setenta e três
Assim, p(x) =
a) p(25,5) = ⋅ 25, 5 + = = 40 → R$ 40,00
b) p(x) = 50 ⇒ = 50 ⇒ ⇒ x = 34,5 → 34,5 km
c) Para obtêr a equação reduzida da reta correspondente ao gráfico da função p, podemos tomar p(x) = y:
y =
Para obtêr a equação geral da reta, inicialmente multiplicamos cada membro da equação reduzida por 9:
9 ⋅ y = 9 ⋅ x + 9 ⋅ ⇒ 9y = 10x + 105 ⇒ 9y − 10x − 105 = 0
36. a) • Considerando quê a reta r passa pêlos pontos de coordenadas (6, 5), (−2, −1), temos quê o coeficiente angular da equação de r é dado por:
ar =
Assim, a equação de r é dada por:
y = y0 + a(x − x0) → y = 5 + (x − 6) ⇒ y = 5 − x ⇒ 3x − 4y = −2
• Considerando quê a reta s passa pêlos pontos de coordenadas (−1, 6), (5, −2), temos quê o coeficiente angular da equação de s é dado por:
as =
Assim, a equação de s é dada por:
y = y0 + a(x − x0) ⇒ y = 6 − [x − (−1)] ⇒ y = 6 − x ⇒ 4x + 3y = 14
b) Isolando y em cada equação e igualando os resultados obtidos, temos:
Segue quê:
Portanto, o ponto em quê as retas r e s se cruzam tem coordenadas (2, 2).
37. a) y = y0 + a(x − x0) ⇒ y = 4 + 3(x − 1) ⇒ y = 3x + 1
b) y = y0 + a(x − x0) ⇒ y = 1 + (− ) (x − 2) ⇒ y = 2 −
38. a) coeficiente angular:
a = = 1
y = y0 + a(x − x0) ⇒ y = 3 + 1(x − 1) ⇒ y = x + 2
b) coeficiente angular:
y = y0 + a(x − x0) ⇒ y = −5 + (−4)(x − 2) ⇒ y = −4x + 3
c) coeficiente angular:
y = y0 + a(x − x0) ⇒ y = 7 + (x −3) ⇒ y = + 6
d) coeficiente angular:
y = y0 + a(x − x0) ⇒ y = 2 + 1(x − 3) ⇒ y = x − 1
39. a) coeficiente angular:
a = = 0
y = y0 + a(x − x0) ⇒ y = 2 + 0(x − 5) ⇒ y = 2
b) coeficiente angular:
a = = 0
y = y0 + a(x − x0) ⇒ y = 5 + 0(x − 0) ⇒ y = 5
c) coeficiente angular:
a = = 0
y = y0 + a(x − x0) ⇒ y = −3 + 0(x − 1) ⇒ y = −3
d) coeficiente angular:
a = = 0
y = y0 + a(x − x0) ⇒ y = −1 + 0(x − 4) ⇒ y = −1
• Resposta esperada: Em cada item, a ordenada dos dois pontos indicados são iguais. Em cada item, a equação ôbitída tem o coeficiente angular igual a zero, o quê implica quê a reta é paralela ao eixo das abscissas e póde sêr expressa na forma y = c, sêndo c a ordenada dos dois pontos indicados.
Integrando com...
1. Alternativas a e d, pois, como a velocidade é constante, não varia com o tempo e, em um mesmo intervalo de tempo, o móvel percórre a mesma distância.
2. a) O ponto de coordenadas (2, 50) representa quê, no tempo correspondente a 2 s, a posição do automóvel era de 50 m.
b) S(12) = 30 + 10 ⋅ 12 = 150 ⇒ 150 m
c) 200 = 30 + 10t ⇒ t = 17 ⇒ 17 s
3. a) Posição inicial: S(0) = 0 → 0 m
Posição no instante 4 s:
S(4) = 200 ⇒ 200 m
b) A velocidade do móvel corresponde à taxa de variação de S:
= 50 ⇒ 50 m/s
c) S(2) − S(0) = 100 − 0 = 100 ⇒ 100 m
d) Como a velocidade dêêsse móvel é 50 m/s e sua posição inicial é 0 m, temos:
S(t) = 0 + 50t ⇒ S(t) = 50t
4. a = = 50
Como o automóvel percórre 50 km a cada hora e parte da posição 10 km, temos:
S(t) = 10 + 50t.
5. a) Analisando o valor da ordenada do ponto cuja abscissa é zero em cada caso, temos: móvel A: 0 m; móvel B: 200 m.
b) O ponto em quê as duas retas se cruzam no gráfico tem abscissa igual a 40. Logo, os móveis se encontram no instante t = 40 s.
c) Móvel A:
Taxa de variação:
a = = 12,5
Como b = 0, temos SA (t) = 12,5t
Móvel B:
Taxa de variação:
a = = 7,5
Como b = 200, temos SB (t) = 200 + 7,5t
Móvel A: SA (80) = 12,5 ⋅ 80 = 1.000 → 1.000 m
Móvel B: SB (80) = 200 + 7,5 ⋅ 80 = 800 → 800 m
d) Móvel A: SA(t) = 12,5t
Móvel B: SB(t) = 200 + 7,5t
6. Resposta pessoal. Espera-se quê os estudantes consigam estabelecer a taxa de variação em cada experimento e considerem possíveis êêrros de medição. A partir da taxa de variação, eles podem comparar, por exemplo, a velocidade da bolha no experimento realizado pêlos grupos.
40. a) • zero de f: 6x − 2 = 0 ⇒ x =
• f é crescente, pois a = 6 > 0
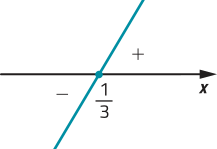
f(x) > 0 para x > , f(x) = 0 para x = e f(x) < 0 para x <
b) • zero de g: −7x + 1 = 0 ⇒ x =
• g é decrescente, pois a = −7 < 0
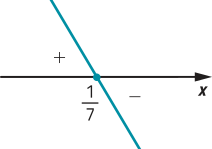
Página trezentos e setenta e quatro
c) • zero de h: 9x − 3 = 0 ⇒ x =
• h é crescente, pois a = 9 > 0
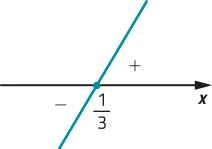
h(x) > 0 para x >, h(x) = 0 para x = e h(x) < 0 para x <
d) • zero de m: −5x − 4 = 0 ⇒ x =
• m é decrescente, pois a = −5 < 0
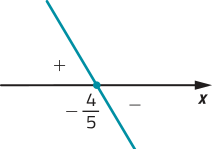
m(x) < 0 para x > , m(x) = 0 para x = e m(x) > 0 para x <
e) • zero de n: 3x + 12 = 0 ⇒ x = −4
• n é crescente, pois a = 3 > 0
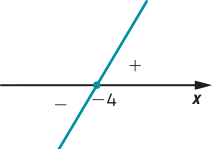
n(x) > 0 para x > −4, n(x) = 0 para x = −4 e n(x) < 0 para x < −4
f) • zero de p: 10x = 0 ⇒ x = 0
• p é crescente, pois a = 10 > 0
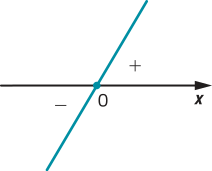
p(x) > 0 para x > 0, p(x) = 0 para x = 0 e p(x) < 0 para x < 0
41. a) Como os pontos de coordenadas (1, 4) e (3, −4) pertencem ao gráfico da função f, podemos determinar quê a lei de formação de f é f(x) = −4x + 8.
Assim, o zero de f é dado por: f(x) = 0 ⇒ −4x + 8 = 0 ⇒ x = 2
Portanto, como f é decrescente (a = −4 < 0), temos f(x) > 0 para x < 2.
b) Como os pontos de coordenadas (2, −3) e (4, 4) pertencem ao gráfico da função f, podemos determinar quê a lei de formação de f é f(x) = x − 10.
Assim, o zero de f é dado por: f(x) = 0 ⇒ x− 10 = 0 ⇒ x =
Portanto, como f é crescente
(a = > 0),temos f(x) > 0 para x > .
42. • f(x) > 0 ⇒ −3x − 12 > 0 ⇒ −3x > 12 ⇒ x < ⇒ x < −4 (A)
• g(x) > 0 ⇒ −4x − 4 > 0 ⇒ −4x > 4 ⇒ x < ⇒ x < −1 (B)
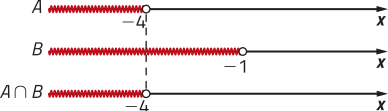
Portanto, ambas as funções são positivas para x ∈]−∞, −4[.
43. Seja f: [0, 10] → ℝ, dada por f(t) = at + b, a função afim quê representa a tempera-túra em função do tempo t de resfriamento. Temos f(2) = 8 e f(8) = −4. Assim:
![]()
Substituindo a = −2 na primeira equação, temos:
2 ⋅ (−2) + b = 8 ⇒ −4 + b = 8 ⇒ b = 12
Assim, f(t) = −2t + 12.
• zero de f: −2t + 12 = 0 ⇒ t = 6
• f é decrescente, pois a = −2 < 0
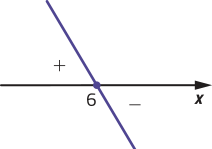
positiva: 0 ≤ t < 6; igual a zero: t = 6;
negativa: 6 < t ≤ 10
44. Para f(x) > 0, temos ax + b > 0 ⇒
⇒ ax > −b. Como f é decrescente, temos a < 0. Assim, dividimos a desigualdade ax > −b por a e invertemos o sentido da desigualdade:
45. a) Como, por 2 horas, no estacionamento A, o motorista pagará R$ 24,00 (2 ⋅ 12 = 24) e, no estacionamento B, pagará R$ 32,00 (20 + 2 ⋅ 6 = 32), é mais vantajoso o estacionamento A para esse período.
b) Considerando quê, no estacionamento A, paga-se R$ 12,00 por hora (sem valor fixo) e quê, no estacionamento B, paga-se R$ 6,00 por hora mais R$ 20,00 fixos, temos:
• Estacionamento A: V(t) = 12t
• Estacionamento B: V(t) = 6t + 20
c) Para determinar o tempo t em quê o estacionamento B é mais vantajoso quê o A, fazemos:
12t > 6t + 20 ⇒ 6t > 20 ⇒ t > .
Como as frações de hora representam uma hora completa na cobrança, temos t > 3.
Portanto, para períodos de até 3 horas de uso, o estacionamento A é mais vantajoso financeiramente para o motorista. Para períodos a partir de 3 horas, o estacionamento B é mais vantajoso.
46. alternativa a
Ana alcança Beatriz quando PA = PB.
Logo:
200 + 25t = 500 + 20t ⇒ 5t = 300 ⇒ t = 60 → 60 minutos.
47. a) Como a figura representa um polígono regular de 7 lados, nomeamos esse polígono heptágono regular.
b) f:]0, +∞[ → ℝ, definida por f(x) = 7x
c) f(4) = 7 ⋅ 4 = 28
Resposta esperada: Esse cálculo indica quê um heptágono regular tem perímetro com 28 unidades de comprimento quando cada um de seus lados méde 4 unidades de comprimento.
48. O polígono regular em quê cada lado méde 2,5 unidades de comprimento tem perímetro de 15 unidades de comprimento; logo, se n é a quantidade de lados do polígono, então:
n ⋅ 2,5 = 15 ⇒ n = = 6
Portanto, o polígono é um hekzágono regular.
49. a) • 1 mês: M = 600(1 + 0,05 ⋅ 1) = 630 → R$ 630,00
• 5 meses: M = 600(1 + 0,05 ⋅ 5) = 750 → R$ 750,00
b) M = = 30t + 600
Assim, temos f: ℕ → ℝ, definida por f(t) = 30t + 600.
c) 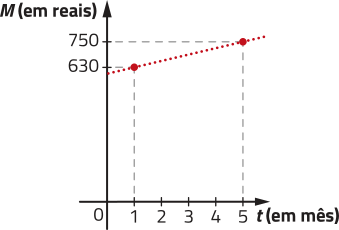
50. a) O perímetro do quadrado corresponde ao quádruplo da medida dos seus lados, e a área, ao quadrado dessas medidas. Assim, os números indicados na coluna correspondente ao perímetro equivalem ao quadruplo dos números indicados na coluna correspondente à medida do lado, e os números indicados na coluna correspondente à área equivalem ao quadrado dos números indicados na coluna correspondente à medida do lado.
b) Perímetro: 4x; área: x2.
c) Não. Por exemplo, um quadrado com 3 cm de lado tem 9 cm2 de área, já um quadrado com 6 cm de lado (o dôbro de 3 cm) tem 36 cm2 de área, e o dôbro de 9 cm2 é 18 cm2.
Página trezentos e setenta e cinco
d) Resposta esperada: Sim, pois, considerando um quadrado cujo lado méde x, temos quê seu perímetro é 4x. Então, ao dobrarmos a medida do lado dele, obtemos 2x, e seu perímetro será de 4 ⋅ 2x = 8x = 2 ⋅ 4x, ou seja, o dôbro do perímetro do quadrado de lado x.
e) p(x) = 4x; s (x) = x2. Apenas p é uma função afim, já quê s tem a variável independente com expoente 2.
51. a) O capital é o montante correspondente ao tempo de aplicação t = 0. Temos:
A: R$ 1.200,00; B: R$ 800,00
b) • instituição A: para t = 20, temos:
j = 2.400 − 1.200 = 1.200
j = c ⋅ i ⋅ t ⇒ 1.200 = 1.200 ⋅ i ⋅ 20 ⇒ i = 0,05 = 5%
• instituição B: para t = 20, temos:
j = 2.400 − 800 = 1.600
j = c ⋅ i ⋅ t ⇒ 1.600 = 800 ⋅ i ⋅ 20 ⇒ i = 0,1 = 10%
c) • instituição A:
M =
Assim, temos f: ℕ → ℝ, definida por f(t) = 60t + 1.200.
• instituição B:
M =
Assim, temos g: ℕ → ℝ, definida por g(t) = 80t + 800.
d) Utilizando as funções determinadas no item c, temos:
• 1 ano (12 meses):
f(12) = 60 ⋅ 12 + 1.200 = 1.920
g(12) = 80 ⋅ 12 + 800 = 1.760
Temos f(12) > g(12); ou seja, o montante na instituição A é maior.
• 2 anos (24 meses):
f(24) = 60 ⋅ 24 + 1.200 = 2.640
g(24) = 80 ⋅ 24 + 800 = 2.720
Temos g(24) > f(24); ou seja, o montante na instituição B é maior.
52. a) Para vendas até R$ 5.000,00, o salário é R$ 2.000,00.
Para vendas maiores quê R$ 5.000,00 e menóres ou iguais a
R$ 10.000,00, temos:
S (v) = 2.000 + 0,10 ⋅ (v − 5.000) = 2.000 + 0,10v − 500 =
= 0,10v + 1.500
Para vendas maiores quê R$ 10.000,00, temos:
S (v) = 2.500 + 0,15 ⋅ (v − 10.000) = 2.500 + 0,15v − 1.500 =
= 0,15v + 1.000
Logo, a lei de formação de S é:
S(v)=
b) 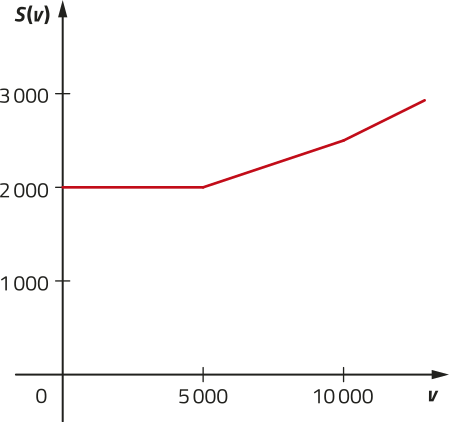
53. a) Para x ≤ 3, temos y = 25.
Para 3 < x ≤ 5, temos um trecho da reta quê passa pêlos pontos de coordenadas (3, 25) e (5, 35). Assim, a taxa de variação é dada por:
y = y0 + a (x − x0) → y = 25 + 5(x − 3) ⇒ y = 5x + 10
Para x > 5, temos o trecho da reta quê passa pêlos pontos de coordenadas (5, 35) e (6, 45). Assim, a taxa de variação é dada por:
y = y0 + a(x − x0) → y = 35 + 10(x − 5) ⇒ y = 10x − 15
Logo, a lei de formação da função V é dada por:
V(x) =
b) Atividade de elaboração do estudante. Espera-se quê os estudantes abordem em suas kestões os conceitos estudados, como taxa de variação, coeficiente angular e linear de uma função afim, função linear, função constante e representação gráfica. Eles podem, ainda, por exemplo, estimar resultados a partir de determinado consumo fictício de metros cúbicos de gás.
54. a) • f(0) = 5 ⋅ 0 − 20 = −20
• f(1) = 5 ⋅ 1 − 20 = −15
• f(2) = 5 ⋅ 2 − 20 = −10
• f(3) = 5 ⋅ 3 − 20 = −5
• f(4) = 5 ⋅ 4 − 20 = 0
−20, −15, −10, −5 e 0
b) r = −15 − (−20) = 5
c) 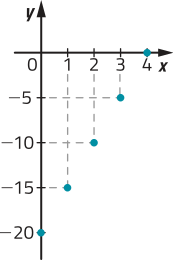
55. a) Sejam a e b números reais tais quê f(x) = ax + b. Então:
f(0) = 10 ⇒ a ⋅ 0 + b = 10 ⇒ b = 10
f(1) = 8 ⇒ a ⋅ 1 + = 8 ⇒ a = −2
Portanto, f(x) = −2x + 10.
b) • f(9) = −2 ⋅ 9 + 10 = −8
• f(19) = −2 ⋅ 19 + 10 = −28
• f(99) = −2 ⋅ 99 + 10 = −188
56. j = c ⋅ i ⋅ t ⇒ 252 = 900 ⋅ 0,07 ⋅ t ⇒ t = 4 → 4 meses
57. a) Resposta pessoal. Espera-se quê os estudantes respondam, por exemplo, quê a quantidade de circunferências corresponde ao dôbro do número da figura e quê a quantidade de quadrados corresponde ao quadrado do número da figura.
b) Resposta pessoal. Espera-se quê os estudantes desenhem uma figura composta de 25 quadrados e 10 circunferências, dispostas de modo quê os quadrados fiquem organizados em 5 fileiras com 5 quadrados cada e quê as circunferências fiquem organizadas em duas fileiras com 5 em cada, sêndo uma fileira acima e outra abaixo dos quadrados.
c) • Resposta esperada: (1, 4, 9, 25,..., n2,...).
• Resposta esperada: (2, 4, 6, 8, 10,..., 2n,...).
d) • 4 − 1 = 3; 9 − 4 = 5
• 4 − 2 = 2; 6 − 4 = 2; 8 − 6 = 2
Resposta esperada: A sequência numérica (2, 4, 6, 8, 10,..., 2n,...) é uma PA, pois, a partir do 2º termo, a diferença entre cada termo e o anterior é igual a 2, quê corresponde à razão da PA.
Página trezentos e setenta e seis
58. Resposta pessoal. Espera-se quê os estudantes reconheçam, em situações do cotidiano deles, uma sequência em quê cada termo, a partir do segundo, seja igual ao anterior adicionado de um valor constante. Observar se eles definem a função relacionada à PA e se determinam elemêntos dessa sequência, como o primeiro termo e a razão.
59. Resposta pessoal. Espera-se quê os estudantes tênham compreendido a PA como uma aplicação particular da função com domínio natural e quê consigam relacionar elemêntos dessa função com a razão da PA às posições dos termos dela.
60. a) f(−3) = |−3 + 5| − 6 = |2| − 6 = 2 − 6 = −4
b) f(4) = |4 + 5| − 6 = |9| − 6 = 9 − 6 = 3
c) g(6) = |6 − 1| + 4 = |5| + 4 = 5 + 4 = 9
d) g(−1) = |−1 − 1| + 4 = |−2| + 4 = 2 + 4 = 6
e) f(0) + g(3) = |0 + 5| − 6 + |3 − 1| + 4 = |5| + |2| − 2 = 5 + 2 − 2 = 5
f) g(−2) − f(2) = |−2 − 1| + 4 − (|2 + 5| − 6) = |−3| − |7| + 10 = 3 − 7 + 10 = 6
61. a) 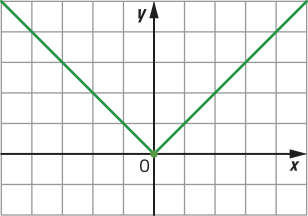
b) 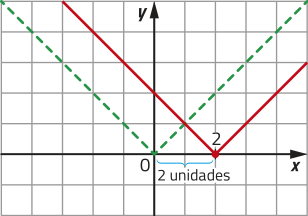
c) 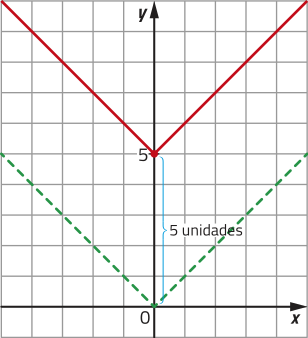
d) 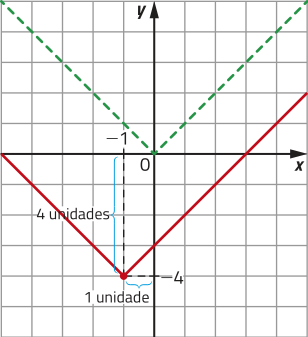
62. 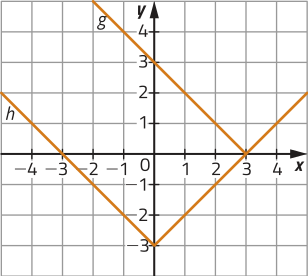
Resposta esperada: O gráfico de h corresponde ao mesmo gráfico de g, deslocado três unidades para a esquerda e três unidades para baixo.
63. a) O gráfico está transladado 4 unidades para a direita; logo, g(x) = |x − 4|.
b) O gráfico está transladado 3 unidades para cima; logo, h(x) = |x| + 3.
c) O gráfico está transladado duas unidades para a esquerda e uma unidade para cima; logo, m(x) = |x + 2| + 1.
• Resposta pessoal. Espera-se quê os estudantes demonstrem, nessa atividade, compreensão a respeito das translações com o gráfico da função modular.
64. a) Como Felipe deslocou o gráfico de f duas unidades para a direita e 5 unidades para cima, temos quê g(x) = |x − 2| + 5.
b) Temos quê:
g(0) = |0 − 2| + 5 = |−2| + 5 = 2 + 5 = 7
Logo, o gráfico cruza o eixo das ordenadas em (0, 7).
65. a) O gráfico de g corresponde ao gráfico de f(x) = |x| transladado 7 unidades para a direita; logo, g(x) = |x − 7|.
b) • g (11) = |11 − 7| = |4| = 4
• g (12) = |12 − 7| = |5| = 5
Logo, os pontos com abscissas 11 ou 12, quê pertencem ao gráfico de g, são (11, 4) e (12, 5). Portanto, o alvo C é o único cujo ponto correspondente pertence ao gráfico da função g.
c) Resposta esperada: 7 pontos, pois x − y = 12 − 5 = 7.
66. alternativa d
Para x = 2, de acôr-do com o fluxograma, temos:
f(2) = 2 + 2 = 4
Para x = −2, de acôr-do com o fluxograma, temos:
f(−2) = −(−2) + 4 = 2 + 4 = 6
A alternativa d é a única quê apresenta uma função em quê f(2) = 4 e f(−2) = 6.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) Considerando quê o valor pago será R$ 0,50 por minuto mais
R$ 2,50 pela ativação do serviço, temos: f(x) = 0,5x + 2,50.
b) • f(5) = 0,5 ⋅ 5 + 2,50 = 5
• f(10) = 0,5 ⋅ 10 + 2,50 = 7,50
Esses resultados indicam quê o aluguel da bicicleta por 5 min e por 10 min custam, respectivamente, R$ 5,00 e R$ 7,50.
c) Como a função é do tipo f(x) = ax + b, com a = 0,5 e b = 2,50, temos quê se trata de uma função afim.
d) Função crescente. Indica quê, ao aumentarmos o tempo de locação da bicicleta, o valor a pagar por esse serviço também aumenta.
e) = = 0,5
Página trezentos e setenta e sete
f) 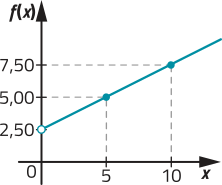
g) Todas as funções têm a taxa de variação igual à da função f, ou seja, a = 0,5, e termo independente b igual à ordenada do ponto cuja reta quê contém o respectivo gráfico intercepta o eixo y. Assim:
• g(x) = 0,5x + 3,5;
• h(x) = 0,5x + 4;
• j(x) = 0,5x + 1,5;
• m(x) = 0,5x.
h) Resposta pessoal. Espera-se quê os estudantes apliquem os conceitos estudados descrevendo uma função afim a partir de valores reais de aluguéis de patinete elétrica, bicicleta ou outro meio de locomoção. Eles ainda podem descrever funções lineares caso não haja custo de ativação do serviço.
i) Resposta pessoal. Espera-se quê os estudantes reflitam a respeito dos meios de transporte utilizados pela população na região em quê moram e sintetizem as informações utilizando, preferencialmente, os conceitos estudados na Unidade. Uma das conclusões possíveis é quê a utilização de transporte coletivo e de meios alternativos menos poluentes póde sêr uma alternativa para um futuro mais sustentável.
Praticando: enêm e vestibulares
1. alternativa b
Sendo x a quantidade de calçados produzidos e R$ 28,00 o valor faturado com cada um deles, tem-se quê o lucro mensal póde sêr expresso por: 28x − 20.000.
2. alternativa a
90% de q é dado por: ⋅ q = 0,9q.
Assim, C = 0,9q.
3. alternativa c
|2⋅16 + b − 63,5| ≤ 1,5 ⇒ |b − 31,5| ≤ 1,5 ⇒ |b − 31,5| − 1,5 ≤ 0
Analisando a função dada por g(b) = |b − 31,5| − 1,5, identificamos quê o gráfico de g corresponde ao gráfico de f(b) = |b| transladado 31,5 unidades para a direita e 1,5 unidade para baixo. Observe o gráfico de g.
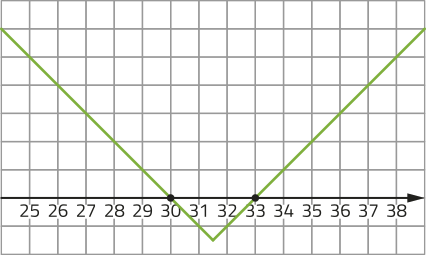
Portanto, g(b) ≤ 0 para 30 ≤ b ≤ 33.
4. alternativa c
A trajetória do projétil B passa pêlos pontos de coordenadas (0, 0) e (4, 2). Calculando o coeficiente angular da função quê descreve essa trajetória, temos:
Para alcançar o objetivo descrito, a nova trajetória do projétil B deve passar pêlos pontos de coordenadas (0, 0) e (4, 16). Assim, o coeficiente angular da função quê descreve essa trajetória deve sêr:
Portanto, o coeficiente angular da função quê descreve a trajetória do projétil B deverá aumentar em duas unidades, pois 4 − 2 = 2.
5. alternativa a
De acôr-do com a equação apresentada, temos as seguintes possibilidades:
• x ≥ 0 e y < 0 → x − (−y) = 1 ⇒ y = −x + 1
• x ≥ 0 e y ≥ 0 → x − y = 1 ⇒ y = x − 1
• x < 0 e y < 0 → −x − (−y) = 1 ⇒ y = x + 1
• x < 0 e y ≥ 0 → −x − y = 1 ⇒ y = −x − 1
Portanto, ao representar a equação dada no plano cartesiano, teremos quatro semirretas.
6. alternativa d
Y = 160 ⋅ (X − 1) + 1.000 ⇒ Y = 160X − 160 + 1.000 ⇒ Y = 160X + 840
7. alternativa d
De acôr-do com os gráficos, temos quê, nessa empresa, a cada hora, são produzidas 20.000 peças e são faturados R$ 4.000,00.
Assim, o faturamento correspondente a cada peça é dado por: 4.000 ∶ 20.000 = 0,2 → R$ 0,20
Desse modo, a quantidade de peças quê devem sêr produzidas para se obtêr um faturamento de R$ 10.000,00 é dada por:
10.000 ∶ 0,2 = 50.000 → 50.000 peças
8. alternativa c
C (48) = 6,00 + 0,50 ⋅ 48 = 6,00 + 24,00 = 30,00 → R$ 30,00
9. alternativa c
Considerando quê a função f passa pêlos pontos de coordenadas (0, 15), e (5, 0), temos quê a taxa de variação de f é dada por:
af = =−3
De f(5) = 0, segue quê:
0 = −3 ⋅ 5 + bf ⇒ bf = 15
Desse modo, f(x) = −3x + 15
Considerando quê a função g passa pêlos pontos de coordenadas (0, 1) e (−1, 0), temos quê a taxa de variação de g é dada por:
ag = =1
De g(−1) = 0, segue quê:
0 = 1 ⋅ (−1) + bg ⇒ bg = 1
Desse modo, g (x) = x + 1.
Como w é abscissa do ponto de interseção das funções f e g, temos:
−3w + 15 = w + 1 ⇒ −4w = 1 − 15 ⇒ w = ⇒ w =
10. alternativa e
Temos quê o gráfico da função m(t) = at + b passa pêlos dois pontos em quê houve correlação perfeita, cujas coordenadas são
(1, 1) e (3, 2). Assim, a taxa de variação dessa função é dada por:
a =
De m(1) = 1, segue quê:
1 = ⋅ 1 + b ⇒ b = 1 − ⇒ b =
Desse modo, m(t) = t + .
Fazendo t = 6, temos:
m(6) = =3,5
Como 210 g = 0,21 kg, segue quê:
3,5 − 0,21 = 3,29 → 3,29 kg
Unidade 4 • Função quadrática
1. São exemplos de leis de formação de funções quadráticas aquelas na forma f(x) = ax2 + bx + c, com a ≠ 0. Assim, temos: a, b, d e e.
Página trezentos e setenta e oito
2. Considerando quê o coeficiente a multiplica o x2, o coeficiente b multiplica o x e c é o termo independente, temos:
a) a = −5; b = 3; c = −9
b) a = 1; b = 0; c = −0,4
c)
d) a = 3,5; b = 0; c = 0
e)
f) a = 4; b = 56; c = 196
3. a) f(2) = 22 + 5 ⋅ 2 − 7 = 7
b) f(−3) = (−3)2 + 5 ⋅ (−3) − 7 = −13
c) g(5) = −2 ⋅ 52 + 4 ⋅ 5 + 3 = −27
d) g(−0,3) = −2 ⋅ (−0,3)2 + 4 ⋅ (−0,3) + 3 = 1,62
e) f(−1) = (−1)2 + 5 ⋅ (−1) − 7 = −11
g(9) = −2 ⋅ 92 + 4 ⋅ 9 + 3 = −123
f(−1) + g(9) = −11 − 123 = −134
f) f(3) = 32 + 5 ⋅ 3 − 7 = 17
g(−1) = −2 ⋅ (−1)2 + 4 ⋅ (−1) + 3 = −3
3 ⋅ f(3) − 2 ⋅ g(−1) = 3 ⋅ 17 − 2 ⋅ (−3) = 57
4. a) figura 1: 5 quadrados; figura 2: 8 quadrados; figura 3: 13 quadrados
b) Substituindo x = 1 em cada lei de formação apresentada, temos:
• f(x) = x2 + 3x + 5
f(1) = 12 + 3 ⋅ 1 + 5 = 9
• f(x) = x2 + 4
f(1) = 12 + 4 = 5
• f(x) = −3x2
f(1) = −3 ⋅ 12 = −3
• f(x) = x2 + 3
f(1) = 12 + 3 = 4
Como há uma única lei de formação em quê f(1) = 5, temos quê a lei de formação quê indica a quantidade de quadrados quê compõe a figura x é dada por f(x) = x2 + 4.
c) f(8) = 82 + 4 = 68
Portanto, 68 quadrados compõem a figura 8 dessa sequência. Resposta pessoal.
5. a) Como a área de um quadrado é dada pelo quadrado da medida do lado, temos: f(x) = x2
b) f(5) = 52 = 25
f(3) = 32 = 9
Resposta esperada: Esses cálculos indicam quê quadrados cujos lados médem 5 u.c. e 3 u.c. têm área com medidas de 25 u.a. e 9 u.a., respectivamente.
c) I: incorréta, pois, se a medida do lado dobra, a medida da área quadruplica.
II: incorréta, pois, pela lei de formação da função, temos a medida do lado elevada ao quadrado, e não multiplicada por dois.
III: correta.
6. a) • d(7) = = 14 → 14 diagonais
• d(14) = = 77 → 77 diagonais
• d(18) = = 135 → 135 diagonais
b)
c) Uma diagonal é um segmento de reta com extremidades em dois vértices não consecutivos de um polígono e, ainda, cada vértice de um polígono convexo tem dois vértices consecutivos a ele. Assim, em um polígono convexo de n lados, temos quê, de cada vértice, partem n − 3 diagonais. Dessa maneira, o total de diagonais é dado pelo produto da quantidade de vértices pela quantidade de diagonais de cada vértice, ou seja, n ⋅ (n − 3). Porém, nesse caso, estamos considerando duas vezes cada diagonal. Assim, o total de diagonais d, de um polígono convexo de n lados, é dado por d(n) = .
7. Resposta pessoal. Espera-se quê os estudantes definam uma função quadrática identificando cada um de seus elemêntos e coeficientes. Eles podem utilizar ou não contextos para a definição da função. Caso utilizem, chamar a atenção para o domínio da função de acôr-do com o contexto escolhido.
8. a) f(15) = 0,2 ⋅ 152 + 5 ⋅ 15 + 200 = 320
f(40) = 0,2 ⋅ 402 + 5 ⋅ 40 + 200 = 720
Portanto, o custo de produção diário dessa cooperativa é R$ 320,00, quando produzem 15 bolsas, e R$ 720,00, quando produzem 40 bolsas.
b) f(35) = 0,2 ⋅ 352 + 5 ⋅ 35 + 200 = 620
lucro: 1.400 − 620 = 780 → R$ 780,00
9. a) f(x) = (x − 4) ⋅ (x − 5) ⇒ f(x) = x2 − 9x + 20
b) g(x) = 2 ⋅ (x − 4) ⋅ (x − 5) + 2 ⋅ (x − 4) ⋅ (x − 2) + 2 ⋅ (x − 5) ⋅ (x − 2) ⇒ g(x) = 6x2 − 44x + 76
c) f(10) = 102 − 9 ⋅ 10 + 20 = 30 → 30 m2
g(10) = 6 ⋅ 102 − 44 ⋅ 10 + 76 = 236 → 236 m2
10. a) 12 ⋅ 4,9 = 4,9
22 ⋅ 4,9 = 19,6
32 ⋅ 4,9 = 44,1
42 ⋅ 4,9 = 78,4
Resposta esperada: Cada número da segunda linha corresponde ao quadrado do respectivo número da primeira linha, multiplicado por 4,9.
b) Considerando a regularidade identificada no item a, temos: 4,9t2.
c) f(t) = 4,9t2. Sim, pois a lei de formação da função é da forma f(t) = at2 + bt + c, com a = 4,9, b = c = 0.
d) f(t) = 4,9 ⋅ 102 = 490 → 490 m
e) Resposta esperada: Não, após determinado tempo, o objeto deixa de estar em queda livre, pois atingirá uma superfícíe.
11. a) 9 ⋅ 0,90 = 8,1 → 8,1 m2
b) 0,9 + 0,5 = 1,4; 1,2 < 1,4 < 1,5
Resposta esperada: Com esse aumento, a rampa passa a ter 1,40 m de largura, o quê a deixa admissível em relação à norma, mas abaixo do recomendado.
c) g(x) = (x + 9) ⋅ (x + 0,90) ⇒ g(x) = x2 + 9,9x + 8,1
d) g(0,6) = (0,6)2 + 9,9 ⋅ 0,6 + 8,1 = 14,4
Resposta esperada: Esse resultado indica quê, aumentando 0,6 m no comprimento e na largura dessa rampa, sua área será de 14,4 m2.
e) Resposta pessoal. Espera-se quê os estudantes analisem rampas de acesso a algum prédio público do município em quê moram e verifiquem a adequação ou não às normas. A pesquisa póde sêr realizada na própria escola. A atividade póde sêr utilizada para proporcionar uma discussão sobre a importânssia do respeito às normas de inclusão.
12. a) Resposta esperada: Porque, ao adicionar os termos extremos dessa sequência, obtêm-se 100 adições, e cada adição foi contada duas vezes. Assim, é preciso dividir por 2 para obtêr a soma correta.
b) = 210
c) s(n) = ou s(n) =
d) s(130) = = 8.515 e s(801) = = 321.201
13. a) f(x) = 5x2 + 3
(delta)" = 02 − 4 ⋅ 5 ⋅ 3 = −60 < 0
Para f, não existem zeros reais.
b) f(x) = 8x − 2x2
(delta)" = 82 − 4 ⋅ (−2) ⋅ 0 = 64
c) f(x) = x2 − 10x + 25
(delta)" = (−10)2 − 4 ⋅ 1 ⋅ 25 = 0
x = = 5
d) f(x) = −2x2 + 3x − 5
(delta)" = 32 − 4 ⋅ (−2) ⋅ (−5) = −31 < 0
Para f, não existem zeros reais.
e) f(x) = 3x2 + 8x + 4
(delta)" = 82 − 4 ⋅ 3 ⋅ 4 = 16
x =
f) f(x) = −2x + 2x + 24
(delta)" = 22 − 4 ⋅ (−2) ⋅ 24 = 196
x =
14. Resposta pessoal. Espera-se quê os estudantes possam resolver as equações da atividade 13 de outra maneira e obtêr os mesmos resultados.
15. g(x) = (2m − 3)x2 + 2x + 2
(delta)" = 22 − 4 ⋅ (2m − 3) ⋅ 2 = 28 − 16m
a) (delta)" > 0 ⇒ 28 − 16m > 0 ⇒ m <
b) (delta)" = 0 ⇒ 28 − 16m = 0 ⇒ m =
c) (delta)" < 0 ⇒ 28 − 16m < 0 ⇒ m >
Página trezentos e setenta e nove
16. a) s(20) = −0,01 ⋅ 202 + 1,2 ⋅ 20 − 11 = 9
Representa quê, se forem vendidas 20 cadeiras na semana, a microempresa terá um lucro de R$ 9,00 por cadeira.
b) s(80) = −0,01 ⋅ 802 + 1,2 ⋅ 80 − 11 = 21
21 ⋅ 80 = 1680 → R$ 1.680,00
c) 0 = −0,01x2 + 1,2x − 11
(delta)" = 1,22 − 4 ⋅ (−0,01) ⋅ (−11) = 1
10 cadeiras ou 110 cadeiras
17. a) v(0)= ⋅ 02 + 48 = 48 → 48 metros cúbicos
b) v(6)= ⋅62 + 48 = 45 → 45 metros cúbicos
c) 0 = t2 + 48 ⇒ t2 = 48 ⇒ t2 = 576 ⇒ t = 24 → 24 horas
18. Ao resolvermos uma equação do 2º grau, analisamos o discriminante (delta)" para avaliar suas raízes reais: se (delta)" > 0, a equação tem duas raízes reais e distintas; se (delta)" = 0, a equação tem duas raízes reais e iguais; se (delta)" < 0, a equação não tem raiz real. Assim, temos:
A: (delta)" > 0?; e B: (delta)" < 0?
19.
20. a) 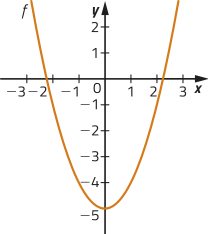
b) 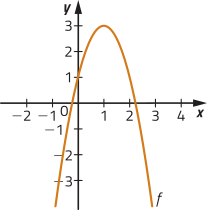
c) 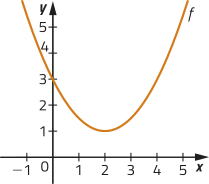
d) 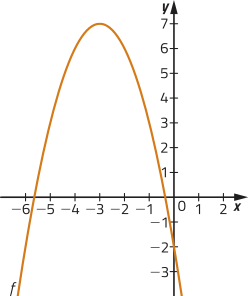
21. a) • Interseção com o eixo x
f(x) = 0 ⇒ 4x2 − 2x − 12 = 0
(delta)" = (−2)2 − 4 ⋅ 4 ⋅ (−12) = 196
• Interseção com o eixo y f(0) = 4 ⋅ 02 − 2 ⋅ 0 − 12 = −12
Portanto, o gráfico de f intersecta o eixo x nos pontos de coordenadas e (2, 0) e o eixo y no ponto de coordenadas (0, −12).
b) • Interseção com o eixo x
f(x) = 0 ⇒ −3x2 + 4x + 7 = 0
(delta)" = 42 − 4 ⋅ (−3) ⋅ 7 = 100
• Interseção com o eixo y
f(0) = −3 ⋅ 02 + 4 ⋅ 0 + 7 = 7
Portanto, o gráfico de f intersecta o eixo x nos pontos de coordenadas (−1, 0) e e o eixo y no ponto de coordenadas (0, 7).
c) • Interseção com o eixo x
f(x) = 0 ⇒ − 3x + 10 = 0
(delta)" = (−3)2 − 4 ⋅ ⋅ 10 = 1
• Interseção com o eixo y
f(0) = − 3 ⋅ 0 + 10 = 10
Portanto, o gráfico de f intersecta o eixo x nos pontos de coordenadas (5, 0) e (10, 0) e o eixo y no ponto de coordenadas (0, 10).
d) • Interseção com o eixo x
f(x) = 0 ⇒ −2x2 + 8x − 8 = 0
(delta)" = 82 − 4 ⋅ (−2) ⋅ (−8) = 0
• Interseção com o eixo y
f(0) = −2 ⋅ 02 + 8 ⋅ 0 − 8 = −8
Portanto, o gráfico de f intersecta o eixo x no ponto de coordenadas (2, 0) e o eixo y no ponto de coordenadas (0, −8).
22. a) Resposta esperada: Temos quê a < 0, pois a parábola tem concavidade voltada para baixo; b < 0, pois a parábola intersecta o eixo y no ramo decrescente; c < 0, pois a parábola intersecta o eixo y abaixo da origem dos eixos.
b) Resposta esperada: Temos quê a > 0, pois a parábola tem concavidade voltada para cima; b > 0, pois a parábola intersecta o eixo y no ramo crescente; c = 0, pois a parábola intersecta o eixo y na origem dos eixos.
c) Resposta esperada: Temos quê a > 0, pois a parábola tem concavidade voltada para cima; b < 0, pois a parábola intersecta o eixo y no ramo decrescente; c > 0, pois a parábola intersecta o eixo y acima da origem dos eixos.
d) Resposta esperada: Temos quê a < 0, pois a parábola tem concavidade voltada para baixo; b = 0, pois a parábola intersecta o eixo y em seu vértice; c > 0, pois a parábola intersecta o eixo y acima da origem dos eixos.
23. Temos quê a função f é definida por f(x) = ax2 + bx + c.
Como o gráfico intersecta o eixo y no ponto de coordenadas (0, −3), temos c = −3.
Já o eixo x é intersectado pelo gráfico nos pontos de coordenadas (−6, 0) e (2, 0), ou seja, −6 e 2 são os zeros de f. Assim:
f(−6) = 0 ⇒ a ⋅ (−6)2 + b ⋅ (−6) + (−3) = 0 ⇒ 36a − 6b − 3 = 0
f(2) = 0 ⇒ a ⋅ 22 + b ⋅ 2 + (−3) = 0 ⇒ 4a + 2b − 3 = 0
Para obtêr os valores de a e b, resolvemos o seguinte sistema de equações:
Logo, f(x) = + x − 3.
Página trezentos e oitenta
24. a) Como o vértice corresponde ao ponto de interseção da parábola com o eixo de simetria dela, temos quê as coordenadas do vértice dessa parábola são V (2, 5). Analisando o gráfico, algumas respostas de pontos simétricos possíveis são os de coordenadas: (0, 4) e (4, 4); (−2, 1) e (6, 1).
b) Em relação aos pontos simétricos de coordenadas (0, 4) e (4, 4), temos:
Em relação aos pontos simétricos de coordenadas (−2, 1) e (6, 1), temos:
Resposta esperada: Quando dois pontos quaisquer do gráfico de uma função quadrática são simétricos em relação ao eixo de simetria, a média aritmética das abscissas dêêsses pontos corresponde à abscissa do vértice da parábola.
25. Considere êste hekzágono regular.
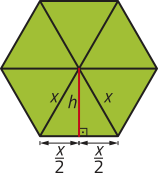
a) Resposta esperada: O hekzágono regular de lado medindo x póde sêr decomposto em seis triângulos equiláteros de lado também medindo x. Assim, inicialmente, determinou-se a altura de cada um dêêsses triângulos. Depois, multiplicou-se por 6 a área de cada triângulo dêêsses, calculada de acôr-do com a medida do lado e da altura.
b) Como os seis lados têm mesma medida e o perímetro é a soma das medidas de todos os lados, temos: f(x) = 6x
c)
d) f: função afim e função linear; g: função quadrática
e) perímetro: f(4) = 6 ⋅ 4 = 24 → 24 cm
área: g(4) = ⋅ 42 = → cm2
perímetro: f(8) = 6 ⋅ 8 = 48 → 48 cm
área: g(8) = ⋅ 82 = → cm2
f) 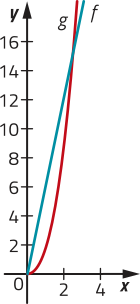
g) I) Resposta esperada: Temos quê o perímetro de um hekzágono regular de lado x é dado por 6x. Ao multiplicarmos x por uma constante real k > 0, o perímetro do hekzágono será igual a 6 ⋅ (kx) = k ⋅ (6x).
II) Resposta esperada: Temos quê a área de um hekzágono regular de lado x é dada por x2 . Ao multiplicarmos x por uma constante real k > 0, a área do hekzágono será igual a ⋅ (kx)2 = k2x2 = k2 ⋅ .
26. a) Como todas as funções são simétricas em relação ao eixo y, temos:
f(−2) = f(2) ⇒ A = 4
g(1) = g(−1) ⇒ B = −2
h(−1) = h(1) ⇒ C =
b) 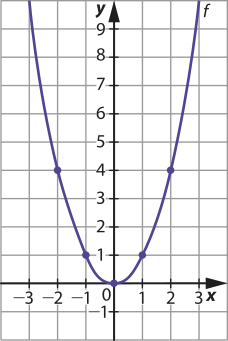
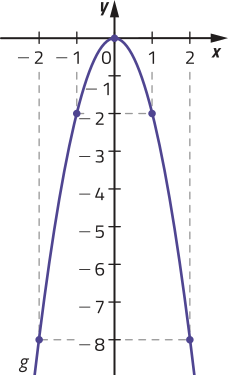
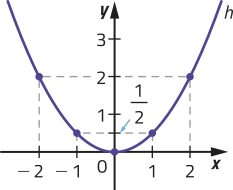
c) f: a > 0, b = 0 e c = 0, pois a parábola tem concavidade voltada para cima, intersecta o eixo das ordenadas no vértice, quê corresponde ao ponto de abscissa igual a 0.
g: a < 0, b = 0 e c = 0, pois a parábola tem concavidade voltada para baixo, intersecta o eixo das ordenadas no vértice, quê corresponde ao ponto de abscissa igual a 0.
h: a > 0, b = 0 e c = 0, pois a parábola tem concavidade voltada para cima, intersecta o eixo das ordenadas no vértice, quê corresponde ao ponto de abscissa igual a 0.
d) Todas as funções são do tipo f(x) = ax2, pois, em todos os casos, os coeficientes b e c são nulos. Assim, conhecendo um ponto da função, é possível determinar o coeficiente a.
• f(1) = 1 ⇒ a ⋅ 12 = 1 ⇒ a = 1
Logo, f(x) = x2.
• g(1) = −2 ⇒ a ⋅ 12 = −2 ⇒ a = −2
Logo, g(x) = −2x2.
• h(1) = ⇒ a ⋅ 12 = ⇒ a =
Logo, h(x) =
Resposta esperada: As três funções quadráticas são definidas por uma lei de formação do tipo y = ax2, com a ≠ 0, e o vértice da parábola correspondente ao gráfico de cada uma delas coincide com a origem O dos eixos cartesianos.
27. Espera-se quê os estudantes escrevam a lei de formação f(x) = ax2 + bx + c, com a < 0 e b < 0, e c um número real qualquer. Alguns exemplos de resposta são: f(x) = −2x2 − 3x; f(x) = −x2 − x + 3.
28. = 5
Resposta esperada: Esse resultado indica quê, no intervalo de tempo de 0 s até 3 s após o momento em quê a bola foi lançada, sua altura variou, em média, 5 m a cada segundo.
29. a) f(−4) = 3 ⋅ (−4)2 + 2 ⋅ (−4) = 40
f(1) = 3 ⋅ 12 + 2 ⋅ 1 = 5
b) f(−3) = −1 ⋅ (−3)2 − 8 ⋅ (−3) + 5 = 20
f(4) = −1 ⋅ 42 − 8 ⋅ 4 + 5 = −43
c) f(−6) = −5 ⋅ (−6)2 + (−6) − 4 = −190
f(0) = −5 ⋅ 02 + 0 − 4 = −4
d)
30. a) • Resposta esperada: Maior chance, pois o uso do celular é uma distração para o condutor.
• Resposta esperada: Redução do tempo de reação (para realizar uma frenagem ou mesmo para perceber e respeitar os sinais de trânsito), dificuldade de manter corretamente o carro na pista e de manter uma distância segura do veículo da frente.
Página trezentos e oitenta e um
b) Resposta esperada: Indica quê, ao pisar no freio dêêsse automóvel, quando ele está a uma velocidade de 40 km/h, o veículo percórre uma distância de 7,6 m antes de parar.
c) Analisando o ponto de abscissa 60 do gráfico, temos 17,1 m.
d) Analisando a abscissa correspondente ao ponto de ordenada 48,1 do gráfico, temos 100 km/h.
e) Temos quê a função d é definida por d(v) = av2 + bv + c.
Como o gráfico intersecta o eixo y no ponto de coordenadas (0; 0,6), segue quê c = 0,6 = .
Como os pontos (40; 7,6) e (60; 17,1) pertencem ao gráfico da função, temos:
d(40) = 7,6 ⇒ a ⋅ (40)2 + b ⋅ 40 + 0,6 = 7,6 ⇒ 1.600a + 40b + 0,6 = 7,6
d (60) = 17,1 ⇒ a ⋅ (60)2 + b ⋅ 60 + 0,6 = 17,1 ⇒ 3.600a + 60b + 0,6 = 17,1
Para obtêr os valores de a e b, resolvemos o seguinte sistema de equações:
Logo, d(v) = .
f) Resposta esperada: Não, pois, de acôr-do com o modelo matemático, calculando d(50) obtemos 11,85, o quê significa quê a distância de frenagem será de 11,85 m, ou seja, maior quê a distância do automóvel até o obstáculo.
31. a) 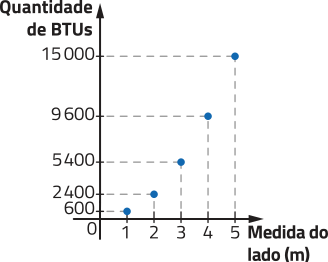
b) • 600 ∶ 600 = 1 e 1 = 12
• 2.400 ∶ 600 = 4 e 4 = 22
• 5.400 ∶ 600 = 9 e 9 = 32
• 9.600 ∶ 600 = 16 e 16 = 42
• 15.000 ∶ 600 = 25 e 25 = 52
Resposta esperada: Cada número da segunda linha corresponde ao quadrado do respectivo número da primeira linha, multiplicado por 600.
c) 600(éli)"2
d) De acôr-do com a expressão ôbitída no item c, temos q((éli)") = 600(éli)"2. Sim, pois a lei de formação da função é da forma q((éli)") = a(éli)"2 + b(éli)" + c, com a = 600 e b = c = 0.
e) • f(2,5) = 600 ⋅ 2,52 = 3.750 → 3.750 BTUs
• f(6) = 600 ⋅ 62 = 21.600 → 21.600 BTUs
• f(10) = 600 ⋅ 102 = 60.000 → 60.000 BTUs
f) 48.600 = 600 ⋅ (éli)"2 ⇒ (éli)" = 9 → 9 m
32. a) • xv = = 20
yv = = −38
Portanto, V (20, −38).
b) xv = = 1
yv = = 11
Portanto, V (1, 11).
c) xv = = −2
yv = = = −8
Portanto, V (−2, −8).
d) xv = = −1
yv = = 2
Portanto, V (−1, 2).
33. a) Como yv = = = −5 e a > 0, então Im(f) = {y ∈ ℝ | y ≥ −5}.
b) Como yv = = e a < 0, então Im(f) = .
c) Como y e a < 0, então Im(f) = {y ∈ ℝ | y ≤ 10}.
d) Como yv = = e a > 0, então Im(f) = .
34. a)
Como xv = −3 e a > 0, então f é decrescente para x < −3 e crescente para x > −3.
b)
Como xv = −1 e a > 0, então f é decrescente para x < −1 e crescente para x > −1.
c)
Como xv = 3 e a < 0, então f é crescente para x < 3 e decrescente para x > 3.
35. a)
• x < −1,5
• x > −1,5
b) Temos a função f definida por f(x) = ax2 + bx + c.
Como o gráfico intersecta o eixo y no ponto de coordenadas (0, 10), temos c = 10.
Já o eixo x é intersectado pelo gráfico nos pontos de coordenadas (−5, 0) e (2, 0), ou seja, −5 e 2 são os zeros de f.
Assim:
f(−5) = 0 ⇒ a ⋅ (−5)2 + b ⋅ (−5) + 10 = 0 ⇒ 25a − 5b + 10 = 0
f(2) = 0 ⇒ a ⋅ (2)2 + b ⋅ (2) + 10 = 0 ⇒ 4a + 2b + 10 = 0
Para obtêr os valores de a e b, resolvemos o seguinte sistema de equações:
Logo, f(x) = −x2 − 3x + 10.
c)
Portanto, V (−1,5; 12,25).
d) Como yv = 12,25 e a < 0, então Im(f) = {y ∈ ℝ | y ≤ 12,25}.
36. alternativa d
Representando o gráfico da parábola correspondente à abóbada, temos:
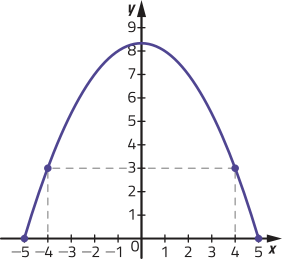
Uma parábola é expressa pela equação y = a ⋅ (x − x1) ⋅ (x − x2), em quê x1 e x2 são as raízes da equação. Pelo gráfico, temos x1 = −5 e x2 = 5. Assim:
y = a ⋅ (x − 5) ⋅ (x + 5) ⇒ y = a ⋅ (x2 − 25)
Como o ponto (4, 3) pertence ao gráfico dessa função, temos:
3 = a ⋅ (42 − 25) ⇒ a =
Assim, y = ⋅ (x2 − 25).
A altura H corresponde ao yv, logo:
Página trezentos e oitenta e dois
Portanto, H = .
37. a) Valor mássimo, pois a < 0.
b) Valor mínimo, pois a > 0.
c) Valor mínimo, pois a > 0.
d) Valor mássimo, pois a < 0.
38. alternativa d
xv = → 2,5 meses ou 2 meses e 15 dias
39. a) h(0) = −0,8 ⋅ 02 + 2 ⋅ 0 + 1,9 = 1,9 → 1,9 m h(2) = −0,8 ⋅ 22 + 2 ⋅ 2 + 1,9 = 2,7 → 2,7 m
b) yv = = = 3, 15 → 3,15 m
xv = = = 1, 25 → 1,25 s
c) = = 0,4
Resposta esperada: Indica quê, em média, a altura da bola variou 0,4 m a cada segundo nesse toque.
40. Sendo x e y as medidas dos lados e A e P a área e o perímetro da região retangular, temos:
A = x ⋅ y
P = 2x + 2y ⇒ 112 = 2x + 2y ⇒ y = 56 − x
Substituindo y na expressão da área temos A = −x2 + 56x. Para determinar as medidas x e y para quê a área seja mássima, calculamos:
xv = =
= 28 → 28 m
y = 56 − x ⇒ y = 56 − 28 ⇒ y = 28
Portanto, as dimensões da horta devem sêr 28 m de comprimento e 28 m de largura.
41. yv = = 0, 5 → 0,5 m
xv = = 2, 5 → 2,5 s
42. a) f(0) = −0,32 ⋅ 02 + 12,8 ⋅ 0 + 70 = 70 → 70 BPM
f(5) = −0,32 ⋅ 52 + 12,8 ⋅ 5 + 70 = 126 → 126 BPM
b) yv = = = 198 → 198 BPM
xv = = 20 → 20 min
c) 70% de 180 → ⋅ 180 = 126
−0,32t2 + 12,8t + 70 > 126 ⇒ −0,32t2 + 12,8t − 56 > 0
(delta)" = 12,82 − 4 ⋅ (−0,32) ⋅ (−56) = 92,16
x = =
a = −0,32 < 0
Logo, o número de batimentos esteve acima do limite entre 5 min e 35 min de treino.
43. alternativa d
yv = = 36 → 36°
Portanto, a tempera-túra no interior da estufa está classificada como alta (30° ≤ 36° ≤ 43°).
44. a) c = 8 + 0,10 ⋅ 280 = 36 → R$ 36,00
p200 = 200 ⋅ 36 = 7.200 → R$ 7.200,00
b) p250 = 250 ⋅ (8 + 0,10 ⋅ 230) = 7.750 → R$ 7.750,00
p400 = 400 ⋅ (8 + 0,10 ⋅ 80) = 6.400 → R$ 6.400,00
Resposta esperada: É mais vantajoso quê compareçam 400 convidados, cujo gasto com a locação será de
R$ 6.400,00, uma vez quê, no caso de comparecerem 250 convidados, o gasto será de R$ 7.750,00.
c) Fazendo P (x) igual ao total a sêr pago pela locação e x igual ao número de convidados quê compareceram, temos:
P (x) = x ⋅ (8 + 0,10 ⋅ (480 − x)) ⇒ P(x) = −0,10x2 + 56x
yv = = 7.840 → R$ 7.840,00
xv = = 280 → 280 convidados
45. a) Analisando a ordenada do ponto em quê o gráfico intercepta o eixo y, temos: 1,3 m.
b) Com base na abscissa do ponto em quê o gráfico intercepta o eixo x, temos: 21,6 s.
c) Temos a função g definida por g(x) = ax2 + bx + c.
Como o gráfico intersecta o eixo y no ponto de coordenadas (0; 1,3), temos: c = 1,3.
Como os pontos (6; 10,3) e (21,6; 0) pertencem ao gráfico da função, temos:
g(6) = 10,3 ⇒ a ⋅ 62 + b ⋅ 6 + 1,3 = 10,3 ⇒ 36a + 6b + 1,3 = 10,3
g(21,6) = 0 ⇒ a ⋅ (21,6)2 + b ⋅ 21,6 + 1,3 = 0 ⇒ 466,56a + 21,6b + 1,3 = 0
Para obtêr os valores de a e b, resolvemos o seguinte sistema de equações:
Logo, g(x) = −0,1x2 + 2,1x + 1,3.
D(g) = {x ∈ ℝ | 0 ≤ x ≤ 21,6}.
d) 12, 325 → 12,325 m
e) A imagem da função corresponde ao intervalo determinado pela altura nula (quando o projétil está no chão) e a altura mássima, determinada no item d. Assim, Im(g) = [0; 12,325].
46. Resposta pessoal. Espera-se quê os estudantes formulem dois problemas quê envolvam a determinação do valor mássimo ou valor mínimo de funções quadráticas. Verificar como os estudantes interprétam cada coordenada do vértice das parábolas.
47. a) Em relação à parte do gráfico correspondente aos valores de x < 1, podemos identificar os pontos da função quadrática de coordenadas (−1, 6), (0, 6) e (1, 2).
Assim, considerando a lei de formação do tipo f(x) = ax2 + bx + c, temos:
I) 6 = a(−1)2 + b ⋅ (−1) + c
II) 6 = a ⋅ 02 + b ⋅ 0 + c ⇒ c = 6
III) 2 = a ⋅ 12 + b + c
De I e II, temos:
IV) 6 = a(−1)2 + b ⋅ (−1) + c ⇒ a − b + 6 = 6 ⇒ a − b = 0 ⇒ a = b
De I, II e IV, temos:
V) 2 = a ⋅ 12 + b + c ⇒ a + a + 6 = 2 ⇒ 2a = − 4 ⇒ a = −2
Assim, a = b = −2
Logo, f(x) = −2x2 − 2x + 6 para x < 1.
Analisando a parte do gráfico correspondente aos valores de x ≥ 1, podemos identificar os pontos da função afim de coordenadas (1, 2) e (2, 1).
Assim, considerando a lei de formação do tipo f(x) = dx + e, temos:
I) 2 = d + e ⇒ e = 2 − d
II) 1 = 2d + e
Substituindo em II o valor de e obtído em I, temos:
Página trezentos e oitenta e três
1 = 2d + e ⇒ 1 = 2d + (2 − d) ⇒ 1 =
= 2d + 2 − d ⇒ 1 − 2 = d ⇒ d = −1
Logo, e = 2 − d = 2 − (−1) = 3.
Assim, f(x) = −x + 3 para x ≥ 1.
Portanto,
f(x) =
b) O valor mássimo da função corresponde a:
48. Pelo caso AA, temos quê os triângulos ABC e CFE são semelhantes. Assim, temos:
Temos quê a área A do retângulo é dada por: A(x) = x ⋅ y = x ⋅ x2 + 2x
Como a área deve sêr a maior possível, calculamos as coordenadas do ponto de mássimo de A(x):
•
• 0,75 → 0,75 m
Assim, temos quê a área mássima do painel retangular é 0,75 m2 e a medida x do lado dêêsse painel para quê isso ocorra é 0,75 m. Logo, a medida do lado y do outro lado dêêsse painel é dada por:
y = 1 → 1 m.
Portanto, um kórti deve sêr realizado paralelo e a 1 m da margem correspondente ao lado , e o outro, paralelo e a 0,75 m da margem correspondente ao lado .
49. a) f(x) > 0 para x < −4 ou x > 3;
f(x) = 0 para x = −4 ou x = 3;
f(x) < 0 para −4 < x < 3
b) f(x) > 0 para −8 < x < 0;
f(x) = 0 para x = −8 ou x = 0;
f(x) < 0 para x < −8 ou x > 0
c) ∄ x ∈ D(f) tal quê f(x) > 0;
f(x) = 0 para x = 3; f(x) < 0 para x ≠ 3
50. a) (delta)" = 52 − 4 ⋅ 4 ⋅ 2 = −7 < 0
A função não tem zeros reais, pois (delta)" < 0. Como a > 0, temos uma parábola com concavidade voltada para cima, sem cruzar o eixo x.
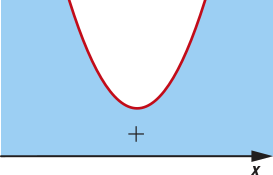
Como a > 0 e (delta)" < 0, f(x) > 0 para todo x ∈ D(f); ∄ x ∈ D(f) | f(x) ≤ 0.
b) (delta)" = 72 − 4 ⋅ (−2) ⋅ (−3) = 25
Como a < 0 e (delta)" > 0, temos uma parábola com concavidade voltada para baixo, intersectando o eixo x em x = 0,5 e x = 3.
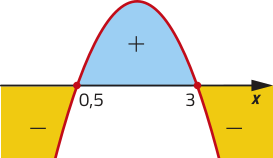
Logo, f(x) > 0 para 0,5 < x < 3;
f(x) = 0 para x = 0,5 oux = 3;
f(x) < 0 para x < 0,5 ou x > 3.
c) (delta)" = (−6)2 − 4 ⋅ (−1) ⋅ (−9) = 0
x = = −3
Como a < 0 e (delta)" = 0, temos uma parábola com concavidade voltada para baixo, intersectando o eixo x em x = −3.

Logo, ∄ x ∈ D(f) | f(x) > 0; f(x) = 0 para x = −3; f(x) < 0 para x ≠ −3.
d) (delta)" = (−1)2 − 4 ⋅ 0,5 ⋅ (−4) = 9
Como a > 0 e (delta)" > 0, temos uma parábola com concavidade voltada para cima, intersectando o eixo x em x = −2 e x = 4.

Logo, f(x) > 0 para x < −2 ou x > 4; f(x) =
= 0 para x = −2 ou x = 4; f(x) < 0 para
−2 < x < 4.
e) (delta)" = (−2)2 − 4 ⋅ 0,4 ⋅ 2,5 = 0
Como a > 0 e (delta)" = 0, temos uma parábola com concavidade voltada para cima, intersectando o eixo x em x = 2,5.

Logo, f(x) > 0 para x ≠ 2,5;
f(x) = 0 para x = 2,5; ∄ x ∈ D(f) | f(x) < 0.
f) (delta)" = 32 − 4 ⋅ ⋅ (−10) = −1 < 0
A função não tem zeros reais, pois (delta)" < 0. Como a < 0, temos uma parábola com concavidade voltada para baixo, sem cruzar o eixo x.

Como a < 0 e (delta)" < 0,
∄ x ∈ D(f) | f(x) ≥ 0;
f(x) < 0 para todo x ∈ D(f).
51. a) Fazendo f(x) = 4x2 − 16x + 12, temos:
(delta)" = (−16)2 − 4 ⋅ 4 ⋅ 12 = 64
Como a > 0 e (delta)" > 0, temos uma parábola com concavidade voltada para cima, intersectando o eixo x em x = 1 e x = 3.

Logo, f(x) > 0 para x < 1 ou x > 3, ou seja, S = {x ∈ ℝ | x < 1 ou x > 3}.
b) x2 + 15 ≤ 0,9x2 − 2x + 45 ⇒ 0,1x2 + 2x − 30 ≤ 0
Fazendo f(x) = 0,1x2 + 2x − 30, temos: (delta)" = 22 − 4 ⋅ 0,1 ⋅ (−30) = 16
Como a > 0 e (delta)" > 0, temos uma parábola com concavidade voltada para cima, intersectando o eixo x em x = −30 e x = 10.
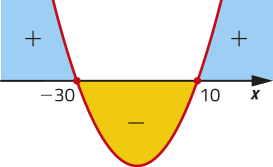
Logo, f(x) ≤ 0 para −30 ≤ x ≤ 10, ou seja, S = {x ∈ ℝ | −30 ≤ x ≤ 10}.
Página trezentos e oitenta e quatro
c) x2 − 10x − < 3x2 + 10x + 13 ⇒ 2x2 + 20x + 25,5 > 0
Fazendo f(x) = 2x2 + 20x + 25,5, temos: (delta)" = 202 − 4 ⋅ 2 ⋅ 25,5 = 196
Como a > 0 e (delta)" > 0, temos uma parábola com concavidade voltada para cima, intersectando o eixo x em x = −8,5 e x = −1,5.
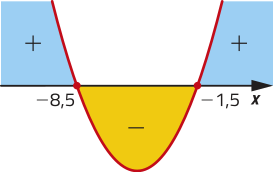
Logo, f(x) > 0 para x < −8,5 ou x > −1,5, ou seja,
S = {x ∈ ℝ | x < −8,5 ou x > −1,5}.
d) x2 − 5x ≤ − 15 ⇒ − 5x + 15 ≤ 0
Fazendo f(x)= − 5x + 15, temos:
(delta)" = (−5)2 − 4 ⋅ 0,5 ⋅ 15 = −5
A função não tem zeros reais, pois (delta)" < 0. Como a > 0, temos uma parábola com concavidade voltada para cima, sem cruzar o eixo x.
Logo, f(x) > 0 para todo x ∈ D(f); ∄ x ∈ D(f) | f(x) ≤ 0, ou seja, S = ∅.
52. 
Resposta esperada: As abscissas dêêsses pontos determinam quê:
• para x < 5 e x > 25 ⇒ f(x) > g(x);
• para x = 5 e x = 25 ⇒ f(x) = g(x);
• para 5 < x < 25 ⇒ f(x) < g(x).
53. (delta)" = 42 − 4 ⋅ (k − 2) ⋅ (−3) = 12k − 8
(delta)" < 0 ⇒ 12k − 8 < 0 ⇒ k <
54. a) A função g é definida por g(x) = ax + b.
Como g = 0 e g(0) = 1, temos:
Assim, g(x) = −2x + 1.
A função f é definida por f(x) = ax2 + bx + c.
Como o gráfico intersecta o eixo y no ponto de coordenadas (0, −8), temos c = −8.
Já o eixo x é intersectado pelo gráfico nos pontos de coordenadas (−2, 0) e (4, 0), ou seja, −2 e 4 são os zeros de f. Assim:
f(−2) = 0 ⇒ a ⋅ (−2)2 + b ⋅ (−2) + (−8) = 0 ⇒ 4a − 2b − 8 = 0
f(4) = 0 ⇒ a ⋅ (4)2 + b ⋅ (4) + (−8) = 0 ⇒ 16a + 4b − 8 = 0
Para obtêr os valores de a e b, resolvemos o seguinte sistema de equações:
Logo, f(x) = x2 − 2x − 8.
b) • f(x) < g(x) ⇒ x2 − 2x − 8 < −2x + 1 ⇒ x2 − 9 < 0 ⇒ −3 < x < 3
• f(x) > g(x) ⇒ x2 − 2x − 8 > −2x + 1 ⇒ x2 − 9 > 0 ⇒ x < −3 ou x > 3
• f(x) = g(x) ⇒ x2 − 2x − 8 = −2x + 1 ⇒ x2 − 9 = 0 ⇒ x = −3 ou x = 3
55. a) T(x) = 0 ⇒ −0,02x2 + 5x − 48 = 0
(delta)" = 52 − 4 ⋅ (−0,02) ⋅ (−48) = 21,16
Como a < 0 e (delta)" > 0, temos uma parábola com concavidade voltada para baixo, intersectando o eixo x em x = 10 e x = 240.
Assim, T(x) > 0 para 10 < x < 240,
T(x) = 0 para x = 10 ou x = 240 e
T(x) < 0 para x < 10 ou x > 240.
• entre 10 min e 240 min
• entre 0 min e 10 min e entre 240 min e 250 min
b)
56. a) 
b) 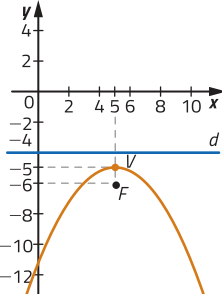
c) 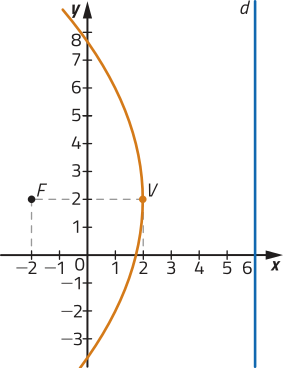
d) 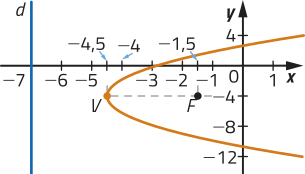
57. a) De acôr-do com o gráfico, temos uma parábola quê tem diretriz paralela ao eixo das ordenadas, vértice V (0, −4) à direita da diretriz e F(1, −4).
Assim, a equação da parábola é da forma (y − yv)2 = 4c(x − xv).
Calculando o valor de c, temos:
A equação da parábola é dada por: (y − (−4))2 = 4 ⋅ 1(x − 0) ⇒ y2 − 4x + 8y = −16
b) De acôr-do com o gráfico, temos uma parábola quê tem diretriz paralela ao eixo das abscissas, vértice V (−1, 1) abaixo da diretriz e F(−1, −1). Assim, a equação da parábola é da forma (x − xv)2 = −4c (y − yv).
Calculando o valor de c, temos:
c = FV = = 2
A equação da parábola é dada por:
(x − (−1))2 = −4 ⋅ 2(y − 1) ⇒ x2 + 2x + 8y = 7
Página trezentos e oitenta e cinco
58. Pelo gráfico apresentado, temos V = (−2, 2) e F = (−1, 2).
A distância focal, de F a V, é c = VF = (−1) − (−2) = 1.
A equação da parábola é da forma (y − yv)2 = 4c (x − xv); assim:
(y − 2)2 = 4 ⋅ 1(x − (−2)) ⇒ y2 − 4y − 4x = 4
Tomando y = 0 e y = 4, podemos determinar dois pontos dessa parábola, utilizando a equação ôbitída anteriormente.
• 02 − 4 ⋅ 0 − 4x = 4 ⇒ x = −1
• 42 − 4 ⋅ 4 − 4x = 4 ⇒ x = −1
Algumas possíveis respostas: (−1, 0), (−1, 4), (2, −2), (2, 6), (7, −4), (7, 8).
Para x = 0, temos: y2 − 4y − 4 ⋅ 0 = 4 ⇒
Logo, yp = 2( +1) ≃ 4,83.
59. Considerando a lei de formação da função dessa parábola como f(x) = ax2 + bx + c e os pontos (0; −1,5), (−2, 0) e (2, −2), pertencentes ao gráfico dessa parábola, temos:
Resolvendo o sistema de equações, temos a = , b = e c = −1,5. Logo, y = x2 − x − 1,5ou ainda, x2 − 4x − 8y = 12.
60. a) Resposta pessoal. Espera-se quê os estudantes construam a parábola a partir das etapas apresentadas. Se necessário, reproduzir cada etapa no qüadro com a turma.
b) As distâncias são iguais, pois a ponta do lápis corresponde a um ponto da parábola, F corresponde ao foco, e a régua, à reta diretriz.
Integrando com...
1. Resposta esperada: Para quê essas pessoas também sêjam inseridas digitalmente e tênham oportunidades de aprendizado, entretenimento e interação.
2. Resposta esperada: A propriedade geométrica do paraboloide garante sêr possível determinar um local para instalar um dispositivo de modo quê êste recepcione a maior quantidade possível do sinal enviado pelo satélite. Por isso, esse formato é escolhido para a transmissão de sinais de Tevê e internet (via satélite), por exemplo.
3. Para essa parábola, temos a lei de formação da função f(x) = ax2 + bx + c e os pontos (3, 0) e (0; 1,25) pertencentes ao gráfico dessa parábola. Temos, ainda, o vértice V(3, 0) e, como o eixo de simetria é paralelo ao eixo das ordenadas, o ponto (6; 1,25), simétrico a (0; 1,25) em relação a esse eixo, também pertence ao gráfico dessa parábola. Assim, temos:
Resolvendo o sistema de equações, temos a = , b = e c = 1,25.
Logo, y = x2 − x + 1, 25 ⇒ 5x2 − 30x − 36y + 45 = 0.
y = x2 − x + 1, 25 ⇒ 5x2 − 30x − 36y + 45 = 0.
4. Resposta pessoal. Espera-se quê os estudantes compreendam quê as tecnologias podem chegar às comunidades indígenas para auxiliar no acesso à informação e no desenvolvimento econômico e social da comunidade, sem quê isso descaracterize sua cultura e de modo quê ela seja valorizada.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) Analisando a ordenada do vértice da parábola, temos: 10 m.
b) Calculamos a diferença entre os zeros da função: 40 − 0 = 40. Assim, temos: 40 m.
c) Temos a função g definida por g(x) = ax2 + bx + c.
Como o gráfico intersecta o eixo y no ponto de coordenadas (0, 0), temos c = 0.
Como os pontos de coordenadas (20, 10) e (40, 0) pertencem ao gráfico de g, temos: g(20) = 10 ⇒ a ⋅ 202 + b ⋅ 20 + 0 = 10 ⇒ 400a + 20b = 10
g(40) = 0 ⇒ a ⋅ 402 + b ⋅ 40 + 0 = 0 ⇒ 1.600a + 40b = 0
Para obtêr os valores de a e b, resolvemos o seguinte sistema de equações:
⇒
Logo, g(x) = + x;
D(g) = {x ∈ ℝ | 0 ≤ x ≤ 40}.
d) • f(x) = (105 + x) ⋅ (68 + x) ⇒ f(x) = x2 + 173x + 7.140
• 7.141,7301 = x2 + 173x + 7.140 ⇒
Como 0,01 m equivale a 1 cm, foi necessário reduzir o campo 1 cm no comprimento e na largura. Resposta esperada: Não, uma vez quê, nesse contexto, a medida de 1 cm no comprimento e na largura póde sêr considerada uma imprecisão relacionada, entre outros motivos, aos instrumentos ou métodos de medição utilizados.
• 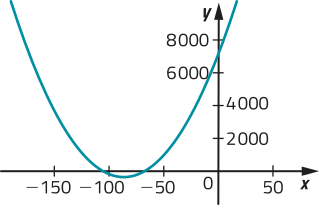
Praticando: enêm e vestibulares
1. alternativa c
Para determinar a medida da base do túnel, inicialmente determinamos as raízes da função:
9 − x2 = 0 ⇒ 9 = x2 ⇒
Assim, a medida da base é dada por: 3 − (−3) = 6 → 6 m.
Para determinar a medida da altura do túnel, calculamos o valor mássimo da função:
Assim, a área procurada é dada por: S = ⋅ 6 ⋅ 9 = = 36 → 36 m2
2. alternativa b
Considerando quê as raízes são os valores de x, em quê a f(x) = 0, o domínio quê faz sentido no contexto é dado pelo intervalo determinado de 0 até a raiz positiva de f. Assim, D(f) = {x ∈ ℝ | 0 ≤ x ≤ x2}, sêndo x2 a raiz positiva de f.
3. alternativa d
Temos de calcular a altura mássima atingida pela bola em relação ao chão, quê é dada, em métro, por: 1,5 + yV. Assim, temos:
Página trezentos e oitenta e seis
Segue quê 1,5 + yv ≃ 1,5 + 20,2 = 21,7 → aproximadamente 21,7 m Portanto, o saque será invalidado nos ginásios I, II, III e IV.
4. alternativa e
Como p = 10 é uma raiz da equação, temos: 102 − S ⋅ 10 + 20 = 0 ⇒ S = 12
5. alternativa c
O mês quê tem maior quantidade de infectados é aquele correspondente à abscissa do vértice tv da função:
Logo, a proposta aceita foi a III.
6. alternativa c
Desconsiderando o desconto, temos quê o valor total seria dado por 2x, para x bôm-bôns vendidos. Como será dado um desconto de x%, temos quê o valor total V em função de x é dado por:
7. alternativa d
A tempera-túra mássima é dada pelo valor mássimo yv da função f:
8. alternativa c
Sendo x o número de pessoas a desistir, temos:
• preêço por pessoa: 800 + 4x
• número de pessoas a voar: 160 − x
• receita em função da quantidade de passagens vendida: (160 − x) ⋅ (800 + 4x) = 128.000 + 640x − 800x − 4x2 = −4x2 − 160x + 128.000
Sabendo quê a receita foi de R$ 125.504,00, temos: 125.504 = −4x2 − 160x + 128.000 ⇒ −4x2 − 160x + 2.496 = 0
Resolvendo a equação ôbitída, temos: ∆ = (−160)2 − 4 ⋅ (−4) ⋅ 2.496 = 25.600 + 39.936 = 65.536
Portando, o número de pessoas quê realizou a viagem é dado por: 160 − 12 = 148 → 148 pessoas
9. alternativa b
−x2 = 2x ⇒ −x2 − 2x = 0
Resolvendo a equação do ôbitída, temos: x (−x −2) = 0 ⇒ x = 0 ou x = − 2
Para x = 0, temos y = 2 ⋅ 0 = 0.
Para x = −2, temos y = 2 ⋅ (−2) = −4.
Portanto, o ponto de coordenadas (−2, −4) corresponde à interseção dos gráficos das funções f e g.
10. alternativa d
Representando a venda de cada produto por p (x) = 400 − x, temos quê a receita ôbitída por sêr expressa por: r (x) = x (400 − x) = 400x − x2
A receita mássima corresponde ao valor mássimo yv da função r:
11. alternativa b
Como o gráfico de f tangencia o eixo das abscissas, temos quê o discriminante (delta)" da equação f(x) = 0 é tal quê (delta)" = 0.
Assim, temos:
Calculando a abscissa do ponto do gráfico de f em quê a ordenada é 9, temos:
Como essa abscissa deve sêr negativa, temos m = 3, de maneira quê x = −2 ⋅ 3 = −6.
12. alternativa d
Como (0, 5) é o ponto em quê o gráfico intersecta o eixo das ordenadas, temos: 5 = a ⋅ 02 + b ⋅ 0 + c ⇒ c = 5
Como xV = 2, temos:
Como o ponto de coordenadas Q (−2, 8) pertence ao gráfico função, temos: 8 = a ⋅ (−2)2 + b ⋅ (−2) + c (II)
Substituindo I em II, temos:
8 = 4a − 2 ⋅ (−4a) + 5 ⇒ a =
Segue quê: b = −4a = −4 ⋅ = −1
Assim, temos f(x) = x2 − x + 5.
Segue quê: y V = f(2) = ⋅ 22 − 2 + 5 = 1 + 3 = 4
13. Fazendo um esboço do gráfico de f(x) = = ax2 + bx + c, quê representa essa situação, temos:
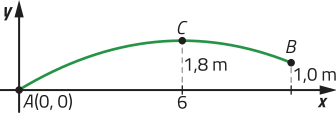
Colocando o ponto A na origem do sistema cartesiano, temos c = 0, pois o gráfico cruza o eixo y em (0, 0).
xv = 6 ⇒ = 6 ⇒ b = −12a
yv = 1,8 ⇒ = 1,8 ⇒ b2 = −7,2a
Substituindo b por −12a na segunda expressão, temos:
(−12a)2 = −7,2a ⇒ 144a2 = −7,2a ⇒
b = −12a ⇒ b = −12 ⋅ ⇒ b =
Assim, f(x) =
f(x) = 1 ⇒ 1 = x ⇒ 20 = −x2 + 12x ⇒ x2 − 12x + 20 = 0 ⇒ x = 2 ou x = 10
Como a abscissa de B deve sêr maior quê 6, tomamos x = 10. Assim, a largura do rio é de 10 metros.
14. alternativa b
f(x) = x(ax + b) ⇒ f(x) = ax2 + bx
Como a e b são números reais positivos, então a parábola quê representa f tem concavidade voltada para cima e corta o eixo y em seu ramo crescente.
15. alternativa c
Logo, para o intervalo [2, 6], temos
Im(f) = [4; 8,5]. Assim:
C (4) = 2(pi)" ⋅ 4 = 8(pi)"
C (8,5) = 2(pi)" ⋅ 8,5 = 17(pi)"
17(pi)" − 8(pi)" = 9(pi)"
16. alternativa c
Considerando x o valor do desconto e F o valor do faturamento, temos: F(x) = (80 − x) ⋅ (1.050 + 105x) = −105x2 + 7.350x + 84.000
80 − 35 = 45 → R$ 45, 00
17. a) d (40) = (402 + 8 ⋅ 40) = ⋅ 1.920 = 16 → 16 m
b) Como a distância de frenagem é de 53,2 m, temos quê:
53,2 = (x2 + 8x) ⇒ 6.384 = x2 + 8x ⇒ x2 + 8x − 6.384 = 0
Resolvendo a equação ôbitída, temos: (delta)" = 82 − 4 ⋅ 1 ⋅ (−6.384) = 25.600
Página trezentos e oitenta e sete
Portanto, a velocidade do automóvel deverá sêr de 76 km/h.
Unidade 5 • Relações métricas e trigonometria no triângulo
1. a)
b)
2. Resposta esperada: Não, pois, para quê João pudesse aplicar o teorema de Tales da maneira como ele fez, r, s e t deveriam formár um feixe de retas paralelas; no entanto, conforme o enunciado, apenas r e s são retas paralelas na figura construída por Isabella.
3. alternativa a
Para x = , as medidas AD e EC seriam negativas; logo, devemos ter x = 5. Segue quê o perímetro do triângulo ABC é:
(x − 2) + 9 + 16 + (5x − 10) + x = + 15 = 7 ⋅ 5 + 13 = 48 → 48 cm
• Resposta esperada: Não, pois a medida DE = 4 cm não foi utilizada.
4. alternativa b
⇒ x + 18 = 48 ⇒ x = 30 → 30 m
5. Como a propriedade tem o formato de um trapézio, os lados de medidas 3 km e 10,84 km são paralelos, pois correspondem às bases do trapézio. Além díssu, como os ângulos indicados são congruentes, a cerca dividindo a propriedade será paralela a essas bases.
Assim, pelo teorema de Tales:
Então, o comprimento total da cerca, em km, quê será construída é: 3 + 3,4 + 1,36 + 10,84 + 2 + 5 + 8,6 = 34,2
Como 34,2 km = 34.200 m, o custo total da cerca será: 34.200 ⋅ 0,20 = 6.840 → R$ 6.840,00
6. Resposta pessoal. Espera-se quê os estudantes elaborem problemas quê envolvam feixes de retas paralelas cortados por transversais e identifiquem quê existe proporção entre as medidas dos segmentos determinados. Um dos contextos possíveis, por exemplo, é o mapa do bairro formado por, no mínimo, três ruas paralelas e duas transversais.
7. De acôr-do com a figura, os ângulos , e são todos congruentes entre si; logo, como dois ângulos adjacentes de um paralelogramo qualquer são suplementares, os ângulos , , e também são congruentes entre si. Além díssu, os lados correspondentes são proporcionais entre si, pois:
•
•
Portanto, os paralelogramos são semelhantes com razão de semelhança igual a 4.
8. • Triângulo a: A medida do ângulo interno não indicada é: 180° − (72° + 66°) = 42°
Notar quê o triângulo c também tem um ângulo com essa medida e os lados quê formam esse ângulo têm medidas tais quê:
Logo, pelo caso LAL, os triângulos a e c são semelhantes.
• Triângulo b: Os três lados do triângulo b são proporcionais aos lados do triângulo e, pois:
Logo, pelo caso LLL, os triângulos b e e são semelhantes.
• Triângulo d: A medida do ângulo interno não indicada é: 180° − (60° + 45°) = 75°
Como os triângulos d e f têm ângulos de 45° e 75°, então, pelo caso AA, esses triângulos são semelhantes.
9. Observe, na figura a seguir, quê os ângulos e são congruentes, pois são opostos pelo vértice.
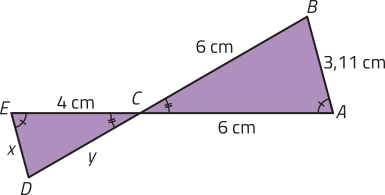
Então, pelo caso de semelhança de triângulos AA, temos quê (delta)"ABC ∼ (delta)"EDC. Assim:
• ⇒ x ≃ 2,07 → aproximadamente 2,07 cm
• ⇒ y = 4 → 4 cm
10. a) 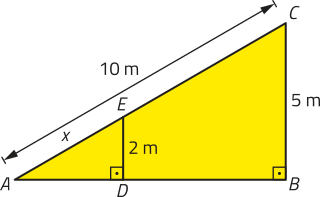
b) Os ângulos e são coincidentes e os ângulos e são congruentes, pois são ambos rétos; logo, pelo caso de semelhança AA, temos quê (delta)"EAD ∼ (delta)"CAB. Assim:
11. a) • A:
• B:
• C:
• D:
• E:
Logo, as resoluções A, B e D são utilizadas em formato de dê vê dê padrão, e as resoluções C e E, em formato widescreen.
b) Resposta esperada: Sim, elas têm formatos de polígonos semelhantes quando obtidas nas resoluções A, B e D e quando obtidas nas resoluções C e E. Nessas situações, têm, respectivamente, ângulos internos congruentes (ângulos retos) e lados correspondentes proporcionais.
12. Atividade de elaboração do estudante. Os estudantes podem abordar as dimensões de telas de smartphone ou táblêti, por exemplo, e outras resoluções diferentes das apresentadas, como 1.280:800 picsels e 1.024:600 picsels. Eles podem comparar a qualidade de diferentes resoluções nos próprios aparelhos e discutir com os côlégas a respeito dos resultados obtidos na pesquisa.
13. a) Utilizando o teorema de Pitágoras, temos: x2 = 12,82 + 9,62 ⇒ x2 = 256 ⇒ x =
Portanto, x corresponde a 16 cm.
b) Utilizando a relação h2 = m ⋅ n, temos: 262 = 15 ⋅ x ⇒ x = ≃ 45
Portanto, x corresponde a aproximadamente 45 mm.
c) Seja c a medida do cateto . Utilizando o teorema de Pitágoras, temos: c2 = 32 + 42 ⇒ c2 = 25 ⇒
Página trezentos e oitenta e oito
Utilizando a relação c ⋅ h = b ⋅ n, temos: 5 ⋅ 4 = x ⋅ 3 ⇒ x = ≃ 6, 67
Portanto, x corresponde a aproximadamente 6,67 m.
d) Utilizando a relação h2 = m ⋅ n, temos: 122 = 16 ⋅ x ⇒ x = 9
Portanto, x corresponde a 9 dm.
14. alternativa a
Utilizando a relação b2 = a ⋅ m, temos: 362 = 45 ⋅ m ⇒ m =
Observe quê m é a medida da projeção do cateto de medida 36 m; logo, a medida da projeção do outro cateto é n = 45 − . Assim: m ⋅ n =
Portanto, o produto das medidas das projeções é de aproximadamente 467.
15. a) Seja x a medida do outro cateto. Pelo teorema de Pitágoras, temos: 62 = x2 + 3,62 ⇒ x2 = 23,04 ⇒ x =
Portanto, o outro cateto méde 4,8 cm.
b) Utilizando a relação a ⋅ h = b ⋅ c, temos: 6 ⋅ h = 3,6 ⋅ 4,8 ⇒ h = 2,88
Portanto, a altura relativa à hipotenusa méde 2,88 cm.
c) Utilizando a relação c2 = a ⋅ n para obtêr a medida n da projeção do cateto de medida 3,6 cm sobre a hipotenusa, temos: 3,62 = 6 ⋅ n ⇒ n = 2,16
Logo, a medida m da projeção do outro cateto é m = 6 − 2,16 = 3,84. Portanto, as medidas das projeções são 2,16 cm e 3,84 cm.
16. a) O raio da circunferência méde, em cm: r = = 14
Logo, o comprimento da circunferência é: 2(pi)" ⋅ 14 = 28(pi)" → 28(pi)" cm ou aproximadamente 87,92 cm
b) Utilizando a relação h2 = m ⋅ n para obtêr a medida h da altura relativa à hipotenusa, temos quê: h2 = 21 ⋅ 7 ⇒ h2 = 3 ⋅ 72 ⇒ h = ⇒
Assim, a área do triângulo é: cm2 ou aproximadamente 169,74 cm2
17. As medidas dos catetos do triângulo retângulo, em centímetro, são dadas por:
• f(59) = 3 ⋅ 59 + 3 = 180
• f(79) = 3 ⋅ 79 + 3 = 240
Assim, pelo teorema de Pitágoras, a medida a da hipotenusa é dada por: a2 = 1802 + 2402 ⇒ a2 = 90.000 ⇒ a = ⇒
Portanto, a hipotenusa méde 300 cm.
18. a) Resposta esperada: Como a soma das áreas dos quadrados construídos sobre os dois menóres lados do triângulo é igual à área do quadrado construído sobre o maior lado, pode-se concluir quê as medidas 3 cm, 4 cm e 5 cm correspondem às medidas dos lados de um triângulo retângulo e quê os números 3, 4 e 5 formam um terno pitagórico.
b) Resposta pessoal. Espera-se quê os estudantes identifiquem, a partir de suas investigações, outros ternos pitagóricos em formatos como: 3k, 4k e 5k; 6k, 8k e 10k; ou 9k, 12k e 15k; sêndo k um número natural positivo.
c) Atividade de elaboração do estudante. Espera-se quê eles compreendam a ideia dos ternos pitagóricos e suas aplicações em problemas quê podem, por exemplo, envolver a área de triângulos ou retângulos.
19. Inicialmente, vamos determinar a medida do lado AB: 432 = AB2 + 352 ⇒ AB2 = 624 ⇒ AB = ⇒
Assim:
•
• _
•
20. a) Como a razão de semelhança é igual a 2, temos: = 2 ⇒ = 2 ⇒ AC = 12
Usando o teorema de Pitágoras no triângulo ABC, temos: 122 = 7,22 + BC2 ⇒ BC2 = 92,16 ⇒ BC = ⇒
Assim, o perímetro do triângulo ABC é: 7,2 + 9,6 + 12 = 28,8 → 28,8 m
E o perímetro do triângulo DEF é: = 14,4 → 14, 4 m
b) •
•
•
c) • 7, 2
•
•
21. A medida (alfa)" corresponde à medida do ângulo interno de um triângulo retângulo de catetos medindo 12 e 5 unidades de comprimento, sêndo 12 a medida do cateto ôpôsto a esse ângulo, conforme a figura.
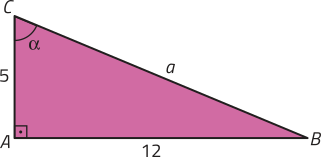
A medida da hipotenusa é dada por: a2 = 52 + 122 ⇒ a2 = 169 ⇒ a = ⇒
Segue quê:
a) sen (alfa)" =
b) cos (alfa)" =
c) (sen (alfa)")2 + (cos (alfa)")2 = = = 1
• Resposta esperada: Infinitos triângulos retângulos, semelhantes, cujos ângulos agudos médem (alfa)" e 90° − (alfa)".
22. a) tg (beta)" =
b) Sabendo quê tg (beta)" = , temos: tg (beta)" = ⇒ AC = 9
Assim: AD + DC = AC ⇒ AD + 6 = 9 ⇒ AD = 3 → 3 m
c) Como AC = 9, a área do triângulo ABC é:
Página trezentos e oitenta e nove
23. De acôr-do com o enunciado, temos o seguinte triângulo retângulo:
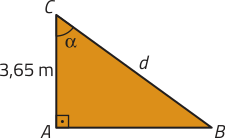
Assim:
Segue quê a distância d percorrida pela bola é, aproximadamente, dada por: d2 ≃ 3,652 + 52 ⇒ d2 ≃ 38,3225 ⇒ d ≃ ⇒
Portanto, a distância percorrida é de aproximadamente 6,19 m.
24. A medida da hipotenusa de um triângulo retângulo é sempre maior quê a medida de qualquer um dos catetos; logo, um triângulo retângulo isósceles só póde ter os dois catetos congruentes. Sejam c a medida comum dos dois catetos e a a medida da hipotenusa. Então, pelo teorema de Pitágoras: a2 = c2 + c2 ⇒ a2 = 2c2
Como a e c são números positivos, segue quê: a =
Além díssu, como o triângulo é isósceles, os dois ângulos internos agudos são congruentes.
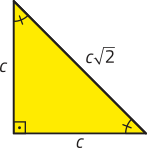
Assim:
• seno:
• cosseno:
• tangente:
25. Resposta pessoal. Para verificar as respostas, os estudantes podem, por exemplo, utilizar relações estudadas, como a quê indica quê os ângulos agudos do triângulo retângulo são complementares.
26. a) • cos 45° = ⇒ x = 22
• tg 45° = ⇒ 1 =
Portanto, x = 22 cm e y = .
b) • cos 20° = ⇒ 0, 940 ≃ ⇒ x ≃ 3,76
• sen 20° = ⇒ 0,342 ≃ ⇒ y ≃ 1,368
Portanto, x ≃ 3,76 m e y ≃ 1,37 m.
27. Observe quê, como a soma dos ângulos internos de um triângulo é igual a 180°, as medidas (alfa)" e (beta)" dos ângulos internos agudos de um triângulo retângulo são tais quê: (alfa)" + (beta)" + 90° = 180° ⇒ (alfa)" + (beta)" = 90°
Ou seja, os ângulos internos agudos de um triângulo retângulo são ângulos complementares.
a) tg (alfa)" =
Como tg 60° = , temos (alfa)" = 60° e
b) tg (alfa)" = = 0,625
Como tg 32° ≃ 0,625, temos (alfa)" ≃ 32° e
28. A situação está representada na seguinte figura:
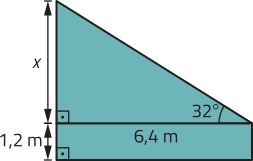
Temos: tg 32° = ⇒ 0, 625 ≃ ⇒ x ≃ 4
A altura do barranco corresponde a x + 1,2, o quê é aproximadamente igual a: 4 + 1,2 = 5,2 → aproximadamente 5,2 m
29. a) 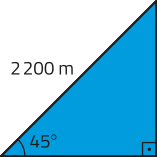
b) Seja h a altura em relação ao solo.
Então: sen 45° =
Portanto, o avião está a uma altura de _ m ou aproximadamente 1.556 m.
30. a) pôdêmos representar parte dessa ponte por um triângulo retângulo ABC e calcular o cosseno do ângulo de 27°, conforme segue.
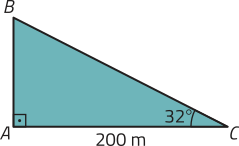
cos 32° =
Consultando a tabéla trigonométrica, temos quê cos 32° ≃ 0,848. Assim:
0,848 ≃
Portanto, o último cabo de sustentação tem aproximadamente 235,85 m de comprimento.
b) Com base no triângulo ABC, representado no item a, temos: tg 32° =
Consultando a tabéla trigonométrica, temos quê tg 32° ≃ 0,625. Assim:
0,625 ≃ ⇒ AB ≃ 200 ⋅ 0,625 = 125
Portanto, o topo do mastro central está a uma altura de aproximadamente 125 m acima do tabuleiro.
31. a) I e III
I) tg (alfa)" = ≃ 0,601
Como tg 31° ≃ 0,601, temos quê (alfa)" ≃ 31°. Logo, a escada atende à norma.
II) tg (beta)" = ≃ 0,675
Como tg 34° ≃ 0,675, temos quê (beta)" ≃ 34°. Logo, a escada não atende à norma.
III) tg θ = ≃ 0,577
Como tg 30° ≃ 0,577, temos quê θ ≃ 30°. Logo, a escada atende à norma.
b) Na figura a seguir, x é o comprimento da projeção horizontal da escada, o qual depende do ângulo de inclinação de medida (alfa)".
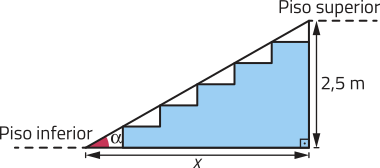
Observe quê a inclinação mínima, com (alfa)" = 26,57°, determina a escada de comprimento mássimo, e a inclinação mássima, com (alfa)" = 32,74°, determina a escada de comprimento mínimo. Vamos calcular x em cada caso:
• Para (alfa)" = 26,57°:
tg 26,57° = ⇒ 0, 500 ≃ ⇒ x ≃ 5
• Para (alfa)" = 32,74°:
tg 32,74° = ⇒ 0, 643 ≃ ⇒ x ≃ 3, 89
Portanto, os comprimentos mínimo e mássimo da projeção horizontal são, respectiva e aproximadamente, 3,89 m e 5 m.
Página trezentos e noventa
32. a) 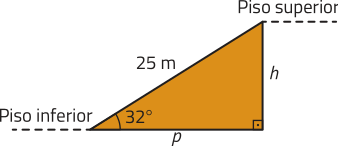
b) O comprimento da projeção horizontal da escada corresponde à medida p indicada na figura. Temos:
cos 32° = ⇒ 0,848 ≃ ⇒ p ≃ 21,2 → aproximadamente 21,20 m
c) A altura do desnível entre os dois pisos corresponde à medida h indicada na figura. Temos: sen 32° = ⇒ 0,530 ≃ ⇒ ⇒ h ≃ 13,25 → aproximadamente 13,25 m
33. Na figura a seguir, a medida x corresponde à largura do lago naquele trecho.
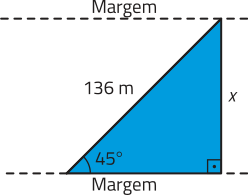
Temos:
sen 45° = ⇒ x = ≃ 96
Portanto, a largura é de aproximadamente m ou aproximadamente 96 m.
34. A altura total do edifício é de 16 ⋅ 3 = 48 metros, porém precisamos subtrair dêêsse valor a altura dos olhos em relação ao solo para obtêr o esquema a seguir:
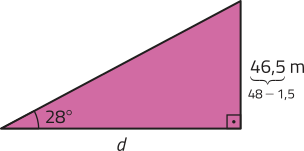
Nesse esquema, a medida d corresponde à distância da pessoa ao edifício e é dada por: tg 28° = ⇒ 0, 532 ≃ ⇒ d ≃ 87,4 → aproximadamente 87,4 m
35. A figura a seguir ilustra o comprimento da sombra c de acôr-do com a medida do ângulo de inclinação (alfa)" quê os raios solares formam com o solo.
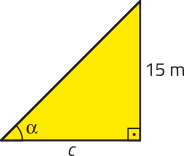
a) Para c = 9 m: tg (alfa)" = ≃ 1,667
Temos tg 59° ≃ 1,664 e tg 60° ≃ 1,732; logo, o ângulo é de aproximadamente 59°.
b) Para c = 18 m: tg (alfa)" = ≃ 0,833
Temos tg 39° ≃ 0,810 e tg 40° ≃ 0,839; logo, o ângulo é de aproximadamente 40°.
c) Para c = 15 m:
tg (alfa)" = = 1
Temos tg 45° = 1; logo, o ângulo é de 45°.
36. A inclinação mínima, com (beta)" = 8°, determina a rampa de extensão mássima, e a inclinação mássima, com (beta)" = 12°, determina a rampa de extensão mínima. Vamos calcular essa extensão em cada caso:
• sen 8° = ⇒ 0,139 ≃ ⇒ x ≃ 43,2
• sen 12° = ⇒ 0,208 ≃ ⇒ x ≃ 28,8
Portanto, a rampa póde ter, aproximadamente, de 28,8 m até 43,2 m de extensão.
37. a) Respostas esperadas: Calculando a razão entre a medida do seno e a medida do cosseno de cada ângulo, obtemos a medida da tangente dêêsse ângulo.
Logo, tg (alfa)" = , com 0° < (alfa)" < 90°; temos quê a medida do seno de um ângulo é igual à medida do cosseno de seu complemento, logo: sen (alfa)" = cos(90° − (alfa)"), com 0° < (alfa)" < 90°.
b) Resposta pessoal. Espera-se quê os estudantes consigam realizar a demonstração utilizando ângulos genéricos. Mas, caso apresentem dificuldades, sugerir quê desenhem um triângulo retângulo com medidas genéricas para os lados e indiquem a medida de um ângulo agudo qualquer e do outro ângulo em função do primeiro. Após isso, pedir quê determinem, utilizando as definições das razões trigonométricas, o seno, o cosseno e a tangente, verificando as relações conjecturadas no item a.
38. Resposta esperada:
a2 = b2 + c2 ⇒ ⇒ 1 = ⇒ 1 = cos2 (alfa)" + sen2 (alfa)"
39. a) Cada placa tem uma área de 1 ⋅ 2 = 2 metros quadrados. Como o painel é formado por duas placas, sua área é de: 2 ⋅ 2 = 4 → 4 m2
b) Como o comprimento da placa é de 2 m, temos: cos (alfa)" = = 0,91
Temos cos 24° ≃ 0,914 e cos 25° ≃ 0,906, logo (alfa)" está entre 24° e 25°. O município com a latitude mais próxima dêêsse ângulo é Guarapuava (PR).
c) Resposta pessoal. Os estudantes podem se basear, por exemplo, na situação descrita no enunciado e realizar os cálculos de modo análogo, ajustando os valores de acôr-do com as coordenadas geográficas pesquisadas.
d) Resposta pessoal. Espera-se quê os estudantes reconheçam quê o investimento em painéis solares tem um retorno financeiro a médio prazo, possibilitando economia na conta de energia elétrica e potencial contribuição ao meio ambiente por sêr uma fonte de energia limpa e renovável. Os estudantes podem, por exemplo, abordar no texto as vantagens dêêsse tipo de geração de energia para o meio ambiente, em comparação com as hidrelétricas e fontes não rêno-váveis.
Integrando com...
1. Algumas respostas possíveis: Construção de rampas; instalação de elevadores; adaptação de banheiros; aplicação de piso tátil em calçadas; disponibilização de transporte coletivo adaptado; instalação de semáforo sonoro; estabelecimento de vagas especiais em estacionamentos. Resposta pessoal. Espera-se quê os estudantes reflitam sobre a necessidade de inclusão por meio da acessibilidade e reconheçam nas melhorias citadas um caminho para uma ssossiedade mais justa.
2. Resposta esperada: As normas de acessibilidade estabelecem critérios e parâmetros técnicos para garantir quê diferentes construções e espaços sêjam acessíveis à maior quantidade possível de pessoas. Resposta pessoal. Espera-se quê esta atividade proporcione um momento de pesquisas e debates a respeito de outras normas de acessibilidade, de modo quê os estudantes possam refletir sobre a legislação de inclusão e o seu cumprimento ou não na comunidade em quê vivem.
3. a) A letra c representa o comprimento da projeção horizontal da rampa, d representa a altura do desnível da rampa e (alfa)" representa o ângulo de inclinação da rampa.
b) alternativa III
Como a altura do desnível é representada por d e o comprimento da projeção horizontal da rampa por c, temos quê a razão representa, no triângulo formado, a razão entre as medidas dos catetos ôpôsto e adjacente a (alfa)", ou seja, tg (alfa)".
4. Resposta esperada: Não, pois a norma estabelece quê a inclinação da rampa não deve ultrapassar 0,0833 e, nesse caso, a inclinação é de 0,1.
Página trezentos e noventa e um
5. a) ![]()
b) De acôr-do com as informações, é necessário quê ≤ 0, 0833, ou seja, tg (alfa)" ≤ 0,0833. Como tg 4° ≃ 0,070 e tg 5° ≃ 0,087, podemos concluir quê a inclinação mássima corresponde a um ângulo com medida aproximadamente igual a 5°.
6. a) Observando o qüadro, podemos estabelecer a seguinte relação: ⇒ c = 12d
Com base nessa relação, completamos o qüadro.
d |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|---|---|---|---|---|---|---|---|---|
c |
1,2 |
2,4 |
3,6 |
4,8 |
6 |
7,2 |
8,4 |
9,6 |
b) Resposta pessoal. Espera-se quê os estudantes coloquem em prática o quê foi estudado na seção. Eles podem, por exemplo, investigar rampas na escola, em alguma edificação no bairro em quê moram ou em outro local do município. Orientar as medições para quê os resultados sêjam próximos da realidade.
c) Resposta pessoal. Espera-se quê os estudantes identifiquem possíveis melhorias nos ambientes em quê circulam visando a acessibilidade e inclusão. Eles podem, por exemplo, apresentar a pesquisa realizada e as conclusões obtidas para a comunidade escolar e, se for o caso, para órgãos governamentais a fim de reivindicar o cumprimento das normas de inclusão.
40. a) A medida x do ângulo Aˆ C Bé dada por: x + 43° + 68° = 180° ⇒ x = 69°
Assim:
• ⇒ ⇒ AC ≃ 4,96
• ⇒ ⇒ BC ≃ 3,65
Portanto, o perímetro do triângulo é, aproximadamente: 5 + 4,96 + 3,65 = 13,61 → aproximadamente 13,61 cm
b) A medida x do ângulo Bˆ A Cé dada por: x + 60° + 80° = 180° ⇒ x = 40°
Assim: • ⇒ ⇒ BC ≃ 5,88
• ⇒ ⇒ AC ≃ 7,91
Portanto, o perímetro do triângulo é, aproximadamente: 9 + 5,88 + 7,91 = 22,79 → aproximadamente 22,79 m
41. a) 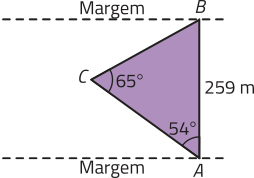
b) A medida x do ângulo Aˆ B Cé dada por: x + 54° + 65° = 180° ⇒ x = 61°
Assim: • ⇒ ⇒ AC ≃ 250,14
• ⇒ ⇒ BC ≃ 231,27
Portanto, a distância aproximada percorrida pelo pescador foi: AC + BC ≃ 250,14 + 231,27 = 481,41 → aproximadamente 481,41 m
42. A medida x do ângulo Aˆ B Cé dada por: x + 58° + 72° = 180° ⇒ x = 50°
Assim: ⇒ ⇒ AB ≃ 276,76
Portanto, a distância do ponto A até a bóia é de aproximadamente 276,76 m.
43. a)
Logo, (alfa)" = 60° ou
• Para (alfa)" = 60°: 60° + (beta)" + 45° = 180° ⇒ (beta)" = 75°
• Para (alfa)" = 120°: 120° + (beta)" + 45° = 180° ⇒ (beta)" = 15°
Portanto, (alfa)" = 60° e (beta)" = 75° ou (alfa)" = 120° e (beta)" = 15°.
b) ⇒
⇒ sen (alfa)" ≃ 0,719 ≃ sen 46°
Logo, (alfa)" ≃ 46° é a única possibilidade, pois, como o ângulo méde 78°, então (alfa)" . Assim: 46° + (beta)" + 78° ≃ 180° ⇒ (beta)" ≃ 56°
Portanto, (alfa)" ≃ 46° e (beta)" ≃ 56°.
c) ⇒ sen (beta)" ≃ 0, 857 ≃ sen 59°
Logo, (beta)" ≃ 59° é a única possibilidade, pois, como o ângulo méde 77°, então (beta)" Assim: (alfa)" + 59° + 77° ≃ 180° ⇒ (alfa)" ≃ 44°
Portanto, (alfa)" ≃ 44° e (beta)" ≃ 59°.
d) ⇒ ⇒ sen (beta)" ≃ 0, 616 ≃ sen 38°
Logo, (beta)" ≃ 38° é a única possibilidade, pois, como o ângulo méde 60°, então (beta)" . Assim: (alfa)" + 38° + 60° ≃ 180° ⇒ (alfa)" ≃ 82°
Portanto, (alfa)" ≃ 82° e (beta)" ≃ 38°.
44. Resposta pessoal. Espera-se quê os estudantes elaborem um problema contextualizado em quê, dado um triângulo, são conhecidas as medidas de dois ângulos e um lado. Eles podem, por exemplo, usar como contexto uma praça de formato triangular, um projeto arquitetônico de um jardim ou ainda a distância entre objetos.
45. A medida x do ângulo é dada por: x + 55° + 44° = 180° ⇒ x = 81°
Assim:
• ⇒ ⇒ BC ≃ 10,78
• ⇒ ⇒ AC ≃ 9,14
Portanto, Maurício estava a aproximadamente 10,78 m de distância do drone e Pamela, a aproximadamente 9,14 m.
46. O ângulo é suplementar de um ângulo de 100°; logo, méde 180° − 100° = = 80°. Seja (beta)" a medida do ângulo . Então, pela lei dos senos: ⇒ sen (beta)" ≃ 0, 770
Temos sen 50° ≃ 0,766 e sen 51° ≃ 0,777; logo, sen (beta)" ≃ sen 50°. Então (beta)" ≃ 50°, pois, como o ângulo méde 80°, temos (beta)" . Segue quê a medida (gama)" do ângulo é dada por:
Página trezentos e noventa e dois
(gama)" + 50° + 80° ≃ 180° ⇒ (gama)" ≃ 50°
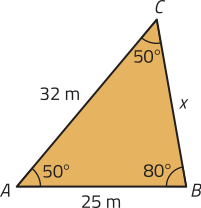
Assim, a medida x é dada, aproximadamente, por: ⇒ x ≃ 25 → aproximadamente 25 m
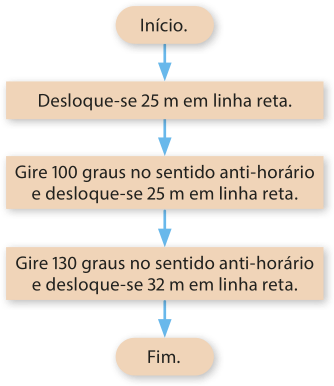
47. 742 = 352 + 452 − 2 ⋅ 35 ⋅ 45 ⋅ cos (alfa)" ⇒ 5.476 = 1.225 + 2.025 − 3.150 ⋅ cos (alfa)" ⇒ −3.150 ⋅ cos (alfa)" = 2.226 ⇒
⇒ cos (alfa)" = ⇒ cos (180° − (alfa)") = ≃ 0,707
Temos cos 45° ≃ 0,707, assim: 180° − (alfa)" ≃ 45° ⇒ (alfa)" ≃ 135°
48. x2 = 32,32 + 302 − 2 ⋅ 32,3 ⋅ 30 ⋅ cos 70° ⇒ x2 ≃ 1.043,29 + 900 − 1.938 ⋅ 0,342 ⇒ x2 ≃ 1.280,494 ⇒ x ≃ ⇒
Portanto, aproximadamente cm ou aproximadamente 35,78 cm.
49. Utilizando a lei dos cossenos, temos:
a) (BC)2 = 62 + 32 − 2 ⋅ 6 ⋅ 3 ⋅ cos 60° ⇒ (BC)2 = 27 ⇒BC = ou BC = (não convém) → BC = cm
b) (AC)2 = 82 + − 2 ⋅ 8 ⋅ ⋅ cos 45° ⇒ (AC)2 = 64 ⇒AC = 8 ou AC = −8 (não convém) → AC = 8 cm
c) (AB)2 = 282 + 202 − 2 ⋅ 28 ⋅ 20 ⋅ cos 120° ⇒ (AB)2 = 1.744 ⇒AB = ou AB = (não convém) → AB = cm ou aproximadamente 41,8 cm
50. a) Seja x a distância de B até C, em métro. Então: x2 = 1502 + 118,22 − 2 ⋅ 150 ⋅ 118,2 ⋅ cos 88° ⇒ x2 ≃ 36.471,24 − 1.241,1 ⇒ x2 ≃ 35.230,14 ⇒ x ≃ ⇒
Portanto, aproximadamente 187,7 m.
b) Seja (alfa)" a medida do ângulo . Então: ⇒ sen (alfa)" ≃ 0,798 ≃ sen 53°
Logo, med = (alfa)" ≃ 53° e med ≃ 180° − 88° − 53° ≃ 39°.
51. Seja (x − 2, x, x + 2) a sequência cujos termos representam as medidas dos lados do triângulo, em centímetro. O maior lado, cuja medida é x + 2, é ôpôsto ao maior ângulo, quê tem 120° de medida. Assim, pela lei dos cossenos:
(x + 2)2 = x2 + (x − 2)2 − 2 ⋅ x ⋅ (x − 2) ⋅ cos 120° ⇒ x2 + 4x + 4 = x2 + x2 − 4x + 4 − (2x2 − 4x) ⋅ (−cos 60°) ⇒ −x2 + 8x = −(2x2 − 4x) ⋅ ⇒ −x2 + 8x = x2 − 2x ⇒ −2x2 + 10x = 0 ⇒ x2 − 5x = 0 ⇒ x(x − 5) = 0 ⇒
Logo, os lados do triângulo médem 3 cm, 5 cm e 7 cm, e seu perímetro é: 3 + 5 + 7 = 15 → 15 cm
52. a) Analisando os vetores apresentados na figura, temos:
• mesma direção: e ; e ; e
• mesmo sentido: e e ; e
• mesmo módulo: e ; e ; e , e
b) O vetor resultante tem módulo igual a: 45 − 25 = 20 → 20 N
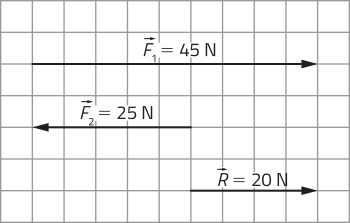
c) Pela lei dos cossenos:
15,042 = 82 + d2 − 2 ⋅ 8 ⋅ d ⋅ ⇒ 226,2016 ≃ 64 + d2 − 12,256d ⇒ d2 − 12,256d − 162,2016 ≃ 0 ⇒
Portanto, d ≃ 20,26 m.
d) 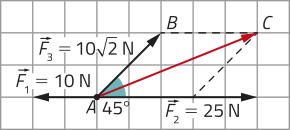
Observe quê BC = 25 − 10 = 15 e med() = 45° + 90° = 135°. Logo, sêndo x o módulo do vetor resultante, representado em vermelho, e utilizando a lei dos cossenos no triângulo ABC, temos:
x2 = ( )2 + 152 − 2 ⋅ ⋅ 15 ⋅ cos 135° ⇒ x2 = 425 − ⋅ (−cos 45°) ⇒ x2 = 425 − ⋅ ⇒ x2 = 425 + 300 ⇒ x2 = 725 ⇒ x = ⇒
Portanto, o módulo do vetor resultante é de aproximadamente 26,93 N.
e) Resposta esperada: Essa diferença acontece porque, ao somar dois vetores, o ângulo considerado entre os vetores é aquele cuja origem coincide com a origem de ambos os vetores. Por exemplo, na imagem a seguir, o ângulo (alfa)" é determinado na soma dos vetores e Entretanto, quando traçamos o vetor resultanteformando um triângulo, o ângulo ôpôsto ao vetor resultante é o suplementar a (alfa)". Como cos (180° − (alfa)") = −cos (alfa)", justificamos a diferença entre as expressões das relações apresentadas.
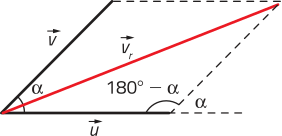
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) Premissas: Os triângulos ABC e A’B’C’ são semelhantes entre si e a razão de semelhança entre esses triângulos é k; conclusão: a razão entre os perímetros dos triângulos ABC e A’B’C’ também é k.
Página trezentos e noventa e três
b) • cos 30° = ⇒ AB = cm
sen 30° = ⇒AC = 4 → 4 cm
• Seja m a medida da projeção do cateto AB sobre a hipotenusa. Então:
cos 30° = ⇒ m = 6 → 6 cm
• A medida n da projeção do cateto AC sobre a hipotenusa é dada por: n + m = BC ⇒ n + 6 = 8 ⇒ n = 2 → 2 cm
c) Nessas condições, os triângulos ADE e ABC serão semelhantes e com razão de semelhança igual a . Assim:
• ⇒ AD =
• ⇒ AE = = 2,5
Portanto, as medidas dos outros lados serão cm e 2,5 cm.
d) Sejam dois quadrados em quê a razão de semelhança entre eles é k. Um deles tem o lado medindo (éli)" e o outro, k ⋅ (éli)", sêndo (éli)" um número positivo.

Assim, a razão entre suas áreas é:
Praticando: enêm e vestibulares
1. alternativa d
R2 = 102 + 102 − 2 ⋅ 10 ⋅ 10 ⋅ cos 120° ⇒ R2 = 100 + 100 − 200 ⋅ ⇒ R2 = 300 ⇒ R = ou R = (não convém) → R = cm ≃ 17 cm
2. alternativa d
x2 = 72 + − 2 ⋅ 7 ⋅ ⋅ cos 135° ⇒ x2 = 49 + 50 − 70 ⋅ ⇒ x2 = 169 ⇒ x = 13 ou x = −13 (não convém) → 13 m
3. alternativa e
Calculando, em métro, a altura do triângulo equilátero de lado 6 m, temos:
Temos quê a parte superior entre o caminhão e o túnel formam outro triângulo, do qual precisamos determinar a altura, quê corresponde à altura mássima do caminhão. Assim, como os triângulos são semelhantes pelo caso AA, temos: ⇒ 6a = ⇒ a =
Logo, a altura mássima do caminhão, em métro, é dada por:
4. alternativa c
Utilizando o teorema de Pitágoras, podemos determinar a altura h do triângulo de lados 3 m, 3 m e 2 m, em relação ao lado de medida 2 m: 32 = h2 + 12 ⇒ h2 = 9 − 1 ⇒ h = ou h = (não convém) → h = m
Assim, a medida x, em métro, é dada por: x = − 0,5
5. alternativa b
Os maiores ângulos internos do triângulo ABC são opostos aos maiores lados, ou seja, AC = 18 cm, BC = 14 cm e AB = 12 cm. Como após a dobra o vértice B ficará sobre , temos quê esse triângulo terá sua altura dividida ao meio, formando triângulos semelhantes, como mostra a figura a seguir.
Pelo caso AA, os triângulos AB’B e DFB são semelhantes. Assim, como a altura BB’ será dividida ao meio (BF = FB’), temos, por consequência, quê AD = DB = 6 cm e BE = EC = 7 cm.
Logo, temos: DB + BE + EC = 6 + 7 + 7 = 20 → 20 cm
6. a) (PR)2 = 32 + 42 ⇒ PR = 5 ou PR = −5 (não convém)
(QS)2 = 32 + (2,25)2 ⇒ QS = 3,75 ou QS = −3,75 (não convém)
Logo, PR = 5 cm e QS = 3,75 cm = 37,5 mm.
b) Vamos, inicialmente, determinar a medida da diagonal do quadrado TSUP. Para isso, construímos a figura a seguir, com as medidas de comprimento indicadas em centímetro.
Do triângulo PQR, temos sen (alfa)" = . Note quê cos ((alfa)" + 90°) = −sen (alfa)". Logo, pela lei dos cossenos aplicada ao triângulo PRS, temos: (PS)2 = 52 + (2,25)2 − 2 ⋅ 5 ⋅ 2,25 ⋅ cos ((alfa)" + 90°) ⇒ (PS)2 =
Como a medida da diagonal do quadrado de lado (éli)" póde sêr expressa por (éli)" , temos quê a área do quadrado TSUP é dada por: = ⇒ 2(éli)"2 = ⇒ (éli)"2 = cm2
7. alternativa b
Da figura, temos: tg (alfa)" =
Assim, a medida p do pilar menor é dada por: tg (alfa)" =
Analisando pela tabéla, temos quê 30° < (alfa)" < 31°.
8. alternativa a
Sendo x e y as medidas, em métro, do menor e do maior lado da região retangular, respectivamente, temos:
• sen 60° = ⇒ x =
• cos 60° =
Assim, a área da região retangular é dada por: x ⋅ y = → m2
9. alternativa b
Calculamos a lei dos cossenos no triângulo ABC em dois casos:
• x = 60°
(AC)2 = 32 + 42 − 2 ⋅ 3 ⋅ 4⋅ cos 60° ⇒ AC = ou AC = (não convém) → AC =
• x = 90°
(AC)2 = 32 + 42 − 2 ⋅ 3 ⋅ 4⋅ cos 90° ⇒ AC = 5 ou AC = −5 (não convém) → AC = 5
Portanto, a variação mínima e mássima da mola são, respectivamente, e 5.
10. alternativa b
Dado o paralelismo indicado no enunciado, pelo caso AA, temos quê são semelhantes os triângulos ABC, SRC e NMC. Além díssu, pelas informações do enunciado, temos - b - R - = RM = x e MC = 2x.
Página trezentos e noventa e quatro
Da semelhança dos triângulos ABC e SRC, temos:
Logo, a área do triângulo SRC corresponde a da área do triângulo ABC.
Já em relação à semelhança dos triângulos ABC e NMC, temos:
Logo, a área do triângulo NMC corresponde a da área do triângulo ABC. A área do trapézio RMNS, em relação à área do triângulo ABC, é dada por: = 0,3125
Portanto, a área do trapézio RMNS corresponde a 31,25% da área do triângulo ABC.
11. De acôr-do com as informações do enunciado, temos a seguinte situação:
Temos OM = OA, pois são raios da mesma circunferência. Além díssu, o triângulo OAM é isósceles, com os ângulos da base medindo 40° (180° − 100° = 80° e 80° ∶ 2 = 180°).
Como as projeções indicadas são ortogonais, , pelo Teorema de Tales, . Logo, pelo caso LAL, os triângulos ADM e ADE são semelhantes. Disso, temos quê = e quê a altura do triângulo AME coincide com o ponto médio do lado ôpôsto, ou seja, esse é um triângulo isósceles. Assim, como = 90° e = 40°, temos = 90° − 40° = 50° e, do mesmo modo, = 40°. Logo, como = 90°, temos = 40°.
12. alternativa b
402 = (PR)2 + 92 ⇒ PR = 40 ou PR = −40 (não convém)
Pelo caso AA, temos quê os triângulos PRQ e PST são semelhantes. Assim, temos: ⇒ 40 ⋅ ST = 9 ⋅ 100 ⇒ ST = 22,5 → 22,5 cm
13. alternativa e
Nomeando os vértices do retângulo correspondente à praça, temos:
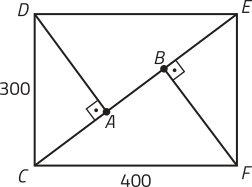
Aplicando o teorema de Pitágoras no triângulo retângulo CDE, temos:
(CE)2 = 3002 + 4002 ⇒ CE = 500 ou CE = −500 (não convém) → CE = 500
Aplicando uma relação métrica no triângulo retângulo CDE, temos: 3002 = CA ⋅ 500 ⇒ CA = 180
Aplicando uma relação métrica no triângulo retângulo CEF, temos: 3002 = BE ⋅ 500 ⇒ BE = 180
Logo, a distância entre os dois póstes é dada por: CE − CA − BE = 500 − 180 − 180 = 140 → 140 m
14. alternativa c
Sendo x a distância entre os prédios, temos: tg 45° = ⇒ x = 20 → 20 m
Unidade 6 • Estatística: gráficos e tabélas
1. a) Analisando a segunda coluna da tabéla simples, temos quê o maior número está na última linha, quê representa o ano de 2023.
b) A resposta depende da região em quê o estudante mora. Espera-se quê o estudante identifique a região em quê mora na primeira coluna e o porcentual de cobertura da vacína contra poliomelite na segunda coluna da tabéla de dupla entrada.
2. a) Verdadeira, pois o porcentual indicado era de 22,8%.
b) Falsa. Resposta esperada: De 2016 para 2022, houve redução no porcentual de pessoas de 14 e 15 anos quê realizavam atividades econômicas em ocupações da Lista TIP.
c) Falsa. Resposta esperada: Em 2022, dentre os setores ocupados pelas pessoas de 5 a 17 anos em situação de trabalho infantil, o de comércio e reparação era o de menor porcentual.
d) Verdadeira, pois, analisando a barra referente a 2022 do grupo de 5 a 13 anos, verificamos quê o porcentual é maior quê 69,4%, enquanto dois terço corresponde a aproximadamente 66,7%.
3. a) De acôr-do com o título do gráfico, de 2017 a 2022.
b) De acôr-do com a fonte indicada, sáiti do Inep.
c) 2017: 42.852 ∶ 56.750 ≃ 0,755 → aproximadamente 75,5%
2022: 28.272 ∶ 44.195 ≃ 0,640 → aproximadamente 64%
d) 44.195 ∶ 9.444.116 ≃ 0,0047 → aproximadamente 0,47%. Resposta pessoal. Espera-se quê os estudantes debatam o baixo porcentual de indígenas matriculados nos cursos superiores, assim como a necessidade de políticas públicas quê garantam o acesso e a permanência de populações historicamente marginalizadas, como os indígenas, em cursos superiores.
4. a) Resposta pessoal. Conversar com os estudantes a respeito da importânssia daqueles quê já têm a idade mínima para tirar o título de eleitor e votar nas eleições.
b) Analisando o gráfico de setores, Ensino Médio. Setor vêrde.
c) 43% de 156 milhões → 0,43 ⋅ 156 milhões ≃ 67,1 milhões Portanto, aproximadamente 67,1 milhões de eleitores tí-nhão o Ensino Médio.
5. a) Observando a última linha da segunda coluna, temos quê 148.920.333 pessoas com 15 anos ou mais não frequentavam a escola.
b) Observando a segunda coluna da segunda linha, temos quê, das pessoas com 15 anos ou mais quê não frequentavam a escola em 2020 no Brasil, 44.108.417 tí-nhão o Ensino Fundamental incompleto ou equivalente.
c) 100% − 52,1% = 47,9%
d) Algumas respostas possíveis: Necessidade de trabalhar ou ajudar nos afazeres domésticos, desinteresse pêlos estudos, ausência de escola na localidade em quê mora, ausência de oferta de turno escolar desejado etc. Algumas respostas possíveis: Implantação de políticas públicas específicas, disponibilização de ambientes escolares acolhedores e inclusivos, construção de novas escolas, ampliação de ofertas de turnos escolares demandados etc.
6. a)
Sítios arqueológicos cadastrados na Região Nordeste, até 24 de março 2024
Estado |
Quantidade de sítios arqueológicos |
|---|---|
Alagoas |
379 |
baía |
1.402 |
Ceará |
589 |
Maranhão |
171 |
Paraíba |
192 |
Pernambuco |
737 |
Piauí |
1.928 |
Rio Grande do Norte |
429 |
Sergipe |
237 |
Fonte dos dados: BRASIL. Instituto do Patrimônio Histórico e Artístico Nacional. Cadastro nacional de sítios arqueológicos CNSA/SGPA. Brasília, DF: Ifan, c2014. Disponível em: https://livro.pw/jvvqs. Acesso em: 23 jul. 2024.
Página trezentos e noventa e cinco
b) Comparando as quantidades apresentadas na segunda coluna da tabéla, temos quê o estado é o Piauí. 1.928 sítios arqueológicos.
c) 379 + 1.402 + 589 + 171 + 192 + 737 + 1.928 + 429 + 237 = 6.064 → 6.064 sítios arqueológicos
d) Resposta pessoal. Espera-se quê os estudantes compreendam o quê são os sítios arqueológicos e descubram alguns próximos da região em quê moram, bem como a história do local. A região em quê moram póde, por exemplo, sêr subdividida para pesquisa, de modo quê duplas distintas façam diferentes pesquisas e compartilhem com a turma. Se necessário, ampliar a extensão geográfica a sêr pesquisada.
7. alternativa b
171 ∶ 6.064 ≃ 0,0282 → aproximadamente 2,82%
⇒ 1 ⋅ x = 360° ⋅ 0,0282 ⇒ x ≃ 10°
8. a) O dado está localizado na terceira linha e terceira coluna e representa quê 65% das crianças e adolescentes de 11 e 12 anos utilizaram a internet para enviar mensagem instantânea em 2023 no Brasil.
b) Analisando o menor índice da última coluna, temos quê a faixa etária de 9 a 10 anos é aquela quê apresentou o menor porcentual de crianças e adolescentes quê conversaram por chamada de vídeo.
c) Comparando a última linha da terceira e da quarta colunas, temos quê enviar mensagem instantânea é o uso da internet quê mais crianças e adolescentes de 15 a 17 anos de idade, em 2023, faziam no Brasil.
d) Resposta esperada: Gráfico de colunas ou de barras, para possibilitar a comparação visual entre os dados pesquisados de cada faixa etária.
e) Resposta esperada: A coluna vêrde mais alta corresponderia ao porcentual de crianças e adolescentes de 15 a 17 anos (95%) quê usou rê-de social, e a coluna amarela mais baixa, ao porcentual de crianças e adolescentes de 9 a 10 anos (45%) quê enviou mensagem instantânea no Brasil em 2023.
f) Resposta pessoal. Espera-se quê os estudantes compreendam as potencialidades dêêsses recursos para a comunicação no mundo globalizado e quê façam sugestões para o uso consciente dêêsses recursos, como um tempo adequado de exposição às telas.
9. a) Analisando a parte vêrde do gráfico, temos quê 17,6% das mortes violentas intencionais no Brasil, em 2021, foram causadas por arma branca.
b) ⇒100x = 6,4⋅360° ⇒ x = ⇒ x ≃ 23°
c) Como 76% das mortes foram por arma de fogo, temos quê esse valor se aproxima de 75% = Logo, a alternativa II é a quê melhor se adequa a um título para o texto.
d) Resposta pessoal. Conversar com os estudantes quê um caminho possível para a redução de mortes violentas a longo prazo é ampliar o acesso à educação, à cultura e ao esporte a toda a população.
e) Resposta pessoal.
10. a) Representa quê 44,3% dos estudantes de 13 a 15 anos quê participaram da pesquisa responderam ter consumido dois ou mais itens de biscoitos e sobremesas industrializadas no dia anterior à pesquisa.
b) Analisando a barra azul dos estudantes de 16 e 17 anos, temos quê 24% deles disseram ter consumido nenhuma bebida ultraprocessada.
Analisando a barra vêrde dos estudantes de 16 e 17 anos, temos quê 28,9% deles disseram ter consumido um item de AUP salgados.
Analisando a barra laranja dos estudantes de 16 e 17 anos, temos quê 39,4% deles disseram ter consumido dois ou mais itens de biscoitos e sobremesas industrializadas.
c) Resposta pessoal. Conversar com os estudantes para quê compreendam quê o consumo excessivo de alimentos ultraprocessados póde prejudicar a saúde.
11. a) Resposta esperada: Não, pois, em 2020 e em 2023, a quantidade de idosos inscritos no enêm aumentou em relação ao ano anterior.
b) 5.900: 11.768 ≃ 0,50 → aproximadamente 50%
50% de 9 cm → 0,50 ⋅ 9 = 4,5 → 4,5 cm
c) Respostas pessoais. Espera-se quê os estudantes pesquisem e identifiquem os serviços referentes ao atendimento especializado aos idosos no enêm, bem como os serviços e programas voltados para pessoas idosas no município em quê moram, e quê discutam a importânssia dêêsses programas quê buscam um processo de envelhecimento ativo e saudável.
12. a) 76,2 − 72,8 = 3,4. 3,4 anos. A redução ocorreu por causa da pandemia de covid-19.
b) Analisando o gráfico de linhas, 1991 e 2010, respectivamente.
c) Resposta esperada: Significa quê, de 1940 a 2022, as mulheres mantiveram o padrão de ter uma expectativa de vida maior quê a dos homens. Resposta pessoal. Espera-se quê os estudantes verifiquem em suas pesquisas quê há diversas razões para quê esse padrão se mantenha na expectativa de vida, como as diferenças genéticas, hormonais e comportamentais. Eles podem, por exemplo, citar algumas dessas diferenças e apresentar resultados de estudos quê as demonstrem.
13. a) O setor azul tem área maior quê o setor roxo, indicando quê, em 26/3/2024, estavam cadastrados no Ifan mais grupos e entidades de capoeira do Rio Grande do Sul quê de Santa Catarina.
b) Paraná: 38,75% de 80:
0,3875 ⋅ 80 = 31 → 31 grupos e entidades; Rio Grande do Sul: 33,75% de 80: 0,3375 ⋅ 80 = 27 → 27 grupos e entidades; Santa Catarina: 27,50% de 80: 0,2750 ⋅ 80 = 22 → 22 grupos e entidades
c) setor vêrde: 38,75% de 360°: 0,3875 ⋅ 360 = 139,5 → 139,5°;
setor azul: 33,75% de 360°: 0,3375 ⋅ 360 = 121,5 → 121,5°;
setor roxo: 27,50% de 360°: 0,2750 ⋅ 360 = 99 → 99°
d) Resposta pessoal. Espera-se quê os estudantes pesquisem e conheçam mais a capoeira, como sua origem, ainda no Brasil Colô-nia, com os africanos escravizados, em resposta à violência quê sofriam. Os estudantes podem pesquisar o Dia Mundial da Capoeira e grupos e entidades cadastrados no Ifan em outras regiões do Brasil.
14. a) De acôr-do com o título do gráfico, o título do eixo horizontal e a legenda, indica a quantidade de denúncias em 2018.
b) ≃ 7,8 → aproximadamente 7,8%
c)
Denúncias por tipo de violação sofridas por crianças e adolescentes no Brasil, 2018-2019
Tipos de violação |
Ano |
|
|---|---|---|
2018 |
2019 |
|
Negligência |
55.375 |
62.019 |
Violência psicológica |
37.160 |
36.304 |
Violência física |
30.962 |
33.374 |
Violência sexual |
17.073 |
17.029 |
Outras violações |
11.608 |
12.558 |
Fonte dos dados: BRASIL. Ministério da Mulher, da Família e dos Direitos Humanos. Disque direitos humanos: relatório 2019. Brasília, DF: MMFDH, 2019. p. 51. Disponível em: https://livro.pw/bkvhv. Acesso em: 23 jul. 2024.
Página trezentos e noventa e seis
Resposta pessoal. Espera-se quê os estudantes consigam utilizar argumentos para defender sua escolha. Por exemplo, eles podem argumentar quê ambos os recursos comunicam igualmente as informações, mas o gráfico tem apelo visual.
d) Resposta esperada: Gráfico de setores, pois esse tipo de gráfico tem como uma de suas características a possibilidade de destacar a relação entre as partes e o todo dos dados representados.
e) Resposta pessoal. A partir da pesquisa realizada, espera-se quê os estudantes consigam aplicar os conhecimentos estudados na Unidade na construção de gráficos e tabélas para comunicar os principais resultados obtidos. É importante verificar se o gráfico ou a tabéla escolhida foi construída compondo todos os elemêntos necessários.
15. a) Analisando o eixo horizontal, temos motocicleta e automóvel, respectivamente.
b) automóveis: velocidade mínima de 20 km/h e mássima de 70 km/h; motocicletas: velocidade mínima de 30 km/h e mássima entre 70 km/h e 80 km/h
c) Como cerca de mêtáde do box-plot correspondente a motocicleta está posicionado acima de 50 km/h, temos quê cerca de 50% das motocicletas pesquisadas trafegaram acima do limite de velocidade permitido.
d) Analisando o box-plot correspondente a automóvel, temos quê aproximadamente 25% dos automóveis pesquisados trafegou entre 40 km/h e 50 km/h.
e) 50 km/h ⋅ 1,2 = 60 km/h
25% de 340 = 0,25 ⋅ 340 = 85 → 85 motocicletas
f) Resposta esperada: A afirmativa é verdadeira, uma vez quê, em relação aos automóveis, o terceiro quartil é igual a 50 km/h, o quê indica quê cerca de 75% dos automóveis (maior parte) trafegaram em uma velocidade menor ou igual ao limite permitido.
16. Atividade de elaboração do estudante. Espera-se quê os estudantes analisem e interpretem as informações contidas no box-plot e, a partir delas, elaborar um texto sintetizando as conclusões a quê chegaram com base nessas informações. Eles podem, por exemplo, discorrer sobre os quartis e sobre o limite superior. É importante quê os estudantes, ao elaborarem o texto e avaliarem o texto elaborado pelo colega, possam expressar a compreensão a respeito da interpretação do recurso.
17. a) Resposta esperada: A estimativa das quantidades de novas vagas de emprego nas áreas de formação industrial com maior demanda por técnicos, em 2023.
b) Algumas respostas possíveis: Construção: carpinteiro, eletricista, encanador; Eletrônica: técnico eletrônico, técnico em eletrônica industrial; Telecomunicações: técnico de telecomunicações, instalador-reparador de rêdes telefônicas e de comunicação de dados, instaladores e reparadores de linhas e cabos elétricos, telefônicos e de comunicação de dados; Tecnologia da informação: programador de internet, técnico de apôio ao usuário de informática, programador de multimídia; Logística e transporte: técnico de planejamento de produção, controlador de entrada e saída, almoxarife; Metalmecânica: forneiro, tecnólogo em manutenção industrial, tecnólogo em mecânica de precisão.
c) Logística e transporte; 38.911 vagas.
d) Algumas respostas possíveis: Gráficos de colunas ou de barras, pois esses tipos de gráfico facilitam visualmente a comparação entre a quantidade de vagas de cada área.
e) Uma resposta possível:
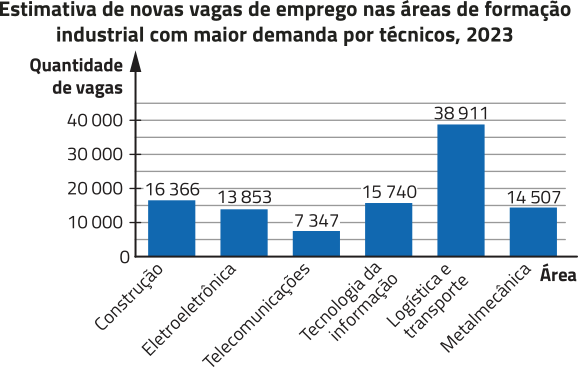
Fonte dos dados:CHMURZYNSKI, Giovanna. Brasil precisa formár mais de 77 mil técnicos industriais em 2023. Agência de Notícias da Indústria, Brasília, DF, 25 jan. 2023. Disponível em: https://livro.pw/hshej. Acesso em: 23 jul. 2024.
Atividade de elaboração do estudante. É importante verificar se a construção do gráfico tem as colunas com mesma largura e alturas proporcionais às quantidades representadas, bem como a inclusão de elemêntos como título, nome dos eixos e fonte dos dados. Espera-se quê os estudantes criem kestões quê envolvam a interpretação do gráfico quê construíram. Eles podem, por exemplo, elaborar kestões de comparação entre as quantidades de vagas de cada área e as alturas das colunas do gráfico.
18. a) Diretores e gerentes: 5.870 ∶ 7.948 ≃ 0,739
Profissionais das ciências e intelectuais: 4.600 ∶ 7.268 ≃ 0,633
Técnicos e profissionais de nível médio: 2.852 ∶ 3.837 ≃ 0,743
Trabalhadores de apôio administrativo: 1.956 ∶ 2.634 ≃ 0,827
Trabalhadores dos serviços, vendedores dos comércios e mercados: 1.552 ∶ 2.374 ≃ 0,654
Resposta esperada: Trabalhadores de apôio administrativo. Razão: aproximadamente 0,827. Essa razão indica quê, dentre os grupos operacionais mostrados no gráfico, o grupo “Trabalhadores de apôio administrativo” é o quê apresenta a menor disparidade entre os rendimentos médios de homens e mulheres; nesse grupo, o rendimento médio das mulheres corresponde a aproximadamente 82,7% (0,827) do rendimento médio dos homens.
b) Resposta esperada: Gráfico de colunas, sêndo cada pilha de dinheiro correspondente a uma coluna.
c) Resposta esperada: As figuras de pilhas de dinheiro utilizadas remetem a valores monetários, associados ao rendimento médio de trabalhos realizados por homens e mulheres, quê é o tema tratado no pictograma.
d) Resposta pessoal. Espera-se quê os estudantes consigam projetar um pictograma a partir de outro gráfico apresentado, utilizando figuras quê possam sêr associadas ao tema tratado nesse gráfico.
e) Resposta pessoal. Espera-se quê os estudantes reconheçam a discriminação de gênero histórica existente no mercado de trabalho e proponham ações como igualdade salarial entre homens e mulheres com mesmas funções e experiência e cotas para inserção das mulheres em cargos de liderança e na política.
f) Resposta pessoal.
19. a) primeiro diagrama: 6 ramos; segundo diagrama: 12 ramos
b) Analisando a quantidade de fô-lhas de cada ramo dos diagramas, temos ramo 3 e ramo 4’, respectivamente.
c) Contabilizando aqueles quê estão nos ramos 4’ acima de 70 e nos ramos 5* e 5’, temos 5 recém-nascidos.
d) 7 ∶ 32 ≃ 0,22 → aproximadamente 22%
• Resposta pessoal. Espera-se quê os estudantes realizem as pesquisas em sáites confiáveis, selecionem e organizem as informações quê julgarem pertinentes para elaborar o material de divulgação dos dados obtidos. Nesse material, espera-se quê os estudantes utilizem recursos estudados na Unidade, como a elaboração de gráficos e tabélas.
Página trezentos e noventa e sete
20. a) Contando as fô-lhas de cada ramo, temos quê 25 estudantes tiveram a freqüência cardíaca aferida.
b) Resposta esperada: Considerar como ramo o algarismo da dezena da freqüência cardíaca de cada estudante, em batimentos por minuto, e a fô-lha, o algarismo da unidade correspondente.
c) Analisando a quantidade de fô-lhas de valor 3 no ramo 8, temos 2 estudantes.
d) Resposta esperada: O ramo 7, indicando quê há mais estudantes com freqüência cardíaca aferida de 70 a 79 bpm do quê nos demais intervalos representados.
e) Analisando a fô-lha com maior freqüência em um mesmo ramo, temos 75 bpm.
f) Uma resposta possível: Dividir cada ramo em dois, compostos de fô-lhas de valores menóres quê 5 e fô-lhas de valores maiores ou iguais a 5.
21. a) Uma resposta possível: Cada ramo corresponde à parte inteira do índice, e as fô-lhas, à parte decimal.
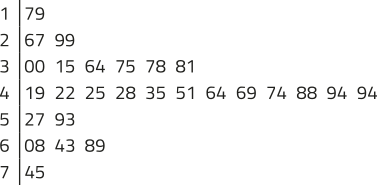
b) Respostas pessoais. Espera-se quê os estudantes incluam nos textos uma análise interpretativa e crítica a respeito do diagrama elaborado, indicando, por exemplo, quê a maior parte das unidades da Federação têm o indicador abaixo de 5, quê 4,94 foi o indicador mais freqüente no período de janeiro a dezembro de 2023.
c) Resposta pessoal. Espera-se quê os estudantes possam dialogar a respeito das análises realizadas e, se necessário, corrigir possíveis equívocos. Caso tênham sido produzidos diferentes diagramas, pedir quê os comparem a fim de opinarem, com base em argumentos, acerca das vantagens e desvantagem de cada diagrama em relação aos demais.
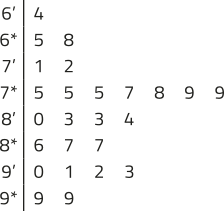
Integrando com...
1. Uma resposta possível: Não, pois póde ocorrer também no ônibus, entre outros locais, por meio da internet, por exemplo.
2. Algumas respostas possíveis: Verbal, física, por escrito, moral, social, virtual.
3. a) Respostas pessoais.
b) Uma resposta possível: O sáiber-búlin ou búlin virtual ocorre por meio das tecnologias da comunicação e informação, como na postagem ou envio de mensagens ofensivas ou difamatórias em rêdes sociais.
4. a) Analisando as informações das páginas 266 a 268, temos quê a resposta da pergunta é meninas.
b) A resposta depende da região do Brasil em quê o estudante mora.
c) Aparência do corpo. 16,5%.
d) Resposta esperada: Incentivar as pessoas a informar os casos; dialogar com os envolvidos; implantar regras contra o búlin.
e) Algumas respostas possíveis: Baixo rendimento escolar, transtôrnos alimentares, comportamentos antissociais, depressão.
5. Resposta pessoal. Espera-se quê os estudantes abordem, na peça publicitária, informações como as apresentadas anteriormente na seção, mas referentes à realidade local. Nessa produção, é importante observar a escolha pelo tipo de gráfico mais adequado para representar a situação, a construção do gráfico ou tabéla e as medidas antibullying propostas pela turma.
22. a) Analisando o gráfico de setores apresentado, temos quê as respostas às kestões são nível intermediário e nível avançado, respectivamente.
b) De acôr-do com o setor vêrde do gráfico, temos quê 16% dos estudantes têm nível de conhecimento avançado.
c) Resposta esperada: Sim, pois 52% dos estudantes estão nos níveis de conhecimento básico ou iniciante, ou seja, mais da mêtáde do total (50%).
d) 105 estudantes; 84%. Resposta esperada: A quantidade de estudantes está indicada na célula correspondente à fa do nível de conhecimento intermediário, e o porcentual, na célula correspondente à far dêêsse mesmo nível de conhecimento.
23. a) II
ME: 9; E: 18; M: 7; B: 1
ME:
b)
Classificação do IDH dos países da América, 2021
Classificação do IDH |
freqüência absoluta (f) |
freqüência acumulada absoluta (fa) |
freqüência relativa (fr) |
freqüência acumulada relativa (far) |
|---|---|---|---|---|
Baixo |
1 |
1 |
2,86% |
2,86% |
Médio |
7 |
8 |
20% |
22,86% |
Elevado |
18 |
26 |
51,43% |
74,29% |
Muito elevado |
9 |
35 |
25,71% |
100% |
Total |
35 |
100% |
Fonte dos dados: PROGRAMA DAS NAÇÕES UNIDAS PARA O DESENVOLVIMENTO. Relatório do desenvolvimento humano 2021/2022: tempos incertos, vidas instáveis: a construir o nosso futuro num mundo em transformação. Nova iórk: pí-núdi, c2022. p. 272-276. Localizável em: Download. Disponível em: https://livro.pw/hsxqp. Acesso em: 23 jul. 2024.
c) 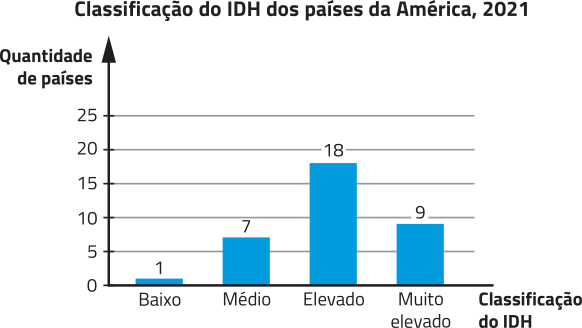
Fonte dos dados: PROGRAMA DAS NAÇÕES UNIDAS PARA O DESENVOLVIMENTO. Relatório do desenvolvimento humano 2021/2022: tempos incertos, vidas instáveis: a construir o nosso futuro num mundo em transformação. Nova iórk: pí-núdi, c2022. p. 272-276. Localizável em: Download. Disponível em: https://livro.pw/hsxqp. Acesso em: 23 jul. 2024.
Página trezentos e noventa e oito
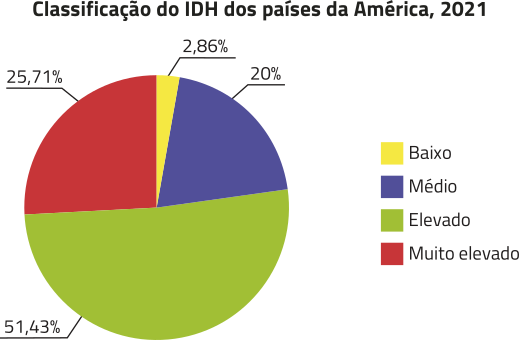
Fonte dos dados: PROGRAMA DAS NAÇÕES UNIDAS PARA O DESENVOLVIMENTO. Relatório do desenvolvimento humano 2021/2022: tempos incertos, vidas instáveis: a construir o nosso futuro num mundo em transformação. Nova iórk: pí-núdi, c2022. p. 272-276. Localizável em: Download. Disponível em: https://livro.pw/hsxqp. Acesso em: 23 jul. 2024.
• Resposta pessoal. Os estudantes podem responder, por exemplo, quê escolheram o gráfico de colunas para facilitar a comparação entre as freqüências absolutas e o gráfico de setores para facilitar a comparação entre o porcentual das partes com o todo.
• Resposta esperada: Gráfico de colunas: freqüência absoluta; gráfico de setores: freqüência relativa.
24. Atividade de elaboração do estudante. Os estudantes podem elaborar quêstionamentos a respeito do IDH da unidade de Federação em que moram e compará-lo com os de outras. É importante quê, ao realizarem comparações, os estudantes ponderem os fatores quê levam àquele IDH, como acesso a educação e saúde pública, e as principais fontes de renda da população.
25. a) Analisando as duas primeiras barras do primeiro histograma, temos quê 14 municípios apresentaram taxa de aprovação escolar menor quê 82 (10 + 4 = 14). De acôr-do com o segundo histograma, quê representa a freqüência relativa, temos 22,6% correspondentes a essa quantidade de municípios amazonenses.
b) Analisando o segundo histograma, de freqüência relativa, temos quê 4,8% de municípios amazonenses apresentaram taxa de aprovação escolar maior ou igual a 94.
c) 82 ⊢ 88
d) Resposta esperada: Não, pois, nessa tabéla de distribuição de freqüências, os dados estão agrupados em intervalos de classe, não apresentando a taxa de aprovação escolar de cada município.
26. a) Igual ou maior quê 20 anos e menor quê 40 anos; 60 anos ou mais.
b) Analisando a terceira linha da coluna freqüência relativa, temos quê 28% dos acidentes notificados foram com pessoas de idade igual ou superior a 40 anos e inferior a 60 anos.
c) De acôr-do com o total apresentado na tabéla, temos quê foram notificados ao todo 196.884 acidentes.
d) De acôr-do com a segunda linha da coluna freqüência relativa acumulada, temos quê 53% dos acidentes foram notificados com pessoas de idade inferior a 40 anos.
e) Resposta pessoal. Espera-se quê os estudantes elaborem kestões quê considerem a interpretação da tabéla com dados agrupados em intervalos de classe. Por exemplo: Qual é o porcentual de acidentes de pessoas com idade superior a 60 anos? E inferior a 20 anos? Os estudantes podem ainda propor quê se compare a faixa etária com mais acidentes notificados e com menos acidentes notificados.
f) Atividade de elaboração do estudante. Os textos devem abordar medidas de prevenção contra esse tipo de acidente. Alguns exemplos são: usar calçados e luvas nas atividades rurais e de jardinagem; examinar calçados, roupas pessoais, de cama e banho antes de usá-las; afastar camas das paredes e evitar pendurar roupas fora de armários; não acumular entulhos e materiais de construção; limpar regularmente móveis, cortinas, quadros, cantos de parede; vedar frestas e buracos em paredes, assoalhos, forros e rodapés; utilizar telas, vedantes ou sacos de areia em portas, janelas e ralos; manter limpos os locais próximos das casas, jardins, quintais, paióis e celeiros; evitar plantas tipo trepadeiras e bananeiras junto às casas e manter a grama sempre cortada; limpar terrenos bâldíos, pelo menos na faixa de um a dois metros junto ao muro ou cercas.
27. a) 35% de 60 → 0,35 ⋅ 60 = 21
20% de 60 → 0,20 ⋅ 60 = 12
15% de 60 → 0,15 ⋅ 60 = 9
30% de 60 → 0,30 ⋅ 60 = 18
Salário mensal, em reais, dos funcionários da empresa, janeiro de 2025
Faixa salarial |
freqüência absoluta (f) |
freqüência acumulada absoluta (fa) |
freqüência relativa (fr) |
freqüência acumulada relativa (far) |
|---|---|---|---|---|
1.500,00 ⊢ 2.000,00 |
21 |
21 |
35% |
35% |
2.000,00 ⊢ 2.500,00 |
12 |
33 |
20% |
55% |
2.500,00 ⊢ .000,00 |
9 |
42 |
15% |
70% |
3.000,00 ⊢ 3.500,00 |
18 |
60 |
30% |
100% |
Total |
60 |
100% |
Fonte: Dados fictícios.
b) Analisando a terceira linha da freqüência absoluta acumulada, 42 funcionários têm salário mensal menor quê R$ 3.000,00.
c) A faixa salarial quê contém a maior freqüência absoluta é 1.500,00 ⊢ 2.000,00.
d) Analisando a freqüência relativa da classe correspondente à faixa salarial 2.000,00 a 2.500,00, temos quê 20% dos funcionários têm salário mensal maior ou igual a R$ 2.000,00 e menor quê R$ 2.500,00.
e) Resposta esperada: Não, pois os salários dos funcionários não foram listados. No entanto, existe a possibilidade de isso ocorrer, pois 21 funcionários têm salário mensal maior ou igual a R$ 1.500,00 e menor quê R$ 2.000,00.
28. a)
IDGM de saneamento e sustentabilidade dos 100 maiores municípios brasileiros, 2021
Resultados dos índices |
freqüência absoluta (f) |
freqüência acumulada absoluta (fa) |
freqüência relativa (fr) |
freqüência acumulada relativa (far) |
|---|---|---|---|---|
0,200 ⊢ 0,400 |
4 |
4 |
4% |
4% |
0,400 ⊢ 0,600 |
12 |
16 |
12% |
16% |
0,600 ⊢ 0,800 |
33 |
49 |
33% |
49% |
0,800 ⊢ 1 |
51 |
100 |
51% |
100% |
Total |
100 |
100% |
Fonte dos dados: DESAFIOS DA GESTÃO MUNICIPAL. IDGM 2021: rã-kin por área: 100+: saneamento e sustentabilidade. [S. l.]: DGM: Macroplan, 2021. Disponível em: https://livro.pw/rxmlq. Acesso em: 23 jul. 2024.
Página trezentos e noventa e nove
b) Respostas possíveis:
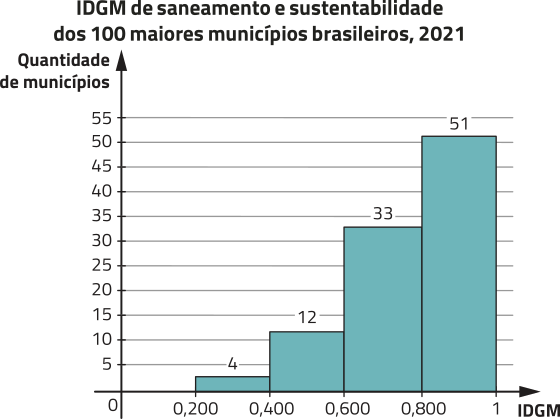
Fonte dos dados: DESAFIOS DA GESTÃO MUNICIPAL. IDGM 2021: rã-kin por área: 100+: saneamento e sustentabilidade. [S. l.]: DGM: Macroplan, 2021. Disponível em: https://livro.pw/rxmlq. Acesso em: 23 jul. 2024.
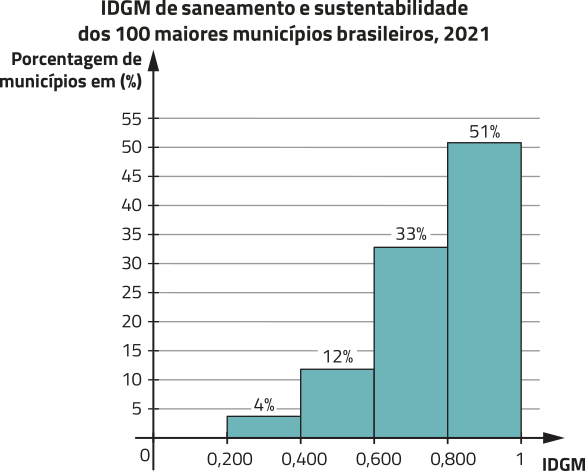
Fonte dos dados: DESAFIOS DA GESTÃO MUNICIPAL. IDGM 2021: rã-kin por área: 100+: saneamento e sustentabilidade. [S. l.]: DGM: Macroplan, 2021. Disponível em: https://livro.pw/rxmlq. Acesso em: 23 jul. 2024.
c) Atividade de elaboração do estudante. Espera-se quê os estudantes interpretem o histograma construído e realizem questionamentos a partir díssu. É importante quê os questionamentos sêjam referentes à temática e quê envolvam a necessidade de interpretar informações a partir do histograma, de modo quê a atividade se torne um instrumento para quê o professor avalie a aprendizagem dos estudantes a respeito dos conceitos estudados.
29. a) Respostas esperadas: Os anos correspondentes aos dados da pesquisa. Crianças e adolescentes, por atividades realizadas na internet e faixa etária (2022).
b) Pesquisou na internet para fazer trabalhos escolares. Resposta esperada: Comparar os comprimentos das barras de cada atividade e identificar a atividade em quê a barra correspondente à faixa etária de 13 a 14 anos é mais comprida quê a de 15 a 17 anos.
c) Resposta esperada: Não, pois as barras correspondentes à atividade “Usou rêdes sociais” não estão com os comprimentos proporcionais aos valores representados por elas.
d) Resposta esperada: O leitor póde acreditar, de maneira incorréta, quê um porcentual menor de crianças e adolescentes usou rêdes sociais do quê realmente foi identificado na pesquisa. Isso, de alguma maneira, póde interferir em tomada de decisões ou ajudar a propagar notícias falsas.
30. Resposta esperada: Na tabéla, não há indicação da fonte, e os dados referentes às regiões Norte e Nordeste estão invertidos entre si; no gráfico de colunas, no título, o ano correspondente aos dados pesquisados está incorréto, os valores da escala do eixo horizontal estão desalinhados com as linhas horizontais correspondentes, de maneira quê as linhas não correspondem aos valores representados no eixo, e os títulos dos eixos estão invertidos entre si.
População quilombola no Brasil, por região, 2022
Região |
População |
|---|---|
Norte |
166 069 |
Nordeste |
905 415 |
sudéste |
182 305 |
Sul |
29 056 |
Centro-Oeste |
44 957 |
Fonte dos dados: BRASIL. Serviços e Informações do Brasil. População quilombola é de 1,3 milhão, indica recorte inédito do censo. Brasília, DF: SIB, 27 jul. 2023. Disponível em: https://livro.pw/uywmm. Acesso em: 23 jul. 2024.
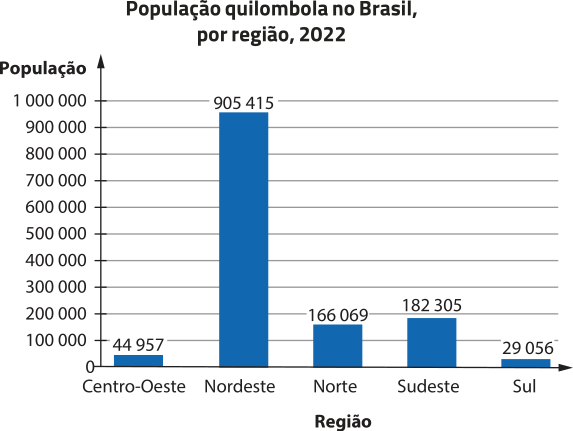
Fonte dos dados: BRASIL. Serviços e Informações do Brasil. População quilombola é de 1,3 milhão, indica recorte inédito do censo. Brasília, DF: SIB, 27 jul. 2023. Disponível em: https://livro.pw/uywmm. Acesso em: 23 jul. 2024.
31. A: 6.500 ∶ 500 = 13. B: 8.000 ∶ 500 = 16. C: 4.500 ∶ 500 = 9
Resposta esperada: Não, pois não está indicado o título do pictograma e, como cada figura de garrafa péti representa 500 garrafas péti, as quantidades arrecadadas correspondentes às escolas B e C foram indicadas incorretamente: a escola B deveria ter 16 figuras de garrafas péti (e está com 15) e a escola C, 9 garrafas (e está com 10).
32. alternativa c
146 + 60 + 40 + 21 + x = 276 ⇒ x = 276 − 267 ⇒ x = 9
33. Resposta pessoal. Espera-se quê os estudantes consigam identificar inadequações em gráficos e tabélas divulgados na mídia, sêjam na estrutura, sêjam na fonte dos dados indicados. É importante quê os estudantes debatam e compreendam as consequências dêêsse tipo de êrro e a importânssia de uma construção fidedigna, de modo a não influenciar em possíveis divulgações de notícias falsas e interpretações equivocadas.
34. a) Resposta esperada: Para construir o gráfico de segmentos, foram utilizadas as freqüências absolutas e, para construir o gráfico de setores, as freqüências relativas.
Página quatrocentos
b) Resposta esperada: Não, pois esse tipo de gráfico costuma sêr utilizado para representar o comportamento de certa variável no decorrer de determinado intervalo de tempo, o quê não é o caso.
• Resposta esperada: Histograma, pois esse tipo de gráfico permite representar dados agrupados em intervalos de classe e comparar visualmente esses dados.
c) Resposta esperada: No gráfico de segmentos, alterar o tipo de gráfico para histograma, pois esse tipo de gráfico permite representar dados agrupados em intervalos de classe, comparar visualmente esses dados; e incluir a fonte dos dados. No gráfico de setores, é necessário indicar no título o ano correspondente aos dados pesquisados e ajustar os elemêntos apresentados na legenda de maneira quê correspondam adequadamente aos respectivos setores.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) 5.840.919 + 19.812.217 + 34.524.858 + 12.050.812 + 5.711.522 = 77.940.328 → 78 milhões de pessoas
b) Mato Grosso do Sul: 18% de 5.711.522 → 0,18 ⋅ 5.711.522 ≃ 1.028.074 → 1.028.074 pessoas
Mato Grosso: 21% de 5.711.522 → 0,21 ⋅ 5.711.522 ≃ 1.199.420 → 1.199.420 pessoas
Goiás: 42% de 5.711.522 → 0,42 ⋅ 5.711.522 ≃ 2.398.839 → 2.398.839 pessoas
Distrito Federal: 19% de 5.711.522 → 0,19 ⋅ 5.711.522 ≃ 1.085.189 → 1.085.189 pessoas
c)
Distribuição da estimativa de pessoas a sêr vacinadas contra a influenza na Região Centro-Oeste, por Unidade da Federação, 2022
Unidade da Federação |
Quantidade de pessoas |
|---|---|
Mato Grosso do Sul |
1 028 074 |
Mato Grosso |
1 199 420 |
Goiás |
2 398 839 |
Distrito Federal |
1 085 189 |
Fonte dos dados: BRASIL. Ministério da Saúde. Informe técnico: 24ª campanha nacional de vacinação contra a influenza. Brasília, DF: MS, mar. 2022. p. 18. Disponível em: https://livro.pw/bopyr. Acesso em: 23 jul. 2024.
d) Resposta esperada: Pode-se, inicialmente, calcular o porcentual da estimativa de pessoas a sêr vacinadas contra influenza correspondente a cada região em relação ao total do país. Em seguida, determinar, de maneira proporcional, a medida do ângulo central de cada setor do gráfico correspondente às regiões. Por fim, colorir os setores do gráfico, elaborar a legenda e indicar o título e a fonte dêêsse gráfico.
e) • Resposta esperada: Quantidade de pessoas quê receberam uma dose da vacína contra influenza em uma unidade básica de saúde, em determinada semana de 2022.
• Uma resposta possível: Gráfico de barras ou de colunas, pois esses tipos de gráfico permitem comparar visualmente a quantidade de pessoas quê receberam a vacína em cada dia dessa semana; ou gráfico de segmentos, pois esse tipo de gráfico permite avaliar a variação da quantidade diária de pessoas quê receberam a vacína nessa semana.
Praticando: enêm e vestibulares
1. alternativa c
7,9% de 240.851.510 = 0,079 ⋅ 240.851.510 ≃ 19.027.269
19.027.269 ∶ 105.051.936 ≃ 0,18 ≃ 18%
2. alternativa c
Considerando a variação entre o 10º e o 20º dia, temos quê, no setor adulto, o volume de vendas diminui em R$ 3.000,00 (18.000 − 15.000 = 3.000). Assim, mantendo essa variação para o período entre o 20º e o 30º dia, temos quê o volume de vendas no 30º dia será dado por: 15.000,00 − 3.000,00 = 12.000 → R$ 12.000,00
Considerando a variação entre o 10º e o 20º dia, temos quê, no setor infantil, o volume de vendas diminui em R$ 1.000,00 (8.000 − 7.000 = 1.000). Assim, mantendo essa variação para o período entre o 20º e o 30º dia, temos quê o volume de vendas no 30º dia será dado por:
7.000,00 − 1.000,00 = 6.000 → R$ 6.000,00
Então, o total de vendas é dado por: 18.000 + 15.000 + 12.000 + 8.000 + 7.000 + 6.000 = 66.000 → R$ 66.000,00
Assim, segue quê: 77.000 − 66.000 = 11.000 → R$ 11.000,00
3. alternativa c
≃ 26,17
Como 25 < 26,17 < 29,9, a pessoa apresenta sobrepeso.
4. alternativa d
30 ⋅ 6 + 40 ⋅ 6 + 50 ⋅ 7 + 30 ⋅ 8 + 25 ⋅ 4 + 25 ⋅ 5 = 180 + 240 + 350 + 240 + 100 + 125 = 1.235
5. alternativa c
13,6% + 45,2% = 58,8%
58,8% de 363.000 → 0,588 ⋅ 363.000 = 213.444
6. alternativa a
a) Correta, pois, analisando o gráfico, temos quê as internações no SUS de todas as regiões foram superiores a 50%.
b) Incorreta, pois a maior parte das internações na Região sudéste foi no SUS (56,40%).
c) Incorreta, pois o porcentual de internações foi 23,80% na Região Norte e 22,20% na Região Nordeste.
d) Incorreta, pois o número de internações pelo SUS nessas regiões foi inferior a 70%.
7. alternativa d
20% de 105 → 0,20 ⋅ 105 = 21
30% de 100 → 0,30 ⋅ 100 = 30
50% de 20 → 0,50 ⋅ 20 = 10
40% de 80 → 0,40 ⋅ 80 = 32
60% de 40 → 0,60 ⋅ 40 = 24
Portanto, o reservatório com maior volume de á gua era o IV.