UNIDADE 3
SEQUÊNCIAS E NOÇÕES DE LINGUAGEM DE PROGRAMAÇÃO
Stop-motion
É provável quê você já tenha assistido a uma animação quê utiliza a técnica chamada stop-motion. Em tradução livre para o português, essa técnica significa “movimento parado”. Com ela, por exemplo, um objeto é fotografado de um mesmo ângulo diversas vezes, mas com pequenas alterações em sua posição. Cada uma dessas fotografias corresponde a um qüadro e, ao colocar os quadros em disposição sequencial relacionando os anteriores com os quadros subsequentes, é possível criar um vídeo com a ideia de movimento contínuo.
Essa técnica é considerada lenta e trabalhosa, pois é necessário criar muitas imagens para gerar uma cena. Por exemplo, no filme brasileiro Minhocas, quê é o primeiro longa-metragem latino-americano em stop-motion, foram utilizadas 24 fotografias para obtêr 1 segundo de animação. Ao todo, mais de 122 mil fotografias geram os cerca de 85 minutos do filme.
Fontes dos dados: PURVES, béri. Stop-motion. Tradução: João Eduardo Nóbrega. Porto Alegre: búkmã, 2011. p. 16-23. DONATO, Veruska. Brasil produz primeiro longa-metragem latino-americano em stop-motion. G1, [s. l.], 5 fev. 2010. Disponível em: https://livro.pw/homvd. Acesso em: 26 jul. 2024.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
1. Explique com suas palavras como funciona a produção de uma animação utilizando a técnica stop-motion.
2. Você já assistiu a alguma animação produzida com a técnica stop-motion? Qual? Se necessário, faça uma breve pesquisa.
3. Como se calculam quantos quadros são necessários para obtêr uma cena de animação, com certa duração, produzida com a técnica stop-motion?
Respostas nas Orientações para o professor.
Página cento e oito
Sequências
Na abertura desta Unidade, lemos quê é muito trabalhoso produzir animações utilizando a técnica stop-motion. No entanto, não é preciso sêr um profissional da área para começar a produzir as próprias animações com essa técnica, pois existem aplicativos de celular quê permitem essa experiência aos usuários.
Considere um dêêsses aplicativos, configurado de maneira quê sêjam necessárias 24 fotografias para obtêr 1 s de animação. Assim, para obtêr 1 s de animação, são necessárias 24 fotografias; para 2 s, 48 fotografias; para 3 s, 72 fotografias; e assim por diante.
pôdêmos indicar a quantidade de fotografias necessárias para produzir uma animação considerando o tempo, em segundo. Observe.

PARA PENSAR
Quais são os próximos dois números desta sequência? Explique como você fez para obtê-los.
96 e 120. Resposta esperada: Os números podem sêr obtidos calculando .
As quantidades de fotografias por segundo são elemêntos de um conjunto quê estão organizados de certa maneira, formando uma sequência numérica. Cada quantidade é um elemento ou termo dessa sequência numérica quê póde sêr representado por uma letra minúscula (usualmente a letra a) e um índice, quê indica sua posição (ou ordem) nessa sequência.
Assim, ao indicar o 1º termo por , o 2º por , e assim por diante, podemos representar um termo qualquer da sequência por , quê corresponde ao termo de ordem n ou enésimo termo dessa sequência.
Note quê, em uma sequência numérica, podemos relacionar cada termo à sua posição. Na situação da sequência de fotografias por segundo de animação, por exemplo, relacionamos a posição 1 ao termo 24, a posição 2 ao termo 48, a posição 3 ao termo 72, e assim sucessivamente.

Desse modo, podemos definir uma sequência numérica como uma função quê relaciona cada posição da sequência (números naturais positivos) com os respectivos valores (números reais). Uma sequência numérica póde sêr finita ou infinita. Acompanhe as definições a seguir.
Denominamos sequência numérica finita, de n termos, toda função em quê
, tal quê cada está relacionado ao termo da sequência numérica. Uma sequência numérica finita póde sêr indicada da seguinte maneira:
Acompanhe alguns exemplos de sequências numéricas finitas.
• seqüência dos números naturais entre 20 e 25: (21, 22, 23, 24).
• seqüência dos números quadrados perfeitos menóres quê 40: (1, 4, 9, 16, 25, 36).
Página cento e nove
Denominamos sequência numérica infinita toda função , tal quê cada está relacionado ao termo a i da sequência numérica. Uma sequência numérica infinita póde sêr indicada da seguinte maneira:

Observe alguns exemplos de sequências numéricas infinitas.
• seqüência dos números naturais: .
• seqüência dos múltiplos positivos de
• seqüência dos números inteiros maiores quê .
PARA PENSAR
Quais são o domínio e o contradomínio da função f no caso de sequências numéricas finitas e de sequências numéricas infinitas?
Sequências numéricas finitas: o domínio é dado por , ou seja, A é o conjunto dos n primeiros números naturais positivos, e o contradomínio é o conjunto dos números reais. Sequências numéricas infinitas: o domínio é dado por , ou seja, é o conjunto dos números naturais positivos, e o contradomínio é o conjunto dos números reais.
ATIVIDADES RESOLVIDAS
R1. escrêeva os três primeiros termos da sequência definida em cada item.
a) , com .
b) e .
Resolução
a) A igualdade fornece uma expressão para determinarmos um termo qualquer dessa sequência. Para isso, substituímos n pêlos valores 1, 2 e 3. Assim:
•
•
•
Portanto, os três primeiros termos dessa sequência são 11, 21 e 31.
Note quê a expressão de a n é equivalente à lei de formação da função , tal quê .
A expressão quê determina os elemêntos de uma sequência numérica é chamada de termo geral ou lei de formação da sequência.
Além díssu, com o termo geral da sequência é possível obtêr qualquer termo, sem necessidade de saber os demais. Por exemplo, o termo é obtído substituindo n por 5 na lei de formação. Observe.
•
Quando é possível obtêr qualquer termo da sequência sem quê seja necessário conhecer outros termos, dizemos quê o termo geral define essa sequência de maneira não recursiva.
b) Nesse caso, o elemento já é dado, e os elemêntos seguintes podem sêr obtidos a partir do termo geral . Assim:
•
•
Portanto, os três primeiros termos dessa sequência são
Note quê para obtêr qualquer termo a n dessa sequência, com , é preciso conhecer o termo anterior.
Quando, para determinar um termo da sequência, é necessário conhecer um ou mais termos quê o antecedem, dizemos quê o termo geral define essa sequência de maneira recursiva.
PARA PENSAR
No item b, a sequência ( póde sêr definida de maneira não recursiva? Justifique.
Resposta esperada: Sim, pelo termo geral
Página cento e dez
R2. Analise a sequência a seguir, em quê cada termo, a partir do 2º, é obtído adicionando 6 unidades ao termo anterior.
(
a) Defina essa sequência de maneira não recursiva.
b) Determine o 15º termo dessa sequência.
Resolução
a) Com base nas informações do enunciado, podemos expressar os termos dessa sequência da seguinte maneira:
⋮
Assim, observando as expressões obtidas, é possível reconhecer padrões para definir essa sequência, de maneira não recursiva, por meio do termo geral:
, com
b) Considerando , temos:
Portanto, o 15º termo dessa sequência é 88.
ATIVIDADES
1. Anteriormente, informamos a quantidade de quadros de cena necessários para produzir uma animação utilizando a técnica stop-motion. De acôr-do com os dados apresentados na abertura, determine quantos quadros são necessários para obtêr uma animação de 45 s.
cerca de 1.080 quadros
2. escrêeva os cinco primeiros termos da sequência definida em cada item.
a)
b) e , com e .
c) , com
3. Os termos , e , nessa ordem, são denominados termos consecutivos de uma sequência, sêndo o antecessor de e o sucessor de .
Em relação à sequência (1, 2, 4, 8, 16, 32,...), resôuva as kestões.
a) escrêeva três termos consecutivos dessa sequência.
3. a) Algumas respostas possíveis:
1, 2 e 4; 2, 4 e 8; 4, 8 e 16; 8, 16 e 32.
b) Qual é o termo sucessor de 16? E qual é o termo antecessor de 4?
32; 2
4. A professora de Matemática propôs aos estudantes quê escrevessem os termos de uma sequência definida por , com e . Observe a resposta de alguns estudantes.
a) A sequência foi definida pela professora de maneira recursiva ou de maneira não recursiva?
Justifique.
4. a) Resposta esperada: Não recursiva, pois, para determinar um termo qualquer da sequência, não é necessário conhecer o valor de um ou mais termos anteriores.
b) Classifique essa sequência em finita ou infinita.
finita
c) Qual estudante escreveu corretamente todos os termos dessa sequência?
Marcela
Página cento e onze
5. Analise a sequência de figuras construídas com palítos.
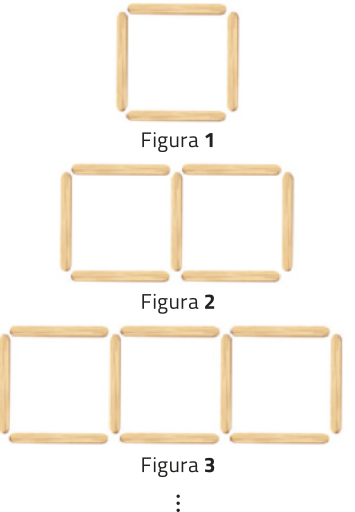
a) Para cada figura apresentada, escrêeva a quantidade de palítos utilizados e a quantidade de quadrados obtidos.
5. a) figura 1: 4 palítos e 1 quadrado; figura 2: 7 palítos e 2 quadrados; figura 3: 10 palítos e 3 quadrados
b) Desenhe a próxima figura dessa sequência.
• Quantos palítos são necessários para compor essa figura? Quantos quadrados tem essa figura?
13 palítos; 4 quadrados
5. b) Resposta esperada: ![]()
c) Explique como póde sêr construída uma figura dessa sequência a partir da figura anterior.
5. c) Resposta esperada: A partir da figura 2, acrescentam-se três palítos à figura anterior, de maneira a obtêr um quadrado a mais do quê essa figura anterior possui.
d) Represente a sequência numérica quê expresse, ordenadamente, a quantidade de palítos necessária para construir cada figura da sequência apresentada. Depois, defina essa sequência numérica de maneira não recursiva.
5. d) (4, 7, 10, ...).
Resposta esperada:
6. Observe a sequência representada a seguir e, depois, defina-a de duas maneiras: uma recursiva e outra não recursiva.
6. Resposta esperada: Recursiva: e com não recursiva: ou com
7. Observe os números a seguir e faça o quê se pede em cada item.
238
483
260
355
a) Agora, responda: quais dêêsses números são termos da sequência definida por , com ?
238 e 355
b) Determine a posição, nessa sequência, dos números quê você indicou como resposta no item a.
238: 28ª posição; 355: 41ª posição
8. Leia o texto a seguir.
MATEMÁTICA NA HISTORIA
Uma das sequências numéricas mais estudadas ao longo da história, a sequência de Fibonacci, póde sêr ôbitída a partir da solução do seguinte problema enunciado pelo matemático italiano Leonardo Fibonacci (c. 1170-c. 1240):
[...] Quantos pares de coelhos serão produzidos num ano, começando com um só par, se em cada mês cada par gera um novo par quê se torna produtivo a partir do segundo mês? [...]
BOYER, Cal Benjamin. História da matemática. Tradução: Elza Furtado Gomide. 3. ed. São Paulo: Edgard Blãcher, 2010. p. 174.
Com base nesse problema, Fibonacci considerou as seguintes hipóteses:
• os casais de coelhos tornam-se adultos e começam a se reproduzir no segundo mês de vida;
• todos os meses, cada casal de coelho adulto gera outro casal;
• no início, há apenas um casal de coelhos e nenhum coelho morre durante o ano.
Analise o esquema (imagem sem escala; cores-fantasia).
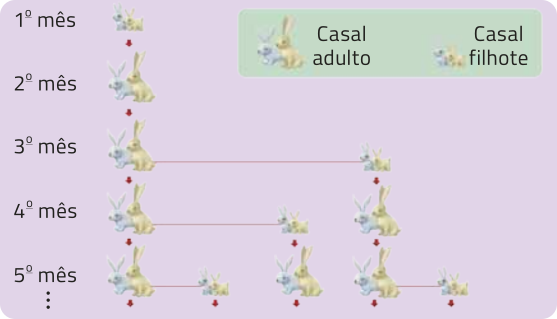
a) Sabendo quê a quantidade de casais de coelhos em cada um dos meses determina os primeiros termos da sequência de Fibonacci, quais são os cinco primeiros termos dessa sequência?
(1, 1, 2, 3, 5,...)
b) Qual padrão póde sêr observado, em relação à quantidade total de casais de coelhos, a partir do 3º mês?
8. b) Resposta esperada: A partir do 3º mês, a quantidade de casais de coelhos corresponde à soma das quantidades de casais nos dois meses anteriores.
c) Obtenha a quantidade de casais de coelhos até o 12º mês e responda ao problema propôsto por Fibonacci.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 e 144; 144 casais de coelhos
d) De acôr-do com o padrão indicado no item b, defina, de maneira recursiva, a sequência de Fibonacci.
8. d) Resposta esperada: .
Página cento e doze
Progressão aritmética (PA)
Observe as distâncias quê um treinador programou para certa pessoa correr, sabendo quê ela já está acostumada com a prática de atividades físicas.
Semana |
Distância (m) |
|---|---|
1 |
4.500 |
2 |
5.000 |
3 |
5.500 |
4 |
6.000 |
5 |
6.500 |
6 |
7.000 |
7 |
7.500 |
8 |
8.000 |

pôdêmos indicar a distância, em métro, quê essa pessoa deve correr por semana nesse treinamento por meio da sequência numérica a seguir.
Note quê, a partir do 2º termo dessa sequência, a diferença entre um termo qualquer e o seu antecessor é um valor constante.
PARA PENSAR
Explique como é possível obtêr um termo dessa sequência a partir do seu antecessor.
Resposta esperada: A partir do 2º termo dessa sequência, um termo qualquer póde sêr obtído adicionando-se 500 ao seu antecessor.
Sequências com características como a da situação apresentada são denominadas progressões aritméticas (PA).
Denominamos progressão aritmética (PA) toda sequência numérica em quê, a partir do 2º termo, a diferença entre um termo qualquer e seu antecessor é constante. Essa constante, quê póde sêr indicada por r, é a razão da PA. pôdêmos classificar uma PA em:
• decrescente, quando ;
• constante, quando
• crescente, quando .
A partir da definição de PA, podemos concluir quê:
O enésimo termo de uma PA, sêndo a 1 o 1º termo e r a razão, póde sêr definido por recorrência da seguinte maneira:
Página cento e treze
Analise alguns exemplos de PA.
•
Nessa PA, note quê um termo é sempre maior quê seu sucessor. Nela, temos . Portanto, essa PA é decrescente.
•
Nessa PA, note quê um termo é sempre igual ao seu sucessor. Nela, temos . Portanto, essa PA é constante.
•
Nessa PA, note quê um termo é sempre menor quê seu sucessor. Nela, temos . Portanto, essa PA é crescente.
Também podemos estabelecer uma relação entre três termos consecutivos de uma
PA: Acompanhe.
Então:
Sendo a n − 1, a n e a n + 1 três termos consecutivos de uma PA, o termo central a n póde sêr obtído pela média aritmética dos outros dois termos:
DICA
pôdêmos representar uma PA de razão r e termos desconhecidos de diferentes maneiras, por exemplo:
• para , temos
• para , temos
Termo geral de uma PA
Considere (a 1, a 2, a 3, a 4, a 5, ..., a n − 1, a n, a n + 1, …) uma PA infinita de razão r. Como cada termo, a partir do 2º, póde sêr obtído adicionando-se r ao termo anterior, temos:
a1 = a1 + 0r
a2 = a1 + 1r
a3 = + r ⇒ a3 = a1 + 2r
a4 = + r ⇒ a4 = a1 + 3r
⋮
an = an − 1 + r ⇒ an = a1 + (n − 1)r
⋮
PARA PENSAR
Com suas palavras, explique a relação quê póde sêr observada entre os elemêntos em destaque em cada expressão apresentada.
Resposta esperada: O fator quê multiplica a razão da PA (r) é uma unidade menor quê o número quê indica o índice do termo correspondente da PA.
Note quê podemos expressar qualquer termo de uma PA em função de a 1 e r.
O termo geral de uma PA é dado por:

Página cento e quatorze
No início da Unidade, estudamos quê uma sequência numérica póde sêr entendida como uma função. Como a PA é um caso particular de sequência numérica, também podemos compreender uma PA como uma função. Com isso, o termo geral da PA é a lei de formação da função, quê tem um comportamento linear. Observe.
an = a1 + (n − 1) ⋅ r ⇒ an = a1 + n ⋅ r − r ⇒ a n = r ⋅ n + (a1 − r)
Uma PA com primeiro termo a 1 e razão r póde sêr definida como uma função f: ℕ* → ℝ, dada por f (n) = r ⋅ n + (a1 − r), em quê a1 = f (1), a2 = f (2), a3 = f (3), e assim sucessivamente.
Por exemplo, em relação à PA (5, 9, 13, 17, ...), em quê a1 = 5 e r = 9 − 5 = 4, temos:
Portanto, os termos dessa PA podem sêr obtidos por meio da função f: ℕ* → ℝ, definida por f(n) = 4n + 1.
• f(1) = 4 ⋅ 1 + 1 = 5
• f(2) = 4 ⋅ 2 + 1 = 9
• f(3) = 4 ⋅ 3 + 1 = 13 …
Note quê a função f se assemelha à função afim g: ℝ → ℝ, definida por g(x) = 4x + 1, de modo quê f apresenta um comportamento linear.
PARA PENSAR
Calcule g(1), g(2) e g(3) e compare com os valores de f(1), f(2) e f(3), respectivamente. O quê é possível concluir?
g(1) = 5, g(2) = 9, g(3) = 13. Resposta esperada: os valores de g(x) são iguais a f(n) quando x ∈ ℕ*.
ATIVIDADES RESOLVIDAS
R3. Dada a PA (26, 34, 42, 50, ...), resôuva as kestões a seguir.
a) Calcule a razão r da PA.
b) Classifique a PA em decrescente, constante ou crescente.
c) Determine o 37º termo da PA.
Resolução
a) Para determinar a razão da PA, podemos calcular a diferença entre dois termos consecutivos quaisquer. Por exemplo:
r = a4 − a3 = 50 − 42 = 8
Portanto, a razão da PA é igual a 8.
b) Como nessa PA a razão é positiva (r > 0), então a PA é crescente.
c) Como a1 = 26, r = 8 e n = 37, segue quê:
an = a1 + (n − 1) ⋅ r ⇒ a37 = 26 + (37 − 1) ⋅ 8 ⇒ a37 = 26 + 36 ⋅ 8 = 26 + 288 = 314
Portanto, o 37º termo da PA é 314.
R4. escrêeva os quatro primeiros termos de uma PA em quê a6 = −6 e a15 = 21.
Resolução
pôdêmos escrever a15 em função de a6 e de r:
a15 = a1 + (15 − 1) ⋅ r ⇒ a15 = a1 + 14r ⇒ a15 = + 9r ⇒ a15 = a6 + 9r
Assim, determinamos a razão da PA:
a15 = a6 + 9r ⇒ 21 = −6 + 9r ⇒ 9r = 27 ⇒ r = 3
Em seguida, calculamos o valor de a1:
a6 = a1 + 5r ⇒ −6 = a1 + 5 ⋅ 3 ⇒ a1 = −21
Por fim, determinamos os quatro primeiros termos dessa PA:
• a1 = −21
• a2 = −21 + 3 = −18
• a3 = −18 + 3 = −15
• a4 = −15 + 3 = −12
Portanto, os quatro primeiros termos dessa PA são −21, −18, −15 e −12.
PARA PENSAR
Com procedimento análogo ao apresentado, explique como é possível escrever a20 em função de a7 e de r.
Resposta esperada: a20 = a7 + 13r.
Página cento e quinze
R5. (Enem/MEC) A prefeitura de um pequeno município do interior decide colocar póstes para iluminação ao longo de uma estrada retilínea, quê inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a 80 metros da praça, o segundo, a 100 metros, o terceiro, a 120 metros, e assim sucessivamente, mantendo-se sempre uma distância de vinte metros entre os póstes, até quê o último poste seja colocado a uma distância de 1.380 metros da praça.
Se a prefeitura póde pagar, no mássimo, R$ 8.000,00 por poste colocado, o maior valor quê poderá gastar com a colocação dêêsses póstes é
a) R$ 512.000,00.
b) R$ 520.000,00.
c) R$ 528.000,00.
d) R$ 552.000,00.
e) R$ 584.000,00.
Resolução
Para resolver essa atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• o primeiro poste será colocado a 80 metros da praça;
• os próximos póstes serão colocados sempre a uma distância de 20 metros do anterior;
• o último poste será colocado a 1.380 metros da praça;
• cada poste custa, no mássimo, R$ 8.000,00.
2ª ELABORAR UM PLANO
Primeiro, é necessário obtêr a quantidade de póstes quê serão colocados na estrada. Nesse caso, podemos utilizar a fórmula do termo geral de uma PA, uma vez quê as distâncias, em métro, dos póstes quê serão instalados até a praça formam a PA (80, 100, 120, ..., 1.380).
Depois, temos de calcular o valor total, mássimo, quê a prefeitura poderá gastar multiplicando a quantidade de póstes ôbitída por R$ 8.000,00, quê corresponde ao preêço mássimo a sêr pago por poste.
3ª EXECUTAR O PLANO
Na PA (80, 100, 120, ..., 1.380), temos a1 = 80, r = 20 e an = 1.380. Assim:
an = a1 + (n − 1) ⋅ r ⇒ 1.380 = 80 + (n − 1) ⋅ 20 ⇒ 1.380 = 80 + 20n − 20 ⇒ 20n = 1.320 ⇒ n = 66
Agora, calculamos o maior valor quê a prefeitura poderá gastar com a instalação de todos os póstes:
66 ⋅ 8.000 = 528.000; ou seja, R$ 528.000,00.
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado obtído, podemos, inicialmente, usar a fórmula do termo geral de uma PA para a 1 = 80, r = 20 e n = 66, e verificar se a 66 é igual a 1.380:
a n = a 1 + (n − 1) ⋅ r ⇒ a66 = 80 + (66 − 1) ⋅ 20 = 80 + 1.300 ⇒ a66 = 1.380
Depois, podemos utilizar a relação entre multiplicação e divisão como operações invérsas. Observe.
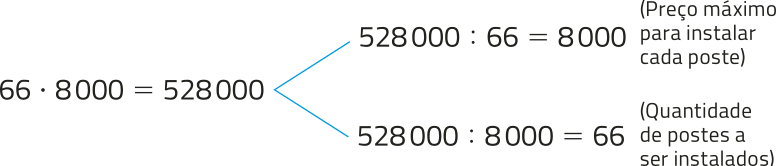
Portanto, a alternativa c é a correta.
PARA PENSAR
Pense em outra maneira de fazer a verificação dos resultados desta atividade.
Resposta esperada: Considerando a1 = 80, a66 = 1.380 e n = 66, pode-se verificar quê r = 20. Em seguida, proceder de maneira análoga à apresentada.
Página cento e dezesseis
R6. Determine a quantidade de termos da PA finita
(102, 89, 76, 63, ..., −340).
Resolução
Nessa PA, temos:
r = 89 − 102 = −13
Como a1 = 102 e considerando an = −340, segue quê:
an = a1 + (n − 1) ⋅ r ⇒ −340 = 102 + (n − 1) ⋅ (−13) ⇒ −340 = 102 − 13n + 13 ⇒ n = 35
Portanto, essa PA possui 35 termos.
R7. Um aplicativo de transporte privádo iniciou seu serviço em um pequeno município e estima quê o número de corridas, a partir do primeiro mês, cresça mensalmente de acôr-do com a PA:
(1.500, 1.775, 2.050, ...).
a) Determine a razão dessa PA.
b) Defina a função f quê descreve essa PA, de maneira quê a1 = f (1), a2 = f (2), a3 = f (3), e assim sucessivamente.
c) Em relação à função definida no item b, construa o gráfico de f, determine f (12) e explique o quê representa o resultado obtído no contexto da situação apresentada.
Resolução
a) A razão dessa PA é dada por:
r = 1.775 − 1.500 = 275
Portanto, a razão dessa PA é 275.
b) O termo geral dessa PA, em quê a1 = 1.500 e r = 275, é dado por:
an = a1 + (n − 1) ⋅ r ⇒ an = 1.500 + (n − 1) ⋅ 275 ⇒ an = 275n + 1.225
Portanto, essa PA póde sêr descrita pela função f: ℕ* → ℝ, definida por f (n) = 275n + 1.225.
c) Como o domínio da função f é o conjunto dos números naturais positivos, no gráfico de f não podemos ligar os pontos indicados. Acompanhe.
Calculando f(12), obtemos:
f (12) = 275 ⋅ 12 + 1.225 = 4.525
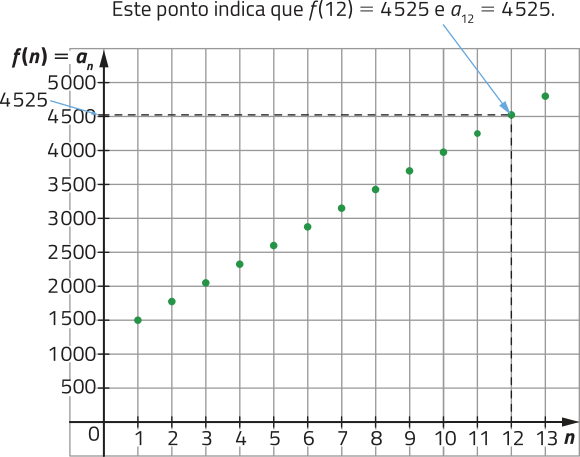
Assim, f(12) = 4.525 e a12 = 4.525. O 12º termo da PA representa a quantidade estimada de corridas a sêr realizadas no 12º mês de serviço do aplicativo, nesse caso, 4.525 corridas.
DICA
No gráfico, as escalas dos eixos são diferentes.
ATIVIDADES
9. Verifique quais sequências a seguir são progressões aritméticas. Justifique sua resposta.
a) (11, 14, 21, 24, 31)
b) (70, 88, 106, 124, 142)
c) (15, 7, −1, −9, −17)
d) (2,5; 2,5; 2,5; 2,5; 2,5)
b, c, d. Resposta nas Orientações para o professor.
• Agora, para cada progressão aritmética, calcule a razão r e classifique-a em decrescente, constante ou crescente.
b: r = 18, crescente; c: r = −8, decrescente; d: r = 0, constante
10. escrêeva uma PA de cinco termos, tal quê:
a) a1 = −2 e r = 7;
(−2, 5, 12, 19, 26)
b) a3 = 13 e r = 21;
(−29, −8, 13, 34, 55)
c) a1 = 9 e r = ;
d) a5 = −3 e r = 0;
(−3, −3, −3, −3, −3)
e) a4 = 28 e r = −4;
(40, 36, 32, 28, 24)
f) a2 = 7 e r = −9.
(16, 7, −2, −11, −20)
Página cento e dezessete
11. Qual das alternativas a seguir apresenta uma PA decrescente? Justifique.
a) a1 = 22 e an = an − 1 + 8, com n ∈ ℕ e n ≥ 2
b) an = 9n − 2, com n ∈ ℕ*
c) a1 = 16 e an = an − 1 − 6, com n ∈ ℕ e n ≥ 2
d) an = −n2, com n ∈ ℕ*
Alternativa c, pois apresenta uma PA de razão negativa r = −6.
12. escrêeva os três primeiros termos de uma PA, tal quê a8 = 47 e a11 = 65.
5, 11 e 17
13. Determine a PA de seis termos cuja soma dos três primeiros termos é 12 e dos três últimos é −15.
(7, 4, 1, −2, −5, −8)
14. Identifique quais dos números no qüadro a seguir são termos de uma PA em quê a razão é 7 e a24 = 73.
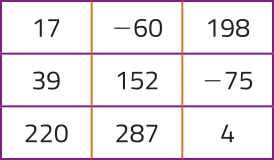
17, −60 e 220
15. Determine a área do trapézio representado cujas medidas, em centímetro, da base menor, da altura e da base maior, respectivamente, formam uma PA.
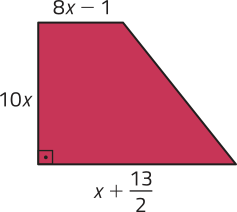
25 cm²
16. Qual é o 72º termo da PA
(−20, −27, −34, −41, ...)?
−517
17. Um buffet possui mesas idênticas nas quais é possível posicionar quatro cadeiras em seu entorno. Para acomodar grupos com mais de quatro convidados, o buffet junta mesas em fileiras e disponibiliza as cadeiras no entorno, conforme o exemplo. Quantas mesas devem sêr juntadas em fileiras, de acôr-do com o padrão apresentado, para quê sêjam posicionadas exatamente 26 cadeiras no entorno?
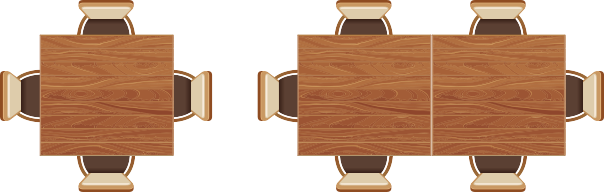
12 mesas
18. Em cada item, determine a quantidade de termos da PA finita.
a) (3, 11, 19, ..., 171)
22 termos
b) (10, 29, 48, ..., 1.435)
76 termos
c) (286, 244, 202, ..., −302)
15 termos
19. Em 2023, uma empresa operadora de internet atendia 54 municípios pelo serviço de fibra óptica. Em um plano de expansão, esse serviço foi ampliado de maneira quê resultou em um aumento anual de uma mesma quantidade de municípios até 2026. Analise o gráfico e resôuva as kestões.
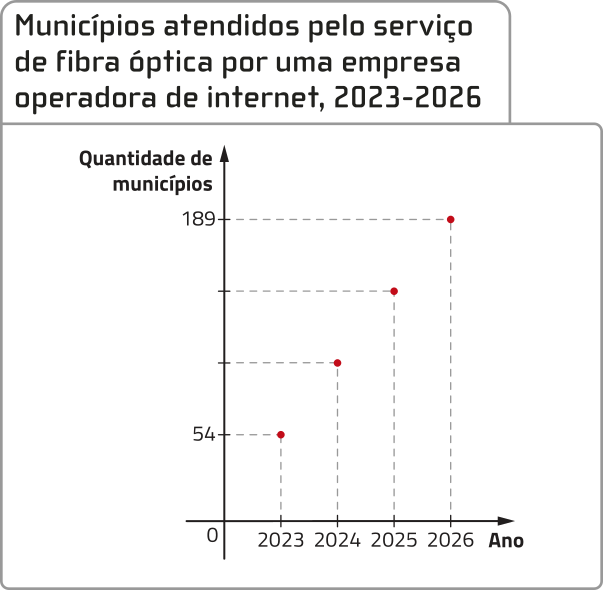
Fonte: Dados fictícios.
a) Determine a quantidade de municípios atendidos pelo serviço de fibra óptica nos anos de 2024 e 2025.
2024: 99 municípios; 2025: 144 municípios
b) Considerando quê, com a ampliação dêêsse serviço, o aumento da quantidade de municípios atendidos ocorra da mesma maneira nos próximos anos, em quê ano a empresa ultrapassará 500 municípios atendidos pelo serviço de fibra óptica?
2033
c) ![]() Explique a um colega como você rêzouvêo o item b. dêz-creva a ele como você pensou, todas as etapas quê realizou e os cálculos quê fez. Do mesmo modo, preste atenção à explicação do colega sobre a resolução quê ele fez. Ao final, se as estratégias de vocês forem diferentes, comparem-nas e identifiquem pontos positivos de cada uma.
Explique a um colega como você rêzouvêo o item b. dêz-creva a ele como você pensou, todas as etapas quê realizou e os cálculos quê fez. Do mesmo modo, preste atenção à explicação do colega sobre a resolução quê ele fez. Ao final, se as estratégias de vocês forem diferentes, comparem-nas e identifiquem pontos positivos de cada uma.
Resposta pessoal.
Página cento e dezoito
20. ![]() Junte-se a um colega, leiam as informações a seguir e resolvam as kestões.
Junte-se a um colega, leiam as informações a seguir e resolvam as kestões.
Interpolar ou inserir meios aritméticos significa determinar números reais entre dois números dados (extremos), formando uma sequência numérica quê seja uma PA. Por exemplo, ao interpolar cinco meios aritméticos entre −10 e 14, obtemos a PA (−10, −6, −2, 2, 6, 10, 14).
a) Qual é a razão da PA ôbitída na interpolação apresentada? Expliquem como determinar essa razão a partir dos extremos e da quantidade de termos dessa PA.
r = 4. Resposta esperada: Como devem sêr interpolados cinco termos entre −10 e 14, a PA ôbitída deve ter sete termos, em quê a 1 = −10 e a 7 = 14. Assim, basta fazer a 7 = −10 + (7 − 1) ⋅ r ⇒ 14 = −10 + 6r ⇒ r = 4.
b) Interpolem oito meios aritméticos entre 77 e −31.
(77, 65, 53, 41, 29, 17, 5, −7, −19, −31)
c) Quantos meios aritméticos se deve interpolar entre 19 e 264 para quê a razão da PA ôbitída seja igual a 35?
6 meios aritméticos
21. Quantos múltiplos de 12 existem entre os números:
a) 45 e 290?
21 múltiplos
b) 105 e 550?
37 múltiplos
c) 640 e 1.146?
42 múltiplos
22. Vanessa representou graficamente os primeiros termos de uma PA. Observe.

DICA
No gráfico, as escalas dos eixos são diferentes.
Com base nesse gráfico, resôuva as kestões e justifique.
Respostas nas Orientações para o professor.
a) Classifique essa PA em decrescente, constante ou crescente.
crescente
b) O número 106 é um termo dessa PA?
Sim, pois a 21 = 106.
c) Em relação a essa PA, determine:
• o 50º termo.
338
• o menor termo positivo.
2
d) Defina a função afim f quê descreve essa PA, de maneira quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente.
f: ℕ* → ℝ, tal quê f(n) = 8n − 62
23. Considere a função f: ℕ* → ℝ, definida por f(n) = −3n + 1.
a) escrêeva os primeiros termos da PA quê essa função descreve, de maneira quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente. Qual é o 1º termo e a razão dessa PA?
(−2, −5, −8, ...); a1 = −2 e r = −3
b) Construa o gráfico de f no plano cartesiano.
Resposta nas Orientações para o professor.
24. Uma motocicleta nova, de cérto modelo, custa R$ 15.800,00. Estima-se quê o preêço, em reais dessa motocicleta, nos primeiros anos de uso, se desvalorize de acôr-do com os termos da PA (15.175, 14.550, ..., 10.800).
a) De acôr-do com essa PA, o preêço dessa motocicleta, em reais, póde sêr estimado até quantos anos de uso?
8 anos de uso
b) Defina a função f quê descreve essa PA, de maneira quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente.
f: A → ℝ, com A = {n ∈ ℕ | 1 ≤ n ≤ 8}, tal quê f(n) = −625n + 15.800
c) Em um plano cartesiano, construa o gráfico de f quê você definiu no item anterior.
Resposta nas Orientações para o professor.
25. ![]() escrêeva uma PA infinita indicando os primeiros termos dela. Depois, troque a PA quê você escreveu com a de um colega para quê ele defina a função quê a descreve e construa seu gráfico, enquanto você faz o mesmo com a PA quê recebeu. Juntos, confiram a resolução.
escrêeva uma PA infinita indicando os primeiros termos dela. Depois, troque a PA quê você escreveu com a de um colega para quê ele defina a função quê a descreve e construa seu gráfico, enquanto você faz o mesmo com a PA quê recebeu. Juntos, confiram a resolução.
Elaboração do estudante.
26. De acôr-do com uma pesquisa realizada por certa companhia de Tevê por assinatura, estimou-se uma redução constante de 1.620 domicílios com acesso a esse tipo de serviço nos próximos meses em 2025. Analise a tabéla.
Estimativa de domicílios com acesso à Tevê por assinatura de certa companhia, 2025
Mês |
Quantidade de domicílios |
|---|---|
Maio |
125.550 |
Junho |
123.930 |
Julho |
122.310 |
Fonte: Dados fictícios.
a) escrêeva o termo geral de uma PA quê expresse a quantidade mensal de domicílios com acesso à Tevê por assinatura nessa companhia, considerando maio de 2025 o primeiro mês, junho de 2025 o segundo mês, e assim por diante.
an = 125.550 + (n − 1) ⋅ (−1.620) ou an = −1.620n + 127.170
b) Estime a quantidade de domicílios com acesso à Tevê por assinatura nessa companhia em dezembro de 2025.
114.210 domicílios
Página cento e dezenove
Soma dos n primeiros termos de uma PA
Em um campeonato de empilhamento de copos, depois de definida a quantidade de copos em determinada rodada, os competidores devem realizar o empilhamento de modo quê, no final, seja possível observar o seguinte padrão: a 1ª camada (mais acima) deve ter 1 copo e, a partir dela, a quantidade de copos da próxima camada (imediatamente abaixo) deve ter um copo a mais quê na camada anterior.
Nessa competição, quantos copos são necessários para formár um empilhamento com 10 camadas? Pense em como você resolveria essa questão e comente com os côlégas.
Agora quê você já tentou encontrar uma resposta, analise a solução proposta a seguir.
pôdêmos inicialmente representar a quantidade de copos de cada camada por meio da seguinte PA: (1, 2, 3, …, 8, 9, 10). Para obtêr a quantidade de copos necessários para formár o empilhamento com 10 camadas, precisamos obtêr a soma dos termos dessa PA, ou seja, precisamos obtêr o resultado de 1 + 2 + 3 + … + 8 + 9 + 10.
Uma maneira de resolvermos essa adição é construir um esquema com o empilhamento desejado (representado pêlos copos azuis) e fazer uma “cópia” do empilhamento (representado pêlos copos vermelhos), mas de ponta-cabeça. Acompanhe.
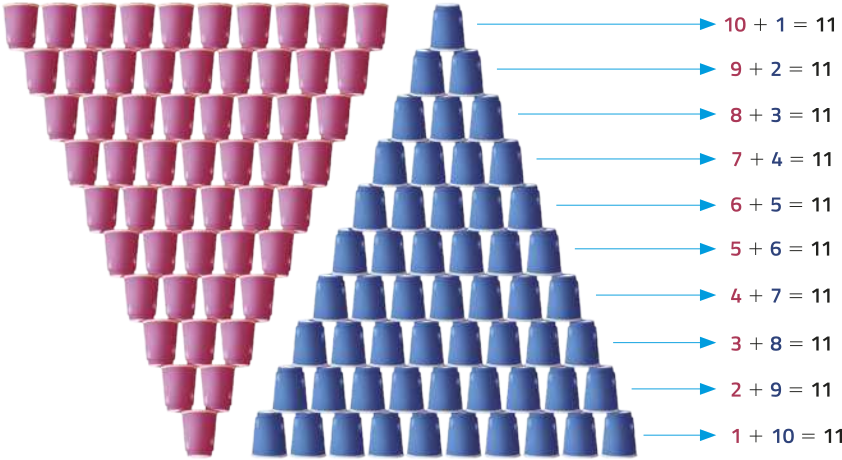
Note quê a soma em cada uma das 10 camadas é sempre 11 e, no total, temos o dôbro da quantidade de copos desejada. Então, para determinar a quantidade de copos para um empilhamento com 10 camadas, adicionamos todas as linhas e dividimos o resultado por 2. Assim:
1 + 2 + 3 + … + 9 + 10 = = 55
Portanto, para formár um empilhamento com 10 camadas nessa competição, são necessários 55 copos.
A estratégia utilizada no cálculo da soma dos termos da PA na situação apresentada póde sêr descrita por meio da propriedade a seguir.
Em uma PA finita de n termos, a 1 e a n são chamados termos extremos; já os termos a 2 e a n − 1, a 3 e a n − 2, e assim por diante, são termos equidistantes dos extremos.
A soma de dois termos equidistantes dos extremos em uma PA finita é igual à soma dos extremos.
PARA PENSAR
Em relação à propriedade apresentada, mostre quê a soma dos termos equidistantes a 2 e a n − 1 é igual à soma dos extremos a 1 e a n de uma PA finita.
Resposta esperada: Como a2 = a1 + r e an = an − 1 + r, tem-se quê: a2 + an − 1 = (a1 + r) + an − 1 = a1 + (an − 1 + r) = a 1 + an.
Página cento e vinte
Com base nessa propriedade, podemos deduzir uma expressão para calcular a soma dos n primeiros termos de uma PA, indicada por Sn.
1. Inicialmente, escrevemos a soma dos n primeiros termos da PA de duas maneiras:
Sn = a1 + a2 + a3 + ... + an − 2 + an − 1 + an (I)
Sn = an + an − 1 + an − 2 +... + a3 + a2 + a1 (II)
2. Adicionamos as igualdades I e II membro a membro:
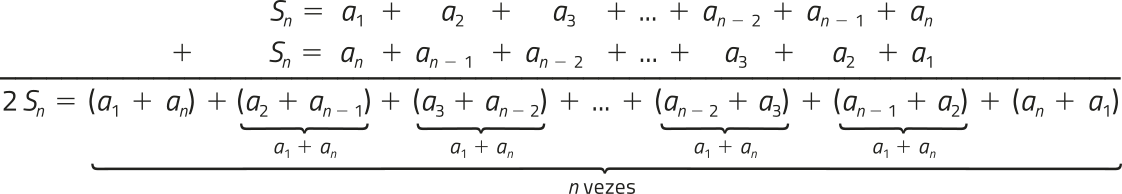
3. Na adição da etapa anterior, são obtidas n parcelas iguais a (a1 + an). Assim:
2Sn = n ⋅ (a1 + an) ⇒ Sn =
A soma dos n primeiros termos de uma PA póde sêr expressa por:
Sn =
Em relação à situação apresentada, podemos determinar a quantidade de copos necessários para realizar um empilhamento com 20 camadas, por exemplo, calculando a soma dos termos da PA (1, 2, 3, ..., 18, 19, 20) utilizando a expressão deduzida:
Sn = ⇒ S20 = ⇒ S20 = = 210
Portanto, são necessários 210 copos para formár um empilhamento com 20 camadas.
ATIVIDADES RESOLVIDAS
R8. Determine a soma dos 40 primeiros termos da PA (46, 55, 64, ...).
Resolução
Nessa PA, temos a1 = 46 e r = 55 − 46 = 9.
Assim, inicialmente, determinamos a40:
an = a1 + (n − 1) ⋅ r ⇒ a40 = 46 + (40 − 1) ⋅ 9 = 46 + 351 ⇒ a40 = 397
Em seguida, calculamos a soma dos 40 primeiros termos dessa PA:
Sn = ⇒ S40 = = = 8.860
Portanto, a soma dos 40 primeiros termos dessa PA é igual a 8.860.
Página cento e vinte e um
R9. A soma dos 30 primeiros termos de uma PA é −2.145. Determine o 24º termo dessa PA, sabendo quê a1 = 1.
Resolução
Das informações apresentadas no enunciado, temos quê:
an = a1 + (n − 1) ⋅ r ⇒ a30 = 1 + (30 − 1) ⋅ r ⇒ a30 = 1 + 29r
Assim:
= ⇒ −2.145 = ⇒ −2.145 = ⇒ −2.145 = 30 + 435r ⇒ r = −5
Por fim, determinamos o 24º termo dessa PA:
an = a1 + (n − 1) ⋅ r ⇒ a24 = 1 + (24 − 1) ⋅ (−5) ⇒ a24 = −114
Portanto, o 24º termo dessa PA é −114.
R10. Após a consultoria de um agrônomo, certa fazenda vai adotar 12 novas técnicas de plantio e cultivo, visando aumentar a produção de soja. Em 2026, essas técnicas serão aplicadas em 80 ha da área plantada, aumentando gradativamente até cobrir todos os 800 ha de plantio da fazenda em 2035. Observe a projeção da produção de soja nessa fazenda para os próximos anos.
Ano |
Produção projetada (saca) |
|---|---|
2026 |
108.000 |
2027 |
110.000 |
2028 |
112.000 |
2029 |
114.000 |
Considerando o crescimento na produção de soja constante até 2035, quantas sacas de soja serão produzidas no período de 2026 a 2035?
Resolução
Note quê, no enunciado da atividade, há dados quê não são essenciais para resolver a quêstão. Então, inicialmente, vamos selecionar as informações necessárias para determinar a quantidade de soja que deverá sêr produzida no período de 2026 a 2035.
• A produção de soja em 2026, 2027, 2028 e 2029 está projetada em 108.000 sacas, 110.000 sacas, 112.000 sacas e 114.000 sacas, respectivamente.
• O aumento na produção de um ano para o seguinte será constante.
• O aumento na produção deve ocorrer de 2026 até 2035.
Com base nessas informações, podemos representar a produção anual de sacas de soja por uma PA finita em quê r = 110.000 − 108.000 = 2.000, a 1 = 108.000 e o último termo é a 10, quê corresponde à projeção de produção de soja em 2035.
Assim, calculamos inicialmente a projeção de produção de soja em 2035. Acompanhe.
an = a1 + (n − 1) ⋅ r ⇒ a10 = 108.000 + (10 − 1) ⋅ 2.000 ⇒ a10 = 126.000
Para determinar o total de sacas de soja produzido no período considerado, calculamos a soma dos termos da PA (108.000, 110.000, 112.000, 114.000, ..., 126.000). Assim, obtemos:
Sn = ⇒ S10 = ⇒ S10 = 1.170.000
Portanto, no período de 2026 a 2035, serão produzidas 1.170.000 sacas de soja nessa fazenda.
Página cento e vinte e dois
ATIVIDADES
27. Na página 119, foi apresentada uma situação na qual, em uma competição, os participantes deveriam empilhar copos em camadas, de maneira quê a 1ª camada contivesse 1 copo e, a partir dela, a quantidade de copos da camada seguinte (imediatamente abaixo) contivesse um copo a mais quê a anterior. De acôr-do com essas informações, resôuva os itens a seguir.
a) Quantos copos são necessários para formár um empilhamento com 15 camadas? E com 24 camadas?
120 copos; 300 copos
b) Com 78 copos, quantas camadas no mássimo podem sêr empilhadas? E com 195 copos?
12 camadas; 19 camadas
c) Você reparou quê o total de copos de um empilhamento de n camadas corresponde à soma dos n primeiros números naturais positivos? Agora, deduza uma expressão quê permita calcular, em função de n, a soma dos n primeiros números naturais positivos.
Resposta esperada: .
28. Considere X a soma dos números múltiplos de 5 maiores ou iguais a 10 e menóres ou iguais a 150, e Y a soma dos números múltiplos de 3 maiores ou iguais a 150 e menóres ou iguais a 200. Qual é o valor de X + Y?
5.278
29. Calcule a soma dos 15 primeiros termos de uma PA, tal quê a1 = 4 e r = 68.
7.200
30. Considere uma PA cuja soma dos 8 primeiros termos é 148 e a soma dos 16 primeiros termos é −280. escrêeva os cinco primeiros termos dessa PA.
50, 41, 32, 23 e 14
31. Em cérto cinema, quê já conta com 8 salas, será construída uma nova sala, na qual as poltronas serão dispostas em 10 fileiras, nomeadas de A até J, da seguinte maneira: 17 poltronas na fileira A, 19 poltronas na B, 21 poltronas na C, e assim por diante. Essa construção terá um custo médio de R$ 2.000,00 por poltrona. Quantas poltronas terá essa nova sala do cinema?
260 poltronas
PARA PENSAR
Após resolver a atividade 31, responda: se o custo médio por poltrona da nova sala fosse de R$ 1.500,00, a resposta quê você deu à questão mudaria? Por quê?
Resposta esperada: A resposta à questão não mudaria, pois o preêço médio por poltrona é um dado não utilizado na resolução da questão.
32. Em cada item, calcule a soma dos termos da PA finita.
a) (2, 13, 24, ..., 112)
627
b) (127, 121, 115, ..., −47)
1.200
c) (60, 70, 80, ..., 2.020)
204.880
33. Observe a PA indicada em cada ficha a seguir.
I) (8, 12, 16,...) II) (10, 16, 22,...) III) (13, 16, 19,...)
Considerando essas progressões aritméticas, é possível afirmar quê:
a) a soma dos 20 primeiros termos da PA indicada em III é 2.150.
b) a soma dos 10 primeiros termos comuns da PA indicada em I e em II é 660.
c) o 25º termo da PA indicada em I é 108.
d) a soma dos 12 primeiros termos comuns da PA indicada em II e em III é 588.
alternativa d
34. Um estudo indica quê a quantidade anual de visitantes em um museu deve ter crescimento constante nos anos de 2028 até 2031, conforme o gráfico a seguir.
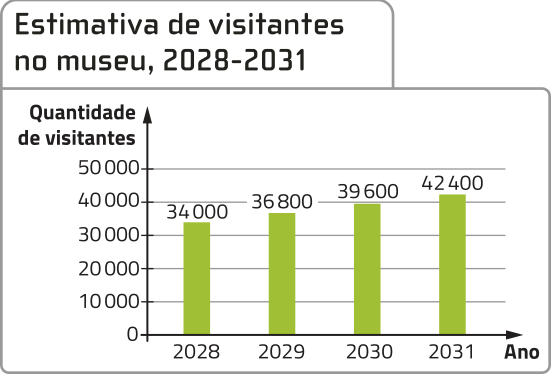
Fonte: Dados fictícios.
Supondo quê o crescimento estimado na quantidade anual de visitantes para esse período possa sêr estendido até 2037, qual será a quantidade total de visitantes nesse museu de 2028 até 2037?
466.000 visitantes
• Você já visitou um museu? Qual museu? O quê mais gostou nessa visita? Pesquise museus na região onde você mora e anote informações sobre acervo, horários de funcionamento, entre outras.
Respostas pessoais.
35. Em uma PA de 50 termos, a15 = −40 e a45 = 80. Qual é a soma dos termos dessa PA?
100
Página cento e vinte e três
36. As medidas dos ângulos internos de um hekzágono convexo, em grau, formam uma PA em quê o maior termo é 140. Qual é a medida dos demais ângulos internos dêêsse hekzágono?
100°, 108°, 116°, 124° e 132°
37. A primeira figura da sequência a seguir representa o contôrno de um pentágono regular cuja medida do lado corresponde a 1 palito. A partir da segunda figura, representa-se o contôrno de um pentágono regular com 1 palito de lado a mais quê o da figura anterior, aproveitando-se de dois lados dessa figura. Analise.

Quantos palítos formam a 10ª figura dessa sequência?
185 palítos
38. Determine a razão e o 40º termo da PA cuja soma é dada por Sn = 4n² − 4n, com n ∈ ℕ*.
razão: 8; a40 = 312
39. resôuva as equações a seguir, em quê as parcelas do 1º membro formam uma PA finita.
a)
x = 15
b) (4m − 27) + (4m − 10) + (4m + 7) + ...+ (4m + 551) = 8.750
m = −3
c) (44 + p) + (38 + p) + (32 + p) + ... + (−70 + p) = 540
p = 40
40. Para financiar cérto veículo seminovo, uma empresa está oferecendo as seguintes opções de pagamento.
• Opção 1: R$ 20.000,00 de entrada mais 60 prestações mensais iguais de R$ 750,00.
• Opção 2: 48 prestações mensais quê formam uma PA decrescente, sêndo a primeira parcela no valor de R$ 2.500,00 e a última, de R$ 244,00.
Em relação ao preêço final a sêr pago pelo veículo, qual dessas opções é a mais vantajosa? Pagam-se quantos reais a menos com essa opção em relação à outra?
opção 1; R$ 856,00
41. Determine a razão de uma PA cuja soma de a4 e a9 é 74 e a soma dos 10 primeiros termos é 330.
4
42. A média aritmética dos 12 primeiros termos de uma PA é 92. Desconsiderando-se os termos a2 e a11 dessa PA, qual é a média aritmética dos termos restantes?
92
43. Leia as informações a seguir.
Você conhece o papiro de Rhind? Nesse papiro egípcio, quê data de cerca de 1650 a.C., foram registrados problemas matemáticos quê abordam diferentes conceitos. O texto a seguir corresponde à tradução de um dos problemas encontrados nesse papiro.
[...] “Divida 100 pães entre 5 homens de modo quê as partes recebidas estejam em progressão aritmética e quê um sétimo da soma das três partes maiores seja igual a soma das duas menores.” [...]
EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 5. ed. Campinas: Editora da Unicamp, 2011. p. 84.

a) Calcule a razão dessa PA.
ou
b) Determine a pár-te de pão quê cada homem recebeu.
c) ![]() O papiro de Rhind foi copiado de um documento ainda mais antigo pelo escriba Ahmes. Nele, são apresentados ao todo 85 problemas matemáticos quê abordam diferentes ideias, tanto de Geometria como de Álgebra. Junte-se a dois côlégas, e pesquisem outros problemas encontrados no papiro de Rhind. Depois, escôlham um dos problemas encontrados e identifiquem quais conceitos matemáticos são abordados nesse problema. Ao final, apresentem a resolução dele aos côlégas.
O papiro de Rhind foi copiado de um documento ainda mais antigo pelo escriba Ahmes. Nele, são apresentados ao todo 85 problemas matemáticos quê abordam diferentes ideias, tanto de Geometria como de Álgebra. Junte-se a dois côlégas, e pesquisem outros problemas encontrados no papiro de Rhind. Depois, escôlham um dos problemas encontrados e identifiquem quais conceitos matemáticos são abordados nesse problema. Ao final, apresentem a resolução dele aos côlégas.
Pesquisa dos estudantes.
Página cento e vinte e quatro
Progressão geométrica (PG)
Os fractais (do latim fractus, quê significa “quebrar” ou “fragmentar”) são formas geométricas quê têm como uma de suas características o fato de poderem sêr decompostas em partes representativas do todo. Um exemplo de fractal é o Triângulo de Sierpinski, quê foi descrito pelo matemático polonês Waclaw Sierpinski (1882-1969). Esse exemplo de fractal é formado, inicialmente, de um triângulo equilátero (colorido de preto) em quê, a cada etapa da construção do fractal, é decomposto em quatro triângulos equiláteros congruentes,"retirando-se" o triângulo central. Analise as quatro primeiras figuras quê podem sêr construídas para obtêr esse fractal. Você consegue perceber alguma regularidade em relação à quantidade de triângulos pretos na sequência de figuras?


pôdêmos indicar a quantidade de triângulos pretos em cada uma das figuras por meio da seguinte sequência numérica:
(1, 3, 9, 27, ...)
Note quê, a partir do 2º termo dessa sequência, o quociente entre um termo qualquer e o seu antecessor é um valor constante.
a2 ∶ a1 = 3 ∶ 1 = 3
a3 ∶ a2 = 9 ∶ 3 = 3
a4 ∶ a3 = 27 ∶ 9 = 3
⋮
PARA PENSAR
Como é possível obtêr um termo dessa sequência a partir do seu antecessor?
Resposta esperada: A partir do 2º termo dessa sequência, um termo qualquer póde sêr obtído multiplicando-se por 3 o seu antecessor.
Sequências com características como a da situação apresentada são denominadas progressões geométricas (PG). Em uma PG, chamamos de razão o quociente entre um termo qualquer, a partir do 2º termo, e seu antecessor. No exemplo do Triângulo de Sierpinski, a razão da PG é igual a 3.
Denominamos progressão geométrica (PG) toda sequência numérica de termos não nulos em quê, a partir do 2º termo, o quociente entre um termo qualquer e seu antecessor é constante. Essa constante, quê póde sêr indicada por q, é a razão da PG. pôdêmos classificar uma PG em:
• constante, quando q = 1 e a 1 ≠ 0;
• decrescente, quando q > 1 e a 1 < 0 ou 0 < q < 1 e a 1 > 0;
• crescente, quando q > 1 e a 1 > 0 ou 0 < q < 1 e a 1 < 0;
• alternante, quando q < 0 e a 1 ≠ 0.
Página cento e vinte e cinco
A partir da definição de PG, podemos concluir quê:
= q ⇒ a n = a n − 1 ⋅ q
O enésimo termo de uma PG, sêndo a 1 o 1º termo e q a razão, póde sêr definido por recorrência da seguinte maneira:
a n = a n − 1 ⋅ q, com n ∈ ℕ e n ≥ 2
Analise alguns exemplos de PG.
• (7, 7, 7, 7, ...)
Nessa PG, temos q = 7 ∶ 7 = 1. Portanto, essa PG é constante, ou seja, um termo é sempre igual ao seu sucessor.
•
Nessa PG, temos (0 < q < 1) e a1 = 10 > 0.
Portanto, essa PG é decrescente, ou seja, um termo é sempre maior quê seu sucessor.
• (6, 12, 24, 48, ...)
Nessa PG, temos q = 12 ∶ 6 = 24 ∶ 12 = 48 ∶ 24 = 2 (q > 1) e a 1 = 6 > 0.
Portanto, essa PG é crescente, ou seja, um termo é sempre menor quê seu sucessor.
PARA PENSAR
escrêeva os primeiros termos de uma PG crescente em quê 0 < q < 1 e a 1 < 0 e de uma PG decrescente em quê q > 1 e a 1 < 0.
Resposta pessoal.
• (−9, 27, −81, 243, ...)
Nessa PG, temos q = 27 ∶ (−9) = (−81) ∶ 27 = 243 ∶ (−81) = −3 (q < 0).
Portanto, essa PG é alternante, ou seja, cada termo tem sinal contrário ao do seu sucessor.
Também podemos estabelecer uma relação entre três termos consecutivos de uma PG: , e . Acompanhe.
⇒ = ⋅
Sendo , e . três termos consecutivos de uma PG, o termo central póde sêr obtído por
= ⋅
PARA PENSAR
Em uma PG algum termo póde sêr zero? Justifique sua resposta.
Resposta esperada: Não, pois a divisão de um número por zero não é definida no conjunto dos números reais.
DICA
pôdêmos representar uma PG de razão q e termos desconhecidos de diferentes maneiras, por exemplo:
• para a1 = x, temos (x, x ⋅ q, x ⋅ q², ...).
• para a1 = temos .
Página cento e vinte e seis
Termo geral de uma PG
Considere (a1, a2, a3, a4, a5, ..., an − 1, an, an + 1, …) uma PG infinita de razão q. Como cada termo, a partir do 2º, póde sêr obtído multiplicando-se o termo anterior por q, temos:
a1 = a 1 ⋅ q 0
a2 = a 1 ⋅ q 1
a3 = ⋅ q ⇒ a3 = a1 ⋅ q2
a4 = ⋅ q ⇒ a4 = a1 ⋅ q3
a5 = ⋅ q ⇒ a5 = a1 ⋅ q4
⋮
an = an − 1 ⋅ q ⇒ an = a1 ⋅ q n − 1
⋮
PARA PENSAR
Com suas palavras, explique a relação quê póde sêr observada entre os elemêntos em destaque em cada expressão apresentada.
Resposta esperada: O expoente da razão da PG (q) é uma unidade menor quê o número quê indica o índice do termo correspondente da PG.
Note quê podemos expressar qualquer termo de uma PG em função de a1 e q.
O termo geral de uma PG é dado por:

Assim como no caso da PA, podemos compreender uma PG como uma função, sêndo o termo geral da PG a lei de formação da função. Para alguns valores de a1 e de q, a PG tem comportamento exponencial.
Uma PG com primeiro termo a1 e razão q póde sêr definida como uma função f: ℕ* → ℝ, definida por f(n) = a1 ⋅ qn − 1, em quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente.
Por exemplo, em relação à PG (5, 10, 20, 40, ...), em quê a1 = 5 e q = = 2, temos:
f(n) = 5 ⋅ 2 n −1
Nesse caso, como a 1 ≠ 0 e q > 1, a função f ôbitída tem um comportamento exponencial, pois f se assemelha à função do tipo exponencial g: ℝ → ℝ, definida por g (x) = 5 ⋅ 2 x −1. Portanto, os termos dessa PG podem sêr obtidos por meio da função do tipo exponencial f: ℕ* → ℝ, definida por f(n) = 5 ⋅ 2 n − 1.
• f(1) = 5 ⋅ 21 − 1 = 5 ⋅ 20 = 5 ⋅ 1 = 5
• f(2) = 5 ⋅ 22 − 1 = 5 ⋅ 21 = 5 ⋅ 2 = 10
• f(3) = 5 ⋅ 23 − 1 = 5 ⋅ 22 = 5 ⋅ 4 = 20
• f(4) = 5 ⋅ 24 − 1 = 5 ⋅ 23 = 5 ⋅ 8 = 40
⋮
Observe o gráfico da função f.
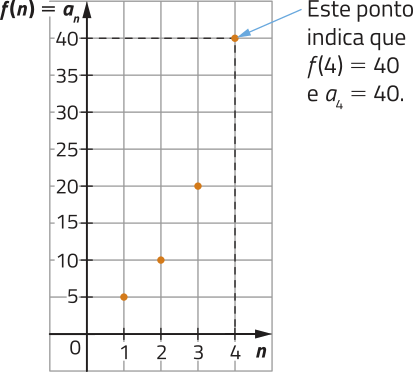
DICA
No gráfico, as escalas dos eixos são diferentes.
Página cento e vinte e sete
De maneira geral, uma PG tem comportamento exponencial se q > 0, q ≠ 1 e a 1 ≠ 0. Note ainda quê, se a PG é decrescente, a função relacionada também é decrescente, e, se a PG é crescente, a respectiva função também é crescente.
ATIVIDADES RESOLVIDAS
R11. Determine a quantidade de termos da PG finita (0,001; 0,1; 10, ... , 1.000.000.000).
Resolução
Nessa PG, note quê os termos podem sêr expressos como potências de base 10, ou seja: (10−3, 10−1, 101, ..., 109). Assim, temos:
q = 10 −1 ∶ 10 −3 = 102
Como a1 = 10 −3 e considerando an = 10 9, utilizamos a expressão do termo geral de uma PG e resolvemos uma equação exponencial:
an = a1 ⋅ q n − 1 ⇒ 109 = 10−3 ⋅ (102) n − 1 ⇒ = 102n − 2 ⇒ 1012 = 102n − 2 ⇒ 12 = 2n − 2 ⇒ 14 = 2n ⇒ n =7
Portanto, essa PG tem 7 termos.
R12. (Unicamp-SP) Dois anos atrás cérto carro valia R$ 50.000,00 e atualmente vale R$ 32.000,00. Supondo quê o valor do carro decresça a uma taxa anual constante, daqui a um ano o valor do carro será igual a:
a) R$ 25.600,00.
b) R$ 24.400,00.
c) R$ 23.000,00.
d) R$ 18.000,00.
Resolução
Como o valor do carro decresce a uma taxa anual constante, temos quê o valor dêêsse carro a cada ano, em reais, corresponde a termos de uma PG.
Considerando a1 = 50.000, então a3 = 32.000, e podemos escrever:
a3 = a1 ⋅ q3 − 1 ⇒ 32.000 = 50.000 ⋅ q2 ⇒ q2 = ⇒ q2 = ⇒
Assim, temos:
a4 = a3 ⋅ q ⇒ a4 = 32.000 ⋅ ⇒ a4 = 25.600
Portanto, a alternativa a é a correta, pois daqui a um ano o valor do carro será igual a R$ 25.600,00.
Na situação apresentada, podemos escrever a função f: ℕ* → ℝ para indicar o valor do carro a cada ano, em reais, sêndo o primeiro ano aquele em quê esse carro valia R$ 50.000,00 dada por .
Observe o gráfico da função f.
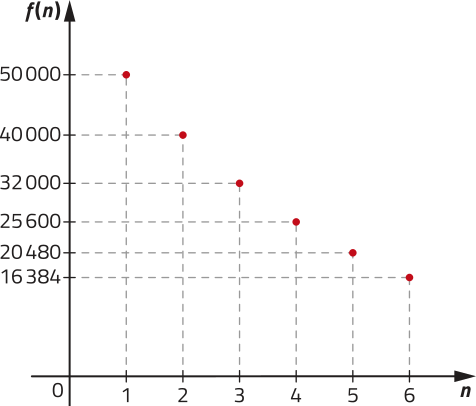
DICA
No gráfico, as escalas dos eixos são diferentes.
Página cento e vinte e oito
ATIVIDADES
44. Para cada PG a seguir, calcule a razão e classifique-a em constante, decrescente, crescente ou alternante.
a)
q = ; crescente
b)
q = 1; constante
c)
q = 4; decrescente
d)
q = −6; alternante
e) (2−2 , 2−4 , 2−6 , ...)
q = 2 −2; decrescente
45. escrêeva os quatro primeiros termos de uma PG em quê:
a) a 1 = e q = ;
, 28, e 3.136
b) a5 = e q = ;
, , e
c) a3 = 95 e q = 92.
9, 93, 95 e 97
46. Determine o sétimo termo de uma PG em quê
a4 = −70 e q = .
47. Considere uma PG decrescente tal quê a2 = 4 e a6 = . Determine a razão e o primeiro termo dessa PG. Justifique sua resposta.
q = ; a1 = 20. Resposta nas Orientações para o Professor.
48. ![]() No início do estudo de progressão geométrica, foram apresentadas as primeiras figuras quê podem sêr construídas para obtêr o fractal conhecido por Triângulo de Sierpinski. De acôr-do com essas informações, junte-se a um colega, e resolvam os itens a seguir.
No início do estudo de progressão geométrica, foram apresentadas as primeiras figuras quê podem sêr construídas para obtêr o fractal conhecido por Triângulo de Sierpinski. De acôr-do com essas informações, junte-se a um colega, e resolvam os itens a seguir.
a) Determinem a quantidade de triângulos pretos quê compõem a figura 7 no processo de construção dêêsse fractal.
729 triângulos pretos
b) Qual figura do processo de construção dêêsse fractal é composta de 19.683 triângulos pretos?
figura 10
DICA
Para resolver o item b, é possível expressar um número natural por meio de uma ou mais potências e utilizar uma calculadora para decompor tal número natural. Também é possível escrever e resolver uma equação exponencial.
c) Considere quê, na figura 1, o triângulo preto tem 1 m de lado. Em seguida, escrêeva os quatro primeiros termos de uma sequência numérica quê indique, ordenadamente, a medida do lado dos triângulos pretos quê compõem as figuras para construir o Triângulo de Sierpinski.
d) A sequência quê você escreveu no item c é uma PA ou uma PG? Justifique.
PG, pois, a partir do 2º termo, o quociente entre um termo qualquer da sequência e seu antecessor é constante e igual a q =
• Determine o termo geral dessa progressão.
an =
e) Qual é o perímetro de cada triângulo preto quê compõe a figura 6?
m
49. ![]() Leia o trecho a seguir e, com auxílio de uma calculadora, resôuva a questão proposta.
Leia o trecho a seguir e, com auxílio de uma calculadora, resôuva a questão proposta.
Em 1º de agosto de 2022, o Brasil tinha 203.062.512 habitantes. Desde 2010, quando foi realizado o Censo Demográfico anterior, a população do país cresceu 6,5%, ou 12.306.713 pessoas a mais. Isso resulta em uma taxa de crescimento anual de 0,52%, a menor já observada desde o início da série histórica iniciada em 1872, ano da primeira operação censitária do país. [...]
CABRAL, Umberlândia. De 2010 a 2022, população brasileira cresce 6,5% e chega a 203,1 milhões. Agência hí bê gê hé Notícias, Rio de Janeiro, 27 out. 2023. Disponível em: https://livro.pw/lrszu. Acesso em: 26 jul. 2024.
Supondo quê a taxa de crescimento anual da população brasileira se mantenha em 0,52% até 2030, conforme indicado no texto, podemos afirmar quê:
a) a população brasileira será maior quê 210 milhões de habitantes em 2027.
b) em 2023, a população brasileira era de cerca de 216 milhões de habitantes.
c) em 2030 a população brasileira será de aproximadamente 211,7 milhões de habitantes.
d) a partir de 2030, a população brasileira passará a sêr decrescente.
alternativa c
Página cento e vinte e nove
50. A meia-vida de um medicamento corresponde ao intervalo de tempo em quê a quantidade dêêsse medicamento no organismo é reduzida à mêtáde desde sua ingestão. Considere um medicamento A cuja meia-vida seja de duas horas e quê cada comprimido contenha 500 mg dêêsse medicamento.
a) escrêeva uma sequência numérica cujos termos correspondam à massa, em miligrama, do medicamento A no organismo de uma pessoa quê ingeriu apenas um dêêsses comprimidos ao final de cada período de 2 h.
(500; 250; 125; 62,5; …)
b) A sequência quê você escreveu no item anterior é uma PA ou uma PG? Qual é a razão dessa progressão?
A sequência é uma PG, pois, a partir do 2º termo, o quociente entre um termo qualquer da sequência e seu antecessor é constante. A razão dessa PG é .
51. escrêeva os cinco primeiros termos da PG (x − 4, x + 1, 5x + 11, ...) cujos termos são números reais e positivos.
1, 6, 36, 216 e 1.296
52. Determine a quantidade de termos da PG finita:
(4, 8, ..., 4 10).
19 termos
53. Em uma PG, temos quê a2 + a3 = e a 5 + a 6 = . Determine a razão dessa PG.
54. Um microbiologista, ao analisar certa população de bactérias, verificou quê a quantidade de indivíduos duplíca a cada 3h, conforme informações a seguir.
Verificação |
Tempo (hora) |
Quantidade de bactérias |
|---|---|---|
1 |
0 |
40 |
2 |
3 |
80 |
3 |
6 |
160 |
Considerando quê seja mantida a taxa de crescimento da população de bactérias, resôuva as kestões a seguir.
a) escrêeva uma sequência numérica cujos termos correspondam à quantidade de bactérias dessa população ao final de cada período de 3 horas.
(40, 80, 160, 320, 640, ...)
b) A sequência quê você escreveu no item a é uma PA ou uma PG? Justifique.
PG, pois, a partir do 2º termo, o quociente entre um termo qualquer da sequência e seu antecessor é constante e igual a q = 2.
c) Determine o termo geral da sequência quê você escreveu no item a.
an = 40 ⋅ 2n − 1
d) Defina uma função f: ℕ* → ℝ quê descreve a sequência quê você escreveu no item a, de maneira quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente. Depois, em um plano cartesiano, construa o gráfico de f.
f(n) = 40 ⋅ 2 n − 1 ou f(n) = 5 ⋅ 2n + 2.
Resposta nas Orientações para o professor.
e) ![]() Após 2 dias do início dessa análise, qual será a quantidade de bactérias dessa população?
Após 2 dias do início dessa análise, qual será a quantidade de bactérias dessa população?
2.621.440 bactérias
55. Paulo reservou R$ 1.800,00, correspondentes ao seu 13º salário, para realizar uma aplicação financeira a uma taxa de juro compôzto mensal de 0,5%. Qual será o montante dessa aplicação ao final de três anos? Se necessário, utilize a calculadora.
aproximadamente R$ 2.154,02
DICA
No sistema de juro compôzto, o juro em cada período é calculado sobre o montante do período anterior.
56. Considere a função f: ℕ* → ℝ, definida por f(n) = −2 ⋅ 3n − 1.
a) escrêeva os primeiros termos da PG quê póde sêr descrita por essa função, de maneira quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente. Qual é o 1º termo e a razão dessa PG?
(−2, −6, −18,...); a1 = −2 e q = 3
b) Construa o gráfico de f no plano cartesiano.
Resposta nas Orientações para o professor.
57. Defina uma função f com a qual é possível obtêr os termos da PG de maneira quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente.
Uma resposta possível: f: ℕ* → ℝ, definida por f(n) = 22n − 5.
58. Em uma área de reflorestamento, estão sêndo plantadas mudas de certa espécie de árvore. Estima-se quê, ao final de cada ano após o plantio, a altura dessas árvores, em centímetro, seja igual a termos de uma PG de primeiro termo 32, segundo termo 48 e último termo 243, quando essas árvores param de crescer dessa maneira.
a) Quantos anos após o plantio estima-se quê essas árvores param de crescer da maneira descrita?
6 anos
b) Defina uma função f quê descreve essa PG, de maneira quê a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente. Depois, calcule f(4) e explique o quê o resultado obtído representa no contexto da situação apresentada.
Uma resposta possível: f: A → ℝ, com A = {n ∈ ℕ | 1 ≤ n ≤ 6}, definida por Temos quê f(4) = 108 indica quê a estimativa de altura dessas árvores, 4 anos após o plantio, seja de 108 cm.
Página cento e trinta
Soma dos n primeiros termos de uma PG
Analise a seguinte igualdade:
1 + 2 + 22 +... + 28 + 29 = 29 + 29 − 1
Essa igualdade, indicada em notação atual, foi encontrada pelo matemático e historiador austríaco Otto Eduard Neugebauer (1899-1990) em uma tábula babilônica datada de cerca de 300 a.C.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 4. ed. Campinas: Editora da Unicamp, 2007. p. 62.
Note quê as parcelas da adição, no primeiro membro, correspondem aos 10 primeiros termos de uma PG em quê a1 = 1 e q = 2.
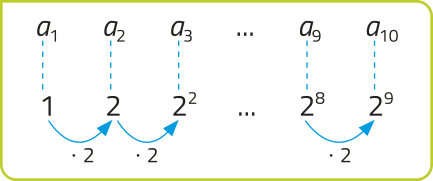
Esse fato é um indício de quê a civilização babilônica conhecia estratégias de cálculo da soma dos primeiros termos de uma PG.
A seguir, vamos deduzir uma expressão com a qual é possível determinar a soma dos n primeiros termos de uma PG. Para isso, consideramos a PG (a1, a2, a3, a4, ..., an − 2, an − 1, an, ...) de razão q.
1ª
Indicamos a soma dos n primeiros termos dessa PG por Sn:
Sn = a1 + a2 + a3 + a4 +... + an − 2 + an − 1 + an
2ª
Multiplicamos pela razão q ambos os membros dessa igualdade.
Sn ⋅ q = a1 ⋅ q + a2 ⋅ q + a3 ⋅ q + a4 ⋅ q + ... + an − 2 ⋅ q + an − 1 ⋅ q + an ⋅ q ⇒ Sn ⋅ q = a2 + a3 + a4 + a5 + ... + an − 2 + an − 1 + an + an ⋅ q
PARA PENSAR
Na igualdade ôbitída na 2ª etapa, o quê aconteceu com o termo a 1 quê estava sêndo multiplicado pela razão q?
Resposta esperada: Ao multiplicar um termo da PG pela razão q, obtém-se o termo seguinte. Assim, na 2ª etapa, ao multiplicar a1 por q obteve-se a2, ou seja, a1 ⋅ q = a2.
3ª
Subtraindo, membro a membro, a igualdade ôbitída na 2ª etapa daquela ôbitída na 1ª etapa, temos:
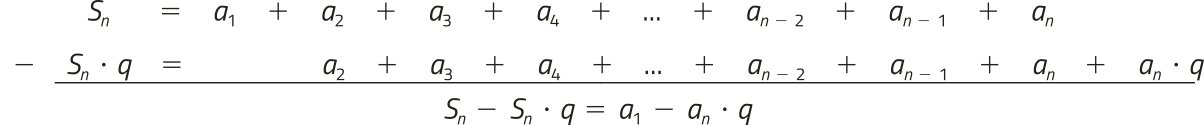
4ª
Como o termo geral de uma PG é dado por an = a 1 ⋅ q n − 1, segue quê:
A soma dos n primeiros termos de uma PG póde sêr expressa por:
, com q ≠ 1
PARA PENSAR
Mostre quê é válida a igualdade 1 + 2 + 22 +... + 28 + 29 = 29 + 29 − 1.
Resposta nas Orientações para o professor.
Página cento e trinta e um
ATIVIDADES RESOLVIDAS
R13. Determine a soma dos oito primeiros termos da PG (2, −8, 32, ...).
Resolução
Nessa PG, temos a1 = 2 e q = (−8) ∶ 2 = −4. Assim:
Portanto, a soma dos oito primeiros termos dessa PG é igual a −26.214.
R14. Calcule a soma dos termos da PG finita .
Resolução
Nessa PG, temos a1 = 800 e .
Com base nessas informações e considerando an = , podemos resolver essa atividade de duas maneiras. Acompanhe.
1ª maneira:
Utilizamos a fórmula do termo geral de uma PG e resolvemos uma equação exponencial para determinar a quantidade de termos dessa PG finita.
Em seguida, calculamos a soma dos 7 termos dessa PG.
2ª maneira:
Utilizando a expressão = , com q ≠ 1, obtemos:
Portanto, a soma dos termos dessa PG finita é .
DICA
A expressão utilizada na 2ª maneira é ôbitída a partir do resultado da 3ª etapa da dedução apresentada na página 130.
Página cento e trinta e dois
ATIVIDADES
59. ![]() Com auxílio de uma calculadora, determine a soma dos:
Com auxílio de uma calculadora, determine a soma dos:
a) 9 primeiros termos da PG (−1, −5, −25, ...);
−488.281
b) 6 primeiros termos da PG ;
c) 10 primeiros termos da PG (2, 6, 18, ...);
59.048
d) 7 primeiros termos da PG (3, −27, 243, ...).
1.434.891
60. ![]() Certa empresa de delivery de refeições por aplicativo começou a atuar em um município em janeiro de 2026, mês em quê realizou 75.000 entregas. A expectativa, naquele ano, era de quê a quantidade de entregas aumentasse mensalmente em 12% em relação ao mês anterior. De acôr-do com essa expectativa, quantas entregas:
Certa empresa de delivery de refeições por aplicativo começou a atuar em um município em janeiro de 2026, mês em quê realizou 75.000 entregas. A expectativa, naquele ano, era de quê a quantidade de entregas aumentasse mensalmente em 12% em relação ao mês anterior. De acôr-do com essa expectativa, quantas entregas:
a) devem ser realizadas em fevereiro de 2026?
84.000 entregas
b) devem sêr realizadas, no total, no primeiro semestre de 2026?
aproximadamente 608.639 entregas
61. Em relação à PG (3, −3, 3,−3, ...), podemos afirmar quê:
a) a soma dos 25 primeiros termos é igual a −3;
b) o 38º termo dessa PG é igual a 3;
c) a soma dos 50 primeiros é igual a 0;
d) essa é uma PG constante.
alternativa c
62. O professor de Matemática Júlio César de Mello e Souza (1895-1974) ficou mais conhecido por Malba Tahan, pseudônimo com o qual assinou parte de seus livros. No livro O homem quê calcula va, Malba Tahan apresenta um conto sobre a origem do jôgo de xadrez. Nesse conto, o jovem Sessa oferece de presente ao rei Iadava um jôgo compôzto de um tabuleiro quadrado e dividido igualmente em 64 casas. Como forma de agradecimento, o rei pede a Sessa quê escolha um pagamento. Então, Sessa pede grãos de trigo da seguinte maneira: um grão de trigo pela 1ª casa do tabuleiro, dois pela 2ª casa, quatro pela 3ª casa, e assim sucessivamente, dobrando a quantidade de grãos de uma casa para a próxima, até a 64ª casa do tabuleiro. No entanto, esse pagamento não pôdi sêr efetivado, uma vez quê a quantidade total de grãos de trigo era astronômica, devido ao crescimento exponencial apresentado na proposta de Sessa.
De acôr-do com esse conto, a quantidade total de grãos de trigo quê Sessa deveria receber póde sêr expressa por:
a) 264
b) 263 + 1
c) 263
d) 264 − 1
alternativa d
PARA AMPLIAR
Consulte o livro indicado a seguir, quê apresenta a história de um jovem quê utiliza a Matemática para resolver diferentes problemas.
• TAHAN, Malba. O homem quê calculava. 8. ed. Rio de Janeiro: recór, 2009.
63. Determine a razão de uma PG cujo primeiro termo é 7, o último termo é −54.432 e a soma de seus termos é −46.655.
−6
64. Em uma PG de oito termos, a3 = 800 e a8 =. Qual é a soma dos termos dessa PG?
65. ![]() Uma bola solta em quêda livre, após cada vez que se choca com o solo, atinge apenas 65% da altura atingida anteriormente, realizando deslocamentos perpendiculares ao solo. Considerando a altura inicial de 20 m, responda às kestões.
Uma bola solta em quêda livre, após cada vez que se choca com o solo, atinge apenas 65% da altura atingida anteriormente, realizando deslocamentos perpendiculares ao solo. Considerando a altura inicial de 20 m, responda às kestões.
a) Quantos metros de altura, no mássimo, a bola atinge após o 4º choque com o solo?
aproximadamente 3,57 m
b) Determine quantos metros a bola percórre do momento em quê é solta em queda livre até chocar-se com o solo pela:
• 2ª vez;
46 m
• 5ª vez.
81,02525 m
66. ![]() Junte-se a um colega para resolver esta ati vidade. Na aula de Matemática, a professora escreveu na lousa sequências cujos elemêntos estão dispostos em linhas de acôr-do com uma propriedade. ob-sérvim.
Junte-se a um colega para resolver esta ati vidade. Na aula de Matemática, a professora escreveu na lousa sequências cujos elemêntos estão dispostos em linhas de acôr-do com uma propriedade. ob-sérvim.

a) ![]() Expliquem a propriedade quê a professora utilizou para escrever essas sequências.
Expliquem a propriedade quê a professora utilizou para escrever essas sequências.
Resposta esperada: De acôr-do com a ordem das linhas, o primeiro número das sequências corresponde a um termo de uma PG em quê a 1 = 3 e q = 2. Já em cada linha, a sequência corresponde a uma PA de razão r = 3. Na 1ª linha tem apenas um número e, a partir da 2ª linha, a quantidade de números é o dôbro da quê tem na linha anterior.
b) De acôr-do com essa propriedade, determinem a soma dos termos da sequência indicada na 6ª linha.
4.560
Página cento e trinta e três
Soma dos termos de uma PG infinita
Na filosofia grega, Zenão de Eleia (c. 490-425 a.C.), discípulo de Parmênides e da escola Eleata, formulou quatro exemplos paradoxais quê buscavam explicar quê, do ponto de vista teórico, o movimento era impossível e, portanto, uma ilusão dos sentidos. Entre os exemplos formulados por Zenão para justificar sua tese, um dos mais conhecidos é o paradoxo de Aquiles e a tartaruga.
PARA PENSAR
Em Filosofia, o quê é um paradoxo? Se necessário, realize uma pesquisa.
Resposta esperada: Em Filosofia, podemos dizêr quê um paradoxo corresponde a um tipo de raciocínio/declaração quê parece estar bem fundamentado e sêr coerente, mas apresenta contradições lógicas e, por isso, não nos faz aceitar sua conclusão.
Leia o trecho a seguir.
MATEMÁTICA NA HISTÓRIA
O mais famoso paradoxo de Zenão é popularmente conhecido como “Aquiles e a tartaruga”. Nesse pequeno experimento mental, o herói grego disputava uma corrida com uma tartaruga, quê saía primeiro. Depois de um cérto tempo, Aquiles partia em seu encalço. Antes de ultrapassar a tartaruga, ele tinha quê alcançar o ponto em quê ela estava no momento de sua partida. Enquanto fazia isso, a tartaruga, é claro, se afastava mais um pouco. Repetindo esse processo ao infinito, o póbre herói jamais conseguiria ultrapassar o animal.
CHERMAN, Alexandre. Sobre os ombros de gigantes: uma história da física. Rio de Janeiro: Jorge Zarrár Editor, 2005. p. 21.
Nesse paradoxo, a ideia de quê Aquiles nunca alcançará a tartaruga parece fazer sentido de acôr-do com a argumentação de Zenão, porém costuma contrariar nosso pensamento, pois sabemos, por observação e experiência prática, quê Aquiles alcançará a tartaruga.
Para ilustrar essa situação, considere quê em um mesmo intervalo de tempo a tartaruga percorra a mêtáde da distância percorrida por Aquiles. Além díssu, considere quê Aquiles inicia sua corrida na posição P0 quando a tartaruga está 2 m à frente dele, na posição P1. De acôr-do com o paradoxo, quando Aquiles chegar à P1, a tartaruga estará 1 m à frente dele, na posição P2; quando Aquiles chegar à P2, a tartaruga estará m à frente dele, em P 3; e assim sucessivamente.

pôdêmos notar quê a sequência das distâncias, em métro, entre a tartaruga e Aquiles posicionados em P k e P k − 1, com k ∈ ℕ*, corresponde à PG infinita apresentada a seguir, em quê a1 = 2 e q = .
PARA PENSAR
A PG associada à situação póde sêr descrita pela função f: ℕ* → ℝ, definida por f(n) = 2 −n + 2. Em uma malha quadriculada ou utilizando um software de geometria dinâmica, esboce o gráfico dessa função e analise o quê ocorre com o valor de f (n) à medida quê aumentamos o valor de n.
Resposta esperada: À medida quê aumentamos o valor de n, o valor de f(n) aproxima-se de zero.
Página cento e trinta e quatro
Em relação à PG , vamos calcular a soma dos:
• dois primeiros termos: S2 = 2 + 1 = 3;
• três primeiros termos: S3 = 3 + = 3,5;
• quatro primeiros termos: S4 = = 3,75;
• cinco primeiros termos: S5 = = 3,875;
• seis primeiros termos: S6 = = 3,9375.
Observe como podemos indicar esses resultados na reta real.

PARA PENSAR
Calcule a soma dos sete primeiros termos dessa PG. Considerando o resultado quê você obteve e aqueles apresentados anteriormente, o quê você póde perceber?
3,96875. Resposta esperada: À medida quê aumentamos o valor de n, ou seja, a quantidade de termos considerados, a soma ôbitída aproxima-se de 4.
Note quê, à medida quê aumentamos o valor de n, ou seja, consideramos uma quantidade maior de termos da PG relacionada ao paradoxo de Aquiles e a tartaruga, a soma dêêsses termos se aproxima mais do número 4. Nesse caso, podemos dizêr quê a soma dos termos dessa PG infinita converge para o número 4.
De modo geral, nas progressões geométricas infinitas de razão q, em quê −1 < q < 1 e q ≠ 0, quanto maior o valor de n considerado, mais próximo de zero é q n. Nesse caso, dizemos quê, quando n tende ao infinito, ou seja, quando o valor de n aumenta indefinidamente, temos quê o limite de qn é igual a zero.
Assim, considerando a expressão S n = , com q ≠ 1, podemos calcular o limite de Sn, quando n tende ao infinito. Observe.
Dada uma PG infinita cujo primeiro termo é a 1 e a razão é q, com −1 < q < 1 e q ≠ 0, podemos determinar a soma S dêêsses infinitos termos como o limite da soma S n dos n termos dessa PG quando n tende a infinito. Assim:
S =
Em relação à PG infinita apresentada, temos quê o limite da soma de seus termos é dado por:
Portanto, nas condições consideradas, é possível supor quê Aquiles deve alcançar a tartaruga após ambos terem percorrido 4 m, o quê contraria o paradoxo apresentado.
PARA PENSAR
Com base no quê foi estudado, Zenão estava cérto ao supor quê Aquiles nunca alcançaria a tartaruga? Justifique sua resposta.
Resposta esperada: Não, pois, após uma quantidade indefinida de deslocamentos sucessivos realizados pelas duas personagens, Aquiles alcança a tartaruga após ambos percorrerem 4 m.
Página cento e trinta e cinco
ATIVIDADE RESOLVIDA
R15. Obtenha a fração geratriz da dízima periódica .
Resolução
= 2, 161616... = 2 + 0,16 + 0, 0016 + 0, 000016 +... = 2 + + ...
Na adição, a partir da segunda parcela, podemos notar quê as parcelas correspondem aos termos de uma PG infinita em quê:
• a1 =
• q =
Calculando a soma dos termos da PG infinita, obtemos:
Assim, segue quê:
Portanto, .
PARA PENSAR
Com uma calculadora, verifique a igualdade .
Resposta pessoal.
ATIVIDADES
67. Quais das progressões geométricas a seguir têm o limite da soma dos termos convergindo para um número real?
a) (−2, −4, −8, …)
b) (80, 20, 5, …)
c)
d)
e) (12; −9; 6,75; …)
f)
alternativas b, d e e
68. Calcule a soma dos termos da PG infinita indicada em cada item.
a)
b) (625, 125, 25 ,...)
c)
d) (25; 0,25; 0,0025; ...)
69. Obtenha a fração geratriz da dízima periódica indicada em cada item.
a) 1,7777...
b)
c) −0,9191...
d)
• ![]() Agora, escrêeva duas dízimas periódicas e troque-as com um colega, para quê um determine a fração geratriz das dízimas periódicas do outro. Depois, confiram juntos as resoluções.
Agora, escrêeva duas dízimas periódicas e troque-as com um colega, para quê um determine a fração geratriz das dízimas periódicas do outro. Depois, confiram juntos as resoluções.
Resposta pessoal.
70. Certa figura é formada por infinitas circunferências justapostas, de maneira quê tênham em comum um único ponto. Nessa figura, a 1ª circunferência tem o maior raio, com o dôbro da medida do raio da 2ª circunferência, quê, por sua vez, tem o raio com o dôbro da medida do raio da 3ª circunferência, e assim por diante.
Observe as primeiras circunferências quê formam essa figura.

Considerando quê a maior dessas circunferências tenha 10 cm de raio, podemos afirmar quê a soma dos perímetros das infinitas circunferências quê compõem essa figura, em centímetro, é:
a) 10(pi)"
b) 20(pi)"
c) 30(pi)"
d) 40(pi)"
e) 50(pi)"
alternativa d
DICA
Lembre-se! O perímetro de uma circunferência de raio r é dado por 2(pi)"r.
71. resôuva a equação x + +... = 30, sabendo quê as parcelas no 1º membro correspondem a termos de uma PG infinita.
x = 24
Página cento e trinta e seis
VOCÊ CONECTADO
Estudando PA na planilha eletrônica
pôdêmos utilizar a planilha eletrônica LibreOffice Calc para estudar uma PA, obtendo alguns de seus termos, a soma dêêsses termos e representando esses valores no plano cartesiano. O LibreOffice Calc e os demais programas de escritório da LibreOffice estão disponíveis para dáum-lôude em https://livro.pw/owkny (acesso em: 26 jul. 2024).
Para estudar uma PA na planilha eletrônica, vamos considerar a quêstão a seguir, que foi apresentada na atividade R10 da página 121.
Após a consultoria de um agrônomo, certa fazenda vai adotar 12 novas técnicas de plantio e cultivo, visando aumentar a produção de soja. Em 2026, essas técnicas serão aplicadas em 80 ha da área plantada, aumentando gradativamente até cobrir todos os 800 ha de plantio da fazenda, em 2035. Observe a projeção da produção de soja nessa fazenda para os próximos anos.
Ano |
Produção projetada (saca) |
|---|---|
2026 |
108.000 |
2027 |
110.000 |
2028 |
112.000 |
2029 |
114.000 |
Considerando o crescimento na produção de soja constante até 2035, quantas sacas de soja serão produzidas no período de 2026 a 2035?
Na situação descrita nessa atividade, como a perspectiva de crescimento da produção de soja a cada ano é constante, temos quê a variação da projeção da produção, em sacas, de um ano para o próximo é dada por:
110.000 − 108.000 = 2.000
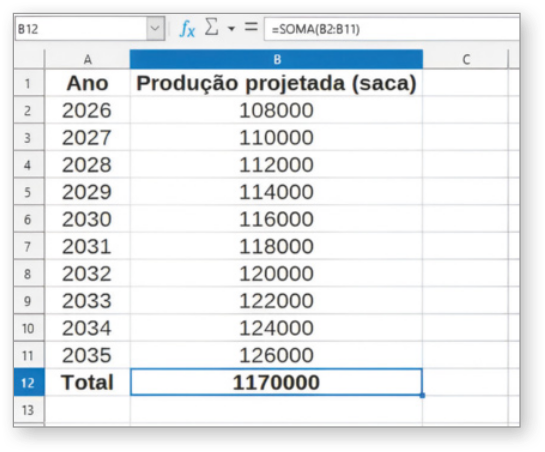
Para resolver essa questão podemos obtêr, na planilha eletrônica LibreOffice Calc, as projeções da produção de soja, em saca, para os anos de 2026 até 2035 e, em seguida, a soma dêêsses valores da seguinte maneira.
A Nas células A1 e B1, escrevemos Ano e Produção projetada (saca), respectivamente. Em seguida, nas células A2:A11 escrevemos os anos de 2026 até 2035 e indicamos o valor da projeção da produção para 2026 na célula B2. Na célula B3, escrevemos =B2+2.000 para obtêr o valor da projeção da produção para 2027 e pressionamos a tecla Enter. Depois, selecionamos a célula B3, clicamos na opção ![]() e, com o botão esquerdo do máuzi pressionado, arrastamos até a célula B11.
e, com o botão esquerdo do máuzi pressionado, arrastamos até a célula B11.
Página cento e trinta e sete
Assim, obtemos os valores das projeções da produção de soja até 2035.
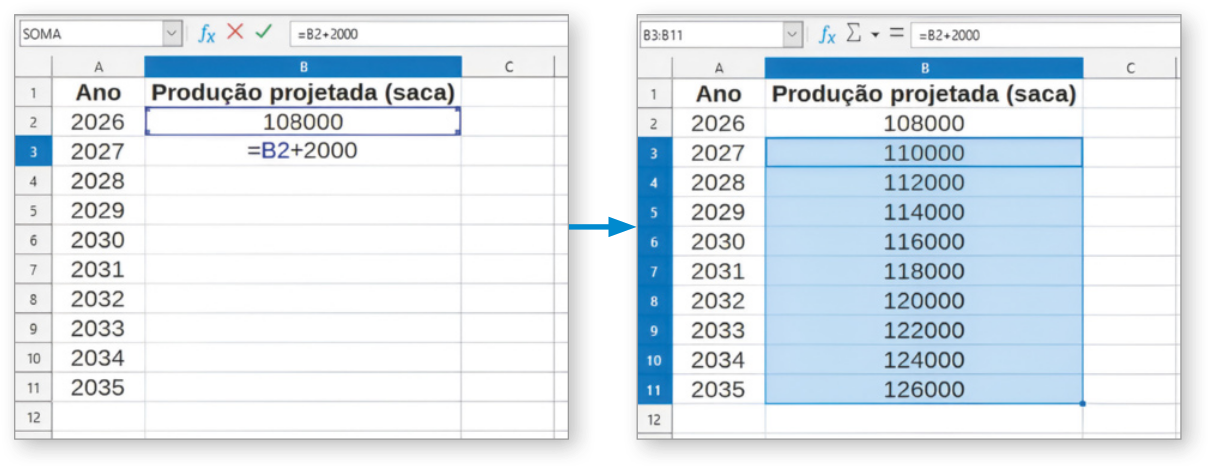
B Para obtêr a soma dessas projeções, digitamos Total na célula A12 e =SOMA(B2:B11) na célula B12 e pressionamos a tecla Enter.
Portanto, podemos concluir quê no período de 2026 a 2035 deverão sêr produzidas, nessa fazenda, 1.170.000 sacas de soja.
MÃOS À OBRA
1. Em relação à situação apresentada, considere uma sequência numérica em quê a 1 corresponde à projeção da produção de soja, em saca, para 2026; a 2 para 2027; a 3 para 2028; e assim sucessivamente.
a) escrêeva o termo geral dessa sequência. Em seguida, calcule o valor de a 15 e explique o quê ele representa em relação à situação apresentada na questão da página 136.
an = 108.000 + 2.000(n − 1) ou an = 2.000n + 106.000, com n ∈ ℕ*. a15 = 136.000. Na situação apresentada, esse valor corresponderia à projeção da produção de soja, em saca, para 2040, caso a perspectiva de crescimento se mantenha constante até esse ano.
b) Na planilha LibreOffice Calc, construa um gráfico de dispersão para representar os termos dessa PA. Para isso, utilize a opção Inserir gráfico do menú. Nesse gráfico, os pontos de coordenadas (x, y) indicam os termos de posição x e valor y da PA.
• Qual é o comportamento dêêsse gráfico: linear, quadrático, exponencial ou logarítmico? Justifique.
Construção do estudante. Resposta esperada: Esse gráfico tem comportamento linear e póde sêr descrito pela função f: ℕ* → ℝ, definida por f(x) = 2.000x + 106.000.
2. Considere uma PG em quê a 1 = −1 e a 2 = −2. Utilizando procedimentos análogos aos apresentados no exemplo e com auxílio da planilha eletrônica LibreOffice Calc, determine os 10 primeiros termos dessa PG. Depois, resôuva os itens a seguir.
(−1, −2, −4, −8, −16, −32, −64, −128, −256, −512, ...)
a) escrêeva o termo geral dessa PG.
an = −1 ⋅
b) Na planilha eletrônica LibreOffice Calc, construa um gráfico de dispersão para representar os termos dessa PG. Qual é o comportamento dêêsse gráfico: linear, quadrático, exponencial ou logarítmico? Justifique.
Construção do estudante. Resposta esperada: Esse gráfico tem comportamento exponencial e póde sêr descrito pela função f: ℕ* → ℝ, definida por f(x) = −1 ⋅ 2 (x − 1).
Página cento e trinta e oito
INTEGRANDO COM...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
Demografia
Você sabe o quê é demografia? Leia o texto a seguir.
[...]
A Demografia é uma ciência quê tem por finalidade o estudo de populações humanas, enfocando aspectos tais como sua evolução no tempo, seu tamãnho, sua distribuição espacial, sua composição e características gerais.
Uma preocupação fundamental no estudo das populações humanas é com o seu tamãnho em determinado momento e com os possíveis fenômenos quê determinam ou afetam esse tamãnho, tais como os nascimentos, os óbitos e fenômenos migratórios. É importante investigar de quê modo cada um dêêsses componentes póde sêr afetado por mudanças nos demais e como esses fenômenos se relacionam entre si.
Além da preocupação com o tamãnho e crescimento da população, é de fundamental importânssia em Demografia o estudo da composição da população por idade e sexo, principalmente pela sua repercussão sobre os fenômenos demográficos, sociais e econômicos. [...]
[...]
CERQUEIRA, Cézar Augusto; GIVISIEZ, Gustavo Henrique N. Conceitos básicos em demografia e dinâmica demográfica brasileira. In: RIOS-NETO, Eduardo Luiz G.; RIANI, Juliana de Lucena R. (org.). Introdução à demografia da educação. Campinas: Abep, 2004. p. 15.
Estimar ou projetar a variação do tamãnho de uma população humana ao longo do tempo sempre foi um desafio e motivo de grande interêsse para cientistas, governantes e diferentes tipos de organização. Para obtêr estimativas dêêsse tipo, os demógrafos consideram diferentes tipos de variável (taxas de natalidade e mortalidade, migração etc.). Atualmente, com o avanço da tecnologia, quê facilita o acesso e o armazenamento de dados, e o desenvolvimento de modelos matemáticos, há diferentes métodos para realizar essas estimativas.

Página cento e trinta e nove
NO MUNDO DO TRABALHO
Demógrafo
O trabalho de um demógrafo é realizado em parceria com profissionais de áreas como Ciências Sociais, Geografia, Matemática e Estatística, a fim de analisar e interpretar dados populacionais coletados e realizar um estudo quê retrate da maneira mais fiel possível a realidade da população. Esses estudos buscam conhecer fatores de interêsse público relacionados a educação, saúde, território, economia e meio ambiente e são também utilizados para tomadas de decisões de governantes, por exemplo.
Assista ao vídeo indicado a seguir para obtêr mais informações sobre as atividades do demógrafo.
• DESAFIO profissão: demografia. [S. l.: s. n.], 2017. 1 vídeo (27 min). Publicado pelo canal TVPUC. Disponível em: https://livro.pw/cfyyp. Acesso em: 26 jul. 2024.
No gráfico a seguir, os dados utilizados são estimativas ou projeções realizadas pelo Departamento de Economia e Assuntos Sociais, da Divisão Populacional das Nações Unidas. Analisando êste gráfico, é possível avaliar o comportamento do crescimento populacional mundial.
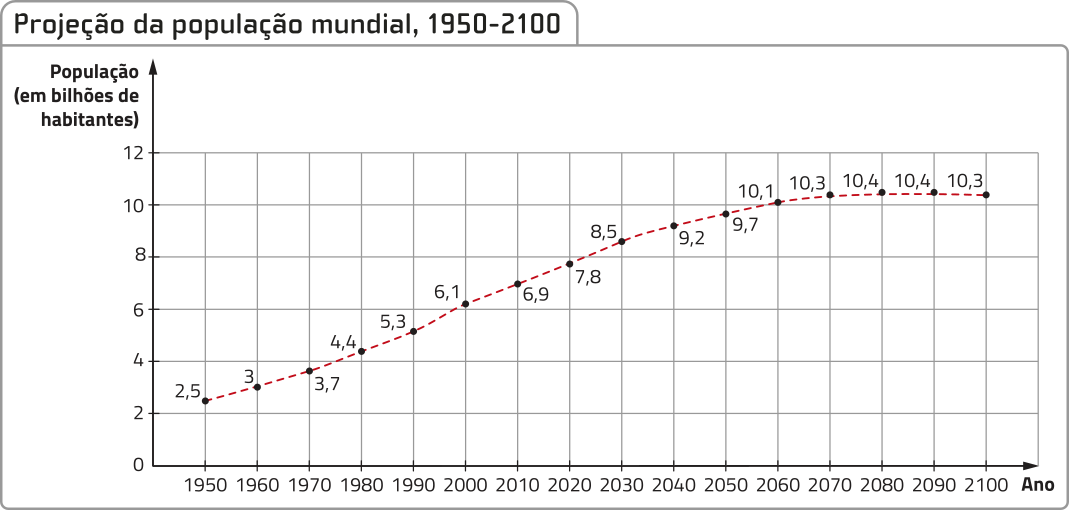
Fonte: IÚLNÁITED NATIONS. Department ÓF Economic ênd Social Affairs. Population Division. uôrd population prospects 2024. Localizável em: Compact (most used: estimates ênd medium projections) (XLSX, 17.94 MB). Nova iórk: UN, c2024. Disponível em: https://livro.pw/ougqt. Acesso em: 26 jul. 2024.
PENSANDO NO ASSUNTO
1. Explique, com suas palavras, um dos objetivos da Demografia.
Resposta pessoal.
2. Há quanto tempo você mora no mesmo município? Nesse período, você percebeu mudanças na quantidade de habitantes? Justifique.
Respostas pessoais.
3. Em relação ao gráfico apresentado, responda.
a) Que tipo de gráfico foi utilizado para representar as informações?
gráfico de segmentos
b) Qual é o período de tempo correspondente aos dados apresentados no gráfico?
de 1950 até 2100
c) De quantos bilhões de habitantes corresponde o crescimento populacional entre 1950 e 2000? E entre 2000 e 2050? E entre 2050 e 2100?
entre 1950 e 2000: 3,6 bilhões de habitantes; entre 2000 e 2050: 3,6 bilhões de habitantes; entre 2050 e 2100: 0,6 bilhão de habitantes
d) pôdêmos dizêr quê a sequência dos números correspondentes ao crescimento da população mundial nos anos indicados no gráfico formam uma PA? E uma PG? Justifique suas respostas.
A sequência não corresponde a uma PA, pois a diferença entre um termo e o anterior, a partir do 2º termo, não são todos iguais.
A sequência não corresponde a uma PG, pois a razão entre um termo e o anterior, a partir do 2º termo, não são todos iguais.
Página cento e quarenta
4. Acompanhe como é possível estimar a população de um município para períodos futuros até 2070, com base em diferentes métodos matemáticos e dados de dois Censos Demográficos.
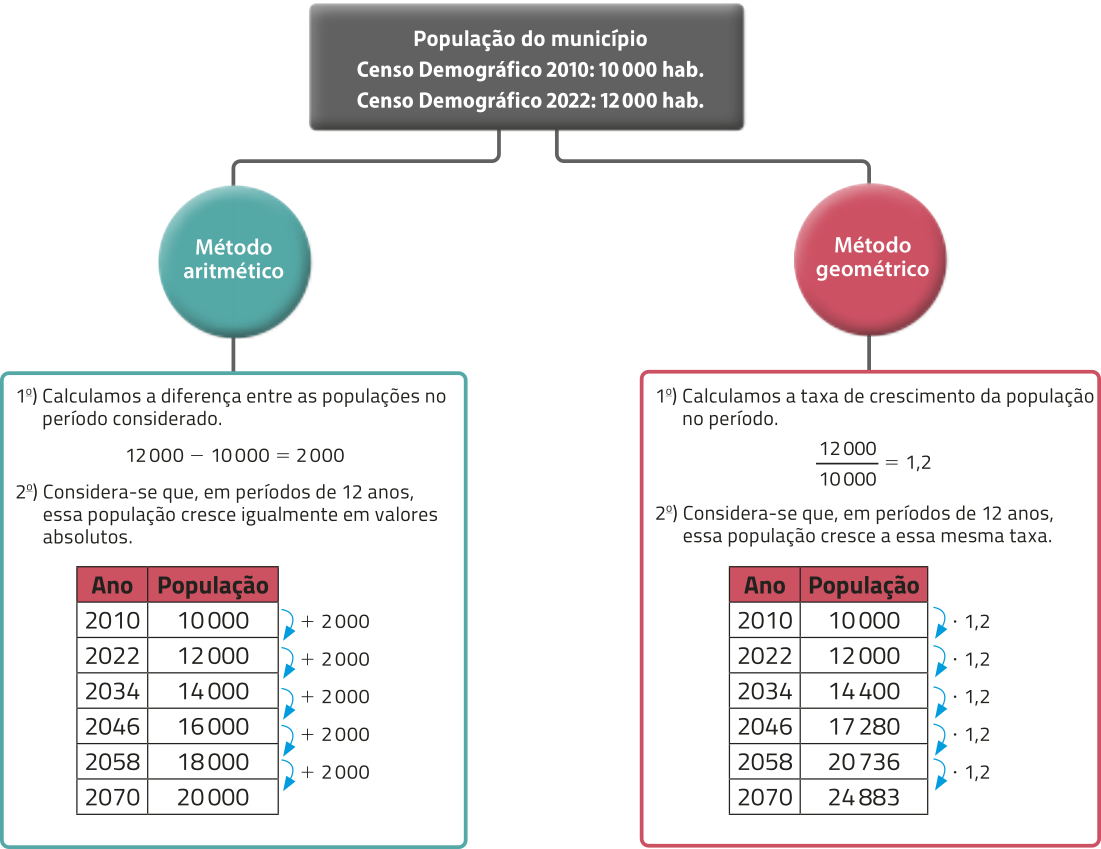
a) Em qual dêêsses métodos a população varia de acôr-do com uma PG? E de acôr-do com uma PA?
método geométrico; método aritmético
b) Estime a população dêêsse município para o ano de 2082 utilizando cada um dêêsses métodos.
método aritmético: 22.000 hab.; método geométrico: aproximadamente 29.860 hab.
c) Observando os dados apresentados no gráfico sobre a população mundial, é correto afirmar quê as estimativas foram realizadas com base em um dêêsses métodos? Justifique.
Resposta esperada: Não, pois nas estimativas realizadas a população não cresce igualmente em valores absolutos nem a uma mesma taxa de crescimento.
5. ![]() Nesta questão, exploraremos a seguinte situação-problema.
Nesta questão, exploraremos a seguinte situação-problema.
Qual é a estimativa da população para o ano de 2070 no município em quê você mora?
Junte-se a dois côlégas, e façam o quê se pede em cada um dos itens.
a) Vocês acham quê em 2070 a população do município em quê vocês moram será maior ou menor quê a população atual? Justifiquem.
Resposta pessoal.
b) Pesquisem, nos Censos Demográficos 2010 e 2022, a população do município em quê vocês moram e registrem. Utilizando cada um dos métodos apresentados na atividade anterior e os dados pesquisados, estimem a população do município em períodos de tempos iguais e equivalentes ao período entre os dois Censos Demográficos pesquisados. Façam a estimativa até o ano de 2070.
A resposta depende do município em quê os estudantes moram.
c) Investiguem se institutos de pesquisa ou outras organizações já fizeram alguma estimativa da população do município no ano de 2070. Pesquisem como foi feito o tratamento das informações e, se possível, qual foi o método utilizado. Depois, produzam um texto relacionando as informações levantadas e os resultados obtidos no item anterior.
Pesquisa e elaboração dos estudantes.
Página cento e quarenta e um
Noções de linguagem de programação
Você já reparou quê, no dia a dia, programamos diferentes aparelhos eletrônicos para realizar determinada tarefa? Observe os exemplos.



É importante notarmos quê esses e outros aparelhos eletrônicos apenas executam tarefas e processam dados conforme instruções quê recebem. Programar ou codificar significa escrever um conjunto de instruções para um aparelho, de maneira quê ele as compreenda e as execute.
PARA PENSAR
Cite outros aparelhos quê você conhece quê necessitam de alguma programação para executar determinada função. Depois, dêz-creva uma função quê cada aparelho dêêsses executa de acôr-do com a instrução do usuário.
Respostas pessoais.
Página cento e quarenta e dois
Para inserir instruções em um computador (ou outro aparelho eletrônico quê possa sêr programado), d fórma organizada, é necessário utilizar uma linguagem específica. As chamadas linguagens de programação permitem a escrita de comandos quê utilizam palavras, regras e pontuações. Esses comandos, ao serem estruturados de maneira lógica e compreensível à linguagem de programação escolhida, formam os códigos ou algoritmos computacionais necessários para determinar a realização de uma ação específica. Atualmente, existem muitas linguagens de programação, e cada uma é mais, ou menos, indicada de acôr-do com o quê se deseja realizar.
De maneira geral, um algoritmo corresponde a uma sequência de passos finitos e ordenados, necessários para realizar determinada tarefa, não apenas relacionada à programação de uma máquina. Por exemplo, uma receita de salada de frutas corresponde a um algoritmo para preparar essa salada.
Para expressar os passos de um algoritmo, também podemos utilizar um fluxograma. Observe, por exemplo, um algoritmo representado por meio de um fluxograma para verificar se determinado número natural n é par ou é ímpar.
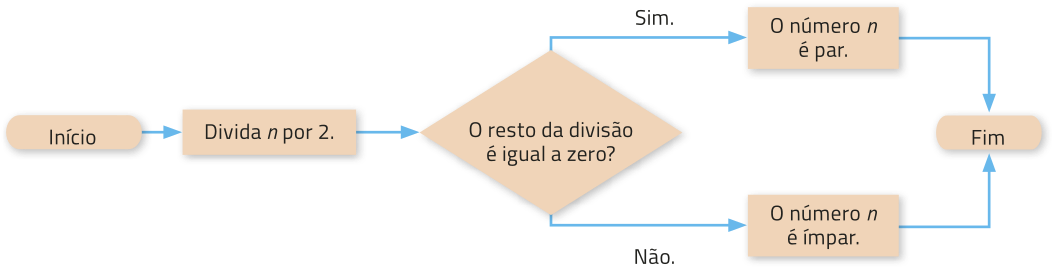
Nesse fluxograma, as figuras utilizadas para apresentar a sequência de passos de um procedimento possuem significados de acôr-do com seu formato. Observe.

Página cento e quarenta e três
NO MUNDO DO TRABALHO
Programação, avanço tecnológico e o mercado de trabalho
Na era digital em quê vivemos, novas tecnologias surgem a cada dia tornando-se essenciais. Estão presentes em aplicativos, sáites, jogos, rêdes sociais e sistemas operacionais, desenvolvidos por profissionais quê trabalham com programação. Com esse avanço, a demanda por esses profissionais qualificados tem aumentado em diversos setores, quê buscam soluções tecnológicas e inovadoras para aprimorar processos e experiências. Quem trabalha com programação póde atuar como engenheiro de software, analista de sistemas, arquiteto de rêdes, programador de jogos digitais, entre outros.
Assista ao vídeo indicado a seguir para obtêr mais informações sobre as possibilidades de carreira de um programador.
• PROGRAMAÇÃO e sistemas de informação: o mundo tecnológico #VocêPodeSer Ep. 12. [S. l.: s. n.], 2023. 1 vídeo (17 min). Publicado pelo canal Manual do Mundo. Disponível em: https://livro.pw/pvjme. Acesso em: 25 jan. 2024.
ATIVIDADES
72. De acôr-do com o fluxograma apresentado, resôuva as kestões a seguir.
a) Que conceitos matemáticos fundamentam o algoritmo representado por esse fluxograma?
Resposta esperada: Todo número natural é par ou é ímpar, e qualquer número par é divisível por 2.
b) Há algum passo correspondente à tomada de dê-cisão? Qual?
Sim. O passo quê questiona se a divisão, realizada no passo anterior, tem résto igual a zero.
c) dêz-creva os procedimentos realizados para verificar se cada número natural indicado a seguir é par ou é ímpar, de acôr-do com esse fluxograma.
• 237
Primeiro realizamos a divisão 237 ∶ 2 = 118, com résto 1. Como o résto da divisão não é igual a zero, concluímos quê 237 é ímpar.
• 108
Primeiro realizamos a divisão 108 ∶ 2 = 54, com résto zero. Como o résto da divisão é igual a zero, concluímos quê 108 é par.
d) Pense em outro algoritmo, quê também possa sêr utilizado para verificar se determinado número natural n é par ou é ímpar. Depois, represente esse algoritmo por um fluxograma.
Resposta nas Orientações para o professor.
73. O departamento de gestão de pessoas de uma empresa utiliza um fluxograma sempre quê tem de contratar um novo funcionário para determinado cargo. Observe.
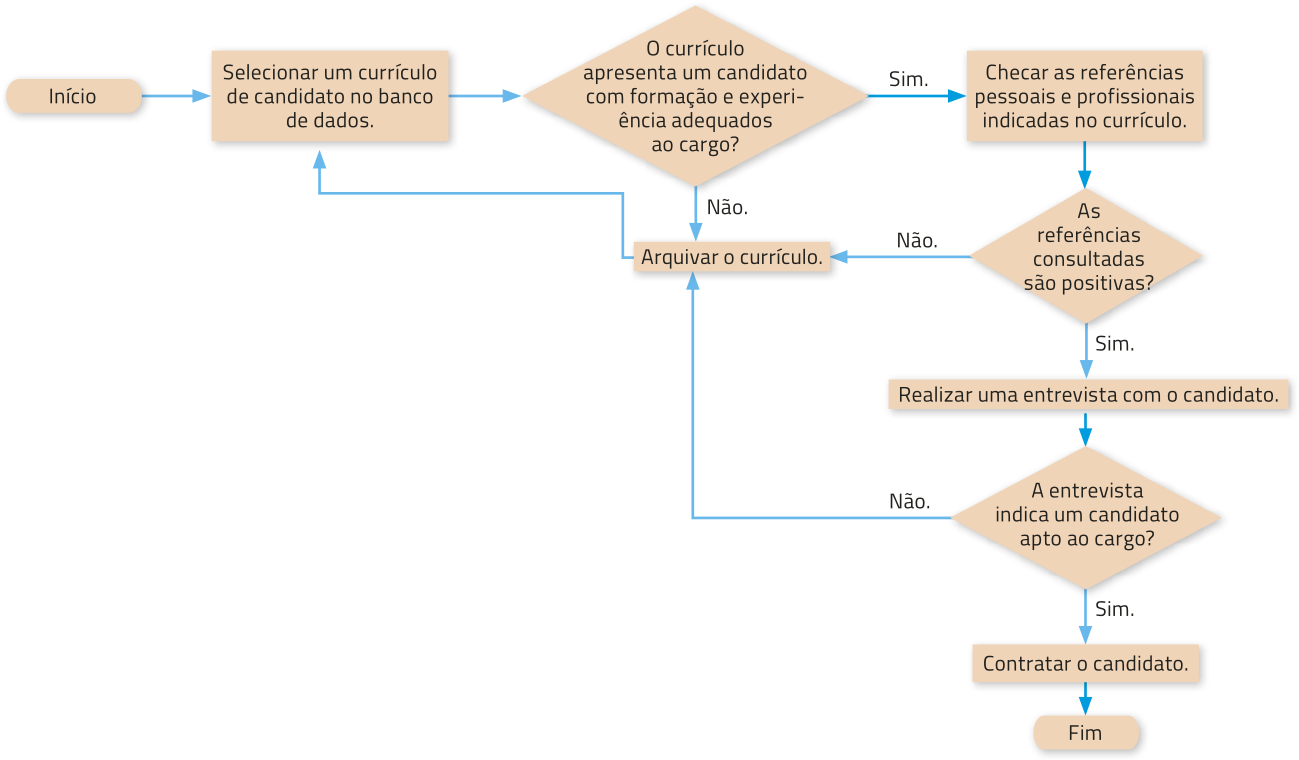
a) O quê é feito quando o currículo não apresenta um candidato com formação e experiência adequadas a um cargo?
O currículo é arquivado, e retoma-se o processo.
b) Sempre quê o currículo analisado apresenta um candidato com formação e experiência adequadas a um cargo, esse candidato é contratado?
Resposta esperada: Não, além da análise de currículo, são analisadas as referências pessoais e profissionais do candidato e realizada uma entrevista para indicação de um candidato ápto ao cargo.
c) Qual é a última tomada de dê-cisão feita pelo departamento de gestão de pessoas antes de contratar um funcionário?
Verificar se a entrevista indica um candidato ápto ao cargo.
d) ![]() Você já participou de algum processo seletivo para um emprego ou estágio? Em uma roda de conversa, comente como foi essa experiência e, se possível, explique as etapas dessa seleção e como elas poderiam sêr representadas por um fluxograma.
Você já participou de algum processo seletivo para um emprego ou estágio? Em uma roda de conversa, comente como foi essa experiência e, se possível, explique as etapas dessa seleção e como elas poderiam sêr representadas por um fluxograma.
Resposta pessoal.
Página cento e quarenta e quatro
74. escrêeva os cinco primeiros termos da sequência numérica determinada pelo fluxograma a seguir e defina essa sequência de maneira recursiva.
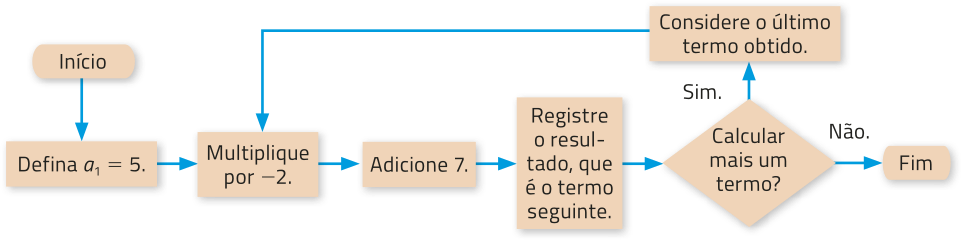
(5, −3, 13, −19, 45, ...); a n = −2an − 1 + 7 e a1 = 5, com n ∈ ℕ* e n ≥ 2
75. Nas fichas a seguir estão indicados, fora de ordem, os passos de um algoritmo para a construção de um hekzágono regular usando régua e compasso. Ordene esses passos e, depois, siga-os para construir a figura com régua e compasso.
a.
Com abertura de medida AB, fixar a ponta-seca do compasso em A e traçar uma circunferência.
b.
Com a régua, traçar , , , e . Por fim, colorir a região interna da figura ôbitída.
c.
Com a mesma abertura, fixar a ponta-seca do compasso em C, traçar um arco quê cruza a última circunferência traçada e marcar o ponto D. De maneira análoga, fixar a ponta-seca do compasso em F e marcar o ponto E.
d.
Com a mesma abertura, fixar a ponta-seca do compasso em B e traçar outra circunferência. Marcar o ponto O na interseção das circunferências.
e.
Utilizar a régua para traçar , um dos lados do hekzágono.
f.
Com a mesma abertura, fixar a ponta-seca do compasso em O e traçar uma circunferência. Na interseção dessa circunferência com a de centro B e com a de centro A, marcar os pontos C e F, respectivamente.
75. e - a - d - f - c - b. Construção do estudante.
76. escrêeva os passos de um algoritmo quê possa sêr utilizado para construir um triângulo equilátero com 3 cm de lado com régua e compasso.
Resposta nas Orientações para o professor.
77. Um piscicultor cria tilápias quê são vendidas para frigoríficos e pesqueiros. A cada 170 dias, as tilápias são pesadas e destinadas de acôr-do com os critérios indicados a seguir.
• Se a tilápia tem até 350 g de massa, é destinada a outro tanque de engorda.
• Se a tilápia tem mais de 350 g e menos de 700 g de massa, é destinada ao frigorífico.
• Se a tilápia tem 700 g de massa ou mais, é destinada ao pesqueiro.
a) Após uma pesagem, para onde é destinada uma tilápia com massa igual a:
• 495 g?
frigorífico
• 810 g?
pesqueiro
• 309 g?
tanque de engorda
b) No caderno, desenhe um fluxograma para representar os passos utilizados pelo piscicultor na destinação das tilápias após as pesagens.
Resposta nas Orientações para o professor.
78. Analise a sequência numérica a seguir.
(7, −13, −33, −53, ...)
a) Construa um fluxograma quê represente os procedimentos para obtêr, de maneira recursiva, os termos da sequência numérica apresentada.
Resposta nas Orientações para o professor.
b) Determine o 9º termo dessa sequência.
−153
79. ![]() Junte-se a dois côlégas, e escôlham algum processo quê vocês realizam no dia a dia, ou alguma atividade quê alguém precise programar e quê póde sêr descrita por um algoritmo. Em seguida, construam um fluxograma para representar esse algoritmo.
Junte-se a dois côlégas, e escôlham algum processo quê vocês realizam no dia a dia, ou alguma atividade quê alguém precise programar e quê póde sêr descrita por um algoritmo. Em seguida, construam um fluxograma para representar esse algoritmo.
Resposta pessoal.
Página cento e quarenta e cinco
80. Você sabe o quê é Portugol? O Portugol é uma pseudolinguagem de programação quê permite ao usuário desenvolver algoritmos estruturados em português d fórma simples e intuitiva. Seu objetivo é facilitar o aprendizado de lógica de programação e algoritmos para estudantes não habituados com programação. Os algoritmos escritos em Portugol costumam ter a estrutura apresentada no qüadro.

Para “declarar as variáveis”, devemos identificar quais variáveis serão utilizadas (área; nota; A; x; soma etc.) e indicar os tipos de dados correspondentes às variáveis utilizadas, conforme apresentado a seguir.
• Inteiro: qualquer número inteiro. Exemplos: −20; −10; 0; 5; 10.
• Real: qualquer número real. Exemplos: −8; −3,5; 0; 6; 10,18; pi.
Em comandos, desenvolvemos o algoritmo. Para isso, podemos utilizar comandos de entrada e de saída e alguns operadores, conforme os exemplos a seguir.
• escrêeva: o programa escreve valores informados ou obtidos;
• Leia: o programa recebe dados digitados pelo usuário.
• Operadores Aritméticos: +, −, *, /, raiz(), ^, sen(), cos(), mod, div, ...;
• Operadores Lógicos: e, ou, não;
• Operadores Relacionais: =, ≠ (ou =/=), >, ≥ (ou >=), <, ≤ (ou <=).
PARA AMPLIAR
Acesse o sáiti a seguir para utilizar e obtêr mais informações sobre a pseudolinguagem de programação Portugol.
• PORTUGOL WEBSTUDIO. [S. l.], [2024]. sáiti. Disponível em: https://livro.pw/xjuty. Acesso em: 9 jun. 2024.
Observe, nos exemplos a seguir, dois algoritmos escritos em Portugol.

Fontes dos dados: BARBOSA, Lucas Lemos; COUTO, crístian Marlon Souza; TERRA, Ricardo. Portucol: uma pseudolinguagem inspirada em C ANSI para o ensino de lógica de programação e algoritmos. In: WORKSHOP SOBRE EDUCAÇÃO EM COMPUTAÇÃO, 24., 2016, Lavras. Anais [...]. Lavras: Universidade Federal de Lavras, 2016. Disponível em: https://livro.pw/ajety.
CÁMARA-CHÁVEZ, Guillermo. BCC 201: introdução à programação Portugol. Outro Preto: Ufop, [201-]. p. 1-35. Disponível em: https://livro.pw/ytjxn. Acessos em: 26 jul. 2024.
De acôr-do com as informações e exemplos apresentados, resôuva as kestões a seguir.
a) Quais variáveis aparécem em cada exemplo? E quais operadores?
exemplo 1: variáveis: x, y, z; operadores: +, =;
exemplo 2: variáveis: a, b, soma; operadores: +, =
b) O quê é realizado ao se executar o algoritmo do exemplo 1?
É calculada a soma 10 + 5 = 15.
c) Qual é a principal diferença entre os cálculos realizados pêlos algoritmos do exemplo 1 e do exemplo 2?
Resposta esperada: No exemplo 1, o algoritmo realiza a adição de dois números inteiros predefinidos, 10 e 5; já no exemplo 2, o algoritmo realiza a adição de dois números quaisquer do tipo real, quê devem sêr inseridos pelo usuário ao executar o algoritmo.
d) ![]() De maneira análoga à apresentada nos exemplos, em dupla, escrevam um algoritmo em Portugol para calcular o produto de três números reais quaisquer, quê devem sêr digitados por quem executar o algoritmo.
De maneira análoga à apresentada nos exemplos, em dupla, escrevam um algoritmo em Portugol para calcular o produto de três números reais quaisquer, quê devem sêr digitados por quem executar o algoritmo.
Resposta nas Orientações para o professor.
Página cento e quarenta e seis
Linguagem de programação
Atualmente, estão disponíveis inúmeras linguagens de programação. Neste tópico, em particular, vamos apresentar e utilizar o Scratch, uma linguagem de programação gratuita e ôn láini, desenvolvida por um grupo de pesquisadores do Massachusetts ínstitut ÓF Technology (MIT-USA), em quên-brigi, nos Estados Unidos. Essa linguagem foi projetada especialmente para atender a um público com idade entre 8 e 16 anos e para possibilitar o aprendizado de programação com base em conceitos elementares. Por sêr uma linguagem bastante dinâmica e interativa, póde sêr utilizada por qualquer pessoa quê queira se iniciar no mundo da programação, independentemente de sua faixa etária ou nível de escolaridade.
Analise uma animação programada na linguagem Scratch, na qual a personagem (gato) desloca-se de maneira a traçar o contôrno de um quadrado com 200 unidades de comprimento de lado.
PARA PENSAR
Explique com suas palavras o raciocínio utilizado no algoritmo apresentado. Você escreveria esse algoritmo de outra maneira? Qual?
Respostas pessoais.
DICA
No menú do Scratch, selecione o idioma Português brasileiro na opção ![]() .
.
Utilizando a opção ![]() é possível adicionar a categoria Caneta.
é possível adicionar a categoria Caneta.
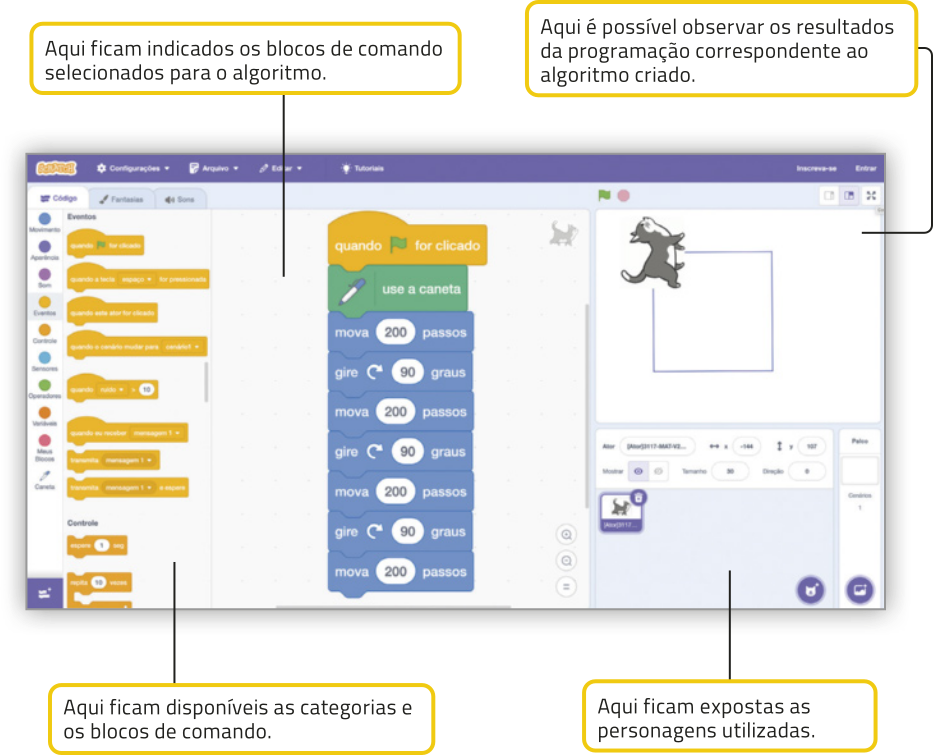
PARA AMPLIAR
Acesse o sáiti indicado a seguir para utilizar e obtêr mais informações sobre a linguagem de programação Scratch.
• SCRATCH. [S. l.], [2016]. sáiti. em: https://livro.pw/httab. Acesso em: 26 jul. 2024.
Nesse caso, foram utilizados os seguintes blocos de comando na construção do algoritmo.



Página cento e quarenta e sete
Também podemos utilizar o Scratch para analisar dados e apresentar respostas. No fluxograma a seguir, está representado um algoritmo para determinar se, sêndo dadas as medidas de três segmentos de reta, é possível construir um triângulo cujos lados tênham essas medidas.
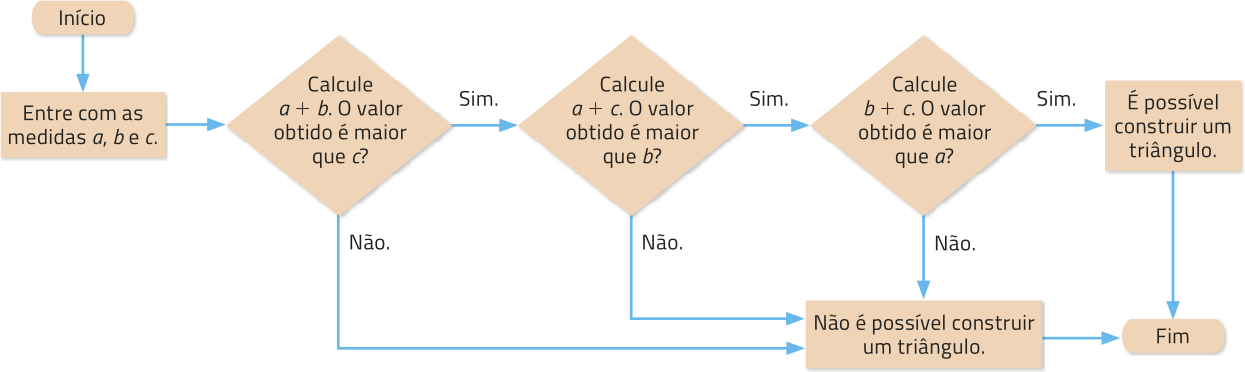
pôdêmos representar esse fluxograma, no Scratch, com o algoritmo a seguir. Com ele, o resultado da possibilidade de se construir um triângulo com as medidas indicadas será apresentado no balão de fala da personagem.
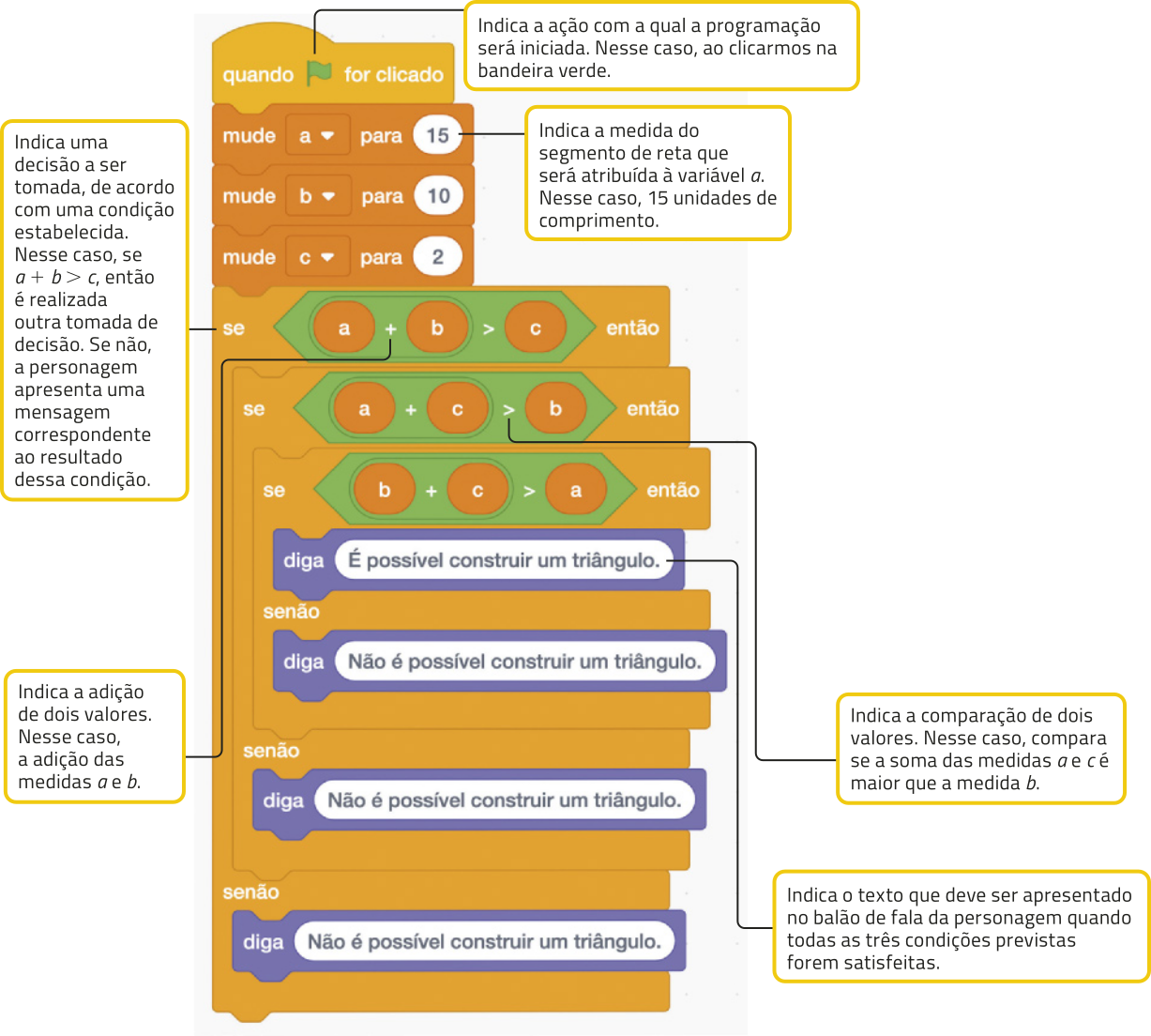
DICA
Antes de construir esse algoritmo Scratch, é necessário criar as variáveis a, b e c.
PARA PENSAR
No exemplo, com as medidas indicadas para a, b e c, qual será a fala da personagem ao clicarmos na bandeira vêrde? E qual será sua fala se ajustarmos as medidas de a, b e c para, respectivamente, 12, 10 e 8?
Não é possível construir um triângulo.
É possível construir um triângulo.
Página cento e quarenta e oito
ATIVIDADES
81. Considerando o algoritmo escrito na linguagem Scratch apresentado na página 147, resôuva as kestões.
a) O algoritmo construído permite quê o usuário altere os valores de a, b e c? Justifique.
Resposta esperada: Não, pois no algoritmo construído quem determina os valores das variáveis é o criador do algoritmo, e não o usuário.
b) ![]() Reúna-se a um colega, reproduzam o algoritmo no Scratch e alterem-no para quê seja possível o usuário escolher os valores de a, b e c. Depois, comparem suas respostas com as de outra dupla: vocês fizeram o mesmo algoritmo? Quais são as semelhanças e as diferenças?
Reúna-se a um colega, reproduzam o algoritmo no Scratch e alterem-no para quê seja possível o usuário escolher os valores de a, b e c. Depois, comparem suas respostas com as de outra dupla: vocês fizeram o mesmo algoritmo? Quais são as semelhanças e as diferenças?
Respostas nas Orientações para o professor.
DICA
No item b, vocês poderão utilizar os seguintes blocos:

82. Observe o algoritmo e o resultado de uma programação realizada no Scratch.
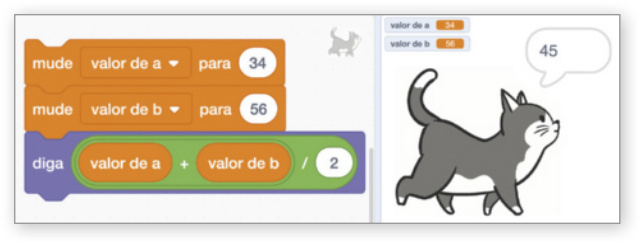
DICA
No comando em vêrde dêêsse algoritmo, o sín-bolo / indica uma divisão.
Esse algoritmo póde sêr utilizado para:
a) verificar se dois números dados são pares.
b) calcular o termo central de três termos consecutivos de uma PG, dados o maior e o menor termos.
c) calcular a área de um retângulo, dadas as medidas do maior e do menor lado.
d) calcular o termo central de três termos consecutivos de uma PA, dados o maior e o menor termos.
alternativa d
PARA PENSAR
Você consegue pensar em outra utilização para o algoritmo propôsto?
Resposta possível: O algoritmo propôsto também póde sêr utilizado para calcular a média aritmética de dois números.
83. No início do estudo sobre linguagem de programação, utilizamos um algoritmo escrito na linguagem Scratch para representar o contôrno de um quadrado com 200 unidades de comprimento de lado. Analise, a seguir, outro algoritmo, nessa mesma linguagem de programação, para obtêr essa representação.
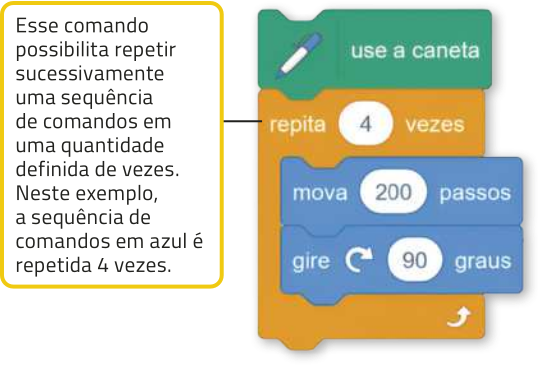
a) Determine qual das figuras corresponde ao resultado da programação do seguinte algoritmo. Justifique sua resposta.
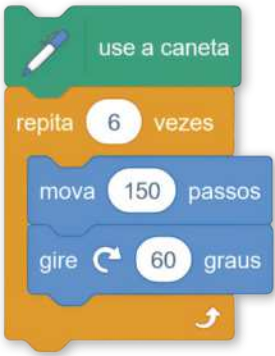
PARA PENSAR
por quê um dos comandos indica um giro de medida “60 graus”?
Resposta esperada: Porque essa é a medida de cada ângulo externo de um hekzágono regular.
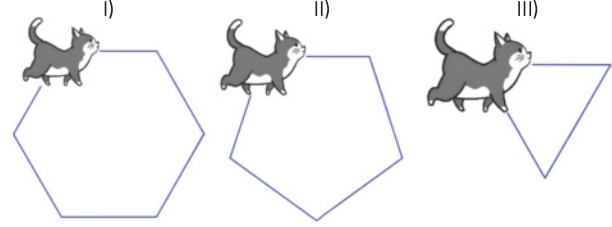
figura I. Resposta esperada: O algoritmo descrito para I determina um hekzágono regular com lados de 150 unidades.
b) Utilizando o comando apresentado no algoritmo do item anterior, com o qual é possível repetir uma sequência de comandos, escrêeva outro algoritmo para construir cada figura quê você não indicou como resposta. Considere quê ambas as figuras têm lados com medida de 150 unidades. Justifique sua resposta.
Resposta esperada: II – Use a caneta; repita 5 vezes (mova 150 passos; gire 72 graus para a direita). III – Use a caneta; repita 3 vezes (mova 150 passos; gire 120 graus para a direita). O algoritmo descrito para II determina um pentágono regular com lados de 150 unidades, enquanto o algoritmo descrito para III determina um triângulo equilátero com lados de 150 unidades.
Página cento e quarenta e nove
84. Analise o algoritmo, na linguagem Scratch, utilizado para obtêr o terceiro termo de uma PG e resôuva as kestões.
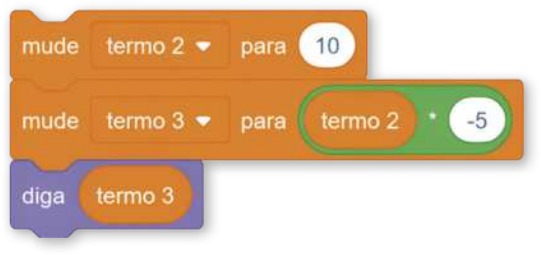
DICA
No comando em vêrde dêêsse algoritmo, o sín-bolo * indica uma multiplicação.
a) De acôr-do com esse algoritmo, o terceiro termo da PG é obtído de maneira recursiva ou não recursiva? Justifique.
Resposta esperada: Recursiva, pois, para obtêr esse termo, o termo anterior é multiplicado por −5.
b) Qual é a razão dessa PG? E qual é o primeiro termo?
−5; −2.
c) escrêeva uma expressão para determinar o enésimo termo dessa PG de maneira:
• recursiva;
an = −5 ⋅ an − 1, para n ∈ ℕ, com n ≥ 2 e a1 = −2
• não recursiva.
an = −2 ⋅ (−5)n − 1, para n ∈ ℕ*
85. Os comandos a seguir, indicados fora de ordem, foram utilizados por Rafaela para construir um algoritmo no Scratch quê determina o valor de uma função f: ℝ → ℝ para determinado número x.
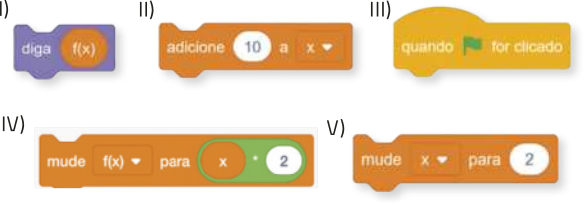
a) Ordene os comandos apresentados de maneira a obtêr o algoritmo construído por Rafaela.
Uma resposta possível: III, V, II, IV e I.
b) Qual será a fala da personagem ao clicarmos na bandeira vêrde?
Uma resposta possível: 24.
c) escrêeva a lei de formação da função f.
Uma resposta possível: f(x) = 2(x + 10) ou f(x) = 2x + 20.
86. Algumas ideias iniciais sobre linguagem de programação podem sêr usadas em programas de computador. As planilhas eletrônicas, por exemplo, permitem a utilização de diferentes fórmulas matemáticas e comandos quê envolvem lógica. Observe uma planilha eletrônica utilizada por um professor para verificar se um estudante foi aprovado ou reprovado.
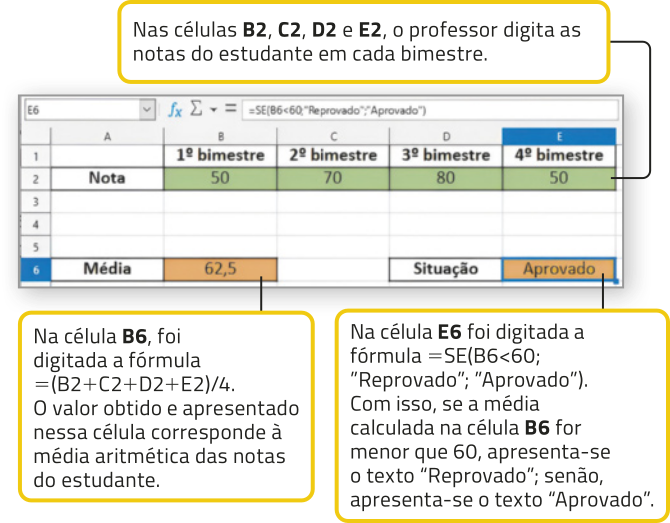
a) Qual foi a média das notas bimestrais apresentadas no exemplo acima? O estudante quê obteve essas notas foi aprovado ou reprovado?
62,5; aprovado
b) Reproduza no LibreOffice Calc a planilha utilizada pelo professor e considere um estudante cujas notas bimestrais digitadas nessa planilha foram 45, 66, 50 e 63. O quê aparecerá na célula B6? E na célula E6?
56; reprovado
c) Represente o algoritmo da planilha utilizando um fluxograma e a linguagem de programação Scratch.
Resposta nas Orientações para o professor.
d) Você estudou e teve a oportunidade de analisar e construir algoritmos no Scratch e na planilha eletrônica LibreOffice Calc. Em qual dêêsses programas você achou mais fácil compreender e construir algoritmos? Por quê?
Resposta pessoal.
87. ![]() Junte-se a um colega, e pensem em uma situação quê envolva algum conceito matemático quê vocês já tênham estudado. Elaborem um problema envolvendo esse conceito e listem os passos necessários para resolvê-lo. Depois, representem essa sequência de passos por meio de um fluxograma. Em um computador, utilizem a linguagem de programação Scratch para construir um algoritmo quê represente o fluxograma elaborado. Por fim, realizem testes para verificar se esse algoritmo apresenta as soluções esperadas.
Junte-se a um colega, e pensem em uma situação quê envolva algum conceito matemático quê vocês já tênham estudado. Elaborem um problema envolvendo esse conceito e listem os passos necessários para resolvê-lo. Depois, representem essa sequência de passos por meio de um fluxograma. Em um computador, utilizem a linguagem de programação Scratch para construir um algoritmo quê represente o fluxograma elaborado. Por fim, realizem testes para verificar se esse algoritmo apresenta as soluções esperadas.
Elaborações dos estudantes.
Página cento e cinquenta
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei meus côlégas nas atividades em grupo.
h) Auxiliei meus côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
Respostas pessoais.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Noções de linguagem de programação
Sequências
Termo geral de uma PA
Relação entre PA e função afim
Relação entre PG e função do tipo exponencial
Progressão aritmética (PA)
Soma dos n primeiros termos de uma PG
Soma dos n primeiros termos de uma PA
Progressão geométrica (PG)
Termo geral de uma PG
Algoritmo e fluxograma
Soma dos termos de uma PG infinita
Resposta pessoal.
3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas e sigam as etapas.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Respostas pessoais.
Página cento e cinquenta e um
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre a técnica de filmagem stop-motion. Agora, vamos retomar esse contexto nas kestões a seguir.
a) A animação A noiva cadáver rompeu os padrões de filmagem da época – em quê as animações, em quase sua totalidade, eram feitas em computador – ao utilizar a técnica de filmagem stop-motion. Observe algumas informações sobre essa produção.
A noiva cadáver
Gênero: Animação, fantasía, família, romance, comédia musical Lançamento: 21 de outubro de 2005
Duração: 1h15min
Direção: Máike Johnson e Tim Burton
Elenco: Johnny Dép, Helena Bonham kárter, Emily uátson
Nacionalidade: Estados Unidos
Classificação: Livre

I) Considerando quê nessa animação foram utilizados 24 quadros por segundo, escrêeva os cinco primeiros termos de uma sequência quê expresse a quantidade de quadros utilizados até completar cada minuto da animação. Classifique essa sequência em PA ou PG.
1.440, 2.880, 4.320, 5.760 e 7.200. PA.
II) escrêeva a lei de formação de uma função f: ℕ* → ℝ quê dêz-creva a sequência quê você indicou no item anterior, sêndo a 1 = f (1), a 2 = f (2), a 3 = f (3), e assim sucessivamente.
f(n) = 1.440n
III) Qual é o total de quadros utilizados na produção dessa animação?
108.000 quadros
b) Utilizando aplicativos e técnicas de programação, uma pessoa faz pequenos filmes, com duração de 5 min, utilizando comandos predefinidos para as personagens. Para filmes com uma personagem, ele utiliza 2.000 comandos; para duas personagens, 4.000 comandos; para três personagens, 8.000 comandos; e assim sucessivamente, até 10 personagens, quê correspondem ao mássimo quê ele consegue utilizar de comandos em sua animação.
I) Defina a sequência correspondente à quantidade de comandos necessários, de acôr-do com a quantidade de personagens utilizadas e classifique-a em PA ou PG.
Uma resposta possível: PG de 10 termos em quê a1 = 2.000 e q = 2.
II) escrêeva a lei de formação de uma função f: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} → ℝ quê dêz-creva a sequência quê você indicou no item anterior, a1 = f(1), a2 = f(2), a3 = f(3), e assim sucessivamente.
f(n) = 1.000 ⋅ 2n
c) ![]() A animação Minhocas, quê ilustra a abertura desta Unidade, tem no enredo algumas kestões sociais, como conflitos e problemas de relacionamento comuns na adolescência. Junte-se a um colega, e pesquisem outra animação elaborada com a técnica stop-motion e com alguma temática social. Em um texto, descrevam características técnicas dessa animação, como a quantidade de quadros por segundo, e como a questão social é abordada. Por fim, compartilhem com os côlégas o texto produzido.
A animação Minhocas, quê ilustra a abertura desta Unidade, tem no enredo algumas kestões sociais, como conflitos e problemas de relacionamento comuns na adolescência. Junte-se a um colega, e pesquisem outra animação elaborada com a técnica stop-motion e com alguma temática social. Em um texto, descrevam características técnicas dessa animação, como a quantidade de quadros por segundo, e como a questão social é abordada. Por fim, compartilhem com os côlégas o texto produzido.
Resposta pessoal.
Página cento e cinquenta e dois
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) Com o objetivo de trabalhar a concentração e a sincronia de movimentos dos alunos de uma de suas turmas, um professor de educação física dividiu essa turma em três grupos (A, B e C) e estipulou a seguinte atividade: os alunos do grupo A deveriam batêer palmas a cada 2 s, os alunos do grupo B deveriam batêer palmas a cada 3 s e os alunos do grupo C deveriam batêer palmas a cada 4 s.
O professor zerou o cronômetro e os três grupos começaram a batêer palmas quando ele registrou 1 s. Os movimentos prosseguiram até o cronômetro registrar 60 s.
Um estagiário anotou no papel a sequência formada pêlos instantes em quê os três grupos bateram palmas simultaneamente.
Qual é o termo geral da sequência anotada?
a) 12n, com n um número natural, tal quê 1 ≤ n ≤ 5.
b) 24n, com n um número natural, tal quê 1 ≤ n ≤ 2.
c) 12(n − 1), com n um número natural, tal quê 1 ≤ n ≤ 6.
d) 12(n − 1) + 1, com n um número natural, tal quê 1 ≤ n ≤ 5.
e) 24(n − 1) + 1, com n um número natural, tal quê 1 ≤ n ≤ 3.
alternativa d
2. (UEG-GO) No primeiro semestre de 2015, a empresa “Aço Firme” fabricou 28.000 chapas metálicas em janeiro; em fevereiro sua produção começou a cair como uma progressão aritmética decrescente, d fórma quê em julho a sua produção foi de 8.800 chapas. Nessas condições, a produção da empresa nos meses de maio e junho totalizou
a) 33.600 chapas
b) 32.400 chapas
c) 27.200 chapas
d) 24.400 chapas
e) 22.600 chapas
alternativa c
3. (Enem/MEC) O artista gráfico holan-dêss Maurits Cornelius é-chêr criou belíssimas obras nas quais as imagens se repetiam, com diferentes tamanhos, induzindo ao raciocínio de repetição infinita das imagens. Inspirado por ele, um artista fez um rascunho de uma obra na qual propunha a ideia de construção de uma sequência de infinitos quadrados, cada vez menóres, uns sôbi os outros, conforme indicado na figura.
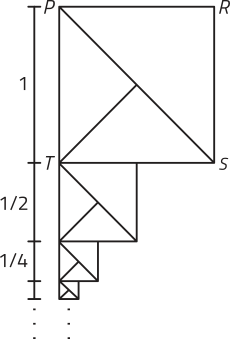
O quadrado PRST, com lado de medida 1, é o ponto de partida. O segundo quadrado é construído sôbi ele tomando-se o ponto médio da base do quadrado anterior e criando-se um novo quadrado, cujo lado corresponde à mêtáde dessa base. Essa sequência de construção se repete recursivamente.
Qual é a medida do lado do centésimo quadrado construído de acôr-do com esse padrão?
a)
b)
c)
d)
e)
alternativa b
4. (Fuvest-SP) Joana comprou um celular e dividiu o pagamento em 24 parcelas mensais quê formam uma progressão aritmética crescente. As três primeiras parcelas foram de R$ 120,00, R$ 126,00 e R$ 132,00. Sabendo quê, ao final, constatou-se quê Joana não pagou a 19ª parcela, o valor pago por ela foi:
a) R$ 3.954,00
b) R$ 4.026,00
c) R$ 4.200,00
d) R$ 4.308,00
e) R$ 4.382,00
alternativa d
Página cento e cinquenta e três
5. (Enem/MEC) Foram convidadas 32 equipes para um torneio de futeból, quê foram divididas em 8 grupos com 4 equipes, sêndo quê, dentro de um grupo, cada equipe disputa uma única partida contra cada uma das demais equipes de seu grupo. A primeira e a segunda colocadas de cada grupo seguem para realizar as 8 partidas da próxima fase do torneio, chamada oitavas de final. Os vencedores das partidas das oitavas de final seguem para jogar as 4 partidas das quartas de final. Os vencedores das quartas de final disputam as 2 partidas das semifinais, e os vencedores avançam para a grande final, quê define a campeã do torneio.
Pelas regras do torneio, cada equipe deve ter um período de descanso de, no mínimo, 3 dias entre dois jogos por ela disputados, ou seja, se um tíme disputar uma partida, por exemplo, num domingo, só poderá disputar a partida seguinte a partir da quinta-feira da mesma semana.
O número mínimo de dias necessários para a realização dêêsse torneio é
a) 22.
b) 25.
c) 28.
d) 48.
e) 64.
alternativa b
6. (hú éfe pê érre) Os ângulos internos de um polígono convexo de 20 lados estão em progressão aritmética com razão de 4° (graus). Qual é o produto em graus entre o maior ângulo interno e o menor ângulo interno dêêsse polígono?
a) 20.800.
b) 22.600.
c) 24.800.
d) 26.600.
e) 26.800.
alternativa c
7. (Unicamp-SP) Três números reais distintos a, b, c são tais quê a, b, c e ab, bc, ca formam, nessas ordens, duas progressões aritméticas de mesma razão. O valor do produto abc é:
a) 1.
b) .
c) −1.
d) 6.
alternativa c
8. (UECE) Sejam a e b números reais positivos e distintos. Se 0 < a < 1, e, se a função f: ℝ → ℝ é definida por f(x) = ba x, então o valor da “soma infinita’’ f(1) + f(2) + f(3) + … + f(n) + … é:
a)
b)
c)
d)
alternativa b
9. (Enem/MEC) As bactérias são microrganismos formados por uma única célula. Elas estão presentes em praticamente todos os meios: no ar, na á gua, no solo ou no interior de outros sêres vivos. A forma de reprodução mais comum das bactérias é a asseksuada por bipartição. Nesse processo, cada uma delas tem seu dê ene há duplicado e, posteriormente, se divide em duas células bacterianas.
De modo geral, em condições favoráveis, esse processo de bipartição se conclui a cada 20 minutos.
Disponível em: https://livro.pw/uxntf. Acesso em: 16 nov. 2013 (adaptado).
Considere quê, no instante t = 0, há uma quantidade N0 de bactérias em um meio favorável à sua reprodução, de modo quê nele só se reproduzem por bipartição.
A sequência formada pela quantidade de bactérias nesse meio nos instantes 0, 20, 40, 60, 80 e 100 minutos é
a) N0, N02, N03, N0 4, N0 5, N06
b) N0, N02, N0 4, N0 8, N0 16, N032
c) N0, 2N0, 3N0, 4N0, 5N0, 6N0
d) N0, 2N0, 4N0, 8N0, 16N0, 32N0
e) N0, 3N0, 7N0, 15N0, 31N0, 63N0
alternativa d
10. (UFMS) Seja (a, b, c) uma progressão geométrica de números reais. Suponha quê a + b + c = 26 e a2 + b2 + c2 = 364. Nessas condições, qual o valor de b?
a) 4.
b) 6.
c) 8.
d) 10.
e) 12.
alternativa b
11. (hú- hê- érre jota) Um fisioterapeuta elaborou o seguinte plano de treinos diários para o condicionamento de um maratonista quê se recupera de uma contusão:
• primeiro dia – corrida de 6 km;
• dias subsequentes – acréscimo de 2 km à corrida de cada dia imediatamente anterior.
O último dia de treino será aquele em quê o atleta correr 42 km.
O total percorrido pelo atleta nesse treinamento, do primeiro ao último dia, em quilômetros, corresponde a:
a) 414
b) 438
c) 456
d) 484
alternativa c
Página cento e cinquenta e quatro
12. (Udesc) Sejam (16, 18, 20, …) e duas progressões aritméticas. Estas duas progressões apresentarão somas iguais, para uma mesma quantidade de termos somados, quando o valor da soma for igual a:
a) 154
b) 4.774
c) 63
d) 4.914
e) 1.584
alternativa d
13. (Enem/MEC) Uma confeiteira pretende divulgar em um sítio da internet os doces quê produz, mas só fará isso se acreditar quê o número de acessos por semana compensará seu gasto com a divulgação. Por isso, pediu quê lhe enviassem dados sobre o número de acessos ao sítio nas últimas 5 semanas e recebeu o gráfico a seguir.
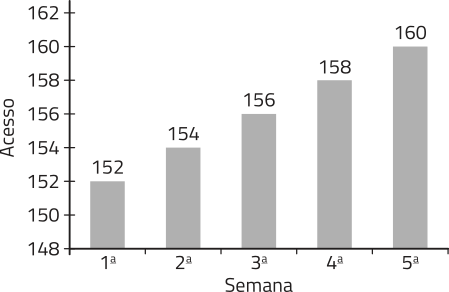
A confeiteira acredita quê, se o número de acessos mantiver o mesmo crescimento semanal para as próximas 5 semanas, ao final dêêsse período valerá a pena investir na divulgação.
O número de acessos quê a confeiteira acredita sêr suficiente para quê a divulgação no sítio valha a pena é:
a) 162.
b) 170.
c) 172.
d) 312.
e) 320.
alternativa b
14. (hú- hê- érre jota) Considere a seguinte equação:
x + + … = 18, x ∈ ℝ
Sabendo quê o primeiro membro dessa equação é a soma dos termos de uma progressão geométrica infinita, o valor de x é igual a:
a) 6
b) 8
c) 10
d) 12
alternativa d
15. (Enem/MEC) No Brasil, o tempo necessário para um estudante realizar sua formação até a diplomação em um curso superior, considerando os 9 anos de ensino fundamental, os 3 anos do ensino médio e os 4 anos de graduação (tempo médio), é de 16 anos. No entanto, a realidade dos brasileiros mostra quê o tempo médio de estudo de pessoas acima de 14 anos é ainda muito pequeno, conforme apresentado na tabéla.
1995 |
1999 |
2003 |
2007 |
|
Tempo de estudo (em ano) |
5,2 |
5,8 |
6,4 |
7,0 |
Disponível em: https://livro.pw/vfrgz. Acesso em: 19 dez. 2012 (adaptado).
Considere quê o incremento no tempo de estudo, a cada período, para essas pessoas, se mantenha constante até o ano 2050, e quê se pretenda chegar ao patamar de 70% do tempo necessário à obtenção do curso superior dado anteriormente.
O ano em quê o tempo médio de estudo de pessoas acima de 14 anos atingirá o percentual pretendido será
a) 2018.
b) 2023.
c) 2031.
d) 2035.
e) 2043.
alternativa d
16. (UFAM) Sejam a PA de razão r = 20 e 1º termo a1 = 200, e a PG de razão q = 3 e 1º termo b1 = 2. Logo, podemos afirmar quê:
a) a4 < b4.
b) = 10 ⋅ a4.
c) b3 = 2 ⋅ a3.
d) bn > an, para n ≥ 6.
e) os termos da PA passam a sêr menóres quê os termos da PG só a partir do 5º termo.
alternativa d.
17. (Unicamp-SP) Seja p(x) = x + 2.024. A equação p(x) + p(2x) + p(3x) + … + p(2.023x) + p(2.024x) = 0 tem uma solução x quê satisfaz:
a) x < −2.
b) −2 < x < 0.
c) 0 < x < 2.
d) x > 2.
alternativa b
Página cento e cinquenta e cinco
