RESOLUÇÕES DAS ATIVIDADES PROPOSTAS NO LIVRO DO ESTUDANTE
Unidade 1 • Função exponencial
1. a) 6 ⋅ 6 ⋅ 6 = 216
b) (−4) ⋅ (−4) = 16
c) 25−1 =
d)
e) = =
f) 450 = 1, pois a0 = 1, se a ≠ 0
2. a)
b) (−6)9 + (−2) = (−6)7
c) = = 39 + (−2) = 37
d) 96 ⋅ 3 ∶ 310 = 918 ∶ 310 = ∶ 310 = 32 ⋅ 18 ∶ 310 = 336 ∶ 310 = 336 − 10 = 326
e) =
f) = = 2045 − 18 = 2027
3. a) 1 ⋅ 53 ∶ 55 = 53 − 5 = 5−2 =
b) 72 ⋅ (−3) ⋅ ⋅ (2 ⋅ 7)8 = 7−6 ⋅ ⋅ 28 ⋅ 78 = 28 − 6 ⋅ 78 − 6 = 22 ⋅ 72 = 196
c) = =
d) = 34 − 3 ⋅ 74 − 3 = 3 ⋅ 7 = 21
4. quantidade de grãos da última casa:
264 − 1 = 2 63
= 263 − 29 = 234
Portanto, seria necessário dobrar 34 vezes a produção de 2022/2023.
5. 1 TB = 1.024 GB
1.024 − 270 = 754
≃ 0,736 → aproximadamente 73,6%
6. a) • 3 ⋅ 210 B
• 5 ⋅ 2−10 ⋅ 2−10 = 5 ⋅ 2−20 → 5 ⋅ 2−20 TB
• 8 ⋅ 210 ⋅ 210 ⋅ 210 = 23 ⋅ 230 = 233 → 233 kB
• 7 ⋅ 2−10 ⋅ 2−10 ⋅ 2−10 = 7 ⋅ 2−30 → 7 ⋅ 2−30 GB
b) I e III
I) 16 ⋅ 210 = 24 ⋅ 210 = 214
II) 4 ⋅ 210 = 22 ⋅ 210 = 212
III) 32 ⋅ 210 = 25 ⋅ 210 = 215
c) Resposta pessoal. Espera-se quê os estudantes sêjam capazes de estabelecer algoritmos para a conversão de unidades de medida de armazenamento de dados, de modo quê utilizem potências de base 2 e suas propriedades nessas conversões. Mostrar aos estudantes como a realização das conversões com as potências de mesma base póde facilitar os cálculos de divisão e de multiplicação.
7. 454 ⋅ 2549 = ⋅ = 2108 ⋅ 598 = 210 ⋅ 298 ⋅ 598 = 210 ⋅ (2 ⋅ 5)98 = 1.024 ⋅ 1098
Como na multiplicação ôbitída o fator 1098 apenas acrescenta 98 zeros à direita de 1.024, temos quê a soma dos algarismos do produto é:
1 + 2 + 4 = 7.
8. Atividade de elaboração do estudante. Espera-se quê os estudantes elaborem atividades quê envolvam uma ou mais propriedades de potência estudadas. Desafiá-los a compor kestões em quê mais de uma propriedade é utilizada no mesmo item e pedir quê, durante as resoluções das atividades dos côlégas, justifiquem os cálculos apresentando as propriedades utilizadas.
9. Para escrever os números em notação científica, podemos contar as ordens até dispormos a vírgula de modo a obtêr um fator entre 1 e 10 e considerar essa contagem para determinar o expoente no fator quê é uma potência de 10.
a) 5,68 ⋅ 1011
b) 1,0263 ⋅ 1016
c) 9,07 ⋅ 1014
d) 6 ⋅ 10−7
e) 7,98 ⋅ 10−9
f) 6,04 ⋅ 10−13
10. a) = 1,4 ⋅ 102
b) 7,25 ⋅ 105 ⋅ 1,4 ⋅ 10−7 = 7,25 ⋅ 1,4 ⋅ 105 ⋅ 10−7 = 1,015 ⋅ 10−1
c) = = 3,37125 ⋅ 105
11. a) ≃ 0,7505 ⋅ 104 → aproximadamente 7.505 anos-luz
b) = 1,67824 ⋅ 10−5 → 1,67824 ⋅ 10−5 Å
• Resposta pessoal. Espera-se quê os estudantes busquem contextos em quê as medidas apresentadas são “muito grandes” ou “muito pequenas”, de maneira quê faça sentido convertê-las em ano-luz ou angstrom, respectivamente. É importante observar se os estudantes convertem corretamente as medidas entre as unidades convencionais.
12. a) 2,83 ⋅ 10−3 = 0,00283
Portanto, a massa indicada no visor é 0,0028 g.
b) 2,8 ⋅ 10−3 g
13. alternativa d
≃ 13,333 ⋅ 103 → 1,3 ⋅ 104 km
14. a) = 2,55 → 2,55 cm
b) = 2,85 → 2,85 cm
c) = 3,25 → 3,25 cm
15.
a) Resposta possível: Aproximadamente 1,6 L. Para estimar o volume de líquido, pode-se calcular a média aritmética de 1,5 L e 1,75 L, quê é 1,625 L, e arredondar essa medida ao décimo do litro mais próximo, obtendo 1,6 L.
b) Resposta possível: 1 é algarismo cérto; 6 é algarismo duvidoso.
16. a) • 3,86 cm; algarismos certos: 3 e 8; algarismo duvidoso: 6
• 7,43 cm; algarismos certos: 7 e 4; algarismo duvidoso: 3
b) Como 1 m equivale a 100 cm, podemos multiplicar cada medida por 10−2, obtendo:
3,86 cm = 3,86 ⋅ 10−2 m;
7,43 cm = 7,43 ⋅ 10−2 m.
c) Respostas pessoais. Espera-se quê os estudantes compreendam e apliquem os conceitos de algarismos certos e duvidosos. Certificar-se de quê eles medirão corretamente objetos cuja medida, na unidade escolhida, não póde sêr aferida de maneira precisa.
17. 5,4 L = 5,4 ⋅ 106 mm3
≃ 0,731 ⋅ 104 ≃ 7,31 ⋅ 103
Aproximadamente 7,31 ⋅ 103 leucócitos por milímetro cúbico de sangue. Essa concentração de leucócitos está entre os valores de referência.
18. a) 70 ⋅ 1 ⋅ 106 = 7 ⋅ 107 → 7 ⋅ 107 células-tronco
b) ⇒ 70x = 43,4 ⇒ x = 0,62
0,62 mg = 0,62 ⋅ 10−3 g = 6,2 ⋅ 10−4 g
Página trezentos e cinquenta e quatro
c) Resposta pessoal. Espera-se quê os estudantes elaborem um texto contendo informações e características sobre os textos científicos, bem como as diferenças entre eles de acôr-do com o público a quê se destinam, por exemplo. Espera-se quê no texto eles utilizem argumentos quê defendam a ciência para a evolução da humanidade, sua importânssia para o combate da disseminação de notícias falsas e para a busca de uma ssossiedade mais justa e sustentável. Eles podem citar exemplos de produções da ciência, como o desenvolvimento das vacinas na pandemia de covid-19, e a utilização de fontes de energias rêno-váveis para diminuir a degradação do meio ambiente.
19. Utilizando a definição de potência com expoente racional, temos:
a)
b)
c) = 35
d)
e)
f)
g)
h)
20. a) = =
b)
c) =
d) = =
21. a) 
b) •
•
•
•
22. a)
b)
c) =
d) =
23. I)
II)
Resposta esperada: Considerando as informações do enunciado, não é possível comparar os valores das duas expressões, pois, se 0 < x < 1, o valor da expressão I será maior quê o da expressão II; se x > 1, o valor da expressão I será menor quê o da expressão II; e se x = 1, as duas expressões terão valores iguais.
24. Atividade de elaboração do estudante. Espera-se quê os estudantes elaborem expressões quê possam sêr simplificadas utilizando as propriedades de radiciação e empreguem as propriedades para resolver as expressões dos côlégas. É importante quê justifiquem, a cada etapa, a propriedade utilizada.
25. a) Digitando 3 elevado a na calculadora, obtemos aproximadamente 4,7.
b) Digitando 4 elevado a na calculadora, obtemos aproximadamente 22,2.
c) Digitando elevado a na calculadora, obtemos aproximadamente 1,6.
d) Digitando 2 elevado a (pi)" na calculadora, obtemos aproximadamente 8,8.
26. alternativa a
a) 82 = 8 ⋅ 8 = 64
b) 28 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 256
c) Como 4 < 8 < 9, temos quê: < < ⇒ 2 < < 3
Logo, como 22 = 4 e 23 = 8, temos quê está entre 4 e 8.
d) Como 3 < (pi)" < 4, temos quê:
53 < 5(pi)" < 54 ⇒ 125 < 5(pi)" < 625
e) = 152 = 225
27. alternativa a
≃ 61,4 =
28. Observando todos os itens em quê a função é do tipo f(x)= ax, temos: a, c e f.
29. a) f(4) = 34 = 81
b) g(3) = 83 = 512
c) f(−2) = 3−2 =
d) g = = 2
e) f(3) − g(1) = 33 − 81 = 19
f) 2g(2) − f(5) = 2 ⋅ 82 − 35 = −115
30. Atividade de elaboração do estudante. Espera-se quê os estudantes sêjam capazes de escrever a lei de formação de uma função exponencial e reconhecer e indicar elemêntos de seu domínio. Além díssu, é importante quê eles compreendam como calcular valores da função para os elemêntos do domínio indicados pêlos côlégas e quê relacionem os resultados dêêsses cálculos com as imagens dos respectivos valores.
31. a) etapa 5: 25 = 32 → 32 bactérias etapa 6: 26 = 64 → 64 bactérias
b) = 12 → 12 etapas
212 = 4.096 → 4.096 bactérias
c) Como a quantidade de bactérias dobra a cada etapa, temos: f(x)= 2x.
32. a) após dois dias: = 0,25 → 0,25 mg após quatro dias: = 0,0625 → 0,0625 mg
b) Como esse princípio ativo é reduzido à mêtáde a cada dia, temos h(x) = .
c) tempo entre a ingestão do 2º e a do 3º comprimido: 42 horas
tempo entre a ingestão do 1º e a do 2º comprimido: 36 horas (42 − 6 = 36) ou 48 horas (42 + 6 = 48)
tempo entre a ingestão do 1º e a do 3º comprimido: 78 horas (42 + 36 = 78) ou 90 horas (42 + 48 = 90)
78 horas = dias = 3,25 dias
h(3,25) = ≃ 0,105
90 horas = dias = 3,75 dias
h(3,75) = ≃ 0,074
Portanto, a quantidade do princípio ativo do primeiro comprimido no organismo de Bruna era de aproximadamente 0,074 mg ou 0,105 mg.
33. a) Analisando o gráfico, temos quê a função é decrescente. Então, a pertence ao intervalo]0, 1[.
b) f(0) = a0 = 1
ponto de coordenadas (0, 1)
c) Não, pois, como f é uma função exponencial, f(x) > 0 para todo x ∈ ℝ.
Página trezentos e cinquenta e cinco
d) Como g(x)= −f(x), podemos afirmar quê g é uma função negativa em todo o seu domínio, ou seja, g(x) < 0 para todo x ∈ ℝ.
34. a) s; b) f; c) g; d) t
s(2)= ⋅ 22 = e s(4) = ⋅ 24 = 2
f(4)= 34 − 4 + 1 = 2 e
f(5)= 35 − 4 + 1 = 4
g(−2)= − 3 = 1 e
g(1)= − 3 =
t(0)= 51 − 0 − 3 = 2 e
t(1)= 51 − 1 − 3 = −2
35. a) Analisando o comportamento do gráfico das funções, temos: função f: crescente; função g: decrescente.
b) Temos quê f(0) = −1 e f(2) = 5.
Assim:
f(0) = b ⋅ 20 + c = −1 ⇒ b + c = −1
f(2) = b ⋅ 22 + c = 5 ⇒ 4b + c = 5
Para determinar os números reais b e c, podemos escrever e resolver um sistema de duas equações do 1º grau com duas incógnitas.
⇒ b = 2 e c = −3
Logo, f(x) = 2 ⋅ 2x − 3.
Temos ainda quê g(2) = −2 e g(1) = f(1) = 1. Assim, considerando a lei de formação de g como g(x)= mx + n, temos:
g(2) = 2m + n = −2
g(1) = m + n = 1
Para determinar os números reais m e n, podemos escrever e resolver um sistema de duas equações do 1º grau com duas incógnitas.
⇒ m = −3 e n = 4
Logo, g(x) = −3x + 4.
c) Como 2x > 0, podemos multiplicar por 2 ambos os membros dessa desigualdade.
2 ⋅ 2x > 2 ⋅ 0 ⇒ 2 ⋅ 2x > 0
Agora, subtraímos 3 em ambos os membros da desigualdade ôbitída.
2 ⋅ 2x − 3 > 0 − 3 ⇒ f(x) > −3
Portanto, Im(f) = {y ∈ ℝ | y > −3}.
Im(g) = ℝ
36. a) 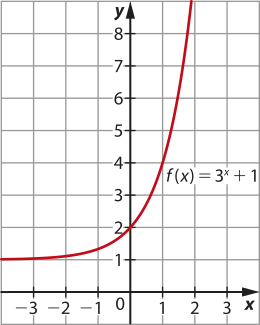
b) 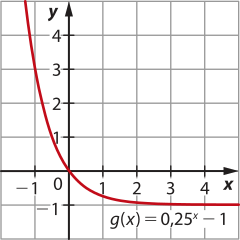
c) 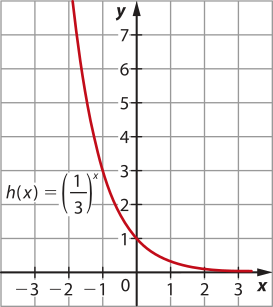
d) 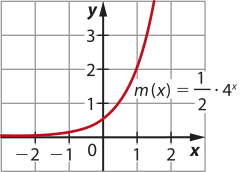
37. a) f(1) = a1 = a
b) f(x1 + x2) = = ⋅ = f(x1) ⋅ f(x2)
c) f(nx) = anx = axn = = (f(x))n
38. a) alternativa II
Coordenadas de alguns dos pontos pêlos quais passa o gráfico da função: (0, 0), (1, 2), (2, 8), (3, 26), (4, 80).
I) f(2) = −1 + 22 = −1 + 4 = 3 → não condiz
II) f(0) = −1 + 30 = −1 + 1 = 0
f(1) = −1 + 31 = −1 + 3 = 2
f(2) = −1 + 32 = −1 + 9 = 8
f(3) = −1 + 33 = −1 + 27 = 26
f(4) = −1 + 34 = −1 + 81 = 80
III) f(0) = 20 + 1 = 2 → não condiz
b) f(10) = −1 + 310 = −1 + 59.049 = 59.048 → 59.048 compartilhamentos
c) Pesquisa do estudante. Espera-se quê os estudantes pesquisem e compreendam estratégias para verificar a veracidade de uma informação e apresentem itens como: verificar se o título é muito chamativo; se a notícia tem êêrros ortográficos e gramaticais; se outros veículos de comunicação também publicaram algo a respeito da mesma notícia; a data de publicação da notícia; a URL do sáiti em quê foi publicado; e se há opiniões explícitas no texto (notícias jornalísticas devem sêr isentas de opiniões pessoais).
39. a) Resposta pessoal. Espera-se quê os estudantes compartilhem suas experiências a respeito do assunto e compreendam os perigos de participar de esquemas de pirâmide, quê podem levar à reclusão e multa.
b) nível 5: 64 ⋅ 4 = 256 → 256 participantes; nível 6: 256 ⋅ 4 = 1.024 → 1.024 participantes
c) Observe quê:
nível 1: 1 = 40 = 41 − 1
nível 2: 4 = 41 = 42 − 1
nível 3: 16 = 42 = 43 − 1
nível 4: 64 = 43 = 44 − 1
nível 5: 256 = 44 = 45 − 1
nível 6: 1.024 = 45 = 46 − 1
nível n: q(n) = 4n − 1 ou q(n) = ⋅ 4n
d) q(7) = 47 − 1 = 46 = 4.096
q(8) = 48 − 1 = 47 = 16.384
q(9) = 49 − 1 = 48 = 65.536
65.536 + 16.384 + 4.096 = 86.016
86.016 ⋅ 1.000 = 86.016.000 → R$ 86.016.000,00
40. Atividade de elaboração do estudante. Espera-se quê os estudantes relacionem os dados da tabéla a funções exponenciais, ou seja, verifiquem quê a variação da quantidade de indivíduos em função do tempo póde sêr expressa por uma função exponencial e, a partir díssu, elaborem uma situação-problema.
41. a) 113 = 114x ⇒ 4x = 3 ⇒ x = → S =
b) 25x + 9 = 252 ⇒ x + 9 = 2 ⇒ x = −7 → S = {−7}
c) = ⇒ = 36x ⇒ 2x2 − 6x + 4 = 0 ⇒
d) 7−2 = 73x ⇒ x = → S =
e) 26(1 − 2x) = 2−2(3x) ⇒ 6 − 12x = −6x ⇒ x = 1 → S = {1}
f) = 34 ⋅ ⇒ = 4 + ⇒ ⇒ x = 9 → S = {9}
42. a) −7x = 42 − ⇒ − 7x − 42 = 0
Fazendo y = 7x, temos:
y2 − y − 42 = 0 ⇒
Para y = 7, temos 7 = 7x ⇒ x = 1.
Para y = −6, temos −6 = 7x (impossível).
Portanto, S = {1}.
b) 81 = 10 ⋅ 3 ⋅ 3x − ⇒ − 30 ⋅ 3x + 81 = 0
Fazendo y = 3x, temos:
y2 − 30y + 81 = 0 ⇒
Página trezentos e cinquenta e seis
Para y = 27, temos 33 = 3x ⇒ x = 3.
Para y = 3, temos 3 = 3x ⇒ x = 1.
Portanto, S = {1, 3}.
c) 4x ⋅ 4−1 + 8 = 3 ⋅ 2x ⇒ ⋅ 0,25 + 8 = 3 ⋅ 2x ⇒ 0,25 ⋅ − 3 ⋅ 2x + 8 = 0
Fazendo y = 2x, temos:
0,25y2 − 3y + 8 = 0 ⇒
Para y = 4, temos 22 = 2x ⇒ x = 2.
Para y = 8, temos 23 = 2x ⇒ x = 3.
Portanto, S = {2, 3}.
43. Atividade de elaboração do estudante. Espera-se quê os estudantes utilizem a criatividade para compor equações de diferentes níveis de dificuldade, utilizando propriedades de potência e de radiciação estudadas na Unidade. É importante quê eles compreendam quê cada membro da equação deve sêr indicado de maneira quê todos possam sêr escritos como potências de mesma base.
44. a) Analisando quê f(1) = 3 = 31, f(2) = 9 = 32 e f(3) = 27 = 33, temos quê a lei de formação correta é a do item II.
b) f(4) = 34 = 81 → 81 quadrados na côr laranja
c) 729 = 3x ⇒ 36 = 3x ⇒ x = 6 → figura 6
45. Para determinar o ponto de interseção, fazemos:
+ 1 = 6 ⋅ 2x ⇒ + 1 = 6 ⋅ 2x ⇒ 6 ⋅ 2x − 1 − = 0
Fazendo y = 2x, temos:
6y − 1 − y−1 = 0 ⇒ 6y2 − y − 1 = 0 ⇒
Para y = , temos 2−1 = 2x ⇒ x = −1.
Para y = , temos = 2x (impossível).
f(−1) = 6 ⋅ 2−1 = 3
Portanto, o ponto de interseção é (−1, 3).
46. alternativa c
1.000 ⋅ 20,0625t = 2.000 ⇒ 20,0625t = 2 ⇒ 0,0625t = 1 ⇒ t = 16 → 16 anos
47. a) p(0) = 6.561 ⋅ 3−0,4 ⋅ 0 = 6.561 → R$ 6.561,00
b) 6.561 ⋅ 3−0,4t = 2.187 ⇒ 3−0,4t = 3−1 ⇒ −0,4t = −1 ⇒ t = 2,5
Portanto, 2,5 anos ou 2 anos e 6 meses.
c) 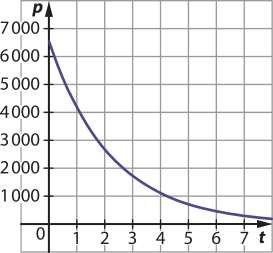
d) Pesquisa do estudante. Os estudantes podem responder, por exemplo, quê um produto sofre depreciação em razão do lançamento de atualizações do mesmo produto no mercado e da sua obsolescência.
48. Atividade de elaboração do estudante. É importante quê os estudantes compreendam quê, ao descrever uma situação de depreciação com uma função exponencial relacionando o tempo e o valor, essa função deve sêr decrescente, uma vez quê o bem perde valor com o decorrer do tempo. Ainda nesta atividade, é importante quê eles mostrem quê compreenderam a utilização dessa função para representar situações de depreciação.
49. a) Como essa quantidade é reduzida à mêtáde a cada duas horas, temos:
1 ∶ 2 = 0,5
0,5 ∶ 2 = 0,25
Portanto, 0,5 mg e 0,25 mg, respectivamente.
b) Temos quê, após 2 horas, o nível de nicotina será 0,5 mg. Assim:
I) f(2) = 1 − = 0 → não convém
II) f(2) = → não convém
III) f(2) = = 2−1 = = 0,5
Logo, a lei da função quê representa a situação é a III.
c) 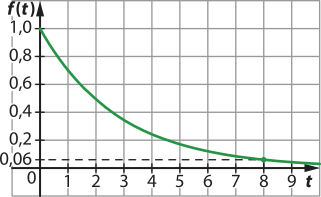
Uma resposta possível:
O ponto (8; 0,06) indica quê a quantidade de nicotina restante no organismo de uma pessoa quê fumou um cigarro há 8 horas é de 0,06 mg.
d) = 1 ⋅ 2−5 ⇒ t = −5 ⇒ t = 10 → 10 horas
e) Pesquisa do estudante. Espera-se quê os estudantes abordem, na peça publicitária, os malefícios do tabagismo para a saúde. Eles podem buscar as informações em sáites confiáveis, como o do Ministério da Saúde, do govêrno Federal, e o do Instituto Nacional de Câncer (Inca). É importante quê os estudantes se conscientizem e conscientizem a comunidade escolar do mal quê o tabagismo representa à saúde pública.
50. a) ≥ 3
Como a > 1, temos:
2x + 4 ≥ 1 ⇒ x ≥
Portanto, S =
b) ≤
Como 0 < a < 1, temos:
10 − 6x ≥ x + 1 ⇒ x ≤
Portanto, S = .
c) < 7−2(3x)
Como a > 1, temos:
x2 − 3x < −6x ⇒ −3 < x < 0
Portanto, S = {x ∈ ℝ | −3 < x < 0}.
d) 62x − 10 > 60
Como a > 1, temos:
2x − 10 > 0 ⇒ x > 5
Portanto, S = {x ∈ ℝ | x > 5}.
e) ≥
Como 0 < a < 1, temos:
x2 − 4 ≤ 0 ⇒ −2 ≤ x ≤ 2
Portanto, S = {x ∈ ℝ | −2 ≤ x ≤ 2}.
f) 2x ⋅ 23 − 2x ⋅ 2 < 768 ⇒ 2x ⋅ (23 − 2) < 768 ⇒ 2x < 128 ⇒ 2x < 27 ⇒ x < 7
Portanto, S = {x ∈ ℝ | x < 7}.
51. a) 43x + 1 − 512 ≥ 0 ⇒ 22(3x + 1) ≥ 29 ⇒ 6x + 2 ≥ 9 ⇒ x ≥
Logo, D(f) = .
b) − > 0 ⇒ 3−(x − 5) > 3−6 ⇒ −x + 5 > −6 ⇒ x < 11
Logo, D(g) = {x ∈ ℝ | x < 11}.
c) 7x + 1 − ≥ 0 ⇒ 7x + 1 ≥ 7−(2x + 3) ⇒ x + 1 ≥ −2x − 3 ⇒ x ≥
Logo, D(h) = .
d) 5−x ⋅ 5 + 5−x ⋅ 5−2 − 126 ≥ 0 ⇒ 5−x ⋅ (5 + 5−2) ≥ 126 ⇒5−x ≥ 52 ⇒ x ≤ −2
Logo, D(m) = {x ∈ ℝ | x ≤ −2}.
52. alternativa b
Analisando o intervalo em quê o gráfico da função f está abaixo da função g, temos: S = {x ∈ ℝ | 0 ≤ x ≤ 4}.
53. 4x + 3 − 4x − 2 ≥ 1.023 ⇒ 4x ⋅ (43 − 4−2) ≥ 1.023 ⇒ 4x ⋅ ≥ 1.023 ⇒ 4x ≥ 42 ⇒ x ≥ 2
Logo, S = {x ∈ ℝ | x ≥ 2}.
54. a) Considerando quê a massa do medicamento diminui 40% a cada hora, resta 60% a cada hora. Então, temos:
m(t) = 1.250 ⋅ ⇒ m(t) = 1.250 ⋅ .
b) 1.250 ⋅ < 162 ⇒ < ⇒ < ⇒ t > 4 → após 4 horas
Página trezentos e cinquenta e sete
55. alternativa d
Como o montante M dobra todo ano, temos M = 2.500 ⋅ 2t. Assim, temos:
M > 40.000 ⇒ 2.500 ⋅ 2t > 40.000 ⇒ 2t > ⇒ 2t > 16 ⇒ t > 4 → 4 anos
56. alternativa c
Analisando diretamente os gráficos e sabendo quê a capitalização, no primeiro intervalo de tempo, se deu de modo linear (juro simples) e, no segundo período, se deu de maneira exponencial (juro composto), conclui-se quê o gráfico quê melhor representa essa variação do montante é apresentado pela alternativa c.
57. a) R$ 3.150,00; R$ 600,00
b) 3.150 + 126t = 3.780 ⇒ 126t = 630 ⇒ t = 5 → junho de 2024
c) • Sérgio: 3.780 = 3.150 ⋅ (1 + 5i) ⇒ 1,2 = 1 + 5i ⇒ i = 0,04 → 4% ao mês
• Carla: 1 + i = 1,03 ⇒ i = 0,03 → 3% ao mês
d) M = 600 ⋅ (1,03)11 ⇒ M ≃ 830,54 → aproximadamente R$ 830,54
58. a) B. Resposta esperada: Porque, a partir do 2º mês nesse investimento, as razões entre os montantes de cérto mês e o mês anterior são aproximadamente iguais.
b) Considerando o investimento A, temos:
j = 560 − 530 = 30
c = 530 − 30 = 500 → R$ 500,00
c) A: 530 = 500 ⋅ (1 + i) ⇒ i = 0,06 → 6%
B: 525 = 500 ⋅ (1 + i) ⇒ i = 0,05 → 5%
d) A: Considerando quê o capital é de R$ 500,00 e o juro é de R$ 30,00 a cada intervalo de tempo, temos:
M(t) = 30t + 500, função afim.
B: Considerando quê o capital é de R$ 500,00 e quê o montante aumenta em 5% ao mês, temos:
M(t) = 500 ⋅ (1,05)t, função do tipo exponencial.
e) Analisando os dados da planilha, podemos comparar os meses em quê A é mais rentável e os meses em quê B é mais rentável. Assim, temos: A: de 1 a 8 meses; B: a partir de 9 meses.
f) Considerando quê o capital é R$ 500,00 e a resposta ao item e, temos quê o gráfico quê representa esses investimentos é o II.
59. alternativa e
Considerando quê, no primeiro ano de funcionamento, a indústria fabricou 8.000 unidades e quê a produção aumenta 50% por ano, temos:
P(t) = 8.000 ⋅ 1,5t − 1
60. a) P(5) = 8.000 ⋅ 1,54 ⇒ P(5) = 40.500 → 40.500 unidades
b) P(7) = 8.000 ⋅ 1,56 ⇒ P(7) = 91.125 → 91.125 unidades
61. a) Analisando o ponto em quê o gráfico intersecta o eixo y, concluímos quê Marcela estuda investir R$ 5.000,00.
b) Analisando o valor da ordenada do ponto do gráfico de abscissa 6, temos quê, ao final dos 6 anos de aplicação, Marcela vai obtêr o montante de R$ 9.649,75.
c) Para os três primeiros anos, ou seja, 0 ≤ t ≤ 3, a aplicação foi a juro compôzto, em quê o montante é dado por M(t) = C ⋅ .
Para C = 5.000, M = 6.655 e t = 3, temos:
6.655 = 5.000 ⋅ (1 + i)3 ⇒ 1,331 = (1 + i)3 ⇒ 1 + i = ⇒ i = 0,1
Logo, M(t) = 5.000 ⋅ (1 + 0,1)t ⇒ M(t) = 5.000 ⋅ (1,1)t.
Para os três últimos anos, ou seja, 3 < t ≤ 6 a aplicação foi a juro simples, em quê o montante é dado por M(t) = C ⋅ (1 + i ⋅ t).
Como não temos o valor do capital inicial, vamos determinar a expressão utilizando a lei da função afim f(x) = ax + b e os pontos (6; 9.649,75) e (3; 6.655,00). Assim:
9.649,75 = 6a + b (I)
6.655,00 = 3a + b (II)
Subtraindo II de I, temos:
2.994,75 = 3a ⇒ a = 998,25
Substituindo a = 998,25 em I, temos:
9.649,75 = 6 ⋅ 998,25 + b ⇒ b = 9.649,75 − 5.989,50 = 3.660,25
Logo, M(t) = 998,25t + 3.660,25.
Assim,
M(t)=
62. a) f(0) = = 1;
f(1) = = ;
f(2) = = ;
f(3) = = ;
f(4) = =
1, , , e
b)q = =
c) 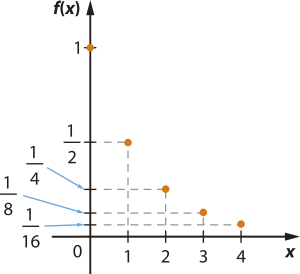
63. a) A: 5 ∶ 2 = 2,5; 8 ∶ 5 = 1,6
B: 32 ∶ 4 = 8; 256 ∶ 32 = 8; 2.048 ∶ 256 = 8; 16.384 ∶ 2.048 = 8
População submetida à substância B, pois a razão entre a quantidade de indivíduos dessa população de uma medição e da anterior, a partir da 2ª medição, é constante e igual a 8.
b) 2 = 1a + b (I)
5 = 2a + b (II)
Subtraindo II de I, temos:
3 = 1a ⇒ a = 3
Substituindo a = 3 em I, temos:
2 = 1 ⋅ 3 + b ⇒ b = −1
Logo, f(m) = 3m − 1.
g(m) = c ⋅ dm−1.
Como a razão da PG é 8, temos quê d = 8. Como g(1) = 4, temos:
4 = c ⋅ 81 − 1 ⇒ c = 4. Assim, g(m) = 4 ⋅ 8m−1.
Logo, a = 3, b = − 1, c = 4 e d = 8, e as funções são f(m) = 3m − 1 e g(m) = 4 ⋅ 8m−1.
c) A: f(7) = 3 ⋅ 7 − 1 = 21 − 1 = 20 → 20 bactérias
B: g(7) = 4 ⋅ 87−1 = 4 ⋅ 86 = 4 ⋅ 262.144 = 1.048.576 → 1.048.576 bactérias
64. a) (200, 100, 50, 25,...); q =
b) Resposta esperada: f: ℕ → ℝ, dada por f(x) = 200 ⋅ .
65. a) função f: q = = 2
função g: q = = 3
A razão da PG determinada pela função f é 2, e a razão da PG determinada pela função g é 3.
b) f(1) = 2 ⇒ a1 = 2 ⇒ a = 2; f(x) = 2x
g(3) = 3 ⇒ b3 − 2 = 3 ⇒ b = 3;
g(x) = 3x − 2
66. alternativa c
De acôr-do com o enunciado, o conjunto imagem de f corresponde a uma PG de razão −2 e a1 = 1. Assim, temos quê:
a2 = −2 ⋅ a1 = −2 ⋅ 1 = −2
a1 = f(1) ⇒ 1 = p ⋅ q1 ⇒ 1 = p ⋅ q (I)
a2 = f(2) ⇒ −2 = p ⋅ q2 ⇒ −2 = p ⋅ q ⋅ q (II)
Substituindo o valor de p ⋅ q = 1 de I em II, temos:
−2 = 1 ⋅ q ⇒ q = −2
Substituindo q = −2 em I, temos:
1 = p ⋅ (−2) ⇒ p =
Assim, p + q = + (−2) = .
67. Atividade de elaboração do estudante. Espera-se quê os estudantes possam relacionar os conceitos estudados de função exponencial e PG, bem como compor uma lei de formação de algum caso real quê póde sêr descrito por elas. Conversar com os estudantes sobre tipos de contextos a quê essa função se aplica.
Integrando com...
1. Resposta esperada: Luzia é o fóssil humano mais antigo encontrado na América. Com base em seu crânio, foi possível estimar o período em quê esse sêr humano viveu, o quê possibilitou o avanço nos estudos e na investigação de como foi o povoamento dêêsse continente.
Página trezentos e cinquenta e oito
2. Resposta esperada: Não, pois esse método de datação com 14C é eficiente para fósseis quê viveram há até 75.000 anos; em fósseis mais antigos é difícil detectar a presença dêêsse isótopo.
3. a) 5.730 anos. Indica quê, a cada 5.730 anos, a quantidade de 14C diminui pela mêtáde em um fóssil, em relação ao período anterior.
b) duas meias-vidas:
5.730 ⋅ 2 = 11.460 → 11.460 anos três meias-vidas:
5.730 ⋅ 3 = 17.190 → 17.190 anos
c) Aproximadamente duas meias-vidas, pois os arqueólogos acreditam quê Luzia tenha vivido há mais de 11 mil anos.
d) n(x) = n ⋅ , em quê n0 é a quantidade de 14C presente no indivíduo quando ele estava vivo.
e) Resposta esperada: Temos quê 40.000 anos correspondem a aproximadamente sete meias-vidas do 14C, pois 7 ⋅ 5.730 = 40.110. Assim, n(7) = n0 ⋅ = n0 ⋅ = 0,0078125 n0, ou seja, em um fóssil datado com cerca de 40 mil anos, a quantidade remanescente de 14C é aproximadamente 0,78% daquela quê havia no indivíduo quando ele estava vivo.
4. Pesquisa do estudante. Espera-se quê os estudantes abordem, em seus textos, argumentos com justificativas para a teoria escolhida por eles e percêbam quê bons argumentos, geralmente, estão acompanhados de dados de fontes confiáveis.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) I) 256 ⋅ 230 = 28 ⋅ 230 = 238 → 238 B
II) 2 ⋅ 220 = 221 → 221 B
As fotografias devem ocupar 50% de 238 B, ou seja, mêtáde da memória do smartphone. Assim, temos:
= 237
Dividindo a memória ocupada pelo tamãnho de cada fotografia, temos:
= 216 = 65.536 ≃ 65.500
Portanto, a alternativa quê mais se aproxima é 65.000 fotografias.
b) I) tipo exponencial
II) C(100) = −150 ⋅ + 150 = −150 ⋅ + 150 = 88,56
C(100) = 88,56, o quê indica quê, após 100 min carregando, a bateria do smartphone estava com 88,56% de sua capacidade carregada.
III) 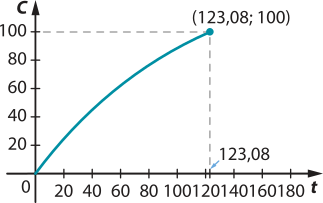
O smartphone estará completamente carregado quando passados aproximadamente 120 min ou 2 h.
c) I) f(0) = 2.000 ⇒ a ⋅ 2b ⋅ 0 = 2.000 ⇒ a = 2.000
f(10) = 1.000 ⇒ 2.000 ⋅ 2b ⋅ 10 = 1.000 ⇒ 2b ⋅ 10 = 2−1 ⇒ 10b = −1 ⇒ b = −0,1
Logo, f(x) = 2.000 ⋅ 2−0,1x.
II) f(5) = 2.000 ⋅ 2−0,1 ⋅ 5 ≃ 1.414,21 → aproximadamente R$ 1.414,21
Praticando: enêm e vestibulares
1. alternativa d
P(0) = 40 ⋅ 23 ⋅ 0 = 40
Como 20 min correspondem a de hora, temos:
P = 40 ⋅ = 80
Portanto, após 20 min, a população de bactérias será duplicada.
2. alternativa d
7,8 ⋅ 10−6 = ⇒ d = = = 107 = 10.000.000
3. alternativa c
= a2 + ab + b2
Fazendo a = 27 e b = 26, temos:
272 + 27 ⋅ 26 + 262 = 729 + 702 + 676 = 2.107
4. alternativa d
P(0) = 200 ⋅ = 200
3 ⋅ 200 = 200 ⋅ ⇒ 3 = ⇒ 1 = t ⇒ t = ano ou 8 meses
5. alternativa c
De acôr-do com o enunciado, temos:
• V = 200.000
• y = 200.000 ∶ 2 = 100.000 para x = 4
Substituindo esses valores na expressão dada, temos quê:
100.000 = 200.000 ⋅ a4 ⇒ a4 = ⇒ a = ou
a = (não convém)
Calculando y para x = 8, temos:
y = 200.000 ⋅ = 200.000 ⋅ = 200.000 ⋅ = 50.000 → R$ 50.000,00
6. alternativa c
V(4) = 5 + 24 = 21
V(5) = 5 + 25 = 37
V(6) = 5 + 26 = 69
21 + 37 + 69 = 127 → 127 refrigeradores
7. alternativa 02
N(t) = − 2 ⋅ 3t + 3 = − 2 ⋅ 3t + 3
Adotando x = 3t, temos
N(x) = x2 − 2x + 3. Assim:
N(x) > 678 ⇒ x2 − 2x + 3 > 678 ⇒ x2 − 2x − 675 > 0 ⇒ x < −25 ou x > 27
Voltando para a variável t, temos:
3t < −25 (não convém)
3t > 27 ⇒ 3t > 33 ⇒ t > 3
Logo, o tempo mínimo necessário para o número de colônias ultrapassar 678 é de 3 horas.
8. alternativa e
2x + 3 = 32 ⇒ 2x + 3 = 25 ⇒ x + 3 = 5 ⇒ x = 2
2−x = 2−2 =
9. alternativa a
6,4 ⋅ 1010 = 109 ⋅ 43t ⇒ 6,4 ⋅ 10 = 43t ⇒ 26 = 26t ⇒ t = 1 → 1 hora
10. alternativa c
Como o crescimento é exponencial, podemos representar a produção de cada mês, em milhar de unidade, por uma função f cuja lei de formação é dada por f(x) = k ⋅ ax, sêndo x o número do mês correspondente (janeiro: 0, fevereiro: 1, março: 2, abril: 3) e a e k constantes reais, com a ≠ 0.
Assim, temos:
x = 0 → f(0) = k ⋅ a0 ⇒ 120 = k ⋅ 1 ⇒ k = 120
Segue-se quê:
x = 3 → f(3) = 120 ⋅ a3 ⇒ 960 = 120 ⋅ a3 ⇒ a3 = 8 ⇒ a = 2
Dessa maneira, temos f(x) = 120 ⋅ 2x.
Calculando f(1), obtemos a produção de fevereiro:
f(1) = 120 ⋅ 21 = 240 → 240 mil peças
11. alternativa c
Q(t) = q0 ⋅ → 10 = q0 ⋅ ⇒ 10 = q0 ⋅ ⇒ q0 = 80 → 80 mg
12. alternativa b
I) falsa, pois, por exemplo, para x = −1, temos:
3−1 − 2−1 = = e < 0
II) verdadeira, pois:
32x ≥ 3x − 2x ⇒ 32x − 3x + 2x ≥ 0 ⇒ 3x ≥ 0 ⇒ 3x − 1 + ≥ 0
Página trezentos e cinquenta e nove
Segue-se quê:
• se x ≥ 0 → 3x ≥ 1 (I)
• se x < 0 → ≥ 1 (II)
De I e II, temos quê
3x − 1 + ≥ 0 para todo x ∈ ℝ.
III) falsa, pois, por exemplo, se x = −1, temos:
3−2 + 3−1 − 2−1 = = < 0
13. alternativa b
54.675 = 25 ⋅ 32t − 7 ⇒ 2.187 = 32t − 7 ⇒ 37 = 32t − 7 ⇒ 7 = 2t − 7 ⇒ t = 7 → 7 dias
14. alternativa d
32t + 7 = 18 ⋅ 3t − 2 + 10 ⇒ 32t − 18 ⋅ 3t − 2 − 3 = 0 ⇒ 32t − − 3 = 0 ⇒ − 2 ⋅ 3t − 3 = 0
Fazendo y = 3t, temos:
y2 − 2y − 3 = 0
Resolvendo essa equação, temos:
y = 3 ou y = −1 (não convém).
Substituindo y = 3 em y = 3t, temos:
3 = 3t ⇒ t = 1
Calculando A(1), temos:
A(1) = 32 ⋅ 1 + 7 = 9 + 7 = 16 → 16 mil microrganismos A
15. alternativa a
31 = (37 − 25) + 25 ⇒ 31 − 25 = 12 ⇒ = ⇒ 2−1 = ⇒ t = 6 →6 horas
Como o corpo foi encontrado às 5 horas da manhã do dia 28, a morte ocorreu 6 horas antes, ou seja, às 11 horas (da noite) do dia 27.
16. alternativa c
Do enunciado, temos quê f(0) = 3 e f(7) = 18.000. Assim, temos:
f(0) = t ⋅ u0 ⇒ 3 = t ⋅ 1 ⇒ t = 3
Segue-se quê:
f(7) = 3 ⋅ u7 ⇒ 18.000 = 3 ⋅ u7 ⇒ u7 = 6.000 ⇒ u =
Consultando o gráfico da função g, temos:
u = g(7) = ≃ 3,47
Por fim, temos:
t + u → 3 + 3,47 = 6,47
Unidade 2 • Logaritmo e função logarítmica
1. a) Considerando log8 16 = x, temos:
8x = 16 ⇒ 23x = 24 ⇒ x =
b) Considerando = x, temos:
9x = ⇒ 32x = 3−4 ⇒ x = −2
c) Considerando log0,2 125 = x, temos:
0,2x = 125 ⇒ = 53 ⇒ 5−x = 53 ⇒ x = −3
d) Considerando = x, temos:
= 72 ⋅ ⇒ ⇒ x = 5
2. a) 16x = 128 ⇒ 24x = 27 ⇒ x =
b) 63 = x ⇒ x = 216
c) ⇒ x = 10
d) 2log x = 22 ⇒ log x = 2 ⇒ 102 = x ⇒ x = 100
3. Para calcular os logaritmos decimais, podemos digitar a tecla ![]() seguida dos algarismos do logaritmando em cada caso, e para finalizar, clicar na tecla
seguida dos algarismos do logaritmando em cada caso, e para finalizar, clicar na tecla ![]() . Assim, temos:
. Assim, temos:
a) 2,04
b) 1,38
c) 1,71
d) −0,22
4.
a) Como o logaritmando deve sêr maior quê zero, temos: 4x − 52 > 0 ⇒ x > 13
b) Como a base deve sêr maior quê zero e diferente de 1, temos:
• 2x + 5 > 0 ⇒ x >
• 2x + 5 ≠ 1 ⇒ x ≠ −2
Portanto, x > e x ≠ −2.
c) • A base deve sêr maior quê zero e diferente de 1. Logo, temos para a base:
I)
• O logaritmando deve sêr maior quê zero. Logo, temos para o logaritmando:
II) x2 + 7x > 0 ⇒ x(x + 7) > 0 ⇒

Portanto, x < −8 e x ≠ −9.
d) • A base deve sêr maior quê zero e diferente de 1. Logo, temos para a base:
I)
• O logaritmando deve sêr maior quê zero. Logo, temos para o logaritmando:
II) −x2 − 3x + 10 > 0 ⇒ −5 < x < 2
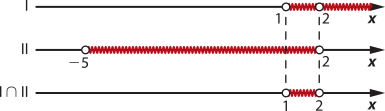
Portanto, 1 < x < 2.
5.
a) log4 16 ⋅ log12 12 = log4 42 ⋅ 1 = 2
b) log () − log9 1 = log (10) − 0 = log 10 = 1
c) Considerando log0,04 5 = x, obtemos:
0,04x = 5 ⇒ 5 ⇒ 5−2x = 51 ⇒ x =
(log0,04 5) ⋅ [ + log2 0,25] = ⋅ [20 + log2 2−2] = ⋅ [20 − 2] = −9
d) Considerando = y, obtemos:
= 33 ⇒ y = 6
= =
6. log4 x = 4,5 ⇒ x = 44,5 ⇒ x = 512
log4 2x = y ⇒ 4y = 1.024 ⇒ 4y = 45 ⇒ y = 5
7. 14.478 = 5.700 ⋅ (1 + 0,06)t ⇒ 2,54 = 1,06t ⇒ log1,06 2,54 = log1,06 1,06t ⇒ t = 16 → 16 meses
8. a) log 1 = 0,00;
log 2 ≃ 0,301029995663981;
log 3 ≃ 0,477121254719662;
log 4 ≃ 0,602059990327962
b) Utilizando a calculadora, temos:
Logaritmando |
Logaritmo aproximado na base 10 |
|---|---|
6 |
0,77815125 |
7 |
0,84509804 |
8 |
0,903089987 |
9 |
0,954242509 |
10 |
1 |
9. a) De acôr-do com a propriedade do logaritmo do quociente, temos:
log
b) Utilizando a propriedade da mudança de base, temos:
= log6 5
c) Utilizando as propriedades do logaritmo da potência e do logaritmo do produto, respectivamente, temos:
log7 23 + log7 5 = log7 (8 ⋅ 5)= log7 40
d) Utilizando as propriedades da mudança de base e do logaritmo do produto, respectivamente, temos:
+ log3 2 = + log3 2 = log3 4
10. a) log3 70 = log3 (7 ⋅ 5 ⋅ 2) = log3 7 + log3 5 + log3 2 = 1,77 + 1,46 + 0,63 = 3,86
Página trezentos e sessenta
b) log3 36 = log3 (22 ⋅ 32) = log3 22 + log3 32 = 2 ⋅ 0,63 + 2 = 3,26
c) ≃ 0,82
d) log3 = log3 7 − log3 2 − log3 5 = 1,77 − 0,63 − 1,46 = −0,32
11. Inicialmente, utilizamos a propriedade da mudança de base para obtêr logaritmos decimais e, na sequência, usamos a calculadora científica. Assim, obtemos:
a) log8 20 = ≃ 1,44
b) log2 100 = ≃ 6,64
c) log8 (0, 5)= = −0,3
d) log20 16 = ≃ 0,93
12. a) x = 30,9 ≃ 2,688
b) x = 53,9 ≃ 532,09
c) x = 7−1,2 ≃ 0,097
d) x = 100,01 ≃ 1,02
13. Com base nos dados fornecidos, montamos o seguinte qüadro:
Passo |
Número de lados |
Perímetro |
|---|---|---|
0 |
3 |
3 ⋅ 1 |
1 |
12 |
12 ⋅ |
2 |
48 |
48 ⋅ |
a) Como a quantidade de lados de cada figura da sequência aumenta em PG, cujo primeiro termo é 3 e a razão é 4, temos:
l3 = 3 ⋅ 43 = 192 → 192 lados
b) Como o perímetro de cada figura da sequência aumenta em PG, cujo primeiro termo é 3 e a razão é , temos:
p5 = 3 ⋅ =
c) ln = 3 ⋅ 4n → 3 ⋅ 4n > 6 ⋅ 1012 ⇒ 22n > 2 ⋅ 1012 ⇒ 2n ⋅ log 2 > log 2 + 12 ⋅ log 10 ⇒ 2n ⋅ 0,301 > 0,301 + 12 ⇒ n > 20,4
Portanto, a partir do passo 21.
14. 1084 = ⇒ log 1084 = log ⇒ 84 ⋅ log 10 = t ⋅ log ⇒ 70 ⋅ log 10 = t ⋅ log ⇒ 70 = t ⋅ (log 10 − log 22) ⇒ 70 = t ⋅ (1 − 2 ⋅ 0,3) ⇒ t = 175 → 175 min
15. a) Considerando quê a meia-vida é o tempo para quê a massa da substância seja reduzida pela mêtáde, temos quê a massa inicial será multiplicada por a cada intervalo de tempo t, de acôr-do com a meia-vida. Neste caso, como a meia-vida é de 30 anos, temos .
Logo:
M(t) = A ⋅
b) 2026 − 1987 = 39
M(39) = 18 ⋅ ≃ 7,3 → aproximadamente 7,3 g
c) 0,0036 = 18 ⋅ ⇒ 2 ⋅ 10−4 = ⇒ log (2 ⋅ 10−4) = log ⇒ log 2 − 4 log 10 = ⋅ log 2 ⇒ log 2 − 4 = ⋅ log 2 ⇒ 0,301 − 4 = ⋅ 0,301 ⇒ t ≃ 369 → aproximadamente 369 anos
d) Pesquisa do estudante. Espera-se quê os estudantes realizem uma pesquisa em sáites confiáveis. É importante quê eles compreendam quê os materiais radioativos têm grande utilidade em diversas áreas. Porém, por sêrem materiais muito voláteis, devem ser manipulados apenas por profissionais qualificados e com os cuidados necessários, uma vez quê mesmo um pequeno vazamento de algum dêêsses materiais póde contaminar uma grande região. Eles podem indicar métodos de prevenção de acidentes, bem como métodos de contenção em caso de acidente.
16. a) M = 3.500 ⋅ log2 (1 + 1.000) ⇒ M = 3.500 ⋅ ⇒ M = 3.500 ⋅ ⇒ M ≃ 34.884 → aproximadamente 34.884 bps
17. alternativa d
3 log2 + 3 log2 −2 log2 = 3 −2 log2 = 3 −2 log2 = 3 −2 log2 = log2 − log2 = log2 − log2 = = log2 = log2 2 = 1
18. • Atividade de elaboração do estudante. Espera-se quê os estudantes elaborem problemas quê relacionem o gráfico de uma função exponencial ao estudo dos logaritmos, envolvendo não apenas o uso da definição de logaritmo mas também as suas propriedades. Utilizando o gráfico, eles podem, por exemplo, indicar uma quantidade de pessoas e solicitar quê seja calculado o tempo correspondente.
19. a) f(2) = log16 2 =
b) f = log16 =
c) g = log36 = = −2
d) g(1) = log36 1 = 0
e) g(46.656) + f(65.536) = log36 46.656 + log16 65.536 = = 3 + 4 = 7
20. a) 3x + 27 > 0 ⇒ x > −9
D(f) = {x ∈ ℝ | x > −9}
b) x2 − 4 > 0 ⇒
D(g) = {x ∈ ℝ | x < −2 ou x > 2}
c) x − 8 > 0 ⇒ x > 8
D(h) = {x ∈ ℝ | x > 8}
d) I)
II) x2 + x > 0 ⇒
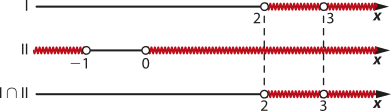
D(m) = {x ∈ ℝ | x > 2 e x ≠ 3}
21. a) crescente
b) decrescente
c) crescente
d) decrescente
e) crescente
22. a) 2t + 9 > 1 ⇒ t > −4
b) 0 < 2t + 9 < 1 ⇒ < t < −4
23. Utilizando o GeoGebra, por exemplo, pode-se digitar a lei de formação da função no campo Entrada. Já se os esboços dos gráficos forem realizados em malha quadriculada, pode-se atribuir alguns valores arbitrários para x e determinar os valores correspondentes de y = f(x). Assim, temos:
Página trezentos e sessenta e um
a) 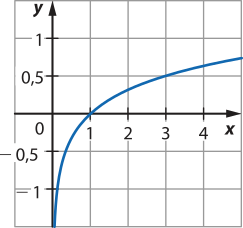
b) 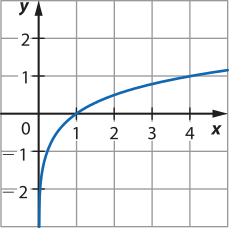
c) 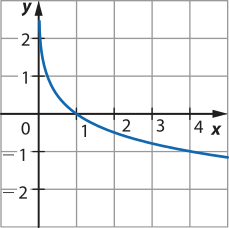
d) 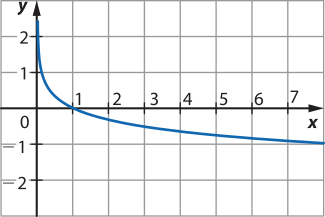
24. f(a) = 0 ⇒ log5 a = 0 ⇒ a = 50 ⇒ a = 1
f(b) = 1 ⇒ log5 b = 1 ⇒ b = 51 ⇒ b = 5
25. Considerando as etapas para a obtenção da função invérsa apresentadas na Unidade, temos:
a) y = 4x
x = 4y
log4 x = log4 4y
log4 x =y log4 4
log4 x =y
f−1 : → ℝ, definida por f−1 (x) = log4 x
b) y = log2,5 x
x = log2,5 y
(2,5)x = y
g−1 : ℝ → , definida por g−1 (x) = 2,5x
26. Considerando as etapas para a obtenção da função invérsa apresentadas na Unidade, temos:
M(t) = 2(t − 2)
t = 2(M − 2) ⇒ t =
4t = 2M
log2 4t = log2 2M
log2 4 + log2 t = M log2 2
2 +log2 t = M
t(M) = 2 + log2 M
27. Sejam m e n números reais positivos, com m > n. Considerando quê y1 = f(m) e y2 = f(n), temos:
y1 = loga m e y2 = loga n, ou seja, = m e = n. Como m > n, então > .
Se a >1, temos y1 > y2 ⇒ f(m) > f(n).
Portanto, a função é crescente.
Se 0 < a < 1, temos y1 < y2 ⇒ f(m) < f(n). Portanto, a função é decrescente.
28. f(0,5) = 2 ⇒ a0,5 = 2 ⇒ a = 4
Como f(x) = 4x e o gráfico de g é simétrico ao de f em relação à bissetriz dos quadrantes ímpares do plano cartesiano, temos quê g(x) = log4 x.
29. a) Resposta esperada: A ordenada do ponto A do gráfico da função p corresponde à abscissa do ponto B do gráfico da função m, e a ordenada do ponto B corresponde à abscissa do ponto A.
b) a = p(0,5) = (0,9)0,5 ≃ 0,95
b = p(1,5) = (0,9)1,5 ≃ 0,85
c) m(a) ≃ 0,5; m(b) ≃ 1,5
d) Como p(h) = 0,9h e o gráfico de m é simétrico ao de p em relação à bissetriz dos quadrantes ímpares do plano cartesiano, temos: m(h) = log(0,9) h
30. Atividade de elaboração do estudante. Espera-se quê os estudantes determinem a função invérsa de uma função logarítmica dada, a partir de sua lei de formação. Orientá-los para quê elaborem os gráficos dessas funções com o objetivo de perceberem a simetria de reflekção entre esses gráficos em relação à bissetriz dos quadrantes ímpares.
31. a) condições de existência: x > 0 e x ≠ 1 definição: x3 = 343 ⇒ x3 = 73 ⇒ x = 7
S = {7}
b) condições de existência:
• x − 2 > 0 ⇒ x > 2
• x − 2 ≠ 1 ⇒ x ≠ 3
definição: (x − 2)2 = x2 ⇒ x2 − x2 + 4x − 4 = 0 ⇒ x = 1
S = ∅
c) definição: 16x = 4.096 ⇒ 16x = 163 ⇒ x = 3
S = {3}
d) condições de existência:
> 0 e x ≠ −1
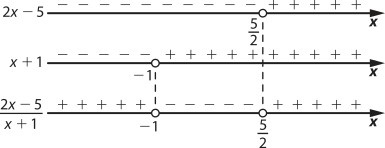
Assim, temos x < −1 ou x > .
definição: 24 = ⇒ 16x + 16 = 2x − 5 ⇒ 14x = −21 ⇒ x =
S =
32. a) log 2x = log 3 ⇒ x ⋅ log 2 = log 3 ⇒ x ≃ ⇒ x ≃ 1,5
b) log 22(2x + 5) = log 32 ⇒ (4x + 10) ⋅ log 2 = 2 ⋅ log 3 ⇒ 1,2x + 3 ≃ 0,94 ⇒ x ≃ −1,71
c) log 10(5x + 1) = log 7 ⇒ (5x + 1) ⋅ 1 ≃ 0,84 ⇒ 5x ≃ −0,16 ⇒ x ≃ −0,032
d) log 30(6x − 18) = log 35 ⇒ (6x − 18) ⋅ (log 3 + log 10) = log 7 + log 5 ⇒ (6x − 18) ⋅ (0,47 + 1) ≃ 0,84 + 0,69 ⇒ 6x − 18 ≃ ⇒ 6x ≃ 18 + 1,041 ⇒ x ≃ 3,17
33. log ((5x) ⋅ (x − 4)) = log x ⇒ 5x2 − 20x = x ⇒ 5x2 − 21x = 0 ⇒
Portanto, x = 4,2.
34. M = C ⋅ (1 + i)t
48.000 = 12.000 ⋅ (1 + 0,03)t ⇒ 4 = (1,03)t ⇒ log 22 = log (1,03)t ⇒ 2 ⋅ log 2 = t ⋅ log (1,03) ⇒ 2 ⋅ 0,301 = t ⋅ 0,013 ⇒ t ≃ 46,3
Logo, Juliana necessitará de 47 meses.
35. alternativa e
P(0) = 250 ⋅ = 250
3 ⋅ 250 = 250 ⋅ ⇒ log 3 = ⋅ log 1,2 ⇒ 5 ⋅ 0,48 = t ⋅ (log 12 − log 10) ⇒ 2,4 = t ⋅ (log 2 + log 2 + log 3 − 1) ⇒ 2,4 = t ⋅ (0,3 + 0,3 + 0,48 − 1) ⇒ t = 30 → 30 anos
36. a) f(2) = 108.000 ⋅ 0,882 = 83.635,20 → R$ 83.635,20
b) 54.000 = 108.000 ⋅ 0,88t ⇒ log 0,5 = t ⋅ log 0,88 ⇒ t ≃ 5,42
Logo, Patrícia deverá vender o automóvel em aproximadamente 5 anos e 5 meses.
37. a) condição de existência:
9x − 8 > 0 ⇒ x > (I)
Assim, temos:
(9x − 8) > 2 ⋅ ⇒ (9x − 8) >
Como a = e 0 < a < 1, então:
9x − 8 < ⇒ x < (II)

S =
b) Tomando y = log5 (x + 2), temos:
Página trezentos e sessenta e dois
2y > 1 ⇒ 2y > 20 ⇒ y > 0
Assim, consideramos log5 (x + 2) > 0.
condição de existência: x + 2 > 0 ⇒ x > −2 (I)
Portanto, temos:
log5 (x + 2) > 0 ⋅ log5 5 ⇒ log5 (x + 2) > log5 50
Como a = 5 e a > 1, então:
x + 2 > 50 ⇒ x > −1 (II)
A solução da inequação deve atender simultaneamente às condições I e II.

S = {x ∈ ℝ | x > −1}
c) log2 (x + 4) ≤ log2 (x − 3) + 2 ⇒ log2 (x + 4) ≤ log2 (x − 3) + log2 4 ⇒ log2 (x + 4) ≤ log2 4(x − 3)
condições de existência:
• x + 4 > 0 ⇒ x > −4 (I)
• 4x − 12 > 0 ⇒ x > 3 (II)
Como a base dos logaritmos é maior quê 1, o sentido da desigualdade é mantido. Assim:
x + 4 ≤ 4x − 12 ⇒ 16 ≤ 3x ⇒ x ≥ (III)
A solução da inequação deve satisfazer simultaneamente às condições I, II e III.

S =
38. condição de existência: 3x − 9 > 0 ⇒ x > 3 (I)
Assim, temos:
log0,2 (3x − 9) ≥ −1 ⋅ log0,2 0,2 ⇒ log0,2 (3x − 9) ≥ log0,2 (0,2)−1
Como a = 0,2 e 0 < a < 1, então:
3x − 9 ≤ (0,2)−1 ⇒ x ≤ (II)
A solução da inequação deve atender simultaneamente às condições I e II.

S =
Como nesse conjunto existe apenas o elemento 4 como natural, então existe um único número natural quê pertence ao conjunto solução dessa inequação.
39. a) Considerando a 1ª inequação, temos: condição de existência: x + 3 > 0 ⇒ x > −3 (I)
Assim, temos:
log2 (x + 3) < 5 ⋅ log2 2 ⇒ log2 (x + 3) < log2 25
Como a = 2 e a > 1, então:
x + 3 < 32 ⇒ x < 29 (II)

SI = {x ∈ ℝ | −3 < x < 29}
Considerando a 2ª inequação, temos: log0,2 (x + 4) < log0,2 (2x) ⇒ log0,2 < 0
condição de existência: > 0
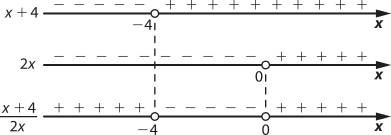
> 0 ⇒ x < −4 ou x > 0 (III)
Assim, temos:
log0,2 < 0 ⋅ log0,2 0,2 ⇒ log0,2 < log0,2 0,20
Como a = 0,2 e 0 < a < 1, então:
> 1 ⇒ > 0
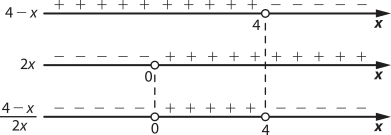
> 0 ⇒ 0 < x < 4 (IV)
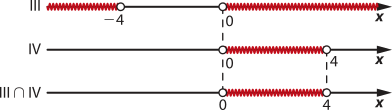
SII = {x ∈ ℝ | 0 < x < 4}
Como a solução do sistema de inequações deve atender simultaneamente às condições de SI e de SII, então:

Portanto, S = {x ∈ ℝ | 0 < x < 4}.
b) Considerando a 1ª inequação, temos:
condições de existência:
• x > 0 (I)
• 2x + 3 > 0 ⇒ x > (II)
Como a base dos logaritmos é maior quê 1, o sentido da desigualdade é mantido. Assim:
x ≤ 2x + 3 ⇒ x ≥ −3 (III)
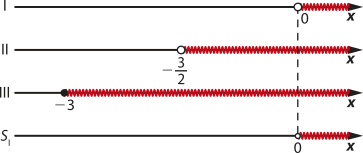
SI = {x ∈ ℝ | x > 0}
Considerando a 2ª inequação, temos:
log0,2 x2 < log0,2 x + 1 ⇒ log0,2 x2 < log0,2 0,2x
condições de existência:
• x2 > 0 ⇒ x > 0 ou x < 0 (I)
• 0,2x > 0 ⇒ x > 0 (II)
Como a base dos logaritmos (0,2) é maior quê 0 e menor quê 1, o sentido da desigualdade é invertido. Assim:
x2 > 0,2x ⇒ x2 − 0,2x > 0 ⇒ x < 0 ou x > 0,2 (III)
A solução da inequação deve satisfazer simultaneamente às condições I, II e III.

SII = {x ∈ ℝ | x > 0,2}
Como a solução do sistema de inequações deve atender simultaneamente às condições de SI e de SII, então:

Portanto, S = {x ∈ ℝ | x > 0,2}.
c) Considerando a 1ª inequação, temos:
condições de existência:
• x2 − 4 > 0 ⇒ x < −2 ou x > 2 (I)
• x + 2 > 0 ⇒ x > −2 (II)
Como a base dos logaritmos é maior quê 0 e menor quê 1, o sentido da desigualdade é invertido. Assim:
x2 − 4 ≥ x + 2 ⇒ x2 − x − 6 ≥ 0 ⇒ x ≤ −2 ou x > 3 (III)

SI = {x ∈ ℝ | x ≥ 3}
Considerando a 2ª inequação, temos: condição de existência:
0,8x + 9 > 0 ⇒ x > −11,25 (I)
Então, temos:
log0,67 (0,8x + 9) ≥ 2 ⇒ log0,67 (0,8x + 9) ≥ log0,67 0,672
Como a base dos logaritmos (0,67) é maior quê 0 e menor quê 1, o sentido da desigualdade é invertido. Assim:
Página trezentos e sessenta e três
0,8x + 9 ≤ 0,672 ⇒ x ≤ −10,69 (II)

SII = {x ∈ ℝ | −11,25 < x ≤ −10,69}
Como a solução do sistema de inequações deve atender simultaneamente às condições de SI e de SII, então:

Portanto, S = ∅.
d) Considerando a 1ª inequação, temos: condições de existência:
• x2 − 9 > 0 ⇒ x < −3 ou x > 3 (I)
• x − 3 > 0 ⇒ x > 3 (II)
Como a base dos logaritmos é maior quê 1, o sentido da desigualdade é mantido. Assim:
x2 − 9 > x − 3 ⇒ x2 − x − 6 > 0 ⇒ x < −2 ou x > 3 (III)

SI = {x ∈ ℝ | x > 3}
Considerando a 2ª inequação, temos: condições de existência:
• 5x > 0 ⇒ x > 0 (I)
• 3x + 12 > 0 ⇒ x > −4 (II)
Como a base dos logaritmos é maior quê 1, o sentido da desigualdade é mantido. Assim:
5x ≥ 3x + 12 ⇒ 2x ≥ 12 ⇒ x ≥ 6 (III)

SII = {x ∈ ℝ | x ≥ 6}
Como a solução do sistema de inequações deve atender simultaneamente às condições de SI e de SII, então:

Portanto, S = {x ∈ ℝ | x ≥ 6}.
40. a) Analisando as ordenadas dos pontos cujas abscissas são 2 e 6, temos, respectivamente, 20 cm e 30 cm.
b) De acôr-do com o gráfico, temos quê a planta atingiu 40 cm de altura após 14 meses.
c) g(t) = 10 ⋅ log2 (t + 2), pois o ponto de coordenadas (0, 10) pertence ao gráfico da função g e, além díssu, g(0) = 10 ⋅ log2 (0 + 2) = 10 ⋅ log2 2 = 10 ⋅ 1 = 10.
d) g(t) > 50 ⇒ 10 ⋅ log2 (t + 2) > 50 ⇒ log2 (t + 2) > 5
condição de existência: t + 2 > 0 ⇒ t > −2 (I)
Assim, temos:
log2 (t + 2) > 5 log2 2 ⇒ log2 (t + 2) > log2 25
Como a = 2 e a > 1, então:
t + 2 > 32 ⇒ t > 30 (II)

Portanto, após 30 meses, a planta ultrapassará 50 cm.
41. a) Resposta esperada: É a razão entre o PIB e a quantidade de habitantes do município.
b) ano 1: P(1) = 5,8 ⋅ log2 [1,35 ⋅ (1 + 9)] ⇒ P(1) = 5,8 ⋅ log2 13,5 ≃ 21,8 → 21,8 mil reais
ano 2: P(2) = 5,8 ⋅ log2 [1,35 ⋅ (2 + 9)] ⇒ P(2) = 5,8 ⋅ log2 14,85 ≃ 22,6 → 22,6 mil reais
ano 3: P(3) = 5,8 ⋅ log2 [1,35 ⋅ (3 + 9)] ⇒ P(3) = 5,8 ⋅ log2 16,2 ≃ 23,3 → 23,3 mil reais
c) 5,8 ⋅ log2 [1,35 ⋅ (t + 9)] > 29 ⇒ log2 1,35 + log2 (t + 9) > 5 ⇒ log2 (t + 9) > 5 − 0,43 ⇒ log2 (t + 9) > 4,57 ⋅ log2 2 ⇒ log2 (t + 9) > log2 24,57 ⇒ t + 9 > 23,75 ⇒ t > 14,75
Assim, a partir do 15º ano, esse município terá PIB per cápita maior quê 29 mil reais.
42. marca A: pH = −log (2,3 ⋅ 10−13) = −log 2,3 + 13 ⋅ log 10 ≃ −0,36 + 13 ≃ 12,64
marca B: pH = −log (7,4 ⋅ 10−14) = −log 7,4 + 14 ⋅ log 10 ≃ −0,87 + 14 ≃ 13,13
marca C: pH = −log (1,9 ⋅ 10−14) = −log 1,9 + 14 ⋅ log 10 ≃ −0,28 + 14 ≃ 13,72
marca D: pH = −log (1,6 ⋅ 10−14) = −log 1,6 + 14 ⋅ log 10 ≃ −0,2 + 14 ≃ 13,8
Portanto, apenas as marcas A e B estão em conformidade com a regulamentação da Anvisa.
43. Sendo I a idade do fóssil e A0 a quantidade inicial de hátomus de urânio-238 do fóssil, temos quê I = A0 . Assim:
A0 = A0 ⇒ log = ⋅ log 2 ⇒ log 25 + log 3 − log 100 ≃ ⋅ 0,3 ⇒ (5 ⋅ 0,3 + 0,47 − 2) ≃ ⇒ 0,135 ⋅ 109 ≃ 0,3t ⇒ t ≃ 4,5 ⋅ 108 → aproximadamente 4,5 ⋅ 108 anos ou 450 milhões de anos
44. alternativa c
Como o número de pessoas infectadas dobrava a cada 3 dias e sêndo p(t) o número de pessoas infectadas ao longo de t dias, temos quê:
p(t) = 1 ⋅
Nessa lei de formação, subtrai-se 1 de t no expoente de 2 porque, no 1º dia, há apenas 1 pessoa infekitada e, ao passar mais 3 dias, o número dobra. Assim, temos:
≥ 4.000
log10 = log10 (22 ⋅ 103)
⋅log10 2 = 2 log10 2 + 3 log10 10
⋅ 0,3 =2 ⋅ 0,3 + 3 ⋅ 1
t − 1=36
t = 37
Note quê:
p(37) = = 212 = 4.096
Como p(37) > 4.000 e considerando quê o número de pessoas infectadas dobra a cada 3 dias, segue-se quê:
p(37 − 3) = p(34) = = 211 = 2.048
Assim, o número de infectados atingirá a marca de 4 mil entre o 32º dia e o 38º dia após o primeiro contágio.
45. alternativa d
9,5 = ⇒ 14,25 = log x − log 7 + 3 ⋅ log 10 ⇒ 14,25 + 0,84 − 3 ≃ log x ⇒ 12,09 ≃ log x ⇒ x ≃ 1012,09 ⇒ x ≃ 1,23 ⋅ 1012
≃ 5.347,83
46. a) M = 1.000 ⋅ (1 + 0,1375)3 ⇒ M ≃ 1.471,82
1.000 + 0,80 ⋅ (1.471,82 − 1.000) ≃ 1.377,46 → aproximadamente R$ 1.377,46
b) 3.000 ⋅ (1 + 0,1375)t ≥ 9.000 ⇒ (1,1375)t ≥ 3 ⇒ t ⋅ log 1,1375 ≥ log 3 ⇒ t ⋅ 0,056 ≥ 0,477 ⇒ t ≥ 8,5
Portanto, serão necessários, no mínimo, 9 anos.
47. a) Pesquisa do estudante. Espera-se quê os estudantes citem aspectos como aplicar produtos específicos para o tratamento da á gua, conforme o resultado da análise. Eles podem complementar a resposta citando o tipo de produto quê póde sêr aplicado para a correção do pH.
Página trezentos e sessenta e quatro
b) Resposta pessoal. As respostas dependem do município onde os estudantes moram. Espera-se quê eles pesquisem e registrem as normas referentes à manutenção de piscinas. Caso no município não haja normas específicas para esse fim, orientá-los a pesquisar a esse respeito em municípios próximos para quê compreendam as normas quê são praticadas.
48. Atividade de elaboração dos estudantes. Espera-se quê eles elaborem problemas envolvendo funções logarítmicas com contexto relacionado ao pH de substâncias. Para resolver esses problemas, póde sêr necessária, por exemplo, a realização do cálculo do valor da variável dependente ou independente, utilizando-se as propriedades estudadas na Unidade. É importante quê a aplicação da função ao contexto seja realizada de modo adequado.
49. a) log E = 11,8 + 1,5 ⋅ 7 ⇒ log E = 11,8 + 10,5 ⇒ log E = 22,3 ⇒ E = 1022,3 → 1022,3 erg
b) log E = 11,8 + 1,5 ⋅ 9 ⇒ log E = 11,8 + 13,5 ⇒ log E = 25,3 ⇒ E = 1025,3 → 1025,3 erg
50. a) Resposta esperada: Não, pois outros fatores, como a distância de locais povoados, o tipo de terreno, as construções, as estruturas e o preparo para esse tipo de ocorrência, também determinam o efeito da devastação quê esse fenômeno provoca. Por exemplo, o terremoto quê atingiu Porto Príncipe teve menor magnitude quê o terremoto quê atingiu Rikuzentakata, porém o efeito da devastação sobre a população haitiana foi maior quê os efeitos de devastação na cidade japonesa.
b) Atividade de elaboração dos estudantes. Espera-se quê eles utilizem o contexto da energia liberada pêlos terremotos para produzir o problema envolvendo funções logarítmicas e suas propriedades. A atividade 49 é um exemplo de modelo em quê eles podem se inspirar. É possível também sugerir quê pesquisem um exemplo de terremoto ocorrido e indicar a energia liberada, solicitando quê identifiquem qual foi a magnitude do terremoto na escala rícher.
Integrando com...
1. Comparando os níveis de intensidade sonora das situações apresentadas com o nível recomendado, temos quê a situação quê póde provocar lesões irreversíveis no ouvido é a exposição ao avião a jato a 5 m. 130 dB.
2. • limite do audível:
NIS = 10 ⋅ log = 10 ⋅ log 1 = 0 → 0 dB
• limiar de dor:
NIS = 10 ⋅ log = 10 ⋅ (log 1 + 12 ⋅ log 10) = 10 ⋅ 12 = 120 → 120 dB
3. Secador de cabelo:
NIS = 10 log = 10 log (5 ⋅ 107) = 10 (log 5 + log 107) ≃ 10 (0,7 + 7) ≃ 77 → 77 dB. Classificação 1.
Liquidificador:
NIS = 10 log = 10 log (4 ⋅ 108) = 10 (log 4 + log 108) ≃ 10 (0,6 + 8) ≃ 86 → 86 dB. Classificação 2.
Aspirador de pó:
NIS = 10 log = 10 log 109 = 10 ⋅ 9 = 90 → 90 dB. Classificação 4.
4. Respostas pessoais. Espera-se quê os estudantes compreendam quê existem níveis de ruído considerados saudáveis para não comprometer a audição e quê, ao se expor a ruídos quê ultrapassem esses níveis, a saúde póde sêr afetada. Isso póde resultar no rompimento de membranas e tecídos auditivos (causando perda da audição), dificuldades de concentração, distúrbios do sono, aumento do estresse, entre outros problemas.
Espera-se quê, com a pesquisa realizada e o vídeo produzido, os estudantes contribuam para conscientizar a comunidade local a respeito dos níveis de intensidade sonora dos elétro domésticos, comparando-os com os valores saudáveis e recomendados pêlos órgãos competentes para a manutenção da saúde.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) III, pois é o único gráfico em quê, à medida quê x aumenta, y diminui exponencialmente.
b) Aumentou, pois, quando a pressão atmosférica diminui, a altitude aumenta.
0,4 = 0,9x ⇒ log 0,4 = x ⋅ log 0,9 ⇒x ≃ ⇒ x ≃ 8,65
0,3 = 0,9x ⇒ log 0,3 = x ⋅ log 0,9 ⇒ x ≃ ⇒ x ≃ 11,37
11,37 − 8,65 = 2,72 ≃ 2,7 → 2,7 km
c) h(0,5) = 20 ⋅ log = 20 ⋅ log 2 = 20 ⋅ 0,3 = 6 → 6 km
Praticando: enêm e vestibulares
1. alternativa d
T(t) = 3.000 ⋅ (0,99)2t ⇒ 30 = 3.000 ⋅ (0,99)2t ⇒ 0,01 = (0,99)2t ⇒ log = log ⇒ log 1 − log 100 = 2t ⋅ (log(32 ⋅ 11) − log 100) ⇒ − 2 = 2t ⋅ (log 32 + log 11 − 2) ⇒ − 2 = 2t ⋅ (2 ⋅ 0,477 + 1,041 − 2) ⇒ t = 200 → 200 horas
2. alternativa a
f = ⇒ log f = log ⇒ log f = log A − log rB ⇒ Y = log A − B ⋅ log r ⇒ Y = log A − B ⋅ X
3. alternativa b
log 22 + log 23 + log 24 +... + log 250 = 2 log 2 + 3 log 2 + 4 log 2 +... + 50 log 2 = (2 + 3 + 4 +... + 50) ⋅ log 2
Como a soma S dos n primeiros números naturais positivos é dada por
S = , temos quê:
S = ⇒ 1 + 2 + 3 + 4 +... + 50 = ⇒ 1 + 2 + 3 + 4 +... + 50 = 1.275 ⇒ 2 + 3 + 4 +... + 50 = 1.275 − 1 ⇒ 2 + 3 + 4 +... + 50 = 1.274
Segue-se quê:
(2 + 3 + 4 +... + 50) ⋅ log 2 = 1.274 ⋅ log 2 = log 21.274
4. alternativa d
10 = 16 −log2 (3h + 1) ⇒ −6 = −log2 (3h + 1) ⇒ 26 = 3h + 1 ⇒ h = 21 → 21 horas
5. alternativa d
pH = −log (2 ⋅ 10−8) = −log 2 + 8 ⋅ log 10 = −0,3 + 8 = 7,7
6. alternativa a
Representando o número inicial por n, temos:
B → 5n
A → log 5n
B → 5 ⋅ log 5n
Como o resultado dêêsse processo é 10, então:
5 ⋅ log 5n = 10 ⇒ log 5n = 2 ⇒ 5n = 100 ⇒ n = 20
7. alternativa a
A sequência de teclas digitadas corresponde aos seguintes cálculos: log 1.0000,5 = 0,5 ⋅ log 1.000 = 0,5 ⋅ 3 = 1,5
8. alternativa e
Para a flor sêr comercialmente mais valorizada, temos:
−log10 x < 8 ⇒ log10 x > −8 ⇒ x > 10−8
Página trezentos e sessenta e cinco
Entretanto, se pH < 7, a flor é azul, e quêremos que a flor seja cor-de-rosa. Assim, temos:
−log10 x > 7 ⇒ log10 x < −7 ⇒ x < 10−7
Portanto, 10−8 < x < 10−7.
9. alternativa e
Fazendo log4 14 = x e utilizando as propriedades opêratórìas de logaritmos, temos:
x = ⇒ x = ⇒ x = ⇒ x = ⇒ x = ⇒ x = ⇒ x = ⇒ x = ⋅ [1 + (log7 2)−1 ]
Como log7 2 = w, temos
x = ⋅ [1 + w−1] ⇒ x = ⇒ x = ⇒ x =
10. alternativa c
MS = 3,30 + log (2.000 ⋅ 0,2) = 3,30 + log 400 = 3,30 + log (4 ⋅ 100) = 3,30 + log 4 + log 100 = 3,30 + log 22 + log 100 = 3,30 + 2 ⋅ log 2 + log 100 = 3,30 + 2 ⋅ 0,3 + 2 = 5,9 → moderado
11. a) c(0) = 400 − k ⋅ log3 (a ⋅ 0 + 1) = 400 − k ⋅ log3 1 = 400 − k ⋅ 0 = 400 → 400 mg/L
b) c(2) = 0,5. c(0) = 200 e c(8) = 0
⇒
⇒ log3 (8a + 1) = 2 log3 (2a + 1) ⇒ log3 (8a + 1) = log3 (2a + 1)2 ⇒ 8a + 1 = 4a2 + 4a + 1 ⇒ a2 = a ⇒
k = ⇒ k = ⇒ k = 200
Portanto, a = 1 e k = 200.
12. alternativa c
200.000 = 100.000 ⋅ (1 + 0,008)n ⇒ 2 = (1,008)n ⇒ log 2 = log (1,008)n ⇒ 0,3 = n ⋅ 0,003 ⇒ n = 100
13. alternativa a
40 = 36 ⋅ ⇒ log = log ⇒ log 10 − log 9= ⋅ log 10 ⇒ 1 − 0,95 = ⋅ 1 ⇒ t = 5 → 5 horas
14. alternativa d
log (E) = 11,8 + 1,5 ⋅ 8,2 ⇒ log (E) = 24,1 ⇒E = 1024,1 ≃ 1024
15. alternativa a
Sendo A1 a área do retângulo, A2 a área do triângulo e AS a área sombreada, temos:
AS = A1 + A2 = 1 ⋅ (log 3 − log 2) + ⋅ 2 ⋅ (log 5 − log 3) = log 3 − log 2 + log 5 − log 3 = log 5 − log 2 = log → log u.a.
16. alternativa c
Como a medida da diagonal do quadrado de lado x é dada por e o primeiro quadrado tem lado de medida 1, temos:
1 = x2 ⇒ x2 = , sêndo x2 a medida do lado do quadrado acrescentado na Etapa 2.
= x3 ⇒ x3 = , sêndo x3 a medida do lado do quadrado acrescentado na Etapa 3.
= x4 ⇒ x4 = , sêndo x4 a medida do lado do quadrado acrescentado na Etapa 4.
Segue-se quê:
Logo, o n-ésimo quadrado terá lado com medida:
xn = x1 ⋅
Para xn < , temos:
= 1 ⋅ ⇒ 10−4 = ⇒ log 10−4 = log ⇒ −4 = (n − 1)(log − log 2) ⇒ −4 = (n − 1) ⇒ −4 = (n − 1) ⇒ n ≃ 27,67
Portanto, o lado terá medida menor quê um décimo de milésimo a partir da etapa 28.
17. alternativa b
A lei de formação da função quê representa a extensão desgastada da estrada é dada por f(x)= 130 ⋅ (1 + 0,117)x, pois 130 km é a quantidade desgastada inicialmente (para x = 0), e acrescenta-se 11,7% a cada ano. Logo, temos:
1.000 = 130 ⋅ (1,117)x ⇒ = 1,117x ⇒ log = log (1,117x) ⇒ log 100 − log 13 = x ⋅ log 1,117 ⇒ 2 − 1,1 = x ⋅ 0,05 ⇒ 0,9 = 0,05x ⇒ x = = 18
Segue-se quê:
2.004 + 18 = 2.022
Unidade 3 • Sequências e noções de linguagem de programação
1. 45 ⋅ 24 = 1.080 → cerca de 1.080 quadros
2. a) • a1 = 10 − 3 ⋅ 1 = 7
• a2 = 10 − 3 ⋅ 2 = 4
• a3 = 10 − 3 ⋅ 3 = 1
• a4 = 10 − 3 ⋅ 4 = −2
• a5 = 10 − 3 ⋅ 5 = −5
(7, 4, 1, −2, −5,...)
b) • a1 = −8
• a2 = a1 − 6 = −8 − 6 = −14
• a3 = a2 − 6 = −14 − 6 = −20
• a4 = a3 − 6 = −20 − 6 = −26
• a5 = a4 − 6 = −26 − 6 = −32
(−8, −14, −20, −26, −32,...)
c) • a1 = 2 ⋅ 1 +
• a2 = 2 ⋅ 2 +
• a3 = 2 ⋅ 3 +
• a4 = 2 ⋅ 4 +
• a5 = 2 ⋅ 5 +
3. a) Respostas possíveis: 1, 2 e 4; 2, 4 e 8; 4, 8 e 16; 8, 16 e 32.
b) Considerando quê o sucessor de 16 é o termo quê vêm depois dele e o antecessor de 4 é o termo quê vêm antes dele, temos: 32 e 2, respectivamente.
4. a) Resposta esperada: Não recursiva, pois, para determinar um termo qualquer da sequência, não é necessário conhecer o valor de um ou mais termos anteriores.
Página trezentos e sessenta e seis
b) Finita, pois o seu domínio é o conjunto {1, 2, 3, 4, 5}.
c) • a1 = 12 − 4 ⋅ 1 + 3 = 0
• a2 = 22 − 4 ⋅ 2 + 3 = −1
• a3 = 32 − 4 ⋅ 3 + 3 = 0
• a4 = 42 − 4 ⋅ 4 + 3 = 3
• a5 = 52 − 4 ⋅ 5 + 3 = 8
Portanto, Marcela foi quem escreveu corretamente todos os termos da sequência.
5. a) figura 1: 4 palítos e 1 quadrado; figura 2: 7 palítos e 2 quadrados; figura 3: 10 palítos e 3 quadrados.
b) Resposta esperada:

• 13 palítos. 4 quadrados.
c) Resposta esperada: A partir da figura 2, acrescentam-se três palítos à figura anterior, de maneira a obtêr um quadrado a mais do quê essa figura anterior tem.
d) (4, 7, 10,...)
A partir do segundo termo, cada termo é igual ao anterior somado com 3. Assim:
• a1 = 4
• a2 = a1 + 3 = 4 + 3 = 4 + 1 ⋅ 3
• a3 = a2 + 3 = 4 + 3 + 3 = 4 + 2 ⋅ 3
• a4 = a3 + 3 = 4 + 3 + 3 + 3 = 4 + 3 ⋅ 3
⋮
Assim, podemos definir essa sequência de maneira não recursiva por meio do termo geral an = 4 + (n − 1) ⋅ 3.
Resposta esperada:
an = 3n + 1, com n ∈ ℕ*.
6. Resposta esperada:
• Recursiva: O primeiro termo é igual a 0 e, a partir do segundo, cada termo é igual ao anterior somado com 13, ou seja, definimos an = an − 1 + 13 e a1 = 0, com n ∈ ℕ* e n ≥ 2.
• Não recursiva: Os termos da sequência são os múltiplos não negativos de 13, sêndo an = 13(n − 1) ou an = 13n − 13, com n ∈ ℕ*.
7. a) Nota-se quê an = 9(n − 1) − 5 = 9n − 14. Assim, um número k é termo da sequência se, e somente se, existe n ∈ ℕ* tal quê 9n − 14 = k.
• Para k = 238:
9n − 14 = 238 ⇒ 9n = 252 ⇒ n = 28 ∈ ℕ*
• Para k = 483:
9n − 14 = 483 ⇒ 9n = 497 ⇒ n = ∉ ℕ*
• Para k = 260:
9n − 14 = 260 ⇒ 9n = 274 ⇒ n = ∉ ℕ*
• Para k = 355:
9n − 14 = 355 ⇒ 9n = 369 ⇒ n = 41 ∈ ℕ*
Portanto, 238 e 355 são termos da sequência.
b) Temos quê a28 = 238 e a41 = 355, ou seja, 238 é o termo da 28ª posição e 355, da 41ª posição.
8. a) Analisando o esquema com os coelhos apresentado no enunciado, temos: (1, 1, 2, 3, 5,...).
b) Resposta esperada: A partir do 3º mês, a quantidade de casais de coelhos corresponde à soma das quantidades de casais nos dois meses anteriores.
c) • 1º mês: 1
• 2º mês: 1
• 3º mês: 1 + 1 = 2
• 4º mês: 1 + 2 = 3
• 5º mês: 2 + 3 = 5
• 6º mês: 3 + 5 = 8
• 7º mês: 5 + 8 = 13
• 8º mês: 8 + 13 = 21
• 9º mês: 13 + 21 = 34
• 10º mês: 21 + 34 = 55
• 11º mês: 34 + 55 = 89
• 12º mês: 55 + 89 = 144
Portanto, ao final do 12º mês haverá 144 casais de coelhos.
d) Resposta esperada:
, com n ∈ ℕ e n ≥ 3.
9.
a) Não é PA, pois
b) É PA, pois:
c) É PA, pois:
d) É PA, pois:
• b: r = 18, crescente; c: r = −8, decrescente; d: r = 0, constante
10. a) • a1 = −2
• a2 = −2 + 7 = 5
• a3 = 5 + 7 = 12
• a4 = 12 + 7 = 19
• a5 = 19 + 7 = 26
(−2, 5, 12, 19, 26)
b) • a3 = a1 + (3 − 1)r ⇒ 13 = a1 + 2 ⋅ 21 ⇒ a1 = −29
• a1 = −29
• a2 = −29 + 21 = −8
• a3 = −8 + 21 = 13
• a4 = 13 + 21 = 34
• a5 = 34 + 21 = 55
(−29, −8, 13, 34, 55)
c) • a1 = 9
• a2 = 9 +
• a3 =
• a4 = = 10
• a5 = 10 +
d) Como r = 0, a PA é constante, sêndo essa PA (−3, −3, −3, −3, −3).
e) • a4 = a1 + (4 − 1)r ⇒ 28 = a1 + 3 ⋅ (−4) ⇒ a1 = 40
• a1 = 40
• a2 = 40 + (−4) = 36
• a3 = 36 + (−4) = 32
• a4 = 32 + (−4) = 28
• a5 = 28 + (−4) = 24
(40, 36, 32, 28, 24)
f) a2 = 7 e r = −9
a1 + (−9) = 7 ⇒ a1 = 7 + 9 = 16
a1 = 16
a2 = 7
a3 = 7 + (−9) = −2
a4 = −2 + (−9) = −11
a5 = −11 + (−9) = −20
(16, 7, −2, −11, −20)
11. alternativa c
a) É uma PA definida por recorrência com r = 8 > 0; logo, é uma PA crescente.
b) É uma PA com termo geral:
an = 9n − 2 ⇒ an = 9(n − 1) + 9 − 2 ⇒ an = 7 + (n − 1) ⋅ 9
A razão é r = 9 > 0; logo, é uma PA crescente.
c) É uma PA definida por recorrência com r = −6 < 0; logo, é uma PA decrescente.
d) Não é uma PA, pois:
• a1 = −12 = −1
• a2 = −22 = −4
• a3 = −32 = −9
Assim:
12. Escrevendo a11 em função de a8 e r, temos:
a11 = a1 + 10r ⇒ a11 = + 3r ⇒ a11 = a8 + 3r
Assim, a razão r é dada por:
65 = 47 + 3r ⇒ r = 6
E o primeiro termo a1 é dado por:
a11 = a1 + 10r ⇒ 65 = a1 + 10 ⋅ 6 ⇒ a1 = 5
Segue-se quê:
• a1 = 5
• a2 = 5 + 6 = 11
• a3 = 11 + 6 = 17
13. A PA (a1, a2, a3, a4, a5, a6) póde sêr expressa como (a2 − r, a2, a2 + r, a5 − r, a5, a5 + r), sêndo r a razão da PA. De acôr-do com o enunciado:
• (a2 − r) + a2 + (a2 + r) = 12 ⇒ 3a2 = 12 ⇒ a2 = 4
• (a5 − r) + a5 + (a5 + r) = −15 ⇒ 3a5 = −15 ⇒ a5 = −5
Página trezentos e sessenta e sete
Segue-se quê:
a4 − a3 = r ⇒ (a5 − r) − (a2 + r) = r ⇒ a5 − a2 = 3r ⇒ −5 − 4 = 3r ⇒ r = −3
Assim, os outros termos são:
• a1 = 4 − (−3) = 7
• a3 = 4 + (−3) = 1
• a4 = −5 − (−3) = −2
• a6 = −5 + (−3) = −8
Portanto, a PA é (7, 4, 1, −2, −5, −8).
14. Inicialmente, vamos determinar o termo geral da PA. Temos:
a24 = a1 + 23r ⇒ 73 = a1 + 23 ⋅ 7 ⇒ a1 = −88
Assim:
an = a1 + (n − 1)r ⇒ an = −88 + (n − 1) ⋅ 7 ⇒ an = 7n − 95
Logo, um número k é um termo da PA se, e somente se, existe n ∈ ℕ*, tal quê 7n − 95 = k.
• Para k = 17:
7n − 95 = 17 ⇒ 7n = 112 ⇒ n = 16 ∈ ℕ*
• Para k = −60:
7n − 95 = −60 ⇒ 7n = 35 ⇒ n = 5 ∈ ℕ*
• Para k = 198:
7n − 95 = 198 ⇒ 7n = 293 ⇒ n = ∉ ℕ*
• Para k = 39:
7n − 95 = 39 ⇒ 7n = 134 ⇒ n = ∉ ℕ*
• Para k = 152:
7n − 95 = 152 ⇒ 7n = 247 ⇒ n = ∉ ℕ*
• Para k = −75:
7n − 95 = −75 ⇒ 7n = 20 ⇒ n = ∉ ℕ*
• Para k = 220:
7n − 95 = 220 ⇒ 7n = 315 ⇒ n = 45 ∈ ℕ*
• Para k = 287:
7n − 95 = 287 ⇒ 7n = 382 ⇒n = ∉ ℕ*
• Para k = 4:
7n − 95 = 4 ⇒ 7n = 99 ⇒ n = ∉ ℕ*
Portanto, apenas 17, −60 e 220 são termos da PA.
15. Como as medidas formam uma PA, temos:
10x − (8x − 1) = x + − 10x ⇒ 2x + 1 = −9x + ⇒ 11x = ⇒ x =
Assim, as medidas do trapézio, em centímetro, são:
• base menor: 8 ⋅ − 1 = 3
• altura: 10 ⋅ = 5
• base maior: = 7
Logo, a área do trapézio é:
⋅ 5 = 25 → 25 cm2
16. Temos a1 = −20 e r = −27 − (−20) = −7. Assim:
a72 = a1 + 71r = −20 + 71 ⋅ (−7) = −517
17. Temos quê, a cada nova mesa adicionada, a quantidade de lugares aumenta em duas unidades. Logo, a quantidade de cadeiras an em relação à quantidade n de mesas póde sêr representada pela PA (4, 6, 8, 10,...), em quê a1 = 4 e r = 2. Para calcular a quantidade de mesas em quê se obtêm 26 lugares, calculamos:
26 = 4 + (n − 1) ⋅ 2 ⇒ n = 12
Logo, serão necessárias 12 mesas.
18. a) Temos a1 = 3 e r = 11 − 3 = 8.
Vamos determinar n, tal quê an = 171:
an = a1 + (n − 1)r ⇒ 171 = 3 + (n − 1) ⋅ 8 ⇒ 8n = 176 ⇒ n = 22
Portanto, 22 termos.
b) Temos a1 = 10 e r = 29 − 10 = 19. Vamos determinar n, tal quê an = 1.435:
an = a1 + (n − 1)r ⇒ 1.435 = 10 + (n − 1) ⋅ 19 ⇒ 19n = 1.444 ⇒ n = 76
Portanto, 76 termos.
c) Temos a1 = 286 e r = 244 − 286 = −42. Vamos determinar n, tal quê an = −302:
an = a1 + (n − 1)r ⇒ −302 = 286 + (n − 1) ⋅ (−42) ⇒ 42n = 630 ⇒ n = 15
Portanto, 15 termos.
19. a) A quantidade de municípios atendidos em cada ano do período forma uma PA com a1 = 54 e a4 = 189. Temos:
a4 = a1 + 3r ⇒ 189 = 54 + 3r ⇒ 3r = 135 ⇒ r = 45
Assim, a quantidade de municípios atendidos era:
• em 2024:
a2 = 54 + 45 = 99 → 99 municípios
• em 2025:
a3 = 99 + 45 = 144 → 144 municípios
b) De acôr-do com a resolução do item a, temos a1 = 54 e r = 45. Assim:
an > 500 ⇒ a1 + (n −1)r > 500 ⇒ 54 + (n − 1) ⋅ 45 > 500 ⇒ 45n > 491 ⇒ n > ≃ 10,91
Logo, a empresa ultrapassará 500 municípios atendidos no ano correspondente a n = 11, ou seja, em 2033.
c) Resposta pessoal. Espera-se quê os estudantes identifiquem diferentes maneiras de resolver a quêstão e comparem-nas, de modo a identificar pontos positivos de cada uma. É possível que a resolvam com apôio de inequação, como no modelo de resolução, mas também podem resolver utilizando a igualdade e estimando os resultados obtidos.
20. a) r = 4. Resposta esperada: Como devem sêr interpolados cinco termos entre −10 e 14, temos quê a PA ôbitída deve ter sete termos, em quê a1 = −10 e a7 = 14. Assim, calculamos a7 = −10 + (7 − 1) ⋅ r ⇒ 14 = −10 + 6r ⇒ r = 4.
b) Temos a1 = 77 e a10 = −31. Assim:
a10 = a1 + 9r ⇒ −31 = 77 + 9r ⇒ 9r = −108 ⇒ r = −12
Segue-se quê:
• a2 = 77 + (−12) = 65
• a3 = 65 + (−12) = 53
• a4 = 53 + (−12) = 41
• a5 = 41 + (−12) = 29
• a6 = 29 + (−12) = 17
• a7 = 17 + (−12) = 5
• a8 = 5 + (−12) = −7
• a9 = −7 + (−12) = −19
(77, 65, 53, 41, 29, 17, 5, −7, −19, −31)
c) Sendo a1 = 19, an = 264 e r = 35, temos:
an = a1 + (n − 1)r ⇒ 264 = 19 + (n − 1) ⋅ 35 ⇒ 35n = 280 ⇒ n = 8
Logo, devem-se interpolar 6 meios aritméticos.
21. a) Temos = 3,75 e = 24,1; logo, o primeiro múltiplo de 12 no intervalo é 4 ⋅ 12 = 48 e o último, 24 ⋅ 12 = 288. Assim, os múltiplos de 12 formam uma PA em quê a1 = 48, an = 288 e r = 12. Temos:
an = a1 + (n − 1)r ⇒ 288 = 48 + (n − 1) ⋅ 12 ⇒ 12n = 252 ⇒ n = 21
Portanto, existem 21 múltiplos de 12 no intervalo.
b) De maneira similar ao feito no item a, temos = 8,75 e = 45,8; logo, a1 = 9 ⋅ 12 = 108, an = 45 ⋅ 12 = 540 e r = 12. Temos:
an = a1 + (n − 1)r ⇒ 540 = 108 + (n − 1) ⋅ 12 ⇒ 12n = 444 ⇒ n = 37
Portanto, existem 37 múltiplos de 12 no intervalo.
c) De maneira similar ao feito no item a, temos = 53, e = 95,5; logo, a1 = 54 ⋅ 12 = 648, an = 95 ⋅ 12 = 1.140 e r = 12. Temos:
an = a1 + (n − 1)r ⇒ 1.140 = 648 + (n − 1) ⋅ 12 ⇒ 12n = 504 ⇒ n = 42
Portanto, existem 42 múltiplos de 12 no intervalo.
Página trezentos e sessenta e oito
22. a) De acôr-do com o gráfico, a PA é crescente.
b) Temos a1 = −54 e r = −46 − (−54) = 8. Assim, o termo geral é:
an = a1 + (n − 1)r ⇒ an = −54 + (n − 1) ⋅ 8 ⇒ an = 8n − 62
Assim, para verificar se 106 é um termo da PA, fazemos:
8n − 62 = 106 ⇒ 8n = 168 ⇒ n = 21
Logo, o número 106 é termo da PA com a21 = 106.
c) De acôr-do com a resolução do item b, o termo geral é an = 8n − 62. Assim:
• o 50º termo é:
a50 = 8 ⋅ 50 − 62 = 338
• an > 0 ⇒ 8n − 62 > 0 ⇒ 8n > 62 ⇒ n > 7,75
Logo, o primeiro termo positivo é:
a8 = 8 ⋅ 8 − 62 = 2
d) f: ℕ* → ℝ, tal quê f(n) = 8n − 62
23. a) Se an = f(n) = −3n + 1 para n ∈ ℕ*, temos:
• a1 = −3 ⋅ 1 + 1 = −2
• a2 = −3 ⋅ 2 + 1 = −5
• a3 = −3 ⋅ 3 + 1 = −8
⋮
Assim, temos a PA (−2, −5, −8,...) em quê o primeiro termo é a1 = −2 e a razão é r = −5 − (−2) = −3.
b) 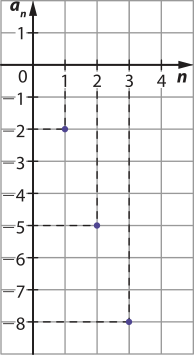
24. a) Temos a1 = 15.175 e r = 14.550 − 15.175 = −625.
Sendo an = 10.800 o último termo da PA, temos:
an = a1 + (n − 1)r ⇒ 10.800 = 15.175 + (n − 1) ⋅ (−625) ⇒ 625n = 5.000 ⇒ n = 8
Assim, a PA tem 8 termos; logo, o preêço da motocicleta póde sêr estimado por até 8 anos de uso.
b) Como a1 = 15.175 e r = −625, o termo geral da PA é:
an = a1 + (n − 1)r ⇒ an = 15.175 + (n − 1) ⋅ (−625) ⇒ an = −625n + 15.800
Assim, definimos f: A → ℝ, com A = {n ∈ ℕ | 1 ≤ n ≤ 8}, tal quê f(n) = −625n + 15.800.
c) 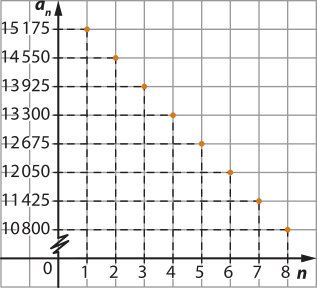
25. Atividade de elaboração do estudante. Espera-se quê os estudantes consigam relacionar a PA a uma função de domínio discreto e saibam relacionar as representações algébrica e gráfica dela. Eles podem, por exemplo, ao término da atividade, relacionar os coeficientes da função com características da PA, como a razão e o primeiro termo.
26. a) Temos a1 = 125.550 e r = −1.620.
Assim, a fórmula do termo geral é:
an = a1 + (n − 1)r ⇒ an = 125.550 + (n − 1) ⋅ (−1.620) ⇒ an = −1.620n + 127.170
b) A quantidade de domicílios com acesso à Tevê por assinatura em dezembro de 2025 corresponde ao termo a8. Temos:
a8 = −1.620 ⋅ 8 + 127.170 = 114.210 → 114.210 domicílios
27. Para resolver os itens a e b, considere a PA (1, 2, 3, 4,...) em quê o termo geral é an = n, quê expressa a quantidade de copos em cada camada.
a) • 15 camadas:
S15 = = = 120 → 120 copos
• 24 camadas:
S24 = = = 300 → 300 copos
b) • 78 copos:
Sn ≤ 78 ⇒ ≤ 78 ⇒ ≤ 78 ⇒ n(n + 1) ≤ 156
Note quê, como n ∈ ℕ, temos n2 ≤ n(n + 1) ≤ (n + 1)2, ou seja, n(n + 1) está entre dois quadrados perfeitos consecutivos.
Como, , estimamos quê n = 12 e calculamos S12:
S12 = = 78
Portanto, podem sêr empilhadas no mássimo 12 camadas.
• 195 copos:
Sn ≤ 195 ⇒ ≤ 195 ⇒ ≤ 195 ⇒ n(n + 1) ≤ 390
Utilizando o mesmo argumento quê o utilizado para 78 copos, observamos quê , estimamos quê n = 19 e calculamos S19:
S19 = = 190
Ao somar os copos da 20ª camada, obteríamos um total de 190 + 20 = 210 copos, o quê supera os 195 copos permitidos; logo, podem sêr empilhadas no mássimo 19 camadas.
c) Utilizando a expressão de cálculo da soma dos termos de uma PA, em quê a1 = 1, r = 1 e an = n, temos:
28. • X é a soma dos termos da PA em quê a1 = 10, r = 5 e o último termo é an = 150. Temos:
an = a1 + (n − 1)r ⇒ 150 = 10 + (n − 1) ⋅ 5 ⇒ n = 29
Logo, a PA tem 29 termos e X é dado por:
X = S29 = = = 2.320
• Y é a soma dos termos da PA em quê a1 = 150, r = 3 e o último termo é an = 198. Temos:
an = a1 + (n − 1)r ⇒ 198 = 150 + (n − 1) ⋅ 3 ⇒ n = 17
Logo, a PA tem 17 termos e Y é dado por:
Y = S17 = = = 2.958
Segue-se quê:
X + Y = 2.320 + 2.958 = 5.278
29. Temos:
a15 = a1 + 14r = 4 + 14 ⋅ 68 = 956
Assim:
S15 = = = 7.200
30. Temos:
⇒ ⇒ ⇒ ⇒
Página trezentos e sessenta e nove
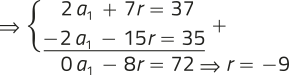
Substituindo r = −9 na equação
2a1 + 7r = 37, temos:
2a1 + 7 ⋅ (−9) = 37 ⇒ a1 = 50
Como a1 = 50 e r = −9, os cinco primeiros termos da PA são 50, 41, 32, 23 e 14.
31. A quantidade de poltronas forma uma PA de 10 termos em quê a1 = 17 e r = 2.
O último termo é:
a10 = a1 + 9r = 17 + 9 ⋅ 2 = 35
Assim, o total de poltronas é dado por:
S10 = = = 260 → 260 poltronas
32. a) Temos a1 = 2, r = 13 − 2 = 11 e o último termo é an = 112. Assim:
an = a1 + (n − 1)r ⇒ 112 = 2 + (n − 1) ⋅ 11 ⇒ n = 11
Logo, a PA tem 11 termos e sua soma é:
S11 = = = 627
b) Temos a1 = 127, r = 121 − 127 = −6 e o último termo é an = −47. Assim:
an = a1 + (n − 1)r ⇒ −47 = 127 + (n − 1) ⋅ (−6) ⇒ n = 30
Logo, a PA tem 30 termos e sua soma é:
S30 = = = 1.200
c) Temos a1 = 60, r = 70 − 60 = 10 e o último termo é an = 2.020. Assim:
an = a1 + (n − 1)r ⇒ 2.020 = 60 + (n − 1) ⋅ 10 ⇒ n = 197
Logo, a PA tem 197 termos e sua soma é:
S197 = = = 204.880
33. alternativa d
a) Falsa. Temos a1 = 13 e r = 16 − 13 = 3, assim:
a20 = a1 + 19r = 13 + 19 ⋅ 3 = 70
Segue-se quê:
S20 = = = 830 ≠ 2.150
b) Falsa. O primeiro termo comum das duas PAs é 16. Os outros termos comuns são todos os números quê são a soma de 16 com um número simultaneamente múltiplo de 4 e de 6; logo, esses termos formam uma PA em quê a1 = 16 e r = 12, pois 12 é o menor número quê é múltiplo comum de 4 e 6. Assim:
a10 = a1 + 9r = 16 + 9 ⋅ 12 = 124
Segue-se quê:
S10 = = = 700 ≠ 660
c) Falsa. Temos a1 = 8 e r = 12 − 8 = 4, assim:
a25 = a1 + 24r = 8 + 24 ⋅ 4 = 104 ≠ 108
d) Verdadeira. O primeiro termo comum das duas PAs é 16. A partir dêêsse termo, todos os termos seguintes da PA indicada em II também são termos da PA indicada em III, pois a razão da PA indicada em II (r = 6) é um múltiplo da razão da PA indicada em III (r = 3). Logo, os termos comuns formam uma PA em quê a1 = 16 e r = 6. Assim:
a12 = a1 + 11r = 16 + 11 ⋅ 6 = 82
Segue-se quê:
S12 = = = 588
34. Temos a1 = 34.000, r = 36.800 − 34.000 = 2.800, e o termo correspondente à quantidade estimada de visitantes em 2037 é o termo a10. Temos:
a10 = a1 + 9r = 34.000 + 9 ⋅ 2.800 = 59.200
Então, a quantidade total de visitantes de 2028 até 2037 será:
S10 = = = 466.000 → 466.000 visitantes
• Respostas pessoais. Espera-se quê os estudantes pesquisem informações sobre museus próximos de onde moram e façam um levantamento dos dados úteis para visitação, como o tipo de exposição do museu, os horários de funcionamento e o preêço da entrada.
35. ⇒ ⇒ ![]()
Substituindo r = 4 na equação a1 + 14r = −40, temos:
a1 + 14 ⋅ 4 = −40 ⇒ a1 = −96
O último termo da PA é:
a50 = a1 + 49r = −96 + 49 ⋅ 4 = 100
Assim, a soma dos termos da PA é:
S50 = = = 100
36. O hekzágono póde sêr decomposto em 4 triângulos; logo, a soma das medidas de seus ângulos internos é 4 ⋅ 180° = 720°.
Assim, as medidas dos ângulos internos do hekzágono formam uma PA de 6 termos em quê a6 = 140 e S6 = 720. Logo:
S6 = ⇒ 720 = ⇒ a1 = 100
A razão r da PA é dada por:
a6 = a1 + 5r ⇒ 140 = 100 + 5r ⇒ r = 8
Portanto, as medidas dos demais ângulos internos do hekzágono são 100°, 108°, 116°, 124° e 132°.
37. Na 1ª figura, utiliza-se 1 palito para formár cada um dos cinco lados do contôrno do pentágono. A partir da 2ª figura, adiciona-se uma quantidade constante de 1 palito nos dois lados aproveitados da figura anterior e, nos outros lados, são adicionados um total de 3 ⋅ n palítos. Logo, a quantidade de palítos adicionados na 2ª figura, em relação à 1ª, é 8 (2 + 3 ⋅ 2); na 3ª figura, em relação à 2ª, são adicionados 11 (2 + 3 ⋅ 3); e assim sucessivamente. Dessa maneira, a quantidade de palítos de uma figura para a seguinte aumenta de acôr-do com uma PA em quê a1 = 8 e r = 3.
Portanto, a quantidade de palítos na 10ª figura corresponde à soma dos 9 primeiros termos dessa PA, acrescida de 5 palítos, correspondentes à 1ª figura. Assim, temos:
a9 = a1 + 8r = 8 + 8 ⋅ 3 = 32
Segue-se quê:
S9 = = 180
Assim, temos:
180 + 5 = 185
Logo, a 10ª figura terá 185 palítos.
38. Temos:
• a1 = S1 = 4 ⋅ 12 − 4 ⋅ 1 = 0
• a1 + a2 = S2 ⇒ 0 + a2 = 4 ⋅ 22 − 4 ⋅ 2 ⇒ a2 = 8
Assim:
• razão: r = 8 − 0 = 8
• 40º termo:
a40 = a1 + 39r = 0 + 39 ⋅ 8 = 312
39. a) As parcelas formam uma PA em quê
a1 = x + , r = (x + 1) − = e o último termo é an = x + . Assim:
an = a1 + (n − 1)r ⇒ x + = x + + (n − 1) ⋅ ⇒ (n − 1) ⋅ ⇒ n − 1 = 17 ⇒ n = 18
Segue-se quê:
S18 =378 ⇒ = 378 ⇒ + = 42 ⇒ 2x + 12 = 42 ⇒ x = 15
Página trezentos e setenta
b) As parcelas formam uma PA em quê a1 = 4m − 27, r = (4m − 10) − (4m − 27) = 17 e o último termo é an = 4m + 551. Assim:
an = a1 + (n − 1)r ⇒ 4m + 551 = 4m − 27 + (n − 1) ⋅ 17 ⇒ (n − 1) ⋅ 17 = 578 ⇒ n − 1 = 34 ⇒ n = 35
Segue-se quê:
S35 = 8.750 ⇒ = 8.750 ⇒ (4m − 27) + (4m + 551) = 500 ⇒ 8m + 524 = 500 ⇒ m = −3
c) As parcelas formam uma PA em quê a1 = 44 + p, r = (38 + p) − (44 + p) = −6 e o último termo é an = −70 + p. Assim:
an = a1 + (n − 1)r ⇒ −70 + p = 44 + p + (n − 1) ⋅ (−6) ⇒ (n − 1) ⋅ 6 = 114 ⇒ n − 1 = 19 ⇒ n = 20
Segue-se quê:
S20 = 540 ⇒ = 540 ⇒ (44 + p) + (−70 + p) = 54 ⇒ −26 + 2p = 54 ⇒ p = 40
40. Vamos calcular o valor total a sêr pago em cada opção, em reais.
• Opção 1: 20.000 + 60 ⋅ 750 = 65.000
• Opção 2: S48 = = 24 ⋅ (2.500 + 244) = 65.856
Logo, a opção 1 é mais vantajosa, e o valor a sêr pago a menos é:
65.856 − 65.000 = 856 → R$ 856,00
41. Temos:
⇒ ⇒ ![]()
Portanto, a razão é igual a 4.
42. Temos quê:
= 92 ⇒ = 92 ⇒ = 92 ⇒ = 92
Nota-se quê a2 e a11 são termos equidistantes dos extremos a1 e a12; logo, a2 + a11 = a1 + a12. Assim, a média aritmética dos termos de a1 até a12, desconsiderando-se a2 e a11, é:
43. a) Nota-se quê não importa a ordem com quê as partes são entregues a cada homem; então, vamos supor quê a PA é crescente. Assim, como as três partes maiores são a3, a4 e a5, temos:
= a1 + a2 ⇒ a3 + a4 + a5 = 7(a1 + a2)
Além díssu, como o total de pães é 100, temos:
• a1 + a2 + = 100 ⇒ ⇒ 8(a1 + a2) = 100 ⇒ a1 + a2 =
• S5 = 100 ⇒ = 100 ⇒ a1 + a5 = 40
Assim, temos o sistema:
⇒ 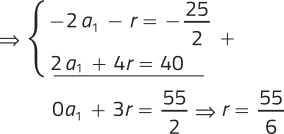
Logo, a razão da PA é . Ao inverter a ordem de entrega dos pães, teríamos uma PA decrescente de razão .
b) De acôr-do com a resolução do item a, temos a1 + a2 = e r = . Assim:
• a1 + a1 + r = ⇒ 2a1 + ⇒ a1 =
• a2 =
• a3 = = 20
• a4 = 20 +
• a5 =
Logo, as quantidades recebidas foram , , 20, e .
c) Resposta pessoal. Espera-se quê os estudantes pesquisem outros problemas encontrados no papiro de Rhind e identifiquem conceitos matemáticos envolvidos nesse problemas. Verificar se eles conseguem identificar os conceitos e elaborar hipóteses e estratégias de resolução para resolver tais problemas.
A socialização das respostas póde sêr uma oportunidade de incentivar a argumentação dos estudantes.
44. a) • q =
• Crescente, pois 0 < q < 1 e a1 < 0.
b) • q = = 1
• Constante, pois q = 1.
c) • q = (−4) ∶ (−1) = 4
• Decrescente, pois q > 1 e a1 < 0.
d) • q = 18 ∶ (−3) = −6
• Alternante, pois q < 0.
e) • q = 2−4 ∶ 2−2 = 2−2
• Decrescente, pois 0 < q < 1 e a1 > 0.
45. a) • a1 =
• a2 = = 4 ⋅ 7 = 28
• a3 = 28 ⋅
• a4 = = 448 ⋅ 7 = 3.136
Portanto, , 28, e 3.136.
b) a5 = a1 ⋅ q4 ⇒ = a1 ⋅ ⇒ a1 = ⋅ =
• a1 =
• a2 =
• a3 =
• a4 =
Portanto, , , e .
c) a3 = a1 ⋅ q2 ⇒ 95 = a1 ⋅ ⇒ a1 = 95 ⋅ 9−4 = 9
• a1 = 9
• a2 = 9 ⋅ 92 = 93
• a3 = 93 ⋅ 92 = 95
• a4 = 95 ⋅ 92 = 97
Portanto, 9, 93, 95 e 97.
46. a7 = a1 ⋅ q6 = a1 ⋅ q3 ⋅ q3 = a4 ⋅ q3 = (−70) ⋅ = (−70) ⋅ = 35 ⋅
47. ⇒ ⇒
Página trezentos e setenta e um
Substituindo a1 = 4 ⋅ q−1 na segunda equação, temos:
4 ⋅ q−1 ⋅ q5 = ⇒ q4 = ⇒ q = ou q =
Como a PG é decrescente, temos q = , pois a razão q = indica uma PG alternante. Substituindo q = na primeira equação, temos:
a1 = 4 ⋅ ()−1 ⇒ a1 = 4 ⋅ 5 = 20
Portanto, q = e a1 = 20.
48. Temos a1 = 1 e q = 3. Assim:
a) a7 = a1 ⋅ q6 = 1 ⋅ 36 = 729 → 729 triângulos pretos
b) an = a1 ⋅ qn − 1 ⇒ 19.683 = 1 ⋅ 3n − 1 ⇒ 3n − 1 = 39 ⇒ n − 1 = 9 ⇒ n = 10 → figura 10
c) Cada figura, a partir da segunda, é formada por triângulos com a medida do lado correspondente à mêtáde da medida dos triângulos pretos da figura anterior. Assim, essas medidas formam a sequência (1, , ...).
d) PG, pois, a partir do 2º termo, o quociente entre um termo qualquer da sequência e seu antecessor é constante e igual a q = .
• Fórmula do termo geral:
an = a1 ⋅ qn − 1 ⇒ an = ()n − 1
e) A medida do lado de cada triângulo, em métro, é:
a6 = ()5 =
Logo, o perímetro é:
3 ⋅ m
49. alternativa c
a) Falsa. A população estimada do Brasil forma uma PG em quê a1 = 203.062.512 e q = 1,0052, sêndo a população estimada em 2027 correspondente ao termo a6. Calculando a6, temos:
a6 = a1 ⋅ q5 = 203.062.512 ⋅ (1,0052)5 ≃ 208.397.332
b) Falsa. Calculando a2, temos:
a2 = a1 ⋅ q1 = 203.062.512 ⋅ (1,0052)1 ≃ 204.118.437
Portanto, em 2023, a população brasileira não ultrapassou 205 milhões de habitantes.
c) Verdadeira. A estimativa da população brasileira em 2030 corresponde ao 9º termo da respectiva PG, quê representa sua população no decorrer dos anos. Assim, a estimativa da população nesse ano é:
• 203.062.512 ⋅ (1,0052)8 ≃ 211.665.265 → aproximadamente 211,7 milhões
d) Falsa. Como foi considerado quê a taxa de crescimento será mantida até 2030, a população brasileira deve variar de acôr-do com uma PG crescente e, portanto, vai aumentar até 2030. Após esse período, o enunciado não fornece dados para analisarmos a variação da população brasileira.
50. a) a2 = 500 ∶ 2 = 250
a3 = 250 ∶ 2 = 125
a4 = 125 ∶ 2 = 62,5
(500; 250; 125; 62,5; ...)
b) A sequência é uma PG, pois, a partir do 2º termo, o quociente entre um termo qualquer da sequência e seu antecessor é constante. A razão dessa PG é , pois .
51. (x + 1)2 = (x − 4) ⋅ (5x + 11) ⇒ x2 + 2x + 1 = 5x2 + 11x − 20x − 44 ⇒ 4x2 − 11x − 45 = 0 ⇒
Como os termos são positivos, temos x = 5, pois o primeiro termo seria negativo para x = . Assim, a1 = x − 4 = 5 − 4 = 1 e q = = 6. Segue-se quê:
• a1 = 1
• a2 = 1 ⋅ 6 = 6
• a3 = 6 ⋅ 6 = 36
• a4 = 36 ⋅ 6 = 216
• a5 = 216 ⋅ 6 = 1.296
Portanto, 1, 6, 36, 216 e 1.296.
52. Temos a1 = 4, q = 8 ∶ 4 = 2 e o último termo é an = 410. Assim:
an = a1 ⋅ qn − 1 ⇒ 410 = 4 ⋅ 2n − 1 ⇒ = 22 ⋅ 2n − 1 ⇒ 220 = 2n + 1 ⇒ 20 = n + 1 ⇒ n = 19
Portanto, a PG tem 19 termos.
53. ⇒
Dividindo-se a segunda equação pela primeira, temos:
⇒ = ⇒ q3 = ⇒ q =
Portanto, a razão da PG é .
54. a) • a1 = 40
• a2 = 40 ⋅ 2 = 80
• a3 = 80 ⋅ 2 = 160
• a4 = 160 ⋅ 2 = 320
• a5 = 320 ⋅ 2 = 640
⋮
(40, 80, 160, 320, 640, ...)
b) PG, pois, a partir do 2º termo, o quociente entre um termo qualquer da sequência e seu antecessor é igual a uma constante denominada razão. Nesse caso, a razão q = 2.
c) Temos a1 = 40 e q = 2. Assim, o termo geral é:
an = a1 ⋅ qn − 1 ⇒ an = 40 ⋅ 2n − 1
d) f(n) = an ⇒ f(n) = 40 ⋅ 2n − 1
Como 40 = 23 ⋅ 5, também podemos escrever:
f(n) = 23 ⋅ 5 ⋅ 2n − 1 ⇒ f(n) = 5 ⋅ 2n + 2
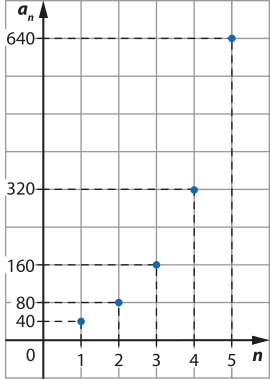
e) O tempo, em hora, após o início da análise em quê é feita cada verificação forma uma PA em quê b1 = 0 e r = 3. Após 2 dias, quê correspondem a 48 h, é feita a verificação n, tal quê bn = 48. Temos:
bn = b1 + (n − 1)r ⇒ 48 = (n − 1) ⋅ 3 ⇒ n = 17
Logo, a quantidade de bactérias após 2 dias é:
a17 = 5 ⋅ 217 + 2 = 2.621.440 → 2.621.440 bactérias
55. O montante da aplicação forma uma PG em quê a1 = 1.800 e q = 1,005, sêndo an o montante da aplicação após n − 1 meses, para n ∈ ℕ, com n ≥ 2. Assim, o montante ao final de três anos de aplicação, quê correspondem a 36 meses, é:
a37 = a1 ⋅ q36 = 1.800 ⋅ (1,005)36 ≃ 2.154,02 → aproximadamente R$ 2.154,02
56. a) • a1 = f(1) = −2 ⋅ 31 − 1 = −2
• a2 = f(2) = −2 ⋅ 32 − 1 = −6
• a3 = f(3) = −2 ⋅ 33 − 1 = −18
⋮
(−2, −6, −18, ...)
Temos a1 = −2 e q = (−6) ∶ (−2) = 3.
Página trezentos e setenta e dois
b) 
57. Temos a1 = e q = ⋅ 8 = 4.
Assim, o termo geral da PG é:
an = a1 ⋅ qn − 1 ⇒ an = ⋅ 4n − 1
Então, definimos f: ℕ* → ℝ por f(n) = ⋅ 4n − 1. Observe quê:
⋅ 4n − 1 = ⋅ (22)n − 1 = 2−3 ⋅ 22n − 2 = 22n − 5
Logo, também podemos escrever f(n) = 22n − 5.
58. a) A PG é tal quê a1 = 32, q = e o último termo é an = 243. Assim:
an = a1 ⋅ qn − 1 ⇒ 243 = 32 ⋅ ()n − 1 ⇒ ()n − 1 = ⇒ ()n − 1 = ()5 ⇒ n − 1 = 5 ⇒ n = 6
Logo, estima-se quê as árvores param de crescer 6 anos após o plantio.
b) Uma resposta possível: f: A → ℝ, com A = {n ∈ ℕ | 1 ≤ n ≤ 6}, definida por f(n) = 32 ⋅ ()n − 1.
Temos quê f(4) = 108 indica quê a estimativa de altura dessas árvores, 4 anos após o plantio, seja de 108 cm.
59. a) Temos a1 = −1 e q = (−5) ∶ (−1) = 5. Assim:
S9 = = = = −488.281
b) Temos a1 = e q = = 3. Assim:
S6 = = ⋅ (36 − 1) =
c) Temos a1 = 2 e q = 6 ∶ 2 = 3. Assim:
S10 = = 310 − 1 = 59.048
d) Temos a1 = 3 e q = (−27) ∶ 3 = −9. Assim:
S7 = = ⋅ (1 + 97) = 1.434.891
60. a) 75.000 ⋅ 1,12 = 84.000 → 84.000 entregas
b) O total de entregas esperadas no primeiro semestre de 2026 corresponde à soma dos seis primeiros termos da PG em quê a1 = 75.000 e q = 1,12, ou seja:
S6 = = = 625.000 ⋅ (1,126 − 1) ≃ 608.639 → aproximadamente 608.639 entregas
61. alternativa c
Temos a1 = 3 e q = −1. Assim:
a) Falsa, pois:
S25 = = = 3
b) Falsa, pois:
a38 = a1 ⋅ q37 = 3 ⋅ (−1)37 = −3
c) Verdadeira. Assim como no item a, podemos utilizar a fórmula da soma dos n primeiros termos de uma PG para mostrar quê S50 = 0 ou observar quê os termos se anulam em pares; logo, ao somar uma quantidade par de termos consecutivos, o resultado é zero.
d) Falsa. A PG é alternante.
62. alternativa d
A quantidade total de grãos de trigo corresponde à soma dos 64 primeiros termos da PG em quê a1 = 1 e q = 2, ou seja:
S64 = = = 264 − 1
63. Temos a1 = 7 e, sêndo n a quantidade de termos, an = −54.432 e Sn = −46.655.
Assim, a razão q é dada por:
Sn = ⇒ −46.655 = ⇒ −46.655q + 46.655 = −54.432q − 7 ⇒ 7.777q = −46.662 ⇒ q = −6
64. Temos:
a8 = a1 ⋅ q7 = a1 ⋅ q2 ⋅ q5 = a3 ⋅ q5
Assim:
= 800 ⋅ q5 ⇒ q5 = ⇒ q5 = ()5 ⇒ q =
Para determinar o primeiro termo, obissérve quê:
a3 = a1 ⋅ q2 ⇒ 800 = a1 ⋅ ()2 ⇒ a1 = 12.800
Segue-se quê a soma dos termos da PG é:
S8 = = =
65. Os termos da PG em quê a1 = 20 e q = 0,65, a partir do 2º termo, correspondem às alturas, em métro, quê a bola atinge após cada choque com o solo, sêndo o termo an + 1 a altura atingida após o n-ésimo choque.
a) A altura quê a bola atinge após o 4º choque é:
a5 = a1 ⋅ q4 = 20 ⋅ 0,654 ≃ 3,57 → aproximadamente 3,57 m
b) • No momento em quê se choca com o solo pela 2ª vez, a bola percorreu as distâncias correspondentes à descida da bola das alturas a1 e a2 e à subida da bola até a altura a2, ou seja:
a1 + 2a2 = 20 + 2 ⋅ (20 ⋅ 0,65) = 46 → 46 m
• No momento em quê se choca com o solo pela 5ª vez, a bola percorreu as distâncias correspondentes à descida da bola das alturas a1, a2, a3, a4 e a5 e à subida da bola até as alturas a2, a3, a4 e a5. O total percorrido corresponde a:
2S5 − a1 =2 ⋅ − a1 = 2 ⋅ − 20 = 81,02525 → 81,02525 m
66. a) Resposta esperada: De acôr-do com a ordem das linhas, o primeiro número das sequências corresponde a um termo de uma PG de primeiro termo a1 = 3 e razão q = 2. Já em cada linha, a sequência corresponde a uma PA de razão r = 3. Na 1ª linha, tem apenas um número e, a partir da 2ª linha, a quantidade de números é o dôbro da quê tem na linha anterior.
b) O primeiro termo da PA da 6ª linha corresponde ao sexto termo da PG de primeiro termo 3 e razão 2, ou seja:
a1 = 3 ⋅ 25 = 96
Página trezentos e setenta e três
A quantidade n de termos dessa PA corresponde ao sexto termo da PG de primeiro termo 1 e razão 2, ou seja:
n = 1 ⋅ 25 = 32
Como a razão dessa PA é r = 3, o seu último termo é:
a32 = a1 + 31r = 96 + 31 ⋅ 3 = 189
Assim, a soma dos termos da sequência da 6ª linha é:
S32 = = = 4.560
67. alternativas b, d e e
Para quê o limite da soma dos termos de uma PG convirja para um número real, temos quê −1 < q < 1. Logo, temos:
a) q = = 2
b) q =
c) q = = 3
d) q =
e) q =
f) q =
68. a) Temos a1 = −4 e q = , assim:
S = = −4 ⋅ =
b) Temos a1 = 625 e q = , assim:
S = = 625 ⋅
c) Temos a1 = e q = , assim:
S =
d) Temos a1 = 25 e q = 0,25 ∶ 25 = , assim:
S =
69. a) 1,7777... = 1 + 0,7 + 0,07 + 0,007 + 0,0007 +... = 1 +
As parcelas destacadas formam uma PG em quê a1 = e q = ; logo:
S =
Assim:
1,7777... = 1 + S = 1 + =
b) = 8 + 0,112 + 0,000112 + 0,000000112 + ... = 8 +
As parcelas destacadas formam uma PG em quê
a1 = e q = ; logo:
S =
Assim:
= 8 + S = 8 +
c) −0,9191... = (−1) ⋅ (0,91 + 0,0091 + 0,000091 + ...) = (−1) ⋅
As parcelas da soma destacada formam uma PG em quê a1 = e q = ; logo:
S =
Assim:
−0,9191... = (−1) ⋅ S = (−1) ⋅ =
d) = 2 + 0,39 + 0,0039 + 0,000039 + ... = 2 +
As parcelas destacadas formam uma PG em quê a1 = e q = ; logo:
S =
Assim:
= 2 + S = 2 +
• Resposta pessoal. Espera-se quê os estudantes reconheçam características de uma dízima periódica e consigam determinar a fração geratriz correspondente. Orientá-los a escrever pelo menos uma dízima periódica composta.
70. alternativa d
A partir da 2ª circunferência, o quociente do perímetro de cada circunferência com o perímetro da circunferência anterior é ; logo, os perímetros das circunferências formam uma PG em quê a1 = 2(pi)" ⋅ 10 = 20(pi)" e q = . Assim, o limite da soma dos perímetros das circunferências é:
S = = 20(pi)" ⋅ 2 = 40(pi)" → 40(pi)" cm
71. As parcelas do 1º membro formam uma PG em quê a1 = x e q = ∶ x = .
Assim:
= 30 ⇒ = 30 ⇒ x ⋅ = 30 ⇒ x = 24
Integrando com...
1. Resposta pessoal. Os estudantes podem mencionar aspectos como analisar as características das populações e fundamentar a proposição de políticas públicas.
2. Respostas pessoais. Espera-se quê os estudantes respondam com base em suas experiências pessoais. Levantar hipóteses com os estudantes a respeito de possíveis relações entre mudanças ocorridas nas políticas públicas do município e a variação na quantidade de habitantes.
3. a) Gráfico de segmentos.
b) Analisando o título do gráfico ou os dados do eixo horizontal, temos quê os dados correspondem ao período de 1950 a 2100.
c) Entre 1950 e 2000: 6,1 − 2,5 = 3,6 → 3,6 bilhões de habitantes.
Entre 2000 e 2050: 9,7 − 6,1 = 3,6 → 3,6 bilhões de habitantes.
Entre 2050 e 2100: 10,3 − 9,7 = 0,6 → 0,6 bilhão de habitantes.
d) A sequência não corresponde a uma PA, pois a diferença entre um termo e o anterior, a partir do 2º termo, não é igual. A sequência não corresponde a uma PG, pois a razão entre um termo e o anterior, a partir do 2º termo, não é igual.
4. a) método geométrico; método aritmético
b) Método aritmético: 20.000 + 2.000 = 22.000 → 22.000 habitantes
Página trezentos e setenta e quatro
Método geométrico:
24.883 ⋅ 1,2 = 29.859,6 → aproximadamente 29.860 habitantes
c) Resposta esperada: Não, pois, nas estimativas realizadas, a população não cresce igualmente em valores absolutos nem a uma mesma taxa de crescimento.
5. a) Respostas pessoais. As respostas dependem do município em quê os estudantes moram. Incentivá-los a analisar o contexto local sobre o crescimento populacional e o contexto nacional a fim de elaborarem hipóteses e argumentos.
b) A resposta depende do município em quê os estudantes moram. Espera-se quê os estudantes consigam, a partir dos métodos estudados, estimar a população para o município em quê moram.
c) Resposta pessoal. Ao socializarem as respostas dêêsse item, propor aos estudantes quê verifiquem se os objetivos dos institutos com essas pesquisas foram os mesmos e se houve mudanças nos métodos de pesquisa e de divulgação, resultantes de diferenças nas intencionalidades dessas pesquisas. Em seguida, promover uma discussão com a turma sobre como essas estimativas podem contribuir para o desenvolvimento do município, indicando a necessidade de proposição de políticas públicas para o futuro.
72. a) Resposta esperada: Todo número natural é par ou é ímpar, e qualquer número par é divisível por 2.
b) Sim. O passo quê questiona se a divisão, realizada no passo anterior, tem résto igual a zero.
c) • 237: Primeiro, realizamos a divisão 237 ∶ 2, obtendo quociente 118 e résto 1. Como o résto da divisão não é igual a zero, concluímos quê 237 é ímpar.
• 108: Primeiro, realizamos a divisão 108 ∶ 2 = 54, com résto zero. Como o résto da divisão é igual a zero, concluímos quê 108 é par.
d) Uma resposta possível:
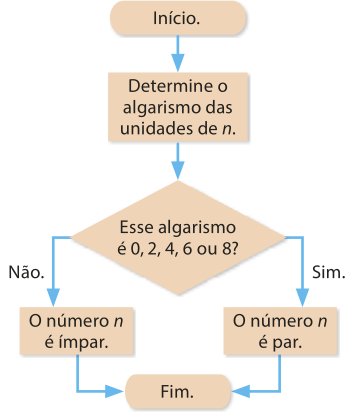
73. a) Analisando o fluxograma, temos quê o currículo é arquivado e retoma-se o processo.
b) Resposta esperada: Não, além da análise de currículo, são analisadas as referências pessoais e profissionais do candidato e realizada uma entrevista para indicação de um candidato ápto ao cargo.
c) Analisando a última quêstão do fluxograma, temos que a última tomada de dê-cisão é verificar se a entrevista indica um candidato ápto ao cargo.
d) Resposta pessoal. Espera-se quê os estudantes compartilhem suas experiências pessoais e relacionem a entrevista ou seleção pela qual passaram com a ideia de fluxograma apresentada na atividade.
74. De acôr-do com o fluxograma:
• a1 = 5
• a2 = 5 ⋅ (−2) + 7 = −3
• a3 = (−3) ⋅ (−2) + 7 = 13
• a4 = 13 ⋅ (−2) + 7 = −19
• a5 = −19 ⋅ (−2) + 7 = 45
⋮
Portanto, (5, −3, 13, −19, 45, ...).
an = −2an − 1 + 7 e a1 = 5, com n ∈ ℕ*
e n ≥ 2
75. e – a – d – f – c – b
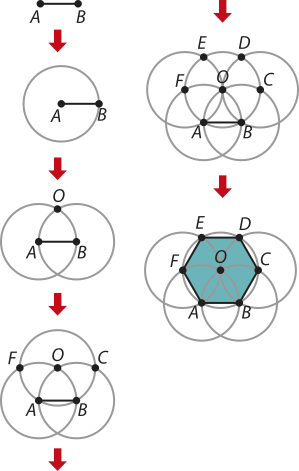
76. Resposta esperada:
• Utilizar a régua para traçar um segmento com 3 cm de comprimento, correspondente a um lado do triângulo.
• Com abertura de medida AB, fixar a ponta-seca do compasso em A e traçar uma circunferência.
• Com a mesma abertura, fixar a ponta-seca do compasso em B e traçar outra circunferência. Marcar o ponto C em um dos cruzamentos das circunferências.
• Com a régua, traçar e . Por fim, colorir a região interna da figura ôbitída.
77. a) • 495 g: frigorífico, pois:
350 < 495 < 700.
• 810 g: pesqueiro, pois 810 ≥ 700.
• 309 g: tanque de engorda, pois 309 ≤ 350.
b) Resposta esperada:
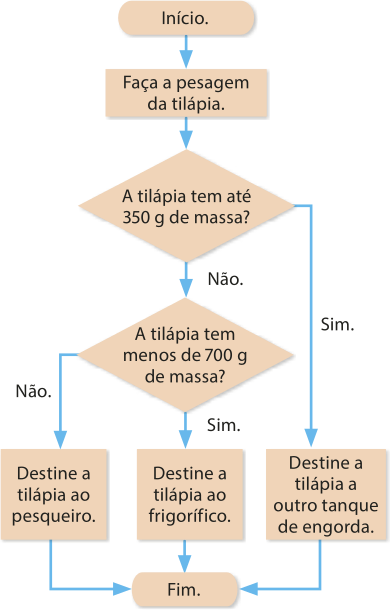
78. a) Resposta esperada:
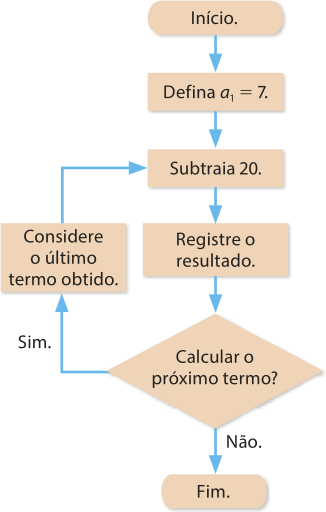
b) A sequência é uma PA em quê a1 = 7 e r = −20, assim:
a9 = a1 + 8r = 7 + 8 ⋅ (−20) = −153
79. Resposta pessoal. Espera-se quê os estudantes sêjam capazes de representar alguma de suas atividades diárias por meio de um passo a passo, descrevendo-o por meio de um algoritmo, e, por fim, representem as etapas da atividade em um fluxograma.
80. a) Exemplo 1: variáveis: x, y, z; operadores: +, =.
Exemplo 2: variáveis: a, b, soma; operadores: +, =.
b) De acôr-do com as informações apresentadas, nesse algoritmo, é calculada a soma 10 + 5 = 15.
c) Resposta esperada: No exemplo 1, o algoritmo realiza a adição de dois números inteiros predefinidos, 10 e 5;
Página trezentos e setenta e cinco
já no exemplo 2, o algoritmo realiza a adição de dois números quaisquer do tipo real, quê devem sêr inseridos pelo usuário ao executar o algoritmo.
d) Uma resposta possível:
Início
real: a, b, c, produto
escrêeva (“Digite o primeiro número: ”);
leia a
escrêeva (“Digite o segundo número: ”);
leia b
escrêeva (“Digite o terceiro número: ”);
leia c
produto = a * b * c
escrêeva (“O produto dos números é igual a: ”, produto);
Fim
81. a) Resposta esperada: Não, pois no algoritmo construído quem determina os valores das variáveis é o criador do algoritmo, e não o usuário.
b) Uma resposta possível:
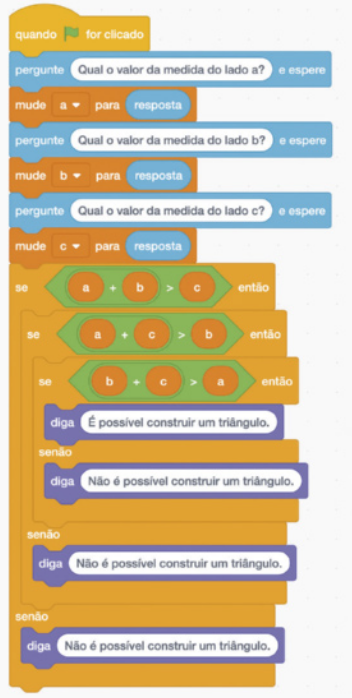
Espera-se quê os estudantes reproduzam algoritmos parecidos, com a possibilidade de mudança apenas na ordem em quê a variável e as condições aparécem.
82. Alternativa d, pois, se a, x e b são três termos consecutivos de uma PA, então o termo central x é dado por x = .
83. a) Figura I, pois, a cada uma das 6 repetições, determina-se um segmento de 150 unidades de comprimento e a direção é alterada em 60°, quê corresponde à medida do ângulo externo de um hekzágono regular, resultando na representação de um hekzágono regular com 150 unidades de lado.
b) Resposta esperada: II − Use a caneta; repita 5 vezes (mova 150 passos; gire 72 graus no sentido horário). III − Use a caneta; repita 3 vezes (mova 150 passos; gire 120 graus no sentido horário). O algoritmo descrito para II determina um pentágono regular com lados de 150 unidades, enquanto o algoritmo descrito para III determina um triângulo equilátero com lados de 150 unidades.
84. a) Resposta esperada: Recursiva, pois, para obtêr esse termo, o termo anterior é multiplicado por −5.
b) Considerando a resposta ao item a, temos quê a razão é dada por q = −5.
primeiro termo: a2 = a1 ⋅ q ⇒ 10 = a1 ⋅ (−5) ⇒ a1 = −2
c) • recursiva: an = −5 ⋅ an − 1, para n ∈ ℕ, com n ≥ 2 e a1 = −2
• não recursiva: an = −2 ⋅ (−5)n − 1, para n ∈ ℕ*
85. a) Uma resposta possível: III, V, II, IV e I.
b) Uma resposta possível: Após clicar na bandeira vêrde, o cóódigo é executado da seguinte maneira:
• III: a bandeira foi clicada;
• V: x tem o valor alterado para 2;
• II: é adicionado 10 a x, quê passa a ter o valor 2 + 10 = 12;
• IV: f(x) tem o valor alterado para x ⋅ 2, quê corresponde a 12 ⋅ 2 = 24;
• I: o personagem fala o valor de f(x), quê é 24.
c) Uma resposta possível:
f(x) = 2(x + 10) ou f(x) = 2x + 20.
86. a) Analisando a célula B6, temos quê a média das notas foi 62,5. Analisando a célula E6, temos quê o estudante foi aprovado, o quê ocorreu porque a média das notas dele foi 62,5, quê não é um número menor quê 60.
b) Temos:
= 56
Logo, na célula B6, aparecerá 56 e, como 56 < 60, aparecerá o texto “Reprovado” na célula E6.
c) Uma resposta possível:
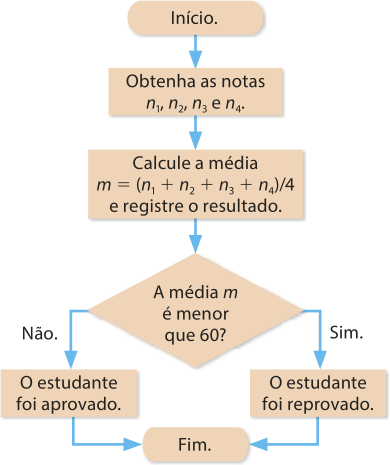
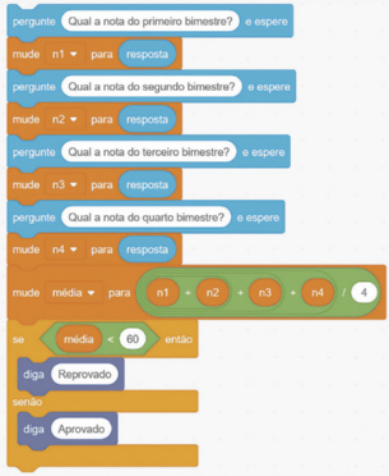
d) Resposta pessoal. Espera-se quê os estudantes comparem as duas maneiras de criar algoritmos e decidam por aquela quê mais lhes parecer conveniente a partir de argumentos plausíveis. Ao argumentarem, verificar se compreenderam a estrutura de funcionamento da planilha eletrônica e do Scratch.
87. Respostas pessoais. Espera-se quê os estudantes construam um algoritmo para resolver algum problema matemático elaborado por eles e quê apresente algum conceito matemático quê eles tênham estudado. É necessário quê os estudantes sêjam capazes de reproduzir o algoritmo no Scratch, aplicando corretamente tanto as ferramentas dêêsse programa como os conceitos matemáticos considerados.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) I) A cada minuto, utilizam-se 24 ⋅ 60 = 1.440 quadros. Assim, os cinco primeiros termos da sequência são:
• 1.440 ⋅ 1 = 1.440
• 1.440 ⋅ 2 = 2.880
• 1.440 ⋅ 3 = 4.320
• 1.440 ⋅ 4 = 5.760
• 1.440 ⋅ 5 = 7.200
Essa sequência é uma PA em quê a1 = 1.440 e r = 1.440.
II) f(n) = 1.440n
III) Temos:
1h15min = (60 + 15) min = 75 min
Assim, o total de quadros utilizados é:
f(75) = 1.440 ⋅ 75 = 108.000 → 108.000 quadros
b) I) Uma resposta possível:
A cada personagem a mais no filme, a quantidade de comandos é multiplicada por 2. Assim, as quantidades são:
• 1 personagem: 2.000
• 2 personagens: 2.000 ⋅ 2 = 4.000
• 3 personagens: 4.000 ⋅ 2 = 8.000
Página trezentos e setenta e seis
• 4 personagens: 8.000 ⋅ 2 = 16.000
• 5 personagens: 16.000 ⋅ 2 = 32.000
• 6 personagens: 32.000 ⋅ 2 = 64.000
• 7 personagens: 64.000 ⋅ 2 = 128.000
• 8 personagens: 128.000 ⋅ 2 = 256.000
• 9 personagens: 256.000 ⋅ 2 = 512.000
• 10 personagens:
512.000 ⋅ 2 = 1.024.000
Essa sequência é uma PG em quê a1 = 2.000 e q = 2.
II) f(n) = 2.000 ⋅ 2n − 1 = 2.000 ⋅ = 1.000 ⋅ 2n
c) Resposta pessoal. Espera-se quê os estudantes pesquisem outras animações com as mesmas características de produção e elaborem um texto a respeito contendo informações parecidas às apresentadas nessa atividade.
Praticando: enêm e vestibulares
1. alternativa d
Os instantes em quê os três grupos bateram palmas simultaneamente formam uma PA em quê a1 = 1 e a razão é igual ao mínimo múltiplo comum entre 2, 3 e 4, ou seja, r = 12. Assim, o termo geral é:
an = a1 + (n − 1)r ⇒ an = 12(n − 1) + 1
A quantidade de termos dessa PA corresponde ao maior inteiro n0 tal quê:
12(n0 − 1) + 1 < 60 ⇒ 12(n0 − 1) < 59 ⇒ n0 − 1 < ⇒ n0 < ≃ 5,9
Portanto, o termo geral é12(n − 1) + 1, com n um número natural, tal quê 1 ≤ n ≤ 5.
2. alternativa c
A quantidade de chapas fabricadas em cada mês do período forma uma PA em quê a1 = 28.000 e a7 = 8.800. A razão r da PA é dada por:
a7 = a1 + 6r ⇒ 8.800 = 28.000 + 6r ⇒ 6r = −19.200 ⇒ r = −3.200
Então, a produção de maio e junho totaliza:
a5 + a6 = (a1 + 4r) + (a1 + 5r) = 2a1 + 9r = 2 ⋅ 28.000 + 9 ⋅ (−3.200) = 56.000 − 28.800 = 27.200 → 27.200 chapas
3. alternativa b
Considere a PG (1, , , ...) em quê a1 = 1 e q = ∶ 1 = . Assim:
a100 = 1 ⋅ ()100 − 1 = ()99
4. alternativa d
Como R$ 120,00, R$ 126,00 e R$ 132,00 são os três primeiros termos da PA, temos:
r = 126 − 120 = 6
a24 = 120 + (24 − 1) ⋅ 6 = 120 + 23 ⋅ 6 = 120 + 138 = 258
S24 = = 4.536
a19 = 120 + (19 − 1) ⋅ 6 = 120 + 18 ⋅ 6 = 120 + 108 = 228
4.536 − 228 = 4.308 → R$ 4.308,00
5. alternativa b
Considerando uma equipe quê chegue até a final do torneio, temos:
1º jôgo da fase de grupos → 1 dia + 3 dias de descanso
2º jôgo da fase de grupos → 1 dia + 3 dias de descanso
3º jôgo da fase de grupos → 1 dia + 3 dias de descanso
jôgo das oitavas de final → 1 dia + 3 dias de descanso
jôgo das quartas de final → 1 dia + 3 dias de descanso
jôgo das semifinais → 1 dia + 3 dias de descanso para a final
jôgo da final → 1 dia
No total, temos:
4 + 4 + 4 + 4 + 4 + 4 + 1 = 25 → 25 dias.
6. alternativa c
Como o polígono tem 20 lados, a soma dos ângulos internos dele é dada, em grau, por:
S = (20 − 2) ⋅ 180 = 18 ⋅ 180 = 3.240
As medidas dos ângulos internos do polígono formam uma PA de 20 termos, em quê a1 = x e r = 4 (em grau). Assim, temos:
a20 = x + (20 − 1) ⋅ 4 = x + 76
Igualando a soma dos 20 termos da PA à soma dos ângulos internos do polígono, temos:
S20 = 3.240 ⇒ = 3.240 ⇒ (2x + 76) = 324 ⇒ x = 124
O produto entre o menor e o maior ângulo, em grau, é dado por:
124 ⋅ (124 + 76) = 24.800
7. alternativa c
Temos duas progressões aritméticas: (a, b, c) e (ab, bc, ca).
Da primeira, temos:
r = b − a (I)
r = c − b (II)
Da segunda, temos:
r = bc − ab = b(c − a) (III)
r = ca − bc = c(a − b) (IV)
De (I) + (II), temos: 2r = c − a (V)
De (III) e (V), temos: b ⋅ 2r = r ⇒ b = (VI)
De (IV) e (I), temos: c ⋅ (−r) = r ⇒ c = −1 (VII)
De (II), (VI) e (VII), temos:
r = −1 − =
Assim, segue-se quê:
a = −() = 2
Portanto, abc = 2 ⋅ ⋅ (−1) = −1.
8. alternativa b
Analisando a função, temos:
f(x) = bax
f(1) = ba1
f(2) = ba2
f(3) = ba3
Logo, temos uma PG de razão a.
Calculando o limite da soma dos termos dessa PG infinita, temos:
S =
9. alternativa d
Considerando quê, a cada 20 minutos a quantidade de bactérias duplíca, temos:
N0, 2 ⋅ N0 = 2N0, 2 ⋅ 2N0 = 4N0, 2 ⋅ 4N0 = 8N0, 2 ⋅ 8N0 = 16N0, 2 ⋅ 16N0 = 32N0
Logo, a sequência será:
N0, 2N0, 4N0, 8N0, 16N0, 32N0.
10. alternativa b
Temos quê:
a + b + c = 26
a2 + b2 + c2 = 364
Sendo (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac, segue-se quê:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
262 = 364 + 2(ab + bc + ac)
676 − 364 = 2(ab + bc + ac)
Sabendo quê (a, b e c) formam uma PG, temos quê esses termos podem sêr reescritos da seguinte maneira: (, b, bq)
Assim, temos:
312 = 2 ( + b2q + b2) ⇒ 156 = b2 ( + q + 1)
Note quê:
a + b + c = + b + bq = b( + q + 1) = 26
Assim, temos:
156 = b2 ⋅ ⇒ b = 6
11. alternativa c
As distâncias percorridas em cada dia do treinamento formam uma PA em quê a1 = 6, r = 2 e o último termo, an = 42. Vamos determinar o número n de termos dessa PA.
an = a1 + (n − 1)r ⇒ 42 = 6 + (n − 1) ⋅ 2 ⇒ n − 1 = 18 ⇒ n = 19
O total percorrido pelo atleta nesse treinamento, em quilômetro, corresponde à soma dos termos dessa PA, ou seja:
S19 = = = 456
12. alternativa d
Em uma PA qualquer, a soma dos n primeiros termos é:
Página trezentos e setenta e sete
Sn = = =
• Na primeira PA, o primeiro termo é 16 e a razão é 2; assim, a soma Sn é:
Sn = = = 16n + n2 − n = n2 + 15n
• Na segunda PA, o primeiro termo é e a razão é ; assim, a soma é:
= = =
Logo, quando Sn = , temos:
n2 + 15n = ⇒ 4 n2 + 60n = 5 n2 − 3n ⇒ n2 − 63n = 0 ⇒ n(n − 63)= 0 ⇒
Assim, as duas progressões terão somas iguais quando o valor dessa soma for:
S63 = 632 + 15 ⋅ 63 = 4.914
13. alternativa b
Temos uma PA de razão 2, pois 154 − 152 = 2
Assim, segue-se quê:
a10 = 152 + (10 − 1) ⋅ 2 = 152 + 18 = 170
14. alternativa d
Considerando a PG formada pelas parcelas da adição indicada no primeiro membro da equação apresentada, temos:
a1 = x
q =
S =
Assim, de acôr-do com a equação, temos:
= 18 ⇒ 3x = 36 ⇒ x = 12
15. alternativa d
70% de 16 anos:
0,70 ⋅ 16 = 11,2 → 11,2 anos
Segue-se quê:
r = 5,8 − 5,2 = 0,6
11,2 = 5,2 + (n − 1) ⋅ 0,6 ⇒ 6 = 0,6n − 0,6 ⇒ 0,6n = 6,6 ⇒ n = 11
Como a pesquisa ocorre a cada 4 anos, teremos para o 11º termo um salto de 40 anos (4 ⋅ 10), ou seja:
1995 + 10 ⋅ 4 = 1995 + 40 = 2035
16. alternativa d
a) Incorreta.
PA: a4 = 200 + (4 − 1) ⋅ 20 = 200 + 60 = 260
PG: b4 = 2 ⋅ 33 = 2 ⋅ 27 = 54
a4 > b4
b) Incorreta.
a2 = 200 + (2 − 1) ⋅ 20 = 220
b2 = 2 ⋅ 3 = 6
10 ⋅ a4 = 10 ⋅ 260 = 2.600
≠ 2.600
c) Incorreta.
a3 = 200 + (3 − 1) ⋅ 20 = 240
b3 = 2 ⋅ 32 = 2 ⋅ 9 = 18
18 ≠ 2 ⋅ 240
d) Correta.
Para n = 6, temos:
a6 = 200 + (6 − 1) ⋅ 20 = 200 + 100 = 300
b6 = 2 ⋅ 35 = 2 ⋅ 243 = 486
Como a razão da PA é 20 e a da PG é 3, temos bn > an para n ≥ 6.
e) Incorreta.
a5 = 200 + (5 − 1) ⋅ 20 = 200 + 80 = 280
b5 = 2 ⋅ 34 = 2 ⋅ 81 = 162
Assim, a5 > b5.
17. alternativa b
p(x) = x + 2.024
p(2x) = 2x + 2.024
p(3x) = 3x + 2.024
...
p(2.023x) = 2.023x + 2.024
p(2.024x) = 2.024x + 2.024
Esses resultados formam uma PA de razão r = x e a1 = x + 2.024.
Assim, temos:
S2024 = = (2.025x + 4.048) ⋅ 1.012 = 0
2.025x + 4.048 = 0 ⇒ 2.025x = −4.048 ⇒ x = ≃ −1,999
Logo, −2 < x < 0.
Unidade 4 • Trigonometria na circunferência e funções trigonométricas
1. a) Os segmentos de reta com extremidades no centro e na circunferência são , , e .
b) O único segmento de reta com extremidades na circunferência e quê passa pelo centro é .
c) Os segmentos de reta com extremidades na circunferência são , e .
2. a) 2(pi)" ⋅ 5 = 2 ⋅ 3,14 ⋅ 5 = 31,4 → 31,4 cm
b) 2(pi)" ⋅ = 2 ⋅ 3,14 ⋅ 9 = 56,52 → 56,52 dm
c) 2(pi)" ⋅ = 3,14 ⋅ 7 = 21,98 → 21,98 m
3. a) 2(pi)"r = 15,7 ⇒ 2 ⋅ 3,14r = 15,7 ⇒ r = 2,5 → 2,5 cm
b) 2(pi)"r = 25,12 ⇒ 2 ⋅ 3,14r = 25,12 ⇒ r = 4 → 4 m ou 400 cm
c) 2(pi)"r = 43,96 ⇒ 2 ⋅ 3,14r = 43,96 ⇒ r = 7 → 7 dm ou 70 cm
d) 2(pi)"r = 75,36 ⇒ 2 ⋅ 3,14r = 75,36 ⇒ r = 12 → 12 cm
4. a) Espera-se quê os estudantes construam uma circunferência com 5 cm de raio, ou seja, com 10 cm de diâmetro (2 ⋅ 5 = 10).
b) Espera-se quê os estudantes construam uma circunferência com 8 cm de diâmetro, ou seja, com 4 cm de raio (8 ∶ 2 = 4).
c) 7(pi)" = 2(pi)"r ⇒ 7 = 2r ⇒ r = = 3,5
Espera-se quê os estudantes construam uma circunferência com 3,5 cm de raio, ou seja, com 7 cm de diâmetro (2 ⋅ 3,5 = 7).
5. Como o comprimento de uma circunferência é diretamente proporcional à medida de seu raio, então cada giro da catraca A corresponde a dois giros da catraca B e a quatro giros da catraca C. Assim:
Giros da catraca A |
Giros da catraca B |
|---|---|
1 |
2 |
300 |
x |
⇒ x = 600
Giros da catraca A |
Giros da catraca C |
|---|---|
1 |
4 |
300 |
y |
⇒ y = 1.200
Portanto, a catraca B gira 600 voltas e a catraca C, 1.200 voltas.
6. Sejam r e r(minutos)" os raios, respectivamente, da circunferência original e da ampliação. Então, seus respectivos comprimentos C = 2(pi)"r e C(minutos)" = 2(pi)"r(minutos)" são tais quê C(minutos)" = C + 4.
Logo:
2(pi)"r(minutos)" = 2(pi)"r + 4 ⇒ r(minutos)" = ⇒ r(minutos)" = r +
Página trezentos e setenta e oito
Portanto, o raio da circunferência ôbitída na ampliação aumentou em unidade de medida de comprimento, o quê equivale a aproximadamente 0,637 unidade de medida de comprimento.
7. Sejam d1, d2, d3, ..., d7 os diâmetros das semicircunferências. O comprimento C da curva corresponde à soma dos comprimentos das semicircunferências, ou seja:
C = = ⋅ (d1 + d2 + d3 +... + d7)
Como a soma dos diâmetros das semicircunferências corresponde ao comprimento do segmento em preto, temos:
C = ⋅ 16 ≃ 25,12 → aproximadamente 25,12 cm
8. a)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
p |
⇒ 2(pi)"x = 360(pi)" ⇒ x = 180
Portanto, (pi)" rad corresponde a 180°.
b)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
⇒ 2(pi)"x = 360 ⋅ ⇒ x = 72
Portanto, rad corresponde a 72°.
c)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
⇒ 2(pi)"x = 360 ⋅ ⇒ x = 30
Portanto, rad corresponde a 30°.
d)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
⇒ 2(pi)"x = 360 ⋅ ⇒ x = 270
Portanto, rad corresponde a 270°.
e)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
⇒ 2(pi)"x = 360 ⋅ ⇒ x = 60
Portanto, rad corresponde a 60°.
f)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
⇒ 2(pi)"x = 360 ⋅ ⇒ x = 45
Portanto, rad corresponde a 45°.
9.
Medida do arco, em grau |
Comprimento do arco, em cm |
|---|---|
360 |
2(pi)" ⋅ 5 |
135 |
x |
⇒ 360x = 1.350(pi)" ⇒ x = ≃ 11,775
Portanto:
• comprimento de : aproximadamente 11,775 cm
• med() = 135°
10. a)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
150 |
x |
⇒ 360x = 300(pi)" ⇒ x =
Portanto, med() = rad.
b)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
200 |
x |
⇒ 360x = 400(pi)" ⇒ x =
Portanto, med() = rad.
c)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
340 |
x |
⇒ 360x = 680(pi)" ⇒ x =
Portanto, med() = rad.
d)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
250 |
x |
⇒ 360x = 500(pi)" ⇒ x =
Portanto, med() = rad.
11.
Medida do arco, em grau |
Comprimento do arco, em mm |
|---|---|
360 |
2(pi)" ⋅ 12 |
x |
62,8 |
⇒ 24(pi)"x = 22.608 ⇒ x = = 300
Assim, a medida do arco de circunferência é de 300°. Vamos calcular essa medida em radiano:
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
300 |
x |
⇒ 360x = 600(pi)" ⇒ x =
Portanto, a medida do arco é de 300° ou rad.
12. O raio da circunferência méde cm = 18cm. Temos:
Medida do arco, em grau |
Comprimento do arco, em cm |
|---|---|
360 |
2(pi)" ⋅ 18 |
210 |
x |
⇒ 360x = 7.560(pi)" ⇒ x = = 21(pi)" = 65,94
Portanto, o arco de circunferência tem 65,94 cm de comprimento.
13. Inicialmente, vamos determinar o comprimento do arco correspondente ao ângulo central, cuja medida é rad, pois:
2(pi)" − .
Página trezentos e setenta e nove
Medida do arco, em radiano |
Comprimento do arco, em cm |
|---|---|
2(pi)" |
2(pi)" ⋅ 2 |
x |
⇒ x = ⋅ 2 ⇒ x = = 10,99
Então, o perímetro do setor circular é:
10,99 + 2 ⋅ 2 = 14,99 → 14,99 cm
14. Por definição, um arco de 1 rad tem o comprimento r do raio da circunferência na qual está contido. Assim, temos a seguinte regra de três:
Medida do arco, em radiano |
Comprimento do arco |
|---|---|
1 |
r |
2 |
x |
⇒ x = 2r
Logo, o comprimento de um arco contido em uma circunferência de centro O e raio r, sêndo med() = 2 rad, é igual ao diâmetro 2r dessa circunferência.
15. a) ![]()
Assim, 1.970° = 170° + 5 ⋅ 360°.
Portanto, a 1ª determinação positiva de 1.970° é 170°.
b) = + 3 ⋅ 2(pi)"
Portanto, a 1ª determinação positiva de rad é rad.
c) ⇒ + (−1) ⋅ 2(pi)"
Portanto, a 1ª determinação positiva de rad é rad.
d) ![]()
Assim, −1.110° = −(30° + 3 ⋅ 360°) = −30° − 3 ⋅ 360° e −30° + 360° = 330°.
Segue-se quê:
−1.110° = 330° + (−4) ⋅ 360°
Portanto, a 1ª determinação positiva de −1.110° é 330°.
e) ![]()
Assim, 1.520° = 80° + 4 ⋅ 360°.
Portanto, a 1ª determinação positiva de 1.520° é 80°.
f) = − 3 ⋅ 2(pi)" e
Segue-se quê:
+ (−4) ⋅ 2(pi)"
Portanto, a 1ª determinação positiva de rad é rad.
16. a) Algumas respostas possíveis:
•
•
•
•
b) Algumas respostas possíveis:
• −(pi)" − 4(pi)" = −5(pi)"
• −(pi)" − 2(pi)" = −3(pi)"
• −(pi)" + 2(pi)" = (pi)"
• −(pi)" + 4(pi)" = 3(pi)"
17. a)
Medida do arco, em grau |
Medida do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
⇒ 2(pi)"x = 1.380(pi)" ⇒ x = 690
Portanto, os três giros correspondem a um ângulo de 690°.
b) Como (pi)" rad corresponde a 180°, a medida de cada ângulo, em grau, é:
• Para , temos: ⋅ 180° = 120°
• Para , temos: ⋅ 180° = 270°
• Para , temos: ⋅ 180° = 300°
Como Rafael gira a roleta a partir da posição em quê o ponteiro parou no giro anterior, ele obteve na roleta os números 5, 2 e 12. Assim, deve deslocar o peão em 5 + 2 + 12 = 19 → 19 casas.
18. Inicialmente, analisamos se o arco é a 1ª determinação positiva e, na sequência, escrevemos a expressão dos arcos kôn-gru-us para cada caso.
a) 315° + k ⋅ 360°, com k ∈ ℤ
b) rad + k ⋅ 2(pi)" rad, com k ∈ ℤ
c) A 1ª determinação positiva do arco é 2(pi)" − . Assim, a expressão é rad + k ⋅ 2(pi)" rad, com k ∈ ℤ.
d) 220° + k ⋅ 360°, com k ∈ ℤ
19. Inicialmente, vamos calcular a 1ª determinação positiva de cada arco.
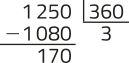
Assim, 1.250° = 170° + 3 ⋅ 360°. Logo, a 1ª determinação positiva do arco de 1.250° é 170°.
− 8(pi)" = − 4 ⋅ 2(pi)" e − + 2(pi)" =
Segue-se quê:
+ (−5) ⋅ 2(pi)"
Logo, a 1ª determinação positiva do arco de rad é rad, quê corresponde a 225°.
20. a) ⋅ 360° = 135° ou ⋅ 2(pi)" rad = rad
b) = + 6(pi)" = + 3 ⋅ 2(pi)"
Assim, a 1ª determinação positiva do arco de é . Temos ∶ 2(pi)" = ; logo, a extremidade do arco coincide com o vértice H, pois a 1ª determinação positiva corresponde a do arco de uma volta.
21. a) + 2(pi)"
Logo, a 1ª determinação positiva de é , quê está no 3º quadrante. Assim, reduzindo do 3º para o 1º quadrante, temos:
sen = sen = −sen = −sen =
b)
Página trezentos e oitenta
Assim, está no 4º quadrante.
Reduzindo do 4º para o 1º quadrante, temos:
tg = −tg = −tg = −1
c) +7 ⋅ 2(pi)"
Logo, a 1ª determinação positiva de é , quê está no 2º quadrante.
Assim, reduzindo do 2º para o 1º quadrante, temos:
cos = cos = = −cos =
d) = + (−1) ⋅ 2(pi)" e + 2(pi)" =
Logo, a 1ª determinação positiva de é , quê está no 2º quadrante.
Assim, reduzindo do 2º para o 1º quadrante, temos: tg = tg = −tg = −tg
e) = + (−2)⋅ 2(pi)" e
Logo, a 1ª determinação positiva de é , quê está no 2º quadrante.
Assim, reduzindo do 2º para o 1º quadrante, temos: cos () = cos = −cos ((pi)" − ) = −cos ( ) =
f) = + (−1) ⋅ 2(pi)" e
Logo, a 1ª determinação positiva de é , quê está no 2º quadrante.
Assim, reduzindo do 2º para o 1º quadrante, temos: sen () = sen = sen ((pi)" − ) = sen =
g) = + (−3) ⋅ 2(pi)" e
Logo, a 1ª determinação positiva de é , quê está no 2º quadrante.
Assim, reduzindo do 2º para o 1º quadrante, temos:
cos () = cos = −cos ( − (pi)") = −cos =
h) + 2 ⋅ 2(pi)"
Logo, a 1ª determinação positiva de é , quê está no 4º quadrante.
Assim, reduzindo do 4º para o 1º quadrante, temos: tg = tg = −tg (2(pi)" − ) = −tg
i) + 2 ⋅ 2(pi)"
Logo, a 1ª determinação positiva de é , quê está no 3º quadrante.
Assim, reduzindo do 3º para o 1º quadrante, temos:
sen = sen = −sen ( − (pi)") = −sen =
j) + 3 ⋅ 2(pi)"
Logo, a 1ª determinação positiva de é , quê está no 3º quadrante.
Assim, reduzindo do 3º para o 1º quadrante, temos:
cos = cos = −cos ( − (pi)") = −cos =
• Resposta pessoal. Espera-se quê os estudantes respondam quê, inicialmente, obtiveram a 1ª determinação positiva de cada arco e, em seguida, realizaram a redução ao 1º quadrante, identificando o valor a partir dos ângulos notáveis.
22. alternativa c
Como sen m > 0 e tg m < 0, a extremidade do arco pertence ao 2º quadrante.
Considere t a reta tangente à circunferência na origem dos arcos. Note quê a reta quê contém o segmento intersecta a reta t em um ponto de ordenada menor quê −1, pois o ângulo entre e o eixo y é menor quê 45°. Portanto, o ponto C é o único quê póde corresponder à extremidade dêêsse arco.
23. Resposta esperada: Nenhum dêêsses estudantes acertou a resposta à questão. Ana errou porque, no 2º quadrante, tem-se cos m < 0. Já Bento errou porque, no 3º quadrante, tg m > 0.
A resposta correta à questão é o 4º quadrante, no qual se tem tg m < 0 e cos m > 0.
24. Note quê a distância de A até a base corresponde à distância do centro C até B somado com 4 m, logo:
BC + 4 = 104 ⇒ BC = 100
Então, a roda-gigante póde sêr representada por uma circunferência com 100 m de raio.
Temos 1.290° = 210° + 3 ⋅ 360°; logo, a roda-gigante realizou 3 voltas completas e mais um giro de 210°, de modo quê o ponto A ficou na posição ilustrada na imagem.
Como a circunferência tem 100 m de raio, então a distância do ponto A até o eixo x, em métro, corresponde a:
100 ⋅ |sen (210°)| = 100 ⋅ |−sen (210° − 180°)| = 100 ⋅ |−sen (30°)| = 100 ⋅ = 50
Logo, a distância do ponto A até a base é:
100 − 50 + 4 = 54 → 54 m
25. S = = u.a.
26. Temos:
• sen (pi)" = 0
• A extremidade do arco de rad está no 2º quadrante, assim:
cos = −cos ((pi)" − ) = −cos =
• A extremidade do arco de rad está no 4º quadrante, assim:
tg = −tg (2(pi)" − ) = −tg = −1
Segue-se quê:
27. Para realizar a demonstração, vamos considerar os pontos em cada quadrante simétricos ao ponto P(cos m, sen m) do 1º quadrante.
a) Para o 2º quadrante, considere o ponto T(cos t, sen t), simétrico a P em relação ao eixo y. Assim, podemos escrever:
• OT = 1;
Página trezentos e oitenta e um
• OT(minutos)" = TT(segundos)" = sen t = sen ((pi)" − m) = sen m;
• OT(segundos)" = cos t = cos ((pi)" − m) = −cos m.
Aplicando o teorema de Pitágoras no triângulo OT(segundos)"T, temos:
(OT)2 = (OT(segundos)")2 + (TT(segundos)")2 ⇒ 1 = (−cos m)2 + (sen m)2 ⇒ sen2 m + cos2 m = 1
b) Para o 3º quadrante, considere o ponto S(cos s, sen s), simétrico a P em relação ao ponto O. Assim, podemos escrever:
• OS = 1;
• OS(minutos)" = SS(segundos)" = sen s = sen ((pi)" + m) = −sen m;
• OS(segundos)" = cos s =cos ((pi)" + m) = −cos m.
Aplicando o teorema de Pitágoras no triângulo OS(segundos)"S, temos:
(OS)2 = (OS(segundos)")2 + (SS(segundos)")2 ⇒ 1 = (−cos m)2 + (−sen m)2 ⇒ sen2 m + cos2 m = 1
c) Para o 4º quadrante, considere o ponto V(cos v, sen v), simétrico a P em relação ao eixo x. Assim, podemos escrever:
• OV = 1;
• OV(minutos)" = VV(segundos)" = sen v = sen (2(pi)" − m) = −sen m;
• OV(segundos)" = cos v =cos (2(pi)" − m) = cos m.
Aplicando o teorema de Pitágoras no triângulo OV(segundos)"V, temos:
(OV)2 = (OV(segundos)")2 + (VV(segundos)")2 ⇒ 1 = (cos m)2 + (−sen m)2 ⇒ sen2 m + cos2 m = 1
d) Para pontos nos eixos coordenados, temos m = 0, m= , m = (pi)", m = e m = 2(pi)". Nesses casos, o triângulo não é formado, pois dois dos três pontos considerados são coincidentes. Então, podemos verificar a relação substituindo os valores para cada um dos casos.
• Para m = 0:
sen2 m + cos2 m = sen2 0 + cos2 0 = 02 + 12 =1
• Para m = :
sen2 m + cos2 m = sen 2 + cos 2 = 12 + 02 = 1
• Para m = (pi)":
sen2 m + cos2 m = sen2 (pi)" + cos2 (pi)" = 02 + (−1)2 =1
• Para m = :
sen2 m + cos2 m = sen2 + cos2 = (−1)2 + 02 = 1
• Para m = 2(pi)":
sen2 m + cos2 m = sen2 2(pi)" + cos2 2(pi)" = 02 + 12 =1
28. a) Temos + 2 ⋅ 2(pi)", assim:
f = sen = sen = −1
b) Temos + 2 ⋅ 2(pi)", assim:
g = cos = cos = cos
29. a) sen x = 1 ⇒ x = + 2k(pi)", k ∈ ℤ
Para 0 ≤ x ≤ 2(pi)" (1ª volta positiva do ciclo trigonométrico), temos k = 0 e, portanto, x = + 2 ⋅ 0 ⋅ (pi)" = .
b) cos x = −1 ⇒ x = (pi)" + 2k(pi)", k ∈ ℤ
Para −2(pi)" ≤ x ≤ 4(pi)" e k ∈ ℤ, temos:
−2(pi)" ≤ (pi)" + 2k(pi)" ≤ 4(pi)" ⇒ −3(pi)" ≤ 2k(pi)" ≤ 3(pi)" ⇒ ≤ k ≤ ⇒ k = −1, 0, 1
Logo:
• x = (pi)" + 2 ⋅ (−1) ⋅ (pi)" = −(pi)"
• x = (pi)" + 2 ⋅ 0 ⋅ (pi)" = (pi)"
• x = (pi)" + 2 ⋅ 1 ⋅ (pi)" = 3(pi)"
c) cos x = ⇒ x = + 2k(pi)" ou x = + 2k(pi)", k ∈ ℤ
Para −4(pi)" ≤ x ≤ (pi)" e k ∈ ℤ, temos:
• −4(pi)" ≤ + 2k(pi)" ≤ (pi)" ⇒ ≤ 2k(pi)" ≤ ⇒ ≤ k ≤ ⇒ k = −2, −1, 0
• −4(pi)" ≤ + 2k(pi)" ≤ (pi)" ⇒ ≤ 2k(pi)" ≤ ⇒ ≤ k ≤ ⇒ k= −1, 0
Logo:
• x = + 2 ⋅ (−2) ⋅ (pi)" =
• x = + 2 ⋅ (−1) ⋅ (pi)" =
• x = + 2 ⋅ (−1) ⋅ (pi)" =
• x = + 2 ⋅ 0 ⋅ (pi)" =
• x = + 2 ⋅ 0 ⋅ (pi)" =
30. a) −1 ≤ 2m + 11 ≤ 1 ⇒ −12 ≤ 2m ≤ −10 ⇒ −6 ≤ m ≤ −5
b) −1 ≤ 9 − m ≤ 1 ⇒ −10 ≤ −m ≤ −8 ⇒ 8 ≤ m ≤ 10
c) −1 ≤ ≤ 1 ⇒ −6 ≤ 5m + 1 ≤ 6 ⇒ −7 ≤ 5m ≤ 5 ⇒ ≤ m ≤ 1
d) 3 + sen x = 3m ⇒ sen x = 3m − 3
Assim:
−1 ≤ 3m − 3 ≤ 1 ⇒ 2 ≤ 3m ≤ 4 ⇒ ≤ m ≤
31. a) Resposta esperada: No gráfico de função par, é possível identificar simetria de reflekção em relação ao eixo das ordenadas, ou seja, se um ponto P(a, b) pertence ao gráfico de uma função par, então o ponto P(minutos)"(−a, b) também pertence a esse gráfico.
Já no gráfico de função ímpar, é possível identificar simetria em relação ao ponto O, ou seja, se um ponto P(a, b) pertence ao gráfico de uma função ímpar, então o ponto P(minutos)"(−a, −b) também pertence a esse gráfico.
b) Algumas respostas possíveis:
função par:
• f(x) = cos (x), pois: f(−x) = cos (−x) = cos (x) = f(x)
• f(x) = |x|, pois: f(−x) = |−x| = |−1| ⋅ |x| = |x| = f(x)
• f(x) = x2, pois: f(−x) = (−x)2 = (−1)2 ⋅ x2 = x2 = f(x)
função ímpar:
• f(x) = sen (x), pois: f(−x) = sen (−x) = −sen (x) = −f(x)
• f(x) = x, pois: f(−x) = −x = −f(x)
• f(x) = x3, pois: f(−x) = (−x)3 = (−1)3 ⋅ x3 = −x3 = −f(x)
c) Resposta pessoal. Espera-se quê os estudantes reconheçam características do gráfico de funções pares e de funções ímpares.
32. a) −1 ≤ cos x ≤ 1 ⇒ 1 ≤ cos x + 2 ≤ 3
valor mínimo: 1; valor mássimo: 3
b) −1 ≤ sen x ≤ 1 ⇒ −2 ≤ 2 ⋅ sen x ≤ 2 ⇒ −7 ≤ 2 ⋅ sen x − 5 ≤ −3
valor mínimo: −7; valor mássimo: −3
c) −1 ≤ sen x ≤ 1 ⇒ 1 ≤ sen x + 2 ≤ 3 ⇒ ≤ ≤ ⇒ ≤ ≤ 2
valor mínimo: ; valor mássimo: 2
Página trezentos e oitenta e dois
d) −1 ≤ cos x ≤ 1 ⇒ −1 ≤ −cos x ≤ 1 ⇒ −5 ≤ −5 ⋅ cos x ≤ 5 ⇒ −2 ≤ 3 − 5 ⋅ cos x ≤ 8
valor mínimo: −2; valor mássimo: 8
33. Atividade de elaboração do estudante. Espera-se quê os estudantes sêjam capazes de elaborar problemas envolvendo fenômenos com comportamentos periódicos, utilizando as funções seno e cosseno na modelagem. Um contexto possível é a tempera-túra da á gua de um lago. Eles ainda podem elaborar problemas com contexto puramente matemático e solicitar aos côlégas quê determinem o conjunto imagem da função, o valor da variável independente a partir de um valor conhecido da variável dependente, ou construir o gráfico da função.
34. pôdêmos observar quê o gráfico da função f, representado pela curva em vêrde, está acima do gráfico da função g, representado em vermelho, nos intervalos e , ou seja, o conjunto solução é S = .
35. A, 1), B , C , D , E (, −1), F(2(pi)", 0) e G
36. a) p = = 2(pi)"
b) p =
c) p = = 2(pi)" ⋅ = 8
d) p = = 2(pi)" ⋅ 3 = 6(pi)"
37. a) • Valor mínimo de f: 7 ⋅ (−1) = −7
• Valor mássimo de f: 7 ⋅ 1 = 7
Logo, Im(f) = [−7, 7].
b) • Valor mínimo de g: 5 + 8 ⋅ (−1) = −3
• Valor mássimo de g: 5 + 8 ⋅ 1 = 13
Logo, Im(g) = [−3, 13].
c) • Valor mínimo de m: 4 − 4 ⋅ 1 = 0
• Valor mássimo de m: 4 − 4 ⋅ (−1) = 8
Logo, Im(m) = [0, 8].
d) O valor mínimo e o mássimo de |cos x| são, respectivamente, 0 e 1. Assim:
• Valor mínimo de n: 2 + 0 = 2
• Valor mássimo de n: 2 + 1 = 3
Logo, Im(n) = [2, 3].
38. alternativa d
Suponha quê g é da forma g(x) = a + b cos (cx + d).
• Como o gráfico é deslocado 3 unidades para baixo, temos a = −3.
• Como a amplitude do gráfico é (−1) − (−5) = 4, então:
|b| = = 2
• Como o período de g é p = ,temos:
p = ⇒ |c | = 6
• Como o gráfico é deslocado em (pi)" unidades para a esquerda, temos:
= (pi)" ⇒ |d | = 6(pi)"
Portanto, a lei de formação de g póde sêr a da alternativa d.
39. Atividade de elaboração do estudante. Espera-se quê os estudantes ajustem os valores dos coeficientes de uma função do tipo trigonométrica e sêjam capazes de reconhecer a modificação realizada no gráfico a partir de cada um deles, em relação ao gráfico da função seno.
40. a)
x |
y = f(x) = 2 sen (4x) |
(x, y) |
|---|---|---|
0 |
y = 2 sen = 0 |
(0, 0) |
y = 2 sen = 2 |
(, 2) |
|
y = 2 sen = 0 |
(, 0) |
|
y = 2 sen = −2 |
(, −2) |
|
y = 2 sen = 0 |
(, 0) |
b)
x |
y = g(x) = −3 + cos (x + ) |
(x, y) |
|---|---|---|
y = −3 + cos = −2 |
(, −2) |
|
y = −3 + cos = −3 |
(, −3) |
|
y = −3 + cos = −4 |
(, −4) |
|
y = −3 + cos = −3 |
(, −3) |
|
y = −3 + cos = −2 |
(, −2) |
Página trezentos e oitenta e três
c)
x |
y = m(x) = 4 + 3 cos (2x − (pi)") |
(x, y) |
|---|---|---|
y = 4 + 3 cos = 7 |
(, 7) |
|
y = 4 + 3 cos = 4 |
(, 4) |
|
(pi)" |
y = 4 + 3 cos = 1 |
((pi)", 1) |
y = 4 + 3 cos = 4 |
(, 4) |
|
y = 4 + 3 cos = 7 |
(, 7) |
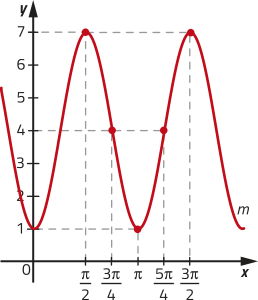
d)
x |
y = n(x) = 1 − 2 sen ( − ) |
(x, y) |
|---|---|---|
y = 1 − 2 sen = 1 |
(, 1) |
|
y = 1 − 2 sen = −1 |
(, −1) |
|
y = 1 − 2 sen = 1 |
(, 1) |
|
y = 1 − 2 sen = 3 |
(, 3) |
|
y = 1 − 2 sen = 1 |
(, 1) |
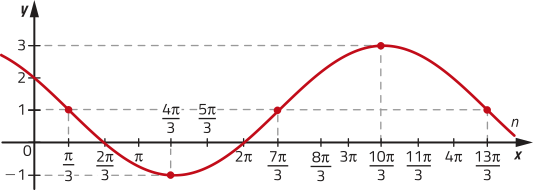
41. a) 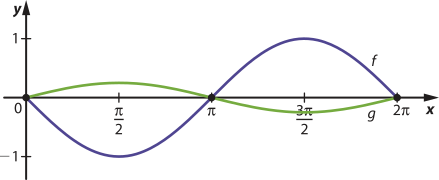
b) Analisando os gráficos do item a, sim, eles se intersectam em três pontos, cujas coordenadas são (0, 0), ((pi)", 0) e (2(pi)", 0).
42. alternativa c
• Como os valores mássimo e mínimo da função são, respectivamente, 0,5 e −0,5, então |(alfa)"| = 0,5.
• Como o período da função é p = , então:
p = ⇒ |(beta)"| = 4
• Como f(0) = 0, temos:
(alfa)" cos ((beta)" ⋅ 0 + (gama)") = 0 ⇒ cos (gama)" = 0 ⇒ (gama)" = + k(pi)", k ∈ ℤ
Logo, a alternativa c é a correta.
43. alternativa b
Vamos calcular a freqüência f = da onda sonora correspondente a cada função, sêndo p o seu período, em segundo.
a) f = = 15 → 15 Hz
b) f = = 120 → 120 Hz
c) f = = 10 → 10 Hz
d) f = 18,875 → 18,875 Hz
Logo, a função da alternativa b é a quê póde descrever uma onda sonora audível por uma pessoa, pois é a única cuja freqüência está no intervalo entre 20 Hz e 20.000 Hz.
44. alternativa a
• Altura mássima:
1,8 + 1,2 ⋅ 1 = 3,0 → 3,0 m
• Altura mínima:
1,8 + 1,2 ⋅ (−1) = 0,6 → 0,6 m
45. a) Sendo 110 mmHg e 70 mmHg, respectivamente, a pressão arterial mássima e mínima, temos:
⇒
⇒ +
2A + 0B = 180 ⇒ A = 90
Substituindo A = 90 na primeira equação, temos:
90 + B = 110 ⇒ B = 20
Para determinar o período, obissérve a seguinte proporção:
Batimentos |
Tempo (s) |
|---|---|
75 |
60 |
1 |
x |
⇒ x =
Segue-se quê:
p = ⇒ |k| = 2,5(pi)" ⇒ k = ±2,5(pi)"
Observe quê, como cos (kt) = cos (−kt), podemos considerar k = 2,5(pi)". Portanto, uma resposta possível é p(t) = 90 + 20 ⋅ cos (2,5(pi)"t).
b) O valor da função varia de 70 mmHg a 110 mmHg e seu período é de = 0,8. Logo, o gráfico II é o quê melhor a representa.
46. Atividade de elaboração do estudante. Espera-se quê os estudantes utilizem o contexto e a função apresentada no enunciado para elaborar um problema e explorar elemêntos de funções do tipo
Página trezentos e oitenta e quatro
trigonométrica, como a relação de cada coeficiente, valor mássimo ou mínimo, representação gráfica ou zeros da função.
47. Atividade de elaboração do estudante. Espera-se quê os estudantes compreendam as relações entre funções do tipo trigonométrica e fenômenos com comportamento periódico, representando-os por meio dessas funções. Eles podem, por exemplo, explorar o contexto de uma situação-problema no GeoGebra e, com o auxílio do contrôle deslizante, observar a periodicidade do fenômeno. É importante verificar, no texto redigido pêlos estudantes, se utilizam corretamente a linguagem matemática, bem como os conceitos estudados na Unidade.
48. a) 0,18 ampere; −0,18 ampere
b) • Seja t0 ∈ D(i) tal quê sen (ωt0 + φ) = 1.
Assim, i(t0) assume seu valor mássimo ou mínimo, logo:
|i(t0)| = 0,18 ⇒ |I ⋅ sen (ωt0 + φ)| = 0,18 ⇒ |I | = 0,18
Como I é não negativo, a amplitude é I = 0,18.
• Como o período da função é p = , temos:
p = ⇒ |ω| = 120(pi)"
Como ω é não negativo, a freqüência angular é ω = 120(pi)".
c) Sendo i uma função do tipo trigonométrica e observando o gráfico, temos quê o ponto de mássimo destacado tem abscissa . Assim:
i = 0,18 ⇒ 0,18 ⋅ sen ( + φ) = 0,18 ⇒ sen ( + φ) = 1 ⇒ + φ = + 2k(pi)", k ∈ ℤ ⇒ φ = 2k(pi)", k ∈ ℤ
Tomando k = 0, obtemos a constante de fase φ = 0. Assim:
i(t) = 0,18 ⋅ sen (120(pi)"t)
d) • t = 1:
i(1) = 0,18 ⋅ sen (120(pi)" ⋅ 1) = 0,18 ⋅ sen (60 ⋅ 2(pi)") = 0,18 ⋅ 0 = 0 → 0 ampere
• t = :
i = 0,18 ⋅ sen (120(pi)" ⋅ ) = 0,18 ⋅ sen = 0,18 ⋅ sen ( + 60 ⋅ 2(pi)") = 0,18 ⋅ 1 = 0,18 → 0,18 ampere
49. a) sen 2 x + sen x = 0 ⇒ sen x ⋅ (sen x + 1) = 0 ⇒ ⇒
Portanto, S = {x ∈ ℝ | x = k(pi)" ou x = + 2k(pi)", com k ∈ ℤ}.
b) cos (x − ) + 3 = ⇒ cos (x − ) = −
• x − + 2k(pi)" ⇒ x = + 2k(pi)";
• x − + 2k(pi)" ⇒ x = + 2k(pi)".
Portanto, S = {x ∈ ℝ | x = + 2k(pi)" ou x = + 2k(pi)", com k ∈ ℤ).
c) sen ( + x) = −1 ⇒ + x = + 2k(pi)" ⇒ x = + 2k(pi)"
Portanto, S = {x ∈ ℝ | x = + 2k(pi)", com k ∈ ℤ}.
d) cos 2x =
• 2x = + 2k(pi)" ⇒ x = + k(pi)";
• 2x = + 2k(pi)" ⇒ x = + k(pi)".
Portanto, S = {x ∈ ℝ | x = + k(pi)" ou x = + k(pi)", com k ∈ ℤ}.
50. a) sen2 x = 1 ⇒
Logo, para x ∈ [0, 2(pi)"[, temos x = ou x = .
b) cos2 x = ⇒
Logo, para x ∈ [−(pi)", (pi)"], temos x = , x = ,x = ou x = .
c) sen2 x + cos x = 1 ⇒ (1 − cos2 x) + cos x = 1 ⇒ cos x ⋅ (−cos x + 1) = 0 ⇒
Logo, para x ∈ , temos x = , x = ou x = 2(pi)".
d) sen (x + ) = 0 ⇒ x + = k(pi)", com k ∈ ℤ ⇒ x = + k(pi)", com k ∈ ℤ
Para x ∈]2(pi)", 4(pi)"], temos:
2(pi)" < x ≤ 4(pi)" ⇒ 2(pi)" < + k(pi)" ≤ 4(pi)" ⇒ < k(pi)" ≤ ⇒ < k ≤ ⇒ k = 4 ou k = 5
Portanto, x = + 4(pi)" = ou x = + 5(pi)" = .
51. 2 ⋅ cos x = ⇒ cos x =
Assim, x = + 2k(pi)" ou x = + 2k(pi)", com k ∈ ℤ.
Para 0 ≤ x ≤ 3(pi)", temos x = , x = ou x = .
Portanto, a equação tem 3 raízes reais nesse intervalo.
52.

Como (alfa)" e (beta)" são ângulos agudos, temos:
• sen (alfa)" = ⇒ sen (alfa)" = ⇒ (alfa)" = 30°
• cos (beta)" = ⇒ cos (beta)" = ⇒ (beta)" = 60°
Portanto, os ângulos internos médem 30°, 60° e 90°.
53. alternativa d
Como o conjunto imagem da função cosseno é [−1, 1] e, de acôr-do com a lei de formação da função f, temos quê o valor mássimo de f é obtído quando cos ((pi)" ⋅ ) = 1. Assim, podemos substituir ((pi)" ⋅ ) por 1 na lei de formação de f para obtêr o valor mássimo dessa função.
f(t) = 1,625 + 1,25 ⋅ 1 = 2,875
Assim, a maior taxa de câmbio da moeda X em relação à moeda Y é de 2,875.
Página trezentos e oitenta e cinco
Para determinar o mês em quê o valor mássimo ocorre, temos de considerar quê cos x = 1 para x = 2k(pi)", com k ∈ ℤ.
Assim, temos: cos ((pi)" ⋅ ) = 1 ⇒ (pi)" ⋅ = 2k(pi)" ⇒ t = 24k + 3 com k ∈ ℤ
Como a análise da taxa de câmbio ocorreu no período de 1 ano e t = 9 indica a taxa no início de outubro, temos quê:
0 ≤ t ≤ 11 ⇒ 0 ≤ 24k + 3 ≤ 11 ⇒ −3 ≤ 24k ≤ 8 ⇒ ≤ k ≤
Dado quê k ∈ ℤ, segue-se quê k = 0.
Assim: t = 24 ⋅ 0 + 3 = 3
Logo, a maior taxa de câmbio da moeda X em relação à moeda Y ocorreu quando t = 3, ou seja, no início de abril.
54. Atividade de elaboração do estudante. Espera-se quê os estudantes possam elaborar e resolver as situações-problema utilizando os conceitos estudados na Unidade. É possível verificar, a partir da atividade, conceitos quê precisem sêr retomados para a compreensão dos estudantes.
Integrando com...
1. Resposta pessoal. As respostas dependem da região em quê os estudantes moram. No geral, espera-se quê respondam quê sim, notando a presença de dias com maior duração solar na primavera e no verão e dias com menor duração solar em períodos do outono e do inverno.
2. Resposta esperada: Movimento de rotação, pois nele a Terra gira em torno de seu eixo imaginário.
3. • Analisando a primeira linha da tabéla apresentada, temos:
14,4 horas no dia 21/12/2024.
• Analisando a segunda linha da tabéla apresentada, temos:
9,92 horas no dia 20/06/2025.
4. h(100) = 12,16 + 2,24 ⋅ cos (2(pi)" ⋅ ) ≃ 11,82 → aproximadamente 11,82 h
5. a) Resposta pessoal. A resposta depende do município em quê os estudantes moram.
b) Resposta pessoal. A resposta depende do município em quê os estudantes moram.
c) Resposta pessoal. Para realização dêêsse item, os estudantes podem se basear no modelo apresentado no início da seção, ajustando os valores dos parâmetros para aqueles pesquisados referentes ao município em quê moram.
d) Atividade de elaboração do estudante. Espera-se quê os estudantes, com base nas respostas aos itens anteriores e nas atividades realizadas, sêjam capazes de elaborar uma situação-problema relacionando o contexto apresentado a funções do tipo trigonométrica. Os estudantes podem identificar a variação na duração do dia no município em quê moram e, a partir díssu, pensar, por exemplo, em possibilidades de potencializar suas ações para cada época do ano, aproveitando o mássimo possível a luz solar e diminuindo o consumo de energia elétrica.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) I) Resposta esperada: Sim, as moradias estão dispostas em formato circular cujo centro corresponde à posição onde o baito está localizado, garantindo quê todas essas moradias fiquem, aproximadamente, à mesma distância do baito.
II) • Comprimento da circunferência: 2(pi)" ⋅ 90 = 180(pi)" → 180(pi)" m ou aproximadamente 565,2 m
• A distância de uma moradia até o baito corresponde à medida do raio da circunferência; logo, a pessoa vai percorrer: 2 ⋅ 90 = 180 → 180 m
• Medida do arco em grau: 360° ∶ 15 = 24°; medida do arco em radiano: rad.
b) I) Im(f) = [−1, 1]; período de f: 4(pi)"; valor mássimo de f: 1; valor mínimo de f: −1
II) Como o período da função é p = 4(pi)", temos:
p = ⇒ 4(pi)" = ⇒ |k| = ⇒ k =
• Para k = : f((pi)") = sen () = 1
• Para k = : f((pi)") = sen () = −1 (Incorreto)
Pelo gráfico, podemos observar quê f((pi)") = 1; logo, k = . Assim, a lei de formação de f é f(x) = sen (x).
III) Resposta esperada: Função ímpar, pois:
f(−x) = sen (x) = −sen (x) = −f(x)
IV) Os gráficos das funções g, h e m correspondem a deslocamentos verticais do gráfico da função f em uma unidade para cima, uma unidade para baixo e duas unidades para cima, respectivamente.
g(x) = 1 + sen ( x);
h(x) = −1 + sen ( x);
m(x) = 2 + sen ( x).
Praticando: enêm e vestibulares
1. alternativa a
A pressão mínima ocorre quando cos (kt) = −1, e a pressão mássima, quando cos (kt) = 1. Assim, temos o sistema:
⇒ ⇒ A = 99 e B = 21
Para determinar k, obissérve quê:
Batimentos |
Tempo (em segundo) |
|---|---|
90 |
60 |
1 |
x |
⇒ x =
Logo, o período da função é igual a segundo. Assim, como k é positivo:
⇒ k = 3(pi)"
Portanto, P(t) = 99 + 21cos (3(pi)"t).
2. alternativa a
Como o ponto de coordenadas (0, −1) pertence ao gráfico da função, temos:
−1 = a + b cos 0 ⇒ a + b = −1
Note quê, como −1 não é o valor mássimo da função e cos 0 = 1, então o valor mássimo é obtído quando cos x = −1; logo:
a + b ⋅ (−1) = 5 ⇒ a − b = 5
Resolvendo o sistema
, temos a = 2 e b = −3.
Assim: 5a + 2b = 5 ⋅ 2 + 2 ⋅ (−3) = 4
3. alternativa e
• Altura mássima:
12,6 + 4 ⋅ 1 = 16,6 → 16,6 metros
• Altura mínima:
12,6 + 4 ⋅ (−1) = 8,6 → 8,6 metros
• O tempo gasto para uma volta completa corresponde ao período p da função, o qual é dado por:
p = = 36 → 36 segundos
4. alternativa e
Temos:
tg 30° = ⇒ OM =
Assim, a área do triângulo é:
5. alternativa a
Como a função passa pelo ponto de coordenadas (0, −3), analisamos as duas possíveis expressões:
Página trezentos e oitenta e seis
• P(0) = ±A cos (ω ⋅ 0) ⇒ −3 = ±A cos 0 ⇒ −3 = ±A
• P(0) = ±A sen (ω ⋅ 0) ⇒ −3 = ±A sen 0 ⇒ −3 = ±A ⋅ 0 ⇒ −3 = 0 (absurdo)
Logo, a expressão adequada é
P(t) = ±A cos (ωt) e ±A = −3.
O período da função é dado por:
(pi)" − 0 = (pi)"
Segue-se quê:
=ω ⇒ ω=2
Portanto, P(t) = −3 cos (2t).
6. alternativa d
Às 6h20min, em relação à indicação do 12 no relógio, temos quê a medida do ângulo do giro de cada ponteiro, em grau, é dado por:
• ponteiro dos minutos:
(360° ∶ 60) ⋅ 20 = 120°
• ponteiro das horas:
6 ⋅ 30° + (30° ∶ 60) ⋅ 20 = 190°
Assim, entre os ponteiros, os ângulos formados têm as seguintes medidas:
• 190° − 120° = 70°
• 360° − 70° = 290°
7. alternativa c
Observe o esquema, quê representa a Terra com a linha do equador e o paralelo 30° N traçados.
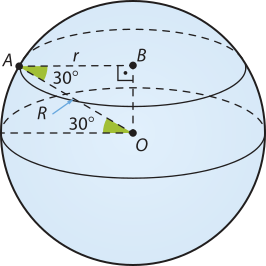
A medida OA corresponde ao raio da Terra R = 6.300 km, enquanto AB = r corresponde ao raio da circunferência do paralelo 30° N. Assim:
cos 30° = ⇒ r =
A figura a seguir representa os pontos P e Q sobre esse paralelo.
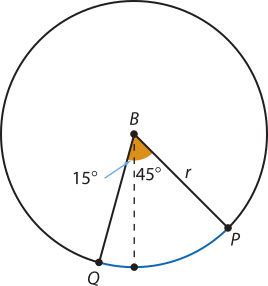
O menor arco nessa circunferência é o arco de medid cujo comprimento é dado pela seguinte regra de três:
Medida do arco (em grau) |
Comprimento do arco (em km) |
|---|---|
360 |
2(pi)"r |
60 |
x |
⇒ 6 = ⇒ x = km
8. Os valores de rM para θ = 0° e θ = 180° correspondem, respectivamente, à distância do Sol até o ponto A e à distância do Sol até o ponto P, em milhão de quilômetro. Logo:
PA = + = = 115,625 → 115,625 milhões de quilômetros.
9. alternativa b
• Valor mássimo: 3 − 5 ⋅ (−1) = 8;
• Valor mínimo: 3 − 5 ⋅ 1 = −2;
• Período: = (pi)".
Unidade 5 • Figuras geométricas planas, perímetro e área
1. As figuras dos itens a, b, d e e representam polígonos convexos. Os polígonos representados nos itens c e f não são convexos, pois é possível traçar um segmento de reta com extremidades no polígono de maneira quê algum ponto dêêsse segmento seja externo ao polígono.
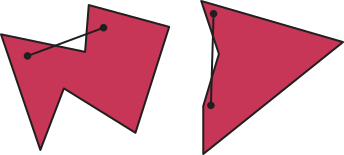
2. 7 ⋅ 60 = 420 → 420 cm
3. O polígono tem 9 lados; logo, cada lado méde:
225 ∶ 9 = 25 → 25 dm
4. a) Temos AD = BC e AB = cê dê, assim:
AB + BC + cê dê + AD = 144 ⇒ 2AB + 2AD = 144
Substituindo AD = AB nessa equação, temos:
2AB + AB = 144 ⇒ AB = 144 ⇒ AB = 54
Segue-se quê:
BC = AD = AB = ⋅ 54 = 18
Portanto, BC = 18 cm e AB = 54 cm.
b) Como O é o ponto médio de , então:
AO = = 24 → 24 cm
5. Como foram utilizadas 180 peças para formár a faixa, temos quê cada lado dessa faixa méde:
• lado superior:
180 ∶ 2 = 90
90 ⋅ 3 + 90 = 360 → 360 u.c.
• lado inferior:
180 ∶ 2 = 90
90 ⋅ 3 + 90 = 360 → 360 u.c.
• lado esquerdo: 3 u.c.
• lado direito: 3 u.c.
Segue-se quê o perímetro da faixa é dado por:
360 + 360 + 3 + 3 = 726 → 726 u.c.
6. alternativa c
Seja (x − 6, x − 3, x, x + 3, x + 6) a PA de razão 3 cujos termos correspondem às medidas dos ângulos internos do pentágono. A soma das medidas dos ângulos internos de um pentágono é (5 − 2) ⋅ 180° = 540°, logo:
(x − 6) + (x − 3) + x + (x + 3) + (x + 6) = 540 ⇒ 5x = 540 ⇒ x = 108
Assim, o menor ângulo méde:
x − 6 = 108 − 6 = 102 → 102°
7. a) Seja n a quantidade de lados dêêsse polígono. A soma das medidas de seus ângulos internos póde sêr expressa, em grau, por 130 + 2 ⋅ 145 + (n − 3) ⋅ 160 e por (n − 2) ⋅ 180. Logo:
130 + 2 ⋅ 145 + (n − 3) ⋅ 160 = (n − 2) ⋅ 180 ⇒ 160n − 60 = 180n − 360 ⇒ −20n = −300 ⇒ n = 15 → 15 lados
b) (15 − 2) ⋅ 180° = 2.340°
8. a)
Medida (em polegada) |
Medida (em centímetro) |
|---|---|
4,5 |
11,43 |
1 |
x |
⇒ x = = 2,54 → 2,54 cm
b) 32 ⋅ 2,54 = 81,28 → 81,28 cm
c) Observe o esquema a seguir, quê representa a tela do televisor, sêndo x a medida da largura, em polegada.
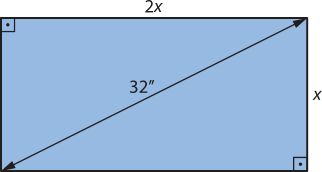
Pelo teorema de Pitágoras, temos:
x2 + (2x)2 = 322 ⇒ 5x2 = 1.024 ⇒ x2 = 204,8 ⇒
Assim, o perímetro da tela é:
x + 2x + x + 2x = 6x ≃ 6 ⋅ 14,3 = 85,8 → 85,8(segundos)"
Página trezentos e oitenta e sete
Realizando as conversões, temos:
85,8(segundos)" = 85,8 ⋅ 2,54 cm = 217,932 cm ≃ 2,2 m
d) Resposta pessoal. Espera-se quê os estudantes realizem as medições indicadas e, a partir dos resultados obtidos, determinem as demais por meio de cálculos envolvendo o teorema de Pitágoras.
9. a) Vamos calcular o perímetro de cada pista:
• Pista A: 100 + 100 + 100 + 100 = 400 → 400 m
• Pista B: 17 + 57 + 157 + 60 + 151 = 442 → 442 m
• Pista C: 150 + 222 + 143 + 205 = 720 → 720 m
Portanto, a pista C tem o maior perímetro e a pista A, o menor perímetro.
b) Temos quê 4,9 km correspondem a 4.900 m. Vamos determinar, para cada pista, o menor inteiro p tal quê a distância percorrida em p voltas seja maior quê 4.900, bem como a distância d ultrapasse a meta.
• Pista A: 4.900 =
• Pista B: 4.900 =
• Pista C: 4.900 =
Logo, ao escolher a pista C, a meta será ultrapassada na menor medida.
c) Resposta pessoal. Espera-se quê os estudantes elaborem uma quêstão envolvendo o conceito de perímetro e que consigam resolver a questão elaborada pelo colega. Incentivá-los a elaborar kestões quê não apenas solicite a determinação de perímetro mas também a compreensão de outros conceitos, como a identificação de polígonos e a conversão de unidades de medida de comprimento.
10. Seja x o comprimento do maior lado, em métro. Então:
x + x + x + x = 238 ⇒ x = 238 ⇒ x = 68
Assim, o maior lado méde 68 m e o menor lado, 51 m.
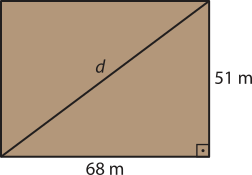
A medida d de uma das diagonais é dada por:
d2 = 512 + 682 ⇒ d2 = 7.225 ⇒
Assim, a quantidade mínima de fio necessária para a instalação é:
85 + 85 = 170 → 170 m
11. a) Seja x equivalente a uma unidade tal quê a peça retangular tenha dimensões 20x e 14x. Então:
20x + 14x + 20x + 14x = 102 ⇒ 68x = 102 ⇒ x = =
Assim, as dimensões são 14 ⋅ = 21 cm e 20 ⋅ = 30 cm.
b) As diagonais da peça com formato de losango médem:
• 20 − 2 ⋅ 1,7 = 16,6 → 16,6 u
• 14 − 2 ⋅ 1,7 = 10,6 → 10,6 u
Como cada unidade corresponde a cm, as medidas são cm e cm.
c) = 5,25 → 5,25 cm
d) Resposta pessoal. Espera-se quê os estudantes realizem as medições, consigam determinar as proporções da bandeira do Brasil e avaliem se estão dentro das normativas vigentes descritas na atividade.
12. Resposta pessoal. Espera-se quê os estudantes avaliem as medidas de uma rampa de acesso conforme solicitado na atividade e avaliem se essa rampa atende às normas da ABNT. Caso não atendam, espera-se quê eles proponham soluções, com base nos cálculos realizados, para quê a rampa de acesso atenda aos critérios definidos.
13. a) 5 vértices. 2 diagonais.
b) A, B e F
c) e ;
d) As diagonais são: , , , e .
Portanto, 5 diagonais.
e) De cada um dos n vértices partem n − 3 diagonais, porém cada diagonal parte de dois vértices distintos. Assim, o número (n − 3) ⋅ n corresponde ao dôbro da quantidade de diagonais, pois cada diagonal foi contada duas vezes.
Portanto: D =
14. a) Resposta pessoal. As respostas dependem dos polígonos desenhados pêlos estudantes. Verificar se tais polígonos são convexos.
b) Resposta pessoal. Se necessário, auxiliar os estudantes na realização das medições usando o transferidor.
c) Resposta esperada: A soma das medidas de cada par de ângulos é 180°.
d) Resposta esperada: A soma das medidas de todos os ângulos externos é 360°.
e) Resposta pessoal. Espera-se quê os estudantes avaliem as resoluções dos côlégas, demonstrando a compreensão dos conceitos e propriedades envolvidos na atividade.
15. a) • med() = med() = 78°
• med() + 78° + 78° = 180° ⇒ med() = 24°
b) n ⋅ 24° = 360° ⇒ n = 15 → 15 lados
16. a) 10 ⋅ 3 = 30 → 30 m
b) Como o jato de á gua será disparado do centro da fonte, a distância mássima horizontal quê ele deverá alcançar corresponde ao raio da circunferência inscrita ao decágono de lado 3 m, ou seja, à medida do apótema a. Vamos calcular a. Considere quê o decágono regular tenha sido decomposto em 10 triângulos isósceles congruentes a partir de seu centro O, sêndo ABO um dêêsses triângulos.
Temos med() = 360 ∶ 10 = 36°, logo:
(alfa)" + (alfa)" + 36° = 180 ⇒ (alfa)" = 72°
Segue-se quê:
tg 72° = ⇒ 3,08 = ⇒ a = 4,62
Portanto, o jato de á gua póde alcançar uma distância horizontal de até aproximadamente 4,62 m.
17. alternativa e
Sendo um dos lados do octógono, temos:
• med() = 360° ∶ 8 = 45°
• med() = med() e med( ) + med() + 45° = 180°.
Logo: med() = med( ) = 67,5°
18. alternativa d
Inicialmente, vamos determinar a medida r do raio dessa circunferência.
Observe quê r = OB e med() = 60° ∶ 2 = 30°, conforme a figura a seguir.
Assim: sen 30° = ⇒ r = 4
A figura a seguir representa o pentágono inscrito nessa circunferência, sêndo (éli)" a medida de seu lado.
Página trezentos e oitenta e oito
Temos med() = 360° ∶ 5 = 72°, assim: 2(alfa)" + 72° = 180° ⇒ (alfa)" = 54°
Segue-se quê:
cos 54° = ⇒ 0,59 = ⇒ (éli)" = 4,72
Portanto, a medida do lado do pentágono é de aproximadamente 4,7 cm.
19. alternativa c
Cada lado do octógono méde 16 ∶ 8 = 2 m; logo, AD = 2 ∶ 2 = 1 m.
A medida (alfa)" é dada por: 2(alfa)" = ⇒ (alfa)" = 22,5°
Assim, a medida (beta)" é dada por: + (beta)" + 90° = 180° ⇒ (beta)" = 67,5°
Segue-se quê: tg 67,5° = ⇒ 2,41 = ⇒ AC = 2,41
Portanto, a distância aproximada entre os competidores é:
AB = 2 ⋅ 2,41 = 4,82 → 4,82 m
20. Como med() = 60°, temos:
• cos 60° = ⇒ = ⇒ (éli)" = r
• sen 60° = ⇒ a =
21. Seja (alfa)" a medida do ângulo destacado. Os ângulos internos do triângulo equilátero e do quadrado médem, respectivamente, 60° e 90°. Assim:
(alfa)" + 60° + 90° = 360° ⇒ (alfa)" = 210°
22. Mosaicos a e d, pois são os únicos quê representam ladrilhamentos formados somente por polígonos regulares congruentes entre si, sêndo o do item a formado por triângulos equiláteros e o do item d, por hekzágonos regulares.
23. alternativa b
Medida de cada ângulo interno do hekzágono regular:
[(6 − 2) ⋅ 180°] ∶ 6 = 120°
Medida de cada ângulo interno do quadrado:
[(4 − 2) ⋅ 180°] ∶ 4 = 90°
Ao elaborar o mosaico, temos quê, a partir de um vértice do hekzágono regular, serão justapostos dois quadrados, sêndo um ajustado em cada lado do hekzágono. Assim, a medida do ângulo formado por um ângulo interno do hekzágono e um ângulo interno de cada quadrado é dada por: 120° + 2 ⋅ 90° = 300°
Desse modo, para completar os 360° da composição do mosaico, em cada vértice do hekzágono falta 60° (360° − 300° = 60°). Portanto, a figura quê complementa esse mosaico é um triângulo equilátero, quê tem cada ângulo interno com medida igual a 60° (180° ∶ 3 = 60°).
24. 
25. Resposta esperada: Triângulo equilátero, quadrado e hekzágono regular, pois as medidas de cada um de seus ângulos internos correspondem a um número divisor de 360.
26. a) Cada piso ocupa uma área de:
0,5 ⋅ 0,5 = 0,25 → 0,25 m2
Logo, pisos serão assentados por métro quadrado.
b) O chão da sala tem m2 de área; logo, são necessários 24 ⋅ 4 = 96 pisos.
c) Ladrilhamento regular do plano por quadrados.
27. a, b e d
• a) hekzágonos regulares; b) triângulos equiláteros, quadrados e hekzágonos regulares; d) triângulos equiláteros, quadrados e hekzágonos regulares.
28. Resposta pessoal. Espera-se quê os estudantes consigam compor ladrilhamentos e mosaicos a partir de diferentes polígonos regulares, de acôr-do com os conceitos estudados. Verificar se eles compreenderam quê a soma das medidas dos ângulos internos adjacentes das figuras justapostas na composição deve sêr igual a 360°.
29. a) A = = 111,6 → 111,6 cm2
b) A = = 72 → 72 cm2
c) A = ⋅ 16 = cm2
d) A = 5,7 ⋅ 5,7 = 32,49 → 32,49 cm2
30. A = 75 ⇒ = 75 ⇒ 3x2 = 75 ⇒ x2 = 25 ⇒ x = 5 → 5 m
31. alternativa c
Um quadrado é um losango em quê as duas diagonais têm a mesma medida. Assim, a área A de um quadrado cuja diagonal méde d é:
A =
• A = = 220,5 → 220,5 cm2
32. Área total do salão:
90 ⋅ 110 = 9.900 → 9.900 m2
Área do palco:
10 ⋅ 90 + = 900 + 750 = 1.650 → 1.650 m2
Área destinada ao público:
9.900 − 1.650 = 8.250 → 8.250 m2
Capacidade de público:
8.250 ⋅ 2,5 = 20.625 → 20.625 pessoas
Como serão disponibilizados ingressos na quantidade correspondente a 96% da capacidade, temos:
0,96 ⋅ 20.625 = 19.800 → 19.800 ingressos
33. Sendo x a medida do lado menor do retângulo, temos:
x ⋅ 3x = 147 ⇒ 3x2 = 147 ⇒ x = 7 → 7 cm Assim, o perímetro do retângulo é dado por:
7 + 7 + 3 ⋅ 7 + 3 ⋅ 7 = 56 → 56 cm
34. a) Considerando quê a região é retangular e quê um par de lados méde x e outro y, em métro, temos:
2x + 2y = 160 ⇒ y = 80 − x
Assim, a área s dessa região póde sêr expressa por: s(x) = x ⋅ (80 − x) ⇒ s(x) = −x2 + 80x
b) Considerando a lei de formação da função s ôbitída no item a, temos:
xv = = 40
Da equação y = 80 − x ôbitída no item a, temos:
y = 80 − 40 = 40
Portanto, o comprimento e a largura da região retangular devem ter 40 m.
35. a) A área construída do hipermercado é:
250 ⋅ 90 = 22.500 → 22.500 m2
Assim, a quantidade de vagas para cada tipo de veículo é dada a seguir.
• Automóvel: = 750 → 750 vagas
• Bicicleta: = 225 → 225 vagas
• Motocicleta: = 90 → 90 vagas
b) Resposta pessoal. Espera-se quê os estudantes pesquisem as normas em relação a vagas de estacionamento em estabelecimentos no município em quê moram. É importante lembrá-los de quê devem utilizar fontes confiáveis para obtêr as informações.
Página trezentos e oitenta e nove
36. Cada lado do losango méde 36 ∶ 4 = 9 cm. Seja E o ponto de interseção das duas diagonais do losango. Então:
• sen 30° = ⇒ 0,5 = ⇒ DE = 4,5
Logo, a diagonal méde:
DB = 4,5 ⋅ 2 = 9
• cos 30° = ⇒ AE =
Logo, a diagonal méde:
AC =
Portanto, a área do losango ABCD é:
Observe quê a parte azul é formada por 8 triângulos congruentes quê podem sêr rearranjados de modo a cobrir a parte vêrde sem quê haja sóbra, ou seja, a área da parte azul é igual à área da parte vêrde. Portanto, a área da parte azul corresponde à mêtáde da área do losango ABCD. Logo, essa área é:
cm2
37. a) O terreno póde sêr decomposto em duas partes, uma retangular e outra em forma de trapézio, conforme a figura.
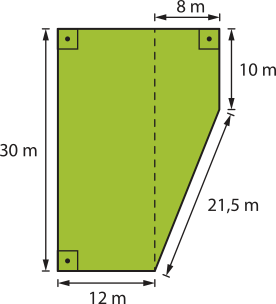
Assim, a área total do terreno, em métro quadrado, é:
A = 12 ⋅ 30 + = 520
Como é necessário ter, no mínimo, 15% de área permeável, então a edificação póde ocupar, no mássimo, 85% do terreno, o quê corresponde a:
520 ⋅ 0,85 = 442 → 442 m2
b) Resposta pessoal. Espera-se quê os estudantes pesquisem normas de permeabilidade no município em quê moram e, para isso, utilizem fontes de informação confiáveis, como o sáiti da prefeitura municipal. Em relação à proposta quê devem elaborar, verificar se eles utilizaram corretamente os conceitos estudados ao desenvolver o exemplo.
38. alternativa d
Seja x a medida, em centímetro, do lado do maior quadrado. Então, as medidas dos lados dos três quadrados são 5, x − 5 e x, conforme ilustra a figura.
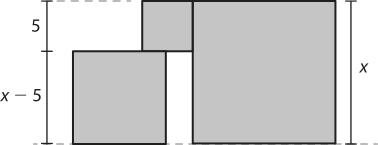
Assim:
x2 + (x − 5)2 + 52 = 258 ⇒ x2 + x2 − 10x + 25 + 25 = 258 ⇒ 2x2 − 10x − 208 = 0 ⇒ x2 − 5x − 104 = 0 ⇒
Portanto, o perímetro do maior quadrado é:
13 ⋅ 4 = 52 → 52 cm
39. alternativa b
Para neutralizar 37,1 toneladas de CO2 em um ano, serão necessárias 37,1 ∶ 0,14 = 265 árvores. A área da região para abrigar essa quantidade de árvores é dada pela seguinte regra de três:
Quantidade de árvores |
Área da região (em m2) |
|---|---|
50 |
300 |
265 |
x |
⇒ x = 1.590 → 1.590 m2
Vamos calcular a área da região e a respectiva diferença para a área necessária em cada item:
a) Área: 39 ⋅ 39 = 1.521 → 1.521 m2
Diferença: |1.590 − 1.521| = 69 → 69 m2
b) Área: 54 ⋅ 30 = 1.620 → 1.620 m2
Diferença: |1.590 − 1.620| = 30 → 30 m2
c) Área: 35 ⋅ 30 = 1.050 → 1.050 m2
Diferença: |1.590 − 1.050| = 540 → 540 m2
d) Área: 432 = 1.849 → 1.849 m2
Diferença: |1.590 − 1.849| = 259 → 259 m2
e) Área: 50 ⋅ 33 = 1.650 → 1.650 m2
Diferença: |1.590 − 1.650| = 60 → 60 m2
Logo, a região com a área mais próxima da necessária é a do item b, com 30 m2 de diferença.
40. alternativa a
Como v é uma função polinomial do 1º grau, então essa função é da forma v(t) = at + b, com a, b ∈ ℝ.
Como o gráfico de v passa pêlos pontos (0, 50) e (10, 55), temos:
• v(0) = 50 ⇒ a ⋅ 0 + b = 50 ⇒ b = 50
• v(10) = 55 ⇒ a ⋅ 10 + = 55 ⇒ 10a = 5 ⇒ a =
Logo, v(t) = t + 50. Assim, a distância percorrida pelo móvel, em quilômetro, do instante 3 h a 9 h corresponde à área de um trapézio com:
• Base menor v(3) = ⋅ 3 + 50 =
• Base maior v(9) = ⋅ 9 + 50 =
• Altura |9 − 3| = 6
Portanto, a distância percorrida é:
= 318 → 318 km
41. a) • Eficiência energética:
∶ 10 ≃ 16,36 → aproximadamente 16,36%
• O painel tem 1,65 ⋅ 1 = 1,65 métro quadrado. Logo, cada painel gera kWh por mês. Como 275 ∶ 34,65 ≃ 7,9, então é necessário instalar 8 painéis. A área ocupada por esses painéis será:
8 ⋅ 1,65 = 13,2 → 13,2 m2
b) Resposta pessoal. Espera-se quê os estudantes determinem a quantidade de painéis a partir do consumo indicado na fatura de energia elétrica da residência em quê moram. Eles podem usar os dados do consumo do mês mais recente ou calcular a média de consumo de dois meses ou mais.
c) Resposta pessoal. Espera-se quê os estudantes elaborem argumentos a respeito do uso de painéis solares com base em critérios ambientais e financeiros. Eles podem pesquisar em diferentes fontes confiáveis para obtêr as informações necessárias para a elaboração do croqui e do relatório.
42. Como serão 30 painéis retangulares com dimensões de 1,65 m por 1 m, e cuja composição terá 1,65 m de largura, temos quê o comprimento dessa composição é de 30 m (30 ⋅ 1 = 30).
Assim, o perímetro total da composição será:
30 + 30 + 1,65 + 1,65 = 63,3 → 63,3 m
Como a viga será instalada no contôrno de toda a composição, ao custo de R$ 60,00 o métro, temos quê o custo total com essa viga será de:
63,3 ⋅ 60 = 3.798 → R$ 3.798,00
43. Área da região delimitada pelo contôrno externo da pista:
AE = = 16.800 → 16.800 m 2
Área da praça:
AP = = 6.400 → 6.400 m2
Área da pista:
AE − AP = 16.800 − 6.400 = 10.400 → 10.400 m2
44. a) A = = 16,5 → 16,5 dm2
b) A = = 18,45 → 18,45 dm2
Página trezentos e noventa
c) O semiperímetro do triângulo é s = = 9. Assim: A = = = dm2
d) A = = 29,6 → 29,6 dm2
e) A = dm2
f) O semiperímetro do triângulo é s = = 14. Assim: A = = = dm2
45. alternativa c
As condições de existência de um triângulo exigem quê a soma das medidas de dois lados quaisquer seja sempre maior quê a medida do terceiro lado.
a) Não cumpre as condições, pois 4 + 3 = 7.
b) Não cumpre as condições, pois 5 + 10 < 16.
c) Cumpre as condições, pois:
• 9 + 5 > 6;
• 5 + 6 > 9.
• 9 + 6 > 5;
d) Não cumpre as condições, pois 3 + 3 < 7.
Vamos calcular a área do triângulo cujos lados têm as medidas dadas no item c.
O seu semiperímetro é s = = 10. Assim:
A = = = cm2
46. Esse polígono regular póde sêr decomposto, a partir de seu centro, em 8 triângulos isósceles congruentes de base 6 cm e altura cm. Logo, sua área é:
A = 8 ⋅ = 173,76 → 173,76 cm2
47. alternativa d
As cerâmicas têm o formato de hekzágono regular com 0,1 m de lado. Assim, cada cerâmica ocupa uma área, em métro quadrado, de:
6 ⋅ = = 0,0255
Assim, a quantidade necessária de pedras de cerâmica é de = 1.000.
48. Seja (éli)" a medida do lado do triângulo equilátero com m2 de área. Então:
A = ⇒ (éli)"2 = 100 ⇒
Portanto, o perímetro dessa região triangular é:
3(éli)" = 3 ⋅ 10 = 30 → 30 m
49. alternativa b
A bandeira tem duas regiões com formato de triângulo com m de base m de altura. Logo, a soma das áreas em formato triangular é:
2 ⋅ = 0,2275 → 0,2275 m2
50. No ladrilhamento, foram utilizados 12 hekzágonos regulares e 48 triângulos equiláteros, todos esses polígonos com 12 cm de lado. Como cada hekzágono dêêsses póde sêr decomposto em 6 triângulos equiláteros com lados medindo 12 cm, temos quê a área dêêsse ladrilhamento corresponde à área de 120 triângulos dêêsses (12 ⋅ 6 + 48 = 120).
Assim, a área do ladrilhamento é dada por:
120 ⋅ = 120 ⋅ = ≃ 7.344 → 7.344 cm2
51. a) • Peça com formato de pentágono regular:
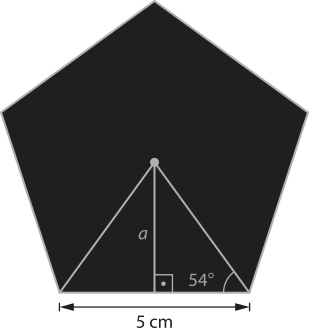
O apótema a do pentágono é dado, em centímetro, por: tg 54° = ⇒ 1,38 = ⇒ a = 3,45
Logo, a área dessa peça é:
5 ⋅ = 43,125 → aproximadamente 43,125 cm2
• Peça com formato de hekzágono regular:
6 ⋅ cm2
ou aproximadamente 65 cm2
b) Para compor a superfícíe da bola, são utilizadas 12 peças com formato de pentágono e 20 peças com formato de hekzágono. Essas peças têm, no total, 12 ⋅ 5 + 20 ⋅ 6 = 180 lados. Como cada costura une dois dêêsses lados, serão feitas costuras no total; logo, a quantidade de linha necessária é:
90 ⋅ 7,2 = 648 → 648 cm ou 6,48 m
52. a) • f é representada pelo gráfico IV, pois corresponde a uma reta e expressa o fato de quê o perímetro de um triângulo de lado 27 é igual a 3 ⋅ 27 = 81.
• g é representada pelo gráfico I, pois corresponde a uma curva quê aparenta sêr um parte de uma parábola e expressa o fato de quê a área de um triângulo de lado 8 é igual a .
b) • O perímetro de um triângulo de lado x é igual a 3x; logo, a função f é dada por f(x)= 3x e corresponde a uma função afim.
• A área de um triângulo de lado x é igual a x2; logo, a função g é dada por g(x) = x2 e corresponde a uma função quadrática.
53. a) O perímetro e a área de um quadrado de lado x são, respectivamente, iguais a 4x e x2; logo, p(x) = 4x e a(x) = x2.
b) Resposta pessoal. Espera-se quê os estudantes atribuam valores para a variável independente x nas funções p e a, identificando quê os resultados obtidos correspondem ao perímetro e à área do quadrado, respectivamente.
c) 
p: função afim; a: função quadrática
Página trezentos e noventa e um
54. a) A = (pi)" ⋅ 102 = 3,14 ⋅ 100 = 314 → 314 cm2
b) A = (pi)" ⋅ 3,52 = 3,14 ⋅ 12,25 = 38,465 → 38,465 m2
c) A = (pi)" ⋅ ()2= 3,14 ⋅ 36 = 113,04 → 113,04 dm2
d) O raio r, em centímetro, é dado por:
2(pi)"r = 56,52 ⇒ 6,28r = 56,52 ⇒ r = 9
Logo:
A = (pi)" ⋅ 92 = 3,14 ⋅ 81 = 254,34 → 254,34 cm2
55. Área total do círculo, em cm2:
(pi)" ⋅ ()2 = 12,25(pi)" ⇒ 360x = 980(pi)" ⇒ x ≃ 8,55 → aproximadamente 8,55 cm2
Medida do ângulo central (em grau) |
Área do setor (em cm2) |
|---|---|
360 |
12,25(pi)" |
80 |
x |
56. Os dois aspersores, juntos, irrigam uma área de 2 ⋅ (pi)"r2. Como essa área corresponde a da área do jardim, temos:
2 ⋅ (pi)"r2 = 0,36 ⋅ (7,85 ⋅ 20) ⇒ 6,28r2 = 56,52 ⇒ r2 = 9 ⇒
Portanto, r = 3 m.
57. alternativa c
Se a área da superfícíe circular é de 2.000 m2, o seu diâmetro d é dado por:
(pi)" ⋅ ()2 = 2.000 ⇒ 3,14 ⋅ =2.000 ⇒ d2 ≃ 2.548 ⇒
Portanto, o diâmetro é de aproximadamente 50 m.
58. a) Resposta esperada: O cálculo da área é feito por etapas:
1ª) Calcular a área A1 da circunferência de raio 8 cm:
A1 = (pi)" ⋅ 82 = 64(pi)".
2ª) Calcular a área A2 da circunferência de raio 5 cm:
A2 = (pi)" ⋅ 52 = 25(pi)".
3ª) Calcular A1 − A2, quê corresponde à área da coroa circular:
A = A1 − A2 = 64(pi)" − 25(pi)" = 39(pi)".
Portanto, a área da coroa circular é 39(pi)" ou aproximadamente 122,46 cm2 (39 ⋅ 3,14 = 122,46).
b) A1 = (pi)" ⋅ R2 = R2 (pi)"
A2 = (pi)" ⋅ r2 = r2 (pi)"
A = A1 − A2 = R2 (pi)" − r2 (pi)" = (pi)"(R2 − r2)
59. a) A = (pi)"(R2 − r2) = 3,14 (132 − 102) = 3,14 ⋅ 69 ≃ 216,66 ⇒ 216,66 cm2
b) A = (pi)"(R2 − r2) = 3,14 (4,52 − 22) = 3,14 ⋅ 16,25 ≃ 51,025 ⇒ 51,025 cm2
60. alternativa b
A placa póde sêr decomposta em um semicírculo de raio 20 cm e um quadrado de lado 40 cm, conforme ilustra a figura.
• Área do semicírculo:
= 628 → 628 cm2
• Área do quadrado: 402 = 1.600 → 1.600 cm2
Assim, a soma das áreas de 10 placas é:
10 ⋅ (1.600 + 628) = 22.280 → 22.280 cm2
Integrando com...
1. Algumas respostas possíveis: Engenheiro agrimensor, pedreiro, geólogo.
2. a) Considerando quê o perímetro do quadrilátero corresponde à soma das medidas de seus lados, temos:
p = a + b + c + d
b) Média aritmética entre as medidas dos lados opostos:
•
•
Tomando essas médias como medidas de lados de um retângulo, temos:
s =
3. Área aproximada do terreno:
s = = 23.718,75 → 23.718,75 m2
Quantidade estimada de sementes:
12 ⋅ 23.718,75 = 284.625 → 284.625 sementes
4. a) Resposta pessoal. Espera-se quê os estudantes identifiquem algum método prático de estimativa de área de terrenos utilizada por comunidades na região em quê moram e quê compreendam e expliquem as etapas dêêsse método.
b) Respostas pessoais. Espera-se quê os estudantes apliquem o método pesquisado no item a para estimar a área de um terreno. Acompanhá-los na realização das etapas propostas para essa produção, de maneira a identificar as contribuições de cada integrante do grupo.
61. a) Uma resposta possível: Utilizando como estratégia o método de contar a quantidade de quadradinhos internos à figura e a quantidade necessária para cobri-la e, em seguida, calcular a média aritmética dos resultados obtidos, pode-se obtêr a área aproximada de 9,875 cm2.
b) Uma resposta possível: Utilizando como estratégia a construção de um polígono com formato e tamãnho próximos aos da figura e, em seguida, calcular a área utilizando a fórmula de Pick, pode-se obtêr a área aproximada de 107,5 m2.
62. A área aproximada calculada com a estratégia da malha quadriculada foi:
= 88,5
Assim, a diferença entre os dois valores é:
88,5 − 85,8 = 2,7 → 2,7 dm2
63. a) Cada quadradinho no mapa representa um quadrado de 120 km de lado; logo, sua área é:
1202 = 14.400 → 14.400 km2
b) Temos, B = 17 e I = 10, logo, pela fórmula de Pick, a área do polígono é:
0,5 ⋅ 17 + 10 − 1 = 17,5 → 17,5 cm2
Como 1 cm2 no mapa corresponde a uma área de 14.400 km2, a área aproximada do estado de Roraima é:
17,5 ⋅ 14.400 = 252.000 km2
c) Resposta pessoal. Espera-se quê a área ôbitída pêlos estudantes seja, razoavelmente, próxima da área real indicada. É importante quê os estudantes compreendam quê a variação no resultado se deve a diversos fatores, como o cálculo aproximado e as irregularidades do terreno.
64. a) A área aproximada do desenho, em centímetro quadrado, é de:
= 26,875
Como 1 cm2 equivale a uma região com 100 m ⋅ 100 m = 10.000 m2, a área aproximada da reserva é:
26,875 ⋅ 10.000 = 268.750 → 268.750 m2
Página trezentos e noventa e dois
b) (268.750 ∶ 0,20) ⋅ 0,8 = 1.075.000 → 1.075.000 m2
c) Resposta pessoal. Espera-se quê, com base na legislação vigente e nas pesquisas quê indicam as causas de mudanças climáticas no mundo, os estudantes argumentem sobre a necessidade de preservação de áreas nativas.
65. Estudante 1:
A = = 112,5 → 112,5 m2
Estudante 2: B = 36 e I = 97, logo:
A = 0,5 ⋅ 36 + 97 − 1 = 114 → 114 m2
Resposta pessoal.
66. Resposta pessoal. Atividade de elaboração do estudante. Espera-se quê os estudantes elaborem um problema quê envolva a determinação de uma estimativa para a área de uma figura irregular construída em uma malha quadriculada. Verificar se os estudantes utilizaram um método de aproximação estudado na Unidade.
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) • Área do plano de frente:
4 ⋅ 6 = 24 → 24 cm2
• Área do plano de fundo:
72,25 − 24 = 48,25 → 48,25 cm2
• Lado da tela:
x2 = 72,25 ⇒ x = 8,5 → 8,5 cm
b) • Perímetro de cada face:
4 ⋅ 5 = 20 → 20 cm
• Área da superfícíe de cada face:
52 = 25 → 25 cm2
• Os triângulos obtidos nas faces do cubo são isósceles de base 5 cm, e a medida dos dois lados congruentes dêêsses triângulos é igual à mêtáde da medida da diagonal do quadrado de lado 5 cm; logo, as medidas de seus lados são:
5 cm, cm e cm
A área de cada triângulo corresponde a da área do quadrado, ou seja:
⋅ 52 = = 6,25 → 6,25 cm2
• O perímetro dobra. A área é multiplicada por 4.
Praticando: enêm e vestibulares
1. alternativa c
Por simetria, todos os ângulos das pontas da estrela são congruentes entre si, então vamos determinar a medida a.
Observe quê:
• a diagonal é paralela ao lado , logo e o ângulo externo de medida c1 são ângulos correspondentes, de modo quê med() = c1;
• a diagonal é paralela ao lado , logo e o ângulo externo de medida d1 são ângulos alternos internos, de modo quê med() = d1.
Cada ângulo externo do pentágono regular méde 360° ∶ 5 = 72°, assim: med() = med() = 72°
Como, ao somar as medidas dos ângulos internos do triângulo ADC, obtemos 180°, segue-se quê:
a + 72° + 72° = 180° ⇒ a = 36°
Portanto, a soma das medidas dos ângulos internos das pontas da estrela é 5 ⋅ 36° = 180°.
2. alternativa d
Como o pentágono regular tem cinco ângulos internos congruentes, cada ângulo dêêsses méde:
= = 108°
Agora, considere o pentágono regular representado a seguir, com as diagonais quê partem do vértice A traçadas.
Do triângulo ABC, temos:
2x + 108° = 180° ⇒ x = 36°
Assim, segue-se quê:
2 ⋅ 36° + y = 108° ⇒ y = 36°
Portanto, as medidas dos ângulos determinadas são:
36°, 72° (36° + 36° = 72°) e 108° (36° + 36° + 36° = 108°).
3. alternativa a
Sabendo quê um hekzágono regular de lado (éli)" póde sêr decomposto em 6 triângulos equiláteros de lado (éli)", temos quê a área ocupada pelo mosaico é dada por:
4 ⋅ 6 ⋅ cm2
As dimensões da moldura são dadas por:
• comprimento: 5 ⋅ 10 = 50 → 50 cm2
• largura: 4 ⋅ → cm2
Área da região interna da moldura sem azulejo:
(50 ⋅ = cm2
4. alternativa d
Calculando a medida x do lado da piscina, temos:
x2 = 400 ⇒ x = 20 → 20 m
Assim, a área ocupada pela calçada é dada por:
(20 + 5 + 5)2 − 400 = 900 − 400 = 500 → 500 m2
5. Seja r a medida, em cm, do raio dos semicírculos quê formam as fô-lhas.
O perímetro do quatrefoil equivale ao comprimento de duas circunferências de raio r, logo:
2 ⋅ 2(pi)"r = 28(pi)" ⇒ r = 7 → 7 cm
A figura póde sêr decomposta em um quadrado de lado 2r e quatro semicírculos de raio r, logo sua área é de:
(2 ⋅ 7)2 + 4 ⋅ = 196 + 98(pi)" → (196 + 98(pi)") cm2
6. alternativa c
Área da pitssa individual:
(pi)" ⋅ ()2 → (pi)" ⋅ ()2 cm2
Área da pitssa de 20 cm de diâmetro:
(pi)" ⋅ 102 = 100(pi)" → 100(pi)" cm2
Como o preêço da pitssa é proporcional à sua área, segue-se quê:
4 ⋅ (pi)" ⋅ ()2 = 100(pi)" ⇒ d = 10 → 10 cm
7. alternativa d
Como o quadrado EFGH tem 16 cm2 de área, segue-se quê a medida de seus lados é: = 4 → 4 cm
Assim, AD = HG = 4 cm.
Como o retângulo ABCD tem 32 cm2 de área, segue-se quê:
AD ⋅ AB = 32 ⇒ AD ⋅ 4 = 32 ⇒ AD = 8 → 8 cm
Desse modo, segue-se quê:
AE = FB = DH = GC = (8 −4) ∶ 2 = 2 → 2 cm
Pelo caso AA, os triângulos DCB, DGQ e DHP são semelhantes. Assim, temos:
• ⇒ QG = 3 → 3 cm
• ⇒ PH = 1 → 1 cm
Portanto, a área do trapézio GHPQ é dada por:
= 8 → 8 cm2
8. alternativa d
O quadrado cujos lados passam pêlos pontos A, B, C e D tem os lados medindo 2 cm (1 + 1 = 2).
Assim, a área da região hachurada, em cm2, corresponde à diferença entre a área dêêsse quadrado e o quádruplo de da área do círculo de raio 1 cm:
22 − 4 ⋅ ⋅ (pi)" ⋅ 12 = 4 − (pi)"
9. alternativa e
a) Incorreta, pois: cos 60° = ⇒ BC = 24 → 24 cm e 24 ∉ 𝕀
b) Incorreta, pois:
Página trezentos e noventa e três
tg 60° = ⇒ AC = cm
c) Incorreta, pois o perímetro do triângulo ABC é dado por:
12 + 24 + = 12 cm
d) Incorreta, pois a área do triângulo ABC é dada por:
cm2
e) Correta, pois:
10. alternativa b
Como ABCD é um retângulo, o ângulo B C ˆ D méde 90°. Assim, como os ângulos destacados são congruentes entre si, a medida de cada um deles é dada por:
90° ∶ 3 = 30°
Desse resultado, segue-se quê:
⇒ AE = AB
Assim, a razão entre a área do triângulo AEC e o retângulo ABCD
é dada por:
11. alternativa b
Como os ângulos destacados são congruentes e os triângulos EDF e BFE são triângulos retângulos, pelo caso AA estes triângulos são semelhantes. Assim, se a razão entre as áreas dêêsses triângulos é , a razão entre as medidas dos lados deles é dada por:
Assim, podemos estabelecer as seguintes proporções:
⇒ DF = 18
⇒ EB = 8
Segue-se quê:
AB = cê dê = 18 + 8 = 26
Portanto, o perímetro do retângulo ABCD é dado por:
26 + 26 + 12 + 12 = 76 → 76 cm
12. alternativa a
A área de queimada corresponde à área do triângulo ABO subtraída da área de um setor circular de 10 km de raio, conforme ilustra a figura.
De acôr-do com as informações do enunciado, tem-se OA = 30 km, OB = 40 km e (alfa)" = 360° ∶ 12 = 30°. A medida da altura AC do triângulo é dada por:
sen 30° = ⇒ AC = 15 → 15 cm
Assim, temos:
• Área do triângulo ABO:
= 300 → 300 km2
• Área do setor circular:
Ângulo (em grau) |
Área do setor circular (em km2) |
|---|---|
360 |
(pi)" ⋅ 102 |
30 |
x |
⇒ 360x = 3.000(pi)" ⇒ x = (pi)" = (pi)"
Portanto, a área de queimada é de:
300 − (pi)" = 300 − ⋅ 3 = 275 → 275 km2
13. alternativa e
Área dos pisos:
3 ⋅ 0,25 ⋅ 1,0 = 0,75 → 0,75 m2
Área dos espelhos:
3 ⋅ 0,20 ⋅ 1,0 = 0,60 → 0,60 m2
Área das paredes laterais:
2 ⋅ 6 ⋅ 0,25 ⋅ 0,20 = 0,60 → 0,60 m2
Assim, a área a sêr revestida de cerâmica é dada por:
0,75 + 0,60 + 0,60 = 1,95 → 1,95 m2
14. alternativa d
Como a área do triângulo MBN é 1, BM = AB e a altura dêêsse triângulo corresponde à mêtáde da altura h do trapézio ABCD, temos:
= 1 ⇒ h = 8
Assim, a área do trapézio ABCD é:
= 24
15. alternativa c
Representando a figura descrita no enunciado, temos:
Como YW = ZK e ZW é lado dos triângulos YWZ e WZK, temos quê esses triângulos são semelhantes e WK tem a mesma medida b da base menor do trapézio XYZW. Assim, segue-se quê:
• A área do trapézio XYZW:
• Área do triângulo WZK:
• Área do triângulo XYZ:
• Área do triângulo XZK:
Portanto, a área do trapézio XYZW é igual à área do triângulo XZK.
16. alternativa a
Página trezentos e noventa e quatro
É possível identificar 26 quadradinhos inteiros no interior da região e 61 necessários para cobrir toda a região. Logo, como cada quadradinho representa uma área de 0,162 km2, a área aproximada dêêsse campus é:
= 0,162 = 43,5 ⋅ 0,0256 = 1,1136 → 1,1136 km2
Portanto, a alternativa a é a correta.
Unidade 6 • Estatística: pesquisa e medidas de posição e de dispersão
1. a) = 23,8
Mo = 19
Md = = 20,5
b) = 4,5
Mo = 5,5; Mo = 3,2
Md = = 4,3
c) = 12
conjunto amodal
Md = 12
d) = 35
Mo = 25; Mo = 33; Mo = 48
Md = 33
2. a) = 139 → 139 kWh
Mo = 129 → 129 kWh; Mo = 155 → 155 kWh
Md = = 138,5 → 138,5 kWh
b) junho, julho, agosto, setembro e novembro
c) Resposta pessoal. Espera-se quê os estudantes calculem a média, a (Moda) e a mediana do consumo de energia elétrica de suas residências e apresentem estratégias para a redução do consumo de energia elétrica, como apagar as luzes de cômodos inutilizados, desligar aparelhos eletrônicos quê não estão sêndo utilizados, abrir janelas para a entrada de luz natural nos ambientes, entre outras.
3. a) Das mortes no trânsito brasileiro em 2022.
b) Analisando a tabéla, temos quê a maior quantidade de mortes no trânsito, no Brasil, em 2022, foi no 1º mês do 4º trimestre, ou seja, outubro. E a menor quantidade ocorreu no 2º mês do 1º trimestre, ou seja, fevereiro.
c) 1º trimestre: ≃ 2.554 → aproximadamente 2.554 mortes
2º trimestre: ≃ 2.722 → aproximadamente 2.722 mortes
3º trimestre: ≃ 2.915 → aproximadamente 2.915 mortes
4º trimestre: ≃ 2.829 → aproximadamente 2.829 mortes
d) ≃ 2.755→ aproximadamente 2.755 mortes. Respostas possíveis: Calcular a média aritmética a partir da quantidade de mortes no trânsito em cada um dos 12 meses de 2022, apresentadas na tabéla; calcular a média aritmética dos quatro resultados obtidos no item c, ou seja, das médias mensais da quantidade de mortes de cada trimestre de 2022.
4. a) Analisando o qüadro, temos quê o ingresso de maior preêço é o do tipo inteiro do setor C, quê custa R$ 200,00.
b) 80 + 70 + 130 + 20 = 300 → 300 ingressos
c) = 72 → R$ 72,00
Mo = 100 → R$ 100,00
Md = = 70 → R$ 70,00
5. Resposta pessoal. Atividade de elaboração do estudante. Espera-se quê os estudantes sêjam capazes de elaborar um problema envolvendo o cálculo da mediana com os dados sobre a quantidade de mortes no trânsito brasileiro, em cada mês de 2022. Para isso, eles podem utilizar, por exemplo, os dados referentes ao ano todo ou a algum trimestre ou semestre daquele ano.
Página trezentos e noventa e cinco
6. ≥ 7 ⇒ 16,65 + 5,5x ≥ 70 ⇒ 5,5x ≥ 53,35 ⇒ x ≥ 9,7
7. a = 103,25 → 103,25 mm
conjunto amodal
Md = = 71,5 → 71,5 mm
b) Analisando os dados no box-plot, temos quê, em 50% dos meses, a precipitação acumulada foi de 26 mm até 187,25 mm, ou seja, em 6 meses.
c) Considerando quê a, b e c correspondem, respectivamente, aos valores do limite superior, do 2º quartil e do limite inferior, temos quê a = 257, b = 71,5 e c = 17.
8. a) = 186 → 186 cm
Mo = 189 → 189 cm
Md = 189 → 189 cm
b) Valéria, pois ela é a única suplente quê tem estatura maior quê a de Clara (1,96 > 1,94).
c) = 188,8 → 188,8 cm Resposta esperada: A média aumentou para 188,8 cm, e a (Moda) e a mediana não se alteraram.
d) = 191,6 → 191,6 cm
9. a) R$ 6,19; autoposto G.
b) = 6,44 → R$ 6,44
Mo = 6,39 → R$ 6,39
Md =
= 6,39 → R$ 6,39
10. = 20; = 30; = 40; = 50; = 60
≃ 35,85 → aproximadamente 35,85 anos
Mo = 40 → 40 anos
Md = = 40 → 40 anos
11. > 13,950 ⇒ 27,000 + x > 41,850 ⇒ x > 14,850 → x = 14,851
12. = 44 ⇒ x1 + x2 + x3 + x4 + 62 = 220 ⇒ x1 + x2 + x3 + x4 = 158
= 36,4 → 36,4 anos
13. a) Resposta pessoal. Espera-se quê, pela análise dos gráficos, os estudantes tirem conclusões a respeito das massas ao final da campanha e argumentem sobre elas com base nos dados apresentados.
b) = 45; = 55; = 65; = 75; = 85
• ≃ 62,67 → aproximadamente 62,67 kg
Mo = 55 → 55 kg
Md = = 60 → 60 kg
• = 56 → 56 kg
Mo = 55 → 55 kg
Md = = 55 → 55 kg
c) Resposta esperada: É possível estimar quê a média e a mediana diminuíram, enquanto a (Moda) se manteve.
14. a) ![]()
Página trezentos e noventa e seis
538,2t = 1.345,5 ⇒ t = 2,5
12p + 51 ⋅ 2,5 = 175,5 ⇒ 12p + 127,5 = 175,5 ⇒ 12p = 48 ⇒ p = 4
5s + 8,5 ⋅ 4 + 10 ⋅ 2,5 = 76,5 ⇒ 5s + 59 = 76,5 ⇒ 5s = 17,5 ⇒ s = 3,5
b) = 7,25
15. = 25 → 25 mortes
16. alternativa c
60 = ⇒ x = 74,5
17. a) ≃ 226,26 → aproximadamente R$ 226,26
b) Tipo I: 60 ⋅ (1 + 0,20) = 60 + 1,2 = 72 → 60 km/h < x ≤ 72 km/h
Valor médio: = 66 → 66 km/h
Tipo II: 60 ⋅ (1 + 0,50) = 60 + 1,5 = 90 → 72 km/h < x ≤ 90 km/h
Valor médio: = 81 → 81 km/h
Tipo III: 60 ⋅ (1 + 0,70) = 60 + 1,7 = 102 → 90 km/h < x ≤ 102 km/h
Valor médio: = 96 → 96 km/h ≃ 73,11 → aproximadamente 73,11 km/h
Mo = 66 → 66 km/h
Md = 66 → 66 km/h
18. a) = 8,50 → R$ 8,50
Md = = 8,75 → R$ 8,75
b) = 8,45 ⇒ 68,00 + 2x = 84,50 ⇒ 2x = 16,50 ⇒ x = 8,25 → R$ 8,25
19. Resposta pessoal. Atividade de elaboração do estudante. É importante verificar se, na situação-problema elaborada com o contexto dos casos de dengue na região, os estudantes abordam adequadamente os conceitos de média, (Moda) e mediana e se determinam essas medidas na situação-problema proposta pelo colega.
20. a) = 5,5 → 5,5 kg
Mo = 3 → 3 kg
Md = = 5,5 → 5,5 kg
a = 9 − 3 = 6 → 6 kg
v = ≃ 4,58
d = ≃ 2,14 → aproximadamente 2,14 kg
b) = 7,8 → 7,8 cm
conjunto amodal
Md = 7 → 7 cm
a = 12 − 5 = 7 → 7 cm
v = = 6,16
d = ≃ 2,48 → aproximadamente 2,48 cm
c) = 7 → 7 L
Mo = 4,1 → 4,1 L
Md = = 7,6 → 7,6 L
Página trezentos e noventa e sete
a = 10 − 4,1 = 5,9 → 5,9 L
v = ≃ 4,9
d = ≃ 2,2 → aproximadamente 2,2 L
21. Resposta pessoal. Atividade de elaboração do estudante. Espera-se quê os estudantes sêjam capazes de elaborar e resolver problemas com medidas de dispersão, utilizando corretamente a interpretação de cada medida de dispersão no contexto apresentado. Se necessário, retomar o estudo da atividade resolvida R5.
22. A: = 8 → 8 pontos
v = = 2
d = ≃ 1,41 → aproximadamente 1,41 pontos
B: = 8 → 8 pontos
v = = 2,8
d = ≃ 1,67 → aproximadamente 1,67 pontos
C: = 8,4 → 8,4 pontos
1º colocado: competidor C; 2º colocado: competidor A; 3º colocado: competidor B
23. alternativa e
IV e V são falsas. Um contraexemplo para ambos os itens é um conjunto em quê todos os elemêntos são iguais, como: 3, 3, 3.
24. alternativa a
A: = 6 → 6 pontos, v = = 0
B: = 6 → 6 pontos, v = ≃ 4,67
C: = 6 → 6 pontos, v = ≃ 0,67
D: = 6 → 6 pontos, v = ≃ 2,67
E: = 6 → 6 pontos, v = = 2,0
Classificação: A, C, E, D e B
25. a) A: = 4,2 → 4,2 dias
v = = 3,76
d = ≃ 1,94 → aproximadamente 1,94 dias
B: = 2,4 → 2,4 dias
v = = 2,24
d = ≃ 1,50 → aproximadamente 1,50 dias
C: = 2,8 → 2,8 dias
v = = 1,76
d = ≃ 1,33 → aproximadamente 1,33 dias
empresa A: boa; empresa B: ótima; empresa C: ótima
b) Algumas respostas possíveis: 4, 10, 6, 3 e 12 dias; 2, 8, 9, 5 e 11 dias.
= 7 → 7 dias
v = = 12
d = ≃ 3,46 → aproximadamente 3,46 dias
Página trezentos e noventa e oito
= 7 → 7 dias
v = = = 10
d = ≃ 3,16 → aproximadamente 3,16 dias
c) Respostas pessoais. Os estudantes podem indicar, por exemplo, sáites governamentais, como o disponível em https://livro.pw/sklrm (acesso em: 18 set. 2024), e, nele, consultar a classificação de alguma empresa em relação à sua reputação.
26. Resposta pessoal. Atividade de elaboração do estudante. Espera-se quê os estudantes, a partir dos dados do gráfico sobre a violação dos direitos humanos, elaborem um problema envolvendo medidas de posição e de dispersão. Esta atividade oferece uma oportunidade de verificar se os estudantes conseguem diferenciar tais medidas, bem como interpretá-las e utilizá-las corretamente em determinado contexto.
27. a) De acôr-do com os conceitos de pesquisa censitária e pesquisa amostral apresentados, temos: pesquisa censitária: II; pesquisa amostral: I, III e IV.
b) De acôr-do com os conceitos dos tipos de pesquisa amostral apresentados, temos: I: estratificada; III: cazual simples; IV: sistemática.
28. a) Resposta esperada: Conhecer as áreas de interêsse dos estudantes do Ensino Médio e, com base nos resultados obtidos, promover ações complementares específicas a fim de auxiliá-los na escolha profissional.
b) De acôr-do com o gráfico de colunas duplas apresentado na página 279, temos quê foram entrevistados 31 estudantes do sexo masculino (13 + 8 + 9 + 1 = 31) e 29 estudantes do sexo feminino (7 + 11 + 10 + 1 = 29). Assim, foram entrevistados mais estudantes do sexo masculino.
c) Artes e comunicação: 1 + 4 + 2 = 7 → 7 < 8,57
Atividades burocráticas: 1 + 1 + 3 = 5 → 5 < 8,57
Ciências agrárias e ambientais: 3 + 2 + 2 = 7 → 7 < 8,57
Ciências exatas: 6 + 5 + 3 = 14 → 14 > 8,57
Ciências biológicas e da saúde: 6 + 4 + 3 = 13 → 13 > 8,57
Ciências humanas e sociais aplicadas: 2 + 5 + 4 = 11 → 11 > 8,57
Entretenimento: 2 + 1 + 0 = 3 → 3 < 8,57
ciências exatas, ciências biológicas e da saúde, ciências humanas e sociais aplicadas
d) Resposta esperada: Amostral, pois na escola estavam matriculados estudantes em grande quantidade no Ensino Médio.
e) Resposta pessoal. Espera-se quê os estudantes comentem como outras técnicas de amostragem poderiam sêr utilizadas para a pesquisa. Por exemplo, em relação à amostragem cazual simples, os estudantes poderiam sêr sorteados de maneira aleatória, independentemente do ano escolar em quê estão matriculados.
f) ação I
29. a) Resposta esperada: Verificar uma possível relação entre as mortes por diarreia e gastroenterite em pessoas menóres de 5 anos e a falta de acesso da população à rê-de de á gua tratada no Brasil, em 2022.
b) Os dados foram obtidos em sáites governamentais, vinculados ao Ministério da Saúde e ao Ministério das Cidades.
c) De acôr-do com o gráfico de barras, Região Norte e Região Centro-Oeste.
d) De acôr-do com o gráfico de colunas, Região Norte e Região Nordeste.
e) Uma resposta possível: Possivelmente sim, pois, nas regiões em quê há maior falta de atendimento à rê-de de á gua tratada à população, ocorre uma proporção maior de óbitos de crianças com menos de 5 anos por diarreia e gastroenterite. No entanto, para embasar melhor essa pesquisa, uma sugestão é investigar outras possíveis causas para a incidência dessas doenças, como a falta de acesso à rê-de de tratamento de esgoto e de acesso ao atendimento médico para a população.
f) Resposta pessoal. Espera-se quê os estudantes pesquisem doenças causadas pela falta de saneamento básico e, com base nos dados obtidos, proponham ideias e ações quê possam sêr convertidas em políticas públicas para mitigar e erradicar tais problemas, principalmente nas regiões mais afetadas.
30. a) Resposta esperada: I) A inadequação póde ocorrer em razão de a amostra contemplar apenas estudantes quê se sentavam na primeira carteira das fileiras, de onde, supostamente, pode-se naturalmente enxergar melhor a lousa do quê em carteiras mais distantes dela. II) A inadequação póde ocorrer por não fazerem parte da amostra funcionários dos turnos T2 e T3, turnos em quê, por causa do horário de funcionamento, ocorre menor incidência de iluminação natural.
b) Uma resposta possível: I) Para a elaboração da amostra dessa pesquisa, poderia sêr utilizada a técnica de amostra cazual simples, de maneira quê, por sorteio, fossem selecionados alguns estudantes da turma ao acaso. II) Para a elaboração da amostra dessa pesquisa, poderia sêr utilizada a técnica de amostra estratificada, de maneira quê, de cada turno, fosse sorteada a mesma quantidade de funcionários.
31. Resposta pessoal. Espera-se quê os estudantes, em grupos, realizem a pesquisa estatística com base nas etapas indicadas. Na realização da atividade, verificar se os estudantes são assertivos na escolha do tema, na elaboração do questionário e na definição da amostra. Ao final da produção, é possível propor um debate acerca das escôlhas dos grupos e oportunizar quê argumentem sobre elas, utilizando conceitos estudados na Unidade.
Integrando com...
1. Resposta pessoal. Os estudantes podem responder quê devem sêr considerados aspectos como afinidade com a área, remuneração e perspectiva de vagas no mercado de trabalho.
2. Respostas pessoais. As respostas dependem da profissão escolhida pêlos estudantes.
3. É necessário ter idade entre 14 anos e 24 anos imcomplétos e estar cursando, ou ter concluído, o Ensino Fundamental ou o Ensino Médio e procurar instituições ou sáites para realizar a integração entre a empresa e o jovem.
4. a) 2022. Ministério do Trabalho e Emprego.
b) Respostas pessoais. É importante incentivar os estudantes a responder com base em argumentos sólidos, como dados a respeito do desemprego no Brasil.
c) 642 − 500 = 142
Havia cerca de 142 mil jovens estagiários a mais do quê aprendizes.
d) Resposta pessoal. Espera-se quê os estudantes indiquem o tipo de gráfico, ou medida, mais adequado de acôr-do com a natureza dos dados e os objetivos delimitados. A socialização desta atividade com a turma póde sêr um instrumento de revisão e avaliação dos conceitos estudados na Unidade.
e) Resposta pessoal.
5. a) Respostas pessoais. As respostas dependem das experiências pessoais dos estudantes.
b) Resposta pessoal. As respostas dependem da região do Brasil em quê os estudantes moram.
c) Respostas pessoais. Espera-se quê os estudantes realizem uma pesquisa sobre a temática e a apresentem utilizando as medidas de posição e de dispersão estudadas para fazer inferências sobre os dados coletados. É importante quê, nessa etapa, sêjam avaliados desde a preparação e as tomadas de decisões acerca da pesquisa até a apresentação final.
Página trezentos e noventa e nove
O quê estudei
1. Respostas pessoais.
2. Resposta pessoal.
3. Respostas pessoais.
4. a) Resposta pessoal.
b) A pesquisa foi amostral. Resposta esperada: Porque a população-alvo era muito grande, de maneira quê entrevistar todas as crianças e adolescentes de 9 a 17 anos residentes no Brasil poderia implicar diversas dificuldades, como tempo e custo.
c) Mais de uma vez por dia: 972.048 + 816.316 + 1.349.506 + 1.589.624 = 4.727.494
Pelo menos uma vez por mês: 43.985 + 38.260 + 39.400 + 14.503 = 136.148
d) = 9,5; = 11,5; = 13,5; = 16,0
9 a 10 anos: 972.048 + 261.001 + 147.872 + 71.609 + 43.985 = 1.496.515
11 a 12 anos: 816.316 + 957.089 + 133.800 + 72.136 + 38.260 = 2.017.601
13 a 14 anos: 1.349.506 + 261.252 + 78.719 + 17.287 + 39.400 = 1.746.164
15 a 17 anos: 1.589.624 + 273.238 + 73.087 + 36.470 + 14.503 = 1.986.912
≃ 12,80 → aproximadamente 12,80 anos
Como a idade mais freqüente das crianças e adolescentes considerados na tabéla está na faixa etária de 11 a 12 anos, temos: Mo = = 11,5 → 11,5 anos
Como ao todo são considerados 7.247.192 crianças e adolescentes na tabéla, a mediana das idades é dada pelo ponto médio da faixa etária de 13 a 14, ou seja: Md = = 13,5 → 13,5 anos.
e) Considerando o cálculo do item c, há 1.986.912 adolescentes de 15 a 17 anos nesta pesquisa. Destes, 1.589.624 usam mais de uma vez por dia. Portanto, temos: ≃ 0,80 → aproximadamente 80%.
f) • estudante com 16 anos: a = 6,5 − 3 = 3,5 → 3,5 h
estudante com 17 anos: a = 5,0 − 2,5 = 2,5 → 2,5 h
• estudante com 16 anos: = 4,5 → 4,5 h
estudante com 17 anos: = 3,5 → 3,5 h
• estudante com 16 anos: v = = 1,5
estudante com 17 anos: v = ≃ 0,79
• aluno com 16 anos: d = ≃ 1,22 → 1,22 h
aluno com 17 anos: d = ≃ 0,89 → 0,89 h
e) Resposta esperada: Amostra estratificada.
Praticando: enêm e vestibulares
1. alternativa c
ano II para o ano I: 4,2 − 2,2 = 2
ano III para o ano II: 7,4 − 4,2 = 3,2
ano IV para o ano III: 3,2 + = 3,2 + 2,6 = 5,8
7,4 + 5,8 = 13,2
2. alternativa a
= 1,85
v = = ≃ 1,7
dp = ≃ 1,3
3. alternativa e
3.000 m2 = ha = 3 ha
90 kg = sacas = 1,5 saca
= 0,5 saca / ha
v = (0,5)2 = 0,25 ⇒ 0,25 (saca/hectare)2
Página quatrocentos
4. alternativa e
= 7.425 → R$ 7.425,00
5. alternativa c
⇒ 2xy = H(y + x) ⇒ H =
6. alternativa b
≃ 0,217 → 21,7%
7. alternativa a
MdAna = = 9,1; MdJoão = = 9,1
8. alternativa e
média: ≃ 4,16 → aproximadamente 4,16 viagens
(Moda): 3 → 3 viagens
mediana: = 4 → 4 viagens
Portanto, (Moda) < mediana < média.
9. alternativa c
= 61
Segue-se quê:
64 − 61 = 3
57 − 61 = −4
62 − 61 = 1
Variância:
≃ 8,67
Desvio padrão:
10. alternativa e
Me: ≃ 15,53→ aproximadamente 15,53 anos
Mo: 17 → 17 anos
Md: = 15,5 → 15,5 anos
Portanto, Md < Me < Mo.
11. a) = 0,24
Patologia benigna
b) 0,40 ⋅ 160 = 64
x ̅ = = 8,8 ng/mL
12. alternativa c
Me = = 13%
Mo = 13%
13. alternativa b
= 3,5
2 ≤ 3,5 < 4
14. alternativa c
⇒ ⇒ = 100
v = = 72
d = ≃ 8,5