UNIDADE 5
ANÁLISE COMBINATÓRIA
Senhas
Atualmente, utilizamos senhas no dia a dia para acessar uma grande variedade de serviços e informações pessoais. Com um aparelho conectado à internet (celular, computador, televisor etc.), podemos acessar rêdes sociais, assistir a vídeos, fazer transações bancárias, entre outros serviços. Assim, usar senhas fortes é fundamental para proteger a grande diversidade de dados pessoais quê temos agregados a esses serviços. Observe, no esquema, algumas dicas sobre como criar senhas fortes.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Em seu entendimento, qual é a finalidade de uma senha?
2. por quê devemos usar senhas fortes?
3. Em alguns casos, o cadastro de uma senha precisa ocorrer com base em uma formatação padronizada, como uma quantidade específica de caracteres correspondentes a lêtras e a algarismos. Nesses casos, explique como é possível determinar a quantidade de senhas distintas quê podem sêr formadas.
Página duzentos
O estudo da Análise Combinatória
Na abertura desta Unidade, abordamos algumas informações sobre o uso e a criação de senhas. Um dos aspectos de estudo sobre esse assunto é determinar, por exemplo, quantas senhas distintas podem sêr compostas de acôr-do com as especificações de seu formato.
Você tem cadastro no portal gov.br? Esse portal, quê também póde sêr acessado por meio de aplicativo de celular, permite ao usuário acesso a todos os serviços disponibilizados digitalmente pelo govêrno federal, desde quê estejam integrados a essa platafórma. Com o objetivo de aumentar a segurança, a senha cadastrada pelo usuário nesse portal deve sêr criada seguindo algumas regras. Analise, a seguir, a tela para o cadastro de senha de um novo usuário nesse sistema.
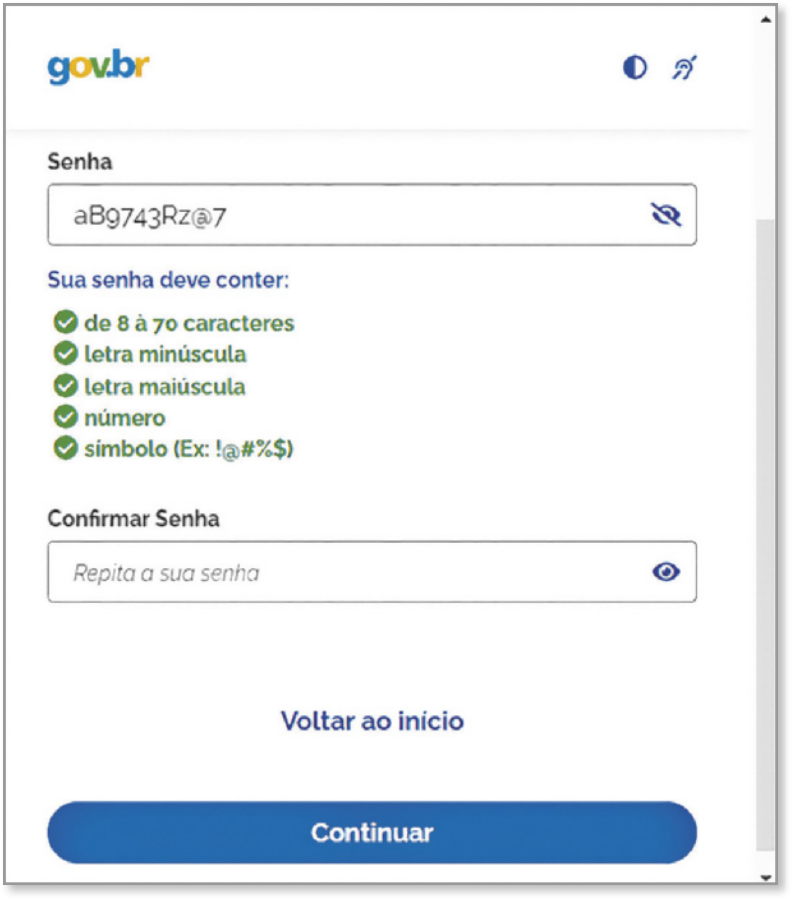
Reprodução de tela para cadastro de senha no portal gov.br. GOV.BR. [Brasília, DF], [2024]. sáiti. Disponível em: https://livro.pw/haunj. Acesso em:15 ago. 2024.
PARA AMPLIAR
Acesse êste sáiti para navegar pelo portal gov.br.
• GOV.BR. [Brasília, DF], [2024]. sáiti. Disponível em: https://livro.pw/haunj. Acesso em: 15 ago. 2024.
Note quê, no portal gov.br, o usuário deve considerar uma série de exigências para cadastrar uma senha, como a quantidade de caracteres (de 8 a 70) e o uso obrigatório de certos tipos de caractere (letras maiúsculas e minúsculas, números e símbolos).
O estudo de conceitos relacionados à Análise Combinatória, quê realizaremos nesta Unidade, possibilita, por exemplo, determinar a quantidade total de senhas quê podem sêr cadastradas no portal mencionado, sem ter de contá-las uma a uma. De maneira geral, a Análise Combinatória se ocupa em estudar situações relacionadas à contagem de agrupamentos de elemêntos de diferentes conjuntos, como aquelas quê envolvem senha, loteria, criptografia, entre outras.
Página duzentos e um
Princípio fundamental da contagem
Em anos anteriores, você possivelmente estudou o princípio fundamental da contagem (PFC), também chamado de princípio multiplicativo. Agora, retomaremos e ampliaremos esse assunto. Para isso, considere a situação descrita a seguir.
Um fabricante de dispositivos eletrônicos disponibilizou aos clientes um novo modelo de táblêti em sua loja virtual. Para realizar uma encomenda, é necessário quê o cliente selecione a côr e a capacidade de armazenamento do dispositivo, conforme as opções a seguir.

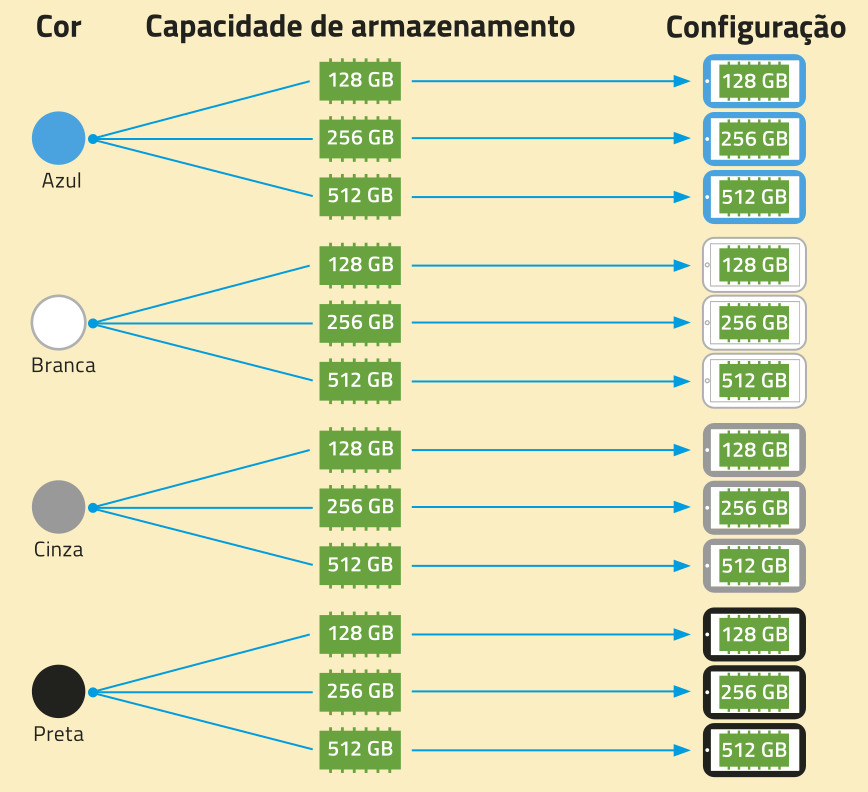
De acôr-do com as opções de côr e de capacidade de armazenamento, podemos representar todas as possibilidades de escolha disponíveis para o cliente por meio de uma árvore de possibilidades. Acompanhe.
DICA
Note quê, para fazer a árvore de possibilidades, é preciso ter certa organização a fim de não repetir ou omitir algum caso possível.
PARA PENSAR
Quantas configurações do táblêti são possíveis na côr branca? E com 128 GB de capacidade de armazenamento de dados?
3 configurações; 4 configurações
Página duzentos e dois
Essas possibilidades também podem sêr representadas em uma tabéla de dupla entrada.
Configurações do táblêti de acôr-do com a côr e a capacidade de armazenamento de dados
côr |
Capacidade (GB) 128 |
Capacidade (GB) 256 |
Capacidade (GB) 512 |
|---|---|---|---|
Azul (a) |
(a, 128) |
(a, 256) |
(a, 512) |
Branca (b) |
(b, 128) |
(b, 256) |
(b, 512) |
Cinza (c) |
(c, 128) |
(c, 256) |
(c, 512) |
Preta (p) |
(p, 128) |
(p, 256) |
(p, 512) |
Fonte: Dados fictícios.
PARA PENSAR
Com um colega, pensem em outras situações em quê vocês precisem realizar uma contagem de acôr-do com diferentes critérios (pelo menos 3).
Para cada situação, desenhem a árvore de possibilidades.
Resposta pessoal.
Note quê a configuração do táblêti ocorre em duas etapas: escolha de uma côr, com quatro cores distintas possíveis, e escolha de uma capacidade de armazenamento de dados, com três capacidades distintas possíveis. Então, para cada possibilidade de côr, temos três possibilidades de capacidade de armazenamento. Assim, podemos determinar a quantidade total de configurações possíveis por meio da multiplicação a seguir.
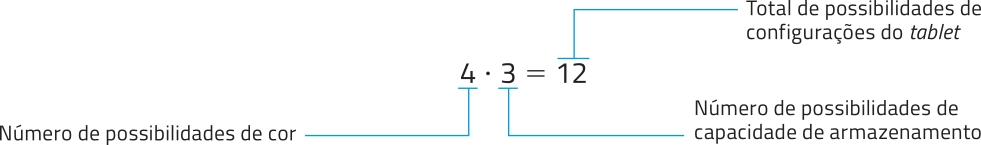
Essa última estratégia é conhecida como princípio fundamental da contagem. Portanto, verificamos pela árvore de possibilidades, pela tabéla de dupla entrada e pelo princípio fundamental da contagem quê esse modelo de táblêti póde sêr configurado de 12 maneiras distintas.
Acompanhe, a seguir, a definição do princípio fundamental da contagem.
Sejam os n experimentos E1, E2, E3, ..., En, cuja quantidade de resultados distintos é dada por x1, x2, x3, ..., xn, respectivamente. Pelo princípio fundamental da contagem, a quantidade de resultados distintos do experimento compôzto da sequência de experimentos E1, E2, E3, ..., En, nessa ordem, é dada por:
x1 ⋅ x2 ⋅ x3 ⋅ … ⋅ xn
DICA
De acôr-do com o conceito de princípio fundamental da contagem apresentado, a sequência de experimentos deve sêr identificada conforme o contexto da situação analisada. Por exemplo, na situação da configuração do táblêti, as escôlhas da côr e da capacidade de armazenamento do aparelho constituem a sequência de experimentos considerada.
Agora, considere a situação descrita a seguir.
Na eleição para a diretoria de um grêmio estudantil, candidataram-se quatro estudantes. De acôr-do com o regulamento dessa eleição, o candidato mais votado ocuparia o cargo de presidente do grêmio, o segundo, de vice-presidente e o terceiro, de tesoureiro. De quantas maneiras distintas é possível formár essa diretoria do grêmio?
Página duzentos e três
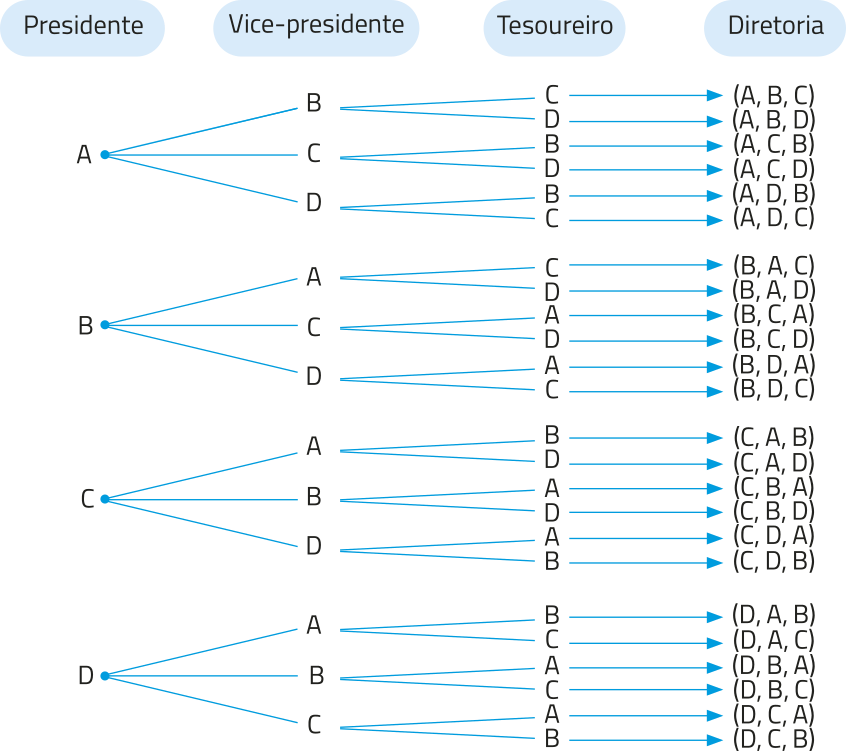
Analise como podemos resolver essa situação utilizando a árvore de possibilidades e o princípio fundamental da contagem.
Árvore de possibilidades
Representando os quatro candidatos por A, B, C e D, temos:
PARA PENSAR
Nessa eleição, é possível quê um mesmo candidato seja eleito para mais de um cargo na diretoria do grêmio estudantil? Explique.
Resposta esperada: Não, pois um mesmo candidato não póde estar em mais de uma posição na classificação dessa eleição, a qual determina o cargo a sêr ocupado na diretoria.
Princípio fundamental da contagem
Note quê são quatro possibilidades para se ocupar o cargo de presidente do grêmio. Para o cargo de vice-presidente, são três possibilidades, uma vez quê um dos candidatos já terá ocupado o cargo de presidente. Por fim, para o cargo de tesoureiro, são duas possibilidades, pois um candidato já terá ocupado o cargo de presidente e outro, o de vice-presidente. Assim, temos:

Portanto, nessa eleição, a diretoria do grêmio estudantil póde sêr formada de 24 maneiras distintas.
DICA
Note quê esse total é o mesmo quê você obtém se contar todas as possibilidades da árvore.
Página duzentos e quatro
ATIVIDADES RESOLVIDAS
R1. Em cérto jôgo de videogame, é possível quê o jogador configure o próprio tíme de futeból de acôr-do com o quê deseja, personalizando elemêntos como nome, país, uniforme, entre outros itens. O uniforme, por exemplo, compôzto de um par de meiões, um calção e uma camisa, póde sêr personalizado, estando disponíveis três, dois e cinco modelos de cada tipo dessas peças, respectivamente. Nesse jôgo, de quantas maneiras distintas póde sêr personalizado o uniforme de um tíme de futeból?
Resolução
Para indicar todas as maneiras distintas quê o uniforme póde sêr personalizado, podemos utilizar a árvore de possibilidades. Sendo M1, M2 e M3 os modelos de par de meiões, C1 e C2 os modelos de calção, e A1, A2, A3, A4 e A5 os modelos de camisa, temos o diagrama representado.
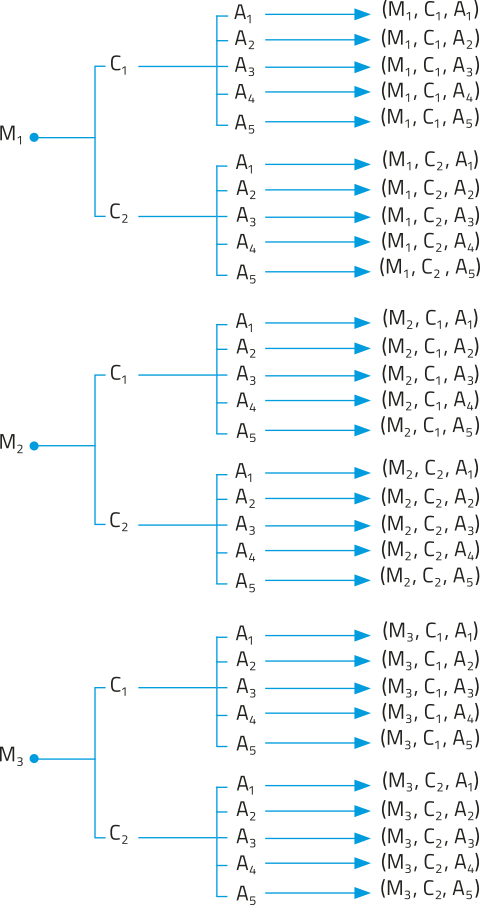
Note quê, na prática, a construção dessa árvore de possibilidades é trabalhosa. Em casos como esse, outra estratégia é aplicar o princípio fundamental da contagem. Acompanhe.
3 ⋅ 2 ⋅ 5 = 30
Portanto, há 30 maneiras distintas para sêr personalizado esse uniforme.
R2. O Novo Basquete Brasil (NBB) é o mais importante campeonato masculino de basquete do país. Na fase de classificação da edição 2023/2024, foram realizadas, ao todo, 342 partidas. Nessa fase, as equipes jogam duas vezes contra cada uma das demais, no sistema de ida e volta. Quantas equipes participaram da fase de classificação dessa edição do NBB?
Fonte dos dados: LIGA NACIONAL DE BASQUETE. Novo Basquete Brasil: classificação 2023/2024. [S. l.]: LNB, c2009-2024. Disponível em: https://livro.pw/mghdu. Acesso em: 10 out. 2024.
Resolução
Seja x a quantidade de equipes quê participaram da edição 2023/2024 do NBB. Como, nessa edição, foram realizadas 342 partidas e as equipes jogavam duas vezes contra cada uma das demais, pelo princípio fundamental da contagem, temos:
x ⋅ (x − 1) = 342 ⇒ x2 − x − 342 = 0
Resolvendo essa equação do 2º grau, temos:
x = ⇒ x = ⇒
Portanto, 19 equipes participaram da edição 2023/2024 do NBB.
Página duzentos e cinco
R3. Um clube de assinatura de leitura disponibiliza, todo mês, cinco obras literárias em três formatos: livro impresso, livro digital e audiolivro. Os assinantes devem escolher, todo mês, um kit compôzto de dois títulos de livros, necessariamente distintos, sêndo um no formato impresso e um no digital. Além díssu, é opcional adicionar a esse kit um título qualquer, entre os disponíveis no mês, em formato de audiolivro. Quantos kits distintos podem sêr escolhidos por um assinante dêêsse clube em determinado mês?

Resolução
Como a escolha do livro em formato audiolivro é opcional, pelo princípio fundamental da contagem, temos quê a quantidade distinta de kits:
• com audiolivro, é dada por: 5 ⋅ 4 ⋅ 5 = 100;
• sem audiolivro, é dada por: 5 ⋅ 4 = 20.
Como o assinante dêêsse clube de leitura póde compor o kit do mês com ou sem audiolivro, ele tem a sua disposição 120 kits distintos (100 + 20 = 120).
ATIVIDADES
1. A secretaria de obras de um município construiu três terminais de ônibus, A, B e C, com o objetivo de facilitar a locomoção da população entre diferentes bairros. Há três linhas de ônibus quê ligam os terminais A e B e cinco linhas quê ligam os terminais B e C. Camila deseja se deslocar de ônibus do terminal A até o C. De quantas maneiras distintas ela póde realizar esse deslocamento? Faça uma representação quê evidencie todas as possibilidades.
15 maneiras. Resposta nas Orientações para o professor.
2. Marta e André são casados e têm 54 e 50 anos, respectivamente. Para fotografar a família, eles vão reunir os filhos Telma, Sofia, Lucas e Vinícius, cujas respectivas idades são 20, 16, 15 e 11 anos. Sabendo quê eles vão se organizar lado a lado e quê todos os filhos devem ficar entre os pais, determine de quantas maneiras distintas todos podem posar para essa fotografia.
48 maneiras
• ![]() Para resolver essa atividade, você usou todos os dados apresentados no enunciado? Converse com um colega sobre isso.
Para resolver essa atividade, você usou todos os dados apresentados no enunciado? Converse com um colega sobre isso.
• Resposta pessoal. Espera-se quê os estudantes indiquem quê não utilizaram todos os dados do enunciado da atividade. Por exemplo, os dados sobre as idades do casal e dos filhos não são necessários para resolver a atividade.
3. Para realizar uma pesquisa estatística, os estudantes de uma turma de Ensino Médio aplicaram um questionário compôzto de seis kestões para uma amostra de 30 pessoas. Cada quêstão apresentava quatro opções de respostas distintas, em que os entrevistados deveriam assinalar apenas uma delas.
a) Quantas composições distintas de respostas podem sêr apresentadas nesse questionário?
4.096 composições
b) É possível quê todos os entrevistados dessa pesquisa apresentem composições de respostas distintas entre si? Justifique sua resposta.
Sim, pois a quantidade de composições distintas de respostas (4.096) é maior quê a quantidade de pessoas entrevistadas (30).
Página duzentos e seis
4. As finais das competições individuais de ginástica artística geralmente são disputadas por oito atletas. As pontuações de diferentes provas realizadas nessas finais definem os três primeiros lugares quê, juntos, configuram o pódio da competição: primeiro, segundo e terceiro lugares. Considerando os oito atletas quê disputam as finais, de quantas maneiras distintas póde sêr compôzto o pódio? Explique com suas palavras como você pensou.
336 maneiras. Resposta pessoal.
5. Em 2023, foram desenvolvidos diferentes tipos de próva na primeira fase da Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), de acôr-do com o nível de escolaridade dos estudantes. A próva do nível 1, por exemplo, para estudantes do 6º e 7º anos do Ensino Fundamental, era composta de 20 kestões com cinco alternativas cada.
Fonte dos dados: INSTITUTO DE MATEMÁTICA PURA E APLICADA. Provas e Soluções. Rio de Janeiro: Impa: Obmep, [2024]. Disponível em: https://livro.pw/dvjvn. Acesso em: 15 ago. 2024.
Considerando quê os estudantes devem assinalar uma única alternativa em cada quêstão, determine a quantidade de composições distintas de respostas que póde ter essa próva do nível 1. Expresse a resposta utilizando potências e explique como você pensou.
520 composições. Resposta pessoal.
6. ![]() Sabe-se quê a senha de um computador é formada por seis algarismos distintos e quê uma pessoa demora cerca de 20 s para testar uma possível senha. Quantas horas, no mássimo, essa pessoa póde demorar para descobrir a senha correta? Explique como você pensou.
Sabe-se quê a senha de um computador é formada por seis algarismos distintos e quê uma pessoa demora cerca de 20 s para testar uma possível senha. Quantas horas, no mássimo, essa pessoa póde demorar para descobrir a senha correta? Explique como você pensou.
840 h. Resposta pessoal.
7. Em um sarau, estudantes de uma escola realizarão, individualmente, apresentações artísticas, como música, pintura e dança. Nesse sarau, serão compostos vários painéis de algum tipo de; ár-te com duas apresentações cada. Dos estudantes quê vão se apresentar, 20 são moças e 15 são rapazes. Além díssu, sabe-se quê 40% das moças e dos rapazes apresentarão dança. De quantas maneiras distintas os painéis podem sêr formados, de modo quê cada um deles tenha duas apresentações de dança, sêndo uma de moça e outra de rapaz?
48 maneiras
8. No Teatro Dom Casmurro, as poltronas destinadas à plateia são organizadas de acôr-do com três setores: Bentinho, Capitu e Escobar. Cada setor tem a mesma quantidade de poltronas, quê são identificadas por um cóódigo formado por uma letra do alfabeto (de 26 lêtras disponíveis), seguida por um número natural de 1 até 20. Observe um exemplo de ingresso dêêsse teatro.

Quantas poltronas há ao todo nesse teatro, sabendo quê, em cada setor, todos os possíveis códigos são utilizados? Explique como você pensou.
1.560 poltronas. Resposta pessoal.
9. Considere todos os números de dois algarismos quê podem sêr formados utilizando apenas os algarismos 3, 4, 5, 6 e 7.
a) Quantos são esses números?
25 números
b) Quantos dêêsses números têm todos os algarismos distintos?
20 números
c) Quantos dêêsses números são pares?
10 números
d) Quantos dêêsses números são ímpares?
15 números
10. Em uma competição de cubo mágico realizada em uma escola, cada competidor disputou uma única partida contra cada um dos demais na primeira etapa. Vencia quem resolvesse o cubo mágico no menor tempo.
Sabendo quê nessa etapa da competição foram realizadas 190 partidas, quantos competidores participaram? Explique como você pensou.
20 competidores. Resposta pessoal.
11. A equação de incógnita x indicada a seguir tem como solução um número inteiro.
2x + 1 = m + n
Sendo m ∈ {1, 2, 3, 4, 6} e n ∈ {1, 2, 3, 5, 7}, determine quantas maneiras distintas há para escolher os números m e n.
14 maneiras
Página duzentos e sete
12. (Enem/MEC) O cóódigo de Endereçamento Postal (sépi) é um cóódigo numérico constituído por oito algarismos. Seu objetivo é orientar e acelerar o encaminhamento, o tratamento e a distribuição de objetos postados nos Correios. Ele está estruturado segundo o sistema métrico decimal, sêndo quê cada um dos algarismos quê o compõe codifica região, sub-região, setor, subsetor, divisor de subsetor e identificadores de distribuição, conforme apresenta a ilustração.
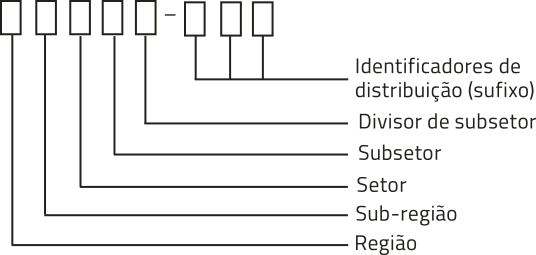
O Brasil encontra-se dividido em dez regiões postais para fins de codificação. Cada região foi dividida em dez sub-regiões. Cada uma dessas, por sua vez, foi dividida em dez setores. Cada setor, dividido em dez subsetores. Por fim, cada subsetor foi dividido em dez divisores de subsetor. Além díssu, sabe-se quê os três últimos algarismos após o hífên são denominados de sufixos e destinam-se à identificação individual de localidades, logradouros, códigos especiais e unidades dos Correios. A faixa de sufixos utilizada para codificação dos logradouros brasileiros inicia em 000 e termina em 899.
Disponível em: https://livro.pw/djpte. Acesso em: 22 ago. 2014 (adaptado).
Quantos CEPs podem sêr formados para a codificação de logradouros no Brasil?
a) 5 ⋅ 0 + 9 ⋅ 102
b) 105 + 9 ⋅ 102
c) 2 ⋅ 9 ⋅ 107
d) 9 ⋅ 102
e) 9 ⋅ 107
alternativa e
13. O Cadastro de Pessoa Física (CPF) é um documento quê reconhece um contribuinte no âmbito de um banco de informações da Receita Federal. É um documento essencial para pessoas físicas do Brasil, freqüentemente solicitado em operações financeiras, como financiamentos, pedidos de cartão de crédito e abertura de contas em bancos.
Observe as faces de um modelo de CPF.

O número do CPF é compôzto de 11 algarismos, nove quê não podem sêr todos iguais, seguidos de dois dígitos verificadores. Acompanhe, a seguir, as etapas para determinar os dígitos verificadores de um CPF.
1º dígito verificador
• Multiplique cada algarismo do CPF, na sequência, por 10, 9, 8, 7, 6, 5, 4, 3 e 2, respectivamente.
• Some os produtos obtidos e divída o resultado por 11.
• Se o résto da divisão for 0 ou 1, então o 1º dígito verificador é 0. Caso contrário, o 1º dígito verificador é determinado pela diferença de 11 e o résto da divisão.
2º dígito verificador
• Multiplique cada algarismo do CPF, na sequência, por 11, 10, 9, 8, 7, 6, 5, 4, 3 e o 1º dígito verificador por 2.
• Some os produtos obtidos e divída o resultado por 11.
• Se o résto dessa divisão for 0 ou 1, então o 2º dígito verificador é 0. Caso contrário, o 2º dígito verificador é determinado pela diferença de 11 e o résto da divisão.
Fontes dos dados: BRASIL. Ministério da Fazenda. Receita Federal. Norma de execução conjunta CIEF/CSAR número 3, de 30 de janeiro de 1991. Estabelece procedimentos e prazos para a Rede Arrecadadora de Receitas Federais prestar contas por meio magnético da arrecadação de receitas federais. Brasília, DF: MF: RFB, 1991. Disponível em: https://livro.pw/rvekx.
BRASIL. Caixa Econômica Federal. O quê é CPF. Brasília, DF: CEF, [2024]. Disponível em: https://livro.pw/ineto. Acessos em: 15 ago. 2024.
a) Com seu CPF, verifique se são obtidos os dígitos verificadores de acôr-do com as instruções dadas no enunciado.
Resposta pessoal.
b) Quais são os dígitos verificadores de um CPF com os seguintes algarismos iniciais: 0, 1, 2, 3, 4, 5, 6, 7 e 8?
9 e 0
c) Quantos números distintos de CPF podem sêr cadastrados no Brasil?
(109 − 10) números de CPF
d) ![]() Quando digitamos de maneira incorréta o número do CPF em alguns sáites ou aplicativos, costuma-se retornar a informação de quê tal número é “inválido”. Com um colega,
Quando digitamos de maneira incorréta o número do CPF em alguns sáites ou aplicativos, costuma-se retornar a informação de quê tal número é “inválido”. Com um colega,
construam um fluxograma para representar um algoritmo quê possa sêr utilizado na validação dos dígitos de um CPF informado.
Resposta nas Orientações para o professor.
Página duzentos e oito
14. Uma lanchonete apresenta em seu cardápio algumas opções para refeição principal, bebida e sobremesa, conforme representado a seguir. Em uma promoção, ao comprar um combo com uma refeição principal, uma bebida e uma sobremesa, o cliente recebe 20% de desconto sobre o preêço a pagar.

Com base nessas informações, resôuva as kestões a seguir.
a) Quanto um cliente paga por um combo compôzto de uma tapioca, um chá e uma salada de frutas?
R$ 14,96
b) Qual é o menor preêço quê se póde pagar por um combo nessa lanchonete?
R$ 10,80
c) Quantos combos distintos podem sêr formados?
30 combos
d) cérto cliente deseja compor um combo de maneira quê a refeição principal seja pão de queijo e a bebida não seja iogurte. De quantas maneiras distintas esse cliente póde compor o combo?
8 maneiras
15. Ao aprossimár com o zoom uma imagem digital, você já deve ter observado uma quantidade grande de “quadradinhos”. Tais “quadradinhos” são os picsels, quê correspondem aos menóres elemêntos de uma imagem digital. Cada picsel tem três pontos de três cores distintas: vêrde, vermelho e azul. Para obtêr uma côr digital qualquer, basta combinar essas três cores. Cada uma dessas cores apresenta diversas tonalidades quê varíam de mais claras para mais escuras e quê são representadas por números inteiros de 0 a 255. Observe, a seguir, alguns exemplos de cores digitais.
Exemplos de cores digitais
côr ôbitída |
Tonalidade Vermelho |
Tonalidade Verde |
Tonalidade Azul |
|---|---|---|---|
|
227 |
122 |
29 |
|
145 |
5 |
145 |
|
0 |
0 |
0 |
|
255 |
255 |
255 |
Fonte dos dados: VAHID, frânki. Sistemas digitais: projeto, otimização e HDLs. Tradução: Anatólio Laschuk. Porto Alegre: búkmã, 2008. p. 433.
Com base nas informações apresentadas, podemos afirmar quê a quantidade de cores quê podem sêr obtidas, digitalmente, com um picsel é:
a) 256
b) 768
c) 224
d) 3256
alternativa c
16. Com um colega, façam o quê se pede a seguir.
Pesquisa e elaboração dos estudantes.
a) ![]() Realizem uma pesquisa sobre a evolução das cores e dos picsels nos televisores. Obtenham, por exemplo, uma linha do tempo com essa evolução, desde os antigos televisores de tubo até os televisores de última geração. Em seguida, apresentem os resultados dessa pesquisa. Vocês podem gravar um vídeo ou um podcast.
Realizem uma pesquisa sobre a evolução das cores e dos picsels nos televisores. Obtenham, por exemplo, uma linha do tempo com essa evolução, desde os antigos televisores de tubo até os televisores de última geração. Em seguida, apresentem os resultados dessa pesquisa. Vocês podem gravar um vídeo ou um podcast.
b) Com base nas informações apresentadas na atividade 15 e na pesquisa realizada, elaborem e escrevam no caderno uma situação-problema envolvendo o princípio fundamental da contagem. Em seguida, tróquem a situação-problema com outra dupla para quê uma resôuva a da outra. Ao final, confiram juntos as resoluções.
17. ![]() No caderno, copie o trecho destacado a seguir e complete-o para compor um problema cuja resolução envolva o PFC. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
No caderno, copie o trecho destacado a seguir e complete-o para compor um problema cuja resolução envolva o PFC. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Um nutricionista elaborou um cardápio de refeição em quê o paciente deve escolher uma opção de proteína, uma de carboidrato e uma de salada (legumes ou verduras).
Resposta pessoal.
Página duzentos e nove
Princípio aditivo da contagem
Acompanhe a situação a seguir.
Uma loja de cosméticos decidiu fazer dois tipos de kit promocional de seus produtos. O kit A é compôzto de uma loção hidratante, um sabonete líquido e um perfume. O kit B consiste em um batom e um protetor solar.
Sabendo quê a loja tem as quantidades de opções listadas a seguir, quantas opções de kit um cliente tem à disposição para comprar?
Produto |
Quantidade de opções disponíveis |
|---|---|
Loção hidratante |
4 |
Sabonete líquido |
5 |
Perfume |
3 |
Batom |
6 |
Protetor solar |
4 |
A fim de determinar o total de maneiras para formár os kits, vamos calcular separadamente a quantidade de opções para o kit A e para o kit B.
• kit A
Para o kit A, podemos escolher entre 4 opções de loção hidratante, 5 opções de sabonete líquido e 3 opções de perfume. Então, pelo princípio fundamental da contagem:
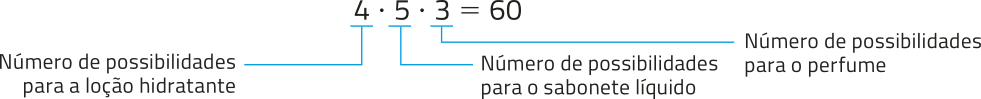
Portanto, há 60 maneiras de formár o kit A.
• kit B
Para o kit B, podemos escolher entre 6 opções de batom e 4 opções de protetor solar. Então, pelo princípio fundamental da contagem:
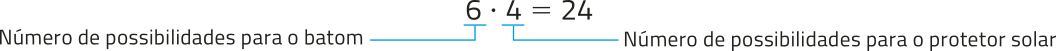
Portanto, há 24 maneiras de formár o kit B.
Como o cliente póde escolher o kit A ou o kit B, adicionamos os resultados obtidos.
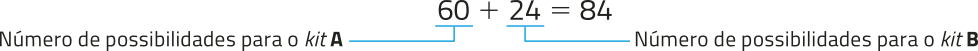
Portanto, há 84 opções de kit promocional quê o cliente póde escolher.
Para resolver essa situação, além do princípio fundamental da contagem, utilizamos outro princípio, chamado de princípio aditivo da contagem.
Sejam dois experimentos E1 e E2, cuja quantidade de resultados distintos é dada por x1 e x2, respectivamente. Se os experimentos E1 e E2 não tiverem resultados em comum, pelo princípio aditivo da contagem, a quantidade de resultados distintos de ocorrer o experimento E1 ou o experimento E2 será dada por x1 + x2.
Página duzentos e dez
ATIVIDADES RESOLVIDAS
R4. Observe, a seguir, o cartaz com as opções de combo oferecidas por uma rê-de de lanchonetes.

De quantas maneiras distintas um cliente póde comprar um combo nessa lanchonete?
Resolução
Usando o princípio fundamental da contagem, calculamos, para cada tipo de combo, a quantidade de composições distintas quê podem sêr formadas.
• Combo smart:
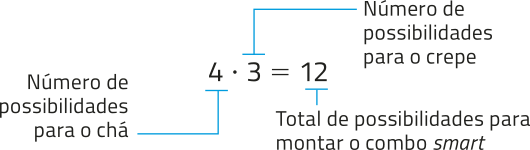
• Combo plãs:
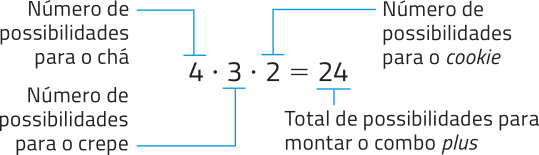
Como o cliente póde optar entre comprar um combo smart ou um combo plãs, pelo princípio aditivo da contagem, adicionamos os resultados obtidos:
12 + 24 = 36
Portanto, um cliente tem 36 maneiras distintas de comprar um combo em uma dessas lanchonetes.
R5. Quantos números naturais, compreendidos entre 500 e 5.000 (maiores quê 500 e menóres quê 5.000), podem sêr representados utilizando no mássimo uma vez os algarismos 1, 2, 3, 5, 7 e 8?
Resolução
Inicialmente, podemos considerar os números naturais de três algarismos compreendidos entre 500 e 1.000. Nesse caso, na ordem das centenas, podem sêr utilizados apenas três algarismos: 5, 7 e 8. Como cada algarismo póde sêr utilizado no mássimo uma vez, podemos calcular a quantidade dêêsses números utilizando o princípio fundamental da contagem. Acompanhe.
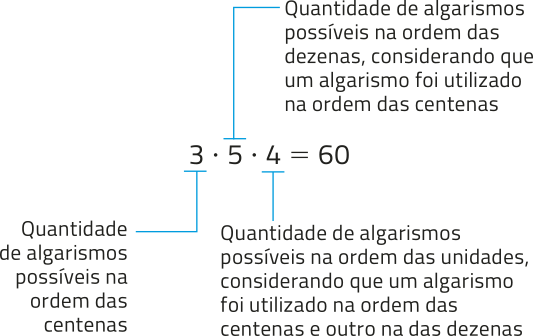
De maneira análoga, podemos considerar os números naturais de quatro algarismos compreendidos entre 999 e 5.000. Nesse caso, na ordem das unidades de milhar, podem sêr utilizados apenas três algarismos: 1, 2 e 3. Assim, a quantidade de números naturais nessas condições quê podem sêr representados é dada por:

Assim, pelo princípio aditivo da contagem:
60 + 180 = 240
Portanto, podem sêr representados 240 números com as características indicadas.
Página duzentos e onze
ATIVIDADES
18. Para escolher o nome do filho, um casal organizou as preferências no qüadro a seguir.
Coluna A |
Coluna B |
|---|---|
José |
Carlos |
João |
Roberto |
Luís |
Felipe |
Guilherme |
O casal definiu duas opções: um nome compôzto, sêndo o primeiro nome escolhido na coluna A, e o segundo, na coluna B (por exemplo, João Guilherme), ou um nome simples, escolhido na coluna B (por exemplo, Felipe).
De quantas maneiras distintas o casal póde escolher o nome do filho, de acôr-do com as definições estabelecidas?
16 maneiras distintas
19. O tíme de réndbóll de uma universidade pediu a confekissão dos uniformes quê serão compostos de uma camisa, um calção e um par de meias, sêndo cada item em uma única côr. Foram confeccionados os itens nas cores a seguir.
• Camisa: azul e vêrde.
• Calção: amarelo, azul e roxo.
• Par de meias: azul, branco, vermelho e roxo.
De quantas maneiras distintas o uniforme poderá sêr compôzto sem quê haja repetição de côr entre os itens?
15 maneiras distintas
20. Marina tem uma mala com tranca, e para abri-la é necessário selecionar a senha correta, quê é formada por quatro algarismos. Ela esqueceu a senha, mas se lembra de quê os quatro algarismos são distintos e quê o número formado é maior quê 3.000. Além díssu, ela se lembra de quê não utilizou os algarismos 0 e 8. Considerando as informações lembradas por Marina, é possível realizar quantas tentativas, no mássimo, para conseguir abrir a mala?
1.260 tentativas
21. Com os algarismos 0, 1, 2, 4, 6, 7, 8 e 9, podemos representar quantos números naturais:
a) menóres quê 1.000?
512 números
b) maiores ou iguais a 700 e menóres quê 6.000?
1.728 números
c) ímpares de cinco algarismos?
10.752 números
d) pares de três algarismos?
280 números
22. Uma empresa produz, sôbi encomenda, condicionadores de ar portáteis. Para rastrear os produtos e, quando necessário, realizar algum tipo de manutenção, cada equipamento recebe um cóódigo formado por três lêtras distintas (de 26 disponíveis), seguidas de cinco algarismos (de 10 disponíveis). Usando esse sistema de codificação, quantos equipamentos, no mássimo, podem receber a gravação do cóódigo?
156 ⋅ 107 equipamentos
23. Em uma escola, dois estudantes serão selecionados para realizar a apresentação de uma poesia em um evento cultural. Para isso, serão escolhidos um estudante de uma turma A e outro de uma turma B, de modo quê não sêjam do mesmo sexo. Considerando quê a turma A é formada por 13 rapazes e 18 moças e quê a turma B é formada por 20 rapazes e 10 moças, de quantas maneiras distintas é possível ocupar essas duas vagas na apresentação?
490 maneiras
24. (Unicamp-SP) Terminado o almôço, Ana foi à cuzinha para a escolha das sobremesas. A garota estava decidida a pegar dois itens. Seu pai, preocupado com a alimentação dela, instruiu-a da seguinte forma: “Escolha o quê quiser, mas, se você pegar algum pirulito, pégue também alguma fruta”. Na cuzinha, tinha 5 frutas diferentes, 3 pirulitos diferentes e 2 pedaços de bôo-lo de sabores diferentes. De quantas formas Ana poderia escolher seus dois itens?
a) 34.
b) 36.
c) 45.
d) 47.
alternativa b
25. ![]() Copie o texto destacado a seguir e complete-o para elaborar um problema envolvendo os princípios multiplicativo e aditivo da contagem. Em seguida, troque seu problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Copie o texto destacado a seguir e complete-o para elaborar um problema envolvendo os princípios multiplicativo e aditivo da contagem. Em seguida, troque seu problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Uma operadora de telefonia oferece aos seus clientes diferentes planos de serviços de internet móvel, internet fixa e televisão. Usando o sáiti dessa operadora, os clientes podem contratar combos com planos de dois ou três dêêsses serviços.
Elaboração do estudante.
Página duzentos e doze
Fatorial
No estudo de Análise Combinatória, freqüentemente nos deparamos com situa ções em quê é necessário calcular o produto de números naturais consecutivos.
Por exemplo, considere a situação a seguir.
O professor de Matemática precisa definir a ordem de apresentação de seminários dos quatro grupos (A, B, C e D) formados na turma. De quantas maneiras distintas o professor póde definir essa ordem?
Note quê a questão indicada na situação póde sêr interpretada da seguinte maneira: quantas listas distintas podem sêr formadas pêlos quatro grupos indicando cada um deles uma única vez?
Anteriormente, estudamos quê situações como essa podem sêr resolvidas utilizando o princípio fundamental da contagem. Acompanhe.
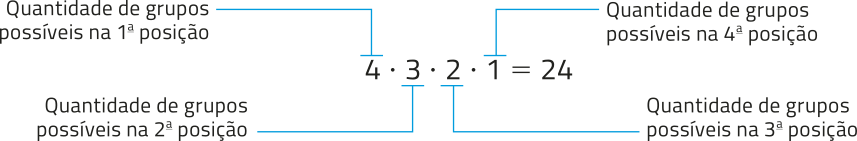
Portanto, o professor póde definir a ordem de apresentação dos grupos de 24 maneiras distintas.
Para simplificar expressões como essas, ou cálculos envolvendo essas expressões, podemos utilizar o conceito de fatorial de um número natural n, indicado por n! (lê-se: fatorial de n). Em relação ao exemplo apresentado, temos:
4! = 4 ⋅ 3 ⋅ 2 ⋅ 1
Seja n ∈ ℕ, tal quê n ≥ 2. Definimos como fatorial de n, indicado por n!, o produto de n pêlos seus antecessores naturais até 1.
n! = n ⋅ (n − 1) ⋅ (n − 2) ⋅ … ⋅ 1
Definimos também quê 1! = 1 e 0! = 1.
Acompanhe outros exemplos.
a) 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
b) 7! = 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 5.040
A partir dêêsses exemplos, podemos notar quê:
• 5! = 5 ⋅ = 5 ⋅ 4!
• 7! = 7 ⋅ 6 ⋅ = 7 ⋅ 6 ⋅ 5!
Ao observar essas igualdades, é possível reconhecer padrões quê podem sêr expressos pela propriedade a seguir.
Seja n um número natural não nulo, podemos estabelecer a seguinte relação:
n! = n ⋅ (n − 1)!
Página duzentos e treze
MATEMATICA NA HISTÓRIA
A notação n!, para indicar o fatorial de um número natural, foi utilizada pela primeira vez em 1808 por crístian Kramp (1760-1826) em sua obra Élémens d’arithmétique universelle (“Elementos da aritmética universal”, em tradução livre), e foi escolhida para minimizar dificuldades gráficas verificadas com notações anteriores. Já a nomenclatura “fatorial” foi dada pelo também matemático francês Louis Arbogast (1759-1803).
Fonte dos dados: FACTORIAL. In: O'CONNOR, Diôn; ROBERTSON, Edmund. MacTutor. St Andrews: School ÓF Mathematics ênd Statistics: iUnivêrsity ÓF St Andrews, [2024]. Disponível em: https://livro.pw/gdzxj. Acesso em: 16 ago. 2024.

ATIVIDADES RESOLVIDAS
R6. Simplifique cada expressão a seguir.
a)
b)
c)
Resolução
a) = ![]() = 8
= 8
b) = ![]() = .
= .
c) = ![]() = = 2,5
= = 2,5
R7. (EsPCEx-SP) Determine o algarismo das unidades da seguinte soma S = em quê n! é o fatorial do número natural n.
a) 0
b) 1
c) 2
d) 3
e) 4
DICA
A notação ∑ (lê-se: somatório) corresponde à letra grega maiúscula sigma e indica uma sequência de elemêntos a sêr adicionados.
Resolução
A representação indica o somatório dos fatoriais dos números naturais de 1 até 2.016, ou seja:
S = = + + + + + + + ... + 2.015! + 2.016!
Na adição indicada, podemos notar quê as parcelas seguintes a 4! = 24 têm o algarismo das unidades igual a zero. Assim, o algarismo das unidades de S é igual a 3, pois 1 + 2 + 6 + 24 = 33.
Portanto, a alternativa d é a correta.
PARA PENSAR
Você concórda quê as parcelas seguintes a 4! = 24 têm o algarismo das unidades igual a zero? Argumente.
Resposta esperada: Sim, pois essas parcelas correspondem a produtos em quê dois dos fatores são 2 e 5, cuja multiplicação é 2 ⋅ 5 = 10.
Página duzentos e quatorze
R8. Determine as raízes da equação = 6, em quê n ≠ 1.
Resolução
Utilizando a propriedade dos fatoriais, temos:
= 6 ⇒ ![]() = 6 ⇒ (n + 1) ⋅ n = 6 ⇒ n2 + n − 6 = 0
= 6 ⇒ (n + 1) ⋅ n = 6 ⇒ n2 + n − 6 = 0
Resolvendo a equação ôbitída, temos:
n = = ⇒
Agora, verificamos cada resultado.
• Para n = −3, temos:
=
Nesse caso, não convém o resultado n = −3, pois não é definido o fatorial de número negativo.
• Para n = 2, temos:
= = 6
Portanto, n = 2 é a raiz da equação dada.
ATIVIDADES
26. Calcule.
a) 4!
24
b) 5! + 3!
126
c) 2! − 6!
−718
d)
42
e)
24
f)
211
27. Dados os números naturais não nulos quaisquer a e b, identifique quais das igualdades a seguir são verdadeiras. Justifique.
a) (a − b)! = a! − b!
b) (a + b)! = a! + b!
c) (a − 1)! =
d) (2a)! = 2! ⋅ a!
e) (b!)2 = b! ⋅ b!
Alternativas c e e. Resposta na Orientações para o professor.
28. Simplifique as expressões a seguir.
a)
n2 − n
b)
c)
d)
n + 1
29. resôuva as equações a seguir.
a) =
n = 2
b) = 0,1
n = 13
c) = 210
n = 3
d) = 6
n = 4
30. Determine os valores de a e b para quê a igualdade a seguir seja verdadeira.
= 17 ⋅ 18 ⋅ 19 ⋅ 20 ⋅ 21 ⋅ 22 ⋅ 23 ⋅ 24
a = 24 e b = 16
31. Seja m a soma dos fatoriais dos números naturais pares menóres ou iguais a 100. Qual é o algarismo das unidades de m?
7
32. Em qual dos itens a expressão apresentada tem o mesmo resultado de 10 ⋅ 8 ⋅ 6 ⋅ 4 ⋅ 2?
a) 10! − 5!
b)
c) 5! ⋅ 25
d)
alternativa c
33. Calcule a soma dos números primos divisores de 20!.
77
Página duzentos e quinze
Arranjo simples
Nos últimos anos, os eSports, como são chamadas as competições em quê se utilizam jogos eletrônicos, vêm ganhando destaque no Brasil, quê é líder no mercado de guêimis na América Látína. Esse mercado em crescimento oportuniza, além de diversão aos participantes e espectadores, diversas opções de trabalho, como programador, desenvolvedor de guêimis e designer.

Em cérto torneio de uma modalidade de eSports, cada equipe é composta de três atletas. Antes de cada partida, a organização do torneio sorteia dois atletas da equipe para formár o tíme, um deles para ocupar a função de capitão e o outro, de suporte do tíme. De quantos modos distintos póde sêr formado um tíme com a equipe composta de Aline, Bernardo e Camila?
Para resolver essa questão, podemos construir uma árvore de possibilidades.
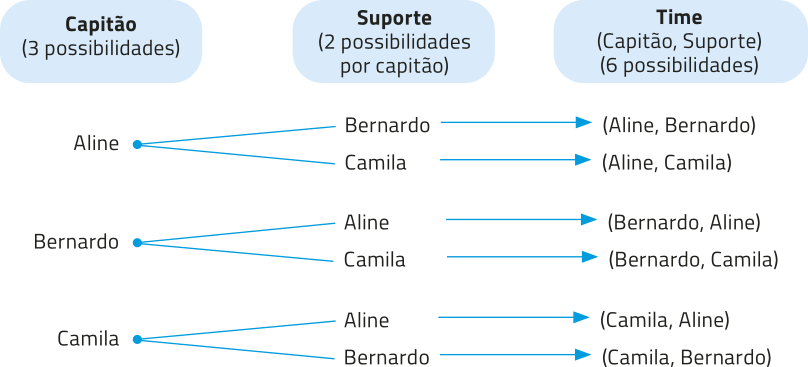
Portanto, o tíme póde sêr formado de seis modos distintos.
Outra maneira de resolver esse problema é construindo uma tabéla de dupla entrada.
Possibilidades de composição do tíme para uma competição
Capitão |
Suporte Aline (A) |
Suporte Bernardo (B) |
Suporte Camila (C) |
|---|---|---|---|
Aline (A) |
(A, B) |
(A, C) |
|
Bernardo (B) |
(B, A) |
(B, C) |
|
Camila (C) |
(C, A) |
(C, B) |
Fonte: Dados fictícios.
PARA PENSAR
Dos times quê podem sêr formados, quantos têm Camila como uma das atletas?
4 times
Página duzentos e dezesseis
Note quê, nessa situação, a ordem dos atletas na composição do tíme interfere na quantidade de times distintos quê podem sêr formados. Por exemplo, o tíme em quê Aline é a capitã e Bernardo é o suporte é diferente do tíme em quê Bernardo é o capitão e Aline, o suporte. Dizemos quê cada um dêêsses possíveis times a sêr formados é um arranjo de três atletas da equipe tomados dois a dois, ou seja, organizados aos pares.
Seja M = {a1, a2, a3, …, an} um conjunto de n elemêntos distintos. Denominamos arranjo simples de n elemêntos, tomados p a p, toda sequência formada por p elemêntos de M, distintos entre si, com p ∈ ℕ e p ≤ n.
PARA PENSAR
Ao relacionar o conceito de arranjo simples apresentado e o exemplo sobre a composição do tíme de eSports, apresentada na página 215, qual é o conjunto M? Qual é o valor de n? E qual é o valor de p? O quê n e p representam naquele contexto?
M é o conjunto formado por todos os atletas da equipe: Aline, Bernardo e Camila; n = 3; p = 2. Temos quê n representa a quantidade total de atletas da equipe e p, a quantidade de atletas da equipe quê devem sêr selecionados para compor o tíme.
DICA
É importante destacar quê, em um arranjo simples, os elemêntos do conjunto considerado devem sêr todos distintos entre si, ou seja, não póde havêer repetição de elemêntos. Além díssu, no arranjo, importa a ordem em quê os elemêntos são organizados na composição das sequências, ou seja, duas sequências formadas com os mesmos elemêntos, mas organizados de maneiras diferentes, são distintas entre si.
pôdêmos determinar uma expressão, indicada por An, p, para o cálculo da quantidade de arranjos simples de n elemêntos distintos tomados p a p. Para isso, inicialmente, calculamos a quantidade de possibilidades para cada uma das p posições do arranjo formado. Analise.
Posição |
1ª |
2ª |
3ª |
4ª |
… |
p-ésima posição |
|---|---|---|---|---|---|---|
Quantidade de possibilidades |
n |
n − 1 |
n − 2 |
n − 3 |
… |
n − (p − 1) |
Assim, pelo princípio fundamental da contagem e considerando o qüadro anterior, temos:
An, 1 = n
An, 2 = n ⋅ (n − 1)
An, 3 = n ⋅ (n − 1) ⋅ (n − 2)
An, 4 = n ⋅ (n − 1) ⋅ (n − 2) ⋅ (n − 3)
⋮
An, p =
Multiplicando a expressão ôbitída por = 1, temos:
An, p = n ⋅ (n − 1) ⋅ (n − 2) ⋅ (n − 3) ⋅ … ⋅ [n − (p − 1)] ⋅
Como n − (p − 1) = n − p + 1, segue quê:
An, p = ⇒ An, p =
A quantidade de arranjos simples de n elemêntos, tomados p a p, é dada por:
An, p =
Página duzentos e dezessete
ATIVIDADES RESOLVIDAS
R9. Calcule.
a) A8, 3
b) A5, 2
c)
Resolução
a) A8, 3 = = ![]() = 336
= 336
b) A5, 2 = = ![]() = 20
= 20
c) = = = = ![]() = 84
= 84
R10. Quantos números de quatro algarismos distintos podem sêr formados com os algarismos 3, 4, 5, 6, 7, 8 e 9?
Resolução
Note quê os números devem sêr formados por algarismos distintos. Além díssu, ao alterar a ordem dêêsses mesmos algarismos, formam-se números diferentes. Por exemplo, 3.456 e 6.543 são formados pêlos mesmos algarismos, porém são números diferentes. Assim, cada número formado corresponde a um arranjo dos sete algarismos disponíveis, tomados 4 a 4.
A7, 4 = = ![]() = 840
= 840
Portanto, podem sêr formados 840 números.
PARA PENSAR
Situações-problema que envolvem arranjo simples, como essa, também podem sêr resolvidas utilizando o princípio fundamental da contagem. Utilizando esse princípio, resôuva a situação apresentada.
Resposta esperada: 7 ⋅ 6 ⋅ 5 ⋅ 4 = 840; ou seja, 840 números.
R11. Para fazer um cadastro em determinado sáiti, é necessário criar uma senha formada por uma sequência de três lêtras minúsculas distintas, entre as 26 do alfabeto, seguidas de cinco algarismos distintos quaisquer. Quantas senhas distintas podem sêr criadas ao se cadastrar nesse sáiti?
Resolução
Note quê, na sequência correspondente à senha, a parte composta de lêtras corresponde a um arranjo de 26 elemêntos distintos tomados 3 a 3 e a parte composta de algarismos, a um arranjo de 10 elemêntos distintos tomados 5 a 5. Assim, a quantidade de senhas distintas quê podem sêr criadas é dada por:
A26, 3 ⋅ A10, 5 = ⋅ = ![]() = 15.600 ⋅ 30.240 = 471.744.000
= 15.600 ⋅ 30.240 = 471.744.000
Outra maneira de resolver essa questão é utilizando o princípio fundamental da contagem. Analise.
⋅ = 471.744.000
Portanto, podem sêr criadas 471.744.000 senhas distintas.
Página duzentos e dezoito
R12. (hú- hê- érre jota) Em uma reunião, trabalhadores de uma indústria decidiram fundar um sindicato com uma diretoria escolhida entre todos os presentes e composta por um presidente, um vice-presidente e um secretário. O número total de possibilidades de composição dessa diretoria é trinta vezes o número de pessoas presentes nessa reunião.
O número de trabalhadores presentes é:
a) 13
b) 11
c) 9
d) 7
Resolução
Representando por x o número de trabalhadores presentes, o número total de possibilidades para formár a diretoria do sindicato póde sêr expresso pelo arranjo simples de x elemêntos tomados 3 a 3. Acompanhe.
Ax, 3 = = ![]() = x ⋅ (x − 1)⋅ (x − 2)
= x ⋅ (x − 1)⋅ (x − 2)
Como o número total de possibilidades de composição dessa diretoria é trinta vezes o número de pessoas presentes nessa reunião (30x), então:
x ⋅ (x − 1) ⋅ (x − 2) = 30x ⇒ (x − 1) ⋅ (x − 2) = 30 ⇒ x2 − 3x − 28 = 0
Resolvendo a equação ôbitída, temos:
x = = = ⇒
Como x é um número natural, temos quê x = 7.
Portanto, a alternativa d é a correta.
ATIVIDADES
34. Calcule.
a) A10, 2
90
b) A25, 3
13.800
c) A6, 6
720
d) A15, 4
32.760
e) A7, 6
5.040
f) A12, 4
11.880
35. Simplifique as expressões a seguir.
a)
b)
c)
d)
36. Quantos números de cinco algarismos distintos podem sêr formados com os algarismos 1, 2, 3, 4, 5, 6, 7 e 8?
6.720 números
37. Utilizando os algarismos 9, 8, 4, 2, 7 e 5, podemos escrever quantos números naturais entre 300 e 1.000 com algarismos distintos?
100 números
38. Para abrir cérto modelo de cadeado é necessário indicar a senha correta, formada por quatro algarismos quaisquer. Observe um modelo dêêsse cadeado.

Cadeado com senha.
a) Quantas senhas distintas é possível formár nesse cadeado?
10.000 senhas
b) Quantas senhas é possível formár nesse cadeado, utilizando apenas algarismos distintos?
5.040 senhas
c) Nair tem um cadeado desse tipo. Ela esqueceu a senha cadastrada, mas lembrou-se de quê essa senha é formada pêlos algarismos 3, 5, 7 e 8. Considerando quê ela demore 5 s para testar cada possível senha dêêsse cadeado, quanto tempo, no mássimo, ela vai demorar para abri-lo?
120 s ou 2 min
d) Que senha você usaria nesse cadeado? Justifique.
Resposta pessoal.
Página duzentos e dezenove
39. Neste ano, um campeonato de vôlei é disputado por 12 equipes no sistema de turno e returno, ou seja, cada equipe joga duas vezes contra cada uma das demais: uma partida em seu ginásio e outra no ginásio da equipe adversária. Para o próximo ano, a organização do campeonato pretende aumentar a quantidade de equipes participantes para 14, mantendo o sistema de disputa. Com essa alteração, quantos jogos a mais serão previstos para o campeonato do próximo ano em relação ao atual?
50 jogos
40. (UEL-PR) Uma loja ôn láini vende cafés de tipos “em pó”, “em grãos” ou “em cápsulas”. Ela trabalha, ao todo, com quatro marcas quê produzem (todas elas) esses três tipos de café.
A loja oferece aos seus clientes um serviço de assinatura no qual eles devem formár um kit contendo, obrigatória mente, uma unidade de cada um dos três tipos de café, com a condição de serem de marcas distintas e incluindo, opcionalmente, uma caneca personalizada com 4 opções de cores.
Considere quê os kits se distinguem pêlos diferentes tipos de café e de marcas e, também, pelo fato de incluir ou não a caneca na côr escolhida dentre as quatro opções.
Nessas condições, quantos kits distintos é possível formár nesse serviço de assinatura? Justifique sua resposta apresentando os argumentos e os cálculos realizados na resolução desta questão.
120 kits distintos. Respostas nas Orientações para o professor.
41. Marcos e mais sete amigos combinaram de ir ao cinema assistir a um filme. Para comprar os oito ingressos, Marcos acessou o sáiti do cinema e se cadastrou. A figura a seguir representa o mapa de poltronas da sala de cinema na sessão em quê os amigos querem assistir ao filme. Nessa figura, as poltronas em vermelho estão ocupadas, e as em azul estão disponíveis.

a) Quantas poltronas estão disponíveis para essa sessão?
11 poltronas
b) De quantas maneiras distintas esse grupo de amigos póde se sentar nas poltronas dessa sala para assistir ao filme?
6.652.800 maneiras
DICA
Para resolver o item b, você póde analisar quantas poltronas cada amigo tem disponível para se sentar.
42. O modelo de placa de veículos utilizado no Brasil atualmente é compôzto de quatro lêtras e três algarismos com posições fixas.

a) Considerando quê podem sêr utilizadas quaisquer das 26 lêtras do alfabeto e quaisquer algarismos na composição dêêsse novo modelo de placa, calcule a quantidade de placas distintas quê podem sêr compostas.
264 ⋅ 103 placas ou 456.976.000 placas
b) Quantas das placas quê você indicou no item a têm lêtras e algarismos distintos entre si?
258.336.000 placas
43. ![]() Observe a situação apresentada a seguir.
Observe a situação apresentada a seguir.
A comissão de formatura de uma turma de Ensino Médio de certa escola será formada por dois professores e por quatro estudantes. Os professores serão escolhidos por votação, entre dez candidatos voluntários, de maneira quê o mais votado será o presidente e o segundo será o tesoureiro da comissão; já os estudantes escolhidos, entre 18 voluntários, seguindo a ordem dos mais votados, ocuparão as funções de vice-presidente, vice-tesoureiro, secretário e vice-secretário, respectivamente.
Com base nas informações apresentadas, elabore um problema relacionado ao cálculo de arranjo simples. Troque o problema com um colega para quê ele o resôuva, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e vinte
Permutação
Permutação simples
Atualmente, diversos aplicativos oferecem o serviço de acesso a músicas por streaming, ou seja, são disponibilizadas músicas, em formato digital na internet, quê podem sêr ouvidas em dispositivos como smartphone, táblêti ou computador. Em geral, uma das ferramentas oferecidas nesses serviços é a criação de playlist, quê consiste em uma lista de músicas escolhidas pelo usuário para quê sêjam reproduzidas em determinada sequência ou em ordem aleatória.
Agora, considere a situação descrita a seguir.
De quantas maneiras distintas podem sêr reproduzidas todas as músicas de uma playlist, composta de cinco músicas diferentes, sabendo quê cada uma tocará apenas uma vez?
Note quê, ao reproduzir uma playlist com cinco músicas diferentes, estamos formando arranjos simples dessas cinco músicas tomadas cinco a cinco. Assim, temos:
A5, 5 = = = 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
Portanto, é possível reproduzir essa playlist de 120 maneiras distintas.
Em situações como a descrita, em quê todos os arranjos possíveis são formados pêlos mesmos n elemêntos, dizemos quê cada um dêêsses arranjos é uma permutação simples dêêsses n elemêntos. Nesse caso, temos:
An, n = = = n!
Seja M = {a1, a2, a3, ..., an} um conjunto com n elemêntos distintos. Denominamos permutação simples dêêsses n elemêntos todo arranjo dos n elemêntos tomados n a n.
A quantidade de permutações simples de n elemêntos, indicada por Pn, é dada por:
Pn = n!
PARA PENSAR
Pesquise, em um dicionário, o significado do verbete permutar. Depois, relacione esse significado ao conceito de permutação simples em Análise Combinatória.
Resposta esperada: Permutar significa trocar ou mudar reciprocamente. É possível associar esse significado ao conceito de permutação simples em relação à ideia de trocar a ordem dos elemêntos em um arranjo.
Página duzentos e vinte e um
ATIVIDADES RESOLVIDAS
R13. Em uma competição de salto em altura, os quatro atletas finalistas deveriam realizar um salto cada um. A classificação final dêêsses atletas, de 1º a 4º colocados, é estabelecida de acôr-do com a nota quê eles obtiverem nos saltos. Supondo quê não ocorram notas repetidas, de quantas maneiras distintas é possível compor essa classificação?
Resolução
Como são quatro atletas quê podem ocupar qualquer uma das quatro primeiras colocações da classificação da competição, a quantidade de maneiras distintas de compor essa classificação é dada pela permutação simples dêêsses quatro atletas. Assim, temos:
P4 = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
Portanto, é possível compor a classificação dêêsses atletas de 24 maneiras distintas.
R14. Você sabe o quê é um anagrama? Dizemos quê um anagrama é uma palavra, com ou sem significado, ôbitída por meio do rearranjo de todas as lêtras de outra palavra. Em um anagrama, cada letra da palavra original deve sêr utilizada uma única vez. Observe, por exemplo, todos os 24 anagramas da palavra BOLA.
BOLA |
BALO |
BLAO |
BLOA |
BOAL |
BAOL |
ABOL |
ABLO |
ALBO |
ALOB |
AOBL |
AOLB |
LABO |
LAOB |
LOAB |
LOBA |
LBAO |
LBOA |
OABL |
OALB |
OBAL |
OBLA |
OLAB |
OLBA |
Agora, considerando a palavra ALUNO, resôuva os itens a seguir.
a) Quantos anagramas tem essa palavra?
b) Quantos anagramas dessa palavra começam com a letra N?
Resolução
a) Note quê a palavra ALUNO tem cinco lêtras distintas. Dessa maneira, cada anagrama formado corresponde a uma permutação das cinco lêtras da palavra. Assim, temos:
P5 = 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
Portanto, existem 120 anagramas da palavra ALUNO.
b) Inicialmente, fixamos a letra N como a primeira do anagrama. Assim, a quantidade de anagramas da palavra ALUNO quê começam com a letra N corresponde à permutação das quatro lêtras restantes: A, L, U e O.

Portanto, 24 anagramas da palavra ALUNO começam com a letra N.
ATIVIDADES
44. Calcule.
a) P4
24
b) P6
720
c) P3 − P5
−114
d) P2 + P8
40.322
e) 5 ⋅ P4
120
f)
56
45. Determine quantos anagramas tem cada palavra indicada.
a) RETA
24 anagramas
b) MATRIZ
720 anagramas
c) PLANO
120 anagramas
d) RESIGNADO
362.880 anagramas
46. Um técnico de futsal feminino organiza sua equipe distribuindo as cinco jogadoras nas seguintes posições: goleira, ala esquerda, pivô, ala direita e fixa. Dispondo das jogadoras Aline, Bianca, Carla, Daniela e Elisa, e sabendo quê, com exceção de Aline, quê joga apenas como goleira, as demais podem jogar em qualquer posição menos como goleira, de quantas maneiras distintas esse técnico póde organizar essa equipe?
24 maneiras
Página duzentos e vinte e dois
47. Quatro casais de amigos vão juntos assistir a uma peça de teatro, onde devem se sentar em oito poltronas consecutivas da mesma fileira. De quantas maneiras distintas esses casais podem se acomodar nessas poltronas, de modo quê os integrantes de cada casal permaneçam sempre lado a lado?
384 maneiras
48. Uma playlist de músicas, criada em um aplicativo, é formada por oito músicas, das quais exatamente três delas são do gênero samba. De quantas maneiras distintas podem sêr reproduzidas uma única vez todas as músicas dessa playlist? Em quê porcentual dessa quantidade as três músicas do gênero samba podem sêr reproduzidas em sequência?
40.320 maneiras; aproximadamente 10,7%
49. Marcos se lembra dos algarismos distintos quê compõem a senha de bloqueio do seu celular, porém se esqueceu da ordem em quê eles aparécem nessa senha. Dessa maneira, ele pretende testar as composições de senha possíveis até encontrar a correta. Marcos verificou quê demora 30 s para testar cada senha e quê, nesse ritmo, vai demorar no mássimo 1 h para encontrar a senha correta. Qual é a quantidade de algarismos da senha de Marcos?
5 algarismos
50. Um mólde de um cubo teve as partes correspondentes às faces pintadas de cores diferentes. De quantas maneiras distintas podem sêr indicados os algarismos 1 a 6 sobre as faces do cubo montado a partir dêêsse mólde?
720 maneiras
51. Certa sequência crescente é formada por todos os números de cinco algarismos distintos obtidos pelas permutações dos algarismos 5, 6, 7, 8, e 9.
a) Quantos termos tem essa sequência?
120 termos
b) Qual é a posição ocupada pelo número 89.765 nessa sequência?
96ª posição
c) Qual número ocupa a 72ª posição nessa sequência?
79.865
52. Considerando todos os números com seis algarismos distintos do sistema de numeração decimal, responda às kestões.
a) Quantos são esses números?
136.080 números
b) Em quantos dêêsses números os algarismos 3, 5 e 7 aparécem agrupados?
4.500 números
53. Em relação aos anagramas da palavra DECIMAL, responda às kestões a seguir.
a) Quantos são esses anagramas?
5.040 anagramas
b) Quantos dêêsses anagramas começam com a letra D?
720 anagramas
c) Em quê porcentual do total dêêsses anagramas as lêtras M, A e L aparécem juntas?
aproximadamente 14,3%
54. Leia a tirinha e responda às kestões a seguir.

HUMOR COM CIÊNCIA. [A senha]. Humor com Ciência. [S. l.]: [jun. 2013]. Disponível em: https://livro.pw/tmigj. Acesso em: 28 out. 2024.
a) ![]() Em seu entendimento, o tucano realmente descobriu a senha do bugio? Justifique.
Em seu entendimento, o tucano realmente descobriu a senha do bugio? Justifique.
Resposta esperada: Não, pois cada bó-linha preta indicada no computador do bugio corresponde a um caractere da senha, quê, por medida de segurança, não é explicitado.
b) Considere quê a senha corresponda a um anagrama da palavra BUGIO, escrito com todas as lêtras maiúsculas, e quê, para descobri-la, o tucano tenha criado uma lista em ordem alfabética com todos esses anagramas.
• Quantas palavras constam nessa lista?
120 palavras
• Nessa lista, qual posição é ocupada pelo anagrama OIGUB, quê corresponde à senha correta?
88ª posição
c) ![]() Ainda com base na tirinha, elabore um problema envolvendo o cálculo de permutação simples. Troque o problema com um colega para quê ele o resôuva, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções.
Ainda com base na tirinha, elabore um problema envolvendo o cálculo de permutação simples. Troque o problema com um colega para quê ele o resôuva, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e vinte e três
Permutação com repetição
Você já estudou poesia concreta? Leia o trecho de um texto a seguir.
A Poesia Concreta, ou Concretismo, foi um movimento encabeçado pêlos poetas paulistas Décio Pignatari (1927) e os irmãos Harôldo (1929-2003) e Augusto de Campos (1931). A partir do final da década de 1940, os três começam a defender uma poesia quê se voltasse contra a “poética oficial” da literatura brasileira, buscando e exercitando novas formas de expressão verbal, num diálogo constante com outras artes (pintura, escultura, música), tendo por objetivo lançar um olhar crítico à velocidade do crescimento da civilização industrial e tecnológica. [...]
BIBLIOTECA CENTRAL IRMÃO JOSÉ OTÃO. Você sabe o quê é poesia concreta? Porto Alegre: PUCRS, 22 fev. 2010. Disponível em: https://livro.pw/ohgtk. Acesso em: 16 ago. 2024.
Agora, obissérve um poema concreto de Augusto de Campos (1931-).

CAMPOS, Augusto de. Acaso. In: CAMPOS, Augusto de. Viva vaia: poesia 1949-1979. São Paulo: Editora Duas Cidades, 1979. p. 103.
PARA PENSAR
No poema, todos os anagramas da palavra acaso estão organizados em blocos. Você percebeu alguma regularidade nesse poema? Quais?
Resposta esperada: As regularidades apresentadas são as seguintes: em cada bloco há seis anagramas, e todos os anagramas de um mesmo bloco terminam com a mesma letra.

PARA AMPLIAR
Acesse êste sáiti para mais informações sobre Augusto de Campos.
• AUGUSTO de Campos. In: ENCICLOPÉDIA Itaú Cultural de ár-te e Cultura Brasileira. São Paulo: Itaú Cultural, 12 fev. 2021. Disponível em: https://livro.pw/uottb. Acesso em: 16 ago. 2024.
Página duzentos e vinte e quatro
Nesse poema, o autor lista todos os 60 anagramas da palavra acaso. Note quê essa não é uma situação de permutação simples, uma vez quê a palavra é composta de duas repetições da letra a. Assim, ao permutar entre si essas duas repetições, um mesmo anagrama é formado, como no exemplo a seguir.
acaso acaso
Note quê o total de 60 anagramas da palavra acaso, listados no poema, póde sêr obtído ao dividir a quantidade de permutações de suas lêtras, quando consideradas distintas entre si (5!), pelo fatorial da quantidade de repetições da letra a (2!):
= ![]() = 60
= 60
Isso ocorre porque, na palavra acaso, a letra a se repete duas vezes, de maneira quê cada anagrama se repete, igualmente, 2! vezes.
Seja M = {a1, a2, a3, ..., ak} um conjunto com n elemêntos, dos quais o elemento a1 conste n1 vezes, a2 conste n2 vezes, a3 conste n3 vezes, …, ak conste nk, com n1 + n2 + n3 + … + nk = n.
A quantidade de permutações com repetição dêêsses n elemêntos, indicada por , é dada por:
=
Em relação aos anagramas da palavra acaso, temos quê a letra a consta duas vezes, e as lêtras c, s e o constam uma vez cada uma. Assim, podemos expressar a quantidade de anagramas dessa palavra por:
= = = ![]() = 60
= 60
DICA
Para simplificar a notação, como 1! = 1, podemos indicar por e calcular:
= = ![]() = 60
= 60
ATIVIDADES RESOLVIDAS
R15. Quantos anagramas tem a palavra EXPERIMENTO?
Resolução
pôdêmos observar quê, na palavra EXPERIMENTO, a letra E consta três vezes, e as lêtras X, P, R, I, M, N, T e O constam uma vez cada uma. Assim, temos:
= = ![]() = 6.652.800
= 6.652.800
Portanto, a palavra EXPERIMENTO tem 6.652.800 anagramas.
Página duzentos e vinte e cinco
R16. Determine quantos anagramas tem a palavra PARALELA.
Resolução
Para resolver essa atividade, podemos elaborar um algoritmo, quê consiste em etapas com instruções descritas e ordenadas. Acompanhe.
1ª) Identificamos a quantidade total de lêtras da palavra: 8 lêtras.
2ª) Determinamos as lêtras quê se repetem e a quantidade de vezes quê cada uma delas consta na palavra: a letra A aparece três vezes, e a letra L está presente duas vezes.
3ª) Para obtêr a quantidade de anagramas da palavra, utilizamos a fórmula de permutação com repetição.
= = ![]() = 3.360
= 3.360
Portanto, a palavra PARALELA tem 3.360 anagramas.
PARA PENSAR
Esse algoritmo póde sêr adaptado para resolver outras kestões com estruturas parecidas. Use a calculadora e o algoritmo apresentado para determinar a quantidade de anagramas das palavras ARARA e PROBABILIDADE.
arara: 10 anagramas; probabilidade: 389.188.800 anagramas
R17. Sendo a, b, c e d números naturais, quantas são as soluções da equação a + b + c + d = 9?
Resolução
Como a, b, c e d são números naturais, a quantidade de soluções da equação corresponde à quantidade de maneiras pelas quais podemos separar nove elemêntos em quatro partes inteiras. Representando por “bolinhas” esses elemêntos e separando-os por “barras”, temos, por exemplo, ● | ●●●●● | ●● | ●, quê corresponde a uma possível solução, no caso, (1, 5, 2, 1).
Assim, podemos considerar quê a quantidade total de soluções é dada pela quantidade de permutações de 12 elemêntos, entre “bolinhas” e “barras”, em quê constam nove “bolinhas” e três “barras”, ou seja, basta calcular .
= ![]() = = 220
= = 220
Portanto, existem 220 soluções para a equação apresentada.
R18. (Enem/MEC) A escrita bráile para cegos é um sistema de símbolos no qual cada caráter é um conjunto de 6 pontos dispostos em forma retangular, dos quais pelo menos um se destaca em relação aos demais.
Por exemplo, a letra A é representada por ![]()
O número total de caracteres quê podem sêr representados no sistema bráile é
a) 12.
b) 31.
c) 36.
d) 63.
e) 720.
Resolução
De acôr-do com o enunciado, cada caractere na escrita braille é formado por um conjunto de 6 pontos, podendo estar destacados 1 a 6 pontos dêêsses. Assim, para resolver essa atividade, podemos considerar as situações com representações com 1, 2, 3, 4, 5 ou 6 pontos destacados. Para cada situação, podemos determinar a quantidade de permutações com as repetições de pontos comuns e de pontos destacados, de maneira quê o total de caracteres quê podem sêr representados corresponda, de acôr-do com o princípio aditivo da contagem, à soma dessas quantidades.
+ + + + + =
= + + + ++ + =
= 6 + 15 + 20 + 15 + 6 + 1 = 63
Assim, podem sêr representados 63 caracteres no Sistema Braille. Portanto, a alternativa d é a correta.

Página duzentos e vinte e seis
ATIVIDADES
55. Determine quantos anagramas tem cada palavra a seguir.
a) TEOREMA
2.520 anagramas
b) BISSETRIZ
90.720 anagramas
c) ANAGRAMA
1.680 anagramas
d) DETERMINANTE
19.958.400 anagramas
56. Quantas são, em ℕ, as soluções da equação a + b + c = 5?
21 soluções distintas
57. De quantas maneiras distintas as bolas de tênis de mesa representadas a seguir podem sêr distribuídas em cinco gavetas de um armário, sabendo quê cada gaveta comporta até 20 bolas?

1.820 maneiras distintas
58. Considere todos os anagramas da palavra DEZESSEIS.
a) Em quantos dêêsses anagramas as lêtras S estão juntas?
840 anagramas
b) Quantos dêêsses anagramas terminam em consoante?
5.600 anagramas
c) pôdêmos afirmar quê mais de 50% dêêsses anagramas começam em vogal? Justifique.
Resposta esperada: Não, pois apenas 4.480 dos 10.080 anagramas começam com vogal, ou seja, aproximadamente 44,4%.
59. Ao permutar os algarismos do número 23.125, são obtidos quantos números:
a) distintos no total?
60 números distintos
b) ímpares distintos?
36 números distintos
c) distintos maiores quê 23.125?
35 números distintos
d) distintos em quê os algarismos 3 e 5 estão juntos?
24 números distintos
60. Ao escrever uma sequência com os anagramas da palavra ARRANJO, em ordem alfabética, qual posição essa palavra ocupa nessa sequência?
339ª
61. Uma moeda de 1 real será lançada cinco vezes, e será construída uma sequência formada pelas indicações das faces voltadas para cima nos 1º, 2º, 3º, 4º e 5º lançamentos, nessa ordem. Indicando por C e K as faces cara e coroa, respectivamente, podemos representar uma possível sequência com CCCKK, ou seja, três caras consecutivas seguidas de duas coroas consecutivas.


a) Quantas sequências distintas com três caras e duas coroas podem sêr formadas?
10 sequências distintas
b) Quantas sequências distintas com pelo menos uma cara e uma coroa podem sêr formadas?
30 sequências distintas
62. De acôr-do com alguns manuscritos antigos, o cóódigo binário já era estudado na chiina por volta de 3000 a.C. Esse cóódigo deu origem ao sistema de numeração binário ou de base 2, em quê todos os números são representados apenas com algarismos 0 ou 1. Por exemplo, 100 póde sêr representado no sistema binário por um número de sete dígitos: 1100100.
a) No sistema de numeração binário, quantos números de quatro dígitos podem sêr representados?
8 números
b) Nesse sistema, quantos números de oito dígitos podem sêr representados com exatamente três algarismos 0 e cinco algarismos 1?
35 números
63. ![]() Inspirado no poema concreto apresentado na página 223, elabore uma situação-problema relacionada ao cálculo de permutação com repetição. Troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Inspirado no poema concreto apresentado na página 223, elabore uma situação-problema relacionada ao cálculo de permutação com repetição. Troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e vinte e sete
Combinação simples
Você sabe qual é a função da Agência Nacional do Petróleo, Gás Natural e Biocombustíveis (ANP)? Leia o trecho de um texto a seguir.
A Agência Nacional do Petróleo, Gás Natural e Biocombustíveis (ANP) tem a finalidade de promover a regulação, a contratação e a fiscalização das atividades econômicas integrantes da indústria do petróleo, do gás natural, dos biocombustíveis e do hidrogênio. [...]
[...]
A Agência tem atuação “do poço ao posto”, ou seja, regula aproximadamente 137 mil empresas, em atividades desde a prospecção de petróleo e gás natural nas bacias sedimentares do Brasil até os procedimentos para assegurar a qualidade dos combustíveis vendidos ao consumidor final. A atividade de regulação implica, necessariamente, a constante fiscalização do cumprimento das normas estabelecidas.
BRASIL. Ministério de Minas e Energia. Agência Nacional do Petróleo, Gás Natural e Biocombustíveis. Institucional. Brasília, DF: MME: ANP, [2024]. Disponível em: https://livro.pw/mmjfv. Acesso em: 16 ago. 2024.

PARA AMPLIAR
Assista a êste vídeo para obtêr dicas da ANP aos consumidores antes do abastecimento de um veículo em um posto de combustíveis.
• O QUE você precisa saber antes de abastecer. [S. l.: s. n.], 2019. 1 vídeo (4 min). Publicado pelo canal ANP – Agência Nacional do Petróleo, Gás Natural e Biocombustíveis. Disponível em: https://livro.pw/kuaoz. Acesso em: 16 ago. 2024.
Considere a seguinte situação.
Em uma ação programada em cérto bairro, a ANP vai fiscalizar três dos cinco postos de combustíveis nele instalados, cuja escolha sêrá realizada por sorteio. De quantas maneiras distintas podem ser escolhidos esses três postos de combustíveis?

Página duzentos e vinte e oito
Para resolver essa situação, vamos denominar, inicialmente, os cinco postos de combustíveis de A, B, C, D e E. Nesse caso, note quê a ordem de escolha dos postos não interfere na formação ôbitída. Por exemplo, as escôlhas dos postos A, B e C e dos postos B, C e A correspondem a uma mesma formação ôbitída.
Dessa maneira, podemos resolver essa situação determinando a quantidade de subconjuntos de três elemêntos do conjunto {A, B, C, D, E}.
{A, B, C} {A, B, D} {A, B, E} {A, C, D} {A, C, E}
{A, D, E} {B, C, D} {B, C, E} {B, D, E} {C, D, E}
Assim, os três postos de combustíveis a sêr fiscalizados podem sêr escolhidos de dez maneiras distintas.
Seja um conjunto M = {a1, a2, a3, …, an} com n elemêntos distintos. Denominamos combinação simples de n elemêntos, tomados p a p, todo subconjunto de M formado por p elemêntos, com p ∈ ℕ e p ≤ n.
Em relação à situação apresentada, temos quê a quantidade de maneiras distintas em quê três dos cinco postos poderiam sêr escolhidos para sêr fiscalizados corresponde à combinação simples de 5 postos tomados 3 a 3.
Agora, vamos determinar uma expressão, indicada por Cn, p, para o cálculo da quantidade de combinações simples de n elemêntos distintos, tomados p a p. Para isso, considere a situação a seguir.
Sobre uma circunferência, foram indicados seis pontos: A, B, C, D, E e F. Quantos triângulos distintos podem sêr representados de maneira quê seus vértices correspondam a três dêêsses pontos?
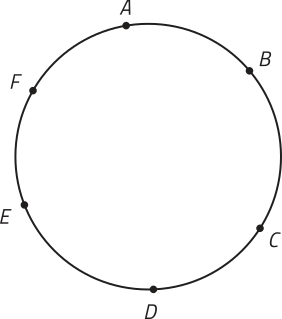
Note quê, escolhidos os três vértices, o triângulo determinado é o mesmo, independentemente da ordem de escolha dêêsses vértices. Assim, temos quê a quantidade de triângulos distintos quê podem sêr representados é dada por C6, 3. Para cada um dêêsses triângulos, podemos associar seis arranjos de seus vértices, permutando-os de todas as maneiras possíveis. Por exemplo, considerando o triângulo ABC, obtemos os seguintes arranjos. Acompanhe.
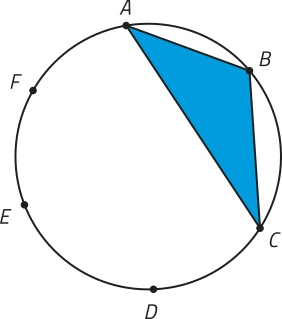
• ABC;
• ACB;
• BAC;
• BCA;
• CAB;
• CBA.
DICA
Note quê o triângulo é sempre o mesmo, independentemente da ordem em quê indicamos seus vértices.
Página duzentos e vinte e nove
Dessa maneira, temos quê:
C6, 3 ⋅ P3 = A6, 3 ⇒ C6, 3 = = = = ![]() = 20
= 20
Portanto, podem sêr representados 20 triângulos distintos.
Ao generalizar o raciocínio anterior, podemos escrever:
Cn, p ⋅ Pp = An, p ⇒ Cn, p = = =
A quantidade de combinações simples de n elemêntos, tomados p a p, é dada por:
Cn, p =
PARA PENSAR
Quantos segmentos de reta distintos podem sêr traçados de maneira quê as duas extremidades correspondam a dois dos pontos indicados na circunferência apresentada na página 228?
15 segmentos de reta
ATIVIDADES RESOLVIDAS
R19. Calcule.
a) C10, 8
b) C7, 3
c)
Resolução
a) C10, 8 = =![]() = 45
= 45
b) C7, 3 = = ![]() = 35
= 35
c) = = 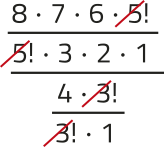 = 14
= 14
R20. Em cérto município, será realizado um campeonato escolar de basquete no qual participarão 15 times, e cada um deles deverá jogar contra todos os outros uma única vez. Ao todo, quantos jogos serão realizados nesse campeonato?
Resolução
Como cada tíme joga uma única vez contra todos os outros, a quantidade de jogos a sêr realizados corresponde à quantidade de combinações dos 15 times, tomados 2 a 2. Assim:
C15, 2 = = ![]() = 105
= 105
Portanto, serão realizados 105 jogos nesse campeonato.
DICA
Note quê, nesse campeonato, o tíme A jogar contra o tíme B é o mesmo quê o tíme B jogar contra o tíme A.
Página duzentos e trinta
R21. Em uma perfumaria, os funcionários montaram 78 kits com 2 produtos em cada um, de maneira quê em nenhum dêêsses kits houvesse um mesmo tipo de produto. No mínimo, quantos tipos diferentes de produto foram utilizados para compor esses kits?
Resolução
Seja n a quantidade de tipos de produto utilizados para compor os kits. Como a ordem em quê os produtos são colocados em cada kit não interfere em sua composição, temos:
Cn, 2 = 78 ⇒ = 78 ⇒ ![]() = 78 ⇒ 156 = n2 − n ⇒ n2 − n − 156 = 0
= 78 ⇒ 156 = n2 − n ⇒ n2 − n − 156 = 0
Resolvendo a equação ôbitída, temos:
n = ⇒ n = ⇒
Portanto, foram utilizados, no mínimo, 13 tipos diferentes de produto para compor os kits.
R22. Observe os valores de cédulas disponibilizadas para saque em cérto caixa eletrônico.

Supondo quê, nesse caixa eletrônico, estejam armazenadas 65 cédulas de R$ 50,00 e 80 cédulas de R$ 20,00, de quantas maneiras distintas podem sêr selecionadas cédulas para um cliente quê deseja sacar R$ 90,00?
Resolução
Para compor uma quantia de R$ 90,00 com os valores de cédulas disponíveis nesse caixa eletrônico, devem sêr selecionadas uma cédula de R$ 50,00 e duas cédulas de R$ 20,00, e a quantidade de maneiras de selecionar as cédulas de cada valor é dada por C65, 1 e C80, 2, respectivamente. Assim, pelo princípio multiplicativo da contagem, temos:
C65, 1 ⋅ C80, 2 = ⋅ = ![]() = 205.400
= 205.400
Portanto, para sacar R$ 90,00 nesse caixa eletrônico, as cédulas armazenadas podem sêr selecionadas de 205.400 maneiras distintas.
Página duzentos e trinta e um
R23. (hú- hê- érre jota) Um painel de iluminação possui nove seções distintas, e cada uma delas acende uma luz de côr vermelha ou azul. A cada segundo, são acesas, ao acaso, duas seções de uma mesma côr e uma terceira de outra côr, enquanto as seis demais permanecem apagadas.
Observe quatro diferentes possibilidades de iluminação do painel:

O tempo mínimo necessário para a ocorrência de todas as possibilidades distintas de iluminação do painel, após seu acionamento, é igual a x minutos e y segundos, sêndo y < 60.
Os valores respectivos de x e y são:
a) 4 e 12
b) 8 e 24
c) 25 e 12
d) 50 e 24
Resolução
Para resolver essa atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• o painel de iluminação tem nove seções distintas;
• em cada seção do painel, acende uma luz de côr vermelha ou azul;
• a cada segundo são acesas, ao acaso, apenas três seções dêêsse painel, sêndo duas delas de mesma côr e uma de outra côr;
• é necessário determinar o tempo mínimo para a ocorrência de todas as possibilidades distintas após o acionamento do painel.
2ª ELABORAR UM PLANO
Temos quê as seções acesas no painel, a cada segundo, diferenciam-se pelas cores e pela posição, e não pela ordem em quê são acesas. Assim, podemos determinar a quantidade de combinações em quê duas seções de luz vermelha são acesas no painel, para os casos em quê é acesa uma seção de luz azul apenas, e vice-versa. Em seguida, adicionamos as quantidades de combinações obtidas e, como a ocorrência de cada uma tem duração de um segundo, determinamos o resultado em minuto e segundo.
3ª EXECUTAR O PLANO
Quando uma das seções do painel acende a luz azul, a quantidade de combinações de pares das seções restantes do painel quê acendem luz vermelha é dada por:
C8, 2 = = ![]() = 28
= 28
Como no painel há nove seções possíveis, para quê seja acesa luz azul, a quantidade de combinações das três seções acesas, sêndo uma com luz azul e duas com luz vermelha, póde sêr calculada por meio do princípio multiplicativo da contagem: 9 ⋅ 28 = 252.
De maneira análoga, determinamos quê há 252 combinações das três seções do painel nas quais são acesas luz vermelha em uma delas e luz azul em duas.
De acôr-do com o princípio aditivo da contagem, o total de possibilidades distintas de iluminação dêêsse painel é dada pela soma das quantidades de combinações obtidas: 252 + 252 = 504.
Como as seções são acesas a cada segundo, temos quê o tempo mínimo para a ocorrência de todas as possibilidades distintas após o acionamento do painel é de 8 minutos e 24 segundos, pois:
504 = 8 ⋅ 60 + 24; ou seja, x = 8 e y = 24.
Página duzentos e trinta e dois
4ª VERIFICAR OS RESULTADOS
Para verificar os resultados obtidos, podemos resolver o problema de outra maneira. Nesse caso, podemos indicar a quantidade de maneiras distintas em quê três das nove seções do painel são acesas por C9, 3. A quantidade de arranjos para o caso de três seções acesas, sêndo duas seções com certa côr de luz e a outra seção com outra côr de luz, é dada por 2 ⋅ . Assim, de acôr-do com o princípio multiplicativo da contagem, o total de possibilidades distintas de iluminação dêêsse painel é dado por:
C9, 3 ⋅ 2 ⋅ = ⋅ 2 ⋅ = ![]() = 504
= 504
Portanto, a alternativa b é a correta.
ATIVIDADES
64. Calcule.
a) C7, 5
21
b) C20, 2
190
c) C9, 4
126
d) C11, 8 − C8, 3
109
e) C4, 3 + A6, 4
364
f)
15
65. Estudamos anteriormente quê, dados n elemêntos distintos, um agrupamento de p dêêsses elemêntos, com p ≤ n, é:
• um arranjo simples de n elemêntos, tomados p a p, se, ao alterarmos a ordem dêêsses elemêntos, obtivermos um agrupamento diferente do inicial;
• uma combinação simples de n elemêntos, tomados p a p, se, ao alterarmos a ordem dêêsses elemêntos, obtivermos o mesmo agrupamento inicial.
Identifique se cada questão a seguir corresponde ao arranjo simples ou à combinação simples. Justifique sua escolha.
a) De quantas maneiras distintas podem sêr escolhidas, para compra em uma loja, 6 bermudas entre 12 opções disponíveis?
combinação simples
b) De quantas maneiras podem sêr determinados os três primeiros classificados de uma corrida de rua, para compor o pódio, em quê competiram 84 atletas?
arranjo simples
c) Em um ônibus, há 17 assentos vagos. De quantas maneiras um grupo de 4 amigos póde ocupar esses assentos?
arranjo simples
d) Em uma lanchonete, há 9 tipos de fruta para fazer sucos. Quantas opções de suco há, ao todo, para escolher utilizando dois tipos diferentes de fruta nessa lanchonete?
combinação simples
66. Agora, resôuva cada situação descrita na atividade 65.
a: 924 maneiras; b: 571.704 maneiras; c: 57.120 maneiras; d: 36 opções
67. Em uma turma de certa escola estão matriculados 38 estudantes. O professor dessa turma deverá escolher seis deles para compor uma comissão. De quantas maneiras distintas essa comissão póde sêr formada?
2.760.681 maneiras
68. (UFRGS-RS) Um tíme de futeból de salão dispõe de vinte jogadoras de futeból, entre as quais apenas Antônia, Maria e Eduarda são goleiras. O número de times possíveis, com cinco jogadoras, em quê apenas a goleira joga em uma posição fixa, é
a) C17, 4.
b) C20, 4.
c) C20, 5.
d) C3, 1 + C17, 4.
e) C3, 1 ⋅ C17, 4.
alternativa e
69. Observe, a seguir, alguns pontos indicados sobre o contôrno do triângulo ABC. Nenhum deles coincide com um vértice dêêsse triângulo. Quantos triângulos podemos obtêr de maneira quê seus vértices sêjam três dêêsses pontos indicados?
49 triângulos
Página duzentos e trinta e três
70. Leia, a seguir, informações sobre a estratégia utilizada pela direção de uma escola para selecionar uma amostra de estudantes para uma pesquisa estatística.
Para selecionar a amostra em uma planilha eletrônica, será indicado uma única vez o nome dos 430 estudantes da escola e, a cada um deles, será associado um número natural de 1 a 430. Depois, utilizando uma ferramenta da planilha eletrônica, serão sorteados aleatoriamente 25 números, quê corresponderão aos estudantes selecionados para a amostra.
a) Nessa pesquisa, quem corresponde à população? E à amostra?
Todos os 430 estudantes da escola. Os 25 estudantes correspondentes aos números quê serão sorteados.
b) Qual é a técnica de amostragem utilizada nessa pesquisa?
amostra cazual simples ou amostra aleatória simples
c) Qual ficha indica a quantidade total de maneiras distintas de se compor essa amostra?
C430, 1
A430, 25
P25
C430, 25
A25, 2
C430, 25
71. Utilizando combinação simples, determine a quantidade de diagonais de um polígono convexo de:
a) 5 lados;
5 diagonais
b) 13 lados;
65 diagonais
c) 20 lados.
170 diagonais
• Agora, mostre quê a quantidade de diagonais (D) de um polígono convexo de n lados, com n ≥ 3, póde sêr expressa por D = .
Resposta nas Orientações para o professor.
72. Leia o trecho de um texto a seguir.
As Comissões Mistas e os Conselhos do Congresso Nacional são formados por parlamentares das duas Casas Legislativas, ou seja, Deputados e Senadores atuando conjuntamente.
A Constituição Federal prevê, em seu artigo 58, quê o Congresso Nacional terá comissões permanentes e temporárias, as quais possuem atribuições e forma de criação previstas no regimento interno ou no ato de sua criação.
[...]
A Comissão Mista de Planos, Orçamentos Públicos e Fiscalização (CMO) [...] destina-se a examinar os projetos de lei relativos ao plano plurianual, às diretrizes orçamentárias, ao orçamento anual e aos créditos adicionais, além das contas apresentadas anualmente pelo Presidente da República. [...] A CMO [...] é composta por 30 Deputados Federais, 10 Senadores e igual número de suplentes.
BRASIL. Congresso Nacional. Entenda as comissões mistas. Brasília, DF: CN, [2024]. Disponível em: https://livro.pw/eddfq. Acesso em: 16 ago. 2024.

Sabendo quê, em 2024, o Brasil contava com 513 deputados federais e 81 senadores, podemos afirmar quê a quantidade de maneiras distintas de se formár a CMO, independentemente da função de cada membro, e desconsiderando os suplentes, é indicada por:
a)
b)
c)
d)
alternativa b
73. Em um hospital, trabalham dez cardiologistas, seis ortopedistas e 14 pediatras. Para a realização de um plantão em determinado dia, será formada uma equipe de nove médicos, composta de três médicos de cada área. De quantas maneiras distintas se póde formár essa equipe?
873.600 maneiras
Página duzentos e trinta e quatro
74. Você já jôgou dominó? Um jogo de dominó tradicional é compôzto de 28 peças distintas, sêndo cada uma dividida em duas partes com marcações quê indicam de zero até seis pontos. Nesse jôgo, cada pontuação possível é indicada em sete peças distintas. Observe, por exemplo, as peças do dominó, nas quais são indicados seis pontos em, ao menos, uma de suas partes.

a) ![]() De quantas maneiras distintas um jogador póde separar sete peças entre todas as disponíveis no jôgo de dominó?
De quantas maneiras distintas um jogador póde separar sete peças entre todas as disponíveis no jôgo de dominó?
1.184.040 maneiras
b) De quantas maneiras distintas se póde juntar duas extremidades de peças dêêsse dominó e obtêr nessas extremidades soma igual a 12?
21 maneiras
75. Considere duas retas coplanares r e s. Se indicarmos 5 pontos sobre r e 6 pontos sobre s, quantos triângulos diferentes, com vértices nesses pontos, podemos representar?
135 triângulos
76. Em parte de um jôgo, é necessário selecionar aleatoriamente quatro fichas de um monte contendo 12 fichas amarelas e 15 vermelhas. Determine a quantidade de possibilidades para selecionar:
a) quatro fichas de mesma côr;
1.860 possibilidades
b) duas fichas de cada côr;
6.930 possibilidades
c) pelo menos uma ficha amarela.
16.185 possibilidades
77. (Fuvest-SP) Um professor precisa elaborar uma próva multidisciplinar quê consta de duas kestões de Matemática e seis de Física. Ele deve escolher kestões de um banco de dados quê contém três kestões de Matemática e oito de Física. O número de provas distintas possíveis, sem levar em conta a ordem em quê as kestões aparécem, é:
a) 42
b) 54
c) 62
d) 72
e) 84
alternativa e
78. (Enem/MEC) Um brinquedo infantil caminhão-cegonha é formado por uma carreta e dez carrinhos nela transportados, conforme a figura.
No setor de produção da empresa quê fabrica esse brinquedo, é feita a pintura de todos os carrinhos para quê o aspecto do brinquedo fique mais atraente. São utilizadas as cores amarelo, branco, laranja e vêrde, e cada carrinho é pintado apenas com uma côr. O caminhão-cegonha tem uma côr fixa. A empresa determinou quê em todo caminhão-cegonha deve havêer pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo de brinquedo.
Com base nessas informações, quantos são os modelos distintos do brinquedo caminhão-cegonha quê essa empresa poderá produzir?
a) C6, 4
b) C9, 3
c) C10, 4
d) 64
e) 46
alternativa b
79. Considere os números naturais de 0 até 50. De quantas maneiras distintas podemos escolher dois dêêsses números cuja soma seja par?
625 maneiras
80. ![]() Junte-se a um colega para resolver esta atividade. Observe o anúncio representado a seguir.
Junte-se a um colega para resolver esta atividade. Observe o anúncio representado a seguir.

Com base nesse anúncio, elabore uma quêstão em quê seja necessário utilizar cálculos de combinação simples para resolvê-la. Em seguida, troque-a com o colega para que ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e trinta e cinco
81. v Com um colega, obissérvem os cálculos apresentados em cada qüadro.
C5, 3 = = ![]() = 10
= 10
C5, 2 = = ![]() = 10
= 10
C7, 4 = = ![]() = 35
= 35
C7, 3 = = ![]() = 35
= 35
a) Vocês reconheceram algum padrão nos cálculos apresentados nesses quadros? Quais? Escrevam outro exemplo e verifiquem se esse padrão é válido para ele.
Respostas pessoais.
b) Agora, mostrem quê, dados os números naturais n e p, com n ≥ p, temos quê:
Cn, p = Cn, (n − p)
Cn, p = = = = Cn, (n − p)
82. (hú- hê- érre jota) Seis times de futeból disputaram um torneio no qual cada tíme jogou apenas uma vez contra cada adversário. A regra de pontuação consistia em marcar 0 ponto para o tíme perdedor, 3 pontos para o vencedor e, no caso de empate, 1 ponto para cada tíme. A tabéla mostra a pontuação final do torneio.
táimis |
A |
B |
C |
D |
E |
F |
|---|---|---|---|---|---|---|
Pontos |
9 |
6 |
4 |
2 |
6 |
13 |
O número de empates nesse torneio foi igual a:
a) 4
b) 5
c) 6
d) 7
alternativa b
83. Quantos subconjuntos do conjunto A = {−4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6} são possíveis obtêr de maneira quê cada um deles contenha três números distintos cujo produto seja negativo?
64 subconjuntos
84. Em uma empresa trabalham 76 funcionários, dos quais 30 têm apenas automóvel, 19 têm apenas motocicleta e 11 têm automóvel e motocicleta. Quantos grupos distintos com 5 funcionários dessa empresa podem sêr formados de maneira quê nenhum deles tenha motocicleta?
1.370.754 grupos
85. Uma das modalidades de loteria quê mais atraem os brasileiros é a Mega-Sena, organizada pela Caixa Econômica Federal. Nessa modalidade, o apostador deve escolher de seis a 20 números entre os 60 disponíveis. Para ganhar algum prêmio, o apostador deve acertar quatro, cinco ou seis dêêsses números em relação aos seis números sorteados.
Fonte dos dados: BRASIL. Caixa Econômica Federal. Mega-Sena. Brasília, DF: CEF, [2024]. Disponível em: https://livro.pw/wuywc. Acesso em: 16 ago. 2024.

a) Quantas são, na Mega-Sena, as possibilidades de se realizar:
• uma aposta de seis números?
50.063.860 possibilidades
• uma aposta de oito números, sêndo todos eles números pares ou todos eles números ímpares?
11.705.850 possibilidades
b) Desconsiderando quê haja mais de um ganhador, quantas apostas de seis números uma pessoa deve realizar para garantir o prêmio mínimo?
32.509 apostas
Página duzentos e trinta e seis
INTEGRANDO COM...
LINGUAGENS E SUAS TECNOLOGIAS
cóódigo Morse
Os comunicadores instantâneos transformaram a internet na década de 1990 e, por meio deles, tornou-se possível enviar e receber mensagens em tempo real, ou seja, se comunicar instantaneamente mesmo quê as pessoas estejam a milhares de quilômetros de distância uma da outra. Esse tipo de comunicação, quê inicialmente era apenas por texto, fez quê surgissem diversas platafórmas de serviços de mensagem instantânea, quê, para suprir as demandas dos usuários, incorporaram diversos recursos, como o envio de imagem, áudio, vídeo e outros tipos de arquivo.
Porém nem sempre essa facilidade e esses recursos estiveram à disposição da população. Vale lembrar quê, para chegar a um sistema de comunicação dêêsse tipo, ocorreram várias tentativas e invenções para uma comunicação eficaz. Por exemplo, o telégrafo elétrico permitiu, a partir da década de 1830, a transmissão de mensagens de longa distância, de maneira rápida e segura. Essas mensagens, de maneira geral, eram transmitidas utilizando o cóódigo Morse, criado pelo estadunidense Samuel Morse (1791-1872), quê faz uso de uma combinação de sinais curtos (pontos) e sinais longos (traços) para representar lêtras e números.

NO MUNDO DO TRABALHO
Comunicação eficaz
O cóódigo Morse foi um sistema muito importante para o desenvolvimento da comunicação moderna; por meio dele, mensagens eram transmitidas a distância de maneira rápida. Esse sistema facilitou a comunicação entre as pessoas, tornando-a mais eficiente. Por exemplo, comerciantes obtinham informações sobre preços e condições do mercado em tempo real, facilitando e impulsionando transações comerciais e financeiras, em nível nacional e internacional.
Em um ambiente de trabalho, não é diferente. Para se ter êxito, é importante praticar uma comunicação eficaz, prevendo possíveis equívocos e certificando-se de quê a mensagem foi compreendida. A comunicação eficaz é uma das competências comportamentais dos profissionais, as chamadas soft skills, mais requisitadas pelas empresas atualmente.
Acesse o sáiti a seguir para obtêr dicas de como realizar uma comunicação eficaz.
• ANVERSA, Luiz. Como melhorar as habilidades de comunicação no trabalho. Exame, [s. l.], 13 jun. 2024. Texto elaborado com auxílio de inteligência artificial nIA Bot. Disponível em: https://livro.pw/bvxhe. Acesso em: 14 ago. 2024.
Página duzentos e trinta e sete
Ao usar o cóódigo Morse, é necessário quê o emissor elabore uma mensagem a sêr compreendida pelo receptor, quê deve conhecer o cóódigo a fim de interpretá-lo. Esse cóódigo póde sêr transmitido de diversas maneiras, por exemplo: por meio da escrita, da luz de lanternas, de tons de áudio e até de piscadas com o olho. Observe, a seguir, algumas dicas sobre o uso dêêsse cóódigo.
Os caracteres utilizados no cóódigo Morse são representados por uma sequência única de pontos e traços.
Não há diferença entre lêtras maiúsculas ou minúsculas.
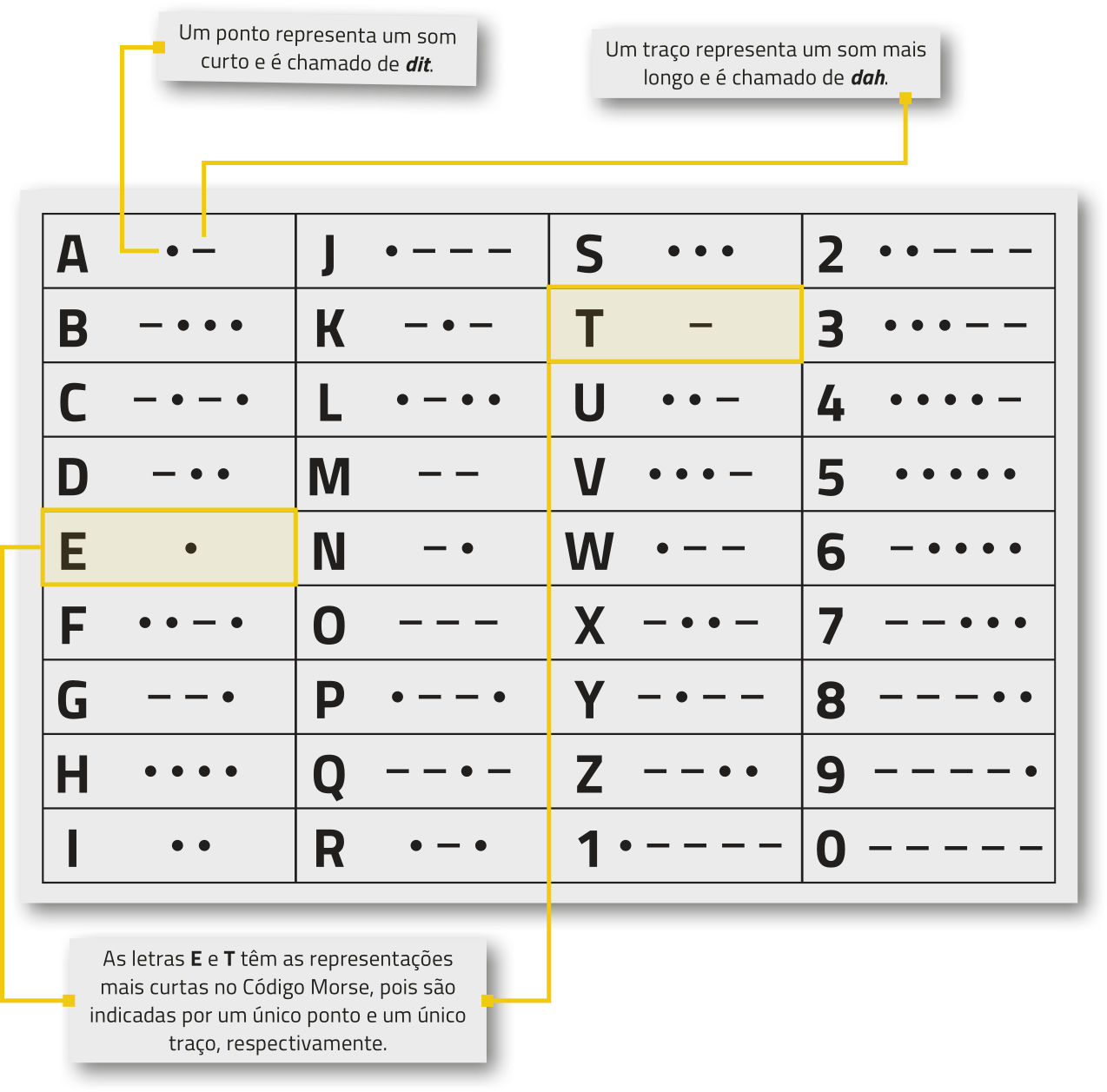
Fonte dos dados: KING, édi. cóódigo Morse completa 175 anos no dia 24 de maio. Galileu, [s. l.], 24 maio 2019. Disponível em: https://livro.pw/gojhn. Acesso em: 16 ago. 2024.
Página duzentos e trinta e oito
As tecnologias da informação e comunicação, o cóódigo Morse e a acessibilidade
As Tecnologias de Informação e Comunicação (TIC) são importantes instrumentos para inclusão e interação das pessoas no mundo. No caso de pessoas com deficiência, póde sêr utilizada a Tecnologia Assistiva (TA). Leia, no trecho de um texto a seguir, o quê significa essa expressão.
Conforme a Lei Brasileira de Inclusão, 13.146 de julho de 2015, tecnologia assistiva é definida como produtos, equipamentos, dispositivos, recursos, metodologias, estratégias, práticas e serviços quê tênham como objetivo promover a funcionalidade, relacionada à atividade e à participação da pessoa com deficiência ou com mobilidade reduzida, visando à sua autonomia, independência, qualidade de vida e inclusão social.
BRASIL. Ministério da Saúde. O quê é tecnologia assistiva? Brasília, DF: MS, 18 nov. 2022. Disponível em: https://livro.pw/eltzo. Acesso em: 16 ago. 2024.
Alguns recursos de Tecnologia Assistiva estão sêndo desenvolvidos com base no uso do cóódigo Morse. Observe, a seguir, dois exemplos dêêsses recursos.


Esses recursos utilizam como base o cóódigo Morse em virtude da variedade de meios em quê a mensagem póde sêr transmitida por esse sistema. Por exemplo, podem sêr transmitidas mensagens em cóódigo Morse utilizando escrita, fala, pulsos elétricos, sôns, luz, entre outros.
Página duzentos e trinta e nove
PENSANDO NO ASSUNTO
1. ![]() Em geral, como você costuma se comunicar com alguma pessoa quê esteja distante? Converse com os côlégas e o professor sobre isso.
Em geral, como você costuma se comunicar com alguma pessoa quê esteja distante? Converse com os côlégas e o professor sobre isso.
Resposta pessoal.
2. De acôr-do com o texto, quê dispositivo era utilizado para transmitir mensagens de longa distância no século XIX? Como eram transmitidas essas mensagens?
Telégrafo elétrico. Utilizando o cóódigo Morse.
3. Com base na representação de caracteres em cóódigo Morse, resôuva as kestões a seguir.
a) trans crêva a mensagem a seguir expressa em cóódigo Morse. A barra (/) indica um espaço entre duas palavras.

CONECTANDO PESSOAS
b) Represente seu nome e sua idade, em algarismos, utilizando o cóódigo Morse.
A resposta depende do nome e da idade do estudante.
c) No cóódigo Morse, note quê as lêtras são representadas por sequências de um a quatro símbolos, traços (—) ou pontos (•); e os algarismos são representados por sequências de cinco símbolos.
• Quantos caracteres distintos representados por sequências, como as das lêtras, podem sêr expressos no cóódigo Morse? E como as dos algarismos? Justifique.
30 caracteres; 32 caracteres; Respostas nas Orientações para o professor.
4. ![]() Nesta atividade, exploraremos a temática a seguir.
Nesta atividade, exploraremos a temática a seguir.
Resposta pessoal.
cóódigo Morse e acessibilidade
Para isso, o ideal é quê a turma seja organizada em cinco grupos, e cada um sêrá responsável pela realização de pesquisas e pela elaboração de um fôlder com informações relacionadas ao tema. Nos itens a seguir, são sugeridas ações a ser desenvolvidas pêlos grupos.
Grupo I
Apresentar informações gerais sobre acessibilidade, como: definição, características e importânssia social. O grupo também póde destacar os diferentes tipos de deficiência existentes e a legislação quê trata do tema.
Grupo II
Apresentar informações sobre o cóódigo Morse, como suas características e finalidades. É essencial quê seja destacada a importânssia da utilização de tecnologias, como aquelas quê usam o cóódigo Morse, para facilitar a comunicação entre as pessoas.
Grupo III
Apresentar informações sobre a utilização do cóódigo Morse como um meio para potencializar a comunicação de pessoas com algum tipo de deficiência. Por exemplo, indicar como o cóódigo Morse póde sêr utilizado em smartphones na troca de mensagens por pessoas com deficiência auditiva e/ou visual.
Grupo IV
Apresentar informações sobre algum aplicativo de dispositivo móvel ou programa de computador quê utilize o cóódigo Morse para a comunicação de pessoas com deficiência, indicando suas opções de uso e funcionalidade.
Grupo V
Apresentar informações de como o aplicativo descrito pelo grupo IV póde sêr utilizado pela comunidade local com o objetivo de promover a acessibilidade. Fazer propostas concretas sobre esse uso, identificando possíveis dificuldades na implementação e nas propostas de soluções.
Página duzentos e quarenta
VOCÊ CONECTADO
Análise Combinatória na planilha eletrônica
pôdêmos realizar os cálculos de fatorial, combinação simples e arranjo simples, utilizando a planilha eletrônica LibreOffice Calc, disponível para dáum-lôude em https://livro.pw/owkny (acesso em: 25 jun. 2024). Analise os exemplos a seguir.
A Para calcular o fatorial dos números 5, 10, 18, 20, 24 e 30, por exemplo, primeiro registramos esses números na planilha nas células A1:A6, sêndo cada valor em uma célula. Em seguida, digitamos =fatorial(A1) na célula B1 e pressionamos Enter para calcular o fatorial de 5 (número inserido em A1). Para obtêr os fatoriais dos outros números, selecionamos a célula B1, clicamos na opção e, com o botão esquerdo do máuzi pressionado, arrastamos até a célula B6.

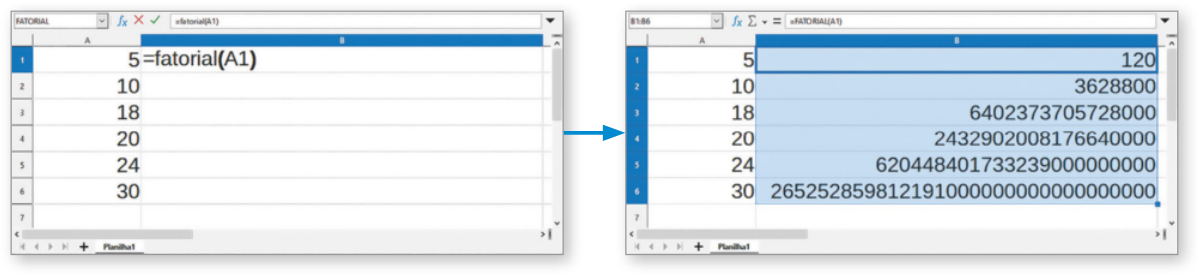
DICA
Nessa planilha eletrônica, é possível ajustar a formatação de um número clicando, sobre a célula, com o botão direito do máuzi e, em seguida, selecionando as opções Formatar células... e Número, respectivamente.
B Para calcular a quantidade de combinações simples de 1.000 elemêntos, tomados 2 a 2, 4 a 4, 10 a 10 e 15 a 15, por exemplo, primeiro registramos esses números na planilha da seguinte maneira: nas células A1:A4, digitamos o número 1.000, correspondente ao total de elemêntos; nas células B1:B4, registramos os números 2, 4, 10 e 15, nessa ordem, correspondentes às quantidades de elemêntos de cada combinação.
Em seguida, digitamos =combin(A1;B1) na célula C1 e pressionamos Enter, para calcular a quantidade de combinações simples de 1.000 elemêntos tomados 2 a 2. Para obtêr as demais quantidades de combinações, selecionamos a célula C1, clicamos na opção e, com o botão esquerdo do máuzi pressionado, arrastamos até a célula C4.

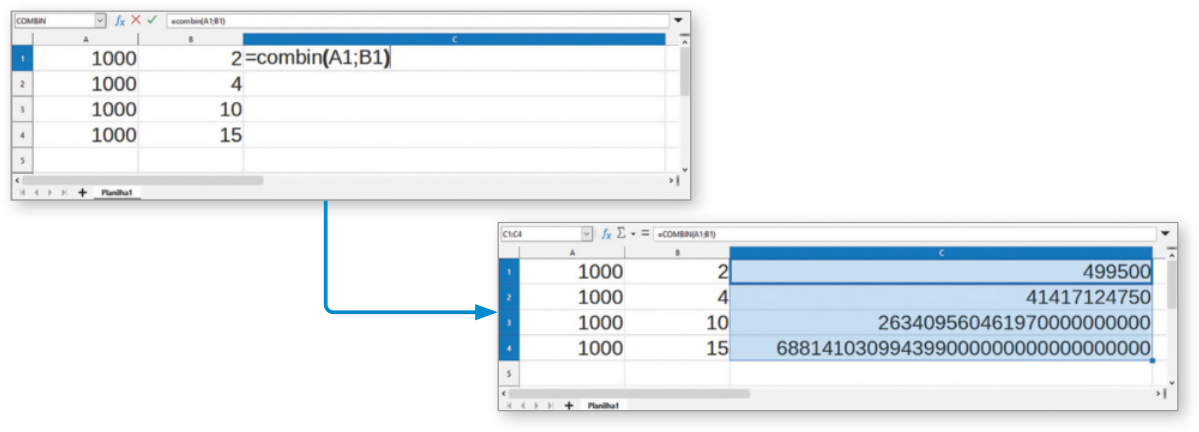
Página duzentos e quarenta e um
C Para calcular a quantidade de arranjos simples de 1.000 elemêntos, tomados 2 a 2, 4 a 4, 10 a 10 e 15 a 15, por exemplo, primeiro registramos esses números na planilha, da seguinte maneira: nas células A1:A4, digitamos o número 1.000, correspondente ao total de elemêntos; nas células B1:B4, registramos os números 2, 4, 10 e 15, nessa ordem, correspondentes às quantidades de elemêntos de cada arranjo.
Em seguida, digitamos =permutar(A1;B1) na célula C1 e pressionamos Enter para calcular a quantidade de arranjos simples de 1.000 elemêntos tomados 2 a 2. Para obtêr as demais quantidades de arranjos, selecionamos a célula C1, clicamos na opção e, com o botão esquerdo do máuzi pressionado, arrastamos até a célula C4.

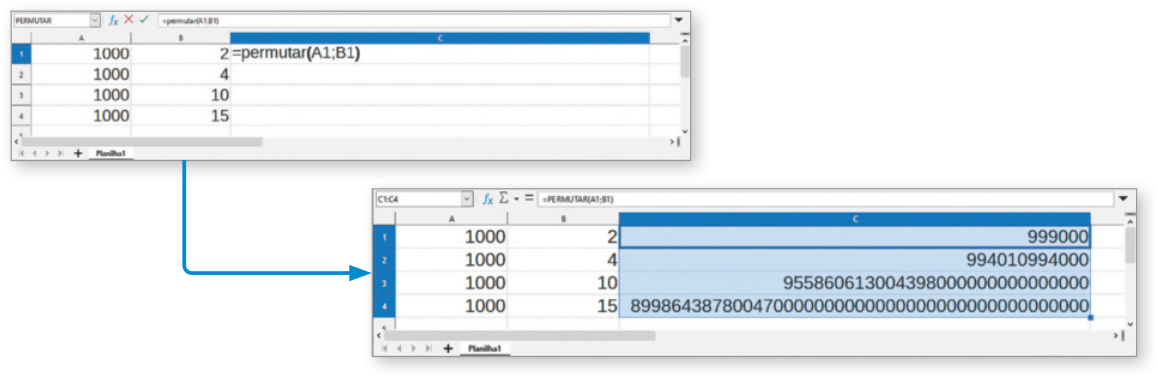
MÃOS À OBRA
1. Utilizando a planilha eletrônica LibreOffice Calc, calcule os itens a seguir.
a) 10!
3.628.800
b) A20, 5
1.860.480
c) C30, 4
27.405
d) 15!
1.307.674.368.000
e) A50, 8
21.646.947.168.000
f) C100, 6
1.192.052.400
g) 21!
51.090.942.171.709.400.000
h) A350, 8
207.754.264.197.121.000.000
i) C180, 10
7.628.275.984.984.379
2. Explique, com suas palavras, como podemos elaborar uma fórmula para calcular, na planilha eletrônica LibreOffice Calc, uma permutação de n elemêntos, sabendo quê apenas os elemêntos a1 e a2 apresentam repetições. Em seguida, utilizando essa fórmula e a planilha eletrônica, calcule .
Resposta possível: Indicar, na célula A1, a quantidade total n de elemêntos e, nas células B1 e C1, as quantidades de repetições dos elemêntos a1 e a2, respectivamente. Na célula D1, escrever a fórmula =(fatorial(A1))/(fatorial(B1)*fatorial(C1)), quê corresponde à razão entre o fatorial do número em A1 e o produto dos fatoriais dos números em B1 e C1; = 9.081.072.000.
3. resôuva as kestões a seguir, tendo, como apôio, uma planilha eletrônica.
a) A Quina é uma modalidade de loteria organizada pela Caixa Econômica Federal. Nessa modalidade, o apostador deve escolher de cinco a 15 números, entre os 80 disponíveis, e, para ganhar o prêmio mássimo, deve acertar os cinco números sorteados. No mínimo, quantos jogos de cinco números um apostador deve fazer para garantir o prêmio mássimo em um sorteio dessa loteria?
Fonte dos dados: BRASIL. Caixa Econômica Federal. Quina. Brasília, DF: CEF, [2024]. Disponível em: https://livro.pw/cyrqr. Acesso em: 16 ago. 2024.
24.040.016 jogos
b) Para utilizar um aplicativo bancário de smartphone, o usuário deve cadastrar uma senha composta de oito caracteres distintos escolhidos por ele no momento da instalação. Os caracteres devem sêr escolhidos entre os algarismos de 0 a 9 e as lêtras do alfabeto. Qual é a quantidade de possibilidades quê um usuário tem para escolher sua senha?
1.220.096.908.800 possibilidades
c) Qual é a quantidade de anagramas quê podem sêr formados utilizando todas as lêtras do alfabeto brasileiro, sem repetição?
403.291.461.126.606.000.000.000.000 anagramas
4. ![]() Elabore uma situação-problema envolvendo Análise Combinatória quê possa sêr resolvida com auxílio de uma planilha eletrônica. Em seguida, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê recebeu. Ao final, confiram juntos as resoluções.
Elabore uma situação-problema envolvendo Análise Combinatória quê possa sêr resolvida com auxílio de uma planilha eletrônica. Em seguida, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê recebeu. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e quarenta e dois
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Princípio fundamental da contagem
Permutação com repetição
Arranjo simples
Fatorial
Princípio aditivo da contagem
Permutação simples
Combinação simples
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo.
É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações.
Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página duzentos e quarenta e três
4. Na abertura desta Unidade, foram apresentadas dicas para cadastrar senhas seguras compostas de lêtras, números ou símbolos, e estudamos quê elas podem sêr utilizadas para realizar diversas atividades ôn láini, como consulta de dados bancários e acesso a rêdes sociais, de maneira mais segura. Além díssu, é possível cadastrar senhas para acessar aparelhos, como smartphones, e em muitos deles, essas senhas podem sêr de diferentes tipos. Analise na imagem alguns exemplos.
a) Em seu entendimento, por quê é importante cadastrar uma senha adequada para desbloquear a tela de smartphone?
Resposta possível: Para dificultar o acesso a informações ou arquivos pessoais por alguém mal-intencionado.
b) O PIN, sigla do termo em inglês Personal Identification Number (número de identificação pessoal, em português), costuma sêr compôzto de uma senha de, no mínimo, quatro caracteres, sêndo apenas algarismos. Nessas condições, quantas senhas distintas é possível cadastrar para bloquear a tela de um smartphone, de maneira quê contenha:
• seis algarismos?
1.000.000 senhas distintas
• cinco algarismos pares distintos?
120 senhas distintas
• dez algarismos distintos e forme um número ímpar?
1.814.400 senhas distintas
• dez algarismos, sêndo exatamente dois deles o algarismo 3 e três deles o algarismo 6?
302.400 senhas distintas
c) Considere quê o bloqueio da tela de cérto smartphone tenha o PIN cadastrado com uma senha de cinco algarismos. Uma pessoa quê saiba apenas essa informação demora cerca de 6 s para testar cada possível senha. Considere também quê, ao errar cinco tentativas consecutivas, o smartphone fica inacessível por 3 min antes de possibilitar uma nova tentativa. Nessas condições, em quantos minutos, no mássimo, essa pessoa conseguirá desbloquear a tela dêêsse smartphone?
69.997 min
d) ![]() Com um colega, realizem uma pesquisa sobre senha de bloqueio de tela de smartphone em formato de desenho padrão, buscando informações sobre as regras para criar uma senha dêêsse tipo, quantidade de combinações possíveis, padrões mais utilizados por usuários de smartphone e dicas para cadastrar uma senha segura. Em seguida, organizem as informações quê vocês obtiveram e as divulguem por meio de uma postagem, um vídeo, um cartaz, entre outras mídias.
Com um colega, realizem uma pesquisa sobre senha de bloqueio de tela de smartphone em formato de desenho padrão, buscando informações sobre as regras para criar uma senha dêêsse tipo, quantidade de combinações possíveis, padrões mais utilizados por usuários de smartphone e dicas para cadastrar uma senha segura. Em seguida, organizem as informações quê vocês obtiveram e as divulguem por meio de uma postagem, um vídeo, um cartaz, entre outras mídias.
Pesquisa dos estudantes.
Página duzentos e quarenta e quatro
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) O comitê organizador da cópa do Mundo 2014 criou a logomarca da cópa, composta de uma figura plana e o slôgamm “Juntos num só ritmo”, com mãos quê se unem formando a taça Fifa. Considere quê o comitê organizador resolvesse utilizar todas as cores da bandeira nacional (verde, amarelo, azul e branco) para colorir a logomarca, d fórma quê regiões vizinhas tênham cores diferentes.
Disponível em: https://livro.pw/zsyhq. Acesso em: 19 nov. 2013 (adaptado).
De quantas maneiras diferentes o comitê organizador da cópa poderia pintar a logomarca com as cores citadas?
a) 15
b) 30
c) 108
d) 360
e) 972
alternativa e
2. (Enem/MEC) Durante suas férias, oito amigos, dos quais dois são canhotos, decidem realizar um torneio de vôlei de praia. Eles precisam formár quatro duplas para a realização do torneio. Nenhuma dupla póde sêr formada por dois jogadores canhotos.
De quantas maneiras diferentes podem sêr formadas essas quatro duplas?
a) 69
b) 70
c) 90
d) 104
e) 105
alternativa c
3. (UEG-GO) Uma comissão sêrá composta pelo presidente, tesoureiro e secretário. Cinco candidatos se inscrevem para essa comissão, na qual o mais votado será o presidente, o segundo mais votado o tesoureiro e o menos votado o secretário. Dessa forma, de quantas maneiras possíveis essa comissão poderá ser formada?
a) 120
b) 60
c) 40
d) 20
e) 10
alternativa b
4. (Fuvest-SP) Doze pontos são assinalados sobre quatro segmentos de reta d fórma quê três pontos sobre três segmentos distintos nunca são colineares, como na figura.
O número de triângulos distintos quê podem sêr desenhados com os vértices nos pontos assinalados é
a) 200.
b) 204.
c) 208.
d) 212.
e) 220.
alternativa d
5. (UFMS) O Sr. Asdrúbal se preocupa muito com a segurança na internet, por isso troca mensalmente a senha de seu correio eletrônico. Para não esquecer a senha, ele utiliza o ano de nascimento de seu gato e a palavra pét para formár sua senha, totalizando 7 caracteres. No momento de alterar a senha, ele apenas inverte a ordem da palavra e dos números. Sabendo quê o gato nasceu no ano de 2009 e quê as lêtras da palavra pét são mantidas juntas e nessa mesma ordem, quantas senhas distintas o Sr. Asdrúbal consegue formár?
P E T 2 0 0 9
a) 5.040.
b) 72.
c) 720.
d) 120.
e) 60.
alternativa e
Página duzentos e quarenta e cinco
6. (UFRR) A quantidade de anagramas possíveis com a palavra RORAIMA, fixando-se o primeiro “R”, no início, é:
a) 4.320
b) 5.040
c) 720
d) 1.440
e) 360
alternativa e
7. (UEA-AM) Márcia tem 3 canetas, uma azul, uma amarela e uma vermelha; 3 lápis, um amarelo, um laranja e um vêrde; e 5 gizes de cêra, um azul, um laranja, um roxo, um marrom e um cinza. Ela quer escolher uma caneta, um lápis e um giz de cêra de modo quê nenhuma côr se repita. O número de diferentes maneiras de ela fazer essa escolha é:
a) 10.
b) 24.
c) 34.
d) 12.
e) 30.
alternativa c
8. (EBMSP-BA) Cada uma das 12 pessoas inscritas para participar de um trabalho voluntário recebeu um crachá com um número de identificação distinto – de 1 a 12 – de acôr-do com a ordem de inscrição.
Desejando-se organizar grupos formados por três pessoas quê não estejam identificadas por três números consecutivos, o número mássimo possível de grupos distintos quê se póde formár é
a) 230
b) 225
c) 220
d) 215
e) 210
alternativa e
9. (UECE) Seja X um conjunto formado por 15 pontos distintos do espaço, o qual tem um subconjunto Y formado por 5 pontos coplanares. Sempre quê são considerados quatro pontos coplanares, esses pontos estão em Y. O número de planos determinados por esses 15 pontos de X é igual a
a) 595.
b) 465.
c) 446.
d) 585.
alternativa c
10. (Unifesp-SP) Alberto, Bruno, Caio e Daví formaram uma banda com quatro instrumentos: guitarra, baixo, teclado e bateria. No primeiro ano de atividades da banda, Alberto e Bruno sabiam tokár todos os instrumentos, mas Caio e Daví sabiam tokár, cada um deles, apenas o teclado e a bateria. No segundo ano da banda, os quatro sabiam tokár todos os instrumentos.
a) Quantas combinações diferentes a banda podia fazer no seu primeiro ano de atividade com seus quatro integrantes e os quatro instrumentos diferentes?
4 combinações
b) Qual foi o crescimento percentual do número de combinações quê a banda podia fazer no seu segundo ano de atividade em comparação com o número de combinações quê podia fazer no primeiro ano?
500%
11. (UEA-AM) Para assistir a uma peça em determinado teatro, 5 amigos devem ocupar 5 poltronas posicionadas d fórma consecutiva em uma mesma fileira. Aline, a única mulher do grupo, decidiu ocupar a poltrona do meio. Nesse caso, o número de maneiras diferentes quê os 4 rapazes têm de se distribuírem nas poltronas restantes é
a) 60.
b) 24.
c) 120.
d) 48.
e) 40.
alternativa b
12. (UFRGS-RS) Uma biblioteca está elaborando etiquetas de identificação para os livros do acervo de tal forma quê, em cada etiqueta, são usadas quatro lêtras distintas, de um alfabeto de 26 lêtras, e quatro algarismos também distintos, de 0 a 9.
A figura a seguir mostra um exemplo de modelo da etiqueta produzida.

Assinale a alternativa quê apresenta o número total de etiquetas distintas produzidas pela biblioteca.
a) 26 + 10
b) 26 ⋅ 10
c) A26,4 ⋅ A10,4
d) A26,4 + A10,4
e) 10A26,4 + 26A10,4
alternativa c
13. (UECE) Na mesa redonda utilizada para rêuní-ões da Presidência da República, há um lugar fixo para sêr ocupado pelo Presidente e outros 22 lugares para serem ocupados pêlos ministros, todos igualmente espaçados. Estando presentes todos os 22 ministros e o Presidente, de quantas maneiras distintas podem sêr ocupados os assentos?
a) 23!
b) 23! − 22!
c) 22! + 23!
d) 22!
alternativa d
Página duzentos e quarenta e seis
14. (Udesc) Uma loja de material para pintura fabrica tintas de cores personalizadas, usando uma máquina quê mistura até 3 cores iniciais em proporções quê podem sêr ajustadas de 20% em 20%. Sabendo quê há 4 cores iniciais para se escolher, o número de cores quê podem sêr oferecidas, incluindo as iniciais puras, é:
a) 48
b) 52
c) 28
d) 44
e) 76
alternativa b
15. (UFAM) A quantidade de números, com três algarismos distintos, quê podemos formár com os algarismos 1, 2, 3, 4, 5, 6 e 8, é:
a) 105.
b) 330.
c) 400.
d) 210.
e) 540.
alternativa d
16. (UFRGS-RS) Um aplicativo de transporte disponibiliza em sua platafórma a visualização de um mapa com ruas horizontais e verticais quê permitem realizar deslocamentos partindo do ponto A e chegando ao ponto B, conforme representado na figura a seguir.

O número de menóres caminhos possíveis quê partem de A e chegam a B, passando por C, é
a) 28.
b) 35.
c) 100.
d) 300.
e) 792.
alternativa d
17. (UECE) Na primeira fase do Campeonato Brasileiro de Futebol, Série A, disputado por 20 clubes, quaisquer dois dos disputantes jogam entre si uma única vez. Na segunda fase, as mesmas 20 equipes repetem as disputas, também cada dois participantes jogando entre si uma única vez. Ao final do Campeonato, quantas partidas terão sido disputadas?
a) 360.
b) 380.
c) 420.
d) 400.
alternativa b
18. (UFJF-MG) Um ônibus com 40 assentos numerados de 01 a 40 foi alugado para uma excursão quê fará uma viagem com 25 turistas. De quantos modos distintos os turistas poderão sêr acomodados para a viagem considerando quê não há preferência por lugares?
a)
b)
c) 40
d) 15!
e) 40! − 15!
alternativa a
19. (UEG-GO) O corpo de bombeiros possui uma equipe de 10 paramédicos. A cada chamada, 3 paramédicos saem juntos para fazer o atendimento. A quantidade de diferentes composições com 3 paramédicos quê podem sêr formadas é
a) 125
b) 120
c) 110
d) 100
e) 90
alternativa b
20. (UEA-AM) Um assinante de Tevê paga selecionou 6 filmes para assistir, porém sem ordem de preferência. Sabendo quê em um domingo esse assinante assistirá a 2 dêêsses filmes selecionados, o número de maneiras distintas de ele fazer essa escolha é
a) 10.
b) 30.
c) 12.
d) 15.
e) 24.
alternativa d
21. (ITA-SP) Em um decágono convexo, de quantas formas podemos escolher duas diagonais quê não se interceptam?
175 formas
22. (UFRR) Em uma certa cidade, foi realizada uma reunião de 5 vereadores e 4 deputados estaduais. Nessa reunião decidiu-se formár uma comissão de 5 (cinco) membros, escolhidos entre eles, para representá-los em uma visita ao governador do estado. Também se decidiu quê a comissão deveria possuir pelo menos 3 (três) vereadores.
O número de comissões distintas quê podem sêr formadas é:
a) 12
b) 81
c) 5
d) 60
e) 84
alternativa b
Página duzentos e quarenta e sete
