Orientações específicas para êsteeste Volume

Uma proposta de cronograma para o desenvolvimento dêstedeste Volume da coleção, considerando um planejamento semestral, trimestral e bimestral, é apresentada a seguir. É importante ressaltar quêque essa proposta é apenas uma sugestão e quêque o cronograma deve sêrser adequado às escôlhasescolhas feitas pela comunidade escolar, de acôr-doacordo com a quantidade de aulas estabelecidas no ano letivo para a área de Matemática e suas Tecnologias.

Página trezentos e trinta330

Unidade 1 Matemática financeira

Quadro-síntese da Unidade

Objetivos da Unidade

• Identificar situações do cotidiano quêque envolvem o uso de porcentagem e contextos relacionados à Matemática Financeira.

• Interpretar e analisar taxas e índices de natureza socioeconômica em diferentes contextos, além de compreender como eles são calculados.

• Compreender e realizar cálculos de atualização de valores financeiros, identificando situações quêque envolvem acréscimos ou descontos sucessivos.

• Reconhecer o uso de tecnologias digitais para criar modelos e promover a economia compartilhada, bem como seus benefícios como alternativa sustentável de geração de renda.

• Compreender o conceito de juro simples e de juro compôztocomposto e interpretar e comparar situações envolvendo esses sistemas de aplicação financeira.

• Relacionar a variação do montante ou do juro obtídoobtido no sistema de juro simples e de juro compôztocomposto a uma função afim ou do tipo exponencial, respectivamente, e representá-las graficamente, com ou sem auxílio de planilha eletrônica.

• Conhecer e compreender os principais sistemas de amortização utilizados em financiamentos: SAC e Price.

• Elaborar orçamentos financeiros e utilizá-los como instrumento para planejar e administrar recursos financeiros de acôr-doacordo com as receitas e despesas envolvidas, com ou sem auxílio de aplicativos ou planilhas eletrônicas.

• Resolver e elaborar problemas, individualmente ou em grupo, envolvendo os tópicos trabalhados nessa Unidade, relacionados ou não a situações do cotidiano.

Orientações didáticas

O trabalho com essa Unidade possibilita desenvolver o pensamento científico e o raciocínio lógico, estabelecendo relações com demandas do cotidiano. Isso ocorre porque, diariamente, é necessário tomar decisões relacionadas ao uso do dinheiro. Além díssudisso, são trabalhadas situações dos mais variados contextos relacionados a porcentagem, aplicações e empréstimos financeiros e sistemas de amortização, o quêque propicíapropicia aos estudantes uma visão da Matemática integrada com temas sociais. Desse modo, o estudo da Unidade pódepode auxiliar os estudantes na tomada de decisões relacionadas a sua vida financeira e, com esse conhecimento, eles podem auxiliar familiares e membros da comunidade.

Página 11

Abertura da Unidade

O trabalho com a abertura da Unidade favorece o desenvolvimento do Tema Contemporâneo Transversal Educação para o Consumo, uma vez quêque trata de kestõesquestões relacionadas ao uso do dinheiro (consumismo) e ao planejamento financeiro por meio de ferramentas matemáticas.

Promover uma roda de conversa com os estudantes e debater os itens propostos e outras kestõesquestões relacionadas ao tema, sempre respeitando a individualidade e as diferenças entre os contextos familiares e sociais deles. Por exemplo, pode-se discutir sobre a diferença entre as palavras necessidade e desejo. De maneira geral, necessidade tem relação com tudo o quêque é preciso para quêque uma pessoa tenha suas principais demandas atendidas, como vestuário, habitação, alimentação, educação, saúde, transporte etc.; e desejo tem relação, entre outras, com o impulso de consumir bens ou serviços quêque não atendem às demandas principais ou não fazem falta a uma pessoa ou família. Solicitar aos estudantes quêque citem exemplos de bens ou serviços quêque estão associados à necessidade e ao desejo e quêque comentem aqueles quêque estão mais relacionados com sua vida. Comentar quêque, algumas vezes, o quêque se julga sêrser necessidade, na realidade, são desejos.

São apresentadas, a seguir, as respostas aos itens propostos.

1. Respostas possíveis: Ao lidar bem com o dinheiro, é possível evitar o endividamento, alcançar objetivos, manter-se estabilizado financeiramente.

2. Em caso afirmativo, espera-se quêque os estudantes comentem, de maneira geral, o destino dessa renda: esporte, cultura, despesas familiares, entre outros. Ainda, eles podem indicar quêque poupam parte da renda.

3. Resposta pessoal. Os estudantes podem, por exemplo, apontar o dado quêque indica quêque 78,10% das famílias brasileiras estavam endividadas em março de 2024, o quêque corresponde a cerca de três em cada quatro famílias brasileiras.

Páginas 12 a 16

Porcentagem

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 1 e da habilidade EM13MAT104 da área de Matemática e suas Tecnologias, pois envolve a interpretação de taxas e tributos de natureza socioeconômica para analisar criticamente a realidade e produzir argumentos.

Nesse tópico, espera-se quêque os estudantes trabalhem com diferentes aplicações de porcentagem em situações financeiras. São apresentados alguns exemplos e atividades em quêque eles devem lidar com porcentagem ou calculá-las interpretando taxas e analisando criticamente a realidade.

Página trezentos e trinta e um331

Antes de iniciar o trabalho com esse tópico, verificar a possibilidade e a necessidade de propor atividades envolvendo cálculos de porcentagem, como uma avaliação diagnóstica. Outra possibilidade é os estudantes explicitarem o quêque conhecem sobre esse tema. Assim, após a análise do dêsempênhodesempenho, a condução do trabalho com esse tópico pódepode atender a possíveis defasagens de aprendizagem.

Ao apresentar a ideia de porcentagem, conversar com os estudantes acerca de pesquisar preços de materiais escolares, fazendo perguntas como: Vocês realizam pesquisas de preços para comprar materiais escolares? Vocês costumam notar grande diferença entre os preços de um mesmo produto em diferentes lojas? Vocês sabem dizêrdizer por quêpor que existe essa diferença de preços? Que critérios utilizam para decidir como comprar materiais escolares? Qual é a importânssiaimportância de realizar pesquisas de preços ao comprar itens como os materiais escolares?

No primeiro boxe Para pensar da página 13, reforçar aos estudantes quêque as porcentagens utilizadas para comparar os preços do caderno são distintas. Se julgar necessário, apresentar exemplos para reforçar essa ideia, como o sugerido a seguir.

• Um aumento de 20% sobre R$ 100,00 determina R$ 120,00; um desconto de 20% sobre R$ 120,00 determina R$ 96,00. por quêPor que isso ocorre? Resposta esperada: Porque os valores sobre os quais incidem o aumento e o desconto dos 20% são diferentes, ou seja, R$ 100,00 e R$ 120,00, respectivamente.

Ao final do trabalho com a atividade resolvida R2, na página 14, solicitar aos estudantes uma pesquisa sobre a cobrança do IPVA na unidade da Federação em quêque moram, destacando as alíquotas aplicadas no ano vigente e as opções de pagamento oferecidas. Depois, estabelecer o valor venal de um veículo e simular o valor a sêrser pago de IPVA para cada opção disponível. Por fim, pedir quêque elaborem um pequeno texto comparando essas formas de pagamento, listando as vantagens e as desvantagens de cada uma delas. Essa proposta pódepode consistir em uma atividade avaliativa.

A seção Atividades das páginas 15 e 16 tem como objetivo trabalhar com cálculos envolvendo porcentagens em diferentes situações, como acréscimos e descontos simples, determinação de lucro, taxa de crescimento e cálculos de tributos.

Páginas 17 a 21

Fatores de atualização

Espera-se quêque os estudantes utilizem as ideias de porcentagem para determinar fatores de atualização e compreendam a sua importânssiaimportância no cálculo de acréscimos e descontos sucessivos relacionado a um bem ou serviço.

Atividade Extra

Propor aos estudantes quêque, organizados em duplas, acessem a Calculadora do cidadão, no sáitisite do Banco Central do Brasil (disponível em: https://livro.pw/beyie; acesso em: 10 out. 2024), e utilizem-na para simular, por exemplo, cálculos de reajustes imobiliários para determinados períodos. Em seguida, pedir quêque elaborem um relatório apresentando as informações utilizadas para os cálculos, como: o índice de correção, as datas (inicial e final), o valor a sêrser corrigido, o porcentual correspondente e o valor na data final. Por fim, os estudantes podem compartilhar os relatórios com os demais côlégascolegas da turma.

A seção Atividades das páginas 20 e 21 tem como objetivo trabalhar com o cálculo de fatores de correção e com acréscimos e descontos sucessivos.

Conexões

Ao trabalhar com a atividade 13, sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para consultar os valores do salário mínimo nominal e do necessário, de acôr-doacordo com o preêçopreço da cesta básica.

• DEPARTAMENTO INTERSINDICAL DE ESTATÍSTICA E ESTUDOS SOCIOECONÔMICOS. Pesquisa nacional da cesta básica de alimentos. São Paulo: Dieese, [2024]. Disponível em: https://livro.pw/ghlxu. Acesso em: 10 out. 2024.

Páginas 22 a 24

Integrando com Ciências Humanas e Sociais Aplicadas

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5 e da competência específica 2 da área de Matemática e suas Tecnologias. Além díssudisso, a seção aborda o Tema Contemporâneo Transversal Ciência e Tecnologia, uma vez quêque explora o uso de platafórmasplataformas digitais para a promoção de uma economia compartilhável, quêque favorece a análise de kestõesquestões sócio-ambientaissocioambientais em relação aos recursos não rêno-váveisrenováveis e à discussão de alternativas tecnológicas para tais kestõesquestões.

Para condução do trabalho com essa seção, fazer uma leitura dos textos e das informações apresentadas com os estudantes e, se possível, trabalhar em parceria com um professor da área de Ciências Humanas e Sociais Aplicadas, uma vez quêque o tema aborda kestõesquestões relacionadas ao mercado de trabalho e à economia compartilhada.

Ao abordar o boxe No mundo do trabalho, verificar a possibilidade de convidar algum profissional quêque atua na área de recursos humanos para conversar com os estudantes a respeito das soft skills. Essa sugestão de abordagem favorece o desenvolvimento da competência geral 6, uma vez quêque valoriza a diversidade de saberes e promove a apropriação dos estudantes em relação a conhecimentos e experiências associados ao mundo do trabalho.

Conexões

Na atividade 5 do Pensando no assunto, sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para auxiliá-los no levantamento de ideias e nortear a elaboração dos projetos.

• WAGNER, TômasThomas éti áuet al. Escutando iniciativas de economia compartilhada. Tradução: fílipPhilip Reed. [S. l.]: CSCP: CBS: Akatu, 2015. Disponível em: https://livro.pw/kdzwq. Acesso em: 10 out. 2024.

Páginas 25 a 31

Juro simples e juro compôztocomposto

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e das habilidades EM13MAT303, EM13MAT304 e EM13MAT305 da área de Matemática e suas Tecnologias, pois envolve interpretação e comparação de situações envolvendo juro simples e juro compôztocomposto, por meio de representações algébricas e gráficas e análise de planilhas eletrônicas, destacando o crescimento linear ou exponencial de cada caso. Além díssudisso, aborda a associação dêêssesdesses sistemas de juro com funções e cálculos envolvendo logaritmo.

Página trezentos e trinta e dois332

Na introdução dêêssedesse tópico, espera-se quêque os estudantes interpretem e comparem situações monetárias quêque envolvem pagamento de empréstimos ou de investimentos em geral. Discutir com eles o significado dos termos capital, juro, taxa de juro, tempo e montante, apresentados no esquema.

Na situação introdutória sobre juro simples, na página 25, envolvendo empréstimo para compra de matérias-primas, propor aos estudantes quêque construam um qüadroquadro para representar o juro e o montante obtidos em cada mês no período de 6 meses.

Explicar aos estudantes quêque a taxa de juro e o tempo devem sêrser expressos em uma mesma unidade de medida de tempo. Em geral, para taxa de juro, usam-se as seguintes abreviações: a.d. (ao dia); a.m. (ao mês); a.b. (ao bimestre); a.t. (ao trimestre); a.s. (ao semestre); e a.a. (ao ano).

No boxe Para pensar da página 25, pedir aos estudantes quêque apresentem exemplos numéricos quêque justifiquem suas respostas.

Na situação inicial da página 27, envolvendo investimento em uma aplicação financeira, propor aos estudantes quêque construam um qüadroquadro para representar o juro e o montante obtidos em cada ano no período de 3 anos (36 meses).

Comentar com os estudantes quêque situações envolvendo o sistema de juro compôztocomposto podem sêrser relacionadas com fatores de atualização, conteúdo tratado anteriormente nessa Unidade. Nesse caso, a cada período de tempo t, são realizados acréscimos sucessivos de uma taxa de juro fixa i ao capital c.

De maneira análoga ao quêque ocorre no sistema de juro simples, em quêque os montantes obtidos em cada período podem sêrser associados a termos de uma PA, os montantes obtidos no sistema de juro compôztocomposto podem sêrser associados a termos de uma PG, em quêque o primeiro termo é c ⋅ (1 + i), a razão é (1 + i) e a quantidade de termos é t. Assim, a expressão do termo geral dessa PG correspondente ao montante é dada por M = c ⋅ (1 + i)^t.

A seção Atividades das páginas 29 a 31 tem como objetivo trabalhar com os elemêntoselementos envolvidos no cálculo de juro (montante, capital, tempo e taxa de juro), no sistema de juro simples e no sistema de juro compôztocomposto, além de trabalhar com a representação gráfica de funções quêque expressam montantes de aplicações em relação ao tempo e a comparação entre o sistema de juro simples e o sistema de juro compôztocomposto em uma situação de aplicação financeira. A atividade 24 pódepode sêrser proposta como uma avaliação formativa dos estudantes, uma vez quêque envolve a compreensão de diversos conceitos estudados, como porcentagem, juro simples e juro compôztocomposto. Uma possibilidade é, ao final da proposta, pedir aos estudantes quêque apresentem suas resoluções para toda a turma.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre tipos de investimento.

• BRASIL. Caixa Econômica Federal. Tipos de investimento. Brasília, DF: CEF [2024]. Disponível em: https://livro.pw/euxtw. Acesso em: 10 out. 2024.

Páginas 32 a 39

Sistemas de amortização

Espera-se quêque os estudantes interpretem e comparem situações monetárias de empréstimos envolvidos em alguns sistemas de amortização, contexto quêque favorece a abordagem do Tema Contemporâneo Transversal Educação para o Consumo.

Enfatizar quêque o trabalho com os sistemas de amortização nessa Unidade considera o sistema de juro compôztocomposto, mais usual na atualidade.

Na situação apresentada na página 33, destacar aos estudantes o procedimento recursivo de cálculo do juro, do saldo devedor e da prestação. Chamar a atenção para o fato de quêque, a cada período, tais valores varíamvariam e devem sêrser recalculados com base no mês anterior.

No segundo boxe Para pensar da página 34, explicar aos estudantes a relação entre a função s e os dados do problema. O termo independente (90.000) corresponde ao valor do crédito obtídoobtido, o produto de −375 pela quantidade n de prestações indica a subtração do valor da amortização a cada prestação paga. Explicar também quêque a função independe da taxa de juro, uma vez quêque, no sistema de amortização constante, o valor amortizado no saldo devedor independe do juro.

Nos cálculos apresentados na página 35, informar quêque foram desconsideradas outras despesas além do juro, as quais costumam sêrser cobradas em um financiamento. No boxe Para pensar dessa página, chamar a atenção dos estudantes para o fato de quêque o valor pago ao final das 60 prestações é quase o dôbrodobro do preêçopreço da motocicleta. Discutir com eles sobre esse fato e relembrar quêque o pagamento à vista pódepode sêrser uma boa opção, considerando o valor final a pagar.

Na planilha eletrônica apresentada na página 36, evidenciar para os estudantes o crescimento da amortização e o decrescimento do juro a cada mês. Explicar quêque isso acontece porque o juro é sempre calculado sobre o valor do saldo devedor do mês anterior.

A seção Atividades das páginas 38 e 39 tem como objetivo trabalhar com o sistema de amortização constante (SAC) e com o sistema Price, por meio do cálculo do montante de uma dívida, do cálculo do valor das prestações de um financiamento, da elaboração de um anúncio de venda parcelada de acôr-doacordo com leis quêque o normatizam e do cálculo de desconto na compra de um produto.

Páginas 40 a 42

Orçamento financeiro

O contexto relacionado à elaboração de orçamento financeiro favorece a abordagem do Tema Contemporâneo Transversal Educação Financeira, uma vez quêque auxilia os estudantes a tomar decisões financeiras com base em conceitos matemáticos.

Espera-se quêque os estudantes conheçam ferramentas para planejar e organizar seu orçamento e o orçamento familiar.

No boxe Para pensar da página 40, é possível promover uma discussão coletiva, de maneira quêque os estudantes respondam oralmente à quêquestão. Pedir a alguns estudantes quêque comentem estratégias quêque utilizam para organizar sua vida financeira, se eles se preocupam com tal organização e se utilizam alguma ferramenta para fazer isso. Durante a discussão, é importante que as individualidades dos estudantes sêjamsejam respeitadas e preservadas.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir, quêque apresenta outra planilha de orçamento.

• PROCON MUNICIPAL DE CAMPINAS. Secretaria Municipal de Justiça. Planilha de orçamento familiar. Campinas: Procon, [2024]. Disponível em: https://livro.pw/ujsqo. Acesso em: 10 out. 2024.

Página trezentos e trinta e três333

Atividade Extra

Com os estudantes organizados em duplas, propor a cada dupla quêque responda à pergunta: Como a análise do resultado do orçamento financeiro de um mês pódepode contribuir com os meses seguintes? Em seguida, orientar uma discussão com toda a turma a respeito dessa questão.

Uma resposta possível: Tendo como base os registros organizados e a análise deles, é possível planejar o orçamento dos meses seguintes estimando um padrão de receitas e despesas mensais, antecipando eventuais dificuldades financeiras e possibilidades de investimentos. Também, com essa análise, pode-se perceber oportunidades de reduzir despesas e aumentar receitas.

A seção Atividades da página 42 tem como objetivo incentivar os estudantes a refletir a respeito da importânssiaimportância do orçamento financeiro por meio de atividades quêque exploram produção textual, classificação de despesas em fixas, variáveis ou eventuais e execução de etapas para construir um orçamento financeiro.

Páginas 43 e 44

Você conectado

Orientar os estudantes a trabalhar com as planilhas eletrônicas e algumas de suas funções. Ao construir a tabélatabela com os dados das aplicações, pedir a eles quêque interpretem as informações inseridas, incluindo as fórmulas, a fim de dar sentido a elas no contexto apresentado.

Se necessário, retomar as expressões para calcular juro simples e juro compôztocomposto apresentadas anteriormente nessa Unidade a fim de quêque os estudantes possam utilizá-las ao realizar os cálculos na planilha eletrônica.

Mãos à obra - página 44

1. Essa questão trabalha a interpretação de informações em uma planilha eletrônica com base em uma situação financeira envolvendo os sistemas de juro simples e juro compôztocomposto. No item d, explicar aos estudantes como construir o gráfico e a linha de tendência. Para obtêrobter uma representação gráfica, selecionar as células com valores referentes ao mês e aos montantes correspondentes e clicar em Inserir gráfico no menúmenu. Ao abrir a caixa de diálogo Assistente de gráficos na opção 1. Tipo de gráfico, selecionar as opções XY (Dispersão) e Somente pontos. Por fim, clicar em Concluir.

Para determinar as linhas de tendência, clicar sobre os pontos do gráfico, selecionar nas opções Inserir e Linha de tendência... no menúmenu. Ao abrir a caixa de diálogo, em Tipo de regressão, selecionar a opção Linear e a opção Exponencial, para os pontos da aplicação a juro simples e para a aplicação a juro compôztocomposto, respectivamente. Por fim, clicar em Concluir.

2. Essa questão contribui para o desenvolvimento da habilidade EM13MAT203 da área de Matemática e suas Tecnologias, pois trabalha com a elaboração, em uma planilha eletrônica, de um simulador para cálculo de montante e de juro em aplicações no sistema de juro simples e sistema de juro compôztocomposto.

No item b, ao elaborar o simulador relacionado ao cálculo de juro compôztocomposto, verificar se os estudantes utilizaram a expressão sistematizada anteriormente [M = c ⋅ (1 + i)^t] e se eles começaram a preencher as células quêque representam o montante para, depois, preencher as células quêque representam o juro (j = M − c).

3. Essa questão trabalha a elaboração de um simulador para determinar o saldo devedor de um financiamento no sistema de amortização constante e no sistema Price.

Páginas 45 e 46

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

Na quêquestão 4, verificar a possibilidade de propor aos estudantes uma roda de conversa para que eles compartilhem com os demais côlégascolegas da turma as estratégias utilizadas para resolver essa questão.

Páginas 47 e 48

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 2 Matrizes, sistemas lineares e transformações de figuras

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender o conceito e a representação de dados em matrizes.

• Compreender e realizar operações com matrizes: adição, subtração, multiplicação por um número real e multiplicação de matrizes.

• Determinar a matriz oposta e a matriz transposta a uma matriz dada.

Página trezentos e trinta e quatro334

• Resolver equações matriciais.

• Compreender e determinar soluções de uma equação linear.

• Reconhecer situações do cotidiano quêque podem sêrser representadas por meio de sistemas lineares.

• Interpretar a solução de um sistema linear, obtendo-a algébrica ou graficamente.

• Identificar sistemas lineares homogêneos e compreender suas propriedades.

• Classificar sistemas lineares de acôr-doacordo com a quantidade de soluções: sistema possível e determinado, sistema possível e indeterminado e sistema impossível.

• Utilizar o método do escalonamento para resolver sistemas lineares.

• Compreender noções de transformações isométricas (simetria de translação, de reflekçãoreflexão e de rotação) e homotéticas de figuras planas, construí-las utilizando instrumentos de desenho ou software de geometria dinâmica e percebê-las em diferentes situações na natureza e em produções humanas.

• Determinar a razão de semelhança entre as figuras obtidas por transformação homotética.

• Resolver e elaborar problemas, individualmente ou em grupo, envolvendo os tópicos trabalhados nessa Unidade, relacionados ou não a situações do cotidiano.

Orientações didáticas

O trabalho com essa Unidade possibilita aos estudantes desenvolver o pensamento algébrico e o pensamento geométrico, estabelecendo relações entre esses tipos de pensamento e demandas do cotidiano, uma vez quêque algumas situações do dia a dia podem sêrser resolvidas por meio de sistemas lineares. Além díssudisso, ideias de transformações de figuras estão presentes em diversas manifestações artísticas, como na pintura, na escultura e na literatura. É possível também quêque os estudantes reconheçam as matrizes como uma das ferramentas quêque podem sêrser utilizadas na resolução de sistemas lineares.

Página 49

Abertura da Unidade

O trabalho com a abertura da Unidade envolve o estudo dos grafos como ponto de partida para o estudo de matriz. Explicar aos estudantes quêque grafos podem sêrser compreendidos como conjuntos de pontos e de ligações entre esses pontos e quêque são utilizados para resolver diversos problemas. Citar como exemplo de problema a criação de uma rota para um carteiro, de modo quêque ele evite passar várias vezes pelo mesmo lugar e consiga entregar todas as encomendas no menor tempo possível.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Leonhard ÓilerEuler. Representar o problema das “pontes de Königsberg” por meio de um esquema.

2. 4 vértices e 4 arestas.

3. Uma resposta possível: Associando as lêtrasletras iniciais dos nomes dos amigos; por exemplo, AB indica quêque Ana é amiga de BétoBeto, e vice-versa. Desse modo, temos: AB, AC, BC e cê dêCD. Outra possibilidade é construir uma tabélatabela de dupla entrada.

Páginas 50 a 54

Matrizes

Nesse tópico, espera-se quêque os estudantes compreendam como representar informações em matrizes, reconheçam seus principais elemêntoselementos e realizem operações com matrizes.

Comentar com os estudantes quêque podem sêrser utilizados outros símbolos para representar matriz em vez de colchetes, como parênteses “()“ e barras duplas “|| ||”. Explicar quêque as linhas de uma matriz são numeradas de cima para baixo e as colunas, da esquerda para a direita, conforme indicado no exemplo a seguir.

No boxe Matemática na história da página 51, explicar aos estudantes quêque as transformações auxiliaram no desenvolvimento do conceito de matrizes. De maneira geral, o estudo das transformações envolve analisar figuras congruentes ou semelhantes em posições distintas.

Na página 52, ao trabalhar com igualdade de matrizes, verificar se os estudantes entenderam quêque, para duas matrizes sêrserem iguais, necessitam ser de mesma ordem. Explicar quêque os elemêntoselementos correspondentes são aqueles de mesmo índice (mesma posição).

Apresentar aos estudantes a definição de igualdade de matrizes, utilizando notação matemática.

A_{m × n} = B_{m × n} ⇔ a_ij = b_ij, com 1 ≤ i ≤ m e 1 ≤ j ≤ n

A seção Atividades das páginas 53 e 54 tem como objetivo trabalhar a elaboração de um grafo, a construção e a interpretação de matrizes, a nomenclatura de matrizes e a determinação de matrizes transpostas. Na atividade 3, comentar com os estudantes quêque o monitoramento dos casos de dengue é realizado por semana epidemiológica.

Páginas 55 a 61

Operações com matrizes

Ao definir adição de matrizes, na página 55, verificar se os estudantes entendem quêque as duas matrizes quêque sêrserão adicionadas devem ser de mesma ordem. Reforçar a escrita algébrica da adição de matrizes, indicando quêque todos os elemêntoselementos da matriz C correspondem à soma dos dois elemêntoselementos correspondentes nas matrizes A e B.

Ao trabalhar matriz oposta, na página 56, retomar a definição de matriz nula apresentada na atividade 5 da página 54. Reforçar quêque o sín-bolosímbolo “−” no nome da matriz oposta −A não indica uma subtração, mas quêque a matriz −A é oposta à matriz A.

Ao trabalhar subtração de matrizes, questionar os estudantes se a igualdade A − B = B − A é verdadeira para quaisquer matrizes A e B de mesma ordem. Espera-se quêque eles percêbampercebam quêque essa igualdade não é válida para toda matriz de mesma ordem e, nesse momento, propor a eles quêque justifiquem essa percepção com exemplos.

Antes de trabalhar a atividade resolvida R3, na página 57, apresentar as seguintes propriedades da multiplicação de uma matriz por um número real, em quêque (alfa)"α e (beta)"β são números reais e A e B duas matrizes de mesma ordem.

• ((alfa)"α + (beta)"β) ⋅ A = (alfa)"αA + (beta)"βA

• (alfa)"α ⋅ (A + B) = (alfa)"αA + (alfa)"αB

• (alfa)"α ⋅ ((beta)"βA) = ((alfa)"α(beta)"β) ⋅ A

• 1 ⋅ A = A

Página trezentos e trinta e cinco335

A seção Atividades das páginas 57 e 58 tem como objetivo trabalhar a igualdade de matrizes e as operações de adição e subtração de matrizes, bem como a multiplicação de uma matriz por um número real.

Ao trabalhar multiplicação de matrizes, na página 59, explicar aos estudantes quêque, em situações quêque requerem esse tipo de operação, cada coluna de uma matriz deve representar dados referentes a um mesmo elemento daqueles representados em cada linha da outra matriz. No exemplo apresentado, os dados referentes à banana e à laranja estão representados nas colunas da matriz A e nas linhas da matriz B. Isso acontece para garantir quêque, ao multiplicar as duas matrizes, a matriz ôbitídaobtida represente a pegada hídrica (nas linhas da matriz A) em cada semana (nas colunas da matriz B) de acôr-doacordo com o consumo de banana e de laranja. O contexto apresentado favorece a abordagem do Tema Contemporâneo Transversal Educação Ambiental, uma vez quêque traz à tona a questão da pegada hídrica.

Antes do início das Atividades Resolvidas da página 60, é trabalhada uma das ideias relacionadas ao pensamento computacional, ao serem apresentadas as condições de existência do produto de duas matrizes por meio de um fluxograma.

A seção Atividades da página 61 tem como objetivo trabalhar com multiplicação de matrizes por meio do cálculo, da análise da possibilidade de realizar uma multiplicação de matrizes, da determinação da ordem do produto entre duas matrizes ou por meio da resolução de uma equação matricial.

Páginas 62 a 69

Sistemas lineares

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3, porque exige procedimentos matemáticos para interpretar, construir modelos e resolver problemas em diversos contextos. Também favorece o desenvolvimento da habilidade EM13MAT301 da área de Matemática e suas Tecnologias, pois envolve a resolução de problemas do cotidiano por meio de equações lineares simultâneas, além de propiciar uma abordagem do Tema Contemporâneo Transversal Saúde.

Antes de iniciar o trabalho com esse tópico, verificar a possibilidade e a necessidade de propor aos estudantes a resolução da atividade 32 da página 68 para utilizá-la como uma avaliação diagnóstica. Isso porque essa atividade aborda o assunto sistemas lineares de duas equações com duas incógnitas, conceito estudado nos Anos Finais do Ensino Fundamental. Assim, é possível identificar indícios do conhecimento prévio dos estudantes a respeito dêêssedesse assunto e, dessa maneira, adequar a prática didática às demandas dos estudantes.

Ao trabalhar com equações lineares, na página 63, espera-se quêque os estudantes compreendam sua definição, reconheçam seus coeficientes, incógnitas e termo independente.

Explicar quêque uma ênupla corresponde a uma sequência ordenada de n elemêntoselementos. Comentar quêque a ordem de apresentação dos elemêntoselementos na ênupla é especificada pêlospelos índices das incógnitas. Quando não há especificação, utiliza-se como convenção a ordem alfabética. Explicar também quêque as ênuplas com dois elemêntoselementos são chamadas de pares ordenados e, com três elemêntoselementos, de ternas.

A seção Atividades das páginas 64 e 65 tem como objetivo trabalhar com a identificação dos termos de uma equação linear, com a solução de um sistema linear e a escrita de uma equação linear a partir de sua representação gráfica.

Ao trabalhar com o conceito e as características de um sistema de equações lineares, a partir da página 65, chamar a atenção dos estudantes para a representação dos coeficientes das incógnitas das equações, quêque segue um padrão análogo ao da representação dos elemêntoselementos de uma matriz.

Para discutir a solução de um sistema linear, enfatizar quêque é necessário quêque uma ênupla seja solução de todas as equações do sistema linear.

Explicar aos estudantes quêque um sistema linear homogêneo pódepode sêrser classificado como SPD (quando a única solução é a trivial) ou SPI (quando existem infinitas outras soluções além da trivial), mas nunca como SI (quando não existe solução).

A seção Atividades das páginas 68 e 69 tem como objetivo trabalhar com escrita, resolução e classificação de um sistema linear.

Na atividade 34, é trabalhada uma das ideias relacionadas ao pensamento computacional, ao sêrser apresentada uma possibilidade de classificar um sistema linear, de acôr-doacordo com a quantidade de soluções, por meio de um fluxograma.

Conexões

Após a resolução da atividade 35, sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para quêque leiam o livreto Mais mulheres na política.

• BRASIL. Senado Federal. Mais mulheres na política. 2. ed. Brasília, DF: Senado Federal: Segraf, 2015. Disponível em: https://livro.pw/zouje. Acesso em: 10 out. 2024.

A atividade 37 favorece uma abordagem do Tema Contemporâneo Transversal Saúde, ao tratar da importânssiaimportância do nutriente ferro no organismo humano. Se possível, desenvolver um trabalho em parceria com um professor da área de Ciências da Natureza e suas Tecnologias para quêque possa orientar uma discussão com os estudantes sobre a importânssiaimportância da ingestão de diferentes nutrientes para a saúde.

Páginas 70 e 71

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, ao relacionar Álgebra com Geometria, da competência geral 5 e da habilidade EM13MAT301, pois aborda a resolução de problemas envolvendo equações lineares simultâneas, usando técnicas algébricas e gráficas com apôioapoio de tecnologias digitais.

Mãos à obra - página 71

1. Verificar se os estudantes se recordam de quêque, quando as retas quêque representam as soluções das equações de um sistema linear 2 × 2 são coincidentes, esse sistema é SPI e, quando as retas não têm ponto em comum, ou seja, quando são paralelas, o sistema é SI.

2. Para a resolução dessa questão, orientar os estudantes a construir uma reta a partir de dois pontos dados. Primeiro, eles devem digitar no campo Entrada as coordenadas de cada um dos pontos. Em seguida, utilizando a opção Reta, clicar no ponto A e no ponto B, obtendo a reta quêque passa por A e B. Fazer o mesmo para os pontos C e D.

Página trezentos e trinta e seis336

3. Uma das possibilidades de escolha de atividade para se resolver essa questão é a atividade 32 da página 68. Nesse caso, reforçar com eles a classificação do sistema de acôr-doacordo com a posição das retas quêque representam suas equações.

4. Orientar os estudantes na elaboração do problema, sugerindo contextos quêque podem sêrser utilizados, como situações envolvendo outras áreas do conhecimento.

Páginas 72 a 79

Escalonamento de um sistema linear

No primeiro boxe Para Pensar da página 72, solicitar aos estudantes quêque compartilhem suas estratégias de resolução. A fim de auxiliá-los na compreensão da definição de um sistema linear escalonado, utilizar as informações do boxe Dica para destacar, no sistema apresentado, cada uma das características mencionadas.

Na resolução da atividade resolvida R9, propor aos estudantes quêque determinem algumas soluções do sistema linear apresentado. Para isso, basta atribuir valores a r e s e obtêrobter os valores correspondentes de p e q. Por exemplo, (−1, 2, 1, 1), (−2, 5, 3, 0) e (−6, 9, 5, −2) são algumas das soluções dêêssedesse sistema.

Para iniciar o trabalho com os procedimentos a fim de escalonar um sistema linear, na página 75, realizar com os estudantes a interpretação do sistema apresentado, de acôr-doacordo com o contexto da questão.

A seção Atividades das páginas 77 a 79 tem como objetivo trabalhar com escrita, resolução e classificação de sistemas lineares, além da elaboração de um problema a partir de um sistema linear.

Páginas 80 a 82

Integrando com Ciências da Natureza e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 1 e da competência específica 3 da área de Matemática e suas Tecnologias e da competência específica 3 da área de Ciências da Natureza e suas Tecnologias, uma vez quêque relaciona conhecimentos matemáticos a tecnologias digitais em um contexto próprio da Ciência. Além díssudisso, essa seção trata do Tema Contemporâneo Transversal Ciência e Tecnologia.

Conexões

Para complementar as informações sobre impressoras 3D, sugerir aos estudantes quêque assistam ao vídeo indicado a seguir.

• SAIBA o quêque é e como funciona uma impressora 3D. [S. l.: s. n.], 2018. 1 vídeo (2 min). Publicado pelo canal UFLA. Disponível em: https://livro.pw/uncss. Acesso em: 10 out. 2024.

O Pensando no assunto tem como objetivo trabalhar com a argumentação, a identificação de pontos pertencentes a um plano e a relação entre as classificações dos sistemas lineares 3 × 3, além das representações geométricas das equações dêêssedesse sistema. Na questão doisquestão 2, incentivar os grupos de estudantes a elaborar uma proposta de uso de impressora 3D relacionada à sustentabilidade do ponto de vista social, econômico ou ambiental. É importante quêque tal proposta apresente benefícios para a comunidade local.

Atividade Extra

O tema trabalhado nessa seção possibilita uma ampliação por meio da realização de um projeto relacionado ao Tema Contemporâneo Transversal trabalho. Uma sugestão é quêque esse projeto contemple a elaboração de um relatório sobre as tendências do uso de impressoras 3D em diferentes profissões. Na parte geral destas Orientações para o professor há informações sobre a metodologia ativa aprendizagem baseada em projetos.

Páginas 83 a 99

Transformações isométricas de figuras

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 1 e da habilidade EM13MAT105 da área de Matemática e suas Tecnologias, pois explora noções de transformações isométricas para construir figuras e analisar produções humanas.

Nas páginas 83 e 84, no início do trabalho com simetria de translação, ao explicar o conceito de vetor, dizêrdizer aos estudantes quêque um vetor indica todos os segmentos de reta orientados de mesmo comprimento, direção e sentido. Reforçar a notação de vetor, explicando quêque $\overrightarrow{AB}$ ≠ $\overrightarrow{BA}$.

A seção Atividades das páginas 87 a 89 tem como objetivo trabalhar com a construção de figuras simétricas por translação, com o cálculo do comprimento de um vetor utilizado para realizar a translação de uma figura no plano, com o cálculo das coordenadas dos vértices de figuras transladadas no plano cartesiano e com a análise de obras artísticas por meio da simetria de translação.

A atividade 52 trabalha uma investigação sobre a simetria de translação presente nos grafismos indígenas e propicíapropicia uma abordagem do Tema Contemporâneo Transversal Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras. Essa atividade pódepode sêrser desenvolvida em parceria com um professor da área de Ciências Humanas e Sociais Aplicadas, para auxiliar na investigação de aspectos culturais e sociais dos povos indígenas da região em quêque os estudantes moram, ou com um professor da área de Linguagens e suas Tecnologias, para auxiliar na produção dos grafismos, com a possibilidade de estender sua aplicação a outros objetos além do papel, como cerâmicas ou tecídostecidos.

No início do trabalho com simetria de reflekçãoreflexão, na página 90, no segundo boxe Para Pensar, retomar com os estudantes a definição de mediatriz de um segmento de reta: a mediatriz de um segmento de reta é o lugar geométrico dos pontos quêque equidistam das extremidades do segmento, ou seja, corresponde à reta perpendicular ao segmento de reta em seu ponto médio.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre o artista Rubem Valentim e suas obras, nas quais podem sêrser identificadas simetrias.

• INSTITUTO RUBEM VALENTIM. [S. l.], c2018. sáitiSite. Disponível em: https://livro.pw/zxmkp. Acesso em: 10 out. 2024.

A seção Atividades das páginas 92 a 94 tem como objetivo trabalhar com a construção de figuras simétricas com régua e compasso, com a identificação do eixo de simetria em uma figura, com a determinação das coordenadas dos vértices de um polígono simétrico a outro por reflekçãoreflexão no plano cartesiano, com a análise da simetria de reflekçãoreflexão em uma obra artística, com a análise da simetria de reflekçãoreflexão em gráficos de funções e com a determinação das coordenadas de pontos simétricos em relação a um eixo cartesiano por meio de equação matricial.

A atividade 58 trabalha a identificação de simetria de reflekçãoreflexão em poema e propicíapropicia uma abordagem do Tema Contemporâneo Transversal Diversidade Cultural. Pode-se planejar uma ampliação dessa atividade em parceria com um professor da área de Linguagens e suas Tecnologias, para explorar com mais dêtálhesdetalhes o gênero

Página trezentos e trinta e sete337

textual, propondo aos estudantes pesquisas sobre outros poemas em quêque seja possível identificar padrões relacionados a diferentes tipos de simetria.

Ao iniciar o trabalho com simetria de rotação, na página 95, propor aos estudantes quêque pesquisem outras obras do artista Maurits Cornelis é-chêrEscher em quêque possam sêrser percebidas ideias de simetria de rotação.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para conhecer outras obras de Maurits Cornelis é-chêrEscher (sáitisite em inglês).

• ESCHER, Maurits Cornelis. Selected works baiby M.C. é-chêrEscher. [S. l.]: M.C. é-chêrEscher Foundation: The M.C. é-chêrEscher cômpãnyCompany, c2024. Disponível em: https://livro.pw/qzulx. Acesso em: 10 out. 2024.

A seção Atividades das páginas 98 e 99 tem como objetivo trabalhar com a construção de polígonos por meio de simetria de rotação, com a identificação de figuras obtidas por simetria central, com a aplicação de diferentes simetrias, com a determinação das coordenadas dos vértices de um polígono obtídoobtido por simetria de rotação e com a construção de mosaico, utilizando conceitos de transformações isométricas de figuras no plano. Ao abordar o boxe Mundo do trabalho, propor aos estudantes quêque pesquisem mais informações relacionadas à profissão de arquiteto. Sugere-se também convidar um profissional da área para conversar com os estudantes a respeito dessa profissão.

Atividade Extra

Em um laboratório de informática, sugerir aos estudantes quêque pesquisem obras de artistas quêque utilizam ideias de transformações isométricas nas composições de suas obras, como o brasileiro Rubem Valentim (1922-1991) e o holan-dêssholandês Maurits Cornelis é-chêrEscher (1898-1972). Pedir a eles quêque escôlhamescolham uma obra com essas características e, por meio de um texto, descrevam como a ideia de transformação isométrica pódepode sêrser percebida nessa obra, identificando os tipos de simetria presentes nela. Em seguida, propor a eles quêque, utilizando um software de geometria dinâmica, como o GeoGebra, elaborem uma composição de figuras inspirada na obra escolhida. Ao final, as produções podem sêrser compartilhadas em uma rê-derede social ou impréssasimpressas e fixadas em um mural da escola.

Páginas 100 a 103

Transformações homotéticas de figuras

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 1 e da habilidade EM13MAT105 da área de Matemática e suas Tecnologias, pois explora noções de transformações homotéticas para construir figuras e analisar produções humanas.

Comentar com os estudantes quêque uma diferença entre transformações isométricas e homotéticas é quêque, com as transformações isométricas, são obtidas figuras congruentes e, com as transformações homotéticas, são obtidas figuras semelhantes. Ou seja, uma transformação isométrica é um caso particular de transformação homotética, pois figuras congruentes são também semelhantes.

A seção Atividades das páginas 102 e 103 tem como objetivo trabalhar com o cálculo da razão de semelhança entre polígonos construídos por transformação homotética, com a construção de polígonos por transformação homotética usando régua e compasso, com o percentual de ampliação de figuras planas e com a relação entre transformação homotética e a perspectiva cônica com um ponto de fuga.

Páginas 104 e 105

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A quêquestão 4 trabalha o uso de matrizes, sistemas lineares e transformações de figuras em uma situação envolvendo grafos, o que permite retomar o tema explorado na abertura dessa Unidade. Se necessário, retomar com os estudantes a ideia de grafo. No item a, realizar outras perguntas sobre a matriz M, explorando, por exemplo, a diagonal principal, a diagonal secundária e a interpretação dos elemêntoselementos da matriz. No item b, perguntar aos estudantes como seria a representação geométrica das soluções do sistema quêque eles escreveram. Resposta: A representação de três planos quêque se intersectam em um único ponto de coordenadas (60, 45, 70). No item c, caso os estudantes optem por utilizar o GeoGebra, orientá-los a escolher as ferramentas adequadas para resolver o item.

Páginas 106 a 108

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 3 Geometria espacial de posição

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender noções primitivas da Geometria Euclidiana e o uso de postulados em demonstrações matemáticas.

• Compreender e identificar as posições relativas entre pontos, ponto e reta, retas contidas em um mesmo plano e ponto e plano.

• Compreender e identificar as posições relativas entre retas no espaço, entre reta e plano e entre planos.

Página trezentos e trinta e oito338

• Compreender o conceito de projeções ortogonais no plano.

• Compreender a ideia de distância envolvendo pontos, retas e planos.

• Compreender ideias quêque envolvem projeções cartográficas e investigar possíveis deformações, com ou sem apôioapoio de tecnologias digitais.

• Determinar a distância entre um ponto e uma reta utilizando um software de geometria dinâmica.

• Resolver e elaborar problemas, individualmente ou em grupo, envolvendo os tópicos trabalhados nessa Unidade, relacionados ou não a situações do cotidiano.

Orientações didáticas

O trabalho com essa Unidade possibilita aos estudantes desenvolver o pensamento geométrico, o raciocínio lógico e a curiosidade. Assim, eles podem constatar a importânssiaimportância de se utilizar conhecimentos historicamente construídos na percepção e na compreensão de procedimentos e ferramentas utilizados em diferentes áreas do conhecimento e da própria Matemática. Além díssudisso, é possível quêque os estudantes reconheçam a existência de diferentes teorias geométricas, como a apresentada no estudo das projeções cartográficas, e comparem conceitos e propriedades relacionadas a essas teorias.

Página 109

Abertura da Unidade

O trabalho com a abertura da Unidade favorece a abordagem da história da Matemática, uma das tendências metodológicas da Educação Matemática, pois apresenta informações históricas a respeito da Geometria Euclidiana e da Geometria não Euclidiana como uma maneira de compreender suas origens e refletir acerca das tentativas de diversos matemáticos na busca de provar a validade do quinto postulado de Euclides. Conversar com os estudantes a respeito de alguns estudiosos quêque tentaram provar o quinto postulado de Euclides, como Girolamo Saccheri (1667-1733), Johann Heinrich lambérLambert (1728-1777), CalCarl fridichiFriedrich Gauss (1777-1855), Nikolai Lobachevsky (1792-1856), János Bolyai (1802-1860) e Georg fridichiFriedrich Bernhard Riemann (1826-1866). Esse tipo de conversa pódepode evidenciar quêque a Matemática é uma construção humana desenvolvida de modo colaborativo.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Respostas possíveis: Ponto; reta; semirreta; segmento de reta; plano; semiplano.

2. A partir de questionamentos sobre a validade única da Geometria Euclidiana, principalmente em relação ao postulado das paralelas de Euclides.

3. Resposta esperada: Por um arco de circunferência.

Atividade Extra

Sugerir aos estudantes quêque realizem um experimento utilizando bolas de isopor esféricas e um pedaço de barbante para representar a menor distância entre dois pontos em uma superfícíesuperfície esférica sem atravessá-la. Para isso, pedir inicialmente quêque márkinmarquem dois pontos na bola de isopor e, depois, ajustem o pedaço de barbante na bola de maneira quêque passe sobre os dois pontos.

Conexões

Acessar o sáitisite indicado a seguir para obtêrobter mais informações sobre a Geometria não Euclidiana.

• ALVES, Sérgio; SANTOS FILHO, Luiz Carlos dos. Encontro com o mundo não euclidiano. Revista do Professor de Matemática, [São Paulo], n. 78, [out./dez. 2012]. Disponível em: https://livro.pw/phsni. Acesso em: 10 out. 2024.

Páginas 110 a 114

Geometria de posição no plano

Ao apresentar o ponto, a reta e o plano na Geometria Euclidiana, comentar com os estudantes quêque esses elemêntoselementos primitivos são abstratos. Porém, geralmente, utiliza-se, para a ideia de ponto, uma marcação com a ponta do lápis e, para a de reta, uma linha traçada com auxílio de uma régua sobre uma fô-lhafolha de papel. Ao imaginar essa fô-lhafolha sêndosendo prolongada em todas as direções, tem-se a ideia de plano.

No boxe Para pensar da página 111, verificar se os estudantes perceberam quêque as retas perpendiculares são um caso particular de retas concorrentes e quêque isso acontece apenas quando retas concorrentes formam ângulos rétosretos (de 90°) entre si.

Ao apresentar o postulado IV, relembrar com os estudantes a notação para a reta: podem-se indicar as lêtrasletras correspondentes a dois diferentes pontos dela e, sobre essas lêtrasletras, uma seta apontando em ambos os sentidos. Nesse caso, $\overleftrightarrow{AB}$ ou reta $\overleftrightarrow{AB}$.

Na demonstração do teorema 1, na página 112, chamar a atenção dos estudantes para o fato de quêque a reta s e o ponto A foram indicados na descrição dêêssedesse teorema. Porém os pontos B e C foram inseridos na demonstração, uma vez quêque, dada uma reta, há infinitos pontos quêque pertencem a ela, assim como há infinitos pontos quêque não pertencem a ela. Logo, podem-se estabelecer dois pontos arbitrários dessa reta.

A seção Atividades da página 114 tem como objetivo trabalhar com relações de pertinência e continência, com análise de afirmações relacionadas aos conceitos primitivos, com posições relativas, com o uso de conceitos geométricos para interpretar e analisar situações do cotidiano e com demonstração da validade de um teorema.

Páginas 115 a 119

Posições relativas no espaço

No boxe Para pensar da página 115, espera-se quêque os estudantes percêbampercebam quêque duas retas distintas, não paralelas, podem sêrser: concorrentes, se forem coplanares; ou reversas, se forem não coplanares. Comentar quêque a interseção entre retas reversas é sempre vazia.

Nas páginas 115 e 116, ao explorar as posições relativas entre reta e plano, conversar com os estudantes sobre a interseção de uma reta com um plano. Espera-se quêque eles percêbampercebam quêque, quando uma reta s está contida em um plano (alfa)"α, a interseção corresponde à própria reta s. Quando uma reta s é paralela a (alfa)"α, a interseção é vazia. E, para uma reta s secante a (alfa)"α, a interseção corresponde a um único ponto.

No trabalho com as posições relativas entre planos, na página 116, explicar aos estudantes quêque, se dois planos secantes não são perpendiculares, eles são chamados de oblíqüosoblíquos.

Página trezentos e trinta e nove339

Comentar com os estudantes quêque, quando dois planos (alfa)"α e (beta)"β, por exemplo, são paralelos, a interseção entre eles é vazia e quêque, quando são secantes, a interseção entre eles corresponde à única reta comum a ambos os planos.

A seção Atividades das páginas 118 e 119 tem como objetivo trabalhar com a análise e a interpretação de afirmações relacionadas a posições relativas no espaço entre planos, retas no espaço e entre reta e plano, assim como com a demonstração de teoremas.

Páginas 120 a 122

Integrando com Linguagens e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento das competências gerais 4 e 9, ao abordar a linguagem do Sistema Braille, quêque pódepode levar os estudantes a exercitar a empatia, promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos.

Além díssudisso, propicíapropicia a abordagem do Tema Contemporâneo Transversal Educação em Direitos Humanos, uma vez quêque aborda diferentes formas de linguagens para se expressar e compartilhar informações, relacionando linguagem matemática e o Sistema Braille.

Promover com os estudantes uma roda de conversa sobre a inclusão de pessoas com deficiência física ou mobilidade reduzida no ambiente escolar. Nesse momento, também é importante debater as atitudes de ameaça e discriminação, conhecidas como búlinbullying, quêque evidenciam preconceitos, como a intolerância às diferenças.

Verificar a possibilidade de realizar um trabalho em parceria com professores da área de Ciências Humanas e Suas Tecnologias a fim de discutir o uso de diferentes linguagens na comunicação, na elaboração de argumentos e na interpretação de situações do cotidiano, incluindo as relacionadas ao entendimento da vida em sua diversidade.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para conhecer as normas técnicas da escrita em Braille.

• BRASIL. Ministério da Educação. Secretaria de Educação Continuada, Alfabetização, Diversidade e Inclusão. Normas técnicas para a produção de textos em Braille. 3. ed. Brasília, DF: MÉCMEC: Secadi, 2018. Disponível em: https://livro.pw/sfrko. Acesso em: 10 out. 2024.

O Pensando no assunto tem como objetivo trabalhar o uso da linguagem verbal na comunicação, a reflekçãoreflexão sobre diferentes formas de se comunicar, a pesquisa e a elaboração de uma peça publicitária sobre acessibilidade atitudinal e a transcrição da linguagem matemática para a linguagem braille.

Atividade Extra

O tema trabalhado nessa seção possibilita uma ampliação por meio da realização de um projeto, quêque também pódepode compor uma avaliação. Uma sugestão é a produção de instrumentos quêque auxiliem no ensino de conhecimentos matemáticos para estudantes com algum tipo de deficiência. Na parte geral destas Orientações para o professor há informações sobre a metodologia ativa aprendizagem baseada em projetos.

1. Organizar os estudantes em grupos de maneira a valorizar os diferentes perfis (colaborativos, criativos, críticos, líderes etc.);

2. Cada grupo deve pesquisar e escolher um instrumento adaptado para pessoas com deficiência a sêrser confeccionado: régua, ábaco, sólidos geométricos etc.). Em seguida, deve investigar como construir esses instrumentos utilizando materiais alternativos.

3. Separar os materiais necessários e produzir o instrumento. Nessa fase, é importante quêque cada grupo produza um instrumento diferente e, além díssudisso, orientar os estudantes na utilização de utensílios cortantes a fim de evitar acidentes e garantir a integridade física dos envolvidos na produção dos instrumentos.

4. Apresentação dos instrumentos produzidos.

Essa apresentação pódepode sêrser feita por meio de uma feira na escola ou da gravação de vídeos com as etapas da produção dos instrumentos e disponibilizados em um blogue ou rê-derede social oficial da escola. Os instrumentos produzidos podem sêrser incorporados a um Laboratório de Ensino de Matemática (LEM) ou doados a uma instituição local.

Ao final do projeto, é importante avaliar a participação individual e coletiva dos estudantes na realização de cada fase do projeto propôstoproposto.

Páginas 123 a 128

Projeções ortogonais

O trabalho com projeções ortogonais é importante para quêque os estudantes desenvolvam a visão espacial, compreendendo quêque a visualização de um objeto tridimensional é possível com base na associação dos diversos pontos de vista, utilizados em sua representação e quêque, a partir dêêssesdesses pontos de vista, pode-se desenhar a figura geométrica espacial ou o objeto correspondente a elas.

Explicar quêque a Geometria Descritiva é o campo de estudo da Matemática quêque tem como um dos objetivos a representação de objetos tridimensionais em um plano bidimensional. O matemático francês Gaspar Monge (1746-1818) é considerado precursor dêêssedesse estudo.

Página trezentos e quarenta340

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações sobre Gaspar Monge e a Geometria Descritiva.

• UNIVERSIDADE ESTADUAL DE LONDRINA. Geometria descritiva. Londrina: Úh-êh-éleUEL: Departamento de Matemática, 2024. Disponível em: https://livro.pw/awayy. Acesso em: 10 out. 2024.

Antes de iniciar o trabalho com esse tópico, verificar a possibilidade e a necessidade de propor aos estudantes a resolução das atividades 19 e 20 da página 127 a fim de utilizá-las como uma avaliação diagnóstica. A resolução dessas atividades não requer conhecimentos teóricos de algum assunto matemático específico. Assim, após a análise do dêsempênhodesempenho, a condução do trabalho com esse tópico pódepode ficar mais personalizada.

Ao definir projeção ortogonal, na página 123, explicar aos estudantes quêque, nesse caso, o plano (alfa)"α corresponde ao plano de projeção e a reta r, quêque passa por P e é perpendicular ao plano (alfa)"α, é a reta projetante do ponto.

Ao trabalhar com distâncias no espaço, nas páginas 124 e 125, verificar a possibilidade de realizar uma atividade prática com os estudantes para quêque eles investiguem a distância entre ponto e reta. Para isso, representar na lousa uma reta r e um ponto P fora dela. Depois, traçar diversos segmentos de reta com uma extremidade em P e outra em algum ponto de r e medir os ângulos formados entre cada um deles e a reta r, conforme a figura a seguir.

Depois, com uma régua, pedir a alguns estudantes quêque, um por vez, meçam os segmentos de reta traçados e registrem o comprimento de cada um deles. Ao final, eles devem identificar o comprimento do menor segmento de reta traçado. Espera-se quêque eles verifiquem quêque, nesse caso, o menor segmento de reta é o quêque forma ângulos de 90° com r e, portanto, o comprimento dêêssedesse segmento de reta corresponde à distância do ponto P à reta r.

A resolução da atividade resolvida R3 utiliza ideias da resolução de problemas, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor. Sugere-se estruturar e executar essas etapas, como foi apresentado, sempre quêque perceber quêque os estudantes estão com dificuldades em determinado problema matemático. Essa estratégia também pódepode sêrser utilizada pêlospelos próprios estudantes quando estiverem diante de um problema matemático a sêrser resolvido.

A seção Atividades das páginas 127 e 128 tem como objetivo trabalhar com a projeção ortogonal de uma figura sobre um plano, com o reconhecimento de projeções ortogonais de um sólido geométrico em diferentes planos, com a análise de afirmações relacionadas à projeção ortogonal e às distâncias no espaço e com a distância entre dois pontos.

Páginas 129 e 130

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, uma vez quêque faz uso de uma tecnologia digital para resolver problemas.

Na etapa A, além da estratégia apresentada para construir os pontos A, B e C, os estudantes podem marcar cada ponto sobre a malha de acôr-doacordo com as respectivas coordenadas. Na etapa B, explicar a eles quêque o valor correspondente à distância apresentada entre $\overleftrightarrow{AB}$ e o ponto C é aproximado.

Mãos à obra - página 130

1. Para construir a reta g, os estudantes podem utilizar a opção Reta paralela e, em seguida, selecionar o ponto C e a reta $\overleftrightarrow{AB}$. De maneira análoga e utilizando a opção Reta perpendicular, eles constroem a reta h. No item b, para marcar o ponto D, os estudantes podem utilizar a opção Interseção de dois objetos e clicar sobre as retas $\overleftrightarrow{AB}$ e h.

2. No item b, orientar os estudantes na construção dos polígonos regulares utilizando a opção Polígono regular. Espera-se quêque eles construam um quadrado, quêque é o polígono regular quêque atende às condições propostas nesse item.

Páginas 131 a 134

Projeções cartográficas

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 5 e da habilidade EM13MAT509 da área de Matemática e suas Tecnologias, pois aborda a deformação de ângulos e áreas provocada pelas diferentes projeções usadas em Cartografia.

Verificar a possibilidade de realizar um trabalho em parceria com um professor da área de Ciências Humanas e Sociais Aplicadas, em particular, para tratar de conceitos relacionados à Geografia, como as principais projeções cartográficas utilizadas para representar o espaço geográfico (projeção de Mercator, projeção de mílerMiller etc.), destacando suas classificações quanto ao método, à superfícíesuperfície de projeção e às propriedades, por exemplo.

A seção Atividades das páginas 133 e 134 tem como objetivo trabalhar com as projeções ortogonal, cartográfica e estereográfica e com a investigação de deformações em mapas.

Ao abordar o boxe Mundo do trabalho, propor aos estudantes quêque pesquisem mais informações relacionadas à profissão de geógrafo. Sugere-se também convidar um profissional da área para conversar com os estudantes a respeito dessa profissão.

Conexões

Ao trabalhar com a atividade 29, sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações sobre como construir uma miniatura do planêtaplaneta Terra.

• hí bê gê héIBGE EDUCA CRIANÇAS. Icosaedro de Fuller. [S. l.]: hí bê gê héIBGE, c2024. Disponível em: https://livro.pw/qpkeg. Acesso em: 10 out. 2024.

Páginas 135 e 136

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o

Página trezentos e quarenta e um341

Trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A questão 4 trabalha a relação entre a Geometria não Euclidiana e as projeções cartográficas. Para a resolução do item a, se necessário, retomar o estudo da área do círculo. No item b, espera-se quêque os estudantes consultem as características das projeções cartográficas apresentadas nessa Unidade. No item c, verificar a possibilidade de trazer para a sala de aula objetos esféricos para auxiliar na interpretação da situação apresentada ou possibilitar aos estudantes acesso a um glôboglobo terrestre digital.

Páginas 137 e 138

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 4 Figuras geométricas espaciais, área de superfícíesuperfície e volume

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender o conceito de poliedro e classificá-lo, de acôr-doacordo com a quantidade de faces, e em convexo ou não convexo.

• Estabelecer e compreender a relação de ÓilerEuler para poliedros convexos.

• Reconhecer os poliedros regulares e os poliedros de Platão.

• Associar figuras geométricas espaciais às planificações correspondentes.

• Compreender os conceitos de prisma, pirâmide, tronco de pirâmide, cilindro circular, cone circular, tronco de cone reto e esféraesfera.

• Compreender a nomenclatura de um prisma de acôr-doacordo com o polígono da base, identificar um prisma regular e classificar um prisma em reto ou oblíquo.

• Compreender a nomenclatura de uma pirâmide de acôr-doacordo com o polígono da base.

• Identificar quando uma pirâmide é regular, bem como determinar o apótema da base da pirâmide e o apótema da pirâmide.

• Classificar cilindros e cones em reto ou oblíquo e identificar um cilindro ou um cone equilátero.

• Estabelecer uma expressão quêque relacione a medida do raio da base, da geratriz e da altura de um cone circular reto.

• Reconhecer sólidos geométricos de revolução.

• Construir figuras geométricas espaciais utilizando um software de geometria dinâmica.

• Compreender e estabelecer expressões para determinar a área da superfícíesuperfície e o volume de prisma, pirâmide, tronco de pirâmide, cilindro reto, cone reto, tronco de cone reto e esféraesfera.

• Compreender o princípio de Cavalieri para determinar o volume de um prisma ou de um cilindro qualquer e outras estratégias para determinar o volume de uma pirâmide, de um cone e de uma esféraesfera.

• Resolver e elaborar problemas, individualmente ou em grupo, envolvendo os tópicos trabalhados nessa Unidade, relacionados ou não a situações do cotidiano.

Orientações didáticas

O trabalho com essa Unidade possibilita aos estudantes desenvolver o pensamento geométrico e o pensamento algébrico, estabelecendo relações entre esses tipos de pensamento e demandas do cotidiano e de outras áreas do conhecimento, uma vez quêque algumas situações do dia a dia e das ciências podem sêrser resolvidas por meio de conceitos associados às ideias de área de superfícíesuperfície e de volume de figuras geométricas espaciais. Além díssudisso, é possível quêque os estudantes percêbampercebam quêque muitas construções e objetos presentes em seu cotidiano lembram figuras geométricas espaciais.

Página 139

Abertura da Unidade

A abertura da Unidade propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia, uma vez quêque trata dos avanços tecnológicos relacionados ao aperfeiçoamento de técnicas nas construções civis, em particular, no uso do concreto armado.

Convidar um professor da área de Ciências da Natureza e suas Tecnologias para conversar com os estudantes acerca do tema trabalhado nessa página, ressaltando as propriedades físico-químicas do concreto quêque o tornam resistente à compressão, assim como o aço da estrutura, quêque é resistente à tração, e como essas características se complementam e são úteis para a construção civil.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

Página trezentos e quarenta e dois342

1. Resposta possível: Sim, em construção de lajes e nas colunas em edificações.

2. Resposta possível: Colunas ou vigas de sustentação.

3. Resposta esperada: O formato e as medidas das dimensões da viga.

Páginas 140 a 145

Poliedros

No trabalho com esse tópico, ao quêquestionar os estudantes sobre construções do bairro ou do município em quêque moram e que podem sêrser associadas a um poliedro, propor a eles quêque compartilhem suas experiências e quêque façam um desenho para representar o poliedro associado a essa construção.

No boxe Para pensar da página 140, espera-se quêque os estudantes percêbampercebam quêque a figura geométrica espacial representada não é poliedro, pois não satisfaz a todas as condições indicadas. Nesse momento, se julgar conveniente, apresentar a eles outros exemplos de figuras geométricas espaciais quêque satisfazem apenas a uma dessas condições. Reforçar, contudo, quêque a figura dada pódepode sêrser ôbitídaobtida da composição de dois poliedros.

Na apresentação da relação de ÓilerEuler, na página 142, comentar com os estudantes quêque há indícios de quêque ela pódepode ter sido conhecida por arquimédisArquimedes (c. 287 a.C.-c. 212 a.C.) e por RenêRené Descartes (1596-1650), porém foi ÓilerEuler quem primeiro a enunciou, em 1752.

Fonte dos dados: EVES, ráuardHoward. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 124.

Conexões

Acessar o sáitisite indicado a seguir para consultar a demonstração da relação de ÓilerEuler, também conhecida por teorema de ÓilerEuler, para poliedros convexos.

• AZAMBUJA FILHO, Zoroastro. Demonstração do teorema de ÓilerEuler para poliedros convexos. Revista do Professor de Matemática, [São Paulo], n. 3, [jan./jun. 1982]. Disponível em: https://livro.pw/wvljw. Acesso em: 11 out. 2024.

Explicar aos estudantes quêque os poliedros para os quais a relação de ÓilerEuler é válida são chamados de poliedros eulerianos. Assim, pode-se afirmar quêque todo poliedro convexo é óilerianoeuleriano, porém nem todo poliedro óilerianoeuleriano é convexo.

Ao abordar a atividade resolvida R2, comentar com os estudantes quêque existem apenas cinco classes de poliedros de Platão, conforme apresentado no qüadroquadro a seguir, em quêque F é a quantidade de faces, A é a quantidade de arestas, V é a quantidade de vértices, n é a quantidade de lados de cada face e q é a quantidade de arestas quêque partem de cada vértice.

A seção Atividades das páginas 144 e 145 tem como objetivo trabalhar com a identificação e o cálculo da quantidade de vértices, faces e arestas de um poliedro, com o formato de suas faces, com a representação de poliedros convexos e não convexos, com a identificação de poliedros regulares e com a relação entre as quantidades de vértices, faces e arestas em um poliedro não convexo.

Páginas 146 a 157

Prismas

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 2, 3 e 5 e das habilidades EM13MAT201, EM13MAT309 e EM13MAT504 da área de Matemática e suas Tecnologias, pois envolve a resolução e a elaboração de problemas com o cálculo de áreas de superfícies e de volumes de prismas em situações contextualizadas, assim como a investigação de processos para a obtenção do volume de prismas, incluindo o princípio de Cavalieri, para a dedução de expressões de cálculo do volume dessa figura.

No boxe Para pensar da página 147, espera-se quêque os estudantes compreendam quêque todo cubo é um paralelepípedo reto-retângulo cujas arestas têm medidas iguais, mas nem todo paralelepípedo reto-retângulo é um cubo. Observe, a seguir, algumas respostas possíveis a esse boxe.

Antes de iniciar o trabalho com área da superfícíesuperfície de um prisma, na página 148, verificar a possibilidade e a necessidade de propor aos estudantes a resolução das atividades 13 a 15 da página 149 para utilizá-la como uma avaliação diagnóstica, pois essas atividades abordam conceitos matemáticos provavelmente estudados em anos anteriores. Assim, é possível identificar indícios do conhecimento prévio dos estudantes a respeito dêêssedesse assunto, ou possíveis defasagens de aprendizagem, e conduzir o trabalho com esse conteúdo de maneira personalizada.

Caso julgar conveniente, trazer para a sala de aula objetos cujos formatos lembram paralelepípedos reto-retângulos, como caixas de sapatos, e propor aos estudantes quêque, em grupos de três ou quatro integrantes, realizem medições para calcular a área da superfícíesuperfície externa dos objetos. Essas medições podem sêrser realizadas com régua, trena, pedaços de barbante etc.

A seção Atividades das páginas 149 e 150 tem como objetivo trabalhar com a obtenção da medida da diagonal do paralelepípedo reto-retângulo em função de suas dimensões, com o cálculo das medidas das arestas de um prisma oblíquo e com cálculos envolvendo a área da superfícíesuperfície de um prisma.

Ao apresentar o princípio de Cavalieri, na página 152, explicar aos estudantes quêque, ao enunciar quêque os sólidos geométricos espaciais estão apoiados em um mesmo plano, isso significa quêque as bases dêêssesdesses sólidos estão contidas nesse plano. A demonstração do princípio de Cavalieri não será apresentada, pois requer o

Página trezentos e quarenta e três343

conhecimento de conceitos matemáticos mais avançados do quêque os propostos nesse nível de ensino. Porém é possível realizar alguma atividade prática para quêque os estudantes compreendam esse princípio, como a proposta a seguir.

Atividade Extra

Providenciar, préviamentepreviamente, fichas retangulares idênticas e, com os estudantes organizados em grupos de três ou quatro integrantes, pedir a eles quêque empilhem as fichas de modo quêque os empilhamentos fiquem com a mesma quantidade de fichas, porém com formatos diferentes. Perguntar a eles se os empilhamentos têm o mesmo volume. Espera-se quêque percêbampercebam quêque o volume de cada empilhamento corresponde à soma dos volumes de cada ficha e, como as fichas são idênticas e os empilhamentos são formados pela mesma quantidade de fichas, pode-se afirmar quêque os empilhamentos têm o mesmo volume, independentemente de como as fichas foram empilhadas.

A resolução da atividade resolvida R6 apresenta ideias da resolução de problemas, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor. Na 3ª etapa, se necessário, retomar o estudo de notação científica, conteúdo abordado na Unidade 1 do Volume 2 desta coleção.

A seção Atividades das páginas 155 a 157 tem como objetivo trabalhar com cálculos envolvendo volume de um prisma reto ou oblíquo, também a partir da sua planificação, além do cálculo do volume de figura geométrica espacial decomposta em prismas.

A atividade 32 propicíapropicia o desenvolvimento da habilidade EM13MAT201 da área de Matemática e suas Tecnologias, pois envolve ações adequadas a uma demanda social abrangendo medidas e cálculo de volume, além de uma abordagem do Tema Contemporâneo Transversal Educação em Direitos Humanos, uma vez quêque aborda aspectos relacionados à acessibilidade, como informações técnicas sobre as rampas de acesso, e propõe a elaboração de uma proposta de construção de rampa na comunidade local.

Páginas 158 a 167

Pirâmides

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 2, 3 e 5 e das habilidades EM13MAT201, EM13MAT309 e EM13MAT504 da área de Matemática e suas Tecnologias, pois envolve a resolução e a elaboração de problemas com o cálculo de áreas de superfícies e de volumes de pirâmides em situações contextualizadas, assim como a investigação de processos para a obtenção do volume de pirâmides.

Comentar com os estudantes quêque uma pirâmide pódepode sêrser classificada em reta ou oblíqua. Na pirâmide reta, a projeção do vértice dessa pirâmide sobre o plano quêque contém sua base coincide com o centro dessa base; na pirâmide oblíqua, isso não ocorre. Se necessário, sugerir aos estudantes quêque retomem o estudo sobre projeções ortogonais no plano, conteúdo tratado na Unidade 3 dêstedeste Volume.

No boxe Para pensar da página 159, questionar os estudantes sobre a diferença entre o cálculo da área da superfícíesuperfície de um prisma e de uma pirâmide. Espera-se quêque eles percêbampercebam quêque a área total da superfícíesuperfície de um prisma corresponde à área lateral mais duas vezes a área da base e quêque a área total da superfícíesuperfície de uma pirâmide corresponde à área lateral mais a área da base.

A seção Atividades das páginas 161 e 162 tem como objetivo trabalhar com o cálculo das medidas do apótema da base, do apótema da pirâmide e da aresta lateral de uma pirâmide regular, além do cálculo da área da superfícíesuperfície de prismas e pirâmides.

Ao trabalhar com o volume de uma pirâmide, na página 163, relembrar aos estudantes quêque dois polígonos são semelhantes se os ângulos internos correspondentes forem congruentes e os lados correspondentes forem proporcionais entre si. Ainda, enfatizar a relação entre a área de quaisquer pares de polígonos semelhantes e, em particular, para polígonos regulares, conforme segue.

Considere um polígono regular de n lados de comprimento (éli)"ℓ e cuja área é A. Ao multiplicar a medida dos lados dêêssedesse polígono por um número real positivo k, obtém-se um polígono regular de n lados de comprimento k ⋅ (éli)"ℓ e área k² ⋅ A.

A seção Atividades das páginas 166 e 167 tem como objetivo trabalhar com cálculos envolvendo volume de pirâmides e de tronco de pirâmides.

Páginas 168 a 174

Cilindro circular

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 2, 3 e 5 e das habilidades EM13MAT201, EM13MAT309 e EM13MAT504 da área de Matemática e suas Tecnologias, pois envolve a resolução e a elaboração de problemas com o cálculo de áreas de superfícies e de volumes de cilindros circulares, assim como a investigação de processos para a obtenção do volume do cilindro circular.

No boxe Matemática na história da página 168, comentar com os estudantes quêque o papiro de Rhind (ou Ahmes) e o papiro de Moscou são as principais fontes de informações acerca da Matemática egípcia antiga. O papiro de Rhind é organizado em proposições e resoluções de problemas e data de cerca de 1650 a.C. Atualmente, esse papiro está exposto no Museu Britânico, em Londres (Inglaterra). O papiro de Moscou data de cerca de 1850 a.C. e contém 25 problemas. êsteEste se encontra no Museu Estatal Pushkin de Belas Artes, em Moscou (Rússia).

Fonte dos dados: EVES, ráuardHoward. Introdução à história da matemática. Tradução Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 69-70.

Ao iniciar o trabalho com a área da superfícíesuperfície de um cilindro reto, na página 170, verificar a possibilidade de reproduzir móldesmoldes de cilindros rétosretos para quêque os estudantes possam manipulá-los e analisar o comprimento do retângulo (correspondente à superfícíesuperfície

Página trezentos e quarenta e quatro344

lateral do cone reto), quêque é igual ao comprimento da circunferência da base do cilindro. Essas medições podem sêrser feitas com pedaços de barbante e régua, por exemplo.

A seção Atividades da página 171 tem como objetivo trabalhar com o cálculo da área da superfícíesuperfície de cilindros. Na atividade 55, explicar aos estudantes quêque a área da superfícíesuperfície ôbitídaobtida ao seccionar um cilindro reto por um plano paralelo ao seu eixo é diretamente proporcional à medida do comprimento do arco de circunferência determinado por essa seção.

Para o trabalho com o volume de um cilindro, na página 172, retomar com os estudantes o princípio de Cavalieri, apresentado nessa Unidade.

A seção Atividades das páginas 173 e 174 tem como objetivo trabalhar com o cálculo do volume de cilindros, cilindros obtidos por revolução e a partir do perímetro de sua seção meridiana, além do cálculo da área da superfícíesuperfície de um cilindro de revolução.

Ao abordar o boxe Mundo do trabalho, propor aos estudantes quêque pesquisem mais informações relacionadas às vantagens do trabalho em equipe. Sugere-se convidar um profissional da área de Recursos Humanos para conversar com os estudantes a respeito das soft skills.

Páginas 175 a 184

Cone circular

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 2, 3 e 5 e das habilidades EM13MAT201, EM13MAT309 e EM13MAT504 da área de Matemática e suas Tecnologias, pois envolve a resolução e a elaboração de problemas com o cálculo de áreas de superfícies e de volumes de cones circulares, assim como a investigação de processos para a obtenção do volume do cone circular. Também propicíapropicia uma abordagem do Tema Contemporâneo Transversal Educação Ambiental, uma vez quêque trata da reciclagem do óleo de cuzinhacozinha. Verificar a possibilidade de promover uma roda de conversa com os estudantes em parceria com um professor da área de Ciências da Natureza e suas Tecnologias para discutir sobre as consequências do descarte incorrétoincorreto do óleo de cuzinhacozinha, como a contaminação de sólossolos e rios.

No boxe Para pensar da página 176, espera-se quêque os estudantes percêbampercebam quêque o raio da base, a altura e a geratriz do cone reto correspondem, nesta ordem, aos dois catetos e à hipotenusa de um triângulo retângulo.

Na página 177, para determinar a área lateral de um cone reto, foi utilizada a propriedade fundamental das proporções; se necessário, retomar o estudo dessa propriedade, conteúdo tratado em anos anteriores. Verificar se os estudantes perceberam quêque 2(pi)"πg e (pi)"πg² correspondem ao comprimento e à área de um círculo de raio g, respectivamente, e quêque 2(pi)"πr e A(éli)"ℓ correspondem ao comprimento e à área do setor circular, respectivamente.

A seção Atividades da página 179 tem como objetivo trabalhar com o cálculo da área da superfícíesuperfície de cones e de seus elemêntoselementos. A atividade 72 propicíapropicia o desenvolvimento da habilidade EM13MAT201, uma vez quêque propõe a elaboração de um mapa virtual identificando pontos de côlétacoleta de óleo de cuzinhacozinha usado.

No trabalho com o volume de um cone circular, na página 180, retomar com os estudantes a relação entre a área de quaisquer pares de polígonos semelhantes, como apresentado nos comentários para o estudo do volume de uma pirâmide.

A seção Atividades das páginas 182 a 184 tem como objetivo trabalhar com o cálculo do volume de cones e de seus elemêntoselementos e cones obtidos por revolução. Para resolver a atividade 78, os estudantes podem utilizar instrumentos de desenho (régua, esquadros, transferidor e compasso) ou um software de geometria dinâmica, como o GeoGebra. A atividade 87 propicíapropicia o desenvolvimento da habilidade EM13MAT201 e uma abordagem do Tema Contemporâneo Transversal Educação para o Consumo, uma vez quêque propõe a investigação de modelos de copos plásticos descartáveis de acôr-doacordo com as especificações da ABNT.

Páginas 185 a 189

esféraEsfera

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 2, 3 e 5 e das habilidades EM13MAT201, EM13MAT309 e EM13MAT504 da área de Matemática e suas Tecnologias, pois envolve a resolução e a elaboração de problemas com o cálculo da área da superfícíesuperfície e do volume de esferas, assim como um processo de investigação para a obtenção do volume da esféraesfera. Além díssudisso, propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia.

Sugerir aos estudantes quêque realizem uma pesquisa para investigar como são calculadas a medida do diâmetro de um planêtaplaneta. Eles devem relacionar os elemêntoselementos de uma esféraesfera ao estudo das linhas imaginárias e das coordenadas geográficas. Essa proposta pódepode sêrser acompanhada por um professor da área de Ciências Humanas e Sociais Aplicadas, em particular, para tratar de conceitos da Geografia.

Ao trabalhar com o volume de uma esféraesfera, na página 186, comentar com os estudantes quêque o sólido geométrico M é conhecido por anticlepsidra. Relembrá-los de quêque uma coroa circular corresponde à região compreendida entre duas circunferências concêntricas. No boxe DICA, verificar se os estudantes perceberam quêque a coroa circular determinada a partir da seção do plano (alfa)"α com o sólido M tem centro O’ e raios d e r, com r > d. Como o plano (alfa)"α é paralelo a (beta)"β e secciona a esféraesfera a uma distância d de seu centro C, analogamente, o plano (alfa)"α também secciona o sólido M a uma mesma distância d do vértice B, ou seja, O’B = d. Além díssudisso, como $\overline{O^{\mathrm{\text{'}}}P}$ é o raio da menor circunferência da coroa circular, tem-se quêque O’P = d. Logo, o triângulo BO’P é isósceles.

Na página 187, ao trabalhar com a área da superfícíesuperfície de uma esféraesfera, comentar com os estudantes quêque, diferentemente do cilindro e do cone, a superfícíesuperfície de uma esféraesfera não pódepode sêrser planificada. A demonstração da expressão para calcular a área da superfícíesuperfície de uma esféraesfera não será apresentada, pois requer o conhecimento de conceitos matemáticos mais avançados do quêque os propostos nesse nível de ensino. No entanto, uma verificação dessa expressão é realizada a partir da decomposição de uma esféraesfera em n sólidos geométricos congruentes. Nesse caso, n pirâmides de base quadrangular congruentes.

Atividade Extra

Ao trabalhar a atividade resolvida R16, propor aos estudantes quêque, em grupos de três integrantes, pesquisem um experimento em quêque seja possível visualizar os sólidos de revolução tratados nessa Unidade, o quêque pódepode sêrser realizado como parte de uma atividade avaliativa. Em seguida, propor a eles quêque investiguem as etapas do experimento, bem como os materiais quêque são

Página trezentos e quarenta e cinco345

necessários para sua realização (dar preferência para materiais simples e acessíveis, como materiais recicláveis). Por fim, eles devem realizar o experimento e apresentá-lo aos demais côlégascolegas da turma. Nesse momento, é importante orientar os estudantes na utilização de utensílios cortantes, por exemplo, a fim de evitar eventuais riscos e garantir a integridade física dos envolvidos no experimento. A apresentação pódepode sêrser feita por meio da gravação de vídeos com as etapas do experimento, disponibilizada em um blogue ou rê-derede social da escola.

A seção Atividades das páginas 188 e 189 tem como objetivo trabalhar com o cálculo do volume e da área da superfícíesuperfície de uma esféraesfera, de um hemisfério e da área de um fuso esférico, além do cálculo da medida aproximada do raio de uma esféraesfera a partir de seu volume e de seu equador. A atividade 97 propicíapropicia o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias, uma vez quêque propõe aos estudantes investigar e estabelecer conjecturas quêque expressem o cálculo da área de um fuso esférico em função de um ângulo de rotação e da medida do raio da esféraesfera correspondente.

Páginas 190 a 192

Integrando com Ciências da Natureza e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento das competências gerais 2 e 6, das competências específicas 2 e 3 e das habilidades EM13MAT201 e EM13MAT309 da área de Matemática e suas Tecnologias e da competência específica 3 da área de Ciências da Natureza e suas Tecnologias, pois envolve ações adequadas a demandas sociais relacionadas a medições e cálculos de área e de volume em situações reais. Além díssudisso, propicíapropicia uma abordagem do Tema Contemporâneo Transversal Educação Ambiental, uma vez quêque propõe uma reflekçãoreflexão sobre os impactos relacionados aos hábitos de consumo, bem como sobre a importânssiaimportância do uso da madeira de reflorestamento e da prática da silvicultura.

Conversar com os estudantes sobre os impactos ambientais causados pêlospelos seus hábitos de consumo, analisando de maneira crítica como a participação efetiva do jovem pódepode contribuir para o consumo consciente e para a preservação do meio ambiente. Essa conversa pódepode sêrser acompanhada por um professor da área de Ciências da Natureza e suas Tecnologias, quêque pódepode apresentar conceitos específicos da área.

O Pensando no assunto tem como objetivo trabalhar a reflekçãoreflexão sobre o consumo consciente a partir dos hábitos de consumo dos estudantes, a pesquisa de produtos provenientes de florestas plantadas e áreas de reflorestamento e a interpretação e a análise de gráficos e métodos de medição do volume de madeira.

O tema trabalhado nessa seção possibilita uma ampliação por meio da realização de um projeto. Uma sugestão é quêque esse projeto promôvapromova a arborização urbana. Na parte geral destas Orientações para o professor há informações sobre a metodologia ativa aprendizagem baseada em projetos. Essa proposta pódepode sêrser acompanhada por um professor da área de Ciências da Natureza e suas Tecnologias. É interessante quêque todo o processo realizado seja gravado em vídeo e disponibilizado, por exemplo, em uma rê-derede social da escola.

Páginas 193 e 194

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, da competência específica 3 e da habilidade EM13MAT309 da área de Matemática e suas Tecnologias, pois envolve a construção e o cálculo da área da superfícíesuperfície e do volume de figuras geométricas espaciais com apôioapoio de tecnologias digitais.

Na etapa A, enfatizar aos estudantes quêque a Janela de visualização 2D é referida apenas como Janela de visualização. Na etapa B, explicar quêque o valor correspondente ao volume do prisma construído, em centímetro cúbico, é aproximado.

Mãos à obra - página 194

1. Se necessário, orientar os estudantes na construção do pentágono regular.

2. Auxiliar os estudantes, inicialmente, na construção de uma das bases do cilindro reto: na Janela de visualização, com a opção Círculo: Centro & Raio selecionada, marcar um ponto qualquer na malha e, na caixa de texto quêque abrir, digitar “3”, quêque corresponde ao raio da base do cilindro, e confirmar com OK. Em seguida, de maneira análoga, eles devem realizar a etapa B, considerando “5” a altura do cilindro.

3. Nessa quêquestão, os estudantes podem investigar situações do cotidiano em que seja necessário utilizar conceitos envolvendo cálculo do volume ou da área da superfícíesuperfície de um prisma reto ou de um cilindro circular reto. Ao final, propor quêque os problemas sêjamsejam reproduzidos na lousa ou em projeção de slides e discutidos com os demais côlégascolegas da turma.

Páginas 195 e 196

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A questão 4 trabalha uma situação envolvendo construções em concreto armado, retomando, assim, o tema da abertura da Unidade. No item b, discutir com os estudantes sobre as partes das colunas e da viga quêque não serão pintadas (regiões de apôioapoio ao solo e regiões de contato entre as colunas e a viga). No item c, explicar aos estudantes quêque a betoneira é uma máquina com recipiente giratório para misturar o concreto, por exemplo. Além díssudisso, no segundo questionamento propôstoproposto nesse mesmo item, chamar a atenção deles para quêque considerem o volume mássimomáximo de concreto produzido em uma única vez na betoneira, e não a capacidade mássimamáxima de seu tambor.

Páginas 197 e 198

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Página trezentos e quarenta e seis346

Unidade 5 Análise Combinatória

Quadro-síntese da Unidade

Objetivos da Unidade

• Compreender as ideias dos princípios multiplicativo e aditivo da contagem.

• Construir árvores de possibilidades e tabélastabelas de dupla entrada para representar os resultados possíveis em um experimento aleatório.

• Compreender o conceito de fatorial de um número natural e resolver e simplificar expressões envolvendo fatoriais.

• Compreender os conceitos de arranjo, combinação e permutação e identificar qual deles utilizar para resolver determinado problema.

• Resolver e elaborar problemas, individualmente ou em grupo, envolvendo os tópicos trabalhados na Unidade, relacionados ou não a situações do cotidiano.

Orientações didáticas

O trabalho com essa Unidade possibilita aos estudantes desenvolver o raciocínio lógico, estabelecendo relações entre esse tipo de raciocínio e demandas do cotidiano, uma vez quêque, em diversas situações do dia a dia, são necessárias reflekçõesreflexões e análises críticas a respeito de possibilidades ou aleatoriedade de eventos para se tomar uma dê-cisãodecisão. Ainda, o trabalho com técnicas de contagem contribui para quêque os estudantes construam significados de ideias próprias da Matemática quêque podem sêrser utilizadas para interpretar e resolver problemas em diferentes contextos. Além díssudisso, é possível quêque os estudantes reconheçam a importânssiaimportância de conhecimentos matemáticos historicamente construídos para o desenvolvimento de diferentes tecnologias utilizadas atualmente.

Página 199

Abertura da Unidade

O trabalho com a abertura da Unidade propicíapropicia uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia, pois trata da necessidade do uso de senhas em serviços ôn láinion-line e contribui para reflekçõesreflexões sobre a importânssiaimportância da criação de senhas, principalmente no quêque diz respeito a segurança e privacidade.

Realizar uma discussão com os estudantes a fim de quêque eles apresentem suas considerações sobre o assunto. Para isso, propor os seguintes questionamentos.

• Vocês têm uma mesma senha para todas as rêdesredes sociais quêque utilizam?

• Vocês utilizam caracteres especiais para compor suas senhas?

• Vocês já observaram como funcionam as senhas de contas bancárias?

• Qual é a importânssiaimportância de ter uma senha difícil de sêrser descoberta?

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre a importânssiaimportância de senhas seguras.

• UNIVERSIDADE ESTADUAL DO NORTE DO PARANÁ. A importânssiaimportância de uma senha segura. [Jacarezinho]: Uenp, 2013. Disponível em: https://livro.pw/klmsw. Acesso em: 11 out. 2024.

São apresentadas, a seguir, as respostas aos itens propostos na abertura.

1. Respostas possíveis: Verificar a identidade do usuário; autenticar o usuário.

2. Respostas esperadas: Para evitar quêque as contas ôn láinion-line sêjamsejam invadidas; para proteger o acesso de cibercriminosos.

3. Resposta esperada: Nesses casos, é preciso considerar as possibilidades existentes para a combinação simultânea de lêtrasletras e algarismos, de acôr-doacordo com a quantidade de caracteres da senha. Por esse motivo, senhas dêêssedesse tipo tendem a sêrser mais seguras.

Página 200

O estudo da Análise Combinatória

Comentar com os estudantes quêque a Análise Combinatória permite determinar a quantidade total de combinações distintas, mesmo quando muitas restrições ou critérios são estabelecidos. Por exemplo, no caso das senhas do portal gov.br, listar todas as senhas distintas possíveis pódepode sêrser compléksocomplexo e trabalhoso. Contudo, a Análise Combinatória possibilita o desenvolvimento de estratégias para determinar a quantidade total de senhas distintas possíveis sem quêque haja necessidade de listar todas elas.

Páginas 201 a 208

Princípio fundamental da contagem

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT310 da área de Matemática e suas Tecnologias, pois envolve a resolução e a elaboração de problemas de contagem por meio do princípio multiplicativo, recorrendo a estratégias diversas, como o diagrama de árvore.

Antes de iniciar o trabalho com esse tópico, verificar a possibilidade e a necessidade de propor aos estudantes a resolução de algumas atividades das páginas 205 e 206 para utilizá-la como uma avaliação diagnóstica, pois essas atividades abordam assuntos matemáticos estudados em anos anteriores. Assim, é possível identificar indícios do conhecimento prévio dos estudantes a respeito dêêssedesse conteúdo e conduzir o trabalho com esse tópico de

Página trezentos e quarenta e sete347

maneira personalizada, realizando recuperações de defasagens, caso seja necessário.

No estudo do princípio fundamental da contagem, discutir com os estudantes quêque a tabélatabela de dupla entrada é uma opção viável para a análise de duas características, como no exemplo apresentado: escolha da côrcor e da capacidade de armazenamento de dados do táblêtitablet. Quando há mais características, outras representações podem sêrser mais viáveis, como a árvore de possiblidades.

Comentar com eles quêque a árvore de possibilidades, também conhecida como diagrama de árvore, é um meio ilustrativo quêque permite visualizar todas as possibilidades de combinação em determinadas condições estabelecidas.

A seção Atividades das páginas 205 a 208 tem como objetivo trabalhar com o princípio fundamental da contagem.

Conexões

Ao abordar a atividade 12, sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre sépiCEP.

• CORREIOS. Tudo sobre sépiCEP. [S. l.]: Correios, c2024. Disponível em: https://livro.pw/kmfhp. Acesso em: 11 out. 2024.

Páginas 209 a 211

Princípio aditivo da contagem

O TRABALHO com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT310 da área de Matemática e suas Tecnologias, pois envolve a resolução e a elaboração de problemas de contagem por meio do princípio aditivo.

A seção Atividades da página 211 tem como objetivo trabalhar com o princípio fundamental da contagem e com o princípio aditivo da contagem. Na atividade 25, é importante avaliar se os problemas elaborados pêlospelos estudantes contemplam as ideias relacionadas aos conceitos propostos. Ao final, alguns dêêssesdesses problemas elaborados podem sêrser reproduzidos na lousa e discutidos com a turma.

Páginas 212 a 214

Fatorial

Ao explorar os exemplos, propor aos estudantes quêque calculem 5 ⋅ 4! e 7 ⋅ 6 ⋅ 5! para verificar se os resultados obtidos correspondem a 120 (5!) e 5.040 (7!), respectivamente. Explicar a eles quêque a relação n! = n ⋅ (n − 1)! é conhecida como propriedade fundamental dos fatoriais.

A seção Atividades da página 214 tem como objetivo trabalhar com o cálculo de expressões, identificação de igualdades verdadeiras, simplificação de expressões e resolução de equações envolvendo o fatorial de um número natural, bem como a ideia de fatorial associada à paridade de um número.

Páginas 215 a 219

Arranjo simples

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT310 da área de Matemática e suas Tecnologias, pois envolve a resolução de problemas de contagem abrangendo agrupamentos ordenáveis, ou seja, em quêque importa a ordem em quêque os elemêntoselementos são agrupados.

Chamar a atenção dos estudantes para o fato de quêque, na tabélatabela de dupla entrada, em alguns momentos, as células da diagonal podem ficar sem a indicação de dados. É importante quêque eles percêbampercebam quêque, de acôr-doacordo com a situação apresentada no exemplo, cada membro da equipe não pódepode ocupar duas funções no tímetime.

Ao explorar a expressão para calcular a quantidade de arranjos simples de n elemêntoselementos distintos tomados p a p, se julgar conveniente, apresentar aos estudantes, de maneira detalhada, o cálculo da quantidade de possibilidades para cada uma das p posições do arranjo formado, como a seguir.

1ª posição: para p = 1, tem-se n − 1 + 1 = n; n possibilidades.

2ª posição: para p = 2, tem-se n − 2 + 1 = n − 1; n − 1 possibilidades.

3ª posição: para p = 3, tem-se n − 3 + 1 = n − 2; n − 2 possibilidades.

4ª posição: para p = 4, tem-se n − 4 + 1 = n − 3; n − 3 possibilidades.

⋮

p-ésima posição: tem-se n − p + 1 = n − (p−1); n − (p−1) possibilidades.

Para justificar aos estudantes a multiplicação da expressão ôbitídaobtida por $\begin{array}{c}\frac{\left(n-p\right)!}{\left(n-p\right)!}\end{array}$,relembrá-los de quêque o número um é o elemento neutro da multiplicação.

A seção Atividades das páginas 218 e 219 tem como objetivo trabalhar com o cálculo de arranjos simples, em situações contextualizadas ou não, e com a simplificação de expressões quêque envolvem arranjos simples.

Ao trabalhar com a atividade 42, verificar a possibilidade de propor a atividade a seguir, quêque pódepode compor o processo avaliativo.

Atividade Extra

Em um laboratório de informática, propor aos estudantes quêque pesquisem informações sobre a Placa de Identificação Veicular (PIV) no padrão merkossúlMercosul, como: a história dessa placa, o motivo pelo qual foi necessária sua implementação, quêque países a utilizam, qual é o diferencial dessa placa em relação ao modelo anterior, em particular, em relação à quantidade de placas distintas quêque podem sêrser formadas nos dois modelos. Além díssudisso, eles podem pesquisar dados estatísticos sobre o uso dessa placa. Pedir quêque registrem os dados da pesquisa em um relatório, quêque pódepode sêrser ilustrado e conter gráficos e tabélastabelas.

Páginas 220 a 222

Permutação simples

Ao explorar o contexto apresentado no início dêêssedesse tópico, promover uma roda de conversa para quêque os estudantes compartilhem suas experiências em relação aos serviços de streaming. Questioná-los sobre quais tipos dêêssesdesses serviços eles conhecem e quais já utilizaram, por exemplo, de vídeos, de músicas, de filmes etc.

Comentar com os estudantes quêque a permutação simples é um caso particular de arranjo simples.

Na atividade resolvida R13, chamar a atenção dos estudantes para o fato de quêque a quantidade de atletas é igual à quantidade de elemêntoselementos dos agrupamentos realizados. Propor a eles quêque resolvam essa atividade utilizando o princípio fundamental da contagem, conforme apresentado a seguir, o quêque possibilita a eles compreender quêque um mesmo problema pódepode sêrser resolvido por meio de diferentes estratégias.

Página trezentos e quarenta e oito348

A seção Atividades das páginas 221 e 222 tem como objetivo trabalhar com o cálculo de permutações simples, em situações contextualizadas ou não.

Caso os estudantes apresentem dificuldade para resolver o item b da atividade 51, sugerir quêque determinem, inicialmente, a quantidade de termos da sequência quêque são maiores quêque 89.765 (1 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24). Em seguida, eles devem subtrair o resultado obtídoobtido de 120, quêque corresponde à posição ocupada pelo último termo dessa sequência (120 − 24 = 96).

Páginas 223 a 226

Permutação com repetição

O contexto apresentado na introdução dêêssedesse tópico propicíapropicia o desenvolvimento da competência geral 3 e uma abordagem do Tema Contemporâneo Transversal Diversidade Cultural, pois trata das manifestações artísticas associadas à poesia concreta. Verificar a possibilidade de realizar um trabalho em parceria com um professor da área de Linguagens e suas Tecnologias para ampliar a discussão sobre as características do Concretismo. Verificar a possibilidade de o professor da área discutir com os estudantes outros movimentos artísticos e literários quêque ocorreram no Brasil.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para escutar um podcast quêque apresenta informações sobre a música e a poesia concreta.

• úspiUSP ESPECIAIS#4: Série Caminhos Sonoros: Música e Poesia Concreta. Apresentadora: Luísa Campelo de Freitas. São Paulo: Rádio úspiUSP, 12 mar. 2020. Podcast. Disponível em: https://livro.pw/xqwmq. Acesso em: 11 out. 2024.

Apresentar aos estudantes outros anagramas da palavra acaso a fim de quêque eles compreendam quêque, ao permutar as lêtrasletras a, obtém-se um mesmo anagrama, como os sugeridos a seguir.

• soaac soaac

• acoas acoas

• acsoa acsoa

Para auxiliar os estudantes a compreender a definição de permutação com repetição, apresentar a eles o esquema a seguir.

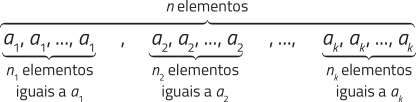
O contexto da atividade resolvida R18 propicíapropicia uma abordagem do Tema Contemporâneo Transversal Educação em Direitos Humanos, uma vez quêque trata da escrita em Braille, um sistema em quêque é possível reconhecer uma tendência de universalização de linguagem, possibilitando a comunicação e a autonomia de pessoas com deficiência visual. Comentar com os estudantes quêque o conjunto de seis pontos dispostos em formato retangular é chamado de cela braille. Como complemento, propor aos estudantes quêque realizem uma pesquisa para representar alguns dos caracteres do Sistema Braille, por exemplo, os símbolos próprios da linguagem matemática.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre o Sistema Braille.

• BRASIL. Ministério da Educação. Secretaria de Educação Especial. cóódigoCódigo matemático unificado para a língua portuguesa – CMU. Brasília, DF: MÉCMEC: Seesp, 2006. Disponível em: https://livro.pw/hctbw. Acesso em: 11 out. 2024.

A seção Atividades da página 226 tem como objetivo trabalhar com o cálculo de permutações com repetição, em situações contextualizadas ou não.

Páginas 227 a 235

Combinação simples

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento da competência específica 3 e da habilidade EM13MAT310 da área de Matemática e suas Tecnologias, pois envolve a resolução de problemas de contagem abrangendo agrupamentos não ordenáveis, ou seja, em quêque não importa a ordem em quêque os elemêntoselementos são agrupados.

Ao explorar a resolução da situação sobre a fiscalização dos cinco postos de combustível, relembrar aos estudantes a ideia de conjunto e de subconjunto.

• Sejam A e B dois conjuntos quaisquer, quando todos os elemêntoselementos do conjunto B também são elemêntoselementos do A, tem-se quêque B está contido em A, ou, ainda, quêque B é um subconjunto de A.

Comentar com os estudantes quêque a combinação simples de n elemêntoselementos, tomados p a p, também pódepode sêrser indicada por $\begin{array}{c}{C}_p^n\end{array}$ ou ($\genfrac{}{}{0pt}{}{n}{p}$).

No boxe Para pensar da página 229, propor aos estudantes quêque justifiquem a resposta. Espera-se quêque eles percêbampercebam quêque, ao escolher dois pontos, o segmento de reta traçado é o mesmo, independentemente da ordem de escolha dêêssesdesses pontos. Por exemplo, considerando os pontos A e B, os segmentos de reta $\overline{AB}$ e $\overline{BA}$ são os mesmos. Assim, a quantidade de segmentos de reta distintos quêque podem sêrser traçados é dado por C_{6, 2}.

A resolução da atividade resolvida R23 utiliza ideias da resolução de problemas, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor.

A seção Atividades das páginas 232 a 235 tem como objetivo trabalhar com o cálculo de combinações simples, em situações contextualizadas ou não, com o cálculo de arranjo simples e de permutação simples, com a identificação de arranjos e combinações simples em diferentes situações e com o reconhecimento de regularidades associadas à combinação simples.

Página trezentos e quarenta e nove349

Na atividade 71, relembrar aos estudantes quêque um polígono é convexo quando qualquer segmento de reta com extremidades no polígono tenha todos os seus pontos pertencentes a esse polígono. Verificar se eles perceberam quêque, para um polígono convexo de n lados, ao calcular C_{n, 2}, o resultado obtídoobtido corresponde ao total de lados e de diagonais dêêssedesse polígono. Assim, é necessário subtrair dêêssedesse resultado a quantidade de lados do polígono.

Na atividade 75, relembrar aos estudantes quêque duas retas r e s são coplanares quando estão contidas em um mesmo plano. Para a resolução, os estudantes podem analisar dois casos: quando dois vértices do triângulo estão sobre a reta r e um vértice está sobre s; e quando dois vértices do triângulo estão sobre a reta s e um vértice está sobre r.

Aproveitar a atividade 85 e promover uma roda de conversa com os estudantes sobre a importânssiaimportância dos cuidados com jogos de aposta, incluindo os jogos digitais de apostas, quêque podem causar problemas de compulsividade. Ressaltar quêque, no Brasil, há programas de saúde quêque oferecem tratamento para pessoas quêque apresentam sinais de dependência de jôgojogo. Para complementar, propor aos estudantes quêque pesquisem informações sobre outra modalidade de loteria organizada pela Caixa Econômica Federal.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre a realização de apostas de maneira responsável.

• BRASIL. Caixa Econômica Federal. jôgoJogo responsável. Brasília, DF: CEF [2024]. Disponível em: https://livro.pw/acljm. Acesso em: 11 out. 2024.

Páginas 236 a 239

Integrando com Linguagens e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento das competências gerais 1 e 9, da competência específica 3 e da habilidade EM13MAT310 da área de Matemática e suas Tecnologias, pois envolve combinações de agrupamentos, e da competência específica 3 da área de Ciências da Natureza e suas Tecnologias. Além díssudisso, o contexto propicíapropicia abordagens dos Temas Contemporâneos Transversais Ciência e Tecnologia e Educação em Direitos Humanos, uma vez quêque trata dos avanços tecnológicos relacionados à comunicação, apresentando conhecimentos historicamente construídos sobre o cóódigoCódigo Morse. Também contribui para a reflekçãoreflexão dos estudantes a respeito das tecnologias digitais da informação e comunicação (TDIC), de maneira a promover o respeito ao outro e aos direitos humanos.

Ao abordar o boxe No mundo do trabalho, verificar a possibilidade de convidar algum profissional de Recursos Humanos quêque trabalha com soft skills para conversar com os estudantes a respeito da comunicação e das outras competências comportamentais. Essa sugestão de abordagem favorece o desenvolvimento da competência geral 6, uma vez quêque valoriza a diversidade de saberes e promove a apropriação dos estudantes em relação a conhecimentos e experiências associados ao mundo do trabalho.

Verificar a possibilidade de promover uma roda de conversa com os estudantes para conversar sobre a história do cóódigoCódigo Morse, identificando, por exemplo, quando foi enviada a primeira mensagem utilizando esse cóódigocódigo. Essa conversa pódepode sêrser acompanhada por um professor da área de Ciências Humanas e Sociais Aplicadas, explorando, também, informações sobre a primeira linha de telégrafo no Brasil. Verificar a possibilidade de o professor da área discutir com os estudantes outros códigos utilizados para compartilhar mensagens no decorrer da história.

Ao abordar as informações sobre Tecnologia Assistiva, conversar com os estudantes sobre as barreiras nas comunicações e na informação quêque limitam ou impedem a inclusão de pessoas com deficiência visual ou auditiva na comunicação e na recepção de mensagens em sáitessites, no uso de softwares etc. Perguntar a eles se conhecem algum tipo de recurso tecnológico quêque promove a acessibilidade, por exemplo, aplicativos em smartphone.

O Pensando no assunto tem como objetivo trabalhar as experiências dos estudantes em relação a comunicação a distância, interpretação do texto apresentado, transcrição e escrita de palavras a partir do cóódigoCódigo Morse, cálculo dos caracteres distintos dêêssedesse cóódigocódigo a partir da Análise Combinatória e elaboração de um fôlder sobre o cóódigoCódigo Morse e acessibilidade.

O tema trabalhado nessa seção possibilita uma ampliação por meio da realização de um projeto, quêque pódepode compor o processo avaliativo da turma. Uma sugestão é quêque as informações dêêssedesse projeto sêjamsejam divulgadas em meios digitais com recursos quêque promovam a acessibilidade. Na parte geral destas Orientações para o professor há informações sobre a metodologia ativa aprendizagem baseada em projetos.

Páginas 240 e 241

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, da competência específica 3 e da habilidade EM13MAT310 da área de Matemática e suas Tecnologias, pois envolve a realização de cálculos utilizados para resolver problemas de contagem e agrupamentos, ordenáveis ou não, de elemêntoselementos com apôioapoio de tecnologias digitais (planilha eletrônica).

Chamar a atenção dos estudantes para a fórmula indicada em cada um dos exemplos. Para os cálculos de combinação e de arranjo simples, ressaltar o uso do ponto e vírgula para separar a indicação das células.

Se julgar conveniente, apresentar aos estudantes outras estratégias para realizar os cálculos de fatorial, combinação e arranjo simples, utilizando a planilha eletrônica LibreOffice Calc, conforme segue.

• Para calcular 5!, digitar “=fatorial(5)” na célula A1 e, em seguida, clicar em Enter.

• Para calcular C_{10, 2}, digitar “=combin(10;2)” na célula A2 e, em seguida, clicar em Enter.

• Para calcular A _{8, 3}, digitar “=permutar(8;3)” na célula A3 e, em seguida, clicar em Enter.

Mãos à obra - página 241

2. Valorizar as estratégias utilizadas pêlospelos estudantes para resolver essa quêquestão. Sugerir que ao menos um deles a apresente para os demais côlégascolegas da turma.

3. Nos itens a, b e c, espera-se quêque os estudantes calculem C_{80, 5}, A_{36, 8} e 26!, respectivamente. Além díssudisso, ao realizar os cálculos na planilha eletrônica, é possível quêque alguns números sêjamsejam arredondá-dosarredondados. Dessa maneira, pode-se redimensionar a célula em quêque o número foi inserido, ou, ainda, utilizar a opção do menúmenu Formatar como número.

Página trezentos e cinquenta350

4. Valorizar as estratégias utilizadas pêlospelos estudantes para resolver essa quêquestão. Sugerir que ao menos um deles a apresente para os demais côlégascolegas da turma.

Páginas 242 e 243

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A questão 4 retoma o tema da abertura da Unidade sobre o cadastro de senhas. No item d, promover um momento para quêque os estudantes compartilhem as informações pesquisadas com os demais côlégascolegas da turma, pois cada grupo pódepode obtêrobter informações sobre padrões de senha de diferentes modelos de smartphones.

Páginas 244 a 246

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Unidade 6 Probabilidade

Quadro-síntese da Unidade

Objetivos da Unidade

• Reconhecer o uso de cálculos de probabilidade em atividades e estudos de diversas áreas do conhecimento e situações do cotidiano.

• Determinar o espaço amostral de um experimento aleatório.

• Identificar quando dois eventos são mutuamente exclusivos.

• Calcular a probabilidade de ocorrência ou não de um evento, considerando um espaço amostral equiprovável.

• Calcular a probabilidade da união de dois eventos e a probabilidade condicional.

• Identificar se eventos de um mesmo espaço amostral são dependentes ou independentes.

• Calcular probabilidades em experimentos binomiais.

• Estimar a probabilidade de ocorrência de um evento a partir de dados estatísticos.

• Resolver e elaborar problemas, individualmente ou em grupo, envolvendo os tópicos trabalhados nessa Unidade, relacionados ou não a situações do cotidiano.

Orientações didáticas

O trabalho com essa Unidade possibilita aos estudantes desenvolver o raciocínio lógico e a curiosidade, ao identificar e aplicar os conceitos trabalhados em diferentes situações cotidianas, em quêque seja necessário investigar e analisar os riscos envolvidos e/ou escolher uma opção dentre outras disponíveis, considerando a probabilidade atrelada a determinado evento. Além díssudisso, é necessário explicitar quêque, por meio do cálculo de probabilidade, é possível prever a chance de ocorrência de um evento, mas não garantir sua ocorrência.

Página 247

Abertura da Unidade

O trabalho com a abertura da Unidade favorece uma abordagem do Tema Contemporâneo Transversal Ciência e Tecnologia, uma vez quêque apresenta informações sobre como são realizados os estudos meteorológicos para a previsão do tempo, bem como o uso de diferentes dispositivos de pesquisa para esse fim.

Promover uma roda de conversa com os estudantes sobre a importânssiaimportância de uma previsão meteorológica de qualidade. Essa conversa pódepode sêrser acompanhada por um professor da área de Ciências da Natureza e suas Tecnologias, pois, além de abordar temas relacionados ao clima, podem sêrser explorados os avanços tecnológicos quêque contribuem para a programação de sistemas de alertas e de ações para minimizar possíveis desastres naturais.

São apresentadas, a seguir, as respostas aos itens propostos nessa seção.

1. Respostas pessoais. As respostas dependem das vivências dos estudantes.

2. Resposta possível: Sim, porque é possível se programar para atividades diárias.

3. Resposta pessoal. A resposta depende do dia e da região em quêque os estudantes residem.

Páginas 248 a 254

O estudo da probabilidade

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 3 e 5 e das habilidades EM13MAT311 e EM13MAT511 da área de Matemática e suas

Página trezentos e cinquenta e um351

Tecnologias, pois envolve a identificação e a descrição do espaço amostral de eventos aleatórios e o reconhecimento da existência de diferentes tipos de espaço amostral.

Explicar aos estudantes quêque jogos de azar são aqueles em quêque ganhar ou perder dependem mais da sorte do quêque de habilidades ou de cálculos, como loteria, bingo e jôgojogo de carteado.

Conexões

Sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter mais informações sobre as aplicações do estudo de probabilidades.

• SILVEIRA, José Francisco Porto da. O desenvolvimento das aplicações das probabilidades. Porto Alegre: IME: (hú f érre gê ésse)UFRGS, 2001. Disponível em: https://livro.pw/udsbs. Acesso em: 11 out. 2024.

Para complementar as informações do boxe Matemática na história da página 248, verificar a possibilidade de propor aos estudantes uma pesquisa sobre como pódepode sêrser enunciado o problema dos pontos.

Conexões

Acessar o sáitisite indicado a seguir para obtêrobter informações sobre o problema dos pontos.

• CARVALHO, Paulo césarCezar Pinto. Métodos de contagem e probabilidade. São Paulo: IME: úspiUSP, 2009. Disponível em: https://livro.pw/rcewt. Acesso em: 11 out. 2024.

Ao discutir com os estudantes sobre experimento aleatório, na página 249, espera-se quêque eles compreendam quêque muitos dos acontecimentos do mundo físico são de natureza aleatória e quêque é possível, em certa medida, identificar prováveis resultados para esses acontecimentos.

Ao explorar o qüadroquadro com as possíveis maneiras quêque os participantes podem esconder os palítospalitos, quêquestionar os estudantes sobre a que corresponde o resultado (x, y). Espera-se quêque eles compreendam quêque o participante I escondeu x palítospalitos e o participante II, y palítospalitos.

Ao definir eventos mutuamente exclusivos, na página 251, relembrar quêque a notação ∅ corresponde ao conjunto vazio. Se necessário, retomar o estudo de operações com conjuntos (interseção).

A seção atividades das páginas 253 e 254 tem como objetivo trabalhar com a identificação de experimentos aleatórios, com a determinação do espaço amostral e de eventos de um experimento aleatório, com a identificação de eventos mutuamente exclusivos e a classificação de um evento em simples, cértocerto ou impossível e com as definições de espaço amostral discreto e contínuo.

Páginas 254 a 262

Cálculo de probabilidade

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 3 e 5 e das habilidades EM13MAT311 e EM13MAT511 da área de Matemática e suas Tecnologias, pois trabalha a identificação e a descrição do espaço amostral de eventos aleatórios, realizando contagem das possibilidades, para resolver e elaborar problemas relacionados ao cálculo da probabilidade, além de investigar implicações no cálculo de probabilidades de acôr-doacordo com o espaço amostral; e da competência específica 2 da área de Ciências da Natureza e suas Tecnologias, uma vez quêque propõe a análise de cálculos probabilísticos para realizar previsões sobre acontecimentos naturais.

Antes de iniciar o trabalho com esse tópico, verificar a possibilidade e a necessidade de propor aos estudantes a resolução das atividades 8 a 11, das páginas 259 e 260, para utilizá-las como uma avaliação diagnóstica, pois essas atividades abordam assuntos matemáticos quêque provavelmente foram tratados em anos anteriores. Assim, é possível identificar indícios do conhecimento prévio dos estudantes a respeito dêêssedesse assunto e conduzir o trabalho com esse tópico de maneira direcionada.

Explicar aos estudantes quêque cada evento simples de um espaço amostral equiprovável é denominado evento equiprovável.

Relembrar aos estudantes, por exemplo, quêque a indicação “n(E)” corresponde à quantidade de elemêntoselementos do conjunto E. Ao apresentar a relação da quantidade de elemêntoselementos dos conjuntos ∅, E e (ômega)"Ω, verificar se eles perceberam quêque a probabilidade de ocorrer algum elemento de E pódepode assumir valores de 0 a 1. Além díssudisso, pode-se indicar a relação 0 ≤ P(E) ≤ 1 por 0% ≤ P(E) ≤ 100%.

Na página 256, enfatizar aos estudantes quêque dois eventos são complementares quando satisfazem a duas condições: sêrser mutuamente exclusivos e a união dêêssesdesses eventos sêrser igual ao espaço amostral.

A resolução da atividade resolvida R6 utiliza ideias da resolução de problemas, uma das tendências metodológicas abordadas na parte geral destas Orientações para o professor.

A seção Atividades das páginas 259 a 262 tem como objetivo trabalhar com o cálculo de probabilidade de eventos aleatórios, com a identificação de espaços amostrais não equiprováveis e com a classificação de um espaço amostral em equiprovável ou não equiprovável.

Ao iniciar o trabalho com a probabilidade da união de dois eventos, na página 263, lembrar aos estudantes o conceito do princípio aditivo da contagem, conteúdo tratado na Unidade 5 dêstedeste Volume. Além díssudisso, relacionar o estudo da união de eventos ao de união de conjuntos, tratado na Unidade 1 do Volume 1 desta coleção.

Na situação apresentada, a expressão “ocorra ao menos um dêêssesdesses eventos” significa quêque pódepode ocorrer apenas o evento A, ou apenas o B, ou ambos os eventos.

A seção Atividades das páginas 265 a 267 tem como objetivo trabalhar com o cálculo envolvendo eventos aleatórios e probabilidade da união de dois eventos, além do cálculo de probabilidade de eventos complementares, da comparação entre a probabilidade de diferentes eventos e da investigação do cálculo da probabilidade da união de eventos mutuamente exclusivos.

Conexões

Ao abordar a atividade 23, sugerir aos estudantes quêque acessem o sáitisite indicado a seguir para obtêrobter informações sobre a participação das mulheres na política.

• BRASIL. Senado Federal. Mais mulheres na política. 2. ed. Brasília, DF: Senado Federal: Segraf, 2015. Disponível em: www12.senado.leg.br/institucional/procuradoria/proc-publicacoes/2a-edicao-do-livreto-mais-mulheres-na-politica. Acesso em: 11 out. 2024.

Página trezentos e cinquenta e dois352

Após trabalhar com a atividade 28, verificar a possibilidade de propor a atividade a seguir, quêque pódepode sêrser realizada como uma avaliação formativa.

Atividade Extra

Propor aos estudantes quêque realizem uma pesquisa estatística amostral em quêque o tema escolhido seja de interêsseinteresse social e o resultado possa contribuir para a melhoria da comunidade escolar. Uma sugestão é a importânssiaimportância do uso consciente das rêdesredes sociais, sobretudo na luta contra a prática de atitudes de ameaça e discriminação em ambientes digitais, conhecidas como sáiber-búlincyberbullying. Após a côlétacoleta e a organização dos dados, propor aos estudantes quêque escôlhamescolham recursos quêque representem os resultados da pesquisa, como tabélastabelas e gráficos, de acôr-doacordo com as características dos dados quêque desê-jamdesejam comunicar ou destacar. Com base nos resultados da pesquisa, os estudantes podem elaborar kestõesquestões quêque envolvam o cálculo de probabilidade, quêque devem sêrser trocadas com as de um colega para quêque um resôuvaresolva as kestõesquestões do outro e, juntos, verifiquem as resoluções.

Ao apresentar a definição de probabilidade condicional, na página 268, salientar aos estudantes quêque esta não se aplica para P(A) = 0. Comentar quêque, nas expressões, admitem-se denominador diferente de n((ômega)"Ω), pois se toma um evento particular do (ômega)"Ω como condição para o cálculo da probabilidade.

A seção Atividades das páginas 270 e 271 tem como objetivo trabalhar com a descrição de probabilidade condicional de eventos e com cálculos envolvendo probabilidade condicional.

A atividade 35 propicíapropicia uma abordagem do Tema Contemporâneo Transversal Processo de envelhecimento, respeito e valorização do Idoso, uma vez quêque trata da melhoria do município, visando o bem-estar dos idosos. Após o trabalho com essa atividade, verificar a possibilidade de propor a atividade a seguir.

Atividade Extra

Pedir aos estudantes quêque, em duplas, investiguem e analisem informações sobre a população idosa do município em quêque vivem, por exemplo: Há campanhas de incentivo à valorização do idoso? As pessoas idosas praticam atividades físicas? Há academias ao ar livre? Com base nessas informações, eles podem elaborar um vídeo ressaltando a importânssiaimportância da valorização do idoso e apresentando os benefícios das atividades físicas para esse público. Sugerir aos estudantes quêque compartilhem as produções com a comunidade local em um blogue ou em uma rê-derede social oficial da escola.

Ao explorar a resolução da questão proposta na página 272, perguntar aos estudantes se eles sabem como obtêrobter a quantidade de resultados possíveis no sorteio com reposição e no sorteio sem reposição utilizando o princípio fundamental da contagem. Espera-se quêque eles compreendam quêque, para o sorteio com reposição, basta calcular 3 ⋅ 3 = 9, uma vez quêque, ao repor na caixa o 1º papel sorteado, ele pódepode sêrser sorteado novamente. E para o sorteio sem reposição, como o 1º papel sorteado não é reposto na caixa antes do sorteio do 2º papel, basta calcular 3 ⋅ 2 = 6.

Comentar quêque, em geral, sorteios sem reposição determinam eventos dependentes e sorteios com reposição, eventos independentes.

A seção Atividades das páginas 275 a 277 tem como objetivo trabalhar com a classificação de eventos em dependentes ou independentes e com o cálculo de probabilidade de ocorrência de eventos dependentes e de eventos independentes.

O contexto da atividade 48 favorece o desenvolvimento da competência específica 2 da área de Ciências da Natureza e suas Tecnologias, uma vez quêque propõe a interpretação e a análise de resultados relacionados ao uso de testes diagnósticos. Verificar a possibilidade de realizar um trabalho em parceria com um professor da área de Ciências da Natureza e suas Tecnologias para quêque ele possa auxiliar na discussão sobre a importânssiaimportância da análise da sensibilidade e da especificidade em testes diagnósticos.

Ao abordar o boxe No mundo do trabalho, verificar a possibilidade de convidar um médico ou outro profissional quêque atua na área da saúde para conversar com os estudantes a respeito da profissão de médico. Essa sugestão de abordagem favorece o desenvolvimento da competência geral 6, uma vez quêque valoriza a diversidade de saberes e promove a apropriação dos estudantes em relação a conhecimentos e experiências associados ao mundo do trabalho.

Para o trabalho com probabilidade em experimentos binomiais, na página 278, se necessário, retomar o estudo de combinação simples, tratado na Unidade 5 dêstedeste Volume. No boxe Para pensar, espera-se quêque os estudantes calculem C_{5, 2} ⋅ ($\frac{1}{3}$)³ ⋅ ($\frac{2}{3}$)². Sugerir quêque um deles apresente a resolução na lousa para a turma.

A seção Atividades das páginas 280 e 281 tem como objetivo trabalhar com o cálculo de probabilidade em experimentos binomiais.

O contexto da atividade 53 propicíapropicia uma abordagem dos Temas Contemporâneos Transversais Educação Financeira e Educação Fiscal, uma vez quêque propõe aos estudantes a realização de uma pesquisa amostral sobre o uso de moedas nas compras do dia a dia na comunidade escolar ou local. Os estudantes podem utilizar diferentes linguagens e ferramentas para compartilhar as informações pesquisadas, como uma apresentação visual digital (slides) ou a produção de um vídeo ou podcast (programa de áudio veiculado na internet).

O contexto da atividade 55 propicíapropicia uma abordagem do Tema Contemporâneo Transversal Saúde, uma vez quêque propõe uma pesquisa sobre como diminuir os riscos de desenvolver diabetes melito. Ao explorar as informações apresentadas, realizar um trabalho em parceria com um professor da área de Ciências da Natureza e suas Tecnologias para discutir conceitos de Biologia relacionados ao diabetes melito e seu tratamento.

Páginas 282 a 286

Probabilidade e estatística

O trabalho com esse tópico favorece, com maior ênfase, o desenvolvimento das competências específicas 1, 3 e 5 e das habilidades EM13MAT106, EM13MAT311 e EM13MAT312 da área de Matemática e suas Tecnologias e da competência específica 2 da área de Ciências da Natureza e suas Tecnologias, pois envolve a identificação de situações da vida cotidiana nas quais é possível fazer escôlhasescolhas considerando-se riscos probabilísticos, realização de contagem para resolver e elaborar problemas relacionados ao cálculo da probabilidade, incluindo a probabilidade de eventos em experimentos aleatórios sucessivos.

É importante quêque os estudantes compreendam a necessidade de utilizar conhecimentos de Probabilidade e Estatística para resolver problemas, de modo quêque apliquem esses conhecimentos

Página trezentos e cinquenta e três353

para apresentar argumentos consistentes ao se depararem com situações do cotidiano em diferentes contextos.

Promover uma roda de conversa com os estudantes para discutir sobre a importânssiaimportância do planejamento familiar e dos direitos reprodutivos no Brasil. Comentar com eles quêque o direito reprodutivo é considerado um dos Direitos Humanos.

A seção Atividades das páginas 284 a 286 tem como objetivo trabalhar com o cálculo de probabilidade estimada, inclusive, em experimentos binomiais e a partir da análise de dados em tabélatabela e gráfico estatísticos.

A atividade 61 propicíapropicia uma abordagem do Tema Contemporâneo Transversal Saúde, uma vez quêque aborda a eficácia de alguns métodos contraceptivos. Verificar a possibilidade de realizar um trabalho em parceria com um professor da área de Ciências da Natureza e suas Tecnologias, em particular, para tratar de conceitos da Biologia, como a produção do hormônio folículo-estimulante (FSH) e do hormônio luteinizante (LH) pela hipófise e discutir sobre a ação dos anticoncepcionais orais combinados (AOCs) no organismo da mulher. Conversar com os estudantes sobre o uso de preservativos, quêque além de serem contraceptivos, previnem doenças sexualmente transmissíveis (DST) e infekiçõesinfecções sexualmente transmissíveis (IST). No item d, enfatizar aos estudantes a importânssiaimportância de realizar pesquisas em fontes confiáveis. Na elaboração do relatório, comentar quêque êsteeste pódepode sêrser ilustrado e conter gráficos e tabélastabelas quêque contribuam com a apresentação das informações.

Páginas 287 a 290

Integrando com Ciências da Natureza e suas Tecnologias

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 2, das competências específicas 1 e 3 e das habilidades EM13MAT106 e EM13MAT312 da área de Matemática e suas Tecnologias e da competência específica 2 da área de Ciências da Natureza e suas Tecnologias, pois envolve a identificação de situações da vida cotidiana quêque englobam ideias probabilísticas e a resolução de problemas com cálculo de probabilidade de eventos em experimentos aleatórios sucessivos. Além díssudisso, propicíapropicia uma abordagem dos Temas Contemporâneos Transversais Saúde e Ciência e Tecnologia, uma vez quêque trata do uso de conceitos e procedimentos matemáticos para interpretar situações envolvendo a Genética, de modo a incentivar os estudantes a recorrer a linguagens próprias da Ciência para analisar criticamente informações sobre os princípios básicos da hereditariedade. Também incentiva a reflekçãoreflexão sobre decisões éticas relacionadas à manipulação genética.

Ao explorar as informações dessas páginas, verificar a possibilidade de realizar um trabalho em parceria com um professor da área de Ciências da Natureza e suas Tecnologias, em particular, para tratar de conceitos relacionados à Biologia, bem como discutir com os estudantes sobre ética e genética, destacando os limites das pesquisas científicas envolvendo sêresseres humanos. Se julgar conveniente, conversar com eles a respeito da bioética, quêque é o estudo dos problemas e implicações morais em pesquisas cientificas.

O Pensando no assunto tem como objetivo trabalhar as aplicações da pesquisa genética, reflekçãoreflexão sobre edições genéticas em humanos, interpretação das informações apresentadas, representação das possibilidades de um organismo homozigoto e o cálculo de probabilidade, incluindo um heredograma da Doença de Huntington (explicar aos estudantes quêque um heredograma é uma representação por meio de diagramas e símbolos da transmissão de doenças e características em uma família).

Páginas 291 e 292

Você conectado

O trabalho com essa seção favorece, com maior ênfase, o desenvolvimento da competência geral 5, pois envolve a utilização de tecnologias digitais para resolver problemas relacionados à realização de sorteio de números.

Comentar com os estudantes quêque, em pesquisas estatísticas, é usual utilizar ferramentas computacionais, como planilhas eletrônicas, na realização dos sorteios para definir os elemêntoselementos de uma amostra.

É importante chamar a atenção dos estudantes para as indicações das fórmulas nas etapas, destacando o uso das pontuações necessárias para os cálculos.

Mãos à obra - página 292

1. No item b, sugerir aos estudantes quêque compartilhem com a turma os números obtidos no sorteio, de modo quêque percêbampercebam a variação de resultado, uma vez quêque os sorteios são aleatórios. Como complemento, propor quêque investiguem uma fórmula para obtêrobter um número real aleatório entre:

• −10 e 0. Resposta: =aleatório()*(−10).

• −10 e 10. Resposta: =aleatório()*20−10.

2. No item d, espera-se quêque os estudantes compreendam quêque, quanto maior a quantidade de números sorteados nesse experimento, a tendência é quêque as freqüênciasfrequências relativas dos números obtidos sêjamsejam ainda mais próximas entre si.

4. No item c, propor aos estudantes quêque comparem a quantidade de ocorrências do número 8 com a de alguns côlégascolegas.

Páginas 293 e 294

O quêque estudei

A seção tem como objetivo possibilitar um momento de reflekçãoreflexão e de autoavaliação para o professor e os estudantes. Para o trabalho com as kestõesquestões 1, 2 e 3, sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, em quêque são apresentadas mais informações sobre como conduzi-la.

A questão 4 trabalha os conceitos tratados nessa Unidade relacionados à previsão do tempo, retomando a abordagem realizada na abertura. No item f, avaliar se os problemas elaborados contemplam cálculos de probabilidade. Ao final, como é possível quêque os estudantes tênhamtenham utilizado diferentes fontes de pesquisa, propor quêque alguns dêêssesdesses problemas sêjamsejam reproduzidos na lousa e discutidos com a turma.

Páginas 295 a 297

Praticando: enêmEnem e vestibulares

Essa seção possibilita a realização de uma avaliação somativa dos estudantes. Sugere-se localizar, na parte geral destas Orientações para o professor, o tópico quêque trata especificamente dessa seção, no qual são apresentadas mais informações sobre como conduzi-la.

Página trezentos e cinquenta e quatro354