RESOLUÇÕES DAS ATIVIDADES PROPOSTAS NO LIVRO DO ESTUDANTE

Unidade 1 • Matemática financeira

1. 310,15 ⋅ 0,02 ≃ 6,20

310,15 + 6,20 = 316,35 → R$ 316,35

2. a) dias 13, 14 e 15

b) • 298,00 ⋅ 0,10 = 29,80

298,00 − 29,80 = 268,20 → R$ 268,20

• 298,00 ⋅ 0,03 = 8,94

298,00 − 8,94 = 289,06 → R$ 289,06

• R$ 298,00

• 298,00 ⋅ 0,05 = 14,90

298,00 + 14,90 = 312,90 → R$ 312,90

c) 312,90 − 268,20 = 44,70

$(início da fração dê) 44,70 (sobre) 312,90 (fim da fração)$ ≃ 0,143 → aproximadamente 14,3%

$(início da fração dê) 44,70 (sobre) 268,20 (fim da fração)$ ≃ 0,167 → aproximadamente 16,7%

Algumas respostas possíveis: O valor do pagamento até dia 8 do mês é aproximadamente 14,3% menor em relação ao valor do pagamento após a data do vencimento. O valor do pagamento após a data do vencimento é aproximadamente 16,7% maior em relação ao valor do pagamento até dia 8 do mês.

3. a) 1.870,00 ⋅ 0,08 = 149,60

149,60 ⋅ 8 = 1.196,80 → R$ 1.196,80

b) x ⋅ 0,02 ⋅ 12 = 239,32 ⇒ 0,24x = 239,32 ⇒ x ≃ 997,17 → aproximadamente R$ 997,17

c) Pesquisa do estudante. Espera-se quê os estudantes compreendam as características do FGTS e as regras para o saque. Essas informações podem sêr obtidas no sáiti disponível em https://livro.pw/jidkv (acesso em: 18 set. 2024).

4. 249,00 − 211,65 = 37,35

$(início da fração dê) 37,35 (sobre) 249,00 (fim da fração)$ = 0,15 → 15%

5. alternativa b

preêço por kg: 400,00 ∶ 50 = 8,00

Lucro: 8,00 ⋅ $(início da fração dê) 200 (sobre) 100 (fim da fração)$ = 8,00 ⋅ 2 = 16,00

8,00 + 16,00 = 24,00 → R$ 24,00

6. a) Resposta pessoal. Espera-se quê os estudantes compartilhem suas experiências com compras ôn láini.

b) $(início da fração dê) 80,4 (sobre) [(x)] (fim da fração)$ = $(início da fração dê) 102 (%) (sobre) 100 (%) (fim da fração)$ ⇒ x ≃ 78,8 → aproximadamente 78,8 bilhões

c) 2% de 80,4 → 0,02 ⋅ 80,4 = 1,608

80,4 + 1,608 ≃ 82 → aproximadamente R$ 82 bilhões

7. Pesquisa dos estudantes. Espera-se quê eles consigam investigar e compreender informações sobre os cálculos realizados na apuração do hí pê tê hú, bem como as taxas e os valores quê envolvem esse imposto. É importante incentivar a realização de cálculos com percentuais a partir da pesquisa realizada.

8. a) 450 ⋅ (1 − 0,2) ⋅ (1 − 0,1) = 324 → R$ 324,00

b) Não. Resposta esperada: Porque o desconto para pagamento à vista é calculado sobre o preêço da armação já considerando o abatimento oferecido na entrega da armação usada.

9. sudéste: 4,89 ∶ 6,61 ≃ 0,740; 5,50 ∶ 4,89 ≃ 1,125

Sul: 5,01 ∶ 6,58 ≃ 0,761; 5,70 ∶ 5,01 ≃ 1,138

Centro-Oeste: 5,03 ∶ 6,63 ≃ 0,759; 5,41 ∶ 5,03 ≃ 1,076

Norte: 4,87 ∶ 6,67 ≃ 0,730; 5,88 ∶ 4,87 ≃ 1,207

Nordeste: 5,04 ∶ 6,65 ≃ 0,758; 5,57 ∶ 5,04 ≃ 1,105

Respostas possíveis: sudéste: aproximadamente 0,740 e 1,125; Sul: aproximadamente 0,761 e 1,138; Centro-Oeste: aproximadamente 0,759 e 1,076; Norte: aproximadamente 0,730 e 1,207; Nordeste: aproximadamente 0,758 e 1,105.

10. x ⋅ (1 − 0,10) ⋅ (1 − 0,07) = 662,00 ⇒ x ⋅ 0,90 ⋅ 0,93 = 662,00 ⇒ 0,837x = 662 ⇒ x ≃ 790,92

790,92 − 662,00 = 128,92 → R$ 128,92

11. (1 − 0,08) ⋅ (1 + 0,10) = 0,92 ⋅ 1,10 = 1,012

1,012 − 1 = 0,012 → acréscimo de 1,2%

12. a) Em 2021: 4,10 ⋅ (1 − 0,037) ⋅ (1 + 0,063) = 4,10 ⋅ 0,936 ⋅ 1,063 ≃ 4,20 → aproximadamente R$ 4,20;

Em 2023: 4,20 ⋅ (1 + 0,048) ⋅ (1 + 0,057) = 4,20 ⋅ 1,048 ⋅ 1,057 ≃ 4,65 → aproximadamente R$ 4,65

b) (1 − 0,037) ⋅ (1 + 0,063) ⋅ (1 + 0,048) ⋅ (1 + 0,057) = 0,963 ⋅ 1,063 ⋅ 1,048 ⋅ 1,057 ≃ 1,134 → aproximadamente 13,4%

c) Pesquisa dos estudantes. Espera-se quê eles apliquem o conceito de fatores de atualização no contexto das variações de preços nas tarifas do transporte coletivo do município ou região em quê moram. A partir díssu, eles podem avaliar as variações e levantar hipóteses sobre tais variações.

13. a) 13 produtos alimentícios. Resposta esperada: Carne, leite, feijão, arrôz, farinha, batata, tomate, pão francês, café em pó, banana, açúcar, banha/óleo e manteiga.

b) 656,88 ⋅ (1 + 0,0125) ⋅ (1 + 0,0024) ⋅ (1 − 0,0057) = 656,88 ⋅ 1,0125 ⋅ 1,0024 ⋅ 0,9943 ≃ 657,63 → aproximadamente R$ 662,89

c) 662,88 ∶ 656,88 ≃ 1,0091

Resposta esperada: Sim, pois esse acréscimo foi de aproximadamente 0,91%.

d) 656,88 ∶ 1.204,35 ≃ 0,55 → aproximadamente 55%

e) Pesquisa e elaboração dos estudantes. Espera-se quê eles compreendam as características e os produtos quê compõem uma cesta básica na região onde moram e o preêço da cesta. A partir díssu, eles podem avaliar a relação com o salário mínimo vigente e analisar os índices obtidos.

Integrando com...

1. Resposta esperada: São iniciativas com foco na atividade de partilha, troca, compra ou venda de qualquer produto ou serviço para atender às necessidades das pessoas, nem sempre em troca de dinheiro, mas procurando benefícios para todos os envolvidos. De modo geral, esses negócios consideram os pilares econômico, ambiental e social da sustentabilidade.

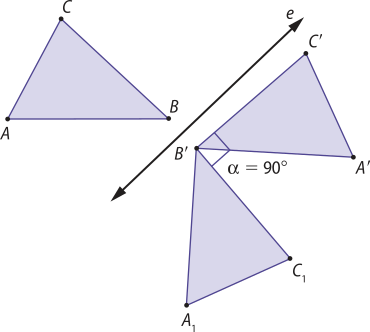
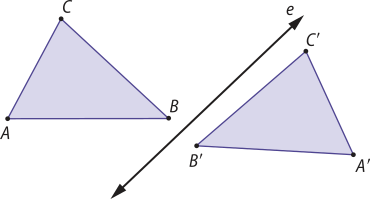
2. Resposta pessoal. Espera-se quê os estudantes comentem e compartilhem suas experiências a respeito da temática, contribuindo com a discussão e apresentando potencialidades dessas iniciativas para um futuro mais sustentável.

3. Resposta esperada: A ideia de compartilhamento visa à otimização do uso de bens produzidos, aproveitando seu tempo ocioso, de maneira quê mais pessoas possam usá-lo, sem ter a necessidade de comprar um novo produto. Com isso, evita-se todo o processo de produção de um novo bem e, consequentemente, reduz-se o uso de recursos naturais, quê já são escassos, além de havêer a diminuição da emissão de gases de efeito estufa envolvidos nesse processo. Isso gera benefícios ambientais para toda a ssossiedade. Além díssu, essa modalidade de compartilhamento gera economia para quem usa e renda para quem fornece.

4. a) 0,94x = 17.540,40 ⇒ x = 18.660,00 → R$ 18.660,00

18.660,00 − 17.540,40 = 1.119,60 → R$ 1.119,60

b) • 18.660,00 ⋅ 0,13 = 2.425,80

18.660,00 ⋅ 0,04 = 746,40

18.660,00 ⋅ 0,09 = 1.679,40

Taxa administrativa: R$ 2.425,80

Parceiro de pagamento: R$ 746,40

Plataforma de financiamento coletivo: R$ 1.679,40.

5. Pesquisa e elaboração dos estudantes. Espera-se quê eles identifiquem estratégias sustentáveis e conscientes de usos coletivos como caminhos para contribuir com o futuro do meio ambiente. É importante avaliar se os projetos idealizados envolvem economia e sustentabilidade.

14. a) j = 1.500,00 ⋅ 0,05 ⋅ 6 ⇒ j = 450,00 → R$ 450,00

Página trezentos e cinquenta e sete

b) j = 1.500,00 ⋅ 0,02 ⋅ 12 ⇒ j = 360,00 → R$ 360,00

c) j = 1.500,00 ⋅ 0,12 ⋅ 3 ⇒ j = 540,00 → R$ 540,00

d) j = 1.500,00 ⋅ 0,15 ⋅ 0,75 ⇒ j = 168,75 → R$ 168,75

• Resposta pessoal. Espera-se quê os estudantes expliquem a maneira como resolveram, seja utilizando a fórmula de cálculo do juro simples, ou calculando a taxa de juro sobre o capital e, posteriormente, multiplicando o resultado pelo tempo da aplicação.

15. a: M = 1.500,00 ⋅ (1 + 0,05)⁶ ⇒ M = 1.500,00 ⋅ (1,05)⁶ ⇒ M ≃ 2.010,14

2.010,14 − 1.500,00 = 510,14 → R$ 510,14

b: M = 1.500,00 ⋅ (1 + 0,02)¹² ⇒ M = 1.500,00 ⋅ (1,02)¹² ⇒ M ≃ 1.902,36

1.902,36 − 1.500,00 = 402,36 → R$ 402,36

c: M = 1.500,00 ⋅ (1 + 0,12)³ ⇒ M = 1.500,00 ⋅ (1,12)³ ⇒ M ≃ 2.107,39

2.107,39 − 1.500,00 = 607,39 → R$ 607,39

d: M = 1.500,00 ⋅ (1 + 0,15)^0,75 ⇒ M = 1.500,00 ⋅ (1,15)^0,75 ⇒ M ≃ 1.665,77

1.665,77 − 1.500,00 = 165,77 → R$ 165,77

16. M = 5.000,00 ⋅ (1 + 0,16 ⋅ 1,5) ⇒ M = 5.000,00 ⋅ 1,24 ⇒ M = 6.200,00

M = 5.000,00 ⋅ (1 + 0,16)^1,5 ⇒ M = 5.000,00 ⋅ (1,16)^1,5 ⇒ M ≃ 6.246,79

juro simples: R$ 6.200,00; juro compôzto: aproximadamente R$ 6.246,79

17. 4c = c ⋅ (1 + 0,04 ⋅ t) ⇒ 4 = 1 + 0,04t ⇒ 3 = 0,04t ⇒ t = 75 → 75 meses

18. a) 1.157,63 = 1.000,00 ⋅ (1 + i)³ ⇒ 1,15763 = (1 + i)³ ⇒ $(início de linha) (início da raíz) 3 (de) 1,15763 (fim da raíz) (fim de linha)$ = 1 + i ⇒ 1,05 ≃ 1 + i ⇒ i ≃ 0,05 → aproximadamente 5%

b) M = 1.000,00 ⋅ (1 + 0,05)¹ ⇒ M = 1.000,00 ⋅ 1,05 ⇒ M = 1.050,00

1.157,63 = 1.050,00 ⋅ (1 + 0,02)^t ⇒ 1,1 ≃ (1,02)^t ⇒ log (1,1) ≃ log (1,02^t) ⇒ log 1,1 ≃ t ⋅ log 1,02 ⇒ 0,04 ≃ 0,008t ⇒ t ≃ 5

5 + 1 = 6 → 6 meses

19. a) c + 1.392,30 = c ⋅ (1 + 0,10)⁴ ⇒ c + 1.392,30 = c ⋅ 1,4641 ⇒ 1.392,30 = 0,4641c ⇒ c = 3.000,00 → R$ 3.000,00

b) M = 3.000,00 ⋅ (1 + 0,10)⁹ ⇒ M ≃ 3.000,00 ⋅ (1,1)⁹ ⇒ M ≃ 7.073,84 → R$ 7.073,84

20. 2.928,20 = 2.000,00 ⋅ (1 + i)⁴ ⇒ 1,4641 = (1 + i)⁴ ⇒ $(início de linha) (início da raíz) 4 (de) 1,4641 (fim da raíz) (fim de linha)$ = 1 + i ⇒ 1,1 = 1 + i ⇒ i = 0,1 → 10%

21. a) 90% de 1.800,00 → 0,9 ⋅ 1.800,00 = 1.620,00 → R$ 1.620,00; 600,00 + 1.632,59 = 2.232,59 → R$ 2.232,59

b) 1.632,59 = 1.200,00 ⋅ (1 + i)⁴ ⇒ 1,3605 = (1 + i)⁴ ⇒ $(início de linha) (início da raíz) 4 (de) 1,3605 (fim da raíz) (fim de linha)$ _ = 1 + i ⇒ 1,08 ≃ 1 + i ⇒ i ≃ 0,08 → aproximadamente 8%

22. a) 90% de 600,00 → 0,90 ⋅ 600,00 = 540,00 → R$ 540,00

b) 2% de 600,00 → 0,02 ⋅ 600,00 = 12,00 → R$ 12,00

c) M = 600,00 ⋅ (1 + 0,01)⁵ ⇒ M = 600,00 ⋅ (1,01)⁵ ⇒ M ≃ 630,61

630,61 + 12,00 = 642,61 → R$ 642,61

d) M = 600,00 ⋅ (1 + 0,01)¹¹ ⇒ M = 600,00 ⋅ (1,01)¹¹ ⇒ M ≃ 669,40

669,40 + 12,00 = 681,40

O valor mássimo pago por esse boleto póde sêr de R$ 681,40. Nesse caso, o atraso seria de 11 meses.

• Pesquisa e elaboração dos estudantes. Espera-se quê eles compreendam as diferenças dos valores pagos no boleto, a depender da data de pagamento, e quê utilizem os conhecimentos sobre acréscimo, desconto, juro e porcentagem para a elaboração do texto e a avaliação do texto produzido pelo colega.

23. a)

Tempo	Aplicação A	Aplicação B
0	5.000,00	5.000,00
1	5.650,00	5.500,00
2	6.300,00	6.050,00
3	6.950,00	6.655,00
4	7.600,00	7.320,50
5	8.250,00	8.052,55
6	8.900,00	8.857,81
7	9.550,00	9.743,59

b) • A: juro simples; B: juro compôzto

• R$ 5.000,00 em ambos os investimentos

• A: 5.650 = 5.000 ⋅ (1 + 1 ⋅ i) ⇒ 1,13 = 1 + i ⇒ i = 0,13 → 13%;

B: 5.500 = 5.000 ⋅ (1 + i)¹ ⇒ 1,1 = 1 + i ⇒ i = 0,1 → 10%

c) f(t) = 5.000 ⋅ (1 + t ⋅ 0,13) ⇒ f(t) = 650t + 5.000;

g(t) = 5.000 ⋅ (1 + 0,1)^t ⇒ g(t) = 5.000 ⋅ (1,1)^t

d) Resposta esperada: Como f(t) > g(t) para 1 ≤ t ≤ 6, a aplicação A é mais rentável quê a B para 6 anos ou menos; como f(t) < g(t) para t ≥ 7, a aplicação B é mais rentável quê a A para 7 anos ou mais.

24. A: M(t) = 3.000,00 ⋅ (1 + 0,15 ⋅ t) ⇒ M(t) = 3.000,00 + 450t, para t em anos.

B: M(t) = 3.000,00 ⋅ (1 + 0,01)^t ⇒ M(t) = 3.000,00 ⋅ (1,01)^t, para t em meses ou M(t) = 3.000,00 ⋅ (1,1268)^t para t em anos.

Obtendo os montantes de cada aplicação e representando em um gráfico, temos:

Aplicação a juro simples
Ano	Montante
1	R$ 3.450,00
2	R$ 3.900,00
3	R$ 4.350,00
4	R$ 4.800,00
5	R$ 5.250,00
6	R$ 5.700,00
7	R$ 6.150,00
8	R$ 6.600,00
9	R$ 7.050,00
10	R$ 7.500,00
Aplicação a juro compôzto
Ano	Montante
1	R$ 3.380,40
2	R$ 3.809,03
3	R$ 4.292,02
4	R$ 4.836,25
5	R$ 5.449,48
6	R$ 6.140,48
7	R$ 6.919,09
8	R$ 7.796,43
9	R$ 8.785,02
10	R$ 9.898,96

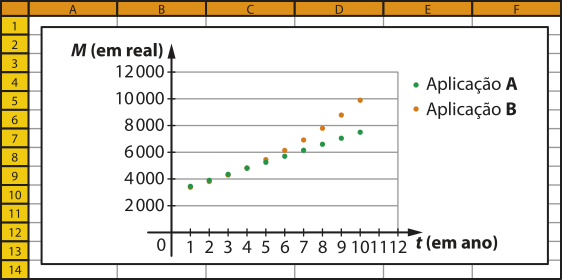
Gráfico de pontos inserido em uma planilha eletrônica. No eixo vertical, temos M, em real, variando de 0 a 12.000. No eixo horizontal, temos T, em ano, variando de 0 a 12. Há duas séries de pontos, representando as aplicações A e B. A curva da aplicação A é linear, com pontos alinhados. Ela parte do ponto correspondente a 1 ano e R$ 3.500 e segue até aproximadamente 10 anos e R$ 7.500. A aplicação B apresenta uma curva crescente, com pontos que sobem de forma acelerada ao longo do tempo. A curva inicia próximo de R$ 3.500 no primeiro ano e atinge R$ 10.000 no décimo ano.

Nesse caso, será mais vantajoso optar por A se o tempo aplicado for de até 3 anos, e por B se a aplicação durar 4 anos ou mais, como podemos observar no gráfico.

25. a) 5.500,00 + 8.000,00 = 13.500,00 → R$ 13.500,00

b) 5.500,00 = c₁ ⋅ 0,10 ⋅ 5 + (8.000,00 − c₁) ⋅ 0,08 ⋅ 10 ⇒ 5.500,00 = 0,5c₁ + 6.400,00 − 0,8c₁ ⇒ −900,00 = −0,3c₁ ⇒ 3.000,00 = c₁

c₂ = 8.000,00 − 3.000,00 ⇒ c₂ = 5.000,00

A: R$ 3.000,00; B: R$ 5.000,00

Página trezentos e cinquenta e oito

c) A: M = 3.000,00 ⋅ (1 + 0,10)⁵ ⇒ M = 3.000,00 ⋅ (1,1)⁵ ⇒ M = 4.831,53

B: M = 5.000,00 ⋅ (1 + 0,08)¹⁰ ⇒ M = 5.000,00 ⋅ (1,08)¹⁰ ⇒ M ≃ 10.794,62

4.831,53 + 10.794,62 = 15.626,15 → R$ 15.626,15

26. 90.000,00 = 30.000,00 ⋅ (1 + 0,03)^t ⇒ 3 = (1,03)^t ⇒ log 3 = log (1,03^t) ⇒ log 3 = t ⋅ log 1,03 ⇒ 0,477 = 0,01284t ⇒ t ≃ 37,15 → 38 meses

27. Resposta esperada: Sim, pois as informações no enunciado da quêstão não são suficientes para resolvê-la. Nesse caso, pode-se ajustar o enunciado indicando o tempo em que a aplicação ocorreu. Por exemplo, caso o tempo indicado seja de 8 meses, o capital aplicado seria de R$ 1.200,00.

28. Pesquisa e elaboração dos estudantes. Espera-se quê eles se apropriem de características de aplicações no sistema de juro compôzto, elaborem e resolvam problemas envolvendo essas aplicações. É importante avaliar se os problemas elaborados contemplam os conceitos estudados na Unidade.

29. alternativa b

200 ⋅ 2 = 400

400 = 200 (1 + 0,05)^t ⇒ 2 = 1,05^t ⇒ log2 = log(1,05^t) ⇒ log2 = t ⋅ log(1,05) ⇒ 0,30 = t ⋅ 0,02 ⇒ t = 15 → 15 meses

30. SAC: b, e, f, g; Price: a, d, e, f

31. p = $(início de linha) (início da fração dê) (c) (vezes) (i) (sobre) 1 (menos) (abre parenteses) 1 + (i) (fécha parenteses) (elevado há) (menos) [(n)] (fim da fração) (fim de linha)$ → p = $(início de linha) (início da fração dê) 3.800 (vezes) 0,1 (sobre) 1 (menos) (abre parenteses) 1 + 0,1 (fécha parenteses) (elevado há) (menos) 4 (fim da fração) (fim de linha)$ = $(início de linha) (início da fração dê) 38 (sobre) 1 (menos) (abre parenteses) 1,1 (fécha parenteses) (elevado há) (menos) 4 (fim da fração) (fim de linha)$ ≃ 1.198,79 → R$ 1.198,79

Resposta esperada: Ao considerar a taxa de juro de 10% a.m. e o sistema Price de amortização (prestações de valores iguais), o valor correto de cada prestação deveria sêr de aproximadamente R$ 1.198,79. A diferença entre o valor anunciado de cada prestação e aquele calculado póde ter ocorrido por diferentes fatores, como a incidência de outras taxas, por exemplo.

32. a) Resposta esperada: O empréstimo A corresponde ao SAC, uma vez quê o valor das prestações é decrescente no período; já o empréstimo B corresponde ao sistema de amortização Price, pois o valor das prestações é fixo.

b) A: 2.250,00 + 2.175,00 + 2.100,00 + 2.025,00 + 1.950,00 + 1.875,00 + 1.800,00 + 1.725,00 + 1.650,00 + 1.575,00 = 19.125,00 → R$ 19.125,00

B: 1.942,57 ⋅ 10 = 19.425,70 → R$ 19.425,70

33. a) 150.000,00 − 30.000,00 = 120.000,00

a = 120.000,00 ∶ 360 ≃ 333,33

p₁ = 333,33 + 120.000 ⋅ 0,005 = 333,33 + 600,00 = 933,33 → R$ 933,33

s₁ = 120.000,00 − 333,33 = 119.666,67

p₂ = 333,33 + 119.666,67 ⋅ 0,005 ≃ 333,33 + 598,33 ≃ 931,66 → aproximadamente R$ 931,66

s₂ = 119.666,67 − 333,33 = 119.333,34

p₃ = 333,33 + 119.333,34 ⋅ 0,005 ≃ 333,33 + 596,67 ≃ 930,00 → aproximadamente R$ 930,00

b) p = $(início de linha) (início da fração dê) [(c)] (vezes) [(i)] (sobre) 1 (menos) (abre parenteses) 1 + (i) (fécha parenteses) (elevado há) (menos) [(n)] (fim da fração) (fim de linha)$ → p = $(início de linha) (início da fração dê) 120.000 (vezes) 0,005 (sobre) 1 (menos) (abre parenteses) 1 + 0,005 (fécha parenteses) (elevado há) (menos) 360 (fim da fração) (fim de linha)$ = $(início da fração dê) 600 (sobre) 1 (menos) (abre parenteses) 1,005 (fécha parenteses) (elevado há) (menos) 360 (fim da fração)$ ≃ $(início da fração dê) 600 (sobre) 1 (menos) 0,16604 (fim da fração)$ ≃ $(início da fração dê) 600 (sobre) 0,83396 (fim da fração)$ ≃

≃ 719,46 → aproximadamente R$ 719,46

719,46 ⋅ 360 = 259.005,60 → aproximadamente R$ 259.005,60

34. Elaboração dos estudantes. Espera-se quê eles elaborem um anúncio de um produto considerando o cóódigo de defesa do consumidor. Eles devem envolver conceitos de juro e sistemas de amortização no anúncio e potencializar os conhecimentos mobilizados com a realização da atividade.

35. alternativa c

c = 0,9 ⋅ 1.200 = 1.080

p = 1.200 ∶ 3 = 400

p = $(início de linha) (início da fração dê) (c) (vezes) (i) (sobre) 1 (menos) (abre parenteses) 1 + (i) (fécha parenteses) (elevado há) (menos) [(n)] (fim da fração) (fim de linha)$ → 400 = $(início de linha) (início da fração dê) 1.080 (vezes) (i) (sobre) 1 (menos) (abre parenteses) 1 + (i) (fécha parenteses) (elevado há) (menos) 3 (fim da fração) (fim de linha)$

Substituindo o valor de i indicado nas alternativas, no segundo membro da equação acima, temos:

a) $(início da fração dê) 1.080 (vezes) 0,005 (sobre) 1 (menos) (abre parenteses) 1 + 0,005 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ = $(início da fração dê) 5,4 (sobre) 1 (menos) (abre parenteses) 1,005 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ ≃ 363,60

b) $(início da fração dê) 1.080 (vezes) 0,03 (sobre) 1 (menos) (abre parenteses) 1 + 0,03 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ = $(início da fração dê) 32,4 (sobre) 1 (menos) (abre parenteses) 1,03 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ ≃ 381,81

c) $(início da fração dê) 1.080 (vezes) 0,05 (sobre) 1 (menos) (abre parenteses) 1 + 0,05 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ = $(início da fração dê) 54 (sobre) 1 (menos) (abre parenteses) 1,05 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ ≃ 396,59

d) $(início da fração dê) 1.080 (vezes) 0,1 (sobre) 1 (menos) (abre parenteses) 1 + 0,1 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ = $(início da fração dê) 108 (sobre) 1 (menos) (abre parenteses) 1,1 (fécha parenteses) (elevado há) (menos) 3 (fim da fração)$ ≃ 434,28

36. Elaboração dos estudantes. Espera-se quê eles identifiquem causas de problemas financeiros no contrôle do orçamento dos brasileiros e discutam estratégias possíveis para não serem parte das estatísticas apresentadas no problema, de modo quê se conscientizem da importânssia do assunto. Para a elaboração do texto dissertativo, é possível solicitar apôio de um professor da área de Linguagens e suas Tecnologias.

37. Resposta esperada: Despesa fixa – assinatura de serviço de streaming, mensalidade do curso de inglês, prestação de financiamento; despesa variável – alimentação, fatura de energia elétrica, fatura de á gua; despesa eventual – manutenção de um noutibúk, viagem a passeio.

38. Respostas pessoais. As respostas dependem do orçamento familiar apresentado pêlos estudantes. Espera-se quê utilizem a planilha para organização e contrôle financeiro levando em consideração as informações das vivências e da realidade deles.

O quê estudei

1. Respostas pessoais.

2. Resposta pessoal.

3. Respostas pessoais.

4. a) 2.640,00 ∶ 3.350,00 ≃ 0,7881 → aproximadamente 78,81%

b) • Moradia. Algumas respostas possíveis: Aluguel, financiamento imobiliário, taxa de condomínio, fatura de á gua, fatura de energia, fatura de gás.

• alimentação: 2.640,00 ⋅ 0,25 = 660,00 → R$ 660,00; educação: 2.640,00 ⋅ 0,13 = 343,20 → R$ 343,20; lazer: 2.640,00 ⋅ 0,06 = 158,40 → R$ 158,40; moradia: 2.640,00 ⋅ 0,40 = 1.056,00 → R$ 1.056,00; transporte: 2.640,00 ⋅ 0,07 = 184,80 → R$ 184,80; outros: 2.640,00 ⋅ 0,09 = 237,60 → R$ 237,60

• 343,20 ⋅ (1 + 0,05) ⋅ (1 + 0,10) = 343,20 ⋅ 1,05 ⋅ 1,10 ≃ 396,40 → aproximadamente R$ 396,40

c) 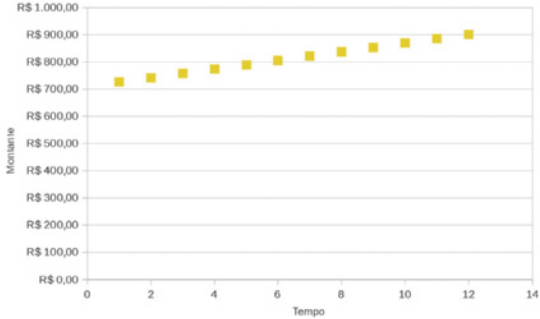Gráfico de pontos. No eixo vertical, temos o montante, em reais, variando de 0 a 1.000. No eixo horizontal, temos o tempo, variando de 0 a 14. Os pontos estão distribuídos de forma alinhada, formando uma linha reta crescente, com início no tempo 1 e valor próximo de R$ 700,00 e término no tempo 12, em R$ 900,00.

Página trezentos e cinquenta e nove

Gráfico de pontos semelhante ao anterior. Os eixos mantêm as mesmas escalas: montante em reais no eixo vertical, de 0 a 1.000, e tempo no eixo horizontal, de 0 a 14. Os pontos estão alinhados e seguem um padrão crescente bastante similar ao gráfico anterior, com pequenas ou nenhuma variação entre os valores.

Construção do estudante. Resposta esperada: Até o 12º mês de investimento, a opção A é a mais vantajosa e, a partir do 13º mês, a opção B é a mais vantajosa.

d) • 100.000,00 ∶ 250 = 400,00

100.000,00 − 2 ⋅ 400,00 = 99.200,00

p₃ = 400,00 + 99.200,00 ⋅ 0,005 = 400,00 + 496,00 = 896,00 → R$ 896,00

• p = $(início da fração dê) (c) (vezes) (i) (sobre) 1 (menos) (abre parenteses) 1 + (i) (fécha parenteses) (elevado há) (menos) [(n)] (fim da fração)$ → p = $(início da fração dê) 100.000 (vezes) 0,005 (sobre) 1 (menos) (abre parenteses) 1 + 0,005 (fécha parenteses) (elevado há) (menos) 250 (fim da fração)$ = $(início de linha) (início da fração dê) 500 (sobre) 1 (menos) (abre parenteses) 1,005 (fécha parenteses) (elevado há) (menos) 250 (fim da fração) (fim de linha)$ ≃ 701,65 → aproximadamente R$ 701,65

Praticando: enêm e vestibulares

1. alternativa a

preêço normal: 1.000 + 1.000 ⋅ 0,10 = 1.100

Desconto para compras com o cartão da loja: 0,02 ⋅ 1.100 = 22

Valor apresentado pela loja: 1.100 − 22 = 1.078

Valor calculado pela cliente: 1.000 + 0,08 ⋅ 1.000 = 1.080

Diferença: 1.080 − 1.078 = 2 → R$ 2,00

2. alternativa b

Dívida ao final do 1º mês: 1.000 ⋅ (1 + 0,10) − 300 = 800

Dívida ao final do 2º mês: 800 ⋅ (1 + 0,10) − 500 = 380

Dívida ao final do 3º mês antes do pagamento: 380 ⋅ (1 + 0,10) = 418 → R$ 418,00

Para aplicar 10% sobre um valor, basta multiplicá-lo por 1,10 (1 + 0,10). Assim, temos:

1º mês: 1.000,00 ⋅ 1,10 = 1.100,00

Após o pagamento: 1.100,00 − 300,00 = 800,00

2º mês: 800,00 ⋅ 1,10 = 880,00; 880,00 − 500,00 = 380,00

3º mês: 380,00 ⋅ 1,10 = 418,00 → R$ 418,00

3. alternativa d

5% de x equivale a R$ 105,00 → 0,05x = 105,00 ⇒ x = 2.100,00

2.100,00 − 105,00 = 1.995,00 → R$ 1.995,00

4. alternativa b

preêço do celular com o desconto: 315 − 0,20 ⋅ 315 = 252

Diferença de preços: 300 − 252 = 48

Percentual de desconto, em relação ao preêço anterior à promoção: 48 ∶ 300 = 0,16 → 16%

5. alternativa a

Rendimento da aplicação básica: (10.000 ⋅ 0,00542) − 0,30 = 53,90 → R$ 53,90

Rendimento da aplicação pessoal: (10.000 ⋅ 0,00560) ⋅ (1 − 0,038) ≃ 53,87 → R$ 53,87

6. alternativa d

0,3x + 0,5 ⋅ 0,7x + 0,2 ⋅ (x − 0,3x − 0,5 ⋅ 0,7x) + 448,00 = x ⇒ 0,72x + 448,00 = x ⇒ 448,00 = 0,28x ⇒ x = 1.600,00 → R$ 1.600,00

7. alternativa a

Montante ao final do 1º mês: 10.404 ⋅ (1 + 0,02) = 10.612,08

Saldo ao final do 1º mês: 10.612,08 − 5.202,00 = 5.410,08

Montante ao final do 2º mês: 5.410,08 ⋅ (1 + 0,02) = 5.518,28

Saldo ao final do 2º mês: 5.518,28 − 5.202,00 = 316,28

Percentual de desconto: 316,28 ∶ 10.404 ≃ 0,03 → aproximadamente 3%

8. alternativa b

202,00 = C₁ ⋅ (1 + 0,01)¹ ⇒ 202,00 = C₁ ⋅ 1,01 ⇒ C₁ = $(início da fração dê) 202,00 (sobre) 1,01 (fim da fração)$ ⇒ C₁ = 200

204,00 = C₂ ⋅ (1 + 0,01)² ⇒ 204,00 = C₂ ⋅ 1,0201 ⇒ C₂ = $(início da fração dê) 204,00 (sobre) 1,0201 (fim da fração)$ ⇒ C₂ = 200

200,00 + 200,00 = 400,00

9. alternativa c

21.405,00 = x ⋅ (1 + 0,08 ⋅ 1) + (20.000,00 − x) ⋅ (1 + 0,05 ⋅ 1) ⇒ 21.405,00 = 1,08x + 21.000,00 − 1,05x ⇒ 405,00 = 0,03x ⇒ x = 13.500,00 → R$ 13.500,00

20.000,00 − 13.500,00 = 6.500,00 → R$ 6.500,00

10. Sendo x o capital investido, temos:

16x = x ⋅ (1 + 1)^t ⇒ 16 = 2^t ⇒ 2⁴ = 2^t ⇒ t = 4

Como t corresponde a um período de 5 anos, temos:

4 ⋅ 5 = 20 → 20 anos

11. alternativa b

1.350 − 1.250 = 1.250 ⋅ 0,01 ⋅ t ⇒ t = 8 → 8 meses

12. alternativa d

M₁ = 1.000

M₂ = 1.000 ⋅ (1 + 0,10) + 1.000 = 2.100

M₃ = 2.100 ⋅ (1 + 0,10) + 0 = 2.310

M₄ = 2.310 ⋅ (1 + 0,10) + 1.000 = 3.541

M₅ = 3.541 ⋅ (1 + 0,10) = 3.895,1 → R$ 3.895,10

Unidade 2 • Matrizes, sistemas lineares e transformações de figuras

1. a) 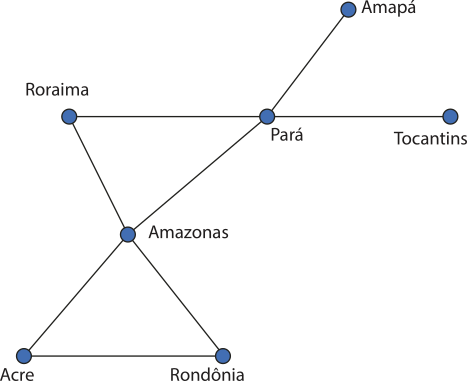Imagem de um diagrama composto por sete pontos, cada um representando um estado da região Norte do Brasil: Acre, Amazonas, Amapá, Pará, Rondônia, Roraima e Tocantins. Alguns desses pontos estão conectados por segmentos de reta: Acre está conectado a Amazonas e Rondônia; Amazonas está conectado a Roraima e Pará; Pará está conectado a Amapá e Tocantins.

Página trezentos e sessenta

Relação de fronteiras entre os estados da região Norte do Brasil

	AC	AM	AP	PA	RO	RR	TO
AC	0	1	0	0	1	0	0
AM	1	0	0	1	1	1	0
AP	0	0	0	1	0	0	0
PA	0	1	1	0	0	1	1
RO	1	1	0	0	0	0	0
RR	0	1	0	1	0	0	0
TO	0	0	0	1	0	0	0

Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: hí bê gê hé, 2018. p. 94.

F = $(início de linha) (grupo) (abre colchete) (grupo)(grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo)(grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 1 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo)(grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo)(grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 1 (grupo)(grupo)(grupo)(grupo) 1 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo)(grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo)(grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 1 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo) 0 (grupo)(grupo)(grupo) (fécha colchete) (grupo) (fim de linha)$

2. a) a₁₁ = (1 − 2)¹ = (−1)¹ = −1

a₁₂ = (1 − 2)² = (−1)² = 1

a₁₃ = (1 − 2)³ = (−1)³ = −1

a₁₄ = (1 − 2)⁴ = (−1)⁴ = 1

a₁₅ = (1 − 2)⁵ = (−1)⁵ = −1

A = [−1 1 −1 1 −1]

b) I) se i ≤ j:

b₁₁ = $(início da fração dê) 4 (vezes) 1 (menos) 1 (sobre) 3 (fim da fração)$ = 1

b₁₂ = $(início da fração dê) 4 (vezes) 1 (menos) 2 (sobre) 3 (fim da fração)$ = $(início da fração dê) 2 (sobre) 3 (fim da fração)$

b₂₂ = $(início da fração dê) 4 (vezes) 2 (menos) 2 (sobre) 3 (fim da fração)$ = 2

II) se i > j:

b₂₁ = 2 + 1 = 3

B = $(início de linha) (abre colchete) 1 (e ainda) (início da fração dê) 2 (sobre) 3 (fim da fração) [(Ê)] 3 (e ainda) 2 (fécha colchete) (fim de linha)$

c) c₁₁ = 3¹^{− 1} = 3⁰ = 1

c₁₂ = 3¹^{− 2} = 3⁻¹ = $(início da fração dê) 1 (sobre) 3 (fim da fração)$

c₁₃ = 3¹^{− 3} = 3⁻² = $(início da fração dê) 1 (sobre) 9 (fim da fração)$

c₂₁ = 3²^{− 1} = 3¹ = 3

c₂₂ = 3²^{− 2} = 3⁰ = 1

c₂₃ = 3²^{− 3} = 3⁻¹ = $(início da fração dê) 1 (sobre) 3 (fim da fração)$

c₃₁ = 3³^{− 1} = 3² = 9

c₃₂ = 3³^{− 2} = 3¹ = 3

c₃₃ = 3³^{− 3} = 3⁰ = 1

c₄₁ = 3⁴^{− 1} = 3³ = 27

c₄₂ = 3⁴^{− 2} = 3² = 9

c₄₃ = 3⁴^{− 3} = 3¹ = 3

C = $(início de linha) (abre colchete) 1 (e ainda) (início da fração dê) 1 (sobre) 3 (fim da fração) (e ainda) (início da fração dê) 1 (sobre) 9 (fim da fração) 3 (e ainda) 1 (e ainda) (início da fração dê) 1 (sobre) 3 (fim da fração) 9 (e ainda) 3 (e ainda) 1 27 (e ainda) 9 (e ainda) 3 (fécha colchete) (fim de linha)$

d) I) se i = j:

d₁₁ = $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$

d₂₂ = $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$

d₃₃ = $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$

d₄₄ = $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$

d₅₅ = $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$

II) se i ≠ j:

d₁₂ = 1³ − 2² = 1 − 4 = −3

d₁₃ = 1³ − 3² = 1 − 9 = −8

d₁₄ = 1³ − 4² = 1 − 16 = −15

d₁₅ = 1³ − 5² = 1 − 25 = −24

d₂₁ = 2³ − 1² = 8 − 1 = 7

d₂₃ = 2³ − 3² = 8 − 9 = −1

d₂₄ = 2³ − 4² = 8 − 16 = −8

d₂₅ = 2³ − 5² = 8 − 25 = −17

d₃₁ = 3³ − 1² = 27 − 1 = 26

d₃₂ = 3³ − 2² = 27 − 4 = 23

d₃₄ = 3³ − 4² = 27 − 16 = 11

d₃₅ = 3³ − 5² = 27 − 25 = 2

d₄₁ = 4³ − 1² = 64 − 1 = 63

d₄₂ = 4³ − 2² = 64 − 4 = 60

d₄₃ = 4³ − 3² = 64 − 9 = 55

d₄₅ = 4³ − 5² = 64 − 25 = 39

d₅₁ = 5³ − 1² = 125 − 1 = 124

d₅₂ = 5³ − 2² = 125 − 4 = 121

d₅₃ = 5³ − 3² = 125 − 9 = 116

d₅₄ = 5³4² = 125 − 16 = 109

D = $(início de linha) (abre colchete) (início da raíz quadrada dê) 5 (fim da raíz) (e ainda) (menos) 3 (e ainda) (menos) 8 (e ainda) (menos) 15 (e ainda) (menos) 24 7 (e ainda) (início da raíz quadrada dê) 5 (fim da raíz) (e ainda) (menos) 1 (e ainda) (menos) 8 (e ainda) (menos) 17 26 (e ainda) 23 (e ainda) (início da raíz quadrada dê) 5 (fim da raíz) (e ainda) 11 (e ainda) 2 63 (e ainda) 60 (e ainda) 55 (e ainda) (início da raíz quadrada dê) 5 (fim da raíz) (e ainda) 39 124 (e ainda) 121 (e ainda) 116 (e ainda) 109 (e ainda) (início da raíz quadrada dê) 5 (fim da raíz) (fécha colchete) (fim de linha)$

3. a) $(início de linha) (abre colchete) 26.603 (e ainda) 46.524 35.453 (e ainda) 28.424 210.460 (e ainda) 69.719 70.116 (e ainda) 38.587 (fécha colchete) (fim de linha)$ ; matriz 4 × 2

b) Respostas esperadas: Casos prováveis de dengue por Unidade da Federação da Região Centro-Oeste do Brasil até a Semana Epidemiológica 52 de 2022. Casos prováveis de dengue no Mato Grosso até a Semana Epidemiológica 52 de 2022 e de 2023.

c) Resposta esperada: Casos prováveis de dengue no Distrito Federal até a Semana Epidemiológica 52 de 2023.

d) Resposta esperada: Sim. Observando se, na linha corresponde à Unidade da Federação, o elemento da 2ª coluna é um número menor do quê o da 1ª coluna.

4. a) Resposta esperada: As linhas indicam a quantidade, em quilograma, de embalagens vendidas de cada modelo no mês de abril. As colunas indicam a quantidade, em quilograma, de embalagens compradas por cliente no mês de abril.

b) x₃₂ = 336

c) Analisando a linha 2 de todas as colunas, temos: cliente 1.

d) cliente 2; 1.836 kg

• cliente 1: 450 + 400 + 216 + 240 = 1.306

• cliente 2: 270 + 750 + 336 + 480 = 1.836

• cliente 3: 225 + 500 + 480 + 384 = 1.589

5. Elaboração do estudante. Espera-se quê os estudantes demonstrem o conhecimento sobre matrizes, de acôr-do com o quê foi estudado na Unidade, para determinar um exemplo de cada tipo indicado.

6. a) Resposta esperada: A transposta de uma matriz A é outra matriz, com os mesmos elemêntos de A, porém em localizações diferentes: ordenadamente, os elemêntos das linhas da matriz A estão localizados nas colunas da sua transposta.

b) matriz 3 × 4; matriz 4 × 3

c) A^t = $(início de linha) (abre colchete) 6 (e ainda) 1 (e ainda) 0 (início da raíz quadrada dê) 14 (fim da raíz) (e ainda) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (e ainda) 10 (menos) 5 (e ainda) 8 (e ainda) (menos) 1 0 (e ainda) 3 (e ainda) 2 (fécha colchete) (fim de linha)$

d) Uma resposta possível: A ordem das matrizes B e (B^t)^t é a mesma, pois B_m_×_n ⇒ B^tn × m ⇒ (B^t)^tm × n e, considerando um elemento b_ij qualquer da matriz B, temos b_ij = (b_ji)^t = ((b_ij)^t)^t.

Página trezentos e sessenta e um

7. a) A − C + B = A + (−C) + B =

= $(abre colchete) 88 (e ainda) (menos) 34 46 (e ainda) 0 (menos) 10 (e ainda) 22 (fécha colchete)$ + $(abre colchete) (menos) 47 (e ainda) (menos) 30 42 (e ainda) 3 20 (e ainda) (menos) 1 (fécha colchete)$ + $(abre colchete) (menos) 14 (e ainda) (menos) 5 6 (e ainda) 28 (menos) 19 (e ainda) 15 (fécha colchete)$ =

= $(abre colchete) 88 + (abre parenteses) (menos) 47 (fécha parenteses) + (abre parenteses) (menos) 14 (fécha parenteses) (e ainda) (menos) 34 + (abre parenteses) (menos) 30 (fécha parenteses) + (abre parenteses) (menos) 5 (fécha parenteses) 46 + 42 + 6 (e ainda) 0 + 3 + 28 (menos) 10 + 20 + (abre parenteses) (menos) 19 (fécha parenteses) (e ainda) 22 + (abre parenteses) (menos) 1 (fécha parenteses) + 15 (fécha colchete)$ =

= $(abre colchete) 27 (e ainda) (menos) 69 94 (e ainda) 31 (menos) 9 (e ainda) 36 (fécha colchete)$

b) A + 3B = $(abre colchete) 88 (e ainda) (menos) 34 46 (e ainda) 0 (menos) 10 (e ainda) 22 (fécha colchete)$ +3 ⋅ $(abre colchete) (menos) 14 (e ainda) (menos) 5 6 (e ainda) 28 (menos) 19 (e ainda) 15 (fécha colchete)$ =

= $(abre colchete) 88 (e ainda) (menos) 34 46 (e ainda) 0 (menos) 10 (e ainda) 22 (fécha colchete)$ + $(abre colchete) (menos) 42 (e ainda) (menos) 15 18 (e ainda) 84 (menos) 57 (e ainda) 45 (fécha colchete)$ =

= $(abre colchete) 88 + (abre parenteses) (menos) 42 (fécha parenteses) (e ainda) (menos) 34 + (abre parenteses) (menos) 15 (fécha parenteses) 46 + 18 (e ainda) 0 + 84 (menos) 10 + (abre parenteses) (menos) 57 (fécha parenteses) (e ainda) 22 + 45 (fécha colchete)$ + $(abre colchete) 46 (e ainda) (menos) 49 64 (e ainda) 84 (menos) 67 (e ainda) 67 (fécha colchete)$

c) B + C − $(início da fração dê) 1 (sobre) 2 (fim da fração)$ (−A) = $(início de linha) (abre colchete) (menos) 14 (e ainda) (menos) 5 6 (e ainda) 28 (menos) 19 (e ainda) 15 (fécha colchete) (fim de linha)$ +

+ $(abre colchete) 47 (e ainda) 30 (menos) 42 (e ainda) (menos) 3 (menos) 20 (e ainda) 1 (fécha colchete)$ − $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⋅ $(abre colchete) (menos) 88 (e ainda) 34 (menos) 46 (e ainda) 0 10 (e ainda) (menos) 22 (fécha colchete)$ = $(abre colchete) (menos) 14 (e ainda) (menos) 5 6 (e ainda) 28 (menos) 19 (e ainda) 15 (fécha colchete)$ +

+ $(abre colchete) 47 (e ainda) 30 (menos) 42 (e ainda) (menos) 3 (menos) 20 (e ainda) 1 (fécha colchete)$ + $(abre colchete) 44 (e ainda) (menos) 17 23 (e ainda) 0 (menos) 5 (e ainda) 11 (fécha colchete)$ =

= $(abre colchete) (menos) 14 + 47 + 44 (e ainda) (menos) 5 + 30 + (abre parenteses) (menos) 17 (fécha parenteses) 6 + (abre parenteses) (menos) 42 (fécha parenteses) + 23 (e ainda) 28 + (abre parenteses) (menos) 3 (fécha parenteses) + 0 (menos) 19 + (abre parenteses) (menos) 20 (fécha parenteses) + (abre parenteses) (menos) 5 (fécha parenteses) (e ainda) 15 + 1 + 11 (fécha colchete)$ = $(abre colchete) 77 (e ainda) 8 (menos) 13 (e ainda) 25 (menos) 44 (e ainda) 27 (fécha colchete)$

d) A^t − 2C^t = $(abre colchete) 88 (e ainda) 46 (e ainda) (menos) 10 [(Ê)] (menos) 34 (e ainda) 0 (e ainda) 22 (fécha colchete)$ − 2 ⋅ $(abre colchete) 47 (e ainda) (menos) 42 (e ainda) (menos) 20 [(Ê)] 30 (e ainda) (menos) 3 (e ainda) 1 (fécha colchete)$ =

= $(abre colchete) 88 (e ainda) 46 (e ainda) (menos) 10 [(Ê)] (menos) 34 (e ainda) 0 (e ainda) 22 (fécha colchete)$ + $(abre colchete) (menos) 94 (e ainda) 84 (e ainda) 40 [(Ê)] (menos) 60 (e ainda) 6 (e ainda) (menos) 2 (fécha colchete)$ =

= $(abre colchete) 88 + (abre parenteses) (menos) 94 (fécha parenteses) (e ainda) 46 + 84 (e ainda) (menos) 10 + 40 [(Ê)] (menos) 34 + (abre parenteses) (menos) 60 (fécha parenteses) (e ainda) 0 + 6 (e ainda) 22 + (abre parenteses) (menos) 2 (fécha parenteses) (fécha colchete)$ = $(abre colchete) (menos) 6 (e ainda) 130 (e ainda) 30 [(Ê)] (menos) 94 (e ainda) 6 (e ainda) 20 (fécha colchete)$

8. a₁₁ = 2 ⋅ 1 − 1 = 2 − 1 = 1

a₁₂ = 2 ⋅ 1 − 2 = 2 − 2 = 0

a₁₃ = 2 ⋅ 1 − 3 = 2 − 3 = −1

a₁₄ = 2 ⋅ 1 − 4 = 2 − 4 = −2

a₂₁ = 2 ⋅ 2 − 1 = 4 − 1 = 3

a₂₂ = 2 ⋅ 2 − 2 = 4 − 2 = 2

a₂₃ = 2 ⋅ 2 − 3 = 4 − 3 = 1

a₂₄ = 2 ⋅ 2 − 4 = 4 − 4 = 0

a₃₁ = 2 ⋅ 3 − 1 = 6 − 1 = 5

a₃₂ = 2 ⋅ 3 − 2 = 6 − 2 = 4

a₃₃ = 2 ⋅ 3 − 3 = 6 − 3 = 3

a₃₄ = 2 ⋅ 3 − 4 = 6 − 4 = 2

a₄₁ = 2 ⋅ 4 − 1 = 8 − 1 = 7

a₄₂ = 2 ⋅ 4 − 2 = 8 − 2 = 6

a₄₃ = 2 ⋅ 4 − 3 = 8 − 3 = 5

a₄₄ = 2 ⋅ 4 − 4 = 8 − 4 = 4

A = $(início de linha) (abre colchete) 1 (e ainda) 0 (e ainda) (menos) 1 (e ainda) (menos) 2 3 (e ainda) 2 (e ainda) 1 (e ainda) 0 5 (e ainda) 4 (e ainda) 3 (e ainda) 2 7 (e ainda) 6 (e ainda) 5 (e ainda) 4 (fécha colchete) (fim de linha)$

a) $(abre colchete) 1 (e ainda) 0 (e ainda) 0 (e ainda) 0 0 (e ainda) 1 (e ainda) 0 (e ainda) 0 0 (e ainda) 0 (e ainda) 1 (e ainda) 0 0 (e ainda) 0 (e ainda) 0 (e ainda) 1 (fécha colchete)$ + $(abre colchete) 1 (e ainda) 0 (e ainda) (menos) 1 (e ainda) (menos) 2 3 (e ainda) 2 (e ainda) 1 (e ainda) 0 5 (e ainda) 4 (e ainda) 3 (e ainda) 2 7 (e ainda) 6 (e ainda) 5 (e ainda) 4 (fécha colchete)$ = $(abre colchete) 2 (e ainda) 0 (e ainda) (menos) 1 (e ainda) (menos) 2 3 (e ainda) 3 (e ainda) 1 (e ainda) 0 5 (e ainda) 4 (e ainda) 4 (e ainda) 2 7 (e ainda) 6 (e ainda) 5 (e ainda) 5 (fécha colchete)$

b) 3 ⋅ $(abre colchete) 1 (e ainda) 3 (e ainda) 5 (e ainda) 7 0 (e ainda) 2 (e ainda) 4 (e ainda) 6 (menos) 1 (e ainda) 1 (e ainda) 3 (e ainda) 5 (menos) 2 (e ainda) 0 (e ainda) 2 (e ainda) 4 (fécha colchete)$ − $(abre colchete) 1 (e ainda) 0 (e ainda) 0 (e ainda) 0 0 (e ainda) 1 (e ainda) 0 (e ainda) 0 0 (e ainda) 0 (e ainda) 1 (e ainda) 0 0 (e ainda) 0 (e ainda) 0 (e ainda) 1 (fécha colchete)$ =

= $(abre colchete) 3 (e ainda) 9 (e ainda) 15 (e ainda) 21 0 (e ainda) 6 (e ainda) 12 (e ainda) 18 (menos) 3 (e ainda) 3 (e ainda) 9 (e ainda) 15 (menos) 6 (e ainda) 0 (e ainda) 6 (e ainda) 12 (fécha colchete)$ + $(abre colchete) (menos) 1 (e ainda) 0 (e ainda) 0 (e ainda) 0 0 (e ainda) (menos) 1 (e ainda) 0 (e ainda) 0 0 (e ainda) 0 (e ainda) (menos) 1 (e ainda) 0 0 (e ainda) 0 (e ainda) 0 (e ainda) (menos) 1 (fécha colchete)$ =

= $(abre colchete) 2 (e ainda) 9 (e ainda) 15 (e ainda) 21 0 (e ainda) 5 (e ainda) 12 (e ainda) 18 (menos) 3 (e ainda) 3 (e ainda) 8 (e ainda) 15 (menos) 6 (e ainda) 0 (e ainda) 6 (e ainda) 11 (fécha colchete)$

9. $(abre colchete) 4 [(ípsilon)] + 1 + (abre parenteses) (menos) 5 (fécha parenteses) (e ainda) 5 + 10 [(Ê)] 11 + (abre parenteses) (menos) 3 [(ípsilon)] (fécha parenteses) (e ainda) 13 + 6 (fécha colchete)$ = $(início de linha) (abre colchete) 4 (e ainda) 15 [(x)] [(Ê)] 5 (e ainda) 19 (fécha colchete) (fim de linha)$ ⇒

⇒ $(abre colchete) 4 [(ípsilon)] (menos) 4 (e ainda) 15 [(Ê)] 11 (menos) 3 [(ípsilon)] (e ainda) 19 (fécha colchete)$ = $(início de linha) (abre colchete) 4 (e ainda) 15 [(x)] [(Ê)] 5 (e ainda) 19 (fécha colchete) (fim de linha)$

15x = 15 ⇒ x = 1

4y − 4 = 4 ⇒ 4y = 8 ⇒ y = 2

10. a₁₁ = 1 + 1 = 2

a₁₂ = a₁₃ = a₂₁ = a₂₃ = a₃₁ = a₃₂ = 0

a₂₂ = 2 + 2 = 4

a₃₃ = 3 + 3 = 6

M + M = $(abre colchete) 2 (e ainda) 0 (e ainda) 0 0 (e ainda) 4 (e ainda) 0 0 (e ainda) 0 (e ainda) 6 (fécha colchete)$ + $(abre colchete) 2 (e ainda) 0 (e ainda) 0 0 (e ainda) 4 (e ainda) 0 0 (e ainda) 0 (e ainda) 6 (fécha colchete)$ = $(início de linha) (abre colchete) 4 (e ainda) 0 (e ainda) 0 0 (e ainda) 8 (e ainda) 0 0 (e ainda) 0 (e ainda) 12 (fécha colchete) (fim de linha)$

11. a) Analisando o elemento b₂₃ da matriz B, temos: 12 estudantes.

b) 5 + 8 + 6 = 19 → 19 estudantes

c) A + B = $(abre colchete) 11 (e ainda) 7 (e ainda) 8 (e ainda) 5 9 (e ainda) 6 (e ainda) 9 (e ainda) 8 14 (e ainda) 5 (e ainda) 10 (e ainda) 6 (fécha colchete)$ + $(abre colchete) 10 (e ainda) 9 (e ainda) 5 (e ainda) 6 8 (e ainda) 10 (e ainda) 12 (e ainda) 3 15 (e ainda) 8 (e ainda) 7 (e ainda) 4 (fécha colchete)$ =

= $(abre colchete) 11 + 10 (e ainda) 7 + 9 (e ainda) 8 + 5 (e ainda) 5 + 6 9 + 8 (e ainda) 6 + 10 (e ainda) 9 + 12 (e ainda) 8 + 3 14 + 15 (e ainda) 5 + 8 (e ainda) 10 + 7 (e ainda) 6 + 4 (fécha colchete)$ =

= $(abre colchete) 21 (e ainda) 16 (e ainda) 13 (e ainda) 11 17 (e ainda) 16 (e ainda) 21 (e ainda) 11 29 (e ainda) 13 (e ainda) 17 (e ainda) 10 (fécha colchete)$

A quantidade total de estudantes das turmas A e B, do 1º, 2º e 3º anos do Ensino Médio, interessados em cada área de atuação profissional.

12. • A + B = B + A

Considerando um elemento a_ij qualquer da matriz A, e b_ij qualquer da matriz B, temos quê o elemento (i, j) da matriz A + B será a_ij + b_ij, e o elemento (i, j) da matriz B + A será b_ij + a_ij. Como a_ij e b_ij são números reais, pela propriedade comutativa da adição, a_ij + b_ij = b_ij + a_ij. Assim, A + B = B + A.

• (A + B) + C = A + (B + C)

Considerando um elemento a_ij qualquer da matriz A, b_ij qualquer da matriz B, e c_ij qualquer da matriz C, temos quê o elemento (i, j) da matriz (A + B) + C será (a_ij + b_ij) + c_ij, e o elemento (i, j) da matriz A + (B + C) será a_ij + (b_ij + c_ij). Como a_ij, b_ij e c_ij são números reais, pela propriedade associativa da adição, (a_ij + b_ij) + c_ij = a_ij + (b_ij + c_ij). Logo, (A + B) + C = A + (B + C).

• A + 0 = A

Considerando U uma matriz em quê A + U = A, sabe-se quê a_ij + u_ij = a_ij. Como a_ij e u_ij são números reais, temos quê esse caso só é verificado se u_ij = 0. Assim, U = 0 e A + 0 = A.

• A + (−A) = 0

Considerando B uma matriz em quê A + B = 0. Considerando b_ij em quê a_ij + b_ij = 0 temos quê esse caso só é verificado se b_ij = −a_ij. Assim, B = −A e A + (−A) = 0.

Página trezentos e sessenta e dois

13. Pesquisa e elaboração dos estudantes. Espera-se quê os estudantes consigam representar as informações das tabélas por meio de matrizes, bem como operar e interpretar o significado das operações realizadas a partir do contexto apresentado no problema, utilizando para isso uma planilha eletrônica.

14. a) $(abre colchete) 3 (e ainda) (menos) 3 (e ainda) 0 2 (e ainda) (menos) 2 (e ainda) 9 5 (e ainda) 4 (e ainda) 1 (fécha colchete)$ ⋅ $(abre colchete) 5 (e ainda) 0 0 (e ainda) 8 (menos) 4 (e ainda) 0 (fécha colchete)$ = $(abre colchete) 3 (vezes) 5 + (abre parenteses) (menos) 3 (fécha parenteses) (vezes) 0 + 0 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (e ainda) 3 (vezes) 0 + (abre parenteses) (menos) 3 (fécha parenteses) (vezes) 8 + 0 (vezes) 0 2 (vezes) 5 + (abre parenteses) (menos) 2 (fécha parenteses) (vezes) 0 + 9 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (e ainda) 2 (vezes) 0 + (abre parenteses) (menos) 2 (fécha parenteses) (vezes) 8 + 9 (vezes) 0 5 (vezes) 5 + 4 (vezes) 0 + 1 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (e ainda) 5 (vezes) 0 + 4 (vezes) 8 + 1 (vezes) 0 (fécha colchete)$ = $(abre colchete) 15 (e ainda) (menos) 24 (menos) 26 (e ainda) (menos) 16 21 (e ainda) 32 (fécha colchete)$

b) $(abre colchete) 5 (e ainda) 0 0 (e ainda) 8 (menos) 4 (e ainda) 0 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha) [(Ê)] (início de linha) (menos) 10 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 5 (vezes) (início da raíz quadrada dê) 3 (fim da raíz) + 0 (vezes) (abre parenteses) (menos) 10 (fécha parenteses) (fim de linha)(início de linha) 0 (vezes) (início da raíz quadrada dê) 3 (fim da raíz) + 8 (vezes) (abre parenteses) (menos) 10 (fécha parenteses) (fim de linha)(início de linha) (abre parenteses) (menos) 4 (fécha parenteses) (vezes) (início da raíz quadrada dê) 3 (fim da raíz) + 0 (vezes) (abre parenteses) (menos) 10 (fécha parenteses) (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 5 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)(início de linha) (menos) 80 (fim de linha)(início de linha) (menos) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha) (fécha colchete)$

c) $(abre colchete) (início de linha) (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha) [(Ê)] (início de linha) (menos) 10 (fim de linha) (fécha colchete)$ ⋅ $(abre colchete) (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) 7 (e ainda) 0 (fécha colchete)$ = $(abre colchete) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 7 (e ainda) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 0 [(Ê)] (menos) 10 (vezes) (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) (menos) 10 (vezes) 7 (e ainda) (menos) 10 (vezes) 0 (fécha colchete)$ = $(abre colchete) 3 (e ainda) 7 (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) 0 [(Ê)] (menos) 10 (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) (menos) 70 (e ainda) 0 (fécha colchete)$

d) $(abre colchete) (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) 7 (e ainda) 0 (fécha colchete)$ ⋅ $(abre colchete) 3 (e ainda) (menos) 3 (e ainda) 0 2 (e ainda) (menos) 2 (e ainda) 9 5 (e ainda) 4 (e ainda) 1 (fécha colchete)$ = $(abre colchete) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 3 + 7 (vezes) 2 + 0 (vezes) 5 (e ainda) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) (abre parenteses) (menos) 3 (fécha parenteses) + 7 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 0 (vezes) 4 (e ainda) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 0 + 7 (vezes) 9 + 0 (vezes) 1 (fécha colchete)$ = $(início de linha) (abre colchete) 3 (início da raíz quadrada dê) 3 (fim da raíz) + 14 (e ainda) (menos) 3 (início da raíz quadrada dê) 3 (fim da raíz) (menos) 14 (e ainda) 63 (fécha colchete) (fim de linha)$

e) $(abre colchete) (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) 7 (e ainda) 0 (fécha colchete)$ ⋅ $(abre colchete) 5 (e ainda) 0 0 (e ainda) 8 (menos) 4 (e ainda) 0 (fécha colchete)$ = $(abre colchete) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 5 + 7 (vezes) 0 + 0 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (e ainda) (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 0 + 7 (vezes) 8 + 0 (vezes) 0 (fécha colchete)$ = $(abre colchete) 5 (início da raíz quadrada dê) 3 (fim da raíz) (e ainda) 56 (fécha colchete)$

f) $(abre colchete) 3 (e ainda) 2 (e ainda) 5 (menos) 3 (e ainda) (menos) 2 (e ainda) 4 0 (e ainda) 9 (e ainda) 1 (fécha colchete)$ ⋅ $(abre colchete) 5 (e ainda) 0 0 (e ainda) 8 (menos) 4 (e ainda) 0 (fécha colchete)$ = $(abre colchete) 3 (vezes) 5 + 2 (vezes) 0 + 5 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (e ainda) 3 (vezes) 0 + 2 (vezes) 8 + 5 (vezes) 0 (abre parenteses) (menos) 3 (fécha parenteses) (vezes) 5 + (abre parenteses) (menos) 2 (fécha parenteses) (vezes) 0 + 4 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (e ainda) (abre parenteses) (menos) 3 (fécha parenteses) (vezes) 0 + (abre parenteses) (menos) 2 (fécha parenteses) (vezes) 8 + 4 (vezes) 0 0 (vezes) 5 + 9 (vezes) 0 + 1 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (e ainda) 0 (vezes) 0 + 9 (vezes) 8 + 1 (vezes) 0 (fécha colchete)$ = $(abre colchete) (menos) 5 (e ainda) 16 (menos) 31 (e ainda) (menos) 16 (menos) 4 (e ainda) 72 (fécha colchete)$

15. Resposta esperada: A ordem de B é 3 × 2 e a ordem de D é 1 × 3. Como a quantidade de colunas de B e a de linhas de D são diferentes, não existe o produto B ⋅ D.

16. a) D_{2 × 3} = (A_p_{× 1} ⋅ B_q_{× 4})_p_{× 4} ⋅ C_r_×_s ⇒ p = 2; q = 1; r = 4; s = 3

b) A = $(início de linha) (abre colchete) (início de linha) [(Há)] (índice) 11 (fim de linha) [(Ê)] (início de linha) [(Há)] (índice) 21 (fim de linha) (fécha colchete) (fim de linha)$

a₁₁ = −1 − 1² = − 1 − 1 = −2

a₂₁ = −1 − 2² = − 1 − 4 = −5

A = $(início de linha) (abre colchete) (início de linha) (menos) 2 (fim de linha) [(Ê)] (início de linha) (menos) 5 (fim de linha) (fécha colchete) (fim de linha)$

B = $(início de linha) (abre colchete) [(b)] (índice) 11 (e ainda) [(b)] (índice) 12 (e ainda) [(b)] (índice) 13 (e ainda) [(b)] (índice) 14 (fécha colchete) (fim de linha)$

b₁₁ = −3 ⋅ 1 + 1 = −3 + 1 = −2

b₁₂ = −3 ⋅ 1 + 2 = −3 + 2 = −1

b₁₃ = −3 ⋅ 1 + 3 = −3 + 3 = 0

b₁₄ = −3 ⋅ 1 + 4 = −3 + 4 = 1

B = $(início de linha) (abre colchete) (menos) 2 (e ainda) (menos) 1 (e ainda) 0 (e ainda) 1 (fécha colchete) (fim de linha)$

C = $(início de linha) (abre colchete) [(C)] (índice) 11 (e ainda) [(C)] (índice) 12 (e ainda) [(C)] (índice) 13 [(C)] (índice) 21 (e ainda) [(C)] (índice) 22 (e ainda) [(C)] (índice) 23 [(C)] (índice) 31 (e ainda) [(C)] (índice) 32 (e ainda) [(C)] (índice) 33 [(C)] (índice) 41 (e ainda) [(C)] (índice) 42 (e ainda) [(C)] (índice) 43 (fécha colchete) (fim de linha)$

c₁₁ = 2 ⋅ 1 − 2 ⋅ 1 = 2 − 2 = 0

c₁₂ = 2 ⋅ 1 − 2 ⋅ 2 = 2 − 4 = −2

c₁₃ = 2 ⋅ 1 − 2 ⋅ 3 = 2 − 6 = −4

c₂₁ = 2 ⋅ 2 − 2 ⋅ 1 = 4 − 2 = 2

c₂₂ = 2 ⋅ 2 − 2 ⋅ 2 = 4 − 4 = 0

c₂₃ = 2 ⋅ 2 − 2 ⋅ 3 = 4 − 6 = −2

c₃₁ = 2 ⋅ 3 − 2 ⋅ 1 = 6 − 2 = 4

c₃₂ = 2 ⋅ 3 − 2 ⋅ 2 = 6 − 4 = 2

c₃₃ = 2 ⋅ 3 − 2 ⋅ 3 = 6 − 6 = 0

c₄₁ = 2 ⋅ 4 − 2 ⋅ 1 = 8 − 2 = 6

c₄₂ = 2 ⋅ 4 − 2 ⋅ 2 = 8 − 4 = 4

c₄₃ = 2 ⋅ 4 − 2 ⋅ 3 = 8 − 6 = 2

C = $(início de linha) (abre colchete) 0 (e ainda) (menos) 2 (e ainda) (menos) 4 2 (e ainda) 0 (e ainda) (menos) 2 4 (e ainda) 2 (e ainda) 0 6 (e ainda) 4 (e ainda) 2 (fécha colchete) (fim de linha)$

D = A ⋅ B ⋅ C

A ⋅ B = $(abre colchete) (início de linha) (menos) 2 (fim de linha) [(Ê)] (início de linha) (menos) 5 (fim de linha) (fécha colchete)$ ⋅ $(abre colchete) (menos) 2 (e ainda) (menos) 1 (e ainda) 0 (e ainda) 1 (fécha colchete)$ = $(abre colchete) (menos) 2 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) (e ainda) (menos) 2 (vezes) (abre parenteses) (menos) 1 (fécha parenteses) (e ainda) (menos) 2 (vezes) 0 (e ainda) (menos) 2 (vezes) 1 [(Ê)] (menos) 5 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) (e ainda) (menos) 5 (vezes) (abre parenteses) (menos) 1 (fécha parenteses) (e ainda) (menos) 5 (vezes) 0 (e ainda) (menos) 5 (vezes) 1 (fécha colchete)$ = $(abre colchete) 4 (e ainda) 2 (e ainda) 0 (e ainda) (menos) 2 [(Ê)] 10 (e ainda) 5 (e ainda) 0 (e ainda) (menos) 5 (fécha colchete)$

(A ⋅ B) ⋅ C = $(abre colchete) 4 (e ainda) 2 (e ainda) 0 (e ainda) (menos) 2 [(Ê)] 10 (e ainda) 5 (e ainda) 0 (e ainda) (menos) 5 (fécha colchete)$ ⋅ $(abre colchete) 0 (e ainda) (menos) 2 (e ainda) (menos) 4 2 (e ainda) 0 (e ainda) (menos) 2 4 (e ainda) 2 (e ainda) 0 6 (e ainda) 4 (e ainda) 2 (fécha colchete)$ = $(abre colchete) 4 (vezes) 0 + 2 (vezes) 2 + 0 (vezes) 4 + (abre parenteses) (menos) 2 (fécha parenteses) (vezes) 6 (e ainda) 4 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 2 (vezes) 0 + 0 (vezes) 2 + (abre parenteses) (menos) 2 (fécha parenteses) (vezes) 4 (e ainda) 4 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) + 2 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 0 (vezes) 0 + (abre parenteses) (menos) 2 (fécha parenteses) (vezes) 2 [(Ê)] 10 (vezes) 0 + 5 (vezes) 2 + 0 (vezes) 4 + (abre parenteses) (menos) 5 (fécha parenteses) (vezes) 6 (e ainda) 10 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 5 (vezes) 0 + 0 (vezes) 2 + (abre parenteses) (menos) 5 (fécha parenteses) (vezes) 4 (e ainda) 10 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) + 5 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 0 (vezes) 0 + (abre parenteses) (menos) 5 (fécha parenteses) (vezes) 2 (fécha colchete)$ =

= $(abre colchete) (menos) 8 (e ainda) (menos) 16 (e ainda) (menos) 24 [(Ê)] (menos) 20 (e ainda) (menos) 40 (e ainda) (menos) 60 (fécha colchete)$

Página trezentos e sessenta e três

17. a) Resposta pessoal. Espera-se quê os estudantes verifiquem numericamente as propriedades apresentadas com matrizes quadradas de ordem 2. É importante comentar com os estudantes quê o exemplo realizado não sérve como demonstração da propriedade, uma vez quê explora apenas um caso particular.

b) Resposta pessoal. Espera-se quê os estudantes consigam elaborar exemplos de matrizes em quê os três casos se verifiquem. Uma matriz possível para o caso da igualdade é tomar uma das matrizes como matriz identidade e a outra como uma matriz de mesma ordem da identidade.

18. P₃_{× 3} ⋅ X_m_×_n = Q₃_{× 1} ⇒ m = 3 e n = 1

$(abre colchete) 10 (e ainda) 3 (e ainda) 11 2 (e ainda) 5 (e ainda) 1 0 (e ainda) 0 (e ainda) (menos) 7 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) [(x)] (fim de linha)(início de linha) [(ípsilon)] (fim de linha)(início de linha) [(z)] (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 12 (fim de linha)(início de linha) 0 (fim de linha)(início de linha) (menos) 14 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) 10 (x) + 3 (ípsilon) + 11 [(z)] (fim de linha)(início de linha) 2 (x) + 5 (ípsilon) + 1 [(z)] (fim de linha)(início de linha) 0 (x) + 0 (ípsilon) + (menos) 7 [(z)] (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 12 (fim de linha)(início de linha) 0 (fim de linha)(início de linha) (menos) 14 (fim de linha) (fécha colchete)$

−7z = −14 ⇒ z = 2

${ (início de linha) 10 (x) + 3 (ípsilon) + 11 (vezes) 2 (igual há) 12 (fim de linha) [(Ê)] (início de linha) 2 (x) + 5 (ípsilon) + 2 (igual há) 0 (fim de linha)$ ⇒ ${ (início de linha) 10 (x) + 3 (ípsilon) (igual há) (menos) 10 (fim de linha) [(Ê)] (início de linha) 2 (x) + 5 (ípsilon) (igual há) (menos) 2 (fécha parenteses) (vezes) (abre parenteses) (menos) 5 (fécha parenteses) (fim de linha)$ ⇒

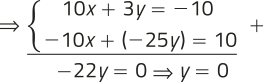
Imagem de um sistema de equações resolvido pelo método da adição. Primeira equação: 10 x mais 3 y igual a menos 0. Segunda equação: menos 10 x mais, abre parênteses, menos 25 y, fecha parênteses, igual a 10. Somando as duas equações, obtemos: menos 22 y igual a zero, resultando em y igual a zero.

10x + 3 ⋅ 0 = −10 ⇒ 10x = −10 ⇒ x = −1

X = $(início de linha) (abre colchete) (início de linha) (menos) 1 (fim de linha)(início de linha) 0 (fim de linha)(início de linha) 2 (fim de linha) (fécha colchete) (fim de linha)$

19. alternativa a

$(abre colchete) 1 (e ainda) 1 (e ainda) 2 3 (e ainda) 3 (e ainda) 1 4 (e ainda) 5 (e ainda) 6 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) 200 (fim de linha)(início de linha) 500 (fim de linha)(início de linha) 300 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 1 (vezes) 200 + 1 (vezes) 500 + 2 (vezes) 300 (fim de linha)(início de linha) 3 (vezes) 200 + 3 (vezes) 500 + 1 (vezes) 300 (fim de linha)(início de linha) 4 (vezes) 200 + 5 (vezes) 500 + 6 (vezes) 300 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 200 + 500 + 600 (fim de linha)(início de linha) 600 + 1500 + 300 (fim de linha)(início de linha) 800 + 2500 + 1800 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 1300 (fim de linha)(início de linha) 2400 (fim de linha)(início de linha) 5100 (fim de linha) (fécha colchete)$

Como os elemêntos da matriz produto indicam medidas em miligrama, convertemos essas medidas para grama dividindo cada elemento por 1.000:

$(início de linha) (abre colchete) (início de linha) 1,3 (fim de linha)(início de linha) 2,4 (fim de linha)(início de linha) 5,1 (fim de linha) (fécha colchete) (fim de linha)$

20. Atividade de elaboração dos estudantes. Espera-se quê eles utilizem as ideias de equação matricial para propor a questão e para resolver a questão recebida do colega.

21. a) $(abre colchete) (menos) 7 (e ainda) 2 [(Ê)] 4 (e ainda) (menos) 1 (fécha colchete)$ ⋅ $(abre colchete) 1 (e ainda) 0 [(Ê)] 0 (e ainda) 1 (fécha colchete)$ = $(abre colchete) (menos) 7 (vezes) 1 + 2 (vezes) 0 (e ainda) (menos) 7 (vezes) 0 + 2 (vezes) 1 [(Ê)] 4 (vezes) 1 + (abre parenteses) (menos) 1 (fécha parenteses) (vezes) 0 (e ainda) 4 (vezes) 0 + (abre parenteses) (menos) 1 (fécha parenteses) (vezes) 1 (fécha colchete)$ = $(abre colchete) (menos) 7 (e ainda) 2 [(Ê)] 4 (e ainda) (menos) 1 (fécha colchete)$

b) $(abre colchete) 1 (e ainda) 0 [(Ê)] 0 (e ainda) 1 (fécha colchete)$ ⋅ $(abre colchete) (menos) 7 (e ainda) 2 [(Ê)] 4 (e ainda) (menos) 1 (fécha colchete)$ = $(abre colchete) 1 (vezes) (abre parenteses) (menos) 7 (fécha parenteses) + 0 (vezes) 4 (e ainda) 1 (vezes) 2 + 0 (vezes) (abre parenteses) (menos) 1 (fécha parenteses) [(Ê)] 0 (vezes) (abre parenteses) (menos) 7 (fécha parenteses) + 1 (vezes) 4 (e ainda) 0 (vezes) 2 + 1 (vezes) (abre parenteses) (menos) 1 (fécha parenteses) (fécha colchete)$ = $(abre colchete) (menos) 7 (e ainda) 2 [(Ê)] 4 (e ainda) (menos) 1 (fécha colchete)$

c) $(abre colchete) (menos) 7 (e ainda) 2 [(Ê)] 4 (e ainda) (menos) 1 (fécha colchete)$ ⋅ $(abre colchete) (menos) 7 (e ainda) 2 [(Ê)] 4 (e ainda) (menos) 1 (fécha colchete)$ = $(abre colchete) (menos) 7 (vezes) (abre parenteses) (menos) 7 (fécha parenteses) + 2 (vezes) 4 (e ainda) (menos) 7 (vezes) 2 + 2 (vezes) (abre parenteses) (menos) 1 (fécha parenteses) [(Ê)] 4 (vezes) (abre parenteses) (menos) 7 (fécha parenteses) + (abre parenteses) (menos) 1 (fécha parenteses) (vezes) 4 (e ainda) 4 (vezes) 2 + (abre parenteses) (menos) 1 (fécha parenteses) (vezes) (abre parenteses) (menos) 1 (fécha parenteses) (fécha colchete)$ = $(abre colchete) 57 (e ainda) (menos) 16 [(Ê)] (menos) 32 (e ainda) 9 (fécha colchete)$

d) $(abre colchete) 57 (e ainda) (menos) 16 [(Ê)] (menos) 32 (e ainda) 9 (fécha colchete)$ − $(abre colchete) 1 (e ainda) 0 [(Ê)] 0 (e ainda) 1 (fécha colchete)$ = $(abre colchete) 57 (e ainda) (menos) 16 [(Ê)] (menos) 32 (e ainda) 9 (fécha colchete)$ + $(abre colchete) (menos) 1 (e ainda) 0 [(Ê)] 0 (e ainda) (menos) 1 (fécha colchete)$ = $(abre colchete) 56 (e ainda) (menos) 16 [(Ê)] (menos) 32 (e ainda) 8 (fécha colchete)$

22. $(abre colchete) (menos) 6 (e ainda) 5 (e ainda) (menos) 1 (fécha colchete)$ ⋅ $(abre colchete) 0 (e ainda) 4 9 (e ainda) [(b)] [(Há)] (e ainda) (menos) 10 (fécha colchete)$ = $(abre colchete) 38 (e ainda) 26 (fécha colchete)$ ⇒ $(abre colchete) (menos) 6 (vezes) 0 + 5 (vezes) 9 + (abre parenteses) (menos) 1 (fécha parenteses) (vezes) [(Há)] (e ainda) (início de linha) (menos) 6 (vezes) 4 + 5 (vezes) (b) + (abre parenteses) (menos) 1 (fécha parenteses) (vezes) (abre parenteses) (menos) 10 (fécha parenteses) (fim de linha) (fécha colchete)$ = $(abre colchete) 38 (e ainda) 26 (fécha colchete)$ ⇒ $(abre colchete) 45 (menos) [(Há)] (e ainda) (menos) 14 + 5 [(b)] (fécha colchete)$ = $(abre colchete) 38 (e ainda) 26 (fécha colchete)$

45 − a = 38 ⇒ a = 7

−14 + 5b = 26 ⇒ b = 8

23. a) incógnitas: x, y e z; coeficientes: 11, 7 e −2; termo independente: 0

b) incógnitas: r, s e t; coeficientes: $(início da fração dê) 1 (sobre) 3 (fim da fração)$ , $(menos) (início da fração dê) 2 (sobre) 5 (fim da fração)$ e −3; termo independente: −1

c) incógnitas: m e n; coeficientes: 4 e −3; termo independente: 7

d) incógnitas: x e y; coeficientes: 8 e 2; termo independente: −5

24. a e d, pois o item b tem uma incógnita de expoente 2 e o item c tem uma incógnita com expoente −1.

25. Para determinar as soluções, em cada caso, pode-se definir o valor de uma das incógnitas e resolver a equação de primeiro grau correspondente. Uma resposta possível: a: (3, $(início da fração dê) 5 (sobre) 4 (fim da fração)$ ), (9, $(início da fração dê) 15 (sobre) 4 (fim da fração)$ ), (0, 0); d: (0, 4), (−2, 0), (−1, 2).

26. a) Para determinar as soluções, em cada caso, pode-se definir o valor de uma das incógnitas e resolver a equação de primeiro grau correspondente. Uma resposta possível: (−1, 3) e (1, −1).

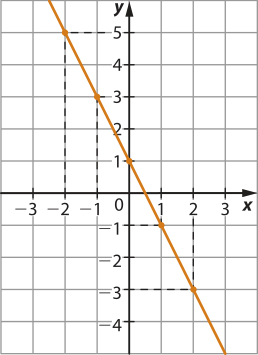
Gráfico de linha sobre malha quadriculada. O eixo y, na vertical, varia de menos 4 a 5. O eixo x, na horizontal, varia de menos 3 a 3. Há uma reta linear decrescente que cruza o eixo vertical em y igual a 1, e cruza o eixo horizontal entre 0 e 1. Há 5 pontos marcados sobre a reta: x igual a menos 2, y igual a 5; x igual a menos 1, y igual a 3; x igual a zero, y igual a 1; x igual a 1, y igual a menos 1; x igual a 2, y igual a menos 3.

b) Uma resposta possível: (−3, −2) e (1, 0).

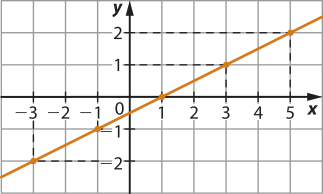
Gráfico de linha sobre malha quadriculada. O eixo y, na vertical, varia de menos 2 a 2. O eixo x, na horizontal, varia de menos 3 a 5. Há uma reta linear crescente que cruza o eixo vertical entre menos 1 e zero, e cruza o eixo horizontal em x igual a 1. Há 5 pontos marcados sobre a reta: x igual a menos 3, y igual a menos 2; x igual a menos 1, y igual a menos 1; x igual a 1, y é igual a zero; x igual a 3, y é igual a 1; x igual a 5, y é igual a 2.

c) Uma resposta possível: (−2, 3) e (2, 0).

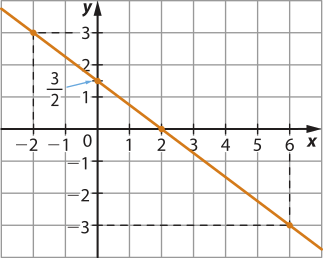
Gráfico de linha sobre malha quadriculada. O eixo y, na vertical, varia de menos 3 a 3. O eixo x, na horizontal, varia de menos 2 a 6. Há uma reta linear decrescente que cruza o eixo vertical em y igual a 3 sobre 2, e cruza o eixo horizontal em x igual a 2. Há 4 pontos marcados sobre a reta: x igual a menos 2, y igual a 3; x igual a zero, y igual a 3 sobre 2; x igual a 2, y igual a zero; x igual a 6, y igual a menos 3.

27. a) −1 + 2 ⋅ 3 = 5;

−5 + 2 ⋅ 5 = 5

−x + 2y = 5

b) Analisando o gráfico apresentado, temos quê uma resposta possível é: (1, 3), (3, 4) e (5, 5).

28. a) 1 + 3 = 4

Uma resposta possível: x + y = 4.

b) 2 ⋅ (−1) + 2 ⋅ 2 − (−4) = 6

Uma resposta possível: 2x + 2y − z = 6.

c) 2 − 2 ⋅ $(início da fração dê) 1 (sobre) 2 (fim da fração)$ = 1

Uma resposta possível: x − 2y = 1.

d) 3 ⋅ $(início da fração dê) 2 (sobre) 3 (fim da fração)$ − 2 ⋅ $(início da fração dê) 1 (sobre) 2 (fim da fração)$ + 3 = 4

Uma resposta possível: 3x − 2y + z = 4.

Página trezentos e sessenta e quatro

29. a) 40x + 20y = 5.000

b) Sim. Uma resposta possível: Considerando quê 100 meias-entradas custam R$ 2.000,00 e quê 75 meias-entradas custam R$ 3.000,00, temos quê 100 pessoas podem ter pagado meia-entrada e 75 pessoas, a entrada inteira.

30. a) A partir das informações do enunciado, temos:

50m + 20n + 10p = 100.

b) Uma resposta possível: (1, 2, 1). Nesse caso, Luan recebe uma cédula de R$ 50,00, duas cédulas de R$ 20,00 e uma cédula de R$ 10,00.

c) Atribuindo valores para m e n, e calculando os valores de p, temos:

m	n	p
0	0	50 ⋅ 0 + 20 ⋅ 0 + 10p = 100 ⇒ p = 10
0	1	50 ⋅ 0 + 20 ⋅ 1 + 10p = 100 ⇒ p = 8
0	2	50 ⋅ 0 + 20 ⋅ 2 + 10p = 100 ⇒ p = 6
0	3	50 ⋅ 0 + 20 ⋅ 3 + 10p = 100 ⇒ p = 4
0	4	50 ⋅ 0 + 20 ⋅ 4 + 10p = 100 ⇒ p = 2
0	5	50 ⋅ 0 + 20 ⋅ 5 + 10p = 100 ⇒ p = 0
1	0	50 ⋅ 1 + 20 ⋅ 0 + 10p = 100 ⇒ p = 5
1	1	50 ⋅ 1 + 20 ⋅ 1 + 10p = 100 ⇒ p = 3
1	2	50 ⋅ 1 + 20 ⋅ 2 + 10p = 100 ⇒ p = 1
2	0	50 ⋅ 2 + 20 ⋅ 0 + 10p = 100 ⇒ p = 0

10 maneiras distintas. Resposta pessoal. Espera-se quê os estudantes atribuam valores para as incógnitas m e n e determinem o valor p correspondente por meio da equação.

31. Resposta esperada: Substituindo, na equação, os valores da ênupla, temos: a₁ ⋅ 0 + a₂ ⋅ 0 + a₃ ⋅ 0 + ... + a_n ⋅ 0 = 0. pôdêmos observar quê o primeiro membro da igualdade ôbitída corresponde a uma adição de n parcelas iguais a zero, o quê determina uma soma igual a zero. Assim, a₁ ⋅ 0 + a₂ ⋅ 0 + a₃ ⋅ 0 + ... + a_n ⋅ 0 = 0 ⇒ 0 = 0. Portanto, a equação linear a₁x₁ + a₂x₂ + a₃x₃ + ... + a_nx_n = 0 admite a ênupla (0, 0, 0, ..., 0) como solução.

32. a) $(início de linha) { (início de linha) (menos) 3 (x) + 4 (ípsilon) (igual há) 14 (vezes) 2 (fim de linha) [(Ê)] (início de linha) 6 (x) (menos) 8 (ípsilon) (igual há) 2 (fim de linha) (fim de linha)$ ⇒

Esse sistema linear é SI.

b) 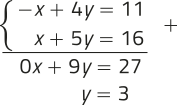Imagem de um sistema de equações resolvido pelo método da adição. Primeira equação: menos x mais 4 y igual a 11. Segunda equação: x mais 5 y igual a 16. Somando as duas equações, obtemos: zero x mais 9 y igual a 27, resultando em y igual a 3.

x + 5y = 16 ⇒ x + 5 ⋅ 3 = 16 ⇒ x = 1 → SPD; (1, 3)

c) $(início de linha) { (início de linha) 3 (x) (menos) 6 (ípsilon) (igual há) (menos) 3 (fim de linha) [(Ê)] (início de linha) (menos) (x) + 2 (ípsilon) (igual há) 1 (vezes) 3 (fim de linha) (fim de linha)$ ⇒

y = $(início da fração dê) (menos) 3 (menos) 3 [(x)] (sobre) (menos) 6 (fim da fração)$ ⇒ y = $(início da fração dê) 1 + (x) (sobre) 2 (fim da fração)$ → SPI, S = {(x, $(início da fração dê) 1 + [(x)] (sobre) 2 (fim da fração)$ ) │ x ∈ ℝ}.

Algumas soluções possíveis são: (−1, 0), (3, 2), (1, 1).

d) $(início de linha) { (início de linha) 3 (x) + 2 (ípsilon) (igual há) 17 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) (fim de linha) [(Ê)] (início de linha) 2 (x) + 3 (ípsilon) (igual há) 18 (vezes) 3 (fim de linha) (fim de linha)$ ⇒

2x + 3 ⋅ 4 = 18 ⇒ 2x = 6 ⇒ x = 3 → SPD; (3, 4)

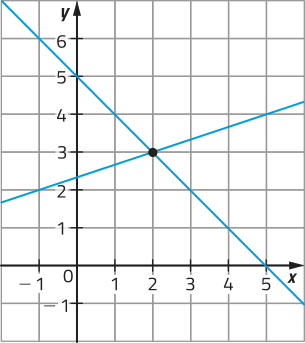
33. Gráfico de linhas sobre malha quadriculada. O eixo y, na vertical, varia de menos 1 a 6. O eixo x, na horizontal, varia de menos 1 a 5. Uma reta crescente cruza o eixo vertical entre 2 e 3. Uma reta decrescente cruza o eixo vertical em y igual a 5, e cruza o eixo horizontal em x igual a 5. As duas retas se cruzam no ponto de coordenadas x igual a 2 e y igual a 3.

Solução do sistema: (2, 3).

Resposta esperada: Inicialmente, representamos cada equação do sistema por uma reta no plano cartesiano. Como as retas se intersectam no ponto de coordenadas (2, 3), temos quê (2, 3) corresponde à única solução do sistema.

34. Caso o sistema linear não tenha solução, ele é classificado como SI.

Caso o sistema linear tenha solução, ele é classificado como SPD se a solução for única, ou como SPI caso a solução não seja única.

35. a) De acôr-do com as informações do enunciado, temos:

$(início de linha) { (início de linha) (h) + (m) (igual há) 5.496 (fim de linha) [(Ê)] (início de linha) (h) (menos) 7 (m) (igual há) 192 (fim de linha) (fim de linha)$

b) $(início de linha) { (início de linha) (h) + (m) (igual há) 5.496 (fim de linha) [(Ê)] (início de linha) (h) (menos) 7 (m) (igual há) 192 (vezes) (abre parenteses) (menos) 1 (fécha parenteses) (fim de linha) (fim de linha)$ ⇒

h + 663 = 5.496 ⇒ h = 4.833

Portanto, foram eleitas 663 mulheres e 4.833 homens.

c) Resposta pessoal.

36. a) Uma resposta possível: $(início de linha) { (início de linha) 2 [(b)] (menos) (p) (igual há) 20 (fim de linha) [(Ê)] (início de linha) [(b)] (menos) 3 (p) (igual há) (menos) 35 (fim de linha) (fim de linha)$

b) $(início de linha) { (início de linha) 2 [(b)] (menos) (p) (igual há) 20 (vezes) (abre parenteses) (menos) 3 (fécha parenteses) (fim de linha) [(Ê)] (início de linha) [(b)] (menos) 3 (p) (igual há) (menos) 35 (fim de linha) (fim de linha)$ ⇒

2b − p = 20 ⇒ 2 ⋅ 19 − p = 20 ⇒ p = 18

19 − 10 = 9 → 9 bolas brancas

18 − 15 = 3 → 3 bolas pretas

37. a) $(início de linha) { (início de linha) 2 (f) + (a) (igual há) 14,1 (fim de linha) [(Ê)] (início de linha) (f) + 4 (a) (igual há) 15,8 (fim de linha) (fim de linha)$ , sêndo f a quantidade de ferro, em miligrama, em cada porção de fígado grelhado e a, a quantidade de ferro, em miligrama, em cada porção de alface roxa (crua).

b) $(início de linha) { (início de linha) 2 (f) + (a) (igual há) 14,1 (fim de linha) [(Ê)] (início de linha) (f) + 4 (a) (igual há) 15,8 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) (fim de linha) (fim de linha)$ ⇒

2f + 2,5 = 14,1 ⇒ 2f = 11,6 ⇒ f = 5,8

Fígado grelhado: 5,8 mg; alface roxa (crua): 2,5 mg

c) $(início da fração dê) 14,1 (sobre) 2,5 (fim da fração)$ = 5,64

Portanto, ela deveria ingerir no mínimo 6 pôr-ções.

d) Resposta pessoal. Espera-se quê os estudantes discutam sobre a importânssia e o cuidado com a quantidade de ferro nos alimentos a partir da pesquisa realizada. Um dos aspectos quê póde sêr citado é a influência dêêsse mineral na perfórmance cognitiva.

38. Pesquisa do estudante. Espera-se quê, a partir da atividade, os estudantes demonstrem compreensão quanto a utilização dos sistemas lineares 2 × 2 para representar situações contextuais, bem como domínio dos métodos de resolução dêêsses sistemas.

Página trezentos e sessenta e cinco

39. a)

−2z = 10 ⇒ z = −5

−7y − 4 ⋅ (−5) = −22 ⇒ −7y = −42 ⇒ y = 6

x + 6 + (−5) = 11 ⇒ x + 1 = 11 ⇒ x = 10

(10, 6, −5); SPD

Esse sistema linear é SI.

−y + 3z = 9 ⇒ y = 3z − 9

2x + 3z − 9 + z = 11 ⇒ 2x = −4z + 20 ⇒ x = −2z + 10

S = {(−2z + 10, 3z − 9, z) | z ∈ ℝ}; SPI

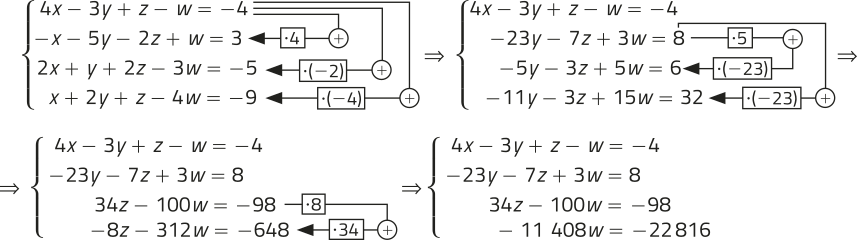
−11.408w = −22.816 ⇒ w = 2

34z − 100 ⋅ 2 = − 98 ⇒ 34z − 200 = −98 ⇒ z = 3

−23y − 7 ⋅ 3 + 3 ⋅ 2 = 8 ⇒ −23y − 15 = 8 ⇒ y = −1

4x − 3 ⋅ (−1) + 3 − 2 = − 4 ⇒ 4x + 4 = − 4 ⇒ x = −2

(−2, −1, 3, 2); SPD

40.

9 − 3(alfa)" = 0 ⇒ (alfa)" = 3

24 + (beta)" ≠ 0 ⇒ (beta)" ≠ −24

41. a) Sendo x, y, z as quantidades de dados consumidos por hora de uso pêlos aplicativos A, B e C, respectivamente, temos:

$(início de linha) { (início de linha) 8 (x) + 5 (ípsilon) + 6 (z) (igual há) 460 (fim de linha)(início de linha) 7 (x) + 4 (ípsilon) + 8 (z) (igual há) 508 (fim de linha)(início de linha) 6 (x) + 7 (ípsilon) + 9 (z) (igual há) 564 (fim de linha) (fim de linha)$

−340z = −13.600 ⇒ z = 40

−13y − 18 ⋅ 40 = −876 ⇒ −13y = −156 ⇒ y = 12

8x + 5 ⋅ 12 + 6 ⋅ 40 = 460 ⇒ 8x + 300 = 460 ⇒ x = 20

Resposta esperada: Em média, por hora de uso, o aplicativo A consome 20 MB, o B consome 12 MB e o C, 40 MB.

c) 10 ⋅ 20 + 15 ⋅ 12 + 5 ⋅ 40 = 200 + 180 + 200 = 580 → 580 MB

d) Pesquisa do estudante. Espera-se quê os estudantes avaliem criticamente o tempo de uso de aplicativos, e comparem os dados obtidos com os dos côlégas. Eles podem refletir, por exemplo, sobre possíveis consequências do tempo elevado de exposição a telas.

42. a) $(início de linha) { (início de linha) (x) + (ípsilon) + (z) (igual há) 38 (fim de linha)(início de linha) 0 (x) + 1 (ípsilon) + 3 (z) (igual há) 70 (fim de linha)(início de linha) 0 (x) + 0 (ípsilon) + 3 (z) (igual há) 60 (fim de linha) (fim de linha)$

b) 3z = 60 ⇒ z = 20

y + 3 ⋅ 20 = 70 ⇒ y = 70 − 60 ⇒ y = 10

x + 10 + 20 = 38 ⇒ x = 8

8 derrotas, 10 empates, 20 vitórias

Página trezentos e sessenta e seis

43.

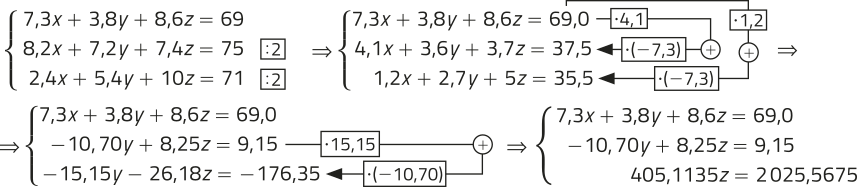
405,1135z = 2.025,5675 ⇒ z = 5

−10,70y + 8,25 ⋅ 5 = 9,15 ⇒ −10,70y + 41,25 = 9,15 ⇒ −10,70y = −32,10 ⇒ y = 3

7,3x + 3,8 ⋅ 3 + 8,6 ⋅ 5 = 69,0 ⇒ 7,3x + 11,4 + 43,0 = 69,0 ⇒ 7,3x = 14,6 ⇒ x = 2

1ª avaliação: 2; 2ª avaliação: 3; 3ª avaliação: 5

44. Elaboração do estudante. Espera-se quê os estudantes consigam representar situações-problema por meio de sistemas de equações lineares 3 × 3, bem como aplicar métodos de resolução dêste tipo de sistema e determinar sua solução.

45. a)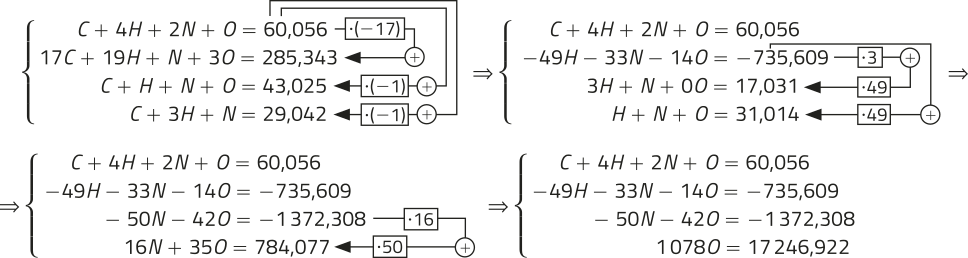

1.078O = 17.246,922 ⇒ O = 15,999

−50N − 42 ⋅ 15,999 = −1.372,308 ⇒ −50N = −700,35 ⇒ N = 14,007

−49H − 33 ⋅ 14,007 − 14 ⋅ 15,999 = −735,609 ⇒ −49H − 686,217 = 735,609 ⇒ −49H = −49,392 ⇒ H = 1,008

C + 4 ⋅ 1,008 + 2 ⋅ 14,007 + 15,999 = 60,056 ⇒ C + 48,045 = 60,056 ⇒ C = 12,011

carbono: 12,011 u; hidrogênio: 1,008 u; nitrogênio: 14,007 u; oxigênio: 15,999 u

b) • 2 ⋅ 1,008 + 15,999 = 2,016 + 15,999 = 18,015 → 18,015 u

• 12,011 + 4 ⋅ 1,008 = 12,011 + 4,032 = 16,043 → 16,043 u

• 2 ⋅ 14,007 + 15,999 = 28,014 + 15,999 = 44,013 → 44,013 u

c) Pesquisa do estudante. Espera-se quê os estudantes utilizem sistemas lineares para determinar as massas moleculares das substâncias pesquisadas.

46. Sendo a o preêço do pacote de arrôz de 2 kg, b o preêço da garrafa de óleo de 900 mL, f o preêço do pacote de feijão de 1 kg e m o preêço do pacote de macarrão de 500 g, temos:

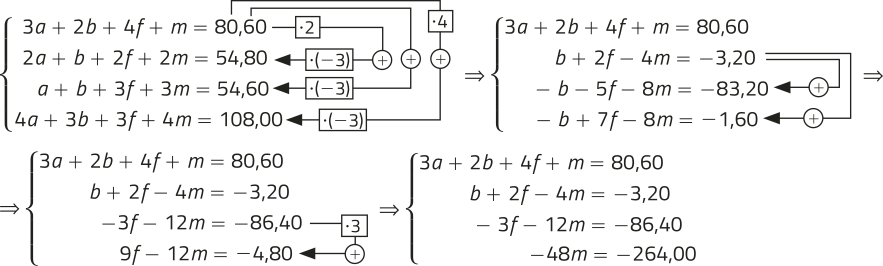
Imagem de um sistema de equações lineares. Há 4 conjuntos de equações lineares. À esquerda, há um sistema com 4 equações e 4 incógnitas. São elas: Equação 1: 3 a mais 2 b mais 4 f mais m igual a 80,60; Equação 2: 2 a mais b mais 2 f mais 2 m igual a 54,80; Equação 3: a mais b mais 3 f mais 3 m igual a 54,60; Equação 4: 4 a mais 3 b mais 3 f mais 4 m igual a 108. Para o segundo conjunto de equações, a primeira linha permanece inalterada. A segunda linha é obtida multiplicando a primeira equação por 2 e somada à segunda equação multiplicada por menos 3. A terceira linha é obtida somando a primeira equação com a terceira equação multiplicada por menos 3. E a quarta linha, multiplicando a primeira equação por 4 e somando à quarta equação multiplicada por menos 3. O sistema resultante é o seguinte: Equação 1: 3 a mais 2 b mais 4 f mais m igual a 80,60; Equação 2: b mais 2 f menos 4 m igual a menos 3,20; Equação 3: menos b menos 5 f menos 8 m igual a menos 83,20; Equação 4: menos b mais 7 f menos 8 m igual a menos 1,60. Para o terceiro conjunto de equações, a primeira e segunda linhas permanecem inalteradas. A terceira linha é obtida somando a segunda e terceira equações. E a quarta linha, somando a segunda e quarta equações. O sistema resultante é o seguinte: Equação 1: 3 a mais 2 b mais 4 f mais m igual a 80,60; Equação 2: b mais 2 f menos 4 m igual a menos 3,20; Equação 3: menos 3 f menos 12 m igual a menos 86,40; Equação 4: 9 f menos 12 m igual a menos 4,80. Para o quarto e último conjunto de equações, as 3 primeiras linhas permanecem inalteradas, e a quarta linha é obtida da seguinte maneira: a terceira equação é multiplicada por 3 e somada à quarta. O sistema resultante é o seguinte: Equação 1: 3 a mais 2 b mais 4 f mais m igual a 80,60; Equação 2: b mais 2 f menos 4 m igual a menos 3,20; Equação 3: menos 3 f menos 12 m igual a menos 86,40; Equação 4: menos 48 m igual a menos 264,00.

−48m = −264,00 ⇒ m = 5,50

−3f − 12 ⋅ 5,50 = −86,40 ⇒ −3f = −20,40 ⇒ f = 6,80

b + 2 ⋅ 6,80 − 4 ⋅ 5,50 = −3,20 ⇒ b −8,40 = −3,20 ⇒ b = 5,20

3a + 2 ⋅ 5,20 + 4 ⋅ 6,80 + 5,50 = 80,60 ⇒ 3a + 43,10 = 80,60 ⇒ 3a =37,50 ⇒ a = 12,50

pacote de arrôz de 2 kg: R$ 12,50; garrafa de óleo de 900 mL: R$ 5,20; pacote de feijão de 1 kg: R$ 6,80; pacote de macarrão de 500 g: R$ 5,50

47. $(início de linha) { (início de linha) (x) + (ípsilon) (igual há) 55 (fim de linha)(início de linha) (x) + (z) (igual há) 60 (fim de linha)(início de linha) (ípsilon) + (z) (igual há) 75 (fim de linha) (fim de linha)$

y + z = 75 ⇒ z = 75 − y

x + 75 − y = 60 ⇒ x − y = −15

$(início de linha) { (início de linha) (x) + (ípsilon) (igual há) 55 (fim de linha) [(Ê)] (início de linha) [(x)] (menos) (ípsilon) (igual há) (menos) 15 (fim de linha) (fim de linha)$ ⇒

20 + y = 55 ⇒ y = 35

z = 75 − 35 ⇒ z = 40

x + y + z = 20 + 35 + 40 = 95

Página trezentos e sessenta e sete

Integrando com...

1. Resposta pessoal. As respostas dependem das experiências dos estudantes.

2. Pesquisa e elaboração dos estudantes. Espera-se quê eles compreendam os benefícios das impressoras 3D e apresentem argumentos para seu uso em contextos sociais ou científicos, de acôr-do com o tema pesquisado.

3. Resposta esperada: Com a primeira coordenada, identificamos a posição de P em relação ao eixo X; com a segunda coordenada, a posição de P em relação ao eixo Y; e, com a terceira coordenada, a posição de P em relação ao eixo Z.

4. A, D e E

A: 2 ⋅ 5 − 3 ⋅ 1 + 8 = 15 ⇒ 15 = 15

B: 2 ⋅ 2 − 3 ⋅ 2 + 5 ≠ 15 ⇒ 3 ≠ 15

C: 2 ⋅ (−3) − 3 ⋅ (−2) + 3 ≠ 15 ⇒ 3 ≠ 15

D: 2 ⋅ 2 − 3 ⋅ (−3) + 2 = 15 ⇒ 15 = 15

E: 2 ⋅ (−1) − 3 ⋅ (−6) + (−1) = 15 ⇒ 15 = 15

F: 2 ⋅ 0 − 3 ⋅ 4 + 3 ≠ 15 ⇒ −9 ≠ 15

5. a) C, D, E e H

b) Resposta esperada: Esses sistemas admitem, ao menos, uma solução.

c) Apenas um ponto em comum; possibilidade H.

SPI; possibilidade C

e) • H

• C, D e E

• A, B, F e G

Elaboração dos estudantes. Espera-se quê eles consigam relacionar um sistema linear 3 × 3 à sua interpretação geométrica e determinar, a partir dessa representação, um sistema linear correspondente.

48. a) Imagem de dois quadrados em uma malha quadriculada com 5 quadrados de altura por 8 quadrados de largura. O primeiro quadrado tem lados medindo 2 quadrados da malha. Abaixo dele, há uma seta na horizontal, apontando 3 quadrados para a esquerda, representando um vetor u. Posicionado 3 quadrados à esquerda, está o outro quadrado, idêntico ao primeiro.

49. $(vetor) [(u)]$ ² = 2² + (1,5)² ⇒ $(vetor) [(u)]$ ² = 4 + 2,25 ⇒ $(vetor) [(u)]$ ² = 6,25 ⇒ $(vetor) [(u)]$ = ± 2,5 → 2,5 cm. Espera-se quê o estudante explique quê determinou o comprimento do vetor utilizando o teorema de Pitágoras.

50. a) A(minutos)"∶ 2 + 3 = 5; 5 + 1 = 6

B(minutos)"∶ 4 + 3 = 7; 4 + 1 = 5

C(minutos)"∶ 2 + 3 = 5; 2 + 1 = 3

A(minutos)"(5, 6), B(minutos)"(7, 5) e C(minutos)"(5, 3)

b) x = 0 − 12 = −12

y = 6 − 8 = −2

E(minutos)" ∶ 6 − 12 = −6; 10 − 2 = 8

F(minutos)" ∶ 16 − 12 = 4; 10 − 2 = 8

G(minutos)" ∶ 16 − 12 = 4; 14 − 2 = 12

H(minutos)" ∶ 6 − 12 = −6; 14 − 2 = 12

E(minutos)"(−6, 8), F(minutos)"(4, 8), G(minutos)"(4, 12) e H(minutos)"(−6, 12)

51. a) Usando A(minutos)" e A como referência: x: 3 − 6 = −3;

y: 2 − 3 = −1 → (−3, −1)

b) $(vetor) [(u)]$ ² = (−3)² + (−1)² ⇒ $(vetor) [(u)]$ ² = 9 + 1 ⇒ $(vetor) [(u)]$ ² = 10 ⇒ $(vetor) [(u)]$ = $(mais ou menos) (início da raíz quadrada dê) 10 (fim da raíz)$ → $(início da raíz quadrada dê) 10 (fim da raíz)$ u.c. ou aproximadamente 3,16 u.c.

52. a) Pesquisa e elaboração do estudante. Espera-se quê, a partir da atividade, os estudantes possam conhecer e explorar elemêntos da cultura de povos indígenas quê vivem próximos de suas regiões. As produções e os grafismos realizados podem sêr socializados entre a turma e com a comunidade escolar em uma exposição.

b) Elaboração do estudante. Espera-se quê os estudantes representem em seus grafismos a simetria de translação das figuras, demonstrando domínio do tema estudado.

53. a) Uma resposta possível:

Imagem de quadrado preenchido por padrões geométricos que lembram a letra T. São 4 T rotacionados em ângulos de 90 graus, e encaixados no interior do quadrado. O sombreamento das formas cria um efeito de relevo e profundidade.

b) 16 ⋅ 5² = 400 → 400 cm²

c) Elaboração dos estudantes. Espera-se quê eles representem um modelo (parte padrão) e utilizem a simetria de translação para compor a tela.

54. $(vetor) [(v)]$ ² = 3² + 2² ⇒ $(vetor) [(v)]$ ² = 9 + 4 ⇒ $(vetor) [(v)]$ ² = 13 ⇒ $(vetor) [(v)]$ = $(mais ou menos) (início da raíz quadrada dê) 13 (fim da raíz)$ ⇒ $(início da raíz quadrada dê) 13 (fim da raíz)$ m ou aproximadamente 3,6 m

55. Posicionar a ponta-seca do compasso em A e traçar um arco de circunferência de maneira a intersectar o eixo e nos pontos P e Q. Posicionar a ponta-seca do compasso em P e, com abertura PB, traçar um arco de circunferência. Em seguida, posicionar a ponta-seca do compasso em Q e, com abertura QB, traçar outro arco de circunferência de maneira a obtêr o ponto B(minutos)", na interseção entre os dois arcos. Proceder de maneira análoga à etapa anterior para obtêr os pontos A(minutos)", C(minutos)", D(minutos)", E(minutos)" e F(minutos)". Por fim, traçar os segmentos de reta quê unem os pontos obtidos e colorir a região interna da figura obtendo o polígono simétrico a ABCDEF por reflekção em torno do eixo e.

Imagem composta por duas figuras geométricas, localizadas acima e abaixo de uma linha horizontal identificada pela letra e. A figura inferior é composta pelos pontos A, B, C, D, E e F. A figura superior é simétrica em relação à reta, com os mesmos formatos e proporções, mas com os vértices identificados como A linha, B linha, C linha, D linha, E linha e F linha.

56. a) Analisando as imagens temos quê as fotografias I, III e V apresentam a ideia de simetria de reflekção.

b) Resposta esperada: Fotografia I: póde sêr traçado um eixo vertical entre as asas da borboleta; fotografia III: póde sêr traçado um eixo horizontal sobre a linha de contato do pato com a á gua; fotografia V: podem sêr traçados 5 eixos de simetria, cada eixo passando por um braço e pelo centro da estrela-do-mar.

Página trezentos e sessenta e oito

c) Resposta pessoal. Espera-se quê os estudantes identifiquem simetria de reflekção em elemêntos da natureza. Eles podem, por exemplo, apresentar as fotografias para a turma e para a comunidade escolar numa exposição, indicando o eixo de simetria identificado.

57. Como o eixo de simetria é paralelo ao eixo y, os vértices simétricos terão a mesma ordenada. Assim, o vértice (−5, 3) será simétrico a B(3, 3). A equação da reta correspondente ao eixo de simetria é dada por:

x = $(início da fração dê) 3 + (abre parenteses) (menos) 5 (fécha parenteses) (sobre) 2 (fim da fração)$ = $(início da fração dê) (menos) 2 (sobre) 2 (fim da fração)$ = −1

Assim:

A(1, 1) → A(minutos)"(−3, 1)

B(3, 3) → B(minutos)"(−5, 3)

C(5, 2) → C(minutos)"(−7, 2)

D(2, −1) → D(minutos)"(−4, −1)

58. a) Resposta esperada: Nesse poema, é possível observar algumas lêtras refletidas, remetendo a um dos sentidos do poema, o reflexo da Lua na á gua.

b) as lêtras L, U, A, N e G

c) nas lêtras A, M e U

d) Resposta pessoal. Os estudantes podem utilizar a mesma ideia representada no poema para compor o texto solicitado, demonstrando compreensão a respeito da simetria de reflekção na literatura e na ár-te.

59. a) Resposta pessoal. Espera-se quê os estudantes reproduzam o qüadro no GeoGebra utilizando a malha quadriculada da Janela de Visualização e a opção Polígono.

b) Resposta esperada: Traçar o eixo de simetria de maneira quê passe pêlos pontos médios dos lados paralelos verticais da tela.

c) O segmento de reta obtído seria congruente aos lados do quadrado correspondente a essa obra, ou seja, sua medida seria 90 cm ou 0,9 m.

d) Resposta pessoal. Espera-se quê os estudantes identifiquem a simetria em outras obras do movimento concretista. Eles podem expor as obras escolhidas e o texto compôzto com a ficha técnica em um mural, apresentando à comunidade escolar uma relação entre ár-te e Matemática.

60. a) 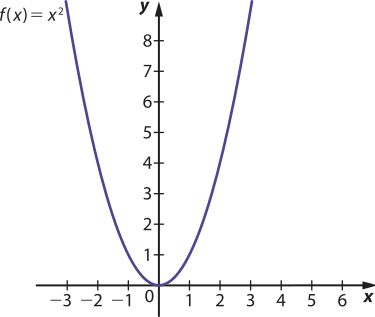Gráfico de linha que representa a função f de x igual a x ao quadrado. O eixo y, na vertical, varia de 0 a 8. O eixo x, na horizontal, varia de menos 3 a 6. O gráfico é uma parábola com concavidade voltada para cima, com vértice na origem, ponto em que x é igual a 0 e y é igual a 0.

Como f(x) = x² e f(−x) = (−x)² = x², então f (x) = f(−x) para todo x ∈ ℝ, ou seja, a função f é par.

b) 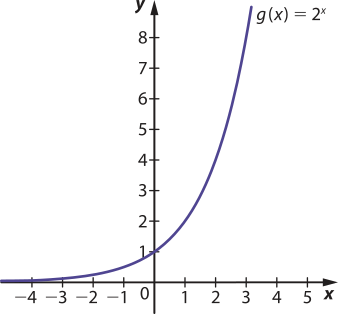Gráfico de linha que representa a função g de x igual a 2 elevado a x. O eixo y, na vertical, varia de 0 a 8, e o eixo x, na horizontal, varia de menos 4 a 5. A curva é crescente e passa pelo ponto de coordenadas x igual a 0 e y igual a 1. À esquerda, aproxima-se do eixo x sem o tocar, e à direita, cresce rapidamente.

Não é função par.

c) 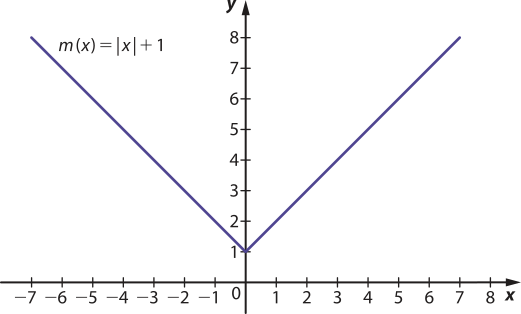Gráfico de linha que representa a função m de x igual a módulo de x mais 1. O eixo y, na vertical, varia de 0 a 8, e o eixo x, na horizontal, varia de menos 7 a 8. O gráfico tem formato de 'V', com vértice no ponto onde x é igual a 0 e y é igual a 1. A partir desse ponto, as linhas sobem de maneira simétrica para a direita e para a esquerda.

Se x ≥ 0, temos m(x) = |x| + 1 = x + 1 e m(−x) = |−x| + 1 = −(−x) + 1 = x + 1. Se x < 0, temos m(x) = |x| + 1 = −x + 1 e m(−x) = |−x| + 1 = −x + 1. Assim, m(x) = m(−x) para todo x ∈ ℝ, ou seja, a função m é par.

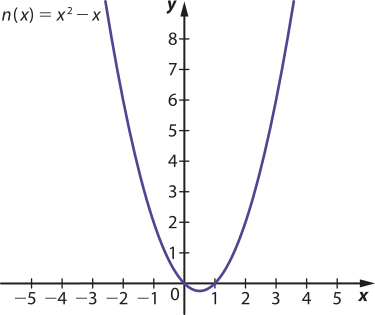
Não é função par.

• Uma resposta possível: b: Como g(1) = 2¹ = 2 e g(−1) = 2⁻¹ = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ , então g(1) ≠ g(−1), ou seja, a função g não é par e, portanto, seu gráfico não é simétrico ao eixo das ordenadas;

d: Como n(1) = 1² − 1 = 0 e n(−1) = (−1)² − (−1) = 2, então n(1) ≠ n(−1), ou seja, a função n não é par e, portanto, seu gráfico não é simétrico ao eixo das ordenadas.

61. A e B são simétricos em relação ao eixo y, com uma distância de 12 u entre eles. Seja E o ponto de interseção entre o segmento AB e o eixo y de simetria:

d_BC² = d_BE² + d_EC² ⇒ 12² = 6² + d_EC² ⇒ d_EC² = 108 ⇒ d_EC = $(início de linha) (mais ou menos) (início da raíz quadrada dê) 108 (fim da raíz) (fim de linha)$ ⇒ d_EC = $(início de linha) (mais ou menos) 6 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$

C(0, 4 + $6 (início da raíz quadrada dê) 3 (fim da raíz)$ ) ou C(0, 4 − $6 (início da raíz quadrada dê) 3 (fim da raíz)$ )

62. a) A(−10, 3)

$(abre colchete) (menos) 1 (e ainda) 0 [(Ê)] 0 (e ainda) 1 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 10 (fim de linha) [(Ê)] (início de linha) 3 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) (menos) 1 (vezes) (abre parenteses) (menos) 10 (fécha parenteses) + 0 (vezes) 3 (fim de linha) [(Ê)] (início de linha) 0 (vezes) (abre parenteses) (menos) 10 (fécha parenteses) + 1 (vezes) 3 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) 10 (fim de linha) [(Ê)] (início de linha) 3 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$

A(minutos)"(10, 3)

B(7, 0)

$(abre colchete) (menos) 1 (e ainda) 0 [(Ê)] 0 (e ainda) 1 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) 7 (fim de linha) [(Ê)] (início de linha) 0 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) (menos) 1 (vezes) 7 + 0 (vezes) 0 (fim de linha) [(Ê)] (início de linha) 0 (vezes) 7 + 1 (vezes) 0 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) (menos) 7 (fim de linha) [(Ê)] (início de linha) 0 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$

B(minutos)"(−7, 0)

C(−2, −5)

$(abre colchete) (menos) 1 (e ainda) 0 [(Ê)] 0 (e ainda) 1 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 2 (fim de linha) [(Ê)] (início de linha) (menos) 5 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) (menos) 1 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 0 (vezes) (abre parenteses) (menos) 5 (fécha parenteses) (fim de linha) [(Ê)] (início de linha) 0 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 1 (vezes) (abre parenteses) (menos) 5 (fécha parenteses) (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) 2 (fim de linha) [(Ê)] (início de linha) (menos) 5 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$

C(minutos)"(2, −5)

D(4, $(menos) (início da fração dê) 3 (sobre) 2 (fim da fração)$ )

Página trezentos e sessenta e nove

$(abre colchete) (menos) 1 (e ainda) 0 [(Ê)] 0 (e ainda) 1 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) 4 (fim de linha) [(Ê)] (início de linha) (menos) (início da fração dê) 3 (sobre) 2 (fim da fração) (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) (menos) 1 (vezes) 4 + 0 (vezes) (abre parenteses) (menos) (início da fração dê) 3 (sobre) 2 (fim da fração) (fécha parenteses) (fim de linha) [(Ê)] (início de linha) 0 (vezes) 4 + 1 (vezes) (abre parenteses) (menos) (início da fração dê) 3 (sobre) 2 (fim da fração) (fécha parenteses) (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) (menos) 4 (fim de linha) [(Ê)] (início de linha) (menos) (início da fração dê) 3 (sobre) 2 (fim da fração) (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$

D(minutos)"(−4, $(menos) (início da fração dê) 3 (sobre) 2 (fim da fração)$ )

b) Como um ponto simétrico em relação ao eixo das abscissas mantém a ordenada do ponto original e a abscissa é o ôpôsto dêêsse ponto, temos:

$(abre colchete) 1 (e ainda) 0 [(Ê)] 0 (e ainda) (menos) 1 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) [(x)] (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) [(x)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (elevado há) ' (fim de linha) (fécha colchete)$

c) Resposta pessoal. Espera-se quê os estudantes apliquem o conhecimento sobre equação matricial para resolver a questão. Ao final, eles podem trocar as produções com os côlégas para verificar se os pontos obtidos são simétricos aos escolhidos anteriormente.

63. Resposta pessoal. As respostas dependem do trapézio desenhado pêlos estudantes. Espera-se quê eles consigam aplicar a ideia de simetria de rotação na produção.

a) Resposta pessoal.

b) Resposta pessoal.

64. Alternativa c, pois é a única em quê a figura I foi rotacionada em 180° em torno do ponto O para determinar a figura II.

65. Resposta pessoal. Espera-se quê os estudantes consigam reconhecer a utilização de diferentes simetrias para determinar os hekzágonos a partir de determinado modelo. É interessante compartilhar com a turma as diferentes respostas, bem como as transformações descritas e os elemêntos identificados em cada tipo de simetria.

66. a) A(minutos)": $(abre colchete) (início de linha) [(x)] (índice) [(Há)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(Há)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) cosseno ⁡ ((alfa)) (e ainda) (menos) seno ((alfa)) [(Ê)] seno ((alfa)) (e ainda) cosseno ⁡ ((alfa)) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 6 (fim de linha) [(Ê)] (início de linha) 2 (fim de linha) (fécha colchete)$ ; B': $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) cosseno ⁡ ((alfa)) (e ainda) (menos) seno ((alfa)) [(Ê)] seno ((alfa)) (e ainda) cosseno ⁡ ((alfa)) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 4 (fim de linha) [(Ê)] (início de linha) 0 (fim de linha) (fécha colchete)$ ; C': $(abre colchete) (início de linha) [(x)] (índice) [(c)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(c)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) cosseno ⁡ ((alfa)) (e ainda) (menos) seno ((alfa)) [(Ê)] seno ((alfa)) (e ainda) cosseno ⁡ ((alfa)) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) 0 (fim de linha) [(Ê)] (início de linha) 4 (fim de linha) (fécha colchete)$

b) A(minutos)": $(abre colchete) (início de linha) [(x)] (índice) [(Há)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(Há)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) cosseno ⁡ (abre parenteses) 120 (graus) (fécha parenteses) (e ainda) (menos) seno (abre parenteses) 120 (graus) (fécha parenteses) [(Ê)] seno (abre parenteses) 120 (graus) (fécha parenteses) (e ainda) cosseno ⁡ (abre parenteses) 120 (graus) (fécha parenteses) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 6 (fim de linha) [(Ê)] (início de linha) 2 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) [(x)] (índice) [(Há)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(Há)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (e ainda) (menos) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) [(Ê)] (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (e ainda) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 6 (fim de linha) [(Ê)] (início de linha) 2 (fim de linha) (fécha colchete)$ ⇒

⇒ $(abre colchete) (início de linha) [(x)] (índice) [(Há)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(Há)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (vezes) (abre parenteses) (menos) 6 (fécha parenteses) + (abre parenteses) (menos) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (fécha parenteses) (vezes) 2 (fim de linha) [(Ê)] (início de linha) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (vezes) (abre parenteses) (menos) 6 (fécha parenteses) + (abre parenteses) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (fécha parenteses) (vezes) 2 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) [(x)] (índice) [(Há)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(Há)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 3 (menos) (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha) [(Ê)] (início de linha) (menos) 3 (início da raíz quadrada dê) 3 (fim da raíz) (menos) 1 (fim de linha) (fécha colchete)$

A(minutos)"(3 − $(início da raíz quadrada dê) 3 (fim da raíz)$ , $(início de linha) (menos) 3 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ − 1)

B(minutos)": $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) cosseno ⁡ (abre parenteses) 120 (graus) (fécha parenteses) (e ainda) (menos) seno (abre parenteses) 120 (graus) (fécha parenteses) [(Ê)] seno (abre parenteses) 120 (graus) (fécha parenteses) (e ainda) cosseno ⁡ (abre parenteses) 120 (graus) (fécha parenteses) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 4 (fim de linha) [(Ê)] (início de linha) 0 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (e ainda) (menos) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) [(Ê)] (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (e ainda) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 4 (fim de linha) [(Ê)] (início de linha) 0 (fim de linha) (fécha colchete)$ ⇒

⇒ $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (vezes) (abre parenteses) (menos) 4 (fécha parenteses) + (abre parenteses) (menos) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (fécha parenteses) (vezes) 0 (fim de linha) [(Ê)] (início de linha) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (vezes) (abre parenteses) (menos) 4 (fécha parenteses) + (abre parenteses) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (fécha parenteses) (vezes) 0 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 2 (fim de linha) [(Ê)] (início de linha) (menos) 2 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha) (fécha colchete)$

B(minutos)"(2, $(início de linha) (menos) 2 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ )

C(minutos)": $(abre colchete) (início de linha) [(x)] (índice) [(c)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(c)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) cosseno ⁡ (abre parenteses) 120 (graus) (fécha parenteses) (e ainda) (menos) seno (abre parenteses) 120 (graus) (fécha parenteses) [(Ê)] seno (abre parenteses) 120 (graus) (fécha parenteses) (e ainda) cosseno ⁡ (abre parenteses) 120 (graus) (fécha parenteses) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) 0 (fim de linha) [(Ê)] (início de linha) 4 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) [(x)] (índice) [(c)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(c)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (e ainda) (menos) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) [(Ê)] (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (e ainda) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) 0 (fim de linha) [(Ê)] (início de linha) 4 (fim de linha) (fécha colchete)$ ⇒

⇒ $(abre colchete) (início de linha) [(x)] (índice) [(c)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(c)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (vezes) 0 + (abre parenteses) (menos) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (fécha parenteses) (vezes) 4 (fim de linha) [(Ê)] (início de linha) (início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (vezes) 0 + (abre parenteses) (menos) (início da fração dê) 1 (sobre) 2 (fim da fração) (fécha parenteses) (vezes) 4 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) [(x)] (índice) [(c)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(c)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) (menos) 2 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha) [(Ê)] (início de linha) (menos) 2 (fim de linha) (fécha colchete)$

C(minutos)"( $(início de linha) (menos) 2 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ , −2)

67. a) quadrados DEFG e CEIH; quadrados FNOJ e IQPK; quadrados LMGJ e SRHK; triângulos FJG e IKH

b) quadrado KPQI

I: (1, 4), J: (−2, 4) → $(vetor) [(v)]$ = 1 − (−2); $(vetor) [(v)]$ = (3, 0) → medida de $(vetor) [(v)]$ é 3 u.c.

quadrado RSKH

H: (2,3), J: (−2, 4) → − 2 − 2 = −4 e 4 − 3 = 1; $(vetor) [(v)]$ = (−4, 1)

x² = (−4)² + 1² ⇒ x² = 16 + 1 ⇒ x² = 17 ⇒ x = $(mais ou menos) (início da raíz quadrada dê) 17 (fim da raíz)$ → medida de $(vetor) [(v)]$ é $(início da raíz quadrada dê) 17 (fim da raíz)$ u.c.

quadrado GJLM

M: (−3, 3), J: (−2, 4) → −2 − (−3) = 1 e 4 − 3 = 1; $(vetor) [(v)]$ = (1, 1)

x² = 1² + 1² ⇒ x² = 2 ⇒ x = $(mais ou menos) (início da raíz quadrada dê) 2 (fim da raíz)$ → medida de $(vetor) [(v)]$ é $(início da raíz quadrada dê) 2 (fim da raíz)$ u.c.

c) Respostas possíveis: O triângulo HIK póde sêr obtído por simetria de rotação do triângulo FGJ, com ângulo de rotação de 90° no sentido horário, em torno do ponto de coordenadas (0, 2); O triângulo FGJ póde sêr obtído por simetria de rotação do triângulo HIK, com ângulo de rotação de 270° no sentido horário, em torno do ponto de coordenadas (0, 2).

d) Respostas esperadas: A cada etapa (iteração) realizada, os triângulos ou os quadrados obtídos correspondem a uma redução do último triângulo ou quadrado obtido em uma etapa anterior. Transformação homotética.

e) Resposta pessoal. Espera-se quê os estudantes compreendam características da árvore pitagórica e de outros fractais quê utilizem transformações isométricas.

68. Elaboração dos estudantes. Espera-se quê eles construam uma figura modelo e utilizem diferentes tipos de transformações isométricas para compor um mosaico. É importante verificar se os estudantes conseguem representar uma figura a partir de uma transformação e, ao avaliarem o mosaico do colega, reconhecer diferentes simetrias.

69. Uma resposta possível: Rotacionar a figura amarela com um dos lados sobre o eixo x em 90° em torno do ponto de coordenadas (4, 2) no sentido anti-horário; transladar a figura ôbitída em relação a $(vetor) [(u)]$ = (−4, 0) e, em seguida, em relação a $(vetor) [(v)]$ = (0, 2).

70. a) II e I: $(início da fração dê) [(Óh)] [(C)] (elevado há) (') (sobre) [(Óh)] [(C)] (fim da fração)$ = $(início da fração dê) 46 (sobre) 23 (fim da fração)$ = 2

III e I: $(início da fração dê) [(Óh)] [(C)] (elevado há) (') (sobre) [(Óh)] [(C)] (fim da fração)$ = $(início da fração dê) 11,5 (sobre) 23 (fim da fração)$ = $(início da fração dê) 1 (sobre) 2 (fim da fração)$

III e II: $(início da fração dê) [(Óh)] [(C)] (elevado há) (') (sobre) [(Óh)] [(C)] (fim da fração)$ = $(início da fração dê) 11,5 (sobre) 46 (fim da fração)$ = $(início da fração dê) 1 (sobre) 4 (fim da fração)$

b) pentágono I: 5 + 5 + 5 + 5 + 5 = 25 → 25 cm

pentágono II: 25 ⋅ 2 = 50 → 50 cm

pentágono III: 25 ⋅ $(início da fração dê) 1 (sobre) 2 (fim da fração)$ = $(início da fração dê) 25 (sobre) 2 (fim da fração)$ = 12,5 → 12,5 cm

71. Construção do estudante. Espera-se quê os estudantes consigam determinar a razão k da homotetia realizada a partir das medidas dos lados correspondentes das figuras.

Página trezentos e setenta

72. a) 98 ∶ 2 = 49

(pi)" ⋅ 49² = 3 ⋅ 49² = 7.203

7.203 ⋅ 5 = 36.015

36.015 = (pi)" ⋅ r² ⇒ 36.015 = 3r² ⇒ 12.055 = r² ⇒ r ≃ 109,6 → aproximadamente 109,6 m

b) 6 ⋅ 24.200 m² = 145.200 m²

$(início da fração dê) 7.203 (sobre) 145.200 (fim da fração)$ ≃ 0,0496 → aproximadamente 4,96%

$(início da fração dê) 36.015 (sobre) 145.200 (fim da fração)$ ≃ 0,248 → aproximadamente 24,8%

73. a) Resposta esperada: Pode-se determinar, por exemplo, as medidas AP e EP e calcular a razão de homotetia k = $(início da fração dê) [(Ê)] [(P)] (sobre) [(Há)] [(P)] (fim da fração)$ Redução.

b) k = $(início da fração dê) 2 (sobre) 5 (fim da fração)$ → $(início da fração dê) 2 (sobre) 5 (fim da fração)$ ou 0,4

c) Resposta pessoal. Espera-se quê os estudantes consigam representar um prisma a partir da perspectiva cônica. Caso seja necessário, retome a representação de alguns prismas.

74. Elaboração do estudante. Espera-se quê os estudantes consigam elaborar e resolver problemas envolvendo transformações homotéticas de figuras. Eles podem, por exemplo, utilizar o contexto de elaboração de um projeto arquitetônico.

O quê estudei

1. Respostas pessoais.

2. Resposta pessoal.

3. Respostas pessoais.

4. a) Relação de ligação entre lojas de uma rê-de varejista

	A	B	C	D	E
A	0	0	1	1	1
B	0	0	1	1	0
C	1	1	0	1	0
D	1	1	1	0	1
E	1	0	0	1	0

Fonte: Dados fictícios.

M = $(início de linha) (abre colchete) 0 (e ainda) 0 (e ainda) 1 (e ainda) 1 (e ainda) 1 0 (e ainda) 0 (e ainda) 1 (e ainda) 1 (e ainda) 0 1 (e ainda) 1 (e ainda) 0 (e ainda) 1 (e ainda) 0 1 (e ainda) 1 (e ainda) 1 (e ainda) 0 (e ainda) 1 1 (e ainda) 0 (e ainda) 0 (e ainda) 1 (e ainda) 0 (fécha colchete) (fim de linha)$

I) De acôr-do com a quantidade de linhas e colunas, temos: matriz 5 × 5.

II) m₃₄ = 1. Indica quê há estrada ligando as lojas C e D.

III) Sim, pois na matriz M as quantidades de linhas e de colunas são iguais.

b) I) Resposta esperada:

$(início de linha) { (início de linha) (x) + (ípsilon) + (z) (igual há) 175 (fim de linha)(início de linha) (ípsilon) + (z) + 55 (igual há) 170 (fim de linha)(início de linha) 65 + 15 + (ípsilon) (igual há) 125 (fim de linha) (fim de linha)$ ou ${ (início de linha) (x) + (ípsilon) + (z) (igual há) 175 (fim de linha)(início de linha) (ípsilon) + (z) (igual há) 115 (fim de linha)(início de linha) [(ípsilon)] (igual há) 45 (fim de linha)$

II) Resposta esperada: Três incógnitas e três equações.

III) ${ (início de linha) (x) + (ípsilon) + (z) (igual há) 175 (fim de linha)(início de linha) (ípsilon) + (z) (igual há) 115 (fim de linha)(início de linha) [(ípsilon)] (igual há) 45 (fim de linha)$

45 + z = 115 ⇒ z = 70

x + 45 + 70 = 175 ⇒ x + 115 = 175 ⇒ x = 60

(60, 45, 70); SPD

IV) Resposta esperada: A estrada entre as lojas A e C tem 60 km, a estrada entre as lojas C e B tem 45 km e a estrada entre as lojas B e D tem 70 km.

c) Imagem de um plano cartesiano com cinco pontos identificados pelas letras A, B, C, D e E, com as seguintes coordenadas: ponto A: x igual a menos 2, y igual a 7; ponto B: x igual a 8, y igual a 2; ponto C: x igual a 3, y igual a 5; ponto D: x igual a 1, y igual a 3; ponto E: x igual a menos 3, y igual a 5.

I) $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) cosseno ⁡ (abre parenteses) 270 (elevado há) ∘ (fécha parenteses) (e ainda) (menos) seno (abre parenteses) 270 (elevado há) ∘ (fécha parenteses) [(Ê)] seno (abre parenteses) 270 (elevado há) ∘ (fécha parenteses) (e ainda) cosseno ⁡ (abre parenteses) 270 (elevado há) ∘ (fécha parenteses) (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 2 (fim de linha) [(Ê)] (início de linha) 8 (fim de linha) (fécha colchete)$ ⇒ $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) 0 (e ainda) 1 [(Ê)] (menos) 1 (e ainda) 0 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) (menos) 2 (fim de linha) [(Ê)] (início de linha) 8 (fim de linha) (fécha colchete)$ ⇒

⇒ $(abre colchete) (início de linha) [(x)] (índice) [(B)] (elevado há) ' (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (índice) [(B)] (elevado há) ' (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 0 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 1 (vezes) 8 (fim de linha) [(Ê)] (início de linha) (menos) 1 (vezes) (abre parenteses) (menos) 2 (fécha parenteses) + 0 (vezes) 8 (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 8 (fim de linha) [(Ê)] (início de linha) 2 (fim de linha) (fécha colchete)$

(8, 2) → ponto B

II) pontos C e E

III) −2 − 1 = −3

8 − 3 = 5

Uma resposta possível: Vetor com origem em O(0, 0) e extremidade em (−3, 5), ou seja, o vetor $(vetor) [(v)]$ = (−3, 5).

Praticando: enêm e vestibulares

1. alternativa a

Banco 1: 0 + 2 + 0 + 2 + 2 = 6

Banco 2: 0 + 0 + 2 + 1 + 0 = 3

Banco 3: 1 + 2 + 0 + 1 + 1 = 5

Banco 4: 0 + 2 + 2 + 0 + 0 = 4

Banco 5: 3 + 0 + 1 + 1 + 0 = 5

2. alternativa a

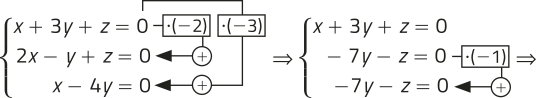
Imagem de um sistema de equações lineares. Há 2 conjuntos de equações lineares. À esquerda, há um sistema com três equações e três incógnitas. São elas: Equação 1: x mais 3 y mais z igual a zero. Equação 2: 2 x menos y mais z igual a zero. Equação 3: x menos 4 y igual a zero. Para o sistema resultante, a primeira linha permanece inalterada. A segunda linha é obtida multiplicando a primeira equação por menos 2 e somando à segunda. E a terceira linha, multiplicando a primeira equação por menos 3 e somando à terceira. O sistema resultante é o seguinte: Equação 1: x mais 3 y mais z igual a zero. Equação 2 é igual à equação 3: menos 7 y menos z igual a zero.

⇒ ${ (início de linha) (x) + 3 (ípsilon) + (z) (igual há) 0 (fim de linha)(início de linha) (menos) 7 (ípsilon) (menos) (z) (igual há) 0 (fim de linha)(início de linha) 0 (ípsilon) (menos) 0 (igual há) 0 (fim de linha)$

SPI

3. alternativa b

${ (início de linha) 2 (x) + 3 (ípsilon) (igual há) 74 (abre parenteses) (vezes) 2 (fécha parenteses) (fim de linha) [(Ê)] (início de linha) 3 (x) (menos) 2 (ípsilon) (igual há) 20 (abre parenteses) (vezes) 3 (fécha parenteses) (fim de linha)$ ⇒

13x = 208 ⇒ x = 16

2 ⋅ 16 + 3y = 74 ⇒ y = 14

x − y = 16 − 14 = 2

4. alternativa c

I) Verdadeira.

II) Falsa. O gráfico da função par é simétrico em relação ao eixo das ordenadas.

III) Falsa. O gráfico da função par é simétrico em relação à origem.

IV) Verdadeira.

V) Falsa.

Página trezentos e setenta e um

5. alternativa b

Considerando quê o polígono será simétrico e terá como eixo de simetria as retas r e s, temos quê, em $(início da fração dê) 1 (sobre) 4 (fim da fração)$ do polígono há 4 lados dele. Assim, como há quatro partes congruentes a essa, teremos ao todo 16 lados (4 ⋅ 4 = 16). Além díssu, temos os lados em quê as retas são mediatrizes, ou seja, mais 4 lados. Portanto, esse polígono terá 20 lados ao todo (16 + 4 = 20).

6. alternativa b

Sentido horário → 45° + 90° = 135°

7. alternativa d

Sendo t o preêço da televisão, e o preêço da estante e s o preêço do sofá, em real, temos:

$(início de linha) { (início de linha) (t) + (s) (igual há) 3.800 (abre parenteses) [(I)] (fécha parenteses) (fim de linha)(início de linha) (s) + (e) (igual há) 3.400 (abre parenteses) [(I)] [(I)] (fécha parenteses) (fim de linha)(início de linha) (t) + (e) (igual há) 4.200 (abre parenteses) [(I)] [(I)] [(I)] (fécha parenteses) (fim de linha) (fim de linha)$

Subtraindo (II) de (I), temos:

t − e = 400 (IV)

Segue quê:

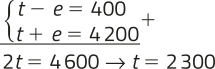
Imagem de um sistema de equações resolvido pelo método da adição. Equação 1: t menos e igual a 400. Equação 2: t mais e igual a 4.200. As equações são somadas e obtemos: 2 t igual a 4.600, resultando em t igual a 2.300.

Substituindo t = 2.300 em (IV) e em (I), temos:

2.300 − e = 400 ⇒ e = 1.900

2.300 + s = 3.800 ⇒ s = 1.500

Segue quê:

2t + s = 2 ⋅ 2.300 + 1.500 = 4.600 + 1.500 = 6.100

Após o desconto de 5%, temos:

0,95 ⋅ 6.100 = 5.795 → R$ 5.795,00

8. alternativa a

A = $(início de linha) (abre colchete) [(Há)] (índice) 11 (e ainda) [(Há)] (índice) 12 (e ainda) [(Há)] (índice) 13 [(Há)] (índice) 21 (e ainda) [(Há)] (índice) 22 (e ainda) [(Há)] (índice) 23 [(Há)] (índice) 31 (e ainda) [(Há)] (índice) 32 (e ainda) [(Há)] (índice) 33 (fécha colchete) (fim de linha)$

I) Para i > j

a₂₁ = a₃₁ = a₃₂ = 0

II) Para i ≤ j

a₁₁ = 4 ⋅ 1 − 5 ⋅ 1 + 2 = 1

a₁₂ = 4 ⋅ 1 − 5 ⋅ 2 + 2 = −4

a₁₃ = 4 ⋅ 1 − 5 ⋅ 3 + 2 = −9

a₂₂ = 4 ⋅ 2 − 5 ⋅ 2 + 2 = 0

a₂₃ = 4 ⋅ 2 − 5 ⋅ 3 + 2 = −5

a₃₃ = 4 ⋅ 3 − 5 ⋅ 3 + 2 = −1

A = $(início de linha) (abre colchete) 1 (e ainda) (menos) 4 (e ainda) (menos) 9 0 (e ainda) 0 (e ainda) (menos) 5 0 (e ainda) 0 (e ainda) (menos) 1 (fécha colchete) (fim de linha)$

9. alternativa c

Sendo v e f o espaço ocupado na memória do cartão em cada minuto de vídeo e cada foto, respectivamente, e x a capacidade de armazenamento do cartão de memória, temos:

$(início de linha) { (início de linha) 10 (v) + 190 (f) (igual há) (x) (fim de linha) [(Ê)] (início de linha) 15 (v) + 150 (f) (igual há) (x) (fim de linha) (fim de linha)$

Multiplicando a primeira equação do sistema por 3 e a segunda por −2, temos:

$(início de linha) { (início de linha) 30 (v) + 570 (f) (igual há) 3 [(x)] (fim de linha) [(Ê)] (início de linha) (menos) 30 [(v)] (menos) 300 (f) (igual há) (menos) 2 [(x)] (fim de linha) (fim de linha)$

Adicionando as equações do sistema obtído, temos:

270f = x

10. alternativa b

$(abre colchete) 0 (e ainda) (menos) 1 [(Ê)] 1 (e ainda) 0 (fécha colchete)$ ⋅ $(abre colchete) (início de linha) [(x)] (fim de linha) [(Ê)] (início de linha) [(ípsilon)] (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) 0 (vezes) (x) + (abre parenteses) (menos) 1 (fécha parenteses) (vezes) [(ípsilon)] (fim de linha) [(Ê)] (início de linha) 1 (vezes) (x) + 0 (vezes) [(ípsilon)] (fim de linha) (fécha colchete)$ = $(abre colchete) (início de linha) (menos) [(ípsilon)] (fim de linha) [(Ê)] (início de linha) [(x)] (fim de linha) (fécha colchete)$ ⇒ (−y, x)

O ponto (−y, x) corresponde a uma rotação de P em 90° no sentido anti-horário e com centro em (0, 0).

11. alternativa b

Sendo g a quantidade de gatos, c a quantidade de cachorros, e p a quantidade de pintinhos, temos:

${ (início de linha) (g) + (p) (igual há) 4 + (c) (fim de linha) [(Ê)] (início de linha) (g) + (c) (igual há) 6 + (p) (fim de linha)$ ⇒

12. alternativa d

I) verdadeira

II) verdadeira

12,2 − 9,4 = 2,8;

10,5 − 8,1 = 2,4;

15 − 12,4 = 2,6;

18,2 − 15,7 = 2,5;

14,2 − 13 = 1,2;

13,1 − 11,7 = 1,4

III) verdadeira

13. alternativa b

• Reflexão em relação ao eixo e.

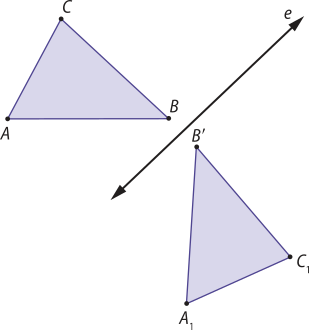
Imagem composta por dois triângulos e uma reta diagonal identificada como 'e'. O primeiro triângulo, com vértices A, B e C, está posicionado na parte superior esquerda da imagem. O segundo triângulo, com vértices Aíndice 1, B linha e Cíndice 1, está na parte inferior direita e é simétrico ao triângulo A B C em relação à reta 'e'.

• Rotação de 90° no sentido anti-horário em torno do ponto B(minutos)".

Imagem anterior. Agora, há um terceiro triângulo, A linha, B linha, C linha, que compartilha o vértice B linha com o segundo triângulo e está rotacionado a um ângulo alfa igual a 90 graus no sentido anti-horário.

Imagem anterior. Agora, o segundo triângulo foi removido, restando apenas os triângulos A, B, C e A linha, B linha, C linha.

Unidade 3 • Geometria espacial de posição

1. a) A ∈ (alfa)"; B ∈ (alfa)"; C ∉ (alfa)"; D ∈ (alfa)"; E ∉ (alfa)"; F ∉ (alfa)" e G ∈ (alfa)"

b) r ⊂ (beta)"; s ⊄ (beta)" e t ⊂ (beta)"

c) A ∈ r; B ∉ r; C ∈ r; D ∉ r; E ∈ r; F ∉ r e G ∉ r; A ∈ s; B ∉ s; C ∉ s; D ∈ s; E ∉ s; F ∉ s e G ∉ s; A ∈ t; B ∈ t; C ∉ t; D ∉ t; E ∉ t; F ∉ t e G ∉ t

2. a) Falsa, pois se os três pontos forem colineares, eles determinam infinitos planos.

b) Verdadeira.

Página trezentos e setenta e dois

c) Falsa, pois postulados são considerados verdadeiros sem a necessidade de serem demonstrados.

d) Falsa, pois duas retas concorrentes tem um único ponto em comum.

e) Verdadeira.

f) Verdadeira.

g) Verdadeira.

3. Respostas esperadas: a) Três pontos não colineares determinam um único plano; c) Os postulados correspondem a afirmações tomadas como verdadeiras sem a necessidade de serem demonstradas; d) Duas retas concorrentes têm apenas um ponto em comum.

4. a) Como os pontos são não colineares três a três, cada conjunto de dois dêêsses pontos determina uma reta quê não contém nenhum dos outros pontos. Como há 6 conjuntos contendo dois dêêsses pontos, {A, B}, {A, C}, {A, D}, {B, C}, {B, D} e {C, D}, então é possível traçar 6 retas distintas contendo dois dêêsses pontos.

b) Cada conjunto de três dêêsses pontos determina um único plano, pois esses pontos não são colineares, são distintos entre si e não são coplanares. Como há 4 conjuntos contendo três dêêsses pontos, {A, B, C}, {A, B, D}, {A, C, D} e {B, C, D}, então existem 4 planos distintos contendo três dêêsses pontos.

5. Resposta esperada: Pelo postulado VII, três pontos não colineares determinam um único plano. Considerando os três pontos correspondentes aos pontos de apôio dos pés dêêsses objetos no piso, podemos afirmar quê esses pontos de apôio determinam um único plano. Assim, mesmo quando apoiados em um piso irregular, esses três pontos de apôio determinam um único plano imaginário quê intersecta esse piso nesses pontos e, portanto, não balançam.

6. Resposta esperada: Considere os pontos A, B e C não colineares, correspondentes à interseção entre as retas r e s, r e t e s e t, respectivamente. Pelo postulado VII esses pontos determinam um único plano (alfa)". Assim, pelo postulado VI podemos afirmar quê as retas r, s e t estão contidas no plano (alfa)".

7. Falsa. Resposta esperada: Vamos supor por hipótese quê exista uma reta t perpendicular à reta r e concorrente à reta s, sêndo r e s perpendiculares entre si. Assim, temos os pontos A, B e C correspondentes às intersecções de r e s, r e t e s e t, respectivamente. Considerando o triângulo ABC, temos, por hipótese, quê med( $(ângulo) [(Há)]$ ) = 90°, med( $(ângulo) [(B)]$ ) = 90° e med( $(ângulo) [(C)]$ ) > 0°. Isso, no entanto, é um absurdo, pois a soma das medidas dos ângulos internos de qualquer triângulo é 180° e med( $(ângulo) [(Há)]$ ) + med( $(ângulo) [(B)]$ ) + med( $(ângulo) [(C)]$ ) > 180°.

8. a) Falsa. Resposta esperada: Duas retas quaisquer quê não têm ponto em comum são reversas ou paralelas.

b) Verdadeira.

c) Falsa. Resposta esperada: Se uma reta é perpendicular a um plano, então essa reta é perpendicular a todas as retas contidas nesse plano e concorrentes a ela.

d) Falsa. Resposta esperada: Se dois planos são coincidentes, então eles correspondem ao mesmo conjunto de pontos.

e) Verdadeira.

9. alternativa e

• As retas $(grupo) [(L)] [(B)] (equivale a) (grupo)$ e $(grupo) [(G)] [(Ê)] (equivale a) (grupo)$ se intersectam nos pontos médios dos segmentos de reta $(segmento) [(L)] [(B)]$ e $(segmento) [(G)] [(Ê)]$ , logo, são concorrentes.

• As retas $(grupo) [(Há)] [(G)] (equivale a) (grupo)$ e $(grupo) [(H)] [(I)] (equivale a) (grupo)$ são coplanares, pois estão contidas no plano quê contém a face correspondente ao pentágono ACIHG, e se intersectam nos prolongamentos dos segmentos de reta $(segmento) [(Há)] [(G)]$ e $(segmento) [(H)] [(I)]$ , logo, essas retas são concorrentes.

• As retas $(grupo) [(Há)] [(Dê)] (equivale a) (grupo)$ e $(grupo) [(G)] [(K)] (equivale a) (grupo)$ não são paralelas, pois os pontos A, D, G e K não são coplanares, e não têm ponto em comum, pois estão contidas, respectivamente, no plano quê contém a face ACDF e no plano quê contém GHKL, quê são paralelos. Logo, essas retas são reversas.

10. Resposta esperada: Não, pois se dois planos distintos têm ponto em comum, então eles são secantes e, portanto, têm uma reta em comum, ou seja, infinitos pontos.

11. a) As retas r e s podem, ou não, ter ponto em comum. Se têm ponto em comum, elas são perpendiculares, caso contrário, são reversas ortogonais.

b) As retas r e s podem, ou não, sêr coplanares. Se forem coplanares, elas são paralelas, caso contrário, são reversas.

c) As retas r e s estão contidas em planos paralelos a (alfa)" e podem, ou não, ter ponto em comum. Se têm ponto em comum, elas são concorrentes, caso contrário, podem sêr paralelas ou reversas.

12. Representando os vértices A, B, D e F nesse cubo, temos:

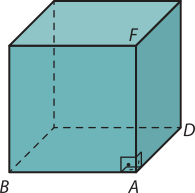
Imagem de um cubo. Há quatro vértices identificados: B, A e D na base inferior, e F na base superior, logo acima do vértice A.

Assim, temos quê os ângulos B $(ângulo) [(Há)]$ D, B $(ângulo) [(Há)]$ F, e D $(ângulo) [(Há)]$ F são rétos. Analisando a figura, temos:

a) retas perpendiculares

b) triângulo

13. a) Respostas possíveis: faces correspondentes aos quadriláteros: ABCD e EFGH; CDEF e ABGH; BCFG e ADEH.

b) Faces correspondentes aos quadriláteros: BCFG e CDEF.

c) $(grupo) [(H)] [(Ê)] (equivale a) (grupo)$ é uma reta contida no plano quê contém a face correspondente ao quadrilátero ADEH e é perpendicular ao plano quê contém a face correspondente ao quadrilátero ABGH.

d) Planos quê contêm as faces correspondentes aos quadriláteros: ABCD, CDEF, EFGH e ABGH.

14. Resposta esperada: Suponha quê os pontos A, B e C sêjam não colineares e pertencentes aos planos distintos (alfa)" e (beta)". Pelo postulado VII, esses pontos determinam um único plano e, assim, (alfa)" e (beta)" devem sêr coincidentes, o quê é um absurdo, pois temos por hipóteses quê (alfa)" e (beta)" são planos distintos. Portanto, os pontos A, B e C são pontos colineares. Nesse caso, (alfa)" e (beta)" são planos secantes.

15. a) A reta $(grupo) [(Há)] [(B)] (equivale a) (grupo)$ tem um ponto pertencente a (alfa)" e um ponto não pertencente a (alfa)", logo, essa reta é secante a (alfa)".

b) A reta $(grupo) [(Há)] [(B)] (equivale a) (grupo)$ tem um ponto pertencente a (beta)" e um ponto não pertencente a (beta)", logo, essa reta é secante a (beta)".

c) As retas $(grupo) [(Há)] [(B)] (equivale a) (grupo)$ e r não podem sêr concorrentes nem paralelas, pois, caso contrário, haveria um plano (gama)" quê as contivesse. Como o plano (alfa)" contém r e A e o plano (beta)" contém r e B, os planos (gama)", (alfa)" e (beta)" seriam coincidentes, o quê é um absurdo. Portanto, $(grupo) [(Há)] [(B)] (equivale a) (grupo)$ e r são retas reversas.

16. alternativa c

a) Falsa, pois essas são retas coplanares.

b) Falsa, pois essas são retas reversas.

c) Verdadeira.

d) Falsa, pois essas são retas reversas.

e) Falsa, pois o ponto H póde sêr posicionado de maneira quê essas retas não sêjam perpendiculares.

17. a) Secantes, pois esses planos contêm faces não paralelas e não perpendiculares da figura.

b) Secantes, pois esses planos contêm faces não paralelas e não perpendiculares da figura.

c) Paralelos, pois esses planos contêm faces paralelas da figura.

d) Secantes e perpendiculares, pois esses planos têm em comum apenas a reta quê passa pêlos pontos B e G.

18. • Teorema I:

Suponha quê a reta r não esteja contida em (alfa)" e seja paralela a uma reta s ⊂ (alfa)". Seja (beta)" o plano determinado pelas retas r e s. Se r não fosse paralela a (alfa)", existiria um ponto A ∈ r ⋃ (alfa)". Tem-se A ∉ s, pois r e s são paralelas. Seja (gama)" o plano determinado por s e pelo ponto A.

Página trezentos e setenta e três

Por um lado, (gama)" coincide com (alfa)", pois s ⊂ (alfa)" e A ∈ (alfa)". Por outro lado, (gama)" também coincide com (beta)", pois s ⊂ (beta)" e A ∈ r ⊂ (beta)". Logo, (alfa)" e (beta)" são coincidentes, o quê é um absurdo, pois concluiríamos quê r ⊂ (alfa)". Portanto, r é paralelo a (alfa)".

• Teorema II:

Suponha, por absurdo, quê uma reta r ⊂ (beta)" não seja paralela a (alfa)". Então r intersecta (alfa)" em um ponto A ∈ (alfa)". Como A ∈ r ⊂ (beta)", então A ∈ (alfa)" ⋃ (beta)", o quê contradiz a hipótese de quê (alfa)" e (beta)" são paralelos.

• Teorema III:

Seja s uma reta qualquer contida em (alfa)". Pelo postulado VII, existe uma reta r quê passa por P e é paralela a s. Assim, pelo Teorema I, r é paralela a (alfa)".

Integrando com...

1. Resposta pessoal. Os estudantes podem citar situações como realizar uma compra, tirar dúvidas na aula, conversar com amigos e familiares, enviar mensagens de áudio, entre outras.

2. Resposta pessoal. Espera-se quê os estudantes discutam sobre a comunicação, percebendo quê a falta dela ou ruídos externos podem atrapalhar as relações e causar conflitos quê poderiam sêr evitados por uma comunicação diréta e objetiva.

3. Pesquisa e produção dos estudantes Espera-se quê os estudantes conheçam, discutam e apresentem à comunidade escolar um pouco sobre acessibilidade atitudinal e quê as discussões sobre a temática proporcionem um ambiente escolar mais inclusivo, democrático e acolhedor.

4. Respostas pessoais. Espera-se quê os estudantes reflitam a respeito da importânssia e da necessidade do Sistema Braille para a inclusão das pessoas com deficiência visual, uma vez quê possibilita a comunicação entre pessoas cegas e viabiliza quê tênham acesso à informação. Portanto é uma ferramenta quê proporciona mais autonomia para essa pessoas.

5. a) De acôr-do com as explicações sobre a escrita em braille, apresentadas na seção, temos:

• livro

• 300

• Euclides

b) Respostas pessoais. Espera-se quê os estudantes consigam transcrever da linguagem materna para o braille o próprio nome e a idade, em anos.

c) •

•

d) Pesquisa dos estudantes. Espera-se quê eles conheçam e compartilhem com os côlégas características técnicas da escrita em braille.

e) Pesquisa dos estudantes. Espera-se quê eles pesquisem diferentes tecnologias quê facilitam a escrita e a leitura de textos em braille, como aplicativos de celular quê transcrevem textos em língua materna para braille (e vice-versa) e impressora quê imprime em braille.

19. alternativa e

Como as lêtras possuem a mesma espessura e estão igualmente espaçadas entre si, as sombras projetadas ortogonalmente no solo terão a forma de retângulos igualmente espaçados como na figura da alternativa e.

20. De acôr-do com a imagem, temos:

a) (gama)"

b) (alfa)"

c) (beta)"

21. a) Falsa, pois, se um segmento de reta for perpendicular a um plano, sua projeção ortogonal sobre esse plano será um ponto.

b) Falsa, pois as projeções ortogonais de duas retas reversas ortogonais, sobre um mesmo plano quê seja perpendicular a uma dessas retas, são um ponto e uma reta.

c) Verdadeira.

d) Falsa, pois a distância entre duas retas concorrentes não é definida.

22. alternativa b

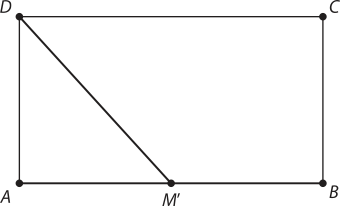
Imagem de um retângulo A B C D, com a base formada pelo lado A B. Do ponto D, localizado no canto superior esquerdo, parte um segmento de reta inclinado até o ponto M linha, que está no ponto médio do lado A B.

A figura representa a projeção ortogonal dos deslocamentos da lagartixa no plano quê contém o chão, sêndo M’ a projeção ortogonal de M, quê corresponde ao ponto médio do segmento $(segmento) [(Há)] [(B)]$ , e sêndo quê D coincide com a projeção ortogonal de H. Assim, a alternativa b é a correta.

23. Como os triângulos AA₁ C e BB₁ C são semelhantes, então:

$(início da fração dê) [(Há)] (índice) 1 [(C)] (sobre) [(Há)] [(Há)] (índice) 1 (fim da fração)$ = $(início da fração dê) [(B)] (índice) 1 [(C)] (sobre) [(B)] [(B)] (índice) 1 (fim da fração)$ ⇒ $(início da fração dê) 4 (sobre) 6 (fim da fração)$ = $(início da fração dê) [(B)] (índice) 1 [(C)] (sobre) 3,6 (fim da fração)$ ⇒ B₁C = 2,4

Assim:

A₁B₁ = A₁C + B₁C = 4 + 2,4 = 6,4 → 6,4 cm

24. De acôr-do com o enunciado, temos quê os lados $(segmento) [(Há)] [(B)]$ e $(segmento) [(B)] [(C)]$ são perpendiculares, uma vez quê B é a projeção ortogonal de C sobre a reta $(grupo) [(Há)] [(B)] (equivale a) (grupo)$ Assim, ABC é um triângulo retângulo. Segue quê:

sen 45° = $(início da fração dê) [(B)] [(C)] (sobre) 10 (fim da fração)$ ⇒ $(início da fração dê) (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 2 (fim da fração)$ = $(início da fração dê) [(B)] [(C)] (sobre) 10 (fim da fração)$ ⇒ BC = $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$

cos 45° = $(início da fração dê) [(Há)] [(B)] (sobre) 10 (fim da fração)$ ⇒ $(início da fração dê) (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 2 (fim da fração)$ = $(início da fração dê) [(Há)] [(B)] (sobre) 10 (fim da fração)$ ⇒ AB = $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$

Assim, o perímetro do triângulo ABC é dado por:

10 + $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ + $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ = 10 + $(início de linha) 10 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ ≃ 10 + 10 ⋅ 1,414 = 24,14 → (10 + $(início de linha) 10 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ ) cm ou aproximadamente 24,14 cm

25. Considere o ponto E sobre o lado $(segmento) [(Há)] [(Dê)]$ de modo quê $(segmento) [(Ê)] [(C)]$ seja paralelo a $(segmento) [(Há)] [(B)]$ , conforme a figura.

Imagem de uma figura plana composta por um retângulo e um triângulo. A parte de baixo da figura é um retângulo A B C E, com base A B e altura de 3 centímetros. Sobre o lado C E do retângulo, está desenhado o triângulo C E D, com vértice D no alto. Esse triângulo tem altura E D de 5 centímetros e hipotenusa D C medindo 13 centímetros.

Então:

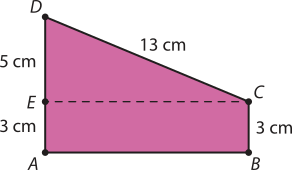
EC² + 5² = 13² ⇒ EC² + 25 = 169 ⇒ EC² = 144 ⇒ $(início de linha) { (início de linha) [(Ê)] (C) (igual há) 12 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) [(Ê)] (C) (igual há) (menos) 12 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim, AB = EC = 12 cm. Segue quê o perímetro do trapézio ABCD é:

8 + 13 + 3 + 12 = 36 → 36 cm

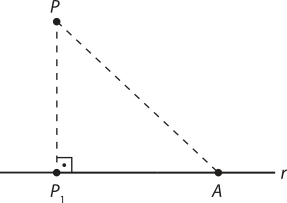
26. Imagem de uma reta horizontal identificada como r, com dois pontos marcados sobre ela: Píndice 1 e A. Acima da reta, fora dela, está o ponto P, alinhado verticalmente a Píndice 1. O ponto P está ligado por linhas tracejadas aos dois pontos sobre a reta, formando um triângulo retângulo.

Resposta esperada: A medida PP₁ é menor quê a medida PA, pois $(segmento) [(P)] [(P)] (índice) 1$ corresponde a um cateto de um triângulo retângulo e $(segmento) [(P)] [(Há)]$ , à hipotenusa dêêsse mesmo triângulo; como a hipotenusa é sempre o maior lado de um triângulo retângulo, então PP₁ é menor quê PA.

27. alternativa d

Imagem de uma esfera apoiada sobre uma superfície retangular, identificada como alfa. Na superfície superior da esfera, estão marcados os pontos A, B e C, ligados por segmentos, formando um triângulo. De cada ponto, partem linhas tracejadas que descem verticalmente até a superfície alfa, sobre a qual há um desenho curvo representando a projeção dos segmentos da esfera.

28. a) Resposta esperada: Projeção cilíndrica, pois essa projeção permite quê os formatos dos territórios representados sêjam mantidos, mas as áreas correspondentes sofram distorções.

Página trezentos e setenta e quatro

b) De acôr-do com o texto, a extensão territorial da Groenlândia corresponde a cerca de um quarto da extensão territorial do Brasil, ou seja, aproximadamente 25%.

c) Resposta esperada: Projeção cônica.

29. Resposta pessoal. Espera-se quê os estudantes compreendam as projeções cartográficas e os elemêntos envolvidos na construção de cada um dos mapas pesquisados, em particular em relação às deformações de ângulos e áreas envolvidas.

30. alternativa a

Trata-se de uma projeção plana sobre um plano tangente à superfícíe do glôbo terrestre no Polo Norte.

31. alternativa d

Sejam O o centro e P_S o Polo Sul do glôbo terrestre, ao projetar o ponto A, quê está na linha do equador, obtendo o ponto A₁ no plano (alfa)", é possível destacar dois triângulos retângulos semelhantes, P_NOA e P_NP_SA₁, conforme mostra a figura a seguir.

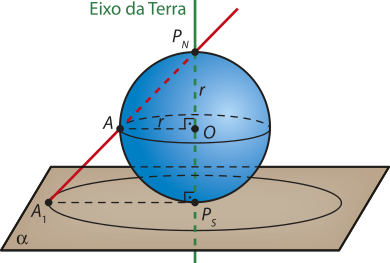
Imagem de uma esfera apoiada sobre uma superfície retangular identificada como alfa. Na parte superior da esfera está o ponto Píndice N, e na parte inferior, o ponto Píndice S. Uma linha vertical liga os pontos Píndice N e Píndice S, passando pelo ponto O, no centro da esfera. Essa linha está identificada como o eixo da Terra. Outra linha, inclinada, liga o ponto Píndice N ao ponto A, localizado na lateral da esfera. Essa linha atravessa a esfera e encontra a superfície alfa no ponto Aíndice 1. A partir do centro O, uma linha horizontal até o ponto A está identificada como raio da esfera. Sobre a superfície alfa, há uma circunferência desenhada ao redor da base da esfera, passando pelo ponto Aíndice 1.

O triângulo menor é isósceles e a medida de seus catetos corresponde à medida do raio da esféra. Assim, o triângulo maior também é isósceles e A₁P_S = P_NP_S = 2r. Portanto, os pontos projetados correspondem à circunferência com centro no Polo Sul e raio 2r, cujo diâmetro é igual a 4r.

O quê estudei

1. Respostas pessoais.

2. Resposta pessoal.

3. Respostas pessoais.

4. a) A = (pi)"r² = (pi)" ⋅ 22² = 484(pi)" → 484(pi)" cm² ou aproximadamente 1.519,76 cm²

b) Resposta esperada: Projeção plana ou azimutal.

c) Como o triângulo está sobre uma superfícíe esférica, a projeção é representada na figura da alternativa III.

Praticando: enêm e vestibulares

1. alternativa b

Como s ⊄ (alfa)", então s é paralela ou secante a (alfa)". Como r ∥ s e r ⊂ (alfa)", então s é paralela ao plano (alfa)".

2. alternativa d

a) Incorreta, pois se os três pontos pertencerem a uma mesma reta (colineares), é possível obtêr dois planos secantes quê contenham essa reta.

b) Incorreta, pois os planos (alfa)" e (beta)" podem sêr coincidentes.

c) Incorreta, dado uma reta e um ponto não pertencente à ela, existe um único plano quê passa por esse ponto e é perpendicular a essa reta.

d) Correta.

e) Incorreta, se uma reta é paralela a um plano, ela não possui ponto comum a nenhuma reta de tal plano.

3. alternativa a

I) Falsa, pois, por exemplo, há retas paralelas contidas nesses planos secantes.

II) Verdadeira.

III) Verdadeira.

IV) Falsa, pois, por exemplo, essas podem sêr retas reversas.

V) Falsa, pois, por exemplo, há retas paralelas contidas nesses planos secantes.

4. alternativa a

Marcando sobre a superfícíe do cubo a continuidade do trajeto do robô, e fazendo a projeção ortogonal do trajeto completo sobre o plano da base do cubo, temos:

Imagem de um cubo. Sobre ele, há um ponto identificado como P, localizado na face superior. Nas demais faces, também há um ponto marcado no centro de cada uma. A partir do ponto P, várias setas indicam deslocamentos em diferentes direções ao longo das faces do cubo, sempre passando pelo ponto central de cada face. O caminho seguido é o seguinte: ponto P na face superior, depois face lateral direita, face de trás, face inferior, face lateral esquerda, face frontal, e por fim, de volta à face superior, no ponto P. A face inferior está dividida em quatro quadrados iguais, sendo destacados os dois quadrados frontais e o quadrado posterior direito.

5. alternativa b

a) Incorreta, pois essa reta é paralela ao plano indicado.

b) Correta.

c) Incorreta, pois o único plano quê atende as condições dadas é aquele quê contém a face CGHD.

d) Incorreta, pois o único plano quê atende as condições dadas é aquele quê contém a face ABCD.

e) Incorreta, pois o único plano quê atende as condições dadas é aquele quê contém a face CGHD.

6. alternativa e

Realizando a projeção ortogonal das duas trajetórias sobre o plano (alfa)", temos:

Imagem de uma esfera apoiada sobre uma superfície identificada como alfa. Na esfera, há uma circunferência horizontal ao redor do seu centro, identificada como linha do Equador, que divide a esfera em partes superior e inferior. Também há duas circunferências verticais que se cruzam perpendicularmente: uma é o Meridiano 1, que separa a esfera em face frontal e posterior; a outra é o Meridiano 2, que separa a esfera em lados direito e esquerdo. No ponto de cruzamento superior entre os meridianos está o ponto N, e no cruzamento inferior, o ponto S. Dois trechos estão destacados na esfera: um na parte frontal inferior esquerda, e o outro na parte posterior superior direita, com as linhas desses trechos projetadas sobre a superfície alfa.

7. alternativa c

De acôr-do com a figura, a projeção ortogonal do triângulo AFC sobre a base BCDE corresponde ao triângulo BDC, cuja área é dada por:

$(início da fração dê) [(B)] (C) (vezes) [(C)] [(Dê)] (sobre) 2 (fim da fração)$ = $(início da fração dê) 2 (vezes) 2 (sobre) 2 (fim da fração)$ = 2 → 2 cm²

8. alternativa d

A imagem mostra a representação parcial do glôbo terrestre com a Antártida no centro da projeção cartográfica, sêndo a superfícíe terrestre projetada sobre um plano tangente. Os paralelos e meridianos são projetados formando círculos concêntricos. Deste modo, fica caracterizada uma projeção plana a partir do Polo Sul da Terra.

Unidade 4 • Figuras geométricas espaciais, área de superfícíe e volume

1. a) 7 vértices; 7 faces; 12 arestas

b) 4 faces triangulares e 3 faces quadrangulares

c) 3 arestas; 4 arestas

2. Construção do estudante. Espera-se quê os estudantes reconheçam poliedros convexos e não convexos, bem como a nomenclatura adequada para cada face dos poliedros apresentados.

3. Cada face possui 5 peças com formato de losango, 5 com formato de trapézio e 1 com formato de pentágono regular. Como o dodecaedro possui 12 faces, o total de peças de cada formato é:

• losango: 12 ⋅ 5 = 60 → 60 peças

• trapézio: 12 ⋅ 5 = 60 → 60 peças

• pentágono regular: 12 ⋅ 1 = 12 → 12 peças

4. a) Resposta esperada: Sim, pois os poliedros regulares são poliedros convexos.

b) No caso do tetraedro, do hexaedro e do octaedro, podemos determinar as quantidades de faces, arestas e vértices por simples contagem e, depois, podemos fazer a verificação utilizando a relação de Óiler para detectar possíveis enganos. Observe no qüadro a seguir essas informações e os cálculos para os outros dois poliedros.

• O dodecaedro possui 12 faces pentagonais.

Como cada aresta é comum a dois lados de polígonos das faces, temos A = $(início da fração dê) 12 (vezes) 5 (sobre) 2 (fim da fração)$ = 30. Como 3 arestas partem de cada vértice e cada aresta parte de dois vértices distintos, então:

V = $(início da fração dê) 2 (vezes) [(Há)] (sobre) 3 (fim da fração)$ = $(início da fração dê) 2 (vezes) 30 (sobre) 3 (fim da fração)$ = 20

Página trezentos e setenta e cinco

• O icosaedro possui 20 faces triangulares. Como cada aresta é comum a dois lados de polígonos das faces, temos A = $(início da fração dê) 20 (vezes) 3 (sobre) 2 (fim da fração)$ = 30. Como 5 arestas partem de cada vértice e cada aresta parte de dois vértices distintos, então:

V = $(início da fração dê) 2 (vezes) [(Há)] (sobre) 5 (fim da fração)$ = $(início da fração dê) 2 (vezes) 30 (sobre) 5 (fim da fração)$ = 12

Poliedro regular	Faces	Arestas	Vértices	Polígono da face	Arestas partindo de cada vértice
Tetraedro	4	6	4	Triângulo	3
Hexaedro	6	12	8	Quadrado	3
Octaedro	8	12	6	Triângulo	4
Dodecaedro	12	30	20	Pentágono	3
Icosaedro	20	30	12	Triângulo	5

c) Resposta esperada: Sim, pois, em um poliedro regular qualquer, todas as faces têm a mesma quantidade de lados, de cada vértice parte a mesma quantidade de arestas e é válida a relação de Óiler.

5. Como há 16 faces triangulares e cada aresta é comum a dois lados de polígonos das faces, então A = $(início da fração dê) 16 (vezes) 3 (sobre) 2 (fim da fração)$ = 24. Assim, pela relação de Óiler:

V + F = A + 2 ⇒ V + 16 = 24 + 2 ⇒ V = 10

Portanto, 10 vértices.

6. alternativa c

A quantidade de faces é F = 5 + 5 + 1 = 11, e, como cada aresta é comum a dois lados de polígonos das faces, então:

A = $(início da fração dê) 5 (vezes) 4 + 5 (vezes) 3 + 5 (sobre) 2 (fim da fração)$ = 20

Assim, pela relação de Óiler:

V + F = A + 2 ⇒ V + 11 = 20 + 2 ⇒ V = 11

Portanto, a alternativa c é a correta.

7. alternativa d

Pela relação de Óiler, o número de faces é dado por:

V + F = A + 2 ⇒ 14 + F = 30 + 2 ⇒ F = 18

Sejam x a quantidade de faces triangulares e y a de faces quadrangulares. Então x + y = 18, e, como cada aresta é comum a dois lados de polígonos das faces, então:

A = $(início da fração dê) 3 (x) + 4 [(ípsilon)] (sobre) 2 (fim da fração)$ ⇒ 3x + 4y = 60

Assim, temos o sistema: $(início de linha) { (início de linha) (x) + (ípsilon) (igual há) 18 (fim de linha) [(Ê)] (início de linha) 3 (x) + 4 (ípsilon) (igual há) 60 (fim de linha) (fim de linha)$ ⇒ x = 12 e y = 6

Portanto, são 12 faces triangulares e 6 faces quadrangulares.

8. a) Como cada aresta é comum a dois lados de polígonos das faces, os quais são todos pentágonos, então A = $(início da fração dê) 5 [(F)] (sobre) 2 (fim da fração)$ . Substituindo na relação de Óiler, temos:

V + F = A + 2 ⇒ V + F = $(início da fração dê) 5 [(F)] (sobre) 2 (fim da fração)$ + 2 ⇒ 2V + 2F = 5F + 4 ⇒ 2V − 3F = 4

Portanto, a alternativa III está correta.

b) Existe uma única classe de poliedro de Platão quê possui as faces com 5 lados: o dodecaedro.

9. O octaedro regular possui 12 arestas. Assim, a quantidade de linha necessária é:

12 ⋅ 9,5 = 114 → 114 cm

10. alternativa e

O poliedro possui 16 vértices, 11 faces e 24 arestas, logo, a alternativa e é a correta, pois $(início de linha) (dado quê) 16 (considerando quê) [(V)] (fim de linha)$ + $(início de linha) (dado quê) 11 (considerando quê) [(F)] (fim de linha)$ + $(início de linha) (dado quê) 24 (considerando quê) [(Há)] (fim de linha)$ + 3.

11. alternativa d

Um dodecaedro regular possui 20 vértices, 12 faces e 30 arestas. Em relação ao procedimento de obtêr o novo poliedro, temos quê:

• 5 vértices de um dodecaedro se justapõem a 5 vértices do outro dodecaedro; logo, o novo poliedro tem 5 vértices a menos quê o total de vértices dos dois dodecaedros, ou seja:

V = 2 ⋅ 20 − 5 = 35

• As faces dos dois dodecaedros passam a sêr faces do novo poliedro, com exceção apenas das duas faces justapostas; logo, o novo poliedro tem 2 faces a menos quê o total de faces dos dois dodecaedros, ou seja:

F = 2 ⋅ 12 − 2 = 22

• 5 arestas de um dodecaedro se justapõem a 5 arestas do outro dodecaedro. Logo, o novo poliedro tem 5 arestas a menos quê o total de arestas dos dois dodecaedros, ou seja:

A = 2 ⋅ 30 − 5 = 55

Portanto:

V + F + A = 35 + 22 + 55 = 112

12. A_A = A_B e V_A = V_B + 8

A_A = $(início de linha) (início da fração dê) 5 (vezes) [(F)] (índice) [(Há)] (sobre) 2 (fim da fração) (fim de linha)$ ; A_B = $(início de linha) (início da fração dê) 3 (vezes) [(F)] (índice) [(B)] (sobre) 2 (fim da fração) (fim de linha)$

$(início da fração dê) 5 (vezes) [(F)] (índice) [(Há)] (sobre) 2 (fim da fração)$ = $(início da fração dê) 3 (vezes) [(F)] (índice) [(B)] (sobre) 2 (fim da fração)$ ⇒ 5 ⋅ F_A = 3 ⋅ F_B ⇒ F_A = $(início de linha) (início da fração dê) 3 (vezes) [(F)] (índice) [(B)] (sobre) 5 (fim da fração) (fim de linha)$

Pela relação de Óiler, temos:

V_A + F_A = A_A + 2 ⇒ V_A = A_A + 2 − F_A

V_B + F_B = A_B + 2 ⇒ V_B = A_B + 2 − F_B

Substituindo as igualdades conhecidas, temos:

V_A = A_A + 2 − F_A ⇒ V_B + 8 = $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 2 (fim da fração) (fim de linha)$ + 2 − $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 5 (fim da fração) (fim de linha)$ ⇒

⇒ A_B + 2 − F_B + 8 = $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 2 (fim da fração) (fim de linha)$ + 2 − $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 5 (fim da fração) (fim de linha)$ ⇒

⇒ $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 2 (fim da fração) (fim de linha)$ + 2 − F_B + 8 = $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 2 (fim da fração) (fim de linha)$ + 2 − $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 5 (fim da fração) (fim de linha)$ ⇒ −F_B + 8 = $(início de linha) (menos) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 5 (fim da fração) (fim de linha)$ ⇒

⇒ −F_B + $(início de linha) (início da fração dê) 3 [(F)] (índice) [(B)] (sobre) 5 (fim da fração) (fim de linha)$ = −8 ⇒ −2F_B = −40 ⇒ F_B = 20

A_B = $(início da fração dê) 3 (vezes) 20 (sobre) 2 (fim da fração)$ = 30; V_B = 30 + 2 − 20 = 12

A_A = A_B = 30; F_A = $(início da fração dê) 3 (vezes) 20 (sobre) 5 (fim da fração)$ = 12; V_A = 30 + 2 − 12 = 20

Poliedro A: dodecaedro; 12 faces, 20 vértices e 30 arestas.

Poliedro B: icosaedro; 20 faces, 12 vértices e 30 arestas.

13. Seja e a medida da diagonal da base e d a medida da diagonal do paralelepípedo, conforme mostra a figura.

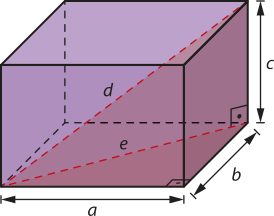
Imagem de um paralelepípedo retângulo, com comprimento medindo a, largura b e altura c. Na face inferior está desenhado um triângulo retângulo, com hipotenusa identificada pela letra e e catetos correspondentes aos lados a e b. A partir de um dos vértices desse triângulo, foi traçado um segmento até o vértice oposto do paralelepípedo, formando a diagonal interna, identificada pela letra d. Essa diagonal forma um triângulo retângulo com hipotenusa d e catetos c e e.

Utilizando o teorema de Pitágoras, temos:

(I) e² = a² + b²

(II) d² = e² + c²

Substituindo (I) em (II), temos: d² = a² + b² + c² ⇒ $(início de linha) { (início de linha) (d) (igual há) (início da raíz quadrada dê) [(Há)] (elevado há) 2 + [(b)] (elevado há) 2 + [(c)] (elevado há) 2 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (d) (igual há) (menos) (início da raíz quadrada dê) [(Há)] (elevado há) 2 + [(b)] (elevado há) 2 + [(c)] (elevado há) 2 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, d = $(início de linha) (início da raíz quadrada dê) [(Há)] (elevado há) 2 + [(b)] (elevado há) 2 + [(c)] (elevado há) 2 (fim da raíz) (fim de linha)$ .

14. A área da superfícíe interna da piscina corresponde à área da base somada com a área lateral do paralelepípedo, ou seja:

Página trezentos e setenta e seis

A = A_b + A(éli)" = (5 ⋅ 4) + (2 ⋅ 1,5 ⋅ 5 + 2 ⋅ 1,5 ⋅ 4) = 20 + 27 = 47

Logo, o azulejista cobrará o revestimento de 47 metros quadrados de superfícíe, o quê irá totalizar:

47 ⋅ 35 = 1.645 → R$ 1.645,00

15. Imagem de um mosaico composto por quatro hexágonos regulares, encaixados dois a dois. Cada hexágono é formado por seis triângulos equiláteros. À esquerda da figura, há uma medida indicando a altura total do mosaico: 127,5 centímetros, valor que corresponde à altura de cinco triângulos equiláteros ou cinco vezes a aresta do hexágono.

Observe quê a medida de 127,5 cm corresponde à altura de cinco triângulos equiláteros congruentes entre si, cuja medida do lado é igual à medida do lado do hekzágono. A figura a seguir ilustra um dêêsses triângulos, cuja altura é 127,5 ∶ 5 = 25,5 cm.

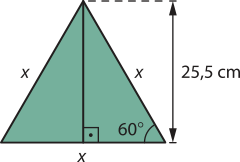
Imagem de um triângulo equilátero de lados x e altura medindo 25,5 centímetros.

Temos:

sen 60° = $(início da fração dê) 25,5 (sobre) [(x)] (fim da fração)$ ⇒ $(início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ = $(início da fração dê) 25,5 (sobre) [(x)] (fim da fração)$ ⇒ x = $(início da fração dê) 51 (sobre) (início da raíz quadrada dê) 3 (fim da raíz) (fim da fração)$ ≃ $(início da fração dê) 51 (sobre) 1,7 (fim da fração)$ = 30

Logo, a parte lateral externa do nicho é formada por 14 retângulos de 30 cm de comprimento e 15 cm de largura, cuja área é igual a:

14 ⋅ 30 ⋅ 15 = 6.300 → 6.300 cm²

16. A área da superfícíe de cada contêiner a sêr pintada, em m², é dada por:

A = + $(início de linha) (dado quê) 2 (vezes) 6,1 (vezes) 2,6 + 2 (vezes) 2,4 (vezes) 2,6 (considerando quê) Área lateral (fim de linha)$ + 2 ⋅ $(início de linha) (dado quê) 6,1 (vezes) 2,4 (considerando quê) Area da base (fim de linha)$ − $(início de linha) (dado quê) 1,2 (elevado há) 2 (considerando quê) Área da janela (fim de linha)$ − $(início de linha) (dado quê) 2,1 (vezes) 2 (considerando quê) Área da porta (fim de linha)$ = 67,84

Logo, a quantidade de tinta necessária para pintar 35 contêineres é dada pela seguinte regra de três:

Área (em m²)	Quantidade de tinta (em L)
14	1
$(dado quê) 2.374,4 (considerando quê) 35 (vezes) 67,84$	x

$(início da fração dê) 14 (sobre) 2374,4 (fim da fração)$ = $(início da fração dê) 1 (sobre) [(x)] (fim da fração)$ ⇒ x = 169,6 → 169,6 L

17. Vamos calcular, em cm², a área da região de personalização de cada modelo:

• Modelo quadrangular:

A = $(início de linha) (dado quê) 35 (elevado há) 2 (considerando quê) Area da base (fim de linha)$ + $(início de linha) (dado quê) 4 (vezes) 4 (vezes) 35 (considerando quê) Area lateral (fim de linha)$ = 1.785

• Modelo octogonal:

Observe quê o apótema do octógono é de 40 ∶ 2 = 20 cm.

A = $(início de linha) (dado quê) 8 (vezes) (início da fração dê) 16,5 (vezes) 20 (sobre) 2 (fim da fração) (considerando quê) Área da base (fim de linha)$ + $(início de linha) (dado quê) 8 (vezes) 16,5 (vezes) 4 (considerando quê) Área lateral (fim de linha)$ = 1.848

Portanto, a diferença entre a área dos dois modelos de tampa é de:

1.848 − 1.785 = 63 → 63 cm²

18. alternativa e

Cada aresta da base méde 10 m e a medida x de cada aresta lateral é dada por:

sen 60° = $(início da fração dê) 18 (sobre) [(x)] (fim da fração)$ ⇒ $(início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ = $(início da fração dê) 18 (sobre) [(x)] (fim da fração)$ ⇒ x = $(início da fração dê) 36 (sobre) (início da raíz quadrada dê) 3 (fim da raíz) (fim da fração)$ = $12 (início da raíz quadrada dê) 3 (fim da raíz)$

Como há duas bases com 6 arestas cada uma e 6 arestas laterais, a soma das medidas de todas as arestas é:

2 ⋅ 6 ⋅ 10 + 6 ⋅ $(início de linha) 12 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ = 120 + $72 (início da raíz quadrada dê) 3 (fim da raíz)$ ≃ 244,7 → aproximadamente 244,7 m

19. alternativa d

A diagonal da base do cubo menor tem a mesma medida da aresta do cubo maior, ou seja, 14 cm. Assim, a medida x da aresta do cubo menor é dada por:

14 = $[(x)] (início da raíz quadrada dê) 2 (fim da raíz)$ ⇒ x = $(início da fração dê) 14 (sobre) (início da raíz quadrada dê) 2 (fim da raíz) (fim da fração)$ = $7 (início da raíz quadrada dê) 2 (fim da raíz)$

Antes da soldagem, as partes externas das duas peças tí-nhão uma área total, em cm², de:

A₁ = 6 ⋅ 14² + 6 ⋅ ( $(início de linha) 7 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ )² = 1.764

Após a soldagem, essa área diminuiu em uma área correspondente à de duas faces do cubo menor, passando a sêr, em cm², de:

A₂ = 1.764 − 2 ⋅ ( $(início de linha) 7 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ )² = 1.568

Logo, a área galvanizada dessa peça é de 1.568 cm².

20. Elaboração do estudante. Espera-se quê os estudantes consigam associar o formato da caixa apresentada a um paralelepípedo e, a partir dele, elaborar e resolver problemas envolvendo área da superfícíe de prismas. Com as informações do qüadro é possível, por exemplo, elaborar um problema quê avalie o modelo de embalagem mais adequado de acôr-do com determinada condição.

21.

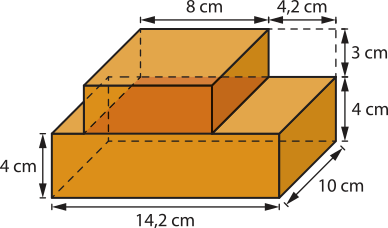
V = 4 ⋅ 14,2 ⋅ 10 + 8 ⋅ 3 ⋅ 10 = 808 → 808 cm³

22. O volume, em m³, do paralelepípedo quê representa a capacidade dêêsse reservatório é:

V = 2 ⋅ 3 ⋅ 1,2 = 7,2

Como 1 m³ equivale a 1.000 L, a capacidade total do reservatório é de 7.200 L. Logo, quando estiver com 80% da capacidade de á gua, haverá $(início de linha) (dado quê) 5.760 (considerando quê) 7.200 (vezes) 0,8 (fim de linha)$ L no reservatório, o quê exigirá uma quantidade de á gua sanitária, em mL, igual a: 2 ⋅ 5.760 = 11.520. Portanto, serão necessários 11,52 L de á gua sanitária.

23. a) • Volume do prisma hexagonal regular:

V₁ = $(início de linha) (dado quê) 6 (vezes) (início da fração dê) 3 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 8 (considerando quê) [(h)] (fim de linha)$ = $108 (início da raíz quadrada dê) 3 (fim da raíz)$ ≃ 108 ⋅ 1,7 ≃ 183,6 → 183,6 cm³

• Volume do paralelepípedo:

V₂ = 3 ⋅ 2 ⋅ 8 = 48 → 48 cm³

Logo, o volume da peça é:

V = V₁ − V₂ = 183,6 − 48 = 135,6 → 135,6 cm³

b) 2,7 ⋅ 135,6 = 366,12 → 366,12 g

24. a) A: V = 36 ⋅ 27 ⋅ 18 = 17.496 → 17.496 cm³

Isso equivale a 17.496 mL ou 17,496 L.

B: V = 54 ⋅ 36 ⋅ 27 = 52.488 → 52.488 cm³

Isso equivale a 52.488 mL ou 52,488 L.

C: V = 27 ⋅ 27 ⋅ 36 = 26.244 → 26,244 cm³

Isso equivale a 26.244 mL ou 26,244 L.

D: V = 27 ⋅ 22,5 ⋅ 13,5 = 8.201,25 → 8.201,25 cm³

Isso equivale a 8.201,25 mL ou aproximadamente 8,201 L.

b) Como a mercadoria ocupa 25 L, ela póde sêr acomodada somente nas caixas do modelo B ou C. Assim, o modelo escolhido deve sêr o B, pois possui um custo de envio menor quê o do modelo C.

Página trezentos e setenta e sete

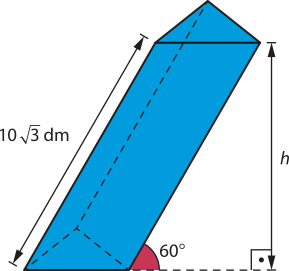
25. Imagem de um prisma oblíquo de base triangular. As bases do prisma são formadas por triângulos equiláteros e as faces laterais são paralelogramos. A aresta lateral do prisma mede 10 raiz de 3 decímetros, e o prisma está inclinado, de modo que a aresta lateral forme um ângulo de 60 graus com a horizontal.

A altura h do prisma, em^_ dm, é dado por: sen 60° = $(início da fração dê) [(h)] (sobre) 10 (início da raíz quadrada dê) 3 (fim da raíz) (fim da fração)$ ⇒ $(início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ = $(início da fração dê) [(h)] (sobre) 10 (início da raíz quadrada dê) 3 (fim da raíz) (fim da fração)$ ⇒ h = 15

Seja x a medida da aresta da base dêêsse prisma. Como V = $(início de linha) 180 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ dm³, temos:

V = A_b ⋅ h ⇒ $180 (início da raíz quadrada dê) 3 (fim da raíz)$ = $(início da fração dê) [(x)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração)$ ⋅ 15 ⇒ x² = 48 ⇒ $(início de linha) { (início de linha) (x) (igual há) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (x) (igual há) (menos) 4 (início da raíz quadrada dê) 3 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, a medida da aresta da base é $(início de linha) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ dm.

26. Cada bloco pavimenta uma área de $(início de linha) (dado quê) 200 (considerando quê) 10 (vezes) 20 (fim de linha)$ cm², o quê equivale a 0,02 m². Como a região a sêr pavimentada tem uma área de $(início de linha) (dado quê) 40 (considerando quê) 8 (vezes) 5 (fim de linha)$ m², são necessários 40 ∶ 0,02 = 2.000 blocos para essa pavimentação, o quê corresponde a um volume de concreto de:

2.000 ⋅ $(início de linha) (dado quê) 0,1 (vezes) 0,2 (vezes) 0,06 (considerando quê) Volume de um bloco, em m (elevado há) 3 (fim de linha)$ = 2,4 → 2,4 m³

27. No triângulo retângulo correspondente à base do prisma, um dos catetos méde 6 cm. Seja x a medida do outro cateto, em cm, então:

x² + 6² = 7,5² ⇒ x² = 20,25 ⇒ $(início de linha) { (início de linha) (x) (igual há) 4,5 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (x) (igual há) (menos) 4,5 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim, o volume do prisma é:

V = $(início de linha) (dado quê) (início da fração dê) 6 (vezes) 4,5 (sobre) 2 (fim da fração) (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 12 (considerando quê) [(h)] (fim de linha)$ = 162 → 162 cm³

28. Pesquisa e elaboração do estudante. Espera-se quê os estudantes elaborem e resolvam problemas envolvendo medida de capacidade em contextos do dia a dia ou de outras áreas do conhecimento. Os problemas podem envolver conversão de unidades de medida de capacidade em uma temática quê seja relevante para a comunidade local, como a capacidade de algum reservatório ou recipiente.

29. alternativa c

A base do prisma póde sêr decomposta em dois trapézios cuja base maior méde, de acôr-do com a vista superior da caçamba, 4 m. A área de cada trapézio, em m², é:

• $(início de linha) (início da fração dê) (abre parenteses) 4 + 3,5 (fécha parenteses) (vezes) 0,5 (sobre) 2 (fim da fração) (fim de linha)$ = 1,875

• $(início de linha) (início da fração dê) (abre parenteses) 4 + 3 (fécha parenteses) (vezes) 1,5 (sobre) 2 (fim da fração) (fim de linha)$ = 5,25

Assim, a área da base do prisma é A_b = 1,875 + 5,25 = 7,125 m, e, de acôr-do com a vista superior da caçamba, a altura dêêsse prisma é h = 2,5 m. O volume mássimo de resíduos quê póde sêr coletado corresponde ao volume dêêsse prisma, quê é igual a:

V = 7,125 ⋅ 2,5 ≃ 17,8 → aproximadamente 17,8 m³

30. Algumas respostas possíveis:

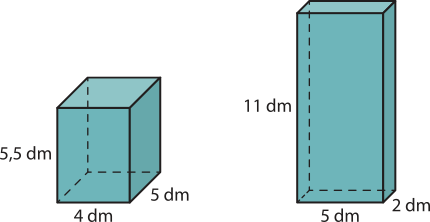
Imagem de dois sólidos. À esquerda, há um prisma retangular com base medindo 4 decímetros por 5 decímetros e altura de 5,5 decímetros. À direita, há outro prisma retangular com base medindo 5 decímetros por 2 decímetros e altura de 11 decímetros.

31. alternativa a

Seja H a medida da altura comum dos dois prismas. O volume de cada prisma é:

• Prisma hexagonal: V₁ = $(início de linha) (dado quê) 6 (vezes) (início da fração dê) [(h)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (considerando quê) [(Há)] (índice) 5 (fim de linha)$ ⋅ H = $(início da fração dê) 3 [(h)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ ⋅ H

• Prisma triangular: V₂ = $(início de linha) (dado quê) (início da fração dê) [(Tê)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ H

Temos V₁ = V₂, logo:

$(início da fração dê) 3 [(h)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ ⋅ H = $(início da fração dê) [(Tê)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração)$ ⋅ H ⇒ 3h² = $(início da fração dê) [(Tê)] (elevado há) 2 (sobre) 2 (fim da fração)$ ⇒ $(início da fração dê) [(h)] (elevado há) 2 (sobre) [(Tê)] (elevado há) 2 (fim da fração)$ = $(início da fração dê) 1 (sobre) 6 (fim da fração)$ ⇒ ( $(início da fração dê) [(h)] (sobre) [(Tê)] (fim da fração)$ )² = $(início da fração dê) 1 (sobre) 6 (fim da fração)$

Como h e t são positivos, segue quê $(início da fração dê) [(h)] (sobre) [(Tê)] (fim da fração)$ = $(início da raíz quadrada dê) (início da fração dê) 1 (sobre) 6 (fim da fração) (fim da raíz)$ = $(início da fração dê) 1 (sobre) (início da raíz quadrada dê) 6 (fim da raíz) (fim da fração)$ .

32. a) i = $(início da fração dê) (h) (vezes) 100 (sobre) [(c)] (fim da fração)$ ⇒ 8 = $(início da fração dê) 0,6 (vezes) 100 (sobre) [(c)] (fim da fração)$ ⇒ c = 7,5 → 7,5 m

b) A rampa terá o formato de um prisma triangular reto de 1,5 m de altura e cuja base é um triângulo retângulo de catetos medindo 0,6 m e 7,5 m. Logo, seu volume é:

V = $(início de linha) (dado quê) (início da fração dê) 0,6 (vezes) 7,5 (sobre) 2 (fim da fração) (considerando quê) Area da base (fim de linha)$ ⋅ $(início de linha) (dado quê) 1,5 (considerando quê) Altura (fim de linha)$ = 3,375 → 3,375 m³

c) Elaboração dos estudantes. Espera-se quê eles compreendam as normas para a construção de rampas apresentadas na atividade e produzam um projeto de acôr-do com elas. Além dos dados técnicos da rampa, propor aos estudantes quê justifiquem o motivo da posição da rampa no local escolhido. É essencial quê eles entendam quê, além de seguir as normas técnicas, é importante quê as rampas sêjam úteis e proporcionem acessibilidade. Para verificar se as medidas indicadas contemplam uma inclinação quê respeita as normas da ABNT, os estudantes podem trocar as propostas entre os grupos.

33. alternativa d

Vamos calcular, em cm³, o volume do prisma quê representa a capacidade de cada recipiente.

• Recipiente I: V_I = $(início de linha) (dado quê) 6 (vezes) (início da fração dê) 12 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 15 (considerando quê) [(h)] (fim de linha)$ = $3.240 (início da raíz quadrada dê) 3 (fim da raíz)$ ≃ 5.612

• Recipiente II: V_II = $(início de linha) (dado quê) 14,5 (elevado há) 2 (considerando quê) [(Há)] (índice) 6 (fim de linha)$ ⋅ $(início de linha) (dado quê) 24 (considerando quê) [(h)] (fim de linha)$ = 5.046

Como 1 cm³ corresponde a 1 mL, podemos concluir quê o recipiente II ficou completamente cheio e transbordou cerca de 5.612 − 5.046 = 566 mL de á gua, ou seja, a alternativa d é a correta.

34. a)

m = 2 ∶ 2 = 1 → 1 cm

g² = 7² + m² ⇒ g² = 7² + 1² ⇒ g² = 50 ⇒ $(início de linha) { (início de linha) (g) (igual há) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) 5 (início da raíz quadrada dê) 2 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ cm ou aproximadamente 7,07 cm.

L² = g² + ( $(início da fração dê) [(l)] (sobre) 2 (fim da fração)$ )² ⇒ L² = ( $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ )² + ( $(início da fração dê) 2 (sobre) 2 (fim da fração)$ )² ⇒ L² = 51 ⇒ $(início de linha) { (início de linha) (L) (igual há) (início da raíz quadrada dê) 51 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (L) (igual há) (menos) (início da raíz quadrada dê) 51 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, $(início de linha) (início da raíz quadrada dê) 51 (fim da raíz) (fim de linha)$ cm ou aproximadamente 7,14 cm.

Página trezentos e setenta e oito

d) A_b = 2² = 4 → 4 cm²

e) A(éli)" = 4 ⋅ $(início de linha) (início da fração dê) 2 (vezes) 5 (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 2 (fim da fração) (fim de linha)$ = $20 (início da raíz quadrada dê) 2 (fim da raíz)$ → $(início de linha) 20 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ cm² ou aproximadamente 28,28 cm²

f) A_t = $(início de linha) 20 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ + 4 = 4( $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ + 1) → 4( $(início de linha) 5 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ + 1) cm² ou aproximadamente 32,28 cm²

35. a)

Polígono da base da pirâmide	Quantidade n	Quantidade V	Quantidade A	Quantidade F
Triângulo	3	4	6	4
Quadrilátero	4	5	8	5
Pentágono	5	6	10	6
hekzágono	6	7	12	7

b) Analisando o qüadro, temos:

• V: 4 = 3 + 1; 5 = 4 + 1; 6 = 5 + 1; 7 = 6 + 1 → V = n + 1

• A: 6 = 2 ⋅ 3; 8 = 2 ⋅ 4; 10 = 2 ⋅ 5; 12 = 2 ⋅ 6 → A = 2n

• F: 4 = 3 + 1; 5 = 4 + 1; 6 = 5 + 1; 7 = 6 + 1 → F = n + 1

36. Como a base da pirâmide é um hekzágono regular, o raio da circunferência quê a circunscreve corresponde à medida do lado do hekzágono. Logo, a medida da aresta da base dessa pirâmide é (éli)" = 2 cm. Assim, se g é a medida do apótema da pirâmide, então:

• A(éli)" = 6 ⋅ $(início da fração dê) 2 (vezes) (g) (sobre) 2 (fim da fração)$ = 6g

• A_b = 6 ⋅ $(início de linha) (início da fração dê) 2 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (fim de linha)$ = $6 (início da raíz quadrada dê) 3 (fim da raíz)$

Como A_t = 6(15 + $(início da raíz quadrada dê) 3 (fim da raíz)$ ) cm², segue quê:

6g + $6 (início da raíz quadrada dê) 3 (fim da raíz)$ = 6(15 + $(início da raíz quadrada dê) 3 (fim da raíz)$ ) ⇒ g + $(início da raíz quadrada dê) 3 (fim da raíz)$ = 15 + $(início da raíz quadrada dê) 3 (fim da raíz)$ ⇒ g = 15 → 15 cm

37. Se x é a medida, em cm, da aresta da peça cúbica, sua área total é 6x², logo:

6x² = 13.824 ⇒ x² = 2.304 ⇒ $(início de linha) { (início de linha) (x) (igual há) 48 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (x) (igual há) (menos) 48 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim, em relação à pirâmide quê representa uma das peças, temos as seguintes medidas:

• aresta da base: (éli)" = $(início da fração dê) 48 (sobre) 2 (fim da fração)$ = 24 → 24 cm

• apótema da base: m = $(início da fração dê) 24 (sobre) 2 (fim da fração)$ = 12 → 12 cm

• apótema da pirâmide: g² = 12² + 40² ⇒ g² = 1.744 ⇒ $(início de linha) { (início de linha) (g) (igual há) 4 (início da raíz quadrada dê) 109 (fim da raíz) (implica em) 4 (início da raíz quadrada dê) 109 (fim da raíz) (cm) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) 4 (início da raíz quadrada dê) 109 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

• área lateral: A(éli)" = 4 ⋅ $(início da fração dê) 24 (vezes) 4 (início da raíz quadrada dê) 109 (fim da raíz) (sobre) 2 (fim da fração)$ = $192 (início da raíz quadrada dê) 109 (fim da raíz)$ → $192 (início da raíz quadrada dê) 109 (fim da raíz)$ cm²

• área da base: A_b = 24² = 576 → 576 cm²

Segue quê a área total da superfícíe da estrutura ôbitída é:

$(início de linha) (dado quê) 13.824 (considerando quê) (início de linha) (Area total) (fim de linha)(início de linha) (da peça) (fim de linha)(início de linha) (cübica) (fim de linha) (fim de linha)$ + $(início de linha) (dado quê) 192 (início da raíz quadrada dê) 109 (fim da raíz) (considerando quê) (início de linha) (Área lateral) (fim de linha) [(Ê)] (início de linha) (da pirâmide) (fim de linha) (fim de linha)$ − $(início de linha) (dado quê) 576 (considerando quê) (início de linha) (Área da) (fim de linha)(início de linha) (base) (fim de linha)(início de linha) (da pirâmide) (fim de linha) (fim de linha)$ =

= 13.248 + $192 (início da raíz quadrada dê) 109 (fim da raíz)$ → (13.248 + $192 (início da raíz quadrada dê) 109 (fim da raíz)$ ) cm² ou aproximadamente 15.252,54 cm²

38. a) • Área de cada face triangular:

Seja g a altura das faces triangulares. Então:

g² + ( $(início da fração dê) 8 (sobre) 2 (fim da fração)$ )² = ( $(início de linha) (início da raíz quadrada dê) 241 (fim da raíz) (fim de linha)$ )² ⇒ g² = 225 ⇒ $(início de linha) { (início de linha) (g) (igual há) 15 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) 15 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Logo, a área de cada face triangular é: $(início da fração dê) 8 (vezes) 15 (sobre) 2 (fim da fração)$ = 60 → 60 cm²

• Área da face quadrangular: 8² = 64 → 64 cm²

• Área da aba maior: $(início de linha) (início da fração dê) (abre parenteses) (início da raíz quadrada dê) 241 (fim da raíz) + 13 (fécha parenteses) (vezes) 1 (sobre) 2 (fim da fração) (fim de linha)$ ≃ 14,26 → aproximadamente 14,26 cm²

• Área da aba menor: $(início de linha) (início da fração dê) (abre parenteses) 8 + 6 (fécha parenteses) (vezes) 1 (sobre) 2 (fim da fração) (fim de linha)$ = 7 → 7 cm²

Portanto, a área aproximada de papel a sêr utilizado na embalagem é:

4 ⋅ 60 + 64 + 14,26 + 3 ⋅ 7 = 339,26 → 339,26 cm²

b) A medida do apótema da pirâmide é g = 15 cm e a do apótema da base é m = $(início da fração dê) 8 (sobre) 2 (fim da fração)$ = 4 cm. Logo, a medida h da altura da pirâmide é dada por:

h² + 4² = 15² ⇒ h² = 209 ⇒ $(início de linha) { (início de linha) (h) (igual há) (início da raíz quadrada dê) 209 (fim da raíz) (aproximadamente igual há) 14,46 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) (início da raíz quadrada dê) 209 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, aproximadamente 14,46 cm.

39. g² = 107² + (146,5)² ⇒ g² =11.449 + 21.462,25 ⇒ g = $(início da raíz quadrada dê) 32.911,25 (fim da raíz)$ ≃ 181,41 → aproximadamente 181,41 m

40. alternativa b

A superfícíe do telhado póde sêr representada por dois pares de triângulos congruentes. Vamos calcular a altura dêêsses triângulos.

• h₁² + ( $(início da fração dê) 24 (sobre) 2 (fim da fração)$ )²= ( $(início de linha) 2 (início da raíz quadrada dê) 61 (fim da raíz) (fim de linha)$ )² ⇒ h₁² = 100 ⇒ $(início de linha) { (início de linha) [(h)] (índice) 1 (igual há) 10 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) [(h)] (índice) 1 (igual há) (menos) 10 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

• h₂² + ( $(início da fração dê) 16 (sobre) 2 (fim da fração)$ )² = ( $(início de linha) 2 (início da raíz quadrada dê) 61 (fim da raíz) (fim de linha)$ )² ⇒ h₂² = 180 ⇒ $(início de linha) { (início de linha) [(h)] (índice) 2 (igual há) 6 (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) [(h)] (índice) 2 (igual há) (menos) 6 (início da raíz quadrada dê) 5 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim, a área do telhado, em m², é:

2 ⋅ $(início da fração dê) 24 (vezes) 10 (sobre) 2 (fim da fração)$ + 2 ⋅ $(início da fração dê) 16 (vezes) 6 (início da raíz quadrada dê) 5 (fim da raíz) (sobre) 2 (fim da fração)$ = 240 + $(início de linha) 96 (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ ≃ 454,66 → 454,66 m²

Como se estima o uso de 12 telhas por m², com desperdício de 10% das telhas, temos quê a quantidade de telhas a serem compradas é dada por:

(12 ⋅ 454,66) ∶ (1 − 0,1) ≃ 6.062 → 6.062 telhas

41. Sejam g e h a altura da face triangular menor e maior, respectivamente, da pirâmide quê representa a parte superior da barraca. Então:

• g² + ( $(início da fração dê) 8 (sobre) 2 (fim da fração)$ )² = ( $3 (início da raíz quadrada dê) 5 (fim da raíz)$ )² ⇒ g² = 29 ⇒ $(início de linha) { (início de linha) (g) (igual há) (início da raíz quadrada dê) 29 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) (início da raíz quadrada dê) 29 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

• h² + ( $(início da fração dê) 10 (sobre) 2 (fim da fração)$ )² = ( $3 (início da raíz quadrada dê) 5 (fim da raíz)$ )² ⇒ h² = 20 ⇒ $(início de linha) { (início de linha) (h) (igual há) (início da raíz quadrada dê) 20 (fim da raíz) (igual há) 2 (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) (início da raíz quadrada dê) 20 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim, a área total de lona em cada barraca é, em m²:

2 ⋅ $(início da fração dê) 8 (vezes) (início da raíz quadrada dê) 29 (fim da raíz) (sobre) 2 (fim da fração)$ + 2 ⋅ $(início da fração dê) 10 (vezes) 2 (início da raíz quadrada dê) 5 (fim da raíz) (sobre) 2 (fim da fração)$ + 2 ⋅ 8 ⋅ 4 + 10 ⋅ 4 = $8 (início da raíz quadrada dê) 29 (fim da raíz)$ + $20 (início da raíz quadrada dê) 5 (fim da raíz)$ + 104 ≃ 191,8

Portanto, o custo aproximado de produção da barraca é:

4 ⋅ 191,8 = 767,2 → R$ 767,20

42. • peça A: V = $(início da fração dê) 144 (vezes) 12 (sobre) 3 (fim da fração)$ = 576 → 576 cm³

• peça B: V = $(início da fração dê) 72 (vezes) 6 (sobre) 3 (fim da fração)$ = 144 → 144 cm³

Página trezentos e setenta e nove

43. alternativa a

pôdêmos decompor o octaedro em duas pirâmides quadrangulares, cuja base comum está destacada em azul na figura a seguir.

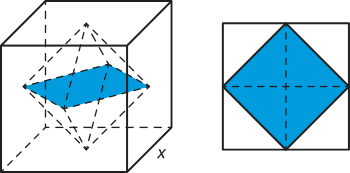
Imagem composta por dois elementos. À esquerda, há um cubo com arestas medindo x e, em seu interior, um octaedro cujos vértices estão localizados no centro de suas faces. Um plano horizontal foi destacado dentro do octaedro, formando um losango, cujos quatro vértices estão posicionados nas laterais do cubo. À direita, há uma figura plana: um quadrado com um losango inscrito, construído pela união dos pontos médios de seus lados. O losango está em destaque.

Se x é a medida da aresta do cubo, temos:

• Volume do cubo: V₁ = x³

• Volume do octaedro: V₂ = 2 ⋅ $(início de linha) (dado quê) (início da fração dê) (abre parenteses) (início da fração dê) [(x)] (sobre) 2 (fim da fração)(início da raíz quadrada dê) 2 (fim da raíz) (fécha parenteses) (elevado há) 2 (vezes) (início da fração dê) [(x)] (sobre) 2 (fim da fração) (sobre) 3 (fim da fração) (considerando quê) Volume de cada pirâmide (fim de linha)$ = 2 ⋅ $(início da fração dê) (início da fração dê) [(x)] (elevado há) 2 (sobre) 2 (fim da fração) (vezes) (início da fração dê) [(x)] (sobre) 2 (fim da fração) (sobre) 3 (fim da fração)$ = $(início da fração dê) [(x)] (elevado há) 3 (sobre) 6 (fim da fração)$ = $(início da fração dê) [(V)] (índice) 1 (sobre) 6 (fim da fração)$

Assim, o volume do objeto em formato de octaedro é $(início da fração dê) 1 (sobre) 6 (fim da fração)$ do volume da caixa cúbica, ou seja:

V₂ = $(início da fração dê) 64 (sobre) 6 (fim da fração)$ = $(início da fração dê) 32 (sobre) 3 (fim da fração)$ → $(início da fração dê) 32 (sobre) 3 (fim da fração)$ L

44. a) • A_b = 6 ⋅ $(início da fração dê) 6 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração)$ = $54 (início da raíz quadrada dê) 3 (fim da raíz)$

• A(éli)" = 6 ⋅ $(início de linha) (dado quê) (início da fração dê) 6 (vezes) 3 (início da raíz quadrada dê) 39 (fim da raíz) (sobre) 2 (fim da fração) (considerando quê) Area de cada (fim de linha)$ = $54 (início da raíz quadrada dê) 39 (fim da raíz)$

Portanto:

A_t = $54 (início da raíz quadrada dê) 3 (fim da raíz)$ + $54 (início da raíz quadrada dê) 39 (fim da raíz)$ = 54( $(início da raíz quadrada dê) 3 (fim da raíz)$ + $(início da raíz quadrada dê) 39 (fim da raíz)$ ) → 54( $(início da raíz quadrada dê) 3 (fim da raíz)$ + $(início da raíz quadrada dê) 39 (fim da raíz)$ ) cm² ou aproximadamente 430,76 cm²

b) O apótema da base corresponde à altura do triângulo equilátero de lado 6 cm, ou seja, $(início da fração dê) 6 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ cm.

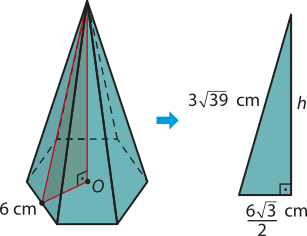
Imagem composta por duas partes. À esquerda, uma pirâmide com base hexagonal, de lados 6 centímetros, e centro da base O. Um triângulo retângulo é desenhado no interior da pirâmide, com vértices no centro O, no ponto médio de uma das arestas e no vértice superior. À direita, triângulo retângulo com hipotenusa medindo 3 raiz de 39 centímetros e com os catetos identificados por h, e por 6 raiz de 3, dividido por 2 centímetros.

Assim, a altura h da pirâmide, em cm, é dada por:

h² + ( $(início de linha) (início da fração dê) 6 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (fim de linha)$ )² = ( $3 (início da raíz quadrada dê) 39 (fim da raíz)$ )² ⇒ h² = 324 ⇒ $(início de linha) { (início de linha) (h) (igual há) 18 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) 18 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

No item a, calculamos A_b = $54 (início da raíz quadrada dê) 3 (fim da raíz)$ .

Assim, o volume da pirâmide é:

V = $(início da fração dê) 54 (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 18 (sobre) 3 (fim da fração)$ = $324 (início da raíz quadrada dê) 3 (fim da raíz)$ → $(início de linha) 324 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ cm³ ou aproximadamente 561,18 cm³

45. a) 12 ⋅ $(início da fração dê) 18 (sobre) 24 (fim da fração)$ = 9 → 9 g

b) V = $(início de linha) (início da fração dê) 1 (elevado há) 2 (vezes) 1,5 (sobre) 3 (fim da fração) (fim de linha)$ = 0,5 → 0,5 cm³

c) $(início da fração dê) 12 (sobre) 0,5 (fim da fração)$ = 24 → 24 g/cm³

46. Sejam x e y as medidas, em decimetro, das arestas da base dessa pirâmide. Como o volume da pirâmide é V = 6 dm³, temos:

$(início da fração dê) (x) (vezes) (ípsilon) (vezes) 1,5 (sobre) 3 (fim da fração)$ = 6 ⇒ xy = 12

Logo, as medidas das duas arestas, em dm, correspondem a números divisíveis por 12 cujo produto é igual a 12. Assim, as únicas possibilidades para essas medidas, sem diferenciar a ordem, são: 1 dm e 12 dm; 2 dm e 6 dm; 3 dm e 4 dm.

47. a) • modelo A:

0,03 ⋅ V = 0,03 ⋅ $(início de linha) (dado quê) 6 (vezes) (início da fração dê) 3 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 5 (considerando quê) [(h)] (fim de linha)$ = $(início de linha) 2,025 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ ≃ 3,51 → R$ 3,51

• modelo B:

0,03 ⋅ V = 0,03 ⋅ $(início de linha) (dado quê) (início da fração dê) 6 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 7 (considerando quê) [(h)] (fim de linha)$ = $(início de linha) 1,89 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ ≃ 3,27 → R$ 3,27

• modelo C:

0,03 ⋅ V = 0,03 ⋅ $(início da fração dê) (início de linha) (dado quê) 6 (vezes) (início da fração dê) 6 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (considerando quê) [(Há)] (índice) [(b)] (fim de linha) (vezes) (início de linha) (dado quê) 12 (considerando quê) [(h)] (fim de linha) (sobre) 3 (fim da fração)$ = $(início de linha) 6,48 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ ≃ 11,22 → R$ 11,22

b) • modelo A:

2,5 ⋅ 3,51 ≃ 8,78 → R$ 8,78

• modelo B:

2,5 ⋅ 3,27 ≃ 8,18 → R$ 8,18

• modelo C:

2,5 ⋅ 11,22 = 28,05 → R$ 28,05

c) O custo de produção das velas vendidas foi de:

800 ∶ 2,5 = 320 → R$ 320,00

Logo, ele lucrou:

800 − 320 = 480 → R$ 480,00

48. a) A superfícíe lateral do tronco é formada por 6 trapézios isósceles congruentes conforme a figura a seguir.

Imagem de um trapézio isósceles com altura representada por t. A base maior mede 5 centímetros, e a base menor, 4 centímetros. A aresta lateral mede x.

A medida x do lado do trapézio é dada por:

x² = 3² + (5 − 4)² ⇒ x² = 10

A altura t do trapézio é dada por:

t² + ( $(início da fração dê) 5 (menos) 4 (sobre) 2 (fim da fração)$ )² = x² ⇒ t² + $(início da fração dê) 1 (sobre) 4 (fim da fração)$ = 10 ⇒ t² = $(início da fração dê) 39 (sobre) 4 (fim da fração)$ ⇒ ${ (início de linha) (t) (igual há) (início da fração dê) (início da raíz quadrada dê) 39 (fim da raíz) (sobre) 2 (fim da fração) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (t) (igual há) (menos) (início da fração dê) (início da raíz quadrada dê) 39 (fim da raíz) (sobre) 2 (fim da fração) (abre parenteses) (não convém) (fécha parenteses) (fim de linha)$

Assim:

• A(éli)" = 6 ⋅ $(início de linha) (dado quê) (início da fração dê) (abre parenteses) 5 + 4 (fécha parenteses) (vezes) (início da fração dê) (início da raíz quadrada dê) 39 (fim da raíz) (sobre) 2 (fim da fração) (sobre) 2 (fim da fração) (considerando quê) Área de cada face lateral (fim de linha)$ = $(início da fração dê) 27 (início da raíz quadrada dê) 39 (fim da raíz) (sobre) 2 (fim da fração)$

• A_B = 6 ⋅ $(início da fração dê) 5 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração)$ = $(início da fração dê) 75 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$

• A_b = 6 ⋅ $(início da fração dê) 4 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração)$ = $24 (início da raíz quadrada dê) 3 (fim da raíz)$

Portanto:

A = $(início da fração dê) 27 (início da raíz quadrada dê) 39 (fim da raíz) (sobre) 2 (fim da fração)$ + $(início da fração dê) 75 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ + $24 (início da raíz quadrada dê) 3 (fim da raíz)$ = $(início de linha) (início da fração dê) 27 (início da raíz quadrada dê) 39 (fim da raíz) + 123 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (fim de linha)$ → ( $(início de linha) (início da fração dê) 27 (início da raíz quadrada dê) 39 (fim da raíz) + 123 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (fim de linha)$ ) cm² ou aproximadamente 190,83 cm²

b) Sendo h a altura da pirâmide menor e H a altura da pirâmide original, temos:

• $(início da fração dê) [(H)] (sobre) [(h)] (fim da fração) (igual há) (início da fração dê) 5 (sobre) 4 (fim da fração) (implica em) (início da fração dê) (h) + 3 (sobre) [(h)] (fim da fração) (igual há) (início da fração dê) 5 (sobre) 4 (fim da fração)$ ⇒ 4h + 12 = 5h ⇒ h = 12

• H = 12 + 3 = 15

Assim, o volume do tronco é:

V_T = V_P − V_p = $(início da fração dê) (início da fração dê) 75 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (vezes) 15 (sobre) 3 (fim da fração)$ − $(início da fração dê) 24 (início da raíz quadrada dê) 3 (fim da raíz) (vezes) 12 (sobre) 3 (fim da fração)$ = $(início da fração dê) (início da fração dê) 549 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (sobre) 3 (fim da fração)$ = $(início da fração dê) 183 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ → $(início da fração dê) 183 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ cm³ ou aproximadamente 158,48 cm³

49. a) A superfícíe lateral do tronco é formada por 4 trapézios isósceles congruentes.

A altura t dêêsses trapézios é dada por:

t² + ( $(início da fração dê) 16 (menos) 8 (sobre) 2 (fim da fração)$ )² = 8² ⇒ t² + 4² = 64 ⇒ t² = 48 ⇒ $(início de linha) { (início de linha) (t) (igual há) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (t) (igual há) (menos) 4 (início da raíz quadrada dê) 3 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim:

• A(éli)" = 4 ⋅ $(início de linha) (dado quê) (início da fração dê) (abre parenteses) 16 + 8 (fécha parenteses) (vezes) 4 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (considerando quê) Área de cada trapézio (fim de linha)$ = $192 (início da raíz quadrada dê) 3 (fim da raíz)$

• A_B = 16² = 256

• A_b = 8² = 64

Portanto:

A_T = $(início de linha) 192 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ + 256 + 64 = 320 + $(início de linha) 192 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ → 320 + $(início de linha) 192 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ dm² ou aproximadamente 652,55 dm²

b) Imagem de um tronco de pirâmide de base quadrada, com altura indicada por Híndice t. A base maior mede 16 decímetros de lado, e a base menor, 8 decímetros. O apótema do tronco, identificado por t, é a hipotenusa de um triângulo retângulo formado pela altura Híndice t e por uma medida horizontal identificada como x.

A medida x indicada na figura corresponde a $(início da fração dê) 16 (menos) 8 (sobre) 2 (fim da fração)$ = 4 dm e a altura t de

Página trezentos e oitenta

cada face lateral foi calculada no item a, sêndo t = $(início de linha) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ _ dm. Assim, a altura H_t do tronco é dada por:

$[(H)] (índice) [(Tê)] (elevado há) 2$ + 4² = ( $(início de linha) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$ )² ⇒ $[(H)] (índice) [(Tê)] (elevado há) 2$ = 32 ⇒ $(início de linha) { (início de linha) [(H)] (índice) [(Tê)] (igual há) 4 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) [(H)] (índice) [(Tê)] (igual há) (menos) 4 (início da raíz quadrada dê) 2 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Sendo h a altura da pirâmide menor e H a altura da pirâmide original, temos:

• $(início da fração dê) [(H)] (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 16 (sobre) 8 (fim da fração)$ ⇒ $(início da fração dê) (h) + 4 (início da raíz quadrada dê) 2 (fim da raíz) (sobre) [(h)] (fim da fração)$ = 2 ⇒ h + $(início de linha) 4 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ = 2h ⇒ h = $(início de linha) 4 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$

• H = $(início de linha) 4 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ + $(início de linha) 4 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ = $(início de linha) 8 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$

Assim, o volume do tronco é:

V_T = V_P − V_p = $(início da fração dê) 16 (elevado há) 2 (vezes) 8 (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 3 (fim da fração)$ − $(início da fração dê) 8 (elevado há) 2 (vezes) 4 (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 3 (fim da fração)$ = $(início da fração dê) 1.792 (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 3 (fim da fração)$ → $(início da fração dê) 1.792 (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 3 (fim da fração)$ dm³

ou aproximadamente 844,76 dm³

50. Elaboração do estudante. Espera-se quê os estudantes consigam relacionar a base do troféu apresentado na imagem a um tronco de pirâmide e, a partir dele, elaborem e resolvam um problema envolvendo o cálculo da área da superfícíe ou do volume do tronco de pirâmide.

51. alternativa a

Sabemos quê o volume da pirâmide (V_p) é 160 m³ e a altura (H) é 4 m. Outra pirâmide será formada ao traçar o plano a 2 m do vértice, de altura (h) 2 m e volume V_s.

Assim, temos:

$(início da fração dê) [(V)] (índice) [(s)] (sobre) [(V)] (índice) [(p)] (fim da fração)$ = ( $(início da fração dê) [(h)] (sobre) [(H)] (fim da fração)$ )³ → $(início da fração dê) [(V)] (índice) [(s)] (sobre) 160 (fim da fração)$ = ( $(início da fração dê) 2 (sobre) 4 (fim da fração)$ )³ ⇒

⇒ $(início da fração dê) [(V)] (índice) [(s)] (sobre) 160 (fim da fração)$ = ( $(início da fração dê) 2 (sobre) 4 (fim da fração)$ )³ ⇒ $(início da fração dê) [(V)] (índice) [(s)] (sobre) 160 (fim da fração)$ = $(início da fração dê) 1 (sobre) 8 (fim da fração)$ ⇒

⇒ V_s = $(início da fração dê) 160 (sobre) 8 (fim da fração)$ = 20 → 20 m³

V_T = V_p − V_s = 160 − 20 = 140 → 140 m³

52. a) A_t = 2 ⋅ $(início de linha) (dado quê) ((pi)) (vezes) 60 (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi)) (vezes) 60 (vezes) 200 (considerando quê) [(Há)] (índice) [(f)] (fim de linha)$ = 2 ⋅ 3.600(pi)" + 24.000(pi)" = 31.200(pi)" → 31.200(pi)" cm² ou aproximadamente 97.968 cm²

b) A_t = 2 ⋅ $(início de linha) (dado quê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 40 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi)) (vezes) (início da fração dê) 40 (sobre) 2 (fim da fração) (vezes) 95 (considerando quê) [(Há)] (índice) [(l)] (fim de linha)$ = 2 ⋅ 400(pi)" + 3.800(pi)" = 4.600(pi)" → 4.600(pi)" cm² ou aproximadamente 14.444 cm²

53. Seja r a medida do raio do cilindro quê representa a caixa. A área total dêêsse cilindro é:

A_t = 2 ⋅ $(início de linha) (dado quê) ((pi)) [(r)] (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi) r) (vezes) 30 (considerando quê) [(Há)] (índice) [(l)] (fim de linha)$ = 2(pi)"r² + 60(pi)"r

A medida mássima do raio corresponde ao valor de r tal quê a área total do cilindro é igual a 350(pi)" cm², ou seja:

2(pi)"r² + 60(pi)"r = 350(pi)" ⇒ r² + 30r − 175 = 0 ⇒ $(início de linha) { (início de linha) (r) (igual há) 5 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (r) (igual há) (menos) 35 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, r = 5 cm.

54. Seja r a medida, em centímetro, do raio do cilindro. Então, sua altura méde 2r cm e sua área total é:

A_t = 2 ⋅ $(início de linha) (dado quê) ((pi)) [(r)] (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi) r) (vezes) 2 [(r)] (considerando quê) [(Há)] (índice) [(l)] (fim de linha)$ = 6(pi)"r²

Como A_t = 48(pi)" cm², temos:

6(pi)"r² = 48(pi)" ⇒ r² = 8 ⇒ $(início de linha) { (início de linha) (r) (igual há) 2 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (r) (igual há) (menos) 2 (início da raíz quadrada dê) 2 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, a altura do cilindro é:

2r = 2 ⋅ $2 (início da raíz quadrada dê) 2 (fim da raíz)$ = $4 (início da raíz quadrada dê) 2 (fim da raíz)$ → $4 (início da raíz quadrada dê) 2 (fim da raíz)$ cm ou aproximadamente 5,66 cm

55. A área lateral do cilindro, em m², do qual foi ôbitída a parte da superfícíe é:

A(éli)" = 2(pi)" ⋅ 15 ⋅ 25 = 2.355

Assim, a área da cobertura é dada pela seguinte regra de três:

Ângulo (em grau)	Área da superfícíe (em m²)
360	2.355
120	x

$(início da fração dê) 360 (sobre) 120 (fim da fração)$ = $(início da fração dê) 2.355 (sobre) [(x)] (fim da fração)$ ⇒ x = 785

Como a manta térmica será instalada na parte interna da cobertura ao preêço de R$ 9,60 por métro quadrado, a quantia a sêr gasta é:

785 ⋅ 9,6 = 7.535 → R$ 7.536,00

56. a) V = (pi)" ⋅ 5² ⋅ 10 = 250(pi)" → 250(pi)" cm³ ou aproximadamente 785 cm³

b) V = (pi)" ⋅ 8² ⋅ 34 = 2.176(pi)" → 2.176(pi)" dm³ ou aproximadamente 6.832,64 dm³

57. Um cilindro equilátero com o raio da base medindo r possui altura h = 2r.

Assim, como a área total do cilindro é A_t = 216(pi)" cm², então:

2A_b + A(éli)" = 216(pi)" ⇒ 2 ⋅ (pi)"r² + 2(pi)"r ⋅ 2r = 216(pi)" ⇒ 6(pi)"r² = 216(pi)" ⇒ r² = 36 ⇒

⇒ $(início de linha) { (início de linha) (r) (igual há) 6 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (r) (igual há) (menos) 6 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, o seu volume é:

V = (pi)"r² ⋅ 2r = 2(pi)"r³ = 2(pi)" ⋅ 6³ = 432(pi)" → 432(pi)" cm³ ou aproximadamente 1.356,48 cm³

58. Vamos calcular a capacidade aproximada de cada modelo de embalagem.

I) V_I = (pi)" ⋅ ( $(início da fração dê) 6 (sobre) 2 (fim da fração)$ )² ⋅ 7,5 = 67,5(pi)" = 211,95 → 211,95 cm³

Portanto, 211,95 mL.

II) V_II = (pi)" ⋅ 3,5² ⋅ 7 = 85,75(pi)" = 269,255 → 269,255 cm³

Portanto, 269,255 mL.

III) V_III = 6 ⋅ $(início de linha) (início da fração dê) 3 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (fim de linha)$ ⋅ 5,4 = $72,9 (início da raíz quadrada dê) 3 (fim da raíz)$ ≃ 126,27 → 126,27 cm³

Portanto, 126,27 mL.

IV) V_IV = 9 ⋅ 6 ⋅ 4,5 = 243 → 243 cm³

Portanto, 243 mL.

Assim, somente o modelo IV poderá sêr utilizado, pois é o único cuja capacidade está entre 230 mL e 250 mL. A área de sua superfícíe é:

A = 2 ⋅ 9 ⋅ 6 + 2 ⋅ 9 ⋅ 4,5 + 2 ⋅ 6 ⋅ 4,5 = 243 → 243 cm²

59. V = (pi)" ⋅ 3² ⋅ 12 = 108(pi)" → 108(pi)" m³ ou aproximadamente 339,12 m³

60. a) V = (pi)" ⋅ ( $(início da fração dê) 3 (sobre) 2 (fim da fração)$ )² ⋅ 130 = 292,5(pi)" → 292,5(pi)" mm³ ou aproximadamente 918,45 mm³

b) 0,9 ⋅ 918,45 ≃ 827 → aproximadamente 827 mm³

Como 1 mL equivale a 1 cm³, o quê corresponde a 10³ mm³ = 1.000 mm³, então esse volume de tinta equivale a:

827 ∶ 1.000 = 0,827 → 0,827 mL

Ou seja, menos do quê 1 mL.

61. O volume de concreto de cada manilha, em m³, é:

(pi)" ⋅ ( $(início da fração dê) 0,4 (sobre) 2 (fim da fração)$ )² ⋅ 1,2 − (pi)" ⋅ ( $(início da fração dê) 0,24 (sobre) 2 (fim da fração)$ ₎⋅ 1,2 = 0,048(pi)" − 0,01728(pi)" = 0,03072(pi)"

Portanto, o volume total de concreto é:

100 ⋅ 0,03072(pi)" = 3,072(pi)" ≃ 9,65 → aproximadamente 9,65 m³

62. a) • cilindro I:

V_I = (pi)" ⋅ 15² ⋅ 6 = 1.350(pi)" → 1.350(pi)" cm³ ou aproximadamente 4.239 cm³

• cilindro II:

V_II = (pi)" ⋅ 6² ⋅ 15 = 540(pi)" → 540(pi)" cm³ ou aproximadamente 1.695,6 cm³

b) Vamos calcular a área total de cada cilindro, em cm².

• cilindro I:

A_I = 2 ⋅ $(início de linha) (dado quê) ((pi)) (vezes) 15 (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi)) (vezes) 15 (vezes) 6 (considerando quê) [(Há)] (índice) [(Ê)] (fim de linha)$ = 630(pi)"

• cilindro II:

A_II = 2 ⋅ $(início de linha) (dado quê) ((pi)) (vezes) 6 (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi)) (vezes) 6 (vezes) 15 (considerando quê) [(Há)] (índice) [(l)] (fim de linha)$ = 252(pi)"

Assim, a diferença é de:

630(pi)" − 252(pi)" = 378(pi)" → 378(pi)" cm² ou aproximadamente 1.186,92 cm²

63. Sejam r a medida do raio da base e h a altura dêêsse cilindro.

• Como sua área lateral é 87,92 cm², temos:

2(pi)"rh = 87,92 ⇒ rh = 14 (I)

• Como o perímetro da seção meridiana é 22 cm, temos:

2 ⋅ (2r + h) = 22 ⇒ 2r + h = 11 ⇒ h = 11 − 2r (II)

Substituindo (II) em (I), temos:

r(11 − 2r) = 14 ⇒

Página trezentos e oitenta e um

⇒ −2r² + 11r − 14 = 0 ⇒ $(início de linha) { (início de linha) (r) (igual há) 2 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (r) (igual há) 3,5 (fim de linha) (fim de linha)$

Segue quê:

• r = 2 ⇒ h = 11 − 2 ⋅ 2 ⇒ h = 7

• r = 3,5 ⇒ h = 11 − 2 ⋅ 3,5 ⇒ h = 4

Assim, há duas possibilidades: r = 2 cm e h = 7 cm; r = 3,5 cm e h = 4 cm.

a) Respostas possíveis: 2 cm ou 3,5 cm.

b) Respostas possíveis: 7 cm ou 4 cm.

c) Respostas possíveis:

• A_t = 2 ⋅ $(início de linha) (dado quê) ((pi)) (vezes) 2 (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi)) (vezes) 2 (vezes) 7 (considerando quê) [(Há)] (índice) [(f)] (fim de linha)$ = 36(pi)" → 36(pi)" cm² (aproximadamente 113,04 cm²)

• A_t = 2 ⋅ $(início de linha) (dado quê) ((pi)) (vezes) 3,5 (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 ((pi)) (vezes) 3,5 (vezes) 4 (considerando quê) [(Há)] (índice) [(l)] (fim de linha)$ = 52,5(pi)" → 52,5(pi)" cm² (aproximadamente 164,85 cm²)

d) Respostas possíveis:

• V = $(início de linha) (dado quê) ((pi)) (vezes) 2 (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 7 (considerando quê) [(h)] (fim de linha)$ = 28(pi)" → 28(pi)" cm³ (aproximadamente 87,92 cm³)

• V = $(início de linha) (dado quê) ((pi)) (vezes) 3,5 (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 4 (considerando quê) [(h)] (com barra) (fim de linha)$ = 49(pi)" → 49(pi)" cm³ (aproximadamente 153,86 cm³)

64. O sólido geométrico obtído será um cilindro com raio da base medindo 6 cm e altura 2 cm, de cujo centro foi retirado um cilindro menor, com raio da base medindo 2 cm e mesma altura. Seu volume será:

V = (pi)" ⋅ 6² ⋅ 2 − (pi)" ⋅ 2² ⋅ 2 = 64(pi)" → 64(pi)" cm³ ou aproximadamente 200,96 cm³

65. a) O volume do cilindro é igual ao volume do cubo, o qual é dado por:

V = ( $(início de linha) 3 (início da raíz) 3 (de) 2 ((pi)) (fim da raíz) (fim de linha)$ )³ = 3³ ⋅ 2(pi)" = 54(pi)" → 54(pi)" cm³ ou aproximadamente 169,56 cm³

b) Seja r a medida do raio da base do cilindro. Então:

$(início de linha) (dado quê) ((pi)) [(r)] (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ ⋅ $(início de linha) (dado quê) 2 [(r)] (considerando quê) [(h)] (fim de linha)$ = 54(pi)" ⇒ 2r³ = 54 ⇒ r³ = 27 ⇒ r = 3 → 3 cm

c) A altura do cilindro é 2 ⋅ 3 = 6 cm.

Assim:

A(éli)" = 2(pi)" ⋅ 3 ⋅ 6 = 36(pi)" → 36(pi)" cm² ou aproximadamente 113,04 cm²

66. Elaboração do estudante. Espera-se quê os estudantes estabeleçam uma capacidade para a embalagem apresentada e apresentem a nova proposta de embalagem e suas respectivas medidas.

67. a) • Área da base:

A_b = (pi)" ⋅ ( $(início da fração dê) 30 (sobre) 2 (fim da fração)$ )² = 225(pi)" → 225(pi)" cm² ou aproximadamente 706,5 cm²

• Área lateral:

A medida g da geratriz é dada por:

g² = ( $(início da fração dê) 30 (sobre) 2 (fim da fração)$ )² + 36² ⇒ g² = 1.521 ⇒ $(início de linha) { (início de linha) (g) (igual há) 39 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) 39 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim:

A(éli)" = (pi)" ⋅ $(início da fração dê) 30 (sobre) 2 (fim da fração)$ ⋅ 39 = 585(pi)" → 585(pi)" cm² ou aproximadamente 1.836,9 cm²

• Área total:

A_t = 225(pi)" + 585(pi)" = 810(pi)" → 810(pi)" cm² ou aproximadamente 2.543,4 cm²

b) • Área da base:

A_b = (pi)" ⋅ 6² = 36(pi)" → 36(pi)" m² ou aproximadamente 113,04 m²

• Área lateral:

A medida g da geratriz é dada por:

g² = 6² + 8² ⇒ g² = 100 ⇒ $(início de linha) { (início de linha) (g) (igual há) 10 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) 10 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim:

A(éli)" = (pi)" ⋅ 6 ⋅ 10 = 60(pi)" → 60(pi)" m² ou aproximadamente 188,4 m²

• Área total:

A_t = 36(pi)" + 60(pi)" = 96(pi)" → 96(pi)" m² ou aproximadamente 301,44 m²

68. a) Seja h a altura do cone. Então:

h² + 15² = ( $(início de linha) 15 (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ )² ⇒ h² = 900 ⇒ $(início de linha) { (início de linha) (h) (igual há) 30 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) 30 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, a altura é 30 cm.

b) A_b = (pi)" ⋅ 15² = 225(pi)" → 225(pi)" cm² ou aproximadamente 706,5 cm²

c) A(éli)" = (pi)" ⋅ 15 ⋅ $15 (início da raíz quadrada dê) 5 (fim da raíz)$ = $225 ((pi)) (início da raíz quadrada dê) 5 (fim da raíz)$ → $(início de linha) 225 ((pi)) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ cm² ou aproximadamente 1.579,78 cm²

d) A_t = 225(pi)" + $(início de linha) 225 ((pi)) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ = 225(pi)"(1 + $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ ) → 225(pi)"(1 + $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ ) cm² ou aproximadamente 2.286,28 cm²

69. A área total de cada parte corresponde à mêtáde da área total do cone original somada com a área da seção meridiana.

Temos:

• Área total do cone original:

A medida g da geratriz é dada por:

g² = 18² + 24² ⇒ g² = 900 ⇒ $(início de linha) { (início de linha) (g) (igual há) 30 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) 30 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim:

A_t = (pi)" ⋅ 18 ⋅ (18 + 30) = 864(pi)" → 864(pi)" cm²

• Área da seção meridiana:

A_m = $(início de linha) (início da fração dê) (abre parenteses) 2 (vezes) 18 (fécha parenteses) (vezes) 24 (sobre) 2 (fim da fração) (fim de linha)$ = 432 → 432 cm²

Assim, a área total de cada parte é:

$(início da fração dê) [(Há)] (índice) [(Tê)] (sobre) 2 (fim da fração)$ + A_m = $(início da fração dê) 864 ((pi)) (sobre) 2 (fim da fração)$ + 432 = 432((pi)" + 1) → 432((pi)" + 1) cm² ou aproximadamente 1.788,48 cm²

70. a) A geratriz possui a mesma medida do diâmetro, ou seja, 14 cm.

b) A(éli)" = (pi)" ⋅ ( $(início da fração dê) 14 (sobre) 2 (fim da fração)$ ) ⋅ 14 = 98(pi)" → 98(pi)" cm² ou aproximadamente 307,72 cm²

c) A_t = $(início de linha) (dado quê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 14 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 98 ((pi)) (considerando quê) [(Há)] (índice) [(Ê)] (fim de linha)$ = 147(pi)" → 147(pi)" cm² ou aproximadamente 461,58 cm²

d) A seção meridiana é um triângulo equilátero de lado 14 cm. Logo, sua área é:

A_m = $(início da fração dê) 14 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração)$ = $49 (início da raíz quadrada dê) 3 (fim da raíz)$ → $49 (início da raíz quadrada dê) 3 (fim da raíz)$ cm² ou aproximadamente 84,77 cm²

e) • Comprimento da circunferência de raio 14 cm:

2 ⋅ (pi)" ⋅ 14 = 28(pi)", ou seja, 28(pi)" cm

• Comprimento do arco de circunferência de raio 14 cm determinado pelo ângulo central de medida (alfa)":

2 ⋅ (pi)" ⋅ ( $(início da fração dê) 14 (sobre) 2 (fim da fração)$ ) = 14(pi)", ou seja, 14(pi)" cm)

Assim, temos a seguinte regra de três:

Medida do ângulo central (em grau)	Comprimento (em cm)
360	28(pi)"
(alfa)"	14(pi)"

$(início da fração dê) 360 (sobre) ((alfa)) (fim da fração)$ = $(início da fração dê) 28 ((pi)) (sobre) 14 ((pi)) (fim da fração)$ ⇒ $(início da fração dê) 360 (sobre) ((alfa)) (fim da fração)$ = 2 ⇒ (alfa)" = 180

Portanto, (alfa)" = 180°.

71. Ao rotacionar o triângulo em torno de um eixo quê contém qualquer um de seus catetos, obtém-se um cone cuja medida g da geratriz é dada por:

g² = 6² + 8² ⇒ g² = 100 ⇒ g = 10 → 10 cm

Vamos calcular a área em cada caso.

• Em torno do maior cateto:

A_t = (pi)" ⋅ 6 ⋅ (6 + 10) = 96(pi)" → 96(pi)" cm² ou aproximadamente 301,44 cm²

• Em torno do menor cateto:

A_t = (pi)" ⋅ 8 ⋅ (8 + 10) = 144(pi)" → 144(pi)" cm² ou aproximadamente 452,16 cm²

72. a) A quantidade de metal necessária para produzir cada coador corresponde à área lateral do cone quê o representa.

Vamos calcular essa área, em cm², para cada modelo.

• modelo A:

g² = ( $(início da fração dê) 12 (sobre) 2 (fim da fração)$ )² + 10² ⇒ g² = 136 ⇒ g = $(início de linha) 2 (início da raíz quadrada dê) 34 (fim da raíz) (fim de linha)$

A(éli)" = (pi)" ⋅ $(início da fração dê) 12 (sobre) 2 (fim da fração)$ ⋅ $2 (início da raíz quadrada dê) 34 (fim da raíz)$ = $12 ((pi)) (início da raíz quadrada dê) 34 (fim da raíz)$ ≃ 219,71

• modelo B:

g² = ( $(início da fração dê) 16 (sobre) 2 (fim da fração)$ )² + 13² ⇒ g² = 233 ⇒ g = $(início de linha) (início da raíz quadrada dê) 233 (fim da raíz) (fim de linha)$

A(éli)" = (pi)" ⋅ $(início da fração dê) 16 (sobre) 2 (fim da fração)$ ⋅ $(início da raíz quadrada dê) 233 (fim da raíz)$ = $8 ((pi)) (início da raíz quadrada dê) 233 (fim da raíz)$ ≃ 383,44

• modelo C:

g² = ( $(início da fração dê) 18 (sobre) 2 (fim da fração)$ )² + 15² ⇒ g² = 306 ⇒ g = $(início de linha) (início da raíz quadrada dê) 306 (fim da raíz) (fim de linha)$

A(éli)" = (pi)" ⋅ $(início da fração dê) 18 (sobre) 2 (fim da fração)$ ⋅ $(início da raíz quadrada dê) 306 (fim da raíz)$ = $9 ((pi)) (início da raíz quadrada dê) 306 (fim da raíz)$ ≃ 494,35

Agora, vamos calcular a quantidade aproximada de metal necessária para produzir os coadores de cada alternativa.

Página trezentos e oitenta e dois

I: 2 ⋅ 219,71 + 3 ⋅ 383,44 = 1.589,74 → 1.589,74 cm²

II: 2 ⋅ 219,71 + 494,35 = 933,77 → 933,77 cm²

III: 383,44 + 494,35 = 877,79 → 877,79 cm²

IV: 219,71 + 383,44 + 494,35 = 1.097,5 → 1.097,5 cm²

Portanto, a única alternativa correta é a II.

b) Resposta pessoal. As respostas dependem das experiências dos estudantes.

c) Pesquisa e elaboração dos estudantes. Espera-se quê eles se conscientizem da importânssia do descarte correto do óleo de cuzinha, bem como prestem serviço à população e comunidade escolar informando sobre os pontos de côléta dêêsse tipo de produto na região em quê moram.

73. a) V = $(início de linha) (início da fração dê) ((pi)) (vezes) 9 (elevado há) 2 (vezes) 12 (sobre) 3 (fim da fração) (fim de linha)$ = 324(pi)" → 324(pi)" cm³ ou aproximadamente 1.017,36 cm³

b) V = $(início de linha) (início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 80 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 96 (sobre) 3 (fim da fração) (fim de linha)$ = 51.200(pi)" → 51.200(pi)" m³ ou aproximadamente 160.768 m³

74. V = $(início de linha) (início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 6 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 11 (sobre) 3 (fim da fração) (fim de linha)$ = 33(pi)" → 33(pi)" cm³ ou aproximadamente 103,62 cm³

75. a) h² + 12² = 20² ⇒ h² = 256 ⇒ $(início de linha) { (início de linha) (h) (igual há) 16 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) 16 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, 16 m.

b) V = $(início de linha) (início da fração dê) ((pi)) (vezes) 12 (elevado há) 2 (vezes) 16 (sobre) 3 (fim da fração) (fim de linha)$ = 768(pi)" → 768(pi)" m³ ou aproximadamente 2.411,52 m³

76. As medidas do raio da base e da geratriz são, respectivamente, r = 13 dm e g = 2 ⋅ 13 = 26 dm, logo, a altura h, em dm, é dada por:

h² + 13² = 26² ⇒ h² = 507 ⇒ $(início de linha) { (início de linha) (h) (igual há) 13 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) 13 (início da raíz quadrada dê) 13 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim:

V = $(início da fração dê) ((pi)) (vezes) 13 (elevado há) 2 (vezes) 13 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração)$ = $(início da fração dê) 2.197 ((pi)) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração)$ → $(início de linha) (início da fração dê) 2.197 ((pi)) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração) (fim de linha)$ dm³ ou aproximadamente 3.982,9 dm³

77. V = $(início da fração dê) ((pi)) [(r)] (elevado há) 2 (vezes) (h) (sobre) 3 (fim da fração)$ ⇒ $(início da fração dê) 81 (sobre) 2 (fim da fração) ((pi))$ = $(início da fração dê) ((pi)) [(r)] (elevado há) 2 (vezes) 6 (sobre) 3 (fim da fração)$ ⇒ 12(pi)"r² = 243(pi)" ⇒ r² = $(início da fração dê) 243 (sobre) 12 (fim da fração)$ =

= $(início da fração dê) 81 (sobre) 4 (fim da fração)$ ⇒ ${ (início de linha) (r) (igual há) (início da fração dê) 9 (sobre) 2 (fim da fração) (igual há) 4,5 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (r) (igual há) (menos) (início da fração dê) 9 (sobre) 2 (fim da fração) (abre parenteses) (não convém) (fécha parenteses) (fim de linha)$

Portanto, a medida é 4,5 cm.

78. Resposta possível: Taça com 12 cm de diâmetro da base e 8 cm de altura na região interna de formato de cone.

79. • Volume do cilindro:

(pi)" ⋅ 14² ⋅ 9 = 1.764(pi)" → 1.764(pi)" cm³

• Volume do cone: $(início de linha) (início da fração dê) ((pi)) (vezes) 6 (elevado há) 2 (vezes) 9 (sobre) 3 (fim da fração) (fim de linha)$ = 108(pi)" → 108(pi)" cm³

Assim, o volume de argila é dado pela diferença:

V = 1.764(pi)" − 108(pi)" = 1.656(pi)" → 1.656(pi)" cm³ ou aproximadamente 5.199,84 cm³

80. • Volume do cilindro: (pi)" ⋅ ( $(início da fração dê) 1 (sobre) 2 (fim da fração)$ )² ⋅ 1,5 = 0,375(pi)" → 0,375(pi)" m³

• Volume do cone: $(início de linha) (início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 1 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 0,24 (sobre) 3 (fim da fração) (fim de linha)$ = 0,02(pi)" → 0,02(pi)" m³

Como 1 m³ corresponde a 1.000 L, a capacidade total do tanque é:

1.000 ⋅ (0,375(pi)" + 0,02(pi)") = 395(pi)" ≃ 1.240,3 → aproximadamente 1.240,3 L

Os cinco geradores consomem, juntos, 5 ⋅ 31 = 155 litros de óleo dízel por hora. Assim, a quantidade de horas quê eles podem funcionar simultaneamente é:

1.240,3 ∶ 155 ≃ 8 → 8 h

81. a) sen 60° = $(início da fração dê) [(h)] (sobre) [(Óh)] [(V)] (fim da fração)$ ⇒ $(início da fração dê) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ = $(início da fração dê) [(h)] (sobre) 9 (fim da fração)$ ⇒ h = $(início da fração dê) 9 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ → $(início da fração dê) 9 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração)$ cm ou aproximadamente 7,79 cm

b) V = $(início da fração dê) ((pi)) (vezes) 3 (elevado há) 2 (vezes) (início da fração dê) 9 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 2 (fim da fração) (sobre) 3 (fim da fração)$ = $(início da fração dê) 27 (início da raíz quadrada dê) 3 (fim da raíz) ((pi)) (sobre) 2 (fim da fração)$ → $(início de linha) (início da fração dê) 27 (início da raíz quadrada dê) 3 (fim da raíz) ((pi)) (sobre) 2 (fim da fração) (fim de linha)$ cm³ ou aproximadamente 73,42 cm³

82. Imagem de um triângulo retângulo A B C, com a hipotenusa A C apoiada sobre uma reta horizontal. Os lados A B e B C medem, respectivamente, 7,5 metros e 10 metros. A altura, identificada por h, vai do vértice B até a base A C, dividindo-a em dois segmentos: m, do vértice A até o ponto onde a altura toca a base; e n, desse ponto até o vértice C.

O sólido de revolução obtído póde sêr decomposto em dois cones quê possuem a medida do raio da base igual à altura h do triângulo e cujas alturas são, respectivamente, m e n, conforme a figura anterior. Sabendo quê as medidas são positivas, temos:

• AC² = 7,5² + 10² ⇒ AC² = 156,25 ⇒ AC = 12,5 → 12,5 m

• $(início da fração dê) 10 (sobre) [(h)] (fim da fração)$ = $(início da fração dê) [(Há)] [(C)] (sobre) 7,5 (fim da fração)$ ⇒ $(início da fração dê) 10 (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 12,5 (sobre) 7,5 (fim da fração)$ ⇒ h = 6 → 6 m

• n² + h² = 10² ⇒ n² + 6² = 10² ⇒ n² = 64 ⇒ n = 8 → 8 m

• m + n = AC ⇒ m + 8 = 12,5 ⇒ m = 4,5 → 4,5 m

Assim, o volume do sólido é:

V = $(início da fração dê) ((pi)) (vezes) 6 (elevado há) 2 (vezes) 4,5 (sobre) 3 (fim da fração)$ + $(início da fração dê) ((pi)) (vezes) 6 (elevado há) 2 (vezes) 8 (sobre) 3 (fim da fração)$ = 54(pi)" + 96(pi)" = 150(pi)" → 150(pi)" m³ ou aproximadamente 471 m³

83. a) A embalagem tem o formato de um cone cuja medida do raio da base é r = 4,8 ∶ 2 = 2,4 cm e cuja geratriz méde g = 7,2 cm. Logo, a área da superfícíe é:

A_t = (pi)" ⋅ 2,4 ⋅ (2,4 + 7,2) = 23,04(pi)" → 23,04(pi)" cm² ou aproximadamente 72,35 cm²

b) A altura h da embalagem, em cm, é dada por:

h² + 2,4² = 7,2² ⇒ h² = 46,08 ⇒ $(início de linha) { (início de linha) (h) (igual há) 4,8 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) 4,8 (início da raíz quadrada dê) 2 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim:

V = $(início de linha) (início da fração dê) ((pi)) (vezes) 2,4 (elevado há) 2 (vezes) 4,8 (início da raíz quadrada dê) 2 (fim da raíz) (sobre) 3 (fim da fração) (fim de linha)$ ≃ 13,03(pi)" → 13,03(pi)" cm³

Portanto, a capacidade aproximada da embalagem é de 13,03(pi)" mL ou 40,91 mL.

84. a) O volume do cone reto é:

V = $(início de linha) (início da fração dê) ((pi)) (vezes) 5 (elevado há) 2 (vezes) 15 (sobre) 3 (fim da fração) (fim de linha)$ = 125(pi)" → 125(pi)" cm³

Logo, se h é a altura do nível da á gua no póte, então:

(pi)" ⋅ 6² ⋅ h = 125(pi)" ⇒ h = $(início da fração dê) 125 (sobre) 36 (fim da fração)$ → $(início da fração dê) 125 (sobre) 36 (fim da fração)$ cm ou aproximadamente 3,47 cm

b) V = (pi)" ⋅ 6² ⋅ 8 = 288(pi)" → 288(pi)" cm³

Portanto, 288(pi)" mL ou aproximadamente 904,32 mL.

c) A á gua ocupará 125(pi)" cm³ do total de 288(pi)" cm³ do póte. Logo, o porcentual é:

$(início da fração dê) 125 ((pi)) (sobre) 288 ((pi)) (fim da fração)$ ≃ 0,434 → aproximadamente 43,4%

85. Um cone equilátero com raio da base medindo r possui geratriz medindo g = 2r e altura h dada por:

h² + r² = (2r)² ⇒ h² = 3r² ⇒ $(início de linha) { (início de linha) (h) (igual há) (r) (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (h) (igual há) (menos) [(r)] (início da raíz quadrada dê) 3 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Assim, seu volume é:

V_c = $(início da fração dê) ((pi)) [(r)] (elevado há) 2 (vezes) (r) (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração)$ = $(início da fração dê) ((pi)) [(r)] (elevado há) 3 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração)$

O volume do paralelepípedo é:

V_p = $6 (início da raíz quadrada dê) 3 (fim da raíz)$ ⋅ 8 ⋅ 12(pi)" = $576 ((pi)) (início da raíz quadrada dê) 3 (fim da raíz)$

Logo, para V_c = V_p, temos:

$(início da fração dê) ((pi)) [(r)] (elevado há) 3 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração)$ = $576 ((pi)) (início da raíz quadrada dê) 3 (fim da raíz)$ ⇒ r³ = 1.728 ⇒ r³ = 2⁶ ⋅ 3³ ⇒ r = 2² ⋅ 3 = 12 → 12 cm

86. Considere o cone do qual se obtém o tronco de cone quê representa o lustre. Se h é a altura, em cm, do cone menor removido do cone original, então:

$(início da fração dê) 30 (sobre) 12 (fim da fração)$ = $(início da fração dê) (h) + 30 (sobre) [(h)] (fim da fração)$ ⇒ 30h = 12h + 360 ⇒

Página trezentos e oitenta e três

⇒ 18h = 360 ⇒ h = 20

Assim, as medidas g e G das geratrizes dos cones menor e original, respectivamente, são dadas por:

• g² =( $(início da fração dê) 12 (sobre) 2 (fim da fração)$ )² + 20² ⇒ g² = 436 ⇒ $(início de linha) { (início de linha) (g) (igual há) 2 (início da raíz quadrada dê) 109 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (g) (igual há) (menos) 2 (início da raíz quadrada dê) 109 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

• $(início da fração dê) 30 (sobre) 12 (fim da fração)$ = $(início da fração dê) [(G)] (sobre) 2 (início da raíz quadrada dê) 109 (fim da raíz) (fim da fração)$ ⇒ G = $5 (início da raíz quadrada dê) 109 (fim da raíz)$

A área da superfícíe externa do lustre corresponde à área lateral do tronco, a qual é igual a:

A(éli)" = (pi)" ⋅ $(início da fração dê) 30 (sobre) 2 (fim da fração)$ ⋅ $5 (início da raíz quadrada dê) 109 (fim da raíz)$ − (pi)" ⋅ $(início da fração dê) 12 (sobre) 2 (fim da fração)$ ⋅ $2 (início da raíz quadrada dê) 109 (fim da raíz)$ = $63 ((pi)) (início da raíz quadrada dê) 109 (fim da raíz)$ ≃ 2.065 → aproximadamente 2.065 cm²

87. a) Vamos calcular a capacidade de cada modelo de copo considerando quê o tronco de cone quê o representa foi obtído a partir de um cone maior de altura H removendo-se um cone menor de altura h.

• Modelo A:

$(início da fração dê) [(H)] (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 12 (sobre) 8 (fim da fração)$ ⇒ $(início da fração dê) (h) + 6,28 (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 3 (sobre) 2 (fim da fração)$ ⇒ 2h + 12,56 = 3h ⇒ h = 12,56

H = 12,56 + 6,28 = 18,84

Assim, o volume do tronco, em cm³, é:

V_T = V_C − V_c = $(início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 12 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 18,84 (sobre) 3 (fim da fração)$ − $(início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 8 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 12,56 (sobre) 3 (fim da fração)$ = $(início da fração dê) 477,28 ((pi)) (sobre) 3 (fim da fração)$ ≃ 500

Logo, o modelo A tem capacidade para 500 mL.

• Modelo B:

$(início da fração dê) [(H)] (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 7,2 (sobre) 4,8 (fim da fração)$ ⇒ $(início da fração dê) (h) + 7 (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 3 (sobre) 2 (fim da fração)$ ⇒ 2h + 14 = 3h ⇒ h = 14

H = 14 + 7 = 21

Assim, o volume do tronco, em cm³, é:

V_T = V_C − V_c = $(início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 7,2 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 21 (sobre) 3 (fim da fração)$ − $(início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 4,8 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 14 (sobre) 3 (fim da fração)$ = $(início da fração dê) 191,52 ((pi)) (sobre) 3 (fim da fração)$ ≃ 200

Logo, o modelo B tem capacidade para 200 mL.

De acôr-do com a tabéla, os modelos A e B devem ter, respectivamente, massa mínima de 6,3 g e 2,2 g. Portanto, o único quê não atende às especificações é o modelo B.

b) Resposta pessoal. Espera-se quê os estudantes consigam avaliar o modelo de copo escolhido utilizando, para isso, argumentos baseados em conhecimentos matemáticos. É importante considerar, nos cálculos realizados, possíveis imprecisões de medição.

88. a) • volume: V = $(início de linha) (início da fração dê) 4 ((pi)) (vezes) 6 (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ = 288(pi)" = 904,32 → 904,32 dm³

• área da superfícíe: A = 4(pi)" ⋅ 6² = 144(pi)" = 452,16 → 452,16 dm²

b) • volume: V = $(início de linha) (início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 30 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ = 4.500(pi)" = 14.130 → 14.130 mm³

• área da superfícíe: A = 4(pi)" ⋅ ( $(início da fração dê) 30 (sobre) 2 (fim da fração)$ )² = 900(pi)" = 2.826 → 2.826 mm²

c) A medida r do raio da esféra, em cm, é dada por:

2(pi)"r = 28,26 ⇒ r = $(início da fração dê) 28,26 (sobre) 6,28 (fim da fração)$ = $(início da fração dê) 9 (sobre) 2 (fim da fração)$

Assim:

• volume: V = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 9 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 243 ((pi)) (sobre) 2 (fim da fração)$ = 381,51 → 381,51 cm³

• área da superfícíe: A = 4(pi)" ⋅ ( $(início da fração dê) 9 (sobre) 2 (fim da fração)$ )² = 81(pi)" = 254,34 → 254,34 cm²

89. • O volume do hemisfério corresponde à mêtáde do volume da esféra correspondente, ou seja:

V = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⋅ $(início da fração dê) 4 ((pi)) (vezes) 9 (elevado há) 3 (sobre) 3 (fim da fração)$ = 486(pi)" = 1.526,04 → 1.526,04 cm³

• A área da superfícíe do hemisfério corresponde à soma da mêtáde da área da superfícíe da esféra com a área do círculo delimitado pelo equador, ou seja:

A = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⋅ 4(pi)" ⋅ 9² + (pi)" ⋅ 9² = 243(pi)" = 763,02 → 763,02 cm²

90. Seja r a medida do raio da base do cone. Então, o volume do cone e o da esféra são, respectivamente:

• V_c = $(início da fração dê) ((pi)) [(r)] (elevado há) 2 (vezes) 25 (sobre) 3 (fim da fração)$ = $(início da fração dê) 25 (sobre) 3 (fim da fração) ((pi)) [(r)] (elevado há) 2$

• V_e = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 10 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 500 (sobre) 3 (fim da fração) ((pi))$

Assim, para V_c = V_e, temos:

$(início da fração dê) 25 (sobre) 3 (fim da fração) ((pi)) [(r)] (elevado há) 2$ = $(início da fração dê) 500 (sobre) 3 (fim da fração) ((pi))$ ⇒ r² = 20 ⇒ $(início de linha) { (início de linha) (r) (igual há) 2 (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (r) (igual há) (menos) 2 (início da raíz quadrada dê) 5 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, o raio da base méde $2 (início da raíz quadrada dê) 5 (fim da raíz)$ cm ou aproximadamente 4,47 cm.

91. V = $(início de linha) (início da fração dê) 4 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ ⇒ 2.304(pi)" = $(início de linha) (início da fração dê) 4 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ ⇒ r³ = 1.728 ⇒ r³ = 2⁶ ⋅ 3³ ⇒ r = 2² ⋅ 3 = 12

Portanto, o raio da esféra méde 12 dm.

92. Inicialmente, vamos determinar a medida r do raio da esféra, em métro. Temos:

A = 4(pi)"r² ⇒ 192(pi)" = 4(pi)"r² ⇒ r² = 48 ⇒ $(início de linha) { (início de linha) (r) (igual há) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (r) (igual há) (menos) 4 (início da raíz quadrada dê) 3 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

a) comprimento do equador:

2(pi)" ⋅ $4 (início da raíz quadrada dê) 3 (fim da raíz)$ = $8 (início da raíz quadrada dê) 3 (fim da raíz) ((pi))$ → $8 (início da raíz quadrada dê) 3 (fim da raíz) ((pi))$ m ou aproximadamente 43,51 m

b) volume:

V = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) 4 (início da raíz quadrada dê) 3 (fim da raíz) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 4 ((pi)) (vezes) 192 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 3 (fim da fração)$ = $256 (início da raíz quadrada dê) 3 (fim da raíz) ((pi))$ → $256 (início da raíz quadrada dê) 3 (fim da raíz) ((pi))$ m³ ou aproximadamente 1.392,29 m³

93. alternativa a

• volume anterior:

V₁ = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 38 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 4 ((pi)) (vezes) 19 (elevado há) 3 (sobre) 3 (fim da fração)$

• volume após as modificações:

V₂ = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 40 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 4 ((pi)) (vezes) 20 (elevado há) 3 (sobre) 3 (fim da fração)$

Página trezentos e oitenta e quatro

Assim, o aumento, em porcentagem, do volume da bola é dado por:

$(início da fração dê) [(V)] (índice) 2 (menos) [(V)] (índice) 1 (sobre) [(V)] (índice) 1 (fim da fração)$ = $(início da fração dê) (início da fração dê) 4 ((pi)) (sobre) 3 (fim da fração) (vezes) (abre parenteses) 20 (elevado há) 3 (menos) 19 (elevado há) 3 (fécha parenteses) (sobre) (início da fração dê) 4 ((pi)) (sobre) 3 (fim da fração) (vezes) 19 (elevado há) 3 (fim da fração)$ = $(início da fração dê) 20 (elevado há) 3 (menos) 19 (elevado há) 3 (sobre) 19 (elevado há) 3 (fim da fração)$ ≃ 0,17 → aproximadamente 17%

94. a) • volume mínimo:

V_mín = $(início de linha) (início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 4,5 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 9 (sobre) 4 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 4 ((pi)) (vezes) (início da fração dê) 729 (sobre) 64 (fim da fração) (sobre) 3 (fim da fração)$ = $(início da fração dê) 243 (sobre) 16 (fim da fração) ((pi))$ → $(início da fração dê) 243 (sobre) 16 (fim da fração) ((pi))$ cm³

• volume mássimo:

V_máx = $(início de linha) (início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 30 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ = $(início da fração dê) 4 ((pi)) (vezes) 3.375 (sobre) 3 (fim da fração)$ = 4.500(pi)" → 4.500(pi)" cm³

Assim, a diferença é:

V_máx − V_mín = 4.500(pi)" − $(início da fração dê) 243 (sobre) 16 (fim da fração)$ (pi)" ≃ 14.082,31 → aproximadamente 14.082,31 cm³

b) 7,85 ⋅ V_mín = 7,85 ⋅ $(início da fração dê) 243 (sobre) 16 (fim da fração)$ (pi)" ≃ 374,36 → aproximadamente 374,36 g

95. A área da superfícíe da tampa corresponde à mêtáde da área da superfícíe da esféra de 4 m de diâmetro, ou seja:

A = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⋅ 4(pi)" ⋅ ( $(início da fração dê) 4 (sobre) 2 (fim da fração)$ )² = 8(pi)" ≃ 25,12

Logo, o pedreiro irá cobrar:

25,12 ⋅ 32 = 803,84 → R$ 803,84

96. Seja a a medida da aresta dêêsse cubo, em cm, a qual corresponde à medida do diâmetro da esféra. A medida d da diagonal do cubo é dada por

d = $(início de linha) (início da raíz quadrada dê) [(Há)] (elevado há) 2 + [(Há)] (elevado há) 2 + [(Há)] (elevado há) 2 (fim da raíz) (fim de linha)$ . Logo, como a > 0, temos:

$21 (início da raíz quadrada dê) 3 (fim da raíz)$ = $(início da raíz quadrada dê) 3 [(Há)] (elevado há) 2 (fim da raíz)$ ⇒ $21 (início da raíz quadrada dê) 3 (fim da raíz)$ = $[(Há)] (início da raíz quadrada dê) 3 (fim da raíz)$ ⇒ a = 21

Assim, o volume da esféra é:

V = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 21 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 4 ((pi)) (vezes) (início da fração dê) 9.261 (sobre) 8 (fim da fração) (sobre) 3 (fim da fração)$ ) = $(início da fração dê) 3.087 (sobre) 2 (fim da fração) (pi)$ = 4.846,59 → 4.846,59 cm³

97. a)

Ângulo (em grau)	Área do fuso (em m²)
360	4(pi)"r²
(alfa)"	A_f

$(início da fração dê) 360 (sobre) ((alfa)) (fim da fração)$ = $(início da fração dê) 4 ((pi)) [(r)] (elevado há) 2 (sobre) [(Há)] (índice) [(f)] (fim da fração)$ ⇒ 360 A_f = 4(pi)"r² (alfa)" ⇒ A_f = $(início de linha) (início da fração dê) ((pi)) [(r)] (elevado há) 2 ((alfa)) (sobre) 90 (fim da fração) (fim de linha)$

b) A_f = $(início de linha) (início da fração dê) ((pi)) (vezes) 10 (elevado há) 2 (vezes) 135 (sobre) 90 (fim da fração) (fim de linha)$ = 150(pi)" = 471 → 471 m²

98. A_f = $(início de linha) (início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 12.756 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 15 (sobre) 90 (fim da fração) (fim de linha)$ = 6.779.814(pi)" ≃ 21.288.616 → 21.288.616 km²

99. • volume:

V = $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 15 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 4 ((pi)) (vezes) (início da fração dê) 3.375 (sobre) 8 (fim da fração) (sobre) 3 (fim da fração)$ = $(início da fração dê) 1.125 (sobre) 2 (fim da fração) ((pi))$ = 1.766,25 → 1.766,25 cm³

• área da superfícíe:

A = 4(pi)" ⋅ ( $(início da fração dê) 15 (sobre) 2 (fim da fração)$ )² = 225(pi)" = 706,5 → 706,5 cm²

100. alternativa e

O volume total das quatro peças iniciais, em mm³, é:

4 ⋅ $(início da fração dê) 4 ((pi)) (vezes) (abre parenteses) (início da fração dê) 32 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 16 (elevado há) 4 ((pi)) (sobre) 3 (fim da fração)$

Assim, se r é a medida do raio da peça esférica maior, então:

$(início da fração dê) 4 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração)$ = $(início da fração dê) 16 (elevado há) 4 ((pi)) (sobre) 3 (fim da fração)$ ⇒ r³ = $(início da fração dê) 16 (elevado há) 4 (sobre) 4 (fim da fração)$ ⇒ r³ = $(início da fração dê) 16 (sobre) 4 (fim da fração)$ ⋅ 16³ ⇒ r³ = 4 ⋅ 16³ ⇒ r = $16 (início da raíz) 3 (de) 4 (fim da raíz)$ → $16 (início da raíz) 3 (de) 4 (fim da raíz)$ mm

101. alternativa e

A medida r do raio do balão, em mm, ao atingir o volume de 500 mm³ é dado por:

$(início de linha) (início da fração dê) 4 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ = 500 ⇒ r³ = $(início da fração dê) 375 (sobre) ((pi)) (fim da fração)$ ⇒ r³ = $(início da fração dê) 5 (elevado há) 3 (vezes) 3 (sobre) ((pi)) (fim da fração)$ ⇒ r = $5 (início da raíz) 3 (de) (início da fração dê) 3 (sobre) ((pi)) (fim da fração) (fim da raíz)$

Assim, o tempo t quê o balão irá levar para atingir esse volume é dado pela seguinte regra de três:

Medida do raio (em mm)	Tempo (em s)
0,5	1
$5 (início da raíz) 3 (de) (início da fração dê) 3 (sobre) (pi) (fim da fração) (fim da raíz)$	t

$(início da fração dê) 0,5 (sobre) 5 (início da raíz) 3 (de) (início da fração dê) 3 (sobre) ((pi)) (fim da fração) (fim da raíz) (fim da fração)$ = $(início da fração dê) 1 (sobre) [(Tê)] (fim da fração)$ ⇒ 0,5t = $(início de linha) 5 (início da raíz) 3 (de) (início da fração dê) 3 (sobre) ((pi)) (fim da fração) (fim da raíz) (fim de linha)$ ⇒ t = $10 (início da raíz) 3 (de) (início da fração dê) 3 (sobre) ((pi)) (fim da fração) (fim da raíz)$ → $10 (início da raíz) 3 (de) (início da fração dê) 3 (sobre) ((pi)) (fim da fração) (fim da raíz)$ s

102. Elaboração do estudante. Espera-se quê os estudantes consigam elaborar e resolver problemas utilizando conhecimentos sobre o cálculo da área da superfícíe e do volume de uma esféra a partir do contexto apresentado. Incentivar a elaboração de problemas criativos e quê envolvam dados reais.

Integrando com...

1. Respostas possíveis: Optar pelo uso do transporte público, comprar produtos quê utilizam a madeira de reflorestamento como matéria-prima, diminuir o tempo de uso do chuveiro e de equipamentos elétricos.

2. Respostas possíveis: Lápis de côr, móveis, palito de denti, palito de fósforo.

3. a) A parte destinada ao cultivo de eucalipto corresponde a cerca de 75% (77,3%) da área de floresta plantada, ou seja, $(início da fração dê) 3 (sobre) 4 (fim da fração)$ da área.

Página trezentos e oitenta e cinco

b) Não, pois, na região Sul, a área ocupada com o plantio de pínus era maior do quê a ocupada com o plantio de eucalipto.

c) Como 1 hectare equivale à área de um quadrado com 100 m de lado, ou 0,1 km de lado, então:

1 ha = (0,1 ⋅ 0,1) km² = 0,01 km²

Assim, a área total aproximada de florestas plantadas, em km², era de:

9.500.000 ⋅ 0,01 = 95.000 → 95.000 km²

Segue quê a área aproximada de floresta plantada de cada tipo era:

• eucalipto:

$(início de linha) (dado quê) 0,773 (considerando quê) 77,3 % (fim de linha)$ ⋅ 95.000 = 73.435 → 73.435 km²

• pínus:

$(início de linha) (dado quê) 0,187 (considerando quê) 18,7 % (fim de linha)$ ⋅ 95.000 = 17.765 → 17.765 km²

• outras espécies:

$(início de linha) (dado quê) 0,040 (considerando quê) 4,0 % (fim de linha)$ ⋅ 95.000 = 3.800 → 3.800 km²

d) Resposta pessoal. As respostas dependem da região em quê os estudantes moram.

4. Pesquisa e elaboração dos estudantes. Espera-se quê eles se conscientizem a respeito da importânssia do reflorestamento para o futuro da humanidade. A atividade póde sêr uma oportunidade para discutir as consequências das mudanças climáticas e a necessidade de políticas públicas quê protejam o meio ambiente.

5. a) Resposta esperada: No método 1, para realizar os cálculos, usa-se um cilindro circular reto. As medições e os cálculos a sêr realizados em relação aos contornos das bases da tora possibilitam determinar a área de um círculo quê corresponde a uma aproximação das áreas das bases dêêsse cilindro. Como o volume de um cilindro é dado pelo produto da área de sua base e da medida da altura, então, pelo método 1, multiplica-se a média das áreas estimadas para as bases pela medida do comprimento dessa tora:

V = ( $(início de linha) (início da fração dê) [(g)] (índice) 1 + [(g)] (índice) 2 (sobre) 2 (fim da fração) (fim de linha)$ ) ⋅ h.

b) Resposta esperada: No método 2, para realizar os cálculos, usa-se um paralelepípedo reto-retângulo. Como o cálculo do volume de um paralelepípedo reto-retângulo é dado pelo produto das medidas das suas três dimensões, então, pelo método 2, multiplica-se as medidas do comprimento, da largura e da altura dêêsse empilhamento de tóras: V = a ⋅ b ⋅ c.

c) Elaboração dos estudantes. Espera-se quê eles consigam elaborar e resolver problemas envolvendo volumes no contexto apresentado. A ideia de empilhamento póde sêr utilizada em outros contextos, como nas indústrias, podendo variar a figura geométrica espacial utilizada para o cálculo do volume.

O quê estudei

1. Respostas pessoais.

2. Resposta pessoal.

3. Respostas pessoais.

4. a) • Volume da viga:

V_v = 5 ⋅ 0,6 ⋅ 0,6 = 1,8 → 1,8 m³

• Volume de cada coluna:

V_c = (pi)" ⋅ ( $(início da fração dê) 0,6 (sobre) 2 (fim da fração)$ )² ⋅ 2 = 0,18(pi)" → 0,18(pi)" m³

Assim, o volume total da estrutura é:

V = V_v + 3V_c = 1,8 + 3 ⋅ 0,18(pi)" = 1,8 + 0,54(pi)" → (1,8 + 0,54(pi)") m³ ou aproximadamente 3,5 m³

b) • Área lateral de cada coluna:

2(pi)" ⋅ $(início da fração dê) 0,6 (sobre) 2 (fim da fração)$ ⋅ 2 = 1,2(pi)" → 1,2(pi)" m²

• Área da base de cada coluna:

(pi)" ⋅ ( $(início da fração dê) 0,6 (sobre) 2 (fim da fração)$ )² = 0,09(pi)" → 0,09(pi)" m²

• Área total da viga:

2 ⋅ 0,6 ⋅ 0,6 + 4 ⋅ 0,6 ⋅ 5 = 12,72 → 12,72 m²

Assim, a área total aproximada da estrutura a sêr pintada é:

3 ⋅ 1,2(pi)" + 12,72 − 3 ⋅ 0,09(pi)" = 3,33(pi)" + 12,72 ≃ 23,18 → 23,18 m²

Considerando as três demãos, será necessária a seguinte quantidade de tinta para pintar:

3 ⋅ 23,18 = 69,54 → 69,54 m²

Como o rendimento da tinta é de 10 m²/L, ou seja, cada litro de tinta é suficiente para pintar 10 m², serão necessários 69,54 ∶ 10 ≃ 7 litros de tinta.

c) • Volume do cilindro:

V_c = (pi)" ⋅ ( $(início da fração dê) 0,9 (sobre) 2 (fim da fração)$ )² ⋅ 0,6 = 0,1215(pi)" → 0,1215(pi)" m³

• Volume do tronco de cone:

Considerando quê o tronco de cone foi obtído a partir de um cone maior de altura H removendo-se um cone menor de altura h, temos:

$(início da fração dê) [(H)] (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 0,9 (sobre) 0,6 (fim da fração)$ ⇒ $(início da fração dê) (h) + 0,3 (sobre) [(h)] (fim da fração)$ = $(início da fração dê) 3 (sobre) 2 (fim da fração)$ ⇒ 2h + 0,6 = 3h ⇒ h = 0,6

H = 0,6 + 0,3 = 0,9

Assim, o volume do tronco é:

V_t = V_C − V_c = $(início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 0,9 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 0,9 (sobre) 3 (fim da fração)$ − $(início da fração dê) ((pi)) (vezes) (abre parenteses) (início da fração dê) 0,6 (sobre) 2 (fim da fração) (fécha parenteses) (elevado há) 2 (vezes) 0,6 (sobre) 3 (fim da fração)$ = 0,04275(pi)" → 0,04275(pi)" m³

Assim, o volume mássimo de concreto quê póde sêr produzido de uma única vez é:

0,75 ⋅ (V_c + V_t) = 0,75 ⋅ (0,1215(pi)" + 0,04275(pi)") ≃ 0,39 → aproximadamente 0,39 m³

• Como a estrutura precisa de aproximadamente 3,5 m³ de concreto para sêr construída e 3,5 ∶ 0,39 ≃ 8,97, então a betoneira será utilizada, no mínimo, 9 vezes.

d) Vamos calcular o volume de cada sólido.

I) V_I = $(início de linha) (início da fração dê) 1 (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração) (fim de linha)$ ⋅ 3 ≃ 1,3 → aproximadamente 1,3 m³

II) V_II = $(início de linha) (início da fração dê) 4 ((pi)) (vezes) 0,94 (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ ≃ 3,48 → aproximadamente 3,48 m³

III) V_III = $(início de linha) (início da fração dê) ((pi)) (vezes) 1,2 (elevado há) 2 (vezes) 3,5 (sobre) 3 (fim da fração) (fim de linha)$ ≃ 5,28 → aproximadamente 5,28 m³

IV) V_IV = $(início de linha) (início da fração dê) 1,8 (elevado há) 2 (vezes) 2,5 (sobre) 3 (fim da fração) (fim de linha)$ = 2,7 → 2,7 m³

Logo, o sólido com volume quê mais se aproxima de 3,5 m³ é o da ficha II.

Praticando: enêm e vestibulares

1. alternativa c

O volume de madeira corresponde à diferença entre o volume do paralelepípedo com as medidas das dimensões externas e o volume interno da caixa. Como a espessura da madeira é de 0,5 cm, então cada medida interna tem 1 cm a menos quê a medida externa correspondente. Assim, o volume de madeira é:

V = 20 ⋅ 20 ⋅ 8 − 19 ⋅ 19 ⋅ 7 = 673 → 673 cm³

2. alternativa a

Inicialmente, a pedra possuía 5 faces, 8 arestas e 5 vértices. Após os cortes, a jóia ficou com:

• 1 face a mais para cada kórti, totalizando 4 faces adicionais;

Página trezentos e oitenta e seis

• 3 arestas a mais para cada kórti, totalizando 12 arestas adicionais;

• 2 vértices a mais para cada kórti, totalizando 8 vértices adicionais.

Portanto, a jóia lapidada ficou com $(início de linha) (dado quê) 9 (considerando quê) 5 + 4 (fim de linha)$ faces, $(início de linha) (dado quê) 20 (considerando quê) 8 + 12 (fim de linha)$ arestas e $(início de linha) (dado quê) 13 (considerando quê) 5 + 8 (fim de linha)$ vértices.

3. alternativa b

Como o diâmetro do cone esculpido é 18 cm e do cone menor retirado é 6 cm, temos quê a razão entre essas medidas é 18 ∶ 6 = 3. Logo, a altura do cone menor a sêr retirado é:

36 ∶ 3 = 12 → 12 cm

Volume do cone esculpido: $(início de linha) (início da fração dê) 3 (vezes) 9 (elevado há) 2 (vezes) 36 (sobre) 3 (fim da fração) (fim de linha)$ = 2.916 → 2.916 cm³

Volume do cone menor retirado: $(início de linha) (início da fração dê) 3 (vezes) 3 (elevado há) 2 (vezes) 12 (sobre) 3 (fim da fração) (fim de linha)$ = 108 → 108 cm³

Volume do cilindro retirado: 3 ⋅ 3² ⋅ 24 = 648 → 648 cm³

Volume da peça: 2.916 − (108 + 648) = 2.916 − 756 = 2.160 → 2.160 cm³

Massa da peça: 2.160 ⋅ 0,6 = 1.296,0 → 1.296,0 g

4. alternativa a

O volume da pirâmide póde sêr expresso por: V_pirâmide = $(início da fração dê) (início da fração dê) [(F)] (G) (vezes) [(G)] [(H)] (sobre) 2 (fim da fração) (vezes) [(B)] [(G)] (sobre) 3 (fim da fração)$ = $(início da fração dê) [(F)] (G) (vezes) (G) (H) (vezes) [(B)] [(G)] (sobre) 6 (fim da fração)$

O produto FG ⋅ GH ⋅ BG corresponde ao volume do paralelepípedo (V_{paralelepípedo}), logo:

V_pirâmide = $(início da fração dê) [(V)] (índice) paralelepipedo (sobre) 6 (fim da fração)$ ⇒ $(início da fração dê) [(V)] (índice) pirämide (sobre) [(V)] (índice) paralelepipedo (fim da fração)$ = $(início da fração dê) 1 (sobre) 6 (fim da fração)$

5. alternativa d

$(início da fração dê) [(Há)] (sobre) [(b)] (fim da fração)$ = $(início da fração dê) 3 (sobre) 4 (fim da fração)$ ⇒ a = $(início da fração dê) 3 [(b)] (sobre) 4 (fim da fração)$

a ⋅ b ⋅ 5 = 540 ⇒ b = 12

a = $(início da fração dê) 3 [(b)] (sobre) 4 (fim da fração)$ = $(início da fração dê) 3 (vezes) 12 (sobre) 4 (fim da fração)$ = 9

Área total:

2 ⋅ (5 ⋅ 9 + 5 ⋅ 12 + 9 ⋅ 12) = 2 ⋅ (45 + 60 + 108) = 426 → 426 cm²

6. alternativa d

r = $(início da fração dê) 1 (sobre) 3 (fim da fração)$ h

$(início de linha) (dado quê) 2 ((pi)) (vezes) (abre parenteses) (início da fração dê) 1 (sobre) 3 (fim da fração) [(h)] (fécha parenteses) (elevado há) 2 (considerando quê) [(Há)] (índice) [(b)] (fim de linha)$ + $(início de linha) (dado quê) 2 (vezes) ((pi)) (início da fração dê) 1 (sobre) 3 (fim da fração) [(h)] (vezes) [(h)] (considerando quê) [(Há)] (índice) [(f)] (fim de linha)$ = 32(pi)" ⇒ $(início da fração dê) 2 ((pi)) [(h)] (elevado há) 2 (sobre) 9 (fim da fração)$ + $(início da fração dê) 2 ((pi)) [(h)] (elevado há) 2 (sobre) 3 (fim da fração)$ = 32(pi)" ⇒

⇒ $(início da fração dê) 2 [(h)] (elevado há) 2 (sobre) 9 (fim da fração)$ + $(início da fração dê) 2 [(h)] (elevado há) 2 (sobre) 3 (fim da fração)$ = 32 ⇒ $(início de linha) (início da fração dê) 8 [(h)] (elevado há) 2 (sobre) 9 (fim da fração) (fim de linha)$ = 32 ⇒ h² = 36 ⇒ h = 6

Área lateral:

2 ⋅ (pi)" ⋅ $(início da fração dê) 1 (sobre) 3 (fim da fração)$ ⋅ h ⋅ h = 2 ⋅ (pi)" ⋅ $(início da fração dê) 1 (sobre) 3 (fim da fração)$ ⋅ 6 ⋅ 6 = 24(pi)" → 24(pi)" cm²

7. alternativa d

Sendo r o raio inicial da bola, temos quê o volume inicial da bola é: $(início de linha) (início da fração dê) 4 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração) (fim de linha)$ .

Temos quê o volume da bola cheia é dado por: $(início da fração dê) 4 ((pi)) (abre parenteses) 2 [(r)] (elevado há) 3 (fécha parenteses) (sobre) 3 (fim da fração)$ = $(início da fração dê) 32 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração)$

Calculando a razão entre os volumes da bola inicial e da bola cheia, temos:

$(início da fração dê) (início da fração dê) 32 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração) (sobre) (início da fração dê) 4 ((pi)) [(r)] (elevado há) 3 (sobre) 3 (fim da fração) (fim da fração)$ = $(início de linha) (início da fração dê) 32 ((pi)) [(r)] (elevado há) 3 (vezes) 3 (sobre) 3 (vezes) 4 ((pi)) [(r)] (elevado há) 3 (fim da fração) (fim de linha)$ = 8

8. O espaço quê ficou vazio no depósito após a retirada do óleo tem o formato de um tronco de cone cujo volume é de 19 m³. Observe quê o triângulo retângulo cujo ângulo interno agudo é de 45° possui os dois catetos congruentes; logo, os raios da base maior e menor dêêsse tronco de cone médem, respectivamente, x + 1 e x. Assim, considerando (pi)" = 3, temos:

V_C − V_c = 19 ⇒ $(início da fração dê) ((pi)) (vezes) (abre parenteses) (x) + 1 (fécha parenteses) (elevado há) 2 (vezes) (abre parenteses) (x) + 1 (fécha parenteses) (sobre) 3 (fim da fração)$ − $(início de linha) (início da fração dê) ((pi)) (vezes) [(x)] (elevado há) 2 (vezes) (x) (sobre) 3 (fim da fração) (fim de linha)$ = 19 ⇒

⇒ (x + 1)² ⋅ (x + 1) − x³ = 19 ⇒

⇒ (x² + 2x + 1) ⋅ (x + 1) − x³ = 19 ⇒

⇒ x³ + 3x² + 3x + 1 − x³ = 19 ⇒ 3x² + 3x − 18 = 0 ⇒

⇒ x² + x − 6 = 0 ⇒ $(início de linha) { (início de linha) (x) (igual há) 2 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (x) (igual há) (menos) 3 (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Portanto, x = 2 m.

9. alternativa c

Seja t o comprimento das arestas do tetraedro e c o comprimento das arestas do cubo. Temos:

• Área da superfícíe do tetraedro: A_tetraedro = 4 ⋅ $(início da fração dê) [(Tê)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 4 (fim da fração)$ = $(início de linha) [(Tê)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (fim de linha)$

• Área da superfícíe do cubo: A_cubo = 6 ⋅ c²

Se A_tetraedro = A_cubo, então:

$(início de linha) (início da fração dê) [(Tê)] (elevado há) 2 (início da raíz quadrada dê) 3 (fim da raíz) (sobre) 6 [(c)] (elevado há) 2 (fim da fração) (fim de linha)$ = 1 ⇒ $(início da fração dê) [(Tê)] (elevado há) 2 (sobre) [(c)] (elevado há) 2 (fim da fração)$ = $(início da fração dê) 6 (sobre) (início da raíz quadrada dê) 3 (fim da raíz) (fim da fração)$ ⇒ ( $(início da fração dê) [(Tê)] (sobre) [(c)] (fim da fração)$ )² = $2 (início da raíz quadrada dê) 3 (fim da raíz)$ ⇒ $(início da fração dê) [(Tê)] (sobre) [(c)] (fim da fração)$ = $(início da raíz quadrada dê) 2 (início da raíz) (de) 3 (fim da raíz) (fim da raíz)$ ⇒ $(início da fração dê) [(Tê)] (sobre) [(c)] (fim da fração)$ = $(início da raíz quadrada dê) 2 (fim da raíz)(início da raíz) 4 (de) 3 (fim da raíz)$

10. alternativa b

• A altura h do cilindro S₃ é dada por:

sen 30° = $(início da fração dê) [(h)] (sobre) 16 (fim da fração)$ ⇒ $(início da fração dê) 1 (sobre) 2 (fim da fração)$ = $(início da fração dê) [(h)] (sobre) 16 (fim da fração)$ ⇒ h = 8 → 8 cm

Assim, o volume de S₃ é:

V₃ = (pi)" ⋅ ( $(início de linha) 2 (início da raíz quadrada dê) 2 (fim da raíz) (fim de linha)$ )² ⋅ 8 = 64(pi)" → 64(pi)" cm³

• Como o cilindro S₁ é equilátero, o raio de sua base méde:

r = $(início da fração dê) [(g)] (índice) 1 (sobre) 2 (fim da fração)$ = $(início da fração dê) 8 (sobre) 2 (fim da fração)$ = 4 → 4 cm

Assim, a medida g₂, em cm, da geratriz do cone S₂ é dada por:

$[(g)] (índice) 2 (elevado há) 2$ = 4² + 8² ⇒ $[(g)] (índice) 2 (elevado há) 2$ = 80 ⇒ $(início de linha) { (início de linha) [(g)] (índice) 2 (igual há) 4 (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) [(g)] (índice) 2 (igual há) (menos) 4 (início da raíz quadrada dê) 5 (fim da raíz) (abre parenteses) (não convém) (fécha parenteses) (fim de linha) (fim de linha)$

Segue quê a área total da superfícíe de S₂ é:

A₂ = (pi)" ⋅ 4 ⋅ (4 + $(início de linha) 4 (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ ) = 16(pi)"(1 + $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ ) → 16(pi)"(1 + $(início de linha) (início da raíz quadrada dê) 5 (fim da raíz) (fim de linha)$ ) cm²

Portanto, a razão procurada é:

$(início da fração dê) [(V)] (índice) 3 (sobre) [(Há)] (índice) 2 (fim da fração)$ = $(início da fração dê) 64 ((pi)) (sobre) 16 ((pi)) (abre parenteses) 1 + (início da raíz quadrada dê) 5 (fim da raíz) (fécha parenteses) (fim da fração)$ = $(início da fração dê) 4 (sobre) (início da raíz quadrada dê) 5 (fim da raíz) + 1 (fim da fração)$ = $(início da fração dê) 4 (abre parenteses) (início da raíz quadrada dê) 5 (fim da raíz) (menos) 1 (fécha parenteses) (sobre) 5 (menos) 1 (elevado há) 2 (fim da fração)$ = $(início da raíz quadrada dê) 5 (fim da raíz)$ − 1 → ( $(início da raíz quadrada dê) 5 (fim da raíz)$ − 1) cm

Unidade 5 • Análise Combinatória

1. 3 ⋅ 5 = 15 → 15 maneiras

Imagem de um diagrama com três pontos identificados como A, B e C, alinhados horizontalmente. Há 3 setas apontando de A para B, e 5 setas de B para C.

2. 2 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 ⋅ 1 = 48 → 48 maneiras.

• Resposta pessoal. Espera-se quê os estudantes indiquem quê não utilizaram todos os dados do enunciado da atividade. Por exemplo, os dados sobre as idades do casal e dos filhos não são necessários para resolver a atividade.

3. a) 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4 = 4.096 → 4.096 composições

b) Sim, pois a quantidade de composições distintas de respostas (4.096) é maior quê a quantidade de pessoas entrevistadas (30).

4. 8 ⋅ 7 ⋅ 6 = 336 → 336 maneiras. Resposta pessoal.

5. 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 = 5²⁰ → 5²⁰ composições. Resposta pessoal.

6. 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 = 151.200

151.200 ⋅ 20 = 3.024.000

$(início da fração dê) 3.024.000 (sobre) 3.600 (fim da fração)$ = 840 → 840 h. Resposta pessoal.

7. 0,40 ⋅ 20 = 8

Página trezentos e oitenta e sete

$(início da fração dê) 2 (sobre) 5 (fim da fração)$ ⋅ 15 = 6

8 ⋅ 6 = 48 → 48 maneiras

8. 3 ⋅ 26 ⋅ 20 = 1.560 → 1.560 poltronas. Resposta pessoal.

9. a) 5 ⋅ 5 = 25 → 25 números

b) 5 ⋅ 4 = 20 → 20 números

c) 5 ⋅ 2 = 10 → 10 números

d) 5 ⋅ 3 = 15 → 15 números

10. $(início de linha) (início da fração dê) (n) (vezes) (abre parenteses) (n) (menos) 1 (fécha parenteses) (sobre) 2 (fim da fração) (fim de linha)$ = 190 ⇒ n² − n − 380 = 0

n = $(início de linha) (início da fração dê) (menos) (abre parenteses) (menos) 1 (fécha parenteses) (mais ou menos) (início da raíz quadrada dê) (abre parenteses) (menos) 1 (fécha parenteses) (elevado há) 2 (menos) 4 (vezes) 1 (vezes) (abre parenteses) (menos) 380 (fécha parenteses) (fim da raíz) (sobre) 2 (vezes) 1 (fim da fração) (fim de linha)$ ⇒ n = $(início da fração dê) 1 (mais ou menos) 39 (sobre) 2 (fim da fração)$ ⇒ ${ (início de linha) (n) (igual há) 20 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (n) (igual há) (menos) 19 (abre parenteses) (não convém) (fécha parenteses) (fim de linha)$

Portanto, participaram 20 competidores. Resposta pessoal.

11. 3 ⋅ 4 + 2 ⋅ 1 = 12 + 2 = 14 → 14 maneiras

12. alternativa e

10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 900 = 9 ⋅ 10⁷

13. a) Resposta pessoal. Espera-se quê os estudantes consigam aplicar o algoritmo apresentado para verificar sua validade com os dígitos do próprio CPF.

b) 0 ⋅ 10 + 1 ⋅ 9 + 2 ⋅ 8 + 3 ⋅ 7 + 4 ⋅ 6 + 5 ⋅ 5 + 6 ⋅ 4 + 7 ⋅ 3 + 8 ⋅ 2 = 156

156 = 11 ⋅ 14 + 2 → 2 (résto)

11 − 2 = 9 → 9 (1º dígito verificador)

0 ⋅ 11 + 1 ⋅ 10 + 2 ⋅ 9 + 3 ⋅ 8 + 4 ⋅ 7 + 5 ⋅ 6 + 6 ⋅ 5 + 7 ⋅ 4 + 8 ⋅ 3 + 9 ⋅ 2 = 210

210 = 11 ⋅ 19 + 1 → 1 (résto)

Como o résto é igual a 1, o 2º dígito verificador é igual a 0.

c) (10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10) − 10 = 10⁹ − 10 → (10⁹ − 10) números de CPF

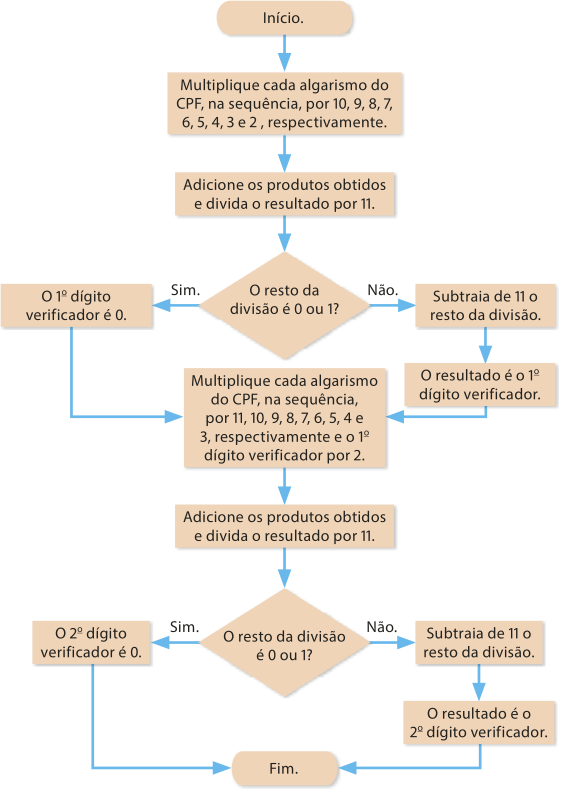
14. a) 7,20 + 5,00 + 6,50 = 18,70

18,70 ⋅ (1 − 0,20) = 18,70 ⋅ 0,80 = 14,96 → R$ 14,96

b) 4,80 + 2,20 + 6,50 = 13,50

13,50 ⋅ 0,80 = 10,80 → R$ 10,80

c) 3 ⋅ 5 ⋅ 2 = 30 → 30 combos

d) 1 ⋅ 4 ⋅ 2 = 8 → 8 maneiras

15. alternativa c

256 = 2⁸

2⁸ ⋅ 2⁸ ⋅ 2⁸ = 2²⁴

16. Pesquisa e elaboração dos estudantes. Espera-se quê eles consigam elaborar e resolver uma situação-problema envolvendo o princípio fundamental da contagem no contexto da evolução dos picsels nos televisores. É importante verificar se eles compreenderam o tipo de situação em quê se aplica esse princípio, ou seja, acontecimentos compostos de etapas sucessivas e independentes.

17. Resposta pessoal. Espera-se quê os estudantes elaborem e resolvam um problema quê envolva o princípio fundamental da contagem no contexto de um cardápio nutricional. Eles podem, por exemplo, completar a parte do enunciado apresentado com quantidades de proteínas, carboidratos e saladas disponíveis e pedir a determinação do número de possibilidades distintas de se compor a refeição.

18. Possibilidades de escolher nome compôzto: 3 ⋅ 4 = 12

Possibilidades de escolher nome simples na coluna B: 4

Total: 12 + 4 = 16 → 16 maneiras distintas

19. Possibilidades distintas: Camisa azul, calção amarelo e par de meias branco, vermelho ou roxo: 3

Camisa azul, calção roxo e par de meias branco ou vermelho: 2

Camisa vêrde, calção amarelo e par de meias azul, branco, vermelho ou roxo: 4

Camisa vêrde, calção azul e par de meias branco, vermelho ou roxo: 3

Camisa vêrde, calção roxo e par de meias azul, branco ou vermelho: 3

Total de possibilidades: 3 + 2 + 4 + 3 + 3 = 15 → 15 maneiras distintas

20. 6 ⋅ 7 ⋅ 6 ⋅ 5 = 1.260 → 1.260 tentativas

21. a) 8 ⋅ 8 ⋅ 8 = 512 → 512 números

b) 700 ≤ x ≤ 999 → 3 ⋅ 8 ⋅ 8 = 192

1.000 ≤ x < 6.000 → 3 ⋅ 8 ⋅ 8 ⋅ 8 = 1.536

192 + 1.536 = 1.728 → 1.728 números

c) 7 ⋅ 8 ⋅ 8 ⋅ 8 ⋅ 3 = 10.752 → 10.752 números

d) 7 ⋅ 8 ⋅ 5 = 280 → 280 números

22. 26 ⋅ 25 ⋅ 24 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 156 ⋅ 10⁷ → 156 ⋅ 10⁷ equipamentos

23. 13 ⋅ 10 + 18 ⋅ 20 = 490 → 490 maneiras

24. alternativa b

Caso Ana escolha um pirulito: 3 ⋅ 5 = 15

Caso Ana não escolha um pirulito, ela terá 7 opções para escolher duas delas. Considerando quê A, B, C, D, E representem as frutas e F, G os pedaços de bôo-lo, temos as seguintes possibilidades: AB, AC, AD, AE, AF, AG, BC, BD, BE, BF, BG, cê dê, CE, CF, CG, DE, DF, DG, EF, EG, FG, ou seja, 21 possibilidades.

Total: 15 + 21 = 36 → 36 formas distintas

25. Elaboração do estudante. Espera-se quê os estudantes consigam elaborar e resolver um problema envolvendo os princípios fundamental e aditivo da contagem. É importante verificar se eles conseguem diferenciar tais princípios, bem como o tipo de situação em quê se aplica cada um.

26. a) 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

b) 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 + 3 ⋅ 2 ⋅ 1 = 120 + 6 = 126

c) 2 ⋅ 1 − 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 2 − 720 = −718

d) $(início da fração dê) 7 (vezes) 6 (vezes) 5 (fatorial) (sobre) 5 (fatorial) (fim da fração)$ = 7 ⋅ 6 = 42

e) $(início da fração dê) 6 (fatorial) (vezes) 14 (fatorial) (sobre) 15 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (vezes) 4 (vezes) 3 (vezes) 2 (fatorial) (vezes) 14 (fatorial) (sobre) 15 (vezes) 14 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (vezes) 4 (vezes) 3 (sobre) 15 (fim da fração)$ = 6 ⋅ 4 = 24

f) $(início da fração dê) 13 (fatorial) + 15 (fatorial) (sobre) 13 (fatorial) (fim da fração)$ = $(início da fração dê) 13 (fatorial) + 15 (vezes) 14 (vezes) 13 (fatorial) (sobre) 13 (fatorial) (fim da fração)$ = $(início de linha) (início da fração dê) 13 (fatorial) (vezes) (abre parenteses) 1 + 15 (vezes) 14 (fécha parenteses) (sobre) 13 (fatorial) (fim da fração) (fim de linha)$ = 211

Página trezentos e oitenta e oito

27. alternativas c e e

a) (a − b)! = (a − b) ⋅ [(a − b) − 1] ⋅ [(a − b) − 2] ⋅... ⋅ [(a − b) − (a − b − 1)] ⇒ (a − b)! ≠ a! − b!

b) (a + b)! = (a + b) ⋅ [(a + b) − 1] ⋅ [(a + b) − 2] ⋅... ⋅ [(a + b) − (a + b − 1)] ⇒ (a + b)! ≠ a! + b!

c) $(início da fração dê) [(Há)] (fatorial) (sobre) [(Há)] (fim da fração)$ = $(início de linha) (início da fração dê) (a) (vezes) (abre parenteses) (a) (menos) 1 (fécha parenteses) (fatorial) (sobre) [(Há)] (fim da fração) (fim de linha)$ = (a − 1)!

d) (2a)! = (2a) ⋅ [(2a) − 1] ⋅ [(2a) − 2] ⋅... ⋅ [(2a) − (2a − 1)] ⇒ (2a)! ≠ 2! ⋅ a!

e) (b!)² = b! ⋅ b!

28. a) $(início da fração dê) [(n)] (fatorial) (sobre) (abre parenteses) (n) (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) [(n)] (fatorial) (abre parenteses) [(n)] (menos) 1 (fécha parenteses) (abre parenteses) [(n)] (menos) 2 (fécha parenteses) (fatorial) (sobre) (abre parenteses) (n) (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = n ⋅ (n − 1) = n² − n

b) $(início da fração dê) (abre parenteses) (n) (menos) 1 (fécha parenteses) (fatorial) (sobre) (abre parenteses) (n) + 1 (fécha parenteses) (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 'fatorial de n menos 1'. No denominador, temos os fatores: 'n mais 1', multiplicado por 'n mais 1 menos 1', multiplicado por 'fatorial de n menos 1'. O 'fatorial de n menos 1' está simplificado.$ = $(início da fração dê) 1 (sobre) (abre parenteses) (n) + 1 (fécha parenteses) (vezes) (n) (fim da fração)$ = $(início da fração dê) 1 (sobre) [(n)] (elevado há) 2 + (n) (fim da fração)$

c) $(início de linha) (início da fração dê) (abre parenteses) (n) + 1 (fécha parenteses) (vezes) (abre parenteses) [(n)] (menos) 1 (fécha parenteses) (fatorial) (sobre) (abre parenteses) (n) + 1 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 'n mais 1', multiplicado por 'fatorial de n menos 1'. No denominador, temos os fatores: 'n mais 1', multiplicado por 'n mais 1 menos 1', multiplicado por 'fatorial de n menos 1'. O 'fatorial de mais 1' e o 'fatorial de n menos 1' estão simplificados.$ = $(início da fração dê) 1 (sobre) [(n)] (fim da fração)$

d) $(início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (fatorial) (sobre) (abre parenteses) (n) + 1 (fécha parenteses) (fatorial) + (n) (fatorial) (fim da fração)$ = $(início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (vezes) (abre parenteses) (n) + 1 (fécha parenteses) (vezes) (n) (fatorial) (sobre) (abre parenteses) (n) + 1 (fécha parenteses) (vezes) (n) (fatorial) + (n) (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados, resultando em outra expressão fracionária. No numerador, temos os fatores: 'n mais 2', multiplicado por 'n mais 1', multiplicado por 'fatorial de n'. No denominador, temos: Abre colchetes, abre parênteses, 'n mais 1', fecha parênteses, mais 1, fecha colchetes, multiplicado por 'fatorial de n'. O 'fatorial de n' está simplificado. Essa expressão é igual a: 'n mais 2', multiplicado por 'n mais 1', tudo dividido por 'n mais 2'.$ = n + 1

29. a) $(início da fração dê) (abre parenteses) (n) (menos) 2 (fécha parenteses) (fatorial) (sobre) [(n)] (fatorial) (fim da fração)$ = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ = $(início da fração dê) (abre parenteses) (n) (menos) 2 (fécha parenteses) (fatorial) (sobre) [(n)] (vezes) (abre parenteses) [(n)] (menos) 1 (fécha parenteses) (vezes) (abre parenteses) [(n)] (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⇒ $(início da fração dê) 1 (sobre) [(n)] (elevado há) 2 (menos) (n) (fim da fração)$ = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⇒ 2 = n² − n ⇒ n² − n − 2 = 0

⇒ n = $(início da fração dê) 1 (mais ou menos) 3 (sobre) 2 (fim da fração)$ ⇒ ${ (início de linha) (n) (igual há) 2 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (n) (igual há) (menos) 1 (abre parenteses) (não convém) (fécha parenteses) (fim de linha)$

b) $(início de linha) (início da fração dê) (abre parenteses) (n) (menos) 4 (fécha parenteses) (fatorial) (sobre) (abre parenteses) (n) (menos) 3 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = 0,1 ⇒ $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 'fatorial de n menos 4'. No denominador, temos os fatores: 'n menos 3', multiplicado por 'fatorial de n menos 4'. O 'fatorial de n menos 4' está simplificado.$ = 0,1 ⇒ $(início da fração dê) 1 (sobre) (n) (menos) 3 (fim da fração)$ = 0,1 ⇒ 1 = 0,1n − 0,3 ⇒ 1,3 = 0,1n ⇒ n = 13

c) $(início de linha) (início da fração dê) (abre parenteses) (n) + 12 (fécha parenteses) (fatorial) (sobre) (abre parenteses) (n) + 10 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = 210 ⇒ $(início de linha) (início da fração dê) (abre parenteses) (n) + 12 (fécha parenteses) (vezes) (abre parenteses) [(n)] + 11 (fécha parenteses) (vezes) (abre parenteses) [(n)] + 10 (fécha parenteses) (fatorial) (sobre) (abre parenteses) (n) + 10 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = 210 ⇒ n² + 23n + 132 = 210 ⇒ n² + 23n − 78 = 0

n = $(início de linha) (início da fração dê) (menos) 23 (mais ou menos) (início da raíz quadrada dê) 23 (elevado há) 2 (menos) 4 (vezes) 1 (vezes) (abre parenteses) (menos) 78 (fécha parenteses) (fim da raíz) (sobre) 2 (vezes) 1 (fim da fração) (fim de linha)$ ⇒ n = $(início da fração dê) (menos) 23 (mais ou menos) 29 (sobre) 2 (fim da fração)$ ⇒ ${ (início de linha) (n) (igual há) 3 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (n) (igual há) (menos) 26 (abre parenteses) (não convém) (fécha parenteses) (fim de linha)$

d) $(início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (fatorial) (menos) 6 [(n)] (fatorial) (sobre) (abre parenteses) (n) + 1 (fécha parenteses) (fatorial) (menos) (n) (fatorial) (fim da fração)$ = 6 ⇒ $(início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (vezes) (abre parenteses) (n) + 1 (fécha parenteses) (vezes) [(n)] (fatorial) (menos) 6 [(n)] (fatorial) (sobre) (abre parenteses) (n) + 1 (fécha parenteses) (vezes) [(n)] (fatorial) (menos) [(n)] (fatorial) (fim da fração)$ = 6 ⇒ $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 'fatorial de n', multiplicado por: abre colchetes, 'n mais 2', multiplicado por 'n mais 1', menos 6, fecha colchetes. No denominador, aparecem: 'fatorial de n', multiplicado por: abre colchetes, 'n mais 1', menos 1, fecha colchetes. O 'fatorial de n' está simplificado.$ = 6 ⇒ $(início de linha) (início da fração dê) [(n)] (elevado há) 2 + 3 [(n)] (menos) 4 (sobre) [(n)] (fim da fração) (fim de linha)$ = 6 ⇒ n² + 3n − 4 = 6n ⇒ n² − 3n − 4 = 0

n = $(início de linha) (início da fração dê) (menos) (abre parenteses) (menos) 3 (fécha parenteses) (mais ou menos) (início da raíz quadrada dê) (abre parenteses) (menos) 3 (fécha parenteses) (elevado há) 2 (menos) 4 (vezes) 1 (vezes) (abre parenteses) (menos) 4 (fécha parenteses) (fim da raíz) (sobre) 2 (vezes) 1 (fim da fração) (fim de linha)$

⇒ n = $(início da fração dê) 3 (mais ou menos) 5 (sobre) 2 (fim da fração)$ ⇒ ${ (início de linha) (n) (igual há) 4 (fim de linha)(início de linha) (ou) (fim de linha)(início de linha) (n) (igual há) (menos) 1 (abre parenteses) (não convém) (fécha parenteses) (fim de linha)$

30. 17 ⋅ 18 ⋅ 19 ⋅ 20 ⋅ 21 ⋅ 22 ⋅ 23 ⋅ 24 = $(início da fração dê) 24 (vezes) 23 (vezes) 22 (vezes) 21 (vezes) 20 (vezes) 19 (vezes) 18 (vezes) 17 (vezes) 16 (fatorial) (sobre) 16 (fatorial) (fim da fração)$ = $(início da fração dê) 24 (fatorial) (sobre) 16 (fatorial) (fim da fração)$

Portanto, a = 24 e b = 16.

31. $(início de linha) (somatória dê) (k) (igual há) 0 (até) 50 (abre parenteses) 2 [(k)] (fécha parenteses) (fatorial) (fim de linha)$ = (2 ⋅ 0)! + (2 ⋅ 1)! + (2 ⋅ 2)! + (2 ⋅ 3)! + ... + (2 ⋅ 50)! =

= $(início de linha) (dado quê) 0 (fatorial) (considerando quê) 1 (fim de linha)$ + $(início de linha) (dado quê) 2 (fatorial) (considerando quê) 2 (fim de linha)$ + $(início de linha) (dado quê) 4 (fatorial) (considerando quê) 24 (fim de linha)$ + $(início de linha) (dado quê) 6 (fatorial) (considerando quê) 720 (fim de linha)$ + ... + 100!

1 + 2 + 4 = 7

32. alternativa c

10 ⋅ 8 ⋅ 6 ⋅ 4 ⋅ 2 = 2 ⋅ 5 ⋅ 2³ ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 2 = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 2³ ⋅ 2 ⋅ 2 = 5! ⋅ 2⁵

33. 20! = 20 ⋅ 19 ⋅ 18 ⋅ 17 ⋅ 16 ⋅ 15 ⋅ 14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1

19 + 17 + 13 + 11 + 7 + 5 + 3 + 2 = 77

34. a) A_{10, 2} = $(início de linha) (início da fração dê) 10 (fatorial) (sobre) (abre parenteses) 10 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 90

b) A_{25, 3} = $(início de linha) (início da fração dê) 25 (fatorial) (sobre) (abre parenteses) 25 (menos) 3 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 13.800

c) A_{6, 6} = $(início de linha) (início da fração dê) 6 (fatorial) (sobre) (abre parenteses) 6 (menos) 6 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 720

d) A_{15, 4} = $(início de linha) (início da fração dê) 15 (fatorial) (sobre) (abre parenteses) 15 (menos) 4 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 32.760

e) A_{7, 6} = $(início de linha) (início da fração dê) 7 (fatorial) (sobre) (abre parenteses) 7 (menos) 6 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $(início da fração dê) 7 (vezes) 6 (vezes) 5 (vezes) 4 (vezes) 3 (vezes) 2 (vezes) 1 (sobre) 1 (fim da fração)$ = 5.040

f) A_{12, 4} = $(início de linha) (início da fração dê) 12 (fatorial) (sobre) (abre parenteses) 12 (menos) 4 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 11.880

35. a) $(início da fração dê) (há) (índice) (abre parenteses) (n) + 1 (fécha parenteses) , (abre parenteses) [(n)] (menos) 1 (fécha parenteses) (sobre) (há) (índice) (abre parenteses) (n) + 2 (fécha parenteses) , [(n)] (fim da fração)$ = $(início da fração dê) (início da fração dê) (abre parenteses) (n) + 1 (fécha parenteses) (fatorial) (sobre) (abre colchete) (abre parenteses) (n) + 1 (fécha parenteses) (menos) (abre parenteses) [(n)] (menos) 1 (fécha parenteses) (fécha colchete) (fatorial) (fim da fração) (sobre) (início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (fatorial) (sobre) (abre colchete) (abre parenteses) (n) + 2 (fécha parenteses) (menos) [(n)] (fécha colchete) (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) (início da fração dê) (abre parenteses) (n) + 1 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração) (sobre) (início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração) (fim da fração)$ = $Imagem de uma operação de expressões fracionárias com elementos simplificados. Expressão 1: 'fatorial de n mais 1', dividido por 2!. Expressão 2: 2!, dividido por 'fatorial de n mais 2'. As expressões 1 e 2 são multiplicadas, e o fator 2! está simplificado, resultando na seguinte expressão fracionária: No numerador, temos: 'fatorial de n mais 1'. No denominador, temos: 'n mais 2', multiplicado por 'fatorial de n mais 1'. O 'fatorial de n mais 1' está simplificado.$ = $(início de linha) (início da fração dê) 1 (sobre) (abre parenteses) (n) + 2 (fécha parenteses) (fim da fração) (fim de linha)$

b) $(início da fração dê) [(Há)] (índice) (abre parenteses) [(n)] (menos) 3 (fécha parenteses) , 2 (sobre) [(Há)] (índice) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) , 1 (fim da fração)$ = $(início da fração dê) (início da fração dê) (abre parenteses) [(n)] (menos) 3 (fécha parenteses) (fatorial) (sobre) (abre colchete) (abre parenteses) [(n)] (menos) 3 (fécha parenteses) (menos) 2 (fécha colchete) (fatorial) (fim da fração) (sobre) (início da fração dê) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) (fatorial) (sobre) (abre colchete) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) (menos) 1 (fécha colchete) (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) (início da fração dê) (abre parenteses) [(n)] (menos) 3 (fécha parenteses) (fatorial) (sobre) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) (fatorial) (fim da fração) (sobre) (início da fração dê) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) (fatorial) (sobre) (abre parenteses) [(n)] (menos) 6 (fécha parenteses) (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) (abre parenteses) [(n)] (menos) 3 (fécha parenteses) (fatorial) (sobre) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ $(início da fração dê) (abre parenteses) [(n)] (menos) 6 (fécha parenteses) (fatorial) (sobre) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 'n menos 3', multiplicado por 'n menos 4', multiplicado por 'fatorial de n menos 5', multiplicado por 'fatorial de n menos 6'. No denominador, aparecem: 'fatorial de n menos 5', multiplicado por 'n menos 5', multiplicado por 'fatorial de n menos 6'. O 'fatorial de n menos 5' e o 'fatorial de n menos 6' estão simplificados.$ = $(início de linha) (início da fração dê) (abre parenteses) [(n)] (menos) 3 (fécha parenteses) (vezes) (abre parenteses) [(n)] (menos) 4 (fécha parenteses) (sobre) (abre parenteses) [(n)] (menos) 5 (fécha parenteses) (fim da fração) (fim de linha)$

c) $(início de linha) (início da fração dê) [(Há)] (índice) [(n)] , (abre parenteses) [(n)] (menos) 1 (fécha parenteses) (vezes) [(Há)] (índice) (abre parenteses) (n) + 3 (fécha parenteses) , (abre parenteses) (n) + 1 (fécha parenteses) (sobre) [(Há)] (índice) (abre parenteses) (n) + 4 (fécha parenteses) , (abre parenteses) (n) + 2 (fécha parenteses) (fim da fração) (fim de linha)$ = $(início da fração dê) (início da fração dê) [(n)] (fatorial) (sobre) (abre colchete) [(n)] (menos) (abre parenteses) [(n)] (menos) 1 (fécha parenteses) (fécha colchete) (fatorial) (fim da fração) (vezes) (início da fração dê) (abre parenteses) (n) + 3 (fécha parenteses) (fatorial) (sobre) (abre colchete) (abre parenteses) (n) + 3 (fécha parenteses) (menos) (abre parenteses) (n) + 1 (fécha parenteses) (fécha colchete) (fatorial) (fim da fração) (sobre) (início da fração dê) (abre parenteses) (n) + 4 (fécha parenteses) (fatorial) (sobre) (abre colchete) (abre parenteses) (n) + 4 (fécha parenteses) (menos) (abre parenteses) (n) + 2 (fécha parenteses) (fécha colchete) (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) (início da fração dê) [(n)] (fatorial) (sobre) 1 (fatorial) (fim da fração) (vezes) (início da fração dê) (abre parenteses) (n) + 3 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração) (sobre) (início da fração dê) (abre parenteses) (n) + 4 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) (início da fração dê) [(n)] (fatorial) (vezes) (abre parenteses) (n) + 3 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração) (sobre) (início da fração dê) (abre parenteses) (n) + 4 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) [(n)] (fatorial) (vezes) (abre parenteses) (n) + 3 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração)$ ⋅ $(início de linha) (início da fração dê) 2 (fatorial) (sobre) (abre parenteses) (n) + 4 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 'n', multiplicado por 'fatorial de n mais 3'. No denominador, aparecem: 'n mais 4', multiplicado por 'fatorial de n mais 3'. O 'fatorial de n mais 3' está simplificado.$ = $(início de linha) (início da fração dê) [(n)] (fatorial) (sobre) (abre parenteses) (n) + 4 (fécha parenteses) (fim da fração) (fim de linha)$

d) $(início da fração dê) [(Há)] (índice) (abre parenteses) (n) + 2 (fécha parenteses) , [(n)] (sobre) [(Há)] (índice) [(n)] , 2 (fim da fração)$ = $(início da fração dê) (início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (fatorial) (sobre) (abre colchete) (abre parenteses) (n) + 2 (fécha parenteses) (menos) [(n)] (fécha colchete) (fatorial) (fim da fração) (sobre) (início da fração dê) [(n)] (fatorial) (sobre) (abre parenteses) [(n)] (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) (início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração) (sobre) (início da fração dê) [(n)] (fatorial) (sobre) (abre parenteses) [(n)] (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (fatorial) (sobre) 2 (fatorial) (fim da fração)$ ⋅ $(início da fração dê) (abre parenteses) [(n)] (menos) 2 (fécha parenteses) (fatorial) (sobre) [(n)] (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 'n mais 2', multiplicado por 'n mais 1', multiplicado por 'fatorial de n', multiplicado por 'fatorial de n menos 2'. No denominador, aparecem: 2 multiplicado por 1 multiplicado por 'fatorial de n'. O 'fatorial de n' está simplificado.$ = $(início de linha) (início da fração dê) (abre parenteses) (n) + 2 (fécha parenteses) (vezes) (abre parenteses) (n) + 1 (fécha parenteses) (vezes) (abre parenteses) [(n)] (menos) 2 (fécha parenteses) (fatorial) (sobre) 2 (fim da fração) (fim de linha)$

Página trezentos e oitenta e nove

36. A_{8, 5} = $(início de linha) (início da fração dê) 8 (fatorial) (sobre) (abre parenteses) 8 (menos) 5 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 6.720 → 6.720 números

37. A_{6, 3} − A_{5, 2} = $(início da fração dê) 6 (fatorial) (sobre) (abre parenteses) 6 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ − $(início da fração dê) 5 (fatorial) (sobre) (abre parenteses) 5 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $Imagem de uma operação de expressões fracionárias com elementos simplificados. Expressão 1: 6 vezes 5 vezes 4 vezes 3 fatorial, tudo sobre 3 fatorial. O 3 fatorial está simplificado. Expressão 2: 5 vezes 4 vezes 3 fatorial, tudo sobre 3 fatorial. O 3 fatorial está simplificado. As expressões 1 e 2 estão subtraídas.$ = 120 − 20 = 100 → 100 números

38. a) 10 ⋅ 10 ⋅ 10 ⋅ 10 = 10.000 → 10.000 senhas

b) A_{10, 4} = $(início de linha) (início da fração dê) 10 (fatorial) (sobre) (abre parenteses) 10 (menos) 4 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 5.040 → 5.040 senhas

c) A_{4, 4} = $(início da fração dê) 4 (fatorial) (sobre) (abre parenteses) 4 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 4 (vezes) 3 (vezes) 2 (vezes) 1 (sobre) 1 (fim da fração)$ = 24

24 ⋅ 5 = 120 → 120 s ou 2 min

d) Resposta pessoal. Espera-se quê os estudantes elaborem a resposta com base nos cálculos realizados e em fatores de segurança sobre senhas tratados na Unidade e de vivências pessoais.

39. Com 12 equipes:

A_{12, 2} = $(início da fração dê) 12 (fatorial) (sobre) (abre parenteses) 12 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 12 (fatorial) (sobre) 10 (fatorial) (fim da fração)$ = $(início da fração dê) 12 (vezes) 11 (vezes) 10 (fatorial) (sobre) 10 (fatorial) (fim da fração)$ = 12 ⋅ 11 = 132

Com 14 equipes:

A_{14, 2} = $(início da fração dê) 14 (fatorial) (sobre) (abre parenteses) 14 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 14 (fatorial) (sobre) 12 (fatorial) (fim da fração)$ = $(início da fração dê) 14 (vezes) 13 (vezes) 12 (fatorial) (sobre) 12 (fatorial) (fim da fração)$ = 14 ⋅ 13 = 182

Assim, segue quê:

182 − 132 = 50 → 50 jogos

40. Kits sem caneca:

A_4,3 = $(início da fração dê) 4 (fatorial) (sobre) (abre parenteses) 4 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 4 (fatorial) (sobre) 1 (fatorial) (fim da fração)$ = $(início da fração dê) 4 (vezes) 3 (vezes) 2 (vezes) 1 (fatorial) (sobre) 1 (fatorial) (fim da fração)$ = 24

Kits com caneca:

24 ⋅ 4 = 96

Assim, segue quê:

24 + 96 = 120 → 120 kits distintos

41. a) 11 poltronas

b) A_{11, 8} = $(início da fração dê) 11 (fatorial) (sobre) (abre parenteses) 11 (menos) 8 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 11 (fatorial) (sobre) 3 (fatorial) (fim da fração)$ = $(início da fração dê) 11 (vezes) 10 (vezes) 9 (vezes) 8 (vezes) 7 (vezes) 6 (vezes) 5 (vezes) 4 (vezes) 3 (fatorial) (sobre) 3 (fatorial) (fim da fração)$ =

= 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 = 6.652.800→ 6.652.800 maneiras

42. a) 26 ⋅ 26 ⋅ 26 ⋅ 26 ⋅ 10 ⋅ 10 ⋅ 10 = 26⁴ ⋅ 10³ → → 26⁴ ⋅ 10³ placas ou 456.976.000 placas

b) A_{26, 4} ⋅ A_{10, 3} = $(início da fração dê) 26 (fatorial) (sobre) (abre parenteses) 26 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ $(início da fração dê) 10 (fatorial) (sobre) (abre parenteses) 10 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $Imagem de uma operação de expressões fracionárias com elementos simplificados. Expressão 1: 26 vezes 25 vezes 24 vezes 23 vezes 22 fatorial, tudo sobre 22 fatorial. O 22 fatorial está simplificado. Expressão 2: 10 vezes 9 vezes 8 vezes 7 fatorial, tudo sobre 7 fatorial. O 7 fatorial está simplificado. As expressões 1 e 2 estão multiplicadas.$ = 258.336.000 → 258.336.000 placas

43. Elaboração do estudante. Espera-se quê os estudantes consigam elaborar e resolver um problema envolvendo arranjo simples no contexto descrito. Verificar se eles compreenderam quê a principal característica do arranjo simples é o fato de serem formados agrupamentos ordenados e quê esse contexto se enquadra pelo fato de a comissão ter cargos específicos, o quê não aconteceria caso eles não fossem nomeados e distintos.

44. a) P₄ = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

b) P₆ = 6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720

c) P₃ − P₅ = 3! − 5! = (3 ⋅ 2 ⋅ 1) − (5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1) = 6 − 120 = −114

d) P₂ + P₈ = 2! + 8! = (2 ⋅ 1) + (8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1) = 2 + 40.320 = 40.322

e) 5 ⋅ P₄ = 5 ⋅ 4! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120

f) $(início da fração dê) [(P)] (índice) 8 (sobre) [(P)] (índice) 6 (fim da fração)$ = $(início da fração dê) 8 (fatorial) (sobre) 6 (fatorial) (fim da fração)$ = = 56

45. a) P₄ = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 → 24 anagramas

b) P₆ = 6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720 → 720 anagramas

c) P₅ = 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120 → 120 anagramas

d) P₉ = 9! = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 362.880 → 362.880 anagramas

46. 1 ⋅ P₄ = 1 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 → 24 maneiras

47. P₄ ⋅ P₂ ⋅ P₂ ⋅ P₂ ⋅ P₂ = 4 ⋅ 3 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 1 = 384 → 384 maneiras

48. P₈ = 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 40.320 → 40.320 maneiras

P₃ ⋅ P₆ = 3 ⋅ 2 ⋅ 1 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 4.320

$(início da fração dê) 4.320 (sobre) 40.320 (fim da fração)$ ≃ 0,107→ aproximadamente 10,7%

49. 1 h → 3.600 s

$(início da fração dê) 3.600 (sobre) 30 (fim da fração)$ = 120

120 = P₅ → 5 algarismos

50. P₆ = 6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720 → 720 maneiras

51. a) P₅ = 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120 → 120 termos

b) 4 ⋅ P₄ = 4 ⋅ 4! = 96 → 96ª posição

c) Para cada algarismo fixado na dezena de milhar, há 24 termos.

$(início da fração dê) 72 (sobre) 24 (fim da fração)$ = 3 → último número quê inicia com 7

79.865

52. a) 9 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 = 136.080 → 136.080 números

b) 3 ⋅ P₃ ⋅ 6 ⋅ 6 ⋅ 5 + P₃ ⋅ 7 ⋅ 6 ⋅ 5 = 4.500 → 4.500 números

53. a) P₇ = 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 5.040 → 5.040 anagramas

b) 1 ⋅ P₆ = 1 ⋅ 6! = 1 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720 → 720 anagramas

c) P₅ ⋅ P₃ = 5! ⋅ 3! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 ⋅ 3 ⋅ 2 ⋅ 1 = 720

$(início da fração dê) 720 (sobre) 5.040 (fim da fração)$ ≃ 0,143 → aproximadamente 14,3%

54. a) Resposta esperada: Não, pois cada bó-linha preta indicada no computador do bugio corresponde a um caractere da senha quê, por medida de segurança, não é explicitado.

b) • P₅ = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120 → 120 palavras

• 3 ⋅ P₄ + 2 ⋅ P₃ + 1 ⋅ P₂ + 2 = 3 ⋅ 4! + 2 ⋅ 3! + 1 ⋅ 2! + 2 = 88 → 88ª posição

c) Elaboração do estudante. Espera-se quê os estudantes consigam elaborar e resolver um problema envolvendo permutação simples no contexto de senhas. Para quê o problema se enquadre no conceito é necessário quê as senhas não tênham repetição de caractere.

55. a) $[(P)] (índice) 7 (elevado há) (abre parenteses) 2 (fécha parenteses)$ = $(início da fração dê) 7 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = = 2.520 → 2.520 anagramas

b) $[(P)] (índice) 9 (elevado há) (abre parenteses) 2,2 (fécha parenteses)$ = $(início da fração dê) 9 (fatorial) (sobre) 2 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 9 vezes 8 vezes 7 vezes 6 vezes 5 vezes 4 vezes 3 vezes 2 fatorial. No denominador, aparecem: 2 vezes 1 vezes 2 fatorial. O 2 fatorial está simplificado.$ = 90.720 → 90.720 anagramas

c) $[(P)] (índice) 8 (elevado há) (abre parenteses) 4 (fécha parenteses)$ = $(início da fração dê) 8 (fatorial) (sobre) 4 (fatorial) (fim da fração)$ = = 1.680 → 1.680 anagramas

d) $[(P)] (índice) 12 (elevado há) (abre parenteses) 2,2 , 3 (fécha parenteses)$ = $(início da fração dê) 12 (fatorial) (sobre) 2 (fatorial) (vezes) 2 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 12 vezes 11 vezes 10 vezes 9 vezes 8 vezes 7 vezes 6 vezes 5 vezes 4 vezes 3 fatorial. No denominador, aparecem: 2 fatorial vezes 2 fatorial vezes 3 fatorial. O 3 fatorial está simplificado.$ = 19.958.400 → 19.958.400 anagramas

56. $[(P)] (índice) 7 (elevado há) (abre parenteses) 5,2 (fécha parenteses)$ = $(início da fração dê) 7 (fatorial) (sobre) 5 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 7 vezes 6 vezes 5 fatorial. No denominador, aparecem: 5 fatorial vezes 2 fatorial. O 5 fatorial está simplificado.$ = $(início da fração dê) 7 (vezes) 6 (sobre) 2 (vezes) 1 (fim da fração)$ = 21 → 21 soluções distintas

57. $[(P)] (índice) 16 (elevado há) (abre parenteses) 12,4 (fécha parenteses)$ = $(início da fração dê) 16 (fatorial) (sobre) 12 (fatorial) (vezes) 4 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 16 vezes 15 vezes 14 vezes 13 vezes 12 fatorial. No denominador, aparecem: 12 fatorial vezes 4 vezes 3 vezes 2 vezes 1. O 12 fatorial está simplificado.$ = 1.820 → 1.820 maneiras distintas

58. a) $[(P)] (índice) 7 (elevado há) (abre parenteses) 3 (fécha parenteses)$ = $(início da fração dê) 7 (fatorial) (sobre) 3 (fatorial) (fim da fração)$ = = 840 → 840 anagramas

b) $[(P)] (índice) 8 (elevado há) (abre parenteses) 3,3 (fécha parenteses)$ ⋅ 5 = $(início da fração dê) 8 (fatorial) (sobre) 3 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ ⋅ 5 = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 8 vezes 7 vezes 6 vezes 5 vezes 4 vezes 3 fatorial vezes 5. No denominador, aparecem: 3 vezes 2 vezes 1 vezes 3 fatorial. O 3 fatorial está simplificado.$ = 5.600 → 5.600 anagramas

c) 4 ⋅ $[(P)] (índice) 8 (elevado há) (abre parenteses) 3,3 (fécha parenteses)$ = 4 ⋅ $(início da fração dê) 8 (fatorial) (sobre) 3 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 4 vezes 8 vezes 7 vezes 6 vezes 5 vezes 4 vezes 3 fatorial. No denominador, aparecem: 3 vezes 2 vezes 1 vezes 3 fatorial. O 3 fatorial está simplificado.$ = 4.480

$[(P)] (índice) 9 (elevado há) (abre parenteses) 3,3 (fécha parenteses)$ = $(início da fração dê) 9 (fatorial) (sobre) 3 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 9 vezes 8 vezes 7 vezes 6 vezes 5 vezes 4 vezes 3 fatorial. No denominador, aparecem: 3 vezes 2 vezes 1 vezes 3 fatorial. O 3 fatorial está simplificado.$ = 10.080

$(início da fração dê) 4.480 (sobre) 10.080 (fim da fração)$ ≃ 0,444 → aproximadamente 44,4%

Página trezentos e noventa

Resposta esperada: Não, pois apenas 4.480 dos 10.080 anagramas começam com vogal, ou seja, aproximadamente 44,4%.

59. a) $[(P)] (índice) 5 (elevado há) (abre parenteses) 2 (fécha parenteses)$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = = 60 → 60 números distintos

b) $[(P)] (índice) 4 (elevado há) (abre parenteses) 2 (fécha parenteses)$ ⋅ 3 = $(início da fração dê) 4 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ ⋅ 3 = = 36 → 36 números distintos

c) 2 ⋅ $[(P)] (índice) 4 (elevado há) (abre parenteses) 2 (fécha parenteses)$ + 2 ⋅ P₃ − 1 = 2 ⋅ $(início da fração dê) 4 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ + 2 ⋅ 3! − 1 = + 2 ⋅ 3 ⋅ 2 ⋅ 1 − 1 = 35 → 35 números distintos

d) $(início de linha) P (índice) 4 (elevado há) (abre parenteses) 2 (fécha parenteses) (fim de linha)$ ⋅ P₂ = = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 → 24 números distintos

60. Começando com AA: $[(P)] (índice) 5 (elevado há) 2$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (vezes) 2 (vezes) 1 (sobre) 2 (vezes) 1 (fim da fração)$ = $(início da fração dê) 120 (sobre) 2 (fim da fração)$ = 60

Começando com AJ: $[(P)] (índice) 5 (elevado há) 2$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (vezes) 2 (vezes) 1 (sobre) 2 (vezes) 1 (fim da fração)$ = $(início da fração dê) 120 (sobre) 2 (fim da fração)$ = 60

Começando com AN: $[(P)] (índice) 5 (elevado há) 2$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (vezes) 2 (vezes) 1 (sobre) 2 (vezes) 1 (fim da fração)$ = $(início da fração dê) 120 (sobre) 2 (fim da fração)$ = 60

Começando com AO: $[(P)] (índice) 5 (elevado há) 2$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (vezes) 2 (vezes) 1 (sobre) 2 (vezes) 1 (fim da fração)$ = $(início da fração dê) 120 (sobre) 2 (fim da fração)$ = 60

Começando com ARA: P₄ = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

Começando com ARJ: P₄ = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

Começando com ARN: P₄ = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

Começando com ARO: P₄ = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

Começando com ARRAJ: P₂ = 2! = 2 ⋅ 1 = 2

Começando com ARRANJO: 1

Assim, segue quê:

4 ⋅ 60 + 4 ⋅ 24 + 2 + 1 = 240 + 96 + 2 + 1 = 339 → 339ª

61. a) $[(P)] (índice) 5 (elevado há) (abre parenteses) 2,3 (fécha parenteses)$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 5 vezes 4 vezes 3 fatorial. No denominador, aparecem: 2 vezes 1 vezes 3 fatorial. O 3 fatorial está simplificado.$ = 10 → 10 sequências distintas

b) (2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2) − 2 ⋅ $(início de linha) [(P)] (índice) 5 (elevado há) (abre parenteses) 5 (fécha parenteses) (fim de linha)$ = 32 − 2 ⋅ $(início da fração dê) 5 (fatorial) (sobre) 5 (fatorial) (fim da fração)$ = 32 − 2 = 30 → 30 sequências distintas

62. a) 1 ⋅ 2 ⋅ 2 ⋅ 2 = 8 → 8 números

b) $[(P)] (índice) 7 (elevado há) (abre parenteses) 3,4 (fécha parenteses)$ = $(início da fração dê) 7 (fatorial) (sobre) 3 (fatorial) (vezes) 4 (fatorial) (fim da fração)$ = 35 → 35 números

63. Elaboração do estudante. Espera-se quê os estudantes elaborem e resolvam um problema envolvendo permutação com repetição a partir do contexto sugerido. Para isso, é necessário quê as palavras escolhidas para a composição tênham, necessariamente, repetições de caracteres.

64. a) C_{7, 5} = $(início de linha) (início da fração dê) 7 (fatorial) (sobre) 5 (fatorial) (vezes) (abre parenteses) 7 (menos) 5 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 7 vezes 6 vezes 5 fatorial. No denominador, aparecem: 5 fatorial vezes 2 vezes 1. O 5 fatorial está simplificado.$ = 21

b) C_{20, 2} = $(início de linha) (início da fração dê) 20 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 20 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 20 vezes 19 vezes 18 fatorial. No denominador, aparecem: 2 vezes 1 vezes 18 fatorial. O 18 fatorial está simplificado.$ = 190

c) C_{9, 4} = $(início de linha) (início da fração dê) 9 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 9 (menos) 4 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 9 vezes 8 vezes 7 vezes 6 vezes 5 fatorial. No denominador, aparecem: 4 vezes 3 vezes 2 vezes 1 vezes 5 fatorial. O 5 fatorial está simplificado.$ = 126

d) C_{11, 8} − C_{8, 3} = $(início da fração dê) 11 (fatorial) (sobre) 8 (fatorial) (vezes) (abre parenteses) 11 (menos) 8 (fécha parenteses) (fatorial) (fim da fração)$ − $(início da fração dê) 8 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 8 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $Imagem de uma operação de expressões fracionárias com elementos simplificados. Expressão 1: 11 vezes 10 vezes 9 vezes 8 fatorial, tudo sobre 8 fatorial vezes 3 vezes 2 vezes 1. O 8 fatorial está simplificado. Expressão 2: 8 vezes 7 vezes 6 vezes 5 fatorial, tudo sobre 3 vezes 2 vezes 1 vezes 5 fatorial. O 5 fatorial está simplificado. As expressões 1 e 2 estão subtraídas.$ = 165 − 56 = 109

e) C_{4, 3} + A_{6, 4} = $(início da fração dê) 4 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 4 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ − $(início da fração dê) 6 (fatorial) (sobre) (abre parenteses) 6 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ = $Imagem de uma operação de expressões fracionárias com elementos simplificados. Expressão 1: 4 vezes 3 fatorial, tudo sobre 3 fatorial vezes 1. O 3 fatorial está simplificado. Expressão 2: 6 vezes 5 vezes 4 vezes 3 vezes 2 fatorial, tudo sobre 2 fatorial. O 2 fatorial está simplificado. As expressões 1 e 2 estão somadas.$ = 4 + 360 = 364

f) $(início da fração dê) [(P)] (índice) 5 (sobre) [(C)] (índice) 8,1 (fim da fração)$ = $(início da fração dê) 5 (fatorial) (sobre) (início da fração dê) 8 (fatorial) (sobre) 1 (fatorial) (vezes) (abre parenteses) 8 (menos) 1 (fécha parenteses) (fatorial) (fim da fração) (fim da fração)$ = $(início da fração dê) 5 (fatorial) (sobre) (início da fração dê) 8 (fatorial) (sobre) 1 (fatorial) (vezes) 7 (fatorial) (fim da fração) (fim da fração)$ = 5! ⋅ $(início da fração dê) 7 (fatorial) (vezes) 1 (fatorial) (sobre) 8 (fatorial) (fim da fração)$ = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 ⋅ $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 7 fatorial vezes 1. No denominador, aparecem: 8 vezes 7 fatorial. O 7 fatorial está simplificado.$ = 15

65. a) Combinação simples, uma vez quê a ordem dos elemêntos nos agrupamentos não importa.

b) Arranjo simples, uma vez quê a ordem dos elemêntos nos agrupamentos importa.

c) Arranjo simples, uma vez quê a ordem dos elemêntos nos agrupamentos importa.

d) Combinação simples, uma vez quê a ordem dos elemêntos nos agrupamentos não importa.

66. a) C_{12, 6} = $(início de linha) (início da fração dê) 12 (fatorial) (sobre) 6 (fatorial) (vezes) (abre parenteses) 12 (menos) 6 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 12 vezes 11 vezes 10 vezes 9 vezes 8 vezes 7 vezes 6 fatorial. No denominador, aparecem: 6 vezes 5 vezes 4 vezes 3 vezes 2 vezes 1 vezes 6 fatorial. O 6 fatorial está simplificado.$ = 924 → 924 maneiras

b) A_{84, 3} = $(início de linha) (início da fração dê) 84 (fatorial) (sobre) (abre parenteses) 84 (menos) 3 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 571.704 → 571.704 maneiras

c) A_{17, 4} = $(início de linha) (início da fração dê) 17 (fatorial) (sobre) (abre parenteses) 17 (menos) 4 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 57.120 → 57.120 maneiras

d) C_{9, 2} = $(início de linha) (início da fração dê) 9 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 9 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 9 vezes 8 vezes 7 fatorial. No denominador, aparecem: 2 vezes 1 vezes 7 fatorial. O 7 fatorial está simplificado.$ = 36 → 36 opções

67. C_{38, 6} = $(início de linha) (início da fração dê) 38 (fatorial) (sobre) 6 (fatorial) (vezes) (abre parenteses) 38 (menos) 6 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 38 vezes 37 vezes 36 vezes 35 vezes 34 vezes 33 vezes 32 fatorial. No denominador, aparecem: 6 vezes 5 vezes 4 vezes 3 vezes 2 vezes 1 vezes 32 fatorial. O 32 fatorial está simplificado.$ = 2.760.681 → 2.760.681 maneiras

68. alternativa e

A escolha das 4 jogadoras de linha será feita entre as 17 profissionais disponíveis. Como não há ordem na posição quê elas ocupam, temos uma situação de combinação simples. A escolha da goleira será feita entre 3 opções disponíveis. Como, para cada possibilidade de escolha da goleira há C_{17, 4} possibilidades de escolha das jogadoras de linha, temos quê o número de times possíveis nas condições dadas será:

C_{3, 1} ⋅ C_{17, 4}.

69. Triângulos com um vértice em $(segmento) [(Há)] [(B)]$ e dois em $(segmento) [(Há)] [(C)]$ :

1 ⋅ C_{7, 2} = $(início da fração dê) 7 (fatorial) (sobre) 2 (fatorial) (abre parenteses) 7 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 7 (vezes) 6 (sobre) 2 (vezes) 1 (fim da fração)$ = 21

Triângulos com um vértice em $(segmento) [(B)] [(C)]$ e dois em $(segmento) [(Há)] [(C)]$ :

Triângulos com um vértice em $(segmento) [(Há)] [(B)]$ , um em $(segmento) [(Há)] [(C)]$ e um em $(segmento) [(B)] [(C)]$ :

1 ⋅ 7 ⋅ 1 = 7

Assim, segue quê:

21 + 21 + 7 = 49 → 49 triângulos

70. a) Todos os 430 estudantes da escola. Os 25 estudantes correspondentes aos números quê serão sorteados.

b) amostra cazual simples ou amostra aleatória simples

c) C_{430, 25}

71. a) C_{5, 2} − 5 = $(início de linha) (início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 5 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ − 5 = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 5 vezes 4 vezes 3 fatorial. No denominador, aparecem: 2 vezes 1 vezes 3 fatorial. O 3 fatorial está simplificado.$ − 5 = 10 − 5 = 5 → 5 diagonais

b) C_{13, 2} − 13 = $(início de linha) (início da fração dê) 13 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 13 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ − 13 = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 13 vezes 12 vezes 11 fatorial. No denominador, aparecem: 2 vezes 1 vezes 11 fatorial. O 11 fatorial está simplificado.$ − 13 = 78 − 13 = 65 → 65 diagonais

c) C_{20, 2} − 20 = $(início de linha) (início da fração dê) 20 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 20 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ − 20 = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 20 vezes 19 vezes 18 fatorial. No denominador, aparecem: 2 vezes 1 vezes 18 fatorial. O 18 fatorial está simplificado.$ − 20 = 190 − 20 = 170 → 170 diagonais

Página trezentos e noventa e um

• Temos quê C_n_{, 2} é a quantidade de lados e diagonais de um polígono de n lados. Assim:

D = C_n_{, 2} − n = $(início de linha) (início da fração dê) [(n)] (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) [(n)] (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ − n =

= $Imagem de uma expressão fracionária com elementos simplificados. No numerador, aparecem os fatores: 'n', multiplicado por 'n menos 1', multiplicado por 'fatorial de n menos 2'. No denominador, aparecem: 2, multiplicado por 1, multiplicado por 'fatorial de n menos 2'. O 'fatorial de n menos 2' está simplificado.$ − n = $(início da fração dê) [(n)] (elevado há) 2 (menos) [(n)] (menos) 2 [(n)] (sobre) 2 (fim da fração)$ = $(início da fração dê) [(n)] (abre parenteses) [(n)] (menos) 3 (fécha parenteses) (sobre) 2 (fim da fração)$

72. alternativa b

C_{513, 30} ⋅ C_{81, 10} = $(início da fração dê) 513 (fatorial) (sobre) 30 (fatorial) (vezes) (abre parenteses) 513 (menos) 30 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ $(início da fração dê) 81 (fatorial) (sobre) 10 (fatorial) (vezes) (abre parenteses) 81 (menos) 10 (fécha parenteses) (fatorial) (fim da fração)$ =

= $(início da fração dê) 513 (fatorial) (vezes) 81 (fatorial) (sobre) 30 (fatorial) (vezes) 483 (fatorial) (vezes) 10 (fatorial) (vezes) 71 (fatorial) (fim da fração)$ = $(início da fração dê) 513 (fatorial) (vezes) 81 (fatorial) (sobre) 483 (fatorial) (vezes) 71 (fatorial) (vezes) 30 (fatorial) (vezes) 10 (fatorial) (fim da fração)$

73. C_{10, 3} ⋅ C_{6, 3} ⋅ C_{14, 3} = $(início da fração dê) 10 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 10 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ $(início da fração dê) 6 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 6 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ ⋅

⋅ $(início da fração dê) 14 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 14 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 10 (fatorial) (vezes) 6 (fatorial) (vezes) 14 (fatorial) (sobre) 3 (fatorial) (vezes) 7 (fatorial) (vezes) 3 (fatorial) (vezes) 3 (fatorial) (vezes) 3 (fatorial) (vezes) 11 (fatorial) (fim da fração)$ =

= $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 10 vezes 9 vezes 8 vezes 'fatorial de 7' vezes 6 vezes 5 vezes 4 vezes 'fatorial de 3' vezes 14 vezes 13 vezes 12 vezes 'fatorial de 11'. No denominador, temos: 3 vezes 2 vezes 1 vezes 'fatorial de 7' vezes 3 vezes 2 vezes 1 vezes 'fatorial de 3' vezes 3 vezes 2 vezes 1 vezes 'fatorial de 11'. Todos os fatoriais estão simplificados: fatorial de 3, de 7 e de 11. E também estão simplificados: o 6 no numerador, com a multiplicação 3 vezes 2 vezes 1, no denominador.$ =

= 873.600 → 873.600 maneiras

74. a) C_{28, 7} = $(início de linha) (início da fração dê) 28 (fatorial) (sobre) 7 (fatorial) (vezes) (abre parenteses) 28 (menos) 7 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 28 vezes 27 vezes 26 vezes 25 vezes 24 vezes 23 vezes 22 vezes 'fatorial de 21'. No denominador, temos: 7 vezes 6 vezes 5 vezes 4 vezes 3 vezes 2 vezes 1 vezes 'fatorial de 21'. O 'fatorial de 21' está simplificado.$ = 1.184.040→ 1.184.040 maneiras

b) C_{7, 2} = $(início de linha) (início da fração dê) 7 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 7 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 21 → 21 maneiras

75. 6 ⋅ C_{5, 2} + 5 ⋅ C_{6, 2} = 6 ⋅ $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 5 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ + 5 ⋅ $(início da fração dê) 6 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 6 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ =

= $Imagem da soma de expressões fracionárias com elementos simplificados. Expressão 1: 6, que multiplica a fração: 5 vezes 4 vezes 3!, tudo dividido por 2 vezes 1 vezes 3!. Expressão 2: 5, que multiplica a fração: 6 vezes 5 vezes 4!, tudo dividido por 2 vezes 1 vezes 4! As expressões 1 e 2 são somadas e os fatores 3! e 4! estão simplificados.$ = 60 + 75 = 135 → 135 triângulos

76. a) C_{12, 4} + C_{15, 4} = $(início da fração dê) 12 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 12 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ + $(início da fração dê) 15 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 15 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ =

= $Imagem da soma de expressões fracionárias com elementos simplificados. Expressão 1: no numerador, temos: 12 vezes 11 vezes 10 vezes 9 vezes 8!; no denominador, temos: 4 vezes 3 vezes 2 vezes 1 vezes 8!. Expressão 2: no numerador, temos: 15 vezes 14 vezes 13 vezes 12 vezes 11!; no denominador, temos: 4 vezes 3 vezes 2 vezes 1 vezes 11!. As expressões 1 e 2 são somadas e os fatores 8! e 11! estão simplificados.$ = 495 + 1.365 = 1.860 → 1.860 possibilidades

b) C_{12, 2} ⋅ C_{15, 2} = $(início da fração dê) 12 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 12 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ $(início da fração dê) 15 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 15 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ =

= $Imagem da multiplicação de expressões fracionárias com elementos simplificados. Expressão 1: no numerador, temos: 12 vezes 11 vezes 10!; no denominador, temos: 2 vezes 1 vezes 10!. Expressão 2: no numerador, temos: 15 vezes 14 vezes 13!; no denominador, temos: 2 vezes 1 vezes 13!. As expressões 1 e 2 são multiplicadas e os fatores 10! e 13! estão simplificados.$ = 66 ⋅ 105 = 6.930 → 6.930 possibilidades

c) C_{27, 4} − C_{15, 4} = $(início da fração dê) 27 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 27 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ − $(início da fração dê) 15 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 15 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ =

= $Imagem da subtração de expressões fracionárias com elementos simplificados. Expressão 1: no numerador, temos: 27 vezes 26 vezes 25 vezes 24 vezes 23!; no denominador, temos: 4 vezes 3 vezes 2 vezes 1 vezes 23!. Expressão 2: no numerador, temos: 15 vezes 14 vezes 13 vezes 12 vezes 11!; no denominador, temos: 4 vezes 3 vezes 2 vezes 1 vezes 11!. A expressão 2 é subtraída da expressão 1 e os fatores 23! e 11! estão simplificados.$ = 17.550 − 1.365 = 16.185 → 16.185 possibilidades

77. alternativa e

C_{3, 2} ⋅ C_{8, 6} = $(início da fração dê) 3 (fatorial) (sobre) 2 (fatorial) (abre parenteses) 3 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ $(início da fração dê) 8 (fatorial) (sobre) 6 (fatorial) (abre parenteses) 8 (menos) 6 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 3 (sobre) 1 (fim da fração)$ ⋅ $(início da fração dê) 8 (vezes) 7 (sobre) 2 (fatorial) (fim da fração)$ = 84

78. alternativa b

$[(P)] (índice) 9 (elevado há) (abre parenteses) 3 , 6 (fécha parenteses)$ = $(início da fração dê) 9 (fatorial) (sobre) 3 (fatorial) (vezes) 6 (fatorial) (fim da fração)$ = $(início da fração dê) 9 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 9 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = C_{9, 3}

79. C_{26, 2} + C_{25, 2} = $(início da fração dê) 26 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 26 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ + $(início da fração dê) 25 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 25 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ =

= $Imagem da soma de expressões fracionárias com elementos simplificados. Expressão 1: no numerador, temos: 26 vezes 25 vezes 24!; no denominador, temos: 2 vezes 1 vezes 24!. Expressão 2: no numerador, temos: 25 vezes 24 vezes 23!; no denominador, temos: 2 vezes 1 vezes 23!. As expressões 1 e 2 são somadas e os fatores 24! e 23! estão simplificados.$ = 325 + 300 = 625 → 625 maneiras

80. Elaboração do estudante. Espera-se quê os estudantes sêjam capazes de elaborar e resolver um problema envolvendo combinação simples no contexto apresentado. É importante quê, no problema elaborado, a ordem dos elemêntos no agrupamento não importe, para caracterizar combinação.

81. a) Respostas pessoais. Espera-se quê os estudantes reconheçam quê o maior fatorial é desenvolvido até quê ele se iguale ao menor, simplificando-os em seguida.

b) C_n_,_p = $(início da fração dê) [(n)] (fatorial) (sobre) [(p)] (fatorial) (vezes) (abre parenteses) [(n)] (menos) [(p)] (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) [(n)] (fatorial) (sobre) (abre parenteses) [(n)] (menos) [(p)] (fécha parenteses) (fatorial) (vezes) [(p)] (fatorial) (fim da fração)$ = $(início de linha) (início da fração dê) [(n)] (fatorial) (sobre) (abre parenteses) [(n)] (menos) [(p)] (fécha parenteses) (fatorial) (vezes) (abre colchete) [(n)] (menos) (abre parenteses) [(n)] (menos) [(p)] (fécha parenteses) (fécha colchete) (fatorial) (fim da fração) (fim de linha)$ = C_n_{, (}_n₋_p₎

82. alternativa b

C_{6, 2} = $(início de linha) (início da fração dê) 6 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 6 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 15

9 + 6 + 4 + 2 + 6 + 13 = 40

Pontuação se não houvesse empates: 3 ⋅ 15 = 45

45 − 40 = 5 → 5 empates

83. C_{4, 3} = $(início de linha) (início da fração dê) 4 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 4 (menos) 3 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 4

4 ⋅ C_{6, 2} = 4 ⋅ $(início de linha) (início da fração dê) 6 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 6 (menos) 2 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = = 60

4 + 60 = 64 → 64 subconjuntos

84. 11 + 19 = 30

76 − 30 = 46

C_{46, 5} = $(início de linha) (início da fração dê) 46 (fatorial) (sobre) 5 (fatorial) (vezes) (abre parenteses) 46 (menos) 5 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 46 vezes 45 vezes 44 vezes 43 vezes 42 vezes 'fatorial de 41'. No denominador, temos: 5 vezes 4 vezes 3 vezes 2 vezes 1 vezes 'fatorial de 41'. O 'fatorial de 41' está simplificado.$ =

= 1.370.754 → 1.370.754 grupos

85. a) • C_{60, 6} = $(início de linha) (início da fração dê) 60 (fatorial) (sobre) 6 (fatorial) (vezes) (abre parenteses) 60 (menos) 6 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 60 vezes 59 vezes 58 vezes 57 vezes 56 vezes 55 vezes 'fatorial de 54'. No denominador, temos: 6 vezes 5 vezes 4 vezes 3 vezes 2 vezes 1 vezes 'fatorial de 54'. O 'fatorial de 54' está simplificado.$ =

= 50.063.860 → 50.063.860 possibilidades

• 2 ⋅ C_{30, 8} = 2 ⋅ $(início de linha) (início da fração dê) 30 (fatorial) (sobre) 8 (fatorial) (vezes) (abre parenteses) 30 (menos) 8 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ =

= $Imagem de uma expressão fracionária com elementos simplificados. A expressão é: 2, que multiplica a fração: no numerador, temos: 30 vezes 29 vezes 28 vezes 27 vezes 26 vezes 25 vezes 24 vezes 23 vezes'fatorial de 22'. No denominador, temos: 8 vezes 7 vezes 6 vezes 5 vezes 4 vezes 3 vezes 2 vezes 1 vezes 'fatorial de 22'. O 'fatorial de 22' está simplificado.$ =

= 11.705.850 → 11.705.850 possibilidades

b) 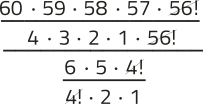$(início da fração dê) [(C)] (índice) 60 , 4 (sobre) [(C)] (índice) 6 , 4 (fim da fração)$ = $(início da fração dê) (início da fração dê) 60 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 60 (menos) 4 (fécha parenteses) (fatorial) (fim da fração) (sobre) (início da fração dê) 6 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 6 (menos) 4 (fécha parenteses) (fatorial) (fim da fração) (fim da fração)$ = $Imagem da divisão de expressões fracionárias com elementos simplificados. Expressão 1: no numerador, temos: 60 vezes 59 vezes 58 vezes 57 vezes 56!; no denominador, temos: 4 vezes 3 vezes 2 vezes 1 vezes 'fatorial de 56'. Expressão 2: no numerador, temos: 6 vezes 5 vezes 'fatorial de 4'; no denominador, temos: 'fatorial de 4' vezes 2 vezes 1. A expressão 1 é dividida pela expressão 2 e os elementos 'fatorial de 56' e 'fatorial de 4' estão simplificados.$ =

= $(início da fração dê) 487.635 (sobre) 15 (fim da fração)$ = 32.509 → 32.509 apostas

Integrando com...

1. Resposta pessoal. As respostas dependem das vivências dos estudantes.

2. De acôr-do com o texto, telégrafo elétrico. Utilizando o cóódigo Morse.

3. a) CONECTANDO PESSOAS

b) A resposta depende do nome e da idade do estudante.

c) lêtras: 2⁴ + 2³ + 2² + 2¹ = 16 + 8 + 4 + 2 = 30 → 30 caracteres algarismos: 2⁵ = 32 → 32 caracteres

4. Resposta pessoal. Espera-se quê os estudantes conheçam um pouco mais sobre o cóódigo Morse e sua relação com a acessibilidade, de modo quê apresentem informações importantes sobre o tema e argumentos a respeito da necessidade de promover acessibilidade para o desenvolvimento de uma ssossiedade inclusiva.

Página trezentos e noventa e dois

O quê estudei

1. Respostas pessoais.

2. Resposta pessoal.

3. Respostas pessoais.

4. a) Resposta possível: Para dificultar o acesso a informações ou arquivos pessoais por alguém mal-intencionado.

b) • 10⁶ = 1.000.000 → 1.000.000 senhas distintas

• P₅ = 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120 → 120 senhas distintas

• P₉ ⋅ 5 = 9! ⋅ 5 = 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 ⋅ 5 = 1.814.400 → 1.814.400 senhas distintas

• $[(P)] (índice) 10 (elevado há) (abre parenteses) 2 , 3 (fécha parenteses)$ = $(início da fração dê) 10 (fatorial) (sobre) 3 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 10 vezes 9 vezes 8 vezes 7 vezes 6 vezes 5 vezes 4 vezes 'fatorial de 3'. No denominador, temos: 'fatorial de 3' vezes 2 vezes 1. O 'fatorial de 3' está simplificado.$ = 302.400 → 302.400 senhas distintas

c) 10⁵ = 100.000

100.000 ⋅ 6 = 600.000

$(início da fração dê) 600.000 (sobre) 60 (fim da fração)$ = 10.000

$(início da fração dê) 100.000 (sobre) 5 (fim da fração)$ = 20.000

(20.000 − 1) ⋅ 3 = 59.997

10.000 + 59.997 = 69.997 → 69.997 min

d) Pesquisa dos estudantes. Espera-se quê eles associem a segurança da senha eletrônica com a quantidade de possibilidades distintas de senhas a serem criadas nas condições determinadas. Ao investigar as possibilidades de senha para o formato padrão, espera-se quê possam comparar com outros tipos de senha e avaliar a mais segura.

Praticando: enêm e vestibulares

1. alternativa e

4 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 972

2. alternativa c

$(início da fração dê) [(C)] (índice) 8,2 (vezes) [(C)] (índice) 6,2 (vezes) [(C)] (índice) 4,2 (vezes) [(C)] (índice) 2,2 (sobre) 4 (fatorial) (fim da fração)$ − $(início da fração dê) 1 (vezes) [(C)] (índice) 6 , 2 (vezes) [(C)] (índice) 4 , 2 (vezes) [(C)] (índice) 2 , 2 (sobre) 3 (fatorial) (fim da fração)$ =

= $(início da fração dê) 28 (vezes) 15 (vezes) 6 (vezes) 1 (sobre) 4 (vezes) 3 (vezes) 2 (vezes) 1 (fim da fração)$ − $(início da fração dê) 1 (vezes) 15 (vezes) 6 (vezes) 1 (sobre) 3 (vezes) 2 (vezes) 1 (fim da fração)$ = 105 − 15 = 90

3. alternativa b

A_{5, 3} = $(início da fração dê) 5 (fatorial) (sobre) (abre parenteses) 5 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (vezes) 2 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = 60

4. alternativa d

C_{12, 3} = $(início de linha) (início da fração dê) 12 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 12 (menos) 3 (fécha parenteses) (fatorial) (fim da fração) (fim de linha)$ = $Imagem de uma expressão fracionária com elementos simplificados. No numerador, temos: 12 vezes 11 vezes 10 vezes 'fatorial de 9'. No denominador, temos: 3 vezes 2 vezes 1 vezes 'fatorial de 9'. O 'fatorial de 9' está simplificado.$ = 220

2 ⋅ C_{4, 3} = 2 ⋅ $(início da fração dê) 4 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 4 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = 2 ⋅ $(início da fração dê) 4 (vezes) 3 (fatorial) (sobre) 3 (fatorial) (vezes) 1 (fim da fração)$ = 8

220 − 8 = 212

5. alternativa e

$[(P)] (índice) 5 (elevado há) (abre parenteses) 2 (fécha parenteses)$ = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (vezes) 2 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = 60

6. alternativa e

$[(P)] (índice) 6 (elevado há) (abre parenteses) 2 (fécha parenteses)$ = $(início da fração dê) 6 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (vezes) 4 (vezes) 3 (vezes) 2 (fatorial) (sobre) 2 (fatorial) (fim da fração)$ = 360

7. alternativa c

Todos os casos possíveis: 3 ⋅ 3 ⋅ 5 = 45

Caneta e lápis amarelo: 1 ⋅ 1 ⋅ 5 = 5

Caneta e giz azuis: 1 ⋅ 3 ⋅ 1 = 3

Lápis e giz laranja: 3 ⋅ 1 ⋅ 1 = 3

Segue quê:

45 − (5 + 3 + 3) = 45 − 11 = 34

8. alternativa e

C_{12, 3} = $(início da fração dê) 12 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 12 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 12 (vezes) 11 (vezes) 10 (vezes) 9 (fatorial) (sobre) 3 (vezes) 2 (vezes) 1 (vezes) 9 (fatorial) (fim da fração)$ = 220

Grupos com crachás de números consecutivos:

E = {(1, 2, 3), (2, 3, 4), (3, 4, 5), (4, 5, 6), (5, 6, 7), (6, 7, 8), (7, 8, 9), (8, 9, 10), (9, 10, 11), (10, 11, 12)} → n(E) = 10

220 − 10 = 210

9. alternativa c

C_{15, 3} = $(início da fração dê) 15 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 15 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 15 (vezes) 14 (vezes) 13 (vezes) 12 (fatorial) (sobre) 3 (vezes) 2 (vezes) 1 (vezes) 12 (fatorial) (fim da fração)$ = 455

C_{5, 3} = $(início da fração dê) 5 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 5 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (vezes) 2 (fatorial) (sobre) 3 (vezes) 2 (vezes) 1 (vezes) 2 (fatorial) (fim da fração)$ = 10

455 − 10 + 1 = 446

10. a) 2 ⋅ 2 ⋅ 1 ⋅ 1 = 4 → 4 combinações

b) 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

24 − 4 = 20; 20 ∶ 4 = 5 → 5 ⋅ 100% = 500%

11. alternativa b

P₄ = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24

12. alternativa c

A escolha das 4 lêtras é um agrupamento ordenado de 4 elemêntos tomados em 26: A_{26, 4}

A escolha dos 4 algarismos é um agrupamento ordenado de 4

elemêntos tomados em 10: A_{10, 4}

Como as escôlhas são etapas sucessivas e independentes, temos: A_{26, 4} ⋅ A_{10, 4}

13. alternativa d

Como o presidente está em um lugar fixo e os ministros podem permutar nos 22 lugares, temos uma permutação simples de 22 elemêntos: 22!

14. alternativa b

$[(P)] (índice) 8 (elevado há) (abre parenteses) 5,3 (fécha parenteses)$ − $[(P)] (índice) 4 (elevado há) (abre parenteses) 3 (fécha parenteses)$ = $(início da fração dê) 8 (fatorial) (sobre) 5 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ − $(início da fração dê) 4 (fatorial) (sobre) 3 (fatorial) (fim da fração)$ = $(início da fração dê) 8 (vezes) 7 (vezes) 6 (vezes) 5 (fatorial) (sobre) 5 (fatorial) (vezes) 3 (vezes) 2 (vezes) 1 (fim da fração)$ − $(início da fração dê) 4 (vezes) 3 (fatorial) (sobre) 3 (fatorial) (fim da fração)$ = 52

15. alternativa d

7 ⋅ 6 ⋅ 5 = 210

16. alternativa d

A até C: $[(P)] (índice) 6 (elevado há) (abre parenteses) 3 , 3 (fécha parenteses)$ = $(início da fração dê) 6 (fatorial) (sobre) 3 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (vezes) 4 (vezes) 3 (fatorial) (sobre) 3 (vezes) 2 (vezes) 1 (vezes) 3 (fatorial) (fim da fração)$ = 20

C até B: $[(P)] (índice) 6 (elevado há) (abre parenteses) 4 , 2 (fécha parenteses)$ = $(início da fração dê) 6 (fatorial) (sobre) 4 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (vezes) 4 (fatorial) (sobre) 4 (fatorial) (vezes) 2 (vezes) 1 (fim da fração)$ = 15

20 ⋅ 15 = 300

17. alternativa b

C_{20, 2} = $(início da fração dê) 20 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 20 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 20 (vezes) 19 (vezes) 18 (fatorial) (sobre) 2 (fatorial) (vezes) 18 (fatorial) (fim da fração)$ = $(início da fração dê) 20 (vezes) 19 (sobre) 2 (fim da fração)$ = 190

190 + 190 = 380

18. alternativa a

Como serão ocupados 25 lugares dos 40 disponíveis, 15 deles serão vagos. Assim, temos uma permutação de 40 elemêntos com repetição de 15 lugares vagos. Deste modo: $[(P)] (índice) 40 (elevado há) 15$ = $(início da fração dê) 40 (fatorial) (sobre) 15 (fatorial) (fim da fração)$

19. alternativa b

C_{10, 3} = $(início da fração dê) 10 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 10 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 10 (vezes) 9 (vezes) 8 (vezes) 7 (fatorial) (sobre) 3 (fatorial) (vezes) 7 (fatorial) (fim da fração)$ = $(início da fração dê) 10 (vezes) 9 (vezes) 8 (sobre) 3 (vezes) 2 (vezes) 1 (fim da fração)$ = $(início da fração dê) 720 (sobre) 6 (fim da fração)$ = 120

20. alternativa d

C_6,2 = $(início da fração dê) 6 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 6 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (vezes) 4 (fatorial) (sobre) 2 (fatorial) (vezes) 4 (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (sobre) 2 (vezes) 1 (fim da fração)$ = $(início da fração dê) 30 (sobre) 2 (fim da fração)$ = 15

21. Imagem de um decágono, com vértices identificados por letras de A a J. A partir do vértice A, partem segmentos de reta ligando-o aos vértices C, D, E e F.

Página trezentos e noventa e três

Dado o decágono da figura apresentada, vamos contar os pares de diagonais possíveis a partir do vértice A.

Diagonal $(segmento) [(Há)] [(C)]$ :

Dentre os 7 vértices restantes, (D, E, F, G, H, I, J) podemos escolher 2 para a outra diagonal e subtrair os 6 lados formados por eles; a quantidade de diagonais é:

C_7,2 − 6 = $(início da fração dê) 7 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 7 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ − 6 = $(início da fração dê) 7 (vezes) 6 (vezes) 5 (fatorial) (sobre) 2 (fatorial) (vezes) 5 (fatorial) (fim da fração)$ − 6 = $(início da fração dê) 42 (sobre) 2 (fim da fração)$ − 6 = 21 − 6 = 15

Diagonal $(segmento) [(Há)] [(Dê)]$ (vértices restantes: E, F, G, H, I, J), de modo análogo, temos:

C_6,2 − 5 = $(início da fração dê) 6 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 6 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ − 5 = $(início da fração dê) 6 (vezes) 5 (vezes) 4 (fatorial) (sobre) 2 (fatorial) (vezes) 4 (fatorial) (fim da fração)$ − 5 = $(início da fração dê) 30 (sobre) 2 (fim da fração)$ − 5 = 15 − 5 = 10

Diagonal $(segmento) [(Há)] [(Ê)]$ (vértices restantes: F, G, H, I, J), de modo análogo, temos:

C_5,2 − 4 = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 5 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ − 4 = $(início da fração dê) 5 (vezes) 4 (vezes) 3 (fatorial) (sobre) 2 (fatorial) (vezes) 3 (fatorial) (fim da fração)$ − 4 = $(início da fração dê) 20 (sobre) 2 (fim da fração)$ − 4 = 10 − 4 = 6

Diagonal $(segmento) [(Há)] [(F)]$ (vértices restantes: G, H, I, J), de modo análogo, temos:

C_4,2 − 3 = $(início da fração dê) 4 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 4 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ − 3 = $(início da fração dê) 4 (vezes) 3 (vezes) 2 (fatorial) (sobre) 2 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ − 3 = $(início da fração dê) 12 (sobre) 2 (fim da fração)$ − 3 = 6 − 3 = 3

Diagonal $(segmento) [(Há)] [(G)]$ (vértices restantes: H, I, J), de modo análogo, temos:

C_3,2 − 2 = $(início da fração dê) 3 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 3 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ − 2 = $(início da fração dê) 3 (vezes) 2 (fatorial) (sobre) 2 (fatorial) (vezes) 1 (fatorial) (fim da fração)$ − 2 = $(início da fração dê) 3 (sobre) 1 (fim da fração)$ − 2 = 3 − 2 = 1

Diagonais $(segmento) [(Há)] [(H)]$ e $(segmento) [(Há)] [(I)]$ : não existe diagonal quê atenda as condições.

Portanto, existem 15 + 10 + 6 + 3 + 1 = 35 pares para o vértice A. Considerando quê, ao contar para todos os vértices, cada par será contado duas vezes, o número total de pares de diagonais quê não se interceptam será dado por:

$(início da fração dê) 35 (vezes) 10 (sobre) 2 (fim da fração)$ = 175 → 175 formas

22. alternativa b

Possibilidades de compor a comissão com 5 vereadores: 1

Possibilidades de compor a comissão com 4 vereadores e 1 deputado:

C_{5, 4} ⋅ 4 = $(início da fração dê) 5 (fatorial) (sobre) 4 (fatorial) (vezes) (abre parenteses) 5 (menos) 4 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ 4 = $(início da fração dê) 5 (vezes) 4 (fatorial) (sobre) 4 (fatorial) (vezes) 1 (fatorial) (fim da fração)$ ⋅ 4 = 5 ⋅ 4 = 20

Possibilidades de compor a comissão com 3 vereadores e 2 deputados:

C_{5, 3} ⋅ C_{4, 2} = $(início da fração dê) 5 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 5 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ ⋅ $(início da fração dê) 4 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 4 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ =

= $(início da fração dê) 5 (vezes) 4 (vezes) 3 (fatorial) (sobre) 3 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ ⋅ $(início da fração dê) 4 (vezes) 3 (vezes) 2 (fatorial) (sobre) 2 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ = 10 ⋅ 6 = 60

Assim, segue quê: 1 + 20 + 60 = 81

Unidade 6 • Probabilidade

1. Considerando experimentos (fenômenos) quê apresentem resultados imprevisíveis, temos: a; c.

2. a) Considerando C a obtenção de cara e K, de coroa, temos (ômega)" = {CC, CK, KC, KK}.

b) A = {KK}; B = {CK, KC}

3. a) proposta I: (ômega)" = {EE, ES, EC, SS, SE, SC, CC, CE, CS}; proposta II: (ômega)" = {ES, EC, SE, SC, CE, CS}

b) proposta I: A = {EE, ES, EC, SE, CE}, B = {EE, SS, CC}; proposta II: A = {ES, EC, SE, CE}, B = ∅

4. a) 15 composições

1 ⋅ 5 = 5 → R$ 5,00

1 ⋅ 10 = 10 → R$ 10,00

1 ⋅ 20 = 20 → R$ 20,00

2 ⋅ 5 = 10 → R$ 10,00

2 ⋅ 10 = 20 → R$ 20,00

2 ⋅ 20 = 40 → R$ 40,00

3 ⋅ 5 = 15 → R$ 15,00

3 ⋅ 10 = 30 → R$ 30,00

3 ⋅ 20 = 60 → R$ 60,00

4 ⋅ 5 = 20 → R$ 20,00

4 ⋅ 10 = 40 → R$ 40,00

4 ⋅ 20 = 80 → R$ 80,00

5 ⋅ 5 = 25 → R$ 25,00

5 ⋅ 10 = 50 → R$ 50,00

5 ⋅ 20 = 100 → R$ 100,00

(ômega)" = {R$ 5,00, R$ 10,00, R$ 15,00, R$ 20,00, R$ 25,00, R$ 30,00, R$ 40,00, R$ 50,00, R$ 60,00, R$ 80,00, R$ 100,00}

c) • A = {R$ 40,00, R$ 50,00, R$ 60,00, R$ 80,00, R$ 100,00};

• B = ∅;

• C = {R$ 5,00, R$ 10,00, R$ 15,00, R$ 20,00, R$ 25,00, R$ 30,00, R$ 40,00, R$ 50,00, R$ 60,00, R$ 80,00, R$ 100,00}

• D = {R$ 5,00}

• E = {R$ 15,00, R$ 20,00, R$ 25,00}

5. a) A e D; A e E; D e E

b) B: impossível; C: cérto; D: simples

6. Alternativa b, pois não há no dado face com número maior quê 12.

7. Elaboração do estudante. Espera-se quê os estudantes consigam estabelecer um exemplo para cada tipo de espaço amostral apresentado. Ao trocarem os experimentos com os côlégas para classificação, os estudantes podem listar os elemêntos de cada espaço amostral discreto (se for possível) e exemplificar alguns elemêntos do espaço amostral contínuo.

8. a) 12 em 25, $(início da fração dê) 12 (sobre) 25 (fim da fração)$ = 0,48 = 48%

b) 13 em 25, $(início da fração dê) 13 (sobre) 25 (fim da fração)$ = 0,52 = 52%

c) 3 em 25, $(início da fração dê) 3 (sobre) 25 (fim da fração)$ = 0,12 = 12%

d) 8 em 25, $(início da fração dê) 8 (sobre) 25 (fim da fração)$ = 0,32 = 32%

Página trezentos e noventa e quatro

e) 15 em 25, $(início da fração dê) 15 (sobre) 25 (fim da fração)$ = 0,6 = 60%

9. (ômega)" = {145, 154, 415, 451, 514, 541}, A = {154, 451}

2 em 6, $(início da fração dê) 2 (sobre) 6 (fim da fração)$ = $(início da fração dê) 1 (sobre) 3 (fim da fração)$ ≃ 0,333 ≃ 33,3%

10. a) 72 + 60 + 68 = 200 → 200 estudantes

b) 72 em 200, $(início da fração dê) 72 (sobre) 200 (fim da fração)$ = $(início da fração dê) 9 (sobre) 25 (fim da fração)$ = 0,36 = 36%

c) 72 + 60 = 132

132 em 200, $(início da fração dê) 132 (sobre) 200 (fim da fração)$ = $(início da fração dê) 33 (sobre) 50 (fim da fração)$ = 0,66 = 66%

d) Resposta esperada: Um estudante do 3º ano, pois há mais estudantes matriculados no 3º ano do quê no 2º ano.

11. a) 60 + 50 + 15 + 25 = 150

60 em 150, $(início da fração dê) 60 (sobre) 150 (fim da fração)$ = $(início da fração dê) 2 (sobre) 5 (fim da fração)$ = 0,4 = 40%

b) 15 em 150, $(início da fração dê) 15 (sobre) 150 (fim da fração)$ = $(início da fração dê) 1 (sobre) 10 (fim da fração)$ = 0,1 = 10%

c) 50 + 15 = 65

65 em 150, $(início da fração dê) 65 (sobre) 150 (fim da fração)$ = $(início da fração dê) 13 (sobre) 30 (fim da fração)$ ≃ 0,433 ≃ 43,3%.

12. (ômega)" = {R$ 0,01, R$ 0,05, R$ 0,10, R$ 0,25, R$ 0,50, R$ 1,00}.

Resposta esperada: Esse não é um espaço amostral equiprovável, pois a probabilidade de sortear cada uma dessas moedas não é a mesma, já quê a massa, o diâmetro e a espessura não são iguais entre si, influenciando o resultado do experimento.

13. a) Observando o primeiro quadrinho da tirinha, temos quê Caco escolheu o número 13. Observando o segundo quadrinho, temos quê o número obtído no lançamento do dado foi 12.

b) Resposta esperada: Porque, considerando a sequência dos números naturais, o número obtído no lançamento do dado (12) é antecessor do número quê Caco escolheu (13).

c) Resposta esperada: Equiprovável, pois o tucano está supondo quê o dado é honesto ao dizêr “A chance de sair 13 é igual pra qualquer outro número do dado”.

d) 1 em 20, $(início da fração dê) 1 (sobre) 20 (fim da fração)$ = 0,05 = 5%

14. a) (ômega)" = {1, 2, 3, 4, 5, 6, 7, 8}. Resposta esperada: Não, pois as probabilidades de ocorrerem os números indicados nas faces não são iguais entre si no lançamento do dado.

b) Resposta esperada: O número 8, pois esse é o maior número indicado nas faces do dado, e a probabilidade de se obtêr cada face é proporcional ao número indicado correspondente.

c) 1p + 2p + 3p + 4p + 5p + 6p + 7p + 8p = 1 ⇒ 36p = 1 ⇒ p = $(início da fração dê) 1 (sobre) 36 (fim da fração)$

6 ⋅ $(início da fração dê) 1 (sobre) 36 (fim da fração)$ = $(início da fração dê) 6 (sobre) 36 (fim da fração)$ = $(início da fração dê) 1 (sobre) 6 (fim da fração)$ ≃ 0,167 ≃ 16,7%

d) Número par, pois a soma dos números pares indicados nas faces é 20, enquanto a soma dos números ímpares é 16, sêndo 20 > 16.

15. Elaboração do estudante. Espera-se quê os estudantes consigam elaborar um problema envolvendo experimento aleatório cuja resolução envolva a construção de uma árvore de possibilidades.

16. alternativa e

n((ômega)") = 20 ⋅ 20 = 400

A = {16 + 20, 17 + 19, 17 + 20, 18 + 18, 18 + 19, 18 + 20, 19 + 17, 19 + 18, 19 + 19, 19 + 20, 20 + 16, 20 + 17, 20 + 18, 20 + 19, 20 + 20} → n(A) = 15

$(início da fração dê) 15 (sobre) 400 (fim da fração)$ = $(início da fração dê) 3 (sobre) 80 (fim da fração)$

17. alternativa d

a) Falso. O número de habitantes com idade menor quê 30 anos é maior quê o número de habitantes quê possuem 60 anos ou mais.

b) Falso.

332.318 + 366.324 = 698.642

$(início da fração dê) 366.324 (sobre) 698.642 (fim da fração)$ ≃ 0,52 → aproximadamente 52%

c) Falso. O número de habitantes do sexo feminino é maior quê o número de habitantes do sexo masculino.

d) Verdadeiro.

$(início da fração dê) 178.547 (sobre) 698.642 (fim da fração)$ ≃ 0,26 → aproximadamente 26%

18. Elaboração do estudante. Espera-se quê os estudantes consigam elaborar e resolver um problema envolvendo o cálculo de probabilidade, utilizando para isso o contexto e os dados da atividade 17. Na elaboração, eles podem se basear nas afirmativas incorrétas da atividade 17.

19. Resposta esperada: Bruna acertou a questão, pois, das 28 peças, em 4 delas a soma das partes é igual a 6, sêndo elas 0 + 6 = 6, 1 + 5 = 6, 2 + 4 = 6 e 3 + 3 = 6. Já élam errou por considerar quê o espaço amostral dêêsse experimento, correspondente à soma dos pontos da peça de dominó sorteada, fosse equiprovável, o quê não ocorre.

20. $(início da fração dê) 100 (sobre) 100 (fim da fração)$ = $(início da fração dê) 85 (sobre) 100 (fim da fração)$ + $(início da fração dê) 20 (sobre) 100 (fim da fração)$ − P(A ⋃ B) ⇒ P(A ⋃ B) = $(início da fração dê) 5 (sobre) 100 (fim da fração)$ → 5%

21. a) Resposta possível: 1ª) Representamos por (ômega)", A e B o espaço amostral compôzto por todos os números naturais de 1 a 100, o evento no qual obtém-se um número ímpar e o evento no qual obtém-se um número menor ou igual a 25, respectivamente. 2ª) Determinamos n((ômega)"), n(A), n(B) e n(A ⋃ B), ou seja, n((ômega)") = 100, n(A) = 50, n(B) = 25 e n(A ⋃ B) = 13. 3ª) Calculamos P (A ⋂ B), correspondente à probabilidade de se obtêr um número natural ímpar ou menor ou igual a 25:

P(A ⋂ B) = P(A) + P(B) − P(A ⋃ B) = $(início da fração dê) 50 (sobre) 100 (fim da fração)$ + $(início da fração dê) 25 (sobre) 100 (fim da fração)$ − $(início da fração dê) 13 (sobre) 100 (fim da fração)$ = $(início da fração dê) 62 (sobre) 100 (fim da fração)$ = $(início da fração dê) 31 (sobre) 50 (fim da fração)$ = 0,62 = 62%

b) • Sendo A o evento no qual obtém-se um número par e B o evento no qual obtém-se um múltiplo de 5, temos:

n(A) = 50, n(B) = 20 e n(A ⋃ B) = 10

P(A ⋂ B) = P(A) + P(B) − P(A ⋃ B) = $(início da fração dê) 50 (sobre) 100 (fim da fração)$ + $(início da fração dê) 20 (sobre) 100 (fim da fração)$ − $(início da fração dê) 10 (sobre) 100 (fim da fração)$ = $(início da fração dê) 60 (sobre) 100 (fim da fração)$ = $(início da fração dê) 3 (sobre) 5 (fim da fração)$ = 0,60 = 60%

• Sendo A o evento no qual obtém-se um número menor ou igual a 15 e B o evento no qual obtém-se um número maior quê 80, temos:

n(A) = 15, n(B) = 20 e n(A ⋃ B) = 0

P(A ⋂ B) = P(A) + P(B) − P(A ⋃ B) = $(início da fração dê) 15 (sobre) 100 (fim da fração)$ + $(início da fração dê) 20 (sobre) 100 (fim da fração)$ − $(início da fração dê) 0 (sobre) 100 (fim da fração)$ = $(início da fração dê) 35 (sobre) 100 (fim da fração)$ = $(início da fração dê) 7 (sobre) 20 (fim da fração)$ = 0,35 = 35%

• Sendo A o evento no qual obtém-se um número múltiplo de 4 e B o evento no qual obtém-se um número divisor de 100, temos:

n(A) = 25, n(B) = 8 e n(A ⋃ B) = 2

P(A ⋂ B) = P(A) + P(B) − P(A ⋃ B) = $(início da fração dê) 25 (sobre) 100 (fim da fração)$ + $(início da fração dê) 8 (sobre) 100 (fim da fração)$ − $(início da fração dê) 2 (sobre) 100 (fim da fração)$ = $(início da fração dê) 31 (sobre) 100 (fim da fração)$ = 0,31 = 31%

22. P(A ⋂ B) = 45%; P(A ⋃ B) = 45%; P(B) = 32%

P(A ⋂ B) = P(A) + P(B) − P(A ⋃ B) ⇒ $(início da fração dê) 45 (sobre) 100 (fim da fração)$ = $(início da fração dê) 32 (sobre) 100 (fim da fração)$ + P(B) − $(início da fração dê) 45 (sobre) 100 (fim da fração)$ ⇒ $(início da fração dê) 90 (sobre) 100 (fim da fração)$ − $(início da fração dê) 32 (sobre) 100 (fim da fração)$ = P(B)⇒ P(B)= $(início da fração dê) 58 (sobre) 100 (fim da fração)$ = 58%

Página trezentos e noventa e cinco

23. a) 1 + 5 + 6 + 3 + 1 = 16

$(início da fração dê) 16 (sobre) 81 (fim da fração)$ ≃ 0,198 ≃ 19,8%

b) 19 + 6 = 25

$(início da fração dê) 25 (sobre) 81 (fim da fração)$ ≃ 0,309 ≃ 30,9%

c) mulher: P(A) = $(início da fração dê) 16 (sobre) 81 (fim da fração)$

ter menos de 55 anos: P(B) = $(início da fração dê) 25 (sobre) 81 (fim da fração)$

P(A ⋃ B) = $(início da fração dê) 6 (sobre) 81 (fim da fração)$

P(A ⋂ B) = $(início da fração dê) 16 (sobre) 81 (fim da fração)$ + $(início da fração dê) 25 (sobre) 81 (fim da fração)$ − $(início da fração dê) 6 (sobre) 81 (fim da fração)$ = $(início da fração dê) 35 (sobre) 81 (fim da fração)$ ≃ 0,432 ≃ 43,2%

24. alternativa c

P(A ⋃ B) = 0

P(A ⋂ B) = 0,38 + 0,24 = 0,62

P(A) = 1 − 0,38 = 0,62

25. a) $(início da fração dê) 1 (sobre) 52 (fim da fração)$ ≃ 0,02 ≃ 2%

b) carta com letra A: P(A) = $(início da fração dê) 4 (sobre) 52 (fim da fração)$ carta de ouros: P(B) = $(início da fração dê) 13 (sobre) 52 (fim da fração)$

P(A ⋃ B) = $(início da fração dê) 1 (sobre) 52 (fim da fração)$

P(A ⋂ B) = $(início da fração dê) 4 (sobre) 52 (fim da fração)$ + $(início da fração dê) 13 (sobre) 52 (fim da fração)$ − $(início da fração dê) 1 (sobre) 52 (fim da fração)$ = $(início da fração dê) 16 (sobre) 52 (fim da fração)$ = $(início da fração dê) 4 (sobre) 13 (fim da fração)$ ≃ 0,31 ≃ 31%

c) carta de espadas: P(A) = $(início da fração dê) 13 (sobre) 52 (fim da fração)$

carta numerada de 2 a 10: P(B) = $(início da fração dê) 36 (sobre) 52 (fim da fração)$

P(A ⋃ B) = $(início da fração dê) 9 (sobre) 52 (fim da fração)$

P(A ⋂ B) = $(início da fração dê) 13 (sobre) 52 (fim da fração)$ + $(início da fração dê) 36 (sobre) 52 (fim da fração)$ − $(início da fração dê) 9 (sobre) 52 (fim da fração)$ = $(início da fração dê) 40 (sobre) 52 (fim da fração)$ = $(início da fração dê) 10 (sobre) 13 (fim da fração)$ ≃ 0,77 ≃ 77%

d) carta quê contém figura: P(A) = $(início da fração dê) 12 (sobre) 52 (fim da fração)$

carta de paus: P(B) = $(início da fração dê) 13 (sobre) 52 (fim da fração)$

P(A ⋃ B) = $(início da fração dê) 3 (sobre) 52 (fim da fração)$

P(A ⋂ B) = $(início da fração dê) 12 (sobre) 52 (fim da fração)$ + $(início da fração dê) 13 (sobre) 52 (fim da fração)$ − $(início da fração dê) 3 (sobre) 52 (fim da fração)$ = $(início da fração dê) 22 (sobre) 52 (fim da fração)$ = $(início da fração dê) 11 (sobre) 26 (fim da fração)$ ≃ 0,42 ≃ 42%

26. a) P(J)= $(início da fração dê) 3 (sobre) 20 (fim da fração)$ = 0,15 = 15%

face vermelha: P(A) = $(início da fração dê) 6 (sobre) 20 (fim da fração)$ = $(início da fração dê) 3 (sobre) 10 (fim da fração)$

número primo: P(B) = $(início da fração dê) 8 (sobre) 20 (fim da fração)$ = $(início da fração dê) 4 (sobre) 10 (fim da fração)$

P(A ⋃ B) = $(início da fração dê) 2 (sobre) 20 (fim da fração)$ = $(início da fração dê) 1 (sobre) 10 (fim da fração)$

P(A ⋂ B) = $(início da fração dê) 3 (sobre) 10 (fim da fração)$ + $(início da fração dê) 4 (sobre) 10 (fim da fração)$ − $(início da fração dê) 1 (sobre) 10 (fim da fração)$ = $(início da fração dê) 6 (sobre) 10 (fim da fração)$ = $(início da fração dê) 3 (sobre) 5 (fim da fração)$ ⇒ P(P) = $(início da fração dê) 3 (sobre) 5 (fim da fração)$ = 0,6 = 60%

face vêrde: P(A) = $(início da fração dê) 4 (sobre) 20 (fim da fração)$

número maior do quê 15: P(B) = $(início da fração dê) 5 (sobre) 20 (fim da fração)$

P(A ⋃ B) = $(início da fração dê) 1 (sobre) 20 (fim da fração)$

P(A ⋂ B) = $(início da fração dê) 4 (sobre) 20 (fim da fração)$ + $(início da fração dê) 5 (sobre) 20 (fim da fração)$ − $(início da fração dê) 1 (sobre) 20 (fim da fração)$ = $(início da fração dê) 8 (sobre) 20 (fim da fração)$ = $(início da fração dê) 2 (sobre) 5 (fim da fração)$ ⇒ P(M) = $(início da fração dê) 2 (sobre) 5 (fim da fração)$ = 0,4 = 40%

Paulo; João

b) face azul: P(A) = $(início da fração dê) 10 (sobre) 20 (fim da fração)$

número múltiplo de 3: P(B) = $(início da fração dê) 6 (sobre) 20 (fim da fração)$

P(A ⋃ B) = $(início da fração dê) 3 (sobre) 20 (fim da fração)$

P(A ⋂ B) = $(início da fração dê) 10 (sobre) 20 (fim da fração)$ + $(início da fração dê) 6 (sobre) 20 (fim da fração)$ − $(início da fração dê) 3 (sobre) 20 (fim da fração)$ = $(início da fração dê) 13 (sobre) 20 (fim da fração)$ = 0,65 = 65%

Não, pois, nesse caso, João teria a maior probabilidade de avançar de nível e Mariana, a menor.

27. 07 (01 + 02 + 04)

01) P(A ⋂ B) = $(início da fração dê) 90 (sobre) 500 (fim da fração)$ + $(início da fração dê) 160 (sobre) 500 (fim da fração)$ − $(início da fração dê) 20 (sobre) 500 (fim da fração)$ = $(início da fração dê) 230 (sobre) 500 (fim da fração)$ = $(início da fração dê) 23 (sobre) 50 (fim da fração)$ = 0,46

02) 1 − 0,46 = 0,54

04) P(A ⋃ B) = $(início da fração dê) 20 (sobre) 500 (fim da fração)$ = $(início da fração dê) 1 (sobre) 25 (fim da fração)$ = 0,04

08) $(início da fração dê) 70 (sobre) 500 (fim da fração)$ = 0,14

28. 80 − 12 = 68

68 = 35 + 43 − n(A ⋃ B) ⇒ n(A ⋃ B) = 10

$(início da fração dê) 35 (sobre) 80 (fim da fração)$ + $(início da fração dê) 43 (sobre) 80 (fim da fração)$ − $(início da fração dê) 10 (sobre) 80 (fim da fração)$ = $(início da fração dê) 68 (sobre) 80 (fim da fração)$ = $(início da fração dê) 17 (sobre) 20 (fim da fração)$ = 0,85 = 85%

29. Resposta esperada: É verdadeira, pois, como A e B são eventos mutuamente exclusivos, temos quê A ⋃ B = ∅ e, por consequência, P(A ⋃ B) = 0.

30. a) $(início da fração dê) 57 (sobre) 120 (fim da fração)$ + $(início da fração dê) 43 (sobre) 120 (fim da fração)$ − $(início da fração dê) 10 (sobre) 120 (fim da fração)$ = $(início da fração dê) 90 (sobre) 120 (fim da fração)$ = $(início da fração dê) 3 (sobre) 4 (fim da fração)$ = 0,75 = 75%

b) $(início da fração dê) 43 (sobre) 120 (fim da fração)$ + $(início da fração dê) 46 (sobre) 120 (fim da fração)$ − $(início da fração dê) 18 (sobre) 120 (fim da fração)$ = $(início da fração dê) 71 (sobre) 120 (fim da fração)$ ≃ 0,592 ≃ 59,2%

c) $(início da fração dê) 46 (sobre) 120 (fim da fração)$ + $(início da fração dê) 57 (sobre) 120 (fim da fração)$ − $(início da fração dê) 21 (sobre) 120 (fim da fração)$ = $(início da fração dê) 82 (sobre) 120 (fim da fração)$ = $(início da fração dê) 41 (sobre) 60 (fim da fração)$ ≃ 0,683 ≃ 68,3%

d) $(início da fração dê) 57 (sobre) 120 (fim da fração)$ + $(início da fração dê) 12 (sobre) 120 (fim da fração)$ = $(início da fração dê) 69 (sobre) 120 (fim da fração)$ = $(início da fração dê) 23 (sobre) 40 (fim da fração)$ ) = 0,575 = 57,5%

31. Elaboração do estudante. Espera-se quê os estudantes elaborem e resolvam um problema envolvendo a probabilidade da união de dois eventos, considerando no contexto o uso dos dois dados apresentados. Incentivar a turma a elaborar problemas envolvendo eventos disjuntos e não disjuntos.

32. 0,5 = $(início de linha) (início da fração dê) 0,4 (sobre) [(P)] (abre parenteses) [(B)] (fécha parenteses) (fim da fração) (fim de linha)$ ⇒ P(B) = $(início da fração dê) 0,4 (sobre) 0,5 (fim da fração)$ = $(início da fração dê) 4 (sobre) 5 (fim da fração)$ = 0,8 ou 80%

33. a) Probabilidade de sortear uma pessoa quê consumiria o produto X, dado quê a pessoa sorteada é um homem.

b) Probabilidade de sortear uma criança, dado quê a pessoa sorteada consumiria o produto Y.

c) Probabilidade de sortear uma mulher, dado quê a pessoa sorteada consumiria o produto X.

d) Probabilidade de sortear um homem, dado quê a pessoa sorteada consumiria o produto Y.

e) Probabilidade de sortear uma pessoa quê consumiria o produto X, dado quê a pessoa sorteada é uma criança.

f) Probabilidade de sortear uma pessoa quê consumiria o produto Y, dado quê a pessoa sorteada é uma mulher.

34. a) a: $(início da fração dê) 53 (sobre) 80 (fim da fração)$ = 0,6625 → 66,25%

b: n(Y) = 36 + 78 + 44 = 158

$(início da fração dê) 44 (sobre) 158 (fim da fração)$ ≃ 0,278 → aproximadamente 27,8%

c: n(X) = 53 + 72 + 28 = 153

$(início da fração dê) 72 (sobre) 153 (fim da fração)$ ≃ 0,471 → aproximadamente 47,1%

d: $(início da fração dê) 36 (sobre) 158 (fim da fração)$ ≃ 0,228 → aproximadamente 22,8%

Página trezentos e noventa e seis

e: $(início da fração dê) 28 (sobre) 50 (fim da fração)$ = 0,56 → 56%

f: $(início da fração dê) 78 (sobre) 120 (fim da fração)$ = 0,65 → 65%

b) Homem: X: $(início da fração dê) 53 (sobre) 80 (fim da fração)$ = 0,6625 → 66,25%

Mulher: Y: $(início da fração dê) 78 (sobre) 120 (fim da fração)$ = 0,65 → 65%

Criança: Y: $(início da fração dê) 44 (sobre) 50 (fim da fração)$ = 0,88 → 88%

Será lançado o produto Y para crianças.

35. a) 100 − 26 = 74

74 = 45 + 58 − n(A ⋃ B) ⇒ n(A ⋃ B) = 29

$(início da fração dê) 29 (sobre) 100 (fim da fração)$ = 0,29 = 29%

b) $(início da fração dê) 29 (sobre) 45 (fim da fração)$ ≃ 0,644 → aproximadamente 64,4%

c) $(início da fração dê) 29 (sobre) 58 (fim da fração)$ = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ = 0,5 = 50%

36. (ômega)" = {(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} → n((ômega)") = 15

n(A) = 5

$(início da fração dê) 5 (sobre) 15 (fim da fração)$ = $(início da fração dê) 1 (sobre) 3 (fim da fração)$ ≃ 0,333 ≃ 33,3%

37. a) n((ômega)") = 28; A = {(3, 3), (4, 2), (5, 1), (6, 0)} → n(A) = 4

$(início da fração dê) 4 (sobre) 28 (fim da fração)$ = $(início da fração dê) 1 (sobre) 7 (fim da fração)$ ≃ 0,143 ≃ 14,3%

b) B = {(5, 0), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)} → n(B) = 7

$(início da fração dê) 3 (sobre) 7 (fim da fração)$ ≃ 0,429 ≃ 42,9%

c) C = {(1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 0), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5, 0), (5, 2), (5, 4), (5, 5), (5, 6)} → n(C) = 18

$(início da fração dê) 2 (sobre) 18 (fim da fração)$ = $(início da fração dê) 1 (sobre) 9 (fim da fração)$ ≃ 0,111 ≃ 11,1%

38. a) rodada 1: $(início da fração dê) 1 (sobre) 5 (fim da fração)$ , 0,20 ou 20%

rodada 2: $(início da fração dê) 1 (sobre) 4 (fim da fração)$ , 0,25 ou 25%

rodada 3: $(início da fração dê) 1 (sobre) 10 (fim da fração)$ , 0,1 ou 10%

b) Opção I: $(início da fração dê) 1 (sobre) 5 (fim da fração)$ , 0,2 ou 20%

Opção II: $(início da fração dê) 1 (sobre) 5 (fim da fração)$ , 0,2 ou 20%

Resposta esperada: Para qualquer uma das dicas, a probabilidade de os estudantes acertarem será a mesma e corresponde a $(início da fração dê) 1 (sobre) 5 (fim da fração)$ , 0,2 ou 20%.

39. alternativa e

0,25 ⋅ 0,20 = 0,05

0,0625 ⋅ 0,80 = 0,05

0,05 + 0,05 = 0,1

$(início da fração dê) 0,05 (sobre) 0,1 (fim da fração)$ = 0,5 → 0,5000

40. Elaboração do estudante. Espera-se quê os estudantes consigam elaborar e resolver um problema envolvendo o conceito de probabilidade condicional a partir do contexto dado. Para isso, o comando do enunciado póde solicitar o cálculo da probabilidade de ocorrer um evento sabendo quê outro já aconteceu.

41. eventos dependentes: b, d; eventos independentes: a, c

42. a) 0,2 ⋅ 0,8 = 0,16

b) $(início da fração dê) 0,16 (sobre) 0,8 (fim da fração)$ = 0,2

c) $(início da fração dê) 0,16 (sobre) 0,2 (fim da fração)$ = 0,8

43. a) Como não há relação entre os giros das roletas, os eventos A e B são independentes.

b) 1 + 1 = 2 → 2 pontos

$(início da fração dê) 1 (sobre) 5 (fim da fração)$ ⋅ $(início da fração dê) 1 (sobre) 5 (fim da fração)$ = $(início da fração dê) 1 (sobre) 25 (fim da fração)$ = 0,04 = 4%

c) $(início da fração dê) 2 (sobre) 5 (fim da fração)$ ⋅ $(início da fração dê) 2 (sobre) 5 (fim da fração)$ = $(início da fração dê) 4 (sobre) 25 (fim da fração)$ = 0,16 = 16%

44. a) sair vermelha apenas no segundo sorteio: $(início da fração dê) 4 (sobre) 12 (fim da fração)$ ⋅ $(início da fração dê) 8 (sobre) 12 (fim da fração)$ = $(início da fração dê) 32 (sobre) 144 (fim da fração)$ = $(início da fração dê) 2 (sobre) 9 (fim da fração)$

sair vermelha nos dois sorteios: $(início da fração dê) 8 (sobre) 12 (fim da fração)$ ⋅ $(início da fração dê) 8 (sobre) 12 (fim da fração)$ = $(início da fração dê) 64 (sobre) 144 (fim da fração)$ = $(início da fração dê) 4 (sobre) 9 (fim da fração)$

$(início da fração dê) 2 (sobre) 9 (fim da fração)$ + $(início da fração dê) 4 (sobre) 9 (fim da fração)$ = $(início da fração dê) 6 (sobre) 9 (fim da fração)$ = $(início da fração dê) 2 (sobre) 3 (fim da fração)$ ≃ 0,667 ≃ 66,7%

b) $(início da fração dê) 4 (sobre) 12 (fim da fração)$ ⋅ $(início da fração dê) 3 (sobre) 11 (fim da fração)$ = $(início da fração dê) 12 (sobre) 132 (fim da fração)$ = $(início da fração dê) 1 (sobre) 11 (fim da fração)$ ≃ 0,091 ≃ 9,1%

c) $(início da fração dê) 4 (sobre) 11 (fim da fração)$ ≃ 0,364 ≃ 36,4%

45. a) $(início da fração dê) 36 (sobre) 52 (fim da fração)$ ⋅ $(início da fração dê) 16 (sobre) 51 (fim da fração)$ = $(início da fração dê) 576 (sobre) 2.652 (fim da fração)$ = $(início da fração dê) 48 (sobre) 221 (fim da fração)$ ≃ 0,217 ≃ 21,7%

b) $(início da fração dê) 12 (sobre) 52 (fim da fração)$ ⋅ $(início da fração dê) 11 (sobre) 51 (fim da fração)$ = $(início da fração dê) 132 (sobre) 2.652 (fim da fração)$ = $(início da fração dê) 11 (sobre) 221 (fim da fração)$ ≃ 0,05 ≃ 5%

c) $(início da fração dê) 13 (sobre) 52 (fim da fração)$ ⋅ $(início da fração dê) 13 (sobre) 51 (fim da fração)$ = $(início da fração dê) 169 (sobre) 2.652 (fim da fração)$ = $(início da fração dê) 13 (sobre) 204 (fim da fração)$ ≃ 0,064 ≃ 6,4%

d) $(início da fração dê) 13 (sobre) 52 (fim da fração)$ = $(início da fração dê) 1 (sobre) 4 (fim da fração)$ = 0,25 = 25%

46.

b	a
b	1	2	3	4	5	6
1	(2, 0)	(3, 1)	(4, 2)	(5, 3)	(6, 4)	(7, 5)
2	(3, −1)	(4, 0)	(5, 1)	(6, 2)	(7, 3)	(8, 4)
3	(4, −2)	(5, −1)	(6, 0)	(7, 1)	(8, 2)	(9, 3)
4	(5, −3)	(6, −2)	(7, −1)	(8, 0)	(9, 1)	(10, 2)
5	(6, −4)	(7, −3)	(8, −2)	(9, −1)	(10, 0)	(11, 1)
6	(7, −5)	(8, −4)	(9, −3)	(10, −2)	(11, −1)	(12, 0)

n((ômega)") = 36

n(E) = 5

$(início da fração dê) 5 (sobre) 36 (fim da fração)$ ≃ 0,139 ≃ 13,9%

47. a) Elaboração do estudante. Espera-se quê os estudantes descrevam dois eventos dependentes entre si. Para isso, eles podem recorrer a contextos parecidos aos apresentados nas atividades anteriores ou recorrer a situações próprias de suas vivências.

b) Elaboração do estudante. Espera-se quê os estudantes descrevam dois eventos independentes entre si. Para isso, eles podem recorrer a contextos parecidos aos apresentados nas atividades anteriores ou recorrer a situações próprias de suas vivências.

• Elaboração do estudante. Espera-se quê os estudantes sêjam capazes de elaborar e resolver problemas envolvendo

Página trezentos e noventa e sete

a probabilidade de eventos dependentes e a probabilidade de eventos independentes. Ao trocarem com os côlégas, propor quê inicialmente identifiquem a relação entre os eventos descritos (dependentes ou independentes) e apontem, no contexto de cada situação, o quê diferencia uma da outra.

48. a) Resposta esperada: Sim, isso é o quê ocorre no chamado resultado falso positivo (FP).

b) Pelo teste A, pois êste apresenta a maior probabilidade de resultado positivo para um paciente enfermo.

c) • 6%; 2%

• $(início da fração dê) 59 % (sobre) 61 % (fim da fração)$ ≃ 0,967 → aproximadamente 0,967 ou 96,7%

• $(início da fração dê) 33 % (sobre) 39 % (fim da fração)$ ≃ 0,846 → aproximadamente 0,846 ou 84,6%

• sensibilidade: $(início da fração dê) 33 % (sobre) 35 % (fim da fração)$ ≃ 0,943 → aproximadamente 0,943 ou 94,3%;

especificidade: $(início da fração dê) 59 % (sobre) 65 % (fim da fração)$ ≃ 0,908 → aproximadamente 0,908 ou 90,8%

49. a) 1 − $(início da fração dê) 3 (sobre) 5 (fim da fração)$ = $(início da fração dê) 5 (sobre) 5 (fim da fração)$ − $(início da fração dê) 3 (sobre) 5 (fim da fração)$ = $(início da fração dê) 2 (sobre) 5 (fim da fração)$

C_{15, 8} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )⁸ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )^{15 − 8} = 6.435 ⋅ $(início da fração dê) 6.561 (sobre) 390.625 (fim da fração)$ ⋅ $(início da fração dê) 128 (sobre) 78.125 (fim da fração)$ ≃ 0,177 → aproximadamente 0,177 ou 17,7%

b) C_{15, 12} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹² ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )^{15 − 12} + C_{15, 13} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹³ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )^{15 − 13} +

C_{15, 14} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹⁴ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )^{15 − 14} + C_{15, 15} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹⁵ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )^{15 − 15} =

C_{15, 12} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹² ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )³ + C_{15, 13} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹³ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )² +

C_{15, 14} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹⁴ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )¹ + C_{15, 15} ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹⁵ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )⁰ =

= 455 ⋅ $(início da fração dê) 531.441 (sobre) 244.140.625 (fim da fração)$ ⋅ $(início da fração dê) 8 (sobre) 125 (fim da fração)$ + 105 ⋅ $(início da fração dê) 1.594.323 (sobre) 1.220.703.125 (fim da fração)$ ⋅ $(início da fração dê) 4 (sobre) 25 (fim da fração)$ + 15 ⋅ $(início da fração dê) 4.782.969 (sobre) 6.103.515.625 (fim da fração)$ ⋅ $(início da fração dê) 2 (sobre) 5 (fim da fração)$ + 1 ⋅ $(início da fração dê) 14.348.907 (sobre) 30.517.578.125 (fim da fração)$ ⋅ 1 ≃

≃ 0,09 → aproximadamente 0,09 ou 9%

c) C_{15, 15} ⋅( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )¹⁵ ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )⁰ = 1 ⋅ $(início da fração dê) 14.348.907 (sobre) 30.517.578.125 (fim da fração)$ ⋅ 1 ≃

≃ 0,00047 → aproximadamente 0,00047 ou 0,047%

50. $(início da fração dê) 100 (sobre) 100 (fim da fração)$ − $(início da fração dê) 30 (sobre) 100 (fim da fração)$ = $(início da fração dê) 70 (sobre) 100 (fim da fração)$

C_{50, 25} ⋅ ( $(início da fração dê) 30 (sobre) 100 (fim da fração)$ )²⁵ ⋅ ( $(início da fração dê) 70 (sobre) 100 (fim da fração)$ )^{50 − 25} = C_{50, 25} ⋅ ( $(início da fração dê) 3 (sobre) 10 (fim da fração)$ )²⁵ ⋅ ( $(início da fração dê) 7 (sobre) 10 (fim da fração)$ )²⁵ ≃

≃ 0,00144 → aproximadamente 0,00144 ou 0,144%

51. alternativa c

1 − $(início da fração dê) 80 (sobre) 100 (fim da fração)$ = $(início da fração dê) 100 (sobre) 100 (fim da fração)$ − $(início da fração dê) 80 (sobre) 100 (fim da fração)$ = $(início da fração dê) 20 (sobre) 100 (fim da fração)$

C_{10, 8} ⋅ ( $(início da fração dê) 8 (sobre) 10 (fim da fração)$ )⁸ ⋅ ( $(início da fração dê) 2 (sobre) 10 (fim da fração)$ )² + C_{10, 9} ⋅ ( $(início da fração dê) 8 (sobre) 10 (fim da fração)$ )⁹ ⋅ ( $(início da fração dê) 2 (sobre) 10 (fim da fração)$ )¹ +

+ C_{10, 10} ⋅ ( $(início da fração dê) 8 (sobre) 10 (fim da fração)$ )¹⁰ ⋅ ( $(início da fração dê) 2 (sobre) 10 (fim da fração)$ )⁰ = 45 ⋅ $(início da fração dê) 16.777.216 (sobre) 100.000.000 (fim da fração)$ ⋅ $(início da fração dê) 4 (sobre) 100 (fim da fração)$ +

+ 10 ⋅ $(início da fração dê) 134.217.728 (sobre) 1.000.000.000 (fim da fração)$ ⋅ $(início da fração dê) 2 (sobre) 10 (fim da fração)$ + 1 ⋅ $(início da fração dê) 1.073.741.824 (sobre) 10.000.000.000 (fim da fração)$ ⋅ 1 ≃

≃ 0,678 → aproximadamente 0,678 ou 67,8%

52. a) 1 − $(início da fração dê) 5 (sobre) 9 (fim da fração)$ = $(início da fração dê) 9 (sobre) 9 (fim da fração)$ − $(início da fração dê) 5 (sobre) 9 (fim da fração)$ = $(início da fração dê) 4 (sobre) 9 (fim da fração)$

C_{7, 5} ⋅ ( $(início da fração dê) 5 (sobre) 9 (fim da fração)$ )⁵ ⋅ ( $(início da fração dê) 4 (sobre) 9 (fim da fração)$ )^{7 − 5} = C_{7, 5} ⋅ ( $(início da fração dê) 5 (sobre) 9 (fim da fração)$ )⁵ ⋅ ( $(início da fração dê) 4 (sobre) 9 (fim da fração)$ )² =

= 21 ⋅ $(início da fração dê) 3.125 (sobre) 59.049 (fim da fração)$ ⋅ $(início da fração dê) 16 (sobre) 81 (fim da fração)$ ≃ 0,22 → aproximadamente 0,22 ou 22%

b) ( $(início da fração dê) 4 (sobre) 9 (fim da fração)$ )⁵ + C_7,1 ⋅ ( $(início da fração dê) 5 (sobre) 9 (fim da fração)$ )¹ ⋅ ( $(início da fração dê) 4 (sobre) 9 (fim da fração)$ )⁶ + C_{7, 2} ⋅ ( $(início da fração dê) 5 (sobre) 9 (fim da fração)$ )² ⋅ ( $(início da fração dê) 4 (sobre) 9 (fim da fração)$ )⁵ =

= $(início da fração dê) 16.384 (sobre) 782.969 (fim da fração)$ + 7 ⋅ $(início da fração dê) 5 (sobre) 9 (fim da fração)$ ⋅ $(início da fração dê) 4.096 (sobre) 531.441 (fim da fração)$ + 21 ⋅ $(início da fração dê) 25 (sobre) 81 (fim da fração)$ ⋅ $(início da fração dê) 1.024 (sobre) 59.049 (fim da fração)$ ≃ 0,146 →

→ aproximadamente 0,146 ou 14,6%

53. a) 1 − $(início da fração dê) 31 (sobre) 100 (fim da fração)$ = $(início da fração dê) 100 (sobre) 100 (fim da fração)$ − $(início da fração dê) 31 (sobre) 100 (fim da fração)$ = $(início da fração dê) 69 (sobre) 100 (fim da fração)$

C_{8, 3} ⋅ ( $(início da fração dê) 69 (sobre) 100 (fim da fração)$ )³ ⋅ ( $(início da fração dê) 31 (sobre) 100 (fim da fração)$ )^{8 − 3} =

= 56 ⋅ $(início da fração dê) 328.509 (sobre) 1.000.000 (fim da fração)$ ⋅ $(início da fração dê) 28.629.151 (sobre) 10.000.000.000 (fim da fração)$ ≃ 0,053 →

→ aproximadamente 0,053 ou 5,3%

b) 1 − $(início da fração dê) 47 (sobre) 100 (fim da fração)$ = $(início da fração dê) 100 (sobre) 100 (fim da fração)$ − $(início da fração dê) 47 (sobre) 100 (fim da fração)$ = $(início da fração dê) 53 (sobre) 100 (fim da fração)$

C_{8, 8} ⋅ ( $(início da fração dê) 47 (sobre) 100 (fim da fração)$ )⁸ ⋅ ( $(início da fração dê) 53 (sobre) 100 (fim da fração)$ )^{8 − 8} ≃ 0,0024 →

→ aproximadamente 0,0024 ou 0,24%

• Pesquisa e elaboração dos estudantes. Espera-se quê os estudantes se envolvam com a temática da pesquisa incentivando, a partir de suas produções, a circulação de moedas no comércio.

54. alternativa b

I) a seta não se móve nas 5 rodadas:

( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )⁵ = $(início da fração dê) 1 (sobre) 243 (fim da fração)$

II) a seta não se móve em 1 rodada, anda para a direita em 2 rodadas e para a esquerda em 2:

$[(P)] (índice) 5 (elevado há) (abre parenteses) 2 , 2 (fécha parenteses)$ ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )¹ ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )² ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )² = $(início da fração dê) 5 (fatorial) (sobre) 2 (fatorial) (vezes) 2 (fatorial) (fim da fração)$ ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )⁵ = 30 ⋅ $(início da fração dê) 1 (sobre) 243 (fim da fração)$ = $(início da fração dê) 30 (sobre) 243 (fim da fração)$

III) a seta não se móve em 3 rodadas e anda para a direita em 1 rodada e para a esquerda em 1:

$[(P)] (índice) 5 (elevado há) (abre parenteses) 3 (fécha parenteses)$ ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )³ ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )¹ ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )¹ = $(início da fração dê) 5 (fatorial) (sobre) 3 (fatorial) (fim da fração)$ ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )⁵ = 20 ⋅ $(início da fração dê) 1 (sobre) 243 (fim da fração)$ = $(início da fração dê) 20 (sobre) 243 (fim da fração)$

$(início da fração dê) 1 (sobre) 243 (fim da fração)$ + $(início da fração dê) 30 (sobre) 243 (fim da fração)$ + $(início da fração dê) 20 (sobre) 243 (fim da fração)$ = $(início da fração dê) 51 (sobre) 243 (fim da fração)$ = $(início da fração dê) 17 (sobre) 81 (fim da fração)$

55.

a) Resposta pessoal. A resposta depende das vivências do estudante.

b) • 1 − $(início da fração dê) 30 (sobre) 100 (fim da fração)$ = $(início da fração dê) 100 (sobre) 100 (fim da fração)$ − $(início da fração dê) 30 (sobre) 100 (fim da fração)$ = $(início da fração dê) 70 (sobre) 100 (fim da fração)$ = $(início da fração dê) 7 (sobre) 10 (fim da fração)$ = 0,7 = 70%

• C_{5, 3} ⋅ ( $(início da fração dê) 7 (sobre) 10 (fim da fração)$ )³ ⋅ ( $(início da fração dê) 3 (sobre) 10 (fim da fração)$ )² + C_{5, 4} ⋅ ( $(início da fração dê) 7 (sobre) 10 (fim da fração)$ )⁴ ⋅ ( $(início da fração dê) 3 (sobre) 10 (fim da fração)$ )¹ +

+ C_{5, 5} ⋅ ( $(início da fração dê) 7 (sobre) 10 (fim da fração)$ )⁵ ⋅ ( $(início da fração dê) 3 (sobre) 10 (fim da fração)$ )⁰ = 10 ⋅ $(início da fração dê) 343 (sobre) 1.000 (fim da fração)$ ⋅ $(início da fração dê) 9 (sobre) 100 (fim da fração)$ +

+ 5 ⋅ $(início da fração dê) 2.401 (sobre) 10.000 (fim da fração)$ ⋅ $(início da fração dê) 3 (sobre) 10 (fim da fração)$ + 1 ⋅ $(início da fração dê) 16.807 (sobre) 100.000 (fim da fração)$ ⋅ 1 ≃ 0,837 →

→ aproximadamente 0,837 ou 83,7%

c) Pesquisa do estudante. Espera-se quê os estudantes compreendam a importânssia do diagnóstico precoce e os cuidados preventivos necessários para diminuir o risco de diabetes melito.

56. Elaboração do estudante. Para elaborar a atividade, os estudantes precisam considerar o contexto da atividade anterior e a realização de experimentos aleatórios binomiais em um espaço amostral equiprovável. Se necessário, revisar conceitos de Análise Combinatória, como combinação simples.

Página trezentos e noventa e oito

57. alternativa e

A, B, D, F: 0,8 ⋅ 0,9 ⋅ 0,3 = 0,216

A, B, C, F: 0,8 ⋅ 0,1 ⋅ 0,6 = 0,048

A, C, F: 0,2 ⋅ 0,6 = 0,120

0,216 + 0,048 + 0,0120 = 0,384

58. a) A: 0,85 ⋅ 0,21 = 0,1785

B: 0,78 ⋅ 0,36 = 0,2808

C: 0,94 ⋅ 0,21 = 0,1974

jogador B

b) 1 − 0,94 = 0,06

0,06 ⋅ 0,21 = 0,0126 → 1,26%

59. C_{2, 1} ⋅( $(início da fração dê) 7 (sobre) 100 (fim da fração)$ )¹ ⋅ ( $(início da fração dê) 93 (sobre) 100 (fim da fração)$ )¹ + C_{2, 2} ⋅ ( $(início da fração dê) 7 (sobre) 100 (fim da fração)$ )² ⋅ ( $(início da fração dê) 93 (sobre) 100 (fim da fração)$ )⁰ = 2 ⋅ $(início da fração dê) 7 (sobre) 100 (fim da fração)$ ⋅ $(início da fração dê) 93 (sobre) 100 (fim da fração)$ + 1 ⋅ $(início da fração dê) 49 (sobre) 10000 (fim da fração)$ ⋅ 1 ≃ 0,0179 → aproximadamente 0,0179 ou 1,79%

C_{4, 1} ⋅ ( $(início da fração dê) 4 (sobre) 100 (fim da fração)$ )¹ _⋅( $(início da fração dê) 96 (sobre) 100 (fim da fração)$ )³ + C_{4, 2} ⋅ ( $(início da fração dê) 4 (sobre) 100 (fim da fração)$ )² ⋅ ( $(início da fração dê) 96 (sobre) 100 (fim da fração)$ )² + C_{4, 3} ⋅ ( $(início da fração dê) 4 (sobre) 100 (fim da fração)$ )³ ⋅ ( $(início da fração dê) 96 (sobre) 100 (fim da fração)$ )¹ + C_{4, 4} ⋅ ( $(início da fração dê) 4 (sobre) 100 (fim da fração)$ )⁴ ⋅ ( $(início da fração dê) 96 (sobre) 100 (fim da fração)$ )⁰ =

= 4 ⋅ $(início da fração dê) 4 (sobre) 100 (fim da fração)$ ⋅ $(início da fração dê) 884.736 (sobre) 1.000.000 (fim da fração)$ + 6 ⋅ $(início da fração dê) 16 (sobre) 10.000 (fim da fração)$ ⋅ $(início da fração dê) 9.216 (sobre) 10.000 (fim da fração)$ + 4 ⋅ $(início da fração dê) 64 (sobre) 1.000.000 (fim da fração)$ ⋅ $(início da fração dê) 96 (sobre) 100 (fim da fração)$ + 1 ⋅ $(início da fração dê) 256 (sobre) 100.000.000 (fim da fração)$ ⋅ 1 =

= 4 ⋅ $(início da fração dê) 4 (sobre) 100 (fim da fração)$ ⋅ $(início da fração dê) 884.736 (sobre) 1.000.000 (fim da fração)$ + 6 ⋅ $(início da fração dê) 16 (sobre) 10.000 (fim da fração)$ ⋅ 9.216/10.000 + 4 ⋅ $(início da fração dê) 64 (sobre) 1.000.000 (fim da fração)$ ⋅ $(início da fração dê) 96 (sobre) 100 (fim da fração)$ + 1 ⋅ $(início da fração dê) 256 (sobre) 100.000.000 (fim da fração)$ ⋅ 1 ≃ 0,151 →

→ aproximadamente 0,151 ou 15,1% medicamento A

60. alternativa b

Probabilidade do tíme 1 chegar à final:

60% ⋅ 50% = 0,6 ⋅ 0,5 = 0,3 = 30%

Probabilidade do tíme 5 chegar à final:

50% ⋅ 50% = 0,5 ⋅ 0,5 = 0,25 = 25%

Probabilidade do tíme 7 chegar à final:

45% ⋅ 50% = 0,45 ⋅ 0,5 = 0,225 = 22,5%

Probabilidade de uma final entre os times 1 e 5:

30% ⋅ 25% = 0,3 ⋅ 0,25 = 0,075 = 7,5%

Probabilidade de uma final entre os times 1 e 7:

30% ⋅ 22,5% = 0,3 ⋅ 0,225 = 0,0675 = 6,75%

Assim, segue quê:

7,5% + 6,75% = 14,25%

61. a) anticoncepcionais orais combinados: $(início da fração dê) 3 (sobre) 1.000 (fim da fração)$ = 0,003 → 0,3%;

pílulas só de progestógeno: 0,3% (caso esteja amamentando) e $(início da fração dê) 9 (sobre) 1.000 (fim da fração)$ = 0,009 → 0,9%(caso não esteja amamentando);

injetáveis só de progestógeno: $(início da fração dê) 3 (sobre) 1.000 (fim da fração)$ = 0,003 → 0,3%;

injetáveis mensais: $(início da fração dê) 5 (sobre) 10.000 (fim da fração)$ = 0,0005 → 0,05%;

implantes: $(início da fração dê) 5 (sobre) 10.000 (fim da fração)$ = 0,0005 → 0,05%;

DIU com cobre: $(início da fração dê) 6 (sobre) 1.000 (fim da fração)$ = 0,006a $(início da fração dê) 8 (sobre) 1.000 (fim da fração)$ = 0,008 → 0,6% a 0,8%;

esterilização feminina: $(início da fração dê) 5 (sobre) 1.000 (fim da fração)$ = 0,005 → 0,5%

b) Injetáveis mensais e implantes, pois são os métodos com os quais a mulher tem a menor probabilidade de engravidar.

c) Anticoncepcionais orais combinados, injetáveis só de progestógeno, injetáveis mensais ou implantes.

d) Pesquisa e elaboração dos estudantes. Espera-se quê os estudantes possam aprofundar o conhecimento sobre um dos métodos contraceptivos e quê compartilhem com os côlégas informações como benefícios, eficácia, efeitos colaterais e riscos à saúde relacionados a tal método.

e) Resposta pessoal.

62. a) n(A) = 411 + 200 + 366 + 271 + 300 + 139 + 113 = 1.800

n((ômega)") = 411 + 200 + 366 + 271 + 300 + 139 + 113 + 412 + 336 + 375 + 97 + 83 + 34 + 24 + 16 + 10 + 5 + 3 + 3 + 0 + 2 = 3.200

$(início da fração dê) 1.800 (sobre) 3.200 (fim da fração)$ = 0,5625 → 56,25%

Faixa etária	Quantidade de acidentes			Probabilidade
Faixa etária	Apenas 1	2 ou mais	Algum acidente	Probabilidade
Até 20 anos	412	16	412 + 16 = 428	$(início da fração dê) 428 (sobre) 3.200 (fim da fração)$ ≃ 13,38%
21 a 25 anos	336	10	336 + 10 = 346	$(início da fração dê) 346 (sobre) 3.200 (fim da fração)$ ≃ 10,81%
26 a 30 anos	375	5	375 + 5 = 380	$(início da fração dê) 380 (sobre) 3.200 (fim da fração)$ ≃ 11,88%
31 a 35 anos	97	3	97 + 3 = 100	$(início da fração dê) 100 (sobre) 3.200 (fim da fração)$ ≃ 3,13%
36 a 40 anos	83	3	83 + 3 = 86	$(início da fração dê) 86 (sobre) 3.200 (fim da fração)$ ≃ 2,69%
41 a 45 anos	34	0	34 + 0 = 34	$(início da fração dê) 34 (sobre) 3.200 (fim da fração)$ ≃ 1,06%
Mais de 45 anos	24	2	24 + 2 = 26	$(início da fração dê) 26 (sobre) 3.200 (fim da fração)$ ≃ 0,81%

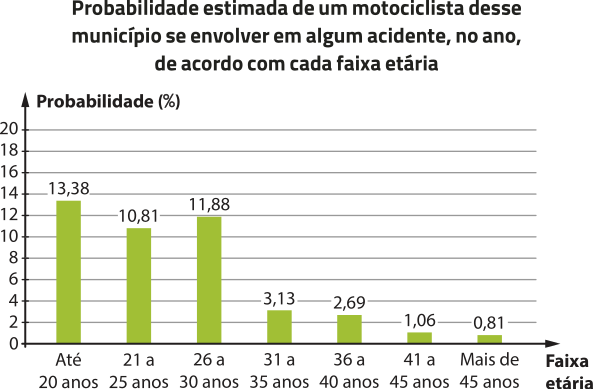
Gráfico de colunas 'Probabilidade estimada de um motociclista desse município se envolver em algum acidente, no ano, de acordo com cada faixa etária', com 7 colunas. No eixo vertical, temos a probabilidade, em porcentagem, de 0 a 20. No eixo horizontal, temos as faixas etárias. Os dados são os seguintes: até 20 anos: 13,38 por cento; 21 a 25 anos: 10,81 por cento; 26 a 30 anos: 11,88 por cento; 31 a 35 anos: 3,13 por cento; 36 a 40 anos: 2,69 por cento; 41 a 45 anos: 1,06 por cento; mais de 45 anos: 0,81 por cento.

c) n((ômega)") = 200 + 336 + 10 + 366 + 375 + 5 = 1.292

n(A) = 336 + 10 + 375 + 5 = 726

$(início da fração dê) 726 (sobre) 1.292 (fim da fração)$ ≃ 0,56 → aproximadamente 56%

63. Elaboração do estudante. Espera-se quê os estudantes elaborem e resolvam um problema envolvendo probabilidade estimada a partir do contexto dado e das informações do gráfico. Essa atividade póde sêr uma oportunidade de avaliar a aprendizagem a respeito dos conceitos estudados na Unidade.

Página trezentos e noventa e nove

Integrando com...

1. Algumas respostas possíveis: Na pesquisa genética pode-se investigar se uma pessoa é mais ou é menos propensa a desenvolver uma doença e, se for o caso, pôdêr preveni-la; avaliar as reações do organismo de uma pessoa a um tratamento ou a um medicamento; entre outras aplicações.

2. Resposta pessoal. Nesta atividade é importante considerar as respostas dos estudantes com base nas argumentações deles, quê devem sêr consistentes e pautadas em fontes confiáveis de informação.

3. São organismos quê possuem ambos os fatores, dominante e recessivo.

4. Resposta esperada: VV ou vv.

5. a) • 1 ou 100%

• 0 ou 0%

• 1 ou 100%

b) • $(início da fração dê) 3 (sobre) 4 (fim da fração)$ 0,75 ou 75%

• $(início da fração dê) 1 (sobre) 4 (fim da fração)$ , 0,25 ou 25%

• $(início da fração dê) 1 (sobre) 2 (fim da fração)$ , 0,5 ou 50%

6. a) Resposta pessoal. A resposta depende das vivências do estudante.

b) • $(início da fração dê) 2 (sobre) 4 (fim da fração)$ = $(início da fração dê) 1 (sobre) 2 (fim da fração)$ → 1 em 2, $(início da fração dê) 1 (sobre) 2 (fim da fração)$ , 0,5 ou 50%

• $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⋅ $(início da fração dê) 1 (sobre) 2 (fim da fração)$ = $(início da fração dê) 1 (sobre) 4 (fim da fração)$ → 1 em 4, $(início da fração dê) 1 (sobre) 4 (fim da fração)$ , 0,25 ou 25%

c) Pesquisa e elaboração dos estudantes. Espera-se quê, ao final da atividade, os estudantes possam compreender as características de diferentes doenças hereditárias cujas informações foram compartilhadas pêlos grupos, os números relativos à incidência, probabilidades de descendentes serem acometidos pela doença e outros aspectos com base em cálculos realizados com a utilização de conceitos estudados na Unidade.

O quê estudei

1. Respostas pessoais.

2. Resposta pessoal.

3. Respostas pessoais.

4. a) sexta-feira (5/7) e domingo (7/7)

b) • 1 − 0,90 = 0,10 → 10%

• 0,05 ⋅ 0,90 ⋅ 0,05 = 0,00225 → 0,225%

• Probabilidade de chover apenas na sexta-feira:

0,05 ⋅ 0,10 ⋅ 0,95 = 0,00475

Probabilidade de chover apenas no sábado:

0,95 ⋅ 0,90 ⋅ 0,95 = 0,81225

Probabilidade de chover apenas no domingo:

0,95 ⋅ 0,10 ⋅ 0,05 = 0,00475

0,00475 + 0,81225 + 0,00475 = 0,82175 → 82,175%

c) A probabilidade é de 5%, uma vez quê na atividade consideram-se independentes os eventos em quê chove ou não chove em cada dia.

d) 100% = 39% + 87% − P(A ⋃ B) ⇒ P(A ⋃ B) = 126% − 100% ⇒ P (A ⋃ B) = 26%

e) 1 − 0,4 = 0,6

• C_{7, 4} ⋅ ( $(início da fração dê) 40 (sobre) 100 (fim da fração)$ )⁴ ⋅ ( $(início da fração dê) 60 (sobre) 100 (fim da fração)$ )^{7 − 4} = C_{7, 4} ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )⁴ ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )³ ≃ 0,19 → aproximadamente 19%

• C_{7, 7} ⋅ ( $(início da fração dê) 40 (sobre) 100 (fim da fração)$ )⁷ ⋅ ( $(início da fração dê) 60 (sobre) 100 (fim da fração)$ )^{7 − 7} = C_{7, 7} ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )⁷ ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )⁰ ≃ 0,0016 → aproximadamente 0,16%

• C_{7, 0} ⋅ ( $(início da fração dê) 40 (sobre) 100 (fim da fração)$ )⁰ ⋅ ( $(início da fração dê) 60 (sobre) 100 (fim da fração)$ )^{7 − 0} = C_{7, 0} ⋅ ( $(início da fração dê) 2 (sobre) 5 (fim da fração)$ )⁰ ⋅ ( $(início da fração dê) 3 (sobre) 5 (fim da fração)$ )⁷ ≃ 0,028 → aproximadamente 2,8%

f) Pesquisa do estudante. Solicitar aos estudantes quê escôlham previsões para dias distintos, de modo quê os problemas e resultados possam sêr compartilhados com toda a turma para discutir as ideias e os resultados obtidos.

Praticando: enêm e vestibulares

1. alternativa d

Probabilidade de não vêr alguma das n placas: ( $(início da fração dê) 1 (sobre) 2 (fim da fração)$ )ⁿ

1 − ( $(início da fração dê) 1 (sobre) 2 (fim da fração)$ )ⁿ > $(início da fração dê) 99 (sobre) 100 (fim da fração)$ ⇒ $(início da fração dê) 1 (sobre) 100 (fim da fração)$ > ( $(início da fração dê) 1 (sobre) 2 (fim da fração)$ )ⁿ

2⁶ = 64 e 2⁷ = 128 → n = 7

7 − 1 = 6

2. alternativa c

0,30 ⋅ 0,50 + (1 − 0,30) ⋅ 0,25 = 0,30 ⋅ 0,50 + 0,70 ⋅ 0,25 = 0,325

3. alternativa b

Probabilidade de uma moeda durar três rodadas:

$(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⋅ $(início da fração dê) 1 (sobre) 2 (fim da fração)$ ⋅ $(início da fração dê) 1 (sobre) 2 (fim da fração)$ = $(início da fração dê) 1 (sobre) 8 (fim da fração)$

Probabilidade de uma moeda não durar três rodadas:

1 − $(início da fração dê) 1 (sobre) 8 (fim da fração)$ = $(início da fração dê) 8 (sobre) 8 (fim da fração)$ − $(início da fração dê) 1 (sobre) 8 (fim da fração)$ = $(início da fração dê) 7 (sobre) 8 (fim da fração)$

Probabilidade de quatro moedas não durarem três rodadas:

$(início da fração dê) 7 (sobre) 8 (fim da fração)$ ⋅ $(início da fração dê) 7 (sobre) 8 (fim da fração)$ ⋅ $(início da fração dê) 7 (sobre) 8 (fim da fração)$ ⋅ $(início da fração dê) 7 (sobre) 8 (fim da fração)$ = $(início da fração dê) 2.401 (sobre) 4.096 (fim da fração)$

Logo, a probabilidade de as quatro moedas durarem pelo menos três rodadas é:

1 − $(início da fração dê) 2.401 (sobre) 4.096 (fim da fração)$ = $(início da fração dê) 4.096 (sobre) 4.096 (fim da fração)$ − $(início da fração dê) 2.401 (sobre) 4.096 (fim da fração)$ = $(início da fração dê) 1.695 (sobre) 4.096 (fim da fração)$

4. alternativa d

$(início da fração dê) 80 (sobre) 90 (fim da fração)$ ≃ 0,89

5. alternativa d

Imagem de três conjuntos, E, F e I, localizados no interior de um quadrado identificado por ômega. Os conjuntos são representados por círculos que se sobrepõem, com interseções entre pares e também entre os três ao mesmo tempo. Há os seguintes números em cada região do diagrama: apenas em E: 16; apenas em F: 8; apenas em I: 22; na interseção entre E e F: 4; na interseção entre E e I: 10; na interseção entre F e I: 6; na interseção entre os três conjuntos: 2; fora dos conjuntos, mas ainda dentro de ômega: 12.

n(E ⋂ F) = 16 + 10 + 2 + 4 + 8 + 6 = 46

n((ômega)") = 16 + 10 + 2 + 4 + 8 + 6 + 22 + 12 = 80

$(início da fração dê) 46 (sobre) 80 (fim da fração)$ = 0,575 → 57,5%

6. alternativa b

Sair duas caras: $(início da fração dê) 2 (sobre) 3 (fim da fração)$ ⋅ $(início da fração dê) 2 (sobre) 3 (fim da fração)$ = $(início da fração dê) 4 (sobre) 9 (fim da fração)$

Página quatrocentos

Sair duas coroas: $(início da fração dê) 1 (sobre) 3 (fim da fração)$ ⋅ $(início da fração dê) 1 (sobre) 3 (fim da fração)$ = $(início da fração dê) 1 (sobre) 9 (fim da fração)$

$(início da fração dê) 4 (sobre) 9 (fim da fração)$ + $(início da fração dê) 1 (sobre) 9 (fim da fração)$ = $(início da fração dê) 5 (sobre) 9 (fim da fração)$

7. alternativa c

Soma 7: {(1, 6), (2, 5), (3, 4)} → P(C) = $(início da fração dê) 3 (sobre) 21 (fim da fração)$ = $(início da fração dê) 1 (sobre) 7 (fim da fração)$

Soma 3: {(1, 2)} → P(J) = $(início da fração dê) 1 (sobre) 21 (fim da fração)$

Soma 4: {(1, 3), (2, 2)} → P(R) = $(início da fração dê) 2 (sobre) 21 (fim da fração)$

8. alternativa e

Possíveis resultados de Ana:

8 + 9 = 9 + 8 = 17

8 + 10 = 10 + 8 = 18

9 + 10 = 10 + 9 = 19

Possíveis resultados de Béto:

3 ⋅ 5 = 5 ⋅ 3 = 15

3 ⋅ 6 = 6 ⋅ 3 = 18

5 ⋅ 6 = 6 ⋅ 5 = 30

O conjunto de pares ordenados (a, b) de possíveis resultados obtidos por Ana e Béto, respectivamente, é:

{(17, 15); (17, 18); (17, 30); (18, 15); (18, 18); (18, 30); (19, 15); (19, 18); (19, 30)}.

Temos a ≥ b em:

(17, 15); (18, 15); (18, 18) (19, 15); (19, 18)

Sendo assim, a probabilidade procurada é dada por: $(início da fração dê) 5 (sobre) 9 (fim da fração)$ .

9. alternativa d

0,25 ⋅ 20 = 5

$(início da fração dê) 5 + (x) (sobre) 20 + (x) (fim da fração)$ = $(início da fração dê) 75 (sobre) 100 (fim da fração)$ ⇒ 500 + 100x = 1.500 + 75x ⇒ 25x = 1.000 ⇒ x = 40

10. alternativa d

Moradores sem telefone móvel na área urbana: 15% dos 86% → 0,15 ⋅ 0,86 = 0,129 → 12,9%

Moradores sem telefone móvel na área rural: 40% dos 14% → 0,40 ⋅ 0,14 = 0,056 → 5,6%

Moradores sem telefone móvel: 12,9% + 5,6% = 18,5%

Assim, segue quê:

P(A | B) = $(início da fração dê) 0,056 (sobre) 0,185 (fim da fração)$ ≃ 0,303 → aproximadamente 30,3%

11. alternativa e

0,9ⁿ ≤ 0,01 ⇒ log 0,9ⁿ ≤ log 0,01 ⇒ n log 0,9 ≤ log 10⁻² ⇒

⇒ n log (9 ⋅ 10⁻¹) ≤ −2 log 10 ⇒ n (log 3² + log 10⁻¹) ≤ −2 ⇒

⇒ n(2 ⋅ 0,477 + (−1)) ≤ − 2 ⇒ −0,046n ≤ −2 ⇒

⇒ n ≥ 43,478 ⇒ n = 44

12. alternativa a

n((ômega)") = 71.114 + 5.344 + 3.961 + 1.935 + 360 + 97 + 1.459 + 324 + 233 = 84.827

n(C) = 1.459 + 324 + 233 = 2.016

n(P) = 71.114 + 1.935 + 1.459 = 74.508

n(C ⋂ P) = 2.016 + 74.508 − 1.459 = 75.065

$(início da fração dê) 75.065 (sobre) 84.827 (fim da fração)$ ≃ 0,885 → aproximadamente 88,5%

13. alternativa b

C_{5, 3} ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )³ ⋅ ( $(início da fração dê) 2 (sobre) 3 (fim da fração)$ )^{5 − 3} = C_{5, 3} ⋅ ( $(início da fração dê) 1 (sobre) 3 (fim da fração)$ )³ ⋅ ( $(início da fração dê) 2 (sobre) 3 (fim da fração)$ )² =

= 10 ⋅ $(início da fração dê) 1 (sobre) 27 (fim da fração)$ ⋅ $(início da fração dê) 4 (sobre) 9 (fim da fração)$ ≃ 0,165 → aproximadamente 0,165 ou 16,5%

14. alternativa b

Para quê o terceiro amigo seja o primeiro a retirar uma bola preta, é necessário quê os dois primeiros amigos retirem bolas brancas. A probabilidade de isso ocorrer é:

$(início da fração dê) 3 (sobre) 5 (fim da fração)$ ⋅ $(início da fração dê) 2 (sobre) 4 (fim da fração)$ ⋅ $(início da fração dê) 2 (sobre) 3 (fim da fração)$ = $(início da fração dê) 12 (sobre) 60 (fim da fração)$ = $(início da fração dê) 1 (sobre) 5 (fim da fração)$ = 0, 20 = 20%

15. alternativa b

Pedrinhas na sacola no momento da parada para o lanche: 25 pedrinhas brancas (60 − 35 = 25) e 15 pedrinhas pretas (40 − 25 = 15), ou seja, 40 pedrinhas ao todo (25 + 15 = 40). Segue quê:

$(início da fração dê) 25 (sobre) 40 (fim da fração)$ ⋅ $(início da fração dê) 24 (sobre) 39 (fim da fração)$ = $(início da fração dê) 5 (sobre) 8 (fim da fração)$ ⋅ $(início da fração dê) 24 (sobre) 39 (fim da fração)$ = $(início da fração dê) 120 (sobre) 312 (fim da fração)$ = $(início da fração dê) 5 (sobre) 13 (fim da fração)$

16. alternativa d

$(início da fração dê) 18 (sobre) 20 (fim da fração)$ ⋅ $(início da fração dê) 17 (sobre) 19 (fim da fração)$ = $(início da fração dê) 306 (sobre) 380 (fim da fração)$ = $(início da fração dê) 153 (sobre) 190 (fim da fração)$

17. alternativa e

Quantidade de maneiras distintas de sortear 3 pessoas dentre 20:

C_{20, 3} = $(início da fração dê) 20 (fatorial) (sobre) 3 (fatorial) (vezes) (abre parenteses) 20 (menos) 3 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 20 (vezes) 19 (vezes) 18 (sobre) 3 (vezes) 2 (vezes) 1 (fim da fração)$ = 1.140

Quantidade de maneiras distintas de sortear 2 pessoas dentre 6 quê tocam violão:

C_{6, 2} = $(início da fração dê) 6 (fatorial) (sobre) 2 (fatorial) (vezes) (abre parenteses) 6 (menos) 2 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 6 (vezes) 5 (sobre) 2 (vezes) 1 (fim da fração)$ = 15

Quantidade de maneiras distintas de sortear 1 pessoa dentre 14 quê não tocam violão:

C_{14, 1} = $(início da fração dê) 14 (fatorial) (sobre) 1 (fatorial) (vezes) (abre parenteses) 14 (menos) 1 (fécha parenteses) (fatorial) (fim da fração)$ = $(início da fração dê) 14 (sobre) 1 (fim da fração)$ = 14

Assim, segue quê:

$(início da fração dê) 14 (vezes) 15 (sobre) 1.140 (fim da fração)$ = $(início da fração dê) 210 (sobre) 1.140 (fim da fração)$ = $(início da fração dê) 7 (sobre) 38 (fim da fração)$

18. alternativa d

Probabilidade de não obtêr face vermelha em nenhum lançamento:

$(início da fração dê) 5 (sobre) 6 (fim da fração)$ ⋅ $(início da fração dê) 5 (sobre) 6 (fim da fração)$ = $(início da fração dê) 25 (sobre) 36 (fim da fração)$

Probabilidade de obtêr face vermelha em ao menos um lançamento:

1 − $(início da fração dê) 25 (sobre) 36 (fim da fração)$ = $(início da fração dê) 36 (sobre) 36 (fim da fração)$ − $(início da fração dê) 25 (sobre) 36 (fim da fração)$ = $(início da fração dê) 11 (sobre) 36 (fim da fração)$

	AC	AM	AP	PA	RO	RR	TO
AC	0	1	0	0	1	0	0
AM	1	0	0	1	1	1	0
AP	0	0	0	1	0	0	0
PA	0	1	1	0	0	1	1
RO	1	1	0	0	0	0	0
RR	0	1	0	1	0	0	0
TO	0	0	0	1	0	0	0

	AC	AM	AP	PA	RO	RR	TO
AC	0	1	0	0	1	0	0
AM	1	0	0	1	1	1	0
AP	0	0	0	1	0	0	0
PA	0	1	1	0	0	1	1
RO	1	1	0	0	0	0	0
RR	0	1	0	1	0	0	0
TO	0	0	0	1	0	0	0

	AC	AM	AP	PA	RO	RR	TO
AC	0	1	0	0	1	0	0
AM	1	0	0	1	1	1	0
AP	0	0	0	1	0	0	0
PA	0	1	1	0	0	1	1
RO	1	1	0	0	0	0	0
RR	0	1	0	1	0	0	0
TO	0	0	0	1	0	0	0