Página 316
UNIDADE 5
MOVIMENTO E O SER HUMANO
Andar, correr, subir escadas, segurar objetos e digitar no teclado do computador. Todos esses movimentos podem parecer simples e corriqueiros em nosso dia a dia, mas exigem o trabalho em conjunto de diversos sistemas do corpo humano. Além disso, por vários motivos, como doenças e acidentes, algumas pessoas são incapazes de realizar tais movimentos ou os realizam de modo limitado.
Algumas pessoas não têm um ou mais membros do corpo, por exemplo. Nesses casos, a falta desses membros impossibilita a realização de alguns movimentos, o que, por sua vez, pode dificultar a realização de algumas tarefas diárias. Pensando em melhorar a qualidade de vida dessas pessoas, foram desenvolvidas próteses biônicas, que visam imitar partes do corpo humano. Ao longo do tempo, com o auxílio da tecnologia, esses itens foram se aperfeiçoando e atualmente permitem a realização de movimentos diversos e cada vez mais precisos, controlados pelo usuário da prótese.
Os movimentos da prótese de mão, como a da imagem, são comandados por estímulos nervosos captados por eletrodos, que se comunicam com os músculos da parte restante do membro superior.
a ) Como os conhecimentos de Física e de outras áreas das Ciências da Natureza podem ser úteis para auxiliar o desenvolvimento de próteses?
b ) Atualmente, há pesquisas para desenvolver robôs humanoides que se movimentam em duas pernas. Em sua opinião, quais são os principais desafios para que os robôs fiquem em pé e/ou se movimentem em duas pernas?
c ) Por que sentimos mais cansaço físico quando corremos certa distância do que quando percorremos a mesma distância andando calmamente?
Respostas nas Orientações para o professor.
Nesta unidade, vamos estudar...
- máquinas simples;
- momento de uma força;
- equilíbrio de um corpo extenso;
- movimento uniforme e uniformemente variado;
- movimento circular;
- trabalho de uma força;
- energia mecânica;
- potência mecânica;
- impulso e quantidade de movimento;
- conservação da quantidade de movimento.
Página 317

Página 318
CAPÍTULO20
Ferramentas e máquinas simples
Desenvolvimento de ferramentas e máquinas simples
Confira a imagem a seguir.

1. Você é capaz de imaginar exemplos de ferramentas e máquinas simples que tenham rodas, polias, planos inclinados ou alavancas e que sejam utilizadas na sociedade moderna? Cite exemplos de aplicações dessas máquinas.
Resposta pessoal. Os estudantes podem citar as rodas de veículos dos mais variados tipos (automóveis, caminhões, ônibus, tratores etc.), parafusos, ferramentas com vários tamanhos de cabos (que facilitam a tarefa de soltar parafusos, como chaves de roda) e sistemas de roldanas para erguer corpos de muita massa. Podem citar ainda exemplos de ferramentas que facilitam a realização de tarefas cotidianas, como tesoura, alicate, martelo, cortador de unha, abridor de latas, macaco para troca de pneus de um automóvel, vara de pescar e carriola.
O guindaste mostrado tem um sistema de roldanas e cabos que possibilita a sustentação e o movimento de corpos de grande massa, aplicando intensidade de força menor do que a necessária para sustentar diretamente o corpo. Diversas máquinas modernas são formadas por partes que utilizam princípios físicos descobertos ou desenvolvidos há muito tempo, como as roldanas, os planos inclinados, os parafusos e as alavancas. Esses componentes são chamados máquinas simples.
As máquinas simples são dispositivos desenvolvidos com o objetivo de facilitar a execução de tarefas do cotidiano, alterando a força aplicada sobre diversos objetos, seja na intensidade, na orientação ou em ambos os fatores.
O desenvolvimento dos elementos aplicados nas máquinas simples provavelmente teve início com as primeiras espécies de hominíneos, que utilizaram rochas a fim de criar ferramentas.
Algumas das ferramentas mais antigas, encontradas por pesquisadores na Etiópia, eram feitas de rochas e têm idade estimada de 2,6 milhões de anos. A fabricação dessas ferramentas foi atribuída ao Homo habilis, uma das espécies de hominíneos relacionada ao surgimento do Homo sapiens (ser humano moderno).

Embora essa espécie de hominíneo ainda seja considerada precursora do desenvolvimento de ferramentas, foram descobertos no Quênia artefatos de rocha ainda mais antigos, produzidos há cerca de 3,3 milhões de anos pelos Kenyanthropus platyops (cerca de 700 mil anos antes daqueles encontrados na Etiópia). A descoberta desses artefatos sugere que hominíneos primitivos eram capazes de produzir ferramentas muito tempo antes do que se acreditava e que membros do gênero Homo não foram os primeiros a criar ferramentas de rocha.
Página 319
Máquinas simples
Suponha que você tenha ganhado uma porção de castanha-do-pará com casca, como as mostradas na fotografia. Portanto, para comê-las, você deve quebrar a casca dura e retirar a castanha de seu interior.
Semente da castanheira-do-pará (Bertholletia excelsa): pode atingir aproximadamente 7 centímetros de comprimento

Imagine que próximo a você haja uma rocha do tamanho aproximado de sua mão e um martelo.
Dica
O uso de ferramentas exige cuidado para que não ocorram acidentes. Peça ajuda a um adulto.
2. Qual desses objetos exige menos esforço para quebrar a casca da castanha-do-pará: um martelo ou uma rocha?
Resposta: O martelo exige menos esforço por causa de seu cabo, o qual proporciona vantagem mecânica.
Na situação proposta na questão, os dois objetos podem ser utilizados como ferramentas para quebrar a casca que envolve a castanha. No entanto, o martelo proporciona uma vantagem em virtude do comprimento do cabo.
Se você utilizasse a rocha para quebrar a casca, ela atingiria a castanha na mesma velocidade que sua mão, pois, nesse caso, você teria de segurá-la diretamente nas mãos. Isso exige a aplicação de uma força para movimentar a rocha com rapidez suficiente para quebrar a casca.
Já com o martelo, ao segurar essa ferramenta pelo cabo e fazer o movimento na direção do alvo, a cabeça do martelo faz um movimento em um arco maior do que o da sua mão e, por isso, ele atinge o alvo a uma velocidade maior do que a da sua mão. Portanto, para produzir o mesmo efeito no alvo, a força aplicada no martelo é menor. Trata-se do efeito de uma alavanca.
Imagens desta página sem proporção.

Dessa maneira, percebemos que o uso de máquinas simples facilita a execução de diversas atividades, alterando a intensidade e/ou a direção e o sentido da força necessária para realizá-las. A seguir, estudaremos diferentes tipos de máquinas simples, como as rodas e polias, as alavancas e o plano inclinado.
Rodas e polias
Já vimos que a invenção da roda data de aproximadamente 3500 anos a.C., na Mesopotâmia, e que ela foi utilizada inicialmente como roda de oleiro para fabricação de objetos de argila.
Esse objeto representa um grande passo para a evolução da tecnologia, contribuindo não apenas para uma cerâmica de melhor qualidade, mas também para o princípio geral de aplicação da roda nos transportes e nas máquinas. Algum tempo depois da invenção da roda, foram encontradas evidências dos primeiros veículos com rodas. Também na Mesopotâmia foram descobertos vestígios das primeiras carroças com rodas de madeira maciça.

Página 320
Ao longo do tempo, a roda passou por uma série de evoluções, modificações e aplicações em diversas outras funções. Por volta do ano 2000 a.C., surgiram no norte da Europa e na Ásia rodas com raios, o que as tornavam mais leves, e elas eram usadas em carruagens e carroças para o transporte de pessoas e cargas. Já no ano 1000 a.C. na Europa Ocidental, os celtas começaram a revestir as rodas de madeira das carruagens com um aro de metal, aumentando a resistência e a durabilidade das rodas. Somente nos séculos XIX e XX, foram desenvolvidas as rodas com pneus de borracha e câmaras de ar e as rodas para serem usadas nos automóveis. Atualmente, utilizam-se ligas metálicas e compostos de carbono nas rodas de veículos.

Compartilhe ideias
Em nosso cotidiano, há diversos equipamentos que utilizam rodas para funcionar.
a ) Converse com seus colegas e cite exemplos de situações do dia a dia em que se utilizam as rodas e imagine como seriam essas tarefas sem elas. Com base nessa discussão, proponham um novo dispositivo que possa substituir a roda em uma das situações citadas.
Resposta pessoal. Os estudantes podem mencionar situações, como em bicicletas, carros, carrinhos de supermercado e até em móveis, como cadeiras de escritório. Ao conversar com os colegas, uma ideia para substituir a roda em carrinhos de supermercado poderia ser o uso de uma espécie de "almofada de ar" ou sistema de levitação magnética, que permitiria ao carrinho flutuar e se mover suavemente sem atrito com o chão, facilitando o transporte de cargas sem a necessidade de rodas tradicionais.
Outra aplicação que pode ser ressaltada é a roda-d'água. Esse equipamento usa o movimento da água para girar uma roda que, por sua vez, movimenta moinhos de grãos ou bombas-d'água.
A transmissão de movimento é feita por engrenagens, também chamadas de rodas dentadas ou polias, que se conectam umas às outras. Dessa forma, o movimento da roda-d'água pode ser transferido alterando-se a direção (de vertical para horizontal, por exemplo), o sentido e a velocidade da rotação.
A transmissão de movimento entre polias pode ser realizada por uma associação coaxial ou por uma associação periférica. Nas imagens a seguir são apresentados esses tipos de associações.

Na associação coaxial, mostrada em A, as polias são conectadas a um eixo comum, de modo que todas girem junto ao eixo.
A.

Na associação periférica, geralmente as polias são conectadas por correias ou correntes (B). No caso de engrenagens, a associação é feita pelo contato direto (C).
B.

C.

Página 321
As polias também podem ser utilizadas para transmitir força por meio de cabos ou correias, como em mastros de bandeiras, equipamentos de ginástica, barcos, elevadores, guindastes e persianas.
Nesses casos, as polias podem ser classificadas em fixas ou móveis, o que altera as características de sua funcionalidade. Além disso, elas podem ser associadas com outras polias, formando sistemas que, por sua vez, têm características diferentes de acordo com a disposição das polias, o número de cordas utilizadas, entre outros fatores.
Considere a situação em que é necessário erguer um balde, com areia, para o andar superior de uma construção, estando um trabalhador no andar de baixo e outro no de cima.
Utilizando uma corda presa no balde e passando-a por uma polia, pode-se aplicar uma força na corda para baixo, fazendo o balde de areia subir até a laje de uma construção.

3. Como os trabalhadores poderiam fazer para subir o balde sem o uso da polia?
Resposta: Os trabalhadores teriam de se deslocar do chão até a laje carregando o balde ou teriam de prender uma corda no balde e subi-lo até a laje superior, puxando a corda para cima.
Note que nessa situação o eixo da polia não pode se deslocar (sofrer translação), por isso ela é classificada como uma polia fixa.
Na polia fixa, o eixo é preso em um suporte de apoio, de modo que ela realiza apenas movimento de rotação em torno do próprio eixo.
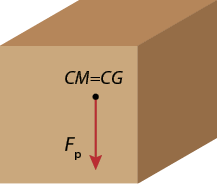
Na imagem a seguir, para manter a caixa em equilíbrio, é necessário aplicar uma força abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses com a mesma intensidade da força peso abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito P fecha parênteses da caixa, isto é, a intensidade da força para realizar a tarefa não é alterada. Considerando que a corda e a polia são ideais, ou seja, a corda tem massa desprezível e não varia seu comprimento (inextensível), e a polia tem massa e atrito desprezíveis, podemos dizer que a força resultante na caixa é nula, pois a força de tensão abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito T fecha parênteses na corda tem a mesma intensidade que a força peso abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito P fecha parênteses.
Imagem sem proporção e em cores fantasia.
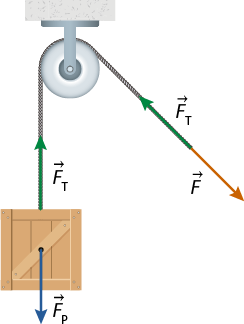
'F' subscrito T é igual a 'F' subscrito P
Se a força peso da caixa tem intensidade de 50 newtons, por exemplo, a força expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima aplicada na corda para manter o conjunto em equilíbrio também tem intensidade de 50 newtons.
Página 322
Diferentemente da polia fixa, as polias móveis têm o eixo livre, ou seja, podem se deslocar com a carga, realizando os movimentos de translação e de rotação.
No sistema mostrado a seguir, o corpo está preso ao eixo da polia de modo que ele é sustentado por duas ou mais forças de tração. Como uma das extremidades está presa ao teto, somente parte da intensidade da força peso expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito P é transmitida para a extremidade livre da corda, onde será aplicada a força.
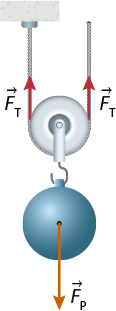
Nessa situação, a intensidade da força aplicada na extremidade livre, para manter o sistema em equilíbrio, tem metade da intensidade da força peso do corpo.
Essa característica da polia móvel faz a força necessária para erguer um corpo ter intensidade menor do que a força peso dele. Em contrapartida, é preciso realizar um deslocamento maior da corda em comparação com o respectivo deslocamento do corpo na direção vertical.
Para obter mais vantagem, podemos realizar uma associação de polias. Assim, aumentamos o efeito da força aplicada no sistema, reduzindo o esforço para levantar uma carga ou mantê-la em equilíbrio.
Nas imagens a seguir há exemplos de associações de polias móveis com polias fixas, conhecidas como talhas exponenciais.
Imagens desta página sem proporção e em cores fantasia.
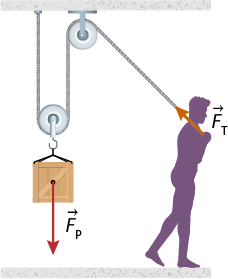
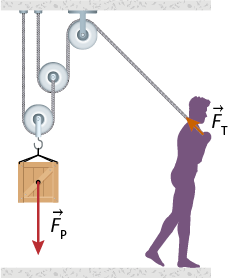
Nas talhas exponenciais, a força necessária para elevar a carga é dividida pela metade entre cada polia móvel utilizada. Assim, a intensidade da força expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito T que deve ser aplicada é dada pela relação a seguir.
'F' subscrito T é igual a início de fração, numerador: 'F' subscrito P, denominador: 2 elevado a n, fim de fração
em que:
- 'F' subscrito P é a intensidade da força peso do corpo, em newton (N);
- 'F' subscrito T é a intensidade da tração que deve ser aplicada na corda, em newton;
- n é a quantidade de polias móveis no sistema.
Em um sistema de polias, pode-se verificar a chamada vantagem mecânica abre parênteses V subscrito mec fecha parênteses, dada pela razão entre a intensidade da força resistente abre parênteses 'F' subscrito res fecha parênteses, que geralmente equivale à força peso do corpo, e a intensidade da força aplicada ou potente abre parênteses 'F' subscrito po fecha parênteses.
V subscrito mec é igual a início de fração, numerador: 'F' subscrito res, denominador: 'F' subscrito p o, fim de fração
em que:
- 'F' subscrito res é a intensidade da força resistente, em newton;
- 'F' subscrito p o é a intensidade da força potente, em newton;
- V subscrito mec é a vantagem mecânica.
Quando a força necessária para erguer um corpo tem intensidade menor do que a força peso do corpo, como no caso da aplicação de polias móveis, a vantagem mecânica é maior do que 1. Para as polias fixas, a vantagem mecânica é igual a 1, pois a força necessária para levantar um corpo nesse sistema tem módulo igual à força peso.
Página 323
ATIVIDADES
1. Explique, com suas palavras, a importância da invenção da roda para o desenvolvimento das máquinas simples, como as polias e as engrenagens.
Resposta pessoal. Espera-se que os estudantes argumentem que o desenvolvimento da roda possibilitou a construção de máquinas baseadas em movimento de rotação, como as polias e as engrenagens, que, por sua vez, passaram a fazer parte de máquinas mais complexas.
2. Um agricultor possui um poço em seu sítio e pre- cisa coletar água dele manualmente, utilizando um balde. Ele pensou em prender uma corda no balde, mergulhá-lo no poço e em seguida puxá-lo para cima, cheio de água. Contudo, seu filho, que é um bom estudante de Física, explicou-lhe que essa tarefa pode se tornar perigosa ao se aproximar demais da borda do poço, pois pode cair dentro dele enquanto puxa a corda para cima. Então, ele sugeriu que seu pai utilizasse uma polia fixa para essa tarefa, diminuindo os riscos. Explique como a utilização de uma polia fixa pode ajudar o agricultor a realizar a atividade de modo mais seguro.
Esse trabalho pode ser realizado de maneira mais segura ao se utilizar uma polia fixa, pois pode-se manter uma distância segura da borda do poço, aplicar uma força em uma direção diferente da vertical, de modo que a polia fixa altere a direção da força, fazendo o balde com água subir até a superfície.
3. Uma estudante que acabou de ter aula de Física sobre associação de polias decidiu fazer um desafio para seu primo: erguer um saco de areia com massa de 70 vírgula 0 quilogramas. O primo topou o desafio, mas foi incapaz de levantar o corpo com tamanha massa. A garota então pegou um sistema composto de cabos passando por uma polia fixa e algumas polias móveis, prendeu uma das extremidades do cabo no saco de areia e segurou a outra extremidade. Começou a puxar a carga com apenas uma mão, erguendo-a sem muitas dificuldades. Considere a aceleração da gravidade dada por 'g' é igual a 10 vírgula 0 metros por segundo quadrado e responda às questões a seguir.
a ) Supondo que a estudante seja capaz de erguer até 15 vírgula 0 quilogramas com apenas uma mão, determine a quantidade mínima de polias mó- veis presentes no sistema.
b ) Considere que o sistema seja composto de quatro polias móveis e que a garota ergueu o saco de areia com velocidade constante. Calcule a vantagem mecânica desse sistema.
4. Para erguer uma bandeira em um mastro, utiliza-se uma corda que passa por uma polia fixa presa em um suporte no alto do mastro. Explique a importância da utilização da polia nesse sistema: como seria a tarefa de hastear uma bandeira sem usar uma polia?
Resposta: A polia fixa tem a função de alterar a direção da força aplicada na corda. Para erguer a bandeira, basta puxar a corda para baixo, enquanto a roldana faz a bandeira subir ao mudar a direção da força aplicada na corda. Para hastear uma bandeira sem utilizar uma polia, seria preciso subir no mastro e puxá-la com uma corda.
5. Para decorar uma festa, foi pendurada uma estrela com massa de 5 kg que ficou suspensa por dois fios inextensíveis fixos um em cada lado da parede, com a decoração no meio. Os fios formaram um ângulo de 60 graus com a horizontal. Para que a estrela fique pendurada e não caia, qual deve ser a tensão individual de cada fio? Considere 'g' é igual a 10 metros por segundo quadrado.
6. Na figura a seguir, uma pessoa está segurando um corpo de massa M suspenso por um sistema de polias contendo três polias móveis e uma fixa, presa ao teto. Considere a aceleração da gravidade sendo 'g' é igual a 10 vírgula 0 metros por segundo quadrado e responda às questões.
Imagens desta página sem proporção e em cores fantasia.
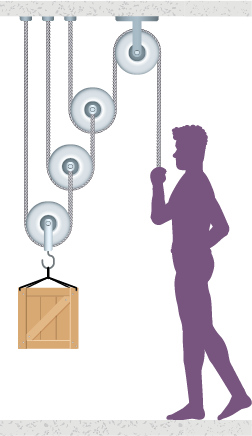
Supondo que a pessoa esteja aplicando uma força de 200 newtons para manter o sistema em equilíbrio, determine a massa M.
7. Observe a montagem a seguir.
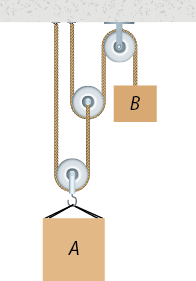
Sabendo que o corpo A tem massa de 24 quilogramas e que o sistema está em equilíbrio, determine a massa do corpo B.
Respostas e resoluções das questões 3, 5, 6 e 7 nas Orientações para o professor.
Página 324
Alavancas
Confira a imagem de um mecânico soltando os parafusos da roda de um carro.

4. A ferramenta utilizada pelo mecânico na imagem pode ter o comprimento de seu cabo aumentado. Qual vantagem isso pode trazer?
Resposta: O objetivo desta questão é verificar os conhecimentos prévios dos estudantes com relação às alavancas. Eles podem citar que a chave de roda atua como uma alavanca e que, aumentando o braço da alavanca, a intensidade da força necessária para retirar o parafuso é menor.
A chave de roda, utilizada pelo mecânico, atua como uma máquina simples conhecida como alavanca.
As alavancas são, geralmente, constituídas de uma barra rígida que gira em torno de um ponto de apoio fixo, chamado fulcro. No exemplo anterior, o fulcro da alavanca coincide com o parafuso.
A vantagem de utilizar alavancas é a redução da intensidade da força necessária para realizar uma tarefa. Essa propriedade é utilizada há muito tempo, para diversas atividades, como mover, sustentar ou carregar objetos.
Em uma alavanca, devemos considerar duas forças: a força aplicada ou força potente abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito po fecha parênteses e a força de resistência da carga ou força resistente abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito res fecha parênteses. Outros fatores importantes são os chamados braços de alavancas, que são determinados com base na posição do ponto de apoio até o ponto de aplicação da força. expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito N é a força normal do apoio sustentando a barra da alavanca.
A distância entre o ponto de apoio e o ponto de aplicação da força potente recebe o nome de braço de potência abre parênteses b subscrito p o fecha parênteses, enquanto a distância entre o ponto de apoio até a força resistente é denominada braço de resistência abre parênteses b subscrito res fecha parênteses.
Imagem sem proporção e em cores fantasia.
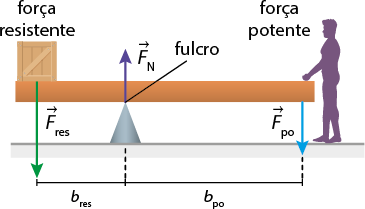
Imagem elaborada com base em: TREFIL, James; HAZEN, Robert Miller. Física viva: uma introdução à física conceitual. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2006. v. 1. p. 147.
A condição de equilíbrio de uma alavanca é dada por:
'F' subscrito p o vezes b subscrito po é igual a 'F' subscrito res vezes b subscrito res
A relação matemática anterior representa a vantagem mecânica das alavancas. Ela revela que, quanto maior o braço de potência em relação ao braço de resistência, menor será a força necessária para equilibrar a carga, ou seja, menor será o esforço para realizar a tarefa. Por isso, há o cabo extensível na chave de roda na fotografia do início da página.
As alavancas são divididas em três tipos principais de acordo com as posições relativas da força potente, da força resistente e do ponto de apoio, sendo classificadas em: interfixa, interpotente e inter-resistente.
Página 325
Uma alavanca interfixa é caracterizada por ter o apoio entre as extremidades nas quais as forças são aplicadas. Alguns exemplos de alavancas interfixas são a tesoura, o alicate e a gangorra.
Imagens desta página sem proporção e em cores fantasia.

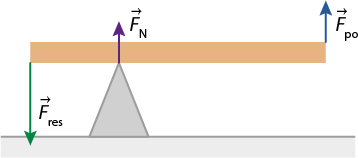
Imagem elaborada com base em: GRUPO DE REELABORAÇÃO DO ENSINO DE FÍSICA. Leituras de física: mecânica. São Paulo: Instituto de Física da USP. v. 1. p. 102. Disponível em: https://s.livro.pro/m5cpmg. Acesso em: 11 set. 2024.
No caso da alavanca interpotente, o ponto de aplicação da força potente se localiza entre o ponto de apoio e o ponto de aplicação da força resistente. Nessa alavanca, a intensidade da força potente pode ser maior do que a intensidade da força resistente. Exemplos de alavancas interpotentes são o pegador de gelo, o pegador de macarrão, a pinça e a vara de pescar.

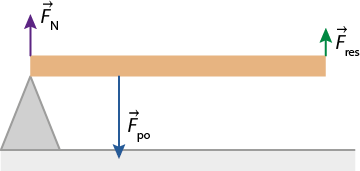
Imagem elaborada com base em: GRUPO DE REELABORAÇÃO DO ENSINO DE FÍSICA. Leituras de física: mecânica. São Paulo: Instituto de Física da USP. v. 1. p. 102. Disponível em: https://s.livro.pro/m5cpmg. Acesso em: 11 set. 2024.
Na alavanca inter-resistente, o ponto de aplicação da força resistente fica entre o apoio e o ponto de aplicação da força potente. São exemplos de alavancas inter-resistentes a carriola (carrinho de mão), o espremedor de alho, o abridor de garrafas e o quebra-nozes.

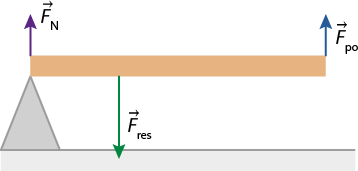
Imagem elaborada com base em: GRUPO DE REELABORAÇÃO DO ENSINO DE FÍSICA. Leituras de física: mecânica. São Paulo: Instituto de Física da USP. v. 1. p. 102. Disponível em: https://s.livro.pro/m5cpmg. Acesso em: 11 set. 2024.
Outra aplicação desse princípio pode ser observada na gangorra. Se duas pessoas de massas muito diferentes forem brincar e ambas se sentarem nas extremidades da gangorra, haverá um desequilíbrio e o brinquedo não vai se movimentar adequadamente. Para solucionar esse problema, a pessoa de maior massa poderia se sentar mais próximo do ponto de apoio, diminuindo seu respectivo braço de alavanca e, assim, equilibrando a gangorra para que possam brincar.

Página 326
PRÁTICA CIENTÍFICA
O princípio das alavancas em instrumentos medievais
Por dentro do contexto
Comentários nas Orientações para o professor.
Ao longo da história, a inovação tecnológica influenciou estratégias militares. Um exemplo disso é o uso de catapultas e trabucos, que são estruturas que revolucionaram a forma como os projéteis eram lançados a grandes distâncias.
O funcionamento dessas armas se baseia no princípio das alavancas, uma vez que elas têm um ponto de apoio e um braço que gira em relação a esse ponto. Um dos fatores que transformou o uso das catapultas foi o desenvolvimento da balística, que é o estudo do movimento de projéteis.
Diversos relatos históricos da Antiguidade e da Idade Média retratam batalhas que foram decididas com o uso de catapultas e trabucos, por exemplo.


a ) Como a balística ajudava na utilização das catapultas e dos trabucos?
Resposta: A balística otimizava o alcance, a precisão e a eficácia dos projéteis, ajustando ângulos, força e condições de lançamento.
b ) Em sua opinião, existe um limite de massa que pode ser arremessada por um trabuco ou uma catapulta com uma determinada dimensão?
Resposta: Sim. Esse limite é determinado pela capacidade das alavancas no mecanismo, pois a força gerada e a estabilidade do lançamento dependem do comprimento e da força aplicada nas alavancas.
Materiais
- 10 lápis número 2
- elásticos
- tampa de garrafa PET
- pistola de cola quente
- pequenos objetos para serem lançados, como bolinhas de papel
- objetos para servir de contrapeso, como chumbadas de pesca
Como proceder
A. Junte dois lápis de modo que fiquem paralelos. Em seguida, posicione um terceiro lápis perpendicularmente aos outros dois, cruzando-o a cerca de um terço do comprimento total dos dois paralelos. Prenda-os com um elástico.
Imagem sem proporção e em cores fantasia.

B. Depois, disponha quatro lápis de modo a formar um quadrado. Prenda-os dois a dois com um elástico em cada uma das pontas.
Dica
Certifique-se de que os lápis paralelos estejam bem alinhados e paralelos para garantir que o braço da catapulta funcione corretamente.
Página 327
Cuidado
As pontas dos lápis podem ser afiadas e causar ferimentos. Manuseie com cuidado para evitar cortes. Evite esticar os elásticos além dos seus limites para prevenir que se rompam e atinjam seu rosto.
Dica
Não atire objetos na direção de seus colegas, professor ou qualquer outra pessoa. Utilizem o equipamento com responsabilidade para evitar acidentes.
C. Junte o lápis perpendicular, passando-o a cerca de um terço do lado superior do quadrado e prendendo com dois elásticos nas pontas. Então, passe um elástico cruzando o quadrado de modo que fique próximo à extremidade do braço da catapulta.
D. Para construir a base, adicione três lápis na parte inferior do quadrado inicial, conectando-os com elásticos e criando um novo quadrado na parte inferior.
E. Depois, adicione um lápis de cada lado conectando os quadrados pelos vértices livres, como mostra a imagem.
F. Para finalizar, peça a um adulto que use a cola quente para prender a tampa na extremidade dos lápis paralelos (braço da catapulta).
Imagem sem proporção e em cores fantasia.
Dica
No caso da produção de um trabuco, o elástico da base do braço da catapulta deve ser substituído por um contrapeso, que pode ser feito com chumbadas para pesca.
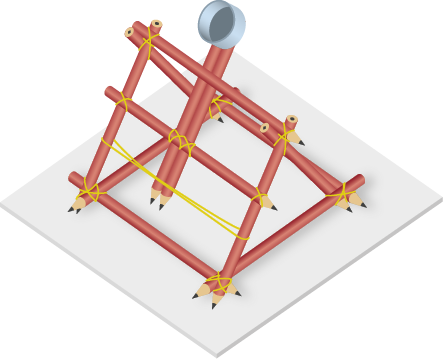
G. Coloque uma bolinha de papel na tampinha. Puxe-a para trás esticando o elástico e solte, lançando o objeto. Meça a distância percorrida pela bolinha em diferentes lançamentos e anote os valores no caderno.
H. Varie a força com que o elástico é esticado (puxando a tampinha mais ou menos) e observe como isso afeta a distância e a velocidade da bolinha.
I. Por fim, registre os dados em uma tabela para diferentes níveis de esticamento.
Análise e divulgação
1. Como o princípio da alavanca pode ser verificado no lançador de projéteis que vocês construíram?
Resposta: Os estudantes devem perceber que onde eles posicionam o projétil há um ponto de apoio e dois locais de aplicação de forças, ligados por uma barra sólida, como uma alavanca. O projétil aplica a força resistente e o dispositivo faz a catapulta funcionar, aplicando a força potente.
2. Qual material faz o equipamento lançar os projéteis?
Resposta: Espera-se que os estudantes citem que o elástico ou o contrapeso faz os objetos serem lançados. Isso dependerá do tipo de projeto que fizerem.
3. O que vocês poderiam alterar, na catapulta ou no trabuco, para lançar objetos a maiores ou menores distâncias?
Resposta: Pode-se alterar o comprimento do braço da catapulta, afetando seu desempenho segundo o princípio das alavancas. O arremesso dos objetos também depende do quanto o braço for girado, pois isso altera a energia armazenada no elástico. Outra possibilidade é alterar o tipo de elástico utilizado como propulsor, assim como o tipo e a massa do projétil. No caso de um trabuco, pode-se alterar também a relação entre os braços da alavanca e o tamanho do contrapeso.
4. Como é possível prever o movimento do projétil para atingir um alvo específico?
Resposta: Espera-se que os estudantes respondam que poderiam prever o movimento do projétil utilizando as relações do lançamento oblíquo, identificando o ângulo e estimando a velocidade do lançamento.
5. O que acontece se trocarmos a bolinha de papel por um objeto de massa diferente? A distância percorrida será a mesma?
Resposta: Não, a distância não será a mesma. Se o objeto tiver uma massa maior, ele tende a percorrer distância menor, porque maior massa exige maior força para atingir a mesma velocidade.
6. Que tipo de energia está armazenada quando o elástico é esticado e que tipo de energia a bolinha tem durante o movimento?
Resposta: Quando o elástico é esticado, este armazena energia potencial elástica. No momento em que é solto, essa energia potencial se transforma em energia cinética, que é transferida para a bolinha, fazendo-a se mover.
7. Agora que você investigou o funcionamento de uma catapulta e analisou sua funcionalidade, assim como os fatores que afetam seu desempenho e sua relação com as alavancas, faça uma postagem em sua rede social mostrando fotografias de seu projeto e as etapas de execução. Componha um texto para legendar as fotografias, descrevendo sua análise e suas conclusões sobre o projeto. Divulgue para outros estudantes terem acesso aos resultados.
Resposta: Espera-se que os estudantes fotografem as etapas do projeto e/ou seu resultado final, descrevendo de forma resumida suas conclusões e os pontos que acharam mais importantes, de forma a divulgar em suas redes sociais
Atividade(s) adaptada(s) acessível(is)
7. Agora que você investigou o funcionamento de uma catapulta e analisou sua funcionalidade, assim como os fatores que afetam seu desempenho e sua relação com as alavancas, junte-se a um colega e façam uma postagem em uma rede social mostrando imagens de seus projetos e as etapas de execução. Elaborem legendas para as imagens, descrevendo as análises e as conclusões sobre o projeto. Divulguem a postagem para outros estudantes terem acesso aos resultados.
Resposta: Espera-se que os estudantes fotografem e descrevam as etapas do projeto e/ou do seu resultado, relatando de forma resumida as conclusões e os pontos que acharam mais importantes, de forma a divulgá-los nas redes sociais.
Orientação para acessibilidade
Professor, professora: Organize os grupos de modo que o estudante não vidente esteja acompanhado de um estudante vidente.
Página 328
ATIVIDADES
Imagens desta página sem proporção e em cores fantasia.
1. Confira as fotografias a seguir.
A.

B.

C.

D.

E.

a ) Classifique as alavancas mostradas em interpotente, inter-resistente e interfixa.
Resposta: O alicate é uma alavanca interfixa; a carriola e o abridor de garrafas são alavancas inter-resistentes; a pinça e o pegador de macarrão são alavancas interpotentes.
b ) Em quais das alavancas a força potente é maior do que a força de resistência?
Resposta: Nas alavancas B (pinça) e E (pegador de macarrão).
2. A noz mostrada na imagem necessita de uma força de 200 newtons para ser quebrada. Qual é a intensidade da força que a pessoa deve aplicar na extremidade do quebrador de nozes?
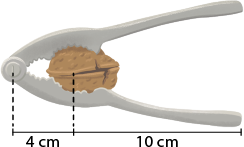
Resposta: 'F' subscrito p o é igual a 57 vírgula 1 newton, aproximadamente. Resolução nas Orientações para o professor.
3. Em uma gangorra com comprimento total de 4 metros, uma pessoa com massa de 60 quilogramas senta-se a uma distância de 1 vírgula 2 metro em relação ao ponto de apoio central. Em qual posição uma pessoa de 80 quilogramas deve se sentar para que a gangorra fique em equilíbrio?
Resposta: b subscrito p o é igual a 0 vírgula 9 metro. Resolução nas Orientações para o professor.
4. Um operário deseja levantar uma caixa de 200 quilogramas usando uma alavanca interfixa. O ponto de apoio da alavanca está localizado a 0 vírgula 5 metro da caixa e a 1 vírgula 5 metro do ponto onde ele aplica a força. Supondo que a aceleração da gravidade seja de 10 metros por segundo quadrado, qual é o menor valor da força 'F' que o operário deve aplicar para levantar a caixa?
Resposta: 'F' subscrito po é aproximadamente igual a 666 vírgula 7 newton, aproximadamente. Resolução nas Orientações para o professor.
5. O corpo humano tem várias alavancas que permitem o movimento eficiente dos nossos membros e de outras partes do corpo. No corpo humano,
os ossos atuam como alavancas e as articulações funcionam como pontos de apoio.
Com base nesse contexto, analise as afirmações a seguir.
I ) No movimento de flexão do braço, a articulação do cotovelo funciona como o ponto de apoio, e o músculo bíceps aplica a força para levantar o antebraço.
II ) O cotovelo funciona como um ponto de apoio em uma alavanca do tipo interpotente quando você levanta um objeto com o braço estendido.
III ) O movimento de elevar o calcanhar, como quando você fica na ponta dos pés, é um exemplo de alavanca do tipo inter-resistente.
IV ) O pescoço, ao inclinar a cabeça para a frente, é um exemplo de alavanca do tipo inter- -resistente.
Estão corretas as afirmações:
a ) I e II.
b ) I e III.
c ) II e III.
d ) II, III e IV.
e ) I, III e IV.
Resposta: Alternativa b.
6. Um pintor precisa equilibrar uma prancha sobre uma viga para alcançar uma área alta de uma parede. Ele coloca a prancha de madeira sobre a viga de modo que ela fique como uma gangorra, com a viga atuando como o ponto de apoio. O pintor e seu assistente, que têm massas diferentes, precisam ficar em lados opostos da prancha para que ela permaneça equilibrada.
Como eles devem se posicionar em relação ao ponto de apoio para garantir que a prancha fique em equilíbrio, horizontalmente?
a ) O pintor de maior massa deve ficar mais perto do ponto de apoio.
b ) O pintor de maior massa deve ficar mais longe do ponto de apoio.
c ) Ambos devem ficar à mesma distância do ponto de apoio.
d ) Como eles têm massas diferentes, eles nunca poderão equilibrar a prancha.
e ) O pintor de menor massa deve ficar mais perto do ponto de apoio.
Resposta: Alternativa a.
7. Um trabalhador está usando um carrinho de mão para transportar sacos de areia. O carrinho de mão tem comprimento total de 2 metros. A roda (apoio) está localizada a 1 vírgula 5 metro da alça do carrinho, e o saco de areia está colocado a 0 vírgula 5 metro do apoio. O trabalhador pode aplicar uma força máxima de 200 newtons na alça do carrinho de mão. Se o peso do saco de areia é 250 newtons, ele conseguirá levantá-lo e transportá-lo usando o carrinho de mão? Justifique sua resposta calculando a força necessária.
Resposta: 'F' subscrito p o é igual a 83 vírgula 3 newtons. Ele consegue transportar o saco de areia. Resolução nas Orientações para o professor.
Página 329
Plano inclinado
O plano inclinado é definido como uma superfície plana com uma inclinação em relação à direção horizontal, ou seja, o início e o fim do plano estão em alturas diferentes.
As rampas de acesso, como a mostrada na fotografia, são exemplos de plano inclinado e devem obedecer às condições de segurança e inclinação estabelecidas pela NBR (Norma Brasileira) 9050/2015.

5. Por que as rampas de acesso têm pequenas inclinações?
Resposta: O objetivo desta questão é resgatar os conhecimentos prévios dos estudantes sobre o plano inclinado. Eles podem citar que subir rampas com pequenas inclinações exige menos esforço físico.
As rampas são utilizadas porque reduzem a intensidade da força necessária para superar o desnível, diminuindo o esforço físico. Por esse motivo, os planos inclinados são considerados máquinas simples.
Em contrapartida, o plano inclinado exige maior deslocamento para superar um desnível. Usando as rampas de acesso como exemplo, para manter o conforto dos usuários, elas devem ter inclinações entre 5% abre parênteses 1 por 20 fecha parênteses e 8,33% abre parênteses 1 por 12 fecha parênteses. Isso quer dizer que, para uma elevação de 1 metro de altura, a projeção horizontal da rampa pode ter entre 20 metros e 12 metros (no mínimo).
Professor, professora: Diga aos estudantes que as adaptações físicas dos ambientes são só um tipo, conhecido como acessibilidade arquitetônica. Há ainda outros, como: instrumental (para diminuir as barreiras nos instrumentos e ferramentas de estudo, trabalho ou lazer); de transportes (para diminuir as barreiras nos veículos e nos pontos de paradas, por exemplo); de comunicações (para eliminar barreiras na comunicação interpessoal); e digital (apresentação do conteúdo digital e informações em sites com formatos alternativos).
Compartilhe ideias
A acessibilidade é um direito de todos para garantir a participação ativa dos cidadãos em todos os aspectos sociais. Rampas de acesso, pisos táteis e indicações em braile são exemplos de adaptações que oferecem condições de autonomia, segurança e conforto para pessoas com deficiência.
a ) Junte-se a dois colegas e analisem os ambientes da sua escola e ao redor dela, identificando adaptações de acessibilidade e a falta delas. Em seguida, discutam se esses ambientes são considerados acessíveis, propondo melhorias que possam ser realizadas.
Resposta: O objetivo dessa questão é levar os estudantes a observar os ambientes que frequentam e verificar suas condições de acessibilidade. Além das adaptações citadas no texto de apoio, podem citar os corrimãos, as barras de apoio nos banheiros, entre outras adaptações. Materiais em braile e aulas em Libras também são exemplos.
Para analisar as forças envolvidas no movimento de um corpo sobre um plano inclinado, adotamos um plano cartesiano como referencial, de modo que o eixo das ordenadas (eixo y) seja perpendicular ao plano e o eixo das abscissas (eixo x) coincida com o plano inclinado, como ilustrado a seguir.
Nessa situação, um recurso útil é a decomposição das forças nas direções dos eixos cartesianos escolhidos para analisar o problema. A força normal expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito N tem direção do eixo das ordenadas, porém a força peso atua em uma direção diagonal, entre as direções dos dois eixos.
Imagem sem proporção e em cores fantasia.
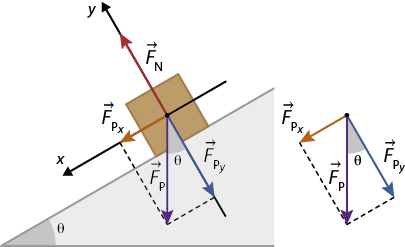
Professor, professora: Ao abordar o conceito de plano inclinado, destaque para os estudantes suas características: superfície plana, rígida, inclinada em relação à horizontal, com o objetivo de multiplicar a força. Caso eles tenham dificuldade em entender a inclinação das rampas, desenhe dois triângulos retângulos na lousa. Um deve ter altura de 1 metro e base de 20 metros, e o outro deve ter altura de 1 metro e base de 12 metros, sendo essas medidas equivalentes aos catetos. A hipotenusa desses triângulos seria equivalente à rampa de acesso.
Então, utilizamos suas projeções perpendiculares sobre os eixos cartesianos. Assim, suas componentes, que podem ser chamadas expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, P subscrito x, fim subscrito e expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima início subscrito, P subscrito y, fim subscrito, serão dadas por:
'F' início subscrito, P subscrito x, fim subscrito é igual a 'F' subscrito P vezes seno teta
'F' início subscrito, P subscrito y, fim subscrito é igual a 'F' subscrito P vezes cosseno teta
Página 330
Para equilibrar o corpo sobre o plano inclinado, é preciso aplicar uma força com intensidade igual à componente 'F' início subscrito, P subscrito x, fim subscrito, que seja no sentido contrário.
ATIVIDADES RESOLVIDAS
R1. João está ajudando seu amigo a carregar uma caixa pesada até a garagem da sua casa. A garagem está situada em um plano inclinado que forma um ângulo teta é igual a 30 graus com a horizontal, como mostra a figura. Se a caixa tem massa de 10 quilogramas, qual é a força necessária para manter a caixa em equilíbrio, impedindo que ela desça pela rampa? Considere que 'g' é igual a 10 metros por segundo quadrado, seno 30 graus é igual a 0 vírgula 5 e cosseno 30 graus é igual a início de raiz quadrada; 3 meios fim de raiz quadrada.
Imagens desta página sem proporção e em cores fantasia.
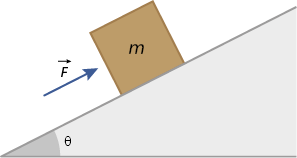
Resolução
Para que a caixa permaneça em equilíbrio, é necessário que a força aplicada seja igual à componente horizontal da força peso, em que 'F' subscrito P é igual a 'm' vezes 'g'. Portanto:
'F' é igual a 'F' início subscrito, P subscrito x, fim subscrito é igual a 'F' subscrito P vezes sen teta é igual a 10 vezes 10 vezes sen 30 graus é igual a 100 vezes 0 vírgula 5 portanto 'F' é igual a 50 newtons
Logo, a força necessária para manter a caixa em equilíbrio é 50 newtons.
Além das rampas de acesso, as cunhas e os parafusos são exemplos de planos inclinados. Objetos como facas, machados e ferramentas de rocha da Antiguidade são exemplos de cunha.
As cunhas geralmente são utilizadas para o corte e são formadas por dois planos inclinados que fazem um ângulo agudo entre si. Essa disposição altera a direção da força aplicada em um objeto. Por exemplo, à medida que a parte afiada do machado é empurrada para o interior da madeira, as laterais da lâmina empurram a madeira para os lados, dividindo-a.
Professor, professora: Diga aos estudantes que o machado ainda tem uma alavanca, o cabo.
Nos parafusos, o plano inclinado tem formato helicoidal (roscas) em torno de um cilindro central. Dessa forma, o parafuso converte o movimento de rotação em um movimento de translação para dentro ou para fora do corpo no qual ele está sendo fixado.

A vantagem de utilizar parafusos para manter dois corpos unidos é que a rosca permite maior superfície de contato com os corpos, evitando que eles escapem com facilidade. Além disso, os parafusos podem ser removidos e reinseridos sem perder sua eficácia.
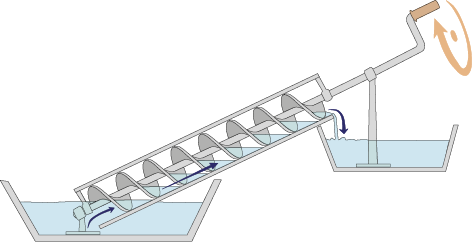
Uma aplicação interessante desse dispositivo é o parafuso de Arquimedes. Ele é utilizado para bombear água de um local mais baixo para um local mais alto.
A extremidade inferior do parafuso é imersa na água e, conforme ele gira, certa quantidade de água é elevada pelo parafuso. Esse dispositivo ainda é usado para irrigação e outras finalidades.

Página 331
Máquinas modernas
Há uma infinidade de máquinas em nosso dia a dia, e elas são compostas de muitos elementos complexos, envolvendo dispositivos eletrônicos, mecânicos, térmicos etc. Ao longo do tempo, houve uma enorme evolução nas técnicas de fabricação das máquinas, bem como a descoberta de novos materiais empregados em sua produção. No entanto, os princípios básicos de funcionamento de muitas máquinas modernas são os mesmos das máquinas simples.
Considerando uma furadeira elétrica como exemplo, observamos que ela é composta de um motor elétrico responsável por aplicar a força para girar a broca. Para que a força de rotação da broca seja maior do que a do motor, há uma associação de polias. É importante notar também que as brocas são feitas com ranhuras laterais em formato de parafuso.

Outro exemplo interessante da importância das máquinas simples na atualidade é o automóvel, uma máquina bastante complexa. Ele envolve muitos dispositivos eletrônicos, além de um motor à combustão interna, cujo funcionamento é explicado pela termodinâmica. Há, ainda, sistemas de lubrificação, arrefecimento, transmissão e muitos outros que utilizam diversas aplicações de máquinas simples.
O dispositivo mais básico que possibilita o deslocamento do carro são suas rodas. Independentemente da potência de seu motor, se não estiver equipado com as rodas, ele não vai a lugar algum.
Já com relação ao motor, para funcionar adequadamente e transmitir seu movimento para as rodas, ele utiliza diversas engrenagens dos mais variados formatos e tamanhos. Essas engrenagens, que são uma adaptação da roda, desempenham diferentes funções dentro de um motor ou de um sistema de transmissão. Há, ainda, os sistemas de polias acopladas com correias.

O que há de comum entre todos esses dispositivos das máquinas modernas é que eles foram desenvolvidos com base em máquinas simples.
a ) Imagine que um amigo diga para você que já não faz sentido estudar as máquinas simples na atualidade, pois elas entraram em desuso há muito tempo. Como você responderia a esse seu amigo?
Resposta pessoal. Após ler o texto do boxe, espera-se que os estudantes reconheçam que, apesar de toda evolução na fabricação das máquinas modernas e no desenvolvimento de novos materiais, o funcionamento de muitos dispositivos ainda se baseia nos princípios de funcionamento das máquinas simples.
b ) Converse com seus colegas sobre outras máquinas modernas (que não foram citadas no texto) que você encontra em sua casa, no caminho para a escola ou em seu dia a dia e que utilizam máquinas simples. Identifiquem e anotem no caderno as partes desses dispositivos que podem ser classificadas como máquinas simples.
Resposta pessoal. Os estudantes devem refletir sobre as máquinas simples que costumam usar (exceto dispositivos simples, como tesoura e faca). Entre as possibilidades, eles podem citar: engrenagens, correias e rodas de uma bicicleta; rodas dos refrigeradores; escada rolante, que aplica uma esteira equipada com polias; e engrenagens, correias e polias de uma máquina de lavar roupas.
Página 332
CONEXÕES com ... HISTÓRIA
Desenvolvimento de ferramentas e máquinas pelos hominíneos
As primeiras ferramentas criadas por alguns de nossos ancestrais eram basicamente rochas quebradas. Com o passar do tempo, os hominíneos passaram a dar melhor acabamento às ferramentas, obtendo artefatos com cantos mais afiados, além de incorporarem o uso de cabos, o que rende vantagem mecânica a essas ferramentas.
Após a descoberta da fundição de metais, elas passaram a ser fabricadas com cobre abre parênteses C u fecha parênteses, bronze e ferro abre parênteses F e fecha parênteses, o que proporcionou ferramentas de melhor qualidade.
O desenvolvimento da agricultura trouxe invenções, como o arado, que permitiram a preparação do solo para o plantio, melhorando o desempenho das colheitas.
Apesar dessas invenções terem sua parcela de importância para o desenvolvimento da humanidade, a invenção da roda significou um grande avanço. Contudo, o tempo necessário desde sua invenção até que surgissem os primeiros veículos equipados com roda é incerto.
Além disso, avanços teóricos e tecnológicos em relação ao uso de novos materiais e o conhecimento de novas fontes de energia, como carvão mineral e petróleo, contribuíram para o desenvolvimento de novas máquinas. Acompanhe a seguir alguns desses avanços tecnológicos.

Idade da Pedra
Paleolítico
2,6 milhões de anos a.C.
Rochas afiadas (ferramentas olduvaienses).
Primeiras ferramentas de rocha fabricadas pelo Homo habilis, obtidas da simples quebra de rochas.
1,5 milhão de anos a.C.
Machado de mão, cutelo e picareta de rocha (ferramentas acheulianas).
Obtidas de lascas de núcleos de rocha, trabalhadas com algo mais macio que a rocha, como madeira ou osso, formando a aresta de corte (técnica bifacial).
80.000 a 40.000 anos a.C.
Lâminas de corte (indústria aurignaciana).
O formato das lâminas permitiu prendê-las a um cabo, proporcionando um efeito de alavanca e, assim, mais eficiência.
Mesolítico
18.000 anos a.C. - Microlâminas afiadas (cultura magdaleniana).
Ferramentas de rocha moldadas em formatos triangulares alongados ou em outras formas. Podiam ser presas a um cabo de osso e usadas como armas, para fins de marcenaria e preparação de alimentos.
Neolítico
11.000 anos a.C.
Machado e cinzel de rocha, foices de madeira ou osso.
Ferramentas produzidas por meio de polimento, mais eficientes e fáceis de afiar. Os padrões de desgaste nas foices revelam que foram usadas para a colheita de grãos.
Fonte de pesquisa: BUNCH, Bryan; HELLEMANS, Alexander. The history of science and technology: a browser's guide to the great discoveries, inventions, and the people who made them from the dawn of time to today. Houghton Mifflin Harcourt, 2004.
Página 333
Idade dos Metais
Cobre - 3.500 anos a.C.
Invenção da roda, possivelmente na Mesopotâmia (atual Iraque).
Inicialmente utilizada para produzir objetos de argila (roda de oleiro) e, em seguida, na construção dos primeiros veículos com rodas.
Bronze - 3.000 anos a.C.
Primeiros machados fabricados na Mesopotâmia por meio da fundição de metais (cobre e, em seguida, bronze).
Apresentam um orifício onde um cabo pode ser inserido. Um arado primitivo é inventado na China, enquanto arados empregando tração animal são utilizados na Mesopotâmia.
Ferro - 2.000 anos a.C.
A picota é inventada no Egito e na Mesopotâmia.
Trata-se de uma máquina simples, baseada no princípio da alavanca, para retirar água de poços.
500 anos a.C.
Surge o primeiro parafuso, supostamente inventado pelo filósofo grego Arquitas de Tarento (428 a.C.-347 a.C.), porém a data exata dessa invenção é incerta.
Trata-se de um plano inclinado em formato helicoidal, inventado para fixar objetos.
Antiguidade
200 anos a.C.
O matemático grego Arquimedes (287 a.C.-212 a.C.) descreve o princípio da alavanca e outras máquinas simples, como as polias.
Ele também inventou o parafuso de Arquimedes, um dos primeiros dispositivos para bombear água de um terreno mais baixo para outro mais alto.
O engenheiro grego Filão de Bizantino (280 a.C.-220 a.C.) descreve uma forma primitiva do acoplamento entre a corrente e a roda dentada (usada hoje em bicicletas), além da descrição de uma roda hidráulica.
Filão também descreveu aquilo que seria o primeiro sistema de engrenagens da história.
60 anos d.C.
O matemático grego Heron de Alexandria (10 d.C.-70 d.C.) descreve um dispositivo para cortar parafusos com roscas fêmeas.
Também descreveu outros dispositivos, como engrenagens helicoidais e válvulas de retenção e de flutuação, bem como os elementos necessários para construir um motor a vapor funcional.
Idade Média
1100
É inventada a catapulta movida a gravidade, chamada pelos europeus de trebuchet (trabuco).
Ela se destaca por aplicar o princípio da alavanca para dar grande velocidade a um projétil por meio de um contrapeso.
Idade Moderna
1698
A máquina inventada pelo engenheiro inglês Thomas Savery (1650-1715), projetada para bombear água de minas de carvão, é considerada a primeira máquina movida a vapor.
Idade Contemporânea
1886
O engenheiro a lemão Karl Benz (1844-1929) patenteou o primeiro automóvel com motor a combustão.
Esse automóvel era um triciclo com motor monocilíndrico, movido a combustível derivado de petróleo.
1891
O inventor estadunidense Thomas Robins Junior (1868-1957) inventa uma correia para o transporte de carvão e minério.
Consiste em uma associação de polias com uma correia em laço fechado, que gira em torno das polias.
1962
Nos Estados Unidos, o primeiro braço robótico produzido em massa (Unimate) é comercializado.
O primeiro robô industrial do mundo foi desenvolvido pelo inventor estadunidense George C. Devol (1912-2011).
a ) Junte-se a um colega e escolham duas ferramentas que vocês consideram importantes para o desenvolvimento e a evolução da sociedade. Em seguida, montem uma apresentação para divulgar as ferramentas escolhidas pela turma.
Resposta pessoal. O objetivo desta questão é incentivar os estudantes a pensar sobre a importância das ferramentas, para a execução de diferentes tarefas cotidianas, para a evolução da sociedade. O desenvolvimento de ferramentas auxiliou a obtenção de alimentos, agricultura, transporte, construção de casas, obtenção de água, entre outras atividades.
Página 334
ATIVIDADES
Imagens desta página sem proporção e em cores fantasia.
1. Considere as afirmações a seguir sobre o plano inclinado. Em seguida, avalie-as como verdadeiras ou falsas, justificando as falsas.
I ) A força necessária para erguer um corpo a uma mesma altura é menor em um plano inclinado do que em um deslocamento vertical. A distância percorrida utilizando o plano inclinado também é menor.
II ) O parafuso não pode ser classificado como exemplo da aplicação de plano inclinado.
III ) O macaco de um automóvel é um tipo de plano inclinado, pois utiliza um parafuso, cujo movimento rotativo faz esse dispositivo levantar o carro, ao custo de um deslocamento menor na vertical.
IV ) Uma ladeira de uma estrada é um plano inclinado, pois permite um deslocamento vertical com menos esforço.
Resposta: I) Falsa. A intensidade da força necessária para erguer um corpo à mesma altura é menor em um plano inclinado do que em um deslocamento vertical, mas a distância percorrida é maior; II) Falsa. O parafuso é um tipo de plano inclinado no formato de uma hélice; III) Verdadeira; IV) Verdadeira.
2. Considere dois planos inclinados, ambos usados para elevar um objeto até uma altura de 3 metros. O plano inclinado A é mais íngreme e tem uma projeção horizontal de 5 metros, enquanto o plano inclinado B é mais suave e tem uma projeção horizontal de 20 metros. Ambos os planos inclinados são máquinas simples que permitem elevar o objeto com menos força do que seria necessário se o objeto fosse levantado verticalmente. Qual plano inclinado exige menos força para levantar o objeto? Justifique sua resposta.
A.

B.

Resposta: O plano inclinado B, porque o ângulo de inclinação dele é menor. Nesse caso, a desvantagem é ter de percorrer uma distância maior.
3. Um carro guinchado encontra-se parado no meio da rampa do caminhão de reboque, sustentado por um cabo de aço inextensível preso no automóvel. Sabendo que a inclinação da rampa forma ângulo de 30 graus com a horizontal, determine a força de tração e a força normal que atua nesse carro, que tem 2.000 quilogramas de massa. Adote 'g' é igual a 10 metros por segundo.
Resposta: 'F' subscrito T é igual a 10.000 newtons, 'F' subscrito N é igual a 10.000 raiz quadrada de 3 newtons.
Resolução nas Orientações para o professor.
4. Uma caixa de 3 quilogramas está no início de um plano inclinado, conforme mostrado na imagem. Desconsiderando o atrito, qual seria a força necessária, aplicada paralelamente ao plano inclinado, para elevar a caixa até a parte mais alta da rampa com velocidade constante? Utilize seno 25 graus é igual a 0 vírgula 42, cosseno 25 graus é igual a 0 vírgula 91 e 'g' é igual a 10 metros por segundo quadrado
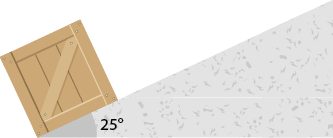
Desprezando o atrito, a força para elevar a caixa com velocidade constante deve ser igual à componente da força peso paralela ao plano inclinado, isto é, 'F' é igual a 'F' início subscrito, P subscrito x, fim subscrito, portanto: 'F' é igual a 'F' início subscrito, P subscrito x, fim subscrito é igual a 'F' subscrito P vezes seno teta é igual a 3 vezes 10 vezes seno 25 graus é igual a 12 vírgula 6 portanto 'F' é igual a 12 vírgula 6 newtons.
5. Um plano inclinado pode nos auxiliar na movimentação de cargas porque a força peso do corpo sofre uma decomposição nas direções paralela e perpendicular ao plano. Considere que uma corda inextensível está sendo utilizada para elevar um bloco de massa 'm', ao longo de um plano inclinado sem atrito que faz um ângulo teta em relação à horizontal. Com base nessas informações, faça a soma das alternativas corretas.
01 ) O bloco se move por causa da segunda lei de Newton, em que a aceleração na direção do plano é dada pelas suas componentes perpendiculares ao plano.
Errada, pois a aceleração ocorre por causa das forças na direção paralela ao plano inclinado.
02 ) Utilizar a direção x ao longo do plano inclinado para a decomposição das forças auxilia na tarefa de determinar a força resultante do sistema.
Correta, a decomposição pode ser usada em outro sistema de referência, porém dificulta a análise matemática.
04 ) A força resultante do sistema será definida pela diferença da tração com a força peso na direção x, paralela ao plano inclinado.
Correta, pois pela decomposição de forças a resultante será 'F' subscrito R é igual a T menos 'F' subscrito P vezes seno teta.
08 ) A componente da força peso na direção x é equilibrada pela força normal, de modo que é necessário dobrar a força de tração para puxar o bloco.
Errada, pois é a componente da força peso na direção y que é equilibrada pela força normal.
16 ) A força de tração necessária para elevar o bloco com velocidade constante, ao longo do plano inclinado, é dada por 'F' subscrito T é igual a 'F' subscrito P vezes seno teta.
Correta.
Resposta: 02 + 04 + 16 = 22
6. Um trabalhador precisa colocar uma caixa de 120 quilogramas na caçamba de um caminhão e dispõe de uma chapa de madeira bem lisa para fazer uma rampa. Ao apoiar a chapa de madeira no solo e na caçamba do caminhão, ela ficou com um ângulo de 30 graus em relação ao solo (horizontal). Qual é a razão entre a força necessária para elevar a caixa empurrando-a pelo plano inclinado e a força para elevar a caixa na vertical?
Adote: 'g' é igual a 10 metros por segundo quadrado, seno 30 graus é igual a 0 vírgula 5 e cosseno 30 graus é igual a 0 vírgula 87.
Resolução nas Orientações para o professor.
Resposta: início de fração, numerador: 'F', denominador: 'F' subscrito P, fim de fração é igual a 0 vírgula 5.
Página 335
CAPÍTULO21
Momento e torque
Momento de uma força
Analise a imagem a seguir.
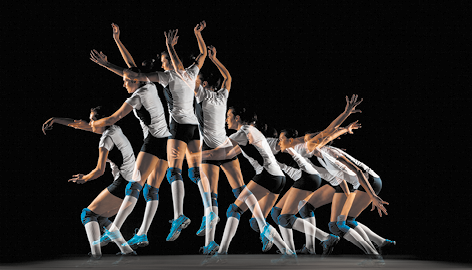
1. Como os esforços dos músculos contribuem para realizar o movimento do corpo humano?
Resposta: O movimento do corpo humano acontece por meio da tração dos músculos sobre os ossos. Quando os músculos se contraem, eles puxam os ossos e geram o movimento.
2. Em quais partes do corpo da atleta podemos identificar o sistema de alavanca?
Resposta: Espera-se que os estudantes identifiquem esse movimento nas seguintes partes: braços, tronco, pernas e pés.
Para golpear uma bola de vôlei, realizando o movimento da imagem, seria necessário aplicar força sobre ela. Para isso, os sistemas do corpo humano (muscular, esquelético, articular e nervoso) trabalham em intensa atividade, formando um sistema de alavanca.
As alavancas são sistemas mecânicos compostos de um corpo extenso e rígido que pode realizar movimentos de rotação em relação a um ponto fixo e multiplicar sua força mecânica. Assim, por meio do movimento de rotação dos braços, a atleta aplica força sobre a bola, alterando seu estado de movimento.
Em academias, é comum a prática de exercícios destinados ao fortalecimento de dois músculos que constituem o braço: o bíceps e o tríceps. Para isso, os exercícios são realizados mantendo o braço imóvel e movimentando o antebraço, formando um sistema de alavanca.
Utilizando um tipo de aparelho que tem como objetivo exercitar o bíceps, uma pessoa deve aplicar força para cima, mantendo os cotovelos imóveis. Assim, observa-se a rotação do antebraço para cima por meio da contração do bíceps, cujo eixo de rotação corresponde ao cotovelo. Nesse tipo de exercício, forma-se um sistema de alavanca interpotente, em que a força potente é concentrada entre o ponto de aplicação da força resistente e o ponto fixo (cotovelo), como mostram as imagens a seguir.

Imagem sem proporção e em cores fantasia.
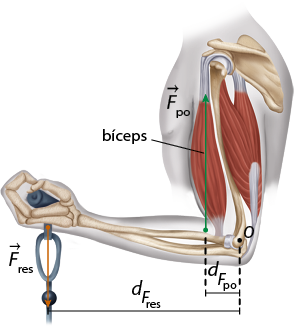
Fonte de pesquisa: UNIVERSIDADE DE SÃO PAULO (USP). Cinesiologia: parte 2: força torque e alavancas. p. 74. Disponível em: https://s.livro.pro/2ot3yj. Acesso em: 8 set. 2024.
Página 336
Entretanto, quando o mesmo aparelho é utilizado para exercitar o tríceps, observa-se que o movimento do antebraço é inverso, isto é, ele executa o movimento de rotação para baixo. Nesse caso, o braço, o antebraço e o cotovelo formam um sistema de alavanca interfixa, em que o ponto fixo (cotovelo) está localizado entre o ponto da ação da força potente e o da força resistente, como mostram as imagens a seguir.

Imagens desta página sem proporção e em cores fantasia.
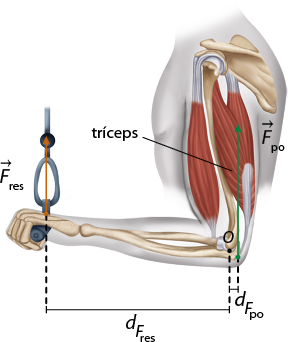
Fonte de pesquisa: UNIVERSIDADE DE SÃO PAULO (USP). Cinesiologia: parte 2: força torque e alavancas. p. 74. Disponível em: https://s.livro.pro/2ot3yj. Acesso em: 8 ago. 2024.
Alguns exercícios são praticados para o fortalecimento do músculo da panturrilha, um importante músculo esforçado quando caminhamos, corremos ou subimos algum degrau. O exercício consiste em manter os dedos do pé fixos no chão e elevar o calcanhar, executando o movimento de rotação do pé. Nesse caso, o calcanhar, a planta do pé e os dedos formam um sistema de alavanca inter-resistente, em que a força resistente está localizada entre o ponto de ação da força potente e o ponto fixo (dedos do pé), conforme as imagens a seguir.

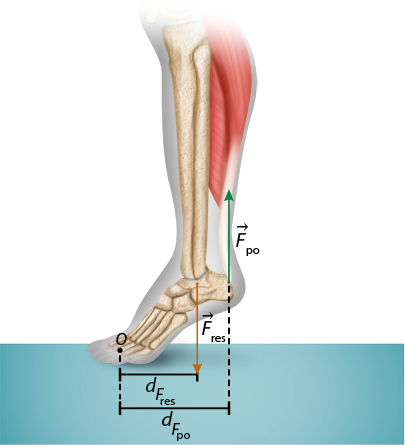
Fonte de pesquisa: UNIVERSIDADE DE SÃO PAULO (USP). Cinesiologia: parte 2: força torque e alavancas. p. 75. Disponível em: https://s.livro.pro/2ot3yj. Acesso em: 25 out. 2024.
Para cada movimento do corpo humano composto de um sistema de alavanca, ocorre a rotação do braço de alavanca (corpo extenso) em torno de um ponto fixo (eixo de rotação). Esse efeito de movimento de rotação causado pela ação das forças potente e resistente é chamado de momento da força ou torque, isto é, a ação das forças tende a produzir o movimento de rotação do corpo extenso.
Página 337
Professor, professora: Analise com os estudantes essa expressão para o cálculo da intensidade do torque. Espera-se que percebam que essa intensidade será máxima quando o ângulo entre a força e a linha que une o ponto de apoio ao ponto em que se aplica a força é igual a 90 graus. A intensidade do torque será nula quando seno teta é igual a 0, ou seja, quando a força é aplicada na mesma direção da linha que une o ponto de apoio ao ponto onde é aplicada a força.
O momento da força ou torque é uma grandeza vetorial que altera o estado de movimento de rotação de um corpo extenso. Sua intensidade é definida por:
M é igual a 'F' vezes d vezes seno teta
em que 'F' é a intensidade do vetor força expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima que tende a produzir a rotação, d é a distância entre o ponto de aplicação da força e o eixo de rotação e teta é o ângulo entre o vetor força e o braço de alavanca, como mostra a imagem a seguir. No Sistema Internacional de Unidades (SI), o momento da força é medido em N vezes m.
Imagens desta página sem proporção e em cores fantasia.

Imagem elaborada com base em: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: mecânica. Tradução: Ronaldo Sérgio de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 1. p. 277.
Somente forças perpendiculares ao braço de alavanca podem produzir torque, por isso a função seno garante que qualquer força aplicada sobre o corpo extenso considere apenas sua componente perpendicular.
Apesar de o momento da força ser uma grandeza vetorial, trataremos apenas do efeito de rotação em torno de um único eixo. Assim, não exploraremos mais detalhes vetoriais. Entretanto, é necessário definir e diferenciar se o movimento de rotação tem sentido horário ou anti-horário. Portanto, por convenção, o momento da força ou torque é definido como positivo quando a rotação ocorre no sentido anti-horário e negativo quando a rotação se dá no sentido horário.
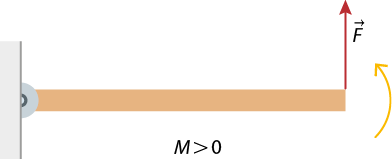
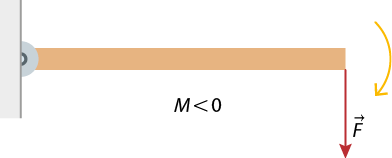
Imagens elaboradas com base em: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: mecânica. Tradução: Ronaldo Sérgio de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 1. p. 277.
ATIVIDADES RESOLVIDAS
R1. Em uma barra é aplicada uma força de módulo 'F', conforme mostrado na figura a seguir.
Sabendo que a intensidade da força 'F' é 50 newtons, qual é o valor do momento da força 'F' em relação ao ponto O?

Resolução
Utilizando a equação do momento de uma força, tem-se:
M é igual a 'F' vezes d vezes seno teta é igual a 50 vezes 2 vezes seno 30 elevado a início expoente, grau, fim expoente é igual a 100 vezes 0 vírgula 5 portanto M é igual a 50 newtons vezes m
Portanto, o momento da força aplicada na barra é 50 newtons vezes m.
Página 338
Equilíbrio de corpo extenso
Para que um corpo esteja em equilíbrio, é necessário que a resultante das forças que agem sobre ele seja nula. Isso garante que o corpo fique em repouso (equilíbrio estático) ou descreva o movimento retilíneo uniforme (equilíbrio dinâmico). Caso contrário, se o corpo não estiver em equilíbrio, isto é, quando a resultante das forças não é nula, ele descreverá um movimento variado, do tipo acelerado ou retardado, ou até mesmo trajetórias curvilíneas.
Para os corpos extensos – cujas dimensões não podem ser desprezadas –, o equilíbrio é atingido quando, além de manter sua velocidade ou rapidez constante, evita-se que o corpo gire. Assim, para que corpos extensos mantenham o estado de equilíbrio, além de a resultante das forças ser nula, o momento resultante (ou torque resultante) também deve ser nulo.
Considera-se que um corpo está em equilíbrio quando ele tem as seguintes propriedades:
1. está em equilíbrio estático (repouso) no qual a intensidade da força resultante (soma das forças) é igual a zero somatório subscrito n 'F' subscrito x subscrito n é igual a 0 e somatório subscrito n 'F' subscrito y subscrito n é igual a 0;
2. está em equilíbrio dinâmico (com velocidade ou rapidez de rotação constante) no qual o torque resultante (soma dos torques) é igual a zero somatório subscrito n M subscrito n é igual a 0.
Analise a fotografia a seguir.

O slackline é um esporte que exige muito equilíbrio. Considerado uma atividade física completa – que envolve resistência física, consciência corporal e concentração –, contribui para o aperfeiçoamento de esportes como atletismo, caminhada, surfe etc., além de oferecer benefícios à saúde.
3. Em sua opinião, qual é a maior dificuldade para a prática desse esporte?
Resposta: Espera-se que os estudantes citem o equilíbrio como o maior fator de dificuldade para a prática de slackline.
4. Você já praticou algum esporte em que teve de manter o equilíbrio? Como o fez?
Resposta pessoal. O objetivo desta questão é explorar os conhecimentos prévios dos estudantes sobre o equilíbrio dos corpos e aproximar o conteúdo de seu cotidiano. Eles podem citar que andaram de bicicleta, patins, skate etc.
Esse esporte consiste em uma fita estreita estendida entre dois pontos distantes do solo, sobre a qual o esportista deve andar mantendo-se em equilíbrio. Para isso, o praticante de slackline deve manter o centro de gravidade na mesma vertical da corda, para não perder o equilíbrio.
O centro de gravidade é a posição geométrica, em um corpo extenso, na qual é possível considerar a ação única da força peso. Assim, em várias situações, define-se o centro de gravidade como uma posição geométrica de equilíbrio.
Imagem sem proporção e em cores fantasia.

Página 339
Nos casos em que o centro de gravidade se localiza fora da linha de gravidade, tem-se o desequilíbrio, o que pode provocar, por exemplo, a queda de uma pessoa.
Na dança, isso pode ser observado quando o dançarino desloca seu peso de forma intencional. Por exemplo, ao executar certos movimentos, como o mostrado na fotografia, o dançarino pode posicionar seu centro de gravidade além da base de apoio, criando um desequilíbrio temporário. Essa manipulação do equilíbrio é utilizada com bastante treino, permitindo que ele execute determinados passos ou transite entre movimentos para retornar a uma posição estável.

Para um campo gravitacional constante, a posição do centro de gravidade – ponto de aplicação da força peso – coincide com o mesmo ponto no qual toda a massa de um corpo pode ser concentrada. Esse ponto é chamado de posição de centro de massa. Em corpos simétricos, cuja massa é uniformemente distribuída, seu centro de massa coincide com seu centro geométrico.
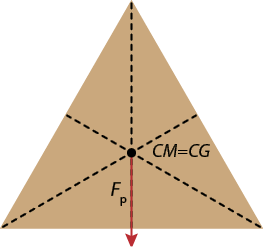
Considerando objetos com massa uniformemente distribuída, para um retângulo, o centro de massa está localizado no ponto de interseção das suas diagonais; para um triângulo, o centro de massa corresponde ao ponto de interseção das medianas (mediana é o segmento de reta que parte de um vértice e vai até o ponto médio do lado oposto a esse vértice), o qual é conhecido como baricentro do triângulo; já para um cubo, o centro de massa está em seu ponto central (centro geométrico).
Imagens desta página sem proporção e em cores fantasia.
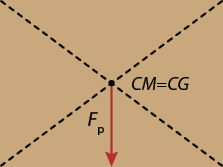
O corpo humano e suas inúmeras articulações atuam em conjunto para que possamos ficar de pé e caminhar. Como um professor de artes marciais bem sabe, o conhecimento sobre o centro de massa de um corpo é fundamental para que o equilíbrio aconteça, principalmente durante os treinos. O centro de massa do corpo humano está localizado nas proximidades do umbigo. O ato de dobrar os joelhos e distanciar os pés contribui para alcançar o equilíbrio ao confrontar o oponente, pois deixa os pontos de apoio mais afastados e o centro de massa mais próximo do solo.
Compartilhe ideias
O centro de gravidade e o centro de massa desempenham um papel importante no cotidiano. A determinação de suas posições relativas pode indicar também o tipo de equilíbrio. Suas aplicações estão em várias situações do dia a dia, como na movimentação de cargas ou no desempenho do corpo humano.
a ) Pesquise os benefícios que o conhecimento do ponto de centro de gravidade e do centro de massa possibilita às pessoas no desenvolvimento de práticas e atividades do cotidiano e converse com um colega sobre eles.
Resposta: Espera-se que os estudantes mencionem a prática de esportes como ginástica e skate, em que entender como distribuir o peso do corpo ajuda a manter o equilíbrio e realizar manobras. Nos transportes, como em carros e aviões, o posicionamento correto do centro de massa melhora a estabilidade e a segurança. Além disso, na construção civil, saber como distribuir o peso em estruturas garante que os edifícios sejam mais resistentes e seguros.
Página 340
PRÁTICA CIENTÍFICA
Equilíbrio em movimento
Por dentro do contexto
O equilíbrio pode ser observado em diversas situações de nosso cotidiano, desde as mais simples, como caminhar ou correr, até as mais complexas, por exemplo, na construção de prédios e esculturas.
Podemos percebê-lo, ainda, em muitos esportes e nas artes circenses, que já eram praticadas há milhares de anos pelas civilizações da Antiguidade.
O circo surgiu como uma forma de espetáculo, reunindo diferentes tipos de atrações e de demonstração de habilidades, como as apresentações em corda bamba. Nelas, os equilibristas caminham sobre uma corda esticada na horizontal, a vários metros de distância do solo. Para auxiliar no equilíbrio, o artista abre os braços ou carrega consigo uma vara comprida, como na imagem a seguir.

a ) Olhando ao seu redor, você seria capaz de identificar situações em que ocorre o equilíbrio de um corpo?
Resposta pessoal. Os estudantes podem citar que o equilíbrio pode ser observado em construções civis, pontes, edifícios; esportes (de maneira geral); andar de bicicleta; entre outros.
Materiais
- colchonete
- fita adesiva
- cones ou objetos para criar obstáculos
- cronômetro
- livro
Como proceder
A. Reúnam-se em grupos e, com a fita adesiva e os cones, elaborem um trajeto composto de obstáculos. Esse trajeto deverá conter segmentos de corrida, de caminhada e saltos.
Dica
Faça a construção do circuito em um ambiente que tenha bastante espaço, de preferência em ambiente aberto.
Imagem sem proporção e em cores fantasia.

B. Agora, um integrante do grupo deverá percorrer o circuito construído na etapa anterior. Para isso, um segundo integrante deverá cronometrar o tempo de execução. Conclua no menor intervalo de tempo que conseguir.
Cuidado
Respeite os limites de seu corpo. Não execute movimentos que possam causar qualquer tipo de lesão.
Página 341
Imagens desta página sem proporção e em cores fantasia.
C. Em seu caderno, faça anotações do que foi mais fácil e do que foi mais difícil de ser realizado durante o percurso. Explique os motivos para as dificuldades encontradas.
D. Agora, o percurso deverá ser completado novamente equilibrando um livro sobre a cabeça. Novamente, um segundo integrante do grupo deverá cronometrar o tempo para concluir o circuito. Caso o livro caia, você deverá retornar ao início.

E. Faça novamente as anotações das observações para a execução do percurso, explicando as dificuldades encontradas e os motivos para isso.
F. Por fim, repita as etapas anteriores utilizando outros tipos de materiais que limitem o movimento, como carregar uma mochila com seu material escolar e realizar os movimentos sobre uma superfície instável (sobre colchonetes).


Análise e divulgação
1. Vocês tiveram dificuldades em manter o equilíbrio do corpo ao realizar algum dos movimentos propostos?
Resposta pessoal. A resposta depende dos movimentos realizados pelos estudantes. O objetivo dessa questão é levá-los a uma experiência em que o corpo seja, ao mesmo tempo, objeto e instrumento de experimentação, buscando compreender, na prática, ao realizar alguns movimentos corporais, a construção inicial dos conceitos de centro de massa e centro de gravidade.
2. Qual foi a interferência dos itens (livro, mochila, entre outros) no tempo de execução do percurso?
Espera-se que os estudantes mencionem que, para manter o equilíbrio do corpo, foi necessário se concentrarem mais para a execução dos movimentos, em razão dos itens que causaram dificuldade. Portanto, o tempo foi maior quando utilizaram esses itens.
3. Qual foi a maneira que vocês encontraram para realizar os movimentos e manter o equilíbrio?
Resposta pessoal. A resposta depende dos movimentos realizados pelos estudantes. Eles podem responder que, na medida em que foi possível deslocar o centro de gravidade do corpo, a linha de ação da força peso passou pela área responsável por seu apoio, não permitindo a ocorrência de torque e mantendo seu equilíbrio.
4. Para que se consiga o equilíbrio estático corporal ao realizar movimentos com o corpo, basta apenas ter vigor muscular para promover a postura ou é necessário considerar os conceitos físicos estudados?
Resposta pessoal. Espera-se que os estudantes respondam que, para um corpo se manter em equilíbrio estático corporal, as resultantes das forças e o torque que atuam sobre ele (no centro de gravidade do corpo) ao realizar determinado movimento devem ser nulos, independentemente de seu vigor muscular.
5. Com base em suas anotações, faça um vídeo contendo a descrição da prática desenvolvida e a relação entre movimento e centro de massa, expondo as dificuldades de locomoção quando o centro de massa é alterado.
Espera-se que os estudantes mencionem no vídeo que, quando o centro de massa está alinhado com nossos apoios, temos mais estabilidade e facilidade para nos mover. Porém, quando esse centro é alterado, seja por massa adicional, seja por mudanças de postura, a locomoção se torna mais difícil, exigindo mais esforço para manter o equilíbrio e aumentar a chance de perda de estabilidade.
Página 342
ATIVIDADES
Imagens desta página sem proporção e em cores fantasia.
1. Exercícios físicos para o fortalecimento dos bíceps são comuns nas academias. Considere que o conjunto de antebraço e mão tem 2 vírgula 5 quilogramas de massa, com a força peso agindo em um ponto a 12 centímetros do cotovelo. A figura mostra a realização de um exercício no qual uma pessoa está equilibrando o antebraço na horizontal, em repouso, e com a mão está sustentando um cabo que exerce sobre ela uma força de resistência com intensidade de 60 newtons para baixo.
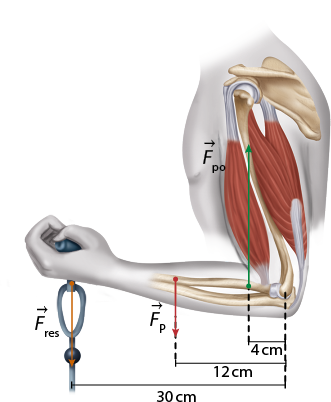
Imagem elaborada com base em: UNIVERSIDADE DE SÃO PAULO (USP). Cinesiologia: parte 2: força torque e alavancas. p. 74. Disponível em: https://s.livro.pro/2ot3yj. Acesso em: 17 ago. 2024.
a ) Qual é a intensidade do torque gerado no antebraço pelas forças peso do antebraço e da mão? A tendência de giro ocorre no sentido horário ou anti-horário? Considere 'g' é igual a 10 metros por segundo elevado ao quadrado.
Resposta: 3 N vezes m; anti-horário. Resoluções nas Orientações para o professor.
b ) Qual é a intensidade do torque gerado no antebraço pela força de resistência? A tendência de giro ocorre no sentido horário ou anti-horário?
Resposta: 18 N vezes m; anti-horário.
c ) Qual é a intensidade da força realizada pelo bíceps para que o antebraço se mantenha em repouso?
Resposta: 525 newtons.
d ) Cite outras partes do corpo humano em que há sistemas de alavanca.
Resposta: Pescoço, calcanhar, joelho, ombro etc.
e ) Você considera importante realizar atividades físicas? Por quê?
Resposta pessoal. O objetivo desta questão é levar os estudantes a refletir sobre os benefícios das atividades físicas para a saúde.
2. Em armários e guarda-roupas, geralmente os puxadores das gavetas são fixados no centro da placa; já os puxadores de porta são colocados na extremidade oposta às dobradiças. Baseando-se nos conceitos estudados, explique por que há essa diferença na montagem da porta.
Resposta: Em relação às gavetas, os puxadores são fixados no centro das placas para garantir que a força aplicada seja distribuída uniformemente ao longo do encaixe. No caso das portas, que normalmente giram em torno de um eixo, quanto mais afastado das dobradiças estiver o puxador, maior será o torque causado pela força aplicada. Isso minimiza o esforço necessário para abrir e fechar portas.
3. As imagens a seguir mostram a vista superior de uma porta em dois momentos distintos em que se aplicam forças para fechá-la. Determine a intensidade do momento provocado pelas forças nas duas situações.
A.

B.
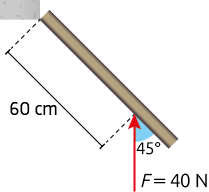
Resolução nas Orientações para o professor.
Resposta: A. 22 vírgula 5 newtons; B. 12 vezes raiz quadrada de 2 N vezes m.
4. O torquímetro é um aparelho que mede o torque aplicado em parafusos ou porcas que exigem precisão em sua fixação, como mostrado na fotografia.
Calcule o valor da força que deve ser aplicada nesse torquímetro para que uma porca receba um torque de 270 N vezes m.

Resposta: 500 newtons. Resolução nas Orientações para o professor.
5. Considere que nove esferas têm mesmo tamanho e mesma cor, e oito delas têm massas idênticas e uma tem massa maior. Explique como identificar a esfera que tem massa diferente utilizando uma balança por apenas duas vezes.
Imagem sem proporção e em cores fantasia.
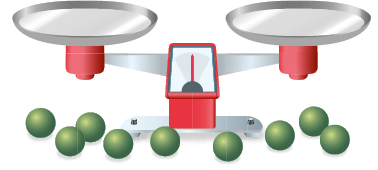
Resposta nas Orientações para o professor.
Página 343
Imagens desta página sem proporção e em cores fantasia.
6. Duas forças são aplicadas na barra ilustrada a seguir. Uma delas abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 2 fecha parênteses, que é aplicada no ponto A, não foi representada, e a outra abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 1 fecha parênteses tem intensidade de 40 newtons. Qual deve ser a intensidade e o sentido de expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 2, se aplicada perpendicularmente à barra, para que não haja rotação da barra em torno do eixo indicado? Considere que o eixo de rotação está fixo.

a ) 10 newtons e sentido horário.
b ) 10 newtons e sentido anti-horário.
c ) 40 newtons e sentido horário.
d ) 40 newtons e sentido anti-horário.
e ) 30 newtons e sentido anti-horário.
Resposta: Alternativa a.
7. Uma criança que tem massa de 25 quilogramas está brincando sobre uma barra de madeira com comprimento que mede 10 metros e com massa de 80 quilogramas apoiada em dois pontos (A e B). Calcule a distância máxima que a criança pode se afastar do apoio B, indicado na figura, sem girar a barra.
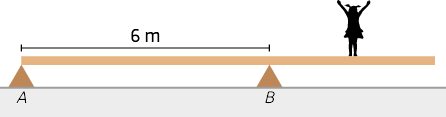
Resposta: 3 vírgula 2 metros.
8. Considere as seguintes afirmações sobre o conceito de torque (momento de uma força). Julgue-as como verdadeiras ou falsas, justificando as incorretas.
I ) O torque é uma grandeza vetorial que depende da força aplicada e da distância entre o ponto de aplicação da força e o eixo de rotação.
II ) O torque é calculado pelo produto entre a distância do ponto de aplicação da força em relação ao eixo de rotação e a força, não importando o ângulo que eles fazem entre si.
III ) Para que um objeto esteja em equilíbrio rotacional, a soma dos torques atuando sobre ele deve ser nula.
IV ) Um objeto pode estar em equilíbrio rotacional, mas não em equilíbrio translacional.
V ) A unidade de medida do torque no SI é o Newton por metro abre parênteses N barra m fecha parênteses.
Resposta: I) Verdadeira. II) Falsa. O ângulo entre o braço girante e a força influencia o torque. III) Verdadeira. IV) Verdadeira. V) Falsa. A unidade de medida no SI é o N vezes m.
9. Seis cubos idênticos de 2 quilogramas cada estão sobre uma barra homogênea de 4 quilogramas suspensa pelas cordas ideais I e II, como mostra a figura. Considere 'g' é igual a 10 metros por segundo elevado ao quadrado.
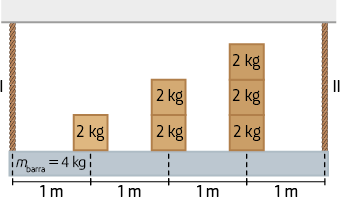
Sabendo que o sistema está em equilíbrio, determine as tensões nas cordas I e II.
Resposta: 70 newtons e 90 newtons, respectivamente.
10. Considere um retângulo no plano cartesiano com os vértices nas seguintes coordenadas: A abre parênteses 1 vírgula 3 fecha parênteses, B abre parênteses 5 vírgula 3 fecha parênteses, C abre parênteses 1 vírgula 1 fecha parênteses e D abre parênteses 5 vírgula 1 fecha parênteses. Calcule as coordenadas do centro de massa desse retângulo.
Resposta: abre parênteses 3 vírgula 2 fecha parênteses.
11. Jogadoras de vôlei cortando uma bola no ar, treinos musculares em uma academia e crianças brincando em balanços no parque são exemplos de sistemas mecânicos que realizam movimentos de rotação. A palavra torque vem do latim "torquere", que significa torcer. Esse termo refere-se a situações em que, quando aplicamos uma força em um objeto a determinada distância, ele tende a girar. A respeito do torque, assinale a(s) alternativa(s) correta(s).
01 ) Para fazermos um corpo girar dependemos apenas da componente tangencial da força, uma vez que a força se encontra perpendicular ao corpo causando um torque no sistema.
02 ) A unidade de medida do torque é N vezes m, e de acordo com a equação do trabalho definida por W é igual a 'F' vezes d vezes cosseno teta, o sistema de medida também apresenta unidade igual a N vezes m, portanto trabalho e torque representam a mesma grandeza física.
04 ) Para um corpo que está sujeito à ação de vários torques, o torque resultante atuando no corpo é a somatória dos torques.
08 ) Os motores de carros utilizam o torque para representar a força que faz o motor funcionar, uma vez que o torque causa um processo de subida e descida dos pistões que está relacionado com a ação de giro realizada pelo torque resultante, implicando na força que o motor pode gerar.
16 ) Para uma barra de comprimento L no eixo horizontal e o ângulo de rotação fixado em uma das extremidades, a força necessária para rotacionar a barra é menor se aplicada na outra extremidade.
Resoluções das questões 6, 7, 9, 10 e 11 nas Orientações para o professor.
Resposta: 04 mais 0 8 mais 16 é igual a 28
Página 344
CAPÍTULO22
Estudando os movimentos dos corpos
Prática de esportes
1. Você pratica ou acompanha alguma modalidade esportiva? Cite a sua preferida.
Resposta pessoal. Espera-se que os estudantes comentem o esporte que mais gostam de praticar ou acompanhar. Caso não tenham o hábito de se exercitar, podem comentar a modalidade que mais chama a atenção deles.
2. Cite benefícios que o esporte traz para a saúde de quem o pratica. Comente com os colegas.
Resposta pessoal. Espera-se que os estudantes mencionem benefícios como agilidade motora e mental e disposição para a realização das tarefas diárias.
A prática de esportes promove uma importante função para a manutenção da saúde do ser humano, contribuindo para o desenvolvimento de aptidões físicas, para a qualidade de vida e até mesmo para a integração social.
O corpo humano é capaz de realizar diversos tipos de movimento – muitos são percebidos na prática de esportes. Por exemplo, em diversas modalidades esportivas, os atletas precisam correr, saltar, arremessar objetos, nadar, pedalar, erguer pesos etc. Em todas as atividades mencionadas, é possível analisar os movimentos do ponto de vista da Física.
Dica
Muitas modalidades esportivas necessitam da utilização de equipamentos de proteção, como capacetes, óculos, tênis apropriados, joelheiras etc. Esses equipamentos protegem a integridade física dos esportistas em casos de acidentes. Portanto, pratique esportes com a devida proteção.
Na natação, por exemplo, a velocidade e a aceleração são conceitos fundamentais que definem um atleta campeão. Nesse tipo de prova, os atletas nadam em raias que delimitam a trajetória do movimento, descrevendo um movimento retilíneo.
No arremesso de martelo, o atleta faz uma esfera maciça de metal presa a um cabo de aço girar rapidamente em torno de seu corpo, adquirindo grande velocidade. A trajetória do movimento da esfera descreve um movimento circular.
Na canoagem de velocidade, após a etapa de largada, os atletas mantêm um ritmo constante de remadas. Nesse momento, a canoa (embarcação a remo) descreve, aproximadamente, um movimento uniforme, isto é, um movimento cuja velocidade é constante.
Já no skate, a velocidade diminui ao realizar o movimento para subir a rampa e aumenta quando desce. Essas variações na velocidade são causadas pela aceleração gravitacional da Terra, que pode ser considerada constante para pontos próximos à superfície terrestre. Um movimento submetido a uma aceleração constante é chamado de movimento uniformemente variado.

Página 345
Leia o trecho de reportagem a seguir, sobre o recorde mundial oficial da maratona, atingido em 2023.
[...]
Para quem gosta de corrida, assistir às maratonas ao longo do ano é sempre emocionante. Em outubro, o queniano Kelvin Kiptum quebrou o recorde mundial ao vencer Chicago em duas horas e 35 segundos. O debate sobre os limites do corpo humano e quando teremos um tempo oficial abaixo de duas horas continua [...].
IZIDRO, Marina. Como será o esporte em 2024. Folha de S.Paulo, 30 dez. 2023. p. B6.
3. A velocidade da corrida realizada pelo atleta queniano Kelvin Kiptum (1999-2024) durante toda a maratona foi a mesma?
Resposta: Espera-se que os estudantes respondam que não, porém os atletas tentam manter sua rapidez média constante.
A velocidade é uma grandeza que representa a rapidez orientada com a qual um móvel (objeto, pessoa, automóvel etc.) se desloca, portanto é uma grandeza vetorial, com módulo, direção e sentido. A velocidade pode ser obtida pela razão entre o deslocamento abre parênteses delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses e o intervalo de tempo abre parênteses delta 't' fecha parênteses para a realização do respectivo deslocamento, ou seja:
expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a início de fração, numerador: delta expressão com detalhe acima, início da expressão, 's', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima, denominador: delta 't', fim de fração
Dica
No Sistema Internacional de Unidades (SI), a velocidade é medida em metro por segundo. Para transformá-la em quilômetro por hora, é necessário multiplicá-la pelo fator 3,6. Caso a transformação ocorra de quilômetro por hora para metro por segundo, divide-se por 3,6.
Para movimentos retilíneos, isto é, movimentos unidimensionais e sem alteração de sentido, a direção do vetor velocidade coincide com a direção da trajetória e com a direção do vetor deslocamento. Assim, o módulo do deslocamento tem o mesmo valor da distância percorrida e podemos utilizar somente a variação do valor numérico da posição, da velocidade e da aceleração. Então, a rapidez do movimento equivale ao módulo da velocidade, que podemos escrever da seguinte maneira.
v é igual a início de fração, numerador: delta 's', denominador: delta 't', fim de fração
No feito alcançado por Kiptum, ele correu 1 quilômetro a cada 2 minutos e 51 segundos, isto é, uma rapidez média em torno de 5 vírgula 8 metros por segundo, que permaneceu aproximadamente constante por toda a prova.
Na modalidade dos 100 metros rasos, o atleta inicia seu movimento a partir do repouso e aumenta sua velocidade com o tempo. O recorde mundial dessa prova pertence ao atleta jamaicano Usain Bolt (1986 -), que completou a prova em 9 segundos e 58 centésimos, em 2009. Ele atingiu a velocidade de 12 metros por segundo após 3 vírgula 78 segundos.

Quando a velocidade de um corpo não é constante ao longo do tempo, significa que ele está sujeito a uma aceleração, que é uma grandeza vetorial, definida pela razão da variação da velocidade abre parênteses delta expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses pelo intervalo de tempo abre parênteses delta 't' fecha parênteses, ou seja:
expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a início de fração, numerador: delta expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima, denominador: delta 't', fim de fração
Novamente, trabalhando apenas com o módulo da aceleração, podemos escrever a relação anterior como:
a é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração
Dica
A aceleração é medida, no SI, em metro por segundo ao quadrado abre parênteses metro por segundo quadrado fecha parênteses.
Professor, professora: Comente com os estudantes que, nessas condições, supondo que Bolt desempenhou uma aceleração constante até atingir a velocidade de 12 metros por segundo, ele aumentou sua velocidade em 3 vírgula 17 metros por segundo a cada segundo, isto é, uma aceleração de aproximadamente 3 vírgula 17 metros por segundo quadrado.
Página 346
Movimento uniforme e movimento uniformemente variado
Como vimos, na prática de esportes ou em algumas situações do cotidiano, podemos perceber a realização de movimentos que são classificados como uniforme, em que módulo, direção e sentido do vetor velocidade permanecem constantes em função do tempo; e uniformemente variado, em que ocorre a variação da velocidade em função do tempo.
Dica
As classificações do movimento em uniforme e uniformemente variado são idealizações que contribuem para a compreensão, a descrição e a previsão dos movimentos observados no cotidiano.
Na maratona corrida por Kelvin Kiptum, mencionada anteriormente, consideramos que sua rapidez foi constante, aproximadamente igual a 21 quilômetros por hora durante todo seu percurso, descrevendo, portanto, um movimento uniforme. Supondo que um cronômetro seja iniciado logo após a largada e que as parciais do atleta sejam anotadas a cada 30 minutos abre parênteses 0 vírgula 5 hora fecha parênteses, podemos construir o esquema a seguir.
Imagem sem proporção e em cores fantasia.

Como conhecemos o valor da velocidade do corredor e da sua posição inicial em relação à linha de largada, é possível fazer o estudo desse movimento com base nas suas posições ocupadas em cada instante de tempo.
A relação entre as posições abre parênteses 's' fecha parênteses e os instantes de tempo abre parênteses 't' fecha parênteses pode ser expressa por meio da equação geral de uma reta, chamada de equação horária das posições do movimento uniforme. Para isso, consideramos a variação de tempo como delta 't' é igual a 't' menos 't' subscrito 0 e a variação da posição como delta 's' é igual a 's' menos 's' subscrito 0. Como o movimento é uniforme, a velocidade média representa a própria velocidade do movimento, já que ela é a mesma em qualquer instante de tempo, isto é, v subscrito m é igual a v. Portanto, com base na definição de velocidade média, a expressão matemática que descreve o movimento uniforme é dada por:
v subscrito m é igual a v é igual a início de fração, numerador: delta 's', denominador: delta 't', fim de fração é igual a início de fração, numerador: 's' menos 's' subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração implica em 's' menos 's' subscrito 0 é igual a v vezes abre parênteses 't' menos 't' subscrito 0 fecha parênteses portanto 's' é igual a 's' subscrito 0 mais v vezes abre parênteses 't' menos 't' subscrito 0 fecha parênteses
Para o caso em que o instante inicial é zero abre parênteses 't' subscrito 0 é igual a 0 fecha parênteses, temos:
's' é igual a 's' subscrito 0 mais v vezes 't'
Essa equação descreve matematicamente o movimento uniforme. Por meio dela, é possível realizar previsões das posições abre parênteses 's' fecha parênteses de um móvel dotado de velocidade constante em qualquer instante de tempo abre parênteses 't' fecha parênteses. Para isso, basta conhecer as condições iniciais, que são a velocidade e a posição inicial.
Sendo a velocidade do atleta v é igual a 20 quilômetros por hora e sua posição inicial 's' subscrito 0 é igual a 0, sua posição s no instante de tempo 't' é igual a 2 horas será:
's' é igual a 0 mais 20 vezes 2 é igual a 40 portanto 's' é igual a 40 quilômetros
Página 347
Na prova de atletismo, mencionada anteriormente, realizada por Usain Bolt, consideraremos que sua aceleração foi constante e aproximadamente 3 vírgula 0 metros por segundo elevado ao quadrado nos primeiros 30 metros de prova, descrevendo, portanto, um movimento uniformemente variado. Supondo que um cronômetro seja iniciado na largada e que as parciais do atleta sejam anotadas a cada segundo, podemos construir o esquema a seguir.
Imagem sem proporção e em cores fantasia.

Como conhecemos o valor de sua aceleração e de sua velocidade inicial, em que começa seu movimento a partir do repouso, é possível fazer o estudo desse movimento com base nas suas velocidades em cada instante de tempo.
De modo similar ao do movimento uniforme, a relação entre as velocidades abre parênteses v fecha parênteses e os instantes de tempo abre parênteses 't' fecha parênteses pode ser expressa por meio da equação geral de uma reta, nesse caso, chamada de equação horária da velocidade do movimento uniformemente variado. Para isso, consideramos a variação da velocidade como delta v é igual a v menos v subscrito 0 e a variação de tempo como delta 't' é igual a 't' menos 't' subscrito 0. Com base na definição de aceleração, a expressão matemática que descreve o comportamento da velocidade de um movimento uniformemente variado é dada por:
a é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração é igual a início de fração, numerador: v menos v subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração implica em v menos v subscrito 0 é igual a a vezes abre parênteses 't' menos 't' subscrito 0 fecha parênteses portanto v é igual a v subscrito 0 mais a vezes abre parênteses 't' menos 't' subscrito 0 fecha parênteses
Para o caso em que o tempo inicial é zero abre parênteses 't' subscrito 0 é igual a 0 fecha parênteses, temos:
v é igual a v subscrito 0 mais a vezes 't'
Essa equação descreve matematicamente a variação da velocidade do movimento uniformemente variado. Por meio dela, é possível realizar previsões das velocidades abre parênteses v fecha parênteses de um móvel sujeito a uma aceleração constante em qualquer instante de tempo abre parênteses 't' fecha parênteses. Para isso, basta conhecer as condições iniciais, que são a velocidade inicial e a aceleração.
Professor, professora: Questione os estudantes sobre movimentos variados, comuns no cotidiano, em que se observa o conceito de aceleração, como na prática de esportes, e a função do acelerador dos veículos. Eles já devem ter percebido que, ao acionar o acelerador de um veículo engrenado, o motorista provoca uma variação na velocidade. Essa é uma situação em que se observa o conceito da aceleração.
Sendo a velocidade inicial do atleta v subscrito 0 é igual a 0 e sua aceleração a é igual a 3 metros por segundo quadrado, sua velocidade v no instante de tempo 't' é igual a 4 vírgula 0 segundos será
v é igual a 0 mais 3 vezes 4 é igual a 12 portanto v é igual a 12 metros por segundo
O aumento da velocidade se deve ao fato de a aceleração ser positiva; nesse caso, o movimento é classificado como acelerado. No entanto, se a aceleração fosse negativa, a velocidade diminuiria e o movimento seria classificado como retardado.
Página 348
No movimento uniformemente variado também é possível obter uma equação que relaciona as posições abre parênteses 's' fecha parênteses do corpo em cada instante abre parênteses 't' fecha parênteses, chamada de equação horária das posições no movimento uniformemente variado. Para isso, considere o diagrama das posições em função do tempo a seguir.
Velocidade em função do tempo de um movimento uniformemente variado

Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: mecânica. Tradução: Ronaldo Sérgio de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 1. p. 29.
O deslocamento realizado por um corpo no intervalo entre 't' subscrito 0 é igual a 0 e 't' é dado pela área da região delimitada pelo gráfico de velocidade pelo tempo, que, nesse caso, corresponde à área de um trapézio:
área expressão com detalhe acima, início da expressão, é igual a, fim da expressão, início do detalhe acima, N, fim do detalhe acima delta 's' é igual a 's' menos 's' subscrito 0 é igual a início de fração, numerador: abre parênteses B maiúsculo mais b minúsculo fecha parênteses vezes 'h', denominador: 2, fim de fração
Portanto, com base na figura, temos:
's' menos 's' subscrito 0 é igual a início de fração, numerador: abre parênteses v mais v subscrito 0 fecha parênteses vezes 't', denominador: 2, fim de fração é igual a início de fração, numerador: abre parênteses v mais v subscrito 0 fecha parênteses vezes 't', denominador: 2, fim de fração
Para representar uma dependência apenas em relação ao tempo, a variável v pode ser substituída pela equação horária das velocidades do movimento uniformemente variável, definida anteriormente. Portanto, isso nos leva à seguinte expressão:
's' menos 's' subscrito 0 é igual a início de fração, numerador: abre parênteses v subscrito 0 mais a vezes 't' mais v subscrito 0 fecha parênteses vezes 't', denominador: 2, fim de fração é igual a início de fração, numerador: abre parênteses 2 vezes v subscrito 0 mais a vezes 't' fecha parênteses vezes 't', denominador: 2, fim de fração portanto 's' é igual a 's' subscrito 0 mais v subscrito 0 vezes 't' mais início de fração, numerador: a vezes 't' elevado ao quadrado, denominador: 2, fim de fração
Por meio dessa equação, é possível realizar previsões das posições do móvel em determinados instantes de tempo.
Ainda em relação à prova do recorde de Bolt, sendo 's' subscrito 0 é igual a 0 e v subscrito 0 é igual a 0 e a é igual a 3 metros por segundo quadrado, a posição que ele ocupou após 4 segundos de prova é dada por:
's' é igual a 0 mais 0 vezes 4 mais início de fração, numerador: 3 vezes 4 elevado ao quadrado, denominador: 2, fim de fração é igual a 48 sobre 2 é igual a 24 portanto 's' é igual a 24 metros
É possível definir uma terceira equação que não apresenta dependência temporal. Para isso, pode-se usar a equação horária das velocidades resolvida para o tempo:
v é igual a v subscrito 0 mais a vezes 't' implica em 't' é igual a início de fração, numerador: abre parênteses v menos v subscrito 0 fecha parênteses, denominador: a, fim de fração
Substituindo a relação anterior na equação horária das posições para o movimento uniformemente variado, tem-se:
's' é igual a 's' subscrito 0 mais v subscrito 0 vezes 't' mais início de fração, numerador: a vezes 't' elevado ao quadrado, denominador: 2, fim de fração é igual a 's' subscrito 0 mais v subscrito 0 vezes abre colchetes início de fração, numerador: abre parênteses v menos v subscrito 0 fecha parênteses, denominador: a, fim de fração fecha colchetes mais início de fração, numerador: a vezes abre colchetes início de fração, numerador: abre parênteses v menos v subscrito 0 fecha parênteses, denominador: a, fim de fração fecha colchetes elevado ao quadrado, denominador: 2, fim de fração
Fazendo os devidos arranjos dos termos, obtemos a relação conhecida como equação de Torricelli, que mostra a dependência entre posição e velocidade, com dependência indireta com o tempo:
v elevado ao quadrado é igual a v subscrito 0 início sobrescrito, 2, fim sobrescrito mais 2 vezes a vezes abre parênteses 's' menos 's' subscrito 0 fecha parênteses
Compartilhe ideias
O estudo e a análise do movimento uniforme e uniformemente variado têm grande aplicação por profissionais no cotidiano.
a ) Junte-se a um colega e pesquisem quais profissionais usam as equações de movimento na sua prática de trabalho. Quais são os objetivos desses profissionais em fazer uso dessas equações? Em seguida, escolham uma das profissões pesquisadas e preparem uma apresentação para o restante da turma, a fim de mostrar a importância do estudo do movimento e sua aplicação.
Resposta: Espera-se que os estudantes citem o emprego das equações de movimento por profissionais ligados ao automobilismo, por peritos criminais, controladores de voo etc. Por meio das análises de movimento utilizando suas equações matemáticas, tais profissionais são capazes de fazer previsões. Isso também possibilita descrever o que ocorreu em uma cena de crime ou acidente automobilístico, por exemplo.
Página 349
Movimento circular
Um movimento é chamado de circular quando o corpo em estudo descreve uma trajetória curva (ou arco de circunferência). Há vários movimentos que podem ser caracterizados como movimento circular, como na modalidade de lançamento de martelo, descrita no início deste capítulo.
4. Em quais outros esportes, além do lançamento de martelo, temos exemplos de movimento circular?
Os estudantes podem citar as provas do atletismo, em que os atletas dão voltas na pista. Também podem citar o ciclismo de pista, manobras de giro na patinação ou no skate, lançamento de disco, entre outros esportes.
O movimento circular é estudado utilizando-se as grandezas já apresentadas, como a posição, a velocidade e a aceleração. Entretanto, essas grandezas são analisadas por meio de suas características angulares, baseadas em elementos da circunferência, tal como o raio e o ângulo.
Por exemplo, a aceleração abre parênteses expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses no movimento circular apresenta duas componentes: a aceleração tangencial abre parênteses expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 't' fecha parênteses e a aceleração centrípeta abre parênteses expressão com detalhe acima, início da expressão, a, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito c fecha parênteses, como mostra a imagem.
Imagens desta página sem proporção e em cores fantasia.
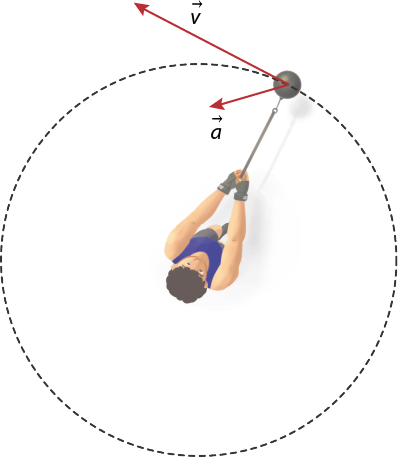
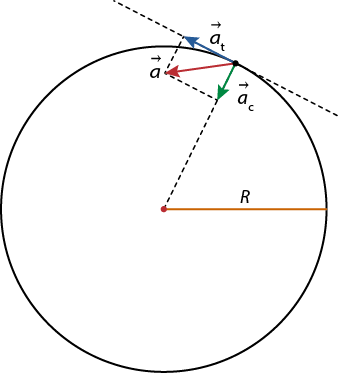
Imagens elaboradas com base em: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: mecânica. Tradução: Ronaldo Sérgio de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 1. p. 78.
A componente tangencial da aceleração está relacionada à variação da intensidade do vetor velocidade do martelo. Ela tem direção tangente à trajetória e seu módulo é dado por:
a subscrito 't' é igual a início de fração, numerador: delta v, denominador: delta 't', fim de fração
Já a componente centrípeta está relacionada com a variação da orientação (direção e sentido) do vetor velocidade do martelo. Ela tem direção radial, com sentido para o centro da trajetória. Seu módulo é calculado por:
a subscrito c é igual a início de fração, numerador: v elevado ao quadrado, denominador: R, fim de fração
Portanto, o módulo da aceleração do martelo é dado por a é igual a início de raiz quadrada; a subscrito t início sobrescrito, 2, fim sobrescrito mais a subscrito c início sobrescrito, 2, fim sobrescrito fim de raiz quadrada.
Supondo que o atleta faça o martelo girar com velocidade cujo módulo seja constante, isto é, com aceleração tangencial nula, o período de rotação do martelo é o mesmo que o período de rotação dos braços do atleta. Entretanto, os comprimentos das trajetórias são diferentes. Esse tipo de movimento descrito é chamado de movimento circular uniforme.
O estudo do movimento circular pode ser realizado com a definição de um referencial bidimensional com a origem sobre o eixo de rotação abre parênteses O fecha parênteses. Considere que determinado corpo executa um movimento circular entre a posição inicial abre parênteses i fecha parênteses e a posição final abre parênteses f fecha parênteses, descrevendo um arco de circunferência, como mostra a imagem do início da próxima página.
Dica
Período de rotação abre parênteses T fecha parênteses é o intervalo de tempo para cada ciclo, isto é, intervalos regulares de tempo em que o móvel retorna à sua posição inicial. Sua relação é inversamente proporcional à frequência abre parênteses f fecha parênteses, que é definida como o número de ciclos por unidade de tempo, medida, no SI, em s elevado a menos 1, denominado hertz hertz.
A relação entre período e frequência é inversamente proporcional, de modo que f é igual a 1 sobre T ou T é igual a 1 sobre f.
Página 350
As posições i e f do corpo são determinadas, respectivamente, pelos segmentos de reta expressão com detalhe acima, início da expressão, O i, fim da expressão, início do detalhe acima, barra horizontal, fim do detalhe acima e expressão com detalhe acima, início da expressão, O f, fim da expressão, início do detalhe acima, barra horizontal, fim do detalhe acima, em relação ao ângulo que elas fazem a partir do eixo x. Nesse caso, denomina-se a posição angular inicial como teta subscrito 0 e a posição angular final como teta. Portanto, o deslocamento angular, que é definido como a diferença entre a posição angular final e inicial, é dado por:
delta teta é igual a teta menos teta subscrito 0
Dica
A posição angular e o deslocamento angular são expressos em radiano abre parênteses rad fecha parênteses, unidade de medida no SI.
Imagem sem proporção e em cores fantasia.
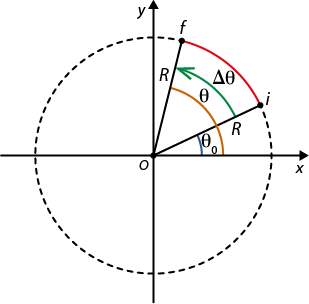
Imagem elaborada com base em: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: mecânica. Tradução: Ronaldo Sérgio de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 1. p. 260.
Conforme o corpo realiza um deslocamento angular delta teta, ele também realiza um deslocamento linear delta s, que corresponde ao arco de circunferência. A relação entre os deslocamentos angular e linear é dada por:
delta teta é igual a início de fração, numerador: delta 's', denominador: R, fim de fração ou delta 's' é igual a delta teta vezes R

Com base na relação anterior, observa-se que a relação entre o deslocamento linear e o raio da circunferência é inversamente proporcional. Por isso, nas provas de atletismo de maiores distâncias, o atleta que ocupa as raias mais externas larga mais à frente dos outros, a fim de compensar o maior comprimento de semicírculo que percorrerá, em razão do maior raio.

A rapidez em que ocorre a mudança na posição angular do móvel define-se como velocidade angular ou frequência angular. A média das diferentes velocidades angulares é chamada de velocidade angular média, que é definida pela razão entre o deslocamento angular abre parênteses delta teta fecha parênteses e o intervalo de tempo abre parênteses delta 't' fecha parênteses para a realização do respectivo deslocamento, ou seja:
ômega subscrito m é igual a início de fração, numerador: delta teta, denominador: delta 't', fim de fração
Dica
A velocidade angular é medida, no SI, em radiano por segundo abre parênteses rad barra s fecha parênteses.
Caso seja um movimento circular uniforme, isto é, movimento cuja velocidade angular seja constante, a velocidade angular média corresponde à velocidade angular do corpo em qualquer ponto da trajetória. Portanto, podemos considerar ômega subscrito m é igual a ômega, ou seja, a velocidade angular média é a própria velocidade angular do movimento. Assim, de forma semelhante ao movimento retilíneo uniforme, podemos escrever a equação horária para a posição angular:
ômega é igual a início de fração, numerador: delta teta, denominador: delta t, fim de fração é igual a início de fração, numerador: teta menos teta subscrito 0, denominador: 't' menos 't' subscrito 0, fim de fração implica em teta menos teta subscrito 0 é igual a ômega vezes t portanto teta é igual a teta subscrito 0 mais ômega vezes t
Com base na relação anterior, é possível descrever e prever as posições angulares do corpo que descreve um movimento circular.
Podemos obter uma relação entre a velocidade abre parênteses v fecha parênteses e a velocidade angular abre parênteses ômega fecha parênteses. Para isso, divide-se a relação entre o deslocamento linear e o deslocamento angular pela variação de tempo, isto é:
delta 's' é igual a delta teta vezes R implica em início de fração, numerador: delta 's', denominador: delta 't', fim de fração é igual a início de fração, numerador: delta teta, denominador: delta 't', fim de fração vezes R portanto v é igual a ômega vezes R
Página 351
ATIVIDADES
1. Um nadador pretende atravessar uma piscina de 50 metros de comprimento em 62 vírgula 5 segundos. Na primeira metade da piscina, ele desenvolve uma velocidade média de módulo 0 vírgula 5 metro por segundo. Qual deve ser sua velocidade média na segunda metade da piscina para seu objetivo ser alcançado?
Resposta: v é igual a 2 metros por segundo
2. Um atleta de salto ornamental abandona a plataforma de salto de 10 metros em queda livre. Estime o tempo que o atleta tem para realizar suas acrobacias e sua velocidade ao entrar na água.
Resposta: delta 't' é aproximadamente igual a 1 vírgula 41 segundo e v é igual a 14 vírgula 1 metros por segundo.
3. Em uma empresa de automóveis, um modelo passa por um teste no qual ele é acelerado em uma pista retilínea, a partir do repouso, até 216 quilômetros por hora em 24 segundos, para então ser freado até parar com uma aceleração média de módulo 10 metros por segundo elevado ao quadrado.
a ) Qual é o módulo da aceleração média do automóvel nos primeiros 24 segundos de teste?
Resposta: a é igual a 2 vírgula 5 metros por segundo quadrado
b ) Quanto tempo dura a frenagem do automóvel no segundo teste?
Resposta: 't' é igual a 6 segundos
4. Um ciclista parte do repouso e acelera a uma taxa constante de 0 vírgula 5 metro por segundo quadrado enquanto pedala em uma pista reta. O ciclista continua acelerando por 12 segundos antes de alcançar uma velocidade constante.
a ) Qual é a velocidade final do ciclista ao final dos 12 segundos?
Resposta: v é igual a 6 metros por segundo
b ) Qual é a distância total percorrida pelo ciclista durante esse tempo?
Resposta: 's' é igual a 36 metros
Resolução das questões 1, 2, 3 e 4 nas Orientações para o professor.
5. Considere a situação representada na imagem a seguir. Um automóvel percorre o trecho de rodovia representado na imagem com velocidade de módulo constante.
Imagem sem proporção e em cores fantasia.
As sentenças a seguir estão relacionadas a essa situação. Avalie as afirmativas como verdadeiras ou falsas, corrigindo as falsas.
a ) A velocidade no trecho AB é constante.
b ) A velocidade durante todo o trecho AD é constante.
c ) O movimento no trecho AD não teve aceleração.
d ) No trecho BC, existe uma aceleração que altera a orientação da velocidade.
e ) No trecho CD, o automóvel manteve a aceleração do trecho BC.
Resposta: a) Verdadeira; b) Falsa. A velocidade é constante nos trechos AB e CD; c) Falsa. O movimento teve aceleração no trecho BC; d) Verdadeira; e) Falsa. No trecho CD, o automóvel não teve aceleração.
6. Analise os gráficos a seguir.
1.
Gráfico da posição × tempo para um móvel
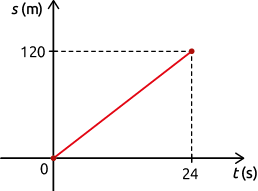
2.
Gráfico da velocidade × tempo para um móvel

3.
Gráfico velocidade × tempo para um móvel

Fonte de pesquisa: TIPLER, Paul Allen; MOSCA, Gene. Física para cientistas e engenheiros: mecânica, oscilações e ondas, termodinâmica. Tradução: Paulo Machado Mors. Rio de Janeiro: LTC, 2009. v. 1. p. 33-38.
Verifique se as afirmações a seguir são verdadeiras ou falsas, corrigindo as falsas.
a ) O gráfico 1 é de um movimento uniforme.
b ) Os gráficos 2 e 3 representam um movimento uniforme.
c ) O gráfico 3 representa um corpo em repouso.
d ) Os gráficos 1 e 3 podem representar o mesmo movimento.
e ) Os gráficos 1 e 2 representam movimentos uniformes diferentes.
Resposta: a) Verdadeira; b) Falsa. O gráfico 2 representa um movimento uniforme e o gráfico 3, um corpo em repouso; c) Verdadeira; d) Falsa. O gráfico 1 representa um movimento uniforme e o gráfico 3, um corpo em repouso; e) Verdadeira.
Página 352
7. Um ciclista se movendo por uma ciclovia retilínea com velocidade de 36 quilômetros por hora avista um galho caído no meio da pista a 10 metros do local onde ele aciona subitamente os freios. Qual é a aceleração mínima, supostamente constante, que ele deve submeter para não bater no galho caído? Escreva a alternativa correta.
a ) 5 metros por segundo quadrado
b ) menos 5 metros por segundo quadrado
c ) 10 metros por segundo elevado ao quadrado
d ) 3 metros por segundo quadrado
e ) menos 3 metros por segundo quadrado
Resposta: Alternativa b.
8. Em 5 de agosto de 2012, o robô Curiosity, da Nasa, chegou a Marte com o objetivo de investigar se o planeta já teve características favoráveis à existência de vida. O Curiosity é capaz de atingir a velocidade máxima de 150 centímetros por minuto. Durante sua primeira movimentação em linha reta, as velocidades desenvolvidas foram registradas no gráfico que segue.
Gráfico de v vezes t do movimento do robô Curiosity
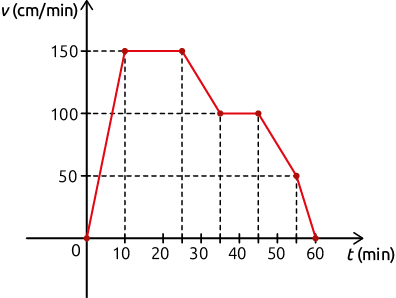
Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: mecânica. Tradução: Ronaldo Sérgio de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 1. p. 37.
a ) Qual é o deslocamento do Curiosity no intervalo de tempo de 10 a 25 minutos? E entre 35 e 45 minutos?
Resposta: De 10 a 25 minutos, delta s é igual a 22 vírgula 5 metros e de 35 a 45 minutos, delta s é igual a 10 metros.
b ) Em quais intervalos de tempo o movimento executado pelo robô foi uniforme? Justifique.
Resposta: Entre 10 e 25 minutos e entre 35 e 45 minutos. Nesses intervalos de tempo, as velocidades desenvolvidas pelo robô foram constantes. Para os outros intervalos de tempo, as velocidades sofreram variações em seus módulos.
9. Em uma rodovia, um automóvel se desloca com velocidade de valor constante e igual a 20 metros por segundo, quando um animal invade subitamente a pista. O motorista que dirigia com atenção aciona imediatamente os freios na posição definida como 's' subscrito 0 é igual a 0 e inicia um movimento uniformemente retardado, parando o veículo em 6 segundos. Determine o valor da aceleração desenvolvida pelo veículo e o deslocamento realizado até o repouso, em unidades do SI.
Resposta: a é aproximadamente igual a menos 3 vírgula 3 metros por segundo elevado ao quadrado
10. A partir de um instante definido como 't' subscrito 0 é igual a 0, as posições ocupadas por um veículo em movimento são dadas pela função 's' é igual a 24 't' menos 0 vírgula 6 't' elevado ao quadrado.
a ) Em qual instante ocorre a inversão de sentido?
Resposta: 't' é igual a 20 segundos
b ) Qual é o deslocamento executado pelo veículo de 't' subscrito 0 é igual a 0 até a inversão do movimento?
Resposta: delta 's' é igual a 240 metros
c ) Esboce o gráfico da velocidade em função do tempo, no intervalo de tempo entre 't' subscrito 0 é igual a 0 e o instante da inversão de sentido. De que forma a resposta da questão b pode ser verificada nesse gráfico?
11. Na aviação, uma curva padrão para um voo de um avião do tipo hélice é aquela em que o avião faz uma curva circular completa em 1,5 minuto. Se a velocidade do avião for 180 metros por segundo, conside- rando pi é igual a 3, determine:
a ) o raio de sua curva.
Resposta: R é igual a 2.700 metros
b ) a aceleração centrípeta do avião.
Resposta: a subscrito c é igual a 12 metros por segundo quadrado
12. Uma partícula que realiza um movimento circular uniforme de raio 1 vírgula 5 metro tem função horária angular teta é igual a pi sobre 4 mais pi sobre 8 vezes 't' (SI). Determine:
a ) a aceleração centrípeta sobre a partícula.
Resposta: a subscrito c é aproximadamente igual a 0 vírgula 23 metro por segundo elevado ao quadrado
b ) a posição angular no instante 't' é igual a 16 segundos.
Resposta: teta é igual a início de fração, numerador: 9 vezes pi, denominador: 4, fim de fração rad
13. Na modalidade esportiva de lançamento de martelo, antes do arremesso, o atleta realiza movimento de rotação fazendo o objeto girar em torno de seu corpo e com o cabo de aço de 1 vírgula 2 metro de comprimento esticado. Suponha que o atleta demore 0 vírgula 5 segundo para completar uma volta. Considerando que esse movimento seja circular uniforme, responda:
a ) Qual é a frequência de seu movimento?
Resposta: f é igual a 2 hertz
b ) Qual é a velocidade angular desse movimento?
Resposta: ômega é igual a 4 vezes pi rad barra s
c ) Antes de iniciar o giro, o atleta posicionou o corpo formando um ângulo pi na posição angular inicial. Escreva a equação para a posição angular horária do giro do atleta.
Resposta: teta é igual a pi mais 4 vezes pi vezes 't'
d ) Qual é a velocidade do martelo na extremidade do cabo se o braço do atleta tiver 75 centímetros de comprimento?
Resposta: v é igual a 7 vírgula 8 vezes pi metros por segundo
14. Duas pessoas correm, com velocidades constantes, em uma pista com formato de circunferência. A raia da pessoa A tem um raio de curvatura de 25 metros, e a raia da pessoa B tem um raio de curvatura de 50 metros. Sabe-se que a pessoa B corre a uma velocidade de 3 metros por segundo, ambas partem do mesmo ponto e completam uma volta juntas. Determine a velocidade de A, a distância percorrida e o tempo para completar uma volta, para ambas. (Utilize pi é igual a 3 vírgula 14)
Resposta: v subscrito A é igual a 1 vírgula 5 metro por segundo; delta 's' subscrito A é igual a 157 metros; delta 's' subscrito B é igual a 314 metros e delta 't' é aproximadamente igual a 104 vírgula 7 segundos.
Resolução das questões 7 a 14 nas Orientações para o professor.
Página 353
CAPÍTULO23
Energia e impulso
Trabalho
Você conhece o bobsled? Trata-se de um esporte coletivo de inverno. Os praticantes dessa modalidade utilizam um trenó para percorrer uma pista de gelo no menor tempo possível. As provas são divididas em categorias com equipes formadas por dois ou quatro atletas.
Antes de começar a descida, os atletas devem empurrar o trenó por cerca de 50 metros, para adquirir certa velocidade, e entrar nele na sequência.
Em razão do impulso inicial e da inclinação da pista, o conjunto trenó e atletas pode atingir uma velocidade máxima de aproximadamente 150 quilômetros por hora.

Para analisar o que acontece enquanto os atletas empurram o trenó, podemos utilizar um diagrama de corpo livre, ou seja, uma representação esquemática em que identificamos todas as forças que atuam em determinado corpo.
Durante a fase de empurrar, os atletas transferem energia para o trenó, deslocando-o por meio da força aplicada.
A grandeza física relacionada à transferência de energia de um sistema ou de um corpo para outro, com base na relação entre força e deslocamento, é denominada trabalho, representado pela letra grega tau abre parênteses tau fecha parênteses.
Imagem sem proporção e em cores fantasia.

Na situação descrita, a força resultante (soma de todas as forças que atuam sobre o corpo) é a responsável por causar o deslocamento. O valor do trabalho realizado por uma força que tem a mesma direção e o mesmo sentido do deslocamento é dado pelo produto entre a intensidade da força e do deslocamento:
tau é igual a 'F' vezes delta 's'
em que:
- tau é o trabalho realizado pela força em newton-metro abre parênteses N vezes m fecha parênteses, unidade denominada joule abre parênteses J fecha parênteses em homenagem ao físico inglês James Prescott Joule (1818-1889), que verificou a transformação de energia mecânica em térmica;
- 'F' é a intensidade da força que atua sobre o corpo em newton N;
- delta 's' é o deslocamento causado pela força em metro metro.
Quando a força aplicada e o deslocamento têm orientações diferentes, somente a componente que está na mesma direção do deslocamento realiza trabalho, de modo que a equação pode ser reescrita como:
tau é igual a 'F' vezes delta 's' vezes cosseno teta
O ângulo teta é medido entre as direções da força e do deslocamento.
Página 354
Se a força ou uma de suas componentes tem o mesmo sentido do deslocamento abre parênteses 0 grau é menor ou igual a teta é menor do que 90 graus fecha parênteses, o trabalho realizado fornece energia ao corpo ou ao sistema e tem sinal positivo. Se a força ou uma de suas componentes tem sentido oposto ao do deslocamento abre parênteses 90 graus é menor do que teta é menor ou igual a 180 graus fecha parênteses, o trabalho realizado retira energia do corpo ou do sistema e tem sinal negativo. Se a força for perpendicular ao deslocamento, temos cosseno 90 graus é igual a 0; isso significa que a força não realiza trabalho sobre o corpo.
Temos ainda que o trabalho é máximo quando a força aplicada ocorre paralelamente ao deslocamento, pois cos 0 grau é igual a 1.
Quando mais de uma força estiver agindo sobre o corpo, devemos calcular o trabalho realizado pela força resultante abre parênteses expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito R fecha parênteses. O ângulo será medido entre a força resultante e o deslocamento.
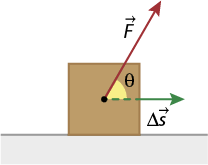
Imagens desta página sem proporção e em cores fantasia.
Outro esporte que podemos analisar é o levantamento de peso, no qual os atletas elevam e descem halteres.

A.
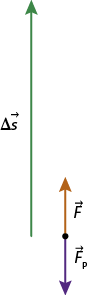
B.

Supondo que um atleta eleve o haltere até certa altura, descendo-o até a posição inicial com velocidade constante, e desprezando pequenas acelerações no início de cada movimento, a força aplicada por ele tem a mesma intensidade que a força peso do haltere abre parênteses 'F' é igual a 'F' subscrito P é igual a 'm' vezes 'g' fecha parênteses, e o deslocamento vertical corresponde à altura atingida pelo haltere abre parênteses delta 's' é igual a 'h' fecha parênteses.
O trabalho realizado por meio da força aplicada pelo atleta na subida é dado por:
tau é igual a 'F' vezes delta 's' vezes cos 0 grau implica em tau é igual a 'F' subscrito P vezes 'h' vezes 1 implica em tau é igual a 'm' vezes 'g' vezes 'h'
Durante a subida, a força peso tem sentido oposto ao deslocamento, de modo que o trabalho realizado pela força peso na subida é dado por:
tau início subscrito, 'F' subscrito P, fim subscrito é igual a 'F' vezes delta 's' vezes cos 180 graus implica em
implica em tau início subscrito, 'F' subscrito P, fim subscrito é igual a 'F' subscrito P vezes 'h' vezes abre parênteses menos 1 fecha parênteses implica em
implica em tau início subscrito, 'F' subscrito P, fim subscrito é igual a menos 'm' vezes 'g' vezes 'h'
Ao descer o haltere com velocidade constante, a força peso atua na mesma direção do deslocamento; o ângulo entre a força peso e o deslocamento é 0 grau e o trabalho realizado por ela durante a descida é dado por:
tau início subscrito, 'F' subscrito P, fim subscrito é igual a 'F' vezes delta 's' vezes cos 0 grau implica em tau início subscrito, 'F' subscrito P, fim subscrito é igual a 'F' subscrito P vezes 'h' vezes 1 implica em
tau início subscrito, 'F' subscrito P, fim subscrito é igual a 'm' vezes 'g' vezes 'h'
Vemos, então, que o trabalho da força peso depende apenas da distância vertical entre os pontos inicial e final, sendo independente da trajetória executada. Essa é uma propriedade das forças conservativas.
Retornando ao caso do bobsled, é fato que o trenó acelera ao longo da descida. Isso é possível por conta do trabalho realizado sobre o trenó pela força peso.
Página 355
Imagens desta página sem proporção e em cores fantasia.
Como o movimento ocorre em uma pista inclinada, a componente da força peso que está na mesma direção da rampa abre parênteses 'F' início subscrito, P subscrito x, fim subscrito fecha parênteses realiza trabalho sobre o trenó durante todo o trajeto da pista.
Entretanto, o valor do trabalho da força peso é independente do trajeto percorrido e pode ser obtido apenas considerando o deslocamento vertical entre o ponto mais alto e o mais baixo da pista.
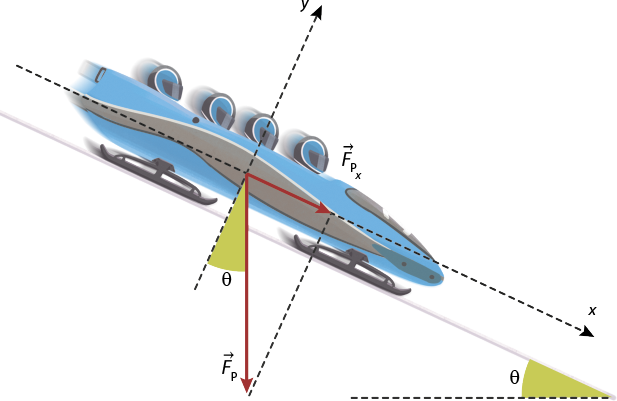
Energias
No tópico anterior, vimos que a realização de trabalho pode adicionar ou retirar energia de um corpo ou sistema.
1. Você já pensou em todos os tipos de energia que utilizamos no cotidiano? Cite pelo menos três tipos de energia, relacionando-os a uma atividade cotidiana.
Resposta pessoal. Os estudantes podem citar energia elétrica para acender uma lâmpada, energia térmica para aquecer alimentos, energia química nos combustíveis e alimentos, energia luminosa para iluminar os ambientes, entre outros tipos.
O conceito de energia não é facilmente definido, no entanto está relacionado a processos de mudanças e transformações em corpos ou sistemas. Em virtude disso, costuma-se estudar as transformações de energia.
Nas práticas esportivas, geralmente há diversas transformações de energia. Vamos analisar o que acontece no salto com vara. Nesse esporte, o atleta usa uma vara flexível para saltar por cima de um obstáculo, chamado sarrafo, que pode estar a mais de 6 metros de altura.
A imagem a seguir mostra diferentes momentos do salto com vara.
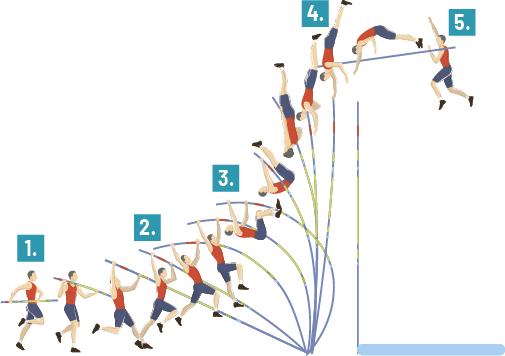
1. No início da prova, o esportista deve correr. Nesse momento, ele utiliza a energia química armazenada em seu corpo (especialmente em seus músculos) graças à alimentação. A energia química é transformada em energia cinética, relacionada à velocidade, e o atleta adiciona um componente vertical à sua velocidade.
2. Na sequência, ele apoia a vara flexível em uma caixa na área de impulsão. O movimento dele faz a vara se curvar, acumulando energia potencial elástica (a mesma energia acumulada nos elásticos e nas molas). É uma energia potencial, pois está armazenada na deformação da vara, que tende a voltar ao seu formato original.
A maneira como o atleta executa o salto faz a energia acumulada arremessá-lo para cima.
3. A velocidade horizontal do atleta diminui, mas ele desenvolve velocidade na vertical, para cima. Isso ocorre em razão de uma nova transformação da energia: a cinética e a potencial elástica transformam-se em energia potencial gravitacional, fazendo-o ganhar altura em relação ao solo.
4. Na altura máxima, ele gira seu corpo para superar o sarrafo, sem derrubá-lo.
5. Enquanto cai, em consequência da ação da força gravitacional, retornando ao solo, a energia potencial gravitacional acumulada é transformada em energia cinética. Para protegê-lo, há um colchão de aterrissagem, que absorve o impacto da queda e dissipa a energia cinética em vibração, calor e som, impedindo que ele se machuque.
Página 356
Nas provas de salto com vara, vence o atleta que superar a maior altura. Ao final dos saltos, todos descansam e se alimentam, repondo a energia consumida.
Vamos descrever agora os diferentes tipos de energia envolvidos no salto com vara e em diversas situações do cotidiano.
Como citado anteriormente, a energia cinética abre parênteses E subscrito c fecha parênteses é relacionada ao movimento. Trata-se de uma grandeza escalar e depende da massa abre parênteses 'm' fecha parênteses em quilograma abre parênteses k g elevado ao cubo fecha parênteses e do módulo da velocidade abre parênteses v fecha parênteses em metro por segundo abre parênteses m barra s fecha parênteses do corpo em movimento, sendo calculada pela relação a seguir.
E subscrito c é igual a início de fração, numerador: 'm' vezes v elevado ao quadrado, denominador: 2, fim de fração
Como todos os tipos de energia, a cinética também é dada, no SI, em joule abre parênteses J fecha parênteses.
Professor, professora: Diga aos estudantes que essas unidades de medida são do Sistema Internacional de Unidades (SI).
Note que a energia cinética é diretamente proporcional à massa e ao quadrado da velocidade. Isso significa que, ao dobrar a massa do objeto, dobramos a energia cinética; mas ao dobrar a velocidade, a energia cinética aumenta em quatro vezes.
Por exemplo, um caminhão, mesmo em baixa velocidade, pode ter grande energia cinética em razão de sua massa. Já um projétil de rifle pode ter grande energia cinética em consequência da alta velocidade, mesmo tendo massa pequena.
Compartilhe ideias
Mesmo dentro do limite de velocidade de uma rodovia, a energia cinética de um carro é muito grande.
a ) Converse com seus colegas sobre como a velocidade dos veículos pode influenciar os danos ocasionados em colisões automotivas, de acordo com a energia cinética. Em seguida, faça um infográfico mostrando como a energia cinética se comporta quando a velocidade aumenta.
Resposta: Espera-se que os estudantes mencionem que, se a velocidade de um carro dobra, a energia cinética quadruplica. Isso significa que, quanto mais rápido um veículo estiver, maior será o impacto e os danos durante uma colisão, pois mais energia precisará ser dissipada no momento do acidente. Por isso, dirigir em alta velocidade aumenta muito o risco de acidentes graves. Para a composição do infográfico, espera-se que eles ilustrem a relação do rápido aumento da energia cinética à medida que a velocidade aumenta.
A energia potencial elástica abre parênteses E subscrito pe fecha parênteses é a energia armazenada em corpos, como molas e elásticos, quando eles são deformados. Esses corpos ou materiais tendem a retornar ao seu estado de equilíbrio após uma deformação, isto é, após sofrer uma expansão ou uma compressão.
A energia potencial elástica armazenada depende do valor da deformação causada, representada por x e medida em metro metro. Ela também depende da constante elástica k do material.
A energia potencial elástica também é medida em joule abre parênteses J fecha parênteses, no SI, e calculada pela relação a seguir.
E subscrito pe é igual a início de fração, numerador: k vezes x elevado ao quadrado, denominador: 2, fim de fração
A constante elástica abre parênteses k fecha parênteses é uma propriedade do corpo elástico que relaciona a intensidade da força aplicada ao corpo com o comprimento da deformação causada. No SI, k é medida em newton por metro abre parênteses N barra m fecha parênteses.
Imagem sem proporção e em cores fantasia.
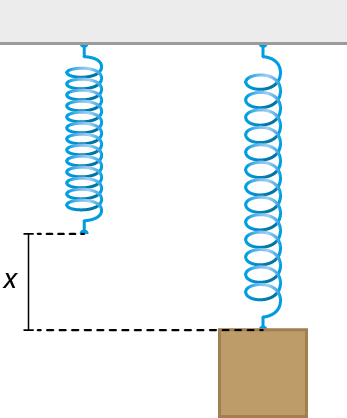
Geralmente, trabalhamos a energia potencial elástica em molas ideais, capazes de armazenar energia e devolvê-la sem perdas.
Já a energia potencial gravitacional abre parênteses E subscrito p g fecha parênteses é acumulada em qualquer objeto que se encontra a certa altura do solo ou em outro nível de referência em relação à Terra, em razão do campo gravitacional terrestre.
Página 357
Para elevar um corpo até certa altura, é necessária uma força que realize trabalho sobre o corpo, atuando no sentido contrário à força peso. Desse modo, o corpo armazena energia potencial gravitacional e, caso seja deixado livre, a força peso atua, realizando trabalho sobre o corpo e transformando a energia potencial gravitacional em cinética.
A energia potencial gravitacional depende da massa do corpo abre parênteses 'm' fecha parênteses em quilograma abre parênteses k g elevado ao cubo fecha parênteses, da altura abre parênteses 'h' fecha parênteses em relação ao nível de referência em metro metro e da aceleração da gravidade local abre parênteses 'g' fecha parênteses, dada pela relação a seguir.
E subscrito p g é igual a 'm' vezes 'g' vezes 'h'
A energia potencial gravitacional também é medida em joule abre parênteses J fecha parênteses.
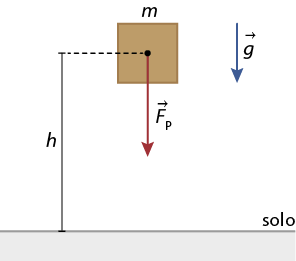
Imagens desta página sem proporção e em cores fantasia.
É importante notar que a energia armazenada, seja ao elevar um corpo no espaço, seja ao comprimir uma mola, será transformada em outros tipos de energia, de modo que a quantidade de energia total do sistema se mantém constante. Ou seja, a energia não é criada nem destruída, apenas se transforma. Esse é o princípio da conservação da energia.
Quando um sistema tem somente as energias cinética, potencial elástica e potencial gravitacional, dizemos que tem uma quantidade de energia mecânica abre parênteses E subscrito m fecha parênteses. O sistema pode ter apenas energia cinética, apenas potencial ou ambas somadas, de modo que podemos expressar a energia mecânica como:
E subscrito m é igual a E subscrito c mais E subscrito pe mais E subscrito p g
Em um sistema conservativo, a energia mecânica mantém-se constante. Isso quer dizer que o valor da energia mecânica final abre parênteses E subscrito m fecha parênteses é igual ao valor da energia mecânica inicial abre parênteses E início subscrito, m subscrito 0, fim subscrito fecha parênteses, ou seja:
E subscrito m é igual a E início subscrito, m subscrito 0, fim subscrito
Professor, professora: Comente com os estudantes que em situações reais não há sistemas conservativos, pois sempre ocorre dissipação de energia. No caso do skatista, a principal forma de dissipar energia é pelo atrito com a pista ou entre os componentes do skate.

Podemos verificar essa transformação ao analisar um skatista que realiza um salto em uma rampa.
Na base da rampa abre parênteses A fecha parênteses, ele tem somente energia cinética em razão da velocidade necessária para subir a rampa.
À medida que ele sobe a rampa baite, sua altura em relação ao solo aumenta e a velocidade diminui, associando energia cinética e energia potencial gravitacional.
Ao atingir a altura máxima abre parênteses 'C' fecha parênteses, o skatista para e, nesse instante, toda a energia cinética inicial é transformada em energia potencial gravitacional.
Em seguida, ele desce a rampa, transformando novamente a energia potencial gravitacional em cinética (ao voltar ao ponto A), o que conservaria a energia mecânica do sistema em um caso ideal.

Devemos observar que as transformações de energia em um sistema conservativo ocorrem por conta das forças elástica e gravitacional (peso), de modo que o trabalho realizado por essas forças pode ser determinado pela variação da energia cinética do corpo, ou seja:
tau é igual a delta E subscrito c implica em tau é igual a E subscrito c menos E início subscrito, c subscrito 0, fim subscrito implica em tau é igual a início de fração, numerador: 'm' vezes v elevado ao quadrado, denominador: 2, fim de fração menos início de fração, numerador: 'm' vezes v subscrito 0 elevado ao quadrado, denominador: 2, fim de fração
na qual E subscrito c é a energia cinética final do corpo e E início subscrito, c subscrito 0, fim subscrito é a energia cinética inicial do corpo.
Página 358
Dica
Acesse o simulador "Energia na pista de skate", desenvolvido pela Universidade de Colorado Boulder, para verificar as transformações de energia no movimento de um skate em uma rampa. Disponível em: https://s.livro.pro/876y08. Acesso em: 12 set. 2024.
É importante ressaltar que a energia se conserva, mas nem sempre se transforma de maneira que possa ser reaproveitada. No caso do skate, em situações não ideais, parte da energia mecânica é transformada em calor (energia térmica) e som (energia sonora) em razão do atrito. Dizemos, então, que a força de atrito é dissipativa, pois ela diminui a energia mecânica do sistema.
Portanto, o trabalho das forças dissipativas pode ser calculado pela seguinte relação:
tau início subscrito, 'F' subscrito d, fim subscrito é igual a delta E subscrito m
Potência e rendimento
Já estudamos diferentes tipos de energia e suas transformações. A partir de agora, estudaremos a relação do conceito de energia com o tempo.
2. Por que subir rapidamente uma escada causa mais cansaço físico do que subi-la lentamente?
Resposta: Eles podem relacionar a subida com o trabalho realizado. Para subir rapidamente, é realizado o mesmo trabalho em um intervalo de tempo menor, ou seja, com maior potência. Em complemento, uma rápida subida exige que a energia química da pessoa seja transformada em energia potencial gravitacional em um curto intervalo de tempo, causando mais cansaço físico.
Imagine que você vai percorrer uma distância de 100 metros. Se você caminhar tranquilamente, isso levaria cerca de 80 segundos e não seria cansativo. Agora, pense na corrida dos 100 metros rasos, modalidade esportiva na qual os atletas podem completar a distância em cerca de 10 segundos. Apesar de a distância ser a mesma, o esportista se cansará muito mais após percorrer os 100 metros do que você em sua caminhada.

O que diferencia essas duas situações é a taxa com a qual o trabalho foi realizado. A grandeza que relaciona o trabalho realizado e o intervalo de tempo para realizá-lo é a potência abre parênteses P fecha parênteses.
A potência média abre parênteses P subscrito m fecha parênteses expressa a taxa média com a qual o trabalho foi realizado por unidade de tempo. Ela é calculada pela razão entre o trabalho realizado abre parênteses tau fecha parênteses e o intervalo de tempo abre parênteses delta 't' fecha parênteses, como mostrado a seguir.
P subscrito m é igual a início de fração, numerador: tau, denominador: delta 't', fim de fração
Dica
Caso o intervalo de tempo seja muito pequeno abre parênteses delta 't' seta para a direita 0 fecha parênteses, isto é, tendendo a zero, a velocidade será a instantânea abre parênteses v fecha parênteses e a potência abre parênteses P fecha parênteses, no instante de tempo abre parênteses 't' fecha parênteses, será a potência instantânea: P é igual a 'F' vezes v.
Como no SI, o trabalho é dado em joule abre parênteses J fecha parênteses e o intervalo de tempo em segundo abre parênteses s fecha parênteses, a potência é dada em joule por segundo abre parênteses J barra s fecha parênteses, unidade que foi renomeada para watt abre parênteses W fecha parênteses em homenagem ao engenheiro escocês James Watt (1736-1819).
Caso uma força constante atue sobre um corpo, realizando trabalho em certo intervalo de tempo, a potência média poderá ser escrita como:
P subscrito m é igual a início de fração, numerador: tau, denominador: delta 't', fim de fração é igual a início de fração, numerador: 'F' vezes delta 's', denominador: delta 't', fim de fração é igual a 'F' vezes início de fração, numerador: delta 's', denominador: delta 't', fim de fração implica em P subscrito m é igual a 'F' vezes v subscrito m
Página 359
O conceito de potência é muito útil para estudar o funcionamento das máquinas.

Todas as máquinas funcionam da mesma maneira: recebem uma potência total abre parênteses P subscrito t fecha parênteses do motor, por exemplo, utilizam uma parte dela para realizar o objetivo da máquina (potência útil P subscrito u) e a outra parte é dissipada (potência dissipada P subscrito d). No caso representado na imagem do guindaste, considera-se potência útil a que efetivamente é usada para erguer a viga. O restante, a potência que causa aquecimento e ruídos sonoros, é considerado potência dissipada, de modo que:
P subscrito t é igual a P subscrito u mais P subscrito d
A relação entre a potência total e a potência útil na máquina ou no sistema fornece o rendimento abre parênteses etá fecha parênteses da máquina, calculado por:
etá é igual a início de fração, numerador: P subscrito u, denominador: P subscrito t, fim de fração
O rendimento é um valor adimensional, ou seja, não tem unidade de medida. Quanto maior o rendimento de uma máquina, maior é a potência útil e menor é a potência dissipada (ou a energia dissipada).
Quantidade de movimento e impulso
Como sabemos, um objeto sob a ação de uma força resultante pode ter seu estado de movimento alterado, sofrendo uma aceleração enquanto a força atuar.
Um saque em uma bola de vôlei, uma tacada de golfe ou o chute em uma bola de futebol ou rugby são exemplos de aplicações de forças que causam aceleração nas bolas utilizadas nos respectivos esportes, fazendo-as se mover com certa velocidade.
Imagem sem proporção e em cores fantasia.

A velocidade de um corpo está relacionada a uma grandeza denominada quantidade de movimento, definida pelo físico inglês Isaac Newton (1643-1727) em sua obra Principia.
[...]
A quantidade de movimento é a medida do mesmo, obtida conjuntamente a partir da velocidade e da quantidade de matéria.
[...]
NEWTON, Isaac. Principia: princípios matemáticos de filosofia natural – Livro I. 2. ed. São Paulo: Edusp, 2012. p. 40.
A quantidade de movimento ou momento linear abre parênteses expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses é uma grandeza vetorial com a mesma direção e o mesmo sentido da velocidade; seu módulo é dado pelo produto entre a massa abre parênteses 'm' fecha parênteses e a velocidade abre parênteses expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses.
expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a 'm' vezes expressão com detalhe acima, início da expressão, v, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima
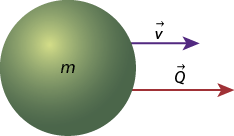
No Sistema Internacional de Unidades (SI), a massa é expressa em quilograma abre parênteses k g elevado ao cubo fecha parênteses, a velocidade, em metro por segundo abre parênteses m barra s fecha parênteses e a quantidade de movimento é dada em quilograma-metro por segundo abre parênteses quilograma vezes metros barra segundo fecha parênteses.
Página 360
Confira a imagem a seguir.
A bola de futebol inicialmente se encontrava em repouso em relação ao solo. Sabendo que ela tem massa de 0 vírgula 42 quilograma, conforme as regras oficiais do esporte, considere que, após o chute, ela passe a ter uma velocidade com módulo de 20 metros por segundo.
Temos que o módulo da quantidade de movimento inicial expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0 é nulo, pois:
Q subscrito 0 é igual a 'm' vezes v subscrito 0 implica em Q subscrito 0 é igual a 0 vírgula 42 vezes 0 portanto Q subscrito 0 é igual a 0
Imagens desta página sem proporção e em cores fantasia.

Depois do chute, a bola passa a ter uma quantidade de movimento final expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima de módulo igual a:
Q é igual a 'm' vezes v implica em Q é igual a 0 vírgula 42 vezes 20 portanto Q é igual a 8 vírgula 4 quilogramas vezes metros barra segundo
Quando um sistema é formado por vários corpos, a quantidade de movimento total abre parênteses expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito t fecha parênteses ou resultante é dada pela soma vetorial das quantidades individuais de movimento.
expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito t é igual a expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 1 mais expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 2 mais expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 3
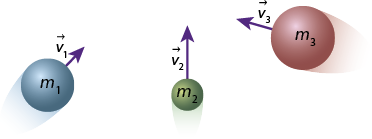
Seguindo o exemplo da bola de futebol, nota-se que houve uma variação na quantidade de movimento dela e a causa disso foi a interação com o pé do jogador. Ao realizar um chute, o pé do jogador aplica uma força na bola durante um intervalo de tempo, provocando o movimento dela.
Considerando que a força aplicada foi constante durante todo o intervalo de tempo, temos uma grandeza denominada impulso da força abre parênteses I fecha parênteses, uma grandeza vetorial que atua na mesma direção e sentido da força, sendo dada pelo produto da força pelo intervalo de tempo no qual ocorre a interação.
expressão com detalhe acima, início da expressão, I, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a expressão com detalhe acima, início da expressão, 'F', fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima vezes delta 't'
No SI, como a força é dada em newton N e o tempo, em segundo abre parênteses s fecha parênteses, o impulso é dado em newton-segundo abre parênteses N vezes s fecha parênteses, unidade equivalente ao quilograma-metro por segundo abre parênteses quilograma vezes metros barra segundo fecha parênteses da quantidade de movimento.
Dica
Se considerarmos somente o módulo da força aplicada, a intensidade do impulso pode ser escrita como:
I é igual a 'F' vezes delta 't'
Existe uma relação entre o impulso e a quantidade de movimento, denominada teorema do impulso. Como a força aplicada sobre um corpo causa uma aceleração, a velocidade do corpo muda e, consequentemente, sua quantidade de movimento também se altera. Dessa maneira, um impulso causa uma variação na quantidade de movimento, sendo descrita como:
expressão com detalhe acima, início da expressão, I, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima é igual a delta expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima
Página 361
3. As bolas de futebol atuais são feitas de materiais impermeáveis. Já as antigas absorviam muita água quando os jogos ocorriam na chuva. Como a absorção de água influencia a intensidade do chute executado pelo jogador?
Resposta: Espera-se que os estudantes respondam que a absorção de água aumenta a massa da bola, de modo que o impulso dado a ela deve ser maior para que atinja a mesma velocidade de quando está seca.
No exemplo da página anterior, a quantidade de movimento da bola de futebol aumentou de Q subscrito 0 é igual a 0 para Q é igual a 8 vírgula 4 quilogramas vezes metros barra segundo, de modo que a variação da quantidade de movimento é:
delta Q é igual a Q menos Q subscrito 0 implica em delta Q é igual a 8 vírgula 4 menos 0 portanto delta Q é igual a 8 vírgula 4 quilogramas vezes metros barra segundo
Se o tempo de atuação da força foi cerca de 0 vírgula 0 4 segundo, podemos determinar a intensidade da força do chute do jogador. Considerando o módulo do impulso, temos:
I é igual a delta Q implica em 'F' vezes delta 't' é igual a delta Q implica em 'F' vezes 0 vírgula 0 4 é igual a 8 vírgula 4 implica em 'F' é igual a início de fração, numerador: 8 vírgula 4, denominador: 0 vírgula 0 4, fim de fração portanto 'F' é igual a 210 newtons
As bolas de futebol e de outros esportes devem seguir padrões de especificação, pois variações na massa podem alterar os efeitos das forças aplicadas.
Imagens desta página sem proporção e em cores fantasia.




O airbag dos automóveis é um exemplo de aplicação do conceito do impulso. Esse dispositivo está relacionado ao impacto e atua de maneira a levar os corpos em movimento ao repouso, variando sua quantidade de movimento.
Se a variação da quantidade de movimento for rápida, a intensidade da força de interação é grande. Mas, se a interação for mais lenta, a intensidade da força de interação diminui. Essa é a forma de atuação do airbag; ele aumenta o tempo de interação e diminui a intensidade da força da colisão, reduzindo os efeitos do impacto no passageiro.

Conservação da quantidade de movimento
Os jogos de bola de gude envolvem muita diversão e variam de acordo com a região do país. Um dos jogos mais comuns é o de acertar as bolas de gude de outros jogadores, envolvendo diversos conceitos das áreas de Física e Matemática, como velocidade, forças, ângulos de reflexão e colisões.

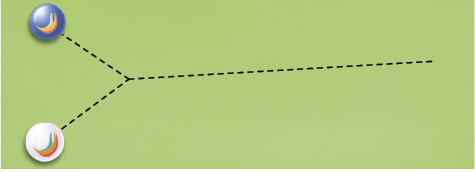
Página 362
Um jogador de bolinhas de gude pode ter desenvolvido suas habilidades principalmente pela prática e pelo treinamento, sem necessariamente se preocupar com os conceitos da Física. No entanto, alguns efeitos das colisões entre as bolinhas de gude são simples de entender. Uma colisão frontal, com os centros das bolas alinhados, faz a bola adversária se mover na mesma direção da trajetória da bola arremessada. Colisões com os centros desalinhados fazem a bola adversária mover-se em certo ângulo em relação à direção inicial e a bola arremessada desviar-se de sua trajetória inicial.
Esses movimentos e interações obedecem ao princípio da conservação da quantidade de movimento ou momento linear. Considerando que não há forças externas atuando no sistema, em uma colisão qualquer, a quantidade de movimento do sistema antes da colisão abre parênteses expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0 fecha parênteses é igual à quantidade de movimento do sistema após a colisão abre parênteses expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima fecha parênteses.
expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima subscrito 0 é igual a expressão com detalhe acima, início da expressão, Q, fim da expressão, início do detalhe acima, seta para a direita, fim do detalhe acima
Dica
Em colisões unidimensionais, podemos desprezar a notação vetorial. A orientação da quantidade de movimento e da velocidade é indicada por um sinal positivo ou negativo. A relação da quantidade de movimento pode ser escrita assim:
Q subscrito 0 é igual a Q
Na situação da imagem a seguir, a bolinha branca ('m' subscrito b é igual a 1 vírgula 5 vezes 10 elevado a menos 2 quilograma) foi lançada com velocidade de 1 vírgula 5 metro por segundo na direção da bolinha azul abre parênteses 'm' subscrito a é igual a 1 vírgula 2 vezes 10 elevado a menos 2 quilograma fecha parênteses em repouso, realizando uma colisão unidimensional. Após a colisão, a bolinha branca adquiriu uma velocidade de 0 vírgula 2 metro por segundo, continuando a se mover na mesma direção e no mesmo sentido.
Imagens desta página sem proporção e em cores fantasia.
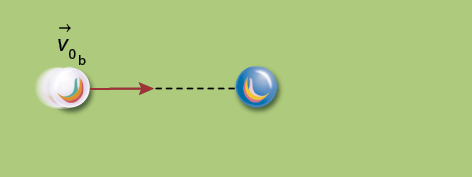
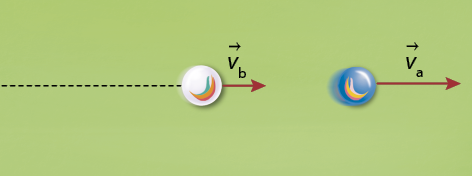
Pela conservação da quantidade de movimento, a velocidade da bolinha azul após a colisão é dada por:
Q subscrito 0 é igual a Q implica em Q início subscrito, 0 subscrito b, fim subscrito mais Q início subscrito, 0 subscrito a, fim subscrito é igual a Q subscrito b mais Q subscrito a implica em 'm' subscrito b vezes v início subscrito, 0 subscrito b, fim subscrito mais 'm' subscrito a vezes v início subscrito, 0 subscrito a, fim subscrito é igual a 'm' subscrito b vezes v subscrito b mais 'm' subscrito a vezes v subscrito a implica em
implica em 1 vírgula 5 vezes 10 elevado a menos 2 vezes 1 vírgula 5 mais 1 vírgula 2 vezes 10 elevado a menos 2 vezes 0 é igual a 1 vírgula 5 vezes 10 elevado a menos 2 vezes 0 vírgula 2 mais 1 vírgula 2 vezes 10 elevado a menos 2 vezes v subscrito a implica em
implica em 2 vírgula 25 vezes 10 elevado a menos 2 é igual a 0 vírgula 3 vezes 10 elevado a menos 2 mais 1 vírgula 2 vezes 10 elevado a menos 2 vezes v subscrito a implica em
implica em 1 vírgula 95 vezes 10 elevado a menos 2 é igual a 1 vírgula 2 vezes 10 elevado a menos 2 vezes v subscrito a portanto v subscrito a é igual a 1 vírgula 625 metro por segundo
Como a velocidade adquirida pela bolinha azul tem sinal positivo, ela se move na mesma direção e no mesmo sentido da bolinha branca, de modo que a quantidade de movimento total do sistema se mantém constante.
Em colisões bidimensionais ou tridimensionais, a análise da conservação da quantidade de movimento deve ser realizada vetorialmente.
Página 363
No exemplo anterior, as duas esferas se mantêm em movimento após a colisão, mas, em outros casos, isso pode não acontecer. O que ocorre depois de colidir depende das massas envolvidas, da velocidade, da quantidade de movimento dos corpos e do tipo de colisão.
Apesar de a conservação da quantidade de movimento levar em conta as orientações dos vetores, nesse momento, vamos trabalhar apenas as colisões unidimensionais.
Considerando que as massas dos corpos não se alteram, as colisões podem ser divididas em três fases.
A primeira é a aproximação relativa entre os corpos.
A segunda é a colisão. Nessa fase, os corpos podem se deformar, transformando energia cinética em outro tipo de energia.
Na terceira, pode ou não ocorrer a fase de restituição dos corpos, na qual eles podem se afastar um do outro, entrar em repouso ou se mover juntos.
Independentemente do que ocorre nas três fases, a quantidade de movimento sempre se conserva, mas a energia cinética (ou mecânica) pode ser dissipada em forma de calor, som e deformações.
Imagem sem proporção e em cores fantasia.
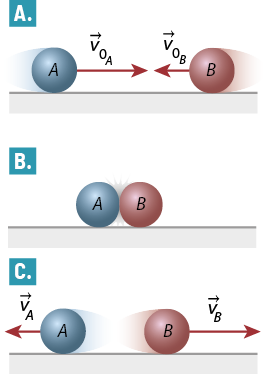
A análise quantitativa e qualitativa, assim como a classificação das colisões, pode ser feita com base no coeficiente de restituição abre parênteses e fecha parênteses, que relaciona a velocidade relativa de aproximação abre parênteses v subscrito a p fecha parênteses entre os corpos antes da colisão, de afastamento abre parênteses v subscrito a f fecha parênteses após colidir e é adimensional, dado por:
e é igual a início de fração, numerador: v subscrito a f, denominador: v subscrito a p, fim de fração implica em e é igual a início de fração, numerador: v subscrito B menos v subscrito A, denominador: v início subscrito, 0 subscrito A, fim subscrito menos v início subscrito, 0 subscrito B, fim subscrito, fim de fração
Classificamos uma colisão como elástica quando o coeficiente de restituição é igual a 1 abre parênteses e é igual a 1 fecha parênteses. Nesse caso, a velocidade de afastamento é igual à velocidade de aproximação abre parênteses v subscrito a f é igual a v subscrito a p fecha parênteses, indicando que não houve dissipação de energia cinética na colisão. Portanto, para uma colisão elástica, temos:
Q subscrito 0 é igual a Q e E início subscrito, c subscrito 0, fim subscrito é igual a E subscrito c
O pêndulo de Newton é um exemplo no qual podemos observar colisões elásticas no cotidiano.

Se o coeficiente de restituição tem valores entre 0 e 1 abre parênteses 0 é menor ou igual a e é menor do que 1 fecha parênteses, a colisão é classificada como inelástica. Nesse caso, há a dissipação de energia cinética na colisão e a velocidade de afastamento é menor do que a de aproximação abre parênteses v subscrito a f é menor do que v subscrito a p fecha parênteses. Nas colisões inelásticas, temos:
Q subscrito 0 é igual a Q e E início subscrito, c subscrito 0, fim subscrito é maior do que E subscrito c
As colisões em que e é igual a 0 são denominadas perfeitamente inelásticas e não há afastamento entre os corpos. Eles podem se mover juntos ou entrar em repouso. Ao entrar em repouso, toda a energia cinética inicial é dissipada.
Página 364
CONEXÕES com ... BIOLOGIA e QUÍMICA
Atividades físicas e saúde
A prática de atividades físicas está intrinsecamente ligada às transformações de energia que ocorrem no corpo humano. Durante a execução de exercícios, o corpo consome energia para realizar uma variedade de ações, como a contração muscular, manutenção da temperatura corporal e reparação celular. A energia é obtida principalmente dos alimentos que ingerimos e é medida em quilocalorias quilocaloria, informação que costuma ser apresentada nas embalagens de alimentos. Para um adulto, o consumo diário recomendado de calorias pode variar conforme fatores como idade, sexo, peso, altura e nível de atividade física.

A ingestão de alimentos é o ponto de partida para a produção de energia no corpo humano. Quando consumimos alimentos, o sistema digestório inicia um processo complexo de digestão, quebrando carboidratos, proteínas e gorduras em suas moléculas menores: glicose, aminoácidos e ácidos graxos, respectivamente. Essas moléculas são absorvidas pelo intestino e transportadas para as células, onde ocorre a conversão em energia.
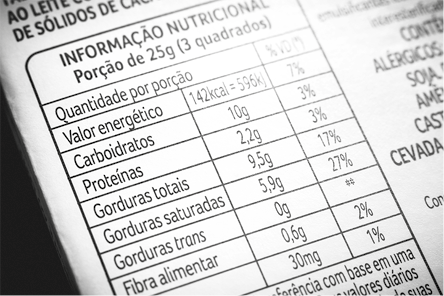
Dentro das células, essas moléculas são metabolizadas em um processo chamado respiração celular, que ocorre nas mitocôndrias. A glicose, por exemplo, passa por uma série de reações químicas conhecidas como glicólise, ciclo de Krebs e cadeia transportadora de elétrons. Durante essas etapas, a energia contida nas ligações químicas das moléculas alimentares é liberada e armazenada na forma de ATP (adenosina trifosfato). Conforme o corpo executa suas funções, o ATP é quebrado, liberando a energia utilizada nesses processos.
Ao longo de uma atividade física, a energia química armazenada no ATP é convertida em outros tipos de energia, como a cinética, diretamente relacionada ao movimento dos músculos e articulações, e a térmica, gerada como subproduto do esforço físico, ajudando a manter a temperatura do corpo. Por exemplo, ao correr ou nadar, os músculos das pernas e dos braços realizam trabalho mecânico ao se contrair e relaxar. Simultaneamente, parte dessa energia é dissipada como calor, o que pode ser observado pelo aumento da temperatura corporal e pela produção de suor, mecanismos que ajudam a regular a temperatura durante o exercício intenso.
O gasto energético do corpo depende do tipo de atividade que está sendo realizada e de quem a realiza. Para uma pessoa de 70 quilogramas, andar de bicicleta consome, em média, de 3 a 5 quilocalorias por minuto. Já o ato de ficar deitado consome aproximadamente 1 vírgula 3 quilocaloria por minuto.
Movimentos como saltar ou subir escadas se relacionam com a energia potencial gravitacional, já que o corpo precisa vencer a força da gravidade ao se mover verticalmente. Ao saltar, o corpo armazena energia potencial gravitacional, que é convertida em energia cinética ao retornar ao solo.
Página 365
Nos esportes que envolvem a interação com objetos, como futebol, voleibol, basquetebol, arremesso de peso e dardo, há uma transferência de energia do corpo para esses objetos. Por exemplo, ao chutar uma bola de futebol, o jogador transfere energia cinética de sua perna para a bola, gerando movimento. De maneira semelhante, no arremesso de peso ou de dardo, a força exercida pelos músculos do corpo é transferida para o objeto, impulsionando-o para cima e para a frente. Essa transferência de energia está diretamente relacionada aos conceitos de impulso e quantidade de movimento, fundamentais na Física. Ao chutar a bola de futebol, o jogador aplica uma força em um curto período e gera um impulso que altera a quantidade de movimento da bola, fazendo-a se deslocar pelo campo.

A prática de atividades físicas desempenha um papel fundamental na saúde, pois está diretamente relacionada ao gasto de energia pelo corpo humano. Durante o exercício, o corpo consome a energia armazenada, principalmente sob a forma de glicose e gordura, para alimentar os músculos em movimento. Esse processo de gasto energético não só auxilia no controle do peso corporal, mas também é essencial para a manutenção da saúde geral. O exercício físico promove o crescimento e a regeneração dos músculos, ajudando a preservar ou aumentar a massa muscular. Além disso, a carga exercida sobre os ossos durante atividades como caminhada, corrida ou levantamento de peso favorece a formação óssea, fortalecendo o esqueleto e ajudando a prevenir doenças como a osteoporose. Manter músculos e ossos saudáveis é essencial para a funcionalidade do corpo, permitindo uma vida ativa e independente. Ademais, o gasto energético contínuo ajuda a regular os níveis de açúcar no sangue e a reduzir o risco de doenças crônicas, como diabetes tipo 2 e hipertensão.
Para as pessoas idosas, a prática de atividade física é especialmente importante. Com o envelhecimento, ocorre uma perda natural de massa muscular e densidade óssea, podendo levar a uma série de problemas de saúde, como fraqueza muscular, redução da mobilidade e aumento do risco de quedas e fraturas. Exercícios regulares, como caminhadas, atividades de resistência e alongamento, podem ajudar a retardar ou a reverter parte dessas perdas, promovendo a manutenção da força muscular, da flexibilidade e da resistência óssea. Além disso, a atividade física contribui para a melhoria do equilíbrio e da coordenação, reduzindo o risco de quedas e ajudando a manter a independência funcional.

a ) Durante uma atividade física intensa, como o levantamento de peso, quais são as principais formas de energia envolvidas e como ocorre a transformação entre elas?
b ) Ao andar de bicicleta em uma subida, o que acontece com a energia cinética do ciclista à medida que ele ganha altitude? Como essa mudança de energia reflete a lei da conservação de energia?
c ) Em maratonas ou triatlos, os atletas podem sofrer de "fadiga muscular" em razão do esgotamento de glicose. Que estratégias nutricionais e de treino podem ser adotadas para evitar essa condição?
d ) De que maneira a quantidade de massa muscular no corpo humano pode influenciar a recuperação de uma doença grave?
Respostas nas Orientações para o professor.
Página 366
ATIVIDADES
Imagens desta página sem proporção e em cores fantasia.
1. Leia os itens a seguir e escreva quais são forças conservativas e quais são forças dissipativas.
a ) Força gravitacional.
Resposta: Conservativa.
b ) Força de atrito cinético.
Resposta: Dissipativa.
c ) Força elástica.
Resposta: Conservativa.
d ) Resistência do ar.
Resposta: Dissipativa.
2. Obedecer às leis de trânsito é essencial para garantir a segurança nas vias, e dirigir dentro do limite de velocidade pode fazer diferença em situações de risco. Suponha que um carro de 1.100 quilogramas se mova com velocidade de 10 metros por segundo. Se a velocidade dele passar para 30 metros por segundo, a energia cinética do carro ficará quantas vezes maior? Como esse aumento de energia influencia no caso de uma colisão?
Resposta: Como a velocidade triplicou, a energia cinética seria multiplicada por 9. No caso de uma colisão, essa quantidade de energia a mais pode ser transferida para os passageiros no interior do carro, podendo causar lesões graves ou até a morte. A menor energia cinética significa maior segurança para os ocupantes do veículo em caso de acidente. Resolução nas Orientações para o professor.
Resposta: início de fração, numerador: E subscrito c, denominador: E início subscrito, c subscrito o, fim subscrito, fim de fração é igual a 9
3. Um acelerador de partículas linear é um dispositivo que acelera partículas subatômicas, como elétrons ou prótons, ao longo de uma trajetória reta. As partículas são injetadas em um tubo longo e reto, e elas passam por uma série de campos elétricos alternados que aceleram as partículas para velocidades próximas à da luz. Suponha que um acelerador de partículas aplica uma força para acelerar um elétron que está em repouso até que ele atinja uma energia cinética final de 5 quiloelétron-volt. Calcule o trabalho realizado pela força do acelerador para executar essa aceleração. Considere 1 e v é igual a 1 vírgula 6 vezes 10 elevado a menos 19 Joule.
Resposta: tau é igual a 8 vírgula 0 vezes 10 elevado a menos 16 Joules.
4. Uma mola tem comprimento de 50 centímetros quando está relaxada. Apoia-se um corpo de 8 quilogramas sobre ela, como mostra a figura a seguir, e o equilíbrio é atingido com a mola no novo comprimento de 40 centímetros. Se a sua constante elástica é k é igual a 800 N barra m, qual é a energia potencial elástica armazenada na mola?

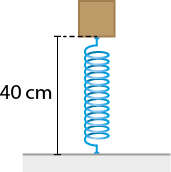
Resposta: E subscrito p e é igual a 4 joules.
5. Em uma pista de skate, você assiste a uma colega e tem uma visão lateral semelhante à da figura a seguir. A atleta de 45 quilogramas sai do ponto A e vai até o 'C'. Lembrando de sua aula de Física, você decide calcular o trabalho realizado pela força peso no deslocamento da garota. Determine o trabalho da força peso entre as posições A e B, depois entre B e 'C' e, por fim, de A até 'C'.
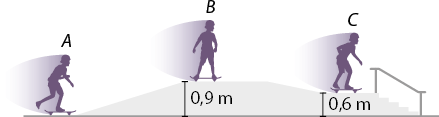
Resposta: tau início subscrito, A B, fim subscrito é igual a menos 405 joules, tau início subscrito, B 'C', fim subscrito é igual a 135 joules e tau início subscrito, A 'C', fim subscrito é igual a menos 270 joules.
6. Nos produtos alimentícios, é obrigatória a tabela de informação nutricional. Nela, estão contidas as quantidades de gorduras, vitaminas, carboidratos e valor energético do produto. A base de uma dieta é 2.000 quilocalorias ou 8.400 quilojoules por dia. Supondo que uma pessoa utilize, em seu metabolismo, a quantidade de calorias indicada no período de um dia, qual é a potência da pessoa?
Resposta: P é aproximadamente igual a 97 vírgula 2 watts.
7. Nas Olimpíadas de 2024, o corredor estadunidense Noah Lyles (1997 -) ganhou a medalha de ouro na prova dos 100 metros rasos com o tempo de 9,784 segundos. Já o segundo colocado, o jamaicano Kishane Thompson (2001 -), completou a prova em 9,789 segundos, uma diferença de 5 milésimos de segundo. Qual é a razão entre a potência mecânica média do estadunidense e a do jamaicano nessa prova? Considere que ambos os corredores têm a mesma massa.
Resposta: início de fração, numerador: P subscrito E, denominador: P subscrito J, fim de fração é aproximadamente igual a 0 vírgula 9987.
8. Um motorista de um carro dirige por uma estrada quando percebe que há um cachorro atravessando a pista. Nesse instante, ele pressiona o pedal do freio, desacelerando o carro, e o animal consegue terminar sua travessia em segurança. Essa desaceleração dura 5 segundos, o carro percorre uma distância de 50 metros e a força de desaceleração realiza um trabalho igual a 30.000 joules. Determine a variação de impulso sofrida pelo carro nesse processo.
Resposta: I é igual a 3.000 N vezes s.
9. Em uma partida de futebol, um atacante que pesa 700 newtons, no momento que recebe a bola, corre em linha reta para o gol com uma aceleração constante de 0 vírgula 3 metro por segundo quadrado. Após percorrer 30 metros, ele colide com o zagueiro do outro time. Qual é a energia cinética do atacante ao colidir com o zagueiro? Adote 'g' é igual a 10 metros por segundo quadrado.
Resolução das questões 2 a 9 nas Orientações para o professor.
Resposta: E subscrito C é igual a 630 joules.
Página 367
10. O gráfico a seguir mostra o valor da energia cinética de dois objetos, A e B, ao longo de 10 segundos; e aos 5 segundos, os objetos colidem. Com base nas informações apresentadas pelo gráfico, descreva o movimento dos objetos ao longo do tempo. Mencione também o tipo de colisão que ocorreu (totalmente elástica, parcialmente elástica, inelástica).
Gráfico da E vezes t para os objetos A e B
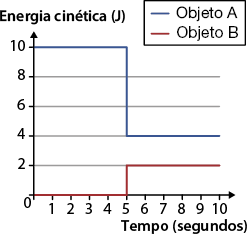
Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: mecânica. Tradução: Ronaldo Sérgio de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 1. p. 244.
Resposta: O objeto B tem energia cinética igual a 0 no tempo 0, logo está em repouso, e o objeto A tem um valor positivo de energia e está em movimento. Após o tempo de 5 segundos, a energia do objeto A diminuiu, enquanto a energia do objeto B aumentou. Logo após a colisão, o objeto A perdeu velocidade enquanto o B ganhou. Como a soma das energias finais dos dois objetos é menor do que a soma das energias iniciais, a colisão foi parcialmente elástica.
11 Uma esfera de 1 quilograma entra em queda livre, a partir do repouso, de uma altura de 9 vírgula 8 metros em relação ao solo. Sendo as forças de resistência desprezíveis, determine a quantidade de movimento da esfera no momento exato em que toca o solo. Considere 'g' é igual a 10 metros por segundo elevado ao quadrado.
Resposta: Q é igual a 14 quilogramas vezes metros por segundo.
12. Algumas pessoas comentam que os carros antigos eram mais resistentes, pois nas colisões eles amassam menos do que os carros novos. No entanto, a deformação das partes dos carros novos é planejada, intencional. Explique como a deformação das partes do carro pode contribuir para a segurança dos passageiros.
Resposta pessoal. Espera-se que os estudantes comentem que a deformação das partes do carro contribui para a dissipação da energia cinética envolvida na colisão do carro, assim, quanto mais energia for dissipada na carroceria do carro, menos energia é transferida para os passageiros, auxiliando na redução dos danos sofridos por eles.
13. Um corpo A, de massa 'm' e velocidade 6 metros por segundo, move-se de encontro a um corpo B, de massa 2 vezes 'm' e velocidade 4 metros por segundo. Após a colisão, o corpo A inverte seu movimento e passa a mover-se com velocidade de 4 metros por segundo.
a ) Determine a velocidade de B após a colisão.
Resposta: v subscrito B é igual a 1 metro por segundo.
b ) Verifique se a colisão foi elástica ou inelástica.
Resposta: A colisão foi inelástica, pois e é igual a 0 vírgula 5.
c ) Considerando 'm' é igual a 2 quilogramas, verifique se houve perda de energia cinética do sistema na colisão.
Resposta: delta E subscrito c é igual a menos 50 joules.
14. Dois blocos se movem no mesmo sentido, o bloco A, de 1 vírgula 6 quilograma, com velocidade 5 vírgula 5 metros por segundo e o bloco B, de 2 vírgula 4 quilogramas, com velocidade 2 vírgula 5 metros por segundo. Imediatamente após a colisão, o bloco B se move com velocidade 4 vírgula 9 metros por segundo.
a ) Qual é a velocidade do bloco A após a colisão?
Resposta: v subscrito A é igual a 1 vírgula 9 metro por segundo.
b ) A colisão foi elástica ou inelástica?
Resposta: A colisão foi elástica, pois e é igual a 1.
15. Um jogador de basquete recebe uma falta durante uma partida e fará um arremesso livre. Ele se posiciona em frente à cesta e arremessa a bola, mas em vez de entrar na cesta, no ponto mais alto da trajetória, a bola acerta a tabela, a uma altura de 3 metros. Em seguida, ela quica no chão e sobe novamente até uma altura de 2 vírgula 4 metros. Descreva as transformações de energia e a perda de energia sofrida pela bola durante esse percurso. Despreze a energia dissipada na colisão da bola com a tabela e desconsidere o atrito com o ar.
Resoluções das questões 11, 13, 14 e 15 nas Orientações para o professor.
Resposta nas Orientações para o professor.
16. Para estudar os princípios de conservação em colisões, um estudante filmou diversas colisões entre bolinhas de gude. Para identificar, no vídeo, o instante das colisões, o estudante utilizou o som emitido em cada colisão. Em relação a essa situação, que conclusão podemos tirar sobre a conservação da quantidade de movimento e sobre a conservação da energia mecânica? Justifique sua resposta.
Resposta: Espera-se que os estudantes concluam que, nessa situação, a quantidade de movimento se conserva, porém a energia mecânica não. O som das colisões indica que parte da energia mecânica está sendo dissipada em energia sonora.
RETOME O QUE ESTUDOU
Refletindo sobre o que estudou nesta unidade, responda às questões a seguir.
1. Como o uso de uma alavanca pode reduzir a quantidade de força necessária para levantar um objeto pesado? Explique a função dos braços de alavanca e o ponto de apoio.
2. O que acontece com o torque aplicado a uma porta se você a empurrar mais próximo da dobradiça? Explique como o comprimento do braço de alavanca influencia o torque.
3. Em um movimento circular uniforme, por que a velocidade tangencial do objeto é constante, mas a aceleração centrípeta não é zero? Qual é a direção dessa aceleração?
4. Se um objeto for lançado para cima, como a energia potencial gravitacional e a energia cinética se comportam ao longo do movimento? O que acontece no ponto mais alto?
5. Durante uma colisão, como o princípio de conservação da quantidade de movimento explica o que acontece com dois objetos de massas diferentes ao colidirem?
Respostas nas Orientações para o professor.
Página 368
MAIS QUESTÕES
1. (Udesc) A Figura 2 mostra dois blocos de massa m minúsculo e M maiúsculo unidos por um fio ideal, suspensos por uma polia ideal. Considere que o fio está o tempo todo tensionado.
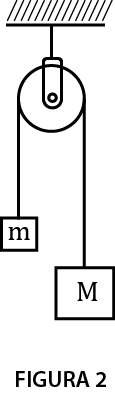
Analise as proposições com relação a figura 2.
I ) A condição de equilíbrio é dada quando m minúsculo é igual a M maiúsculo, portanto a aceleração do sistema é nula.
II ) Para M maiúsculo é maior do que m minúsculo, a quantidade M maiúsculo menos m minúsculo é inversamente proporcional à aceleração do sistema.
III ) Para M maiúsculo é maior do que m minúsculo, a quantidade M maiúsculo mais m minúsculo é diretamente proporcional à aceleração do sistema.
IV ) Fora da condição de equilíbrio, a aceleração do sistema é diretamente proporcional à aceleração gravitacional.
V ) Fora do equilíbrio, o modulo das acelerações dos blocos são iguais, no entanto, as acelerações têm sentidos opostos.
Assinale a alternativa correta.
a ) Somente as afirmativas IV e V são verdadeiras.
b ) Somente as afirmativas I, II e III são verdadeiras.
c ) Somente as afirmativas I, III e V são verdadeiras.
d ) Somente as afirmativas II, III e IV são verdadeiras.
e ) Somente as afirmativas I, IV e V são verdadeiras.
Resposta: Alternativa e.
2. (UECE) Considere duas massas iguais penduradas por uma corda flexível e inextensível que passa por uma polia presa ao teto. Desconsiderando-se todos os atritos, de modo que as massas possam subir ou descer livremente, e considerando, nesse arranjo, a situação em que uma das massas está subindo com velocidade constante, é correto afirmar que o módulo da soma vetorial dos momentos lineares das massas é
a ) o dobro do módulo do momento linear de uma das massas.
b ) o triplo do modulo do momento linear de uma das massas.
c ) igual ao módulo do momento linear de uma das massas.
d ) zero.
Resposta: Alternativa d. Resoluções nas Orientações para o professor.
3. (IME-RJ)
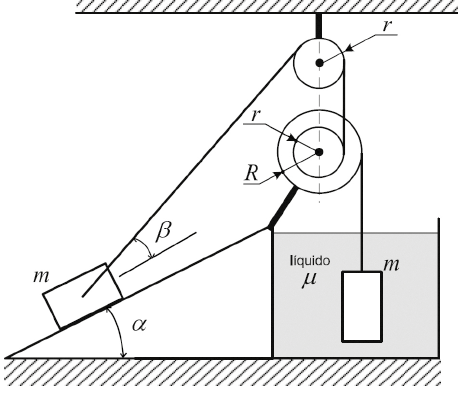
Como mostra a figura, dois corpos de massa m e volume V estão em equilíbrio estático. Admita que mi é a massa específica do líquido, que não existe atrito entre o corpo e o plano inclinado e que as extremidades dos fios estão ligadas a polias, sendo que duas delas são solidárias, com raios menor e maior r e R, respectivamente. A razão R maiúsculo barra r minúsculo para que o sistema esteja em equilíbrio é:
Resolução nas Orientações para o professor.
a ) início de fração, numerador: 'm' vezes sen abre parênteses alfa mais beta fecha parênteses, denominador: 'm' menos mi V, fim de fração
b ) início de fração, numerador: 'm' vezes cosseno abre parênteses alfa mais beta fecha parênteses, denominador: 'm' menos mi V, fim de fração
c ) início de fração, numerador: seno abre parênteses alfa fecha parênteses, denominador: cosseno abre parênteses beta fecha parênteses, fim de fração vezes abre parênteses 1 menos início de fração, numerador: mi V, denominador: 'm', fim de fração fecha parênteses elevado a menos 1
d ) início de fração, numerador: cosseno abre parênteses alfa fecha parênteses, denominador: seno abre parênteses beta fecha parênteses, fim de fração vezes abre parênteses 1 menos início de fração, numerador: mi V, denominador: 'm', fim de fração fecha parênteses elevado a menos 1
e ) cosseno abre parênteses alfa mais beta fecha parênteses vezes abre parênteses 1 menos início de fração, numerador: mi V, denominador: 'm', fim de fração fecha parênteses
Resposta: Alternativa c.
Página 369
4. (IFBA) Na montagem experimental abaixo, os blocos A, B e C têm massas m subscrito A é igual a 2 vírgula 0 quilogramas, m subscrito B é igual a 3 vírgula 0 quilogramas e m subscrito C é igual a 5 vírgula 0 quilogramas. Desprezam-se os atritos e a resistência do ar. Os fios e as polias são ideais e adote 'g' é igual a 10 metros por segundo quadrado
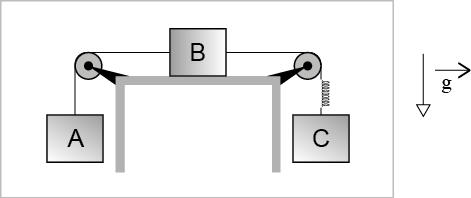
No fio que liga o bloco B com o bloco C, está intercalada uma mola leve de constante elástica 3 vírgula 5 vezes 10 elevado ao cubo N barra m. Com o sistema em movimento, a deformação da mola é?
Resolução nas Orientações para o professor.
a ) 2 vírgula 0 centímetros
b ) 1 vírgula 0 centímetro
c ) 1 vírgula 5 centímetro
d ) 2 vírgula 8 centímetros
e ) 4 vírgula 2 centímetros
Resposta: Alternativa b.
5. (Epcar-MG) O sistema representado na figura seguinte é composto por um bloco de dimensões desprezíveis e de massa m apoiado em um plano inclinado, que forma um ângulo alfa com a direção horizontal. O sistema possui uma mola ideal de constante elástica k e comprimento natural x subscrito 0
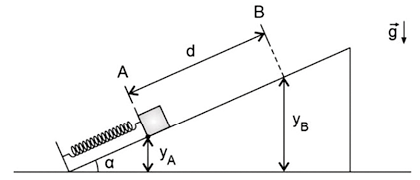
O bloco se encontra apenas encostado na mola e em equilíbrio, na posição A, a uma altura y subscrito A. Nesse momento, a mola está travada e comprimida de um valor x. Quando a mola é destravada, o bloco, pela ação da força elástica, percorre a distância d, sem atrito, indicada na figura, até atingir o ponto B, a uma altura y subscrito B, onde ocorre a inversão do sentido de seu deslocamento. Considerando grama o módulo da aceleração da gravidade, a distância d percorrida pelo bloco é dada na alternativa
Resolução nas Orientações para o professor.
a ) início de fração, numerador: k x subscrito 0 início sobrescrito, 2, fim sobrescrito, denominador: m g seno alfa, fim de fração
b ) início de fração, numerador: k x elevado ao quadrado, denominador: 2 m g sen alfa, fim de fração
c ) início de fração, numerador: k abre parênteses y subscrito B menos y subscrito A fecha parênteses elevado ao quadrado, denominador: m g seno alfa, fim de fração
d ) início de fração, numerador: k abre parênteses y subscrito B menos y subscrito A fecha parênteses elevado ao quadrado, denominador: 2 m g seno alfa, fim de fração
Resposta: Alternativa b.
6. (UECE) Espacate é um movimento ginástico que consiste na abertura das pernas até que formem um ângulo de 180 graus entre si, sem flexionar os joelhos. Considere uma posição intermediária, em que um(a) atleta de 70 quilogramas faça uma abertura de 120 graus. A força normal feita pelo solo no pé do(a) atleta exerce um torque sobre sua perna em relação a um ponto no centro do seu quadril. Pode-se estimar esse torque assumindo que a distância entre o ponto de aplicação da força e o ponto central é 1 metro e que a aceleração da gravidade é 10 metros por segundo elevado ao quadrado.
Assim, é correto dizer que esse torque, em Newton-metro, é aproximadamente
Resolução nas Orientações para o professor.
a ) 350 cosseno abre parênteses 60 graus fecha parênteses.
b ) 350 cosseno abre parênteses 120 graus fecha parênteses.
c ) 350 seno abre parênteses 60 graus fecha parênteses.
d ) 700 cosseno abre parênteses 60 graus fecha parênteses.
Resposta: Alternativa c.
7. (Uesb-BA) Um objeto se movimenta em uma trajetória retilínea, com velocidade constante, quando sofre ação de uma força externa paralela ao plano do seu movimento, porém sua velocidade permanece sem alteração do seu módulo.
Sobre a situação descrita, analise as assertivas e assinale a alternativa que aponta as corretas.
I ) A direção da velocidade necessariamente sofreu alteração.
II ) O módulo da quantidade de movimento do objeto permaneceu inalterado.
III ) A força externa exerceu o impulso que provocou a variação da quantidade de movimento do objeto.
IV ) Se a força exercida for perpendicular à direção inicial do movimento do objeto, a nova trajetória descrita será circular.
a ) Apenas I, II e III.
b ) I, II, III e IV.
c ) Apenas I, II e IV.
d ) Apenas I e III.
e ) Apenas I e IV.
Resposta: Alternativa
a.
I) Correta
II) Correta,
símbolo de uma barra vertical Q símbolo de uma barra vertical é igual a 'm' vezes símbolo de uma barra vertical v símbolo de uma barra vertical
III) Correta, pois o
Impulso é definido por
I subscrito 'F' é igual a delta Q
IV) Errada,
't' é igual a x sobre v
e no eixo
y
temos:
y é igual a início de fração, numerador: a 't' elevado ao quadrado, denominador: 2, fim de fração
a é igual a início de fração, numerador: 'F' x elevado ao quadrado, denominador: 2 'm' v elevado ao quadrado, fim de fração, como
F,
metro
e
v
são constantes temos uma função quadrática logo terá a forma de
uma parábola.
Página 370
8. (EsPCEx-SP) Uma plataforma circular plana está girando em um plano horizontal, em torno de um eixo fixo vertical, que passa pelo ponto O, a 30 rotações por minuto, conforme representado no desenho abaixo. Sobre a plataforma giratória, encontra-se uma pequena moeda. Sabendo que o coeficiente de atrito estático entre a moeda e a plataforma é 0,18, a máxima distância do centro da plataforma, em 'm', que a moeda poderá ficar sem deslizar é:
Dados: Despreze a resistência do ar e as dimensões da moeda; considere o módulo da aceleração da gravidade igual a 10 metros por segundo quadrado e pi é igual a 3.
Resolução nas Orientações para o professor.
a ) 0,20
b ) 0,25
c ) 0,30
d ) 0,36
e ) 0,54
Resposta: Alternativa a.
9. (UPE) Duas esferas metálicas idênticas de massas iguais estão penduradas por fios ideais de mesmo comprimento, conforme ilustra a figura abaixo. A esfera 1 é abandonada de uma altura h, colidindo com a esfera 2, que está inicialmente em repouso.
Acerca desse experimento e considerando apenas a primeira colisão entre as esferas, é CORRETO afirmar que
a ) após uma colisão elástica, as duas esferas sobem unidas até uma altura igual a h barra 2.
b ) as duas esferas sobem unidas até uma altura h após uma colisão inelástica.
c ) após uma colisão elástica, as esferas se movem em sentidos opostos, alcançando uma altura h barra 2 cada uma.
d ) em uma colisão completamente inelástica, a esfera 1 recua e alcança uma altura h barra 2.
e ) a esfera 1 fica em repouso após uma colisão elástica com a esfera 2.
Resposta: Alternativa b.
10. (UEA) Uma criança constrói uma rampa para brincar com seu carrinho, conforme a figura.
O carrinho é, então, abandonado no início da rampa, com velocidade nula. Considerando uma condição em que não haja atrito ou nenhuma outra forma de dissipação de energia, o carrinho obterá sua maior velocidade no ponto
a ) 5.
b ) 3.
c ) 4.
d ) 1.
e ) 2.
Resposta: Alternativa b.
11. (Udesc) Um objeto move-se em uma trajetória circular com módulo da velocidade constante.
Assinale a alternativa que explica por que o trabalho realizado pela força centrípeta é zero.
a ) A força centrípeta é perpendicular à velocidade.
b ) A força média para cada revolução é zero.
c ) Não há atrito.
d ) A magnitude da aceleração é zero.
e ) O deslocamento para cada revolução é zero.
Resposta: Alternativa a.
Página 371
12. (Fuvest-SP) Uma das modalidades de skate é o bowl, disputado em um espaço em formato aproximado de bacia. Supondo um bowl com profundidade de 2 vírgula 45 metros, qual a máxima velocidade que um skatista, partindo do repouso no ponto mais alto da bacia, poderia alcançar no ponto mais baixo?

Note e adote: Aceleração da gravidade abre parênteses g fecha parênteses é igual a 10 metros por segundo quadrado
Resolução nas Orientações para o professor.
a ) 3 metros por segundo
b ) 5 metros por segundo
c ) 7 metros por segundo
d ) 9 metros por segundo
e ) 11 metros por segundo
Resposta: Alternativa c.
13. (UFRGS-RS) Um corpo com massa M é igual a 1 quilograma, inicialmente em repouso sobre uma superfície horizontal sem atrito, está preso a uma mola de massa desprezível e de constante elástica k é igual a 16 N barra m, conforme representado na figura abaixo.
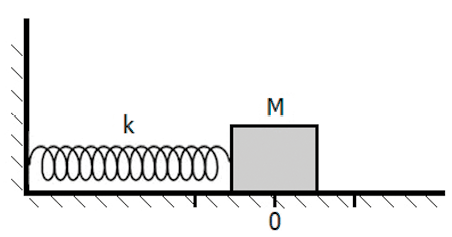
O corpo recebe um impulso para a direita de módulo I é igual a 2 N vezes s e passa a descrever um movimento oscilatório.
A amplitude de oscilação, em metro, é
Resolução nas Orientações para o professor.
a ) 1 barra 8.
b ) 1 barra 4.
c ) 1 barra 2.
d ) 1.
e ) 2.
Resposta: Alternativa c.
14. (UEL-PR) A RioBotz, equipe de robótica da PUC-Rio, foi criada em 2003, quando estudantes, orientados pelo professor Marco Antônio Meggiolaro, decidiram construir robôs de combate. Hoje a RioBotz é uma das 32 equipes que entraram na chave do Battlebots, programa de televisão norteamericano de luta de robôs. A equipe foi a única da América Latina a participar da competição. Suponha que o robô da RioBotz tenha massa de 18 quilogramas e possua uma lança cuja ponta tenha uma área de secção transversal de 1 milímetro quadrado. Admita que a lança atinja uma parede perpendicularmente com velocidade de 15 metros por segundo, recue com uma velocidade de 3 metros por segundo e que o período da colisão tenha durado 9 milissegundos.
Com base nos conhecimentos de física mecânica, assinale a alternativa que apresenta, corretamente, a pressão (em pascal) exercida pela lança sobre a parede, desconsiderando atritos e deformações.
Resolução nas Orientações para o professor.
a ) 3 vírgula 6 vezes 10 elevado a 10
b ) 2 vírgula 7 vezes 10 elevado a 9
c ) 5 vírgula 4 vezes 10 elevado a 9
d ) 5 vírgula 4 vezes 10 elevado a 10
e ) 3 vírgula 6 vezes 10 elevado a 9.
Resposta: Alternativa a.
15. (UEPG-PR) Considere duas esferas pequenas, uma feita de borracha, possuindo uma massa de 100 gramas, e a outra feita de massa de modelar possuindo uma massa de 200 gramas. As duas são largadas, simultaneamente a partir do repouso, de uma altura de 5 metros. Considere que a colisão da esfera de borracha com o solo é perfeitamente elástica e a da esfera feita de massa de modelar é perfeitamente inelástica. Desconsiderando a resistência do ar, assinale o que for correto.
Dados: aceleração da gravidade g é igual a 10 metros por segundo elevado ao quadrado
Resolução nas Orientações para o professor.
01 ) Os impulsos devidos aos choques de cada uma das esferas com o solo são iguais.
02 ) Podemos afirmar que a conservação da quantidade de movimento sempre terá como consequência a conservação da energia cinética.
04 ) O coeficiente de restituição para a colisão da esfera feita de massa de modelar é igual a zero.
08 ) As duas esferas irão atingir o solo ao mesmo tempo e terão neste instante valores de energias cinéticas.
16 ) Podemos afirmar que no caso da colisão da esfera feita de borracha com o solo, a energia cinética da esfera é conservada.
Resposta: Soma: 01 mais 0 4 mais 16 é igual a 21