CAPÍTULO 1
CONJUNTOS
A ideia de conjunto está presente em várias situações do dia a dia. Ao organizar a lista de amigos para uma festa, ao reunir o material escolar e ao formár um tíme, por exemplo, estamos constituindo conjuntos.
Neste Capítulo, estudaremos os conjuntos do ponto de vista matemático, analisando algumas de suas propriedades e operações, além de retomar os conjuntos numéricos já estudados no Ensino Fundamental e ampliar os conteúdos associados a esses conjuntos. Esses conteúdos auxiliam na compreensão da linguagem utilizada para expressar conceitos matemáticos e serão utilizados na apresentação de outros conteúdos.

Página onze
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. Citem outros exemplos em quê a ideia de conjunto esteja presente no dia a dia de vocês.
Resposta pessoal. Exemplo de resposta: Conjunto de pótes para guardar alimentos, conjunto de brinquedos etc.
2. O quê são conjuntos numéricos? Quais deles vocês conhecem? Escrevam um pequeno texto a respeito do assunto.
Respostas pessoais. Espera-se quê os estudantes relembrem o quê já estudaram a respeito dos números naturais, inteiros e racionais no Ensino Fundamental.
3. Como vocês definiriam o quê é um conjunto infinito? Escrevam com suas próprias palavras.
Resposta pessoal.
Página doze
Introdução
Professor, apresentar o quêstionamento do primeiro parágrafo para a turma e deixar quê os estudantes debatam por um tempo para que percêbam facilidades e dificuldades de uma escrita e de outra. Incentivar quê justifiquem suas respostas e, caso necessário, apresentar outros exemplos. Esse momento de discussão e investigação é importante para despertar o interêsse no assunto a sêr tratado, antes de prosseguir com o conteúdo.
Você já parou para pensar em como escreveria uma simples conta de adição, como 2 + 3 = 5, se não houvesse os símbolos “+” e “=” e os numerais “2”, “3” e “5” para representar os números? Uma opção seria escrever na língua materna, quê, no caso do português, seria: “dois mais três é igual a cinco”.
Esses símbolos foram desenvolvidos e aprimorados ao longo do tempo, à medida quê estudiosos da área perceberam a necessidade de tê-los para simplificar e condensar a escrita e para representar os conceitos, as definições e as propriedades matemáticas, mantendo, porém, a precisão e o rigor necessários.
Neste Capítulo, estudaremos a linguagem dos conjuntos, quê é bastante útil ao tratar de diferentes assuntos, por exemplo, as funções, as relações entre entes geométricos (como ponto, reta e plano) e a lógica. Também estudaremos propriedades e operações quê podem sêr feitas nessa estrutura de conjuntos.
Saiba quê...
Utilizamos a expressão "língua materna" relacionando-a ao português; é importante destacar quê, para os estudantes surdos brasileiros, além do português, a Língua Brasileira de Sinais (Libras) também é considerada língua materna.
Conceitos iniciais
Um conjunto é uma coleção qualquer de objetos, e cada um deles é chamado de elemento. No exemplo apresentado na abertura dêste Capítulo, cada jogadora é um elemento do conjunto tíme de futeból.
Representações de um conjunto
Geralmente, nomeamos os conjuntos utilizando lêtras maiúsculas (por exemplo: A, B, C, D,..., X, Y, Z) e adotamos lêtras minúsculas para representar seus elemêntos (por exemplo: a, b, c, d,..., x, y, z).
Um conjunto póde sêr representado de várias maneiras. Por exemplo, podemos representar o conjunto A, formado pelas vogais do nosso alfabeto, dos seguintes modos:
a) Os elemêntos do conjunto são colocados entre chaves e separados por vírgula ou ponto e vírgula:
A = {a, e, i, o, u}
b) Os elemêntos do conjunto são indicados por uma ou mais propriedades quê os caracterizam:

Professor, se julgar necessário, comentar com os estudantes quê os dois-pontos (:) ou o ponto e vírgula (;) também podem sêr usados para representar as expressões “tal que” e “tais que”.
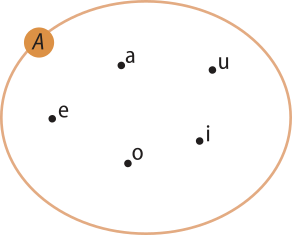
c) Os elemêntos do conjunto são representados em um diagrama de Venn, como mostra a imagem.
Saiba quê...
O diagrama de Venn foi desenvolvido pelo matemático inglês Diôn Venn (1834-1923).
Página treze
Observe outros exemplos de conjuntos:
• conjunto das consoantes da palavra “avião”:
A = {v};
• conjunto dos números naturais pares:
B = {b | b é um número natural par};
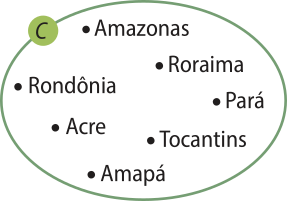
• conjunto dos estados da Região Norte:
Para indicar quê um elemento faz parte de determinado conjunto, usamos o sín-bolo ∈ (pertence) e, para indicar quê ele não faz parte, usamos o sín-bolo ∉ (não pertence). Por exemplo, dado o conjunto das vogais A = {a, e, i, o, u}, temos:
• i ∈ A (lê-se: i pertence a A);
• d ∉ A (lê-se: d não pertence a A).
Pense e responda
Uma reta é formada por infinitos pontos. Como você escreveria, usando símbolos, quê “um ponto A pertence a uma reta r”?
A ∈ r
Tipos de conjuntos
Quanto ao número de elemêntos, os conjuntos podem sêr classificados em finitos ou infinitos.
Um conjunto é finito quando é possível contar seus elemêntos.
Quando dizemos “contar”, significa quê a contagem finaliza em algum número natural. Vamos retomar o exemplo do conjunto A das vogais de nosso alfabeto:
A = {a, e, i, o, u}
Ao contar os elemêntos do conjunto, chegamos até o número 5. Logo, esse conjunto é finito e tem cinco elemêntos. Utilizamos a notação n(A) para indicar a quantidade de elemêntos do conjunto finito A. Nesse exemplo, temos n(A) = 5.
Um conjunto é infinito quando não é finito.
Ou seja, um conjunto é infinito quando não é possível contar todos os seus elemêntos e finalizar a contagem até cérto número. Por exemplo, dado o conjunto B dos números naturais ímpares, temos:

Saiba quê...
As reticências também podem sêr usadas entre dois elemêntos de um conjunto para indicar os elemêntos entre eles (sejam finitos ou infinitos). Por exemplo, o conjunto finito N dos números naturais de 1 a 90 póde sêr representado por N = {1, 2, 3, 4,..., 88, 89, 90}.
Página quatorze
Um conjunto é unitário quando é formado por um único elemento.
Observe, a seguir, um exemplo de um conjunto unitário.
H = {x | x é um número natural maior do quê 6 e menor do quê 8}
Como só existe um número natural maior do quê 6 e menor do quê 8, temos: H = {7}. Logo, H é um conjunto unitário.
O conjunto vazio é aquele quê não possui elemêntos.
Representamos um conjunto vazio por {} ou ∅. Por exemplo:
V = {x | x é um número natural menor do quê zero}
Como não existe número natural menor do quê zero, o conjunto V é vazio. Logo, V = ∅. Por definição, o conjunto vazio é um conjunto finito.
Pense e responda
Qual é o valor de n(H)?
E o de n(V)?
n(H) = 1; n(V) = 0
Igualdade de conjuntos
Analisando os conjuntos A = {vogais da palavra “livro”} e B = {i, o}, observamos quê eles possuem exatamente os mesmos elemêntos. Nesse caso, dizemos quê A e B são iguais.
Agora, obissérve os conjuntos C = {1, 2, 3} e D = {0, 1, 2, 3}. Como existe um elemento em D quê não pertence a C, dizemos quê C e D são diferentes.
Dois conjuntos A e B são iguais quando todos os elemêntos pertencentes a A também pertencem a B e todos os elemêntos pertencentes a B também pertencem a A. Indicamos A = B.
Dois conjuntos A e B são diferentes se, pelo menos, um dos elemêntos de um dos conjuntos não pertence ao outro. Indicamos A ≠ B.
A ordem em quê os elemêntos estão dispostos nos conjuntos não os diferencia. Por exemplo, os conjuntos X = {p, a, t, o} e W = {a, o, t, p} das lêtras da palavra “pato” têm os mesmos elemêntos, então X = W.
Da mesma maneira, os conjuntos P = {a, r, n, h} e Q = {a, r, a, n, h, a} das lêtras da palavra “aranha” também são iguais, ou seja, têm os mesmos elemêntos, pois elemêntos repetidos não diferenciam um conjunto de outro. Apesar de a palavra ter três lêtras “a”, elas não precisam aparecer todas as vezes na representação do conjunto das lêtras quê a compõem.
Subconjuntos
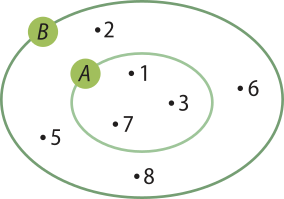
Considerando os conjuntos A = {1, 3, 7} e B = {1, 2, 3, 5, 6, 7, 8}, observamos quê todo elemento do conjunto A também é elemento de B. Nesse caso, dizemos quê A é um subconjunto de B. Observe a representação dêêsses conjuntos por meio de um diagrama.
De maneira geral:
Um conjunto A é subconjunto de um conjunto B quando todos os elemêntos de A também pertencem a B.
Página quinze
Quando um conjunto A é subconjunto de um conjunto B, temos uma relação de inclusão e dizemos quê A está contido em B. pôdêmos dizêr, também, quê B contém A.
Indica-se:

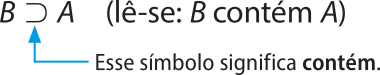
Observe alguns exemplos:
a) Sendo A = {1, 2} e B = {0, 1, 2, 3}, tem-se A ⊂ B.
b) {1, 2, 3, 4, 5, 6} ⊃ {3, 4, 5}
c) {4, 5, 6} ⊂ {4, 5, 6}
d) {2, 4, 6, 8} ⊃ {8}
e) {a, b} ⊂ {a, b, x, y}
f) Sendo M = {m | m é um mês do ano quê tem 30 dias} e Q = {junho, setembro}, então Q ⊂ M.
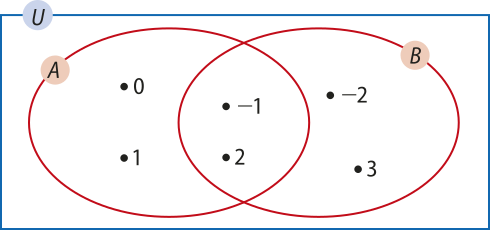
O conjunto universo, representado por U, é o conjunto quê contém todos os elemêntos considerados em uma situação ou um problema. Por exemplo:
Os conjuntos A = {−1, 0, 1, 2} e B = {−2, −1, 2, 3} são subconjuntos do conjunto universo U, formado pêlos números inteiros. Nos diagramas, é usual representar o conjunto universo por um retângulo.
Propriedades da relação de inclusão
É possível demonstrar quê são válidas as seguintes propriedades para a relação de inclusão de conjuntos:
1ª) Propriedade reflexiva: A ⊂ A, para qualquer A, ou seja, um conjunto sempre é subconjunto dele mesmo.
2ª) Propriedade antissimétrica: Se A ⊂ B e B ⊂ A, então A = B, ou seja, dados dois conjuntos, se cada um deles é subconjunto do outro, então eles são iguais.
3ª) Propriedade transitiva: Se A ⊂ B e B ⊂ C, então A ⊂ C, ou seja, se um conjunto é subconjunto de um segundo, quê, por sua vez, é subconjunto de um terceiro conjunto, então o primeiro é subconjunto do terceiro.
Observações:
• A relação de pertinência (x ∈ A) se estabelece entre elemento e conjunto, enquanto a relação de inclusão (A ⊂ B) se estabelece entre dois conjuntos.
• Se existir pelo menos um elemento de A quê não pertença a B, dizemos quê A não está contido em B ou quê B não contém A.
• O sín-bolo ⊄ significa não está contido.
• O sín-bolo ⊍ significa não contém.
• O conjunto vazio é subconjunto de qualquer conjunto, ou seja, ∅ ⊂ A, qualquer quê seja o conjunto A.
Página dezesseis
ATIVIDADES RESOLVIDAS
1. dêz-creva os conjuntos a seguir, listando seus elemêntos:
a) V = {x | x é vogal da palavra “estacionamento”}.
b) P = {y | y é um número natural primo menor do quê 30}.
Resolução
a) As vogais do nosso alfabeto são: a, e, i, o, u. Na palavra “estacionamento”, as vogais são: a, e, i, o. Portanto, V = {a, e, i, o}.
b) Os números primos são aqueles quê possuem apenas dois divisores distintos, o número 1 e ele mesmo. Logo, os números naturais primos menóres do quê 30 são: 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29. Portanto, P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}.
2. Verifique se o conjunto A = {0, 3, 5} é subconjunto de B = {0, 1, 2, 3, 4}.
Resolução
Comparando, um a um, os elemêntos dos conjuntos A e B, verificamos quê o elemento 5 do conjunto A não pertence a B, ou seja, 5 ∉ B. Logo, A não está contido em B, isto é, A ⊄ B. Portanto, A não é subconjunto de B.
3. Determine todos os subconjuntos de A = {1, 2, 3}.
Resolução
O conjunto vazio é subconjunto de qualquer conjunto. Além díssu, os subconjuntos de A serão todas as combinações possíveis dos elemêntos de A.
Então, os subconjuntos de A são os seguintes:
• o conjunto vazio: ∅
• os conjuntos com apenas 1 elemento: {1}, {2}, {3};
• os conjuntos com 2 elemêntos: {1, 2}, {1, 3}, {2, 3};
• o próprio conjunto A, com 3 elemêntos: {1, 2, 3}.
4. Observe o diagrama, em quê E, F e H são conjuntos não vazios:
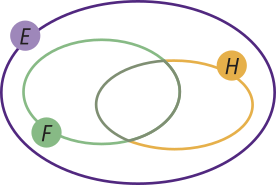
Quais afirmativas são verdadeiras? Justifique sua resposta.
a) E ⊄ F
b) F ⊃ E
c) H ⊂ F
d) E ⊃ H
e) F ⊄ H
f) H ⊂ E
Resolução
Analisando as afirmativas, uma a uma, temos:
a) Verdadeira, pois existem elemêntos quê pertencem a E e não pertencem a F.
b) Falsa, pois existem elemêntos quê pertencem a E e não pertencem a F.
c) Falsa, pois existem elemêntos quê pertencem a H e não pertencem a F.
d) Verdadeira, pois todos os elemêntos de H pertencem a E.
e) Verdadeira, pois existem elemêntos quê pertencem a F e não pertencem a H.
f) Verdadeira, pois todos os elemêntos de H pertencem a E.
ATIVIDADES
1. escrêeva os conjuntos descritos em cada item.
a) O conjunto A representado pêlos números naturais múltiplos de 3 menóres do quê 20.
A = {0, 3, 6, 9, 12, 15, 18}
b) O conjunto B representado pêlos números naturais primos menóres do quê 27.
B = {2, 3, 5, 7, 11, 13, 17, 19, 23}
c) O conjunto C representado pêlos números naturais menóres do quê 50 e múltiplos de 7.
C = {0, 7, 14, 21, 28, 35, 42, 49}
d) D = {x | x é satélite natural da Terra}.
D = {Lua}
e) E = {y | y é consoante da palavra “pedra”}.
E = {p, d, r}
2. Dado o conjunto B = {1, −1, 2, −2}, responda se as proposições a seguir são verdadeiras ou falsas.
a) 1 ∈ B
b) {1} ∈ B
c) 2 ∈ B
d) −1 ∈ B
e) 1 ∉ B
f) 3 ∈ B
V F V V F F
• ![]() Agora reúna-se a um colega, e reescrevam as alternativas falsas alterando-as para quê se tornem verdadeiras.
Agora reúna-se a um colega, e reescrevam as alternativas falsas alterando-as para quê se tornem verdadeiras.
Exemplo de resposta: b) 1 ∈ B; e) 4 ∉ B; f) 3 ∉ B
Página dezessete
3. Considere o conjunto A = {3, 4, 5, 6, 7, 8, 9, 10, 11}. Represente os subconjuntos de A formados:
a) pêlos números maiores do quê 5 e menóres do quê 10;
{6, 7, 8, 9}
b) pêlos números pares;
{4, 6, 8, 10}
c) pêlos números ímpares maiores do quê ou iguais a 7.
{7, 9, 11}
4. Dado o conjunto E = {2, 4, 6, 8}, liste todos os subconjuntos de E formados por:
a) 3 elemêntos;
{2, 4, 6}; {2, 4, 8}; {2, 6, 8}; {4, 6, 8}
b) 4 elemêntos.
{2, 4, 6, 8}
5. Sejam a e b números naturais, determine o valor de a + b, tal quê {0, 1, 2} = {2, a, b}.
1
6. Uma pessoa tem quatro opções de música para escutar: a, b, c e d. Considerando o conjunto {a, b, c, d} formado por essas músicas, resôuva os itens.
a) Indique todos os subconjuntos possíveis com apenas duas músicas.
{a, b}; {a, c}; {a, d};
{b, c}; {b, d}; {c, d}
b) Se uma pessoa quiser ouvir apenas duas músicas por dia, quantas possibilidades de pares ela tem para escolher?
6 pares
7. No diagrama a seguir, A, B e C são três conjuntos não vazios.
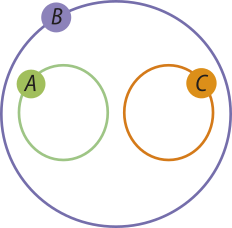
Associe V ou F a cada uma das seguintes sentenças, conforme ela seja verdadeira ou falsa.
a) A ⊂ B
V
b) C ⊂ B
V
c) B ⊂ A
F
d) A ⊂ C
F
e) B ⊄ A
V
f) A ⊄ C
V
g) B ⊃ A
V
h) A ⊍ B
V
8. Dados os conjuntos A = {1}, B = {0, 1}, C = {1, 2, 3} e D = {0, 1, 2, 4}, relacione cada par de conjuntos a seguir usando o sín-bolo ⊂ ou ⊄.
a) A e B
A ⊂ B
b) A e C
A ⊂ C
c) A e D
A ⊂ D
d) B e C
B ⊄ C
e) B e D
B ⊂ D
f) C e D
C ⊄ D
9. Sejam A, B e C os conjuntos a seguir:
A = {x | x é número natural par compreendido entre 3 e 15};
B = {x | x é número natural par menor do quê 15};
C = {x | x é número natural par diferente de 2}.
Relacione cada par a seguir usando o sín-bolo
⊂ ou ⊄.
a) A e B
A ⊂ B
b) A e C
A ⊂ C
c) B e C
B ⊄ C
10. Dado o conjunto A = {0, 2, 3}, diga se as proposições são verdadeiras ou falsas.
a) 0 ∈ A
V
b) 1 ⊂ A
F
c) 3 ∈ A
V
d) {3} ⊂ A
V
e) {1, 2} ⊂ A
F
f) ∅ ⊂ A
V
g) ∅ ∈ A
F
h) {3} ∈ A
F
11. Indique apenas as afirmações verdadeiras.
a) {5} ⊂ {0, 5, 10, 15}
b) {a, b, c} ⊃ {b, a, c}
c) 2 ⊂ {0, 2, 4}
d) 8 ∈ {2, 4, 6, 8, 10}
e) {1, 2, 3} ⊃ {1, 2}
f) {−1, 6} ⊄ {n | n é um número natural}
g) 3 ∈ {0, 3, 6, 9}
h) ∉ {n | n é um número natural}
alternativas a, b, d, e, f, g e h
12. Sendo P e Q dois conjuntos não vazios, de modo quê P ⊂ Q, indique apenas as afirmações verdadeiras.
alternativa d
a) Existe x ∈ P, tal quê x ∉ Q.
b) Existe x ∈ Q, tal quê x ∉ P.
c) Se x ∈ Q, então x ∈ P.
d) Se x ∉ Q, então x ∉ P.
e) P e Q não têm elemêntos em comum.
13. Quantos conjuntos M satisfazem à sentença a seguir?
{1, 2} ⊂ M ⊂ {1, 2, 3, 4}
4 conjuntos
14. Qual deve sêr a relação entre os conjuntos A, B e C para quê A ⊂ B, B ⊂ C e C ⊂ A?
A = B = C
Página dezoito
Operações entre conjuntos
Agora quê já estudamos como representar conjuntos, vamos aprender a realizar operações entre eles e conhecer a simbologia utilizada para isso. Por exemplo, em um grupo de pessoas quê estão participando de um processo seletivo, algumas delas informaram quê têm conhecimentos de inglês; outras afirmaram ter habilidades com um programa específico de computador. Os recrutadores desê-jam saber quantos candidatos apresentam as duas características juntas e quantos não apresentam nenhuma das duas características. O quê vamos estudar auxiliará na resolução de situações como essa.

União de conjuntos
A união (também chamada de reunião) de dois conjuntos A e B, quê indicamos por A ∪ B, é o conjunto formado pela junção dos elemêntos quê pertencem ao conjunto A com os elemêntos quê pertencem ao conjunto B:
A ∪ B = {x | x ∈ A ou x ∈ B}
Por exemplo, dados os conjuntos A = {0, 2, 4, 6} e B = {0, 1, 2, 3, 4}, a união dêêsses conjuntos é o conjunto cujos elemêntos pertencem a pelo menos um dêêsses conjuntos, isto é:
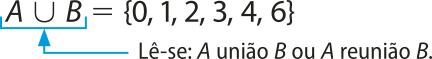
Observe quê, qualquer quê seja o elemento de A ⋂ B, ele pertence ao conjunto A ou ao conjunto B ou a ambos.
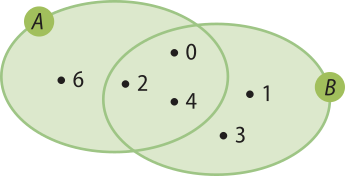
Intersecção de conjuntos
A intersecção de dois conjuntos A e B, quê indicamos por A ⋃ B, é o conjunto formado pêlos elemêntos quê pertencem a A e também pertencem a B:
A ∩ B = {x | x ∈ A e x ∈ B}
Por exemplo, a intersecção dos conjuntos A e B do exemplo anterior é o conjunto cujos elemêntos pertencem, ao mesmo tempo, ao conjunto A e ao conjunto B. Observe:
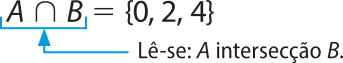
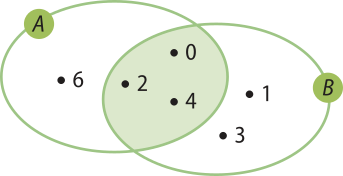
Página dezenove
Observação:
Se os conjuntos A e B não têm elemêntos comuns (A ⋃ B = ∅), dizemos quê A e B são conjuntos disjuntos. Acompanhe alguns exemplos:
a) Considere os conjuntos: A = {0, 2, 4, 6, 8, 10} e B = {1, 3, 5, 7, 9}
Temos A ⋂ B = ∅, então os conjuntos A e B são disjuntos.
b) Considere os conjuntos: P = {p | p é mês do ano com 30 dias} e Q = {dezembro}
O mês de dezembro tem 31 dias, então os conjuntos P e Q são disjuntos, pois P ⋂ Q = ∅.
Saiba quê...
Usualmente, as operações de união e de intersecção de conjuntos são associadas aos conectivos ou e e, respectivamente. Na Matemática, dizêr quê um elemento pertence a um conjunto ou a outro significa dizêr quê ele pertence a pelo menos um dos conjuntos, mas póde pertencer a ambos. Já dizêr quê um elemento pertence a um conjunto e a outro significa, necessariamente, quê ele pertence aos dois conjuntos considerados.
Propriedades da união e da intersecção de conjuntos
Dados três conjuntos, A, B e C, é possível demonstrar quê valem as seguintes propriedades:
1ª) Propriedade comutativa
A ⋃ B = B ⋃ A
propriedade comutativa da união
A ⋂ B = B ⋂ A
propriedade comutativa da intersecção
2ª) Propriedade associativa
(A ⋃ B) ⋃ C = A ⋃ (B ⋃ C)
propriedade associativa da união
(A ⋂ B) ⋂ C = A ⋂ (B ⋂ C)
propriedade associativa da intersecção
3ª) Propriedade distributiva
A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂C)
propriedade distributiva da intersecção em relação à união
A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃C)
propriedade distributiva da união em relação à intersecção
4ª) Propriedade
Se A ⊂ B, então A ⋃ B = B e A ⋂B = A.
Da mesma maneira, se A ⋃ B = B ou A ⋂ B = A, então A ⊂ B.
Quantidade de elemêntos da união de conjuntos
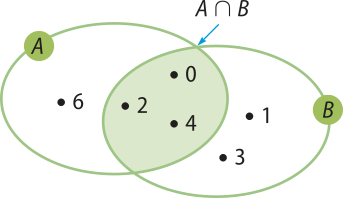
Acompanhe o exemplo a seguir. Dados os conjuntos A = {0, 2, 4, 6} e B = {0, 1, 2, 3, 4}, qual é a quantidade de elemêntos do conjunto A ⋃ B?
Observe o diagrama e note quê, se adicionarmos a quantidade de elemêntos de A à quantidade de elemêntos de B, a quantidade de elemêntos de A ⋂ B será contada duas vezes, pois os elemêntos 0, 2 e 4 estão presentes nos dois conjuntos.
Assim, precisamos descontar essa repetição, de modo quê concluímos quê o conjunto A ⋃ B tem 6 elemêntos.
Página vinte
De maneira geral, sêndo A e B dois conjuntos finitos, a quantidade de elemêntos do conjunto
A ⋂ B, quê indicamos por n(A ⋂ B), é dada pela seguinte relação:
n(A ⋂ B) = n(A) + n(B) − n(A ⋃ B)
Aplicando essa igualdade para o exemplo anterior, temos:
n(A ⋂ B) = 4 + 5 − 3 ⇒ n(A ⋂ B) = 6
Observação:
Se A ⋃ B = ∅, temos: n(A ⋃ B) = 0 e n(A ⋂ B) = n(A) + n(B).
Diferença de conjuntos
A diferença de dois conjuntos A e B, quê indicamos por
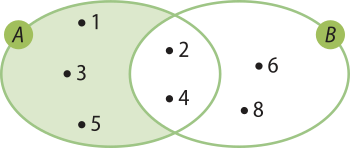
A − B, nessa ordem, é o conjunto dos elemêntos quê pertencem a A e não pertencem a B:
A − B = {x | x ∈ A e x ∉ B}
Por exemplo, dados os conjuntos A = {1, 2, 3, 4, 5} e B = {2, 4, 6, 8}, a diferença A − B é formada por todos os elemêntos quê pertencem a A, mas não pertencem a B.
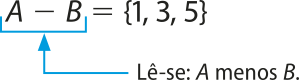
Acompanhe outros exemplos:
a) Dados M = {m, n, p, q, r} e P = {p, q}, temos:
M − P = {m, n, r}
b) Seja E o conjunto formado pêlos seguintes esportes: basquete, vôlei, futeból, réndbóll, judô, xadrez, natação e atletismo. Temos:
E = {basquete, vôlei, futeból, réndbóll, judô, xadrez, natação, atletismo}
Considere também o conjunto C, formado pêlos esportes coletivos. Ao realizarmos E − C, temos:
E − C = {judô, xadrez, natação, atletismo}
Se B ⊂ A, a diferença A − B é denominada complementar de B em relação a A e é indicada por:
= A − B
Página vinte e um
Por exemplo, se B = {2, 3} e A = {0, 1, 2, 3, 4}, o complementar de B em relação a A é dado por:
= A − B = {0, 1, 4}
No caso de termos determinado conjunto universo U, do qual A é subconjunto, o complementar de A em relação a U é indicado por:
A(minutos)" = = U − A
FÓRUM
O Brasil nos jogos Parapan-Americanos 2023
O Brasil se despediu dos Jogos Parapan-Americanos de Santiago 2023 com o maior dêsempênho de todos os tempos. Foram 343 medalhas no total, com 156 ouros, 98 pratas e 89 bronzes [...]. Desde o Parapan do Rio 2007, o Brasil termina no topo do qüadro de medalhas.
[...]
O dêsempênho brasileiro [...] foi histórico por diversos motivos, como a melhor campanha em todas as edições e conkistas inéditas. E um dado foi muito importante para quê isso acontecesse: o Brasil subiu ao pódio em todas as 17 modalidades em quê esteve presente na competição na capital chilena.
[...] Fosse no badminton, halterofilismo, natação ou qualquer outro esporte, ao menos um atleta brasileiro ocupou um dos três lugares do pódio pelo menos em uma ocasião em Santiago.
[...]
COMITÊ PARALÍMPICO BRASILEIRO. Saiba 23 motivos quê fizeram do Parapan de Santiago 2023 inesquecível. [S. I.]: CPB, 27 nov. 2023. Disponível em: https://livro.pw/ypyhz. Acesso em: 25 jun. 2024.

![]() Após ler o texto, faça o quê se pede.
Após ler o texto, faça o quê se pede.
• Reúna-se a mais dois côlégas, e pesquisem o quê são os jogos Parapan-Americanos e quais foram as 17 modalidades esportivas presentes na edição de Santiago (Chile) em 2023. Depois, promovam um fórum para discutir as diferentes modalidades de esportes adaptados para pessoas com deficiência (PcD).
Ver as Orientações para o professor.
Página vinte e dois
ATIVIDADES RESOLVIDAS
5. Dados os conjuntos A = {0, 1, 2, 3, 4} e B = {1, 3, 5, 7}, determine os conjuntos A ⋃ B, A ⋂ B, A − B e represente cada um deles por meio de um diagrama.
Resolução
Juntando todos os elemêntos quê pertencem a A com os elemêntos quê pertencem a B, temos: A ⋃ B = {0, 1, 2, 3, 4, 5, 7}
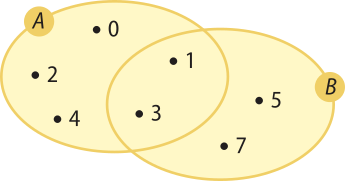
Tomando os elemêntos comuns a A e a B, temos: A ⋂ B = {1, 3}
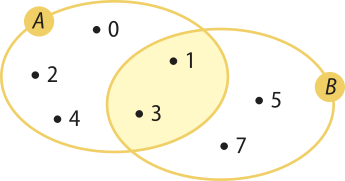
Considerando os elemêntos quê pertencem a A e não pertencem a B, temos:
A − B = {0, 2, 4}
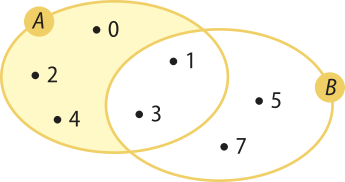
6. Determinada empresa de perfume deseja saber como está o consumo de seus produtos. Assim, fez uma pesquisa de mercado para levantar quantas pessoas consomem o seu produto (P) e quantas consomem o produto (S) da sua principal concorrente. Os dados obtidos na pesquisa foram os seguintes:
Produto consumido |
S |
P |
S e P |
Nenhum dos dois |
|---|---|---|---|---|
Número de consumidores |
210 |
180 |
50 |
40 |
Fonte: Dados fictícios.
Quantas pessoas foram consultadas nessa pesquisa?
Resolução
Vamos considerar o conjunto universo U de todas as pessoas quê responderam à pesquisa e os conjuntos S e P das pessoas quê consomem os produtos S e P, respectivamente. Fazemos o diagrama e o preenchemos do seguinte modo:
• Colocamos 50 na região S ⋃ P, pois 50 pessoas consomem os dois produtos. É importante começar pela intersecção, pois, assim, não corremos o risco de contar mais de uma vez essas 50 pessoas.
• Das 210 pessoas quê consomem o produto S, 50 consomem também o produto P, então o número de pessoas quê consomem somente o produto S é:
210 − 50 = 160
Portanto, colocamos 160 na região S − P.
• Das 180 pessoas quê consomem o produto P, temos 50 quê também consomem o produto S. Então, o número de pessoas quê consomem somente o produto P é:
180 − 50 = 130
Portanto, colocamos 130 na região P − S.
• Por último, acrescentamos as 40 pessoas quê não consomem nenhum dos produtos.
Observe como fica o diagrama de Venn com essas informações.
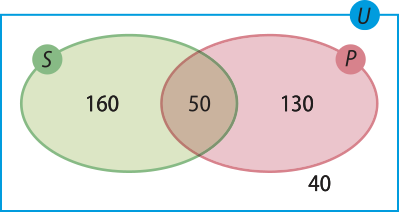
Para determinar quantas pessoas foram consultadas, adicionamos os números marcados no diagrama:
160 + 50 + 130 + 40 = 380
Assim, foram consultadas 380 pessoas nessa pesquisa.
Página vinte e três
ATIVIDADES
15. Sendo A = {0, 11, 12, 13, 14}, B = {11, 12}, C = {x | x é número natural par compreendido entre 11 e 19} e D = {x | x é número natural ímpar compreendido entre 10 e 16}, determine:
a) A ⋂ B
A ⋂ B = {11, 12}
b) A ⋂ C
A ⋂ C = {12, 14}
c) B ⋃ C
B ⋃ C = {11, 12, 14, 16, 18}
d) C ⋃ D
C ⋃ D = {11, 12, 13, 14, 15, 16, 18}
e) (A ⋃ B) ⋃ C
(A ⋃ B) ⋃ C = {0, 11, 12, 13, 14, 16, 18}
f) (A ⋂ C) ⋂ D
(A ⋂ C) ⋂ D = ∅
16. Dados os conjuntos A = {m, n, p, q}, B = {n, p, q} e C = {p, q, r, s}, cujos elemêntos são lêtras, determine:
a) A − B
A − B = {m}
b) A − C
A − C = {m, n}
c) B − C
B − C = {n}
d) (A ⋂ B) − C
(A ⋂ B) − C = {n}
e) (A − C) ⋂ (B − C)
(A − C) ⋂ (B − C) = {n}
f) A − ∅
A − ∅ = {m, n, p, q}
17. Considere o diagrama.
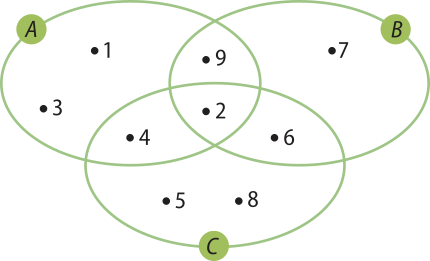
Determine:
a) A ⋃ B
A ⋃ B = {1, 2, 3, 4, 6, 7, 9}
b) A ⋃ C
A ⋃ C = {1, 2, 3, 4, 5, 6, 8, 9}
c) A ⋃ B ⋃ C
A ⋃ B ⋃ C = {1, 2, 3, 4, 5, 6, 7, 8, 9}
d) B ⋂ C
B ⋂ C = {2, 6}
e) A ⋂B ⋂ C
A ⋂ B ⋂ C = {2}
f) A − C
A − C = {1, 3, 9}
g) (A ⋂ C) − B
(A ⋂ C) − B = {4}
18. Liste os elemêntos dos conjuntos resultantes de cada operação dada.
a) {10, 11, 12} ⋂ {7, 8, 9, 10, 11}
{10, 11}
b) {−3, −2, −1, 0} ⋂ {0, 1, 2, 3}
{0}
c)
∅
19. Os conjuntos A, B e E são tais quê
A ⋃ B = {1, 2, 3, 4, 5, 6, 7}, A ⋂ B = {4, 5},
E − B = {1, 2}, B − A = {6, 7}, E ⋂ B = ∅
e E ⊂ A. Calcule
= A − E = {3, 4, 5}
20. Dados U = {0, 1, 2, 3, 4, 5, 6, 7}, A = {0, 2, 5}, B = {1, 3, 5, 7} e E = {2, 4, 6}, determine:
a)
a) = U − A = {1, 3, 4, 6, 7}
b)
b) = U − B = {0, 2, 4, 6}
c)
c) = U − E = {0, 1, 3, 5, 7}
21. Representamos M(a) o conjunto dos múltiplos de a e D(a) o conjunto dos divisores de a, com a sêndo um número natural. Liste os elemêntos dos conjuntos resultantes das operações a seguir.
a) M(3) ⋂ D(30)
{3, 6, 15, 30}
b) M(2) ⋂ M(4)
{0, 4, 8,...}
c) D(100) ⋂ D(50)
{1, 2, 5, 10, 25, 50}
d) M(7) ⋂ M(5)
{0, 35, 70,...}
22. (hú éfi éssi cê) Sejam A e B dois conjuntos, onde (A ⋃ B) possui 134 elemêntos e (A ⋂ B) possui 49 elemêntos. Se A possui 15 elemêntos a mais do quê B, então o número de elemêntos de A é: _____
99 elemêntos
23. Uma pesquisa revelou quê, das pessoas consultadas, 100 liam o jornál A, 150 liam o jornál B, 20 liam os dois jornais (A e B) e 110 não liam nenhum jornál. Quantas pessoas foram consultadas?
340 pessoas
24. Em uma escola de idiomas, há 630 estudantes, dos quais 350 optaram pelo curso de Inglês, 210 escolheram o de Espanhol e 90 optaram pêlos dois cursos (Inglês e Espanhol). Pergunta-se:
a) Quantos estudantes cursam apenas Inglês?
260 estudantes
b) Quantos estudantes cursam apenas Espanhol?
120 estudantes
c) Quantos estudantes cursam Inglês ou Espanhol?
470 estudantes
d) Quantos estudantes não cursam nenhum dos dois idiomas?
160 estudantes
25. Em um grupo de 99 esportistas, 40 jogam vôlei, 20 jogam vôlei e xadrez, 22 jogam xadrez e tênis, 18 jogam vôlei e tênis e 11 jogam as três modalidades. O número de pessoas quê jogam xadrez é igual ao número de pessoas quê jogam tênis. Quantos esportistas jogam:
a) tênis e não jogam vôlei?
36 esportistas
b) xadrez ou tênis e não jogam vôlei?
59 esportistas
c) vôlei e não jogam xadrez?
20 esportistas
Página vinte e quatro
Conjuntos numéricos
Ao longo da história humana, conforme as sociedades foram se desenvolvendo, o uso dos números evoluiu da simples necessidade de contar e registrar quantidades para concepções e escritas cada vez mais abrangentes quê pudessem atender a necessidades matemáticas mais compléksas quê foram surgindo. É nesse contexto quê os números foram organizados em conjuntos numéricos.
Estudaremos os conjuntos dos números naturais, dos números inteiros, dos números racionais, dos números irracionais e dos números reais, com algumas de suas propriedades e aplicações.

Conjunto dos números naturais
Os números naturais são utilizados para indicar contagens, como idade, dias de mês ou, ainda, para representar o número de uma residência.
Começando por zero e acrescentando sempre uma unidade, obtemos os elemêntos do conjunto dos números naturais, indicado por ℕ.
ℕ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,...}
O conjunto dos números naturais é infinito, e podemos representá-lo em uma reta orientada sobre a qual marcamos pontos equidistantes. A cada ponto marcado, fazemos corresponder, ordenadamente, um número natural, e cada número natural é representado por um dêêsses pontos, como mostra a figura a seguir.

Página vinte e cinco
A respeito dos números naturais:
• Todo número natural n tem seu sucessor n + 1, quê é o número natural quê vêm imediatamente depois dele. Por exemplo, o sucessor de 5 é 6; o sucessor de 29 é 30.
• O número natural quê vêm imediatamente antes de um número natural diferente de zero é denominado antecessor. Por exemplo, o antecessor de 10 é 9; o antecessor de 231 é 230.
• Os números naturais n e n + 1 são denominados consecutivos. Analogamente, dizemos quê os números naturais n, n + 1, n + 2,... são consecutivos. Por exemplo, 4 e 5 são consecutivos, e 18, 19 e 20 também são consecutivos.
• O subconjunto de ℕ formado por todos os números naturais diferentes de zero é denotado assim:
ℕ* = {1, 2, 3, 4, 5, 6,...} = ℕ − {0}
No conjunto ℕ, as operações de adição e de multiplicação estão bem definidas, pois, quaisquer quê sêjam dois números naturais, essas operações sempre resultam em um número natural. Porém, a subtração de dois números naturais nem sempre resulta em um número natural. Por exemplo: 5 − 7 = −2 e −2 ∉ ℕ.
Pense e responda
Qual é o único número natural quê não tem antecessor?
o zero
Saiba quê...
O asterisco (*), colocado junto ao sín-bolo quê representa um conjunto numérico, indica quê o número zero foi retirado do conjunto.
Conjunto dos números inteiros
Professor, enfatizar a facilidade de se usar a notação de conjuntos com o sín-bolo de “não pertence” para a escrita de algumas sentenças matemáticas.
Durante o Renascimento (entre os séculos XIV e XVI), a circulação de dinheiro aumentou, por causa da expansão comercial. Isso fez com quê comerciantes se envolvessem com situações de lucro e prejuízo e, para facilitar a representação dessa movimentação financeira, começaram a utilizar os símbolos + (mais), para representar um valor positivo ou lucro, e − (menos), para representar um valor negativo ou prejuízo.
Ao incluirmos os números negativos −1, −2, −3, −4,... no conjunto {0, 1, 2, 3, 4,...}, formamos o conjunto dos números inteiros, representado por ℤ.
ℤ = {..., −4, −3, −2, −1, 0, +1, +2, +3, +4,...}
ou
ℤ = {..., −4, −3, −2, −1, 0, 1, 2, 3, 4,...}
Todos os números naturais pertencem ao conjunto dos números inteiros, ou seja, o conjunto dos números naturais é um subconjunto do conjunto dos números inteiros, como mostra o diagrama. pôdêmos escrever ℕ ⊂ ℤ.
Na reta orientada, o conjunto ℤ póde sêr assim representado:
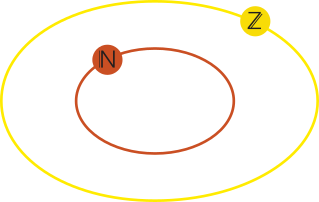

Note quê cada ponto marcado na reta está associado a um único número inteiro e quê, reciprocamente, cada número inteiro está associado a apenas um dêêsses pontos.
Página vinte e seis
Pense e responda
Todo número natural também é um número inteiro? E todo número inteiro é um número natural? Justifique.
Sim, todo número natural é um número inteiro. Entretanto, nem todo número inteiro é um número natural, por exemplo, −1 não é um número natural.
A respeito dos números inteiros:
• Todo número inteiro tem um antecessor e um sucessor. Por exemplo: o antecessor de −10 é −11, e o sucessor de −1 é 0.
• Dois números inteiros são opostos ou simétricos quando a soma deles é igual a zero. Por exemplo: o ôpôsto de 1 é −1, e o ôpôsto de −3 é 3. O ôpôsto de zero é o próprio zero.
Na reta orientada, identificamos dois números opostos quando eles são simétricos em relação ao zero, ou seja, estão a uma mesma distância da origem. Observe:
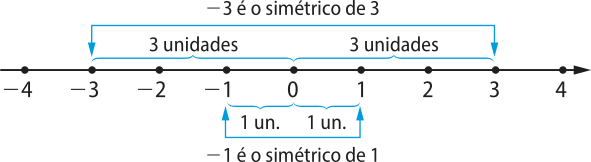
Destacamos, agora, importantes subconjuntos de ℤ:
• números inteiros não nulos: ℤ* = {..., −4, −3, −2, −1, 1, 2, 3, 4,...} = ℤ − {0}
• números inteiros não negativos: ℤ+ = {0, 1, 2, 3, 4,...}
• números inteiros não positivos: ℤ− = {0, −1, −2, −3, −4,...}
• números inteiros positivos: = {1, 2, 3, 4,...}
• números inteiros negativos: = {−1, −2, −3, −4,...}
• números pares: P = {..., −4, −2, 0, 2, 4,...}, ou seja, são os números quê, divididos por 2, têm résto 0.
• números ímpares: I = {..., −3, −1, 1, 3,...}, ou seja, são os números quê, divididos por 2, têm résto 1.
No conjunto ℤ, as operações de adição, subtração e multiplicação estão bem definidas. Isso significa quê, quaisquer quê sêjam dois números inteiros, essas operações sempre resultam em um número inteiro. Observe alguns exemplos:
a) −5 + 8 = 3
b) 25 + (−2) = 25 − 2 = 23
c) 10 − (−17) = 10 + 17 = 27
d) −40 − 21 = −61
e) −7 ⋅ 3 = −21
f) 4 ⋅ (−9) = −36
No entanto, no conjunto dos números inteiros, não é possível obtêr um número inteiro como quociente de algumas divisões exatas, como 7 ∶ 2, por exemplo. Desse modo, surge a necessidade de definir novos conjuntos numéricos.
Conjunto dos números racionais
Como mencionamos, os resultados de algumas divisões não pertencem ao conjunto dos números inteiros. Por causa díssu, surgiu a necessidade de complementar os conjuntos numéricos, o quê deu origem ao conjunto dos números racionais.
O conjunto dos números racionais, quê indicamos por ℚ, é aquele formado pêlos números quê podem sêr expressos na forma , sêndo a e b inteiros e b ≠ 0:
ℚ =
Página vinte e sete
Exemplos:
• 7 =
• 0,6 =
• −0,13 =
• 1,3333... =
• 0,4777... =
Professor, reforçar com os estudantes o uso da linguagem de conjuntos já estudada para estabelecer e indicar a relação entre os conjuntos numéricos.
pôdêmos escrever os números inteiros como frações com denominador 1. Assim, todos os números inteiros pertencem ao conjunto dos números racionais, ou seja, o conjunto ℤ é um subconjunto do conjunto ℚ, como mostra o diagrama. pôdêmos escrever ℤ ⊂ ℚ.
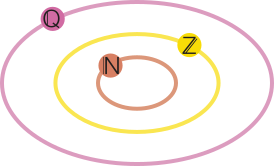
Um número racional póde sêr representado de duas maneiras: na forma fracionária, sêndo o denominador não nulo; e na forma decimal, caso em quê a parte decimal tem uma quantidade finita de algarismos ou é infinita e periódica.
Exemplos:
• = 0,25
• = 2,8
• = 2,1666...
Ao realizar uma divisão para obtêr a forma decimal de um número racional, temos duas possibilidades:
1. O resultado é um número decimal com uma quantidade finita de algarismos depois da vírgula. Nesse caso, temos um número decimal exato.
Exemplos:
• = 3
• = 4,5
• = 0,75
• = −0,375
2. O resultado é um número decimal com uma quantidade infinita de algarismos depois da vírgula, com um grupo deles se repetindo periodicamente. Nesse caso, temos uma dízima periódica, e o grupo de algarismos quê se repetem infinitamente é chamado de período da dízima.
Exemplos:
• = 2,1666... = 2, (o período é 6)
• = 0,404040... =0, (o período é 40)
Saiba quê...
Colocamos um traço sobre o período da dízima para indicar quê ela se repete indefinidamente. Por exemplo:
• 0,333... = 0,
• 0,171717... = 0,
• 3,1454545... = 3,
Pense e responda
Observando o résto da divisão de dois números inteiros positivos, você consegue perceber se o quociente dêêsses dois números é um decimal exato ou uma dízima periódica? Explique.
Espera-se quê os estudantes percêbam quê, se em algum momento o número 0 aparecer como résto da divisão entre dois inteiros, o quociente é finito; portanto, trata-se de um decimal exato.
Página vinte e oito
Pense e responda
Como obtemos a fração irredutível equivalente a um número decimal exato?
Espera-se quê os estudantes percêbam quê, se o número for inteiro, basta escrevê-lo como uma fração de denominador 1. Para um número na forma decimal, é possível escrevê-lo como uma fração cujo denominador é uma potência de 10 e simplificá-la até obtêr a fração irredutível equivalente.
Acabamos de aprender a obtêr a forma decimal de um número racional a partir de sua forma fracionária. Também podemos obtêr uma fração de inteiros equivalente a um número racional, seja ele um decimal exato, seja ele uma dízima periódica.
Essa fração é chamada de fração geratriz. Acompanhe como obtêr a fração geratriz da dízima 2,313131...
x = 2,313131... I
Como o período tem 2 algarismos quê se encontram logo após a vírgula, multiplicamos por 100 ambos os membros da igualdade:
100x = 231,313131... II
Fazemos II − I, subtraindo, membro a membro, as duas igualdades:
100x − x = 231,313131... − 2,313131...
Portanto:
99x = 229 ⇒ x =
Logo, é a fração geratriz da dízima periódica 2,313131...
Professor, comentar com os estudantes quê o conjunto dos números racionais é formado pêlos decimais exatos e pelas dízimas periódicas.
Um número racional escrito na forma decimal póde ter uma quantidade finita ou infinita e periódica de algarismos depois da vírgula. Na forma fracionária, um número racional tem uma representação quê é uma fração formada por números inteiros com denominador não nulo.
Na reta orientada, é possível marcar pontos quê representem números racionais. Acompanhe alguns exemplos de localização de números racionais na reta orientada:
a) Como o número = 1,25 está localizado entre 1 e 2, dividimos o intervalo entre os números 1 e 2 em quatro partes iguais e tomamos o ponto da divisão quê fica mais próximo de 1. Nesse ponto, localizamos o número 1,25.

b) O número −0,2 = está localizado entre 0 e −1; então, dividimos o intervalo entre os números −1 e 0 em cinco partes iguais e tomamos o ponto da divisão quê fica mais próximo do 0. Nesse ponto, localizamos o número −0,2.
Professor, comentar com os estudantes quê é comum localizar números na reta numérica utilizando pequenos traços, em vez de pontos, como aparécem nesses exemplos.

Observe um trecho da reta orientada com alguns pontos quê estão associados a alguns números racionais:
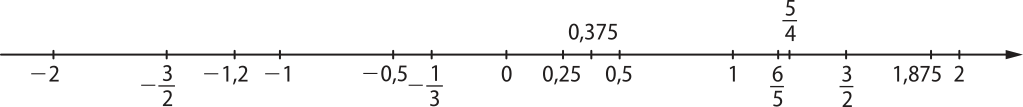
Todos os números racionais estão associados a um único ponto da reta orientada. No entanto, nem todos os pontos da reta orientada correspondem a um número racional, como é o caso das dízimas não periódicas. Isso significa quê os números racionais não são suficientes para “preencher” toda a reta, ou seja, há “buracos” na reta quê precisam sêr preenchidos com outros números. Esses números serão estudados mais adiante neste Capítulo.
Página vinte e nove
A respeito dos números racionais:
a) A soma de dois números racionais é um número racional. Exemplos:
•
• 7,4 + 3,6 = 11,0
b) A diferença de dois números racionais é um número racional. Exemplos:
• 1, − 0, = 1,
•
c) O produto de dois números racionais é um número racional. Exemplos:
• 45, ⋅ 2 = 90,
•
d) O quociente de dois números racionais, sêndo o divisor diferente de zero, é um número racional. Exemplos:
• 0,5 ∶ 2,25 = 0,
•
e) Dois números racionais são opostos ou simétricos quando a soma deles é igual a zero. Exemplos:
• O ôpôsto de 0,5 é −0,5, pois 0,5 + (−0,5) = 0,5 − 0,5 = 0.
• O ôpôsto de é , pois = 0.
f) Dois números racionais são inversos um do outro quando o produto deles é igual a 1. Exemplos:
• O inverso de é , pois = 1.
• O inverso de −7 é − pois −7 ⋅ − = 1.
Pense e responda
Qual é o único número racional quê não possui inverso?
o zero
g) Entre dois números racionais distintos sempre existe outro número racional. Daí a impossibilidade de se escreverem todos os números racionais situados entre dois números quaisquer. Exemplos:
• Entre os números 0,2 = e 0, = existem, entre outros, os números racionais 0,25; 0,2 e .
Exemplo de resposta: 4,51; 4,6 e 4,799. Os estudantes podem utilizar a estratégia da média aritmética apresentada ou outra quê desejarem.
Pense e responda
Determine três números racionais quê estejam entre 4,5 e 4,8.
• Um procedimento possível para se obtêr um número racional entre dois outros números racionais é calcular a média aritmética entre eles. No caso do exemplo anterior, temos:
= 0, ou
Destacamos, agora, importantes subconjuntos de ℚ:
• números racionais não nulos: ℚ* = ℚ − {0}
• números racionais não negativos: ℚ+
• números racionais não positivos: ℚ−
• números racionais positivos:
• números racionais negativos:
Aprendemos quê a soma, a diferença, o produto e o quociente de números racionais são números racionais. Além díssu, todo número racional, quando não nulo, possui ôpôsto e inverso.
Página trinta
ATIVIDADES RESOLVIDAS
7. Considere os conjuntos A = {x ∈ ℕ | x ≤ 5} e
B = {x ∈ ℤ | −2 ≤ x < 3}. Em seguida:
a) dêz-creva os elemêntos dos conjuntos A e B.
b) determine A ⋃ B.
c) determine A ⋂ B.
Resolução
a) No conjunto A, a notação x ≤ 5 significa quê x é um número menor do quê ou igual a 5, ou seja, sêndo x ∈ ℕ, x póde assumir qualquer valor natural entre 0 e 5, incluindo os dois extremos. Logo, A = {0, 1, 2, 3, 4, 5}.
No conjunto B, a notação −2 ≤ x < 3 significa quê x ≥ −2 e, também, x < 3, sêndo x ∈ ℤ, ou seja, x póde assumir qualquer valor inteiro entre −2 e 3, incluindo o extremo −2, mas não incluindo o extremo 3. Assim, B = {−2, −1, 0, 1, 2}.
b) A união dos conjuntos A e B é o conjunto formado por todos os elemêntos quê pertencem a A ou a B. Logo, A ⋃ B = {−2, −1, 0, 1, 2, 3, 4, 5}.
c) A intersecção dos conjuntos A e B é o conjunto formado pêlos elemêntos quê pertencem a A e também pertencem a B.
Portanto, A ⋂ B = {0, 1, 2}.
8. Considere os conjuntos:
A = {x ∈ ℕ | x é par};
B = {x ∈ ℕ | x = 2k + 1, com k ∈ ℕ} e
C = {…,−3, −2, −1, 0, 1, 2, 3, …}.
O conjunto C − (A ⋃ B) é o conjunto:
a) ℕ*
b) ℤ−
c) ℚ−
d)
e)
Resolução
O conjunto A é formado pêlos números naturais pares, portanto A = {0, 2, 4, 6, …}.
O conjunto B é formado por x natural, tal quê x é da forma x = 2k + 1, com k natural.
Atribuindo valores naturais para k, obtemos valores de x:
k = 0 ⇒ x = 2 ⋅ 0 + 1 ⇒ x = 1
k = 1 ⇒ x = 2 ⋅ 1 + 1 ⇒ x = 3
k = 2 ⇒ x = 2 ⋅ 2 + 1 ⇒ x = 5
k = 3 ⇒ x = 2 ⋅ 3 + 1 ⇒ x = 7
⋮
Note quê, ao atribuir valores naturais para k, obtemos valores naturais ímpares para x.
Então, o conjunto B é formado pêlos números naturais ímpares. Portanto, B = {1, 3, 5, 7, …}.
Sendo assim, temos A ⋃ B = {0, 1, 2, 3, 4, 5, 6, …}.
Fazendo C − (A ⋃ B), temos:
{…, −3, −2, −1, 0, 1, 2, 3, …} − {0, 1, 2, 3, 4, 5, 6, …} = {…, −3, −2, −1}
Então, o conjunto C − (A ⋃ B) é formado por números inteiros negativos, ou seja,
C − (A ⋃ B) = .
Portanto, e é a alternativa correta.
9. escrêeva, em ordem crescente, os números racionais:
; ; 1,333...; ; e
Resolução
Primeiro, determinamos a forma decimal das frações:
= −0,666...
= 2,125
= −2,25
= 3,5
= 2,15
Agora, observando os números na forma decimal, escrevemos esses números racionais em ordem crescente:
< 1,333...
10. Dois números inteiros x e y, com x < y, são consecutivos e somam 153. Quais são os valores de x e y?
Resolução
Se x e y são números consecutivos e x < y, então podemos escrever quê:
y = x + 1
Como a soma de x com y é 153, temos:
x + y = 153 ⇒ x + x + 1 = 153 ⇒
⇒ 2x = 152 ⇒ x = 76
Sendo assim, temos y = 76 + 1 ⇒ y = 77.
Portanto, x = 76 e y = 77.
Página trinta e um
ATIVIDADES
26. escrêeva os seguintes conjuntos, listando seus elemêntos:
a) A = {x ∈ ℕ | x < 8}
A = {0, 1, 2, 3, 4, 5, 6, 7}
b) C = {z ∈ ℤ* | −3 < z < 4}
C = {−2, −1, 1, 2, 3}
27. dêz-creva cada um dos conjuntos de números, definindo-os por uma propriedade de seus elemêntos.
Exemplo de resposta:
a) M = {6, 7, 8}
M = {x ∈ ℕ | 6 ≤ x ≤ 8}
b) T = {..., −5, −4, −3, −2, −1}
T = {x ∈ ℤ | x ≤ −1}
28. Considere os conjuntos A = {x ∈ ℕ | x é par e x < 9} e B = {x ∈ ℕ | x é ímpar e x < 9}. Utilize os símbolos ∈ ou ∉ para relacionar cada par a seguir.
a) 4 e A
∈
b) 5 e A
∉
c) 8 e A
∈
d) 2 e B
∉
e) 1 e B
∈
f) 10 e A
∉
29. Sendo ℕ = {0, 1, 2, 3,...}, escrêeva os seguintes conjuntos, listando seus elemêntos.
a) A = {x ∈ ℕ | x = 2k, k ∈ ℕ}
A = {0, 2, 4,...}
b) B = {x ∈ ℕ | x = k2, k ∈ ℕ}
B = {0, 1, 4, 9,...}
30. Dados os conjuntos A = {x ∈ ℕ* | x = 2k, k ∈ ℕ} e B = {x ∈ ℕ | x ≤ 10}, determine o número de elemêntos de A ⋃ B.
n(A ⋂ B) = 5
31. Verifique se os conjuntos a seguir são iguais.
Sim, são iguais.
A = {x ∈ ℕ | 2 ≤ x < 4}
B = {x ∈ ℕ | (x − 2)(x − 3) = 0}
32. Usando os símbolos ∈ ou ∉, relacione:
a) −7 e ℕ.
∉
b) 4 e ℤ.
∈
c) e ℤ.
∉
d) 0,166... e ℚ.
∈
33. Determine a fração geratriz dos números a seguir.
a) 0,323232...
b) 2,715715715...
34. Sendo A o conjunto dos divisores naturais de 18 e B o conjunto dos divisores naturais de 30, escrêeva:
a) o conjunto A;
A = {1, 2, 3, 6, 9, 18}
b) o conjunto B;
B = {1, 2, 3, 5, 6, 10, 15, 30}
c) o conjunto C dos divisores comuns de 18 e 30;
C = {1, 2, 3, 6}
d) o mássimo divisor comum de 18 e 30.
6
35. (UFAL) No universo ℕ, sêjam A o conjunto dos números pares, B o conjunto dos números múltiplos de 3 e C o conjunto dos números múltiplos de 5. Determine os 10 menóres números quê pertencem ao conjunto B − (A ⋃ C).
3, 9, 21, 27, 33, 39, 51, 57, 63 e 69
36. (Unicamp-SP) Ache dois números inteiros positivos e consecutivos sabendo quê a soma de seus quadrados é 481.
15 e 16
37. Determine os seguintes conjuntos, listando seus elemêntos.
a) M = {x ∈ ℚ | −2x − 9x + 5 = 0}
M=
b) N =
N=
c) P = {y ∈ ℤ | (y − 1)(y + 2)(y − 3) = 0}
P = {−2, 1, 3}
d) S = {x ∈ ℕ | x2 − 25 = 0}
S = {5}
38. (hú éfe ême gê) Considere x, y e z números naturais. Na divisão de x por y, obtém-se quociente z e résto 8. Sabe-se quê a representação decimal de é a dízima periódica 7,363636...
Então, o valor de x + y + z é
alternativa d
a) 190.
b) 193.
c) 191.
d) 192.
39. (OBMEP) A figura representa parte de uma régua graduada de meio em meio centimetro, onde estão marcados alguns pontos. Qual deles melhor representa o número 2x − 2?
alternativa d
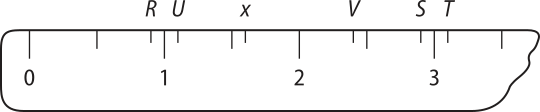
a) R
b) S
c) T
d) U
e) V
40. O valor de é
a) 20,0
b) 18,18...
c) 18,0
d) 2,2...
e) 2,0
alternativa c
41. (Cesgranrio-RJ) Ordenando os números racionais p = , q = e r = , obtemos:
a) p < r < q
b) p < q < r
c) r < p < q
d) q < r < p
e) r < q < p
alternativa a
Página trinta e dois
Conjunto dos números irracionais
Antigamente, o conjunto dos números racionais parecia sêr ideal para todas as situações quê envolviam operações aritméticas. E, de fato, durante algum tempo, acreditou-se quê os números racionais resolveriam todos os problemas quê envolviam medições. No entanto, já na época de Pitágoras e seus discípulos, cerca de VI a.C., alguns problemas desafiavam essa teoria, como o apresentado a seguir.
Qual é a medida da diagonal d do quadrado ABCD cujo lado méde uma unidade de comprimento?
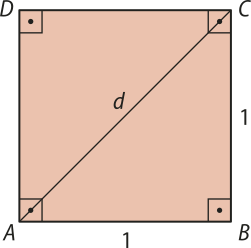
Usando o teorema de Pitágoras no triângulo ABC, temos:
d2 = 12 + 12 ⇒ d2 = 2
Para determinar o valor de d, devemos responder à seguinte questão: qual é o número cujo quadrado é igual a 2? Inicialmente, vamos tentar calcular o valor de d usando aproximações por números racionais.
12 = 1
22 = 4
Logo, d é um valor quê está entre 1 e 2 (1 < d < 2).
Em seguida, com o auxílio de uma calculadora, vamos determinar a primeira casa decimal de d.
(1,1)2 = 1,21
(1,2)2 = 1,44
(1,3)2 = 1,69
(1,4)2 = 1,96
(1,5)2 = 2,25
Logo, d está entre 1,4 e 1,5, ou seja, 1,4 < d < 1,5.
Então, 1,4 é um valor aproximado de d, por falta, com uma casa decimal.
Usando o mesmo procedimento, determinamos a segunda casa decimal de d.
(1,41)2 = 1,9881 (1,42)2 = 2,0164
Logo, d está entre 1,41 e 1,42, ou seja, 1,41 < d < 1,42.
Aqui, 1,41 é um valor aproximado de d, por falta, com duas casas decimais.
Mediante outras tentativas, percebemos quê a medida d da diagonal está entre 1,414 e 1,415, ou seja, 1,414 < d < 1,415. Observe:
(1,414)2 = 1,999396 (1,415)2 = 2,002225
Nesse caso, 1,414 é um valor aproximado de d, por falta, com três casas decimais.
Se continuarmos repetindo esse processo, vamos obtêr quantas casas decimais quisérmos, mas encontraremos sempre um valor aproximado para d, por falta, pois esse valor, elevado ao quadrado, é sempre um número menor do quê 2.
Poderíamos também obtêr o valor aproximado de d por excésso, ou seja, utilizando as aproximações para d tais quê, elevadas ao quadrado, ultrapassam o valor 2.
Representamos o valor exato para a medida da diagonal do quadrado de lado 1 por . Utilizando uma calculadora científica, é possível obtêr as primeiras casas decimais de , quê indicamos assim:
= 1,414213562...
Pense e responda
• Com base nos cálculos feitos, indique uma aproximação, por excésso, para a medida d da diagonal do quadrado apresentado com três casas decimais.
1,415
• Utilizando uma calculadora e o raciocínio apresentado aqui, determine uma aproximação com duas casas decimais para o número irracional .
Exemplo de resposta: Aproximação por falta: 1,73; aproximação por excésso: 1,74
Página trinta e três
Esse número tem uma infinidade de casas decimais quê não apresentam padrão de repetição; logo, não é uma dízima periódica, e é possível demonstrar quê números dêêsse tipo não podem sêr escritos na forma de fração com números inteiros (com denominador não nulo). Portanto, não é um número racional; é um número irracional, quê faz parte do conjunto dos números irracionais.
O conjunto dos números irracionais, quê indicamos por 𝕀, é o conjunto formado pêlos números quê têm uma representação decimal infinita e não periódica.
Saiba quê...
Uma calculadora científica é capaz de realizar outras operações e funções além das operações aritméticas básicas. Além da versão física, também está disponível digitalmente na maioria dos sistemas operacionais dos computadores e celulares.
Para realizar cálculos aproximados, podemos utilizar os números irracionais em sua representação decimal com quantas casas decimais desejarmos. Por exemplo:
≃ 1,73205 e ≃ 1,41
≃ Esse sín-bolo significar aproximadamente igual a.
Observe outros exemplos de números irracionais e suas primeiras casas decimais, obtidas com o auxílio de uma calculadora científica:
• = 3,605551275...
• = 1,709975946...
• (pi)" = 3,141592653...
A respeito dos números irracionais, é possível demonstrar quê:
a) as raízes quadradas de números naturais quê não são quadrados perfeitos são números irracionais. Exemplos:
• = 3,162277660...
• = 4,898979485...
b) em particular, as raízes quadradas de números primos positivos são números irracionais. Exemplos:
• = 1,732050807...
• = 2,645751311...
• = 7,810249675...
c) a soma de um número racional com um número irracional é um número irracional. Exemplos:
• 3 + = 3 + 1,414213562... = 4,414213562...
• + 1,5 = 2,236067977... + 1,5 = 3,736067977...
d) o resultado da subtração entre um número racional e um número irracional, e vice-versa, é um número irracional. Exemplos:
• 1 − (pi)" = 1 − 3,141592653... = −2,141592653...
• − 4 = 2,449489742... − 4 = −1,550510257...
e) o produto de um número racional não nulo por um número irracional é um número irracional. Exemplos:
• 2 ⋅ = 2 ⋅ 2,645751311... = 5,291502622...
• ⋅ (pi)" = = −1,047197551...
f) o quociente de um número racional não nulo por um número irracional é um número irracional. Exemplos:
Professor, se julgar interessante, comentar com os estudantes quê o quociente de um número irracional por um número racional não nulo também é um número irracional.
• 5 ∶ = 2,886751345...
• 7 ∶ = 4,949747468...
Destacamos dois subconjuntos de 𝕀:
• Números irracionais positivos: 𝕀+
• Números irracionais negativos: 𝕀−
Saiba quê...
• Um número irracional não póde sêr expresso por uma fração formada por números inteiros, com denominador não nulo.
• Número quadrado perfeito é o número natural cuja raiz quadrada é um número natural. Assim, 1, 9, 25 e 64 são exemplos de quadrados perfeitos, pois: = 1; = 3; = 5; = 8.
Pense e responda
• A soma de dois números irracionais sempre é um número irracional? Justifique.
Não. Espera-se quê os estudantes apresentem algum contraexemplo, como: _ _ = 1.
• O produto de dois números irracionais sempre é um número irracional? Justifique.
Não. Espera-se quê os estudantes apresentem algum contraexemplo, como: _ _ = 5.
Página trinta e quatro
Alguns números irracionais famosos
O número pi ((pi)")
O número representado pela letra grega (pi)" (pi) é um dos números irracionais mais conhecidos no meio matemático. O número (pi)" é a constante ôbitída da razão entre o comprimento de uma circunferência e a medida de seu diâmetro. Essa razão não póde sêr expressa na forma de fração com números inteiros (com denominador não nulo), isto é, (pi)" é um número irracional e sua representação decimal é infinita e não periódica: (pi)" = 3,141592653....
As aproximações do número (pi)" já eram conhecidas por muitas civilizações antigas, como a babilônica e a egípcia, quê sabiam quê essa razão era maior do quê 3. Por exemplo, essa constante aparece com o valor 3,16 (na notação atual) no papiro de Ahmes (cerca de 1650 a.C.) e com o valor 3,14 no papiro de Moscou (cerca de 1850 a.C.).
No entanto, a designação dessa constante pela letra grega (pi)" apareceu apenas em 1706, quando o matemático inglês uílhãm Jones (1675-1749) usou esse sín-bolo pela primeira vez para expressar essa razão. Óiler adotou o sín-bolo em 1737, o qual rapidamente se tornou uma notação padrão.
O número de Óiler (e)
O número irracional e, chamado de número de Óiler, cujo valor é 2,718281828..., tem diversas aplicações na Matemática, bem como em outras ciências, como Economia, Biologia e Estatística. Esse número irracional também é chamado de número de Napier, graças aos estudos relacionados aos logaritmos feitos pelo matemático Diôn Napier (1550-1617).
A primeira referência a esse número foi publicada em 1618, em um trabalho sobre logaritmos realizado por esse matemático. O valor da constante não aparece nesse trabalho, há apenas uma lista de logaritmos naturais de diversos números.
Anos depois, Jacob Bernoulli (1655-1705) indicou um possível valor aproximado para esse número, enquanto estudava soluções para problemas de juro compôzto no campo financeiro.
Leonhard Óiler (1707-1783) adotou a letra e para representar a constante em sua obra Mechanica, publicada em 1736, quê descreve analiticamente a matemática quê rege os movimentos em Física. O número e é bastante utilizado no cálculo de logaritmos e de funções exponenciais e logarítmicas.

Para assistir
• PARA quê sérve o pi e por quê esse número causa tanto fascínio? [S. I.: s. n.], 2020. 1 vídeo (3 min). Publicado pelo canal BBC nius Brasil. Disponível em: https://livro.pw/hqglb. Acesso em: 26 jun. 2024.
O vídeo apresenta curiosidades sobre o número (pi)" e suas casas decimais.
Página trinta e cinco
A razão áurea
A razão áurea está relacionada à divisão de um segmento de reta em média e extrema razão. Acompanhe.
Dado um segmento AB de medida a, dividi-lo em média e extrema razão é determinar o ponto C tal quê .
Indicando a medida do segmento por c, a proporção fica:
c2 + ac − a2 = 0

A equação c2 + ac − a2 = 0 é uma equação do 2º grau, cujo método de resolução será apresentado posteriormente neste Volume.
A partir da resolução dessa equação na incógnita c, obtém-se a razão:
Essa razão é conhecida como razão áurea, e o número irracional , cujo valor é 1,618033988..., é chamado de número de ouro, representado pela letra grega maiúscula φ (lê-se: fi).
A “divisão de um segmento em média e extrema razão” foi um dos assuntos da escola pitagórica, grupo de estudos criado por Pitágoras, responsável por grandes descobertas por volta do século VI a.C. Séculos mais tarde, essa razão ficou conhecida como razão áurea.
A razão áurea também esteve presente nos trabalhos de outros matemáticos, principalmente naqueles desenvolvidos por Fibonacci (1170-1250) e por Luca Pacioli (1445-1517).
Outra denominação para a razão áurea é proporção áurea, considerada harmônica entre dois segmentos de reta, ou seja, considerada o perfeito equilíbrio, ou proporcionalidade, entre as medidas de dois segmentos de reta. Por exemplo, um retângulo áureo é aquele quê possui a razão entre suas medidas igual a φ. Nesta figura, o retângulo tem medidas próximas às de um retângulo áureo.
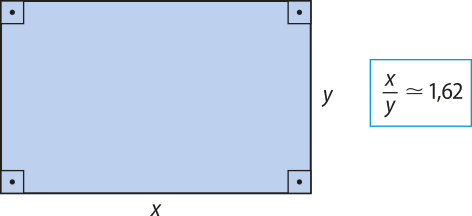
A razão áurea foi objeto de grande admiração e estudo desde a Antigüidade, pois é encontrada em diversas formas de; ár-te e na arquitetura, como na pirâmide de Quéops, na arquitetura egípcia; no Parthenon (construído entre 447 a.C. e 433 a.C.), na arquitetura grega; na obra Homem vitruviano, de Leonardo da Vinci (1452-1519); entre outras.
Página trinta e seis
Conjunto dos números reais
Reunindo os números racionais aos números irracionais, formamos o conjunto dos números reais, representado por ℝ.
Assim, os conjuntos dos números naturais, inteiros, racionais e irracionais estão contidos no conjunto dos números reais, ou seja, são subconjuntos de ℝ. Observe o diagrama.
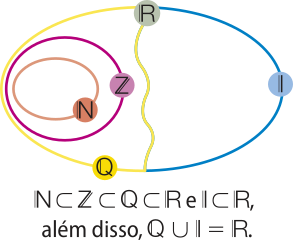
Já aprendemos a marcar, na reta orientada, pontos quê representam números racionais. Aprendemos, também, quê os números racionais não são suficientes para preencher toda a reta orientada. É possível marcar pontos na reta quê representam números irracionais. Observe alguns números racionais e irracionais representados na reta orientada:

Saiba quê...
O ponto quê representa o número zero também é chamado de origem da reta real.
Agora, com os números irracionais na reta orientada, podemos dizêr quê ela está completa e quê não há mais “buracos” em seu preenchimento. pôdêmos demonstrar quê, ao marcarmos os números racionais e os irracionais na reta orientada, ela fica completa, com todos os números reais. A reta assim construída é denominada reta numérica ou reta real.
Cada ponto da reta numérica póde sêr associado a um único número real, e cada número real póde sêr associado a um único ponto da reta numérica, ou seja, dizemos quê há uma correspondência biunívoca dos números reais com os pontos da reta.
A respeito dos números reais:
a) A soma de dois números reais é um número real.
b) A diferença de dois números reais é um número real.
c) O produto de dois números reais é um número real.
d) O quociente de dois números reais, sêndo o divisor diferente de zero, é um número real.
e) Os conceitos de números opostos e de números inversos estudados nos conjuntos numéricos anteriores também são válidos para os números reais.
Exemplos:
• O ôpôsto de é pois = 0
• O inverso de (pi)" é , pois (pi)" = 1.
No conjunto ℝ dos números reais, destacamos os seguintes subconjuntos:
• números reais não nulos: ℝ* = ℝ − {0}
• números reais não negativos: ℝ+ = {x ∈ ℝ | x ≥ 0}
• números reais não positivos: ℝ− = {x ∈ ℝ | x ≤ 0}
• números reais positivos: = {x ∈ ℝ | x > 0}
• números reais negativos: = {x ∈ ℝ | x < 0}
Saiba quê...
As lêtras ℕ, ℚ e ℝ são as iniciais das palavras número (ou natural), quociente e real. A letra ℤ é inicial da palavra zahl, quê significa número em alemão.
LIMA, Elon L. éti áu. A Matemática do Ensino Médio. 11. ed. Rio de Janeiro: SBM, 2016. (Coleção Professor de Matemática, v. 1, p. 58).
Página trinta e sete
Intervalos reais
Existem subconjuntos de ℝ, chamados de intervalos reais, quê são determinados por desigualdades. Os intervalos podem sêr representados de diversas maneiras, como mostrado a seguir.
Dados dois números reais a e b, chamados de extremos do intervalo, com a < b, temos:
Representação na reta real |
Representação por notação de conjuntos |
|
|---|---|---|
Intervalo aberto |
|
{x ∈ ℝ | a < x < b} ou ]a, b[ |
Intervalo fechado |
|
{x ∈ ℝ | a ≤ x ≤ b} ou [a, b] |
Intervalos semiabertos |
|
{x ∈ ℝ | a ≤ x < b} ou [a, b[ |
|
{x ∈ ℝ | a < x ≤ b} ou ]a, b] |
|
Intervalos ilimitados |
|
{x ∈ ℝ | x < a} ou ] −∞, a[ |
|
{x ∈ ℝ | x ≤ a} ou ] −∞, a] |
|
|
{x ∈ ℝ | x > a} ou ]a, +∞ [ |
|
|
{x ∈ ℝ | x ≥ a} ou [a, +∞ [ |
|
|
ℝ = ] −∞ , +∞ [ |
Observações:
• A bó-linha vazia (ο) indica quê os extremos não pertencem ao intervalo.
• A bó-linha cheia (•) indica quê os extremos pertencem ao intervalo.
• O sín-bolo +∞ lê-se “mais infinito”.
• O sín-bolo −∞ lê-se “menos infinito”.
• Os símbolos +∞ e −∞ não são números reais, são apenas símbolos usados na notação de intervalos ilimitados.
Observe alguns exemplos de intervalos reais a seguir.
a) [−4, 3[ ou
{x ∈ ℝ | −4 ≤ x < 3} ou

b)]−∞, −2] ou
{x ∈ ℝ | x ≤ −2} ou

c)]0, +∞[ ou
{x ∈ ℝ | x > 0} ou

Saiba quê...
Outra maneira de representar os intervalos abertos é utilizando parênteses. Observe:
]a, b[ = (a, b)
]a, b] = (a, b]
[a, b[ = [a, b)
Página trinta e oito
ATIVIDADES RESOLVIDAS
11. Determine a área, o perímetro e a diagonal do retângulo ABCD. As medidas obtidas são números irracionais?
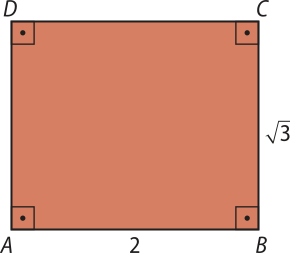
Resolução
Vamos calcular a área A do retângulo dada pelo produto da medida da base pela medida da altura:
A = 2 ⋅
A medida da área do retângulo é irracional, pois o produto de um número racional (não nulo) por um número irracional é um número irracional.
O perímetro P do retângulo é dado pela soma das medidas de seus lados:
P = 2 + + 2 + ⇒ P = 4 + 2
A medida do perímetro do retângulo é irracional, pois a soma de um número racional com um número irracional é um número irracional.
Para determinarmos a medida da diagonal d do retângulo, aplicamos o teorema de Pitágoras no triângulo ABD:
d2 = 22 + ⇒ d2 = 4 + 3 = 7 ⇒ d = √ 7
A medida da diagonal do retângulo é irracional, pois a raiz quadrada de um número primo positivo é um número irracional.
12. Se A =]2, 5[ e B = [3, 8[, determine A ⋃ B e A ⋂ B.
Resolução
As operações de união e intersecção com intervalos reais funcionam da mesma maneira quê as operações de união e intersecção com conjuntos estudadas anteriormente neste Capítulo. No caso dos intervalos, é interessante começar pela análise dos extremos. Assim, a união dos intervalos A e B é dada por:
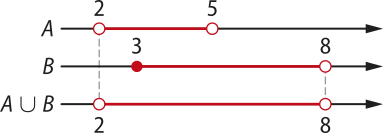
Para a intersecção, também vamos analisar os extremos dos intervalos. Observe quê 3 é elemento de A e também de B; e 5 é elemento de B e não é elemento de A.
Os elemêntos de 3 até 5, excluído êste último, pertencem a A e a B. Logo:
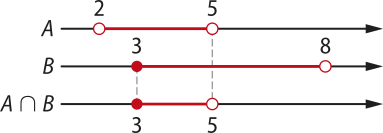
Assim, temos: A ⋃ B =]2, 8[ e A ⋂ B = [3, 5[.
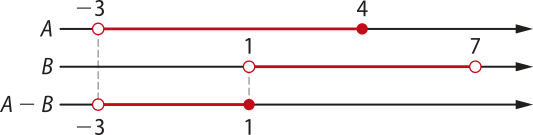
13. Dados A = {x ∈ ℝ | −3 < x ≤ 4} e B = {x ∈ ℝ | 1 < x < 7}, calcule A − B.
Resolução
O conjunto A − B é formado pêlos elemêntos quê pertencem a A e não pertencem a B.
Observe quê o número 1 pertence ao conjunto A, mas não pertence ao conjunto B; portanto, ele pertence ao conjunto A − B.
A diferença dos conjuntos é A − B = {x ∈ ℝ | −3 < x ≤ 1}.
Página trinta e nove
ATIVIDADES
42. Determine os elemêntos dos conjuntos.
a) A = {x ∈ ℕ | 3x − 4x − 4 = 0}
A = ∅
b) B = {y ∈ 𝕀 | y2 − 7 = 0}
B =
c) C = { a ∈ ℕ | + 0,25a + = 2}
C = {1}
d) D = {x ∈ ℚ | 3 + x2 = 4}
D = {−1, 1}
e) E = { x ∈ ℚ | + = }
E =
f) F = {x ∈ ℝ | x2 − 4 = 0}
F = {−2, 2}
43. Sendo ≃ 1,732, calcule um valor aproximado de:
a)
aproximadamente 1,866
b)
aproximadamente 0,616
44. Sejam a e b números irracionais quaisquer. As seguintes afirmações são FALSAS:
Exemplo de resposta:
a) a ⋅ b sempre é um número irracional;
a) a = _ e b =
b) a + b sempre é um número irracional.
b) a = e b = −
Em cada caso, dê um exemplo quê indica quê as afirmações são falsas.
45. Assinale a afirmação verdadeira.
a) é irracional e 0,999...
é racional.
b) é racional e 0,999...
é racional.
c) é racional e 0,999...
é irracional.
d) é irracional e 0,999...
é irracional.
e) e 0,999... não são números reais.
alternativa b
46. Usando a notação de conjuntos, escrêeva os intervalos a seguir.
a) [6, 10]
{x ∈ ℝ | 6 ≤ x ≤ 10}
b)]−1, 5]
{x ∈ ℝ | −1 < x ≤ 5}
c)]−6, 0[
{x ∈ ℝ | −6 < x < 0}
d) [0, +∞[
{x ∈ ℝ | x ≥ 0}
e)]−∞, 3[
{x ∈ ℝ | x < 3}
47. Represente, na reta real, os intervalos a seguir.
a) [2, 8]
b)]−∞, 2]
c) [−6, −1[
d) [2, +∞[
e) {x ∈ ℝ | 2 < x < 5}
f) {x ∈ ℝ | −2 ≤ x ≤ 2}
Ver as Orientações para o professor.
48. Usando a notação de conjuntos, escrêeva os intervalos a seguir, quê estão representados na reta real.
a)

{x ∈ ℝ | 2 ≤ x ≤ 4}
b)

{x ∈ ℝ | x > 1}
c)

{x ∈ ℝ | < x < 5}
d)

.
49. Determine A ⋃ B em cada caso.
a) A = {x ∈ ℝ | 0 < x < 3} e
B = {x ∈ ℝ | 1 < x < 5}
{x ∈ ℝ | 0 < x < 5}
b) A = {x ∈ ℝ | −4 < x ≤ 1} e
B = {x ∈ ℝ | 2 ≤ x ≤ 3}
{x ∈ ℝ | −4 < x ≤ 1
ou 2 ≤ x ≤ 3}
c) A = {x ∈ ℝ | 2 < x < 5} e
B = {x ∈ ℝ | 1 < x < 4}
{x ∈ ℝ | 1 < x < 5}
d) A = {x ∈ ℝ | −2 ≤ x < 2} e
B = {x ∈ ℝ | x > 0}
{x ∈ ℝ | x ≥ −2}
50. Dados os conjuntos A = [−1, 6[, B =]−4, 2] e E =]−2, 4[, calcule:
a) (B ⋃ E) − A
]−4,−1[
b) E − (A ⋂ B)
]−2,−1[⋃]2, 4[
51. (Fuvest-SP) Na figura abaixo estão representados geometricamente os números reais 0, x, y e 1. A posição do número real x ⋅ y é:
alternativa b

a) à esquerda do zero
b) entre zero e x
c) entre x e y
d) entre y e 1
e) à direita de 1
Página quarenta
HISTÓRIA DA MATEMÁTICA
Incomensurabilidade e números irracionais
Um dos assuntos quê gerou muita discussão entre os estudiosos da Antigüidade foi o conceito de grandezas incomensuráveis, advindo da descoberta de quê os números racionais não eram suficientes para medir tudo o quê se desejava. Leia o trecho de um texto quê trata dêêsse assunto.
Grandezas incomensuráveis e números irracionais
Existem, em Matemática, conceitos quê parecem muito simples a uma visão superficial, mas quê, submetidos a uma análise mais cuidadosa, revelam aspectos verdadeiramente surpreendentes.
[...] Exploremos alguns fatos notáveis e inesperados, quê estão ligados à primeira grande crise do desenvolvimento da Matemática, ocorrida no final do 5º século a.C.
Uma quêstão com que lidavam os matemáticos gregos daquela época era a de comparar grandezas da mesma espécie, como dois segmentos de reta, duas áreas ou dois volumes. No caso de dois segmentos retilíneos AB e cê dê, dizêr quê a razão é o número racional significava para eles (e ainda significa para nós) quê existia um terceiro segmento EF tal quê AB fosse m vezes EF e cê dê n vezes esse mesmo segmento EF. Na Fig. 1 ilustramos essa situação com m = 8 e n = 5.
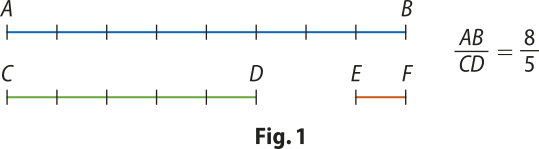
No tempo de Pitágoras (580 – 500 a.C. aproximadamente) – e mesmo durante boa parte do 5º século a.C. – pensava-se quê os números racionais fossem suficientes para comparar segmentos de reta; isto é, dados dois segmentos AB e cê dê, seria sempre possível encontrar um terceiro segmento EF contido um número inteiro de vezes em AB e outro número inteiro de vezes em cê dê, situação esta quê descrevemos dizendo quê EF é um submúltiplo comum de AB e cê dê. Uma simples reflekção revela quê essa é uma ideia muito razoável. Afinal, se EF não sérve, podemos imaginar um segmento menor, outro menor ainda, e assim por diante. Nossa intuição geométrica parece dizer-nos quê há de existir um cérto segmento EF, talvez muito pequeno, mas satisfazendo aos propósitos desejados. Na Fig. 2 ilustramos uma situação com segmento EF bem menor quê o da Fig. 1. O leitor deve ir muito além, imaginando um segmento EF tão pequeno que nêm possa mais desenhar, para se convencer, pela sua intuição geométrica, da possibilidade de sempre encontrar um submúltiplo comum de AB e cê dê.
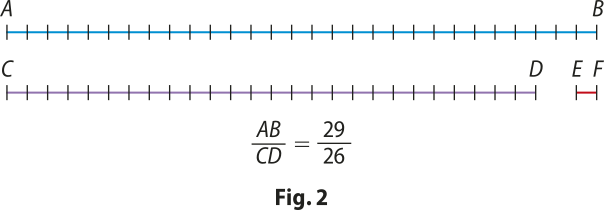
Página quarenta e um
Dois segmentos nessas condições são ditos comensuráveis, justamente por sêr possível medi-los ao mesmo tempo, com a mesma unidade EF. Entretanto, não é verdade quê dois segmentos quaisquer sêjam sempre comensuráveis. Em outras palavras, existem segmentos AB e cê dê sem unidade comum EF, os chamados segmentos incomensuráveis. Esse é um fato quê contraria nossa intuição geométrica, e por isso mesmo a descoberta de grandezas incomensuráveis na Antigüidade representou um momento de crise no desenvolvimento da Matemática.
Foram os próprios pitagóricos quê descobriram grandezas incomensuráveis, provavelmente entre 450 e 400 a.C.; e, ao quê tudo indica, isto se fez através de um argumento geométrico, [...] demonstrando quê o lado e a diagonal de um quadrado são segmentos incomensuráveis.
[...]
A descoberta dos incomensuráveis representou, no 5º século a.C., uma derrota para os pitagóricos. De fato, para eles o número era a essência de tudo. Eles acreditavam na possibilidade de explicar todos os fenômenos do mundo sensível em termos dos números e de suas relações, tanto na Geometria como na Música, na Astronomia ou na Física, enfim, o número sêria a essência última do ser e de todos os fenômenos. Mas por número eles entendiam apenas o quê chamamos hoje de “números naturais”, ou inteiros positivos: 1, 2, 3, 4,.... Nem as frações eram números, já quê elas apareciam como relações entre grandezas da mesma espécie. Agora quê haviam sido descobertas grandezas incomensuráveis, estava claro quê os números (naturais) eram insuficientes até mesmo para definir a razão entre duas grandezas, o quê se constituía num sério entrave à Filosofia Pitagórica.
Ao mesmo tempo em quê essas coisas aconteciam, outros argumentos propostos pêlos filósofos da época [...] também apontavam dificuldades na suposta harmonía entre a Geometria e os números. Tudo isso culminou numa crise no desenvolvimento da Matemática, crise essa quê só foi definitivamente superada com a criação da teoria dos números reais (racionais e irracionais) no século passado, devido, sobretudo aos trabalhos do matemático alemão ríchard Dedekind (1831-1916).
ÁVILA, Geraldo. Grandezas incomensuráveis e números irracionais. Revista do Professor de Matemática (RPM), São Paulo, n. 5, [201-]. Disponível em: https://livro.pw/nfpou. Acesso em: 16 jul. 2024.

Para ler
• STEWART, Ian. O fantástico mundo dos números: a matemática do zero ao infinito. Rio de Janeiro: Zarrár, 2016.
Um livro quê traz informações interessantes a respeito de diversos números por meio de textos leves e divertidos. Por exemplo, você sabia quê 43.252.003.274.489.856.000 é o número de maneiras possíveis de rearranjar um cubo mágico?

Página quarenta e dois
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Alimentação
Hábitos saudáveis, como exercícios regulares, sono adequado e alimentação balanceada, são alguns dos fatores para uma vida com qualidade. Leia o trecho de um texto a respeito de uma alimentação saudável e faça o quê se pede em cada questão.
Alimentação saudável
A alimentação para os sêres humanos possui significado maior do quê apenas garantir as necessidades do corpo. O ato de comer está relacionado a valores sociais, culturais, afetivos e sensoriais. Na maioria das vezes, comer é um momento de prazer e confraternização com nóssos amigos e familiares.
O alimento torna-se, assim, muito mais do quê uma fonte de nutrientes. Apreciamos as cores e gostamos de sentir a textura e o sabor da comida. Mas isso não é tudo! Nesse jôgo de sensações, precisamos lembrar quê uma alimentação saudável:
• não precisa sêr cara, pois póde sêr feita com alimentos naturais, produzidos na região em quê vivemos;
• deve sêr colorida e composta por alimentos variados;
• é saborosa;
• precisa ter qualidade e sêr consumida na quantidade certa;
• deve sêr segura para o consumo, ou seja, estar livre de contaminação.
[...]
Mudanças na alimentação ao longo do tempo e seu impacto na saúde
Com a evolução da ssossiedade, muitos tipos de alimentos foram criados e, para garantir maior aceitação da população, foram introduzidos novos ingredientes. Com isso, surgiram produtos cada vez mais atraentes e saborosos.

Página quarenta e três
Açúcar: é fonte de energia para o sêr humano. Mas, quando comemos em ezagêro, póde causar aumento de peso e excésso de gordura no sangue.
Gordura saturada: é um tipo de gordura muito encontrado em alimentos de origem animal. Comê-la excessivamente póde provocar o acúmulo de gordura nos vasos sangüíneos e causar doenças do coração.
Gordura trans: é produzida pela transformação de óleos vegetais em gordura vegetal hidrogenada. Está presente em produtos como biscoitos e chocolates. Consumida em excésso póde causar problemas de saúde, principalmente ao coração.
Sódio: faz parte do sal de cuzinha e é acrescentado aos alimentos, pelas indústrias, para dar um sabor mais salgado e aumentar o tempo de conservação [...] do produto. Comer muito sódio póde causar pressão alta.
Por exemplo: açúcar para adoçar; gordura saturada e gordura trans para dar maior maciez, leveza e cremosidade; sódio para acentuar o sabor; corantes para dar côr especial e aromatizantes para criar um cheirinho irresistível.
[...]
No entanto, todos esses novos produtos reduziram a qualidade nutricional dos alimentos. Alguns deles têm se tornado tão populares quê passaram a sêr cada vez mais desejados, como os salgadinhos, refrigerantes, sorvetes, biscoitos e muitos outros.
Então, parte da população habituou-se a comer esses alimentos somente para saciar desejos e estar “na moda”, sem considerar quê os excessos podem trazer problemas à saúde, como a obesidade, a pressão alta, o diabetes e as doenças do coração.
AGÊNCIA NACIONAL DE VIGILÂNCIA SANITÁRIA. Alimentação saudável: fique esperto! Brasília, DF: Anvisa, 2018. p. 4-7. Disponível em: https://livro.pw/cextq. Acesso em: 16 jul. 2024.
Professor, esta obra está atualizada conforme a grafia estabelecida pelo SI na publicação: BRASIL. Instituto Nacional de Metrologia, Qualidade e Tecnologia; PORTUGAL. Instituto Português da Qualidade. O Sistema Internacional de Unidades (SI): tradução luso-brasileira da 9 ª edição. Brasília, DF: Inmetro; Caparica: IPQ, 2021.
Agora, faça o quê se pede nas atividades a seguir.
1. De acôr-do com o texto, responda:
a) Quais são as características de uma alimentação saudável?
Conter, em sua composição, alimentos naturais, sêr colorida e composta de alimentos variados, sêr saborosa, ter qualidade, sêr consumida na quantidade certa e estar livre de contaminação.
b) Quais problemas de saúde estão associados ao consumo excessivo de produtos quê contêm açúcares, sódio e gorduras saturadas e trans?
Doenças como obesidade, pressão alta, diabetes e doenças do coração.
c) Reflita sobre seus hábitos alimentares. O quê póde sêr melhorado para quê você tenha uma alimentação saudável?
Resposta pessoal. Espera-se quê os estudantes consigam, com base nas informações apresentadas no texto, identificar e apontar hábitos alimentares ruins quê eles possam estar reproduzindo.
2. Você já ouviu falar sobre hí eme cê? O Índice de Massa Corpórea (hí eme cê) é adotado pela Organização Mundial da Saúde (hó ême ésse) para o cálculo da massa ideal de um indivíduo adulto. O cálculo póde sêr realizado por meio da relação hí eme cê = , com a massa indicada em kilograma, e a altura, em métro. O valor obtído póde sêr interpretado conforme a tabéla.
a) Determine a classificação do hí eme cê de uma pessoa de 80 kg e 1,70 m de altura.
sobrepeso
b) pôdêmos escrever a faixa do hí eme cê quê determina a classificação “magro” como hí eme cê < 18,5. Utilizando essa mesma simbologia, escrêeva as demais faixas.
normal: 18,5 ≤ hí eme cê ≤ 24,9; sobrepeso: 25,0 ≤ hí eme cê ≤ 29,9; obesidade: 30,0 ≤ hí eme cê ≤ 39,9; obesidade grave: hí eme cê ≥ 40,0
hí eme cê |
Classificação |
|---|---|
Menor do quê 18,5 |
Magro |
Entre 18,5 e 24,9 |
Normal |
Entre 25,0 e 29,9 |
Sobrepeso |
Entre 30,0 e 39,9 |
Obesidade |
Maior do quê ou igual a 40,0 |
Obesidade grave |
Fonte dos dados: ASSOCIAÇÃO BRASILEIRA PARA O ESTUDO DA OBESIDADE E DA SÍNDROME METABÓLICA. Diretrizes brasileiras de obesidade 2016. 4. ed. São Paulo: Abeso, 2016. p. 16. Disponível em: https://livro.pw/yanvz. Acesso em: 16 jul. 2024
3. ![]() Reúna-se a mais dois côlégas, e pesquisem a respeito de alimentos industrializados, alimentação balanceada e hábitos saudáveis. Elaborem um material informativo sobre esse assunto para sêr apresentado aos demais côlégas e membros da comunidade escolar.
Reúna-se a mais dois côlégas, e pesquisem a respeito de alimentos industrializados, alimentação balanceada e hábitos saudáveis. Elaborem um material informativo sobre esse assunto para sêr apresentado aos demais côlégas e membros da comunidade escolar.
Pesquisa dos estudantes.
Pense e responda
Que conceitos estudados neste Capítulo você utilizou para realizar as atividades desta seção?
Resposta esperada: Cálculos com números racionais; intervalos reais
Página quarenta e quatro
EXPLORANDO A TECNOLOGIA
Algoritmos e fluxogramas
Um algoritmo é uma sequência simples e objetiva de instruções quê póde sêr utilizada para resolver um problema. Além díssu, essa sequência deve sêr finita e não póde permitir mais de uma interpretação. Já o fluxograma é um diagrama quê é usado para uma representação visual de um algoritmo, utilizando, para isso, uma simbologia própria.
Vamos analisar um algoritmo quê resólve o seguinte problema sobre conjuntos; depois, vamos construir um fluxograma quê represente esse algoritmo.
O aplicativo de agendamento de aulas de uma academia registrou, em certa manhã, a seguinte movimentação de 68 alunos:
• 25 agendaram musculação
• 29 agendaram aula de step
• 30 agendaram aula de jump
• 9 agendaram musculação e aula de step
• 7 agendaram musculação e aula de jump
• 5 agendaram aulas de step e jump
• 3 agendaram musculação e aulas de step e jump
Determine quantos alunos agendaram somente musculação.
Um algoritmo quê resólve o problema é:
I. Construa um diagrama de Venn para representar os três conjuntos (musculação, step e jump).
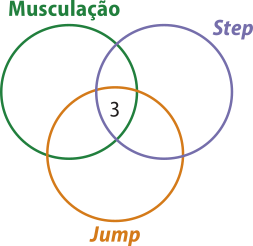
II. Indique o número de alunos quê agendaram as três aulas na região do diagrama quê representa a intersecção dos três conjuntos.
III. Registre no diagrama o número de alunos quê agendaram duas aulas em cada uma das regiões quê representa a intersecção de apenas dois conjuntos; porém, subtraia o número de alunos quê agendaram as três aulas.
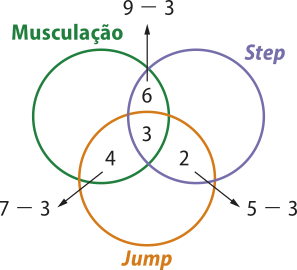
IV. Complete o diagrama com o número de alunos quê agendaram apenas uma aula, subtraindo o número de alunos indicados anteriormente no diagrama.
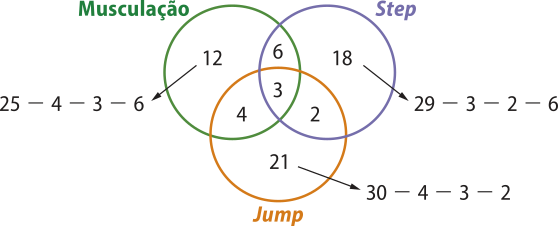
Página quarenta e cinco
V. Adicione todos os números do diagrama e verifique se o total é igual ao total de alunos registrados no aplicativo da academia.
12 + 6 + 18 + 4 + 3 + 2 + 21 = 66; portanto, há uma diferença de 2 alunos.
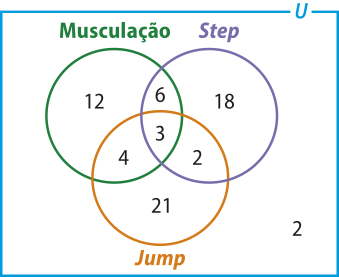
VI. Se a soma for diferente, significa quê alguns alunos não fizeram agendamento para musculação, step ou jump. Nesse caso, desenhe um retângulo, quê representa o conjunto universo U, contendo os 3 conjuntos, e indique dentro dele, mas fora dos 3 conjuntos, a diferença ôbitída.
VII. Observe os valores em cada região do diagrama e responda à pergunta inicial do problema.
Existem símbolos específicos quê devem sêr usados na construção de um fluxograma. A seguir, apresentamos alguns dêêsses símbolos.

A seguir, analise um fluxograma quê mostra os passos para a resolução de problemas como o apresentado.
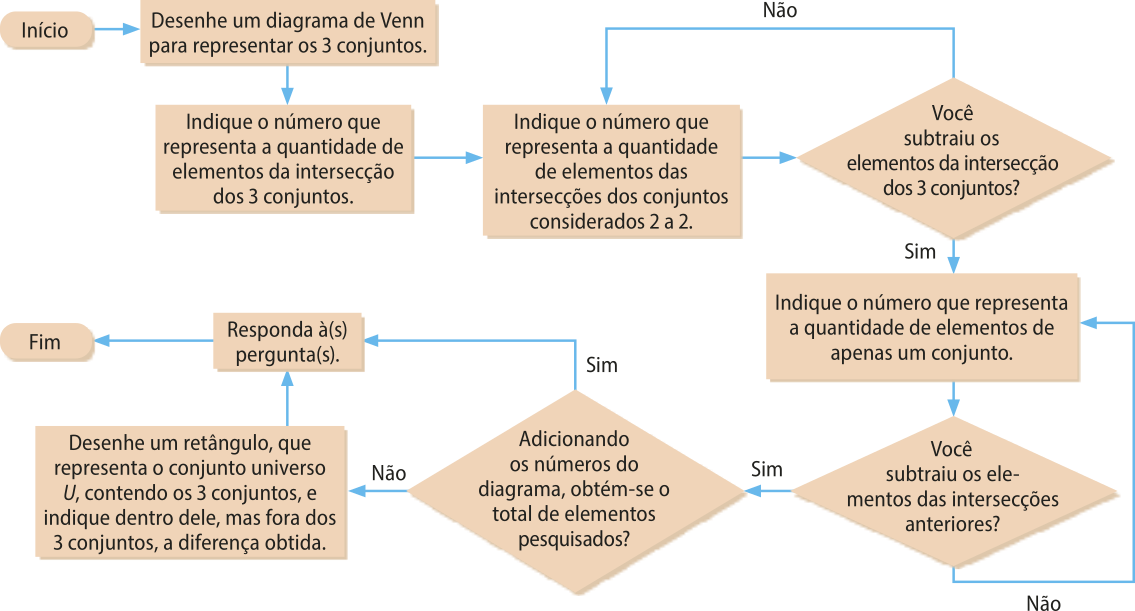
Agora, faça o quê se pede nas atividades a seguir.
1. Na situação apresentada, obissérve o diagrama e determine quantos alunos agendaram:
a) somente musculação.
12 alunos
b) somente step.
18 alunos
c) somente jump.
21 alunos
2. Crie um algoritmo e, depois, um fluxograma para descrever como escovar os dentes.
Resposta pessoal. Ver as Orientações para o professor.
3. Construa um fluxograma para resolver o problema a seguir.
Em uma escola de Artes, estudam 400 alunos. Destes, 50 fazem curso de desenho, 35 fazem curso de canto e 6 fazem os dois cursos. Quantos alunos não fazem nenhum dos dois cursos?
Espera-se quê os estudantes consigam, por meio de um fluxograma, obtêr o resultado 321.
Página quarenta e seis
ATIVIDADES COMPLEMENTARES
1. (IFS-SE) O quê podemos afirmar sobre os conjuntos A, B e C quê satisfazem as seguintes condições:
alternativa c
a) A = C
b) B = {a, b, c, f, g}
c) A = {e, f, g, h, i}
d) A ⋂ B ⋂ C = {b, e, f, g}
2. (PUC-RJ) Uma próva com duas kestões foi dada a uma classe de quarenta alunos. Dez alunos acertaram as duas kestões, 25 acertaram a primeira e 20 acertaram a segunda questão. Quantos alunos erraram as duas kestões?
alternativa e
a) 40
b) 10
c) nenhum
d) 8
e) 5
3. (Enem/MEC) Um grupo sangüíneo, ou tipo sangüíneo, baseia-se na presença ou ausência de dois antígenos, A e B, na superfícíe das células vermelhas do sangue. Como dois antígenos estão envolvidos, os quatro tipos sangüíneos distintos são:
• Tipo A: apenas o antígeno A está presente;
• Tipo B: apenas o antígeno B está presente;
• Tipo AB: ambos os antígenos estão presentes;
• Tipo O: nenhum dos antígenos está presente.
Disponível em: https://livro.pw/icxzl Acesso em: 15 abr. 2012 (adaptado)
Foram coletadas amostras de sangue de 200 pessoas e, após análise laboratorial, foi identificado quê em 100 amostras está presente o antígeno A, em 110 amostras há presença do antígeno B e em 20 amostras nenhum dos antígenos está presente. Dessas pessoas quê foram submetidas à côléta de sangue, o número das quê possuem o tipo sangüíneo A é igual a
alternativa c
a) 30.
b) 60.
c) 70.
d) 90.
e) 100.
4. (UFS-SE) Os senhores A, B e C concorriam à liderança de cérto partido político. Para escolher o líder, cada eleitor votou apenas em dois candidatos de sua preferência. Houve 100 votos para A e B, 80 votos para B e C e 20 votos para A e C. Em consequência:
alternativa e
a) venceu A, com 120 votos.
b) venceu A, com 140 votos.
c) A e B empataram em primeiro lugar.
d) venceu B, com 140 votos.
e) venceu B, com 180 votos.
5. (UFRGS-RS) Em uma escola, sabe-se quê dos estudantes gostam de praticar somente o esporte A, dos estudantes gostam de praticar somente o esporte B, e dos estudantes gostam de praticar os esportes A e B.
A fração quê representa a quantidade de estudantes dessa escola quê não praticam o esporte A e não praticam o esporte B é
alternativa a
a) .
b) .
c) .
d) .
e) .
6. (IFPI) O professor Antônio desenhou a seguinte reta numérica.
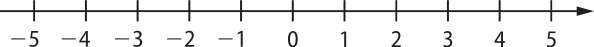
O número foi marcado entre quê pontos dessa reta numérica?
alternativa d
a) 2 e 3
b) 3 e 4
c) −3 e −2
d) −4 e −3
e) −5 e −4
7. (UFF-RJ) O número (pi)" − pertence ao intervalo:
alternativa c
a)
b)
c)
d)]−1, 1[
e)
8. (UFRGS-RS) Dados a e b números reais positivos, considere as afirmações abaixo.
I. Se a > b, então _ .
II. Para quaisquer a e b, + é um núme ro irracional.
III. Para quaisquer a e b, > 1.
Quais estão corretas?
alternativa a
a) Apenas I.
b) Apenas III.
c) Apenas I e II.
d) Apenas II e III.
e) I, II e III.
Página quarenta e sete
9. (PUC-MG) A diferença A − B, sêndo A = {x ∈ ℝ | −4 ≤ x ≤ 3} e B = {x ∈ ℝ | −2 ≤ x < 5} é igual a:
a) {x ∈ ℝ | −4 ≤ x < −2}
b) {x ∈ ℝ | −4 ≤ x ≤ −2}
c) {x ∈ ℝ | 3 < x < 5}
d) {x ∈ ℝ | 3 ≤ x ≤ 5}
e) {x ∈ ℝ | −2 ≤ x < 5}
alternativa a
10. (UFSM-RS) Assinale verdadeira (V) ou falsa (F) em cada uma das afirmações a seguir.
( ) A letra grega (pi)" representa o número racional quê vale 3,14159265.
( ) O conjunto dos números racionais e o conjunto dos números irracionais são subconjuntos dos números reais e possuem apenas um ponto em comum.
( ) Toda dízima periódica provém da divisão de dois números inteiros, portanto é um número racional.
A sequência correta é:
alternativa d
a) F – V – V.
b) V – V – F.
c) V – F – V.
d) F – F – V.
e) F – V – F.
11. (PUCCamp-SP) Considere os conjuntos:
alternativa d
ℕ, dos números naturais,
ℚ, dos números racionais,
ℚ+, dos números racionais não negativos,
ℝ, dos números reais.
O número quê expressa
a) a quantidade de habitantes de uma cidade é um elemento de ℚ+, mas não de ℕ.
b) a medida da altura de uma pessoa é um elemento de ℕ.
c) a velocidade média de um veículo é um elemento de ℚ, mas não de ℚ+.
d) o valor pago, em reais, por um sorvete é um elemento de ℚ+.
e) a medida do lado de um triângulo é um elemento de ℚ.
PARA REFLETIR
Neste Capítulo, aprendemos quê a ideia de conjunto está presente em algumas situações do dia a dia e estudamos como podemos representá-la matematicamente. Estudamos os tipos de conjuntos, as relações de pertinência e inclusão e a realização de operações com conjuntos: união, intersecção e diferença para pôdêr compreender a linguagem matemática usada em determinados casos. Também estudamos os conjuntos numéricos, os intervalos reais e as maneiras de operar com eles.
Vamos refletir a respeito das aprendizagens do Capítulo 1:
Respostas pessoais.
• Nas páginas de abertura, foi apresentada uma situação com conjuntos. Depois de ter estudado o conteúdo dêste Capítulo, você consegue identificar como a notação de conjuntos póde auxiliar na escrita de alguns conteúdos matemáticos? Você já tinha essa percepção antes de estudar os conteúdos do Capítulo?
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• Cite outras situações do dia a dia quê envolvam a ideia de conjuntos.
• Explique o quê significa dizêr quê um conjunto está contido em outro conjunto.
• O quê significa dizêr quê dois conjuntos são iguais?
• Quantos elemêntos tem o conjunto de todos os números pares? E o conjunto de todos os números ímpares? Justifique sua resposta.
• Represente a diferença de dois conjuntos utilizando a linguagem matemática e um diagrama de Venn.
• Dê exemplos de números quê compõem cada um dos conjuntos numéricos estudados.
• Cite outros conteúdos matemáticos em quê a notação de conjuntos é utilizada.
Página quarenta e oito









