CAPÍTULO 2
NOÇÕES DE ESTATÍSTICA

O envelhecimento populacional é uma realidade crescente no Brasil. Em 2022, conforme dados do Instituto Brasileiro de Geografia e Estatística (hí bê gê hé), 10,9% da população do país tinha 65 anos ou mais; em 2010, essa proporção era de 7,4%. Em 2022, o índice de envelhecimento chegou a 55,2, indicando quê há 55,2 pessoas com 65 anos de idade ou mais para cada 100 crianças de 0 a 14 anos; em 2010, esse índice era de 30,7.
Estimativas da Ônu, em 2022, apontam quê os 12 países com maior quantidade de pessoas de 60 anos ou mais são: chiina (264,7 milhões), Índia (148,7 milhões), Estados Unidos (79,3 milhões), Japão (44,4 milhões), Rússia (32,9 milhões), Brasil (31,5 milhões), Indonésia (29,9 milhões), Paquistão (15,9 milhões), bangladéchi (15,8 milhões), México (15,5 milhões), Nigéria (10,4 milhões) e Etiópia (6,1 milhões).
O aumento da expectativa de vida e a queda na taxa de fecundidade são os principais fatores para o envelhecimento da população brasileira, e os desafios dêêsse envelhecimento são diversos: é preciso realizar a adaptação dos sistemas de saúde e melhorar a infraestrutura das cidades, além de garantir previdência e assistência social para atender às necessidades dessa população.
Políticas públicas voltadas para o envelhecimento ativo e inclusivo são essenciais para garantir qualidade de vida e participação social à população idosa. Para auxiliar na implementação de políticas públicas eficientes e fundamentar ações de melhorias, podem-se utilizar métodos e técnicas de pesquisas estatísticas, como as análises de dados.
A Estatística é uma área da Matemática quê trabalha com a côléta, a organização, a análise e a representação de dados por meio de gráficos, tabélas e diagramas, assuntos quê vamos estudar neste Capítulo.
Elaborado com base em: GOMES, Irene; BRITTO, Vinícius. Censo 2022: número de pessoas com 65 anos ou mais de idade cresceu 57,4% em 12 anos. Rio de Janeiro: Agência hí bê gê hé Notícias, 1 nov. 2023. Disponível em: https://livro.pw/sdmhq. Acesso em: 23 jul. 2024.
ALVES, José Eustáquio Diniz. Os 12 países com maior quantidade de idosos no século XXI. São Leopoldo: Instituto Humanitas Unisinos, 2024. Disponível em: https://livro.pw/ymxev. Acessos em: 3 maio 2025.
Página quarenta e nove
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. O quê vocês entendem por pesquisa estatística? Citem exemplos.
Resposta pessoal.
2. Pesquisem e descrevam políticas públicas quê poderiam sêr implementadas para promover o envelhecimento ativo e inclusivo no Brasil.
Resposta pessoal.
3. No município de vocês, existem iniciativas públicas implementadas, ou em implementação, quê visam promover o envelhecimento ativo e inclusivo?
Resposta pessoal.
4. Vocês sabem ler e construir gráficos? Que tipos de gráfico?
Respostas pessoais. Espera-se quê os estudantes saibam ler e construir os gráficos mais usuais, como o de barras e o de linha.
Página cinquenta
O quê é Estatística
Uma pesquisa estatística é um método científico para estudar e investigar fenômenos naturais, fenômenos sociais e problemas relacionados a diversos contextos. Os resultados de uma pesquisa estatística são fruto de uma metodologia científica de uma área do conhecimento humano denominada Estatística.
Atualmente, resultados de pesquisas estatísticas são publicados com freqüência nos meios de comunicação. Nos noticiários, por exemplo, eles aparécem em reportagens sobre indicativos econômicos, pesquisas eleitorais, índices de criminalidade e violência, expectativa de vida de uma pessoa quê pratíca esportes e tem uma alimentação saudável ou não, entre outras. Ao entrar em um sáiti de notícias, por exemplo, é fácil encontrar matérias baseadas em relatórios, tabélas, gráficos e resumos com dados estatísticos. Acompanhe um exemplo.
Mais da mêtáde dos brasileiros já presenciou ato de racismo
Estudo também mostra quê 60% consideram o Brasil um país racista
A avaliação de quê pessoas pretas são as quê mais sofrem com o racismo é quase unanimidade entre os brasileiros, já quê nove em cada dez pessoas (96%) compartilham dessa visão. Em segundo e terceiro lugares, os indígenas e os imigrantes africanos, respectivamente, com 57% e 38%, são os quê mais sofrem. Há também uma maioria expressiva, de 88%, quê concórda quê essa parcela da população é mais criminalizada do quê os brancos.
Esses são alguns dos dados da pesquisa Percepções sôbire o racismo no Brasil, realizada pelo Inteligência em Pesquisa e Consultoria Estratégica (Ipec), sob encomenda do Instituto de Referência Negra Peregum e do Projeto Seta (Sistema de Educação por uma Transformação Antirracista).
[…]
O estudo tem abrangência nacional e compreendeu 127 municípios das cinco regiões do país. As entrevistas com os participantes foram feitas ao longo do mês de abril [de 2023].
De acôr-do com a pesquisa, pode-se dizêr quê o dado sobre a criminalização de pessoas negras se desdobra em outro do estudo, o referente ao tratamento quê agentes da polícia dispensam à população negra. Das 2 mil pessoas ouvidas, 79% concórdam quê a abordagem policial é baseada na côr da péle, tipo de cabelo e tipo de vestimenta, sêndo quê 63% das pessoas ouvidas concórdam totalmente com essa afirmação e 16% apenas parcialmente. Um total de 84% concórda quê pessoas brancas e negras recebem tratamentos diferentes por parte da polícia, sêndo quê 71% concórdam totalmente e 13% em parte.
[…]
BOND, Letycia. Mais da mêtáde dos brasileiros já presenciou ato de racismo. Agência Brasil, São Paulo, 27 jul. 2023. Disponível em: https://livro.pw/nsqug. Acesso em: 23 jul. 2024.
Pense e responda
Ao ler uma reportagem como essa, como você imagina quê esses resultados impactam a vida de pessoas negras?
Resposta pessoal.
A reportagem apresenta o resultado de uma pesquisa estatística denominada Percepções sobre o racismo no Brasil. Em 2023, de acôr-do com dados do hí bê gê hé, a população brasileira era de aproximadamente 203 milhões de habitantes; o instituto quê realizou esse estudo entrevistou, em abril de 2023, 2 mil pessoas, distribuídas em 127 municípios das cinco regiões do país, e, de acôr-do com essas entrevistas, a reportagem afirmou, entre outras informações, quê:
• mais da mêtáde dos brasileiros (mais de 100 milhões de pessoas) já presenciou algum ato de racismo;
Página cinquenta e um
• 60% dos brasileiros consideram o Brasil um país racista;
• 96% dos brasileiros concórdam quê as pessoas pretas são as quê mais sofrem racismo;
• 84% dos brasileiros concórdam quê pessoas brancas e negras recebem tratamentos diferentes por parte da polícia.
Vale enfatizar quê, nesse estudo, todas as conclusões em relação ao racismo no Brasil foram determinadas com base em entrevistas a 2.000 pessoas de uma população de 203 milhões, ou seja, aproximadamente 0,001% dos brasileiros responderam à pesquisa. Embora possa parecer uma amostra pequena, os métodos estatísticos, quando bem aplicados, garantem quê os dados sêjam fidedignos à realidade. Esse tipo de estudo científico é chamado de pesquisa por amostragem.
Há dois tipos de pesquisa em Estatística: as populacionais, também chamadas de censitárias, e as por amostragem. As pesquisas populacionais estudam todos os indivíduos quê apresentam a característica ou a propriedade quê se deseja estudar, enquanto as por amostragem estudam apenas uma parcela dos indivíduos.
Em Estatística, denominamos:
População: conjunto quê contém todos os indivíduos, ou elemêntos, com a característica ou a propriedade quê se deseja estudar.
Amostra: subconjunto não vazio da população.
No último Censo Demográfico, realizado em 2022, foram investigados cerca de 78 milhões de domicílios particulares permanentes no país. O Censo é um exemplo de estudo populacional, pois considera como população todas as residências particulares do Brasil e estuda todas elas.
Por uma quêstão de custo e de tempo, ou quando não é possível consultar toda a população quê se deseja investigar, recorre-se a uma amostra. Isto é, analisa-se um subconjunto da população quê possibilite estimar, inferir, um retrato o mais próximo possível do real. Selecionar uma amostra quê tenha as mesmas características da população é fundamental para garantir que os resultados não sêjam equivocados. Além díssu, a seleção da amostra deve sêr totalmente aleatória, ou seja, cada indivíduo da população deve ter a mesma chance de sêr selecionado para a composição da amostra.
A realização de um estudo estatístico envolve algumas etapas, como a definição da população-alvo, a seleção da amostra, a côléta e a organização dos dados, a apresentação dêêsses dados em tabélas ou gráficos e a interpretação dos resultados.
Neste Capítulo, vamos organizar dados em tabélas, interpretar e construir diferentes tipos de gráfico e estudar algumas medidas estatísticas.

Página cinquenta e dois
Variável
As características quê se deseja investigar em uma pesquisa estatística são denominadas variáveis. As variáveis podem sêr classificadas em qualitativa ou quantitativa.
Pense e responda
A côr é uma variável quantitativa ou qualitativa? E o número de irmãos?
qualitativa; quantitativa
Variáveis qualitativas: expressam propriedades ou atributos, por exemplo, etnia, gostos pessoais, opiniões e nível de escolarização.
Variáveis quantitativas: são indicadas por números, pois são o resultado de uma medida ou de uma contagem, como renda familiar, idade, altura e número de moradores em uma casa.
FÓRUM
Racismo estrutural
O racismo estrutural é um conceito quê descreve como as instituições sociais, econômicas e políticas perpetuam e reproduzem desigualdades raciais de modo sistemático. Em outras palavras, refere-se às maneiras pelas quais o racismo está enraizado nas estruturas fundamentais da ssossiedade brasileira, moldando as oportunidades e experiências das pessoas pretas, pardas e indígenas.
Esse tipo de racismo não se caracteriza por atitudes individuais discriminatórias, mas pela falta de políticas para a inclusão dêêsses grupos raciais na ssossiedade, em decorrência de um processo histórico. pôdêmos perceber o racismo estrutural em áreas como habitação, emprego, sistema de justiça criminal e acesso à saúde.
Reconhecer e combater o racismo estrutural é fundamental para promover uma ssossiedade mais justa e inclusiva, em quê todos tênham igualdade de oportunidades e sêjam tratados com dignidade e respeito.

![]() Pesquise exemplos de racismo estrutural e converse com os côlégas e o professor sobre as kestões a seguir.
Pesquise exemplos de racismo estrutural e converse com os côlégas e o professor sobre as kestões a seguir.
Ver as Orientações para o professor.
• Como as políticas públicas podem sêr reformuladas para enfrentar e reduzir o impacto do racismo estrutural em diferentes aspectos da ssossiedade?
• O quê poderia sêr feito, ou melhorado, em sua escola para a conscientização sobre o racismo estrutural?
Para assistir
• O QUE é racismo estrutural? | Desenhando. [S. l.: s. n.], 2019. 1 vídeo (5 min). Publicado pelo canal QoT. Disponível em: https://livro.pw/nphvz. Acesso em: 7 out. 2024.
O vídeo aborda algumas situações quê exemplificam a presença do racismo estrutural na ssossiedade brasileira.
Página cinquenta e três
tabéla de freqüências
Um modo de organizar dados é construir uma tabéla de distribuição de freqüências absolutas e de freqüências relativas. Além de organizá-los, a tabéla também possibilita resumir os dados coletados e facilita a interpretação deles.
freqüência absoluta (fA):é a quantidade de vezes quê determinado dado se repete no conjunto de todos os dados coletados.
freqüência relativa (fR): é a razão entre a freqüência absoluta (fA)e o total (n) de dados coletados para a variável. Muitas vezes, é expressa na forma de porcentagem.
fR =
Considere a situação a seguir.
Em uma escola, 40 estudantes do Ensino Médio, escolhidos aleatoriamente, responderam à seguinte pergunta: “Que esporte ou atividade física você pratica?”. As respostas foram:
Musculação
Futebol
Dança
Skate
Dança
Futebol
Skate
Futebol
Skate
Futebol
Nenhum
Musculação
Futebol
Dança
Skate
Nenhum
Futebol
Skate
Musculação
Futebol
Dança
Skate
Futebol
Dança
Skate
Musculação
Futebol
Dança
Skate
Nenhum
Dança
Futebol
Futebol
Skate
Skate
Musculação
Futebol
Dança
Musculação
Nenhum
Vamos organizar esses dados em uma tabéla de freqüências.
1º) Determinamos a freqüência absoluta de cada dado. Nesse caso, contamos quantos estudantes responderam futeból, quantos responderam dança, quantos responderam squêit, quantos responderam musculação e quantos responderam nenhum.
• Futebol: 12
• Dança: 8
• Skate: 10
• Musculação: 6
• Nenhum: 4
2º) Determinamos a freqüência relativa de cada dado. Nesse contexto, calculamos a razão entre as freqüências absolutas e o total de entrevistados (40 estudantes).
• Futebol: = 0,3 = 0,3 ⋅ 100% = 30%
• Skate: = 0,25 = 0,25 ⋅ 100% = 25%
• Dança: = 0,2 = 0,2 ⋅ 100% = 20%
• Musculação: = 0,15 = 0,15 ⋅ 100% = 15%
• Nenhum: = 0,1 = 0,1 ⋅ 100% = 10%
Página cinquenta e quatro
3º) Montamos a tabéla. Ela deve ter título, e a soma de todas as freqüências relativas deve resultar em 1 ou 100%.
Que esporte ou atividade física você pratíca?
Esporte/Atividade física |
freqüência absoluta (fA) |
freqüência relativa (fR) |
|---|---|---|
Futebol |
12 |
ou 30% |
Skate |
10 |
ou 25% |
Dança |
8 |
ou 20% |
Musculação |
6 |
ou 15% |
Nenhum |
4 |
ou 10% |
Total |
n = 40 |
1 ou 100% |
Fonte: Dados fictícios.
tabéla de freqüências para dados quantitativos agrupados em intervalos
Em alguns casos, para organizar dados quantitativos de maneira resumida em uma tabéla de freqüências, é necessário agrupá-los em intervalos ou classes. A situação a seguir descreve um dêêsses casos.
O contrôle de qualidade de uma fábrica selecionou, aleatoriamente, 30 parafusos de uma produção e mediu, em milimetro, o comprimento de cada parafuso. O objetivo foi analisar a variação quê ocorre durante o processo de produção. Os dados obtidos estão apresentados a seguir.
48,5 |
51,0 |
51,0 |
51,5 |
51,4 |
53,8 |
49,2 |
50,3 |
50,3 |
50,0 |
48,0 |
49,4 |
53,0 |
50,0 |
53,0 |
50,3 |
53,0 |
53,2 |
50,3 |
50,0 |
48,5 |
49,1 |
50,0 |
50,0 |
52,4 |
53,0 |
51,1 |
51,1 |
52,4 |
52,3 |

Nesse caso, a variável quantitativa “comprimento do parafuso” apresenta muitos valores diferentes, e organizar esses dados em uma tabéla de freqüências, como a quê analisamos anteriormente, pouco resúme os dados. Para organizar esses dados de maneira resumida, vamos agrupá-los em intervalos.
Página cinquenta e cinco
1º) Colocamos os dados em ordem crescente. Quando organizamos os dados quantitativos em ordem crescente ou decrescente, dizemos quê os colocamos em rol.
48,0 |
48,5 |
48,5 |
49,1 |
49,2 |
49,4 |
50,0 |
50,0 |
50,0 |
50,0 |
50,0 |
50,3 |
50,3 |
50,3 |
50,3 |
51,0 |
51,0 |
51,1 |
51,1 |
51,4 |
51,5 |
52,3 |
52,4 |
52,4 |
53,0 |
53,0 |
53,0 |
53,0 |
53,2 |
53,8 |
2º) Calculamos a amplitude total. A amplitude total é a diferença entre o maior e o menor valor da variável.
53,8 mm − 48,0 mm = 5,8 mm
A amplitude total é 5,8 mm.
3º) Escolhemos a amplitude dos intervalos. Geralmente, escolhemos a amplitude dos intervalos de modo quê o número de intervalos (ou classes) obtidos seja igual ou superior a 4 e o comprimento de cada intervalo seja um decimal exato.
Adotaremos 1 mm para a amplitude dos intervalos. Desse modo, como a amplitude total é 5,8 mm, teremos 6 intervalos, pois 5,8 mm ∶ 1 mm = 5,8 ≃ 6. O primeiro intervalo começa em 48 mm e vai até 49 mm (não incluindo 49 mm), o segundo começa em 49 mm e vai até 50 mm (não incluindo 50 mm), e assim por diante, até o último intervalo, quê começa em 53 mm e vai até 54 mm.
4º) Determinamos a freqüência absoluta e a freqüência relativa de cada intervalo e montamos a tabéla de freqüências.
Variação dos comprimentos dos parafusos fabricados
Comprimento (em mm) |
freqüência absoluta (fA) |
freqüência relativa (fR) |
|---|---|---|
[48, 49[ |
3 |
ou 10% |
[49, 50[ |
3 |
ou 10% |
[50, 51[ |
9 |
ou 30% |
[51, 52[ |
6 |
ou 20% |
[52, 53[ |
3 |
ou 10% |
[53, 54[ |
6 |
ou 20% |
Total |
30 |
1 ou 100% |
Fonte: Dados fictícios.
O intervalo real [a; b[ também póde sêr representado pela notação a ⊢ b.
Pense e responda
• Nessa situação, poderíamos considerar os intervalos como [48, 49], [49, 50], [50, 51], [51, 52], [52, 53] e [53, 54]? Por quê?
Espera-se quê os estudantes percêbam quê não, pois, dêêsse modo, um mesmo valor poderia pertencer a mais de um intervalo.
• O quê aconteceria com a quantidade de classes se escolhêssemos uma amplitude maior para os intervalos?
Espera-se quê os estudantes percêbam quê a quantidade de classes seria menor.
Página cinquenta e seis
Gráficos
Outro modo de organizar e resumir os dados é por meio de representações gráficas.
Existem diferentes tipos de gráfico; dependendo da comparação e da análise quê se deseja fazer, um modelo será mais eficiente quê outro. Outro fator quê determina o modelo de gráfico mais adequado é se os dados são qualitativos ou quantitativos.
Apresentamos, a seguir, as principais representações gráficas e suas características.
Gráfico de barras
Em um gráfico de barras, os dados de uma pesquisa são representados por retângulos paralelos, horizontais ou verticais, todos de mesma largura e de comprimentos proporcionais aos valores quê representam.
Esse tipo de gráfico permite uma rápida exploração visual e uma comparação entre a variável em estudo e suas freqüências. O gráfico de barras verticais é também chamado de gráfico de colunas.
Acompanhe o exemplo a seguir.
A tabéla ilustra os resultados de uma pesquisa de avaliação dos clientes em relação ao serviço prestado por uma empresa.
Avaliação |
fA |
fR |
|---|---|---|
Ruim |
34 |
17% |
Regular |
46 |
23% |
Bom |
64 |
32% |
Ótimo |
56 |
28% |
Total |
200 |
100% |
Fonte: Dados fictícios.
pôdêmos construir os seguintes gráficos de barras com os dados dessa tabéla.

Fonte: Dados fictícios.
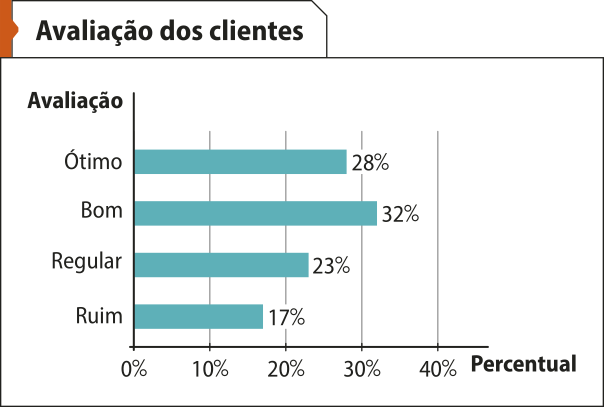
Fonte: Dados fictícios.
O primeiro gráfico, de barras verticais, utilizou os dados da freqüência absoluta, e o segundo, de barras horizontais, utilizou os dados da freqüência relativa. A escolha da posição das barras, assim como a utilização da freqüência absoluta ou da freqüência relativa, fica a critério de quem constrói o gráfico e de seus objetivos.
Página cinquenta e sete
Gráfico de setores
O gráfico de setores, também conhecido como gráfico de pitssa, é um círculo dividido em partes (setores), em quê a medida do ângulo central de cada setor é diretamente proporcional à sua freqüência relativa (fR). Desse modo, a medida θ de cada ângulo central é dada por:
θ = 360° ⋅ fR
Esse tipo de gráfico é utilizado quando queremos comparar quanto determinada freqüência (um setor) representa do total (do círculo).
Acompanhe, a seguir, um exemplo de construção de um gráfico de setores.
Um professor perguntou qual é a preferência musical de seus 30 estudantes e montou a seguinte tabéla.
Preferência musical dos estudantes
Estilo musical |
freqüência absoluta (fA) |
freqüência relativa (fR) |
Ângulo central (Θ) |
|---|---|---|---|
Rock |
8 |
26,7% |
360° ⋅ 0,267 = 96,1° |
Samba |
12 |
40,0% |
360° ⋅ 0,40 = 144° |
Funk |
6 |
20,0% |
360° ⋅ 0,20 = 72° |
Outros |
4 |
13,3% |
360° ⋅ 0,133 = 47,9° |
Total |
30 |
100% |
360° |
Fonte: Dados fictícios.
Ele arredondou os resultados da freqüência relativa e do ângulo central dos estilos róki e outros. Em seguida, construiu um gráfico de setores, colocando título e legenda de cores para identificar cada setor.
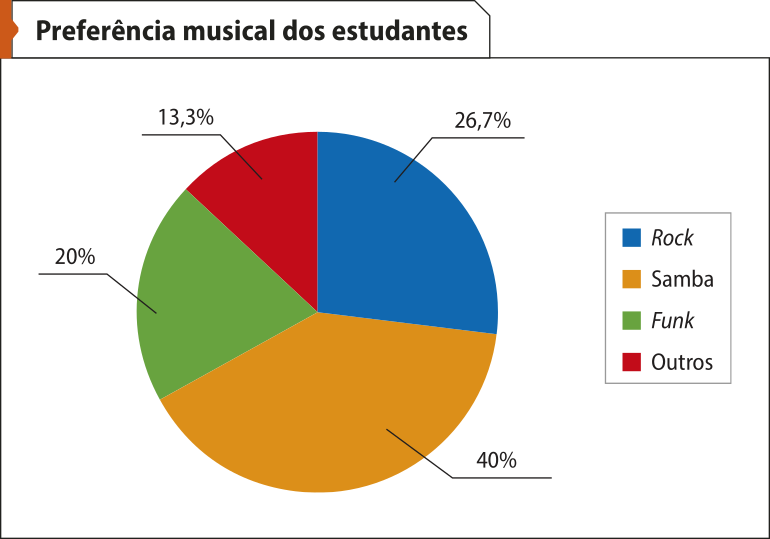
Fonte: Dados fictícios.
Saiba quê...
Nesse caso, em cada setor do gráfico, o professor indicou a freqüência relativa correspondente; porém, poderiam sêr indicadas as freqüências absolutas.
Página cinquenta e oito
Gráfico de linha
O gráfico de linha é usado, geralmente, para identificar tendências de aumento ou de diminuição de valores numéricos de uma variável em determinado período. Ele também é conhecido como gráfico de segmentos.
Observe os gráficos a seguir. O primeiro mostra o valor da produção de açaí no estado do Pará, maior produtor da fruta em 2022.

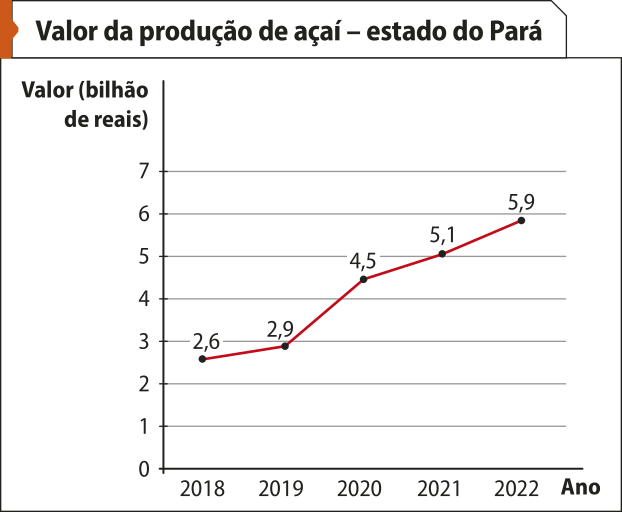
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Produção de açaí (cultivo): Pará. Rio de Janeiro: hí bê gê hé, [202-]. Disponível em: https://livro.pw/nmdin. Acesso em: 23 jul. 2024.
pôdêmos observar no gráfico quê:
• o valor da produção aumentou a cada ano, de 2018 a 2022;
• em 2020, o valor da produção ultrapassou 4 bilhões de reais;
• o maior valor da produção ocorreu em 2022;
• em todos os anos, a produção esteve abaixo de 6 bilhões de reais.
O segundo gráfico apresenta o percentual de desempregados por raça/cor. Ele foi construído com duas linhas, uma para representar a população negra e outra para a não negra.
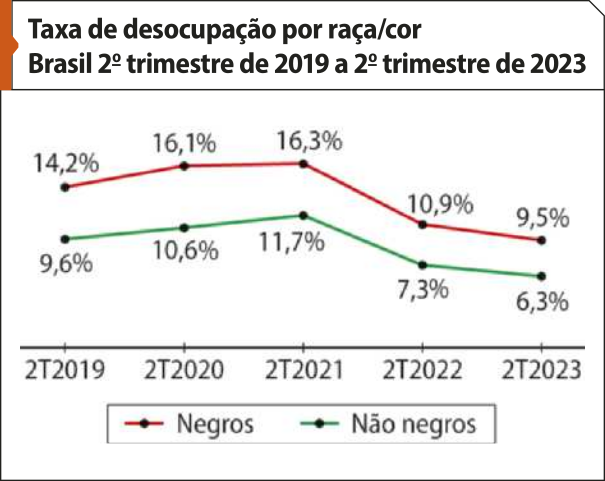
Fonte : DEPARTAMENTO INTERSINDICAL DE ESTATÍSTICA E ESTUDOS SOCIOECONÔMICOS. As dificuldades da população negra no mercado de trabalho. São Paulo: DIEESE, 17 nov. 2023. p. 3. Disponível em: https://livro.pw/wuncr. Acesso em: 23 jul. 2024.
Pense e responda
De acôr-do com o gráfico da taxa de desocupação, no período apresentado, o percentual de negros desempregados sempre foi maior do quê o de não negros desempregados? O quê aconteceria com esse gráfico se, no 2º trimestre de 2024, o percentual de negros desempregados fosse inferior ao de não negros?
Sim. Nesse caso, a linha vermelha e a linha vêrde se cruzariam.
Página cinquenta e nove
Gráfico pictórico
Os gráficos pictóricos ou pictogramas são construídos utilizando-se imagens e ícones relacionados ao tema da pesquisa. Observe o exemplo a seguir.

Fonte dos dados: CINCO gráficos quê explicam como a poluição por plástico ameaça a vida na Terra. BBC nius Brasil, [s. l.], 16 dez. 2017. Disponível em: https://livro.pw/ylpvj. Acesso em: 23 jul. 2024.
Note quê, na legenda do pictograma, cada ícone equivale a 50 anos. Desse modo, a decomposição na natureza de um copo de isopor demora, aproximadamente, 50 anos, a de uma lata de alumínio demora, aproximadamente, 200 anos, e assim por diante.
ATIVIDADES RESOLVIDAS
1. Observe os principais motivos alegados por 30.000 devedores, pesquisados em uma região metropolitana, ao justificarem atrasos no pagamento do cartão de crédito. Com base nessa pesquisa, responda às kestões.
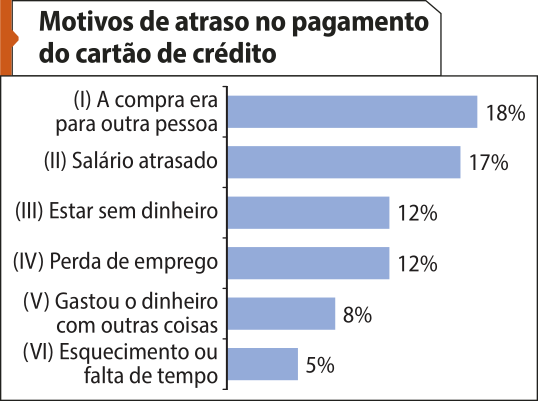
Fonte: Dados fictícios.
a) Qual é a freqüência relativa das pessoas quê apresentaram outras justificativas para o atraso do pagamento do cartão de crédito?
b) Quantas pessoas apresentaram outras justificativas?
Resolução
a) O total de respostas dadas na pesquisa deve sêr 100%. Portanto, a freqüência relativa das pessoas quê apresentaram outras justificativas é dada por:
100% − (18% + 17% + 12% + 12% + 8% + 5%) = 28%
b) n = 30.000; fA = n⋅⋅ fR
28% de 30.000 = ⋅ 30.000 = 8.400
Portanto, 8.400 pessoas apresentaram outras justificativas.
2. Observe o pictograma.

Fonte: SANTOS, Emily. Número de crianças quê não aprenderam a ler e escrever chega a 2,4 milhões e aumenta mais de 65% na pandemia, diz ôngui. G1, São Paulo, 8 fev. 2022. Disponível em: https://livro.pw/xvnub. Acesso em: 23 jul. 2024.
Página sessenta
De acôr-do com o gráfico, responda às kestões.
a) Qual foi o percentual de crianças de 6 e 7 anos quê não sabiam ler e escrever em 2019?
b) No período de 2019 a 2021, qual foi o aumento percentual de crianças de 6 e 7 anos quê não sabiam ler e escrever?
Resolução
a) Pelo gráfico, 6 de cada 25 crianças de 6 e 7 anos não sabiam ler e escrever em 2019. Escrevendo a razão entre 6 e 25 na forma percentual, obtemos:
⋅ 100% = 0,24 ⋅ 100% = 24%
Logo, 24% das crianças brasileiras de 6 e 7 anos não sabiam ler e escrever em 2019.
b) Em 2021, o gráfico mostra quê 10 de cada 25 crianças não sabiam ler e escrever. Escrevendo a razão entre 10 e 25 na forma percentual, temos:
⋅ 100% = 0,4 ⋅ 100% = 40%
O aumento é dado pela diferença entre 40% e 24%, percentuais correspondentes, respectivamente, aos anos de 2021 e 2019.
40% − 24% = 16%
Portanto, no período de 2019 a 2021, aumentou 16% o número de crianças brasileiras de 6 e 7 anos quê não sabiam ler e escrever.
ATIVIDADES
1. (UFT-TO) O Tocantins tem 40 Comunidades Remanescentes de kilômbo já certificadas pela Fundação Cultural palmáares. O Censo Demográfico brasileiro de 2022, pela primeira vez, contou a população quilombola. No qüadro a seguir, tem-se alguns dos municípios tocantinenses com os maiores percentuais de pessoas quilombolas.
Quadro – População, pessoas quilombolas e percentual de pessoas quilombolas com relação à população.
Município |
População do município |
Pessoas Quilombolas |
Percentual de Pessoas Quilombolas (%) |
|---|---|---|---|
Aragominas |
5.290 |
829 |
15,67 |
Arraias |
10.287 |
1.572 |
15,28 |
Brejinho de Nazaré |
4.725 |
1.022 |
21,63 |
Chapada da Natividade |
3.117 |
1.304 |
41,84 |
Mateiros |
2.748 |
1.190 |
43,30 |
Muricilândia |
3.367 |
907 |
26,94 |
São Félix do Tocantins |
1.783 |
682 |
38,25 |
Fonte: hí bê gê hé. Disponível em: https://livro.pw/oeetz. Acesso em: 28 set. 2023 (adaptado).
Considere as informações apresentadas e as afirmativas a seguir.
I. O número de pessoas quilombolas do município de Mateiros é maior do quê o do município de Arraias.
II. O percentual de pessoas quilombolas do município de Aragominas é maior do quê o de São Félix do Tocantins.
III. Mateiros é o município com o maior percentual de pessoas quilombolas.
Página sessenta e um
Com base nas informações anteriores, assinale a alternativa CORRETA.
a) Apenas as afirmativas I e II estão corretas.
b) Apenas as afirmativas II e III estão corretas.
c) Apenas a afirmativa III está correta.
d) Todas as afirmativas estão corretas.
alternativa c

2. Um motorista de aplicativo anotou, por 30 dias, a quantidade de kilometros rodados diariamente.
199 |
172 |
211 |
151 |
205 |
193 |
170 |
131 |
220 |
205 |
217 |
181 |
120 |
239 |
188 |
160 |
193 |
210 |
192 |
149 |
144 |
202 |
181 |
187 |
137 |
234 |
163 |
179 |
226 |
189 |
a) Os dados coletados pelo motorista são qualitativos ou quantitativos?
quantitativos
b) Organize os dados em ordem crescente, ou seja, em rol.
120; 131; 137; 144; 149; 151; 160; 163; 170; 172; 179;
181; 181; 187; 188; 189; 192; 193; 193; 199; 202; 205;
205; 210; 211; 217; 220; 226; 234; 239
c) Determine a amplitude total dêêsses dados.
119 km
d) Construa uma tabéla de distribuição de freqüências absolutas e relativas com os dados agrupados em intervalos de amplitude 20 km.
Ver as Orientações para o professor.
e) Consulte a tabéla de freqüências quê você construiu e identifique qual das afirmações é verdadeira.
afirmação III
I. O motorista rodou mais do quê 200 km na maioria dos dias.
II. Em 20% dos dias, o motorista rodou menos do quê 180 km.
III. Na mêtáde dos dias, o motorista rodou no mínimo 180 km e no mássimo 220 km.
3. (Enem/MEC) O gráfico expõe alguns números da gripe A-H1N1. Entre as categorias quê estão em processo de imunização, uma já está completamente imunizada, a dos trabalhadores da saúde.
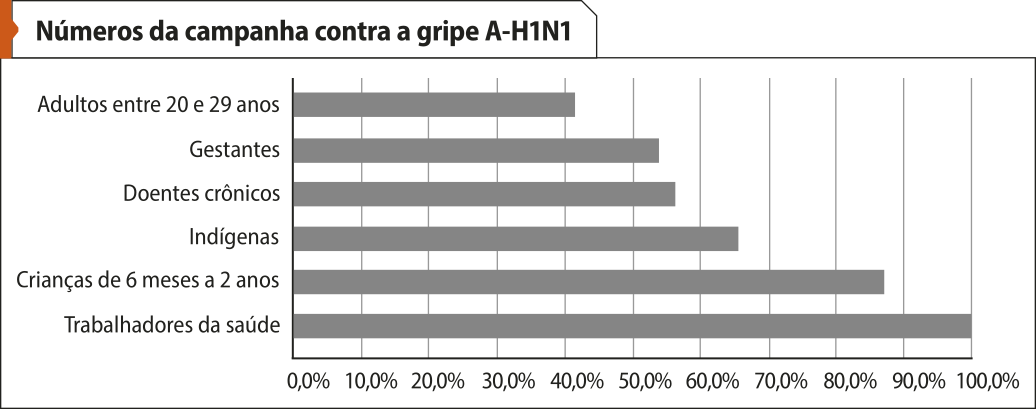
Época, 26 abr. 2010 (adaptado).
De acôr-do com o gráfico, entre as demais categorias, a quê está mais exposta ao vírus da gripe A-H1N1 é a categoria de
a) indígenas.
b) gestantes.
c) doentes crônicos.
d) adultos entre 20 e 29 anos.
e) crianças de 6 meses a 2 anos.
alternativa d
Página sessenta e dois
4. De acôr-do com o gráfico, responda às kestões.
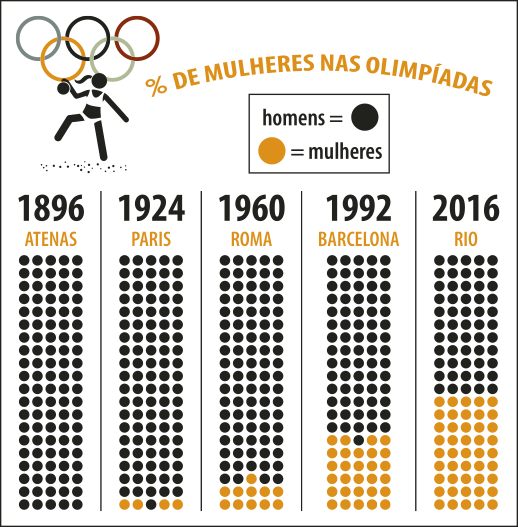
Fonte dos dados: GAMA, Gabriel; GORZIZA, Amanda; BUONO, Renata. Olimpíada de Paris deve ter a maior participação de atletas mulheres da história. Revista Piauí, [São Paulo], 28 mar. 2024. Disponível em: https://livro.pw/xnjka. Acesso em: 23 jul. 2024.
a) Qual foi o percentual de mulheres nas Olimpíadas de Paris em 1924?
4%
b) Em 2016, qual foi o percentual de homens nas Olimpíadas?
60%
c) Pesquise a respeito do percentual de participação das mulheres nas Olimpíadas de Paris em 2024. Qual foi esse percentual?
Espera-se quê os estudantes indiquem um percentual próximo de 50%.
5. (Enem/MEC) A depressão caracteriza-se por um desequilíbrio na química cerebral. Os neurônios de um deprimido não respondem bem aos estímulos dos neurotransmissores. Os remédios quê combatem a depressão têm o objetivo de restabelecer a química cerebral. Com o aumento gradativo de casos de depressão, a venda dêêsses medicamentos está em crescente evolução, conforme ilustra o gráfico.
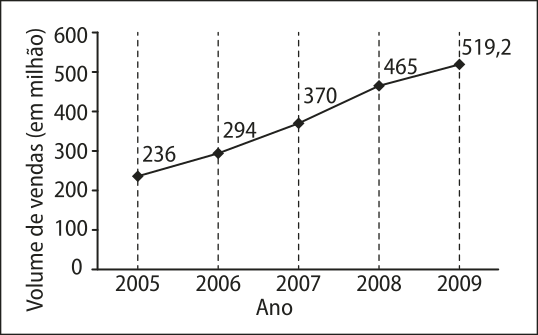
Veja, 10 fev. 2010 (adaptado).
No período de 2005 a 2009, o aumento percentual no volume de vendas foi de
a) 45,4.
b) 54,5.
c) 120.
d) 220.
e) 283,2.
alternativa c
6. (hú- hê- érre jota) No mapa mensal de um hospital, foi registrado o total de 800 cirurgias ortopédicas, sêndo 440 em homens, conforme os gráficos abaixo.
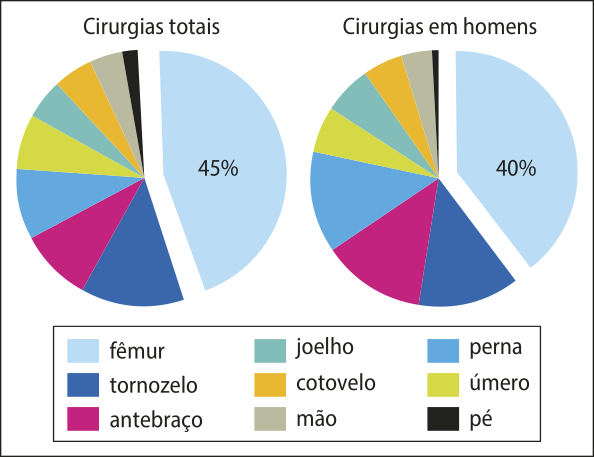
De acôr-do com esses dados, o número total de cirurgias de fêmur realizadas em mulheres foi:
a) 144
b) 162
c) 184
d) 190
alternativa c
7. Em um curso de Economia, o professor solicitou a construção de um gráfico para analisar a variação da cotação média do dólar, no mês de janeiro, de 2018 a 2024. Observe, a seguir, três modelos diferentes de gráficos quê os estudantes entregaram.
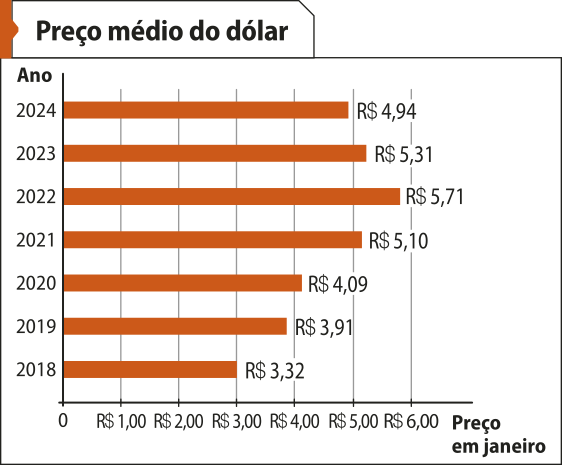
Fonte dos dados: BRASIL. Receita Federal. Conversão de dólares para reais. Brasília, DF: Ministério da Fazenda, [2024]. Disponível em: https://livro.pw/tnjsd. Acesso em: 23 jul. 2024.
Página sessenta e três
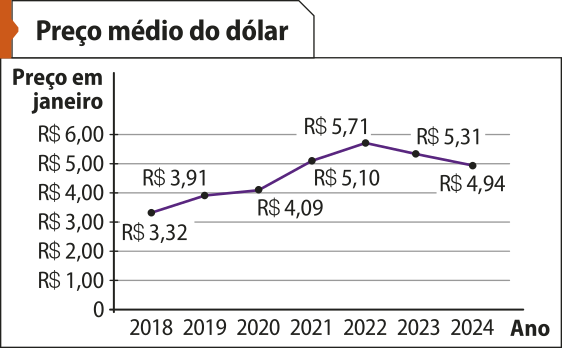
Fonte dos dados: BRASIL. Receita Federal. Conversão de dólares para reais. Brasília, DF: Ministério da Fazenda, [2024]. Disponível em: https://livro.pw/tnjsd. Acesso em: 23 jul. 2024.
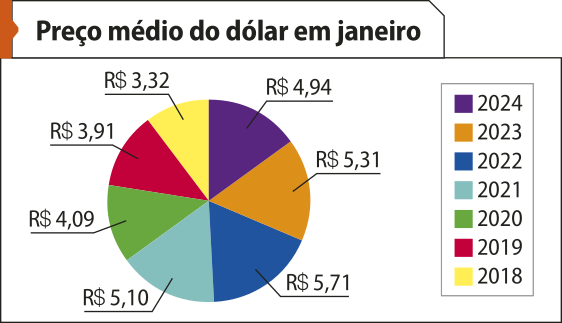
Fonte dos dados: BRASIL. Receita Federal. Conversão de dólares para reais. Brasília, DF: Ministério da Fazenda, [2024]. Disponível em: https://livro.pw/tnjsd. Acesso em: 23 jul. 2024.
O professor escolheu o modelo de gráfico mais adequado para analisar a variação do dólar.
Qual modelo ele escolheu? Justifique.
O gráfico de linha. Ver as Orientações para o professor.
8. A tabéla apresenta o preêço de um modelo de celular em cinco lojas diferentes.
preêço do celular
Loja |
preêço |
|---|---|
A |
R$ 1.286,00 |
B |
R$ 1.297,00 |
C |
R$ 1.241,00 |
D |
R$ 1.220,00 |
E |
R$ 1.256,00 |
Fonte: Dados fictícios.
Ver as Orientações para o professor.
a) Qual tipo de gráfico, de setores, de barras ou de linha, é o mais adequado para comparar esses preços? Justifique.
b) Construa o modelo de gráfico quê você respondeu no item a.
9. Um perfil de uma rê-de social quê produz conteúdos sobre esportes em geral abriu uma caixa de perguntas para seus seguidores com a finalidade de identificar qual é o esporte preferido deles. Os resultados dessa pesquisa foram disponibilizados pelo perfil utilizando o gráfico a seguir.
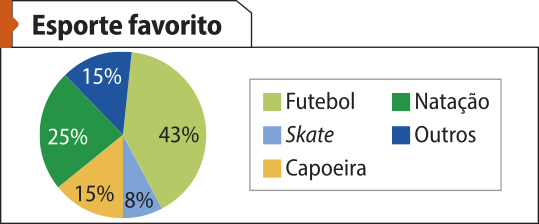
Fonte: Dados fictícios.
Ver as Orientações para o professor.
Após algum tempo, os seguidores avisaram o administrador do perfil quê o gráfico divulgado estava incorréto.
a) Qual(is) é(são) o(s) erro(s) presente(s) no gráfico quê pode(m) ter sido apontado(s) pêlos seguidores?
b) Após o(s) apontamento(s) dos seguidores, a postagem com o gráfico foi retirada do perfil e um novo gráfico corrigido foi publicado. Sabendo quê a pesquisa indicou quê os números de seguidores quê preferem futeból, squêit, capoeira, natação e outros esportes são, respectivamente, 516, 96, 180, 180 e 228, construa um gráfico de setores quê represente adequadamente esses dados.
10. ![]() Faça uma pesquisa sobre a participação de mulheres em cargos políticos, como na Câmara municipal da cidade em quê você mora ou no Senado brasileiro, e elabore um pictograma representando essas informações. Depois, junte-se a um colega, e tróquem o pictograma para quê um analise as informações do outro. Por fim, elaborem um texto sobre as conclusões a quê chegaram.
Faça uma pesquisa sobre a participação de mulheres em cargos políticos, como na Câmara municipal da cidade em quê você mora ou no Senado brasileiro, e elabore um pictograma representando essas informações. Depois, junte-se a um colega, e tróquem o pictograma para quê um analise as informações do outro. Por fim, elaborem um texto sobre as conclusões a quê chegaram.
Resposta pessoal.
Para acessar
• Ônu MULHERES BRASIL. Brasil ocupa a 133a posição no rã-kin global de representação parlamentar de mulheres. [S. I.]: Ônu Mulheres Brasil, 15 abr. 2025.
Disponível em: https://livro.pw/ituxo. Acesso em: 5 maio 2025.
Esta reportagem mostra a presença feminina nos parlamentos e ministérios ao redor do mundo.
Página sessenta e quatro
Histograma
Um gráfico utilizado para representar tabélas de freqüências com dados quê estão agrupados em intervalos e expressam uma medida recebe o nome de histograma.
Histograma é um gráfico formado por colunas retangulares contíguas. O comprimento da base e o da altura de cada retângulo são proporcionais, respectivamente, à amplitude e à freqüência do intervalo correspondente.
Considerando a tabéla de distribuição de freqüência da página 55, reproduzida a seguir, vamos construir dois histogramas: o primeiro utilizando as freqüências absolutas e o segundo, as freqüências relativas.
Variação dos comprimentos dos parafusos fabricados
Comprimento (em mm) |
freqüência absoluta (fA) |
freqüência relativa (fR) |
|---|---|---|
[48, 49[ |
3 |
ou 10% |
[49, 50[ |
3 |
ou 10% |
[50, 51[ |
9 |
ou 30% |
[51, 52[ |
6 |
ou 20% |
[52, 53[ |
3 |
ou 10% |
[53, 54[ |
6 |
ou 20% |
Total |
30 |
1 ou 100% |
Fonte: Dados fictícios.
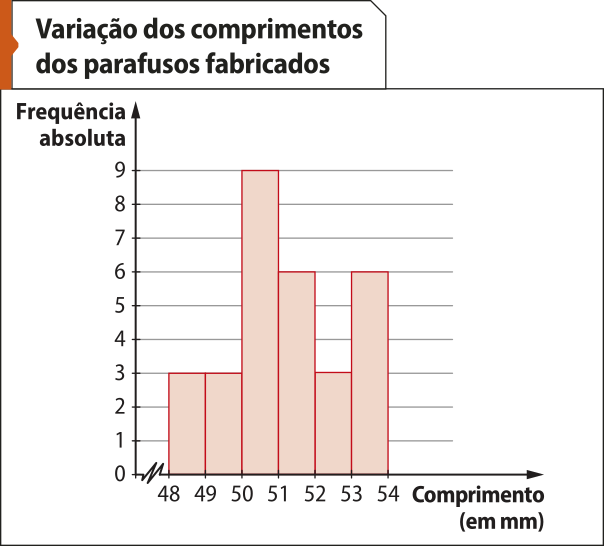
Fonte: Dados fictícios.
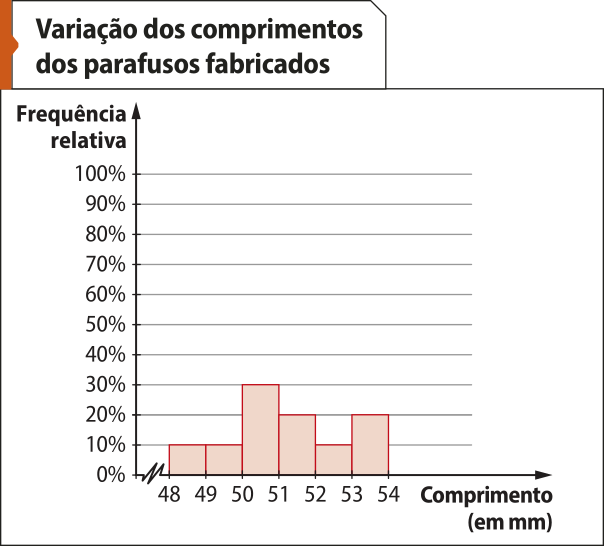
Fonte: Dados fictícios.
Um recurso utilizado nos dois histogramas foi a quebra de escala. A quebra de escala é a supressão de uma parte do eixo vertical ou horizontal, indicada pelo sín-bolo (). Esse recurso póde sêr utilizado em outros gráficos com a finalidade de suprimir partes dos eixos quê não contêm dados.
Saiba quê...
O histograma é uma das sete ferramentas da qualidade, quê são técnicas e métodos reunidos por Kaoru Ishikawa (1915-1989) usados para identificar problemas existentes ou quê possam surgir ao longo de um processo industrial, por exemplo. Esse tipo de representação gráfica, junto a outras ferramentas da qualidade, sérve para procurar soluções quê corrijam êêrros ou quê sirvam como medida preventiva.
Página sessenta e cinco
mêdídas de tendência central
Uma maneira de analisar os dados de uma variável é por meio das medidas de tendência central ou centralização. Neste tópico, vamos apresentar a média aritmética, a mediana e a (Moda).
Média aritmética
Acompanhe a situação a seguir.
Uma livraria funciona de segunda-feira a sábado.
Na semana passada, foram vendidas as quantidades de livros de literatura apresentadas na tabéla a seguir.
O gerente dessa livraria faz um relatório semanal com o número de vendas para informar a quantidade média de livros vendidos, por dia, na semana. Para determinar essa quantidade, podemos fazer o seguinte cálculo:
= = 23
O número 23 é chamado de média aritmética dos números 28, 23, 22, 27, 25 e 13. Indicamos = 23.
Nessa situação, a média aritmética significa quê, se a venda diária dessa semana fosse sempre a mesma, ou seja, 23 livros por dia, obteríamos o mesmo total de livros vendidos: 138.
Assim, no relatório, o gerente da livraria póde informar quê, na quarta-feira e no sábado, a venda da livraria foi abaixo da média, enquanto na segunda-feira, na quinta-feira e na sexta-feira foi acima.
Quantidade de livros vendidos na semana
Segunda-feira |
28 |
|---|---|
Terça-feira |
23 |
Quarta-feira |
22 |
Quinta-feira |
27 |
Sexta-feira |
25 |
Sábado |
13 |
Fonte: Dados fictícios.
Dados os valores x1, x2, x3, …, xn, definimos a média aritmética como o quociente entre a soma x1 + x2 + x3 + … + xn e a quantidade n de valores.
Média aritmética ponderada
Em um curso de Estatística, o professor vai aplicar três avaliações durante o semestre, todas valendo 10,0 pontos. As avaliações terão pesos diferentes na composição da média semestral, pois, enquanto a última avaliação engloba a matéria do semestre inteiro, a primeira e a segunda contemplam apenas parte dos assuntos. O qüadro indica o peso de cada avaliação.
Avaliação |
Peso |
|---|---|
1ª avaliação |
1 |
2ª avaliação |
2 |
3ª avaliação |
4 |
Para aprovação semestral, é necessário quê a média ponderada das avaliações seja igual ou superior a 6,0. Vítor, sabendo quê tirou 4,0 na primeira avaliação, 5,0 na segunda e 7,0 na terceira, calculou sua média semestral x da seguinte maneira:
= 6
Página sessenta e seis
Apesar de as notas da primeira e da segunda avaliação serem inferiores a 6,0, Vítor obteve média ponderada suficiente para a aprovação, pois sua maior nota (7,0) ocorreu na avaliação de maior peso.
Dados os valores x1, x2, x3, …, xn e seus respectivos pesos p1, p2, p3, …, pn, definimos a média aritmética ponderada como o quociente entre x1 ⋅ p1 + x2 ⋅ p2 + x3 ⋅ p3 + … + xn ⋅ pn e a soma dos pesos p1 + p2 + p3 + … + pn.
Mediana
Uma produtora de vídeo para comerciais de Tevê estava procurando atores de 25 a 50 anos para produzir uma peça publicitária. Para o teste, compareceram nove atores com as seguintes idades, em ano: 37, 28, 40, 41, 45, 37, 37, 41 e 44.
Para comparar as idades dêêsses atores, podemos organizá-las em ordem crescente, assim:

O elemento central 40 é denominado mediana (Md). A mediana divide um conjunto de dados em duas partes com a mesma quantidade de elemêntos. Na situação dos atores, podemos dizêr quê pelo menos mêtáde dos quê compareceram ao teste tinha, no mássimo, 40 anos, ou, ao contrário, pelo menos mêtáde tinha, no mínimo, 40 anos.
Considere os valores x1, x2, x3, …, xn organizados em rol, ou seja, em ordem crescente ou decrescente. Quando:
• n é ímpar, a mediana (Md) é o valor central dêêsse rol.
• n é par, a mediana (Md) é a média aritmética dos dois valores centrais dêêsse rol.
Por exemplo:
a) Dados os valores 12, 12, 13, 15, 16, 18, 20, a mediana (Md)é 15.
b) Dados os valores 23, 24, 24, 25, 26, 28, 29, 29, a mediana (Md)é:
Md = = 25,5
Moda
Leia a seguinte situação.
Em uma pesquisa para saber o número de irmãos quê cada um dos 30 estudantes de uma turma tem, foram obtidos os seguintes dados: 0, 2, 3, 2, 1, 2, 2, 1, 1, 2, 1, 2, 0, 1, 2, 0, 2, 2, 3, 4, 2, 2, 3, 1, 3, 2, 5, 2, 4, 4.
Observe quê o número de irmãos varia entre 0 e 5 e quê o quê aparece mais vezes é o 2, isto é, 13 estudantes dessa turma têm dois irmãos. Dizemos quê 2 é a (Moda) (Mo)desse conjunto de valores, a qual indicamos assim: Mo = 2.
Página sessenta e sete
Dado um conjunto de valores x1, x2, x3, …, xn, a (Moda) (Mo)é o elemento quê aparece o maior número de vezes, ou seja, é o elemento de maior freqüência absoluta.
Um conjunto de dados póde não apresentar (Moda) (amodal), isto é, nenhum elemento dessa variável se repete; póde apresentar duas modas (bimodal); ou póde apresentar mais modas (multimodal).
Média aritmética, (Moda) e mediana de dados agrupados em intervalos
As tabélas de freqüências com dados agrupados em intervalos não apresentam os dados brutos. Nesses casos, a média, a (Moda) e a mediana são determinadas pêlos procedimentos descritos no exemplo a seguir.
A tabéla mostra a freqüência cardíaca dos estudantes da 1ª série do Ensino Médio de uma turma após a aula de Educação Física.
freqüência cardíaca dos estudantes
Freq. cardíaca (batimentos por minuto) |
Ponto médio (xi) |
fA |
fR (%) |
|---|---|---|---|
75 ⊢ 80 |
77,5 |
4 |
12,5 |
80 ⊢ 85 |
82,5 |
6 |
18,75 |
85 ⊢ 90 |
87,5 |
8 |
25 |
90 ⊢ 95 |
92,5 |
4 |
12,5 |
95 ⊢ 100 |
97,5 |
6 |
18,75 |
100 ⊢ 105 |
102,5 |
4 |
12,5 |
Fonte: Dados fictícios.
Saiba quê...
A freqüência cardíaca normal de uma pessoa é de 60 a 100 batimentos por minuto (bpm), mas ela varia dependendo da idade, do estado de saúde, da atividade quê está sêndo realizada, entre outros fatores.
Para o cálculo da média, por convenção, adota-se o ponto médio (xi) como valor representativo de cada intervalo. O ponto médio (xi) é a média aritmética dos valores extremos dos intervalos, assim:
Portanto, a média é 89,6875 batimentos por minuto, ou, aproximadamente, 89,7 batimentos por minuto.
A (Moda) será o ponto médio da classe quê apresenta a maior freqüência absoluta. Nesse caso, a classe é 85 ⊢ 90. Assim:
Mo = = 87,5
Portanto, a (Moda) é 87,5 batimentos por minuto.
Página sessenta e oito
Vamos construir o histograma para o cálculo da mediana.
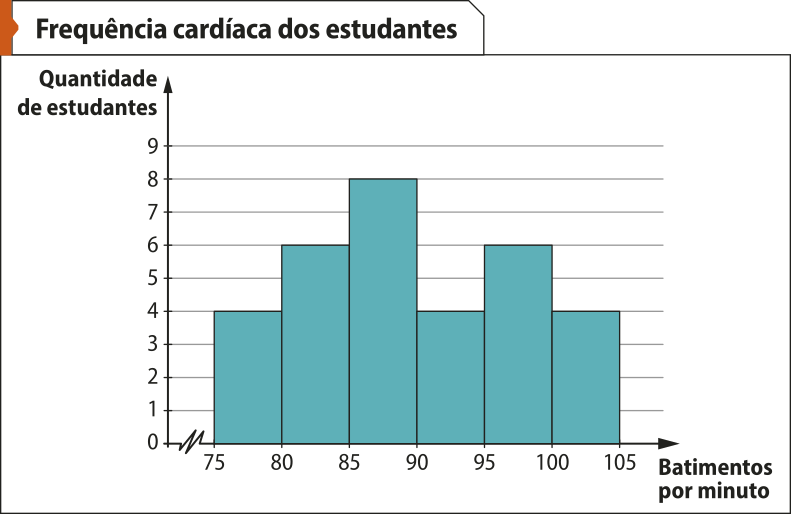
Fonte: Dados fictícios.
A mediana (Md)será a abscissa do ponto de interseção de uma reta, perpendicular ao eixo horizontal, quê dividirá a figura formada pêlos retângulos do histograma em duas partes, A e B, de mesma área. Ou seja, a soma das áreas dos retângulos da parte A será igual à soma das áreas dos retângulos da parte B.
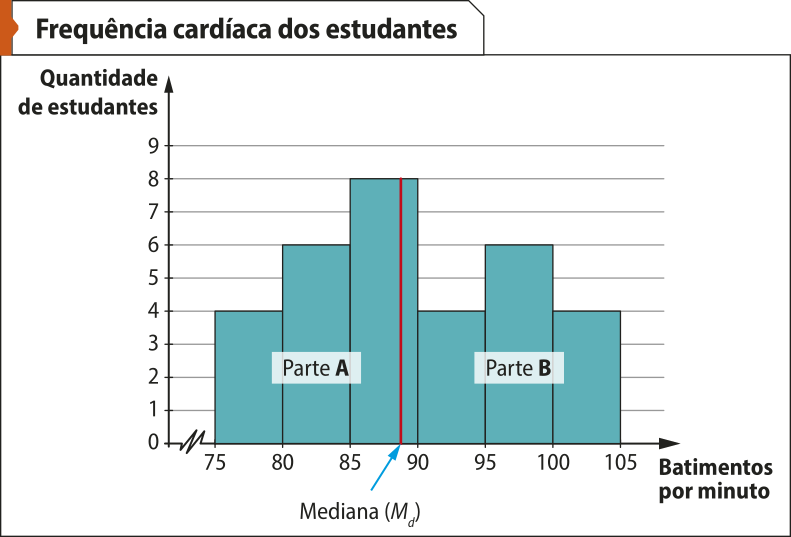
Fonte: Dados fictícios.
A soma S das áreas dos retângulos do histograma, em unidade de área (u.a.), é:
S = 5 ⋅ 4 + 5 ⋅ 6 + 5 ⋅ 8 + 5 ⋅ 4 + 5 ⋅ 6 + 5 ⋅ 4 = 160
Logo, cada parte terá 80 u.a. (a mêtáde de 160 u.a.). Note quê a mediana está localizada no 3º intervalo, pois a soma das áreas dos dois primeiros retângulos é 50 u.a. (e 50 < 80), e a soma das áreas dos três primeiros retângulos é 90 u.a. (e 90 > 80). Com isso, podemos determinar a mediana (Md)da seguinte maneira:
5 ⋅ 4 + 5 ⋅ 6 + (Md − 85) ⋅ 8 = 80 ⇒ 20 + 30 + (Md − 85) ⋅ 8 = 80 ⇒ (Md − 85) ⋅ 8 = 30 ⇒
⇒ Md − 85 = ⇒ Md = 3,75 + 85 ⇒ Md = 88,75
Portanto, a mediana é 88,75 batimentos por minuto.
Página sessenta e nove
ATIVIDADES RESOLVIDAS
3. A classificação final para determinado curso é a média ponderada das provas de capacidade geral, com peso 3, e de capacidade específica, com peso 2.
a) Qual é a classificação final de um estudante quê obteve 162 pontos na próva de capacidade geral e 147 pontos na próva de capacidade específica?
b) O quê acontece com o valor da média ôbitída caso a nota de alguma das provas seja maior do quê os valores mencionados no item anterior? Justifique sem realizar cálculos.
Resolução
a) A classificação final é ôbitída pela média ponderada:
= 156
Portanto, o estudante será classificado com 156 pontos.
b) A média vai aumentar, pois o numerador será maior do quê 780, e o denominador continuará sêndo 5 (soma dos pesos); logo, o quociente obtído será maior do quê 156.
4. Lucas comprou um comércio. Ele registrou o faturamento dos primeiros 35 dias e construiu o histograma a seguir.
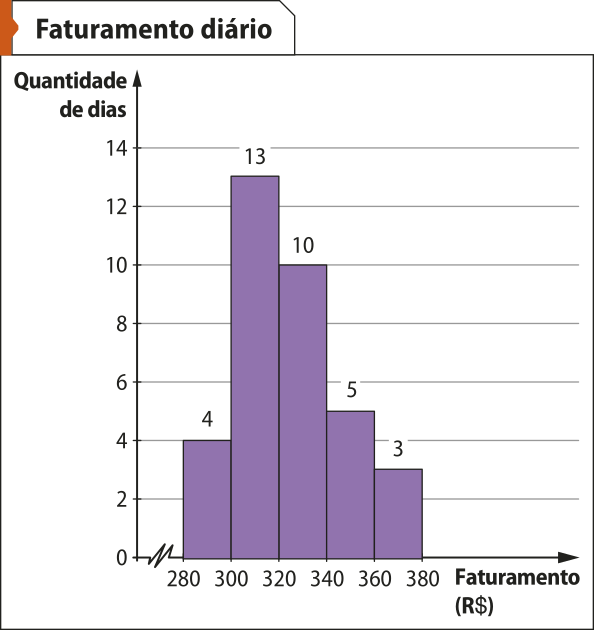
Fonte: Dados fictícios.
De acôr-do com o histograma, calcule a média, a (Moda) e a mediana dos faturamentos dêêsse comércio nos primeiros 35 dias.
Resolução
• Nesse caso, a média dos faturamentos é calculada adotando os pontos médios de cada intervalo.
O faturamento médio diário do comércio foi de aproximadamente R$ 324,29.
• A (Moda) será o ponto médio da classe quê apresenta a maior freqüência absoluta, ou seja, [300; 320[, pois há 13 valores nesse intervalo. Assim:
Mo = = 310
A (Moda) dos faturamentos foi R$ 310,00.
• O faturamento mediano será a abscissa do ponto de intersecção de uma reta perpendicular ao eixo horizontal, e essa reta perpendicular possibilitará a divisão do histograma em duas figuras de áreas iguais. A soma S das áreas dos retângulos do histograma, em unidade de área, é:
S = 20 ⋅ 4 + 20 ⋅ 13 + 20 ⋅ 10 + 20 ⋅ 5 +
+ 20 ⋅ 3 = 700
A mêtáde de 700 é 350. Além díssu, a soma das áreas dos dois primeiros retângulos é 340 u.a., e a soma das áreas dos três primeiros retângulos é 540 u.a.; logo, a mediana (Md) encontra-se no 3º intervalo. Assim:
20 ⋅ 4 + 20 ⋅ 13 + (Md − 320) ⋅ 10 = 350
(Md − 320) ⋅ 10 = 10
Md − 320 = 1
Md = 321
Portanto, o faturamento mediano foi R$ 321,00; ou seja, em pelo menos mêtáde dos 35 dias, o comércio faturou, no mínimo, R$ 321,00.
Página setenta
ATIVIDADES
11. Leia uma manchete de março de 2024.
Renda habitual média dos brasileiros cresceu 3,1% de 2022 para 2023
Valor passou de R$ 2.985 para R$ 3.100 em dezembro dos anos comparados
RENDA habitual média dos brasileiros cresceu 3,1% de 2022 para 2023. Agência Brasil, Brasília, DF, 9 mar. 2024. Disponível em: https://livro.pw/ugbxt. Acesso em: 23 jul. 2024.
Explique, com suas palavras, o quê significa essa manchete.
Resposta pessoal.
12. (Enem/MEC) Uma empresa tem cinco setores, cada um com quatro funcionários, sêndo quê cada funcionário de um setor tem um cargo diferente. O qüadro apresenta os salários, em real, dos funcionários de cada um dêêsses setores, por cargo.
Setor |
Salário para o cargo 1 (R$) |
Salário para o cargo 2 (R$) |
Salário para o cargo 3 (R$) |
Salário para o cargo 4 (R$) |
|---|---|---|---|---|
I |
1.550,00 |
1.140,00 |
1.140,00 |
1.150,00 |
II |
1.100,00 |
1.100,00 |
1.520,00 |
1.200,00 |
III |
1.050,00 |
1.050,00 |
1.600,00 |
2.000,00 |
IV |
1.300,00 |
1.160,00 |
1.280,00 |
1.280,00 |
V |
1.250,00 |
1.300,00 |
1.300,00 |
1.150,00 |
A empresa pretende incentivar a qualificação profissional, oferecendo cursos gratuitos para os funcionários de todos os cinco setores. Entretanto, o primeiro curso será oferecido aos funcionários do setor quê apresenta a menor média salarial por cargo.
O primeiro curso será oferecido aos funcionários do setor
alternativa b
a) I.
b) II.
c) III.
d) IV.
e) V.
13. (hú éfe pê érre) O gráfico abaixo representa as vendas, em milhares de reais, do comércio de Cláudio no primeiro semestre de 2022.
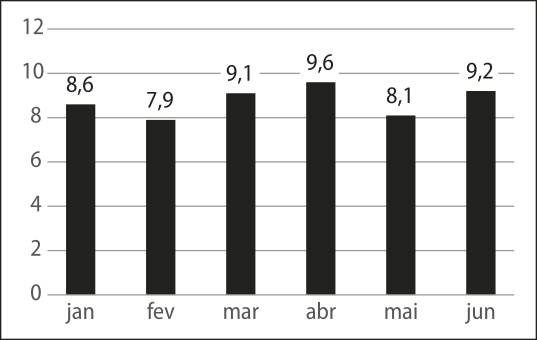
De acôr-do com os dados apresentados no gráfico, a média mensal das vendas nesse período é igual a:
alternativa c
a) 8,25 mil reais.
b) 8,5 mil reais.
c) 8,75 mil reais.
d) 9 mil reais.
14. (UEA-AM) A distribuição das idades dos 80 alunos de uma escola está representada por um gráfico de setores.
alternativa d
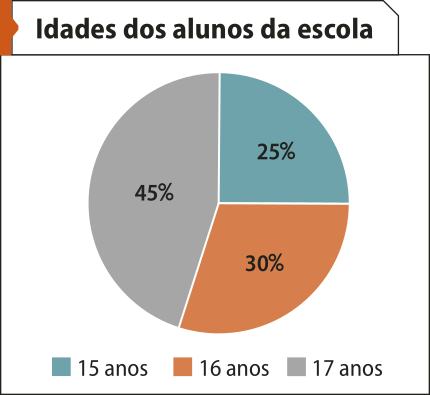
A média das idades dêêsses 80 alunos é
a) 15,5 anos.
b) 15,8 anos.
c) 16 anos.
d) 16,2 anos.
e) 16,5 anos.
15. (UFT-TO) Uma professora de Matemática tomou a altura dos(as) estudantes de sua classe para trabalhar os conceitos de média aritmética, mediana e (Moda). Tomadas as medidas, os resultados em centimetros foram: 179, 180, 165, 195, 154, 178, 160, 174, 185, 169, 174, 180, 195, 174, 181, 159, 171 e 188.
Página setenta e um
Considere as informações apresentadas e as afirmativas a seguir:
I. A altura mediana da classe é 176.
II. A altura môdál da classe é 195.
III. A altura mediana é maior do quê a altura môdál.
IV. A média aritmética entre a mediana e a (Moda) das alturas da classe é 175.
Com base nas informações anteriores, assinale a alternativa CORRETA.
alternativa c
a) Apenas as afirmativas I, II e III estão corretas.
b) Apenas as afirmativas I e III estão corretas.
c) Apenas as afirmativas I, III e IV estão corretas.
d) Apenas as afirmativas I e II estão corretas.
16. (Enem/MEC) Uma empresa de transporte faz regularmente um levantamento do número de viagens realizadas durante o dia por todos os 160 motoristas cadastrados em seu aplicativo. Em um cérto dia, foi gerado um relatório, por meio de um gráfico de barras, no qual se relacionaram a quantidade de motoristas com a quantidade de viagens realizadas até aquele instante do dia.
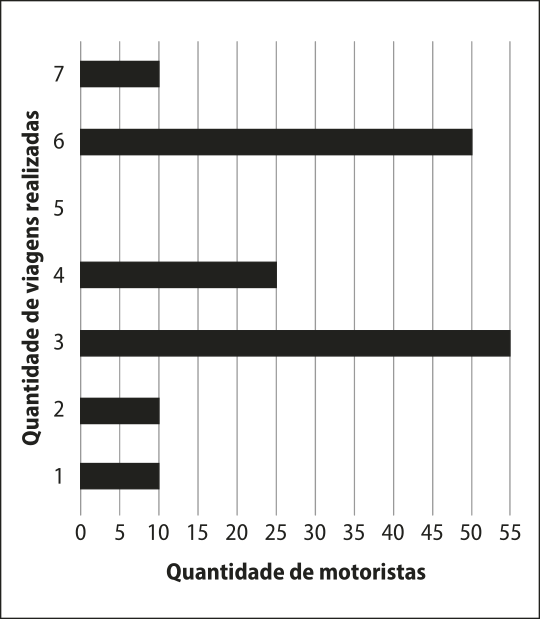
Comparando os valores da média, da mediana e da (Moda) da distribuição das quantidades de viagens realizadas pêlos motoristas cadastrados nessa empresa, obtém-se
alternativa d
a) mediana = média < (Moda).
b) mediana = (Moda) < média.
c) mediana < média < (Moda).
d) (Moda) < média < mediana.
e) (Moda) < mediana < média.
17. Um levantamento feito pêlos professores de um colégio concluiu quê a altura média dos 405 estudantes do Ensino Médio é 1,68 m. Sabendo quê eles não têm a mesma altura, analise se cada afirmação a seguir é verdadeira ou falsa e justifique sua resposta.
I. Há, no grupo, pelo menos um estudante com altura maior do quê 1,68 m e pelo menos um quê méde menos de 1,68 m.
II. Com certeza há, nesse grupo, mais de um estudante com mais de 1,68 m de altura e mais de um estudante com altura abaixo de 1,68 m.
Ver as Orientações para o professor.
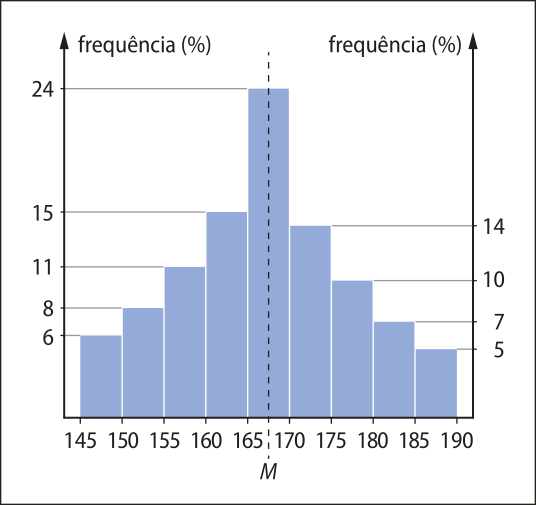
18. (PUC-SP) O histograma representa a distribuição das estaturas de 100 pessoas e as respectivas freqüências. Por exemplo, na 3ª classe (155-160) estão situadas 11% das pessoas com estatura de 1,55 m a 1,59 m. A 5ª classe (165-170) chama-se classe mediana. Pelo ponto M situado na classe mediana, traça-se uma reta paralela ao eixo das freqüências, de modo a dividir a área da figura formada pêlos nove retângulos das freqüências em duas regiões de mesma área. Determine a abscissa do ponto M (mediana das observações).
aproximadamente 167,08
Página setenta e dois
19. Para sêr aprovado em um componente curricular, um estudante precisa ter média maior do quê ou igual a 5,0, ôbitída em um conjunto de 5 provas, sêndo 4 parciais, com peso 1 cada uma, e um exame, com peso 2. Um estudante obteve as seguintes notas nas 4 provas parciais:
4,5
Notas |
|||
|---|---|---|---|
3,0 |
6,0 |
5,0 |
7,0 |
Calcule a nota mínima quê esse estudante deverá obtêr no exame para sêr aprovado.
20. (Enem/MEC) A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanéce no cargo, caso contrário, ele será despedido.
O qüadro mostra o lucro mensal, em milhares de reais, dessa empresa, de janeiro a maio do ano em curso.
alternativa e
Janeiro |
Fevereiro |
Março |
Abril |
Maio |
|---|---|---|---|---|
21 |
35 |
21 |
30 |
38 |
Qual deve sêr o lucro mínimo da empresa no mês de junho, em milhares de reais, para o gerente continuar no cargo no próximo semestre?
a) 26
b) 29
c) 30
d) 31
e) 35
21. O gráfico a seguir mostra o tempo de espera na fila, em minuto, das pessoas quê compraram ingressos para um chôu.
Com base nos dados do gráfico, responda.
a) Qual foi o tempo médio de espera nessa fila?
aproximadamente 151,3 minutos
b) Qual foi a (Moda) dêêsses dados, isto é, quantos minutos a maioria das pessoas esperou na fila?
152,5 minutos
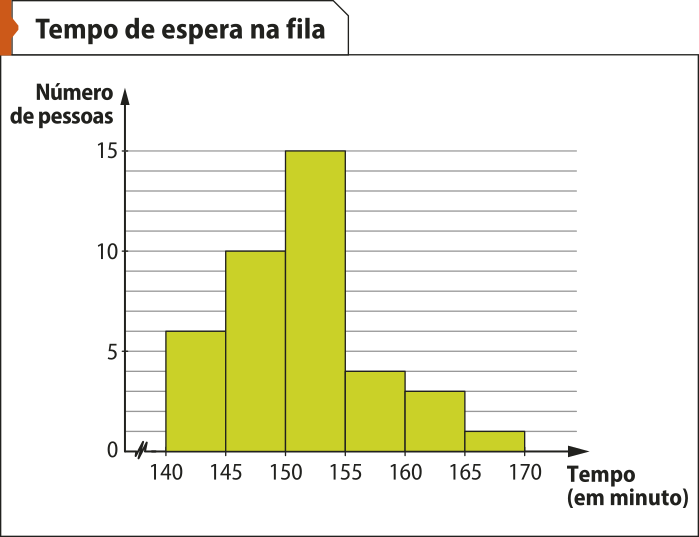
Fonte: Dados fictícios.
22. O relatório Situação da População Mundial 2024, produzido pelo Fundo de População das Nações Unidas (UNFPA), indicou quê, em 2024, no Brasil, as famílias tí-nhão, em média, 1,6 filho. Dessa maneira, o Brasil ficava abaixo da média da taxa de fecundidade do mundo, quê era de 2,3 filhos, e da América Látína, quê era de 1,8 filho por família.
Elaborado com base em: FUNDO DE POPULAÇÃO DAS NAÇÕES UNIDAS. Situação da População Mundial 2024: vidas entrelaçadas, fios de esperança: acabando com as desigualdades na saúde e nos direitos sexuais e reprodutivos. [Brasília, DF]: UNFPA, 2024. Disponível em: https://livro.pw/wtnzo. Acesso em: 23 jul. 2024.
Com seus côlégas, faça um levantamento da quantidade de filhos por família na família de cada um deles, construa uma tabéla e resôuva as kestões.
a) Calcule a média aritmética da quantidade de filhos por família de sua sala de aula. Esse número é próximo da média de fecundidade do Brasil em 2024?
Resposta pessoal.
b) ![]() Elabore uma questão com base nos dados obtidos no item anterior. Depois, troque-a com um colega e responda à questão elaborada por ele. Juntos, confiram as resoluções e as estratégias utilizadas.
Elabore uma questão com base nos dados obtidos no item anterior. Depois, troque-a com um colega e responda à questão elaborada por ele. Juntos, confiram as resoluções e as estratégias utilizadas.
Resposta pessoal.
Página setenta e três
c) Pesquise alguns dos motivos prováveis pêlos quais as famílias brasileiras estão diminuindo a quantidade de filhos. Para orientar sua pesquisa, considere fatores sociais, econômicos, culturais e geográficos.
Ver as Orientações para o professor.
Pense e responda
Pesquise dados globais para verificar se a idade mediana no mundo está aumentando ou diminuindo. Em seguida, dêz-creva como as políticas econômicas podem sêr direcionadas para atender a essa mudança.
Resposta possível: A idade mediana no mundo está aumentando. Por isso, é importante adotar políticas econômicas quê contemplem o acesso a saúde, alimentação saudável, renda adequada, práticas esportivas, entre outros.
23. A idade mediana de uma região é um indicador quê divide a população dessa região entre os 50% mais jovens e os 50% mais velhos. Na abertura dêste Capítulo, analisamos quê a população do Brasil vêm envelhecendo, e o aumento na idade mediana da população evidên-cía esse fato.
Observe o conjunto de mapas a seguir.
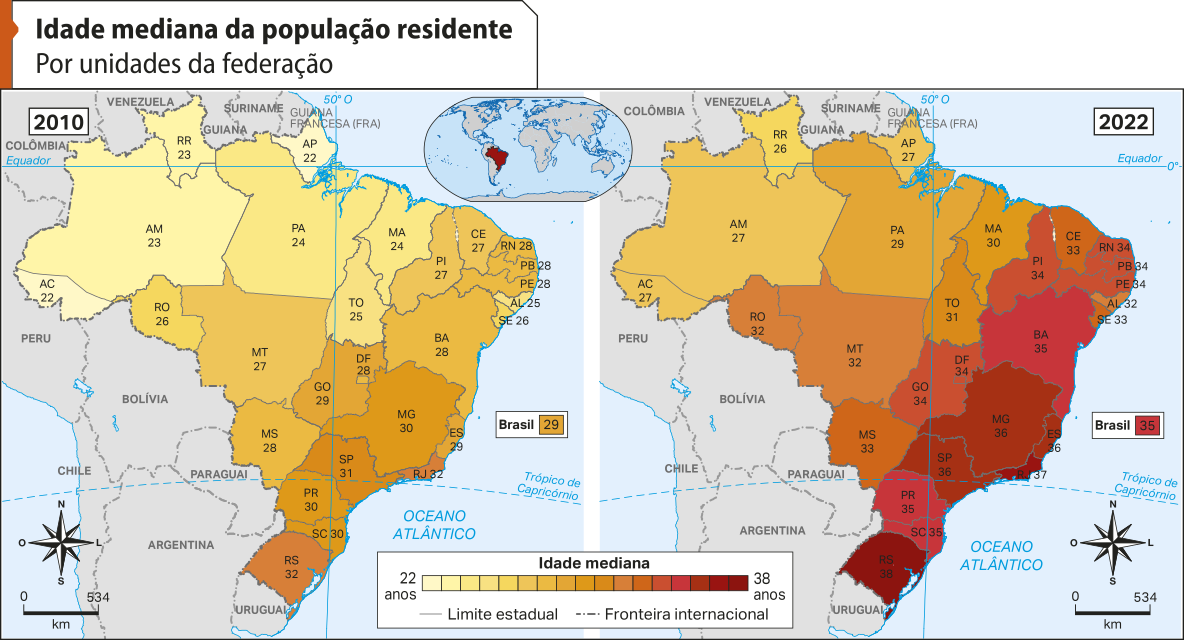
Elaborados com base em: GOMES, Irene; BRITTO, Vinícius. Censo 2022: número de pessoas com 65 anos ou mais de idade cresceu 57,4% em 12 anos. Rio de Janeiro: Agência hí bê gê hé Notícias, 1 nov. 2023. Disponível em: https://livro.pw/sdmhq. Acesso em: 23 jul. 2024.
Agora, faça o quê se pede em cada item.
a) Somente comparando as cores nos mapas, o quê você póde dizêr sobre a idade mediana no Brasil e em cada uma das Unidades da Federação?
Espera-se quê os estudantes percêbam quê, no mapa de 2022, as tonalidades de todas as regiões são mais escuras quê no mapa de 2010, indicando quê a idade mediana aumentou em todas as Unidades da Federação.
b) Compare agora os valores em cada Unidade da Federação. Houve algum local onde a idade mediana diminuiu?
Não. Em todos os locais indicados, a idade mediana aumentou.
c) A idade mediana no Brasil aumentou quantos anos de 2010 para 2022?
Aumentou 6 anos.
d) Procure nos mapas o estado em quê você mora e compare a idade mediana nos anos de 2010 e 2022. De quanto foi a variação na idade mediana?
Resposta pessoal.
e) ![]() Elabore uma pergunta quê possa sêr respondida com os mapas. Em seguida, troque-a com um colega para quê você responda à pergunta quê ele elaborou e ele responda à sua pergunta.
Elabore uma pergunta quê possa sêr respondida com os mapas. Em seguida, troque-a com um colega para quê você responda à pergunta quê ele elaborou e ele responda à sua pergunta.
Resposta pessoal.
Para assistir
• FECUNDIDADE no Brasil: hí bê gê hé Explica. [S. l.: s. n.], 2019. 1 vídeo (3 min). Publicado pelo canal hí bê gê hé. Disponível em: https://livro.pw/xjgyv. Acesso em: 23 jul. 2024.
O vídeo explica o quê é taxa de fecundidade e como esse índice influencía o envelhecimento da população.
Página setenta e quatro
mêdídas de dispersão
As medidas de tendência central nem sempre são suficientes para a análise de um conjunto de dados. Acompanhe o exemplo.
A tabéla apresenta os índices pluviométricos, em milimetro, nos seis primeiros meses do ano em duas regiões, A e B.
Índice pluviométrico (em milimetro)
Mês Jan. |
Mês Fev. |
Mês Mar. |
Mês Abr. |
Mês Maio |
Mês Jun. |
Média semestral |
|
|---|---|---|---|---|---|---|---|
Região A |
52,3 |
44,7 |
36,8 |
37,4 |
26,0 |
18,8 |
36,0 |
Região B |
80,6 |
58,6 |
35,4 |
20,1 |
12,3 |
9,0 |
36,0 |
Fonte: Dados fictícios.
Saiba quê...
O índice pluviométrico refere-se à quantidade de chuva por métro quadrado em determinada região e por determinado período. Cada 1 mm de chuva indica quê, para cada métro quadrado da região, choveu 1 litro de á gua.
Comparando os dados da tabéla, obissérve quê a região B apresentou os dois maiores (em vermelho) e os dois menóres (em azul) índices pluviométricos, por isso sua variação pluviométrica foi maior do quê a variação da região A. Em outras palavras, podemos dizêr quê a região A, em relação à região B, apresentou índices mais regulares (mais homogêneos), com menóres oscilações pluviométricas durante esse período.
No exemplo, a média aritmética não foi suficiente para indicar qual das regiões teve as maiores, ou menóres, oscilações pluviométricas. Quando precisamos caracterizar o grau de dispersão, ou de homogeneidade, de um conjunto de dados, utilizamos as medidas de dispersão.
Neste tópico, vamos estudar quatro medidas de dispersão: amplitude, desvio médio, variância e desvio padrão.
Amplitude
Você estudou, anteriormente, como calcular a amplitude total e a de cada intervalo quando agrupou os dados em classes para construir uma tabéla de freqüências. Essa medida póde sêr usada para verificar a dispersão dos dados observados. Acompanhe, por exemplo, a seguinte situação.
Em uma produção de peças de metal para cérto equipamento, o contrôle de qualidade precisa verificar o comprimento, em milimetro, dessas peças. Para isso, foram selecionadas, em dois dias, nove dessas peças, conforme indicado a seguir.
1º dia |
234 |
234 |
231 |
233 |
235 |
234 |
234 |
234 |
234 |
|---|---|---|---|---|---|---|---|---|---|
2º dia |
234 |
231 |
234 |
240 |
234 |
234 |
239 |
234 |
234 |
Para calcular a amplitude dos dados obtidos em cada dia, vamos identificar o menor e o maior valor observado em cada dia; depois, calculamos a diferença entre eles.
• 1º dia: o menor valor é 231 mm, e o maior, 235 mm; portanto, a amplitude é:
235 mm − 231 mm = 4 mm
• 2º dia: o menor valor é 231 mm, e o maior, 240 mm; portanto, a amplitude é:
240 mm − 231 mm = 9 mm
Página setenta e cinco
Observe quê a amplitude do primeiro dia foi 4 mm, e a do segundo dia foi 9 mm. Isso indica quê as peças produzidas no primeiro dia tiveram menor variação de medida.
Por se tratar de uma produção de peças de metal, provavelmente se tem uma tolerância aceitável de variação de medida, mas note quê, no 2º dia, essa variação foi quase de 10 mm, ou seja, 1 cm.

Pense e responda
O contrôle de qualidade identificou quê a maioria das peças dessa amostra está com a medida ideal para o funcionamento do equipamento em quê essa peça será acoplada. Observando os valores de cada dia, qual é a medida ideal? Como é chamado, em Estatística, esse valor?
234 mm; (Moda)
Desvio médio
Para estudar o desvio médio, vamos considerar as notas bimestrais de um estudante de Matemática durante um ano letivo.
Bimestre |
1º |
2º |
3º |
4º |
|---|---|---|---|---|
Notas |
5 |
8 |
6 |
9 |
Agora, vamos calcular a média aritmética das notas dêêsse estudante:
= 7
Calculamos, em seguida, as diferenças entre cada uma das notas e a média aritmética. Essas diferenças são chamadas de desvios em relação à média, ou simplesmente desvios.
• x1 − = 5 − 7 = −2
• x2 − = 8 − 7 = 1
• x3 − = 6 − 7 = −1
• x4 − = 9 − 7 = 2
Definimos o desvio médio (dm) como a média aritmética dos valores absolutos dos desvios .
dm =
Saiba quê...
O sín-bolo indica o somatório, ou seja, a soma dos valores de índice 1 até n para a expressão Ai. Por exemplo, indica 12 + 22 + 32 = 14.
Página setenta e seis
Em nosso exemplo, temos:
dm =
dm = = 1,5
Assim, o desvio médio das notas é 1,5. Isso significa quê, na média, cada nota ficou 1,5 distante da nota média.
Variância e desvio padrão
A variância e o desvio padrão, assim como o desvio médio, são medidas quê quantificam o grau de dispersão de um conjunto de dados em relação à média. Quanto maiores são a variância e o desvio padrão, maior é a dispersão dos dados em relação à média e vice-versa.
Definimos a variância (Va) como a média aritmética dos quadrados dos desvios (xi− .
Va =
O desvio padrão (Dp) é dado pela raiz quadrada da variância.
Dp =
A unidade de medida do desvio padrão é a mesma dos dados analisados.
Para exemplificar, obissérve a quantidade e a média de pontos quê dois jogadores de basquete fizeram em quatro partidas de um campeonato.
Jogador |
Partida 1 |
Partida 2 |
Partida 3 |
Partida 4 |
Média de pontos |
|---|---|---|---|---|---|
A |
12 |
20 |
8 |
32 |
18 |
B |
15 |
19 |
17 |
21 |
18 |
Observe, no qüadro, quê os dois jogadores têm a mesma média de 18 pontos. No entanto, a pontuação mínima e a mássima do jogador B foram 15 e 21 pontos, enquanto as do jogador A foram 8 e 32. Vamos analisar o grau de dispersão dessas pontuações em relação à média por meio da variância e do desvio padrão.
Va (jogador A) = = 84
Dp (jogador A) = ≃ 9, 2
Va (jogador B) = = 5
Dp (jogador B) = ≃ 2, 2

Pense e responda
A variância póde sêr um número negativo? O quê significa um desvio padrão igual a zero?
Não, a variância é sempre um número não negativo.
Se o desvio padrão é zero, então a variância também é zero; isso só acontece quando todos os valores do conjunto de dados são iguais.
O jogador B apresentou a menor variância e, consequentemente, o menor desvio padrão de pontuações. Isso aconteceu porque os menóres desvios de pontos marcados em relação à média foram do jogador B. Nesse contexto, os dois jogadores tiveram a mesma média de pontos, mas podemos afirmar quê o jogador B teve um dêsempênho mais equilibrado, mais regular, de pontos marcados nas quatro partidas ou quê o dêsempênho do jogador A foi mais inconsistente, isto é, a quantidade de pontos marcados variou mais em cada partida.
Página setenta e sete
ATIVIDADES RESOLVIDAS
5. Uma empresa, para aumentar a produção de anéis de vedação de borracha, comprou duas máquinas. O contrôle de qualidade registrou as massas, em grama, dos oito primeiros anéis fabricados por cada máquina.
Máquina 1 |
20 |
19 |
20 |
20 |
21 |
20 |
19 |
21 |
|---|---|---|---|---|---|---|---|---|
Máquina 2 |
20 |
20 |
19 |
20 |
20 |
20 |
21 |
20 |
Calcule os desvios médios das massas dos anéis de borracha produzidos em cada máquina.
Em seguida, compare os dois valores e explique o quê eles indicam.
Resolução
Primeiro, vamos calcular as massas médias dos anéis produzidos em cada máquina.
O desvio médio (dm)é a média aritmética dos valores absolutos dos desvios, logo:
dm máquina 1 =
dm máquina 2 =
O desvio médio da máquina 1 foi 0,5 grama e o da máquina 2 foi 0,25 grama. Isso mostra quê a máquina 2 foi mais eficiente em garantir pouca variação das massas dos anéis de borracha confeccionados.
6. Nos últimos anos, por causa das mudanças climáticas e da sazonalidade, produtos alimentícios têm sofrido grandes variações de preêço. Observe o preêço por kilograma de dois alimentos no primeiro semestre de 2024.
preêço por kilograma no primeiro semestre de 2024
Mês Jan. |
Mês Fev. |
Mês Mar. |
Mês Abr. |
Mês Maio |
Mês Jun. |
|
|---|---|---|---|---|---|---|
Alimento A |
R$ 12,00 |
R$ 15,00 |
R$ 12,00 |
R$ 16,00 |
R$ 14,00 |
R$ 15,00 |
Alimento B |
R$ 12,00 |
R$ 11,00 |
R$ 18,00 |
R$ 9,00 |
R$ 19,00 |
R$ 15,00 |
Fonte: Dados fictícios.
a) Calcule o desvio padrão dos preços de cada alimento. Em seguida, responda: qual dos dois alimentos sofreu a maior variação de preêço?
b) Elabore um fluxograma com as etapas para calcular o desvio padrão de um conjunto de dados.
Resolução
a) Inicialmente, vamos calcular o preêço médio por kilograma dos dois alimentos no semestre.
Página setenta e oito
Em seguida, calculamos os desvios e os quadrados dos desvios.
A |
Xi − |
12 − 14 = −2 |
15 − 14 = 1 |
12 − 14 = −2 |
16 − 14 = 2 |
14 − 14 = 0 |
15 − 14 = 1 |
|---|---|---|---|---|---|---|---|
(Xi −)2 |
(−2)2 = 4 |
(1)2 = 1 |
(−2)2 = 4 |
(2)2 = 4 |
(0)2 = 0 |
(1)2 = 1 |
|
B |
Xi − |
12 − 14 = −2 |
11 − 14 = −3 |
18 − 14 = 4 |
9 − 14 = −5 |
19 − 14 = 5 |
15 − 14 = 1 |
(Xi − )2 |
(−2)2 = 4 |
(−3)2 = 9 |
(4)2 = 16 |
(−5)2 = 25 |
(5)2 = 25 |
(1)2 = 1 |
Agora, vamos determinar as variâncias.
Por fim, determinamos os desvios padrão.
O alimento B sofreu a maior variação de preços, pois seu desvio padrão foi superior ao desvio padrão do alimento A.
b) Para calcular o desvio padrão de um conjunto de dados, podemos seguir as etapas indicadas no fluxograma a seguir.
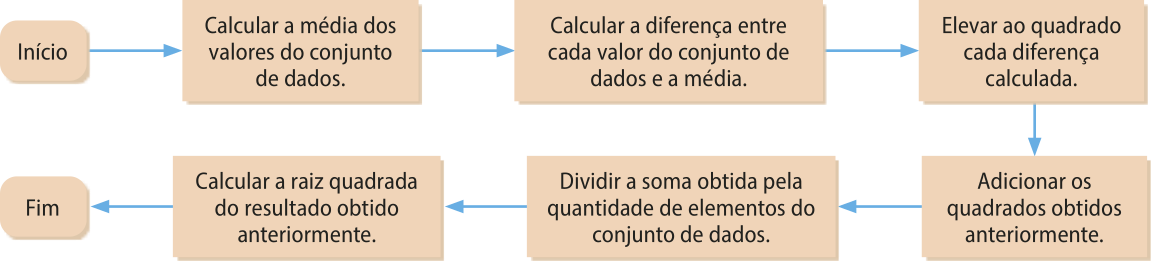
ATIVIDADES
24. Dois atletas anotaram seus tempos, em minuto, das cinco últimas meias maratonas.
Atleta 1 |
112 |
120 |
130 |
117 |
121 |
|---|---|---|---|---|---|
Atleta 2 |
115 |
124 |
122 |
120 |
119 |
a) Calcule o desvio médio dos tempos de cada atleta.
dm1 = 4,4 dm2 = 2,4
b) Calcule a variância e o desvio padrão dos tempos de cada atleta.
Va1 = 34,8; Dp1 ≃ 5,9
Va2 = 9,2; Dp2 ≃ 3,03
c) Qual dos atletas teve uma perfórmance mais regular nessas corridas? Justifique.
O atleta 2, pois tanto o desvio médio quanto o desvio padrão dêêsse atleta foram inferiores ao desvio médio e ao desvio padrão do atleta 1.

Página setenta e nove
25. Um teste de qualidade estimou o tempo de duração, em mil horas, de cinco lâmpadas LED de duas marcas diferentes.
Marca 1 |
32 |
28 |
41 |
48 |
36 |
|---|---|---|---|---|---|
Marca 2 |
26 |
49 |
45 |
31 |
34 |
a) De acôr-do com essas estimativas, determine, para cada marca de lâmpada, a amplitude, o desvio médio e o desvio padrão dêêsses tempos.
A1 = 20; dm1 = 6; Dp1 ≃ 6,99 A2 = 23; dm2 = 8; Dp2 ≃ 8,65
b) Qual das marcas apresentou o dêsempênho mais regular? Por quê?
A marca 1, pois as durações das lâmpadas dessa marca tiveram amplitude, desvio médio e desvio padrão inferiores às medidas correspondentes das lâmpadas da marca 2.
26. Duas empresas fizeram anúncios fora do padrão em suas rêdes sociais para incentivar profissionais a se candidatarem às vagas oferecidas.


Se você pudesse escolher uma dessas empresas para trabalhar, considerando apenas os salários, qual você escolheria? Justifique.
Resposta pessoal. Ver as Orientações para o professor.
27. (Enem/MEC) Em uma corrida de regularidade, a equipe campeã é aquela em quê o tempo dos participantes mais se aproxima do tempo fornecido pêlos organizadores em cada etapa. Um campeonato foi organizado em 5 etapas, e o tempo médio de próva indicado pêlos organizadores foi de 45 minutos por próva. No qüadro, estão representados os dados estatísticos das cinco equipes mais bem classificadas.
Dados estatísticos das equipes mais bem classificadas (em minutos)
Equipes |
Média |
Moda |
Desvio padrão |
|---|---|---|---|
Equipe I |
45 |
40 |
5 |
Equipe II |
45 |
41 |
4 |
Equipe III |
45 |
44 |
1 |
Equipe IV |
45 |
44 |
3 |
Equipe V |
45 |
47 |
2 |
Fonte: Dados fictícios.
Utilizando os dados estatísticos do qüadro, a campeã foi a equipe
alternativa c
a) I.
b) II.
c) III.
d) IV.
e) V.
28. Anote a medida da altura, em centimetro, de todos os estudantes da sua turma e faça o quê se pede.
Respostas pessoais.
a) Construa uma tabéla de distribuição de freqüências de dados agrupados, considerando intervalos com 2 cm de amplitude.
b) Calcule as medidas da altura média e da mediana.
c) Calcule o desvio padrão das medidas das alturas.
d) O quê se póde concluir com base nos cálculos feitos?
29. ![]() Elabore um problema envolvendo a comparação de dois conjuntos de dados por meio de medidas estatísticas. Troque seu problema com um colega e resôuva o problema elaborado por ele.
Elabore um problema envolvendo a comparação de dois conjuntos de dados por meio de medidas estatísticas. Troque seu problema com um colega e resôuva o problema elaborado por ele.
Resposta pessoal. Ver as Orientações para o Professor.
Página oitenta
Box-plot
O box-plot, ou diagrama de caixa, é utilizado para representar a dispersão de dados de uma variável quantitativa. Sua estrutura consiste em uma caixa retangular com linhas saindo de suas extremidades e limitadas superior e inferiormente.
Ao construir um box-plot, usa-se um eixo real para localizar os pontos correspondentes aos valores: mínimo; mássimo; discrepantes; do primeiro quartil (Q1); do segundo quartil (Q2); e do terceiro quartil (Q3). Observe.
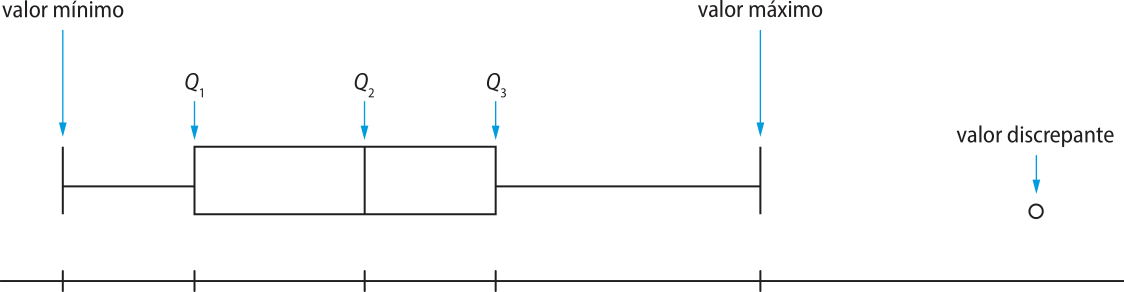
Fonte: Dados fictícios.
Para determinar os quartis, os dados quantitativos devem sêr organizados em ordem crescente. Os quartis dividem o conjunto em quatro partes com a mesma quantidade de elemêntos. Para isso, Q2 é a mediana do conjunto de dados, Q1 é a mediana dos dados inferiores a Q2, e Q3 é a mediana dos dados superiores a Q2.
O exemplo a seguir mostra como construir um box-plot.
Em uma sala com 27 estudantes, o professor registrou, em ordem crescente, o tempo, em minuto, quê cada um levou para fazer sua avaliação.
5; 21; 25; 25; 25; 28; 30; 32; 32; 32; 35; 36; 36; 38; 39; 40; 40; 40; 41; 43; 44; 45; 45; 45; 45; 50; 50
Para representar esses valores em um box-plot, podemos seguir os passos apresentados.
1º) Determinamos o valor do segundo quartil (Q2).
Q2 é a mediana do conjunto de dados. Como temos 27 dados em ordem crescente, a mediana será o 14º dado, então Q2 = 38.
2º) Determinamos o valor do primeiro quartil (Q1).
Q1 é a mediana dos dados inferiores a Q2. Há 13 dados inferiores a Q2; logo, a mediana será o 7º dado, ou seja, Q1 = 30.
3º) Determinamos o valor do terceiro quartil (Q3).
Q3 é a mediana dos dados superiores a Q2. Nesse caso, a mediana será o 21º dado, isto é, Q3 = 44.
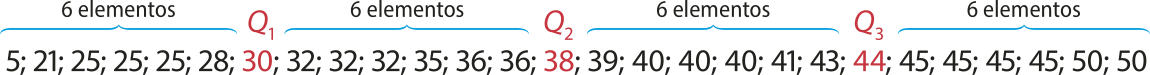
4º) Verificamos se existem valores discrepantes.
Um valor é considerado discrepante se for menor do quê Q1 − 1,5(Q3 − Q1) ou maior do quê Q3 + 1,5(Q3 − Q1), assim:
Q1 − 1,5(Q3 − Q1) = 30 − 1,5(44 − 30) = 9
Q3 + 1,5(Q3 − Q1)= 44 + 1,5(44 − 30) = 65
O valor 5 é um dado menor do quê 9, portanto 5 é um valor discrepante.
Página oitenta e um
5º) Identificamos os valores mínimo e mássimo desconsiderando os valores discrepantes.
Valor mínimo = 21
Valor mássimo = 50
6º) Desenhamos o box-plot considerando os valores encontrados.
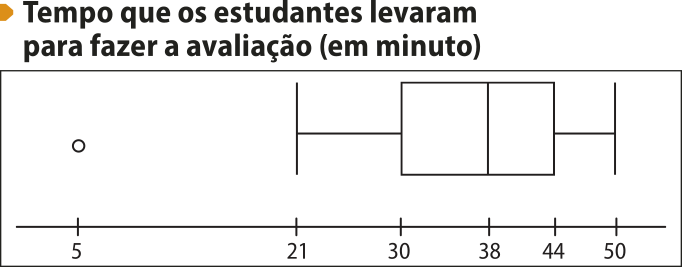
Fonte: Dados fictícios.
Saiba quê...
O box-plot póde sêr representado na vertical ou na horizontal. Os valores discrepantes podem sêr representados no diagrama por uma bó-linha ou um asterisco.
Pelo diagrama, podemos identificar, por exemplo, quê mêtáde dos estudantes rêzouvêo a avaliação em até 38 minutos, 25% dos estudantes demoraram, no mínimo, 44 minutos para solucionar a próva e 50% resolveram a avaliação no intervalo de 30 a 44 minutos.
Diagrama de ramo e fô-lhas
Um modo de organizar dados de uma variável quantitativa em ordem crescente e, ao mesmo tempo, mostrar sua distribuição de freqüências é confeccionando um diagrama de ramo e fô-lhas.
Acompanhe o exemplo.
Idade dos professores |
|||||||
|---|---|---|---|---|---|---|---|
50 |
45 |
62 |
70 |
45 |
50 |
48 |
37 |
47 |
48 |
60 |
44 |
48 |
58 |
53 |
47 |
56 |
75 |
38 |
39 |
37 |
65 |
72 |
71 |
50 |
63 |
49 |
50 |
45 |
39 |
40 |
61 |
Uma faculdade registrou em um qüadro a idade de seus 32 professores.
Para montar um diagrama de ramo e fô-lhas com esses dados, podemos executar os seguintes passos.
1º) Colocamos as idades em ordem crescente.
37; 37; 38; 39; 39; 40; 44; 45; 45; 45; 47; 47; 48; 48; 48; 49; 50; 50; 50; 50; 53; 56; 58; 60; 61; 62; 63; 65; 70; 71; 72; 75
2º) Escrevemos em cada linha apenas as idades com dezenas iguais.
37; 37; 38; 39; 39
40; 44; 45; 45; 45; 47; 47; 48; 48; 48; 49
50; 50; 50; 50; 53; 56; 58
60; 61; 62; 63; 65
70; 71; 72; 75
3º) Montamos o diagrama em duas colunas, separadas por um traço vertical. Na primeira coluna, escrevemos os algarismos das dezenas de cada idade e, na segunda coluna, escrevemos os algarismos correspondentes das unidades de cada idade.

Fonte: Dados fictícios.
Página oitenta e dois
Pelo diagrama de ramo e fô-lhas construído, podemos concluir quê:
• três professores têm 48 anos;
• a (Moda) (Mo)das idades é 50 anos;
• 11 professores têm de 40 a menos de 50 anos;
• a amplitude das idades é 38 anos, pois 75 − 37 = 38.
A primeira coluna do diagrama é denominada ramo, e a segunda, fô-lhas. Os ramos e as fô-lhas podem representar qualquer ordem de grandeza; por isso, o diagrama deve sempre ter uma legenda, indicando o quê significam o ramo e as fô-lhas. Observe alguns exemplos de legenda.
Legenda: 3 | 21 = 3,21 cm
Legenda: 42 | 6 = 426 kg
ATIVIDADES RESOLVIDAS
7. O diagrama de caixa representa as distâncias, em kilometro, das 50 entregas quê um mótobói fez em um mês.
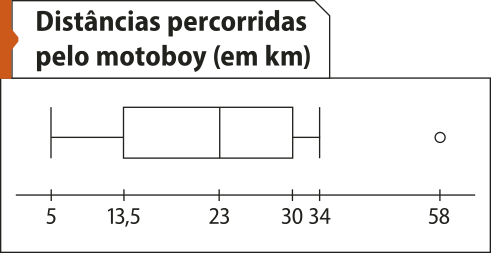
Fonte: Dados fictícios.
De acôr-do com o gráfico, classifique cada afirmação em verdadeira (V) ou falsa (F) e justifique sua resposta.
I. A viagem mais curta quê o mótobói fez tinha 5 km, e a mais longa tinha 34 km.
II. Na mêtáde das viagens, o mótobói percorreu, no mínimo, 23 km.
III. Em 49 das 50 entregas, o mótobói percorreu, no mássimo, 30 km.
IV. Em 75% das viagens, o mótobói percorreu, pelo menos, 13,5 km.
Resolução
I. Falsa. A distância da viagem mais curta está correta. No entanto, a viagem mais longa tinha 58 km.
II. Verdadeira. O valor do segundo quartil, Q2 = 23, é a mediana do conjunto de dados.
III. Falsa. Em 49 das 50 entregas, o mótobói percorreu, no mássimo, 34 km.
IV. Verdadeira. 25% dos dados estão antes do primeiro quartil, Q1 = 13,5; logo, em 75% das viagens, o mótobói percorreu, pelo menos, 13,5 km.
8. O diagrama de ramo e fô-lhas a seguir apresenta a quantidade de passageiros quê uma linha de ônibus transportou durante 41 dias seguidos.
Analise o diagrama e responda às kestões.

Fonte: Dados fictícios.
a) Qual foi a quantidade mínima de passageiros transportados? E a mássima?
b) Quantos passageiros essa linha de ônibus transportou na maioria dos dias?
c) Qual é a mediana dêêsse conjunto de dados? O quê ela representa?
Resolução
a) A quantidade mínima foi 155 passageiros, e a mássima, 192.
b) Na maioria dos dias, a linha transportou 169 passageiros.
c) Há 41 dados em ordem crescente no diagrama, logo a mediana (Md) é o 21º dado, isto é, Md = 169. Ela indica quê, na mêtáde dos dias, foram transportados, no mássimo, 169 passageiros.
Página oitenta e três
ATIVIDADES
30. No qüadro a seguir, apresenta-se o número de kestões acertadas por estudante em determinado exame aplicado a 43 estudantes do Ensino Médio.
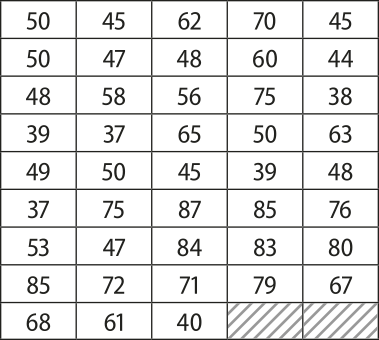
a) Apresente esses dados em um diagrama de ramo e fô-lhas.
Ver as Orientações para o professor.
b) Determine a mediana e a (Moda) de kestões acertadas.
mediana: 56 kestões; (Moda): 50 kestões
c) Calcule o percentual da turma quê acertou, no mínimo, 70 kestões.
aproximadamente 30,23%
d) Agora, construa um histograma com esses dados considerando o primeiro intervalo como [30, 40[ e representando as freqüências absolutas no eixo vertical.
Ver as Orientações para o professor.
e) Qual das representações gráficas você achou quê é mais adequada para representar os dados: o histograma ou o diagrama de ramo e fô-lhas?
Resposta pessoal. Espera-se quê os estudantes percêbam quê as duas representações são adequadas, dependendo da intenção de quem está fazendo o gráfico. O histograma permite visualizar de maneira mais imediata a freqüência de cada intervalo, já o diagrama de ramo e fô-lhas preserva cada dado da amostra.
31. Observe o diagrama de caixa quê representa as idades, em ano, dos estudantes de uma turma de Educação de Jovens e Adultos (EJA) e responda.
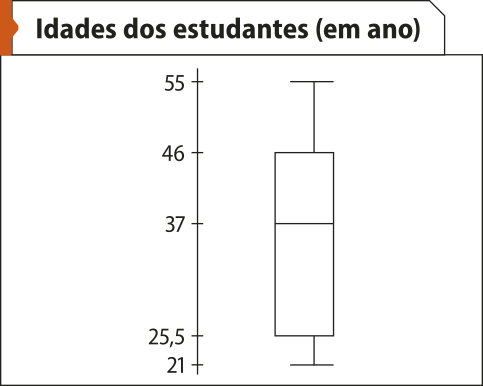
Fonte: Dados fictícios.
a) Qual é a idade do estudante mais novo matriculado nessa turma? E a do estudante mais velho?
21 anos. 55 anos
b) pôdêmos dizêr quê 75% dos estudantes dessa turma têm menos do quê 46 anos? Explique sua resposta.
Ver as Orientações para o professor.
c) Há mais estudantes com idade entre 21 e 25,5 anos ou entre 46 e 55 anos? Justifique sua resposta.
Ver as Orientações para o professor.
d) O quê 37 indica nesse gráfico?
Ver as Orientações para o professor.
32. ![]() Elabore uma situação-problema envolvendo o diagrama de ramo e fô-lhas a seguir. Troque sua situação-problema com a de um colega e resôuva a situação proposta por ele. Depois, verifiquem se as resoluções estão corretas. Não se esqueça de dar um título ao diagrama e de adicionar uma legenda condizente com sua situação-problema.
Elabore uma situação-problema envolvendo o diagrama de ramo e fô-lhas a seguir. Troque sua situação-problema com a de um colega e resôuva a situação proposta por ele. Depois, verifiquem se as resoluções estão corretas. Não se esqueça de dar um título ao diagrama e de adicionar uma legenda condizente com sua situação-problema.
Resposta pessoal.

Fonte: Dados fictícios.
33. ![]() Os dados indicam a validade, em meses, de 32 medicamentos estocados em uma farmácia.
Os dados indicam a validade, em meses, de 32 medicamentos estocados em uma farmácia.
Resposta pessoal.
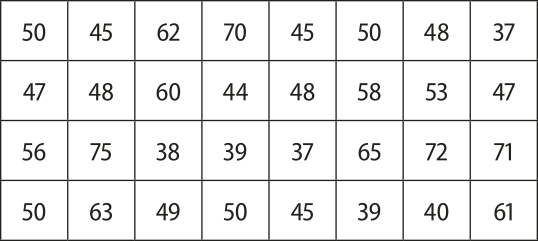
Represente esses dados em um diagrama de caixa. Depois, elabore duas kestões sobre seu diagrama e peça a um colega quê as responda, enquanto você responde às kestões dele. Por fim, confiram juntos as resoluções.
Página oitenta e quatro
EXPLORANDO A TECNOLOGIA
Conhecendo o GeoGebra
Orientar os estudantes a navegar pelo sáiti do GeoGebra, pois nele há uma comunidade de discussão e muitas informações disponíveis, inclusive alguns tutoriais e materiais produzidos por professores.
O GeoGebra é um software de Matemática dinâmica quê póde sêr utilizado em todos os níveis de ensino. Trata-se de uma multiplataforma, pois tem portabilidade em todos os sistemas operacionais e póde sêr instalada em computadores, tablets e smartphones.
Sua instalação deve sêr feita por meio do sáiti oficial https://livro.pw/jtbfa (acesso em: 23 jul. 2024), baixando-se o software GeoGebra Clássico 6 e seguindo-se as orientações de instalação.
O GeoGebra também póde sêr usado em sua versão ôn láini, sem a necessidade de instalação, pelo sáiti https://livro.pw/otpjb (acesso em: 23 jul. 2024).
Ao abrir o software instalado ou a versão ôn láini, aparece uma tela inicial composta de várias janelas, com ferramentas e exibições específicas de acôr-do com a utilização. A seguir, apresentamos a tela inicial com algumas de suas funções.

Página oitenta e cinco
Além da janela de Álgebra e da janela de visualização, quê são mostradas na tela inicial padrão, o GeoGebra tem outras janelas, quê, dependendo da construção quê se deseja realizar, podem sêr acionadas no menú Exibir. Quando necessário, essas outras janelas serão exibidas durante a realização das construções.
Todas as janelas do GeoGebra estão relacionadas dinamicamente, ou seja, ao se realizar uma alteração em algum objeto em uma delas, todas as representações dêêsse mesmo objeto nas demais janelas serão alteradas automaticamente.
O GeoGebra utiliza linguagem e notação próprias, quê podem diferir um pouco das utilizadas nesta Coleção. Por exemplo, para a separação da parte decimal de um número, o software usa o ponto no lugar da vírgula; para indicar as coordenadas de um ponto A qualquer, a notação é A = (0,0), em vez de A(0, 0). Ao longo da Coleção, conforme necessário, apresentaremos outras particularidades do GeoGebra.
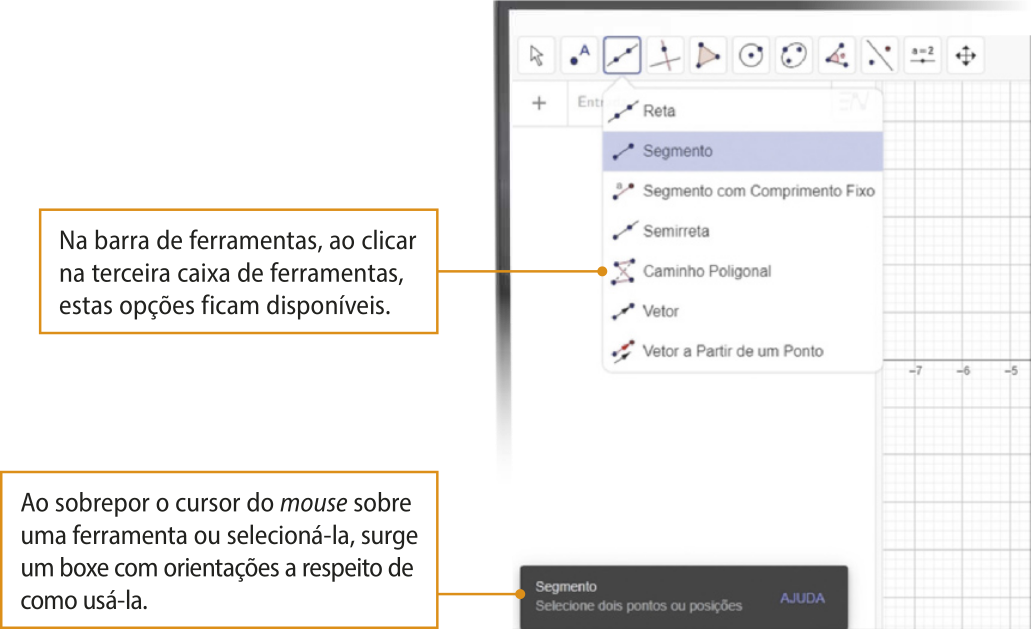
Criando diagrama de ramo e fô-lhas e box-plot no GeoGebra
Neste Capítulo, estudamos como construir e interpretar um diagrama de ramo e fô-lhas e um box-plot. Essas são importantes representações gráficas quê sérvem para analisar a distribuição dos dados de um conjunto. Agora, vamos utilizar o GeoGebra para criar esses diagramas.
Inicialmente, devemos configurar o GeoGebra para auxiliar nossas construções.
Depois de abri-lo, clique em Exibir e, em seguida, selecione Planilha. Vai aparecer uma janela com uma planilha ao lado da janela de visualização. Na sequência, clique no menú Configurações e, no ícone ![]() , clique na opção EixoY e desabilite a visualização do eixo y. Nessa construção, usaremos apenas o eixo horizontal.
, clique na opção EixoY e desabilite a visualização do eixo y. Nessa construção, usaremos apenas o eixo horizontal.
Página oitenta e seis
Diagrama de ramo e fô-lhas
Para criar um diagrama de ramo e fô-lhas, vamos considerar como exemplo a seguinte amostra das idades de 15 pessoas e seguir os passos indicados.
A = {2, 5, 10, 12, 15, 17, 22, 23, 28, 31, 34, 35, 42, 47, 51}
I. Digitamos na planilha os dados de nossa amostra na coluna A da seguinte forma: o número 2 na célula A1, o número 5 na célula A2, o número 10 na célula A3, e assim por diante.
II. Após digitar todos os elemêntos de nossa amostra, ela vai ocupar as células A1 a A15. Em seguida, digitamos, no campo de entrada, o comando "DiagramaDeCauleEFolhas(A1:A15)". Pressionando Enter, o diagrama de ramo e fô-lhas será criado na janela de Álgebra e aparecerá na janela de visualização.
É importante observar quê podemos digitar os dados em qualquer coluna e indicar a célula inicial e a final da nossa lista de elemêntos, desde quê eles ocupem uma mesma coluna.
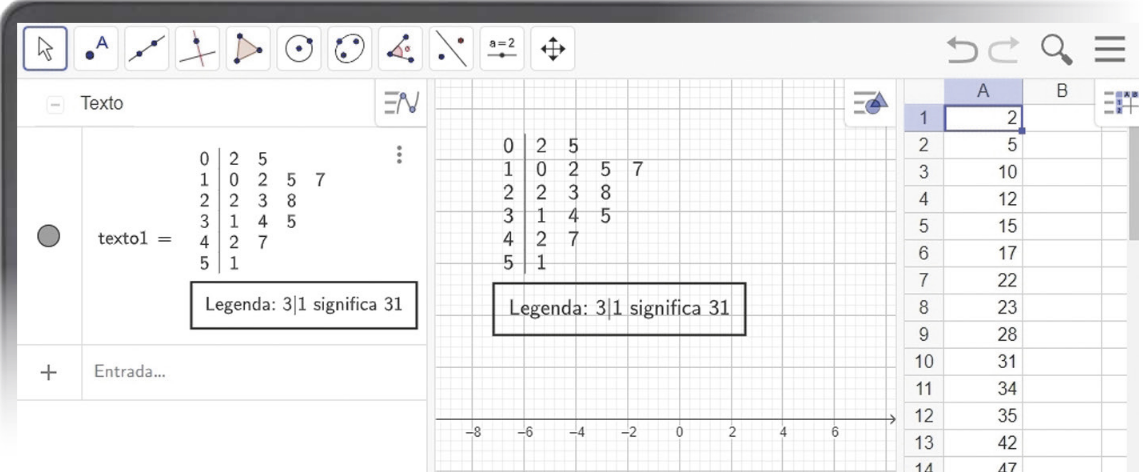
Por sêr um texto, você póde deslocar o diagrama pela janela de visualização de acôr-do com sua necessidade.
Box-plot
Para criar um box-plot, vamos utilizar o mesmo conjunto A = {2, 5, 10, 12, 15, 17, 22, 23, 28, 31, 34, 35, 42, 47, 51} e o quê já produzimos para o diagrama de ramo e fô-lhas, acompanhando o seguinte passo.
I. Como os valores já estão digitados na planilha do GeoGebra, digitamos, no campo de entrada, o comando"BoxPlot(a,b,A1:A15)" e pressionamos Enter.
Página oitenta e sete
Depois dêêsse processo, o GeoGebra apresentará o box-plot referente à nossa amostra na janela de visualização. póde sêr quê, por causa dos dados da amostra, o diagrama não apareça totalmente na tela. Caso isso ocorra, talvez seja necessário ajustar as dimensões da janela usando o botão Reduzir ![]() ou a ferramenta Mover janela de visualização
ou a ferramenta Mover janela de visualização ![]() conforme a necessidade.
conforme a necessidade.
Observe quê serão criados dois controles deslizantes na janela de Álgebra. O contrôle deslizante a sérve para deslocar o box-plot na vertical. Já o contrôle deslizante b sérve para ajustar a largura do box-plot, a fim de facilitar ou permitir sua leitura.
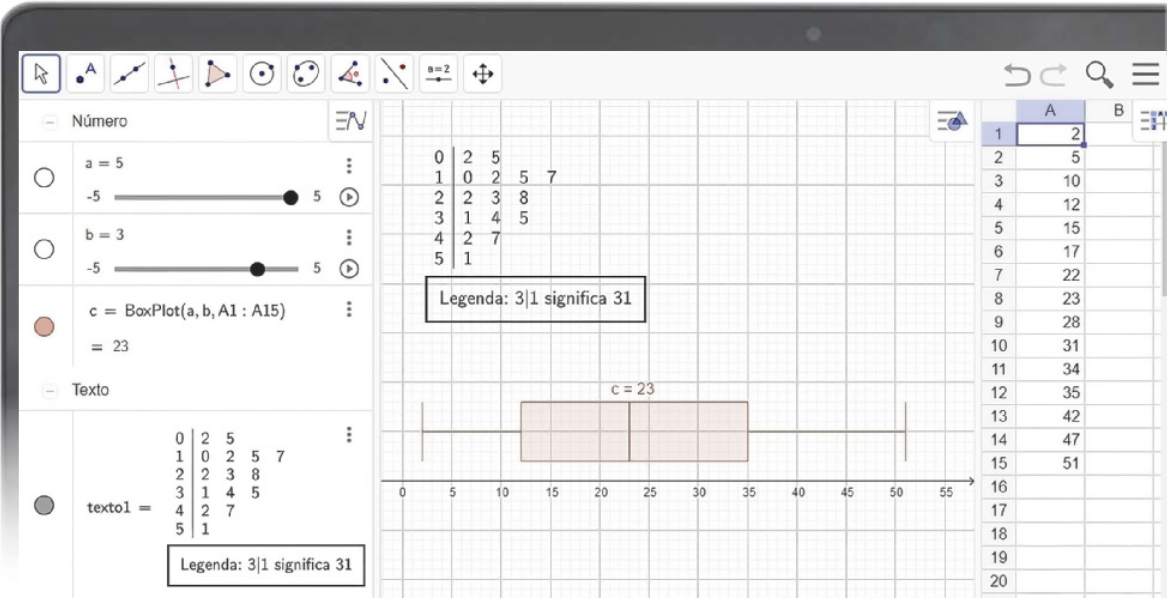
Agora, faça o quê se pede nas atividades a seguir.
1. Qual dos dois diagramas você achou quê representa melhor os dados? Caso você precisasse identificar posteriormente a freqüência absoluta de cada uma das idades, qual dos dois tipos de gráfico você escolheria? Em qual deles você acha quê é possível identificar com mais facilidade a mediana do conjunto de dados?
1. Respostas pessoais. Espera-se quê os estudantes percêbam quê somente no diagrama de ramo e fô-lhas é possível identificar a freqüência absoluta de cada dado e quê no box-plot é mais fácil identificar a mediana, apesar de sêr possível identificá-la também no diagrama de ramo e fô-lhas.
2. Anote a idade de 10 pessoas de cada turma do Ensino Médio da escola em quê você estuda. Escolha essas pessoas aleatoriamente. Em seguida, usando o GeoGebra, construa um diagrama de ramo e fô-lhas e um box-plot com os dados coletados. Por fim, escrêeva uma conclusão a respeito do quê você pôdi observar por meio dos gráficos.
Resposta pessoal.
3. ![]() Reúna-se a um colega, e comparem os gráficos construídos. Vocês, provavelmente, selecionaram pessoas diferentes para a amostra. Os gráficos ficaram parecidos?
Reúna-se a um colega, e comparem os gráficos construídos. Vocês, provavelmente, selecionaram pessoas diferentes para a amostra. Os gráficos ficaram parecidos?
Resposta pessoal.
Página oitenta e oito
CONEXÕES com...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS e CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Amazônea Legal
Você já ouviu falar sobre a Amazônea Legal? Leia, a seguir, algumas informações sobre ela.
[…] há o termo Amazônea Legal […] instituído pelo govêrno brasileiro em 1953, buscando promover o desenvolvimento socioeconômico de estados da Região Amazônica quê compartilhavam historicamente os mesmos desafios econômicos, políticos e sociais. Engloba a totalidade de oito estados (Acre, Amapá, Amazonas, Mato Grosso, Pará, Rondônia, Roraima e Tocantins) e parte do Maranhão (a oeste do meridiano de 44°W), totalizando 5 milhões de km2. […]
[...]
Amazônea? Rio Amazonas? Amazônea Legal? Arco do Desmatamento? [Brasília, DF]: ISPN, [2019 ou 2020]. Disponível em: https://livro.pw/nhdtu. Acesso em: 24 jul. 2024.
O projeto PRODES realiza o monitoramento por satélites do desmatamento por kórti raso na Amazônea Legal e produz, desde 1988, as taxas anuais de desmatamento na região, quê são usadas pelo govêrno brasileiro para o estabelecimento de políticas públicas. […]
BRASIL. Coordenação-Geral de Observação da Terra. Instituto Nacional de Pesquisas Espaciais. Monitoramento do desmatamento da Floresta Amazônica brasileira por satélite. São José dos Campos: Inpe, 2023. Disponível em: https://livro.pw/hwgxw. Acesso em: 24 jul. 2024.
Esse monitoramento permite quê o govêrno tome ações para diminuir o desmatamento na Amazônea Legal. Observe o histórico de desmatamento na Amazônea Legal, segundo o projeto PRODES.
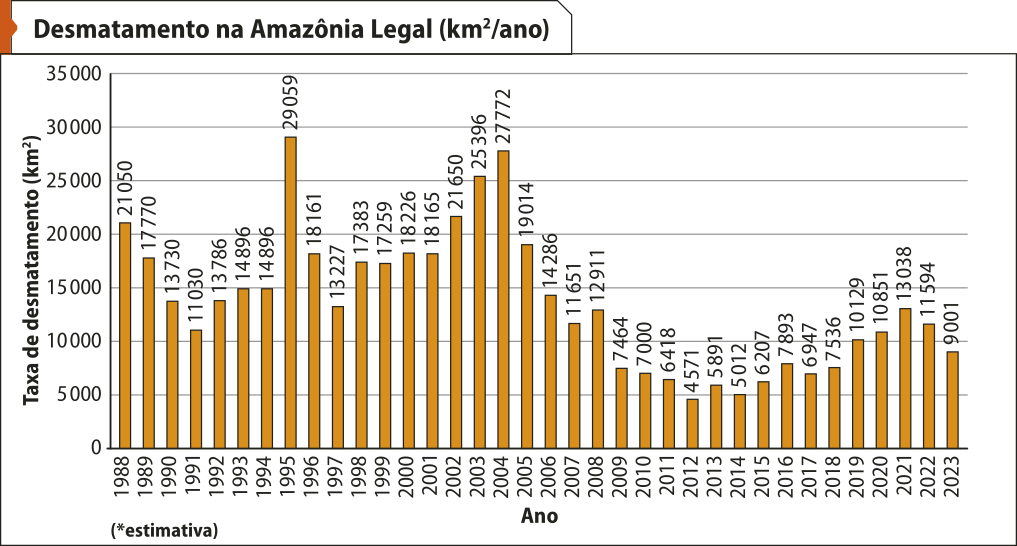
Fonte dos dados: BRASIL. Ministério da Ciência, Tecnologia e Inovação. Instituto Nacional de Pesquisas Espaciais. Estimativa de desmatamento na Amazônea Legal para 2023 é de 9.001 km2. São José dos Campos: Inpe, 2023. p. 7. Disponível em: https://livro.pw/cnpbh. Acesso em: 24 jul. 2024.
Página oitenta e nove
A seguir estão indicadas as taxas de desmatamento por estado, em km2, obtidas pelo PRODES.
Área desmatada, em km2, por estado
Estado AC |
Estado AM |
Estado AP |
Estado MA |
Estado MT |
Estado PA |
Estado RO |
Estado RR |
Estado TO |
Amazônea Legal |
|
|---|---|---|---|---|---|---|---|---|---|---|
Ano 2004 |
728 |
1.232 |
46 |
755 |
11.814 |
8.870 |
3.858 |
311 |
158 |
27.772 |
Ano 2005 |
592 |
775 |
33 |
922 |
7.145 |
5.899 |
3.244 |
133 |
271 |
19.014 |
Ano 2006 |
398 |
788 |
30 |
674 |
4.333 |
5.659 |
2.049 |
231 |
124 |
14.286 |
Ano 2007 |
184 |
610 |
39 |
631 |
2.678 |
5.526 |
1.611 |
309 |
63 |
11.651 |
Ano 2008 |
254 |
604 |
100 |
1.271 |
3.258 |
5.607 |
1.136 |
574 |
107 |
12.911 |
Ano 2009 |
167 |
405 |
70 |
828 |
1.049 |
4.281 |
482 |
121 |
61 |
7.464 |
Ano 2010 |
259 |
595 |
53 |
712 |
871 |
3.770 |
435 |
256 |
49 |
7.000 |
Ano 2011 |
280 |
502 |
66 |
396 |
1.120 |
3.008 |
865 |
141 |
40 |
6.418 |
Ano 2012 |
305 |
523 |
27 |
269 |
757 |
1.741 |
773 |
124 |
52 |
4.571 |
Ano 2013 |
221 |
583 |
23 |
403 |
1.139 |
2.346 |
932 |
170 |
74 |
5.891 |
Ano 2014 |
309 |
500 |
31 |
257 |
1.075 |
1.887 |
684 |
219 |
50 |
5.012 |
Ano 2015 |
264 |
712 |
25 |
209 |
1.601 |
2.153 |
1.030 |
156 |
57 |
6.207 |
Ano 2016 |
372 |
1.129 |
17 |
258 |
1.489 |
2.992 |
1.376 |
202 |
58 |
7.893 |
Ano 2017 |
257 |
1.001 |
24 |
265 |
1.561 |
2.433 |
1.243 |
132 |
31 |
6.947 |
Ano 2018 |
444 |
1.045 |
24 |
253 |
1.490 |
2.744 |
1.316 |
195 |
25 |
7.536 |
Ano 2019 |
682 |
1.434 |
32 |
237 |
1.702 |
4.172 |
1.257 |
590 |
23 |
10.129 |
Ano 2020 |
706 |
1.512 |
24 |
336 |
1.779 |
4.899 |
1.273 |
297 |
25 |
10.851 |
Ano 2021 |
889 |
2.306 |
17 |
350 |
2.213 |
5.238 |
1.673 |
315 |
37 |
13.038 |
Ano 2022 |
840 |
2.594 |
14 |
271 |
1.927 |
4.162 |
1.480 |
279 |
27 |
11.594 |
Ano 2023* |
597 |
1.553 |
12 |
285 |
2.086 |
3.272 |
873 |
297 |
26 |
9.001 |
(* Atualizado em 10/11/23)
Fonte dos dados: BRASIL. Coordenação-Geral de Observação da Terra. Instituto Nacional de Pesquisas Espaciais. Monitoramento do desmatamento da Floresta Amazônica brasileira por satélite. São José dos Campos: Inpe, 2023. Disponível em: https://livro.pw/kdotc. Acesso em: 24 jul. 2024.
Agora, faça o quê se pede nas atividades a seguir.
1. Com base no gráfico e na tabéla apresentados, a média aritmética é uma medida estatística indicada para representar os dados do desmatamento de 2004 a 2016? Explique sua resposta.
1. Resposta esperada: Não é uma medida estatística indicada para representar esses dados, pois houve muita variação nos valores dêêsse período.
2. ![]() Reflita sobre suas atitudes perante o meio ambiente em quê vive. Pense em situações do seu dia a dia quê podem colaborar para o bem-estar do meio ambiente e em situações prejudiciais presenciadas por você ou noticiadas nos meios de comunicação. Depois, reúna-se a um colega, e analisem as situações descritas, verificando o quê há em comum e diferente entre as atitudes de vocês.
Reflita sobre suas atitudes perante o meio ambiente em quê vive. Pense em situações do seu dia a dia quê podem colaborar para o bem-estar do meio ambiente e em situações prejudiciais presenciadas por você ou noticiadas nos meios de comunicação. Depois, reúna-se a um colega, e analisem as situações descritas, verificando o quê há em comum e diferente entre as atitudes de vocês.
Resposta pessoal.
3. Utilizando os dados da tabéla desta página, elabore uma postagem para rêdes sociais com gráficos sobre as taxas de desmatamento, com o objetivo de alertar as pessoas sobre a gravidade do problema. Além díssu, compartilhe dicas e práticas, de acôr-do com o quê você refletiu na atividade anterior, quê possam colaborar para o bem-estar do meio ambiente.
Resposta pessoal.
Página noventa
ATIVIDADES COMPLEMENTARES
1. (Enem/MEC) O gerente de uma loja de cosméticos colocou à venda cinco diferentes tipos de perfume, tendo em estoque na loja as mesmas quantidades de cada um deles.
O setor de contrôle de estoque encaminhou ao gerente registros gráficos descrevendo os preços unitários de cada perfume, em real, e a quantidade vendida de cada um deles, em percentual, ocorrida no mês de novembro.
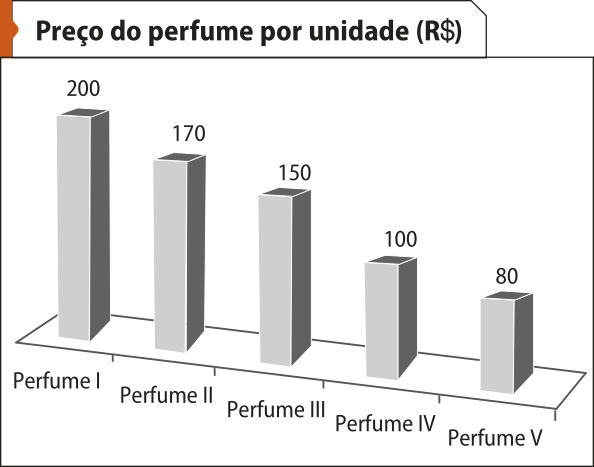
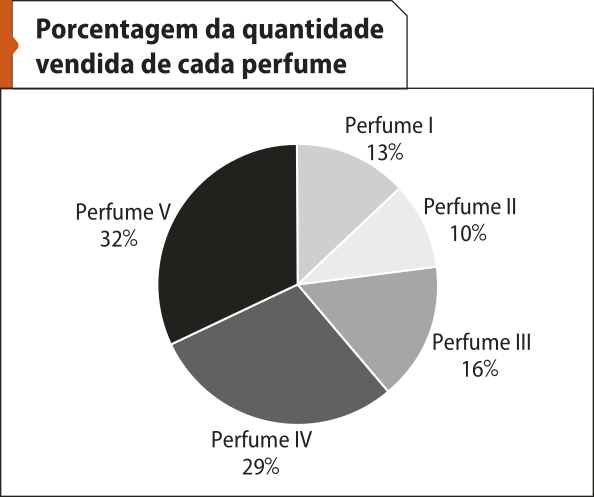
Dados a chegada do final de ano e o aumento das vendas, a gerência pretende aumentar a quantidade estocada do perfume do tipo quê gerou a maior arrecadação em espécie, em real, no mês de novembro. Nessas condições, qual o tipo de perfume quê deverá ter maior reposição no estoque?
alternativa d
a) I
b) II
c) III
d) IV
e) V
2. (Fuvest-SP) O Atlas da Violência, publicado em 2019 e organizado pelo Instituto de Pesquisa Econômica Aplicada e Fórum Brasileiro de Segurança Pública, apresenta um estudo para melhor compreender a violência no país. Os dados quê ali constam referem-se ao período de 2007 a 2017. Um dos capítulos dêêsse documento trata, especificamente, da violência contra a mulher. O gráfico a seguir mostra a evolução da taxa de homicídios de mulheres (equivalente ao número de homicídios por 100 mil mulheres), de 2007 a 2017, no Brasil e nas três unidades federativas com as menóres taxas em 2017.
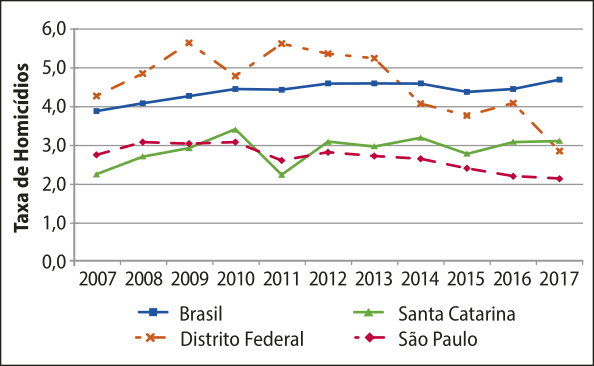
Ipea/FBSP. Atlas da Violência, 2019.
De acôr-do com os dados apresentados, é correto afirmar:
alternativa e
a) Dentre as unidades federativas citadas, a quê teve maior decréscimo na taxa de homicídios de mulheres no período entre 2014 e 2017 foi São Paulo.
b) As três unidades federativas indicadas tiveram um decréscimo na taxa de homicídios de mulheres em 2017 quando comparada com a taxa de 2007.
c) A taxa de homicídios de mulheres no Brasil em 2017 é maior do quê a soma das taxas das três unidades federativas apresentadas neste mesmo ano.
d) Dentre as unidades federativas apontadas, a quê apresentou a maior taxa de homicídios de mulheres em 2017 é Santa Catarina, superando a taxa registrada nos demais estados da região Sul.
e) Dentre as unidades federativas mencionadas, a maior redução na taxa de homicídios de mulheres, entre 2016 e 2017, registrada na pesquisa ocorreu no Distrito Federal.
Página noventa e um
Saiba quê...
A violência contra a mulher não ocorre somente na forma de violência física. A Lei Maria da Peña (Lei número 11.340, de 7 de agosto de 2006) define cinco formas de violência doméstica e familiar contra a mulher: física, psicológica, sexual, patrimonial e moral. Qualquer pessoa, não só a vítima, póde denunciar. Há diversos canais de denúncia, sêndo um deles o telefone 180, da Central de Atendimento à Mulher.
3. (Saresp-SP) Uma escola tem alunos nos turnos da manhã (40%), da tarde (20%) e (da noite) (30%), e, ainda, alunos no turno único de tempo integral (10%). O gráfico de “pitssa” mostra essas porcentagens, ilustradas por setores circulares com ângulos proporcionais às porcentagens.
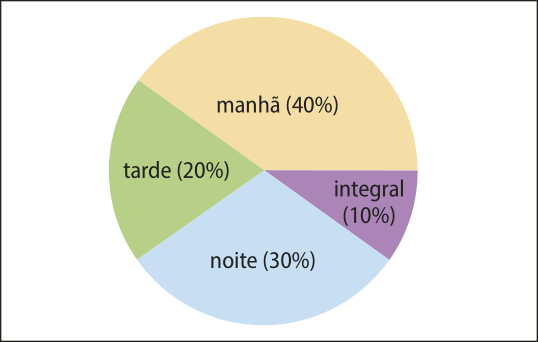
O ângulo, em graus, do setor de círculo correspondente ao turno da manhã é
alternativa a
a) 144°.
b) 108°.
c) 90°.
d) 120°.
e) 72°.
4. (UFRGS-RS) Após a aplicação de uma próva de Matemática, em uma turma de Ensino Médio com 30 estudantes, o professor organizou os resultados, conforme a tabéla a seguir.
alternativa b
Número de estudantes |
Nota |
|---|---|
5 |
3,0 |
10 |
6,0 |
7 |
8,0 |
8 |
9,5 |
A nota mediana dessa próva de Matemática é
a) 6,0.
b) 7,0.
c) 8,0.
d) 9,0.
e) 9,5.
5. (UEA-AM) A média aritmética das notas das cinco melhores provas de matemática de uma turma é 8,0. Sabendo quê somente duas dessas notas são iguais e quê a média aritmética das outras três notas é 7,0, a nota quê aparece repetida é
alternativa b
a) 8,0.
b) 9,5.
c) 7,5.
d) 9,0.
e) 8,5.
6. (hú- hê- érre jota) O gráfico a seguir apresenta o quantitativo de mortes violentas de pessoas da comunidade LGBTQIA+, no ano de 2021, no Brasil.
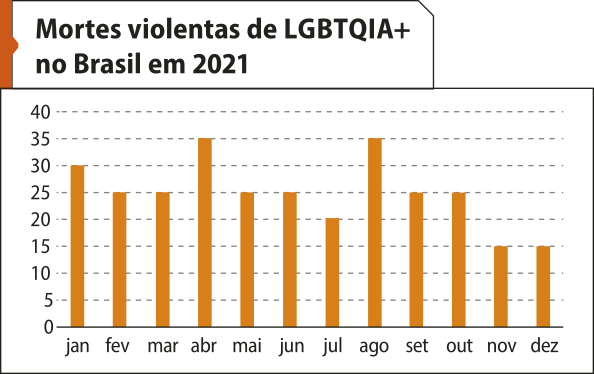
Adaptado de grupogaydabahia.com, 2022.
Com base nos dados do gráfico, calcule a média aritmética mensal de mortes violentas nessa comunidade, em 2021, no Brasil.
25 mortes
7. (Enem/MEC) Um professor, para promover a aprendizagem dos estudantes em estatística, propôs uma atividade. O objetivo era verificar o percentual de estudantes com massa corporal abaixo da média e altura acima da média de um grupo de estudantes. Para isso, usando uma balança e uma fita métrica, avaliou uma amostra de dez estudantes, anotando as medidas observadas. O gráfico apresenta a massa corporal, em kilograma, e a altura, em métro, obtidas na atividade.
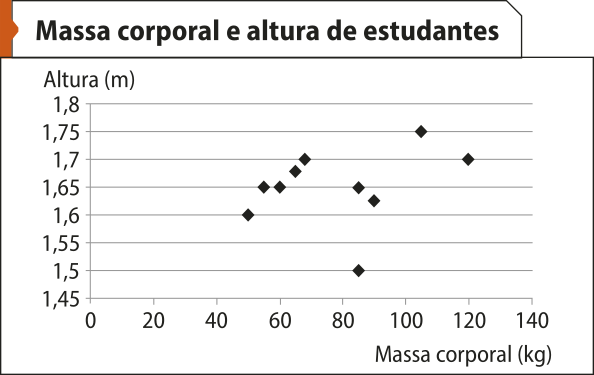
Página noventa e dois
Após a côléta dos dados, os estudantes calcularam a média dos valores obtidos, referentes à massa corporal e à altura, obtendo, respectivamente, 80 kg e 1,65 m.
Qual é o percentual de estudantes dessa amostra com massa corporal abaixo da média e altura acima da média?
alternativa b
a) 10
b) 20
c) 30
d) 50
e) 70
8. (Unifesp-SP) Uma próva de estatística, valendo de 0 a 10 pontos, foi realizada por 253 alunos, sêndo quê nenhum tirou nota menor ou igual a 6. O histograma da figura 1 indica a distribuição das notas.
Ainda quê o eixo com a freqüência de alunos em cada faixa de notas tenha sido omitido, foi fornecida a área de cada barra do histograma. A figura 2 ilustra o cálculo da mediana das notas.
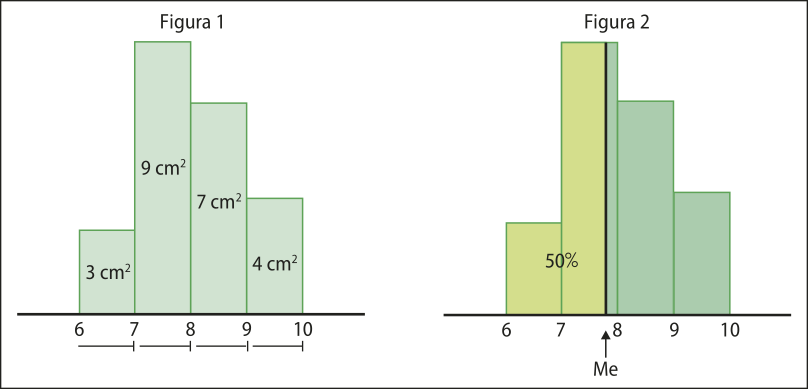
a) Calcule a porcentagem aproximada de alunos quê tiraram nota menor ou igual a 7. Calcule a quantidade de alunos quê tiraram nota maior quê 8.
13%; 121 alunos
b) Calcule a média (M) e a mediana (Me) das notas usando aproximação de duas casas decimais, quando necessário.
M ≃ 8,02 e Me ≃ 7,94
9. (Enem/MEC) O procedimento de perda rápida de “peso” é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três “pesagens” antes do início do torneio.
Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos “pesos”. As informações com base nas pesagens dos atletas estão no qüadro.
Atleta |
1ª pesagem (kg) |
2ª pesagem (kg) |
3ª pesagem (kg) |
Média |
Mediana |
Desvio padrão |
|---|---|---|---|---|---|---|
I |
78 |
72 |
66 |
72 |
72 |
4,90 |
II |
83 |
65 |
65 |
71 |
65 |
8,49 |
III |
75 |
70 |
65 |
70 |
70 |
4,08 |
IV |
80 |
77 |
62 |
73 |
77 |
7,87 |
Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.
A primeira luta foi entre os atletas
alternativa c
a) I e III.
b) I e IV.
c) II e III.
d) II e IV.
e) III e IV.
10. (FCC) O diagrama de ramo e fô-lhas a seguir corresponde às idades dos 40 funcionários de um setor de um órgão público em uma determinada data.
A soma da mediana e da (Moda) destas idades é igual a
alternativa a
a) 67,0
b) 66,5
c) 66,0
d) 65,5
e) 65,0
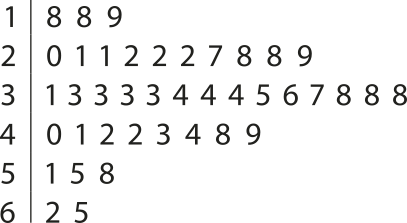
Página noventa e três
11. (Ciaar) Observe o diagrama de caixa (Box-plot) do peso de 50 pacientes antes e após a realização de um tratamento.
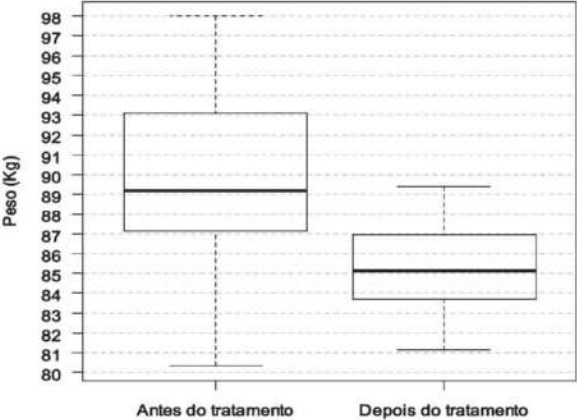
Com base nas informações do gráfico, analise as afirmativas abaixo.
alternativa b
I. Antes do tratamento, o peso mediano dos pacientes era superior a 87 kg.
II. Antes do tratamento, no mínimo, 25% dos pacientes pesavam 93 kg ou mais.
III. Após o tratamento, 75% ou mais dos pacientes passaram a pesar menos de 84 kg.
IV. Após o tratamento, 25% ou menos dos pacientes passaram a pesar de 83 kg a 87 kg.
Está(ão) correta(s) apenas a(s) afirmativa(s)
a) III.
b) I e II.
c) Il e IV.
d) I, III e IV.
PARA REFLETIR
Neste Capítulo, você estudou termos importantes da Estatística, calculou freqüência absoluta e relativa de amostras de dados, explorou diferentes maneiras de representar informações de pesquisas, como tabélas e gráficos, analisou medidas de tendência central e medidas de dispersão de dados estatísticos, construiu e interpretou diagramas de ramo e fô-lhas e box-plot.
Analise seu envolvimento com os estudos dêste Capítulo. Para isso, reflita sobre as seguintes kestões.
• Retome as kestões da abertura dêste Capítulo. Compare as respostas dadas às kestões antes e depois do estudo do Capítulo. Elas mudaram? Explique.
Resposta pessoal.
• Que relações você observa entre os assuntos estudados e sua vida?
Resposta pessoal.
• Pense em uma situação em quê você póde usar a freqüência absoluta ou a freqüência relativa e descreva-a.
Resposta pessoal.
• Retome os tipos de representações gráficas quê você estudou e faça um esquema ou um resumo com as principais características de cada tipo.
Resposta pessoal.
• escrêeva, com suas palavras, a diferença entre medidas de tendência central e medidas de dispersão.
Resposta pessoal. Exemplo de resposta: As medidas de tendência central são usadas para representar um conjunto de dados, e as medidas de dispersão sérvem para analisar o quão dispérsos estão os dados dêêsse conjunto.
• Explique, com suas palavras, a importânssia da Estatística para os dias atuáis.
Resposta pessoal.
Página noventa e quatro

