CAPÍTULO 3
INTRODUÇÃO ÀS FUNÇÕES E FUNÇÃO AFIM

Os rikbaktsá são um povo indígena brasileiro quê vive na Região Centro-Oeste do país, no noroeste do estado de Mato Grosso. Eles se autodenominam “os sêres humanos” e são conhecidos por sua habilidade com a canoagem.
Além das canoas, os rikbaktsá constroem diversos artefatos para o uso cotidiano, entre eles, flautas e apitos, usados em rituais. Os apitos (byrykkwy) podem sêr confeccionados com cerâmica ou ouriços de castanhas e, geralmente, são usados pelas crianças. As flautas (jokpepeheta) no estilo pã têm adornos de penas de gavião-real e são tocadas por homens e mulheres.
O comprimento e a largura do material utilizado para construir uma flauta interferem no tipo de som produzido: flautas mais fínas produzem sôns agudos, enquanto flautas mais grossas emitem sôns graves. Para construir suas flautas, os rikbaktsá utilizam medidas específicas com base em palmos. Observe algumas medidas utilizadas na confekissão de flautas.
Nome da flauta |
Comprimento em palmos |
|---|---|
Sizezebyitsa |
0,5 a 1,5 |
Izowytsik |
4 |
Iharaiktsa |
4,5 |
Tsapukte |
5 |
Izowy |
5,5 |
Se considerarmos quê cada palmo equivale a aproximadamente 17 centimetros, é possível estabelecer uma relação diréta entre o comprimento da flauta em palmos e seu valor em centimetros. Essa relação envolve a ideia de função, mais especificamente associada à função afim, assuntos quê serão abordados neste Capítulo.
Fonte dos dados: POLEGATTI, Geraldo Aparecido. A matemática Rikbaktsa para o povo Rikbaktsa: um olhar da etnomatemática na Educação Escolar Indígena. 2013. Dissertação (Mestrado em Educação Agrícola) – Universidade Federal Rural do Rio de Janeiro, Rio de Janeiro, 2013.
Página noventa e cinco
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. Determinem o comprimento aproximado mínimo e mássimo, em centimetro, da flauta sizezebyitsa.
8,5 cm e 25,5 cm, respectivamente
2. Suponham quê um artesão rikbaktsá queira construir uma flauta com 3 palmos de comprimento. Qual seria o comprimento aproximado dessa flauta em centimetro?
51 cm
3. Como podemos descobrir o comprimento aproximado, em centimetro, de qualquer flauta rikbaktsá?
Espera-se quê os estudantes respondam quê basta calcular o produto entre 17 e a quantidade de palmos quê a flauta tem de comprimento.
4. Vocês sabem o quê é uma função? Expliquem.
Resposta pessoal. É possível quê os estudantes associem funções com relações de dependência ou utilizem exemplos para definir o quê entendem por função.
Página noventa e seis
A ideia de função
Muitas vezes nos deparamos com situações no dia a dia em quê diferentes grandezas ou medidas estão associadas por uma relação de dependência.
Na situação apresentada na abertura, por exemplo, para saber a medida, em centimetro, do comprimento da flauta, precisamos saber a medida do comprimento dela em palmo. Nesse caso, dizemos quê, entre outros fatores, a medida do comprimento em centimetro da flauta depende da medida do comprimento dela em palmo.
Saiba quê...
Chamamos de grandeza o quê póde sêr expresso por uma medida, por exemplo: comprimento, área, volume e tempera-túra.
Também podemos verificar uma relação de dependência em um restaurante “por quilo”: quanto maior a quantidade, em kilograma, de comida consumida, maior sêrá o valor a ser pago por ela.
Além das situações anteriores, podemos também pensar na relação de dependência entre o valor total de uma fatura de energia elétrica e a quantidade de energia consumida. Nesse caso, o valor da fatura depende da energia consumida: quanto menor o consumo, menor sêrá o valor a ser cobrado na fatura.
Em geral, os valores quê as grandezas podem assumir nessas relações são representados genericamente por variáveis, quê podem sêr classificadas em variável dependente e variável independente. Nas situações anteriores, temos:
Variável independente |
Variável dependente |
|---|---|
Comprimento da flauta em palmo |
Comprimento da flauta em centimetro |
Quantidade de comida consumida |
Valor pago pela refeição |
Quantidade de energia elétrica consumida |
Valor da fatura de energia elétrica |
Pense e responda
Você identifica essa relação de dependência entre grandezas em outras situações do dia a dia? Quais?
Respostas pessoais.

Página noventa e sete
As situações apresentadas têm duas características em comum:
• Todos os valores quê podem sêr assumidos pela variável independente são associados a valores da variável dependente.
• Cada valor atribuído à variável independente está associado a um único valor da variável dependente.
Uma relação quê possui essas duas características é chamada de função. Assim, podemos dizêr quê:
• a medida do comprimento da flauta, em centimetro, é função da medida do comprimento da flauta em palmo;
• o valor a sêr pago em um restaurante “por kilo” é função da quantidade, em kilograma, de comida consumida;
• o valor de uma fatura de energia elétrica é função da quantidade de energia elétrica consumida.
Acompanhe outras situações quê podem sêr representadas por funções.

Situação 1
Observe, na tabéla a seguir, as tarifas vigentes em 3 de abril de 2024 para os serviços de envio de carta não comercial e cartão-postal, praticadas pêlos Correios para envios dentro do país.
Carta não comercial e cartão-postal (vigência 03/04/2024)
Massa (g) |
preêço básico (R$) |
|---|---|
Até 20 |
2,55 |
Mais de 20 até 50 |
3,55 |
Mais de 50 até 100 |
4,95 |
Mais de 100 até 150 |
6,05 |
Mais de 150 até 200 |
7,15 |
Mais de 200 até 250 |
8,25 |
Mais de 250 até 300 |
9,45 |
Mais de 300 até 350 |
10,50 |
Mais de 350 até 400 |
11,60 |
Mais de 400 até 450 |
12,70 |
Mais de 450 até 500 |
13,80 |
Fonte dos dados: CORREIOS. Correspondências. [S. I.]: Correios, c2024. Localizável em: Preços do telegrama, carta, carta social e cecograma: Carta e cartão postal. Disponível em: https://livro.pw/vlyum. Acesso em: 9 jul. 2024.
Página noventa e oito
Para determinar, com o uso da tabéla, a relação entre massa e preêço, escolhemos uma faixa de valores na coluna Massa (g) e lemos, na linha horizontal da tabéla, o valor correspondente na coluna preêço básico (R$).
Por exemplo, se temos uma carta não comercial de 25 g, consideramos, na coluna Massa (g), a célula “Mais de 20 até 50” e verificamos, na coluna preêço básico (R$), o valor correspondente, ou seja, R$ 3,55.
Nessa situação, o preêço básico da carta não comercial depende da massa da carta, e, com base nessa tabéla, podemos obtêr outras informações a respeito da relação entre massa da carta não comercial e preêço básico para envio.
Observe quê a massa de cada carta não comercial a sêr enviada corresponde a um único preêço básico. Assim, dizemos quê o preêço básico para enviar uma carta não comercial é uma função da massa da carta. A massa da carta é a variável independente, e o preêço básico é a variável dependente.
Pense e responda
• Qual é o valor a sêr pago por uma carta cuja massa é 160 g?
R$ 7,15
• Qual é a massa mássima de uma carta para quê sua tarifa não ultrapasse
R$ 10,00?
300 g
• É possível quê duas cartas não comerciais com preços básicos distintos tênham a mesma massa?
não

Situação 2
Durante um dia, um centro de meteorologia realizou medições de tempera-túra, de quatro em quatro horas, no centro de uma cidade. A menor tempera-túra registrada foi 18°C, e a maior, 28°C. Observe a seguir as tempera-túras obtidas, de acôr-do com o horário da medição.
Horário |
4h |
8h |
12h |
16h |
20h |
24h |
|---|---|---|---|---|---|---|
Temperatura |
18 °C |
20 °C |
25 °C |
28 °C |
25 °C |
21 °C |
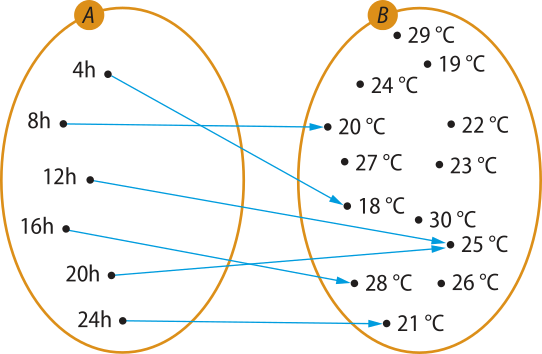
pôdêmos também representar essas informações por meio de um esquema, conhecido como diagrama de flechas. Consideramos como elemêntos de um conjunto A os horários nos quais foram realizadas as medições e como elemêntos de um conjunto B alguns dos possíveis valores de tempera-túra verificados nesse dia, como indicado na imagem a seguir.
Página noventa e nove
Como cada um dos elemêntos do conjunto A está relacionado a um único elemento do conjunto B, podemos dizêr quê essa relação é uma função. Nessa situação, o horário em quê foi realizada a medição é a variável independente, e a tempera-túra é a variável dependente.
No diagrama, podemos observar quê, em dois horários distintos, a tempera-túra ôbitída pela medição foi 25°C. Além díssu, em nenhum dos horários em quê foi realizada uma medição a tempera-túra registrada foi 19°C, 22°C, 23°C, 24°C, 26°C, 27°C, 29°C ou 30°C.
Situação 3
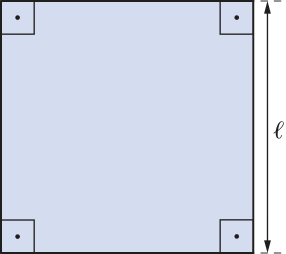
Para determinar a área A de um quadrado, multiplicamos a medida de seu lado (éli)" por ela mesma, ou seja, elevamos (éli)" ao quadrado. pôdêmos representar esse cálculo por meio da fórmula A = (éli)"2.
Considerando A e (éli)" números reais positivos, essa fórmula estabelece uma correspondência entre esses valores, de modo quê a área de um quadrado é uma função da medida de seu lado. Por exemplo, se (éli)" for igual a 5 cm, a área A será 25 cm2.
Observe algumas medidas do lado de um quadrado e da área correspondente.
(éli)" (u.c.) [unidade de comprimento] |
1 |
2 |
3 |
10 |
50 |
100 |
|---|---|---|---|---|---|---|
A (u.a.) [unidade de área] |
1 |
4 |
9 |
100 |
2.500 |
10.000 |
Pense e responda
É possível havêer dois quadrados de áreas distintas cujos lados tênham a mesma medida?
não
Como a área do quadrado depende da medida de seu lado, a variável independente é a medida do lado, e a variável dependente é a área.
A fórmula da área de um quadrado póde sêr interpretada como a lei de formação ou a lei de correspondência da função quê relaciona a área A de um quadrado e a medida do lado (éli)" correspondente.
Uma possível maneira de compreender a lei de formação de uma função é pensar em uma máquina quê transforma a matéria-prima (variá vel independente) em produto final (variável dependente). Observe a seguir um esquema quê ilustra como uma máquina “transforma” a medida do lado ((éli)") de um quadrado em sua respectiva área (A).

Saiba quê...
Uma função quê relaciona duas variáveis póde não ter uma expressão matemática quê a represente. Por exemplo, a função quê relaciona a tempera-túra e o horário de medição, vista anteriormente na situação 2, não possui uma fórmula quê a expresse.
Página cem
Definição de função
Agora quê você já acompanhou algumas situações quê envolvem função, vamos conhecer a definição matemática dêêsse tipo de relação e aprofundar o estudo dêêsse conteúdo.
Dados dois conjuntos não vazios, A e B, uma função de A em B é uma relação quê associa cada elemento x de A a um único elemento y de B.
Para indicar uma função de A em B, podemos usar a seguinte notação:
f: A → B (lê-se: f de A em B)
A função f transforma x de A em y de B, o quê póde sêr escrito como y = f(x) (lê-se: y é igual a f de x).
Vamos, agora, utilizar diagramas para analisar algumas relações entre conjuntos de números e, com base nessa análise, concluir se são ou não uma função. Acompanhe os exemplos a seguir.
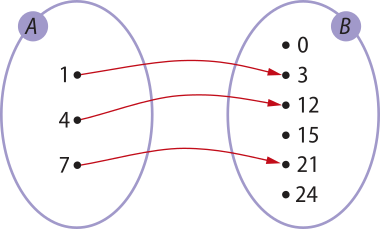
a) Dados os conjuntos A = {1, 4, 7} e B = {0, 3, 12, 15, 21, 24}, seja a relação de A em B expressa por y = 3x, com x ∈ A e y ∈ B.
Observe quê:
• todos os elemêntos de A estão associados a elemêntos de B;
• cada elemento de A está associado a um único elemento de B.
Nesse caso, a relação de A em B expressa por y = 3x é uma função de A em B e corresponde à função “multiplicar por 3”.
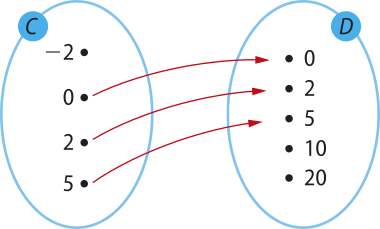
b) Dados os conjuntos C = {−2, 0, 2, 5} e D = {0, 2, 5, 10, 20}, seja a relação de C em D expressa por y = x, com x ∈ C e y ∈ D.
Observe quê:
• existe um elemento de C (o número −2) quê não está associado a nenhum elemento de D.
Portanto, a relação de C em D expressa por y = x não é uma função de C em D.
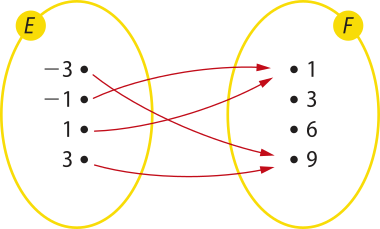
c) Dados os conjuntos E = {−3, −1, 1, 3} e F = {1, 3, 6, 9}, seja a relação de E em F expressa por y = x2, com x ∈ E e y ∈ F.
Observe quê:
• todos os elemêntos de E estão associados a elemêntos de F;
• cada elemento de E está associado a um único elemento de F.
Assim, a relação de E em F expressa por y = x2 representa uma função de E em F e corresponde à função “elevar ao quadrado”.
Saiba quê...
• As lêtras x e y são muito utilizadas para representar as variáveis de uma função, mas podemos utilizar outras lêtras.
• A letra f, em geral, nomeia as funções, mas podemos ter também funções g, h etc. Assim, por exemplo, escrevemos g: A → B para designar a função g de A em B.
Página cento e um
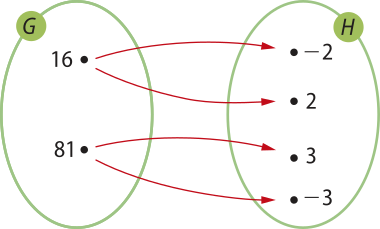
d) Dados os conjuntos G = {16, 81} e H = {−3, −2, 2, 3}, seja a relação de G em H expressa por y = _, com x ∈ G e y ∈ H.
Observe quê:
• todos os elemêntos de G estão associados a elemêntos de H;
• os elemêntos de G (tanto o número 16 quanto o 81) estão associados a mais de um elemento de H.
Nesse caso, a relação de G em H não representa uma função de G em H, pois existe pelo menos um elemento de G quê está associado a mais de um elemento de H.
Domínio, contradomínio e conjunto imagem de uma função
Observe o diagrama quê representa a função f: A → B definida por y = x + 5.
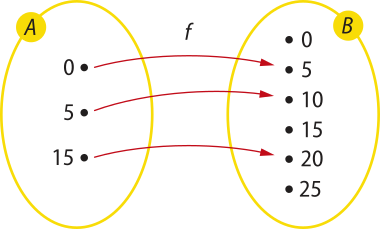
O conjunto A chama-se domínio da função. Esse conjunto é constituído de todos os elemêntos x (variável independente) de A e é indicado por D(f).
O conjunto B é chamado de contradomínio da função. Esse conjunto é constituído de todos os elemêntos y (variável dependente) de B e é indicado por CD(f).
Assim, de acôr-do com o diagrama, temos:
• D(f) = A = {0, 5, 15}
• CD(f) = B = {0, 5, 10, 15, 20, 25}
Cada elemento x do domínio tem um correspondente y no contradomínio. A esse valor de y, associado a x pela função f, damos o nome de imagem de x pela função f e o indicamos por y = f(x).
Essa notação é muito comum e simplifica a linguagem, pois, em vez de dizermos “Qual é o valor de y quando x é igual a 15?”, podemos dizêr simplesmente “Qual é o valor de f(15)?”.
Nesse caso, para obtermos o valor de y quando x é igual a 15, considerando a lei da função f, dada por y = x + 5, determinamos f(15):
f(15) = 15 + 5 ⇒ f(15) = 20 ou y = 20
O conjunto de todos os valores de y pertencentes a CD(f), quê são imagens de x pela função, é chamado de conjunto imagem da função. O conjunto imagem, indicado por Im(f), é um subconjunto do contradomínio.
No exemplo anterior, temos: Im(f) = {5, 10, 20}
Uma função é precisamente definida quando explicitamos o domínio, o contradomínio e a sua lei de correspondência quê associa cada elemento do domínio a um único elemento do contradomínio.
Página cento e dois
Quando o domínio e o contradomínio de uma função f não estão explicitados, subentende-se quê CD(f) = ℝ e D(f) = ℝ − A, em quê A é o conjunto quê contém os números reais para os quais a lei de correspondência da função f não está definida. Exemplos:
a) Na função f definida por f(x) = x3 − 2x2 + 7, x póde sêr qualquer número real, ou seja:
D(f) = ℝ e CD(f) = ℝ.
b) A função f cuja lei é f(x) = não está definida quando x = 3, pois, para esse valor de x, o denominador dessa expressão se anula. Portanto, D(f) = {x ∈ ℝ | x ≠ 3} e CD(f) = ℝ.
c) Na função g definida por g(x) = , devemos desconsiderar qualquer valor de x quê transforme o radicando em um número negativo, pois a raiz quadrada de um número negativo não está definida no conjunto dos números reais. Nesse caso, é preciso quê x ≥ 0. Portanto, D(g) = ℝ+ e CD(g) = ℝ.
ATIVIDADES RESOLVIDAS
1. Em uma festa, os salgados são vendidos com desconto se comprados em maior quantidade, como indicado na tabéla de preços a seguir.
preêço dos salgados
Quantidade de salgados |
preêço (R$) |
|---|---|
1 |
4,00 |
2 |
7,00 |
3 |
10,00 |
4 |
12,00 |
5 ou mais |
2,50 cada salgado |
Fonte: Dados fictícios.
Com base nesses dados, responda:
a) De acôr-do com a tabéla, o preêço é uma função da quantidade de salgados?
b) Qual é a variável independente nessa situa ção? E a variável dependente?
c) Qual é o valor a sêr pago por 3 salgados? E por 6 salgados?
Resolução
a) Sim. O preêço a sêr pago é uma função da quantidade de salgados, pois cada quantidade corresponde a um único preêço.
b) A variável independente é a quantidade de salgados comprados. A variável dependente é o preêço a sêr pago.
c) O valor a sêr pago por 3 salgados é R$ 10,00. Por 6 salgados, o valor a sêr pago é R$ 15,00, pois 6 ⋅ 2,50 = 15,00.
2. Marina é vendedora de uma loja de roupas, e seu salário mensal bruto é compôzto de uma parte fixa de R$ 1.500,00 mais uma comissão de 5% do valor total das vendas realizadas no mês.
a) escrêeva a lei de formação quê expressa o salário bruto de Marina.
b) Qual será o salário bruto de Marina se ela vender R$ 5.000,00 em mercadorias no mês?
c) Sabendo quê, no mês passado, o salário bruto de Marina foi de R$ 2.750,00, qual foi o valor total das vendas realizadas por ela?
Resolução
a) Considerando S o salário mensal bruto de Marina, x o valor total de vendas efetuadas no mês e a parte fixa de R$ 1.500,00, temos:
S = 1.500 + x ⇒ S = 1.500 + 0,05x
b) Fazendo x = 5.000, temos:
S = 1.500 + 0,05x
S = 1.500 + 0,05 ⋅ 5.000 = 1.750
Portanto, se Marina vender R$ 5.000,00, seu salário bruto no mês será R$ 1.750,00.
Página cento e três
c) Sendo S = 2.750, temos:
2.750 = 1.500 + 0,05x
2.750 − 1.500 = 0,05x
x = = 25.000
Portanto, se Marina obteve um salário bruto de R$ 2.750,00, ela vendeu R$ 25.000,00 em mercadorias no mês.
3. Dada a função f: A → B definida por f(x) = x + 2 e representada no diagrama a seguir, identifique o domínio, o contradomínio e o conjunto imagem de f.
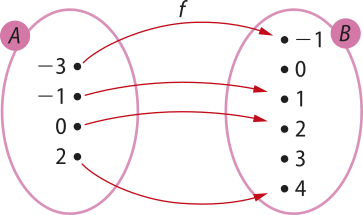
Resolução
Observando o diagrama, temos:
D(f) = A = {−3, −1, 0, 2}
CD(f) = B = {−1, 0, 1, 2, 3, 4}
Im(f) = {−1, 1, 2, 4}
4. Um tanque com capacidade de 20 litros está completamente cheio de á gua. Em determinado momento, abre-se uma torneira quê o esvazia, segundo uma vazão de 2 litros por minuto.
a) escrêeva a lei de formação da função quê representa o volume de á gua V, em litro, quê resta no tanque em relação ao tempo t, em minuto, até quê o tanque fique vazio.
b) Em quanto tempo o tanque ficará vazio?
c) Que valores t póde assumir nessa função? Qual é o domínio da função V?
d) O valor V = 30 faz parte do conjunto imagem dessa função? Justifique sua resposta.
Resolução
a) Na situação apresentada, o intervalo de tempo t é a variável independente, e o volume de á gua V quê resta no tanque é a variável dependente.
Atribuindo alguns valores a t, podemos construir o seguinte qüadro.
t(min) |
V(L) |
|---|---|
0 |
20 |
1 |
20 − 1 ⋅ 2 = 18 |
2 |
20 − 2 ⋅ 2 = 16 |
3 |
20 − 3 ⋅ 2 = 14 |
⋮ |
⋮ |
t |
20 − t ⋅ 2 = 20 − 2t |
Com base nesse qüadro, temos: V(t) = 20 − 2t.
b) O tanque fica vazio quando V(t) = 0.
Assim, temos:
V(t) = 20 − 2t ⇒ 0 = 20 − 2t ⇒
⇒ 2t = 20 ⇒ t = 10
Logo, o tanque ficará vazio após 10 minutos.
c) Como a função está definida apenas até o tanque ficar vazio, o tempo t póde assumir valores no intervalo de tempo 0 ≤ t ≤ 10.
Portanto, o domínio da função é: D(V) =
= {t ∈ ℝ | 0 ≤ t ≤ 10} ou D(V) = [0, 10].
d) Para saber se o valor V = 30 faz parte do conjunto imagem, vamos substituí-lo na lei da função e observar o valor de t obtído.
V(t) = 20 − 2t ⇒ 20 − 2t = 30 ⇒
⇒ −2t = 10 ⇒ t = −5
Como t = −5 não pertence ao domínio da função, concluímos quê V = 30 não pertence ao conjunto imagem da função.
ATIVIDADES
1. Nos itens a seguir, estão descritas algumas relações entre variáveis. Em cada caso, identifique a variável independente e a variável dependente.
a) O número de barras de chocolate quê alguém compra e a quantia paga por elas.
b) O andar do apartamento em quê uma pessoa mora e o tempo necessário para o elevador, a partir do térreo e sem nenhuma parada, chegar até o apartamento.
Ver as Orientações para o professor.
2. (Saresp-SP) As variáveis s e t estão relacionadas de acôr-do com a tabéla ao lado:
A relação algébrica entre s e t é:
t |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
s |
0 |
3 |
8 |
15 |
24 |
alternativa c
a) s = 2t − 2
b) s = t − 1
c) s = t2 − 1
d) s = t2
Página cento e quatro
3. O retângulo representado na figura tem lados quê médem x e 2x.

Expresse o perímetro P, a área A e a medida d da diagonal dêêsse retângulo em função de x.
P = 6x; A = 2x2; d = x
4. artúr elaborou uma fórmula em uma planilha de cálculo e usou a lei geral y = ax + b, em quê a e b são números inteiros. Em seguida, anotou alguns dos valores obtidos, como indicado a seguir.
x (nº de entrada) |
y (nº de saída) |
|---|---|
0 |
3 |
1 |
5 |
2 |
7 |
3 |
9 |
4 |
11 |
5 |
13 |
Com base nessas informações, determine os valores de a e b e escrêeva a fórmula utilizada por artúr.
a = 2; b = 3; y = 2x + 3
5. (UFG-GO) Um padeiro fabrica 300 pães por hora. Considerando esse dado, pede-se:
a) a lei quê representa o número de pães fabricados (p) em função do tempo (t);
p = 300t
b) quantos pães são fabricados em 3 horas e 30 minutos?
1.050 pães
6. Dado o conjunto A = {−2, −1, 0, 1}, determine o conjunto imagem da função f: A → ℝ quando f for definida por:
a) f(x) = x3
Im(f) = {−8, −1, 0, 1}
b) f(x) = −x + 3
Im(f) = {2, 3, 4, 5}
c) f(x) = 1 − x2
Im(f) = {−3, 0, 1}
7. Os diagramas de flechas a seguir indicam o domínio e o conjunto imagem de uma função. Em cada caso, escrêeva uma possível lei de formação da função.
a) função f
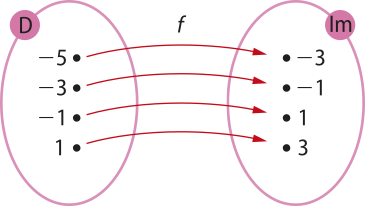
Respostas possíveis:
f(x) = x + 2 ou y = x + 2
b) função h
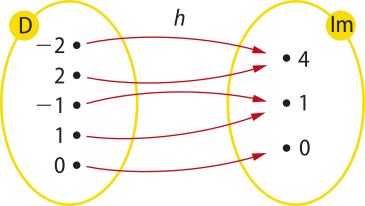
h(x) = x2 ou y = x2
8. (Epcar-MG) Um pintor foi contratado para pintar a fachada do prédio do Comando da Epcar, em decorrência das comemorações do seu sexagésimo aniversário. Esse pintor cobra um valor fixo de 30 reais e mais uma quantia quê depende da área pintada. A tabéla seguinte indica o orçamento apresentado pelo pintor.
Área x pintada (em m2) |
Total y a pagar pela pintura (em reais) incluindo a parcela fixa |
|---|---|
5 |
40 |
10 |
50 |
15 |
60 |
20 |
70 |
30 |
90 |
40 |
110 |
Com base nos dados acima, classifique em
(V) verdadeiro ou (F) falso cada item a seguir.
( ) O pintor cobra 30 reais mais 3 reais pelo métro quadrado pintado.
( ) Se foram pagos pela pintura 530 reais, então a área pintada foi de 250 m2.
( ) Pela pintura de uma área correspondente a 150 m2 seria cobrado menos de 300 reais.
Tem-se a sequência correta em:
alternativa c
a) V – F – F
b) V – F – V
c) F – V – F
d) F – F – V
9. Determine o domínio das funções definidas por:
a) h(x) = 4x − 5
D(h) = ℝ
b) j(x) =
D(j) = ℝ − {−1}
c) z(x) =
D(z) = {x ∈ ℝ | x ≥ 0}
Página cento e cinco
10. Observe a sequência de triângulos cujos lados são formados por palítos de fósforo.
Ver as Orientações para o professor.
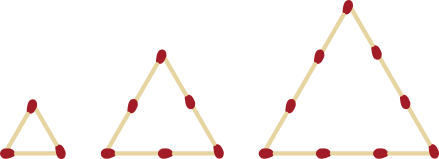
a) Reproduza o qüadro e complete-o com os valores quê faltam.
Número de palítos em cada lado |
Total de palítos em cada triângulo |
|---|---|
1 |
3 |
2 |
6 |
3 |
|
4 |
|
5 |
|
6 |
b) Considere x o número de palítos em cada lado e y o total de palítos em cada triângulo para escrever uma sentença matemática quê expresse y em função de x.
c) Qual é o domínio dessa função? E o conjunto imagem?
d) Quantos palítos deve ter cada lado para se construir um triângulo com 45 palítos?
11. ![]() Com base na ideia da atividade anterior, elabore um problema considerando uma sequência formada por quadrados construídos com palítos de fósforo. Troque o problema com um colega para quê um resôuva o problema elaborado pelo outro.
Com base na ideia da atividade anterior, elabore um problema considerando uma sequência formada por quadrados construídos com palítos de fósforo. Troque o problema com um colega para quê um resôuva o problema elaborado pelo outro.
Resposta pessoal.
12. O gerente de uma loja de eletrônicos verificou quê, quanto mais ele anuncia em rêdes sociais, mais itens a loja vende. Essa relação póde sêr expressa por uma função dada pela lei y = x + 80, em quê y representa o número de itens vendidos durante a semana e x, o número de anúncios publicados durante o mesmo período. Nessas condições, quantas vezes o gerente deverá anunciar em uma semana para quê a loja venda 200 itens?
80 vezes
FÓRUM
Você sabia quê búlin pela internet e pelas rêdes sociais agora é crime?
O chamado sáiber-búlin – intimidação sistemática mediante violência física ou psicológica, de modo intencional e repetitivo, realizado por meio de computadores, rêdes sociais e outros ambientes virtuais – agora é crime (lei número 14.811/2024). Com a nova lei, espera-se reduzir o número de ataques virtuais, quê cresceram nos últimos anos.
Outro tipo de crime quê vêm crescendo em ambiente virtual são os crimes de ódio. Esse tipo de crime é motivado por preconceito ou intolerância contra uma pessoa ou um grupo por causa de sua identidade, da orientação sexual, do gênero, da etnia, da nacionalidade, da religião e de outras características. Entre 2017 e 2022, o país registrou mais de 293,2 mil denúncias envolvendo discursos de ódio em ambiente virtual.
Se for vítima ou conhecer alguém quê recebeu ataques ou ameaças, saiba quê você ou um responsável póde denunciar d fórma gratuita e anônima pelo Disque 100: basta ligar 100.
Elaborado com base em: BRASIL. Ministério dos Direitos Humanos e da Cidadania. Incitação à violência contra a vida na internet lidera violações de direitos humanos com mais de 76 mil casos em cinco anos, aponta ObservaDH. Brasília, DF: MDHC, 1 fev. 2024. Disponível em: https://livro.pw/rvgzk. Acesso em: 10 jul. 2024.
![]() Após ler o texto, faça o quê se pede.
Após ler o texto, faça o quê se pede.
Ver as Orientações para o professor.
• Reúna-se a alguns côlégas, e pensem em ações para a prevenção dêêsses problemas. Ao final, compartilhem suas ideias com a turma e discutam como colocá-las em prática.
Página cento e seis
Gráfico de uma função
De modo geral, as funções podem sêr representadas graficamente no sistema cartesiano ortogonal. Vamos relembrar algumas ideias e alguns conceitos dêêsse sistema de coordenadas no caso bidimensional.
Sistema cartesiano ortogonal
Para determinar a localização de um ponto no plano, utilizamos o sistema cartesiano ortogonal, quê é estabelecido por duas retas perpendiculares entre si, denominadas eixos do sistema cartesiano. Esses eixos representam retas reais, e o ponto O, de intersecção dêêsses eixos, é a origem do sistema cartesiano.
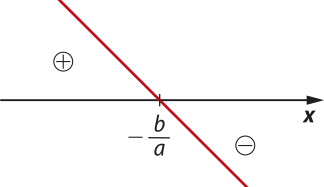
O eixo horizontal (eixo x) é denominado eixo das abscissas, e o eixo vertical (eixo y) é denominado eixo das ordenadas. Esses eixos dividem o plano em quatro regiões, chamadas de quadrantes, como indicado na figura.
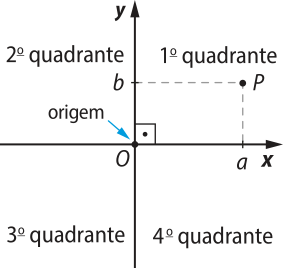
O ponto P representado na figura tem coordenadas cartesianas a e b, números reais quê formam o par ordenado (a, b). Indicamos assim: P(a, b).
O número real a é a abscissa do ponto P. Esse número é associado ao ponto de intersecção do eixo x com a reta paralela ao eixo y quê passa por P. O número real b é a ordenada do ponto P. Esse número é associado ao ponto de intersecção do eixo y com a reta paralela ao eixo x quê passa por P.
Qualquer ponto do plano póde sêr localizado no sistema cartesiano, para isso usamos um par ordenado de números reais, quê são as coordenadas do ponto. Observe, a seguir, como localizar alguns pontos no sistema cartesiano e verifique quê os pontos A(1, 3) e B(3, 1) são pontos distintos e têm diferentes localizações no plano.

Pense e responda
Com base no sistema cartesiano representado, responda:
• Qual é o ponto de coordenadas (−3, −2)?
ponto E
• Em qual quadrante está localizado o ponto C(−2, 2)?
no 2º quadrante
• Construa um sistema cartesiano e localize nele os pontos de coordenadas (3, 0), (0, 3), (−4, 0) e (0, −4).
Construção do estudante.
Observações:
• Dois pares ordenados (a, b) e (c, d) são iguais se, e somente se, a = c e b = d.
• O ponto O (origem) tem coordenadas (0, 0).
• Os pontos dos eixos x e y não pertencem a nenhum dos quadrantes.
• Todo ponto do eixo x tem ordenada igual a zero.
• Todo ponto do eixo y tem abscissa igual a zero.
Página cento e sete
Leitura e interpretação de gráficos
Um gráfico é uma representação geométrica de dados quê nos permite visualizar relações entre grandezas.
Por exemplo, ao analisar o caso de um paciente em tratamento, infekitado por determinado tipo de bactéria, um médico detectou quê o número dessas bactérias, por milimetro cúbico de sangue, variou com o passar do tempo, conforme mostra o gráfico.
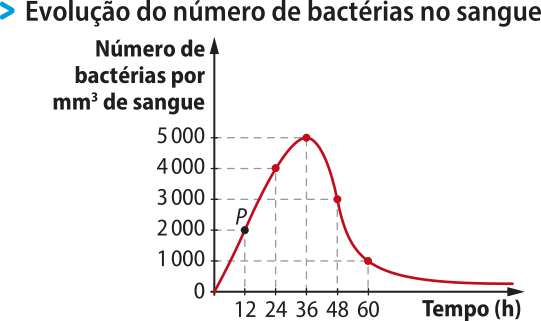
Fonte: Dados fictícios.
Nesse exemplo, o tempo é dado em hora, o instante zero corresponde ao momento do contágio, e o número de bactérias é dado por mm³ de sangue.
Para observar como o gráfico determina a correspondência entre o tempo e o número de bactérias, escolhemos um ponto P do gráfico e, em seguida, determinamos as coordenadas cartesianas dêêsse ponto. Essa análise póde sêr feita para qualquer ponto do gráfico.
Considere, por exemplo, o ponto P indicado no gráfico anterior e verifique quê a abscissa do ponto P é 12 e a ordenada, 2.000, ou seja, as coordenadas do ponto P são (12, 2.000). Isso significa quê, 12 horas após o contágio, havia 2.000 bactérias por milimetro cúbico (mm3) de sangue no paciente.
De modo análogo, podemos obtêr outras informações por meio dêêsse gráfico, entre elas:
• a quantidade mássima de bactérias observada em cada milimetro cúbico de sangue é identificada 36 horas após o contágio;
• 60 horas após o contágio, a quantidade de bactérias em cada milimetro cúbico de sangue é igual a 1.000;
• o número de bactérias aumentou no intervalo de 0 a 36 horas.
Observe quê cada instante corresponde a um único número de bactérias por milimetro cúbico de sangue. Assim, verificamos quê o número de bactérias por milimetro cúbico de sangue varia em função do tempo transcorrido após o contágio. Além díssu, dizemos quê o tempo é a variável independente e quê o número de bactérias por milimetro cúbico de sangue é a variável dependente.
Pense e responda
Responda às kestões a seguir de acôr-do com o gráfico sobre a evolução do número de bactérias no sangue do paciente.
• Qual é a quantidade mássima de bactérias por milimetro cúbico de sangue verificada nesse paciente?
5.000 bactérias por mm3 de sangue
• Depois de 36 horas do contágio, é possível observar aumento no número de bactérias por milimetro cúbico de sangue nesse paciente?
não
Página cento e oito
Construção de gráficos
Para construir gráficos de funções no sistema cartesiano ortogonal, devemos considerar os valores do domínio da função no eixo x (eixo das abscissas) e as respectivas imagens no eixo y (eixo das ordenadas).
O gráfico da função é o conjunto de todos os pontos (x, y) do plano cartesiano tais quê y = f(x) com x ∈ D(f).
Como exemplo, vamos construir o gráfico da função f: A → ℝ dada por y = x + 1, em quê A = {0, 1, 2, 3}.
Iniciamos construindo o qüadro com os valores de x pertencentes ao domínio e determinando as imagens de x pela função f, ou seja, os valores de y = f(x), para representar os pontos obtidos no plano cartesiano.
x |
y |
|
|---|---|---|
0 |
1 |
→ B(0, 1) |
1 |
2 |
→ C(1, 2) |
2 |
3 |
→ D(2, 3) |
3 |
4 |
→ E(3, 4) |
Observe quê D(f) = A = {0, 1, 2, 3} e Im(f) = {1, 2, 3, 4}.
Como o conjunto A é finito, o gráfico de f é formado apenas pêlos quatro pontos obtidos por meio do qüadro: B(0, 1), C(1, 2), D(2, 3) e E(3, 4). Para concluir, representamos esses pontos no sistema cartesiano, como mostra a figura.
Agora, vamos construir o gráfico da função f dada por f(x) = 2x + 3, considerando três domínios distintos, e observar as semelhanças e as diferenças entre esses gráficos.
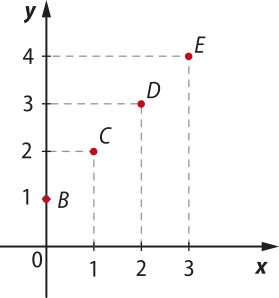
a) Considerando D(f) = {−1, 0, 1, 2, 3}.
Inicialmente, construímos um qüadro com os valores de x ∈ D(f) e determinamos as imagens de x pela função f, ou seja, os valores de y = f(x), para obtêr os respectivos pares ordenados.
x |
y = 2x + 3 |
(x, y) |
|---|---|---|
−1 |
y = 2 ⋅ (−1) + 3 = −2 + 3 = 1 |
(−1, 1) |
0 |
y = 2 ⋅ 0 + 3 = 0 + 3 = 3 |
(0, 3) |
1 |
y = 2 ⋅ 1 + 3 = 2 + 3 = 5 |
(1, 5) |
2 |
y = 2 ⋅ 2 + 3 = 4 + 3 = 7 |
(2, 7) |
3 |
y = 2 ⋅ 3 + 3 = 6 + 3 = 9 |
(3, 9) |
Página cento e nove
Em seguida, representamos, no sistema cartesiano, os pontos cujas coordenadas são os pares ordenados do qüadro.
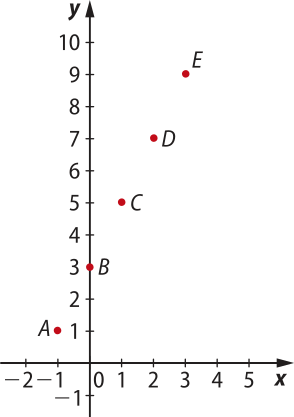
Como o domínio da função é o conjunto {−1, 0, 1, 2, 3}, o gráfico de f é formado pêlos pontos A(−1, 1), B(0, 3), C(1, 5), D(2, 7) e E(3, 9), representados na figura.
b) Considerando D(f) = [−1, 3].
Nesse caso, o domínio da função é um intervalo real, e os valores de x considerados no exemplo anterior pertencem a esse intervalo. Entretanto, no intervalo [−1, 3], existem infinitos valores de x quê têm imagem correspondente pela função f.
Quando representamos esses infinitos pontos no sistema cartesiano, obtemos um segmento de reta, quê é o gráfico da função f quando D(f) = [−1, 3].

Observe quê essa função não está definida para valores de x menóres do quê −1 nem para valores de x maiores do quê 3.
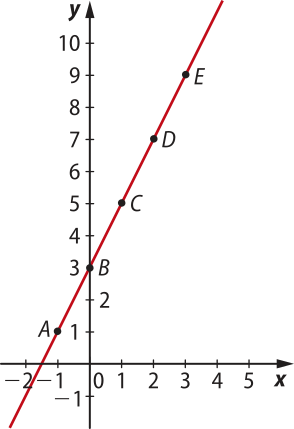
c) Considerando D(f) = ℝ.
Nesse caso, o domínio de f é todo o conjunto dos números reais e, como nos exemplos anteriores, os pontos A, B, C, D e E fazem parte do gráfico da função. Além dêêsses pontos, existem infinitos pontos quê satisfazem à lei da função f.
O gráfico de f é uma reta em quê todo valor de x ∈ ℝ tem uma imagem pela função f, expressa por y = f(x). Observe o gráfico da função f quando D(f) = ℝ.
Portanto, apesar de a lei quê define a função sêr a mesma nos três casos apresentados, os gráficos são diferentes, pois dependem do domínio considerado.
Página cento e dez
Domínio e imagem no gráfico de uma função
Considere o gráfico a seguir, quê representa uma função f.
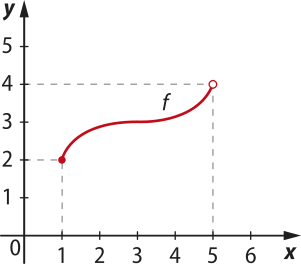
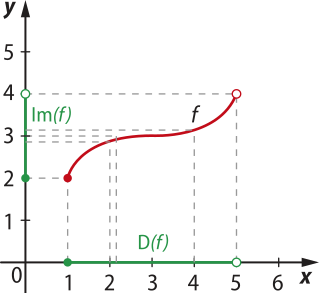
Para determinar o domínio e o conjunto imagem de f, projetamos os pontos do gráfico sobre os eixos x e y, como indicado a seguir.
Saiba quê...
A projeção ortogonal de um ponto P sobre uma reta r é o ponto P(minutos)" determinado pela intersecção da reta r com a reta perpendicular a ela, passando por P.
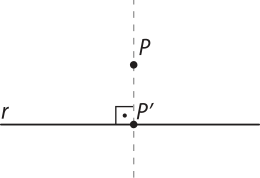
Se o ponto P é um ponto da reta r, a projeção ortogonal de P sobre r é o próprio P.
O domínio da função f é o conjunto das abscissas de todos os pontos do gráfico. Note quê o ponto (5, 4) não faz parte do gráfico. Portanto, a abscissa 5 não pertence ao domínio de f.
Sendo assim, temos:
D(f) = [1, 5[ ou D(f) = {x ∈ ℝ | 1 ≤ x < 5}
O conjunto imagem da função f é o conjunto das ordenadas de todos os pontos do gráfico. Como o ponto (5, 4) não faz parte do gráfico, então a ordenada 4 não pertence ao conjunto imagem de f. Sendo assim, temos:
Im(f) = [2, 4[ ou Im(f) = {y ∈ ℝ | 2 ≤ y < 4}
ATIVIDADE RESOLVIDA
5. Os pares ordenados (a − 1, 3) e (−2, 2b + 1) representam o mesmo ponto P no sistema cartesiano.
a) Determine os valores de a e b.
b) escrêeva as coordenadas do ponto P.
Resolução
a) Como os pares ordenados representam o mesmo ponto P, as abscissas a − 1 e −2 são iguais, assim como as ordenadas 3 e 2b + 1. Então, obtemos os valores de a e de b resolvendo as seguintes equações:
a − 1 = −2 ⇒ a = −2 + 1 ⇒ a = −1
2b + 1 = 3 ⇒ 2b = 3 − 1 ⇒ b = 1
Portanto, a = −1 e b = 1.
b) Com os valores de a e b, substituímos em um dos pares ordenados para obtêr as coordenadas do ponto P.
a − 1 = −1 − 1 = −2
Portanto, as coordenadas de P são (−2, 3).
Página cento e onze
ATIVIDADES
13. Determine as coordenadas dos pontos indicados na figura.

A(2, 2); B(0, 0); C(5, 0); D(0, 6); E(−3, 0); F(0, −2); G(−2, 4); H(−5, −5); I(5, −3); J(−5, 1)
14. Dados os pares ordenados (2a − 3, b + 2) e (5a − 1, 2b − 3) e sabendo quê ambos representam o mesmo ponto no sistema cartesiano, quais são os valores de a e b?
a = e b = 5
15. (OBMEP) Manoel testa sua pontaria lançando 5 flechas quê atingiram o alvo nos pontos A, B, C, D e E de coordenadas A = (1, −1), B = (2,5; 1), C = (−1, 4), D = (−4, −4) e E = (6, 5).
A tabéla mostra quantos pontos se ganha quando a flecha acerta um ponto dentro de cada uma das três regiões, conforme mostra a figura.
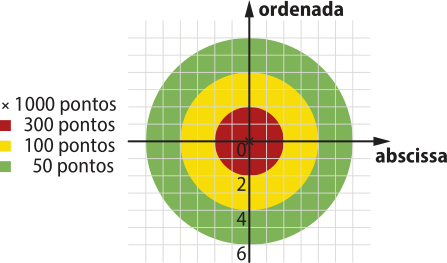
a) Marque os pontos A, B, C, D e E.
Ver as Orientações para o professor.
b) Quantas flechas ele acertou no interior do menor círculo?
1 flecha
c) Ao todo, quantos pontos Manoel fez?
500 pontos
16. Os esboços dos gráficos a seguir representam funções reais de variável real. Observando-os, determine o domínio D(f) e o conjunto imagem Im(f) de cada função.
a)
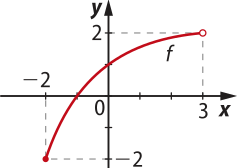
D(f) = {x ∈ ℝ | −2 ≤ x < 3}
e Im(f) = {y ∈ ℝ | −2 ≤ y < 2}
b)
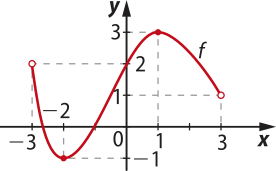
D(f) = {x ∈ ℝ | −3 < x < 3}
e Im(f) = {y ∈ ℝ | −1 ≤ y ≤ 3}
c)
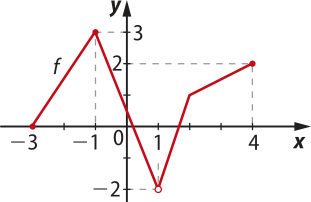
D(f) = {x ∈ ℝ | −3 ≤ x ≤ 4 e x ≠ 1}
e Im(f) = {y ∈ ℝ | −2 < y ≤ 3}
d)
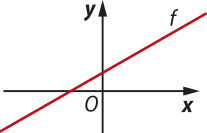
D(f) = ℝ e Im(f) = ℝ
e)
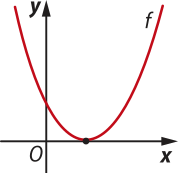
D(f) = ℝ e Im(f) = {y ∈ ℝ | y ≥ 0}
f)
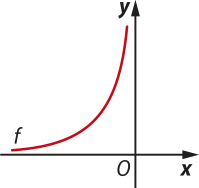
D(f) = {x ∈ ℝ | x < 0} e Im(f) = {y ∈ ℝ | y > 0}
17. (UFV-MG) O gráfico a seguir ilustra a evolução da tempera-túra T (°C), em uma região ao longo de um período de 24 horas.
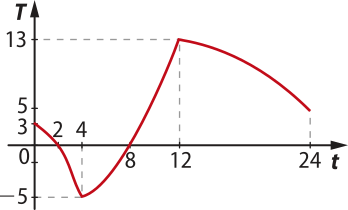
Determine:
a) os horários em quê a tempera-túra atinge 0 °C;
às 2 h e às 8 h
b) o intervalo de variação da tempera-túra ao longo das 24 horas;
A tempera-túra varia de −5 °C a 13 °C.
c) os intervalos de tempo em quê a tempera-túra é positiva.
de 0 h às 2 h e de 8 h às 24 h
Página cento e doze
Função afim
Você sabe como é calculado o valor de uma corrida de táxi? Tudo depende de onde você está e para onde quer ir.
O valor de uma corrida de táxi está relacionado a duas tarifas: uma tarifa fixa, conhecida como bandeirada, e outra variável, quê é cobrada por kilometro rodado e por outros fatores quê possam influenciar esse valor, como o tempo do veículo parado no trânsito e o período do dia em quê acontece a corrida.
A determinação dessas tarifas é incumbência das prefeituras; por isso, estados e até cidades dentro do mesmo estado podem ter valores diferentes. Como exemplo, conforme regulamentado pela Prefeitura de São Paulo, em 2024, no município de São Paulo (SP), na categoria Táxi Comum, o preêço da bandeirada para o período das 6 h às 20 h era de R$ 6,00, e a taxa por kilometro rodado era de R$ 4,25. Além díssu, havia a tarifa de R$ 51,00 por hora parada.
Desse modo, o preêço p a sêr cobrado por uma corrida de táxi depende, entre outros fatores, da distância x percorrida pelo táxi. Vamos estudar agora como podemos utilizar o conceito de função para analisar a relação entre esses valores.
Levando em consideração os dados apresentados do município de São Paulo (SP), suponha uma situação em quê o táxi não cobre adicionalmente a hora parada e cujo período da corrida esteja dentro do horário das 6 h às 20 h. Nesse caso, o preêço p a sêr cobrado é compôzto de uma parte fixa, quê é a bandeirada, e uma parte variável, correspondente à distância x percorrida.
Considerando R$ 6,00 o valor da bandeirada e R$ 4,25 o valor de cada kilometro rodado, podemos escrever a seguinte lei de formação para representar o preêço p em função da distância x:
p(x) = 6,00 + 4,25x ou y = 4,25x + 6
Observe quê p(x) ou y é o preêço a sêr cobrado (em reais) e x é a distância percorrida (em kilometro).
Pense e responda
Utilizando a lei de formação apresentada, calcule o preêço cobrado por uma corrida de táxi cuja distância percorrida foi de 8 km.
R$ 40,00

Página cento e treze
Acompanhe, agora, outra situação quê póde sêr modelada e analisada por meio de uma função.
Um encanador foi contratado para resolver o problema de vazamento em uma residência e, para ter noção da quantidade de á gua desperdiçada e localizar o vazamento, fechou todos os registros até quê a caixa-d’água de 1.000 litros ficasse completamente cheia. Na rê-de em quê detectou o vazamento, ele percebeu quê 8 litros de á gua eram desperdiçados a cada hora.
A quantidade de á gua q (em litro) quê resta na caixa-d’água é uma função do tempo t (em hora) e póde sêr representada pela lei:
q(t) = 1.000 − 8t ou y = −8t + 1.000
Pense e responda
Determine quantos litros de á gua restarão na caixa se o vazamento durar 24 horas.
808 litros
As leis de formação utilizadas para representar cada situação descrita anteriormente são exemplos de leis de função afim, quê podemos definir da seguinte maneira:
Uma função f: ℝ → ℝ definida por f(x) = ax + b, com a e b reais, é chamada de função afim.
Observe outros exemplos de leis de função afim.
a) f(x) = 5x + 1 ou y = 5x + 1
b) g(x) = − 1 ou y = − − 1
c) h(x) = x ou y =
d) z(x) = 14,90 ou y = 14,90

Lembre-se de quê x é a variável independente e y é a variável dependente na função afim dada por y = ax + b. Ao atribuir valores para a variável independente x, obtemos y, o valor da função. Observe alguns exemplos.
• Considerando a função dada por f(x) = 5x + 1, podemos calcular f(3) da seguinte maneira: f(3) = 5 ⋅ 3 + 1 ⇒ f(3) = 16
Portanto, 16 é o valor da função f para x = 3.
• Considerando a função dada por h(x) = podemos calcular h(−20) da seguinte maneira: h(−20) = ⋅ (−20) ⇒ h(−20) = 8 Portanto, 8 é o valor da função h para x = −20.
Em uma função afim dada por f(x) = ax + b, os números reais a e b são chamados coeficientes e, de acôr-do com seus valores, a função afim recebe alguns nomes particulares, quê estudaremos a seguir.
Página cento e quatorze
Função polinomial do 1º grau
Quando o coeficiente a da função afim é diferente de zero, a função recebe o nome de função polinomial do 1º grau, pois a relação entre a variável dependente e a variável independente é expressa por um polinômio do 1º grau.
Uma função f: ℝ → ℝ definida por f(x) = ax + b, com a e b reais e a ≠ 0, é chamada de função polinomial do 1 º grau.
Observe alguns exemplos de leis de função polinomial do 1º grau:
a) f(x) = 2x − 1, em quê a = 2 e b = −1;
b) y = 0,5x + , em quê a = 0,5 e b = ;
c) y = + 2x, em quê a = 2 e b = ;
d) f(x) = 4x, em quê a = 4 e b = 0.
Função linear
Considere, agora, a situação a seguir.
cérto modelo de veículo blindado consome, aproximadamente, 0,25 litro de combustível por kilometro rodado. pôdêmos dizêr quê a quantidade y de combustível consumido (em litro) é função da distância x percorrida (em kilometro) e póde sêr indicada pela lei:
y = 0,25x
A lei para representar essa função é a lei de um tipo de função afim, conhecida também como função linear, quê definimos da seguinte maneira:
Uma função f: ℝ → ℝ definida por f(x) = ax, com a real e a ≠ 0, é chamada de função linear.
Pense e responda
por quê uma função linear é uma função afim?
Porque ela também é da forma f(x) = ax + b, com a e b reais.
Observe alguns exemplos de leis de função linear
a) f(x) = −7x, em quê a = −7;
b) y = , em quê a = ;
c) y = , em quê a = ;
d) y = x, em quê a = 1.

Pense e responda
• Quantos litros de combustível são necessários para quê esse modelo de veículo blindado percorra 20 km?
5 litros
Página cento e quinze
Função identidade
Quando a = 1 e b = 0, a função polinomial do 1º grau é expressa pela lei f(x) = x e é chamada função identidade.
A função f: ℝ → ℝ definida por f(x) = x é chamada de função identidade.
A função identidade recebe esse nome por associar cada valor de x ∈ ℝ a ele mesmo. Por exemplo:
• f(1) = 1;
• f(0,5) = 0,5;
• f(−3) = −3;
•
Função linear e proporcionalidade
Retomando a situação quê relaciona o consumo de combustível y (em litro) de um modelo de carro blindado e a distância x quê ele percórre (em kilometro) por meio de uma função linear dada por y = 0,25x, podemos construir um qüadro para analisar a relação entre alguns valores.
Observe.
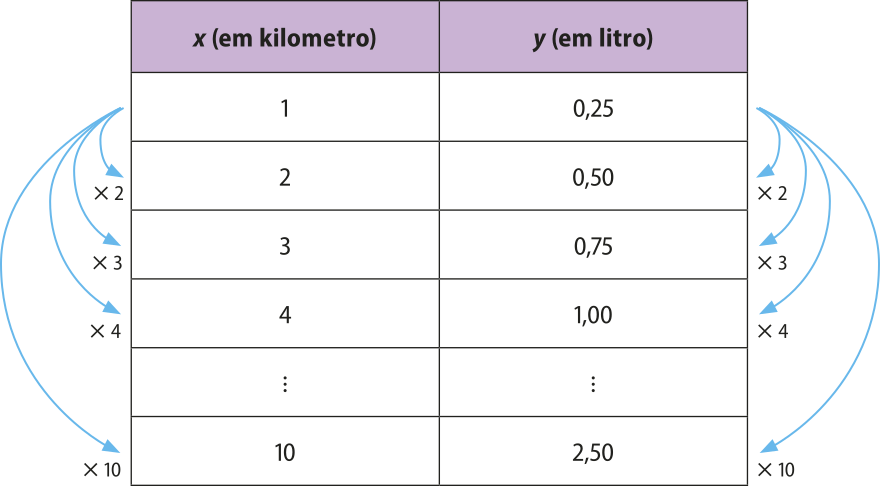
Perceba quê, ao dobrarmos o valor de x, o valor correspondente de y também dobra. Se multiplicarmos x por 3, o valor correspondente de y também será multiplicado por 3, e assim sucessivamente.
Nesse caso, dizemos quê as variáveis x e y representam grandezas diretamente proporcionais, e a constante de proporcionalidade k póde sêr ôbitída pela razão , quando x ≠ 0.
… = 0,25, ou seja, k = 0,25
Em uma função linear, cuja lei de formação é dada por y = ax, quando a > 0, dizemos quê as variáveis x e y representam grandezas diretamente proporcionais. A constante de proporcionalidade k é o coeficiente a da função.
Página cento e dezesseis
Função constante
Outro tipo de função afim é a função constante, definida a seguir.
A função f: ℝ → ℝ definida por f(x) = b, com b real, é chamada de função constante.
Saiba quê...
Se b = 0, a função constante f é dada por f(x) = 0 para todo x real. Essa função é conhecida como função nula.
A função constante associa cada valor de x ∈ ℝ sempre ao mesmo valor b. Nesse caso, o conjunto imagem da função constante é Im(f) = {b}.
Por exemplo, para a função constante f dada por f(x) = 12, todos os elemêntos de D(f) têm imagem igual a 12. Observe alguns casos.
• f(0) = 12
• f(−3) = 12
• f = 12
• f = 12
ATIVIDADES RESOLVIDAS
6. Vinícius trabalha como di gêi e cobra um valor fixo de R$ 250,00, além de um valor adicional de R$ 110,00 por hora, para animar uma festa.

a) Indicando por y o valor total cobrado por Vinícius, em reais, e por x a quantidade de horas trabalhadas, escrêeva a lei da função quê relaciona y e x.
b) Essa lei de formação é de uma função afim? Justifique sua resposta.
c) Qual é o valor, em reais, quê Vinícius receberá se trabalhar durante 2 horas em uma festa?
d) Sabendo quê Vinícius recebeu R$ 635,00 pelo trabalho em determinada festa, por quantas horas ele prestou seu serviço?
Resolução
a) O valor y recebido por Vinícius depende da quantidade x de horas quê ele trabalhou animando a festa. Assim, a lei quê relaciona essas duas variáveis póde sêr escrita como:
y = 250 + 110x ou y = 110x + 250
b) Sim, essa lei de formação é de uma função afim, pois é do tipo y = ax + b, com a e b reais. Nesse caso, a = 110 e b = 250.
c) Se o tempo de animação da festa for de 2 horas, então substituímos x por 2 na lei da função e determinamos o valor de y correspondente:
y = 250 + 110 ⋅ 2 ⇒ y = 250 + 220 ⇒ y = 470
Portanto, Vinícius receberá R$ 470,00 por 2 horas de trabalho na festa.
d) Sabendo quê ele recebeu R$ 635,00, substituímos y por 635 na lei da função e determinamos o valor de x:
635 = 250 + 110x ⇒ 110x = 385 ⇒ x = 3,5
Portanto, ele prestou serviço nessa festa por 3,5h ou 3h30min.
Pense e responda
Observe a afirmação a seguir.
“O valor quê Vinícius recebe é diretamente proporcional ao número de horas quê trabalhou”.
Reúna-se a um colega, e discutam-na. Ela é verdadeira? Justifiquem.
Não, pois a relação entre o valor quê ele recebe e o número de horas trabalhadas não é dada por uma função linear.
Página cento e dezessete
7. (UEG-GO) Em uma fábrica, o custo de fabricação de 500 unidades de camisetas é de R$ 2.700,00, enquanto o custo para produzir 1.000 unidades é de R$ 3.800,00. Sabendo quê o custo das camisetas é dado em função do número produzido através da expressão C(x) = qx + b, em quê x é a quantidade produzida e b é o custo fixo, determine:
a) Os valores de b e de q.
b) O custo de produção de 800 camisetas.
Resolução
a) De acôr-do com o enunciado:
• quando x = 500, temos C(500) = 2.700;
• quando x = 1.000, temos C(1.000) = 3.800.
Para determinar os valores de b e q, utilizamos essas informações, substituindo os valores correspondentes na lei C(x) = qx + b, e resolvemos o sistema a seguir.
Multiplicamos por (−1) a primeira equação do sistema e adicionamos membro a membro as duas equações, como indicado a seguir.
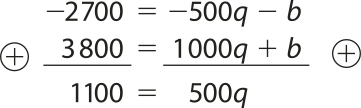
Se 500q = 1.100, então q = .
Substituindo q por na primeira equação do sistema, temos:
2.700 = 500 ⋅ + b ⇒ b = 1.600
Portanto, b = 1.600 e q = .
b) A lei da função quê representa o custo das camisetas é C(x) = x + 1.600.
Substituindo x = 800 na lei da função, determinamos C(800).
C(800) = ⋅ 800 + 1.600 ⇒ C(800) = 3.360
Portanto, o custo de produção de 800 camisetas é R$ 3.360,00.
8. Marcelo mora em um município onde é possível alugar patinetes elétricos para se locomover. A velocidade mássima permitida dêêsses aparelhos é de 20 km/h, mas é recomendado quê pessoas sem experiência não ultrapassem 12 km/h. Fazendo alguns cálculos para estimar o tempo quê levaria utilizando um patinete elétrico de uma estação de metrô até o local onde trabalha, Marcelo considerou quê manteria uma velocidade constante de 3 metros por segundo e fez um qüadro para relacionar a distância percorrida, em métro, em função do tempo, em segundo.
Distância d (em metro) |
3 |
6 |
9 |
12 |
15 |
… |
|---|---|---|---|---|---|---|
Tempo t (em segundo) |
1 |
2 |
3 |
4 |
5 |
… |
Com base nessas informações, responda:
a) Qual é a lei da função quê relaciona a distância d, em métro, a sêr percorrida por Marcelo e o tempo t, em segundo?
b) As grandezas representadas por d e t são diretamente proporcionais? Justifique sua resposta.
c) Marcelo levou 10 minutos para realizar o deslocamento quê pretendia nas condições quê tinha planejado. Qual distância ele percorreu?
Resolução
a) De acôr-do com os dados apresentados, verifica-se quê, a cada segundo, Marcelo vai percorrer 3 metros de distância.
Essa relação corresponde a uma função linear, quê póde sêr representada pela lei d(t) = 3t.
b) Sim. Essa função é linear, e o coeficiente a da função é igual a 3. Como 3 ≠ 0 e 3 > 0, as grandezas representadas por d e t são grandezas diretamente proporcionais.
Também podemos verificar quê, se multiplicarmos o valor de t por um número natural n, o valor correspondente de d também será multiplicado pelo mesmo número natural n.
c) Como Marcelo levou 10 minutos para realizar o percurso, isso equivale a 600 segundos, pois 10 ⋅ 60 = 600.
Substituindo t = 600 na lei da função, temos:
d(600) = 3 ⋅ 600 ⇒ d(600) = 1.800
Portanto, Marcelo percorreu 1.800 metros.
Página cento e dezoito
ATIVIDADES
18. Karina trabalha em um ateliê quê confeksiona sapatos e usa uma fórmula para calcular a numeração deles, de acôr-do com a medida de comprimento dos pés dos clientes.

A fórmula utilizada por Karina é dada por y = 1,25x + 7, em quê y é a numeração do sapato e x, a medida de comprimento do pé, em centimetro. Quando o resultado não é um número natural, ela o arredonda para o número natural imediatamente maior do quê o valor calculado.
a) Determine a numeração do sapato de um cliente de Karina cujo pé méde 27 cm.
41
b) ![]() Considere, agora, sua numeração de sapato e utilize essa fórmula para calcular a medida de comprimento x correspondente. Depois, use uma régua para medir o comprimento do seu pé e confira se o valor calculado é um valor aproximado da medida verificada.
Considere, agora, sua numeração de sapato e utilize essa fórmula para calcular a medida de comprimento x correspondente. Depois, use uma régua para medir o comprimento do seu pé e confira se o valor calculado é um valor aproximado da medida verificada.
Resposta pessoal.
19. Considere as funções reais definidas a seguir.
I. f(x) = 3x2 − 5x + 4
II. g(x) = −2x + X
III. h(x) =
IV. i(x) = 0,01
Ver as Orientações para o professor.
a) Qual(is) dessas leis é(são) de função afim?
b) Classifique as funções afins em função polinomial do 1º grau, função linear e/ou função constante.
c) Para as funções afins, identifique os valores dos coeficientes a e b.
20. Dada a função definida por f(x) = 5x − 2, determine:
a) f(2);
8
b) o valor de x para f(x) = 0.
x =
21. (Enem/MEC) Para concretar a laje de sua residência, uma pessoa contratou uma construtora. Tal empresa informa quê o preêço y do concreto bombeado é compôzto de duas partes: uma fixa, chamada de taxa de bombeamento, e uma variável, quê depende do volume x de concreto utilizado. Sabe-se quê a taxa de bombeamento custa R$ 500,00 e quê o métro cúbico do concreto bombeado é de R$ 250,00.
A expressão quê representa o preêço y em função do volume x, em métro cúbico, é
alternativa d
a) y = 250x
b) y = 500x
c) y = 750x
d) y = 250x + 500
e) y = 500x + 250
22. Considere uma função afim dada por y = h(x). Sabendo quê h(1) = 4 e h(−2) = 10, escrêeva a lei da função h e calcule h .
h(x) = −2x + 6; h = 7
23. Dada a função f definida por f(x) = ax + 2, determine o valor de a para quê se tenha f(4) = 20.
24. Sofia quer produzir folhetos com a propaganda de sua empresa. Na gráfica A, o valor da impressão dêêsse folheto, por unidade, é R$ 0,30, e, na gráfica B, o valor, também por unidade, é R$ 0,25.
a) escrêeva a fórmula quê relaciona o valor y a sêr pago pela impressão, em reais, com o número x de folhetos impressos em cada uma dessas gráficas.
yA = 0,30x e yB = 0,25x
Página cento e dezenove
b) Na gráfica A, o valor pago pela impressão é diretamente proporcional ao número de unidades impréssas? E na gráfica B? Justifique.
Ver as Orientações para o professor.
c) Se Sofia encomendar 1.000 folhetos na gráfica B, quantos reais gastará?
R$ 250,00
25. Sabendo quê f é uma função linear e quê f(−3) = 4, determine o valor de f(6).
−8
26. Os lados de um retângulo médem x e (x + 5), em métro.
a) escrêeva a fórmula matemática quê relaciona o perímetro p dêêsse retângulo com a medida x.
p = 4x + 10
b) Reproduza o qüadro a seguir e complete-o com os valores quê faltam.
x (em metro) |
5 |
10 |
20 |
30 |
||
|---|---|---|---|---|---|---|
p (em metro) |
162 |
210 |
Ver as Orientações para o professor.
c) As grandezas p e x são diretamente proporcionais? Por quê?
Não, pois a razão não é constante.
d) Quais devem sêr as medidas dos lados dêêsse retângulo para quê o perímetro seja de 78 metros?
17 m e 22 m
27. (FGV-SP) Uma função polinomial f do 1º grau é tal quê f(3) = 6 e f(4) = 8. Portanto, o valor de f(10) é:
a) 16
b) 17
c) 18
d) 19
e) 20
alternativa e
28. Considere quê uma pessoa, caminhando a uma velocidade constante, percorra, em média, 80 centimetros a cada 1 segundo.

a) escrêeva a fórmula quê indica a distância percorrida d, em centimetro, em função do tempo t, em segundo.
d = 80t
b) Nessa situação, a distância (d) e o tempo (t) são grandezas diretamente proporcionais? Justifique sua resposta.
Ver as Orientações para o professor.
c) Quantos metros uma pessoa nessas condições percorrerá em 10 segundos? E em 40 segundos?
8m; 32m
d) Quantos segundos uma pessoa nessas condições levará para percorrer 100 metros?
125 s
29. (UFC-CE) Seja f uma função real, de variável real, definida por f(x) = ax + b. Se f(1) = −9 e b2 − a2 = 54, calcule o valor de a − b.
6
Saiba quê...
O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
(b + a) ⋅ (b − a) = b2 − a2
30. (Enem/MEC) Um experimento consiste em colocar certa quantidade de bolas de vidro idênticas em um copo com á gua até cérto nível e medir o nível da á gua, conforme ilustrado na figura a seguir. Como resultado do experimento, concluiu-se quê o nível da á gua é função do número de bolas de vidro quê são colocadas dentro do copo. O qüadro a seguir mostra alguns resultados do experimento realizado.

número de bolas (x) |
nível da á gua (y) |
|---|---|
5 |
6,35 cm |
10 |
6,70 cm |
15 |
7,05 cm |
Disponível em: ww w.penta.ufrgs.b r. Acesso em: 13 jan. 2009 (adaptado).
Qual a expressão algébrica quê permite calcular o nível da á gua (y) em função do número de bolas (x)?
alternativa e
a) y = 30x.
b) y = 25x + 20,2.
c) y = 1,27x.
d) y = 0,7x.
e) y = 0,07x + 6.
Página cento e vinte
Gráfico da função afim
Estudamos quê o gráfico de uma função f é o conjunto de todos os pontos (x, y) tais quê x ∈ D(f) e y = f(x).
Em relação ao gráfico da função afim, pode-se demonstrar o seguinte teorema.
O gráfico da função afim f: ℝ → ℝ tal quê f(x) = ax + b é uma reta.
Quando o domínio de uma função f, tal quê f(x) = ax + b, é um subconjunto de ℝ diferente do próprio ℝ, o gráfico de f póde sêr uma semirreta, um segmento de reta ou pontos de uma reta, como ocorre nos exemplos a e b das páginas 108 e 109.
Com base no teorema, podemos localizar, no sistema cartesiano, dois pontos distintos pertencentes ao gráfico da função afim e traçar a reta correspondente.
Inicialmente, construímos um qüadro com dois valores de x ∈ ℝ e determinamos os valores de y = f(x) para obtêr os pares ordenados dêêsses pontos. Em seguida, localizamos esses pontos no sistema cartesiano e traçamos a reta determinada por eles, quê é o gráfico da função f.
Acompanhe alguns exemplos.
a) Gráfico da função afim definida por f(x) = 2x − 1
Primeiro, escolhemos dois valores reais para x e obtemos os pares ordenados de dois pontos pertencentes ao gráfico de f. Em seguida, traçamos o gráfico.
x |
y = 2x − 1 |
(x, y) |
|---|---|---|
−1 |
y = 2 ⋅ (−1) − 1 = −3 |
(−1, −3) |
2 |
y = 2 ⋅ 2 − 1 = 3 |
(2, 3) |
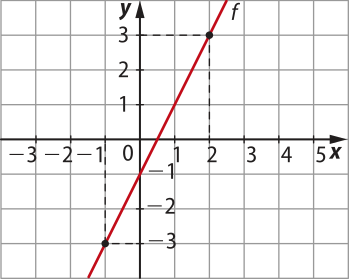
b) Gráfico da função afim definida por g(x) = −2x − 1
Inicialmente, escolhemos dois valores reais para x e obtemos os pares ordenados de dois pontos pertencentes ao gráfico de g. Em seguida, traçamos o gráfico.
x |
y = −2x − 1 |
(x, y) |
|---|---|---|
−1 |
y = −2 ⋅ (−1) − 1 = 1 |
(−1, 1) |
1 |
y = −2 ⋅ 1 − 1 = −3 |
(1, −3) |
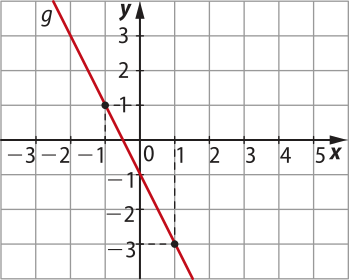
Pense e responda
Compare o gráfico da função f com o da função g. Depois, obissérve as leis dessas funções. Você identifica alguma semelhança e alguma diferença entre esses gráficos? Explique.
Espera-se quê os estudantes percêbam quê o gráfico da função f e o da função g cruzam o eixo y no mesmo ponto, cuja ordenada corresponde ao coeficiente b dessas funções. O coeficiente a da função g é o ôpôsto do coeficiente a da função f, e as retas são simétricas em relação ao eixo y.
Página cento e vinte e um
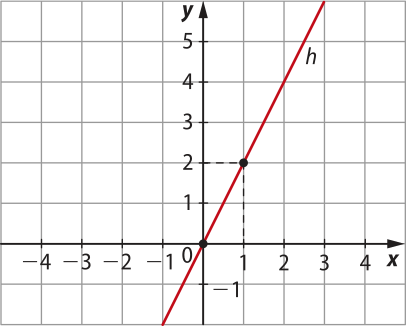
c) Gráfico da função afim definida por h(x) = 2x
Observe quê a função h é uma função linear. Como a lei de formação de uma função linear é da forma y = ax, substituindo x = 0 nessa lei, temos y = a ⋅ 0 = 0.
Portanto, o gráfico da função linear sempre passa pelo ponto (0, 0), origem do sistema cartesiano.
x |
y = 2x |
(x, y) |
|---|---|---|
0 |
y = 2 ⋅ 0 = 0 |
(0, 0) |
1 |
y = 2 ⋅ 1 = 2 |
(1, 2) |
d) Gráfico da função afim definida por i(x) = x
Observe quê a função i é a função identidade, quê associa cada valor de x do domínio a ele mesmo. O gráfico da função i também passa pela origem do sistema cartesiano.
x |
y = x |
(x, y) |
|---|---|---|
−2 |
y = −2 |
(−2, −2) |
3 |
y = 3 |
(3, 3) |
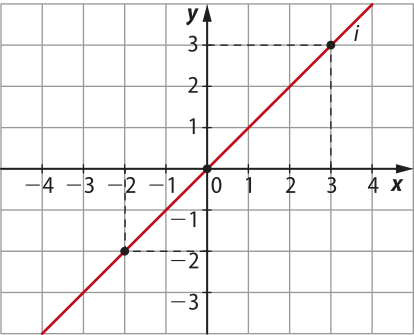
O gráfico da função identidade é a reta quê contém a bissetriz dos quadrantes ímpares do plano cartesiano.
e) Gráfico da função afim definida por j(x) = 4
Observe quê a função j é uma função constante. Para qualquer valor de x no domínio da função, y é igual a 4. Portanto, o gráfico é uma reta paralela ao eixo x quê intersecta o eixo y no ponto (0, 4).
x |
y = 4 |
(x, y) |
|---|---|---|
−1 |
y = 4 |
(−1, 4) |
3 |
y = 4 |
(3, 4) |
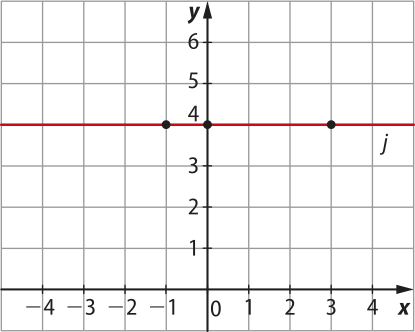
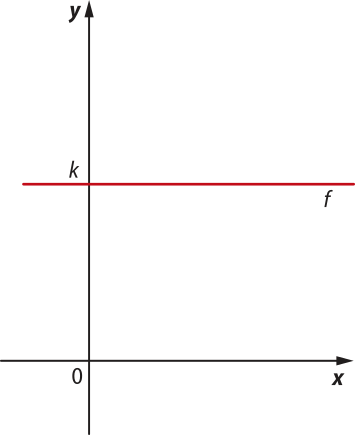
O gráfico de uma função constante definida por y = k, em quê k ∈ ℝ, é uma reta paralela ao eixo x quê intersecta o eixo y no ponto (0, k).
Pense e responda
Sobre os exemplos apresentados, responda:
O exemplo c, cuja constante de proporcionalidade é 2, e o exemplo d, cuja constante de proporcionalidade é 1.
• Em quais deles as variáveis x e y representam grandezas diretamente proporcionais? Justifique sua resposta.
• Nesse(s) caso(s), qual é a constante de proporcionalidade?
Página cento e vinte e dois
Zero da função afim
Estudaremos, agora, o valor da variável independente quê anula a função afim, mas, antes, apresentamos a seguinte definição.
Em uma função f: A → B, um valor de x ∈ A tal quê f(x) = 0 é chamado zero da função f.
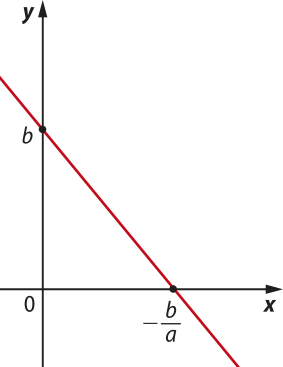
No caso da função afim, definida por f(x) = ax + b, quando a ≠ 0, resolvemos a equação f(x) = 0, ou seja, ax + b = 0 para determinar o zero da função f. Nesse caso, temos:
ax + b = 0 ⇒ ax = −b ⇒ x =
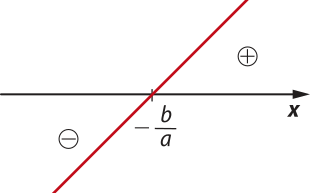
Logo, quando a ≠ 0, o zero de uma função afim é dado por x = . O zero da função afim é a abscissa do ponto em quê o gráfico intersecta o eixo x, como indicado na figura.
Se a = 0, temos duas situações:
• b ≠ 0: nesse caso, temos uma função constante cujo gráfico não intersecta o eixo x; portanto, não há zero da função;
• b = 0: nesse caso, temos uma função constante dada por y = 0, conhecida também como função nula, cujo gráfico é uma reta coincidente com o eixo x; portanto, todo x ∈ ℝ é zero da função nula.
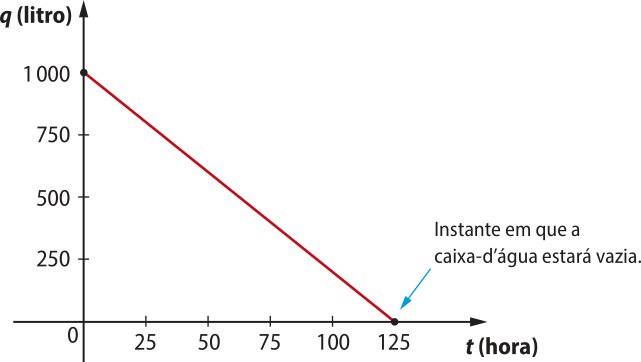
Acompanhamos, em uma situação apresentada anteriormente, quê, por causa de um vazamento, a quantidade de á gua q em uma caixa-d’água, em litro, varia em função do tempo t, em hora, de acôr-do com a lei q(t) = −8t + 1.000.
Para saber em quanto tempo esse vazamento esvaziará a caixa-d'água, considerando quê o registro de entrada de á gua na caixa permaneça fechado, podemos determinar o zero dessa função. Nesse caso, temos:
−8t + 1.000 = 0 ⇒ −8t = −1.000 ⇒ t = 125
Portanto, nas condições apresentadas, o vazamento esvaziará essa caixa-d’água em 125 horas.
Geometricamente, essa situação também póde sêr interpretada por meio do gráfico da função, como indicado a seguir.
Pense e responda
Analisando o gráfico da função q e a relação quê ela representa, quais são o domínio e a imagem da função q?
D(q) = [0, 125] e Im(q) = [0, 1000]
Página cento e vinte e três
Taxa de variação
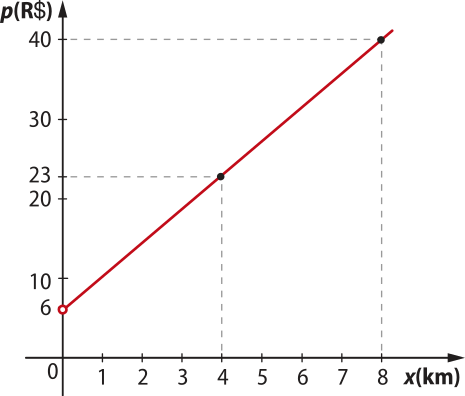
Utilizamos, neste Capítulo, uma função dada por p(x) = 4,25x + 6 para representar a relação entre o preêço de uma corrida de táxi, em reais, e a distância percorrida, em kilometro.
Observe a seguir o gráfico dessa função, verificando quê, nessa situação, temos x > 0.
Pense e responda
• por quê, nessa situação, o domínio da função é o conjunto formado pêlos valores reais de x maiores do quê 0?
Espera-se quê os estudantes respondam quê o domínio da função é o conjunto formado pêlos valores reais maiores do quê 0, porque x representa a distância percorrida pelo táxi, e a distância percorrida pelo táxi é um valor positivo.
• Nessa função, qual é o acréscimo verificado no valor de p a cada variação de 1 km no valor de x?
R$ 4,25
Perceba quê, na situação apresentada, há uma variação nos valores da função p à medida quê os valores correspondentes de x também varíam. Estudaremos, agora, uma maneira de fazer essa análise utilizando a taxa de variação média.
Considerando uma função f: ℝ → ℝ e dois números reais x1 e x2, tais quê x1 < x2,a taxa de variação média da função no intervalo [x1,x2] é dada por .
pôdêmos determinar a taxa de variação média da função afim f: ℝ → ℝ, dada por f(x) = ax + b, em um intervalo [x1, x2], com x1 ≠ x2, da seguinte maneira:
Logo, a taxa de variação média da função afim definida por f(x) = ax + b, em relação a x, é dada pelo coeficiente a.
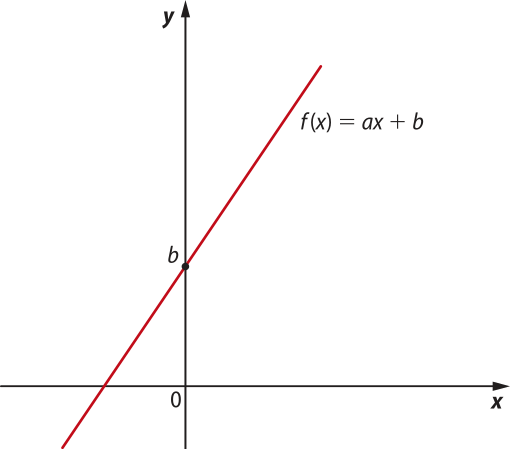
O coeficiente a é também conhecido como coeficiente angular ou declividade da reta, pois esse coeficiente está relacionado ao ângulo de inclinação da reta em relação ao eixo x quando os eixos coordenados apresentam a mesma escala.
O coeficiente b, denominado coeficiente linear dessa reta, é a ordenada do ponto em quê o gráfico da função afim intersecta o eixo y.
Página cento e vinte e quatro
Observe e compare, em um mesmo sistema cartesiano, o gráfico de algumas funções afins, considerando diferentes valores de a.
• f(x) = x + 1
• g(x) = 2x + 1
• h(x) = 5x + 1
• i(x) = + 1
• j(x) = −x + 1
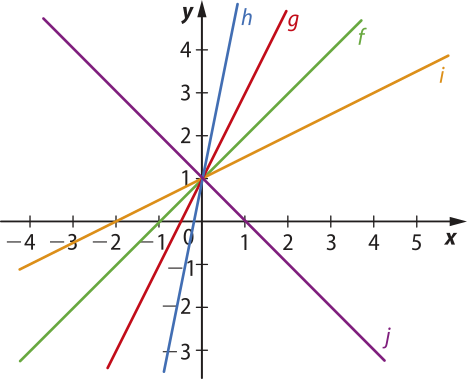
Observe e compare, agora, em um mesmo sistema cartesiano, o gráfico de algumas funções afins, considerando diferentes valores de b.
• m(x) =
• n(x) = + 1
• p(x) = − 1
• q(x) = − 2
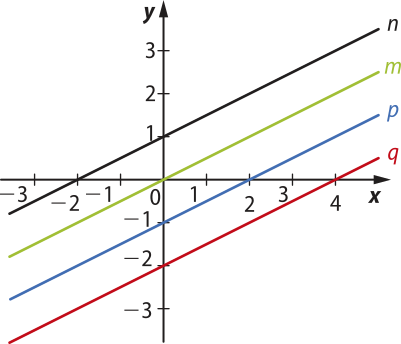
Note quê os gráficos das funções afins com o mesmo coeficiente a têm a mesma inclinação em relação ao eixo x, ou seja, são retas paralelas entre si.
Pense e responda
Em qual das representações é possível obtêr o gráfico de uma função por meio de um movimento de translação vertical do gráfico de outra: quando variamos o coeficiente a e fixamos o b, ou quando fixamos o coeficiente a e variamos o b?
A representação com o coeficiente a fixo e o coeficiente b variando.
Agora, acompanhe a situação a seguir.
Interessado em comprar um apartamento, Maurício fez uma pesquisa em sáites de vendas de imóveis focando as buscas em uma região de interêsse. Após verificar uma grande quantidade de opções, ele calculou a média dos preços dos apartamentos por área e, com os dados, construiu o seguinte qüadro.
Área do imóvel (em m2) |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|---|---|---|---|---|---|---|---|
Valor médio (em milhares de reais) |
200 |
250 |
320 |
440 |
510 |
620 |
690 |
Página cento e vinte e cinco
Ele colocou os valores médios dos apartamentos em função da área em um aplicativo e observou, no gráfico gerado, quê os pontos obtidos não estavam sobre uma única reta (Figura 1), mas quê era possível obtêr uma reta (Figura 2) quê o auxiliasse a analisar o comportamento dêêsses valores.
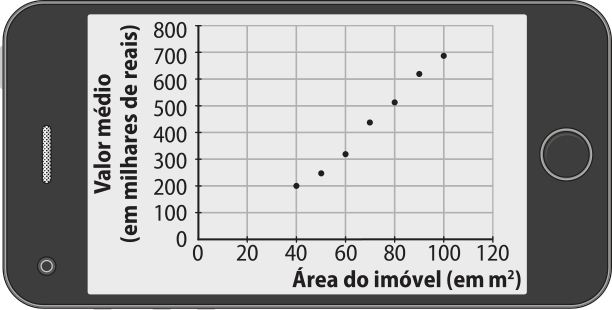
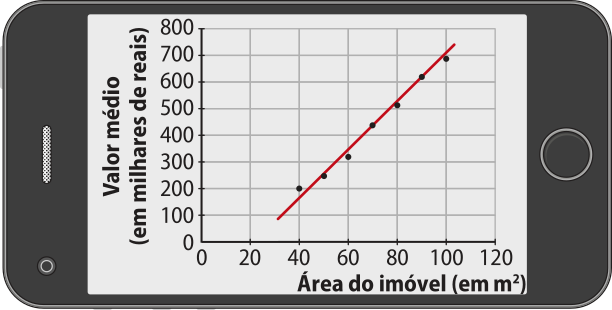
Maurício obteve a lei de uma função afim para quê pudesse modelar essa situação e fazer uma estimativa do valor médio de apartamentos com área de 150 m2. Observe como ele fez isso.
Inicialmente, Maurício utilizou os pontos (70, 440) e (90, 620), pertencentes à reta, para calcular o coeficiente a.
Assim, ele escreveu a lei da função como y = 9x + b.
Em seguida, calculou o coeficiente linear b substituindo as coordenadas do ponto (70, 440) na lei da função.
440 = 9 ⋅ 70 + b ⇒ b = 440 − 630 ⇒ b = −190
Desse modo, obteve a lei da função dada por f(x) = 9x − 190 e calculou f(150).
f(150) = 9 ⋅ 150 − 190 = 1.350 − 190 = 1.160
Portanto, a estimativa de Maurício é de quê um apartamento com 150 m2 de área tenha um valor médio próximo de R$ 1.160.000,00.
Pense e responda
Você identifica uma situação do dia a dia envolvendo a relação entre duas variáveis numéricas cujo comportamento póde sêr analisado com o auxílio de uma função afim? Qual?
O preêço de serviços em função do tempo é um exemplo de situação do dia a dia em quê a relação entre duas variáveis numéricas póde sêr representada por uma função afim.
ATIVIDADES RESOLVIDAS
9. Considere a função afim dada por f(x) = −3x + 5 e determine:
a) o valor da função para x = 0;
b) o zero da função.
Resolução
a) Para determinar f(0), substituímos o valor de x na lei da função dada.
f(0) = −3 ⋅ 0 + 5 ⇒ f(0) = 5
Portanto, o valor da função para x = 0 é f(0) = 5.
b) Para determinar o zero da função, devemos calcular x para quê f(x) = 0. Assim, temos:
−3x + 5 = 0 ⇒ −3x = −5 ⇒ x =
Portanto, o zero da função é x = .
Página cento e vinte e seis
10. Um automóvel anda a 72 km/h, o quê equivale a 20 m/s, até o momento em quê é freado. Com isso, sua velocidade v, em métro por segundo, varia em função do tempo t, em segundo, de acôr-do com a lei v = 20 − 4t, até o instante em quê o automóvel para completamente (v = 0 m/s).
a) Qual é o instante em quê o automóvel para completamente?
b) Qual é o domínio dessa função?
c) Construa o gráfico dessa função.
d) Qual é a taxa de variação da função v?
Resolução
a) Para obtêr o instante no qual o automóvel para completamente, determinamos o zero da função v.
0 = 20 − 4t ⇒ 4t = 20 ⇒ t = 5
Portanto, o automóvel para completamente no instante t = 5s.
b) A situação ocorre do instante inicial (t = 0 s) até o momento em quê o automóvel para completamente (t = 5 s). Portanto, o domínio da função é D(v) = [0, 5].

c) Como a lei da função v é da forma y = ax + b e 0 ≤ t ≤ 5, o gráfico de v é um segmento de reta. Para construí-lo, escolhemos dois valores de t no domínio de v, obtemos os pares ordenados de dois pontos pertencentes ao gráfico, localizamos esses pontos no sistema cartesiano e traçamos o segmento, como indicado a seguir.
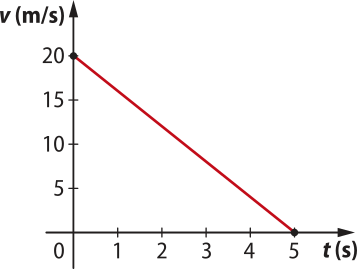
t |
v |
(t, v) |
|---|---|---|
0 |
20 |
(0, 20) |
5 |
0 |
(5, 0) |
Observe quê D(v) = [0, 5] e Im(v) = [0, 20].
d) Como a função v é dada na forma y = ax + b, a taxa de variação de v é dada pelo coeficiente a. Logo, a taxa de variação de v é −4.
11. Observe a seguir o gráfico da função afim f e determine a lei de formação dessa função.
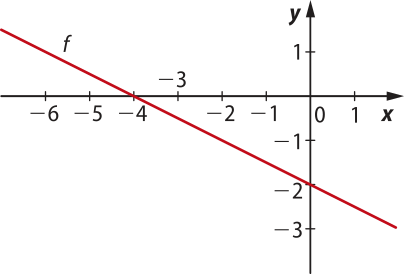
Resolução
Como f é uma função afim, sua lei de formação é do tipo f(x) = ax + b.
Observando o gráfico, temos:
• −4 é o zero da função f, pois f(−4) = 0;
• −2 é o coeficiente linear do gráfico, pois é a ordenada do ponto em quê o gráfico de f intersecta o eixo y. Assim, b = −2.
Substituindo esses valores na lei y = ax + b, obtemos o valor de a.
0 = a ⋅ (−4) + (−2) ⇒ −4a = 2 ⇒ a =
Portanto, a lei de formação da função f é f(x) = − 2.
Página cento e vinte e sete
ATIVIDADES
31. Construa, no sistema cartesiano ortogonal, gráfico das funções afins dadas por:
Ver as Orientações para o professor.
a) f(x) = 2x + 1
b) g(x) = −x + 4
c) y = − x
d) h(x) = −2x
32. Determine o valor de p de modo quê o gráfico da função definida por f(x) = 3x + p − 2 cruze o eixo y no ponto de ordenada 4.
p = 6
33. Determine m de modo quê o gráfico da função f dada por f(x) = −2x + 4m + 5 cruze o eixo x no ponto de abscissa 3.
m =
34. Determine o zero de cada uma das funções afins definidas a seguir.
a) f(x) = −3x + 4
b) y =
0
c) y = 2x + 8
−4
d) y = 6 +
−24
35. (Ufop-MG) O custo total da fabricação de determinado artigo depende do custo de produção, quê é de R$ 45,00 por unidade fabricada, mais um custo fixo de R$ 2.000,00.
Pede-se:
Ver as Orientações para o professor.
a) A função quê representa o custo total em relação à quantidade fabricada.
b) O custo total da fabricação de 10 unidades.
c) O número de unidades quê deverão sêr fabricadas para quê o custo total seja de R$ 3.800,00.
d) O gráfico da função custo total, destacando-se os dados obtidos nos itens anteriores.
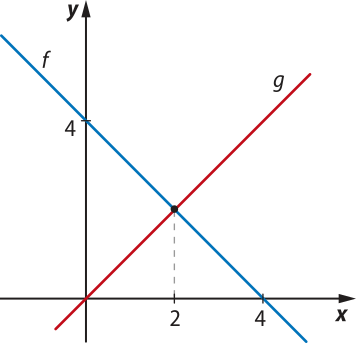
36. Observe os gráficos das funções f e g e determine a lei de formação de cada uma delas.
f(x) = −x + 4 e g(x) = x
37. O gerente de uma loja de artigos para pets fez um levantamento das vendas da loja ao longo dos últimos cinco anos e observou quê os valores poderiam sêr aproximados por uma reta. Com base nos dados obtidos, construiu o gráfico quê representa as vendas (em milhares de reais) em função do tempo (em ano).
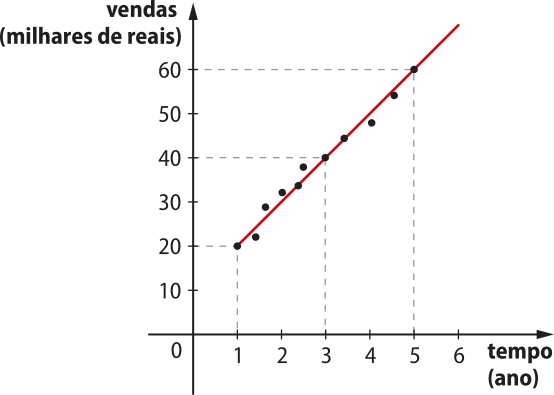
Observe o gráfico e faça o quê se pede em cada caso.
a) Determine a lei de formação da função representada pelo gráfico.
y = 10x + 10
b) Se as vendas da loja mantiverem a evolução apresentada nos últimos cinco anos, qual será a projeção de vendas para o sétimo ano de observação?
R$ 80.000,00
c) ![]() Reúna-se a um colega, e respondam: as informações disponíveis são suficientes para responder aos itens anteriores? Há algum dado quê não foi utilizado? Justifiquem suas respostas.
Reúna-se a um colega, e respondam: as informações disponíveis são suficientes para responder aos itens anteriores? Há algum dado quê não foi utilizado? Justifiquem suas respostas.
Ver as Orientações para o professor.

Página cento e vinte e oito
EXPLORANDO A TECNOLOGIA
Analisando os coeficientes da função afim
Vamos utilizar o GeoGebra para visualizar de quê forma os coeficientes a e b de uma função afim influenciam o gráfico e verificar como esses coeficientes estão relacionados com transformações no plano.
Inicialmente, vamos observar como o coeficiente a influencía o gráfico da função, considerando a função linear f, definida por f(x) = ax. Para isso, siga os passos a seguir.
I. No campo de entrada do GeoGebra, digite “f(x) = ax” e pressione Enter. O programa criará automaticamente um contrôle deslizante para o coeficiente a. Esse contrôle permitirá alterar o valor de a d fórma dinâmica e ficará exibido na janela de Álgebra.

II. Inicialmente, o programa exibirá o gráfico da função f com o coeficiente a valendo 1. Altere a posição do ponto ao longo do contrôle para alterar o valor de a e obissérve o quê acontece com o gráfico de f.
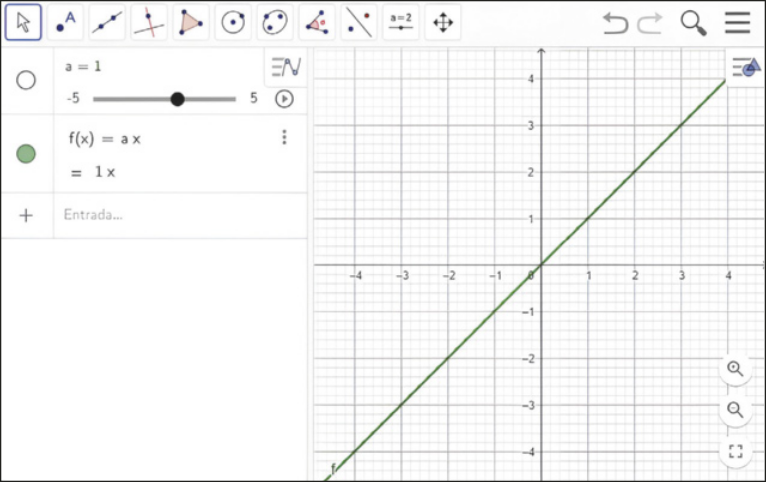
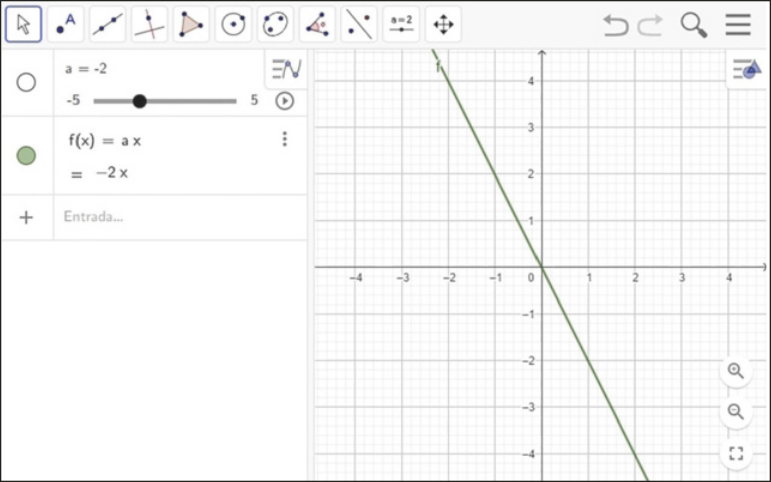
Página cento e vinte e nove
III. Por padrão, o contrôle deslizante é criado limitado ao intervalo [−5, 5]. Para alterá-lo, clique em cima do número −5 ou do 5. Com isso, o programa permitirá alterar esses números para os valores desejados.
Para analisar a influência do coeficiente b, digitamos “g(x) = x + b” no campo de entrada. Observe quê um contrôle deslizante será criado também para o coeficiente b. Para facilitar a visualização da função g, oculte o gráfico da função f. Para isso, basta clicar no círculo colorido quê aparece ao lado da lei de f na janela de Álgebra.
Comentar com os estudantes quê, ao digitar números decimais no campo de entrada do GeoGebra, deve-se utilizar ponto, em vez da vírgula. Por exemplo, para 2,5, deve-se digitar 2.5.
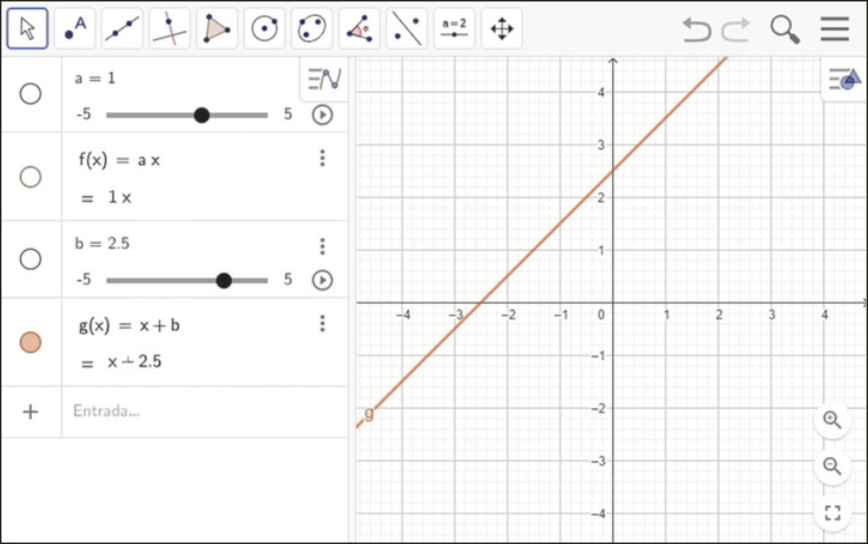
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Após ocultar a visualização do gráfico da função g e ativar novamente a visualização do gráfico da função f, deslize o contrôle para alterar o coeficiente a e obissérve as mudanças quê ocorrem na reta. dêz-creva o quê acontece com o gráfico.
2. Após ocultar a visualização do gráfico da função f e reativar a visualização do gráfico da função g, deslize o contrôle para alterar o coeficiente b e obissérve as mudanças no gráfico. O quê acontece com a reta?
3. Até agora, analisamos cada coeficiente separadamente. Nesta atividade, vamos analisar os coeficientes a e b juntos em uma mesma função. Para facilitar, exclua as funções f e g clicando em cada reta e, em seguida, pressionando a tecla Delete do teclado. Observe quê os controles deslizantes de a e b não serão excluídos. Após isso, digite “h(x) = ax + b” no campo de entrada. Movimente os controles e verifique a influência dos coeficientes juntos em uma única função. Considerando a = −3 e b = 6, em quê ponto o gráfico da função h intersecta o eixo x?
DICA: Você póde usar a ferramenta Interseção de Dois Objetos, ![]() , para determinar o ponto solicitado.
, para determinar o ponto solicitado.
Página cento e trinta
Crescimento e decrescimento da função afim
Estudar o comportamento de uma função à medida quê os valores do domínio aumentam ou diminuem nos permite verificar se essa função é crescente ou decrescente em um intervalo do seu domínio.
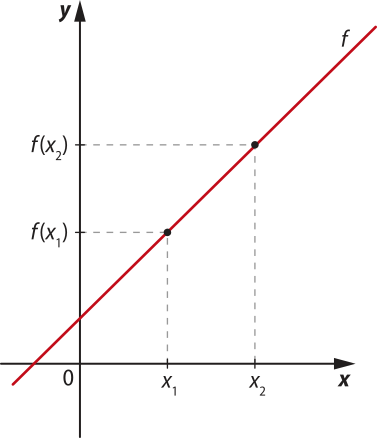
Uma função f é crescente em um intervalo [a, b] de seu domínio D(f) quando, para quaisquer valores de x1 e x2 dêêsse intervalo, com x1 < x2, temos f(x1) < f(x2).
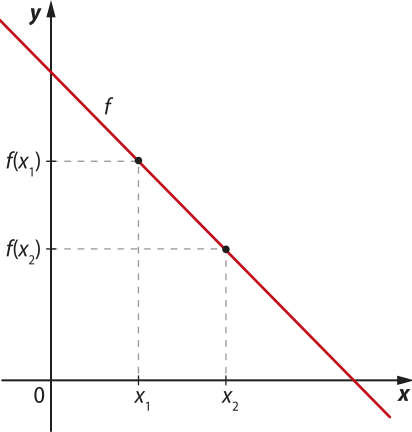
Uma função f é decrescente em um intervalo [a, b] de seu domínio D(f) quando, para quaisquer valores de x1 e x2 dêêsse intervalo, com x1 < x2, temos f(x1) > f(x2).
No caso da função afim, temos as seguintes propriedades.
• Propriedade 1: A função afim é crescente se, e somente se, a taxa de variação for positiva.
Demonstração
Se f(x) = ax + b é crescente, então, para quaisquer valores x1 e x2 do domínio de f, temos quê:
x2 > x1 ⇔ f(x2) > f(x1)⇔ f(x2) − f(x1)> 0 ⇔ ax2 + b − (ax1 + b) > 0 ⇔ ax2 + b − ax1 − b > 0 ⇔ a(x2 − x1)> 0 ⇔ a > 0
• Propriedade 2: A função afim é decrescente se, e somente se, a taxa de variação for negativa.
Demonstração
Se f(x) = ax + b é decrescente, então, para quaisquer valores x1 e x2 do domínio de f, temos quê:
x2 > x1 ⇔ f(x2) < f(x1)⇔ f(x2) − f(x1)< 0 ⇔ ax2 + b − (ax1 + b) < 0 ⇔ ax2 + b − ax1 − b < 0 ⇔ a(x2 − x1)< 0 ⇔ a < 0
Observe os exemplos a seguir.
a) f(x) = 2x + 1 (a > 0)
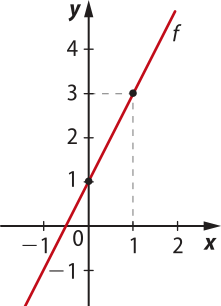
b) g(x) = −2x + 1 (a < 0)
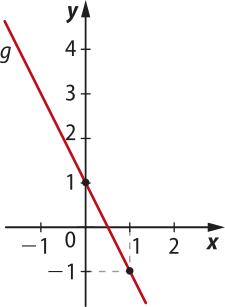
Página cento e trinta e um
De modo geral, para uma função afim definida por f(x) = ax + b, temos:
• se a > 0, então a função f é crescente;
• se a < 0, então a função f é decrescente;
• se a = 0, então a função f é constante.
pôdêmos também identificar se uma função afim é crescente ou decrescente observando a inclinação da reta quê constitui o gráfico da função.
Pense e responda
Das situações quê você já estudou neste Capítulo, identifique uma na qual a função afim correspondente é decrescente. Que relação podemos fazer entre a taxa de variação da função afim e o fato de ela sêr decrescente?
Resposta pessoal. Resposta possível: A situação do vazamento de á gua, apresentada na página 113. A função q(t) = −8t + 1.000 é decrescente, pois a = −8, ou seja, sua taxa de variação é negativa.
a > 0 |
a < 0 |
a = 0 |
|---|---|---|
|
|
|
• O gráfico de uma função afim crescente é uma reta ascendente. • f é crescente se, e somente se: ∀x1, x2 ∈ D(f), x2 > x1 ⇒ f(x2) > f(x1) |
• O gráfico de uma função afim decrescente é uma reta descendente. • f é decrescente se, e somente se: ∀x1, x2 ∈ D(f), x2 > x1 ⇒ f(x2) < f(x1) |
• O gráfico de uma função constante é uma reta paralela ao eixo x. • f é constante se, e somente se: ∀x ∈ D(f), f(x) = k, para algum k ∈ ℝ |
Estudo do sinal da função afim
Para estudar o sinal de uma função, verificamos os elemêntos do seu domínio para os quais a imagem da função é um valor positivo, um valor negativo ou um valor nulo.
Considerando uma função f, de domínio D(f), temos quê:
• f é positiva para os valores de x ∈ D(f) em quê f(x) > 0;
• f é negativa para os valores de x ∈ D(f) em quê f(x) < 0;
• f é nula para os valores de x ∈ D(f) em quê f(x) = 0 (zeros da função).
Para estudar o sinal de uma função afim dada por f(x) = ax + b, considerando a ≠ 0, podemos inicialmente determinar o zero da função, quê genericamente póde sêr escrito como x = .
Página cento e trinta e dois
Em seguida, desenhamos um esboço do gráfico da função afim, levando em consideração o fato de ela sêr crescente (a > 0) ou decrescente (a < 0). Por fim, analisamos esse esboço, como indicado a seguir.
a > 0 |
a < 0 |
||
|---|---|---|---|
|
f(x) = 0 para x = f(x) > 0 para x > f(x) < 0 para x < |
|
f(x) = 0 para x = f(x) > 0 para x < f(x) < 0 para x > |
• Se a = 0 e b ≠ 0, a função afim é a função constante dada por f(x) = b. Nesse caso, temos:
Observações:
b > 0 |
b < 0 |
|---|---|
f(x) > 0 para todo x ∈ D(f) |
f(x) < 0 para todo x ∈ D(f) |
• Se a = 0 e b = 0, a função afim é a função nula dada por f(x) = 0. Portanto, a função é nula para todos os valores de x do domínio.
Inequações polinomiais do 1º grau
Denominamos inequação do 1º grau na incógnita x toda desigualdade quê póde sêr escrita em uma das formas a seguir, com a, b ∈ ℝ e a ≠ 0.
• ax + b ≥ 0
• ax + b > 0
• ax + b ≤ 0
• ax + b < 0
Solucionar uma inequação polinomial do 1º grau é estudar o sinal de uma função afim, por exemplo, resolver, em ℝ, a inequação −x − 1 ≥ 0 é determinar para quais valores x ∈ D(f) a função f(x) = −x − 1 assume valores positivos ou nulo, ou seja, quando f(x) ≥ 0. Seguindo os procedimentos de estudo do sinal da função afim, fazemos:
1) Determinamos o zero da função.
−x − 1 = 0 ⇒ −x = 1 ⇒ x = −1
2) Esboçamos parcialmente o gráfico de f quê é decrescente (a < 0).
Pelo gráfico, identificamos quê f(x) ≥ 0 quando x ≤ −1. Logo, o conjunto solução da inequação é S = {x ∈ ℝ | x ≤ −1}.
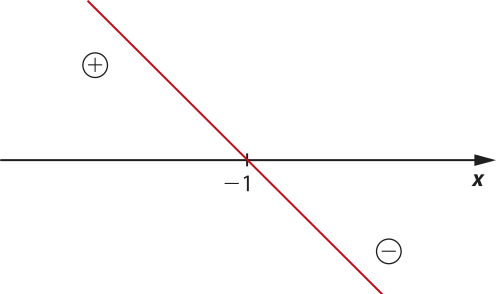
Página cento e trinta e três
ATIVIDADES RESOLVIDAS
12. Estude o sinal da função afim f definida por f(x) = 2x − 4.
Resolução
Essa função é crescente, pois a > 0.
O zero da função afim f é dado por:
2x − 4 = 0 ⇒ x = = 2
Logo, a reta intersecta o eixo x no ponto de abscissa x = 2.
Esboçando o gráfico, temos:

Analisando o esboço do gráfico, concluímos quê:
f(x) = 0 para x = 2;
f(x) > 0 para x > 2;
f(x) < 0 para x < 2.
13. O faturamento líquido relativo de cérto produto, em reais, é calculado por f(x) = 4x − 1.000. Nessa lei, f(x) representa o faturamento líquido de x unidades vendidas. Determine a quantidade mínima de unidades quê devem sêr vendidas para quê haja lucro nessa indústria.
Resolução
Determinar a quantidade mínima de unidades vendidas para quê a indústria tenha lucro é determinar o valor mínimo de x para quê se tenha f(x) > 0.
Observe quê o domínio de f(x) é o conjunto ℕ, pois x representa o número de unidades vendidas. Assim, o gráfico de f é formado por pontos alinhados, mas, como faremos apenas um esboço dêêsse gráfico, traçaremos uma reta como se o domínio fosse o conjunto ℝ.
Essa função é crescente, pois a > 0.
Determinamos o zero da função:
4x − 1.000 = 0 ⇒ 4x = 1.000 ⇒ x = 250
Esboço do gráfico:

Analisando o esboço feito, temos:
f(x) = 0 para x = 250 (lucro zero);
f(x) > 0 para {x ∈ ℕ | x > 250} (lucro);
f(x) < 0 para {x ∈ ℕ | x < 250} (prejuízo).
Portanto, para havêer lucro, é necessário vender pelo menos 251 unidades dêêsse produto.
14. resôuva, em ℝ, a inequação 4x − 1 + 2(1 − 3x) ≤ 0.
Resolução
Primeiro, manipulamos algebricamente a inequação para deixá-la na forma ax + b ≤ 0.
4x − 1 + 2(1 − 3x) ≤ 0
4x − 1 + 2 − 6x ≤ 0
−2x + 1 ≤ 0
Resolver a inequação −2x + 1 ≤ 0 é estudar o sinal da função f(x) = −2x + 1 e determinar para quais valores x ∈ D(f) temos f(x) ≤ 0.
O zero dessa função é:
−2x + 1 = 0 ⇒ −2x = −1 ⇒ x =
Esboçando parcialmente o gráfico de f, quê é decrescente (a < 0), temos:
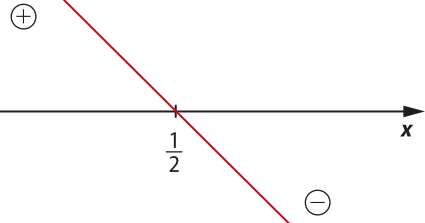
Pelo gráfico, identificamos quê f(x) ≤ 0 quando x ≥ . Portanto, o conjunto solução da inequação é S = .
15. Paula vai estacionar seu carro e estava analisando os preços de dois estacionamentos.
• Estacionamento A: R$ 10,00 fixos mais R$ 4,00 por hora com o carro estacionado.
• Estacionamento B: R$ 16,00 fixos mais R$ 2,00 por hora com o carro estacionado.
Página cento e trinta e quatro
Sabendo quê a previsão é de quê o carro fique estacionado durante 5 horas, qual é a opção mais vantajosa para Paula?
Resolução
pôdêmos escrever a lei quê representa o valor cobrado pelo estacionamento, em reais, em função do tempo x, em hora, em cada caso e calcular o valor da função quando x = 5.
Estacionamento A
f(x) = 10 + 4x
f(5) = 10 + 4 ⋅ 5 = 30
Estacionamento B
g(x) = 16 + 2x
g(5) = 16 + 2 ⋅ 5 = 26
Nessas condições, a opção mais vantajosa para Paula é o estacionamento B.
pôdêmos representar essas duas funções em um mesmo sistema cartesiano e interpretá-las geometricamente, conforme apresentado a seguir.
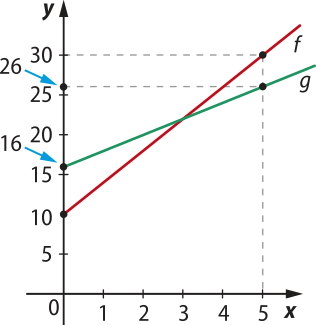
Também é possível determinar o valor de x para o qual f(x) = g(x):
10 + 4x = 16 + 2x ⇒ 2x = 6 ⇒ x = 3
Nesse caso, se o carro ficar estacionado durante 3 horas, o valor pago será o mesmo em ambos os estacionamentos.
Se x < 3, f(x) < g(x), portanto o estacionamento A é mais vantajoso.
Se x > 3, g(x) < f(x), portanto o estacionamento B é mais vantajoso.
ATIVIDADES
38. Identifique como crescente, decrescente ou constante cada função afim definida a seguir.
a) y = + 1
crescente
b) y = −2x + 3
decrescente
c) f(x) =
constante
d) f(x) = 3,5 − 0,4x
decrescente
e) y = −5x
decrescente
f) f(x) = −6
constante
39. Observe o gráfico da função afim a seguir e faça o quê se pede.
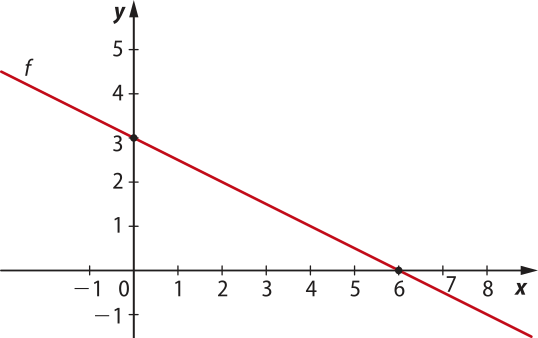
a) A função representada é crescente, decrescente ou constante? Justifique sua resposta.
A função é decrescente, pois a reta é descendente.
b) Determine a lei dessa função.
f(x) = + 3
c) Estude o sinal dessa função.
f(x) > 0 para x < 6; f(x) < 0 para x > 6; f(x) = 0 para x = 6
40. Seja f uma função real de variável real definida por f(x) = x(3 − x) + (x − 1)2.
a) Mostre quê f é uma função afim.
Ver as Orientações para o professor.
b) Determine o zero da função f.
x = −1
c) Determine x de modo quê f(x) > 0.
x > −1
41. Estude o sinal de cada função a seguir.
Ver as Orientações para o professor.
a) f(x) = x + 5
b) y = −3x + 9
c) y = − 1
d) f(x) = 2 −
42. Uma função afim f é tal quê seu gráfico intersecta o eixo x no valor de abscissa −3 e passa pelo ponto (1, 2). A partir dessas informações, faça o quê se pede.
a) Esboce o gráfico dessa função.
Ver as Orientações para o professor.
b) Determine a lei de formação da função f.
f(x) =
c) Estude o sinal dessa função.
f(x) > 0 para x > −3; f(x) < 0 para x < −3; f(x) = 0 para x = −3
Página cento e trinta e cinco
43. Uma barra de metal com tempera-túra inicial de −10 °C foi aquecida até 30 °C. O gráfico a seguir representa a tempera-túra da barra em função do tempo.
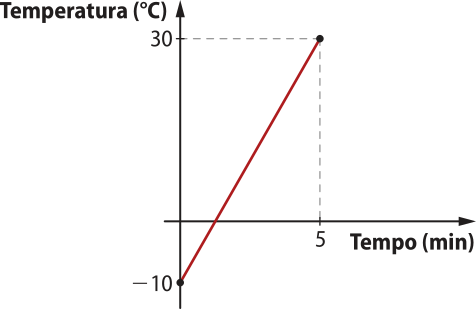
a) Quanto tempo após o início da experiência a tempera-túra atingiu 0 °C?
1min15s
b) Em qual intervalo de tempo a tempera-túra da barra ficou positiva? E negativa?
positiva: 1,25 < t ≤ 5; negativa: 0 ≤ t < 1,25
44. (Vunesp-SP) Uma pessoa obesa, pesando num cérto momento 156 kg, recolhe-se a um spa onde se anunciam perdas de peso de até 2,5 kg por semana. Suponhamos quê isso realmente ocorra. Nessas condições:
a) Encontre uma fórmula quê expresse o peso mínimo, P, quê essa pessoa poderá atingir após n semanas.
P = 156 − 2,5n
b) Calcule o número mínimo de semanas completas quê a pessoa deverá permanecer no spa para sair de lá com menos de 120 kg de peso.
15 semanas
45. resôuva, em ℝ, as inequações a seguir.
a) 5x − 2(x + 2) ≥ 1 − (3 − 4x)
S = {x ∈ ℝ | x ≤ −2}
b)
S = {x ∈ ℝ| x ≤ −1}
46. Quais são os valores de x, no conjunto dos números naturais, quê satisfazem à inequação 7x − 8 < 4x + 1?
S = {0, 1, 2}
47. As medidas do comprimento e da largura de um retângulo são 10 cm e x cm, respectivamente. Calcule x para quê:
a) a área do retângulo seja maior do quê 50 cm2;
x > 5
b) o perímetro do retângulo não seja menor do quê 32 cm.
x ≥ 6
48. Observe a figura e, sabendo quê MNPR é um trapézio retângulo, responda às kestões a seguir.
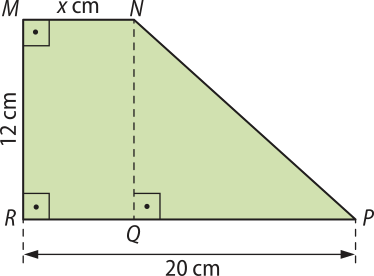
a) Determine o maior valor inteiro de x de modo quê a área do trapézio seja maior do quê o dôbro da área do retângulo MNQR.
6
b) Caso a medida do lado não fosse fornecida, ainda assim seria possível resolver o problema? Justifique sua resposta.
Sim, pois a medida MR não interfere nos cálculos da atividade.
49. (FGV-SP) A figura fornece os gráficos dos lucros anuais LA e LB de duas empresas (em milhares de reais) em função da quantidade anual produzida e vendida (x).
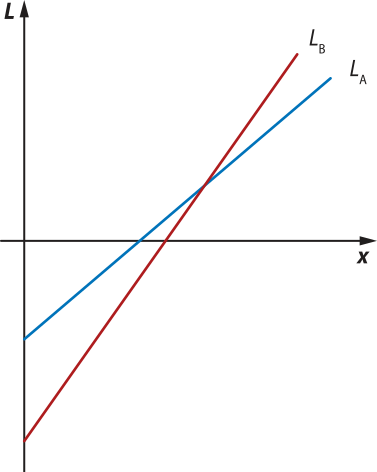
As intersecções dos gráficos com os eixos são:
LA |
LB |
|
|---|---|---|
eixo x |
(50, 0) |
(60, 0) |
eixo y |
(0, −500) |
(0, −1.000) |
a) Obtenha LA em função de x.
LA(x) = 10x − 500, para x ≥ 0
b) Para quê valores de x o lucro LB é superior ao LA?
x > 75
Página cento e trinta e seis
CONEXÕES com..
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Transporte público sustentável
O setor de transportes no Brasil é responsável por uma parcela considerável das emissões dos gases de efeito estufa (GEE). Uma das iniciativas para a redução dessa parcela é a substituição de veículos a combustão por veículos elétricos, os quais têm, como principais vantagens, a não emissão de GEE e o baixo custo para carregamento e manutenção. Em contrapartida, o custo de aquisição, comparado ao de veículos a combustão, é bem maior.
Uma possibilidade quê vêm sêndo fomentada pelo govêrno é a substituição da frota de ônibus a combustão por ônibus elétricos no transporte público para mobilidade urbana. No texto a seguir, são apresentadas algumas informações sobre o assunto.
[…]
A eletrificação do transporte público por ônibus é um dos grandes desafios do setor no país, principalmente para a mobilidade urbana coletiva. […]
No Brasil, o transporte é responsável por 40% a 60% das emissões de gases de efeito estufa nas cidades, e tem potencial para diminuir em torno de 45% do total dessas emissões até 2050, de acôr-do com estudo da Coalition for Urban Transitions. A eletrificação das frotas, especialmente do sistema de transporte público coletivo, é apontada por especialistas em mobilidade como medida mais efetiva nesse sentido, com impacto positivo direto na saúde pública, mas também em outros, como uma melhor experiência dos usuários.
sôb o acôr-do de Paris, o Brasil enfrenta o grande desafio de reduzir suas emissões de gases de efeito estufa em 43% nos próximos oito anos. Uma das medidas necessárias para atingir esse objetivo é a eletrificação do transporte público, quê também póde gerar benefícios sociais de R$ 290 bilhões, segundo estudo quê avalia cenários para a eletrificação de ônibus no Brasil. O relatório foi desenvolvido pela Plataforma Nacional de Mobilidade Elétrica (PNME) […].
[…] O relatório do PNME sugere quê, a longo prazo, os veículos movidos a energia elétrica irão substituir totalmente a frota de veículos movidos a dízel. Esta mudança irá refletir-se na redução das emissões de carbono na atmosféra, afetando também a qualidade de vida dos cidadãos por meio da melhoria da qualidade do ar.
No entanto, a Avaliação Prospectiva da Eletrificação dos Ônibus no Brasil orienta algumas mudanças para incentivar o uso de veículos elétricos.

Página cento e trinta e sete
No Brasil, essas políticas focaram na redução dos custos de aquisição de veículos, com pouco investimento em infraestrutura. Por exemplo, disponibilizar pontos de carregamento para veículos elétricos é um dos principais obstáculos à eletrificação dos transportes públicos. […]
[…]
[…] O Brasil precisa tornar-se um país livre de carbono até 2060, e a eletrificação do transporte público contribuirá para essa transição energética, garantindo o cumprimento do acôr-do de Paris e do relatório do Fórum Brasileiro de Mudanças Climáticas “Zero Carbon brézíl 2060”. […]
SERVIÇO BRASILEIRO DE APOIO ÀS MICRO E PEQUENAS EMPRESAS. Eletrificação do setor de transporte: futuro das cidades sustentáveis. [S. l.]: Sebrae, 11 fev. 2023. Disponível em: https://livro.pw/nhwte. Acesso em: 11 jul. 2024.
Agora, faça o quê se pede.
1. De acôr-do com o texto, por quê a eletrificação do transporte público deve acontecer?
1. Espera-se quê os estudantes respondam quê se trata de uma medida quê impacta drasticamente a redução da emissão de carbono e poluentes locais, trazendo consequências positivas ao combate às mudanças climáticas e benefícios significativos para a saúde da população. Além díssu, o Brasil deve cumprir o acôr-do de Paris e o relatório do Fórum Brasileiro de Mudanças Climáticas “Zero Carbon brézíl 2060”.
2. Pesquise e obtenha informações sobre o acôr-do de Paris e o Brasil Carbono Zero em 2060 (Zero Carbon brézíl 2060). Em seguida, escrêeva um pequeno texto com as informações encontradas.
2. Resposta pessoal. Os estudantes podem pesquisar informações em sáites confiáveis, como o do Ministério do Meio Ambiente (disponível em: https://livro.pw/lnfgp; acesso em: 11 jul. 2024) e o da Agência Brasil (disponível em: https://livro.pw/elqmg; acesso em: 11 jul. 2024). Os estudantes podem apresentar informações a respeito de outras medidas, além da eletrificação do transporte, relacionadas com a redução das emissões de GEE quê estão sêndo ou serão adotadas pelo Brasil para atingir a meta do acôr-do.
3. Os gráficos apresentam o custo médio de consumo de um ônibus a combustão (dízel) e de um ônibus elétrico (energia elétrica) em função da distância percorrida.
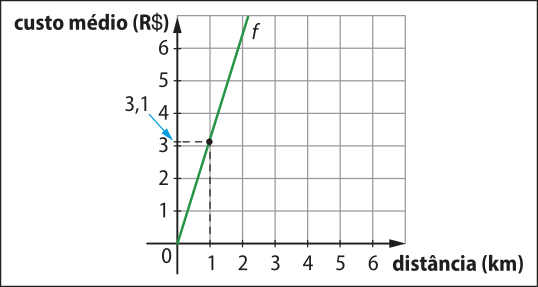
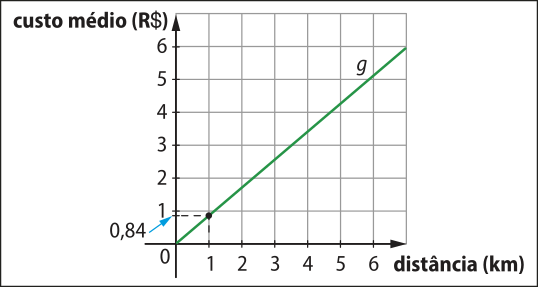
Elaborados com base em: GONZAGA, Bernardo; BARROS, Rafaella. Eletrificação de frotas de ônibus esbarra em custo bilionário. [S. I.]: Poder 360, 30 maio 2022. Disponível em: https://livro.pw/abdsu. Acesso em: 11 jul. 2024.
a) Qual é o custo médio de consumo por kilometro percorrido de um ônibus a combustão e de um ônibus elétrico?
ônibus a combustão: R$ 3,10; ônibus elétrico: R$ 0,84
b) escrêeva as leis de formação das funções apresentadas nos gráficos. Em seguida, calcule o custo médio de consumo para cada tipo de ônibus apresentado percorrer 5 mil kilometros.
gráfico 1: f(x) = 3,1x; R$ 15.500,00
gráfico 2: g(x) = 0,84x; R$ 4.200,00
c) Considerando uma distância x percorrida, calcule a razão aproximada entre o custo médio dado pela função do gráfico 1 e o custo médio dado pela função do gráfico 2. Explique o quê essa razão significa.
Resposta possível: Aproximadamente 3,69. Significa quê o custo médio para um veículo a combustão percorrer determinada distância é de 3,69 vezes o de um veículo elétrico.
4. ![]() Junte-se a dois côlégas, e pesquisem características dos veículos a combustão e dos veículos elétricos e, em seguida, confeccionem um cartaz comparativo entre eles. Essas informações podem estar relacionadas ao consumo, à potência, à eficiência, à manutenção, à emissão de gás carbônico, entre outras características.
Junte-se a dois côlégas, e pesquisem características dos veículos a combustão e dos veículos elétricos e, em seguida, confeccionem um cartaz comparativo entre eles. Essas informações podem estar relacionadas ao consumo, à potência, à eficiência, à manutenção, à emissão de gás carbônico, entre outras características.
Resposta pessoal. Cada grupo deve confeksionar um cartaz comparando os veículos a combustão e os elétricos. Algumas vantagens dos veículos elétricos em relação aos de combustão estão relacionadas a maior potência e eficiência, menor manutenção, não emissão de gás carbônico e maior economia para abastecimento. Entre as desvantagens estão o custo de aquisição, a demora para carregar e o acesso a fontes de abastecimento.
Página cento e trinta e oito
HISTÓRIA DA MATEMÁTICA
O surgimento dos gráficos
Leia o texto a seguir para conhecer um pouco mais sobre o uso dos gráficos em Matemática e em outras áreas de conhecimento, bem como sobre os primeiros estudiosos a usar esse tipo de representação em seus trabalhos e a repercussão díssu ao longo da história.
Na matemática são utilizados gráficos para visualizar funções. Em outros campos, como o da biologia e da economia, os gráficos são utilizados principalmente para a apresentação de dados. Normalmente, as curvas matemáticas são representadas em um conjunto de dois eixos perpendiculares, denominados x e y, em duas dimensões. Todo ponto do plano póde sêr identificado a partir de um “par ordenado” (x, y) quê especifica sua distância aos eixos y e x. O mesmo conceito é utilizado para apresentar uma informação em três dimensões, acrescentando um terceiro eixo quê se denomina convencionalmente z.
Esse sistema recebe o nome de coordenadas cartesianas em homenagem ao seu inventor, o matemático e filósofo francês Renê Descartes. Seu contemporâneo, Piérre de Fermat, desenvolvê-u ao mesmo tempo ideias semelhantes. Entretanto, seria mais lógico conceder o crédito da invenção a Nicole d’Oresme, quêm, três séculos antes, utilizou eixos horizontais e verticais para demonstrar graficamente uma lei relativa à distância percorrida por dois objetos que se moviam em velocidades diferentes.
O descobrimento de Descartes do potencial de gráficos foi fundamental para o desenvolvimento da história da matemática, já quê relacionou números a figuras geométricas. O quê tornou possível representar figuras por meio de equações, unindo a álgebra à geometria para criar o campo da geometria analítica.
BROWN, ríchard. 50 teorías matemáticas: creadoras e imaginativas. Barcelona: Blume, 2012. p. 108. Tradução nossa.

Para assistir
• PLANO cartesiano na arquitetura. [S. l.: s. n.], 2014. 1 vídeo (4 min). Publicado pelo canal Nova Escola.
Disponível em: https://livro.pw/gsqhs. Acesso em: 11 jul. 2024. Assista ao vídeo para conhecer um pouco mais a respeito do plano cartesiano e de seu uso na Arquitetura.
Página cento e trinta e nove
ATIVIDADES COMPLEMENTARES
1. (UECE) Um equipamento eletrônico utilizado por uma indústria tem seu valor monetário continuamente reduzido em função do uso e do surgimento de novas tecnologias, dentre outros fatores. Se o valor monetário do equipamento decresce linearmente com o tempo, sabendo-se quê foi adquirido há três anos pelo valor de R$ 180.000,00 e quê hoje está avaliado em R$ 135.000,00, é correto afirmar quê o valor monetário do equipamento daqui a dois anos será
alternativa a
a) R$ 105.000,00.
b) R$ 115.000,00.
c) R$ 108.000,00.
d) R$ 112.000,00.
Uma função real de variável real decresce linearmente se é do tipo f(x) = ax + b, com a e b números reais constantes e a < 0.
2. (Enem/MEC) Muitas vezes o objetivo de um remédio é aumentar a quantidade de uma ou mais substâncias já existentes no corpo do indivíduo para melhorar as defesas do organismo. Depois de alcançar o objetivo, essa quantidade deve voltar ao normal.
Se uma determinada pessoa ingére um medicamento para aumentar a concentração da substância A em seu organismo, a quantidade dessa substância no organismo da pessoa, em relação ao tempo, póde sêr mais bem representada no gráfico:
alternativa d
a)
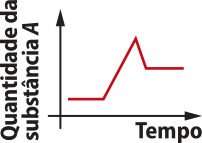
b)
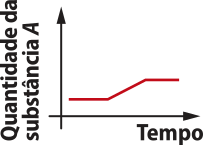
c)
d)
e)
3. (FEI-SP) Durante o tratamento térmico de uma peça metálica, sua tempera-túra varia de acôr-do com o gráfico abaixo.
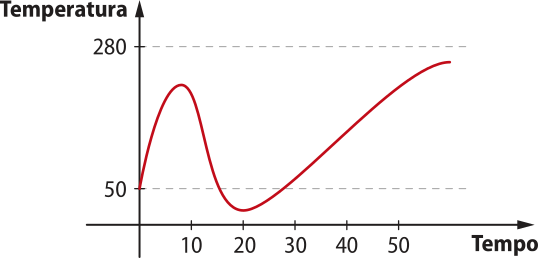
É válido afirmar:
alternativa c
a) a partir do instante t = 10, as tempera-túras são crescentes.
b) a partir do instante t = 5, as tempera-túras são decrescentes.
c) a partir do instante t = 20, as tempera-túras são crescentes.
d) todas as tempera-túras observadas são maiores do quê 50.
e) há um determinado valor de tempera-túra quê foi observado em 5 instantes diferentes.
4. (UEA-AM) A reta r passa pêlos pontos (4, 6) e (0, −4) e intersecta o eixo das abscissas no ponto P, conforme mostra a figura.
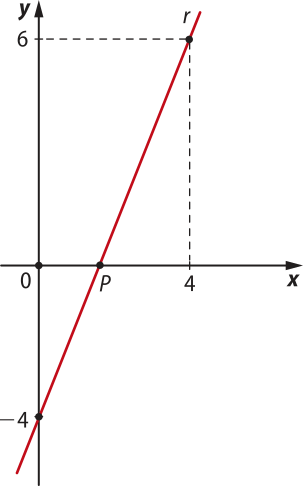
O valor da abscissa do ponto P é
alternativa d
a) 2
b)
c)
d)
e)
Página cento e quarenta
5. (Enem/MEC)
VENDEDORES JOVENS
Fábrica de LONAS
Vendas no Atacado 10 vagas para estudantes, 18 a 20 anos, sem experiência.
Salário: R$ 300,00 fixo + comissão de R$ 0,50 por m2 vendido.
Contato: 0xx97 – 43421167 ou atacadista@lonaboa.com.br
Na seleção para as vagas dêste anúncio, feita por telefone ou correio eletrônico, propunha-se aos candidatos uma questão a sêr resolvida na hora.
Deveriam calcular seu salário no primeiro mês, se vendessem 500 m de tecido com largura de 1,40 m, e no segundo mês, se vendessem o dôbro.
Foram bem-sucedidos os jovens quê responderam, respectivamente,
alternativa c
a) R$ 300,00 e R$ 500,00.
b) R$ 550,00 e R$ 850,00.
c) R$ 650,00 e R$ 1000,00.
d) R$ 650,00 e R$ 1300,00.
e) R$ 950,00 e R$ 1900,00.
6. (Epcar-MG) Para fazer uma instalação elétrica em sua residência, Otávio contatou dois eletricistas.
O Sr. Luiz, quê cobra uma parte fixa pelo orçamento mais uma parte quê depende da quantidade de metros de fio requerida pelo serviço. O valor total do seu serviço está descrito no seguinte gráfico:
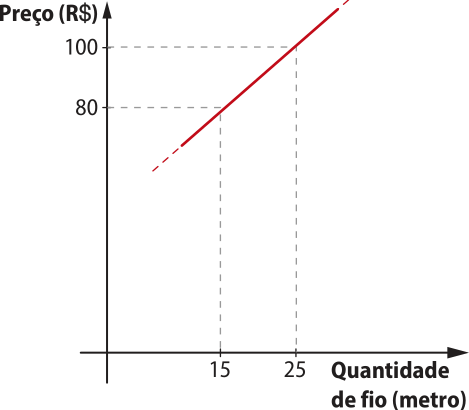
Já o Sr. José cobra, apenas, R$ 4,50 por métro de fio utilizado e não cobra a parte fixa pelo orçamento.
Com relação às informações acima, é correto afirmar quê:
alternativa d
a) o valor da parte fixa cobrada pelo Sr. Luiz é maior do quê R$ 60,00.
b) o Sr. Luiz cobra mais de R$ 2,50 por métro de fio instalado.
c) sempre será mais vantajoso contratar o serviço do Sr. José.
d) se forem gastos 20 m de fio não haverá diferença de valor total cobrado entre os eletricistas.
7. (UFPI) A função real de variável real, definida por f(x) = (3 − 2a) ⋅ x + 2, é crescente quando:
a) a > 0.
b) a .
c) a =.
d) a >.
e) a < 3.
alternativa b
8. (Enem/MEC) Uma fatura mensal de á gua é composta por uma taxa fixa, independentemente do gasto, mais uma parte relativa ao consumo de á gua, em métro cúbico. O gráfico relaciona o valor da fatura com o volume de á gua gasto em uma residência no mês de novembro, representando uma semirreta.
alternativa a
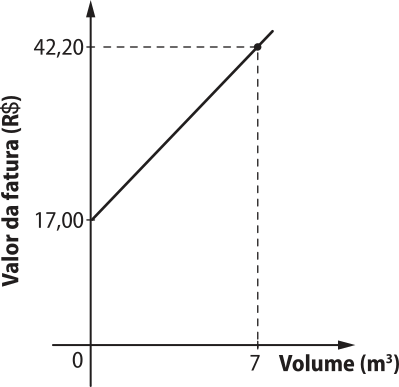
Observa-se quê, nesse mês, houve um consumo de 7 m3 de á gua. Sabe-se quê, em dezembro, o consumo de á gua nessa residência, em métro cúbico, dobrou em relação ao mês anterior.
Página cento e quarenta e um
O valor da fatura referente ao consumo no mês de dezembro nessa residência foi
a) superior a R$ 65,00 e inferior a R$ 70,00.
b) superior a R$ 80,00 e inferior a R$ 85,00.
c) superior a R$ 90,00 e inferior a R$ 95,00.
d) superior a R$ 95,00.
e) inferior a R$ 55,00.
9. (IFPE) Os volumes de á gua V, medidos em litros, em dois reservatórios A e B, varíam em função do tempo t, medido em minutos, de acôr-do com as seguintes relações:
VA(t) = 200 + 3t e VB(t) = 5.000 − 3t
Determine o instante t em quê os reservatórios estarão com o mesmo volume.
alternativa d
a) t = 500 minutos.
b) t = 600 minutos.
c) t = 700 minutos.
d) t = 800 minutos.
e) t = 900 minutos.
10. (UEA-AM) Considere as funções polinomiais do 1º grau f(x) = 2x + 3 e g(x) = −x + 6. Sobre essas funções, afirma-se quê
alternativa d
a) possuem pontos de mássimo.
b) são crescentes.
c) possuem domínios diferentes.
d) têm o ponto (1, 5) em comum.
e) suas representações gráficas não se intersectam.
PARA REFLETIR
Neste Capítulo, estudamos quê, em algumas situações do dia a dia, o comportamento de uma grandeza depende do comportamento de outra. Estudamos também como podemos utilizar a ideia de função e o conceito de função afim para representar e analisar essas relações entre grandezas e entre conjuntos. Isso nos permite construir modelos quê podem sêr utilizados para fazer estimativas e possibilitar algumas tomadas de dê-cisão d fórma mais consciente.
Estudamos o conceito de função, bem como o domínio, o contradomínio e a imagem de funções, e aprendemos sobre função afim, representações gráficas, taxa de variação da função afim, zero da função, crescimento e decrescimento de funções, estudo de sinais da função afim e inequação do 1º grau.
Vamos refletir a respeito das aprendizagens do Capítulo 3:
Respostas pessoais.
• Nas páginas de abertura, foi apresentada uma situação quê póde sêr modelada por uma função afim. Depois de ter estudado o conteúdo dêste Capítulo, você consegue reconhecer quê esses conceitos podem auxiliá-lo a compreender e a analisar a situação apresentada na abertura? Você já tinha essa percepção antes de estudar esses conceitos?
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• Cite outras situações do dia a dia quê envolvem a ideia de função e de função afim.
• Explique, com suas palavras, qual é a relação existente entre função linear e grandezas diretamente proporcionais.
• Explique, com suas palavras, o quê é a variação em situações envolvendo grandezas.
• Cite uma situação envolvendo a variação entre duas grandezas e diga qual delas representa a variável dependente e qual representa a variável independente.
Página cento e quarenta e dois