CAPÍTULO 4
FUNÇÃO QUADRÁTICA

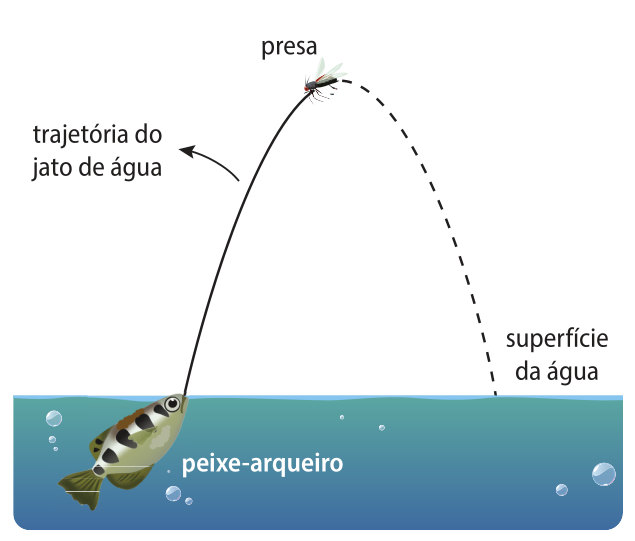
O Toxotes jaculatrix, também conhecido como “peixe-arqueiro”, é uma espécie quê habita as á guas do oceano Índico e do Pacífico Sul. Sua habilidade notável de caça consiste em atirar jatos de água em insetos, aranhas e até mesmo pequenos pássaros quê estejam próximos à superfícíe da á gua. Com uma precisão incrível, esse peixe é capaz de ajustar o ângulo e a fôrça do jato de á gua, derrubando suas presas e garantindo sua refeição.
Como parte de sua técnica, o peixe-arqueiro cria um vácuo em sua bôca e, em seguida, dispara um jato de á gua com sua língua em direção à presa. Essa habilidade de arremesso de á gua é uma adaptação surpreendente quê torna o peixe dessa espécie um mestre na ár-te da caça, demonstrando a engenhosidade e a versatilidade das criaturas aquáticas em seu ambiente natural.
A trajetória do jato de á gua é semelhante a uma parte de uma curva conhecida como parábola, quê póde sêr representada matematicamente por uma função quadrática, assunto quê será estudado neste Capítulo.
Elaborado com base em: OCEANÁRIO DE LISBOA. Peixe-arqueiro, um mestre da física. Um oceano para ensinar, Lisboa, n. 30, p. 1-6, jul. 2024. Disponível em: https://livro.pw/imcph. Acesso em: 11 out. 2024.
![]() Agora, reúna-se a um colega, e, juntos, façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e, juntos, façam o quê se pede em cada questão.
1. Como vocês acham quê o ângulo de lançamento afeta a trajetória do jato de á gua lançado pelo peixe-arqueiro?
Resposta pessoal. Espera-se quê os estudantes percêbam quê, quanto maior o ângulo de lançamento, maior a altura do jato de á gua. O ângulo ideal para maior alcance horizontal é 45°.
2. Em uma função quê associa o instante x, em segundo, a uma altura y, em centimetro, quê o jato de á gua atinge após o lançamento, qual é a variável dependente e qual é a independente?
Como a altura em quê o jato se encontra depende do instante após sêr lançado, então x é a variável dependente e y, a variável independente.
3. Citem outras situações em quê é possível observar uma curva semelhante à curva da trajetória do jato de á gua.
Resposta pessoal. Os estudantes podem citar lançamentos de bola, arcos na estrutura de algumas pontes, saltos de um atleta olímpico, entre outros exemplos.
4. Resolvam as equações.
a) x2 = 25
S = {−5, 5}
b) x2 − 4x = 0
S = {0, 4}
c) x2 + 2x + 1 = 9
S = {−4, 2}
Página cento e quarenta e três
Página cento e quarenta e quatro
Introdução
No Capítulo anterior, você estudou algumas ideias associadas aos conceitos de função e de função afim e aprendeu como esses conceitos matemáticos podem contribuir para a compreensão e a análise de situações do dia a dia. Neste Capítulo, ampliaremos esse estudo abordando as funções quadráticas.
Situações envolvendo trajetórias parabólicas, como lançamentos de projéteis, podem sêr modeladas por meio de funções quadráticas, assim como certos tipos de movimentos estudados pela Física. Além díssu, alguns objetos, como antenas parabólicas e faróis de veículos, são construídos utilizando-se propriedades da parábola, a curva quê representa o gráfico de funções quadráticas. Na Arquitetura e na Engenharia, há muitos exemplos de construções quê utilizam a curva da parábola.

Função quadrática
A função quadrática também póde sêr denominada função polinomial do 2º grau, pois as relações entre a variável dependente e a variável independente são expressas por polinômios do 2º grau.
Uma função f: ℝ → ℝ definida por f(x) = ax2 + bx + c, com a, b, c reais e a ≠ 0, é chamada de função quadrática.
Os números a, b e c são os coeficientes (ou parâmetros) da função, sêndo a o coeficiente do termo x2, b o coeficiente do termo x e c o coeficiente independente.
Pense e responda
por quê precisamos cumprir a condição a ≠ 0 para definir a função quadrática?
Porque, para quê um polinômio seja de 2º grau, é preciso quê exista o termo em x2. Caso tivéssemos a = 0, o termo ax2 se anularia, e teríamos uma função definida por f(x) = bx + c, quê é a lei de uma função afim.
Página cento e quarenta e cinco
Observe a seguir a lei de formação de algumas funções quadráticas.
a) f(x) = x2 − 3x + 2, em quê os coeficientes são: a = 1, b = −3 e c = 2.
b) g(x) = 0,8x2 − 1, em quê os coeficientes são: a = 0,8, b = 0 e c = −1.
c) y = −x2 + ,em quê os coeficientes são: a = −1, b = e c = 0.
d) y = −5x2, em quê os coeficientes são: a = −5, b = 0 e c = 0.
Não são leis de funções quadráticas:
• h(x) = 7x
• y = x4 + 2x2
• y = 5x
Agora, considere a situação a seguir.
Elisa possui uma loja quê vende capas para celular. Estudando como maximizar os seus lucros, ela obteve uma função quadrática quê modela o lucro diário L, em reais, da loja em relação ao preêço pelo qual cada capa é vendida, também em reais. Essa função é dada pela lei L(x) = −x2 + 55x − 250.
Saiba quê...
A fórmula utilizada por Elisa considera cérto preêço de custo da capa e uma relação de dependência entre a quantidade de vendas e o preêço de venda de cada capa.

Utilizando essa lei, Elisa calculou o lucro diário de sua loja supondo quê cada capa fosse vendida a R$ 20,00. O cálculo quê ela fez está representado a seguir.
L(20) = −(20)2 + 55 ⋅ 20 − 250
L(20) = −400 + 1.100 − 250
L(20) = 450
Assim, Elisa verificou quê vender cada capa a R$ 20,00 gera um lucro diário de R$ 450,00, considerando a função L.
Pense e responda
Com os dados apresentados na situação, é possível calcular quantas capas de celular a loja precisa vender diariamente para obtêr esse lucro de R$ 450,00? Justifique.
Não, pois, na lei da função, não há uma variável quê corresponda à quantidade de capas.
Página cento e quarenta e seis
Gráfico da função quadrática
Tomás utilizou o GeoGebra para observar como é o gráfico de uma função quadrática. Ele utilizou a lei de duas funções para representar os respectivos gráficos e obteve duas curvas, chamadas de parábolas, como podemos verificar a seguir.
a) Gráfico da função f: ℝ → ℝ definida por f(x) = x2 − 2x − 3.
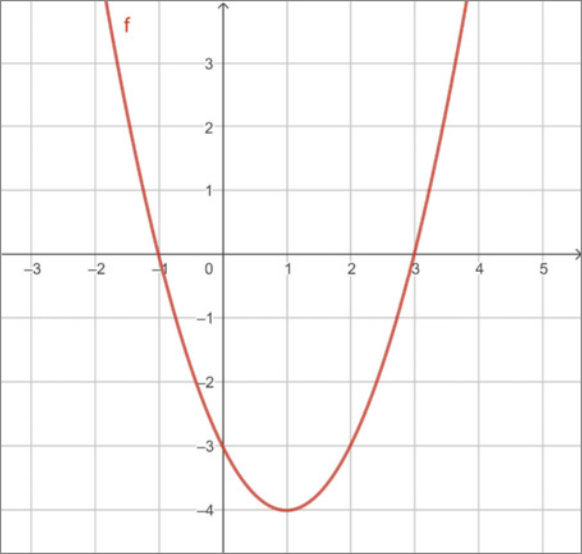
b) Gráfico da função g: ℝ → ℝ definida por g(x) = −x2 + 6x − 5.
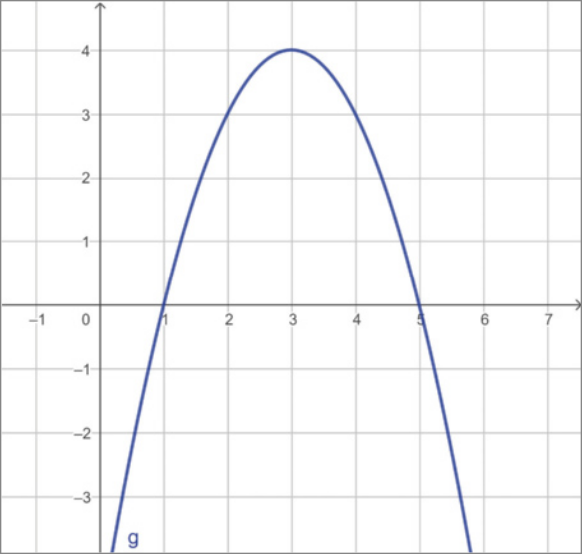
Pense e responda
Comparando o gráfico da função f com o gráfico da função g, quê diferença você identifica?
Espera-se quê os estudantes respondam quê o gráfico da função f tem a "abertura" voltada para cima, e o gráfico da função g tem a"abertura" voltada para baixo.
É possível demonstrar quê o gráfico de uma função quadrática é uma parábola quê póde ter sua concavidade voltada para cima, se o coeficiente a for positivo, ou para baixo, se a for negativo.
Destacamos também quê, para qualquer função quadrática, o ponto de intersecção da parábola com o eixo y é o ponto de coordenadas (0, c), em quê c é o coeficiente independente na lei da função quadrática. Observe:
Considerando a lei f(x) = ax2 + bx + c, temos f(0) = a ⋅ 02 + b ⋅ 0 + c; portanto, f(0) = c.
Página cento e quarenta e sete
Assim como aprendemos no estudo de função afim, para construir o gráfico da função quadrática, podemos elaborar uma tabéla com alguns valores de x e calcular os valores de y correspondentes para obtermos alguns pontos pertencentes ao gráfico da função dada. No entanto, no caso da função quadrática, precisamos de mais do quê dois pontos para termos uma noção do traçado da parábola.
Acompanhe alguns exemplos.
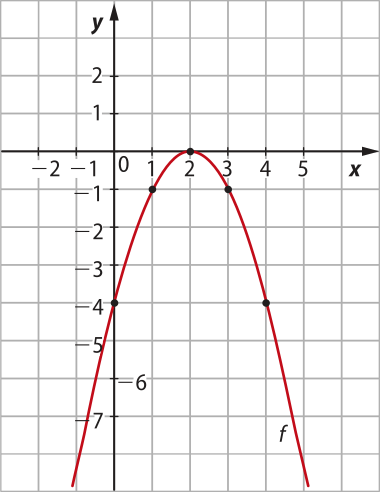
a) Gráfico da função quadrática definida por f(x) = −x2 + 4x − 4.
Inicialmente, construímos uma tabéla com alguns valores de x e calculamos y = f(x).
Em seguida, localizamos, no sistema cartesiano, os pontos (x, y) pertencentes ao gráfico da função f e esboçamos a parábola quê contém esses pontos.
Como a < 0, a parábola terá concavidade voltada para baixo.
x |
y = −x2 + 4x − 4 |
(x, y) |
|---|---|---|
0 |
y = −(0)2 + 4 ⋅ 0 − 4 = −4 |
(0, −4) |
1 |
y = −(1)2 + 4 ⋅ 1 − 4 = −1 + 4 − 4 = −1 |
(1, −1) |
2 |
y = −(2)2 + 4 ⋅ 2 − 4 = −4 + 8 − 4 = 0 |
(2, 0) |
3 |
y = −(3)2 + 4 ⋅ 3 − 4 = −9 + 12 − 4 = −1 |
(3, −1) |
4 |
y = −(4)2 + 4 ⋅ 4 − 4 = −16 + 16 − 4 = −4 |
(4, −4) |
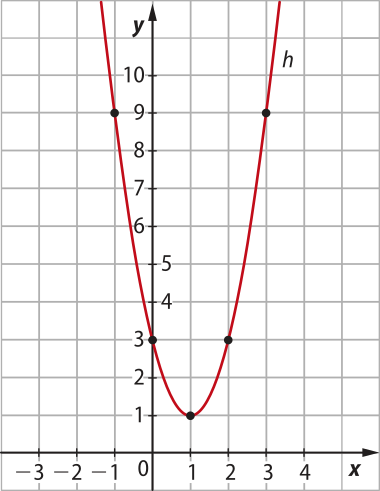
b) Gráfico da função quadrática definida por h(x) = 2x2 − 4x + 3.
Assim como no exemplo anterior, construímos uma tabéla com alguns valores de x e calculamos y = h(x). Em seguida, localizamos, no sistema cartesiano, os pontos (x, y) pertencentes ao gráfico da função h e esboçamos a parábola quê contém esses pontos.
Como a > 0, nesse caso, a parábola terá concavidade voltada para cima.
x |
y = 2x2 − 4x + 3 |
(x, y) |
|---|---|---|
−1 |
y = 2 ⋅ (−1)2 − 4 ⋅ (−1) + 3 = 2 + 4 + 3 = 9 |
(−1, 9) |
0 |
y = 2 ⋅ (0)2 − 4 ⋅ 0 + 3 = 0 − 0 + 3 = 3 |
(0, 3) |
1 |
y = 2 ⋅ (1)2 − 4 ⋅ 1 + 3 = 2 − 4 + 3 = 1 |
(1, 1) |
2 |
y = 2 ⋅ (2)2 − 4 ⋅ 2 + 3 = 8 − 8 + 3 = 3 |
(2, 3) |
3 |
y = 2 ⋅ (3)2 − 4 ⋅ 3 + 3 = 18 − 12 + 3 = 9 |
(3, 9) |
Página cento e quarenta e oito
ATIVIDADES RESOLVIDAS
1. Considere o gráfico de uma função quadrática f representado a seguir e faça o quê se pede em cada item.
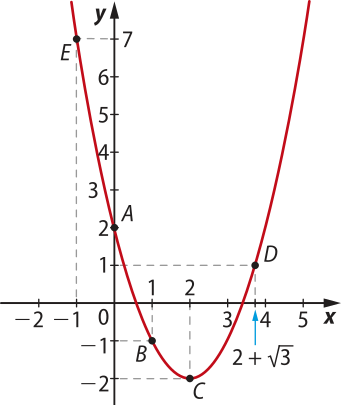
a) Sabendo quê os pontos A, B, C, D e E pertencem ao gráfico de f, escrêeva a lei de formação dessa função.
b) Calcule f(10) − f(6) + f(−1).
c) Todos os dados fornecidos pelo enunciado foram utilizados na resolução do item a? O quê teria acontecido caso outros pontos tivessem sido escolhidos?
Resolução
a) A lei de formação da função quadrática é dada por f(x) = ax² + bx + c. Para determinar a lei de formação da função representada pelo gráfico dado, precisamos obtêr os coeficientes a, b e c.
Inicialmente, escrevemos os pares ordenados dos pontos A, B, C, D e E:
A(0, 2); B(1, −1); C(2, −2); ; E(−1, 7).
Sendo assim, verificamos quê f(0) = 2, f(1) = −1, f(2) = _ = 1 e f(−1) = 7.
Sabemos quê o ponto de intersecção da parábola com o eixo y é o ponto de coordenadas (0, c), quê corresponde ao ponto A(0, 2). Então, concluímos quê c = 2.
Para determinar os coeficientes a e b, escolhemos outros dois pontos quaisquer e substituímos suas coordenadas na lei de formação. Escolhendo os pontos B e C, temos:
f(1) = −1 ⇒ a ⋅ 12 + b ⋅ 1 + 2 = −1 ⇒
⇒ a + b = −3 I
f(2) = −2 ⇒ a ⋅ 22 + b ⋅ 2 + 2 = −2 ⇒
⇒ 4a + 2b = −4 II
As equações I e II formam um sistema de equações:
Multiplicando ambos os membros da primeira equação por −2, temos:
Adicionando, membro a membro, essas equações, temos:
2a = 2
a = 1
Substituindo a = 1 em I, temos:
1 + b = −3
b = −4
Como a = 1, b = −4 e c = 2, a lei de formação da função f é f(x) = x2 − 4x + 2.
b) f(10) = 102 − 4 ⋅ 10 + 2 = 100 − 40 + 2 = 62
f(6) = 62 − 4 ⋅ 6 + 2 = 36 − 24 + 2 = 14
f(−1) = (−1)2 − 4 ⋅ (−1) + 2 = 1 + 4 + 2 = 7
Portanto:
f(10) − f(6) + f(−1) = 62 − 14 + 7 = 55
c) Observando a resolução do item a, percebemos quê foram utilizadas as informações a respeito dos pontos A, B e C. Os pontos D e E não foram utilizados.
Caso tivéssemos escolhido os pontos D e E, em vez dos pontos B e C, teríamos chegado à mesma resposta.
2. Considere uma função quadrática h, definida por h(x) = (3m − 15)x2 + 6x ,com m ∈ ℝ.
Determine o valor de m para quê a parábola correspondente ao gráfico de h tenha concavidade voltada para cima.
Resolução
Para quê o gráfico da função h tenha a concavidade voltada para cima, o coeficiente do termo x2 deve sêr maior do quê zero. Nesse caso, temos:
3m − 15 > 0
3m > 15
m > 5
Portanto, o gráfico de h terá a concavidade voltada para cima para todo número real m > 5.
Página cento e quarenta e nove
ATIVIDADES
1. Considere a função definida por f(x) = x2 − 5x + 4 e calcule:
a) f(0)
4
b) f(−4)
40
c)
d)
6 −
2. Um objeto é lançado para cima, a partir do solo, e sua altura h, em métro, varia em função do tempo t, em segundo, decorrido após o lançamento. Supondo quê a lei dessa função seja h(t) = 30t − 5t2, qual será a altura do objeto 3 segundos após o lançamento?
45 metros
3. A soma S dos n primeiros números naturais diferentes de zero (1 + 2 + 3 + 4 +... + n) póde sêr calculada utilizando a função quadrática dada por S(n) = .
Qual é a soma dos 50 primeiros números naturais diferentes de zero?
1.275
4. Mensalmente, uma fábrica produz x unidades de cérto produto. Sua produção é vendida por (500 − x) reais a unidade. Cada unidade dêêsse produto tem um custo de R$ 100,00. Além díssu, a fábrica tem uma despesa mensal fixa de R$ 10.000,00.
a) Sabendo quê o lucro é calculado pela diferença entre a receita das vendas e a despesa, escrêeva a lei da função quê determina o lucro mensal L dessa fábrica, em reais, em função de x.
L(x) = −x2 + 400x − 10.000
b) De quantos reais será o lucro quando a fábrica vender 100 produtos?
R$ 20.000,00
5. Uma função quadrática f é tal quê f(0) = 6, f(1) = 2 e f(−2) = 20. Determine o valor de .
6. Esboce, no sistema cartesiano, o gráfico de cada função quadrática definida a seguir.
a) y = −x2
c) y = −x2 + 6x − 9
b) y = x2 − 4
d) y = x2 − 5x
Ver as Orientações para o professor.
7. Determine o valor de m para quê a parábola quê representa a função definida por y = 3x2 − x + m passe pelo ponto (1, 6).
m = 4
8. (UEA-AM) A representação gráfica, no plano cartesiano, da função f(x) = x2 − bx + c, em quê b e c são números reais, passa pêlos pontos A(0, 5), C(5, 0) e D.
alternativa d
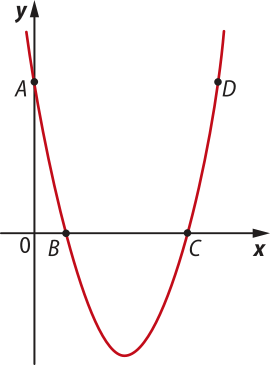
Sabendo quê os pontos A e D possuem a mesma ordenada, as coordenadas do ponto D são:
a) (5, 6)
b) (6, 0)
c) (5, 5)
d) (6, 5)
e) (6, 6)
Página cento e cinquenta
EXPLORANDO A TECNOLOGIA
Os coeficientes da função quadrática e a parábola
Aprendemos quê o sinal do coeficiente a indica se a concavidade da parábola correspondente ao gráfico de uma função quadrática está voltada para cima ou para baixo.
Agora, vamos utilizar o GeoGebra para analisar como outras mudanças nos coeficientes da lei de uma função quadrática influenciam no gráfico correspondente.
Para isso, realize, inicialmente, a sequência de passos a seguir.
I. No campo de entrada do GeoGebra, digite “f(x) = x^2” e pressione Enter.
II. No campo de entrada, digite “g(x) = ax^2” e pressione Enter. Será criado, automaticamente, um contrôle deslizante para o coeficiente a. Altere a posição do ponto ao longo do contrôle para alterar o valor de a e obissérve o quê acontece com o gráfico de g, comparando-o com o gráfico de f.
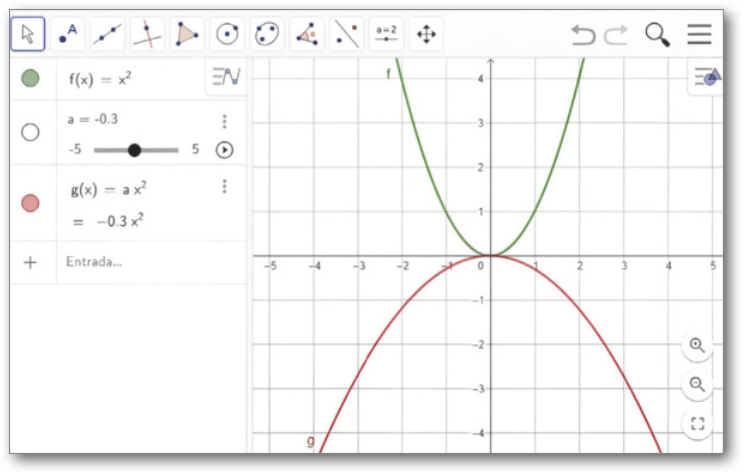
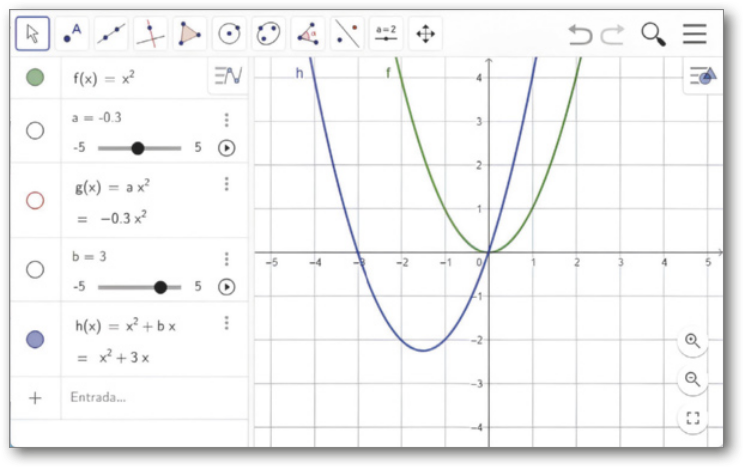
III. Na janela de Álgebra, clique na bó-linha colorida da lei da função g para ocultar o gráfico de g. Em seguida, no campo de entrada do GeoGebra, digite “h(x) = x^2 + bx” e pressione Enter. Um contrôle deslizante para o coeficiente b será criado. Altere a posição do ponto ao longo do contrôle para alterar o valor de b e obissérve o quê acontece com o gráfico de h, comparando-o com o gráfico de f.
Página cento e cinquenta e um
IV. Na janela de Álgebra, clique na bó-linha colorida da lei da função h para ocultar o gráfico da função. No campo de entrada, digite “j(x) = x^2 + c” e pressione Enter. Um contrôle deslizante será criado para o coeficiente c. Altere a posição do ponto ao longo do contrôle para alterar o valor de c e obissérve o quê acontece com o gráfico de j, comparando-o com o gráfico de f.
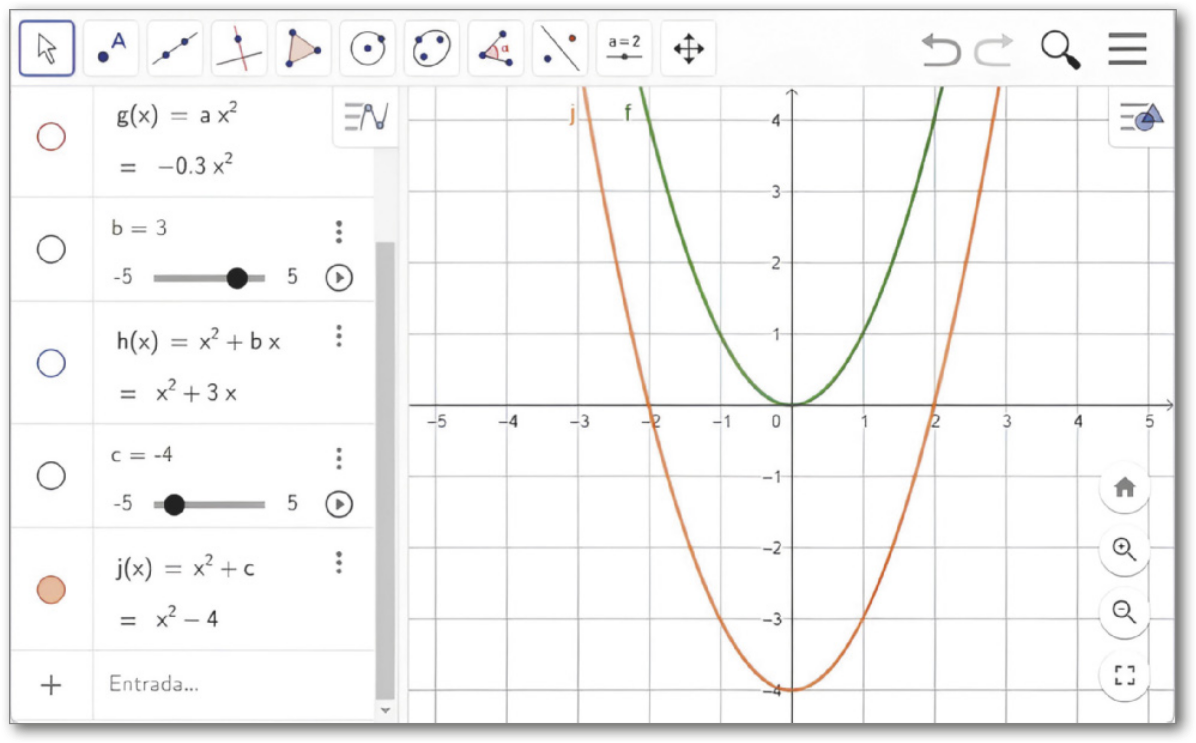
V. Na janela de Álgebra, clique nas bó-linhas para ocultar ou exibir os gráficos construídos. Manipule-os e faça comparações, analisando o comportamento das funções.
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Ao deslizar o contrôle do coeficiente a, comparando o gráfico da função g com o da função f, o quê você observou?
2. Ao deslizar o contrôle do coeficiente b, comparando o gráfico da função h com o da função f, o quê você observou?
3. Ao deslizar o contrôle do coeficiente c, comparando o gráfico da função j com o da função f, o quê você observou?
4. Na janela de Álgebra, clique nas bó-linhas para ocultar os gráficos das funções f, g, h e j.
Em seguida, no campo de entrada, digite “t(x) = ax^2 + bx + c” e pressione Enter.
Manipule os controles para verificar o gráfico de diferentes funções, aproveitando para representar os gráficos de funções apresentadas anteriormente neste Capítulo.
Página cento e cinquenta e dois
Zeros da função quadrática
Já estudamos quê o zero de uma função é um valor de x quê anula a função, ou seja, o valor de x para o qual f(x) = 0. Aprendemos também quê, considerando a função afim, é possível determinar o zero da função definida por f(x) = ax + b resolvendo a equação ax + b = 0.
Para determinar os zeros de uma função quadrática, devemos proceder de maneira análoga: os zeros da função quadrática dada por y = ax2 + bx + c são as raízes da equação ax2 + bx + c = 0.
Agora, vamos explorar como resolver equações polinomiais do 2º grau aplicando uma fórmula resolutiva, também conhecida como fórmula de Bhaskara, na qual os coeficientes a, b e c são utilizados. Acompanhe como obtêr a fórmula.
Considere a equação ax2 + bx + c = 0, com a, b, c ∈ ℝ e a ≠ 0.
Procedimentos |
|
|---|---|
Considerar a equação ax2 + bx + c = 0. |
ax2 + bx + c = 0 |
Multiplicar a equação por 4a. |
4a ⋅ ax2 + 4a ⋅ bx + 4a ⋅ c = 4a ⋅ 0 |
Adicionar b2 aos dois membros da equação. |
4a2x2 + 4abx + 4ac + b2 = 0 + b2 |
Subtrair 4ac dos dois membros da equação. |
4a2x2 + 4abx + 4ac − 4ac + b2 = b2 − 4ac |
Identificar o trinômio quadrado perfeito. |
(2ax)2 + 2 ⋅ 2ax ⋅ b + b2 = b2 − 4ac |
Fatorar o trinômio quadrado perfeito. |
(2ax + b)2 = b2 − 4ac |
Extrair a raiz quadrada dos dois membros da equação. |
= ± |
Subtrair b dos dois membros da equação. |
2ax + b − b = −b ± |
Dividir a equação por 2a para isolar a incógnita x. |
= x = |
Portanto, a fórmula resolutiva da equação ax2 + bx + c = 0 é dada por:
em quê (delta)" = b2 − 4ac
A expressão b2 − 4ac, indicada pela letra grega (delta)" (delta), é denominada discriminante da equação polinomial do 2º grau. Determinar _ só tem sentido quando (delta)" ≥ 0, caso contrário, a equação não possui raízes reais.
Saiba quê...
A fatoração de um trinômio quadrado perfeito resulta no produto notável quadrado da soma de dois termos ou no produto notável quadrado da diferença de dois termos.
p2 + 2pq + q2 = (p + q)2
p2 − 2pq + q2 = (p − q)2
Saiba quê...
O motivo pelo qual apareceu o sinal± no desenvolvimento da equação póde sêr entendido por meio do seguinte exemplo simplificado.
Na equação x2 = 9, busca-se um valor x quê, elevado ao quadrado, resulte em 9.
Nesse caso, há duas soluções, −3 e 3, pois(−3)2 = 9 e 32 = 9.
Desse modo, tem-se:
x2 = 9 ⇒ x = = ±3
De modo geral,
x2 = m ⇒ x = .
Página cento e cinquenta e três
Quando resolvemos a equação ax2 + bx + c = 0, com a, b, c ∈ ℝ e a ≠ 0, utilizando a fórmula resolutiva, deparamo-nos com uma das três situações a seguir.
I. Se (delta)" > 0, então a equação possui duas raízes reais e distintas.
Portanto, a função quadrática correspondente tem dois zeros:
x(minutos)" = _ e x(segundos)" =
II. Se (delta)" = 0, então a equação possui duas raízes reais iguais.
Portanto, a função quadrática correspondente tem um zero:
x(minutos)" = x(segundos)" =
III. Se (delta)" < 0, então a equação não possui raízes reais.
Portanto, a função quadrática correspondente não tem zero.
(delta)" > 0 |
(delta)" = 0 |
(delta)" < 0 |
|
|---|---|---|---|
a > 0 |
|
|
|
a < 0 |
|
|
|
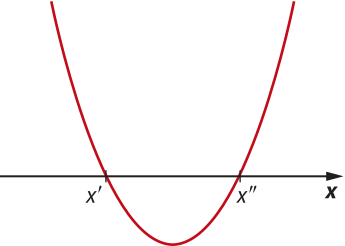
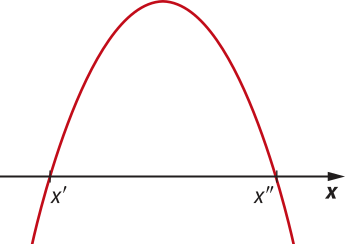
■ Nesse caso, os zeros da função, x’ e x’’, são as abscissas dos dois pontos de intersecção do gráfico da função com o eixo x. |
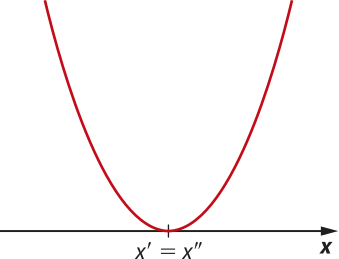
■ Nesse caso, o zero da função é a abscissa do ponto de tangência do gráfico da função com o eixo x. |
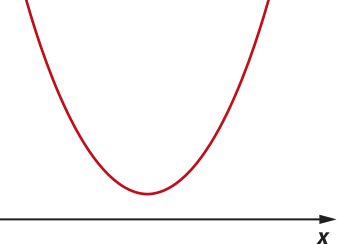
■ Nesse caso, como não há zero da função, não há intersecção do gráfico da função com o eixo x. |
Página cento e cinquenta e quatro
Soma e produto das raízes de uma equação do 2º grau
Pense e responda
A soma das raízes reais de uma equação do 2º grau é −1 e o produto é −6. Quais são essas raízes?
−3 e 2
Considerando x(minutos)" e x(segundos)" as raízes reais da equação ax2 + bx + c = 0, ou seja, x(minutos)" = e x(segundos)" = , podemos calcular a soma e o produto dessas raízes, como se verifica a seguir.
x(minutos)" + x(segundos)" = ⇒ x(minutos)" + x(segundos)" = ⇒ x(minutos)" + x(segundos)" =
x(minutos)" ⋅ x(segundos)" = ⇒ x(minutos)" ⋅ x(segundos)" = ⇒
⇒ x(minutos)" ⋅ x(segundos)" = ⇒ x(minutos)" ⋅ x(segundos)" = ⇒ x(minutos)" ⋅ x(segundos)" =
Portanto, a soma e o produto das raízes de uma equação de 2º grau são, respectivamente, x(minutos)" + x(segundos)" = e x(minutos)" ⋅ x(segundos)" =.
Forma fatorada da equação do 2º grau
Saiba quê...
A forma “fatorada” de um polinômio é assim chamada porque resulta em uma expressão algébrica na forma de uma multiplicação. O adjetivo “fatorada” vêm de “fatores” de uma multiplicação.
Vamos utilizar a soma e o produto das raízes x(minutos)" e x(segundos)" de uma equação ax2 + bx + c = 0, com a ≠ 0, para obtêr a forma fatorada da lei de formação da função quadrática correspondente, quê é dada por f(x) = ax2 + bx + c. Acompanhe a seguir.
Colocando em evidência o coeficiente a na lei da função, temos:
f(x) = ⇒ f(x) =
Como x(minutos)" + x(segundos)" = e x(minutos)" ⋅ x(segundos)" = , temos:
f(x) = a [x2 − (x(minutos)" + x(segundos)")x + x(minutos)" ⋅ x(segundos)"]
Desenvolvendo e fatorando essa expressão, temos:
f(x) = a[x2 − x(minutos)"x − x(segundos)"x + x(minutos)"x(segundos)"]
f(x) = a[x(x − x(minutos)") − x(segundos)"(x − x(minutos)")]
f(x) = a(x − x(minutos)")(x − x(segundos)")
Portanto, a forma fatorada da lei da função quadrática é:
f(x) = a(x − x(minutos)")(x − x(segundos)")
Página cento e cinquenta e cinco
ATIVIDADES RESOLVIDAS
3. Determine os zeros das funções quadráticas definidas a seguir.
a) f(x) = x2 − 25
b) g(x) = x2 + 8x
c) h(x) = x2 + 3x − 4
Resolução
As equações do 2º grau em quê algum dos coeficientes, b, c ou ambos, é nulo são chamadas de equações do 2º grau incompletas. Quando temos esse tipo de equação, é possível resolvê-la utilizando outros métodos, além da fórmula resolutiva, como será feito nos itens a e b a seguir.
a) Para encontrar os zeros da função f, devemos obtêr os valores de x para os quais f(x) = 0. Assim, devemos encontrar as raízes da equação do 2º grau:
x2 − 25 = 0
Nesse caso, como b = 0, a equação é incompleta e póde sêr resolvida isolando-se x diretamente:
x2 − 25 = 0 ⇒ x2 = 25 ⇒
⇒ x = ⇒ x = ±5
Portanto, a equação possui duas raízes,
x(minutos)" = −5 e x(segundos)" = 5. Sendo assim, os zeros da função f são −5 e 5.
b) Para encontrar os zeros da função g, basta encontrar as raízes da equação:
x2 + 8x = 0
Nesse caso, como c = 0, a equação é incompleta e póde sêr resolvida utilizando-se fatoração. Acompanhe.
x2 + 8x = 0 ⇒ x(x + 8) = 0
Como o produto entre os fatores x e x + 8 é zero, então:
x = 0 ou x + 8 = 0 ⇒ x = −8
Portanto, a equação possui duas raízes, x(minutos)" = 0 e x(segundos)" = −8. Sendo assim, os zeros da função g são 0 e −8.
c) Para encontrar os zeros da função h, basta encontrar as raízes da equação:
x2 + 3x − 4 = 0
Nesse caso, como a = 1, b = 3 e c = −4, a equação do 2º grau é completa. Ela póde sêr resolvida usando a fórmula resolutiva x = , em quê (delta)" = b2 − 4ac.
Desse modo, tem-se:
(delta)" = 32 − 4 ⋅ 1 ⋅ (−4) = 25
x = ⇒ x =
x(minutos)" = = −4 e x(segundos)" = = 1
Portanto, a equação possui duas raízes, x(minutos)" = −4 e x(segundos)" = 1. Assim, os zeros da função h são −4 e 1.
4. Elabore um fluxograma quê retórne, se houver, os zeros de uma função quadrática.
Resolução
Considerando quê, dependendo do valor de (delta)", a função quadrática terá dois zeros distintos, um único zero ou não possuirá zeros reais; então, um possível fluxograma seria:
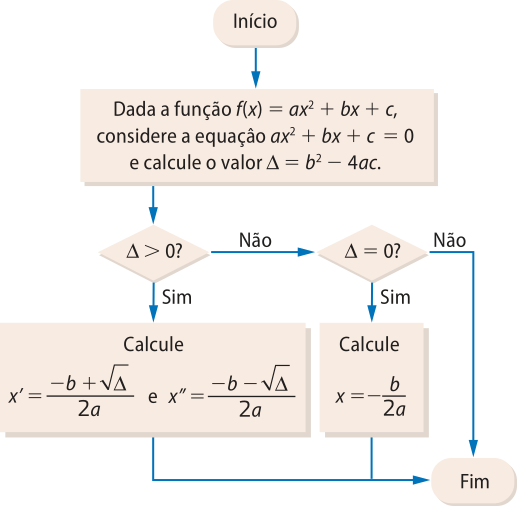
5. Seja a função definida por h(x) = x2 − 2x + 3k.
Sabendo quê essa função tem um único zero, determine o valor real de k.
Resolução
A condição para quê a função tenha apenas um zero é (delta)" = 0.
(delta)" = b2 − 4ac ⇒ (delta)" = (−2)2 − 4 ⋅ 1 ⋅ 3k ⇒
⇒ (delta)" = 4 − 12k
Fazendo (delta)" = 0 em (delta)" = 4 − 12k, temos:
4 − 12k = 0 ⇒ −12k = −4 ⇒
⇒ k = ⇒ k =
Portanto, para quê h tenha um único zero, devemos ter k = .
Página cento e cinquenta e seis
6. (UEA-AM) Durante um tratamento com medicina alternativa, uma pessoa deverá ingerir, apenas uma vez ao dia, durante os 10 primeiros dias do mês, determinado número de gotas de um medicamento. Sabendo quê o número de gotas foi calculado através da função dada por g(x) = −x2 + 10x, sêndo g(x) o número de gotas e x o dia do mês, com x ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, é correto afirmar quê essa pessoa ingeriu 16 gotas nos dias:
a) 2 e 8.
b) 2 e 9.
c) 3 e 8.
d) 3 e 9.
e) 5 e 6.
Resolução
Como g(x) representa o número de gotas, considera-se g(x) = 16. Assim, temos:
16 = −x2 + 10x ⇒ x2 − 10x + 16 = 0
(delta)" = (−10)2 − 4 ⋅ 1 ⋅ 16 = 36
x = _
Logo, x(minutos)" = 2 e x(segundos)" = 8.
Portanto, a resposta é a alternativa a.
ATIVIDADES
9. Determine, se existirem, os zeros das funções quadráticas definidas a seguir.
a) y = x2 − 6x + 5
x(minutos)" = 1; x(segundos)" = 5
b) y = 3x2 − 4x
x(minutos)" = 0; x(segundos)" =
c) y = −x2 + x − 3
A função não tem zeros.
d) y = x2 − 9
x(minutos)" = −3; x(segundos)" = 3
e) y = −6x2
x(minutos)" = x(segundos)" = 0
f) y = 4x2 − x +
A função não tem zeros.
10. Calcule k de modo quê a função dada por y = kx2 − 2x + 3 admita o valor 2 como um de seus zeros.
k =
11. Considerando a função definida por f(x) = ax2 + bx + 10, determine a e b, sabendo quê seus zeros são −2 e 5. Em seguida, faça um esboço do gráfico dessa função.
Ver as Orientações para o professor.
12. Considere a função f: ℝ → ℝ definida por f(x) = x2 + 2mx + 16. Determine m ∈ ℝ de modo quê:
a) a função f tenha um único zero;
m = ±4
b) o gráfico da função f passe pelo ponto (2, −4).
m = −6
13. Determine o parâmetro real k de modo quê a função f(x) = x2 − 2x + k tenha:
a) dois zeros;
k < 1
b) um único zero;
k = 1
c) nenhum zero.
k > 1
14. (hú éfe ême gê) Um cérto reservatório, contendo 72 m3 de á gua, deve sêr drenado para limpeza. Decorridas t horas após o início da drenagem, o volume de á gua quê saiu do reservatório, em m3, é dado por V(t) = 24t − 2t2. Sabendo-se quê a drenagem teve início às 10 horas, o reservatório estará completamente vazio às:
alternativa b
a) 14 horas.
b) 16 horas.
c) 19 horas.
d) 22 horas
Página cento e cinquenta e sete
15. Dadas as funções definidas por f(x) = (x + 1)(x − 3) e g(x) = + 3, determine:
a) os pontos de intersecção da parábola com o eixo das abscissas;
(−1, 0) e (3, 0)
b) o ponto de intersecção da parábola com o eixo das ordenadas;
(0, −3)
c) o ponto de intersecção da reta com o eixo das ordenadas;
(0, 3)
d) o ponto de intersecção da reta com a parábola situado no 2º quadrante.
16. (hú éfe pê érre) A distância quê um automóvel percórre a partir do momento em quê um condutor pisa no freio até a parada total do veículo é chamada de distância de frenagem. Suponha quê a distância de frenagem d, em metros, possa sêr calculada pela fórmula d(v) = (v2 + 8v), sêndo v a velocidade do automóvel, em kilometros por hora, no momento em quê o condutor pisa no freio.
a) Qual é a distância de frenagem de um automóvel quê se desloca a uma velocidade de 40 km/h?
16 m
b) A quê velocidade um automóvel deve estar para quê sua distância de frenagem seja de 53,2 m?
76 km/h
FÓRUM
Riscos do uso de celulares ao dirigir
Dirigir exige atenção plena. Quando o motorista desvia o foco para o celular, ao ler mensagens ou atender a chamadas, sua capacidade de reação fica comprometida, resultando em tempos de resposta mais longos. Esses segundos extras necessários para reagir podem fazer toda a diferença entre evitar um acidente ou se envolver em uma situação perigosa; por esse motivo, destaca-se a importânssia de manter o foco total na condução. Portanto, é essencial se conscientizar sobre os perigos associados à utilização do celular ao volante e reconhecer a importânssia de manter os olhos na estrada para prevenir acidentes e preservar vidas.
![]() Converse com os côlégas sobre a questão a seguir.
Converse com os côlégas sobre a questão a seguir.
• Que estratégia você adotaria para conscientizar pessoas da comunidade sobre os perigos de usar o celular ao dirigir e a importânssia de manter o foco total na condução?
Ver as Orientações para o professor.

Página cento e cinquenta e oito
Vértice da parábola
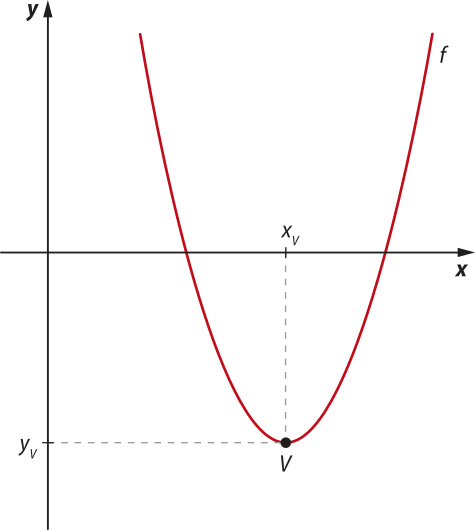
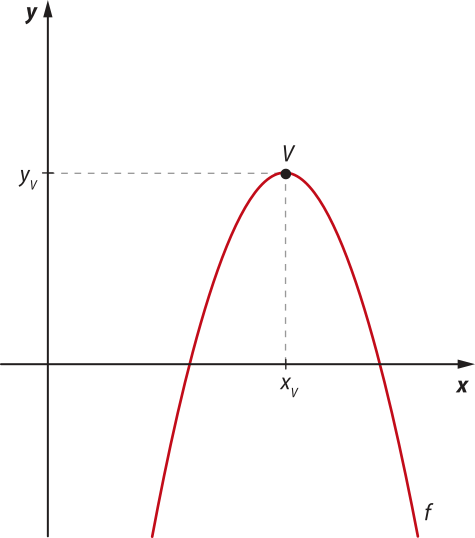
O vértice V da parábola de uma função quadrática f é um ponto do gráfico no qual identificamos uma mudança de comportamento de crescente para decrescente ou, ao contrário, de decrescente para crescente da função f. Isto é, seja V(xV, yV) o vértice da parábola da função quadrática f: ℝ → ℝ, se f é decrescente no intervalo]−∞, xV], ela é crescente em [xv, +∞[, ou se f é crescente no intervalo]−∞, xV], ela é decrescente em [ xV, +∞[.
O eixo de simetria da parábola de uma função quadrática é a reta r, perpendicular ao eixo x, quê passa pelo vértice V.
Observe, na figura 1, o gráfico de uma função quadrática f e o vértice V(xV, yV) destacado.
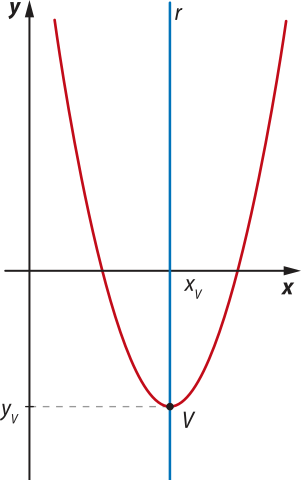
Acompanhe a seguir uma maneira de obtêr as coordenadas do vértice.
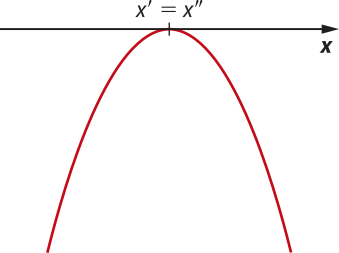
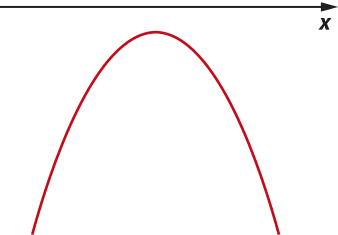
Considere f uma função quadrática dada por f(x) = ax2 + bx + c e dois pontos pertencentes ao gráfico de f quê têm ordenadas iguais. Sabemos quê esses pontos estão à mesma distância do eixo de simetria da parábola e quê êste, por sua vez, é perpendicular ao eixo x e cruza esse mesmo eixo no ponto de abscissa xV do vértice.
pôdêmos, então, indicar as coordenadas dêêsses dois pontos por P(xV − k, y0) e Q(xV + k, y0), em quê k ≠ 0 é a diferença entre as abscissas de V e de P, e de Q e de V, como póde sêr verificado na figura 2.
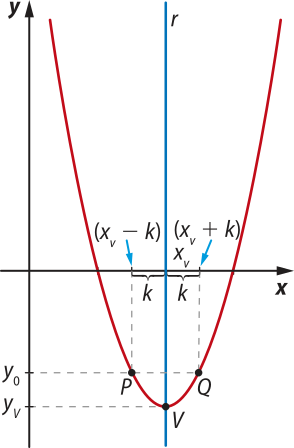
Como as ordenadas dos pontos P e Q são iguais, temos:
f(xV − k) = f(xV + k)
Substituindo esses valores na lei da função f, temos:
a(xV − k)2 + b(xV − k) + c = a(xV + k)2 + b(xV + k) + c ⇒
⇒ ![]() ⇒
⇒
⇒ ![]() ⇒
⇒
⇒ −2axVk − 2axVk = bk + bk ⇒ −4axVk = 2bk ⇒
⇒ xV = ⇒ xV =
Para calcular a ordenada yV do vértice, substituímos, na lei da função, o valor de xV obtído. Nesse caso, temos:
yV = f(xV) = + c ⇒
⇒ yV = a ⋅ + c ⇒ yV = + c ⇒
⇒ yV = ⇒ yV = ⇒ yV =
Portanto, as coordenadas do vértice da parábola são .
Saiba quê...
Para facilitar o esboço do gráfico de uma função quadrática, podem-se utilizar pontos específicos, como o vértice da parábola, o ponto em quê a parábola intersecta o eixo y e, se houver, os zeros da função.
Página cento e cinquenta e nove
Valor mínimo e valor mássimo da função quadrática
Ao esboçarmos o gráfico de uma função quadrática f, dada por f(x) = ax2 + bx + c, consideramos o sinal do coeficiente a para identificar se a concavidade da parábola será voltada para cima ou voltada para baixo.
Utilizando esse esboço, podemos verificar, entre outras propriedades, quê a função f tem um valor mínimo ou um valor mássimo, quê corresponde à ordenada do vértice da parábola.
Nesse caso, se a > 0, a concavidade da parábola é voltada para cima, e temos três situações possíveis para o gráfico:
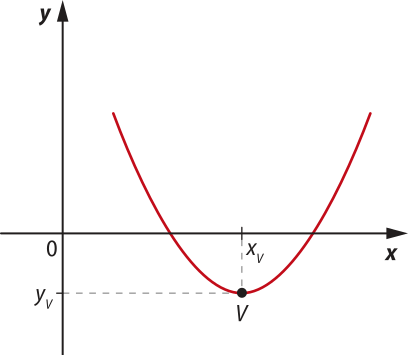
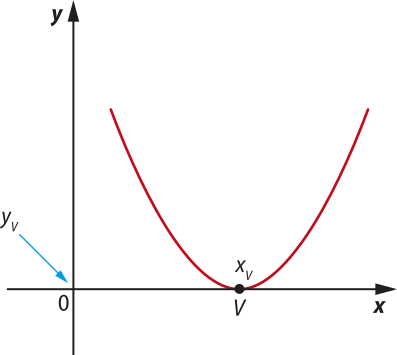
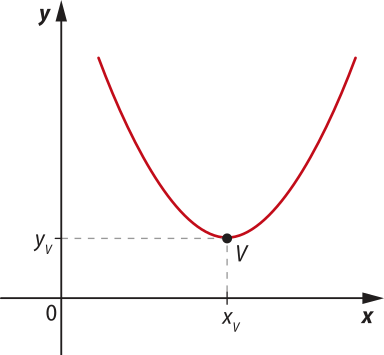
Observe quê, nos três casos, o vértice V da parábola é o ponto cuja ordenada é o menor valor assumido pela função para todo x ∈ D(f), chamado também de ponto de mínimo da função. A ordenada de V, quê póde sêr ôbitída por yV = , é o valor mínimo da função, quê ocorre quando xV = .
De maneira análoga, se a < 0, a concavidade da parábola é voltada para baixo, e temos outras três possibilidades para o gráfico da função:
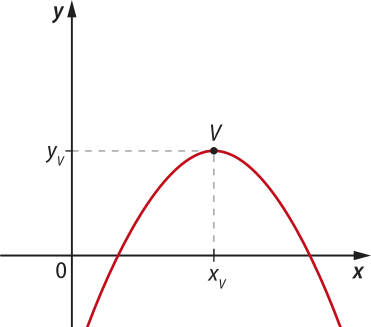
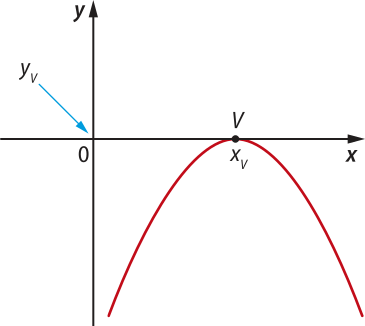
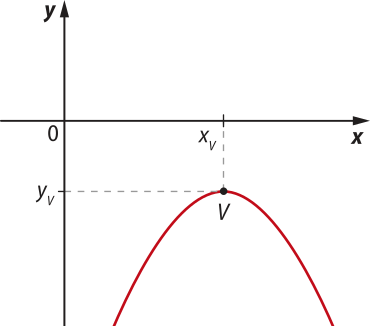
Considerando esses três casos, o vértice V da parábola é o ponto cuja ordenada é o maior valor assumido pela função para todo x ∈ D(f), chamado também de ponto de mássimo da função. A ordenada de V, quê póde sêr ôbitída por yV = , é o valor mássimo da função, quê ocorre quando xV = .
Página cento e sessenta
Pense e responda
De acôr-do com a função L, qual é o lucro diário mássimo quê Elisa, a dona da loja de capas para celular, póde obtêr?
R$ 506,25
Exploramos, no início dêste Capítulo, uma situação na qual o lucro diário de uma loja de capas para celular é modelado por uma função quadrática. Nessa situação, o lucro L, em reais, é função do preêço x pelo qual cada capa é vendida, também em reais, e é expresso por L(x) = −x2 + 55x − 250.
Como, nesse caso, a < 0, a ordenada do vértice V da parábola é o maior valor assumido pela função.
Utilizando a coordenada xV do vértice, podemos determinar o preêço pelo qual cada capa deve sêr vendida para quê a loja obtenha o maior lucro diário, de acôr-do com essa função.
xV = − ⇒ xV = ⇒ xV = ⇒ xV = 27,5
Logo, para quê a loja obtenha o maior lucro diário, cada capa de celular deve sêr vendida por R$ 27,50.
Imagem da função quadrática
Utilizando as coordenadas do vértice da parábola correspondente ao gráfico de uma função quadrática f, podemos determinar o seu conjunto imagem.
Aprendemos quê, quando a > 0, o vértice V é o ponto de mínimo da função, e yV = é o valor mínimo quê a função assume, ou seja, é o menor valor de imagem da função.
Por outro lado, quando a < 0, o vértice V é o ponto de mássimo da função, e yV = é o valor mássimo quê a função assume, ou seja, é o maior valor de imagem da função.
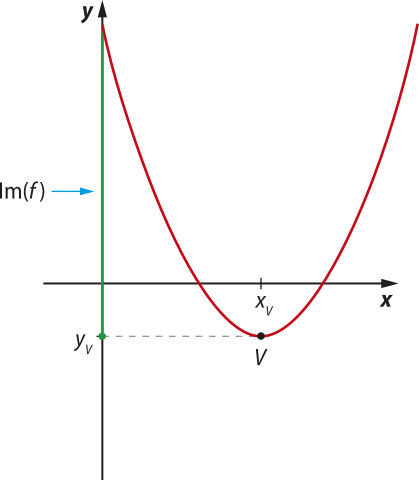
Im(f) = {y ∈ ℝ | y ≥ yV}.
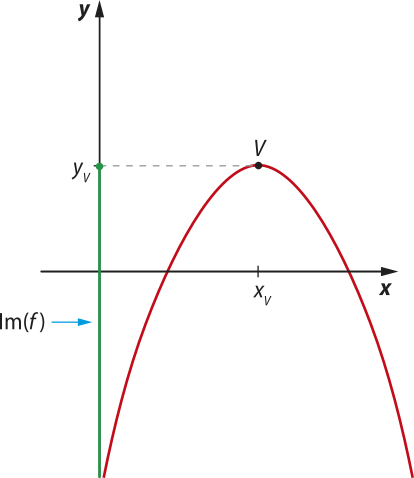
Im(f) = {y ∈ ℝ | y ≤ yV}.
Página cento e sessenta e um
Crescimento e decrescimento da função quadrática
Estudamos anteriormente quando uma função real de variável real é crescente em um intervalo e quando ela é decrescente. Estudaremos, agora, o comportamento da função quadrática em relação a crescimento e decrescimento.
Acompanhe a situação a seguir.
Em determinado momento de uma coreografia de ginástica rítmica, uma bola é lançada do solo verticalmente para cima. A altura h da bola em relação ao solo, em métro, varia de acôr-do com o tempo t, em segundo, conforme a lei h(t) = −5t2 + 10t, considerando 0 ≤ t ≤ 2.
Observe o gráfico quê representa a função h.
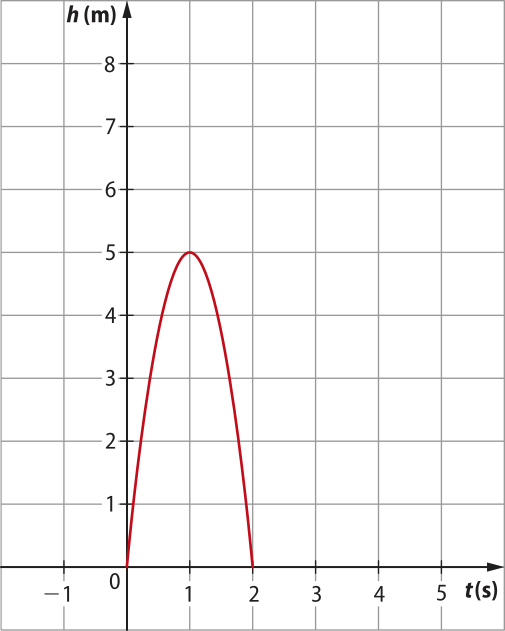
A função h é crescente no intervalo [0, 1], pois, à medida quê t aumenta nesse intervalo, h(t) também aumenta. Em outras palavras, para quaisquer valores de t1 e t2 pertencentes a [0, 1], com t1 < t2, temos h(t1) < h(t2).
Por outro lado, a função h é decrescente no intervalo [1, 2], pois, à medida quê t aumenta nesse intervalo, h(t) diminui. Em outras palavras, para quaisquer valores de t1 e t2 pertencentes a [1, 2], com t1 < t2, temos h(t1) > h(t2).

Pense e responda
• Qual é a altura mássima alcançada pela bola? Em quê instante isso é observado?
5 metros. Isso acontece em t = 1 s.
• pôdêmos dizêr quê, à medida quê t aumenta no intervalo [0, 2], h(t) também aumenta?
Não. A partir de t = 1, à medida quê t aumenta, h(t) diminui.
Página cento e sessenta e dois
De modo geral, podemos estudar o crescimento e o decrescimento da função quadrática definida por f(x) = ax2 + bx + c com base no valor de a e na abscissa xV do vértice da parábola, como indicado a seguir.
a > 0 |
a < 0 |
|---|---|
|
|
• A função f é decrescente no intervalo ]−∞, xV]. • A função f é crescente no intervalo [xV, +∞[. |
• A função f é crescente no intervalo ]−∞, xV]. • A função f é decrescente no intervalo [xV, +∞[. |
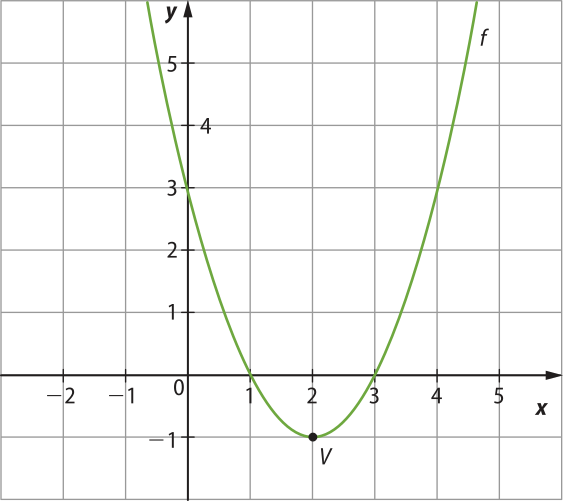
Considere, por exemplo, a função definida por f(x) = x2 − 4x + 3.
Calculando a abscissa xV do vértice da parábola correspondente, temos:
xV = ⇒ xV = ⇒ xV = 2
Assim, como a > 0, essa função é decrescente no intervalo]−∞, 2] e crescente no intervalo [2, +∞[. Isso também póde sêr observado por meio do gráfico a seguir.
Página cento e sessenta e três
ATIVIDADES RESOLVIDAS
7. Determine as coordenadas do vértice V da parábola quê representa a função dada por f(x) = −5x2 + 3x − 1.
Resolução
Os coeficientes da lei da função são a = −5, b = 3 e c = −1.
Além díssu, (delta)" = 32 − 4 ⋅ (−5) ⋅ (−1) = −11.
Calculando as coordenadas do vértice, obtemos:
xV =
yV =
Logo, as coordenadas do vértice são
8. Determine as coordenadas do vértice da parábola quê representa a função quadrática f cujos zeros são −5 e −3 e o coeficiente a é igual a 1.
Resolução
pôdêmos utilizar os zeros da função para escrever a lei de f na sua forma fatorada.
f(x) = 1(x + 5)(x + 3) ⇒ f(x) = x2 + 8x + 15
Assim, os coeficientes da lei dessa função são a = 1, b = 8 e c = 15.
Calculando as coordenadas do vértice, obtemos:
xV = = −4
yV = f(xV) ⇒ yV = f(−4) ⇒
⇒ yV = (−4)2 + 8 ⋅ (−4) + 15 ⇒
⇒ yV = 16 − 32 + 15 = −1
Portanto, o vértice da parábola quê representa a função f tem coordenadas (−4, −1).
9. Uma empresa calculou quê a produção mensal de x unidades de um cérto produto gera um lucro mensal, em reais, de 150 − por unidade do produto. Responda aos itens.
a) Qual é a lei da função quê representa o lucro, em reais, em relação à quantidade de produtos produzidos por mês?
b) Qual é o lucro mássimo mensal quê essa empresa póde ter com a venda dêêsse produto?
Resolução
a) Para obtêr a lei dessa função, multiplicamos a quantidade de produtos produzidos por mês pelo valor correspondente ao lucro unitário. Assim, temos:
L(x) = x ⋅ ⇒ L(x) = 150x
A lei da função é L(x) = 150x .
b) O lucro mássimo mensal é obtído pelo cálculo da ordenada do vértice do gráfico dessa função.
yv =
= = 22.500
Assim, o lucro mássimo mensal é de R$ 22.500,00.
10. Considere uma função quadrática f: ℝ → ℝ, definida por f(x) = x2 − 3x + 2.
a) Em qual intervalo real essa função é crescente?
b) Determine o conjunto imagem dessa função.
Resolução
a) Como a > 0, a função f é crescente no intervalo [xV,+∞[.
Calculando a abscissa xV do vértice da parábola, temos:
xV =
Logo, a função f é crescente no intervalo
b) Para determinar o conjunto imagem da função f, determinamos inicialmente a ordenada yV do vértice da parábola. Nesse caso, temos:
yV =
yV =
Página cento e sessenta e quatro
Como a > 0, o gráfico de f tem concavidade voltada para cima, e yV é o valor mínimo da função, como podemos verificar a seguir.
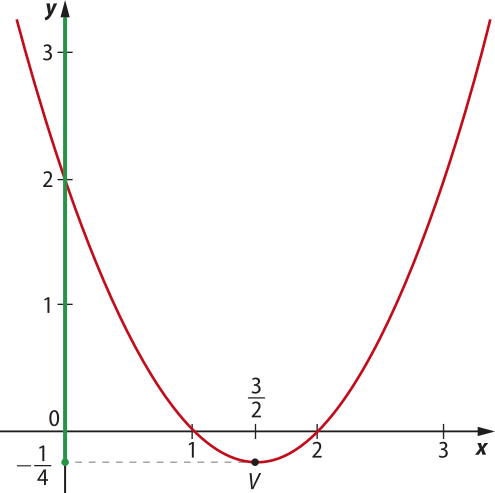
Assim, f(x) ≥ para todo x ∈ ℝ.
Portanto, Im(f) = .
11. (EsPCEx-SP) Uma indústria produz mensalmente x lotes de um produto. O valor mensal resultante da venda dêste produto é V(x) = 3x2 − 12x e o custo mensal da produção é dado por C(x) = 5x2 − 40x − 40.
Sabendo quê o lucro é obtído pela diferença entre o valor resultante das vendas e o custo da produção, então o número de lotes mensais quê essa indústria deve vender para obtêr lucro mássimo é igual a
a) 4 lotes.
b) 5 lotes.
c) 6 lotes.
d) 7 lotes.
e) 8 lotes.
Resolução
Inicialmente, determinamos a expressão do lucro L(x) dessa indústria em função do número de lotes x produzidos em um mês.
Do enunciado, temos L(x) = V(x) − C(x).
Assim:
L(x) = 3x2 − 12x − (5x2 − 40x − 40)
L(x) = 3x2 − 12x − 5x2 + 40x + 40
L(x) = −2x2 + 28x + 40
O gráfico da função correspondente ao lucro é uma parábola com a concavidade voltada para baixo, pois a < 0.
Portanto, o número de lotes mensais quê devem sêr produzidos para quê a indústria obtenha lucro mássimo é o valor da abscissa xV do vértice.
Logo, a resposta é a alternativa d.
ATIVIDADES
17. A trajetória de uma bola de futeból em uma cobrança de falta foi descrita por uma função quadrática quê relaciona a altura h alcançada pela bola, em relação ao solo, e o deslocamento horizontal x da bola, sêndo h e x dados em métro. Essa função é expressa por h(x) = + 0,5x.
a) Qual é a distância entre o ponto em quê a bola sai do solo e o ponto em quê a bola chega ao solo?
30 metros
b) Qual é a altura mássima atingida pela bola nessa trajetória?
3,75 metros

18. Faça um esboço do gráfico das funções quadráticas a seguir. Indique o vértice da parábola, o ponto de intersecção da parábola com o eixo y e, se existirem, os zeros da função.
Ver as Orientações para o professor.
a) y = x2 − 5x + 6
b) y = −x2 + 4
c) y = x2 − 4x + 4
d) y = x2 + 2x + 5
Página cento e sessenta e cinco
19. Determine o conjunto imagem das funções quadráticas definidas a seguir.
a) f(x) = 3x2 − 2x − 1
Im(f) = { y ∈ ℝ | y ≥ }
b) g(x) = −2x2 + 1
Im(g) = {y ∈ ℝ | y ≤ 1}
20. Murilo comprou 40 metros de cerca para fazer um cercado em formato de retângulo para seu cachoorro no quintal de sua moradia. Ele vai aproveitar uma parede como um dos lados do cercado, de acôr-do com a figura a seguir.
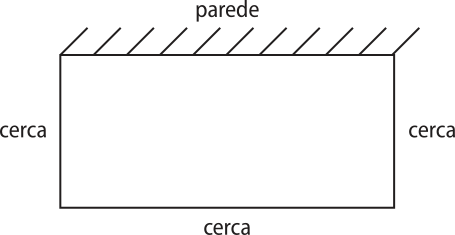
Sabendo quê ele vai utilizar toda a cerca comprada, qual é a área mássima quê esse cercado poderá ter?
200 m2
21. (UFJF-MG) Sobre os lados do retângulo ABCD, de dimensões 30 cm e 50 cm, marcam-se os pontos M, N, P e Q d fórma quê a distância dos pontos M e N ao vértice A e dos pontos P e Q ao vértice C sêjam iguais a x centimetros.
Veja a figura abaixo:
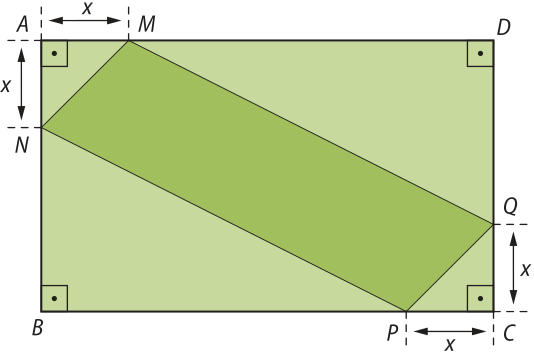
Determine o valor de x de modo quê o quadrilátero MNPQ tenha área mássima.
20 cm
22. (FEI-SP) Durante o processo de tratamento, uma peça de metal sofre uma variação de tempera-túra descrita pela função f(t) = 2 + 4t − t2, 0 < t < 5. Em quê instante t a tempera-túra atinge seu valor mássimo?
t = 2
23. (Fuvest-SP) A dona de uma lanchonete observou quê, vendendo um combo a R$ 10,00,200 deles são vendidos por dia, e quê, para cada redução de R$ 1,00 nesse preêço, ela vende 100 combos a mais. Nessas condições, qual é a mássima arrecadação diária quê ela espera obtêr com a venda dêêsse combo?
alternativa c
a) R$ 2.000,00.
b) R$ 3.200,00.
c) R$ 3.600,00.
d) R$ 4.000,00.
e) R$ 4.800,00.
24. (UEG-GO) O lucro de uma empresa é dado pela relação R = L + C, em quê L é o lucro, R é a receita e C é o custo de produção. Numa empresa quê produziu x unidades de um produto, verificou-se quê C(x) = 2x2 + 2.500x + 3.000 e R(x) = x2 + 7.500x + 3.000.
a) Esboce o gráfico da função L.
Ver as Orientações para o professor.
b) Quantas unidades essa empresa deve produzir para obtêr o maior lucro possível?
2.500
25. (UEA-AM) Em um plano cartesiano, a parábola descrita pela função quadrática f(x) = x2 − 4x + 3 tem vértice no ponto V, de abscissa 2, e passa pelo ponto P de abscissa 4.
alternativa e
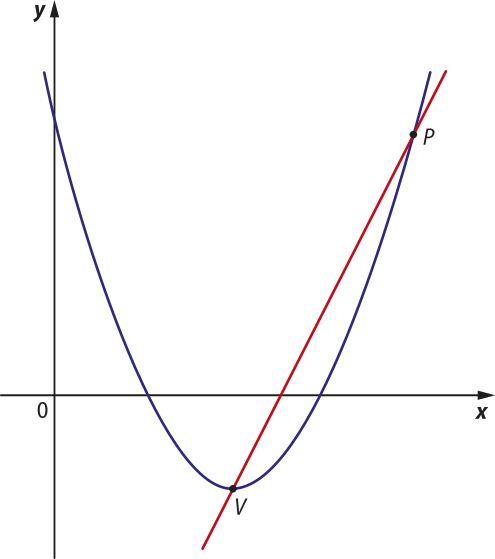
A reta quê passa pêlos pontos P e V intersecta o eixo y no ponto de ordenada igual a
a) −2.
b) −1.
c) −4.
d) −3.
e) −5.
Página cento e sessenta e seis
EXPLORANDO A TECNOLOGIA
Valor mássimo e valor mínimo
Estudamos como os coeficientes da lei de uma função quadrática influenciam no gráfico correspondente. Agora, vamos utilizar o GeoGebra para analisar também como esses coeficientes estão relacionados ao valor mássimo e ao valor mínimo quê uma função quadrática póde assumir.
Para isso, realize, inicialmente, a sequência de passos a seguir.
I. No campo de entrada do GeoGebra, digite “y = ax^2 + bx + c” e pressione Enter.
II. Serão exibidos o gráfico da função e os controles deslizantes dos coeficientes a, b e c.
Observe quê esses controles indicam, inicialmente, a = b = c = 1. Nesse caso, temos a representação do gráfico da função definida por y = x2 + x + 1.
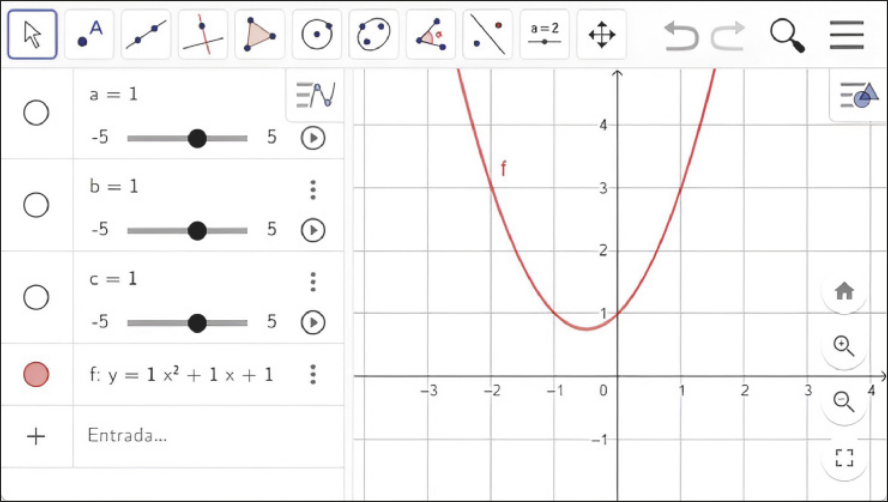
III. Agora, no campo de entrada, digite “Vértice(f)” e obissérve quê será exibido o ponto A, pertencente ao gráfico da função, correspondente ao vértice da parábola. Nesse caso, o vértice da parábola é o ponto de coordenadas xV = −0,5 e yV = 0,75.
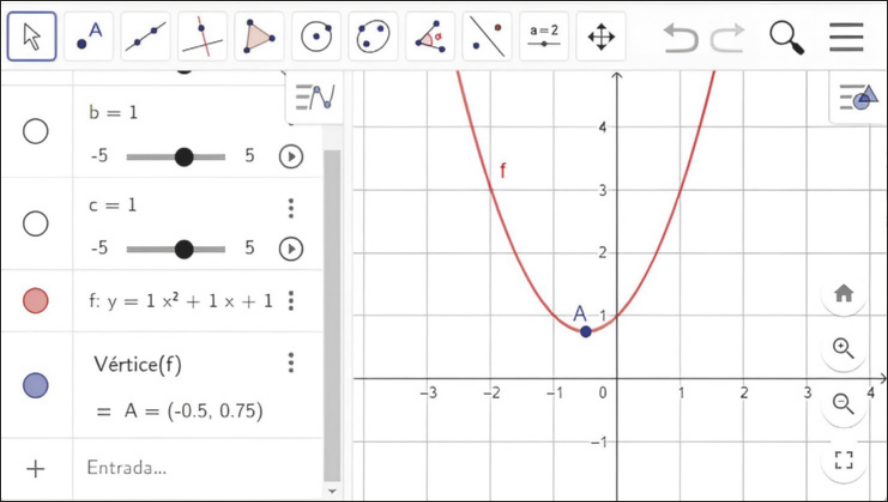
Página cento e sessenta e sete
IV. Mova o cursor do contrôle deslizante de cada coeficiente, observando as alterações no gráfico da função e nas coordenadas do ponto A.
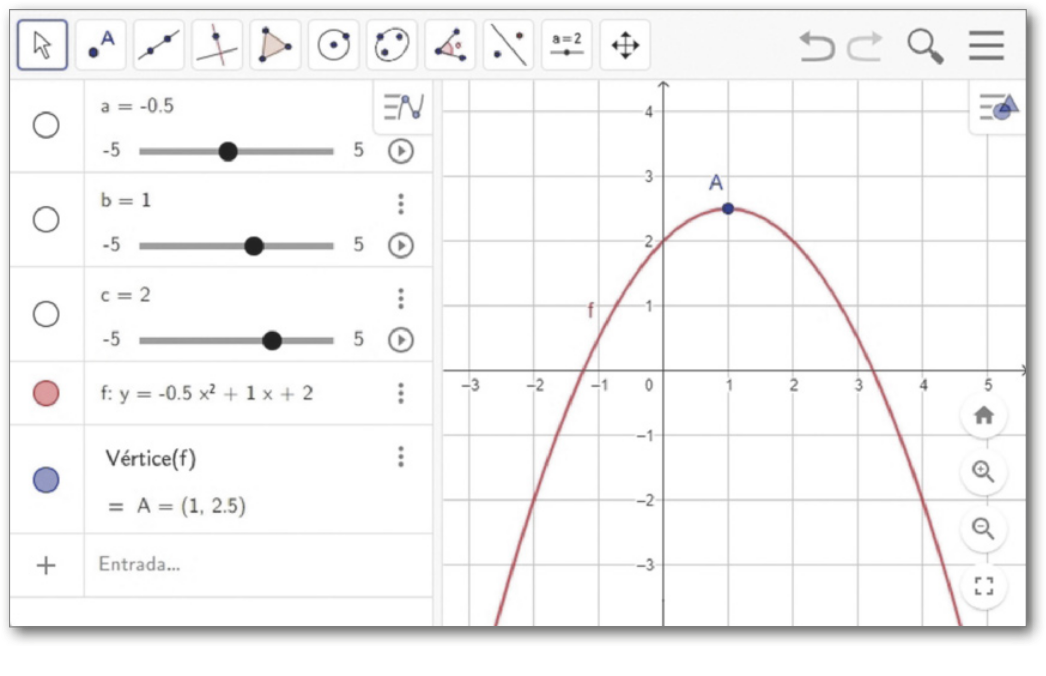
■ Gráfico de f para a = −0,5, b = 1 e c = 2. Nesse caso, o vértice tem coordenadas xV = 1 e yV = 2,5.
Agora, aproveite a construção quê você fez para realizar as atividades a seguir.
1. Qual coeficiente da lei da função quadrática devemos verificar para saber se o gráfico da função possui um ponto de mássimo ou um ponto de mínimo? Justifique sua resposta.
Ver as Orientações para o professor.
2. Utilizando o GeoGebra, indique o vértice da parábola, considerando os coeficientes a seguir.
a) a = 2, b = 0 e c = 2
V(0, 2)
b) a = −1, b = 2 e c = −1
V(1, 0)
c) a = −2, b = −4 e c = −3
V(−1, −1)
d) a = 2, b = 4 e c = −1
V(−1, −3)
3. Manipulando os controles deslizantes, determine os valores dos coeficientes a, b e c para os quais o vértice da parábola esteja localizado:
a) no terceiro quadrante;
Uma resposta possível: a = 2, b = 4 e c = −1
b) sobre o eixo y;
Uma resposta possível: a = 3, b = 0 e c = 1
c) sobre o eixo x.
Uma resposta possível: a = 1, b = 0 e c = 0
4. Clique com o botão direito do máuzi em cima do vértice da parábola e selecione a opção Exibir Rastro. Depois, anime o coeficiente b clicando em ![]() na janela de Álgebra. O vértice descreve uma curva, qual você acha quê é? Por quê?
na janela de Álgebra. O vértice descreve uma curva, qual você acha quê é? Por quê?
Respostas pessoais.
DICA: É possível alterar a côr do vértice para melhorar a visualização do rastro, se necessário. As opções de cores podem sêr encontradas nas configurações do vértice.
Página cento e sessenta e oito
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Gestão de resíduos
Na ssossiedade atual, cada vez mais industrializada, utilizar os recursos naturais d fórma sustentável é primordial para manter o meio ambiente em equilíbrio e não esgotar os recursos disponíveis no planêta. A Matemática póde contribuir para o planejamento realizado por empresas, considerando, por exemplo, a otimização do uso de matérias-primas.
Sobre o assunto, leia o texto a seguir.
Política Nacional de Resíduos Sólidos
A Lei número 12.305/10, quê institui a Política Nacional de Resíduos Sólidos (PNRS) [...] contém instrumentos importantes para permitir o avanço necessário ao País no enfrentamento dos principais problemas ambientais, sociais e econômicos decorrentes do manejo inadequado dos resíduos sólidos.
Prevê a prevenção e a redução na geração de resíduos, tendo como proposta a prática de hábitos de consumo sustentável e um conjunto de instrumentos para propiciar o aumento da reciclagem e da reutilização dos resíduos sólidos (aquilo quê tem valor econômico e póde sêr reciclado ou reaproveitado) e a destinação ambientalmente adequada dos rejeitos (aquilo quê não póde sêr reciclado ou reutilizado).

Institui a responsabilidade compartilhada dos geradores de resíduos: dos fabricantes, importadores, distribuidores, comerciantes, o cidadão e titulares de serviços de manejo dos resíduos sólidos urbanos na Logística Reversa dos resíduos e embalagens pré-consumo e pós-consumo.
Cria metas importantes quê irão contribuir para a eliminação dos lixões e institui instrumentos de planejamento nos níveis nacional, estadual, microrregional, intermunicipal e metropolitano e municipal; além de impor quê os particulares elaborem seus Planos de Gerenciamento de Resíduos Sólidos.
Também coloca o Brasil em patamar de igualdade aos principais países desenvolvidos no quê concerne ao marco legal e inova com a inclusão de catadoras e catadores de materiais recicláveis e reutilizáveis, tanto na Logística Reversa quanto na Coleta Seletiva.
[…]
BRASIL. Ministério do Meio Ambiente. Política Nacional de Resíduos Sólidos. Brasília, DF: MMA, [201-]. Disponível em: https://livro.pw/fmvdi. Acesso em: 18 ago. 2024.
Página cento e sessenta e nove
Logística reversa
[…]
[…] A PNRS define a logística reversa como um “instrumento de desenvolvimento econômico e social caracterizado por um conjunto de ações, procedimentos e meios destinados a viabilizar a côléta e a restituição dos resíduos sólidos ao setor empresarial, para reaproveitamento, em seu ciclo ou em outros ciclos produtivos, ou outra destinação final ambientalmente adequada”.
[…]
BRASIL. Ministério do Meio Ambiente. Logística reversa. Brasília, DF: MMA, [201-]. Disponível em: https://livro.pw/cnjqu. Acesso em: 18 ago. 2024.

Ver as Orientações para o professor.
Agora, faça o quê se pede nas atividades a seguir.
1. De acôr-do com os textos, quais são as propostas previstas na PNRS para a redução na geração de resíduos?
2. Uma fábrica de embalagens, considerando as propostas previstas na PNRS para a redução na geração de resíduos, está procurando otimizar a utilização de papelão na produção de caixas.
Os engenheiros construíram um modelo matemático quê relaciona a quantidade de material desperdiçado com o tempo de produção de cada lote, utilizando a lei de uma função quadrática. Que conceito eles poderão utilizar para calcular o tempo de produção mais adequado para cumprir o objetivo?

3. ![]() Reúna-se a dois côlégas, e, juntos, pesquisem os conceitos de consumo consciente e de desperdício. Discutam o tema com os demais côlégas e construam com a turma um painel expondo ações sustentáveis quê podem sêr adotadas por todos para minimizar o desperdício de recursos na moradia de cada um e na escola.
Reúna-se a dois côlégas, e, juntos, pesquisem os conceitos de consumo consciente e de desperdício. Discutam o tema com os demais côlégas e construam com a turma um painel expondo ações sustentáveis quê podem sêr adotadas por todos para minimizar o desperdício de recursos na moradia de cada um e na escola.
Para assistir
• CONHEÇA a Política Nacional de Resíduos Sólidos. [S. l.: s. n.], 2022. 1 vídeo (4 min). Publicado pelo canal SENAI Play. Disponível em: https://livro.pw/fudqb. Acesso em: 25 jul. 2024.
O vídeo apresenta algumas definições relacionadas ao tema de resíduos sólidos.
Página cento e setenta
Investigando o comportamento de variáveis
Considere a situação proposta a seguir.
Um treinador está fazendo medições do tempo t, em segundo, quê um atleta leva para atingir uma distância d, em métro, após iniciar uma corrida de treinamento para uma próva dos 100 metros rasos.
Observe, a seguir, os dados obtidos pelo treinador para o arranque do atleta nos primeiros 5 segundos.
Saiba quê...
Na situação, o corredor parte da largada com aceleração constante até atingir a linha de chegada.
Tempo (em segundo) |
Distância (em metro) |
|---|---|
0 |
0 |
1 |
1 |
2 |
4 |
3 |
9 |
4 |
16 |
5 |
25 |
Após a obtenção dos dados, o treinador representou os valores obtidos em um plano cartesiano e obteve o esboço a seguir.

Pense e responda
• Com base nas observações do treinador, pode-se afirmar quê, nessa situação, as grandezas tempo e distância são grandezas diretamente proporcionais?
Não são grandezas diretamente proporcionais.
• A resposta ao item anterior póde sêr dada com base na análise do gráfico de pontos obtído pelo treinador? Justifique.
Sim, o gráfico mostra quê as grandezas envolvidas não são diretamente proporcionais, pois os pontos destacados não fazem parte de uma mesma reta.
• Que padrão póde sêr observado nos valores referentes às medidas de distância obtidas?
Espera-se quê os estudantes respondam quê os valores das distâncias são formados por números quadrados.
Com base na tabéla e observando o gráfico, o treinador notou quê, ao dobrar a medida do tempo, a distância percorrida era multiplicada por 4, ou seja, era multiplicada por 22, e quê, ao triplicar o tempo, a distância era multiplicada por 9, ou seja, por 32.
Sendo t o tempo, em segundo, e d a distância, em métro, observando-se os valores da tabéla, nota-se quê:
Para t = 0, tem-se d = 0 = 02.
Para t = 1, tem-se d = 1 = 12.
Para t = 2, tem-se d = 4 = 22.
Para t = 3, tem-se d = 9 = 32.
Para t = 4, tem-se d = 16 = 42.
Para t = 5, tem-se d = 25 = 52.

Página cento e setenta e um
Portanto, percebe-se quê, em cada medição, a medida da distância corresponde ao quadrado da medida do tempo. Desse modo, nessa situação, a lei da função quê relaciona as variáveis t, em segundo, e d, em métro, póde sêr expressa por d(t) = t2.
Conforme acompanhamos, na situação apresentada, a relação entre a medida da distância e a medida do tempo póde sêr expressa pela lei d(t) = t2, quê tem a forma da lei de uma função quadrática do tipo y = ax2. Observamos também quê, ao dobrar o valor de t, o valor correspondente de d fica multiplicado por 22. Ao triplicar o valor de t, o valor correspondente de d fica multiplicado por 32.
Isso acontece porque se trata de uma propriedade das funções quadráticas do tipo y = ax2. Quando multiplicamos a variável x por uma constante real k, o valor correspondente de y é multiplicado por k2.
Considere, agora, outra situação.
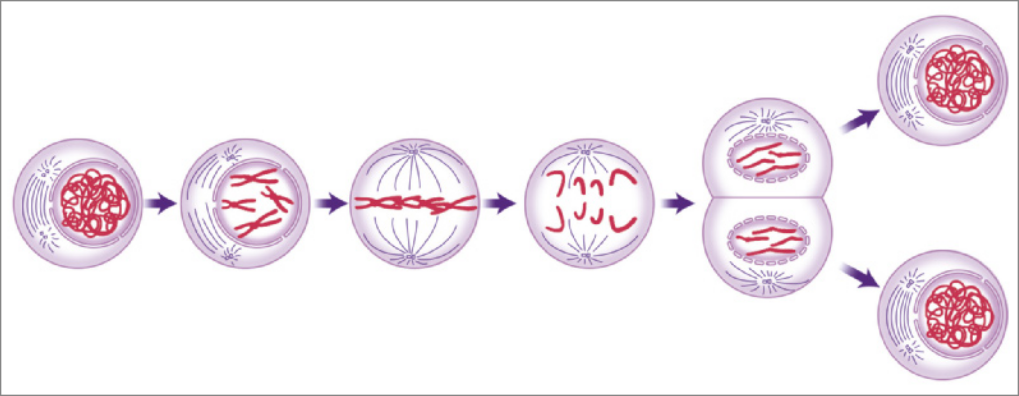
No processo de divisão celular conhecido como mitose, uma célula-mãe dá origem a duas células-filhas iguais a ela. Cada uma dessas células-filhas, por sua vez, póde se dividir em outras duas novas células, e assim sucessivamente, em diversas divisões.
Pense e responda
• A curva quê contém os pontos do gráfico obtído pelo treinador é uma parábola? Por quê?
Sim, pois os pontos obtidos satisfazem à lei d(t) = t2, quê é a lei de uma função quadrática.
• De acôr-do com a lei da função, quantos metros o atleta percórre em 10 segundos?
100 metros
• Pesquise a respeito do récorde mundial para a próva dos 100 metros rasos e, com base nos dados encontrados, responda se você considera quê a medida ôbitída no item anterior indica quê o atleta da situação é de alto dêsempênho ou não.
O resultado anterior indica quê o atleta é de alto dêsempênho, pois apresenta valores próximos aos de recordistas mundiais.
Na tabéla, verificamos um modelo quê conta a quantidade de células obtidas por meio dêêsse tipo de divisão celular, considerando um processo contínuo a partir de uma única célula.
Quantidade de divisões |
Quantidade de células |
|---|---|
1 |
2 |
2 |
4 |
3 |
8 |
4 |
16 |
5 |
32 |
Essa contagem não póde sêr modelada por uma função quadrática quê relaciona a quantidade de divisões no processo e a quantidade de células obtidas.
Verifique quê, quando multiplicamos um número de divisões no processo por uma constante k, o número correspondente de células não fica multiplicado por k2.
Comentar com os estudantes quê, no estudo da função exponencial, realizado no Ensino Médio, eles terão um modelo matemático quê poderá sêr utilizado para representar essa situação.
Página cento e setenta e dois
Estudo do sinal da função quadrática
Aprendemos quê estudar o sinal de uma função definida por y = f(x) significa determinar os valores reais de x ∈ D(f) quê tornam a função positiva (f(x) > 0), negativa (f(x) < 0) ou nula (f(x) = 0).
O estudo do sinal de uma função quadrática póde sêr feito observando o esboço de sua representação gráfica, quê, como já estudamos, é uma parábola.
De acôr-do com a concavidade da parábola, relacionada ao coeficiente a, e com a quantidade de zeros da função, relacionada ao valor de (delta)", podemos esboçar o gráfico de uma função quadrática e fazer o estudo de sinais, como verificado a seguir.
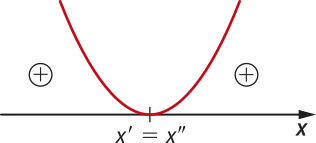
• Considerando a > 0, temos as seguintes possibilidades:
(delta)" > 0 |
(delta)" = 0 |
(delta)" < 0 |
|---|---|---|
A função quadrática admite dois zeros reais distintos.
Nesse caso, temos: f(x) > 0 para x < x’ ou x > x’’; f(x) < 0 para x’ < x < x’’; f(x) = 0 para x = x’ ou x = x’’. |
A função quadrática admite dois zeros reais iguais.
Nesse caso, temos: f(x) = 0 para x = x’ = x’’; f(x) > 0 para x ≠ x’. |
A função quadrática não admite zeros reais.
Nesse caso, temos: f(x) > 0 para todo x real. |
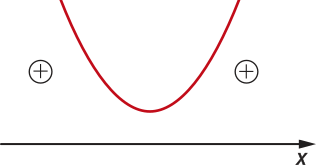
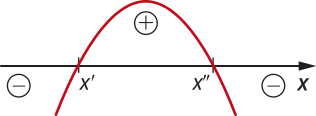
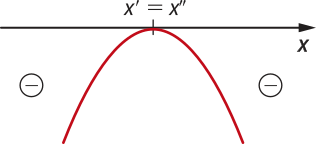
• Considerando a < 0, temos as seguintes possibilidades:
(delta)" > 0 |
(delta)" = 0 |
(delta)" < 0 |
|---|---|---|
A função quadrática admite dois zeros reais distintos.
Nesse caso, temos: f(x) < 0 para x < x’ ou x > x’’; f(x) > 0 para x’ < x < x’’; f(x) = 0 para x = x’ ou x = x’’. |
A função quadrática admite dois zeros reais iguais.
Nesse caso, temos: f(x) = 0 para x = x’ = x’’; f(x) < 0 para x ≠ x’. |
A função quadrática não admite zeros reais.
Nesse caso, temos: f(x) < 0 para todo x real. |
Página cento e setenta e três
Inequações polinomiais do 2º grau
Acompanhe a situação a seguir.
Um pequeno produtor de mel de abelha deseja vender sua produção em pótes de mel. Dadas cértas condições, como o custo de produção e a quantidade de unidades vendidas, ele sabe quê o lucro semanal L, em reais, obtído com a venda do produto é modelado pela função L(x) = −x2 + 100x − 600, em quê x representa o preêço, em reais, de cada póte de mel vendido.
Vamos, agora, resolver a seguinte questão:
Por quantos reais cada póte de mel deve sêr vendido para quê o produtor obtenha um lucro semanal maior do quê R$ 1.000,00?
Para responder a essa questão, precisamos resolver a inequação L(x) > 1.000.
Denominamos inequação polinomial do 2º grau na incógnita x toda desigualdade quê póde sêr reduzida a uma das formas a seguir, com a, b, c ∈ ℝ e a ≠ 0.
• ax2 + bx + c ≥ 0
• ax2 + bx + c > 0
• ax2 + bx + c ≤ 0
• ax2 + bx + c < 0
• ax2 + bx + c ≠ 0
Pense e responda
Utilizando o GeoGebra, represente o gráfico dessa função e descubra pelo menos um valor de x para o qual temos o lucro diário maior do quê R$ 1.000,00.
Espera-se quê, pela observação do gráfico construído, os estudantes deem como resposta algum valor de x entre 20 e 80.
Observe alguns exemplos:
a) x2 − 3x + 1 ≥ 0
b) ≤ 0
c) 2x2 − 5x < 0
Ao resolver uma inequação do 2º grau, é preciso determinar os valores reais de x quê satisfazem à inequação dada, o quê é feito por meio do estudo do sinal da função quadrática correspondente.
Para determinar os valores de x para os quais L(x) > 1.000, temos:
−x2 + 100x − 600 > 1.000 ⇒ −x2 + 100x − 1.600 > 0
Precisamos, então, estudar o sinal da função dada por: f(x) = −x2 + 100x − 1.600. Para isso, vamos obtêr os zeros da função e esboçar o seu gráfico.
Considerando −x2 + 100x − 1.600 = 0, temos:
(delta)" = 1002 − 4 ⋅ (−1) ⋅ (−1.600) = 3.600 (a função tem dois zeros reais distintos).
x =
Logo, x(minutos)" = 20 e x(segundos)" = 80.
Como a < 0, a concavidade da parábola é voltada para baixo. Fazendo um esboço da parábola, temos:

Assim, −x2 + 100 − 1.600 > 0 para todos os valores reais de x tais quê 20 < x < 80.
Para quê o produtor obtenha um lucro semanal maior do quê R$ 1.000,00, o preêço unitário de póte de mel deve sêr maior do quê R$ 20,00 e menor do quê R$ 80,00.

Página cento e setenta e quatro
ATIVIDADES RESOLVIDAS
12. Considerando a função definida por f(x) = −3x2 + 2x + 1, para quais valores de x verifica-se f(x) ≤ 0?
Resolução
Para determinar os valores de x para os quais f(x) ≤ 0, estudamos o sinal da função. Nesse caso, vamos obtêr os zeros da função e esboçar o seu gráfico.
Considerando −3x2 + 2x + 1 = 0, temos:
(delta)" = 22 − 4 ⋅ (−3) ⋅ 1 = 16
Como (delta)" > 0, a função tem dois zeros reais distintos.
x =
Logo, x(minutos)" = e x(segundos)" = 1.
Como a < 0, a concavidade da parábola é voltada para baixo. Assim, temos:
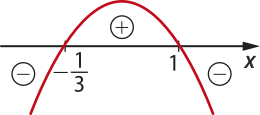
Portanto, f(x) ≤ 0 para .
13. Determine p de modo quê a função dada por f(x) = px2 + (2p − 1)x + p assuma valores positivos para todo x real.
Resolução
Como se deseja quê a função assuma valores positivos para todo x real, devemos ter f(x) > 0 para x ∈ ℝ. Fazendo um esboço do gráfico de f, temos:
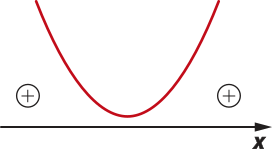
Como a parábola tem concavidade voltada para cima, p > 0. I
Como f não tem zero, (delta)" < 0. Assim, temos:
(delta)" < 0 ⇒ (2p − 1)2 − 4 ⋅ p ⋅ p < 0 ⇒
⇒ 4p2 − 4p + 1 − 4p2 < 0 ⇒ p > II
Considerando as desigualdades I e II, obtemos:
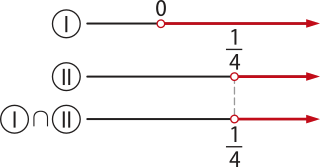
Logo, para quê a função f seja sempre positiva, devemos ter p > , com p ∈ ℝ.
14. (FGV-SP) O custo diário de produção de um artigo é C = 50 + 2x + 0,1x2, onde x é a quantidade diária produzida. Cada unidade do produto é vendida por R$ 6,50. Entre quê valores deve variar x para não havêer prejuízo?
a) 19 ≤ x ≤ 24
b) 20 ≤ x ≤ 25
c) 21 ≤ x ≤ 26
d) 22 ≤ x ≤ 27
e) 23 ≤ x ≤ 28
Resolução
Considerando quê a quantidade diária produzida x seja vendida, a receita arrecadada R(x) com a venda diária deve sêr maior ou igual ao custo diário para quê não haja prejuízo.
A receita póde sêr expressa por R(x) = 6,5x.
Nesse caso, temos:
R(x) ≥ C(x) ⇒ R(x) − C(x) ≥ 0
Logo:
6,5x − (50 + 2x + 0,1x2) ≥ 0
6,5x − 50 − 2x − 0,1x2 ≥ 0
−0,1x2 + 4,5x − 50 ≥ 0
Na resolução dessa inequação, obtemos os zeros da função dada por y = −0,1x2 + 4,5x − 50 e esboçamos o gráfico correspondente.
Considerando −0,1x2 + 4,5x − 50 = 0, temos:
(delta)" = (4,5)2 − 4 ⋅ (−0,1) ⋅ (−50) = 0,25
Como (delta)" > 0, a função tem dois zeros reais distintos.
x =
Logo, x(minutos)" = 20 e x(segundos)" = 25.
Como a < 0, a concavidade da parábola é voltada para baixo. Assim, temos:
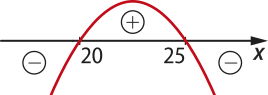
Portanto, não haverá prejuízo quando 20 ≤ x ≤ 25.
A resposta é a alternativa b.
Página cento e setenta e cinco
ATIVIDADES
26. Estude os sinais das funções definidas a seguir.
a) f(x) = x2 − 3x − 10
b) f(x) = −x2 + 2x
c) f(x) = −4x2 + 4x −1
d) f(x) = x2 − x + 10
Ver as Orientações para o professor.
27. Dada a função definida por:
f(x) = x2 − (2m + 1)x + m2, determine m de modo quê f(x) > 0 para todo x real.
28. Considerando uma função dada por
f(x) = kx2 − 2kx + k − 1, calcule os valores de k para quê f(x) assuma valores negativos para todo x real.
{k ∈ ℝ | k < 0}
29. resôuva as seguintes inequações do 2º grau.
a) x2 − 2x − 8 < 0
S = {x ∈ ℝ | −2 < x < 4}
b) 9x2 − 8x − 1 ≥ 0
S =
c) −3x2 + 2x − 1 > 0
S = ∅
d) −x2 + 4x − 4 < 0
S = {x ∈ ℝ | x ≠ 2}
30. Determine o conjunto solução da inequação:
(2x − 5)(x − 4) − 7 ≥ (x − 2)(x − 3)
S = {x ∈ ℝ | x ≤ 1 ou x ≥ 7}
31. Sabendo quê f(x) = x2 − 3x + 8, determine o conjunto solução da inequação f(x) ≥ 2f(1).
S = {x ∈ ℝ | x ≤ −1 ou x ≥ 4}
32. (UFJF-MG) Considere a função h: ℝ → ℝ, definida por h(t) = −5t2 + 7t + 6.
a) Para quais valores de t tem-se h(t) ≥ 8?
b) Determine o conjunto imagem da função h.
Im(h) =]−∞, 8,45]
33. (FGV-SP) O lucro mensal de uma empresa é dado por L = −x2 + 30x − 5, onde x é a quantidade mensal vendida.
a) Qual o lucro mensal mássimo possível?
R$ 220,00
b) Entre quais valores deve variar x para quê o lucro mensal seja, no mínimo, igual a 195?
S = {x ∈ ℝ | 10 ≤ x ≤ 20}
34. (hú- hê- érre jota) Considere as seguintes funções, relativas a uma ninhada de pássaros:
C = 5 + 10n
C = custo mensal, em reais, para a manutenção de n pássaros
V = −5n2 + 100n − 320
V = valor mensal arrecadado, em reais, com a venda de n pássaros, para 4 ≤ n ≤ 16
Sabe-se quê o lucro mensal obtído é determinado pela diferença entre os valores de venda V e custo C.
a) Determine os possíveis valores de n para quê haja lucro nas vendas.
5 < n < 13
b) Calcule o valor de n quê proporciona o maior lucro possível e o valor, em reais, dêêsse lucro.
n = 9; R$ 80,00
35. (UFPB) Um fabricante de picolés distribui diariamente, com seus vendedores, caixas contendo, cada uma, 300 picolés. O lucro diário, em reais, na venda dêêsses picolés, é dado pela função L(n) = −200n2 + 1.600n − 2.400, onde n é o número de caixas vendidas. Considere as afirmações relativas ao lucro diário:
I. Para 2 < n < 6 o fabricante terá lucro.
II. O lucro não poderá sêr superior a R$ 1.000,00.
III. O lucro será mássimo quando forem vendidos 1.500 picolés.
Está(ão) correta(s) apenas:
alternativa a
a) I e II.
b) I e III.
c) II e III.
d) I.
e) III.
36. (Mack-SP) Se f: ℝ → ℝ é uma função definida por f(x) = −2x2 + x + 1, então os valores de x para os quais f assume valores positivos são
a) −2 < x < 1
b) −1 < x < 2
c) −1 ≤ x ≤
d) −1 < x <
e) < x < 1
alternativa e
Página cento e setenta e seis
HISTÓRIA DA MATEMÁTICA
Galileu Galilei
Leia a seguir um texto sobre Galileu Galilei e algumas de suas contribuições para a Ciência. Observe a expressão quê ele usou para descrever a relação entre a distância percorrida por um corpo em queda livre e o tempo de queda. Nessa lei, g é uma constante correspondente à aceleração gravitacional.
[...]
Galileu, filho de um nobre florentino empobrecido, nasceu em Pisa em 1564, no dia em quê faleceu Miquelângelo. Aos dezessete anos de idade foi encaminhado pêlos pais à Universidade de Pisa para estudar medicina. Um dia, quando assistia a um serviço na Catedral de Pisa, seu espírito se distraiu observando o grande lustre de bronze suspenso da elevada abóbada. A lâmpada tinha sido posta para fora a fim de iluminar mais facilmente e, solta, oscilava para cá e para lá com amplitude quê decrescia gradualmente. Usando as batidas de seu pulso para marcar o tempo, ele ficou surpreso ao verificar quê o período de uma oscilação da lâmpada independia da amplitude do arco de oscilação. Posteriormente, por experiências, ele mostrou quê o período de um pêndulo em movimento também independe do peso de sua massa oscilante, dependendo assim apenas do comprimento de sua hás-te. Relata-se quê o interêsse de Galileu pela ciência e pela matemática surgiu dêêsse problema e foi estimulado, posteriormente, pela oportunidade de assistir a um curso de geometria na Universidade. Como resultado solicitou da família (e conseguiu) permissão para abandonar a medicina e dedicar-se à ciência e à matemática, campos para os quais possuía forte talento natural.
Aos vinte e cinco anos de idade Galileu foi indicado professor de matemática da Universidade de Pisa, tendo, segundo consta, realizado experiências públicas sobre a queda dos corpos enquanto exerceu essa função. Conta uma história quê, perante uma multidão de estudantes, professores e religiosos, ele deixou cair dois pedaços de metal, um deles com peso dez vezes o do outro, do alto da torre de Pisa. Os dois pedaços chocaram-se contra o chão praticamente no mesmo momento, contrariando assim Aristóteles, segundo quêm o corpo mais pesado teria de cair muito mais rapidamente do quê o outro. Galileu estabeleceu a lei segundo a qual a distância percorrida por um corpo em queda livre é proporcional ao quadrado do tempo de queda, e que se traduz na fórmula familiar s = .
[...]
Devemos a Galileu o moderno espírito científico na forma de uma harmonía entre experiência e teoria. Ele fundou a mecânica dos corpos em queda livre, lançou os fundamentos da dinâmica em geral, e sobre esses fundamentos mais tarde níltom foi capaz de construir uma ciência.
EVES, ráuard. Introdução à história da matemática. Tradução: Hygino H. Domingues. Campinas: Editora da Unicamp, 2004. p. 352-355.

Página cento e setenta e sete
ATIVIDADES COMPLEMENTARES
1. (UFMS) Um retângulo inicial, de perímetro 200 centimetros, sofre uma modificação tal quê a medida de sua largura aumenta 20%, e a medida do seu comprimento diminui 20%. Determine a função quê define a área A do novo retângulo, em centimetros quadrados, em relação à medida da largura do retângulo inicial x, em centimetros.
a) A(x) = 120x − 0,8x2
b) A(x) = 120x + 0,8x2
c) A(x) = 98x − 0,98x2
d) A(x) = 80x − 1,2x2
e) A(x) = 96x − 0,96x2
alternativa e
2. (UEPB) Um setor de uma metalúrgica produz uma quantidade N de peças dada pela função N(x) = x2 + 10x, x horas após iniciar suas atividades diárias. Iniciando suas atividades às 6 horas, o número de peças produzidas no intervalo de tempo entre as 7 e as 9 horas será igual a:
a) 50.
b) 28.
c) 25.
d) 16.
e) 39.
alternativa b
3. (PUCCamp-SP) Considere quê a curva quê fornece os níveis de oxigênio dissolvido, em μg/L, no período de 1900 a 1950, seja o arco de parábola definido por , em quê x representa o número de dékâdâs contadas a partir de 1900 (x = 0, 1, 2, 3, 4, 5). Nessas condições, no período de 1910 a 1930, o nível de oxigênio dissolvido decresceu em:
a) 0,24 μg/L.
b) 0,25 μg/L.
c) 0,26 μg/L.
d) 0,27 μg/L.
e) 0,28 μg/L.
alternativa e
4. (PUC-RS) A função quadrática tem diversas aplicações no nosso dia a dia. Na construção de antenas parabólicas, superfícies de faróis de carros e outras aplicações, são exploradas propriedades da parábola, nome dado à curva quê é o gráfico de uma função quadrática.
Seja p(x) = mx2 + nx + 1. Se p(2) = 0 e p(−1) = 0, então os valores de m e n são, respectivamente, iguais a
a) e .
b) −1 e 1.
c) 1 e .
d) −1 e .
alternativa a
5. (Fuvest-SP) Considere a função polinomial f: ℝ → ℝ definida por f(x) = ax2 + bx + c, em quê a, b, c ∈ ℝ e a ≠ 0. No plano cartesiano xy, a única intersecção da reta y = 2 com o gráfico de f é o ponto (2, 2) e a intersecção da reta x = 0 com o gráfico f é ponto (0, −6).
O valor de a + b + c é
a) −2.
b) 0.
c) 2.
d) 4.
e) 6.
alternativa b
6. (Fuvest-SP) Os funcionários de um salão de beleza compraram um presente no valor de R$ 200,00 para a recepcionista do estabelecimento. No momento da divisão igualitária do valor, dois deles desistiram de participar e, por causa díssu, cada pessoa quê ficou no grupo precisou pagar R$ 5,00 a mais quê a quantia originalmente prevista. O valor pago por pessoa quê permaneceu na divisão do custo do presente foi:
a) R$ 10,00.
b) R$ 15,00.
c) R$ 20,00.
d) R$ 25,00.
e) R$ 40,00.
alternativa d
7. (UEA-AM) As funções f, g e h são funções reais, tais quê f(x) = −x + 2, g(x) = x + 1 e h(x) = f(x) ⋅ g(x). Com base nessas funções, é correto afirmar quê a soma das raízes da função h é igual a
a) 1.
b) 2.
c) −2.
d) −1.
e) 3.
alternativa a
8. (Udesc) A função quadrática cujo gráfico contém os pontos (0, −9), (1, 0) e (2, 15) tem vértice em:
a) (−2, −13).
b) (1, 0).
c) (0, −9).
d) (2, 15).
e) (−1, −12).
alternativa e
Página cento e setenta e oito
9. (Enem/MEC) Em jogos de voleibol, um saque é invalidado se a bola atingir o teto do ginásio onde ocorre o jôgo. Um jogador de uma equipe tem um saque quê atinge uma grande altura. Seu récorde foi quando a batida do saque se iniciou a uma altura de 1,5 m do piso da quadra, e a trajetória da bola foi descrita pela parábola ,em quê y representa a altura da bola em relação ao eixo x (das abscissas) quê está localizado a 1,5 m do piso da quadra, como representado na figura. Suponha quê em todas as partidas algum saque dêêsse jogador atinja a mesma altura do seu récorde.
alternativa d
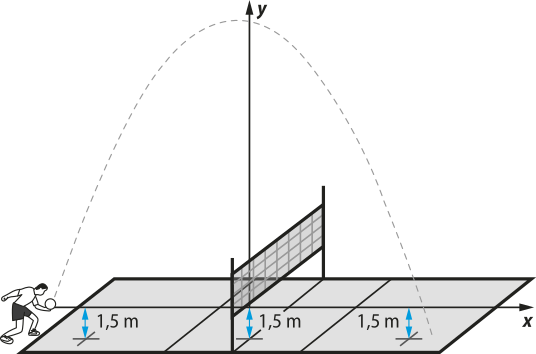
A equipe dêêsse jogador participou de um torneio de voleibol no qual jogou cinco partidas, cada uma delas em um ginásio diferente. As alturas dos tetos dêêsses ginásios, em relação aos pisos das quadras, são:
• ginásio I: 17 m;
• ginásio II: 18 m;
• ginásio III: 19 m;
• ginásio IV: 21 m;
• ginásio V: 40 m.
O saque dêêsse atleta foi invalidado
a) apenas no ginásio I.
b) apenas nos ginásios I e II.
c) apenas nos ginásios I, II e III.
d) apenas nos ginásios I, II, III e IV.
10. (UEG-GO) Um lava jato tem 50 clientes fixos por semana e cada lavagem custa R$ 20,00. Sabe-se quê a cada um real quê o dono dêêsse lava jato aumenta no preêço da lavagem, ele perde 2 clientes. O valor do aumento quê maximiza a arrecadação semanal dêêsse lava jato é de
a) R$ 25,00.
b) R$ 20,00.
c) R$ 2,50.
d) R$ 10,00.
e) R$ 2,00.
alternativa c
11. (Acafe-SC) Um clube recreativo possui 800 sócios e cobra uma mensalidade de R$ 200,00 de cada sócio. Uma pesquisa de mercado indica quê a cada R$ 1,00 de redução na mensalidade, há um aumento de 10 sócios. O valor da mensalidade quê gera a maior receita é de:
a) R$ 120,00.
b) R$ 60,00.
c) R$ 140,00.
d) R$ 160,00.
alternativa c
12. (Ifal) cérto fabricante, segundo levantamentos estatísticos, percebe quê seus clientes não têm comprado mais de 100 de seus produtos por compras. Para incentivar as compras em maior quantidade, ele estabelece um preêço unitário p por produto dado por p(x) = 400 − x, onde x é a quantidade de produtos comprados, considerando uma compra de, no mássimo, 300 produtos. Sabendo-se quê a receita de uma empresa é o valor arrecadado com a venda de uma certa quantidade de produtos, qual a receita mássima quê essa empresa póde ter quando fechar uma venda com um determinado cliente, na moeda corrente no Brasil?
a) R$ 200,00.
b) R$ 400,00.
c) R$ 20.000,00.
d) R$ 40.000,00.
e) R$ 80.000,00.
alternativa d
13. (hú- hê- érre jota) Um número N, inteiro e positivo, quê satisfaz à inequação N2 − 17N + 16 > 0 é:
a) 2.
b) 7.
c) 16.
d) 17.
alternativa d
14. (Uneb-BA) Um paciente compareceu a um Posto de Saúde apresentando febre de 40 °C, foi atendido e, duas horas depois, a febre havia diminuído para 38 °C. Sabendo-se quê, nesse período, sua tempera-túra variou como uma função F do 2º grau, atingindo seu valor mássimo, Fm, 30 min após o início do atendimento, é correto afirmar quê o valor de (Fm − 3,00) é
01) 36,25 °C.
02) 37,25 °C.
03) 38,25 °C.
04) 39,25 °C.
05) 40,25 °C.
alternativa 02
Página cento e setenta e nove
15. (Enem/MEC) A Igreja de São Francisco de Assis, obra arquitetônica modernista de Óscar Niemáiêr, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólicas.
A seta na Figura 1 ilustra uma das abóbadas na entrada principal da capela. A Figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos.
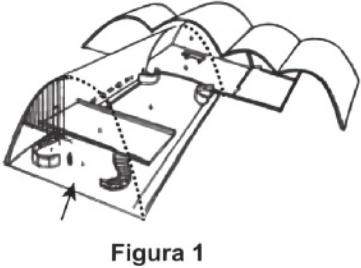
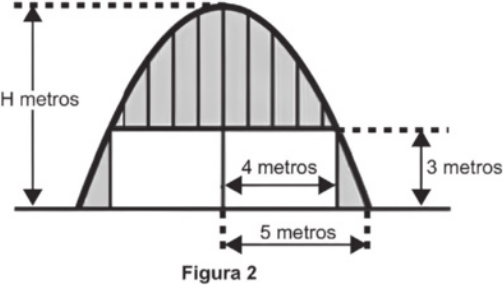
Qual a medida da altura H, em métro, indicada na Figura 2?
a)
b)
c)
d)
e)
alternativa d
PARA REFLETIR
Neste Capítulo, aprendemos quê as funções quadráticas podem sêr utilizadas para modelar situações, bem como para descrever alguns tipos de movimento e de trajetórias estudados pela Física.
Estudamos o conceito matemático de função quadrática, as representações gráficas dêêsse tipo de função, os vértices da parábola, os zeros da função quadrática, o crescimento e o decrescimento, o valor mássimo e o valor mínimo quê uma função quadrática póde assumir em um intervalo, bem como o estudo de sinais da função quadrática e as inequações do 2º grau.
Nas páginas de abertura, foi apresentada uma curiosa espécie de peixe quê utiliza o lançamento de jatos de á gua para caçar. Depois de ter estudado o conteúdo dêste Capítulo, você consegue reconhecer quê a trajetória do jato de á gua póde sêr modelada por uma função? Que tipo de função?
Vamos refletir a respeito das aprendizagens do Capítulo 4:
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• Cite outras situações do dia a dia quê envolvem a ideia de função quadrática.
• Identifique a relação entre o estudo da função quadrática e os conteúdos estudados na disciplina de Física ou em outra disciplina da área de Ciências da Natureza.
• Como o estudo de valor mássimo e de valor mínimo de uma função quadrática póde sêr usado para planejar formas de economizar e otimizar processos?
• Cite situações em quê os conceitos estudados podem ajudar a tomar decisões e a resolver problemas do dia a dia.
Respostas pessoais.
Página cento e oitenta