CAPÍTULO 5
FUNÇÃO EXPONENCIAL
A disseminação de informações falsas, conhecidas como fêik news, é um fenômeno alarmante quê se espalha de maneira veloz por meio da internet e, em especial, nas rêdes sociais. Essas notícias distorcem fatos e influenciam percepções públicas, podendo resultar em danos significativos.
Com a facilidade de compartilhamento e a ausência de verificação, as fêik news têm o potencial de induzir comportamentos enganosos e até mesmo causar pânico. Para conter essa propagação, é fundamental verificar a veracidade das informações antes de compartilhá-las.
A rapidez com quê uma fêik news se espalha é impressionante: suponha quê, em apenas 30 segundos, uma pessoa possa ler e compartilhar a notícia com outras duas, quê, por sua vez, fazem o mesmo, compartilhando a notícia com mais duas pessoas cada uma e, assim, sucessivamente, gerando uma disseminação para mais de 1.000 indivíduos em menos de cinco minutos! Esse padrão de propagação póde sêr analisado por meio de uma função exponencial, conteúdo quê será estudado neste Capítulo.
Elaborado com base em: AMARAL, Inês; SANTOS, Sofia José. Algoritmos e rêdes sociais: a propagação de fêik news na era da pós-verdade. In: FIGUEIRA, João; SANTOS, Sílvio (org.). As fêik news e a nova ordem (des)informativa na era da pós-verdade. Coimbra: Imprensa da Universidade de Coimbra, 2019. p. 63-85. Disponível em: https://livro.pw/feghr. Acesso em: 1 ago. 2024.
![]() Agora reúna-se a um colega, e respondam às kestões.
Agora reúna-se a um colega, e respondam às kestões.
1. por quê as fêik news são criadas?
Resposta pessoal. Os estudantes podem citar objetivos diversos, como: favorecer ideologias, disseminar preconceito, gerar pânico, promover difamação, entre outros.
2. Como podemos evitar a propagação de notícias falsas? Deem exemplos de ações de combate às fêik news.
2. Resposta pessoal. Espera-se quê os estudantes indiquem ações como verificação de fontes, validação das ideias descritas na publicação em outros materiais, verificação do respeito aos direitos humanos, entre outras.
3. Uma pessoa compartilhou uma notícia falsa em seu perfil de uma rê-de social. Se essa notícia for compartilhada para duas pessoas no primeiro minuto e depois o compartilhamento dobrar a cada minuto, quantos compartilhamentos ocorrerão no 3º minuto? E no 5º minuto?
8 e 32 compartilhamentos, respectivamente
4. Efetue as operações e escrêeva as respostas em notação científica.
a) 64
1,296 ⋅ 103
b) 0,53
1,25 ⋅ 10−1
c)
21 ⋅ 102
d)
5,0 ⋅ 10−2
Página cento e oitenta e um

Página cento e oitenta e dois
Introdução
Nos alimentos derivados do leite fermentado, há bactérias quê colabóram para o equilíbrio da flora intestinal, evitando a proliferação de bactérias nocivas, melhorando a absorção de nutrientes e fortalecendo nosso sistema imunológico.
Apesar de esses alimentos serem benéficos, o consumo em excésso póde acarretar alguns efeitos indesejados ao nosso organismo. Esses efeitos podem estar relacionados ao aumento do número de bactérias, quê se reproduzem muito rapidamente.
Em geral, o crescimento de uma população de bactérias póde sêr modelado por um tipo de função quê estudaremos neste Capítulo: a função exponencial.
FÓRUM
Conservação de alimentos
A conservação de alimentos é um processo essencial para garantir a disponibilidade de alimentos seguros e nutritivos em todas as épocas do ano. Dentro dêêsse vasto universo, os laticínios ocupam um lugar de destaque, oferecendo uma rica fonte de nutrientes, como cálcio e proteínas. No entanto, a composição específica dêêsses alimentos torna-os particularmente suscetíveis à rápida proliferação de microrganismos, o quê póde levar a uma perda acelerada e ao desperdício, se não forem armazenados corretamente.
Além díssu, é importante observar atentamente o prazo de validade dos alimentos e consumi-los antes de seu vencimento. O prazo de validade é uma indicação da segurança e da qualidade dos alimentos e deve sêr respeitado para garantir quê não causem qualquer dano, pois ignorar esse aspecto póde resultar em riscos para a saúde, como o risco de infekição por bactérias, além de contribuir para o desperdício de alimentos quê ainda estão próprios para consumo.
Para evitar o desperdício de laticínios e de alimentos em geral, devemos adotar práticas de compra e armazenamento conscientes. Comprar apenas a quantidade necessária de alimentos e armazená-los adequadamente póde ajudar a prolongar sua vida útil e reduzir a necessidade de descarte precoce. Além díssu, é importante planejar as refeições com antecedência e usar técnicas de reaproveitamento criativas.
• ![]() Converse com os côlégas e professores a respeito de outras práticas quê podem sêr utilizadas no dia a dia para evitar o desperdício de alimentos, especialmente produtos perecíveis, como os laticínios.
Converse com os côlégas e professores a respeito de outras práticas quê podem sêr utilizadas no dia a dia para evitar o desperdício de alimentos, especialmente produtos perecíveis, como os laticínios.
Ver as Orientações para o professor.
Página cento e oitenta e três
Potenciação e radiciação
Antes de abordar o conteúdo de função exponencial, vamos retomar conhecimentos sobre potenciação e radiciação, pois serão essenciais no estudo dêêsse tipo de função.
Potência com expoente natural
Acompanhe, a seguir, a definição de potenciação quando o expoente é um número natural.
Sendo a um número real e n um número natural, com n ≥ 2, definimos a potência de base a e expoente n como o produto de n fatores iguais a a.
an =
Além díssu, considerando a um número real, tem-se quê:
• para n = 1, definimos a1 = a.
• para a ≠ 0 e n = 0, definimos a0 = 1.
Exemplos:
a) 25 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32
b) =
c)
d) (−3)0 = 1
Potência com expoente inteiro
Para estender o conceito de potência para expoentes inteiros, vamos definir o quê significa uma potência de expoente inteiro negativo.
Sendo a um número real não nulo (a ≠ 0) e n um número inteiro, define-se:
a−n =
Exemplos:
a) 6−1 =
b) = 64
Página cento e oitenta e quatro
Propriedades da potenciação
É possível demonstrar quê, dados a e b reais não nulos e m e n inteiros, são válidas as seguintes propriedades opêratórìas com expoentes inteiros.
1ª propriedade:
am ⋅ an = am+n
Exemplo: 34 ⋅ 32 = 34 + 2 = 36 = 729
2ª propriedade:
= am ∶ an = am−n
Exemplo: = 45−3= 42 = 16
3ª propriedade:
(am)n = am⋅n
Exemplo: (62)3 = 62⋅3= 66 = 46.656
4ª propriedade:
=
Exemplo: (5 ⋅ 4)3 = 53 ⋅ 43 = 125 ⋅ 64 = 8.000
5ª propriedade:
Exemplo:
Notação científica
No meio científico, é comum nos depararmos com números muito grandes, como as distâncias entre os planêtas, ou muito pequenos, como o tamãnho de uma célula.
Quando queremos expressar números como esses, recorremos ao uso da notação científica, utilizando potências na base 10 para simplificar essas representações.
Sendo a um número real, tal quê 1 ≤ a < 10, e n um número inteiro, a forma em notação científica de um número real não nulo é dada por: a ⋅ 10n
Exemplos:
a) O raio médio do Sol é de aproximadamente 696.000.000 metros; em notação científica, temos: 696.000.000 metros = 6,96 ⋅ 108 metros (note quê n = 8 e a = 6,96).
b) O diâmetro do átomo de hidrogênio é de aproximadamente 0,0000000001 métro; em notação científica, temos: 0,0000000001 métro = 1,0 ⋅ 10−10 métro (note quê n = −10 e a = 1,0).
Pense e responda
Pesquise sobre o nanometro e expresse 1 nanometro em métro, utilizando notação científica.
1 nanometro = 1 ⋅ 10−9 métro
Para assistir
• O QUE é a nanotecnologia? [S. l.: s. n.], 2014. 1 vídeo (3 min). Publicado pelo canal stãri Inalberta. Disponível em: https://livro.pw/hlxts. Acesso em: 1 ago. 2024.
A palavra nano póde significar pequeno, muito pequeno. Quando nos referimos a medidas de comprimento, 1 nanometro equivale a 1 milionésimo de milimetro. Assista ao vídeo para saber mais.
Página cento e oitenta e cinco
Radiciação
Antes de abordarmos o conteúdo de potência com expoente racional, vamos retomar a definição de raiz enésima e as propriedades da operação de radiciação.
Sendo a um número real não negativo e n um número natural não nulo, a raiz enésima de a é o número real não negativo b, tal quê bn = a. Em símbolos, podemos escrever:
_

se, e somente se, bn = a
• Para n ímpar e a um número real negativo, a raiz enésima de a é o número real negativo b, tal quê bn = a.
• Para n par e a um número real negativo, não podemos definir a raiz enésima real de a, pois não existe número real b, tal quê bn = a.
Exemplos:
a) = 2 se, e somente se, 24 = 16.
b) = 3 se, e somente se, 3² = 9.
c) se, e somente se, = .
d) = −2, porque (−2)3 = −8.
e) ∄ b ∈ ℝ, tal quê = b.
Propriedades da radiciação
Dados a e b números reais não negativos, m inteiro e n, p e q naturais não nulos, sêndo q um divisor comum de n e m, apresentamos as seguintes propriedades.
1ª propriedade:
Exemplo:
2ª propriedade:
Exemplo: = 34 = 81
3ª propriedade:
Exemplo:
4ª propriedade:
e
Exemplo: e
5ª propriedade:
Exemplo:
Página cento e oitenta e seis
Potência com expoente racional
Acompanhe a seguir a definição de potência com expoente fracionário, sêndo o numerador inteiro e o denominador natural diferente de 0.
Se a é um número real positivo, m é inteiro e n é natural não nulo, define-se:
Exemplos:
a)
b) =
c)
d)
Observação:
As potências com expoente racional têm as mesmas propriedades opêratórìas quê as potências com expoente inteiro.
Exemplo:
= = 16 ou = 24 = 16
Potência com expoente irracional
Neste tópico, vamos aprender como calcular o valor de uma potência com expoente irracional.
Por exemplo, como calcular ?
Para responder a essa pergunta, vamos considerar, inicialmente, aproximações racionais de _ por falta, tomando os valores 1,4; 1,41; 1,414;..., e por excésso, tomando os valores 1,5; 1,42; 1,415;...
Usando uma calculadora científica, vamos listar alguns resultados e obtêr a melhor aproximação para .
n |
10n |
|---|---|
1,4 |
25,11886432 |
1,41 |
25,70395783 |
1,414 |
25,94179362 |
1,4142 |
25,95374301 |
1,41421 |
25,95434062 |
1,414213 |
25,95451991 |
n |
10n |
|---|---|
1,5 |
31,62277660 |
1,42 |
26,30267992 |
1,415 |
26,00159563 |
1,4143 |
25,95971977 |
1,41422 |
25,95493825 |
1,414214 |
25,95457967 |
De acôr-do com os resultados obtidos nos dois quadros, uma aproximação racional para com quatro casas decimais é 25,9545.
25,95451991 < < 25,95457967
Página cento e oitenta e sete
Continuando esse processo, podemos encontrar uma aproximação racional para com quantas casas decimais se deseje.
Sendo a um número real positivo e x um número irracional, podemos obtêr aproximações racionais para o valor de ax, com quantas casas decimais quisérmos, atribuindo a x valores aproximados por falta e por excésso.
Para potências com expoente irracional, valem as mesmas propriedades opêratórìas das potências com expoente inteiro.
Exemplos:
a) = 102 = 100
b) 2(pi)" ⋅ 23(pi)" = 2(pi)"+3(pi)" = 24(pi)"
c)
d)
Calculando com o auxílio de uma calculadora
Geralmente, as calculadoras mais simples têm a tecla ![]() . Com ela, podemos calcular a raiz quadrada de um número real maior do quê ou igual a 0. Por exemplo: para calcular , pressionamos
. Com ela, podemos calcular a raiz quadrada de um número real maior do quê ou igual a 0. Por exemplo: para calcular , pressionamos ![]() e obtemos 1,414213562.
e obtemos 1,414213562.
Agora, para calcular outras potências quaisquer, diferentes de , será necessário utilizar uma calculadora científica quê tenha a tecla ![]() . Em alguns modelos, essa tecla aparece como
. Em alguns modelos, essa tecla aparece como ![]() (com y representando a base da potência, e x, o expoente) ou
(com y representando a base da potência, e x, o expoente) ou ![]() (com x representando a base da potência, e y, o expoente). Por exemplo: para calcular 210, pressionamos
(com x representando a base da potência, e y, o expoente). Por exemplo: para calcular 210, pressionamos ![]() ou
ou ![]() ou
ou ![]() e obtemos 1.024.
e obtemos 1.024.
Entre as diferentes opções quê uma calculadora científica póde oferecer, estão:
• o cálculo de uma raiz enésima. Por exemplo: para calcular , pressionamos ![]() e obtemos 1,988647795;
e obtemos 1,988647795;
• a utilização do número irracional (pi)". Por exemplo: para calcular 24(pi)", pressionamos ![]() e obtemos 6.065,330793.
e obtemos 6.065,330793.
Observações:
A tecla ![]() permite acionar as opções escritas acima das teclas na mesma côr da palavra Shift.
permite acionar as opções escritas acima das teclas na mesma côr da palavra Shift.
As teclas ![]() e
e ![]() devem sêr utilizadas para indicar a ordem de cálculo das operações e identificar corretamente os termos de uma expressão a serem considerados.
devem sêr utilizadas para indicar a ordem de cálculo das operações e identificar corretamente os termos de uma expressão a serem considerados.
Saiba quê...
Os passos indicados e a quantidade de casas decimais em todos os exemplos podem variar ligeiramente dependendo do modelo da calculadora.
Página cento e oitenta e oito
ATIVIDADES RESOLVIDAS
1. Calcule o valor de .
Resolução
Decompondo o número 243 em fatores primos, obtemos: 243 = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3
Logo, 243 = 35.
Então:
Como o expoente é negativo, aplicamos a definição a−n = . Assim:
Aplicando a propriedade (am)n = am⋅n, obtemos: = = 32 = 9
Portanto, = 9.
2. Aplicando as propriedades da potenciação, calcule (53 ⋅ 56): 510.
Resolução
Usando as propriedades, temos: (53 ⋅ 56): 510 = 53+6 : 510 = 59 : 510 = 59−10 = 5−1 =
3. Simplifique a expressão .
Resolução
Substituindo os números decimais por frações decimais e aplicando as propriedades de potências, temos:
4. (PUCCamp-SP) Efetuando-se , obtém-se:
a)
b)
c)
d)
e)
Resolução
Resolvendo as operações e aplicando as propriedades da radiciação, temos:
Logo, .
A resposta correta é a alternativa d.
5. ![]() Utilize uma calculadora científica e determine valores reais aproximados para e
Utilize uma calculadora científica e determine valores reais aproximados para e
Resolução
Para calcular ,pressionamos ![]() e obtemos 18.514,08427.
e obtemos 18.514,08427.
Para calcular , pressionamos ![]() e obtemos 0,204525605.
e obtemos 0,204525605.
Página cento e oitenta e nove
ATIVIDADES
1. ![]() escrêeva, sôbi a forma de radical, as potências a seguir. Depois, com o auxílio de uma calculadora, calcule seu valor com aproximação de três casas decimais.
escrêeva, sôbi a forma de radical, as potências a seguir. Depois, com o auxílio de uma calculadora, calcule seu valor com aproximação de três casas decimais.
a)
; 3,344
b)
; 3,162
c)
; 1,260
d) 3 0,25
; 1,316
e)
; 1,331
f)
; 0,577
2. Aplicando as propriedades gerais das potências, reduza a uma só potência os itens a seguir. Considere a ≠ 0.
a) 34 ⋅ 35
39
b) (x3)4
x12
c) 79 ⋅ 74
7 13
d)
107
e) (103)2
106
f) an+1 ⋅ an−2
a2n − 1
3. escrêeva os números a seguir na forma de potência com expoente inteiro negativo. Considere a ≠ 0.
a)
3−2
b)
10−4
c)
2−5
d)
6−2
e)
2−1
f)
a−2
4. ![]() Usando uma calculadora científica, calcule cada potência com aproximação de três casas decimais.
Usando uma calculadora científica, calcule cada potência com aproximação de três casas decimais.
a) 51,5
11,180
b)
1,861
c) 280,25
2,300
d) 34,5
140,296
e) 22,6
6,063
f)
1,894
g)
11,665
h)
53,957
5. Leia os itens a seguir e escrêeva os números em notação científica. Utilize a aproximação de três casas decimais.
a) A velocidade da luz no vácuo é igual a 299.793.458 m/s.
2,998 ⋅ 108
b) O diâmetro da Terra é cerca de 12.742 km.
1,274 ⋅ 104
c) O vírus influenza é uma partícula esférica quê tem um diâmetro interno de aproximadamente 0,00011 mm.
1,1 ⋅ 10−4
6. Efetue os cálculos a seguir e dê as respostas em notação científica.
a) (2,0 ⋅ 103) ⋅ (4,0 ⋅ 10−5)
8 ⋅ 10−2
b) (5,2 ⋅ 106) ∶ (1,3 ⋅ 10−3)
4 ⋅ 109
c) (1,5 ⋅ 103) ⋅ (2,0 ⋅ 10−5) ⋅ (4,0 ⋅ 10−8)
1,2 ⋅ 10−9
7. (Unicamp-SP)
a) Calcule as seguintes potências: a = 33, b = (−2)3, c = 3−2 e d = (−2)−3.
a = 27; b = −8; c = ;d =
b) escrêeva os números a, b, c e d em ordem crescente.
−8; ;27
8. Qual é a mêtáde de 22012?
22011
9. Determine o número quê representa a expressão:
(4x + 2 ∶ 4x − 2) ∶ (4x ∶ 4x − 1)
64
10. Determine o valor da expressão .
1
11. Sendo A = 12n, com 78 ≤ n ≤ 155, qual é o maior valor natural de n para quê o algarismo das unidades de A seja 6?
n = 152
12. Calcule o valor das expressões a seguir, utilizando as propriedades da potenciação.
a)
b)
243
c)
d)
49
e)
13. Ao se resolver a expressão apresentada, cometeu-se um êrro em uma das passagens. Descubra qual é esse êrro, corrija-o e dê a resposta correta.
(passagem 1)
(passagem 2)
(passagem 3)
= 50 = 1 (passagem 4)
13. O êrro foi cometido na passagem 3:
= 52 = 25
14. (UFSM-RS) Determine o valor da expressão
.
30
15. (FEI-SP) Que número real representa a expressão ?
16. (Fuvest-SP) Sendo x = (22)3, y = e z = , qual é a potência quê representa a expressão xyz?
223
17. (UFRGS-RS) Simplifique a expressão:
10−10
18. (PUC-SP) escrêeva a expressão abaixo, em quê n ∈ ℤ, em sua forma mais simples:
Página cento e noventa
Função exponencial
Uma vez revisadas as propriedades básicas da potenciação e da radiciação, vamos agora estudar a função exponencial, quê é um tipo de função real cuja definição apresentamos a seguir.
A função f: ℝ → dada por f(x) = ax, com a ∈ ℝ, a > 0 e a ≠ 1, é denominada função exponencial de base a.
Exemplos:
a) f(x) = 2x
b) f(x) = (0,4)x
c) f(x) =
d) f(x) =
Em uma função exponencial dada por f(x) = ax, a base a deve sêr positiva e diferente de 1, pois:
• Se a < 0, então f(x) = ax não estaria definida para todo x real. Por exemplo, supondo a = −2 e x = ,teríamos a potência quê não está definida em ℝ.
• Se a = 1, então f(x) = ax é uma função constante, pois: f(x) = 1x ⇒ f(x) = 1 para todo x real.
• Se a = 0, então f(x) = ax não estaria definida para todo x real. Por exemplo, considerando x = −2, teríamos a potência (0)−2 quê não está definida em ℝ.
Além díssu, para a = 0 e x > 0, a função f seria constante e igual a zero.
Gráfico da função exponencial
Vamos, agora, esboçar o gráfico de algumas funções exponenciais. Observe os exemplos a seguir.
• Esboço do gráfico de g(x) = 2x.
x |
g(x) = 2x |
|---|---|
−3 |
|
−2 |
|
−1 |
|
0 |
1 |
1 |
2 |
2 |
4 |
3 |
8 |
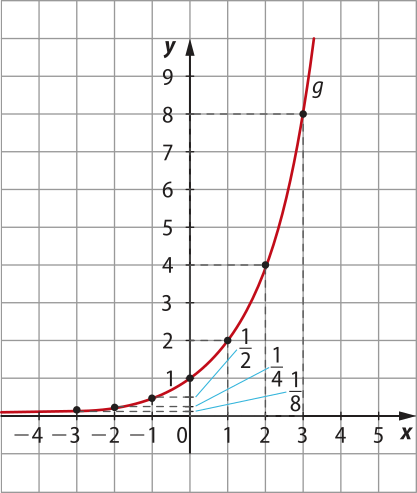
Observe quê os valores de 2x aumentam conforme o valor de x aumenta. Essa característica póde sêr observada sempre quê a > 1.
Página cento e noventa e um
• Esboço do gráfico de h(x) = .
x |
h(x) = |
|---|---|
−3 |
8 |
−2 |
4 |
−1 |
2 |
0 |
1 |
1 |
|
2 |
|
3 |
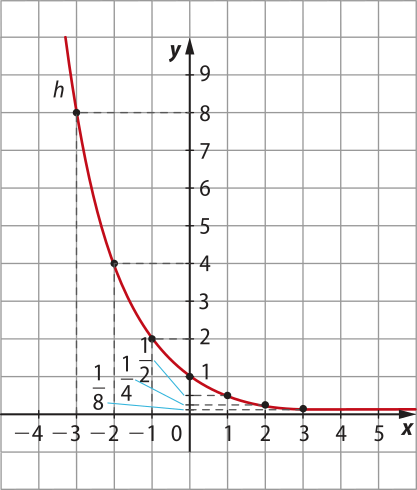
Observe quê os valores de diminuem conforme o valor de x aumenta. Essa característica póde sêr observada sempre quê 0 < a < 1.
Considerando a função exponencial dada por f(x) = ax (com a > 0 e a ≠ 1), temos:
• o domínio da função é D(f) = ℝ;
• o contradomínio da função é CD(f) = ;
• o conjunto imagem da função é Im(f) = .
Saiba quê...
Os gráficos das funções g e h se aproximam do eixo x, mas não o tocam, e intersectam o eixo y no ponto (0, 1).
Pense e responda
pôdêmos dizêr quê os gráficos das funções g e h, representados em um mesmo sistema cartesiano, são simétricos com relação ao eixo y?
sim, pois g(x) = h(−x) e g(−x) = h(x)
A função f(x) = ex
Vamos, agora, conhecer a função f: ℝ → definida por f(x) = ex, quê é uma função exponencial cuja base é o número e. Vários fenômenos das Ciências da Natureza podem sêr modelados tomando-se como base essa função e ela também é utilizada em diversas aplicações dentro da própria Matemática.
Observe, a seguir, como é o gráfico dessa função.
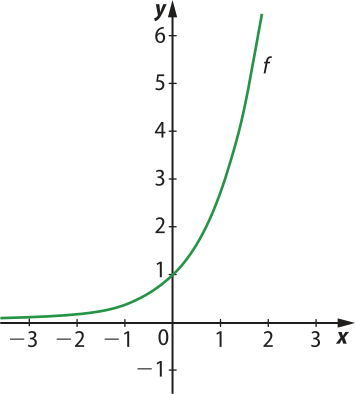
Saiba quê...
Conforme estudamos no Capítulo 1, o número e, conhecido como número de Óiler, é um número irracional cujo valor é 2,718281...
Pense e responda
• Em quê ponto o gráfico da função intersecta o eixo y?
• Qual é o valor de f(1)?
(0, 1); f(1) = e
Página cento e noventa e dois
EXPLORANDO A TECNOLOGIA
A base da potenciação e o gráfico da função exponencial
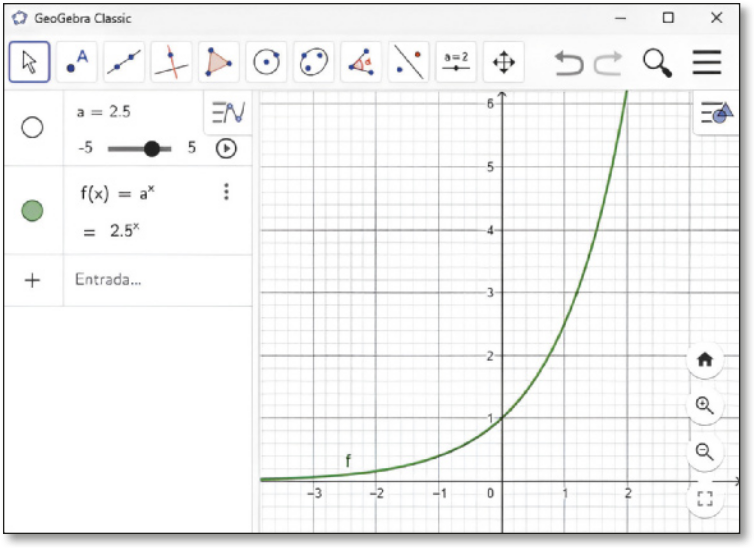
Vamos utilizar o GeoGebra para analisar a influência da base a da potenciação no gráfico da função exponencial.
Para isso, acompanhe os passos a seguir.
Se achar necessário, lembrar aos estudantes quê, por padrão, o contrôle deslizante é criado limitado ao intervalo [−5, 5] e quê, para alterar esse intervalo, basta clicar em cima do número −5 ou do 5 no contrôle deslizante e alterar esses números para os valores desejados.
I. No campo de entrada do GeoGebra, digite “f(x) = a ^ x” e pressione Enter.
II. O programa vai criar, na janela de Álgebra, um contrôle deslizante para o coeficiente a e exibirá, na janela de visualização, o gráfico da função f de acôr-do com o valor indicado no contrôle deslizante.
Ao sêr criado, o contrôle aparece indicando a = 1. Mova o cursor do contrôle deslizante, alterando o valor de a, e obissérve o quê acontece com o gráfico de f.
Observe quê o valor indicado no contrôle, quando a > 0 e a ≠ 1, representa o valor da base da função exponencial dada por f(x) = ax.
Note quê, quando f é a função exponencial, ela tem valores muito próximos de zero, mas nunca assume o valor zero, ou seja, não existe x tal quê f(x) = 0. Você póde conferir esse fato dando zoom na tela do GeoGebra para aprossimár o gráfico e verificar quê ele nunca encosta no eixo x. Para isso, basta movimentar o botão Scroll do máuzi para a frente ou utilizar o ícone.
Agora, faça o quê se pede nas atividades a seguir.
1. Movimente o cursor do contrôle deslizante e altere o valor de a. Analise as alterações no gráfico e registre o quê acontece em cada caso a seguir.
a) Para a < 0;
Nenhum gráfico é exibido, pois a < 0 não é um valor válido para a na função.
b) Para 0 < a < 1;
O gráfico representa uma função decrescente.
c) Para a = 1;
O gráfico é uma reta paralela ao eixo x, pois a função definida é a função constante dada por f(x) = 1x = 1.
d) Para a > 1.
O gráfico representa uma função crescente.
2. Em uma nova janela do GeoGebra, construa, agora, o gráfico da função definida por g(x) = 2b ⋅ x
Para isso, digite “g(x) = 2 ^ (b * x)” no campo de entrada.
Altere o valor de b e analise o quê acontece quando:
a) b < 0;
A função é decrescente.
b) b > 0.
A função é crescente.
Página cento e noventa e três
Crescimento e decrescimento da função exponencial
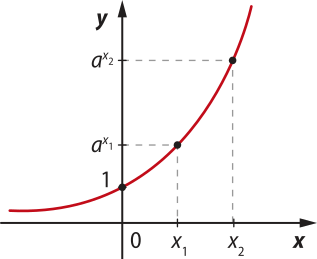
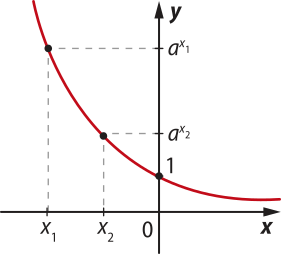
De acôr-do com os exemplos apresentados nas páginas 190 e 191 e com o estudo feito na página 192, podemos perceber quê a base da potência ax influencía o comportamento da função exponencial dada por f(x) = ax.
De modo geral, considerando a função exponencial dada por f(x) = ax, temos:
a > 1 |
0 < a < 1 |
|---|---|
|
|
■ Quando a > 1, a função é crescente. ∀x1, x2 ∈ D(f), x1 > x2 ⇒ f(x2) > f(x1) |
■ Quando 0 < a < 1, a função é decrescente. ∀x1, x2 ∈ D(f), x1 > x2 ⇒ f(x2) < f(x1) |
ATIVIDADES RESOLVIDAS
6. O gráfico representado a seguir mostra a evolução do número de bactérias em certa cultura.
Quantas bactérias haverá, aproximadamente, nessa cultura decorridos 30 minutos do início das observações?
Resolução
A partir da observação do gráfico, verificamos quê a função é do tipo f(t) = a ⋅ bt e contém os pontos (0, 104) e (3, 8 ⋅ 104).
Dessa maneira:
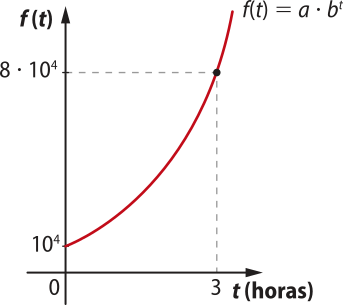
• f(0) = a ⋅ b0 = 104 ⇒ a = 104
• f(3) = a ⋅ b3 = 8 ⋅ 104 ⇒ a ⋅ b3 = 8 ⋅ 104
Como a = 104, temos: 104 ⋅ b³ = 8 ⋅ 104 ⇒ b3 = ⇒ b3 = 8 ⇒ b = 2
Portanto, f(t) = 104 ⋅ 2t.
Adotamos t = para descobrir a quantidade de bactérias após 30 minutos (meia hora) do início das observações:
f = 104 ⋅ = 104 ⋅ ≃ 104 ⋅ 1,41 ≃ 14.100
Assim, haverá aproximadamente 14.100 bactérias nessa cultura.
Página cento e noventa e quatro
7. (Unifei-MG) Sendo f(x) = para x ∈ ℝ, pode-se afirmar quê:
a) o gráfico de f intersecta o eixo x em apenas um ponto.
b) f é decrescente.
c) o conjunto imagem de f é dado por Im(f) =]0, +∞[.
d) o gráfico de f intersecta o eixo y no ponto (0, .
e) f(−1) =
Resolução
Vamos esboçar o gráfico da função f(x) = .Como a > 1, a função é crescente.
x |
−2 |
−1 |
0 |
1 |
2 |
|---|---|---|---|---|---|
f(x) = |
1 |
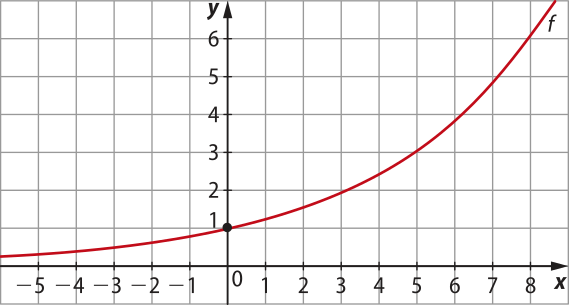
Observamos quê:
a) o gráfico de f não tem intersecção com o eixo x.
b) f é crescente.
c) o conjunto imagem de f é Im(f) =]0, +∞[.
d) o gráfico de f intersecta o eixo y no ponto (0, 1).
e) f(−1) =
Portanto, a única afirmativa verdadeira é a correspondente à alternativa c.
8. Utilize uma calculadora científica e encontre valores reais aproximados para 24e e .
Resolução
Para calcular 24e, pressionamos ![]() e obtemos 1.875,588098.
e obtemos 1.875,588098.
Para calcular ,pressionamos ![]() e obtemos 4,481689070; ou pressionamos
e obtemos 4,481689070; ou pressionamos ![]() e obtendo o mesmo resultado.
e obtendo o mesmo resultado.
Saiba quê...
Assim como a tecla
![]() ,a tecla
,a tecla![]() permite acionar as opções escritas acima das teclas na mesma côr da palavra Alpha.
permite acionar as opções escritas acima das teclas na mesma côr da palavra Alpha.
Para ler
• ROBSON, Daví. Contágio por coronavírus: o quê é o viés matemático quê dificulta o combate à pandemia de covid-19. BBC nius Brasil, [s. l.], 19 ago. 2020. Disponível em: https://livro.pw/mjtty. Acesso em: 1 ago. 2024.
O texto aborda o “viés do crescimento exponencial” e comenta a dificuldade quê nós, sêres humanos, temos de compreender o rápido crescimento exponencial em comparação com o crescimento linear. Ele discute como essa percepção errônea dos dados impactou o enfrentamento da pandemia de covid-19.
Página cento e noventa e cinco
ATIVIDADES
19. Identifique como crescente ou decrescente as funções exponenciais definidas a seguir.
a) f(x) = 5x
crescente
b) f(x) =
decrescente
c) f(x) = 2−x
decrescente
d) f(x) =
crescente
20. Esboce o gráfico das funções definidas a seguir. Depois, determine o domínio e a imagem de cada uma delas.
Ver as Orientações para o professor.
a) f(x) = 3x
D(f) = ℝ; Im(f) =
b) f(x) = 2x + 1
D(f) = ℝ; Im(f) =
c) f(x) =
D(f) = ℝ; Im(f) =
d) f(x) = 2x + 1
D(f) = ℝ; Im(f) = {y ∈ ℝ | y > 1}
21. Durante a aula de Matemática, o professor comentou sobre uma função quê representava o crescimento de uma população de bactérias e escreveu na lousa f(t) = 2t, para t ≥ 0, em quê t é dado em horas e f(t) em milhares de bactérias.
Um estudante distraído copiou f(t) = 2t e, portanto, seus cálculos não deram cérto.
a) Esboce os gráficos das duas funções em um mesmo sistema de coordenadas.
Ver as Orientações para o professor.
b) Observando os gráficos construídos no item a, existe algum valor de t para o qual as duas funções assumem valor igual? Se sim, qual(is)?
sim, para t = 1 h e t = 2 h
c) O quê você póde concluir sobre o crescimento dessas duas funções?
Ambas são funções crescentes.
d) Para t = 3 h, qual é a diferença entre o número de bactérias nas duas funções?
2.000 bactérias
22. Uma amostra de bactérias foi estudada quanto ao seu crescimento e decrescimento populacional P, em centenas de milhares, em relação ao aumento da tempera-túra t, em°C. Nesse experimento, a tempera-túra foi aumentada progressivamente, partindo de 0°C e terminando em 120°C, em um período de 24 horas. Observe, a seguir, a tabéla e o gráfico quê descrevem a variação populacional dessa amostra.
Variação de uma população de bactérias em relação à tempera-túra
Temperatura (°C) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
|---|---|---|---|---|---|---|---|
Quantidade de bactérias |
2 ⋅ 105 |
2 ⋅ 105 |
8 ⋅ 105 |
32 ⋅ 105 |
32 ⋅ 105 |
2 ⋅ 105 |
0,125 ⋅ 105 |
Fonte: Dados fictícios.
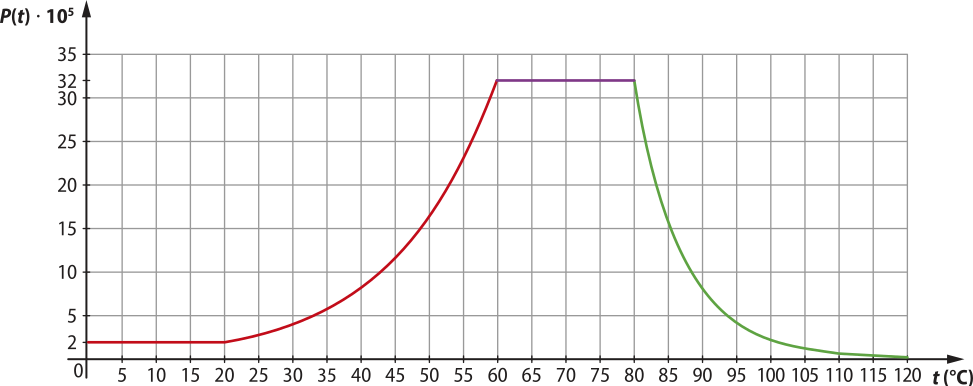
a) Para quais intervalos de tempera-túra a população de bactérias estudada aumentou, diminuiu ou se manteve estável?
Aumentou no intervalo entre 20 °C e 60 °C; diminuiu no intervalo entre 80°C e 120°C; manteve-se estável nos intervalos entre 0°C e 20°C e entre 60°C e 80°C.
b) Se o aumento da população de bactérias é dado por f(t) = 20,1(t −10) e a diminuição, por g(t) = 32 ⋅ 2−0,2(t −80), calcule a quantidade aproximada de bactérias nessa amostra, quando a tempera-túra atingiu:
• 30°C;
400.000 bactérias
• 50°C;
1.600.000 bactérias
• 90°C;
800.000 bactérias
• 110°C.
50.000 bactérias
Página cento e noventa e seis
23. Para quais valores reais de k a função dada por f(x) = (k − 3)x é decrescente?
3 < k < 4
24. Copie o qüadro a seguir, referente às funções definidas por f(x) = 3x, g(x) = 3x + 2 e h(x) = 3x − 2, e complete-o.
x = −2 |
x = −1 |
x = 0 |
x = 1 |
x = 2 |
x = 3 |
|
|---|---|---|---|---|---|---|
lei da função: f(x) = 3x |
1 |
3 |
9 |
27 |
||
lei da função: g(x) = 3x + 2 |
3 |
5 |
11 |
29 |
||
lei da função: h(x) = 3x − 2 |
1 |
3 |
Agora, faça o quê se pede.
Ver as Orientações para o professor.
a) Utilizando o GeoGebra, construa, em um mesmo sistema cartesiano, o gráfico de f, de g e de h.
b) Ao analisar os gráficos construídos, podemos dizêr quê f, g e h são funções crescentes ou decrescentes?
crescentes
c) Determine o domínio e o conjunto imagem dessas funções.
D(f) = ℝ, D(g) = ℝ e D(h) = ℝ; Im(f) =
Im(g) = {y ∈ ℝ | y > 2} e Im(h) =
d) dêz-creva como seria o gráfico da função dada por m(x) = 3x − 2, em relação ao gráfico de f, sem construí-lo.
Ver as Orientações para o professor.
e) dêz-creva como seria o gráfico da função dada por q(x) = 3x + 2, em relação ao gráfico de f, sem construí-lo.
Ver as Orientações para o professor.
f) Construa, em um mesmo sistema cartesiano, os gráficos das funções f, m e q e comprove as respostas dadas nos itens d e e.
Ver as Orientações para o professor.
25. Um banco possui taxa de rendimento na poupança de 0,35% ao mês. Um cliente quê possui poupança nesse banco depositou R$ 1.000,00 no mês de janeiro e, ao longo de 6 meses, não realizou saques nem depositou quantia a mais. Conforme os dados da tabéla, responda às kestões.
Valor disponível em poupança após 6 meses de aplicação
Mês |
Poupança (R$) |
|---|---|
Janeiro |
1.000,00 |
Fevereiro |
1.000,00 ⋅ 1,0035 = 1.003,50 |
Março |
1.003,50 ⋅ 1,0035 = 1.007,01 |
Abril |
1.007,01 ⋅ 1,0035 = 1.010,53 |
Maio |
1.010,53 ⋅ 1,0035 = 1.014,07 |
Junho |
1.014,07 ⋅ 1,0035 = 1.017,62 |
Fonte: Dados fictícios.
a) Qual é a taxa de variação média aproximada da poupança entre o sexto e o primeiro mês dêêsse ano?
R$ 3,52
b) Considerando quê não houve saques nem depósitos nessa aplicação, determine a lei da função quê representa o valor disponível em poupança em relação ao número de meses em quê o valor inicial foi aplicado.
f(x) = 1.000 ⋅ (1,0035)x
c) Quanto esse cliente terá aproximadamente na poupança após 12 meses sem realizar saques ou depósitos?
R$ 1.042,82
Saiba quê...
Quando uma pessoa deposita o dinheiro em uma poupança e o deixa lá por algum tempo, dizemos quê ela fez uma aplicação, recebendo juro por esse investimento. É como se o banco estivesse pagando pelo dinheiro emprestado.
Página cento e noventa e sete
Equações exponenciais
Toda equação cuja incógnita se apresenta no expoente de pelo menos uma potência de base real, positiva e diferente de 1, é denominada equação exponencial. Assim, são exemplos de equações exponenciais:
a) 2x = 8
b) = 0,25
c) 52x + 5x = 30
d)
Vamos resolver as equações exponenciais nas quais ambos os membros da igualdade podem sêr representados como potências de mesma base. Para isso, utilizamos a seguinte propriedade:
ax1 = ax2 ⇔ x1 = x2
Assim, para resolver, por exemplo, a equação 2x = 8, escrevemos o segundo membro da equação como uma potência de base 2:
2x = 8 ⇒ 2x = 23
Aplicando a propriedade descrita, temos:
2x = 23 ⇒ x = 3
Portanto, o conjunto solução da equação 2x = 8 é S = {3}.
Inequações exponenciais
Toda desigualdade quê apresenta incógnita no expoente de, pelo menos, uma potência de base real positiva e diferente de 1 é denominada inequação exponencial. Assim, são exemplos de inequações exponenciais:
a) 5x < 1
b) > 4x
c) 10x ≥ −0,1
d) ⋅ ≤
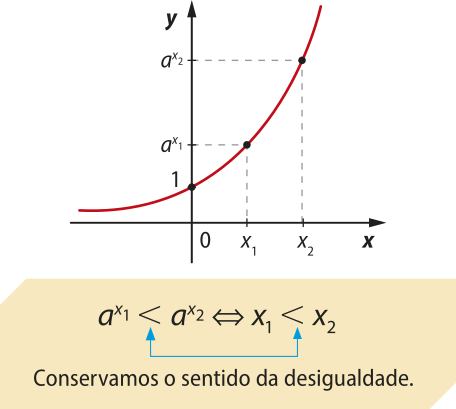
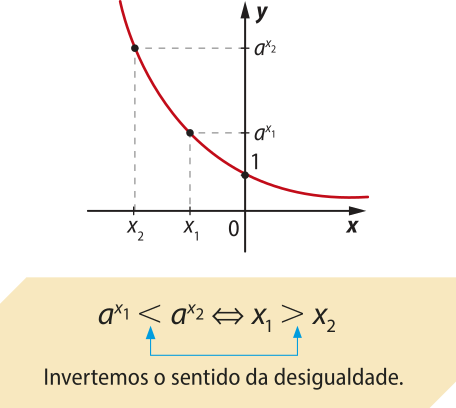
Vamos resolver as inequações exponenciais nas quais ambos os membros da desigualdade podem sêr representados como potências de mesma base. Com base no crescimento e no decrescimento da função exponencial, dada por f(x) = ax, aplicamos as propriedades a seguir.
1º caso: a > 1 (função crescente) |
2º caso: 0 < a < 1 (função decrescente) |
|---|---|
Quando a base da potência é maior do quê 1, a relação de desigualdade entre as potências se mantém entre os expoentes.
|
Quando a base da potência está entre 0 e 1, a relação de desigualdade entre as potências se inverte entre os expoentes.
|
Página cento e noventa e oito
ATIVIDADES RESOLVIDAS
9. Uma pesquisa feita por biólogos de uma reserva florestal mostrou quê a população de uma espécie de cérto animal está diminuindo a cada ano. A partir do ano em quê se iniciou a pesquisa, o número dêêsses animais seguia a lei matemática N = N0⋅ 3−0,05t, com t em anos (t ≥ 0) e N0 > 0 correspondendo ao número de animais no início da pesquisa.
a) Calcule em quantos anos a população dessa espécie de animal estará reduzida à terça parte.
b) Qual era o número de animais dessa população quando a pesquisa foi iniciada, sabendo quê, após 80 anos, restam apenas 12 indivíduos?
Resolução
a) Sendo N o número de animais no decorrer do tempo, podemos obtêr t resolvendo a equação:
N = ⇒ = N0 ⋅ 3−0,05t ⇒ = 3−0,05t ⇒ = ⇒ =
Como as bases são iguais, positivas e diferentes de 1, concluímos quê os expoentes são iguais. Assim:
0,05t = 1 ⇒ t = ⇒ t =20
Portanto, a população de animais será reduzida à terça parte após 20 anos.
b) Sabemos quê, para t = 80, temos N = 12. Assim, para obtermos N0, basta substituirmos t e N na lei de formação da função.
N = N0 ⋅ 3−0,05t ⇒ 12 = N0 ⋅ 3−0,05 ⋅80 ⇒ 12 = N0 ⋅ 3−4 ⇒ 12 = N0 ⋅ ⇒ 12 = ⇒ N0 = 972
Portanto, havia 972 animais dessa espécie no início da pesquisa.
10. resôuva a equação 125x+1 =
Resolução
Usando as propriedades de potências, vamos expressar o 1º e o 2º membros da equação como potências de mesma base.
125x + 1 = ⇒ (53)x + 1 = ⇒ 53x + 3 =
Como as bases são iguais, positivas e diferentes de 1, podemos igualar os expoentes:
3x + 3 = ⇒ ⇒ 9x = −13 ⇒ x =
Portanto, o conjunto solução é S = .
11. resôuva a equação 4x − 5 ⋅ 2x + 4 = 0.
Resolução
Aplicando as propriedades de potência, vamos reescrever o termo 4x na base 2: 4x = (22)x = (2x)2
Assim, podemos escrever a equação 4x − 5 ⋅ 2x + 4 = 0 como: (2x)2 − 5 ⋅ 2x + 4 = 0
Fazendo 2x = y, obtemos a equação do 2º grau na incógnita y: y2 − 5y + 4 = 0
Resolvendo essa equação, obtemos:
(delta)" = (−5)2 − 4 ⋅ 1 ⋅ 4 ⇒ (delta)" = 9
y = ⇒ y(minutos)" = 4 e y(segundos)" = 1
Voltando à igualdade 2x = y, temos:
• para y = 4, temos: 2x = 4 ⇒ 2x = 22 ⇒ x = 2;
• para y = 1, temos: 2x = 1 ⇒ 2x = 20 ⇒ x = 0.
Portanto, o conjunto solução da equação é S = {0, 2}.
Página cento e noventa e nove
12. resôuva a inequação .
Resolução
Como a base está entre 0 e 1, o sentido da desigualdade entre os expoentes se inverte:
⇒ 3x − 1 > x + 5 ⇒ 2x > 6 ⇒ x > 3
Portanto, S = {x ∈ ℝ | x > 3}.
13. Determine o conjunto solução da inequação 22x + 2 − 0,75 ⋅ 2x + 2 < 1.
Resolução
Aplicando as propriedades de potências, temos:
4 ⋅ 22x − 0,75 ⋅ 4 ⋅ 2x − 1 < 0
Fazendo 2x = y, obtemos: 4y2 − 3y − 1 < 0
Fazendo o estudo do sinal da função dada por f(y) = 4y2 − 3y − 1, temos o gráfico a seguir.
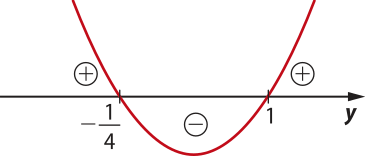
Logo: < y < 1
Lembrando quê 2x = y, temos: 2x < 1 ⇒ 2x < 20 ⇒ x < 0 I
Como 2x será sempre um número positivo, independentemente do valor de x, temos:
2x > para todo x ∈ ℝ II
Fazendo I ∩ II, temos a seguinte representação:
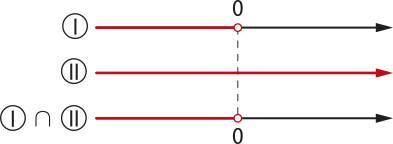
Portanto, S = {x ∈ ℝ | x < 0}.
14. O valor de um automóvel daqui a t anos é dado pela função V(t) = 40.000 ⋅ (0,8)t. Após quantos anos de uso o valor dêêsse automóvel será menor do quê R$ 20.480,00?
Resolução
Do enunciado, temos:
V(t) < 20.480 ⇒ 40.000 ⋅ (0,8)t < 20.480
Resolvendo essa inequação, obtemos:
40.000 ⋅ (0,8)t < 20.480 ⇒ (0,8)t < ⇒ (0,8)t < ⇒ (0,8)t < ⇒ (0,8)t < (0,8)3
Como as bases são iguais a 0,8, quê é maior do quê zero e menor do quê 1, temos: t > 3.
Portanto, o valor do automóvel será menor do quê R$ 20.480,00 após 3 anos de uso.
Página duzentos
ATIVIDADES
26. resôuva as equações exponenciais a seguir.
a) 2x = 64
S = {6}
b) 10x = 1.000
S = = {3}
c) 9x = 243
s =
d)
S = {5}
e) = 0,25
S =
f) 4x =
S = {−3}
g) 3x =
S =
h) 4x =
S =
27. Seja uma função definida por f(x) = 52x − 1, com x ∈ ℝ. Determine x para quê:
a) f(x) = 125
x = 2
b) f(x) = 1
x =
c) f(x) = 0
∄ x ∈ ℝ | 52x − 1 = 0
d) f(x) =
x = 0
28. resôuva as equações apresentadas.
a) 2x − 2 =
S = {4}
b) 252x + 2 =
S =
c) 5x2 − 2 ∶ 25 =
S = {−1, 4}
d)
S =
29. Qual é o valor de x na equação = 2?
1
30. (ú éfi érri jóta) Considere quê num recipiente, no instante t = 0, um número N0 de bactérias está se reproduzindo normalmente. É aceito cientificamente quê o número de bactérias num cérto instante t > 0 é dado pela equação
N(t) = N0Kt,
sêndo N(t) o número de bactérias no instante t e K uma constante quê depende do tipo de bactéria. Suponhamos quê, num cérto instante, observou-se quê havia 200 bactérias no recipiente reproduzindo-se normalmente. Passadas 12 horas, havia 600 bactérias. Após 48 horas do início da observação, quantas bactérias existirão?
16.200 bactérias
31. (Uespi) Determine o conjunto solução da equação 2x + 1 + 2x + 2 + 2x + 3 = 224.
S = {4}
32. (PUC-MG) Determine o valor de x para satisfazer a equação 33x − 1 ⋅ 92x + 3 = 273 − x.
x =
33. Qual é a solução da equação 8x + 8x − 1 + 8x + 1 = 292 no universo ℝ?
S =
34. (hú éfe pê érre) resôuva a equação exponencial 1x + 5x + 25x = 3.
S = {0}
35. resôuva a equação: .
S =
36. (UFAL) Devido à desintegração radioativa, uma massa m0 de carbono 14 é reduzida a uma massa m em t anos. As duas massas estão relacionadas pela fórmula m = m0 ⋅ . Nessas condições, em quantos anos 5 g da substância serão reduzidos a 1,25 g?
10.800 anos
37. (ITA-SP) Dê o conjunto verdade da equação exponencial 3 ⋅ 5x2 + 3x2 + 1 − 8 ⋅ 3x2 = 0.
S = {−1, 1}
38. (ITA-SP) resôuva a equação = −1.
S = {0, 1}
39. (PUC-SP) Sejam f(x) = 3x−1, g(x) = 3x e s(x) = f(x) + g(x). Qual é o valor de x, tal quê s(x) = 4?
x = 1
40. (UFV-MG) Seja a função f: ℝ → ℝ definida por f(x) = 3x. Determine os valores de x ∈ ℝ tais quê f(x + 1) + f(−x + 4) = 36.
x = 2 ou x = 1
41. Uma represa utilizada como reservatório para o abastecimento de á gua de uma determinada região tem capacidade aproximada de 16.000.000 m³ num período de normalidade de chuvas. Após o início de um período de seca, a variação da quantidade de á gua dêêsse reservatório passou a sêr dada pela função V(t) = V0 ⋅ 2−0,05t, sêndo V0 a capacidade da represa em um período de normalidade, t o número de meses de estiagem e V(t) a quantidade de á gua nesse reservatório em m³ após t meses.
• ![]() Elabore uma questão com base nos dados do enunciado apresentado. Depois, troque a atividade criada por você com um colega e responda à questão elaborada por ele. Juntos, confiram as resoluções e as estratégias utilizadas por cada um.
Elabore uma questão com base nos dados do enunciado apresentado. Depois, troque a atividade criada por você com um colega e responda à questão elaborada por ele. Juntos, confiram as resoluções e as estratégias utilizadas por cada um.
Resposta pessoal.
Página duzentos e um
42. Determine o conjunto solução das inequações.
a) 2x2 − 3x ≥
S = {x ∈ ℝ | x ≤ 1 ou x ≥ 2}
b)
S =
c) (0,2)x − 2 > 1
S = {x ∈ ℝ | x < 2}
d) 2x + 1 ⋅ 4x − 1 ≤
S =
e)
S =
f) ≥ 0,008
S = {x ∈ ℝ | −1 ≤ x ≤ 3}
43. Determine os valores reais de x quê verificam a inequação 3x + 1 + 32 + x > 108.
S = {x ∈ ℝ | x > 2}
44. Para quais valores de x a expressão representa um número real?
S = {x ∈ ℝ | x ≥ 2}
45. Determine o domínio D da função definida por:
a) f(x) =
D(f) =
b) g(x) =
D(g) =
46. Determine a solução da inequação 4x − 10 ⋅ 2x + 16 < 0.
S = {x ∈ ℝ | 1 < x < 3}
47. resôuva em ℝ a inequação 21 + x + √ 8 ≥ .
S =
48. Quais valores inteiros de x satisfazem a desigualdade 1 < ≤ 64?
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
49. (UFAL) No universo ℝ, qual o conjunto solução da inequação 5x 2 ⋅ 52x − 1 ⋅ 5−3 < ?
S = {x ∈ ℝ | −3 ≤ x ≤ 1}
50. Um botânico anotou diariamente o crescimento de uma planta e verificou quê esse crescimento obedecia, de maneira aproximada, a uma função exponencial dada por h(t) = 2,52 + 0,04 ⋅ 30,14t, em quê t representa o número de dias aferidos, a partir do primeiro registro, e h(t) indica a altura, em centimetro, da planta no dia t.
Resposta pessoal.
• ![]() Elabore uma questão com base nos dados dêêsse enunciado, utilizando as expressões tempo mínimo ou tempo mássimo.
Elabore uma questão com base nos dados dêêsse enunciado, utilizando as expressões tempo mínimo ou tempo mássimo.
Depois, troque a atividade criada por você com um colega e responda à questão elaborada por ele. Juntos, confiram as resoluções e as estratégias utilizadas por cada um.
51. (Unimontes-MG) Todos os valores de x quê satisfazem a inequação estão no intervalo
alternativa d
a) [2, 4].
b)]1, 2].
c) [0, 2].
d)]1, 3[.
52. (EsPCEx-SP) A quantidade de números inteiros ímpares quê pertencem ao intervalo quê satisfaz a inequação exponencial > 4 é de:
alternativa b
a) um número ímpar.
b) dois números ímpares.
c) três números ímpares.
d) quatro números ímpares.
e) cinco números ímpares.
53. (UFRN) Os modelos matemáticos quê representam os crescimentos populacionais, em função do tempo, de duas famílias de microrganismos, B1 e B2, são expressos, respectivamente, por meio das funções F1(t) = t2 + 96 e F2(t) = 9 ⋅ 2t + 64, para t ≥ 0.
Com base nestas informações, é correto afirmar quê:
alternativa b
a) após o instante t = 2, o crescimento populacional de B1 é maior quê o de B2.
b) após o instante t = 2, o crescimento populacional de B1 é menor quê o de B2.
c) quando t varia de 2 a 4, o crescimento populacional de B1 aumenta 10% e o de B2 aumenta 90%.
d) quando t varia de 4 a 6, o crescimento populacional de B1 cresce 20 vezes menos quê o de B2.
Página duzentos e dois
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Radioatividade
Usinas nucleares para geração de energia e aparelhos de radioterapia para uso em Medicina Nuclear são algumas das aplicações da radioatividade. No entanto, elemêntos radioativos também podem sêr matéria-prima para a produção de armamentos nucleares, quê têm grande potencial de destruição. Para saber um pouco mais sobre o assunto, leia, a seguir, o trecho de um texto sobre decaimento radioativo.
Radioatividade
O esquecimento de uma rocha de urânio sobre um filme fotográfico virgem levou à descoberta de um fenômeno interessante: o filme foi velado (marcado) por “alguma coisa” quê saía da rocha, na época denominada raios ou radiações.
Outros elemêntos pesados, com massas próximas à do urânio, como o rádio e o polônio, também tí-nhão a mesma propriedade.
O fenômeno foi denominado radioatividade e os elemêntos quê apresentavam essa propriedade foram chamados de elemêntos radioativos.
Comprovou-se quê um núcleo muito energético, por ter excésso de partículas ou de carga, tende a estabilizar-se, emitindo algumas partículas.
[...]
O lixo atômico
Os materiais radioativos produzidos em Instalações Nucleares (Reatores Nucleares, Usinas de Beneficiamento de Minério de urânnio e Tório, Unidades do Ciclo do Combustível Nuclear), Laboratórios e Hospitais, nas formas sólida, líquida ou gasosa, quê não têm utilidade, não podem sêr simplesmente “jogados fora” ou “no lixo”, por causa das radiações quê emitem. Esses materiais, quê não são utilizados em virtude dos riscos quê apresentam, são chamados de Rejeitos Radioativos.
Na realidade, a expressão “lixo atômico” é um pleonasmo, porque qualquer lixo é formado por hátomus e, portanto, é atômico. Ele passa a ter essa denominação popular quando é radioativo.
Tratamento de rejeitos radioativos
Os rejeitos radioativos precisam sêr tratados, antes de sêrem liberados para o meio ambiente, se for o caso. Eles podem ser liberados quando o nível de radiação é igual ao do meio ambiente e quando não apresentam toxidez química.

Página duzentos e três
Rejeitos sólidos, líquidos ou gasosos podem sêr, ainda, classificados, quanto à atividade, em rejeitos de baixa, média e alta atividade.
Os rejeitos de meia-vida curta são armazenados em locais apropriados (preparados), até sua atividade atingir um valor semelhante ao do meio ambiente, podendo, então, sêr liberados. Esse critério de liberação leva em conta somente a atividade do rejeito. É evidente quê materiais de atividade ao nível ambiental mas quê apresentam toxidez química para o sêr humano ou quê são prejudiciais ao éco-sistema não podem sêr liberados sem um tratamento químico adequado.
Rejeitos sólidos de baixa atividade, como partes de maquinaria contaminadas, luvas usadas, sapatilhas e aventais contaminados, são colocados em sacos plásticos e guardados em tambores ou caixas de aço, após classificação e respectiva identificação. Os produtos de fissão, resultantes do combustível nos reatores nucleares, sofrem tratamento especial em Usinas de Reprocessamento, onde são separados e comercializados, para uso nas diversas áreas de aplicação de radioisótopos. Os materiais radioativos restantes, quê não têm justificativa técnica e/ou econômica para serem utilizados, sofrem tratamento químico especial e são vitrificados, guardados em sistemas de contenção e armazenados em Depósitos de Rejeitos Radioativos.
[...]
CARDOSO, Eliezer de Moura. Apostila educativa: radioatividade. Rio de Janeiro: Comissão Nacional de Energia Nuclear, [2004]. p. 5; 14-15. Disponível em: https://livro.pw/uhzaa. Acesso em: 23 ago. 2024.
Agora, faça o quê se pede nas atividades a seguir.
1. De acôr-do com o texto, a descoberta da radioatividade se deu a partir de um fato ocorrido com qual tipo de rocha?
rocha de urânio
2. Os hátomus de um elemento químico radioativo possuem naturalmente a tendência de se desintegrarem, emitindo partículas e se transformando em outro elemento. Dessa maneira, com o passar do tempo, a quantidade original dêêsse elemento diminui.
Suponha quê certa quantidade de um elemento radioativo se decomponha conforme a função M(t) = 50 ⋅ ,na qual M(t) é a quantidade de massa radioativa (em grama) no tempo t (em anos).
a) Esboce o gráfico dessa função, identificando os pontos da função em quê t = 0, t = 35 e t = 70.
b) Com base no gráfico esboçado, estime a quantidade de massa radioativa dêêsse elemento quando t = 10.
c) Verifique se a sua estimativa estava correta, calculando M(10) com o auxílio da calculadora.
Ver as Orientações para o professor.
3. As substâncias radioativas, ao atingirem a meia-vida, têm as suas massas iniciais reduzidas pela mêtáde. Tomemos hoje 16 gramas de uma substância radioativa, cuja meia-vida é de 5 anos. A massa dessa substância, em grama, é uma função do tempo, em anos, contado a partir de hoje, dada por M(n) = 16 ⋅ .Se daqui a n anos sua massa for 2−111 gramas, qual será o valor de n?
575 anos
4. ![]() Reúna-se a mais dois côlégas, e pesquisem alguns dos acidentes radioativos quê marcaram a história.
Reúna-se a mais dois côlégas, e pesquisem alguns dos acidentes radioativos quê marcaram a história.
Quais foram as causas e consequências dêêsses acidentes?
Produzam um podcast contando um pouco sobre os acidentes quê vocês pesquisaram.
Ver as Orientações para o professor.
Página duzentos e quatro
ATIVIDADES COMPLEMENTARES
1. (PUC-RJ) Se = x, quanto vale x2 + 1?
a) 1
b)
c)
d)
e)
alternativa b
2. (Unifor-CE) Simplificando a expressão , na qual n ∈ ℝ, obtém-se:
a) 0
b) 23n
c)
d)
e)
alternativa e
3. (Uneb-BA) Se , para x e y números reais, y > 0, então o valor de y + 3x é
01) 33
02) 48
03) 56
04) 69
05) 77
alternativa 04
4. (IFMS) Um professor desafiou seus estudantes a resolverem a seguinte expressão:
(2−3,5 × _) + 0,125 +
Assinale a alternativa quê apresenta o resultado correto dessa expressão.
a) 1
b) _
c) 2−1
d) 1,8
e) 2
alternativa a
5. (Enem/MEC) A côr de uma estrela tem relação com a tempera-túra em sua superfícíe.
Estrelas não muito kemtes (cerca de 3.000 K) nos parecem avermelhadas. Já as estrelas amarelas, como o Sol, possuem tempera-túra em torno dos 6.000 K; as mais kemtes são brancas ou azuis porque sua tempera-túra fica acima dos 10.000 K.
A tabéla apresenta uma classificação espectral e outros dados para as estrelas dessas classes.
Estrelas da seqüência Principal
Classe Espectral |
O5 |
B0 |
A0 |
G2 |
M0 |
|---|---|---|---|---|---|
Temperatura |
40.000 |
28.000 |
9.900 |
5.770 |
3.480 |
Luminosidade |
5 ⋅ 105 |
2 ⋅ 104 |
80 |
1 |
0,06 |
Massa |
40 |
18 |
3 |
1 |
0,5 |
Raio |
18 |
7 |
2,5 |
1 |
0,6 |
■ Temperatura em kélvin. Luminosidade, massa e raio, tomando o Sol como unidade.
Se tomarmos uma estrela quê tenha tempera-túra 5 vezes maior quê a tempera-túra do Sol, qual será a ordem de grandeza de sua luminosidade?
alternativa a
a) 20.000 vezes a luminosidade do Sol.
b) 28.000 vezes a luminosidade do Sol.
c) 28.850 vezes a luminosidade do Sol.
d) 30.000 vezes a luminosidade do Sol.
e) 50.000 vezes a luminosidade do Sol.
6. (AFA-SP) A função real f definida por f(x) = a ⋅ 3x + b, sêndo a e b constantes reais, está graficamente representada abaixo.
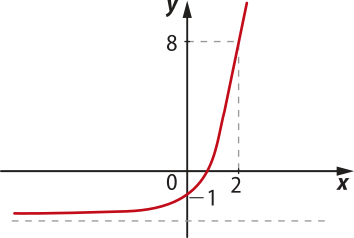
Pode-se afirmar quê o produto (a ⋅ b) pertence ao intervalo real
alternativa a
a) [−4, −1[
b) [−1, 2[
c) [2, 5[
d) [5, 8]
Página duzentos e cinco
7. (Enem/MEC) O govêrno de uma cidade está preocupado com a possível epidemia de uma doença infectocontagiosa causada por bactéria. Para decidir quê medidas tomar, deve calcular a velocidade de reprodução da bactéria. Em experiências laboratoriais de uma cultura bacteriana, inicialmente com 40 mil unidades, obteve-se a fórmula para a população:
p(t) = 40 ⋅ 23t
em quê t é o tempo, em hora, e p(t) é a população, em milhares de bactérias.
Em relação à quantidade inicial de bactérias, após 20 min, a população será
a) reduzida a um terço.
b) reduzida à mêtáde.
c) reduzida a dois terços.
d) duplicada.
e) triplicada.
alternativa d
8. (Enem/MEC) Um modelo de automóvel tem seu valor depreciado em função do tempo de uso segundo a função f(t) = b ⋅ at, com t em ano. Essa função está representada no gráfico.
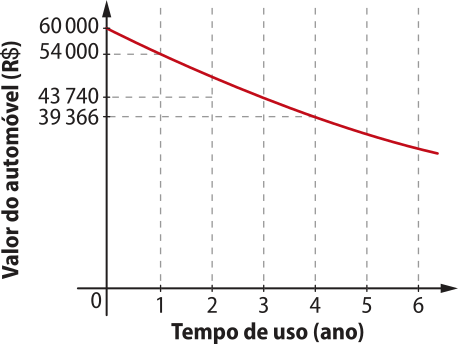
Qual será o valor dêêsse automóvel, em real, ao completar dois anos de uso?
a) 48.000,00
b) 48.114,00
c) 48.600,00
d) 48.870,00
e) 49.683,00
alternativa c
9. (Unemat-MT) Certa substância se desintegra obedecendo à seguinte expressão:
Q(t) = k ⋅ 2−0,5t, em quê t é o tempo (em horas), k é uma constante real e Q(t) é a quantidade da substância (em gramas), no tempo t.
Considerando quê no instante inicial, t = 0, a quantidade de substância é de 800 g, assinale a alternativa quê corresponde ao tempo necessário para quê a quantidade dessa substância esteja reduzida a 25% do seu valor inicial.
a) 2 h
b) 4 h
c) 6 h
d) 8 h
e) 10 h
alternativa b
10. (Mack-SP) O valor de x na equação
é:
a) tal quê 2 < x < 3.
b) negativo.
c) tal quê 0 < x < 1.
d) múltiplo de 2.
e) 3.
alternativa d
11. (UEL-PR) Se o número real k satisfaz à equação 32k − 4 ⋅ 3k + 3 = 0, então k2 é igual a:
a) 0 ou
b) 0 ou 1
c) ou 1
d) 1 ou 2
e) 1 ou 3
alternativa b
12. (UECE) Se o número real k é a solução da equação − 8 ⋅ − 9 = 0, então, o número k cumpre a seguinte condição:
a) 1,5 < k < 3,5.
b) 7,5 < k < 9,5.
c) 5,5 < k < 7,5.
d) 3,5 < k < 5,5.
alternativa d
13. (EsPCEx-SP) Na pesquisa e desenvolvimento de uma nova linha de defensivos agrícolas, constatou-se quê a ação do produto sobre a população de insetos em uma lavoura póde sêr descrita pela expressão N(t) = N0 ⋅ 2kt, sêndo N0 a população no início do tratamento, N(t), a população após t dias de tratamento e k uma constante, quê descreve a eficácia do produto. Dados de campo mostraram quê, após dez dias de aplicação, a população havia sido reduzida à quarta parte da população inicial. Com estes dados, podemos afirmar quê o valor da constante de eficácia dêste produto é igual a:
a) 5−1
b) −5−1
c) 10
d) 10−1
e) −10−1
alternativa b
Página duzentos e seis
14. (IFPR) Alguns objetos de uso contínuo sofrem desvalorização comercial, devido ao uso e desgaste ao longo do tempo. Ao comprar uma moto, temos quê o valor de venda V(t) da mesma, em função do tempo t de uso em anos, é dado pela seguinte função: V(t) = 10.000 ⋅ (0,9)t. Dessa forma, essa moto poderá sêr vendida por R$ 8.100,00, após quanto tempo de uso?
a) 2 anos.
b) 1 ano.
c) 18 meses.
d) 36 meses.
alternativa a
15. (UFPB) Uma determinada indústria constatou quê o gás expelido na fabricação dos seus produtos continha o poluente alfa em quantidade acima do recomendado, quê é de no mássimo 4 mg/L.
Visando resolver esse problema, instalou filtros para purificação do gás. Estudos mostram quê, com esses filtros, a quantidade (q) do poluente alfa presente no gás, t horas após o processo de purificação ter sido iniciado, é dada por q(t) = 25 − 0,5t mg/L. Com base nessas informações, identifique as afirmativas corretas:
I, II, IV e V
I. A quantidade do poluente alfa presente no gás no instante em quê o processo de purificação foi iniciado era de 32 mg/L.
V
II. A quantidade do poluente alfa presente no gás, quatro horas após o início do processo de purificação, corresponde a um quarto da quantidade existente no instante em quê o processo foi iniciado.
V
III. A função utilizada para determinar a quantidade de poluentes no gás, q(t), é crescente.
F
IV. O tempo de purificação necessário para quê a quantidade do poluente alfa presente no gás fique reduzida à mêtáde da existente no instante em quê o processo foi iniciado é de 2 horas.
V
V. A quantidade do poluente alfa presente no gás estará conforme o recomendado a partir da 6ª hora após o instante em quê o processo de purificação foi iniciado.
V
16. (Vunesp-SP) Uma lagoa tem sofrido as consequências da poluição do ambiente e os pescadores reclamam, há muito tempo, da diminuição na quantidade de peixes. Após anos de denúncias, a prefeitura contratou, na última década, um pesquisador quê vêm acompanhando o desenvolvimento da vida aquática e da quantidade de peixes na lagoa. Após terminar suas experiências, ele concluiu quê a quantidade n de peixes poderia sêr calculada pela fórmula n(T) = 10.000 − ,sendo T o tempo, em anos, medido a partir dêste exato momento. De acôr-do com esse pesquisador, o número de peixes será igual a 9.271 daqui a:
a) 15 anos
b) 18 anos
c) 24 anos
d) 27 anos
e) 30 anos
alternativa c
17. (Unicamp-SP) O processo de resfriamento de um determinado corpo é descrito por:
T(t) = TA+ (alfa)" ⋅ 3(beta)"t, onde T(t) é a tempera-túra do corpo, em graus célcius, no instante t, dado em minutos, TA é a tempera-túra ambiente, suposta constante, e (alfa)" e (beta)" são constantes. O referido corpo foi colocado em um congelador com tempera-túra de −18°C. Um termômetro no corpo indicou quê ele atingiu 0°C após 90 minutos e chegou a −16°C após 270 minutos.
a) Encontre os valores numéricos das constantes (alfa)" e (beta)".
(beta)" = ; (alfa)" = 54
b) Determine o valor de t para o qual a tempera-túra do corpo no congelador é apenas °C superior à tempera-túra ambiente.
360 minutos
18. (UECE) Uma cultura de bactérias cresce obedecendo à função f(t) = c32t, onde c é uma constante positiva e t é o tempo medido em horas.
O valor de t para quê a quantidade inicial de bactérias fique multiplicada por nove é
a) 1 hora.
b) hora
c) 1 hora e meia.
d) 2 horas.
alternativa a
19. (UEA-AM) O ponto A(5, 4) pertence à função f(x) = 2x − k, e o ponto B(2, 4) pertence à função g(x) = k ⋅ x + c, em quê c e k são números reais. O valor de f(k) + g(1) é
a) 3.
b) 2.
c) 0.
d) 4.
e) 1.
alternativa b
Página duzentos e sete
20. (Enem/MEC) Enquanto um sêr está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ele morre, essa quantidade vai diminuindo. Sabe-se quê a meia-vida do carbono 14 é de 5.730 anos, ou seja, num fóssil de um organismo quê morreu há 5.730 anos haverá mêtáde do carbono 14 quê existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado:
Q(t) = Q0⋅⋅ em quê t é o tempo, medido em ano, Q(t) é a quantidade de carbono 14 medida no instante t e Q0 é a quantidade de carbono 14 no sêr vivo correspondente.
Um grupo de arqueólogos, numa de suas expedições, encontrou 5 fósseis de espécies conhecidas e mediram a quantidade de carbono 14 neles existente. Na tabéla temos esses valores juntamente com a quantidade de carbono 14 nas referidas espécies vivas.
Fóssil |
Q0 |
Q(t) |
|---|---|---|
1 |
128 |
32 |
2 |
256 |
8 |
3 |
512 |
64 |
4 |
1.024 |
512 |
5 |
2.048 |
128 |
O fóssil mais antigo encontrado nessa expedição foi
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
alternativa b
PARA REFLETIR
Neste Capítulo, revisamos as propriedades da potenciação e da radiciação e apresentamos as potências com expoente real. Estudamos, também, quê medidas muito grandes ou muito pequenas podem sêr expressas em notação científica e quê função, equações e inequações exponenciais são utilizadas para modelar o crescimento de uma população de bactérias, o decaimento de substâncias radioativas, além de outros fenômenos sociais e naturais.
Nas páginas de abertura, foram apresentadas informações sobre fêik news e como sua rápida disseminação póde sêr relacionada ao rápido crescimento de uma função exponencial. Você conseguiu reconhecer essa relação? Se sim, qual é a importânssia de estudá-la? Se não, retome o texto de abertura do Capítulo e as perguntas iniciais. Se possível, pesquise também em livros, revistas, jornais e sáites sobre as fêik news.
Vamos refletir sobre as aprendizagens do Capítulo 5:
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
Respostas pessoais.
• Cite exemplos de outras situações em quê podemos utilizar notação científica para expressar medidas.
Resposta pessoal.
• Como podemos obtêr a aproximação de uma potência com expoente real?
Fazemos sucessivas aproximações com um expoente racional, por falta e por excésso, e tomamos um valor quê se repita nos dois casos e quê atenda à necessidade.
• Qual é a condição para quê uma função exponencial seja crescente? E decrescente?
base a maior do quê 1; base a entre 0 e 1
• ![]() Elabore um passo a passo sobre como calcular a raiz enésima de um número natural e de potências do tipo ex com o auxílio de uma calculadora científica.
Elabore um passo a passo sobre como calcular a raiz enésima de um número natural e de potências do tipo ex com o auxílio de uma calculadora científica.
Resposta pessoal.
Página duzentos e oito