CAPÍTULO 7
PROPORCIONALIDAD E SEMELHANÇA
Você sabia quê as televisões são comercializadas por polegadas? Você sabe o quê significa, por exemplo, uma televisão de 60 polegadas?
A polegada, quê equivale a 2,54 centimetros, é uma unidade de medida de comprimento usada em países como a Inglaterra e os Estados Unidos. A quantidade de polegadas anunciada em um aparelho corresponde à medida da diagonal da tela, ou seja, anunciar uma Tevê de 70 polegadas significa dizêr quê a medida da diagonal da tela tem 70 polegadas ou, aproximadamente, 177,8 cm.
Além das televisões, essa unidade de medida é usada para descrever o tamãnho de monitores de computador e de dispositivos móveis, como smartphones e tablets. As telas mais comuns de celulares varíam de 4 a 5,5 polegadas, enquanto as de televisores podem variar entre 24 e 100 polegadas.
A medida da diagonal de um retângulo está diretamente relacionada às dimensões dêêsse retângulo. Portanto, conhecendo as medidas da base e da altura de uma tela, podemos aplicar o teorema de Pitágoras para saber quantas polegadas ela tem. Neste Capítulo, vamos explorar esse teorema e as propriedades de semelhança de figuras geométricas.

Página duzentos e quarenta e cinco
![]() Forme dupla com um colega, e façam o quê se pede em cada questão.
Forme dupla com um colega, e façam o quê se pede em cada questão.
1. Pesquisem por quê a unidade de medida se chama “polegadas”.
Porque a origem da medida está ligada ao uso de dedos polegares.
2. Qual é, aproximadamente, a medida de comprimento da diagonal de uma Tevê de 100 polegadas em centimetros?
aproximadamente 254 cm
3. Com o auxílio de régua e esquadro ou compasso, desenhem um retângulo de dimensões 6,5 × 14 centimetros para representar a tela de um celular. Utilizando o teorema de Pitágoras, calculem quantas polegadas, aproximadamente, tem a tela de celular desenhada.
Espera-se quê os estudantes encontrem valores próximos a 6 polegadas. A diagonal do retângulo tem aproximadamente 15,4 cm.
Página duzentos e quarenta e seis
Proporcionalidade
Nesta coleção, já estudamos algumas razões, como a razão áurea e razões entre grandezas de naturezas distintas, por exemplo, a velocidade e a densidade. Vamos agora estudar o conceito de razão entre segmentos de reta.
Segmentos de reta proporcionais
pôdêmos comparar as medidas de dois segmentos de reta por meio de uma razão. Definimos quê a razão entre dois segmentos de reta é o quociente entre as respectivas medidas dêêsses segmentos, tomadas na mesma unidade. Por exemplo, a razão entre dois segmentos de reta, e , de medidas respectivamente iguais a 16 cm e 80 cm, é dada por:
= = ou 0,2
Dizemos quê a razão entre AB e cê dê é ou 0,2. A ordem de leitura e escrita de uma razão é importante. Assim, a razão entre cê dê e AB é = 5, ou seja, se AB = cê dê, temos quê .
Agora, considere os segmentos de reta , , e . Dizemos quê, nessa ordem, , , e são proporcionais se, e somente se, a razão entre as medidas dos dois primeiros segmentos de reta for igual à razão entre as medidas dos dois últimos, ou seja: .
Feixe de retas paralelas
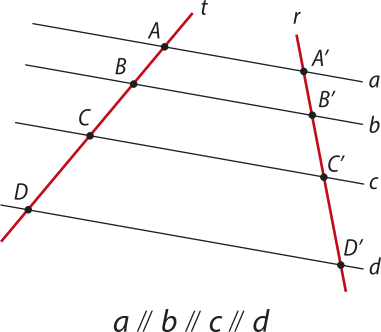
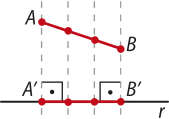
Duas ou mais retas paralelas entre si, pertencentes a um mesmo plano, formam um feixe de retas paralelas. Uma reta quê intersecta esse feixe de paralelas é chamada de reta transversal. Na figura, as retas a, b, c e d formam um feixe de retas paralelas, e as retas r e t são as transversais. Além díssu, definimos:
• A e A(minutos)" são pontos correspondentes, assim como B e B(minutos)", C e C(minutos)", D e D(minutos)".
• e são segmentos correspondentes, assim como
e , e , e , e , e .
Saiba quê...
Para simplificar a escrita e quando isso não causar dificuldade de entendimento, em alguns momentos desta coleção não faremos distinção entre segmentos e suas medidas, bem como entre ângulos e suas medidas. Assim, usaremos com o mesmo significado expressões como “circunferência de raio de medida r” e “circunferência de raio r”, assim como “lado de medida L” e “lado L” ou “altura de medida h” e “altura h”, por exemplo.
Página duzentos e quarenta e sete
Teorema de Tales
A proporcionalidade póde sêr utilizada em diversos casos do nosso cotidiano. Nesse sentido, o teorema de Tales, quê será apresentado a seguir, trata da relação entre os segmentos de reta determinados por um feixe de retas paralelas e duas retas transversais. Por meio dêêsse teorema, podemos realizar cálculos para determinar, por exemplo, distâncias quê não podem sêr medidas diretamente.
Vamos enunciar o teorema e, em seguida, apresentar sua demonstração.
Se duas retas são transversais a um feixe de retas paralelas, então dois segmentos quaisquer de uma das retas transversais são proporcionais aos segmentos correspondentes da outra reta.
Observe a figura e uma possível proporção ôbitída pelo teorema de Tales.
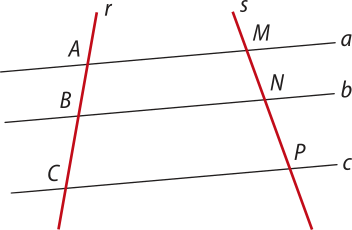
a // b // c ⇒ =
Pense e responda
A partir da figura apresentada, quais outras proporções podem sêr consideradas pelo teorema de Tales?
;
Com base nessa figura, podemos considerar outras proporções, como: ou .
Demonstração
Primeiro, vamos apresentar duas propriedades dos triângulos, quê serão usadas na demonstração do teorema de Tales.
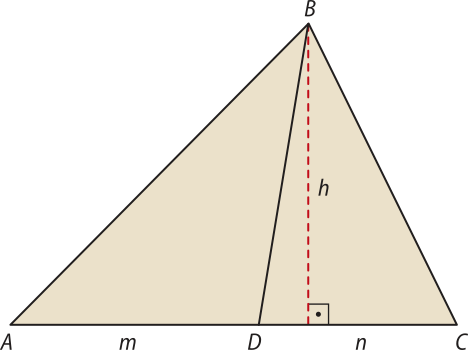
• 1ª propriedade
Considere o triângulo ABC, uma ceviana qualquer, com extremidade no vértice B, e a altura h do triângulo, de modo quê a área do triângulo ABD é igual a A1, a área do triângulo BDC é igual a A2,
AD = m e DC = n.
Temos quê:
A1 = e A2 =
Dividindo A1 por A2, tem-se: -
Saiba quê...
• Tales, matemático e filósofo quê viveu no século VI a.C., era natural da cidade de Mileto, na Grécia, por isso ficou conhecido como Tales de Mileto.
• Ceviana de um triângulo é um segmento de reta quê tem como extremidades um dos vértices do triângulo e um ponto no lado ôpôsto a esse vértice.
Página duzentos e quarenta e oito
• 2ª propriedade
Dadas duas retas paralelas r e s, considere um triângulo HIJ e outro HI(minutos)"J, ambos com a base pertencente a s e vértices I e I(minutos)" como pontos da reta r.
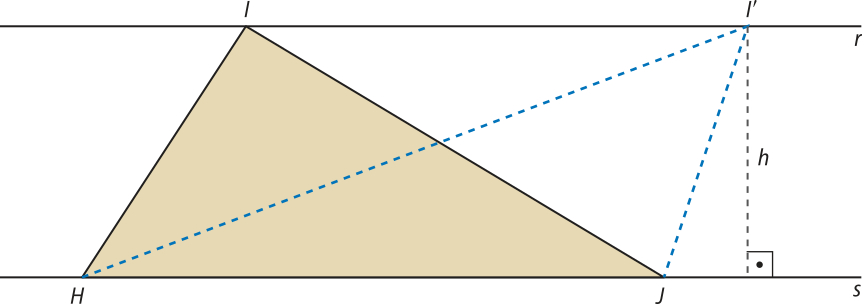
pôdêmos concluir quê a área do triângulo HIJ é igual à área do triângulo HI(minutos)"J, pois ambos têm a mesma base e a mesma altura h. Portanto, qualquer triângulo formado pela base quê tenha o vértice ôpôsto a essa base como um ponto da reta r terá a mesma área do triângulo HIJ.
• Demonstração do teorema de Tales
Dados um feixe de retas paralelas e duas transversais quê intersectam esse feixe, obtemos os pontos A, B, C, D, E e F, conforme a figura a seguir.
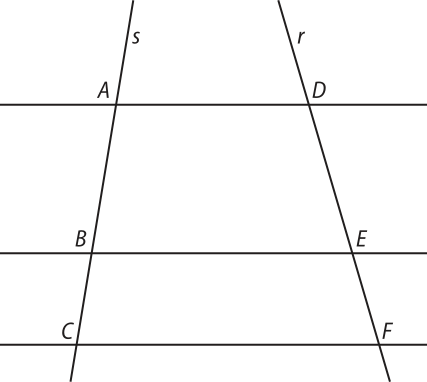
Vamos provar quê os segmentos de reta formados são proporcionais, de modo quê .
Para isso, vamos construir os triângulos ACE e DFB, conforme a figura a seguir.
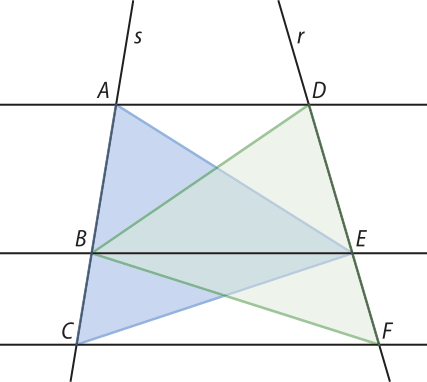
Sejam as áreas S1, S2, S3 e S4 dos triângulos AEB, BEC, DBE e EBF, respectivamente. Pela 1ª propriedade, temos:
e
De acôr-do com a 2ª propriedade: S1 = S3 e S2 = S4
Portanto: ⇒
Página duzentos e quarenta e nove
ATIVIDADES RESOLVIDAS
1. A figura a seguir representa dois terrenos cujas laterais são paralelas. De acôr-do com a figura, determine as medidas x e y.
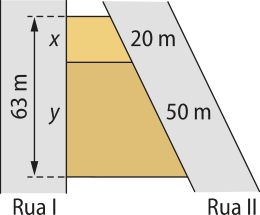
Resolução
Pelo teorema de Tales, temos:
I
II
Substituindo x + y por 63 em I, temos:
⇒ ⇒ 7x = 126 ⇒ x = 18
Substituindo x + y por 63 em II, temos:
⇒ ⇒ 7y = 315 ⇒ y = 45
Portanto, as medidas são x = 18 m e y = 45 m.
2. Na figura a seguir, a // b // c. Determine a medida do segmento .
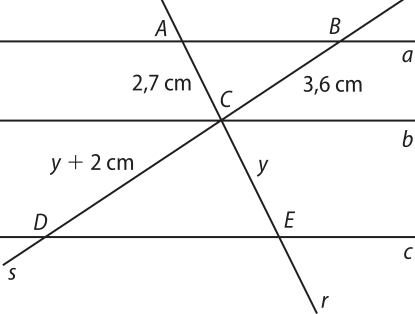
Resolução
Aplicando o teorema de Tales, temos:
⇒ 2,7 ⋅ (y + 2) = 3,6y ⇒
⇒ 2,7y + 5,4 = 3,6y ⇒ 3,6y − 2,7y = 5,4 ⇒
⇒ 0,9y = 5,4 ⇒ y = ⇒ y = 6
Portanto, cê dê = 6 cm + 2 cm = 8 cm.
ATIVIDADES
1. Uma pessoa tem 1,95 m de altura e, em determinado instante, sua sombra méde 2,60 m. Calcule a razão entre a medida da altura da pessoa e a medida de sua sombra naquele instante.
2. Na figura a seguir, as retas r, s, t e u são paralelas. Com as informações fornecidas, deseja-se calcular as medidas x e y indicadas.
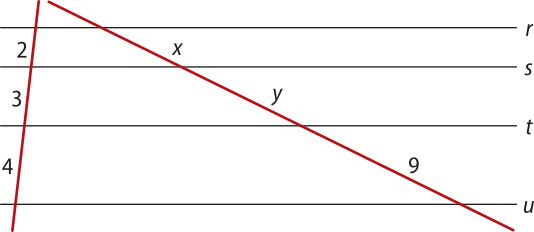
a) A partir das informações dadas, é possível resolver o problema?
Sim. Ver as Orientações para o professor.
b) Se for possível, resôuva o problema. Se não for possível, indique quais informações estão faltando para quê as medidas possam sêr encontradas.
x = 4,5; y = 6,75
3. Duas avenidas se encontram em um ponto A.
Essas avenidas intersectam três ruas, r1, r2 e r3, quê são paralelas entre si. Os segmentos de reta , e representam quarteirões da avenida 2. Na figura, estão indicados os comprimentos, em métro, de alguns quarteirões.
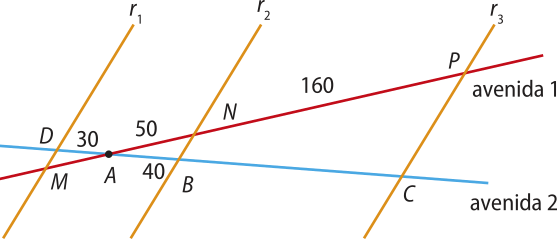
Determine os comprimentos dos quarteirões representados pêlos segmentos de reta e .
BC = 128 m; AM = 37,5 m
4. Considerando quê , , e são proporcionais nessa ordem e sabendo quê AB = (x + 3) cm, cê dê = (x − 2) cm, MN = 40 cm e PQ = 30 cm, calcule as medidas dos segmentos e .
AB = 20 cm; cê dê = 15 cm
Página duzentos e cinquenta
5. Observe a figura a seguir, em quê as retas a, b e c são paralelas, e as medidas são dadas em centimetro.
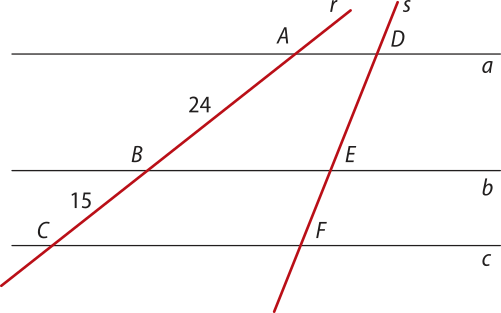
Deseja-se determinar as medidas dos segmentos e .
a) A partir das informações dadas, é possível resolver o problema?
Não. Ver as Orientações para o professor.
b) Se for possível, resôuva o problema. Se não for possível, indique quais informações estão faltando para quê as medidas possam sêr encontradas.
Resposta possível: É preciso saber a medida do segmento , ou .
6. Os segmentos , , e são proporcionais. A soma das medidas dos dois primeiros segmentos equivale a 12, e a diferença entre essas medidas é igual a 2. Com relação aos dois últimos segmentos, sabemos quê a medida do primeiro é o triplo da medida do segundo menos duas unidades. Nessas condições, determine a soma das medidas de todos os segmentos.
15
7. ![]() Clara precisa resolver o seguinte problema em sua aula de Matemática:
Clara precisa resolver o seguinte problema em sua aula de Matemática:
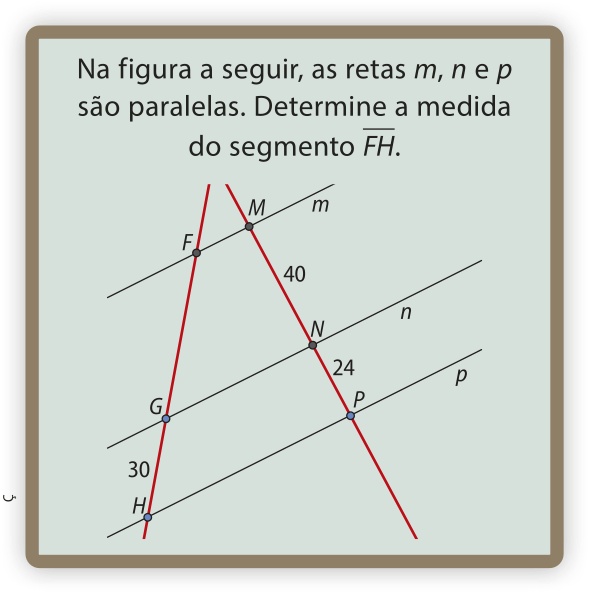
Para resolver o problema, Clara utilizou a proporção . Reúna-se a um colega, e respondam às kestões.
a) A proporção apresentada por Clara está correta? Justifiquem a resposta.
Sim. Espera-se quê os estudantes justifiquem utilizando o teorema de Tales.
b) Essa proporção resólve o problema? Justifiquem a resposta.
Sim. Ver as Orientações para o professor.
c) Existe outra proporção quê resólve o problema?
Se sim, escrevam-na.
Sim. Resposta possível: .
8. A unidade de medida de tempera-túra usada no Brasil é o grau célcius (°C). Em alguns países do mundo, como nos Estados Unidos, a unidade de medida padrão é o grau farenrráiti (°F). Para converter uma medida de tempera-túra de uma unidade para outra, usamos uma escala de correspondência, como indica a figura a seguir.
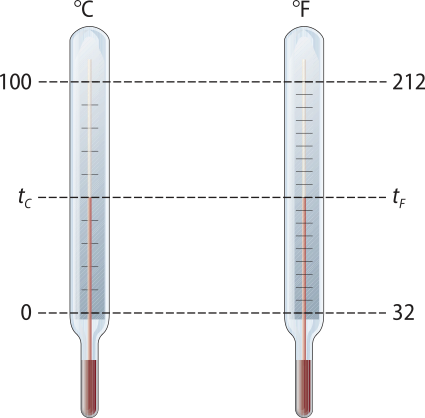
Agora, obissérve a fotografia.
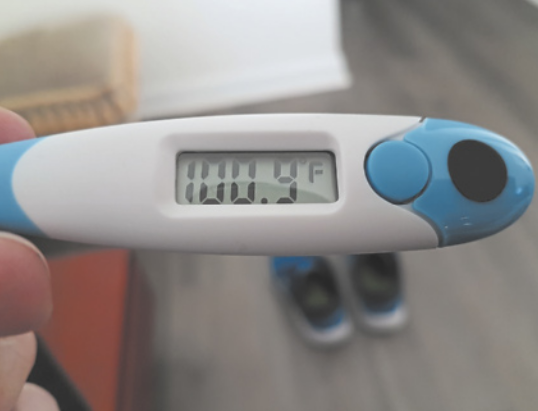
Qual é a tempera-túra indicada na fotografia na escala célcius?
aproximadamente 38,28 °C
Página duzentos e cinquenta e um
Figuras semelhantes
Semelhança é a característica do quê é semelhante. Na linguagem do dia a dia, dois objetos são semelhantes quando são"parecidos".
Em Matemática, o conceito de semelhança usado em figuras geométricas é diferente daquele de uso cotidiano. pôdêmos associar a ideia de figuras semelhantes à ampliação ou redução de uma imagem, mantendo proporcionalmente a sua forma.
É o quê acontece, por exemplo, quando damos zoom em uma fotografia no celular ou no computador: ela é ampliada, mas as proporções são mantidas.
Agora, obissérve as imagens a seguir em quê a fotografia foi ampliada da situação A para a situação B.

Quando ampliamos (ou reduzimos) a fotografia proporcionalmente, as medidas dos ângulos são preservadas e as medidas dos segmentos correspondentes aos da fotografia original são aumentadas (ou reduzidas) na mesma razão.
No caso do exemplo, essa razão de ampliação é dada por:
ou
Assim, dizemos quê a fotografia original e a ampliada (ou a reduzida) são figuras semelhantes. A seguir, vamos formalizar esse conceito de semelhança para os polígonos.
Página duzentos e cinquenta e dois
Polígonos semelhantes
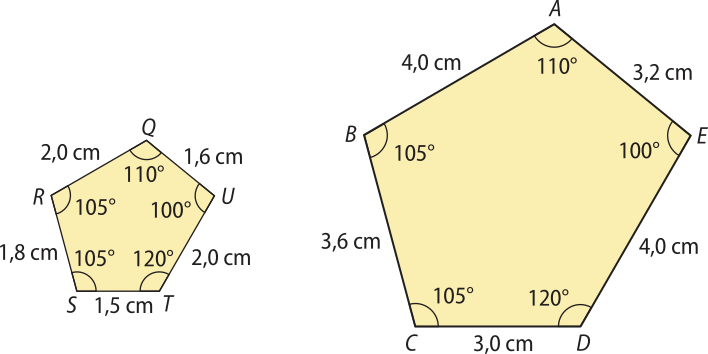
Considere os pentágonos QRSTU e ABCDE representados a seguir.
Saiba quê...
Os ângulos e são ângulos correspondentes, assim como os pares de ângulos e , e , e , e .
Vamos analisar alguns de seus elemêntos.
Comparando as medidas dos ângulos internos, obissérve quê e possuem a mesma medida: 110°. Isso também póde sêr indicado como:
med( ) = med( ) = 110°
Comparando os demais pares de ângulos, ordenadamente, temos:
med( ) = med( ) = 105°
med( ) = med( ) = 105°
med() = med( ) = 120°
med() = med( ) = 100°
Note quê os ângulos correspondentes dos pentágonos têm a mesma medida, isto é, são congruentes. Nesse caso, escrevemos:
Analisando as medidas dos lados correspondentes, QR e AB, temos:
QR = 2,0 cm e AB = 4,0 cm
Comparando, ordenadamente, as medidas dos pares de lados correspondentes, temos:
RS = 1,8 cm e BC = 3,6 cm
ST = 1,5 cm e cê dê = 3,0 cm
TU = 2,0 cm e DE = 4,0 cm
UQ = 1,6 cm e EA = 3,2 cm
Perceba quê os lados correspondentes são proporcionais:
Como os ângulos internos são ordenadamente congruentes e os lados correspondentes dos pentágonos são proporcionais, dizemos quê os pentágonos QRSTU e ABCDE são semelhantes.
Indicamos: pentágono QRSTU ∼ pentágono ABCDE
∼ sín-bolo de semelhança
Página duzentos e cinquenta e três
pôdêmos definir quê:
Dois polígonos são semelhantes quando satisfazem duas condições: os ângulos correspondentes são congruentes e os lados correspondentes são proporcionais.
Observações:
• Os lados (ou ângulos) correspondentes também são chamados de lados (ou ângulos) homólogos.
• O número k obtído pela razão entre as medidas dos lados homólogos é chamado de razão de semelhança. No exemplo dado, temos k = .
• Se dois polígonos são semelhantes e têm razão de semelhança k, então a razão entre as respectivas alturas, entre os perímetros ou entre quaisquer outras medidas lineares correspondentes também é k.
Dois polígonos são congruentes se eles são semelhantes e a razão de semelhança é 1.
Saiba quê...
Se duas figuras A e B são semelhantes e têm, nessa ordem, razão de semelhança k > 1, então a figura A é uma ampliação da figura B. Se a razão de semelhança for k < 1, então a figura A será uma redução da figura B.
ATIVIDADE RESOLVIDA
3. Os pentágonos ABCDE e MNOPQ são semelhantes. Sabendo quê o perímetro do pentágono ABCDE é 8,7 cm, determine a medida de seus lados.
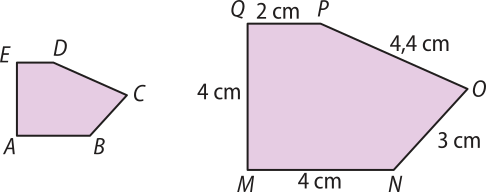
Resolução
Indicando as medidas dos lados do pentágono ABCDE por x, y, z, v e w, como mostrado na imagem, escrevemos a expressão quê indica a razão de semelhança:
Indicando o perímetro dos polígonos por P, temos:
PMNOPQ = 2 + 4,4 + 3 + 4 + 4 = 17,4
Como observado anteriormente, a razão entre os perímetros de polígonos semelhantes é igual à razão de semelhança entre eles.
Assim:
Além díssu, podemos escrever:
⇒ x = 2
⇒ y = 1,5
⇒ z = 2,2
⇒ v = 1
⇒ w = 2
Portanto, AB = 2 cm, BC = 1,5 cm, cê dê = 2,2 cm, DE = 1 cm e EA = 2 cm.
Página duzentos e cinquenta e quatro
ATIVIDADES
9. Verifique se os paralelogramos ABCD e XYZW são semelhantes.
São semelhantes.
10. Os quadriláteros ABCD e MNPQ a seguir são semelhantes, e o lado do primeiro corresponde ao lado do segundo. Se a razão de semelhança do quadrilátero ABCD para o quadrilátero MNPQ é de , determine a medida do lado do quadrilátero MNPQ.
10
11. Sobre polígonos semelhantes e congruentes, é correto afirmar quê:
a) se as medidas dos lados de um dos polígonos são iguais às medidas dos lados do outro, eles são congruentes.
b) dois polígonos com número de lados diferentes podem sêr semelhantes.
c) dois polígonos semelhantes são sempre congruentes.
d) dois polígonos congruentes são sempre semelhantes.
e) dois polígonos são semelhantes se as somas das medidas dos ângulos internos dêêsses polígonos são iguais.
alternativa d
12. A razão de semelhança entre dois decágonos regulares é . Se o perímetro do decágono quê possui o maior lado é 720 mm, qual é a medida do lado, em centimetro, do outro decágono?
4,32 cm
13. Os tampos de duas mesas retangulares são semelhantes. A razão de semelhança entre as medidas dos lados do maior para o menor é 1,5. Se as dimensões do tampo da mesa menor são 3,5 m e 2,5 m, determine o perímetro do tampo da mesa maior.
18 m
14. ![]() Os trapézios ABCD e MNPQ representados a seguir são semelhantes.
Os trapézios ABCD e MNPQ representados a seguir são semelhantes.
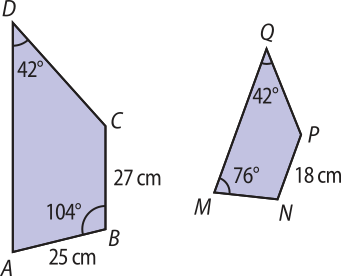
Reúna-se a um colega, elaborem duas perguntas quê envolvam os dados dessas figuras e respondam-nas.
Resposta pessoal. Ver as Orientações para o professor.
Semelhança de triângulos
Aprendemos quê, estabelecida uma correspondência entre os vértices, dois polígonos são semelhantes quando se verificam duas condições: os ângulos correspondentes são congruentes e os lados homólogos são proporcionais.
Entretanto, os triângulos constituem um caso especial. É possível estabelecer um conjunto de critérios mínimos quê garantam a semelhança entre dois triângulos sem quê seja necessário verificar as três congruências dos ângulos e a proporcionalidade entre todos os lados. Esses conjuntos de critérios podem sêr demonstrados e são conhecidos como casos de semelhança.
A seguir, apresentamos três deles.
Página duzentos e cinquenta e cinco
Casos de semelhança de triângulos
1º caso: Ângulo, Ângulo (AA)
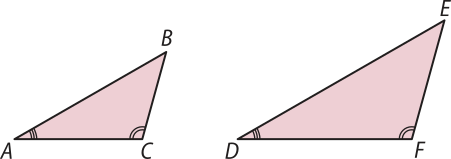
⇒ (triângulo)" ABC ∼ (triângulo)" DEF
Se dois triângulos possuem dois ângulos internos ordenadamente congruentes, então esses triângulos são semelhantes.
2º caso: Lado, Ângulo, Lado (LAL)

⇒ (triângulo)" ABC ∼ (triângulo)" DEF
Se dois triângulos possuem dois lados correspondentes proporcionais e os ângulos formados por esses lados são congruentes, então esses triângulos são semelhantes.
3º caso: Lado, Lado, Lado (LLL)
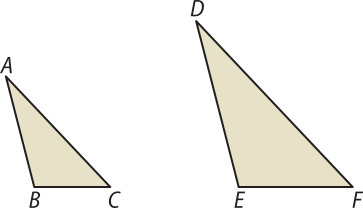
⇒ (triângulo)"ABC ∼(triângulo)"DEF
Se dois triângulos possuem os três lados correspondentes proporcionais, então esses triângulos são semelhantes.
Propriedade da semelhança de triângulos
Consideremos o triângulo ABC. Nele, vamos traçar uma reta r, paralela ao lado , quê vai intersectar o lado no ponto P e o lado no ponto Q.
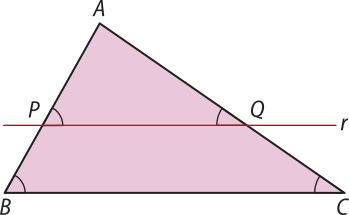
Do paralelismo de r com o lado , temos e , quê são ângulos correspondentes.
Assim, os triângulos APQ e ABC têm ângulos ordenadamente congruentes. Portanto, pelo caso AA de semelhança, concluímos quê (triângulo)"APQ ∼ (triângulo)"ABC.
De maneira geral, temos quê:
Toda reta paralela a um lado de um triângulo quê intersecta os outros dois lados em pontos distintos determina um novo triângulo semelhante ao primeiro.
Página duzentos e cinquenta e seis
Consequências da semelhança de triângulos
A partir da semelhança de triângulos, algumas consequências podem sêr demonstradas.
A seguir, apresentamos duas delas.
1ª consequência
Se a razão de semelhança entre as medidas dos lados de dois triângulos é igual a k, então:
• a razão entre os perímetros também é k;
• a razão entre as medidas de duas alturas homólogas também é k;
• a razão entre as medidas de duas bissetrizes homólogas também é k;
• a razão entre as áreas é igual a k2.
Vamos demonstrar quê a razão entre as áreas de dois triângulos semelhantes (de razão de semelhança k) é k2.
Demonstração
Considere os triângulos ABC e DEF, tais quê (triângulo)"ABC ∼ (triângulo)"DEF, como mostram as figuras. Então, pela semelhança de triângulos, temos:
Considerando as alturas homólogas AG e DH, temos, pelo caso AA de semelhança, (triângulo)"ABG ∼ (triângulo)"DEH. Então, podemos escrever:
Calculando as respectivas áreas, indicadas por S, temos:
• Área (triângulo)"ABC: S1 =
• Área (triângulo)"DEF: S2 =
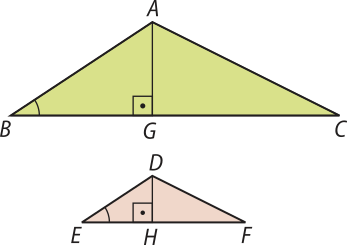
2ª consequência
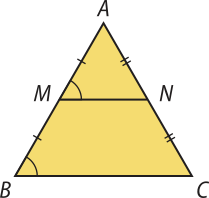
Se um segmento de reta une os pontos médios de dois lados de um triângulo, então esse segmento de reta é paralelo ao terceiro lado, e sua medida é mêtáde da medida do terceiro lado.
Demonstração
Os pontos M e N são os pontos médios dos lados e , respectivamente. Daí, temos quê AM = MB e AN = NC.
Assim, os triângulos AMN e ABC são semelhantes pelo caso LAL, pois o ângulo A ˆ é comum aos dois triângulos e .
Logo, pela semelhança dos triângulos, temos quê:
•
•
•
Portanto, como os ângulos e são congruentes, assim como o par de ângulos e , temos quê // .
Página duzentos e cinquenta e sete
ATIVIDADES RESOLVIDAS
4. Considere um triângulo ABC e uma reta r paralela ao lado . As intersecções de r com e são os pontos D e E, respectivamente, de modo quê AD = 6 cm e DB = 9 cm. Se o lado do triângulo méde 20 cm, determine as medidas dos segmentos de reta formados pela intersecção da reta r com o lado .
Resolução
Por meio das informações presentes no enunciado, é possível construir a seguinte figura, em quê x e y representam as medidas dos segmentos de reta e , respectivamente, determinados em pela reta r.
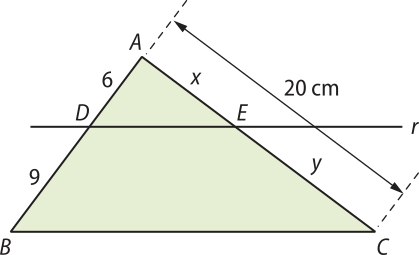
Pela propriedade da semelhança, os triângulos ABC e ADE são semelhantes. Então, podemos escrever:
⇒ 15x = 120 ⇒ x = 8
x + y = 20 ⇒ 8 + y = 20 ⇒
⇒ y = 20 − 8 ⇒ y = 12
Portanto, AE = 8 cm e EC = 12 cm.
5. Observe a figura a seguir e determine o valor de x.
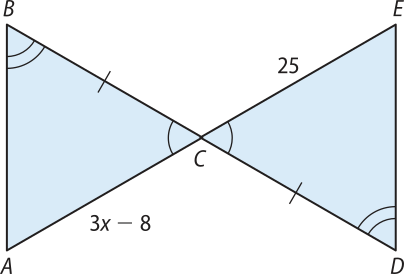
Resolução
De acôr-do com a figura, os lados e são congruentes, assim como os ângulos e e os ângulos B A e D E(opostos pelo vértice).
Então, pelo caso AA de semelhança, podemos afirmar quê (triângulo)"BCA ∼ (triângulo)" DCE, com razão de semelhança igual a 1, pois = 1.
Portanto, os triângulos são também congruentes. Assim, temos:
⇒ 3x − 8 = 25 ⇒
⇒ 3x = 25 + 8 ⇒ 3x = 33 ⇒ x = 11
6. Conta-se quê Tales de Mileto foi desafiado a medir a altura da grande pirâmide de Quéops.
Para isso, ele usou os seus conhecimentos de proporcionalidade e semelhança de triângulos e a ideia de quê os raios solares são paralelos e incidem com a mesma inclinação sobre a superfícíe terrestre. Observe a figura a seguir.
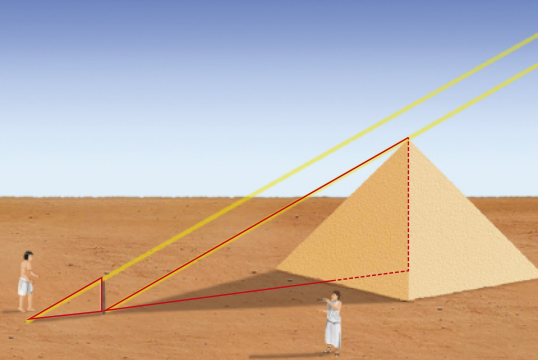
Supondo quê a estaca fincada no chão tinha altura igual a 1,5 métro e a sombra dessa estaca, 2,3 metros, e sabendo quê o lado da base quadrada da pirâmide tem medida igual a 230 metros e quê a altura encontrada por Tales foi de 146 metros, determine a medida da sombra da pirâmide no solo no momento da medição.
Página duzentos e cinquenta e oito
Resolução
Como os raios solares incidem com a mesma inclinação sobre a superfícíe terrestre, podemos representar a situação com o esquema a seguir.
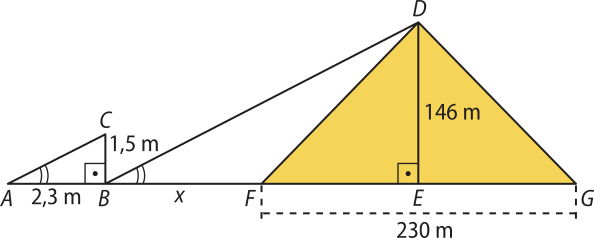
Nesse esquema, BC é a medida da altura e AB é a medida da sombra da estaca; BF = x é a medida da sombra da pirâmide; FE = 115 m é a distância do centro da pirâmide ao lado quê está de frente para a estaca; e DE é a altura da pirâmide.
Os triângulos ABC e BED são semelhantes pelo caso AA. Logo, temos a seguinte proporção:
⇒
⇒ 1,5 ⋅ (x + 115) = 2,3 ⋅ 146 ⇒
⇒ 1,5x + 172,5 = 335,8 ⇒ 1,5x = 335,8 − 172,5 ⇒
⇒ 1,5x = 163,3 ⇒ x ≃ 108,9
Portanto, a medida da sombra da pirâmide de Quéops no momento da medição era aproximadamente igual a 108,9 metros.
ATIVIDADES
15. (UEMA) Um prédio e um poste projetam simultaneamente sombras de 20 m e 4 m, respectivamente. Se a altura do poste é 5 m, pode-se concluir quê a altura do prédio é:
a) 25 m
b) 20 m
c) 16 m
d) 15 m
e) 10 m
alternativa a
16. A moradia de Júlia está situada na mêtáde do caminho entre a escola e o local de trabalho dela. Júlia observou quê a moradia também fica exatamente na mêtáde do caminho entre o supermercado e o parque. Sabe-se quê a distância entre a escola e a moradia de Júlia é de (2x + 7) km, e a distância da moradia de Júlia até o local de trabalho dela é de 21 km. Além díssu, a distância entre o supermercado e a moradia de Júlia é x km, conforme a imagem a seguir. Para ir até o parque, saindo da moradia dela, quantos kilometros Júlia deverá percorrer?
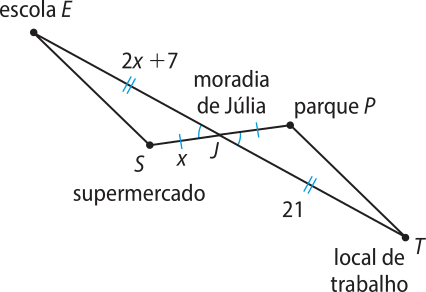
7 km
17. (UFV-MG) Para determinar o comprimento de uma lagoa, utilizou-se o esquema indicado pela figura abaixo, onde os segmentos e são paralelos.
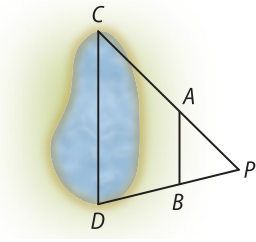
Sabendo-se quê AB = 36 m, BP = 5 m e DP = 40 m, o comprimento cê dê da lagoa, em metros, é:
a) 248
b) 368
c) 288
d) 208
e) 188
alternativa c
18. Considere o triângulo ABC a seguir, de modo quê AB = 5 cm e AC = 7 cm. O polígono AFDE é um quadrado, tal quê os pontos D, E e F pertencem aos lados , e , respectivamente. De acôr-do com as informações, qual é a medida do lado do quadrado?
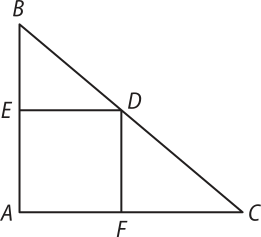
a) 2 cm
b) 3 cm
c) cm
d) cm
e) 1,5 cm
alternativa c
Página duzentos e cinquenta e nove
19. (Cefet-MG) A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 m, respectivamente. Um jogador deve lançar a bola branca do ponto B e acertar a preta no ponto P, sem acertar em nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto L, de modo quê a mesma possa rebater e colidir com a preta.
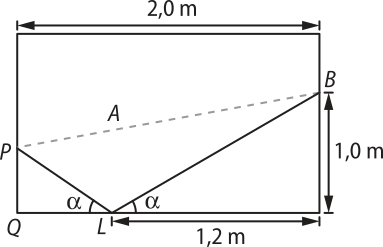
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de P a Q, em cm, é aproximadamente
a) 67
b) 70
c) 74
d) 81
alternativa a
20. (UEA-AM) Considere o retângulo ABCD e o triângulo retângulo BEF, com a hipotenusa intersectando o lado do retângulo, no ponto Q, e os pontos B, C e E alinhados, conforme a figura.
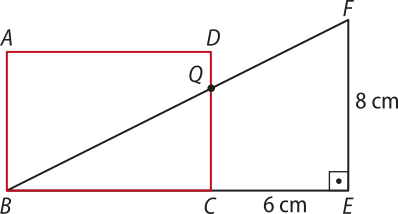
Sabendo quê EF = 8 cm, BE = 15 cm, CE = 6 cm e DQ = 1,2 cm, a área do retângulo ABCD é igual a
a) 72,0 cm2.
b) 54,0 cm2.
c) 63,0 cm2.
d) 67,5 cm2.
e) 58,5 cm2.
alternativa b
21. (Unicamp-SP) Uma rampa de inclinação constante, como a quê dá acesso ao Palácio do Planalto em Brasília, tem 4 metros de altura na sua parte mais alta. Uma pessoa, tendo começado a subi-la, nota quê após caminhar 12,3 métros sobre a rampa está a 1,5 metro de altura em relação ao solo.
a) Faça uma figura ilustrativa da situação descrita.
Ver as Orientações para o professor.
b) Calcule quantos metros a pessoa ainda deve caminhar para atingir o ponto mais alto da rampa.
20,5 m
22. (Fuvest-SP) Um marceneiro possui um pedaço de madeira no formato de um triângulo retângulo, cujos catetos médem 12 cm e 35 cm. A partir desta peça, ele precisa extrair o maior quadrado possível, de tal forma quê um dos ângulos rétos do quadrado coincida com o ângulo reto do triângulo. A medida do lado do quadrado desejado pelo marceneiro está mais próxima de
a) 8,0 cm.
b) 8,5 cm.
c) 9,0 cm.
d) 9,5 cm.
e) 10,0 cm.
alternativa c
23. (Enem/MEC) O dono de um sítio pretende colocar uma hás-te de sustentação para melhor firmar dois póstes de comprimentos iguais a 6 m e 4 m. A figura representa a situação real na qual os póstes são descritos pêlos segmentos AC e BD e a hás-te é representada pelo segmento EF, todos perpendiculares ao solo, quê é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço quê serão instalados.
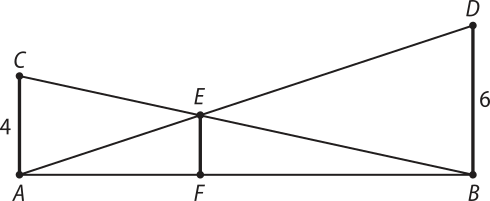
Qual deve sêr o valor do comprimento da hás-te EF?
a) 1 m
b) 2 m
c) 2,4 m
d) 3 m
e)2√ 6 m
alternativa c
24. Os lados de um triângulo médem 10 cm, 12 cm e 18 cm. Determine as medidas dos lados de um triângulo semelhante ao anterior cujo perímetro é 60 cm.
15 cm, 18 cm e 27 cm
• ![]() Elabore uma atividade parecida com essa, alterando as medidas dos lados do triângulo e o perímetro do triângulo semelhante.
Elabore uma atividade parecida com essa, alterando as medidas dos lados do triângulo e o perímetro do triângulo semelhante.
Depois, troque-a com a atividade de um colega e resolvam as atividades um do outro.
Resposta pessoal.
Página duzentos e sessenta
CONEXÕES com...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
Picos mais altos do Brasil
Você conhece os picos mais altos do Brasil? O Instituto Brasileiro de Geografia e Estatística (hí bê gê hé) fez a última atualização das altitudes dos picos em março de 2018. Leia o texto a seguir sobre esse assunto.
Geociências: hí bê gê hé revê as altitudes de sete pontos culminantes
[…]
A determinação da altitude em locais de difícil acesso sempre representou um grande desafio para o campo das geociências. No passado, a alternativa era o nivelamento barométrico, realizado com o barôometro, instrumento criado no século 17 e utilizado para medir a pressão atmosférica, altitude e mudanças no tempo. No entanto, os valores obtidos apresentavam imprecisões da ordem de metros. Com o advento das técnicas de posicionamento associadas aos Sistemas Globais de Navegação por Satélites (GNSS), em especial ao Sistema de Posicionamento Global (GPS), os levantamentos passaram a fornecer coordenadas (latitude, longitude e altitude) com alta precisão.
Utilizando a tecnologia GPS, em maio de 2004, o hí bê gê hé iniciou o projeto Pontos Culminantes, com o objetivo de determinar altitudes mais precisas para os picos mais elevados do Brasil, utilizando equipamentos de rastreamento GPS associados às modernas técnicas de posicionamento preciso por satélites. O projeto, executado em cooperação com o Instituto Militar de Engenharia (IME), foi concluído em 2005, com a medição do Monte Roraima (Serra de Pacaraíma, RR, divisa entre Brasil, Venezuela e Guiana) e outros seis pontos culminantes: Pico da Neblina (Serra do Imeri, AM), Pico 31 de Março (Serra do Imeri), Pico da Bandeira (Serra do Caparaó), Pico Pedra da Mina (Serra da Mantiqueira), Pico das Agulhas Negras (Serra da Mantiqueira) e Pico Cristal (Serra do Caparaó).
[…]
GEOCIÊNCIAS: hí bê gê hé revê as altitudes de sete pontos culminantes. Rio de Janeiro: Agência hí bê gê hé notícias, 19 mar. 2018. Disponível em: https://livro.pw/xhpui. Acesso em: 29 set. 2024.
Observe a altitude dos picos mais altos do Brasil.
Altitude anterior e revista de sete pontos culminantes no Brasil
Ponto culminante |
Nova altitude (m) |
Altitude anterior (m) |
|---|---|---|
Pico da Neblina |
2.995,30 |
2.993,78 |
Pico 31 de março |
2.974,18 |
2.972,66 |
Pico da Bandeira |
2.891,32 |
2.891,98 |
Pico Pedra da Mina |
2.798,06 |
2.798,39 |
Pico das Agulhas Negras |
2.790,94 |
2.791,55 |
Pico do Cristal |
2.769,05 |
2.769,76 |
Monte Roraima |
2.734,05 |
2.734,06 |
Fonte dos dados: GEOCIÊNCIAS: hí bê gê hé revê as altitudes de sete pontos culminantes. Rio de Janeiro: Agência hí bê gê hé Notícias, 19 mar. 2018. Disponível em: https://livro.pw/mxfum. Acesso em: 9 set. 2024.
Página duzentos e sessenta e um

O Pico da Neblina está localizado na serra do Imeri, no Amazonas, na fronteira com a Venezuela e a Colômbia, e dá nome ao Parque Nacional do Pico da Neblina, quê foi criado em 1979 com o objetivo de proteger a riqueza natural da região amazônica.
Você sabia quê existem alguns métodos para calcular grandes comprimentos sem aparelhos sofisticados e, ainda assim, obtêr resultados confiáveis? Tal medição utiliza conceitos da semelhança de triângulos, quê estudamos neste Capítulo.
Agora, faça o quê se pede nas atividades a seguir.
1. De acôr-do com a tabéla quê acompanha o texto, percebe-se quê houve uma diferença entre as medidas antigas e as atuáis dos pontos culminantes. Qual foi o motivo dessa diferença?
Ver as Orientações para o professor.
2. ![]() Essa mesma tabéla traz dados sobre sete picos. Reúna-se a mais um colega, e pesquisem a localização de cada um deles. Depois, respondam:
Essa mesma tabéla traz dados sobre sete picos. Reúna-se a mais um colega, e pesquisem a localização de cada um deles. Depois, respondam:
a) Em quais estados do Brasil esses picos estão localizados?
Picos da Neblina e 31 de março – Amazonas; Pico da Bandeira – Espírito Santo/Minas Gerais; Pico Pedra da Mina – Minas Gerais/São Paulo; Pico das Agulhas Negras – Rio de Janeiro; Pico do Cristal – Minas Gerais; Monte Roraima – Roraima.
b) Pesquisem se há algum pico próximo da cidade em quê vocês moram. Qual é a altura dele?
A resposta depende do local em quê os estudantes residem.
3. Em determinada hora do dia, Cláudio estava passeando pelo Parque Nacional do Pico da Neblina e reparou quê a sua sombra tinha um comprimento de 1,5 m. Nesse mesmo momento, qual seria a distância entre a extremidade da sombra produzida pelo Pico da Neblina e a projeção no solo do ponto mais alto do pico, considerando quê a altura do pico é 2 995,3 m e quê a altura de Cláudio é 1,8 m?
A distância seria de, aproximadamente, 2 496,08 m.
4. ![]() Reúna-se a alguns côlégas e façam uma pesquisa na internet para saber o quê é um relatório de experimento científico e como se realiza o método de medição de alturas utilizando um prato com á gua.
Reúna-se a alguns côlégas e façam uma pesquisa na internet para saber o quê é um relatório de experimento científico e como se realiza o método de medição de alturas utilizando um prato com á gua.
Depois, façam o quê se pede em cada item.
Ver as Orientações para o professor.
a) Escolham um edifício, uma torre ou uma construção de seu município e empreguem o método de medição do prato com á gua. Feito isso, façam um relatório do experimento, quê deve conter: materiais usados, tipo e local da construção medida, procedimento detalhado, incluindo a teoria matemática, e, por fim, conclusões obtidas.
b) Apresentem o relatório do experimento para a turma de vocês em sala de aula. Depois, conversem sobre a experiência.
Página duzentos e sessenta e dois
Relações métricas no triângulo retângulo
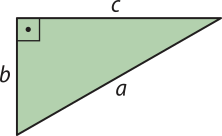
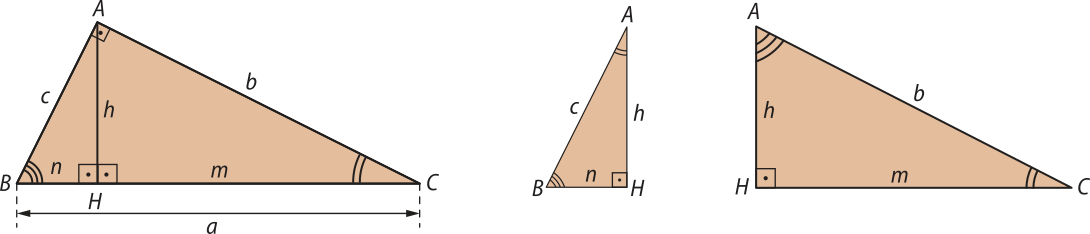
No Ensino Fundamental, você estudou quê, na Geometria Euclidiana, a soma das medidas dos ângulos internos de um triângulo qualquer é igual a 180°. Assim, como um triângulo retângulo tem um ângulo interno medindo 90°, podemos concluir quê a soma das medidas dos outros dois ângulos agudos também é 90°, ou seja, esses ângulos agudos do triângulo retângulo são complementares. Além díssu, o lado ôpôsto ao ângulo reto é o maior lado, chamado de hipotenusa. Os outros dois lados, perpendiculares entre si, são chamados de catetos.

(alfa)" + (beta)" = 90°
(beta)" = 90° − (alfa)"
Teorema de Pitágoras
Provavelmente você estudou no Ensino Fundamental o teorema de Pitágoras, uma conhecida relação entre as medidas dos lados de um triângulo retângulo. Vamos relembrar esse teorema:
Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos:
a2 = b2 + c2

Em quê:
• a é a medida da hipotenusa;
• b e c são as medidas dos catetos.
Observe, a seguir, uma das muitas demonstrações dêêsse teorema.
Demonstração
Considere o triângulo retângulo representado na figura 1, em quê a é a medida da hipotenusa e b e c são as medidas dos catetos. Queremos provar quê a2 = b2 + c2.
Com quatro triângulos retângulos congruentes a esse, construímos um quadrado MNPQ, cujo lado méde (b + c).
Página duzentos e sessenta e três
Na figura 2, obissérve quê, inscrito ao quadrado MNPQ, temos o quadrilátero TRSV. Vamos mostrar quê o quadrilátero TRSV é um quadrado. Acompanhe:
• Os quatro lados de TRSV são congruentes, pois são as hipotenusas dos triângulos retângulos.
• Os ângulos internos de TRSV são rétos, pois, em cada um dos seus vértices, por exemplo, em R, temos três ângulos adjacentes suplementares, sêndo dois deles os ângulos agudos do triângulo retângulo, e o outro, o ângulo interno de TRSV com vértice em R. Como os ângulos agudos do triângulo retângulo médem (alfa)" e 90° − (alfa)", o ângulo interno do quadrilátero TRSV méde 90°. De maneira análoga, podemos provar quê os outros ângulos internos − , e − do quadrilátero TRSV são rétos.
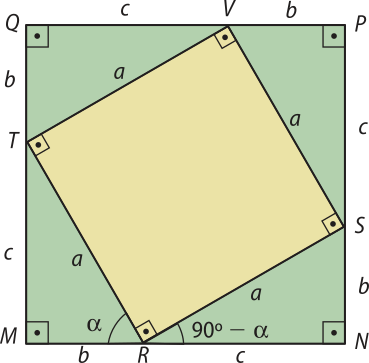
Assim, fica demonstrado quê o quadrilátero TRSV é um quadrado.
Agora, considere:
• AMNPQ a área do quadrado MNPQ;
• ATRSV a área do quadrado TRSV;
• A(triângulo)" a área do triângulo retângulo dado.
Da figura 2, obtemos:
AMNPQ = ATRSV + 4 ⋅ A(triângulo)"
(b + c)2 = a2 + 4 ()
Desenvolvendo essa expressão, temos:
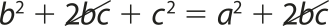
Portanto: a2 = b2 + c2
Para assistir
• TEOREMA de Pitágoras: diferentes demonstrações. [S. I.: s. n.], 2017. 1 vídeo (1 min). Publicado pelo canal IVEPESP. Disponível em: https://livro.pw/xflcu. Acesso em: 9 set. 2024.
Assista a uma animação quê apresenta alguns modos diferentes de mostrar a validade do teorema de Pitágoras.
Outras relações métricas no triângulo retângulo
Além do teorema de Pitágoras, existem outras relações métricas entre os elemêntos de um triângulo retângulo. Inicialmente, vamos identificar esses elemêntos.
Consideremos o triângulo retângulo ABC a seguir, em quê:
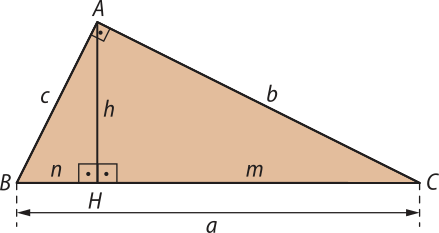
• é a hipotenusa de medida a.
• é o cateto de medida b.
• é o cateto de medida c.
• é a altura relativa à hipotenusa de medida h.
• é a projeção ortogonal, de medida n, do cateto sobre a hipotenusa.
• é a projeção ortogonal, de medida m, do cateto sobre a hipotenusa.
Saiba quê...
A projeção ortogonal de um segmento de reta sobre uma reta r é um segmento de reta obtído pela projeção ortogonal de todos os seus pontos sobre a reta r.
é a projeção ortogonal do segmento de reta sobre a reta r.
Página duzentos e sessenta e quatro
pôdêmos observar quê dividiu o triângulo retângulo ABC em outros dois triângulos também retângulos: HBA e HAC.
Provemos quê os triângulos ABC, HBA e HAC são semelhantes.
Os triângulos ABC e HAC são semelhantes pelo caso AA, pois eles têm o ângulo em comum e um ângulo reto. O mesmo ocorre com os triângulos ABC e HBA, semelhantes pelo caso AA, pois têm o ângulo em comum e um ângulo reto.
Como os triângulos ABC e HBA são retângulos e os ângulos agudos de um triângulo retângulo são complementares, tem-se:
med( ) + med( ) = med( ) + med( B H), em quê − B He, novamente, pelo caso de semelhança AA, os triângulos HBA e HAC são semelhantes.
Assim, concluímos quê os três triângulos são semelhantes.
A partir da semelhança entre os triângulos formados, podemos estabelecer as relações apresentadas a seguir.
Em qualquer triângulo retângulo, o quadrado da medida de um cateto é igual ao produto da medida da hipotenusa pela medida da respectiva projeção do cateto sobre a hipotenusa:
• Como (triângulo)"ABC ∼ (triângulo)"HAC, temos: ⇒ b2 = a ⋅ m
• Como (triângulo)"ABC ∼ (triângulo)"HBA, temos: ⇒ c2 = a ⋅ n
Em qualquer triângulo retângulo, o quadrado da altura relativa à hipotenusa é igual ao produto das medidas das projeções ortogonais dos catetos sobre a hipotenusa:
• Como (triângulo)"HAC ∼ (triângulo)"HBA, temos: ⇒ h2 = m ⋅ n
Em qualquer triângulo retângulo, o produto das medidas dos catetos é igual ao produto da medida da hipotenusa pela medida da altura relativa à hipotenusa:
• Como (triângulo)"ABC ∼ (triângulo)"HAC, temos: ⇒ a ⋅ h = b ⋅ c
Com as duas primeiras relações métricas obtidas, podemos também demonstrar o teorema de Pitágoras. Note quê, com a adição das equações, temos:
b2 + c2 = a ⋅ m + a ⋅ n ⇒ b2 + c2 = a ⋅ (m + n)
Como m + n = a, e fazendo a substituição necessária na equação encontrada, finalizamos a demonstração:
b2 + c2 = a ⋅ a ⇒ a2 = b2 + c2
Página duzentos e sessenta e cinco
ATIVIDADES RESOLVIDAS
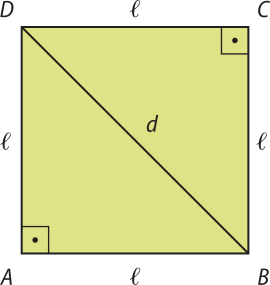
7. Considere o quadrado, cujo lado méde (éli)" e cuja diagonal méde d. Calcule o valor de d em função de (éli)".
Resolução
Aplicando o teorema de Pitágoras no triângulo retângulo BCD, temos:
d2 = (éli)"2 + (éli)"2 ⇒ d2 = 2(éli)"2 ⇒ d = ⇒
⇒ d = _
8. A circunferência tem raio desconhecido.
Sobre ela, marcam-se uma kórda de 8 cm de comprimento e um segmento perpendicular a de 2 cm de comprimento, de modo quê M é um ponto de e O é o centro da circunferência. Com esses dados, determine a medida do raio da circunferência.
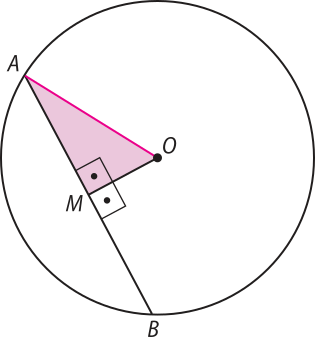
Resolução
Na figura dada, traçando-se um raio de O a B, forma-se o triângulo isósceles AOB, pois OA = OB (raios) e, como é perpendicular à base , temos AM = MB. Logo, M é ponto médio da kórda . Então:
AM = ⇒ AM = 4
Considerando o triângulo retângulo OMA e aplicando o teorema de Pitágoras, temos:
(OA)2 = (OM)2 + (AM)2 ⇒ (OA)2 = 22 + 42 ⇒
⇒ OA2 = 20 ⇒ OA = _ = 2
Portanto, o raio da circunferência méde 2 cm.
ATIVIDADES
25. (Enem/MEC) Na figura apresentada abaixo, quê representa o projeto de uma escada com 5 degraus da mesma altura, o comprimento total do corrimão é igual a:
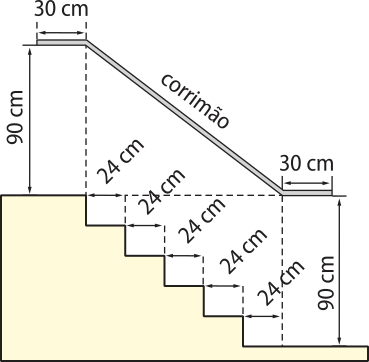
a) 1,8 m
b) 1,9 m
c) 2,0 m
d) 2,1 m
e) 2,2 m
alternativa d
26. ![]() No triângulo retângulo ABC, determine as medidas m, n, h e c indicadas.
No triângulo retângulo ABC, determine as medidas m, n, h e c indicadas.
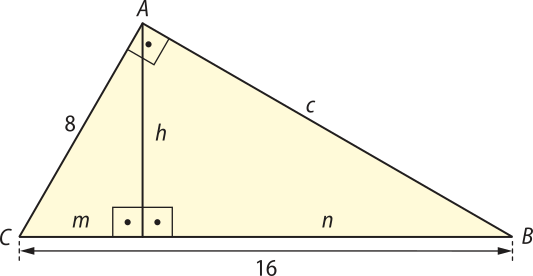
m = 4; n = 12; h = ; c =
27. (UnB-DF) Em um triângulo retângulo, um dos catetos méde 16 metros. Determine, em metros, a medida da hipotenusa, sabendo quê a medida desta excede a medida de outro cateto em oito metros.
20 m
Página duzentos e sessenta e seis
28. Um triângulo retângulo tem sua hipotenusa medindo 5 cm e a altura relativa a essa hipotenusa com medida de 2,4 cm. Com as informações fornecidas, é possível determinar as medidas, em centimetro, dos catetos?
Justifique. Se não for possível, explicite pelo menos uma informação quê tornaria possível resolver o problema.
Não, pois faltam dados. Ver as Orientações para o professor.
29. (FGV-SP) Na figura a seguir, ABCD é um retângulo e AMCN é um losango.
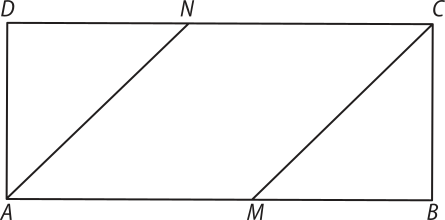
Determine a medida do segmento , sabendo quê AB = 2AD = 20 cm.
aproximadamente 16 cm
30. (hú- hê- érre jota) Segundo historiadores da matemática, a análise de padrões como os ilustrados a seguir possibilitou a descoberta das triplas pitagóricas.

Observe quê os números inteiros 32, 42 e 52, representados respectivamente pelas 2ª, 3ª e 4ª figuras, satisfazem ao Teorema de Pitágoras.
Dessa forma (3, 4, 5) é uma tripla pitagórica.
Os quadrados representados pelas 4ª, 11ª e n ª figuras determinam outra tripla pitagórica, sêndo o valor de n igual a:
a) 10
b) 12
c) 14
d) 16
alternativa b
31. (Unitau-SP) Uma rê-de de á gua potável ligará uma central de abastecimento, situada à margem de um rio de 400 m de largura (considerada constante), a um conjunto habitacional, situado na outra margem, através dos pontos USR, como mostra a figura.
O custo da instalação da tubulação através do rio é de R$ 830,00 o métro, enquanto, em térra, custa R$ 400,00.
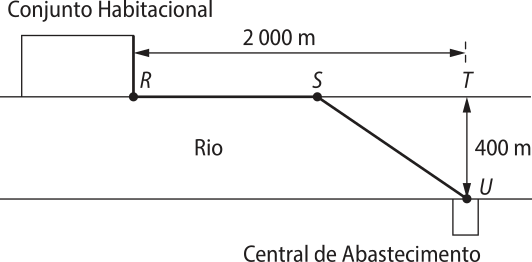
Se a distância do conjunto habitacional até o ponto S for igual a 1.700 metros, pode-se afirmar, CORRETAMENTE, quê o custo de instalação da rê-de de á gua potável será de:
a) R$ 1.611.000,00
b) R$ 1.012.000,00
c) R$ 1.132.000,00
d) R$ 1.095.000,00
e) R$ 1.321.000,00
alternativa d
32. (Unichristus) Um drone, em um ponto A, foi utilizado para localizar os focos de um incêndio na mata. Esse drone está a uma altura H do solo e detecta dois focos de incêndio nos pontos B e C, de acôr-do com a figura abaixo.
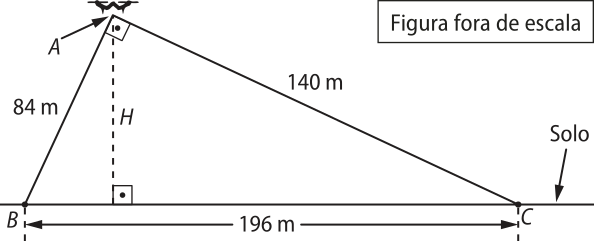
A distância do ponto A (drone) até o ponto B é de 84 m, a distância do ponto A (drone) até o ponto C é de 140 m, e a distância entre os pontos B e C é de 196 m. Se o triângulo ABC é retângulo em A, a altura H do drone em relação ao solo é igual a
a) 45 m.
b) 50 m.
c) 55 m.
d) 60 m.
e) 65 m.
alternativa d
33. ![]() Elabore um problema quê possa sêr resolvido usando uma ou mais relações métricas em um triângulo retângulo. Passe seu problema para um colega resolver e resôuva o problema elaborado por ele.
Elabore um problema quê possa sêr resolvido usando uma ou mais relações métricas em um triângulo retângulo. Passe seu problema para um colega resolver e resôuva o problema elaborado por ele.
Resposta pessoal.
Página duzentos e sessenta e sete
FÓRUM
Uso de drones e conservação ambiental
Você sabe o quê são drones? Também chamados de veículos aéreos não tripulados (vants), esses equipamentos têm sido utilizados em muitos setores, desde entregas de compras ôn láini, passando por inteligência policial, até manejo e fiscalização de áreas de conservação ambiental. Leia a reportagem a seguir, quê trata dêêsse último uso.
Resex usará drone para identificar desmatamento
[…]
A Resex Ipaú-Anilzinho contará agora com drone para ajudar a preservar a Unidade de Conservação [UC]. O objetivo é melhorar a capacidade de monitoramento aéreo das alterações da cobertura vegetal da Resex. O trabalho é fruto da parceria entre o Instituto Chico Mendes de Conservação da Biodiversidade (í cê ême bíu) e o Instituto Federal do Pará (IFPA), do Campus Tucuruí.
[…]
Um dos diferenciais dêêsse tipo de equipamento é a capacidade de capturar imagens do alto e realizar a gravação de vídeos com estabilidade. Há também o Sistema de Detecção de Obstáculos para quê o quadricóptero possa desviar de objetos e evitar acidentes e a função Smart Return Home para quê, com ajuda do GPS, o equipamento volte automaticamente para o ponto inicial.
De acôr-do com o chefe da Resex, a implementação de tecnologias de aerolevantamento no combate ao desmatamento ilegal na região da UC garante maior celeridade de atuação da equipe de trabalho e, até mesmo, otimização de recursos. […]
INSTITUTO CHICO MENDES DE CONSERVAÇÃO DA BIODIVERSIDADE. Resex usará drone para identificar desmatamento. Brasília, DF: í cê ême bíu, 5 abr. 2019. Disponível em: https://livro.pw/ohqtf. Acesso em: 9 set. 2024.
Saiba quê...
• Resex é a abreviação de reserva extrativista. As reservas extrativistas são áreas protegidas pelo govêrno federal. Elas são implementadas com o objetivo de conservar o bioma e a população originária local.
• Ipaú-Anilzinho é uma resex localizada na Vila Anilzinho, na cidade de Baião, no estado do Pará.
Após ler o texto, faça o quê se pede a seguir.
Ver as Orientações para o professor.
• ![]() Em pequenos grupos, pesquisem sobre as Unidades de Conservação (UCs) no Brasil: o quê são, quais são seus objetivos e sua importânssia ecológica e como são classificadas. Listem exemplos dessas unidades localizadas em nosso país. Depois, promovam um fórum, em grupos maiores ou com toda a turma, para apresentar o resultado das pesquisas e debater a importânssia da preservação dos éco-sistemas e da biodiversidade.
Em pequenos grupos, pesquisem sobre as Unidades de Conservação (UCs) no Brasil: o quê são, quais são seus objetivos e sua importânssia ecológica e como são classificadas. Listem exemplos dessas unidades localizadas em nosso país. Depois, promovam um fórum, em grupos maiores ou com toda a turma, para apresentar o resultado das pesquisas e debater a importânssia da preservação dos éco-sistemas e da biodiversidade.

Página duzentos e sessenta e oito
EXPLORANDO A TECNOLOGIA
O picsel e a formação da imagem
O computador é uma máquina quê póde sêr programada, o quê significa quê é possível criar uma sequência de instruções para quê ele execute determinada função. Para programá-lo, é necessário usar uma linguagem de programação, a fim de garantir quê as instruções sêjam passadas de maneira precisa e coesa. Essas linguagens de programação são escritas por nós, sêres humanos, e interpretadas pelo computador como uma linguagem de máquina, quê é uma grande sequência de números.
Se os computadores só armazenam números, como eles reproduzem as imagens? Primeiro, é necessário pensar em como são as telas. Os visores dos computadores são compostos de uma grade de pontos, e cada um dêêsses pontos é chamado de picsel. Em uma tela em preto e branco, o picsel póde assumir uma dessas duas cores. Dessa maneira, as imagens, assim como tudo quê aparece em uma tela, são formadas por uma junção de picsels pretos e brancos, como a letra J a seguir.

Portanto, para quê o computador armazene a imagem, basta quê ele guarde quais picsels são de cada côr. Uma possível maneira de fazer isso é associar uma sequência de números a cada linha, de maneira quê se dêz-creva quais picsels devem sêr brancos e quais devem sêr pretos. Investigue a imagem a seguir e obissérve como essa associação é feita para a letra J!
Pense e responda
Observe a sequência descrita para armazenar a imagem da letra J e responda às kestões.
• Qual é o motivo de esses valores estarem atrelados a essas linhas?
Os números indicam as quantidades de quadrinhos quê serão pintados de branco ou de preto.
• por quê algumas linhas começam com zero? Qual é o impacto díssu na imagem?
Quando a sequência começa com zero, isso significa quê o primeiro quadradinho da linha será preto.
• O quê as linhas com o mesmo cóódigo têm em comum?
As linhas com o mesmo cóódigo produzem imagens iguais.
Página duzentos e sessenta e nove
O primeiro dígito do cóódigo se refere à quantidade de picsels brancos quê estão mais à esquerda da tela. Já o segundo dígito descreve quantos picsels pretos existem depois dos brancos. O terceiro indica quantos brancos há a seguir, e assim por diante até obtêr toda a informação da linha dessa sequência numérica. Esse processo é feito linha a linha. Observe quê, se o primeiro picsel for preto, o cóódigo começará com um zero.
As imagens na tela podem sêr ampliadas, e as proporções são mantidas. Observe como ficaria a ampliação de um picsel em cinco vezes, isto é, a figura semelhante a um único picsel com razão de semelhança 5.
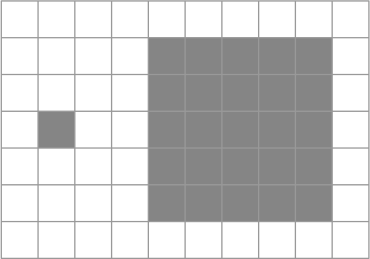
Da mesma maneira, as imagens podem sêr reduzidas. Observe agora como seria a redução de um retângulo 6 × 2 com razão de semelhança 0,5.

Agora, faça o quê se pede na atividade a seguir.
• Em uma malha quadriculada:
Ver as Orientações para o professor.
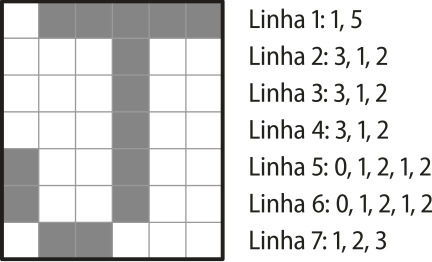
a) desvende a imagem armazenada por um computador com o seguinte cóódigo:
Linha 1: 0, 7
Linha 2: 0, 1, 5, 1
Linha 3: 0, 1, 5, 1
Linha 4: 0, 1, 5, 1
Linha 5: 0, 1, 1, 3, 1, 1
Linha 6: 0, 1, 1, 1, 1, 1, 1, 1
Linha 7: 0, 1, 1, 1, 1, 1, 1, 1
Linha 8: 0, 7
b) crie uma nova figura, com base na imagem do item anterior, com razão de semelhança 2 e escrêeva o cóódigo de armazenamento dessa imagem.
Ver as Orientações para o professor.
Página duzentos e setenta
HISTÓRIA DA MATEMÁTICA
Na Babilônia, mil anos antes de Pitágoras
Leia a seguir o trecho de um texto sobre a Matemática na Babilônia.
Uma vez, vi um carpinteiro marcar dois cortes perpendiculares na madeira: pegou um barbante de comprimento 12 dm, formou um triângulo com lados de comprimentos 3, 4 e 5 dm, e usou o fato de quê o ângulo entre os lados menóres é reto. Não sei se sabia por quê funciona, mas aposto quê ignorava quê a técnica já era usada 4.000 anos atrás.
Plimpton 322, uma tábua de argila encontrada nas escavações da Mesopotâmia e datada de 1800 a.C., é um dos mais famosos documentos matemáticos antigos. Tem inscrita uma tabéla com 15 linhas e 4 colunas de números (na notação sexagesimal da Babilônia) quê formam triplas pitagóricas, ou seja, triplas de números inteiros a, b e c (por exemplo, a = 3, b = 4 e c = 5) tais quê a² + b² = c².
A maioria dos especialistas acredita quê se trata de uma lista de exemplos para uso em sala de aula. Mas a inscrição também aponta um método de cálculo das triplas – mais de mil anos antes de Pitágoras! – quê mostra um conhecimento de geometria quê se pensava só ter sido alcançado na Grécia.

Um leitor chamou a minha atenção para outro documento matemático da Babilônia identificado recentemente. A peça, uma placa circular de argila chamada Si.427, data de 1900 a 1600 a.C. Ela foi escavada em Bagdá em 1894, mas foi dada como perdida até quê o pesquisador australiano Daniel Mansfield a localizou no Museu Arqueológico de Istambul.
Si.427 contém um dos exemplos mais antigos de aplicação da trigonometria, a um dos problemas quê mais motivaram o avanço da matemática no Egito e na Mesopotâmia: a redistribuição de terras. Ela é uma espécie de registro de imóvel, contendo informações legais e geométricas sobre um terreno quê foi dividido para quê fosse vendida a mêtáde dele.
Para fazer essa divisão d fórma precisa, é importante saber traçar perpendiculares a uma reta dada. É aí quê os dois documentos se conéctam: um método prático de obtêr a perpendicularidade é construindo triângulos cujos lados têm comprimentos dados por alguma tripla pitagórica, tal como fez o meu carpinteiro.
Assim, os problemas práticos colocados por Si.427 podem sêr resolvidos utilizando a “teoria” contida em Plimpton 322. […]
VIANA, Marcelo. Na Babilônia, mil anos antes de Pitágoras. Folha de São Paulo, São Paulo, 17 ago. 2021. Disponível em: https://livro.pw/pnmdt. Acesso em: 29 jun. 2024.

Página duzentos e setenta e um
ATIVIDADES COMPLEMENTARES
1. (Unifor-CE)
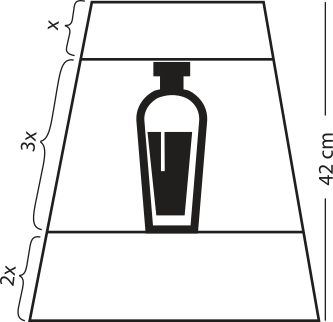
A figura acima mostra um armário de banheiro quê tem o formato de um trapézio. A altura total do armário é de 42 cm e ele está dividido em três compartimentos. As medidas de um dos lados de cada compartimento estão indicadas na figura.
Desprezando a espessura das divisórias, podemos afirmar quê no compartimento do meio podemos colocar um produto com altura mássima de
a) 10 cm.
b) 14 cm.
c) 18 cm.
d) 21 cm.
e) 25 cm.
alternativa d
2. (Unemat-MT) A sombra de uma pessoa quê tem 1,80 m de altura méde 60 cm. No momento, a seu lado, a sombra projetada de um poste méde 2,00 m. Se mais tarde, a sombra do poste diminuir 50 cm, a sombra da pessoa passará a medir:
a) 30 cm
b) 45 cm
c) 48 cm
d) 36 cm
e) 25 cm
alternativa b
3. (IFSC) Para determinar a altura de um poste, Ana utilizou o seguinte artifício, com o auxílio de uma colega: mediu sua sombra e a do poste, obtendo 2,4 m e 3,7 m, respectivamente. Se Ana tem 1,5 m de altura, então é CORRETO afirmar quê a altura do poste é de:
a) 1,0 m
b) 2,3 m
c) 5,9 m
d) 2,6 m
e) 2,0 m
alternativa b
4. (Epcar-MG) Observe a figura a seguir:
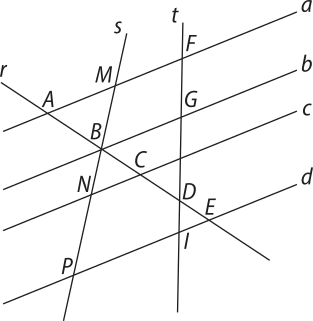
Nela, as retas a, b, c e d são paralelas e são interceptadas pelas retas transversais r, s e t.
Assim, as medidas dos segmentos, em cm, são:
AB = y
DE = 4
HD = 5
BN = 6
BC = 9
FG = z
DI = 2
BP = x
cê dê = 10
GH = m
MN = 16
A soma AB + FH, em cm, é dada por um número divisível por:
a) 3
b) 4
c) 7
d) 11
alternativa a
5. (UFU-MG) Uma área delimitada pelas Ruas 1 e 2 e pelas Avenidas A e B tem a forma de um trapézio ADD(minutos)"A(minutos)", com AD = 90 m e A(minutos)"D(minutos)" = 135 m, como mostra o esquema da figura abaixo.
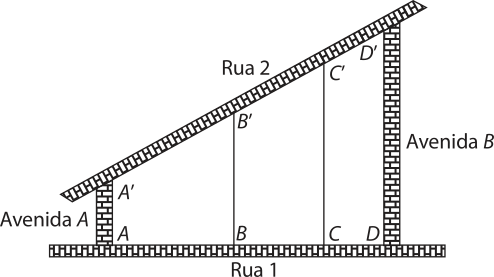
Tal área foi dividida em terrenos ABB(minutos)"A(minutos)", BCC(minutos)"B(minutos)" e cê dê dê(minutos)"C(minutos)", todos na forma trapezôidáu, com bases paralelas às avenidas tais quê AB = 40 m, BC = 30 m e cê dê = 20 m.
De acôr-do com essas informações, a diferença, em metros, A(minutos)"B(minutos)" − C(minutos)"D(minutos)" é igual a:
a) 20.
b) 30.
c) 15.
d) 45.
alternativa b
Página duzentos e setenta e dois
6. (UEA-AM) A circunferência (gama)" está inscrita no triângulo isósceles ABC de altura 12 cm e base medindo 10 cm, conforme a figura:
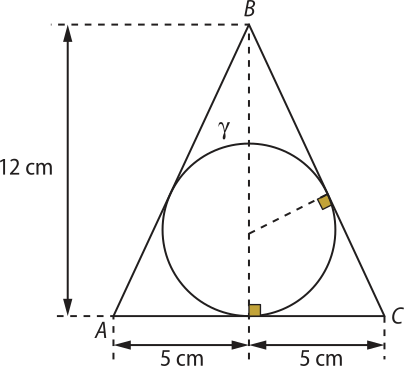
O raio da circunferência (gama)" méde
a) cm
b) cm
c) cm
d) cm
e) cm
alternativa d
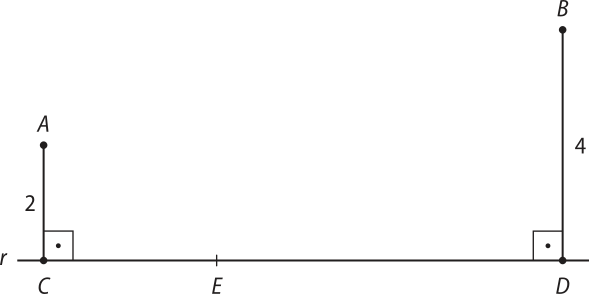
7. (Fuvest-SP) Na figura abaixo, as distâncias dos pontos A e B à reta r valem 2 e 4. As projeções ortogonais de A e B sobre essa reta são os pontos C e D. Se a medida de é 9, a quê distância de C deverá estar o ponto E, do segmento , para quê C A − D B?
a) 3
b) 4
c) 5
d) 6
e) 7
alternativa a
8. (IFPE) Ramon, Alexandre e Milton são alunos do curso de Informática no Campus Afogados da Ingazeira e estão testando um robô para participar de olimpíadas de robótica. Um dos exercícios testes consistia em fazer o robô realizar os seguintes comandos:
I. andar 30 cm em linha reta;
II. realizar um giro de 90° à direita;
III. andar mais 40 cm em linha reta;
IV. retornar ao ponto inicial no menor percurso possível.
Sobre o trajeto percorrido pelo robô, neste teste, é CORRETO afirmar quê:
a) forma um triângulo retângulo cuja hipotenusa méde 50 cm.
b) forma um triângulo retângulo cujo perímetro méde 100 cm.
c) forma um triângulo retângulo e isósceles.
d) forma um paralelogramo cujo perímetro méde 140 cm.
e) forma um paralelogramo cujas diagonais médem 50 cm.
alternativa a
9. (UFRGS-RS) Considere o retângulo ABCD de lados AB = 4 e AD = 2 e o ponto médio M de . Traçando a reta mediatriz do lado , determina-se o segmento , com N na intersecção da mediatriz com . Considere um ponto P construído sobre o segmento , e os segmentos e , como mostra a figura abaixo.
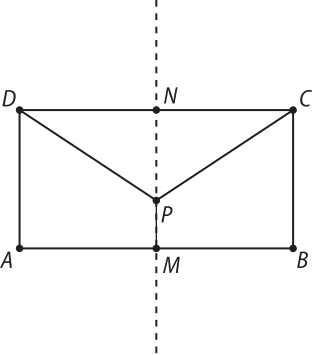
Tomando x como a medida do segmento , considere S(x) a função quê expressa a soma das medidas dos segmentos , e em função de x.
Para 0 ≤ x ≤ 2, S(x), entre as alternativas abaixo, é
a) S(x) = x + .
b) S(x) = (2 − x) + 2(x2 + 4).
c) S(x) = (2 − x) + _.
d) S(x) = x + _.
e) S(x) = (2 − x) + _ .
alternativa e
Página duzentos e setenta e três
10. (Cefet-MG) Na figura a seguir, o segmento representa uma parede cuja altura é 2,9 m. A medida do segmento é 1,3 m, o segmento representa o beiral da casa. Os raios de sól r1 e r2 passam ao mesmo tempo pela casa e pelo prédio, respectivamente.
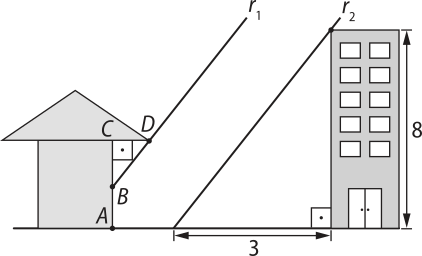
Se r1 é paralelo com r2, então, o comprimento do beiral, em metros, é:
a) 0,60
b) 0,65
c) 0,70
d) 0,75
alternativa a
11. (FGV-SP) O paralelogramo ABCD, indicado na figura, é tal quê BE = , DF = e G é a intersecção de com .
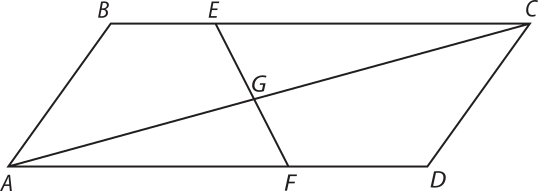
A área do triângulo GCE supera a do triângulo GAF em, aproximadamente:
a) 27%
b) 25%
c) 21%
d) 11%
e) 6%
alternativa a
PARA REFLETIR
Neste Capítulo, estudamos o conceito de proporcionalidade aplicado à Geometria. Conhecemos o teorema de Tales, quê tem como princípio a proporcionalidade entre medidas de segmentos de reta e póde sêr aplicado a diversas situações de cálculo de distâncias, inclusive as inacessíveis ou de difícil medição.
Trabalhamos as noções de figuras congruentes e figuras semelhantes, em particular os triângulos. Além díssu, trabalhamos as relações métricas no triângulo retângulo e o teorema de Pitágoras.
Nas páginas de abertura, fizemos uma discussão sobre a medida de polegadas no comércio de televisões e sobre o quê representa essa medida. Você conseguiu responder às perguntas?
Vamos refletir a respeito das aprendizagens do Capítulo 7:
Respostas pessoais.
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• Cite algumas situações do dia a dia nas quais póde sêr aplicado o teorema de Tales.
• Explique a diferença entre congruência e semelhança.
• Dê exemplos de situações do dia a dia nas quais póde sêr aplicado o teorema de Pitágoras.
Página duzentos e setenta e quatro
