PARTE ESPECÍFICA
Comentários e sugestões de abordagem para êsteeste Volume

O objetivo dêstedeste material é oferecer subsídios para a atividade docente, quêque assume um papel relevante dentro do compléksocomplexo processo de ensino-aprendizagem, d fórmade forma articulada com as propostas apresentadas no Livro do estudante.

Nas Orientações para o professor, há uma descrição explicando de quêque forma estão sêndosendo contempladas neste Volume as habilidades, as competências específicas e as competências gerais da BNCC. Em seguida, são apresentadas estratégias para auxiliar o processo de ensino-aprendizagem, d fórmade forma a contribuir para o desenvolvimento dessas competências e habilidades. Além díssudisso, há sugestões de atividades complementares, instrumentos avaliativos e referências de outros materiais atualizados quêque podem sêrser utilizados. Vale ressaltar quêque esta obra não pretende sêrser a única referência de consulta nem apresentar soluções completas para os desafios enfrentados pêlospelos professores, mas sim constituir uma alternativa para auxiliar a atividade docente e o processo de ensino-aprendizagem, contribuindo para a otimização do planejamento de aulas, sem deixar de respeitar a autonomia do docente quêque age de acôr-doacordo com os desafios reais da comunidade escolar e da turma em quêque atua lecionando.

êsteEste Volume é organizado em 8 capítulos. O qüadroquadro a seguir apresenta uma sugestão de cronograma, considerando 200 dias letivos, consequentemente, 40 semanas de aula. A proposta contempla 34 semanas, considerando 6 semanas para ajustes, avaliações e outras demandas pedagógicas.

Para planejamentos bimestrais, recomenda-se considerar 9 semanas de aula para cada bimestre; para planejamentos trimestrais, 12 semanas; e, para planejamentos semestrais, 17 semanas. No entanto, é importante quêque o professor avalie sua realidade e realize as adequações necessárias conforme o calendário escolar, de modo a privilegiar o desenvolvimento dos estudantes de acôr-doacordo com suas necessidades e com as escôlhasescolhas feitas pela comunidade escolar.

Página trezentos e vinte e nove329

Para todos os blocos semanais, estão disponíveis atividades resolvidas e atividades propostas. Recomenda-se a seleção de parte das atividades para sêrser desenvolvida em sala de aula (individualmente, em duplas ou grupos maiores) e outra parte para sêrser realizada fora do horário de aula.

Professor, caso tenha alunos PcD (Pessoa com Deficiência), recomenda-se a leitura dos textos a seguir.

• SILVA, Luciene de Castro. O lúdico e o conteúdo adaptado: uma proposta para o ensino de matemática voltada ao aluno surdo incluso no ensino médio. 2016. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Departamento de Matemática e Estatística (Demat), Universidade Federal de São João Del-Rei, São João Del-Rei, 2016. Disponível em: https://livro.pw/ncbls. Acesso em: 30 out. 2024.

• BORGES, José AntônioAntonio; BORGES, Pedro Paixão. Matemática para alunos cegos: novas tecnologias desenvolvidas na ú éfi érri jótaUFRJ ampliam o acesso de estudantes com deficiência visual à disciplina, inclusive no ensino superior. Ciência hoje, Rio de Janeiro, n. 348, out. 2018. Infinitas possibilidades. Disponível em: https://livro.pw/zbprg. Acesso em: 30 out. 2024.

No sáitisite Educ@, disponível em: https://livro.pw/rtdcl (acesso em: 30 out. 2024), é possível encontrar trabalhos acadêmicos e artigos relacionados à inclusão de alunos PcD.

Capítulo 1
Conjuntos

Orientações

Neste Capítulo, são estudados conceitos relacionados a Conjuntos. Pretende-se quêque os estudantes possam se apropriar dêêssesdesses conceitos, das propriedades relacionadas, da linguagem utilizada, retomando e ampliando a compreensão sobre conjuntos numéricos, de modo quêque sêjamsejam capazes de fazer uso dêêssedesse conhecimento nos diversos campos da Matemática e na análise de problemas sociais. As discussões e atividades propostas visam contribuir para o desenvolvimento das competências específicas 2, 4 e 5 da área de Matemática e suas Tecnologias. Os estudantes também são convidados a discutir sobre alimentação saudável, o quêque possibilita desenvolver a competência geral 8, destacando o autoconhecimento e o cuidado da saúde física e mental.

No tópico Propriedades da relação de inclusão, recomenda-se explicar quêque:

• a propriedade antissimétrica é utilizada quando se deseja demonstrar quêque dois conjuntos A e B são iguais. Para isso, prova-se quêque todo elemento do conjunto A pertence ao conjunto B e quêque todo elemento do conjunto B pertence ao conjunto A;

• a propriedade transitiva é a base do raciocínio dedutivo, denominado silogismo.

Acompanhe um exemplo de silogismo: Todo sêrser vivo é mortal. Os gatos são sêresseres vivos, logo são mortais. Esse raciocínio é expresso por meio da linguagem de conjuntos do seguinte modo:

Considere A o conjunto dos mortais, B o conjunto dos sêresseres vivos e C o conjunto dos gatos. A primeira afirmação é representada pela relação de inclusão B ⊂ A (B é um subconjunto de A), e a afirmação “os gatos são sêresseres vivos” é representada por C ⊂ B (C é um subconjunto de B). Logo, pela propriedade transitiva, C ⊂ A (C é um subconjunto de A), o quêque significa quêque “os gatos são mortais”.

No tópico Operações entre conjuntos, o primeiro boxe Saiba que… apresenta informações sobre a distinção entre os conectivos ou e e, assim como a relação entre as operações de união e de intersecção de conjuntos. É importante enfatizar essa reflekçãoreflexão, de modo quêque o estudante compreenda os conceitos envolvidos. Esse estudo incentiva a competência geral 7, pois auxilia os estudantes no desenvolvimento da capacidade argumentativa. Sugere-se propor a eles atividades complementares quêque incentivem essa reflekçãoreflexão. Uma possibilidade é apresentada a seguir.

Leia a afirmação a seguir e, com base nela, responda às kestõesquestões em cada item.

Flávia estuda Matemática às segundas-feiras ou às sextas-feiras.

a) Flávia pódepode ter estudado Matemática somente na segunda-feira? Resposta: Sim.

b) Flávia pódepode ter estudado Matemática somente na sexta-feira? Resposta: Sim.

Página trezentos e trinta330

c) Flávia pódepode ter estudado Matemática somente na quarta-feira? Resposta: Não.

d) Flávia pódepode ter estudado Matemática na segunda-feira e na sexta-feira também? Resposta: Sim.

e) Flávia pódepode ter estudado Matemática na segunda-feira, na quarta-feira e na sexta-feira? Resposta: Sim.

A mesma atividade pódepode sêrser refeita, mas com a frase “Flávia estuda Matemática nas segundas-feiras e nas sextas-feiras.”. Nesse caso, as respostas são: a) Não; b) Não; c) Não; d) Sim; e) Sim.

A situação do item d pódepode gerar dúvidas, pois é possível entender equivocadamente quêque o conectivo ou admite apenas uma das possibilidades (apenas A ou apenas B). Para quêque a primeira afirmação seja verdadeira, basta quêque Flávia estude em um dos dois dias (segunda-feira ou sexta-feira), mas isso não exclui outras possibilidades. Da mesma maneira, na situação do item e, ambas as afirmações são verdadeiras.

Para melhor compreensão das Propriedades da união e da intersecção de conjuntos, recomenda-se propor uma atividade complementar aos estudantes: elaborar diagramas de Venn para representar algumas das propriedades enunciadas. O software InteractiVenn, disponível em https://livro.pw/adfhc (acesso em: 1 out. 2024), é uma ferramenta ôn láinion-line quêque pódepode sêrser utilizada para essa finalidade.

Exemplos:

• Propriedade comutativa da união: A ⋃ B = B ⋃ A

Observar se os estudantes compreendem quêque fazer a união dos elemêntoselementos do conjunto A com os elemêntoselementos do conjunto B é equivalente a fazer a união dos elemêntoselementos do conjunto B com os do conjunto A.

• Propriedade associativa da união: (A ⋃ B) ⋃ C =

= A ⋃ (B ⋃ C)

Observar se os estudantes compreendem quêque fazer primeiro a união dos elemêntoselementos dos conjuntos A e B e depois acrescentar a essa união os elemêntoselementos do conjunto C é equivalente a fazer a união dos elemêntoselementos dos conjuntos B e C e depois juntá-los aos elemêntoselementos do conjunto A.

Além díssudisso, o tópico Propriedades da união e da intersecção de conjuntos é uma oportunidade para se iniciar um trabalho com demonstrações. Pode-se, por exemplo, apresentar as demonstrações das propriedades comutativa da união e associativa da intersecção, conforme apresentado a seguir, e solicitar aos estudantes as demonstrações das demais propriedades.

Propriedade comutativa da união:

x ∈ A ⋃ B ⇒ x ∈ A ou x ∈ B ⇒ x ∈ B ou x ∈ A ⇒ x ∈ B ⋃ A

Propriedade associativa da intersecção:

x ∈ (A ⋂ B) ⋂ C ⇒ x ∈ A ⋂ B e x ∈ C ⇒ x ∈ A e x ∈ B e x ∈ C ⇒ x ∈ A e x ∈ B ⋂ C ⇒ x ∈ A ⋂ (B ⋂ C)

O boxe Fórum oportuniza o desenvolvimento de reflekçõesreflexões a respeito das diferenças entre as pessoas, mostrando como é possível promover estratégias quêque permítampermitam a inclusão de todas elas em diferentes aspectos da vida. Além díssudisso, o debate permite conhecer diferentes tipos de esporte e refletir sobre campeonatos. Essa atividade pódepode sêrser mais bem aprofundada se feita com o professor de Educação Física, da área de Linguagens e suas Tecnologias, em um trabalho interdisciplinar.

Propõe-se aos estudantes quêque, em grupos, pesquisem sobre os jogos Parapan-Americanos, a fim de quêque exercitem suas autonomias no processo de aprendizagem e quêque desenvolvam a competência de buscar informações em fontes confiáveis.

Esses jogos são um evento multidesportivo, realizado a cada quatro anos e organizado pelo Comitê Paralímpico das Américas.

Para ampliar a preparação para o debate, sugere-se propor aos estudantes quêque, em duplas ou trios, pesquisem a respeito de um dos esportes adaptados presentes nesse evento para apresentá-lo ao restante da turma, de modo a ampliar o conhecimento de todos.

No debate, recomenda-se incentivar reflekçõesreflexões visando à empatia e ao acolhimento às pessoas com deficiência, promovendo o respeito e estimulando a troca de saberes e culturas. Pode-se orientar uma conversa sobre cooperação, de modo quêque se estimule o respeito às diferenças, a valorização da diversidade de indivíduos e a eliminação de preconceitos. Desse modo, colabora-se para o desenvolvimento da competência geral 9.

No boxe Pense e responda do tópico Conjunto dos números inteiros, espera-se quêque os estudantes compreendam quêque o conjunto dos números naturais está contido no conjunto dos números inteiros. Assim, todo número natural também é um número inteiro. Também se espera quêque eles entendam quêque existem elemêntoselementos no conjunto dos números inteiros quêque não fazem parte do conjunto dos números naturais. Pode-se propor aos estudantes quêque representem cada situação em um diagrama de Venn. É interessante quêque eles se conscientizem de quêque, para justificarem a negativa ao segundo questionamento dêêssedesse boxe, precisam apenas apresentar um exemplo do fato, como “−2 é um número inteiro, mas não é um número natural”. Desse modo, os estudantes dêsênvólvemdesenvolvem capacidade de argumentação e de formação matemática, contribuindo para o desenvolvimento da competência específica 5 da área

Página trezentos e trinta e um331

de Matemática e suas Tecnologias. Nesse sentido, e refletindo sobre o pensamento dedutivo, recomenda-se trabalhar com os estudantes o vídeo Conclusões precipitadas, do sáitisite Matemática Multimídia da Unicamp, disponível em https://livro.pw/ndptq (acesso em: 1 out. 2024).

Para aprofundar o trabalho sobre implicações e lógica, recomenda-se o material O quêque é lógica matemática?, disponível em https://livro.pw/btxdp (acesso em: 1 out. 2024).

No tópico Alguns números irracionais famosos, uma possibilidade para se iniciar o estudo do número pi ((pi)"π) é a realização da atividade a seguir.

Materiais: régua, compasso, barbante e calculadora (opcional).

Modo de fazer: com o uso da régua e do compasso, cada estudante constrói uma circunferência com determinada medida de diâmetro. Colocando o barbante sobre a circunferência, é possível medir, de modo aproximado, o comprimento dela. Na lousa, recomenda-se construir um qüadroquadro com três colunas: diâmetro (d), comprimento (C) e razão $\begin{array}{c}\left(\frac{C}{d}\right)\end{array}$. Em seguida, preencher o qüadroquadro com os dados de cada estudante e, com o auxílio da calculadora, realizar a divisão entre C e d, ou seja, escrever a fração $\begin{array}{c}\left(\frac{c}{d}\right)\end{array}$ na sua representação correspondente na forma decimal. Após preencher o qüadroquadro, é importante realizar uma reflekçãoreflexão sobre as semelhanças e as diferenças observadas. Espera-se quêque os valores fiquem próximos de 3,14, porém êêrroserros de medição causarão discrepâncias. Caso haja diferenças muito grandes, convém orientar os estudantes a refazer as medições, o quêque será uma oportunidade para auxiliá-los na aprendizagem.

Para explorar demais aspectos do número (pi)"π, sugere-se a leitura dos seguintes artigos:

• DIA do pi: para quêque se usa a mais famosa constante matemática. BBC niusNews Brasil, [s. l.], 14 mar. 2018. Disponível em: https://livro.pw/ksjfk. Acesso em: 1 out. 2024.
O artigo apresenta curiosidades, como a data de comemoração do número, e explica sua importânssiaimportância para além da Geometria: em celulares, GPS (Sistema de Posicionamento Global) e relógios.

• ORTEGA, Rodrigo. Para quêque sérveserve a sequência do (pi)"π? Mundo Estranho, São Paulo, 22 fev. 2024. Disponível em: https://livro.pw/iejpo. Acesso em: 1 out. 2024.
O artigo apresenta exemplos de aplicação do número (pi)"π na Física e no automobilismo.

Após a leitura, pode-se propor aos estudantes quêque, em grupos, pesquisem sobre as aplicações citadas nos artigos, aprofundando os estudos.

Sobre o tópico O número de ÓilerEuler (e), recomendam-se os artigos:

• PRECIOSO, Juliana Conceição; PEDROSO, érmesHermes AntônioAntonio. História do número e: gênese e aplicações. Matemática e Estatística em Foco, Uberlândia, v. 1, n. 1, p. 31-44, 2013. Disponível em: https://livro.pw/gavnp. Acesso em: 1 out. 2024.

• POMMER, Wagner M. O número de ÓilerEuler: possíveis abordagens no ensino básico. Nilson José Machado, São Paulo, p. 1-14, 2010. Seminário sobre Ensino de Matemática apresentado no Programa de pós-graduação da Faculdade de Educação da úspiUSP (Feusp). Disponível em: https://livro.pw/veauj. Acesso em: 1 out. 2024.

Esses dois artigos apresentam aspectos históricos quêque podem sêrser trabalhados com os estudantes. Além díssudisso, eles relacionam o número de ÓilerEuler com aspectos da Matemática financeira, da função logarítmica, das funções exponenciais e da hipérbole, indicando possibilidades para o trabalho em aula. As sugestões podem sêrser, em um primeiro momento, indicadas aos estudantes e, posteriormente, aprofundadas, quando o foco do estudo for as funções exponenciais, por exemplo.

Outra possibilidade de aprofundamento no tema é trabalhar o texto a seguir, em parceria com o professor de Língua Inglesa, da área de Linguagens e suas Tecnologias.

• O’CONNOR, J. J.; ROBERTSON, E. F. The number e. Escócia: MacTutor: Universidade St. Andrews, 2001. Disponível em: https://livro.pw/dqzbp. Acesso em: 1 out. 2024.
No tópico Intervalos reais, são apresentados dois diferentes modos de representar intervalos reais, bem como seus respectivos símbolos, contribuindo para o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias.

A seção História da Matemática trata da descoberta, pêlospelos pitagóricos, do conceito de grandezas incomensuráveis e de sua relação com os números irracionais, contribuindo para a competência geral 1.

Conforme exemplificado na seção, duas grandezas de mesma espécie são comensuráveis quando a razão entre elas pódepode sêrser expressa por um número racional. Caso contrário, se a razão entre essas duas grandezas não pódepode sêrser expressa por um número racional, dizemos quêque são incomensuráveis.

A descoberta de quêque duas grandezas de mesma natureza podem não ter uma medida em comum teve consequências importantes, pois ajudou a explicar, por exemplo, o caráter formal e abstrato da Geometria, à medida quêque as grandezas incomensuráveis desafiam os sentidos ao admitir quêque sempre é possível encontrar um segmento tão pequeno, quêque seja múltiplo comum de ambos os segmentos quêque se queira comparar.

Página trezentos e trinta e dois332

Além do exemplo de quêque o lado e a diagonal do quadrado são segmentos incomensuráveis, também é possível citar a incomensurabilidade do diâmetro de uma circunferência e do comprimento de uma circunferência.

Para se aprofundar no assunto, a seguinte leitura é sugerida:

• ROQUE, Tatiana. História da matemática: uma visão crítica, desfazendo mitos e lendas. Rio de Janeiro: ZarrárZahar, 2012.

Nessa obra, a autora explica algumas hipóteses sobre a descoberta da incomensurabilidade e sobre como a pesquisa das grandezas incomensuráveis foi positiva, possibilitando o desenvolvimento contínuo da Matemática e de novas técnicas para lidar com razões e proporções.

A partir do Tema Contemporâneo Transversal Educação Alimentar e Nutricional na seção Conexões com…, são propostos textos e atividades quêque permitem refletir sobre a importânssiaimportância de uma alimentação balanceada para a saúde e sobre a tomada de decisões conscientes quêque melhorem a qualidade de vida, contribuindo, assim, para a competência específica 2 da área de Ciências da Natureza e suas Tecnologias.

Esse trabalho pódepode sêrser feito com os professores de Educação Física, da área de Linguagens e suas Tecnologias, e de Biologia, da área de Ciências da Natureza e suas Tecnologias, favorecendo a aprendizagem.

Recomenda-se quêque a atividade 1 seja realizada a partir de uma conversa coletiva, de modo quêque os estudantes possam compartilhar suas ideias e escutar as dos côlégascolegas, ampliando suas considerações. Outras perguntas relacionadas aos hábitos alimentares dos estudantes podem contribuir com a discussão: Como são seus hábitos alimentares? Isso é uma preocupação na vida de vocês? Quais são as possibilidades e as dificuldades para melhorar esses hábitos? Dessa maneira, essa atividade permite desenvolver a competência geral 8, uma vez quêque esse é um momento de examinar e pensar sobre o cuidado de si com auto críticaautocrítica.

Na atividade 2, estuda-se o Índice de Massa Corpórea (hí eme cêIMC) como uma maneira de a Matemática contribuir para a investigação de problemas de saúde e fornecer indicativos para a tomada de dê-cisãodecisão com fundamento, desenvolvendo, assim, a competência específica 2 da área de Matemática e suas Tecnologias. Após a compreensão do cálculo do hí eme cêIMC, sugere-se trabalhar o texto a seguir, da Associação Brasileira para o Estudo da Obesidade e da Síndrome Metabólica (Abeso), quêque mostra as conclusões da análise de diversas pesquisas realizadas com adultos (de 46 anos, em média) sobre hí eme cêIMC alto. Tem-se quêque:

[…]

[…] Cada 5 kg/m² adicional [no IMC] traduziu-se em um aumento de 40% na mortalidade por doenças do coração, derrames e demais problemas vasculares; de 60% a 120% para diabetes, doenças de fígado e rins; de 10% na mortalidade por câncer; e de 20% de aumento em pessoas com doenças pulmonares.

[…]

SANTOS, Beth. hí eme cêIMC alto leva a aumento da mortalidade. São Paulo: Abeso, 20 mar. 2009. Disponível em: https://livro.pw/qfqji. Acesso em: 1 out. 2024.

Apesar dos apontamentos das pesquisas citadas anteriormente, é importante observar quêque o hí eme cêIMC tem limitações e quêque seu resultado não deve sêrser interpretado isoladamente, pois não diz respeito aos índices de gordura, os quais varíamvariam de acôr-doacordo com a idade, o sexo, a etnia e a prática esportiva. As Diretrizes Brasileiras de Obesidade, também da Abeso, dispõem o seguinte:

[…]

O hí eme cêIMC (calculado através da divisão do peso em kg pela altura em metros elevada ao quadrado, kg/m²) é o cálculo mais usado para avaliação da adiposidade corporal. O hí eme cêIMC é um bom indicador, mas não totalmente correlacionado com a gordura corporal. É simples, prático, sem custo. pódePode havêerhaver diferenças na composição corporal em função do sexo, idade, etnia, no cálculo de indivíduos sedentários quando comparados a atletas, na presença de perda de estatura em idosos devido à cifose, em edemaciados, etc. O hí eme cêIMC não distingue massa gordurosa de massa magra, podendo sêrser menos preciso em indivíduos mais idosos, em decorrência da perda de massa magra e diminuição do peso, e superestimado em indivíduos musculosos. O hí eme cêIMC não reflete a distribuição da gordura corporal. […] a medida da distribuição de gordura é importante na avaliação de sobrepeso e obesidade porque a gordura visceral (intra-abdominal) é um fator de risco potencial para a doença, independentemente da gordura corporal total. Indivíduos com o mesmo hí eme cêIMC podem ter diferentes níveis de massa gordurosa visceral. A distribuição de gordura abdominal é claramente influenciada pelo sexo: para algum acúmulo de gordura corporal, o homem tem, em média, o dôbrodobro da quantidade de gordura abdominal em relação à mulher antes da menopausa. Além díssudisso, o hí eme cêIMC não é indicador do mesmo grau de gordura em populações diversas, particularmente por causa das diferentes proporções corporais.

[…]

[…] Portanto, o ideal é quêque o hí eme cêIMC seja usado em conjunto com outros métodos de determinação de gordura corporal. A combinação de hí eme cêIMC com medidas da distribuição de gordura

Página trezentos e trinta e três333

pódepode ajudar a resolver alguns problemas do uso do hí eme cêIMC isolado.

[…]

ASSOCIAÇÃO BRASILEIRA PARA O ESTUDO DA OBESIDADE E DA SÍN-DROME METABÓLICA. Diretrizes brasileiras de obesidade 2016. 4. ed. São Paulo: Abeso, 2016. Disponível em: https://livro.pw/yanvz. Acesso em: 1 out. 2024.

No boxe Pense e responda, propõe-se aos estudantes quêque identifiquem os conceitos matemáticos mobilizados durante o estudo da seção Conexões com…. Essa identificação é importante para quêque os estudantes percêbampercebam a utilidade dos conceitos matemáticos na compreensão dos Temas Contemporâneos Transversais.

A seção Explorando a tecnologia contribui para o desenvolvimento da habilidade EM13MAT315, pois os estudantes aprenderão como escrever um algoritmo quêque resólveresolve problemas quêque envolvem a quantidade de elemêntoselementos de um conjunto e registrar, por meio de um fluxograma, um algoritmo quêque resólveresolve um conjunto de problemas do mesmo tipo.

É importante quêque os passos do algoritmo sêjamsejam lidos, um a um, com o diagrama quêque o representa. Sugere-se quêque os estudantes identifiquem os símbolos no fluxograma e sigam as etapas para resolver o problema apresentado. É válido solicitar aos estudantes quêque busquem as informações de cada passo no enunciado do problema. Recomenda-se quêque os estudantes comparem o fluxograma com o algoritmo apresentado.

Na atividade 2, espera-se quêque os estudantes escrevam, minimamente, quêque é necessário ter uma escôvaescova e um creme dental, abrir o creme dental, colocar o creme dental na escôvaescova, abrir a torneira, molhar a parte da escôvaescova com o creme, fechar a torneira, escovar os dentes, abrir a torneira novamente, enxaguar a bôcaboca e a escôvaescova, fechar a torneira, guardar a escôvaescova, fechar e guardar o creme. Depois, os estudantes devem elaborar um fluxograma com base no algoritmo quêque eles fizeram. O desenvolvimento dessa atividade estimula a competência específica 3 da área de Matemática e suas Tecnologias. É interessante quêque os estudantes tróquemtroquem os algoritmos e o fluxograma entre si para quêque um colega possa testá-los e apontar melhorias, se necessário.

Na atividade 3, é importante compartilhar com a turma os diferentes fluxogramas criados pêlospelos estudantes e validá-los. Se julgar oportuno, organizar os estudantes em duplas ou trios para resolver essa tarefa.

Avaliação

A atividade 2 da Abertura do Capítulo possibilita uma avaliação diagnóstica das seguintes habilidades relacionadas aos conjuntos numéricos quêque foram trabalhadas no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah zero umEF09MA01) Reconhecer quêque, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).

(ê éfe zero nove ême ah zero doisEF09MA02) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica.

No tópico Conjuntos numéricos são estudadas as principais propriedades e aplicações dos conjuntos dos números naturais, dos números inteiros, dos números racionais, dos números irracionais e dos números reais. Ao término dos estudos, pode-se propor uma atividade interativa sobre conjuntos numéricos, disponível em https://livro.pw/kfkox (acesso em: 1 out. 2024). Dessa maneira, é possível verificar se os estudantes compreenderam as relações entre os conjuntos e as características dos elemêntoselementos quêque os compõem.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 9 e 13 (página 17).

2ª avaliação formativa: atividades 17 e 24 (página 23).

3ª avaliação formativa: atividades 32 e 38 (página 31).

4ª avaliação formativa: atividades 44 e 47 (página 39).

Capítulo 2
Noções de Estatística

Orientações

Neste Capítulo, os estudantes exploram noções de Estatística, a fim de utilizarem estratégias, conceitos e procedimentos matemáticos para interpretar várias situações a partir da análise de tabélastabelas, gráficos e pesquisas estatísticas divulgadas por diferentes meios, o quêque favorece principalmente o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias e, de modo particular, o desenvolvimento da habilidade EM13MAT102. Além díssudisso, esse estudo possibilita compreender e utilizar, com flexibilidade e precisão, diferentes registros de representação matemáticos para construir modelos e resolver problemas, analisando os resultados e colaborando com o desenvolvimento das competências específicas 3 e 4 da área de Matemática e suas Tecnologias e, em particular, o desenvolvimento das habilidades EM13MAT316, EM13MAT406 e EM13MAT407.

A Abertura do Capítulo apresenta dados estatísticos relacionados ao envelhecimento populacional no Brasil.

Página trezentos e trinta e quatro334

O texto possibilita um diálogo com os estudantes a respeito dos desafios enfrentados pela ssossiedadesociedade brasileira acerca dêêssedesse assunto. Pode-se explicar aos estudantes quêque o Brasil possui o Estatuto da Pessoa Idosa, quêque foi instituído pela lei númeronº 10.741, garantindo à pessoa idosa diversos direitos, como o direito à vida, à dignidade, ao respeito e à convivência familiar e comunitária. Vale ressaltar quêque o termo “pessoa” é utilizado para combater a desumanização do envelhecimento. O Estatuto é uma medida quêque visa confrontar o preconceito quêque existe contra o envelhecimento e trazer dignidade e respeito a essa parcela da população, além de assegurar-lhe gratuitamente o acesso aos medicamentos e ao transporte público. O Estatuto completo está disponível em https://livro.pw/llkve (acesso em: 1 out. 2024).

Espera-se quêque, ao realizarem as atividades 2 e 3, os estudantes identifiquem se os direitos das pessoas idosas com as quais convivem são respeitados e assegurados. Tanto o diálogo quanto a realização dessas atividades trabalham o desenvolvimento da competência geral 9 da BNCC.

No tópico O quêque é Estatística, recomenda-se explicar quêque a Estatística é imprescindível para os estudos científicos em diversas áreas do conhecimento e está muito presente no dia a dia, como em notícias diversas, por exemplo. Desse modo, compreendê-la se faz necessário tanto para a formação de um cidadão crítico como para a formação de pesquisadores e cientistas. O texto a seguir destaca a importânssiaimportância da Estatística na análise de situações em diferentes campos de estudo.

[…] Sua principal função é evitar determinados êêrroserros analíticos quêque são comuns quando utilizamos métodos heurísticos.

Por exemplo, muitas pessoas resolvem incentivar seus filhos a treinarem basquete durante a infância esperando quêque esse esporte os tornem mais altos quando chegarem à vida adulta. O raciocínio simplista dessas pessoas está baseado na constatação de quêque a maioria dos atletas profissionais de basquete é formada por atletas muito altos. Na verdade, o quêque ocorre é exatamente o contrário, sêndosendo chamado viés de sobrevivência: apenas as crianças quêque começam a ficar mais altas do quêque os côlégascolegas ganham destaque nos times juvenis de basquete e, com isso, têm maiores chances de chegar às ligas profissionais, enquanto as crianças de estatura mediana tentam escolher outras profissões. De outra forma, vários estudos médicos comprovaram quêque a maioria dos jogadores de basquete quêque são altos também possuem os pais altos, o quêque aponta fatores genéticos como principais influenciadores da altura de uma pessoa na vida adulta.

Outro exemplo comum quêque podemos destacar é o uso da Estatística para analisar se determinadas políticas públicas atingiram ou não seus objetivos.

Hoje em dia, os métodos estatísticos são usados em diversos campos de investigação científica, como Medicina, Demografia, Meteorologia, Economia etc.

[…]

HOLANDA, Francisco Bruno. Estatística básica: o início. Rio de Janeiro: Portal da Matemática OBMEP, 4 fev. 2019. p. 1. Disponível em: https://livro.pw/huvvm. Acesso em: 1 out. 2024.

Pode-se dizêrdizer quêque a Estatística é formada por duas áreas principais. A primeira é a Estatística descritiva, quêque tem como objetivo coletar dados, organizá-los e analisá-los. A segunda área é a Estatística inferencial (ou Inferência estatística), quêque permite realizar conclusões sobre todo um grupo a partir de dados de uma parte da população. O vídeo O quêque é Estatística?, disponível em https://livro.pw/ohlrj (acesso em: 1 out. 2024), pódepode sêrser utilizado nesse momento inicial, pois apresenta as principais características dessa ciência.

A reportagem Mais da mêtádemetade dos brasileiros já presenciou ato de racismo e o conteúdo do boxe Pense e responda podem sêrser trabalhados com o boxe Fórum. Essa é uma possibilidade de ampliar a discussão dêêssedesse tema, pois, tanto a seção quanto o boxe exploram o Tema Contemporâneo Transversal Cidadania e Civismo, desenvolvendo a competência geral 9. O tema racismo também pódepode sêrser trabalhado em parceria com os professores da área de Ciências Humanas e Sociais Aplicadas, colaborando com o desenvolvimento da competência específica 5 dessa área.

Ler a reportagem Mais da mêtádemetade dos brasileiros já presenciou ato de racismo ou apresentar o vídeo O quêque é racismo estrutural? | Desenhando é uma forma de introduzir o tema. Sugere-se incentivar os estudantes a discutir e a debater sobre as políticas públicas existentes e sobre como elas podem contribuir para o fim do racismo estrutural, quêque afeta diferentes grupos d fórmade forma desigual. É provável quêque os estudantes citem o sistema de cotas, quêque está presente nos vestibulares de universidades públicas. Pode-se aproveitar o momento para abordar o assunto de como as cotas são uma medida para amenizar desigualdades sociais e promover a igualdade de oportunidades.

Os estudantes podem, por exemplo, trazer discussões a respeito da reforma do sistema de justiça criminal brasileiro, de modo a reduzir o viés racial, de programas de habitação acessível e equitativa, de iniciativas de inclusão no mercado de trabalho e de políticas de saúde quêque visam reduzir disparidades raciais.

Página trezentos e trinta e cinco335

Eles podem considerar também algumas formas de se envolverem ativamente com o processo político para promover mudanças na ssossiedadesociedade. Isso pódepode incluir a elaboração de propostas para serem enviadas a representantes políticos, a participação de atos pacíficos, o apôioapoio a organizações comunitárias e o envolvimento em campanhas de conscientização sobre o racismo estrutural.

A promoção de uma educação antirracista é fundamental no combate ao racismo estrutural e envolve a conscientização sobre a história do racismo e suas manifestações contemporâneas. Além díssudisso, incentiva à reflekçãoreflexão crítica sobre as estruturas sociais quêque perpetuam a desigualdade racial. É importante não só abordar explicitamente o racismo e a discriminação racial nos currículos escolares, mas também quêquestionar as normas e as práticas institucionais que mantêm o estátusstatus quo racial. Uma educação antirracista tem como objetivo habilitar as pessoas a reconhecer e contestar o racismo em todas as suas formas.

Além díssudisso, a educação antirracista deve promover a empatia, o respeito e a valorização da diversidade racial. Isso pódepode sêrser alcançado, por exemplo, por meio da promoção de ambientes escolares inclusivos e acolhedores para todos os estudantes, independentemente de sua raça ou etnia. Ao promover a consciência e a ação antirracistas, é possível trabalhar juntos para a construção de um mundo onde a igualdade racial seja uma realidade.

No tópico tabélaTabela de freqüênciasfrequências, se necessário, retomar o conceito de porcentagem estudado no Ensino Fundamental – Anos Finais. É essencial quêque os estudantes saibam a equivalência entre a escrita na forma de porcentagem, fracionária e decimal, por exemplo, 37% = $\frac{37}{100}$ = 0,37.

O estudo das tabélastabelas e dos gráficos explorados ao longo do Capítulo contribui para o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias, em particular, da habilidade EM13MAT406, uma vez quêque são exploradas diferentes maneiras de registro matemático.

No tópico Gráficos, abordam-se características de diferentes gráficos, assunto estudado no Ensino Fundamental – Anos Finais, e quêque agora é retomado e aprimorado. O tema possibilita desenvolver a competência geral 4, à medida quêque se amplia a análise de diferentes gráficos, fornecendo subsídios para quêque essa linguagem seja compreendida e utilizada pêlospelos estudantes para compartilhar informações em diferentes contextos. Além díssudisso, possibilita exercitar a investigação, a análise crítica e o estabelecimento de conclusões embasadas em dados.

Ao trabalhar a construção do Gráfico de setores, é oportuno realizar as construções com transferidor e compasso, observando, cuidadosamente, a relação entre a medida do ângulo central do setor circular e a parte do todo quêque esse setor representa.

Ao estudar o Gráfico de linha, ressaltar a característica temporal dêêssedesse tipo de gráfico, quêque permite realizar uma análise de dados em relação ao crescimento ou decrescimento no decorrer do tempo. Para estudar a característica de séries temporais, para as quais o gráfico de linha é adequado, recomenda-se realizar o experimento Séries temporais, disponível em https://livro.pw/glnkw (acesso em: 1 out. 2024). Nele, os estudantes vão coletar dados ao longo de determinado intervalo de tempo e, posteriormente, analisar tais informações. É possível aproveitar o contexto trabalhado no boxe Pense e responda para reforçar o tema abordado anteriormente sobre racismo estrutural.

Ao analisar o pictograma apresentado, enfatizar a importânssiaimportância da legenda nesse tipo de gráfico.

O estudo do Histograma contribui para o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias, em particular a habilidade EM13MAT407, pois amplia as possibilidades de interpretação e comparação de dados estatísticos por meio de um novo tipo de gráfico.

O estudo do tópico mêdídasMedidas de tendência central permite desenvolver a competência específica 3 da área de Matemática e suas Tecnologias, em particular a habilidade EM13MAT316, pois envolvem os conceitos de média, (Moda)moda e mediana.

Para finalizar esse tópico, recomenda-se propor aos estudantes as atividades interativas Média, (Moda)moda e mediana e Entre médias, disponíveis em https://livro.pw/ohlmu (acesso em: 19 set. 2024). Desse modo, com base nelas, os estudantes podem verificar quêque a média, sózínhasozinha, pódepode não sêrser uma boa representante de um conjunto de dados; por isso, outras medidas auxiliam essa descrição.

O estudo do tópico mêdídasMedidas de dispersão permite trabalhar a competência específica 3 da área de Matemática e suas Tecnologias, em particular a habilidade EM13MAT316, pois envolve os conceitos de amplitude, variância, desvio médio e desvio padrão.

No tópico Amplitude, explorar a situação apresentada envolvendo as medidas das peças usinadas. Um exemplo cotidiano quêque pódepode sêrser citado é a amplitude térmica diária.

No tópico Desvio médio, apresentar exemplos do sín-bolosímbolo somatório mencionado no boxe Saiba que…, a fim de quêque os estudantes se familiarizem com a utilização dêêssedesse sín-bolosímbolo.

Ao trabalhar com o tópico Variância e desvio padrão, enfatizar as kestõesquestões propostas no boxe Pense e responda, a fim de quêque os estudantes compreendam quêque essas medidas estatísticas não podem ter como resultado um valor negativo.

Ao estudar os tópicos Box-plot e Diagrama de ramo e fô-lhasfolhas, os estudantes têm a oportunidade de desenvolver a competência específica 4 da área de Matemática e suas Tecnologias, em particular a habilidade EM13MAT407.

Página trezentos e trinta e seis336

Para acompanhar o estudo do tópico Box-plot, sugere-se utilizar o objeto de aprendizagem Conhecendo o Box-plot, disponível em https://livro.pw/fknjn (acesso em: 1 out. 2024). De forma interativa, os estudantes visualizam quais são as características e etapas da construção de um box-plot, além de responderem a perguntas quêque auxiliam em seus estudos. Além díssudisso, recomenda-se ao professor o artigo Sobre o Box-plot no GeoGebra, disponível em https://livro.pw/rdbvq (acesso em: 1 out. 2024), quêque faz uma análise do uso do software GeoGebra para a construção do box-plot.

O diagrama de ramo e fô-lhasfolhas facilita a localização de medidas estatísticas, como a mediana e a (Moda)moda, além de ajudar o cálculo da amplitude. Ele é similar a um histograma, com a diferença de quêque, nesse tipo de gráfico, não se perdem informações sobre cada um dos elemêntoselementos do conjunto de dados. Recomenda-se enfatizar a necessidade de uma legenda, pois a escolha da composição dos ramos e das fô-lhasfolhas pódepode variar (décimos, unidades, dezenas etc.).

Para a construção dêêssedesse diagrama, sugere-se utilizar papel quadriculado indicando quêque o espaço ocupado por cada dígito deve sêrser o mesmo, para quêque não ocorram distorções visuais das informações. O mesmo pódepode sêrser feito com a utilização de planilhas eletrônicas.

Na seção Explorando a tecnologia, utiliza-se o GeoGebra para criar diagramas de ramo e fô-lhasfolhas e box-plot, ampliando o repertório dos estudantes, de modo quêque se comuniquem por meio de diferentes linguagens a partir da utilização de tecnologias digitais, o quêque permite o desenvolvimento das competências gerais 4 e 5. Além díssudisso, contribui também para o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias, em particular as habilidades EM13MAT406 e EM13MAT407, uma vez quêque permite aos estudantes construir, interpretar e analisar diferentes tipos de gráfico.

Recomenda-se orientar os estudantes a fazer o dáum-lôudedownload do GeoGebra, conforme mencionado, caso eles ainda não o tênhamtenham utilizado.

As atividades 2 e 3 propostas na seção dependem da pesquisa realizada pêlospelos estudantes. Na atividade 2, eles devem selecionar 10 pessoas aleatoriamente e construir um diagrama de ramo e fô-lhasfolhas e um box-plot com as idades dessas pessoas. Na atividade 3, eles precisam comparar os gráficos elaborados na atividade anterior para verificar semelhanças e diferenças entre eles. Sugere-se destinar um tempo de aula para uma discussão a respeito dos gráficos construídos pêlospelos estudantes, a fim de quêque possam apresentar conclusões a partir das informações obtidas.

A seção Conexões com… trabalha o Tema Contemporâneo Transversal Educação Ambiental. Essa seção aborda o tema AmazôneaAmazônia Legal, o quêque é uma oportunidade para desenvolver um trabalho mais aprofundado com os professores de Biologia e Geografia.

Ao explorar o texto, o gráfico e a tabélatabela apresentados, conversar com os estudantes a respeito das informações sobre o desmatamento, levando-os a refletir com criticidade o total de área desmatada ao longo dos anos cujos dados são apresentados. As kestõesquestões dessa seção ajudam a aprofundar essa conversa com o apôioapoio de dados e a aplicar conceitos matemáticos nas análises propostas, contribuindo para o trabalho com as competências gerais 4 e 7.

Na atividade 1, espera-se quêque os estudantes indiquem quêque a média não é suficiente para representar esses dados. Sugere-se, como atividade complementar, solicitar aos estudantes quêque calculem outras medidas estatísticas, como a (Moda)moda e a mediana, além de medidas de dispersão.

A atividade 2 propicíapropicia uma discussão ampla a respeito das atitudes pessoais perante o meio ambiente. Caso se estabêlêçaestabeleça a parceria sugerida com outros componentes curriculares, pode-se orientar a discussão e abordar aspectos do aquecimento global ou das reservas indígenas, as quais têm importante colaboração no quêque se refere à preservação do meio ambiente. Recomenda-se incentivar os estudantes a compartilhar com a comunidade escolar, nas rêdesredes sociais, as postagens por eles elaboradas na atividade 3.

Os contextos apresentados nas atividades complementares 2 e 6 podem servir de discussão a respeito, respectivamente, dos temas violência contra a mulher e violência contra a comunidade LGBTQIAPN+, reforçando a importânssiaimportância do respeito e do combate à violência. Pode-se apresentar dados mais recentes sobre a violência contra a mulher a partir do relatório Atlas da violência, elaborado pelo Instituto de Pesquisa Econômica Aplicada (Ipea), disponível em https://livro.pw/ivqef (acesso em: 1 out. 2024).

Avaliação

As atividades 1 e 4 da Abertura do Capítulo permitem uma avaliação diagnóstica das seguintes habilidades quêque foram trabalhadas no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah dois umEF09MA21) Analisar e identificar, em gráficos divulgados pela mídia, os elemêntoselementos quêque podem induzir, às vezes propositadamente, êêrroserros de leitura, como escalas inapropriadas, legendas não explicitadas corretamente, omissão de informações importantes (fontes e datas), entre outros.

(ê éfe zero nove ême ah dois doisEF09MA22) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.

Página trezentos e trinta e sete337

(ê éfe zero nove ême ah dois trêsEF09MA23) Planejar e executar pesquisa amostral envolvendo tema da realidade social e comunicar os resultados por meio de relatório contendo avaliação de medidas de tendência central e da amplitude, tabélastabelas e gráficos adequados, construídos com o apôioapoio de planilhas eletrônicas.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2 e 9 (páginas 61 e 63, respectivamente).

2ª avaliação formativa: atividades 15 e 16 (páginas 70 e 71, respectivamente).

3ª avaliação formativa: atividades 26 e 29 (página 79). Na atividade 26, um estudante pódepode preferir a empresa X, porque ela paga os maiores e os menóresmenores salários. Nesse caso, se ele seguir carreira dentro da empresa, receberá salários maiores do quêque a empresa Z. Por outro lado, um estudante pódepode escolher a empresa Z, pois a chance de ele receber salário próximo de R$ 9.000,00 é maior do quêque na outra empresa. Verificar essas justificativas é importante para perceber a compreensão dos estudantes acerca do conceito de desvio padrão.

Capítulo 3
Introdução às funções e função afim

Orientações

O trabalho com Função afim é propôstoproposto em diversos contextos. Com isso, pretende-se quêque os estudantes desenvolvam a capacidade de interpretar e fazer uso das funções afins para resolver problemas e modelar situações da realidade. Nesse aspecto, os estudantes são convidados a analisar a dependência entre variáveis numéricas em situações envolvendo consumo, variação de tempera-túratemperatura, entre outros, desenvolvendo as habilidades EM13MAT101, EM13MAT302, EM13MAT401 e EM13MAT501.

Na Abertura do Capítulo, é importante introduzir os estudantes à etnomatemática. Pode-se comentar quêque existem diferentes matemáticas presentes no cotidiano, por exemplo, a matemática do pedreiro, a matemática do costureiro, entre outras. De acôr-doacordo com suas necessidades, esses profissionais dêsênvólvemdesenvolvem saberes matemáticos diferentes dos conhecimentos acadêmico e escolar. A etnomatemática compreende quêque existem diferentes sistemas culturais quêque dêsênvólvemdesenvolvem suas técnicas, habilidades e práticas matemáticas, valorizando-as. O modo como os rikbaktsá construíram suas flautas é um exemplo dessas técnicas. Assim, o trabalho na Abertura do Capítulo desen vólvedesenvolve as competências gerais 1 e 3 e a competência específica 3 da área de Matemática e suas Tecnologias.

As flautas dos rikbaktsá sérvemservem de elo entre sua cultura e a Matemática escolar, conforme descrito no artigo Etnomatemática em três dimensões na educação escolar indígena. Leia um trecho:

Os professores rikbaktsá de matemática nos informaram quêque eles precisavam encontrar éloselos entre conceitos da matemática escolar do “branco” com “coisas” de sua cultura, para quêque sêjamsejam providos encontros culturais nas suas aulas de matemática tornando a compreensão dêêssesdesses conceitos matemáticos relacionais mais significativos para os alunos indígenas. Olhando um artefato da cultura rikbaktsá, quêque é a sua flauta, vislumbramos quêque poderíamos relacionar os comprimentos das mesmas, medidas por eles em palmos, com suas medidas em centimetros, dando origem a uma função linear, quêque eles passaram a chamar de função das flautas.

MATTOS, José Roberto L. de; POLEGATTI, Geraldo Aparecido. Etnomatemática em três dimensões na educação escolar indígena. In: CONGRESO DE EDUCACIÓN MATEMÁTICA DE AMÉRICA CENTRAL Y EL CARIBE, 1., 2013, República Dominicana. Memorias […]. Santo Domingo: Pontificia Universidad Católica Madre y Maestra, 2013. p. 1-8. Disponível em: https://livro.pw/gnmln. Acesso em: 2 out. 2024.

As atividades 1, 2 e 3 da Abertura do Capítulo ilustram exemplos de como os professores rikbaktsá de Matemática construíram uma relação entre os conceitos matemáticos escolares e a cultura deles.

O tópico A ideia de função trabalha gradualmente a ideia de dependência entre grandezas em diferentes contextos, identificando quais são as variáveis dependente e independente, de acôr-doacordo com Barufi e Lauro:

[…] a palavra função foi introduzida na Matemática por Leibniz (1646-1716), quêque utilizou esse termo para designar um cértocerto tipo de fórmula matemática. Mais tarde, viu-se quêque a ideia de função desenvolvida por Leibniz tinha um alcance muito reduzido, e, posteriormente, o significado da palavra função foi experimentando generalizações sucessivas, até chegar à conceituação atual.

Assim, num curso de nível médio, não podemos ter a pretensão de alcançar uma formalização completa no estabelecimento de um conceito quêque traz dentro de si um grau de dificuldade epistemológica muito grande para os alunos, fato quêque pódepode sêrser historicamente comprovado. Essa pretensão, pódepode, inclusive, sêrser nociva, se provocar a falta de uma vivência mais prática e significativa do conceito, por parte dos alunos.

BARUFI, Maria Cristina B.; LAURO, Maira M. Funções elementares, equações e inequações: uma abordagem utilizando microcomputador. 1. ed. São Paulo: CAEM-IME/USP, 2001. v. 1, p. 5.

Página trezentos e trinta e oito338

A atividade 10 da página 105 possibilita articular e desenvolver as seguintes habilidades da área de Matemática e suas Tecnologias: EM13MAT302, uma vez quêque se utiliza de funções para analisar e resolver o problema; EM13MAT501, ao identificar padrões e criar conjecturas para generalizar e expressar algebricamente a situação; e EM13MAT510, por analisar o comportamento relacionado às variáveis número de palítospalitos em cada lado e total de palítospalitos em cada triângulo.

O boxe Fórum tem a finalidade de enfatizar quêque, em 2024, foi sancionada a lei númeronº 14.811, quêque inclui, no cóódigocódigo penal, os crimes de búlinbullying e sáiber-búlincyberbullying, com penas proporcionais às condutas. Para a intimidação sistemática, a pena é multa e, para a intimidação sistemática virtual, a pena é reclusão de dois a quatro anos e de multa, se a conduta não constituir crime mais grave. Para mais dêtálhesdetalhes, consulte o sáitisite https://livro.pw/inehz (acesso em: 2 out. 2024). Entende-se quêque a temática búlinbullying e sáiber-búlincyberbullying é de grande relevância, deve envolver toda a comunidade escolar e sêrser norteada pelo seu projeto político pedagójikôpedagógico. Uma possibilidade é verificar com o corpo docente se a atividade proposta na seção pódepode sêrser uma das diversas ações pedagógicas relacionadas a esse tema. Assim, é trabalhado o desenvolvimento das competências gerais 8, 9 e 10, pois o estudante é levado a se conhecer e a cuidar de sua saúde emocional, reconhecendo suas emoções e as dos outros, com auto críticaautocrítica e capacidade para lidar com elas. Além díssudisso, é necessário exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, com acolhimento, sem preconceitos de qualquer natureza.

O tópico Leitura e interpretação de gráficos apresenta uma situação relacionada à área de Ciências da Natureza e suas Tecnologias, na qual a utilização do gráfico de funções contribui para a análise, a investigação e soluções de problemas, o quêque contribui para o desenvolvimento da habilidade EM13MAT101 e da competência específica 1 da área de Matemática e suas Tecnologias. Além díssudisso, ao interpretar a situação-problema sobre bactérias no sanguesangue por meio de um modelo matemático e perceber a utilidade dele para tratamentos de saúde, desenvolve-se a competência específica 3 da área de Ciências da Natureza e suas Tecnologias.

Para ampliar o conhecimento a respeito da interpretação e leitura de gráficos, sugere-se realizar com os estudantes as atividades complementares e interativas propostas no Portal da OBMEP, disponíveis em https://livro.pw/higbk (acesso em: 2 out. 2024). Na atividade Vou de táxi, por exemplo, os estudantes podem visualizar duas retas quêque descrevem, cada uma, uma bandeira de taxímetro diferente e realizar a interpretação dos gráficos. Da mesma forma, a atividade Tanque cheio possibilita interpretar gráficos quêque descrevem o esvaziamento e o enchimento de tanques. Convém retomar essas atividades posteriormente, quando o estudante tiver ferramentas suficientes para escrever a forma algébrica das funções e puder realizar uma atividade complementar cujo objetivo é descrever tais funções algebricamente com base no gráfico.

O tópico Gráfico da função afim favorece o desenvolvimento das competências específicas 4 e 5 da área de Matemática e suas Tecnologias, em específico, as habilidades EM13MAT401 e EM13MAT501, ao explorar a relação entre as diferentes representações de uma função, gráfica e algébrica, e trabalhar a observação de padrões em tabélastabelas quêque expressam relações entre grandezas.

[…]

No estágio atual – nível médio – os alunos não têm condição de fazer a construção do gráfico de uma função, no sentido de não sêrser evidente para eles se os pontos, obtidos na prática, ou seja, êsperimentalmenteexperimentalmente, são ligados por segmentos de retas ou de curvas, com tal ou qual concavidade, uma vez quêque não possuem o instrumento necessário, fornecido por um posterior curso universitário de Cálculo Diferencial.

[…]

BARUFI, Maria Cristina B.; LAURO, Maira M. Funções elementares, equações e inequações: uma abordagem utilizando microcomputador. 1. ed. São Paulo: CAEM-IME/USP, 2001. v. 1, p. 8.

Uma alternativa para estudar esse tópico é utilizar o software GeoGebra. Com ele, é possível verificar visualmente quêque os gráficos da função afim são retas. Além díssudisso, pode-se utilizar o software para reproduzir, de modo dinâmico, os exemplos de gráficos indicados no Livro do estudante. Esse recurso pódepode sêrser apresentado para os estudantes em um projetor, não sêndosendo necessário quêque ele esteja instalado em um computador. No entanto, é necessário enfatizar aos estudantes quêque as visualizações do GeoGebra são apenas verificações empíricas, diferentemente de uma próvaprova lógica-dedutiva. A seguir, uma demonstração de quêque o gráfico da função afim é uma reta. Essa demonstração utiliza a fórmula da distância entre dois pontos no plano cartesiano, ôbitídaobtida por meio do teorema de Pitágoras.

Teorema: o gráfico de uma função afim é uma reta.

Demonstração:

Considere a função real afim f (x) = ax + b e três pontos quaisquer do gráfico de f, P₁ (x₁, ax₁ + b), P₂ (x₂, ax₂ + b) e P₃ (x₃, ax₃ + b), tal quêque x₁ < x₂ < x₃. Para demonstrar quêque esses três pontos são colineares, vamos provar quêque:

d(P₁, P₂) + d(P₂, P₃) = d(P₁, P₃)

Página trezentos e trinta e nove339

Pela fórmula da distância entre dois pontos, temos:

$$\begin{array}{c}\begin{array}{c}d(P_1,P_3)=\sqrt[]{{(x_3-x_1)}^2+{(a{x}_3+b-a{x}_1-b)}^2}=\\ =\sqrt[]{{(x_3-x_1)}^2+a^2{(x_3-x_1)}^2}=\sqrt[]{{(x_3-x_1)}^2\cdot (1+a^2)}=\\ =(x_3-x_1)\sqrt[]{1+a^2}\end{array}\end{array}$$

$$\begin{array}{c}\begin{array}{c}d(P_1,P_2)=\sqrt[]{{(x_2-x_1)}^2+{(a{x}_2+b-a{x}_1-b)}^2}=\\ =(x_2-x_1)\sqrt[]{1+a^2}\end{array}\end{array}$$

$$\begin{array}{c}\begin{array}{c}d(P_{2^{\text{'}}},P_3)=\sqrt[]{{(x_3-x_2)}^2+{(a{x}_3+b-a{x}_2-b)}^2}=\\ =(x_3-x_2)\sqrt[]{1+a^2}\end{array}\end{array}$$

Desse modo, obtemos:

d(P₁, P₂) + d(P₂, P₃) =
= (x₂ − x₁) $\begin{array}{c}\sqrt[]{1+a^2}\end{array}$ + (x₃ − x₂) $\begin{array}{c}\sqrt[]{1+a^2}\end{array}$ =
= (x₃ − x₁) $\begin{array}{c}\sqrt[]{1+a^2}\end{array}$
d(P₁, P₂) + d(P₂, P₃) = d(P₁, P₃)

Portanto, os pontos são colineares, e o gráfico da função é uma reta.

Sugere-se a leitura do material disponível no línkilink https://livro.pw/cehux (acesso em: 2 out. 2024), para consultar outra demonstração, entre outras informações. Também recomenda-se realizar a atividade complementar Conteúdo do Universo, disponível em https://livro.pw/iltvw (acesso: 2 out. 2024). Essa atividade baseia-se em áudios, apresentando informações sobre a Cosmologia moderna e o uso do gráfico de uma função linear nesse contexto. No línkilink, há um guia do professor, quêque contém atividades para serem realizadas antes ou depois da exibição dos áudios. Esse conteúdo pódepode ainda sêrser trabalhado com o professor de Física, da área de Ciências da Natureza e suas Tecnologias.

Na seção Explorando a tecnologia, a ferramenta contrôleControle deslizante (ou seletor) é utilizada. Além da sequência proposta, pode-se empregar essa opção da seguinte forma: clique no ícone dessa ferramenta, nomeie o seletor como a e escolha valores de mássimomáximo e de mínimo. Repita a operação para criar um seletor b.

Na caixa de entrada, digite “y = a*x + b” (note quêque é necessário colocar o *, quêque representa a multiplicação). Assim, para cada movimentação realizada no seletor referente às constantes a e b, o programa mostrará a reta correspondente à função.

Na atividade 1, espera-se quêque os estudantes verifiquem quêque, ao se alterar o valor do coeficiente a da função definida por f(x) = ax utilizando a ferramenta contrôleControle deslizante, modifica-se a inclinação da reta, porém ela continua passando pela origem do plano cartesiano (0, 0).

Para resolver a atividade 2, os estudantes terão de observar o gráfico da função definida por g(x) = x + b e as mudanças quêque ocorrem ao utilizar a ferramenta contrôleControle deslizante. Espera-se quêque obissérvemobservem quêque apenas o coeficiente b se altera, ou seja, a reta não sofre alteração em sua inclinação, mas ela é transladada. Essa atividade auxilia a percepção de quêque b corresponde à ordenada do ponto em quêque a reta da função afim cruza o eixo y.

Na atividade 3, considerando quêque a função h seja definida por h(x) = −3x + 6, a reta quêque a representa cruza o eixo x no ponto (2, 0).

Em Crescimento e decrescimento da função afim, explicar aos estudantes quêque as demonstrações das propriedades 1 e 2 são exemplos do método dedutivo característico da Matemática. De maneira gradual e criteriosa, é importante quêque os estudantes desenvolvam a capacidade de demonstrar teoremas e propriedades matemáticas e diferenciar as demonstrações dos processos de descobertas e verificações empíricas.

Nos tópicos Estudo do sinal da função afim e Inequações polinomiais do 1º grau, apresenta-se o estudo do sinal de uma função afim como um método para a resolução de inequações polinomiais do 1º grau. Essa relação amplia o significado das inequações ao exigir construção e interpretação gráfica da função.

O Tema Contemporâneo Transversal Educação Ambiental é trabalhado na seção Conexões com…. Nela propõe-se uma reflekçãoreflexão sobre o efeito estufa e sobre o aquecimento global, desenvolvendo a competência específica 3 da área de Ciências da Natureza e suas Tecnologias, pois parte da interpretação de texto é com base em informações científicas.

Na atividade 2, os estudantes devem pesquisar o acôr-doAcordo de Paris, quêque teve 195 países signatários. Entre os maiores poluidores do mundo, só não constam no acôr-doacordo os Estados Unidos. A comunidade internacional se comprometeu a manter o aumento da tempera-túratemperatura média global abaixo de 2°C e a continuar os esforços para limitar o aumento da tempera-túratemperatura a 1,5°C. Uma das medidas seria reduzir a emissão de gases de efeito estufa originada por atividades humanas. A atividade 3 possibilita desenvolver a competência específica 1 da área de Matemática e suas Tecnologias e a habilidade EM13MAT101, uma vez quêque analisa a situação por meio de gráficos. A produção da atividade 4 favorece a competência geral 4 ao se buscar comparar informações confiáveis quêque promovam uma consciência sócio-ambientalsocioambiental. Além díssudisso, propicíapropicia quêque a Educação Midiática seja inserida como uma camada no trabalho pedagójikôpedagógico desenvolvido. Para consultar mais informações acerca da Educação Midiática, recomenda-se a leitura do Guia da Educação Midiática, quêque foi publicado pelo Instituto Palavra Aberta, disponível em https://livro.pw/zkbal (acesso em: 29 out. 2024). Conheça também a Estratégia Brasileira de Educação Midiática, quêque foi publicada em 2023 pelo govêrnogoverno federal, disponível em https://livro.pw/ayufc (acesso em: 29 out. 2024).

Página trezentos e quarenta340

A seção História da Matemática aborda o surgimento dos gráficos, versando, inicialmente, sobre sua aplicabilidade não só na Matemática, mas também em outros campos, como o da Biologia e o da Economia, para apresentação e análise de dados, trabalhando, assim, a competência geral 1. Em seguida, é introduzida uma explicação sobre o sistema de coordenadas cartesianas, assim chamado em homenagem ao filósofo e matemático francês RenêRené Descartes (1596-1650).

Embora o diagrama de Nicole d’Oresme, quêque utiliza duas linhas para representar grandezas envolvidas no movimento, seja considerado um dos antecedentes do plano cartesiano, não havia nenhuma menção à sua interpretação algébrica. Foi Descartes quem uniu a Álgebra e a Geometria, criando o campo da Geometria Analítica, possibilitando maior desenvolvimento dessa área da Matemática.

Para saber mais sobre a vida, a importânssiaimportância e as descobertas de RenêRené Descartes, sugere-se acessar o línkilink https://livro.pw/ohqwk (acesso em: 2 out. 2024).

Avaliação

A atividade 4 da Abertura do Capítulo permite uma avaliação diagnóstica da seguinte habilidade relacionada às funções, quêque foram trabalhadas no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah zero seisEF09MA06) Compreender as funções como relações de dependência unívoca entre duas variáveis e suas representações numérica, algébrica e gráfica e utilizar esse conceito para analisar situações quêque envolvam relações funcionais entre duas variáveis.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 3, 5 e 6 (página 104).

2ª avaliação formativa: atividades 13 e 18 (páginas111 e 118, respectivamente).

3ª avaliação formativa: atividades 22, 25 e 32 (páginas 118, 119 e 127, respectivamente).

4ª avaliação formativa: atividade 37 (página 127).

5ª avaliação formativa: atividades 41 e 45 (páginas 134 e 135, respectivamente).

Capítulo 4
Função quadrática

Orientações

O trabalho com a Função quadrática é propôstoproposto em diferentes contextos. Desse modo, espera-se quêque os estudantes desenvolvam a capacidade de interpretar e fazer uso das funções polinomiais do 2º grau para resolver problemas e modelar situações da realidade, contribuindo, principalmente, para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, com destaque para a habilidade EM13MAT302.

Estudar o Gráfico da função quadrática desen vólvedesenvolve as competências específicas 4 e 5 da área de Matemática e suas Tecnologias e as habilidades EM13MAT402 e EM13MAT502. Além díssudisso, contribui para o desenvolvimento da competência geral 2, uma vez quêque instiga, nos estudantes, a curiosidade e a investigação.

Recomenda-se aprofundar os estudos sobre parábolas apresentando a definição geométrica delas, quêque permite compreender os motivos pêlospelos quais utilizamos as parábolas no cotidiano, como nas antenas parabólicas de televisão e nos faróis de automóveis com esse formato. O texto a seguir apresenta uma ampliação possível.

[…]

[…] vamos partir da definição dessa curva chamada parábola, descobrir sua equação e investigar algumas de suas propriedades, quêque vão justificar por quêpor que as antenas e os espelhos precisam sêrser parabólicos.

Por kestõesquestões de simplicidade, tudo o quêque dissermos de agora em diante se passa num plano.

DEFINIÇÃO

Consideremos uma reta d e um ponto F. Parábola de foco F e diretriz d é o conjunto de todos os pontos cuja distância à reta d é igual à distância ao ponto F.

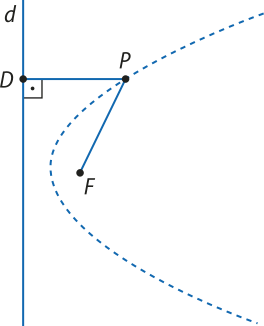
Na figura acima, se PD = PF, então P é um ponto da parábola de foco F e diretriz d.

Para obtêrobter diversos pontos de uma parábola, dados o foco F e a diretriz d, trace por F uma reta r perpendicular à diretriz e seja D o ponto de interseção de r e d.

O segmento DF chama-se parâmetro da parábola e o ponto V, médio de DF, é o vértice da parábola. Para cada ponto A da semirreta VF, trace a reta s, perpendicular a r. A circunferência de centro F e raio AD corta s nos pontos P e P’, quêque pertencem à parábola.

Página trezentos e quarenta e um341

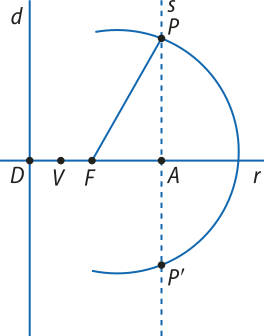
Como PF = AD, a distância de P ao foco é igual à sua distância à diretriz.

[…]

WAGNER, Eduardo. Porque as antenas são parabólicas? Revista do Professor de Matemática (RPM), São Paulo, n. 33, [201-]. Disponível em: https://livro.pw/hsxxe. Acesso em: 2 out. 2024.

No GeoGebra, a definição de parábola pódepode sêrser explorada, e os estudantes podem fazer uma atividade complementar. Primeiro, eles devem construir o gráfico da função quadrática definida por f(x) = $\begin{array}{c}\frac{x^2}{4}\end{array}$ .Em seguida, no mesmo sistema de coordenadas cartesianas, eles devem construir o lugar geométrico dos pontos (x, y), de modo quêque a distância à reta y = −1 seja igual à distância ao ponto (0, 1), ou seja, a parábola deve ter foco em (0, 1) e diretriz y = −1. Para isso, solicitar a eles quêque construam a reta y = −1, colocando esse comando na caixa de entrada, e, da mesma maneira, construam o ponto A(0, 1). Na barra de ferramentas, selecionar, no ícone Cônicas, a opção Parábola e clicar na reta diretriz e no foco já construídos (esses termos farão sentido aos estudantes se foi trabalhada, anteriormente, a definição geométrica de parábola). Tal construção resultará na mesma parábola quêque corresponde ao gráfico de f construída inicialmente. Para quêque isso fique mais visível, na janela de visualização, clicar no gráfico da parábola e modificar a côrcor, alterando também a côrcor da equação correspondente, facilitando a identificação. Recomenda-se ocultar um dos gráficos para visualizar o gráfico da outra função e, assim, evidenciar quêque ambos são idênticos.

Como atividade complementar para os estudantes, pode-se solicitar a eles quêque demonstrem quêque o gráfico da função definida por g(x) = x^² é uma parábola com foco em $(0,\frac{1}{4})$ e diretriz y = $-\frac{1}{4}$.Orientar quêque utilizem a definição da parábola como lugar geométrico e o teorema de Pitágoras.

A seção Explorando a tecnologia proporciona aos estudantes um momento para explorar as relações entre a forma algébrica e a forma gráfica das funções quadráticas. Esse estudo possibilita o desenvolvimento das competências específicas 3 e 4 da área de Matemática e suas Tecnologias e as habilidades EM13MAT302 e EM13MAT402, uma vez quêque compreender tais relações é necessário para quêque sêjamsejam realizadas, posteriormente, modelagens matemáticas com o uso de funções quadráticas.

Para a realização das atividades, recomenda-se realizar perguntas para mediar a investigação dos estudantes, de acôr-doacordo com suas percepções iniciais.

Na atividade 1, espera-se quêque os estudantes percêbampercebam quêque, ao modificar o valor do coeficiente a da função de 2º grau, a parábola terá alterações em sua concavidade: voltada para cima, se a for positivo, e voltada para baixo, se a for negativo.

Na atividade 2, espera-se quêque os estudantes notem quêque h é uma função quadrática incompleta cujo coeficiente c é nulo, portanto os zeros dessa função são x = 0 ou x = −b, pois: x^² + bx = 0 ⇒ x(x + b) = 0 ⇒ x’ = 0 e x” = −b (Valor ôpôstooposto ao do ajustado no contrôlecontrole deslizante.)

Na atividade 3, ao utilizar o contrôleControle deslizante referente ao coeficiente c nas duas funções f e j, nota-se quêque c é a ordenada do ponto em quêque as funções intersectam o eixo y. Além díssudisso:

• quando c é negativo, tem-se quêque o gráfico de j é uma translação do gráfico de f para baixo;

• quando c é positivo, tem-se quêque o gráfico de j é uma translação do gráfico de f para cima.

Por fim, a atividade 4 propõe uma investigação em quêque todos os coeficientes são manipulados. Recomenda-se incentivar os estudantes a realizar testes e anotar suas observações, instigando, assim, a competência geral 2. Uma atividade quêque pódepode complementar a investigação é propor aos estudantes quêque criem perguntas de investigação para quêque um colega possa respondê-las. Por exemplo: Fixando o valor de a, o quêque acontece se aumentarmos os valores de b e de c?

No boxe Fórum, os estudantes podem sugerir a criação de campanhas de conscientização, na escola ou na comunidade, por meio de cartazes, panfletos e palestras quêque destaquem os riscos de se usar celular ao dirigir e promovam a importânssiaimportância de se manter o foco na condução, desenvolvendo, assim, a competência geral 10. Os estudantes podem também compartilhar histoóriashistórias pessoais ou de pessoas próximas quêque tênhamtenham sofrido algum tipo de acidente causado pelo uso do celular ao dirigir. Esses relatos podem causar um impacto emocional significativo e podem ajudar a sensibilizar os côlégascolegas sobre os perigos envolvidos. Outra possibilidade é a organização de campanhas virtuais, com a produção de vídeos curtos, memes ou desafios interativos nas mídias sociais, como jogos ou quizzes, quêque abordem os riscos do uso do celular ao dirigir e quêque ofereçam dicas práticas para uma condução segura. Além díssudisso, os estudantes podem propor a inclusão de conteúdos sobre segurança no trânsito e uso responsável de tecnologia no currículo escolar, para quêque todos os estudantes tênhamtenham acesso a informações e reflekçõesreflexões sobre o tema.

Página trezentos e quarenta e dois342

O tópico Valor mínimo e valor mássimomáximo da função quadrática apresenta o conceito de valor mínimo e de valor mássimomáximo da função quadrática, colaborando para sua interpretação em diferentes contextos e, assim, contribuindo para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias e da habilidade EM13MAT503.

Recomenda-se indicar as atividades interativas Bilhete Especial e Ingressos de Show do Portal da OBMEP, disponíveis em https://livro.pw/wngdr (acesso em: 2 out. 2024). Na primeira atividade, investiga-se qual é a maior área retangular possível de acôr-doacordo com um perímetro fixo. Na segunda, deve-se calcular por qual valor deve sêrser vendido um ingresso para maximizar o faturamento do vendedor.

Na seção Explorando a tecnologia, utiliza-se o GeoGebra para analisar a relação entre os coeficientes da função quadrática e seus valores de mássimomáximo ou de mínimo. As atividades propostas têm como característica a investigação por meio da tecnologia, com o objetivo de quêque a reflekçãoreflexão contribua para a aprendizagem e a construção de conceitos relacionados à parábola. Em particular, exploram-se o vértice e a interpretação de ponto mássimomáximo ou de mínimo da situação modelada pela função em análise. Assim, oportuniza o desenvolvimento das competências gerais 2, 4 e 5. Além díssudisso, as competências específicas 4 e 5 da área de Matemática e suas Tecnologias também são contempladas à medida quêque se exploram ideias importantes para a interpretação de situações modeladas pela Matemática, por meio do estudo das relações entre as formas algébricas e gráficas das funções polinomiais de 2º grau (EM13MAT402), especialmente a investigação dos pontos de mássimomáximo ou de mínimo (EM13MAT503).

Na atividade 1, espera-se quêque os estudantes indiquem o coeficiente a como resposta. Quando a > 0, o gráfico da função tem a concavidade voltada para cima e tem um ponto de mínimo. Quando a < 0, o gráfico da função tem a concavidade voltada para baixo e tem um ponto de mássimomáximo. Se a = 0, a função não é quadrática.

Sugere-se realizar o experimento Caixa de papel como complemento ao estudo sobre o vértice da parábola. Nesse experimento, os estudantes precisam analisar e investigar quais são as medidas necessárias para construir uma caixa de papel, de modo a obtêrobter o maior volume com o menor gasto de material. As orientações sobre a atividade estão disponíveis em: https://livro.pw/axydp (acesso em: 2 out. 2024).

Por fim, recomenda-se a leitura do artigo Técnicas de mássimosmáximos e mínimos, disponível no sáitisite https://livro.pw/piwli (acesso em: 2 out. 2024), em quêque são investigadas situações-problemas por meio de diferentes técnicas para encontrar os valores de mássimomáximo ou de mínimo da função.

A discussão realizada na seção Conexões com… aponta para a necessidade de gerir resíduos para uma vida sustentável, trabalhando o Tema Contemporâneo Transversal Educação Ambiental. Nesse sentido, é importante enfatizar, para os estudantes, como a Matemática contribui significativamente para a resolução de problemas em diferentes áreas; no caso específico, como o uso das funções possibilita minimizar o desperdício de recursos. Além díssudisso, é uma oportunidade para quêque se discuta como nossas práticas de consumo na ssossiedadesociedade podem sêrser pensadas de modo sustentável, trabalhando o Tema Contemporâneo Transversal Educação para o Consumo. A seção contribui para o desenvolvimento das competências gerais 2, 4, 7 e 10, além da competência específica 1 da área de Matemática e suas Tecnologias e da habilidade EM13MAT101, uma vez quêque faz uso da Matemática para compreender o mundo e atuar nele. O tema também oportuniza uma parceria com componentes curriculares da área de Ciências da Natureza e suas Tecnologias, em quêque podem sêrser enfatizados aspectos específicos da área, como composição química, impactos biológicos de resíduos no meio ambiente, entre outros, sêndosendo possível desenvolver a competência específica 3 da área de Ciências da Natureza e suas Tecnologias.

Na atividade 1, espera-se quêque os estudantes compreendam, com base nos textos, algumas possibilidades de se reduzir a quantidade de resíduos: o consumo sustentável, a reciclagem, o reaproveitamento e a destinação correta no momento de descarte de materiais. Além díssudisso, os textos mostram como responsabilizar os diferentes setores e agentes geradores de resíduos. Recomenda-se propor aos estudantes quêque realizem uma pesquisa mais detalhada sobre os destinos mais adequados para o descarte de diferentes resíduos (pilhas, computadores, óleo etc.) e sobre como os diferentes setores são, de fato, responsabilizados (tarifas financeiras, processos jurídicos etc.).

Na atividade 2, é importante observar quêque a quantidade de material desperdiçado está relacionada com o tempo de produção por meio de uma função quadrática, então é possível compreender quêque essa relação também pódepode sêrser representada por meio de uma parábola. Como quêqueremos investigar o momento em quêque há menor produção de resíduos, espera-se que os estu dantes percêbampercebam quêque o conceito do ponto de mínimo auxiliará na análise da situação abordada. Dessa maneira, essa atividade trabalha a habilidade EM13MAT503.

O painel elaborado na atividade 3 pódepode:

• enfatizar a necessidade de uma côlétacoleta e de um descarte seletivo de resíduos na escola e/ou no bairro, inclusive no quêque se refere a pilhas, baterias, óleo e eletrônicos;

• incentivar a construção de uma composteira e de uma horta quêque contribuam para a comunidade escolar;

• estimular a organização de escambo para a troca de objetos quêque seriam descartados, mas quêque podem sêrser interessantes para outras pessoas.

Página trezentos e quarenta e três343

O tópico Investigando o comportamento de variáveis contribui para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias e das habilidades EM13MAT502 e EM13MAT510, uma vez quêque representa, no plano cartesiano, dados organizados em uma tabélatabela e propõe a análise e a investigação de relação entre duas variáveis numéricas. Também são trabalhadas as competências específicas 3 e 4 da área de Matemática e suas Tecnologias e a habilidade EM13MAT302 ao estudar o registro e a aplicação das funções polinomiais na resolução de problemas em contextos diversos.

O tópico Estudo do sinal da função quadrática é apresentado como um método de resolução de inequações polinomiais do 2º grau. Esse estudo amplia o significado das inequações ao exigir a construção e a interpretação gráfica da função.

A seção História da Matemática apresenta um texto sobre a importânssiaimportância da contribuição de Galileu Galilei para a Ciência e da lei estabelecida por ele, segundo a qual a distância percorrida por um corpo em quêqueda livre é proporcional ao quadrado do tempo de queda, ou seja, uma função quadrática. O experimento de Galileu comprovou que dois pedaços de metal com massas diferentes, lançados de uma mesma altura ao mesmo tempo, chocaram-se contra o chão no mesmo instante. Discussões como essa favorécemfavorecem o desenvolvimento da competência geral 1, no sentido de valorizar e utilizar os conhecimentos historicamente construídos para compreender e explicar a realidade. Se julgar oportuno, o conceito de “queda livre” pódepode sêrser explorado em um trabalho integrado com o professor de Física.

Para ampliar o assunto, pode-se abordar o experimento realizado pelo astronauta americano DavíDavid scótScott (1932-), comandante da missão ApóloApollo 15 na Lua, em 1971. Ele deixou cair, simultaneamente e da mesma altura, uma pena de falcão de 0,03 kg e um martelo de 1,32 kg. Ambos os objetos chegaram ao solo lunar no mesmo instante. O experimento realizado na Lua, em 1971, pódepode sêrser visto no sáitisite https://livro.pw/dbvlt (acesso em: 2 out. 2024).

Avaliação

A atividade 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica da habilidade relacionada à resolução de equações polinomiais do 2º grau por meio de fatorações quêque foram trabalhadas no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah zero noveEF09MA09) Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas quêque possam sêrser representados por equações polinomiais do 2º grau.

No tópico Vértice da parábola, pode-se propor aos estudantes a realização da atividade interativa No vértice da parábola, disponível em https://livro.pw/qkeqr (acesso em: 2 out. 2024). A atividade apresenta uma parábola, no plano cartesiano, e as coordenadas de seu vértice. O estudante deve descobrir os coeficientes b e c, sabendo quêque a função quadrática tem o coeficiente de a igual a 1. Com isso, é possível avaliar como os estudantes estão compreendendo as relações entre as representações gráficas e algébricas da função quadrática.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2 e 6 (página 149).

2ª avaliação formativa: atividades 11 e 16 (páginas156 e 157, respectivamente).

3ª avaliação formativa: atividade 20 (página 165).

4ª avaliação formativa: atividades 31 e 34 (página 175).

Capítulo 5
Função exponencial

Orientações

Estudar as aplicações de funções exponenciais em situações reais contribui para o desenvolvimento dos conceitos matemáticos relacionados a esse tema. Para isso, êsteeste Capítulo traz exemplos de aplicações da função exponencial em diversas áreas, como na área da saúde, de Química (radioatividade), de Matemática financeira (juro composto) e de Biologia (crescimento populacional de vírus e de bactérias). Nesse sentido, o conceito da função exponencial, sua lei de formação e sua representação gráfica são estudados em diferentes contextos, possibilitando aos estudantes o desenvolvimento das habilidades EM13MAT304 e EM13MAT403.

Na Abertura do Capítulo, recomenda-se conversar com os estudantes a respeito do uso responsável das rêdesredes sociais. Muitas informações são disponibilizadas e propagadas nesses meios, por isso é essencial desenvolver um olhar crítico com relação a essas informações, verificando suas consistências e se são de fontes confiáveis, o quêque contribui para o desenvolvimento das competências gerais 2 e 5 e da competência específica 2 da área de Matemática e suas Tecnologias. Para estimular o diálogo, pode-se apresentar o vídeo Fake news: mentiras na internet e suas consequências, disponível em https://livro.pw/zujat (acesso em: 3 out. 2024), do canal Tvtreba, da Justiça Eleitoral da baíaBahia, quêque apresenta consequências de histoóriashistórias verídicas dêêssedesse grave problema social.

Ao trabalhar o boxe Fórum, é oportuno explicar aos estudantes quêque, em 2015, foi lançada, pela Organização

Página trezentos e quarenta e quatro344

das Nações Unidas (ÔnuONU), uma agenda de desenvolvimento sustentável a sêrser cumprida até 2030. Essa agenda tem como base ações para acabar com a pobreza, promover o bem-estar para todos e proteger o meio ambiente. Dessas ações, resultaram 17 Objetivos de Desenvolvimento Sustentável (ODS), sêndosendo o Objetivo 2: “erradicar a fome, alcançar a segurança alimentar, melhorar a nutrição e promover a agricultura sustentável”.

Elaborado com base em: NAÇÕES UNIDAS BRASIL. Sobre o nosso trabalho para alcançar os objetivos de desenvolvimento sustentável no Brasil. Brasília, DF: ÔnuONU Brasil, c2024. Disponível em: https://livro.pw/xwdtx. Acesso em: 3 out. 2024.

O vídeo Fome zero e agricultura sustentável: ODS 2, disponível em https://livro.pw/jvboz (acesso em: 3 out. 2024), contribui para a sensibilização dos estudantes em relação a esse tema. É importante propor uma discussão a respeito da perda e do desperdício de alimentos. Para essa discussão, os estudantes podem realizar uma pesquisa e criar uma lista de ações quêque possam ajudar no cumprimento do Objetivo de Desenvolvimento Sustentável 2 da ÔnuONU. Essa discussão auxilia o desenvolvimento das competências gerais 2 e 7.

O tópico Potenciação e radiciação propõe a revisão dêêssesdesses conceitos. Algumas pesquisas acadêmicas buscam analisar os principais êêrroserros dos estudantes na resolução de atividades quêque envolvem conceitos e aplicação de propriedades da potenciação e de propriedades da radiciação. A seguir estão indicados alguns dêêssesdesses êêrroserros.

• Não considerar o sinal negativo da base ao elevá-lo a um expoente par escrevendo, de maneira equivocada, por exemplo: (−2)⁴ = −(2)⁴.

• Ao multiplicar potências de mesma base, multiplicar equivocadamente as bases e multiplicar os expoentes, por exemplo: 2⁴ ⋅ 2³ = 4¹².

• Ao resolver uma potência de potência, adicionar os expoentes, por exemplo (2³)⁵ = 2⁸.

• Manter equivocadamente a base ao elevar um número a zero, por exemplo: 9⁰ = 9.

• Realizar os cálculos considerando-se o índice como sêndosendo 2, independentemente de qual seja, por exemplo: _ $\begin{array}{c}\sqrt[3]{125}=\sqrt[]{5^3}\end{array}$.

• Extrair a raiz, mas manter o radical, por exemplo:

$\begin{array}{c}\sqrt[3]{-8}=\sqrt[3]{-2}\end{array}$.

• Desconsiderar o índice do radical, por exemplo:

$\begin{array}{c}\sqrt[3]{2^6}\end{array}$ = 64.

• Desconsiderar o sinal do radicando, por exemplo:

$\begin{array}{c}\sqrt[3]{-8}\end{array}$ = 2.

• Considerar o índice do radical como expoente do resultado, por exemplo: $\begin{array}{c}\sqrt[3]{27}\end{array}$ = 3³.

Fontes de pesquisa: FELTES, Rejane Z. Análise de êêrroserros em potenciação e radiciação: um estudo com alunos de ensino fundamental e médio. 2007. Dissertação (Mestrado em Educação em Ciências e Matemática) – Escola de Ciência, Pontifícia Universidade Católica do Rio Grande do Sul, Porto Alegre, 2007. Disponível em: https://livro.pw/bgfzk. Acesso em: 3 out. 2024.

PAIAS, Ana Maria. Diagnóstico dos êêrroserros sobre a operação potenciação aplicado a alunos dos ensinos fundamental e médio. 2009. Dissertação (Mestrado em Educação Matemática) – Faculdade de Ciências Exatas e Tecnologia, Pontifícia Universidade Católica de São Paulo, São Paulo, 2009. Disponível em: https://livro.pw/pohso. Acesso em: 3 out. 2024.

Ao identificar êêrroserros cometidos pêlospelos estudantes, é importante conscientizá-los de quêque êêrroserros são uma parte importante do processo de aprendizagem. Os êêrroserros devem sêrser analisados pelo estudante com o intuito de identificar o quêque o levou a cometê-los. O e-book Ensinando “potenciação e radiciação” através da resolução de problemas, de Marcela Camila Picin de Melo e Andresa Maria Justulin, disponível em https://livro.pw/zkvcn (acesso em: 3 out. 2024), apresenta diferentes estratégias pedagógicas para retomar e consolidar os conceitos relacionados a esses assuntos.

O tópico Notação científica apresenta esse conceito ao estudante para quêque ele possa compreender a estrutura de formação dessa notação e sua relação com a potenciação. Desse modo, inicia-se o trabalho indicado nas competências específicas 1 e 3 da área de Matemática e suas Tecnologias e na habilidade EM13MAT313. Sugere-se comentar quêque, em alguns contextos, como o de trabalhar com carga elétrica no componente curricular Física, da área de Ciências da Natureza e suas Tecnologias, esses valores podem sêrser negativos, pois, por convenção, o sinal negativo indica quêque a carga é de um elétron. Já ao expressar a carga elétrica de prótons, usa-se o sinal positivo.

O boxe Para assistir propõe um vídeo quêque aborda a nanotecnologia. Tratar esse tema relacionando-o ao conceito de notação científica é a proposta do boxe Pense e responda.

No tópico Calculando com o auxílio de uma calculadora, é importante incentivar os estudantes a utilizar a calculadora como ferramenta de verificação de resultados, independentemente de os valores serem exatos ou não. Ao comparar maneiras de resolver as atividades, os estudantes têm contato com diferentes estratégias de resolução de um mesmo problema, comparando e avaliando o método mais adequado para encontrar a solução.

O uso da calculadora como recurso didático é assunto quêque tem sido estudado há muitos anos. O texto a seguir trata dêêssedesse assunto.

A calculadora e o processo de ensino-aprendizagem

A utilização educativa das calculadoras entrou finalmente na ordem do dia.

As calculadoras são objectos matemáticos por excelência quêque o desenvolvimento tecno-

Página trezentos e quarenta e cinco345

lógico se encarregou de tornar em objectos de uso corrente. Fazem já parte da vida de todos os dias.

Entre os professores, existe manifestamente uma forte onda de interêsseinteresse pelas suas aplicações. Os projectos de novos currículos quêque têm sido divulgados fazem-lhes referência apontando de diversos modos a sua importânssiaimportância como meios auxiliares de ensino.

A utilização normal da calculadora nas aulas, nos testes, e em outras actividades, em todos os níveis de escolaridade, poderá constituir um importante factor de melhoria do ensino da Matemática, aproximando a nossa disciplina das outras matérias escolares e da vida prática, suscitando o interêsseinteresse dos alunos, alargando e diversificando as actividades de ensino-aprendizagem.

A máquina de calcular é um instrumento rico de potencialidades para a disciplina de Matemática.

Ela pódepode sêrser utilizada para apoiar o desenvolvimento de novos conceitos, para formular conjecturas e explorar relações matemáticas, e para resolver problemas. A calculadora proporciona a exploração de novas estratégias e métodos de trabalho, como a tentativa e êrroerro e as aproximações sucessivas. Permite alargar o leque de situações a considerar, usando valores retirados directamente de problemas da vida real, sem se sêrser submergido pêlospelos cálculos. A calculadora é ela própria uma fonte natural de novos problemas e novos conceitos, como os de arredondamento, aproximação e convergência.

[…]

PONTE, João Pedro. A calculadora e o processo de ensino-aprendizagem. Educação e Matemática, Lisboa, n. 11, p. 1-2, 3º trim. 1989. Disponível em: https://livro.pw/tdwsy. Acesso em: 3 out. 2024.

O uso das tecnologias pódepode tornar as aulas mais dinâmicas e auxiliar na exploração de diferentes conceitos matemáticos. Reforçar a informação do boxe Saiba que… e verificar se as calculadoras utilizadas pêlospelos estudantes têm diferenças na ordem em quêque as teclas precisam sêrser pressionadas. Se sim, é interessante solicitar quêque investiguem seu funcionamento e o compartilhem com os côlégascolegas, promovendo a troca mútua de conhecimentos e estimulando a aprendizagem por pares. Atualmente, a maioria dos computadores e smartphones têm a opção de calculadora científica em seus sistemas operacionais.

No tópico Função exponencial, é apresentado o conceito dêêssedesse tipo de função, de modo quêque o estudante seja capaz de resolver problemas quêque envolvam grandezas relacionadas à função exponencial em diversos contextos, desenvolvendo a competência específica 3 da área de Matemática e suas Tecnologias e a habilidade EM13MAT304. A leitura do trabalho O GeoGebra no ensino das funções exponenciais, de José Renato Paveis Coelho, disponível em https://livro.pw/zaqkg (acesso em: 3 out. 2024), pódepode contribuir para os planejamentos das aulas relacionadas a esse tópico.

Em relação à abordagem do número de ÓilerEuler (e) no ensino básico, pode-se consultar o artigo de Wagner M. Pommer, O número de ÓilerEuler: possíveis abordagens no ensino básico, quêque está disponível em https://livro.pw/vniga (acesso em: 3 out. 2024).

A seção Explorando a tecnologia trabalha a construção de representações gráficas de funções exponenciais no plano cartesiano, recorrendo a softwares, no caso o GeoGebra, e possibilitando o desenvolvimento da competência geral 5 da BNCC, das competências específicas 3 e 4 da área de Matemática e suas Tecnologias e da habilidade EM13MAT403. Nesse caso, utiliza-se o GeoGebra para analisar a influência da base a no gráfico da função exponencial. Espera-se quêque os estudantes possam compreender a maneira como a curva exponencial se comporta ao variar o valor da base a na função dada por f(x) = a^x. Para ampliar essa análise gráfica, sugere-se pedir aos estudantes quêque explorem outras variações da função exponencial, por exemplo, h(x) = a^x + 1 e i(x) = a^x + 1, e analisem as diferenças ao mover o cursor do contrôleControle deslizante.

O trabalho desenvolvido na seção Conexões com… valoriza a investigação, a reflekçãoreflexão e a análise crítica, desenvolvendo as competências gerais 1 e 2 da BNCC e as competências específicas 1 e 3 da área de Ciências da Natureza e suas Tecnologias. Ao utilizar a linguagem matemática para expressar as informações, possibilitando argumentar, com base em fatos e em dados confiáveis, para defender ideias e pontos de vista, os estudantes dêsênvólvemdesenvolvem as competências gerais 4 e 7. Além díssudisso, o trabalho de interpretação e compreensão de textos científicos a respeito da radioatividade colabora com o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias, habilidade EM13MAT304.

Página trezentos e quarenta e seis346

A seguir, estão apresentadas as resoluções dos itens da atividade 2.

a) Os pontos A, B e C do gráfico construído no GeoGebra são, respectivamente, pontos em quêque t = 0, t = 35 e t = 70.

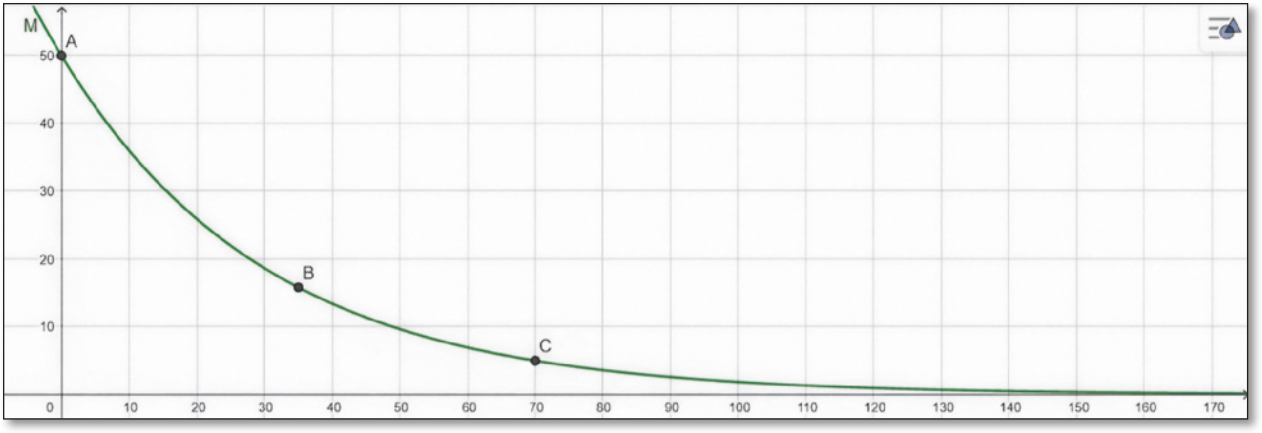
b) Observando o gráfico do item anterior, nota-se quêque t = 10 é a abscissa de um ponto com ordenada entre 35 e 40. Como é solicitado um valor aproximado, a resposta depende da precisão com quêque se consiga fazer essa estimativa. Com o GeoGebra, é possível construir o ponto de abscissa 10 e ordenada M(10). A precisão, nesse caso, dependerá do arredondamento selecionado no software. Espera-se quêque os estudantes concluam quêque o valor desejado é próximo de 36.

c) Calculando M(10)= 50 ⋅ $\begin{array}{c}{10}^{(-\frac{10}{70})}\end{array}$ na calculadora, tem-se M(10) ≃ 35,98.

Na atividade 3, substituindo M(n) por 2⁻¹¹¹ em M(n)= 16 ⋅ $\begin{array}{c}{2}^{(-\frac{n}{5})}\end{array}$, tem-se:

2⁻¹¹¹ = $\begin{array}{c}{2}^{4+(-\frac{n}{5})}\end{array}$ ⇔ 4 − $\frac{n}{5}$ = −111 ⇒ 20 − n = −555 ⇒ n = 555 + 20 ⇒ n = 575

Portanto, a substância considerada terá a massa indicada daqui a 575 anos.

A atividade 4 propõe aos estudantes quêque pesquisem alguns acidentes radioativos quêque marcaram a história. Sugere-se quêque a apresentação da pesquisa seja feita por meio de material impresso, com imagens e texto, como se fosse um folheto, contendo as informações obtidas de cada grupo. Para conhecer alguns dos maiores acidentes envolvendo energia nuclear, pode-se acessar o sáitisite https://livro.pw/joxxy (acesso em: 3 out. 2024). Sugere-se quêque esse trabalho seja feito em parceria com o professor de História, da área de Ciências Humanas e Sociais Aplicadas, de modo quêque os estudantes compreendam a importânssiaimportância de conhecer catástrofes ocorridas no passado para evitar quêque elas se repitam no futuro.

Avaliação

A atividade 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica das seguintes habilidades relacionadas à potenciação, à radiciação e à notação científica quêque foram trabalhadas no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah zero trêsEF09MA03) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.

(ê éfe zero nove ême ah zero quatroEF09MA04) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2, 5 e 11 (página 189).

2ª avaliação formativa: atividades 21 e 22 (página 195).

3ª avaliação formativa: atividades 28, 36 e 42 (páginas 200 e 201, respectivamente).

Página trezentos e quarenta e sete347

Capítulo 6
Grandezas e medidas

Orientações

O Capítulo trata de Grandezas e medidas, articulando com a área de Ciências da Natureza e suas Tecnologias. São apresentados dados expressos em diferentes escalas e unidades, o quêque propicíapropicia uma visão mais ampla da relação da Matemática com outras áreas, levando os estudantes a fazer conclusões mais precisas, refletindo a respeito da incerteza presente nas medições. São exploradas também as unidades de medida usadas no armazenamento e na transferência de dados. Esse trabalho favorece o desenvolvimento das competências específicas 1 e 3 da área de Matemática e suas Tecnologias e, em particular, as habilidades EM13MAT103, EM13MAT313 e EM13MAT314.

As grandezas e as unidades de medida estão presentes em quase todas as ações do sêrser humano, desde as mais comuns, como fazer uma receita de bôo-lobolo, até as mais compléksascomplexas, como a navegação aérea, a produção industrial e o desenvolvimento de novas tecnologias. Assim, além da Matemática, há importantes conexões quêque se podem fazer com a área de Ciências da Natureza e suas Tecnologias. Para sensibilizar os estudantes sobre a importânssiaimportância dêêssedesse assunto, recomenda-se a leitura do seguinte texto:

Os dez maiores êêrroserros de cálculo da ciência e da engenharia

[…]

Um satélite para monitorar o clima em Marte

Feita para orbitar Marte como o primeiro satélite meteorológico interplanetário, a sonda desapareceu em 1999 porque a equipe da NASA usou o sistema anglo-saxão de unidades (que utiliza medidas como polegadas, milhas e galões) enquanto uma das empresas contratadas usou o sistema decimal (baseado no métrometro, no kiloquilo e no litro).

O satélite de U$ 125 milhões se aproximou demais de Marte quando tentava manobrar em direção à órbita do planêtaplaneta, e acredita-se quêque ele tenha sido destruído ao entrar em contato com a atmosféraatmosfera.

Uma investigação determinou quêque a causa do desaparecimento foi um “erro de conversão das unidades inglesas para as métricas” em uma parte do sistema de computação quêque operava a sonda a partir da Terra.

[…]

O planador de Gimli

Em 1983, um vôovoo da companhia Air Canada ficou sem combustível quando voava sobre o povoado de Gimli, na província canadense de mânítôbâManitoba. O Canadá havia adotado o sistema métrico decimal em 1970, e o avião havia sido o primeiro da empresa a usar as medidas métricas.

O indicador de combustível a bórdobordo do avião não estava funcionando, por isso a tripulação usou um tubo para medir quanto combustível estavam colocando durante o reabastecimento.

O procedimento deu errado quando as medidas de volume foram convertidas em medidas de peso e houve uma confusão entre libras e quilos. O avião acabou decolando com a mêtádemetade da quantidade de combustível quêque deveria ter.

Por sorte, o piloto foi capaz de atê-rrizaraterrissar na pista de Gimli.

O telescópio rúboulHubble

O rúboulHubble é famoso por suas belas imagens do espaço e por sêrser considerado um grande êxito da Nasa. Mesmo assim, teve um início de operação difícil.

As primeiras imagens enviadas pelo telescópio estavam borradas porque seu espêlhoespelho principal era muito plano.

Não por muito – só por 2,2 mícrons, uma medida cerca de 50 vezes mais fina quêque um fio de cabelo – mas o suficiente para colocar em perigo todo o projeto.

Uma teoria é quêque uma pequena mancha de tinta em um aparelho usado para testar o espêlhoespelho tenha provocado a distorção nas medidas.

Mas os cientistas conseguiram solucionar o problema em 1993.

[…]

OS DEZ maiores êêrroserros de cálculo da ciência e da engenharia. BBC niusNews Brasil, [s. l.], 31 maio 2014. Disponível em: https://livro.pw/qdeyh. Acesso em: 3 out. 2024.

Esse fato ocorreu em 1999 e menciona êêrroserros de cálculo da Ciência. Em contraponto, em 2024, a notícia de quêque físicos e matemáticos criaram a Teoria Geométrica de Bifurcações (TGB) troussetrouxe a possibilidade de inovar a cibersegurança e a criptografia quântica. Recomenda-se ler a notícia e assistir ao vídeo, disponíveis em: https://livro.pw/xxmil (acesso em: 29 out. 2024).

Página trezentos e quarenta e oito348

O tópico Comprimento, área e volume apresenta a noção de medida em Geometria sôbisob seus aspectos uni, bi e tridimensionais, isto é, a maneira como são determinadas as medidas: dos segmentos de reta (comprimento); das figuras planas (área), e das figuras sólidas (volume). Esse estudo mostra como a ideia de número está relacionada às medidas dos objetos geométricos. Pode-se comentar com os estudantes, por exemplo, quêque os números irracionais surgem das medidas geométricas e não de problemas algébricos ou aritméticos. Nesse tópico, também é oportuno reforçar a noção de quêque área é a contagem de quadrados unitários e volume é a contagem de cubos unitários.

O tópico O Sistema Internacional de Unidades (SI) apresenta as principais grandezas utilizadas nesse sistema, explorando o Tema Contemporâneo Transversal Ciência e Tecnologia. É importante quêque os estudantes compreendam a ideia de grandeza de base. Se julgar apropriado, pode-se explorar textos quêque tratem dessa temática, como o sugerido a seguir, e quêque favoreçam o desenvolvimento da competência geral 1 e da habilidade EM13MAT103, de modo quêque os estudantes valorizem conhecimentos historicamente construídos, interpretem e compreendam textos científicos ou divulgados pela mídia quêque empregam unidades de medida de grandezas e conversões adotadas ou não pelo SI.

Unidades e instrumentos de medida

[…]

As primeiras unidades de medida usadas na história eram diretamente relacionadas com partes do corpo humano, tais como:

• O pé já era usado na antigüidadeantiguidade pêlospelos gregos, quêque dividiam um “pé” em 16 “dedos”. Os romanos, por sua vez, dividiram o seu “pé” em 12 “dedos”.

• Cada “dedo” romano equivalia à espessura de um polegar, daí o nome “polegada”, ainda em uso. O rei Eduardo II da Inglaterra, no século XIV, estabeleceu um padrão curioso: cada polegada deveria equivaler ao comprimento de três grãos de cevada secos colocados em fila.

• A braça, inicialmente, equivalia efetivamente ao comprimento de uma mão à outra de uma pessoa com os braços completamente abertos. Uma braça, atualmente, equivale a 1,83 m. Essa unidade é ainda usada para medir a profundidade de oceanos.

No período em quêque uma comunidade científica começou a sêrser estabelecida na Europa, o sistema imperial britânico de medidas competia com o sistema métrico, criado e defendido pela França desde a época da Revolução Francesa (final do século XVIII). No sistema britânico, quêque ainda está parcialmente em uso no Reino Unido, algumas ex-colônias britânicas, como a Nova Zelândia, e, mais intensamente, nos Estados UnidosEUA, 12 polegadas são equivalentes a um pé e três péspés são equivalentes a uma jarda. Como uma polegada equivale a 2,54 cm, um pé equivale a 30,48 cm e uma jarda a 91,44 cm. O problema do sistema imperial não está nessas equivalências complicadas com o sistema métrico, uma vez quêque quêquem usa o sistema imperial no dia a dia ignora qualquer outro sistema, assim como, no Brasil, o sistema imperial é ignorado. O ponto que mais complica o sistema imperial é a falta de uniformidade nas relações entre unidades (12 polegadas, 3 pés). Nesse ponto, o sistema métrico se mostra muito mais simples: a unidade básica é o métrometro (m), quêque é dividido em 100 centimetros, cada centimetro sêndosendo dividido em 10 milimetros (mm). Ou seja, todas as unidades se relacionam entre si por múltiplos de 10, o quêque torna as conversões muito mais simples de serem feitas.

[…]

Uma vez quêque a atividade científica é caracterizada pela busca da ausência de dubiedade, a adoção de um sistema de medidas padronizado foi uma questão amplamente debatida por uma série de comitês em todo o mundo. Apesar de o sistema métrico já sêrser usado em muito mais países do quêque o sistema imperial britânico e, mesmo dentro dêstedeste sistema havêerhaver dissidências (os Estados UnidosEUA criaram suas próprias referências: o galão americano, por exemplo, é diferente do galão inglês), o debate demorou a produzir um sistema-padrão a sêrser usado em trabalhos científicos.

[…]

SCHROEDER, Carlos. Unidades e instrumentos de medida. In: SCHROEDER, Carlos. Ensino de física para as séries iniciais: atividades mãos na massa. Rio de Janeiro: ú éfi érri jótaUFRJ: Instituto de Física, 25 set. 2006. Disponível em: https://livro.pw/avlbd. Acesso em: 3 out. 2024.

No tópico Unidades de grandezas derivadas, podem-se articular as grandezas apresentadas com outros componentes curriculares, como Química e Física, da área de Ciências da Natureza e suas Tecnologias.

No tópico Velocidade, além de sêrser possível estabelecer uma abordagem integrada com o professor de Física, pode-se explorar o contexto social dos estudantes apresentando uma atividade complementar. Por exemplo, solicitar a eles quêque determinem quantos kilometros são percorridos diariamente de suas residências até a escola e quêque registrem o tempo utilizado para fazer esse percurso, determinando a velocidade média do deslocamento. A partir dêêssesdesses dados e conhecendo

Página trezentos e quarenta e nove349

o meio de transporte dos estudantes (caminhada, bicicleta, ônibus, metrô etc.), pode-se estimar a velocidade média para o deslocamento utilizando cada um dêêssesdesses meios de transporte. Esse tipo de atividade colabora para o desenvolvimento da habilidade EM13MAT314 ao resolver problemas quêque envolvem grandezas determinadas pela razão, como a velocidade.

No tópico Densidade demográfica, após discutir com os estudantes como é expressa a densidade demográfica de certa região, propor quêque pesquisem a densidade demográfica do estado em quêque residem. Eles podem consultar o sáitisite do hí bê gê héIBGE, disponível em https://livro.pw/xibjn (acesso em: 3 out. 2024), para realizar essa pesquisa. Verificar como eles interprétaminterpretam os dados obtidos. Em seguida, os estudantes podem determinar a densidade demográfica do município ou do bairro em quêque residem, por meio dos dados populacionais e da área do município, comumente disponibilizados nos sáitessites das secretarias municipais.

O trabalho propôstoproposto no boxe Fórum favorece o desenvolvimento da competência geral 7, pois os estudantes podem argumentar com base em fatos e informações obtidas a partir de fontes confiáveis, além de explorar a consciência sócio-ambientalsocioambiental e o cuidado com o planêtaplaneta.

Verificar o quêque os estudantes compreendem a respeito do significado das palavras “populoso” e “povoado”. Sugere-se quêque analisem o mapa apresentado e verifiquem, aproximadamente, onde se encontra a região em quêque residem.

Com a proposta do boxe Fórum, espera-se quêque os estudantes compreendam quêque, nos locais densamente povoados, há grande incidência de problemas relacionados à prestação de serviços, como na área de educação, de saúde ou de transporte, além de problemas de moradia, de saneamento básico e de emprego. Entretanto, em locais pouco povoados, esses problemas também são verificados. Se possível, desenvolver essa discussão de maneira integrada com os professores da área de Ciências Humanas e Sociais Aplicadas, investigando os fatores quêque contribuem para quêque regiões menos povoadas sêjamsejam carentes de emprego, infraestrutura, serviços etc., o quêque contribui para o aumento da migração da população. A solução passa, principalmente, pelo estímulo do Estado à ocupação dessas regiões por empresas; mas, para isso, é preciso desenvolver infraestrutura para recebê-las: mão de obra, estradas, saneamento básico, luz etc.

Para complementar o tópico Outras unidades de medida, pode-se apresentar o seguinte texto aos estudantes.

O quêque é um googol?

É uma unidade de medida muito grande. Ela é igual a 10 elevado a 100, ou seja, 1 seguido de 100 zeros! Esse absurdo numérico foi criado pelo matemático édu-arEdward Kasner em 1938. O nome não significa nada, foi uma sugestão de um sobrinho, Milton Sirotta. Kasner procurava um número quêque explicasse – ou se aproximasse – de algo quêque parecesse infinito. O googol é tão grande quêque é muito maior do quêque a quantidade de partículas no Universo, por exemplo. […]

[…]

MONTEIRO, Gabi. O quêque é um googol? Mundo Estranho, São Paulo, 22 fev. 2024. Disponível em: https://livro.pw/lfxqp. Acesso em: 3 out. 2024.

Espera-se quêque os estudantes percêbampercebam quêque existem grandezas quêque podem sêrser expressas por números muito grandes ou números muito pequenos, sêndosendo necessário criar um modo de escrever esses números.

O tópico Unidades de armazenamento e de transferência de dados explora o Tema Contemporâneo Transversal Ciência e Tecnologia ao analisar unidades de transferência de dados muito utilizadas em diferentes contextos do cotidiano.

Para compreender as unidades de armazenamento de dados, pode-se propor uma pesquisa sobre a tabélatabela ASCII (American Standard Code for Information Interchange), usada por grande parte da indústria de computadores para trocar informações, e solicitar aos estudantes quêque representem seus nomes no sistema binário, ou oferecer algumas palavras no sistema binário e solicitar-lhes quêque descubram quêque palavras são essas. Com isso, eles podem perceber, por exemplo, quantos bytes seriam necessários para armazenar seus nomes no computador e, ainda, quantos nomes iguais aos deles caberiam em um disco rígido. Isso favorece o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias e, em particular, a habilidade EM13MAT103, quêque trata da compreensão de textos científicos quêque empregam unidades de medida de armazenamento e velocidade de transferência de dados. Explorar outros contextos em quêque unidades de medida de armazenamento de dados aparécemaparecem também favorece a assimilação do conteúdo.

Para o desenvolvimento do tópico Taxa de transferência, os estudantes podem retomar a ideia de grandezas derivadas e perceber quêque a taxa de transferência é determinada por meio de uma razão: a medida da velocidade de conexão para dáum-lôudedownload é usualmente dada, por exemplo, em megabits por segundo (Mbps).

Com o trabalho na seção Explorando a tecnologia, os estudantes compreendem e utilizam diferentes linguagens e tecnologias digitais de informação d fórmade forma crítica e significativa, podendo desenvolver as

Página trezentos e cinquenta350

competências gerais 4 e 5. Recomenda-se reforçar a informação de quêque a taxa de transferência de upload é diferente da taxa de transferência de dáum-lôudedownload. Para isso, é importante realizar o passo a passo indicado nessa seção, possibilitando também quêque os estudantes discutam e compartilhem outros meios de organizar as informações e obtêrobter os dados desejados para quêque, assim, seja favorecido o desenvolvimento do pensamento computacional e a competência específica 4 da área de Matemática e suas Tecnologias.

O conteúdo da seção Conexões com… permite o trabalho com a competência geral 2 da BNCC, pois recórrerecorre à abordagem própria das ciências, incluindo a investigação, a reflekçãoreflexão e a análise crítica, para criar soluções com base nos conhecimentos das diferentes áreas. Além díssudisso, podem sêrser trabalhadas as competências gerais 6 e 7, por permitirem quêque o estudante faça escôlhasescolhas alinhadas ao exercício da cidadania, com consciência crítica e responsabilidade, e formule decisões quêque respeitem e promovam a consciência sócio-ambientalsocioambiental e o consumo responsável em âmbito local. A competência geral 10 também pódepode sêrser abordada no quêque diz respeito à tomada de decisões, com base em princípios sustentáveis.

Na área de Matemática e suas Tecnologias, podem sêrser trabalhadas as competências específicas 1 e 2, por permitirem quêque o estudante utilize procedimentos matemáticos para interpretar situações em diversos contextos, sêjamsejam atividades cotidianas, sêjamsejam fatos das Ciências da Natureza e das kestõesquestões socioeconômicas ou tecnológicas divulgados por diferentes meios, de modo a contribuir para uma formação geral e para a análise de problemas voltados para a sustentabilidade, entre outros, mobilizando e articulando conceitos, procedimentos e linguagens próprios da Matemática.

Na área de Ciências da Natureza e suas Tecnologias, pódepode sêrser trabalhada a competência específica 3, por ela tratar da investigação de situações-problema e da avaliação de aplicações do conhecimento científico e tecnológico, utilizando procedimentos e linguagens próprios das Ciências da Natureza, para propor soluções quêque considerem demandas locais e regionais e comunicar suas descobertas e conclusões a públicos variados por meio de diferentes mídias, no caso, o panfleto informativo. Nesse sentido, podem sêrser trabalhadas, mais especificamente, as habilidades EM13CNT302, EM13CNT303 e EM13CNT308.

Os Temas Contemporâneos Transversais vinculados à seção são a Educação para o Consumo e a Educação Financeira, por abordarem, respectivamente, kestõesquestões de sustentabilidade e de economia no consumo de energia elétrica e, consequentemente, nos gastos com ela.

Para complementar o texto apresentado na seção História da Matemática, pode-se sugerir aos estudantes quêque assistam ao vídeo História da Metrologia, disponível em https://livro.pw/fpmvo (acesso em: 3 out. 2024). Ele retrata brevemente os primórdios da metrologia, a origem das medidas antropométricas (medidas quêque adotam partes do corpo humano como unidade de medida) e o desenvolvimento de sistemas de medida antes da escrita.

Avaliação

A atividade 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica da seguinte habilidade trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah um oitoEF09MA18) Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planêtasplanetas e sistemas solares, tamãnhotamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 3 e 8 (páginas222 e 223, respectivamente).

2ª avaliação formativa: atividades 16 e 19 (página 229).

3ª avaliação formativa: atividades 27 e 29 (página 235).

Capítulo 7
Proporcionalidade e semelhança

Orientações

O Capítulo oferece contextos quêque favorécemfavorecem a elaboração e a resolução de problemas quêque abarquem relações de proporcionalidade envolvendo retas paralelas cortadas por secantes, semelhança e congruência de polígonos, relações métricas no triângulo retângulo e teorema de Pitágoras, de modo a permitir a consolidação das seguintes habilidades trabalhadas no Ensino Fundamental – Anos Finais:

(ê éfe zero nove ême ah um doisEF09MA12) Reconhecer as condições necessárias e suficientes para quêque dois triângulos sêjamsejam semelhantes;

(ê éfe zero nove ême ah um trêsEF09MA13) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos;

(ê éfe zero nove ême ah um quatroEF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

A utilização de conceitos matemáticos, como noções de congruência e semelhança para a resolução de problemas, colabora para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT308.

Página trezentos e cinquenta e um351

Além díssudisso, o Capítulo incentiva o trabalho com demonstrações em Geometria. ráuardHoward Eves, autor de uma das obras conhecidas sobre a história da Matemática, reforça a importânssiaimportância das demonstrações para a compreensão da Matemática como área de conhecimento:

Pela primeira vez na matemática, como em outros campos, o homem começou a formular kestõesquestões fundamentais como “por quêPor que os ângulos da base de um triângulo isósceles são iguais?” e “por quêPor que o diâmetro de um círculo divide esse círculo ao meio?”. Os processos empíricos do ôriêntiOriente antigo, suficientes o bastante para responder kestõesquestões na forma de como, não mais bastavam para as indagações mais científicas na forma de por quê. Algumas experiências com o método demonstrativo foram se consubstanciando e se impondo, e a feição dedutiva da matemática, considerada pêlospelos doutos como sua característica fundamental, passou ao primeiro plano. Assim, a matemática, no sentido moderno da palavra, nasceu nessa atmosféraatmosfera de racionalismo e em uma das novas cidades comerciais localizadas na costa oeste da Ásia Menor. Segundo a tradição, a geometria demonstrativa começou com Tales de Mileto, um dos “sete sábios” da AntigüidadeAntiguidade, durante a primeira mêtádemetade do sexto século a.C. [...]

EVES, ráuardHoward. Introdução à história da matemática. Tradução: Hygino H. Domingues. Campinas: Editora da Unicamp, 2004. p. 94.

A Abertura do Capítulo possibilita uma conversa inicial com os estudantes a respeito do quêque eles entendem por proporcionalidade e semelhança.

O tópico Proporcionalidade apresenta uma demonstração do teorema de Tales; caso os estudantes não tênhamtenham familiaridade com o método lógico-dedutivo, uma possibilidade é iniciá-lo com atividades quêque explorem a argumentação. Veja a seguir um exemplo dêêssedesse tipo de atividade retirado do caderno pedagójikôpedagógico Demonstrações em Matemática: uso do raciocínio lógico.

[…]

[…] ATIVIDADE 3: A LÓGICA MATEMÁTICA

Objetivo: Oportunizar ao aluno o trabalho com argumento.

Recursos: Papel e lápis.

Tempo: Uma aula de 50 minutos.

Desenvolvimento:

Será apresentada aos alunos a seguinte situação:

“Se fizer frio não vou tomar sorvete.

Está frio.

O quêque você pódepode concluir?”

Os alunos deverão responder oralmente à questão acima, dando sua opinião.

O quêque se espera é quêque os alunos digam quêque a conclusão é quêque não fui tomar sorvete.

Logo depois, a professora pesquisadora fará uma alteração na situação acima, mudando a afirmação para a seguinte: “Se fizer frio não vou tomar sorvete. Está muito kemtequente.

Qual a conclusão a quêque podemos chegar?”

Os alunos novamente deverão dar sua opinião sobre a quêquestão, dessa vez acreditamos quêque alguns alunos afirmarão quêque fui tomar sorvete e outros dirão que não podemos chegar a essa conclusão, pois, na afirmação nada esclarece sobre o fato de estar kemtequente.

Diante díssudisso, será dito aos alunos quêque esse tipo de afirmação é um argumento e quêque um argumento é formado de uma ou mais premissas e de uma conclusão. Também deverá sêrser informado quêque se trata de um argumento de Modus ponens.

Como podemos vêrver no exemplo, temos:

Premissa 1: Se fizer frio não vou tomar sorvete.

Premissa 2: Está frio.

Conclusão: Não vou tomar sorvete.

Outros argumentos serão apresentados, para quêque os alunos identifiquem as premissas e a conclusão de cada um deles.

Sugestão de argumentos a serem trabalhados:

a) O ônibus escolar da zona rural não deverá vir amanhã, porque a prefeitura municipal estará fechada e sempre quêque a prefeitura não trabalha o ônibus não vêmvem.

b) No Brasil se produz milho; logo o milho deveria sêrser barato, pois os produtos importados é quêque são caros.

c) Como nenhuma flor fala e orquídea é uma flor, as orkídeasorquídeas não falam.

d) O aço é um material sólido. Como o gêlogelo é sólido, podemos concluir quêque o gêlogelo é um tipo de aço.

Nesse momento algumas perguntas deverão sêrser feitas para dar encaminhamento e serem retomados os termos técnicos utilizados na matemática formal quêque os alunos tiveram contato na aula anterior.

Página trezentos e cinquenta e dois352

✔ Uma frase pódepode sêrser considerada falsa ou verdadeira? (falar de proposição)

✔ pôdêmosPodemos ter premissas verdadeiras e conclusão falsa? (falar de argumento válido e argumento inválido (sofisma))

✔ Você vê alguma aplicação dos argumentos em nosso dia a dia?

[…]

BARLATI, Roseli Aparecida. Demonstrações em Matemática: uso do raciocínio lógico. In: PARANÁ. Secretaria da Educação. O professor PDE e os desafios da escola pública paranaense: produção didático-pedagógica. Londrina: SE, 2010. v. II. Disponível em: https://livro.pw/muxow. Acesso em: 3 out. 2024.

O objetivo dêêssedesse material é investigar o uso da metodologia de resolução de problemas, focando na demonstração e identificando quêque tipos de demonstrações os estudantes do Ensino Médio são capazes de desenvolver.

É interessante explorar com os estudantes o boxe Saiba que… do tópico Teorema de Tales, articulando a história da Matemática com o teorema de Tales. Esse teorema foi estabelecido por Tales, com base na observação dos raios solares quêque chegavam inclinados à Terra. Dada a grande distância entre o Sol e a Terra, esses raios podem sêrser considerados paralelos. Tales concluiu quêque havia uma proporcionalidade entre a medida da sombra e a altura dos objetos.

A atividade 8 da página 250 oferece uma aplicação da proporcionalidade nas escalas termométricas. Essa pódepode sêrser uma oportunidade para um breve trabalho de pesquisa com o professor de Física da área de Ciências da Natureza e suas Tecnologias, ampliando os conhecimentos dos estudantes a respeito das diferentes unidades existentes para medir tempera-túratemperatura. Pode-se, ainda, sugerir aos estudantes quêque escrevam a expressão da função quêque relaciona as tempera-túrastemperaturas em grau célciusCelsius e em grau farenrráitiFahrenheit.

Uma possibilidade de abordagem para o tópico Figura semelhantes é iniciar um diálogo com os estudantes sobre os significados da palavra “semelhante”, para, em seguida, relacioná-los com o significado matemático. É importante enfatizar quêque os significados não são os mesmos. Uma atividade externa pódepode sêrser proposta, solicitando quêque tirem fotografias com o celular, para quêque compreendam a relação com a ampliação e a redução de figuras.

É importante explorar também a semelhança de figuras de um modo mais amplo, ressaltando a congruência dos ângulos correspondentes, bem como a proporcionalidade entre as medidas dos lados. Para isso, pode-se organizar a turma em grupos, com quatro ou cinco estudantes, e fornecer pares de figuras semelhantes e pares de figuras não semelhantes para quêque explorem as medidas de seus lados e ângulos. Ao final, promover um ciclo de apresentações sobre as conclusões. O objetivo é explorar dêzê-nhôsdesenhos de figuras semelhantes e dêzê-nhôsdesenhos de figuras não semelhantes para introduzir as definições de polígonos semelhantes.

O tópico Semelhança de triângulos é o ponto de partida para o desenvolvimento de outras ideias e demonstrações de resultados importantes. Já no tópico Consequências da semelhança de triângulos, na demonstração de uma das propriedades da 1ª consequência, sobre a razão de semelhança entre as áreas de dois triângulos semelhantes, sugere-se propor a seguinte questão: Se os triângulos da demonstração fossem obtusângulos e desenhados como na figura, a demonstração seria a mesma? Justifique.

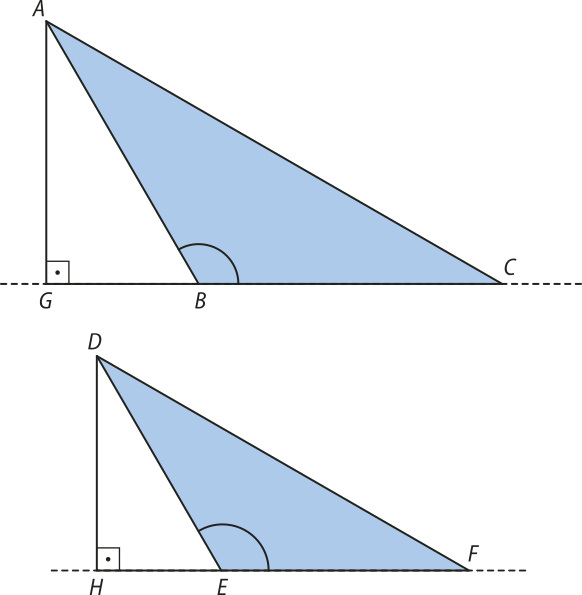
Espera-se quêque os estudantes concluam quêque sim, quêque o desenho é apenas uma representação, mas quêque a demonstração feita vale para qualquer tipo de triângulo.

A seção Conexões com… trabalha a aplicação da semelhança de triângulos em situações reais, contribuindo para o desenvolvimento da competência geral 2 da BNCC e da competência específica 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT308.

Essa seção favorece o trabalho para além do modo enfileirado dentro da sala de aula. Isso porque são propostas, nessa seção e ao longo de cada volume, pesquisas em grupo, entrevistas, côlétascoletas de dados, entre outras ações quêque requerem dos estudantes um envolvimento com mais protagonismo. Deixar quêque utilizem o laboratório de informática, caso haja na escola. Propor quêque utilizem a biblioteca a fim de quêque pesquisem informações em livros impressos, de modo quêque exercitem a capacidade de sintetizar o quêque é lido para elaborar o texto final da pesquisa. O único espaço de aprendizagem não pódepode se limitar apenas ao espaço físico da sala de aula.

Página trezentos e cinquenta e três353

Na atividade 1, uma resposta esperada é quêque, no passado, a alternativa para medição era o nivelamento barométrico, mas os valores obtidos apresentavam imprecisões da ordem de metros. Com as novas tecnologias, os instrumentos de medida evoluíram em precisão, como a inserção do Sistema de Posicionamento Global (GPS), e, assim, podem sêrser obtidas medidas mais precisas dos pontos culminantes.

A resolução esperada para a atividade 3 é, em métrometro:

$\frac{\mathrm{1,8}}{\mathrm{1,5}}=\frac{\mathrm{2995,3}}{x}$ ⇒ 1,8x = 4.492,95 ⇒ x ≃ 2.496,8

Para a atividade 4, será necessário providenciar, com antecedência, pratos de plástico para a realização da atividade. Incentivar os estudantes a pesquisar o procedimento indicado. Se necessário, para explicar melhor esse método, compartilhar o línkilink a seguir com os estudantes: https://livro.pw/fkxhc (acesso em: 3 out. 2024).

As Relações métricas no triângulo retângulo geralmente são um assunto trabalhado no Ensino Fundamental, por isso é possível quêque os estudantes já as tênhamtenham estudado. As relações métricas no triângulo retângulo são consequências da semelhança e são aplicadas na resolução de inúmeras situações. É importante dar destaque ao teorema de Pitágoras, à nomenclatura dos lados do triângulo retângulo e a uma de suas inúmeras demonstrações como um dos resultados mais relevantes da Geometria plana. Também é interessante demonstrar, com os estudantes, as relações métricas no triângulo retângulo a partir da semelhança de triângulos, contribuindo, assim, para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT308.

O boxe Fórum apresenta uma oportunidade para quêque os estudantes pesquisem e promovam discussões entre os pares e com os professores de outras áreas do conhecimento em uma oportunidade de trabalho multidisciplinar. Podem sêrser organizados pequenos seminários e momentos de exposição das ideias dos estudantes.

O desenvolvimento da competência geral 5 é favorecido à medida quêque se compreende quêque a tecnologia digital dos drones é usada para a obtenção de informações de monitoramento de áreas, especialmente as de difícil acesso. As competências gerais 7 e 9 são contempladas ao se realizar a atividade em grupo e promover o debate, o quêque permite exercitar a argumentação, a defesa de ideias e pontos de vista, a consciência sócio-ambientalsocioambiental e de cuidado com o planêtaplaneta, a empatia, o diálogo e a cooperação entre os estudantes. A discussão sobre o tema desmatamento também contribui para o desenvolvimento da competência específica 1 da área de Ciências da Natureza e suas Tecnologias, bem como do Tema Contemporâneo Transversal Educação Ambiental.

Para contribuir com a pesquisa proposta na seção, podem sêrser sugeridas aos estudantes algumas fontes para complementar as informações sobre as Unidades de Conservação. Algumas sugestões são:

• INSTITUTO CHICO MENDES DE CONSERVAÇÃO DA BIODIVERSIDADE. Planos de manejo. Brasília, DF: í cê ême bíuICMBio, 11 abr. 2024. Disponível em: https://livro.pw/glzrd. Acesso em: 3 out. 2024.

• O QUE são unidades de conservação. Dicionário ambiental. O Eco, Rio de Janeiro, 19 abr. 2013. Disponível em: https://livro.pw/hmugn. Acesso em: 3 out. 2024.

A seção Explorando a tecnologia é uma oportunidade de promover o aprofundamento de conhecimentos matemáticos associados às noções de linguagem de programação, proporcionando novas formas de resolver uma atividade. É uma ocasião para quêque seja explorada a competência específica 4 da área de Matemática e suas Tecnologias, habilidade EM13MAT405, relacionada ao pensamento computacional.

A atividade dessa seção tem como proposta explorar o pensamento computacional sem a utilização de computadores. Para a realização dos itens a e b, providenciar fô-lhasfolhas de papel quadriculado cujas dimensões dos quadradinhos sêjamsejam 1 cm × 1 cm. Uma sugestão é organizar os estudantes em duplas e permitir quêque realizem as representações. Após terem realizado as construções, fazer a mediação das conclusões obtidas e verificar se estabeleceram relação com a proporcionalidade. Caso haja possibilidade, incentivar quêque cada dupla crie uma figura para quêque outra dupla a amplie, usando os comandos trabalhados nessa atividade. A seguir estão as respostas esperadas.

a)

b)

Página trezentos e cinquenta e quatro354

cóódigoCódigo de armazenamento para a imagem ampliada.

Linha 1: 0, 14

Linha 2: 0, 14

Linha 3: 0, 2, 10, 2

Linha 4: 0, 2, 10, 2

Linha 5: 0, 2, 10, 2

Linha 6: 0, 2, 10, 2

Linha 7: 0, 2, 10, 2

Linha 8: 0, 2, 10, 2

Linha 9: 0, 2, 2, 6, 2, 2

Linha 10: 0, 2, 2, 6, 2, 2

Linha 11: 0, 2, 2, 2, 2, 2, 2, 2

Linha 12: 0, 2, 2, 2, 2, 2, 2, 2

Linha 13: 0, 2, 2, 2, 2, 2, 2, 2

Linha 14: 0, 2, 2, 2, 2, 2, 2, 2

Linha 15: 0, 14

Linha 16: 0, 14

pódePode sêrser interessante, ao terminar a atividade, fomentar a discussão sobre a comparação dos códigos antes e depois da redução. Algumas sugestões de perguntas são: O quêque aconteceu com os dígitos dos códigos? E com as linhas?; Se o objetivo fosse ampliar a imagem original em sete vezes, como ficariam os códigos?

A seção História da Matemática apresenta fatos históricos relacionados à Matemática com o intuito de contextualizar conteúdos e contribuir para a compreensão da evolução de ideias e de teorias ao longo do tempo. Para aprofundar o quêque foi exposto nessa seção, pode-se solicitar aos estudantes quêque realizem pesquisas sobre Tales de Mileto e propor um momento de exposição sobre o quêque descobriram. Em meio às informações trazidas por eles, certamente haverá diversas conexões com os temas abordados neste Capítulo.

Avaliação

A atividade 3 da Abertura do Capítulo possibilita uma avaliação diagnóstica da seguinte habilidade relacionada ao teorema de Pitágoras, quêque foi trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah um quatroEF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividade 8 (página 250).

2ª avaliação formativa: atividade 13 (página 254).

3ª avaliação formativa: atividades 18 e 21 (páginas 258 e 259, respectivamente).

Capítulo 8
Trigonometria no triângulo retângulo

Orientações

As atividades propostas neste Capítulo ilustram as aplicações da Trigonometria nos mais variados contextos, estimulando a resolução e a elaboração de problemas quêque envolvem triângulos em diferentes áreas do conhecimento. Todas as situações contribuem para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias e a habilidade EM13MAT308, especificamente. Nesse sentido, espera-se quêque os estudantes reconheçam a aplicação das razões trigonométricas para a obtenção de medidas inacessíveis em diferentes áreas.

As atividades propostas na Abertura do Capítulo incentivam uma análise, do ponto de vista técnico, da construção de rampas de acessibilidade, conforme a norma NBR 9050 cujo texto pódepode sêrser acessado por meio do línkilink https://livro.pw/wdwbn (acesso em: 4 out. 2024). Espera-se quêque os estudantes concluam quêque, se a medida do ângulo formado pela inclinação de uma rampa em relação à horizontal for maior quêque a inclinação mássimamáxima permitida mencionada no texto, a rampa ficará muito íngreme e sem condições de uso, pois nem pedestres nem cadeirantes conseguirão subi-la. Por isso, é necessário quêque haja uma norma para delimitar o ângulo mássimomáximo de inclinação da rampa, de modo quêque ela seja de fato acessível. As discussões propostas valorizam os conhecimentos construídos sobre o mundo, incentivando, ao mesmo tempo, a empatia e o acolhimento, desenvolvendo as competências gerais 1 e 9.

O assunto abordado na Introdução fornece informações sobre a importânssiaimportância da Trigonometria e dos seus procedimentos de cálculo ao longo da história, reforçando a competência geral 1.

Ao abordar o tópico Razões trigonométricas no triângulo retângulo, pode-se retomar, por meio da semelhança de triângulos, as demonstrações das relações métricas no triângulo retângulo.

As demonstrações do tópico Relações entre razões trigonométricas possibilitam aos estudantes um avanço em relação ao método dedutivo, quêque é característico da Matemática para validar resultados. Isto é, compreender essas demonstrações ajuda no desenvolvimento da capacidade de distinguir a diferença entre uma próvaprova lógico-dedutiva e uma verificação empírica. Esta última pódepode envolver a visualização de dêzê-nhôsdesenhos, a construção de modelos materiais, simuladores virtuais ou a medição de grandezas.

Na atividade 15 da página 284, é esperado quêque os estudantes elaborem uma atividade usando um modelo parecido com o da atividade 14. Isto é, com uma pessoa no solo e dois drones no ar, de modo a compor dois triângulos justapostos; dessa maneira, uma das perguntas quêque pódepode sêrser feita tem a vêrver com a distância entre os dois drones.

O Tema Contemporâneo Transversal propôstoproposto no boxe Fórum é Direitos da Criança e do Adolescente. O Estatuto da Criança e do Adolescente (ECA), sancionado em 13 de julho de 1990, estabelece, entre ou-

Página trezentos e cinquenta e cinco355

tros itens, o direito à educação de todas as crianças e dos adolescentes, sem discriminação de qualquer natureza. Isso inclui as pessoas com deficiência, entre elas aquelas quêque fazem uso de cadeira de rodas, chamadas, no contexto coloquial, de cadeirantes. No línkilink https://livro.pw/btzdb (acesso em: 4 out. 2024), é possível ter acesso ao texto do ECA na íntegra.

Em relação à discussão proposta, é possível quêque os estudantes destaquem quêque crianças e adolescentes têm necessidades e vulnerabilidades específicas, quêque não são abordadas pêlospelos direitos concedidos aos adultos. Eles podem argumentar quêque as crianças e os adolescentes têm diferentes capacidades cognitivas e níveis de autonomia em comparação com os adultos. Portanto, são necessários direitos e proteções quêque lévemlevem em consideração essas diferenças e os ajudem a se desenvolverem de maneira saudável e segura. Ao incentivar quêque os estudantes defendam suas ideias e argumentem com informações confiáveis, a atividade colabora para o desenvolvimento da competência geral 7.

No trabalho com o tópico Ângulos de 30°, de 45° e de 60°, verificar, inicialmente, se os estudantes já conhecem algo relacionado a essa temática. Se possível, organizar breves momentos para quêque eles apresentem, uns aos outros, as formas de se obterem os valores, observando se compreenderam os cálculos desenvolvidos em cada caso. Sugere-se propor a questão: Observe quêque, conhecidos o seno, o cosseno e a tangente de 30°, ficam também determinados o seno, o cosseno e a tangente de 60°. Por quê? Justifique. Espera-se quêque os estudantes respondam quêque os ângulos são complementares, logo sen 60° = cos 30°, cos 60° = sen 30° e tg 60° = $\begin{array}{c}\frac{1}{\mathrm{t}\mathrm{g}{30}^{\circ }}\end{array}$.

Pode-se, ainda, solicitar aos estudantes quêque, em duplas, elaborem dois fluxogramas diferentes cujas instruções permítampermitam a construção, com régua não graduada e compasso, de dois triângulos retângulos quêque tênhamtenham um ângulo agudo de 30°. A ideia de pedir dois fluxogramas diferentes está relacionada ao fato de possibilitar aos estudantes uma reflekçãoreflexão sobre como usar conhecimentos matemáticos amparados em diferentes conceitos. Eles poderão, por exemplo, utilizar o quêque está sêndosendo verificado no estudo de Trigonometria; nesse caso, construindo um segmento de meia unidade de comprimento, perpendicular a uma reta suporte, e, posteriormente, construindo a hipotenusa do triângulo, com uma unidade de comprimento, intersectando a reta suporte mencionada anteriormente, quêque vai determinar o outro cateto do triângulo, utilizando, nessa construção, o fato de quêque sen 30° = $\frac{1}{2}$ ; ou ainda utilizar a construção do triângulo equilátero para obtêrobter um ângulo de 60° e, com isso, determinar o ângulo de 30°. Incentive os estudantes a compartilhar as soluções para essa atividade.

A atividade 28 da página 289 propõe a construção e a utilização de um teodolito artesanal cuja finalidade é a de os estudantes conhecerem esse instrumento d fórmade forma prática e vivencial. No sáitisite https://livro.pw/lthfq (acesso em: 4 out. 2024), há um livro digital, Modelagem matemática: Ensinando Matemática com teodolito caseiro, de Cláudio Lima da Silva, Lucas Ferreira Rodrigues e Fábio José da Costa Alves, com sugestões de atividades e descrição, passo a passo, de como construir um teodolito caseiro. Ao seguir o passo a passo dêêssedesse material sugerido, alertar aos estudantes, no passo 5, para quêque tênhamtenham cuidado ao utilizar a cola kemtequente a fim de quêque não se queimem.

Uma estratégia possível para essa atividade é solicitar aos estudantes quêque assistam ao vídeo antecipadamente em casa e, além díssudisso, quêque leiam o material sugerido para quêque reúnam e tragam os materiais necessários para a aula, durante a qual montarão seus teodolitos. Caso tênhamtenham dificuldade de obtêrobter os materiais ou na montagem, uma opção é construir um modelo mais simples, com transferidores e canudos (de preferência, com materiais recicláveis ou biodegradáveis). Durante a aula, os estudantes podem selecionar pontos, como: altura de uma árvore, altura dos prédios, comprimento da quadra entre outros. Os cálculos serão realizados por meio das razões trigonométricas do triângulo retângulo. Se possível, apresentar as medidas reais posteriormente para quêque os estudantes as comparem com os resultados quêque obtiveram em suas medidas e seus cálculos com o teodolito construído por eles. No caso de resultados muito diferentes das medidas reais, pódepode ter havido êêrroserros de observação, de cálculo ou mesmo de construção do equipamento.

Outra possibilidade para o uso do teodolito é a realização do seguinte experimento:

• SOARES, Maria Zoraide M. C. éti áuet al. A altura da árvore: experimento. Campinas: Matemática Multimídia, [201-]. Disponível em: https://livro.pw/jdrxq. Acesso em: 4 out. 2024.

A seção Explorando a tecnologia é uma oportunidade para promover o aprofundamento de conhecimentos matemáticos associados ao uso de recursos tecnológicos disponíveis, utilizando diferentes linguagens e proporcionando novas formas de resolver uma atividade, colaborando para as competências gerais 4 e 5. O cálculo das razões trigonométricas com base na semelhança de triângulos, na prática e por meio da utilização do aplicativo sugerido, permite aos estudantes quêque consigam resolver e elaborar problemas quêque envolvam triângulos em diferentes contextos com maior desenvoltura.

Página trezentos e cinquenta e seis356

Na atividade 1, espera-se quêque os estudantes indiquem o caso de semelhança AA (ângulo-ângulo), pois os ângulos C $\widehat{A}$ B e E $\widehat{A}$ D são congruentes e os ângulos C $\widehat{B}$ Ae E $\widehat{D}$ A são rétosretos.

Na atividade 2, j e m representam a razão trigonométrica seno entre o cateto ôpôstooposto e a hipotenusa; k e n representam a razão trigonométrica cosseno entre o cateto adjacente e a hipotenusa; l e o representam a razão trigonométrica tangente entre o cateto ôpôstooposto e o cateto adjacente. Todas tomam como referência os ângulos congruentes C $\widehat{A}$ Be E $\widehat{A}$ D, permitindo quêque se conclua quêque são constantes, mantendo-se a medida do ângulo.

Na atividade 3, é esperado quêque os estudantes percêbampercebam quêque as razões não mudam de valor. Assim, a conclusão é quêque não importa a medida dos lados do triângulo, pois qualquer triângulo retângulo quêque tenha um ângulo agudo de mesma medida do ângulo relativo ao vértice A terá os mesmos valores para as razões observadas na construção.

Na atividade 4, é esperado quêque os estudantes respondam quêque todas as razões terão seus valores alterados com a mudança de posição do ponto C, pois, ao mudar o ponto C, muda-se a medida do ângulo relativo ao vértice A. Outra observação importante é quêque as duas razões seno sempre terão o mesmo valor. Isso também sérveserve para as duas razões cosseno e as duas razões tangente. Pode-se concluir quêque os valores obtidos nas razões dependem da medida do ângulo, nesse caso, o ângulo relativo ao vértice A.

Outra atividade possível a sêrser feita no GeoGebra é a construção de um teodolito virtual quêque permita medições de objetos em cenário virtual em 3D. As instruções podem sêrser consultadas em:

• ZILKHA, êstérEsther. Utilização do GeoGebra na construção de instrumentos: teodolito. 2014. Trabalho de Conclusão de Curso (Mestrado profissional em Matemática em Rede Nacional) – Instituto de Matemática Pura e Aplicada, Rio de Janeiro, 2014. Disponível em: https://livro.pw/tkpge. Acesso em: 4 out. 2024.

A seção Conexões com… oferece possibilidades interessantes para explorar temas diversos e promover a interdisciplinaridade, quando possível. Contribui também para desenvolver a competência leitora e o senso crítico, capacidades essenciais para a participação cidadã dos estudantes.

Nesse caso, a proposta é trabalhar aplicações da Trigonometria em situações reais, contribuindo para o desenvolvimento das competências gerais 2, 3 e 9, quando se recórrerecorre à abordagem própria da Matemática para resolver problemas e criar uma solução tecnológica para a construção da pista de squêitskate. Os textos e as atividades apresentados nessa seção valorizam a manifestação do squêitskate como esporte, cultura de rua e ár-tearte, a técnica envolvida na marcenaria e a destreza nos movimentos, além de exercitar o diálogo, o respeito e a cooperação na atividade em grupo, valorizando aspectos relacionados às culturas juvenis.

Para a atividade 3, pódepode sêrser mostrada aos estudantes a construção de algumas pistas feitas com material reciclável, encontrada no seguinte artigo:

• SILVA, Adnielson L. da éti áuet al. Skate de dedo e as relações trigonométricas no triângulo retângulo. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 12., 2016, São Paulo. Anais […]. São Paulo: Sociedade Brasileira de Educação Matemática, 2016. Disponível em: https://livro.pw/bsaen. Acesso em: 4 out. 2024.

A seguir, outros línkislinks sobre o assunto quêque podem subsidiar o trabalho propôstoproposto nessa atividade:

• SKATEPARKS DO BRASIL. [S. l.], c2024. sáitiSite. Disponível em: https://livro.pw/dnbvy. Acesso em: 4 out. 2024. sáitiSite quêque reúne imagens, fornece a localização e dicas sobre pistas de squêitskate pelo Brasil.

• CONFEDERAÇÃO BRASILEIRA DE SKATEBOARDING. São Paulo, c2024. sáitiSite. Disponível em: https://livro.pw/uhxnt. Acesso em: 4 out. 2024. sáitiSite da Confederação Brasileira de Skateboarding, com informações sobre torneios, regulamentos entre outras.

Avaliação

A atividade 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica da seguinte habilidade trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah um seteEF09MA17) Reconhecer vistas ortogonais de figuras espaciais e aplicar esse conhecimento para desenhar objetos em perspectiva.

Reconhecer vistas ortogonais é uma habilidade importante para a utilização da Trigonometria em objetos tridimensionais.

A seguir, sugestões de atividades cujas análises de suas resoluções podem contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 4 e 13 (páginas 283 e 284, respectivamente).

2ª avaliação formativa: atividades 17 e 24 (páginas 288 e 289, respectivamente).

Página trezentos e cinquenta e sete357