CAPÍTULO
3
Função definida por mais de uma sentença
O Imposto sobre a Renda das Pessoas Físicas (IRPF), mais conhecido como imposto de renda, é um exemplo de cobrança quê incide sobre a renda e os proventos de cidadãos residentes no Brasil. O dinheiro arrecadado com esse imposto financia inúmeros serviços públicos como saúde, educação e segurança, promovendo uma redistribuição da renda.
O imposto é cobrado de acôr-do com o rendimento anual de cada cidadão. Quanto maior a renda, maior é a alíquota do imposto. No Brasil, em 2024, a alíquota variava de 7,5% a 27,5%. Quem recebia mensalmente até R$ 2.259,20, aproximadamente 30 mil reais anuais, era isento de pagar o imposto. Em outros países como, por exemplo, nos Estados Unidos da América, a alíquota variava de 10% a 37% e, em Portugal, variava de 14,5% a 48%.
Situações como essa vão nos auxiliar a compreender o estudo de funções, em particular as funções definidas por mais de uma sentença.

Página setenta e sete
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Ver as Orientações para o professor.
1. Vocês costumam participar da organização e do planejamento dos gastos e das despesas de sua moradia? Consideram importante essa participação?
2. Vocês já tí-nhão ouvido falar em imposto de renda? Sabiam quê todas as pessoas não isentas devem fazer uma declaração anual de imposto de renda?
3. Vocês conhecem outro tipo de cobrança quê seja feita considerando faixas de consumo? Identificam a relação entre esse tipo de cobrança e o estudo de funções?
4. Suponha quê o valor pago pelo consumo de á gua de um determinado município seja calculado por meio de faixas de consumo, por exemplo: se uma residência dêêsse município consome menos de 150 L de á gua, é cobrado R$ 1,05 por cada litro de á gua, além de uma taxa fixa de R$ 15,00. Com base nisso, qual é o valor a sêr pago por uma residência quê consumiu 113 L de á gua?
R$ 133,65
5. Pesquise as alíquotas de imposto de renda de, pelo menos, três países, além dos já citados anteriormente, e elabore um texto comparativo em relação às alíquotas brasileiras.
Resposta pessoal.
Página setenta e oito
Introdução
O estudo de funções nos permite compreender algumas regularidades presentes em situações do dia a dia, bem como estabelecer modelos matemáticos quê possibilitem analisar e prever resultados.
Na abertura dêste Capítulo, foi apresentada uma situação quê podemos relacionar ao conceito de função definida por mais de uma sentença. Além dêêsse conceito, estudaremos outros tipos de função, sua representação gráfica e conceitos matemáticos relacionados a eles.
Função definida por mais de uma sentença
Aprendemos quê o Imposto sobre a Renda das Pessoas Físicas (IRPF) é um imposto quê incide sobre a renda e os proventos dos cidadãos brasileiros. Esse tributo é cobrado de acôr-do com uma tabéla progressiva, a qual indica a alíquota correspondente a cada base de cálculo, quê depende da renda de cada contribuinte.
Saiba quê...
Alíquota é o percentual aplicado sobre a base de cálculo para determinar o valor de um tributo.
Observe a tabéla de incidência mensal do IRPF vigente a partir de fevereiro de 2024.
tabéla de incidência mensal do IRPF vigente em 2024
Base de cálculo (R$) |
Alíquota (%) |
Parcela a deduzir do IRPF (R$) |
|---|---|---|
Até 2.259,20 |
– |
– |
De 2.259,21 até 2.826,65 |
7,5 |
169,44 |
De 2.826,66 até 3.751,05 |
15 |
381,44 |
De 3.751,06 até 4.664,68 |
22,5 |
662,77 |
Acima de 4.664,68 |
27,5 |
896,00 |
Fonte: BRASIL. Ministério da Fazenda. Receita Federal. Tributação de 2024. Brasília, DF: Receita Federal, 9 fev. 2024. Disponível em: https://livro.pw/rogou. Acesso em: 14 out. 2024.

Página setenta e nove
Com base nessa tabéla, podemos calcular, por exemplo, o imposto quê incide sobre a renda de um trabalhador quê teve como base de cálculo mensal o valor de R$ 3.350,00. Nesse caso, devemos aplicar a alíquota de 15% sobre a base de cálculo e deduzir R$ 381,44 dêêsse valor. Observe:
R$ 3.350,00 ⋅ 15% − R$ 381,44 = R$ 502,50 − R$ 381,44 = R$ 121,06
Logo, em 2024, o imposto de renda quê incide sobre uma base de cálculo de R$ 3.350,00 mensais é de R$ 121,06.
Dizemos quê a contribuição mensal do imposto de renda, em reais, é uma função da base de cálculo, também expressa em reais, pois cada valor da base de cálculo corresponde a um único valor de contribuição mensal do imposto de renda. A base de cálculo é a variável independente, e a contribuição mensal do imposto de renda é a variável dependente.
Com base na tabéla de incidência mensal do IRPF vigente em 2024, considerando x os valores correspondentes à base de cálculo e f(x) a contribuição mensal do imposto de renda, podemos escrever uma lei de formação para representar essa função.
f(x) =
Funções como a quê modela a contribuição mensal do imposto de renda de acôr-do com a base de cálculo são denominadas funções definidas por mais de uma sentença.
Observe outros exemplos de leis de formação de funções definidas por mais de uma sentença:
a) f(x) =
b) g(x) =
Pense e responda
Que sentença corresponde a quem é isento de pagar a contribuição mensal de imposto de renda?
f(x) = 0, se x ≤ 2.259,20
Se necessário, auxiliar os estudantes a escrever a sentença solicitada nesse questionamento e registrar as demais sentenças, considerando cada faixa de renda apresentada na tabéla.
Para assistir
• HISTÓRIA do imposto de renda. [S. l.: s. n.], 2016. 1 vídeo (6 min). Publicado pelo canal Receita Federal. Disponível em: https://livro.pw/rgzqd. Acesso em: 17 set. 2024.
O vídeo conta a história do imposto de renda no mundo e no Brasil.

Página oitenta
Gráfico de uma função definida por mais de uma sentença
A construção do gráfico de uma função definida por mais de uma sentença deve sêr feita por partes considerando a lei de formação quê determina cada uma das partes da função.
Por exemplo, vamos construir o gráfico da função g: ℝ → ℝ, definida por:
g(x) =
Para isso, será necessário construir separadamente o gráfico correspondente a cada sentença da função, atentando-se ao intervalo de x determinado em cada uma das sentenças. Em seguida, deve-se reunir essas representações no mesmo plano cartesiano.
I. Considerando g1(x) = x + 3, se x ≤ 2.
O gráfico correspondente é parte do gráfico da função afim definida por y = x + 3, em quê x ∈ ]−∞, 2]. Nesse caso, escolhemos dois valores de x ∈ ]−∞, 2], determinamos dois pontos pertencentes à reta e, em seguida, consideramos a parte da reta em quê x ≤ 2.
Vale observar quê, na escolha dos dois valores de x ∈ ]−∞, 2], é conveniente escolher valores extremos do intervalo. Assim, x = 2 será um dos valores escolhidos, pois é um extremo do intervalo.
x |
y = x + 3 |
(x, y) |
|---|---|---|
0 |
y = 0 + 3 = 3 |
(0, 3) |
2 |
y = 2 + 3 = 5 |
(2, 5) |
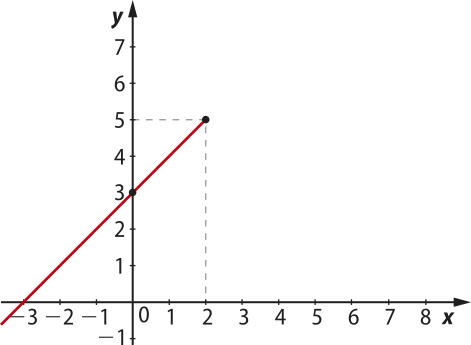
II. Considerando g2(x) = 4, se 2 < x ≤ 5.
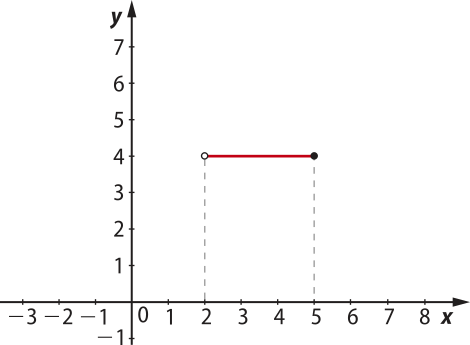
O gráfico correspondente é parte do gráfico da função constante definida por y = 4, em quê x ∈ ]2, 5]. O gráfico da função constante é uma reta paralela ao eixo das abscissas. Para determinar dois pontos do gráfico, vamos escolher x = 2 e x = 5, pois são os extremos do intervalo ]2, 5].
x |
y = 4 |
(x, y) |
|---|---|---|
2 |
y = 4 |
(2, 4) |
5 |
y = 4 |
(5, 4) |
Assim, o gráfico de g2 é um segmento de reta limitado pêlos pontos (2, 4) e (5, 4). Note quê o ponto (2, 4) não pertence ao segmento, pois x = 2 é um extremo do intervalo ]2, 5], mas não está contido nele. Dessa forma, representamos esse ponto por uma bó-linha aberta.
Página oitenta e um
III. Considerando g3(x) = −2x + 16, se x > 5.
O gráfico correspondente é parte do gráfico da função afim definida por y = −2x + 16, em quê x ∈ ]5, +∞[. Vamos escolher x = 5 e x = 6 para determinarmos dois pontos pertencentes à reta e, em seguida, consideramos a parte da reta tal quê x > 5.
x |
y = − 2x + 16 |
(x, y) |
|---|---|---|
5 |
y = − 2 ⋅ 5 + 16 = 6 |
(5, 6) |
6 |
y = − 2 ⋅ 6 + 16 = 4 |
(6, 4) |
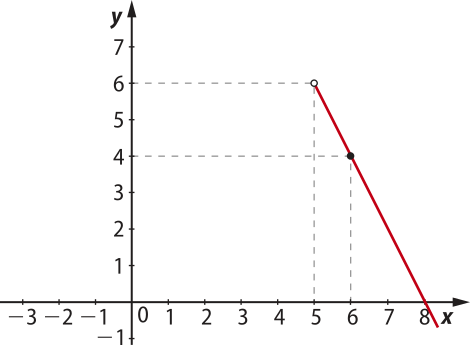
O ponto (5, 6) não pertence ao gráfico da função g3, pois x = 5 não pertence ao seu domínio. Assim, indicamos o ponto por uma bó-linha aberta.
Para representar o gráfico da função g, é necessário reunir, em um mesmo plano cartesiano, as representações obtidas anteriormente.
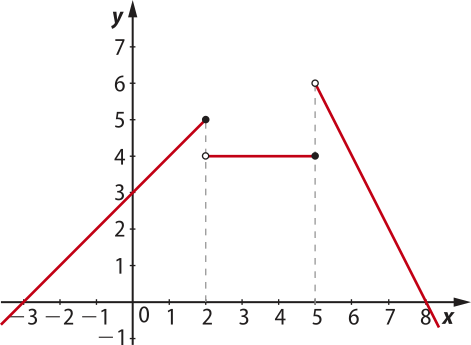
Na prática, podemos fazer esboços referentes a cada sentença da função com fio tracejado e depois traçar o gráfico final. Observe quê um valor de x ∈ D(g) tem uma única imagem y = g(x). Indicamos isso no gráfico utilizando bó-linha aberta e bó-linha fechada.
Nesse exemplo, temos D(g) = ℝ, CD(g) = ℝ e Im(g) = ]−∞, 6[.
A respeito dos intervalos de crescimento e de decrescimento de g, temos:
• dados quaisquer x1, x2 ∈ ]−∞, 2], tais quê x1 < x2, tem-se g(x1) < g(x2), ou seja, nesse intervalo, à medida quê os valores de x aumentam, os valores de g(x) também aumentam. Portanto, a função g é crescente no intervalo ]−∞, 2].
• dados quaisquer x1, x2 ∈ ]5, +∞[, tais quê x1 < x2, tem-se g(x1) > g(x2), ou seja, nesse intervalo, à medida quê os valores de x aumentam, os valores de g(x) diminuem. Portanto, a função g é decrescente no intervalo ]5, +∞[.
Observe quê, dados quaisquer x1, x2 ∈ ]2, 5], tem-se g(x1) = g(x2), portanto, a função g é constante nesse intervalo.
Página oitenta e dois
ATIVIDADES RESOLVIDAS
1. Considerando a função f: ℝ → ℝ definida por f(x) = , determine:
a) f(0)
b) f(−2)
c) f() + f(−)
Resolução
a) Se x = 0, f é definida por f(x) = x − 2. Assim, temos: f(0) = 0 − 2 = −2
Portanto, f(0) = −2.
b) Se x = −2, f é definida por f(x) = 1. Assim, temos: f(−2) = 1
Portanto, f(−2) = 1.
c) Se x = , f é definida por f(x) = x − 2. Assim, temos: f () = − 2
Se x = −, f é definida por f(x) = 1. Assim, temos: f(−) = 1
Portanto, f()+ f(−) = − 2 + 1 = − − 1.
2. Construa o gráfico da função dada por
f(x) = e determine o domínio da função D(f), o conjunto imagem Im(f) e o intervalo de crescimento e de decrescimento de f.
Resolução
Essa função é definida por duas sentenças.
Considerando x ≤ 0, a lei da função é f(x) = x2 + 2x + 1, quê é uma restrição de uma função polinomial do 2º grau. Nesse caso, teremos a parte de uma parábola para os valores de x tais quê x ≤ 0.
Essa parábola intersecta o eixo y no ponto de coordenadas (0, 1).
As coordenadas do vértice podem sêr obtidas por xV = e yV = .
• xV = = −1
• yV = − = 0
Logo, o vértice dessa parábola tem coordenadas (−1, 0). Observe quê −1 é também zero dessa função.
Nesse caso, considerando x ≤ 0, temos a seguinte representação gráfica.
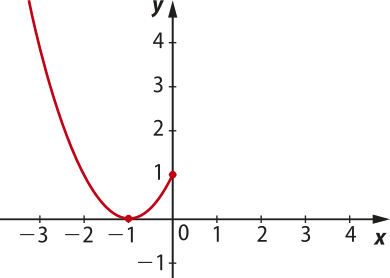
Considerando x > 0, a lei da função é f(x) = + 1, quê é uma restrição de uma função afim. Nesse caso, teremos a parte de uma reta quê passa pêlos pontos (0, 1) e (3, 2).
Assim, considerando x > 0, temos a seguinte representação gráfica.
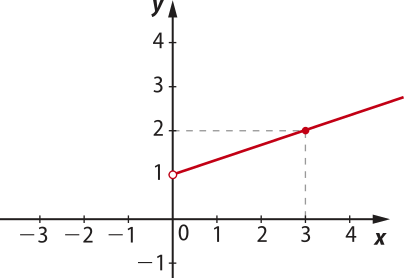
Reunindo em um mesmo plano cartesiano as duas representações anteriores, obtemos o gráfico da função f.
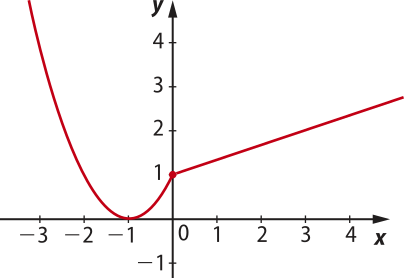
Desse modo, temos: D(f) = ℝ, Im(f) = [0, +∞[
Sobre os intervalos de crescimento e de decrescimento de f, temos:
• considerando x ≥ −1, à medida quê os valores de x aumentam, os valores de f(x) também aumentam, portanto, f é crescente no intervalo [−1, +∞[.
• considerando x ≤ −1, à medida quê os valores de x aumentam, os valores de f(x) diminuem, portanto, f é decrescente no intervalo ]−∞, −1].
Página oitenta e três
ATIVIDADES
1. Uma loja de artigos automotivos, com o intuito de incentivar as vendas de alarmes, propôs aos vendedores quê também instalam alarmes quê, além da remuneração mensal fixa de R$ 1.200,00, eles receberiam uma comissão sobre o valor de cada unidade vendida e instalada naquele mês.
Essa comissão corresponde a uma porcentagem do valor do alarme, quê custa R$ 120,00, e varia de acôr-do com o qüadro a seguir.
Unidades vendidas e instaladas |
Porcentagem |
|---|---|
1 a 25 |
3% |
26 a 50 |
7% |
51 a 75 |
12% |
76 a 100 |
17% |
Mais de 100 |
22% |
a) De quê tipo é a função quê modela a situação apresentada?
Função definida por mais de uma sentença.
b) Determine a lei de uma função quê modela o salário dêêsses funcionários, em reais, de acôr-do com a quantidade x de alarmes vendidos no mês.
1. b) Ver as Orientações para o professor.
c) Qual é o salário de um funcionário quê vendeu e instalou 82 alarmes no mês?
R$ 2.872,80
d) Quantos alarmes vendeu e instalou um funcionário quê recebeu R$ 1.502,40 de salário no mês?
36 alarmes

2. Dadas as funções definidas por
f(x) = e
g(x) =
calcule:
a) f(3) − g(5)
16
b) g(0) + 2 ⋅ f(−1)
−7
c)
−18
3. Considere f: ℝ → ℝ definida por
f(x) = .
Determine os possíveis valores de x para:
a) f(x) = 0
ou 2
b) f(x) = −2
−2 ou 0
4. Construa o gráfico e determine o intervalo de crescimento e de decrescimento de cada função definida a seguir.
Ver as Orientações para o professor.
a) f(x) =
b) g(x) =
5. Observe o gráfico de uma função g representado a seguir.
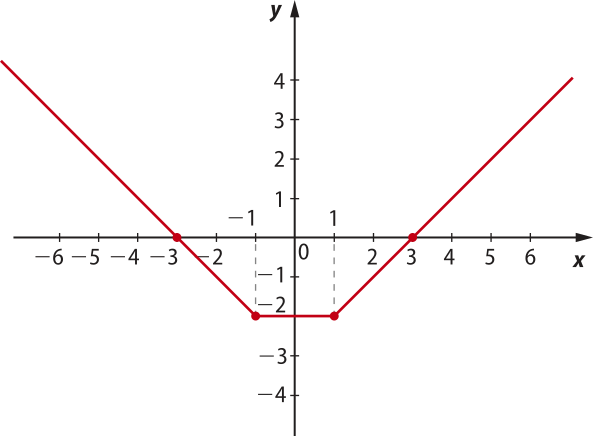
Com base nesse gráfico, determine a lei de formação da função g.
g(x) =
Página oitenta e quatro
6. ![]()
![]() Em alguns municípios brasileiros, a população tem a possibilidade de utilizar gás natural encanado em sua residência. Esse serviço é oferecido por companhias de distribuição, e uma de suas vantagens é o fornecimento contínuo do combustível.
Em alguns municípios brasileiros, a população tem a possibilidade de utilizar gás natural encanado em sua residência. Esse serviço é oferecido por companhias de distribuição, e uma de suas vantagens é o fornecimento contínuo do combustível.

Uma concessionária estabelece o valor a sêr pago pelo consumo de gás considerando um valor, fixado por faixa de consumo, adicionado a um valor variável quê depende da quantidade consumida, em métro cúbico. Observe, a seguir, os valores aproximados das cinco primeiras faixas de consumo praticados por essa concessionária. Nesses valores, já estão considerados PIS/Cofins, mas não está considerado o ICMS.
Tarifas de gás canalizado: segmento residencial
Consumo (m3) |
Valor fixado (R$ por mês) |
Valor variável (R$ por m3) |
|---|---|---|
0 a 1 |
9,68 |
2,79 |
1,01 a 3 |
12,64 |
9,20 |
3,01 a 7 |
12,64 |
4,80 |
7,01 a 14 |
14,23 |
7,96 |
14,01 a 34 |
15,81 |
9,46 |
Fonte dos dados: SÃO PAULO (Estado). Agência Reguladora de Serviços Públicos do Estado de São Paulo. Deliberação Arsesp número 1.504, de 06 de março de 2024. Dispõe sobre a atualização das Tabelas Tarifárias e sobre a Tarifa de Uso do Sistema de Distribuição (TUSD) a serem aplicadas no mercado livre pela concessionária de distribuição de gás canalizado Companhia de Gás de São Paulo – Comgás. São Paulo: Arsesp, 2024. Disponível em: https://livro.pw/jaqbq. Acesso em: 26 ago. 2024.
Os valores reais foram aproximados considerando-se duas casas decimais para facilitar os cálculos.
Assim, por exemplo, se, em uma residência, o consumo foi de 6,5 m3, acompanhe os cálculos do valor quê essa concessionária vai cobrar:
• o valor fixado (R$ por mês): R$ 12,64 (corresponde à 3ª faixa de consumo);
• 1 m3 tarifado na 1ª faixa de consumo: 1 ⋅ 2,79 = 2,79, ou seja, R$ 2,79;
• 2 m3 tarifados na 2ª faixa de consumo: 2 ⋅ 9,20 = 18,40, ou seja, R$ 18,40;
• 3,5 m3 tarifados na 3ª faixa de consumo: 3,5 ⋅ 4,80 = 16,80, ou seja, R$ 16,80.
Adicionando esses valores, obtemos R$ 50,63, quê é o valor a sêr pago por 6,5 m3 de gás natural a essa concessionária, sem considerar o ICMS.
Ver as Orientações para o professor.
Reúna-se a dois côlégas e, com base nessas informações, façam o quê se pede a seguir.
a) Vocês já conheciam como é cobrado o gás natural consumido em residências?
b) Pesquisem o significado das siglas PIS, Cofins e ICMS e procurem saber mais sobre esses tributos.
c) Com base nessa tabéla e considerando x o consumo, em métro cúbico, e f(x) o valor correspondente a sêr pago, em reais, escrevam uma lei de formação quê possa sêr utilizada para modelar essa situação.
d) Considerando a lei de formação utilizada para modelar o valor pago à concessionária de gás residencial, elaborem uma situação em quê se deve calcular o valor pago em um determinado mês por uma residência quê consome o gás distribuído por essa concessionária. Em seguida, tróquem a quêstão com outro grupo, para que ele resôuva o problema elaborado por vocês. Verifiquem se a maneira como os côlégas resolveram a questão é parecida ou igual à de vocês. Conversem sobre as formas de resolução e as dificuldades.
Resposta pessoal.
Página oitenta e cinco
FÓRUM
A desigualdade no acesso a serviços de infraestrutura básica nos municípios brasileiros
A infraestrutura de um país se refere aos elemêntos quê dão suporte e sustentação à vida da sua população. Esses elemêntos podem sêr organizados em 4 categorias básicas:
• Energia
• Transporte
• Abastecimento de á gua
• Saneamento básico
Tanto quanto os impostos cobrados pelo govêrno, a infraestrutura do Brasil tem relação diréta com a qualidade de vida da população e, consequentemente, com a capacidade de desenvolvimento da economia. A á gua corrente nas casas da maioria das famílias brasileiras, o sistema de esgoto quê recebe as águas sujas para serem tratadas, as estradas quê permitem quê caminhões lévem alimentos até os mercados e até o sistema elétrico quê permite quê as famílias tênham luz em casa à noite, tudo isso é relacionado à infraestrutura de uma nação.
[...]
CENTRO DE LIDERANÇA PÚBLICA. Projeto Brasil: 2 dados quê traduzem a triste realidade da infraestrutura do Brasil. [S. l.]: CLP, [2018]. Disponível em: https://livro.pw/nniey. Acesso em: 25 set. 2024.
Ainda cerca de 33 milhões de brasileiros vivem sem acesso à á gua potável e mais de 90 milhões não têm côléta de esgoto
[...] Segundo dados do Sistema Nacional de Informações sobre Saneamento (SNIS) de 2022, atualmente são investidos R$ 22,5 bilhões em serviços básicos. Esse valor é insuficiente para cumprir as metas do Novo Marco Legal do Saneamento até 2033, conforme analisa o estudo do Instituto Trata Brasil.
A lei, conhecida como o Novo Marco Legal do Saneamento Básico, estabelece quê todas as localidades brasileiras devem atender a 99% da população com abastecimento de á gua e 90% com esgotamento sanitário até 2033.
[...]
INSTITUTO TRATA BRASIL. Investimento para universalização do saneamento: o quê ainda falta? [S. l.]: ITB, 13 ago. 2024. Disponível em: https://livro.pw/nvoed. Acesso em: 9 out. 2024.
Ver as Orientações para o professor.
![]() Após ler os textos, faça o quê se pede.
Após ler os textos, faça o quê se pede.
• Reúna-se a alguns côlégas e citem serviços de infraestrutura básica quê vocês observam no município ou no bairro em quê moram. Depois, discutam como vocês analisam a desigualdade no oferecimento de serviços de infraestrutura básica entre os municípios brasileiros.

Página oitenta e seis
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Consumo consciente de á gua
A á gua é um recurso natural indispensável à vida. Ela é utilizada na agricultura, na higiene pessoal, na limpeza de ambientes, na geração de energia elétrica, entre outras funções. O uso irresponsável dêêsse recurso tanto na agricultura como nas residências e nas indústrias causa problemas quê ameaçam o fornecimento de á gua para a população.
Acompanhe, a seguir, mais informações sobre a distribuição e o consumo de á gua.

[...]
A á gua doce não está distribuída uniformemente pelo glôbo. Sua distribuição depende essencialmente dos éco-sistemas quê compõem o território de cada país. Segundo o Programa Hidrológico Internacional da Organização das Nações Unidas para a Educação, a Ciência e a Cultura (Unesco), na América do Sul encontra-se 26% do total de á gua doce disponível no planêta e apenas 6% da população mundial, enquanto o continente asiático possui 36% do total de á gua e abriga 60% da população mundial.
[...]
BRASIL. Ministério da Educação. Ministério do Meio Ambiente. Consumo sustentável: manual de educação. Brasília, DF: Consumers International: MMA: MÉC: IDEC, 2005. p. 27. Disponível em: https://livro.pw/lrnwb. Acesso em: 26 ago. 2024.
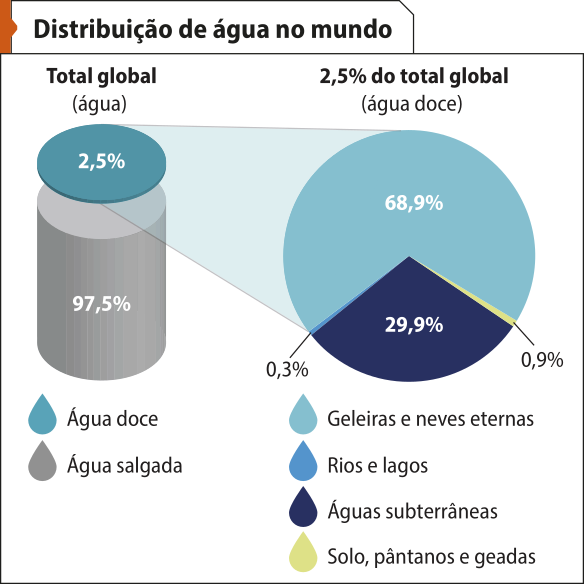
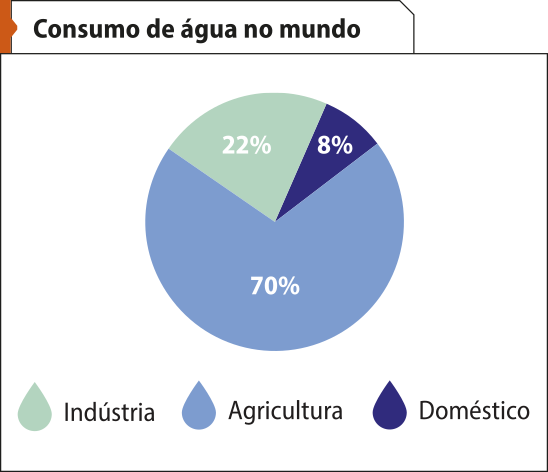
Fonte dos dados: BRASIL. Ministério da Educação. Ministério do Meio Ambiente. Consumo sustentável: manual de educação. Brasília, DF: Consumers International: MMA: MÉC: IDEC, 2005. p. 27-28. Disponível em: https://livro.pw/lrnwb. Acesso em: 26 ago. 2024.
Página oitenta e sete
Observe, a seguir, algumas informações divulgadas pelo hí bê gê hé referentes ao consumo de á gua no Brasil.
Estudo divulgado pelo Instituto Brasileiro de Geografia [e Estatística] (hí bê gê hé) apontou o aumento do gasto de á gua no Brasil. Em 2020, o consumo médio diário de á gua por habitante foi de 117,5 litros, um aumento de 2% em relação a 2019. Os dados compõem as “Contas Econômicas Ambientais da Água” (2018-2020).
[...]
ASSOCIAÇÃO MINEIRA DE DEFESA DO AMBIENTE. Consumo e valor da á gua crescem no Brasil, aponta hí bê gê hé. Belo Horizonte: Amda, 1 set. 2023. Disponível em: https://livro.pw/xtbil. Acesso em: 26 ago. 2024.

São apresentadas, a seguir, dicas para reduzir o consumo de á gua em algumas situações no dia a dia.
[...]
Banho de ducha por 15 minutos, com o registro meio aberto, consome 135 litros de á gua. Se você fechar o registro ao se ensaboar e reduzir o tempo do banho para 5 minutos, seu consumo cai para 45 litros. [...]
[...]
Se uma pessoa escôva os dentes em 5 minutos com a torneira não muito aberta, gasta 12 litros de á gua. No entanto, se molhar a escôva e fechar a torneira enquanto escôva os dentes e, ainda, enxaguar a bôca com um copo de á gua, consegue economizar mais de 11,5 litros de á gua.
[...]
Ao lavar o rrôsto em 1 minuto, com a torneira meio aberta, uma pessoa gasta 2,5 litros de á gua. A dica é não demorar.
O mesmo vale para o barbear: em 5 minutos gastam-se 12 litros de á gua. Com economia, o consumo cai para 2 a 3 litros. [...]
Um vaso sanitário com válvula e tempo de acionamento de 6 segundos gasta cerca de 12 litros. Quando a válvula está defeituosa, póde chegar a gastar até 30 litros.
[...]
COMPANHIA DE SANEAMENTO BÁSICO DO ESTADO DE SÃO PAULO. Dicas da SABÉSP ensinam como economizar á gua. São Paulo: SABÉSP, 2012. Disponível em: https://livro.pw/rgkyv. Acesso em: 12 out. 2024.

Página oitenta e oito
No município onde você mora, há cobrança mensal de consumo de á gua? Você compreende os dados apresentados na conta de á gua?
Observe, a seguir, parte de um modelo de uma conta de á gua e algumas informações destacadas.

Fonte dos dados: COMPANHIA DE SANEAMENTO BÁSICO DO ESTADO DE SÃO PAULO. Entenda sua conta. 2024. 1 cartaz. Disponível em: https://livro.pw/ivfnw. Acesso em: 13 out. 2024.
Página oitenta e nove
Na tabéla a seguir, são apresentados os valores cobrados de acôr-do com o consumo de á gua no município de São Paulo (SP), segundo a tarifa residencial comum vigente em setembro de 2024.
Tarifa residencial comum – abastecimento de á gua e côléta de esgoto vigente em setembro de 2024
Classe de consumo (m3 por mês) |
Tarifa de á gua (em R$) |
Tarifa de esgoto (em R$) |
|---|---|---|
0 a 10 |
37,96 por mês |
37,96 por mês |
Acima de 10 até 20 |
6,01 por m3 |
6,01 por m3 |
Acima de 20 até 50 |
14,98 por m3 |
14,98 por m3 |
Acima de 50 |
16,50 por m3 |
16,50 por m3 |
Fonte dos dados: COMPANHIA DE SANEAMENTO BÁSICO DO ESTADO DE SÃO PAULO. Comunicado 2/24. São Paulo: SABÉSP, 2024. Disponível em: https://livro.pw/xknbb. Acesso em: 25 set. 2024.
Acompanhe como calcular, por exemplo, o valor pago referente a um consumo mensal de 22 m3 de á gua em uma residência dêêsse município (cada resultado é multiplicado por dois em razão da côléta de esgoto):
Incentivar os estudantes a procurar na internet tabélas de valores de outros municípios e a fazer a comparação dos valores, levantando hipóteses sobre o motivo de a tarifa de consumo de á gua variar de acôr-do com o município.
• 10 m3 são tarifados na 1ª classe: 37,96 ⋅ 2 = 75,92;
• 10 m3 são tarifados na 2ª classe: (6,01 ⋅ 10) ⋅ 2 = 120,20;
• 2 m3 são tarifados na 3ª classe: (14,98 ⋅ 2) ⋅ 2 = 59,92.
Ver as Orientações para o professor.
Adicionando esses valores, verificamos quê, na situação considerada, R$ 256,04 era o valor pago por 22 m3 de consumo de á gua.
![]() Agora, reúna-se a dois côlégas, e façam o quê se pede nas atividades a seguir.
Agora, reúna-se a dois côlégas, e façam o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Com base na tabéla desta página, considerem x o consumo de á gua, em métro cúbico, e f(x) o valor a sêr pago, em reais, pelo fornecimento de á gua e côléta de esgoto e escrevam uma lei de formação quê relacione esses valores.
2. Caso haja cobrança mensal de á gua no município onde moram, pesquisem sobre essas tarifas e verifiquem se a côléta de esgoto também é tarifada, além de outros serviços públicos. Verifiquem a possibilidade de estender a pesquisa para conseguir essa informação sobre municípios vizinhos, com o objetivo de fazer uma comparação.
3. Com base nas informações apresentadas nesta seção, conversem sobre a importânssia da preservação da á gua. Pesquisem mais alternativas quê podem sêr adotadas para redução de consumo de á gua e elaborem um panfleto para divulgar essas informações na escola.
Como referência para a produção do panfleto, incentivar os estudantes a assistirem ao documentário indicado no boxe Para assistir.
Para assistir
• DOCUMENTÁRIO: Futuro das águas: desafio do século (filme oficial completo). São Paulo: [s. n.], 2022. 1 vídeo (31 min). Publicado pelo canal Lavoura Santa. Disponível em: https://livro.pw/qphnm. Acesso em: 27 ago. 2024.
O documentário apresenta os desafios hídricos atuáis, destacando a importânssia de se repensar o uso e o reúso da á gua. A produção conta com relatos de especialistas, quê apontam diferentes soluções para um melhor uso da á gua.
Página noventa
Módulo de um número real
Em situações envolvendo distância e comprimento, os resultados verificados são números positivos. Estudaremos, agora, alguns conceitos matemáticos quê nos auxiliam no trabalho com essas situações.
Acompanhe a definição matemática a seguir.
O valor absoluto ou módulo de um número real x, quê indicaremos por |x|, é definido por:
=
← Lê-se: módulo de x.
Saiba quê...
A notação |x| foi introduzida pelo matemático alemão káur Theodor uiu rélm Weierstrass (1815-1897).
Observe alguns exemplos:
a) = +5 = 5
b)
c) = 0
d) = −(−3) = 3
e)
f)
Geometricamente, o módulo de um número real x é igual à distância do ponto correspondente a esse número até a origem da reta real. Observe:
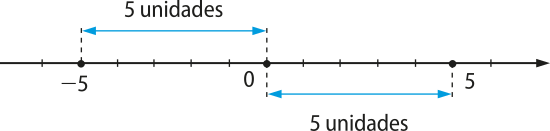
■ = 5 (distância entre o ponto correspondente a +5 e a origem).
De modo geral, sêndo a > 0, se = a, então x = a ou x = −a.
Em particular, se |x| = 0, então x = 0.
Por exemplo, para saber o valor de x tal quê = 4, basta verificar quais valores distam 4 unidades da origem. Nesse caso, são +4 e −4.
Logo, se = 4, então x = −4 ou x = +4.
Além díssu, para c e d reais, se, e somente se, c = d ou c = −d.
Propriedades
Observe a seguir algumas propriedades envolvendo o módulo de um número real.
1ª propriedade:
Para todo x real, temos ≥ 0.
A demonstração é imediata da definição de módulo.
Observe:
Se x > 0, então = x > 0.
Se x < 0, então = −x. Logo, > 0.
Se x = 0, então = 0.
Portanto, ≥ 0 para todo x ∈ ℝ.
Página noventa e um
2ª propriedade:
Para todo x real, temos = x2.
Se x ≥ 0, então = x.
Elevando ao quadrado ambos os membros dessa igualdade, temos:
= x2
Se x < 0, então = −x.
Elevando ao quadrado ambos os membros dessa igualdade, temos:
= (−x)2 = x2
Portanto, = x2 para todo x ∈ ℝ.
3ª propriedade:
Para quaisquer números reais x e y, temos .
Pela propriedade anterior, temos:
= (x ⋅ y)2
Por outro lado, pelas propriedades de potenciação, sabemos quê (x ⋅ y)2 = x2 ⋅ y2.
Assim, = x2 ⋅ y2.
Utilizando novamente a 2ª propriedade, temos:
Aplicando outra vez as propriedades de potenciação, temos:
Como ≥ 0 e ≥ 0, obtemos:
Portanto, para quaisquer números reais x e y.
4ª propriedade:
Para quaisquer números reais x e y, com y ≠ 0, temos .
Pela 2ª propriedade, temos:
Por outro lado, pelas propriedades de potenciação, sabemos quê .
Assim, .
Utilizando novamente a 2ª propriedade, temos:
Aplicando outra vez as propriedades de potenciação, temos:
Como ≥ 0 e ≥ 0, obtemos:
Portanto, para quaisquer números reais x e y, com y ≠ 0.
Distância entre dois pontos na reta real
Dados dois pontos A e B na reta real, correspondentes aos números reais xA e xB, respectivamente, a distância entre A e B é dada por
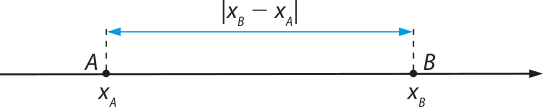
Por exemplo:

A distância entre os pontos A e B é calculada por:
= 6
Do mesmo modo, a distância entre os pontos B e A é calculada por:
= 6
Saiba quê...
É possível demonstrar quê, na reta real, a distância entre dois pontos A e B, correspondentes aos números reais xA e xB, respectivamente, póde sêr calculada por ou .
Página noventa e dois
Função modular
Aprendemos quê, para cada número real x, existe um único número correspondente. Com base nisso, podemos determinar uma função f: ℝ → ℝ quê associa cada número real ao seu módulo. Essa função é um caso particular de função definida por mais de uma sentença.
A função f: ℝ → ℝ definida por f(x) = é denominada função modular ou função módulo.
Aplicando-se a definição de módulo de um número real, a função modular póde sêr escrita como:
f(x) =
Gráfico da função modular
Para construir o gráfico da função modular, podemos traçar separadamente o gráfico de cada sentença quê compõe a lei da função no sistema cartesiano e, posteriormente, reunir as representações.
Considerando a função dada por f(x) = , temos:
• f(x) = x, para x ≥ 0
x |
y = f(x) |
|---|---|
0 |
0 |
1 |
1 |
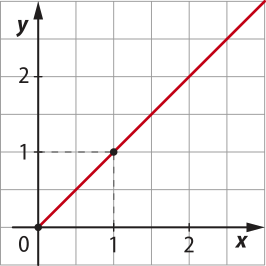
• f(x) = −x, para x < 0
x |
y = f(x) |
|---|---|
−1 |
1 |
−2 |
2 |
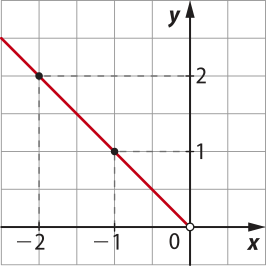
Reunindo em um mesmo sistema cartesiano as duas representações anteriores, temos o gráfico da função modular definida por f(x) = .
Observe quê o domínio dessa função é D(f) = ℝ e quê o conjunto imagem é Im(f) = {y ∈ ℝ | y ≥ 0}.
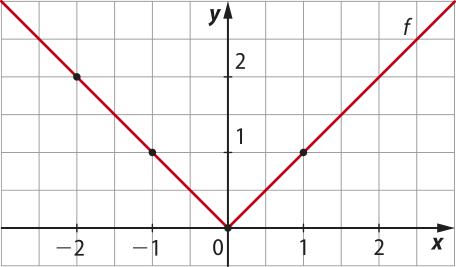
Página noventa e três
Outros gráficos de funções envolvendo módulo
Com base no gráfico da função dada por f(x) = , podemos construir gráficos de outras funções quê envolvem o módulo de um número real.
Observe, por exemplo, o gráfico das funções a seguir em um mesmo sistema cartesiano:
Professor, verificar a possibilidade de trabalhar o tópico Outros gráficos de funções envolvendo módulo utilizando o GeoGebra.
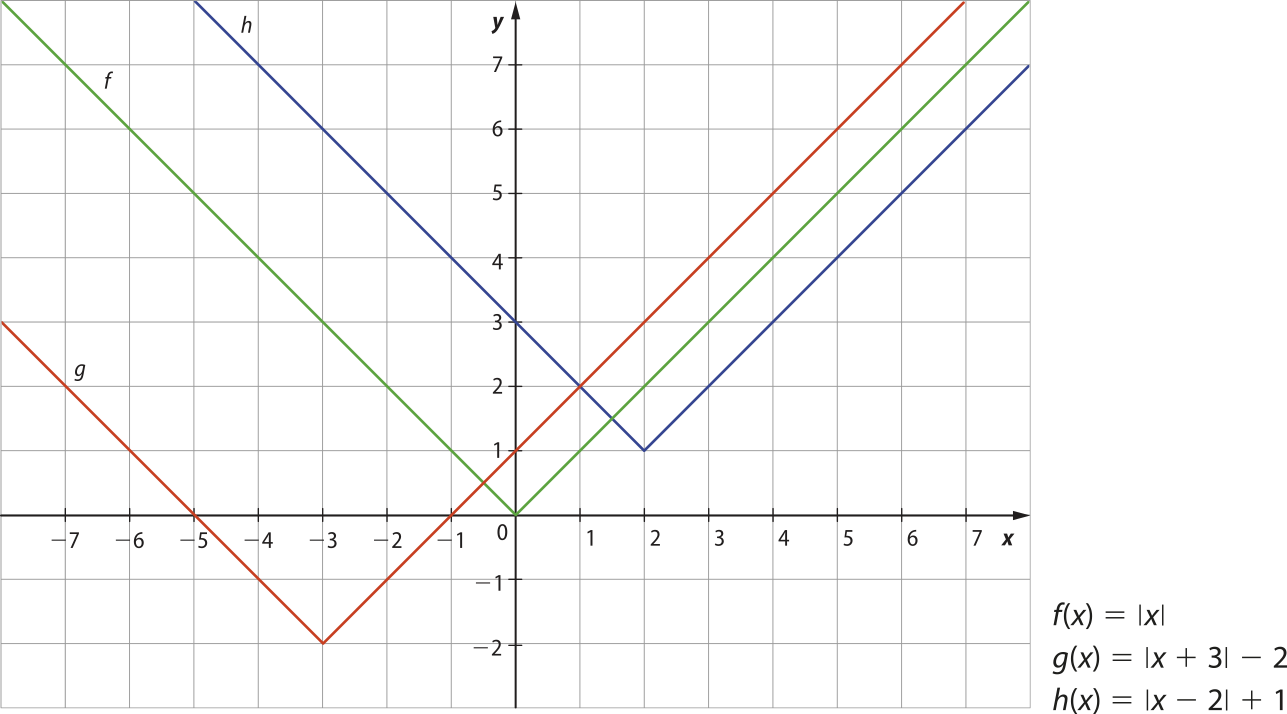
Fazendo translações do gráfico da função f, podemos obtêr os gráficos de g e de h. O procedimento é o seguinte:
• o gráfico da função g, dada por g(x) = − 2, é obtído após o gráfico de f sofrer uma translação horizontal de 3 unidades para a esquerda, seguida de uma translação vertical de duas unidades para baixo;
• o gráfico da função h, dada por h(x) = + 1, é obtído após o gráfico de f sofrer uma translação horizontal de duas unidades para a direita, seguida de uma translação vertical de uma unidade para cima.
De modo geral, considerando uma função f: ℝ → ℝ dada por f(x) = + b, o gráfico dessa função póde sêr obtído por meio de translações do gráfico da função definida por f(x) = .
Para isso, podemos considerar os seguintes casos:
• b > 0: o gráfico é transladado para cima em b unidades;
• b < 0: o gráfico é transladado para baixo em unidades;
• a > 0: o gráfico é transladado para a esquerda em a unidades;
• a < 0: o gráfico é transladado para a direita em unidades.
Página noventa e quatro
Equações modulares
Toda equação quê apresenta o módulo de pelo menos uma expressão quê tenha incógnita é denominada equação modular. Por exemplo:
a) = 8
b) = x + 1
c) = 0
d)
Com base na definição do módulo de um número real, considerando a ≥ 0, podemos escrever a seguinte propriedade:
= a ⇔ x = a ou x = −a
Utilizamos essa propriedade na resolução de equações modulares.
Considerando o exemplo do item a, temos = 8.
Como 8 > 0, para resolver essa equação, calculamos:
• x + 5 = 8 ⇒ x = 3
• x + 5 = −8 ⇒ x = −13
Assim, os números 3 e −13 são soluções da equação = 8.
ATIVIDADES RESOLVIDAS
3. Em cada caso, simplifique a expressão sabendo quê x é um número real tal quê:
a) x ≥ 3
b) 1 ≤ x < 3
c) x < 1
Resolução
Pela definição de módulo, temos:
a) Para x ≥ 3, temos:
= x − 1 + x − 3 = 2x − 4
b) Para 1 ≤ x < 3, temos:
= x − 1 − x + 3 = 2
c) Para x < 1, temos:
= −x + 1 − x + 3 = −2x + 4
4. Construa o gráfico da função f: ℝ → ℝ dada por f(x) = e determine o conjunto imagem.
Resolução
pôdêmos reescrever a lei da função f como uma função definida por mais de uma sentença. Para isso, vamos estudar o sinal de y = x² − 4 para definir os intervalos de x para cada sentença da lei de f. Nesse caso, temos:
x2 − 4 = 0 ⇒ x2 = 4 ⇒ x = ±2
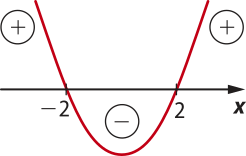
x2 − 4 ≥ 0, para x ≤ −2 ou x ≥ 2
x2 − 4 < 0, para −2 < x < 2
Logo, a função f é dada por:
f(x) =
Vamos traçar separadamente o gráfico de cada sentença quê compõe a lei da função e, posteriormente, reunir em um mesmo sistema cartesiano as representações obtidas.
I f(x) = x2 − 4, se x ≤ −2 ou x ≥ 2
x |
f(x) |
|---|---|
−3 |
5 |
−2 |
0 |
2 |
0 |
3 |
5 |
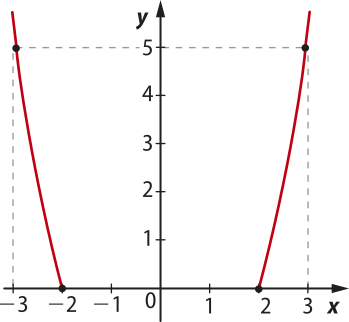
Página noventa e cinco
II f(x) = −x2 + 4, se −2 < x < 2
x |
f(x) |
|---|---|
−1 |
3 |
0 |
4 |
1 |
3 |

Reunindo em um mesmo sistema cartesiano as partes obtidas em I e II, temos o gráfico da função f.
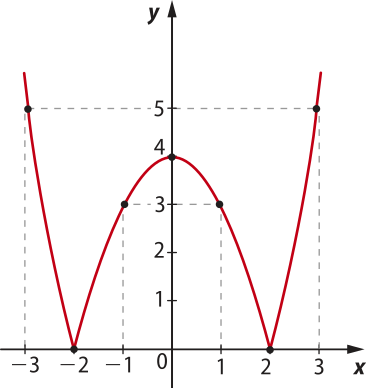
O conjunto imagem da função é dado por Im(f) = {y ∈ ℝ | y ≥ 0} ou, simplesmente, Im(f) = ℝ+. Outra maneira de traçar um gráfico quê poderia sêr utilizada para construir o gráfico de f seria realizar uma reflekção em relação ao eixo x da parte quê representa os valores negativos da função real dada por g(x) = x2 − 4, pois o módulo de um número negativo é o ôpôsto dêêsse número.
5. resôuva as equações a seguir no conjunto dos números reais.
a) = 6
b)
Resolução
a) Como 6 > 0, utilizamos a propriedade = a ⇔ x = a ou x = −a na resolução da equação modular = 6.
Assim, temos: u = 6 ⇒
De I, temos:
x2 − 5x − 6 = 0
Resolvendo essa equação do 2º grau, obtemos x(minutos)" = 6 e x(segundos)" = −1.
De II, temos:
x2 − 5x + 6 = 0
Resolvendo essa equação do 2º grau, obtemos x(minutos)" = 3 e x(segundos)" = 2.
Portanto, S = {−1, 2, 3, 6}.
b) Como ≥ 0, ∀ x ∈ ℝ, utilizamos a propriedade = a ⇔ x = a ou x = −a na resolução da equação modular = .
Assim, temos:
⇒
De I, temos: x − 2 = 3 − 2x ⇒ 3x = 5 ⇒ x =
De II, temos: x − 2 = −3 + 2x ⇒ −x = −1 ⇒ x = 1
Portanto, S =
6. Determine o conjunto solução da equação = x − 3.
Resolução
Como o módulo de um número real x é sempre maior do quê ou igual a 0, é necessário quê x − 3 ≥ 0. Logo, x ≥ 3.
Supondo x − 3 ≥ 0, utilizamos a propriedade |x| = a ⇔ x = a ou x = −a na resolução da equação modular = x − 3.
Assim, temos:
= x − 3 ⇒
De I, obtemos: 2x + 1 = x − 3 ⇒ x = −4
De II, obtemos: 2x + 1 = −x + 3 ⇒ 3x = 2 ⇒ x =
Como x = −4 e x = não satisfazem a condição x ≥ 3, não existe x ∈ ℝ quê seja solução da equação, ou seja, o conjunto solução é vazio. Portanto, S = ∅.
Página noventa e seis
ATIVIDADES
7. De acôr-do com a definição de módulo, calcule:
a)
2
b)
2
c)
8
d)
7
e)
5
f)
−8
8. Considere os pontos A, B, C e D representados na reta real a seguir.
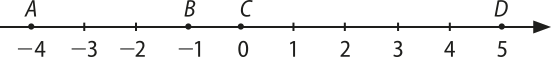
Calcule a distância entre os pontos indicados nos itens a seguir.
a) A e B
3
b) B e C
1
c) B e D
6
d) A e D
9
9. Aplicando a definição de módulo, determine o valor numérico de:
a) 2x − , para x = −4.
−12
b) , para x = −1.
c) , para x = −2.
−1
10. Simplifique a expressão algébrica A = + para os seguintes valores de x:
a) x < −2
−2x − 2
b) −2 ≤ x < 0
2
c) x ≥ 0
2x + 2
11. escrêeva a expressão sem os módulos, para x > 3.
3x + 2
12. Qual é o conjunto de valores assumidos pela expressão sêndo a, b e c números reais não nulos e:
a) a, b e c positivos?
3
b) a, b e c negativos?
−3
13. Considere a função definida por f(x) = e faça o quê se pede.
a) Há algum valor de x ∈ ℝ para o qual a função não está definida? Se sim, qual é esse valor?
sim, x = 3
b) Calcule o valor de f
14. Construa o gráfico de cada função definida a seguir.
Ver as Orientações para o professor.
a) f(x) =
b) g(x) = + 4
c) h(x) =
d) j(x) = − 3
e) m(x) = − 5
15. Observe a seguir o gráfico da função f.
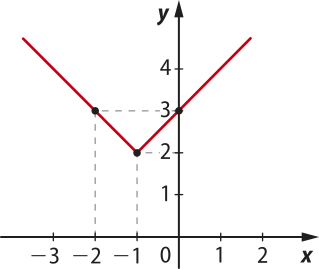
Utilizando módulo, determine a lei da função f, o domínio D(f) e o conjunto imagem Im(f).
f(x) = + 2; D(f) = ℝ; Im(f) = {y ∈ ℝ | y ≥ 2}
16. O preêço médio de cérto produto agrícola é dado em função do mês do ano em quê é comercializado. Se P é o preêço médio em reais e n é o número correspondente ao mês do ano, P em função de n é dado por P(n) = 8 − . Determine para qual valor de n ocorre o valor mínimo de P.
n = 12
17. Construa o gráfico das funções definidas a seguir e determine o domínio e o conjunto imagem de cada uma.
Ver as Orientações para o professor.
a) f(x) =
b) g(x) =
18. resôuva as seguintes equações modulares:
a) = 6
18. a) S =
b) = 1
S = {−1, 5}
c) = 12
S = {−6, 2}
19. (Udesc) A soma das raízes distintas da equação x2 − 5x + 6 = é:
a) 10
b) 7
c) 0
d) 3
e) 4
alternativa e
20. (Epcar-MG) Considere a equação = x − 6. Com respeito à solução real dessa equação, pode-se afirmar quê a:
a) solução pertence ao intervalo fechado [1, 2].
b) solução pertence ao intervalo fechado [−2, −1].
c) solução pertence ao intervalo aberto ]−1, 1[.
d) equação não tem solução.
alternativa d
Página noventa e sete
21. (Fafeod-MG) Sejam S1 e S2 os conjuntos solução das seguintes equações modulares, respectivamente:
(i) = 1 − 2x
(ii) = 6 − 2x
Assim sêndo, é CORRETO afirmar, então, quê o conjunto S1 ∩ S2 é igual a:
a) {x ∈ ℝ | x < −1}
b) {−4, 2}
c) {x ∈ ℝ | x < 3}
d) {−4}
e) {x ∈ ℝ | x < 0}
alternativa d
22. Um posto de combustível está localizado em determinado ponto de uma rodovia de 350 km de comprimento. A distância de um viajante quê está nessa rodovia até o posto póde sêr determinada por uma função definida por d(x) = em quê d(x) é a distância, em kilometro, e x indica o km da rodovia onde o viajante se encontra. De acôr-do com essas informações, responda:
a) Em qual km dessa rodovia está localizado o posto?
No kilometro 200 da rodovia.
b) Em quais pontos da rodovia póde estar uma pessoa quê se encontra a uma distância de 135 km do posto de combustível?
No kilometro 65 ou no 335.
23. (ITA-SP) O produto das raízes reais da equação é igual a:
a) −5
b) −1
c) 1
d) 2
e) 5
alternativa a
24. (Furg-RS) O produto de todas as raízes da equação − 4 = 0 é:
a) 4.
b) −4.
c) −8.
d) −48.
e) 48.
alternativa e
25. (UECE) Se f(x) = x2 − 2, então as raízes irracionais da equação = 8 são:
a) 2 e 2
b) 3 e
c) 4 e 4
d) 5 e 5
alternativa c
26. (Insper-SP) A figura a seguir mostra o gráfico da função f(x).
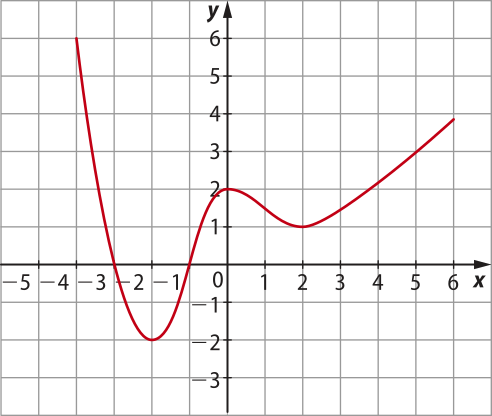
O número de elemêntos do conjunto solução da equação = 1, resolvida em ℝ, é igual a:
a) 6
b) 5
c) 4
d) 3
e) 2
alternativa b
27. (Mack-SP) Observando, na figura, os esboços dos gráficos das funções f(x) = e g(x) = + 1, considere as afirmações:
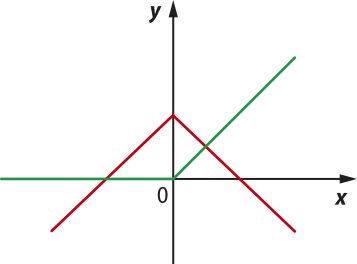
I. Não existe x < 0, tal quê g(x) > f(x).
II. As soluções de f(x) ≥ g(x) são todas positivas.
III. A soma das raízes da equação f(x) = g(x) é .
Então:
a) Todas são falsas.
b) Todas são verdadeiras.
c) Somente I e II são verdadeiras.
d) Somente I e III são verdadeiras.
e) Somente II e III são verdadeiras.
alternativa a
Página noventa e oito
Funções sobrejetora, injetora e bijetora
Vamos estudar agora quando uma função é sobrejetora (ou sobrejetiva), injetora (ou injetiva) e bijetora (ou bijetiva). Com esse estudo, pretendemos facilitar a compreensão do conceito de função invérsa, quê será explorado mais à frente.
Função sobrejetora
Uma função f: A → B é sobrejetora (ou sobrejetiva) quando, para qualquer y ∈ B, existe x ∈ A tal quê f(x) = y.
Em outras palavras, uma função f é sobrejetora quando todo elemento do contradomínio é imagem de pelo menos um elemento do domínio da função, ou seja, quando Im(f) = CD(f).
Por exemplo:
a) Considere a função f: A → B, definida por f(x) = x2, representada por meio do diagrama.
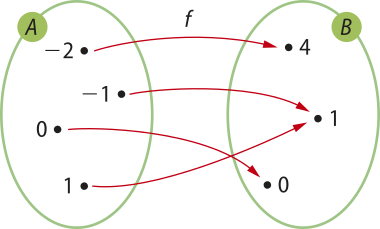
A função f é sobrejetora, pois todo elemento de B é imagem de pelo menos um elemento de A.
b) Considere agora a função g: ℕ → ℕ definida por g(x) = 2x + 3.
Observe alguns valores assumidos pela função g.
x = 0 ⇒ g(0) = 2 ⋅ 0 + 3 = 3
x = 1 ⇒ g(1) = 2 ⋅ 1 + 3 = 5
x = 2 ⇒ g(2) = 2 ⋅ 2 + 3 = 7
⋮ ⋮ ⋮
Existem números naturais quê não são imagem de nenhum elemento do domínio da função g. Por exemplo, os valores 0, 1 e 2 não pertencem ao conjunto imagem de g, pois não existe x ∈ ℕ tal quê 2x + 3 = 0, 2x + 3 = 1 ou 2x + 3 = 2. Nesse caso, a função g não é sobrejetora.
Na verdade, basta quê haja pelo menos um elemento do contradomínio quê não seja imagem de algum elemento do domínio da função para quê ela não seja sobrejetora.
Função injetora
Uma função f: A → B é injetora (ou injetiva) quando, para quaisquer x1, x2 ∈ A, com x1 ≠ x2, tem-se f(x1) ≠ f(x2).
Em outras palavras, uma função f é injetora quando não existe elemento do contradomínio quê seja imagem de mais de um elemento do domínio da função.
Página noventa e nove
Por exemplo:
a) Considere a função f: A → B, definida por f(x) = x + 1, representada por meio do diagrama a seguir.
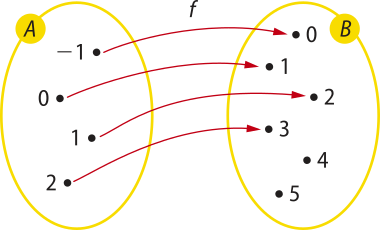
A função f é injetora, pois elemêntos distintos de A são associados pela função a elemêntos distintos de B.
b) Considere agora a função g: ℝ → ℝ definida por g(x) = x2 + 1 e obissérve o cálculo de dois valores assumidos por essa função.
g(1) = 12 + 1 ⇒ g(1) = 2
g(−1) = (−1)2 + 1 ⇒ g(−1) = 2
Note quê o número 2, pertencente ao contradomínio da função, é imagem de dois elemêntos distintos do domínio, (1 e −1). Nesse caso, a função g não é injetora.
Função bijetora
Uma função f: A → B é bijetora (ou bijetiva) quando é sobrejetora e injetora simultaneamente.
Quando f: A → B é uma função bijetora, dizemos quê há uma bijeção entre A e B, ou, ainda, uma correspondência biunívoca entre A e B.
Por exemplo:
a) Considere a função f: A → B, definida por f(x) = 2x + 1, representada por meio do diagrama a seguir.
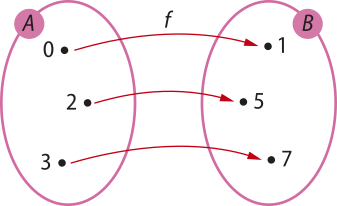
Com base nessa representação, temos:
• a função f é sobrejetora, pois todo elemento de B é imagem de pelo menos um elemento de A;
• a função f é injetora, pois elemêntos distintos de A são associados por f a elemêntos distintos de B.
Portanto, a função f é bijetora, ou seja, temos uma correspondência biunívoca entre A e B.
b) Considere agora a função g: ℝ → ℝ definida por g(x) = x2.
• A função g não é sobrejetora, pois existe pelo menos um elemento no contradomínio quê não é imagem de nenhum elemento do domínio da função g. Por exemplo, o número −1 (não há número real x tal quê x2 = −1).
• A função g não é injetora, pois existem elemêntos distintos do domínio de g quê têm imagens iguais por essa função. Por exemplo: g(−2) = g(2) = 4
Portanto, a função g não é bijetora.
Outra maneira de reconhecer se uma função é ou não bijetora é por meio do gráfico quê a representa. Para isso, traçamos retas paralelas ao eixo x, quê passam por pontos de ordenadas pertencentes ao contradomínio da função, verificando se elas intersectam esse gráfico. Caso isso aconteça, observamos quantos pontos de intersecção existem em cada reta traçada.
Página cem
Observe alguns exemplos.
a) Função f: A → B, em quê A = [1, 5] e B = [2, 7], representada no gráfico a seguir. Observe quê o domínio D(f) foi destacado em azul e o contradomínio CD(f), em vêrde.
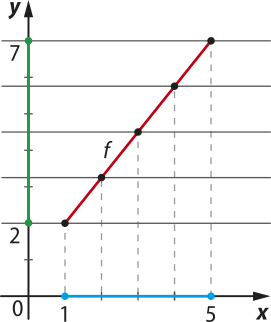
Nesse exemplo, qualquer quê seja a reta traçada paralelamente ao eixo x, passando por pontos de ordenadas pertencentes ao contradomínio da função, intersecta o gráfico em um único ponto.
Nesse caso, a função f é bijetora.
Pense e responda
Observe o gráfico da função f e explique por quê essa função é injetora e sobrejetora.
Ver as Orientações para o professor.
b) Função g: A → B, em quê A = [1, 6] e B = [2, 6], representada no gráfico a seguir. Observe quê o domínio D(g) foi destacado em azul e o contradomínio CD(g), em vêrde.
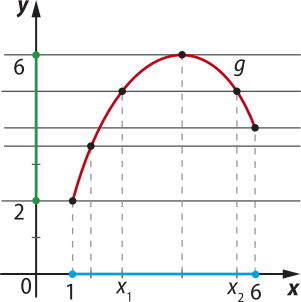
Nesse exemplo, qualquer quê seja a reta traçada paralelamente ao eixo x, passando por pontos de ordenadas pertencentes ao contradomínio da função, intersecta o gráfico. Entretanto, pelo menos uma dessas retas intersecta o gráfico em mais de um ponto.
Nesse caso, a função g é sobrejetora, mas não é injetora. Portanto, a função g não é bijetora.
Pense e responda
Observe o gráfico da função g e explique por quê essa função não é injetora.
Ver as Orientações para o professor.
c) Função h: A → B, em quê A = [1, 8] e B = [1, 6], representada no gráfico a seguir. Observe quê o domínio D(h) foi destacado em azul e o contradomínio CD(h), em vêrde.
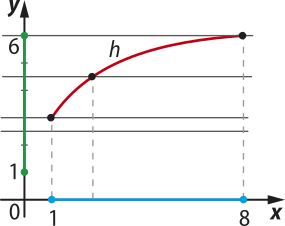
Nesse exemplo, existe pelo menos uma reta paralela ao eixo x, passando por um ponto de ordenada pertencente ao contradomínio da função, quê não intersecta o gráfico.
Nesse caso, a função h não é sobrejetora. Portanto, não é bijetora.
Pense e responda
Observe o gráfico da função h e responda: essa função é injetora? Por quê?
Ver as Orientações para o professor.
Página cento e um
ATIVIDADES RESOLVIDAS
7. Observe o gráfico de uma função f: ℝ → ℝ e verifique se essa função é injetora.
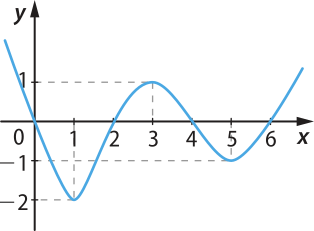
Resolução
Traçando retas paralelas ao eixo x quê passam por pontos de ordenadas pertencentes ao contradomínio da função, temos:
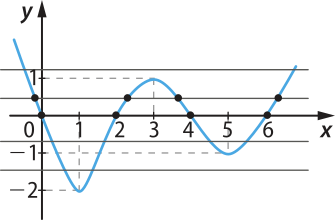
Observe quê a função f não é injetora, pois há pelo menos uma reta paralela ao eixo x, passando por um ponto de ordenada pertencente ao contradomínio da função, quê intersecta o gráfico de f em mais de um ponto.
Isso significa quê, para diferentes valores de x ∈ D(f), temos imagens iguais. Por exemplo: f(0) = f(2) = f(4) = f(6) = 0
8. Verifique se o gráfico da função g: [−2, 8] → [0, 8] a seguir representa uma função bijetora.
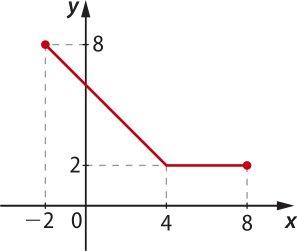
Resolução
A função g não é sobrejetora, pois há pelo menos um elemento do contradomínio de g quê não é imagem de nenhum elemento do domínio de g pela função. Por exemplo, não existe x ∈ D(g) tal quê g(x) = 1 e 1 ∈ CD(g).
Portanto, a função g não é bijetora.
Perceba também quê essa função não é injetora, pois elemêntos distintos do domínio, por exemplo, 4 e 8, são associados, pela função, à mesma imagem, pois f(4) = f(8) = 2.
ATIVIDADES
28. Verifique se a função f: A → B representada em cada diagrama a seguir é bijetora, apenas sobrejetora, apenas injetora ou nenhuma dessas classificações.
a) 
apenas sobrejetora
b) 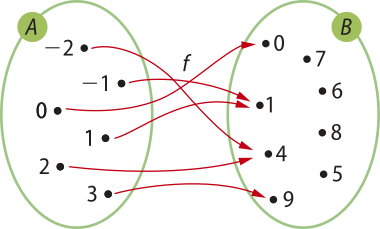
nem sobrejetora nem injetora
c) 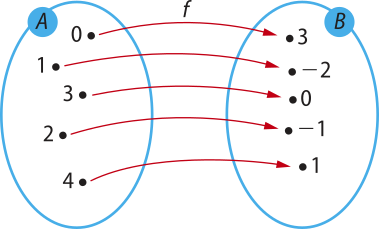
bijetora
d) 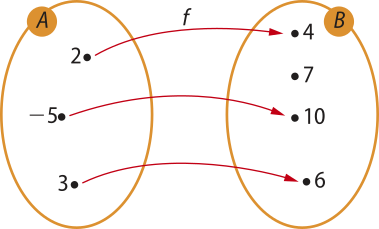
apenas injetora
Página cento e dois
29. Considerando os gráficos a seguir, indique aquele quê representa uma função bijetora, sabendo quê o domínio é ℝ e o contradomínio é ℝ também.
a) 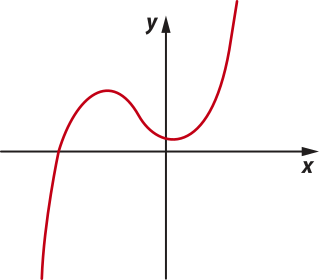
b) 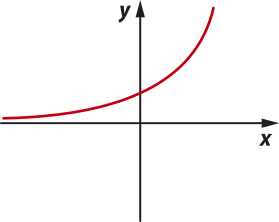
c) 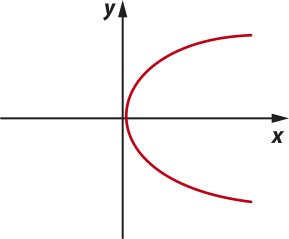
d) 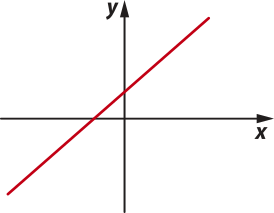
alternativa d
30. (UFMT) A figura a seguir representa o gráfico de uma função y = f(x).
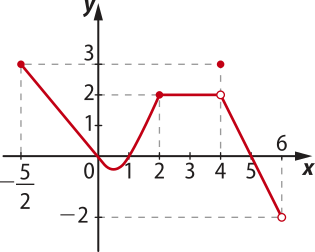
A partir das informações contidas no gráfico, indique V para as afirmativas verdadeiras e F para as falsas.
• f é uma função injetora.
• O domínio de f é o intervalo ]−2; 3].
• f(x) = 2, para todo 2 ≤ x ≤ 4.
• f(x) ≥ 0, para ∀ x ∈ ∪ [1; 5].
A sequência correta é:
a) F, F, F, V.
b) F, V, V, F.
c) V, F, V, V.
d) V, V, V, F.
e) F, V, F, F.
alternativa a
Função composta
Acompanhe a situação a seguir.
Em uma fábrica de calçados, o lucro L obtído com a venda de cada par é função do preêço V de venda de cada par para os varejistas. Essa função é expressa por L(V) = 0,4 ⋅ V. Por sua vez, o preêço V, referente à venda de cada par, é função do valor P, gasto com a matéria-prima necessária para produzir o par, e é expresso por V(P) = 20 + 2P.
Como seria possível determinar o lucro L com base no valor gasto em matéria-prima P?
Observe como podemos fazer isso utilizando uma composição entre as duas funções. Temos as seguintes leis:
L(V) = 0,4 ⋅ V I e V(P) = 20 + 2P II
Substituindo II em I, obtemos:
L(P) = 0,4 ⋅ (20 + 2P) ⇒ L(P) = 8 + 0,8P
Com isso, a função dada por L(P) = 8 + 0,8P relaciona diretamente o lucro L, obtído com a venda de cada par de calçados, e o valor P, gasto com a matéria-prima necessária para produzir cada par.
Página cento e três

Nessa situação, observamos quê a variável L (lucro) é função da variável V (preço de venda), quê, por sua vez, é função de uma terceira variável, P (valor da matéria-prima).
Essas cadeias de dependência podem sêr matematicamente modeladas pela composição de funções.
Acompanhe a definição matemática de função composta e obissérve o diagrama a seguir, quê representa esse conceito.
Dadas as funções f: A → B e g: B → C, chamamos de função composta de g com f a função g ∘ f: A → C, tal quê (g ∘ f)(x) = g(f(x)) para ∀ x ∈ A.
(g ∘ f)(x) = g(f(x)), ∀ x ∈ A
(g ∘ f)(x) ← Lê-se: g de f de x.
g(f(x)) ← Lê-se: g composta com f.
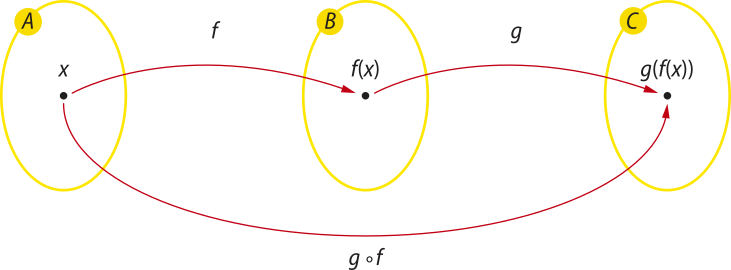
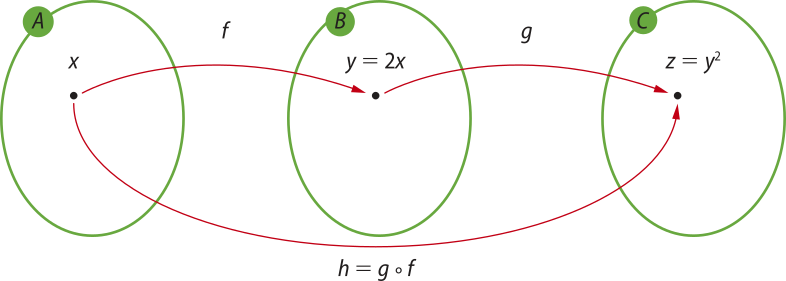
Considere, por exemplo, as funções f e g, definidas por:
• f: A → B, quê, a cada x ∈ A, associa um único valor de y ∈ B, tal quê y = 2x;
• g: B → C, quê, a cada y ∈ B, associa um único z ∈ C, tal quê z = y2.
Considere uma terceira função, h: A → C, quê, a cada x ∈ A, associa um único valor de z ∈ C, dada pela composição g ∘ f. Observe como podemos usar um diagrama para representá-la.
z = y2 = (2x)2 = 4x2
Saiba quê...
Dadas duas funções, f e g, para quê exista g ∘ f, o domínio de g deve sêr igual ao contradomínio de f, ou seja, D(g) = CD(f).
Página cento e quatro
Note quê as leis das funções f e g podem sêr expressas, respectivamente, por f(x) = 2x e g(y) = y². Com isso, podemos obtêr a lei da função h, composta de g com f, do seguinte modo:
h = g ∘ f = g(f(x)) = g(2x) = (2x)2 = 4x2
Assim, a lei da função h é expressa por g(f(x)) = 4x2.
Pense e responda
Considerando as funções f e g do exemplo dado, existe a função f ° g, isto é, a função composta de f com g? Justifique.
Não existe a função f ∘ g, pois CD(g) = C e D(f) = A, logo CD(g) ≠ D(f).
Função invérsa
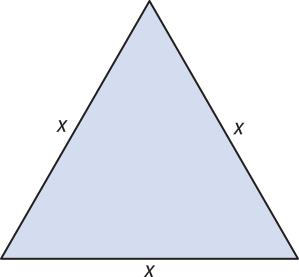
Ao considerarmos um triângulo equilátero, podemos relacionar o perímetro dêêsse triângulo e a medida dos lados por meio de uma função.
Observe quê, dado um lado x do triângulo equilátero, para obtermos o perímetro y associado a esse lado, basta calcular 3 ⋅ x. Entretanto, dado o perímetro y, para obtermos o lado x, basta calcular
pôdêmos representar essa situação pelas seguintes funções:
• Uma função bijetora p: A → B, quê associa cada lado x ∈ A a um único perímetro y ∈ B, expressa por y = 3x.
• Uma função bijetora q: B → A, quê associa cada perímetro y ∈ B a um único lado x ∈ A, expressa por x = .
Escolhendo alguns valores numéricos, representamos os diagramas a seguir.
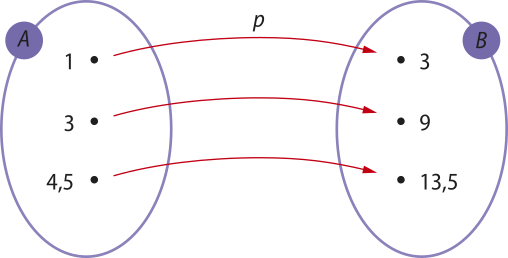
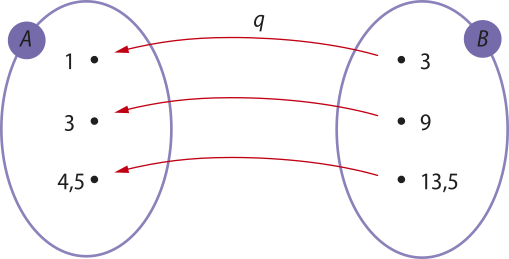
Note, por exemplo, quê:
• p(1) = 3 e q(3) = 1
• p(3) = 9 e q(9) = 3
• p(4,5) = 13,5 e q(13,5) = 4,5
A função p relaciona cada x de A a um y de B, e a função q relaciona cada y de B a um x de A, de modo quê p(x) = y e q(y) = x para todo x ∈ A e y ∈ B.
Quando observamos situações como essa, dizemos quê uma função é invérsa da outra. Sendo assim, a funções p e q são inversas uma da outra.
Acompanhe a seguir como podemos definir matematicamente a função invérsa.
Dada uma função bijetora f: A → B, denomina-se função invérsa de f a função g: B → A, tal quê, se f(a) = b, então g(b) = a para todo a ∈ A e b ∈ B.
Página cento e cinco
A função g póde sêr indicada por f−1 (lê-se: função invérsa de f).
O número −1 na notação f−1 não é um expoente, ou seja, f−1 (x) ≠
Considerando a função invertível f: ℝ → ℝ dada por f(x) = 2x − 1, podemos determinar a lei de sua invérsa f−1. Observe a seguir como proceder.
• Reescrevemos a lei da função f mudando a variável dependente f(x) para y:
y = 2x − 1
• Trocamos a variável x por y e a variável y por x:
x = 2y − 1
• Para determinarmos a nova lei, isolamos y:
x = 2y − 1 ⇒ x + 1 = 2y ⇒ y =
A lei da função invérsa de f é dada por f−1(x) = .
Saiba quê...
Uma função f só admite função invérsa f−1 se for bijetora. Nesse caso, dizemos quê a função f é invertível.
Gráfico da função invérsa
Considere a função f: ℝ+ → ℝ+ invertível dada por f(x) = 3x e a função invérsa de f, f−1: ℝ+ → ℝ+, definida por f−1 (x) = .
Como o gráfico de f e o de f–1 são semirretas, atribuímos alguns valores para x e obtemos os pares ordenados de alguns pontos para traçar a semirreta correspondente a cada função.
x |
y = f(x) |
|---|---|
0 |
0 |
1 |
3 |
2 |
6 |
x |
y = f−1(x) |
|---|---|
0 |
0 |
3 |
1 |
6 |
2 |
Traçando o gráfico de f e o de f−1 no mesmo sistema de coordenadas, obtemos:
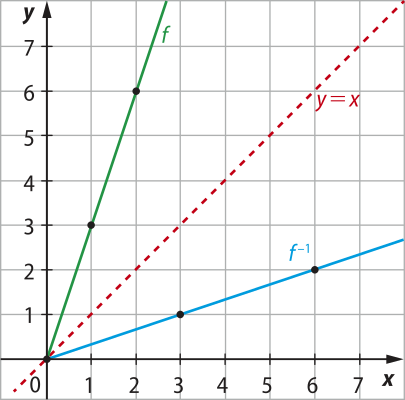
Saiba quê...
Um ponto de coordenadas (x, y) e um ponto de coordenadas (y, x) são simétricos em relação à bissetriz dos quadrantes ímpares.
Observe quê o gráfico de f e o de f−1 são simétricos em relação à bissetriz dos quadrantes ímpares (y = x) do sistema cartesiano ortogonal. É possível demonstrar quê essa propriedade é válida para toda função invertível e sua invérsa.
Página cento e seis
ATIVIDADES RESOLVIDAS
9. Considerando as funções reais f e g, definidas respectivamente por f(x) = x + 1 e g(x) = 2x2 − 3, determine:
a) f(g(x)) e g(f(x));
b) os valores de x para quê se tenha f(g(x)) = g(f(x)).
Comentar com os estudantes quê a composição de funções não é comutativa. Esta atividade resolvida mostra isso.
Resolução
a) Para determinar f(g(x)), fazemos:
f(g(x)) = f(2x2 − 3)
f(g(x)) = 2x2 − 3 + 1
f(g(x)) = 2x2 − 2
Para determinar g(f(x)), fazemos:
g(f(x)) = g(x + 1)
g(f(x)) = 2(x + 1)2 − 3
g(f(x)) = 2(x2 + 2x + 1) − 3
g(f(x)) = 2x2 + 4x − 1
b) Igualando as leis de f ∘ g e de g ∘ f, temos: 2x2 − 2 = 2x2 + 4x − 1 ⇒ 4x = −1 ⇒ x =
Logo, x = .
10. Dadas as funções de domínio real definidas por f(x) = x2 − 5x + 6 e g(x) = x + 1, determine os valores de x para quê tenhamos f(g(x)) = 0.
Resolução
Como g(x) = x + 1, então f(g(x)) = f(x + 1).
f(x + 1) = (x + 1)2 − 5(x + 1) + 6 = x2 + 2x + 1 − 5x − 5 + 6 = x2 − 3x + 2
Para determinar os valores de x para os quais f(g(x)) = 0, precisamos resolver a equação x2 − 3x + 2 = 0.
Utilizando a fórmula resolutiva, temos:
(delta)" = b2 − 4ac = (−3)2 − 4 ⋅ 1 ⋅ 2 = 9 − 8 = 1
Assim:
x = ⇒ x = ⇒ x =
Logo, x = 1 ou x = 2.
Portanto, f(g(x)) = 0 para x = 1 ou x = 2.
11. Sabendo quê f(x) = 3x − 1 e f(g(x)) = 6x + 8, determine g(x).
Resolução
f(x) = 3x − 1 ⇒ f(g(x)) = 3 ⋅ g(x) − 1 ⇒ 3 ⋅ g(x) − 1 = 6x + 8 ⇒ 3 ⋅ g(x) = 6x + 9 ⇒ g(x) = ⇒ g(x) = 2x + 3
Logo, g(x) = 2x + 3.
12. Considerando a função real f bijetora dada por f(x) = x + 2, determine a lei da função invérsa g e esboce os gráficos de f e g em um mesmo plano cartesiano.
Resolução
Como a função f é bijetora, é invertível.
Admitindo g como a função invérsa de f, temos:
f(x) = y ⇒ y = x + 2
Trocando a variável x por y e a variável y por x e isolando y, temos:
x = y + 2 ⇒ y = x − 2
Portanto, a lei da função invérsa g é g(x) = x − 2.
Para construir os gráficos, podemos representar o gráfico da função f e, em seguida, determinar o gráfico de g, simétrico ao gráfico de f em relação à bissetriz dos quadrantes ímpares (y = x).
Para isso, determinamos alguns pontos pêlos quais passa a reta quê representa a função f e esboçamos os gráficos em um mesmo sistema de coordenadas.
x |
y = f(x) |
|---|---|
−1 |
1 |
0 |
2 |
1 |
3 |
2 |
4 |
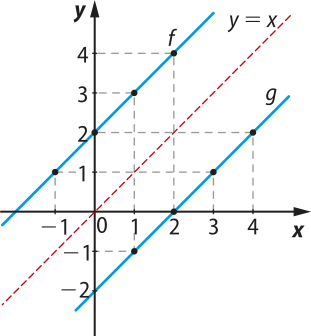
Página cento e sete
ATIVIDADES
31. Sendo f e g funções de domínio real, com f(x) = x2 + 2x e g(x) = 1 − 3x, determine:
a) f(g(x))
9x2 − 12x + 3
b) g(f(x))
−3x2 − 6x + 1
c) (f ∘ f)(x)
x4 + 4x3 + 6x2 + 4x
d) (g ∘ g)(x)
9x − 2
32. Dados f(x) = 3x + 5 e g(x) = 2x − 3, calcule x para quê se tenha:
a) f(g(x)) = 0
x =
b) g(f(x)) = 0
x = −
33. Se f(x) = , qual é o valor de x para quê f(f(x)) = 1?
x =
34. Considere as funções f: ℝ → ℝ e g: ℝ → ℝ definidas por f(x) = x2 − 2x − 3 e g(x) = 4x + m. Sabendo quê f(g(−1)) = 12, calcule m.
1 ou 9
35. (UEPB) Sendo f(x) = , x ≠ 1 e g(x) = 2x − 4, o valor de f(g(2)) + g é igual a:
a) 1
b) −8
c) −9
d) 1
e) −2
alternativa c
36. (hú éfi éssi cê) Considere as funções f, g: ℝ → ℝ tais quê g(x) = 2x + 1 e g(f(x)) = 2x2 + 2x + 1. Calcule f(7).
56
37. Determine a lei da função invérsa de cada função bijetora definida a seguir, considerando o domínio e o contradomínio como ℝ.
a) f(x) = x − 3
f−1(x) = x + 3
b) g(x) =
g–1(x) = 4x − 2
38. Seja f: ℝ → ℝ, definida por f(x) = ax − 2 e g a função invérsa de f. Sabendo quê f(−2) = 10, determine a lei da função g.
g(x) =
39. Considere uma função invertível dada por f(x) = com D(f) = ℝ − {3}, e determine:
a) f−1(x)
f−1 (x) =
b) o domínio de f−1
D(f−1) = {x ∈ ℝ | x ≠ 2}
c) f−1 (−3)
2
40. Em cada item a seguir, estão representados, em um mesmo sistema cartesiano ortogonal, os gráficos de duas funções. Determine se as funções representadas são uma a invérsa da outra. Justifique sua resposta.
a) 
Não são inversas.
b) 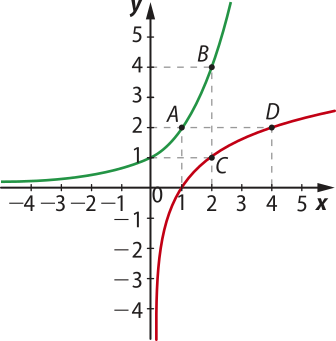
São inversas.
c) 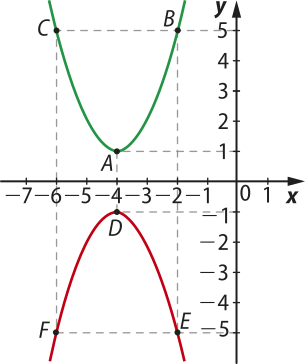
Não são inversas.
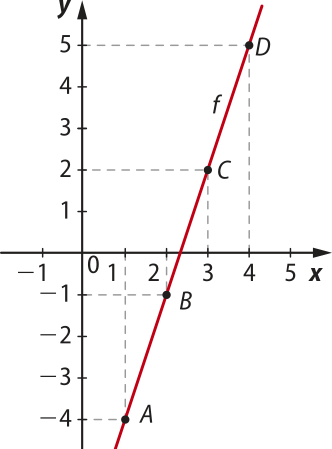
41. Uma função bijetora f está representada no gráfico a seguir. Com base nele, esboce o gráfico da função invérsa f−1.
Ver as Orientações para o professor.
Página cento e oito
EXPLORANDO A TECNOLOGIA
Conhecendo o GeoGebra
Orientar os estudantes a navegar pelo sáiti do GeoGebra, pois nele há uma comunidade de discussão e muitas informações disponíveis, inclusive alguns tutoriais e materiais produzidos por professores.
O GeoGebra é um software de Matemática dinâmica quê póde sêr utilizado em todos os níveis de ensino. Trata-se de uma multiplataforma, pois tem portabilidade em todos os sistemas operacionais e póde sêr instalada em computadores, tablets e smartphones.
Sua instalação deve sêr feita por meio do sáiti oficial https://livro.pw/jtbfa (acesso em: 23 jul. 2024), baixando-se o software GeoGebra Clássico 6 e seguindo-se as orientações de instalação.
O GeoGebra também póde sêr usado em sua versão ôn láini, sem a necessidade de instalação, pelo sáiti https://livro.pw/otpjb (acesso em: 23 jul. 2024).
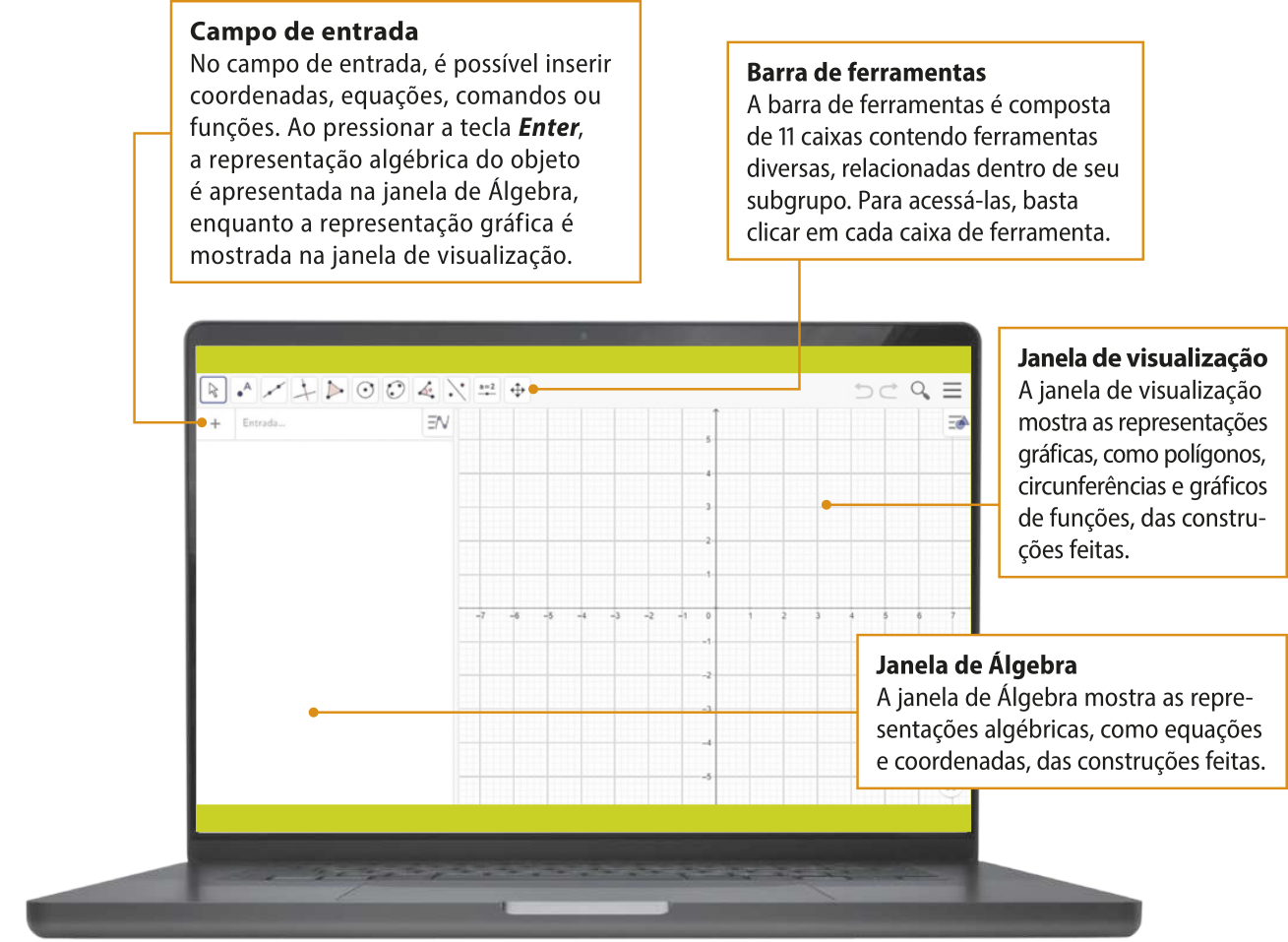
Ao abrir o software instalado ou a versão ôn láini, aparece uma tela inicial composta de várias janelas, com ferramentas e exibições específicas de acôr-do com a utilização. A seguir, apresentamos a tela inicial com algumas de suas funções.
Página cento e nove
Além da janela de Álgebra e da janela de visualização, quê são mostradas na tela inicial padrão, o GeoGebra tem outras janelas, quê, dependendo da construção quê se deseja realizar, podem sêr acionadas no menú Exibir. Quando necessário, essas outras janelas serão exibidas durante a realização das construções.
Todas as janelas do GeoGebra estão relacionadas dinamicamente, ou seja, ao se realizar uma alteração em algum objeto em uma delas, todas as representações dêêsse mesmo objeto nas demais janelas serão alteradas automaticamente.
O GeoGebra utiliza linguagem e notação próprias, quê podem diferir um pouco das utilizadas nesta Coleção. Por exemplo, para a separação da parte decimal de um número, o software usa o ponto no lugar da vírgula; para indicar as coordenadas de um ponto A qualquer, a notação é A = (0,0), em vez de A(0, 0). Ao longo da Coleção, conforme necessário, apresentaremos outras particularidades do GeoGebra.
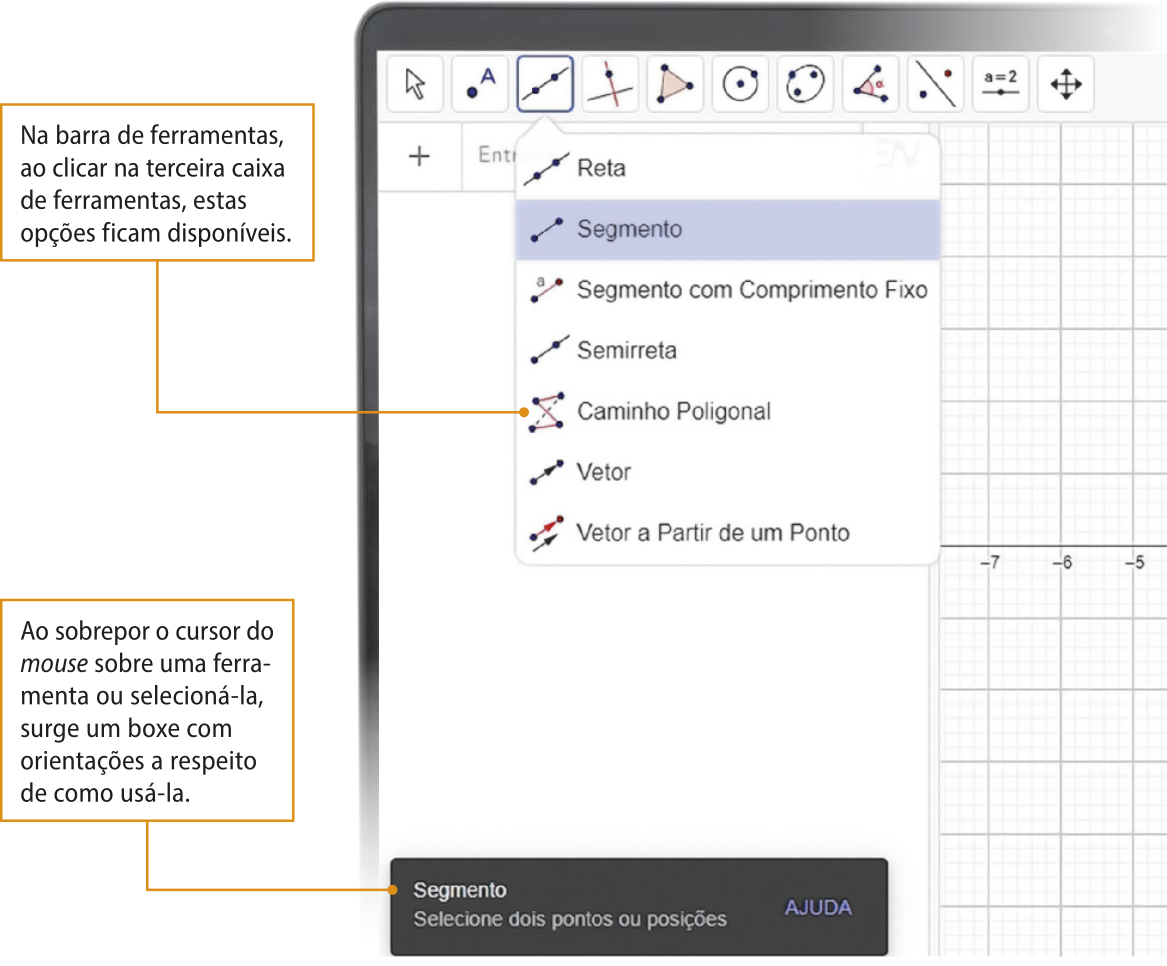
Página cento e dez
Explorando função invérsa com o GeoGebra
Estudamos quê uma função f precisa sêr bijetora para admitir função invérsa. No entanto, nem todas as funções são bijetoras, por exemplo, a função f: ℝ → ℝ+ dada por f(x) = x2.
Porém, se restringirmos de maneira conveniente o domínio e o contradomínio de f, podemos obtêr uma correspondência biunívoca.
pôdêmos considerar, por exemplo, uma função f1: ℝ+ → ℝ+, definida por f1(x) = x2, e uma função f2: ℝ− → ℝ+, definida por f2(x) = x2, cujos gráficos estão representados a seguir.
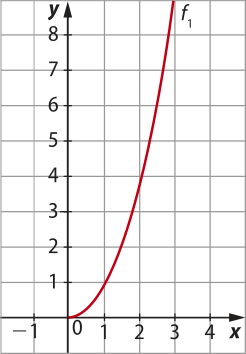
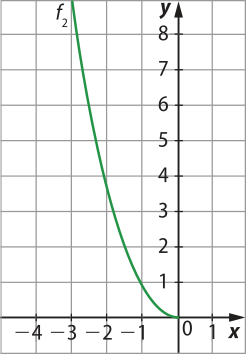
Vamos, agora, utilizar o GeoGebra para representar o gráfico da função invérsa de f1 e o da função invérsa de f2. Para isso, execute os passos a seguir.
I. No campo de entrada, digite “f1(x)=x^2, 0<=x” e pressione Enter. O acento circunflexo indica para o programa quê o número 2 é um expoente.
Será representada, na janela de visualização, a função dada por f1(x) = x2 para 0 ≤ x.
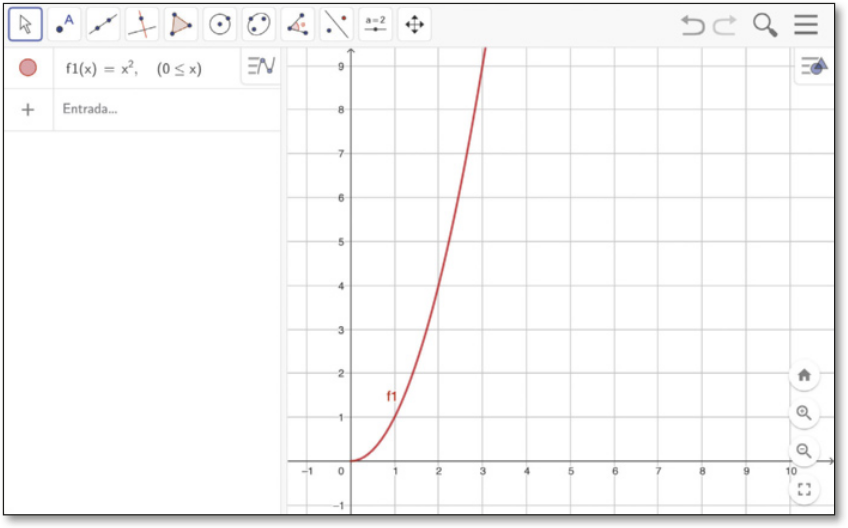
Página cento e onze
II. Estudamos quê o gráfico de uma função e o de sua invérsa são simétricos em relação à bissetriz dos quadrantes ímpares.
Para representar essa reta, digite "y=x" no campo de entrada e pressione Enter.
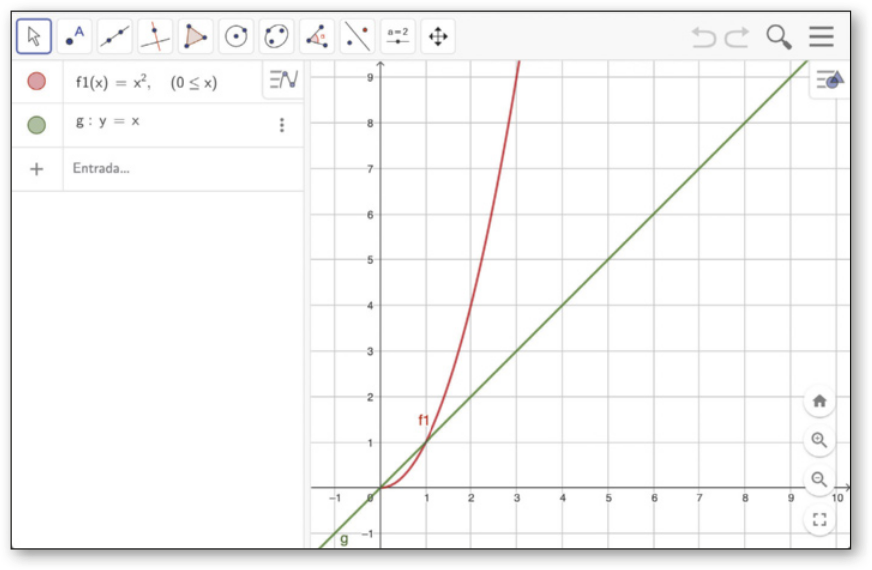
III. Para obtêr a função invérsa de f1, selecione a ferramenta ![]() (Reflexão em Relação a uma Reta). Em seguida, clique sobre o gráfico de f1 e, posteriormente, sobre a bissetriz dos quadrantes ímpares. O gráfico obtído é o da função invérsa de f1, representado em azul na imagem.
(Reflexão em Relação a uma Reta). Em seguida, clique sobre o gráfico de f1 e, posteriormente, sobre a bissetriz dos quadrantes ímpares. O gráfico obtído é o da função invérsa de f1, representado em azul na imagem.
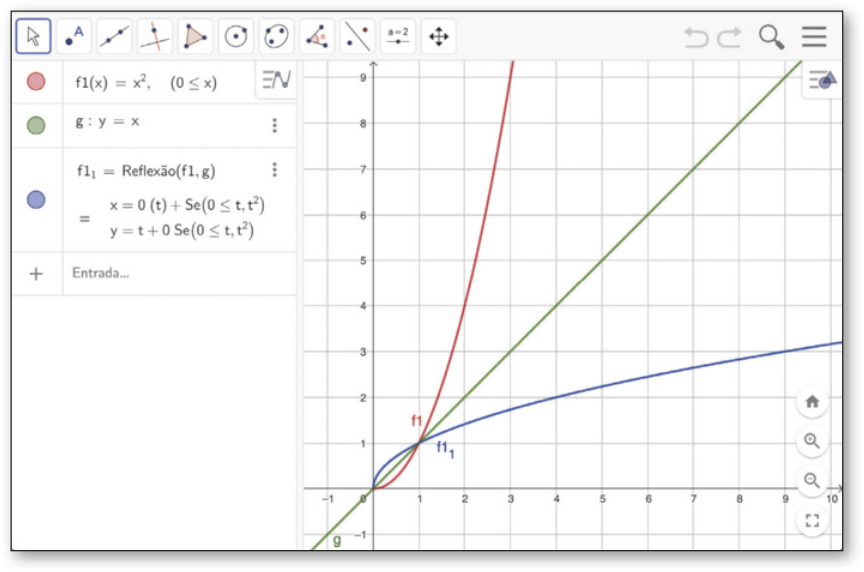
Para obtêr o gráfico da função invérsa de f2, repita a sequência de passos apresentada digitando “f2(x)=x^2, x<=0” no passo I.
Agora, faça o quê se pede nas atividades a seguir.
1. Construa no GeoGebra o gráfico da função definida por g(x) = x3. Para isso, digite "y=x^3" no campo de entrada. Observe o gráfico obtído e responda: a função g é bijetora? Justifique sua resposta.
1. A função g é bijetora, pois, traçando-se retas paralelas ao eixo x quê passem por quaisquer pontos cuja ordenada pertença a CD(g), elas intersectam o gráfico em um único ponto, o quê significa quê a função g é injetora e sobrejetora.
2. Para construir o gráfico da função invérsa de g, é necessário restringir o domínio, como foi feito para a função f1 observada no início da seção?
Não, pois g é uma função bijetora; portanto, admite função invérsa.
3. Represente o gráfico da função g–1 na mesma janela de visualização em quê g foi representada. Quantos pontos de intersecção há entre os gráficos de g e de g–1?
3
Página cento e doze
ATIVIDADES COMPLEMENTARES
1. (IFSul-RS) O gráfico quê descreve a função
f(x) = é:
a) 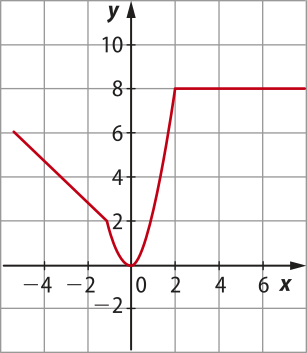
b) 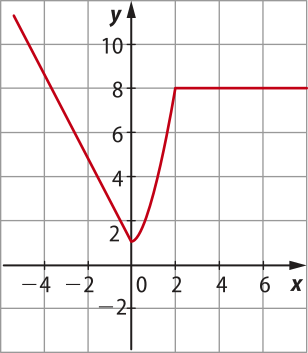
c) 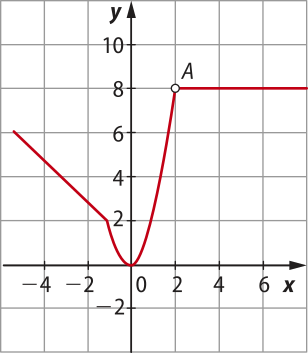
d) 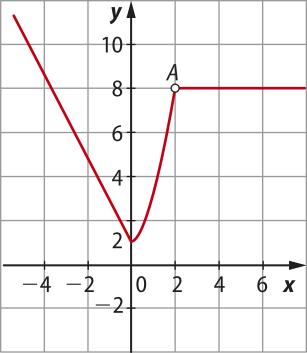
alternativa a
2. (UFRGS-RS) O gráfico da função f definida por:
f(x) = é
a) 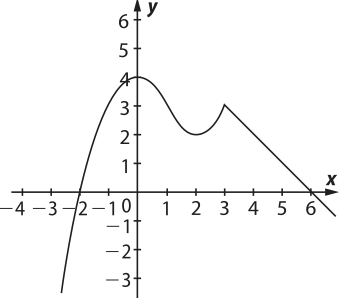
b) 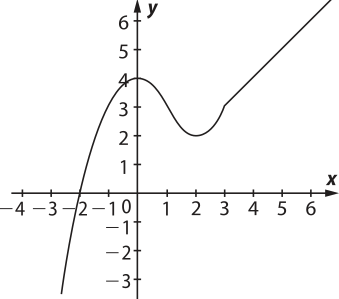
c) 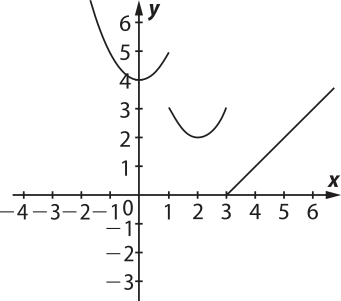
d) 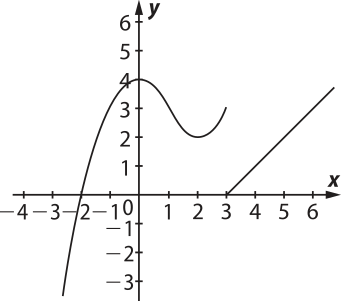
e) 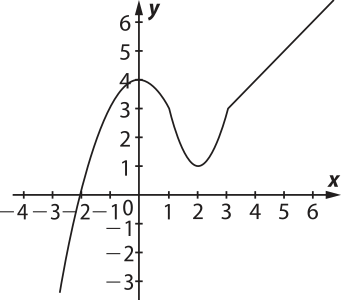
alternativa b
Página cento e treze
3. (UEL-PR) Leia o texto a seguir.
Em 1970, o matemático Diôn Conway inventou o “Jogo da Vida”, exemplo teórico de como regras fixas e simples permitem, com o passar das gerações, a criação, a sobrevivência e o fim de vidas simuladas. Daí o nome do jôgo!
Adaptado de: https://livro.pw/uabes.
Admita uma variação do jôgo da Vida como dada a seguir.
Para cada geração t ∈ ℕ = {1, 2, …}, há uma sequência numérica infinita a1, a2, a3, …, an, … tal quê an ∈ {0, 1} para todo n ∈ ℕ. O número 1 indica quê há vida naquela posição e 0 o contrário.
As gerações se sucedem da seguinte forma:
se a1, a2, a3,…, an,… é a sequência da geração t, então a sequência , , , …, , … da geração t + 1 é dada por:
=
Por exemplo,
Geração |
seqüência numérica |
||||||||
|---|---|---|---|---|---|---|---|---|---|
t |
n = 1, |
n = 2, |
n = 3, |
n = 4, |
n = 5, |
n = 6, |
n = 7, |
n = 8, |
… |
1 |
1, |
1, |
0, |
0, |
1, |
0, |
0, |
0, |
… |
2 |
1, |
1, |
1, |
1, |
0, |
1, |
0, |
0, |
… |
3 |
1, |
0, |
0, |
1, |
0, |
0, |
1, |
0, |
… |
Supondo agora quê 1, 0, 0, 0, 0, 0, … é a sequência da geração t, assinale a alternativa quê apresenta, corretamente, a sequência da geração t + 1.
a) 0, 0, 0, 0, 0, …
b) 0, 1, 0, 0, 0, …
c) 1, 1, 0, 0, 0, …
d) 1, 1, 0, 1, 0, …
e) 1, 1, 1, 1, 1, …
alternativa b
4. (UECE) Se f: ℝ → ℝ é a função definida por
f(x) = ,
então, considerando o sistema de coordenadas usual com o métro (m) sêndo a unidade de comprimento, a medida da área, em m2, da região do plano limitada pelo gráfico de f e pelo eixo x é
a) 12.
b) 10.
c) 9.
d) 11.
alternativa b
5. (PUC-PR) Um economista, no início de 2007, fez uma projeção sobre a situação financeira de um grupo de investidores quê aplicam na bolsa de valores, e observou quê a variação dos ganhos dessas aplicações é alterada diariamente; assim, concluiu quê o lucro diário é dado pela função f(x) = ⋅ 50, onde x representa cada dia do ano, (x = 1, 2, 3, …, 365), e o lucro é dado em real.
Se o grupo de investidores pretende um lucro de R$ 5.750,00, em quais meses isso será possível?
a) Abril e novembro.
b) Março e outubro.
c) Março e novembro.
d) Maio e outubro.
e) Abril e outubro.
alternativa c
6. (UECE) Considerando, no plano, o sistema de coordenadas cartesianas usual, usando o métro (m) como unidade de comprimento, é correto dizêr quê a medida da área da região limitada pelo gráfico da função f: [0, 4] → ℝ definida por f(x) = − 2 e pelo eixo das abscissas, em metros quadrados, é igual a
a) 6.
b) 8.
c) 3.
d) 4.
alternativa d
Página cento e quatorze
7. (UFRGS-RS) O gráfico de f(x) está esboçado na imagem a seguir.

O esboço do gráfico de + 2 está representado na alternativa
a) 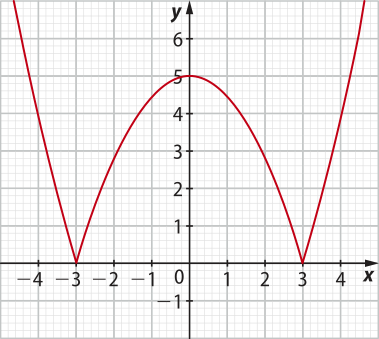
b) 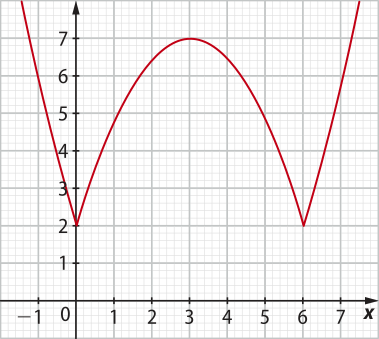
c) 
d) 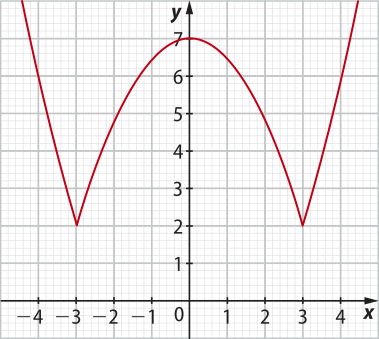
e) 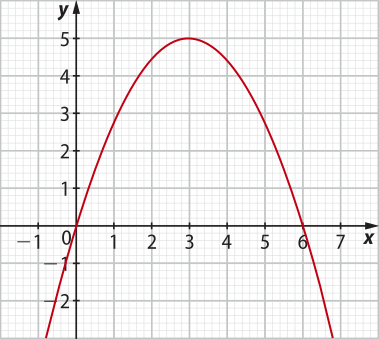
alternativa b
8. (Udesc) Considere os gráficos ilustrados na figura:
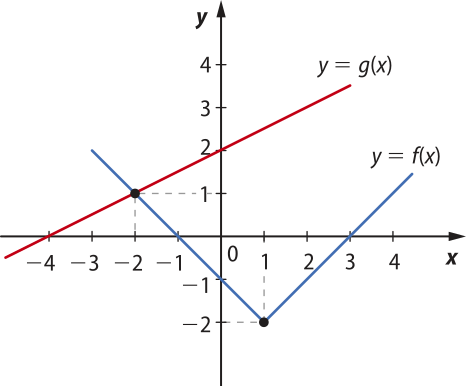
Classifique cada sentença abaixo em verdadeira
(V) ou falsa (F).
() O valor de g(f(−1)) − f(g(−2) + 2) é igual a 2.
() O valor de f(g(−4) + 1) + 3 é igual a 1.
() A lei de formação de y = f(x) é y = − 2.
Assinale a alternativa quê contém a sequência correta, de cima para baixo:
a) V – F – V
b) V – V – V
c) F – V – F
d) F – V – V
e) V – V – F
alternativa b
Página cento e quinze
9. (IFSul-RS) Considere a função f: [−5, 3] → A ⊂ ℝ, definida por f(x) = − 3. Se f é sobrejetora, então
a) A = [−6, 2].
b) A = [−5, 2].
c) A = [−4, 2].
d) A = [−3, 2].
alternativa d
10. (ESPM-SP) Sejam f e g funções reais tais quê f(2x + 1) = 2x + 4 e g(x + 1) = 2x − 1 para todo x ∈ ℝ. pôdêmos afirmar quê a função f ∘ g(x) é dada por:
a) 2x − 1
b) x + 2
c) 3x + 1
d) 2x
e) x − 3
alternativa d
11. (IFSul-RS) A função f: [0, +∞[ → [4, +∞[, definida por f(x) = (x + 2)2, possui invérsa f−1: [4, +∞[ → [0, +∞[, definida por
a) f−1 (x) =
b) f−1 (x) =
c) f−1 (x) = + 2
d) f−1 (x) = − 2
alternativa d
12. (UEPB) Dada a função bijetora tal quê f(x) = , D(f) = ℝ − {1}, o domínio de f−1 é:
a) ℝ
b) ℝ − {3}
c) ℝ − {1}
d) ℝ − {−1}
e) ℝ −
alternativa b
PARA REFLETIR
Neste Capítulo, aprendemos quê, em algumas situações do dia a dia, o comportamento de uma grandeza depende do comportamento de outra, mas essa relação é estabelecida de acôr-do com classes ou faixas de valores. Estudamos também como podemos utilizar a ideia de função para estabelecer modelos quê podem sêr utilizados para fazer estimativas e possibilitar algumas tomadas de dê-cisão de maneira mais consciente.
Estudamos o conceito de função definida por mais de uma sentença e a representação gráfica dêêsse tipo de função, bem como função composta e função invérsa, módulo de números reais, função modular e equações modulares.
Nas páginas de abertura, foi apresentada uma situação envolvendo uma discussão sobre imposto de renda, quê foi retomada um pouco mais adiante. Depois de ter estudado o conteúdo dêste Capítulo, você consegue reconhecer quê esses conceitos podem auxiliá-lo a compreender e a analisar a situação apresentada na abertura? Você já tinha essa percepção antes de estudar esses conceitos?
Vamos refletir a respeito das aprendizagens do Capítulo 3:
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• Cite outras situações do dia a dia quê envolvam as ideias de função definida por mais de uma sentença e de função modular.
• Explique como você acredita quê seu entendimento sobre o conceito de função se aprofundou em relação ao quê você conhecia anteriormente.
• Você utiliza os conceitos estudados para analisar situações antes de tomar decisões e de resolver problemas do dia a dia?
Respostas pessoais.
Página cento e dezesseis