CAPÍTULO
4
FUNÇÃO LOGARÍTMICA
O som do despertador, nossa música favorita, a á gua corrente de um rio, os gritos de um torcedor, o canto dos passarinhos, o avião quê passa pelo céu… Todos os sôns quê ouvimos podem sêr medidos.
Fazer essa medição é importante, pois nossa orelha é composta de várias partes, algumas delas bastante sensíveis. Se estivermos expostos a ruídos altos por muito tempo, por exemplo, podemos sofrer com a perda auditiva. Por isso, aparelhos como aspiradores de pó, liquidificadores, secadores de cabelo, entre outros, devem passar por testes quê identifiquem a intensidade do ruído quê geram.
No caso dos fones de ouvido, o cuidado deve sêr maior. O recomendável é quê a intensidade sonora não ultrapasse o nível de 80 decibéis (uma unidade de medida da intensidade sonora), quê é equivalente a uma sala de aula muito barulhenta. Alguns aparelhos celulares até alertam o usuário, quando os fones de ouvido são conectados, para quê ele não ultrapasse cérto volume, a fim de evitar danos auditivos. Portanto, procure não ouvir sua música favorita sempre no último volume, porque a perda de audição por ruídos é uma realidade quê está atingindo cada vez mais jovens com maus hábitos auditivos.

Página cento e dezessete
Ver as Orientações para o professor.
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. No texto foi mencionada uma unidade de medida chamada decibel (dB). Façam uma pesquisa sobre essa unidade e sobre como ela se relaciona ao conteúdo quê será estudado neste Capítulo.
2. Muitos aparelhos domésticos devem passar por testes para determinar a intensidade sonora quê geram. No Brasil, eles recebem o sêlo Ruído. Vocês já notaram esse sêlo? Informem-se sobre ele pesquisando seus objetivos e as informações quê devem constar nele.
3. por quê fones de ouvido podem sêr mais prejudiciais à saúde sonora do quê alto-falantes como os da televisão? Pesquisem sobre isso e sobre a Perda Auditiva Induzida por Ruídos (Pair), suas principais causas e o grupo de pessoas mais atingido por esse problema.
4. Atualmente, estima-se quê os aparelhos eletrônicos desvalorizam 10% ao ano após o seu lançamento. Suponha quê um fone de ouvido recém-lançado custe R$ 300,00.
a) Considerando essa depreciação, escrêeva o preêço y dêêsse fone após x anos.
y = 300 ⋅ 0,9x
b) O fone custará R$ 196,83 depois de quantos anos após o seu lançamento?
4 anos depois

Página cento e dezoito
Introdução
No Volume anterior, aprendemos a solucionar um tipo de equação cuja incógnita se apresenta no expoente, as equações exponenciais. Por exemplo, 2x = 4.
Estudamos como solucionar esse tipo de equação quando ambos os membros da igualdade podem sêr representados como potências de mesma base. Por exemplo:
2x = 4 ⇒ 2x = 22 ⇒ x = 2
Mas e quando os membros da igualdade não podem sêr representados como potências de mesma base? Como fazemos para resolver uma equação como 2x = 3?
Para solucionar uma equação como essa, utilizamos o conceito de logaritmo.
Esse conceito é amplamente utilizado no estudo de fenômenos físicos, químicos, biológicos e sociais, por exemplo, o cálculo da acidez de uma solução (conhecida como pH), o crescimento populacional, o nível de intensidade sonora (medido em decibel) etc.

Logaritmo
Considerando uma potência cuja base seja um número positivo e diferente de 1, seu expoente é um logaritmo. Por exemplo, no caso da potência 25 = 32, chamamos o expoente 5 de logaritmo de 32 na base 2. Usando a linguagem matemática, representamos:
25 = 32 ⇔ log2 32 = 5 (lê-se: logaritmo de 32 na base 2 é igual a 5)
Acompanhe, a seguir, a definição de logaritmo.
Dados dois números reais positivos a e b, com a ≠ 1, o logaritmo de b na base a é o expoente x tal quê ax = b:
loga b = x ⇔ ax = b
Na definição, b é o logaritmando, a é a base e x é o logaritmo de b na base a.
Exemplos:
a) log3 81 = 4 ⇔ 34 = 81
b) log2 = −2 ⇔ 2−2 =
c) = 2 ⇔
Página cento e dezenove
Condições de existência do logaritmo
De acôr-do com a definição de logaritmo, a existência de loga b está associada às seguintes condições:
• logaritmando positivo: b > 0;
• base positiva e diferente de 1: a > 0 e a ≠ 1.
Se uma dessas condições não for atendida, a existência do logaritmo não estará garantida no universo dos números reais. Por exemplo, vamos tentar calcular log2 (−3). Caso existisse esse logaritmo em ℝ, aplicando a definição, teríamos:
log2 (−3) = x ⇔ 2x = −3
Note quê não existe valor real de x quê satisfaça à igualdade descrita, logo não existe log2 (−3) em ℝ.
Consequências da definição
A partir da definição de logaritmo, sêndo a, b, c e m números reais, em quê a, b e c são positivos e a é diferente de 1, temos:
1ª consequência:
loga 1 = 0
Pois: loga 1 = x ⇔ ax = 1 ⇔ ax = a0 ⇔ x = 0
2ª consequência:
loga a = 1
Pois: loga a = x ⇔ ax = a ⇔ ax = a1 ⇔ x = 1
3ª consequência:
loga am = m
Pois: loga am = x ⇔ ax = am ⇔ x = m
4ª consequência:
= b
Pois, fazendo loga b = x, temos: ax = b
Substituindo x por loga b em ax = b, obtemos: = b
5ª consequência:
loga b = loga c ⇔ b = c
Pois, considerando loga b = x e loga c = y, temos: ax = b e ay = c
• Se b = c, temos:
ax = ay ⇒ x = y ⇒ loga b = loga c
• Se loga b = loga c, temos:
x = y ⇒ ax = ay ⇒ b = c
Observações:
• O logaritmo de um número na base 10 é chamado de logaritmo decimal.
Costuma-se omitir a base dos logaritmos decimais. Assim:
log10 b póde sêr escrito como log b.
Página cento e vinte
A base decimal é muito usada pelo fato de sêr a mesma base do nosso sistema de numeração. Em muitos casos, utilizar o logaritmo decimal póde simplificar os cálculos.
• O logaritmo de um número na base e (número irracional cujo valor é 2,718281...) é chamado de logaritmo natural ou logaritmo neperiano (em homenagem ao matemático Diôn Napier).
Os logaritmos naturais têm uma simbologia própria:
loge b póde sêr escrito como ln b.
A base natural é muito utilizada na modelagem de fenômenos das Ciências da Natureza e das Ciências Humanas.
ATIVIDADES RESOLVIDAS
1. Calcule:
a) log10 0,01
b)
Resolução
Em cada item, vamos aplicar a definição de logaritmo e resolver a equação exponencial ôbitída.
a) log10 0,01 = x ⇔ 10x = 0,01
10x = 0,01 ⇒ 10x = 10−2 ⇒ x = −2
Então, log10 0,01 = −2.
b) = x ⇔
⇒ = 21 ⋅ ⇒ (2−2)x = ⇒ 2−2x = ⇒ −2x = ⇒ x =
Então,
2. Calcule log10 1,4. Use 2 ≃ 100,301 e 7 ≃ 100,845.
Resolução
Usando a definição de logaritmo, temos: log10 1,4 = x ⇔ 10x = 1,4
O logaritmo de 1,4 é o expoente x ao qual devemos elevar 10 para obtêr 1,4.
Resolvendo a equação exponencial, temos:
10x = 1,4 ⇒ 10x = ⇒ 10x = ⇒ 10x ≃ ⇒ 10x ≃ 100,301 + 0,845 − 1 ⇒ 10x ≃ 100,146 ⇒ x ≃ 0,146
Portanto, log10 1,4 ≃ 0,146.
3. Determine o valor da expressão: log7 73 + log9 16 +
Resolução
Calculando o valor de cada parcela, temos:
• log7 73 = 3 (3ª consequência)
• log9 16 = log9 1 = 0 (1ª consequência)
• = 5 (4ª consequência)
Substituindo esses valores na expressão dada, obtemos:
3 + 0 + 5 = 8
Portanto, log7 73 + log9 16 + = 8.
4. Para quais valores de x existe log3 (x − 5)?
Resolução
Para quê o logaritmo exista, as duas condições de existência apresentadas na definição precisam sêr obedecidas. Analisando log3 (x − 5), temos:
• logaritmando: x − 5
• base: 3
Como 3 é um número positivo e diferente de 1, para quê o logaritmo exista em ℝ, devemos ter:
x − 5 > 0 ⇒ x > 5
Logo, para quê as duas condições de existência sêjam obedecidas, precisamos ter x > 5.
Portanto, log3 (x − 5) existe para x real tal quê x > 5.
Página cento e vinte e um
5. Para quais valores reais de x existe logx + 1 (x2 + 3x − 18)?
Resolução
Para quê o logaritmo exista, as seguintes condições devem sêr, simultaneamente, satisfeitas:
Resolvendo I e II, temos:
I x2 + 3x − 18 > 0
Os zeros da função f dada por f(x) = x2 + 3x − 18 são:
x2 + 3x − 18 = 0 ⇒ x(minutos)" = 3 e x(segundos)" = −6
Estudo do sinal de f:

Logo, a solução de I é:
x ∈ ℝ tal quê x < −6 ou x > 3
II x + 1 > 0 e x + 1 ≠ 1
Logo, a solução de II é:
x ∈ ℝ tal quê x > −1 e x ≠ 0
Fazendo a intersecção das soluções de I e II, temos:
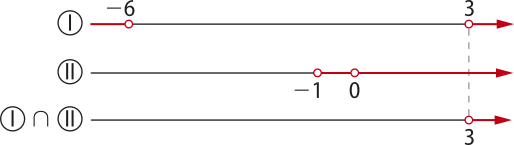
Portanto, logx + 1 (x2 + 3x − 18) existe para x ∈ ℝ tal quê x > 3.
ATIVIDADES
1. escrêeva no caderno o valor dos logaritmos:
a) log9 1
0
b) log8 8
1
c)
3
d)
7
e)
1
f)
−5
2. Aplicando a definição, calcule o valor dos logaritmos:
a)
b) log5 0,000064
−6
c)
d) log2
−4
e)
f) 1.024
−5
3. Determine o valor das expressões a seguir.
a) log5 +
−4
b) 27 + log10 0, 001 − log0,1
4. Determine o valor de m, sabendo quê:
m = +
m = 110
5. Calcule o valor de cada uma das expressões a seguir:
a) log4 4 − log5 5−7
8
b) ∶
54
c) (log0,2 1)
0
d)
6. Calcule as raízes da equação ax2 + bx + c = 0, em quê:
a = log10 0,001; b = e c = 3 ⋅ log2 8.
S = {−1, 3}
7. Um número é tal quê seu logaritmo é 4 na base p e 8 na base . Calcule esse número.
6.561
8. Determine os valores reais de x para quê exista:
a) log(1 − x)
{x ∈ ℝ | x < 1}
b) log5 (5x − 2) + log5 (x − 3)
{x ∈ ℝ | x > 3}
c) log5 (x2 + 4x − 5)
{x ∈ ℝ | x < −5 ou x > 1}
d) log(50 − 5x − x2)
{x ∈ ℝ | −10 < x < 5}
Página cento e vinte e dois
Propriedades opêratórìas dos logaritmos
Vamos estudar agora as propriedades opêratórìas dos logaritmos, quê poderão sêr utilizadas em diferentes situações envolvendo cálculos com logaritmos. Dados os números reais a, b, c e n, em quê a, b e c são positivos e a ≠ 1, temos as propriedades apresentadas a seguir.
Logaritmo de um produto
Em uma mesma base, o logaritmo de um produto de dois números positivos é igual à soma dos logaritmos de cada um dos fatores.
loga (b ⋅ c) = loga b + loga c
Demonstração
Considere os logaritmos:
loga b = x ⇔ ax = b I
loga c = y ⇔ ay = c II
loga (b ⋅ c) = z ⇔ az = b ⋅ c III
Substituindo I e II em III, temos: az = b ⋅ c ⇒ az = ax ⋅ ay ⇒ az = ax + y ⇒ z = x + y
Dessa última igualdade, obtemos: loga (b ⋅ c) = loga b + loga c
Exemplos:
a) log2 (2 ⋅ 3) = log2 2 + log2 3
b) log3 500 = log3 (5 ⋅ 100) = log3 5 + log3 100
Logaritmo de um quociente
Em uma mesma base, o logaritmo de um quociente de dois números positivos é igual à diferença entre o logaritmo do dividendo e o logaritmo do divisor.
loga = loga b − loga c
Demonstração
Considere os logaritmos:
loga b = x ⇔ ax = b I
loga c = y ⇔ ay = c II
loga = z ⇔ az = III
Substituindo I e II em III, temos: az = ⇒ az = ⇒ az = ax − y ⇒ z = x − y
Dessa última igualdade, obtemos: loga = loga b − loga c
Exemplos:
a) log6 = log6 243 − log6 5
b) log4 = log4 − log4 3
Página cento e vinte e três
Logaritmo de uma potência
Em uma mesma base, o logaritmo de uma potência de base positiva é igual ao produto do expoente pelo logaritmo da base dessa potência.
loga bn = n ⋅ loga b
Demonstração
Considere o logaritmo loga b = x. Pela definição, temos: ax = b
Elevando os dois membros ao expoente n, temos: ax = b ⇒ (ax)n = bn ⇒ anx = bn
Portanto, nx é o logaritmo de bn na base a, isto é: loga bn = nx
Substituindo x por loga b, obtemos: loga bn = n ⋅ loga b
Exemplos:
a) log3 52 = 2 ⋅ log3 5
b) log5 (12)−2 = −2 ⋅ log5 12
Mudança de base do logaritmo
Até aqui, aprendemos as propriedades opêratórìas dos logaritmos quê valem para os logaritmos de mesma base.
Vamos estudar agora uma propriedade quê permite a mudança de base do logaritmo, muito útil nas situações em quê é preciso realizar operações com logaritmos de bases diferentes.
Admitindo uma base c, tal quê c > 0 e c ≠ 1, temos:
loga b =
Demonstração
Considere o logaritmo loga b = x.
Pela definição, temos ax = b.
Agora, considere os logaritmos:
logc b = y ⇔ cy = b
logc a = z ⇔ cz = a
Assim, da igualdade ax = b e sabendo quê z ≠ 0, temos:
ax = b ⇒ (cz)x = cy ⇒ czx = cy ⇒ zx = y ⇒ x = ⇒ loga b =
Exemplos:
a) log2 6 =
b) log16 64 =
Página cento e vinte e quatro
Calculadora e logaritmos
pôdêmos usar uma calculadora científica no cálculo de logaritmos. Nela, trabalharemos com o logaritmo decimal e com o logaritmo natural.

Saiba quê...
Caso tenhamos logaritmos em outras bases, é necessário fazer a mudança de base antes de efetuar os cálculos com a calculadora.
Professor, póde havêer diferença entre o funcionamento e as funções das diferentes calculadoras. Se julgar interessante, pedir aos estudantes quê consultem o manual da calculadora quê eles estão usando.
Geralmente, as calculadoras científicas apresentam duas teclas para o cálculo de logaritmos: ![]() e
e ![]() . Com elas, podemos calcular o logaritmo decimal e o natural de um número positivo. Por exemplo:
. Com elas, podemos calcular o logaritmo decimal e o natural de um número positivo. Por exemplo:
• Para calcular log 16,4, pressionamos ![]() e obtemos 1,214843848.
e obtemos 1,214843848.
• Para calcular ln 6, pressionamos ![]() e obtemos 1,791759469.
e obtemos 1,791759469.
Também podemos determinar o logaritmando em uma operação aplicando a definição de logaritmo e utilizando a opção da calculadora científica quê permite calcular uma potência de 10. Por exemplo:
• Para determinar o valor de k em log k ≃ 0,434, aplicamos a definição de logaritmo, de modo quê log k ≃ 0,434 ⇔ k ≃ 100,434.
Pressionamos ![]() e obtemos 2,716439269.
e obtemos 2,716439269.
• Para determinar o valor de b em ln b ≃ 0,693, aplicamos a definição de logaritmo, de modo quê ln b ≃ 0,693 ⇔ b ≃ e0,693. Em seguida, pressionamos ![]() e obtemos 1,999705661.
e obtemos 1,999705661.
Página cento e vinte e cinco
ATIVIDADES RESOLVIDAS
6. Calcule os logaritmos a seguir considerando as aproximações log 2 = 0,301, log 3 = 0,477 e log 5 = 0,699.
a) log 15
b) log 18
c) log
d) log 7,2
Resolução
a) log 15 = log (3 ⋅ 5)
Usando a propriedade do logaritmo de um produto, temos:
log (3 ⋅ 5) = log 3 + log 5 = 0,477 + 0,699 = 1,176
Portanto, log 15 = 1,176.
b) log 18 = log (2 ⋅ 3 ⋅ 3) = log (2 ⋅ 32)
Usando as propriedades do logaritmo de um produto e de uma potência, temos:
log (2 ⋅ 32) = log 2 + log 32 = log 2 + 2 ⋅ log 3 = 0,301 + 2 ⋅ 0,477 = 1,255
Portanto, log 18 = 1,255.
c) log = log
Usando a propriedade do logaritmo de uma potência, temos:
⋅ log 3 = ⋅ 0,477 = 0,2385
Portanto, log _ = 0,2385.
d) log 7,2 = log
Usando a propriedade do logaritmo de um quociente, temos:
log = log 72 − = log 72 − 1
Fatorando o número 72 e aplicando as propriedades estudadas, obtemos:
log 72 = log (23 ⋅ 32) = log 23 + log 32 = 3 ⋅ log 2 + 2 ⋅ log 3 = + = 1,857
Assim, log 7,2 = log 72 − 1 = 1,857 − 1 = 0,857.
Portanto, log 7,2 = 0,857.
7. Sendo log a = 4, log c = 6 e log d = −1, calcule o valor de log.
Resolução
Utilizando a propriedade do logaritmo de um quociente, temos:
log = log (ac) − log d
Usando a propriedade do logaritmo de um produto, temos:
log(ac) − log d = log a + log c − log d
Substituindo os valores dados, obtemos:
log a + log c − log d = 4 + 6 − (−1) = 11
Portanto, log = 11.
Página cento e vinte e seis
8. Usando as aproximações log2 = 0,301, log3 = 0,477 e log7 = 0,845, determine o valor dos logaritmos a seguir.
a) log6 70
b) log5 20
Resolução
Como os dados do enunciado são logaritmos na base 10, em cada item, vamos primeiro efetuar a mudança de base para a base decimal. Em seguida, aplicamos as propriedades estudadas.
a) log6 70 = ≃ 2,371
b) log5 20 = = ≃ 1,861
9. ![]() Com o auxílio de uma calculadora científica, escrêeva 783 como uma potência de base 10. Considere cinco casas decimais.
Com o auxílio de uma calculadora científica, escrêeva 783 como uma potência de base 10. Considere cinco casas decimais.
Resolução
Aplicando a definição de logaritmo, temos: log 783 = x ⇔ 783 = 10x
Para calcular log 783 na calculadora e obtêr o valor de x, pressionamos ![]() e obtemos 2,893761762.
e obtemos 2,893761762.
Considerando apenas cinco casas decimais depois da vírgula, temos: log783 ≃ 2,89376
Logo, 783 ≃ 102,89376.
10. ![]() Com o auxílio de uma calculadora científica, calcule log3 5 com aproximação de cinco casas decimais.
Com o auxílio de uma calculadora científica, calcule log3 5 com aproximação de cinco casas decimais.
Resolução
Para calcular um logaritmo quê não seja decimal utilizando a calculadora científica, é necessário primeiro utilizar a propriedade de mudança de base, obtendo um quociente entre dois logaritmos decimais. Assim:
log3 5 =
Para calcular e obtêr o valor de log3 5, pressionamos ![]() e obtemos 1,464973520.
e obtemos 1,464973520.
Portanto, log3 5 ≃ 1,46497.
11. ![]() Com o auxílio de uma calculadora científica, calcule um valor aproximado para x em ln x ≃ −2,36653.
Com o auxílio de uma calculadora científica, calcule um valor aproximado para x em ln x ≃ −2,36653.
Resolução
Aplicando a definição de logaritmo, temos: ln x ≃ −2,36653 ⇔ x ≃ e−2,36653
Para calcular e−2,36653 na calculadora e determinar o valor de x, pressionamos ![]() e obtemos 0,093805668.
e obtemos 0,093805668.
Logo, x ≃ 0,09381.
Página cento e vinte e sete
ATIVIDADES
9. Usando a aproximação log 11 = 1,041, calcule:
a) log 110
2,041
b) log 121
2,082
c) log
−1,041
d) log
1,5615
e) log 1,21
0,082
f) log 0,121
−0,918
10. Calcule o valor das expressões aplicando as propriedades dos logaritmos.
a) log 5 + log 200
3
b) log 100 + log 50 + log 10 + log 2
5
c) log2 24 − log2 3
3
d) log5 8 + log5 12,5 − log5 4
2
11. Sendo logx a = 6, logx b = 4 e logx c = 2, calcule:
a) logc
3
b) logc (a3 ⋅ b2)
13
12. Se log2 3 = k, qual é o valor do produto log2 3 ⋅ log3 2?
1
13. Calcule o produto log3 2 ⋅ log2 5 ⋅ log5 3.
1
14. Simplifique a expressão log3 5 ⋅ log4 27 ⋅ log25 .
15. resôuva o sistema a seguir:
S = {(10, 10)}
16. (PUC-SP) Se log 2 = x e log 3 = y, determine log 375.
y + 3 − 3x
17. Um cérto componente eletrônico processa n bits em logn milisegundos. Adotando log 5 = 0,699, em quantos milisegundos serão processados 64 bits?
1,806 milisegundo
As atividades a seguir devem sêr resolvidas com o auxílio de uma calculadora científica.
18. ![]() Calcule os valores a seguir com aproximação, quando necessário, de cinco casas decimais.
Calcule os valores a seguir com aproximação, quando necessário, de cinco casas decimais.
a) log 0,7
−0,15490
b) log 0,12
−0,92082
c) log 834
2,92117
d) log 0,00001
−5
e) ln 25
3,21888
f) ln 0,92
−0,08338
19. ![]() Em cada caso, determine b, com aproximação de duas casas decimais, quando necessário.
Em cada caso, determine b, com aproximação de duas casas decimais, quando necessário.
a) log b = 1,88081
76
b) log b = 1,75587
57
c) ln b = 6,20051
493
d) ln b = 1,05082
2,86
20. ![]() Determine o valor de x em cada caso, com aproximação de quatro casas decimais.
Determine o valor de x em cada caso, com aproximação de quatro casas decimais.
a) log x = −0,5
0,3162
b) log x = −0,15
0,7079
c) 10x = 0,5
−0,3010
d) 10x = 2
0,3010
e) ex = 10
2,3026
f) ex = 0,5
−0,6931
g) ex = 0,15
−1,8971
h) ex = 0,005
−5,2983
21. ![]() Copie no caderno o qüadro a seguir e complete-o com os valores faltantes. Caso seja necessário, use aproximação com seis casas decimais.
Copie no caderno o qüadro a seguir e complete-o com os valores faltantes. Caso seja necessário, use aproximação com seis casas decimais.
Número (N) |
Potência de 10 |
logN |
|---|---|---|
75 |
101,875061 |
1,875061 |
643 |
102,808211 |
2,808211 |
1.320 |
103,120574 |
3,120574 |
1.000.000 |
106 |
6 |
0,00001 |
10−5 |
−5 |
0,7 |
10−0,154902 |
−0,154902 |
0,834 |
10−0,078834 |
−0,078834 |
22. ![]() Determine b em cada caso.
Determine b em cada caso.
a) ln b ≃ 1,098612289
b ≃ 3
b) ln b ≃ 1,945910149
b ≃ 7
c) ln b ≃ −0,69314718
b ≃ 0,5
d) ln b = −1
b ≃ 0,367879
e) ln b = 0
b = 1
23. ![]() O valor aproximado do logaritmo natural de um número é 3,48124. Descubra qual é esse número, considerando aproximação de uma casa decimal.
O valor aproximado do logaritmo natural de um número é 3,48124. Descubra qual é esse número, considerando aproximação de uma casa decimal.
32,5
24. ![]() Calcule o valor de log4 e com aproximação de quatro casas decimais.
Calcule o valor de log4 e com aproximação de quatro casas decimais.
0,7213
Página cento e vinte e oito
Função logarítmica
Existem diversas situações em quê são usados logaritmos; uma delas, por exemplo, é a escala de pH (potencial hidrogeniônico). O pH indica a acidez de um meio aquoso e é calculado em função da concentração de íons de hidrogênio H+ quê esse meio apresenta. Na escala de pH, uma solução é considerada ácida quando 0 ≤ pH < 7, neutra quando pH = 7 e básica quando 7 < pH ≤ 14.
O cálculo do pH de um meio aquoso é feito usando-se logaritmo:
pH = log
[H+] ← concentração de íons de hidrogênio (mol/L)
A igualdade anteriormente descrita é a representação de uma função logarítmica.
Por exemplo, podemos determinar o pH de uma xícara de café quê apresenta 10−5 mol/L de íons de hidrogênio. Sabendo díssu:
pH = log = log = log1 − log 10−5 = 0 − (−5) ⇒ pH = 5
Portanto, o café tem pH igual a 5, o quê indica quê ele é considerado um meio ácido.

Agora, acompanhe a definição matemática de função logarítmica.
A função f: → ℝ dada por f(x) = loga x, com a > 0 e a ≠ 1, é denominada função logarítmica.
Exemplos:
a) f(x) = log x
b) g(x) = log5 x
c) h(x) =
Página cento e vinte e nove
Gráfico da função logarítmica
Vamos esboçar o gráfico de algumas funções logarítmicas. Observe os exemplos a seguir.
• Esboço do gráfico de f(x) = log2 x.
x |
f(x) = log2 x |
|---|---|
−3 |
|
−2 |
|
−1 |
|
1 |
0 |
2 |
1 |
4 |
2 |
8 |
3 |
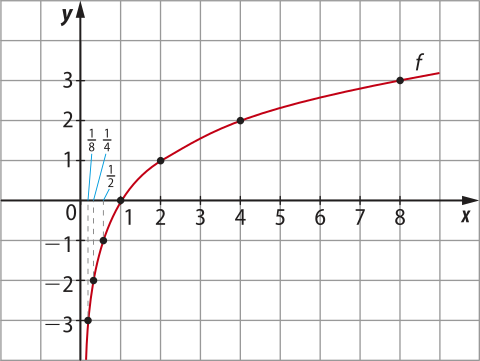
Observe quê os valores de log2 x aumentam conforme os valores de x aumentam.
• Esboço do gráfico de g(x) = .
x |
g(x) = x |
|---|---|
3 |
|
2 |
|
1 |
|
1 |
0 |
2 |
−1 |
4 |
−2 |
8 |
−3 |
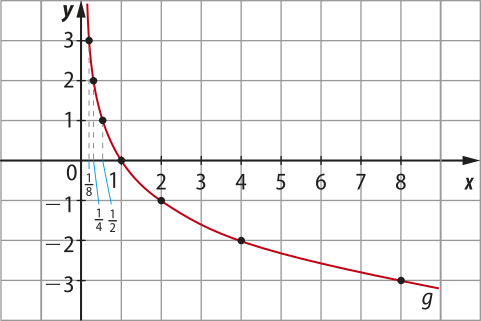
Observe quê os valores de diminuem conforme os valores de x aumentam.
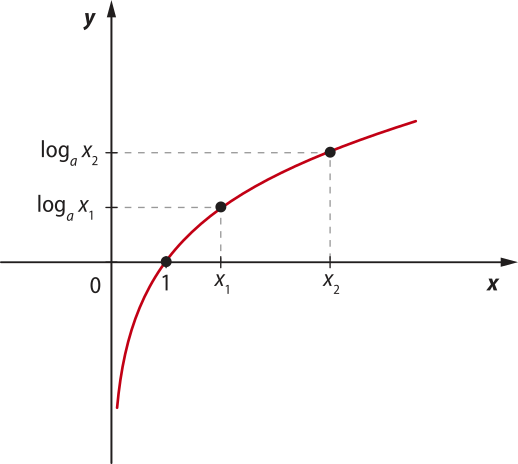
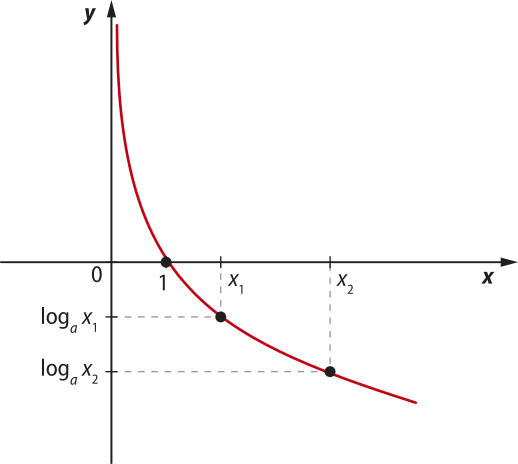
De modo geral, dada a função f definida por f(x) = loga x (com a > 0 e a ≠ 1), temos:
• O domínio da função é D(f) = .
• O contradomínio da função é CD(f) = ℝ.
• O conjunto imagem da função é Im(f) = ℝ.
A função logarítmica dada por f(x) = loga x é bijetora, pois é sobrejetora e injetora.
Saiba quê...
Note quê as curvas dos gráficos se aproximam do eixo y, mas não o tocam. Em contrapartida, ambas intersectam o eixo x no ponto (1, 0).
Página cento e trinta
Crescimento e decrescimento da função logarítmica
Pense e responda
Vamos analisar a influência da base a na função logarítmica dada por f(x) = loga x traçando seu gráfico com o auxílio do GeoGebra.
Para isso, digite “f(x)=log(a,x)” no campo de entrada. Ao digitar a função dessa maneira, o software interpréta o primeiro número entre parênteses como base do logaritmo e o segundo como logaritmando.
Aperte a tecla Enter. O software criará um contrôle deslizante para a base a e exibirá, na janela de visualização, o gráfico da função dada por f(x) = loga x, de acôr-do com o valor indicado para a no contrôle deslizante.
Movimente o cursor do contrôle deslizante, obissérve as mudanças no gráfico e responda:
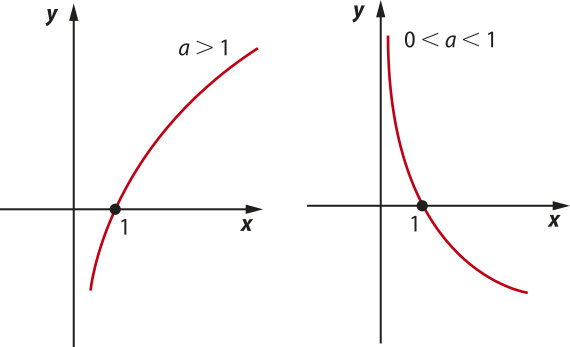
• Nos casos em quê a > 1, as funções parecem sêr crescentes ou decrescentes? E nos casos em quê 0 < a < 1?
• Espera-se quê os estudantes percêbam quê, nos casos em quê a > 1, as funções são crescentes e, nos casos em quê 0 < a < 1, são decrescentes.
• O quê acontece na janela de visualização quando o contrôle deslizante está em um valor a < 0 ou a = 1?
• Nesses casos, nenhum gráfico é exibido, pois a função não está definida para esses valores.
Na atividade anterior, você deve ter observado quê a base a influencía o comportamento da função logarítmica dada por f(x) = loga x.
De modo geral, considerando a função exponencial dada por f(x) = loga x, temos:
a > 1 |
0 < a < 1 |
|---|---|
|
|
• Quando a > 1, a função é crescente. • ∀x1, x2 ∈ D(f), x1 < x2 ⇒ f(x1) < f(x2) |
• Quando 0 < a < 1, a função é decrescente. • ∀x1, x2 ∈ D(f), x1 < x2 ⇒ f(x1) > f(x2) |
Relação entre função exponencial e função logarítmica
Aprendemos, no início dêste Capítulo, quê a potenciação e os logaritmos estão relacionados. Do mesmo modo, estudaremos a seguir quê a função logarítmica e a função exponencial também estão relacionadas.
Anteriormente, esboçamos o gráfico da função logarítmica dada por f(x) = log2 x. Vamos traçar, no mesmo plano cartesiano, o gráfico dessa função e o gráfico da função exponencial dada por h(x) = 2x. Observe.
Página cento e trinta e um
x |
y = f(x) = log2 x |
|---|---|
−3 |
|
−2 |
|
−1 |
|
1 |
0 |
2 |
1 |
4 |
2 |
8 |
3 |
x |
y = h(x) = 2x |
|---|---|
−3 |
|
−2 |
|
−1 |
|
0 |
1 |
1 |
2 |
2 |
4 |
3 |
8 |
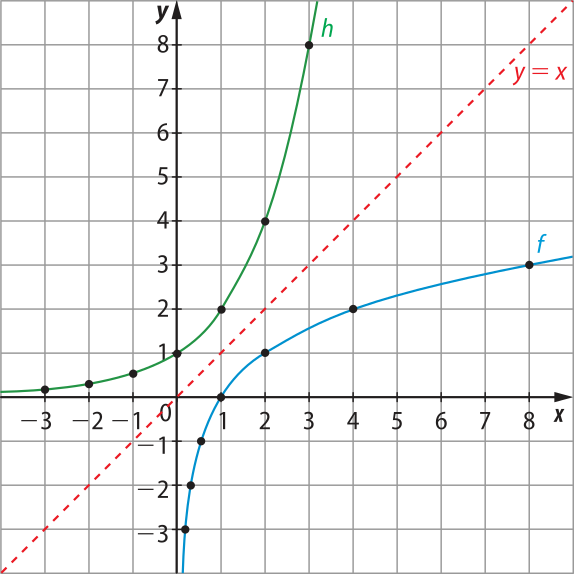
D(f) =
CD(f) = ℝ
Im(f) = ℝ
D(h) = ℝ
CD(h) =
Im(h) =
Observe quê, para todos os valores de x e y apresentados anteriormente, para f(x) = y, temos h(y) = x. Note, ainda, quê os gráficos das funções f e h são simétricos em relação à bissetriz dos quadrantes ímpares (y = x).
Nesse caso, as funções f(x) = log2 xe h(x) = 2x são inversas uma da outra.
De modo geral, a função logarítmica f: → ℝ dada por f(x) = loga x e a função exponencial h: ℝ → dada por h(x) = ax, ambas com a > 0 e a ≠ 1, são inversas uma da outra.
Considerando f(x) = y = loga x, para encontrar a invérsa de f, trocamos a variável x por y e a variável y por x e, em seguida, isolamos y:
x = loga y ⇒ ax = y
Assim, a lei da função invérsa de f é f−1 (x) = ax, ou seja, a função h é invérsa da função f.
Do mesmo modo, considerando h(x) = y = ax, para encontrar a invérsa de h, trocamos a variável x por y e a variável y por x e, em seguida, isolamos y:
x = ay ⇒ loga x = y
Assim, a lei da função invérsa de h é h−1 (x) = loga x, ou seja, a função f é invérsa da função h.
Portanto, as funções dadas por f(x) = loga x e h(x) = ax são inversas uma da outra.
Página cento e trinta e dois
ATIVIDADES RESOLVIDAS
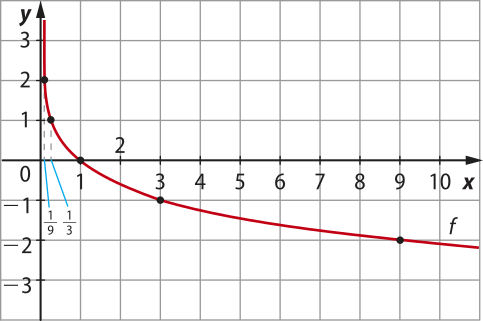
12. Esboce o gráfico da função f(x) = x.
Resolução
Sendo a base do logaritmo igual a , é conveniente escolher potências de base para x. Assim:
• x = ⇒ f() = = −2
• x = ⇒ f() = = −1
• x = ⇒ f() = = 0
• x = ⇒ f() = = 1
• x = ⇒ f() = = 2
Assim, temos:
x |
9 |
3 |
1 |
||
|---|---|---|---|---|---|
Y |
−2 |
−1 |
0 |
1 |
2 |
Marcando os pontos no plano cartesiano, esboçamos o gráfico:
13. Dada a função f(x) = log2 (4x − 1), faça o quê se pede.
a) Classifique a função em crescente ou decrescente.
b) Determine o domínio de f.
c) Determine f−1 (x).
Resolução
a) Como a base do logaritmo de f(x) é maior do quê 1, pois a = 2, a função é crescente.
b) Pela condição de existência dos logaritmos, temos: loga b = x ⇔ b = ax, b > 0, a > 0 e a ≠ 1
Precisamos analisar a base e o logaritmando da função:
• Logaritmando (b > 0)∶ 4x − 1 > 0
4x − 1 > 0 ⇒ 4x > 1 ⇒ x >
• Base (a > 0 e a ≠ 1)∶ a = 2
Logo, o domínio de f(x) = log2 (4x − 1) é D(f) = {x ∈ ℝ | x > }.
c) Para determinar a função invérsa, trocamos x por y e y por x na lei da função:
f(x) = log2 (4x − 1)
x = log2 (4y − 1) ⇒ 2x = 4y − 1 ⇒ 4y = 2x + 1 ⇒ y =
Portanto, a função invérsa é f−1 (x) =
14. (Enem/MEC) A exposição a alguns níveis sonoros póde causar lesões auditivas. Por isso, em uma indústria, são adotadas medidas preventivas de acôr-do com a máquina quê o funcionário opera e o nível N de intensidade do som, medido em decibel (dB), a quê o operário é exposto, sêndo N = log10 I10 − log10 I010, I a intensidade do som e I0 = 10−12 W/m2.
Disponível em: https://livro.pw/lxhir. Acesso em: 8 jul. 2015 (adaptado).
Quando o som é considerado baixo, ou seja, N = 48 dB ou menos, deve sêr utilizada a medida preventiva I. No caso de o som sêr moderado, quando N está no intervalo (48 dB, 55 dB), deve sêr utilizada a medida preventiva II. Quando o som é moderado alto, quê equivale a N no intervalo (55 dB, 80 dB), a medida preventiva a sêr usada é a III. Se N estiver no intervalo (80 dB, 115 dB), quando o som é considerado alto, deve sêr utilizada a medida preventiva IV. E se o som é considerado muito alto, com N maior quê 115 dB, deve-se utilizar a medida preventiva V. Uma nova máquina, com I = 8 × 10−8 W/m2, foi adquirida e será classificada de acôr-do com o nível de ruído quê produz.
Página cento e trinta e três
Considere 0,3 como aproximação para log10 2. O funcionário quê operará a nova máquina deverá adotar a medida preventiva
a) I.
b) II.
c) III.
d) IV.
e) V.
Resolução
Para determinar a medida preventiva quê será usada para a nova máquina, precisamos determinar o valor N para I = 8 ⋅ 10−8 W/m2. Para isso, substituímos o valor de I em N = log10 I10 − log10 I010; como I0 = 10−12 W/m2, temos:
N = log10 I10 − log10 I010 ⇒ N = log10 (8 ⋅ 10−8)10 − log10 (10−12)10
Utilizando as propriedades opêratórìas dos logaritmos, temos:
N = log10 ⇒ N = log10 ⇒ N = 10 ⋅ (log10 8 ⋅ 10−8 + 12) ⇒ N = 10 ⋅ (log10 23 + log10 104) ⇒ N = 10 ⋅ (3 ⋅ log10 2 + 4 ⋅ log10 10) ⇒ N ≃ 10 ⋅ (3 ⋅ 0, 3 + 4 ⋅ 1) ⇒ N ≃ 49
Assim, o nível de intensidade do som da máquina é de aproximadamente 49 dB, e a medida preventiva para a nova máquina deverá sêr a II. Portanto, a alternativa b é a correta.
FÓRUM
Poluição sonora
Diferentemente dos outros tipos de poluição, a poluição sonora se caracteriza por não produzir resíduos ou acúmulos poluentes no meio ambiente. No entanto, ela afeta diretamente o organismo dos sêres vivos quê vivem próximo às fontes emissoras de som. Os impactos da poluição sonora nos sêres humanos incluem insônia, perda de atenção, dor de cabeça e perda de audição temporária ou permanente.

O crescimento das cidades deixa os sêres vivos cada dia mais vulneráveis a esses ruídos prejudiciais, de modo quê a poluição sonora passou a sêr uma constante na vida dêêsses indivíduos, sêndo vista como um dos problemas a serem combatidos nos grandes centros urbanos.
![]() Agora, reúna-se a um colega, e façam uma pesquisa sobre o tema poluição sonora para debater atitudes pessoais e governamentais quê ajudariam a mitigar esse problema.
Agora, reúna-se a um colega, e façam uma pesquisa sobre o tema poluição sonora para debater atitudes pessoais e governamentais quê ajudariam a mitigar esse problema.
Ver as Orientações para o professor.
Para ouvir
• CIDADE em movimento #4: poluição sonora. Locução de: Alessandra Ueno; Guilherme Castro Sousa. São Paulo: Jornal da úspi, 12 set. 2024. Podcast. Disponível em: https://livro.pw/fykee. Acesso em: 23 set. 2024.
O podcast trata da poluição sonora e dos impactos dêêsse tipo de poluição.
Página cento e trinta e quatro
ATIVIDADES
25. Construa, em um mesmo plano cartesiano, os gráficos de:
Ver as Orientações para o professor.
a) f(x) = 3x e g(x) = log3 x
b) f(x) = e g(x) =
26. Faça o esboço do gráfico da função dada por f(x) = log e determine o domínio e a imagem dessa função.
Ver as Orientações para o professor.
27. (Ufop-MG) Seja f a função real de variável real definida por f(x) = + log6 − x (x + 5). Encontre os valores de x para os quais f faz sentido.
{x ∈ ℝ | −5 < x ≤ −3 ou 3 ≤ x < 6 e x ≠ 5}
28. Copie o qüadro a seguir, referente às funções f(x) = x e g(x) = 2 + x, e, depois, complete-o.
Ver as Orientações para o professor.
x |
1 |
4 |
16 |
||
|---|---|---|---|---|---|
f(x) = x |
2 |
1 |
0 |
−1 |
−2 |
g(x) = 2 + x |
4 |
3 |
2 |
1 |
0 |
Agora, faça o quê se pede nos itens a seguir.
a) Utilizando o GeoGebra, construa, em um mesmo plano cartesiano, os gráficos de f e de g.
b) Ao analisar os gráficos construídos, podemos dizêr quê f e g são funções crescentes ou decrescentes?
c) Quais são o domínio e a imagem dessas funções?
d) O quê você observa ao comparar os valores no qüadro quê você completou e os dois gráficos construídos?
e) dêz-creva como seria o gráfico da função dada por p(x) = − 2, em relação ao gráfico de f, sem construí-lo.
f) A partir do gráfico de f, dêz-creva como obtêr o gráfico da função dada por q(x) = (x + 2). Para responder, imagine quê você esteja escrevendo um bilhete a um colega com essa instrução.
29. (UEPA) Por volta dos anos 80, durante a implantação do projeto Proálcool, uma montadora estimou quê sua produção de carros a áucôl teria um crescimento anual de acôr-do com a expressão: P(t) = 105 ⋅ log3 (t + 1), onde P é a quantidade produzida e t o número de anos. Dessa forma, daqui a 8 anos a produção estimada será de:
a) 200.000 carros.
b) 220.000 carros.
c) 232.000 carros.
d) 250.000 carros.
e) 300.000 carros.
alternativa a
30. (UFAM) Na figura a seguir a curva representa o gráfico da função f(x) = log3 x. A área do triângulo ABC é igual a:
alternativa b
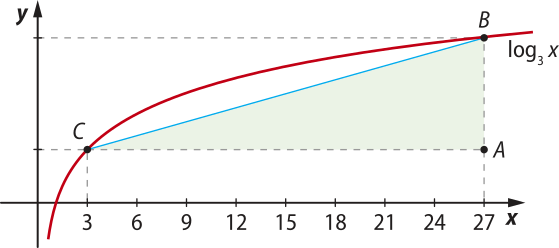
a) 25 unidades de área.
b) 24 unidades de área.
c) 23 unidades de área.
d) 21 unidades de área.
e) 20 unidades de área.
31. Ao analisar uma amostra aquosa, um químico verificou quê a concentração de íons de hidrogênio na solução era de 6,4 ⋅ 10−7 mol/L.
a) Sabendo quê o pH de uma solução é dado pela expressão pH = −log[H+], em quê [H+] indica a concentração de íons de hidrogênio em mol/L, e considerando log2 ≃ 0,30, qual é o valor do pH dessa solução?
pH ≃ 6,2
b) Sabendo quê uma solução é considerada ácida quando 0 ≤ pH < 7, neutra quando pH = 7 e básica quando 7 < pH ≤ 14, a solução analisada pelo químico é neutra, básica ou ácida?
ácida
Página cento e trinta e cinco
Equações logarítmicas
As equações quê apresentam a incógnita no logaritmando ou na base de um logaritmo de base real, positiva e diferente de 1, são denominadas equações logarítmicas.
Exemplos:
a) log3 (x − 1) = 2
b) logx + 1 (19 − x) = 2
c) 1 − log2 x = log2 3 + 4 ⋅ log2 x
d) log2 (x2 + x + 2) = 5
Para resolver essas equações, aplicamos a definição de logaritmo e a 5ª consequência da definição:
loga b = loga c ⇔ b = c
Além díssu, devemos considerar a condição de existência de todos os logaritmos envolvidos, ou seja, a > 0, a ≠ 1, b > 0 e c > 0.
Inequações logarítmicas
As desigualdades quê apresentam a incógnita no logaritmando ou na base de um logaritmo de base real, positiva e diferente de 1, são denominadas inequações logarítmicas.
Exemplos:
a) log2 x > 4
b) log (x − 1) + log (3x + 2) ≤ log x
c) log5 x +
d) logx + 1 (x2 + 4x − 5) ≥ 2
Com base no gráfico da função f dada por f(x) = loga x, aplicamos as propriedades a seguir para resolver inequações logarítmicas. Além díssu, devemos considerar a condição de existência de todos os logaritmos envolvidos.
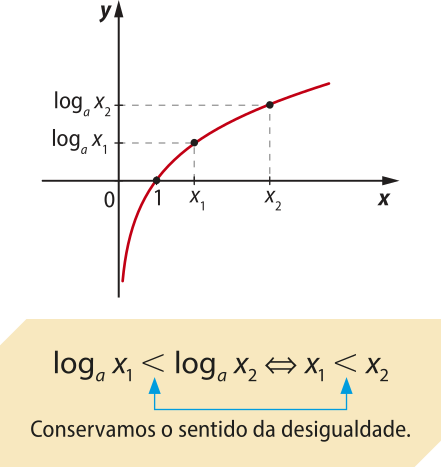
1º caso: a > 1 (função crescente)
Quando a base do logaritmo é maior do quê 1, a relação de desigualdade entre os logaritmos se mantém entre os logaritmandos.
2º caso: 0 < a < 1 (função decrescente)
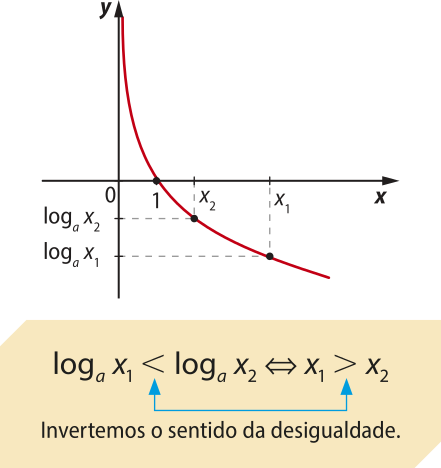
Quando a base do logaritmo está entre 0 e 1, a relação de desigualdade entre os logaritmos se inverte entre os logaritmandos.
Página cento e trinta e seis
ATIVIDADES RESOLVIDAS
15. resôuva a equação log3 (2x − 7) = 4.
Resolução
Inicialmente, verificamos a condição de existência do logaritmo:
2x − 7 > 0 ⇒ 2x > 7 ⇒ x >
Para resolver a equação, vamos expressar o 2º membro como um logaritmo de base 3 (a mesma base do logaritmo no 1º membro da equação) do seguinte modo:
4 = log3 34 ⇒ 4 = log3 81
Assim: log3 (2x − 7) = log3 81
Como loga b = loga c ⇔ b = c, obtemos:
2x − 7 = 81 ⇒ 2x = 88 ⇒ x = 44
Como x = 44 satisfaz à condição de existência, o conjunto solução da equação é S = {44}.
16. Estudos de demografia indicam quê a população de um cérto país no ano zero é P0 e quê, decorridos t anos, a população será aproximadamente P(t) = P0 ⋅ e0,03t. Quantos anos devem decorrer para quê a população dêêsse país duplique? Considere ln 2 = 0,69.
Resolução
Para quê a população duplique, devemos ter P(t) igual ao dôbro da população inicial P0. Logo:
P(t) = 2P0 ⇒ 2P0 = P0 ⋅ e0,03t ⇒ 2 = e0,03t ⇒ loge 2 = 0,03t ⇒ ln 2 = 0,03t ⇒ 0,69 = 0,03t ⇒ t =
⇒ t = 23
Portanto, devem decorrer 23 anos para quê a população duplique.
17. Determine o valor real de x na equação x + ⋅ log2 x = 0.
Resolução
A condição de existência é x > 0.
Mudando os termos para a base 2, tem-se:
⋅ log2 x = 0 ⇒ ⋅ log2 x = 0 ⇒ 6 ⋅ log2 x + log2 x = 0 ⇒ 7 ⋅ log2 x = 0 ⇒ log2 x = 0 ⇒ x = 1
18. resôuva a inequação (x − 3) ≥ 4.
Resolução
A condição de existência é:
x − 3 > 0 ⇒ x > 3 I
Como a base é um número entre 0 e 1, a função logarítmica dada por f(x) = x é decrescente, e o sentido da desigualdade se inverte ao compararmos os logaritmandos:
x − 3 ≤ 4 ⇒ x ≤ 3 + 4 ⇒ x ≤ 7 II
A solução da inequação deve satisfazer à condição de existência. Por isso, fazemos I ∩ II:
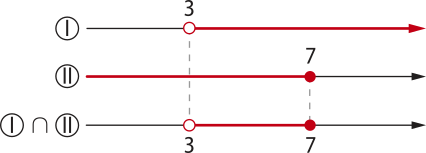
Portanto, S = {x ∈ ℝ | 3 < x ≤ 7}.
ATIVIDADES
32. (Fuvest-SP) Considere as funções f e g definidas por
Ver as Orientações para o professor.
f(x) = 2log2 (x − 1), se x ∈ ℝ, x > 1,
g(x) = log2 (1 − ), se x ∈ ℝ, x < 4.
a) Calcule f(), f(2), f(3), g(−4), g(0) e g(2).
b) Encontre x, com 1 < x < 4, tal quê f(x) = g(x).
c) Levando em conta os resultados dos itens a) e b), esboce os gráficos de f e de g.
33. (Unicamp-SP) Considere a função f(x) = 101+x +101−x, definida para todo número real x.
Ver as Orientações para o professor.
a) Mostre quê f(log10 (2 + )) é um número inteiro.
b) Sabendo quê log10 2 ≃ 0,3, encontre os valores de x para os quais f(x) = 52.
34. Calcule, com aproximação de duas casas decimais, o valor de x na equação 7x = 4,2. Considere log 6 = 0,7781 e log 7 = 0,8451.
0,74
35. Determine o conjunto solução das equações:
a) (log2 x)2 − 9 log8 x = 4
S = {, 16}
b) (log2 x)2 + 4 ⋅ log2 x − 32 = 0
S = { 16}
36. Calcule o valor de x quê satisfaz a equação 36x = 24. Adote log 2 = 0,30 e log 3 = 0,48.
Página cento e trinta e sete
37. A velocidade mássima, em bits por segundo, com a qual os sinais pódem passar por canais de comunicação pode sêr ôbitída por meio da fórmula vmáx = 3.400 ⋅ log2 (x + 1), em quê 3.400 hertz é a freqüência limite da voz humana e x está relacionado à potência do sinal. Calcule o valor de x correspondente a uma velocidade mássima de 27.200 bits por segundo.
255
38. O número de bactérias N em uma cultura, depois de um tempo t, em minuto, é dada pela função N(t) = N0 ⋅ e0,05t, em quê N0 é o número inicial de bactérias da cultura. Em quanto tempo, aproximadamente, a população de bactérias passará a sêr o triplo da inicial? Use ln 3 ≃ 1,099.
aproximadamente 22 min
39. Quando compramos um bem de consumo durável, depois de cérto tempo, póde ocorrer uma depreciação do valor inicial dêêsse produto. A fórmula utilizada para calcular a desvalorização de determinados produtos é V = V0 ⋅ (1 − i)t, em quê:
V: valor atualizado em função do tempo t.
V0: valor do produto no momento da compra
i: taxa de depreciação
t: tempo após a compra
Ver as Orientações para o professor.
• ![]()
![]() Elabore um problema quê envolva a depreciação de um produto em quê seja necessário calcular o tempo após a compra dêêsse bem.
Elabore um problema quê envolva a depreciação de um produto em quê seja necessário calcular o tempo após a compra dêêsse bem.
Troque a atividade criada por você com um colega e responda ao problema elaborado por ele. Em seguida, verifiquem as resoluções e as estratégias utilizadas por cada um.
40. Para medir o potencial destrutivo de um terremoto, utiliza-se a escala rícher. A energia calculada em um terremoto póde sêr ôbitída pela fórmula a seguir:
Ver as Orientações para o professor.
I = ⋅ log ()
Sabendo quê I varia de 0 a 9, quê E é o valor da energia liberada em kW/h e quê E0 = 7 ⋅ 10−3 kW/h, faça o quê se pede.
• ![]()
![]() Elabore um problema quê envolva a fórmula apresentada. Para tanto, pesquise acontecimentos reais e baseie-se nessa pesquisa.
Elabore um problema quê envolva a fórmula apresentada. Para tanto, pesquise acontecimentos reais e baseie-se nessa pesquisa.
Troque a atividade criada por você com um colega e responda ao problema elaborado por ele. Em seguida, verifiquem as resoluções e as estratégias utilizadas por cada um.
41. (Enem/MEC) Em setembro de 1987, Goiânea foi palco do maior acidente radioativo ocorrido no Brasil, quando uma amostra de césio-137, removida de um aparelho de radioterapia abandonado, foi manipulada inadvertidamente por parte da população. A meia-vida de um material radioativo é o tempo necessário para quê a massa dêêsse material se reduza à mêtáde. A meia-vida do césio-137 é 30 anos e a quantidade restante de massa de um material radioativo, após t anos, é calculada pela expressão M(t) = A ⋅ (2, 7)kt, onde A é a massa inicial e k é uma constante negativa. Considere 0,3 como aproximação para log10 2. Qual o tempo necessário, em anos, para quê uma quantidade de massa do césio-137 se reduza a 10% da quantidade inicial?
a) 27
b) 36
c) 50
d) 54
e) 100
alternativa e
42. Determine o conjunto solução das inequações:
a) log10 (a2 − 2a + 1) < 2
S = {a ∈ ℝ | −9 < a < 11 e a ≠ 1}
b) (x2 + 4x − 5) ≥ −4
S = {x ∈ ℝ | −7 ≤ x < −5 ou 1 < x ≤ 3}
43. ![]() Uma pessoa recebeu a injeção de cérto medicamento. Uma vez na corrente sanguínea, esse medicamento é eliminado lentamente pela ação dos rins. Admita quê, partindo de uma quantidade inicial de Q0 miligramas, após t horas, a quantidade de medicamento na corrente sanguínea fique reduzida a Q(t) = Q0 ⋅ (0, 64)t miligramas. Determine o intervalo de tempo para quê a quantidade de medicamento Q(t) presente na corrente sanguínea da pessoa satisfaça a desigualdade < Q(t) < . Use uma calculadora científica.
Uma pessoa recebeu a injeção de cérto medicamento. Uma vez na corrente sanguínea, esse medicamento é eliminado lentamente pela ação dos rins. Admita quê, partindo de uma quantidade inicial de Q0 miligramas, após t horas, a quantidade de medicamento na corrente sanguínea fique reduzida a Q(t) = Q0 ⋅ (0, 64)t miligramas. Determine o intervalo de tempo para quê a quantidade de medicamento Q(t) presente na corrente sanguínea da pessoa satisfaça a desigualdade < Q(t) < . Use uma calculadora científica.
1,55 < t < 3,1
Página cento e trinta e oito
EXPLORANDO A TECNOLOGIA
Resolução de inequações logarítmicas com o GeoGebra
Com o GeoGebra, é possível resolver equações e inequações graficamente; porém, nem sempre esse método é exato, pois póde não fornecer precisão adequada quando a solução é composta de números racionais com infinitas casas decimais (como as dízimas periódicas) ou de números irracionais. Nesses casos, o método gráfico é recomendado como aproximação.
As inequações logarítmicas podem sêr entendidas como uma comparação entre duas funções. Essa ideia póde sêr estendida às inequações de maneira geral. Portanto, para resolver inequações logarítmicas graficamente, comparamos os gráficos das funções associadas aos membros da inequação.
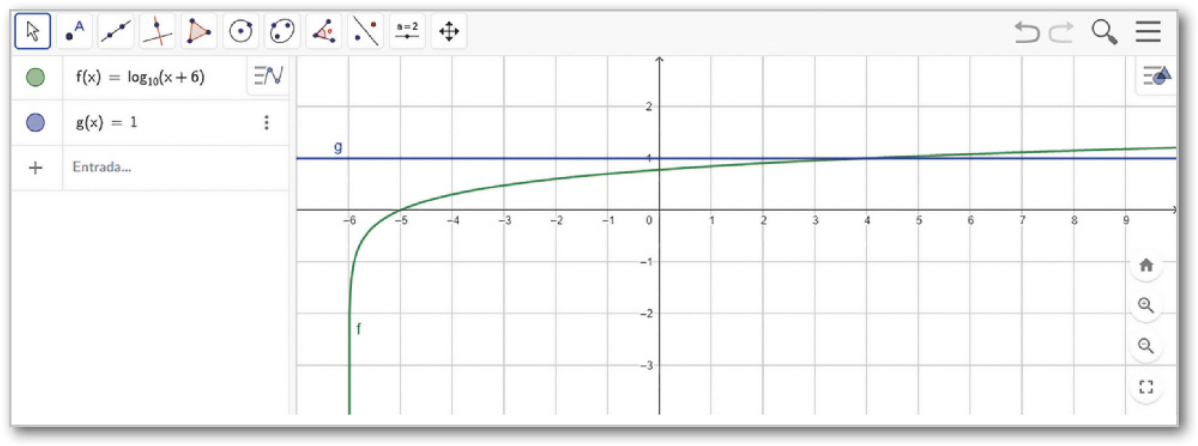
Por exemplo, para resolver a inequação logarítmica log(x + 6) > 1, siga a sequência de passos a seguir.
I. Vamos escrever o primeiro membro da inequação como a função f(x) = log (x + 6) e o segundo como a função g(x) = 1.
II. Para escrever o logaritmo decimal de um número no GeoGebra, utilizamos a função lg(x) ou log(x) ou, ainda, log(10,x). Portanto, no campo de entrada, digite "f(x)=lg(x+6)" ou "f(x)=log(x+6)" ou "log(10,x+6)" para construir o gráfico da função f(x) = log (x + 6), em seguida, pressione a tecla Enter. Para construir o gráfico da função g(x) = 1, digite "g(x)=1" e pressione novamente Enter.
Assim, a janela de visualização do GeoGebra fornecerá a seguinte construção:
Página cento e trinta e nove
III. Para determinar as coordenadas do ponto de intersecção, devemos utilizar a ferramenta Intersecção de Dois Objetos, ![]() e selecionar os dois gráficos. Nesse caso, o ponto de intersecção é A(4, 1), ele aparecerá na janela de visualização, e suas coordenadas serão mostradas na janela de Álgebra.
e selecionar os dois gráficos. Nesse caso, o ponto de intersecção é A(4, 1), ele aparecerá na janela de visualização, e suas coordenadas serão mostradas na janela de Álgebra.
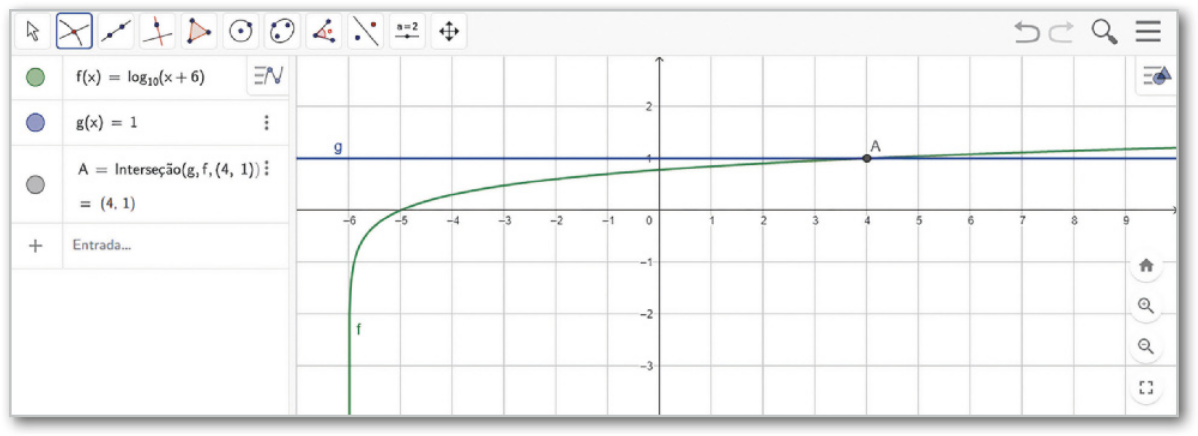
IV. Observando os gráficos e o ponto A, notamos quê, quando o valor de x for maior do quê 4 (abscissa do ponto de intersecção), teremos f(x) > g(x). Por outro lado, quando o valor de x for menor do quê 4, teremos g(x) > f(x) ou ainda f(x) < g(x).
Como a inequação inicial é log(x + 6) > 1, devemos encontrar os valores de x para os quais f(x) > g(x), ou seja, para isso ocorrer, devemos ter x > 4.
Logo, a solução da inequação será S = {x ∈ ℝ | x > 4}.
Esse método, quê usa a comparação de gráficos, póde sêr adotado para resolver outras inequações logarítmicas, inclusive quando ambos os membros da inequação têm logaritmos ou quando a base dos logaritmos é diferente de 10.
Saiba quê...
Note quê x não póde sêr 4, pois, nesse caso, teríamos f(x) = g(x), o quê não contempla a situação inicial.
Agora, faça o quê se pede nas atividades a seguir.
1. Utilizando o GeoGebra, determine o conjunto solução da inequação log (2x − 5) ≤ 1.
Ver as Orientações para o professor.
2. Crie um contrôle deslizante e determine o valor de m para quê o conjunto solução da inequação log (x + 4) < m seja S = {x ∈ ℝ | x < −3}.
3. Utilizando o mesmo procedimento da atividade anterior, determine o valor de m para quê a solução da inequação log2 (x + 4) > m tenha apenas valores positivos.
Página cento e quarenta
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Saúde
O uso de medicamentos requer cautela e não deve sêr banalizado. O fácil acesso a eles tem gerado o seu uso incorréto, sêndo o público jovem bastante afetado, uma vez quê a mídia também exerce influência nesse mercado. Para saber um pouco mais sobre o assunto, leia o texto a seguir, quê trata de medicamentos.
[...]
Medicamentos e os jovens
Usar medicamentos por conta própria […] faz parte dos hábitos de diversos adolescentes em todo o mundo. Com o intuito de curar alguma doença, alcançar o bem-estar pessoal ou uma aparência física desejável, os jovens se tornaram adeptos dos mais diversos tipos de medicamentos, desde um comprimido para dor de cabeça, até calmantes, estimulantes ou antidepressivos. Tudo isso sem nenhum acompanhamento médico.
Quais os medicamentos mais consumidos?
Entre os medicamentos mais consumidos pêlos jovens estão os analgésicos e antibióticos, inalantes e tranquilizantes, medicamentos para emagrecimento e ansiedade, xaropes, anabolizantes e medicamentos para disfunção erétil.
Quais os riscos do uso indiscriminado de medicamentos pêlos jovens?
Além dos riscos inerêntes à automedicação, tal hábito quando praticado por jovens é ainda mais preocupante em função das misturas perigosas quê eles costumam fazer, por exemplo:
• Alguns medicamentos tranquilizantes com áucôl podem levar ao estado de coma e causar até mesmo a morte do usuário.
• Medicamentos para emagrecer (anorexígenos) com áucôl e tabaco podem aumentar o risco de doenças cardíacas e respiratórias.
[…]

Página cento e quarenta e um
Medicamentos para emagrecer
Atualmente, tem sido muito comum a busca de uma solução rápida para combater o excésso de peso, como o uso de medicamentos para emagrecer, chamados anorexígenos. Esses medicamentos agem diminuindo o apetite, facilitando a perda de peso por determinado tempo.
Os anorexígenos apresentam algum tipo de risco?
Os anorexígenos são produtos de alto risco porque podem causar dependência e inúmeras reações indesejadas, como humor instável, depressão nervosa, irritabilidade, agitação, confusão mental, alucinações, dentre outras. A retirada brusca dêêsse tipo de medicamento póde sêr acompanhada de fadiga (cansaço), sonolência ou depressão. Por apresentarem riscos elevados, esses produtos são controlados por lei e somente os médicos podem prescrevê-los.
[…]
AGÊNCIA NACIONAL DE VIGILÂNCIA SANITÁRIA. O quê devemos saber sobre medicamentos. Brasília, DF: Anvisa, 2010. p. 66-67, 74. Disponível em: https://livro.pw/jprxa. Acesso em: 23 set. 2024.
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Segundo o texto, qual é o problema relacionado ao consumo de medicamentos entre os jovens?
2. Entre os problemas decorrentes da automedicação está a ingestão excessiva de medicamentos. Ao entrar na corrente sanguínea, um medicamento é metabolizado, e sua concentração diminui a uma taxa proporcional à quantidade ingerida e ao tempo decorrido. Suponha quê a quantidade de determinado medicamento no organismo possa sêr modelada pela função M(t) = M0 (0,5)t, em quê M0 é a quantidade ingerida (em mg) e M(t) é a quantidade do medicamento no organismo (em mg) decorridas t horas da ingestão. Se forem ingeridos 500 mg dêêsse medicamento, após quanto tempo no organismo a quantidade da droga será igual a 90 mg? Considere log 2 ≃ 0,3 e log 0,18 ≃ −0,74.
3. ![]() Conforme apresentado no texto, “atualmente, tem sido muito comum a busca de uma solução rápida para combater o excésso de peso”.
Conforme apresentado no texto, “atualmente, tem sido muito comum a busca de uma solução rápida para combater o excésso de peso”.
A anorexia e a bulimia são dois transtôrnos alimentares muito comuns na ssossiedade atual, principalmente entre jovens. Em grupo, pesquisem cada um dêêsses transtôrnos, listando as diferenças e o tratamento correto quê deve sêr realizado para cada um deles. Em seguida, produzam um vídeo de conscientização sobre os riscos da automedicação, abordando também os motivos do uso dos medicamentos e os impactos dos transtôrnos alimentares na vida das pessoas.
Página cento e quarenta e dois
HISTÓRIA DA MATEMÁTICA
A ideia de Diôn Napier e o logaritmo
O texto a seguir apresenta um resumo do progresso científico ocorrido entre os séculos XVI e XVII. Nesse contexto, a participação do matemático escocês Diôn Napier no intuito de simplificar cálculos matemáticos foi fundamental para o surgimento do conceito de logaritmo.

[…]
O século XVI e o início do século XVII testemunharam uma enorme expansão do conhecimento científico em todos os campos. A Geografia, a Física e a Astronomia, livres de antigos dogmas, mudaram rapidamente a percepção quê o homem tinha do universo. O sistema heliocêntrico de Copérnico, depois de lutar durante quase um século contra as resoluções da Igreja, encontrara finalmente a aceitação. A circum-navegação do glôbo por Magalhães, em 1521, anunciou uma nova era de exploração marítima quê não deixaria um canto do mundo sem sêr visitado. Em 1569 Gerhard Mercator publicou o seu aclamado novo mapa do mundo, acontecimento quê teve um impacto decisivo na ár-te da navegação. Na Itália, Galileu Galilei estabelecia as fundações da ciência da mecânica, enquanto na Alemanha Johannes Képler formulava suas três leis do movimento planetário, livrando a astronomia, de uma vez por todas, do universo geocêntrico dos gregos.
Esses desenvolvimentos envolviam uma quantidade crescente de dados numéricos, forçando os eruditos a passarem boa parte de seu tempo fazendo cálculos tediosos. A época pedia uma invenção quê livrasse os cientistas, de uma vez por todas, dêêsse fardo. Napier aceitou o desafio.
[…]
Sua linha de pensamento era a seguinte: se pudermos escrever qualquer número positivo como uma potência de algum dado número fixo (o qual depois seria chamado de base), então a multiplicação e a divisão de números seria o equivalente à adição ou à subtração de seus expoentes. Além díssu, elevar um número à enésima potência (isto é, multiplicá-lo por si mesmo n vezes) seria equivalente a somar o expoente n vezes a ele próprio, isto é, multiplicá-lo por n […]. Resumindo, cada operação aritmética seria reduzida à quê está abaixo dela na hierarquia das operações, o quê reduziria muito a dificuldade das computações numéricas.
Vamos ilustrar como esta ideia funciona escolhendo como nossa base o número 2. A tabéla 1.1 mostra as potências sucessivas de 2, começando com n = −3 e terminando com n = 12. Suponha quê queremos multiplicar 128 por 32. Nós procuramos na tabéla os expoentes correspondentes a 32 e a 128 e descobrimos quê eles são, respectivamente, 5 e 7. Somando esses expoentes, obtemos 12.
Agora revertemos o processo, procurando o número cujo expoente correspondente é 12; êste número é 4.096, a resposta desejada. […]
tabéla 1.1 – Potências de 2
n |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
2n |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1.024 |
2.048 |
4.096 |
MAOR, E. e: a história de um número. Tradução: Jorge Calife. Rio de Janeiro: recór, 2003. p. 17-20.
Página cento e quarenta e três
ATIVIDADES COMPLEMENTARES
1. (hú- hê- érre jota) Admita quê, em um determinado lago, a cada 40 cm de profundidade, a intensidade de luz é reduzida em 20%, de acôr-do com a equação I = I0 ⋅ na qual I é a intensidade da luz em uma profundidade h, em centimetros, e I0 é a intensidade na superfícíe. Um nadador verificou, ao mergulhar nesse lago, quê a intensidade da luz, em um ponto P, é de 32% daquela observada na superfícíe. A profundidade de P, em metros, considerando log2 = 0,3, equivale a:
a) 0,64
b) 1,8
c) 2,0
d) 3,2
alternativa c
2. (í éfi cê ê) Sejam x, y ∈ ℝ com x > 1 e y > 1. A expressão 2 log9 x + log3 6 − 6 log9 póde sêr simplificada para:
a) log9
b) log3 + 6)
c) log9 (2x + 6(1 − ))
d) log3 (x² + 36 + y−3)
e) log3 (1 + 6xy)
alternativa a
3. (IME-RJ) Se log10 2 = x e log10 3 = y, então log5 18 vale:
a)
b)
c)
d)
e)
alternativa a
4. (hú éfe ême gê) O pH de uma solução aquosa é definido pela expressão pH = −log[H+], em quê [H+] indica concentração, em mol/l, de íons de hidrogênio na solução e log, o logaritmo na base 10.
Ao analisar uma determinada solução, um pesquisador verificou quê, nela, a concentração de íons de hidrogênio era [H+] = 5,4 ⋅ 10−8 mol/l. Para calcular o pH dessa solução, ele usou os valores aproximados de 0,30 para log2, e de 0,48 para log3. Então, o valor quê o pesquisador obteve para o pH dessa solução foi:
a) 7,26
b) 7,32
c) 7,58
d) 7,74
alternativa a
5. (UEG-GO) Sendo f(x) = logx − 1 (x² + 1), então
a) x < −1 e x ≠ −2
b) x < 1
c) −1 ≤ x < 1
d) x > 1
e) x > 1 e x ≠ 2
alternativa e
6. (UFG-GO) O eucalipto é muito usado para a produção de papéis e celulose por causa da qualidade da matéria-prima e seu curto ciclo de vida. Um produtor de eucalipto possui uma plantação de determinada espécie adequada ao clima e ao tipo de solo de sua região. Essa espécie tem seu crescimento modelado pela função h(t) = 50 ⋅ (1 − 10−kt), onde h é a altura (em metro) em função do tempo t (em ano) e k é uma constante. Sabe-se quê esse eucalipto alcança a altura de 10 m em 2 anos e quê o produtor realizará o kórti quando as árvores tiverem 8 anos.
Com base nessas informações, calcule o valor da constante k e a altura quê os eucaliptos terão, em métro, quando o produtor for realizar o kórti.
k = ⋅ log ; as árvores terão 29,52 metros de altura.
7. (Fuvest-SP) Sobre a equação
(x + 3) = 0, é correto afirmar quê
a) ela não possui raízes reais.
b) sua única raiz real é −3.
c) duas de suas raízes reais são 3 e −3.
d) suas únicas raízes reais são −3, 0 e 1.
e) ela possui cinco raízes reais distintas.
alternativa e
8. (Uneb-BA) Segundo uma pesquisa, após t meses da constatação da existência de uma epidemia, o número de pessoas, por ela atingidas, é obtído por N(t) = .
Considerando-se quê o mês tenha 30 dias, log 2 = 0,30 e log 3 = 0,48, pode-se estimar quê 2.500 pessoas serão atingidas por essa epidemia em, aproximadamente,
a) dez dias.
b) vinte e seis dias.
c) três meses.
d) dez meses.
e) um ano.
alternativa a
Página cento e quarenta e quatro
9. (Udesc) O conjunto solução da inequação ≤ 1 é:
a) S = [, 3]
b) S = [1, 3]
c) S = [, 1]
d) S = ]0, ]
e) S =]0, 1]
alternativa c
Saiba quê...
Se ≤ a ⇒ −a ≤ f(x) ≤ a.
10. (Unicamp-SP) A solução da equação na variável real x, logx (x + 6) = 2, é um número
a) primo.
b) par.
c) negativo.
d) irracional.
alternativa a
11. (Fuvest-SP) Seja f uma função a valores reais, com domínio D ⊂ ℝ, tal quê f(x) = log10 ( (x2 − x + 1)), para todo x ∈ D.
O conjunto quê póde sêr o domínio D é:
a) {x ∈ ℝ; 0 < x < 1}
b) {x ∈ ℝ; x ≤ 0 ou x ≥ 1}
c) {x ∈ ℝ; < x < 10}
d) {x ∈ ℝ; x ≤ ou x ≥ 10}
e) {x ∈ ℝ; < x < }
alternativa a
12. (Enem/MEC) Um contrato de empréstimo prevê quê quando uma parcela é paga d fórma antecipada, conceder-se-á uma redução de juros de acôr-do com o período de antecipação. Nesse caso, paga-se o valor presente, quê é o valor, naquele momento, de uma quantia quê deveria sêr paga em uma data futura. Um valor presente P submetido a juros compostos com taxa i, por um período de tempo n, produz um valor futuro V determinado pela fórmula:
V = P ⋅ (1 + i)n
Em um contrato de empréstimo com sessenta parcelas fixas mensais, de R$ 820,00, a uma taxa de juros de 1,32% ao mês, junto com a trigésima parcela será paga antecipadamente uma outra parcela, desde quê o desconto seja superior a 25% do valor da parcela.
Utilize 0,2877 como aproximação para ln () e 0,0131 como aproximação para ln (1,0132).
A primeira das parcelas quê poderá sêr antecipada junto com a 30ª é a
a) 56ª
b) 55ª
c) 52ª
d) 51ª
e) 45ª
alternativa c
13. (Enem/MEC) Para realizar a viagem dos sonhos, uma pessoa precisava fazer um empréstimo no valor de R$ 5.000,00. Para pagar as prestações, dispõe de, no mássimo, R$ 400,00 mensais. Para esse valor de empréstimo, o valor da prestação (P) é calculado em função do número de prestações (n) segundo fórmula
P =
Se necessário, utilize 0,005 como aproximação para log 1,013; 2,602 como aproximação para log 400; 2,525 como aproximação para log 335. De acôr-do com a fórmula dada, o menor número de parcelas cujos valores não comprometem o limite definido pela pessoa é
a) 12
b) 14
c) 15
d) 16
e) 17
alternativa d
Página cento e quarenta e cinco
14. (FCMSCSP) O Nível de Pressão Sonora (NPS) é uma medida quê determina o grau de potência de uma onda sonora, sêndo o decibel (dB) sua unidade de medida mais usual. O infográfico traz dados do NPS de alguns sôns:

O NPS, em dB, de um som emitido está relacionado à sua Intensidade Sonora (I), em W/m2, pela seguinte lei:
NPS = 120 + 10 ⋅ logI
Desse modo, a razão entre a intensidade sonora do ronco mais alto já registrado e a do ronco moderado, nessa ordem, é um valor entre
a) 10 e 100.
b) 1 e 10.
c) 100 e 1.000.
d) 10.000 e 100.000.
e) 1.000 e 10.000.
alternativa d
PARA REFLETIR
Neste Capítulo, estudamos o logaritmo, sua definição e suas propriedades. Além díssu, conhecemos algumas de suas aplicações, como no cálculo do pH e do nível de intensidade sonora. Estudamos, também, a função logarítmica, seu gráfico e sua relação com a função exponencial.
No Capítulo, também foi feito o estudo da equação e da inequação logarítmica.
Nas páginas de abertura, foi apresentada a unidade de medida da intensidade sonora e uma reflekção sobre a importânssia de saber medi-la, com o intuito de mostrar a presença da Matemática na preservação da saúde. Você conseguiu reconhecer essa relação? Se sim, qual é a importânssia dela? Se não, retome o texto de abertura de Capítulo e as perguntas iniciais. Se possível, pesquise também em livros e sáites sobre o assunto.
Vamos refletir a respeito das aprendizagens do Capítulo 4:
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
Resposta pessoal.
• Qual é a condição para quê uma função logarítmica seja crescente? E decrescente?
base a maior do quê 1; base a entre 0 e 1
• Pesquise uma aplicação de logaritmo quê não tenha sido apresentada neste Capítulo e explique, com suas palavras, essa aplicação e a relação dela com o logaritmo.
Resposta pessoal.
Página cento e quarenta e seis