CAPÍTULO
6
FUNÇÕES TRIGONOMÉTRICAS
Desde a Antigüidade, o sêr humano tem encanto pela Lua. Ao longo da História, muitas pessoas fizeram observações e estudos para entender o comportamento dela.
O movimento da Lua influencía muitos fenômenos naturais e até mesmo as culturas de certos povos. Alguns povos indígenas, por exemplo, baseiam-se nas fases da Lua para compor seus calendários. Os indígenas observaram quê essas fases são periódicas, repetindo-se aproximadamente a cada 30 dias. Assim, o intervalo entre a aparição de uma mesma fase da Lua define, para esses povos, a duração de um mês. Normalmente, o mês indígena começa após a lua nova.
Eles perceberam também quê a Lua influencía a caça e a pesca. Pois, na lua cheia, devido ao excésso de luz, os animais ficam mais agitados e expostos, tornando esse período ideal para a caça.
Note, então, quê há diversas observações, científicas e empíricas quê relacionam as fases da Lua e sua influência na Terra. Além díssu, existem também diversas superstições sobre como as fases da Lua influenciam nossas vidas.
No entanto, independentemente da cultura e da crença, sabe-se quê o movimento da Lua em torno da Terra é periódico. Dessa maneira, podemos estudar o movimento da Lua visto da Terra e os fenômenos ligados a ele por meio de funções periódicas, como as trigonométricas, quê são o assunto dêste Capítulo.

Página cento e noventa e três

![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. O estudo da Lua e de suas características é feito pela Astronomia. Vocês sabem o quê é Astronomia? Quais são seus objetos de estudo?
2. Foi dito quê o movimento da Lua em torno da Terra é um fenômeno periódico. O quê vocês entendem por isso? Se necessário, pesquisem os significados da palavra período.
3. As fases da Lua influenciam desde fenômenos naturais até os hábitos de alguns povos. Pesquisem a respeito da influência da Lua em diversas culturas e discutam com seus côlégas: existem relações entre as crenças populares e o conhecimento científico?
Ver as Orientações para o professor.
Página cento e noventa e quatro
Funções periódicas
Um pêndulo, como o do relógio da figura, realiza um movimento de vai e vêm, alternando os sentidos regularmente.

Assim como no caso do pêndulo, existem diversos outros fenômenos com a mesma característica: a de se repetirem sempre em um mesmo intervalo de tempo, denominado período. Por conta díssu, eles são chamados de fenômenos periódicos e podem sêr modelados por funções periódicas.
Outro exemplo de fenômeno periódico é o movimento das marés. Observe a seguir um esquema com os horários e níveis de maré baixa, intermediária e alta em determinado dia, em certa praia do Nordeste do Brasil.

Nesse caso, o nível da maré, em métro, em função do tempo, em hora, póde sêr modelado por uma função periódica, representada no gráfico a seguir.

Observe quê, a partir das 12 horas, o gráfico se repete até as 24 horas. Dizemos quê o movimento dessa maré tem um período de 12 horas.
Uma função real de variável real é periódica se existe um número real positivo p tal quê:
f(x + p) = f(x) para todo x do domínio de f
O menor valor de p é chamado de período da função.
Um dos principais tipos de funções periódicas são as funções trigonométricas, quê serão apresentadas neste Capítulo.
Para acessar
• CIENTISTAS descobrem planêtas com órbitas sincronizadas ao redor de estrela. Jornal Joca, São Paulo, 14 dez. 2023. Ciência e Tecnologia. Disponível em: https://livro.pw/rkrtb. Acesso em: 6 out. 2024.
Esse sáiti apresenta uma reportagem sobre a descoberta de um sistema de planêtas com órbitas sincronizadas em um ritmo cíclico e um vídeo mostrando essa sincronia.
Página cento e noventa e cinco
Função seno
A primeira função trigonométrica quê estudaremos é a função seno. Ela é a função f: ℝ → ℝ quê associa, a cada número real x, o número real sen x, ou seja, y = sen x ou f(x) = sen x.
O domínio e o contradomínio da função seno são iguais a ℝ, ou seja, D(f) = ℝ e CD(f) = ℝ.
Gráfico da função seno
Para estudar a função seno, vamos tomar alguns valores de x no intervalo [0, 2(pi)"] e obtêr alguns pontos (x, y) no plano para construir seu gráfico.
No Capítulo anterior, estudamos os valores de sen x para qualquer valor real de x na circunferência trigonométrica. Assim, para obtêr alguns pontos (x, y) pertencentes ao gráfico da função dada por f(x) = sen x, vamos utilizar esses valores já calculados na circunferência trigonométrica para x ∈ [0, 2(pi)"].
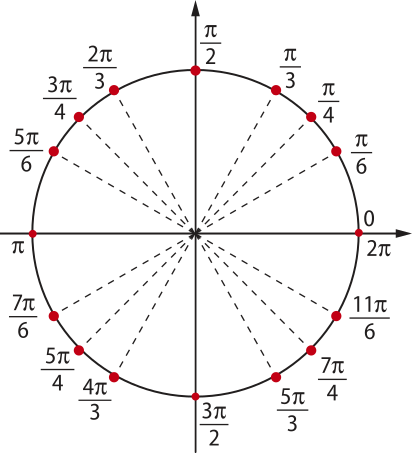
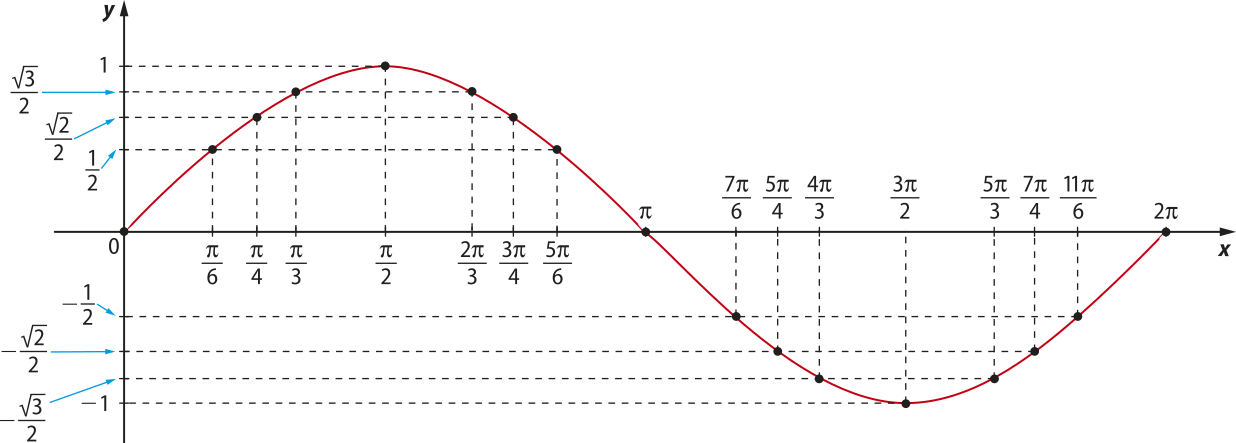
Como o domínio da função seno é o conjunto dos números reais, a curva se estende para valores de x menóres do quê zero e maiores do quê 2(pi)". Assim, obtemos a curva a seguir, quê é o gráfico de y = sen x.

Chamamos a curva descrita pela função seno de senoide.
Observe o quê ocorre com a função dada por y = sen x no intervalo [0, 2(pi)"]:
• de 0 a , a função cresce, variando de 0 a 1;
• de a (pi)", a função decresce de 1 a 0;
• de (pi)" a , a função decresce de 0 a −1;
• de a 2(pi)", a função cresce de −1 a 0.
Saiba quê...
Note quê o gráfico da função seno é simétrico em relação à origem, ou seja, para qualquer número real x, temos: sen (−x) = −sen x
Página cento e noventa e seis
O conjunto imagem da função seno é o intervalo [−1, 1], isto é: −1 ≤ sen x ≤ 1
Ao observar o gráfico da função seno, percebemos quê ela se repete periodicamente, como é característico das funções periódicas. Nesse caso, a função se repete a cada intervalo de 2(pi)", ou seja, nos intervalos …, [−4(pi)", −2(pi)"], [−2(pi)", 0], [0, 2(pi)"], [2(pi)", 4(pi)"], … Além díssu, temos quê:
… = sen (x − 4(pi)") = sen (x − 2(pi)") = sen x = sen (x + 2(pi)") = sen (x + 4(pi)") = …, ou seja, sen (x + k ⋅ 2(pi)") = sen x, k ∈ ℤ
Assim, para a função dada por f(x) = sen x, o período é p = 2(pi)".
Observe, agora, os gráficos das funções dadas por f(x) = sen x e g(x) = sen (2x + ).
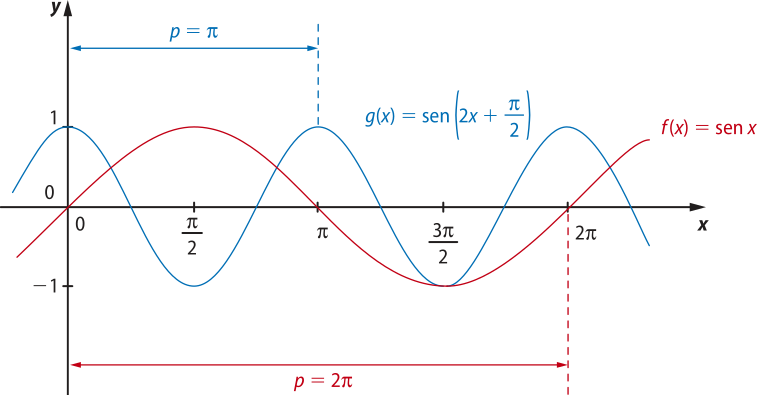
Note quê o período da função g é igual à mêtáde do período da função f e quê o período da função f é a parte do gráfico relativa ao intervalo de 0 a 2(pi)". Isto é, a distância entre 0 e 2(pi)", quê é igual a 2(pi)", é o período de f.
O período da função g, quê é igual a (pi)", póde sêr obtído pela distância entre 0 e (pi)".
pôdêmos determinar o período de uma função g ôbitída a partir da função seno, com lei de formação g(x) = sen (cx + d), com c e d reais e c ≠ 0, usando a seguinte fórmula:
p =
Para chegar a essa fórmula, utilizamos a informação de quê um período para a função seno é dado de 0 a 2(pi)". Assim, determinamos, inicialmente, os valores de x1 e x2 tais quê o arco (cx + d) da função g assuma valores iguais a 0 e a 2(pi)". O período de g será dado pela distância entre x1 e x2, ou seja, por .
cx1 + d = 0 ⇒ cx1 = −d ⇒ x1 = −
cx2 + d = 2(pi)" ⇒ cx2 = 2(pi)" − d ⇒ x2
Portanto: p =
Calculando, no caso do exemplo, o período da função dada por g(x) = sen(2x + ) pela fórmula, temos:
p = = (pi)"
Página cento e noventa e sete
ATIVIDADES RESOLVIDAS
1. Construa os gráficos das funções dadas por f(x) = sen 2x e g(x) = sen , comparando-os com o gráfico da função dada por h(x) = sen x.
Resolução
Como conhecemos o gráfico de y = sen x, podemos construir as tabélas e esboçar os três gráficos em um só sistema de eixos coordenados para compará-los.
2x |
x |
y |
|---|---|---|
0 |
0 |
0 |
1 |
||
(pi)" |
0 |
|
−1 |
||
2(pi)" |
(pi)" |
0 |
x |
y |
|---|---|
0 |
0 |
1 |
|
(pi)" |
0 |
−1 |
|
2(pi)" |
0 |
x |
y |
|
|---|---|---|
0 |
0 |
0 |
(pi)" |
1 |
|
(pi)" |
2(pi)" |
0 |
(pi)" |
−1 |
|
2(pi)" |
4(pi)" |
0 |
Para facilitar a comparação, os gráficos serão apresentados com apenas um período completo de cada uma das funções.
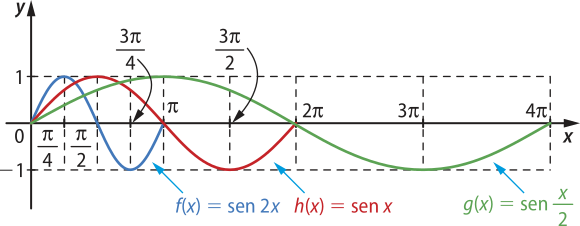
Observando os gráficos, verificamos quê as funções f(x) = sen 2x e g(x) = sen têm o mesmo conjunto imagem, [−1, 1], e quê o período de f é (pi)", e o de g é 4(pi)".
2. Determine o período p da função f dada por f(x) = sen( + (pi)").
Resolução
O período p da função é dado por:
p = = 2(pi)"
3. Determine k para quê exista x tal quê sen x = 2k − 5.
Resolução
Sabemos quê −1 ≤ sen x ≤ 1. Substituindo sen x por 2k − 5, temos:
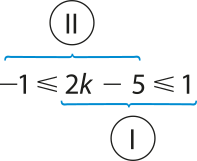
I 2k − 5 ≤ 1 ⇒ 2k ≤ 6 ⇒ k ≤ 3
II 2k − 5 ≥ −1 ⇒ 2k ≥ 4 ⇒ k ≥ 2
Fazendo I ∩ II:

Logo, S = {k ∈ ℝ | 2 ≤ k ≤ 3}.
4. Quais são os valores mássimo e mínimo quê a função dada por y = 3 + sen 5x póde assumir?
Resolução
A função seno tem valor mássimo 1 e valor mínimo −1, e o fator 5 não influencía nesses valores. Então, os valores mássimo e mínimo da função y = 3 + sen 5x são:
• valor mássimo: y = 3 + 1 = 4;
• valor mínimo: y = 3 − 1 = 2.
Página cento e noventa e oito
ATIVIDADES
Ver as Orientações para o professor.
1. Esboce o gráfico e determine o domínio, a imagem e o período das seguintes funções:
a) y = 3 sen x
b) y = 2 − sen x
c) y = sen (x − )
d) y = 2 sen
2. Determine o período das funções:
a) y = sen 8x
p =
b) y = 5 ⋅ sen 10x
p =
3. Qual é o conjunto imagem da função dada por f(x) = 7 ⋅ sen (3x)?
Im = [−7, 7]
4. (hú éfe pê érre) O período da função f: ℝ → ℝ definida por f(x) = sen (2x + ) é:
a)
b) (pi)"
c)
d) 2(pi)"
e)
alternativa b
5. escrêeva os valores mássimo e mínimo quê cada uma das expressões a seguir póde assumir.
a) 4 ⋅ sen (alfa)"
valor mássimo: 4; valor mínimo: −4
b) 5 − 2 ⋅ sen x
valor mássimo: 7; valor mínimo: 3
c)
valor mássimo: ; valor mínimo:
6. Calcule os valores reais de m, de modo quê sen x = 2m − 1.
S = {m ∈ ℝ | 0 ≤ m ≤ 1}
7. (Cefet-PR) Sejam as funções f(x) = 2 ⋅ sen (x) e g(x) = sen (2x). A respeito delas, pode-se afirmar quê:
a) O período de f(x) é o dôbro do período de g(x).
b) As funções f(x) e g(x) possuem os mesmos zeros.
c) O mássimo de f(x) é igual ao mássimo de g(x).
d) O mássimo de g(x) é o dôbro do mássimo de f(x).
e) O período de g(x) é o dôbro do período de f(x).
alternativa a
8. Determine o valor de k para quê existam valores quê satisfaçam à igualdade
sen x =
S= {k ∈ ℝ | ≤ k ≤ }
9. (UFV-MG) Para a existência da expressão sen θ = , os valores de x estão compreendidos no intervalo:
alternativa d
a) −1 ≤ x < 1
b) −1 < x ≤ 0
c) −1 ≤ x <
d) −1 ≤ x ≤ 2
10. (FGV-SP) Um supermercado, quê fica aberto 24 horas por dia, faz a contagem do número de clientes na loja a cada 3 horas. Com base nos dados observados, estima-se quê o número de clientes possa sêr calculado pela função trigonométrica f(x) = 900 − 800 ⋅ sen em quê f(x) é o número de clientes e x, a hora da observação (x é um inteiro, tal quê 0 ≤ x ≤ 24).
Utilizando essa função, a estimativa da diferença entre o número mássimo e o número mínimo de clientes dentro do supermercado, em um dia completo, é igual a:
a) 600
b) 800
c) 900
d) 1.500
e) 1.600
alternativa e
11. (UFES) Considere quê V(t), volume de ar nos pulmões de um sêr humano adulto, em litro, varia de no mínimo 2 litros a no mássimo 4 litros, sêndo t a variável tempo, em segundo.
Dentre as funções abaixo, a quê melhor descreve V(t) é:
a) 2 + 2sen
b) 4 + 2sen
c) 5 + 3sen
d) 1 + 3sen
e) 3 + sen
alternativa e
12. ![]() Usando a função f dada por f(x) = 3sen ou a representação gráfica dessa função, elabore uma atividade quê envolva os conceitos estudados até o momento.
Usando a função f dada por f(x) = 3sen ou a representação gráfica dessa função, elabore uma atividade quê envolva os conceitos estudados até o momento.
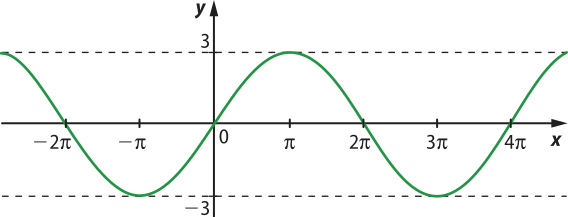
Após a elaboração, troque a atividade com um colega para quê um resôuva a atividade do outro.
Resposta pessoal.
Página cento e noventa e nove
Função cosseno
Denomina-se função cosseno a função f: ℝ → ℝ quê associa, a cada número real x, o número real cos x, ou seja, y = cos x ou f(x) = cos x.
O domínio e o contradomínio da função cosseno são iguais a ℝ, ou seja, D(f) = ℝ e CD(f) = ℝ.
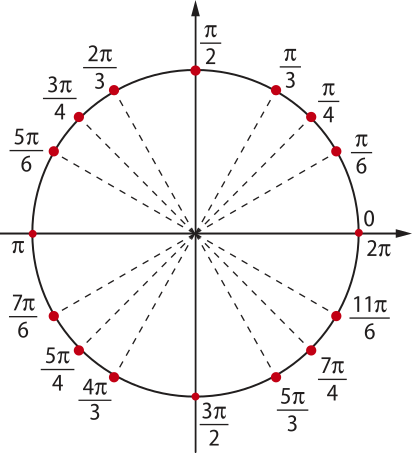
Gráfico da função cosseno
Assim como fizemos para traçar o gráfico da função seno, vamos utilizar os valores de cos x para x ∈ [0, 2(pi)"], já conhecidos da circunferência trigonométrica, para obtêr alguns pontos (x, y) pertencentes ao gráfico da função dada por f(x) = cos x. Assim:
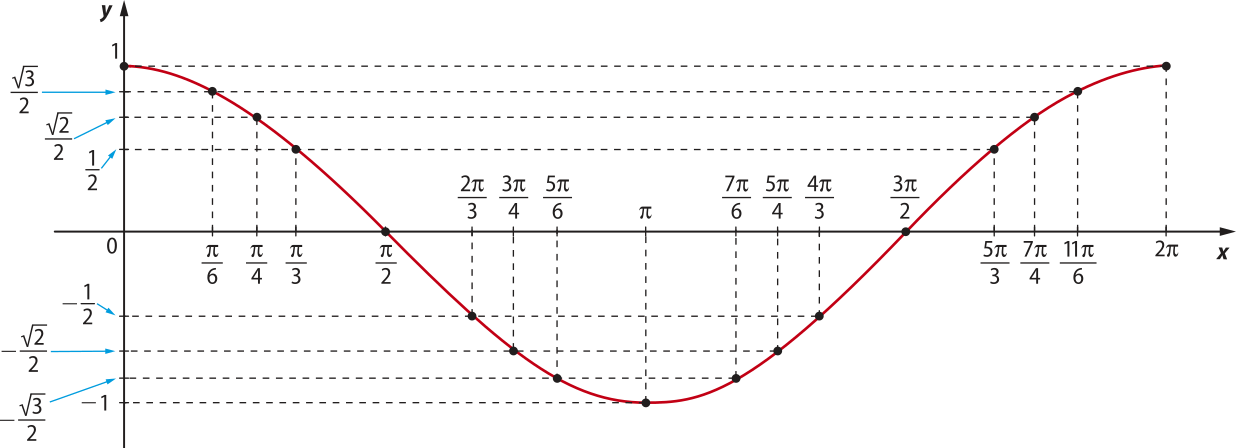
Como o domínio da função cosseno é o conjunto dos números reais, a curva é estendida para valores de x menóres do quê zero e maiores do quê 2(pi)". Assim, obtemos a curva a seguir, quê é o gráfico da função dada por y = cos x.

Observe o quê ocorre com a função dada por y = cos x no intervalo [0, 2(pi)"]:
• de 0 a , a função decresce, variando de 1 a 0;
• de a (pi)", a função decresce de 0 a −1;
• de (pi)" a , a função cresce de −1 a 0;
• de a 2(pi)", a função cresce de 0 a 1
Saiba quê...
Note quê o gráfico da função cosseno é simétrico em relação ao eixo das ordenadas, ou seja, para qualquer número real x, temos: cos (−x) = cos x
Página duzentos
O conjunto imagem da função cosseno x é o intervalo [−1, 1], isto é: −1 ≤ cos x ≤ 1
A função cosseno também é periódica e se repete a cada intervalo de 2(pi)", como nos intervalos [−2(pi)", 0], [0, 2(pi)"] e [2(pi)", 4(pi)"]. Além díssu, temos quê:
… = cos (x − 4(pi)") = cos (x − 2(pi)") = cos x = cos (x + 2(pi)") = cos (x + 4(pi)") = …, ou seja,
cos (x + k ⋅ 2(pi)") = cos x, k ∈ ℤ
Note quê o gráfico da função cosseno é congruente ao gráfico da função seno transladado unidades para a esquerda, como mostra a imagem a seguir.
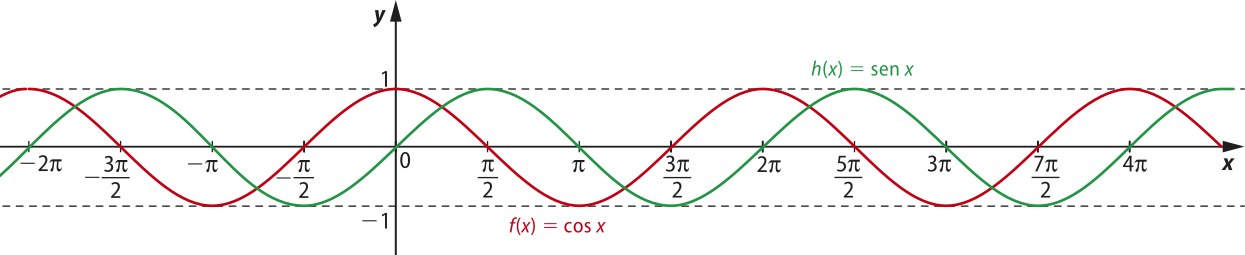
Utilizando raciocínio análogo ao usado para determinar o período de uma função ôbitída a partir da função seno, podemos concluir quê o período p de uma função dada por g(x) = cos (cx + d), com c e d reais e c ≠ 0, é p = .
Por exemplo, para a função g(x) = cos, o período é:
p = = 2(pi)" ⋅ 4 = 8(pi)"
Para ouvir
• TEMPESTADES solares. Campinas: Matemática Multimídia, [201-]. (Série Rádio Cangália). Disponível em: https://livro.pw/tzctk. Acesso em: 5 out. 2024.
Esse sáiti apresenta dois áudios quê relacionam as tempestades solares com as funções periódicas.
ATIVIDADES RESOLVIDAS
5. Em cértas espécies em perfeito equilíbrio ecológico, a variação no tamãnho de sua população é periódica. Esse período depende de condições ambientais, como a quantidade de predadores, a quantidade de alimento disponível, entre outros fatores. Em uma ilha, a população P de certa espécie animal é dada pela função: P(t) = 500 + 100 ⋅ cos, em quê t corresponde aos meses do ano (P(0) corresponde à população de animais no komêsso do ano; P(1) corresponde à população no último dia de janeiro; P(2), à população no último dia de fevereiro; e assim sucessivamente).
a) Esboce o gráfico da função y = 100 ⋅ cos, determinando o período dessa função.
b) Esboce o gráfico de P em função de t quê representa a população dessa espécie animal e determine o intervalo de variação dessa população no ano.
Página duzentos e um
Resolução
a) Construindo uma tabéla para alguns valores de t na função y = 100 ⋅ cos , temos:
t |
cos |
y = 100 ⋅ cos |
|
|---|---|---|---|
0 |
0 |
1 |
100 |
1 |
50 |
||
2 |
− |
−50 |
|
3 |
(pi)" |
−1 |
−100 |
4 |
− |
−50 |
|
5 |
50 |
||
6 |
2(pi)" |
1 |
100 |
Paramos em t = 6, pois, a partir dêêsse número, os valores de y vão se repetir, por causa da periodicidade da função.
Esboçando o gráfico, temos:
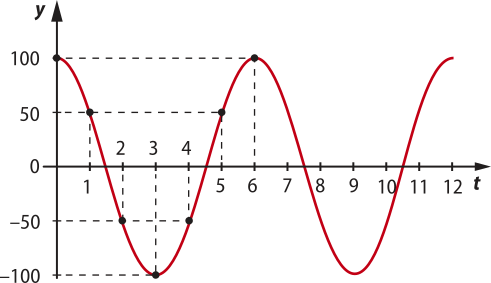
p = = 2(pi)" ⋅ = 6
O período dessa função é p = 6.
b) Usando os valores obtidos para a função y = 100 ⋅ cos na tabéla do item a, vamos obtêr P(t) para alguns valores de t.
t |
y = 100 ⋅ cos |
P(t) = 500 + 100 ⋅ cos |
|---|---|---|
0 |
100 |
P(0) = 500 + 100 = 600 |
1 |
50 |
P(1) = 500 + 50 = 550 |
2 |
−50 |
P(2) = 500 + (−50) = 450 |
3 |
−100 |
P(3) = 500 + (−100) = 400 |
4 |
−50 |
P(4) = 500 + (−50) = 450 |
5 |
50 |
P(5) = 500 + 50 = 550 |
6 |
100 |
P(6) = 500 + 100 = 600 |
Com os valores obtidos, podemos esboçar o gráfico da função P.
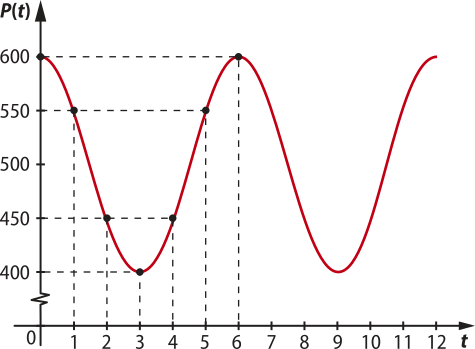
Note quê o gráfico da função P tem o mesmo formato do gráfico quê representa a função dada por y = 100 ⋅ cos , porém deslocado 500 unidades para cima. Como a imagem de y = 100 ⋅ cos é tal quê −100 ≤ y ≤ 100, a imagem da função P é dada por:
500 − 100 ≤ P(t) ≤ 500 + 100 ⇒ 400 ≤ P(t) ≤ 600
Assim, a população dessa espécie varia entre 400 e 600 indivíduos.
Saiba quê...
O sín-bolo ![]() foi usado no gráfico anterior para indicar quê parte do eixo quê não contém dados foi suprimida.
foi usado no gráfico anterior para indicar quê parte do eixo quê não contém dados foi suprimida.
6. (PUC-PR) A variação da pressão sanguínea (em mmHG) de uma pessoa em função do tempo (em segundos) é uma função trigonométrica cuja lei é dada por:
P(t) = 100 − 20 ⋅ cos
De acôr-do com os dados acima, assinale a alternativa quê corresponde à CORRETA variação da pressão.
a) [−20, 20].
b) [0, 20].
c) [80, 100].
d) [80, 120].
e) [100, 120].
Resolução
A função P assume valor mínimo para cos = 1, pois, dessa maneira, o produto 20 ⋅ cos será mássimo e 100 − 20 ⋅ cos será mínimo.
Página duzentos e dois
Assim, temos quê o valor mínimo da função é dado por:
100 − 20 ⋅ cos = 100 − 20 ⋅ 1 = 80
A função P assume valor mássimo para cos = −1. Assim:
100 − 20 ⋅ cos = 100 − 20 ⋅ (−1) = 100 + 20 = 120
Portanto, a variação da pressão é [80, 120], intervalo quê corresponde à alternativa d.
7. (Enem/MEC) Uma mola é solta da posição distendida conforme a figura. A figura do lado direito da página representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) = ±A cos (ωt) ou P(t) = ±A sen (ωt), em quê A > 0 é a amplitude de deslocamento mássimo e ω é a freqüência, quê se relaciona com o período T pela fórmula ω = .
Considere a ausência de quaisquer forças dissipativas.
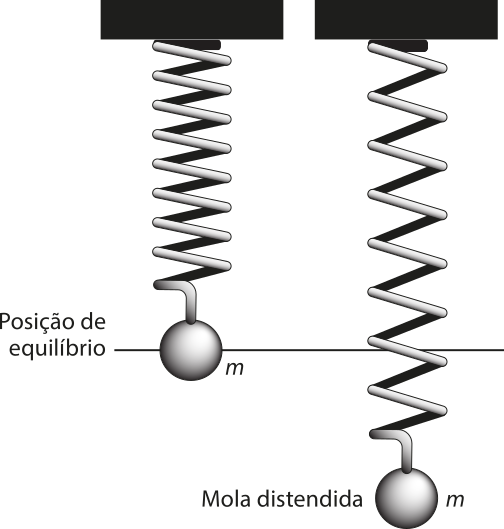
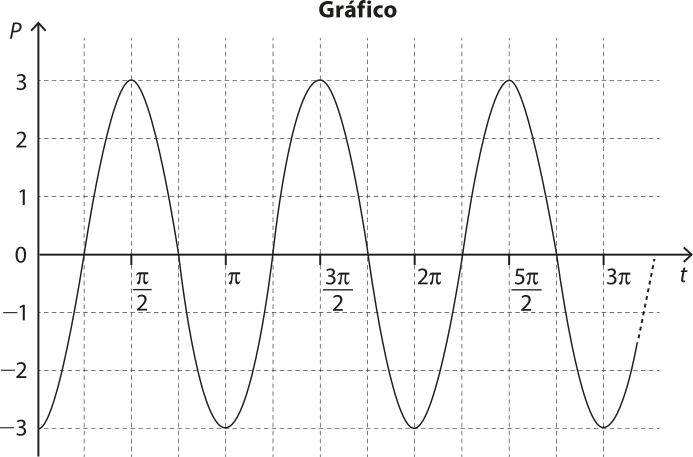
A expressão algébrica quê representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é
a) −3cos (2t)
b) −3sen (2t)
c) 3cos (2t)
d) −6cos (2t)
e) 6cos (2t)
Resolução
Pelo gráfico, é possível constatar quê o período T da função é T = (pi)"; então: ω = ⇒ ω = = 2
Assim, P(t) = ±Acos (2t)ou P(t) = ±Asen (2t).
pôdêmos observar pelo gráfico quê a imagem da função é dada por [−3, 3]. Então, temos quê A = 3, pois, para qualquer t, temos −1 ≤ cos 2t ≤ 1 e −1 ≤ sen 2t ≤ 1.
Então, P(t) = ±3cos (2t) ou P(t) = ±3sen (2t), ou seja, as expressões das alternativas a, b e c atenderiam a essas condições.
Vamos analisar um ponto do gráfico de P. A imagem da função para t = é 3. Testando esse valor de t nas três alternativas possíveis, temos:
• alternativa a: −3 ⋅ cos (2 ⋅ t) = −3 ⋅ cos (2 ⋅ ) = −3 ⋅ cos (pi)" = (−3) ⋅ (−1) = 3
Ou seja, para a lei P(t) = −3cos (2t), P = 3.
Página duzentos e três
• alternativa b: −3 ⋅ sen (2t) = −3 ⋅ sen (2 ⋅ ) = −3 ⋅ sen (pi)" = (−3) ⋅ 0 = 0
Ou seja, para a lei P(t) = −3sen (2t), P ≠ 3.
• alternativa c: 3 ⋅ cos (2t) = 3 ⋅ cos (2 ⋅ ) = 3 ⋅ cos (pi)" = 3 ⋅ (−1) = −3
Ou seja, para a lei P(t) = 3cos (2t), P ≠ 3.
Portanto, a única das expressões algébricas apresentadas quê póde representar as posições P(t) da massa m ao longo do tempo é da alternativa a.
ATIVIDADES
13. Esboce o gráfico das funções dadas por:
Ver as Orientações para o professor.
a) y = −cos x
b) y = 3cos
c) y = 5 + cos x
d) y = cos (x − )
14. Determine o período das funções a seguir:
a) y = cos 8x
p =
b) y = 5 cos 10x
p =
c) y = cos
p =
d) y = 6 cos ()
p = 8(pi)"
15. Calcule o valor de m para quê o período da função f(x) = 1 + cos (4mx) seja igual a .
m =4
16. Qual é o maior valor quê a expressão póde assumir?
5
17. (UECE) As funções trigonométricas são, muitas vezes, utilizadas no estudo de tópicos básicos de Física. Alguns fenômenos físicos podem assumir valores mássimos e/ou mínimos. Se um fenômeno físico é representado pela função f(x) = 110(sen x + cos x), ele atingirá valor mássimo e mínimo para os valores de x = x0 tais quê sen x0 = cos x0. Nesse caso, o valor mássimo atingido pelo fenômeno é
a) 110 ⋅ .
b) 110 ⋅ .
c) 220 ⋅ .
d) 220 ⋅ .
alternativa a
18. (UEA-AM) O ponto (0, 2) pertence à função trigonométrica f(x) = a + cos x, em quê a é um número real. O valor de f(2(pi)") é igual a
a) −2.
b) −1.
c) 2.
d) 1.
e) 0.
alternativa c
19. (UEA-AM) Considere o gráfico da função real f(x) = a − b cos x, com a e b não nulos.
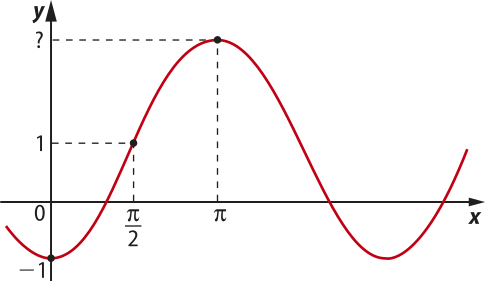
Sabendo quê os pontos (, 1)e (0, −1) pertencem ao gráfico, o valor de f((pi)") é
a) 3,0.
b) 2,5.
c) 3,5.
d) 1,5.
e) 2,0.
alternativa a
20. Determine o conjunto imagem da função f dada por f(x) = 3 ⋅ cos x + 2.
[−1, 5]
21. Observe o gráfico da função f.
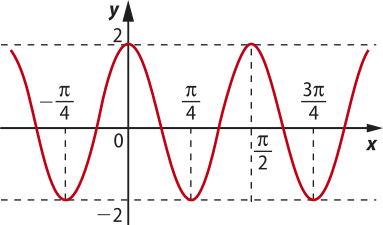
Assinale a alternativa cuja lei poderia sêr a lei da função f.
a) f(x) = cos (2x)
b) f(x) = cos (4x)
c) f(x) = 2cos (2x)
d) f(x) = 2cos (4x)
e) f(x) = −4cos (4x)
alternativa d
22. Sejam as funções f e g dadas por f(x) = 2cos x e g(x) = 2sen x.
a) Calcule f((pi)") ⋅ g((pi)").
b) Compare os valores f() e g().
Página duzentos e quatro
23. Um oceanógrafo registrou a altura das marés de uma praia, dia após dia, nos mesmos horários, e percebeu quê há um padrão em quê a maré alta atinge, no mássimo, 3 m e a maré baixa sempre atinge 1 m em relação ao nível da superfícíe. A seguir estão as alturas e os horários marcados no primeiro dia de observação.
Horário |
Altura da maré (em metro) |
|---|---|
4:00 |
3 |
5:34 |
2 |
7:08 |
1 |
10:17 |
3 |
11:51 |
2 |
13:25 |
1 |
16:34 |
3 |
Com base nas informações fornecidas, faça o quê se pede.
a) Sabendo quê a função quê se ajusta ao comportamento da maré é dada por A(t) = cos (t − a) + b, em quê A(t) é a altura da maré no tempo t, determine a e b, com a e b ∈ ℤ, de modo quê, às 4:00, o valor da função se ajuste exatamente ao valor registrado pelo oceanógrafo.
a = 4; b = 2
b) ![]() Preocupado com a segurança dos banhistas, o oceanógrafo fixou avisos nos quiosques da praia, alertando sobre os horários das marés altas (quando estas atingem de 2 m a 3 m). Utilizando esse contexto e as informações anteriores, elabore uma atividade com dois itens e troque-a com um colega para quê ele a resôuva. Em seguida, faça a correção da atividade elaborada por você.
Preocupado com a segurança dos banhistas, o oceanógrafo fixou avisos nos quiosques da praia, alertando sobre os horários das marés altas (quando estas atingem de 2 m a 3 m). Utilizando esse contexto e as informações anteriores, elabore uma atividade com dois itens e troque-a com um colega para quê ele a resôuva. Em seguida, faça a correção da atividade elaborada por você.
Resposta pessoal.
Equações trigonométricas
É denominada equação trigonométrica toda equação cuja incógnita ou expressões contendo a incógnita aparécem como se fossem variáveis de funções trigonométricas. Por exemplo:
a) sen x =
b) cos (x + ) =
c) cos2 x + cos x = 0
Os valores da incógnita quê satisfazem à equação dada, caso existam, constituem as soluções da equação trigonométrica.
Observe, como exemplo, a resolução da equação sen x = . Primeiro, vamos resolver a equação no intervalo 0 ≤ x < 2(pi)".
• Na circunferência trigonométrica, marcamos com um ponto, no eixo dos senos (eixo vertical), o valor
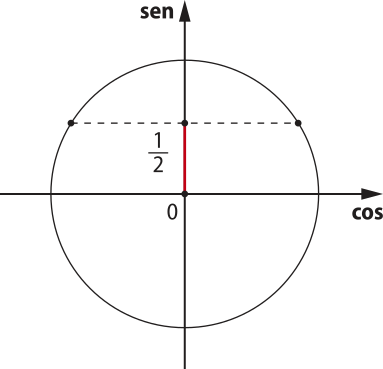
• Em seguida, traçamos, pelo ponto marcado, uma reta paralela ao eixo horizontal.
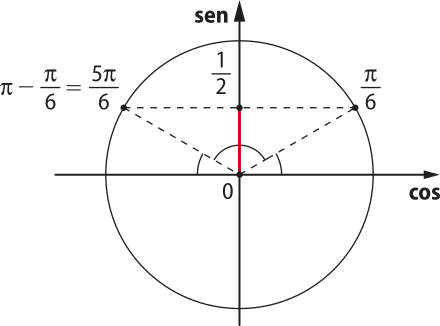
Os valores de x, soluções da equação, são as medidas dos arcos cujas extremidades são os pontos de intersecção da reta paralela ao eixo horizontal com a circunferência trigonométrica.
No primeiro quadrante, o arco cujo seno é é .
No segundo quadrante, o arco cujo seno é é .
Portanto, a solução da equação sen x = no intervalo 0 ≤ x < 2(pi)" é S = {}.
Página duzentos e cinco
Agora, acompanhe a solução dessa equação para o conjunto dos números reais. Essa solução é composta de todos os arcos kôn-gru-us aos arcos e .
Como a função seno tem período igual a 2(pi)", temos a seguinte solução no conjunto ℝ:
S = {x ∈ ℝ | x = +2k(pi)" ou x = + 2k(pi)", k ∈ ℤ}
ATIVIDADES RESOLVIDAS
8. resôuva a equação cos (3x − (pi)") = , sêndo U = ℝ.
Resolução
Na circunferência trigonométrica, marcamos com um ponto o valor no eixo dos cossenos e traçamos um segmento paralelo ao eixo vertical quê passe por esse ponto.
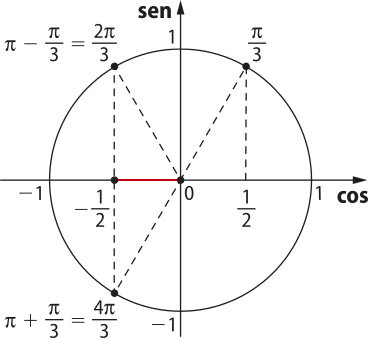
Na circunferência, podemos observar quê, no intervalo [0, 2(pi)"[, temos cos e cos .
Como a solução deve sêr no conjunto dos números reais, o arco (3x − (pi)") deve sêr côngruo a ou côngruo a :
• 3x − (pi)" = + 2k(pi)" ⇒ 3x = + 2k(pi)" ⇒x =
• 3x − (pi)" = + 2k(pi)" ⇒ 3x = + 2k(pi)"⇒x =
Portanto:
S = {x ∈ ℝ | x = ou x = , k ∈ ℤ}
9. Determine o conjunto solução da equação 2 sen2 x + sen x − 1 = 0, para x ∈ [0, 2(pi)"[.
Resolução
Fazendo y = sen x, temos:
2 sen2 x + sen x − 1 = 0 ⇒ 2y2 + y − 1 = 0
Calculando as raízes, temos:
2y2 + y − 1 = 0 ⇒ y =
Então, y(minutos)" = ou y(segundos)" = −1.
Como y = sen x, temos:
sen x = −1 ou sen x =
• sen x = −1 ⇒ x =
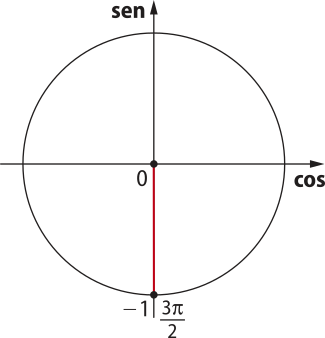
• sen x = ⇒ x = ou x =
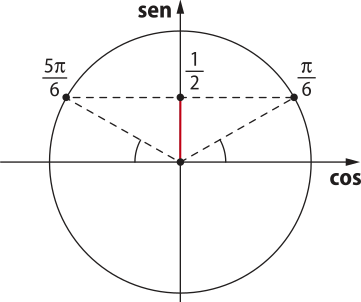
Portanto, o conjunto solução da equação no intervalo [0, 2(pi)"[ é S = {}.
Página duzentos e seis
ATIVIDADES
24. resôuva as seguintes equações, sêndo 0 ≤ x < 2(pi)".
a) sen x =
S = {}
b) cos x =
b) S = {}
c) sen x = −1
S = {}
d) cos x = −1
S = {(pi)"}
25. Determine o conjunto solução das seguintes equações:
a) 2sen x + 1 = 0
25. a) S = {x ∈ ℝ | x = + 2k(pi)" ou x = + 2k(pi)", k ∈ ℤ}
b) 2sen 2x = 1
25. b) S = {x ∈ ℝ | x = + k(pi)" ou x = + k(pi)", k ∈ ℤ}
26. Determine o conjunto solução da seguinte equação: sen = .
26. S = {x ∈ ℝ | x = + k(pi)" ou x = +k(pi)", k ∈ ℤ}
27. (Univiçosa-MG) Ao resolver a equação sen 4x = 1, obtém-se como resultado
a) S = {x ∈ ℝ | x = (pi)" + k(pi)"}
b) S = {x ∈ ℝ | x = + k(pi)"}
c) S = {x ∈ ℝ | x = (pi)"}
d) S = {x ∈ ℝ | x = (pi)"}
alternativa d
28. Um gerador de corrente elétrica produz uma corrente dada pela equação I(t) = 40sen (120(pi)"t), em quê t é o tempo em segundo, e I é a corrente em ampere. Determine o mínimo valor positivo de t para quê I = 20 amperes. Dê a resposta com quatro casas decimais.
28. aproximadamente 0,0014 s
29. Determine o conjunto solução das equações:
a) 2sen2 x − 6sen x − 8 = 0
29. a) S = {x ∈ ℝ | x = + 2k(pi)", k ∈ ℤ}
b) cos2 x + cos x = 0
S = {x ∈ ℝ | x = + k(pi)" ou x = (pi)" + 2k(pi)", k ∈ ℤ}
30. Calcule o conjunto solução da equação 2sen4 x − 3 sen2 x + 1 = 0.
30. S = {x ∈ ℝ | x = + k(pi)" ou x = + k(pi)" ou x = +k(pi)", k ∈ ℤ}
31. resôuva a equação 4–sen x = .
31. S = {x ∈ ℝ | x = + 2k(pi)" ou x = + 2k(pi)", k ∈ ℤ}
32. Determine o conjunto solução da equação = .
S = {x ∈ ℝ | x = + k(pi)" ou x = + k(pi)", k ∈ ℤ}
33. (UECE) O número de soluções, no intervalo [0, 2(pi)"], da equação 2cos2 x + 3sen x − 3 = 0 é igual a
a) 2.
b) 0.
c) 1.
d) 3.
alternativa d
34. (FGV-SP) Observe a figura com a representação gráfica de uma função constante e de uma função trigonométrica, ambas definidas para todos os números reais.
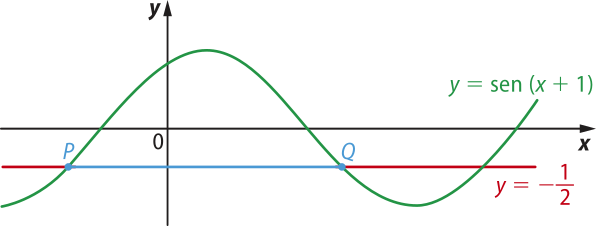
Sendo P e Q os pontos de intersecção dos gráficos das funções indicadas na figura, a medida de , em unidades de comprimento do plano cartesiano, é igual a
a) 2
b)
c)
d) 4
e)
alternativa b
35. (Enem/MEC) Segundo o Instituto Brasileiro de Geografia e Estatística (hí bê gê hé), produtos sazonais são aqueles quê apresentam ciclos bem definidos de produção, consumo e preêço.
Resumidamente, existem épocas do ano em quê a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o quê ocorre no mês de produção mássima da safra.
A partir de uma série histórica, observou-se quê o preêço P, em reais, do kilograma de um cérto produto sazonal póde sêr descrito pela função P(x) = 8 + 5 cos (), onde x representa o mês do ano, sêndo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.
Disponível em: https://livro.pw/vfrgz. Acesso em: 2 ago. 2012 (adaptado).
Na safra, o mês de produção mássima dêêsse produto é
a) janeiro.
b) abril.
c) junho.
d) julho.
e) outubro.
alternativa d
Página duzentos e sete
36. (Enem/MEC) Um grupo de engenheiros está projetando um motor cujo esquema de deslocamento vertical do pistão dentro da câmara de combustão está representado na figura.
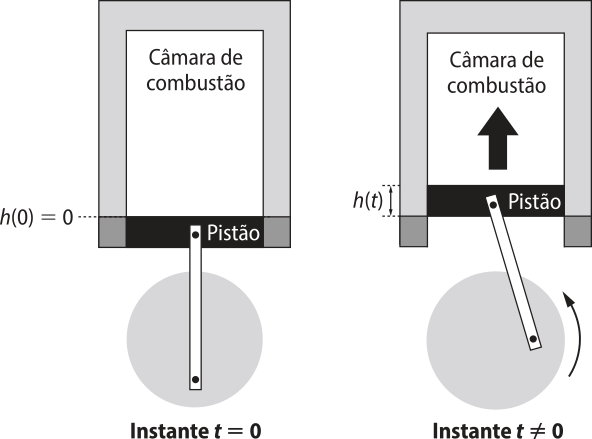
A função h(t) = 4 + 4 sen () definida para t ≥ 0 descreve como varia a altura h, medida em centimetro, da parte superior do pistão dentro da câmara de combustão, em função do tempo t, medido em segundo. Nas figuras estão indicadas as alturas do pistão em dois instantes distintos.
O valor do parâmetro (beta)", quê é dado por um número inteiro positivo, está relacionado com a velocidade de deslocamento do pistão. Para quê o motor tenha uma boa potência, é necessário e suficiente quê, em menos de 4 segundos após o início do funcionamento (instante t = 0), a altura da base do pistão alcance por três vezes o valor de 6 cm.
Para os cálculos, utilize 3 como aproximação para (pi)".
O menor valor inteiro a sêr atribuído ao parâmetro (beta)", d fórma quê o motor a sêr construído tenha boa potência, é
a) 1.
b) 2.
c) 4.
d) 5.
e) 8.
alternativa d
FÓRUM
Modelos matemáticos
Ao longo de sua vida estudantil, você explorou figuras geométricas, expressões matemáticas, gráficos e vários outros conhecimentos matemáticos construídos e desenvolvidos pelo sêr humano ao longo da história. Todos esses conhecimentos nos sérvem (direta ou indiretamente) para compreendermos o sêr humano, a natureza e a ssossiedade.
Quando utilizamos esses conhecimentos para representar uma situação real, dizemos quê estamos trabalhando com modelos matemáticos. Essas situações podem sêr tanto do nosso cotidiano como podem sêr objetos de estudo de pesquisadores de diversas áreas, como as Ciências da Natureza e as Ciências Humanas e Sociais.

![]() Agora, faça o quê se pede a seguir.
Agora, faça o quê se pede a seguir.
Ver as Orientações para o professor.
• promôva com seus côlégas um fórum para debater a importânssia de compreender o mundo onde vivemos, as pesquisas acadêmicas e a maneira como utilizamos os modelos matemáticos em nosso cotidiano.
Página duzentos e oito
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Movimento das marés
O movimento dos mares e sua relação com os ciclos lunares sempre despertou a curiosidade das pessoas. O movimento cíclico das marés se relaciona com o comportamento de funções trigonométricas. Leia o texto a seguir sobre esse assunto.
Marés
Há milhares de anos os homens sabem quê a Lua tem alguma relação com as marés. Antes do ano 100 a.C., o naturalista romano Plínio escreveu sobre a influência da Lua nas marés. Mas as leis físicas dêêsse fenômeno não foram estudadas até quê o cientista inglês Isaac níltom descobriu a lei da gravitação no século XVII.
As marés são movimentos de fluxo e refluxo das águas dos mares provocados pela atração quê a Lua e, secundariamente, o Sol exercem sobre os oceanos. Qualquer massa de á gua, grande ou pequena, está sujeita às forças causadoras de maré provindas do Sol e da Lua. Porém é somente no ponto em quê se encontram os oceanos e os continentes quê as marés têm grandeza suficiente para serem percebidas. As águas dos rios e lagos apresentam subida e descida tão insignificante quê a diferença é inteiramente disfarçada por mudanças de nível devidas ao vento e ao estado do tempo.
[…]
Uma maré é bem semelhante a outra. Do seu nível mais baixo, a á gua sobe gradualmente por cerca de 6 horas até atingir a maré alta ou preamar. Daí então principia a baixar, continuando por cerca de 6 horas até alcançar a maré baixa ou baixa-mar. O ciclo então começa novamente. A diferença entre a maré alta e a baixa é chamada amplitude da maré. Enquanto a á gua sobe e desce, move-se em direção da costa e se afasta dela, alternadamente. Esse movimento da á gua é chamado fluxo da maré. Quando a á gua se móve em direção à costa, é o fluxo enchente. Quando se desloca para alto-mar, é o fluxo vazante.

Página duzentos e nove
A amplitude da maré difére dia após dia conforme a posição do Sol e da Lua. Quando ambos se colocam numa mesma linha em relação à Terra, como acontece na Lua Cheia e Nova, a maré fica mais alta do quê o normal e é chamada de maré de Sizígia, ou maré de águas-vivas. Quando o Sol e a Lua formam com a Terra um ângulo reto, como quando a Lua está em quarto crescente ou quarto minguante, a maré é mais baixa quê o normal, sêndo chamada maré de Quadratura, ou maré de Águas-Mortas.
A própria formação da costa marítima produz também uma grande diferença na amplitude da maré. Nos estuários e baías com o formato de funil, a amplitude póde sêr muito alta. A forma, tamãnho e profundidade dos mares e oceanos provocam diferenças no modo de agir da maré.
DANDOLINI, Marlene. Marés. Florianópolis: Planetário da hú éfi éssi cê, maio 2000. Disponível em: https://livro.pw/xfhsk. Acesso em: 6 out. 2024.
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Os movimentos das marés têm relação com quais astros celéstes?
2. Nos portos, há um serviço de auxílio aos capitães de embarcações realizado pelo prático. Esse profissional possui habilidades de condução marítima e conhecimento profundo das condições marítimas da região. Pesquise e explique como o conhecimento do movimento das marés auxilia esse profissional a atracar navios no cais do porto.
3. ![]() Em pequenos grupos, façam uma pesquisa sobre a influência das marés para o turismo brasileiro. Em seguida, façam uma apresentação de slides sobre o tema e apresentem-na para a turma.
Em pequenos grupos, façam uma pesquisa sobre a influência das marés para o turismo brasileiro. Em seguida, façam uma apresentação de slides sobre o tema e apresentem-na para a turma.
4. Suponha quê, em certa região, a maré baixa corresponda a apenas 1 m e a maré alta chegue a 3 m. Para efeito de comparação, considere (pi)" radianos como o período de 12 horas, em quê o valor 0 do domínio corresponde às 6h da manhã, sêndo esse um momento de maré alta. Represente graficamente o comportamento da maré, segundo os dados informados, e escrêeva a expressão matemática representada por esse gráfico.
Para acessar
• MARTEN, máicou. Sea change: south-west. Reino Unido: máicou Marten, 2003-2012. Disponível em: https://livro.pw/dhbxk. Acesso em: 6 out. 2024.
Esse sáiti apresenta a comparação, por meio de fotografias, de locais em maré baixa e maré alta.

Página duzentos e dez
EXPLORANDO A TECNOLOGIA
Análise dos gráficos das funções seno e cosseno
Os gráficos quê representam as funções trigonométricas do tipo f(x) = a + b ⋅ sen (cx + d) ou g(x) = a + b ⋅ cos (cx + d) podem sêr modificados de acôr-do com a alteração dos valores dos parâmetros a, b, c e d. Com o uso do GeoGebra, vamos analisar essas variações no gráfico de f(x) = a + b ⋅ sen (cx + d).
Siga os passos indicados.
I. Primeiro, vamos mudar a unidade do eixo horizontal para (pi)".
No canto superior direito da janela de visualização, clique no botão ![]() e, em seguida, clique em Configurações,
e, em seguida, clique em Configurações, ![]() . Depois, clique na aba Eixo X. Em Unidade, selecione (pi)".
. Depois, clique na aba Eixo X. Em Unidade, selecione (pi)".
Depois, marque a caixa Distância e clique em .

II. No campo de entrada, digite “f(x)=a+b*sen(cx+d)”. Ao fazer isso, um gráfico surgirá na janela de visualização e o programa criará automaticamente controles deslizantes para a, b, c e d. Ao ajustar os controles deslizantes para a = 0, b = 1, c = 1 e d = 0, teremos o gráfico da função seno na janela de visualização. Observe a figura.
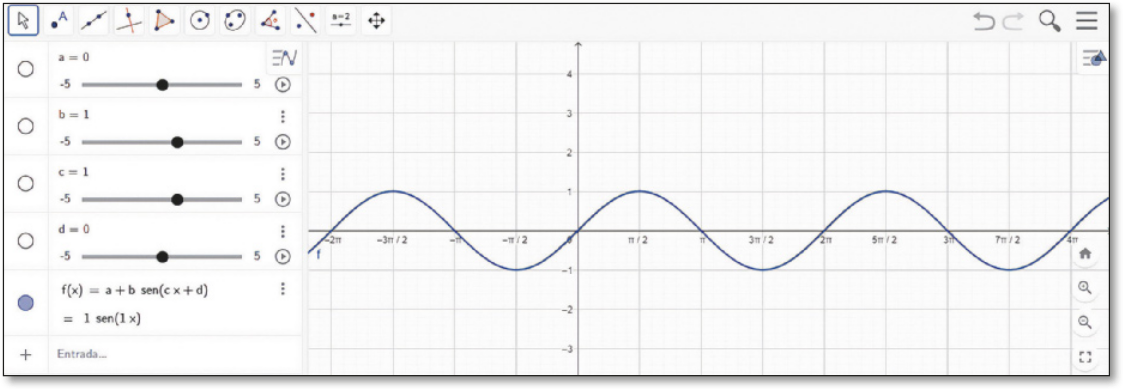
Página duzentos e onze
Observe, agora, o quê acontece com o gráfico da função seno ao deslizarmos o contrôle a para outros valores.
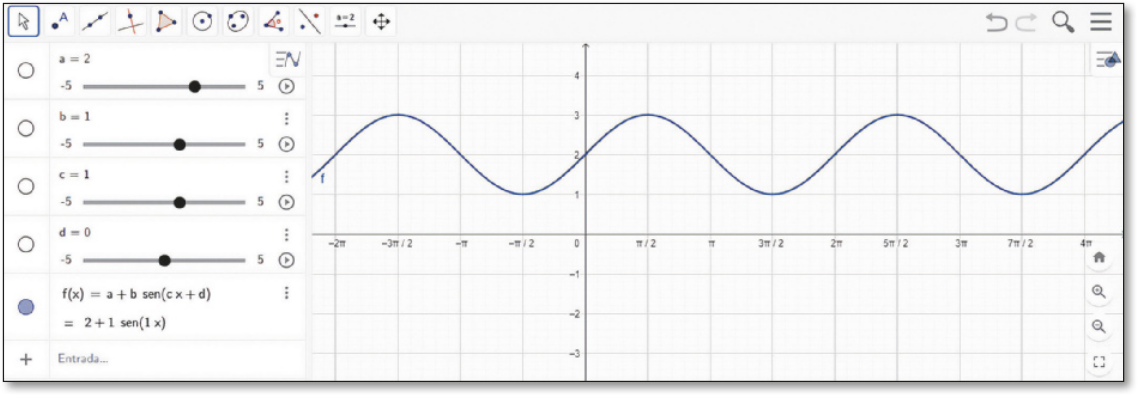
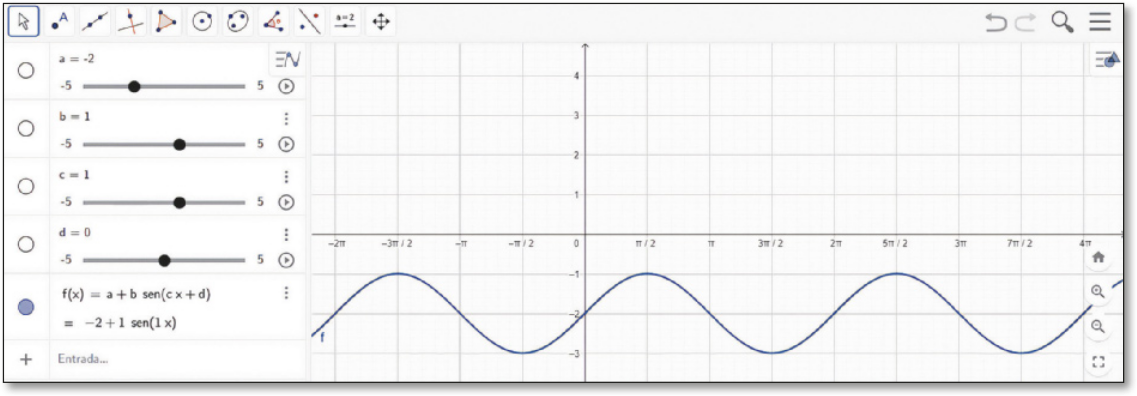
Agora, manipule os controles deslizantes para observar o quê acontece com o gráfico e faça o quê se pede nas atividades a seguir.
1. dêz-creva o quê acontece com o gráfico da função dada por f(x) = a + b ⋅ sen (cx + d) ao:
a) se manterem os parâmetros b, c e d fixos em b = 1, c = 1 e d = 0 e deslizar o contrôle do parâmetro a para valores positivos e negativos.
Para valores positivos, o gráfico se desloca verticalmente a unidades para cima e, para valores negativos, o gráfico se desloca verticalmente a unidades para baixo.
b) se manterem os parâmetros a, c e d fixos em a = 0, c = 1 e d = 0 e deslizar o contrôle do parâmetro b para valores positivos.
Os valores de mássimo e mínimo da função se alteram. Porém, o período permanéce o mesmo.
c) se manterem os parâmetros a, b e d fixos em a = 0, b = 1 e d = 0 e deslizar o contrôle do parâmetro c para valores positivos.
Ocorrem alterações no período da função.
d) se manterem os parâmetros a, b e c fixos em a = 0, b = 1 e c = 1 e deslizar o contrôle do parâmetro d para valores positivos e negativos.
Para valores positivos, o gráfico se desloca horizontalmente para a esquerda e, para valores negativos, o gráfico se desloca horizontalmente para a direita.
2. Em uma nova janela do GeoGebra, construa o gráfico da função dada por g(x) = a + b ⋅ cos (cx + d) e repita os itens da atividade 1 para essa função. Verifique se as alterações nos parâmetros a, b, c e d interferem da mesma maneira no gráfico da função cosseno.
Espera-se quê os estudantes concluam quê os parâmetros interferem da mesma maneira no gráfico da função.
Página duzentos e doze
ATIVIDADES COMPLEMENTARES
1. (UEA-AM) Considere a função f(x) = 4 ⋅ sen (2x). O valor de f() é
a)
b)
c)
d)
e)
alternativa c
2. (UECE) Considere as funções reais de variável real definidas por f(x) = sen (1 + )(pi)" e g(x) = sen(1 − )(pi)". Se K = f(9) ⋅ g(9), então, pode-se afirmar corretamente quê o valor de K é igual a
a) 1.
b) −1.
c) 0.
d) −2.
alternativa b
3. (Uneb-BA) Admitindo-se quê o peso de determinada pessoa, ao longo de um ano, possa sêr modelado pela função P(t) = 65 − 5cos (()(pi)"), em quê t = 1, …, 12 corresponde aos meses de janeiro a dezembro e, considerando = 1,7, pode-se estimar quê, de maio até agosto, o peso dessa pessoa
01) diminuiu 4,50 kg.
02) aumentou 4,50 kg.
03) diminuiu 6,75 kg.
04) aumentou 6,75 kg.
05) diminuiu 7,56 kg.
alternativa 03
4. (UEPA) A altura das ondas em determinado trecho de um oceano varia de acôr-do com a expressão H(t) = 5 + 3 ⋅ sen (2t), onde t (em segundo) é o tempo e H (em metro), a altura dessas ondas. A altura mássima (crista da onda) atingida por essas ondas é de:
a) 9 m
b) 3 m
c) 5 m
d) 6 m
e) 8 m
alternativa e
5. (UEG-GO) Seja f(x) uma função definida para todos os números reais. Dada a expressão f(x) cos( + (pi)") + 3 = f(x − )(x − (pi)"sen(x)), o valor de f() é
a) (pi)"2 − 1
b) 0
c) (pi)" −
d) (pi)" + 3
e)
alternativa e
6. (UEG-GO) Duas ondas sonóras são descritas pelas funções y = 1 + sen x e y = 1 − cos x. Considerando 0 ≤ x ≤ 2(pi)", os gráficos dessas funções se interceptam em:
a) e
b) e
c) e
d) e
e) e
alternativa e
7. (UECE) No plano, com o sistema de coordenadas cartesianas usual, a interseção dos gráficos das funções reais de variável real f(x) = sen (x) e g(x) = cos (x) são, para cada número inteiro k, os pontos P(xk, yk). Então, os possíveis valores para yk são
a) e .
b) e .
c) e .
d) e .
alternativa a
8. (UFRGS-RS) Um ponto A, quê se movimenta sobre uma circunferência, tem sua posição p(t), considerada na vertical, no instante t, descrita pela relação p(t) = 100 − 20sen (t), para t ≥ 0. Nesse caso, a medida do diâmetro dessa circunferência é:
a) 30
b) 40
c) 50
d) 80
e) 120
alternativa b
9. (UFRGS-RS) Considere a função real de variável real f(x) = 3 − 5sen (2x + 4). Os valores de mássimo, mínimo e o período de f(x) são, respectivamente,
a) −2, 8, (pi)"
b) 8, −2, (pi)"
c) (pi)", −2, 8
d) (pi)", 8, −2
e) 8, (pi)", −2
alternativa b
10. (UECE) Se M e m são respectivamente os valores mássimo e mínimo quê a função f: ℝ → ℝ definida por f(x) = 3 sen2 x + 7 cos2 x póde assumir, então o produto M ⋅ m é igual a
a) 24.
b) 15.
c) 21.
d) 18.
alternativa c
11. (PUC-SP) A imagem da função f: ℝ → ℝ definida por f(x) = 2 − 3 cos x é o intervalo:
a) [−1; 2]
b) [−1; 0]
c) [3; 5]
d) [2; 3]
e) [−1; 5]
alternativa e
Página duzentos e treze
12. (UFES) O período e a imagem da função f(x) = 5 − 3 cos() são, respectivamente:
a) 2(pi)" e [−1, 1]
b) 2(pi)" e [2, 8]
c) 2(pi)"2 e [2, 8]
d) 2(pi)" e [−3, 3]
e) 2(pi)"2 e [−3, 3]
alternativa c
13. (UFRGS-RS) Se f(x) = a + b ⋅ sen x tem como gráfico
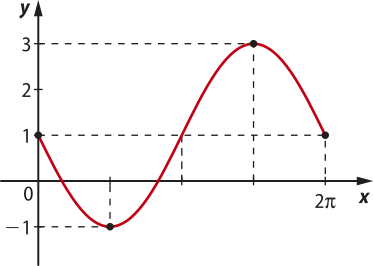
Então:
a) a = −2 e b = 1
b) a = −1 e b = 2
c) a = 1 e b = −1
d) a = 1 e b = −2
alternativa d
14. (Enem/MEC) Um cientista, em seus estudos para modelar a pressão arterial de uma pessoa, utiliza uma função P(t) = A + B cos (kt), em quê A, B e k são constantes reais positivas e t representa a variável tempo, medida em segundo. Considere quê um batimento cardíaco representa o intervalo de tempo entre duas sucessivas pressões mássimas.
Ao analisar um caso específico, o cientista obteve os dados:
Pressão mínima |
78 |
|---|---|
Pressão mássima |
120 |
Número de batimentos por minuto |
90 |
A função P(t) ôbitída, por êste cientista, ao analisar o caso específico foi:
a) P(t) = 99 + 21cos (3(pi)"t)
b) P(t) = 78 + 42cos (3(pi)"t)
c) P(t) = 99 + 21cos (2(pi)"t)
d) P(t) = 99 + 21cos (t)
e) P(t) = 78 + 42cos (t)
alternativa a
15. (Fuvest-SP)
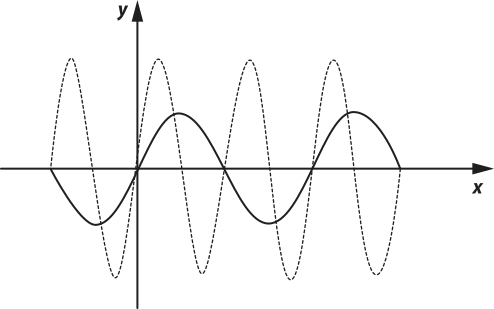
Admitindo quê a linha pontilhada represente o gráfico da função f(x) = sen (x) e quê a linha contínua represente o gráfico da função g(x) = (alfa)" sen ((beta)"x), segue quê:
a) 0 < (alfa)" < 1 e 0 < (beta)" < 1.
b) (alfa)" > 1 e 0 < (beta)" < 1.
c) (alfa)" = 1 e (beta)" > 1.
d) 0 < (alfa)" < 1 e (beta)" > 1.
e) 0 < (alfa)" < 1 e (beta)" = 1.
alternativa a
16. (Enem/MEC) Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Lás Végas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:
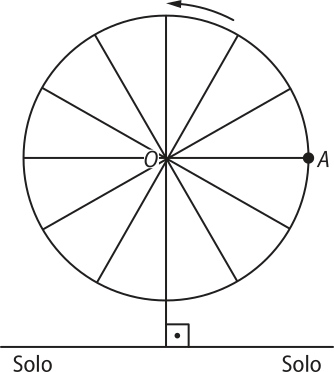
Disponível em: https://livro.pw/hjmki. Acesso em: 22 abr. 2014 (adaptado)
A partir da posição indicada, em quê o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função quê descreve a altura do ponto A, em relação ao solo, em função de t.
Página duzentos e quatorze
Após duas voltas completas, f tem o seguinte gráfico:
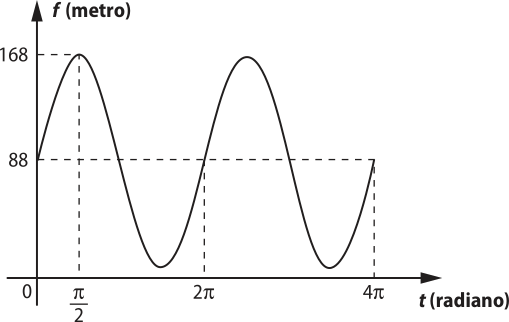
A expressão da função altura é dada por:
a) f(t) = 80sen (t) + 88
b) f(t) = 80cos (t) + 88
c) f(t) = 88cos (t) + 168
d) f(t) = 168sen (t) + 88cos (t)
e) f(t) = 88sen (t) + 168cos (t)
alternativa a
Saiba quê...
Em 2021, foi inaugurada a roda-gigante Ain Dubai, em Dubai, nos Emirados Árabes, com 250 m de altura, tirando o posto da High Roller de maior roda-gigante do mundo.
17. (UFPE) Admita quê a pressão arterial P(t) de uma pessoa no instante t, medido em segundo, seja dada por: P(t) = 96 + 18 cos (2(pi)"t), t ≥ 0.
Considerando esses dados, analise a veracidade das seguintes afirmações:
I. O valor mássimo da pressão arterial da pessoa é 114.
II. O valor mínimo da pressão arterial da pessoa é 78.
III. A pressão arterial da pessoa se repete a cada segundo, ou seja, P(t + 1) = P(t), para todo t ≥ 0.
IV. Quando t = de segundo, temos P() = 105.
V. O gráfico de P(t) para 0 ≤ t ≤ 4 é:
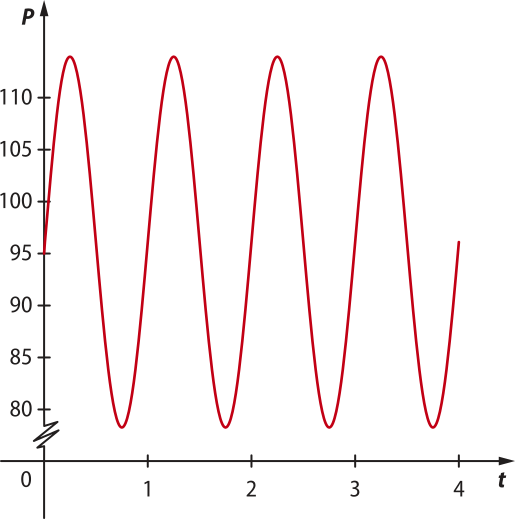
I: V; II: V; III: V; IV: F; V: F
18. (UEFS-BA) Em um parque de diversões, uma roda-gigante de raio r = 10 m, tendo 12 cadeiras igualmente espaçadas ao longo de seu perímetro, faz uma volta completa em 30 segundos. Além díssu, o ponto mais baixo atingido ao longo do percurso circular está a 0,5 m do solo. cérto dia, depois de todos os assentos estarem ocupados, o assento 1 se encontrava na posição indicada na figura, quando a roda começa a girar no sentido anti-horário.
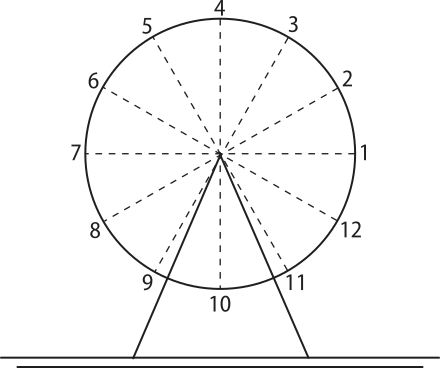
Sendo a distância dêêsse assento ao solo, t segundos após a roda ter começado a girar, dada pela expressão D(t) = M + N sen ((alfa)"t), (alfa)" > 0, é correto afirmar quê M − N é igual a
a) cos (5(alfa)")
b) sen (5(alfa)")
c) cos (10(alfa)")
d) sen (10(alfa)")
e) cos (15(alfa)")
alternativa a
Página duzentos e quinze
19. (UECE) O valor da soma sen(x) + sen(x + (pi)") + sen(x + 2(pi)") + sen(x + 3(pi)") + … + sen(x + n(pi)"), onde n é um número natural par e menor do quê 100 é:
a) sen (x)
b) cos (x)
c) 0
d) 1
alternativa a
20. (UEG-GO) Resolvendo-se a equação sen 2x = 1, encontramos a 1ª determinação positiva de x igual a
a)
b)
c)
d)
e)
alternativa c
21. (IFPR) Em uma determinada região litorânea, a maré oscila segundo a função h(t) = 3 − 2 sen(), sêndo h a altura em metros, quê a maré atinge no tempo t em horas, medido a partir de 6 h da manhã. Uma embarcação, quê se encontra encalhada às 11 h da manhã, precisa de uma profundidade mínima de 2 metros para navegar. Assinale a alternativa quê apresenta quantas horas os tripulantes dessa embarcação ainda terão quê esperar para prosseguirem viagem.
a) 4 h.
b) 5 h.
c) 6 h.
d) 7 h.
alternativa b
22. (Enem/MEC) Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r kilometros de distância do centro da Terra. Quando r assume seus valores mássimo e mínimo, diz-se quê o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha quê, para esse satélite, o valor de r em função de t seja dado por r(t) =
Um cientista monitora o movimento dêêsse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir quê, periodicamente, S atinge o valor de
a) 12.765 km.
b) 12.000 km.
c) 11.730 km.
d) 10.965 km
e) 5.865 km.
alternativa b
PARA REFLETIR
Nas páginas de abertura, foram apresentadas algumas informações sobre a Lua e sobre como o seu ciclo é um exemplo de fenômeno periódico. Ao longo do Capítulo, estudamos quê fenômenos como esse podem sêr modelados por funções periódicas, como a função seno e a função cosseno. Você conseguiu reconhecer essa relação? Se sim, qual é a importânssia dela? Se não, retome o texto de abertura do Capítulo e as perguntas iniciais. Se possível, pesquise também em livros e sáites a modelagem de fenômenos periódicos.
Estudamos também o quê são funções periódicas (mais especificamente as funções trigonométricas seno e cosseno) e estudamos seus gráficos e suas aplicações na modelagem de fenômenos oscilatórios.
Além díssu, estudamos as equações trigonométricas.
Vamos refletir a respeito das aprendizagens do Capítulo 6:
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
Respostas pessoais.
• Explique o quê significa dizêr quê uma função é periódica.
Resposta esperada: É uma função cujo valor se repete após determinado intervalo.
• Quais exemplos de situações ou fenômenos podem sêr modelados utilizando a função seno e a função cosseno?
Algumas respostas possíveis: O movimento pendular, o movimento lunar e outros fenômenos oscilatórios.
• Qual é o valor mássimo e o mínimo da função f(x) = sen x? E da função g(x) = cos x?
1 e −1, tanto para f(x) quanto para g(x)
Página duzentos e dezesseis
