CAPÍTULO
7
ÁREAS
No Brasil, assim como em outros países do mundo, o acesso à moradia ainda é um desafio para muitas pessoas. Inúmeras famílias não têm condições dignas de habitação e, muitas vezes, com poucos recursos disponíveis, acabam vivendo em locais inadequados. As organizações não governamentais (ônguis) são entidades sem fins lucrativos quê, entre outros propósitos, auxiliam na captação de verbas e na distribuição do orçamento para auxiliar as camadas menos favorecidas da população.
Algumas dessas ônguis promóvem campanhas específicas voltadas para esse fim e realizam projetos para a construção de moradias populares e para a reconstrução de lares de pessoas quê sofreram com alguma catástrofe natural, como enchentes, terremotos, furacões e tsunâmis.
Muitos conjuntos habitacionais concebidos por meio de programas sociais, governamentais ou não, seguem uma série de especificações quê ajudam a padronizar as construções. Entre essas especificações, encontram-se, por exemplo, a área útil da residência (espaço interno sem considerar a área das paredes) e as dimensões de tanques, pias, corredores e cômodos. Essas medidas são muito importantes para garantir conforto e acessibilidade aos moradores.
Página duzentos e dezessete
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Ver as Orientações para o professor.
1. Vocês já ouviram falar sobre trabalhos desenvolvidos por ônguis? Pesquisem se, na região onde vocês moram, há alguma ôngui quê se dedique à construção ou à reforma de moradias populares.
2. Vocês acham relevante quê haja especificações para a construção de moradias de programas sociais? O quê poderia acontecer, na opinião de vocês, se as dimensões das moradias pudessem sêr livres?
3. Vocês já fizeram algum trabalho voluntário ou participaram de uma organização quê ajuda outras pessoas? Se estiveram ou estão envolvidos nesse tipo de ação, compartilhem suas experiências com os côlégas. Caso não tênham participado, vocês têm vontade de fazer parte de projetos de voluntariado? Debatam a importânssia dêêsse tipo de trabalho para a ssossiedade.
4. Como vocês fariam para calcular a área útil de uma sala quadrada? E a de um quarto retangular?

Página duzentos e dezoito
Introdução
Na abertura dêste Capítulo, compreendemos como algumas ônguis auxiliam na construção de moradias para famílias sem recursos. Nesse processo de construção ou na reforma de um imóvel, muitas atividades envolvem medições e cálculos de áreas e perímetros. Neste Capítulo, estudaremos o cálculo da área de algumas figuras planas.
As áreas quê precisamos determinar no dia a dia nem sempre são regiões poligonais, por exemplo, a piscina cuja vista aérea é mostrada na fotografia desta página ocupa uma região não poligonal no deck.
Para calcular a área ocupada pela superfícíe dessa piscina, pode-se considerar o contôrno dela em uma malha quadriculada e tomar a área de um quadradinho da malha como unidade de área.
Inicialmente, contamos na malha a quantidade de quadradinhos quê estão inteiramente contidos na região cuja área pretendemos determinar e dizemos quê essa é a área por falta (Sfalta)dessa região. Na figura com legenda área por falta, temos Sfalta = 47 unidades de área (u.a.). Note quê há espaços dentro do contôrno cuja área é desprezada nessa contagem. Isso significa quê a área real da figura é maior do quê a área por falta.
Em seguida, contamos na malha a quantidade de quadradinhos quê estão inteiramente ou parcialmente contidos na região cuja área pretendemos determinar e dizemos quê essa é a área por excésso (Sexcésso)dessa região. Na figura com legenda área por excésso, temos Sexcésso = 88 u.a. Note quê há espaços fora do contôrno cuja área é considerada nessa contagem. Isso significa quê a medida da área real da figura é menor do quê a medida da área por excésso.

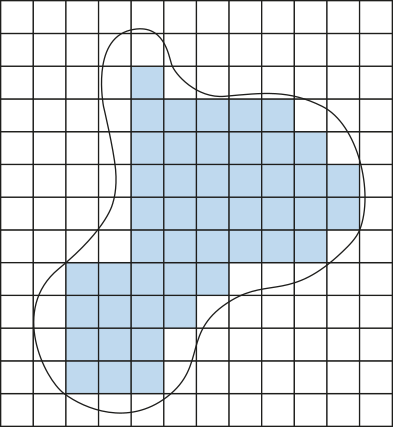
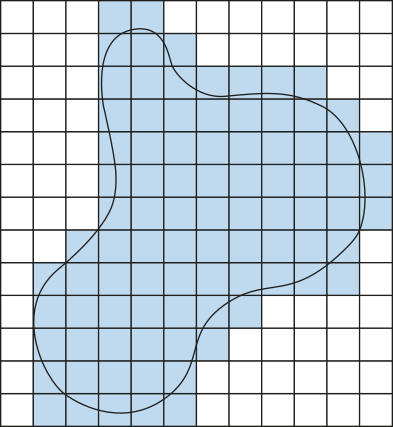
Para obtêr a área aproximada da superfícíe da piscina, podemos calcular a média aritmética entre a área por falta e a área por excésso. Assim, temos 67,5 u.a., pois:
S = ⇒ S = = 67,5
Quanto menóres forem as unidades de área (u.a.), correspondentes aos quadradinhos da malha nesse exemplo, mais precisas se tornam as áreas por falta e por excésso e melhor será a aproximação, uma vez quê a área interna desprezada na medida da área por falta e a área externa considerada na medida da área por excésso serão menóres.
Página duzentos e dezenove
Área de polígonos
A grafiteira Gugie Cavalcanti (1993-) é uma artista brasileira quê retrata, em suas obras, o quêstionamento sobre os processos de criação de afetos, como nos sensibilizamos na construção das relações e do estar no mundo. Observe o mural "Triunfo " que está localizado em Santa Catarina. Esse mural foi pintado por Gugie, no ano de 2024, e ocupa uma superfícíe retangular da parede lateral do Edifício Dona Izabel, no centro de Florianópolis. Com dimensões de 21 m de altura por 8 m de largura, a artista retrata akilo quê, na visão dela, é o triunfo verdadeiro: "ver a mãe de um amigo no centro da cidade com a neta no colo".

Para determinar a área do mural "Triunfo", precisamos retomar o cálculo da área de um retângulo, assunto quê foi estudado no Ensino Fundamental. A seguir, acompanhe a maneira de se determinar a área dêêsse e de outros polígonos.
Pense e responda
Como você determinaria a área do muro da fachada de sua escola?
Resposta pessoal.
Área do retângulo
A área S de um retângulo de lados de medidas b e h, com b e h reais positivos, é dada pelo produto da medida da base b pela medida da altura h.
S = b ⋅ h

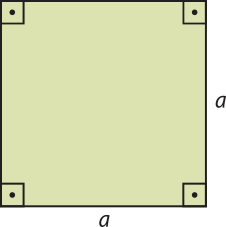
Área do quadrado
Todo quadrado é um retângulo com lados de medidas iguais. Logo, a área S de um quadrado de lado de medida a é igual ao produto das medidas de dois de seus lados.
S = a ⋅ a = a2
Página duzentos e vinte
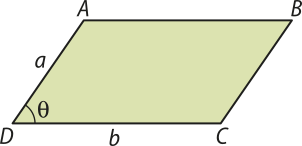
Área do paralelogramo
Vamos considerar um paralelogramo ABCD cuja base méde b e cuja altura méde h, conforme a figura.
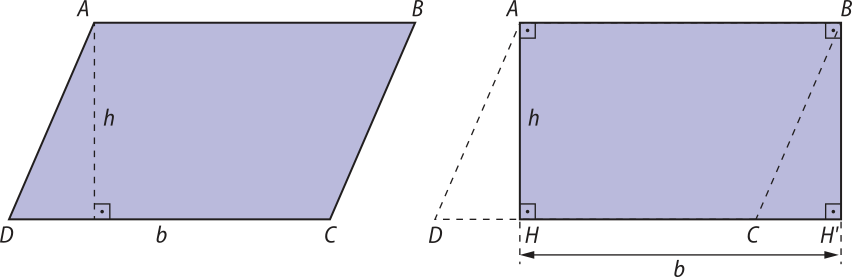
Projetando ortogonalmente os vértices A e B dêêsse paralelogramo sobre a reta quê passa pêlos pontos D e C, obtemos os pontos H e H(minutos)", respectivamente, determinando o retângulo ABH(minutos)"H, como indicado na figura. Os triângulos AHD e BH(minutos)"C são congruentes pelo caso LAAO (Lado, Ângulo, Ângulo Oposto). Desse modo, eles têm a mesma área.
Logo, a área S do paralelogramo ABCD é igual à área do retângulo ABH(minutos)"H:
S = b ⋅ h
O resultado obtído independe do lado escolhido para sêr a base do paralelogramo. Caso tivéssemos escolhido outro lado do paralelogramo como base e sua respectiva altura, o resultado seria o mesmo.
Pense e responda
Partindo da expressão S = b ⋅ h para o cálculo da área do paralelogramo, como chegar à expressão S = b ⋅ a ⋅ sen θ?
Ver as Orientações para o professor.
Fórmula trigonométrica para o paralelogramo
A área de um paralelogramo também póde sêr calculada em função das medidas de dois de seus lados consecutivos e da medida do ângulo formado por eles.
Considerando o paralelogramo ABCD, sua área S é dada por:
S = b ⋅ a ⋅ sen θ
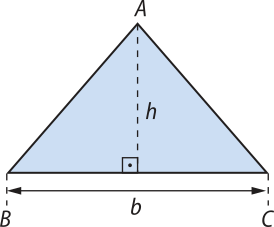
Área do triângulo
Vamos considerar um triângulo ABC cuja base méde b, e a altura relativa a essa base méde h.
A área S do triângulo ABC é igual à mêtáde do produto da medida da base pela altura relativa a essa base.
S =
Página duzentos e vinte e um
Fórmula de Heron
Outra maneira de calcular a área de um triângulo qualquer é a partir da medida de seus três lados.
Seja um triângulo ABC, em quê a, b e c são as medidas dos lados, como mostra a figura.
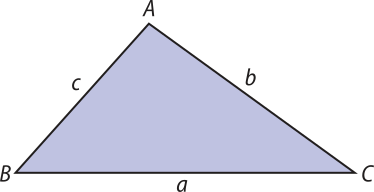
Sendo p = o semiperímetro do triângulo ABC, a área S do triângulo é dada por:
S =
Essa expressão para o cálculo da área de um triângulo é conhecida como fórmula de Heron, ou fórmula de Herão.
Saiba quê...
Heron de Alexandria foi um matemático grego quê viveu entre, aproximadamente, 150 a.C. e a segunda mêtáde do século I d.C. Ele ficou conhecido pela fórmula quê calcula a área de um triângulo, a qual leva seu nome. O livro em quê apresenta essa fórmula, A métrica, só foi encontrado em 1896.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 5. ed. Campinas: Editora da Unicamp, 2011. p. 194, 205.
Para acessar
• OLIMPÍADA BRASILEIRA DE MATEMÁTICA DAS ESCOLAS PÚBLICAS. Fórmula de Herão. In: OBMEP. Clubes de Matemática da OBMEP. Rio de Janeiro, 2019. Disponível em: https://livro.pw/jzntx. Acesso em: 4 set. 2024.
Esse línki apresenta várias demonstrações da fórmula de Heron.
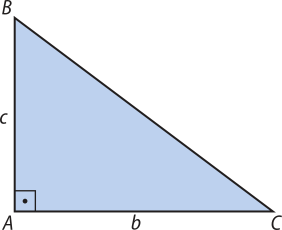
Área do triângulo retângulo
Em um triângulo retângulo ABC, o cateto é a altura relativa ao lado , e o cateto é a altura relativa ao lado AB. Assim, sêndo AB = c, AC = b e S a área do triângulo retângulo ABC, temos:
S =
Área do triângulo equilátero
Em um triângulo equilátero, todos os lados são congruentes, todos os ângulos internos são congruentes e toda altura é também bissetriz interna e mediana. Vamos considerar um triângulo equilátero ABC, como mostra a figura.
A área S do triângulo equilátero ABC é dada por:
S =
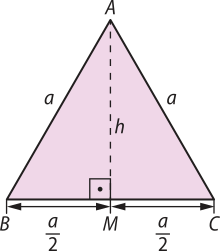
Pense e responda
Partindo da expressão S = para o cálculo da área do triângulo, como chegar à expressão S = para o cálculo da área do triângulo equilátero?
DICA: Use o teorema de Pitágoras para determinar a medida da altura h em função do lado a.
Ver as Orientações para o professor.
Página duzentos e vinte e dois
Fórmula trigonométrica para o triângulo
Assim como ocorre com os paralelogramos, a área de um triângulo também póde sêr calculada em função das medidas de dois de seus lados consecutivos e da medida do ângulo formado por eles.
Considerando o triângulo ABC, sua área S é dada por:
S =
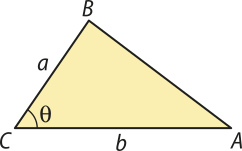
Conforme estudamos no Capítulo 5, essa é uma maneira de calcular a área de um triângulo qualquer.
Área do losango
Todo losango é um paralelogramo cujas medidas dos lados são iguais e as diagonais d e D são perpendiculares entre si.
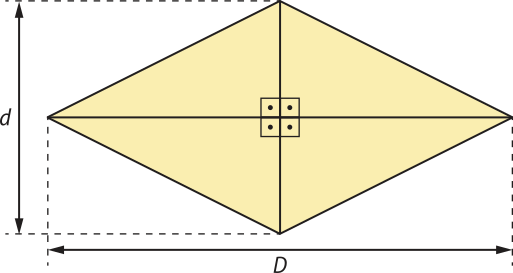
Saiba quê...
Em um losango:
• os ângulos opostos são congruentes;
• as diagonais são bissetrizes dos ângulos internos;
• as diagonais se intersectam no ponto médio.
Observe quê o losango póde sêr decomposto em quatro triângulos congruentes de mesma área. Assim, a área S de um losango é dada pelo produto de 4 pela área de um dêêsses quatro triângulos:
S = 4 ⋅ S(triângulo)" = 4 ⋅
Portanto, a área de um losango é igual à mêtáde do produto das medidas das diagonais, ou seja:
S =
Área do trapézio
Vamos considerar um trapézio cujas base maior, base menor e altura médem B, b e h, respectivamente. Traçando uma diagonal nesse trapézio, obtemos dois triângulos: um de base B e altura h e outro de base b e altura h, como mostra a figura.
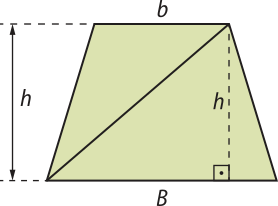
Página duzentos e vinte e três
A área S do trapézio é a soma das áreas dêêsses dois triângulos:
S =
Portanto, a área de um trapézio é igual à mêtáde do produto da soma das medidas das bases pela medida da altura, ou seja:
S =
Para acessar
• MORAES, Máike. Teorema de Pick. [S. l.]: GeoGebra, c2024. Disponível em: https://livro.pw/gmfza. Acesso em: 4 set. 2024.
Esse línki apresenta o teorema de Pick, quê permite calcular a área de um polígono qualquer em um geoplano.
FÓRUM
Você sabe o quê é uma horta comunitária?
Hortas comunitárias são áreas públicas nas quais são plantadas hortaliças, legumes e alguns frutos para consumo dos moradores locais. Nos espaços urbanos, existem muitas áreas públicas inutilizadas, quê não têm uma destinação definida e acabam se tornando depósitos de entulhos e focos de contaminação, enquanto muitas famílias menos favorecidas não têm acesso a alimentos saudáveis. Por meio da implantação de hortas comunitárias, o solo urbano passa a sêr aproveitado para a produção de alimentos livres de agrotóxicos, quê servirão para alimentar essas famílias, minimizando os problemas de falta de alimentos e de carência nutricional e gerando renda com a venda do excedente. Muitas hortas comunitárias são construídas por estudantes em ambientes escolares ou próximas a escolas.
Fonte dos dados: OLIVEIRA, Giovanna B. de; CALVO, Paloma A. N.; CASTRO, Patrícia G. de. Horticultura urbana. Boletim de inovação e sustentabilidade, São Paulo, v. 1, p. 1-43, 2018. Disponível em: https://livro.pw/pmzqv. Acesso em: 4 set. 2024.

![]() Após ler o texto, reúna-se a um colega, e façam o quê se pede a seguir.
Após ler o texto, reúna-se a um colega, e façam o quê se pede a seguir.
• Inicialmente, respondam às kestões: vocês conhecem alguma horta comunitária? Já participaram da organização e da manutenção dêêsse tipo de projeto?
• Em seguida, iniciem uma roda de conversa com a turma e com o professor e debatam os benefícios de uma horta comunitária para a comunidade local e seus impactos sociais e na saúde.
Respostas pessoais.
Página duzentos e vinte e quatro
ATIVIDADES RESOLVIDAS
1. As bases de um trapézio médem 10 cm e 2,8 cm. Se a medida de cada um dos outros dois lados é 6 cm, qual é a área dêêsse trapézio?
Resolução
Como os lados não paralelos têm medidas iguais, o trapézio é isósceles.
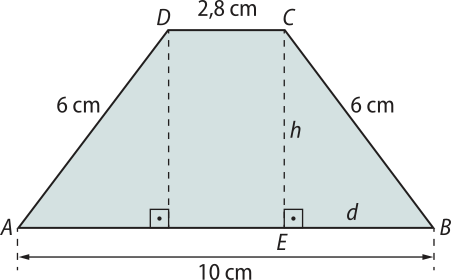
Calculando a medida d no triângulo CEB, temos:
d = = 3,6
Logo, d = 3,6 cm.
Aplicando o teorema de Pitágoras no triângulo CEB, temos:
h2 + 3,62 = 62 ⇒ h2 = 23,04
Logo, h = 4,8 cm.
Cálculo da área do trapézio:
S = = 30,72
Portanto, S = 30,72 cm2.
2. Calcule a área do triângulo ABC.

Resolução
A base do triângulo méde 8 cm, pois 10 − 2 = 8, e a altura, 4 cm, pois 6 − 2 = 4. Logo:
S = ⇒ S = = 16
Assim, a área do triângulo ABC é 16 cm2.
3. Determine a área do quadrilátero ILHA representado a seguir.
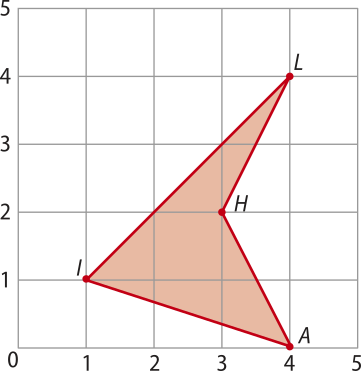
Resolução
Inicialmente, observamos quê o quadrilátero é não convexo.
Precisamos, então, decompor a figura em polígonos cuja área sabemos calcular. Uma possibilidade é considerar os triângulos ILA e LHA.
A área do quadrilátero ILHA é a área do triângulo ILA menos a área do triângulo LHA.
No triângulo ILA, considerando-se a base como o lado , a altura relativa a esse lado póde sêr ôbitída com o auxílio da malha quadriculada e vale 3 u.c. (unidades de comprimento). Assim:
SILA = = 6
Logo, SILA = 6 u.a. (unidades de área).
Usamos raciocínio análogo no triângulo LHA e determinamos sua área:
SLHA = = 2
Logo, SLHA = 2 u.a.
De posse dêêsses valores, conseguimos determinar a área do quadrilátero ILHA:
SILHA = SILA − SLHA = 6 − 2 = 4
Portanto, a área do quadrilátero ILHA é 4 u.a.
Página duzentos e vinte e cinco
ATIVIDADES
1. Calcule a área das figuras a seguir.
a) 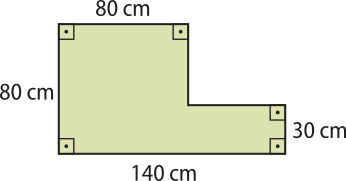
8.200 cm2
b) 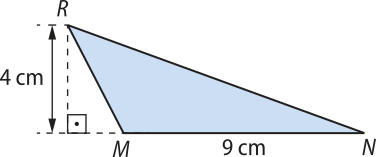
18 cm2
c) 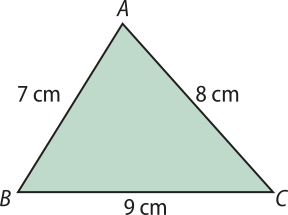
12 cm2
d) 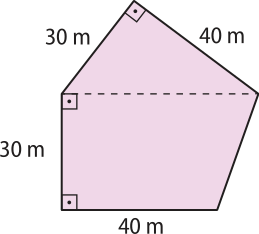
1.950 m2
2. Conforme observamos anteriormente, neste Capítulo, as dimensões do mural “Triunfo”, da grafiteira Gugie Cavalcanti, são 21 m de altura e 8 m de largura. Qual é a área, em métro quadrado, ocupada por esse mural?
168 m2
3. Considere a figura representada na malha quadriculada a seguir e considere quê cada quadradinho tem 1 cm de lado.
Calcule:
a) A área da figura por falta.
100 cm2
b) A área da figura por excésso.
148 cm2
c) Uma medida aproximada da área da figura.
124 cm2
d) Qual é o êrro percentual entre a medida aproximada calculada no item c e a medida real da área dessa figura, quê, com aproximação até décimos, é 119,6 cm2?
aproximadamente 3,68%
4. Se aumentarmos a medida do lado de um quadrado em 4 cm, sua área será aumentada em 56 cm2. Qual é a medida da diagonal do quadrado inicial?
5 cm
5. O quê ocorre com a área de um quadrado se aumentarmos em 20% a medida de seu lado?
aumenta 44%
6. (Vunesp-SP) Uma parede de 350 cm de altura e 500 cm de comprimento será revestida de azulejos quadrados iguais. Desprezando-se a necessidade de deixar espaço entre os azulejos e supondo-se quê não haverá perdas provenientes do kórti deles:
a) determine o número de azulejos de 20 cm de lado necessários para revestir a parede;
437,5 azulejos
b) encontre a maior dimensão de cada peça de azulejo para quê não haja necessidade de cortar nenhum deles.
50 cm
7. (Enem/MEC) Um agricultor utilizava toda a área de uma região plana, em formato retangular, com 50 m de largura e 240 m de comprimento, para o plantio de mudas. Seguindo recomendações técnicas, cada muda é plantada no centro de uma pequena região retangular de 10 cm de largura por 20 cm de comprimento.
Esse agricultor decidiu ampliar a área destinada ao plantio de mudas, utilizando agora um terreno, também plano, em formato retangular, com 100 m de comprimento por 200 m de largura. As mudas deverão sêr plantadas respeitando-se as mesmas recomendações técnicas.
Com o aumento da área destinada ao plantio, a quantidade mássima de mudas quê poderão sêr plantadas a mais é
a) 100.000.
b) 400.000.
c) 600.000.
d) 1.000.000.
e) 1.600.000.
alternativa b
Página duzentos e vinte e seis
8. Considere o retângulo ABCD a seguir.
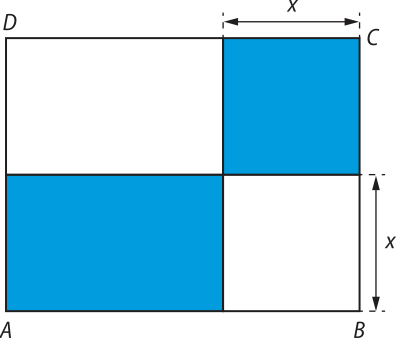
Sabendo-se quê AB = 27 cm e AD = 21 cm, calcule o valor de x, de modo quê a soma das áreas dos retângulos em azul seja a maior possível.
12 cm
9. (Enem/MEC) Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1 m, conforme a figura a seguir.
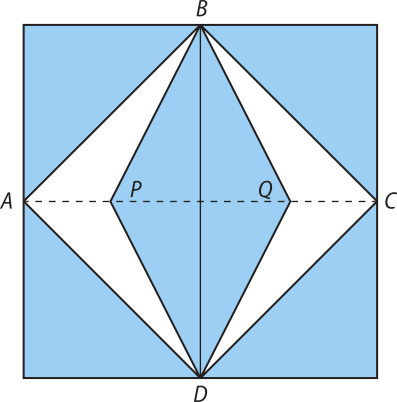
Nesta figura, os pontos A, B, C e D são pontos médios dos lados do quadrado e os segmentos e médem da medida do lado do quadrado. Para confeksionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, quê custa R$ 30,00 o m2, e outro para a parte mais clara (regiões ABPDA e BCDQB), quê custa R$ 50,00 o m2.
De acôr-do com esses dados, qual é o custo dos materiais usados na fabricação de um vitral?
a) R$ 22,50
b) R$ 35,00
c) R$ 40,00
d) R$ 42,50
e) R$ 45,00
alternativa b
10. (Udesc) Maria precisa comprar piso para o seu apartamento, cuja planta baixa póde sêr vista na figura. Devido aos rekórtis necessários para a colocação do piso, o mestre de obras solicitou 10% a mais da metragem total do apartamento.
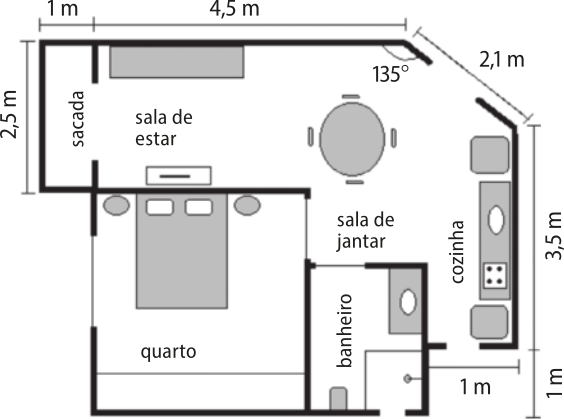
De acôr-do com as instruções do mestre de obras, Maria deve comprar aproximadamente:
a) 38 m2
b) 37 m2
c) 40 m2
d) 39 m2
e) 42 m2
alternativa c
11. (UFRGS-RS) No retângulo ABCD, representado na figura abaixo, os três ângulos destacados com vértice em C são iguais.
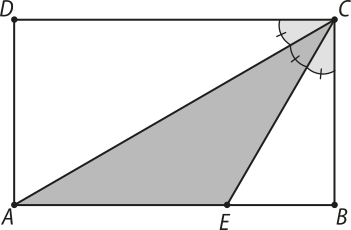
A área do triângulo sombreado AEC, em relação à área total do retângulo, corresponde a:
a) .
b) .
c) .
d) .
e) .
alternativa b
12. ![]() Reúna-se a dois côlégas, e elaborem uma proposta de construção de uma horta comunitária na sua escola. Essa proposta deve apresentar:
Reúna-se a dois côlégas, e elaborem uma proposta de construção de uma horta comunitária na sua escola. Essa proposta deve apresentar:
Ver as Orientações para o professor.
• a indicação do local onde a horta poderia sêr implementada na escola, bem como os alimentos e temperos quê poderiam sêr cultivados;
• a planta baixa da horta comunitária, com cálculos de área para cada cultivo;
• os cálculos de perímetro para a construção de cercas em locais pertinentes.
Página duzentos e vinte e sete
Área do círculo e de suas partes
Atualmente, a agricultura tem recorrido a equipamentos cada vez mais tecnológicos para aumentar e melhorar a produtividade. O sistema chamado de pivô central, quê faz irrigação de culturas, é um deles. Trata-se de uma máquina quê irriga a plantação, cobrindo uma área circular do campo considerado.

Para assistir
• ENTENDA como o braço de um pivô central de irrigação gira. [S. I.]: glôboplay, c2024. 1 vídeo (3 min). Publicado pelo canal Globo Rural. Disponível em: https://livro.pw/phxbj. Acesso em: 11 set. 2024.
Esse vídeo mostra como funciona o sistema de irrigação de um pivô central.
No exemplo apresentado no vídeo do boxe Para assistir, o pivô central tem um braço de 580 m e é capaz de irrigar uma área de 100 hectares. Para estabelecer essa relação entre as dimensões do pivô central e a área atendida, é preciso saber calcular a área de um círculo. É o quê compreenderemos a seguir.
Área do círculo
Vamos considerar um círculo cujo raio méde r. Dividindo-o em um número par de partes iguais, como feito a seguir, podemos observar quê essas partes podem formár uma figura quê lembra um paralelogramo. Quanto mais aumentarmos a quantidade dessas partes quê dividem o círculo, mais a base da figura formada se aproximará de (pi)"r, ou seja, da mêtáde do comprimento da circunferência.
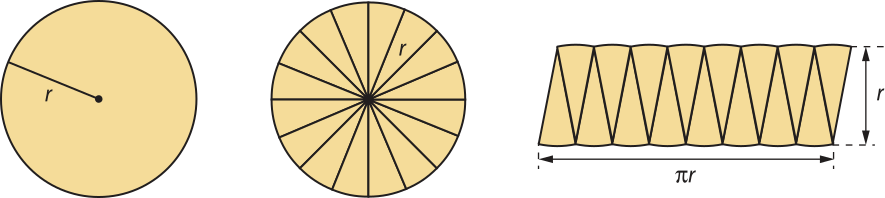
Dessa forma, quanto mais aumentarmos a quantidade de partes, mais a área da figura se aproximará da área de um paralelogramo com base de medida (pi)"r e altura de medida r.
Portanto, ao aumentar indefinidamente a quantidade de partes quê dividem o círculo, a área do círculo e a da figura vão coincidir, concluindo-se quê a área do círculo é dada por: S = (pi)"r ⋅ r = (pi)"r2
Logo, a área de um círculo de raio r é dada por:
S = (pi)"r2
Página duzentos e vinte e oito
Área do setor circular
Denominamos setor circular a região do círculo delimitada por um de seus ângulos centrais.
Vamos calcular a área de um setor circular relativo a um ângulo central (alfa)", montando uma regra de três simples quê relacione a medida do ângulo central e a área:
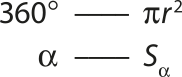
Portanto: S(alfa)" =
Área da coroa circular
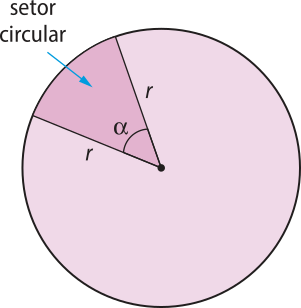
A coroa circular é a região compreendida entre duas circunferências concêntricas, isto é, de mesmo centro, quê estão em um mesmo plano e quê têm as medidas de seus raios diferentes.
A área S de uma coroa circular é igual à diferença entre a área do círculo maior e a do círculo menor, cujos raios médem, respectivamente, R e r. Nesse caso, temos: S = (pi)"R2 − (pi)"r2 = (pi)"(R2 − r2)
Assim: S = (pi)"(R2 − r2)
Pense e responda
Reúna-se a um colega para realizar as atividades a seguir.
• Pesquisem o quê é um segmento circular.
• Debatam e registrem uma maneira de calcular a área de um segmento circular. Em seguida, compartilhem-na com os demais côlégas e com o professor. Vocês pensaram da mesma maneira?
Ver as Orientações para o professor.
ATIVIDADE RESOLVIDA
4. Na figura, ABCD é um quadrado e é um arco de circunferência de centro A. Qual é, aproximadamente, a área da parte colorida de vêrde?
Considere (pi)" ≃ .
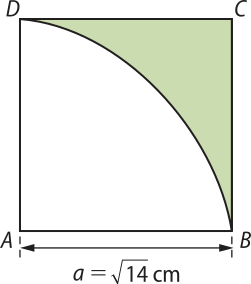
Resolução
A área S da parte colorida de vêrde é igual à área do quadrado ABCD menos a quarta parte da área do círculo de raio a.
• Squadrado = a2 ⇒ Squadrado = = 14
• = 11
Assim: S = Squadrado − ≃ 14 − 11 = 3
Portanto, a área da parte colorida de vêrde é aproximadamente 3 cm2.
Página duzentos e vinte e nove
ATIVIDADES
13. Qual é a medida do diâmetro de um círculo de área 100(pi)" dm2?
20 dm
14. (ESPM-SP) Da área de um quadrado, retiramos a área correspondente a um círculo de diâmetro igual à mêtáde da medida do lado do quadrado. A área restante, em percentagem da área original do quadrado, vale aproximadamente:
a) 50%
b) 60%
c) 75%
d) 80%
e) 90%
alternativa d
15. Em 2009, foi instalado, no estado do Tocantins, o maior pivô central do mundo, com um raio de 1.300 m. Qual é a área irrigada, em hectare (ha), por esse pivô? (Considere 1 ha = 1 hm2 e (pi)" ≃ 3,14.)
aproximadamente 530,660 ha
16. Sabendo quê r = 10 cm, calcule a área da região colorida de azul na figura. (Adote (pi)" ≃ 3,14.)
aproximadamente 628 cm2
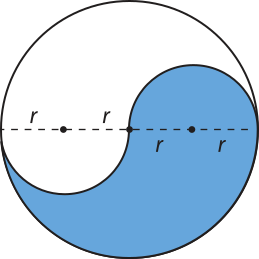
17. (Insper-SP) Uma pizzaria vende pitssas circulares com 32 cm de diâmetro, divididas em 8 pedaços iguais. O dono do estabelecimento pensou em criar uma pitssa de tamãnho maior, a sêr dividida em 12 pedaços iguais, de modo quê a área de cada um deles seja igual à área de um pedaço da pitssa menor. Para isso, o diâmetro da pitssa de 12 pedaços deve sêr aproximadamente igual a:
a) 36 cm
b) 40 cm
c) 44 cm
d) 48 cm
e) 52 cm
alternativa b
18. Determine a área da região colorida de laranja da figura. (Dados: R1 = 3 m, R2 = 5 m.)
16(pi)" m2
19. Duas circunferências concêntricas têm raios iguais a 50 cm e 40 cm, conforme indica a figura. Calcule a área destacada em vêrde.
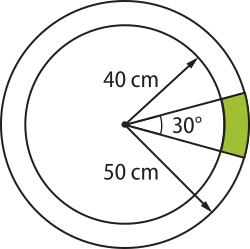
75(pi)" cm2
20. Uma praça é formada por um retângulo de comprimento 100 m e largura 40 m e por dois semicírculos com diâmetros coincidindo com os lados menóres do retângulo.
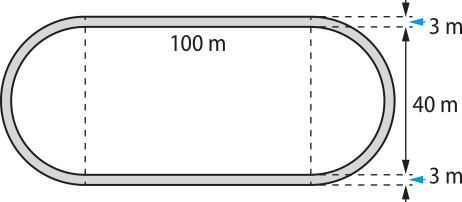
Em torno da praça, será construída uma calçada de 3 m de largura, cujo preêço, por métro quadrado, é R$ 50,00. Calcule o custo total dêêsse projeto. (Adote (pi)" ≃ 3,14.)
aproximadamente R$ 50.253,00
21. (UFRGS-RS) Considere um quadrado de lado 1. Foram construídos dois círculos de raio R com centros em dois vértices opostos do quadrado e tangentes entre si; dois outros círculos de raio r com centros nos outros dois vértices do quadrado e tangentes aos círculos de raio R, como ilustra a figura abaixo.
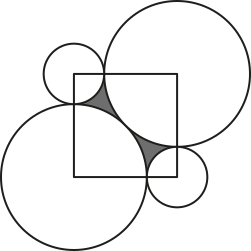
A área da região sombreada é
a) ( +1)(pi)".
b) ( − 1)(pi)".
c) 1 + ()(pi)".
d) 1+( − 1)(pi)".
e) 1+ ( −1)(pi)".
alternativa e
Página duzentos e trinta
Polígonos regulares

No Ensino Fundamental, você já estudou algumas características dos polígonos regulares. Agora, vamos aprender outras, inclusive o cálculo de suas áreas. Mas, antes, obissérve alguns exemplos de situações quê envolvem polígonos regulares.
Você conhece uma chave de bôca? Sabe para quê ela sérve?
A chave de bôca é uma ferramenta muito utilizada por profissionais de mecânica de automóvel quando precisam soltar ou apertar porcas ou parafusos dos carros. Porcas e parafusos, em sua maioria, têm o formato sextavado, ou seja, quando vistos de cima, lembram um hekzágono regular.
No esporte também podemos identificar polígonos regulares. Por exemplo, os tatames de competição do UFC (sigla de Ultimate Fighting Championship, uma organização estadunidense de artes marciais mistas, também conhecida como Mixed Martial Arts – MMA), são conhecidos como octógonos.
Um polígono é regular se, e somente se, apresenta todos os seus lados congruentes e todos os ângulos internos congruentes. Um fato bastante significativo é quê todo polígono regular póde sêr inscrito em uma circunferência, como ilustram os polígonos regulares representados a seguir.

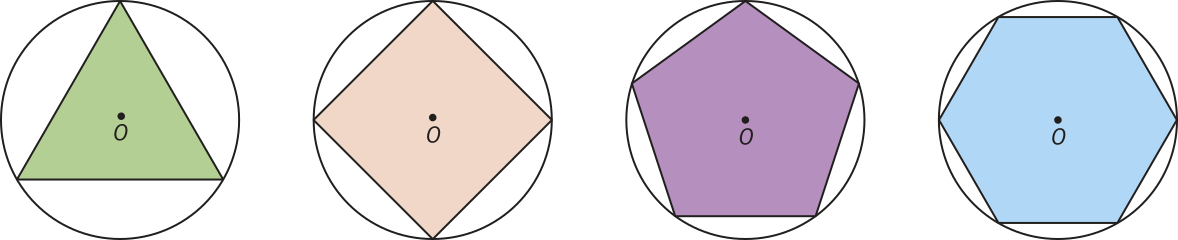
A seguir, vamos estudar alguns polígonos regulares e relacionar seus elemêntos com os da circunferência na qual cada um deles está inscrito.
Elementos de um polígono regular inscrito em uma circunferência
O centro O da circunferência na qual o polígono regular está inscrito é denominado centro do polígono.
A distância m do centro O até o ponto médio M de um lado do polígono regular é denominada apótema do polígono.
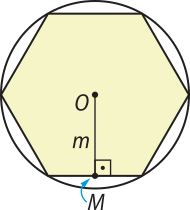
Página duzentos e trinta e um
Os ângulos cujos lados são dois lados consecutivos do polígono são chamados de ângulos internos do polígono. A medida de cada ângulo interno de um polígono regular de n lados é dada por (beta)" = .

Um ângulo (alfa)" cujo vértice está no centro da circunferência circunscrita ao polígono regular e cujos lados passam por dois vértices consecutivos dêêsse polígono é chamado de ângulo central do polígono.
A medida de um ângulo central de um polígono regular é dada por (alfa)" = , sêndo n o número de lados do polígono.
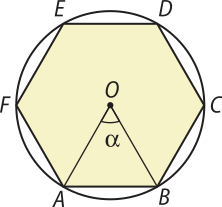
Relações métricas nos polígonos regulares
Quando consideramos a medida (éli)" do lado de um polígono regular, a medida m do apótema do mesmo polígono e a medida r do raio da circunferência na qual esse polígono está inscrito, podemos estabelecer relações métricas entre essas medidas.
Vamos estudar como obtêr essas relações no quadrado, no hekzágono regular e no triângulo equilátero inscritos em uma circunferência.
Quadrado
Considere o quadrado ABCD, inscrito em uma circunferência de raio r, representado na figura. Aplicando o teorema de Pitágoras no triângulo AOD, temos:
(éli)"2 = r2 + r2 ⇒ (éli)"2 = 2r2 ⇒(éli)" = r
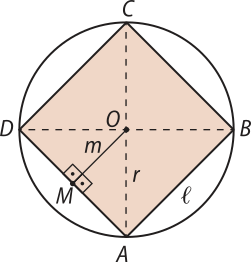
Assim:
(éli)" =
O segmento de reta é congruente aos segmentos e .
Observe, na figura anterior, quê:
m + m = (éli)" ⇒ 2m = (éli)" ⇒ m = ⇒ m =
Portanto:
m =
Pense e responda
Analise a representação do quadrado ABCD, inscrito na circunferência de raio r, e justifique por quê os segmentos e são congruentes.
Essa é uma característica quê só vale para os quadrados? Justifique.
Ver as Orientações para o professor.
Página duzentos e trinta e dois
hekzágono regular
Considere o hekzágono regular ABCDEF, inscrito em uma circunferência de raio r, representado na figura. Observe quê:
• med() = = 60°
• e (pois o triângulo OAF é isósceles)
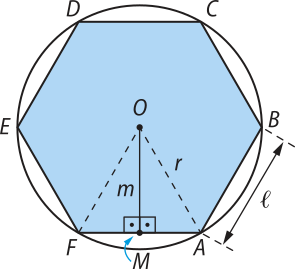
Assim, med() = med() = 60°, pois = 60°, de modo quê podemos concluir quê o triângulo OAF é equilátero.
Como AOF é um triângulo equilátero, então:
(éli)" = r
Como MA = , do teorema de Pitágoras aplicado no triângulo AOM, obtemos:
(OA)2 = (OM)2 + (MA)2 ⇒ r2 = m2 + ()2 ⇒ r2 = m2 + ⇒ m2 = ⇒ m =
Assim:
m =
Triângulo equilátero
Considere o triângulo equilátero ABC, inscrito em uma circunferência de raio r, representado na figura. Observe quê é o lado de um hekzágono regular inscrito nessa circunferência; então, pelo quê estudamos, AD = r. Aplicando o teorema de Pitágoras no triângulo BDA, temos:
(BD)2 = (éli)"2 + (DA)2 ⇒ (2r)2 = (éli)"2 + r2 ⇒ 4r2 = (éli)"2 + r2 ⇒ (éli)"2 = 3r2 ⇒ (éli)" = r
Assim:
(éli)" =
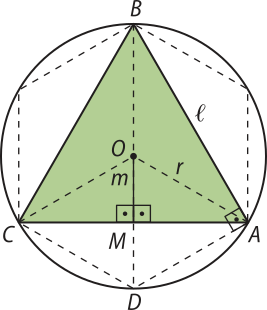
Agora, aplicando o teorema de Pitágoras no triângulo OMA, temos:
(OA)2 = (OM)2 + (MA)2 ⇒ r2 = m2 + ()2 ⇒ m2 = r2 − ⇒ m2 = ⇒ m =
Portanto:
m =
Saiba quê...
Se um lado do triângulo for o diâmetro da semicircunferência na qual ele está inscrito, então o triângulo é retângulo.
Página duzentos e trinta e três
Área de um polígono regular
Vamos considerar os polígonos regulares a seguir, em quê:
• (éli)" é a medida do lado;
• m é a medida do apótema;
• O é o centro do polígono;
• n é a quantidade de lados;
• n ⋅ (éli)" é o perímetro;
• p é o semiperímetro, ou seja, n ⋅ (éli)" = 2p.
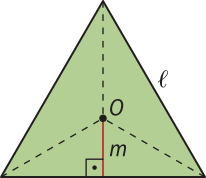

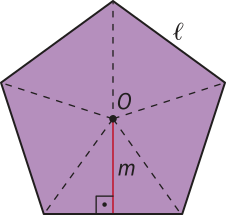
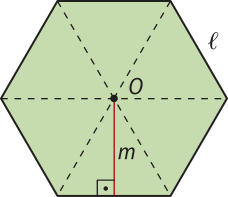
Unindo o centro O de um polígono regular de n lados a cada um dos seus vértices, esse polígono fica decomposto em n triângulos isósceles congruentes.
Como a medida da altura de cada um dêêsses triângulos é igual à medida do apótema do polígono, a área S de cada um dêêsses polígonos é igual a n vezes a área do triângulo formado:
S = n ⋅
Como n ⋅ (éli)" é a medida do perímetro do polígono, a área S também póde sêr expressa por:
S = = p ⋅ m
Portanto, a área de um polígono regular de n lados é igual ao produto da medida p, do semiperímetro, pela medida m, do apótema, ou seja:
S = p ⋅ m
Saiba quê...
Em um hekzágono regular de lado (éli)", o semiperímetro é p = = 3(éli)" e o apótema é m = .
Assim, usando a fórmula apresentada, concluímos quê a área S de um hekzágono regular é:
S = p ⋅ m = 3(éli)" ⋅ =
Variação no perímetro e na área de um polígono regular
Considere a situação a seguir.
Para cercar um terreno quadrado de 4 metros de lado, Antônio usou 16 metros de arame. Seu cliente, satisfeito com o trabalho realizado, pediu quê ele colocasse cerca em outro terreno, também quadrado, mas com o quádruplo da área do primeiro. Antônio ficou pensando se usaria, então, o quádruplo da metragem de arame.
Pense e responda
Junte-se a um colega, e avaliem a suposição de Antônio. Ele estava correto? Justifiquem a resposta.
Não. Espera-se quê os estudantes respondam quê, se a área quadruplica, o perímetro dobra.
Página duzentos e trinta e quatro
Para compreender melhor o problema, vamos relacionar o perímetro P e a área S de um quadrado em função da medida x do seu lado:
x (em metro) |
P (em metro) |
S (em métro quadrado) |
|---|---|---|
1 |
4 |
1 |
2 |
8 |
4 |
3 |
12 |
9 |
4 |
16 |
16 |
5 |
20 |
25 |
6 |
24 |
36 |
7 |
28 |
49 |
8 |
32 |
64 |
n |
4n |
n2 |
Assim, voltando para o problema de Antônio, concluímos quê o novo terreno tem área de 64 m2, pois 4 ⋅ 16 = 64; portanto, ele precisará de 32 metros de arame para cercá-lo, ou seja, o dôbro da metragem anterior.
Analisando os dados do qüadro apresentado, podemos perceber quê, quando dobramos a medida do lado do quadrado, seu perímetro também dobra; porém, sua área quadruplica. Quando triplicamos a medida do lado, o perímetro triplica, mas a área passa a sêr multiplicada por 9, ou seja, 32.
Agora, vamos observar essas variações graficamente:
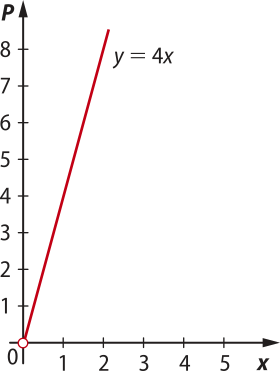
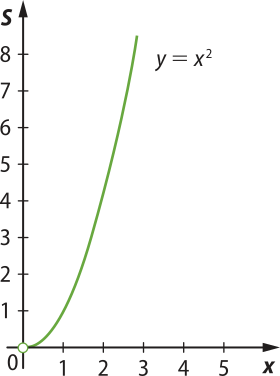
Para construir esses gráficos, consideramos apenas valores de x > 0, pois x representa a medida do lado do quadrado.
O perímetro P de um quadrado é diretamente proporcional à medida de seu lado e póde sêr modelado pela lei da função afim definida por P(x) = 4x, restrita ao domínio D = {x ∈ ℝ | x > 0}. Já a área S do quadrado, em função da medida x do lado, póde sêr modelada pela lei da função quadrática definida por S(x) = x2, restrita ao domínio D. Assim, podemos perceber quê a variação do perímetro do quadrado em função do lado é linear, enquanto a variação da área é quadrática.
Página duzentos e trinta e cinco
Considerando agora o caso do triângulo equilátero, temos P(x) = 3x e S(x) = , de modo quê a variação de seu perímetro em função do lado é linear e a variação de sua área é quadrática. O mesmo ocorre com o hekzágono regular, uma vez quê, para esse polígono, P(x) = 6x e S(x) = .
Saiba quê...
Em polígonos semelhantes cuja razão de semelhança é k, a razão entre lados, alturas e apótemas homólogos é k. Além díssu, a razão entre os perímetros também é k, enquanto a razão entre as áreas é k2. Isso vale para quaisquer dois polígonos semelhantes, inclusive para o caso de eles serem regulares. Portanto, se multiplicarmos as medidas de todos os lados de um polígono por k, obteremos um polígono semelhante ao primeiro e observaremos quê a variação do perímetro ocorrerá linearmente, enquanto a variação da área ocorrerá de maneira quadrática.
ATIVIDADES RESOLVIDAS
5. Determine a medida R do raio da circunferência inscrita no hekzágono regular cujo lado méde 4 cm.
Resolução
A medida do raio da circunferência inscrita em um polígono regular é igual à medida do apótema dêêsse polígono. Assim, R = m.
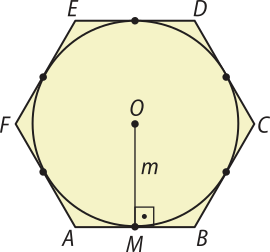
Para o hekzágono regular, temos: (éli)" = r e m = , em quê r é a medida do raio da circunferência circunscrita ao hekzágono.
De acôr-do com o enunciado, temos (éli)" = r = 4 cm. Assim: m =
Logo, a medida R do raio da circunferência inscrita é cm.
6. Observe o gráfico representado e faça o quê se pede a seguir.
a) escrêeva a lei de formação da função representada.
b) Considerando quê essa função representa a variação do perímetro P de um polígono regular em função da medida do seu lado, identifique esse polígono e justifique sua resposta.
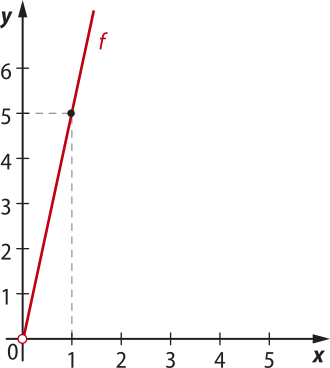
Resolução
a) Conhecemos dois pares ordenados da reta suporte do gráfico: (0, 0) e (1, 5). Vamos considerar quê a equação dessa reta é y = ax + b. Como a reta passa por (0, 0), b = 0. Assim, y = ax. Para x = 1, y = 5. Logo, a = 5. Assim, a equação da reta é y = 5x.
Portanto, a lei de formação da função é f(x) = 5x, com x > 0.
b) A lei da função é f(x) = 5x. Isso quer dizêr quê, para uma medida x do lado dêêsse polígono, o perímetro é 5x. Como se trata de um polígono regular, todos os lados têm a mesma medida, então concluímos quê esse polígono é um pentágono regular.
Página duzentos e trinta e seis
ATIVIDADES
22. Dado um triângulo equilátero, cujo lado méde 6 cm, calcule:
a) a medida do raio da circunferência circunscrita;
cm
b) a medida do apótema.
cm
23. Em uma circunferência de raio 2 cm está inscrito um hekzágono regular. Qual é a área dêêsse polígono? (Adote ≃ 1,73.)
aproximadamente 10,38 cm²
24. Calcule as áreas dos polígonos regulares representados a seguir.
a) 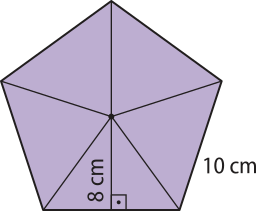
200 cm2
b) 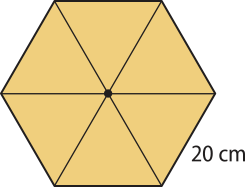
600 cm2
25. A figura a seguir foi recortada de uma cartolina e é formada por um hekzágono regular e seis quadrados. Cada lado do hekzágono méde 10 cm.
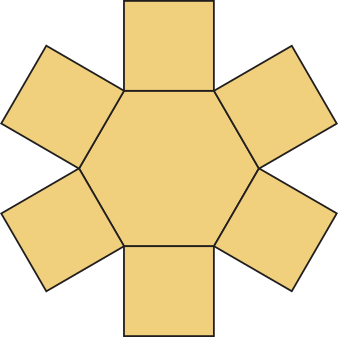
Considerando ≃ 1,73, quantos centimetros quadrados de cartolina foram usados para fazer a figura?
aproximadamente 859,5 cm²
26. Calcule a área de um triângulo equilátero, sabendo quê seu apótema méde 3 cm.
cm2
27. São dados dois quadrados: um inscrito e outro circunscrito à mesma circunferência.
Determine a razão entre:
a) o perímetro do quadrado inscrito e o do quadrado circunscrito;
b) a área do quadrado inscrito e a do quadrado circunscrito.
28. O apótema de um hekzágono regular méde cm. Nessas condições, determine:
a) a medida do seu lado;
12 cm
b) sua área.
cm2
29. Na figura a seguir, o quadrado ABCD está inscrito em uma circunferência. Sabendo quê o lado dêêsse quadrado méde a, expresse, em função de a, a área da região sombreada.

a2 ( − 1) u.a.
30. Observe a relação entre a medida dos lados e o perímetro de um polígono regular.
Identifique qual é esse polígono regular e justifique sua resposta.
Medida do lado |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
Perímetro |
20 |
30 |
40 |
50 |
Decágono; a medida do lado é x e o perímetro, 10x.
31. ![]() Considerando os estudos sobre a variação da área e do perímetro de um polígono regular em função da medida do lado, elabore um problema e resolva-o. Depois, troque-o com um de seus côlégas e resôuva o problema propôsto por ele. Em seguida, discutam as soluções, verificando se chegaram às mesmas conclusões e quais procedimentos utilizaram.
Considerando os estudos sobre a variação da área e do perímetro de um polígono regular em função da medida do lado, elabore um problema e resolva-o. Depois, troque-o com um de seus côlégas e resôuva o problema propôsto por ele. Em seguida, discutam as soluções, verificando se chegaram às mesmas conclusões e quais procedimentos utilizaram.
Resposta pessoal.
32. (Ence-RJ) A figura abaixo representa um hekzágono regular.
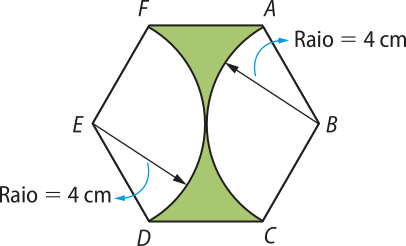
Cal cule:
a) a medida do seu apótema;
cm
b) a área da região colorida de vêrde.
cm2
Página duzentos e trinta e sete
33. Calcule a área de um hekzágono regular cujo lado méde 6 cm.
cm2
34. (UEL-PR) Algumas figuras geométricas são utilizadas em símbolos, como, por exemplo, a “Estrela de David” (Figura 1).


A partir das Figuras 1 e 2, desenhou-se um esquema, representado na Figura 3, quê não obedece a uma escala. Sabe-se quê, na Figura 3, estão representados uma circunferência de centro no ponto O e um triângulo equilátero (ABC), inscrito nessa circunferência.
Considerando quê o raio da circunferência é de cm, responda aos itens a seguir.
a) Determine a medida do lado do triângulo ABC. Justifique sua resposta apresentando os cálculos realizados na resolução dêste item.
12 cm
b) Determine a área representada pela côr cinza na Figura 3. Justifique sua resposta apresentando os cálculos realizados na resolução dêste item.
aproximadamente 88 cm2
35. Em alguns municípios, serão construídas praças na forma de octógono regular. Para isso, foi elaborado um projeto em quê consta a medida m do lado do octógono, uma vez quê o comprimento do lado poderia variar conforme o local para a construção da praça.
a) Faça um esboço do polígono regular quê representa a praça.
Ver as Orientações para o professor.
b) Qual é a função quê relaciona o perímetro P e a medida do lado m do octógono regular?
P(m) = 8m
c) Construa o gráfico quê representa essa função.
Ver as Orientações para o professor.
36. Considere os polígonos regulares representados na Figura 1 e na Figura 2.


a) escrêeva as funções P1 e S1 quê descrevem, respectivamente, o perímetro e a área da Figura 1 em função da medida a do seu lado.
36. a) P1(a) = 3a, com a > 0; S1(a) = , com a > 0
b) Esboce os gráficos das funções P1 e S1.
Ver as Orientações para o professor.
c) escrêeva as funções P2 e S2 quê descrevem, respectivamente, o perímetro e a área da Figura 2 em função da medida b do seu lado.
P2(b) = 6b, com b > 0; S2(b) = , com b > 0.
d) Esboce os gráficos das funções P2 e S2.
Ver as Orientações para o professor.
37. (Enem/MEC) Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas quadradas de 2 metros de lado, conforme a figura. Para 1 tampa grande, a empresa produz 4 tampas médias e 16 tampas pequenas.

Área do círculo: (pi)"r2
As sóbras de material de produção diária das tampas grandes, médias e pequenas dessa empresa são doadas, respectivamente, a três entidades: I, II e III, para efetuarem reciclagem do material. A partir dessas informações, pode-se concluir quê:
a) a entidade I recebe mais material do quê a entidade II;
b) a entidade I recebe mêtáde do material da entidade III;
c) a entidade II recebe o dôbro de material da entidade III;
d) as entidades I e II recebem, juntas, menos material do quê a entidade III;
e) as três entidades recebem iguais quantidades de material.
alternativa e
Página duzentos e trinta e oito

Ladrilhamento do plano
Na instalação de pisos e azulejos em cozinhas e banheiros, por exemplo, o termo usado pêlos profissionais da construção civil é "assentar" (o piso ou o azulejo). Nesse processo, para obtêr um bom acabamento, os profissionais precisam recobrir a maior área possível, utilizando apenas peças inteiras. Porém, normalmente, é necessário fazer o quê se chama de "recorte", assentando pedaços dessas peças para recobrir totalmente a superfícíe.
Em Matemática, a ideia de ladrilhamento está associada ao recobrimento do plano utilizando determinadas composições de polígonos.
Considere a situação a seguir.
Carlos foi contratado para assentar pisos na superfícíe plana de um pátio retangular. Para obtêr um bom acabamento, ele pretende recobrir a maior área possível da superfícíe dêêsse pátio, utilizando apenas pisos inteiros e de um único modelo, A ou B, conforme representado pelas figuras.

Se Carlos utilizar o piso do modelo A, poderá compor um ladrilhamento seguindo o padrão indicado a seguir, à esquerda. Note quê, para determinar esse padrão, não é necessário realizar nenhum recorte do piso do modelo A. Porém, se Carlos utilizar o piso do modelo B, ele teria a situação indicada a seguir, à direita.

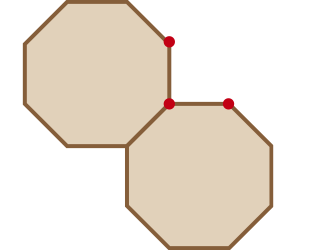
Observe quê, na composição com pisos do modelo B, não é possível encaixar um novo piso dêêsse mesmo modelo na região triangular determinada pêlos pontos destacados em vermelho.
Assim, ao utilizar o modelo B, seria necessário fazer rekórtis nos pisos para conseguir recobrir toda a superfícíe plana do pátio. Portanto, o modelo A é o mais adequado à necessidade de Carlos.
Saiba quê...
A ideia de ladrilhamento é utilizada em diferentes manifestações artísticas. Por exemplo, o artista gráfico holan-dêss é-chêr (1898-1972), em suas obras de tesselação, partia de figuras geométricas para criar imagens, como de peixes ou de aves, quê se encaixavam perfeitamente. A tesselação é um tipo de pavimentação, com peças de mosaico, de uma superfícíe plana.
Página duzentos e trinta e nove
A situação anterior nos dá ideia do quê, em Matemática, denominamos ladrilhamento do plano, quê é o recobrimento do plano com base em determinado padrão geométrico. Esse padrão póde sêr compôzto de um único tipo de polígono ou da combinação de diferentes tipos de polígonos.
Os polígonos utilizados para fazer o ladrilhamento devem obedecer às seguintes condições:
• A intersecção entre os polígonos é sempre um vértice ou um lado ou é vazia;
• A distribuição ao redor de cada vértice é sempre a mesma, obedecendo a um padrão.
Considere um triângulo equilátero ABC. É possível compor um ladrilhamento com seis triângulos equiláteros congruentes ao triângulo ABC, todos com vértice A.
Observe outros exemplos de ladrilhamento do plano com polígonos regulares:


Vamos, agora, investigar se é possível ladrilhar o plano utilizando outro polígono regular. Primeiro, vamos estudar os casos do pentágono e do eneágono regulares, cujas medidas dos ângulos internos estão destacadas nas figuras a seguir.
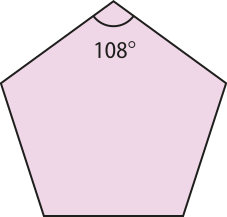
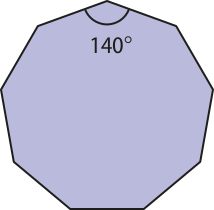
Ao dispor três pentágonos regulares em torno de um vértice, percebemos quê, na região não preenchida, forma-se um ângulo de 36°, quê não comporta um quarto pentágono regular. No caso do eneágono regular, ao dispor duas dessas figuras em torno de um vértice, é formado um ângulo de 80° na região não preenchida, de modo quê não é possível dispor um terceiro eneágono regular em torno dêêsse vértice.
Página duzentos e quarenta
Pense e responda
• Qual é a medida dos ângulos internos do heptágono regular?
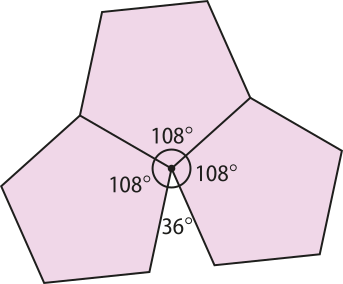
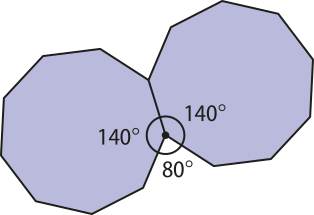
Com isso, é possível perceber quê, para obtêr um ladrilhamento do plano, a soma das medidas dos ângulos internos dos polígonos, relativos aos vértices coincidentes, deve sêr 360°.
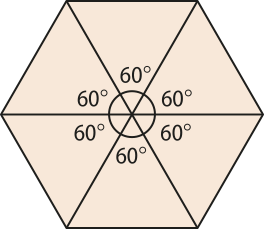
Além díssu, no caso de ladrilhamentos utilizando apenas um tipo de polígono regular, a medida dos ângulos internos do polígono deve sêr um divisor de 360°. Portanto, há apenas três possibilidades de escolha para o tipo de polígono regular: triângulos equiláteros, quadrados ou hekzágonos regulares.
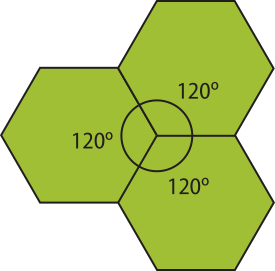
O ladrilhamento do plano também póde sêr feito por meio da composição de dois ou mais polígonos regulares convexos com lados congruentes, de modo quê o padrão de cada vértice obedeça sempre à mesma ordem.
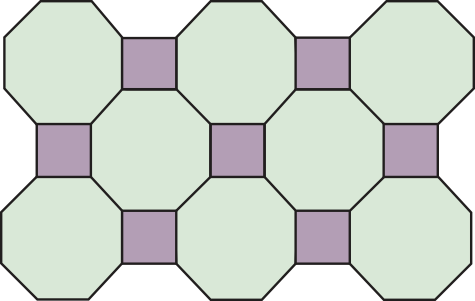
A figura a seguir representa uma maneira de se obtêr o ladrilhamento do plano, utilizando octógonos regulares e quadrados.
Pense e responda
Quais são as medidas dos ângulos internos dos polígonos regulares quê compõem essa figura?
135º (do octógono regular); 90º (do quadrado)
Página duzentos e quarenta e um
Os ladrilhamentos também podem sêr feitos com alguns polígonos congruentes, ainda quê sêjam não regulares. Na figura a seguir, por exemplo, o padrão geométrico utilizado é compôzto de triângulos quê não são regulares.

Para assistir
• ISTO é Matemática: T05E09: o estranho mundo de é-chêr. [S. I.: s. n.], 2013. 1 vídeo (8 min). Publicado pelo canal sigma3web. Disponível em: https://livro.pw/ctdey. Acesso em: 4 set. 2024.
O vídeo apresenta noções básicas de ladrilhamento por meio de contextualização com azulejos e com as obras de é-chêr.
ATIVIDADE RESOLVIDA
7. Para fazer o ladrilhamento de uma superfícíe, Caio comprou pisos em formato de octógonos regulares. Ao iniciar o trabalho de revestimento, notou quê não seria possível recobrir todo o piso. Observe:
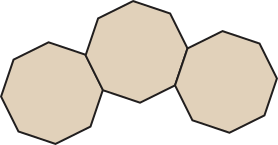
a) Explique o motivo pelo qual Caio não conseguirá ladrilhar a superfícíe usando somente pisos nesse formato.
b) Caio rêzouvêo voltar à loja para comprar algum outro piso quê se encaixe perfeitamente ao ladrilhamento já iniciado. Ele deve procurar pisos no formato de qual polígono regular?
Resolução
a) A medida do ângulo interno do octógono regular é dada por (beta)" = = 135°, e 135 não é divisor de 360.
Com dois octógonos regulares, a soma dos ângulos justapostos em um mesmo vértice é 270°; com três octógonos regulares, essa soma passa a 405°. Assim, usando somente octógonos regulares, não é possível ladrilhar o piso.
b) Sabemos quê a medida de cada ângulo interno do octógono regular é igual a 135°. Assim, temos: 2 ⋅ 135° + x = 360°, em quê x é a medida do ângulo do polígono regular desconhecido.
Assim, temos: x = 360° − 270°
Logo, x = 90°.
O polígono regular quê possui ângulos iguais a 90° é o quadrado, portanto Caio deve procurar pisos quadrados.
Página duzentos e quarenta e dois
ATIVIDADES
38. Ao utilizarmos a combinação de dois hekzágonos regulares e dois triângulos equiláteros, cujos lados tênham a mesma medida, é possível ladrilhar o plano? Justifique sua resposta.
Sim. Ver as Orientações para o Professor.
39. Uma construtora decidiu inovar e encomendou ladrilhos no formato de dodecágonos regulares (polígonos de 12 lados congruentes). Ao se depararem com esses ladrilhos de formato inusitado, alguns pedreiros disseram quê não seria possível usar apenas esse ladrilho, pois sobraria espaço entre eles. Ao ouvir os côlégas, o mestre de obras encontrou a solução para esse problema. Ele afirmou quê somente com os ladrilhos no formato de dodecágonos regulares, de fato, não era possível recobrir todo o piso, mas se esses ladrilhos fossem combinados com outro tipo de ladrilho poligonal, o problema estaria resolvido.
a) Explique por quê não é possível usar somente os ladrilhos em formato de dodecágono regular para cobrir todo o piso, sem deixar espaço. Se possível, utilize um software de Geometria Dinâmica para auxiliar sua explicação.
Ver as Orientações para o professor.
b) Considerando a solução dada pelo mestre de obras, quê tipo de ladrilho seria possível combinar com o dodecágono regular para satisfazer às condições de ladrilhamento?
triângulo equilátero
40. (Saresp-SP) Uma parede precisa sêr revestida com azulejos em formato de polígonos regulares. Para tanto, será escolhido um tipo de azulejo, de modo a se obtêr um ladrilhamento. Das alternativas a seguir, qual é a forma de azulejo ideal para revestir essa parede?
a) Um heptágono (7 lados).
b) Um pentágono (5 lados).
c) Um octógono (8 lados).
d) Um decágono (10 lados).
e) Um hekzágono (6 lados).
alternativa e
41. (Fuvest-SP) Um ladrilhamento é chamado de uniforme se é compôzto por polígonos regulares quê preenchem todo o plano sem sobreposição e, além díssu, o padrão é o mesmo em cada vértice. Para classificá-los, utilizamos uma notação dada por uma sequência de números quê é definida desta forma: escolhemos um vértice qualquer e indicamos o número de lados de cada polígono quê contém êste vértice, seguindo o sentido anti-horário, iniciando com os polígonos de menos lados, conforme os exemplos:
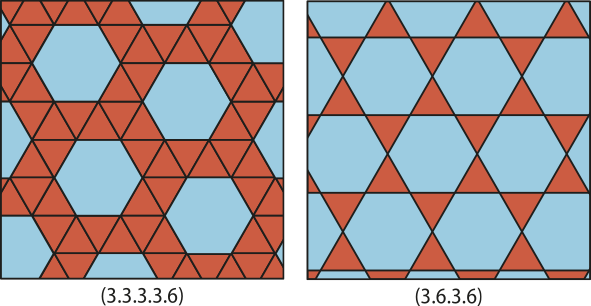
A foto mostra o piso de um museu em Sevilha.

A notação quê representa o padrão do ladrilhamento do piso é:
a) (3. 3. 3. 4)
b) (3. 3. 4. 6)
c) (3. 4. 4. 4)
d) (3. 4. 4. 6)
e) (3. 4. 6. 4)
alternativa e
Página duzentos e quarenta e três
42. (Enem/MEC) Na construção civil, é muito comum a utilização de ladrilhos ou azulejos com a forma de polígonos para o revestimento de pisos ou paredes. Entretanto, não são todas as combinações de polígonos quê se prestam a pavimentar uma superfícíe plana, sem quê haja falhas ou superposições de ladrilhos, como ilustram as figuras:

A tabéla traz uma relação de alguns polígonos regulares, com as respectivas medidas de seus ângulos internos.

Se um arquiteto deseja utilizar uma combinação de dois tipos diferentes de ladrilhos entre os polígonos da tabéla, sêndo um deles octogonal, o outro tipo escolhido deverá ter a forma de um
a) triângulo.
b) quadrado.
c) pentágono.
d) hekzágono.
e) eneágono.
alternativa b
43. (CPII-RJ) Alguns polígonos regulares, quando postos juntos, preenchem o plano, isto é, não deixam folga, espaço entre si. Por outro lado, outras combinações de polígonos não preenchem o plano.
A seguir, exemplos dêêsse fato: a Figura 1, formada por hekzágonos regulares, preenche o plano; a Figura 2, formada por pentágonos e hekzágonos regulares, não preenche o plano.
Na Figura 2, a medida x do ângulo é igual a
a) 14°.
b) 12°.
c) 10°.
d) 8°.
alternativa b
Página duzentos e quarenta e quatro
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Áreas verdes urbanas
As áreas verdes, em centros urbanos, são fundamentais para diversos aspectos, entre eles, a melhora na qualidade do ar. Leia o texto a seguir.
A importânssia das áreas verdes nas cidades
Desde a Antigüidade, as áreas verdes e jardins tí-nhão finalidades de passeio, lugar para expor luxo e de repouso. Atualmente com os problemas gerados pelas cidades modernas, elas e os parques e jardins são uma exigência não só para a ornamentação urbana, mas também como necessidade higiênica, de recreação e principalmente de defesa do meio ambiente diante da degradação das cidades.
[…]
Além de servirem como equilíbrio do ambiente urbano e de locais de lazer, também podem oferecer um colorido e plasticidade ao meio urbano.
Outro fator importante referente à vegetação é a arborização das vias públicas quê sérve como um filtro para atenuar ruídos, retenção de pó, reoxigenação do ar, além de oferecer sombra e a sensação de frescor.
[…]
LIMA, Valéria; AMORIM, Margarete C. de C. T. A importânssia das áreas verdes para a qualidade ambiental das cidades. Revista Formação, Presidente Prudente, v. 1, n. 13, p. 69-82. 2006. p. 71. Disponível em: https://livro.pw/aqxrd. Acesso em: 4 set. 2024.

Página duzentos e quarenta e cinco
Índice de Áreas Verdes
Indicadores e índices são números quê procuram descrever um determinado aspecto da realidade, ou apresentam uma relação entre vários deles […]. Dentre alguns indicadores quê expressam a qualidade ambiental de uma cidade, destaca-se: o Índice de Áreas Verdes (IAV) quê méde a relação entre a quantidade de área vêrde (m²) e a população quê vive em determinada cidade.
[…]
[…] em termos gerais, o IAV é aquele quê denota a quantidade de espaços livres de uso público, em km² (kilometro quadrado) ou m² (metro quadrado) dividido pela quantidade de habitantes de uma cidade. […]
[…]
TAVC = ∑ áreas de parques (m²) + ∑ áreas de praças (m²)
IAV =
Onde:
TAVC = Total de áreas verdes consideradas (parques e praças)
IAV = Índice de áreas verdes
NH = Número de habitantes
[…]
TOLEDO, Fabiane dos S.; MAZZEI, Kátia; SANTOS, Douglas G. dos. Um índice de áreas verdes (IAV) na cidade de Uberlândia/MG. REVSBAU, Piracicaba, v. 4, n. 3, p. 86-97, 2009. p. 91, 99. Disponível em: https://livro.pw/zydmr. Acesso em: 4 set. 2024.
A Organização Mundial da Saúde (hó ême ésse) recomenda um mínimo de 12 m2 de área vêrde por habitante.
Fonte dos dados: ÁREA vêrde por habitante. [S. I.]: Programa Cidades Sustentáveis, 2016. Disponível em: https://livro.pw/gawhq. Acesso em: 4 set. 2024.
Saiba quê...
∑ é o sín-bolo utilizado para o somatório, quê indica a soma de determinados números. É também a décima oitava letra do alfabeto grego, quê corresponde ao S maiúsculo.
Agora, faça o quê se pede nas atividades a seguir.
1. ![]() Em sua opinião, por quê é importante havêer áreas verdes na cidade? Há áreas verdes em sua cidade? Converse com seus côlégas sobre esses espaços.
Em sua opinião, por quê é importante havêer áreas verdes na cidade? Há áreas verdes em sua cidade? Converse com seus côlégas sobre esses espaços.
Respostas pessoais.
2. Uma cidade quê tinha, em 2023, 62.961.882 m2 de áreas verdes (praças e parques), tinha, na mesma data, a população de 1.409.351 habitantes.
Calcule o índice de áreas verdes (IAV) dessa cidade em 2023 e compare-o com o índice mínimo estabelecido pela Ônu.
IAV = 44,6744 m2/hab. O índice está acima do recomendado pela Ônu.
3. ![]() Junte-se a três côlégas, e façam uma pesquisa sobre os parques urbanos do Brasil, incluindo aqueles quê vocês já tênham visitado. Em seguida, organizem uma apresentação sobre o assunto, utilizando fotografias para ilustrar os parques pesquisados.
Junte-se a três côlégas, e façam uma pesquisa sobre os parques urbanos do Brasil, incluindo aqueles quê vocês já tênham visitado. Em seguida, organizem uma apresentação sobre o assunto, utilizando fotografias para ilustrar os parques pesquisados.
Pesquisa do estudante.

Página duzentos e quarenta e seis
EXPLORANDO A TECNOLOGIA
Explorando polígonos inscritos na circunferência
De acôr-do com o quê estudamos, a área (S) de um polígono regular é o produto de seu apótema (m) pelo semiperímetro (p), S = p ⋅ m. Aprendemos, também, quê todo polígono regular póde sêr inscrito em uma circunferência.
Utilizando essas informações, podemos criar um arquivo no GeoGebra, em quê é possível construir um polígono regular com tantos lados quanto desejarmos. Em seguida, o programa calcula o valor de sua área. Desse modo, podemos comparar o valor obtído com a fórmula anterior.
Para isso, siga os passos a seguir.
I. Utilizando a ferramenta Ponto, ![]() clique na origem do sistema de coordenadas, definindo, assim, o ponto A(0, 0).
clique na origem do sistema de coordenadas, definindo, assim, o ponto A(0, 0).
II. Em seguida, ainda utilizando a ferramenta Ponto, ![]() , clique no ponto (1, 0) sobre o eixo x, ficando definido o ponto B(1, 0).
, clique no ponto (1, 0) sobre o eixo x, ficando definido o ponto B(1, 0).
III. Utilizando a ferramenta Círculo dados Centro e Um de seus Pontos, ![]() , clique primeiro no ponto A e, depois, no ponto B. O programa fornecerá uma circunferência de raio 1, cujo centro é o ponto A, e B é um de seus pontos.
, clique primeiro no ponto A e, depois, no ponto B. O programa fornecerá uma circunferência de raio 1, cujo centro é o ponto A, e B é um de seus pontos.
Pode-se, então, utilizar a ferramenta Ampliar, ![]() , e clicar sobre a circunferência até quê ela se ajuste ao espaço disponível, ou simplesmente utilizar o scroll do máuzi para ampliar a imagem visível na janela de visualização.
, e clicar sobre a circunferência até quê ela se ajuste ao espaço disponível, ou simplesmente utilizar o scroll do máuzi para ampliar a imagem visível na janela de visualização.
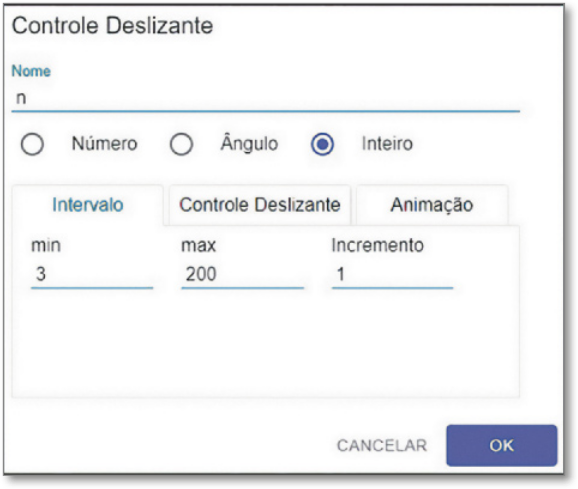
IV. Utilize a ferramenta contrôle deslizante, ![]() , e clique em qualquer lugar da janela de visualização. Na caixa de diálogo aberta (Figura 1), nomeie-o como n e selecione a opção Inteiro. Além disso, altere os valores min e max para 3 e 200, respectivamente. Mantenha o incremento em 1.
, e clique em qualquer lugar da janela de visualização. Na caixa de diálogo aberta (Figura 1), nomeie-o como n e selecione a opção Inteiro. Além disso, altere os valores min e max para 3 e 200, respectivamente. Mantenha o incremento em 1.
V. Para criar outro ponto na circunferência, vamos defini-lo de modo quê sua distância ao ponto B coincida com a medida do lado do polígono regular de n lados. Para isso, digite “C=(cos(2*pi/n),sen(2*pi/n))” no campo de entrada para criar o ponto C.
Página duzentos e quarenta e sete
VI. Utilizando a ferramenta Polígono Regular, ![]() , clique primeiro no ponto B e, depois, no ponto C. Para o número de lados, digite “n”. Assim, o valor do contrôle deslizante n vai determinar o número de lados do polígono regular. Surgirá, na janela de visualização, o triângulo equilátero inscrito na circunferência recém-criada (Figura 2).
, clique primeiro no ponto B e, depois, no ponto C. Para o número de lados, digite “n”. Assim, o valor do contrôle deslizante n vai determinar o número de lados do polígono regular. Surgirá, na janela de visualização, o triângulo equilátero inscrito na circunferência recém-criada (Figura 2).
Observe quê, na janela de Álgebra, aparece um objeto chamado pol1 e, ao lado, um número. Esse número representa a área do polígono regular construído inscrito na circunferência de raio unitário.
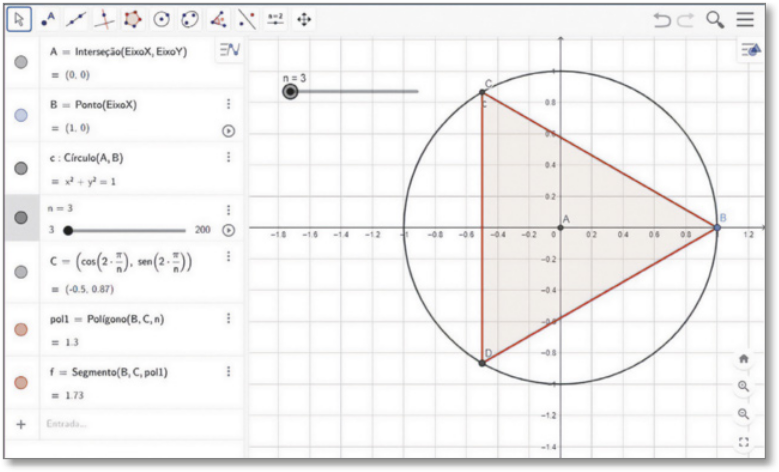
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Durante a construção, definimos o intervalo do contrôle deslizante de 3 a 200. Explique por quê faz sentido o valor mínimo para essa construção sêr n = 3.
2. Para n = 3, o polígono na tela será um triângulo equilátero.
• Utilizando a ferramenta Reta Perpendicular, ![]() trace uma reta perpendicular a um dos lados do triângulo, a partir do ponto A.
trace uma reta perpendicular a um dos lados do triângulo, a partir do ponto A.
• Marque o ponto de intersecção dessa reta com o lado do triângulo, utilizando a ferramenta
Interseção de Dois Objetos, ![]() . A distância entre esse ponto e o ponto A é o apótema dêêsse triângulo.
. A distância entre esse ponto e o ponto A é o apótema dêêsse triângulo.
a) Utilizando a ferramenta Distância, Comprimento ou Perímetro, ![]() meça o apótema e anote.
meça o apótema e anote.
b) Com a mesma ferramenta anterior, meça um dos lados do triângulo e anote.
c) Calcule a área do triângulo equilátero usando a fórmula do semiperímetro.
d) Compare o valor calculado com o valor fornecido pelo GeoGebra.
3. O quê acontece com o valor da área quando aumentamos o número de lados?
4. Ao definir n = 200, o polígono inscrito se parece com qual figura? O quê podemos afirmar sobre o valor da área do polígono para esse caso?
Página duzentos e quarenta e oito
HISTÓRIA DA MATEMÁTICA
Pentágonos convexos quê pavimentam o plano
Leia o texto a seguir sobre Marjorie Rice, uma dona de casa autodidata estadunidense quê descobriu novas formas de ladrilhar o plano usando pentágonos. Observe quê, mesmo sem uma formação acadêmica na disciplina, Rice pôdi contribuir com a Matemática.

[…]
Em julho de 1975, mártim Gardner publicou na Saentífic Américam, uma revista de divulgação científica, o problema de pavimentação do plano por polígonos convexos e a lista dos oito tipos de pentágonos convexos quê conhecidamente pavimentam o plano. Essa publicação permitiu quê um público mais amplo tivesse contato com o problema e, como veremos, estimulou a descoberta de novas pavimentações.
ríchard diêmes III, um cientista da área de computação, leu o artigo publicado por mártim Gardner e decidiu […] tentar descobrir sózínho algum pentágono convexo quê pavimentasse o plano. Após algumas tentativas, conseguiu encontrar um exemplo e o enviou para mártim Gardner […].
Esse resultado foi publicado por Gardner no exemplar de dezembro de 1975 da Saentífic Américam, elevando para nove o total de tipos de pentágonos quê pavimentam o plano.
[…] essa descoberta despertou a curiosidade de outra leitora da Saentífic Américam: uma dona de casa de Sã Diego, Califórnia, Marjorie Rice, com cinco filhos, sem formação matemática específica além daquela ôbitída no ensino médio. Após ler o artigo de mártim Gardner de dezembro de 1975, começou a desenvolver sua própria pesquisa sistemática sobre quais tipos de pentágonos convexos podem pavimentar o plano. Dentre os vários resultados obtidos por ela, destaca-se a descoberta, em 1976 e em 1977, de quatro novos tipos de pavimentações do plano por pentágonos convexos […].

O décimo quarto tipo de pentágono convexo quê pavimenta o plano foi descoberto somente em 1985 por Rolf Stein, um estudante de Matemática da Universidade de Dortmund, Alemanha.
[…]
Fonte: DUTENHEFNER, Francisco; CASTRO, Rosiene de F. C. R. Uma história sobre pavimentações do plano euclidiano: acêrrrtos e êêrros. Revista do Professor de Matemática (RPM), São Paulo, n. 70, [200-]. Disponível em: https://livro.pw/lgsgf. Acesso em: 4 set. 2024.
Página duzentos e quarenta e nove
ATIVIDADES COMPLEMENTARES
1. (UFRGS-RS) Considere um segmento de comprimento 10 e M um ponto dêêsse segmento, distinto de A e de B, como na figura abaixo. Em qualquer posição do ponto M, AMDC é quadrado e BME é triângulo retângulo em M.
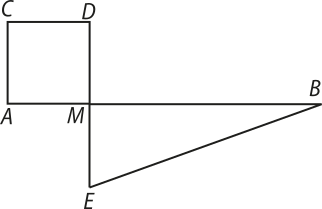
Tomando x como a medida dos segmentos e para quê valor(es) de x as áreas do quadrado AMDC e do triângulo BME são iguais?
a) 0 e .
b) 0, 2 e 3.
c) .
d) 0, e 10.
e) 5.
alternativa c
2. (Unicamp-SP) No triângulo ABC exibido na figura a seguir, M é o ponto médio do lado AB, e N é o ponto médio do lado AC.
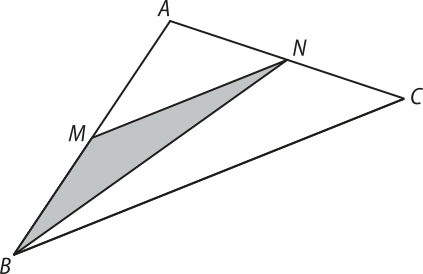
Se a área do triângulo MBN é igual a t, então a área do triângulo ABC é igual a
a) 3t.
b) t.
c) 4t.
d) t.
alternativa c
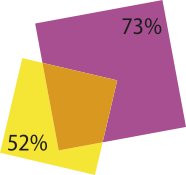
3. (OBMEP) Dois quadrados de papel se sobrepõem como na figura. A região não sobreposta do quadrado menor corresponde a 52% de sua área e a região não sobreposta do quadrado maior corresponde a 73% de sua área. Qual é a razão entre o lado do quadrado menor e o lado do quadrado maior?
a)
b)
c)
d)
e)
alternativa a
4. (Unifor-CE) Um pequeno terreno retangular tem área de 104 m2. Sabendo quê seu comprimento tem 3 m a menos quê o dôbro de sua largura, é correto concluir quê a medida dêêsse comprimento está entre:
a) 14 m e 16 m
b) 12 m e 14 m
c) 10 m e 12 m
d) 8 m e 10 m
e) 6 m e 8 m
alternativa b
5. (Udesc) O projeto de uma casa é apresentado em forma retangular e dividido em quatro cômodos, também retangulares, conforme ilustra a Figura 3.
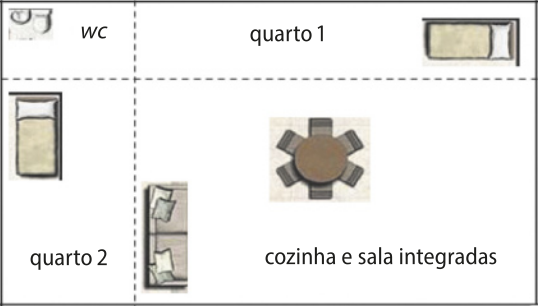
Sabendo quê a área do banheiro (wc) é igual a 3 m2 e quê as áreas dos quartos 1 e 2 são, respectivamente, 9 m2 e 8 m2, então a área total do projeto desta casa, em metros quadrados, é igual a:
a) 24
b) 32
c) 44
d) 72
e) 56
alternativa c
6. (UFABC-SP) Observe a figura. As duas áreas retangulares são utilizadas para o plantio de cana-de-açúcar, sêndo quê a área R está para a área H na razão de 9 para 5. Sabe-se quê um hectare (ha) de cana produz 8 mil litros de etanol. Dado: 1 ha = 10.000 m2
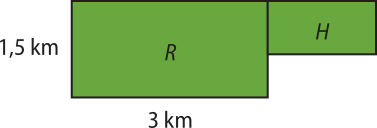
Pode-se concluir, então, quê as áreas R e H, juntas, produzem:
a) 2,5 ⋅ 106 litros de etanol.
b) 3,6 ⋅ 106 litros de etanol.
c) 4,5 ⋅ 106 litros de etanol.
d) 5,6 ⋅ 106 litros de etanol.
e) 6,2 ⋅ 106 litros de etanol.
alternativa d
Página duzentos e cinquenta
7. (UFRN) Miguel pintará um painel retangular com motivos geométricos. As duas regiões destacadas, a região 1 (FGKM), contida no quadrado FGLM, e a região 2 (HILK), contida no paralelogramo HILM, conforme figura abaixo, serão pintadas de vermelho. Sabe-se quê a tinta utilizada para pintar uma região qualquer depende proporcionalmente de sua área.
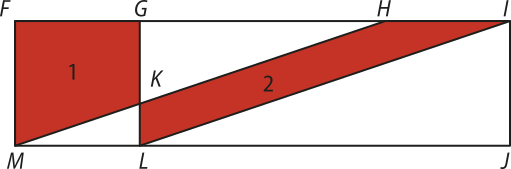
Se Miguel gastasse, na pintura da região 1, da tinta vermelha de quê dispõe, poderíamos afirmar quê
alternativa d
a) o restante de tinta vermelha daria, exatamente, para a pintura da região 2.
b) o restante de tinta vermelha seria insuficiente para a pintura da região 2.
c) a região 2 seria pintada e ainda sobrariam de tinta vermelha.
d) a região 2 seria pintada e ainda sobraria de tinta vermelha.
8. (FCMSCSP) Na figura, vê-se uma forma geométrica em vermelho quê foi ôbitída pela junção de um setor circular de raio 3 cm e ângulo 90° com um setor de uma coroa circular de raio interno 3 cm, raio externo 4 cm e ângulo 270°.

O círculo cuja área é igual à área da forma geométrica em vermelho tem raio igual a
a) cm
b) cm
c) cm
d) cm
e) cm
alternativa a
9. (Enem/MEC) O dono de uma loja pretende usar cartões imantados para a divulgação de sua loja. A empresa quê fornecerá o serviço lhe informa quê o custo de fabricação do cartão é de R$ 0,01 por centimetro quadrado e quê disponibiliza modelos tendo como faces úteis para impressão:
• um triângulo equilátero de lado 12 cm;
• um quadrado de lado 8 cm;
• um retângulo de lados 11 cm e 8 cm;
• um hekzágono regular de lado 6 cm;
• um círculo de diâmetro 10 cm.
O dono da loja está disposto a pagar, no mássimo, R$ 0,80 por cartão. Ele escolherá, dentro dêêsse limite de preêço, o modelo quê tiver maior área de impressão.
Use 3 como aproximação para (pi)" e use 1,7 como aproximação para .
Nessas condições, o modelo quê deverá sêr escolhido tem como face útil para impressão um
a) triângulo.
b) quadrado.
c) retângulo.
d) hekzágono.
e) círculo.
alternativa e
10. (FGV-SP) A figura indica um hekzágono regular ABCDEF, de área S1, e um hekzágono regular GHIJKL, de vértices nos pontos médios dos apótemas do hekzágono ABCDEF e área S2.
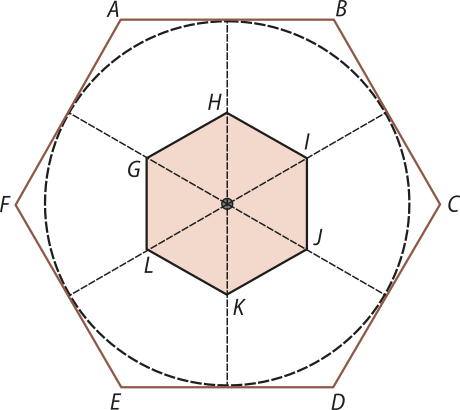
Nas condições descritas, é igual a
a)
b)
c)
d)
e)
alternativa e
Página duzentos e cinquenta e um
11. (UFRGS-RS) Considere um retângulo ABCD, de lados = 12 e = 8, e um ponto P construído sobre o lado . Traçando a reta r perpendicular ao lado quê passa pelo ponto P, determina-se o polígono ADEF, em quê E e F são pontos de interseção de r com os segmentos e , respectivamente, como mostra a figura abaixo.
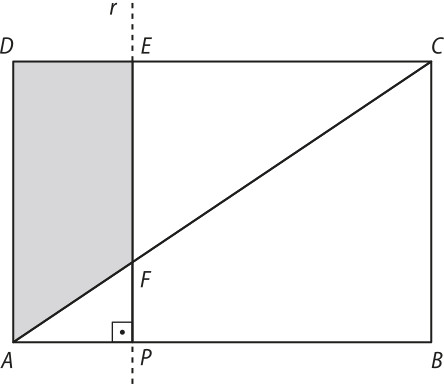
Tomando x como a medida do segmento AP, a função A(x) quê expressa a área de ADEF em função de x, entre as alternativas abaixo, é
a) A(x) = 8x − , para 0 ≤ x ≤ 12.
b) A(x) = 8x − , para 0 ≤ x ≤ 12.
c) A(x) = 16x − , para 0 ≤ x ≤ 12.
d) A(x) = 8x − , para 0 ≤ x ≤ 12.
e) A(x) = 8x − para 0 ≤ x ≤ 12.
alternativa d
12. (OBMEP) A figura a seguir é formada por quatro quadrados. A medida do segmento destacado em vermelho é 2. Qual é a soma das áreas dos quadrados azuis?
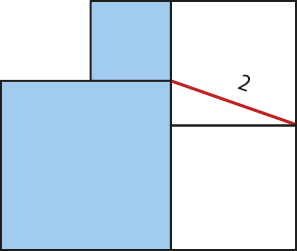
a) 2
b) 4
c) 6
d) 8
e) 10
alternativa d
13. (OBMEP) A área do polígono amarelo com vértices em pontos do quadriculado é 30 cm2. Qual é a área, em cm2, de cada quadradinho do quadriculado?

a) 2
b) 3
c) 4
d) 5
e) 6
alternativa e
14. (IFRN) Como lembrança da Cúpula da Amazônea, uma empresa entregou uma miniatura retangular do parque estadual Mangal das Garças. Sabendo quê essa miniatura tinha dimensões de 2 cm de comprimento por 8 cm de largura e quê foi feita numa escala de 1:5.000, a área real do mangal das garças, quê foi representada, em m2, na miniatura é
a) 40.000.
b) 30.000.
c) 25.000.
d) 35.000.
alternativa a
15. (Epcar-MG) A figura abaixo é um losango e as medidas indicadas estão em metros.
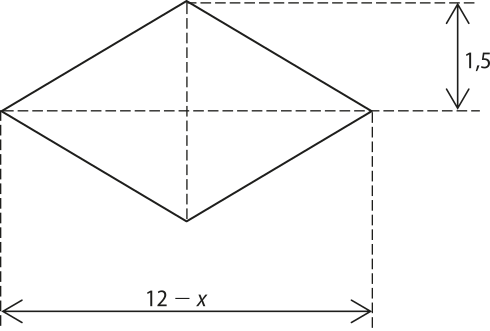
Todos os possíveis valores reais de x para quê a área dêêsse losango seja maior ou igual a 72 m2, são tais quê
a) x ≥ −84
b) x ≥ −36
c) x ≤ −84
d) x ≤ −36
alternativa d
Página duzentos e cinquenta e dois
16. (PUC-RJ) Seja R um retângulo com base igual a 24 e altura igual a 12. Um triângulo retângulo ABC com ângulo reto em B e base AB com comprimento igual ao dôbro da altura BC deve sêr construído dentro do retângulo R, d fórma quê a base AB fique sobre a base do retângulo R. Considere x o comprimento da base AB.
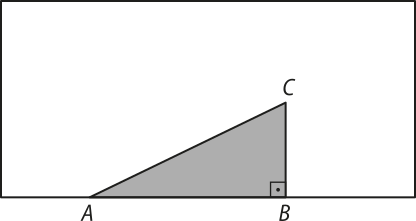
a) Para quais valores de x é possível construir esse triângulo?
0 < x ≤ 24
b) Encontre a expressão da hipotenusa do triângulo retângulo ABC em termos de x.
16. b) AC =
c) Determine o valor de x para o qual a área do triângulo ABC é igual a 64.
x = 16
17. (Unicamp-SP) Na figura a seguir, ABCD é um trapézio com AB = 1 e cê dê = 5. Os pontos M e N são pontos médios de AB e BC, respectivamente.
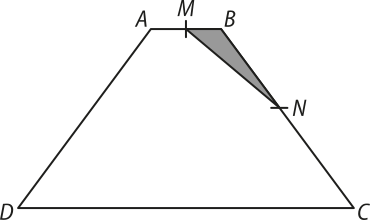
Sabendo quê a área de MBN é 1, a área do trapézio é:
a) 18.
b) 20.
c) 22.
d) 24.
alternativa d
18. (UFJF-MG) Um restaurante vende pitssas tamãnho família quê são produzidas em formas quadradas de 40 centimetros de lado e circulares de 40 centimetros de diâmetro. Para estimular a venda das pitssas quadradas, o dono do restaurante utiliza a frase: “Leve mais pitssa pelo mesmo preêço: compre pitssa quadrada!”. Ao optar pela pitssa quadrada, quantos cm2 a mais de pitssa o cliente está comprando? (Utilize (pi)" = 3,14).
a) 34,4 cm2
b) 91,2 cm2
c) 344 cm2
d) 912 cm2
e) 1.348,8 cm2
alternativa c
19. (IFSC) Marcelo recortou dois retângulos, um de dimensões 10 cm × 12 cm e outro de dimensões 11 cm × 13 cm. Em seguida, Marcelo colocou um retângulo sobre o outro, como mostra a imagem, e percebeu quê a região cinza tinha uma área equivalente a 58 cm2.
Sendo assim, a área da região hachurada é:
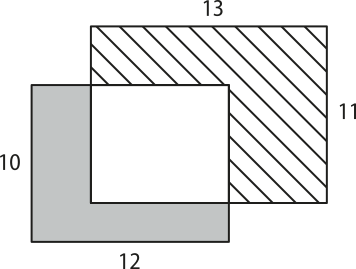
a) 62 cm2.
b) 92 cm2.
c) 79 cm2.
d) 84 cm2.
e) 81 cm2.
alternativa e
20. (IFMA) Suponha quê uma sala de aula esteja sêndo construída para sêr utilizada sem o apôio de recursos digitais, conforme a Figura 1. Sabendo quê, nessa sala de aula, cada aluno necessita de um espaço correspondente a 1,50 m2, o número mássimo de alunos quê podem estar presentes, simultaneamente, nesse ambiente, considerando a área destinada aos alunos, é
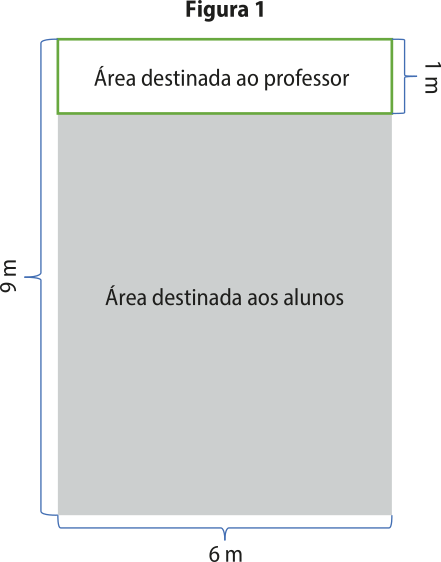
Fonte: Elaboração própria.
a) 36.
b) 28.
c) 32.
d) 40.
alternativa c
Página duzentos e cinquenta e três
21. (UFRGS-RS) Na figura abaixo, o triângulo ABC é equilátero de lado 4. O ponto D pertence ao lado AB, o ponto E pertence ao lado BC, o ponto F pertence ao lado AC, e os segmentos AD, BE e CF têm medida x.
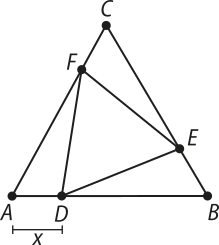
A função A(x) quê expressa a área do triângulo equilátero DEF, para 0 ≤ x ≤ 4, é
a) A(x) = (3x2 − 6x + 8).
b) A(x) = (3x2 + 12x + 16).
c) A(x) = (3x2 + 12x − 16).
d) A(x) = (3x2 + 12x + 16).
e) A(x) = (3x2 − 12x + 16).
alternativa e
PARA REFLETIR
Neste Capítulo, retomamos o conceito de área de polígonos e de área do círculo e de suas partes. Aprofundamos nosso estudo refletindo sobre a variação da área e do perímetro de polígonos regulares em função do comprimento dos lados. Aprendemos quê a medida do ângulo interno de polígonos regulares está diretamente relacionada à possibilidade de ladrilhamento do plano.
Nas páginas de abertura, abordamos o trabalho das ônguis e os programas sociais direcionados à construção e à reforma de moradias populares.
Na seção Conexões, conhecemos o conceito de índice de áreas verdes (IAV) de um município e pudemos pensar sobre a importânssia de parques e praças arborizados nas grandes cidades.
Vamos refletir a respeito das aprendizagens do Capítulo 7:
Respostas pessoais.
• Você lembrava como calcular a área de figuras como o quadrado, o triângulo e o losango?
• A partir da área do círculo, podemos calcular a área de uma coroa circular e do setor circular. Você recorda como?
• Aprendemos quê a variação da área de um polígono regular em função da medida do comprimento do seu lado é modelada pela função quadrática restrita ao domínio dos números reais positivos. Qual função modela a relação entre o perímetro e a medida do lado de um polígono regular?
• Ao escolher polígonos regulares para ladrilhar um plano, qual critério geométrico devemos considerar?
• Sobre o estudo relacionado às áreas de polígonos regulares inscritos na circunferência, as atividades da seção Explorando a tecnologia ajudaram você a compreender melhor esse tema?
Página duzentos e cinquenta e quatro

