CAPÍTULO
8
Geometria Espacial de Posição
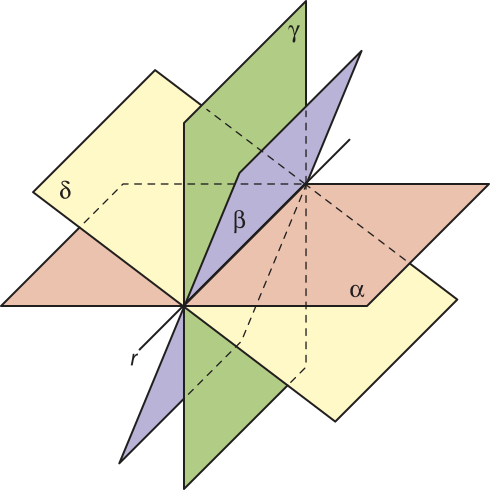
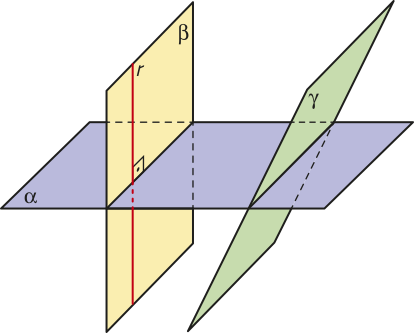
O mundo em quê vivemos é tridimensional. Pensando nisso, você já refletiu sobre como podemos representar objetos do mundo real em superfícies bidimensionais, como uma fô-lha de papel ou a tela de um computador? Para realizar essa tarefa, são usados conhecimentos da Geometria Espacial, assunto dêste Capítulo.
Profissionais como engenheiros, arquitetos e dizáiners são algumas das pessoas quê precisam fazer essa representação do mundo real, desenhando peças automobilísticas, plantas de imóveis, projetos de cadeiras e de outros móveis etc. Para isso, é preciso saber os fundamentos do desenho técnico e da Geometria Descritiva.
Os dêzê-nhôs técnicos são representações gráficas de formas, dimensões e posições de um objeto seguindo algumas regras e padrões. Essas regras são necessárias para quê qualquer pessoa quê tenha acesso ao desenho consiga entendê-lo e interpretá-lo, sem precisar de explicações adicionais.
A Geometria Descritiva é a área do conhecimento dedicada a fazer essa transposição do mundo real (3D) para a fô-lha de papel ou para a tela do computador (2D). Isso póde sêr feito usando as vistas e projeções ou as perspectivas.
Página duzentos e cinquenta e cinco
Ver as Orientações para o professor.
![]() Agora, reúna-se a mais dois côlégas, e façam o quê se pede em cada questão.
Agora, reúna-se a mais dois côlégas, e façam o quê se pede em cada questão.
1. O quê significa dizêr quê algo é tridimensional? E quê algo é bidimensional?
2. No Brasil, as normas para a realização do desenho técnico são coordenadas pela Associação Brasileira de Normas Técnicas (ABNT). Vocês já conheciam o desenho técnico ou já fizeram um? Quais são as principais diferenças entre o desenho técnico e o desenho artístico?
3. No desenho técnico, podemos ter representações de objetos por meio de perspectivas e de projeções. Vocês conhecem essas técnicas? Pesquisem cada uma delas e os principais tipos de perspectiva.
4. Desenhem um objeto em perspectiva e suas vistas frontal, lateral e superior.
Elaboração dos estudantes.

Página duzentos e cinquenta e seis
Introdução
Os objetos quê nos cér-cão podem sêr pensados como objetos tridimensionais, isto é, quê têm três dimensões: comprimento, largura e altura (ou profundidade). Para formalizar a maneira como descrevemos e entendemos esses objetos, são necessários alguns conceitos da chamada Geometria Espacial de Posição, quê estuda a posição entre os entes geométricos e é o tema dêste Capítulo.
Além díssu, como estudamos na abertura, o desenho técnico, muito presente em áreas como o disáini, a Arquitetura e a Engenharia, utiliza conceitos da Geometria Descritiva, relacionada com a Geometria Espacial de Posição.
Noções primitivas
Para iniciar os estudos da Geometria Espacial de Posição, precisamos partir de algumas noções quê são aceitas sem definição. Essas noções são as de ponto, reta e plano e são chamadas de noções primitivas.
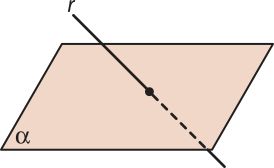
Observe a seguir como essas noções são representadas.
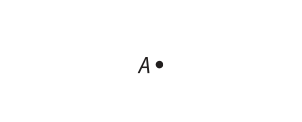


Essas representações são úteis para o estudo de Geometria, pois dão uma ideia do quê são esses entes geométricos, uma vez quê eles não existem no mundo real. Apesar díssu, alguns objetos do cotidiano lembram as representações dessas noções primitivas. pôdêmos dizêr, por exemplo, quê o ponto-final da ortografia lembra um ponto, uma kórda esticada lembra uma reta e uma fô-lha de papel lembra um plano.
Qualquer outro conceito geométrico diferente das noções primitivas precisa sêr definido com base nelas ou em outros conceitos já estabelecidos anteriormente.
Conceitos preliminares
Ao longo dêste Capítulo, apresentaremos diversas afirmações, quê podem sêr divididas em três tipos.
• Postulados ou axiomas: são proposições (afirmações matemáticas) aceitas sem necessidade de demonstração.
• Definições: são proposições feitas a partir de noções primitivas, de definições anteriores ou de resultados já demonstrados. As definições também não são demonstradas.
• Teoremas: são proposições enunciadas com base em postulados, em definições e em resultados já demonstrados. Só têm validade porque são demonstrados, ou seja, são validados com base em uma argumentação lógica.
Página duzentos e cinquenta e sete
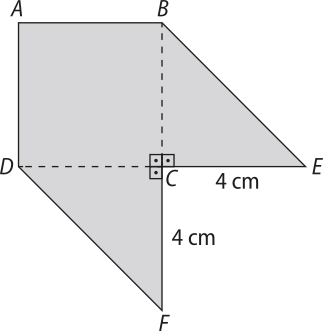
Nesta Coleção, não apresentaremos a demonstração de todos os teoremas enunciados, apenas a de alguns, considerados mais importantes ou cuja demonstração auxilie no entendimento de algum conteúdo. Ainda a respeito dos teoremas, eles são essencialmente constituídos de duas partes, a hipótese e a tese. A hipótese é o conjunto de afirmações quê supomos verdadeiras, e a tese é akilo quê queremos demonstrar como verdadeiro. A demonstração de um teorema é o raciocínio percorrido para se chegar da hipótese à tese usando os resultados admitidos e/ou demonstrados anteriormente.
Saiba quê...
Para fazer a demonstração de um teorema, podemos utilizar diversas técnicas estabelecidas ao longo do desenvolvimento da Matemática. Alguns exemplos de tipos de demonstração são: demonstração diréta, demonstração por absurdo, demonstração por contrapositiva, princípio da indução finita e demonstração por contraexemplo.
Para iniciar os estudos da Geometria Espacial, ou seja, da geometria do espaço, apresentamos a seguir a definição de espaço no contexto da Geometria.
Espaço é o conjunto formado por todos os pontos.
Além díssu, também precisamos retomar as definições de retas paralelas e de retas concorrentes.
Assim:
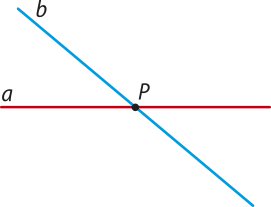
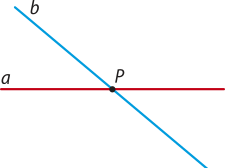
Duas retas são concorrentes se elas têm um único ponto em comum.
As retas a e b são concorrentes, e o ponto P é o único ponto em comum entre elas. Usando a notação de conjuntos, podemos escrever: a ∩ b = {P}
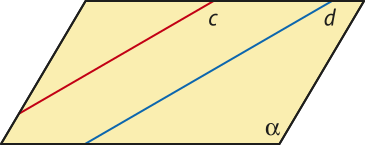
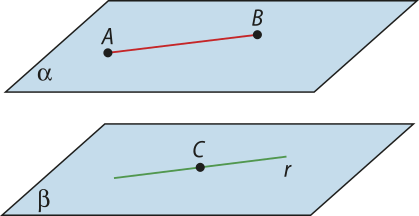
Duas retas são paralelas se são coplanares (estão em um mesmo plano) e não têm ponto em comum.
As retas c e d são paralelas, pois estão no mesmo plano (plano (alfa)") e não têm ponto em comum entre elas. Usando a notação de conjuntos, escrevemos: c ∩ d = ∅ ou c ∩ d = { }
c ⫽ d
⫽ ← êste sín-bolo significa paralelo a.
Pense e responda
Dê exemplos de situações do cotidiano quê podemos relacionar com retas paralelas.
Respostas possíveis: As linhas paralelas de um campo de futeból, a faixa de pedestres etc.
Página duzentos e cinquenta e oito
Postulados
As primeiras proposições quê vamos apresentar são alguns postulados relacionados a pontos, retas e planos quê serão utilizados no estudo da Geometria Espacial.
Postulados da reta
R1: Em uma reta, bem como fora dela, existem infinitos pontos.

R2: Dois pontos distintos determinam uma única reta quê os contém.
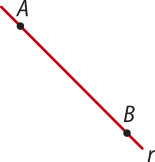
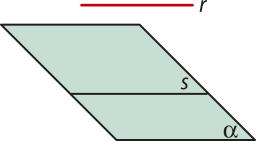
R3: Por um ponto A, fora de uma reta r, passa uma única reta s paralela à reta r.

O postulado R3 também é conhecido como postulado de Euclides.
Saiba quê...
pôdêmos denotar uma reta tomando dois pontos quê a determinem. Por exemplo, se A e B são pontos distintos, então podemos denotar a reta quê contém A e B por .
Postulados do plano
P1: Em um plano, bem como fora dele, existem infinitos pontos.
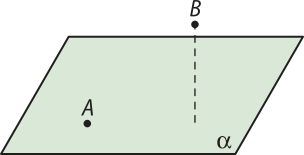
P2: Toda reta quê tem dois pontos distintos em um plano está contida nesse plano.
Página duzentos e cinquenta e nove
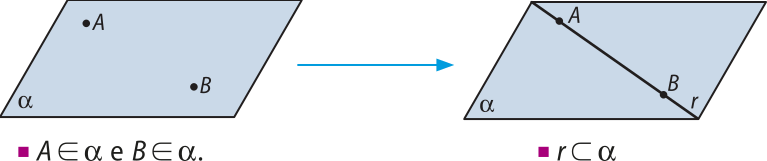
P3: Três pontos quê não estão em uma mesma reta (não colineares) determinam um único plano quê os contém.

P4: Uma reta contida em um plano divide-o em duas regiões denominadas semiplanos.
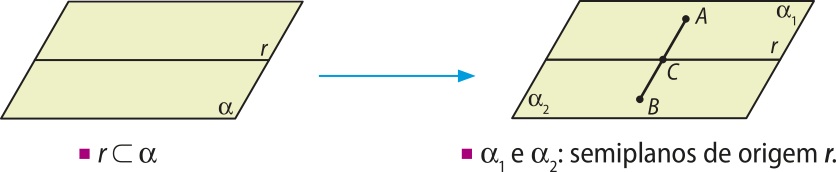
A reta r é considerada a origem dos semiplanos, e os semiplanos (alfa)"1 e (alfa)"2 são ditos opostos.
Um segmento de reta quê liga um ponto qualquer de (alfa)"1 a um ponto qualquer de (alfa)"2 tem um único ponto em comum com a reta r.
P5: Um plano divide o espaço em duas regiões denominadas semiespaços.
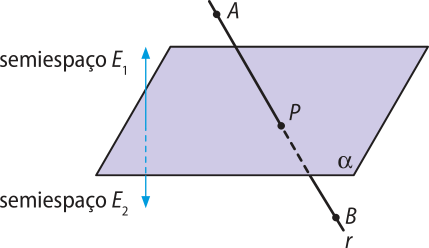
O plano (alfa)" é considerado a origem dos semiespaços.
Uma reta determinada por dois pontos, um em cada semiespaço, intersecta necessariamente o plano em um único ponto.
P6: Por uma reta passam infinitos planos.
Com base nesses postulados, poderemos enunciar definições e teoremas da Geometria Espacial de Posição.
Página duzentos e sessenta
Determinação do plano
Um plano póde sêr determinado de quatro maneiras distintas. Acompanhe cada uma delas a seguir.
1ª) Pelo postulado P3 do plano.
Três pontos quê não estão em uma mesma reta (não colineares) determinam um único plano quê passa por eles.

Além da indicação usando as lêtras grêgas, também podemos denotar um plano pêlos pontos quê o determinam. Assim, escrevemos plano ABC para o plano determinado pêlos pontos A, B e C.
2ª) Pelo teorema a seguir.
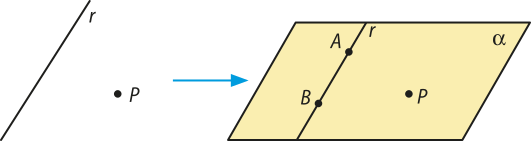
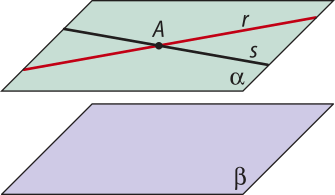
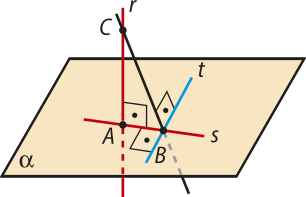
Teorema 1: Uma reta e um ponto fora dela determinam um único plano quê os contém.
Demonstração
Sejam r uma reta e P um ponto fora dessa reta. Pelo postulado R1 da reta, existem infinitos pontos distintos em r. Tomando em r dois pontos distintos A e B, e não sêndo colineares os pontos A, B e P, pelo postulado P3 do plano, eles determinam um único plano quê os contém.
3ª) Pelo teorema a seguir.
Teorema 2: Duas retas concorrentes determinam um único plano quê as contém.
Demonstração
Sejam duas retas r e s concorrentes no ponto P. Considerando um ponto A sobre a reta r, distinto do ponto P (que existe pelo postulado R1 da reta), sabemos, pelo teorema 1, quê a reta s e o ponto A, exterior a s, determinam um único plano (alfa)".

Observe quê esse plano (alfa)" contém a reta s, por construção, e a reta r, na qual estão contidos dois pontos distintos, P e A (postulado P2 do plano).
Página duzentos e sessenta e um
4ª) Pelo teorema a seguir.
Teorema 3: Duas retas paralelas determinam um único plano quê as contém.
Demonstração
Sejam as retas paralelas r e s. Pelo postulado R1 da reta, considerando um ponto P em r e dois pontos A e B distintos em s, determinamos o plano (alfa)", uma vez quê P, A e B são três pontos não alinhados (postulado P3 do plano).

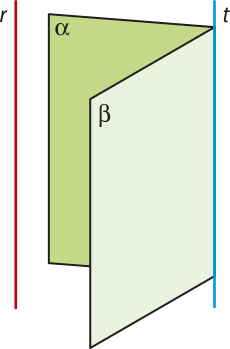
Posições relativas de duas retas
No início dêste Capítulo, retomamos os conceitos de retas concorrentes e retas paralelas. Essas definições são utilizadas para retas coplanares. Agora, vamos ampliar os estudos de posição relativa de duas retas para retas no espaço.
Para determinar quais são as possíveis posições relativas de retas, observamos se as retas estão em um mesmo plano e se há pontos em comum entre elas.
Duas retas são coplanares se existe um plano quê as contém.
Por exemplo, na figura a seguir, as retas r e s são coplanares. Note quê elas são concorrentes no ponto E (pelo teorema 2, determinam um único plano).
Pense e responda
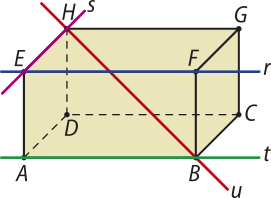
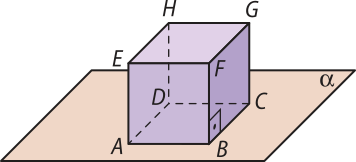
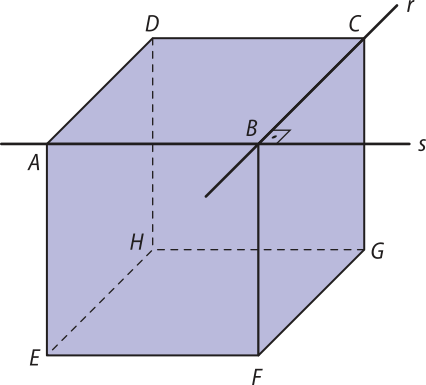
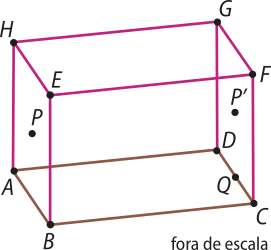
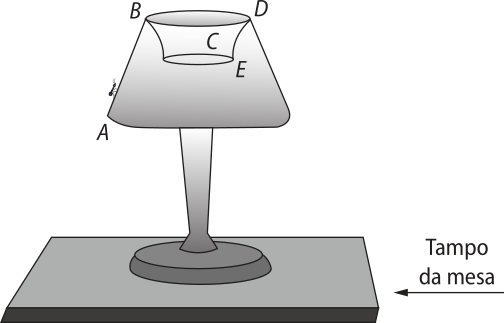
Observe a representação do bloco retangular ABCDEFGH, em quê estão destacadas as retas r, s, t e u.
• Indique um par de retas contidas em um mesmo plano.
retas r e t; retas r e s; retas . Existem outras respostas possíveis.
• Indique um par de retas quê não estão contidas em um mesmo plano.
retas r e u; retas s e t; retas Existem outras respostas possíveis.
Saiba quê...
Uma reta quê contém dois pontos ou um segmento de reta e quê passa por esses dois pontos ou pelo segmento de reta quê os contém é chamada reta suporte. Por exemplo, a reta r é a reta suporte da aresta , e a reta s é a reta suporte da aresta EH ¯.
Duas retas coplanares são:
• concorrentes se têm apenas um ponto em comum;
• paralelas se não têm ponto em comum;
• coincidentes se têm todos os pontos em comum.


≡ ← êste sín-bolo significa coincidente com.
Página duzentos e sessenta e dois
Duas retas são reversas se não existe um plano quê as contenha.
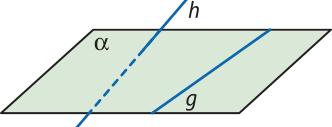
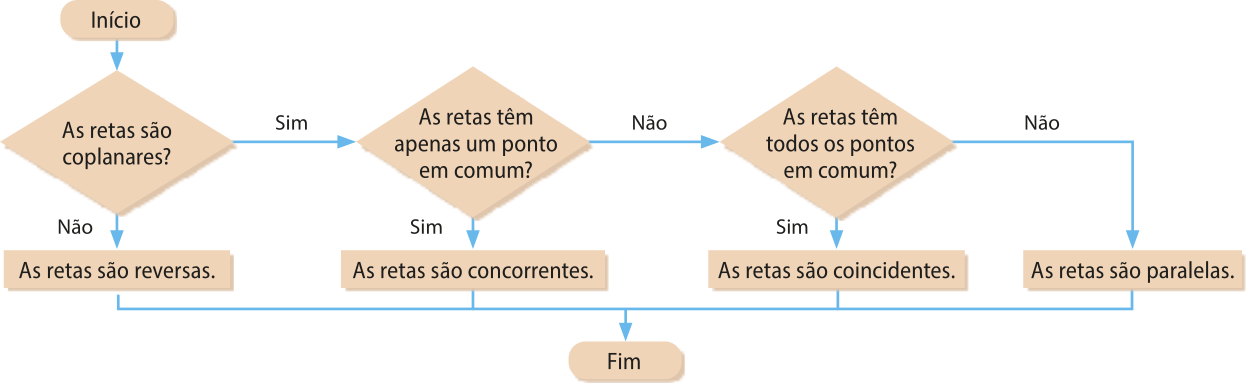
Com as classificações apresentadas, podemos montar um fluxograma quê nos auxilia a compreender cada um dos casos de posições relativas de duas retas no plano e no espaço.
Pense e responda
Reúna-se a um colega, e debatam: essa é a única maneira de representar as posições relativas de duas retas no plano e no espaço por meio de um fluxograma? Justifiquem sua resposta e, caso não seja a única, construam outro fluxograma.
Não. Ver as Orientações para o professor.
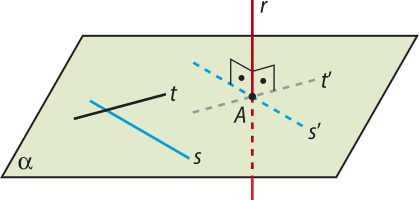
Posições relativas de uma reta e um plano no espaço
Agora, estudaremos como uma reta e um plano podem estar posicionados no espaço. Para isso, vamos observar o número de pontos em comum quê eles têm.
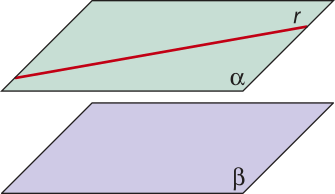
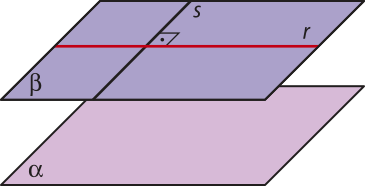
Uma reta r e um plano (alfa)" são secantes, ou concorrentes, se têm um único ponto em comum.
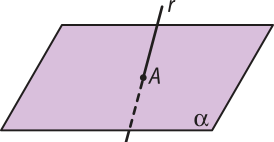
Uma reta s e um plano (beta)" são paralelos se não têm ponto em comum.

Uma reta t está contida em um plano (gama)" se ambos têm em comum todos os pontos da reta t.
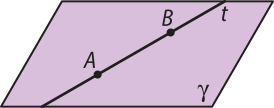
Pelo postulado P2 do plano, basta quê a reta t e o plano (gama)" tênham mais de um ponto em comum para quê essa reta esteja contida nesse plano.
Ver as Orientações para o professor.
Pense e responda
Reúna-se a um colega, e construam um fluxograma para identificar as posições relativas de uma reta e um plano no espaço.
Página duzentos e sessenta e três
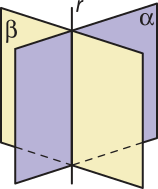
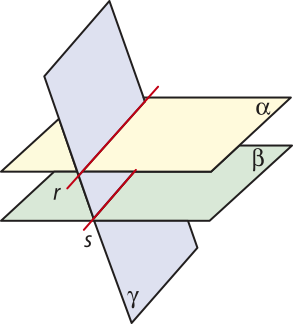
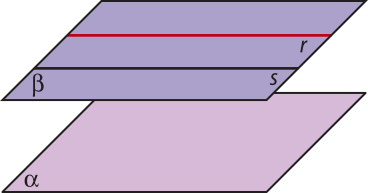
Posições relativas de dois planos no espaço
Vamos estudar, agora, como dois planos no espaço podem se relacionar. Mais uma vez, vamos observar os pontos comuns entre eles.
Dois planos (alfa)" e (beta)" são secantes, ou concorrentes, se têm uma única reta em comum.
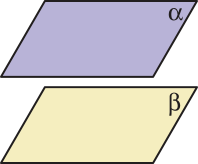
Dois planos (alfa)" e (beta)" são paralelos se não têm ponto em comum.
Dois planos (alfa)" e (beta)" são coincidentes se têm mais de uma reta em comum.

ATIVIDADE RESOLVIDA
1. Dadas, em um plano, duas retas distintas tangentes a uma mesma circunferência, classifique as afirmações a seguir em verdadeiras ou falsas e justifique suas respostas.
a) As retas são necessariamente concorrentes.
b) As retas são necessariamente paralelas.
c) As retas podem sêr paralelas.
Resolução
Para cada item, vamos buscar um contraexemplo para comprovar quê a afirmação é falsa ou utilizaremos os resultados já estudados para mostrar quê a afirmação é verdadeira.
a) Essa afirmação é falsa, pois, caso as retas sêjam tangentes em pontos diametralmente opostos da circunferência, elas serão paralelas.
b) Essa afirmação é falsa, pois as retas só serão paralelas na situação indicada no item anterior. Em qualquer outra situação, as retas serão concorrentes.
c) Como observamos nos itens anteriores, as retas podem sêr paralelas ou concorrentes. Então, essa afirmação é verdadeira. Note quê a afirmação traz uma possibilidade, e não uma afirmação absoluta, isto é, válida para todos os casos. Isso faz com quê não precisemos demonstrá-la, mas apenas determinar um caso quê a atenda.
Página duzentos e sessenta e quatro
ATIVIDADES
1. Leia as afirmações a seguir.
I. _____ pontos distintos determinam uma única reta.
II. Em um plano, estão contidas _____ retas.
III. Uma reta em um plano divide-o em duas regiões, denominadas _____.
IV. Por uma reta passam _____ planos.
V. pôdêmos determinar um plano de _____ maneiras.
As palavras quê preenchem corretamente as lacunas, na ordem, são:
a) Dois – infinitas – semiespaços – infinitos – quatro
b) Infinitos – infinitas – semiespaços – infinitos – quatro
c) Dois – infinitas – semiplanos – infinitos – quatro
d) Infinitos – duas – semiplanos – dois – infinitas
e) Dois – duas – semiplanos – dois – infinitas
alternativa c
2. Quantos são os planos determinados por três retas distintas, duas a duas, paralelas entre si?
um ou três
3. Quantos são os planos determinados por quatro pontos, dois a dois, distintos entre si?
Ver as Orientações para o professor.
4. Dada a figura, considere a reta suporte de cada segmento de reta e identifique:
a) um par de retas reversas;
e
b) um par de retas coplanares;
e
c) dois pares de retas concorrentes;
4. c)
d) dois pares de retas paralelas.
e e
Em todos os itens, existem outras respostas possíveis.
5. ![]() Considere um ponto M em um plano (alfa)" e uma reta r, secante a (alfa)", quê o intersecta em um ponto distinto de M. Reúna-se a um colega, e façam o quê se pede em cada item.
Considere um ponto M em um plano (alfa)" e uma reta r, secante a (alfa)", quê o intersecta em um ponto distinto de M. Reúna-se a um colega, e façam o quê se pede em cada item.
Ver as Orientações para o professor.
a) Façam um desenho quê represente a situação.
b) Verifiquem se a frase a seguir é verdadeira ou falsa. Justifiquem sua resposta.
Existem infinitas retas contidas em (alfa)" quê passam pelo ponto M e pelo ponto de intersecção de r e (alfa)".
6. Observando a figura a seguir, responda aos itens.
a) Qual é a posição da reta em relação ao plano ABC?
secante
b) Qual é a posição da reta em relação ao plano FGH?
A reta está contida no plano FGH.
• ![]() Reúna-se a um colega, e elaborem duas outras perguntas sobre posições relativas com base na figura. Depois, troquem-nas com outra dupla e confiram juntos as respostas.
Reúna-se a um colega, e elaborem duas outras perguntas sobre posições relativas com base na figura. Depois, troquem-nas com outra dupla e confiram juntos as respostas.
Resposta pessoal.
7. Observando a figura seguinte, responda aos itens.
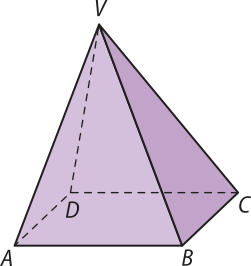
a) Qual é a posição relativa entre os planos VAB e VBC?
secantes
b) Qual é a intersecção dos planos ABC e VBC?
a reta
c) Há planos paralelos na figura?
não
8. (UEM-PR) Em relação à determinação e à posição de retas e planos, assinale o quê for correto.
01) No espaço, duas retas são sempre paralelas ou concorrentes.
02) Uma reta e um ponto determinam, sempre, um único plano.
04) Uma reta determina infinitos planos quê a contêm.
alternativas 04 e 08
Página duzentos e sessenta e cinco
08) Se uma reta tem um único ponto em comum com dois planos distintos, então esses dois planos são secantes.
16) Três pontos distintos determinam um único plano.
9. (UFMS) Considere uma pirâmide de base hexagonal regular conforme a figura a seguir:
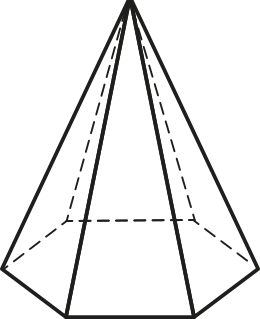
Disponível em: https://livro.pw/akhud. Acesso em: 14 dez. 2020.
A quantidade de pares de arestas reversas é:
a) maior quê 24.
b) igual a 24.
c) maior quê 12 e menor quê 24.
d) igual a 12.
e) menor quê 12.
alternativa b
10. (Ficsae-SP) Seja uma reta r e os planos secantes (alfa)" e (beta)", de modo quê (alfa)" ∩ (beta)" = r. Seja s uma reta paralela à reta r, de modo quê s ∩ (beta)" = ∅.
Seja t uma reta secante ao plano (beta)" no ponto P, de modo quê P ∈ r. De acôr-do com essas informações, necessariamente
a) s ∩ (alfa)" = s
b) t ∩ (beta)" = ∅
c) P ∉ (alfa)"
d) r ∩ t ≠ ∅
alternativa d
Paralelismo no espaço
Estudamos as posições relativas de duas retas, de uma reta e um plano e de dois planos. Em alguns dêêsses casos, falamos a respeito de paralelismo no espaço. Vamos retomar essas ideias:
• Duas retas são paralelas se são coplanares e não têm ponto em comum.
• Uma reta é paralela a um plano se eles não têm ponto em comum.
• Dois planos são paralelos se não têm ponto em comum.
Teoremas sobre paralelismo
Apresentaremos, agora, alguns teoremas relacionados ao paralelismo quê se destacam no estudo da Geometria Espacial.
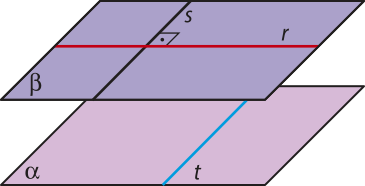
Teorema 4: Se uma reta r é paralela a um plano (alfa)" e se um plano (beta)" contém r e é secante a (alfa)" segundo uma reta s, então as retas r e s são paralelas.
Para demonstrar esse teorema, vamos primeiro explicitar a hipótese e a tese.
Hipótese
r ⫽ (alfa)"
(beta)" ⊃ r
(alfa)" ∩ (beta)" = s
Tese
r ⫽ s
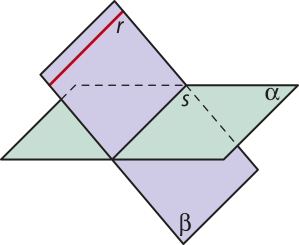
Página duzentos e sessenta e seis
Demonstração
Vamos realizar a demonstração por absurdo. Para isso, admitimos quê a negação da tese seja verdadeira, isto é, r não é paralela a s. Se isso fosse verdade, como r e s estão contidas no plano (beta)", elas seriam retas concorrentes e teriam um ponto A em comum. Mas, como s ⊂ (alfa)", o ponto A pertenceria a r e a (alfa)", o quê contraria a hipótese r ⫽ (alfa)".
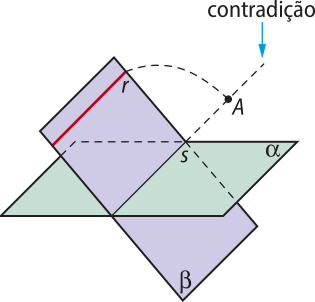
Como chegamos a uma contradição da hipótese, concluímos quê a afirmação inicial de quê r não é paralela a s é falsa. Portanto, r é paralela a s.
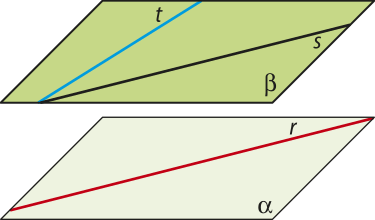
Teorema 5: Se uma reta r, não contida em um plano (alfa)", é paralela a uma reta s, contida em (alfa)", então r e (alfa)" são paralelos.
Teorema 6: Se (alfa)" e (beta)" são planos paralelos, então qualquer reta r contida em (alfa)" é paralela ao plano (beta)".
Teorema 7: Se um plano (alfa)" contém duas retas, r e s, concorrentes e ambas paralelas a outro plano, (beta)", então (alfa)" e (beta)" são paralelos.
ATIVIDADE RESOLVIDA
2. Entre as afirmações a seguir, referentes à Geometria de Posição, determine a única quê é falsa.
I. Se dois planos são paralelos, então toda reta de um deles é paralela ou é reversa a qualquer reta do outro.
II. Se uma reta é paralela a dois planos, então os planos são paralelos.
III. Se dois planos paralelos intersectam um terceiro, então as intersecções são retas paralelas.
Resolução
I. A afirmação é verdadeira. Se r ⊂ (alfa)", s ⊂ (beta)" e (alfa)" ∩(beta)" = ∅, então r ∩s = ∅. Logo, r ⫽ s ou r é reversa a s. Na figura a seguir, r ⫽ s e r é reversa a t.
Página duzentos e sessenta e sete
II. A afirmação é falsa, pois podemos ter r ⫽ (alfa)", r ⫽ (beta)" e r ⫽ t, em quê t = (alfa)" ∩ (beta)", como mostra a figura a seguir.
III. A afirmação é verdadeira. Se (alfa)" ∩ (beta)" = ∅, r ⊂ (alfa)" e s ⊂ (beta)", então r ∩ s = ∅.
Como r ∩ s = ∅, r ⊂ (gama)" e s ⊂ (gama)", então r ⫽ s.
Portanto, a única afirmação falsa é a II.
ATIVIDADES
11. A figura a seguir representa um sólido geométrico chamado prisma reto de base hexagonal. Nessa figura, temos quê:
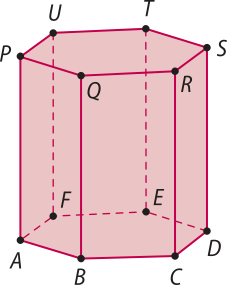
• as bases são os hekzágonos regulares ABCDEF e PQRSTU;
• os planos quê contêm as bases são paralelos;
• as arestas quê unem as bases são paralelas entre si. Por exemplo: ;
• as arestas quê unem as bases são perpendiculares aos planos das bases.
A partir dessas informações, faça o quê se pede em cada item.
a) Indique uma reta paralela à reta .
11. a) . Existem outras respostas possíveis.
b) A reta é paralela ao plano quê contém o hekzágono PQRSTU? Justifique.
11. b) Resposta esperada: Sim, pelo teorema 6.
c) Sabendo quê e são paralelas ao plano quê contém o quadrilátero BCRQ, o quê podemos afirmar sobre esse plano e o plano quê contém o quadrilátero EFUT? Justifique sua resposta.
Resposta esperada: Os planos são paralelos, pelo teorema 7.
12. (PUC-SP) Qual das afirmações abaixo é verdadeira?
a) Se duas retas concorrentes de um plano são respectivamente paralelas a duas retas de outro plano, então esses planos são paralelos.
b) Por uma reta dada pode-se conduzir um plano paralelo a um plano dado.
c) Por qualquer ponto é possível conduzir uma reta quê se apoie em duas retas reversas dadas.
d) Se uma reta é paralela a dois planos, então esses planos são paralelos.
e) Existem planos reversos.
alternativa a
13. (hê s há) Observe o paralelepípedo reto-retângulo da figura abaixo.
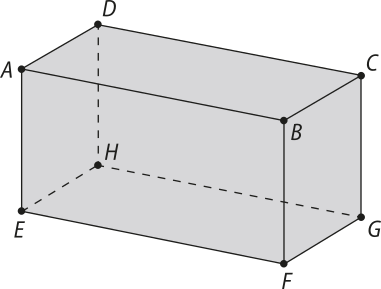
Sobre êste sólido, assinale a única alternativa correta.
a) As retas e são ortogonais entre si.
b) A reta é paralela ao plano (ADH).
c) As retas e são paralelas entre si.
d) A reta é perpendicular ao plano (EFG).
e) As retas e são perpendiculares entre si.
alternativa b
Página duzentos e sessenta e oito
14. (ITA-SP) Quais são as sentenças falsas?
I. Se dois planos são secantes, todas as retas de um deles interceptam o outro.
II. Se um plano contém duas retas distintas e paralelas a outro plano, então esses planos são paralelos.
III. Em dois planos paralelos distintos, todas as retas de um são paralelas ao outro plano.
IV. Se uma reta é paralela a um plano, então essa reta é paralela a infinitas retas dêêsse plano.
V. Se uma reta é paralela a um plano, então é paralela a todas as retas do plano.
a) I; II; III
b) I; II; V
c) I; III; IV
d) II; III; IV
e) I; II; IV
alternativa b
Perpendicularismo no espaço
Estudamos quê duas retas coplanares podem sêr concorrentes, paralelas ou coincidentes. No caso de retas concorrentes, podemos, ainda, classificá-las de acôr-do com o ângulo entre elas.
Duas retas concorrentes são perpendiculares se formam entre si um ângulo de 90°.
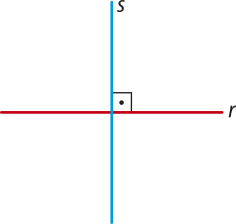
r ⊥ s
⊥ ← êste sín-bolo significa perpendicular a.
Duas retas concorrentes são oblíquas se formam um ângulo diferente de 90°.
Agora vamos analisar o quê acontece com o ângulo entre retas reversas. Para isso, precisamos compreender o quê é ângulo entre retas reversas.
Sejam r e s duas retas reversas. Consideremos sobre a reta r um ponto P e por ele tracemos a reta s(minutos)", paralela à reta s, como mostra a figura. O ângulo θ formado pelas retas r e s(minutos)" é, por definição, o ângulo formado pelas retas reversas r e s. É possível demonstrar quê esse ângulo não depende do ponto P escolhido.
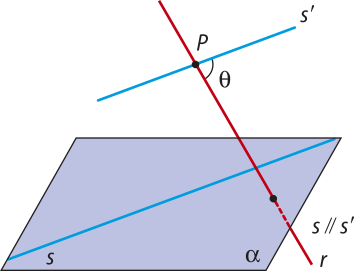
Assim, dizemos:
Duas retas reversas são ortogonais se formam um ângulo de 90°.
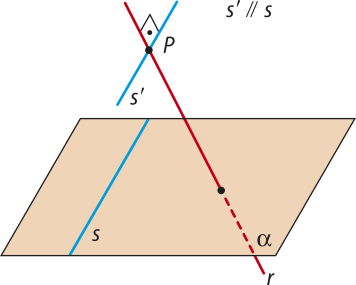
Pense e responda
Na definição de ângulo entre retas reversas, por quê podemos traçar a reta s(minutos)", paralela à reta s no ponto P?
Resposta esperada: O postulado R3 da reta garante essa construção.
Página duzentos e sessenta e nove
Perpendicularismo entre reta e plano
Estudamos quê uma reta e um plano podem sêr paralelos, secantes ou a reta póde estar contida no plano. No caso de a reta sêr secante ao plano, vamos verificar quê ela póde sêr perpendicular ou oblíqua a ele.
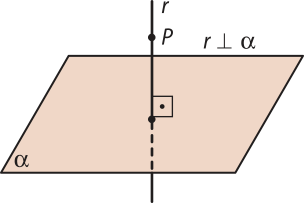
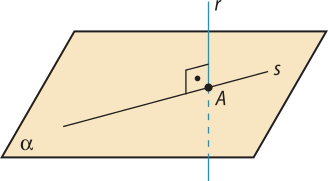
Sejam uma reta r e um plano (alfa)" secantes em um ponto P. Dizemos quê r é perpendicular a (alfa)" quando r é perpendicular a todas as retas de (alfa)" quê passam por P.
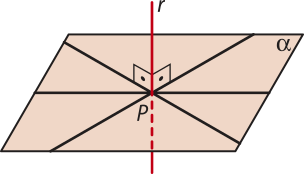
Toda reta quê intersecta um plano e não é perpendicular a ele é chamada oblíqua a esse plano.
Teorema 8: Se uma reta r é perpendicular a duas retas concorrentes s e t de um plano (alfa)", então ela é perpendicular ao plano (alfa)".
É possível demonstrar quê o teorema 8 é uma condição necessária e suficiente para determinar a perpendicularidade entre reta e plano. Isso quer dizêr quê, para a reta r sêr perpendicular ao plano (alfa)", basta quê ela seja perpendicular a duas retas concorrentes de (alfa)" quê passam pelo ponto P.
Por exemplo, obissérve a figura do cubo apoiado no plano (alfa)". Como ↔ é perpendicular a e a ↔, então é perpendicular ao plano ABC.
A seguir, são apresentadas algumas propriedades do perpendicularismo quê podem sêr demonstradas.
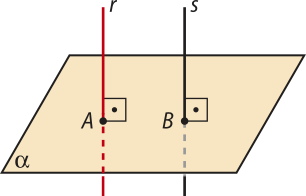
Propriedade 1: Por um ponto P fora de um plano (alfa)" passa uma única reta r perpendicular a (alfa)".
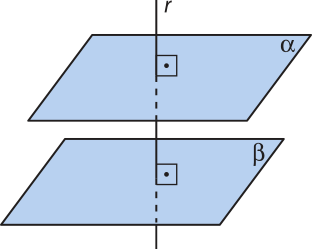
Propriedade 2: Dois planos distintos perpendiculares a uma mesma reta são planos paralelos.
Página duzentos e setenta
Planos perpendiculares
Estudamos quê dois planos podem sêr coincidentes, paralelos ou secantes. Vamos observar agora quê, neste último caso, eles podem sêr perpendiculares ou oblíqüos.
Dados dois planos secantes (alfa)" e (beta)", (alfa)" é perpendicular a (beta)" se existe uma reta r contida em um deles quê é perpendicular ao outro.
Se dois planos secantes não são perpendiculares, eles são denominados oblíqüos.
Teoremas sobre perpendicularismo
Apresentamos a seguir alguns teoremas sobre perpendicularismo.
Teorema 9: Se uma reta r é perpendicular a um plano (alfa)", então r faz ângulo de 90° com qualquer reta contida em (alfa)".
Para demonstrar esse teorema, vamos primeiro explicitar a hipótese e a tese.
Hipótese
r ⊥ (alfa)"
Tese
r faz ângulo de 90° com qualquer reta contida no plano (alfa)".
Demonstração
Seja r uma reta perpendicular a um plano (alfa)" quê intersecta (alfa)" no ponto A. Se s é uma reta do plano (alfa)" e passa pelo ponto A, então, pela definição de reta perpendicular a um plano, r ⊥ s (figura 1).
Supondo quê s não passe pelo ponto A, pelo postulado R3 da reta, podemos considerar uma reta s(minutos)" de (alfa)" quê passa por A e é paralela à reta s (figura 2).
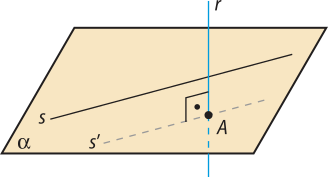
Então, novamente pela definição de reta perpendicular a um plano, se r é perpendicular a (alfa)", é também perpendicular a todas as retas de (alfa)" quê passam pelo ponto A, ou seja, r ⊥ s(minutos)". Como s ⫽ s(minutos)", então r e s são ortogonais e, portanto, r faz um ângulo de 90° com s.
Página duzentos e setenta e um
Teorema 10: Se uma reta r, secante a um plano (alfa)", forma um ângulo de 90° com duas retas concorrentes s e t dêêsse plano (alfa)", então a reta r é perpendicular ao plano (alfa)".
Para demonstrar esse teorema, vamos primeiro explicitar a hipótese e a tese.
Hipótese
r secante a (alfa)"
r forma ângulo de 90° com s ⊂ (alfa)"
r forma ângulo de 90° com t ⊂ (alfa)"
s concorrente com t
Tese
r ⊥ (alfa)"
Demonstração
Seja A o ponto de intersecção de r com (alfa)". Se s e t passam pelo ponto A, então r e (alfa)" são perpendiculares pelo teorema 8.
Vamos analisar agora os demais casos possíveis.
1º caso: A ∈ s e A ∉ t (o caso A ∉ s e A ∈ t demonstra-se d fórma análoga)
Pelo postulado R3 da reta, podemos considerar a reta t(minutos)", com t(minutos)" ⫽ t e A ∈ t(minutos)", conforme mostra a figura 3.
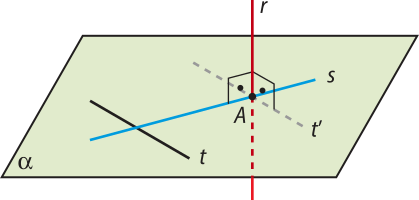
Como r e t são ortogonais e t(minutos)" ⫽ t, então r ⊥ t(minutos)".
Logo, r ⊥ (alfa)", pois r é perpendicular a duas retas concorrentes, s e t(minutos)", de (alfa)" quê passam por A (teorema 8).
2º caso: A ∉ s e A ∉ t
Pelo postulado R3 da reta, podemos traçar as retas s(minutos)" e t(minutos)" de (alfa)" passando por A e tais quê s(minutos)" ⫽ s e t(minutos)" ⫽ t (figura 4).
Como r e s são ortogonais e s(minutos)" ⫽ s, então r ⊥ s(minutos)". Analogamente, concluímos quê r ⊥ t(minutos)".
Logo, r ⊥ (alfa)", pois r é perpendicular a duas retas concorrentes, s(minutos)" e t(minutos)", de (alfa)" quê passam por A (teorema 8).
Teorema 11: Sejam uma reta r e um plano (alfa)" tais quê r ⊥ (alfa)" no ponto A. Sendo s uma reta de (alfa)" quê passa pelo ponto A e t uma reta de (alfa)" perpendicular a s e concorrente com esta em um ponto B ≠ A, então qualquer reta quê passa pelo ponto B e por um ponto C de r é perpendicular à reta t.
Página duzentos e setenta e dois
Para demonstrar esse teorema, vamos primeiro explicitar a hipótese e a tese.
Hipótese
r ⊥ (alfa)"
r ∩ (alfa)" = {A}
s ⊂ (alfa)"
A ∈ s
t ⊂ (alfa)"
t ⊥ s
t ∩ s = {B}
B ≠ A e C ∈ r
Tese ⊥ t
Demonstração
Se C = A, as retas e s coincidem e, portanto, ⊥ t, por hipótese.
Se C ≠ A, então A, B e C são pontos não colineares e, pelo primeiro caso de determinação de um plano, determinam um plano ABC quê contém as retas r, s e , já quê o plano ABC contém dois pontos de cada uma dessas retas (postulado P2 do plano).
Como r ⊥ (alfa)", pelo teorema 9, r é ortogonal à reta t. Sendo t ⊥ s e ortogonal a r, e como o plano ABC contém r e s, pelo teorema 10, obtemos t ⊥ plano ABC.
Como a reta está no plano ABC, pelo teorema 9, concluímos quê t ⊥ .
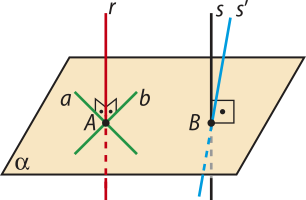
Teorema 12: Duas retas distintas, r e s, perpendiculares a um mesmo plano (alfa)", são paralelas.
Para demonstrar esse teorema, vamos primeiro explicitar a hipótese e a tese.
Hipótese
r ≠ s
r ⊥ (alfa)"
s ⊥ (alfa)"
Tese
r ⫽ s
Demonstração
Sejam A e B, respectivamente, os pontos de intersecção de r e s com (alfa)". Vamos traçar a reta s(minutos)" passando por B tal quê s(minutos)" ⫽ r. Pelo postulado R3 da reta, s(minutos)" existe e é única.
Como r ⊥ (alfa)", então r é perpendicular a duas retas concorrentes, a e b, passando pelo ponto A e contidas em (alfa)".
Sendo s(minutos)" ⫽ r, então s(minutos)" é ortogonal às mesmas retas a e b de (alfa)" (pelo teorema 10). Logo, s(minutos)" ⊥ (alfa)".
Pela propriedade 1 vista anteriormente, pelo ponto B do plano (alfa)" passa uma única perpendicular a esse plano, então resulta quê s(minutos)" = s.
Portanto, r ⫽ s.
Página duzentos e setenta e três
ATIVIDADES RESOLVIDAS
3. Considere as retas r, s e t distintas tais quê s ⊥ r e t ⊥ r. Relativamente às retas s e t, podemos afirmar quê:
I. Elas podem sêr unicamente paralelas ou concorrentes.
II. Elas podem sêr unicamente paralelas ou reversas.
III. Elas podem sêr unicamente concorrentes ou reversas.
IV. Elas podem sêr paralelas, concorrentes ou reversas.
V. Elas podem sêr unicamente reversas.
Qual dessas afirmações é verdadeira?
Resolução
Uma das maneiras de resolver esse problema é desenhando as retas como retas suporte de arestas de um cubo. No cubo ABCDEFGH, representado na figura a seguir, sêjam r a reta quê passa por B e C, quê indicaremos por e s a reta quê passa por A e B, quê indicaremos por . Note quê s ⊥ r.
Nas condições do enunciado, podemos ter:
• t = então s ⊥ r, t ⊥ r e s ⫽ t.
• t = , então s ⊥ r, t ⊥ r e s e t são retas concorrentes.
• t = , então s ⊥ r, t ⊥ r e s e t são retas reversas.
Portanto, a afirmação verdadeira é a IV.
4. Sejam um plano (alfa)" e uma reta r, paralela a (alfa)". Verifique se as proposições a seguir são verdadeiras.
I. Toda reta paralela a r está contida em (alfa)".
II. Toda reta perpendicular a r é perpendicular a (alfa)".
III. Toda reta ortogonal a r é perpendicular a (alfa)".
Resolução
Ilustrando o enunciado, temos a figura a seguir.

Agora, analisaremos cada uma das afirmações.
I. Falsa, pois existe um plano (beta)" ⫽ (alfa)" quê contém r. Em (beta)" existe uma reta s, s ⫽ r e s não está contida em (alfa)".
II. Falsa. Considerando o plano (beta)" do item I, existe s ⊥ r, s ⊂ (beta)" e s ⫽ (alfa)"; logo, s não é perpendicular a (alfa)".
III. Falsa. Considerando a reta s do item II, existe uma reta t, t ⊂ (alfa)" e t ⫽ s; t é ortogonal a r e não é perpendicular a (alfa)".
Portanto, nenhuma das proposições é verdadeira.
Página duzentos e setenta e quatro
ATIVIDADES
15. A figura a seguir mostra uma porta entreaberta e o canto de uma sala.
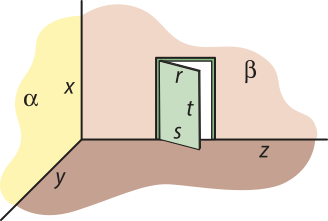
a) Que posições relativas têm as retas suporte quê contêm r e s; s e t; x e r; y e t?
15. a) As retas são, respectivamente, paralelas, perpendiculares, reversas e reversas.
b) Que posições relativas têm a reta suporte de t e o plano suporte de (alfa)"? E a reta suporte de r e o plano suporte de (beta)"?
São, respectivamente, paralelos e secantes.
16. A figura seguinte representa um cubo. Observando-a, determine as posições relativas:
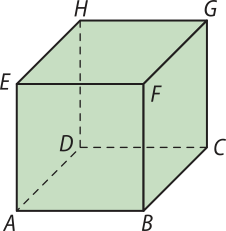
a) das retas e .
As retas são perpendiculares.
b) das retas e .
As retas são reversas ortogonais.
17. (EsPCEx-SP) Considere duas retas r e s no espaço e quatro pontos distintos, A, B, C e D, de modo quê os pontos A e B pertencem à reta r e os pontos C e D pertencem à reta s. Dentre as afirmações abaixo:
I. Se as retas e são concorrentes, então r e s são necessariamente concorrentes.
II. Os triângulos ABC e ABD serão sempre coplanares.
III. Se e forem concorrentes, então as retas r e s são coplanares.
Pode-se concluir quê:
a) somente a I é verdadeira.
b) somente a II é verdadeira.
c) somente a III é verdadeira.
d) as afirmações II e III são verdadeiras.
e) as afirmações I e III são verdadeiras.
alternativa c
18. ![]() Reúna-se a um colega, e refaçam o fluxograma feito na página 262, no boxe Pense e responda, para identificar as posições relativas de uma reta e um plano no espaço, considerando agora também o caso de uma reta perpendicular a um plano.
Reúna-se a um colega, e refaçam o fluxograma feito na página 262, no boxe Pense e responda, para identificar as posições relativas de uma reta e um plano no espaço, considerando agora também o caso de uma reta perpendicular a um plano.
Ver as Orientações para o professor.
19. ![]() Reúna-se a um colega, e façam um fluxograma para identificar as posições relativas de dois planos no espaço, considerando também o caso de dois planos perpendiculares.
Reúna-se a um colega, e façam um fluxograma para identificar as posições relativas de dois planos no espaço, considerando também o caso de dois planos perpendiculares.
Ver as Orientações para o professor.
20. (EEM-SP)
I. Duas retas reversas podem sêr ambas perpendiculares a uma mesma reta t.
II. Se r é uma reta de um plano e s uma paralela ao mesmo plano, então, certamente, r e s são paralelas.
III. Se uma reta é perpendicular a um plano, então ela é perpendicular a qualquer reta do plano.
Relativamente às afirmações acima, podemos afirmar quê:
a) todas são verdadeiras.
b) somente I e II são verdadeiras.
c) somente II e III são verdadeiras.
d) somente II é verdadeira.
e) somente I é verdadeira.
alternativa e
21. (Fuvest-SP) É correta a afirmação:
a) Se dois planos forem perpendiculares, todo plano perpendicular a um deles será paralelo ao outro.
b) Se dois planos forem perpendiculares, toda reta paralela a um deles será perpendicular ao outro.
c) Duas retas paralelas a um plano são paralelas.
d) Se duas retas forem ortogonais reversas, toda reta ortogonal a uma delas será paralela à outra.
e) Se duas retas forem ortogonais, toda paralela a uma delas será ortogonal ou perpendicular à outra.
alternativa e
Página duzentos e setenta e cinco
Projeção ortogonal
Na abertura dêste Capítulo, conhecemos algumas ideias do desenho técnico. Uma delas é a projeção, quê consiste em projetar as vistas de um objeto em planos. As mais conhecidas são as vistas frontal, superior e lateral.
Observe, a seguir, um exemplo de uma peça e suas vistas.
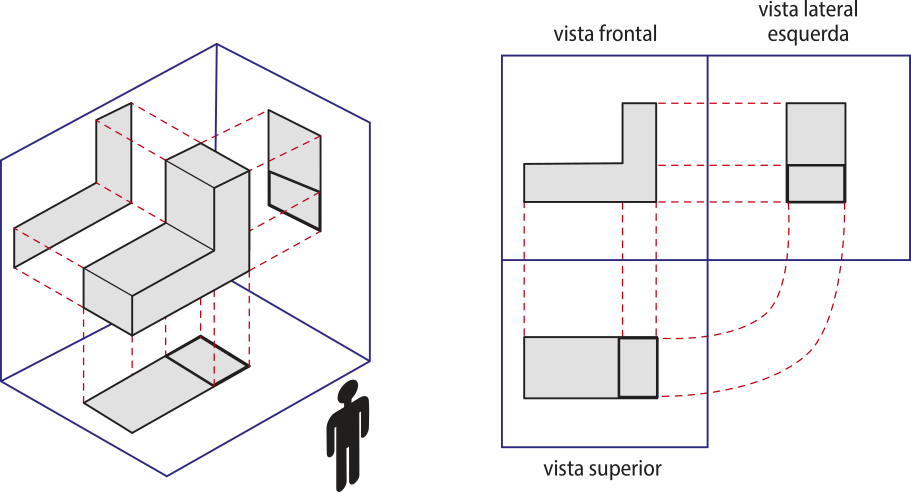
Essa projeção é chamada de projeção ortogonal, pois é feita perpendicularmente ao plano de projeção, e as vistas são chamadas de ortográficas. Ela é muito utilizada nos projetos de fabricação de peças industriais.
Estudaremos, a seguir, os conceitos de projeção ortogonal relativa a um ponto, a uma reta e a uma figura qualquer, quê são a base para a execução dos projetos.
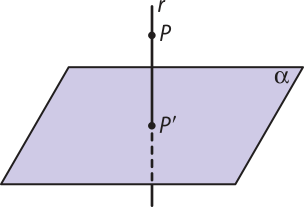
Projeção ortogonal de um ponto sobre um plano
Consideremos um ponto P e um plano (alfa)", P ∉ (alfa)".
Pelo ponto P, tracemos a reta r, perpendicular ao plano (alfa)". Pela propriedade 1, essa reta é única e intersecta (alfa)" no ponto P(minutos)".
A projeção ortogonal de um ponto P sobre um plano (alfa)" é o ponto P(minutos)", P(minutos)" ∈ (alfa)", de modo quê ⊥ (alfa)". Se P ∈ (alfa)", definimos P(minutos)" ≡ P.
Para acessar
• BORTOLOSSI, Humberto J.; EL ADJI, Victor I. S. Projeções ortogonais: matemática: geometria. Rio de Janeiro: UFF: Conteúdos digitais para o ensino e aprendizagem de matemática e estatística, [201-]. Disponível em: https://livro.pw/hlbdo. Acesso em: 9 set. 2024.
Nesse línki, é possível explorar diversas projeções ortogonais.
Página duzentos e setenta e seis
Projeção ortogonal de uma reta sobre um plano
A projeção ortogonal de uma reta r sobre um plano (alfa)" é a figura ôbitída pelas projeções ortogonais, sobre (alfa)", de todos os pontos de r.
Consideremos, primeiro, o caso em quê a reta r é oblíqua a um plano (alfa)" e intersecta o plano no ponto A, conforme mostra a figura 1.
Tomando outro ponto, B de r, determinamos o ponto B(minutos)", quê é a projeção ortogonal de B sobre o plano (alfa)", conforme mostra a figura 2.
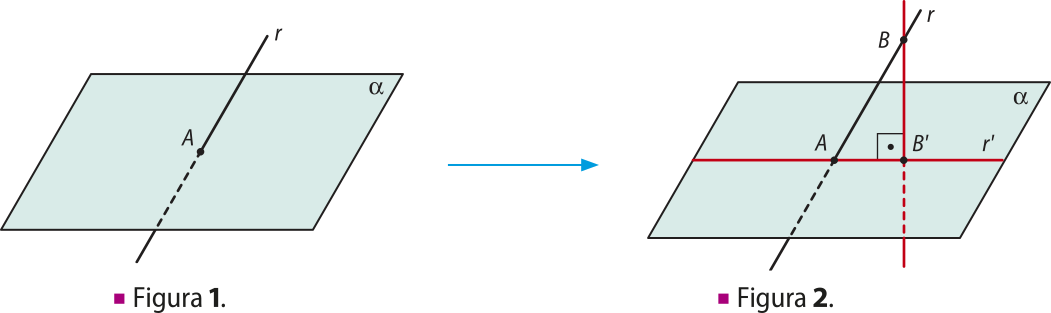
Pelo postulado R2 da reta, obtemos, então, a reta r(minutos)", determinada pêlos pontos A e B(minutos)", quê é a projeção ortogonal da reta r sobre o plano (alfa)".
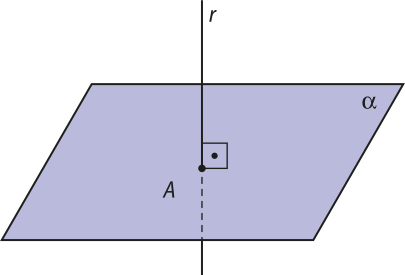
Vamos considerar agora o caso em quê r é perpendicular a (alfa)". Nesse caso, a projeção ortogonal de r sobre (alfa)" é o ponto em quê a reta r intersecta o plano (alfa)".
Vamos analisar, por fim, casos em quê a reta r não é secante ao plano (alfa)".
B(minutos)": projeção ortogonal de B sobre (alfa)".
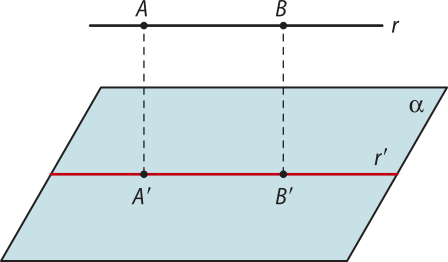
• Se r é paralela a (alfa)", então a projeção ortogonal de r sobre (alfa)" é uma reta r(minutos)" no plano (alfa)" paralela a r.
• Se r está contida em (alfa)", então r(minutos)" coincide com r.
Página duzentos e setenta e sete
Projeção ortogonal de uma figura sobre um plano
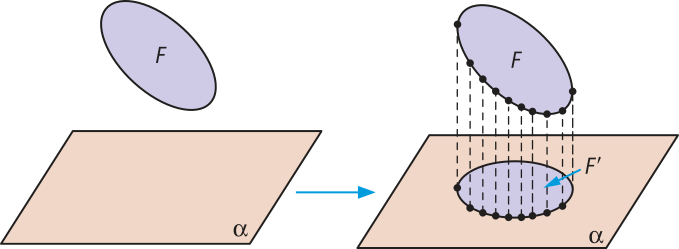
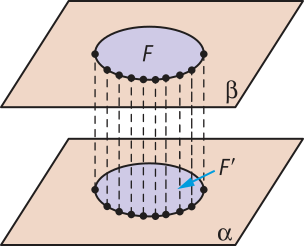
A projeção ortogonal de uma figura F sobre um plano (alfa)" é a figura F(minutos)" ôbitída pelas projeções ortogonais de todos os pontos de F sobre (alfa)".
Saiba quê...
Se a figura F está contida em um plano (beta)" paralelo ao plano (alfa)", então F(minutos)" é congruente a F.
ATIVIDADE RESOLVIDA
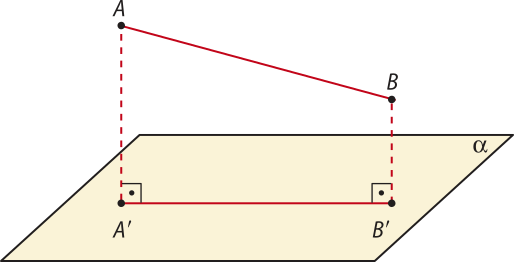
5. Mostre quê a projeção ortogonal de um segmento de reta oblíquo a um plano, sobre esse plano, é menor do quê o segmento.
Resolução
Para demonstrar esse resultado, vamos primeiro identificar a hipótese e a tese.
Hipótese
oblíquo a (alfa)"
é a projeção ortogonal de sobre (alfa)".
Tese
A(minutos)"B(minutos)" < AB
Primeiro, vamos considerar o caso em quê A ∉ (alfa)", B ∉ (alfa)" e AA(minutos)" > BB(minutos)" (o caso AA(minutos)" < BB(minutos)" é análogo).
Traçamos um segmento paralelo ao segmento passando por B, o qual intersecta o segmento no ponto P.
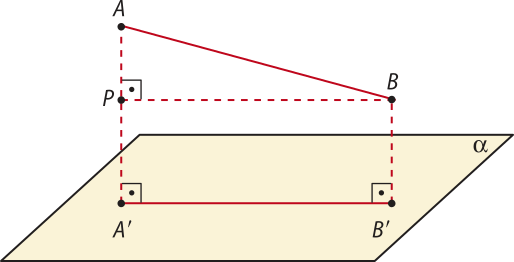
Por construção, A(minutos)"B(minutos)"BP é um retângulo, portanto A(minutos)"B(minutos)" = PB.
Também por construção, (triângulo)"ABP é retângulo em Então, PB < AB, pois é a hipotenusa dêêsse triângulo.
Portanto, de A(minutos)"B(minutos)" = PB e PB < AB, concluímos quê A(minutos)"B(minutos)" < AB.
Agora, vamos considerar o caso em quê A ∉ (alfa)" e B ∈ (alfa)" (o caso A ∈ (alfa)" e B ∉ (alfa)" é análogo).
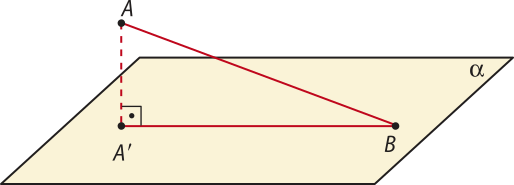
Nesse caso, (triângulo)"ABA(minutos)" é retângulo em .
Então, A(minutos)"B < AB, pois é a hipotenusa dêêsse triângulo. Como B ∈ (alfa)", B(minutos)" ≡ B.
Portanto, A(minutos)"B(minutos)" < AB.
Página duzentos e setenta e oito
ATIVIDADES
22. Como é a projeção ortogonal de um polígono convexo sobre um plano (alfa)", sabendo quê ele está contido em um plano (beta)", perpendicular a (alfa)"?
um segmento de reta
23. Observando o cubo da figura, responda às perguntas.
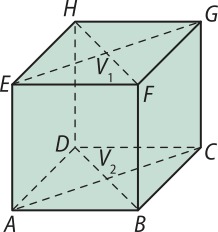
a) Qual é a projeção ortogonal do ponto G sobre o plano ABC?
o ponto C
b) Qual é a projeção ortogonal do ponto A sobre o plano BCF?
o ponto B
c) Qual é a projeção ortogonal do ponto V1 sobre o plano ABC?
o ponto V2
24. (UEA-AM) Uma hás-te de metal foi presa entre dois muros, ambos perpendiculares ao solo, nos pontos A e B, conforme mostra a figura.
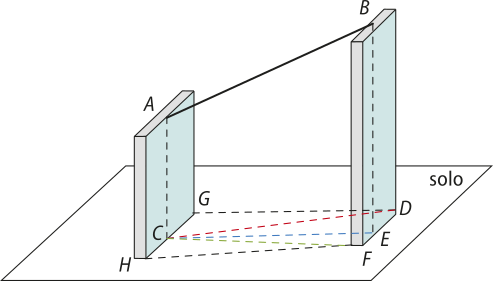
A projeção ortogonal dessa hás-te, no solo, é representada na figura pelo segmento
a)
b)
c)
d)
e)
alternativa d
25. (Enem/MEC) Na figura estão destacadas duas trajetórias sobre a superfícíe do glôbo terrestre, descritas ao se percorrer parte dos meridianos 1, 2 e da Linha do Equador, sêndo quê os meridianos 1 e 2 estão contidos em planos perpendiculares entre si. O plano (alfa)" é paralelo ao quê contém a Linha do Equador.
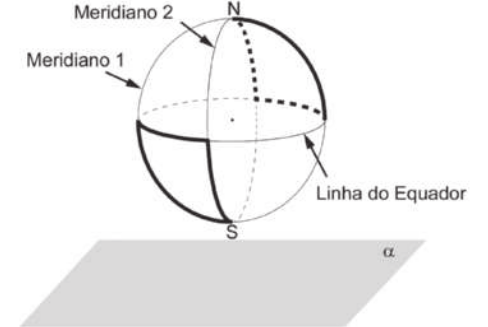
A vista superior da projeção ortogonal sobre o plano (alfa)" dessas duas trajetórias é
a) 
b) 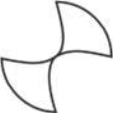
c) 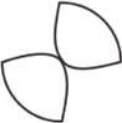
d) 
e) 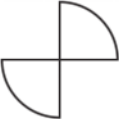
alternativa e
26. Leia o texto a seguir.
[…]
As áreas públicas ou de uso comum em edificações, espaços e equipamentos urbanos devem ter sinalização tátil de alerta no piso para:
a) informar à pessoa com deficiência visual sobre a existência de desníveis ou outras situações de risco permanente, como objetos suspensos não detectáveis pela bengala longa;
b) orientar o posicionamento adequado da pessoa com deficiência visual para o uso de equipamentos como elevadores, equipamentos de autoatendimento ou serviços;
c) informar as mudanças de direção ou opções de percursos […];
d) indicar o início e o término de escadas e rampas;
e) indicar a existência de patamares, nas situações indicadas;
f) indicar o local de travessia de pedestres.
[…]
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 16537: acessibilidade: sinalização tátil no piso: diretrizes para elaboração de projetos e instalação. 1. ed. Rio de Janeiro: ABNT, 2016. Disponível em: https://livro.pw/fmnxw. Acesso em: 9 set. 2024.
A figura na página seguinte mostra um objeto suspenso quê requer sinalização tátil de alerta ao seu redor com as medidas indicadas em métro.
Página duzentos e setenta e nove
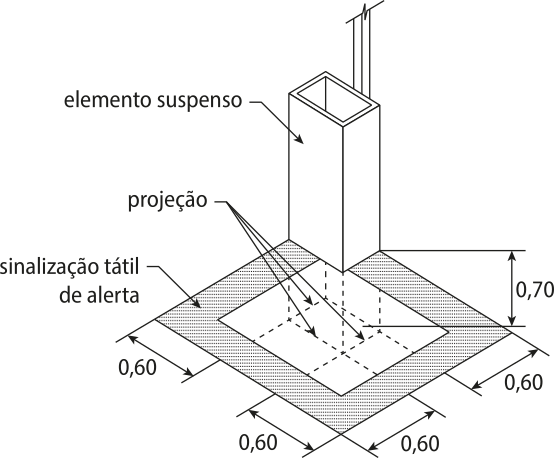
Sabendo quê o elemento suspenso tem altura igual a 1,50 m, largura igual a 0,25 m e comprimento igual a 0,55 m, responda:
a) Quais dimensões do elemento suspenso são relevantes para a instalação do piso tátil?
largura e comprimento
b) Qual é a área da projeção do elemento suspenso sobre o piso?
0,1375 m2
c) Qual é o perímetro externo da sinalização tátil de alerta?
6,4 m
FÓRUM
A importânssia das normas de acessibilidade para pessoas com deficiência
Viver em uma ssossiedade verdadeiramente inclusiva requer o reconhecimento e a implementação de normas de acessibilidade quê garantam igualdade de oportunidades para todas as pessoas, independentemente de suas habilidades físicas ou cognitivas. Conforme destacado pela Associação Brasileira de Normas Técnicas (ABNT), as normas de acessibilidade não se reférem apenas à presença física de elemêntos como rampas ou elevadores, mas também à conformidade com regras técnicas específicas.
Além de melhorar o acesso físico, as normas de acessibilidade também abrangem aspectos como comunicação, tecnologia e transporte. Por exemplo, a disponibilização de informações em formatos acessíveis, como braille, áudio ou linguagem simples, garante quê as pessoas com deficiência possam compreender e participar plenamente da ssossiedade. Da mesma forma, o desenvolvimento de tecnologias assistivas e de aplicativos acessíveis permite quê essas pessoas realizem tarefas diárias, como se comunicar, estudar e trabalhar, d fórma mais independente e eficaz.
É importante ressaltar quê a acessibilidade beneficia a ssossiedade como um todo. As normas de acessibilidade promóvem a inovação e a criatividade, incentivando o desenvolvimento de soluções e produtos quê atendam às necessidades de uma variedade maior de pessoas.

![]() Após ler o texto, faça um fórum com os côlégas e o professor para discutir as kestões a seguir.
Após ler o texto, faça um fórum com os côlégas e o professor para discutir as kestões a seguir.
Ver as Orientações para o professor.
• Acessibilidade vai muito além de fornecer rampas ou elevadores em espaços físicos. Discutam outras soluções de acessibilidade.
• Na sua escola, vocês observam algumas dessas soluções de acessibilidade? Se sim, quais? Discutam estratégias quê poderiam sêr implementadas na sua escola para torná-la mais acessível para todos.
Página duzentos e oitenta
Distâncias
Observemos agora algumas definições envolvendo distâncias.
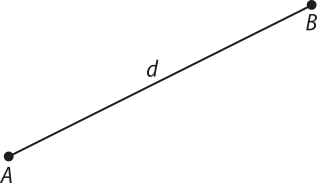
Distância entre dois pontos
A distância entre dois pontos distintos A e B é igual à medida do segmento .
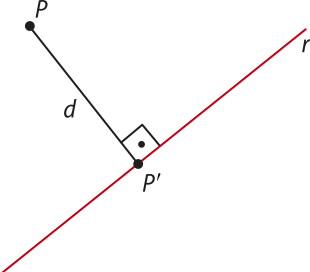
Distância entre ponto e reta
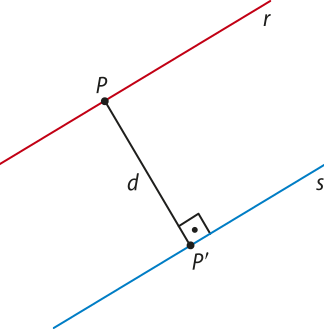
A distância entre um ponto P e uma reta r quê não o contém é igual à medida do segmento , em quê P(minutos)" é a projeção ortogonal de P sobre r.
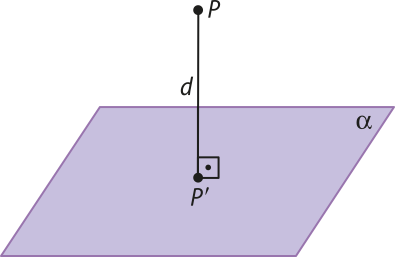
Distância entre ponto e plano
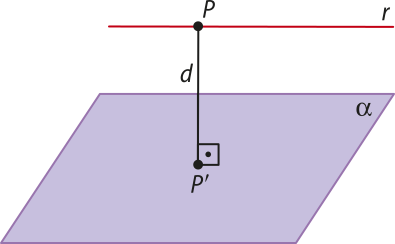
A distância entre um ponto P e um plano (alfa)" quê não o contém é igual à medida do segmento , em quê P(minutos)" é a projeção ortogonal de P sobre (alfa)".
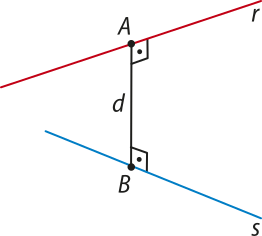
Distância entre duas retas
A distância entre duas retas reversas r e s é igual à medida do segmento , em quê A ∈ r, B ∈ s e é perpendicular a r e a s.
Página duzentos e oitenta e um
A distância entre duas retas paralelas é igual à medida do segmento , em quê P é um ponto qualquer de uma das retas e P(minutos)" é a projeção ortogonal de P sobre a outra reta.
Saiba quê...
A distância entre retas quê têm pelo menos um ponto em comum é zero. Assim, tanto a distância entre retas concorrentes quanto a distância entre retas coincidentes são iguais a zero.
Distância entre reta e plano paralelos
A distância entre uma reta r e um plano (alfa)" paralelo a ela é igual à medida do segmento , em quê P é um ponto qualquer de r e P(minutos)" é a projeção ortogonal de P sobre (alfa)".
Distância entre dois planos paralelos
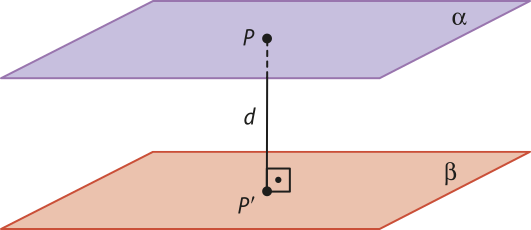
A distância entre dois planos paralelos é igual à medida do segmento , em quê P é um ponto qualquer de um dos planos e P(minutos)" é a projeção ortogonal de P sobre o outro plano.
Página duzentos e oitenta e dois
ATIVIDADES RESOLVIDAS
6. O cubo ABCDEFGH tem aresta de 2 cm.
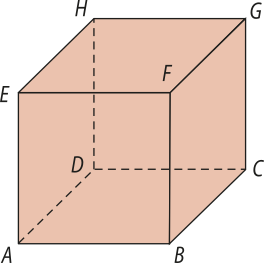
Calcule:
a) a distância entre os pontos A e C.
b) a distância entre o ponto B e a reta .
c) a distância entre o ponto C e o plano EFG.
d) a distância entre as retas reversas e .
e) a distância entre as retas paralelas e .
f) a distância entre a reta e o plano EFG.
g) a distância entre os planos paralelos ADE e BCF.
Resolução
a) A distância entre os pontos A e C é d = AC.
Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, obtemos:
AC2 = AB2 + BC2
d2 = 22 + 22
d2 = 8
d =
Portanto, a distância entre os pontos A e C é cm.
b) A distância entre o ponto B e a reta é d = BG. Aplicando o teorema de Pitágoras no triângulo retângulo BCG, obtemos:
BG2 = CG2 + BC2
d2 = 22 + 22
d2 = 8
d =
Portanto, a distância entre o ponto B e a reta é cm.
c) A distância entre o ponto C e o plano EFG é d = CG, ou seja, igual a 2 cm.
d) A distância entre as retas reversas e é d = EF, ou seja, igual a 2 cm.
e) A distância entre as retas paralelas e é d = CF. Aplicando o teorema de Pitágoras ao triângulo retângulo CFG, obtemos:
CF2 = CG2 + FG2
d2 = 22 + 22
d2 = 8
d =
Portanto, a distância entre as retas paralelas e é cm.
f) A distância entre a reta e o plano EFG é d = CG, ou seja, igual a 2 cm.
g) A distância entre os planos paralelos ADE e BCF é d = AB, ou seja, igual a 2 cm.
7. (UEA-AM) Considere dois planos paralelos distintos (alfa)" e (beta)", o segmento contido no plano (alfa)", a reta r contida no plano (beta)" e um ponto C, tal quê C ∈ r, conforme mostra a figura.
De acôr-do com essas informações, pode-se afirmar quê
a) a distância do ponto C ao plano (alfa)" é igual à distância do ponto A ao plano (beta)".
b) a projeção ortogonal do ponto C sobre o plano (alfa)" está sobre o segmento .
c) a projeção ortogonal do ponto A sobre o plano (beta)" não está sobre a reta r.
d) a projeção do segmento sobre o plano (beta)" coincide com a reta r.
e) a distância do ponto C ao plano (alfa)" é igual à distância do ponto C ao ponto B.
Resolução
A distância de qualquer ponto do plano (alfa)" ao plano (beta)" é igual à distância de qualquer ponto do plano (beta)" ao plano (alfa)". Portanto, podemos afirmar quê a distância do ponto C ao plano (alfa)" é igual à distância do ponto A ao plano (beta)", de modo quê a alternativa a está correta.
Página duzentos e oitenta e três
ATIVIDADES
27. Considere o paralelepípedo reto-retângulo ABCDEFGH e calcule o quê se pede.

a) A distância entre os pontos C e H.
13 cm
b) A distância entre o ponto D e a reta .
27. b) 4 cm
c) A distância entre o ponto F e o plano ADH.
27. c) 12 cm
d) A distância entre as retas reversas e .
27. d) 4 cm
e) A distância entre as retas paralelas e .
13 cm
f) A distância entre a reta e o plano CDG.
27. f) 4 cm
g) A distância entre os planos paralelos ABC e EFG.
5 cm
28. (UEA-AM) Considere dois planos distintos e paralelos, (alfa)" e (beta)", uma reta r contida no plano (alfa)", um ponto Q pertencendo ao plano (alfa)", mas com Q não pertencendo à reta r, e um ponto P pertencendo ao plano (beta)", conforme mostra a figura.

alternativa c
De acôr-do com essas informações, afirma-se quê
a) a distância do ponto Q ao ponto P é igual à distância do ponto Q ao plano (beta)".
b) a projeção ortogonal da reta r sobre o plano (beta)" passará pelo ponto P.
c) a distância do ponto Q ao plano (beta)" é igual à distância de qualquer ponto da reta r ao plano (beta)".
d) ao se projetar ortogonalmente a reta r e o ponto Q sobre o plano (beta)", os pontos Q e P ficarão sobre a reta r.
e) a distância entre o ponto Q e sua projeção ortogonal no plano (beta)" é igual à distância entre os pontos Q e P.
29. (UEA-AM) Seja (alfa)" o plano quê passa pêlos pontos C, D, G e F. Seja P um ponto distante 8 cm de (alfa)", tal quê a sua projeção ortogonal sobre (alfa)" é o ponto P(minutos)".
Sabendo quê o ponto Q pertence ao plano (alfa)" e quê a distância entre os pontos P e Q é igual a cm, a distância entre os pontos P(minutos)" e Q é igual a
a) 4 cm.
b) 5 cm.
c) 8 cm.
d) 9 cm.
e) 12 cm.
alternativa b
30. (EsPCEx-SP) Considere um plano (alfa)" e os pontos A, B, C e D tais quê
• O segmento AB tem 6 cm de comprimento e está contido em (alfa)".
• O segmento BC tem 24 cm de comprimento, está contido em (alfa)" e é perpendicular a AB.
• O segmento AD tem 8 cm de comprimento e é perpendicular a (alfa)".
Nessas condições, a medida do segmento cê dê é
a) 26 cm
b) 28 cm
c) 30 cm
d) 32 cm
e) 34 cm
alternativa a
31. (ESPM-SP) Na figura plana abaixo, ABCD é um quadrado de área 10 cm2. Os segmentos CE e CF médem 4 cm cada. Essa figura deverá sêr dobrada nas linhas tracejadas, fazendo com quê os pontos E e F coincidam com um ponto P do espaço. A distância dêêsse ponto P ao ponto A é igual a:
a) 6 cm
b) 5 cm
c) cm
d) cm
e) cm
alternativa a
Página duzentos e oitenta e quatro
CONEXÕES com...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
Arquitetura e Urbanismo
A Arquitetura é uma das áreas em quê são feitos muitos projetos utilizando conceitos do desenho técnico. Para tornar-se arquiteto, é necessário realizar o curso de Arquitetura e Urbanismo. Mas você sabe o quê faz um arquiteto? Leia o texto a seguir para conhecer um pouco mais a respeito dessa profissão.
O arquiteto-urbanista lida basicamente com o espaço, seja ele interno ou externo. Cabe a ele projetar, planejar, organizar e intervir em empreendimentos, áreas urbanas, restaurações do patrimônio histórico e arquitetura de interiores. É o profissional responsável por elaborar a planta e determinar os materiais quê serão utilizados na obra, levando em conta funcionalidade, estética e conforto. Para isso, pensa no uso do imóvel, disposição dos ambientes e dos objetos, acústica, ventilação e iluminação.
Com uma formação técnica, humanista e com interfaces social e artística, o arquiteto-urbanista póde ir além da área de edificações. Respaldado pela legislação quê regulamenta a profissão, o profissional póde buscar especialização em arquitetura paisagística, cenografia, conjuntos arquitetônicos e monumentos, projetos de interiores, planejamento físico, urbano e regional. Além díssu, póde trabalhar em planos de orientação do crescimento das cidades; projetos de habitação, de transportes, de saneamento; dêzê-nhôs industriais e comunicação visual.
[…]
ARQUITETURA e urbanismo. Fortaleza: Portal da Universidade Federal do Ceará, c2024. Disponível em: https://livro.pw/gpqxa. Acesso em: 23 set. 2024.

Durante a execução de um projeto arquitetônico, o profissional precisa fazer diversos dêzê-nhôs para quê a obra sáia como o planejado; para isso, são usadas as vistas e as projeções. Além da forma do edifício, sua intencionalidade também deve sêr levada em conta. Nesse sentido, kestões como inovação e sustentabilidade podem nortear o projeto.
Página duzentos e oitenta e cinco
Leia o texto a seguir, quê mostra a visão do arquiteto quê projetou o Museu do Amanhã, no Rio de Janeiro, exemplo de inovação e sustentabilidade.
[…]
“A ideia é quê o edifício fosse o mais etéreo possível, quase flutuando sobre o mar, como um barco, um pássaro ou uma planta”, explica o autor do projeto, o arquiteto espanhol Santiago Calatrava […].
[…]
O edifício, em sua arquitetura e diretrizes de sustentabilidade, integra-se como parte do conteúdo do Museu do Amanhã, incentivando a discussão de temas como utilização da energia solar, novas formas da arquitetura moderna, relação com a paisagem da cidade e recuperação da Baía de Guanabara. “Um passeio ao redor do Museu é uma lição de sustentabilidade, de botânica, uma aula do quê significa energia solar”, exemplifica Calatrava. […]
[…]
A ARQUITETURA de Santiago Calatrava. Rio de Janeiro: Museu do Amanhã, [202-]. Disponível em: https://livro.pw/rluse. Acesso em: 9 set. 2024.

Para acessar
• MUSEU do Amanhã: visitas virtuais. [S. l.]: gúgou Arts & Culture, [202-]. Disponível em: https://livro.pw/fiqpm. Acesso em: 9 set. 2024.
Por meio do sáiti, é possível fazer Turs virtuais pelo Museu do Amanhã, tanto para navegar pela parte externa do edifício e apreciar sua arquitetura como para visitar algumas exposições feitas no museu.
Agora, faça o quê se pede nas atividades a seguir.
1. Você já tinha ouvido falar na profissão arquiteto? Na região onde você mora, existe alguma universidade quê disponibilize esse curso de graduação? Pesquise a respeito do curso: qual é a duração dele, quantas vagas há, qual é o processo de ingresso etc.
Resposta pessoal.
2. Você conhece outras profissões quê utilizem desenho técnico e projeções no seu dia a dia? Pesquise sobre o assunto e compartilhe os resultados com os demais côlégas da turma.
2. Resposta pessoal. Resposta possível: Profissões como engenheiro e designer (de interiores, de embalagens, por exemplo).
3. ![]() Reúna-se a dois côlégas, e escôlham um monumento ou um edifício quê seja conhecido na sua cidade. Pesquisem quem foi o responsável pela concepção do projeto: foi um arquiteto? Ele tem outros projetos na cidade? Façam um vídeo para apresentar os resultados da pesquisa feita para o restante da turma.
Reúna-se a dois côlégas, e escôlham um monumento ou um edifício quê seja conhecido na sua cidade. Pesquisem quem foi o responsável pela concepção do projeto: foi um arquiteto? Ele tem outros projetos na cidade? Façam um vídeo para apresentar os resultados da pesquisa feita para o restante da turma.
Respostas pessoais.
4. ![]() Reúna-se a dois côlégas, e escôlham um objeto para fazer a projeção ortogonal das vistas frontal, superior e lateral.
Reúna-se a dois côlégas, e escôlham um objeto para fazer a projeção ortogonal das vistas frontal, superior e lateral.
Resposta pessoal.
Página duzentos e oitenta e seis
EXPLORANDO A TECNOLOGIA
Programando posições relativas de retas e de planos
Para quê os computadores executem tarefas, é necessário quê sêjam programados para isso. Essa programação póde sêr feita por meio de diversas linguagens e formas. Para esta atividade, vamos utilizar o Scratch, um software quê póde sêr usado ôn láini, pelo línki https://livro.pw/kxboe (acesso em: 9 set. 2024), ou póde sêr realizado o dáum-lôude no computador e usado off-line.
O Scratch utiliza uma linguagem de programação em blocos. Basta identificar, à esquerda da tela, os comandos quê se deseja executar e arrastar os blocos para a área de trabalho no centro da tela. Não se esqueça de garantir quê seu bloco, isto é, sua sequência de comandos, seja coerente e atenda a seu objetivo. Antes de começar, lembre-se de alterar o idioma para o Português, clicando, consecutivamente, em Settings, Language e Português Brasileiro.
Nesta atividade, será explorada a posição relativa entre duas retas com base nas propriedades verificadas, isto é, será construído um programa quê vai perguntar sobre uma série de propriedades envolvendo duas retas e, com base nas respostas fornecidas, retornará um resultado sobre a posição relativa entre essas retas.
Para construir esse programa, é preciso pensar em quais são as perguntas necessárias para determinar precisamente a posição relativa entre duas retas. Usaremos o fluxograma construído na página 262 para isso, acompanhando os passos a seguir.
I. Adicione, na área de trabalho, o bloco alaranjado, conforme imagem a seguir, quê está na barra lateral na categoria Eventos. Esse bloco indica quê, ao clicar na bandeira vêrde no topo direito, ao lado da figura cor-de-rosa, o programa será executado.
II. Na categoria Sensores, arraste o bloco azul, conforme imagem a seguir, encaixe-o no bloco alaranjado e altere a pergunta para "As retas são coplanares? Responda sim ou não.".

Página duzentos e oitenta e sete
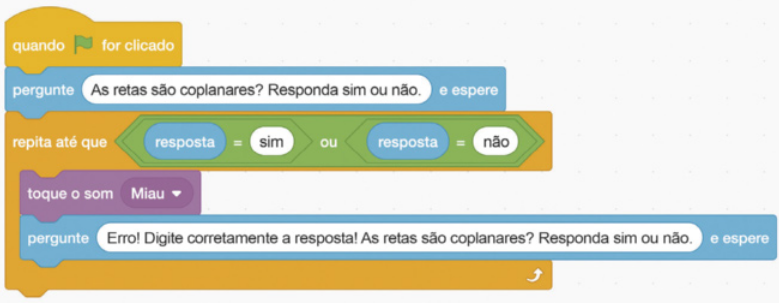
III. Se a resposta dada pelo usuário for diferente de "sim" ou "não", o programa póde interpretar as informações equivocadamente, apresentando um êrro ou chegando a uma conclusão incorréta. Para quê isso não aconteça, vamos garantir quê as únicas respostas possíveis sêjam "sim" ou "não", clicando em contrôle e arrastando o bloco "repita até que", também alaranjado, para o cóódigo.
IV. Clique em Som e arraste o bloco roxo "toque o som", encaixando-o no bloco alaranjado "repita até que" anterior. Repita a pergunta, colocando um aviso de êrro no início da frase. Para isso, arraste um novo bloco de criação de pergunta e escrêeva "Erro! Digite corretamente a resposta! As retas são coplanares? Responda sim ou não.", conforme a imagem a seguir.
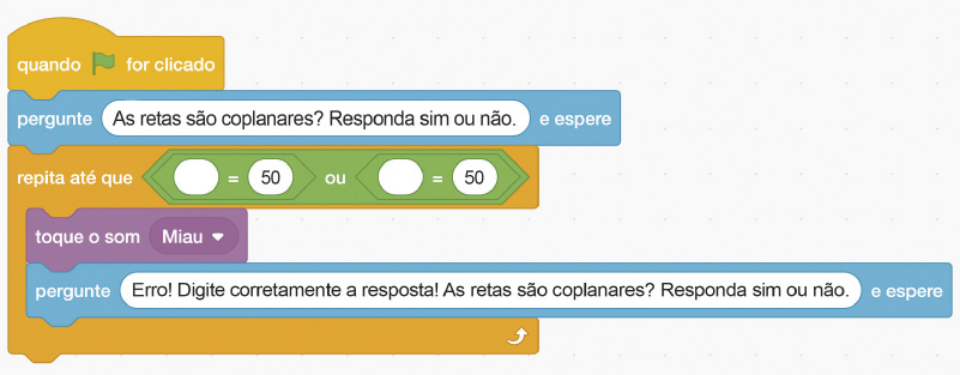
V. É preciso restringir o programa para quê não seja repetida a notificação de êrro e siga com o cóódigo quando a resposta "sim" ou "não" for dada. Para fazer isso, adicione essa verificação no espaço vazio logo após "repita até que". Como há duas respostas possíveis, em Operadores, arraste o bloco vêrde "ou", encaixando-o nesse espaço vazio, e, na sequência, arraste outros dois blocos vêrdes com "= 50", encaixando-os no bloco verde "ou", conforme figura a seguir.
VI. Clique em Sensores, arraste o bloco azul "resposta", encaixando-o na primeira igualdade e substitua o "50" por "sim". Repita o processo para a segunda igualdade e troque o "50" por "não".
Página duzentos e oitenta e oito
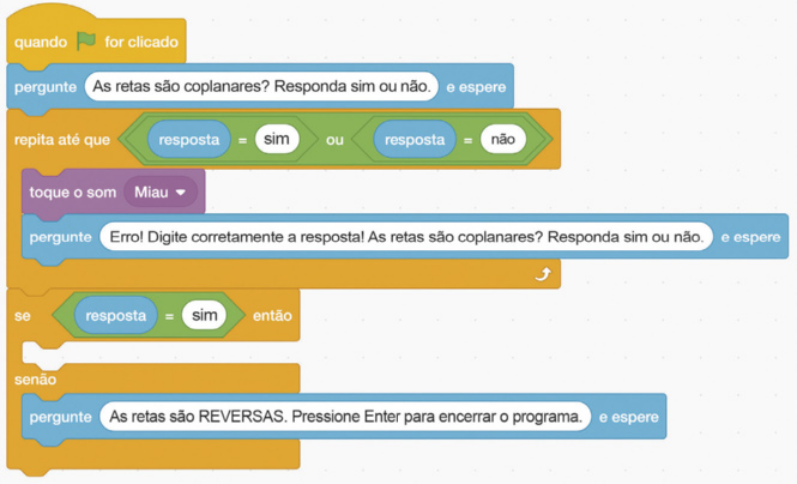
VII. Agora quê as respostas foram dadas, é necessário instruir o programa sobre o quê fazer com elas. Se a resposta for "sim", é necessário perguntar se as retas têm um único ponto em comum. Para isso, em contrôle, arraste o bloco alaranjado "se <espaço> então" para o fim do bloco anterior e preencha esse espaço vazio com os blocos verde"= sim" e azul "resposta", conforme imagem a seguir.
VIII. Caso a resposta seja "não", as retas são reversas, e precisamos notificar o usuário sobre isso. Para isso, clique em Sensores, arraste o bloco azul "pergunte e espere", encaixando-o ao bloco alaranjado "senão" e digite "As retas são REVERSAS. Pressione Enter para encerrar o programa.", conforme imagem a seguir.
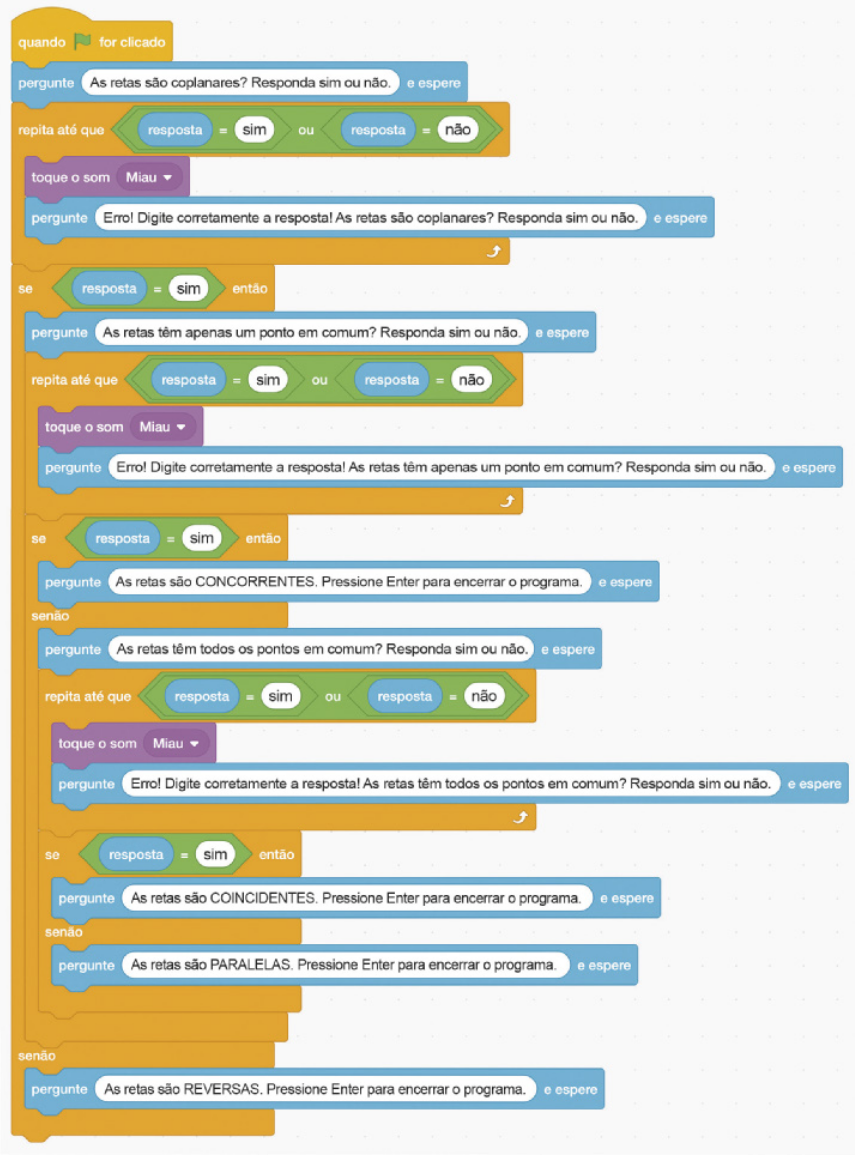
IX. Com isso, finalizamos a primeira pergunta a sêr feita para descobrir a posição relativa entre duas retas. Para fazer as demais perguntas, a estrutura é muito parecida com a da primeira. Assim, repita o quê foi criado até aqui. Vá até a primeira pergunta, clique com o botão direito, selecione Duplicar e arraste o bloco copiado para dentro do "se". Troque as perguntas para "As retas têm apenas um ponto em comum? Responda sim ou não.". Não se esqueça de trocar a pergunta na mensagem de êrro também.
Se a resposta for "sim", a conclusão é de quê as retas são concorrentes. Para notificar essa resposta ao usuário, mova o bloco copiado do "senão" para o "se" e altere o texto para "As retas são CONCORRENTES. Pressione Enter para encerrar o programa.".
Para o caso em quê a resposta seja "não", precisamos perguntar se as retas têm todos os pontos em comum. Para isso, repita os passos anteriores para copiar o bloco da pergunta e altere as perguntas e respostas correspondentes.
Página duzentos e oitenta e nove
X. O programa final ficará assim:
XI. Pressione a bandeira vêrde e teste as perguntas quê aparecerão na tela da direita. essperimênte dar respostas erradas também, para observar as mensagens de êrro.
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. Crie um programa para determinar a posição relativa entre uma reta e um plano.
2. Crie um cóódigo quê diga qual é a posição relativa entre dois planos considerados.
Página duzentos e noventa
ATIVIDADES COMPLEMENTARES
1. Analise as afirmações a seguir e indique qual delas é falsa.
a) Três pontos distintos de uma circunferência definem um plano.
b) O centro e os extremos de um diâmetro de uma circunferência não definem um plano.
c) Dois diâmetros distintos de uma circunferência definem um plano.
d) Se dois pontos de uma circunferência pertencem a um plano, então a circunferência está contida nesse plano.
e) Dadas uma reta e uma circunferência em um mesmo plano, as quais não se intersectam, há somente uma reta paralela à reta dada quê passa pelo centro da circunferência.
alternativa d
2. (Vunesp-SP) Considere o cubo da figura. Das alternativas abaixo, aquela correspondente a pares de vértices quê determinam três retas, duas a duas reversas, é:
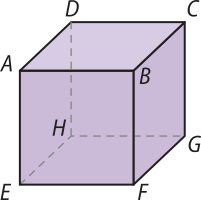
a) (A, D), (C, G), (E, H)
b) (A, E), (H, G), (B, F)
c) (A, H), (C, F), (F, H)
d) (A, E), (B, C), (D, H)
e) (A, D), (C, G), (E, F)
alternativa e
3. (UERN) Seja um plano (alfa)" e uma reta s secante a (alfa)". Para qualquer reta r contida em (alfa)", é correto afirmar:
a) r e s podem sêr paralelas, apenas.
b) r e s podem sêr reversas, apenas.
c) r e s podem sêr concorrentes, apenas.
d) r e s podem sêr paralelas ou reversas.
e) r e s podem sêr reversas ou concorrentes.
alternativa e
4. (FURRN) Um plano é determinado por:
a) uma única reta.
b) duas retas quaisquer.
c) três pontos quaisquer.
d) uma reta e um ponto não pertencente a ela.
e) uma reta e um ponto a ela pertencente.
alternativa d
5. (Vunesp-SP) Entre todas as retas suportes das arestas de um cérto cubo, considere duas, r e s, reversas. Seja t a perpendicular comum a r e a s. Então:
a) t é a reta suporte de uma das diagonais de uma das faces do cubo.
b) t é a reta suporte de uma das diagonais do cubo.
c) t é a reta suporte de uma das arestas do cubo.
d) t é a reta quê passa pêlos pontos médios das arestas contidas em r e s.
e) t é a reta perpendicular a duas faces do cubo, por seus pontos médios.
alternativa c
6. (Enem/MEC) O acesso entre dois andares de uma casa é feito através de uma escada circular (escada caracol), representada na figura. Os cinco pontos A, B, C, D e E sobre o corrimão estão igualmente espaçados, e os pontos P, A e E estão em uma mesma reta. Nessa escada, uma pessoa caminha deslizando a mão sobre o corrimão do ponto A até o ponto D.
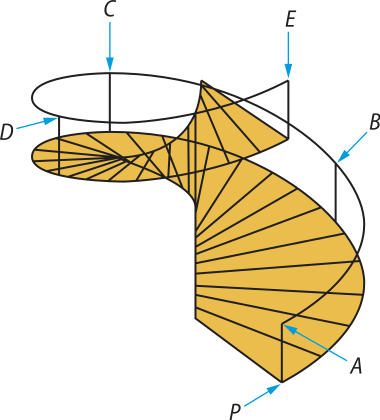
A figura quê melhor representa a projeção ortogonal sobre o piso da casa (plano) do caminho percorrido pela mão dessa pessoa é:
a) 
b) 
c) 
d) 
e) 
alternativa c
Página duzentos e noventa e um
7. (UFAM) Assinale a alternativa CORRETA:
a) Dois planos quê possuem três pontos em comum são coincidentes.
b) Se dois planos (alfa)" e (beta)" são perpendiculares ao plano (gama)", então os planos (alfa)" e (beta)" são paralelos.
c) Existem dois planos distintos, passando ambos por um mesmo ponto e perpendiculares a uma reta.
d) Duas retas perpendiculares a um plano são paralelas.
e) Toda reta paralela a um plano é perpendicular a infinitas retas dêêsse plano.
alternativa d
8. (UFAL) Sejam (alfa)" e (beta)" dois planos perpendiculares entre si. A reta r é perpendicular ao plano (alfa)" e a reta s é perpendicular ao plano (beta)".
Nessas condições:
a) a reta r não póde ter pontos em comum com o plano (beta)".
b) as retas r e s são concorrentes.
c) as retas r e s podem sêr reversas.
d) a reta s está contida em um plano perpendicular a (alfa)".
e) as retas r e s são paralelas entre si.
alternativa c
9. (Enem/MEC) A figura representa o glôbo terrestre e nela estão marcados os pontos A, B e C. Os pontos A e B estão localizados sobre um mesmo paralelo, e os pontos B e C, sobre um mesmo meridiano. É traçado um caminho do ponto A até C, pela superfícíe do glôbo, passando por B, d fórma quê o trecho de A até B se dê sobre o paralelo quê passa por A e B e, o trecho de B até C se dê sobre o meridiano quê passa por B e C. Considere quê o plano (alfa)" é paralelo à linha do equador na figura.
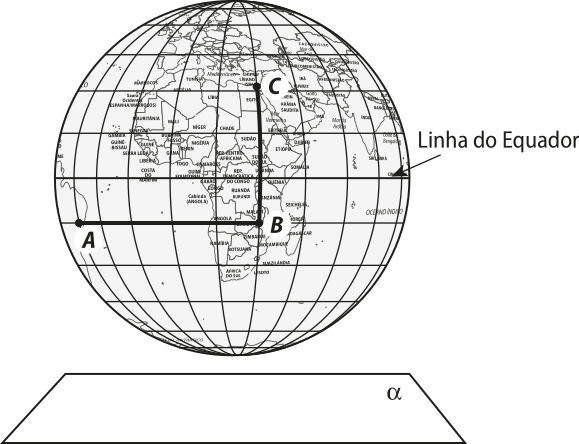
A projeção ortogonal, no plano a, do caminho traçado no glôbo póde sêr representada por
a) 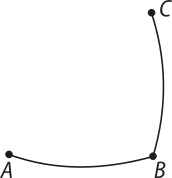
b) 
c) ![]()
d) ![]()
e) ![]()
alternativa e
10. (Enem/MEC) Um grupo de países criou uma instituição responsável por organizar o Programa Internacional de Nivelamento de Estudos (PINE) com o objetivo de melhorar os índices mundiais de educação. Em sua sede foi construída uma escultura suspensa, com a logomarca oficial do programa, em três dimensões, quê é formada por suas iniciais, conforme mostrada na figura.

Essa escultura está suspensa por cabos de aço, de maneira quê o espaçamento entre lêtras adjacentes é o mesmo, todas têm igual espessura e ficam dispostas em posição ortogonal ao solo, como ilustrado a seguir.

Ao meio-dia, com o sól a pino, as lêtras quê formam essa escultura projetam ortogonalmente suas sombras sobre o solo.
A sombra projetada no solo é
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
alternativa e
Página duzentos e noventa e dois
11. (Enem/MEC) No desenho técnico, é comum representar um sólido por meio de três vistas (frontal, perfil e superior), resultado da projeção do sólido em três planos, perpendiculares dois a dois.
A figura representa as vistas de uma torre.
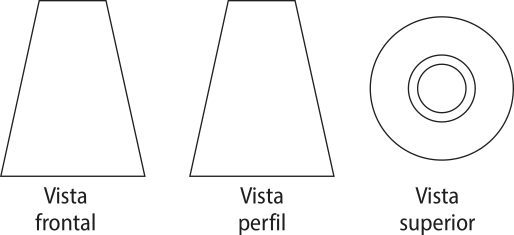
Disponível em: https://livro.pw/mvygw. Acesso em: 11 dez. 2012 (adaptado).
Com base nas vistas fornecidas, qual figura melhor representa essa torre?
a) 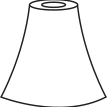
b) 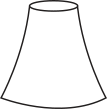
c) 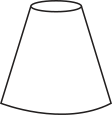
d) 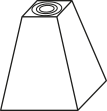
e) 
alternativa e
12. (Enem/MEC) Uma formiga move-se sobre um castiçal de vidro transparente, do ponto A para B em linha reta, percórre o arco circular BCD, sêndo C localizado na parte da frente do castiçal, e desce o arco DE, como representado na figura.
Os pontos A, B, D e E estão sobre um mesmo plano perpendicular à mesa sobre a qual se encontra o castiçal. A projeção ortogonal, sobre o plano da mesa, do trajeto percorrido pela formiga, do ponto A até o ponto E, é melhor representada por
a) 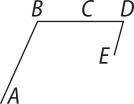
b) 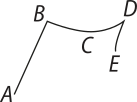
c) ![]()
d) ![]()
e) ![]()
alternativa c
13. (Enem/MEC) Em um jôgo desenvolvido para uso no computador, objetos tridimensionais vão descendo do alto da tela até alcançarem o plano da base. O usuário póde mover ou girar cada objeto durante sua descida para posicioná-lo convenientemente no plano horizontal. Um dêêsses objetos é formado pela justaposição de quatro cubos idênticos, formando assim um sólido rígido, como ilustrado na figura.
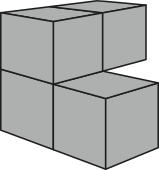
Para facilitar a movimentação do objeto pelo usuário, o programa projéta ortogonalmente esse sólido em três planos quadriculados perpendiculares entre si, durante sua descida.
A figura quê apresenta uma possível posição dêêsse sólido, com suas respectivas projeções ortogonais sobre os três planos citados, durante sua descida é
a) 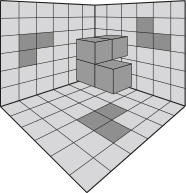
b) 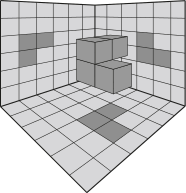
c) 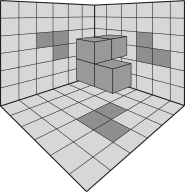
d) 
e) 
alternativa e
Página duzentos e noventa e três
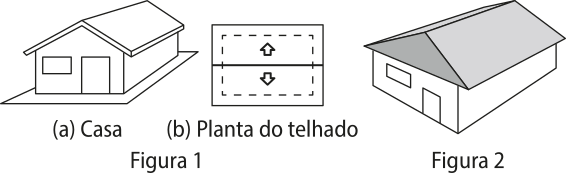
14. (Enem/MEC) A Figura 1 apresenta uma casa e a planta do seu telhado, em quê as setas indicam o sentido do escoamento da á gua de chuva. Um pedreiro precisa fazer a planta do escoamento da á gua de chuva de um telhado quê tem três caídas de á gua, como apresentado na Figura 2.
A figura quê representa a planta do telhado da Figura 2 com o escoamento da á gua de chuva quê o pedreiro precisa fazer é
a) 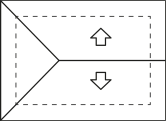
b) 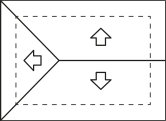
c) 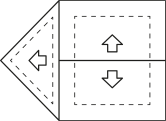
d) 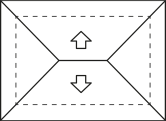
e) 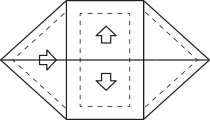
alternativa b
PARA REFLETIR
Neste Capítulo, estudamos noções primitivas, definições, postulados e teoremas da Geometria Espacial de Posição. Estudamos também as posições relativas entre os principais entes geométricos (ponto, reta e plano) no plano e no espaço.
Compreendemos os conceitos de paralelismo e de perpendicularismo e como eles se relacionam. Analisamos também alguns teoremas e propriedades relacionados a esses conceitos. Outro conteúdo abordado foi o de projeção ortogonal e sua relevância para projetistas e para o trabalho com vistas e projeções. Por fim, estudamos o conceito de distância entre pontos, retas e planos.
Nas páginas de abertura, foi discutido como o desenho técnico é importante para representarmos o nosso mundo tridimensional em um suporte bidimensional (como a fô-lha de papel). Depois de ter estudado o conteúdo dêste Capítulo, você consegue reconhecer quê esses conceitos podem auxiliá-lo a fazer essa transposição utilizando o desenho técnico e a Geometria Descritiva?
Vamos refletir a respeito das aprendizagens do Capítulo 8:
Respostas pessoais.
• Você já conhecia algum dos conteúdos apresentados neste Capítulo? Qual(is)?
• Você se sente confiante para realizar uma demonstração em Matemática?
• Você consegue reconhecer se houve um aprofundamento em relação ao quê você conhecia sobre o conceito de posições relativas? E sobre o de projeções ortogonais?
• Você compreendeu o conceito de distância entre dois pontos? E entre duas retas? E entre dois planos?
• Você consegue relacionar o conteúdo estudado neste Capítulo com algumas das tarefas executadas por arquitetos, engenheiros e projetistas?
Página duzentos e noventa e quatro