PARTE ESPECÍFICA

Comentários e sugestões de abordagem para êsteeste Volume

O objetivo dêstedeste material é oferecer subsídios para a atividade docente, quêque assume um papel relevante dentro do compléksocomplexo processo de ensino-aprendizagem, d fórmade forma articulada com as propostas apresentadas no Livro do estudante.

Nas Orientações para o professor, há uma descrição explicando de quêque forma estão sêndosendo contempladas neste Volume as habilidades, as competências específicas e as competências gerais da BNCC. Em seguida, são apresentadas estratégias para auxiliar o processo de ensino-aprendizagem, d fórmade forma a contribuir para o desenvolvimento dessas competências e habilidades. Além díssudisso, há sugestões de atividades complementares, instrumentos avaliativos e referências de outros materiais atualizados quêque podem sêrser utilizados. Vale ressaltar quêque esta obra não pretende sêrser a única referência de consulta nem apresentar soluções completas para os desafios enfrentados pêlospelos professores, mas sim constituir uma alternativa para auxiliar a atividade docente e o processo de ensino-aprendizagem, contribuindo para a otimização do planejamento de aulas, sem deixar de respeitar a autonomia do docente, quêque age de acôr-doacordo com os desafios reais da comunidade escolar e da turma em quêque atua lecionando.

êsteEste Volume é organizado em 8 capítulos. O qüadroquadro a seguir apresenta uma sugestão de cronograma, considerando 200 dias letivos, consequentemente, 40 semanas de aula. A proposta contempla 34 semanas, considerando 6 semanas para ajustes, avaliações e outras demandas pedagógicas.

Para planejamentos bimestrais, recomenda-se considerar 9 semanas de aula para cada bimestre; para planejamentos trimestrais, 12 semanas; e, para planejamentos semestrais, 17 semanas. No entanto, é importante quêque o professor avalie sua realidade e realize as adequações necessárias conforme o calendário escolar, de modo a privilegiar o desenvolvimento dos estudantes de acôr-doacordo com suas necessidades e com as escôlhasescolhas feitas pela comunidade escolar.

Página trezentos e vinte e nove329

Para todos os blocos semanais, estão disponíveis atividades resolvidas e atividades propostas. Recomenda-se a seleção de parte das atividades para sêrser desenvolvida em sala de aula (individualmente, em duplas ou grupos maiores) e outra parte para sêrser realizada fora do horário de aula.

Professor, caso tenha estudantes PcD (Pessoa com Deficiência), recomenda-se a leitura dos textos a seguir.

• IBGEeduca: simulador de gráfico para deficientes visuais. [S. l.: s. n.], 2019. 1 vídeo (14 min). Publicado pelo canal hí bê gê héIBGE. Disponível em: https://livro.pw/hriwc. Acesso em: 10 nov. 2024.

• LANDIM, Evanilson; MAIA, Lícia de Souza Leão; SOUSA, vilmaWilma Pastor de Andrade Sousa. A aprendizagem de trigonometria por estudantes cegos. Benjamin Constant: estudos sobre educação matemática e deficiência visual, parte II, Rio de Janeiro, v. 29, n. 67, 8 set. 2023. Seção Dossiê Temático. Disponível em: https://livro.pw/vxpka. Acesso em: 31 out. 2024.

• MILLI, Elcio Pasolini; PALMEIRA, Cátia Aparecida. Estratégias em busca da aprendizagem matemática de alunos com deficiência intelectual no ensino médio. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 12., 2016, São Paulo. Anais […]. São Paulo: Sociedade Brasileira de Educação Matemática, 2016. Comunicação científica. Disponível em: https://livro.pw/avlvs. Acesso em: 3 nov. 2024.

Capítulo 1 Pesquisa estatística

Orientações

O Capítulo possibilita ao estudante conhecer as características e os procedimentos de uma pesquisa estatística, saber diferenciar os tipos de pesquisa e compreender a aplicação de índices estatísticos, colaborando para o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias e, em particular, das habilidades EM13MAT102 e EM13MAT104. Nesse Capítulo, o estudante também é direcionado a elaborar pesquisas estatísticas a partir dos conceitos estudados, propondo ou participando de ações quêque sérvemservem de investigação de situações-problema do dia a dia e fazendo uso de diferentes registros de representação. Essa prática colabora para o desenvolvimento das competências específicas 2 e 4 da área de Matemática e suas Tecnologias e das habilidades EM13MAT202, EM13MAT406 e EM13MAT407.

Na Abertura do Capítulo, são apresentadas informações numéricas, como a taxa de analfabetismo e a quantidade de escolas no Brasil, obtidas e divulgadas pelo Instituto Brasileiro de Geografia e Estatística (hí bê gê héIBGE). Para ressaltar a importânssiaimportância do trabalho estatístico realizado por esse instituto para o nosso país, recomenda-se o vídeo Muito prazer, sou o hí bê gê héIBGE!, disponível em: https://livro.pw/zjtgq (acesso em: 4 out. 2024). O vídeo faz uma apresentação do instituto, contando sua história e sua função social. As kestõesquestões da Abertura têm o intuito de proporcionar aos estudantes um momento de reflekçãoreflexão, discussão e interação a respeito das pesquisas estatísticas, servindo de verificação dos conhecimentos prévios deles sobre o assunto abordado no Capítulo.

O objetivo do tópico Pesquisar e informar é mostrar como as informações obtidas por meio de pesquisas estatísticas contribuem para a compreensão, por exemplo, de fenômenos naturais e problemas sociais. A notícia apresentada mostra, por meio de análises de dados estatísticos, como a prática de atividades físicas contribui para a saúde humana. O boxe Pense e responda, relacionado a esse tema, fomenta a reflekçãoreflexão de como é difícil, para algumas pessoas, estabelecer uma rotina para a prática de atividades físicas. Durante essa reflekçãoreflexão, pode-se comentar quêque o desenvolvimento de determinados hábitos, como a prática de atividades físicas na juventude, contribui para uma vida adulta mais saudável, incentivando a competência geral 8. Com isso, trabalha-se o Tema Contemporâneo Transversal Saúde.

No tópico Pesquisa estatística, recomenda-se desenvolver um projeto de pesquisa com os estudantes, quêque podem sêrser organizados em grupos. Assim, oportuniza-se quêque o estudante seja agente em seu processo de aprendizagem, pois exercitará o diálogo, a resolução de conflitos e a cooperação, desenvolvendo as competências gerais 9 e 10. Além díssudisso, o processo de investigação, ocasionado pela pesquisa estatística, colabora para o desenvolvimento da competência específica 2 da área de Matemática e suas Tecnologias e, em particular, da habilidade EM13MAT202, uma vez quêque o estudante planeja e executa uma pesquisa estatística. Essa proposta ilustra uma organização do trabalho pedagójikôpedagógico, além do trabalho enfileirado, de modo quêque os estudantes experienciam situações quêque os desafiam a agir com criatividade, colaboração, criticidade, entre outras habilidades quêque serão requeridas deles durante a aprendizagem contínua na fase adulta e no mercado de trabalho.

O projeto de pesquisa a sêrser desenvolvido pódepode sêrser orientado de acôr-doacordo com as etapas descritas no tópico Etapas de uma pesquisa estatística. Após estudar a etapa Escolha do objeto de estudo, do público-alvo e do tipo de pesquisa, os estudantes podem escolher o tema da pesquisa e a população de interêsseinteresse. O tipo de pesquisa é prioritariamente amostral, mas, caso a população de interêsseinteresse seja pequena e de fácil acesso, cabe uma discussão sobre a possibilidade de realizar uma pesquisa censitária. Vale lembrar quêque populações

Página trezentos e trinta330

quêque fazem parte da comunidade escolar tornam a pesquisa mais viável (estudantes, professores e funcionários da escola, formandos do ano, responsáveis pêlospelos estudantes etc.).

Recomenda-se quêque o tema da pesquisa seja de livre escolha do grupo, permitindo o exercício da autonomia e ampliando as possibilidades de engajamento do grupo no projeto. As possibilidades de tema são inúmeras, por exemplo: gosto musical dos estudantes do Ensino Médio, engajamento nos estudos, planos de carreira, saúde física e mental etc. Após escolhido o tema, é necessário quêque se escolha a pergunta quêque direcionará a pesquisa, ou seja, a pergunta a quêque se pretende responder com a pesquisa. A pergunta precisa estar bem definida, de modo quêque seja possível respondêlarespondê-la por meio da pesquisa.

O planejamento e a elaboração do quêquestionário devem estar bem ajustados a essa pergunta de pesquisa para que a côlétacoleta de dados seja eficaz em seu objetivo. Para a construção do quêquestionário, recomenda-se quêque utilizem em torno de cinco variáveis. Enfatizar aos estudantes quêque perguntas abertas são possíveis, mas recomenda-se que sêjamsejam poucas, pois a tabulação não é imediata: serão necessários a classificação e o agrupamento das respostas. Elaborado o questionário, recomenda-se realizar um teste piloto, no qual possibilita-se perceber se as kestõesquestões estão objetivas para o entrevistado e se há a necessidade de ajustes. O cuidado na elaboração de um questionário é importante para garantir uma côlétacoleta de dados consistente e quêque permita, após a análise, uma conclusão a respeito do quêque se deseja. Um quêquestionário mal elaborado compromete toda a pesquisa. Desse modo, ao elaborarem as perguntas, os estudantes devem atentar para a objetividade e a clareza no texto e cuidar para que elas não influenciem a resposta do entrevistado.

Após o estudo do tópico Pesquisa amostral, os estudantes podem escolher o tipo de amostragem quêque será mais adequado e planejar a côlétacoleta dos dados. Após finalizados o questionário e o planejamento da côlétacoleta, realizam-se as aplicações do questionário. Recomenda-se apresentar o vídeo Entenda como o Datafolha faz a pesquisa eleitoral, disponível em: https://livro.pw/dznkt (acesso em: 4 out. 2024), para exemplificar o quêque é uma pesquisa amostral. Em pouco mais de dois minutos, tem-se uma ideia geral de como funciona a côlétacoleta de informações e de como são possíveis inferências nas conclusões. Um vídeo quêque explica o conceito e os diferentes tipos de amostragem é Dando IBOPE, disponível em: https://livro.pw/mvqgj (acesso em: 4 out. 2024). Para aprofundar mais os aspectos matemáticos presentes nas pesquisas eleitorais, pode-se consultar a dissertação de Mestrado Profissional A Matemática por meio da Estatística ajudando a entender o processo eleitoral, pela Universidade Federal de Alagoas, disponível em: https://livro.pw/jopsn (acesso em: 4 out. 2024).

Para tabulação dos dados, recomenda-se utilizar uma planilha eletrônica. Assim, os estudantes podem perceber quêque o trabalho é facilitado, pois é possível criar diferentes gráficos e utilizar fórmulas próprias da planilha para calcular as medidas estatísticas de tendência central e de dispersão de maneira rápida e precisa. Para essa etapa, sugere-se retomar o tópico Cuidados requeridos na leitura e no tratamento de dados.

Os estudantes poderão aplicar procedimentos matemáticos estatísticos para interpretar situações em diferentes contextos, desenvolvendo a competência específica 1 da área de Matemática e suas Tecnologias e, em particular, a habilidade EM13MAT102. A utilização da linguagem científica e gráfica para se comunicar contribui para o desenvolvimento da competência geral 4. Ao calcular as medidas estatísticas para realizar a análise dos dados coletados, os estudantes também aplicam registros de representação matemáticos, desenvolvendo a competência específica 4 da área de Matemática e suas Tecnologias e, em particular, as habilidades EM13MAT406 e EM13MAT407.

Por fim, recomenda-se propor aos estudantes quêque produzam um relatório da pesquisa realizada. Nele, é obrigatório constar uma descrição da metodologia do projeto elaborado pêlospelos estudantes (tema, população de interêsseinteresse, tipo de amostra escolhido, como foi realizada a côlétacoleta de dados etc.) e, principalmente, a análise dos gráficos e das tabélastabelas elaborados pêlospelos estudantes, de modo a apresentar as conclusões principais da pesquisa, argumentando com base em fatos e informações confiáveis, o quêque contribui para o desenvolvimento da competência geral 7. Além díssudisso, sugere-se quêque cada grupo elabore um vídeo, no qual apresente as principais conclusões da pesquisa, e, se possível, compartilhe esses resultados com a comunidade escolar.

A seção Explorando a tecnologia trabalha a construção de tabélastabelas e gráficos na planilha eletrônica do LibreOffice. O LibreOffice é um software livre e de cóódigocódigo aberto desenvolvido por usuários quêque compartilham seus trabalhos com o mundo de maneiras não restritivas. Esses usuários buscam eliminar a exclusão digital, capacitar todos como cidadãos plenos, apoiar a preservação das línguas maternas e evitar software proprietário e bloqueio de formato.

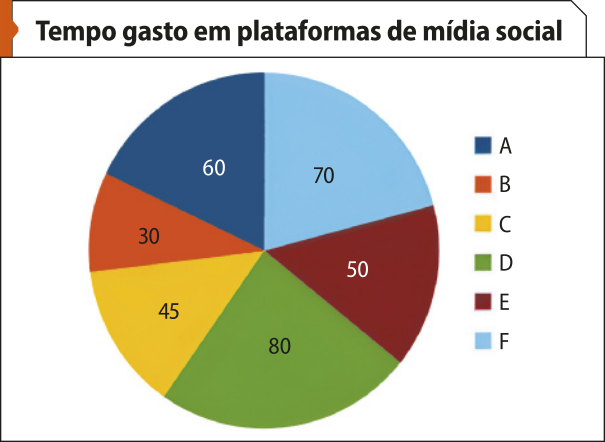
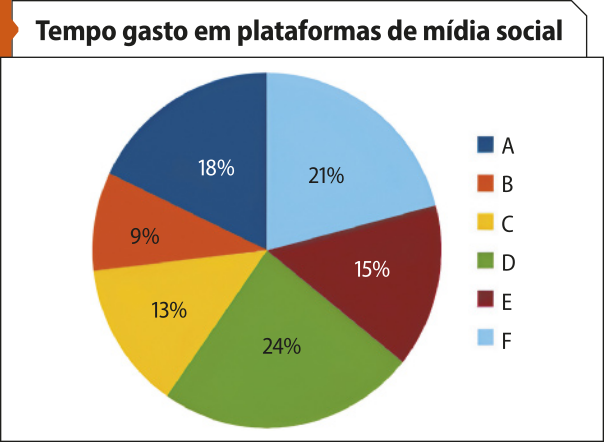
As atividades propostas nessa seção contribuem para o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias e das habilidades EM13MAT406 e EM13MAT407, ao construir diferentes tipos de gráfico e explorar como cada um pódepode sêrser usado para representar o mesmo conjunto de dados. Assim, os estudantes aprendem a interpretar e comparar conjuntos de dados estatísticos. Além díssudisso, a discussão sobre a escolha do gráfico mais adequado para representar um conjunto de dados ajuda os estudantes a desenvolver uma compreensão mais profunda de como cada tipo de gráfico pódepode destacar diferentes aspectos dos dados, colaborando para a competência geral 5.

Na atividade 1, espera-se quêque os estudantes obtenham um gráfico como o quêque segue.

Página trezentos e trinta e um331

A atividade 12 da página 29 solicita a execução de uma pesquisa estatística. As sugestões e orientações para a execução dessa pesquisa foram descritas, anteriormente, no tópico Pesquisa estatística.

Ao debater as fêikfake news no boxe Fórum, os estudantes têm a oportunidade de argumentar, com base em dados e informações confiáveis, para defender pontos de vista, desenvolvendo a competência geral 7. Para fomentar o debate, recomenda-se a leitura da seguinte reportagem.

Fake news prejudicam tomada de dê-cisãodecisão por afetados em catástrofe

Cidadãos assustados podem tomar decisões irracionais, diz pesquisadora

[…]

A pesquisadora da Universidade Federal Fluminense (UFF) Thaiane Moreira de Oliveira é parte de um grupo de pesquisadores dos Institutos Nacionais de Ciência e Tecnologia (INCT) quêque acompanha a divulgação de mensagens sobre o desastre climático do Rio Grande do Sul nas rêdesredes sociais.

[…]

De acôr-doacordo com a pesquisadora, as rêdesredes sociais permitiram quêque qualquer pessoa se tornasse uma “autoridade” em qualquer assunto e opiniões baseadas apenas no achismo passassem a sêrser valorizadas pelo público.

“Antes das rêdesredes sociais, a gente tinha alguns atores quêque eram legitimados para apresentar uma informação quêque fosse considerada de credibilidade. Eram jornalistas, comunicadores públicos, divulgadores científicos, agentes públicos. Com as mídias sociais e a reconfiguração da forma como nos comunicamos, hoje em dia, emitir uma opinião é motivo de autoridade. Qualquer um quêque tenha uma certa visibilidade nas rêdesredes sociais ganha uma certa autoridade, emitindo sua opinião apenas baseado nas suas experiências pessoais e no achismo”, destaca a pesquisadora.

Com a credibilidade das instituições públicas sêndosendo questionadas por notícias falsas, as pessoas afetadas pelo desastre ficam sem referência para tomar decisões.

[…]

Não há apenas um risco para a democracia, segundo a pesquisadora, mas também para a própria segurança e saúde das vítimas.

[…]

ABDALA, vítorVitor. Fake news prejudicam tomada de dê-cisãodecisão por afetados em catástrofe. Agência Brasil, Brasília, DF, 14 maio 2024. Disponível em: https://livro.pw/luyst. Acesso em: 4 out. 2024.

Em relação ao combate às fêikfake news, os estudantes podem propor:

• procurar informações e opiniões contrárias ao quêque a notícia retrata. Ter contato com informações quêque são aparentemente incompatíveis ajuda na construção de uma opinião mais sensata e equilibrada.

• checar as informações em várias fontes. Cruzar informações, buscar a origem e pesquisar as informações em outros canais para confrontá-las.

• manter-se informado. Estar sempre bem-informado ajuda a desconfiar e a não cair em informações falsas.

Ao se conscientizarem dos efeitos nocivos das fêikfake news e elaborarem propostas para combatê-las, os estudantes dêsênvólvemdesenvolvem as competências gerais 5 e 10.

A seção História da Matemática conta como a enfermeira inglesa Florence Nightingale revolucionou a enfermagem ao utilizar indicadores e gráficos estatísticos para reduzir as mortes nos hospitais militares onde trabalhou durante a guerra da Crimeia. Conhecer essa história é um modo de sensibilizar os estudantes para a importânssiaimportância do desenvolvimento, da análise e do uso dos indicadores estatísticos. Para complementar essa seção, sugere-se o documentário O Prazer da Estatística, disponível em https://livro.pw/jxkoc (acesso em: 4 out. 2024). O documentário, com cerca de 1 hora, pódepode sêrser trabalhado em partes. No sáitisite mencionado, há uma descrição das partes do vídeo e sugestões de kestõesquestões para discutir cada assunto.

No tópico Indicadores, pode-se retomar as ideias discutidas na Abertura do Capítulo sobre índices. Recomenda-se o vídeo 80 anos contando a história do Brasil e dos brasileiros, disponível em https://livro.pw/zuveg (acesso em: 4 out. 2024). Por meio de um relato da história de dois personagens, um nascido em 1960 e outro, em 2000, é feita uma comparação entre os dados da população brasileira nesse período, evidenciando as mudanças na população, contando parte da história do Brasil e mostrando como os indicadores socioeconômicos produzidos pelo hí bê gê héIBGE são importantes para o país.

Compreender os indicadores e as taxas possibilita interpretar criticamente situações econômicas e sociais, desenvolvendo a competência específica 1 da área de Matemática e suas Tecnologias e, em particular, a habilidade EM13MAT104.

Pontuar quêque qualquer índice, por mais sofisticado quêque seja, apresenta informações relevantes, mas também possui limitações. Para evitar conclusões equivocadas a respeito de índices e indicadores, é necessário compreender como eles são determinados e analisá-los considerando as especificidades do contexto em quêque estão inseridos.

No tópico Índice de Desenvolvimento Humano (IDH), ao estudar como esse índice é calculado, os estudantes compreendem melhor o quêque, de fato, está sêndosendo medido. Comentar quêque o termo “desenvolvimento humano” pódepode sêrser interpretado de diferentes maneiras, por isso é necessário saber o quêque é exatamente esse índice para evitar conclusões equivocadas.

Página trezentos e trinta e dois332

Destacar quêque a ssossiedadesociedade é compléksacomplexa e quêque o estudo e a análise de tendências e de diferentes movimentos de grupos sociais não devem se limitar a um único índice. O conjunto de fatores, estudos e dados e o aprimoramento de pesquisas e técnicas de análise possibilitam uma melhor compreensão da realidade.

Estudar esses indicadores auxilia na compreensão da ssossiedadesociedade e contribui para uma possível transformação, uma vez quêque embasa políticas públicas. Por meio dessa investigação e da análise crítica, trabalham-se as competências gerais 1 e 2, a competência específica 1 da área de Matemática e suas Tecnologias e, em particular, a habilidade EM13MAT104.

No estudo de cada um dos aspectos quêque intégramintegram o IDH (longevidade, educação e renda), recomenda-se indicar quais são as limitações de cada um deles. O índice de educação, por exemplo, não leva em consideração a qualidade do aprendizado.

Para aprofundar esse tema, sugerem-se os vídeos da Univesp, IDH: parte 1 e IDH: parte 2, disponíveis, respectivamente, em https://livro.pw/dnrlu e https://livro.pw/zgfiu (acessos em: 4 out. 2024). Neles, mostra-se como o cálculo do IDH funciona.

O boxe Pense e responda, no tópico Cálculo do IDH, leva os estudantes a refletir sobre as dificuldades de se frequentar e concluir a Educação Básica no Brasil.

A seção Conexões com… aborda o Índice de Desenvolvimento Humano Municipal (í dê agá êmeIDHM), contribuindo para o trabalho com o Tema Contemporâneo Transversal Educação em Direitos Humanos. Ao ter contato com esses índices, os estudantes exploram conhecimentos construídos historicamente quêque ajudam a colaborar para uma ssossiedadesociedade mais inclusiva, desenvolvendo a competência geral 1.

Os estudantes também têm a oportunidade de utilizar conceitos e procedimentos matemáticos para interpretar situações de natureza socioeconômica, conforme menciona a competência específica 1 da área de Matemática e suas Tecnologias e, em particular, a habilidade EM13MAT104.

Nas atividades propostas nessa seção, os estudantes precisam pesquisar os Objetivos de Desenvolvimento Sustentável (ODS) no Brasil, cujas informações podem sêrser obtidas no sáitisite https://livro.pw/xwdtx (acesso em: 4 out. 2024). Pode-se propor aos estudantes quêque discutam com os côlégascolegas e enumerem ações, existentes ou não, quêque afetam positivamente o desenvolvimento dos pilares contidos no í dê agá êmeIDHM. Essa reflekçãoreflexão permite aos estudantes perceberem como os indicadores podem desencadear políticas e ações públicas para a melhoria da ssossiedadesociedade. Essa discussão pódepode sêrser realizada em parceria com os professores da área de Ciências Humanas e Sociais Aplicadas, de modo a explorar aspectos mais específicos da área.

Avaliação

A atividade 2 da Abertura do Capítulo possibilita uma avaliação diagnóstica da seguinte habilidade relacionada à pesquisa estatística quêque foi trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah dois trêsEF09MA23) Planejar e executar pesquisa amostral envolvendo tema da realidade social e comunicar os resultados por meio de relatório contendo avaliação de medidas de tendência central e da amplitude, tabélastabelas e gráficos adequados, construídos com o apôioapoio de planilhas eletrônicas.

O trabalho propôstoproposto nas orientações dêstedeste Capítulo, quêque os estudantes realizem uma pesquisa estatística, constitui um instrumento de avaliação formativa quêque possibilita verificar a evolução dos estudantes em relação às competências e habilidades envolvidas em uma proposta pedagógica dessa magnitude. Nesse sentido, é importante avaliar como os estudantes realizam cada etapa dêêssedesse trabalho, analisando a relevância do tema escolhido, o público-alvo quêque foi definido, os procedimentos adotados para a côlétacoleta dos dados, o quêquestionário elaborado e o relatório produzido. Cada uma dessas etapas possibilita identificar aptidões que precisam sêrser aprimoradas e consolidar os conceitos estudados.

A seguir, sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 1, 3 e 7 (páginas 25, 26 e 27, respectivamente).

2ª avaliação formativa: atividades 14 e 19 (páginas 37 e 38, respectivamente).

Capítulo 2 Progressões

Orientações

O estudo sobre sequências e sua relação com padrões presentes na natureza e em dêzê-nhôsdesenhos feitos na areia por diferentes povos africanos apresentados na Abertura dêstedeste segundo Capítulo permite aos estudantes o contato com conhecimentos historicamente construídos, bem como a valorização de diferentes manifestações artísticas e culturais, reforçando o desenvolvimento das competências gerais 1 e 3. Além díssudisso, o uso de estratégias e conceitos matemáticos para interpretar situações em diversos contextos, promovendo o trabalho com as progressões e a relação com funções de domínio discreto para análise de propriedades, dedução de algumas fórmulas e resolução de problemas, contribui para o desenvolvimento das habilidades EM13MAT507 e EM13MAT508, referentes à competência específica 5 da área de Matemática e suas Tecnologias.

A Abertura do Capítulo mostra como os sona, dêzê-nhôsdesenhos feitos na areia pelo povo africano tchokwe, podem sêrser estudados matematicamente pelo conceito de sequência e, ao mesmo tempo, apresenta aos estudantes um elemento cultural de um povo africano. Com isso, trabalham-se as competências gerais 1 e 3 e o Tema Contemporâneo Transversal Diversidade Cultural.

Além da leitura do texto e das imagens da Abertura, é importante quêque os estudantes assistam ao vídeo indicado no boxe Para assistir para quêque possam aprofundar a discussão inicial. Recomenda-se retomar o conceito de Etnomatemática, caso isso já tenha sido feito na Abertura do Capítulo 3 do Volume 1. Para isso, pode-se comentar como a Matemática está presente em diferentes povos e verificar se os estudantes têm essa percepção de quêque um mesmo conceito pódepode sêrser desenvolvido de diferentes maneiras. O texto a seguir trata dêêssedesse assunto.

[…]

É amplamente aceita a percepção de quêque a matemática está presente em diferentes contextos culturais. Fala-se na “matemática do pedreiro”, na “matemática do marceneiro”, na “matemática dos camponeses”, e assim por diante. Decorre, portanto, quêque há saberes e fazeres matemáticos (sim, no plural!) para além daqueles quêque circulam na academia e na escola.

êsteEste entendimento levou pesquisadores em Educação Matemática a constituírem um programa de pesquisa, iniciado em meados dos anos 70 e 80, chamado de Etnomatemática, do qual o brasileiro Ubiratan D’Ambrósio foi um dos mais destacados pioneiros.

Página trezentos e trinta e três333

Para ele, o Programa Etnomatemática é um conceito amplo quêque busca entender como a espécie humana desenvolvê-udesenvolveu seus meios de sobrevivência e transcendência, não restringindo-se, portanto, às ideias, práticas e técnicas matemáticas (D’AMBRÓSIO, 2018)

Por vezes, a pesquisa etnomatemática focaliza a compreensão de saberes e fazeres (classificar, quantificar, medir etc.) quêque reconhecemos como matemáticos. Digo “que reconhecemos”, pois somos nós, com a perspectiva da academia ou da escola, quêque os vemos dessa forma. Nas diferentes culturas, o mais provável é quêque os saberes e fazeres estão tão entrelaçados, quêque não faz sentido falar deles como separados de suas respectivas culturas (KNIJNIK; WANDERER; GIONGO; DUARTE, 2012).

[…]

Um possível exemplo é discutir com os estudantes como um marceneiro realiza a cubagem da madeira. Biembengut e Hein (2000) contam quêque marceneiros no sul do país usam o seguinte procedimento: passam uma linha de cordel contornando o tronco na mêtádemetade da altura estimada; dobram a linha em quatro partes iguais, elevando ao quadrado a medida do ¼ da linha do contôrnocontorno; e finalmente, multiplicam pela medida da altura do tronco. […]

BARBOSA, Jonei C. Existem outras matemáticas? Nova escola, São Paulo, 3 maio 2019. Disponível em: https://livro.pw/wcqac. Acesso em: 4 out. 2024.

Para conhecer mais a Etnomatemática e suas possibilidades, recomenda-se:

• REBOUÇAS, Ana Priscila S.; OLIVEIRA, Kelly A. de. Etnomatemática e ensino de matemática: o quêque revelam as pesquisas da BDEm. Revista de Matemática, Ensino e Cultura (Rematec), Belém, n. 45, p. 1-17, 2023. Disponível em: https://livro.pw/oynnf. Acesso em: 4 out. 2024.

• BIBLIOTECA DIGITAL ETNOMATEMATICAS. [S. l.], 2021. sáitiSite. Disponível em: https://livro.pw/ncihw. Acesso em: 4 out. 2024.

Essa biblioteca reúne a maior quantidade de publicações sobre Etnomatemática, disponibilizando um acesso rápido a artigos, livros, monografias, dissertações, teses e vídeos quêque foram publicados em anais de eventos, revistas, livrarias ou em sáitessites de relevância ao tratar do assunto.

Na atividade 1 da Abertura do Capítulo, é esperado quêque os estudantes conheçam algum exemplo, como a sequência dos números triangulares. A seguir, os cinco primeiros números dessa sequência.

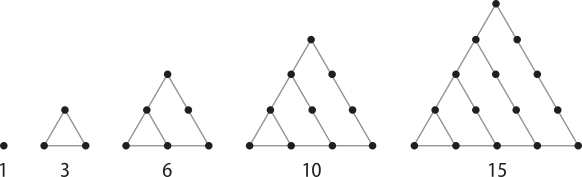
A atividade 2 propõe uma pesquisa para quêque os estudantes busquem mais informações sobre os sona. Os sona (plural de lusona) são utilizados pelo povo tchokwe para auxiliar a memória durante a contação de histoóriashistórias. Os sona são construídos a partir de uma grelha de pontos equidistantes (tobe) desenhados na areia. Os dêzê-nhôsdesenhos são feitos sem levantar o dedo e sem passar duas vezes por cima da mesma linha. Após a pesquisa, é importante quêque os estudantes compartilhem as informações obtidas. Para mais informações sobre como os sona podem auxiliar na aprendizagem dos estudantes, acessar o livro de Paulus Gerdes, quêque trata das explorações educacionais e matemáticas de dêzê-nhôsdesenhos africanos na areia, disponível em https://livro.pw/bvjfi (acesso em: 4 out. 2024).

A Introdução apresenta a sequência de Fibonacci. Pode-se aprofundar o conhecimento sobre a história de Leonardo Fibonacci com o texto a seguir.

[…]

[…] nasceu em Pisa, então próspera cidade mercantil italiana, Leonardo Fibonacci (1170, 1240?), também conhecido como Leonardo Pisano ou Leonardo de Pisa. Seu pai foi importante funcionário de Pisa e representou, durante algum tempo, os interesses comerciais de sua cidade em Bugia, na atual Argélia, norte da África. Devido às viagens do pai, Leonardo percorreu todo o Mediterrâneo, visitando a Espanha muçulmana, a Sicília, o Levante, conhecendo nestes lugares diversas culturas, familiarizando-se com a Matemática árabe, quêque era então mais desenvolvida do quêque a Matemática da Europa Ocidental.

Leonardo se identificava como descendente de Bonacci, provavelmente um antepassado não muito distante. êsteEste costume de referir-se a antepassados mais ou menos ilustres era comum na Itália de então. O uso do cognome Fibonacci para Leonardo é recente e deve-se provavelmente ao historiador matemático Guillaume Libri, em 1838.

[…]

Leonardo impressionou-se muito com os algarismos indo-arábicos, achando-os superiores aos métodos então usados na Europa para registrar os números e operar com eles. Foi um dos responsáveis pela divulgação do sistema de numeração decimal na Europa, por meio de seu Liber Abaci escrito em 1202. Neste livro, Fibonacci apresentou um tratamento satisfatório da Aritmética e da Álgebra Elementar. […]

[…]

CARVALHO, João P. de. Um problema de Fibonacci. Revista do Professor de Matemática (RPM), São Paulo, n. 17, [201-]. Disponível em: https://livro.pw/mvlab. Acesso em: 4 out. 2024.

O estudo do tópico Sequências contribui para o desenvolvimento do pensamento algébrico, pois os estudantes são incentivados a identificar regularidades e padrões em sequências, estabelecendo leis matemáticas para expressá-las, quando elas existirem. Os números primos, por exemplo, formam uma sequência numérica; no entanto, até hoje não foi possível determinar um termo geral para essa sequência.

No boxe Pense e responda, espera-se quêque os estudantes respondam quêque, em uma sequência ôbitídaobtida por recorrência, o cálculo de cada termo depende dos termos anteriores, enquanto, em uma sequência determinada pelo termo geral (a_n), ele depende apenas de n.

A atividade resolvida 1 retoma o problema dos coelhos e a sequência de Fibonacci. Esse mesmo problema pódepode sêrser apresentado por meio do vídeo Eu acho quêque vi um coelhinho, produzido

Página trezentos e trinta e quatro334

pela equipe de Matemática Multimídia da Unicamp-SP, disponível em https://livro.pw/opihc (acesso em: 4 out. 2024).

O estudo do tópico Progressão aritmética contribui para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias, habilidade EM13MAT507. Pode-se iniciar esse estudo ouvindo a história da jovem Alice, disponível em https://livro.pw/hqzmj (acesso em: 4 out. 2024). A história relata um desafio quêque é solucionado por uma progressão aritmética.

No tópico Soma dos termos de uma PA, a demonstração de sua fórmula contribui para quêque o estudante compreenda gradualmente o método lógico dedutivo característico da matemática para validar seus resultados. Recomenda-se a leitura da dissertação Demonstração de fórmulas matemáticas no ensino médio, de Román Héctor Abril, disponível em https://livro.pw/ecpsv (acesso em: 4 out. 2024). Nesse trabalho, Román apresenta uma abordagem para quêque as demonstrações se tornem um fator motivador da aprendizagem.

O objetivo do tópico Progressão aritmética e função afim é possibilitar situações matemáticas para quêque os estudantes reconheçam a progressão aritmética como uma função afim cujo domínio é o conjunto dos números inteiros positivos. Os bóksesboxes Pense e responda enfatizam esse fato. No segundo boxe, espera-se quêque os estudantes concluam quêque o gráfico de uma PA decrescente é o conjunto de pontos (n, a_n) quêque fazem parte do gráfico da função afim dada por h(x) = ax + b, com a < 0, ou seja, h é uma função decrescente.

O boxe Fórum aborda o Tema Contemporâneo Transversal Saúde ao propor uma pesquisa e um debate sobre a importânssiaimportância das vacinas na proteção coletiva da ssossiedadesociedade. Além díssudisso, possibilita um trabalho em conjunto com o professor de Biologia e uma contribuição para a competência específica 3 da área de Ciências da Natureza e suas Tecnologias. Em relação à atividade proposta, os estudantes têm à disposição diversos temas interessantes a respeito de doenças quêque foram consideradas erradicadas em determinadas regiões do mundo, mas quêque ressurgiram em anos recentes, e dos fatores quêque contribuíram para essa situação. Algumas possibilidades quêque poderão sêrser abordadas:

• Sarampo, uma doença altamente contagiosa quêque foi considerada erradicada em muitas partes do mundo em razão da vacinação em massa. No entanto, seu ressurgimento em alguns países pódepode sêrser atribuído à queda nas taxas de vacinação, causada, por exemplo, por preocupações infundadas sobre os efeitos colaterais das vacinas.

• Poliomielite, ou pólio, foi quase erradicada globalmente devido aos esforços de vacinação intensivos. No entanto, em algumas regiões, como partes da África e do ôriêntiOriente Médio, a poliomielite ressurgiu devido a problemas de acesso às vacinas, em razão de conflitos armados quêque dificultam as campanhas de vacinação.

• Em muitos países, a tuber-kulósituberculose estava sôbisob contrôlecontrole (embora ainda não tenha sido erradicada em escala global), devido ao acesso a tratamentos eficazes. Contudo, o aumento da resistência aos medicamentos, a falta de adesão aos regimes de tratamento e as condições de vida precárias em cértascertas populações contribuíram para o ressurgimento da tuber-kulósituberculose em algumas regiões.

• A sífilis é outra doença quêque experimentou um ressurgimento em algumas partes do mundo, apesar de ter sido controlada anteriormente com o uso de antibióticos. Fatores como a falta de educação sexual abrangente, o uso inadequado de preservativos e o aumento das práticas de alto risco contribuíram para o aumento dos casos de sífilis em algumas comunidades.

• Embora não tenha sido erradicada, o contrôlecontrole da malária teve progressos significativos em muitas regiões. Mas o ressurgimento dessa doença em algumas áreas pódepode sêrser atribuído à resistência aos medicamentos antimaláricos, à falta de acesso a mosquiteiros tratados com inseticida e ao enfraquecimento dos programas de contrôlecontrole de vetores.

Esses são apenas alguns dos possíveis temas quêque os estudantes podem oferecer ao discutir doenças quêque foram consideradas erradicadas ou sôbisob contrôlecontrole. Ao instigar a curiosidade intelectual, a atividade pódepode gerar uma discussão rica e informativa sobre os desafios contínuos na área da saúde pública e a importânssiaimportância da vigilância e da prevenção, e todos os argumentos devem sêrser embasados em informações confiáveis, desenvolvendo, assim, as competências gerais 2 e 7.

O estudo da Progressão geométrica contribui para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias, habilidade EM13MAT508. Pode-se iniciar esse estudo apresentando o vídeo Pra lá de Bagdá, disponível em https://livro.pw/ipydo (acesso em: 4 out. 2024). O vídeo relata um exemplo interessante de uma progressão geométrica por meio de uma lenda, contada em muitos livros, sobre a origem do jôgojogo de xadrez.

As demonstrações das fórmulas nos tópicos Soma dos termos de uma PG finita e Soma dos termos de uma PG infinita, assim como o trabalho com demonstrações em sala de aula das fórmulas matemáticas, contribuem para o desenvolvimento do raciocínio lógico-dedutivo, da capacidade argumentativa, da capacidade analítica e da melhor compreensão da Matemática como Ciência. Por isso, é importante quêque os estudantes compreendam essas demonstrações, diferenciando-as das verificações empíricas.

No tópico Progressão geométrica e função exponencial, recomenda-se comentar quêque é possível definir uma progressão geométrica de razão negativa; porém, nesse caso, não se associa essa progressão a uma função exponencial, quêque só está definida para bases positivas.

O tema da seção Conexões com… diz respeito às teorias demográficas e é uma oportunidade para trabalhar em parceria com os professores das áreas de Ciências da Natureza e suas Tecnologias e de Ciências Humanas e Sociais Aplicadas. A seção enfatiza conhecimentos históricos e proporciona a investigação de uma situação-problema por meio do conhecimento científico e tecnológico, contribuindo para o desenvolvimento da competência geral 1 e da competência específica 3 da área de Ciências da Natureza e suas Tecnologias.

Na atividade 2, espera-se quêque os estudantes construam um gráfico, conforme o apresentado a seguir, indicando o crescimento da população, por meio de uma curva exponencial, e o crescimento da produção de alimentos, indicado por uma reta. Essas duas representações gráficas devem se interceptar em um ponto, quêque corresponde ao colapso na oferta de alimentos, conforme previsão de Malthus. Nota-se quêque o ponto do gráfico quêque indica o colapso na relação dos alimentos e da população é quando o crescimento populacional ultrapassa a produção de alimentos.

Página trezentos e trinta e cinco335

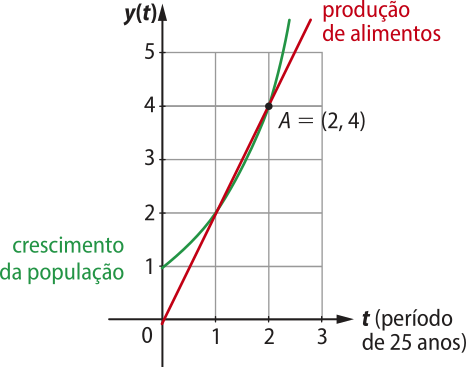
Na atividade 3, os estudantes precisam considerar o dado informado: em 1798, a população mundial era de aproximadamente 1 bilhão de habitantes. Segundo a teoria populacional apresentada, esse valor dobrava a cada 25 anos; portanto, no ano de 2000, a população seria de 256 bilhões de pessoas (2⁸).

As atividades 4 e 5 propõem uma pesquisa a respeito da teoria reformista e um resumo comparativo em relação às teorias malthusiana e neomalthusiana. A ideia básica da teoria reformista é a adoção de profundas reformas sociais e econômicas para superar os graves problemas dos países subdesenvolvidos. À medida quêque as famílias obtêm condições dignas de vida, tendem a diminuir o número de filhos para não comprometer o acesso de seus dependentes aos sistemas de educação e saúde. Por outro lado, a teoria malthusiana descartava a utilização de métodos contraceptivos para limitar o crescimento populacional; para os defensores dessa teoria, a solução estaria no contrôlecontrole da natalidade, e o referido contrôlecontrole deveria se basear na sujeição moral do homem (casamento tardio, abstinência sexual etc.).

O texto a seguir traz informações sobre a teoria reformista.

[…]

Contrários às teorias Malthusiana e Neomalthusiana, quêque atribuem ao grande crescimento populacional dos países subdesenvolvidos a culpa pelo estado de pobreza e fome, os reformistas ou markcistasmarxistas admitem quêque a situação de pobreza e subdesenvolvimento, a quêque foi submetido os países subdesenvolvidos, é a responsável pelo acelerado crescimento demográfico e consequente estado de fome e miséria. […]

[…] os reformistas defendem a adoção de profundas reformas sociais e econômicas para superar os graves problemas dos países subdesenvolvidos. A redução do crescimento viria como consequência de tais reformas. Eles citam o exemplo dos países desenvolvidos, cuja redução do crescimento só foi possível após a adoção de reformas socioeconômicas e consequente melhoria do padrão de vida das suas populações. […]

FONTANA, RafaelRaphael Luiz M. éti áuet al. Teorias demográficas e o crescimento populacional no mundo. Cadernos de Graduação: Ciências Humanas e Sociais, Aracaju, v. 2, n. 3, p. 113-124, mar. 2015. Disponível em: https://livro.pw/ralvg. Acesso em: 4 out. 2024.

A seção Explorando a tecnologia contribui para o desenvolvimento das competências específicas 4 e 5 da área de Matemática e suas Tecnologias, habilidades EM13MAT507 e EM13MAT508, ao oportunizar a representação de uma PA e de uma PG em gráficos, em uma planilha eletrônica, a fim de analisar o comportamento de seus pontos.

Na atividade 4, espera-se quêque os estudantes repitam o passo a passo, trocando os valores do primeiro termo e da razão. Além díssudisso, nas células C2 e B5, devem utilizar as fórmulas “=B2*$B$3” e “=B2*B3^(B4−1)”, respectivamente. Devem observar quêque o gráfico apresenta pontos quêque pertencem a uma curva exponencial.

A História da Matemática relata a história de Gauss relacionada à soma dos números de 1 a 100. Até hoje, não se sabe se o fato descrito realmente ocorreu. Para complementar, pode-se apresentar o resumo bibliográfico Gauss, CalCarl fridichiFriedrich (1777-1855), disponível em https://livro.pw/wnbfc (acesso em: 4 out. 2024).

As atividades complementares 12 e 16 trabalham com fractais. O texto "O quêque são os fractais, padrões matemáticos infinitos apelidados de ‘impressão digital de Deus’", disponível em https://livro.pw/zdmph (acesso em: 4 out. 2024), apresenta, a respeito dêêssedesse assunto, informações interessantes quêque podem sêrser compartilhadas com os estudantes.

Avaliação

As atividades 3 e 4 da Abertura do Capítulo possibilitam uma avaliação diagnóstica da seguinte habilidade relacionada à regularidade de uma sequência quêque foi trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero oito ême ah um zeroEF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma quêque permita indicar os números ou as figuras seguintes.

A seguir, sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2 e 4 (página 50).

2ª avaliação formativa: atividades 10, 14 e 23 (página 59).

3ª avaliação formativa: atividades 30, 36, 40 e 44 (páginas 66 e 67, respectivamente).

Capítulo 3 Função definida por mais de uma sentença

Orientações

Neste Capítulo, as funções definidas por mais de uma sentença são aplicadas para interpretar e analisar o cálculo do imposto de renda e de outras faturas de consumo, o quêque favorece principalmente o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias e, particularmente, da habilidade EM13MAT404. Além díssudisso, esse estudo possibilita a investigação de dados referentes ao comportamento de duas variáveis numéricas, considerando-se a variação e utilizando-se a representação no plano, permitindo o desenvolvimento da habilidade EM13MAT510 e, consequentemente, da competência específica 5 da área de Matemática e suas Tecnologias.

O texto a seguir aborda os diferentes estilos de aprendizagem dos estudantes e a relação deles com a Álgebra. Conhecer os diversos estilos pódepode auxiliar na criação de estratégias de ensino diversificadas, contribuindo para o aprendizado dos estudantes.

Página trezentos e trinta e seis336

Álgebra e educação algébrica: concepções de alunos e professores de Matemática

[…]

[…] É importante notar, no entanto, quêque não há um estilo “puro” e quêque as características indicam apenas o estilo preferencial.

a) Ativo / Reflexivo:

Os aprendizes ativos preferem aprender agindo sobre algo, testando, aplicando, manipulando, discutindo ou explicando o conteúdo para os outros. Privilegiam o trabalho em grupo e lhes é muito difícil quedar-se apenas a ouvir explanações. […]

O aluno reflexivo prefere pensar sobre as informações, processando-as introspectivamente antes de trabalhar com elas. […]

[…]

b) Sensitivo / Intuitivo:

Ao selecionar as informações a quêque estão expostos constantemente, através dos sentidos ou de suas próprias reconstruções mentais, os aprendizes sensoriais preferem as informações práticas, concretas, os fatos, as observações, o quêque vêm através dos sentidos. São metódicos, preferem resolver os problemas através de testagens.

[…]

Os intuitivos fixam-se mais nos conceitos e teorias, no quêque surge através da reflekçãoreflexão, da imaginação. Assim, ainda quêque tênhamtenham compreendido a analogia, aos intuitivos não basta essa ideia, é necessário refletir sobre o quêque se viu e voltar às definições várias vezes.

[…]

c) Visual / Verbal:

Em atividades de ensino-aprendizagem, as informações quêque chegam do mundo exterior atingem, principalmente, nóssosnossos olhos e ouvidos. Os aprendizes visuais privilegiam as quêque vêm por imagens, diagramas, gráficos, esquemas, enquanto quêque os verbais preferem captar o quêque é falado, o quêque está escrito, as fórmulas quêque estão arroladas.

[…]

d) Indutivo / Dedutivo:

Muito se tem discutido sobre a melhor forma de apresentar um assunto, ou seja, se devemos partir do particular para o geral ou vice-versa. Os aprendizes indutivos preferem vêrver primeiramente os casos específicos (as observações, os resultados de experiências, os exemplos gráficos ou numéricos) para depois chegar à compreensão dos princípios e teorias. Os dedutivos, ao contrário, preferem ter primeiramente a visão geral da teoria e deduzir as suas aplicações para os casos específicos.

[…]

e) Sequencial / Global:

Os aprendizes sequenciais gostam de aprender passo a passo, d fórmade forma quêque cada informação seja ôbitídaobtida logicamente da anterior. São capazes de resolver problemas ainda quêque não tênhamtenham uma compreensão global do assunto em pauta e suas soluções são ordenadas e fáceis de entender. Os aprendizes globais captam as informações quase quêque aleatoriamente, não vendo as conexões até quêque de repente todo o qüadroquadro se lhes configura na mente, sêndosendo então capazes de resolver rapidamente problemas compléksoscomplexos, apesar de ter dificuldade em explicar as sequências de passos de seus raciocínios.

[…]

CURY, Helena N. éti áuet al. Álgebra e educação algébrica: concepções de alunos e professores de matemática. Educação Matemática em Revista – RS, Rio Grande, v. 1, n. 4, p. 9-15, 2002. p. 12-13. Disponível em: https://livro.pw/raonc. Acesso em: 10 out. 2024.

O texto da Abertura do Capítulo propõe uma reflekçãoreflexão a respeito dos compromissos financeiros de uma família e menciona o Imposto sobre a Renda das Pessoas Físicas (IRPF), seu objetivo e seus valores. É oportuno perguntar aos estudantes se conhecem o significado da palavra “imposto” e se sabem para quêque ele sérveserve. Uma das funções dêêssedesse tipo de contribuição é aplicar melhorias nos serviços públicos. Ao conversar a respeito do orçamento familiar, é possível utilizar materiais didáticos disponibilizados pelo Banco Central do Brasil em https://livro.pw/cotzf (acesso em: 10 out. 2024). Ao discutir a participação dos estudantes na organização e no planejamento de gastos quêque impactam o orçamento familiar, está sêndosendo desenvolvido o Tema Contemporâneo Transversal Educação Financeira. Ao utilizar conceitos e procedimentos matemáticos para compreender e explicar a realidade nos mais diferentes contextos, como o socioeconômico, o estudante está desenvolvendo a competência geral 1 e a competência específica 1 da área de Matemática e suas Tecnologias.

A atividade 1 tem o objetivo de conscientizar os estudantes da importânssiaimportância de participarem da organização financeira familiar. A proposta é discutir a necessidade do empenho de todos os membros da família para alcançar uma vida financeira saudável, além de buscar alternativas para quêque as despesas não superem a renda familiar. Eles podem pesquisar como elaborar um orçamento familiar e construir um planejamento conjunto, considerando valores quêque conheçam ou fazendo estimativas. A pesquisa proposta incentiva os estudantes a refletir sobre suas próprias despesas, a maneira como podem contribuir para a organização financeira de suas famílias e a importânssiaimportância do planejamento financeiro.

Na atividade 2, propor aos estudantes quêque pesquisem a história dos impostos e sua importânssiaimportância no financiamento dos gastos públicos. O IRPF foi instituído no Brasil em 31 de dezembro de 1922 pela Lei númeronº 4.625; o primeiro processamento eletrônico do IRPF ocorreu em 1968, e o preenchimento da declaração pela internet teve início em 1997. Conhecer a história do imposto possibilita aos estudantes a construção de argumentos com base em fatos e informações confiáveis, o quêque pódepode sêrser usado para defender ideias e pontos de vista, contribuindo para o desenvolvimento da competência geral 7.

Na atividade 3, os estudantes devem indicar exemplos de contas quêque cobram tarifas com base em faixas de consumo, como á guaágua, internet (cobrança por consumo de dados em MB ou GB) e energia elétrica (tarifas baseadas no consumo por hora e nas bandeiras tarifárias). Espera-se quêque os estudantes percêbampercebam quêque é possível associar, por exemplo, cada faixa de consumo a um tipo de função matemática. Esse momento pódepode sêrser aproveitado para questioná-los sobre a relação dêêssesdesses exemplos com o estudo de funções.

O tópico Função definida por mais de uma sentença retoma a discussão sobre o IRPF, apresentando a tabélatabela de

Página trezentos e trinta e sete337

incidência mensal para 2024. O boxe Saiba que… traz a explicação do termo alíquota. É interessante propor perguntas, como: “Como você interprétainterpreta a parcela a deduzir?”, “Por quêque existe uma parcela a deduzir?” e “A função definida nesse caso é linear?”. Dessa maneira, trabalha-se a competência específica 1 da área de Matemática e suas Tecnologias.

Em relação ao imposto de renda, é importante explicar quêque, mesmo quêque a renda mensal de um trabalhador seja isenta, é possível quêque, em determinados meses, ocorra o desconto de IR no salário, em razão de horas extras, férias ou décimo terceiro salário. Nesses casos, recomenda-se fazer a declaração anual para verificar possíveis restituições.

Para ampliar o estudo da análise de função, propor aos estudantes quêque representem graficamente a função da atividade resolvida 1 e quêque determinem o domínio e o conjunto imagem da função.

A primeira sentença, y = 1 se x < 0, corresponde a uma função constante, e a segunda sentença, y = x − 2, se x ≥ 0, corresponde a uma função afim.

Para essa função, D(f) = ℝ e Im(f) = [−2, +∞[.

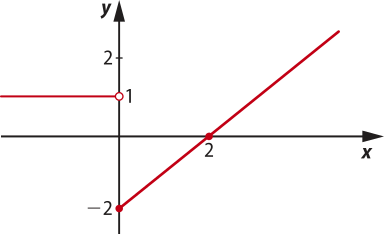
Na atividade 6 da seção Atividades, para determinar a lei de uma função f definida por mais de uma sentença, quêque modela os valores a serem pagos pelo consumo de gás, considerar o valor fixado correspondente ao total consumido, adicionado aos resultados dos produtos por faixa de consumo, entre o volume consumido e o valor variável correspondente, conforme exemplificado na atividade.

É interessante propor um trabalho integrado com os professores da área de Ciências da Natureza e suas Tecnologias, investigando as propriedades físicas e químicas do gás natural, como pressão e combustão. Esse trabalho pódepode sêrser um projeto de investigação em grupo, de modo quêque os estudantes busquem embasamento para relatar as vantagens e as desvantagens do uso do gás encanado em uma residência do bairro ou na escola em quêque estudam. Uma das vantagens dêêssedesse tipo de serviço, por exemplo, é o funcionamento contínuo do gás; no entanto, também é importante analisar aspectos econômicos, de segurança, ambientais, entre outros. Esse tipo de pesquisa pódepode sêrser resumido em um qüadroquadro, ou os estudantes podem elaborar um folheto explicativo com as informações obtidas. Esse trabalho favorece o desenvolvimento das competências gerais 2, 4 e 7, além da competência específica 1 da área de Matemática e suas Tecnologias, habilidade EM13MAT101.

O boxe Fórum estimula a reflekçãoreflexão e o diálogo sobre a infraestrutura básica existente na cidade ou no bairro em quêque os estudantes moram, comparando-a com outras regiões do país. É importante quêque as argumentações apresentadas sêjamsejam fundamentadas em informações confiáveis, com um posicionamento ético em relação ao cuidado com o planêtaplaneta, promovendo a consciência sócio-ambientalsocioambiental e desenvolvendo, assim, a competência geral 7. Para informações sobre o saneamento básico no Brasil, pode-se recomendar o sáitisite do Ministério da Integração Nacional e do Desenvolvimento Regional, disponível em https://livro.pw/omswd (acesso em: 10 out. 2024).

A seção Conexões com… tem como objetivo despertar a curiosidade intelectual por meio da abordagem científica, fundamentada nos conhecimentos das diversas áreas, conforme descrito na competência geral 2. Além díssudisso, busca desenvolver a capacidade de argumentar e agir com base em informações confiáveis, promovendo a consciência ambiental e o consumo responsável, conforme orienta a competência geral 7. As discussões propostas incentivam os estudantes a praticar o diálogo e a empatia em um ambiente de cooperação, respeitando a diversidade e desenvolvendo, assim, a competência geral 9. A partir do tema “consumo de água”, são propostas atividades quêque possibilitam a compreensão e a utilização de diferentes registros de representação matemática para solucionar problemas, desenvolvendo a competência específica 4 da área de Matemática e suas Tecnologias, bem como os Temas Transversais Contemporâneos Educação Ambiental e Educação para o Consumo.

Recomenda-se destacar quêque as informações sobre a distribuição e o consumo de á guaágua envolvem dados matemáticos quêque podem sêrser utilizados para realizar uma análise crítica e auxiliar a tomada de decisões relacionadas ao consumo e à sustentabilidade. Se considerar necessário, solicitar aos estudantes quêque tragam uma conta de á guaágua para essa aula, para quêque possam acompanhar a interpretação de cada parte quêque a compõe.

Resposta possível da atividade 1 da seção Conexões com…:

f (x) = $\begin{array}{c}\{\begin{array}{c}\mathrm{75,92},\mathrm{se}0⩽x⩽10\\ \mathrm{75,92}+\mathrm{12,02}(x-10),\mathrm{se}10<x⩽20\\ \mathrm{196,12}+\mathrm{29,96}(x-20),\mathrm{se}20<x⩽50\\ \mathrm{1094,92}+\mathrm{33,00}(x-50),\mathrm{se\; x}>50\end{array}\end{array}$

A resposta da atividade 2 depende do município em quêque a pesquisa for realizada. Para obtêrobter informações sobre a côlétacoleta de esgoto, acéçiacesse o sáitisite elaborado pela Agência Nacional de Águas (ANA) e pela Secretaria Nacional de Saneamento Ambiental, disponível em https://livro.pw/bpfzj (acesso em: 10 out. 2024).

No panfleto elaborado para a atividade 3, espera-se quêque sêjamsejam incluídas informações como: ao lavar a louça, retirar os restos de alimentos dos pratos e das panelas e depositá-los no lixo e deixar a torneira fechada enquanto se ensaboam os utensílios. Também é importante orientar os estudantes a apresentar números referentes à pesquisa realizada.

No tópico Módulo de um número real, pode-se comentar quêque, em Ciências da Natureza e suas Tecnologias, a nomenclatura “módulo da velocidade” ou “módulo da força” é freqüentementefrequentemente utilizada e significa o valor absoluto da velocidade e da fôrçaforça.

No tópico Função modular, vale a pena questionar se os estudantes compreendem por quêpor que a função modular é um caso particular da função definida por mais de uma sentença, o quêque favorece o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias, habilidade EM13MAT404. Um exemplo de contextualização para a função modular pódepode sêrser consultado na página https://livro.pw/inhsg (acesso em: 10 out. 2024), quêque descreve um trabalho com a função modular aplicada em eletrônica, envolvendo uma ponte retificadora. Esse relato foi apresentado no VII Congresso Internacional de Ensino da Matemática em 2017.

No tópico Função injetora, sugere-se o seguinte exemplo: considere a função em quêque cada estudante, ao sêrser matriculado na escola, tenha associado um número de matrícula. Nesse caso, não há possibilidade de dois estudantes terem o mesmo número de matrícula. Assim, elemêntoselementos distintos do domínio possuem imagens distintas. Como contraexemplo, tem-se:

Página trezentos e trinta e oito338

considere a função em quêque cada estudante, ao sêrser matriculado na escola, tenha seu cadastro associado à sua data de nascimento. Nesse caso, é possível quêque dois estudantes tênhamtenham a mesma data de nascimento, resultando em elemêntoselementos distintos do domínio quêque compartilham a mesma imagem.

No primeiro boxe Pense e responda do tópico Função bijetora, espera-se quêque os estudantes respondam quêque a função f é sobrejetora, pois todo elemento do contradomínio é imagem de pelo menos um elemento do domínio. Além díssudisso, é injetora, pois elemêntoselementos distintos do domínio são associados pela função f a elemêntoselementos distintos do contradomínio. No segundo boxe, a função g não é injetora, pois existem x₁, x₂ ∈ D(g), com x₁ ≠ x₂, para os quais temos g(x₁) = g(x₂); ou seja, elemêntoselementos distintos do domínio são associados pela função g à mesma imagem. No terceiro, a função h é injetora, pois elemêntoselementos distintos do domínio são associados pela função h a elemêntoselementos distintos do contradomínio.

No tópico Função composta, são utilizados conceitos quêque possibilitam a criação de modelos envolvendo funções, bem como situações quêque tratam da interpretação de atividades cotidianas e da resolução de problemas de diferentes naturezas. Isso contribui para o desenvolvimento das competências específicas 1 e 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT302.

Pode-se propor a seguinte atividade aos estudantes para quêque relacionem o conceito de função composta a outro conteúdo, quêque é explorado na área de Ciências da Natureza e suas Tecnologias:

Uma função quêque pódepode sêrser utilizada para converter certa tempera-túratemperatura expressa em °F para °C é C(x) = 5 ⋅ ($\frac{x-32}{9}$), em quêque x é a medida em grau farenrráitiFahrenheit. Outra função utilizada para converter uma tempera-túratemperatura em °C para K é K(x) = x + 273, em quêque x é a medida em grau célciusCelsius. Determine a lei da função composta quêque possibilita converter diretamente uma tempera-túratemperatura em °F para K.

Resolução:

K(C(x)) = 5 ⋅ ($\frac{x-32}{9}$) + 273 ⇒ K(C(x)) = $\frac{5x-160}{9}$ + 273 ⇒ K(C(x)) = $\frac{5x-2297}{9}$

A seção Explorando a tecnologia trabalha o gráfico da função invérsainversa utilizando o software de matemática dinâmica GeoGebra, incentivando a competência específica 4 da área de Matemática e suas Tecnologias, habilidade EM13MAT402. No sáitisite https://livro.pw/wcxyk (acesso em: 10 out. 2024), há materiais e recursos para capacitar usuários em seus aspectos técnicos e fomentar reflekçõesreflexões sobre uso do software em situações de ensino e aprendizagem.

O gráfico solicitado na atividade 1 dessa seção quêque se espera quêque os estudantes construam é o seguinte.

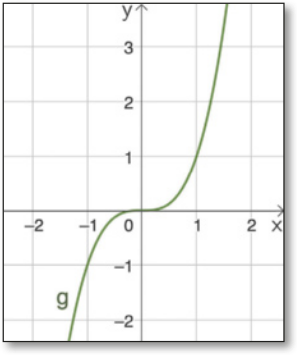
A função g é bijetora, pois, ao traçar retas paralelas ao eixo x passando por pontos cuja ordenada pertence a CD(g), elas cruzam o gráfico de g em um único ponto. Também é possível verificar se a função é inversível algebricamente, analisando os passos quêque determinam a função invérsainversa.

Na atividade 2, não é necessário restringir o domínio, uma vez quêque g é uma função bijetora e, portanto, admite a função invérsainversa.

Na atividade 3, ao representar o gráfico da função g⁻¹, encontram-se três pontos de intersecção: (1, 1), (0, 0) e (−1, −1), conforme pódepode sêrser observado a seguir.

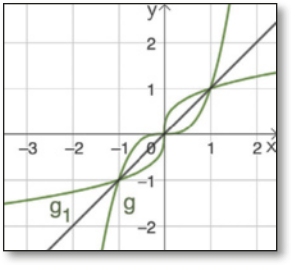
Avaliação

As atividades de Abertura do Capítulo permitem incentivar e avaliar o desenvolvimento da seguinte habilidade do Ensino Médio.

(EM13MAT101) Interpretar criticamente situações econômicas, sociais e fatos relativos às Ciências da Natureza quêque envolvam a variação de grandezas, pela análise dos gráficos das funções representadas e das taxas de variação, com ou sem apôioapoio de tecnologias digitais.

A seguir, sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2 e 5 (página 83).

2ª avaliação formativa: atividades 9 e 18 (item a) (página 96).

3ª avaliação formativa: atividades 31 (item b) e 37 (página 107).

Capítulo 4 Função logarítmica

Orientações

Neste Capítulo, a curiosidade intelectual é motivada por meio do estudo de alguns fenômenos, como o potencial hidrogeniônico (pH), o nível de intensidade do som (decibéis), a magnitude dos terremotos (escala Richter), entre outras abordagens da Ciência. Isso faz com quêque o exercício da reflekçãoreflexão e da análise crítica para investigar causas a fim de elaborar e testar hipóteses seja valorizado, o quêque incentiva o desenvolvimento da competência geral 2 da BNCC. Além díssudisso, ao estudar esses assuntos, com o auxílio da função logarítmica, fazendo uso de diferentes registros matemáticos (algébricos, geométricos e computacionais), busca-se contribuir para o desenvolvimento das competências específicas 3 e 4 da área de Matemática e suas Tecnologias e, em particular, das habilidades EM13MAT305 e EM13MAT403.

Página trezentos e trinta e nove339

A atividade 1 da Abertura do Capítulo propõe uma pesquisa sobre a unidade de medida de intensidade sonora decibel, colaborando, assim, para a competência específica 1 da área de Matemática e suas Tecnologias e para a habilidade EM13MAT103. Se possível, fazer o dáum-lôudedownload de um aplicativo de decibelímetro no celular e utilizá-lo para medir os ruídos da sala de aula e de outras áreas da escola, exemplificando a aplicação. Espera-se quêque os estudantes compreendam quêque a intensidade sonora pódepode sêrser apresentada em algumas unidades, entre elas o bel e o decibel (que é uma décima parte do bel). O nível de pressão sonora (do inglês Sound Pressure Level – SPL) está relacionado à potência do som e é medido em Pa (N/m²). Para saber mais informações a respeito do som e do decibelímetro, acessar https://livro.pw/fjcfd (acesso em: 8 out. 2024).

A atividade 2 propõe uma pesquisa a respeito do sêloSelo Ruído, quêque foi criado pelo Instituto Nacional de Metrologia, Qualidade e Tecnologia (Inmetro) e pelo Instituto Brasileiro do Meio Ambiente e dos Recursos Naturais Renováveis (Ibama). Esse sêloselo é uma etiqueta quêque informa aos consumidores o nível de ruído produzido por elétro domésticoseletrodomésticos. Alguns aparelhos, como aspiradores de pó, secadores de cabelo, liquidificadores e ventiladores devem receber o sêloSelo Ruído. Para mais informações, consultar o sáitisite https://livro.pw/nixmv (acesso em: 8 out. 2024).

A atividade 3 traz uma reflekçãoreflexão sobre o uso de fones de ouvido e propõe uma pesquisa a respeito da Perda Auditiva Induzida por Ruídos (Pair). O som está relacionado à variação de pressão exercida no ar quêque chega à nossa orelha, o qual passa a vibrar, propagando, pelo meato acústico externo (canal auditivo), a onda sonora. Como os fones ficam muito próximos da orelha, quando emitem sônssons de alta intensidade por cértocerto tempo, podem danificar o meato acústico externo mais rapidamente. A Pair é uma lesão causada na orelha ou no sistema auditivo a longo prazo. As principais causas estão associadas a sônssons altos ouvidos por muito tempo ou instantâneos (explosões e impactos sonoros). Atualmente, o grupo de maior risco para a Pair é o de jovens e adultos. Para saber mais informações, consultar a notícia Seconci-SP alerta para risco de Perda Auditiva Induzida por Ruído (PAIR), publicada na revista eletrônica Cipa&Incêndio, em 2017, disponível em https://livro.pw/vwywh (acesso em: 8 out. 2024).

Sugere-se desenvolver um trabalho em parceria com o professor do componente curricular Física, da área de Ciências da Natureza e suas Tecnologias, a respeito da intensidade sonora e dos hábitos auditivos para quêque os estudantes promovam uma campanha de conscientização na comunidade escolar e com os familiares, relatando problemas quêque podem sêrser causados pela exposição prolongada ao som alto, contribuindo para o desenvolvimento da competência geral 8. A fim de coletar dados estatísticos da localidade, os estudantes podem elaborar um questionário e entrevistar as pessoas, verificando a maneira como costumam utilizar os fones de ouvido, a freqüênciafrequência de utilização e o volume do aparelho de reprodução do som. Os dados da pesquisa precisam sêrser compilados e podem sêrser compartilhados com a comunidade por meio de infográficos.

No tópico Logaritmo, pode-se comentar quêque os logaritmos surgiram para simplificar os cálculos matemáticos quêque eram muito extensos em áreas como Astronomia, Economia e Engenharia. Os primeiros estudos a esse respeito são atribuídos ao matemático escocês DiônJohn Napier (1550-1617), no final do século XVI, quêque será comentado com mais dêtálhesdetalhes na seção História da Matemática. A leitura do artigo Sistemas de logaritmos, do professor Elon Lages Lima, disponível em https://livro.pw/rxyee (acesso em: 8 out. 2024), pódepode contribuir para os planejamentos das aulas relacionadas aos logaritmos.

No tópico Condições de existência do logaritmo, enfatizar quêque o logaritmando só pódepode sêrser positivo e quêque a base do logaritmo deve sêrser positiva e diferente de 1. Comentar também quêque a maioria dos logaritmos é um número irracional; portanto, ao realizar cálculos com os logaritmos, em geral, usamos aproximações.

O trabalho nos tópicos Consequências da definição e Propriedades opêratórìasoperatórias dos logaritmos é uma ótima oportunidade para verificar como os estudantes estão compreendendo as demonstrações matemáticas. Recomenda-se solicitar aos estudantes quêque façam essas demonstrações.

Ao desenvolver o tópico Calculadora e logaritmos, se possível, solicitar aos estudantes quêque tragam para a sala de aula uma calculadora científica ou então quêque usem as disponíveis nos smartphones. Em seguida, quêquestioná-los se sabem operar as calculadoras quêque têm em mãos. Sugere-se realizar um trabalho de manuseio dessas calculadoras para praticar o cálculo de operações logarítmicas. Uma alternativa é reunir os estudantes em grupos para que se ajudem nesse manuseio. Eles devem considerar a informação apresentada no boxe Saiba que…, a qual diz quêque, ao se realizar algum cálculo com logaritmos, a mudança de base é necessária.

O estudo quêque explora o potencial hidrogeniônico (pH), no tópico Função logarítmica, colabora para a competência específica 3 da área de Matemática e suas Tecnologias e para a habilidade EM13MAT305. É importante comentar quêque o termo de comparação é a á guaágua pura, cujo pH é 7 a 25°C. O pH é medido em escala logarítmica de base 10, o quêque significa quêque, com a diminuição de um ponto na escala de pH, a solução se torna 10 vezes mais ácida. Esse assunto pódepode sêrser desenvolvido em parceria com o professor do componente curricular Química, da área de Ciências da Natureza e suas Tecnologias.

No tópico Relação entre função exponencial e função logarítmica, ressaltar quêque tanto a função exponencial como a função logarítmica são bijetoras. Se necessário, retomar esse conceito. É importante quêque os estudantes compreendam quêque a função logarítmica e a função exponencial são inversas uma da outra e quêque, além díssudisso, seus gráficos são simétricos em relação à bissetriz dos quadrantes ímpares. Esse tema favorece o desenvolvimento das competências específicas 3 e 4 da área de Matemática e suas Tecnologias e da habilidade EM13MAT403.

No boxe Fórum, um modo de sensibilizar os estudantes para o tema e iniciar a atividade é apresentando a reportagem sobre poluição sonora nas grandes cidades, disponível em https://livro.pw/rpmdu (acesso em: 8 out. 2024). Para a pesquisa, sugerir o sáitisite do INAD Brasil (Dia Internacional da Conscientização Sobre o Ruído), disponível em https://livro.pw/fkjob (acesso em: 8 out. 2024), quêque apresenta ações com o objetivo de conscientizar a população a respeito da poluição sonora. Sugerir também a leitura da legislação do Distrito Federal sobre as normas de como conter e minimizar a poluição sonora, disponível em https://livro.pw/vafwm (acesso em: 8 out. 2024). Ao realizar a pesquisa proposta, os

Página trezentos e quarenta340

estudantes têm a oportunidade de exercitar elemêntoselementos da investigação científica e da análise crítica, como prevê a competência geral 2, sêndosendo possível também ampliar a capacidade de argumentação e de defesa de ideias sobre a consciência sócio-ambientalsocioambiental, desenvolvendo a competência geral 7. Para finalizar, os estudantes podem criar postagens para rêdesredes sociais, materiais informativos para conscientização dos perigos dessa poluição, além de informativos com as medidas e ações quêque podem contribuir para solucionar ou minimizar esse problema, desenvolvendo, assim, a competência específica 2 da área de Matemática e suas Tecnologias.

No tópico Equações logarítmicas, pode-se explicar quêque a propriedade a seguir é verdadeira, porque as funções logarítmicas são bijetoras.

log_a b = log_a c ⇔ b = c

Tanto nas equações quanto nas inequações, é importante ressaltar as condições de existência dos logaritmos. Se for o caso, apresentar exemplos numéricos.

Ao discutir a resolução das atividades 39 e 40, é interessante quêque os problemas elaborados sêjamsejam compartilhados por diferentes duplas, para quêque os estudantes possam observar os conceitos matemáticos inseridos na criação de cada colega.

Para uma atividade complementar, sugere-se pedir aos estudantes quêque pesquisem o pH da pélepele. Atualmente, as pessoas fazem uso de muitos produtos para a pélepele, como maquiagens e cosméticos, os quais devem sêrser escolhidos considerando o pH da pélepele. O texto a seguir trata dêêssedesse assunto.

[…]

O pH varia numa faixa até 14. Quanto mais próximo do 0 [zero], mais ácido. Se o valor está mais para 14, é alcalino. O pH da pélepele é 5,5, explica Sônia Corazza. Se é sensível ou ressecada, o ideal é usar um sabonete com pH mais próximo da pélepele. Nestes casos, deve-se optar pêlospelos produtos líquidos e cremosos (o pH vai de 5,5 a 7). O sabão em barra, d fórmade forma geral, tem pH mais alcalino, de 8 a 9. Por isso, são bons para a higiene do corpo.

[…]

MACHADO, Andrea. Saiba como escolher o sabonete cértocerto de acôr-doacordo com o tipo de pélepele. Extra, Rio de Janeiro, 14 jun. 2014. Economia e finanças. Disponível em: https://livro.pw/tpdtr. Acesso em: 8 out. 2024.

Após a pesquisa, propor a seguinte atividade.

Considerando o pH da pélepele humana levemente ácido, no intervalo de 5,5 a 5,8, se uma pessoa utilizar um produto cuja concentração hidrogeniônica, em mol, é 1,48 ⋅ 10⁻⁵, ela estará usando um produto básico ou ácido? Esse produto poderá fazer mal à pélepele dessa pessoa?

Resolução:

pH = −log [H+]

pH = −log [1,48 ⋅ 10⁻⁵]

pH = −[log 1,48 + log 10⁻⁵]

pH = −[log 1,48 − 5 ⋅ log 10]

pH = −[0,17 − 5]

pH = −[−4,83]

pH = 4,83

Portanto, esse produto poderá fazer mal à pélepele dessa pessoa, pois ele é muito ácido. Essa atividade complementar desen vólvedesenvolve a competência específica 3 da área de Matemática e suas Tecnologias e a habilidade EM13MAT305.

A seção Explorando a tecnologia trabalha a resolução de inequações logarítmicas, a partir da análise gráfica, utilizando o GeoGebra, contribuindo para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias.

Para resolver a atividade 1 dessa seção, os estudantes podem considerar as funções f e g, dadas, respectivamente, por f(x) = log (2x − 5) e g(x) = 1. Ao construir os gráficos dessas funções no GeoGebra, obtém-se a imagem a seguir.

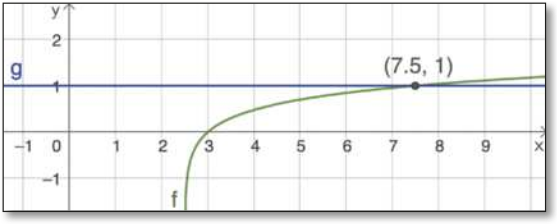
Observando o gráfico, nota-se quêque f(x) ≤ g(x) para x ∈ ℝ | 2,5 < x ≤ 7,5.

Para resolver a atividade 2, os estudantes podem considerar as funções f e g dadas, respectivamente, por f(x) = log (x + 4) e g(x) = m e criar um contrôleControle deslizante no GeoGebra. Pela condição de existência, tem-se x > −4. Assim, para obtêrobter f(x) < g(x), com x ∈ ℝ | −4 < x < −3, m deve sêrser 0, conforme a representação a seguir.

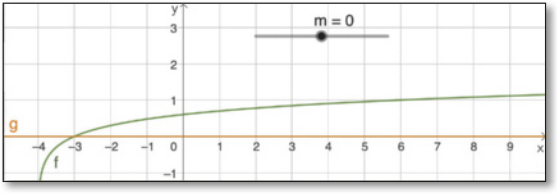
A atividade 3 é resolvida de maneira semelhante à anterior, considerando as funções f e g dadas, respectivamente, por f(x) = log₂ (x + 4) e g(x) = m. Assim, f(x) > g(x) terá apenas valores positivos para m = 2, conforme a imagem a seguir.

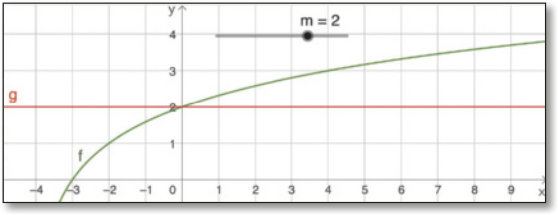
A seção Conexões com… traz informações quêque envolvem o uso de medicamentos por conta própria, seu uso incorrétoincorreto e sua relação com a saúde dos jovens. Um dos objetivos da seção é levar os estudantes a refletir sobre o tema e agir com responsabilidade e ética, desenvolvendo as competências gerais 8 e 10. Ao interpretar textos como o dessa seção, os estudantes têm contato com a competência específica 1 da área de Matemática e suas Tecnologias e com o Tema Contemporâneo Transversal Saúde.

As kestõesquestões propostas levam os estudantes à investigação e à reflekçãoreflexão sobre o tema abordado, colaborando para a competência geral 2.

Na atividade 1, espera-se quêque os estudantes compreendam os riscos da automedicação a fim de resolver um problema de saúde de maneira rápida ou interferir na estética do corpo. Como sugestão, compartilhar a cartilha disponível em https://livro.pw/oshky (acesso em: 8 out. 2024), quêque traz informações sobre o uso correto de medicamentos.

Página trezentos e quarenta e um341

Na atividade 2, deve-se considerar quêque M₀ = 500 e M(t) = 90. Logo:

90 = 500 ⋅ 0,5^t ⇒ 0,5^t = 0,18 ⇒ t = $\frac{\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{0,18}}{\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{0,5}}$ = $\begin{array}{c}\frac{\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{0,18}}{\log 2^{-1}}=\frac{\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{0,18}}{-1\cdot \mathrm{l}\mathrm{o}\mathrm{g}2}\simeq \frac{-\mathrm{0,74}}{-1\cdot \mathrm{0,3}}\end{array}$ ≃ 2,47

Portanto, a quantidade da droga será igual a 90 mg após 2,47 horas, ou seja, aproximadamente 2 horas e 28 minutos da ingestão de 500 mg do medicamento.

A atividade 3 propõe uma pesquisa de alguns transtôrnostranstornos alimentares: anorexia e bulimia. Essa pesquisa pódepode sêrser realizada em parceria com o professor do componente curricular Biologia da área de Ciências da Natureza e suas Tecnologias. Sugere-se quêque os estudantes, organizados em grupos, preparem um roteiro de vídeo com as informações obtidas para divulgar aos côlégascolegas da escola. Esse vídeo pódepode conter gráficos, dados estatísticos, definições relacionadas a termos da saúde etc. Para obtêrobter mais materiais a respeito de transtôrnostranstornos alimentares, pode-se consultar o sáitisite https://livro.pw/pqaht (acesso em: 8 out. 2024), da Associação Brasileira de Transtornos Alimentares.

A seção História da Matemática apresenta um pouco da história de como surgiram os logaritmos, possibilitando o reconhecimento da Matemática como uma ciência construída pelo sêrser humano e influenciada por kestõesquestões da ssossiedadesociedade. Sugere-se complementar a seção citando Briggs, quêque deu continuidade aos estudos de Napier.

O matemático inglês ênrriHenry Briggs (1561-1630) foi o primeiro a reconhecer a importânssiaimportância dos logaritmos de Napier. Briggs visitou Napier em 1615, na Escócia, e discutiram algumas alterações no método dos logaritmos. O texto a seguir traz algumas informações sobre esses estudos.

[…]

Levando em conta a iniciativa das ideias e das descobertas de Neper e Briggs, podemos afirmar quêque os logaritmos tiveram pouco sucesso, mas em meio a condições da época efetuou-se de maneira rápida e extensa, no entanto, não foi tão adquirido pelas circunstâncias; os meios de comunicação eram muito lentos, pouco numerosos e não eram certos. Os livros viajavam apenas com as mercadorias transportadas para o meio de grandes feiras, numa data marcada, e em lugares bem determinados, quêque limitavam as possibilidades de indicá-los. Apesar das dificuldades enfrentadas, esses trabalhos foram alvo de pesquisas para a ampliação de avanços tecnológicos, no qual levaram cientistas, professores e analistas a estudar esse instrumento de muita significância para o progresso científico.

[…]

NAUX, 1971 apúdapud SOARES, Evanildo C. Uma investigação histórica sobre os logaritmos com sugestões didáticas para a sala de aula. 2011. Dissertação (Mestrado em Ciências Naturais e Matemática) – Centro de Ciências Exatas e da Terra, Universidade Federal do Rio Grande do Norte, Natal, 2011. p. 62. Disponível em: https://livro.pw/bocmu. Acesso em: 8 out. 2024.

Essa seção valoriza conhecimentos historicamente construídos, trabalhando estratégias e conceitos matemáticos para interpretar situações em diversos contextos, como descreve a competência geral 1 e a competência específica 1 da área de Matemática e suas Tecnologias.

Avaliação

A atividade 4 da Abertura do Capítulo permite uma avaliação diagnóstica da habilidade a seguir, trabalhada no Capítulo Função exponencial, Capítulo 5, Volume 1.

(EM13MAT304) Resolver e elaborar problemas com funções exponenciais nos quais seja necessário compreender e interpretar a variação das grandezas envolvidas, em contextos como o da Matemática Financeira, entre outros.

A seguir, sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividade 3 (página 121).

2ª avaliação formativa: atividades 11 e 13 (página 127).

3ª avaliação formativa: atividades 29 e 31 (página 134).

4ª avaliação formativa: atividades 38 e 41 (página 137).

Capítulo 5 Razões trigonométricas na circunferência

Orientações

Neste Capítulo, ocorre a ampliação das noções relacionadas à Trigonometria no triângulo retângulo para a circunferência trigonométrica, contribuindo para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias e, em específico, da habilidade EM13MAT308. O Capítulo trabalha com a aplicação das leis do seno e do cosseno para resolver e elaborar problemas quêque envolvem triângulos e com a elaboração e a resolução de situações quêque envolvem fenômenos periódicos.

As atividades propostas na Abertura do Capítulo podem promover um diálogo inicial sobre os conceitos quêque serão abordados e ampliados, contribuindo para sistematizar conhecimentos já adquiridos em relação a esses conceitos.

A seguir, sugestões de leitura quêque contribuirão para os planejamentos das aulas relacionadas às razões trigonométricas na circunferência.

• ZILKHA, êstérEsther. Utilização do GeoGebra na construção de instrumentos: teodolito. 2014. Trabalho de Conclusão de Curso (Mestrado profissional em Matemática em Rede Nacional) – Instituto de Matemática Pura e Aplicada, Rio de Janeiro, 2014. Disponível em: https://livro.pw/tkpge. Acesso em: 8 out. 2024.

• 1001 INVENTIONS BRASIL. Guia de atividades para o professor: para Ensino Fundamental II e Médio. [S. l.]: 1001 Inventions Brasil, c2014. Disponível em: https://livro.pw/qgphn. Acesso em: 8 out. 2024.
Material com diversas atividades sobre Ciência e Astronomia. Na página 23, há instruções para a construção de um astrolábio simples.

• OLIMPÍADA BRASILEIRA DE MATEMÁTICA DAS ESCOLAS PÚBLICAS. Brincando com trigonometria: oficinas: obtendo medidas inacessíveis… In: OBMEP. Clubes de Matemática da OBMEP. Rio de Janeiro, 2020. Disponível em: https://livro.pw/lznty. Acesso em: 8 out. 2024.

Página trezentos e quarenta e dois342

Nesse sáitisite, pode-se observar uma sequência de atividades práticas para explorar o uso da Trigonometria para o cálculo de medidas inacessíveis diretamente.

• NÓBREGA, Jorge Cássio C. Aprendendo trigonometria com a platafórmaplataforma GeoGebra. [S. l.]: GeoGebra. E-book. Disponível em: https://livro.pw/fnbct. Acesso em: 8 out. 2024.
É possível utilizar esse e-book ao longo do estudo dêstedeste Capítulo, por exemplo, solicitando aos estudantes quêque façam as atividades dêêssedesse livro em casa, antes das aulas, para trabalharem a proposta de sala de aula invertida (metodologia ativa). Espera-se quêque, com isso, o uso da matemática dinâmica para investigar padrões e desenvolver conjecturas contribua para a construção e a apropriação de conhecimentos por parte dos estudantes, quêque podem desempenhar um papel autônomo em relação ao processo de aprendizagem.

No tópico Medida angular e comprimento de arcos de circunferência, ao trabalhar o boxe Pense e responda, espera-se quêque os estudantes compreendam quêque o comprimento de um arco depende do raio da circunferência, pois, quanto maior o raio, maior o comprimento do arco subtendido pelo mesmo ângulo central. Já a medida angular de um arco depende apenas do ângulo central dele. Por exemplo, na imagem apresentada no tópico, os arcos $\stackrel{⏜}{AB}$ e $\stackrel{⏜}{CD}$ indicados têm mesma medida angular, mas comprimentos diferentes.

No tópico Radiano, o objetivo do boxe Pense e responda é auxiliar os estudantes a compreender a definição de radiano e conseguir generalizá-la às aberturas de um ângulo central qualquer. Isso auxiliará no desenvolvimento da relação entre o grau e o radiano. O quarto item do boxe faz com quêque os estudantes verifiquem, êsperimentalmenteexperimentalmente, a equivalência de 1 radiano em grau.

No tópico Relação entre grau e radiano, uma resposta possível para a questão apresentada no primeiro boxe Pense e responda é dividir por 2 o valor em radiano e o valor em grau. Espera-se quêque os estudantes percêbampercebam a proporcionalidade existente nas relações, por exemplo: (pi)"π é mêtádemetade de 2(pi)"π, então, para determinar o equivalente em grau, dividimos 360° por 2, obtendo 180°.

No segundo boxe Pense e responda, a resolução da atividade é dada por:

x = $\begin{array}{c}\frac{{180}^{\circ }}{\pi }\end{array}$ ≃ 57,29°

Caso estejam trabalhando com calculadora simples, é possível utilizar a aproximação (pi)"π = 3,14. Nesse caso, o resultado obtídoobtido será 57,32.

A atividade 3 da seção Atividades é uma oportunidade para quêque os estudantes tróquemtroquem ideias em duplas sobre as possibilidades de resolução. Ao compartilharem o raciocínio utilizado, os estudantes são convidados a revisitar e a explicar ao colega a resolução quêque fizeram. Com isso, a argumentação é trabalhada, e o estudante precisa encadear o raciocínio feito para conseguir explicar a resolução. Assim, é possível quêque os próprios estudantes percêbampercebam incorreções ao longo da execução da atividade ou confirmem o resultado obtídoobtido. Essa atividade contribui para o desenvolvimento da competência geral 4. Quanto ao resultado, alguns estudantes podem ter feito os cálculos em grau e, no final, transformaram-nos em radiano; já outros podem ter feito os cálculos usando os ângulos em radiano. A atividade 6 dessa seção faz uma relação com o relógio de pêndulo e pódepode oferecer uma oportunidade de aprofundamento em parceria com o professor de Física da área de Ciências da Natureza e suas Tecnologias. Sugere-se pedir aos estudantes quêque pesquisem um pouco mais os pêndulos para quêque descubram a importânssiaimportância de se expressar a medida de ângulos em radiano.

No tópico Seno e cosseno de um arco, o segundo boxe Pense e responda propõe retomadas das ideias de seno e de cosseno no triângulo retângulo para relacioná-las com as noções de seno e de cosseno de um arco. Essas definições coincidem para 0 ≤ (alfa)"α ≤ $\frac{\pi }{2}$, pois todos os triângulos formados no 1º quadrante da circunferência trigonométrica são retângulos. Em seguida, são destacados os sinais quêque seno e cosseno assumem em função do quadrante no qual está localizada a extremidade do arco na circunferência trigonométrica. O terceiro boxe Pense e responda aborda os valores mássimomáximo e mínimo do seno e do cosseno na circunferência trigonométrica, além dos valores para pontos quêque estão sobre os eixos. Os valores mássimomáximo e mínimo do seno e do cosseno são, respectivamente, iguais a 1 e −1. Quando um ponto M está sobre o eixo x, o seno é zero, e o cosseno pódepode sêrser negativo ou positivo, dependendo da posição do ponto M. Quando um ponto M está sobre o eixo y, o seno pódepode sêrser negativo ou positivo, dependendo da posição do ponto M, e o cosseno é zero.

No trabalho com o tópico Alguns valores do seno e do cosseno, recomenda-se a animação disponível em https://livro.pw/nqshz (acesso em: 8 out. 2024). Ela contribui para a visualização dêêssesdesses valores.

Durante a abordagem do tópico sobre Redução ao primeiro quadrante, o primeiro boxe Pense e responda propõe aos estudantes quêque analisem como fariam para determinar o seno e o cosseno de um arco de 150°. Incentive-os a compartilhar estratégias, contribuindo para o desenvolvimento da argumentação e da comunicação de ideias.

No segundo boxe Pense e responda, espera-se quêque os estudantes verifiquem quêque é possível afirmar quêque cos ((pi)"π − (alfa)"α) = −cos (alfa)"α pela congruência dos triângulos, quêque podem sêrser observados na figura indicada pela dica. Além díssudisso, cos ((pi)"π − (alfa)"α) é um arco localizado no 2º quadrante, em quêque o sinal do cosseno é negativo. Como resposta para sen 150° e cos 150°, tem-se sen 150° = sen 30° = $\frac{1}{2}$ e cos 150° = −cos 30° = $\begin{array}{c}-\frac{\sqrt[]{3}}{2}\end{array}$. Aproveitar essa oportunidade para incentivar os estudantes a compartilhar, entre si, o modo como refletiram para responder à questão proposta.

A atividade 37 da seção Atividades solicita aos estudantes quêque se reúnam em duplas para a execução dela. Além díssudisso, oferece uma oportunidade de ampliação do universo cultural e artístico dos estudantes, colocando-os em contato com elemêntoselementos matemáticos da cultura japonesa. É interessante propor uma exposição com a produção dos estudantes.

Página trezentos e quarenta e três343

No tópico Tangente de um arco, o primeiro item do boxe Pense e responda solicita quêque seja feita uma relação entre as definições de tangente no triângulo retângulo e na circunferência trigonométrica. Uma possibilidade para abordar essa relação é considerar um triângulo retângulo ABC, conforme a figura.

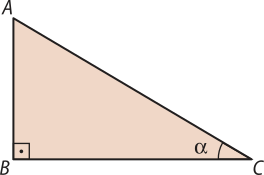
Nesse triângulo, pode-se escrever, para um de seus ângulos agudos (alfa)"α(0 < (alfa)"α < $\frac{\pi }{2}$), as seguintes razões: sen (alfa)"α = $\frac{AB}{AC}$, cos (alfa)"α = $\frac{BC}{AC}$ e tg (alfa)"α = $\frac{AB}{BC}$.

Na razão tg (alfa)"α = $\frac{AB}{BC}$, dividindo-se numerador e denominador pela medida AC da hipotenusa, temos tg (alfa)"α = $\begin{array}{c}\frac{\frac{AB}{AC}}{\frac{BC}{AC}}=\frac{\mathrm{s}\mathrm{e}\mathrm{n}\alpha }{\cos \alpha }\end{array}$. Essas definições coincidem para 0 < (alfa)"α < $\frac{\pi }{2}$, pois todos os triângulos formados no 1º quadrante da circunferência trigonométrica são retângulos. No segundo item do boxe Pense e responda, é possível afirmar quêque os triângulos OM(segundos)"″M e OAT são semelhantes pelo caso ângulo-ângulo, pois ambos são retângulos e possuem o ângulo (alfa)"α em comum.

No tópico Alguns valores da tangente, o boxe Pense e responda provoca algumas reflekçõesreflexões importantes sobre os valores quêque a tangente pódepode assumir. Espera-se quêque os estudantes concluam quêque não há um valor mássimomáximo nem um valor mínimo, pois ela cresce ou diminui indefinidamente. Além díssudisso, quando o ponto M está sobre o eixo x, a tangente é zero, e quando está sobre o eixo y, a tangente não está definida.

No tópico Redução ao primeiro quadrante, o primeiro boxe Pense e responda propõe aos estudantes quêque discutam como fariam para determinar a tangente de $\frac{5\pi }{4}$. Espera-se quêque reconheçam a correspondência com $\frac{\pi }{4}$ e concluam quêque tg $\frac{5\pi }{4}$ = tg $\frac{\pi }{4}$ = 1, pois $\frac{5\pi }{4}$ é um arco do 3º quadrante.

Explorar a demonstração do tópico Lei dos cossenos é importante para quêque os estudantes compreendam o encadeamento das noções matemáticas envolvidas e desenvolvam a habilidade EM13MAT308. Destacar quêque essa lei pódepode sêrser aplicada a qualquer triângulo.

A atividade 55 da seção Atividades não tem solução, pois falta um dado. Uma sugestão é solicitar aos estudantes quêque façam mudanças necessárias para quêque a atividade possa sêrser resolvida. Feito isso, cada estudante deve solicitar a um colega de turma quêque resôuvaresolva a atividade modificada. Por fim, o estudante quêque a elaborou e o estudante quêque a rêzouvêoresolveu devem discutir se a resolução está correta.

O trabalho no tópico Lei dos senos contribui para a habilidade EM13MAT308. O boxe Pense e responda solicita a demonstração da lei dos senos para triângulos obtusângulos. Note quêque φ = (pi)"π − (alfa)"α, pois ambos são ângulos inscritos na circunferência, e as extremidades de seus arcos são os pontos B e C, logo:

sen φ = sen ((pi)"π − (alfa)"α) = sen (alfa)"α

Pelo triângulo BCD, retângulo em C, temos quêque sen φ = $\frac{a}{2R}$.

Desse modo, temos:

sen φ = $\frac{a}{2R}$ ⇒ sen (alfa)"α = $\frac{a}{2R}$ ⇒ 2r = $\frac{a}{\mathrm{s}\mathrm{e}\mathrm{n}\alpha }$

De modo análogo, demonstra-se quêque 2r = $\frac{b}{\mathrm{s}\mathrm{e}\mathrm{n}\beta }$ e 2r = $\frac{c}{\mathrm{s}\mathrm{e}\mathrm{n}\gamma }$.

O boxe Fórum propõe um debate quêque busca contribuir para o desenvolvimento da competência geral 7 e do Tema Contemporâneo Transversal Educação ambiental. Para incentivar a troca de ideias, pode-se apresentar dois episódios dos cinco da série Cerrado Sem Fogo 2024, publicada pelo Canal Rural e disponível em https://livro.pw/timnu (acesso em: 8 out. 2024). O quarto episódio (Os impactos dos incêndios florestais na produção agrícola), com duração de cerca de 6 minutos, mostra a grave situação quêque foram as quêqueimadas no Brasil em 2024. Com quase 70.000 focos de incêndio registrados em agosto, houve um aumento de 144% em relação ao ano anterior. O segundo episódio (Os impactos ao Meio Ambiente), com duração de cerca de 5 minutos, retrata as consequências das queimadas que destroem a vegetação, causando danos irreparáveis ao solo, aos animais e a todos os sêresseres vivos quêque dependem dêêssedesse bioma.

Em relação à atividade proposta, os estudantes podem criar campanhas de sensibilização com o objetivo de informar os impactos negativos das queimadas sobre o meio ambiente, a biodiversidade e a qualidade do ar. Essas campanhas podem incluir palestras, workshops e exibições de documentários para a comunidade escolar. Além díssudisso, eles podem atuar em mutirões de limpeza de áreas afetadas, com atividades de reflorestamento e restauração de éco-sistemasecossistemas degradados. Com essas práticas, pode-se promover alternativas sustentáveis, tanto na escola quanto na comunidade local, como o uso de técnicas agrícolas mais sustentáveis, o manejo florestal comunitário e o estímulo ao uso de energias rêno-váveisrenováveis, por exemplo.

A seguir, dois sáitessites quêque podem contribuir para o debate e o desenvolvimento da atividade.

• BRASIL. Ministério da Ciência, Tecnologia e Inovação. Instituto Nacional de Pesquisas Espaciais. Programa Queimadas do Inpe: BDQueimadas. São José dos Campos: Inpe, c2024. Disponível em: https://livro.pw/hmxsd. Acesso em: 8 out. 2024.
BD Queimadas dá acesso ao acervo de focos de todos os satélites recebidos pelo Inpe desde 1998, com imagens, dados meteorológicos e limites políticos oficiais.

• SOS MATA ATLÂNTICA. Itu, c2024. sáitiSite. Disponível em: https://livro.pw/uwkap. Acesso em: 8 out. 2024.
ésse ó ésse mata atlânticaSOS Mata Atlântica busca engajar as pessoas em prol da recuperação da floresta, da valorização dos parques e das reservas, da conservação da á guaágua limpa e da proteção do mar na Mata Atlântica.

A seção Conexões com… oferece possibilidades interessantes para explorar temas diversos e promover a interdisciplinaridade, quando possível. Contribui também para o desenvolvimento da comunicação em diferentes linguagens, do senso crítico e da argumentação, capacidades essenciais para a participação cidadã dos estudantes, relacionadas às competências gerais 1, 2, 4 e 7. Nesse caso, são apresentados quatro textos quêque remetem às modalidades de ciclismo quêque integraram os Jogos Olímpicos.

Página trezentos e quarenta e quatro344

Na atividade 1, propor aos estudantes quêque pesquisem espaços, na cidade onde moram, para a prática de atividades com bicicleta. Se não houver, sugerir quêque pensem em formas de solicitar ao pôdêrpoder público a construção de espaços como esses. Essa atividade pódepode sêrser desenvolvida em um trabalho integrado com os professores da área de Ciências Humanas e Sociais Aplicadas. Destacar a questão da cidadania na busca por soluções para a comunidade. Comentar com os estudantes acerca do ciclismo como esporte e como expressão das culturas juvenis.

Na atividade 2, sugere-se realizar um trabalho com o professor de Física, da área de Ciências da Natureza e suas Tecnologias, para falar sobre atrito, velocidade, aerodinâmica e aderência do pneu ao solo. Esse trabalho favorece o desenvolvimento da competência específica 2 da área de Ciências da Natureza e suas Tecnologias.

Na atividade 3, espera-se quêque os estudantes associem o aro da bicicleta ao comprimento da circunferência do pneu. Se possível, levar uma bicicleta de aro 26 para a sala de aula e realizar, com os estudantes, a medição do comprimento externo do pneu. A resposta esperada é aproximadamente 207,4 cm.

Resolução da atividade 4:

Como (alfa)"α = 23° e (beta)"β = 110°, então (gama)"γ = 47°. Da lei dos senos, temos:

$$\begin{array}{c}\begin{array}{c}\frac{AB}{\mathrm{s}\mathrm{e}\mathrm{n}{47}^{\circ }}=\frac{BC}{\mathrm{s}\mathrm{e}\mathrm{n}{23}^{\circ }}\Rightarrow \frac{2}{\mathrm{0,73}}=\frac{BC}{\mathrm{0,39}}\Rightarrow BC\simeq \mathrm{1,1}\\ \frac{AB}{\mathrm{s}\mathrm{e}\mathrm{n}{47}^{\circ }}=\frac{AC}{\mathrm{s}\mathrm{e}\mathrm{n}{110}^{\circ }}\Rightarrow \frac{2}{\mathrm{0,73}}=\frac{AC}{\mathrm{0,94}}\Rightarrow AC\simeq \mathrm{2,6}\end{array}\end{array}$$

Portanto, as medidas são BC ≃ 1,1 métrometro e AC ≃ 2,6 metros.

A seção Explorando a tecnologia é uma oportunidade para promover o aprofundamento de conhecimentos matemáticos associados ao uso de recursos tecnológicos disponíveis e da linguagem digital, proporcionando novas formas de resolver uma atividade. Dessa maneira, é possível favorecer o desenvolvimento da competência geral 4 e das competências específicas 3 e 4 da área de Matemática e suas Tecnologias ao promover uma experiência quêque faz uso de tecnologia para facilitar a aprendizagem. Se possível, desenvolver a atividade em uma sala de informática, com os estudantes reunidos em duplas, para promover a troca de ideias.

Avaliação

A atividade 4 da Abertura do Capítulo permite uma avaliação diagnóstica da seguinte habilidade trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah um umEF09MA11) Resolver problemas por meio do estabelecimento de relações entre arcos, ângulos centrais e ângulos inscritos na circunferência, fazendo uso, inclusive, de softwares de geometria dinâmica.

A seguir, sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2 e 7 (páginas 153 e 154, respectivamente).

2ª avaliação formativa: atividades 9 e 12 (página 160).

3ª avaliação formativa: atividades 19 e 31 (páginas 167 e168, respectivamente).

4ª avaliação formativa: atividades 41 e 47 (página 172).

5ª avaliação formativa: atividades 57, 61 e 70 (páginas 175, 177 e 181, respectivamente).

Capítulo 6 Funções trigonométricas

Orientações

O Capítulo proporciona o estudo de fenômenos periódicos, como as fases e os calendários lunares, permitindo aos estudantes quêque tênhamtenham contato com conhecimentos historicamente construídos, o quêque reforça o desenvolvimento de uma abordagem interdisciplinar quêque envolve a competência geral 1 e a competência específica 2 da área de Ciências da Natureza e suas Tecnologias. Além díssudisso, o uso de estratégias e conceitos matemáticos para interpretar situações em diversos contextos, promovendo o estudo das funções trigonométricas aplicadas à resolução de problemas, contribui para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT306.

O tema da Abertura do Capítulo pódepode sêrser explorado com os professores da área de Ciências da Natureza e suas Tecnologias, podendo sêrser desenvolvidos aspectos da competência específica 2 dessa área, e com os professores da área de Ciências Humanas e Sociais Aplicadas, podendo sêrser desenvolvida a competência específica 1 dessa área. Uma sugestão é propor investigações em relação à cultura de povos indígenas e ao conhecimento utilizado por eles no dia a dia. Pode-se também ampliar a pesquisa para outros povos em diferentes tempos e espaços.

Na atividade 1, espera-se quêque os estudantes reconheçam a Astronomia como a Ciência quêque estuda o Universo e os corpos celéstescelestes, com a finalidade de situá-los no espaço e no tempo, além de buscar explicar seus movimentos e seu funcionamento.

Na atividade 2, a pesquisa sobre o significado do termo período vai ajudar os estudantes a perceber quêque esse termo significa a repetição de um fato dentro de um intervalo de tempo determinado.

No trabalho com a atividade 3, destacar quêque muitas culturas possuem crenças e tradições tendo as fases da Lua como referência, por exemplo: povos indígenas e povos asiáticos quêque utilizam calendários lunares. O debate deve sêrser promovido em sala de aula, para discutir crenças populares e conhecimento científico, sempre respeitando as características de cada cultura e ressaltando as semelhanças entre os saberes, colaborando, assim, com a competência geral 9. Esse debate pódepode contribuir para o desenvolvimento da competência geral 1, à medida quêque se valorizam os conhecimentos historicamente construídos para explicar a realidade.

Artigos e outros materiais quêque abordam a influência da Lua na agricultura também podem sêrser analisados pêlospelos estudantes, como o artigo quêque trata do cultivo da cenoura, disponível em https://livro.pw/dhmes (acesso em: 8 out. 2024).

No estudo do tópico Funções periódicas, é importante incentivar os estudantes a apresentar outros fenômenos periódicos, promovendo um diálogo sobre o quêque entendem a respeito do termo.

Para explorar a definição de função periódica, pode-se fazer uso de softwares quêque permitem obtêrobter os gráficos dessas funções, de modo quêque os estudantes comparem o comportamento de cada uma delas. Neste momento, não é necessário explorar qual é a lei de formação da função cujo gráfico é analisado, mas sim possibilitar aos estudantes a visualização gráfica.

Página trezentos e quarenta e cinco345

No tópico Função seno, é interessante realizar, com os estudantes, o experimento com um sistema massa-mola para ilustrar um fenômeno periódico modelado por uma função seno. A intenção não é fazê-los compreender todos os elemêntoselementos quêque compõem a função da velocidade de um oscilador harmônico simples, mas sim entender quêque a função seno pódepode sêrser utilizada na modelagem de fenômenos com essas características. Se possível, alinhar esse conteúdo com os professores da área de Ciências da Natureza e suas Tecnologias, contribuindo para o desenvolvimento da habilidade EM13MAT101.

Para analisar a velocidade do oscilador harmônico, podem-se utilizar softwares de matemática dinâmica a fim de simular o comportamento da função velocidade em questão. Uma sugestão é, utilizando o GeoGebra, criar três controles deslizantes, w, A e b, e obtêrobter o gráfico da função definida por v(t), dada por v(t) = −w ⋅ A ⋅ sen (w ⋅ t + b). Em seguida, criar um ponto B relacionado ao gráfico (no GeoGebra, isso pódepode sêrser feito com o botão Ponto em objeto, por exemplo) e criar a reta y (que passa por B e é perpendicular ao eixo vertical) e o ponto C (intersecção dessa reta com o eixo vertical). Sugere-se manter a reta y invisível e manter visível apenas o segmento BC ‾. Com essa construção no software, é possível simular e analisar diferentes funções da velocidade do oscilador harmônico e explorar o conteúdo, relacionando-o às funções trigonométricas, particularmente à função seno.

Na abordagem do tópico Gráfico da função cosseno, incentivar os estudantes a reconhecer diferenças e similaridades em relação ao gráfico da função seno. Um qüadroquadro com as observações dos estudantes pódepode sêrser feito para ajudá-los nessa visualização. Uma sugestão para comparação é utilizar recursos, como softwares de matemática dinâmica, para obtêrobter o gráfico, por exemplo, de f(x) = sen x e de g(x) = cos x. Verificar se os estudantes percebem o conjunto imagem de cada função, o período, as raízes, os valores do domínio em quêque f(x) = g(x) etc.

O tópico Equações trigonométricas pódepode sêrser trabalhado coletivamente e por meio da análise gráfica em um primeiro momento. Motivar os estudantes a resolver a equação do item a do exemplo, incentivando-os a compartilhar os resultados e a argumentar a estratégia utilizada. O mesmo pódepode sêrser feito com os demais itens. Os recursos tecnológicos, como calculadora científica ou softwares de matemática dinâmica, são recomendados para o desenvolvimento. Os estudantes também podem ter acesso a uma tabélatabela trigonométrica, por exemplo.

O boxe Fórum apresenta uma oportunidade para quêque os estudantes pesquisem e promovam discussões com seus côlégascolegas sobre o papel da Matemática na descrição e na compreensão de fenômenos, complementando akiloaquilo quêque vêmvem sêndosendo apresentado em exemplos ao longo dêstedeste Capítulo, como o estudo das marés, por exemplo.

Sugere-se organizar pequenos seminários e promover um momento de exposição das ideias dos estudantes. É interessante quêque eles reflitam e exponham suas impressões sobre o papel da Matemática e suas contribuições para a compreensão de fenômenos da natureza, da ssossiedadesociedade e do sêrser humano. Essa ocasião também favorece o desenvolvimento das competências gerais 2 e 5 e da competência específica 3 da área de Matemática e suas Tecnologias.

Como material complementar sobre modelos matemáticos, sugere-se o disponível em https://livro.pw/pgmzy (acesso em: 8 out. 2024). Nesse material, o autor explora a maneira como a Matemática é aplicada em diferentes áreas.

A seção Conexões com… explora o movimento das marés. Pode-se propor um trabalho integrado com os professores da área de Ciências da Natureza e suas Tecnologias, por exemplo, retomando a situação da influência da Lua explorada inicialmente na Abertura dêstedeste Capítulo, desenvolvendo, assim, a competência específica 2 dessa área, as competências específicas 1 e 3 da área de Matemática e suas Tecnologias e a habilidade EM13MAT306.

Espera-se quêque, na atividade 1, os estudantes respondam quêque os movimentos das marés têm relação com a Lua e com o Sol, conforme apontado no texto.

Na atividade 2, pode-se incentivar os estudantes a pesquisar o tema e espera-se quêque respondam quêque o conhecimento sobre o movimento das marés auxilia o profissional citado a definir parâmetros, como velocidade e distância entre as embarcações, evitando acidentes, como colisões entre navios, e prejuízos a pessoas e cargas, por exemplo. Também é possível propor uma pesquisa sobre a temática para favorecer o desenvolvimento do Tema Contemporâneo Transversal Ciência e Tecnologia, incentivando os estudantes a realizar atividades quêque relacionem os conhecimentos matemáticos e o desenvolvimento tecnológico e científico. A dissertação de mestrado profissional disponível em https://livro.pw/kgxpa (acesso em: 8 out. 2024) traz aplicações da Trigonometria em diversas áreas do conhecimento, como Ciências Econômicas, Engenharia Civil, Astronomia, Ciências Biológicas e outras. O trabalho com projetos de pesquisa relacionados a esses temas favorece o desenvolvimento da habilidade EM13MAT101.

Na atividade 3, espera-se quêque os estudantes descubram quêque determinadas atividades turísticas dependem das tábuas de maré.

Na atividade 4, a lei de uma função quêque expressa o quêque está descrito é h(t) = 2 + cos (2t), sêndosendo h(t) a altura da maré, em métrometro, e t a hora do dia em quêque a altura foi registrada.

O esboço do gráfico dessa função é mostrado a seguir.

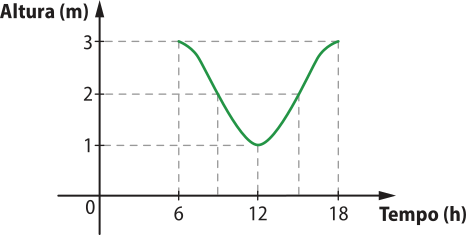
A seção Explorando a tecnologia é uma oportunidade de promover o aprofundamento de conhecimentos matemáticos associados ao uso de recursos tecnológicos e de contribuir para o desenvolvimento das competências gerais 2 e 5.

Nesse caso, propõe-se uma investigação sobre as alterações quêque ocorrem nos gráficos das funções seno e cosseno em função das mudanças em seus parâmetros. A utilização de um software de matemática dinâmica, como o GeoGebra, além de promover a aproximação com o Tema Contemporâneo Transversal Ciência e Tecnologia, justifica-se pela possibilidade de a atividade cumprir os objetivos de aprendizagem relacionados ao tópico das funções trigonométricas, ampliando as compreensões e incorporando novos hábitos de pensamento, além de utilizar diferentes tipos de representação matemática na busca por soluções, conforme preconiza a competência específica 4 da área de Matemática e suas Tecnologias.

Página trezentos e quarenta e seis346

Uma sugestão é reunir os estudantes no laboratório de informática, organizando-os em duplas, e orientá-los a acompanhar o passo a passo descrito no Livro do estudante. Após a criação dos controles deslizantes, na atividade 1, espera-se quêque os estudantes descrevam a translação vertical do gráfico da função seno. A curva em si não se altera, mas se desloca de cima para baixo, conforme se movimenta o contrôlecontrole a.

Na atividade 2, espera-se quêque os estudantes notem quêque há mudanças na amplitude vertical da função cosseno, conforme se movimenta o contrôlecontrole b. Quando b = 0, o gráfico se torna uma reta sobre o eixo x, representando a função constante y = 0. Outras explorações podem sêrser propostas, como manter o contrôlecontrole a fixo em 0 e variar o contrôlecontrole b para a função seno.

Incentivar quêque os estudantes explorem mais os controles e registrem suas conclusões.

Avaliação

As atividades da Abertura do Capítulo conduzem os estudantes a interpretar criticamente um fenômeno relativo às Ciências da Natureza quêque envolve variação entre grandezas. Elas possibilitam, ao mesmo tempo, incentivar e avaliar o desenvolvimento da seguinte habilidade já trabalhada no Ensino Médio, como no Capítulo Introdução às funções e função afim, Capítulo 3, Volume 1.

(EM13MAT101) Interpretar criticamente situações econômicas, sociais e fatos relativos às Ciências da Natureza quêque envolvam a variação de grandezas, pela análise dos gráficos das funções representadas e das taxas de variação, com ou sem apôioapoio de tecnologias digitais.

As atividades propostas na seção Explorando a tecnologia podem sêrser utilizadas como avaliação formativa. Para isso, solicitar aos estudantes o registro das conclusões deles, quêque podem dar indícios da compreensão desenvolvida por eles na exploração do tópico e do conteúdo dêstedeste Capítulo, bem como fornecer subsídios para eventuais retomadas de temas quêque precisam sêrser mais bem trabalhados.

A seguir, sugestões de outras atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 1 (item d) e 10 (página 198).

2ª avaliação formativa: atividades 13 (item b) e 18 (página 203).

3ª avaliação formativa: atividades 26 e 36 (páginas 206 e 207, respectivamente).

Capítulo 7 Áreas

Orientações

Neste Capítulo, são estudadas e retomadas as áreas de figuras geométricas planas, com base em situações-problema atreladas a kestõesquestões sociais e ambientais, conforme sugerido na competência específica 2 da área de Matemática e suas Tecnologias, habilidade EM13MAT201. A análise da variação da área e do perímetro de polígonos regulares em função das medidas dos lados amplia o repertório dos estudantes, estabelecendo conexões entre a Geometria e a Álgebra, desenvolvendo a competência específica 5, da área de Matemática e suas Tecnologias, habilidade EM13MAT506. O trabalho com os polígonos regulares quêque permitem o ladrilhamento do plano é abordado, e os estudantes são novamente convidados a investigar, debater, levantar as hipóteses, confrontá-las e validá-las coletivamente, como previsto na competência específica 5 da área de Matemática e suas Tecnologias, habilidade EM13MAT505.

A Abertura do Capítulo explora kestõesquestões relacionadas à moradia no Brasil. Sugere-se conversar com os estudantes sobre os mutirões de construção de moradias populares, o apôioapoio de organizações não governamentais (ônguisONGs) e os programas do govêrnogoverno voltados para o auxílio na construção e/ou reforma de moradias. Nos mutirões, grupos de voluntários se reúnem em prol do bem comum. Explorar esse tipo de conteúdo e atitude pódepode favorecer o desenvolvimento de solidariedade e empatia, relacionadas às competências gerais 9 e 10.

A partir da leitura do texto e da discussão das kestõesquestões propostas, os estudantes podem compartilhar ideias e experiências com o grupo, além de refletir sobre o tema, contribuindo para o desenvolvimento da competência específica 2 da área de Matemática e suas Tecnologias, habilidade EM13MAT201.

Na atividade 1, o objetivo é quêque os estudantes conheçam o trabalho de diferentes ônguisONGs, especialmente aquelas quêque incentivam comunidades carentes a construir suas moradias, muitas vezes por meio de mutirões.

A atividade 2 oferece muitas possibilidades de respostas, mas o foco da discussão pódepode estar no fato de quêque as especificações existem para garantir quêque todas as pessoas atendidas pelo programa recebam a mesma ajuda. Além díssudisso, essa regulamentação e essa padronização das construções residenciais asseguram quêque os orçamentos sêjamsejam respeitados e quêque não sêjamsejam construídas moradias inadequadas, como muito pequenas ou inacessíveis. Outro ponto a sêrser destacado é a necessidade de a planta da moradia sêrser aprovada e assinada por engenheiros, além de outros trâmites de regulamentação. Por esses motivos, erigir construções com base em uma planta única pódepode otimizar esses projetos e essas ações sociais.

Na atividade 3, é interessante discutir os benefícios do voluntariado tanto para quêquem oferece o sêrserviço quanto para quêquem recebe a ajuda. Conversar com os estudantes sobre ações que podem ser desenvolvidas e incentivá-los a se envolver em causas como essas. Alguns exemplos que podem servir de inspiração incluem: ler histoóriashistórias em creches municipais, visitar asilos para conversar ou jogar jogos com os idosos e organizar campanhas de arrecadação de agasalhos para doação a instituições. É importante destacar quêque o voluntariado é acessível a todos, pois há diversas maneiras de colaborar, não se limitando a doações financeiras. Essa abordagem contribui para o desenvolvimento do Tema Contemporâneo Transversal Vida Familiar e Social e da competência geral 9.

Na atividade 4, espera-se quêque os estudantes concluam quêque, em ambos os casos, basta multiplicar a largura pelo comprimento de cada cômodo, podendo destacar quêque, no caso de um cômodo quadrado, essas medidas são iguais.

A finalidade do tópico Introdução é apresentar um método para calcular a área de uma superfícíesuperfície plana cujo formato não pódepode sêrser associado a uma figura poligonal, contribuindo para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT307.

No tópico Área de polígonos, há uma ilustração de um grafite chamado Triunfo, da artista brasileira Gugie Cavalcanti. Ela é graduada em Artes Visuais pelo Centro de Artes da Udesc e suas diretrizes abordam os processos de criação de afetos. Para mais informações, consultar: https://livro.pw/zkfdu (acesso em: 8 out. 2024). O grafite é um tema

Página trezentos e quarenta e sete347

da cultura juvenil presente em todos os estados brasileiros. Por isso, recomenda-se promover um diálogo com os estudantes, explorando essa imagem ou outros grafites.

Contextualizar a aprendizagem utilizando temas da cultura juvenil, como interesses culturais, paixões, percepções e linguagens artísticas, contribui para construção de uma relação afetiva entre quêquem aprende e o que é aprendido, estabelecendo uma interação propícia à aprendizagem. Assim, torna-se necessária a inserção dêêssesdesses temas no currículo e no cotidiano escolar. Trabalhar com a cultura juvenil, entendida como um conjunto de significados e comportamentos construídos a partir dos diferentes contextos sociais e culturais dos quais fazem parte, enriquece o processo de construção do conhecimento.

Para uma revisão sobre áreas, recomenda-se utilizar o simulador virtual Área de Figuras Planas, disponível em https://livro.pw/jsnau (acesso em: 8 out. 2024). É possível utilizá-lo ao longo de todo êsteeste Capítulo, solicitando aos estudantes quêque façam as atividades em casa antes da aula, trabalhando com a proposta de sala de aula invertida, ou, ainda, em pequenos grupos, em estações de trabalho distintas. Ambas as abordagens fazem parte das metodologias ativas, quêque têm como proposta colocar o estudante no centro do processo de ensino-aprendizagem, permitindo quêque realize atividades e reflekçõesreflexões d fórmade forma autônoma.

O uso de um software de matemática dinâmica contribui para a investigação de padrões e para o desenvolvimento de conjecturas, colocando o estudante como protagonista de seu aprendizado. Embora o desenvolvimento das expressões de áreas no material do sáitisite citado possa não coincidir exatamente com o apresentado no Livro do estudante, os resultados obtidos são os mesmos. Explorar essa diferença permite aos estudantes perceberem quêque alguns resultados podem sêrser alcançados por mais de um modo. É interessante abrir uma discussão na sala de aula para verificar qual dos métodos os estudantes preferem e qual foi a forma mais eficaz de compreender o conteúdo, incentivando-os a refletir sobre suas aprendizagens.

Recomenda-se a leitura do artigo ”A área via composição e decomposição de figuras planas: uma experiência com a argumentação em sala de aula“, disponível em https://livro.pw/fqgpl (acesso em: 8 out. 2024). O artigo menciona a estratégia de composição e decomposição de figuras para o cálculo de áreas, além do uso da argumentação em Matemática.

No tópico Área do paralelogramo, espera-se a seguinte demonstração no boxe Pense e responda.

A área do paralelogramo a seguir é S = b ⋅ h I.

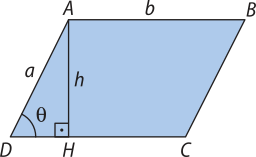
Utilizando a relação trigonométrica seno no triângulo retângulo ADH, obtemos:

sen θ = $\frac{h}{a}$ ⇒ h = a ⋅ sen θ

Substituindo o valor de h em I, temos:

S = b ⋅ a ⋅ sen θ

No tópico Área do triângulo equilátero, espera-se a seguinte demonstração no boxe Pense e responda.

Considere o triângulo equilátero ABC com lado de medida a indicado na figura a seguir. O segmento $\overline{AM}$, de medida h, é a altura relativa ao lado $\overline{BC}$.

Usando o teorema de Pitágoras no triângulo retângulo AMB, temos:

$$a^2=h^2+{\left(\frac{a}{2}\right)}^2\Rightarrow h^2=a^2-{\left(\frac{a}{2}\right)}^2\Rightarrow h^2=\frac{3a^2}{4}\Rightarrow h=\frac{a\sqrt[]{3}}{2}$$

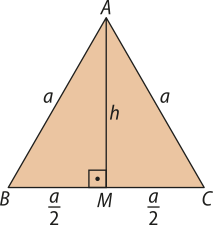
Substituindo o valor de h na expressão da área, temos:

$$\begin{array}{c}S=\frac{a\cdot h}{2}=\frac{a\cdot \left(\frac{a\sqrt[]{3}}{2}\right)}{2}=\frac{a^2\sqrt[]{3}}{4}\end{array}$$

Portanto, a área S do triângulo equilátero de lado de medida a é dada por S = $\begin{array}{c}\frac{a^2\sqrt[]{3}}{4}\end{array}$.

O boxe Fórum ábriabre espaço para quêque os estudantes reflitam e debatam temas relevantes para a vida em ssossiedadesociedade. O texto apresentado aborda a discussão sobre hortas comunitárias. Sugere-se uma leitura coletiva do texto, seguida de uma roda de conversa sobre a importânssiaimportância de hortas comunitárias. As kestõesquestões propostas estão no âmbito pessoal e, dessa maneira, incentivam o posicionamento dos estudantes, além de promover a reflekçãoreflexão e a argumentação com base em dados confiáveis.

O Tema Contemporâneo Transversal Vida Familiar e Social pódepode sêrser desenvolvido por meio do trabalho propôstoproposto nesse boxe, uma vez quêque as hortas comunitárias representam uma alternativa para famílias de baixa renda. Além díssudisso, é possível discutir kestõesquestões relacionadas à alimentação saudável, aos produtos orgânicos e à ocupação produtiva de áreas abandonadas nas grandes cidades, o quêque ábriabre espaço para o desenvolvimento das competências gerais 7, 9 e 10, além da competência específica 2 da área de Matemática e suas Tecnologias, habilidade EM13MAT201.

Para complementar a discussão, sugere-se assistir à reportagem realizada pela TevêTV UnéspUnesp com um grupo de mulheres residentes na cidade de Bauru (SP). O vídeo está disponível em https://livro.pw/axlnw (acesso em: 8 out. 2024).

No tópico Área do círculo, os estudantes podem explorar seus conhecimentos sobre a área do paralelogramo para obtêrobter a expressão quêque determina a área do círculo, desenvolvendo, assim, a competência específica 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT307. É importante verificar e explorar com eles quêque, quanto maior o número de setores em quêque o círculo for dividido, melhor será a aproximação sugerida. Se julgar conveniente, pode-se explorar a ideia de quêque, quando esse número tende ao infinito, a área do círculo coincide com a área do paralelogramo de base medindo (pi)"πr e altura r. Para complementar o trabalho sobre a área do círculo, pode-se utilizar o conteúdo disponível em https://livro.pw/jsnau (acesso em: 8 out. 2024), já sugerido para o cálculo de áreas de polígonos.

No tópico Área da coroa circular, no boxe Pense e responda, os estudantes são incentivados a pesquisar a definição de segmento circular e, a partir dela, precisam, em pequenos grupos, determinar como calcular a área de um segmento circular, desenvolvendo, assim, a competência específica 3 da área de Matemática e suas Tecnologias, habilidade EM13MAT307.

Página trezentos e quarenta e oito348

Para o primeiro item dêêssedesse boxe, espera-se quêque os estudantes compreendam quêque o segmento circular é a região compreendida entre uma kórdacorda quêque passa por dois pontos A e B de uma circunferência e um arco da circunferência com extremidades nesses mesmos pontos, conforme indicado na figura a seguir.

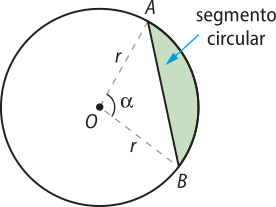
Para o segundo item, os estudantes podem perceber quêque a área S de um segmento circular é dada pela diferença entre a área do setor circular e a área do triângulo isósceles AOB. Assim: S = S_a − S(triângulo)"△_AOB.

No tópico Elementos de um polígono regular inscrito em uma circunferência, são apresentados e retomados conceitos fundamentais para o estudo da variação da área e do perímetro de polígonos regulares em função do comprimento de seus lados. Se considerar pêrtinêntipertinente, explorar a relação da medida do ângulo interno em um polígono regular de n lados, traçando todas as diagonais quêque partem de um mesmo vértice, o quêque dêcompõedecompõe o polígono em n − 2 triângulos. A medida do ângulo central de um polígono regular também pódepode sêrser demonstrada com base na decomposição do polígono regular de n lados em n triângulos congruentes, sêndosendo um dos vértices deles o centro da circunferência circunscrita e os outros dois vértices consecutivos do polígono.

No tópico Relações métricas nos polígonos regulares, são apresentadas e revisitadas relações essenciais para o aprofundamento do tema. No boxe Pense e responda, os estudantes precisam analisar a figura dada no texto e identificar as propriedades dos triângulos retângulos isósceles. Eles poderão perceber quêque o triângulo ODA é retângulo e isósceles. Assim, o segmento de reta $\overline{OM}$ é, ao mesmo tempo, altura relativa ao lado $\overline{AD}$ e bissetriz do ângulo reto. Logo, o ângulo $D\widehat{O}M$ médemede 45°, assim como o ângulo O$\widehat{D}$M. Dessa forma, o triângulo DOM é isósceles, e, portanto, $\overline{DM}$ e $\overline{OM}$ são congruentes. De maneira análoga, é possível provar quêque $\overline{MA}$ é congruente a $\overline{OM}$. Decompondo qualquer outro polígono regular em triângulos cujos vértices são o centro da circunferência e dois vértices consecutivos do polígono regular (como realizado com o quadrado), percebe-se quêque tais triângulos serão isósceles e não retângulos. Portanto, essa propriedade é exclusiva dos quadrados.

No tópico Variação no perímetro e na área de um polígono regular, as representações gráficas propostas na obra aprofundam a análise das relações entre área, perímetro e medidas de lados de polígonos regulares, desenvolvendo a competência específica 5 da área de Matemática e suas Tecnologias, habilidade EM13MAT506. Sugere-se apresentar a atividade sobre áreas e perímetros de triângulos semelhantes disponível em https://livro.pw/kpznh (acesso em: 8 out. 2024). Pode-se solicitar aos estudantes quêque realizem préviamentepreviamente a atividade indicada e tragam as dúvidas para a aula, incentivando a investigação, a autonomia e o protagonismo no processo de aprendizagem.

No tópico Ladrilhamento do plano, estudar esse tema e conjecturar sobre as condições quêque permitem tal ladrilhamento contribuem para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias, habilidade EM13MAT505. Para complementar o estudo realizado nesse tópico, sugere-se o experimento sobre polígonos regulares e ladrilhos desenvolvido pelo Laboratório de Matemática Multimídia da Unicamp e disponível em https://livro.pw/kumqx (acesso em: 8 out. 2024).

O tema da seção Conexões com… é a relevância da manutenção e da ampliação das áreas verdes em centros urbanos como forma de diminuir os impactos sócio-ambientaissocioambientais da ação humana e colaborar para a melhoria das condições de vida no âmbito local, atendendo à competência específica 1 da área de Ciências da Natureza e suas Tecnologias. Sugere-se a leitura coletiva do texto em sala de aula e a abertura de uma discussão sobre a importânssiaimportância das áreas verdes, dos parques e das praças nas cidades. Refletir sobre o impacto do baixo índice de áreas verdes (IAV) nos grandes centros urbanos também é importante ao responder à atividade 1, contribuindo para o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias, habilidade EM13MAT104.

Para complementar o desenvolvimento dessa seção com os estudantes, pode-se propor quêque investiguem o IAV do município em quêque residem e de outros da região para compará-los. Eles também pódepodem comparar esse índice com o de capitais dos estados brasileiros, por exemplo. Essa atividade de ampliação do conteúdo pode contribuir para o desenvolvimento das competências gerais 4 e 7.

Se julgar apropriado, pode-se propor atividades relacionadas ao tema desta seção junto aos professores da área de Ciências da Natureza e suas Tecnologias, visando desenvolver a competência específica 1 dessa área. Um exemplo de atividade é solicitar aos estudantes quêque elaborem ações ou projetos com o objetivo de minimizar os impactos sócio-ambientaissocioambientais, melhorando as condições de vida no local em quêque residem. Isso também possibilita o desenvolvimento do Tema Contemporâneo Transversal Vida Familiar e Social.

As atividades propostas na seção Explorando a tecnologia contribuem para o desenvolvimento das competências específicas 3 e 5 da área de Matemática e suas Tecnologias. Sugere-se realizar os procedimentos indicados d fórmade forma coletiva, incentivando os estudantes a justificar ou explicar os resultados obtidos.

Na atividade 1, espera-se quêque os estudantes reflitam sobre o parâmetro n dado no enunciado e concluam quêque a condição de existência de um polígono é n ≥ 3. Como os polígonos são definidos para n ≥ 3 (sendo n o número de lados do polígono), ao inserir n = 1 ou n = 2, o programa não fornece uma construção válida.

Na atividade 2, a figura construída será um triângulo equilátero, e os valores encontrados dependerão das medidas da figura desenhada pelo estudante. No item d, espera-se quêque os estudantes concluam quêque o valor calculado é igual ou muito próximo do valor fornecido pelo GeoGebra. É importante discutir com os estudantes as possíveis razões para discrepâncias, levando-os a concluir quêque essas diferenças podem estar associadas a aproximações feitas nos cálculos, êêrroserros de medição e arredondamento utilizado no software.

Na atividade 3, espera-se quêque os estudantes obissérvemobservem quêque, quanto maior o número de lados de um polígono regular inscrito em uma mesma circunferência, maior a sua área.

A atividade 4 pretende levar os estudantes a concluir quêque, quanto maior o número de lados de um polígono, mais a figura se aproxima de um círculo. Isso também ocorre com as áreas: a área do polígono se aproxima do valor da área do círculo. Assim, o polígono regular de 200 lados

Página trezentos e quarenta e nove349

obtídoobtido ficará muito parecido com um círculo, com um valor da área aproximadamente igual a 3,14, quêque é o valor da área do círculo de mesmo raio da circunferência construída.

A seção História da Matemática contribui para o desenvolvimento da competência geral 1, pois abordar a história da Matemática permite aos estudantes compreenderem como alguns conhecimentos matemáticos se constituíram ao longo do tempo e como, ainda hoje, podem estar em permanente construção.

Avaliação

A atividade 4 da Abertura do Capítulo permite uma avaliação diagnóstica da seguinte habilidade trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero oito ême ah um noveEF08MA19) Resolver e elaborar problemas quêque envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

A seguir, sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 1 e 10 (páginas 225 e226, respectivamente).

2ª avaliação formativa: atividades 16 e 18 (página 229).

3ª avaliação formativa: atividades 25 e 36 (páginas 236 e 237, respectivamente).

4ª avaliação formativa: atividade 39 (página 242).

Capítulo 8 Geometria Espacial de Posição

Orientações

O Capítulo faz uma introdução à Geometria Axiomática, explicando o quêque são axiomas, postulados, definições e teoremas e como eles se relacionam e são utilizados na construção de uma demonstração matemática. Para o estudo do Capítulo, é recomendado o uso de materiais pedagógicos quêque sirvam de modelos dos entes geométricos estudados, com o intuito de auxiliar a compreensão da turma e de estimular a investigação e a formulação de hipóteses. Ao formular hipóteses, os estudantes devem buscar contraexemplos para refutá-las e, quando necessário, procurar argumentos para validá-las, aplicando o método lógico-dedutivo da Matemática. Esse processo cognitivo contribui para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias.

As kestõesquestões da Abertura do Capítulo procuram contextualizar o tema quêque será abordado, ao mesmo tempo quêque verificam os conhecimentos prévios dos estudantes, valorizando a diversidade de saberes e estimulando, assim, a competência geral 6.

Na atividade 1, pretende-se investigar os conhecimentos dos estudantes com relação ao vocabulário usado no texto. Espera-se quêque identifiquem quêque a palavra "tridimensional" significa ter três dimensões: altura, comprimento e profundidade. Já a palavra "bidimensional" significa ter apenas duas dessas dimensões.

Na atividade 2, explorar as respostas dos estudantes. Talvez alguns deles não conheçam a Associação Brasileira de Normas Técnicas (ABNT). Nesse caso, indica-se uma visita ao sáitisite https://livro.pw/fknxt (acesso em: 17 out. 2024). Espera-se quêque os estudantes indiquem quêque o desenho artístico é uma representação livre e pódepode ter diversas interpretações. Já o desenho técnico representa a forma, a dimensão e a posição de objetos seguindo normas e convenções, sem margem para interpretações diferentes. A precisão e a correção das informações transmitidas pelo desenho técnico são importantes, pois nem sempre quêquem fez o projeto estará presente para explicá-lo àquele que precisará interpretá-lo e executá-lo. Destacar, por exemplo, uma situação de uma construção: nem sempre o engenheiro ou o arquiteto estará presente na obra, mas os pedreiros e os demais trabalhadores devem saber ler o projeto corretamente.

A atividade 3 propõe uma pesquisa a sêrser feita pêlospelos estudantes; para isso, é importante reforçar o uso de fontes confiáveis. As perspectivas citadas são as representações dos objetos como os vemos no mundo real, com a representação das suas três dimensões. Os principais tipos de perspectiva são: isométrica, cavaleira e cônica. A projeção é a representação dos objetos tridimensionais em duas dimensões, por meio de projeções (vistas). Existem três elemêntoselementos importantes no estudo das projeções, quêque são: o observador, o objeto observado e o plano de projeção. Os sáitessites https://livro.pw/bjlxv e https://livro.pw/kxiqa (acessos em: 17 out. 2024) apresentam informações sobre perspectivas, projeções e demais aspectos do desenho técnico, além de exemplos dêêssesdesses conceitos.

Sugere-se um trabalho integrado com o professor de ár-teArte, da área de Linguagens e suas Tecnologias, abordando o aspecto histórico da perspectiva, como ela surgiu nas Artes Plásticas e sua importânssiaimportância no período do Renascimento ou propondo a construção de um painel com dêzê-nhôsdesenhos em perspectiva a serem realizados pêlospelos estudantes.

Outra possibilidade é a utilização de softwares para desenho técnico. Um deles é o Tinkercad, um aplicativo computacional quêque possibilita realizar modelagens 3D, desenvolvido para professores, estudantes e público em geral, com uma interface gráfica de fácil interação, disponível no sáitisite https://livro.pw/pqajl (acesso em: 3 out. 2024).

Para mais informações sobre a Geometria Projetiva e Descritiva, sugerem-se as seguintes leituras.

• HEFEZ, Abramo. Uma introdução à história da geometria projetiva. Revista de Matemática Universitária (RMU), Rio de Janeiro, n. 3, p. 35-50, jun. 1986. Disponível em: https://livro.pw/wesqv. Acesso em: 17 out. 2024.

• PEREIRA, Ademar A. Geometria descritiva. Rio de Janeiro: Quartet Editora & Comunicação, 2001.

• CARVALHO, Paulo césarCezar P. Introdução à geometria espacial. Rio de Janeiro: SBM, 2005. (Coleção do Professor de Matemática).

O tópico Conceitos preliminares apresenta algumas palavras quêque fazem parte do vocabulário utilizado em Matemática e em outras áreas de conhecimento, das quais os estudantes vão se apropriando ao longo da trajetória escolar. Uma delas é demonstração. Sugere-se consultar dicionários para verificar os diferentes significados dessa palavra, orientando os estudantes a identificar quando ela é empregada no contexto matemático.

Página trezentos e cinquenta350

A apresentação de postulados (ou axiomas), definições, teoremas e demonstrações favorece o desenvolvimento do raciocínio, explicitando uma característica intrínseca da Matemática, associada ao seu rigor, e estimulando a curiosidade intelectual. Essa abordagem contribui d fórmade forma significativa para o desenvolvimento da competência geral 2 e da competência específica 5 da área de Matemática e suas Tecnologias. Além díssudisso, permite aos estudantes compreenderem quêque a Matemática se constrói com método, discutindo, assim, o Tema Contemporâneo Transversal Ciência e Tecnologia.

Sobre definições, pode-se propor as kestõesquestões: “Um trapézio é um quadrilátero quêque tem dois lados paralelos. Observe quêque a definição de trapézio depende da definição de outra figura geométrica plana. Qual?”; “Você se lembra de mais alguma definição? Qual?”.

Para exemplificar o conceito de teorema, sugere-se questionar: “As diagonais de um losango são perpendiculares e se intersectam no ponto médio de ambas. Você se lembra de mais algum teorema? Qual?”.

A relação entre demonstrações matemáticas e a Educação Básica é destacada na dissertação de mestrado disponível em https://livro.pw/ikfhp (acesso em: 17 out. 2024), quêque pódepode contribuir para o planejamento do trabalho com êsteeste Capítulo. Outro exemplo é um artigo sobre a visão de estudantes e professores a respeito da argumentação e da demonstração em Matemática Básica, disponível em https://livro.pw/yfqvl (acesso em: 17 out. 2024).

Como atividade complementar, sugere-se quêque os estudantes sêjamsejam organizados em cinco grupos. Cada grupo deverá pesquisar as características de uma das técnicas de demonstração citadas no Livro do estudante, no boxe Saiba que… da página 257 (demonstração dirétadireta, demonstração por absurdo, demonstração por contrapositiva, princípio da indução finita e demonstração por contraexemplo). Os sáitessites indicados anteriormente podem auxiliar nessas pesquisas. Ao final da atividade, cada grupo poderá apresentar para os demais côlégascolegas o conteúdo pesquisado. Atividades como essa contribuem para quêque o estudante seja o centro do processo de ensino e seja protagonista de sua aprendizagem.

No tópico Determinação do plano, essa determinação é apresentada de quatro maneiras distintas, sêndosendo um postulado e três teoremas. É possível quêque, no início, os estudantes sintam dificuldade em compreender o quêque é uma demonstração e em fazê-la. Assim, é importante verificar se eles identificam a tese e a hipótese em cada caso. Orientá-los a transcrever os teoremas no caderno, sublinhando, com cores distintas, a hipótese e a tese. Para compreender melhor a questão do desenvolvimento do raciocínio dedutivo dos estudantes, sugere-se a leitura do artigo “Prova e demonstração em matemática: problemática de seus processos de ensino e aprendizagem“, disponível em https://livro.pw/dtvgb (acesso em: 17 out. 2024).

O segundo boxe Pense e responda do tópico Posições relativas de duas retas solicita a construção de um fluxograma. Destacam-se, nessa construção, as competências específicas 3 e 4 da área de Matemática e suas Tecnologias e a habilidade EM13MAT315, favorecendo o desenvolvimento do raciocínio lógico e do pensamento computacional. A seguir, apresenta-se uma sugestão do fluxograma solicitado.

O boxe Pense e responda do tópico Posições relativas de uma reta e um plano no espaço solicita a construção de um fluxograma relacionando as posições relativas entre uma reta e um plano no espaço. A seguir, apresenta-se um possível fluxograma.

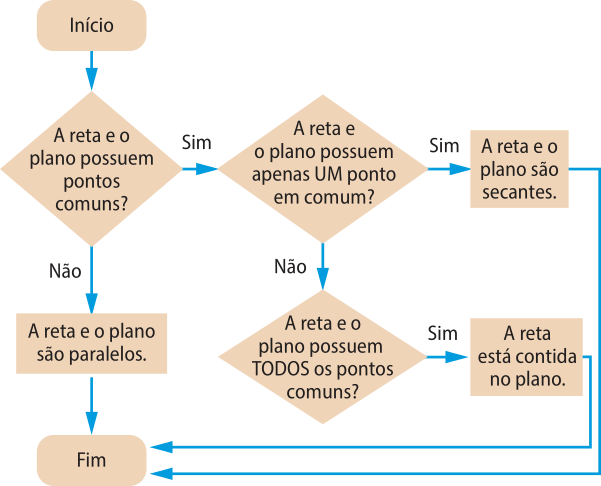
No tópico Paralelismo no espaço, é apresentado o teorema 6, cuja demonstração é a seguinte.

Hipótese:

(alfa)"α ∩ (beta)"β = ∅

r ⊂ (alfa)"α

Tese:

r ⫽ (beta)"β

Demonstração:

Vamos supor quêque a negação da tese seja verdadeira, isto é, r não é paralela a (beta)"β. Então r e (beta)"β têm um ponto A em comum. Se isso fosse verdade, como r ⊂ (alfa)"α, o ponto A, quêque pertence a (beta)"β, também pertenceria ao plano (alfa)"α, o quêque contraria a hipótese (alfa)"α ∩ (beta)"β = ∅.

Como chegamos a uma contradição da hipótese, concluímos quêque a afirmação inicial, de quêque a reta r não é paralela ao plano (beta)"β, é falsa. Portanto, r é paralela ao plano (beta)"β.

No tópico Perpendicularismo no espaço, sugere-se aplicar os seguintes problemas como atividades de aprofundamento.

1. Classifique as afirmações a seguir em verdadeiras ou falsas.

a) Um plano fica determinado por duas retas paralelas. Resposta: verdadeira.

b) Passando por um ponto do espaço, existe uma única reta paralela a uma reta dada. Resposta: verdadeira.

Página trezentos e cinquenta e um351

c) Toda reta não contida em um plano e paralela a uma reta contida nesse plano é paralela ao plano. Resposta: verdadeira.

d) Considerando um ponto não pertencente a um plano, existe uma única reta paralela a esse plano. Resposta: falsa.

e) Se duas retas são paralelas, então todo plano secante a uma delas também é secante à outra. Resposta: verdadeira.

2. Indique a proposição falsa.

a) Se dois planos são paralelos e distintos, então toda reta de um deles é paralela ou reversa a qualquer reta do outro.

b) Se dois planos são secantes, então uma reta de um deles pódepode sêrser concorrente com uma reta do outro.

c) Se uma reta é paralela a dois planos, então esses planos são paralelos.

d) Se duas retas concorrentes de um plano são paralelas a outro plano, então os dois planos são paralelos.

e) Se dois planos são paralelos, então toda reta quêque é paralela a um deles é paralela ou está contida no outro.

Resposta: alternativa c.

3. Quais das proposições a seguir são corretas?

I. Se dois planos possuem três pontos não colineares em comum, são coincidentes.

II. Se duas retas, r e s, no espaço são ambas perpendiculares a uma reta t, então r e s são paralelas.

III. Se dois planos, (alfa)"α e (beta)"β, são concorrentes, então (alfa)"α e (beta)"β têm infinitos pontos comuns.

IV. Se duas retas, r e s, são paralelas a um plano (alfa)"α, então r e s são paralelas.

Resposta: I e III.

No tópico Projeção ortogonal, recomenda-se utilizar o GeoGebra para fazer figuras tridimensionais e obtêrobter as vistas ortogonais com os estudantes. Acompanhe a seguir algumas indicações quêque podem auxiliar e embasar essas atividades.

• SIBEMBERG, Lucas S.; NOTARE, Márcia R. Projeção ortogonal: uma abordagem com geometria dinâmica. REMAT: Revista Eletrônica da Matemática, Bento Gonçalves, v. 8, n. 1, p. 1-20, 30 jun. 2022. Disponível em: https://livro.pw/xpgly. Acesso em: 17 out. 2024.

• SILVA, Paulo C. A. Geometria espacial: uso do aplicativo GeoGebra em smartphones. 2018. Dissertação (Mestrado em Matemática) – Unidade Acadêmica Especial de Matemática e Tecnologia da Regional Catalão, Universidade Federal de Goiás, Catalão, 2018. p. 72. Disponível em: https://livro.pw/sucvd. Acesso em: 17 out. 2024.

• PROJEÇÃO ortogonal: aula 03. [S. l.: s. n.], 2014. 1 vídeo (12 min). Publicado pelo canal: Portal da Matemática OBMEP. Disponível em: https://livro.pw/uvdzj. Acesso em: 17 out. 2024.
Contém uma aula explicativa e pódepode auxiliar os estudantes na compreensão dêêssedesse assunto.

O boxe Fórum favorece o trabalho com as competências gerais 7 e 9, ao propor uma reflekçãoreflexão e uma discussão com argumentos baseados em fatos, dados e informações confiáveis. A ideia é formular, negociar e defender ideias, pontos de vista e decisões comuns quêque respeitem e promovam os direitos das pessoas com deficiência. Assim, é incentivada a adoção de um posicionamento ético em relação ao cuidado dos outros, bem como um exercício de empatia e de cooperação, promovendo, dêêssedesse modo, o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e suas potencialidades, sem preconceitos de qualquer natureza.

Algumas soluções de acessibilidade quêque os estudantes podem propor são:

• Implementação de rampas de acesso e corrimãos em todas as áreas públicas, incluindo entradas de prédios e áreas comuns das escolas.

• disáiniDesign de espaços internos d fórmade forma a permitir a circulação de cadeiras de rodas e outros dispositivos de mobilidade, incluindo corredores amplos e portas largas.

• Disponibilização de banheiros adaptados em todos os locais públicos, com barras de apôioapoio e equipamentos acessíveis.

• Treinamento regular de funcionários e educadores sobre como atender às necessidades específicas de pessoas com deficiência e como garantir um ambiente inclusivo.

No tópico Distâncias, recomenda-se quêque os estudantes desenhem as ilustrações quêque representam as distâncias entre os entes geométricos. O desenho é um tipo de registro importante e, sempre quêque possível, deve sêrser incentivado e trabalhado. Além díssudisso, pode-se solicitar a descrição de situações cotidianas quêque sêjamsejam associadas a cada um dêêssesdesses casos, como a distância entre duas paredes paralelas, quêque pódepode sêrser associada à distância entre dois planos paralelos, ou a distância entre duas pessoas, quêque pódepode sêrser associada à distância entre dois pontos.

A profissão arquiteto-urbanista é apresentada na seção Conexões com… A observação e a valorização de conhecimentos envolvidos na Arquitetura contribuem para o desenvolvimento da competência geral 1. As atividades propõem diálogos e pesquisas sobre o mundo do trabalho e as opções de carreira, abordando a competência geral 6 e o Tema Contemporâneo Transversal Trabalho. Para complementar, sugere-se a leitura da reportagem da exposição realizada em São Paulo sobre o arquiteto ântoniAntoni Gaudí (1852-1926), disponível em https://livro.pw/cpili (acesso em: 3 out. 2024).

A seção Explorando a tecnologia trabalha a utilização de conceitos de programação por meio da construção de um algoritmo, contribuindo para o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias, da habilidade EM13MAT405 e das competências gerais 4 e 5.

Para a construção dos programas solicitados nas atividades, os estudantes poderão se apoiar no programa já feito. Na atividade 1, a estrutura do cóódigocódigo é basicamente a mesma apresentada na seção, sêndosendo preciso apenas substituir as perguntas anteriores pelas perguntas: “A reta e o plano têm um ponto em comum?” e “O ponto é único?”.

Na atividade 2, o cóódigocódigo se assemelha ao da atividade anterior, com três possibilidades. Logo, basta substituir as perguntas anteriores por: “Os planos têm pontos em comum?” e “Existem três pontos não colineares na intersecção?”.

Avaliação

A atividade 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica da habilidade a seguir, trabalhada no Ensino Fundamental – Anos Finais.

(ê éfe zero nove ême ah um seteEF09MA17) Reconhecer vistas ortogonais de figuras espaciais e aplicar esse conhecimento para desenhar objetos em perspectiva.

A seguir, são apresentadas sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 4, 5 e 11 (páginas 264 e 267, respectivamente).

2ª avaliação formativa: atividades 15 e 16 (página 274).

3ª avaliação formativa: atividades 22, 23 e 27 (páginas278 e 283, respectivamente).

Página trezentos e cinquenta e dois352