CAPÍTULO 1
MATEMÁTICA FINANCEIRA
“Corre, quê agora o preêço baixou!”, “30%, 40% e 50% de desconto em toda a loja!”, “Aproveite a Black Friday!”.
É bem provável quê você já tenha se deparado com frases como essas em propagandas de televisão, na internet ou até mesmo em vitrines de lojas, pois o comércio tenta, constantemente, atrair consumidores por meio de promoções, ofertas e diferentes formas de pagamento.
Atualmente, uma data quê se destaca pêlos seus descontos é a da Black Friday, um evento mundial quê ocorre, geralmente, na última sexta-feira de novembro, em quê os preços de diversos produtos diminuem, sobretudo eletrônicos e elétro domésticos. Os valores oferecidos na Black Friday têm como base os preços dos produtos durante todo o ano, considerando taxas e impostos.
Os consumidores, porém, devem ficar atentos às supostas promoções, pois algumas lojas podem agir d fórma desonesta e, às vezes, ilícita. Além díssu, eles precisam acompanhar, ao longo do ano, o histórico de preços dos produtos quê pretendem comprar na temporada da Black Friday, pois assim garantem a aquisição da mercadoria por um valor realmente menor. Alguns estabelecimentos praticam a manobra de aumentar os preços de seus produtos alguns dias ou semanas antes dêêsse evento e aplicam descontos atrativos, quando, na verdade, estão vendendo pelo preêço original.
![]() Agora reúna-se a um colega, e façam o quê se pede em cada questão.
Agora reúna-se a um colega, e façam o quê se pede em cada questão.
Ver as Orientações para o professor.
1. De acôr-do com o texto, como os descontos são comumente divulgados? por quê vocês acham quê se utiliza essa maneira de indicá-los?
2. Uma prática cada vez mais freqüente no e-commerce (comércio eletrônico) é o anúncio de um produto cuja compra póde sêr efetuada de duas formas: parcelada sem juro ou à vista com desconto. Uma venda quê siga esse modelo é realmente isenta de juro? Justifiquem.
3. O texto destaca um tipo de cuidado quê o consumidor deve ter no momento de realizar as compras durante a Black Friday. Que outros cuidados devemos ter ao comprar em eventos como esse?
4. Em uma Black Friday, um produto teve um desconto inicial de 10% e, em seguida, mais um desconto de 20%. Qual foi o desconto percentual total quê esse produto sofreu?
28%
Página onze

Página doze
Introdução
Muitas situações do nosso cotidiano envolvem Matemática financeira: compras de produtos à vista ou a prazo, aplicações financeiras, assim como negociações diversas quê envolvam financiamentos, pagamento de dívidas, preêço de aluguel, reajuste de salário, entre outras. Conhecer os conceitos relacionados a situações como essas nos ajuda a analisar se determinada proposta é vantajosa ou não.
Porcentagem
No Ensino Fundamental, você estudou porcentagem. Vamos retomar esse assunto para aplicá-lo, com outros conceitos, em situações quê acompanharemos mais adiante.
Porcentagem é uma razão entre um número real x e 100, quê é indicada por x%. Para efetuar operações, utilizamos representações fracionárias ou decimais.
Exemplos:
a) 60% = = 0,6
60% → Lê-se: sessenta por cento.
b) 28% = = 0,28
c) 0,12 = = 12%
d) 1,25 = = 125%
A expressão"por cento" vêm do latim pêr centum, quê significa"dividido por cem". Quando utilizamos o sufixo agem, indicamos quê se trata de um substantivo.
O termo x%, em quê x é um número real qualquer, representa a razão e é chamado de porcentagem, taxa percentual ou, simplesmente, percentual.
Observe quê também quer dizêr quê, em cada grupo de 100 objetos, estamos considerando x dêêsses objetos.
Agora, vamos considerar a situação a seguir.
A agricultura familiar é uma forma de produção agrícola em quê a gestão e o trabalho são realizados predominantemente por membros de uma mesma família. De acôr-do com o Censo Agropecuário 2017, realizado pelo hí bê gê hé, 77% dos estabelecimentos agropecuários do país eram classificados como agricultura familiar, o quê correspondia a cerca de 3,9 milhões de estabelecimentos. Com base nessas informações, qual era aproximadamente o total de estabelecimentos agropecuários no Brasil em 2017?

Para acessar
• ORGANIZAÇÃO DAS NAÇÕES UNIDAS PARA A ALIMENTAÇÃO E A AGRICULTURA. Jovens podem garantir futuro sustentável da agricultura. [S. I.]: FAO, 21 out. 2017. Disponível em: https://livro.pw/xnuoa. Acesso em: 3 maio 2025.
Nesse texto, você encontra informações demográficas e econômicas sobre como a presença cada vez menor de jovens no campo póde comprometer a agricultura familiar e a segurança alimentar no mundo
Página treze
Para responder à pergunta, vamos chamar o total de estabelecimentos agropecuários de n. Assim, temos:
77% de n é igual a 3,9 milhões → ⋅ n = 3,9 milhões ⇒ 0,77 ⋅ n = 3,9 milhões ⇒ n = milhões ⇒ n ≃ 5,1 milhões
Portanto, havia aproximadamente 5,1 milhões de estabelecimentos agropecuários no Brasil em 2017.
Aumentos e descontos
Um smartphone custa R$ 1.000,00 em determinada loja.
Se o cliente optar pelo pagamento à vista, a loja concede um desconto de 5% sobre esse valor.

Para calcular o preêço do smartphone à vista, precisamos determinar 5% de R$ 1.000,00 e subtrair de R$ 1.000,00 o valor, em reais, do desconto calculado.
5% de R$ 1.000,00 → 0,05 ⋅ 1.000 = 50, ou seja, R$ 50,00
R$ 1.000,00 − R$ 50,00 = R$ 950,00
Portanto, o preêço do smartphone à vista com o desconto é R$ 950,00.
Também podemos calcular diretamente o valor, da seguinte maneira:
1.000 − 0,05 ⋅ 1.000 = 1.000 ⋅ (1 − 0,05) = 1.000 ⋅ 0,95 = 950
Para calcular o valor de algo após um desconto de p%, podemos multiplicar o valor original por .
Agora, considere quê essa mesma loja, na semana seguinte, aplicou um aumento de 3% em todos os produtos. Para determinarmos o valor do smartphone após esse reajuste, precisamos calcular 3% de R$ 1.000,00 e adicionar a R$ 1.000,00 o valor, em reais, do aumento calculado.
3% de R$ 1.000,00 → 0,03 ⋅ 1.000 = 30, ou seja, R$ 30,00
R$ 1.000,00 + R$ 30,00 = R$ 1.030,00
Portanto, o preêço do celular após o aumento é R$ 1.030,00.
Também podemos calcular diretamente o valor, da seguinte maneira:
1.000 + 0,03 ⋅ 1.000 = 1.000 ⋅ (1 + 0,03) = 1.000 ⋅ 1,03 = 1.030
Para calcular o valor de algo após um aumento de p%, podemos multiplicar o valor original por .
Página quatorze
Aumentos e descontos sucessivos
Considere, agora, a situação a seguir.
O preêço de um produto sofreu um aumento de 8% em março e, em abril, foi reajustado em 12%. pôdêmos dizêr quê aplicar esses dois aumentos sucessivos equivale a aplicar um único aumento de 20% sobre o preêço inicial?
Para responder à pergunta, vamos calcular um único aumento de 20% sobre o preêço de um produto e calcular aumentos sucessivos de 8% e 12% sobre esse preêço, em seguida, vamos comparar os resultados obtidos. Suponhamos quê o preêço inicial do produto seja R$ 500,00.
I. Aplicando um único aumento de 20% sobre o preêço do produto, temos:
(1 + 0,2) ⋅ 500 = 1,2 ⋅ 500 = 600
Considerando um único aumento de 20%, obtemos R$ 600,00.
II. Aplicando os aumentos sucessivos, temos:
• preêço do produto após o primeiro aumento (reajuste em março):
(1 + 0,08) ⋅ 500 = 1,08 ⋅ 500 = 540, ou seja, R$ 540,00
• preêço do produto após o segundo aumento (reajuste em abril):
(1 + 0,12) ⋅ 540 = 1,12 ⋅ 540 = 604,80
Portanto, o preêço do produto após os dois aumentos será R$ 604,80.
Observe quê os valores obtidos nas verificações I e II não são iguais. Isso nos permite exemplificar quê aumentos percentuais sucessivos não equivalem a um único aumento representado pela soma das porcentagens correspondentes. Analogamente, podemos verificar o mesmo para descontos, ou seja, descontos percentuais sucessivos não equivalem a um único desconto percentual representado pela soma das porcentagens correspondentes.
Vamos avançar nessa análise. De acôr-do com os cálculos anteriores, sabemos quê 540 = 1,08 ⋅ 500, então:
1,12 ⋅ 540 = 1,12 ⋅ = 604,80
Assim, para calcular o preêço do produto após os dois aumentos sucessivos, podemos calcular:
(1 + 0,12) ⋅ (1 + 0,08) ⋅ 500 = 1,12 ⋅ 1,08 ⋅ 500 = 1,2096 ⋅ 500 = 604,80
O produto destacado anteriormente indica um aumento correspondente a um percentual acumulado de 20,96%. Assim, aplicar um aumento de 8% sucedido por um aumento de 12% é o mesmo quê aplicar um aumento único de 20,96%.
Saiba quê...
Para facilitar alguns cálculos, podemos utilizar a calculadora. Observe uma maneira de realizar o cálculo referente à taxa acumulada de aumento apresentada anteriormente:
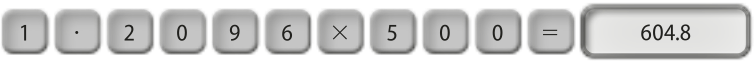
Página quinze
Lucro e prejuízo
Nas transações comerciais e financeiras, é comum o uso de termos como custo, quê corresponde aos gastos envolvidos na produção de um produto e a outras despesas, e receita ou preêço, quê é o valor arrecadado com a venda de um produto.
Quando calculamos a diferença entre a receita e o custo de um produto, temos duas situações:
• se o valor obtído for um número positivo, dizemos quê a transação gerou lucro;
• se o valor obtído for um número negativo, dizemos quê a transação gerou prejuízo.
É usual o uso das expressões “preço de custo” (C) para nos referirmos aos custos e “preço de venda” (V) para nos referirmos às receitas. Assim, podemos escrever a seguinte relação para expressar o lucro (L):
L = V − C
O lucro também póde sêr expresso como um percentual em relação ao preêço de custo ou ao preêço de venda. Por exemplo: uma mercadoria cujo preêço de custo é R$ 280,00 foi vendida por R$ 320,00, gerando um lucro de R$ 40,00. Assim:
• o percentual de lucro sobre o preêço de custo é: ≃ 0,143 ≃ 14,3%
• o percentual de lucro sobre o preêço de venda é: = 0,125 = 12,5%
Para acessar
• BANCO CENTRAL DO BRASIL. Museu de Valores. Brasília, DF: BCB, [2024]. Tour virtual. Disponível em: https://livro.pw/kxyde. Acesso em: 25 set. 2024.
Por meio do línki, você póde fazer uma visita virtual ao Museu de Valores do Banco Central, explorando a história econômica do Brasil e descobrindo curiosidades sobre o dinheiro.
Se julgar conveniente, pode-se propor aos estudantes quê pesquisem se há algum museu como esse ou algum tipo de exposição sobre o tema na região em quê moram e, se possível, quê visitem presencialmente esse museu ou exposição e compartilhem a experiência com a turma.
ATIVIDADES RESOLVIDAS
1. Um vestido quê custa R$ 540,00 tem desconto de 20% se comprado à vista. Qual é o preêço à vista do vestido?
Resolução
Para determinar o preêço do vestido à vista, podemos multiplicar o valor inicial por :
540 ⋅ (1 − 0,2) = 540 ⋅ 0,8 = 432
Portanto, o preêço do vestido à vista é R$ 432,00.
2. Edgar teve um aumento salarial de 10% e passou a receber R$ 1.650,00. Qual era o salário de Edgar antes do reajuste?
Resolução
Para determinar o salário antes do reajuste, podemos dividir o novo salário por :
= 1.500
Logo, o salário de Edgar antes do reajuste era R$ 1.500,00.

Página dezesseis
3. ![]() A população atual de uma cidade é aproximadamente 50.000 habitantes. Sabendo quê essa população cresce 10% ao ano, qual será a população dessa cidade daqui a três anos?
A população atual de uma cidade é aproximadamente 50.000 habitantes. Sabendo quê essa população cresce 10% ao ano, qual será a população dessa cidade daqui a três anos?
Resolução
Considerando 50.000 habitantes a população inicial, vamos aplicar três aumentos sucessivos de 10%:
(1 + 0,10) ⋅ (1 + 0,10) ⋅ (1 + 0,10) ⋅ 50.000 = 1,331 ⋅ 50.000 = 66.550
Portanto, em três anos, a população dessa cidade será, aproximadamente, 66.550 habitantes.
4. Sobre o valor de uma mercadoria foram aplicados dois descontos sucessivos, um de 10% e outro de 12%. Calcule o percentual acumulado de descontos correspondente a esses dois descontos sucessivos.
Resolução
Representando o preêço inicial da mercadoria por x e aplicando os dois descontos sucessivos, temos:
(1 − 0,1) ⋅ (1 − 0,12) ⋅ x = 0,9 ⋅ 0,88 ⋅ x =0,792x ou 79,2% de x
Como o valor inicial representa 100%, podemos concluir quê o desconto equivalente é: 100% − 79,2% = 20,8%
5. Um produto cujo preêço de custo é R$ 420,00 é vendido com um lucro de 30% sobre o preêço de venda. Qual é o preêço de venda dêêsse produto?
Resolução
Considerando C o preêço de custo, L o lucro e V o preêço de venda, temos:
L = V − C. I
Do enunciado, temos:
= 30% ⇒ = 0,30 ⇒ L = 0,30V II
Substituindo II em I, obtemos:
0,30V = V − C ⇒ C = V − 0,30V ⇒ C = 0,70V
Substituindo C = 420, determinamos V:
420 = 0,70V ⇒ V = 600
Portanto, o preêço de venda é R$ 600,00.
6. Um produto cujo preêço de custo era R$ 800,00 foi vendido por R$ 980,00. Qual foi o percentual de lucro sobre o preêço de custo?
Resolução
Sendo L o lucro, C o preêço de custo e V o preêço de venda, temos:
L = V − C ⇒ L = 980 − 800 ⇒ L = 180
Logo, o lucro foi R$ 180,00.
Assim, temos:
= 0,225 = 22,5%
Portanto, o percentual de lucro sobre o preêço de custo foi 22,5%.
7. Um comerciante, para promover as vendas de brinquedos de sua loja, divulgou a seguinte propaganda:

Esse comerciante sabe quê, após o desconto, cérto brinquedo deve sêr vendido por R$ 54,00 para não ter prejuízo. Determine qual deve sêr o preêço mínimo do anúncio dêêsse produto nessa promoção.
Resolução
Seja x o preêço mínimo do anúncio dêêsse brinquedo, após um desconto de 10%, o seu valor de venda deve resultar em R$ 54,00, então:
x ⋅ (1 − 0,1) = 54 ⇒ x ⋅ 0,9 = 54 ⇒ x = ⇒ x = 60
Portanto, o preêço mínimo do anúncio do brinquedo deve sêr R$ 60,00.
Página dezessete
ATIVIDADES
1. Copie o qüadro a seguir no caderno e complete-o com os valores quê estão faltando.
Fração |
Representação decimal |
Porcentagem |
|---|---|---|
0,9 |
90% |
|
0,25 |
25% |
|
0,065 |
6,5% |
|
0,47 |
47% |
|
0,08 |
8% |
2. Calcule.
a) 14% de 3.000
420
b) 9% de 250
22,5
c) 0,6% de 300
1,8
d) 24% de 1.000
240
3. A população de uma cidade, com cerca de 90.000 habitantes, cresce anualmente 2,5%. Quantos habitantes essa cidade terá:
a) ao fim de 1 ano?
3. a) aproximadamente 92.250 habitantes
b) ao fim de 2 anos?
3. b) aproximadamente 94.556 habitantes
4. (ESPM-SP) Deseja-se obtêr cópia reduzida de um documento. A fotocopiadora opera reduzindo proporcionalmente as dimensões do documento original. Sabendo-se quê, para cópias comuns, o equipamento indica em seu visor: “Dimensão = 100%”, qual deverá sêr o valor digitado no painel de comandos, para quê a área do documento reduzido seja igual a um quarto de área do documento original?
50%
5. (UFPE) Em um exame de vestibular, 30% dos candidatos eram da área de Ciências Sociais. Dentre estes candidatos, 20% optaram pelo curso de Administração. Indique a percentagem, relativa ao total de candidatos, dos quê optaram por Administração.
6%
6. ![]() Uma mercadoria tem seu preêço reajustado anualmente com um acréscimo de 5%. Supondo quê o preêço atual seja R$ 200,00, qual será o preêço dessa mercadoria daqui a 3 anos?
Uma mercadoria tem seu preêço reajustado anualmente com um acréscimo de 5%. Supondo quê o preêço atual seja R$ 200,00, qual será o preêço dessa mercadoria daqui a 3 anos?
aproximadamente R$ 231,52
7. (UFV-MG) A viação No Leito do Asfalto faz a linha entre duas cidades quê distam 800 km uma da outra. Por questão de segurança, foram determinadas duas paradas obrigatórias para o revezamento dos motoristas. O primeiro trecho da viagem corresponde a 40% de todo o trajeto e o segundo trecho, a 55% do restante. Calcule:
a) A distância quê é percorrida no primeiro trecho da viagem.
320 km
b) A distância quê é percorrida no segundo trecho da viagem.
264 km
c) O tempo de percurso do terceiro trecho, caso o motorista mantenha uma velocidade média de 90 km/h.
2,4h ou 2h24min
8. (Enem/MEC) Em janeiro do ano passado, a direção de uma fábrica abriu uma creche para os filhos de seus funcionários, com 10 salas, cada uma com capacidade para atender 10 crianças a cada ano. As vagas são sorteadas entre os filhos dos funcionários inscritos, enquanto os não contemplados pelo sorteio formam uma lista de espera. No ano passado, a lista de espera teve 400 nomes e, neste ano, esse número cresceu 10%.
A direção da fábrica realizou uma pesquisa e constatou quê a lista de espera para o próximo ano terá a mesma quantidade de nomes da lista de espera dêste ano. Decidiu, então, construir, ao longo dêêsse ano, novas salas para a creche, também com capacidade de atendimento para 10 crianças cada, de modo quê o número de nomes na lista de espera no próximo ano seja 25% menor quê o dêste ano. O número mínimo de salas quê deverão sêr construídas é
a) 10.
b) 11.
c) 13.
d) 30.
e) 33.
alternativa b
9. Em uma loja, um aparelho de ar-condicionado custa R$ 8.000,00 à vista.
Vendido a prazo, o valor dêêsse aparelho sofre um acréscimo de 8%, e o total é dividido em duas prestações iguais. Qual é o valor de cada prestação?
R$ 4.320,00
10. (UFPel-RS) Uma raquete custa na loja A R$ 15,00 mais caro quê na loja B. O proprietário da loja A, percebendo a diferença, lança uma promoção oferecendo desconto de 10% para quê o preêço de sua mercadoria se torne o mesmo preêço da loja B. Quanto custa a raquete na loja B?
R$ 135,00
Página dezoito
11. (FGV-SP) Uma mercadoria, cujo preêço de tabéla é R$ 8.000,00, é vendida à vista com desconto de x%, ou em duas parcelas iguais de R$ 4.000,00, sêndo a primeira no ato da compra e a segunda um mês após a compra. Suponha quê o comprador dispõe do dinheiro necessário para pagar à vista e quê ele sabe quê a diferença entre o preêço à vista e a primeira parcela póde sêr aplicada no mercado financeiro a uma taxa de 25% ao mês. Nessas condições:
a) se x = 15, será vantajosa para ele a compra a prazo? Explique.
não
b) Qual é o valor de x quê torna indiferente comprar à vista ou a prazo? Explique.
x = 10
12. (hú éfe pê érre) Numa loja de automóveis usados, a comissão paga a cada um dos vendedores consiste num percentual sobre o total de vendas do vendedor mais um bônus por meta atingida, conforme a tabéla abaixo:
Total de vendas no mês |
Percentual sobre o total de vendas |
Bônus por meta atingida |
|---|---|---|
Até R$ 80.000,00 |
0,8% |
R$ 0,00 |
Entre R$ 80.000,00 e R$ 200.000,00 |
1,0% |
R$ 600,00 |
Acima de R$ 200.000,00 |
1,2% |
R$ 900,00 |
a) Qual é a comissão paga a um vendedor quê consegue vender R$ 120.000,00 em um mês?
R$ 1.800,00
b) Quanto um vendedor precisará vender em um mês para receber uma comissão de R$ 3.900,00?
R$ 250.000,00
c) Um dos vendedores apresentou uma reclamação ao gerente da loja porque havia recebido R$ 1.000,00 de comissão. Explique por quê esse valor está errado.
12. c) Uma resposta possível: Porque o valor mássimo de comissão correspondente à primeira faixa do total de vendas é R$ 640,00, e o valor mínimo de comissão correspondente à segunda faixa é R$ 1.400,00.
13. Uma mercadoria teve seu preêço reajustado em 18%. A pedido de um cliente, foi dado um desconto de 5% sobre o novo preêço, passando a mercadoria a custar R$ 302,50 a mais quê seu preêço inicial. Qual era o preêço inicial dessa mercadoria?
R$ 2.500,00
14. Amélia fixou em 18% o lucro sobre o preêço de custo de uma mercadoria quê comprou para revender. Sabendo quê o custo dessa mercadoria foi R$ 250,00, por quanto deverá sêr revendida?
R$ 295,00
15. Certa mercadoria foi comprada por R$ 860,00. Por quanto deve sêr revendida para quê o lucro seja de 20% sobre o preêço de custo?
R$ 1.032,00
16. Um comerciante comprou dez sacas de batatas por R$ 210,00. Por quanto ele deve revender cada saca para obtêr um lucro de 20% sobre o preêço de venda?
R$ 26,25
17. (PUCCamp-SP) O preêço pedido pêlos 18 volumes da enciclopédia Tesouro da Juventude em um sebo é uma verdadeira “pechincha”. Com os 17% de desconto já embutidos no preêço, a enciclopédia toda póde sêr comprada por R$ 478,08. Supondo quê cada volume tenha o mesmo preêço, conclui-se quê o preêço quê o sebo anunciou, por volume, antes do desconto, era de
a) R$ 28,00.
b) R$ 26,00.
c) R$ 38,00.
d) R$ 36,00.
e) R$ 32,00.
alternativa e
18. O preêço de um produto em uma loja é R$ 39,00. O dono da loja, mesmo pagando um imposto de 20% sobre o preêço de venda, obtém lucro de 30% sobre o preêço de custo. Qual é o preêço de custo dêêsse produto?
R$ 24,00
19. Qual é o preêço de custo de um produto vendido por R$ 240,00 em cuja transação o comerciante teve um lucro de 20% sobre a venda?
R$ 192,00
20. (Vunesp-SP) A diferença entre o preêço de venda anunciado de uma mercadoria e o preêço de custo é igual a R$ 2.000,00. Se essa mercadoria for vendida com um desconto de 10% sobre o preêço anunciado, dará ainda um lucro de 20% ao comerciante. Determine seu preêço de custo.
R$ 6.000,00
Página dezenove
Juros
No Brasil, existem duas modalidades de compra: com pagamento à vista e com pagamento a prazo. Resumindo, a compra à vista significa quê o valor total da mercadoria ou do serviço é pago no momento da compra; já a compra a prazo significa quê o valor total não é pago no ato da compra, é parcelado em prestações ou pago integralmente após um tempo.
A compra a prazo póde vir acompanhada de juro, de modo quê o valor a sêr pago ao final póde sêr maior do quê o valor à vista.
Acompanhe a situação a seguir.

O preêço à vista de uma geladeira é R$ 1.450,00. Bruno comprou essa geladeira e pagará todo o valor daqui a 30 dias, ou seja, um mês após a compra. Nessas condições, a loja cobrou juros de 8% sobre o preêço à vista.
Ao fazer essa compra, Bruno assumiu o compromisso de pagar um valor adicional chamado de juro, quê corresponde a uma porcentagem do preêço à vista e depende do prazo para pagamento.
Juro (J) é uma compensação financeira quê se paga pela utilização de uma quantia por determinado período.
Observe, por exemplo, uma maneira de calcular o valor adicional quê Bruno vai pagar na compra da geladeira. pôdêmos usar uma calculadora para fazer esse cálculo.

Ou seja, a loja cobrou R$ 116,00 de juros na venda dessa geladeira a prazo.
Além da palavra juro, os termos apresentados a seguir são muito freqüentes no estudo de Matemática financeira.
• Capital (C): quantia monetária investida ou disponível para investimento também denominada valor presente ou principal.
• Taxa de juros (i): taxa percentual quê se paga ou se recebe pela compensação da aplicação de um capital. Essa taxa deve vir acompanhada da unidade de tempo a quê se refere. Exemplo: 5% ao dia, quê póde sêr escrita como 5% a.d.; 2% ao mês ou 2% a.m.; 8% ao ano ou 8% a.a.
• Tempo (t): período quê decorre desde o início até o fim de uma operação financeira.
• Montante (M): investimento rentabilizado, ou seja, é o capital acrescido dos juros acumulados em determinado período (capital + juros). Também é denominado valor futuro.
Página vinte
Assim, o juro (J) é o valor obtído ao se aplicar uma taxa percentual (i) sobre um capital (C) em determinado período de tempo (t).
É importante observar quê, se a taxa i for mensal, o tempo t deverá sêr expresso em meses. Se i for uma taxa anual, t deverá sêr expresso em anos.
Saiba quê...
Nas operações financeiras, o tempo póde sêr classificado em:
• exato: usa o ano civil de 365 ou 366 (ano bissexto) dias, em quê os dias dos meses são contados pelo calendário (28, 29, 30 ou 31 dias).
• comercial: usa o ano comercial, no qual o mês tem sempre 30 dias, e o ano, 360 dias.
Neste Capítulo, caso não esteja indicado, vamos considerar o tempo comercial.
Juro simples
Nos tempos atuáis, raramente é adotado o regime de juro simples em transações. Quando utilizado, ele é praticado em operações de curtíssimos prazos, como cálculos de multas por atraso de pagamento, por exemplo, de faturas.
Denominamos juro simples aquele calculado sempre sobre o capital inicial.
Suponha, por exemplo, quê uma quantia de R$ 2.000,00 tenha sido aplicada a juro simples, segundo uma taxa de 4,5% ao mês, durante 3 meses. Para obtêr o valor correspondente aos juros nesse período, calculamos:
juros = + +
juros = 0,045 ⋅ 2.000 + 0,045 ⋅ 2.000 + 0,045 ⋅ 2.000
juros = (2.000 ⋅ 0,045) ⋅ 3 = 270
Portanto, nesse período, o capital de R$ 2.000,00 gerou R$ 270,00 de juros.
Como o juro simples (J) é diretamente proporcional ao capital (C), à taxa de juros (i) e ao tempo (t), podemos usar a seguinte relação:
J = C ⋅ i ⋅ t
Para determinar o montante, ou valor total obtído pela aplicação, adicionamos o juro ao capital, ou seja, utilizamos a relação:
M = C + J ou M = C + C ⋅ i ⋅ t ou M = C ⋅ (1 + i ⋅ t)
Aplicando essas relações à situação anterior, temos:
J = C ⋅ i ⋅ t
J = 2.000 ⋅ 0,045 ⋅ 3 = 270
Logo, M = C + J, ou seja, M = 2.000 + 270 = 2.270.
Portanto, ao final da aplicação, o montante será R$ 2.270,00.
Página vinte e um
ATIVIDADES RESOLVIDAS
8. Uma pessoa aplicou R$ 3.000,00 à taxa de 2% a.m. durante 5 meses no regime de juro simples.
a) Quanto receberá de juros ao final dêêsse período?
b) Que montante terá ao final dessa aplicação?
Resolução
a) Sendo C = 3.000, i = 2% = 0,02 e t = 5, temos:
J = 3.000 ⋅ 0,02 ⋅ 5 ⇒ J = 300
Portanto, a pessoa receberá R$ 300,00 de juros.
b) O montante é a soma do capital com os juros:
M = 3.000 + 300 ⇒ M = 3.300
Logo, o montante será R$ 3.300,00.
9. (Unimontes-MG) A quê taxa mensal de juros simples um capital de R$ 500,00, aplicado durante 10 meses, produz R$ 150,00 de juros?
Resolução
Seja i a taxa mensal de juro simples dessa aplicação. Pelo enunciado, temos:
• juro J obtído na aplicação: R$ 150,00;
• capital C aplicado: R$ 500,00;
• tempo t de aplicação: 10 meses.
Substituindo esses valores em J = C ⋅ i ⋅ t, obtemos:
150 = 500 ⋅ i ⋅ 10 ⇒ 150 = 5.000 ⋅ i ⇒ i = ⇒ i = 0,03 ⇒ i = 3%
Portanto, a taxa i mensal de juros simples deve sêr 3%.
ATIVIDADES
21. (UEA-AM) Ronaldo fez um empréstimo de R$ 1.000,00. Ao final do primeiro mês, foram aplicados juros de 10% sobre o valor da dívida, e ele fez um pagamento de R$ 300,00. Ao final do segundo mês, foram aplicados juros de 10% sobre o saldo da dívida, e ele fez um pagamento de R$ 500,00. Ao final do terceiro mês, foram aplicados juros de 10% sobre o saldo da dívida, e ele fez um pagamento para quitá-la. O valor do último pagamento feito por Ronaldo foi de
a) R$ 418,00.
b) R$ 309,00.
c) R$ 500,00.
d) R$ 531,00.
e) R$ 200,00.
alternativa a
22. (ITA-SP) Uma loja oferece um computador e uma impressora por R$ 3.000,00 à vista ou por 20% do valor à vista como entrada e mais um pagamento de R$ 2.760,00 após 5 meses. Qual é a taxa de juro simples cobrada?
3% a.m.
23. Qual é o juro simples quê um capital de R$ 7.000,00 rende quando aplicado:
a) durante 4 meses, a uma taxa de 2,5% a.m.?
R$ 700,00
b) durante 1 ano, a uma taxa de 3% a.m.?
R$ 2.520,00
c) durante 3 meses, a uma taxa de 0,15% a.d.?
R$ 945,00
24. (Ufop-MG) José deposita mensalmente em um fundo, a partir de 1º de janeiro, a quantia de 200 reais, a juros simples de 1,5% ao mês. Calcule o seu montante no fim de um ano, para um total de 12 depósitos.
R$ 2.634,00
25. Calcule o juro simples quê um capital de R$ 1.800,00 rende à taxa de 2,7% a.m., quando aplicado durante 2 meses.
R$ 97,20
26. Calcule o capital quê se deve empregar à taxa de 6% a.m., a juro simples, para obtêr
R$ 6.000,00 de juros em 4 meses.
R$ 25.000,00
27. Determine o montante obtído na aplicação de um capital de R$ 12.000,00, à taxa de 1,5% ao mês, a juro simples, pelo prazo de 9 meses.
R$ 13.620,00
28. Um capital de R$ 8.000,00, aplicado durante 6 meses, resulta em um montante de
R$ 9.200,00. Determine a taxa mensal de juro simples dessa aplicação.
2,5% a.m.
Página vinte e dois
Juro compôzto
A maioria das operações financeiras, como compras a médio e a longo prazo, compras com cartão de crédito, aplicações financeiras, empréstimos bancários, entre outras, utiliza o regime de juro compôzto, também conhecido como juro sobre juro.

Denominamos juro compôzto o valor de juro gerado em um período e incorporado ao capital, passando a participar da composição de juro no período seguinte.
Acompanhe a situação a seguir.
Mariana investiu R$ 800,00 à taxa de 0,8% ao mês, durante 4 meses, no regime de juro compôzto. Quanto Mariana terá ao final dessa aplicação?
No regime de juro compôzto, devemos considerar o juro calculado em cada período e adicioná-lo ao capital anterior para constituir um novo capital, sobre o qual será calculado o juro do período posterior. Nesse exemplo, temos o seguinte:
• Cálculo do juro obtído no 1º mês:
0,8% de 800 = 0,008 ⋅ 800 = 6,40
800 + 6,40 = 806,40 (montante do 1º mês)
Ao final do 1º mês, Mariana terá R$ 806,40.
• Cálculo do juro obtído no 2º mês:
0,8% de 806,40 = 0,008 ⋅ 806,40 ≃ 6,45
806,40 + 6,45 = 812,85 (montante do 2º mês)
Ao final do 2º mês, Mariana terá R$ 812,85.
• Cálculo do juro obtído no 3º mês:
0,8% de 812,85 = 0,008 ⋅ 812,85 ≃ 6,50
812,85 + 6,50 = 819,35 (montante do 3º mês)
Ao final do 3º mês, Mariana terá R$ 819,35.
• Cálculo do juro obtído no 4º mês:
0,8% de 819,35 = 0,008 ⋅ 819,35 ≃ 6,55
819,35 + 6,55 = 825,90 (montante do 4º mês)
Assim, ao final do 4º mês, Mariana terá R$ 825,90.
Pense e responda
Observe o cálculo do montante de Mariana no 2º mês. Veja quê o juro obtído é um valor aproximado e, mesmo assim, afirmamos quê Mariana terá uma quantia exata com duas casas decimais. Pense na situação real e explique por quê isso acontece.
Ver as Orientações para o professor.
Página vinte e três
Pense e responda
Suponha essa mesma quantia aplicada em regime de juro simples, considerando uma taxa de 0,8% ao mês, durante 4 meses. Use uma calculadora para determinar o montante obtído nessa situação e o compare com o valor obtído na aplicação feita por Mariana. O quê você observa?
R$ 825,60. É um valor menor quando comparado ao montante obtído considerando a mesma taxa e o mesmo período em regime de juro compôzto.
Observe quê a maneira apresentada para resolver esse problema é trabalhosa e necessita de muitos passos para quê seja ôbitída a resposta. Imagine realizar esse cálculo se Mariana deixar essa quantia aplicada por um período de 36 meses.
Vamos, agora, obtêr uma fórmula quê deixará a resolução mais prática.
Considere M o montante de um capital C aplicado em um regime de juro compôzto a uma taxa i.
Como M = C + J = C + C ⋅ i, temos:
• Montante obtído no 1º período:
M1 = C + C ⋅ i = C(1 + i) ⇒ M1 = C(1 + i)
• Montante obtído no 2º período:
M2 = M1 + M1 ⋅ i = M1(1 + i) = C(1 + i)(1 + i) = C(1 + i)2 ⇒ M2 = C(1 + i)2
• Montante obtído no 3º período:
M3 = M2 + M2 ⋅ i = M2(1 + i) = C(1 + i)2 (1 + i) = C(1 + i)3 ⇒ M3 = C(1 + i)3
• Montante obtído no 4º período
M4 = M3 + M3 ⋅ i = M3(1 + i) = C(1 + i)3 (1 + i) = C(1 + i)4 ⇒ M4 = C(1 + i)4
Considerando uma quantidade de períodos t, o montante obtído nesse período póde sêr calculado pela expressão:
M = C(1 + i)t
Utilizando a fórmula apresentada para calcular o montante obtído na aplicação feita por Mariana, temos:
M = 800 ⋅ (1 + 0,008)4 ⇒ M = 800 ⋅ (1,008)4
pôdêmos realizar esse cálculo utilizando uma calculadora científica, como indicado a seguir.
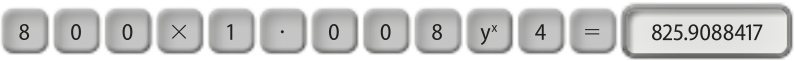
Logo, o montante obtído por Mariana ao final dessa aplicação será aproximadamente R$ 825,91.
Lembre-se de quê, quando fazemos aproximações, podemos obtêr diferentes resultados para um mesmo problema. Compare, por exemplo, o resultado obtído por meio da expressão com os cálculos anteriores.
Muitas vezes temos o capital e o montante e desejamos saber o juro obtído na aplicação. Se necessário, podemos calcular o valor do juro utilizando a fórmula M = C + J, pela qual temos:
J = M − C
Saiba quê...
Utilizar uma calculadora científica em situações envolvendo juro compôzto torna os cálculos mais práticos. Em alguns modelos de calculadora científica, é necessário realizar primeiro o cálculo envolvendo a potenciação e, posteriormente, multiplicar o resultado pelo capital.
Página vinte e quatro
Juros e funções
Existe uma inter-relação entre o juro simples e a função afim e entre o juro compôzto e a função exponencial, como veremos a seguir.
Um capital de R$ 1.000,00 foi aplicado a uma taxa de 12% ao ano. Vamos calcular o montante obtído, ano a ano, para os regimes de juro simples e de juro compôzto e analisar os resultados.
Para calcular o montante, ano a ano, da aplicação em regime de juro simples, vamos utilizar a relação M = C + C ⋅ i ⋅ t, na qual, ao substituirmos os valores C = 1.000 e i = 0,12, obtemos:
M = 1.000 + 1.000 ⋅ 0,12 ⋅ t, ou seja, M = 1.000 + 120t
Observamos quê a expressão ôbitída é a lei de uma função afim, com variável dependente M e variável independente t. Atribuindo a t os valores 1, 2, 3, 4, 5, ..., obtemos os valores correspondentes de M:
t (em ano) |
1 |
2 |
3 |
4 |
5 |
… |
|---|---|---|---|---|---|---|
M (em reais) |
1.120 |
1.240 |
1.360 |
1.480 |
1.600 |
… |
Nesse caso, os valores do montante obtidos, ano a ano, são termos da progressão aritmética (1.120, 1.240, 1.360, 1.480, 1.600, …), de razão r = 120, com termo geral an = 1.000 + 120n, correspondente à lei de uma função afim, com n restrito ao conjunto dos números naturais não nulos.
Assim, dados o capital e a taxa de juros, o montante obtído pelo regime de juro simples relaciona-se com a ideia de função afim, na qual o montante varia em função do tempo. Como isso ocorre para todos os casos em quê há regime de juro simples, podemos associar o cálculo do montante à lei da função afim dada por: M = C + C ⋅ i ⋅ t
Considerando a situação enunciada, na qual o capital de R$ 1.000,00 é aplicado à taxa de 12% ao ano, o montante, a juro compôzto, póde sêr obtído pela relação:
M = 1.000(1 + 0,12)t, ou seja, M = 1.000 ⋅ 1,12t
Observamos quê a expressão ôbitída é a lei de uma função exponencial, com variável dependente M e variável independente t. Atribuindo a t os valores 1, 2, 3, 4, 5, …, obtemos os valores correspondentes de M:
t (em ano) |
1 |
2 |
3 |
4 |
5 |
… |
|---|---|---|---|---|---|---|
M (em reais) |
1.120 |
1.254,40 |
1.404,93 |
1.573,52 |
1.762,34 |
… |
Nesse caso, os valores do montante obtído, ano a ano, são termos da progressão geométrica (1.120; 1.254,40; 1.404,93; 1.573,52; 1.762,34; …), de razão q = 1,12, com termo geral an = 1.000 ⋅ (1,12) n, correspondente à lei de uma função exponencial, com n restrito ao conjunto dos números naturais não nulos.
Página vinte e cinco
Assim, dados o capital e a taxa de juros, o montante obtído pelo regime de juro compôzto relaciona-se à ideia de função exponencial, na qual o montante varia em função do tempo. Como isso ocorre para todos os casos em quê há regime de juro compôzto, podemos associar o cálculo do montante à lei da função exponencial dada por M = C(1 + i)t.
Vamos, agora, analisar o gráfico das duas funções em um mesmo plano cartesiano e analisar os valores obtidos.
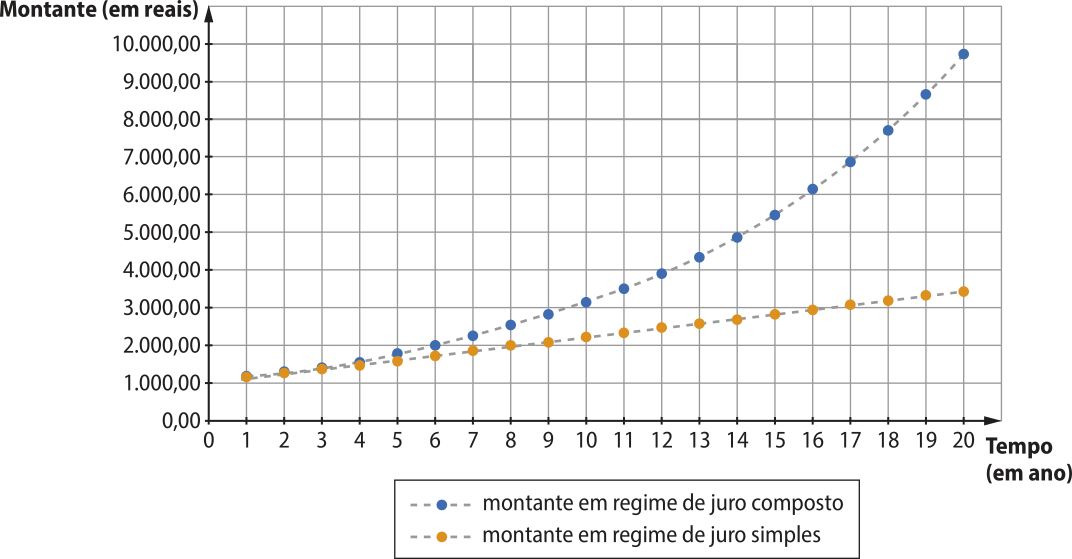
No gráfico estão indicados alguns pontos pertencentes aos gráficos das funções. Note quê não traçamos a reta nem a curva da função exponencial com linhas contínuas, pois o domínio de ambas as funções é ℕ*. O tracejado apenas indica a tendência da curva e auxilia na visualização dos resultados.
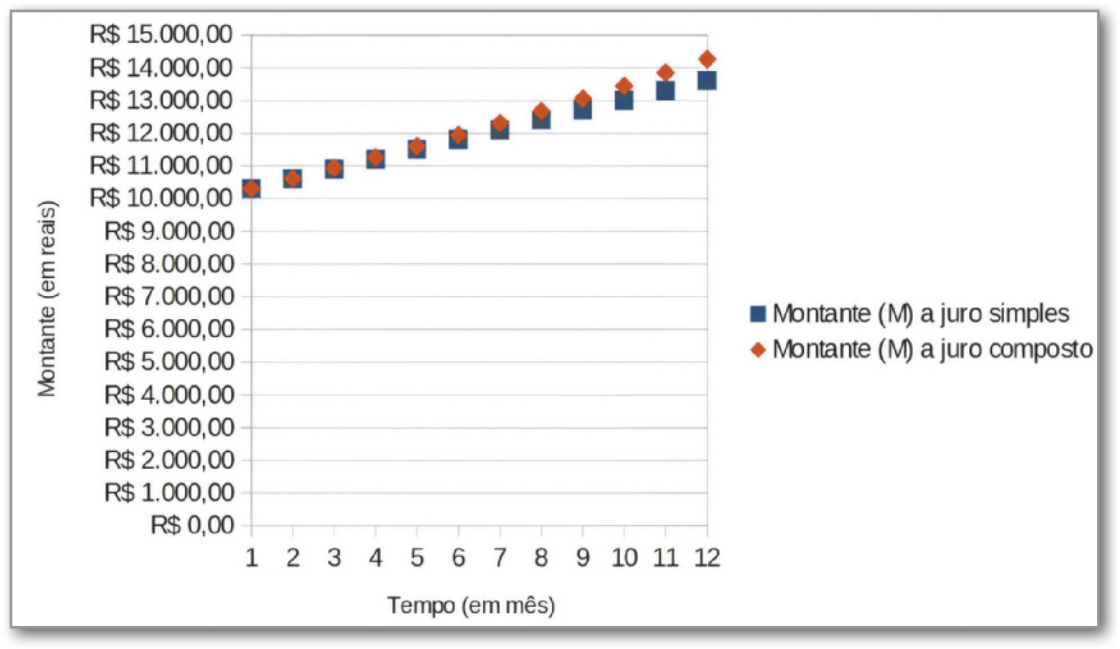
Observando os gráficos, percebemos quê, para t = 1, o montante obtído é o mesmo para os dois regimes de juro. A partir daí, quanto maior o tempo de aplicação, maior a diferença entre os montantes obtidos no regime de juro compôzto e no de juro simples.
Assim, para o caso de um investimento, a rentabilidade em regime de juro compôzto será maior do quê a rentabilidade em regime de juro simples a partir do segundo período de investimento. Se a situação for de empréstimo, a dívida aumenta mais a cada período, a partir do segundo, no regime de juro compôzto em relação ao mesmo empréstimo em regime de juro simples.
Para acessar
• VENTURA, Dalia. O quê são juros compostos, a"bola de neve" matemática da qual os super-ricos tiram proveito. BBC nius Brasil, [s. l.], 26 fev. 2023. Disponível em: https://livro.pw/ulnpj. Acesso em: 26 set. 2024.
A reportagem explora o conceito de juro compôzto, destacando seu crescimento exponencial por meio de exemplos.
Página vinte e seis
ATIVIDADES RESOLVIDAS
10. Um investidor aplicou R$ 500.000,00 a juros compostos de 2% ao mês. Quantos reais ele terá após 5 meses de aplicação? Qual será o valor dos juros obtidos?
Resolução
Utilizando a expressão apresentada, determinamos o montante obtído pelo investidor após 5 meses de aplicação.
M = C(1 + i)t ⇒ M = 500.000 ⋅ (1 + 0,02)5 ⇒ M ≃ 552.040,40
Para calcular o juro obtído, utilizamos a expressão J = M − C.
J = 552.040,40 − 500.000,00
J = 52.040,40
Assim, após 5 meses, o investidor terá R$ 552.040,40, e os juros obtidos serão de R$ 52.040,40.
11. (Vunesp-SP) Um capital de R$ 1.000,00 é aplicado durante 4 meses.
a) Encontre o rendimento de aplicação, no período, considerando a taxa de juro simples de 10% ao mês.
b) Determine o rendimento da aplicação, no período, considerando a taxa de juro compôzto de 10% ao mês.
Resolução
Do enunciado, temos C = 1.000, t = 4 meses, e a taxa, em ambos os casos, é i = 10%.
a) Para o cálculo do rendimento no regime de juro simples, temos:
J = C ⋅ i ⋅ t ⇒ J = 1.000 ⋅ 0,1 ⋅ 4 = 400
O rendimento da aplicação ao final de 4 meses no regime de juro simples será R$ 400,00.
b) Para o cálculo do montante no regime de juro compôzto, temos:
M = C(1 + i)t ⇒ M = 1.000 ⋅ (1 + 0,1)4 = 1.000 ⋅ 1,14 = 1.464,1
Porém, como devemos encontrar o rendimento, temos:
J = M − C ⇒ J = 1.464,1 − 1.000 = 464,1
O rendimento da aplicação, ao final de 4 meses, no regime de juro compôzto, será R$ 464,10.
12. Calcule o valor dos juros compostos quê o banco cobra em um empréstimo de
R$ 25.000,00 a 26% ao ano durante 24 meses.
Resolução
Inicialmente, vamos calcular o montante dêêsse empréstimo. Do enunciado, temos:
C = 25.000; i = 26% a.a. = 0,26 a.a.; t = 24 meses = 2 anos
Usando a fórmula do montante, obtemos o valor de M:
M = C(1 + i)t ⇒ M = 25.000 ⋅ (1 + 0,26)2 ⇒ M = 25.000 ⋅ (1,26)2 ⇒ M = 39.690
Como M = C + J, temos:
J = M − C ⇒ J = 39.690 − 25.000 = 14.690
Portanto, o banco cobra R$ 14.690,00 de juros.
13. ![]() Por quanto tempo Jorge deve deixar aplicada a quantia de R$ 6.000,00 para quê ela gere um montante de R$ 9.348,00, quando aplicada à taxa de 3% ao mês no regime de juro compôzto?
Por quanto tempo Jorge deve deixar aplicada a quantia de R$ 6.000,00 para quê ela gere um montante de R$ 9.348,00, quando aplicada à taxa de 3% ao mês no regime de juro compôzto?
Resolução
Os dados do problema são: C = 6.000, M = 9.348 e i = 3% a.m.
Usando a fórmula do montante, temos:
M = C(1 + i)t
Logo: 9.348 = 6.000 ⋅ (1 + 0,03)t
Assim: (1,03)t = ⇒ (1,03)t = 1,558 ⇒ t = log1,031,558
Aplicando a propriedade de mudança de base, temos:
t =
Utilizando uma calculadora científica, obtemos os valores dos logaritmos:
log 1,588 ≃ 0,19257 e log 1,03 ≃ 0,01284
Assim:
t ≃ ≃ 15
Portanto, Jorge deve aplicar seu capital por 15 meses.
Página vinte e sete
ATIVIDADES
29. ![]() Um investidor aplicou a quantia de R$ 200.000,00 à taxa de juro compôzto de 0,7% ao mês. Que montante esse capital vai gerar após 6 meses?
Um investidor aplicou a quantia de R$ 200.000,00 à taxa de juro compôzto de 0,7% ao mês. Que montante esse capital vai gerar após 6 meses?
aproximadamente R$ 208.548,38
30. Um capital de R$ 20.000,00 foi aplicado a juro compôzto durante oito meses à taxa mensal de 0,6% ao mês. Que montante será obtído ao final dessa aplicação? (Use: 1,0068 ≃ 1,0490.)
aproximadamente R$ 20.980,00
31. ![]() Valter fez um empréstimo no banco no valor de R$ 30.000,00 pelo prazo de 24 meses. Sabendo quê a taxa de juros compostos cobrada pelo banco é 0,95% a.m., qual é o montante quê ele pagará ao final do empréstimo?
Valter fez um empréstimo no banco no valor de R$ 30.000,00 pelo prazo de 24 meses. Sabendo quê a taxa de juros compostos cobrada pelo banco é 0,95% a.m., qual é o montante quê ele pagará ao final do empréstimo?
aproximadamente R$ 37.642,03
32. ![]() Qual é o valor a sêr aplicado hoje, a uma taxa de juro compôzto de 2% a.m., para quê uma pessoa receba R$ 8.000,00 ao final de 6 meses?
Qual é o valor a sêr aplicado hoje, a uma taxa de juro compôzto de 2% a.m., para quê uma pessoa receba R$ 8.000,00 ao final de 6 meses?
aproximadamente R$ 7.103,77
33. João deseja comprar um carro cujo preêço à vista, com todos os descontos possíveis, é R$ 21.000,00, valor quê não será reajustado nos próximos meses. Ele tem R$ 20.000,00, quê podem sêr aplicados a uma taxa de juro compôzto de 2% ao mês, e escolhe deixar todo o seu dinheiro aplicado até quê o montante atinja o valor do carro.
Para ter o carro, João deverá esperar:
a) dois meses e terá a quantia exata.
b) três meses e terá a quantia exata.
c) três meses e ainda sobrarão, aproximadamente, R$ 225,00.
d) quatro meses e terá a quantia exata.
e) quatro meses e ainda sobrarão, aproximadamente, R$ 430,00.
alternativa c
34. ![]() Luís vai aplicar certa quantia em um fundo imobiliário a uma taxa de juro compôzto de 5% a.a., ele deseja quê, após 6 anos, essa quantia gere um montante de R$ 25.000,00. Qual valor aproximadamente Luís deve aplicar?
Luís vai aplicar certa quantia em um fundo imobiliário a uma taxa de juro compôzto de 5% a.a., ele deseja quê, após 6 anos, essa quantia gere um montante de R$ 25.000,00. Qual valor aproximadamente Luís deve aplicar?
a) R$ 18.000,00.
b) R$ 18.655,38.
c) R$ 18.910,15.
d) R$ 19.328,45.
e) R$ 19.230,77.
alternativa b
35. Celina aplicou R$ 40.000,00 em um banco, a juros compostos de 16% a.a., capitalizados anualmente. Qual é o valor dos juros obtído ao final de 2 anos?
aproximadamente R$ 13.824,00
36. ![]() Qual é o montante quê um capital de R$ 4.000,00 produz quando aplicado:
Qual é o montante quê um capital de R$ 4.000,00 produz quando aplicado:
a) durante 3 meses, a uma taxa de 4% a.m. de juro compôzto?
aproximadamente R$ 4.499,46
b) durante 10 anos, a uma taxa de 2% a.m. de juro compôzto?
aproximadamente R$ 43.060,65
c) durante 15 meses, a uma taxa de 0,02% a.d. de juro compôzto?
aproximadamente R$ 4.376,66
37. ![]() Cláudio aplicou R$ 5.000,00 à taxa de 3% ao mês durante 5 meses. Que montante esse capital vai gerar, se o regime for de juro compôzto? Quantos reais de juro ele obterá nessa operação?
Cláudio aplicou R$ 5.000,00 à taxa de 3% ao mês durante 5 meses. Que montante esse capital vai gerar, se o regime for de juro compôzto? Quantos reais de juro ele obterá nessa operação?
aproximadamente R$ 5.796,37;
aproximadamente R$ 796,37
38. (Saresp-SP) Um negociante pediu emprestados R$ 2.000,00 por três meses, sêndo R$ 1.000,00 de um amigo e R$ 1.000,00 de uma casa bancária. O amigo lhe propôs cobrar juros simples, à taxa de 10% ao mês. A casa bancária impôs a cobrança de juros compostos à taxa de 10% ao mês.
Veja, na tabéla abaixo, a evolução mensal da dívida, com valores em reais.
Capital |
Dívida após 1 mês |
Dívida após 2 meses |
Dívida após 3 meses |
|
|---|---|---|---|---|
Amigo |
1.000 |
1.100 |
1.200 |
1.300 |
Banco |
1.000 |
1.100 |
1.210 |
1.331 |
É correto afirmar quê esses valores formam uma progressão:
a) aritmética de razão R$ 100,00 na casa bancária e geométrica de razão R$ 100,00 com seu amigo.
b) geométrica de razão 10 na casa bancária e aritmética de razão 10 com seu amigo.
c) geométrica de razão 10 com seu amigo e aritmética de razão 10 na casa bancária.
d) aritmética de razão R$ 100,00 com seu amigo e geométrica de razão 1,1 na casa bancária.
alternativa d
Página vinte e oito
39. João aplicou seu capital durante 3 anos, à taxa de 12% a.a., no regime de juro simples. Caso houvesse aplicado a juro compôzto, à mesma taxa, teria recebido R$ 2.633,36 a mais. Quantos reais João recebeu de juros?
aproximadamente R$ 1.544,49
40. (Vunesp-SP) Cássia aplicou o capital de R$ 15.000,00 a juros compostos, pelo período de 10 meses e à taxa de 2% a.m. (ao mês). Considerando a aproximação (1,02)5 = 1,1, Cássia computou o valor aproximado do montante a sêr recebido ao final da aplicação. Esse valor é:
a) R$ 18.750,00
b) R$ 18.150,00
c) R$ 17.250,00
d) R$ 17.150,00
e) R$ 16.500,00
alternativa b
41. (FGV-SP) César aplicou R$ 10.000,00 num fundo de investimentos quê rende juros compostos a uma certa taxa de juro anual positiva i. Após um ano, ele saca dêêsse fundo R$ 7.000,00 e deixa o restante aplicado por mais um ano, quando verifica quê o saldo é R$ 6.000,00. O valor de (4i − 1)² é:
a) 0,01
b) 0,02
c) 0,03
d) 0,04
e) 0,05
alternativa d
42. (í éfi cê ê) Um capital foi aplicado a uma taxa anual de juros compostos e rende um montante de R$ 2.012,85 em 2 anos e um montante de R$ 2.314,77 em 3 anos. Indique o valor aproximado do capital investido.
a) R$ 1.102,00
b) R$ 1.237,00
c) R$ 1.522,00
d) R$ 1.933,00
e) R$ 1.252,00
alternativa c
43. ![]() Uma pessoa aplicou R$ 18.000,00 à taxa de juro compôzto de 2,81% ao mês e obteve um rendimento de R$ 6.390,00. Qual é o prazo dessa aplicação?
Uma pessoa aplicou R$ 18.000,00 à taxa de juro compôzto de 2,81% ao mês e obteve um rendimento de R$ 6.390,00. Qual é o prazo dessa aplicação?
aproximadamente 11 meses
44. ![]() Qual é a taxa mensal de juro compôzto quê, aplicada ao capital de R$ 24.000,00, o transforma em um montante de R$ 36.087,00 em 7 meses?
Qual é a taxa mensal de juro compôzto quê, aplicada ao capital de R$ 24.000,00, o transforma em um montante de R$ 36.087,00 em 7 meses?
6% ao mês
45. (UFS-SE) Para analisar a veracidade das afirmações abaixo, considere quê para estimar o crescimento populacional dos municípios de cérto Estado é usada a expressão P(t) = P(0) ⋅ (1 + i)t, em quê P(0) é a população considerada em cérto ano, P(t) a população observada t anos depois e i a taxa anual de crescimento da população.
I. Se em 2004 um município dêêsse Estado tinha 50.000 habitantes e, a partir dêêsse ano, a população aumentou anualmente à taxa de 2%, então em 2007 tal município deverá ter 50.604 habitantes.
F
II. Sabe-se quê, anualmente, a população de um município X cresce à taxa de 2%, enquanto quê a de um município Y cresce à taxa de 5%. Se hoje X e Y têm, respectivamente, 19.600 e 28.900 habitantes, daqui a dois anos a razão entre seus respectivos números de habitantes será .
F
III. Atualmente, os municípios X e Y têm 129.600 e 122.500 habitantes, respectivamente. Supondo quê a população de X cresça a uma taxa anual de 5% e a de Y cresça a uma taxa anual de 8%, então daqui a dois anos X e Y terão o mesmo número de habitantes.
V
IV. A taxa anual de crescimento da população de um município póde sêr calculada pela expressão i = − 1.
F
V. Se atualmente um município tem 44.100 habitantes e nos últimos cinco anos sua população cresceu à taxa anual de 5%, então há dois anos o seu número de habitantes era menor quê 42.000.
V
46. ![]() Um investidor aplicou R$ 80.000,00 a juros compostos de 2,2% ao mês.
Um investidor aplicou R$ 80.000,00 a juros compostos de 2,2% ao mês.
a) Daqui a quantos meses terá um montante de R$ 85.400,00?
aproximadamente 3 meses
b) Após quantos anos terá um montante de R$ 134.868,80?
aproximadamente 2 anos
Página vinte e nove
47. (UFPel-RS) Um dos motivos quê leva as pessoas a enfrentarem o problema do desemprego é a busca, por parte das empresas, de mão de obra qualificada, dispensando funcionários não habilitados e pagando a indenização a quê têm direito. Um funcionário quê vivenciou tal problema recebeu uma indenização de R$ 57.000,00 em três parcelas, em quê a razão da primeira para a segunda é de e a razão da segunda para a terceira, de .
(Dados: log 1,06 = 0,0253; log 1,01 = 0,0043.)
Com base no texto e em seus conhecimentos, determine:
a) o valor de cada parcela;
R$ 12.000,00;
R$ 15.000,00;
R$ 30.000,00
b) o tempo necessário para quê o funcionário aplique o valor da primeira parcela, a juro compôzto, a uma taxa de 1% ao mês, para acumular um montante de R$ 12.738,00;
aproximadamente 6 meses
c) a taxa mensal quê deve sêr aplicada, a juro simples, à segunda parcela, para quê o funcionário, no final de 2 anos, obtenha o montante de R$ 25.800,00.
3% a.m.
48. ![]() Observe, no qüadro a seguir, os juros do cartão de crédito e do cheque especial vigentes em março de 2024.
Observe, no qüadro a seguir, os juros do cartão de crédito e do cheque especial vigentes em março de 2024.
Modalidade |
Taxa (em % ao ano) |
|---|---|
Cartão de crédito |
421,3 |
Cheque especial |
127,6 |
Fonte dos dados: MARTELLO, Alexandro. Cartão de crédito: juro volta a subir em março, mesmo com medida quê limita dívida no rotativo. G1, Brasília, DF, 3 maio 2024. Disponível em: https://livro.pw/dkysl Acesso em: 23 out. 2024.
De acôr-do com o conteúdo estudado, elabore um problema utilizando os dados dêêsse qüadro. Depois, troque-o com um colega, para quê ele resôuva seu problema, enquanto você resólve o problema elaborado por ele. Compare as taxas apresentadas e converse com familiares, côlégas e o professor sobre o cuidado quê devemos ter ao usar essas modalidades de crédito.
Resposta pessoal.
49. (UECE) Um investidor aplicou, no sistema de juros compostos, certa quantia em uma instituição financeira quê remunera as aplicações à taxa de 1% mensal. Assim, é correto afirmar quê o número de meses, a partir da aplicação, em quê o capital inicial será dobrado é igual a
a) 74.
b) 68.
c) 72.
d) 70.
Use os valores aproximados: log(1,01) = 0,0043 e log(2) = 0,30103.
alternativa d
50. (hú- hê- érre jota) Os clientes de um banco podem realizar apenas duas operações financeiras:
• fazer investimentos quê rendem juros compostos a uma taxa mensal de 1%; ou
• pegar empréstimos com juros compostos a uma taxa mensal de 5%.
O banco usa o dinheiro dos investimentos para conceder os empréstimos, obtendo lucro nessas transações.
Considere quê um cliente X investiu R$ 1.000,00 e quê o banco emprestou esse valor a um cliente Y. Após 12 meses, o cliente X recebeu o montante pela aplicação nesse período e Y quitou o empréstimo.
Admitindo (1,01) 12 = 1,13 e (1,05) 12 = 1,80, o lucro, em reais, obtído pelo banco com essas duas operações financeiras é igual a:
a) 470
c) 670
b) 520
d) 820
alternativa c
51. (UECE) Ana Sofia foi às compras dispondo de R$ 300,00. Ao entrar em uma loja magazine, gostou de uma blusa no valor de R$ 180,00 e de uma sandália quê custava R$ 130,00. O custo das duas peças excedia o dinheiro de quê Ana Sofia dispunha. O vendedor informou quê uma promoção da loja garantia quê, se ela comprasse as duas peças, teria um desconto de 15% na peça de maior valor e 20% na peça de menor valor. Tendo aceitado a promoção, após o pagamento, Ana Sofia recebeu um Trôco correspondente a x% do quê dispunha ao entrar na loja. O valor de x está entre:
a) 14 e 15.
b) 12 e 13.
c) 15 e 16.
d) 13 e 14.
alternativa a
Página trinta
EXPLORANDO A TECNOLOGIA
Conhecendo a planilha eletrônica
A planilha eletrônica é uma ferramenta muito útil em diversas situações do dia a dia e na resolução de problemas matemáticos. Com ela, cálculos recorrentes, por exemplo, podem sêr feitos rapidamente com a criação de uma fórmula adequada ou utilizando uma fórmula disponível no banco de dados do software.
Existem planilhas eletrônicas de diversos fabricantes, mas todas elas funcionam de maneira muito semelhante. Aqui, vamos utilizar a planilha eletrônica do LibreOffice, quê póde sêr baixada gratuitamente no sáiti oficial https://livro.pw/nigol (acesso em: 26 set. 2024).
Cálculo de juros
Leia o problema a seguir.
Sandro aplicou um capital (C) de R$ 10.000,00 em dezembro de 2023 a uma taxa de juros (i) de 3% a.m. Ao final de dezembro de 2024, Sandro verificou seu extrato. Considerando os montantes obtidos do regime de juro compôzto e do regime de juro simples, qual foi a diferença, em reais, entre esses montantes?
Agora, siga os passos quê podem sêr realizados para resolver esse problema usando uma planilha eletrônica.
I. Abra uma planilha no LibreOffice e organize as colunas da planilha, digitando “Mês”, “Tempo (t)”, “Montante (M) a juro simples” e “Montante (M) a juro composto”, como indicado a seguir.
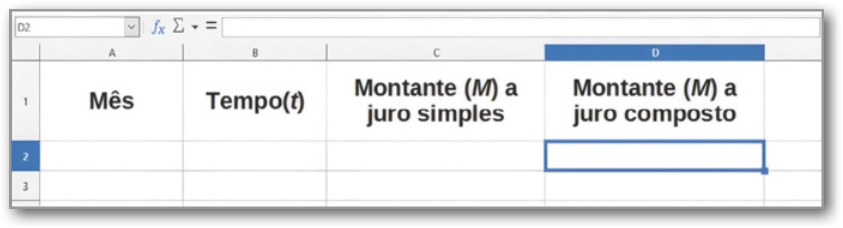
II. Digite o nome dos meses do ano e o número correspondente a cada mês.
Conforme estudamos, o montante (M) em regime de juro simples póde sêr obtído por meio da relação M = C ⋅ (1 + i ⋅ t) e, em regime de juro compôzto, póde sêr obtído por M = C ⋅ (1 + i)t.
Página trinta e um
Vamos utilizar essas fórmulas para realizar os cálculos, lembrando quê C é o capital, quê, nesse caso, é R$ 10.000,00, a taxa de juros (i) é 3% ou 0,03, e o tempo (t) será representado pelo número correspondente ao mês.
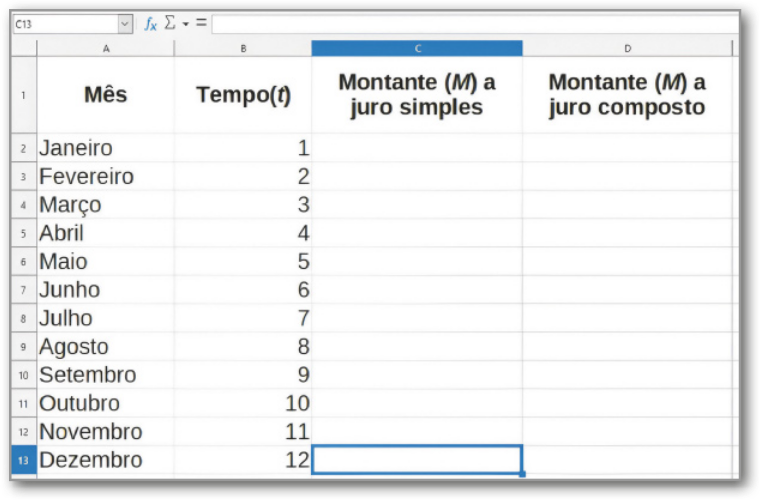
III. Para calcular o montante (M) em janeiro, em regime de juro simples, na célula C2, digite: “=10000*(1+0,03*B2)” e pressione Enter.
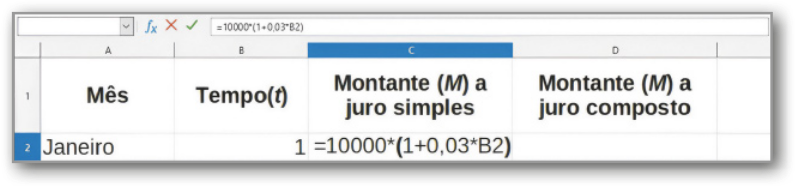
IV. Para calcular o montante (M) em janeiro, em regime de juro compôzto, na célula D2, digite: “=10000*(1+0,03)^B2” e pressione Enter.
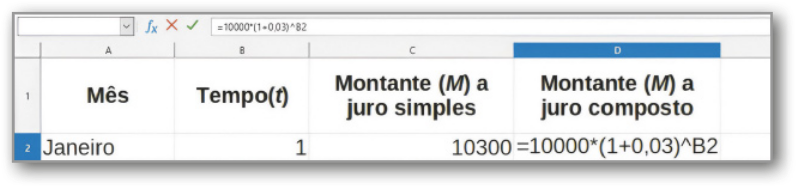
V. Para obtêr o montante (M) gerado nos demais meses, selecione as células C2 e D2 e, em seguida, clique no quadradinho destacado em vermelho, ![]() , arrastando a seleção até a linha de dezembro. Ainda com as células dos valores de montante selecionadas, para deixar os valores em formato monetário, clique na ferramenta Formatar como moeda:
, arrastando a seleção até a linha de dezembro. Ainda com as células dos valores de montante selecionadas, para deixar os valores em formato monetário, clique na ferramenta Formatar como moeda: ![]()
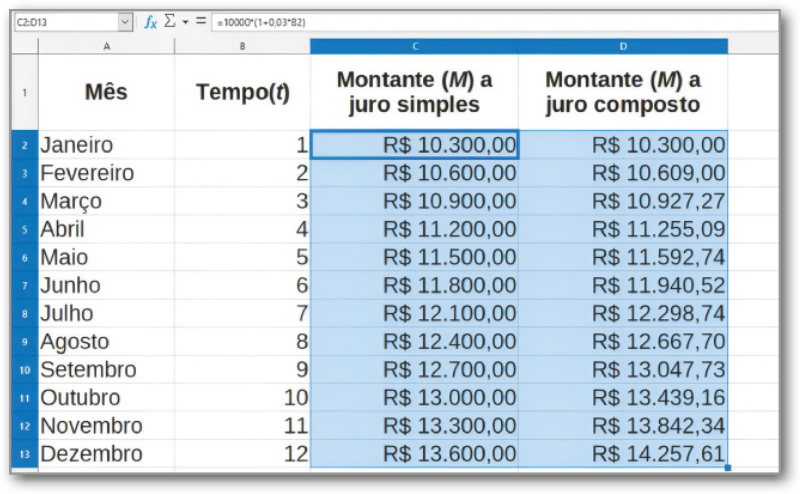
VI. Observe a planilha com os valores obtidos nesse passo a passo. Repare quê, pelo regime de juro compôzto, o montante obtído é maior do quê o obtído considerando o regime de juro simples, ainda quê o período e a taxa sêjam iguais em ambos os casos.
Página trinta e dois
Construindo gráficos
I. Primeiro, selecione as colunas referentes aos montantes. Para fazer isso, clique na célula C1, depois pressione e segure a tecla Shift e clique na célula D13.
II. Clique no menú Inserir e, em seguida, clique em Gráfico.... Uma janela de assistente de gráficos será aberta, como esta da imagem.
No assistente, você póde escolher o tipo de gráfico quê desejar. Vamos escolher gráfico de Linha e a opção Somente pontos. Em seguida clique em Finalizar.
III. Depois de inserir o gráfico, você póde personalizá-lo conforme necessário. Para isso você póde clicar com o botão direito sobre o elemento quê deseja personalizar. Por exemplo, po demos mudar a escala do eixo vertical e acrescentar nomes aos eixos. Dessa maneira, podemos obtêr um gráfico como o seguinte.
Agora, faça o quê se pede nas atividades a seguir.
1. Na situação apresentada, qual é a diferença, em reais, entre o montante obtído em dezembro em regime de juro compôzto e o obtído nesse mesmo mês em regime de juro simples?
R$ 657,61
2. No mês de janeiro, os valores do montante gerado em regime de juro simples e em regime de juro compôzto são iguais. Explique o motivo.
Resposta possível: Como o mês de janeiro corresponde a t = 1, ao substituirmos t por 1 na fórmula, em ambos os casos, obtemos M = C ⋅ (1 + i).
3. Construa uma planilha eletrônica para determinar o montante considerando um capital de R$ 20.000,00 aplicado a uma taxa de 2% a.m. Calcule o montante obtído ao final de um ano, considerando os dois sistemas: juro simples e juro compôzto.
juro simples: R$ 24.800,00; juro compôzto: aproximadamente R$ 25.364,84
Página trinta e três
Valor presente e valor futuro
O mundo financeiro póde parecer complékso, mas entender alguns conceitos póde ajudar a compreen-dê-lo melhor. Dois dêêsses conceitos são o valor presente e o valor futuro. Eles são fundamentais para entender como o dinheiro muda de valor ao longo do tempo.
O valor presente é o valor de um capital em determinado momento, enquanto o valor futuro é o valor dêêsse capital após cérto período de tempo, ou seja, o montante. É importante lembrar quê todo valor futuro inclui juros.
Vamos considerar uma situação prática. Imagine quê você esteja indeciso e não sabe se paga sua compra de R$ 200,00 hoje ou se paga R$ 220,00 daqui a um mês, pois póde utilizar essa quantia em outra despesa. Como saber qual seria a melhor opção? Para responder a essa pergunta, precisamos analisar o valor da quantia R$ 200,00 ao longo do tempo.
Suponha quê o banco no qual você tem uma conta lhe ofereceu um investimento quê faz seu dinheiro render 7% ao mês. E agora, o quê fazer? Paga sua compra de R$ 200,00 hoje ou investe esse valor a essa taxa e paga R$ 220,00 daqui a um mês?
Sabemos quê, no regime de juro compôzto, um capital C, aplicado por t período de tempo a uma taxa i, resulta em um montante M = C ⋅ (1 + i)t. Assim:
• o valor futuro (VF) de um capital é dado por:
VF = VP ⋅ (1 + i)t
• o valor presente (VP) de um capital é dado por:
VP =
Retomando a situação, aplicando a relação do valor futuro (VF), temos:
VF = 200 ⋅ (1 + 0,07)1 = 200 ⋅ 1,07 = 214
Logo, obtemos um valor futuro igual a R$ 214,00. Portanto, em vez de investir a quantia, seria mais vantajoso pagar R$ 200,00 hoje do quê R$ 220,00 daqui a um mês, pois o valor de R$ 200,00 aplicado a 7% ao mês será menor do quê R$ 220,00 após um mês.
Agora, considere outra situação. Lorena está planejando comprar uma moto quê custa R$ 30.000,00. No entanto, ela não tem esse valor disponível no momento. Assim, ela planeja economizar para comprar a moto daqui a 12 meses. Ela encontrou um investimento quê oferece uma taxa de juro compôzto de 5% ao mês. Quantos reais aproximadamente Lorena precisaria investir hoje para ter exatamente R$ 30.000,00 daqui a 12 meses?
Para responder a essa pergunta, podemos usar a relação do valor presente (VP):
VP = ≃ 16.705,12
Portanto, Lorena precisaria investir aproximadamente R$ 16.705,12 hoje em um investimento quê renda 5% ao mês para ter R$ 30.000,00 daqui a 12 meses.
Página trinta e quatro
ATIVIDADES RESOLVIDAS
14. Ao planejar a compra de um novo computador, uma pessoa tem as seguintes opções de pagamento:
• Opção 1: à vista, por R$ 3.000,00.
• Opção 2: em cinco prestações mensais de R$ 605,00 cada, com a primeira parcela paga no ato da compra.
Sabendo quê o dinheiro dessa pessoa rende 2% ao mês, qual seria a melhor opção para ela?
Resolução
Para saber a melhor opção, vamos construir esquemas de pagamento.
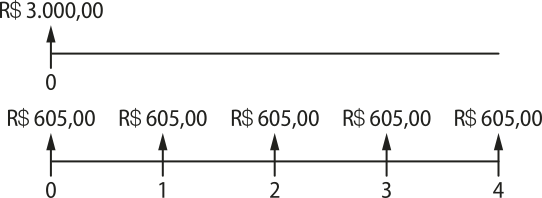
Em seguida, determinamos o valor presente dos conjuntos de pagamentos, considerando o período 0, e por fim comparamos as opções.
• Opção 1: 3.000
• Opção 2: 605 + ≃ 2.908,68
Portanto, optar pelo pagamento em cinco prestações é mais vantajoso, pois R$ 2.908,68, rendendo 2% ao mês, é suficiente para pagar as cinco prestações.
15. Humberto pegou emprestados R$ 800,00 a uma taxa de juro compôzto de 5% ao mês. Para quitar essa dívida, ele combinou quê:
• após 2 meses do empréstimo, pagaria
R$ 350,00;
• após 2 meses do 1º pagamento, pagaria
R$ 200,00;
• após 2 meses do 2º pagamento, quitaria a dívida.
Qual será aproximadamente o valor do último pagamento de Humberto?
Resolução
Para determinarmos o valor x do último pagamento, vamos construir esquemas de pagamento:

Agora, trazemos todas as prestações para o valor presente e igualamos a soma dêêsses valores ao valor da dívida:
800 = ⇒ x ≃ 426,15
Portanto, o último pagamento de Humberto será aproximadamente R$ 426,15.
ATIVIDADES
52. ![]() Uma pessoa quer quitar uma dívida três meses antes do vencimento. O valor futuro dessa dívida é de R$ 20.000,00, e a taxa de juro compôzto fixada pelo banco é de 3% ao mês. Determine qual é aproximadamente o valor presente da dívida, isto é, o valor quê a pessoa deve pagar para quitá-la.
Uma pessoa quer quitar uma dívida três meses antes do vencimento. O valor futuro dessa dívida é de R$ 20.000,00, e a taxa de juro compôzto fixada pelo banco é de 3% ao mês. Determine qual é aproximadamente o valor presente da dívida, isto é, o valor quê a pessoa deve pagar para quitá-la.
aproximadamente R$ 18.302,83
53. ![]() Lúcia fez um empréstimo de R$ 4.000,00 a uma taxa de juro compôzto de 8% ao mês. Ela quitou esse empréstimo da seguinte maneira: dois meses após o empréstimo, ela pagou R$ 1.500,00; três meses após o primeiro pagamento, ela quitou a dívida. Qual foi o valor do último pagamento de Lúcia?
Lúcia fez um empréstimo de R$ 4.000,00 a uma taxa de juro compôzto de 8% ao mês. Ela quitou esse empréstimo da seguinte maneira: dois meses após o empréstimo, ela pagou R$ 1.500,00; três meses após o primeiro pagamento, ela quitou a dívida. Qual foi o valor do último pagamento de Lúcia?
aproximadamente R$ 3.987,74
54. ![]() Fabiano vai comprar uma Tevê de 75 polegadas quê custa R$ 5.400,00. A loja em quê ele vai comprar oferece três opções de pagamento.
Fabiano vai comprar uma Tevê de 75 polegadas quê custa R$ 5.400,00. A loja em quê ele vai comprar oferece três opções de pagamento.
• Opção 1: à vista, com 5% de desconto.
• Opção 2: em três parcelas de R$ 1.800,00 por mês, sêndo a primeira parcela um mês após a compra.
• Opção 3: em oito parcelas de R$ 675,00 por mês, sêndo a primeira parcela paga no ato da compra.
Se o dinheiro de Fabiano rende 1,5% ao mês, qual é a opção de pagamento mais vantajosa para ele?
opção 3
Página trinta e cinco
Orçamento familiar
Pense sobre a seguinte questão: como as pessoas ou grupos familiares sabem quando são capazes de arcar financeiramente com a parcela de um financiamento ou com a prestação de uma compra parcelada?
Uma maneira seria visualizar todos os ganhos e gastos da família e fazer um orçamento, reunindo as informações referentes à quantia recebida e à quantia gasta em determinado período.
O orçamento familiar bem organizado possibilita quê as pessoas de uma família tênham o conhecimento e o contrôle de suas finanças, para quê possam avaliar se a compra de um bem ou serviço póde sêr realizada.
Para a elaboração do orçamento familiar, é importante entender seus elementos-chave e envolver todos os membros da família quê são capazes de tomar decisões relacionadas ao uso do dinheiro naquele grupo. A seguir apresentamos alguns dêêsses elemêntos.
• Receita: rendimento quê a família ganha durante um período específico. A receita póde vir de várias fontes, como salários, aposentadorias, rendimentos de investimentos e auxílios ou doações, ou seja, é qualquer valor ganho quê se agrega ao saldo da família.
• Despesa: qualquer valor quê a família gasta durante um período específico. As despesas podem incluir alimentação, serviços e taxas (como, por exemplo, á gua, luz, telefone e internet), vestuário, assistência médica, entre outros.
• Saldo: valor quê resta depois de serem subtraídas as despesas do total de receitas. É uma medida importante da saúde financeira da família.
Quando elaboramos um orçamento familiar, consideramos algumas despesas quê são fixas e outras quê são variáveis.
As despesas fixas, como aluguel, prestação do imóvel, mensalidade escolar, entre outras, são aquelas cujo valor não depende da quantidade consumida.
As despesas variáveis, como a conta de á gua e a de energia elétrica, a alimentação, o transporte, entre outras, são aquelas cujo valor depende da quantidade consumida.

Pense e responda
Se fosse necessário fazer algum ajuste no orçamento familiar por conta de um imprevisto financeiro, o quê você faria?
Resposta pessoal
Página trinta e seis
Acompanhe a situação a seguir.
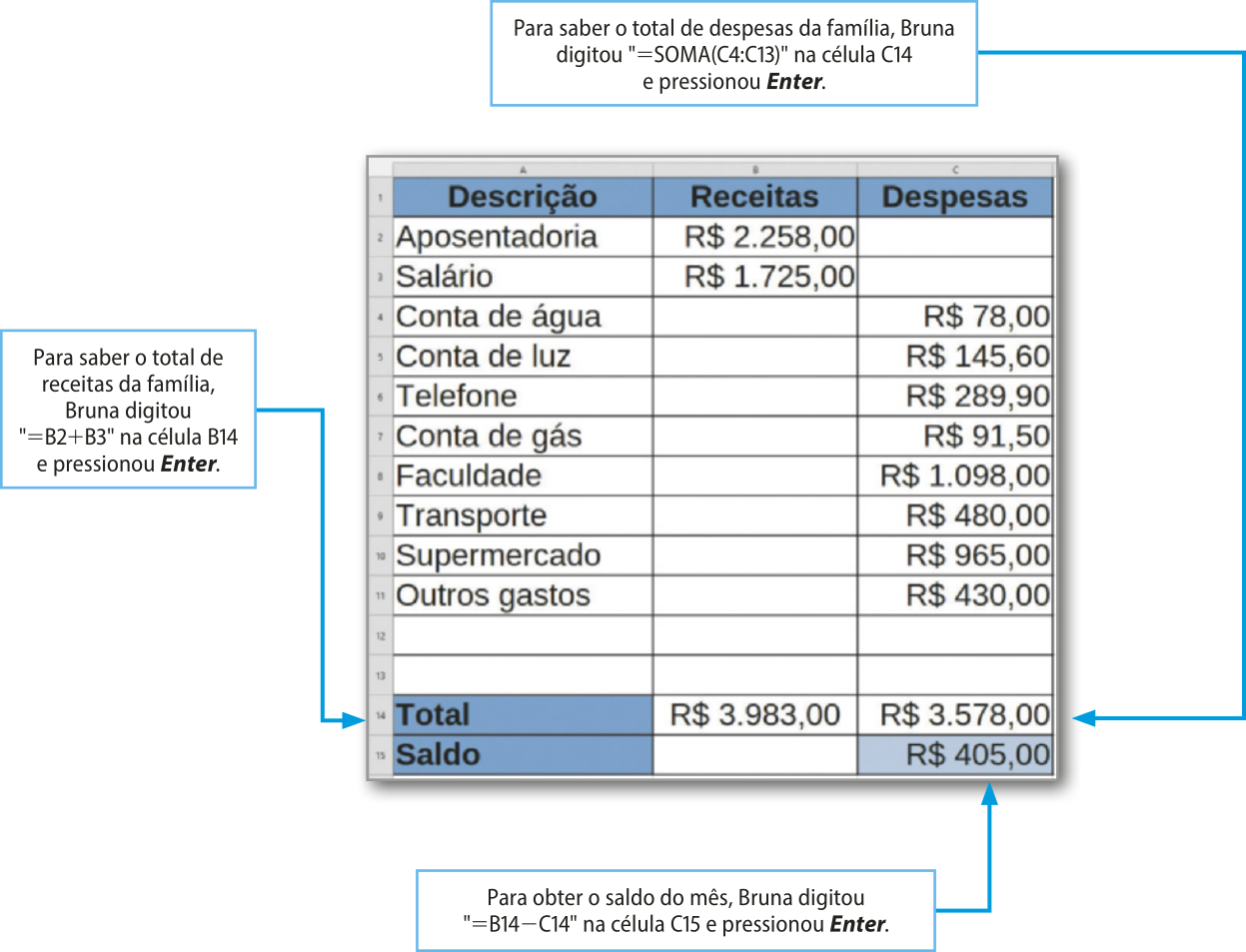
Alice mora com o filho, Sérgio, e a neta, Bruna. Essa família paga suas despesas juntando a aposentadoria de Alice, no valor líquido de R$ 2.258,00, e o salário de Sérgio, no valor líquido de R$ 1.725,00.
Conversando com a avó, Bruna propôs quê fizéssem juntas uma planilha para reunir as informações sobre os gastos mensais da família, de modo a fazer um orçamento e planejar uma viagem. Elas construíram uma planilha como a mostrada a seguir.
Pense e responda
O saldo póde sêr um valor negativo? Em quê situação isso acontece?
Sim. Quando o total de despesas é maior do quê o total de receitas.
Utilizando esses dados, a família de Alice póde antecipar seus gastos para o próximo mês. Eles podem fazer isso por meio de um orçamento quê detalha os valores previstos e, depois, registrar os valores reais para verificar se conseguiram cumprir as metas financeiras quê estabeleceram. Isso póde sêr feito mês a mês, a fim de analisar quais despesas podem sêr reduzidas e, com isso, gerar maior economia de dinheiro. Eles podem definir, inclusive, uma quantia a sêr poupada e fixar isso como se fosse uma"despesa" incluída na planilha.
Pense e responda
Com base nas informações sobre a família de Alice, é possível fazer uma previsão de gastos para o mês seguinte. Em sua opinião, qual(is) despesa(s) pode(m) sêr reduzida(s)?
Resposta pessoal.
Página trinta e sete
FÓRUM
Consumo sustentável
Atualmente, somos constantemente incentivados a consumir e muitas vezes compramos algo de quê não precisamos. Mas será quê o simples fato de um produto estar com um preêço mais baixo do quê o habitual é suficiente para justificar a compra? Ou deveríamos ir além e considerar também o impacto ambiental dessa compra?
Leia o texto a seguir e reflita sobre a informação apresentada.
[...]
O Consumo Sustentável envolve a escolha de produtos quê utilizaram menos recursos naturais em sua produção, quê garantiram o emprego decente aos quê os produziram, e quê serão facilmente reaproveitados ou reciclados. Significa comprar akilo quê é realmente necessário, estendendo a vida útil dos produtos tanto quanto possível. Consumimos de maneira sustentável quando nossas escôlhas de compra são conscientes, responsáveis, com a compreensão de quê terão consequências ambientais e sociais – positivas ou negativas.
[...]
Consumo consciente, consumo vêrde, consumo responsável são nuances do Consumo Sustentável, cada um focando uma dimensão do consumo. O consumo consciente é o conceito mais amplo e simples de aplicar no dia a dia: basta estar atento à forma como consumimos – diminuindo o desperdício de á gua e energia, por exemplo – e às nossas escôlhas de compra – privilegiando produtos e empresas responsáveis. A partir do consumo consciente, a ssossiedade envia um recado ao setor produtivo de quê quêr que lhe sêjam ofertados produtos e serviços quê tragam impactos positivos ou reduzam significativamente os impactos negativos [...]
[...]
BRASIL. Ministério do Meio Ambiente. Consumo sustentável: o quê é consumo sustentável. Brasília, DF: MMA, [2011]. Disponível em: https://livro.pw/ugwka. Acesso em: 26 set. 2024.

![]() Converse com os côlégas e o professor sobre a questão a seguir.
Converse com os côlégas e o professor sobre a questão a seguir.
• Como o impacto ambiental de um produto póde influenciar nossas decisões de compra? Como a sua turma ou a escola poderiam se organizar e pensar em um projeto quê valorize e divulgue práticas de consumo sustentável?
Ver as Orientações para o professor.
Página trinta e oito
Sistemas de amortização
Quando adquirimos um bem de maior valor, como um automóvel ou um imóvel, é comum fazermos um empréstimo ou financiamento por meio de uma instituição financeira. Nesse tipo de transação, o valor acordado, conhecido como capital, é devolvido à instituição com um acréscimo, o juro.
Uma vez contratado o financiamento, o processo para saldar a dívida se dá por meio de pagamentos periódicos, conhecidos como parcelas ou prestações, quê são pagas em intervalos de tempo constantes, normalmente mensais. Alguns financiamentos também incluem o pagamento de quantias preestabelecidas, quê são pagas em datas combinadas préviamente.
Em um empréstimo ou financiamento, o valor de cada prestação é compôzto de uma parte do capital adquirido e do juro calculado sobre o saldo devedor. Essa parte do capital adquirido é também chamada de amortização ou valor amortizado.
Assim, considerando P o valor da prestação, A o valor amortizado e J o juro sobre o saldo devedor, podemos escrever:
P = A + J
As diferentes maneiras de se realizar esse cálculo caracterizam o quê chamamos de sistema de amortização. Alguns dos sistemas mais utilizados são: Sistema Price ou Francês, Sistema de Amortização Constante (SAC), Sistema de Amortização Misto (SAM), entre outros.
Vamos estudar o Sistema Price e o Sistema de Amortização Constante, quê costumam sêr os mais praticados no mercado consumidor.
Sistema Price
O Sistema Price, ou Sistema de Amortização Francês, é aquele quê prevê o pagamento em prestações iguais, de valor fixo, durante todo o período de quitação do valor emprestado ou financiado. Normalmente é mais utilizado em contratos de curto prazo, como a compra de automóveis.
Acompanhe a situação a seguir.
Aline vai comprar um carro no valor de R$ 39.500,00 e pretende pagar R$ 7.500,00 como valor de entrada e financiar o restante da dívida em 36 prestações.
Ela conseguiu uma proposta de financiamento em um banco, a uma taxa de 2,5% ao mês, considerando o Sistema Price de amortização. O gerente enviou a ela uma planilha com algumas informações sobre as prestações. Observe as primeiras linhas dessa planilha.
Esclarecer aos estudantes quê o mês 0 indica a ocasião em quê o contrato foi celebrado.
Mês |
Prestação |
Amortização |
Juros |
Saldo devedor |
|---|---|---|---|---|
0 |
R$ 32.000,00 |
|||
1 |
R$ 1.358,45 |
R$ 558,45 |
R$ 800,00 |
R$ 31.441,55 |
2 |
R$ 1.358,45 |
R$ 572,41 |
R$ 786,04 |
R$ 30.869,14 |
3 |
R$ 1.358,45 |
R$ 586,72 |
R$ 771,73 |
R$ 30.282,42 |
Pense e responda
Sabendo quê os juros são calculados sobre o saldo devedor, quantos reais Aline vai pagar de juros na quarta prestação? Utilize uma calculadora para obtêr o resultado.
Saiba quê...
No Sistema Price, ao observar os valores quê compõem a prestação, verifica-se quê o valor correspondente à amortização aumenta e o juro diminui com o passar do tempo.
R$ 757,06
Página trinta e nove
Acompanhe uma situação em quê deduzimos o valor da prestação P no sistema Price considerando um valor V, financiado a uma taxa de juro i, quê será pago em 3 prestações.
Ao fim do primeiro mês, deve-se à instituição financiadora: V ⋅ (1 + i) e paga-se P. Assim, o saldo devedor é:
V(1 + i) − P
Ao fim do segundo mês, deve-se à instituição financiadora [V(1 + i) − P] ⋅ (1 + i) e paga-se P. Assim, o saldo devedor é:
[V(1 + i) − P] ⋅ (1 + i) − P = V(1 + i)2 − (1 + i)P − P
Ao fim do terceiro mês, deve-se à instituição [V(1 + i)2 − (1 + i)P − P] ⋅ (1 + i) e paga-se P. Assim, o saldo devedor é:
[V(1 + i)2 − (1 + i)P − P] ⋅ (1 + i) − P = V(1 + i)3 − (1 + i)2 P − (1 + i)P − P
Como a terceira prestação é a última, o saldo devedor ao fim do terceiro mês é igual a zero. Logo:
V(1 + i)3 − (1 + i)2 P − (1 + i)P − P = 0
Isolando o valor de P, obtemos:
P =
Substituindo (1 + i)2 + (1 + i) + 1 por , temos:
P =
Generalizando esse resultado, apresentamos a seguir uma forma de calcular o valor da prestação nesse sistema de amortização.
Saiba quê...
Dados os números a e b, podemos escrever a diferença de a e b elevados ao cubo como:
a3 − b3 = (a − b) ⋅ (a2 + ab + b2)
Isolando o segundo fator do segundo membro da igualdade, temos:
a2 + ab + b2 =
Repare quê, na dedução da fórmula do valor da prestação no Sistema Price, temos a = (1 + i) e b = 1.
O valor P da prestação no Sistema Price póde sêr calculado utilizando-se a expressão P = V ⋅ , em quê V é o valor financiado, i é a taxa de juro ao mês e n é a quantidade de prestações a serem quitadas.

Atualmente, os softwares de planilhas eletrônicas apresentam funções quê permitem criar uma tabéla com os valores envolvidos em todo o financiamento, quê é também conhecida como tabéla Price.
■ Conhecer o valor a sêr pago todo mês e a vantagem de a primeira parcela não sêr tão alta quando comparada a outros sistemas de amortização são fatores quê atraem as pessoas a optar pelo Sistema Price.
Página quarenta
Sistema de Amortização Constante (SAC)
Assim como o nome sugere, o Sistema de Amortização Constante (SAC) é aquele no qual a amortização A é constante, caracterizando um sistema mais acelerado de amortização, quando comparado ao Price. Com isso, as parcelas iniciais costumam sêr mais altas.
Nesse sistema, a amortização de uma dívida é calculada pela razão entre o capital C contratado e a quantidade n de parcelas, indicada por:
Geralmente, esse sistema é mais utilizado em contratos de longo prazo, envolvendo quantias muito grandes, como a compra de imóveis.
Acompanhe a situação a seguir.
Pedro e Amanda são sócios em uma loja de móveis e aproveitaram uma oportunidade para investir no imóvel onde a loja funciona atualmente, quê é um local alugado. Para isso, precisaram fazer um empréstimo de R$ 70.000,00, a juro de 0,65% ao mês, pelo SAC.
Quando analisaram as possibilidades e a proposta da instituição financeira, optaram por um período de 10 anos de financiamento.
Como a amortização é um valor fixo quê compõe parte do valor de cada prestação, o saldo devedor diminuirá a cada mês, de acôr-do com o pagamento das parcelas. Consequentemente, o valor do juro quê sêrá calculado sobre o saldo devedor também diminuirá, fazendo o valor da próxima parcela ser inferior ao valor da parcela anterior.
Nesse caso, o valor amortizado em cada prestação é R$ 583,33:
R$ 70.000,00 ∶ 120 = R$ 583,33
O valor de juro pago na primeira parcela é calculado sobre o saldo devedor, quê corresponde a todo o valor emprestado. Nesse caso, a taxa é de 0,65% ao mês. Assim temos:
J = 0,0065 ⋅ R$ 70.000,00 = R$ 455,00
A primeira prestação é ôbitída pela adição do valor da amortização e o do juro correspondentes:
P1 = R$ 583,33 + R$ 455,00 = R$ 1.038,33
A segunda prestação é ôbitída pela adição do valor da amortização (R$ 583,33) e o do juro correspondente, quê é calculado sobre o saldo devedor (R$ 69.416,67):
69.416,67 ⋅ 0,0065 = 451,21
Assim:
P2 = R$ 583,33 + R$ 451,21 = R$ 1.034,54
O saldo devedor, para o cálculo de P3, é:
R$ 69.416,67 – R$ 583,33 = R$ 68.833,34

Página quarenta e um
Observe como podemos organizar esses valores em uma planilha e calcular os valores das cinco primeiras prestações.
Mês |
Saldo devedor |
Amortização |
Juros |
Prestação |
|---|---|---|---|---|
0 |
R$ 70.000,00 |
|||
1 |
R$ 69.416,67 |
R$ 583,33 |
R$ 455,00 |
R$ 1.038,33 |
2 |
R$ 68.833,34 |
R$ 583,33 |
R$ 451,21 |
R$ 1.034,54 |
3 |
R$ 68.250,01 |
R$ 583,33 |
R$ 447,42 |
R$ 1.030,75 |
4 |
R$ 67.666,68 |
R$ 583,33 |
R$ 443,62 |
R$ 1.026,95 |
5 |
R$ 67.083,35 |
R$ 583,33 |
R$ 439,83 |
R$ 1.023,16 |
Saiba quê...
No SAC, o saldo devedor sofre redução mais acelerada em comparação com o Sistema Price. Como o juro é calculado sobre esse valor, o montante de juro gerado por um capital financiado no SAC será menor do quê o montante de juro gerado pelo mesmo capital ao fim de um mesmo financiamento no Sistema Price, ao sêr considerado o mesmo período.
ATIVIDADES RESOLVIDAS
16. ![]() Marília vai fazer um empréstimo de R$ 50.000,00 para uma reforma em seu estúdio de fotografia e está analisando qual sistema de amortização vai utilizar, de acôr-do com as propostas de uma agência financiadora, quê trabalha com uma taxa de 0,95% ao mês. Ela pretende saldar a dívida em 6 anos.
Marília vai fazer um empréstimo de R$ 50.000,00 para uma reforma em seu estúdio de fotografia e está analisando qual sistema de amortização vai utilizar, de acôr-do com as propostas de uma agência financiadora, quê trabalha com uma taxa de 0,95% ao mês. Ela pretende saldar a dívida em 6 anos.
a) Qual será o valor amortizado em cada parcela se Marília decidir pelo SAC? De quanto será a 1ª prestação nesse caso?
b) Se decidir pelo Sistema Price, qual será o valor de cada prestação? Qual será o valor amortizado na primeira prestação?
Resolução
a) Como no SAC o valor amortizado é constante em todo o período de quitação, dividimos o capital pela quantidade de prestações. Assim, temos:
A = ≃ 694,44
Portanto, o valor amortizado em cada parcela será R$ 694,44.
O juro pago na primeira prestação é calculado considerando todo o capital emprestado, pois ainda não houve amortização. Nesse caso, temos:
J = 0,0095 ⋅ R$ 50.000,00 = R$ 475,00
Logo: P1 = R$ 694,44 + R$ 475,00 = R$ 1.169,44
Então, no SAC, a primeira prestação será R$ 1.169,44.
b) No Sistema Price, o valor da prestação é constante em todo o período de quitação e póde sêr obtído por meio da expressão:
P = V ⋅
Substituindo V por 50.000, i por 0,0095 e n por 72 e utilizando uma calculadora científica, obtemos o valor de P:
P = 50.000 ⋅ ≃ 961,98
Desse modo, o valor de cada prestação será R$ 961,98 no sistema Price.
Assim como no SAC, o juro pago na primeira prestação é calculado sobre todo o valor tomado como empréstimo. Recuperando o valor calculado no item a, temos:
J = R$ 475,00
Logo:
A = R$ 961,98 − R$ 475,00 = R$ 486,98
Portanto, o valor amortizado na primeira prestação é R$ 486,98.
Página quarenta e dois
17. Construa uma planilha eletrônica simulando os valores das prestações de amortização e dos juros cobrados pela agência financiadora da atividade anterior para auxiliar Marília a analisar a situação proposta.
Resolução
Inicialmente, vamos construir uma tabéla considerando o Sistema Price, utilizando o passo a passo a seguir.
I. Abrimos uma planilha no LibreOffice, e nas células A1, A2 e A3, digitamos “Valor emprestado”, “Taxa” e “Número de meses”, respectivamente. Em seguida, organizamos as colunas da planilha digitando “Mês”, “Prestação”, “Amortização”, “Juro” e “Saldo devedor”. Com a ferramenta côr do plano de fundo, ![]() formatamos as células preenchidas anteriormente com a côr desejada, como na imagem.
formatamos as células preenchidas anteriormente com a côr desejada, como na imagem.

II. Com a ferramenta Formatar como moeda, ![]() formatamos as células B1, B6, C6, D6 e E6. Também formatamos a célula B2, clicando em Formatar como porcentagem,
formatamos as células B1, B6, C6, D6 e E6. Também formatamos a célula B2, clicando em Formatar como porcentagem, ![]() Depois, digitamos “50000”, “0,95” e “72” nas células B1, B2 e B3, respectivamente.
Depois, digitamos “50000”, “0,95” e “72” nas células B1, B2 e B3, respectivamente.
III. Nas células A6, B6, C6 e D6, digitamos “0” (zero). Na célula E6 digitamos “=$B$1” e pressionamos Enter (o $ sérve para deixar fixa a célula indicada). Essa linha corresponde ao início do contrato.
IV. Na célula A7, digitamos “=A6+1” e pressionamos Enter para indicar o mês 1, ou seja, a primeira prestação.
V. Em B7, vamos usar a função PGTO. Essa função calcula o valor de cada prestação no Sistema Price dados a taxa, o número de prestações e o valor total da dívida. Para isso, digitamos “=PGTO($B$2;$B$3;−$B$1)” e pressionamos Enter. Atenção: é necessário digitar o sinal de menos antes de “$B$1”.
VI. Para calcular o juro, vamos digitar, em D7, “=$B$2*E6” e pressionar Enter. Na célula C7, digitamos “=B7−D7” e Enter.
VII. Por fim, na célula E7, digitamos “=E6−C7” e pressionamos Enter. Para obtêr as próximas linhas, selecionamos as células A7 a E7, posicionamos o cursor do máuzi no quadradinho no canto inferior direito da última célula, clicamos e arrastamos a seleção para baixo até obtermos a linha correspondente ao mês 72.
Na imagem, são mostradas as primeiras linhas da planilha construída dessa maneira.
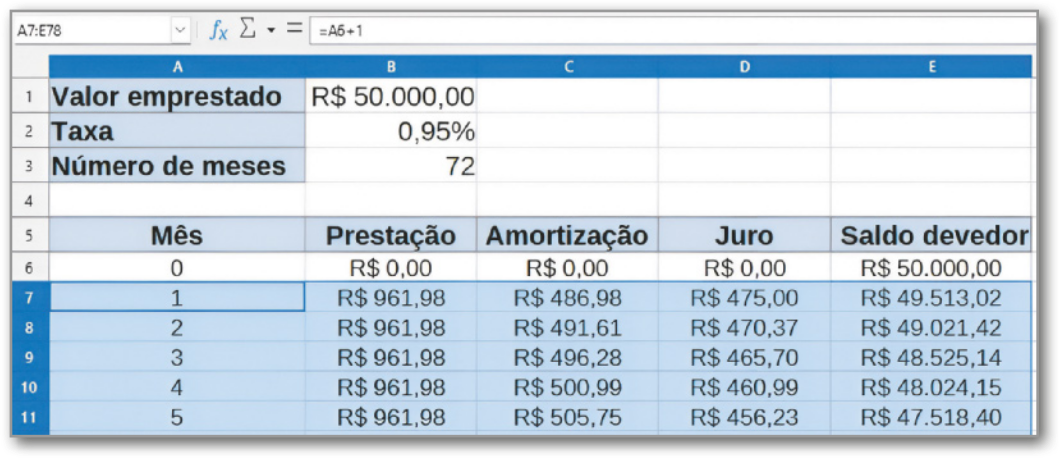
Página quarenta e três
Vamos construir agora uma tabéla considerando o SAC, utilizando o passo a passo a seguir.
I. Vamos construir essa tabéla à direita da tabéla construída anteriormente, utilizando as colunas G a K. Selecionamos as células A1 a B3, pressionamos as teclas Ctrl + C para copiá-las e as colamos nas células G1 a H3 pressionando as teclas Ctrl + V. Trocamos a côr das células para diferenciá-las da tabéla anterior. Digitamos, nas células G5 a K5, o título de cada coluna: “Mês”, “Saldo devedor”, “Amortização”, “Juro” e “Prestação”, como indicado na imagem.
Observe quê invertemos a ordem das colunas, o quê foi feito apenas por uma questão de organização.
II. Formatamos as células H6, I6, J6 e K6, clicando na ferramenta ![]() .
.
III. Nas células G6, I6, J6 e K6, digitamos “0” (zero). Na célula H6, digitamos “=$H$1” e pressionamos Enter. Essa linha corresponde ao início do contrato.
IV. Na célula G7, digitamos “=G6+1” e pressionamos Enter para indicar o mês 1, ou seja, a primeira prestação.
V. Em I7, vamos calcular a amortização, quê é constante nesse sistema, digitando “=$H$1/$H$3” e pressionando Enter. Na célula H7, digitamos “=H6−I7”, pressionando Enter na sequência, para obtêr o saldo devedor depois de realizado o pagamento da primeira prestação.
VI. Para calcular o juro, digitamos, na célula J7, “=$H$2*H6” e pressionamos Enter.
VII. Por fim, na célula K7, digitamos “=I7+J7” e pressionamos Enter para o obtêr o valor da primeira parcela. Para obtêr as próximas linhas, selecionamos as células G7 a K7, posicionamos o cursor do máuzi no quadradinho no canto inferior direito da última célula, clicamos e arrastamos a seleção para baixo até obtêr a linha correspondente ao mês 72.
Na imagem, são mostradas as primeiras linhas da planilha construída dessa maneira.
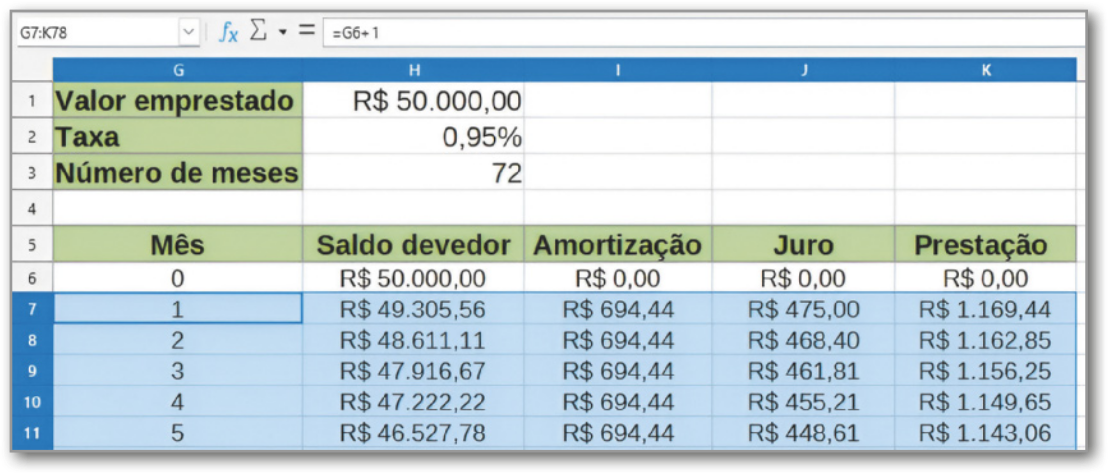
Página quarenta e quatro
ATIVIDADES
55. Retome a situação apresentada na página 36 sobre a família formada por Alice, Sérgio e Bruna. Reproduza a planilha de receitas e despesas dessa família e amplie essa planilha conforme as orientações.
a) Na quarta coluna, coloque o título “Despesas previstas – próximo mês” e estime os valores imaginando quê Bruna quisesse quê o saldo previsto fosse de R$ 560,00.
b) Na quinta coluna, inclúa o título “Despesas realizadas – próximo mês” e estime os valores imaginando quanto a família gastou, de modo quê o saldo tenha sido de R$ 510,00. Em seguida, compartilhe sua resolução com os côlégas.
Ver as Orientações para o professor.
56. Responda às kestões a seguir com base em alguns resultados das atividades resolvidas na seção anterior.
a) Em qual dos sistemas de amortização a primeira prestação é mais alta? Em sua opinião isso póde influenciar a dê-cisão de Marília?
A primeira prestação é mais alta no SAC. Resposta pessoal.
b) Comparando os valores amortizados nas primeiras prestações, o quê você percebe? Esse fato interfere no montante de juro pago em todo o período de quitação da dívida?
Resposta possível: Nas primeiras prestações, o valor amortizado no SAC é maior do quê no Sistema Price. Sim.
57. Em cada situação a seguir, considerando o SAC, calcule o valor amortizado a cada prestação.
a) Em um empréstimo de R$ 25.000,00 quê deve sêr pago em 8 prestações.
R$ 3.125,00
b) Em um financiamento de R$ 40.000,00 quê deve sêr pago em 10 prestações, porém considerando uma entrada de R$ 12.000,00.
R$ 2.800,00
58. ![]() Um veículo no valor de R$ 75.000,00 está à venda de acôr-do com as condições do cartaz.
Um veículo no valor de R$ 75.000,00 está à venda de acôr-do com as condições do cartaz.
Entrada de 25% do valor; o restante pago em 48 prestações com juros de 2% a.m.
De acôr-do com essas informações, responda.
a) Qual é o valor a sêr financiado?
R$ 56.250,00
b) Se o financiamento for feito pelo Sistema Price de amortização, qual será o valor da prestação?
aproximadamente R$ 1.833,85
c) Caso a opção seja pelo financiamento segundo o SAC, qual será o valor amortizado em cada prestação?
aproximadamente R$ 1.171,88
d) Utilizando uma planilha eletrônica para simular os valores do financiamento no Sistema Price e no SAC, qual será o montante de juro pago em todo o período?
Sistema Price: R$ 31.774,96; SAC: R$ 27.562,50
59. ![]() Sandro vai comprar um noutibúk e se interessou pelo modelo a seguir.
Sandro vai comprar um noutibúk e se interessou pelo modelo a seguir.

Sabendo quê a loja trabalha com o Sistema Price de amortização, se Sandro comprar esse noutibúk a prazo, deverá pagar 10 prestações de:
a) R$ 176,80.
b) R$ 206,80.
c) R$ 209,59.
d) R$ 229,59.
e) R$ 249,49.
alternativa c
Página quarenta e cinco
HISTÓRIA DA MATEMÁTICA
Luca Pacioli, um dos precursores dos processos contábeis
O Renascimento foi um período importante na história da humanidade, por ter favorecido o desenvolvimento da criatividade humana em diversas áreas. Considerando as inúmeras ideias quê surgiram nesse período, podemos destacar as novas concepções na Astronomia, a noção da perspectiva nas artes, os estudos sobre o comportamento da luz, o desenvolvimento da Álgebra e dos processos contábeis, entre outras.
Nessa perspectiva, o papel do frade Luca Pacioli foi importante, em razão de suas inúmeras contribuições para a Matemática e para a área contábil.

Saiba quê...
Embora o método de partidas dobradas seja um pensamento aparentemente simples, no qual, em síntese, não existe devedor sem credor, ele é aplicado até hoje em instituições financeiras, no comércio e em empresas em geral, sêndo a base teórica quê desen vólve as Ciências Contábeis.
[...]
[...] Pacioli, quê foi professor de matemática e colaborador de Leonardo da Vinci, publicou em 1494 o livro de Summa de Arithmetica, Geometria, Proporzioni di Proporzionalita (Compêndio de Aritmética, Geometria, Proporções e Proporcionalidade), escrito em idioma vernacular. A obra abordava quatro assuntos: aritmética, álgebra, geometria euclidiana elementar e contabilidade. O livro, síntese de boa parte do conhecimento matemático de então, foi o primeiro livro impresso a tratar de álgebra, retomando a classificação das equações de segundo grau dos árabes. No quê diz respeito à contabilidade, introduziu o chamado método das partidas dobradas, também conhecido como método veneziano. Esse é o sistema padrão usado em empresas e outras organizações para registrar transações financeiras, em quê todos os movimentos são lançados em pelo menos duas contas, com o total de débitos devendo se igualar ao total de créditos. A contribuição de Pacioli veio a atender algumas necessidades de técnicas aritméticas surgidas com o desenvolvimento do sistema bancário nas cidades mercantis italianas.
[...]
MOL, Rogério S. Introdução à história da matemática. Belo Horizonte: CAED-UFMG, 2013. p. 90. Disponível em: https://livro.pw/upvsb. Acesso em: 24 set. 2024.
Página quarenta e seis
CONEXÕES com...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
Inflação e seus impactos na vida da população
Ir ao mesmo supermercado e comprar os mesmos produ com a mesma quantia com quê se comprava há alguns meses uma tarefa pouco provável. Isso acontece porque os preços dos produtos, em geral, aumentam ao longo do tempo, e a inflação é uma das responsáveis por isso.
Mas você sabe o quê é inflação e como ela é calculada? Leia o texto a seguir, quê trata dêêsse assunto.

Inflação
O quê é inflação
Inflação é o nome dado ao aumento dos preços de produtos e serviços. Ela é calculada pêlos índices de preços, comumente chamados de índices de inflação.
O hí bê gê hé produz dois dos mais importantes índices de preços: o IPCA, considerado o oficial pelo govêrno federal, e o INPC.
Para quê sérvem o IPCA e o INPC?
O propósito de ambos é o mesmo: medir a variação de preços de uma cesta de produtos e serviços consumida pela população. O resultado mostra se os preços aumentaram ou diminuíram de um mês para o outro.
A cesta é definida pela Pesquisa de Orçamentos Familiares – POF, do hí bê gê hé, quê, entre outras kestões, verifica o quê a população consome e quanto do rendimento familiar é gasto em cada produto: arrôz, feijão, passagem de ônibus, material escolar, médico, cinema, entre outros.
Os índices, portanto, levam em conta não apenas a variação de preêço de cada item, mas também o peso quê ele tem no orçamento das famílias.
[…]
Qual é a diferença entre eles?
A sigla INPC corresponde ao Índice Nacional de Preços ao Consumidor. A sigla IPCA corresponde ao Índice Nacional de Preços ao Consumidor Amplo.
A diferença entre eles está no uso do termo “amplo”.
O IPCA engloba uma parcela maior da população. Ele aponta a variação do custo de vida médio de famílias com renda mensal de 1 a 40 salários mínimos.
O INPC verifica a variação do custo de vida médio apenas de famílias com renda mensal de 1 a 5 salários mínimos. Esses grupos são mais sensíveis às variações de preços, pois tendem a gastar todo o seu rendimento em itens básicos, como alimentação, medicamentos, transporte etc.
[…]
Página quarenta e sete
por quê se fala tanto em IPCA?
O govêrno federal usa o IPCA como o índice oficial de inflação do Brasil. Portanto, ele sérve de referência para as metas de inflação e para as alterações na taxa de juros.
Como ele é calculado?
O hí bê gê hé faz um levantamento mensal, em 13 áreas urbanas do País, de, aproximadamente, 430 mil preços em 30 mil locais. Todos esses preços são comparados com os preços do mês anterior, resultando num único valor quê reflete a variação geral de preços ao consumidor no período.
Índice pessoal de inflação
Sua cesta de compras, ou seja, os produtos e serviços quê você consome regularmente, póde sêr bem diferente da cesta média da população brasileira. Com isso, o seu índice pessoal de inflação póde sêr maior ou menor do quê o IPCA.
Por exemplo, uma família quê não consome carne vermelha e não tem filhos em idade escolar terá, com certeza, um índice de inflação pessoal diferente do oficial, cujo cálculo coloca peso considerável na variação do preêço da carne e da mensalidade escolar.
Poder de compra
Se a variação do seu salário, de um ano para o outro, for menor do quê o IPCA, você perde seu pôdêr de compra, pois os preços sóbem mais do quê a sua renda. Se a inflação e o seu salário têm a mesma variação, seu pôdêr de compra se mantém. Se você, porém, receber um aumento acima do IPCA, seu pôdêr de compra aumentará.
Curiosidades do IPCA
O hí bê gê hé produz e divulga o IPCA, sistematicamente, desde 1980. Entre 1980 e 1994, ano de implantação do Plano Real, o índice acumulado foi de 13.342.346.717.671,70%!
A maior variação mensal do IPCA foi em março de 1990 (82,39%), enquanto a menor variação, em julho de 2022 (−0,68%).
[…]
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Inflação. Rio de Janeiro: hí bê gê hé, 2024. Disponível em: https://livro.pw/fzobu. Acesso em: 23 out. 2024.
Em outubro de 2024, a inflação acumulada dos últimos doze meses do Brasil foi 4,8%. Alguns países apresentaram índices de inflação anualizada maior quê a do Brasil nesse mesmo período, tais como, Argentina (193%), Turquia (48,6%), Rússia (8,5%) e Índia (6,2%). Outros países tiveram inflação menor quê a brasileira, por exemplo, Estados Unidos (2,6%), Alemanha (2%), Arábia Saudita (1,9%) e chiina (0,3%).
Fonte dos dados: TRAIDING ECONOMICS. Taxa de inflação: lista de países: G20. [S. I.]: Trading Economics, 2025.
Disponível em: https://livro.pw/qlxxp. Acesso em: 3 maio 2025.

Página quarenta e oito
O gráfico a seguir apresenta o IPCA acumulado nos últimos 12 meses em dezembro de cada ano, de 2010 a 2023.
Fonte de dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. IPCA: Índice Nacional de Preços ao consumidor amplo. Rio de Janeiro: hí bê gê hé, [2024]. Disponível em: https://livro.pw/knmil. Acesso em: 27 set. 2024.
Para determinar a atualização de um valor de um ano para outro, é preciso calcular o índice acumulado no período. Por exemplo, a atualização de R$ 100,00 em janeiro de 2010 para dezembro de 2011 deve sêr calculada com aumentos sucessivos de 5,91% e 6,5%:
100 ⋅ 1,0591 ⋅ 1,065 = 112,74415
Portanto, em dezembro de 2011, o valor atualizado era R$ 112,74.
Agora, faça o quê se pede nas atividades a seguir.
1. Explique como a inflação impacta a vida do consumidor.
Ver as Orientações para o professor.
2. De acôr-do com o IPCA de dezembro de 2022, qual seria o preêço, no final de dezembro de 2022, de uma cesta básica de produtos quê, no início do mês, custava R$ 672,07?
R$ 667,50
3. ![]() De acôr-do com o gráfico apresentado, faça o quê se pede.
De acôr-do com o gráfico apresentado, faça o quê se pede.
a) Atualize o valor de R$ 500,00 em janeiro de 2020 para dezembro de 2023.
R$ 636,59
b) Responda: qual foi o aumento, em porcentagem, do IPCA de janeiro de 2010 a dezembro de 2023? Arredonde o índice para um valor inteiro.
124%
4. Além dos índices apresentados no texto, pesquise outros índices quê são referência para o cálculo do índice de inflação e investigue a particularidade de cada um. Compartilhe sua resposta com os côlégas.
Ver as Orientações para o professor.
5. ![]() Em duplas, realizem uma entrevista com uma pessoa quê era adulta no final da década de 1980 e no início de 1990. Previamente, preparem um roteiro com kestões quê estejam relacionadas à hiperinflação da época. Gravem um vídeo ou um áudio da entrevista e apresentem os resultados para a turma. Não se esqueçam de pedir ao entrevistado autorização para uso da imagem e da entrevista cedida por ele.
Em duplas, realizem uma entrevista com uma pessoa quê era adulta no final da década de 1980 e no início de 1990. Previamente, preparem um roteiro com kestões quê estejam relacionadas à hiperinflação da época. Gravem um vídeo ou um áudio da entrevista e apresentem os resultados para a turma. Não se esqueçam de pedir ao entrevistado autorização para uso da imagem e da entrevista cedida por ele.
Resposta pessoal. Ver as Orientações para o professor.
Para assistir
• O QUE é inflação: hí bê gê hé explica IPCA e INPC. [S. l.: s. n.], 2015. 1 vídeo (5 min). Publicado pelo canal hí bê gê hé. Disponível em: https://livro.pw/voyju. Acesso em: 27 set. 2024.
O vídeo apresenta informações sobre como são calculados o INPC e o IPCA, além de explicar para quê sérvem esses índices e suas diferenças.
Página quarenta e nove
ATIVIDADES COMPLEMENTARES
1. ![]() (IFSC) O Produto Interno Bruto (PIB) é uma representação da soma dos valores monetários de todos os bens e serviços produzidos em uma determinada região em um determinado espaço de tempo. O Balinsky (país fictício) tinha em 2016 um PIB quê em comparação com o PIB de 2015 cresceu 2%. Já em 2017 o PIB de Balinsky diminui 5% em relação a 2016. A previsão para 2018 é de um crescimento de 3% em relação a 2017. Dessa forma, se a previsão para 2018 se confirmar, podemos afirmar quê a variação do PIB de Balinsky do período de 2015 a 2018 foi: Assinale a alternativa CORRETA.
(IFSC) O Produto Interno Bruto (PIB) é uma representação da soma dos valores monetários de todos os bens e serviços produzidos em uma determinada região em um determinado espaço de tempo. O Balinsky (país fictício) tinha em 2016 um PIB quê em comparação com o PIB de 2015 cresceu 2%. Já em 2017 o PIB de Balinsky diminui 5% em relação a 2016. A previsão para 2018 é de um crescimento de 3% em relação a 2017. Dessa forma, se a previsão para 2018 se confirmar, podemos afirmar quê a variação do PIB de Balinsky do período de 2015 a 2018 foi: Assinale a alternativa CORRETA.
a) Um decrescimento de aproximadamente 0,2%.
b) Não cresceu nem diminuiu.
c) Um aumento de aproximadamente 1,8%.
d) Um decrescimento de mais de 2%.
e) Um acréscimo de menos de 1%.
alternativa a
2. (UEA-AM) Ricardo comprou uma bicicleta e conseguiu revendê-la por um preêço 20% maior do quê pagou, o quê correspondeu a um lucro de R$ 150,00. O valor quê Ricardo recebeu pela venda dessa bicicleta foi
a) R$ 700,00.
b) R$ 750,00.
c) R$ 800,00.
d) R$ 850,00.
e) R$ 900,00.
alternativa e
3. (Epcar-MG) À taxa anual de 15%, em quê tempo, aproximadamente, o capital R$ 8.000,00 produz R$ 3.600,00 de juros simples?
a) 2 anos
b) 3 anos
c) 4 anos
d) 5 anos
e) 6 anos
alternativa b
4. (UFPE) Uma loja de eletrônicos oferece duas opções de pagamento:
• à vista, com 10% de desconto no preêço anunciado;
• em duas prestações mensais iguais, sem desconto sobre o preêço anunciado, sêndo a primeira prestação paga no momento da compra.
Qual a taxa de juros mensais embutida nas vendas a prazo?
a) 25%
b) 30%
c) 10%
d) 15%
e) 20%
alternativa a
5. (ESPM-SP) O sr. Paulo aplicou um cérto capital à taxa de juros simples de 4% ao mês durante 3 meses. O montante dessa aplicação, ele reaplicou à taxa de juros simples de 3% ao mês durante 9 meses. Se ele tivesse feito uma única aplicação dêêsse capital a juros simples durante 1 ano, para obtêr o mesmo rendimento final, a taxa mensal deveria sêr de:
a) 3,28%
b) 3,36%
c) 3,43%
d) 3,52%
e) 3,64%
alternativa d
6. (Ufersa-RN) Qual foi o capital aplicado a 6% ao mês, juros simples, quê deu origem ao montante de R$ 1.960,00 de 1 ano e 4 meses?
a) R$ 1.000,00
b) R$ 1.400,00
c) R$ 1.200,00
d) R$ 1.900,00
alternativa a
7. (UEPA) Um carro flex de R$ 30.000,00 foi vendido por uma concessionária da seguinte forma: 60% de entrada e o restante em 5 prestações mensais iguais com juro simples de 2% ao mês. O valor de cada prestação será de:
a) R$ 2.400,00
b) R$ 2.500,00
c) R$ 2.640,00
d) R$ 2.860,00
e) R$ 3.960,00
alternativa c
8. (UERN) Uma pessoa possui uma quantia aplicada a juros compostos de 1% ao mês, da qual, em meses alternados, ela retira R$ 100,00 e doa a uma instituição de caridade. Sabendo-se quê, no início de cérto mês, a quantia aplicada era de R$ 10.000 e, no final daquele mês, ela fez a doação, pode-se concluir quê a quantia aplicada após 3 meses era igual a
a) R$ 10.100,00
b) R$ 10.101,00
c) R$ 10.110,00
d) R$ 10.200,00
e) R$ 10.201,00
alternativa b
9. (EsPCEx-SP) O valor de revenda de um carro é dado por V(t) = V0(0,8)t, em quê V0 é o valor inicial e V(t) é o valor após t anos de uso. A alternativa quê mais se aproxima do percentual de desvalorização dêêsse carro, em relação ao valor inicial, após 3 anos exatos de uso, é:
a) 24%
b) 47%
c) 49%
d) 50%
e) 51%
alternativa c
Página cinquenta
10. (Enem/MEC) Um investidor deseja aplicar R$ 10.000,00 durante um mês em um dos fundos de investimento de um banco. O agente de investimentos dêêsse banco apresentou dois tipos de aplicações financeiras: a aplicação Básica e a aplicação Pessoal, cujas informações de rendimentos e descontos de taxas administrativas mensais são apresentadas no qüadro.
Aplicação |
Taxa de rendimento mensal |
Taxa administrativa mensal |
|---|---|---|
Básica |
0,542% |
R$ 0,30 |
Pessoal |
0,560% |
3,8% sobre o rendimento mensal |
Consideradas as taxas de rendimento e administrativa, qual aplicação fornecerá maior valor de rendimento líquido a esse investidor e qual será esse valor?
a) Básica, com rendimento líquido de R$ 53,90.
b) Básica, com rendimento líquido de R$ 54,50.
c) Pessoal, com rendimento líquido de R$ 56,00.
d) Pessoal, com rendimento líquido de R$ 58,12.
e) Pessoal, com rendimento líquido de R$ 59,80.
alternativa a
11. (Enem/MEC) Uma loja vende seus produtos de duas formas: à vista ou financiado em três parcelas mensais iguais. Para definir o valor dessas parcelas nas vendas financiadas, a loja aumenta em 20% o valor do produto à vista e divide esse novo valor por 3. A primeira parcela deve sêr paga no ato da compra, e as duas últimas, em 30 e 60 dias após a compra. Um cliente da loja decidiu comprar, d fórma financiada, um produto cujo valor à vista é R$ 1.500,00.
Utilize 5,29 como aproximação para .
A taxa mensal de juros compostos praticada nesse financiamento é de
a) 6,7%
b) 10%
c) 20%
d) 21,5%
e) 23,3%
alternativa d
12. (Uesc-BA) Em uma aplicação financeira a uma taxa de juros compostos de 2% ao mês, em quê foram efetuados três depósitos mensais de R$ 2.300,00 cada, o valor acumulado na data do último depósito é igual a:
a) R$ 6.900,00.
b) R$ 7.038,00.
c) R$ 7.038,92.
d) R$ 7.178,76.
e) R$ 7.178,80.
alternativa c
13. (Unifor-CE) A expressão M = A ⋅ (1 + i) n permite o cálculo do montante produzido por um capital A, aplicado a juros compostos e à taxa unitária i, ao final de n períodos. Assim, se o capital de R$ 1.370,00 for aplicado à taxa anual de 25%, ao final de quantos anos ele produzirá o montante de R$ 5.480,00? (Use: log 2 = 0,30)
a) 6
b) 5
c) 4
d) 3
e) 2
alternativa a
14. (FGV-SP) Um empréstimo sêrá quitado em 5 anos com pagamentos consecutivos anuais postecipados de R$ 6.720,00, segundo o Sistema Francês de Amortização (Tabela Price). Se a taxa de juros efetiva a ser utilizada é de 16% a.a., então a amortização no saldo devedor decorrente do pagamento da primeira prestação será de (Considere 1,165 = 2,1)
a) R$ 3.000,00.
b) R$ 3.050,00.
c) R$ 3.100,00.
d) R$ 3.150,00.
e) R$ 3.200,00.
alternativa e
15. (UFAL) Um dos maiores problemas enfrentados pêlos governos é a inflação. Felizmente, para a Economia Brasileira, a inflação está controlada; porém, não deixa de dar sinais de sua persistência. Pode-se definir inflação como:
a) o aumento contínuo e generalizado de todos os preços da economia.
b) o aumento rápido e incontrolável das variáveis de demanda, como o consumo.
c) o excésso de gastos, principalmente, os de investimento, em relação ao produto de uma economia.
d) o aumento contínuo da massa salarial da economia, provocando elevação da demanda e, consequentemente, dos preços.
e) o aumento do crédito na economia, provocando elevação da demanda agregada.
alternativa a
Página cinquenta e um
16. (Enem/MEC) O ganho real de um salário, r, é a taxa de crescimento do pôdêr de compra dêêsse salário. Ele é calculado a partir do percentual de aumento dos salários e da taxa de inflação, referidos a um mesmo período. Algebricamente, pode-se calcular o ganho real pela fórmula
1 + r =
em quê i é o percentual de aumento no valor dos salários e f é a taxa de inflação, ambos referidos a um mesmo período.
Considere quê uma categoria de trabalhadores recebeu uma proposta de aumento salarial de 10%, e quê a taxa de inflação do período correspondente tenha sido 5%. Para avaliar a proposta, os trabalhadores criaram uma classificação em função dos ganhos reais conforme o qüadro.
Ganho real |
Classificação |
|---|---|
Igual ou superior a 5% |
Boa |
Maior ou igual a 1,5% e menor do quê 5% |
Regular |
Maior do quê 0% e menor do quê 1,5% |
Ruim |
Igual ou menor do quê 0% |
Inaceitável (ganho real negativo significa perda do pôdêr de compra dos salários) |
Eles classificaram a proposta de aumento e justificaram essa classificação apresentando o valor do ganho real quê obteriam.
A classificação, com sua respectiva justificativa, foi
a) inaceitável, porque o ganho real seria mais próximo de −5%.
b) ruim, porque o ganho real seria mais próximo de 1,05%.
c) regular, porque o ganho real seria mais próximo de 4,7%.
d) boa, porque o ganho real seria mais próximo de 9,5%.
e) boa, porque o ganho real seria mais próximo de 5%.
alternativa c
PARA REFLETIR
Nas páginas de abertura, apresentamos a Black Friday, com o intuito de mostrar como a Matemática financeira contribui para o consumo consciente. Você conseguiu reconhecer essa relação?
Fizemos, neste Capítulo, um retrospecto do assunto porcentagem, quê você já deve ter estudado no Ensino Fundamental. Estudamos também juro simples e juro compôzto e como eles se relacionam com as funções afim e exponencial, respectivamente.
Além díssu, estudamos como fazer um orçamento familiar e conhecemos o Sistema Price e o Sistema de Amortização Constante.
Vamos refletir sobre as aprendizagens do Capítulo 1:
• Você já conhecia algum dos conteúdos apresentados? Qual(is)?
• Imagine quê você tivesse X reais para fazer uma aplicação e pudesse escolher entre duas opções com a mesma taxa: uma sôbi o regime de juro simples, e a outra, sôbi o regime de juro compôzto. Qual das aplicações você escolheria? Justifique.
• Dê exemplos de outras situações do dia a dia quê envolvem sistemas de amortização e orçamento familiar.
• Como você póde utilizar os conceitos estudados para analisar situações antes de tomar decisões e de resolver problemas do dia a dia?
Respostas pessoais.
Página cinquenta e dois
