CAPÍTULO 2
POLIEDROS
A beleza dos cristais é impressionante, não é mesmo? Os cristais, na sua forma mais pura, lembram poliedros, assunto dêste Capítulo.
A ciência quê estuda os cristais é chamada Cristalografia, cujos estudos são importantes para o avanço tecnológico de diversas áreas, entre elas, a Engenharia dos Materiais.
Para classificar esses minerais, os cristalógrafos avaliam o sistema de acôr-do com as células unitárias quê formam sua estrutura. Uma célula unitária consiste em um agrupamento de hátomus quê formam um padrão repetitivo. Então, com base no sistema cristalino ao qual pertence, um mineral póde sêr classificado em: cúbico, tetragonal, hexagonal, trigonal, ortorrômbico, monoclínico ou triclínico.
O arranjo dêêsses hátomus garante algumas propriedades ao cristal, como a dureza e o formato. O tipo de arranjo atômico, por exemplo, é o quê diferencia um frágil carbono de um diamante inquebrável.
Ver as Orientações para o professor.
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. ob-sérvim a imagem. Que formas geométricas, planas ou espaciais, vocês conseguem identificar?
2. O formato de um determinado cristal lembra um bloco retangular com dimensões 3 cm, 4 cm e 5 cm. Qual é o volume, em cm3, dêêsse cristal?
60 cm3
3. Na região onde vocês moram, há mineração de algum tipo de cristal? Qual(is)? Caso não haja, façam uma breve pesquisa a respeito da mineração de cristais no Brasil, indicando locais onde ocorre, principais cristais extraídos e o destino dêêsses recursos.
4. Escolham um dos sistemas cristalinos citados no texto e respondam às kestões.
• Qual foi o sistema escolhido?
• por quê vocês acham quê esse sistema recebe esse nome?
• Qual é o formato das células unitárias do sistema escolhido? Pesquisem em livros ou na internet a respeito do formato das células do sistema cristalino e encontrem o nome de um cristal quê pertença a ele.
Página cinquenta e três

Para assistir
• VOCÊ disse cristalografia? Campinas: Matemática Multimídia, 2012. 1 vídeo (12 min). Publicado pelo canal M3 Matemática Multimídia. (Série Matemática na escola). Disponível em: https://livro.pw/ywmtg. Acesso em: 17 set. 2024.
O vídeo fala sobre Cristalografia, um estudo quê descreve as formas geométricas e as simetrias dos cristais.
Página cinquenta e quatro
Poliedros
É comum encontrarmos no dia a dia objetos cujos formatos lembram sólidos geométricos. Basta observarmos ao nosso redor, pois eles estão presentes na Arquitetura, na Engenharia, nas Artes Plásticas, entre outras áreas do nosso cotidiano. Neste Capítulo, vamos estudar os sólidos geométricos conhecidos como poliedros.
Frequentemente, na Arquitetura e na Engenharia, os projetos e as construções utilizam formatos quê lembram poliedros para, por exemplo, obtêr o melhor aproveitamento da área ou mesmo para criar ambientes mais agradáveis à vista. Observe a seguir o prédio da Biblioteca Nacional de Belarus, país do Leste Europeu. Obra dos arquitetos Viktor Kramarenko (1945-) e Mi káil Vinogradov (1944-2020), o prédio é conhecido como"diamante bielorrusso" e tem formato de um poliedro.
Os poliedros são sólidos formados por um número finito de polígonos e pela região do espaço limitada por eles, em quê:
• cada lado de um dêêsses polígonos é comum a dois, e somente dois, polígonos;
• a intersecção de dois dêêsses polígonos é um lado comum ou um vértice comum ou é vazia.

Página cinquenta e cinco
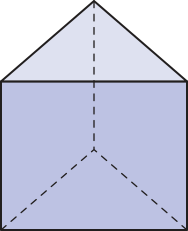
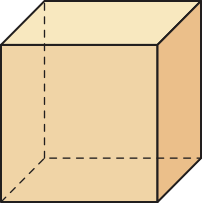
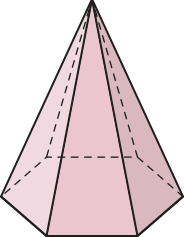
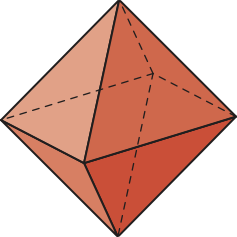
Observe alguns exemplos de poliedros:
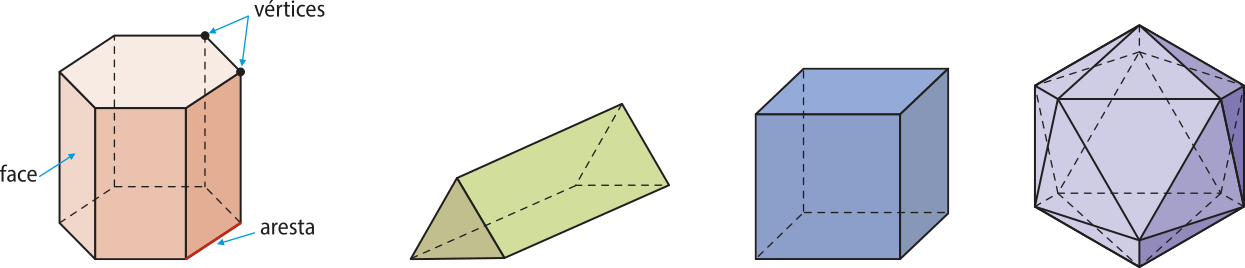
Em um poliedro, destacamos os seguintes elemêntos:
• Faces: são os polígonos quê formam a superfícíe do poliedro;
• Arestas: são os lados comuns a duas faces do poliedro;
• Vértices: são os pontos de intersecção de três ou mais arestas.
Assim como os polígonos são nomeados com base em seu número de lados, os poliedros são nomeados com base em seu número de faces. Observe a seguir o nome e o respectivo número de faces de alguns poliedros.
Nome do poliedro |
Número de faces |
|---|---|
tetraedro |
4 |
pentaedro |
5 |
hexaedro |
6 |
heptaedro |
7 |
octaedro |
8 |
eneaedro |
9 |
decaedro |
10 |
undecaedro |
11 |
dodecaedro |
12 |
icosaedro |
20 |

Saiba quê...
A palavra"poliedro" é formada por poli, do grego polys (muitos ou vários), e edro, do grego hedra (face), ou seja, um poliedro seria um sólido de muitas faces.
Poliedros convexos e poliedros não convexos
Em um poliedro, se qualquer reta não paralela a nenhuma das faces intersecta suas faces em, no mássimo, dois pontos, dizemos quê ele é convexo; caso contrário, é não convexo.
Observe os exemplos.
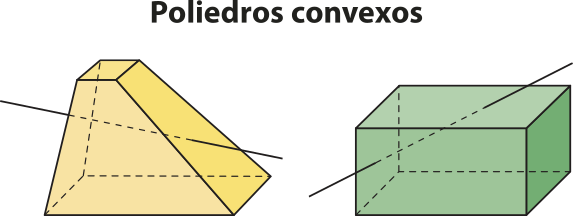
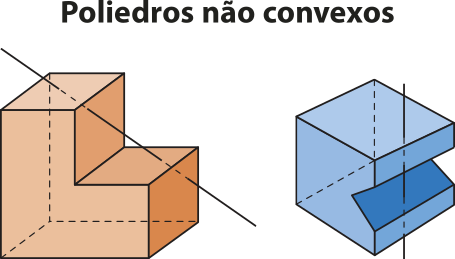
Neste Capítulo, concentraremos nóssos estudos nos poliedros convexos
Página cinquenta e seis
Relação de Óiler
Existe uma relação importante quê envolve o número de faces (F), o número de arestas (A) e o número de vértices (V) de um poliedro convexo. Essa relação é válida para todo poliedro convexo e recebe o nome de relação de Óiler, em homenagem ao matemático suíço Leonhard Óiler (1707-1783).
V − A + F = 2

Observe alguns exemplos.
Poliedro |
|
|
|
|
|---|---|---|---|---|
F |
5 |
6 |
7 |
8 |
A |
9 |
12 |
12 |
12 |
V |
6 |
8 |
7 |
6 |
V − A + F |
6 − 9 + 5 = 2 |
8 − 12 + 6 = 2 |
7 − 12 + 7 = 2 |
6 − 12 + 8 = 2 |
A relação de Óiler póde sêr empregada para determinar o número de um dos elemêntos (faces, arestas ou vértices) de um poliedro convexo, desde quê os outros dois sêjam conhecidos.
Um poliedro em quê é válida a relação de Óiler é conhecido como poliedro óileriano.
Os poliedros convexos são todos eulerianos.
Observação:
Há poliedros não convexos para os quais vale a relação de Óiler. Na figura, temos um exemplo.
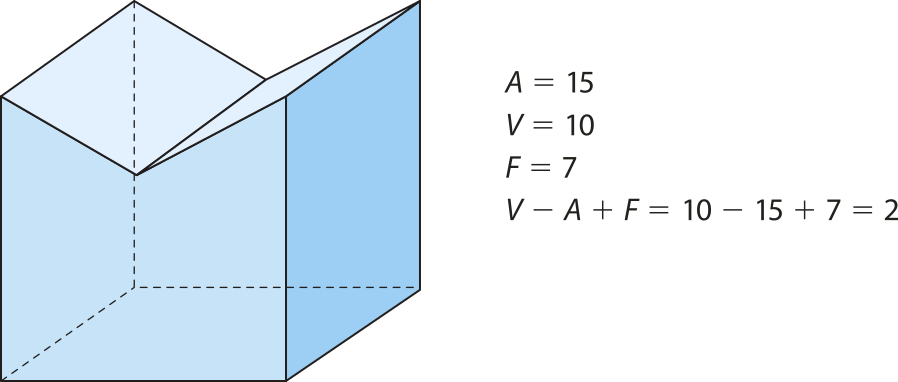
Ver as Orientações para o professor.
Página cinquenta e sete
Poliedro regular
Um poliedro convexo é regular quando suas faces são polígonos regulares e congruentes entre si e quando, em todos os vértices, concorre o mesmo número de arestas.
É possível provar quê existem somente cinco poliedros regulares: tetraedro, hexaedro, octaedro, dodecaedro e icosaedro.
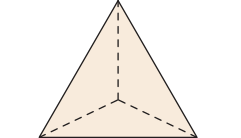
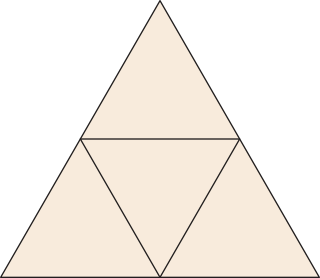
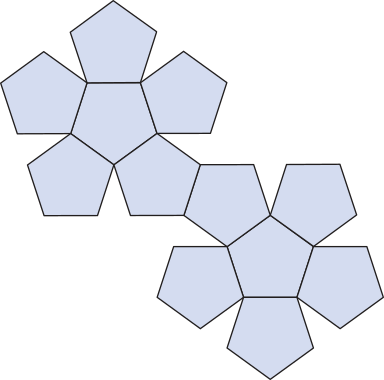
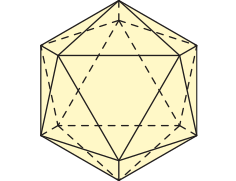
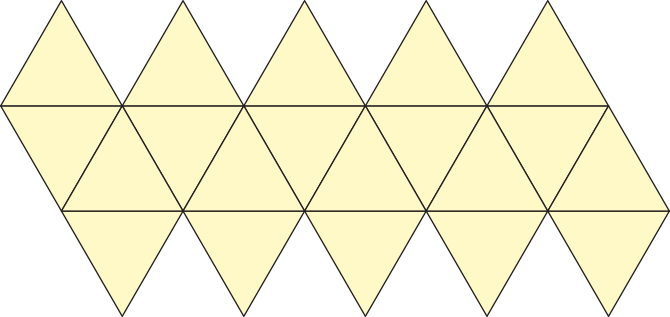
Observe a seguir representações dos cinco poliedros regulares e as respectivas planificações de suas superfícies.

• 4 faces triangulares
• 4 vértices
• 6 arestas
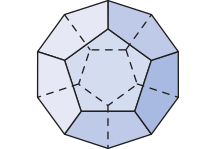
• 12 faces pentagonais
• 20 vértices
• 30 arestas
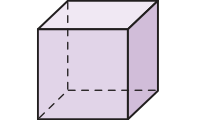
• 6 faces quadrangulares
• 8 vértices
• 12 arestas

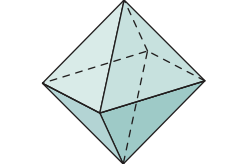
• 8 faces triangulares
• 6 vértices
• 12 arestas
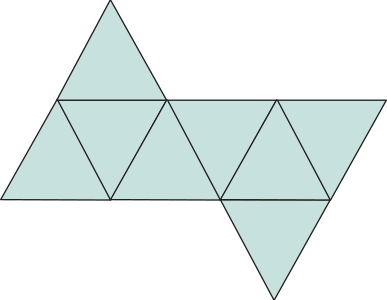
• 20 faces triangulares
• 12 vértices
• 30 arestas
Página cinquenta e oito
Poliedros de Platão
Os poliedros de Platão levam o nome do filósofo grego Platão (c. 427 a.C.-347 a.C.), quê os utilizava para explicar alguns fenômenos naturais.
Para quê um poliedro seja considerado um poliedro de Platão, é necessário quê as faces dêêsse poliedro tênham o mesmo número de arestas, quê, em todos os vértices, concorra o mesmo número de arestas e quê seja válida a relação de Óiler. Assim, os poliedros de Platão englobam todos os poliedros regulares convexos. Existem somente cinco classes de poliedros de Platão: tetraedros, hexaedros, octaedros, dodecaedros e icosaedros.
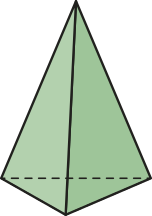
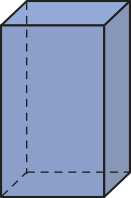
Nos poliedros de Platão, as faces não precisam sêr polígonos regulares; logo, nem todo poliedro de Platão é regular.
Observe alguns exemplos de poliedros de Platão quê não são regulares.
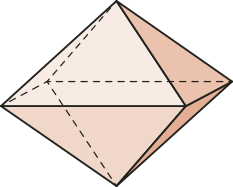
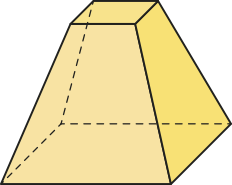
ATIVIDADES RESOLVIDAS
1. Em um poliedro convexo, o número de faces é 11 e o número de vértices é 18. Calcule o número de arestas dêêsse poliedro.
Resolução
Pela relação de Óiler, V − A + F = 2, válida para qualquer poliedro convexo, temos:
F = 11 e V = 18. Logo:
V − A + F = 2 ⇒ 18 − A + 11 = 2 ⇒ A = 27
Portanto, o poliedro tem 27 arestas.
2. Um poliedro convexo tem seis faces quadrangulares e duas hexagonais. Calcule o número de vértices dêêsse poliedro.
Resolução
Pelo enunciado, o poliedro tem oito faces, sêndo seis quadrangulares e duas hexagonais. Vamos determinar o número de arestas:
Seis faces quadrangulares: 6 ⋅ 4 = 24 arestas.
Duas faces hexagonais: 2 ⋅ 6 = 12 arestas.
Como cada aresta foi contada duas vezes, temos:
2A = 24 + 12 ⇒ 2A = 36 ⇒ A = 18
Aplicando a relação de Óiler, temos:
V − A + F = 2 ⇒ V − 18 + 8 = 2 ⇒ V = 12
Assim, o número de vértices é 12.
ATIVIDADES
1. Em um poliedro convexo, o número de arestas é 16 e o número de faces é 9. Determine o número de vértices.
9 vértices
2. Um poliedro convexo tem cinco faces quadrangulares e duas faces pentagonais. Determine o número de arestas e o número de vértices.
15 arestas e 10 vértices
3. (Fatec-SP) Um poliedro convexo tem 3 faces com 4 lados, 2 faces com 3 lados e 4 faces com 5 lados. Calcule o número de vértices dêêsse poliedro.
12 vértices
4. (Mack-SP) Determine o número de vértices de um poliedro quê tem três faces triangulares, uma face quadrangular, uma pentagonal e duas hexagonais.
10 vértices
Página cinquenta e nove
5. (Unifesp-SP) Considere o poliedro cujos vértices são os pontos médios das arestas de um cubo. O número de faces triangulares e o número de faces quadradas dêêsse poliedro são, respectivamente:
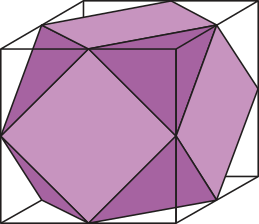
a) 8 e 8.
b) 8 e 6.
c) 6 e 8.
d) 8 e 4.
e) 6 e 6
alternativa b
6. (UEL-PR) Leia o texto a seguir.
Originalmente os dados eram feitos de osso, marfim ou argila. Há evidências da existência deles no Paquistão, Afeganistão e noroeste da Índia, datando de 3500 a.C. Os dados cúbicos de argila continham de 1 a 6 pontos, dispostos de tal maneira quê a soma dos pontos de cada par de faces opostas é sete.
(Adaptado de: Museu Arqueológico do Red Fort. Delhi, Índia.)
Atualmente, além dos dados em forma de cubo (hexaedro), encontram-se dados em vários formatos, inclusive esféricos, como mostram as figuras a seguir.

Apesar do formato esférico, ao sêr lançado, o dado mostra pontos de um a seis, como se fosse um dado cúbico. Isso acontece porque no interior da esféra existe uma cavidade em forma de octaedro, na qual existe um peso (um chumbinho) quê se aloja em um dos vértices do octaedro.
Assinale a alternativa quê apresenta, corretamente, a propriedade dos poliedros regulares quê justifica o fato de a cavidade no interior da esféra sêr octaédrica.

a) O número de vértices do octaedro é igual ao número de faces do hexaedro.
b) O número de vértices do octaedro é diferente do número de faces do hexaedro.
c) O número de arestas do octaedro é igual ao número de arestas do hexaedro.
d) O número de faces do octaedro é igual ao número de vértices do hexaedro.
e) O número de faces do octaedro é diferente do número de vértices do hexaedro.
alternativa a
7. Indique qual das afirmações a seguir é falsa.
a) A relação de Óiler é válida para todos os poliedros de Platão.
b) Todo poliedro de Platão é um poliedro regular convexo.
c) Todas as faces de um poliedro de Platão têm o mesmo número de arestas.
d) As faces de um poliedro regular são polígonos regulares e congruentes entre si.
alternativa b
8. Em 1985, foi divulgada a descoberta de uma molécula tridimensional de carbono, na qual os hátomus ocupam os vértices de um poliedro convexo cujas faces são 12 pentágonos e 20 hekzágonos regulares. Em homenagem ao arquiteto estadunidense Buckminster Fuller, a molécula foi denominada buckminsterfulereno. Algum tempo depois, passou-se a denominá-la simplesmente fulereno.
Fonte dos dados: SINDICATO DOS FARMACÊUTICOS DO ESTADO DA PARAÍBA. [Fulerenos]. João Pessoa: Sifep, c2016. Disponível em: https://livro.pw/idtda. Acesso em: 17 set. 2024.
Determine o número de hátomus de carbono nessa molécula e o número de ligações representadas pelas arestas do poliedro.
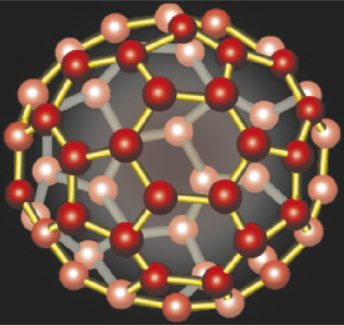
60 hátomus e 90 ligações
Página sessenta
Prismas
Agora, vamos estudar os prismas, suas características, seus elemêntos e as maneiras de calcular a área da superfícíe e o volume de um prisma.
Vamos considerar dois planos paralelos (alfa)" e (beta)", um polígono convexo, contido em (alfa)", e uma reta r secante a esses planos quê não intersecta o polígono.
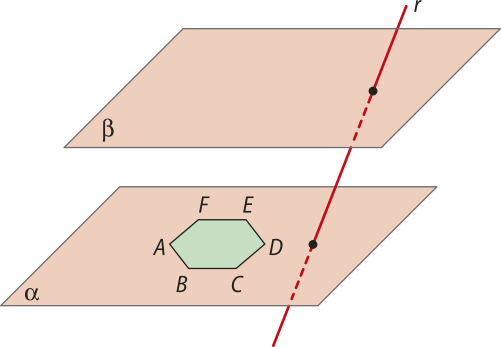
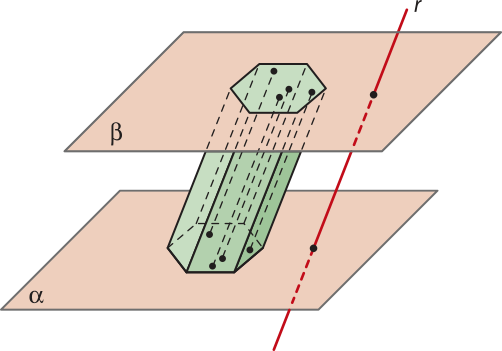
A figura geométrica formada pela reunião de todos os segmentos de reta paralelos à reta r, com uma extremidade em um ponto do polígono convexo e a outra no plano (beta)", é denominada prisma.
Considerando o prisma representado na figura a seguir, destacamos os seguintes elemêntos:
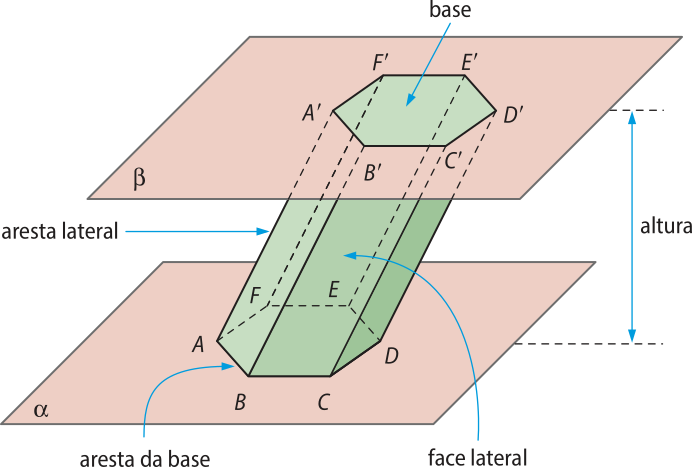
• Bases: são os polígonos convexos congruentes ABCDEF e A’B’C’D’E’F’ situados nos planos paralelos (alfa)" e (beta)" (planos das bases);
• Faces laterais: são os paralelogramos ABB’A’, BCC’B’, cê dê dê’C’, DEE’D’, EFF’E’ e AFF’A’;
• Vértices: são os vértices das faces do prisma, A, B, C, D, E, F, A’, B’, C’, D’, E’ e F’;
• Arestas das bases: são os lados dos polígonos das bases , , , , , , , e ;
• Arestas laterais: são os segmentos de reta , , , , e ;
• Diagonais: são os segmentos de reta quê ligam dois vértices não pertencentes à mesma face do prisma, ou seja, , , , , , , , , , , , , , , , , e ;
• Altura: é a distância entre os planos das bases.
pôdêmos classificar os prismas de acôr-do com o número de lados dos polígonos das bases. Por exemplo, os prismas podem sêr triangulares, quando as bases são triângulos; quadrangulares, quando as bases são quadriláteros; pentagonais, quando as bases são pentágonos; e assim por diante.

Página sessenta e um
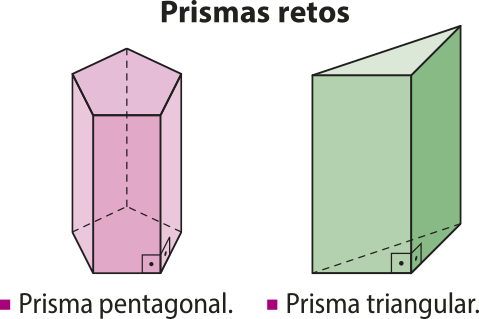
De acôr-do com a inclinação das arestas laterais em relação aos planos das bases, os prismas podem sêr rétos ou oblíqüos.
Em um prisma reto, as arestas laterais são perpendiculares aos planos das bases, e, em um prisma oblíquo, as arestas laterais são oblíquas aos planos das bases.
Observe os exemplos a seguir.

Prisma regular
Se o prisma for reto e as bases forem polígonos regulares, o prisma é dito regular. Um exemplo é a figura a seguir, quê representa um prisma hexagonal regular.
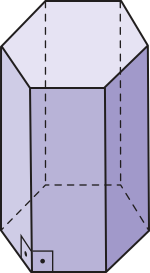
Pense e responda
Sabendo quê a figura apresenta um prisma hexagonal regular, quê figuras geométricas compõem suas bases e suas faces laterais?
As bases de um prisma hexagonal regular são hekzágonos regulares; suas faces laterais são retângulos congruentes.
Paralelepípedos
Os prismas cujas bases são paralelogramos recebem nomes especiais.

• Paralelepípedo: é um prisma cujas bases são paralelogramos.
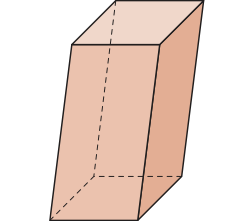
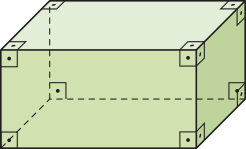
• Paralelepípedo reto-retângulo ou bloco retangular: é um prisma reto cujas bases e faces laterais são retângulos. O paralelepípedo reto-retângulo é um caso particular do paralelepípedo.
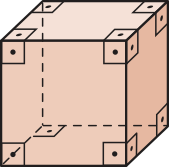
• Cubo ou hexaedro regular: é um prisma reto cujas faces são todas quadradas. O cubo é um caso particular do paralelepípedo reto-retângulo.
Página sessenta e dois
Diagonal de um paralelepípedo reto-retângulo
Considere o paralelepípedo reto-retângulo a seguir, em quê estão indicadas algumas medidas.
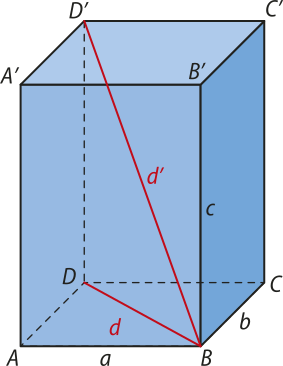
Conhecendo as dimensões a, b e c, podemos calcular as medidas d da diagonal da base e d’ da diagonal do paralelepípedo pelo teorema de Pitágoras.
Considerando o triângulo retângulo ABD, temos:
a2 + b2 = d ⇒ d =
Do triângulo retângulo BDD’, temos:
c2 + d2 = d’2 ⇒ d’ = ⇒ d’ =
Portanto, a medida da diagonal de um paralelepípedo reto-retângulo de dimensões a, b e c é:
Pense e responda
Como podemos expressar a medida d da diagonal de um cubo em função da medida a de sua aresta?
Área da superfícíe de um prisma
Em um prisma, definimos:
• área da base (Sb) como a área de um dos dois polígonos quê formam as bases;
• área lateral (S(éli)") como a soma das áreas de todas as faces laterais;
• área total (St) como a soma da área lateral e das áreas das bases.
Assim, podemos escrever:
St = S(éli)" + 2Sb
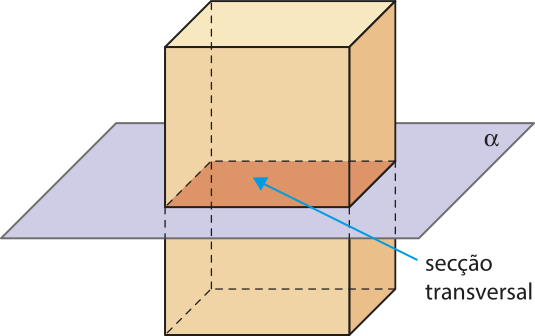
Secção transversal de um prisma
A intersecção de um prisma com um plano paralelo às suas bases é denominada secção transversal do prisma.
Observe na figura quê a secção transversal de um prisma é um polígono congruente aos polígonos das bases.
Página sessenta e três
ATIVIDADES RESOLVIDAS
3. Determine a área total da superfícíe de um paralelepípedo reto-retângulo de dimensões 5 cm, 4 cm e 3 cm.
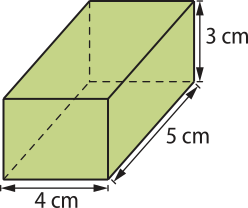
Resolução
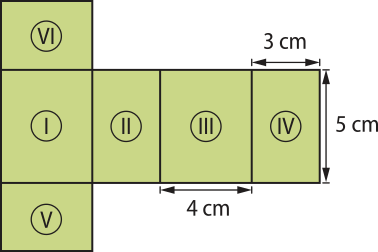
A superfícíe do paralelepípedo é formada por seis faces retangulares, indicadas na planificação anterior. Note quê I ≅ III, II ≅ IV e V ≅ VI.
Calculando cada área, temos:
SI = 4 cm ⋅ 5 cm = 20 cm2
SII = 3 cm ⋅ 5 cm = 15 cm2
SV = 4 cm ⋅ 3 cm = 12 cm2
Então:
St = 2SI + 2SII + 2SV
St = 2 ⋅ (20 + 15 + 12) = 2 ⋅ 47 = 94
Portanto, a área total da superfícíe é de 94 cm2.
4. Em um prisma triangular regular, a medida a da aresta da base é igual à medida h da altura do prisma. Sabendo quê a área lateral é 10 m2, calcule a área total do prisma.
Resolução
Planificando a superfícíe do prisma, temos:
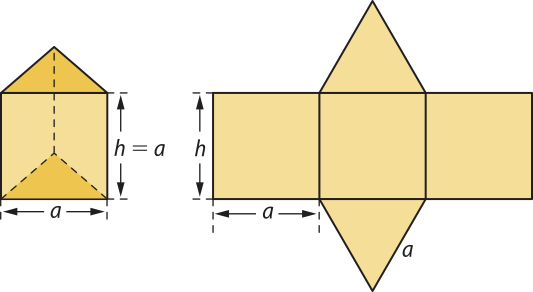
A face lateral é um retângulo de dimensões a e h.
S(éli)" = 3 ⋅ (a ⋅ h) ⇒ S(éli)" = 3 ⋅ (a ⋅ a) ⇒ S(éli)" = 3a2
Como S(éli)" = 10 m2, temos:
3a2 = 10 ⇒ a2 =
A base é um triângulo equilátero cujo lado méde a. Assim:
Sb = ⇒ Sb =
Cálculo da área total:
St = S(éli)" + 2 ⋅ Sb = 10 + 2 ⋅ = 10 (1 + )
Portanto, St = 10 (1 + ) m2.
5. Felipe está construindo uma piscina no quintal da casa dele no formato de um bloco retangular quê tem, intérnamente, 8 métros de comprimento, 4 metros de largura e 1,5 metro de profundidade. O revestimento escolhido por Felipe para cobrir a área interna da piscina é formado por quadrados de cerâmica com 25 cm de lado vendidos por R$ 1,50 a unidade. Considerando quê não haverá espaço entre os quadrados, calcule o valor quê Felipe deve gastar para comprar a quantidade exata de revestimento necessário para cobrir a área interna da piscina.
Resolução
A área total de um paralelepípedo reto-retângulo é dada por St = S(éli)" + 2 ⋅ Sb.
Por se tratar de uma piscina, o revestimento não será colocado em uma das faces do paralelepípedo. Assim, a área total, em métro quadrado, é:
St = 8 ⋅ 4 + 2 ⋅ (4 ⋅ 1,5) + 2 ⋅ (8 ⋅ 1,5) = 68
A área de cada revestimento, em métro quadrado, é:
AR = 0,25 ⋅ 0,25 = 0,0625
O total de unidades necessárias para o revestimento é de = 1.088.
Felipe precisará comprar 1.088 unidades. Como cada unidade custa R$ 1,50, então o custo total do revestimento é dado por:
1.088 ⋅ 1,5 = 1.632
Assim, o custo do revestimento será de R$ 1.632,00.
Página sessenta e quatro
ATIVIDADES
9. Calcule a área total de um cubo cuja aresta méde 8 cm.
384 cm2
10. A diagonal de um paralelepípedo reto-retângulo méde 13 dm, e a diagonal da base, 5 dm. Determine as três dimensões do paralelepípedo, sêndo a soma das medidas de todas as arestas igual a 76 dm.
3 dm, 4 dm e 12 dm
11. Um prisma pentagonal regular tem 20 cm de altura. A aresta da base do prisma méde 4 cm. Determine a área lateral dêêsse prisma.
400 cm2
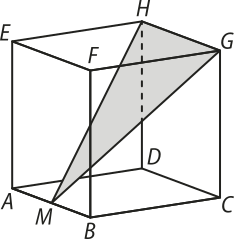
12. (UFRGS-RS) Considere o cubo ABCDEFGH, representado na figura abaixo, cuja aresta méde 4 e M é o ponto médio da aresta .
A área do triângulo MHG é
a)
b)
c)
d)
e)
alternativa c
13. Um prisma reto tem por base um triângulo isósceles com as medidas indicadas na figura.
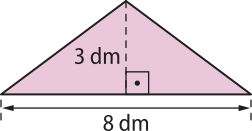
Sabendo quê a altura do prisma é igual a do perímetro da base, calcule a área total da superfícíe do prisma.
St = 132 dm2
14. Em um paralelepípedo reto-retângulo, o comprimento é o dôbro da largura, e a altura é 15 cm. Sabendo quê a área total é 424 cm2, calcule as dimensões desconhecidas dêêsse paralelepípedo.
8 cm; 4 cm
15. As dimensões de um paralelepípedo reto-retângulo são números consecutivos. Sabendo quê a soma das medidas de todas as arestas é 84 cm, calcule a área total da superfícíe dêêsse paralelepípedo.
292 cm2
16. (UFRN) Atualmente, uma das técnicas muito utilizadas no cultivo de hortaliças é a produção em estufas (plasticultura), pois, entre outros fatores, possibilita a proteção contra chuvas, frio, insetos e um aumento da produtividade, quê póde atingir até 200%, como no exemplo da abóbora italiana.
1.192 m2
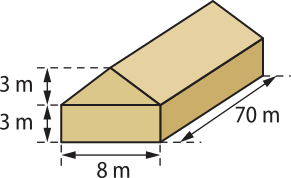
Considerando uma estufa como a representada acima, em quê o triângulo da fachada é isósceles, calcule a área de plástico utilizado para revesti-la totalmente (exceto o piso).
17. (UnB-DF) Em um prisma triangular regular, a área lateral é o quádruplo da área da base. Sabendo quê o triângulo da base póde sêr inscrito em uma circunferência de raio 2 dm, calcule a área total do prisma em decimetros quadrados e multiplique o resultado por .
54 dm2
18. Calcule a área total dos prismas rétos ilustrados.
a) 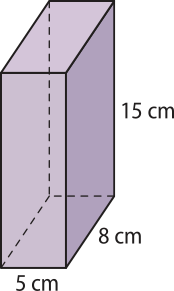
470 cm2
b) 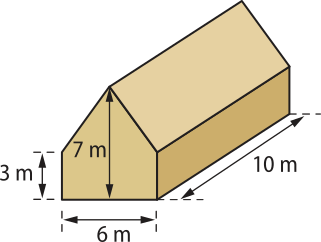
280 m2
19. (UFPE) Uma formiga (ignore seu tamanho) encontra-se no vértice A do paralelepípedo reto ilustrado a seguir.
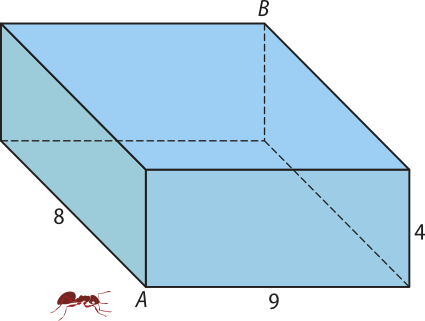
Qual a menor distância quê ela precisa percorrer para chegar ao vértice B (caminhando sobre a superfícíe do paralelepípedo)?
15 unidades de comprimento
Página sessenta e cinco
Volume de um paralelepípedo reto-retângulo
Para medir o volume do espaço ocupado por um sólido S, precisamos comparar esse sólido com uma unidade de medida de volume.
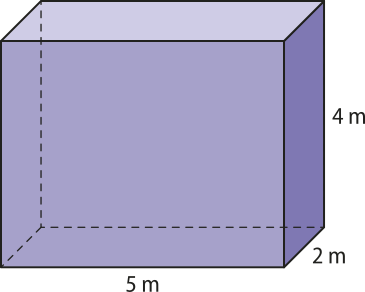
Vamos considerar, por exemplo, um paralelepípedo reto-retângulo com dimensões 5 m, 2 m e 4 m.
Note quê, ao dividir esse bloco retangular em cubos com arestas medindo 1 m, podemos determinar a quantidade de cubos quê o compõem da seguinte maneira:
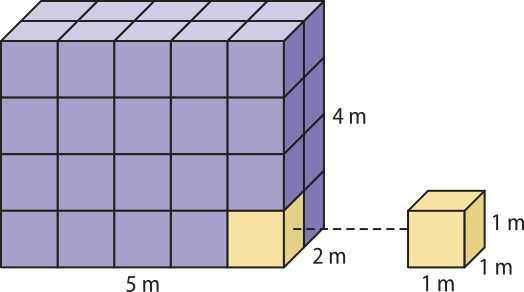
⋅ = 40
Portanto, esse paralelepípedo é compôzto de 40 cubos com 1 m3 de volume cada. Assim, o volume total é igual a 40 m3.
Note quê o volume V do paralelepípedo, nesse caso, poderia sêr obtído multiplicando-se suas três dimensões: comprimento, largura e altura. Observe:
V = 5 m ⋅ 2 m ⋅ 4 m = 40 m3
No caso geral de um paralelepípedo reto-retângulo qualquer, prova-se quê o volume V dêêsse paralelepípedo de dimensões com medidas a, b e c é dado por:
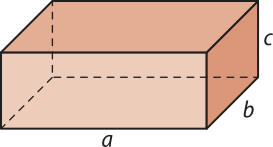
V = a ⋅ b ⋅ c
Saiba quê...
A grandeza volume se relaciona com a grandeza capacidade; dêêsse modo, podemos também relacionar suas unidades de medida. Observe um exemplo: 1 m3 = 1.000 L
Como o produto a ⋅ b equivale à área da base Ab e c é a medida h da altura, podemos dizêr quê o volume do paralelepípedo é igual ao produto da área da base pela medida da altura:
V = Sb ⋅ h
Observe como calcular o volume de um paralelepípedo reto-retângulo de dimensões 5,32 m, 2,08 m e 2,2 m.
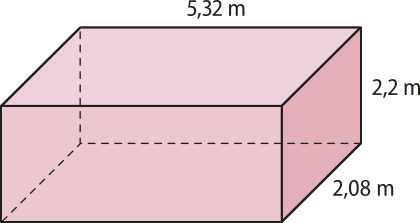
V = 5,32 m ⋅ 2,08 m ⋅ 2,2 m ≃ 24,34 m3
Página sessenta e seis
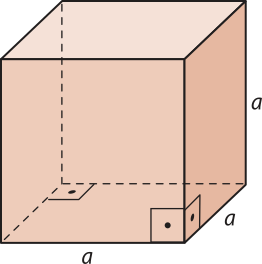
Volume de um cubo
Em um cubo, as três dimensões têm a mesma medida e, indicando cada uma delas por a, seu volume é dado por:
V = a ⋅ a ⋅ a ⇒ V = a3
Princípio de Cavalieri
Apresentamos o cálculo quê determina o volume do paralelepípedo reto-retângulo e do cubo. No entanto, a fórmula para o cálculo do volume de outros sólidos póde não sêr tão simples e, para estabelecê-la, precisamos de um resultado matemático, conhecido como princípio de Cavalieri.
Vamos considerar duas pilhas de papel sulfite idênticas, com a mesma quantidade de fô-lhas em cada uma, colocadas sobre uma mesa.
Saiba quê...
O princípio de Cavalieri foi desenvolvido pelo matemático italiano Frantiesco Bonaventura Cavalieri (1598-1647).
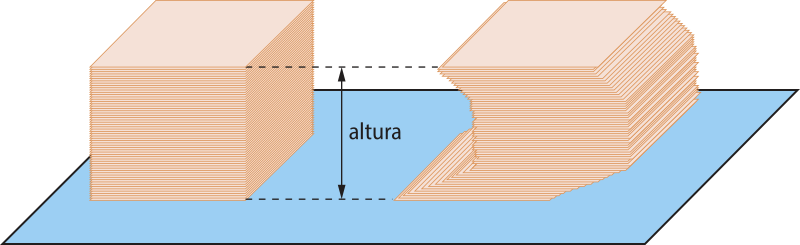
Observando as duas pilhas, podemos destacar algumas características: a altura é a mesma, pois cada uma tem a mesma quantidade de fô-lhas; as fô-lhas de cada pilha quê ficam à mesma distância da mesa têm a mesma área; e as duas pilhas têm o mesmo volume, uma vez quê são formadas pela mesma quantidade de fô-lhas.
Essa ideia ilustra o princípio de Cavalieri, apresentado a seguir.
Considere dois sólidos A e B de mesma altura com as bases contidas em um mesmo plano horizontal (alfa)". Traçando um plano (beta)", paralelo a (alfa)" e secante aos sólidos, determinamos duas secções transversais, cujas áreas são S1 e S2.
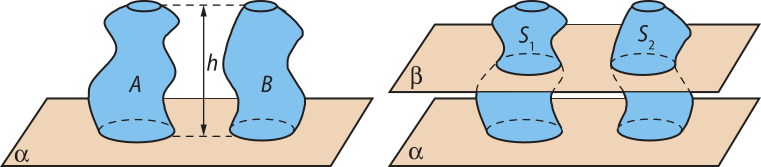
O princípio de Cavalieri afirma quê, se, para todo plano (beta)", nas condições anteriores, tivermos S1 = S2, então os sólidos A e B terão o mesmo volume.
O princípio de Cavalieri póde sêr demonstrado; no entanto, não o faremos aqui, por esse cálculo envolver conceitos matemáticos quê não são estudados no Ensino Médio. Vamos considerá-lo verdadeiro e aplicá-lo para a determinação do volume de alguns sólidos.
Página sessenta e sete
Volume de um prisma
cérto fabricante de itens alimentícios tem, em seu catálogo, um produto cuja embalagem lembra um prisma de base hexagonal, como podemos observar na imagem.

Para propósitos de armazenamento, o fabricante precisa saber qual é o volume ocupado por cada embalagem. Como ele póde determinar isso?
Para responder a essa pergunta, vamos usar o princípio de Cavalieri e determinar uma fórmula para calcular o volume de um prisma.
Seja A um sólido de altura h e área da base Sb. Considere, ainda, um paralelepípedo reto-retângulo B de mesma altura h e área da base também Sb. Ambos estão apoiados no plano (alfa)".
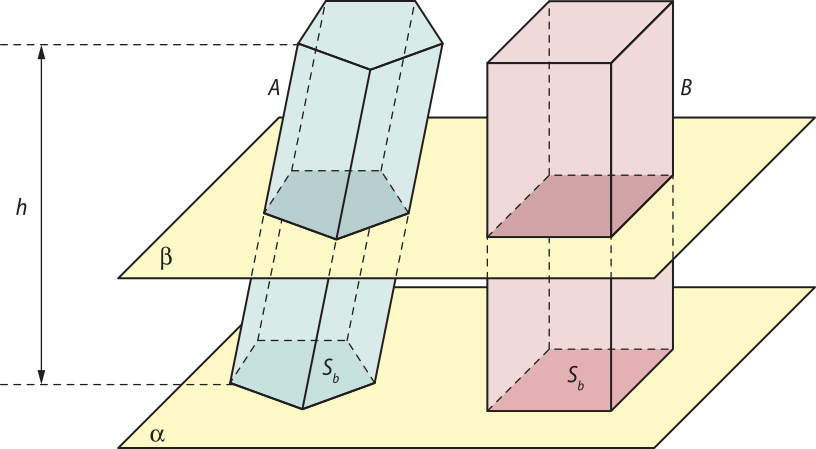
Qualquer plano (beta)", paralelo ao plano (alfa)", quê intersecte os sólidos A e B determina secções transversais congruentes às respectivas bases. Como as áreas das bases de A e B são iguais e valem Sb, então as secções transversais também têm área igual a Sb. Portanto, pelo princípio de Cavalieri, concluímos quê o volume do prisma A é igual ao volume do paralelepípedo reto-retângulo B.
Como o volume do paralelepípedo reto-retângulo é dado pelo produto da área da base Sb pela medida da altura h, então o volume do prisma Vprisma também será calculado da mesma maneira. Assim, podemos escrever:
Vprisma = Sb ⋅ h
Pense e responda
Qual é o volume ocupado pela embalagem, sabendo quê a área de sua base é igual a 6 cm2 e quê cada embalagem tem 10 cm de altura?
60 cm3
Página sessenta e oito
FÓRUM
O impacto das embalagens e o desafio dos resíduos sólidos
As embalagens dêsempênham papel essencial na ssossiedade moderna, facilitando o transporte, a proteção e a preservação de produtos, bem como trazem importantes informações para o consumidor. No entanto, o uso excessivo e inadequado de embalagens tem gerado uma série de problemas ambientais e sociais, principalmente relacionados à produção de resíduos sólidos.
Esses resíduos, muitas vezes feitos de plástico, podem levar centenas de anos para se decompor, prejudicando éco-sistemas terrestres e aquáticos e representando uma ameaça à vida selvagem. Além díssu, visando ao aperfeiçoamento das técnicas de conservação de produtos, novos materiais têm sido incorporados às embalagens para torná-las mais eficientes. Entretanto, essas misturas freqüentemente dificultam tanto a sua degradação natural como a sua reciclagem.
Muitos dêêsses resíduos acabam sêndo descartados de maneira incorréta, poluindo rios, oceanos e áreas naturais e contribuindo para a formação de lixões e atêerros sanitários sobrecarregados. Esse cenário não apenas compromete a qualidade do ar, da á gua e do solo, mas também representa um desafio para as comunidades locais e os governos, quê enfrentam dificuldades na côléta, no tratamento e na disposição adequada dêêsses resíduos.
O excésso de embalagens também tem consequências econômicas e sociais. O aumento dos custos relacionados à gestão de resíduos representa um ônus para empresas, governos e consumidores, enquanto a poluição resultante afeta negativamente o turismo, a pesca e outras atividades econômicas dependentes de éco-sistemas saudáveis.
Diante dêêsses desafios, é fundamental adotar medidas eficazes para mitigar os problemas causados pelas embalagens e pêlos resíduos sólidos gerados por elas. Isso inclui a promoção de práticas de disáini e produção sustentáveis, a implementação de políticas de redução, reutilização e reciclagem de embalagens, o investimento em infraestrutura de gestão de resíduos e a conscientização pública sobre o impacto ambiental do consumo excessivo e do desperdício. Um país quê se destaca nesse sentido é a Alemanha, onde os resíduos quê não podem sêr reciclados ou compostados vão para usinas modernas, nas quais são incinerados em altas tempera-túras, gerando calor, quê é convertido em energia elétrica e térmica, reduzindo assim a dependência de fontes de energia não rêno-váveis.
Fonte dos dados: PORTAL SUSTENTABILIDADE. 5 países reconhecidos por boas práticas na gestão de resíduos sólidos urbanos. [S. l.]: Portal Sustentabilidade, 22 jun. 2023. Disponível em: https://livro.pw/pqiez. Acesso em: 3 maio 2025.
![]() Após ler o texto, converse com seus côlégas sobre as kestões a seguir.
Após ler o texto, converse com seus côlégas sobre as kestões a seguir.
• Como vocês costumam descartar as embalagens após o uso do conteúdo? Já pensaram em como suas escôlhas de consumo afetam o meio ambiente? Que tipo de ações vocês acham quê poderiam sêr realizadas na escola ou na comunidade para abordar essas kestões?
Ver as Orientações para o professor.

Página sessenta e nove
ATIVIDADE RESOLVIDA
6. (Enem/MEC) Um petroleiro possui reservatório em formato de um paralelepípedo retangular com as dimensões dadas por 60 m × 10 m de base e 10 m de altura. Com o objetivo de minimizar o impacto ambiental de um eventual vazamento, esse reservatório é subdividido em três compartimentos, A, B e C, de mesmo volume, por duas placas de aço retangulares com dimensões de 7 m de altura e 10 m de base, de modo quê os compartimentos são interligados, conforme a figura. Assim, caso haja rompimento no casco do reservatório, apenas uma parte de sua carga vazará.
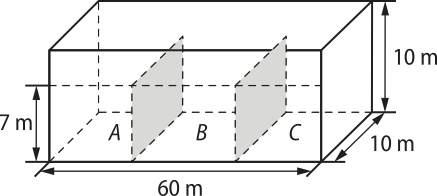
Suponha quê ocorra um desastre quando o petroleiro se encontra com sua carga mássima: ele sofre um acidente quê ocasiona um furo no fundo do compartimento C. Para fins de cálculo, considere desprezíveis as espessuras das placas divisórias. Após o fim do vazamento, o volume do petróleo derramado terá sido de
a) 1,4 × 103 m3
b) 1,8 × 103 m3
c) 2,0 × 103 m3
d) 3,2 × 103 m3
e) 6,0 × 103 m3
Resolução
Vamos calcular o volume da região acima das placas e do compartimento C, onde está o furo quê provocará o vazamento.
Assim, temos:
V = 60 ⋅ 10 ⋅ (10 − 7) + (60 ∶ 3) ⋅ 10 ⋅ 7
V = 1.800 + 1.400
V = 3.200
Dessa maneira, o volume de petróleo derramado é igual a 3,2 ⋅ 103 m3.
Outro modo de resolver a questão é calcular o volume total do reservatório e subtrair o volume dos compartimentos A e B.
V = 60 ⋅ 10 ⋅ 10 − 2 ⋅ (60 ∶ 3) ⋅ 10 ⋅ 7
V = 6.000 − 2.800
V = 3.200
A resposta correta é a alternativa d.
ATIVIDADES
20. Qual é o volume, em métro cúbico, de argila necessário para produzir 5.000 tijolos, tendo cada tijolo a forma de um paralelepípedo reto-retângulo com dimensões 18 cm, 9 cm e 6 cm?
4,86 m3

21. As medidas das arestas de um paralelepípedo reto-retângulo formam uma progressão geométrica. Se a menor das arestas méde cm e o volume de tal paralelepípedo é 64 cm3, calcule as medidas das outras arestas.
4 cm e 32 cm
22. (UEPB) Um reservatório em forma de cubo, cuja diagonal méde m, tem capacidade igual a:
a) 4.000 litros
b) 6.000 litros
c) 8.000 litros
d) 2.000 litros
e) 1.000 litros
alternativa c
23. Uma empresa alimentícia vai começar a produzir bôm-bôns de chocolate em formatos de cubo de aresta 4 cm e de paralelepípedo reto-retângulo com comprimento de 6 cm, largura de 5 cm e altura de 2 cm. Serão produzidos três tipos: chocolate ao leite, meio amargo e branco. A seguir, temos as dimensões dos bôm-bôns e os custos de produção dos chocolates.
Tipo |
1 |
2 |
|---|---|---|
Dimensões (cm) |
4 × 4 × 4 |
6 × 5 × 2 |
Tipos |
Ao leite |
Meio amargo |
Branco |
|---|---|---|---|
Custo (R$/cm3) |
0,03 |
0,05 |
0,04 |
Elabore um problema quê associe as dimensões dos bôm-bôns ao custo por cm3.
Resposta pessoal.
Página setenta
24. (UEPG-PR) As medidas internas de uma caixa-d’água em forma de paralelepípedo retângulo são: 1,2 m, 1 m e 0,7 m. Sua capacidade é de:
a) 8.400 L
b) 84 L
c) 840 L
d) 8,4 L
e) n.d.a.
alternativa c
25. (UFRN) Quando se diz quê, numa região, caiu uma chuva com precipitação de 10 mm de á gua, isso significa quê cada métro quadrado dessa região recebeu 10 litros de á gua da chuva. Uma caixa-d’água de 1,5 m de altura, 0,8 m de largura e 1,4 m de comprimento, com uma abertura na face superior, na forma de um quadrado com 40 cm de lado, recebeu á gua diretamente de uma chuva de 70 mm.
Admitindo-se quê a caixa só tenha recebido á gua da chuva, pode-se afirmar quê o nível da á gua nessa caixa aumentou:
a) 0,8 cm
b) 1 cm
c) 1,2 cm
d) 2 cm
alternativa b
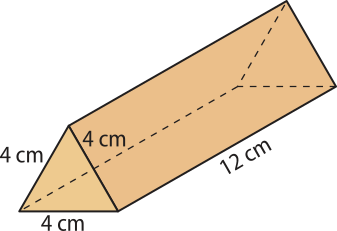
26. Uma barra de chocolate tem o formato da figura a seguir. Calcule o volume de chocolate contido nessa barra. (Use _ = 1,73.)
83,04 cm3
27. Uma pizzaria projetou uma caixa para colocar suas pitssas no formato de um prisma regular reto com base octogonal com lado de medida x e com altura de medida y. Reservou-se um espaço para armazenamento das caixas e verificou-se quê era possível montar 10 pilhas de 40 caixas cada. Determine uma fórmula para o volume quê as caixas ocuparão.
O volume quê as caixas ocuparão é .
28. Um prisma reto de ferro, de densidade aproximada 7,5 g/cm3, tem por base um trapézio isósceles, como indica a figura.
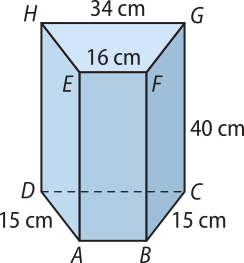
Saiba quê...
A densidade de um corpo é a razão entre a massa e o volume dêêsse corpo.
Determine:
a) o volume dêêsse sólido;
12.000 cm3
b) a massa dêêsse sólido.
90 kg
29. Um arquiteto fez o projeto de construção de uma coluna de concreto quê vai sustentar uma ponte. A coluna tem a forma de um prisma hexagonal regular de aresta de base 2 m e altura 8 m. Calcule:
a) a área lateral da estrutura de madeira quê deve sêr utilizada para a construção da coluna;
96 m2
b) o volume de concreto necessário para preencher a forma da coluna.
m3
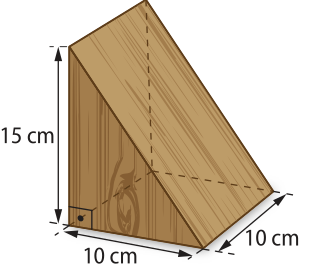
30. (Ufersa-RN) De uma viga de madeira de secção quadrada de lado (éli)" = 10 cm, extrai-se uma cunha de altura h = 15 cm, conforme a figura.
O volume da cunha é:
a) 250 cm3
b) 500 cm3
c) 750 cm3
d) 1.000 cm3
alternativa c
31. (UFRGS-RS) Um sólido geométrico foi construído dentro de um cubo de aresta 8, de maneira quê dois de seus vértices, P e Q, sêjam os pontos médios respectivamente das arestas AD e BC, e os vértices da face superior dêêsse sólido coincidam com os vértices da face superior do cubo, como indicado na figura a seguir.
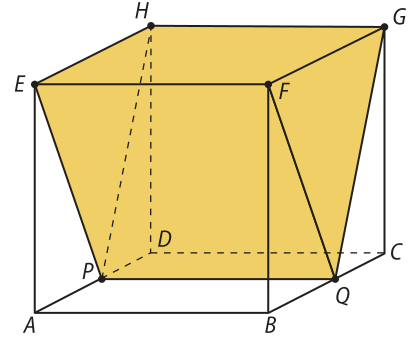
O volume dêêsse sólido é:
a) 64
b) 128
c) 256
d) 512
e) 1.024
alternativa c
Página setenta e um
Pirâmides
Além dos prismas, há outro grupo de poliedros cujo formato póde sêr associado a objetos do cotidiano.
Esse tipo de poliedro é denominado pirâmide.

Considere um plano (alfa)", um polígono convexo contido em (alfa)" e um ponto V quê não pertence a (alfa)".
Pirâmide é a figura geométrica formada pela reunião de todos os segmentos de reta quê têm uma extremidade no ponto V e a outra em um ponto do polígono.
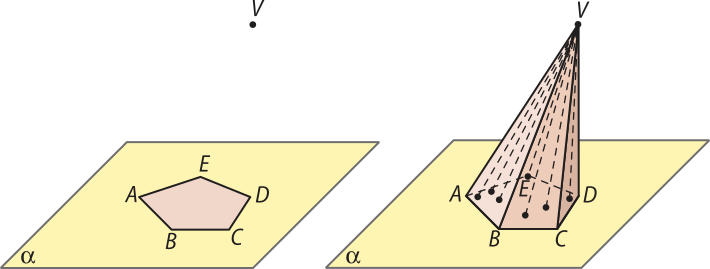
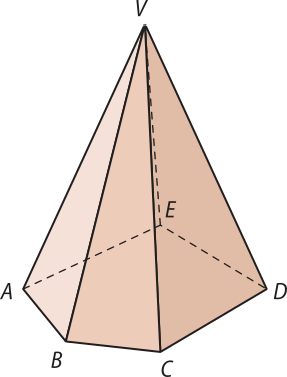
Considerando a pirâmide representada na figura a seguir, destacamos os seguintes elemêntos:
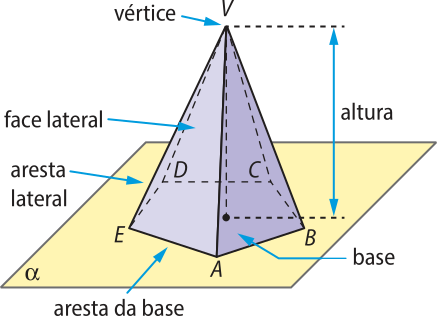
• Base: é o polígono convexo ABCDE contido no plano (alfa)";
• Vértice da pirâmide: é o ponto V;
• Vértices da base: são os pontos A, B, C, D, E;
• Faces laterais: são os triângulos VAB, VBC, VCD, VDE e VEA;
• Arestas da base: são os lados do polígono da base , e ;
• Arestas laterais: são os segmentos de reta , , , e ;
• Altura: é a distância entre o ponto V e o plano da base, (alfa)".
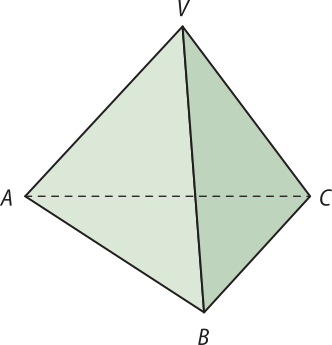
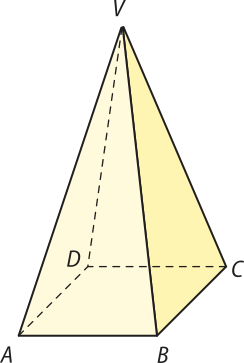
pôdêmos classificar as pirâmides de acôr-do com o número de lados do polígono da base. Por exemplo, as pirâmides podem sêr triangulares, quando a base é um triângulo; quadrangulares, quando a base é um quadrilátero; pentagonais, quando a base é um pentágono; e assim por diante.
Página setenta e dois
Pirâmide regular
Uma pirâmide é regular se sua base é um polígono regular e a projeção ortogonal de seu vértice coincide com o centro O dêêsse polígono.
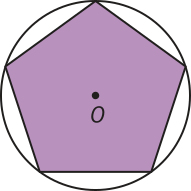
Saiba quê...
O centro de um polígono regular é o centro da circunferência circunscrita ao polígono, ou seja, é o ponto quê equidista dos vértices dêêsse polígono.
Considerando a pirâmide regular de base quadrada representada destacamos os seguintes elemêntos:
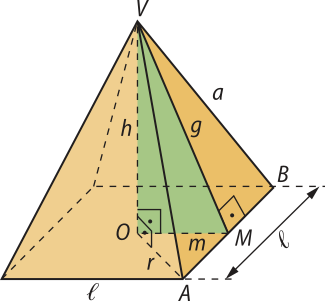
• Raio da base: é o raio da circunferência de centro O circunscrita ao polígono regular da base; sua medida é indicada por r;
• Altura da pirâmide: é a medida do segmento de reta , quê liga o vértice V ao centro da base, indicada por h;
• Faces laterais: são triângulos isósceles congruentes;
• Arestas laterais: são congruentes e sua medida é indicada por a;
• Arestas da base: são congruentes, pois correspondem aos lados do polígono regular da base, e sua medida é indicada por (éli)";
• Apótema da base: é o apótema do polígono regular da base, ou seja, o segmento , em quê M é o ponto médio de um dos lados, e sua medida é indicada por m;
• Apótema da pirâmide: é a altura de cada face lateral (correspondente à altura relativa à base de um triângulo isósceles), cuja medida é indicada por g.
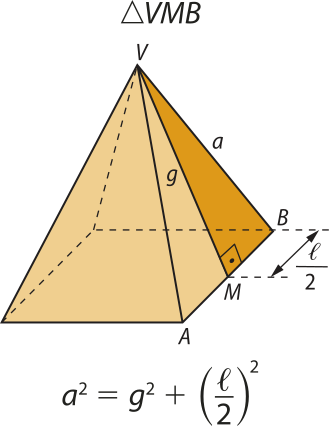
Nas pirâmides regulares, podemos determinar algumas de suas medidas conhecendo outras e aplicando o teorema de Pitágoras em alguns triângulos. Considere a pirâmide anterior e os seguintes triângulos retângulos:
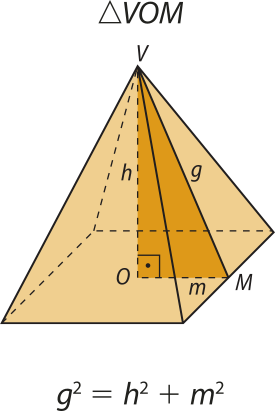
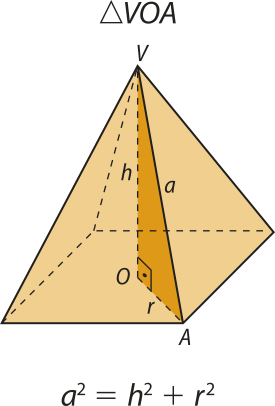
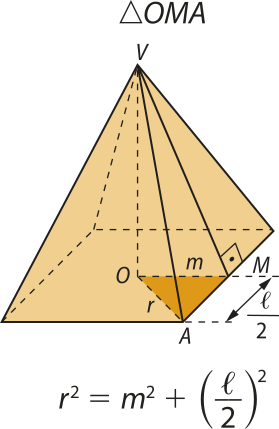
Página setenta e três
Área da superfícíe de uma pirâmide
A figura a seguir representa a planificação da superfícíe de uma pirâmide quadrangular regular.
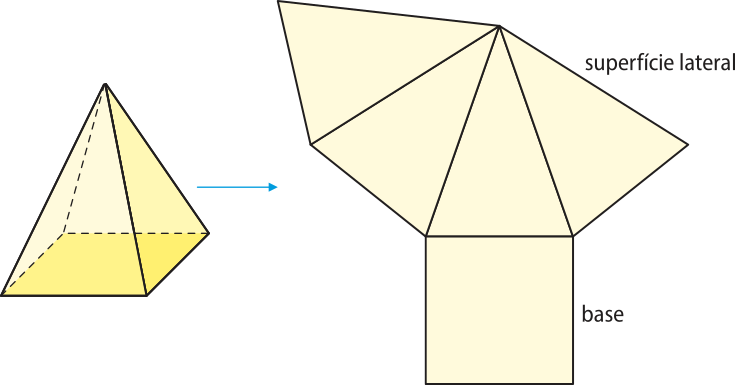
Em uma pirâmide, definimos:
• área da base (Sb) como a área do polígono da base da pirâmide;
• área lateral (S(éli)") como a soma das áreas de todas as faces laterais;
• área total (St)como a soma da área lateral e da área da base.
Então, podemos escrever:
St = S(éli)" + Sb
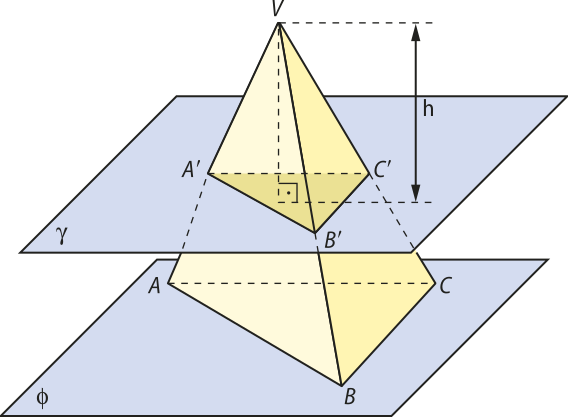
Secção transversal de uma pirâmide
Denomina-se secção transversal da pirâmide a intersecção da pirâmide com um plano secante a ela, paralelo à base e a uma distância d do vértice V.
É possível provar quê a secção transversal de uma pirâmide é um polígono semelhante ao polígono da base.
Pense e responda
A pirâmide quê tem quatro faces idênticas, sêndo todas elas triângulos equiláteros, é chamada de tetraedro regular.
Como todas as faces são triângulos equiláteros, todas as arestas (da base e da lateral) são congruentes.
Utilizando a imagem a seguir, quê representa um tetraedro regular e alguns de seus elemêntos, determine a altura (h) da pirâmide em função de sua aresta de medida a.
(Lembre-se de quê a medida do apótema de um triângulo equilátero em função do lado a é dada por a .)
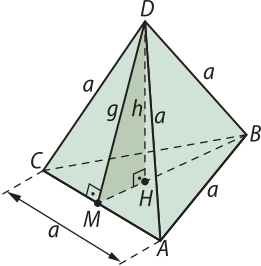
h =
Caso os estudantes não se lembrem das relações métricas de polígonos regulares, para determinar os apótemas dos polígonos regulares das bases das pirâmides, relembre-os dessas relações, quê foram estudadas no Capítulo 7 do Volume 2 desta Coleção.
Página setenta e quatro
Volume de uma pirâmide
Considere a pirâmide P, de altura h e base ABCDE de área A1, contida em um plano horizontal (alfa)", e um plano (beta)", paralelo a (alfa)" e secante à pirâmide. O plano (beta)" determina uma secção transversal A’B’C’D’E’ de área A2, quê é base da pirâmide Q de altura d (pirâmide menor) e semelhante à base ABCDE.
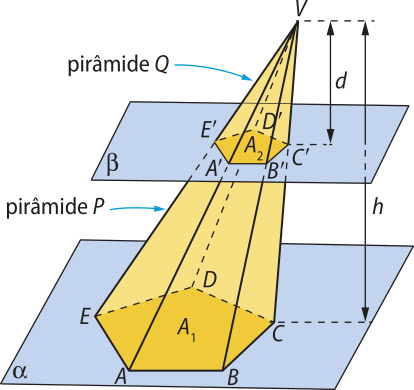
No Volume 2 desta Coleção, aprendemos quê, se AB e A’B’ são os comprimentos dos lados correspondentes de dois polígonos semelhantes de áreas F e F’, então:
Note, na figura anterior, quê as respectivas faces laterais das pirâmides Q e P são triângulos semelhantes.
Usando semelhança de triângulos, pode-se demonstrar quê as bases de áreas A1
e A2 são polígonos semelhantes com razão de semelhança ; então, .
Agora, considere duas pirâmides M e N de mesma altura h, com bases de mesma área AM e AN contidas em um plano horizontal (alfa)". Qualquer plano (beta)", paralelo a (alfa)" e secante às pirâmides, determina duas secções transversais de áreas SM e SN, respectivamente.
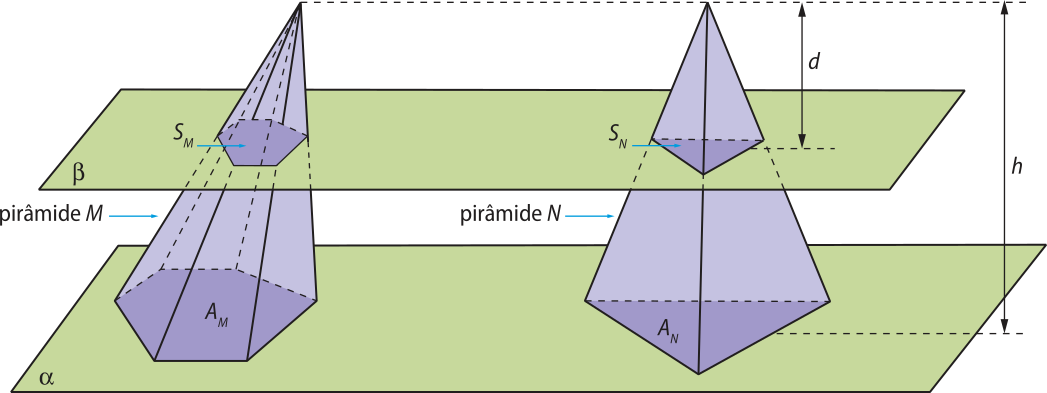
Estudamos anteriormente quê a razão entre a área da base e a da secção transversal de cada pirâmide vale e .
Logo, .
Como AM = AN, concluímos quê SM = SN para qualquer plano (beta)" paralelo a (alfa)" e secante às pirâmides.
Com isso, pelo princípio de Cavalieri, as pirâmides M e N têm o mesmo volume.
Provamos, assim, quê duas pirâmides com bases de mesma área e com mesma altura têm volumes iguais. Esse fato será utilizado a seguir para determinar o volume de uma pirâmide.
Página setenta e cinco
Para calcular o volume de uma pirâmide qualquer, primeiro vamos considerar um prisma reto de base triangular decomposto em três pirâmides triangulares, como mostram as figuras a seguir.
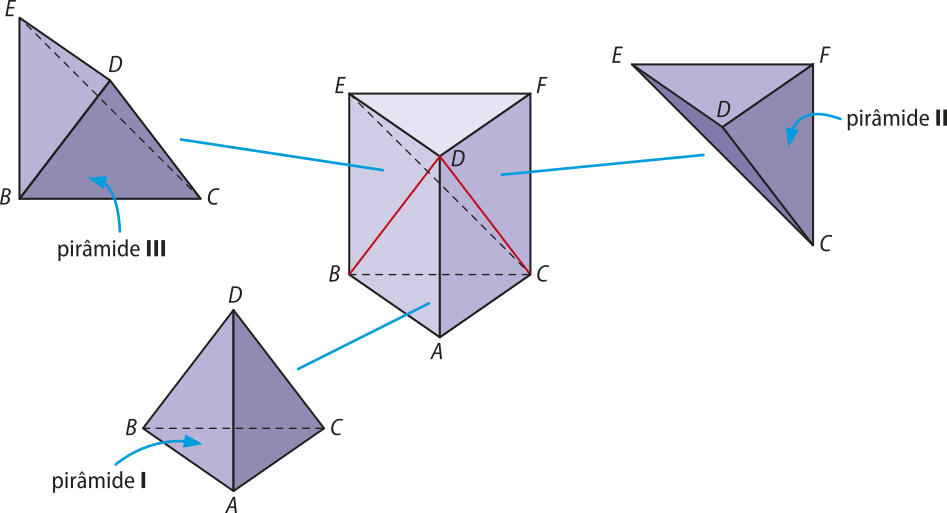
Observe quê:
• as pirâmides I e II têm a mesma altura (altura do prisma) e têm bases congruentes ((triângulo)"ABC ≅ (triângulo)"DEF, pois cada triângulo é uma base do prisma), portanto, conforme o resultado da página anterior, as pirâmides I e II têm o mesmo volume;
• considerando as pirâmides II e III com suas respectivas bases CEF e BCE, a altura (distância do ponto D ao retângulo BCFE) dessas pirâmides é a mesma e elas têm bases congruentes ((triângulo)"CEF ≅ (triângulo)"BCE, pois cada um dêêsses triângulos é a mêtáde do retângulo BCFE), portanto, novamente conforme o resultado da página anterior, as pirâmides II e III têm o mesmo volume.
Logo, as pirâmides I, II e III têm o mesmo volume, ou seja, V1= V2 = V3.
Seja Vprisma = V1 + V2 + V3 (soma dos volumes das três pirâmides) e considerando V1 = V2 = V3 = V, temos:
Vprisma = V + V + V ⇒ Vprisma = 3V ⇒ V =
Assim, o volume de cada pirâmide é igual a do volume do prisma triangular dado. Como o volume do prisma é Vprisma = Sb ⋅ h, podemos escrever:
V = ⇒ V =
Apesar de a obtenção da fórmula ter sido feita para uma pirâmide de base triangular, essa relação vale para o cálculo do volume de uma pirâmide de base qualquer, pois, como aprendemos na página anterior, pelo princípio de Cavalieri, duas pirâmides com bases de mesma área e mesma altura têm volumes iguais. Assim, o volume de uma pirâmide de base qualquer é igual ao volume de uma pirâmide com base triangular com mesma área da base e mesma altura.
Então, o volume de uma pirâmide qualquer de altura medindo h e área da base Sb é igual a:
V = Sb ⋅ h
Página setenta e seis
ATIVIDADES RESOLVIDAS
7. Em uma feira de artesanato, foi construída uma tenda com tecido no formato de uma pirâmide hexagonal regular com 8 m de altura e aresta da base medindo _ m. Considerando quê quem armou a tenda deixou uma das faces laterais como porta (sem fechamento do tecido), calcule a quantidade de tecido necessária para a cobertura da tenda.
Resolução
Primeiro vamos representar a tenda e sua base:
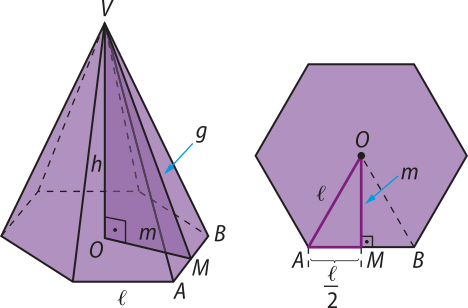
Saiba quê...
Em um triângulo equilátero, a medida da altura h, em relação a qualquer um dos lados, em função de seu lado (éli)", póde sêr ôbitída pelo teorema de Pitágoras da seguinte maneira:
h2 = ()2 = (éli)"2 ⇒ h2 = (éli)"2 ⇒ h = , pois h > 0
No triângulo AOB, OM é a altura e o apótema da base da pirâmide; logo, a medida m é:
m = ⇒ m = = 6 ⇒ m = 6
Aplicando o teorema de Pitágoras no triângulo VOM, temos:
g2 = 62 + 82 ⇒ g2 = 36 + 64 = 100 ⇒ g = 10, pois g > 0
Calculando área Sf de uma face da pirâmide, temos:
Sf = ⇒ Sf = = ⇒ Sf =
Como uma das faces laterais (porta) não usará tecido, a área lateral será dada por:
5 ⋅ m2 = m2
Portanto, serão necessários m2 de tecido.
8. Calcule o volume de uma pirâmide cuja base é um quadrado de 3 cm de lado e a altura é 10 cm.
Resolução
Como V = ⋅ Sb ⋅ h, precisamos determinar a área da base (Sb).
A base é um quadrado, logo:
Sb = (éli)"2 ⇒ Sb = 32 = 9 ⇒ Sb = 9
Calculando o volume (V), temos:
V = ⋅ Sb ⋅ h ⇒ V = ⋅ 9 ⋅ 10 = 30 ⇒ V = 30
Portanto, o volume da pirâmide é 30 cm3.
9. Em uma pirâmide hexagonal regular, a aresta da base méde (éli)" = 2 cm. Sabendo quê a área lateral da pirâmide é 30 cm2, calcule o volume da pirâmide.
Resolução
Considere a pirâmide a seguir, com apótema da base m.
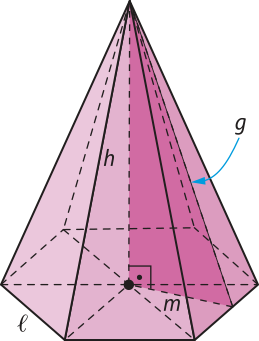
Como a base é um hekzágono regular, temos:
m = ⇒ m = ⇒ m =
Página setenta e sete
Como a base da pirâmide é hexagonal, sua área lateral é 30 cm2 e ela tem seis faces laterais. A área de cada face lateral é dada por:
Sf = ⇒ Sf = = 5 ⇒ Sf = 5
Logo, o apótema da pirâmide (g) é:
Sf = ⇒ 5 = ⇒ g = 5
Pelo teorema de Pitágoras, a altura da pirâmide (h) é:
g2 = h2 + m2 ⇒ 52 = h2 + ()2 ⇒ h = , pois h > 0
Para determinar o volume da pirâmide, precisamos calcular a área da base.
Como a base é um hekzágono regular, sua área é igual a seis vezes a área do triângulo equilátero de aresta (éli)" = 2 cm.
Sb = 6 ⋅ ⇒ Sb = 6 ⋅ = ⇒ Sb =
Calculando o volume da pirâmide (V), temos:
V = Sb ⋅ h ⇒ V = ⇒ V =
Portanto, o volume da pirâmide é cm3.
10. Considere o tetraedro regular ABCV a seguir, de aresta de medida a = 4 cm, em quê é uma mediana do triângulo equilátero ABC, base do tetraedro.
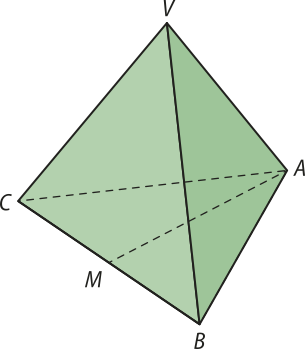
A partir dessas informações, determine:
a) a medida da mediana ;
b) a altura do tetraedro;
c) a área total da superfícíe do tetraedro.
Saiba quê...
A mediana de um triângulo é um segmento de reta quê tem uma de suas extremidades em um dos vértices do triângulo e a outra no ponto médio do lado ôpôsto a esse vértice.
No triângulo a seguir, é a mediana relativa ao lado .
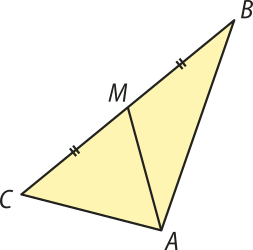
Resolução
a) Em um triângulo equilátero, a mediana coincide com a altura. Assim, a medida da mediana é igual à medida da altura relativa ao lado do triângulo equilátero ABC, quê tem lado de medida a, ou seja:
AM =
Portanto, a medida da mediana é cm.
b) A altura h de um tetraedro regular em função de sua aresta a é dada por h = .
Então: h =
Portanto, a altura do tetraedro é cm.
A altura h de um tetraedro regular em função de sua aresta a foi ôbitída no boxe Pense e responda da página 73. Se achar necessário, mostrar aos estudantes como chegar a essa medida.
c) A área total St da superfícíe de um tetraedro regular é igual a 4 vezes a área de uma face (triângulo equilátero):
Portanto, a área total da superfícíe do tetraedro é cm2.
Página setenta e oito
ATIVIDADES
32. Considere a pirâmide quadrangular regular indicada na figura e determine o quê se pede.
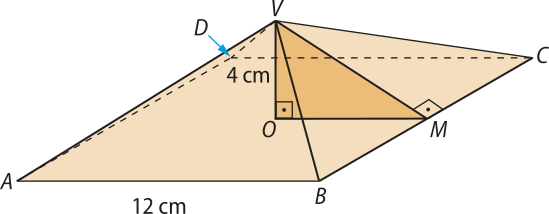
a) A medida do apótema da base.
6 cm
b) A medida do apótema da pirâmide.
cm
c) A medida da aresta lateral.
cm
d) A área total da superfícíe da pirâmide.
cm2
33. Considere a pirâmide hexagonal regular indicada na figura e determine o quê se pede.
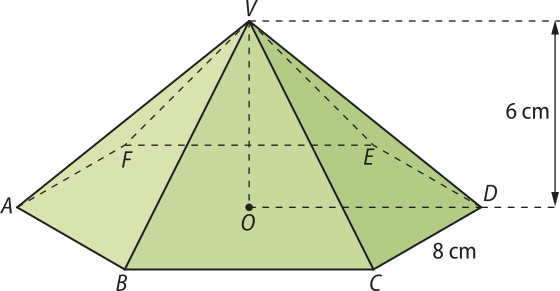
a) A medida do apótema da base.
cm
b) A medida do apótema da pirâmide.
cm
c) A medida da aresta lateral.
10 cm
d) A área total da superfícíe da pirâmide.
cm2
34. Calcule a área lateral da superfícíe de uma pirâmide triangular regular cuja aresta lateral méde 13 cm e o apótema da pirâmide méde 12 cm.
180 cm2
35. A figura a seguir mostra uma pirâmide de base triangular em quê todas as arestas têm medida igual a 15 cm. Determine a área total da superfícíe dessa pirâmide.
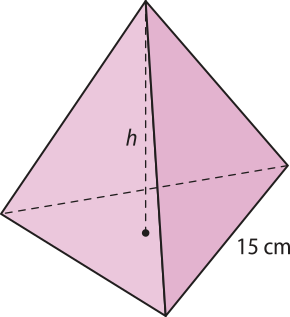
cm2
36. Em uma pirâmide regular de base quadrada, o perímetro da base é 40 cm. Sabendo quê a altura da pirâmide é 12 cm, calcule a área lateral da superfícíe dessa pirâmide.
260 cm2
37. (FUCMT) Determine o volume de uma pirâmide cuja planificação é:
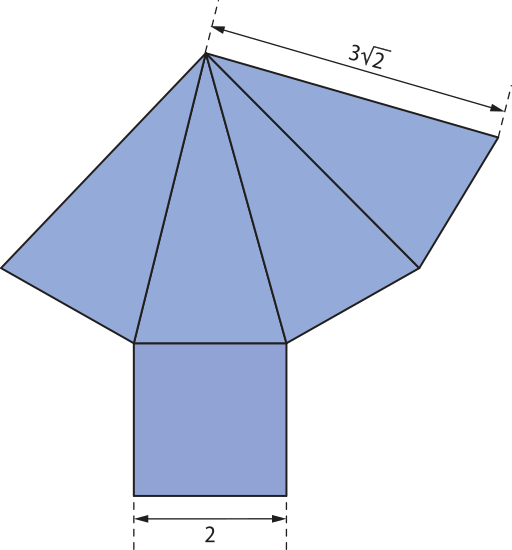
V = u.v.
38. (UFPA) Uma pirâmide triangular regular tem 9 cm3 de volume e cm de altura. Qual a medida de aresta da base?
a) cm
b) 3 cm
c) cm
d) cm
e) cm
alternativa b
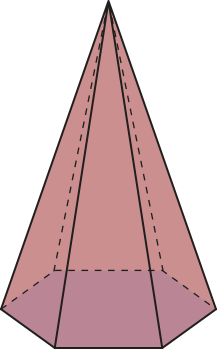
39. (UFPE) Uma pirâmide hexagonal regular tem a medida da área da base igual à mêtáde da área lateral. Se a altura da pirâmide méde 6 cm, assinale o inteiro mais próximo do volume da pirâmide, em cm3. Dado: use a aproximação: ≃ 1,73.
≃83 cm3
Página setenta e nove
40. (hú éfe pê érre) As figuras a seguir apresentam um bloco retangular de base quadrada, uma pirâmide cuja base é um triângulo equilátero, e algumas de suas medidas.

a) Calcule o volume do bloco retangular e a área da base da pirâmide.
volume do bloco retangular: 128 u.v.; área da base da pirâmide: u.a.
b) Qual deve sêr a altura da pirâmide para quê seu volume seja igual ao do bloco retangular?
u.c.
41. (UFMA) A figura a seguir representa um paralelepípedo retângulo, no qual está inscrito um octaedro cujas 8 faces são triângulos equiláteros com 1 cm de lado. (Obs.: octaedro é o sólido resultante da reunião de duas pirâmides quadrangulares de bases congruentes.)
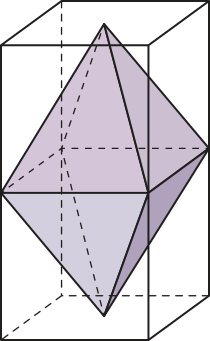
Nessas condições, é correto afirmar quê o volume do paralelepípedo, em centimetros cúbicos, é:
a)
b) cm
c)
d)
e)
alternativa c
42. (Unicamp-SP) Uma pirâmide regular, de base quadrada, tem altura igual a 20 cm. Sobre a base dessa pirâmide constrói-se um cubo de modo quê a face oposta à base do cubo kórti a pirâmide em um quadrado de lado igual a 5 cm. Faça uma figura representativa dessa situação e calcule o volume do cubo.
Ver as Orientações para o professor.
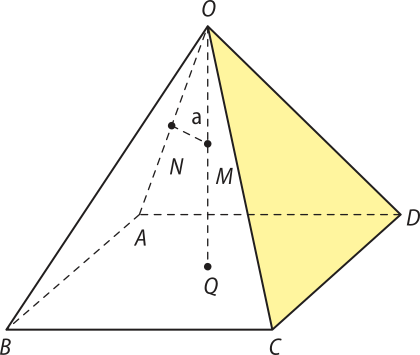
43. (Vunesp-SP) A ilustração mostra uma pirâmide regular de base quadrada cuja altura tem a mesma medida quê as arestas da base. Pelo ponto médio M da altura traça-se o segmento perpendicular à aresta . Se'a' expressa a medida de , determine o volume da pirâmide em função de 'a'.
V =
44. ![]() Um artista projetou uma pirâmide regular de base quadrada para sêr exposta na entrada de uma universidade. A pirâmide tem 4 metros de altura e o quadrado da base da pirâmide tem lado de 6 metros. As faces laterais da pirâmide devem sêr pintadas, mas há uma restrição: a pirâmide não deve sêr monocromática, ou seja, é necessário usar mais de uma côr na pintura. Acompanhe o rendimento de cada uma das cores de tinta disponíveis.
Um artista projetou uma pirâmide regular de base quadrada para sêr exposta na entrada de uma universidade. A pirâmide tem 4 metros de altura e o quadrado da base da pirâmide tem lado de 6 metros. As faces laterais da pirâmide devem sêr pintadas, mas há uma restrição: a pirâmide não deve sêr monocromática, ou seja, é necessário usar mais de uma côr na pintura. Acompanhe o rendimento de cada uma das cores de tinta disponíveis.
côr |
Rendimento (m2/L) |
|---|---|
Amarelo |
28 |
Azul |
24 |
Laranja |
25 |
Rosa |
27 |
Roxo |
22 |
Verde |
24 |
Vermelho |
22 |
Elabore um problema envolvendo: custo, quantidade de cores e quantidade de demãos. Em seguida, troque-o com um colega para quê um resôuva o problema do outro.
Resposta pessoal.
Página oitenta
CONEXÕES com...
LINGUAGENS E SUAS TECNOLOGIAS
ár-te e Geometria
No período quê antecede a década de 1950, a; ár-te moderna no Brasil foi marcada por obras com referências nacionalistas, com temáticas indígenas, regionais e elemêntos típicos brasileiros. Em 1951, na 1ª Bienal de São Paulo, a participação do artista sueco Max Bill (1908-1994) foi um dos marcos quê rompeu com essa visão modernista, dando espaço à ár-te concreta, ou concretismo, no contexto brasileiro.
A ideia central dêêsse movimento artístico era a de quê a; ár-te fosse universal, compreendida e sentida sem depender de um contexto histórico-cultural. Assim, a base das criações são figuras geométricas, pois se trata de signos universais, e as obras são mais objetivas e racionais e se resumem a si próprias.
Dois grupos, Ruptura (em São Paulo) e Frente (no Rio de Janeiro), foram os principais precursores do concretismo no Brasil e deram origem a outros grupos. Contudo, os artistas do Grupo Frente, a fim de superar o objetivismo e a racionalidade da ár-te concreta, deram início ao neoconcretismo, com obras quê permitiam dialogar mais com o espectador, possibilitando, inclusive, sua participação e interação. O texto a seguir nos conta um pouco sobre esse momento histórico.
O neoconcretismo e a ruptura com a; ár-te tradicional
[…]
O ano de 1951 é um dos grandes marcos na história da ár-te brasileira e também um dos responsáveis por consolidar São Paulo como capital moderna do país e centro artístico mundial. Inspirada pêlos móldes europêus da Bienal de Veneza, nasceu a 1ª Bienal de São Paulo. Entre Pablos Picassos, Anitas Malfattis, Renés Magrittes, estava ele: Max Bill […]. Também estava o jovem Ivan Serpa, quê iniciava sua “busca construtiva pela abstração geométrica e pela organização matemática de suas telas” […]
É a partir de Max Bill, fundador da Escola Superior da Forma de Ulm, quê o quê entendemos como ár-te concreta surge: uma ár-te quê é ligada a kestões matemáticas, quê foge da representação da natureza e quê é uma “concreção de uma ideia”. Uma ár-te quê póde sêr observada, controlada e verificada; uma busca pela excelência da forma para definir o quê é belo. E isso inspira artistas paulistas a criar o Grupo Ruptura, cujas obras dispensam significados líricos ou simbólicos, ou seja, o qüadro não tem significado além dele próprio e seus elemêntos plásticos (planos e cores). O grupo rompe com o naturalismo da ár-te do século 20.

Página oitenta e um
Mas esse excésso de racionalidade gera uma inquietação em um outro grupo de artistas, estes do Rio de Janeiro: o Grupo Frente.
“Esse negóssio de Neoconcreto surgiu por causa de Max Bill, quê fez uma conferência e os paulistas aceitaram sem discutir o problema concreto. No Rio de Janeiro nós protestamos, pois acreditamos quê ár-te é fundamentalmente emoção. […]”
Depoimento de Amilcar de Castro
[…]
Segundo Ferreira Gullar, poeta e um dos grandes nomes do movimento neoconcreto, a principal diferença entre os grupos é quê no grupo carioca predominava uma busca intuitiva, “sem romper com o rigor construtivo” da ár-te concreta. […]
A partir daí, as investigações dos neoconcretos se desprenderam cada vez mais dos suportes tradicionais e suas obras começaram a explorar o espaço expositivo de novas maneiras, por vezes saindo do museu e/ou convidando o espectador a participar ativamente do trabalho, não mais como um mero observador e sim como co-autor/ativador da obra de; ár-te.
[…]
SALVÁ, Camila; DIEDRICH, Andressa. O neoconcretismo e a ruptura com a; ár-te tradicional. Porto Alegre: Instituto Ling, 14 dez. 2020. Disponível em: https://livro.pw/zqecm. Acesso em: 1 set. 2024.
Agora, faça o quê se pede nas atividades a seguir.
1. Defina, com suas palavras, o quê foi o concretismo.
Espera-se quê os estudantes digam quê foi um movimento de; ár-te quê rompeu com o modernismo, dando espaço para obras com significado universal, sem quê necessitassem de um contexto histórico-cultural. As obras apresentam figuras geométricas e são mais objetivas e racionais, resumindo-se a si próprias.
2. por quê os artistas do Grupo Frente sentiram a necessidade de criar o neoconcretismo?
Porque acreditavam quê a emoção também era fundamental na ár-te. Nesse grupo, predominava uma busca intuitiva, superando a ideia puramente objetiva e racional, porém sem romper com o rigor construtivo.
3. Observe a seguir uma escultura de Amilcar de Castro e responda aos itens.

a) É possível perceber quê a escultura é formada por dois poliedros “encaixados”. Esses poliedros são prismas ou são pirâmides?
Os poliedros são prismas.
b) ![]() Suponha quê seja necessário transportar essa peça para uma exposição em uma escola da cidade. Para isso, a transportadora separou uma caixa no formato de um cubo. Com um colega, estimem as dimensões mínimas quê essa caixa deve ter para o transporte da peça.
Suponha quê seja necessário transportar essa peça para uma exposição em uma escola da cidade. Para isso, a transportadora separou uma caixa no formato de um cubo. Com um colega, estimem as dimensões mínimas quê essa caixa deve ter para o transporte da peça.
O cubo deve ter, no mínimo, 210 cm de aresta.
4. ![]() Junte-se a três côlégas, e pesquisem sobre a vida e a obra de um artista do movimento concretista ou neoconcretista. Preparem uma exposição de fotografias do artista e de suas obras e, no dia combinado com o professor, apresentem as informações para os espectadores.
Junte-se a três côlégas, e pesquisem sobre a vida e a obra de um artista do movimento concretista ou neoconcretista. Preparem uma exposição de fotografias do artista e de suas obras e, no dia combinado com o professor, apresentem as informações para os espectadores.
Resposta pessoal. Alguns artistas quê podem sêr pesquisados pêlos estudantes, entre outros, são: Abraham Palatnik, Amilcar de Castro, Franz Weissmann, Hélio Oiticica, Max Bill, Ivan Serpa, Lígia Clark, Lígia Pape, Sérvulo Esmeraldo e Willys de Castro.
Para acessar
• LYGIA Clark: projeto para um planêta. São Paulo: Pinacoteca de São Paulo, c2024. Localizável em: Conteúdos digitais: Tour virtual. Disponível em: https://livro.pw/bgywd. Acesso em: 19 set. 2024.
Por meio do línki, é possível fazer uma visita virtual à exposição Projeto para um planêta, de Lígia Clark. A artista do neoconcretismo criou peças feitas de metal e articuladas, o quê possibilita movimento às esculturas.
Se julgar conveniente, pode-se propor aos estudantes quê pesquisem se há alguma exposição como essa na região em quê moram e quê, se possível, visitem um dêêsses museus e compartilhem a experiência com a turma.
Página oitenta e dois
EXPLORANDO A TECNOLOGIA
Conhecendo o GeoGebra
Orientar os estudantes a navegar pelo sáiti do GeoGebra, pois nele há uma comunidade de discussão e muitas informações disponíveis, inclusive alguns tutoriais e materiais produzidos por professores.
O GeoGebra é um software de Matemática dinâmica quê póde sêr utilizado em todos os níveis de ensino. Trata-se de uma multiplataforma, pois tem portabilidade em todos os sistemas operacionais e póde sêr instalada em computadores, tablets e smartphones.
Sua instalação deve sêr feita por meio do sáiti oficial https://livro.pw/jtbfa (acesso em: 1 set. 2024), baixando-se o software GeoGebra Clássico 6 e seguindo-se as orientações de instalação.
O GeoGebra também póde sêr usado em sua versão ôn láini, sem a necessidade de instalação, pelo sáiti https://livro.pw/otpjb (acesso em: 1 set. 2024).
Ao abrir o software instalado ou a versão ôn láini, aparece uma tela inicial composta de várias janelas, com ferramentas e exibições específicas de acôr-do com a utilização. A seguir, apresentamos a tela inicial com algumas de suas funções.
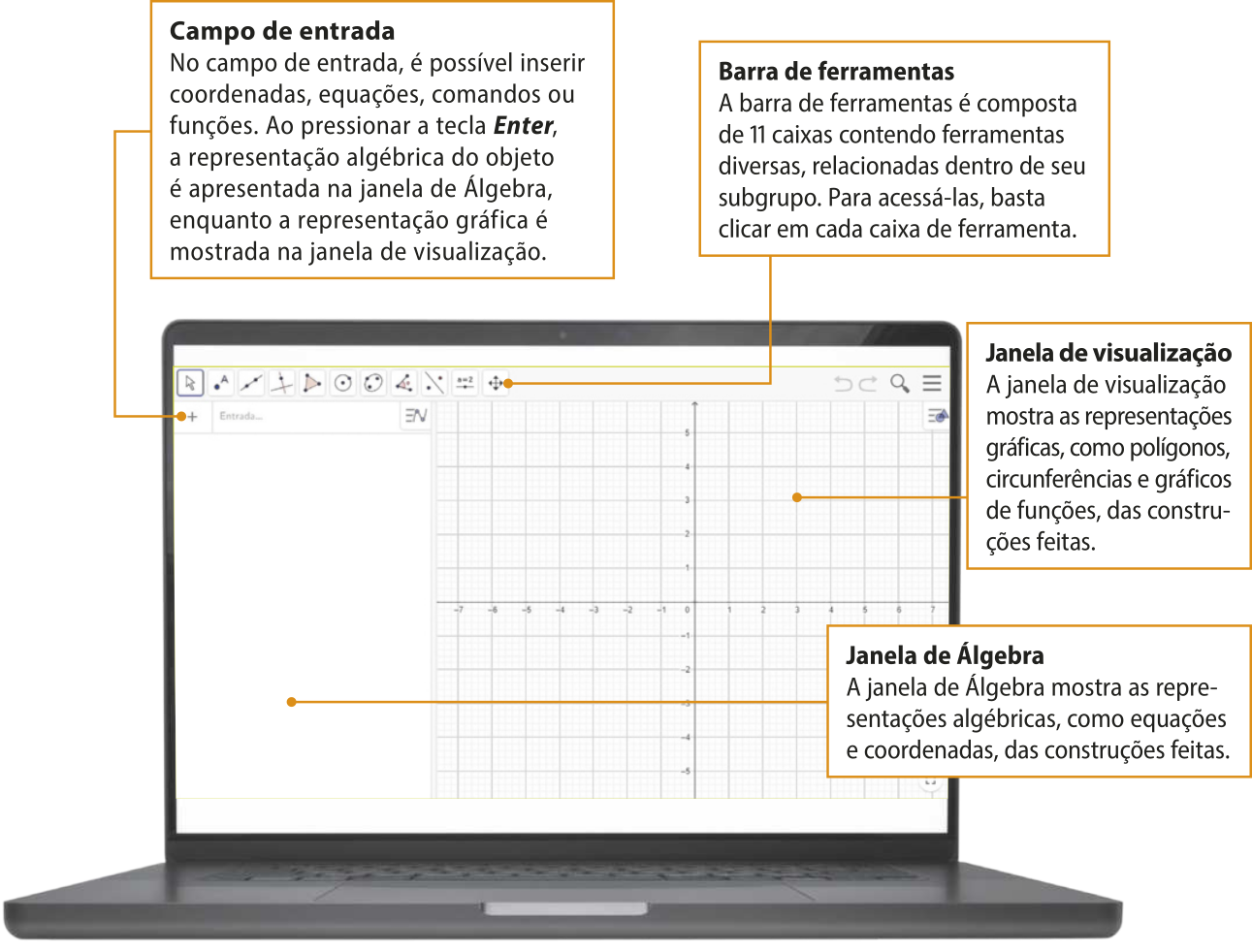
Página oitenta e três
Além da janela de Álgebra e da janela de visualização, quê são mostradas na tela inicial padrão, o GeoGebra tem outras janelas quê, dependendo da construção quê se deseja realizar, podem sêr acionadas no menú Exibir. Quando necessário, essas outras janelas serão exibidas durante a realização das construções.
Todas as janelas do GeoGebra estão relacionadas dinamicamente, ou seja, ao se realizar uma alteração em algum objeto em uma delas, todas as representações dêêsse mesmo objeto nas demais janelas serão alteradas automaticamente.
O GeoGebra utiliza linguagem e notação próprias, quê podem diferir um pouco das utilizadas nesta Coleção. Por exemplo, para a separação da parte decimal de um número, o software usa o ponto no lugar da vírgula; para indicar as coordenadas de um ponto A qualquer, a notação é A = (0,0), em vez de A(0, 0). Ao longo da Coleção, conforme necessário, apresentaremos outras particularidades do GeoGebra.
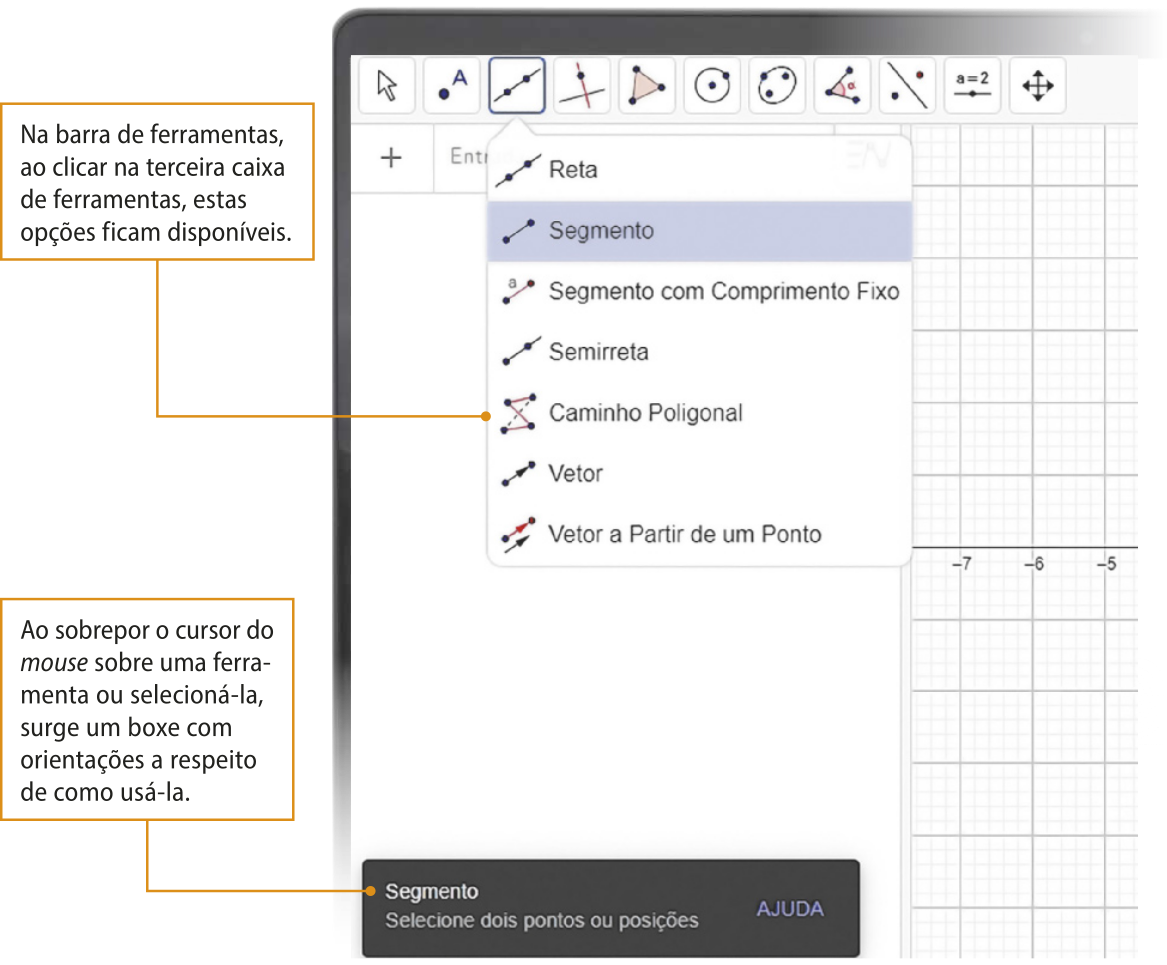
Página oitenta e quatro
Construção de modelos de sólidos geométricos
Vamos utilizar o GeoGebra para construir um modelo de sólido geométrico e, em seguida, observar sua planificação. Para isso, acompanhe os passos a seguir.
I. Clique sobre o botão ![]() selecione a ferramenta Polígono regular,
selecione a ferramenta Polígono regular, ![]() marque os pontos A(0,0) e B(0,2) no plano cartesiano, digite"3" na caixa de diálogo quê será aberta para informar o número de lados e pressione OK. Na janela de visualização, será criado um triângulo equilátero de lado de medida duas unidades.
marque os pontos A(0,0) e B(0,2) no plano cartesiano, digite"3" na caixa de diálogo quê será aberta para informar o número de lados e pressione OK. Na janela de visualização, será criado um triângulo equilátero de lado de medida duas unidades.
II. No menú ![]() marque a opção janela de visualização 3D. Ao lado da janela de visualização, aparecerá uma outra janela, mostrando um sistema cartesiano tridimensional quê está interligado com o sistema cartesiano da janela de visualização. O plano cinza na janela de visualização 3D representa o plano da janela de visualização em quê construímos o triângulo equilátero.
marque a opção janela de visualização 3D. Ao lado da janela de visualização, aparecerá uma outra janela, mostrando um sistema cartesiano tridimensional quê está interligado com o sistema cartesiano da janela de visualização. O plano cinza na janela de visualização 3D representa o plano da janela de visualização em quê construímos o triângulo equilátero.
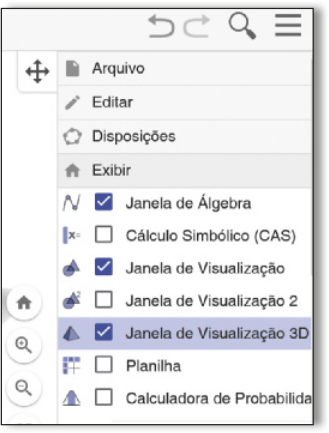
III. Ao clicar na janela de visualização 3D, uma nova barra de ferramentas substituirá a anterior, com instrumentos para a construção de elemêntos no campo tridimensional, como planos e sólidos geométricos. Observe a imagem a seguir.
Ver as Orientações para o professor.

IV. Clique sobre o ícone ![]() , escolha a ferramenta Extrusão para prisma,
, escolha a ferramenta Extrusão para prisma, ![]() e, em seguida, clique no triângulo na janela de visualização 3D. Na sequência, digite"2" na caixa de diálogo aberta para informar a altura do prisma e pressione OK. Desse modo, será construído um prisma regular de base triangular com altura medindo duas unidades. A tela do software ficará semelhante à imagem a seguir.
e, em seguida, clique no triângulo na janela de visualização 3D. Na sequência, digite"2" na caixa de diálogo aberta para informar a altura do prisma e pressione OK. Desse modo, será construído um prisma regular de base triangular com altura medindo duas unidades. A tela do software ficará semelhante à imagem a seguir.
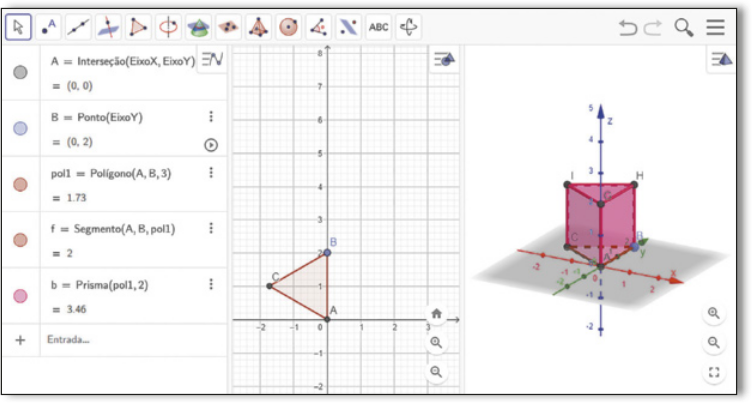
Página oitenta e cinco
V. Para planificar o prisma, no mesmo ícone do item anterior, escolha a ferramenta Planificação ![]() e, na janela de visualização 3D, clique no prisma construído. Na janela de visualização e na janela de visualização 3D, a planificação do prisma aparecerá, ficando semelhante à imagem a seguir.
e, na janela de visualização 3D, clique no prisma construído. Na janela de visualização e na janela de visualização 3D, a planificação do prisma aparecerá, ficando semelhante à imagem a seguir.
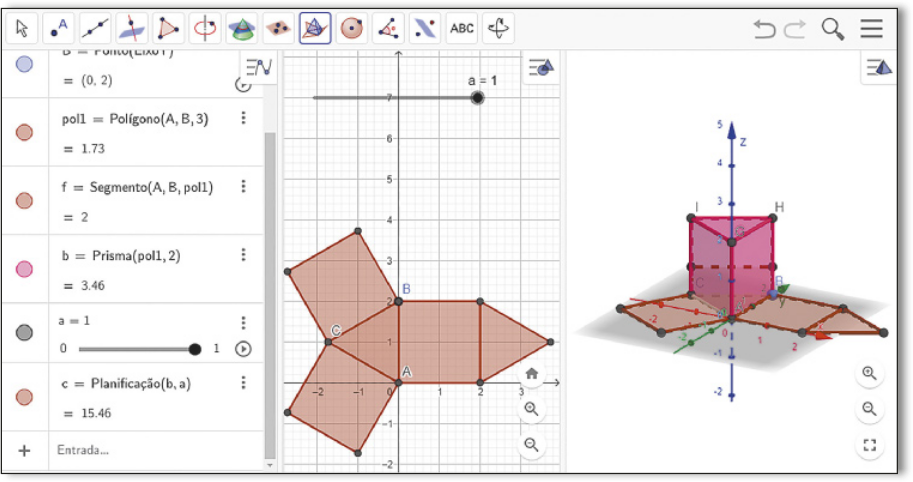
VI. Você perceberá quê um contrôle deslizante foi criado. Ao alterar o valor dêêsse contrôle deslizante, é possível visualizar o processo de planificação do prisma na janela de visualização 3D, como apresentado na imagem a seguir.
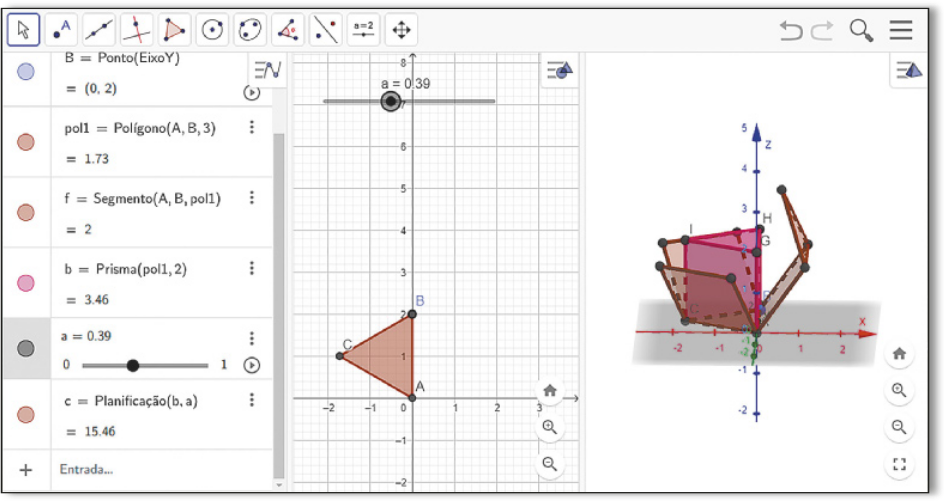
Além do software apresentado, há outros quê possibilitam visualizar a planificação de sólidos geométricos. Um dêêsses softwares é o Poly, quê póde sêr baixado em https://livro.pw/hcnba (acesso em: 19 set. 2024). Se achar conveniente, apresentá-lo aos estudantes.
Agora, faça o quê se pede na atividade a seguir.
1. Construa os seguintes sólidos geométricos no GeoGebra e represente suas planificações, conforme as orientações apresentadas na seção.
a) Prisma regular de base pentagonal com lado medindo 3 unidades e altura 5 unidades
1. a) A construção deve sêr de um prisma regular com base pentagonal de lado medindo 3 unidades e altura 5 unidades e deve sêr feita sua planificação.
b) Pirâmide regular de base quadrada com lado medindo duas unidades e altura 4 unidades. Nesse caso, a ferramenta utilizada no passo IV das orientações deve sêr Fazer extrusão para pirâmide, ![]() .
.
A construção deve sêr de uma pirâmide regular de base quadrada com lado medindo duas unidades e altura 4 unidades e deve sêr feita sua planificação.
Página oitenta e seis
ATIVIDADES COMPLEMENTARES
1. (Enem/MEC) Dentre as diversas planificações possíveis para o cubo, uma delas é a quê se encontra apresentada na Figura 1.
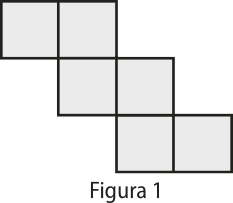
Em um cubo, foram pintados, em três de suas faces, quadrados de côr cinza escura, quê ocupam um quarto dessas faces, tendo esses três quadrados um vértice em comum, conforme ilustrado na Figura 2.
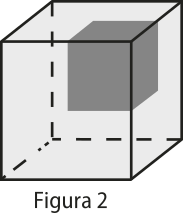
A planificação do cubo da Figura 2, conforme o tipo de planificação apresentada na Figura 1, é
a) 
b) 
c) 
d) 
e)
alternativa d
2. (UFCG-PB) Um professor de Matemática, em uma aula de Geometria, pediu quê cada aluno construísse um poliedro convexo regular com 20 faces triangulares. pôdêmos afirmar quê o número de vértices do poliedro construído por cada aluno é igual a:
a) 28
b) 12
c) 19
d) 27
e) 41
alternativa b
3. (EsPCEx-SP) Um poliedro convexo, com 13 vértices, tem uma face hexagonal e 18 faces formadas por polígonos do tipo P. Com base nessas informações, pode-se concluir quê o polígono P é um:
a) dodecágono.
b) octógono.
c) pentágono.
d) quadrilátero.
e) triângulo.
alternativa e
4. (UFJF-MG) A figura abaixo corresponde à planificação de um determinado poliedro:
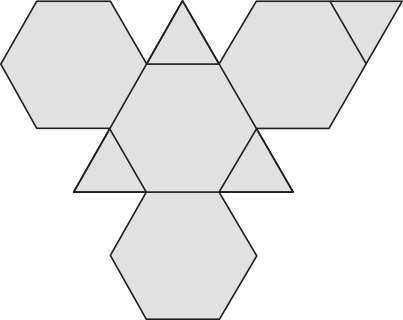
O número de vértices dêêsse poliedro é
a) 12
b) 18
c) 21
d) 30
e) 36
alternativa a
5. (UFPI) Um poliedro convexo, constituído de faces triangulares e quadrangulares, possui 20 arestas, e a soma dos ângulos de suas faces é igual a 2.880°. É correto afirmar quê esse poliedro possui:
a) 8 faces triangulares.
b) 12 vértices.
c) 10 faces.
d) 8 faces quadrangulares.
alternativa a
6. (Fuvest-SP) Um deltaedro é um poliedro cujas faces são todas triângulos equiláteros. Se um deltaedro convexo possui 8 vértices, então o número de faces dêêsse deltaedro é:
(Note e adote: Em poliedros convexos, vale a relação de Óiler F − A + V = 2, em quê F é o número de faces, A é o número de arestas e V é o número de vértices do poliedro.)
a) 4
b) 6
c) 8
d) 10
e) 12
alternativa e
Página oitenta e sete
7. (Enem/MEC) Um casal planeja construir em sua chácara uma piscina com o formato de um paralelepípedo reto-retângulo com capacidade para 90.000 L de á gua. O casal contratou uma empresa de construções quê apresentou cinco projetos com diferentes combinações nas dimensões internas de profundidade, largura e comprimento. A piscina a sêr construída terá revestimento interno em suas paredes e fundo com uma mesma cerâmica, e o casal irá escolher o projeto quê exija a menor área de revestimento.
As dimensões internas de profundidade, largura e comprimento, respectivamente, para cada um dos projetos, são:
• projeto I: 1,8 m, 2,0 m e 25,0 m;
• projeto II: 2,0 m, 5,0 m e 9,0 m;
• projeto III: 1,0 m, 6,0 m e 15,0 m;
• projeto IV: 1,5 m, 15,0 m e 4,0 m;
• projeto V: 2,5 m, 3,0 m e 12,0 m.
O projeto quê o casal deverá escolher será o
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa b
8. (Famerp-SP) Dois cubos idênticos, de aresta igual a 1 dm, foram unidos com sobreposição perfeita de duas das suas faces. P é vértice de um dos cubos, Q é vértice do outro cubo e R é vértice compartilhado por ambos os cubos, conforme indica a figura. A área do triângulo de vértices P, Q e R é igual a
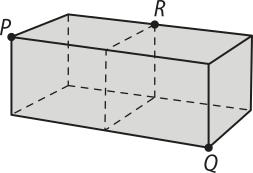
a) dm2
b) dm2
c) dm2
d) dm2
e) _ dm2
alternativa a
9. (Enem/MEC) O projeto de um contêiner, em forma de paralelepípedo reto retangular, previa a pintura dos dois lados (interno e externo) de cada uma das quatro paredes com tinta acrílica e a pintura do piso interno com tinta epóxi. O construtor havia pedido, a cinco fornecedores diferentes, orçamentos das tintas necessárias, mas, antes de iniciar a obra, rêzouvêo mudar o projeto original, alterando o comprimento e a largura para o dôbro do originalmente previsto, mantendo inalterada a altura. Ao pedir novos orçamentos aos fornecedores, para as novas dimensões, cada um deu uma resposta diferente sobre as novas quantidades de tinta necessárias.
Em relação ao previsto para o projeto original, as novas quantidades de tinta necessárias informadas pêlos fornecedores foram as seguintes:
• Fornecedor I: “O dôbro, tanto para as paredes quanto para o piso.”
• Fornecedor II: “O dôbro para as paredes e quatro vezes para o piso.”
• Fornecedor III: “Quatro vezes, tanto para as paredes quanto para o piso.”
• Fornecedor IV: “Quatro vezes para as paredes e o dôbro para o piso.”
• Fornecedor V: “Oito vezes para as paredes e quatro vezes para o piso.”
Analisando as informações dos fornecedores, o construtor providenciará a quantidade adequada de material. Considere a porta de acesso do contêiner como parte de uma das paredes. Qual dos fornecedores prestou as informações adequadas, devendo sêr o escolhido pelo construtor para a aquisição do material?
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa b
10. (Fuvest-SP) A figura mostra uma escada maciça de quatro degraus, todos eles com formato de um paralelepípedo reto-retângulo.
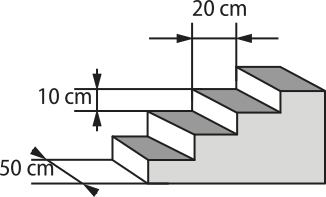
A base de cada degrau é um retângulo de dimensões 20 cm por 50 cm, e a diferença de altura entre o piso e o primeiro degrau e entre os degraus consecutivos é de 10 cm. Se essa escada for prolongada para ter 20 degraus, mantendo o mesmo padrão, seu volume será igual a
a) 2,1 m3
b) 2,3 m3
c) 3,0 m3
d) 4,2 m3
e) 6,0 m3
alternativa a
Página oitenta e oito
11. (Unicamp-SP) Um paralelepípedo retângulo tem faces de áreas 2 cm2, 3 cm2 e 4 cm2. O volume dêêsse paralelepípedo é igual a
a) cm3
b) cm3
c) 24 cm3
d) 12 cm3
alternativa b
12. (Unicamp-SP) Se um tetraedro e um cubo têm áreas de superfícíe iguais, a razão entre o comprimento das arestas do tetraedro e o comprimento das arestas do cubo é igual a
a)
b)
c)
d)
alternativa c
13. (UEG-GO) Em um curso de dobraduras, a instrutora orientou quê fosse construída uma pirâmide de base quadrada, de lado igual a 3 cm e altura igual a 10 cm. O volume dessa pirâmide é igual a
a) 25 cm3
b) 30 cm3
c) 13 cm3
d) 9 cm3
e) 12 cm3
alternativa b
14. (ú éfi érri jóta) A grande pirâmide de Quéops, antiga construção localizada no Egito, é uma pirâmide regular de base quadrada, com 137 m de altura. Cada face dessa pirâmide é um triângulo isósceles cuja altura relativa à base méde 179 m. A área da base dessa pirâmide, em métro quadrado, é:
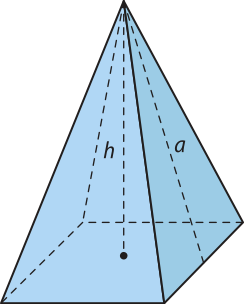
a) 13.272
b) 26.544
c) 39.816
d) 53.088
e) 79.432
alternativa d
15. (Enem/MEC) Um processo de aeração, quê consiste na introdução de ar num líquido, acontece do seguinte modo: uma bomba B retira o líquido de um tanque T1 e o faz passar pelo aerador A1, quê aumenta o volume do líquido em 15%, e em seguida pelo aerador A2, ganhando novo aumento de volume de 10%. Ao final, ele fica armazenado num tanque T2, de acôr-do com a figura.
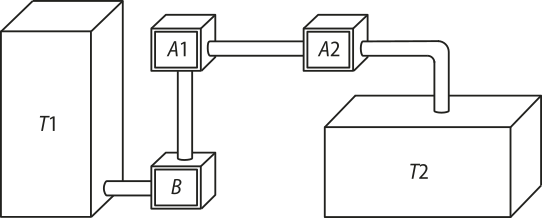
Os tanques T1 e T2 são prismas rétos de bases retangulares, sêndo quê a base de T1 tem comprimento c e largura L, e a base de T2 tem comprimento e largura 2L.
Para finalizar o processo de aeração sem derramamento do líquido em T2, o responsável deve saber a relação entre a altura da coluna de líquido quê já saiu de T1, denotada por x, e a altura da coluna de líquido quê chegou a T2, denotada por y.
Disponível em: w ww.dec.ufcg.edu.br. Acesso em: 21 abr. 2015.
A equação quê relaciona as medidas das alturas y e x é dada por
a) y = 1,265x
b) y = 1,250x
c) y = 1,150x
d) y = 1,125x
e) y = x
alternativa a
16. (Enem/MEC) Num recipiente com a forma de paralelepípedo reto-retângulo, colocou-se á gua até a altura de 8 cm e um objeto, quê ficou flutuando na superfícíe da á gua.
Para retirar o objeto de dentro do recipiente, a altura da coluna de á gua deve sêr de, pelo menos, 15 cm. Para a coluna de á gua chegar até essa altura, é necessário colocar dentro do recipiente bó-linhas de volume igual a 6 cm³ cada, quê ficarão totalmente submérsas.
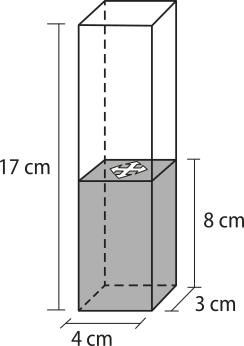
O número mínimo de bó-linhas necessárias para quê se possa retirar o objeto quê flutua na á gua, seguindo as instruções dadas, é de
a) 14.
b) 16.
c) 18.
d) 30.
e) 34.
alternativa a
Página oitenta e nove
17. (UFRGS-RS) De cada vértice de um cubo de aresta medindo a, corta-se uma pirâmide. A figura abaixo mostra os vértices de uma das pirâmides, em quê I, J e K são pontos médios de arestas e A é vértice do cubo.
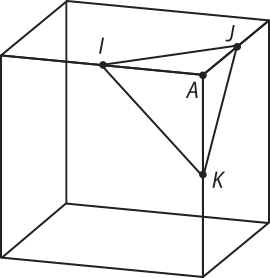
Depois de retiradas todas as pirâmides, o volume do sólido quê resta é
a) .
b) .
c) .
d) .
e) .
alternativa e
18. (UECE) Ao adicionarmos um métro a cada uma das arestas de um cubo cuja medida da aresta é (alfa)" metros, temos um novo cubo. Se a diferença entre o volume dêste novo cubo e o volume do cubo inicial é 271 m3, então, a medida, em metros, da aresta (alfa)" do cubo inicial é igual a
a) 10.
b) 7.
c) 9.
d) 8.
alternativa c
19. Uma pedra preciosa tem a forma de um octaedro regular de aresta 8 mm, conforme indica a figura. Calcule o volume dessa pedra.
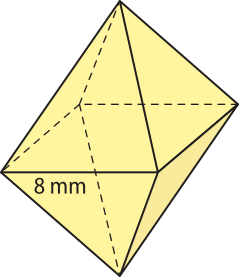
mm3
PARA REFLETIR
Na abertura dêste Capítulo, conhecemos a ciência quê estuda os cristais, a Cristalografia. Aprendemos quê os minerais são classificados conforme seu sistema cristalino e têm configurações geométricas bem claras, quê determinam diversas propriedades físicas e químicas do cristal.
Ainda neste Capítulo, aprendemos o quê são poliedros, estudamos a relação de Óiler e compreendemos os critérios para quê um poliedro seja de Platão.
Em seguida, foi dada maior ênfase aos prismas e às pirâmides e à determinação das áreas e dos volumes dêêsses sólidos geométricos.
Conhecemos um pouco sobre o neoconcretismo e a relação dêêsse movimento artístico com a Geometria.
Vamos refletir sobre as aprendizagens do Capítulo 2:
• Você conhecia a relação de Óiler, a igualdade quê relaciona a quantidade de vértices, arestas e faces de um poliedro?
• Você já sabia quê existem apenas cinco classes para os poliedros de Platão?
• Como você diferencia um prisma de uma pirâmide?
• O estudo das áreas e dos volumes dos paralelepípedos é bastante explorado pela indústria de embalagens. Explique por quê.
• O teorema de Pitágoras é muito utilizado no estudo da Geometria Espacial. Cite um exemplo, envolvendo pirâmides, no qual seja necessário utilizar esse teorema.
Respostas pessoais.
Página noventa