CAPÍTULO 4
ANÁLISE COMBINATÓRIA
Em 1961, foi publicado o livro Cent mille milliards de poèmes (Cem mil bilhões de poemas), do escritor francês Raymond Queneau (1903-1976), quê encantou os amantes de poesia e da Matemática. A obra rompeu com a estrutura convencional dos livros e explorou a criatividade do leitor, por meio de uma experiência interativa com os versos.
Esse livro contém dez sonetos impressos na frente de cada página. Como um soneto é um poema compôzto de 14 versos, as páginas são divididas em 14 tiras horizontais, permitindo quê os versos de uma página sêjam combinados com os de outras páginas. Essa ideia engenhosa no formato físico do livro deixa fluir a criatividade do leitor, quê póde compor, com base nas possibilidades de combinações, sonetos distintos, todos com a mesma estrutura, ou, como sugere o título, “cem mil bilhões de poemas”.
A ideia é possibilitar a criação de sonetos clássicos regulares (dois quartêtos e dois tercetos) bem construídos, por meio de uma “máquina de produzir poemas”.
Ver as Orientações para o professor.
![]() Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
Agora, reúna-se a um colega, e façam o quê se pede em cada questão.
1. Vocês gostam de poesia? Conversem sobre obras e autores quê escrevem esse tipo de texto.
2. De acôr-do com o texto e a imagem apresentados, qual foi a inovação do livro Cem mil bilhões de poemas?
3. Inspirando-se em Raymond Queneau, criem um livro interativo. Separem três fô-lhas de papel sulfite e criem, em cada uma, uma estrofe com quatro versos, de modo quê as rimas sêjam alternadas (a primeira com a terceira e a segunda com a quarta). Em seguida, colem ou grampeiem as fô-lhas na margem esquerda e recortem os versos em tiras, da mesma maneira apresentada no livro de Queneau.
4. Com base no livro confeccionado na atividade anterior, qual é a quantidade de combinações possíveis para criar uma estrofe com quatro versos? Como vocês calcularam essa quantidade?
Página cento e trinta e sete

Página cento e trinta e oito
Introdução
Diariamente, inserimos em nóssos computadores, smartphones ou tablets uma série de dados pessoais protegidos por senhas. Uma senha póde conter lêtras, maiúsculas ou minúsculas, números e símbolos. Dependendo da quantidade de caracteres utilizados, o número de possibilidades de senhas diferentes póde sêr da ordem dos milhões; por exemplo: existem 11.881.376 senhas diferentes compostas de exatamente cinco lêtras minúsculas do nosso alfabeto.
Quantificar o número de possibilidades de senhas é um assunto da Combinatória, área da Matemática quê analisa e estuda problemas de contagem de possibilidades, além de outros conteúdos. Neste Capítulo, vamos estudar e conhecer algumas técnicas de contagem de possibilidades da Combinatória, como o princípio multiplicativo, a permutação, o arranjo simples e a combinação simples.
Princípio multiplicativo
Antes de apresentarmos a definição do princípio multiplicativo, vamos analisar dois problemas.
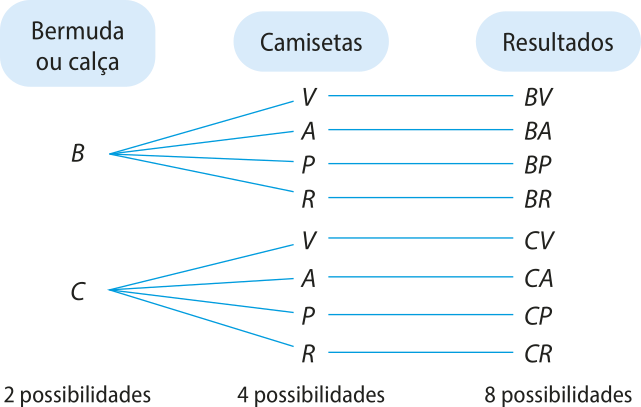
Problema 1: De quantos modos distintos Adelaide póde vestir o manequim de sua loja, sabendo-se quê ela separou, para a realização dessa tarefa, uma calça, uma bermuda e quatro camisetas?
Todas as possibilidades de vestir esse manequim estão representadas no diagrama a seguir, denominado árvore de possibilidades ou diagrama de árvore. Para isso, consideramos: as indicações bermuda (B) e calça (C); as quatro camisetas, nas cores vêrde (V), azul (A), preta (P) e rosa (R); e o resultado BV, por exemplo, quê representa a composição do manequim com a bermuda e a camiseta vêrde.

Página cento e trinta e nove
Pelo diagrama, há 8 possibilidades diferentes de se vestir o manequim. Outro modo de solucionar esse problema é efetuando a seguinte multiplicação:
2 ⋅ 4 = 8
Nessa multiplicação:
• o fator 2 é o número de possibilidades para vestir a parte de baixo do manequim (bermuda ou calça);
• o fator 4 é o número de possibilidades para vestir a parte de cima do manequim (camiseta).
Problema 2: Usando apenas os algarismos 2, 3, 7 e 9, sem repeti-los, quantos números naturais podemos formár de modo quê sêjam maiores do quê 400 e menóres do quê 999?
O diagrama de árvore a seguir mostra todos os números quê podemos formár respeitando as condições do problema.
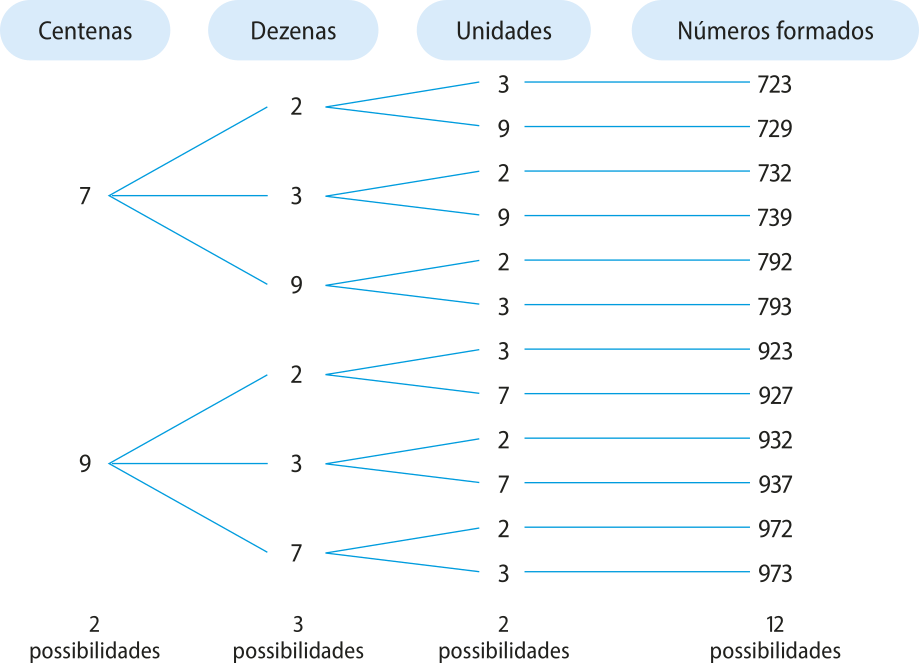
Portanto, há 12 possibilidades de números naturais quê podemos formár respeitando as condições impostas. Outro modo de solucionar esse problema é efetuando a seguinte multiplicação:
2 ⋅ 3 ⋅ 2 = 12
Nessa multiplicação:
• o primeiro fator 2 é o número de possibilidades de algarismos para a centena (7 ou 9), uma vez quê os números devem sêr maiores do quê 400;
• o fator 3 é o número de possibilidades para a dezena, pois, uma vez definido o algarismo da centena, ele não póde sêr repetido na dezena;
• o último fator 2 é o número de possibilidades para a unidade, já quê, uma vez definidos o algarismo da centena e o algarismo da dezena, nenhum deles póde sêr repetido na unidade.
Página cento e quarenta
Os problemas anteriores exemplificam o princípio multiplicativo, também conhecido como princípio fundamental da contagem, quê póde sêr definido do seguinte modo:
Se um evento E póde ocorrer em k etapas sucessivas, de modo quê:
• há p1 possibilidades diferentes de ocorrer a primeira etapa;
• definida a primeira etapa, há p2 possibilidades diferentes de ocorrer a segunda etapa;
• definida a segunda etapa, há p3 possibilidades diferentes de ocorrer a terceira etapa;
⋮
• definida a penúltima etapa, há pk possibilidades diferentes de ocorrer a última etapa; então, o número de possibilidades diferentes de o evento E acontecer é:
p1 ⋅ p2 ⋅ p3 ⋅ … ⋅ pk
O princípio multiplicativo é uma das ferramentas básicas de contagem e é uma das mais utilizadas para solucionar problemas dêêsse tipo. Para utilizá-lo, é necessário identificar o evento, estabelecer em quantas etapas ele póde acontecer e, para cada uma das etapas, quantificar suas possibilidades de ocorrência. Além díssu, dependendo das condições impostas pelo problema, devemos adotar determinadas estratégias para a utilização dêêsse princípio.
Observe, a seguir, cinco exemplos.
Exemplo 1: Uma pesquisa elaborou um questionário contendo 8 perguntas de múltipla escolha, com 4 alternativas cada uma. Se o entrevistado deve responder a todas as perguntas, escolhendo uma única alternativa, quantas respostas diferentes para esse questionário a pesquisa póde receber?
Identificar o evento, estabelecer em quantas etapas ele póde acontecer e quantificar as possibilidades de ocorrência de cada etapa é um processo de criatividade e imaginação.
Neste exemplo, imagine quê você responderá às 8 perguntas dêêsse quêstionário na ordem em que elas são apresentadas. Desse modo, temos o evento “responder ao questionário” sêndo executado em 8 etapas, sêndo quê cada etapa é a seleção da resposta para uma pergunta. Além díssu, como há 4 alternativas em cada pergunta, há 4 possibilidades em cada etapa.

Assim, pelo princípio fundamental da contagem, a quantidade de respostas diferentes para esse questionário é dada pela multiplicação a seguir.

Portanto, a pesquisa póde receber 65.536 respostas diferentes para o questionário.
Página cento e quarenta e um
Exemplo 2: De quantos modos diferentes quatro pessoas podem se sentar em um banco de cinco lugares?

Para determinar o evento dêêsse exemplo, vamos imaginar quê as quatro pessoas se sentam no banco uma após a outra, isto é, a primeira pessoa escolhe um lugar e se senta no banco; depois, a segunda pessoa faz o mesmo; em seguida, a terceira pessoa; e, por fim, a quarta pessoa. Desse modo, temos o evento “sentar-se em um banco de cinco lugares” sêndo executado em 4 etapas. Além díssu, há:
• 5 possibilidades diferentes de ocorrer a primeira etapa, pois havia inicialmente 5 lugares vazios no banco para a primeira pessoa escolher;
• 4 possibilidades de ocorrer a segunda etapa, pois sobraram 4 lugares vazios no banco para a segunda pessoa escolher, uma vez quê a primeira pessoa já ocupou um lugar;
• 3 possibilidades de ocorrer a terceira etapa, pois sobraram 3 lugares vazios no banco após as duas primeiras pessoas ocuparem seus lugares;
• 2 possibilidades de ocorrer a quarta etapa, pois sobraram 2 lugares vazios no banco após as três primeiras pessoas ocuparem seus lugares.
Logo, a quantidade de modos diferentes como quatro pessoas podem se sentar em um banco de cinco lugares é expressa pela seguinte multiplicação:

Portanto, existem 120 modos diferentes de as quatro pessoas se sentarem no banco.
Exemplo 3: Quantas senhas de quatro algarismos distintos podem sêr criadas de modo quê o número formado seja par?
Imagine quê você tenha de criar uma senha com essas características. Nesse caso, o evento “criar uma senha” póde ocorrer em 4 etapas, sêndo a primeira escolher o algarismo da unidade; a segunda escolher o algarismo da dezena; a terceira escolher o algarismo da centena; e a quarta escolher o algarismo da unidade de milhar.
Como a senha criada deve sêr um número par, o número de possibilidades de ocorrer a primeira etapa – escolher o algarismo da unidade – é 5, uma vez quê os únicos algarismos quê podem sêr escolhidos são 0, 2, 4, 6 e 8.

Página cento e quarenta e dois
Como existem, no total, 10 algarismos (0, 1, 2, 3, 4, 5, 6, 7, 8 e 9) e a senha deve conter quatro algarismos distintos, o número de possibilidades da segunda etapa é 9, pois, uma vez definido o algarismo da unidade, ele não póde sêr utilizado novamente. Pelo mesmo raciocínio, o número de possibilidades da terceira etapa é 8, e o número de possibilidades da quarta etapa é 7, uma vez quê os algarismos definidos nas etapas anteriores não podem sêr utilizados novamente.
Assim, a quantidade de senhas com as características impostas pelo problema é dada pela multiplicação:
5 ⋅ 9 ⋅ 8 ⋅ 7 = 2.520
Portanto, 2.520 senhas pares podem sêr criadas com quatro algarismos distintos.
Note quê, nesse exemplo, definimos como primeira etapa aquela em quê havia a maior quantidade de restrições (a escolha do algarismo da unidade era mais restrita do quê as escôlhas dos demais algarismos). Essa é uma estratégia para a utilização do princípio multiplicativo: quantificar primeiro as possibilidades da etapa quê contém o maior número de restrições.
Exemplo 4: Utilizando cinco cores diferentes, de quantas maneiras é possível colorir a figura de modo quê as regiões adjacentes, quê possuem um lado em comum, tênham cores distintas?

Observe, a seguir, uma das possibilidades de colorir a figura obedecendo às condições estabelecidas no enunciado.

Como a figura é composta de 6 regiões, uma horizontal (A) e cinco verticais (B, C, D, E e F), o evento “colorir a figura” póde ocorrer em 6 etapas, quê recebem o mesmo nome da região a sêr colorida, conforme indica o esquema a seguir.
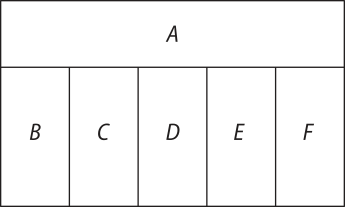
Iniciando a quantificação das possibilidades pela etapa A, obtemos:
• 5 possibilidades para a etapa A, pois há 5 opções de cores para pintar a região horizontal;
• 4 possibilidades para a etapa B, pois a côr definida para a região horizontal não póde mais sêr utilizada;
• 3 possibilidades para a etapa C, pois a região C deve ter uma côr diferente das cores das regiões A e B;
Página cento e quarenta e três
• 3 possibilidades para a etapa D, pois a região D deve ter uma côr diferente das cores das regiões A e C (perceba quê a região D póde ter a mesma côr da região B);
• 3 possibilidades para a etapa E, pois a região E deve ter uma côr diferente das cores das regiões A e D;
• 3 possibilidades para a etapa F, pois a região F deve ter uma côr diferente das cores das regiões A e E.
Logo, a multiplicação a seguir expressa o número de maneiras possíveis de colorir a figura.
5 ⋅ 4 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 1.620
Portanto, a figura póde sêr colorida de 1.620 maneiras diferentes.
Exemplo 5: Quantos números pares com três algarismos distintos podemos formár?
O evento “formar um número par com três algarismos" póde ocorrer em 3 etapas, sêndo a primeira escolher o algarismo da centena; a segunda escolher o algarismo da dezena; e a terceira escolher o algarismo da unidade. Além de escolhermos algarismos distintos para cada etapa, na primeira não podemos escolher o 0 para a centena, pois, nesse caso, o número não teria três algarismos; já na última etapa, temos de escolher 0, 2, 4, 6 ou 8 como algarismo da unidade para formár um número par.
Começando pela última etapa, quê tem o maior número de restrições, há 5 possibilidades para o algarismo da unidade; com isso, o número de possibilidades da centena depende do quê foi definido para a unidade. Se foi escolhido o 0 para a unidade, há 9 possibilidades para a centena; caso contrário, há 8 possibilidades. Quando esse impasse acontece, é necessário dividir a ocorrência do evento em dois casos mutuamente excludentes, ou seja, se ocorrer um dos casos, o outro não ocorrerá. Acompanhe os casos a seguir.
• Caso 1: Quando o algarismo da unidade é 0.
Nesse caso, há 1 possibilidade para o algarismo da unidade (o algarismo 0), 9 possibilidades para o algarismo da centena e 8 possibilidades para o algarismo da dezena, pois o número formado deve ter três algarismos distintos. Pelo princípio multiplicativo, a quantidade de números com três algarismos distintos quê terminam em 0 é:
9 ⋅ 8 ⋅ 1 = 72
• Caso 2: Quando o algarismo da unidade é 2, 4, 6 ou 8.
Nesse caso, há 4 possibilidades para o algarismo da unidade (2, 4, 6 ou 8), 8 possibilidades para o algarismo da centena (não póde sêr 0 nem sêr igual ao algarismo da unidade) e 8 possibilidades para o algarismo da dezena (pode sêr 0, mas não póde sêr igual aos algarismos da unidade e da centena). Pelo princípio multiplicativo, a quantidade de números dêêsse caso é:
8 ⋅ 8 ⋅ 4 = 256
Como o número par ou termina em 0 ou termina em 2, 4, 6, ou 8, pelo princípio aditivo podemos adicionar as quantidades dos dois casos.
72 + 256 = 328
Portanto, podemos formár 328 números pares com três algarismos distintos.
Nesse exemplo, para a aplicação do princípio multiplicativo, utilizamos a estratégia de dividir o evento em dois casos mutuamente excludentes. Ao final, aplicamos o princípio aditivo de conjuntos disjuntos.
Saiba quê...
Princípio aditivo
Se dois conjuntos A e B são finitos e disjuntos, ou seja, A ∩ B = ∅, o número de elemêntos da união A ∪ B é dado por: n(A ∪ B) = n(A) + n(B)
Página cento e quarenta e quatro
Fatorial
Neste tópico, vamos apresentar o número fatorial. Ele será utilizado nas técnicas de contagem, permutação, arranjo simples e combinação simples. Acompanhe sua definição.
Sendo n um número natural, com n ≥ 2, definimos o fatorial de n como o produto dos n números naturais consecutivos de 1 a n e o indicamos por n! (lê-se: n fatorial ou fatorial de n).
n! = n ⋅ (n − 1) ⋅ (n − 2) ⋅ … ⋅ 3 ⋅ 2 ⋅ 1
Definem-se também 1! = 1 e 0! = 1
Por exemplo:
• 2! = 2 ⋅ 1 = 2
• 3! = 3 ⋅ 2 ⋅ 1 = 6
• 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
• 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
A partir da definição de fatorial, podemos escrever, para qualquer n natural maior do quê ou igual a 2:
n! = n ⋅
Portanto: n! = n ⋅ (n − 1)!
pôdêmos escrever, por exemplo, 8! = 8 ⋅ 7!, pois:
8! = 8 ⋅ = 8 ⋅ 7!
Saiba quê...
As calculadoras científicas possuem uma tecla específica para o cálculo do fatorial, normalmente indicada por"x!".
ATIVIDADES RESOLVIDAS
1. Fernanda precisa organizar 15 livros, um do lado do outro, em uma prateleira. De quantas maneiras diferentes ela póde realizar essa tarefa?
Resolução
O evento “organizar 15 livros um do lado do outro" póde ocorrer em 15 etapas, sêndo cada etapa a colocação de um livro na prateleira. A primeira etapa tem 15 possibilidades, pois Fernanda deve escolher um dos 15 livros para sêr colocado primeiro na prateleira. A segunda etapa tem 14 possibilidades, uma vez quê um livro já foi colocado. A terceira etapa tem 13 possibilidades, e assim por diante, até a décima quinta etapa, quê é a colocação do último livro na prateleira. Desse modo, pelo princípio fundamental da contagem, o número de maneiras diferentes de organizar esses livros é:
15 ⋅ 14 ⋅ 13 ⋅ … ⋅ 3 ⋅ 2 ⋅ 1 = 15!
Portanto, Fernanda póde organizar esses livros de 15! maneiras diferentes.
Dependendo da ordem de grandeza, é comum respostas de problemas de contagem serem expressas por números fatoriais, por exemplo: 15! = 1.307.674.368.000
Página cento e quarenta e cinco
2. (Enem/MEC) Um modelo de telefone celular oferece a opção de desbloquear a tela usando um padrão de toques como senha.

Os toques podem sêr feitos livremente nas 4 regiões numeradas da tela, sêndo quê o usuário póde escolher entre 3, 4 ou 5 toques ao todo.
Qual expressão representa o número total de códigos existentes?
a) 45 − 44 − 43
b) 45 + 44 + 43
c) 45 × 44 × 43
d) (4!)5
e) 45
Resolução
Como a senha para desbloquear a tela do celular póde conter 3, 4 ou 5 toques, o evento “criar uma senha” para desbloquear a tela do celular póde sêr dividido em três casos mutuamente excludentes.
Caso 1: A senha contém 3 toques.
Nesse caso, o evento póde ocorrer em 3 etapas, uma para cada toque, e há 4 possibilidades em cada etapa, pois a tela do celular apresenta 4 regiões numeradas de 1 a 4. Logo, pelo princípio multiplicativo, o número de senhas possíveis quê contém 3 toques é expresso por:
4 ⋅ 4 ⋅ 4 = 43
Caso 2: A senha contém 4 toques.
Nesse caso, o evento póde ocorrer em 4 etapas, uma para cada toque, e há 4 possibilidades em cada etapa. Logo, o número de senhas possíveis quê contém 4 toques é expresso por:
4 ⋅ 4 ⋅ 4 ⋅ 4 = 44
Caso 3: A senha contém 5 toques.
Nesse caso, o evento póde ocorrer em 5 etapas, uma para cada toque, e há 4 possibilidades em cada etapa. Logo, o número de senhas possíveis quê contém 5 toques é expresso por:
4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4 = 45
Como os casos 1, 2 e 3 constituem conjuntos disjuntos, isto é, eles não possuem elemêntos em comum, pelo princípio aditivo, o número total de códigos existentes é dado por:
43 + 44 + 45
Portanto, está correta a alternativa b.
3. Simplifique.
a)
b)
c)
Resolução
a) = 420
b) = = 91
c) = n2 − n
4. Determine o conjunto solução da equação (n − 4)! = 120.
Resolução
(n − 4)! = 120 ⇒ (n − 4)! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 ⇒ (n − 4)! = 5!
Pela igualdade entre números fatoriais, obtemos:
(n − 4)! = 5! ⇒ n − 4 = 5 ⇒ n = 9
Portanto, o conjunto solução da equação é S = {9}.
Página cento e quarenta e seis
ATIVIDADES
1. Catarina e Virgínia combinaram ir juntas a um chôu. Catarina mora na rua A e vai buscar a amiga Virgínia, quê mora na rua B. De lá, seguirão para o endereço onde ocorrerá o chôu, na rua C. Para Catarina chegar à casa de Virgínia, ela tem três caminhos diferentes (x, y ou z). Já para ir da casa de Virgínia ao chôu, elas têm duas opções diferentes (caminho 1 ou caminho 2).
a) Quais são os caminhos quê Catarina póde percorrer para ir ao chôu, saindo de sua casa e passando pela casa de Virgínia?
As possibilidades de caminho são (x, 1), (x, 2), (y, 1), (y, 2), (z, 1) e (z, 2).
b) Como você calcularia o total de opções de caminho listadas no item a aplicando o princípio multiplicativo?
3 ⋅ 2 = 6
c) Desenhe o diagrama de árvore dos possíveis caminhos quê Catarina póde percorrer para ir ao chôu, passando pela casa de Virgínia.
Ver as Orientações para o professor.
2. Uma moeda tem duas faces: cara (K) e coroa (C). Lança-se essa moeda três vezes seguidas e observa-se qual das faces fica voltada para cima.
a) Represente, em um diagrama de árvore, todos os resultados possíveis dêêsse experimento.
Ver as Orientações para o Professor.
b) Pelo princípio fundamental da contagem, escrêeva a multiplicação quê expressa a quantidade de resultados possíveis dêêsse experimento.
2 ⋅ 2 ⋅ 2
3. No cardápio de café da manhã de uma lanchonete, há quatro sabores de suco, três opções de lanche e dois tipos de fruta. Pagando um valor fixo, o cliente póde escolher um suco, um lanche e uma fruta. De quantas maneiras diferentes é possível compor um café da manhã nessa lanchonete?
24 maneiras
4. (UECE) Uma próva do exame válido para seleção de vagas visando ao ingresso em Instituições de Ensino Superior é elaborada da seguinte forma:
I. 40 kestões são formuladas no formato objetivo, com alternativas de respostas ou conclusões das quais apenas uma é correta.
II. Cada quêstão disponibiliza 5 alternativas para identificação, pelo candidato, daquela que é a única correta.
Assim, é correto concluir-se quê o número de gabaritos quê podem sêr construídos para essa próva é
a) 540.
b) 405.
c) 5 ⋅ (60!).
d) 60 ⋅ (5!).
alternativa a
5. escrêeva uma situação-problema de Combinató ria cuja resolução possa sêr expressa pelo diagrama de possibilidades a seguir.
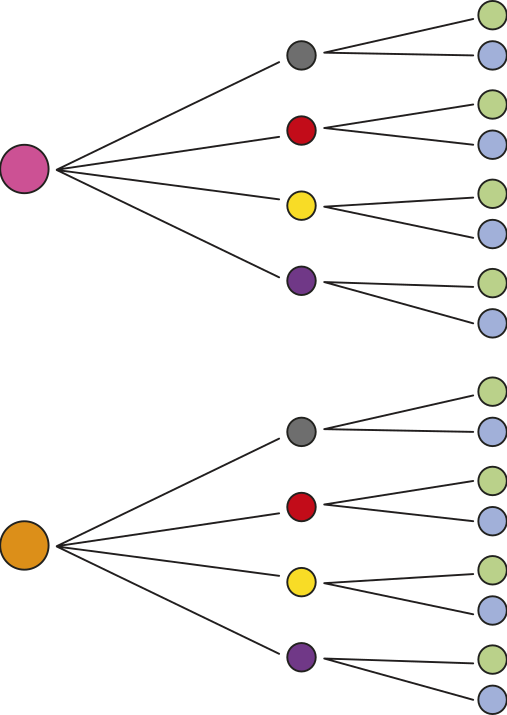
Resposta pessoal.
6. Oito cavalos disputam uma corrida. Quantas são as possibilidades de chegada para os 3 primeiros lugares?
336 possibilidades
7. Em uma sala de espera, há seis cadeiras dispostas lado a lado. De quantos modos distintos quatro pessoas podem ocupar esses lugares?
360 modos
Página cento e quarenta e sete
8. A figura ilustra oito vagas vazias de um estacionamento. De quantas maneiras diferentes quatro carros podem ocupar quatro dessas vagas?

1.680 maneiras
9. (UFAL) Quantos números inteiros positivos divisíveis por 5, de 4 algarismos distintos, podem sêr escritos com os algarismos 1, 3, 5, 7, 9?
24 números
10. (UFG-GO) Utilizando as notas dó, ré, mi, fá, sól, lá e si, um músico deseja compor uma melodia com 4 notas, de modo quê tenha notas consecutivas distintas. Por exemplo: {dó, ré, dó, mi} e {si, ré, mi, fá} são melodias permitidas, enquanto quê {ré, ré, dó, mi} não, pois possui duas notas ré consecutivas.
a) escrêeva cinco melodias diferentes, de acôr-do com o critério dado.
Ver as Orientações para o professor.
b) Qual o número de melodias quê podem sêr compostas nessas condições?
1.512 melodias
11. Determine a quantidade de números:
a) com quatro algarismos.
9.000 números
b) com quatro algarismos distintos.
4.536 números
c) divisíveis por 5, com quatro algarismos distintos.
952 números
12. (UEG-GO) Maria tem 5 saias, sêndo uma de cada côr: azul, vermelha, branca, preta e lilás. Ela possui ainda 4 blusas: azul, rosa, marfim e preta. De quantas formas diferentes ela poderá se vestir de modo a não usar sáia e blusa da mesma côr?
a) 10
b) 09
c) 18
d) 12
e) 16
alternativa c
13. Calcule.
a) 6!
720
b) 10!
3.628.800
c)
336
d)
272
e)
f)
21
14. Flávia tem seis lápis de cores diferentes. De quantas maneiras distintas ela póde colorir a figura a seguir de modo quê os quadrados com um lado em comum não tênham cores iguais?

630 maneiras
15. Simplifique as expressões:
a)
n
b)
16. resôuva as equações:
a) (n − 2)! = 720
S = {8}
b) (n − 2)! = 2(n − 4)!
S = {4}
17. (Ufop-MG) resôuva a equação = 6n − 4
S = {2}
18. Para proteger seus dados em um aplicativo bancário no celular, Flávia criou uma senha com seis caracteres diferentes. Ela escolheu vogais minúsculas para os três primeiros caracteres e algarismos para os três últimos. Quantas senhas distintas podem sêr criadas com essas características?
43.200 senhas
Página cento e quarenta e oito
FÓRUM
Segurança digital: o papel fundamental das senhas
Desde a era dos primeiros computadores até a atualidade, as senhas têm sido a primeira linha de defesa contra invasores cibernéticos interessados em acessar informações confidenciais. A importânssia de criar senhas seguras não póde sêr subestimada. Uma senha robusta, quê combina lêtras maiúsculas e minúsculas, números e caracteres especiais, funciona como uma fortaleza digital, o quê dificulta tentativas de invasão.
Contudo, a segurança digital vai além da criação de senhas compléksas. Muitos sáites e aplicativos têm adotado medidas adicionais para garantir a proteção dos dados de seus usuários. A autenticação em duas etapas, por exemplo, adiciona uma camada ésstra de segurança, exigindo um segundo método de verificação, como um cóódigo enviado por mensagem de texto ou gerado por um aplicativo específico. Essa abordagem reduz significativamente o risco de acesso não autorizado, mesmo se a senha principal for comprometida.
Outra medida de proteção adicional é o uso de tecnologias biométricas, como impressão digital ou reconhecimento facial. Portanto, é essencial quê os usuários verifiquem quais medidas estão disponíveis em cada caso e as utilizem d fórma eficaz. Ao adotar essas práticas de segurança digital, o usuário aumentará a garantia da integridade dos seus dados.

Com base na leitura do texto, reúna-se a um colega, e façam o quê se pede.
![]() • Discutam outras estratégias quê possam aumentar a segurança digital e comentem os riscos quê uma pessoa corre ao ter seus dados violados.
• Discutam outras estratégias quê possam aumentar a segurança digital e comentem os riscos quê uma pessoa corre ao ter seus dados violados.
Ver as Orientações para o professor.
Página cento e quarenta e nove
Permutação simples
Alguns problemas de Combinatória quê aparécem com muita freqüência consistem em determinar a quantidade de sequências (ou filas) quê é possível formár com n objetos distintos apenas trocando-os de lugar. Acompanhe o exemplo.
Quatro atletas, A, B, C e D, disputam uma corrida feminina de 100 m rasos. De quantas maneiras póde ocorrer a ordem de chegada dessa corrida, sabendo-se quê não há empates em nenhuma das posições?
Saiba quê...
Permutar é sinônimo de trocar.

A resolução dêêsse problema pelo princípio fundamental da contagem é dada pela multiplicação:
4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
Note quê, nessa multiplicação, os fatores 4, 3, 2 e 1 correspondem, respectivamente, ao número de possibilidades de se definirem, nesta ordem, o 1º, o 2º, o 3º e o 4º lugares. Observe quê essa resolução também póde sêr representada pelo seguinte número fatorial:
4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
As 24 ordens possíveis de chegada dessas quatro atletas estão representadas no qüadro a seguir, e cada uma delas é chamada de permutação simples das atletas A, B, C e D.
ABCD ACDB BACD BCDA CABD CBDA DABC DBCA
ABDC ADBC BADC BDAC CADB CDAB DACB DCAB
ACBD ADCB BCAD BDCA CBAD CDBA DBAC DCBA
Seja E um conjunto com n elemêntos distintos, com n ∈ ℕ*. Cada sequência diferente dos n elemêntos de E é denominada permutação simples, e o número de permutações simples dos n elemêntos é indicado por Pn, em quê:
Pn = n!
Página cento e cinquenta
Observe a seguir outros exemplos em quê a permutação simples é empregada.
a) As sequências (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2) e (3, 2, 1) são as permutações simples do conjunto {1, 2, 3}. Note quê o número de permutações dêêsse conjunto é:
P3 = 3! = 3 ⋅ 2 ⋅ 1 = 6
b) De quantas maneiras é possível dispor 10 livros distintos, lado a lado, em uma prateleira? Cada sequência diferente em quê os livros são colocados na prateleira é uma permutação simples dêêsses 10 livros. Logo, o número de maneiras de dispor esses livros é:
P10 = 10! = 3.628.800
Permutação com repetição
Um anagrama é formado pela troca de posição das lêtras de uma palavra, podendo ou não ter significado na língua de origem. Por exemplo, os anagramas da palavra CABO são:
CABO CBOA ACBO ABOC BCAO BAOC OCAB OABC
CAOB COAB ACOB AOCB BCOA BOCA OCBA OBCA
CBAO COBA ABCO AOBC BACO BOAC OACB OBAC
Cada anagrama da palavra CABO é uma permutação simples das lêtras C, A, B e O. Logo, o número de anagramas dessa palavra é dado por:
P4 = 4! = 24
Considere, agora, os anagramas da palavra PIPA, quê contém 4 lêtras – a mesma quantidade da palavra CABO. Como a letra P se repete na palavra, quando trocamos um P pelo outro, obtemos o mesmo anagrama, e não um diferente. Com isso, o número de permutações simples P4 = 4! conta cada anagrama duas vezes, uma vez quê há 2! maneiras de trocar as lêtras P entre si. Desse modo, o número de anagramas da palavra PIPA é obtído pela seguinte divisão:
= 12
Os 12 anagramas da palavra PIPA são:
PIPA PPIA PAPI IPPA IAPP APPI
PIAP PPAI PAIP IPAP APIP AIPP
De forma análoga, o número de anagramas da palavra ABACATE, quê tem 7 lêtras, sêndo uma delas (a letra A) repetida três vezes, é dado pela divisão a seguir.
= 840
Isso ocorre porque o número de permutações simples, 7!, conta o mesmo anagrama 3! vezes, uma vez quê há 3! maneiras de trocar as lêtras A entre si.
Página cento e cinquenta e um
Para solucionar problemas de permutações com repetição, podemos utilizar a seguinte fórmula:
O número de permutações de n elemêntos, com n ∈ ℕ*, em quê um dos elemêntos se repete (alfa)" vezes, outro se repete (beta)" vezes, e assim por diante, até o último elemento, quê se repete (gama)" vezes, é dado por:
Vamos agora considerar mais um exemplo: quantos anagramas tem a palavra RIGOROSO?
Essa palavra tem 8 lêtras, com a letra R se repetindo duas vezes, e a letra O se repetindo 3 vezes. Assim, o número de permutações das suas lêtras é:
Portanto, a palavra RIGOROSO tem 3.360 anagramas.
ATIVIDADES RESOLVIDAS
5. Quantos números de cinco algarismos distintos podem sêr formados usando-se os algarismos 1, 3, 5, 7 e 8?
Resolução
pôdêmos solucionar esse exercício de dois modos.
1º modo: Qualquer um dos cinco algarismos dados póde ocupar a ordem das dezenas de milhar, restando, então, quatro algarismos para a unidade de milhar, três para a centena, dois para a dezena e, finalmente, um para a unidade. Então, pelo princípio multiplicativo, temos:
5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
2º modo: Observe quê cada permutação simples dos algarismos 1, 3, 5, 7 e 8 gera um número diferente. O número de permutações simples de 5 elemêntos é:
P5 = 5! = 120
Portanto, podemos formár 120 números.
6. Considere os anagramas da palavra LIVRO.
a) Quantos deles começam com L e terminam com O?
b) Quantos começam com I ou terminam com V?
Resolução
a) Os anagramas quê se iniciam com a letra L e têm a letra O no final são do tipo:

Fixadas essas duas lêtras, obissérve quê cada permutação simples das outras 3 lêtras gera um anagrama diferente. Determinando P3, temos:
P3 = 3! = 3 ⋅ 2 ⋅ 1 = 6
Portanto, há 6 anagramas quê começam com L e terminam com O.
b) Considere:
• x o número de anagramas quê começam com I;
• y o número de anagramas quê terminam com V;
• z o número de anagramas quê começam com I e terminam com V.
Desse modo, o número de anagramas quê começam com I ou terminam com V é expresso por: x + y − z
Note quê é necessário subtrair z, pois os anagramas quê começam com I e terminam com V, por exemplo ILROV, são quantificados tanto pelo número x quanto pelo número y; consequentemente, a adição x + y conta duas vezes esses anagramas.
Vamos calcular cada um dêêsses números.
Página cento e cinquenta e dois
• Anagramas quê começam com I:

x = P4 = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
• Anagramas quê terminam com V:

y = P4 = 4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
• Anagramas quê começam com I e terminam com V:

z = P3 = 3! = 3 ⋅ 2 ⋅ 1 = 6
• Anagramas quê começam com I ou terminam com V:
x + y − z = 24 + 24 − 6 = 42
Portanto, 42 anagramas de LIVRO começam com I ou terminam com V.
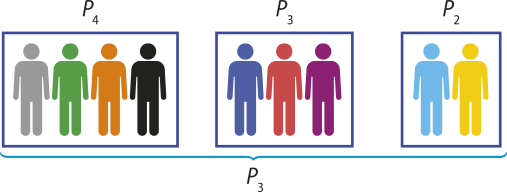
7. Nove estudantes do Ensino Médio de uma escola, sêndo quatro do 1º ano, três do 2º e dois do 3º, farão uma apresentação musical. De quantas maneiras eles podem se posicionar lado a lado para essa apresentação, de modo quê os estudantes do mesmo ano permaneçam juntos?
Resolução
Decidir a posição dêêsses nove estudantes póde ocorrer em quatro etapas. A primeira é definir a posição em quê os 4 estudantes do 1º ano estarão juntos, formando um bloco do 1º ano. A segunda é definir a posição em quê os 3 estudantes do 2º ano estarão juntos, formando um bloco do 2º ano. A terceira é definir a posição em quê os 2 estudantes do 3º ano estarão juntos, formando um bloco do 3º ano. Por fim, definir a posição dêêsses três blocos lado a lado.

• O número de possibilidades da 1ª etapa é P4, pois há 4 estudantes do 1º ano.
• O número de possibilidades da 2ª etapa é P3.
• O número de possibilidades da 3ª etapa é P2.
Como se trata de três blocos, o número de possibilidades de dispor lado a lado esses blocos é P3.
Pelo princípio multiplicativo, temos:
P4 ⋅ P3 ⋅ P2 ⋅ P3 = 4! ⋅ 3! ⋅ 2! ⋅ 3! = 24 ⋅ 6 ⋅ 2 ⋅ 6 = 1.728
Portanto, há 1.728 maneiras de os estudantes se posicionarem lado a lado de modo quê os estudantes do mesmo ano permaneçam juntos.
8. De quantas maneiras diferentes é possível colorir as cinco bandeirinhas ilustradas a seguir de modo quê quaisquer duas delas tênham a côr azul e as demais tênham as cores vêrde, amarelo e vermelho?

Resolução
Considere quê as lêtras Z, D, A e V representam as cores:
• azul (Z)
• vêrde (D)
• amarelo (A)
• vermelho (V).
Com isso, podemos indicar a forma como as bandeirinhas poderão sêr pintadas por anagramas compostos pelas lêtras Z, Z, D, A e V. Por exemplo, o anagrama DVZAZ indica quê as cinco bandeirinhas serão pintadas, da esquerda para a direita, nas cores vêrde (D), vermelho (V), azul (Z), amarelo (A) e azul (Z). Determinando o número de permutações dessas 5 lêtras, em quê a letra Z se repete duas vezes, temos:
Logo, há 60 maneiras diferentes de colorir essas bandeirinhas.
Página cento e cinquenta e três
9. Uma formiga, inicialmente no vértice A, anda sobre as linhas do quadriculado da figura, sempre para a direita ou para baixo, até chegar ao vértice B. De quantas maneiras diferentes ela póde fazer esse percurso?

Resolução
Vamos indicar o deslocamento da formiga entre dois vértices consecutivos pela letra D, se ela for para a direita, e pela letra B, se ela for para baixo.
Alguns caminhos possíveis são: DDDDBBBB, BBBBDDDD, BDBDBDBD e BBDDBBDD.
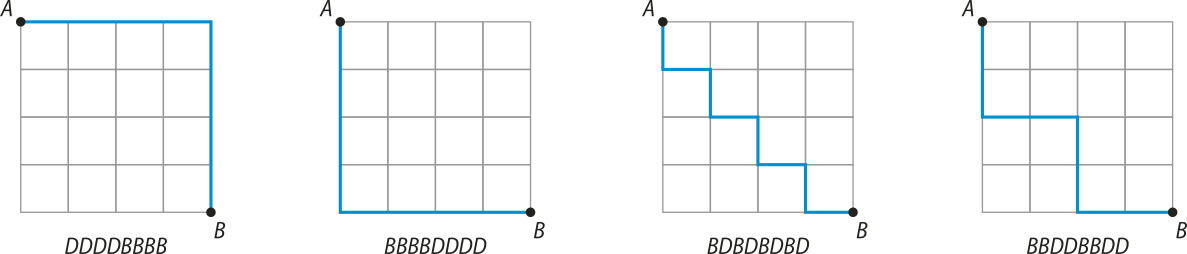
Observe quê, para ir do ponto A ao ponto B, independentemente do caminho escolhido, a formiga sempre fará 4 deslocamentos entre dois vértices consecutivos para a direita (DDDD) e 4 deslocamentos entre dois vértices consecutivos para baixo (BBBB). Desse modo, cada anagrama formado pelas lêtras D, D, D, D, B, B, B e B representa um percurso diferente quê a formiga póde fazer.
Calculando o número de permutações dessas 8 lêtras, em quê há 4 repetições da letra D e 4 da letra B, temos:
Logo, a formiga póde fazer esse percurso de 70 maneiras diferentes.
ATIVIDADES
19. escrêeva os seis anagramas da palavra PAZ.
PAZ, PZA, APZ, AZP, ZPA e ZAP
20. (UFSM-RS) Para cuidar da saúde, muitas pessoas buscam atendimento em cidades maiores, onde há centros médicos especializados e hospitais mais equipados. Muitas vezes, o transporte até essas cidades é feito por vans disponibilizadas pelas prefeituras.
Em uma vã com 10 assentos, viajarão 9 passageiros e o motorista. De quantos modos distintos os 9 passageiros podem ocupar suas poltronas na vã?
a) 4.032.
b) 36.288.
c) 40.320.
d) 362.880.
e) 403.200.
alternativa d
21. Quantos anagramas da palavra EDITORA:
a) começam com A?
720 anagramas
b) começam com A e terminam com E?
120 anagramas
22. Considere a palavra FELINO.
a) Quantos são os anagramas dessa palavra?
720
b) Quantos começam com N?
120
c) Quantos terminam com vogal?
360
d) Quantos apresentam as lêtras E, L e I juntas e nessa ordem?
24
e) Quantos apresentam as lêtras E, L e I juntas e em qualquer ordem?
144
Página cento e cinquenta e quatro
23. (hú éfe ême gê) Permutando-se os algarismos do número 123.456, formam-se números de seis algarismos.
Supondo-se quê todos os números formados com esses seis algarismos tênham sido colocados numa lista em ordem crescente,
a) DETERMINE quantos números possui essa lista.
720
b) DETERMINE a posição do primeiro número quê começa com o algarismo 4.
361
c) DETERMINE a posição do primeiro número quê termina com o algarismo 2.
34
24. Um estudante ganhou quatro livros diferentes de Matemática, três livros diferentes de Física e dois livros diferentes de Química. De quantos modos distintos esses livros podem sêr enfileirados em uma prateleira de uma estante mantendo-se juntos os da mesma disciplina?
1.728 modos
25. escrêeva os dez anagramas da palavra ARARA.
AAARR, AARAR, AARRA, ARARA, ARAAR, ARRAA, RRAAA, RARAA, RAARA e RAAAR
26. Quantos anagramas tem cada palavra a seguir?
a) PATA
12
b) PARALELOGRAMO
129.729.600
c) GUANABARA
15.120
27. Determine a quantidade de números distintos obtidos pela permutação dos algarismos dos números:
a) 73.431
20
b) 343.434
60
28. Alfredo, Armando, Ricardo, Renato e ernésto querem criar uma sigla com cinco símbolos, sêndo cada sín-bolo a primeira letra de seus nomes. Qual é o número total de siglas possíveis de se formár?
30
29. Uma cesta contém dez frutas: seis ma-ssãns e quatro peras. Ana quer retirar, uma a uma, as dez frutas dessa cesta. De quantas maneiras ela poderá retirá-las?
210 maneiras
30. Quantos anagramas tem a palavra ARAPONGA com a letra P ocupando o último lugar?
840 anagramas
31. (hú éfi éssi cê) Calcule o número de anagramas da palavra CLARA em quê as lêtras AR aparécem juntas e nessa ordem.
24 anagramas
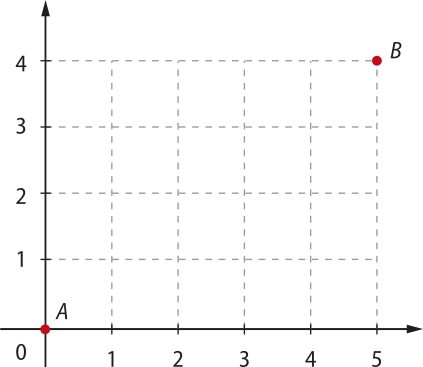
32. Na figura a seguir, deslocando-se uma unidade de cada vez, para cima ou para a direita, quantos caminhos diferentes podem sêr feitos de A até B?
126 caminhos
33. (Unifimes-MG) Cinco amigos compraram ingressos para uma peça de teatro, de modo quê as poltronas ficavam na mesma fileira, uma ao lado da outra. Sabendo quê no dia da peça um dos amigos não pôdi comparecer, e quê as poltronas do teatro são numeradas, o número de maneiras distintas dos quatro amigos quê foram ao teatro se sentarem nessas poltronas era
a) 30.
b) 60.
c) 20.
d) 5.
e) 120.
alternativa e
34. Para uma apresentação de dança, oito dançarinos formarão uma fila de modo quê Julia e Guilherme fiquem lado a lado. De
quantas maneiras distintas eles poderão formár essa fila?
a) 7! ⋅ 2!
b)
c) 6! ⋅ 2!
d)
e) 8! ⋅ 2!
alternativa a
35. Elabore uma situação-problema cuja resolução seja dada pela multiplicação P4 ⋅ P3.
Resposta pessoal.
Página cento e cinquenta e cinco
Arranjo simples
Todos os problemas de arranjo simples são solucionados pelo princípio multiplicativo. Acompanhe o exemplo.
Saiba quê...
Arranjar significa colocar em ordem, organizar.
Uma turma de 3º ano do Ensino Médio deve eleger um representante, um vice-representante e um suplente. Se apenas cinco estudantes, Maria, Paula, João, Carolina e Everaldo, candidataram-se para esses cargos, de quantas maneiras distintas três dêêsses cinco estudantes podem sêr escolhidos?
Pelo princípio multiplicativo, o número de maneiras distintas de escolher três dêêsses cinco estudantes é dado pela multiplicação:
5 ⋅ 4 ⋅ 3 = 60
Nessa multiplicação, os fatores 5, 4 e 3 são, nessa ordem, o número de possibilidades de eleger o representante, o vice-representante e o suplente.
Dizemos quê esse tipo de problema é um arranjo simples de 5 elemêntos tomados 3 a 3, pois havia 5 candidatos para 3 cargos distintos (representante, vice-representante e suplente). Cada um dos 60 resultados possíveis dessa eleição é denominado arranjo simples de 3 estudantes dos 5 candidatos.
É importante ressaltar quê, mudando apenas os cargos dos estudantes eleitos, temos um resultado diferente da eleição. Por exemplo, o trio Maria (M), Paula (P) e João (J) poderiam sêr eleitos de seis maneiras distintas. Considerando quê a primeira letra da sigla é a inicial do nome do representante, a segunda letra é a inicial do nome do vice-representante e a terceira letra é a inicial do nome do suplente, temos as seguintes opções:
MPJ MJP
JMP JPM
PMJ PJM
Seja E um conjunto com n elemêntos distintos, com n ∈ ℕ*. Cada sequência de p elemêntos distintos de E é denominada arranjo simples de E.
A seguir, apresentamos outros exemplos de arranjos simples.
a) As sequências (M, P, J), (M, J, P), (J, M, P) e (E, C, J) são alguns dos arranjos simples de três elemêntos do conjunto {M, P, J, C, E}.
b) As sequências (1, 3, 5, 7), (7, 5, 3, 1), (1, 9, 5, 11) e (5, 1, 3, 7) são alguns dos arranjos simples de quatro elemêntos do conjunto {1, 3, 5, 7, 9, 11}.
Página cento e cinquenta e seis
Fórmula do arranjo simples
Apesar de todos os problemas de arranjo simples poderem sêr quantificados por meio do princípio multiplicativo, também é possível fazer essa quantificação por meio de fórmula específica.
Dado um conjunto E = {x1, x2, x3, …, xn}com n elemêntos, com n ∈ ℕ*, pelo princípio multiplicativo, o número de arranjos simples An, p (lemos: arranjo de n elemêntos tomados p a p) de p elemêntos distintos do conjunto E, ou seja, o número de sequências com p elemêntos distintos de E, é dado pela seguinte multiplicação:
Note quê, nessa multiplicação, o fator n é o número de possibilidades de escolher o primeiro elemento da sequência; definido o primeiro elemento, (n − 1) é o número de possibilidades de escolher o segundo elemento; definidos o primeiro e o segundo elemento, (n − 2) é o número de possibilidades de escolher o terceiro elemento; e assim por diante, até o número de possibilidades (n − p + 1) de escolher o último elemento dessa sequência.
Para indicar o número An, p utilizando fatoriais, vamos multiplicar a expressão anterior por . Acompanhe.
Saiba quê...
Observe quê: = 1
An, p = n ⋅ (n − 1) ⋅ (n − 2) ⋅ … ⋅ (n − p + 1) ⋅
An, p =
An, p =
Portanto, o número de arranjos simples An, p de n elemêntos tomados p a p, em quê n e p são números naturais diferentes de zero e p ≤ n, póde sêr determinado pela fórmula:
Acompanhe a aplicação dessa fórmula por meio do exemplo a seguir.
Para calcular o número de arranjos de 7 elemêntos tomados 3 a 3, podemos:
• utilizar o princípio multiplicativo: A7, 3 = 7 ⋅ 6 ⋅ 5 = 210
• ou utilizar a fórmula: A7, 3 = = 7 ⋅ 6 ⋅ 5 = 210
Para assistir
• O jôgo da imitação. Direção: Morten Tyldum. Estados Unidos: Bristol Automotive; Reino Unido: Black Bear, 2014. Streaming (114 min).
Essa ficção aborda a vida e a contribuição do matemático inglês élam Turing (1912-1954) para desvendar o cóódigo nazista durante a Segunda Guerra Mundial.

Página cento e cinquenta e sete
ATIVIDADES RESOLVIDAS
10. Quantos números de três algarismos distintos podemos formár com os algarismos 1, 2, 3, 4, 5 e 7?
Comentar com os estudantes quê, de modo geral, as atividades de análise combinatória podem sêr resolvidas de diferentes maneiras.
Resolução
pôdêmos solucionar esse exercício de dois modos.
1º modo: Qualquer um dos seis algarismos dados póde ocupar a ordem das centenas, restando, então, dois algarismos para a dezena e, por fim, um algarismo para a unidade. Então, pelo princípio multiplicativo, temos:
6 ⋅ 5 ⋅ 4 = 120
2º modo: Cada número formado com as características impostas pelo enunciado é um arranjo simples de 3 elemêntos dêêsses 6 algarismos. O número de arranjos simples de 6 elemêntos tomados 3 a 3 é:
A6, 3 = = 120
Logo, podemos formár 120 números.
11. Vinte pessoas se candidataram para uma comissão quê sêrá composta de um presidente, um vice-presidente, um tesoureiro e um secretário. De quantas maneiras essa comissão poderá ser formada, sabendo-se quê cargos distintos não podem sêr ocupados pela mesma pessoa e quê o candidato Lucas foi selecionado, mas seu cargo ainda não foi definido?
Resolução
A formação dessa comissão póde ocorrer em duas etapas. A primeira etapa é definir o cargo do candidato já selecionado, Lucas, e a segunda é definir os candidatos para os outros três cargos. Há 4 possibilidades para a primeira etapa, porque Lucas póde assumir qualquer um dos 4 cargos da comissão. Definida a primeira etapa, sobram 3 cargos e 19 candidatos. Cada arranjo simples de 3 dos 19 candidatos é um modo de preencher as vagas dos 3 cargos quê faltam. Por isso, o número de possibilidades da segunda etapa é a quantidade de arranjos simples A19, 3. Pelo princípio multiplicativo, temos:
4 ⋅ A19, 3 = 4 ⋅ = 23.256
Portanto, há 23.256 maneiras de compor essa comissão.
12. Uma próva de natação é disputada por 10 competidores, dos quais 4 são brasileiros. Qual é o número de resultados possíveis para a próva, de modo quê pelo menos um brasileiro fique em uma das três primeiras colocações?
Resolução
Cada arranjo simples de 3 dos 10 nadadores é um resultado possível das três primeiras colocações dessa competição. Logo, o total de possibilidades das três primeiras colocações é:
A10, 3 = = 720
Dos 10 competidores, 4 são brasileiros, consequentemente, 6 não são. Assim, cada arranjo simples de 3 dos 6 competidores não brasileiros é um resultado da competição na qual não ocorre a presença de brasileiros nas três primeiras colocações. Logo, o total de possibilidades das três primeiras colocações, sem quê haja a presença de brasileiros, é:
A6, 3 = = 120
Subtraindo 120 do total de possibilidades, quê é 720, temos:
720 − 120 = 600
Portanto, há 600 resultados possíveis em quê pelo menos um brasileiro fique em uma das três primeiras colocações.
ATIVIDADES
36. resôuva os problemas a seguir de duas maneiras. A primeira utilizando o princípio multiplicativo, e a segunda utilizando a fórmula do arranjo simples. Em seguida, responda: qual método de resolução você prefere? Por quê?
Resposta pessoal.
a) De quantas maneiras três pessoas podem se sentar em nove cadeiras numeradas de 1 a 9?
504 maneiras
b) Quantos números de cinco algarismos distintos podem sêr formados com os algarismos 1, 2, 3, 4, 5, 6, 7, 8 e 9?
15.120 números
Página cento e cinquenta e oito
37. Elabore uma situação-problema cuja resolução possa sêr determinada calculando-se o número de arranjos simples de 12 elemêntos tomados 4 a 4.
Resposta pessoal.
38. Copie o qüadro no caderno e complete-o com todos os arranjos simples, todas as sequências, de 3 elemêntos do conjunto E = {A, B, C, D}.

39. (UFJF-MG) Um ônibus com 40 assentos numerados de 01 a 40 foi alugado para uma excursão quê fará uma viagem com 25 turistas. De quantos modos distintos os turistas poderão sêr acomodados para a viagem considerando quê não há preferência por lugares?
a)
b)
c) 40
d) 15!
e) 40! − 15!
alternativa a
40. (Enem/MEC) Uma família composta por sete pessoas adultas, após decidir o itinerário de sua viagem, consultou o sáiti de uma empresa aérea e constatou quê o vôo para a data escolhida estava quase lotado. Na figura, disponibilizada pelo sáiti, as poltronas ocupadas estão marcadas com X e as únicas poltronas disponíveis são as mostradas em branco.
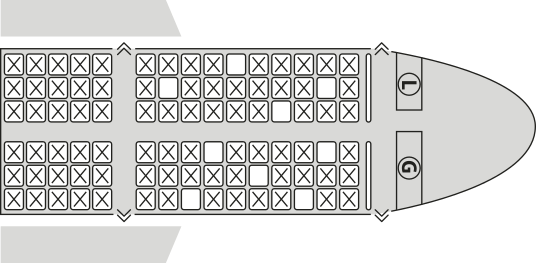
Disponível em: https://livro.pw/qcysz. Acesso em: 30 out. 2013 (adaptado).
O número de formas distintas de se acomodar a família nesse vôo é calculado por
a)
b)
c) 7!
d)
e)
alternativa a
41. Quantos números de três algarismos distintos podemos formár com os algarismos 1, 2, 3, 4, 5, 6, 7, 8 e 9, incluindo sempre o algarismo 4?
168 números
42. Sabendo-se quê uma bandeira tem quatro faixas horizontais:
a) quantas são as possibilidades de pintá-la com quatro cores distintas, escolhendo entre vermelho, laranja, amarelo, vêrde, azul, roxo e marrom?
840 possibilidades
b) quantas bandeiras podem sêr pintadas se, além da condição do item a, a côr amarela estiver sempre presente?
480 bandeiras
43. Em uma gincana escolar, cinco meninos e sete meninas disputaram uma competição. Em quantos resultados possíveis dessa competição há, pelo menos, um menino em uma das três primeiras colocações?
1.110 resultados
44. (Enem/MEC) Um determinado campeonato de futeból, compôzto por 20 tímes, é disputado no sistema de pontos corridos. Nesse sistema, cada tíme joga contra todos os demais times em dois turnos, isto é, cada time joga duas partidas com cada um dos outros times, sêndo quê cada jôgo póde terminar empatado ou havêer um vencedor.
Sabendo-se quê, nesse campeonato, ocorreram 126 empates, o número de jogos em quê houve ganhador é igual a
a) 64.
b) 74.
c) 254.
d) 274.
e) 634.
alternativa c
45. (UFRGS-RS) Uma biblioteca está elaborando etiquetas de identificação para os livros do acervo de tal forma quê, em cada etiqueta, são usadas quatro lêtras distintas, de um alfabeto de 26 lêtras, e quatro algarismos também distintos, de 0 a 9.
A figura abaixo mostra um exemplo de modelo da etiqueta produzida.

Assinale a alternativa quê apresenta o número total de etiquetas distintas produzidas pela biblioteca.
a) 26 + 10
b) 26 ⋅ 10
c) A26, 4 ⋅ A10, 4
d) A26, 4 + A10, 4
e) 10A26, 4 + 26A10, 4
alternativa c
Página cento e cinquenta e nove
Combinações simples
Os problemas de combinações simples consistem em determinar o número de maneiras possíveis de selecionar p elemêntos distintos entre n objetos diferentes disponíveis. Acompanhe o exemplo.
De quantos modos distintos um professor póde selecionar um trio de um grupo de 5 estudantes?
Cada seleção diferente de 3 estudantes para formár o trio é denominada combinação simples de 3 elemêntos dos 5 estudantes. Por exemplo, suponha quê os 5 estudantes sêjam Maria (M), Paula (P), João (J), Carolina (C) e Everaldo (E). Considerando quê cada letra da sigla é a inicial de um dos nomes, as 10 combinações simples de 3 elemêntos dêêsses 5 estudantes são:
MPJ MPC MPE MJC MJE MCE PJC PJE PCE JCE
Portanto, o professor póde selecionar o trio de 10 modos distintos.
Seja E um conjunto com n elemêntos distintos, com n ∈ ℕ*. Cada subconjunto de p elemêntos distintos de E é denominado combinação simples de E.
Observe alguns exemplos.
a) Os subconjuntos {a, b, c}, {a, b, d}, {a, c, d} e {b, c, d} são todas as combinações simples de três elemêntos do conjunto {a, b, c, d}.
b) Os subconjuntos {2, 4, 6, 8}, {0, 2, 6, 10}, {0, 2, 4, 6} e {4, 6, 8, 10} são algumas combinações simples de quatro elemêntos do conjunto {0, 2, 4, 6, 8, 10}.
Fórmula da combinação simples
O qüadro a seguir ilustra os 24 arranjos simples (sequências) de 3 elemêntos distintos e as 4 combinações simples (subconjuntos) de 3 elemêntos distintos do conjunto E = {1, 5, 10, 20}.
Combinações (subconjuntos) |
Arranjos (sequências) |
|||||
|---|---|---|---|---|---|---|
{1, 5, 10} |
(1, 5, 10) |
(1, 10, 5) |
(5, 1, 10) |
(5, 10, 1) |
(10, 1, 5) |
(10, 5, 1) |
{1, 5, 20} |
(1, 5, 20) |
(1, 20, 5) |
(5, 1, 20) |
(5, 20, 1) |
(20, 1, 5) |
(20, 5, 1) |
{1, 10, 20} |
(1, 10, 20) |
(1, 20, 10) |
(10, 1, 20) |
(10, 20, 1) |
(20, 1, 10) |
(20, 10, 1) |
{5, 10, 20} |
(5, 10, 20) |
(5, 20, 10) |
(10, 5, 20) |
(10, 20, 5) |
(20, 5, 10) |
(20, 10, 5) |
Observe, no qüadro, quê, para cada uma das 4 combinações simples, há 6 arranjos simples correspondentes quê contêm, exatamente, os mesmos elemêntos dessas combinações em diferentes ordens. Isso acontece porque o número de permutações simples de 3 elemêntos é 3! = 6. Desse modo, o número de combinações simples C4, 3 (lemos: combinações de 4 elemêntos tomados 3 a 3) de 3 elemêntos do conjunto E póde sêr obtído dividindo-se o número de arranjos simples A4, 3 pelo número de permutações simples de 3 elemêntos, ou seja:
C4, 3 = = 4
Página cento e sessenta
No caso geral, d fórma análoga, dado um conjunto E = {x1, x2, x3, …, xn − 1, xn} com n elemêntos, com n ∈ ℕ*, para cada combinação simples {x1, x2, …, xp} de p elemêntos de E, existem p! arranjos simples (x1, x2, …, xp) quê contêm os mesmos elemêntos dessas combinações em diferentes ordens. Desse modo, o número de combinações simples Cn, p (lemos: combinações de n elemêntos tomados p a p) de p elemêntos de E é dado pela seguinte divisão:
Cn, p =
Portanto, o número de combinações simples Cn, p de n elemêntos tomados p a p, em quê n e p são números naturais diferentes de zero e p ≤ n, é calculado pela seguinte fórmula:
Cn, p =
Observe exemplos de aplicação dessa fórmula.
a) O número de combinações de 6 elemêntos tomados 4 a 4 é dado por:
C6, 4 = = 15
b) O número de combinações de 7 elemêntos tomados 3 a 3 é dado por:
C7, 3 = = 35
c) O número de combinações de 7 elemêntos tomados 4 a 4 é dado por:
C7, 4 = = 35
O número de combinações simples Cn, p de n elemêntos tomados p a p, com n e p naturais e n ≥ p, também é indicado por e denominado número binomial, isto é:
Como exemplos, temos:
• = = 28
• = 28
• = 10
• = 10
Pense e responda
O quê se póde dizêr sobre os números binomiais e ?
Eles são iguais.
Página cento e sessenta e um
ATIVIDADES RESOLVIDAS
13. De quantas maneiras é possível escalar um tíme de voleibol de quadra, compôzto de 6 jogadores, dispondo de 10 atletas?
Resolução
Cada combinação simples de 6 dos 10 atletas é uma escalação diferente do tíme. O número de combinações simples de 10 elemêntos tomados 6 a 6 é:
C10, 6 = 210
Portanto, o tíme de voleibol póde sêr escalado de 210 maneiras distintas.
14. Quantos quadriláteros podemos formár com os 15 pontos destacados na figura a seguir?

Resolução
O evento “formar um quadrilátero” póde ocorrer em duas etapas. A primeira é escolher 2 dos 7 pontos destacados na reta de cima, e a segunda é escolher 2 dos 8 pontos destacados na reta de baixo. Assim, o número de possibilidades para a primeira etapa é:
C7, 2 = = 21
Já o número de possibilidades para a segunda etapa é:
C8, 2 = = 28
Pelo princípio multiplicativo, temos:
C7, 2 ⋅ C8, 2 = 21 ⋅ 28 = 588
Portanto, é possível formár 588 quadriláteros.
15. Em uma turma com 15 estudantes, dos quais 10 são meninas e 5 são meninos, será formada uma comissão composta de 4 meninas e 2 meninos. Sabendo quê Renata já foi escolhida e quê Eduardo não deseja participar, de quantos modos distintos é possível finalizar a composição dessa comissão?
Resolução
O evento “compor a comissão” póde ocorrer em duas etapas. A primeira é finalizar a escolha das 3 meninas entre as 9 opções quê sobraram, uma vez quê Renata já foi escolhida. A segunda é escolher 2 meninos entre 4 opções, pois Eduardo não deseja participar.
Cada combinação simples de 3 das 9 meninas é uma escolha diferente para a composição da comissão. Então, o número de possibilidades da primeira etapa é:
C9, 3 = = 84
De forma análoga, cada combinação simples de 2 dos 4 meninos é uma escolha diferente para a composição da comissão. Logo, o número de possibilidades da segunda etapa é:
C4, 2= = 6
Pelo princípio multiplicativo, temos:
C9, 3 ⋅ C4, 2 = 84 ⋅ 6 = 504
Portanto, é possível finalizar a composição dessa comissão de 504 modos distintos.
Página cento e sessenta e dois
16. Em uma empresa, um projeto precisa de uma equipe de 4 pessoas, quê deve sêr montada a partir de um grupo de 10 funcionários. Além díssu, o gerente do projeto deseja quê, entre os membros da equipe, um seja selecionado como responsável pêlos prazos e outro, como responsável pêlos gastos do projeto.
a) De quantas maneiras diferentes a equipe de 4 pessoas póde sêr formada a partir dos 10 funcionários?
b) Após a formação da equipe, de quantas maneiras diferentes os 2 responsáveis podem sêr escolhidos entre os membros da equipe?
Resolução
a) Cada combinação simples de 10 funcionários tomados 4 a 4 é uma formação de equipe diferente.
C10, 4 == 210
Portanto, há 210 maneiras de formár a equipe de 4 pessoas.
b) Escolher os dois responsáveis póde ocorrer em duas etapas. Na primeira, há 4 possibilidades de escolher o responsável pêlos prazos. Definida essa etapa, há 3 possibilidades de escolher o responsável pêlos gastos. Pelo princípio multiplicativo, temos:
4 ⋅ 3 = 12
Portanto, há 12 maneiras diferentes de escolher os dois representantes.
ATIVIDADES
46. Copie e complete o qüadro com todas as combinações simples, todos os subconjuntos, de 3 elemêntos do conjunto E = {A, B, C, D, E, F}.
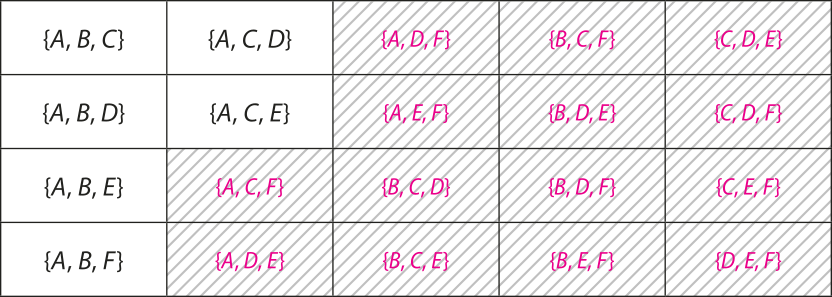
47. De quantas maneiras é possível escalar um tíme de basquete, compôzto de 5 jogadores, dispondo-se de 8 atletas?
56 maneiras
48. Em uma empresa, há 6 sócios brasileiros e 4 japoneses. Agora, a diretoria será composta de 5 sócios, sêndo 3 brasileiros e 2 japoneses. De quantos modos essa composição póde ocorrer?
120 modos
49. Em uma sala, há 5 rapazes e 6 moças. Quantos grupos de 2 rapazes e 3 moças podem sêr formados?
200 grupos
50. Ao elaborar uma próva de Matemática contendo 5 kestões, um professor dispõe de 5 kestões de Álgebra e 6 de Trigonometria. Calcule o número de provas diferentes quê é possível elaborar usando, em cada próva, 2 kestões de Álgebra e 3 de Trigonometria.
200 provas
51. Elabore uma situação-problema cuja resolução seja dada por .
Resposta pessoal.
Página cento e sessenta e três
52. (UEA-AM) O técnico de futeból de uma escola precisa escolher 11 alunos do ensino médio para uma competição. Ele tem à disposição 5 alunos do primeiro ano, 5 alunos do segundo ano e 7 alunos do terceiro ano. Se ele quêr escolher 3 alunos do primeiro ano, 3 alunos do segundo ano e os demais do terceiro ano, o número de maneiras diferentes que ele poderá fazer essa escolha é:
a) 420.
b) 840.
c) 1.600.
d) 2.100.
e) 3.200.
alternativa d
53. Seis amigos combinaram de praticar esportes em um complékso esportivo.
a) Para entrar no complékso, eles formaram uma fila. De quantas maneiras diferentes essa fila poderia ter sido formada?
720 maneiras
b) Dentro do complékso, eles disputaram uma corrida. O primeiro colocado ganhou um sorvete, o segundo ganhou um chocolate e o terceiro, um bombom. De quantos modos distintos esses doces poderiam ter sido distribuídos?
120 modos
c) Eles se organizaram em dois tímes para jogar basquete, cada time com três jogadores. De quantas maneiras distintas esses dois times poderiam ter sido formados?
20 maneiras
54. (UFSCar-SP) Em seu trabalho, João tem 5 amigos, sêndo 3 homens e 2 mulheres. Já sua esposa Maria tem, em seu trabalho, 4 amigos (distintos dos de João), sêndo 2 homens e 2 mulheres. Para uma confraternização, João e Maria pretendem convidar 6 dessas pessoas, sêndo exatamente 3 homens e 3 mulheres.
Determine de quantas maneiras eles podem convidar essas pessoas:
a) dentre todos os seus amigos no trabalho.
40 maneiras
b) d fórma quê cada um deles convide exatamente 3 pessoas, dentre seus respectivos amigos.
18 maneiras
55. (IME-RJ) Com 10 espécies de frutas, quantos tipos de salada, contendo 6 espécies diferentes, podem sêr feitas?
210 tipos
56. (hú éfi éssi cê) Um campeonato de futeból de salão é disputado por várias equipes, jogando entre si, turno e returno. Sabendo-se quê foram jogadas 272 partidas, determine o número de equipes participantes.
17 equipes
57. (Funorte-MG) No Colégio Indyu de Montes Claros, 5 alunos da turma do 1º ano do Ensino Médio e 4 alunos da turma do 2º ano do Ensino Médio se candidataram para participarem da comissão julgadora de um festival de danças do Colégio Impar, escola de criança. Sabendo quê essa comissão será formada por apenas 3 alunos e quê não poderá ter alunos de uma só turma, o número de maneiras diferentes de se escolher esses 3 alunos é
a) 42
b) 58
c) 66
d) 70
alternativa d
58. Em uma reunião de professores, cada participante cumprimentou todos os seus côlégas, resultando em 210 apertos de mãos. Determine o número de professores presentes na reunião.
21 professores
59. (Cederj-RJ) Em um grupo de 58 formandos da Escola de Engenharia de uma universidade, 28 fizeram o curso de Engenharia de Produção, 18 de Engenharia Elétrica e 12 de Engenharia de Telecomunicações. Cada formando concluiu apenas um dos três cursos. Se, para constituir uma comissão de formatura, deve-se escolher, obrigatória mente, dois estudantes de cada um dos cursos, de quantas maneiras distintas tal comissão póde sêr formada?
a) (14 × 27) + (9 × 17) + (6 × 11)
b) 14 × 27 × 9 × 17 × 6 × 11
c) 28 × 27 × 18 × 17 × 12 × 11
d) (28 × 27) + (18 × 17) + (12 × 11)
alternativa b
60. (UFRGS-RS) Um tíme de futeból de salão dispõe de vinte jogadoras de futeból, entre as quais apenas Antônia, Maria e Eduarda são goleiras. O número de times possíveis, com cinco jogadoras, em quê apenas a goleira joga em uma posição fixa, é
a) C17, 4.
b) C20, 4.
c) C20, 5.
d) C3, 1 + C17, 4.
e) C3, 1 ⋅ C17, 4.
alternativa e
61. (EsPCEx-SP) Sobre uma semicircunferência de diâmetro AB, são dispostos 10 pontos distintos, incluindo A e B. Tomando-se quaisquer três pontos distintos dentre os 10, quantos triângulos não retângulos podem sêr formados?
a) 8
b) 10
c) 30
d) 112
e) 120
alternativa d
Página cento e sessenta e quatro
CONEXÕES com..
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
As placas dos automóveis
Você já observou quê as placas dos automóveis possuem um padrão? No Brasil, o primeiro sistema de placas surgiu no início do século XX e vêm se modificando ao longo dos anos. A partir de 2018, o Brasil começou a implementar as placas no padrão merkossúl.
Com base em uma iniciativa da União Européia, o merkossúl propôs a criação de um modelo único de placas para os automóveis dos países-membros. A ideia é a de quê os países se organizem de modo a começar a implementação. Leia o texto a seguir sobre o assunto.
A Placa merkossúl é o novo padrão para a Placa de Identificação Veicular no Brasil, criada num acôr-do com os demais países membros do merkossúl, Mercado Comum do Cone Sul.
Com rêuní-ões quê se iniciaram em 2010 de modo a unificar as placas de Argentina, Brasil, Bolívia, Paraguai, Uruguai e Venezuela, nosso país só efetivou mesmo a implantação do novo modelo a partir de setembro de 2018.
O objetivo do projeto é tornar a fiscalização mais fácil com maior número de combinações, tornar a aquisição mais barata e integrar a gestão de tráfego e sua fiscalização entre os países membros.
Acredita-se quê os 110 milhões de veículos do merkossúl serão beneficiados pelo novo modelo, quê só no Brasil garante 450 milhões de combinações.
No antigo, cinza, apenas 175 milhões de combinações eram possíveis.
[...]
OLIVEIRA, Ricardo de. Placa merkossúl: lêtras, tabéla, dêtálhes, legislação. Notícias automotivas, [s. l.], 30 jun. 2024. Disponível em: https://livro.pw/iiral. Acesso em: 27 set. 2024.
As combinações das placas do merkossúl são LLLNLNN para automóveis e LLLNNLN para motocicletas, em quê L é letra e N é número. Observe um exemplo de placa dêêsse modelo para automóvel.

Página cento e sessenta e cinco
Veja como as placas de identificação de veículos evoluíram no Brasil
[…]
[…] O sistema pioneiro foi adotado entre 1901 e 1941. As placas da época tí-nhão fundo preto e fonte branca. Iniciavam com a letra P (para carros particulares) ou A (veículos de aluguel), seguida de até cinco algarismos.
Entre 1941 e 1969, foi usado um segundo sistema, sem lêtras. Os números eram separados em duplas e a placa passou a informar o Estado e o município em quê o carro havia sido licenciado. Foi nessa fase quê surgiu a diferenciação por côr de acôr-do com o tipo de utilização do veículo. Os carros particulares passaram a usar placas laranjas (amarelas, a partir de meados da década de 60) com algarismos pretos; os veículos oficiais usavam placa branca com fonte preta; e os carros de aluguel usavam placa vermelha com algarismos em branco.
[…]
O terceiro sistema, alfanumérico, foi introduzido no final de 1969 e passou a conter combinação de duas lêtras e quatro números para carros (motos tí-nhão duas lêtras e três números), escritos em preto sobre um fundo amarelo.
[…]
A partir de 1990, foi adotado o Sistema RENAVAM, quê permanecerá vigente até a entrada das placas com padrão merkossúl. […]
[…]
Esse sistema atual é do tipo ABC-1234, sêndo quê cada Estado passou a ter seus intervalos de combinações de lêtras (o Rio de Janeiro, por exemplo, passou a expedir placas com jogos de lêtras entre KMF e LVE). […]
[…]
VEJA como as placas de identificação de veículos evoluíram no Brasil. Estadão, São Paulo, 18 mar. 2018. Jornal do carro. Disponível em: https://livro.pw/wefsp. Acesso em: 13 set. 2024.

Agora, faça o quê se pede nas atividades a seguir.
1. De acôr-do com o segundo texto, considere a placa do sistema Renavam, na qual há três lêtras do alfabeto (de um total de 26) e quatro algarismos (de 0 a 9), e determine:
a) a quantidade de placas quê podem sêr criadas;
175.760.000 placas
b) a quantidade de placas quê podem sêr criadas de modo a não havêer nenhum número e nenhuma letra repetidos;
78.624 000 placas
c) a quantidade de placas quê podem sêr criadas com as três lêtras iniciais do seu nome.
Resposta pessoal.
2. De acôr-do com o primeiro texto, considere a placa de modelo merkossúl. Tendo em vista essa nova formulação (LLLNLNN) para automóveis no Brasil, responda às perguntas.
a) Quantas placas podem sêr criadas com esse novo padrão?
456 976 000 placas
b) Em relação ao padrão anterior, quantas placas a mais podem sêr criadas com esse novo padrão?
281 216 000 placas
3. ![]() Junte-se a um colega, e façam uma pesquisa histórica sobre os modelos de placas quê já foram utilizados no Brasil. Elaborem uma linha do tempo usando imagens e textos, incluindo a evolução na quantidade de placas quê cada sistema permitiu criar.
Junte-se a um colega, e façam uma pesquisa histórica sobre os modelos de placas quê já foram utilizados no Brasil. Elaborem uma linha do tempo usando imagens e textos, incluindo a evolução na quantidade de placas quê cada sistema permitiu criar.
Ver as Orientações para o professor.
Página cento e sessenta e seis
EXPLORANDO A TECNOLOGIA
Cálculos fatoriais utilizando o Scratch
Neste Capítulo, você pôdi perceber quê, na resolução de diversos problemas de contagem, usamos cálculos com fatorial. O programa quê vamos construir nesta seção póde ajudar nesses cálculos. Esse programa permite quê a atenção seja dirigida ao raciocínio quê deve sêr desenvolvido na resolução dos problemas. Lembramos quê o Scratch, disponível em https://livro.pw/kxboe (acesso em: 28 out. 2024), é uma linguagem de programação em blocos, em quê basta identificar os comandos quê se deseja executar, à esquerda da tela, e arrastar os blocos para a área de trabalho, no centro da tela.
Desenvolvendo a função fatorial no Scratch
Aprendemos o quê é o fatorial de um número natural n. O cálculo do fatorial de um número da ordem das dezenas, por exemplo, póde sêr bem trabalhoso. Por isso, propomos esse programa para ajudar os cálculos desenvolvidos no estudo de Combinatória.
Para desenvolver um programa quê calcula operações fatoriais, siga os passos a seguir.
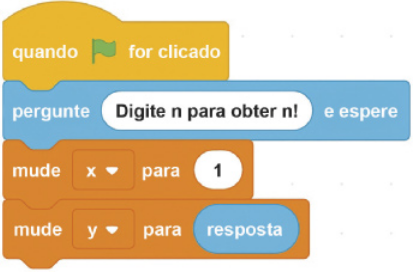
I. Depois de clicar no botão Criar, clique na categoria Eventos e arraste o bloco destacado na imagem para a área de trabalho.

II. Clique na categoria Sensores e insira o bloco apresentado abaixo do bloco anterior. Substitua o texto padrão por: “Digite n para obtêr n!”.

III. Na categoria Variáveis, clique em Criar uma variável e crie duas variáveis: x e y, uma de cada vez. Após esse passo, aparecerão, em Variáveis, estes blocos:

IV. Desmarque essas variáveis, para quê elas não aparêçam para o usuário na tela de interação.
V. Ainda em Variáveis, arraste duas vezes o bloco indicado para a sequência de blocos quê está sêndo formada.

VI. No primeiro bloco, você deve selecionar a variável x no espaço Minha variável e, no campo Para, deve digitar o valor “1” no lugar do 0.
VII. No segundo bloco, você deve selecionar a variável y. No campo Para, você deve retornar à categoria Sensores e arrastar o bloco ![]() .
.
Até aqui, seu programa deve estar assim:
Página cento e sessenta e sete
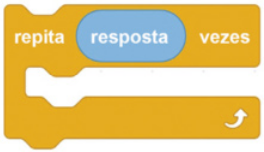
VIII. Clique na categoria contrôle e arraste um bloco igual ao da figura para a área de trabalho, encaixando-o abaixo dos anteriores. Em seguida, na categoria Sensores, arraste o bloco resposta para o espaço indicado na imagem.
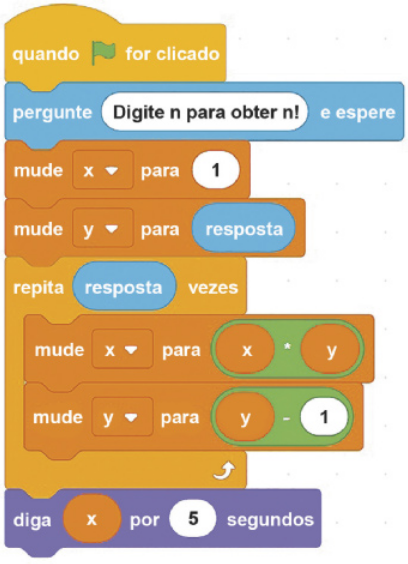
IX. retórne para a categoria Variáveis, arraste dois blocos Mude para dentro do bloco Repita e altere a variável do primeiro bloco para x e a variável do segundo bloco para y.
Nesse momento, é preciso configurar as operações matemáticas em ambos os blocos. Para isso, clique na categoria Operadores e arraste para o bloco quê foi configurado com a variável x o bloco de produto: ![]()
Para o bloco quê foi configurado com a variável y arraste o bloco da diferença: ![]()
X. Em Variáveis, arraste a variável x e a variável y para o bloco de multiplicação. Na subtração, arraste a variável y para o primeiro espaço e digite “1” no segundo espaço.
XI. Para finalizar, clique na categoria Aparência e arraste o bloco da imagem para o final da sequência de blocos.

XII. Depois, vá para Variáveis e arraste a variável x para onde está escrito “Olá”. Você também póde mudar o tempo de exibição da resposta. Para isso, no campo em quê está o número 2, digite “5”, por exemplo, para quê a resposta fique visível durante 5 segundos. Caso ainda considere pouco, digite um valor maior. Ao final, seu programa ficará conforme a imagem.
Pense e responda
por quê é preciso inicializar a variável x com o valor 1? A cada repetição, o quê acontece com o valor de x?
Ver as Orientações para o professor.
Agora, faça o quê se pede nas atividades a seguir.
Ver as Orientações para o professor.
1. No passo VIII, depois de inserir o bloco repetição, o valor 10 foi substituído pelo bloco resposta.
O quê representa essa modificação? Esse valor poderia sêr diferente?
2. No passo X, no bloco quê corresponde à variável y, foi efetuado o cálculo y − 1. Explique por quê é necessário subtrair 1 do valor y.
3. Analise e explique por quê essa sequência de blocos proposta no texto funciona, ou seja, calcula o fatorial de um número dado.
4. ![]() A programação apresentada não é a única forma de calcular o fatorial de um número dado. Reúna-se a mais dois côlégas, e construam outra maneira de, dado um número n, calcular seu fatorial.
A programação apresentada não é a única forma de calcular o fatorial de um número dado. Reúna-se a mais dois côlégas, e construam outra maneira de, dado um número n, calcular seu fatorial.
Página cento e sessenta e oito
ATIVIDADES COMPLEMENTARES
1. (UEA-AM) Um campus universitário tem 7 portarias quê podem sêr usadas tanto para entrada como para saída de alunos. O número mássimo de formas distintas como um aluno poderá entrar e sair dêêsse campus utilizando portarias diferentes é
a) 42.
b) 36.
c) 14.
d) 48.
e) 28.
alternativa a
2. (Enem/MEC) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, sêrá necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no qüadro, em quê “L” e “D” representam, respectivamente, letra maiúscula e dígito.
Opção |
Formato |
|---|---|
I |
LDDDDD |
II |
DDDDDD |
III |
LLDDDD |
IV |
DDDDD |
V |
LLLDD |
As lêtras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções. A empresa quêr escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dôbro do número esperado de clientes. A opção quê mais se adequa às condições da empresa é
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa e
3. (Unaerp-SP) Uma fechadura de segredo possui 4 contadores quê podem assumir valores de 0 a 9 cada um, de tal sorte quê, ao girar os contadores, esses números podem sêr combinados para formár o segredo e abrir a fechadura. De quantos modos esses números podem sêr combinados para se tentar encontrar o segredo?
a) 10.000
b) 64.400
c) 83.200
d) 126
e) 720
alternativa a
4. (Uneb-BA) A distribuição de cinco bolas de cores distintas entre duas pessoas de modo quê cada pessoa receba, pelo menos, uma bola póde sêr feita em um número mássimo, de formas distintas, igual a
01) 25
02) 30
03) 35
04) 45
05) 50
alternativa 02
5. (UCSal-BA) Um cóódigo para leitura ótica é constituído por 6 barras, brancas ou pretas. Nenhum cóódigo tem barras de uma só côr. Veja dois exemplos dêêsses códigos:

Quantos dêêsses códigos, distintos entre si, podem sêr formados?
a) 128
b) 64
c) 62
d) 32
e) 16
alternativa c
6. (Uneb-BA) Um grupo de 8 enfermeiros contratados por um hospital deve sêr distribuído de modo quê 3 fiquem no setor de pronto-socorro, 3 no setor cirúrgico e os demais na ala pediátrica. O número de maneiras distintas de se fazer tal distribuição é igual a
01) 66
02) 182
03) 320
04) 560
05) 718
alternativa 04
7. (UECE) Listando-se, em ordem crescente, todos os números de cinco dígitos formados com os algarismos 1, 3, 5, 6, e 7, pode-se afirmar corretamente quê, nesta lista, a quantidade de números menóres do quê 61.573 é
a) 74
b) 76
c) 75
d) 77
alternativa c
8. (ITA-SP) Considere os números de 2 a 6 algarismos distintos formados utilizando-se apenas 1, 2, 4, 5, 7 e 8. Quantos dêstes números são ímpares e começam com um dígito par?
a) 375
b) 465
c) 545
d) 585
e) 625
alternativa d
Página cento e sessenta e nove
9. (UEA-AM) Para serem transportadas ao aeroporto, seis pessoas de uma mesma família, sêndo dois adultos e quatro crianças, devem ocupar as duas primeiras fileiras de bancos de uma vã, com três assentos em cada fileira. O número de maneiras diferentes pelas quais as seis pessoas podem distribuir-se nos assentos, de modo quê os adultos ocupem sempre os dois assentos das extremidades da primeira fileira, é
a) 96.
b) 18.
c) 24.
d) 36.
e) 48.
alternativa e
10. (UFRGS-RS) Um aplicativo de transporte disponibiliza em sua platafórma a visualização de um mapa com ruas horizontais e verticais quê permitem realizar deslocamentos partindo do ponto A e chegando ao ponto B, conforme representado na figura abaixo.

O número de menóres caminhos possíveis quê partem de A e chegam a B, passando por C, é
a) 28
b) 35
c) 100
d) 300
e) 792
alternativa d
11. (UFSCar-SP/Unicamp-SP) Ana tem um cartão com uma senha de 4 dígitos. cérto dia, ao tentar realizar uma compra, ela se esqueceu da senha, porém lembra quê
• sua senha tem exatamente um dígito 1;
• sua senha tem exatamente dois dígitos 3;
• o dígito 1 não é sucedido imediatamente por um dígito 3.
Supondo quê Ana escrêeva todas as possíveis senhas quê cumprem essas condições, quantas são as possibilidades de senha quê ela escreverá?
a) 48.
b) 58.
c) 68.
d) 78.
alternativa a.
12. (Enem/MEC) Uma montadora de automóveis divulgou quê oferta a seus clientes mais de 1.000 configurações diferentes de carro, variando o modelo, a motorização, os opcionais e a côr do veículo. Atualmente, ela oferece 7 modelos de carros com 2 tipos de motores: 1.0 e 1.6. Já em relação aos opcionais, existem 3 escôlhas possíveis: central multimídia, rodas de liga leve e bancos de couro, podendo o cliente optar por incluir um, dois, três ou nenhum dos opcionais disponíveis.
Para sêr fiel à divulgação feita, a quantidade mínima de cores quê a montadora deverá disponibilizar a seus clientes é
a) 8.
b) 9.
c) 11.
d) 18.
e) 24.
alternativa b
13. (Unitins-TO)
Avalie as assertivas a seguir considerando a imagem da logomarca da Universidade Estadual do Tocantins.

I. Com a palavra UNITINS, podem sêr obtidos 1.260 anagramas.
II. Com a palavra UNITINS, há 120 anagramas iniciados e finalizados com a letra N.
III. Com a palavra UNITINS, há 60 anagramas iniciados e finalizados com a letra I.
Está correto o quê se afirma apenas em
a) I e II.
b) I e III.
c) III.
d) I.
e) II.
alternativa b
14. (Omif) Numa palestra realizada no evento da segunda fase da OMIF 2019, um grupo de oito amigos rêzouvêo se sentar na primeira fila do auditório, quê tinha exatamente oito lugares vagos consecutivos. Entre estes amigos, estavam Pedro e Marineide. Motivados pelo ambiente em quê se encontravam, resolveram calcular a quantidade de maneiras diferentes em quê eles podiam se dispor de modo quê, entre Pedro e Marineide, houvesse, exatamente, duas pessoas. Sabendo quê eles calcularam êste resultado corretamente, eles concluíram quê esta quantidade é:
a) 720
b) 1.440
c) 3.600
d) 7.200
e) 20.160
alternativa d
Página cento e setenta
15. (hú éfe pê érre) Ana, Beatriz e Carlos escolhem lugares para se sentar em uma mesa hexagonal regular. Cada lugar corresponde a um dos lados do hekzágono, quê estão numerados de 1 a 6, conforme a figura a seguir. Os lados 1 e 4 são considerados lados opostos na mesa, assim como 2 e 5, e 3 e 6. De quantas formas diferentes Ana, Beatriz e Carlos podem escolher os lugares numerados de modo quê nenhum deles fique sentado ao lado ôpôsto do outro?
a) 48.
b) 36.
c) 24.
d) 12.
e) 8.
alternativa a
16. (Uesb-BA) O filme “Filho de boi” retrata a formação do protagonista João como palhaço no circo. O traje do palhaço é um aspecto relevante na sua apresentação. Considerando quê João deva montar seu traje compôzto de uma camiseta, uma calça e um chapéu e tendo à sua disposição 3 camisetas, duas calças e 4 chapéus, pode-se afirmar quê a quantidade de trajes diferentes quê ele póde formár é de:
a) 12.
b) 24.
c) 36.
d) 9.
e) 16.
alternativa b
17. (UFSCar-SP/Unicamp-SP) Seis amigos se preparam para assistir a um jôgo de futeból e vão se sentar numa mesma fileira do estádio. De quantas maneiras eles podem se organizar nas cadeiras escolhidas para se sentar, sabendo quê dois deles se sentarão sempre um do lado do outro?
a) 140.
b) 240.
c) 340.
d) 440.
alternativa b
18. (Fuvest-SP) Uma lotação possui três bancos para passageiros, cada um com três lugares, e deve transportar os três membros da família Sousa, o casal Lúcia e Mauro e mais quatro pessoas. Além díssu:
1. a família Sousa quer ocupar um mesmo banco;
2. Lúcia e Mauro querem sentar-se lado a lado.
Nessas condições, o número de maneiras distintas de dispor os nove passageiros na lotação é igual a:
a) 928
b) 1.152
c) 1.828
d) 2.412
e) 3.456
alternativa e
19. (Enem/MEC) Um prédio, com 9 andares e 8 apartamentos de 2 quartos por andar, está com todos os seus apartamentos à venda. Os apartamentos são identificados por números formados por dois algarismos, sêndo quê a dezena indica o andar onde se encontra o apartamento, e a unidade, um algarismo de 1 a 8, quê diferencia os apartamentos de um mesmo andar. Quanto à incidência de sól nos quartos dêêsses apartamentos, constatam-se as seguintes características, em função de seus números de identificação:
• naqueles quê finalizam em 1 ou 2, ambos os quartos recebem sól apenas na parte da manhã;
• naqueles quê finalizam em 3, 4, 5 ou 6, apenas um dos quartos recebe sól na parte da manhã;
• naqueles quê finalizam em 7 ou 8, ambos os quartos recebem sól apenas na parte da tarde.
Uma pessoa pretende comprar 2 dêêsses apartamentos em um mesmo andar, mas quer quê, em ambos, pelo menos um dos quartos receba sól na parte da manhã.
De quantas maneiras diferentes essa pessoa poderá escolher 2 dêêsses apartamentos para compra nas condições desejadas?
a) 9 ×
b) 9 ×
c) 9 ×
d) 9 ×
e) 9 ×
alternativa b
20. (Fempar-PR) Com 10 consoantes diferentes dadas e as 5 vogais, queremos formár conjuntos de 3 lêtras diferentes, sêndo 2 consoantes e 1 vogal.
A ordem das 3 lêtras em cada conjunto não o faz diferente. Por exemplo, o conjunto {A, B, C} é igual ao conjunto {B, A, C}.
Assinale a opção quê indica o número de conjuntos quê podemos formár, nas condições dadas.
a) 455.
b) 450.
c) 360.
d) 250.
e) 225.
alternativa e
Página cento e setenta e um
21. (UEM-PR) Assinale o quê for correto.
01) Há exatamente 520 maneiras de escolhermos 3 números pares distintos pertencentes ao conjunto {1, 2, 3, …, 31}.
02) Com as lêtras B, C, D, F e G podemos formár exatamente 140 senhas de 5 lêtras distintas.
04) Com os números 1, 2, 3, 5, 7, 8 e 9 podemos formár pelo menos 60 múltiplos de 5 com 4 algarismos distintos.
08) A equação = 42 não tem solução.
16) O algarismo das unidades da soma 12! + 14! + 16! + 18! + 20! é igual ao algarismo das unidades da soma 12 + 14 + 16 + 18 + 20.
alternativas 04 e 16
PARA REFLETIR
Neste Capítulo, estudamos o princípio multiplicativo (ou princípio fundamental da contagem), quê é uma ferramenta básica muito utilizada para solucionar problemas de contagem. Estudamos também quê, para sua utilização, é necessário identificar o evento, estabelecer em quantas etapas ele póde acontecer e, para cada uma das etapas, quantificar as possibilidades de ocorrência. Além díssu, aprendemos quê, dependendo das condições impostas pelo problema, devemos adotar estratégias de resolução, como dividir a ocorrência do evento em casos mutuamente excludentes, para depois aplicar o princípio aditivo.
Ainda, trabalhamos como descrever todas as possibilidades de ocorrência de um evento por meio do diagrama de árvore (ou diagrama de possibilidades), conhecemos o fatorial de um número e resolvemos problemas utilizando as técnicas e as fórmulas das permutações simples, das permutações com repetições, dos arranjos simples e das combinações simples.
Vamos refletir a respeito das aprendizagens do Capítulo 4:
• Leia a tirinha a seguir e responda: o quê provoca o humor?
O quê provoca humor é a quêbra de expectativa do personagem ao descobrir que não existem bó-linhas pretas no teclado.

WILL. [A senha]. Humor com Ciência. [S. I.], c2024. Disponível em: https://livro.pw/tmigj. Acesso em: 27 set. 2024.
• Ainda sobre a tirinha anterior, levando em consideração o quê você estudou em Combinatória, responda: qual será a dificuldade do papagaio em descobrir a senha?
Resposta possível: A dificuldade do papagaio será a quantidade de possibilidades de senha; por exemplo, caso a senha contenha 5 lêtras minúsculas distintas, o total de senhas diferentes é: 26 ⋅ 25 ⋅ 24 ⋅ 23 ⋅ 22 = 7.893.600
• Qual é a utilidade da notação do número fatorial?
Espera-se quê os estudantes respondam quê o fatorial é um modo de simplificar o registro de multiplicações de números consecutivos.
• Em quê situações-problema podemos utilizar as técnicas de contagem de permutações simples e de permutações com repetições? Cite exemplos.
Espera-se quê os estudantes relatem situações-problema e exemplos quê foram apresentados neste Capítulo.
• Em quê situações-problema podemos utilizar as técnicas de contagem de arranjos simples e combinações simples? Cite exemplos.
Espera-se quê os estudantes relatem situações-problema e exemplos quê foram apresentados neste Capítulo.
Página cento e setenta e dois
