CAPÍTULO 5
PROBABILIDADE
Já reparou quê os cães labradores podem sêr amarelos, chocolate ou pretos? Ou quê existe um número muito grande de cores, espessuras e tipos de cabelo em sêres humanos? Que, de modo geral, os gatos de três cores são fêmeas? Pois é, a natureza é mesmo interessante e diversificada, em parte pela combinação genética, e a Probabilidade nos ajuda a entender como isso funciona.
Os famosos experimentos com ervilhas, quê foram realizados por Gregor Mendel (1822-1884), desenvolveram as bases dos estudos sobre hereditariedade. Desde então, os estudos genéticos avançaram, e hoje temos muitas informações quê nos ajudam a compreender um pouco mais o sêr humano. Sabemos, por exemplo, quê características como côr de péle, lóbulo auricular aderente ou não, habilidade de dobrar a língua em formato de"U", entre outras, são hereditárias.
Atualmente, a Genética conta com a tecnologia, principalmente na seleção de genes para produção agrícola. Para essa seleção, há muitos estudos probabilísticos quê ajudam a prever as características quê se manifestarão nas próximas gerações a partir das características das gerações parentais.
Fonte dos dados: TREVILATTO, P. C. éti áu. Introdução ao estudo da genética. In: KRIGER, L.; MOYSÉS, S. J.; MOYSÉS, S. T. (org.). Genética odontológica. São Paulo: Artes Médicas, 2014. (Série Abeno).
![]() Agora reúna-se a um colega, e façam o quê se pede em cada questão.
Agora reúna-se a um colega, e façam o quê se pede em cada questão.
Ver as Orientações para o professor.
1. O quê são organismos geneticamente modificados? Pesquisem e descrevam os prós e contras da produção e do consumo de plantas geneticamente modificadas.
2. A côr de certa espécie de planta é uma característica genética quê póde se manifestar entre vermelha e branca. Ao cruzar essa espécie, temos 75% de probabilidade de ocorrer flor vermelha e de o restante sêr branca.
a) Suponham quê um floricultor tenha semeado essa espécie e quê tênham florescido 80 indivíduos, quê mantiveram as proporções descritas. Como vocês fariam para determinar qual é a quantidade esperada, nessa colheita, de indivíduos com flores de côr vermelha? E de indivíduos com flores de côr branca?
b) Pode-se afirmar quê haverá, com certeza, na colheita, a quantidade esperada de cada côr? Justifique.
3. Descrevam ou deem exemplos do quê vocês compreendem por:
• experimentos aleatórios;
• cálculo de probabilidade como a razão entre o número de resultados favoráveis e o total de resultados possíveis;
• espaço amostral e eventos equiprováveis.
• eventos dependentes e eventos independentes de um espaço amostral.
Página cento e setenta e três

Página cento e setenta e quatro
Introdução
Quando estamos ao nível do mar e aquecemos um pouco de á gua, a quê tempera-túra ela entra em ebulição? Se soltarmos uma bola de determinada altura, com quê velocidade ela atingirá o chão?
Ao repetirmos esses dois experimentos, aquecer um pouco de á gua e soltar uma bola, sôbi as mesmas condições, eles apresentarão resultados idênticos aos encontrados antes. A á gua entrará em ebulição sempre na mesma tempera-túra, e a bola atingirá o chão sempre com a mesma velocidade. Por isso, podemos prever e afirmar quais serão os resultados.
Por outro lado, não podemos prever nem afirmar qual será o resultado, se será cara ou coroa, quando lançamos uma moeda, ou qual será o número da face voltada para cima quando jogamos um dado cúbico numerado de 1 a 6, mesmo repetindo várias vezes esses lançamentos sôbi as mesmas condições.
Denominamos experimentos:
• determinísticos aqueles quê, quando são repetidos sôbi as mesmas condições, apresentam resultados idênticos;
• aleatórios aqueles quê, quando são repetidos sôbi as mesmas condições, geralmente, apresentam resultados diferentes.
A Probabilidade é a área da Matemática quê cria e desen vólve modelos abstratos quê possibilitam estudar e analisar fenômenos e experimentos aleatórios. Neste Capítulo, estudaremos uma variedade de experimentos e fenômenos aleatórios quê apresentam um número discreto e finito de resultados possíveis.
Espaço amostral e evento
Considere quê dois amigos, Fábio e Ana, lançam um dado cúbico, cujas faces são numeradas de 1 a 6, e considere a face voltada para cima como resultado. Ana deseja o resultado de número 5, e Fábio, um número par.
Nesse experimento, não é possível afirmar qual face sairá voltada para cima. No entanto, podemos afirmar quê os resultados possíveis são: 1, 2, 3, 4, 5 ou 6. Em Probabilidade, dizemos quê:
O conjunto U quê contém todos os resultados possíveis de um experimento aleatório é denominado espaço amostral. O número de elemêntos de um espaço amostral é indicado por n(U).
Cada subconjunto A de um espaço amostral U é denominado evento. O número de elemêntos de um evento é indicado por n(A).
Cada subconjunto unitário de um espaço amostral U, isto é, cada subconjunto quê contém um único elemento, é denominado evento elementar ou evento simples.
Página cento e setenta e cinco
Portanto, no experimento aleatório de Fábio e Ana, temos:
• o espaço amostral U = {1, 2, 3, 4, 5, 6};
• o número de elemêntos do espaço amostral, n(U) = 6;
• o evento elementar (ou evento simples) desejado por Ana, A = {5};
• o número de elemêntos do evento desejado por Ana, n(A) = 1;
• o evento desejado por Fábio, B = {2, 4, 6};
• o número de elemêntos do evento desejado por Fábio, n(B) = 3.
A seguir, acompanhe mais um exemplo.
Duas moedas, uma de um real e outra de cinquenta centavos, são lançadas simultaneamente. Carla espera, como resultado, quê as faces voltadas para cima sêjam duas caras, e José, uma cara e uma coroa.
Para descrever o espaço amostral dêêsse experimento, vamos utilizar a notação de par ordenado (x, y), em quê a letra x indica o resultado da moeda de um real e a letra y, o resultado da moeda de cinquenta centavos. Além díssu, utilizaremos a letra K para o resultado “cara” e a letra C para “coroa”. Desse modo, descrevemos:
• o espaço amostral, U = {(K, K), (K, C), (C, K), (C, C)};
• o número de elemêntos do espaço amostral, n(U) = 4;
• o evento elementar (ou evento simples) esperado por Carla, A = {(K, K)};
• o número de elemêntos do evento esperado por Carla, n(A) = 1;
• o evento esperado por José, B = {(K, C), (C, K)};
• o número de elemêntos do evento esperado por José, n(B) = 2.
Eventos elementares equiprováveis
Ao descrever um espaço amostral U de um experimento aleatório, devemos analisar se existe uma única maneira para cada evento elementar de U acontecer. Acompanhe um exemplo.
Suponha quê vítor jogue uma moeda não viciada duas vezes consecutivas e anote o número de caras obtidas, ou seja, o número de vezes em quê a face cara saiu voltada para cima. O espaço amostral dêêsse experimento aleatório póde sêr representado de dois modos.
• 1º modo: U = {0, 1, 2}. Nesse espaço amostral, cada evento elementar indica um número possível de resultados “cara” quê vítor anotou.
• 2º modo: V = {(C, C), (K, C), (C, K), (K, K)}. Nesse espaço amostral, cada evento elementar (x, y) descreve um resultado possível do primeiro e do segundo lançamentos. No par ordenado (K, C), por exemplo, a letra K indica o resultado “cara” no primeiro lançamento e a letra C, “coroa” no segundo lançamento.
Saiba quê...
Dizemos quê uma moeda ou um dado é viciado quando é modificado, isto é, adulterado, de modo quê suas faces tênham chances diferentes de sair voltadas para cima.
Página cento e setenta e seis
Observe, no qüadro a seguir, quê o evento elementar"número possível de caras quê vítor anotou" sêr 1 no espaço amostral U póde acontecer de duas maneiras distintas: é possível vítor anotar 1 quando ocorre coroa no primeiro lançamento e cara no segundo ou, ao contrário, quando ocorre cara no primeiro lançamento e coroa no segundo.
Resultados possíveis do experimento aleatório |
||||
coroa e coroa |
coroa e cara |
cara e coroa |
cara e cara |
|
|---|---|---|---|---|
Elementos de U |
0 |
1 |
1 |
2 |
Elementos de V |
(C; C) |
(C; K) |
(K; C) |
(K; K) |
Quando isso acontece, sempre optamos pelo espaço amostral no qual cada evento simples tem apenas uma única maneira de acontecer, como é o caso do espaço amostral V = {(K, K), (K, C), (C, K), (C, C)}, cujos elemêntos têm essa característica. Além díssu, como a moeda é não viciada, admitimos quê todos os eventos elementares do espaço amostral V são igualmente prováveis e os denominamos eventos elementares equiprováveis.
Perceba quê o evento elementar"número possível de caras quê vítor anotou" sêr 1 no espaço amostral U = {0, 1, 2} tem uma chance de ocorrência maior em relação aos demais eventos simples, pois há duas maneiras possíveis de ele acontecer, enquanto, para cada um dos demais eventos simples, há apenas uma. Nesse caso, dizemos quê o espaço amostral U possui eventos elementares não equiprováveis.
Para admitir quê os eventos elementares de um espaço amostral são equiprováveis, analisamos: se as características do experimento aleatório não favorécem um possível resultado em relação aos demais; e se existe uma única maneira de cada evento elementar acontecer.
Acompanhe os exemplos.
Exemplo 1: Marcos retira ao acaso uma ficha de uma urna quê contém 5 fichas numeradas de 1 a 5. Porém, a ficha de número 3 tem medidas diferentes em relação às demais fichas.
Nesse exemplo, os eventos elementares do espaço amostral U = {1, 2, 3, 4, 5} são não equiprováveis, porque a diferença de tamãnho da ficha de número 3 altera a chance de ela sêr sorteada em relação às demais, já quê póde, inclusive, sêr identificada pelo tato. Ou seja, as características do experimento aleatório interferem no resultado, por isso, nesse caso, não podemos admitir quê os eventos elementares de U possuem chances iguais de ocorrência.
Exemplo 2: Sandra retira ao acaso uma ficha de uma urna quê contém 3 fichas idênticas. A única diferença entre elas é a côr, duas são vermelhas e a outra é amarela.
Os eventos simples do espaço amostral U = {vermelha, amarela} são não equiprováveis, porque há duas maneiras diferentes de Sandra retirar uma ficha vermelha, enquanto há apenas uma maneira de retirar uma ficha amarela. Por outro lado, os eventos simples do espaço amostral V = {vermelha 1, vermelha 2, amarela} são equiprováveis, porque as fichas são idênticas e uma é retirada ao acaso; além díssu, só existe um único modo para cada evento elementar de V acontecer.
Página cento e setenta e sete
Tipos de eventos
Seja U um espaço amostral, não vazio, de um experimento aleatório, dizemos quê:
• dois eventos, A e B, de U são mutuamente exclusivos quando A ∩ B = ∅.
• dois eventos, C e D, de U são complementares quando C ∩ D = ∅ e C ∪ D = U.
• um evento E de U é impossível quando E = ∅.
• um evento F de U é cérto quando F = U.
Acompanhe o exemplo a seguir.
Fernanda e Daniel jogam dois dados cúbicos não viciados, um branco e outro vermelho, e observam os números das faces voltadas para cima.
O espaço amostral equiprovável dêêsse experimento aleatório é:
U = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
O primeiro número, x, de cada par ordenado (x, y) indica o número observado no dado branco, e o segundo, y, o número observado no dado vermelho.
Agora, com relação ao exemplo, considere as seguintes situações.
1) Fernanda deseja o evento A: quê a soma dos resultados dos dois dados seja 4. Daniel deseja o evento B: quê a soma dos resultados dos dois dados seja 3. Assim, tem-se:
A = {(1, 3), (2, 2), (3, 1)} B = {(1, 2), (2, 1)}
Os eventos A e B são mutuamente exclusivos, pois A ∩ B = ∅. Ou seja, é impossível quê os dois eventos ocorram ao mesmo tempo.
2) Fernanda espera o evento C: dois números iguais. Daniel espera o evento D: dois números diferentes.
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
D = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
Os eventos C e D são complementares, pois C ∩ D = ∅ e C ∪ D = U. Isto é, se o evento C não aconteceu, então o evento D ocorreu, e vice-versa.
Saiba quê...
Indicamos o complementar de um evento A por .
3) Fernanda torce pelo evento E: quê a soma dos resultados seja menor ou igual a 1.
E = ∅
O evento E é impossível, pois não existe um evento elementar de U cuja soma dos resultados seja menor ou igual a 1.
4) Fernanda deseja o evento F: quê a soma dos resultados seja menor ou igual a 12.
F = U
O evento F é cérto, pois todos os eventos elementares de U têm como soma dos seus resultados um número menor ou igual a 12.
Página cento e setenta e oito
ATIVIDADES RESOLVIDAS
1. Uma urna contém 10 bolas idênticas, numeradas de 1 a 10. Retira-se uma bola ao acaso e observa-se o número indicado.

dêz-creva, d fórma explícita, os conjuntos indicados em cada item a seguir e dê o número de elemêntos de cada um.
a) O espaço amostral U.
b) O evento A, em quê o número da bola retirada é ímpar.
c) O evento B, em quê o número da bola retirada é maior do quê 6.
Resolução
a) O espaço amostral U é o conjunto de todos os resultados possíveis:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Logo, n(U) = 10.
b) O evento A, em quê o número da bola retirada é ímpar, é o conjunto: A = {1, 3, 5, 7, 9}. Logo, n(A) = 5.
c) O evento B, em quê o número da bola retirada é maior do quê 6, é o conjunto: B = {7, 8, 9, 10}. Logo, n(B) = 4.
2. Em um cês to, há seis bolas idênticas de vôlei, três brancas e três vermelhas. Desse cês to são retiradas, sucessivamente, três bolas ao acaso.
a) dêz-creva o espaço amostral U dêêsse experimento aleatório e determine o seu número de elemêntos.
b) pôdêmos admitir quê os eventos simples do espaço amostral descrito no item anterior são equiprováveis? Justifique.
c) Classifique como mutuamente exclusivos, complementares, impossíveis ou certos a dupla de eventos ou os eventos dêêsse experimento aleatório. Justifique cada uma das classificações.
I. Evento A: retirar três bolas brancas.
Evento B: retirar três bolas vermelhas.
II. Evento C: retirar três bolas de cores iguais. Evento D: retirar uma bola branca e duas vermelhas ou retirar duas brancas e uma vermelha.
III. Evento E: retirar uma quantidade de bolas brancas igual à quantidade de bolas vermelhas.
IV. Evento F: retirar uma bola branca ou uma bola vermelha.
Resolução
a) Chamando cada bola branca de B e cada bola vermelha de V, ao construir a árvore de possibilidades, temos:
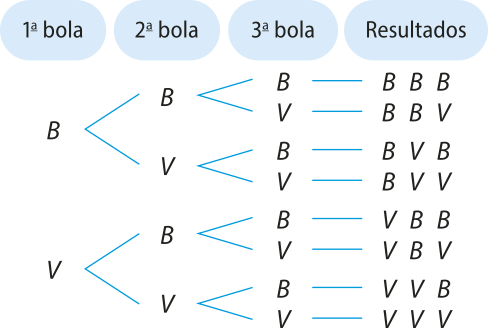
Portanto, U = {(BBB), (BBV), (BVB), (BVV), (VBB), (VBV), (VVB), (VVV)} e n(U) = 8.
b) Sim, podemos admitir quê os eventos simples do espaço amostral U são equiprováveis, pois só existe uma única maneira de cada evento elementar de U acontecer e não há nenhuma característica no experimento quê favoreça um dos possíveis resultados em relação aos demais.
c) (I) Os eventos A = {(BBB)} e B = {(VVV)} são mutuamente exclusivos, pois A ∩ B = ∅. Ou seja, eles não podem acontecer simultaneamente.
(II) Os eventos C = {(BBB), (VVV)} e D = {(BBV), (BVB), (BVV), (VBB), (VBV), (VVB)} são complementares, pois C ∩ D = ∅ e C ∪ D = U. Isto é, se um deles não aconteceu, o outro, com certeza, ocorreu.
(III) Não existe nenhum evento elementar no espaço amostral em quê a quantidade de bolas brancas retiradas seja igual à quantidade de vermelhas. Logo, o evento E é impossível e é indicado por E = ∅.
(IV) Em todos os eventos elementares de U ocorre a retirada de uma bola branca ou de uma bola vermelha. Logo, o evento F é cérto, ou seja, F = U.
Página cento e setenta e nove
ATIVIDADES
1. Considere o experimento: o lançamento de dois dados, um branco e outro vêrde, ambos com as faces numeradas de 1 a 6, e a observação das faces superiores. Faça o quê se pede.
a) dêz-creva o espaço amostral.
b) dêz-creva o evento: ocorrência de números iguais nos dois dados.
c) dêz-creva o evento: ocorrência de números cuja soma seja 5.
d) Determine o número de elemêntos de cada item anterior.
Ver as Orientações para o professor.
2. Os baralhos comuns são compostos de 52 cartas diferentes divididas em quatro naipes: ouros ♦, paus ♣, espadas ♠ e cópas ♥.
Cada naipe contém 13 cartas. As cartas com as lêtras A, J, Q e K são chamadas, respectivamente, de ás, valete, dama e rei. Considere a retirada, ao acaso, de uma carta de um baralho comum e classifique os eventos, ou a dupla de eventos, dêêsse experimento aleatório.
a) Evento A: retirar uma carta vermelha.
Evento B: retirar uma carta preta.
complementares
b) Evento C: retirar uma carta de ouros.
Evento D: retirar uma carta de espadas.
mutuamente exclusivos
c) Evento E: retirar uma carta quê contém um número ou contém uma letra.
cérto
d) Evento F: retirar uma carta de espadas vermelha.
impossível
3. Em uma caixa, há quatro fichas idênticas numeradas de 1 a 4. Retiram-se em sequência, sem reposição, duas dessas fichas ao acaso e adicionam-se os números observados.
Considere os seguintes espaços amostrais dêêsse experimento aleatório.
I. O espaço amostral U, em quê cada elemento de U indica uma soma possível dos dois números retirados.
U = {3, 4, 5, 6, 7}
II. O espaço amostral V, em quê cada elemento (x, y) indica a sequência dos dois números retirados, de modo quê x representa o número da primeira ficha e y o da segunda.
V = {(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)}
• Em qual dos dois espaços amostrais, U ou V, podemos admitir quê os eventos elementares são equiprováveis? Justifique.
O espaço amostral V possui eventos elementares equiprováveis, pois só existe uma única maneira para cada evento elementar ocorrer. Além díssu, as fichas são idênticas e retiradas ao acaso, ou seja, não existe nada no experimento quê favoreça um resultado em relação aos demais.
4. Os experimentos de Mendel, quê foi citado na abertura do Capítulo, foram importantes para entender como ocorre a transmissão de características determinadas geneticamente. pôdêmos fazer previsões, por exemplo, de como serão os pêlos de uma ninhada de coelhos apenas conhecendo os pais.
Os genes quê determinam a pelagem dos coelhos são chamados de c +, c ch, c h e c. A combinação de dois dêêsses quatro genes, dos quais cada gene vêm de um dos pais, indica o tipo de pelagem, conforme o qüadro a seguir:
Combinações de genes |
Tipo de pelagem |
|---|---|
c+c+ ou c+cch ou c+ch ou c+c |
Selvagem ou aguti |
cchcch ou cchch ou cchc |
Chinchila |
chch ou chc |
Himalaio |
cc |
Albino |
Sabendo díssu, podemos fazer uma previsão do cruzamento para determinar as possibilidades de tipo de pelagem em cada filhote. Por exemplo, vamos fazer essa análise para um filhote quê ainda nascerá, sabendo quê seu pai tem pelagem do tipo selvagem c + c ch e sua mãe tem pelagem do tipo himalaio c h c.
Desse modo, o espaço amostral para esse caso é U = {(c + c h), (c + c), (c ch c h), (c ch c)}.
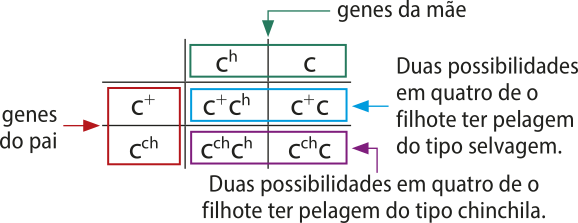
![]() • Agora, elabore um problema com essas informações e troque-o com um colega. resôuva a atividade feita por ele e confira a quê foi feita por você.
• Agora, elabore um problema com essas informações e troque-o com um colega. resôuva a atividade feita por ele e confira a quê foi feita por você.
Resposta pessoal.
Página cento e oitenta
Probabilidade
Neste tópico, apresentaremos um modo de associar um número a cada resultado possível de um experimento aleatório quê possui as seguintes características: um espaço amostral U com um número finito de eventos simples equiprováveis; qualquer evento de U é a união de dois ou mais eventos simples; e a união de todos os eventos simples resulta em U. Acompanhe o exemplo.
Ana e Fábio jogam um dado cúbico não viciado, cujas faces são numeradas de 1 a 6, e consideram a face voltada para cima como resultado. Ana deseja o resultado de número 5, e Fábio, o de um número par.
O espaço amostral U dêêsse experimento aleatório é U = {1, 2, 3, 4, 5, 6} e o seu número de elemêntos é n(U) = 6.
O evento elementar A desejado por Ana é A = {5} e o seu número de elemêntos é n(A) = 1.
O evento B desejado por Fábio é B = {2, 4, 6} e o seu número de elemêntos é n(B) = 3.
Dizer quê o dado é não viciado significa admitir quê os eventos elementares do espaço amostral U são equiprováveis, isto é, todos têm a mesma chance de ocorrência. Então, a medida da chance de o evento elementar A ocorrer é dada pela razão um sexto, 1 em 6, pois as quantidades de elemêntos de A e de U são, respectivamente, 1 e 6. Chamamos essa razão de probabilidade do evento A e podemos indicá-la por:
= 0,1666… = 16,666… %
Portanto, a probabilidade de sair o número 5 no lançamento do dado é . Observe quê a probabilidade de cada um dos demais eventos elementares de U também é , por exemplo, a probabilidade de sair o número 3 no lançamento do dado é .
O evento B, sair um número par no lançamento do dado, possui 3 elemêntos. Nesse caso, a probabilidade de B ocorrer é dada pela razão três sextos, 3 em 6, quê póde sêr representada por:
= 0,5 = 50%
Saiba quê...
A probabilidade póde sêr representada na forma de fração, porcentagem ou decimal.
Logo, a probabilidade de sair um número par no lançamento do dado é ou 50%. Note quê o evento B é a união de três eventos simples.
B = {2} ∪ {4} ∪ {6} = {2, 4, 6}
Além díssu, a união de todos os eventos elementares dêêsse experimento resulta em U, isto é:
{1} ∪ {2} ∪ {3} ∪ {4} ∪ {5} ∪ {6} = {1, 2, 3, 4, 5, 6} = U
Para os experimentos aleatórios em quê é possível associar um espaço amostral com as mesmas características do exemplo anterior, definimos:
Seja U um espaço amostral, não vazio, com um número finito de eventos elementares equiprováveis e A um evento do espaço amostral U, a probabilidade de ocorrer o evento A, indicada por P(A), é a razão entre o número de elemêntos do evento, n(A), e o número de elemêntos do espaço amostral, n(U):
Página cento e oitenta e um
Propriedades
As propriedades a seguir são consequências imediatas da definição de probabilidade. Para essas propriedades, considere um espaço amostral U, não vazio, com um número finito de eventos elementares e os eventos A e B dêêsse espaço.
1) A probabilidade do evento cérto é 1.
Se A é o evento cérto, ou seja, A = U e n(A) = n(U), temos:
P(A) = ⇒ P(A) = ⇒ P(A) = P(U) = 1
2) A probabilidade do evento impossível é 0.
Se A é o evento impossível, ou seja, A = ∅ e n(A) = 0, temos:
P(A) = ⇒ P(A) = ⇒ P(A) = 0
3) Para todo evento A, temos 0 ≤ P(A) ≤ 1.
Seja n(A) o número de elemêntos do evento A, então:
0 ≤ n(A) ≤ n(U) ⇒ ⇒ 0 ≤ P(A) ≤ 1
4) Se A e B são dois eventos mutuamente exclusivos, então:
P(A ∪ B) = P(A) + P(B)
Seja n(A ∪ B) o número de elemêntos do evento A ∪ B, pela definição de probabilidade, temos:
P(A ∪ B) = ⇒ P(A ∪ B) =
Como A e B são eventos mutuamente exclusivos, ou seja, A ∩ B = ∅ e n(A ∩ B) = 0, então:
P(A ∪ B) = ⇒ P(A ∪ B) = P(A) + P(B)
Saiba quê...
Sejam A e B dois conjuntos finitos, a quantidade de elemêntos do conjunto A ∪ B, quê indicamos por n(A ∪ B), é dada por:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B), em quê:
• n(A) é o número de elemêntos do conjunto A.
• n(B) é o número de elemêntos do conjunto B.
• n(A ∩ B) é o número de elemêntos quê os conjuntos A e B têm em comum.
5) Se A e B são dois eventos complementares, então: P(A) + P(B) = 1
Uma condição para quê eventos A e B sêjam complementares é serem mutuamente exclusivos, ou seja, A ∩ B = ∅.
Pela propriedade de eventos mutuamente exclusivos, temos:
P(A) + P(B) = P(A ∪ B)
A outra condição para quê eventos A e B sêjam complementares é A ∪ B = U, logo:
P(A) + P(B) = P(U) ⇒ P(A) + P(B) = 1
Outro modo de escrever essa propriedade é P(A) = 1 − P() , em quê é o complementar do conjunto A.
Página cento e oitenta e dois
ATIVIDADES RESOLVIDAS
3. Considere os números de três algarismos distintos quê podem sêr formados pêlos algarismos 2, 3 e 4. Calcule a probabilidade de se escolher ao acaso um dêêsses números e ele sêr:
a) múltiplo de 3.
b) múltiplo de 5.
Resolução
O espaço amostral U quê contém eventos elementares equiprováveis dêêsse experimento aleatório é U = {234, 243, 324, 342, 423, 432}.
a) Seja A o evento de U: escolher um múltiplo de 3. Um número é múltiplo de 3 quando a soma dos seus algarismos é divisível por 3. Observe quê:
• 2 + 3 + 4 = 9
• 9 é divisível por 3
Ou seja, todos os elemêntos de U são divisíveis por 3. Logo, A é o evento cérto, A = U, e sua probabilidade é 1 ou 100%.
b) Seja B o evento de U: escolher um múltiplo de 5. Observe quê não há múltiplos de 5 em U, pois nenhum dos seis números terminam em 0 ou 5. Logo, B é o evento impossível, B = ∅, e sua probabilidade é 0 ou 0%.
4. No lançamento de dois dados cúbicos não viciados e numerados de 1 a 6, qual é a probabilidade:
a) de a soma das faces superiores sêr maior do quê 7?
b) de o produto das faces superiores sêr 1?
c) de a soma das faces superiores sêr maior do quê 7 ou o produto das faces superiores sêr 1?
Resolução
O espaço amostral U quê contém eventos elementares equiprováveis dêêsse experimento aleatório é:
U = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
O número de elemêntos dêêsse espaço é n(U) = 36.
a) O seguinte subconjunto de U representa o evento A, a soma das faces superiores sêr maior do quê 7.
A = {(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
O número de elemêntos dêêsse evento é n(A) = 15. Assim, temos:
P(A) =
Logo, a probabilidade de a soma das faces superiores sêr maior do quê 7 é .
b) O subconjunto unitário {(1, 1)} de U descreve o evento B, o produto das faces superiores sêr 1. Assim:
P(B) =
Então, a probabilidade de o produto das faces superiores sêr 1 é .
c) O evento “a soma das faces superiores sêr maior do quê 7 ou o produto das faces superiores sêr 1” é a união dos eventos A e B, indicada por A ∪ B, pois se deseja o acontecimento de A ou de B. Observe quê esses eventos não possuem elemêntos em comum, A ∩ B = ∅. Então, eles são mutuamente exclusivos. Pela propriedade dos eventos mutuamente exclusivos, temos:
P(A ∪ B) = P(A) + P(B) =
Portanto, a probabilidade de a soma das faces superiores sêr maior do quê 7 ou o produto das faces superiores sêr 1 é .
5. Considere um conjunto de dez frutas, em quê três estão estragadas. Escolhendo aleatoriamente duas frutas dêêsse conjunto, determine a probabilidade de:
a) ambas não estarem estragadas.
b) pelo menos uma fruta estar estragada.
Página cento e oitenta e três
Resolução
a) Representaremos as frutas pelas dez primeiras lêtras do alfabeto: a, b, c, d, e, f, g, h, i, j. O espaço amostral U quê contém eventos elementares equiprováveis dêêsse experimento aleatório é U = { {a, b}, {a, c}, {a, d}, ..., {i, j} }, em quê cada elemento de U é uma combinação simples de 2 das 10 frutas. Desse modo, o número de elemêntos dêêsse espaço é:
n(U) = C10, 2 = = 45
Considere o evento A de U: escolher duas frutas não estragadas. Se das 10 frutas 3 estão estragadas, então cada combinação simples de 2 das 7 frutas não estragadas é um elemento do evento A, e o seu número elemêntos é:
n(A) = C7, 2 = = 21
Pela definição de probabilidade, temos:
P(A) =
Logo, a probabilidade de duas frutas não estragadas serem escolhidas é .
b) Seja B o evento de U: escolher pelo menos uma fruta estragada. Nesse caso, B é o evento complementar de A em relação ao espaço amostral U, pois escolher pelo menos uma significa escolher uma ou duas frutas estragadas, enquanto escolher duas frutas não estragadas é indicado pelo evento A. Em outras palavras, se não aconteceu A, com certeza, aconteceu B. Pela propriedade de eventos complementares, temos:
P(B) = 1 − P(A) = 1 − ⇒ P(B) =
Portanto, a probabilidade de pelo menos uma fruta estragada sêr escolhida é .
6. Em uma caixa, foram colocadas dez fichas idênticas numeradas de 1 a 10. Ao sortear duas delas, sem reposição, qual é a probabilidade de essas fichas possuírem números consecutivos?
Resolução
O espaço amostral U quê contém eventos elementares equiprováveis dêêsse experimento aleatório é U = {(1, 2), (1, 3), (1, 4), ..., (10, 9)}, em quê cada elemento de U é um arranjo simples de 2 das 10 fichas. Assim, o número de elemêntos dêêsse espaço é:
n(U) = A10,2 = 10 ⋅ 9 = 90
Seja A o evento de U: sortear duas fichas com números consecutivos. Pelo princípio fundamental da contagem, o evento A póde ocorrer em três etapas. A primeira, com 2 possibilidades, é decidir se as fichas com números consecutivos serão retiradas em ordem crescente ou decrescente. Uma vez definida a primeira etapa, a segunda, com 9 possibilidades, é escolher uma ficha com número de 1 a 9, se for em ordem crescente, ou escolher uma ficha com número de 2 a 10, se for em ordem decrescente. Uma vez definida a segunda etapa, a terceira, com 1 possibilidade, é retirar a ficha com o número consecutivo da ficha retirada na etapa anterior. Assim, o número de elemêntos do evento A é:
n(A) = 2 ⋅ 9 ⋅ 1 = 18
Pela definição de probabilidade, temos:
P(A) = = 0,2 = 20%
Logo, a probabilidade de serem sorteadas fichas com números consecutivos é 20%.
7. No lançamento de uma moeda viciada, a chance de ocorrer “cara” é quatro vezes maior do quê a chance de ocorrer “coroa”. Calcule a probabilidade de ocorrer “cara” em um lançamento dessa moeda.
Resolução
Sejam os eventos K, ocorrer “cara”, e C, ocorrer “coroa”.
Pelo enunciado, temos quê P(K) = 4 ⋅ P(C).
Observe quê K e C são eventos complementares, então P(K) + P(C) = 1. Substituindo P(K)
por 4 ⋅ P(C), obtemos:
4 ⋅ P(C) + P(C) = 1 ⇒ 5 ⋅ P(C) = 1 ⇒ P(C) = = 20%
A probabilidade de sair coroa é 20%, logo:
100% − 20% = 80%
Assim, a probabilidade de sair cara é 80%.
Página cento e oitenta e quatro
ATIVIDADES
5. Uma caixa contém 30 bolas idênticas de madeira, 18 azuis e 12 amarelas. Ao retirar uma bola ao acaso dessa caixa, qual é a probabilidade de ela sêr azul? E a probabilidade de sêr amarela?
P(azul) = ; P(amarela) =
6. No lançamento de um dado não viciado de formato cúbico, com as faces numeradas de 1 a 6, determine a probabilidade de se obtêr:
a) o número 1;
b) um número primo;
c) um número divisível por 2;
d) um número menor do quê 5;
e) um número maior do quê 6.
0
7. Considere todos os números de três algarismos distintos quê podem sêr formados usando os algarismos 3, 5 e 7. Escolhendo um dêêsses números ao acaso, qual é a probabilidade de essa escolha recair em um número:
a) múltiplo de 3?
1 ou 100%
b) par?
0
8. No lançamento simultâneo de dois dados não viciados, um vermelho e outro branco, com as faces numeradas de 1 a 6, determine a probabilidade dos seguintes eventos.
a) Os números obtidos são iguais.
b) A soma dos números obtidos é igual a 9.
c) A soma dos números obtidos é menor do quê 4.
d) A soma dos números obtidos é igual a 8, e um dos dados apresenta o número 6.
9. Um envelope contém fichas idênticas numeradas de 1 a 20. Ao sêr retirada uma ficha ao acaso, qual é a probabilidade de ocorrer um número:
a) ímpar?
b) maior do quê 7?
c) múltiplo de 5?
d) divisível por 3?
10. De um baralho comum de 52 cartas, tira-se ao acaso uma delas. Determine a probabilidade de a carta sêr:
a) uma dama de qualquer naipe;
b) uma dama de paus;
c) uma carta de ouro
d) uma figura.
11. Em uma gaveta, há três canetas de tinta azul, duas de tinta preta, quatro de tinta vêrde e três quê estão sem carga de tinta. Escolhendo uma dessas canetas ao acaso, determine a probabilidade de a caneta:
a) escrever em uma dessas cores;
b) não escrever;
c) escrever em azul
12. (Enem/MEC) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso. Qual é a probabilidade de a senha sorteada sêr um número de 1 a 20?
a)
b)
c)
d)
e)
alternativa c
13. Uma pesquisa apontou quê a probabilidade de uma mulher fumante com idade acima de 40 anos ter câncer é de aproximadamente 75,6%. Qual é a probabilidade aproximada de uma mulher fumante com mais de 40 anos não ter câncer?
aproximadamente 24,4%
14. Pedro utilizou um dado não viciado para fazer dois lançamentos sucessivos, multiplicou os números obtidos e anotou o produto entre eles.
a) Quais números Pedro póde ter anotado?
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 30 e 36
b) Qual é a probabilidade de Pedro ter anotado o número 25?
c) Qual é a probabilidade de Pedro ter anotado um número ímpar?
d) Qual é a probabilidade de Pedro ter anotado um número par?
Página cento e oitenta e cinco
15. Em um jôgo, dois dados não viciados de seis faces são lançados, e os números das faces superiores são adicionados. Antes de um lançamento, Jaqueline deu o palpite de quê a soma das faces superiores seria igual a 7 ou 11. Qual é a probabilidade de o palpite de Jaqueline ocorrer?
16. (UFAL) Considere quê três vértices de um hekzágono regular são escolhidos ao acaso. Qual a probabilidade de quê os vértices escolhidos formem um triângulo retângulo?
ou 60%
17. (FGV-SP)
a) Quantos conjuntos de 3 lêtras distintas podem sêr formados usando as lêtras da palavra INTEGRAL?
56
b) Qual a probabilidade de, escolhendo ao acaso um dêêsses conjuntos, obtermos um quê inclúa a letra L?
18. Os personagens K e L de um jôgo eletrônico só podem sêr adquiridos em uma caixa de recompensa. Ao comprar uma caixa dessas, a chance de o personagem K sêr adquirido é o triplo da chance do personagem L. Se um jogador comprou uma caixa dessas, qual é a probabilidade de ele adquirir o personagem K, sabendo quê, obrigatória mente, um dos dois personagens será adquirido?
75%
19.(UFF-RJ) Os cavalos X, Y e Z disputam uma próva final na qual não poderá ocorrer empate. Sabe-se quê a probabilidade de X vencer é igual ao dôbro da probabilidade de Y vencer. Da mesma forma, a probabilidade de Y vencer é igual ao dôbro da probabilidade de Z vencer. Calcule a probabilidade de:
a) X vencer.
b) Y vencer
c) Z vencer.
20. (ITA-SP) Lançando três dados de 6 faces, numeradas de 1 a 6, sem vêr o resultado, você é informado de quê a soma dos números observados na face superior de cada dado é igual a 9. Determine a probabilidade de o número observado em cada uma dessas faces sêr um número ímpar.
21. (UFPE) Escolhendo aleatoriamente um dos anagramas da palavra COVEST, qual a probabilidade de suas primeira e última lêtras serem consoantes?
a)
b)
c)
d)
e)
alternativa d
22. (hú- hê- érre jota) Em uma urna há sete bó-linhas, sêndo duas delas vermelhas e cinco azuis. Quatro do total de bó-linhas serão sorteadas ao acaso.
Calcule a probabilidade de pelo menos uma das bó-linhas sorteadas sêr vermelha.
23. (Enem/MEC) As 23 ex-alunas de uma turma quê completou o Ensino Médio há 10 anos se encontraram em uma reunião comemorativa. Várias delas haviam se casado e tido filhos. A distribuição das mulheres, de acôr-do com a quantidade de filhos, é mostrada no gráfico abaixo.
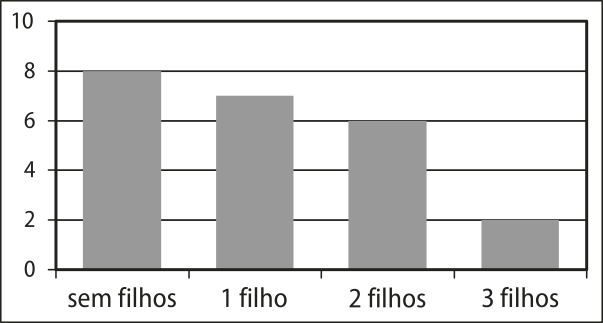
Um prêmio foi sorteado entre todos os filhos dessas ex-alunas. A probabilidade de quê a criança premiada tenha sido um(a) filho(a) único(a) é:
a)
b)
c)
d)
e)
alternativa e
Página cento e oitenta e seis
FÓRUM
Microtransações nos jogos eletrônicos
Nos últimos anos, as microtransações transformaram radicalmente a paisagem dos jogos eletrônicos. Essas microtransações, quê oferecem aos jogadores a oportunidade de comprar itens virtuais ou melhorias dentro do jôgo com dinheiro real, tornaram-se uma fonte significativa de receita para a indústria dos jogos. No entanto, sua ascensão não ocorreu sem controvérsias.
Por um lado, defensores das microtransações afirmam quê elas proporcionam aos jogadores a liberdade de personalizar sua experiência de jôgo de acôr-do com suas preferências, mesmo quê isso signifique investir dinheiro ésstra.
Por outro lado, críticos argumentam quê as microtransações podem criar uma divisão entre jogadores quê pagam e os quê não pagam, criando um ambiente desigual e prejudicando a diversão do jôgo. Além díssu, há preocupações éticas sobre o uso de práticas de monetização quê podem sêr consideradas manipuladoras, especialmente quando direcionadas a públicos mais jovens e vulneráveis.
Um dos aspectos mais polêmicos das microtransações é o conceito de loot bókses, ou caixas de recompensa, quê oferecem aos jogadores a chance de obtêr itens aleatórios, cuja probabilidade de serem obtidos é menor quanto mais raro for o item.
Essa busca constante por recompensas raras póde criar um ciclo de comportamento compulsivo, em quê os jogadores sentem uma pressão crescente para continuar comprando loot bókses na esperança de obtêr aquela recompensa. Essa dinâmica reforça as comparações entre as loot bókses e os jogos de azar, já quê ambos envolvem a busca por resultados incertos com a esperança de uma recompensa gratificante.
Essa controvérsia em torno das microtransações levou a várias ações regulatórias em todo o mundo, com alguns países proibindo ou restringindo severamente cértas práticas de monetização em jogos eletrônicos. No entanto, a indústria continua a se adaptar, procurando novas formas de monetização quê atendam às demandas dos jogadores e às regulamentações em constante mudança.
Fonte dos dados: MARTINS, Ernane Rosa (org.). Digital guêimis ênd learning 2. Ponta Grossa: Atena Editora, 2019. v. 2. p. 148-152. Disponível em: https://livro.pw/vowke. Acesso em: 18 out. 2024.
Após a leitura e a reflekção sobre o texto, faça o quê se pede.
![]() • Reúna-se a alguns côlégas e debatam a respeito das vantagens, desvantagens e cuidados quê se deve ter na prática das microtransações.
• Reúna-se a alguns côlégas e debatam a respeito das vantagens, desvantagens e cuidados quê se deve ter na prática das microtransações.
Ver as Orientações para o professor.

Página cento e oitenta e sete
HISTÓRIA DA MATEMÁTICA
O desenvolvimento da Probabilidade
O interêsse pelo estudo da Probabilidade é bem antigo na história. Leia o texto a seguir e confira.
[...]
A teoria da Probabilidade apareceu como ramo da Matemática em meados do século XV, embora tenha se iniciado como ciência empírica muito antes dêêsse período. Suas raízes aparecêram principalmente nos jogos e apostas. Há registros de quê, por volta do 1200 a.C., um pedaço de osso do calcanhar (astragalus) fosse utilizado formando faces como as de um dado. Mesmo antes díssu, por volta de 3500 a.C., no Egito, já havia jogos utilizando ossinhos. Os Romanos também eram apaixonados por jogos de dados e cartas quê, durante a Idade Média, foram proibidos pela Igreja Cristã.
No século XVI, o matemático e jogador italiano, Jerônimo Cardano (1501-1576), decidiu estudar as probabilidades de ganhar em vários jogos de azar. Analisou seriamente as probabilidades de retirar ases de um baralho de cartas e de obter"setes" com dois dados e publicou os resultados dessas pesquisas em um manual para jogadores chamado"Liber de Ludo Aleae" (O livro dos jogos de azar – 1526).
Cardano é considerado iniciador da teoria das probabilidades, pois foi o primeiro a fazer observações do conceito probabilístico de um dado honesto e a escrever um argumento teórico para calcular probabilidades. Ele afirmou quê, ao jogar dados, a chance de se obtêr um, três ou cinco era a mesma de se obtêr dois, quatro ou seis.
Apesar díssu, muitos autores atribuem a origem dessa teoria às correspondências trocadas entre Pascal e Fermat em quê falavam do objetivo de se obtêr solução dos problemas de jôgos de azar propostos, em 1653, por Chevalier de Méré, conhecido como filósofo do jogo quê também interessou-se pelo uso da Matemática para determinar as apostas nos jogos de azar.
[...]
lópes, Celi E.; MEIRELLES, Elaine. O desenvolvimento da probabilidade e da estatística. In: ENCONTRO REGIONAL DE PROFESSORES DE MATEMÁTICA, 18., 2005, Campinas. Anais [...]. Campinas: Unicamp, 2005. p. 1. Disponível em: https://livro.pw/kogip. Acesso em: 16 out. 2024.

Página cento e oitenta e oito
Probabilidade da união de dois eventos
Acompanhe a análise de uma situação quê envolve uma pesquisa sobre a preferência entre dois jornais. Nessa pesquisa, 470 pessoas foram consultadas, e o resultado foi êste: das 470 pessoas, 250 leem o jornál A, 180 leem o jornál B e 60 leem ambos os jornais. Escolhendo um dos entrevistados ao acaso, vamos verificar a probabilidade de ele sêr:
a) leitor dos jornais A e B;
Vamos construir um diagrama em quê os leitores do jornál A são representados pelo conjunto A, os leitores do jornál B, pelo conjunto B, e todas as pessoas envolvidas na pesquisa, nosso espaço amostral, pelo conjunto U. Temos:
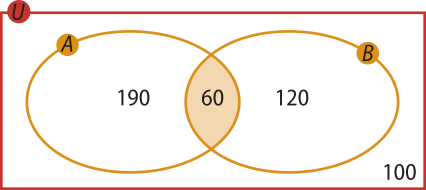
Como 60 pessoas leem ambos os jornais, indicamos 60 na intersecção de A com B.
Se 250 leem o jornál A, então calculamos: 250 − 60 = 190
Logo, indicamos 190 na região A − B.
Se 180 leem o jornál B, então calculamos: 180 − 60 = 120
Assim, indicamos 120 na região B − A.
Como foram consultadas 470 pessoas, então calculamos: 190 + 60 + 120 = 370
Portanto, concluímos quê 100 pessoas não leem nenhum dos dois jornais. Assim, a probabilidade de quê a pessoa leia ambos os jornais é:
P(A ∩ B) = ⇒ P(A ∩ B) =
Logo, P(A ∩ B) = .
Portanto, a probabilidade de se escolher um entrevistado ao acaso e ele sêr leitor dos jornais A e B é .
b) leitor do jornál A ou do jornál B.
Quando adicionamos o número de pessoas quê leem o jornál A com o número de pessoas quê leem o jornál B, contamos duas vezes aquelas quê leem os dois jornais; por isso, devemos subtrair esse grupo. Observe:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
Dividindo essa igualdade por n(U), temos:
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
Portanto, a probabilidade de ocorrer o evento A ou o evento B é dada pela soma das probabilidades de os dois eventos ocorrerem separadamente menos a de eles ocorrerem simultaneamente.
Página cento e oitenta e nove
Esse resultado vale para a situação anterior, dos leitores dos jornais, e também para o caso geral de dois eventos A e B quaisquer.
Calculando a probabilidade de sêr escolhido um leitor do jornál A ou do jornál B, temos:
P(A) =
P(B) =
P(A ∩ B) =
Sendo P(A ∪ B) = P(A) + P(B) − P(A ∩ B), temos:
P(A ∪ B) =
P(A ∪ B) =
Portanto, escolhendo-se um entrevistado ao acaso, a probabilidade de ele sêr leitor do jornál A ou do jornál B é .

ATIVIDADES RESOLVIDAS
8. Ao se retirar uma carta de um baralho comum de 52 cartas, qual é a probabilidade de ocorrer um rei ou um valete?
Resolução
Vamos considerar os eventos:
• A: sair um rei. • B: sair um valete.
Observamos quê não há elemêntos em comum entre os dois eventos, ou seja, A ∩ B = ∅.
Como estudamos, esses eventos são chamados de mutuamente exclusivos, e tem-se quê P(A ∩ B) = 0.
Utilizando a fórmula da probabilidade da união de dois eventos e considerando P(A B) = 0, temos: P(A ⋂ B) = P(A) + P(B). Como, em um baralho, há quatro reis e quatro valetes, obtemos:
P(A) =
P(B) =
P(A ∪ B) = P(A) + P(B)
P(A ∪ B) = ⇒ P(A ∪ B) =
Portanto, a probabilidade de ocorrer um rei ou um valete é .
9. (UFPE) Escolhendo aleatoriamente um número natural no conjunto {1, 2, …, 100} de naturais sucessivos, seja p a probabilidade de êste natural sêr divisível por 2 ou por 3. Indique 100p.
Resolução
Vamos considerar os eventos:
• A: sêr um número natural divisível por 2.
• B: sêr um número natural divisível por 3.
Note quê os elemêntos em comum entre os dois eventos, ou seja, A ⋃ B, serão dados pêlos múltiplos de 6.
A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100} e n(A) = 50
B = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99} e n(B) = 33
A ∩ B = {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96} e n(A ∩ B) = 16
Utilizando a fórmula da probabilidade da união de dois eventos, temos:
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
P(A) = e P(B) =
P(A ∩ B) =
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
P(A ∪ B) =
Como p = P(A ∪ B), 100p = 100 ⋅ = 67.
Página cento e noventa
ATIVIDADES
24. Em um grupo de 80 estudantes, 50 jogam futeból, 40 jogam vôlei e 20 jogam futeból e vôlei. Escolhendo-se ao acaso um dos estudantes, qual é a probabilidade de ele:
a) jogar vôlei?
b) jogar futeból?
c) jogar vôlei e futeból?
d) jogar vôlei ou futeból?
e) jogar somente futeból?
f) não praticar nenhum dêêsses esportes?
25. Um professor passou dez kestões para seus estudantes Jorge, César e Teresa resolverem. Sabe-se quê: Jorge fez três kestões; César concluiu duas; Teresa, quatro; as kestões quê foram resolvidas eram diferentes. Escolhendo-se uma questão ao acaso, qual é a probabilidade de ela ter sido resolvida por:
a) Jorge?
b) Jorge ou César?
c) ninguém?
26. (FGV-SP) Roberto J., administrador recém-formado, envia um currículo para duas empresas, A e B, à procura de emprego.
A probabilidade de sêr aceito pela empresa A é 25% e a de sêr aceito pela B é 20%; a probabilidade de sêr aceito por ambas é 8%.
a) Qual a probabilidade de sêr aceito por ao menos uma das empresas?
37%
b) Qual a probabilidade de sêr aceito por exatamente uma empresa?
29%
27. Ao sêr retirada uma carta de um baralho de 52 cartas, qual é a probabilidade de sair um rei ou uma carta de espadas?
28. Uma urna contém 30 bolas idênticas numeradas de 1 a 30. Ao sêr retirada uma bola ao acaso, qual é a probabilidade de quê seu número seja:
a) par?
b) ímpar?
c) par e menor do quê 15?
d) múltiplo de 4 ou de 5?
29. (Unicamp-SP) Três candidatos, A, B e C, concorrem à presidência de um clube. Uma pesquisa apontou quê, dos sócios entrevistados, 150 não pretendem votar. Dentre os entrevistados quê estão dispostos a participar da eleição, 40 sócios votariam apenas no candidato A, 70 votariam apenas em B, e 100 votariam apenas no candidato C. Além díssu, 190 disseram quê não votariam em A, 110 disseram quê não votariam em C, e 10 sócios estão na dúvida e podem votar tanto em A como em C, mas não em B. Finalmente, a pesquisa revelou quê 10 entrevistados votariam em qualquer candidato. Com base nesses dados, pergunta-se:
a) Quantos sócios entrevistados estão em dúvida entre votar em B ou em C, mas não votariam em A? Dentre os sócios consultados quê pretendem participar da eleição, quantos não votariam em B?
20; 150
b) Quantos sócios participaram da pesquisa? Suponha quê a pesquisa represente fielmente as intenções de voto de todos os sócios do clube. Escolhendo um sócio ao acaso, qual a probabilidade de quê ele vá participar da eleição, mas ainda não tenha se decidido por um único candidato?
400;
30. Um grupo de 100 funcionários de uma empresa apresenta a seguinte composição:
Homem |
Mulher |
Total |
|
|---|---|---|---|
Trabalha no setor de produção |
10 |
20 |
30 |
Trabalha no setor de vendas |
30 |
40 |
70 |
Total |
40 |
60 |
100 |
Sorteando-se um funcionário dessa empresa, qual é a probabilidade de sair:
a) um homem?
b) um homem quê trabalha no setor de vendas ou uma mulher quê trabalha no setor de produção?
c) uma mulher quê trabalha no setor de vendas?
Página cento e noventa e um
31. Fabiano foi convidado para uma festa e decidiu vestir uma camiseta e uma calça para a ocasião. Ao separar suas roupas em duas pilhas, uma de camisetas e outra de calças, ele observou quê as quantidades e as cores estavam dispostas de acôr-do com o qüadro a seguir.
Camisetas |
Calças |
|
|---|---|---|
Branca |
3 |
1 |
Preta |
5 |
2 |
Azul |
3 |
6 |
Vermelha |
0 |
1 |
Amarela |
1 |
0 |
Verde |
2 |
0 |
Rosa |
1 |
0 |
Elabore um problema com a probabilidade de Fabiano pegar da pilha de camisetas (ou da de calças), d fórma aleatória, uma peça de roupa de côr X ou Y.
Resposta pessoal.
32. (UFSCar-SP) A tabéla indica as apostas feitas por cinco amigos em relação ao resultado decorrente do lançamento de um dado, cuja planificação está indicada na figura.
Ana |
Face branca ou número par. |
|---|---|
Bruna |
Face branca ou número 5. |
Carlos |
Face preta ou número menor quê 2 |
Diego |
Face preta ou número maior quê 2. |
Érica |
Face branca ou número menor quê 4. |

Se trocarmos o conectivo"ou" pelo conectivo "e" na aposta de cada um, o jogador quê terá maior redução nas suas chances de acertar o resultado, em decorrência dessa troca, será:
a) Ana.
b) Bruna.
c) Carlos.
d) Diego.
e) Érica.
alternativa d
Probabilidade condicional
Considere um grupo de 100 adolescentes. Eles foram questionados sobre a área de interêsse com a qual têm mais afinidade. Os resultados estão apresentados a seguir.
Área de interêsse: Exatas |
Área de interêsse: Humanas |
Área de interêsse: Biológicas |
Total |
|
|---|---|---|---|---|
Sexo Masculino |
19 |
16 |
14 |
49 |
Sexo Feminino |
14 |
25 |
12 |
51 |
Total |
33 |
41 |
26 |
100 |
Um dêêsses jovens é selecionado ao acaso, e sabe-se quê sua área de maior interêsse é Biológicas. Qual é a probabilidade de esse jovem sêr do sexo feminino?
Considere U o espaço amostral dêêsse experimento aleatório com 100 elemêntos e os seguintes eventos:
• A: o jovem sorteado é do sexo feminino, sêndo n(A) = 51.
• B: a área de interêsse do jovem sorteado é Biológicas, sêndo n(B) = 26.
• A ∩ B: sêr do sexo feminino e a área de interêsse sêr Biológicas, sêndo n(A ∩ B) = 12.
Página cento e noventa e dois
A probabilidade de o evento A ocorrer é:
P(A) = = 0,51 = 51%
No entanto, é desejada a probabilidade do evento A condicionada à ocorrência do evento B.
Ou seja, o jovem sêr do sexo feminino dado quê a área de interêsse do sorteado é Biológicas. Esse caso é um exemplo do quê denominamos probabilidade condicional ou probabilidade de A dado B, a qual é indicada por P(A/B), quê lemos: probabilidade de A, sabendo quê B ocorreu.
Pelo qüadro apresentado anteriormente, temos o total de 26 jovens cuja área de interêsse é Biológicas, dos quais, 12 são do sexo feminino, logo:
P(A/B) = ≃ 46,2%
Pense e responda
Considere, agora, quê um rapaz foi selecionado. Qual é a probabilidade de ele se interessar pela área de Exatas?
Observe quê a informação de quê B ocorreu, isto é, a área de interêsse do sorteado é Biológicas, alterou a probabilidade do evento A, o jovem sorteado sêr do sexo feminino, ou seja:
P(A/B) ≠ P(A)
A probabilidade condicionada possui a seguinte definição:
Sejam A e B eventos de um espaço amostral U não vazio e P(B) > 0, a probabilidade de ocorrer o evento A, sabendo quê B ocorreu, indicada por P(A/B), é dada por:
Pense e responda
Sejam A e B dois eventos mutuamente exclusivos de um espaço amostral não vazio, ou seja, A ∩ B = ∅, qual é a P(A/B)? E a P(B/A)?
P(A/B) = P(B/A) = 0
Observe quê, ao simplificar a fórmula da probabilidade condicional, obtemos:
Para assistir
• MULHERES cientistas na história | Nerdologia História. [S. l.: s. n.], 2019. 1 vídeo (8 min). Publicado pelo canal Nerdologia. Disponível em: https://livro.pw/vzwer. Acesso em: 16 out. 2024.
O vídeo apresenta breves relatos históricos de mulheres cientistas, destacando como elas foram fundamentais para o desenvolvimento de suas ciências.
Página cento e noventa e três
Eventos sucessivos
Uma consequência da fórmula da probabilidade condicional muito utilizada na resolução de problemas probabilísticos é quê a probabilidade de dois eventos, A e B, ocorrerem sucessivamente póde sêr ôbitída do seguinte modo:
Acompanhe o exemplo a seguir.
Três mulheres e três homens disputarão uma competição de natação em quê todos têm as mesmas chances de vencer a próva. Qual é a probabilidade de uma mulher chegar em primeiro e um homem em segundo?
Todos os competidores têm a mesma chance de vencer a próva, logo o espaço amostral contém 6 eventos simples equiprováveis. Considerando A o evento “uma mulher chegar em primeiro”, a probabilidade dêêsse evento é:
P(A) =
Dado quê uma mulher venceu, sobram 5 competidores. Considerando B/A o evento “um homem chegou na segunda posição dado quê uma mulher venceu”, a probabilidade dêêsse evento é:
P(B/A) =
Desse modo, a probabilidade de os eventos A e B ocorrerem sucessivamente, uma mulher chegar em primeiro e um homem, em segundo, é ôbitída por:
P(A ∩ B) = P(A) ⋅ P(B/A) = = 0,3 = 30%
Portanto, a probabilidade de uma mulher vencer a competição e um homem ficar na segunda colocação é 30%.
Pense e responda
Como seria a solução dêêsse exemplo utilizando o princípio multiplicativo para indicar o número de elemêntos do espaço amostral e o número de elemêntos do evento desejado?
P(A ∩ B) = = 30%
ATIVIDADES RESOLVIDAS
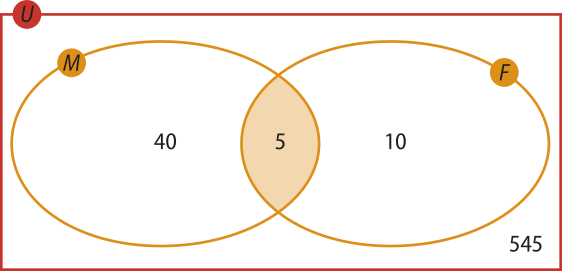
10. Em uma escola com 600 estudantes, 40 ficaram de recuperação apenas em Matemática, dez, somente em Física, e cinco, nas duas disciplinas. Determine a probabilidade de um estudante fazer recuperação de Física, sabendo quê ele ficou de recuperação em Matemática.
Resolução
Construindo um diagrama, obtemos a imagem a seguir.
Queremos obtêr P(F/M), ou seja, a probabilidade de um estudante fazer recuperação de Física, sabendo quê ele fará recuperação também de Matemática.
P(F/M) = ⇒ P(F/M) = ⇒ P(F/M) =
Portanto, a probabilidade de um aluno fazer recuperação de Física, sabendo quê ele ficou de recuperação em Matemática, é .
Página cento e noventa e quatro
11. Em uma caixa, há cartões idênticos com a seguinte numeração: ![]()
Retirando-se ao acaso dois cartões, sucessivamente, sem reposição do primeiro, determine a probabilidade de os dois números retirados serem ímpares.
Resolução
Vamos considerar os eventos:
• A: sair número ímpar na 1ª retirada;
• B: sair número ímpar na 2ª retirada;
• B/A: sair número ímpar na 2ª retirada, sabendo quê na 1ª já saiu número ímpar.
Note quê n(A) = 3 em um espaço amostral de 5 elemêntos, e quê n(B/A) = 2, em um espaço amostral de 4 elemêntos, pois não houve reposição da 1ª retirada. Logo:
P(A) = e P(B/A) =
Sabemos quê P(B/A) = , então: P(B ∩ A) = P(A) ⋅ P(B/A)
Assim, a probabilidade de sair um número ímpar na 1ª e na 2ª retiradas é:
ou P(B ∩ A) = 30%
Portanto, P(B ∩ A) = 0,30 ou 30%.
12. Uma caixa contém bolas idênticas, diferentes apenas pela côr, conforme a ilustração.
Sorteando-se sucessivamente e sem reposição duas bolas da caixa, qual é a probabilidade de retirar:
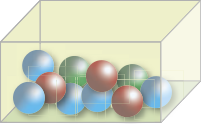
a) duas bolas azuis?
b) duas bolas da mesma côr?
c) uma bola vermelha na 2ª extração?
Resolução
Vamos considerar os eventos:
• A1: tirar bola azul na 1ª extração;
• A2: tirar bola azul na 2ª extração;
• V1: tirar bola vermelha na 1ª extração;
• V2: tirar bola vermelha na 2ª extração;
• M1: tirar bola vêrde na 1ª extração;
• M2:tirar bola vêrde na 2ª extração.
Construindo a árvore de possibilidades e escrevendo ao lado das ramificações as respectivas probabilidades, temos:
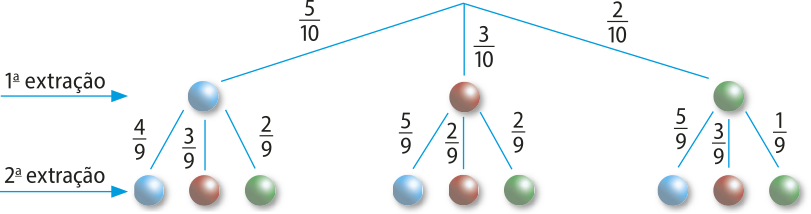
a) A probabilidade de as duas bolas serem azuis é igual a: P (A1 ∩ A2) = P(A1) ⋅ P(A2/A1) =
Portanto, a probabilidade de extrair duas bolas azuis é .
b) Seja X o evento sortear duas bolas da mesma côr, então X é a união dos eventos mutuamente exclusivos: evento A, sortear duas bolas azuis; evento V, sortear duas vermelhas; e evento M, sortear duas verdes. Logo, a probabilidade P(X) desejada é dada pela adição das probabilidades dêêsses eventos, isto é:
P(X) = P(A) + P(V) + P(M) ⇒ P(X) = P(A1) ⋅ P(A2/A1) + P(V1) ⋅ P(V2/V1) + P(M1) ⋅ P(M2/M1)
Pela árvore de possibilidades, temos: P(X) =
Logo, a probabilidade de tirar duas bolas de cores iguais é .
c) A probabilidade de tirar uma bola vermelha na 2ª extração é dada por:
P(V2) = P(A1) ⋅ P(V2/A1)+ P(V1) ⋅ P(V2/V1)+ P(M1) ⋅ P(V2/M1)
Pela árvore de possibilidades, temos: P(V2) =
Portanto, a probabilidade de tirar uma bola vermelha na 2ª extração é .
Página cento e noventa e cinco
ATIVIDADES
33. Jogando-se um dado e sabendo-se quê foi obtído um número maior do quê 4, qual é a probabilidade de ele sêr um número par?
50%
34. (PUCCamp-SP) Lança-se um par de dados não viciados. Se a soma nos dois dados é 8, calcule a probabilidade de ocorrer a face 5 em um deles.
35. Na extração de uma carta de um baralho de 52 cartas, considere os eventos:
• A: sair um rei;
• B: sair uma carta de paus.
Determine:
a) P(A) e P(B)
;
b) P(A/B) e P(B/A)
;
36. Retirando-se duas cartas ao acaso, sem reposição, de um baralho de 52 cartas, qual é a probabilidade de o naipe da primeira sêr de paus e o da segunda sêr de cópas?
37. (Enem/MEC) Numa escola com 1.200 alunos foi realizada uma pesquisa sobre o conhecimento dêêsses em duas línguas estrangeiras, inglês e espanhol. Nessa pesquisa constatou-se quê 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um dêêsses idiomas. Escolhendo-se um aluno dessa escola ao acaso e sabendo-se quê ele não fala inglês, qual a probabilidade de quê esse aluno fale espanhol?
a)
b)
c)
d)
e)
alternativa a
38. (Famema-SP) Uma confekissão de roupas produziu um lote com um total de 150 camisetas, distribuídas entre os tamanhos P e M, sêndo 59 lisas e as demais êstampádas. Nesse lote, havia 100 camisetas tamãnho P, das quais 67 eram êstampádas. Retirando-se, ao acaso, uma camiseta dêêsse lote e sabendo quê seu tamãnho é M, a probabilidade de quê seja uma peça estampada é igual a
a) 36%.
b) 24%.
c) 48%.
d) 60%.
e) 72%.
alternativa c
39. (hú- hê- érre jota) Um instituto de pesquisa colheu informações para saber as intenções de voto no segundo turno das eleições para governador de um determinado estado. Os dados estão indicados no qüadro abaixo:
Intenção de voto |
Percentual |
|---|---|
Candidato A |
26% |
Candidato B |
40% |
Votos nulos |
14% |
Votos brancos |
20% |
Escolhendo aleatoriamente um dos entrevistados, verificou-se quê ele não vota no candidato B. A probabilidade de quê esse eleitor vote em branco é:
a)
b)
c)
d)
e)
alternativa d
40. (Enem/MEC) Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes 20% das declarações de imposto de renda quê lhe foram encaminhadas. Uma declaração é classificada como inconsistente quando apresenta algum tipo de êrro ou conflito nas informações prestadas. Essas declarações consideradas inconsistentes foram analisadas pêlos auditores, quê constataram quê 25% delas eram fraudulentas. Constatou-se ainda quê, dentre as declarações quê não apresentaram inconsistências, 6,25% eram fraudulentas. Qual é a probabilidade de, nesse ano, a declaração de um contribuinte sêr considerada inconsistente, dado quê ela era fraudulenta?
a) 0,0500
b) 0,1000
c) 0,1125
d) 0,3125
e) 0,5000
alternativa e
Página cento e noventa e seis
41. (Enem/MEC) A senha de um cofre é uma sequência formada por oito dígitos, quê são algarismos escolhidos de 0 a 9. Ao inseri-la, o usuário se esqueceu dos dois últimos dígitos quê formam essa senha, lembrando somente quê esses dígitos são distintos.
Digitando ao acaso os dois dígitos esquecidos, a probabilidade de quê o usuário acerte a senha na primeira tentativa é
a)
b)
c)
d)
e)
alternativa b
42. (Unicamp-SP) João e Maria estão passeando pela floresta. Para não se perderem no caminho, levaram consigo uma sacola com 100 pedrinhas, sêndo 60 pedrinhas brancas e 40 pedrinhas pretas. A cada 5 passos eles retiram aleatoriamente uma pedrinha da sacola e jogam-na no chão para marcar o caminho. Quando eles pararam para fazer um lanche, notaram quê já tí-nhão sido jogadas 35 pedrinhas brancas e 25 pedrinhas pretas. Qual a probabilidade de as próximas duas pedrinhas jogadas serem brancas?
alternativa b
a) .
b) .
c)
d) .
43. (hú- hê- érre jota) Para fazer o sorteio de um livro, quatro amigos colocaram três bolas brancas e duas pretas em uma caixa. Decidiram quê o primeiro a retirar uma bola preta ficará com o livro. Na ordem alfabética de seus nomes, cada um retira uma bola, ao acaso, sem devolvê-la à caixa. A probabilidade de o terceiro amigo retirar a primeira bola preta e ficar com o livro é igual a:
a) 10%
b) 20%
c) 30%
d) 40%
alternativa b
44. Elabore um problema em quê seja solicitada a probabilidade de ocorrência de dois eventos sucessivos, A e B, cuja resolução possa sêr determinada por:
P(A ∩ B) = P(A) ⋅ P(B/A)
Resposta pessoal.
45. O gerente de uma loja de brinquedos alugou uma “máquina de pelúcia”, na qual uma garra pega, aleatoriamente, um dos três bichos de pelúcia disponíveis: cachoorro, gato ou urso. Evandro e Mariana vão receber, cada um, um brinde dessa máquina e perceberam quê há exatamente 14 bichos de pelúcia na máquina, sêndo sete cachorros, cinco gatos e dois ursos. Qual é a probabilidade de Evandro e Mariana receberem bichos de pelúcia do mesmo tipo?
46. (Unésp)
Combate ao aédis egípti
O Ministério da Saúde convoca a população brasileira a manter permanentemente a mobilização nacional pelo combate ao aédis egípti, mosquito transmissor de quatro tipos de dengue, zika, chikungunya e febre amarela.
O período do verão é o mais propício à proliferação do mosquito, por causa das chuvas, e consequentemente é a época de maior risco de infekição por essas doenças. No entanto, a recomendação é não descuidar nenhum dia do ano.

(https://livro.pw/qeqei. Adaptado.)
Uma pessoa contraiu febre amarela, tratou-se e, algum tempo depois, contraiu dengue tipo 2. Supondo quê essa pessoa resida em uma cidade onde circulam com a mesma prevalência os vírus causadores de todas essas doenças, e quê essa pessoa venha a adquirir duas delas, a probabilidade de quê essas doenças sêjam dengue e chikungunya, nessa ordem, é
a) 25%.
b) 5%.
c) 15%.
d) 10%.
e) 30%.
alternativa c
Página cento e noventa e sete
Eventos independentes
A probabilidade condicional de um evento A, sabendo quê B ocorreu, geralmente, não é igual à probabilidade de A. Em notação matemática, indicamos esse fato por:
P(A/B) ≠ P(A)
Além díssu, dizemos quê os eventos A e B são dependentes.
Existem situações em quê a probabilidade condicional de um evento A, sabendo quê B ocorreu, é igual à probabilidade de A, isto é:
P(A/B) = P(A)
Nesse caso, dizemos quê o evento A é independente do evento B. Em outras palavras, a informação de quê B ocorreu não altera em nada a chance de ocorrência do evento A. Acompanhe o exemplo.
São jogados uma moeda e um dado cúbico cujas faces são numeradas de 1 a 6, ambos não viciados. Qual é a probabilidade de se obtêr o resultado de número 5 no dado, sabendo quê o resultado da moeda foi “cara”?
Adotando C para “coroa” e K para “cara”, o espaço amostral U com 12 eventos simples equiprováveis dêêsse experimento aleatório é:
U = {(C, 1), (C, 2), (C, 3), (C, 4), (C, 5), (C, 6), (K, 1), (K, 2), (K, 3), (K, 4), (K, 5), (K, 6)}
Considere os seguintes eventos de U:
• A: obtêr o resultado 5 no dado, note quê n(A) = 2;
• B: obtêr o resultado “cara” na moeda, note quê n(B) = 6;
• A ⋃ B: obtêr como resultado 5 no dado e “cara” na moeda, note quê n(A ∩ B) = 1.
• A/B: obtêr o resultado 5 no dado, sabendo quê saiu “cara” na moeda.
• A probabilidade do evento A, obtêr o resultado 5 no dado, é:
P(A) =
A probabilidade condicional do evento A dado B, obtêr 5 no dado, sabendo quê saiu “cara” na moeda, é:
P(A/B) =
Logo, a ocorrência do evento B não mudou a probabilidade do evento A, pois:
P(A/B) = P(A) =
Por isso, dizemos quê o evento A é independente de B.
Suponha quê A e B sêjam dois eventos independentes, isto é, P(A/B) = P(A). Substituindo P(A/B) por P(A) na fórmula da probabilidade condicional, temos:
P(A/B) = ⇒ P(A) = ⇒ P(A ∩ B) = P(A) ⋅ P(B)
Desse modo, definimos:
Se A e B são eventos independentes de um espaço amostral U, então:
P(A ∩ B) = P(A) ⋅ P(B)
Página cento e noventa e oito
ATIVIDADES RESOLVIDAS
13. Considere uma caixa contendo dez bolas idênticas, sêndo diferentes apenas pela côr, quatro são pretas e seis são azuis. Sorteando-se duas bolas, de modo quê a primeira bola retirada é recolocada na caixa antes de sêr sorteada a segunda, qual é a probabilidade:
a) de a primeira bola sêr preta e a segunda, azul?
b) de as duas bolas serem pretas?
Resolução
Seja U o espaço amostral com 10 eventos simples equiprováveis dêêsse experimento aleatório contendo os eventos:
• A: a primeira bola sorteada é preta;
• B: a segunda bola sorteada é azul;
• C: a segunda bola sorteada é preta.
a) Há 4 bolas pretas na caixa, logo a probabilidade do evento A é P(A) = .
Há 6 bolas azuis, e a primeira bola retirada retorna à caixa antes de sêr sorteada a segunda, então a probabilidade do evento B é P(B) = .
Por causa da reposição, a primeira bola retirada não interfere na probabilidade do segundo sorteio, ou seja, os eventos A e B são independentes, portanto:
P(A ∩ B) = P(A) ⋅ P(B) = = 0,24 = 24%
A probabilidade de sortear uma bola preta e, em seguida, uma azul é 24%.
b) Como a primeira bola sorteada retorna à caixa, a probabilidade do evento C é P(C) = .
Por causa da reposição, os eventos A e C são independentes, logo:
P(A ∩ C) = P(A) ⋅ P(C) = = 0,16 = 16%
A probabilidade de serem sorteadas duas bolas pretas é 16%.
14. (Unifesp) Um jovem possui dois despertadores. Um deles funciona em 80% das vezes em quê é colocado para despertar e o outro em 70% das vezes. Tendo um compromisso para daqui a alguns dias e preocupado com a hora, o jovem pretende colocar os dois relógios para despertar.
a) Qual é a probabilidade de quê os dois relógios venham a despertar na hora programada?
b) Qual é a probabilidade de quê nenhum dos dois relógios venha a despertar na hora programada?
Resolução
a) Sejam os eventos A e B, respectivamente, relógio 1 despertar e relógio 2 despertar. Logo, P(A) = e P(B) = . Assim, a probabilidade de ambos os relógios despertarem simultaneamente é:
P(A ∩ B) = = 0,56 = 56%
b) A probabilidade de quê nenhum dos dois relógios desperte é dada pelo cálculo das probabilidades dos eventos complementares. Logo, P() = e P() = .
Assim, a probabilidade de quê ambos os relógios não despertem é:
) = = 0,06 = 6%
Página cento e noventa e nove
15. Uma moeda é lançada quatro vezes. Qual é a probabilidade de sair pelo menos uma vez"cara"?
Resolução
Considere o evento A: sair pelo menos uma vez"cara".
Adotando K para"cara" e C para"coroa", temos a seguinte árvore de possibilidades:

dêsses 16 resultados possíveis, 15 apresentam pelo menos uma"cara". Portanto: P(A) = .
Um modo mais prático de resolver essa questão é calcular inicialmente a probabilidade dos casos desfavoráveis ao evento A, isto é, a probabilidade de"não sair nenhuma cara" (evento complementar de A). A única maneira de não sair"cara" é sair"coroa" nos quatro lançamentos. Assim:
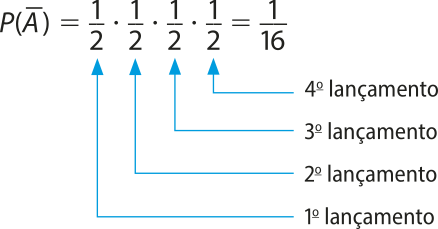
Portanto, a probabilidade de sair pelo menos uma"cara" é:
P(A) + P() = 1 ⇒ P(A) = 1 − P()
P(A) = 1 − ⇒ P(A) =
Página duzentos
ATIVIDADES
47. Um dado com as faces numeradas de 1 a 6, não viciado, é lançado duas vezes. Qual é a probabilidade de saírem números menóres do quê 3 nos dois lançamentos?
48. No lançamento de um dado e de uma moeda, qual é a probabilidade de obtermos"cara" e um número maior do quê 3?
49. Qual é a probabilidade de um casal ter quatro filhos, todos do sexo feminino?
50. Retirando-se duas cartas ao acaso, com reposição, de um baralho com 52 cartas, qual é a probabilidade de a primeira sêr de ouros e a segunda, de espadas?
51. Na gaveta de um armário, há duas chaves tipo A e uma tipo B. Em outra gaveta, há um cadeado quê é aberto pelas chaves do tipo A e três quê são abertos pelas chaves do tipo B. Uma pessoa escolhe, ao acaso, uma chave da primeira gaveta e um cadeado da segunda gaveta. Qual é a probabilidade de o cadeado sêr aberto pela chave escolhida?
52. (OBMEP) Em um jôgo, Pedro lança uma moeda para decidir quantas casas avançar. Quando sai cara, ele avança uma casa; quando sai coroa, ele avança duas casas. O jôgo acaba quando Pedro alcança ou ultrapassa a última casa. Faltam três casas para Pedro terminar o jôgo. Qual é a probabilidade de quê ele tire coroa em sua última jogada?
a)
b)
c)
d)
e)
alternativa d
53. (FGV-SP) Uma moeda é viciada de tal forma quê os resultados possíveis, cara e coroa, são tais quê a probabilidade de sair cara num lançamento é o triplo da de sair coroa.
a) Lançando-se uma vez a moeda, qual a probabilidade de sair cara?
b) Lançando-se três vezes a moeda, qual a probabilidade de sair exatamente uma cara?
54. (Inatel-MG) Uma caixa contém 4 cubos brancos e 2 pretos; outra contém 3 cubos brancos e 5 pretos. Extrai-se um cubo de cada caixa. Calcule a probidade de ambos os cubos serem branco
55. (Unésp) Um piloto de Fórmula 1 estima quê suas chances de subir ao pódio numa dada próva são de 60% se chover no dia da próva e de 20% se não chover. O Serviço de Meteorologia prevê quê a probabilidade de chover durante a próva é de 75%. Nessas condições, calcule a probabilidade de quê o piloto venha a subir ao pódio.
ou 50%
56. (Fuvest-SP) Uma urna contém 5 bolas brancas e 3 bolas pretas. Três bolas são retiradas ao acaso, sucessivamente, sem reposição. Determine
a) a probabilidade de quê tênham sido retiradas duas bolas pretas e uma bola branca.
b) a probabilidade de quê tênham sido retiradas duas bolas pretas e uma bola branca, sabendo-se quê as três bolas retiradas não são da mesma côr.
57. (Enem/MEC) Uma competição esportiva envolveu 20 equipes com 10 atletas cada. Uma denúncia à organização dizia quê um dos atletas havia utilizado substância proibida. Os organizadores, então, decidiram fazer um exame antidópim. Foram propostos três modos diferentes para escolher os atletas quê irão realizá-lo:
Modo I: sortear três atletas dentre todos os participantes;
Modo II: sortear primeiro uma das equipes e, desta, sortear três atletas;
Modo III: sortear primeiro três equipes e, então, sortear um atleta de cada uma dessas três equipes.
Considere quê todos os atletas têm igual probabilidade de serem sorteados e quê P(I), P(II) e P(III) sêjam as probabilidades de quê o atleta quê utilizou a substância proibida seja um dos escolhidos para o exame no caso do sorteio sêr feito pelo modo I, II ou III. Comparando-se essas probabilidades obtém-se
a) P(I) < P(III) < P(II)
b) P(II) < P(I) < P(III)
c) P(I) < P(II) = P(III)
d) P(I) = P(II) < P(III)
e) P(I) = P(II) = P(III)
alternativa e
Página duzentos e um
Probabilidades em espaços amostrais não discrétos
Os experimentos aleatórios estudados até o momento possuíam espaços amostrais discrétos com um número finito de eventos elementares. Entretanto, existem experimentos quê possuem espaços amostrais não discrétos, quê são indicados por intervalos reais, por exemplo.
Um ônibus chega sempre ao seu destino em qualquer instante entre 17 horas e 17 horas e 20 minutos. Qual é a probabilidade de, em determinado dia, ele chegar antes das 17 horas e 5 minutos?
pôdêmos considerar o intervalo real [0, 20], em quê 0 indica quê o ônibus chegou às 17 horas e 20 indica quê o ônibus chegou às 17 horas e 20 minutos, como o espaço amostral U dêêsse experimento aleatório, ou seja, U = [0, 20]. Além díssu, d fórma análoga, o evento A, chegar antes das 17 horas e 5 minutos, póde sêr indicado pelo intervalo real A = [0, 5[.
Para calcular a probabilidade de eventos em espaços amostrais expressos por intervalos reais, podemos admitir quê todos os pontos do intervalo são equiprováveis e considerar a porcentagem quê o evento representa em relação ao espaço amostral. No exemplo do ônibus, obissérve quê o comprimento do intervalo A em relação ao comprimento do espaço amostral U representa:
= 25%
Desse modo, podemos dizêr quê a probabilidade de o ônibus chegar antes das 17 horas e 5 minutos é 25%.
Para ler
• ABUCHAIBE, Rafael. Como é calculada chance de chuva quê serviços de meteorologia divulgam. BBC nius Brasil, [s. l.], 29 abr. 2023. Disponível em: https://livro.pw/kmhdu. Acesso em: 7 ago. 2024.
A reportagem relata algumas características das previsões meteorológicas e como devem sêr interpretadas.
ATIVIDADE RESOLVIDA
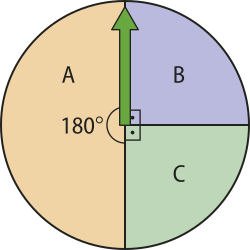
16. Um jôgo possui uma roleta dividida em 3 setores, A, B e C, cujos ângulos centrais estão indicados na figura. Após um giro, se o ponteiro parar sobre uma linha compartilhada por setores adjacentes, quê possuem um lado em comum, ele é girado novamente. Calcule a probabilidade de o ponteiro apontar para cada um dos setores após um giro aleatório.
Resolução
Vamos indicar por A, B e C, respectivamente, os eventos “o ponteiro apontar para o setor A”, “apontar para o setor B” e “apontar para o setor C”.
Como o giro é aleatório, admitiremos quê, após um giro, as posições finais do ponteiro possuem chances iguais. Além díssu, vamos considerar quê o comprimento do espaço amostral U é 360, pois uma volta completa do ponteiro possui 360°. De forma análoga, o comprimento do evento A é 180, o do evento B é 90 e o do evento C é 90. Calculando o percentual de quanto cada evento representa do espaço amostral, temos:
= 0,5 = 50%
= = 0,25 = 25%
Logo, a probabilidade de o ponteiro apontar para o setor A é 50%, para o setor B é 25% e para o setor C é 25%.
Página duzentos e dois
ATIVIDADES
58. (Enem/MEC) Em uma campanha promocional de uma loja, um cliente gira uma roleta, conforme a apresentada no esquema, almejando obtêr um desconto sobre o valor total de sua compra. O resultado é o quê está marcado na região apontada pela seta, sêndo quê todas as regiões são congruentes. Além díssu, um dispositivo impede quê a seta venha a apontar exatamente para a linha de fronteira entre duas regiões adjacentes. Um cliente realiza uma compra e gira a roleta, torcendo para obtêr o desconto mássimo.
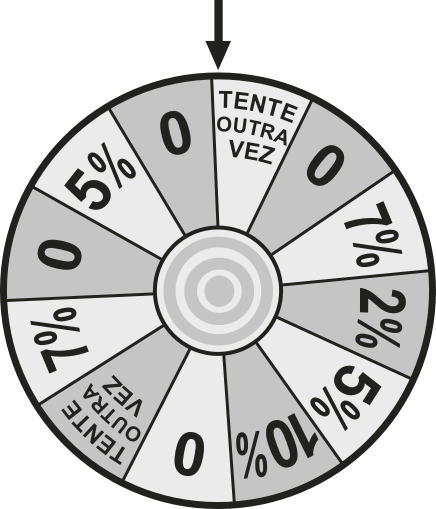
A probabilidade, em porcentagem, de esse cliente ganhar o desconto mássimo com um único giro da roleta é melhor aproximada por
a) 8,3.
b) 10,0.
c) 12,5.
d) 16,6.
e) 50,0.
alternativa a
59. (ú éfi érri jóta) Um ponto P é aleatoriamente selecionado num retângulo S de dimensões 50 cm por 20 cm. Considere, a partir de S, as seguintes regiões:
Região A – retângulo de dimensões 15 cm por 4 cm com centro no centro de S e
Região B – círculo de raio 4 cm com centro no centro de S.
Suponha quê a probabilidade de quê o ponto P pertença a uma região contida em S seja proporcional à área da região.
Determine a probabilidade de quê P pertença simultaneamente às regiões A e B.
60. (Unésp) A figura indica uma roleta circular, dividida em cinco setores. As posições finais do ponteiro giratório da roleta, após um giro aleatório em torno do centro do círculo, possuem mesmas probabilidades. Se, após o giro, o ponteiro para sobre a linha compartilhada por setores circulares contíguos, ele é girado novamente.
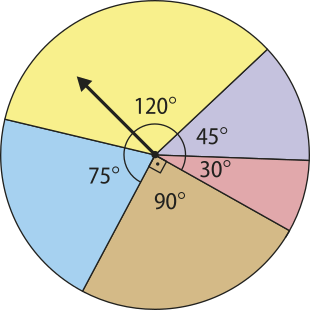
a) Girando-se ao acaso o ponteiro da roleta até quê ele pare em uma região do interior de algum dos cinco setores, qual a probabilidade de quê o ângulo central do setor seja obtuso? E qual a probabilidade de quê esse ângulo seja agudo?
A probabilidade de quê o ângulo central do setor seja obtuso é e a de quê seja agudo é .
b) Girando-se ao acaso duas vezes o ponteiro da roleta e anotando-se os dois ângulos obtidos, qual é a probabilidade de quê ao menos um deles seja ângulo interno de um polígono regular?
61. (Enem/MEC) Num determinado bairro há duas empresas de ônibus, ANDABEM e BOMPASSEIO, quê fazem o trajeto levando e trazendo passageiros do subúrbio ao centro da cidade. Um ônibus de cada uma dessas empresas parte do terminal a cada 30 minutos, nos horários indicados na tabéla.
Horário do ônibus
ANDABEM |
BOMPASSEIO |
|---|---|
... |
... |
6h00min |
6h10min |
6h30min |
6h40min |
7h00min |
7h10min |
7h30min |
7h40min |
... |
... |
Página duzentos e três
Carlos mora próximo ao terminal de ônibus e trabalha na cidade. Como não tem hora certa para chegar ao trabalho nem preferência por qualquer das empresas, toma sempre o primeiro ônibus quê sai do terminal. Nessa situação, pode-se afirmar quê a probabilidade de Carlos viajar num ônibus da empresa ANDABEM é:
a) um quarto da probabilidade de ele viajar num ônibus da empresa BOMPASSEIO.
b) um terço da probabilidade de ele viajar num ônibus da empresa BOMPASSEIO.
c) mêtáde da probabilidade de ele viajar num ônibus da empresa BOMPASSEIO.
d) duas vezes maior do quê a probabilidade de ele viajar num ônibus da empresa BOMPASSEIO.
e) três vezes maior do quê a probabilidade de ele viajar num ônibus da empresa BOMPASSEIO.
alternativa d
62. (hú- hê- érre jota) Para construir um alvo de dardos como o da figura 1, foram traçados dois círculos de centro D, um de raio r e outro de raio 2r, conforme ilustra a figura 2. Duas regiões são observadas no alvo: I, definida pelo círculo menor; II, a da coroa circular.
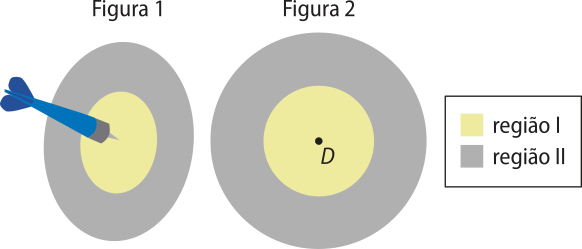
Considere quê um dardo lançado por uma pessoa sempre atinge o alvo em qualquer ponto das regiões I ou II, sêndo a probabilidade de acertar cada região diretamente proporcional à sua respectiva área. Assim, ao lançar um dardo, a probabilidade de essa pessoa acertar a região II é igual a:
a)
b)
c)
d)
alternativa c
63. (UPE) A figura a seguir é composta por três roletas em formato circular, cada uma dividida em três regiões A, B e C e com uma seta com origem em seus centros. Após girar a seta, a chance de quê esta pare em qualquer parte da roleta é sempre a mesma.
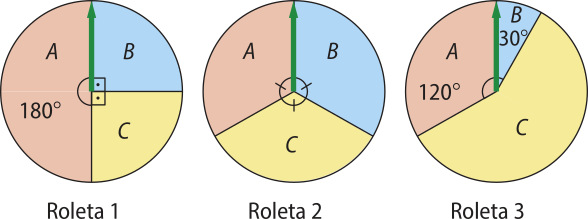
As setas nas três roletas são giradas simultaneamente e sabe-se quê todas pararam em exatamente uma das regiões A, B ou C. Seja P(A) a probabilidade de as três setas pararem na região A, P(B) a probabilidade de as três setas pararem na região B e P(C) a probabilidade de as três setas pararem na região C. É CORRETO afirmar quê
a) P(A) = P(B) = P(C)
b) P(A) > P(B) > P(C)
c) P(A) > P(C) > P(B)
d) P(C) > P(A) > P(B)
e) P(C) > P(B) > P(A)
alternativa c
64. (FGV-SP) Duas pessoas combinaram de se encontrar entre 12h00 e 13h00. Elas também combinaram de esperar até 20 minutos pela outra pessoa depois de chegar ao local do encontro. Assumindo quê os horários de chegada ao local de encontro são uniformemente distribuídos no intervalo de uma hora, quê vai das 12h00 às 13h00, a probabilidade de quê elas se encontrem no intervalo combinado é igual a
a)
b)
c)
d)
e)
alternativa c
Página duzentos e quatro
CONEXÕES com...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Prevenção da gravidez na adolescência
A gravidez na adolescência é um grave problema de saúde pública, por causa das diversas consequências para a mãe, para o bebê e para todo o núcleo familiar. Uma gravidez não planejada póde trazer uma série de impactos físicos, psicológicos e sociais.
A Organização Mundial de Saúde (hó ême ésse) considera gravidez na adolescência a gestação quê ocorre entre 10 e 20 anos de idade. Os riscos para a menina gestante são mortalidade materna, eclâmpsia, diabetes gestacional, hipertensão, anemia, infekições urinárias e infekições sexualmente transmissíveis (ISTs). Para o bebê, existe maior probabilidade de parto prematuro, baixo peso ao nascer (menos de 2,5 kg), desnutrição fetal nos casos em quê a mãe tem anemia, malformações e síndrome de Down.
Em relação aos impactos psicológico e social, é preciso lidar com a quêstão da autoimagem, porque ocorre uma rápida mudança corporal na gestação. A permanência na escola também é dificultada, 70% das adolescentes que engravidam abandonam a escola e, consequentemente, anulam ou adiam o sonho de cursar uma universidade. Além díssu, há a dificuldade de arrumar e conciliar um emprego e cuidar de uma criança.
No Brasil, a taxa de nascimentos de crianças filhas de mães entre 15 e 19 anos é 50% maior do quê a média mundial – a taxa mundial é estimada em 46 nascimentos a cada mil meninas, enquanto no Brasil estão estimadas 68,4 gestações nessa fase da vida.
A situação ainda é mais preocupante quando é analisado o recorte de crianças e adolescentes entre 10 e 14 anos. Em 2020, foram registradas 17,5 mil mães nessa faixa etária. Na última década, a Região Nordeste foi a quê mais teve casos de gravidez com esse perfil, totalizando 61,2 mil casos, seguida pela Região sudéste, com 42,8 mil. Observe os dados no gráfico a seguir.
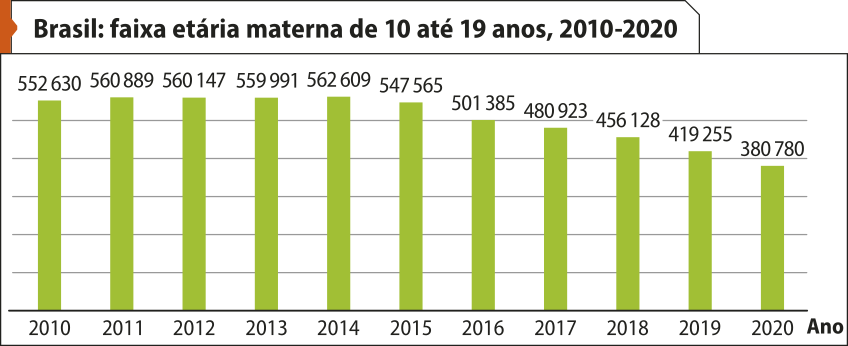
Fonte: BRASIL. Ministério dos Direitos Humanos e da Cidadania. Casos de gravidez na adolescência diminuíram, em média, 18% desde 2019. Brasília, DF: MDHC, 31 out. 2022. Disponível em: https://livro.pw/hjylg. Acesso em: 16 out. 2024.
Por isso, há a necessidade de ações para a prevenção da gravidez na adolescência, como a Semana Nacional de Prevenção da Gravidez na Adolescência, quê acontece anualmente na primeira semana de fevereiro, voltada para adolescentes, jovens, pais ou responsáveis.
Há também uma campanha de distribuição de métodos contraceptivos, como preservativo masculino ou feminino, anticoncepcionais, entre outros, realizada pelo Sistema Único de Saúde (SUS), quê ajuda no planejamento familiar e na prevenção de algumas infekições sexualmente transmissíveis.
Página duzentos e cinco
Evitar uma gravidez indesejada é responsabilidade do homem e da mulher. Existem vários métodos anticoncepcionais, obissérve alguns a seguir.
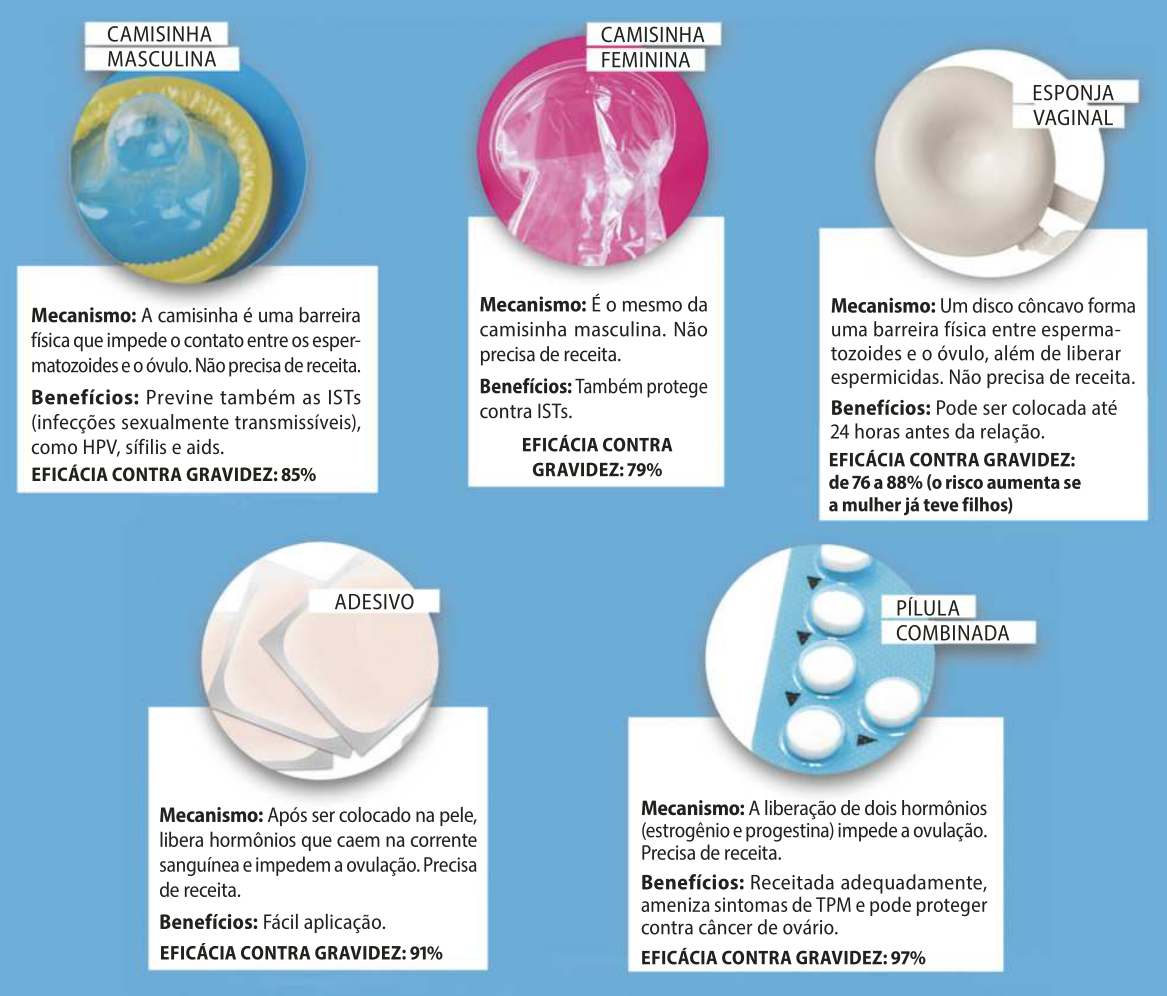
Fontes dos dados: RIBEIRO, Maiara. Gravidez na adolescência: quais são os impactos? [S. l.]: Portal Drauzio varélla, 28 dez. 2022. Disponível em: https://livro.pw/exkmj.
FUJITA JUNIOR, Luiz. Principais métodos anticoncepcionais de fácil acesso: infográfico. [S. l.]: Portal Drauzio varélla, 2 jan. 2024. Infográfico. Disponível em: https://livro.pw/dacsw.
BRASIL. Ministério dos Direitos Humanos e da Cidadania. Casos de gravidez na adolescência diminuíram, em média, 18% desde 2019. Brasília, DF: MDHC, 31 out. 2022. Disponível em: https://livro.pw/hjylg. Acessos em: 16 out. 2024.
Ver as Orientações para o professor.
![]() Agora, reúna-se a mais 3 ou 4 côlégas, e façam as atividades a seguir.
Agora, reúna-se a mais 3 ou 4 côlégas, e façam as atividades a seguir.
1. Como uma pessoa póde determinar qual método contraceptivo utilizará? Somente a eficácia é suficiente para determinar o método a sêr utilizado?
2. Levantem hipóteses para explicar os motivos quê levam o Brasil a ter índices 50% maiores de gravidez na adolescência do quê a média mundial.
3. Produzam e publiquem um material em suas rêdes sociais para conscientização sobre a prevenção da gravidez na adolescência.
Página duzentos e seis
EXPLORANDO A TECNOLOGIA
freqüência relativa e Probabilidade
Imagine jogar uma moeda não viciada n vezes e calcular a freqüência relativa do resultado “cara”, ou seja, o número de vezes quê saiu “cara” dividido por n. A probabilidade de sêr ôbitída “cara” ao jogar essa moeda é 0,5. Desse modo, à medida quê o número de repetições n dêêsse experimento aumenta indefinidamente, é esperado quê a freqüência relativa do resultado “cara” tenda a se estabilizar próximo de 0,5. Em uma linguagem matemática, dizemos quê ela vai convergir para 0,5.
Nesta seção, vamos construir um programa de computador quê sorteia um número de 1 a 50. Inicialmente, ele repetirá esse experimento aleatório 30 vezes e calculará a freqüência relativa dos números pares sorteados, ou seja, a quantidade de pares sorteados dividida por 30. Depois, ele será reprogramado para repetir esse procedimento 100, 1.000 e 10.000 vezes. Com isso, você poderá observar como a freqüência relativa dos números pares sorteados tende a se estabilizar e se aprossimár da probabilidade 0,5, pois a probabilidade de sortear um número par de 1 a 50 é 0,5.
Vamos realizar a atividade no Scratch, e a programação final terá a configuração indicada na imagem a seguir. Durante as etapas da programação, consulte essa configuração sempre quê necessário.
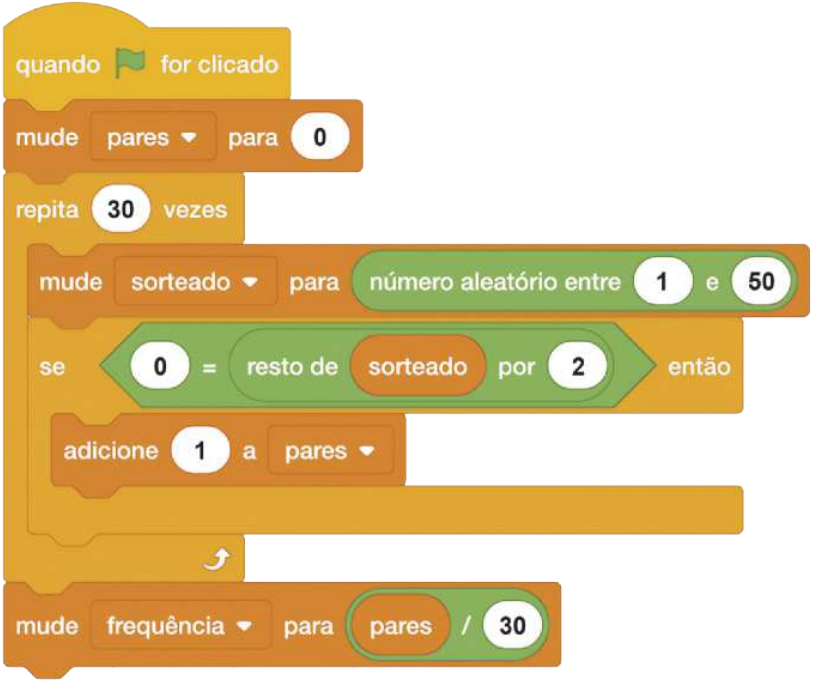
I. Para iniciar, acéçi o línki https://livro.pw/jqetp (acesso em: 2 nov. 2024), clique em Criar, altere o idioma para Português Brasileiro no menú Configurações, ![]() , e siga as etapas.
, e siga as etapas.
Clique na categoria Eventos e arraste para a área de trabalho o bloco indicado na imagem.

Página duzentos e sete
II. Clique na categoria contrôle e arraste o bloco indicado na imagem, encaixando-o no bloco do passo anterior. Essa repetição será referente ao sorteio dos 30 números aleatórios. Portanto, substitua o número 10, quê aparece automaticamente no comando, por 30; para isso, clique em cima do 10 e digite “30”.

III. Clique na categoria Variáveis, em seguida clique em Criar uma variável e crie a variável"sorteado". Além díssu, é necessário contar quantos números pares foram sorteados; assim, criaremos outra variável e a nomearemos"pares". Por fim, é necessária, ainda, uma variável quê armazenará a freqüência relativa de o número sorteado sêr par. Essa variável será a"frequência". Após a criação das três variáveis, deixe selecionada em azul apenas a variável"frequência". Dessa maneira, apenas ela ficará visível para o usuário.
IV. Ainda em Variáveis, arraste o bloco indicado na imagem e substitua o texto “minha variável” preestabelecido por"sorteado". Arraste-o para dentro do bloco Repita.

V. Desejamos sortear números entre 1 e 50. Assim, vá à categoria Operadores, escolha o comando indicado na imagem e substitua o valor 10 preestabelecido por “50”.

Depois, encaixe-o no lugar do 0 no bloco quê foi apresentado em IV, de modo quê fique como na imagem a seguir.

VI. Para verificar se um número natural é par, o résto da divisão dêêsse número por 2 deve sêr igual a zero. Assim, vamos introduzir um comando condicional. Na categoria contrôle, selecione o comando indicado na imagem e encaixe-o dentro do bloco Repita.
VII. Na categoria Operadores, arraste o bloco indicado na côr vêrde na imagem para dentro do bloco Se, formando a seguinte estrutura.
Página duzentos e oito
VIII. No lugar do 50, é preciso colocar o operador indicado na imagem, quê vai analisar o résto da divisão.

Depois, arraste a variável"sorteado" para dentro do campo vazio depois de "resto de" e preencha com"0" o campo vazio antes do sinal de igualdade e com"2" o campo vazio depois de"por", para quê a condição seja atendida.Esse bloco ficará como indicado na imagem a seguir.

IX. Se a condição imposta for satisfeita, deverá sêr adicionada uma unidade à variável"par". Para isso, clique na categoria Variáveis e, depois, selecione o comando a seguir, substituindo"minha variável" pela variável"pares".

Encaixe esse bloco dentro do bloco Se e será ôbitída a configuração a seguir.
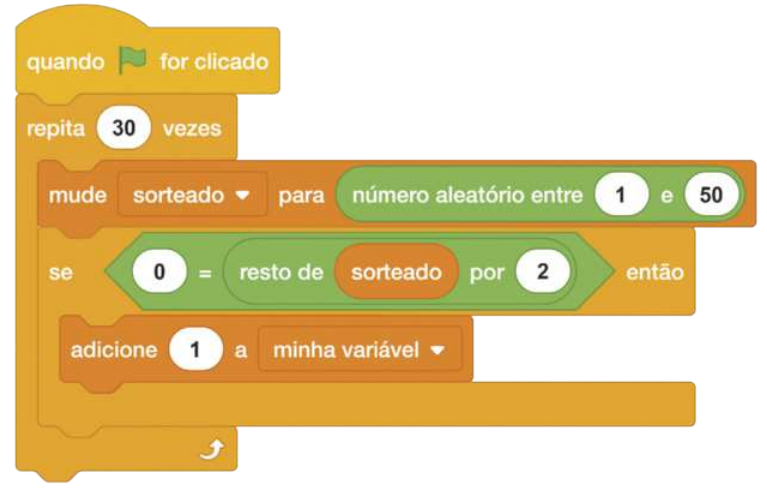
X. Sintetizando o quê foi feito até aqui: o programa inicia quando a bandeira vêrde é clicada. Na sequência, é repetido 30 vezes o processo de:
• sortear um número entre 1 e 50;
• verificar se o número sorteado é par;
• se for par, adicionar 1 ao contador de números pares.
Página duzentos e nove
XI. Para calcular a freqüência relativa dos números pares sorteados, clique em
Variáveis e arraste o bloco de côr laranja indicado na imagem para quê fique abaixo do bloco Repita.

Substitua o texto “minha variável” preestabelecido por"frequência". Depois selecione, na categoria Operadores, o comando indicado na côr vêrde na imagem e coloque-o no bloco de côr laranja, no lugar do 0. No primeiro espaço vazio, insira a variável "pares" e, no segundo, o número"30".

XII. Clicando na bandeira vêrde, no topo da área de trabalho, a variável"frequência" apresentará a freqüência relativa dos números pares sorteados. Ao clicar novamente na bandeira vêrde, o novo experimento vai sêr feito adicionando os novos pares ao número de pares do experimento anterior. Para evitar esse problema, é necessário colocar, no início do programa, uma linha quê deixe o contador de número de pares zerado antes de realizar um novo experimento. Assim, clique em Variáveis e arraste o bloco indicado na imagem para antes do bloco Repita.

Troque o texto"minha variável" preestabelecido por"pares", deixando o 0 como está. Assim, a cada novo experimento, o contador de números pares será zerado.
Agora, faça o quê se pede nas atividades a seguir.
1. Utilize o programa criado para responder aos itens.
a) Clique na bandeira vêrde e registre a freqüência relativa dos números pares sorteados ao repetir o experimento 30 vezes. Que freqüência você obteve?
A resposta depende do experimento.
b) Mude a configuração da programação para repetir 100 vezes o experimento, ou seja, mude os campos quê contêm o número 30 para 100. Clique novamente na bandeira vêrde e registre a freqüência relativa. Que freqüência você obteve?
A resposta depende do experimento.
c) Altere novamente a configuração para repetir o experimento 1.000 vezes e depois 10.000 vezes e anote as freqüências relativas observadas em cada configuração. Que freqüências você obteve?
A resposta depende do experimento.
d) De acôr-do com as respostas obtidas nos itens anteriores, o quê aconteceu com a freqüência relativa dos números pares sorteados durante esse processo?
Espera-se quê os estudantes respondam quê, conforme configurou-se um número maior para o número de repetições do experimento, obteve-se uma freqüência relativa mais próxima de 0,5.
2. Crie um programa quê calcule a chance de, ao sortearmos 50 números entre 1 e 100, ele sêr múltiplo de 2 ou múltiplo de 3.
Elaboração do estudante.
Página duzentos e dez
ATIVIDADES COMPLEMENTARES
1. (UFRR) O Role Playing Game (RPG) de mesa possui um dado conhecido entre os jogadores como D8. êste dado honesto possui 8 faces pentagonais, enumeradas de 1 a 8, com arestas de mesma medida. Jogando duas vezes êste dado, a probabilidade da soma das faces resultar em 8 é de
a)
b)
c)
d)
e)
alternativa e
2. (Cesgranrio-RJ) Em uma amostra de 500 peças, existem exatamente quatro defeituosas. Retirando-se ao acaso uma peça dessa amostra, a probabilidade de ela sêr perfeita é de:
a) 99,0%
b) 99,1%
c) 99,2%
d) 99,3%
e) 99,4%
alternativa c
3. (Vunesp-SP) Numa pesquisa feita com 200 homens, observou-se quê 80 eram casados, 20 separados, 10 eram viúvos e 90 eram solteiros. Escolhido um homem ao acaso, a probabilidade de ele não sêr solteiro é:
a) 0,65
b) 0,6
c) 0,55
d) 0,5
e) 0,35
alternativa c
4. (UFRGS-RS) Considere um hekzágono regular convexo com vértices, A, B, C, D, E e F. Tomando dois vértices ao acaso, a probabilidade de eles serem extremos de uma diagonal do hekzágono é
a)
b)
c)
d)
e) 1
alternativa c
5. (UEG-GO) Um jôgo de programa de auditório entre dois participantes consiste em rodar dois piões idênticos, em forma de prisma regular hexagonal, cujas faces laterais estão numeradas de 1 a 6, conforme ilustra a figura.

Ganha o prêmio do jôgo o participante quê obtiver, na soma das faces dos dois piões, a maior pontuação. Por exemplo: se um participante rodar os piões e obtiver face 3 no primeiro pião e face 4 no segundo pião, ele soma 7 pontos. Em caso de mesma pontuação (empate), nenhum participante ganha o prêmio. Dessa forma, se o primeiro participante roda os piões e obtém face 4 no primeiro pião e face 5 no segundo pião, a probabilidade de ele ganhar o prêmio dêêsse jôgo é de
a)
b)
c)
d)
e)
alternativa d
6. (Fuvest-SP) Em uma urna, há bolas amarelas, brancas e vermelhas. Sabe-se quê:
I. A probabilidade de retirar uma bola vermelha dessa urna é o dôbro da probabilidade de retirar uma bola amarela.
II. Se forem retiradas 4 bolas amarelas dessa urna, a probabilidade de retirar uma bola vermelha passa a sêr .
III. Se forem retiradas 12 bolas vermelhas dessa urna, a probabilidade de retirar uma bola branca passa a sêr
A quantidade de bolas brancas na urna é
a) 8.
b) 10.
c) 12.
d) 14.
e) 16.
alternativa c
7. (Unicamp-SP) Um dado não tendencioso de seis faces será lançado duas vezes. A probabilidade de quê o maior valor obtído nos lançamentos seja menor do quê 3 é igual a
a)
b)
c)
d)
alternativa d
Página duzentos e onze
8. (Enem/MEC) Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima em 30% a probabilidade da ocorrência de chuva nessa região.
Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
a) 0,075
b) 0,150
c) 0,325
d) 0,600
e) 0,800
alternativa c
9. (Uneb-BA) Das pessoas quê procuraram atendimento em um posto de saúde cérto dia, constatou-se quê 60% eram mulheres, 60% tí-nhão mais de 18 anos e 85% eram mulheres ou tí-nhão mais de 18 anos. Escolhendo-se, ao acaso, a ficha de um dêêsses pacientes, a probabilidade de ele sêr um homem, se tiver mais de 18 anos, é igual a
a)
b)
c)
d)
e)
alternativa e
10. (UFRGS-RS) As máquinas A e B produzem o mesmo tipo de parafuso. A porcentagem de parafusos defeituosos produzidos, respectivamente, pelas máquinas A e B é de 15% e de 5%. Foram misturados, numa caixa, 100 parafusos produzidos por A e 100 produzidos por B. Se tirarmos um parafuso ao acaso e ele for defeituoso, a probabilidade de quê tenha sido produzido pela máquina A é de
a) 10%
b) 15%
c) 30%
d) 50%
e) 75%
alternativa e
11. (EsPCEx-SP) A probabilidade de um casal ter um filho de olhos azuis é igual a . Se o casal pretende ter 4 filhos, a probabilidade de quê no mássimo dois tênham olhos azuis é:
a)
b)
c)
d)
e)
alternativa c
12. (UniCesumar-PR) O professor de Anatomia de um curso de Medicina preparou 20 kestões para uma próva oral, sêndo 12 sobre Sistema Respiratório, das quais 9 são difíceis, e preparou, também, 8 kestões sobre Sistema Digestivo, das quais 6 são difíceis. Escreveu cada quêstão em um cartão e misturou todos eles sobre a mesa, de modo quê os alunos não podiam identificar seus registros. Um dos alunos do curso pegou, ao acaso, um dos cartões. Sabendo que nesse cartão há uma questão difícil, qual é a probabilidade de essa questão tratar sobre Sistema Respiratório?
a) 55%.
b) 60%.
c) 65%.
d) 70%.
e) 80%.
alternativa b
13. (IFMA) Um professor de matemática solicitou aos seus alunos quê identificassem a quantidade de anagramas possíveis de serem formados com as lêtras da palavra chatbot. Se cada um dêêsses anagramas fosse escrito em um pedaço de papel e sorteado, aleatoriamente, apenas um papel, a probabilidade de o anagrama sorteado iniciar e terminar com lêtras iguais é, aproximadamente, de
a) 4,8%.
b) 11,9%.
c) 2,4%.
d) 14,3%
alternativa a
14. (FMABC-SP) Considere três caixas contendo cartelas de cérto medicamento. A caixa P tem 10 cartelas, das quais 4 já ultrapassaram o prazo de validade. A caixa Q tem 6 cartelas, das quais 1 já ultrapassou o prazo de validade, e a caixa R tem 9 cartelas, das quais 3 já ultrapassaram o prazo de validade. Tomando-se aleatoriamente uma das caixas e retirando-se ao acaso uma cartela dessa caixa, a probabilidade de quê essa cartela contenha medicamento com prazo de validade ultrapassado é de
a)
b)
c)
d)
e)
alternativa d
15. (hú- hê- érre jota)
População agredida fisicamente no Brasil em 2009
côr ou raça |
Homens |
Mulheres |
|---|---|---|
Branca |
567.000 |
474.000 |
Preta |
880.000 |
608.000 |
Adaptado de IBGE/PNAD, 2009.
A partir dos dados da tabéla, escolhe-se ao acaso uma pessoa dessa população. Sabendo quê essa pessoa é uma mulher, a probabilidade de ela sêr preta é mais próxima de:
a) 0,64
b) 0,56
c) 0,44
d) 0,36
alternativa b
Página duzentos e doze
16. (Enem/MEC) Em um colégio público, a admissão no primeiro ano se dá por sorteio. Neste ano há 55 candidatos, cujas inscrições são numeradas de 01 a 55. O sorteio de cada número de inscrição será realizado em etapas, utilizando-se duas urnas. Da primeira urna será sorteada uma bola, dentre bolas numeradas de 0 a 9, quê representará o algarismo das unidades do número de inscrição a sêr sorteado e, em seguida, da segunda urna, será sorteada uma bola para representar o algarismo das dezenas dêêsse número. Depois do primeiro sorteio, e antes de se sortear o algarismo das dezenas, as bolas quê estarão presentes na segunda urna serão apenas aquelas cujos números formam, com o algarismo já sorteado, um número de 01 a 55.
As probabilidades de os candidatos de inscrição número 50 e 02 serem sorteados são, respectivamente,
a) e
b) e
c) e
d) e
e) e
alternativa a
17. (Enem/MEC) No alojamento de uma universidade, há alguns quartos com o padrão superior ao dos demais. Um dêêsses quartos ficou disponível, e muitos estudantes se candidataram para morar no local. Para escolher quem ficará com o quarto, um sorteio será realizado. Para esse sorteio, cartões individuais com os nomes de todos os estudantes inscritos serão depositados em uma urna, sêndo quê, para cada estudante de primeiro ano, sêrá depositado um único cartão com seu nome; para cada estudante de segundo ano, dois cartões com seu nome; e, para cada estudante de terceiro ano, três cartões com seu nome. Foram inscritos 200 estudantes de primeiro ano, 150 de segundo ano e 100 de terceiro ano. Todos os cartões têm a mesma probabilidade de serem sorteados. Qual a probabilidade de o vencedor do sorteio ser um estudante de terceiro ano?
a)
b)
c)
d)
e)
alternativa e
18. (IFMG) Um determinado jôgo com várias cartas com dêzê-nhôs de animais é jogado com as seguintes regras, em ordem:
(1) A banca sorteia e mostra 4 cartas, ainda sem uma ordem definida;
(2) Cada jogador recebe outras 3 cartas e as coloca lado a lado em uma ordem quê não poderá sêr mudada;
(3) A banca agora pega as 4 cartas sorteadas no komêsso e as coloca lado a lado d fórma aleatória;
(4) Vence o jogador quê conseguir enxergar exatamente sua sequência, da esquerda para direita, dentro da sequência da banca.
Considere agora as cartas sorteadas pela banca em determinada partida, ainda fora de ordem, conforme regra (1):

■ CARTAS DA BANCA
Nesta partida, cérto jogador recebeu e organizou suas 3 cartas na seguinte sequência, conforme regra (2):

■ SEQUÊNCIA DO JOGADOR
Note quê se, por exemplo, a sequência da banca fosse a apresentada, o jogador ganharia a partida, pois sua sequência aparece dentro da sequência da banca.
A banca então embaralha suas quatro cartas sorteadas e irá colocá-las em ordem d fórma aleatória.
Neste momento, a probabilidade dêste jogador vencer a partida conforme as regras é de, aproximadamente,
a) 4%
b) 8%
c) 17%
d) 75%
alternativa c
Página duzentos e treze
19. (OBMEP) Em um teatro, cinco garotos e cinco garotas escolheram aleatoriamente seus lugares em uma fila com exatamente 10 cadeiras. Dado quê as cinco garotas estão em 5 cadeiras adjacentes, qual é a probabilidade de quê os cinco garotos também estejam em 5 cadeiras adjacentes?

a) 1
b)
c)
d)
e)
alternativa c
20. (IFMG) JORGE, um namorado muito dedicado, mandou fazer para presentear sua amada uma coleção de cinco moedas em quê em uma das faces foram desenhadas as lêtras de seu nome e na outra as lêtras do nome de ALINE. Elas foram feitas d fórma quê a primeira moeda tenha a letra J em uma das faces e a letra A na outra, a segunda moeda tenha a letra O em uma face e a letra L na outra, e assim sucessivamente. A probabilidade de lançadas todas as moedas, uma por vez, na ordem dos nomes, e se formár exatamente JORGE ou ALINE é igual a
a)
b)
c)
d)
alternativa c
PARA REFLETIR
Neste Capítulo, estudamos e analisamos uma diversidade de fenômenos e experimentos aleatórios por meio de um modelo probabilístico. Para isso, aprendemos a descrever e associar a cada experimento aleatório um espaço amostral com eventos elementares equiprováveis, a classificar os eventos de um espaço amostral e a determinar suas probabilidades.
Estudamos também probabilidade condicional, probabilidade de eventos sucessivos e probabilidade de eventos independentes. Além díssu, na seção Explorando a tecnologia, trabalhamos as relações entre a freqüência relativa e a probabilidade.
Agora, vamos refletir a respeito das aprendizagens dêste Capítulo.
• Quando associamos um espaço amostral a um experimento aleatório, o quê devemos analisar?
• Liste os diferentes tipos de evento de um espaço amostral e explique como você faz para identificar cada um.
• Elabore um texto explicando as relações e as diferenças entre os conceitos de probabilidade condicional, probabilidade de eventos sucessivos e probabilidade de eventos independentes.
• Qual é a diferença entre o cálculo de uma probabilidade e o cálculo de uma freqüência relativa?
• As informações presentes na seção Conexões com..., sobre os métodos contraceptivos quê auxiliam tanto na prevenção da gravidez precoce quanto na prevenção contra as ISTs contribuíram para esclarecer alguma dúvida quê você tinha sobre o tema?
• Na seção História da Matemática, você leu quê Jerônimo Cardano se apoiou na observação dos resultados dos jogos de azar para construir sua teoria. No seu entendimento, como estudar probabilidade póde contribuir para quê as pessoas tênham consciência de quê jogos de azar as prejudicam em vários aspectos?
Respostas pessoais.
Página duzentos e quatorze
