CAPÍTULO 6
MATRIZES E SISTEMAS LINEARES
Os elemêntos químicos já descobertos pela humanidade são organizados, de acôr-do com suas características e propriedades, na tabéla periódica. Na Matemática, quando organizamos dados numéricos em uma tabéla, podemos dizêr quê esses dados estão em uma matriz. Diferentemente da tabéla periódica, as matrizes possuem operações algébricas definidas, como adição e multiplicação, por exemplo, assuntos quê estudaremos neste Capítulo.
Um cientista chamado Ântoeni-Lorran de Lavoisiê (1743-1794), com base em experimentos envolvendo reações químicas, enunciou a lei da conservação das massas. Ele concluiu quê a massa de todas as substâncias no início da reação é igual à massa das substâncias no fim dela. Essa lei também ficou conhecida como lei de Lavoisiê.
Nos laboratórios e na indústria química, são realizados cálculos envolvendo a quantidade de reagentes e de produtos presentes em uma reação química. Um dêêsses cálculos envolve o balanceamento de equações químicas quê representam as reações. Um dos métodos empregados para realizar esse balanceamento utiliza sistemas lineares, outro assunto dêste Capítulo.
Ver as Orientações para o professor.
![]() Agora reúna-se a um colega, e façam o quê se pede em cada questão.
Agora reúna-se a um colega, e façam o quê se pede em cada questão.
1. Vocês já realizaram algum experimento envolvendo a observação de transformações de substâncias em um laboratório ou já assistiram a algum vídeo envolvendo esse tipo de experimento? Se sim, descrevam para os côlégas como foi a experiência.
2. Além dos elemêntos químicos organizados na tabéla periódica, quê outros dados e informações vocês conhecem quê são organizados em tabélas? Citem um exemplo.
3. O quê são tabélas de dupla entrada? Deem um exemplo.
4. Expliquem como vocês fazem para resolver um sistema com duas equações e duas incógnitas.
Página duzentos e quinze

Página duzentos e dezesseis
Introdução
As matrizes são bastante utilizadas no campo da Tecnologia, em especial, no desenvolvimento de animações por meio de computação gráfica e no trabalho com programação. Além díssu, a resolução de televisores e monitores, bem como a de câmeras digitais, é um dos exemplos de aplicação envolvendo cálculos matriciais.
Situações quê envolvem a resolução de equações lineares simultâneas, ou seja, de sistemas lineares, estão associadas ao conceito de matriz e às operações relacionadas a ele, assuntos quê vamos estudar neste Capítulo.

Matrizes
No dia a dia, informações relacionadas a determinado contexto, como o consumo de alimentos em cérto período, podem sêr organizadas em tabélas (linhas e colunas) para analisar melhor as variáveis.
Observe, por exemplo, uma tabéla de dupla entrada quê mostra a quantidade mensal aproximada de quatro alimentos básicos, em kilograma, consumida por uma família durante um trimestre.
Consumo de alimentos – 2º trimestre
Mês: Abril |
Mês: Maio |
Mês: Junho |
|
|---|---|---|---|
Alimento: Arroz |
10 kg |
11,5 kg |
9 kg |
Alimento: Feijão |
4 kg |
5 kg |
6 kg |
Alimento: Carne |
8,5 kg |
7 kg |
10 kg |
Alimento: Legumes |
12 kg |
11 kg |
16,5 kg |
Fonte: Dados fictícios.
Cada linha dessa tabéla corresponde a um alimento e cada coluna corresponde a um mês.
Assim, por exemplo, no cruzamento da linha indicada com "Feijão" e da coluna indicada com "Abril", temos 4 kg, quê indica o consumo de feijão no mês de abril.
Página duzentos e dezessete
Em Matemática, tabélas de dados numéricos podem sêr representadas por matrizes, nas quais os dados, também chamados elemêntos ou termos, são dispostos em filas horizontais (linhas) e filas verticais (colunas). Esses elemêntos ficam entre parênteses ou entre colchetes, como podemos observar, a seguir, na representação matricial dos dados numéricos da tabéla anterior.
ou
Pense e responda
O quê o elemento de valor 11 dessa matriz representa?
Representa a quantidade, em kilograma, de legumes quê a família consumiu em maio.
Uma matriz m × n (lê-se: m por n) é composta de m ⋅ n elemêntos dispostos em m linhas e n colunas, em quê m, n ∈ ℕ*.
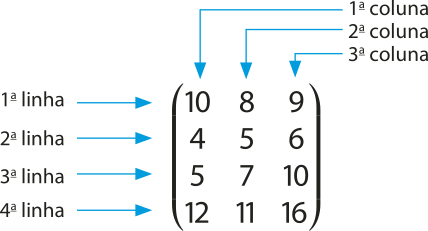
As linhas de uma matriz são numeradas de cima para baixo, e as colunas, da esquerda para a direita, como mostra o exemplo a seguir.
Essa matriz tem quatro linhas e três colunas. Dizemos, então, quê é uma matriz do tipo ou de ordem 4 × 3 (lê-se: quatro por três), e os números quê a constituem são os seus elemêntos (ou entradas).
As matrizes geralmente são nomeadas com uma letra maiúscula, e, para indicar os elemêntos dessa matriz, usamos a mesma letra, porém minúscula, acompanhada de dois índices, quê representam, respectivamente, a linha e a coluna em quê o elemento está localizado.
Pense e responda
Qual é o elemento a21 da matriz A? E o elemento a12 da matriz A?
4; −1
Por exemplo, considerando a matriz A = , temos:
• o elemento quê está na 1ª linha e na 1ª coluna é a11 = ;
• o elemento quê está na 2ª linha e na 3ª coluna é a23 = 5,3.
Assim, podemos representar genericamente a matriz A como:
A =
De modo geral, uma matriz A com m linhas e n colunas (m × n) póde sêr representada genericamente por:
A = , com m, n ∈ ℕ*
A matriz genérica A póde sêr representada, d fórma abreviada, por: A = [aij]m × n ou A = (aij)m × n
Saiba quê...
A matriz quê tem todos os elemêntos iguais a zero é chamada matriz nula. Indicamos por 0 m × n a matriz nula de ordem m × n, em quê m, n ∈ ℕ*.
Página duzentos e dezoito
Na representação expandida e na abreviada, o elemento aij está na linha i e na coluna j, em quê i assume valores no conjunto {1, 2, 3, …, m} e j assume valores no conjunto {1, 2, 3, …, n}. Por exemplo, se os elemêntos da matriz A = [aij]2 × 3 são obtidos pela lei de formação aij = 3i + j, podemos calcular o valor de cada elemento e determinar a matriz A.
A =
• a11 = 3 ⋅ 1 + 1 = 3 + 1 ⇒ a11 = 4
• a12 = 3 ⋅ 1 + 2 = 3 + 2 ⇒ a12 = 5
• a13 = 3 ⋅ 1 + 3 = 3 + 3 ⇒ a13 = 6
• a21 = 3 ⋅ 2 + 1 = 6 + 1 ⇒ a21 = 7
• a22 = 3 ⋅ 2 + 2 = 6 + 2 ⇒ a22 = 8
• a23 = 3 ⋅ 2 + 3 = 6 + 3 ⇒ a23 = 9
Portanto, A = .
Matriz quadrada
Matriz quadrada é aquela quê possui o número de linhas igual ao número de colunas. Nesse caso, chamamos de matriz n × n ou, simplesmente, matriz quadrada de ordem n.
Observe alguns exemplos.
a) A matriz A = é uma matriz quadrada de ordem 2.
b) A matriz B = é uma matriz quadrada de ordem 3.
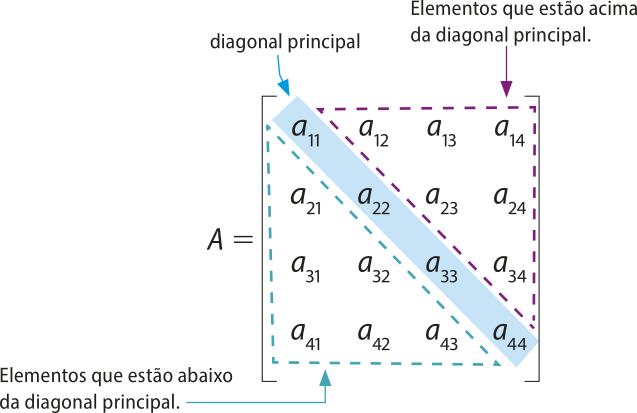
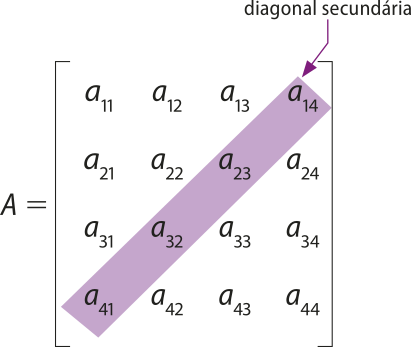
Em uma matriz quadrada, os elemêntos aij para os quais i = j formam uma diagonal denominada diagonal principal da matriz. Os elemêntos aij para os quais i + j = n + 1 formam uma diagonal chamada diagonal secundária da matriz.
Quando i > j, o elemento aij está abaixo da diagonal principal.
Quando i < j, o elemento aij está acima da diagonal principal.
Por exemplo, para uma matriz quadrada de ordem 4, temos:
Página duzentos e dezenove
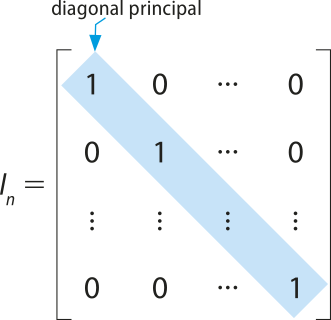
A matriz quadrada de ordem n na qual aij = 0 para i ≠ j e aij = 1 para i = j é chamada matriz identidade de ordem n e é indicada por In.
Pense e responda
Na matriz identidade de ordem n, quê número real verificamos em todas as entradas quê estão na diagonal principal? E em todas as entradas quê não estão na diagonal principal?
1; 0
ATIVIDADES RESOLVIDAS
1. Observe as matrizes e responda às kestões.
A =
B =
C =
a) Qual é a ordem da matriz B?
b) O elemento a12 da matriz A é igual a qual elemento bij da matriz B?
c) Qual é o produto da diagonal principal da matriz A?
d) Qual é a soma dos elemêntos da diagonal secundária da matriz identidade?
Resolução
a) A matriz B possui 3 linhas e 2 colunas, portanto sua ordem é 3 × 2.
b) O elemento a12 está na primeira linha e na segunda coluna da matriz A, logo a12 = 3. O número 3 na matriz B está na terceira linha e na primeira coluna, ou seja, b31 = 3. Portanto, a12 = b31.
c) Os elemêntos da diagonal principal da matriz A são a11 = 2 e a22 = 5, logo: a11 ⋅ a22 = 2 ⋅ 5 = 10
Portanto, o produto da diagonal principal é 10.
d) A matriz identidade é a C, e os elemêntos da sua diagonal secundária são a13 = 0, a22 = 1 e a31 = 0, logo: a13 + a22 + a31 = 0 + 1 + 0 = 1
Assim, a soma da diagonal secundária é 1.
2. Construa a matriz B = (bij)3x3, em quê:
bij =
Resolução
Para construir a matriz B, é necessário calcular cada entrada, de acôr-do com os índices referentes à linha e à coluna, utilizando a expressão correspondente.
Inicialmente, representamos genericamente a matriz B.
B =
• Para determinar b11, verificamos quê i = 1 e j = 1; nesse caso, i = j.
Assim, b11 = 2i + j = 2 ⋅ 1 + 1 = 3.
Logo, b11 = 3.
• Para determinar b12, verificamos quê i = 1 e j = 2; nesse caso, i < j.
Assim, b12 = 2j − i = 2 ⋅ 2 − 1 = 3.
Logo, b12 = 3.
• Para determinar b13, verificamos quê i = 1 e j = 3; nesse caso, i < j.
Assim, b13 = 2j − i = 2 ⋅ 3 − 1 = 5.
Logo, b13 = 5.
• Para determinar b21, verificamos quê i = 2 e j = 1; nesse caso, i > j.
Assim, b21 = 2i + j = 2 ⋅ 2 + 1 = 5.
Logo, b21 = 5.
• Para determinar b22, verificamos quê i = 2 e j = 2; nesse caso, i = j.
Página duzentos e vinte
Assim, b22 = 2i + j = 2 ⋅ 2 + 2 = 6.
Logo, b22 = 6.
• Para determinar b23, verificamos quê i = 2 e j = 3; nesse caso, i < j.
Assim, b23 = 2j − i = 2 ⋅ 3 − 2 = 4.
Logo, b23 = 4.
• Para determinar b31, verificamos quê i = 3 e j = 1; nesse caso, i > j.
Assim, b31 = 2i + j = 2 ⋅ 3 + 1 = 7.
Logo, b31 = 7.
• Para determinar b32, verificamos quê i = 3 e j = 2; nesse caso, i > j.
Assim, b32 = 2i + j = 2 ⋅ 3 + 2 = 8.
Logo, b32 = 8.
• Para determinar b33, verificamos quê i = 3 e j = 3; nesse caso, i = j.
Assim, b33 = 2i + j = 2 ⋅ 3 + 3 = 9.
Logo, b33 = 9.
Portanto, a matriz B é:
B =
ATIVIDADES
1. (Unimontes-MG) Ao associarmos as lêtras do alfabeto aos números, segundo a correspondência
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
podemos afirmar quê a palavra UNIMONTES póde sêr codificada pela matriz 3 × 3 dada por
a)
b)
c)
d)
alternativa b
2. Obtenha a matriz A = (aij)3 × 3, sabendo quê aij = 3i − j2.
Ver as Orientações para o professor.
3. Dizemos quê uma matriz quadrada é um quadrado mágico se as somas dos elemêntos de cada linha, de cada coluna e de cada diagonal, principal e secundária, são todas iguais. Qual(is) das matrizes a seguir corresponde(m) a um quadrado mágico?
A =
B =
C =
A e B
Para ler
• lópes, Tânia Isabel D. A história dos quadrados mágicos. Coimbra: Departamento de Matemática da Universidade de Coimbra, 21 jun. 2012. Disponível em: https://livro.pw/ykuln. Acesso em: 20 set. 2024.
Leia o texto indicado para conhecer um pouco da história dos quadrados mágicos.
4. Determine cada matriz definida a seguir.
a) A = (aij)1 × 3, tal quê aij = 2i − j
b) B = (bij)4 × 2, tal quê bij =
c) C = (cij)3 × 3, tal quê cij =
Ver as Orientações para o professor.
Página duzentos e vinte e um
5. (UEPA) A tabéla abaixo, regularmente disposta em linhas (atleta) e colunas (dia), representa os registros dos tempos de treinamento dos atletas A, B e C em 3 dias. Sendo i a ordem das linhas e j a ordem das colunas e aij = 30i + 10j o elemento genérico desta tabéla, com i e j dados em minutos, o tempo de treinamento gasto pelo atleta B no terceiro dia foi de:
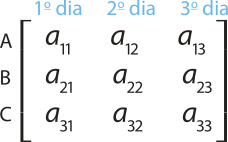
a) 1 hora e 30 minutos.
b) 1 hora e 50 minutos.
c) 2 horas.
d) 2 horas e 10 minutos.
e) 2 horas e 30 minutos.
alternativa a
6. (Unimep-SP) É dado um quadrado de lado medindo uma unidade, numerado conforme a figura. A matriz 4 × 4, tal quê aij é a distância entre os vértices de números i e j, é:

a)
b)
c)
d)
e) nenhuma das alternativas anteriores.
alternativa b
7. Determine a soma dos elemêntos da diagonal principal com os elemêntos da diagonal secundária da matriz quadrada A = (aij)4 × 4 em quê aij = i − j.
zero
Igualdade de matrizes
Quando consideradas duas matrizes de mesma ordem, os elemêntos quê ocupam a mesma posição em cada uma delas, ou seja, quê têm o mesmo índice, são denominados elemêntos correspondentes.
Por exemplo, nas matrizes A = e B = , os elemêntos a11 e b 11 são correspondentes, assim como os elemêntos a 12 e b 12, a 21 e b 21 e a 22 e b 22.
Duas matrizes de mesma ordem, A = (aij) e B = (bij)m × n são iguais se cada elemento de A for igual ao elemento correspondente de B. Denotamos isso por:
A = B ⇔ aij = bij, para todo i ∈ {1, 2, …, m} e todo j ∈ {1, 2, …, n}
Exemplo:
Considere as matrizes a seguir.
A = e B =
Se A = B, então x = 1 e y = 4.
Página duzentos e vinte e dois
Adição de matrizes
Uma livraria fez uma doação para as bibliotecas de duas escolas do bairro. Os títulos foram selecionados de acôr-do com a faixa etária, visando atender a estudantes do Ensino Fundamental – Anos Iniciais (EFAI), do Ensino Fundamental – Anos Finais (EFAF) e do Ensino Médio (EM). Nessa doação, os exemplares eram livros de autores internacionais (AI) e de autores brasileiros (AB).
Observe o número de livros doados para cada biblioteca.

Livros doados para a Biblioteca Cecília Meireles
Segmento EFAI |
Segmento EFAF |
Segmento EM |
|
|---|---|---|---|
Autor AI |
36 |
45 |
75 |
Autor AB |
60 |
72 |
120 |
Fonte: Dados fictícios.
Livros doados para a Biblioteca Raquel de Queiroz
Segmento EFAI |
Segmento EFAF |
Segmento EM |
|
|---|---|---|---|
Autor AI |
24 |
60 |
54 |
Autor AB |
52 |
98 |
100 |
Fonte: Dados fictícios.
Pense e responda
Quantos livros de autores brasileiros destinados a estudantes do Ensino Médio foram doados por essa livraria na situação apresentada? Como você fez para descobrir isso?
220 livros. Espera-se quê os estudantes respondam quê, para descobrir o resultado, foram adicionados os números das células do cruzamento da linha AB e da coluna EM nas duas tabélas.
Para se obtêr a quantidade de livros doados pela livraria, de acôr-do com cada característica especificada na tabéla, basta adicionar os valores correspondentes às células das duas tabélas.
Considerando a matriz A, formada pêlos números de livros doados para a Biblioteca Cecília Meireles, e a matriz B, formada pêlos números de livros doados para a Biblioteca Raquel de Queiroz, temos:
A = e B =
Nesse caso, para se obtêr o total de livros doados pela livraria às duas bibliotecas, de acôr-do com as características especificadas nas tabélas, basta adicionar os elemêntos correspondentes das matrizes A e B, ou seja, determinar a matriz C = A + B da seguinte maneira:
C =
A matriz C = é o resultado da adição das matrizes A e B, quê, de modo geral, definimos a seguir.
Dadas as matrizes de mesma ordem A = (aij)m × n e B = (bij)m × n, a matriz soma de A com B, indicada por A + B, é a matriz C = (cij)m × n, tal quê cij = aij + bij para todo i ∈ {1, 2, 3, …, m} e todo j ∈ {1, 2, 3, …, n}.
Página duzentos e vinte e três
Multiplicação de um número real por uma matriz
O qüadro a seguir mostra o estoque de alguns produtos de um supermercado no início da semana.
Marca A |
Marca B |
Marca C |
|
|---|---|---|---|
Produto Sabão em barra |
60 |
105 |
129 |
Produto Detergente |
112 |
170 |
220 |
Para o fim de semana, o supermercado precisa dobrar a quantidade dêêsses produtos. Observe quê, multiplicando por 2 cada número do qüadro, as novas quantidades são determinadas.
Marca A |
Marca B |
Marca C |
|
|---|---|---|---|
Produto Sabão em barra |
2 ⋅ 60 = 120 |
2 ⋅ 105 = 210 |
2 ⋅ 129 = 258 |
Produto Detergente |
2 ⋅ 112 = 224 |
2 ⋅ 170 = 340 |
2 ⋅ 220 = 440 |
Na Matemática, definimos:
Dados uma matriz A = (aij)m × n e um número real k, o produto de k por A, indicado por k ⋅ A, é a matriz B = (b ij)m × n, em quê b ij = k ⋅ a ij, para todo i ∈ {1, 2, 3, ..., m} e todo j ∈ {1, 2, 3, ..., n}.
Em outras palavras, efetuamos o produto de um número real por uma matriz multiplicando cada elemento da matriz por esse número. O resultado é uma matriz de mesma ordem.
Acompanhe o exemplo do estoque inicial e final do supermercado na situação apresentada no início dêste tópico.
Matriz oposta
Dada uma matriz A de ordem m × n, dizemos quê a matriz oposta de A, denotada por −A, é aquela quê, quando adicionada à matriz A, resulta na matriz nula de ordem m × n. No exemplo a seguir, acompanhe a adição de duas matrizes opostas.
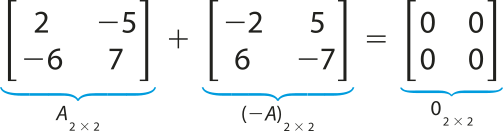
Observe quê, ao multiplicarmos uma matriz A de ordem m × n por −1, obtemos como resposta a matriz oposta −A, ou seja:
−1 ⋅ A = −A
Definimos a subtração A − B de duas matrizes de mesma ordem como uma adição entre a matriz A e a matriz oposta de B, isto é:
Página duzentos e vinte e quatro
Propriedades da adição de matrizes
Dadas as matrizes A, B, C e 0 (matriz nula) de mesma ordem m × n, valem as propriedades seguintes:
1ª) Propriedade comutativa: A + B = B + A
2ª) Propriedade associativa: (A + B) + C = A + (B + C)
3ª) Propriedade do elemento neutro: A + 0 = 0 + A = A
4ª) Propriedade do elemento ôpôsto: A + (−A) = (−A) + A = 0
ATIVIDADE RESOLVIDA
3. Dada a matriz A = (aij)3 × 3 em quê:
Calcule A + I3.
Resolução
Inicialmente, escrevemos a representação genérica da matriz A:
A =
Com base na definição da matriz A, temos:
A =
Como I3 é a matriz identidade de ordem 3, a soma A + I3 é calculada da seguinte maneira:
A + I3 =
Portanto: A + I3 =
ATIVIDADES
8. Uma escola fez um levantamento para identificar a quantidade de estudantes matriculados por sexo e por turno. Observe.
Quantidade de estudantes matriculados
Ensino Fundamental |
Ensino Médio |
|||
|---|---|---|---|---|
Sexo Masculino |
Sexo Feminino |
Sexo Masculino |
Sexo Feminino |
|
Turno Manhã |
340 |
410 |
180 |
152 |
Turno Tarde |
105 |
87 |
64 |
36 |
Turno Noite |
96 |
134 |
113 |
88 |
Fonte: Dados fictícios.
a) Organize esses dados em duas matrizes, A3 × 2 e B3 × 2, de modo quê a matriz A represente os estudantes do Ensino Fundamental por turno e sexo, e a matriz B represente os estudantes do Ensino Médio por turno e sexo.
b) Determine a matriz C = A + B, em quê C representa o total de estudantes da escola de acôr-do com o turno e o sexo.
Ver as Orientações para o professor.
9. Considerando A = , B = e C = , verifique quê:
a) A + B = B + A
b) A + (B + C) = (A + B) + C
c) B + 0 2 × 2 = B
d) C + (−C) = 0 2 × 2
Ver as Orientações para o professor.
10. Considere as seguintes matrizes:
• A = (aij) 2 × 3, definida por aij = i + j
• B = (bij)2 × 3, definida por bij = i − j
Determine o elemento c23 da matriz C = A + B.
c23 = 4
Página duzentos e vinte e cinco
Multiplicação de matrizes
Os quadros a seguir apresentam as quantidades de produtos vendidos por uma loja no primeiro trimestre do ano e os preços dêêsses produtos.
Produto I |
Produto II |
|
|---|---|---|
Janeiro |
10 |
5 |
Fevereiro |
20 |
10 |
Março |
15 |
20 |
preêço (R$) |
|
|---|---|
Produto I |
80,00 |
Produto II |
100,00 |
Para calcular o faturamento de cada mês com a venda dêêsses produtos, temos de efetuar as seguintes operações:
Faturamento (R$) |
|
|---|---|
Janeiro |
10 ⋅ 80,00 + 5 ⋅ 100,00 = 1.300,00 |
Fevereiro |
20 ⋅ 80,00 + 10 ⋅ 100,00 = 2.600,00 |
Março |
15 ⋅ 80,00 + 20 ⋅ 100,00 = 3.200,00 |
A situação descrita póde sêr representada pela seguinte multiplicação matricial:
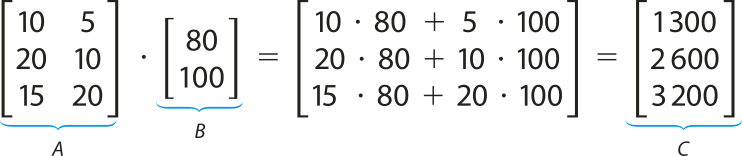 , em quê:
, em quê:
• os elemêntos da matriz A, de ordem 3 × 2, representam as quantidades vendidas de cada produto;
• os elemêntos da matriz B, de ordem 2 × 1, representam os preços dos produtos;
• os elemêntos da matriz C, de ordem 3 × 1, resultado da multiplicação da matriz A pela matriz B, representam os faturamentos de cada mês.
Apresentamos a seguir a definição de multiplicação de matrizes.
Dadas uma matriz A = (aij)m × n e uma matriz B = (bij)n × p o produto de A por B, indicado por A ⋅ B ou AB, é a matriz C = (c ij)m × p, em quê cada elemento cij é dado por: c ij = a i1 ⋅ b 1j + a i2 ⋅ b 2j + a i3 ⋅ b 3j + … + a in ⋅ b nj
Com base na definição, obissérve exemplos de como calcular a multiplicação de matrizes.
a) A multiplicação das matrizes A = e B = resulta em:
A ⋅ B =
Página duzentos e vinte e seis
b) Dadas as matrizes C = e D = , efetuamos C ⋅ D do seguinte modo:
C ⋅ D =
C ⋅ D =
Para realizar a multiplicação de matrizes A ⋅ B, é necessário quê a quantidade de colunas da matriz A seja igual ao número de linhas da matriz B. O resultado será uma matriz com tantas linhas quanto a matriz A e tantas colunas quanto a matriz B, ou seja:
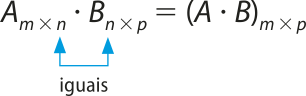
Por exemplo, dadas as matrizes A3 × 4 e B4 × 2, temos:
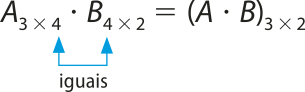

Acompanhe a seguir um exemplo.
Considere as matrizes E = e F = . Não existe o produto E ⋅ F, pois a matriz E tem 2 colunas e a matriz F tem apenas 1 linha. No entanto, existe o produto F ⋅ E, porque a matriz F tem 2 colunas e a matriz E tem 2 linhas. O resultado dêêsse produto é:
F ⋅ E =
F ⋅ E =
Propriedades da multiplicação de matrizes
Dadas as matrizes A, B e C, de modo quê as somas e os produtos estejam definidos, valem as propriedades:
1ª) Propriedade associativa: A ⋅ (B ⋅ C) = (A ⋅ B) ⋅ C
2ª) Propriedade distributiva: (B + C) ⋅ A = B ⋅ A + C ⋅ A (à esquerda)
A ⋅ (B + C) = A ⋅ B + A ⋅ C (à direita)
3ª) Propriedade do elemento neutro para matrizes quadradas: A ⋅ I n = A e I n ⋅ A = A, em quê A é uma matriz quadrada de ordem n e In é a matriz identidade de ordem n.
Saiba quê...
Na multiplicação de matrizes, também póde sêr utilizada a notação de potência. Por exemplo, o produto A ⋅ A também póde sêr indicado por A2.
Página duzentos e vinte e sete
Observações:
a) A multiplicação de matrizes não é comutativa, ou seja, póde não valer a propriedade AB = BA. Por exemplo: se e , então AB ≠ BA, pois e .
b) Se ocorrer AB = BA, dizemos quê as matrizes A e B comutam.
Por exemplo: e comutam, pois e .
Observe quê é necessário quê as matrizes A e B sêjam quadradas para quê existam tanto o produto AB como o produto BA.
c) Diferentemente do quê ocorre com os números reais, o produto de duas matrizes não nulas póde resultar em uma matriz nula.
Por exemplo: considerando e , temos A ≠ 0, B ≠ 0 e
ATIVIDADES RESOLVIDAS
4. Sendo A = e B = , determine, se possível:
a) A ⋅ B
b) B ⋅ A
Resolução
a) Como A é uma matriz de ordem 2 × 2 e B, de ordem 2 × 3, existe a matriz C tal quê
C = AB. A matriz C é de ordem 2 × 3. Nesse caso, temos:
C =
c11 = a11 ⋅ b11 + a12 ⋅ b21 = 2 ⋅ 0 + 1 ⋅ 1 = 1
c12 = a11 ⋅ b12 + a12 ⋅ b22 = 2 ⋅ 4 + 1 ⋅ (−3) = 5
c13 = a11 ⋅ b13 + a12 ⋅ b23 = 2 ⋅ (−2) + 1 ⋅ 5 = 1
c21 = a21 ⋅ b11 + a 22 ⋅ b 21 = 3 ⋅ 0 + (−1) ⋅ 1 = −1
c22 = a 21⋅ b 12 + a 22 ⋅ b 22= 3 ⋅ 4 + (−1) ⋅ (−3) = 15
c23 = a 21 ⋅ b 13 + a 22 ⋅ b 23 = 3 ⋅ (−2) + (−1) ⋅ 5 = −11
Logo: C =
b) Como B é uma matriz de ordem 2 × 3 e A, de ordem 2 × 2, temos a quantidade de colunas de B diferente da quantidade de linhas de A. Nesse caso, não existe a matriz produto B ⋅ A.
5. (UFPB) As mensagens entre duas agências de espionagem, Gama e Rapa, são trocadas usando uma linguagem de códigos, onde cada número inteiro entre 0 e 25 representa uma letra, conforme mostra a tabéla a seguir:
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
7 |
10 |
22 |
9 |
5 |
4 |
18 |
2 |
17 |
25 |
23 |
12 |
14 |
8 |
1 |
19 |
15 |
20 |
21 |
11 |
3 |
16 |
24 |
6 |
13 |
0 |
Página duzentos e vinte e oito
A agência Gama enviou para a Rapa o nome de um espião codificado na matriz . Para decodificar uma palavra de cinco lêtras, dada por uma matriz A, de ordem 5 × 1, formada por inteiros entre 0 e 25, deve-se multiplicá-la pela matriz de conversão e, usando-se a tabéla dada, converter os números em lêtras.
Utilizando-se esse processo, conclui-se quê o nome do espião é:
a) DIEGO
b) SHUME
c) SADAN
d) RENAN
e) RAMON
Resolução
De acôr-do com as informações do enunciado, calculamos o produto C ⋅ A.
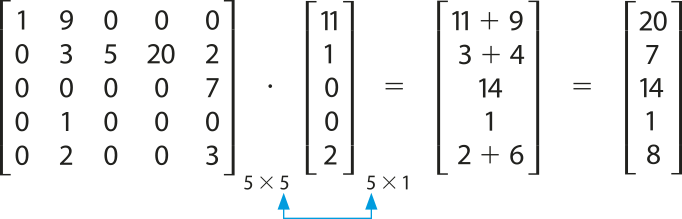
Com base na linguagem de códigos utilizada pelas agências, decodificam-se os elemêntos da matriz ôbitída:
• 20 corresponde à letra R;
• 7 corresponde à letra A;
• 14 corresponde à letra M;
• 1 corresponde à letra O;
• 8 corresponde à letra N.
Logo, o nome do espião é RAMON.
Resposta: alternativa e.
ATIVIDADES
11. Considerando as matrizes e , calcule:
a) 2A
b) −3B
c) B
d) 3A + 2B
Ver as Orientações para o professor.
12. Sendo , , (alfa)" = 2 e (beta)" = 3, verifique quê:
a) (alfa)"((beta)"X) = ((alfa)"(beta)")X
b) (alfa)"(X + Y) = (alfa)"X + (alfa)"Y
c) ((alfa)" + (beta)")X = (alfa)"X + (beta)"X
d) 1 ⋅ Y = Y
Ver as Orientações para o professor.
13. Dadas as matrizes e , determine, se possível:
a) (A + B)
b) −4A − B
Ver as Orientações para o professor.
Página duzentos e vinte e nove
14. Sejam as matrizes:
A = (aij)2 × 2, em quê aij =
B = (bij)2 × 2, em quê bij =
Calcule:
a) C = 2A − 3B
b)
Ver as Orientações para o professor.
15. Determine, quando possível, a matriz quê resulta das multiplicações indicadas a seguir.
a)
b)
Não é possível determinar êste produto.
c) ⋅ (2 4 −1)
16. Dados e , calcule AB e BA. As matrizes A e B comutam?
Ver as Orientações para o professor.
17. (hú éfi éssi cê) Sejam A= (aij)4 × 3 e B = (bij)3 × 4 duas matrizes definidas por aij = i + j e bij = 2i + j, respectivamente. Se A ⋅ B = C, então qual é o elemento c32 da matriz C?
c32 = 94
18. Uma fábrica de mochilas utiliza três tamanhos de zíper na confekissão de dois modelos de mochilas, conforme indicado no qüadro a seguir.
Modelo X |
Modelo Y |
|
|---|---|---|
Pequeno |
4 |
2 |
Médio |
2 |
3 |
Grande |
1 |
2 |
Essa fábrica recebeu a seguinte encomenda para o último trimestre do ano.
Outubro |
Novembro |
Dezembro |
|
|---|---|---|---|
Mochila X |
50 |
100 |
200 |
Mochila Y |
50 |
150 |
100 |

a) escrêeva a matriz T3 × 2, quê representa a quantidade de zíperes, por tamãnho, utilizada em cada modelo de mochila.
Ver as Orientações para o professor.
b) escrêeva a matriz E2 × 3 para representar a quantidade de mochilas, por modelo, encomendada para o último trimestre do ano.
Ver as Orientações para o professor.
c) Calcule o produto T ⋅ E e responda: quantos zíperes de tamãnho médio serão necessários para confeksionar as mochilas encomendadas no mês de novembro?
650 zíperes
d) Elabore um problema quê possa sêr respondido com as informações apresentadas nesta atividade.
Resposta pessoal.
19. (hú éfe pê érre) Calcule o valor de a de modo quê exista somente uma matriz , tal quê o produto seja igual a .
a = 2
20. (UEG-GO) Tatiana e Tiago comunicam-se entre si por meio de um cóódigo próprio dado pela resolução do produto entre as matrizes A e B, ambas de ordem 2 × 2, onde cada letra do alfabeto corresponde a um número, isto é, a = 1, b = 2, c = 3, …, z = 26. Por exemplo, se a resolução de A ⋅ B for igual a , logo a mensagem recebida é amor. Dessa forma, se a mensagem recebida por Tatiana foi flor e a matriz , então a matriz A é
a)
b)
c)
d)
alternativa b
Página duzentos e trinta
CONEXÕES com...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
Mobilidade urbana e matrizes
Leia o texto a seguir.
[…]
O transporte veicular é um artifício indispensável para a mobilidade humana, do qual a maioria da população mundial usufrui para se deslocar d fórma rápida e segura, sêndo estas características as mais importantes para se classificar um bom meio de transporte. […] a má qualidade do transporte público e o aumento populacional constituem-se em fatores decisórios para o acúmulo de veículos nos centros urbanos. Em razão do aumento contínuo da frota veicular, os sistemas de trânsito atuáis da maioria das cidades acabam não comportando o grande número de veículos existentes. Por consequência, surgem os inevitáveis congestionamentos e, com esses, vários problemas à ssossiedade, como alto nível de estresse, poluição, acidentes e prejuízos econômicos, sêndo estes últimos decorrentes do alto consumo de combustível e desperdício de tempo. […]
[…]
LACORTT, M.; KRIPKA, M.; KRIPKA, R. M. L. Modelos matemáticos para otimização do tráfego urbano semaforizado. Tendências em Matemática Aplicada e Computacional, São Carlos, v. 14, n. 3, p. 359-372, 2013. p. 359. Disponível em: https://livro.pw/zsugg. Acesso em: 17 set. 2024.
Uma preocupação crescente no planejamento das cidades são as estratégias para organizar o fluxo de veículos. Isso mobiliza engenheiros de tráfego e órgãos reguladores de trânsito, quê utilizam alguns modelos matemáticos para otimizar o tráfego urbano.
Observe a seguir uma situação envolvendo o fluxo de carros em um cruzamento, analisada por meio de matrizes.
Em um cruzamento de ruas de mão dupla, o fluxo de automóveis nos pontos 1, 2 e 3 é organizado por três conjuntos de semáforos, de modo quê o ciclo dêêsses semáforos dura 4 minutos. Os engenheiros de tráfego fizeram um modelo para descobrir quantos carros passam por hora, em cada semáforo, nesse cruzamento. Observe-o a seguir.
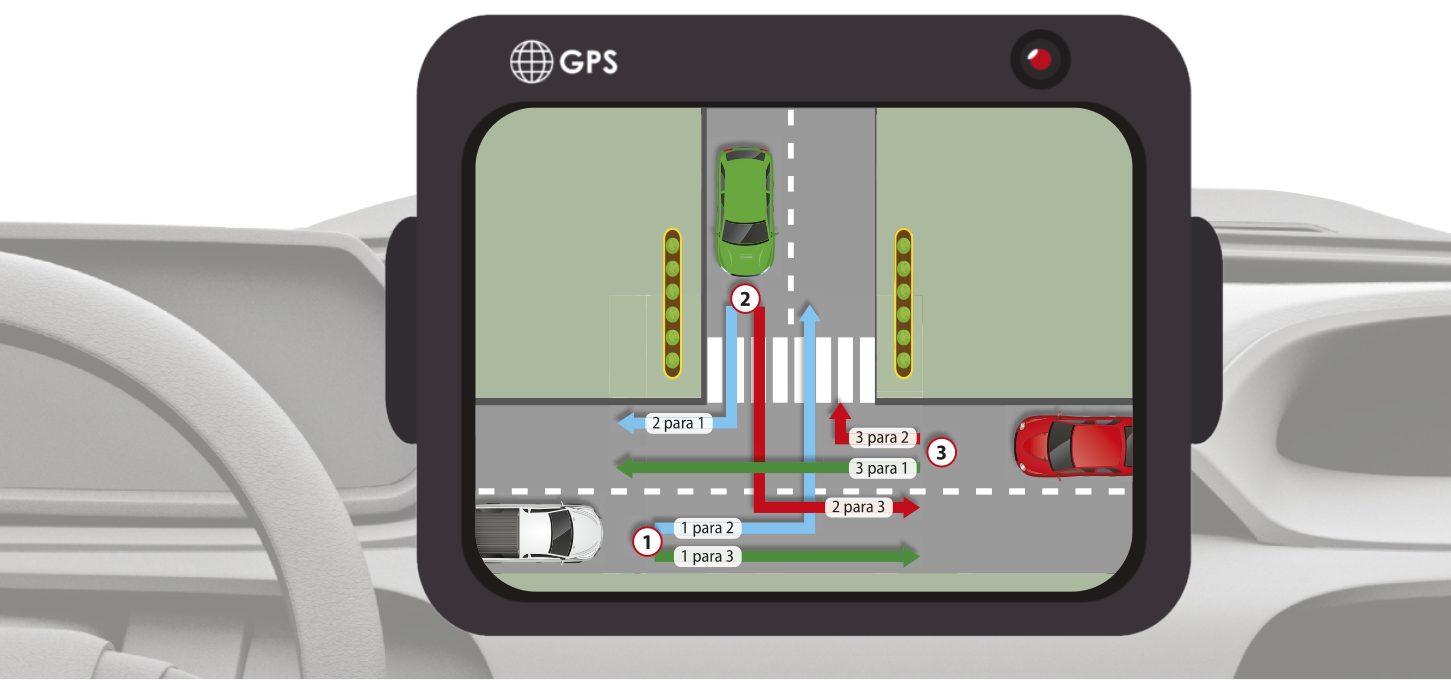
Página duzentos e trinta e um
Nesse modelo, foram construídas inicialmente as matrizes M1, M2 e M3, quê indicam o tempo mij, em minuto, pelo qual alguns semáforos se mantêm simultaneamente abertos, permitindo o fluxo de i para j.
Durante os primeiros dois minutos do ciclo, ficam verdes os semáforos de (1) para (2), de (1) para (3) e de (2) para (1).
Em seguida, durante um minuto, ficam verdes os semáforos de (2) para (1), de (2) para (3) e de (3) para (2).
Por fim, durante o último minuto do ciclo, ficam verdes os semáforos de (3) para (1), de (3) para (2) e de (1) para (3).
Para saber o intervalo de tempo quê cada semáforo fica aberto no ciclo de 4 minutos, adicionamos M1, M2 e M3, obtendo a matriz M.
Com base nessa matriz, quê corresponde a um ciclo de 4 minutos, é possível fazer uma estimativa da quantidade de veículos quê póde passar nesse cruzamento, considerando determinados períodos, e buscar resolver problemas de engarrafamento.
Por exemplo: se considerarmos quê, em 1 minuto, passam cerca de 15 veículos pelo cruzamento, para saber quantos veículos passam em 1 hora, fazemos:
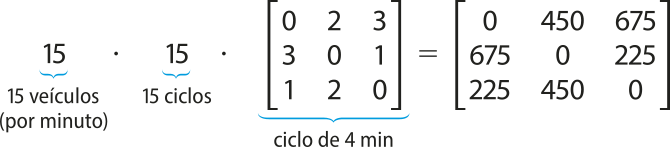
Note quê 15 ciclos de 4 minutos equivalem a 1 hora, pois 15 ⋅ 4 = 60, 60 minutos.
Nesse caso, se o número de carros em alguma das direções for maior do quê a quantidade calculada, teremos um engarrafamento, quê póde ou não sêr resolvido se forem alterados os intervalos de tempo de abertura dos semáforos, isto é, se forem modificados os valores nas matrizes M1, M2 e M3.
Ver as Orientações para o professor.
![]() Agora, reúna-se a mais côlégas, e façam o quê se pede nas atividades a seguir.
Agora, reúna-se a mais côlégas, e façam o quê se pede nas atividades a seguir.
1. Nos grandes centros urbanos, os congestionamentos são freqüentes. Descrevam as possíveis causas e pensem em uma alternativa quê possibilite diminuir o tráfego de veículos nas vias. Pesquisem sobre mobilidade urbana e identifiquem cidades ao redor do mundo quê têm apresentado políticas públicas e propostas inovadoras nesse sentido.
2. O quê vocês sabem sobre Engenharia de Tráfego? Pesquisem sobre essa área de trabalho e verifiquem instituições quê oferecem curso nessa área. Indiquem qual é o órgão responsável pela engenharia de tráfego de sua cidade. Descrevam o quê essa área tem a vêr com mobilidade urbana.
3. Utilizando o exemplo apresentado, pesquisem um cruzamento quê seja de mão dupla. Elaborem um problema considerando ciclos de semáforos, utilizando a matriz quê representa o tempo durante o qual cada semáforo fica aberto em cada um dos sentidos. Compartilhem com os outros grupos o problema quê vocês elaboraram.
Página duzentos e trinta e dois
Sistemas lineares
Você já estudou e rêzouvêo sistemas de equações com duas equações e duas incógnitas na sua vida estudantil. Neste tópico, vamos aprofundar esse estudo, apresentando as classificações de um sistema linear e o método do escalonamento para solucionar sistemas com três ou mais incógnitas e com três ou mais equações.
Equação linear
Acompanhe a situação a seguir, em quê apresentamos uma aplicação de equação linear.
Andréa percebeu quê o saldo de seu cartão escolar de transporte era R$ 120,00. Na cidade onde mora, os estudantes pagam R$ 3,00 na viagem de ônibus, R$ 2,50 na de metrô e R$ 2,00 na viagem de trem. Com esse saldo do cartão, quantas viagens Andréa póde fazer utilizando esses meios de transporte?
Uma situação como essa póde sêr traduzida para a linguagem matemática. Para isso, podemos utilizar incógnitas (valores desconhecidos), representadas por meio de lêtras, relacionando-as com as informações apresentadas na situação analisada.
Considerando x, y e z, respectivamente, o número de viagens de ônibus, de metrô e de trem, podemos escrever a seguinte sentença:
3,00 ⋅ x + 2,50 ⋅ y + 2,00 ⋅ z = 120,00 ou 3x + 2,5y + 2z = 120
Toda equação quê póde sêr escrita na forma geral a1x1 + a2x2 + a3x3 + … + anxn = b, em quê a1, a2, a3, …, an e b são números reais e x1, x2, x3, …, xn são incógnitas, é denominada equação linear.
Na equação linear a1x1 + a2x2 + a3x3 + … + anxn = b:
• a1, a2, …, an são números reais chamados coeficientes (ou parâmetros);
• x1, x2, …, xn são as incógnitas;
• b é o termo (ou parâmetro) independente.
Uma ênupla, ou seja, uma sequência ordenada de n números reais ((alfa)"1, (alfa)"2, …, (alfa)" n) quê, substituindo, respectivamente, por x1, x2, …, xn, tornam verdadeira a igualdade a1x1 + a2x2 + … + anxn = b, é uma solução da equação.
Por exemplo, a sentença 3x + 2,5y + 2z = 120 é uma equação linear em quê 3; 2,5 e 2 são os coeficientes; x, y e z são as incógnitas; e 120 é o termo independente. Essa equação apresenta várias soluções, entre as quais as ternas ordenadas (20, 20, 5), (16, 16, 16) e (25, 18, 0), pois cada uma delas torna verdadeira a igualdade 3x + 2,5y + 2z = 120.
Pense e responda
Imagine quê Andréa não vai utilizar o metrô e quê a quantidade de viagens de ônibus quê vai fazer será o dôbro da quantidade de viagens de trem. Qual é a solução da equação 3x + 2,5y + 2z = 120 considerando essa condição?
S = {(30, 0, 15)}
Página duzentos e trinta e três
Observe outros exemplos de equações lineares:
a) 2x − y = 4
Nessa equação, 2 e −1 são os coeficientes; x e y são as incógnitas; e 4 é o termo independente. Duas das soluções dessa equação são, por exemplo, os pares ordenados (2, 0) e (3, 2), pois, substituindo, respectivamente, os valores de x e y na equação, obtemos uma sentença verdadeira.
• Para x = 2 e y = 0, temos:
2 ⋅ 2 − 0 = 4, ou seja, o par ordenado (2, 0) torna verdadeira a sentença 2x − y = 4.
• Para x = 3 e y = 2, temos:
2 ⋅ 3 − 2 = 4, ou seja, o par ordenado (3, 2) também torna verdadeira a sentença 2x − y = 4.
b) x + 2y − z = 0
Não são exemplos de equações lineares:
a) xy = 15
b) x2 + y2 = 1
Pense e responda
• Determine duas das possíveis soluções da equação:
x + 2y − z = 3
Algumas respostas possíveis: (1, 1, 0) e (−1, 1, −2).
• A terna ordenada (2, 3, 0) é solução da equação x + 2y − z = 3? Justifique sua resposta.
Ver as Orientações para o professor.
FÓRUM
Auxílio em passagem estudantil
Diversos países ao redor do mundo oferecem descontos em passagens de ônibus para os estudantes, e no Brasil isso não é diferente. Contudo, as políticas varíam de um estado para outro e até mesmo entre municípios.
No município de São Paulo, por exemplo, estudantes podem ter direito à gratuidade ou à meia-tarifa no transporte público. Já em Fortaleza, todos os estudantes do município quê têm carteirinha de estudante válida por uma unidade escolar da cidade têm direito a duas passagens gratuitas no transporte público por ônibus em dias úteis do ano letivo.
Fontes dos dados: UNIÃO BRASILEIRA DOS ESTUDANTES SECUNDARISTAS. Bilhete único SPTrans Estudante, tire suas dúvidas! São Paulo: Ubes, c2024. Disponível em: https://livro.pw/nhnsm. PASSE Livre Estudantil oferta passagens grátis a partir desta segunda; veja como funciona. G1, Ceará, 12 nov. 2023. Disponível em: https://livro.pw/sdxib. Acessos em: 27 set. 2024.

Agora, faça o quê se pede a seguir.
1. No município onde você mora, existe esse tipo de auxílio para estudantes? Você conhece alguma pessoa quê não póde estudar por dificuldade de acesso ao local da escola, por residir em região afastada ou local com acesso apenas por embarcação?
Resposta pessoal. A resposta depende de onde o estudante mora.
2. ![]() No seu entendimento, qual é a importânssia dêêsse tipo de auxílio, considerando o orçamento das famílias e o direito de acesso aos estudos? Reúna-se a mais côlégas para discutirem esse assunto.
No seu entendimento, qual é a importânssia dêêsse tipo de auxílio, considerando o orçamento das famílias e o direito de acesso aos estudos? Reúna-se a mais côlégas para discutirem esse assunto.
Ver as Orientações para o professor.
Página duzentos e trinta e quatro
Equação linear homogênea
Quando o termo independente b de uma equação linear é igual a zero, ela é denominada equação linear homogênea. Nesse caso, temos:
a1x1 + a2x2 + … + anxn = 0
A ênupla (0, 0, …, 0) é uma das soluções de qualquer equação linear homogênea.
Por exemplo, a equação 2x − y + 3z = 0 é homogênea, e (0, 0, 0) é uma de suas soluções, pois: 2 ⋅ 0 − 0 + 3 ⋅ 0 = 0
Equações lineares equivalentes
Quando duas ou mais equações lineares têm o mesmo conjunto solução, elas são denominadas equações equivalentes.
Por exemplo, as equações lineares 4x + y − 2z = −7 e −8x − 2y + 4z = 14 são equações equivalentes, pois qualquer solução de uma também é solução da outra.
Sistemas lineares m × n
Denominamos sistema linear m × n, de m equações com n incógnitas, todo conjunto de m equações lineares quê póde sêr representado como:
Nesse caso:
• x1, x2, …, xn são as incógnitas;
• a11, a12, a13, …, a1n, a21, a22, …, a2n, …, amn são números reais chamados coeficientes;
• b1, b2, …, bm são os termos independentes.
Quando uma ênupla ordenada ((alfa)"1, (alfa)"2, …, (alfa)"n) é solução de cada uma das equações de um sistema linear, ou seja, torna simultaneamente verdadeiras todas as sentenças quê o compõem, ((alfa)"1, (alfa)"2, …, (alfa)"n) é solução do sistema linear.
Acompanhe os exemplos.
a)
O sistema linear é 3 × 3, pois possui 3 equações e 3 incógnitas (x, y e z).
b)
O sistema linear é 2 × 3, pois possui 2 equações e 3 incógnitas (m, n e p).
Página duzentos e trinta e cinco
Classificação de sistemas lineares
Um sistema linear é classificado em:
• sistema possível e determinado (SPD) quando possui uma única solução;
• sistema possível e indeterminado (SPI) quando possui infinitas soluções;
• sistema impossível (SI) quando não possui solução.
Acompanhe as resoluções, as classificações e as representações gráficas de três sistemas lineares 2 × 2.
a)
Resolução algébrica pelo método da adição.
× −2 ⇒ 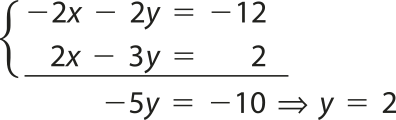
Substituindo y por 2 em x + y = 6, temos:
x + y = 6 ⇒ x + 2 = 6 ⇒ x = 4
Portanto, o sistema é possível e determinado (SPD), pois possui solução única, sêndo seu conjunto solução expresso por S = {(4, 2)}.
Representação gráfica
Equações lineares da forma ax + bai = c são representadas no plano cartesiano por uma reta. Cada ponto pertencente à reta satisfaz à equação, portanto representa uma solução dela. Nesse caso, o sistema linear com duas equações d fórma ax + bai = c é representado graficamente por duas retas no mesmo plano cartesiano.
A equação x + y = 6 tem como solução o par ordenado (4, 2) e o par ordenado (0, 6), além de outros, como (1, 5), (3, 3), (−1, 7), …. Logo, a reta do plano cartesiano quê passa pêlos pontos (4, 2) e (0, 6) representa graficamente a equação x + y = 6. Da mesma forma, a equação 2x − 3y = 2 será representada pela reta do plano cartesiano quê passa pêlos pontos (4, 2) e (1, 0), pois as coordenadas (x, y) dêêsses pontos são soluções dessa equação.
Com isso, temos a seguinte representação gráfica do sistema:
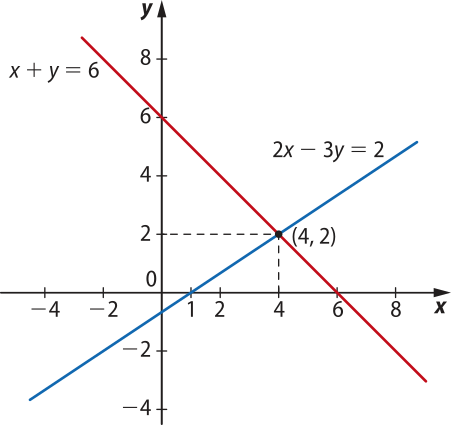
pôdêmos observar quê essas retas são concorrentes, ou seja, elas se cruzam em um único ponto. Isso indica quê há um único par ordenado, nesse caso, (4, 2), quê é a solução do sistema.
Página duzentos e trinta e seis
b)
Resolução algébrica pelo método da substituição.
Manipulando a equação I, temos:
x − 2y = 2 ⇒ x = 2 + 2y
Substituindo a incógnita x por 2 + 2y na equação II, obtemos:
2x − 4y = 0 ⇒ 2 ⋅ (2 + 2y) − 4y = 0 ⇒ 4 + 4y − 4y = 0 ⇒ 4 = 0 (uma igualdade falsa)
Ao resolver o sistema pelo método da substituição, obtivemos uma igualdade falsa. Nesse caso, o sistema é impossível (SI), pois não admite solução. Sendo assim, seu conjunto solução é S = ∅.
Representação gráfica
Note quê a equação x − 2y = 2 é representada pela reta do plano cartesiano quê passa pêlos pontos (0, −1) e (2, 0), duas soluções dessa equação. Da mesma forma, a equação 2x − 4y = 0 é representada pela reta quê passa pêlos pontos (0, 0) e (2, 1).
O plano cartesiano apresentado ilustra a representação do sistema:
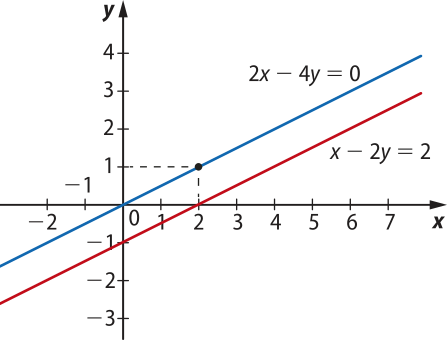
pôdêmos observar quê essas retas são paralelas, ou seja, elas não se cruzam. Isso indica quê não existe um par ordenado quê seja solução do sistema.
c)
Resolução algébrica pelo método da substituição.
Manipulando a equação I, temos:
−x + 2y = 1 ⇒ x = 2y − 1
Substituindo a incógnita x por 2y − 1 na equação II, obtemos:
3x − 6y = −3 ⇒ 3 ⋅ (2y − 1) − 6y = −3 ⇒ 6y − 3 − 6y = −3 ⇒ −3 = −3 (uma igualdade verdadeira)
Ao resolver o sistema, obtivemos uma igualdade verdadeira. Nesse caso, o sistema é possível e indeterminado (SPI), isto é, admite infinitas soluções.
Representação gráfica
Os pares ordenados (−1, 0) e (1, 1) são soluções do sistema pois:
e
Página duzentos e trinta e sete
Nesse caso, a representação gráfica do sistema é dada por duas retas coincidentes, pois ambas as retas passam pêlos pontos (−1, 0) e (1, 1). Observe:
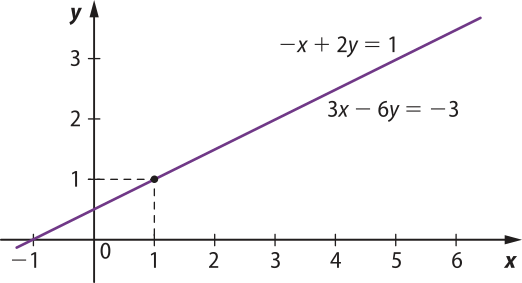
Como as retas são coincidentes, elas têm infinitos pontos de intersecção, quê representam as infinitas soluções do sistema linear possível e indeterminado.
ATIVIDADES RESOLVIDAS
6. Verifique se a terna ordenada (3, −2, 4) é solução da equação linear 4x − 3y + 5z = 36.
Resolução
Substituindo x = 3, y = −2 e z = 4 no primeiro membro da equação, temos:
4 ⋅ 3 − 3(−2) + 5 ⋅ 4 = 12 + 6 + 20 = 38
Como 38 ≠ 36, a terna ordenada (3, −2, 4) não é uma solução da equação linear 4x − 3y + 5z = 36.
7. resôuva e classifique os sistemas a seguir.
a)
b)
Resolução
a) Vamos resolver esse sistema usando o método da substituição.
Isolando b na equação I, temos:
b = 2a − 5
Substituímos b por 2a − 5 em II:
4a − 2 ⋅ (2a − 5) = 10 ⇒ 4a − 4a + 10 = 10
Logo, 0a = 0.
Observe quê qualquer número real colocado no lugar de a torna verdadeira a sentença. Isso significa quê o sistema tem infinitas soluções, ou seja, ele é possível e indeterminado.
Como b = 2a − 5, então cada uma das infinitas soluções é um par ordenado cujo 1º elemento é um número real qualquer e cujo 2º elemento é o dôbro do 1º menos 5, ou seja, as soluções são pares ordenados da forma (k, 2k − 5), para qualquer número real k.
Algumas das soluções dêêsse sistema são:
(1, −3), (−3, −11), (0, −5) e
Como estamos trabalhando com números reais, temos:
S = {(k, 2k − 5) | k ∈ ℝ}
b) Vamos resolver o sistema utilizando o método da adição. Multiplicando a primeira equação por (−2), temos:
Adicionando, membro a membro, essas equações, temos: 0x + 0y = −8
Observe quê não há valores reais de x e de y quê tornam verdadeira essa sentença. Por isso, dizemos quê não existe solução, e, nesse caso, temos um sistema impossível. Portanto, o conjunto solução é vazio, indicado por S = ∅.
De fato, observando as duas equações do sistema, é possível perceber quê não há solução, pois as equações 2x + 3y = 9 e 4x + 6y = 10 são incompatíveis:
Página duzentos e trinta e oito
multiplicando por 2 a primeira equação, obtemos 4x + 6y = 18, ou seja, 4x + 6y não póde, simultaneamente, sêr igual a 10 e a 18.
8. Calcule m e n, de modo quê os sistemas
e
tênham o mesmo conjunto solução.
Resolução
Empregando o método da adição, vamos resolver o primeiro sistema.
Adicionando, membro a membro, as equações I e II, obtemos: 3x = 6
Logo, x = 2.
Substituindo x por 2 na equação I, temos y = 1.
Como os sistemas devem ter o mesmo conjunto solução, quê, nesse caso, é constituído de uma única solução, o par ordenado (2, 1) é também solução do segundo sistema.
Substituindo as incógnitas do segundo sistema por esses valores, determinamos m e n.
Multiplicando por −2 a equação IV e adicionando, membro a membro as equações, temos:
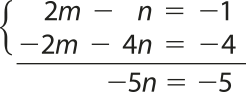
Logo, n = 1.
Substituindo n por 1 na equação III, obtemos m.
2m − 1 = −1 ⇒ 2m = 0
Logo, m = 0.
Assim, para quê esses sistemas tênham o mesmo conjunto solução, devemos ter m = 0 e n = 1.
9. (UFPE) Uma fábrica de automóveis utiliza três tipos de aço, A1, A2 e A3, na construção de três tipos de carro, C1, C2 e C3. A quantidade dos três tipos de aço, em tonelada, usados na confekissão dos três tipos de carro está na tabéla a seguir.
C1 |
C2 |
C3 |
|
|---|---|---|---|
A1 |
2 |
3 |
4 |
A2 |
1 |
1 |
2 |
A3 |
3 |
2 |
1 |
Se foram utilizadas 26 toneladas de aço do tipo A1, 11 toneladas do tipo A2 e 19 toneladas do tipo A3, qual o total de carros construídos dos tipos C1, C2 ou C3?
Resolução
Considerando x, y e z os respectivos números de carros dos tipos C1, C2 e C3 quê foram construídos e utilizando as informações fornecidas, representamos a situação por meio de um sistema linear 3 × 3 (3 equações e 3 incógnitas), como indicado a seguir.
Isolando x na equação II, temos:
x = 11 − y − 2z IV
Substituindo x por 11 − y − 2z na equação I, temos:
2 ⋅ (11 − y − 2z) + 3y + 4z = 26
22 − 2y − 4z + 3y + 4z = 26
Logo, y = 4.
Substituindo x por 11 − y − 2z na equação III, temos:
3 ⋅ (11 − y − 2z) + 2y + z = 19
33 − 3y − 6z + 2y + z = 19
y + 5z = 14 V
Substituindo y por 4 na equação V, obtemos z:
4 + 5z = 14
Logo, z = 2.
Substituindo y por 4 e z por 2 na equação IV, determinamos x:
x = 11 − 4 − 2 ⋅ 2
Logo, x = 3.
Portanto, foram construídos 3 carros do tipo C1, 4 carros do tipo C2 e 2 carros do tipo C3, totalizando 9 carros.
Página duzentos e trinta e nove
ATIVIDADES
21. Considerando x, y e z as incógnitas, qual(is) das seguintes equações é(são) linear(es)?
alternativa a
a) 4x − y + = 0
c) 2x + 3y − z2 = 0
b) 5x + 2yz = 0
d) xyz = 1
22. Dos pares ordenados (0, −3), (1, 2), e , quais são soluções da equação 2x − 3y = 9?
(0, −3) e
23. A equação linear 0x + 0y = 4 possui solução? Justifique.
Resposta esperada: Não, pois, qualquer quê seja o par ordenado (a, b), temos 0a + 0b ≠ 4.
24. Determine m, de modo quê (−1, 2, −3) seja solução da equação linear: 2a − 4b + mc = 0
25. Determine os valores de m para quê a equação x − 4y + z = m2 − 4 seja homogênea.
m = 2 ou m = −2
26. Verifique se (−1, 2) é solução do sistema:
É solução.
27. Determine o conjunto solução do sistema a seguir.
S = {(10, 5)}
28. (UFG-GO) Para se deslocar de casa até o seu trabalho, um trabalhador percórre 550 km por mês. Para isso, em alguns dias, ele utiliza um automóvel e, em outros, uma motocicleta. Considerando quê o custo do kilometro rodado é de 21 centavos para o automóvel e de 7 centavos para a motocicleta, calcule quantos kilometros o trabalhador deve andar em cada um dos veículos para quê o custo total mensal seja de R$ 70,00.
motocicleta: 325 km; automóvel: 225 km
29. Um caminhão-baú póde transportar, em uma mesma viagem, no mássimo, 58 caixas.
Essas caixas podem sêr de um tipo A ou de um tipo B, de modo quê elas têm, respectivamente, 56 kg e 72 kg. Sabendo quê a carga mássima quê esse caminhão póde transportar por viagem é de 3,84 toneladas, responda às kestões a seguir.
a) Quais equações representam essa situação, considerando o caminhão com a capacidade mássima ocupada?
b) Quantas caixas de cada tipo são transportadas por esse caminhão quando ele viaja com a capacidade mássima ocupada?
21 caixas do tipo A e 37 do tipo B
30. Elabore um problema quê possa sêr resolvido por um dos sistemas a seguir. Em seguida, resolva-os e responda: esses sistemas têm o mesmo conjunto solução?
Resposta pessoal.
S = {(4, 3)}; sim
31. Utilizando o GeoGebra, interpréte geometricamente cada sistema a seguir e o classifique em possível e determinado, possível e indeterminado ou impossível.
a)
possível e determinado
b)
impossível
c)
possível e indeterminado
32. Considere o sistema linear a seguir.
Verifique se as ternas ordenadas a seguir são soluções dêêsse sistema.
a) (2, −1, 1)
É solução.
b) (0, 0, 0)
Não é solução.
33. (UECE) Um hotel possui exatamente 58 unidades de hospedagem assim distribuídas: m quartos duplos, p quartos triplos e q suítes para quatro pessoas. A capacidade mássima de lotação do hotel é 166 pessoas, sêndo quê, dessas, 40 lotam completamente todas as suítes. A diferença entre o número de quartos triplos e o número de quartos duplos é:
a) 8
c) 12
b) 10
d) 14
alternativa c
Página duzentos e quarenta
34. (UFG-GO) Em um determinado parque, existe um circuito de caminhada, como mostra a figura a seguir.
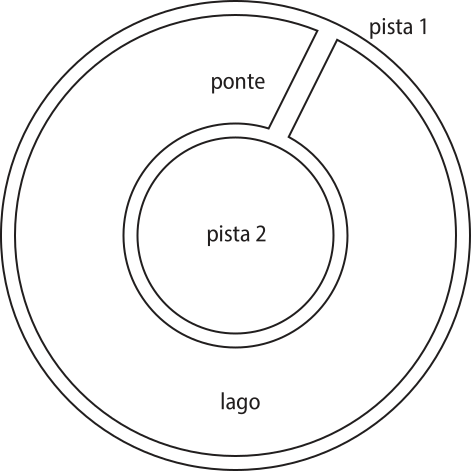
Um atleta, utilizando um podômetro, percórre em um dia a pista 1 duas vezes, atravessa a ponte e percórre a pista 2 uma única vez, totalizando 1.157 passos. No dia seguinte, percórre a pista 1 uma única vez, atravessa a ponte e percórre a pista 2, também uma única vez, totalizando 757 passos. Além díssu, percebe quê o número de passos necessários para percorrer sete voltas na pista 1 equivale ao número de passos para percorrer oito voltas na pista 2. Diante do exposto, conclui-se quê o comprimento da ponte, em passos, é:
a) 5.
b) 6.
c) 7.
d) 8.
e) 15.
alternativa c
35. Foi exposto, na abertura dêste Capítulo, quê o balanceamento de equações químicas póde sêr realizado por meio de um sistema de equações. A equação química I, não balanceada, indica quê uma reação de moléculas compostas de dois hátomus de hidrogênio (H2) com moléculas compostas de dois hátomus de oxigênio (O2) formam moléculas de á gua (H2O).
I (alfa)"H2 + (beta)"O2 → ωH2O
Para balancear essa equação, é necessário determinar as quantidades mínimas de moléculas, expressas pelas incógnitas (alfa)", (beta)" e ω, de modo quê o número de hátomus de hidrogênio e de oxigênio seja igual antes e depois da reação. Observe quê:
• a quantidade de hátomus de hidrogênio (H) antes da reação é 2(alfa)" e, depois da reação, é 2ω;
• a quantidade de hátomus de oxigênio (O) antes da reação é 2(beta)" e, depois da reação, é 1ω.
Desse modo, a menor solução inteira positiva do sistema linear II torna a equação química I balanceada.
II
a) Classifique e dê a solução geral do sistema linear II.
sistema possível e indeterminado; S =
b) Determine a menor solução inteira positiva do sistema linear II.
S = {(2, 1, 2)}
c) escrêeva a equação química I balanceada.
2H2 + O2 → 2H2 O
Sistemas lineares escalonados
Estudaremos agora um processo conhecido como escalonamento, quê também nos permite resolver e classificar sistemas lineares. Antes, porém, vamos apresentar o quê é um sistema escalonado.
Observe o sistema linear escalonado.
Pense e responda
• Como você resolveria esse sistema linear?
• Comparando com os sistemas quê você já rêzouvêo neste Capítulo, resolver esse sistema foi mais prático? Por quê?
Ver as Orientações para o professor.
Página duzentos e quarenta e um
Note quê a equação I tem 4 incógnitas, a equação II tem 3 incógnitas, a equação III, 2 incógnitas e a equação IV, 1 incógnita. Além díssu, todas as equações apresentam as incógnitas na mesma ordem (x, y, z e w). No entanto, consideramos quê o coeficiente da incógnita x da equação II é zero; do mesmo modo, os coeficientes das incógnitas x e y da equação III são zero; e os coeficientes das incógnitas x, y e z da equação IV também são zero. Ou seja, o sistema poderia sêr escrito da seguinte forma:
Porém, para simplificar a escrita, não registramos as incógnitas cujos coeficientes são nulos.
Identificamos quê um sistema linear de m equações com n incógnitas está escalonado quando todas as equações apresentam as incógnitas na mesma ordem e a quantidade de incógnitas com coeficientes nulos aumenta a cada equação. Observe outros exemplos de sistemas escalonados.
a)
b)
c)
Resolução de um sistema linear escalonado
Observe, a seguir, três exemplos de como resolver e classificar um sistema escalonado.
Exemplo 1. O sistema linear escalonado dêste exemplo tem a quantidade de equações igual ao número de incógnitas. Sua resolução é feita da última para a primeira equação, primeiro, é determinado o valor da incógnita z pela equação III, em seguida, é substituído o valor encontrado de z na equação II, então, é obtído o valor da incógnita y e assim por diante. Acompanhe:
Começando pela equação III, temos:
−z = 7 ⇒ z = −7
Substituindo z por −7 na equação II, obtemos:
5y + (−7) = 1 ⇒ 5y = 8 ⇒ y =
Substituindo z por −7 e y por na equação I, temos:
x + 2 ⋅ () − (−7) = 2 ⇒ x = 2 − ⇒ x =
Portanto, o sistema é possível e determinado (SPD), pois possui a solução única:
S =
Página duzentos e quarenta e dois
Exemplo 2. O sistema linear escalonado dêste exemplo apresenta uma quantidade de equações menor do quê o número de incógnitas: 2 equações e 3 incógnitas (a, b e c).
Nesse caso, a solução geral dêêsse sistema será expressa em função de uma variável real (alfa)". Para isso, vamos admitir quê a última incógnita c seja igual a (alfa)", isto é:
c = (alfa)", em quê (alfa)" ∈ ℝ
Em seguida, substituindo c por (alfa)" na equação II, temos:
b − 2 ⋅ (alfa)" = −1 ⇒ b = 2(alfa)" − 1
Por fim, substituindo c por (alfa)" e b por 2(alfa)" − 1 na equação I, obtemos:
7a − (2(alfa)" − 1) + 5 ⋅ (alfa)" = 0 ⇒ 7a = −3(alfa)" − 1 ⇒ a =
Portanto, o sistema linear é possível e indeterminado (SPI), e sua solução geral é:
S =
Exemplo 3. Não existe nenhum valor real de w quê torne a última equação do sistema linear dêste exemplo verdadeira.
Como a última equação 0w = 6 não tem solução real, o sistema linear é impossível (SI), e o seu conjunto solução é indicado por:
S = ∅
Sistemas equivalentes
Quando dois sistemas lineares admitem o mesmo conjunto solução, dizemos quê são sistemas equivalentes.
Por exemplo: e são sistemas equivalentes, pois ambos os sistemas lineares 3 × 3 têm o mesmo conjunto solução, S = {(1, 2, 3)}.
e
Indicamos quê dois sistemas são equivalentes usando o sín-bolo ∼.
Página duzentos e quarenta e três
Escalonamento de sistemas lineares
Sempre é possível escalonar um sistema linear transformando o sistema inicial em um sistema escalonado equivalente, ou seja, quê possui o mesmo conjunto solução. Para isso, podem sêr realizadas as seguintes etapas:
a) Trocar de lugar duas ou mais equações de um sistema linear.
b) Reescrever uma equação para alinhar as incógnitas correspondentes.
c) Multiplicar ou dividir ambos os membros de uma equação por um número real qualquer não nulo.
d) Substituir uma equação do sistema por sua soma com um múltiplo de outra equação do mesmo sistema.
Acompanhe, a seguir, o processo de escalonamento de um sistema linear.
1º) Vamos reescrever a equação I para alinhar as incógnitas correspondentes e colocar a equação III no lugar da equação I, obtendo as equações L1, L2 e L3.
2º) Vamos substituir a equação L2 pela equação L4, em quê L4 é resultado da adição de L2 com o produto de L1 por 3. Em seguida, vamos substituir a equação L3 pela equação L5, em quê L5 é resultado da adição de L3 com o produto de L1 por 2.
3º) Vamos dividir a equação L5 por 3 para obtermos a equação L6, quê colocaremos, em seguida, na posição da equação L4.
4º) Para finalizar o escalonamento, vamos substituir a equação L4 pela equação L7, em quê L7 é o resultado da adição da equação L4 com o produto da equação L6 por −2.
Resolvendo o sistema escalonado, encontramos a solução S = {(−1; 0; 1)}. Portanto, o sistema é possível e determinado (SPD).
Página duzentos e quarenta e quatro
ATIVIDADE RESOLVIDA
10. resôuva e classifique os sistemas lineares pelo método do escalonamento.
a)
b)
Resolução
a)
Primeiro, vamos substituir a equação L2 pela equação L4, em quê L4 é resultado da adição de L2 com o produto de L1 por −2. Em seguida, vamos substituir a equação L3 pela equação L5, em quê L5 é resultado da adição de L3 com o produto de L1 por −1. Observe:
Note quê as equações L4 e L5 são idênticas. Logo, temos um sistema escalonado com três incógnitas e duas equações. Admitindo quê a incógnita z = (beta)", em quê (beta)" ∈ ℝ, podemos usar a equação L4 para determinar o valor da incógnita y em função de (beta)".
Substituindo z por (beta)" e y por na equação L1, vamos obtêr o valor da incógnita x em função de (beta)".
x − 2 ⋅ () + (beta)" = 4
Portanto, o sistema é possível e indeterminado (SPI), e sua solução geral é:
S =
b)
Vamos substituir a equação L2 pela equação L4, em quê L4 é resultado da adição de L2 com o produto de L1 por 2. Em seguida, vamos substituir a equação L3 pela equação L5, em quê L5 é resultado da adição de L3 com o produto de L1 por 3. Acompanhe:
Agora, vamos substituir a equação L5 pela equação L6, em quê L6 é resultado da adição de L5 com o produto de L4 por −2.
A equação L6 do sistema linear escalonado não tem solução. Portanto, o sistema é impossível (SI), e seu conjunto solução é indicado por S = ∅.
Página duzentos e quarenta e cinco
ATIVIDADES
36. Em cada caso, resôuva os sistemas escalonados.
a)
S = {(10, 20)}
b)
S = {(−12, 7, 3)}
c)
S = {(1, 1, 1, 1)}
d)
S = ∅
e)
f)
S = ∅
37. O sistema seguinte tem o número de equações menor do quê o número de incógnitas. Determine a solução geral dêêsse sistema.
Ver as Orientações para o professor.
38. resôuva os sistemas a seguir por escalonamento e classifique-os.
a)
S = {(1, −2, 3, 4)}; sistema possível e determinado
b)
S = {(3 − 2λ, 1, λ) | λ ∈ ℝ}; sistema possível e indeterminado
39. resôuva, por escalonamento, os seguintes sistemas lineares.
a)
S = {(−2; 3; 0)}
b)
S = {(1, −2, 2)}
40. (UFPE) Um nutricionista pretende misturar três tipos de alimentos (A, B e C) d fórma quê a mistura resultante contenha 3.600 unidades de vitaminas, 2.500 unidades de minerais e 2.700 unidades de gorduras. As unidades por grama de vitaminas, minerais e gorduras dos alimentos constam da tabéla a seguir:
Vitaminas |
Minerais |
Gordura |
|
|---|---|---|---|
A |
40 |
100 |
120 |
B |
80 |
50 |
30 |
C |
120 |
50 |
60 |
Quantos gramas do alimento C devem compor a mistura?
20 gramas
41. (FGV-SP) Para trabalhar na feira internacional do livro, a editora contratou três funcionários: Ana, Béto e Carlos, com salários x, y e z reais, respectivamente. O salário de Ana é igual à soma dos salários de Béto e Carlos. No final da feira, a editora pagou uma gratificação, de valor igual ao salário de Béto, a cada um dos três. Assim, Ana recebeu no total R$ 2.300,00, e a soma dos valores quê os três receberam foi de R$ 5.400,00. Qual foi o valor da gratificação quê receberam?
R$ 800,00
Página duzentos e quarenta e seis
EXPLORANDO A TECNOLOGIA
Utilizando o Mêitrix calculator
Nesta seção, você vai explorar o sáiti Mêitrix calculator e utilizá-lo para conferir resoluções de sistemas de equações lineares pelo método do escalonamento. Mas, para isso, vamos compreender antes o modo como um sistema linear é representado na forma matricial.
Considere o sistema linear de m equações com n incógnitas:
A matriz na qual cada linha é formada, ordenadamente, pêlos coeficientes e termos independentes de cada equação, é denominada matriz completa do sistema.
A matriz formada pêlos coeficientes ordenados de cada equação, é denominada matriz dos coeficientes do sistema.
Exemplo:
• Sistema linear
• Matriz completa
• Matriz dos coeficientes
Consideremos, ainda, as seguintes matrizes associadas ao sistema:
• X = , formada pelas incógnitas.
• B = , formada pêlos termos independentes.
Ao multiplicarmos a matriz dos coeficientes pela matriz das incógnitas, obtemos a matriz dos termos independentes:
Dizemos quê essa é a forma matricial do sistema linear considerado.
Página duzentos e quarenta e sete
Em notação simplificada, temos: A ⋅ X = B, em quê A é a matriz de ordem m × n formada por todos os coeficientes do sistema, X é a matriz de ordem n × 1 formada por todas as incógnitas, e B é a matriz de ordem m × 1 formada por todos os termos independentes.
Quando um sistema linear tem o número de equações igual ao número de incógnitas, a matriz dos coeficientes do sistema é uma matriz quadrada. Observe o exemplo.
• Sistema linear
• Forma matricial
Agora, vamos utilizar o Mêitrix calculator.
Você póde acessar o sáiti por meio do línki matrixcalc.org/pt (acesso em: 21 set. 2024). A vantagem de utilizar essa platafórma está no fato de quê todo o processo quê envolve a resolução é apresentado em etapas, permitindo quê a revisão da resolução seja mais rápida.
Ao digitar esse línki no navegador, você terá acesso à seguinte página inicial.
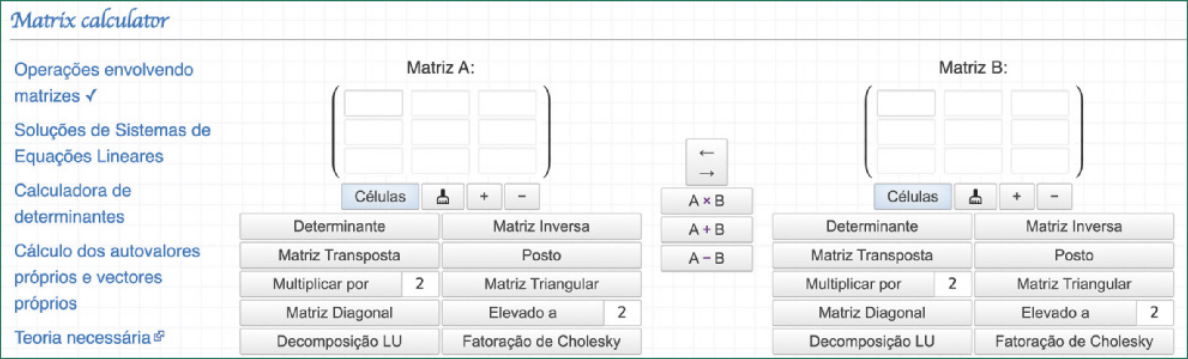
Inicialmente, acompanhe a resolução de um sistema linear de três equações com três incógnitas pelo método do escalonamento. Nesse escalonamento, em uma das passagens, foi cometido um êrro, quê, posteriormente, vamos identificar e corrigir com o auxílio do Mêitrix calculator.
O sistema a sêr resolvido é o seguinte:
Primeiro, vamos substituir a equação L2 pela equação L4, em quê L4 é resultado da adição de L2 com o produto de L1 por −2. Em seguida, vamos substituir a equação L3 pela equação L5, em quê L5 é resultado da adição de L3 com o produto de L1 por −2.
Página duzentos e quarenta e oito
Agora, vamos substituir a equação L5 pela equação L6, em quê L6 é resultado da adição da equação L5 com o produto da equação L4 por .
Resolvendo as equações do sistema, de baixo para cima, temos:
z = , y = e x =
Por outro lado, ao verificarmos se os resultados obtidos tornam verdadeiras as sentenças quê formam o sistema, observamos quê isso não acontece, o quê indica quê há êrro na resolução.
Como, em geral, essas verificações são muito trabalhosas, vamos utilizar o Mêitrix calculator para nos auxiliar na verificação da resolução.
Para isso, siga os passos a seguir.
I. Em um navegador, digite o línki apresentado anteriormente e clique na opção Solução de Sistemas de Equações Lineares, conforme o destaque em vermelho.

II. O sáiti apresenta a seção desejada, na qual você vai inserir os coeficientes das equações do sistema. Mas, antes, verifique se a ordem do sistema é a quê você precisa. Você póde aumentar ou diminuir a quantidade de células clicando nos botões destacados em azul, como na imagem a seguir.
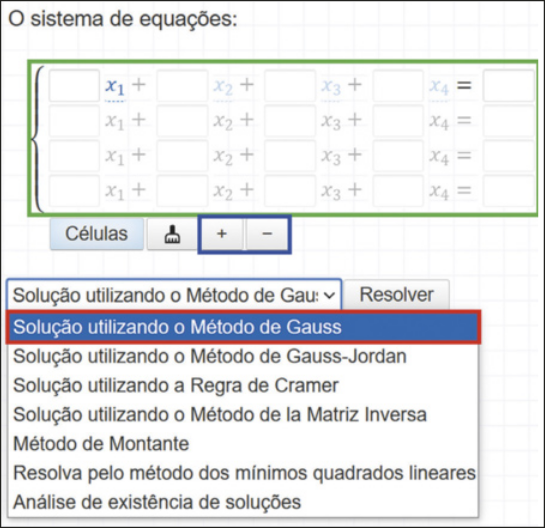
Página duzentos e quarenta e nove
III. Ajuste a quantidade de células, para quê o sistema fique com três equações e três incógnitas, e complete os quadrinhos, na parte destacada em vêrde na imagem anterior, com os coeficientes das equações. Caso a equação linear tenha algum coeficiente nulo, preencha o quadrinho da incógnita correspondente com o número 0.
Depois de completar o sistema com os coeficientes, clique em Solução utilizando o Método de Gauss, destacado em vermelho na imagem anterior, quê também é conhecido como método de escalonamento de matrizes.
IV. O sáiti apresenta o escalonamento da matriz completa do sistema e o sistema linear escalonado equivalente ao sistema inicial, como póde sêr verificado na imagem a seguir.

V. Explore o sáiti, lendo as explicações sobre cada passo, e compare o escalonamento apresentado com o escalonamento feito no início desta seção. Observe quê o sistema linear escalonado corretamente é êste:
Resolvendo as equações do sistema, têm-se as soluções z = 1, y = −1 e x = 1.
Agora, faça o quê se pede nas atividades a seguir.
1. Qual foi o êrro cometido no escalonamento da matriz no início da seção?
Ver as Orientações para o professor.
2. Determine o sistema linear escalonado equivalente ao sistema a seguir. Utilize o Mêitrix calculator para conferir a sua resolução.
S = {(1, 2, 3)}
Página duzentos e cinquenta
ATIVIDADES COMPLEMENTARES
1. (Cesupa) Aproveitando o recesso do mês de julho, o Cesupa pretende alterar parte do sistema de refrigeração em 3 de seus prédios, num período de uma semana. Para tanto, convida 3 firmas para submeter orçamentos para o trabalho envolvido em cada um dos prédios. As propostas recebidas estão representadas na matriz abaixo:
A =
onde aij é o orçamento em unidades de mil reais da firma i para o prédio j.
Como cada firma, no período previsto de uma semana, só consegue fazer o serviço em um dos prédios, será preciso então contratar uma firma diferente para cada prédio.
A contratação firma/prédio, dentre as abaixo apresentadas, quê levará o Cesupa a uma despesa mínima é:
a) a11, a22, a33
b) a11, a23, a32
c) a12, a23, a31
d) a13, a22, a31
alternativa a
2. (Unicruz-RS) Dadas as matrizes A = e B = , a matriz quê resulta da operação 2A − B é:
a)
b)
c)
d)
e)
alternativa b
3. (Vunesp-SP) Considere três lojas, L1, L2 e L3, e três tipos de produtos, P1, P2 e P3. A matriz a seguir descreve a quantidade de cada produto vendido por cada loja na primeira semana de dezembro. Cada elemento aij da matriz indica a quantidade do produto Pi vendido pela loja Lj, i, j = 1, 2, 3.
Analisando a matriz, podemos afirmar quê:
a) a quantidade de produtos do tipo P2 vendidos pela loja L2 é 11.
b) a quantidade de produtos do tipo P1 vendidos pela loja L3 é 30.
c) a soma das quantidades de produtos do tipo P3 vendidos pelas três lojas é 40.
d) a soma das quantidades de produtos do tipo Pi vendidos pelas lojas Li, i = 1, 2, 3 é 52.
e) a soma das quantidades dos produtos dos tipos P1 e P2 vendidos pela loja L1 é 45.
alternativa e
4. (UCDB-MS) Dadas as matrizes
e ,
tem-se quê o produto A ⋅ B é igual a:
a)
b)
c)
d)
e)
alternativa a
5. (UFC-CE) O valor de 2A2 + 4B2 quando e é igual a:
a)
b)
c)
d)
e)
alternativa b
6. (UFABC-SP) Duas bicicletas dêsênvólvem movimentos retilíneos e uniformes sobre a mesma trajetória, com suas grandezas em unidades do Sistema Internacional. Suas funções horárias estão representadas matricialmente por:
Nessas condições, as duas bicicletas se encontrarão no instante:
a) 1,0 s.
b) 1,4 s.
c) 2,0 s.
d) 3,5 s.
e) 5,0 s.
alternativa c
7. (ESA-MG) Os Batalhões de Inteligência Militar dêsênvólvem formas para o envio de mensagens secretas, sêndo uma delas os códigos matemáticos quê seguem os passos a seguir:
Página duzentos e cinquenta e um
1. O destinatário e o remetente possuem uma matriz chave C;
2. O destinatário recebe do remetente uma matriz P, tal quê MC = P, onde M é a matriz da mensagem a sêr codificada;
3. Cada número da matriz M corresponde a uma letra do alfabeto:
1 = a, 2 = b, 3 = c, …, 23 = z;
4. Consideramos o alfabeto com 23 lêtras, excluindo as lêtras k, w e y;
5. O número zero corresponde ao ponto de exclamação;
6. A mensagem é lida, encontrando a matriz M, fazendo correspondência número/letra e ordenando as lêtras por linhas da matriz conforme segue:
m11 m12 m13 m21 m22 m23 m31 m32 m33.
Considere as matrizes:
e
Com base nas informações descritas, qual alternativa apresenta a mensagem enviada por meio da matriz M?
a) Brasil!
b) Território!
c) Pantanal!
d) Montanha!
e) Guerreiro!
alternativa c
8. (UEL-PR) Com a criação da tela sensível ao toque e sensores de movimento, foi possível utilizar gestos humanos como interface de comunicação com a máquina. Por conta díssu, pode-se girar uma imagem em um celular.
Admita quê um aplicativo receba o gesto para girar a ilustração de Emil Lendof, quê faz uma releitura do fragmento A Criação de Adão de Miquelângelo, por um ângulo θ = radianos no sentido anti-horário. O aplicativo considera a imagem em um plano cartesiano de origem O de modo quê cada ponto P é rotacionado até um ponto P’ no mesmo sistema de coordenadas, conforme imagens a seguir.
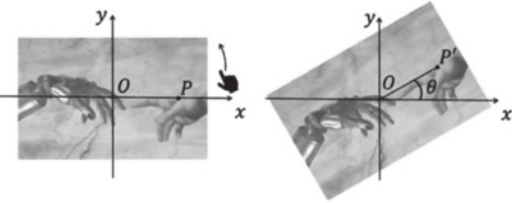
Sabendo quê se P = (a, b), P’ = (a’, b’) e M = , então = M × assinale a alternativa quê apresenta, corretamente, as coordenadas do ponto P’.
a)
b)
c)
d)
e)
alternativa e
9. (Fuvest-SP) Matrizes podem sêr usadas para se obtêr informações sobre uma rê-de social. Para compreender como isso póde sêr feito, consideremos como exemplo uma pequena rê-de social formada por 4 pessoas: P1, P2, P3, P4. A matriz associada a essa rê-de social é a matriz 4 × 4:
O valor 1 (um) na posição a32 (linha 3, coluna 2) da matriz significa quê a pessoa P3 segue a pessoa P2 , ao passo quê o valor 0 (zero) na posição a24 (linha 2, coluna 4) significa quê a pessoa P2 não segue a pessoa P4. O valor 0 (zero) será atribuído às posições aii. O significado do valor da posição bmn da matriz produto M × M = M2 é a quantidade de conexões da pessoa Pm até a pessoa Pn passando exatamente por uma pessoa, diferente delas duas, quê chamaremos de conexão de grau 2. Dessa forma, os valores das posições da matriz M2 podem refletir o alcance da rê-de social, suas potencialidades e fraquezas, a influência de certos membros dela, dentre outros aspectos. Com relação à rê-de social apresentada, é correto afirmar quê:
a) Existem 5 pares de pessoas diferentes (Pi ≠ Pj) quê não possuem conexões de grau 2.
Página duzentos e cinquenta e dois
b) Existem 6 pares de pessoas diferentes (Pi ≠ Pj) quê possuem apenas uma conexão de grau 2.
c) Existem 3 pares de pessoas diferentes (Pi ≠ Pj) quê possuem 2 conexões de grau 2 diferentes.
d) Existem 3 pessoas quê possuem conexões de grau 2 com todas as outras pessoas da rê-de social.
e) Existe apenas 1 pessoa Pi (i ≠ 3) tal quê Pi e P3 seguem-se mutuamente.
(Note e adote: A posição bmn da matriz produto M × M = M2 é dada pela expressão
bmn = am1a1n + am2a2n + am3a3n + am4a4n.)
alternativa b
10. (Enem/MEC) Diante de um sanduíche e de uma porção de batatas fritas, um garoto, muito interessado na quantidade de calorias quê póde ingerir em cada refeição, analisa os dados de quê dispõe. Ele sabe quê a porção de batatas tem 200 g, o quê equivale a 560 calorias, e quê o sanduíche tem 250 g e 500 calorias. Como ele deseja comer um pouco do sanduíche e um pouco das batatas, ele se vê diante da questão: “Quantos gramas de sanduíche e quantos gramas de batata eu posso comer para ingerir apenas 462 calorias permitidas para esta refeição?”
Considerando quê x e y representam, respectivamente, em grama, as quantidades do sanduíche e das batatas quê o garoto póde ingerir, indique a alternativa correspondente à expressão algébrica quê relaciona corretamente essas quantidades.
a) 2x + 2,8y = 462
b) 2,8x + 2y = 462
c) 1,8x + 2,3y = 1.060
d) x + 0,4y = 462
e) 0,4x + y = 462
alternativa a
11. (Fuvest-SP) Considere o sistema linear . Assinale a alternativa quê representa graficamente esse sistema.
a) 
b) 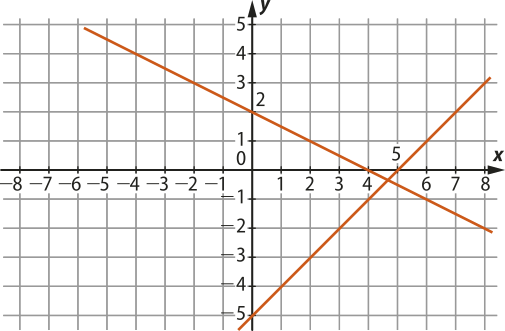
c) 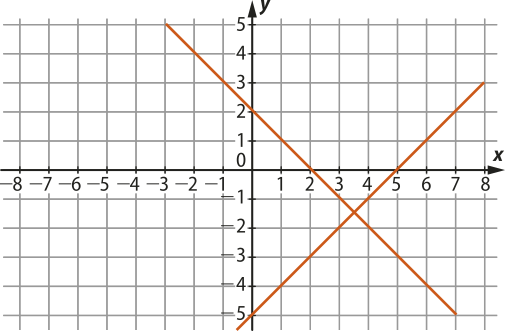
d) 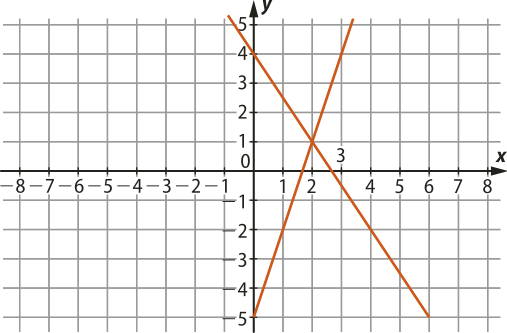
e) 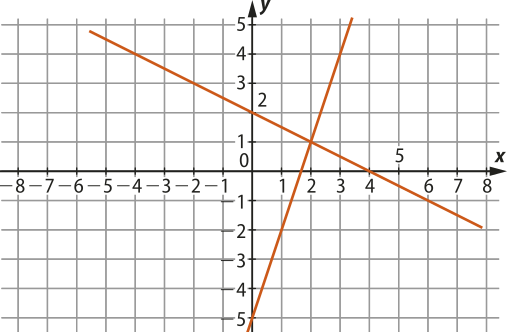
alternativa e
Página duzentos e cinquenta e três
12. (EsPCEx-SP) Dado o sistema:
Sendo x, y, z ∈ ℝ, então o valor de x + y + z é igual a:
a) 20
b) 30
c) 40
d) 50
e) 60
alternativa c
13. (hú- hê- érre jota) Uma nutricionista recomendou, para uma pessoa adulta, a ingestão de pão, fruta e iogurte no café da manhã. Os três alimentos, em conjunto, devem conter, exatamente, 16 g de proteínas, 124 g de carboidratos e 10 g de gorduras. Admita a seguinte quantidade de nutrientes, em gramas, em uma porção de 100 g de cada alimento:
QUANTIDADE DE NUTRIENTE (EM G) |
PORÇÃO DE 100 G |
||
|---|---|---|---|
PÃO |
FRUTA |
IOGURTE |
|
proteínas |
8 |
0 |
4 |
carboidratos |
60 |
20 |
2 |
gorduras |
4 |
0 |
3 |
A partir da tabéla, calcule quantas pôr-ções de cada alimento essa pessoa deve ingerir de modo a consumir as quantidades de nutrientes recomendadas para seu café da manhã.
uma pôr-ção de pão, 3 pôr-ções de fruta e duas pôr-ções de iogurte
PARA REFLETIR
Neste Capítulo, estudamos o conceito de matrizes e operações envolvendo matrizes. Também foram apresentados os sistemas lineares e suas classificações.
Vamos refletir a respeito das aprendizagens do Capítulo 6:
• Você já conhecia algum dos conteúdos apresentados ao longo dêste Capítulo? Qual(is)?
• Você consegue pensar em outras situações do dia a dia quê podem sêr resolvidas utilizando sistemas de equações lineares?
• Você consegue reconhecer se houve um aprofundamento em relação ao quê você conhecia sobre o conceito de sistemas de equações?
• Monte um qüadro comparativo entre as propriedades da adição de matrizes e as propriedades da adição de números reais. Depois, faça o mesmo para as propriedades da multiplicação.
Respostas pessoais.
Página duzentos e cinquenta e quatro

