PARTE ESPECÍFICA
Comentários e sugestões de abordagem para êsteeste Volume

O objetivo dêstedeste material é oferecer subsídios para a atividade docente, quêque assume um papel relevante dentro do compléksocomplexo processo de ensino-aprendizagem, d fórmade forma articulada com as propostas apresentadas no Livro do estudante.

Nas Orientações para o professor, há uma descrição explicando de quêque forma estão sêndosendo contempladas neste Volume as habilidades, as competências específicas e as competências gerais da BNCC. Em seguida, são apresentadas estratégias para auxiliar o processo de ensino-aprendizagem, d fórmade forma a contribuir para o desenvolvimento dessas competências e habilidades. Além díssudisso, há sugestões de atividades complementares, instrumentos avaliativos e referências de outros materiais atualizados quêque podem sêrser utilizados. Vale ressaltar quêque esta obra não pretende sêrser a única referência de consulta nem apresentar soluções completas para os desafios enfrentados pêlospelos professores, mas sim constituir uma alternativa para auxiliar a atividade docente e o processo de ensino-aprendizagem, contribuindo para a otimização do planejamento de aulas, sem deixar de respeitar a autonomia do docente quêque age de acôr-doacordo com os desafios reais da comunidade escolar e da turma em quêque atua lecionando.

êsteEste Volume é organizado em 7 capítulos. O qüadroquadro a seguir apresenta uma sugestão de cronograma, considerando 200 dias letivos, consequentemente, 40 semanas de aula. A proposta contempla 34 semanas, considerando 6 semanas para ajustes, avaliações e outras demandas pedagógicas.

Para planejamentos bimestrais, recomenda-se considerar 9 semanas de aula para cada bimestre; para planejamentos trimestrais, 12 semanas; e, para planejamentos semestrais, 17 semanas. No entanto, é importante quêque o professor avalie sua realidade e realize as adequações necessárias conforme o calendário escolar, de modo a privilegiar o desenvolvimento dos estudantes de acôr-doacordo com suas necessidades e com as escôlhasescolhas feitas pela comunidade escolar.

Página trezentos e vinte e nove329

Para todos os blocos semanais, estão disponíveis atividades resolvidas e atividades propostas. Recomenda-se a seleção de parte das atividades para sêrser desenvolvida em sala de aula (individualmente, em duplas ou grupos maiores) e outra parte para sêrser realizada fora do horário de aula.

Professor, caso tenha estudantes PcD (Pessoa com Deficiência), recomenda-se a leitura dos textos a seguir.

• SILVEIRA, Ingrid Machado. Desenvolvimento de recurso tátil no ensino da matemática financeira para alunos com deficiência visual. Revista Educação Pública, v. 21, n. 43, 30 nov. 2021. Disponível em: https://livro.pw/fqjar. Acesso em: 4 nov. 2024.

• SANTOS, Cristina Paludo; LOOSE, Luis Carlos. Estratégias tecnológicas de interação e mediação para o ensino de geometria espacial: um estudo de caso com alunos surdos. In: WORKSHOP DE INFORMÁTICA NA ESCOLA (WIE), 23., 2017, Recife. Anais […]. Porto Alegre: Sociedade Brasileira de Computação, 2017. p. 11-20. Disponível em: https://livro.pw/kefkg. Acesso em: 4 nov. 2024.

• LEAL, Simone de Almeida Delphim; ABAD, Alberto (org.). A formação de professores em educação matemática na perspectiva da educação especial e inclusiva. Macapá: Unifap, 2019. Disponível em: https://livro.pw/aeujs. Acesso em: 4 nov. 2024.

Capítulo 1 Matemática financeira

Orientações

O Capítulo explora a porcentagem e os conceitos de aumentos e descontos percentuais sucessivos, juros simples e juros compostos, alguns índices de inflação, sistemas de amortização de financiamento e empréstimo e orçamento familiar, favorecendo a reflekçãoreflexão e a análise crítica de kestõesquestões ligadas à construção de nossa ssossiedadesociedade, colaborando, assim, para o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias, em particular, a habilidade EM13MAT104. O uso de tecnologias digitais para fazer simulações envolvendo problemas do dia a dia relacionados a esse contexto favorece a compreensão e o trabalho com esses conceitos, desenvolvendo as competências específicas 2 e 3 da área de Matemática e suas Tecnologias, em particular, as habilidades EM13MAT203 e EM13MAT303.

O texto da Abertura do Capítulo e as kestõesquestões propostas permitem trabalhar os Temas Contemporâneos

Página trezentos e trinta330

Transversais Educação para o Consumo e Educação Financeira. Também colabóramcolaboram para o desenvolvimento da competência geral 6, pois os estudantes podem compartilhar e valorizar a diversidade dos saberes e vivências culturais, explorando aspectos de autonomia e de responsabilidade no quêque se refere ao tema.

Na atividade 1, espera-se quêque os estudantes digam quêque as promoções divulgam descontos percentuais. Pode-se incentivar a troca de situações vivenciadas por eles relacionadas à venda e à compra de produtos e serviços em quêque as propagandas anunciam descontos.

A atividade 2 leva os estudantes a explicar como escolhem a melhor forma de pagamento. Uma resposta possível é comparar os valores correspondentes nas condições dadas com base no tempo e na quantidade de vezes em quêque o bem é parcelado. Há situações em quêque os valores não são diferentes, considerando as duas opções de pagamento indicadas.

Aproveitar a atividade 3 para promover uma discussão acerca dos cartões oferecidos por lojas quêque visam fidelizar o cliente. Muitas lojas oferecem descontos e baixos juros para quêquem paga com esse tipo de cartão, o que costuma sêrser viável para quem tem o hábito de comprar no mesmo estabelecimento com freqüênciafrequência ou realizar compras de grandes valores. Em alguns casos, a loja cobra uma taxa mensal ou anual pelo uso do cartão, por isso é importante analisar se há realmente vantagem em adquirir esse serviço. Cada loja estipula suas regras de uso do cartão, conforme estabelece sua instituição credora.

Na atividade 4, espera-se quêque os estudantes respondam 28%.

A finalidade do tópico Porcentagem é revisar e aprofundar esse assunto, quêque é de grande importânssiaimportância para o exercício da cidadania.

No estudo do tópico Aumentos e descontos sucessivos, pode-se explicar quêque, após aumentos (ou descontos) percentuais sucessivos, o aumento médio percentual é calculado pela média geométrica. Para isso, pode-se apresentar o exemplo a seguir.

Em 2024, um produto custava R$ 100,00. Aumentou 100% em 2025, tendo seu preêçopreço elevado para R$ 200,00, e aumentou 28% em 2026, elevando seu preêçopreço para R$ 256,00. O aumento percentual médio anual quêque ocorreu nesse período é dado pela média geométrica M_G a seguir.

M_G = $\begin{array}{c}\sqrt[]{\left(2\cdot \mathrm{1,28}\right)}=\sqrt[]{\mathrm{2,56}}\end{array}$ = 1,60

Portanto, o aumento médio anual foi 60%, pois:

100 ⋅ 1,6 ⋅ 1,6 = 256.

No estudo do tópico Lucro e prejuízo, pode-se verificar se os estudantes compreendem o significado de lucro propondo o problema a seguir.

João comprou um relógio por R$ 50,00 e o vendeu para seu amigo por R$ 60,00. Meses depois, João comprou de seu amigo o mesmo relógio por R$70,00 e o revendeu a outra pessoa por R$ 80,00. Ao final dessas duas transações, João teve lucro ou prejuízo? Explique.

Espera-se quêque os estudantes respondam quêque João teve um lucro total de R$ 20,00, sêndosendo R$ 10,00 de lucro na primeira transação e mais R$ 10,00 de lucro na segunda.

Ao desenvolver o tópico Juro simples, propor aos estudantes quêque pesquisem, em boletos de compras, de condomínio, entre outros documentos financeiros, o percentual correspondente à multa e ao juro de mora, para quêque percêbampercebam quêque o juro simples, em geral, é aplicado em dívidas de curto prazo, de no mássimomáximo 30 dias.

No primeiro boxe Pense e responda do tópico Juro compôztocomposto, explicar aos estudantes quêque, em cálculos envolvendo quantias monetárias, usamos apenas duas casas decimais após a vírgula, quêque indicam os centavos de real. Por isso, para obtêrobter o resultado, realiza-se o arredondamento para a ordem dos centésimos (segunda ordem da parte decimal do número) e, dêêssedesse modo, a quantia correspondente é expressa em centavo. Se necessário, recordar as regras de arredondamento: se o algarismo da ordem dos milésimos (terceira ordem da parte decimal) for menor do quêque 5, o algarismo da ordem dos centésimos (segunda ordem da parte decimal) não se altera; já se o algarismo da ordem dos milésimos (terceira ordem da parte decimal) for igual ou maior do quêque 5, o algarismo da ordem dos centésimos (segunda ordem da parte decimal) é aumentado em um centésimo. Orientar os estudantes a proceder dessa maneira ao trabalhar com valores monetários nas atividades propostas.

O segundo boxe Pense e responda dêêssedesse mesmo tópico leva os estudantes a perceber a diferença entre a aplicação a juro compôztocomposto e a aplicação a juro simples, considerando uma mesma taxa e um mesmo período.

No tópico Juros e funções, os estudantes comparam representações gráficas de funções associadas a juro simples e a juro compôztocomposto. Com isso, eles dêsênvólvemdesenvolvem a competência específica 3 da área de Matemática e suas Tecnologias, com destaque para a habilidade EM13MAT303.

Nesse tópico, recomenda-se enfatizar a associação da função afim ao juro simples e da função exponencial ao juro compôztocomposto, considerando como domínio os números naturais não nulos. Comentar quêque a representação gráfica ajuda a comparar visualmente duas aplicações, seja em uma mesma modalidade, seja em modalidades diferentes.

Página trezentos e trinta e um331

A seção Explorando a tecnologia trabalha o uso de planilhas eletrônicas para auxiliar o cálculo e a análise do juro simples e do juro compôztocomposto. Dessa forma, colabora-se para o desenvolvimento da competência geral 5, pois os estudantes utilizam tecnologias digitais de maneira crítica, reflexiva e ética para se comunicar e resolver problemas. Na seção, estão também envolvidas as competências específicas 1, 2 e 3 da área de Matemática e suas Tecnologias, pois os estudantes são levados a utilizar estratégias, conceitos e procedimentos matemáticos para interpretar situações em variados contextos, seja em kestõesquestões socioeconômicas, seja tecnológicas, além de aplicar esses conceitos para resolver problemas e avaliar a plausibilidade dos resultados. Os estudantes exploram, ainda, as habilidades EM13MAT203 e EM13MAT303, ao aplicar conceitos matemáticos no planejamento, na execução e na análise de ações quêque envolvem a utilização de aplicativos e a criação de planilhas para simular cálculos de juro simples e juro compôztocomposto, comparando os montantes obtidos em cada um dos regimes por meio de representações gráficas.

Na atividade 1, os estudantes comparam o montante obtídoobtido nas modalidades de juro simples e de juro compôztocomposto. Espera-se quêque eles calculem a diferença ôbitídaobtida em dezembro, bastando, para isso, realizar a subtração: 14.257,61 − 13.600,00 = 657,61, obtendo, então, R$ 657,61.

Na atividade 2, espera-se quêque eles percêbampercebam quêque, no primeiro mês, o montante obtídoobtido é o mesmo nas duas modalidades de juro, pois, ao considerar t = 1 nas duas fórmulas, obtém-se o mesmo resultado, conforme mostrado a seguir.

Juro simples: M = C ⋅ (1 + i ⋅ t) ⇒ M = 10.000 ⋅ (1 + 0,03 ⋅ 1) = 10.300

Juro compôztocomposto: M = C ⋅ (1 + i)^t ⇒ M = 10.000 ⋅ (1 + 0,03) ¹ = 10.300

Na atividade 3, os estudantes precisam construir uma planilha considerando um capital de R$ 20.000,00 aplicado a uma taxa de 2% a.m. durante um ano. A seguir, reproduzimos uma possível resposta.

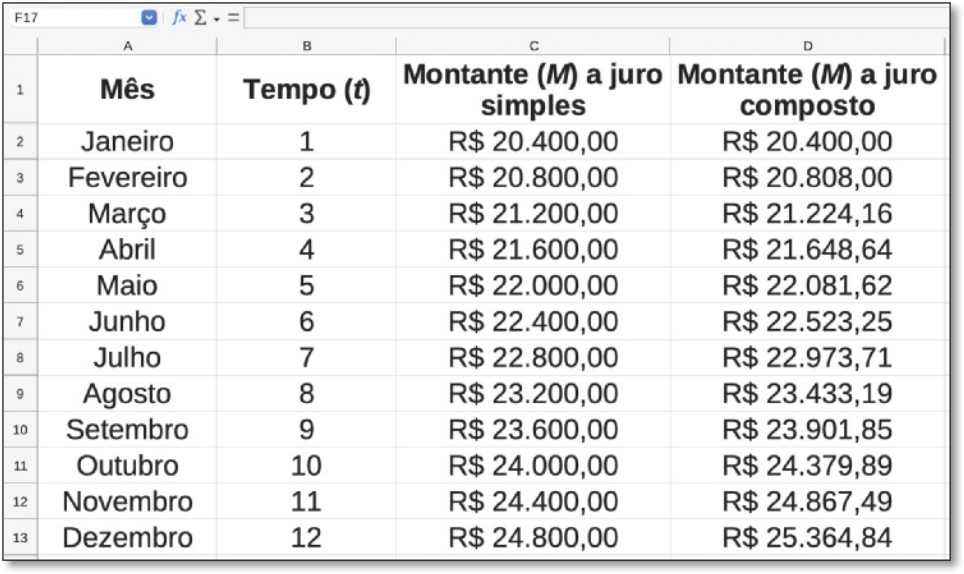
Na atividade resolvida 14, no tópico Valor presente e valor futuro, explicar aos estudantes quêque o valor determinado na opção 2, de um total de R$ 2.908,68, é a quantia necessária, rendendo 2% ao mês, para pagar as 5 parcelas de R$ 605,00, como ilustra o qüadroquadro.

Página trezentos e trinta e dois332

O tópico Orçamento familiar colabora para o desenvolvimento das competências específicas 1 e 2 da área de Matemática e suas Tecnologias, com ênfase nas habilidades EM13MAT104 e EM13MAT203, respectivamente, pois os estudantes interprétaminterpretam taxas e índices de natureza socioeconômica, investigando os processos de cálculo dêêssesdesses números, e aplicam conceitos matemáticos no planejamento, na execução e na análise de ações envolvendo a criação de planilhas para contrôlecontrole de orçamento familiar. Com isso, exploram-se os Temas Contemporâneos Transversais Educação Financeira, Educação para o Consumo e Vida Familiar e Social.

Uma possibilidade de atividade complementar para esse tópico é propor aos estudantes quêque elaborem uma planilha com o orçamento da família deles, incluindo todos os gastos. Para isso, sugere-se a leitura do conteúdo disponível em: https://livro.pw/chuyr (acesso em: 24 out. 2024), do Banco Central do Brasil, quêque explica, em texto e vídeo, como montar um orçamento familiar.

O trabalho com o consumo sustentável, no boxe Fórum, aborda o Tema Contemporâneo Transversal Educação para o Consumo. Com ele, podem sêrser desenvolvidas as competências gerais 4 e 7 da BNCC, pois os estudantes utilizam diferentes linguagens para se expressar e partilhar informações, experiências e ideias, argumentando com base em fatos, dados e informações confiáveis para defender pontos de vista e decisões comuns quêque respeitem e promovam os direitos humanos e a consciência sócio-ambientalsocioambiental. Também permite desenvolver a competência específica 2 da área de Matemática e suas Tecnologias, ao propor a participação em ações quêque investigam o mundo contemporâneo para tomar decisões voltadas à sustentabilidade, e as competências específicas 2 e 3 da área de Ciências da Natureza e suas Tecnologias, pois os estudantes precisam se perceber como parte da dinâmica da vida e do planêtaplaneta e elaborar argumentos com base em decisões éticas e responsáveis para propor soluções de demandas locais, comunicando-as por diferentes meios. Esse trabalho pódepode sêrser desenvolvido em parceria com o professor de Biologia, da área de Ciências da Natureza e suas Tecnologias.

Uma opção de trabalho é incentivar os estudantes a discutir com suas famílias o desperdício de alimentos e apresentar a eles o sáitisite https://livro.pw/qxrum (acesso em: 24 out. 2024), quêque traz diferentes materiais com objetivo de incentivar a redução de perdas de alimentos.

O trabalho com o tópico Sistemas de amortização colabora para o desenvolvimento das competências específicas 2 e 3 da área de Matemática e suas Tecnologias, pois os estudantes investigam ações do mundo contemporâneo relacionadas às finanças, fazendo uso de tecnologias para mobilizar conceitos e procedimentos matemáticos, a fim de aplicá-los na interpretação e na resolução de problemas em diversos contextos. Esse tópico também contribui para trabalhar as habilidades EM13MAT203, pois os estudantes aplicam conceitos matemáticos no planejamento, na execução e na análise de ações quêque envolvem o contrôlecontrole de orçamento familiar e utilizam simuladores de juros para tomar decisões, e EM13MAT303, pois interprétaminterpretam e comparam situações envolvendo juros.

No boxe Pense e responda do tópico Sistema Price, para calcular o valor dos juros na quarta prestação, os estudantes devem determinar 2,5% de R$ 30.282,42, quêque é o saldo devedor correspondente à terceira parcela, como indicado na planilha, obtendo o valor de R$ 757,06.

No tópico Sistema de Amortização Constante (SAC), comentar quêque esse modelo costuma sêrser utilizado no financiamento de bens com valores altos, por exemplo, imóveis.

A seção História da Matemática contribui para o desenvolvimento da competência geral 1, pois são valorizados os conhecimentos historicamente construídos sobre o mundo físico, social e cultural para entender e explicar a realidade, e da competência geral 6, pois permite valorizar a diversidade dos saberes e vivências culturais para apropriar-se de conhecimentos e experiências quêque possibilitam entender as relações próprias do mundo do trabalho. Para mais informações sobre o método das partidas dobradas, pode-se consultar o artigo “Epistemologia do método das partidas dobradas: considerações sobre aspectos históricos e métodos de ensino”, disponível em: https://livro.pw/zfotg (acesso em: 24 out. 2024), em quêque os autores apresentam reflekçõesreflexões sobre o método em seus aspectos teóricos e conceituais.

Uma possibilidade nesse momento é verificar se os estudantes conhecem ou têm interêsseinteresse em seguir carreira na área das Ciências Contábeis e apresentar a descrição de um curso de Ensino Superior destinado a essa formação específica; para isso, pode-se apresentar o sáitisite: https://livro.pw/hopbs (acesso em: 24 out. 2024), quêque contém uma descrição dessa Ciência.

O trabalho com a seção Conexões com… aborda o Tema Contemporâneo Transversal Educação Financeira. Esse trabalho possibilita desenvolver a competência específica 1 da área de Matemática e suas Tecnologias, ao utilizar estratégias, conceitos e procedimentos

Página trezentos e trinta e três333

matemáticos para interpretar situações socioeconômicas. Em particular, também pódepode sêrser desenvolvida a habilidade EM13MAT104, quêque diz respeito à interpretação de taxas e índices, como a inflação.

A seguir, apresentam-se comentários e soluções das atividades.

1. Resposta possível: Por se tratar da alteração de preços e serviços, a inflação impacta basicamente o pôdêrpoder de compra das pessoas: quando os índices aumentam, por exemplo, de um mês para o outro, uma mesma cesta de produtos já não pódepode mais sêrser comprada com a mesma quantia do mês anterior.

2. 672,07 ⋅ (1 − 0,0068) ≃ 667,50, ou seja, R$ 667,50

3. a) 500,00 ⋅ 1,0452 ⋅ 1,1006 ⋅ 1,0579 ⋅ 1,0462 ≃ 636,59, ou seja, R$ 636,59

b) 1,0591 ⋅ 1,065 ⋅ 1,0584 ⋅ 1,0591 ⋅ 1,0641 ⋅ 1,1067 ⋅ 1,0629 ⋅ 1,0295 ⋅ 1,0375 ⋅ 1,0431 ⋅ 1,0452 ⋅ 1,1006 ⋅ 1,0579 ⋅ 1,0462 ≃ 2,24

Como 2,24 corresponde a 224%, tem-se quêque o aumento foi 124% (224 −100).

4. Respostas possíveis: IPCA-15: diféredifere do IPCA apenas pelo período de côlétacoleta, quêque abrange, em geral, do dia 16 do mês anterior ao dia 15 do mês de referência; IPP (Índice de Preços ao Produtor): mais voltado para a indústria, médemede a variação de preços de venda recebidos pêlospelos produtores de bens e serviços; Sinapi (Sistema Nacional de Pesquisa de Custos e Índices da Construção Civil): produzido em conjunto com a Caixa Econômica Federal, médemede a variação de preços para o setor habitacional e de construção; IGP-M (Índice Geral de Preços – Mercado): calculado pela Fundação Getúlio Vargas (FGV), é formado por três outros índices, o Índice de Preços ao Produtor Amplo – Mercado (IPA-M), o Índice de Preços ao Consumidor – Mercado (IPC-M) e o Índice Nacional de Custo da Construção – Mercado (INCC-M).

5. Auxiliar os estudantes na realização da entrevista sobre o período de hiperinflação no Brasil, primeiramente, na seleção da pessoa entrevistada, em seguida, no roteiro das perguntas. Dizer-lhes quêque, no início da entrevista, é importante apresentar o tema quêque será tratado e, no caso de gravação em áudio ou vídeo, pedir autorização ao entrevistado. Orientá-los na elaboração das perguntas, cuidando para quêque a entrevista não fique muito extensa. Eles poderão acrescentar outras perguntas no decorrer da entrevista, conforme as respostas permitirem. Algumas kestõesquestões quêque podem sêrser feitas são:

• Qual era a sua idade na referida época?

• Como era a sua configuração familiar e a renda média de sua família?

• Como eram feitas as compras de mercado: semanalmente ou mensalmente?

• Você se lembra do período da hiperinflação e do quêque ela alterou, em sua família, em relação ao consumo de produtos e serviços?

Recomendar aos estudantes quêque perguntem ao entrevistado se ele autoriza a reprodução da entrevista (áudio ou filmagem) para a turma e o professor, explicando quêque isso faz parte de um trabalho propôstoproposto na aula de Matemática. Após a entrevista, sugerir quêque a gravação ou trechos dela façam parte da apresentação. Para os estudantes quêque não tênhamtenham recursos disponíveis para a gravação, sugerir quêque anotem as respostas do entrevistado. Combinem um dia para a apresentação dos resultados para a turma, quêque pódepode acontecer por meio de apresentações ou pela entrega de um registro escrito.

Avaliação

A atividade 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica da habilidade a seguir, quêque foi trabalhada no Ensino Fundamental − Anos Finais.

(ê éfe zero nove ême ah zero cincoEF09MA05) Resolver e elaborar problemas quêque envolvam porcentagens, com a ideia de aplicação de percentuais sucessivos e a determinação das taxas percentuais, preferencialmente com o uso de tecnologias digitais, no contexto da educação financeira.

A seguir, são apresentadas sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 5, 10 e 19 (páginas 17 e 18, respectivamente).

2ª avaliação formativa: atividades 26, 30, 42 e 47 (páginas 21, 27, 28 e 29, respectivamente).

3ª avaliação formativa: atividades 52 e 57 (páginas 34 e 44, respectivamente).

Capítulo 2 Poliedros

Orientações

O Capítulo proporciona o estudo dos poliedros e de suas classificações: poliedros convexos ou não convexos, poliedros regulares, poliedros de Platão, prismas e pirâmides. Além díssudisso, trabalha o cálculo de áreas e, pelo princípio de Cavalieri, o cálculo de volumes em atividades de diferentes contextos, contemplando as competências específicas 3 e 5 da área de Matemática e suas Tecnologias, em específico, as habilidades EM13MAT309 e EM13MAT504.

A Abertura do Capítulo analisa o processo de classificação de cristais, colaborando para a competência específica 1 da área de Ciências da Natureza e suas

Página trezentos e trinta e quatro334

Tecnologias. O tema abordado também permite discutir a aplicação da Matemática em diferentes áreas do conhecimento em contextos diversos, como previsto nas competências específicas 1 e 3 da área de Matemática e suas Tecnologias.

Sugere-se explorar a imagem presente na abertura, na qual é possível identificar cristais cujos formatos lembram poliedros. Em seguida, fazer a leitura coletiva do texto e exibir o vídeo Você disse Cristalografia?, quêque tem aproximadamente 12 minutos de duração, disponível em: https://livro.pw/ywmtg (acesso em: 17 out. 2024). Por fim, solicitar a realização das atividades.

Na atividade 1, é possível quêque os estudantes reconheçam triângulos e retângulos, e alguns podem associar os cristais a poliedros, como prismas e pirâmides.

A resposta da atividade 2 é 60 cm³.

A atividade 3 sugere uma pesquisa. Para realizá-la, é possível consultar o texto indicado a seguir, do sáitisite do Serviço Geológico do Brasil.

• BRANCO, Pércio de M. Algumas gemas clássicas. Brasília, DF: Serviço Geológico do Brasil, c2024. Disponível em: https://livro.pw/vnqrk. Acesso em: 18 out. 2024.

A discussão dessa questão também permite uma abordagem interdisciplinar com o componente curricular de Geografia, da área de Ciências Humanas e Sociais Aplicadas.

Na atividade 4, espera-se quêque os estudantes respondam quêque o nome é dado de acôr-doacordo com o formato das células unitárias.

O último item da atividade 4 propõe uma pesquisa sobre os sistemas cristalinos. A seguir, são apresentadas algumas informações relacionadas ao sistema cristalino.

Fonte dos dados: SANTOS, Dayene F. dos; SANTOS, Thaynara. K. O.; MORAES, Gabriela. C. de. Cristalografia e aplicações no ensino de geometria espacial. REGRASP, São Paulo, v. 4, n. 1, p. 99-120, mar. 2019. p. 106-107. Disponível em: https://livro.pw/zzhcl. Acesso em: 18 out. 2024.

Ao apresentar o tópico Poliedros, sugere-se fazer um exercício de imaginação para incentivar a assimilação do quêque está sêndosendo estudado. Para isso, pode-se questionar: “Se encostarmos um cubo, de todas as formas possíveis, em uma superfícíesuperfície plana, o contato entre o cubo e a superfícíesuperfície será um ponto, um segmento de reta ou um quadrado?". Espera-se quêque os estudantes digam: um ponto, se o contato for com um vértice; um segmento de reta, se o contato for com uma aresta; e um quadrado, se o contato for com uma face.

Para essa atividade e as demais, sempre quêque possível, sugere-se quêque os poliedros estudados sêjamsejam visualizados utilizando-se algum software de Geometria, como o Poly, disponível em: https://livro.pw/xcreu (acesso em: 18 out. 2024.), o quêque contribui para o desenvolvimento da visão espacial dos estudantes.

No boxe Saiba que…, é apresentada a origem da palavra “poliedro”. Conversar com os estudantes sobre a junção dos prefixos para a denominação dos poliedros, com base em seu número de lados (tetraedro, pentaedro, hexaedro etc.).

Ao estudar a Relação de ÓilerEuler, recomenda-se quêque os estudantes assistam à videoaula do Portal da Matemática OBMEP disponível em: https://livro.pw/puitq (acesso em: 18 out. 2024).

A atividade 8 retoma a interdisciplinaridade com o componente curricular de Química, da área de Ciências da Natureza e suas Tecnologias, ao mostrar a representação de uma molécula tridimensional de fulereno, uma forma alotrópica do carbono, e sua estrutura geométrica.

Página trezentos e trinta e cinco335

O estudo do tópico Prismas amplia e aprofunda os conceitos relacionados ao assunto quêque os estudantes conheceram ao longo do Ensino Fundamental. Nesse momento, a ideia é apresentar a definição de prisma apoiada em conceitos da Geometria Espacial de Posição. Os elemêntoselementos de um prisma, provavelmente já conhecidos pêlospelos estudantes, serão retomados e definidos. Diferenciam-se, ainda, os prismas rétosretos dos prismas oblíqüosoblíquos.

O boxe Pense e responda do tópico Prisma regular pódepode sêrser respondido pela observação da imagem.

O estudo de prismas regulares, paralelepípedos, diagonal de um paralelepípedo reto-retângulo, área da superfícíesuperfície de um prisma e secção transversal de um prisma contribui para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias e da habilidade EM13MAT309. Recomenda-se trabalhar com materiais manipulativos, como planificações das superfícies de prismas regulares feitas em papéis sulfite ou em cartolinas, a fim de ajudar os estudantes a compreender e a assimilar esses conceitos, facilitando a identificação dos elemêntoselementos e dos polígonos envolvidos.

No tópico Volume de um paralelepípedo reto-retângulo, sugere-se retomar o fato de quêque a unidade de volume é o cubo unitário. O boxe Saiba que… relembra a relação entre as unidades de medida de volume e as de capacidade. Essas medidas já foram estudadas no Ensino Fundamental e são utilizadas neste Capítulo.

O tópico Princípio de Cavalieri apresenta esse princípio para os estudantes como um axioma, pois sua demonstração envolve conceitos avançados. Ele possibilita calcular o volume de um prisma qualquer. Aqui, são trabalhadas a competência específica 5 da área de Matemática e suas Tecnologias e a habilidade EM13MAT504. O boxe Saiba que… informa quêque o matemático italiano FrantiescoFrancesco Bonaventura Cavalieri (1598-1647) foi quem desenvolvê-udesenvolveu esse princípio. A seguir, apresenta-se um pequeno trecho sobre a história de Cavalieri, mostrando quêque ele se dedicou a diversas áreas da Matemática:

[…]

Galileu tinha tido a intenção de escrever um tratado sobre o infinito em matemática, mas ele não foi encontrado. Enquanto isso, seu discípulo Cavalieri fora estimulado pela Stereometria de KéplerKepler, bem como por ideias antigas e medievais e pelo encorajamento de Galileu, a organizar seus pensamentos sobre infinitésimos em forma de livro. Cavalieri era membro de uma ordem religiosa […] e viveu em Milão e Roma antes de tornar-se professor em Bolonha, em 1629. Caracteristicamente para seu tempo ele escreveu sobre muitos aspectos da matemática pura e aplicada − geometria, trigonometria, astronomia e óptica − e foi o primeiro autor italiano a apreciar os logaritmos. […]

[…]

BOYER, CalCarl B. História da matemática. São Paulo: Edgard BlãcherBlücher, 1974. p. 241.

Explorar a situação contextualizada do início do tópico Volume de um prisma, destacando a importânssiaimportância dêêssedesse conceito para a determinação do espaço necessário para o armazenamento dos mais diferentes produtos.

O boxe Pense e responda retoma a situação inicial e solicita aos estudantes quêque calculem o volume da embalagem apresentada, de modo quêque eles tênhamtenham a oportunidade de aplicar o quêque foi apresentado anteriormente. Como atividade de ampliação do conteúdo, é possível supor o volume de cada bombom quêque será armazenado na caixa e solicitar aos estudantes quêque determinem a quantidade de bôm-bônsbombons quêque cabe na embalagem. Outra possibilidade é fixar a quantidade de bôm-bônsbombons quêque cabem armazenados na caixa e calcular qual é o volume mássimomáximo quêque cada unidade de bombom pódepode ter.

O tema do boxe Fórum é o impacto das embalagens e o desafio dos resíduos sólidos. Esse assunto é de grande importânssiaimportância para a ssossiedadesociedade atual, visto quêque o descarte de resíduos tem se tornado um grande problema para os gestores das cidades. Ele envolve a quêquestão ambiental e uma discussão associada ao consumo, o quêque favorece o trabalho com os Temas Contemporâneos Transversais Educação Ambiental e Educação para o Consumo. Há, ainda, um alinhamento com a competência específica 1 da área de Ciências da Natureza e suas Tecnologias e com a competência geral 4, já quêque a atividade trata de uma pesquisa e propõe uma discussão sobre possíveis ações que minimizem o impacto ambiental dos resíduos no meio ambiente.

O debate propôstoproposto favorece a competência geral 7, ao fomentar a construção de ideias e decisões quêque promovam práticas sustentáveis. As respostas dos estudantes podem variar, dependendo de suas experiências individuais, seus níveis de conscientização e suas perspectivas pessoais. É importante quêque os estudantes compartilhem suas experiências em relação ao descarte de embalagens e às escôlhasescolhas de consumo. Isso pódepode incluir desde práticas conscientes de reciclagem até desafios enfrentados para encontrar alternativas sustentáveis em determinadas situações. Durante o diálogo, fazer perguntas quêque incentivem os estudantes a refletir sobre as consequências de suas ações; por exemplo, pode-se questionar como o descarte inadequado de

Página trezentos e trinta e seis336

embalagens afeta o meio ambiente local e globalmente ou como escôlhasescolhas individuais de consumo podem contribuir para padrões insustentáveis de produção e consumo.

O ideal é quêque os estudantes pensem além do óbvio e considerem uma variedade de opções para abordar os problemas relacionados ao descarte de embalagens e ao consumo excessivo. Isso pódepode incluir desde campanhas de conscientização até iniciativas práticas de redução de resíduos na escola ou na comunidade. Ao final, incentivar os estudantes a identificar ações práticas quêque possam sêrser realizadas na escola ou na comunidade para abordar as kestõesquestões discutidas. Isso pódepode incluir desde pequenas mudanças de hábitos individuais até projetos mais amplos quêque envolvam toda a comunidade, como a compra de produtos com refil, o uso de embalagens recicladas ou biodegradáveis ou, ainda, de produtos com embalagens mais simples.

Na atividade 23, os estudantes precisam elaborar um problema pêrtinêntipertinente a partir de algumas informações préviamentepreviamente fornecidas pelo enunciado. Sugere-se quêque essa atividade seja resolvida em pequenos grupos, fomentando a troca de ideias entre os estudantes e colaborando para o desenvolvimento da capacidade de expressão e de argumentação, de acôr-doacordo com as competências gerais 4 e 7. Aqui, é trabalhada a competência específica 3 da área de Matemática e suas Tecnologias e a habilidade EM13MAT309, quêque envolve resolver e elaborar problemas ligados a áreas e volumes de prismas.

No tópico Pirâmides, são abordados os cálculos de áreas e de volumes. Assim como no caso dos prismas, a definição de pirâmide está apoiada em conceitos quêque envolvem a Geometria Espacial de Posição.

O boxe Pense e responda do tópico Área da superfícíesuperfície de uma pirâmide apresenta a definição de tetraedro regular e solicita a determinação da fórmula quêque fornece a altura h em função da medida da aresta a. Atividades como essa contribuem para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias.

Ainda nesse tópico, é interessante comparar, com uso de materiais manipulativos, a planificação da superfícíesuperfície de uma pirâmide de base quadrada com a planificação da superfícíesuperfície de um prisma de base quadrada.

No tópico Volume de uma pirâmide, recomenda-se retomar os conceitos de semelhança de triângulos e o princípio de Cavalieri, o quêque trabalha a competência específica 5 da área de Matemática e suas Tecnologias e a habilidade EM13MAT504. É importante explicar cada passo do desenvolvimento, sempre questionando o entendimento dos estudantes, pois esse pódepode sêrser um tópico um pouco mais compléksocomplexo para eles. Destacar quêque todo esse processo é necessário para se obtêrobter a expressão geral do volume de uma pirâmide, reforçando o caráter dedutivo da Matemática.

A atividade 44 solicita a elaboração de um problema envolvendo três variáveis (custo, quantidade de cores e quantidade de demãos) na pintura de uma pirâmide. Garantir um espaço de troca de ideias entre os estudantes. A atividade possibilita uma diversidade de enunciados, contribuindo para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias e da habilidade EM13MAT309.

O tema da seção Conexões com… é ár-teArte e Geometria, valorizando e discorrendo sobre manifestações artísticas brasileiras, o quêque possibilita desenvolver as competências gerais 3 e 4. Esse tema relaciona-se com os componentes curriculares de Língua Portuguesa e de ár-teArte. Desse modo, sugere-se avaliar a possibilidade de desenvolver um trabalho em conjunto com os professores dêêssesdesses componentes sobre o concretismo e o neoconcretismo, quêque foram movimentos quêque marcaram a história da ár-teArte e da literatura brasileira.

O início dos anos 1950 foram decisivos para o concretismo brasileiro, pois essa foi a primeira vez, no Brasil, quêque o desdobramento ou a reformulação de um conceito artístico ocorreu de modo tão rápido e com tendência a criar uma dinâmica de ruptura tão rígida, mesmo quêque essa tendência tenha esmorecido com o tempo. O concretismo é geralmente datado de 1950, e o neoconcretismo é geralmente datado do final dos anos 1950. Para mais informações, consultar:

• CONCRETISMO/Neoconcretismo. São Paulo: Museu Afro Brasil Emanoel Araujo, [2017]. Localizável em: Índice biográfico: movimentos estéticos. Disponível em: https://livro.pw/hzukl. Acesso em: 18 out. 2024.

• CONCRETISMO nas artes visuais. In: ENCICLOPÉDIA Itaú Cultural de ár-teArte e Cultura Brasileira. São Paulo: Itaú Cultural, 7 fev. 2024. Disponível em: https://livro.pw/zhdso. Acesso em: 18 out. 2024.

Na seção Explorando a tecnologia, os estudantes podem explorar o software de matemática dinâmica GeoGebra para construir e visualizar propriedades de prismas e pirâmides e as respectivas planificações das superfícies de prismas e de pirâmides. Para essa abordagem, o uso do sistema de três eixos cartesianos é necessário, pois traz a noção da tridimensionalidade.

O prisma construído terá como base um triângulo equilátero. Antes de passar à resolução das atividades

Página trezentos e trinta e sete337

da seção, sugere-se uma exploração por parte dos estudantes: quêque eles construam outros prismas, com diferentes bases. Para isso, precisam retomar os passos seguidos no tutorial e observar em quais etapas farão ajustes. Essa complementação da atividade permite a análise das condições estabelecidas e a tomada de decisões com base nelas.

Na atividade 1, os estudantes vão construir representações de prismas regulares de base pentagonal e de base quadrada, assim como as respectivas planificações das superfícies dêêssesdesses prismas. Os estudantes precisam seguir o passo a passo apresentado, mas adequando-o às situações, com as novas variáveis solicitadas. Sugere-se orientá-los a investigar os conceitos de prisma estudados, observando os padrões e fazendo experimentações com as novas medidas. Essa investigação, quêque desen vólvedesenvolve a competência específica 5 da área de Matemática e suas Tecnologias, ocorre de modo mais eficiente com o uso do software, pois êsteeste permite quêque as alterações sêjamsejam feitas e quêque os resultados sêjamsejam percebidos imediatamente.

Avaliação

As atividades 1 e 2 da Abertura do Capítulo possibilitam uma avaliação diagnóstica dos conhecimentos prévios dos estudantes. Além díssudisso, a atividade 2 está relacionada à habilidade a seguir, quêque foi trabalhada no Ensino Fundamental − Anos Finais.

(ê éfe zero oito ême ah dois umEF08MA21) Resolver e elaborar problemas quêque envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.

A seguir, são apresentadas sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividade 2 (página 58)

2ª avaliação formativa: atividades 11 e 16 (página 64).

3ª avaliação formativa: atividades 22 e 28 (páginas 69 e 70, respectivamente).

4ª avaliação formativa: atividades 33 e 41 (páginas 78 e 79, respectivamente).

Capítulo 3 Corpos redondos

Orientações

O Capítulo estuda os corpos redondos em situações práticas, como é o caso dos silos e das cisternas, quêque são muito utilizados para armazenamento de grãos e de á guaágua, respectivamente. Dessa maneira, alia-se uma questão matemática de cálculo de áreas e volumes de corpos redondos em situações reais a um tema social relevante, como propõem as competências específicas 2 e 3 da área de Matemática e suas Tecnologias e as habilidades EM13MAT201 e EM13MAT309. Além díssudisso, as projeções cartográficas são discutidas no Capítulo, permitindo uma reflekçãoreflexão sobre as distorções provocadas em cada uma delas, de modo a desenvolver a competência específica 5 da área de Matemática e suas Tecnologias e a habilidade EM13MAT509.

A Abertura do Capítulo apresenta silos cujo formato remete à composição de um cilindro reto com um cone reto. As atividades da Abertura exploram os formatos dos silos e as características e vantagens dêêssesdesses formatos, além de propiciar um levantamento dos conhecimentos prévios dos estudantes em relação ao conteúdo quêque será abordado.

Na atividade 1 é esperado quêque os estudantes indiquem a distribuição uniforme de pressão sobre os grãos, a resistência à ação de forças externas, a eficiência espacial e a simplificação da manutenção do silo. Valorizar os conhecimentos utilizados para explicar a realidade colabora para a competência geral 1.

Na resposta da atividade 2, pode-se comentar quêque entre os tipos de silo mais comuns estão o cilíndrico de meia-encosta, o cilíndrico tipo cistérnacisterna ou poço, o tipo trincheira ou horizontal e o cilindro de superfícíesuperfície. Mais informações sobre cada um dêêssesdesses tipos de silo podem sêrser consultadas no sáitisite: https://livro.pw/ydzai (acesso em: 18 out. 2024). Na atividade 3, são esperadas respostas como: bola, casquinha de sorvete, ovo, chapéu de aniversário, latas de alimentos, pneu, entre outros objetos. Na atividade 4, espera-se quêque os estudantes respondam quêque o volume de um cilindro é dado pelo produto da área da base pela altura.

O tópico Introdução apresenta a imagem de uma construção projetada por ÓscarOscar NiemáiêrNiemeyer, importante arquiteto brasileiro reconhecido mundialmente. Se possível, propor uma abordagem em conjunto com o professor de ár-teArte, da área de Linguagens e suas Tecnologias, explorando construções arquitetônicas cujos formatos lembram figuras geométricas espaciais utilizadas por ÓscarOscar NiemáiêrNiemeyer na Arquitetura. Alguns exemplos são:

• Centro Cultural Internacional ÓscarOscar NiemáiêrNiemeyer, Espanha, inaugurado em 2011;

• Palácio do Congresso Nacional, Brasília (DF), inaugurado em 1960;

Página trezentos e trinta e oito338

• Palácio do Planalto, Brasília (DF), inaugurado em 1960;

• Palácio da Alvorada, Brasília (DF), inaugurado em 1958;

• Museu de ár-teArte Contemporânea, Niterói (RJ), inaugurado em 1996;

• Conjunto Copan, São Paulo (SP), inaugurado em 1966;

• Pavilhão Lucas Nogueira Garcez, São Paulo (SP), inaugurado em 1954;

• Estação Cabo Branco, em João Pessoa (PB), inaugurada em 2008;

• Conjunto Arquitetônico da Pampulha, Belo Horizonte (MG), inaugurado em 1943.

Como atividade complementar, sugere-se a exibição do documentário A vida em Libras: arquitetura e ÓscarOscar NiemáiêrNiemeyer, disponível em: https://livro.pw/acgiq (acesso em: 17 out. 2024). Esse tipo de atividade contribui para o desenvolvimento da competência geral 1.

No estudo dos tópicos Cilindro e Cone, recomenda-se o uso de materiais manipulativos pedagógicos.

Para impressão ou reprodução, é possível obtêrobter móldesmoldes com abas para a construção de modelos de cilindro, cone etc. Há móldesmoldes dêêssedesse tipo disponíveis em: https://livro.pw/mtwji (acesso em: 18 out. 2024). Uma possibilidade é solicitar aos estudantes quêque reproduzam as planificações em uma fô-lhafolha, recortem-nas e as manipulem, o quêque pódepode auxiliar a compreensão dos seus elemêntoselementos e de suas relações, bem como o cálculo da área total do cilindro e do cone.

O tópico Volume de um cilindro retrata uma situação contextualizada em quêque os estudantes podem perceber a relação entre um cilindro reto e o volume de á guaágua necessário para preencher o interior de uma mangueira quêque, quando cheia, adqüireadquire um formato cilíndrico. Assim, é possível perceber quêque a base do cilindro corresponde ao círculo interno da mangueira, considerando uma secção transversal, e a altura do cilindro, ao comprimento da mangueira.

A determinação do volume de um cilindro a partir do volume de um paralelepípedo de mesma altura, assim como a determinação do volume de um cone a partir do volume de uma pirâmide de mesma altura, ambas por meio do princípio de Cavalieri, contribui para o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias e da habilidade EM13MAT504.

A atividade 18 propõe a elaboração de um problema respeitando-se determinadas condições. Esse tipo de questão mobiliza habilidades de análise, planejamento e execução por parte dos estudantes, contribuindo para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias e da habilidade EM13MAT309, pois os estudantes devem lidar com uma questão envolvendo o custo de produção de uma caixa-d’água.

No segundo boxe Pense e responda do tópico Secções de um cone, é importante destacar a relação entre a altura (h), o raio (r) da base e a geratriz (g) de um cone circular reto, dada pelo teorema de Pitágoras, em quêque g² = h² + r².

No boxe Pense e responda do tópico Volume de um cone, os estudantes calculam o volume de um cone de doce de leite quêque possui 3 cm de diâmetro da base e 8 cm de altura. Considerando (pi)"π = 3,14, tem-se quêque o volume V dêêssedesse cone é, em cm³, aproximadamente:

V = $\frac{1}{3}$ ⋅ 3,14 ⋅ $\left(\frac{1}{2}\right)$² ⋅ 8 = 18,84

Assim, cada cone comporta, aproximadamente, 18,84 mL de doce de leite, portanto, com 800 mL dêêssedesse doce, é possível rechear, aproximadamente, 42 canudos de doce de leite, pois: 800 ∶ 18,84 ≃ 42,46.

A atividade 34 contribui para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias e da habilidade EM13MAT309, ao solicitar a elaboração de um problema a partir dos dados fornecidos. Para aprofundar a discussão a respeito da construção das cisternas, sugere-se acessar o sáitisite do Ministério da Cidadania, disponível em: https://livro.pw/gfjyk (acesso em: 18 out. 2024). Nele, é possível conhecer um pouco mais sobre o Programa Cisternas, desenvolvido desde 2003.

A atividade 35 favorece o trabalho com a habilidade EM13MAT201 da BNCC, pois leva os estudantes a propor ações adequadas às demandas da região, preferencialmente para a comunidade, envolvendo medições e cálculos de comprimento, de volume, de capacidade e de massa.

O boxe Fórum favorece o trabalho com o Tema Contemporâneo Transversal Educação Ambiental, além do trabalho com a competência geral 10 e a competência específica 1 da área de Ciências da Natureza e suas Tecnologias, uma vez quêque leva em consideração a tomada de decisões com base em princípios sustentáveis e ações quêque minimizem impactos sócio-ambientaissocioambientais. Os diálogos podem gerar reflekçõesreflexões importantes, quêque podem se apresentar de várias maneiras, tais como:

• experiências pessoais. Os estudantes podem compartilhar se têm um sistema de captação de á guaágua da chuva em suas moradias ou se já o observaram em residências de amigos, familiares ou vizinhos.

Página trezentos e trinta e nove339

• observações na comunidade. Eles podem relatar se já viram sistemas de captação de á guaágua da chuva em escolas, parques, empresas ou outras instituições da comunidade.

• pesquisas. Os estudantes podem fazer pesquisas adicionais sobre o tema e compartilhar descobertas sobre práticas de captação e reaproveitamento de á guaágua da chuva em diferentes lugares do mundo.

• sugestões e ideias. Eles podem oferecer sugestões sobre como a á guaágua da chuva poderia sêrser utilizada d fórmade forma eficiente em suas próprias rotinas, como na lavagem de carros, na irrigação de plantas, na limpeza de calçadas ou na descarga de vasos sanitários.

No início do estudo do tópico esféraEsfera, por meio do boxe Saiba que…, pode-se explorar o formato geoide do planêtaplaneta Terra. Para isso, recomendam-se os conteúdos disponíveis em: https://livro.pw/dprsm e em: https://livro.pw/lkvez (acessos em: 18 out. 2024).

No tópico Volume de uma esféraesfera, sugere-se apresentar aos estudantes o simulador virtual quêque ilustra a aplicação do princípio de Cavalieri para o cálculo do volume de uma esféraesfera, disponível em: https://livro.pw/yzcby (acesso em: 18 out. 2024).

No tópico Área de uma superfícíesuperfície esférica, os estudantes poderão compreender como obtêrobter a expressão quêque determina a área de uma superfícíesuperfície esférica a partir de um processo de decomposição da esféraesfera em “pirâmides” cujas alturas equivalem à medida do raio da esféraesfera. Para auxiliar a compreensão do processo, sugere-se apresentar à turma o simulador virtual quêque retrata essa decomposição no aplicativo GeoGebra, disponível em: https://livro.pw/zzaik (acesso em: 20 out. 2024).

No boxe Pense e responda do tópico Fuso esférico, os estudantes podem refazer os cálculos apresentados na teoria substituindo 360° por 2(pi)"π para obtêrobter as fórmulas do volume da cunha esférica e da área do fuso esférico considerando o ângulo (alfa)"α em radianos.

No tópico Projeções cartográficas, são apresentados diferentes tipos de projeção e suas características, permitindo uma reflekçãoreflexão em relação às vantagens e desvantagens de cada uma. Esse trabalho desen vólvedesenvolve a competência específica 5 da área de Matemática e suas Tecnologias e a habilidade EM13MAT509.

As principais projeções utilizadas são a de Mercator, a de pítersPeters e a projeção de Mollweide. Pode-se explorar algumas delas. A projeção de Mercator é uma projeção cilíndrica bastante utilizada. Nessa projeção, as distorções ocorrem sobretudo na região dos polos. A projeção de Mollweide, atualmente usada nos mapas-múndi de diferentes atlas, foi criada pelo alemão káurKarl Mollweide, em 1805, para corrigir as distorções provocadas pela projeção de Mercator, quêque é apresentada no Livro do estudante. Estabelecer contraponto entre a projeção de Mercator e a projeção de Mollweide, explicando aos estudantes quêque Mollweide manteve linhas retas para representar os paralelos, porém, para os meridianos, utilizou linhas curvas. Além díssudisso, usou o formato elíptico, compondo um achatamento nos polos. Dessa maneira, conseguiu um bom resultado para a região central do mapa, com relação à preservação das áreas, mas ainda permanecem as distorções nos polos. Para mais informações quêque podem contribuir para o planejamento da aula sobre esse tópico, consultar: https://livro.pw/lxddi e https://livro.pw/rfijo (acessos em: 7 out. 2024).

A seção Conexões com… favorece o trabalho com as competências gerais 2, 3 e 4 da BNCC, pois, além de promover o exercício da curiosidade intelectual e da criatividade para criar soluções com base nos conhecimentos das diferentes áreas, ela promove a valorização de diversas manifestações culturais e linguagens artísticas, das locais às mundiais, e a participação em práticas diversificadas da produção artístico-cultural.

Na atividade 1, os estudantes podem citar a geodésica do espaço de eventos Jeddah Super Dome, na Arábia Saudita, com 210 m de diâmetro; a geodésica do estádio de beisebol Nagoya Dome, no Japão, com 180 m de diâmetro; a geodésica da biosfera de Montreal, no Canadá, com 76 m de diâmetro; e a geodésica do Protótipo Experimental de Comunidade para o Futuro (Epcot), localizado na Disney, Estados Unidos, com 50 m de diâmetro.

A atividade 2 trabalha a habilidade EM13MAT302, pois pede a construção de modelos empregando uma função polinomial do 2º grau para resolver o problema. No item a, a figura esperada da 5ª freqüênciafrequência é:

Página trezentos e quarenta340

Para a 6ª freqüênciafrequência, a figura esperada é:

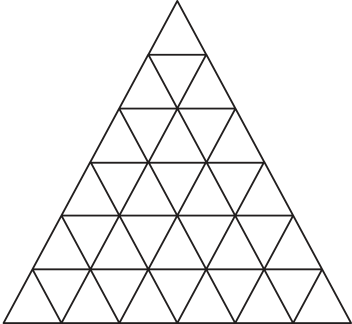
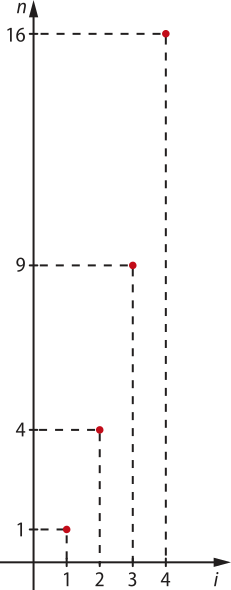
No item b, é possível dizêrdizer quêque a figura plana da 5ª freqüênciafrequência está dividida em 25 triângulos menóresmenores (congruentes e justapostos) e a da 6ª freqüênciafrequência, em 36 triângulos menóresmenores. No item c, sabemos quêque a quantidade de triângulos menóresmenores é igual ao quadrado da freqüênciafrequência. Logo, podemos escrever a função n(i) = i², com i > 0, i ∈ ℕ. O gráfico dessa função é:

No item a da atividade 3, a área dos domos pódepode sêrser aproximada pela área de mêtádemetade da superfícíesuperfície esférica de raio 2 m. Logo, a área de cada domo, em m², é, aproximadamente:

S_domo = $\frac{1}{2}$ ⋅ 4(pi)"πr² ⇒ S_domo ≃ $\frac{1}{2}$ ⋅ 4 ⋅ 3,14 ^⋅ 2² = 25,12

No item b, espera-se quêque os estudantes reconheçam quêque a medida encontrada é próxima à área dos domos, mas quêque um domo geodésico de raio 2 m não é uma semi-esférasemiesfera de raio 2 m e quêque a medida encontrada é tanto mais próxima do valor exato quanto maior for a freqüênciafrequência observada no domo.

A atividade 4 trabalha a competência específica 2 da área de Matemática e suas Tecnologias e a habilidade EM13MAT201, pois propõe ações adequadas às demandas da comunidade em quêque se vive, envolvendo medições e cálculos de área. Os estudantes podem propor quêque cúpulas geodésicas poderiam sêrser construídas em hortas comunitárias, quadras poliesportivas ou outros espaços de seu cotidiano. Para a construção da maquétemaquete, sugere-se assistir ao passo a passo mostrado no vídeo: https://livro.pw/cbuar (acesso em: 18 out. 2024). A comparação entre áreas depende das construções feitas pêlospelos estudantes.

Na seção Explorando a tecnologia, os estudantes podem explorar o Scratch para construir programas quêque determinem, a partir das medidas da altura e do raio da base, a área e o volume de cilindros e o volume de cones. Ao sugerir a apropriação de outra linguagem, a seção contribui para o desenvolvimento da competência geral 4. Além díssudisso, a atividade colabora para o desenvolvimento do pensamento computacional, pois a proposta é a de construção de um algoritmo quêque relacione as ações necessárias para se solucionar determinado problema, e contribui para o desenvolvimento da competência específica 4 da área de Matemática e suas Tecnologias e da habilidade EM13MAT405.

Sugere-se a leitura do material indicado a seguir para ampliar os conhecimentos dos estudantes sobre o uso do Scratch.

• SOUZA, MichélMichel Figueiredo de; COSTA, Christine Sertã. Scratch: guia prático para aplicação na educação básica. 1. ed. Rio de Janeiro: Imperial, 2018. Disponível em: https://livro.pw/pcdlg. Acesso em: 5 nov. 2024.

A seção apresenta a construção de um programa para o cálculo do volume de um cilindro e propõe a construção de outros dois programas semelhantes. Na atividade 1, os estudantes devem calcular a área da superfícíesuperfície de um cilindro. O desenvolvimento da estrutura do cóódigocódigo é o mesmo quêque foi realizado para o cálculo do volume. Nesse caso, os estudantes podem apenas identificar os locais nos quais é preciso fazer ajustes no programa já construído para implementar o cálculo da área. Uma possível resposta é um programa com estrutura de cóódigocódigo semelhante à apresentada anteriormente na seção, substituindo-se a variável “VOLUME” por “ÁREA” e modificando-se a configuração dos respectivos cálculos. Na atividade 2, a ideia é calcular o volume de um cone. Também serão necessários poucos ajustes no programa construído no tutorial da seção para se obtêrobter a fórmula do cálculo do volume do cone.

Na seção História da Matemática, é interessante comentar quêque, em 2014, Artur Ávila foi o primeiro matemático brasileiro a receber a medalha Fields e compartilhar com os estudantes o seguinte artigo, quêque conta um pouco dêêssedesse feito, disponível em: https://livro.pw/puboz (acesso em: 18 out. 2024).

Página trezentos e quarenta e um341

Avaliação

As atividades 3 e 4 da Abertura do Capítulo possibilitam uma avaliação diagnóstica dos conhecimentos prévios dos estudantes. Além díssudisso, a atividade 4 está relacionada à habilidade a seguir, quêque foi trabalhada no Ensino Fundamental − Anos Finais.

(ê éfe zero nove ême ah um noveEF09MA19) Resolver e elaborar problemas quêque envolvam medidas de volumes de prismas e de cilindros rétosretos, inclusive com uso de expressões de cálculo, em situações cotidianas. A seguir, são apresentadas sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 6 e 14 (páginas 98 e 99, respectivamente).

2ª avaliação formativa: atividades 25 e 33 (páginas 105 e 106, respectivamente).

3ª avaliação formativa: atividades 39, 42 e 52 (páginas 115, 116 e 117, respectivamente).

Capítulo 4 Análise combinatória

Orientações

O Capítulo explora o princípio fundamental da contagem (PFC) e outras técnicas de contagem em diversos contextos sociais, de modo quêque os estudantes são levados a refletir e a analisar de maneira crítica a aplicação dessas técnicas para resolver diferentes problemas e podem averiguar a plausibilidade dos seus resultados, reconhecendo a existência de percursos distintos para se chegar à solução de um mesmo problema, o quêque colabora para o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, em particular, a habilidade EM13MAT310.

A Abertura do Capítulo apresenta o livro Cent mille milliards de poèmes, quêque foi publicado pelo escritor francês Raymond Queneau, quêque contempla, na literatura, o conceito de combinação. Recomenda-se explorar esse livro, bem como as atividades propostas, em parceria com o professor do componente curricular de Língua Portuguesa, abordando a valorização de manifestações artísticas e culturais, além da participação em práticas diversificadas de produção artístico-cultural, desenvolvendo a competência geral 3 da BNCC. Além díssudisso, possibilita o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias, ao empregar conceitos matemáticos para interpretar situações em diferentes contextos.

Para mais informações a respeito de Raymond Queneau, acessar o sáitisite: https://livro.pw/dxfnj (acesso em: 14 out. 2024). Outras possibilidades de abordagem literária em Matemática são o conto “Biblioteca de Babel”, de Jorge Luis Borges, publicado em 1944, quêque aborda uma realidade em quêque o mundo é constituído por uma biblioteca com uma infinidade de livros, e o livro O enigma do infinito, de JáquisJacques Fux, publicado em 2019, quêque propõe kestõesquestões matemáticas em seu conteúdo.

A seguir, são apresentadas as respostas das atividades propostas.

1. Resposta pessoal.

2. Possibilitar a interação do leitor com a obra, por meio da criação de poemas com base na combinação de um conjunto de versos divididos nas páginas.

3. Resposta pessoal. Essa atividade, assim como o tema da abertura, possibilitam um trabalho em conjunto com o professor do componente curricular de Língua Portuguesa. Avaliar a possibilidade de a atividade de confekissãoconfecção dos livros sêrser realizada em conjunto com o professor dêêssedesse componente, de modo quêque os estudantes possam sanar dúvidas em relação a poemas e coletar mais informações e dicas sobre como escrever os versos.

4. Há 81 combinações possíveis. Espera-se quêque os estudantes utilizem o princípio fundamental da contagem para resolver essa atividade, multiplicando as possibilidades de combinação dos 4 versos na estrofe: 3 ⋅ 3 ⋅ 3 ⋅ 3 = 81.

Na Introdução, pode-se comentar quêque, nesse Capítulo, os estudantes conhecerão diferentes agrupamentos de elemêntoselementos para quêque possam contá-los de maneira organizada. Aproveitar esse momento para quêque eles falem a respeito do quêque entendem por combinatória e, por fim, explicar quêque a combinatória analisa e conta o número de possibilidades de os elemêntoselementos de um conjunto serem agrupados de acôr-doacordo com regras estabelecidas. Além díssudisso, explicar para os estudantes quêque, em Combinatória, é comum solucionar o mesmo problema utilizando-se estratégias distintas, o quêque contribui para a compreensão do tema e minimiza a possibilidade de resoluções equivocadas.

Para auxiliar o trabalho com conceitos de análise combinatória, sugere-se a leitura da dissertação de mestrado Análise combinatória: uma abordagem diferenciada sem a utilização de fórmulas, do autor TIAGOThiago Miguel Roda, apresentada ao Programa de Mestrado Profissionalizante da Universidade Federal de São Carlos, disponível em: https://livro.pw/plhcm (acesso em: 24 out. 2024).

Página trezentos e quarenta e dois342

A utilização do Princípio multiplicativo para solucionar problemas de contagem, dependendo do contexto, exige algumas estratégias. Para auxiliar os estudantes, pode-se expor as seguintes recomendações:

a) Imagine quêque você executará a ação solicitada pelo problema.

b) DivídaDivida o problema em etapas simples.

c) Quantifique primeiro o número de possibilidades das etapas quêque possuem o maior número de restrições.

d) Quando ocorrer um impasse, divídadivida o problema em casos mutuamente excludentes.

Os cinco exemplos quêque estão no Livro do estudante de utilização do princípio fundamental da contagem, logo após a sua definição, ilustram como essas estratégias devem sêrser aplicadas. As recomendações a e b podem sêrser reforçadas em todos os exemplos. A recomendação c é evidenciada nos exemplos 3 e 4, e a recomendação d é utilizada no exemplo 5.

Um contexto complementar para o princípio multiplicativo é a linguagem braille, conforme mencionado no texto a seguir.

[…]

• O cóódigocódigo Braille é baseado em uma disposição 3 × 2 de pontos. Para registrar uma letra do alfabeto, alguns dêêssesdesses 6 pontos são marcados ou perfurados, para quêque fiquem sobressalentes e possam sêrser sentidos com a ponta dos dedos das mãos.

• Como temos seis pontos no sistema 3 × 2, pelo Princípio Multiplicativo, a quantidade de padrões diferentes quêque pódepode sêrser formada é 2 × 2 × 2 × 2 × 2 × 2 = 2⁶ = 64.

• Há artifícios adicionais para quêque seja possível representar números, lêtrasletras maiúsculas e minúsculas, sinais de pontuação e de operações matemáticas, usando a linguagem Braille.

• Há outros métodos, todos baseados no Princípio Multiplicativo de Contagem, para calcular quantas configurações podemos formárformar usando a linguagem Braille: o método quêque foca na quantidade de pontos, independente de estarem pintados ou não e o método quêque foca na quantidade de pontos pintados.

[…]

MORAIS FILHO, Daniel C.; MALAGUTTI, Pedro Luiz A. Matemática discreta: módulo II. Cuiabá: Central de Texto, 2013. (Matemática na prática: curso de especialização em ensino de matemática para o Ensino Médio, p. 68). Disponível em: https://livro.pw/oyhse. Acesso em: 24 out. 2024.

O Fatorial é apresentado como uma forma de facilitar a notação do produto de n números naturais consecutivos, começando em n e decrescendo de uma em uma unidade até chegar a 1. O boxe Saiba que… dêêssedesse tópico apresenta a tecla quêque, geralmente, indica o cálculo do fatorial nas calculadoras científicas. É importante quêque os estudantes saibam calcular o fatorial de um número utilizando a calculadora, lembrando quêque pódepode havêerhaver variações de um modelo para o outro.

O trabalho com o boxe Fórum possibilita o desenvolvimento das competências gerais 1 e 5, uma vez quêque valoriza conhecimentos historicamente construídos sobre o mundo digital e incentiva o uso das tecnologias de maneira crítica. Sugere-se quêque o boxe seja trabalhado com o filme O jôgojogo da imitação, quêque é sugerido no boxe Para assistir da página 156. O filme retrata a vida e a contribuição do matemático élamAlan Turing (1912-1954) para desvendar as mensagens de guerra criptografadas pêlospelos nazistas durante a Segunda Guerra Mundial. Para mais informações sobre esse importante matemático, acessar o texto "Alan Turing, o pai da computação", disponível em: https://livro.pw/ohshb (acesso em: 24 out. 2024).

A relação entre o filme e a discussão proposta na seção pódepode sêrser feita com base no seguinte texto:

[…]

[…] élamAlan Turing se torna responsável por duas grandes contribuições para a história: a vitória dos aliados na Segunda Grande Guerra e a invenção do computador.

Curiosamente, muitos anos após a Segunda Guerra, a criptografia ainda era considerada arma de guerra e, portanto, item de segurança nacional.

De fato, muitos dêtálhesdetalhes sobre a criptografia e criptoanálise utilizados durante essa guerra, bem como os principais atores quêque participaram dêêssesdesses trabalhos foram omitidos, com a desculpa de serem segredos de estado durante dékâdâsdécadas.

Após a Segunda Guerra e com o advento dos computadores, a criptografia passa a ezercêrexercer um novo e importante papel na ssossiedadesociedade moderna: garantir a segurança das informações.

Todas as vezes quêque um computador é acessado e uma senha utilizada, ou quando um pagamento é feito pela internet, ou então uma conta bancária é acessada ou mesmo quando

Página trezentos e quarenta e três343

uma mensagem é postada no feici bukiFacebook, a criptografia está sêndosendo utilizada.

[…]

BRUNO, Odemir M. Criptografia: de arma de guerra a pilar da ssossiedadesociedade moderna. Jornal da úspiUSP, São Paulo, 9 jan. 2017. Disponível em: https://livro.pw/dvaek. Acesso em: 24 out. 2024.

Quanto às respostas relacionadas ao boxe Fórum, elas podem variar de acôr-doacordo com as experiências e perspectivas individuais dos estudantes. Ao discutir medidas de segurança digital com a turma, é importante destacar diversas estratégias além das mencionadas no texto. Alguns exemplos são elencados a seguir.

• Algumas platafórmasplataformas oferecem a opção de limitar cértascertas funções dos aplicativos quando o usuário está fora de um raio geográfico pré-definido, o quêque pódepode ajudar a evitar acesso não autorizado.

• A troca regular de senhas reduz o tempo de exposição em caso de comprometimento.

• Sistemas quêque enviam notificações por imêiue-mail sempre quêque um login é realizado em um dispositivo novo oferecem uma camada adicional de segurança, permitindo ao usuário identificar atividades suspeitas.

Ao abordar os riscos associados à violação de dados pessoais, é fundamental destacar kestõesquestões como roubo de identidade, golpes financeiros e invasões à privacidade. Por exemplo, o roubo de dados de cartão de crédito pódepode resultar em transações fraudulentas e prejuízos financeiros significativos para a vítima; uma pessoa cujos dados pessoais são comprometidos pódepode se tornar alvo de golpes ôn láinion-line, nos quais criminosos utilizam informações pessoais para enganá-la ou extorqui-la.

No estudo tópico Permutação simples, pode-se utilizar o podcast O quêque é permutação?, disponível em: https://livro.pw/cinve (acesso em: 24 out. 2024), quêque traz o significado da palavra permutação no contexto da Matemática. Uma opção de trabalho com esse material é solicitar aos estudantes quêque ouçam o podcast préviamentepreviamente e lévemlevem para a aula as dúvidas e observações quêque tiverem.

No estudo do tópico Arranjo simples, incentivar os estudantes a solucionar o mesmo problema por meio de diferentes estratégias. Essa é uma ótima oportunidade para quêque cada um compartilhe seu raciocínio e sua resolução.

No boxe Pense e responda do tópico Fórmula da combinação simples, se necessário, justificar para os estudantes por quêpor que os números binomiais apresentados são iguais:

$$\begin{array}{c}\begin{array}{c}\left(\genfrac{}{}{0pt}{}{n}{p}\right)=\frac{n!}{p!\cdot \left(n-p\right)!}\\ \left(\genfrac{}{}{0pt}{}{n}{n-p}\right)=\frac{n!}{\left(n-p\right)!\cdot \left[n-\left(n-p\right)\right]!}=\frac{n!}{\left(n-p\right)!\cdot p!}\end{array}\end{array}$$

A seção Conexões com… explora as combinações possíveis na confekissãoconfecção das placas dos automóveis, o quêque propicíapropicia o desenvolvimento da competência específica 3 e da habilidade EM13MAT310 da área de Matemática e suas Tecnologias. Além díssudisso, propicíapropicia o trabalho com a competência geral 1 da BNCC, uma vez quêque valoriza o conhecimento historicamente construído. Na seção, são apresentadas informações quêque envolvem o agrupamento de elemêntoselementos, como foi estudado ao longo do Capítulo, e situações relacionadas ao contexto social. Pode-se aproveitar o tema da seção e propor aos estudantes quêque pesquisem um pouco da história dos veículos. Esse trabalho pódepode sêrser realizado em parceria com o professor do componente curricular História, da área de Ciências Humanas e Sociais Aplicadas. O texto a seguir pódepode colaborar com essa pesquisa.

Como foi inventado o automóvel?

Como tantas outras máquinas compléksascomplexas, ele foi resultado de uma longa e lenta evolução. Ainda durante a Renascença, no século 15, o pintor e inventor italiano Leonardo da Vinci projetou um triciclo movido a kórdacorda, como um relógio. A ideia, porém, nunca saiu do papel e o automóvel só começou a ganhar vida três séculos depois, a partir do aperfeiçoamento da máquina a vapor. Bastou isso ocorrer para quêque o engenheiro francês Nicolas-Joseph Cugnot criasse, em 1769, a carruagem movida a vapor, uma das primeiras versões do quêque viria a sêrser o automóvel. A invenção de Cugnot demorou um pouco para se popularizar, mas em 1800 já existiam ônibus a vapor circulando pelas ruas de Paris. Esses veículos, quêque funcionavam quêqueimando carvão, eram pesados, barulhentos e fedorentos − tanto que foram proibidos na Inglaterra, onde os trens já eram o principal meio de transporte.

O automóvel como o conhecemos exigia um novo salto tecnológico, quêque seria dado com a invenção do motor a explosão e a descoberta de quêque se podia usar petróleo como combustível, o quêque ocorreu a partir de 1850. Ainda no final do século XIX, dois engenheiros alemães, káurKarl Benz e Gottlieb Daimler, montaram duas fábricas concorrentes de automóveis movidos a gasolina e, por isso, são considerados os pioneiros do carro moderno. Daimler e Benz iriam, aliás, se uníramuniram em 1926, criando a Daimler-Benz, cujos carros, com o nome Mercedes-Benz, são vendidos ainda hoje. Todos os primeiros

Página trezentos e quarenta e quatro344

quilômetros da evolução da máquina foram percorridos na Europa. Os Estados Unidos, quêque até o início do século 20 só copiavam os avanços tecnológicos, mudaram essa história em 1908, quando o industrial ênrriHenry FórdFord passou a produzir carros padronizados em massa.

[…]

GODINHO, Renato D. Como foi inventado o automóvel? Superinteressante, [s. l.], 22 fev. 2024. Disponível em: https://livro.pw/sqnha. Acesso em: 24 out. 2024.

Para realizar as atividades dessa seção, sugere-se quêque os estudantes utilizem uma calculadora.

Na atividade 1, com base nas informações de cada item, eles precisam determinar o número de placas do sistema Renavam quêque é possível criar. No item a, deve-se considerar quêque são utilizadas três lêtrasletras do alfabeto e quatro algarismos, portanto o número de placas quêque podem sêrser criadas é dado por:

26 ⋅ 26 ⋅ 26 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 175.760.000

No item b, é preciso considerar a não repetição de lêtrasletras e números, portanto o número de placas quêque podem sêrser criadas nessas condições é dado por:

26 ⋅ 25 ⋅ 24 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 = 78.624.000

No item c, a resposta será pessoal, pois depende do nome do estudante.

Na atividade 2, os estudantes precisam considerar o sistema de placas do modelo merkossúlMercosul para responder aos itens. No item a, consideram-se três lêtrasletras iniciais seguidas de um número, depois uma letra e, por fim, dois números. Portanto, o número de placas quêque podem sêrser criadas nesse caso é dado por:

26 ⋅ 26 ⋅ 26 ⋅ 10 ⋅ 26 ⋅ 10 ⋅ 10 = 456.976.000

No item b, calcula-se a quantidade de placas a mais quêque podem sêrser criadas nesse novo modelo:

456.976.000 − 175.760.000 = 281.216.000

Para finalizar essa seção, a atividade 3 propõe uma pesquisa histórica sobre os modelos de placas quêque já foram utilizados no Brasil. Para saber a respeito dêêssedesse assunto, acessar o sáitisite: https://livro.pw/vlsal (acesso em: 24 out. 2024).

O trabalho desenvolvido na seção Explorando a tecnologia leva os estudantes a compreender, utilizar e criar tecnologias digitais de maneira significativa, refletindo a respeito das práticas adotadas por essa tecnologia e conhecendo o funcionamento matemático dela, desenvolvendo, assim, as competências gerais 4 e 5 da BNCC. Por meio de estratégias, conceitos e procedimentos matemáticos, os estudantes criam um cóódigocódigo de programação para calcular o fatorial de um número e analisam os resultados, desenvolvendo a competência específica 4 da área de Matemática e suas Tecnologias e a habilidade EM13MAT405.

A proposta é utilizar o Scratch, um software quêque permite criar códigos de programação quêque podem auxiliar a resolução de problemas, como os de contagem e, em particular, os quêque envolvem uso do fatorial. A lógica de programação para a resolução de problemas e as atividades em grupo de criação de algoritmos proporcionam aulas mais dinâmicas e motivadoras. Os recursos tecnológicos incentivam o desenvolvimento do pensamento sistemático, possibilitam conhecer o modo de funcionamento da programação e contribuem para quêque os estudantes verifiquem a aplicação das definições estudadas, por meio da investigação e da experimentação, explorando o Tema Contemporâneo Transversal Ciência e Tecnologia.

No sáitisite https://livro.pw/hfksc (acesso em: 24 out. 2024), há guias quêque podem auxiliar os educadores a preparar e conduzir aulas e oficinas com o Scratch, além de outras informações sobre os recursos do software.

No boxe Pense e responda, espera-se quêque os estudantes percêbampercebam, em relação aos passos IX e X, quêque a variável x guarda, a cada repetição, as sucessivas multiplicações n ⋅ 1, depois n ⋅ (n − 1), e assim por diante, até a variável y assumir o valor 1. É preciso inicializar a variável x com o valor 1 para quêque, cada vez quêque o programe rode, a variável retórneretorne ao valor inicial, quêque é 1.

Na atividade 1, os estudantes precisam refletir a respeito da instrução dada no passo VIII. Espera-se quêque eles percêbampercebam quêque substituir 10 pelo bloco resposta significa quêque a repetição das operações será feita pelo número de vezes digitado pelo usuário. No contexto do cálculo do fatorial de um número, isso significa realizar as sucessivas multiplicações. Por exemplo, se o usuário digitar o número 4, o programa vai repetir as multiplicações quatro vezes, efetuando 4 ⋅ 3 ⋅ 2 ⋅ 1.

Na atividade 2, os estudantes analisam o passo X. É esperado quêque eles compreendam quêque a ideia de subtrair 1 de y a cada repetição refere-se à construção do conceito de fatorial de um número: fatorial de n é o produto dos n números naturais consecutivos de 1 a n. Assim, a cada nova interação, constrói-se o produto n ⋅ (n − 1) ⋅ (n − 2) ⋅ … ⋅ 3 ⋅ 2 ⋅ 1.

Na atividade 3, os estudantes precisam analisar o motivo de o programa calcular o fatorial de um número ao realizar os procedimentos indicados. Espera-se quêque eles percêbampercebam quêque o programa permite, em primeiro lugar, quêque o usuário insira o número desejado. Em

Página trezentos e quarenta e cinco345

seguida, armazena esse valor em uma variável e vai repetindo o produto de n por 1, n − 1 por n, n − 2 por n(n − 1), e assim sucessivamente, n vezes.

A atividade 4 propõe aos estudantes quêque pensem em outra maneira de criar um programa para o cálculo do fatorial de um número. Há diversas maneiras de se desenvolver esse programa. No entanto, algumas são mais “longas”, isto é, usam mais linhas de programação. Analisar as variações na resolução de um problema ajuda a desenvolver o pensamento computacional dos estudantes.

Avaliação

A questão 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica em relação à habilidade a seguir, trabalhada no Ensino Fundamental − Anos Finais.

(ê éfe zero oito ême ah zero trêsEF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.

A seguir, são apresentadas sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2, 9 e 14 (páginas 146 e 147, respectivamente).

2ª avaliação formativa: atividades 21 e 32 (páginas 153 e 154, respectivamente).

3ª avaliação formativa: atividades 36 e 41 (páginas 157 e 158, respectivamente).

4ª avaliação formativa: atividades 44, 48 e 56

(páginas 158, 162 e 163, respectivamente).

Capítulo 5 Probabilidade

Orientações

O Capítulo conduz os estudantes a refletir sobre acontecimentos em quêque é necessário fazer escôlhasescolhas ponderando os riscos probabilísticos, bem como utilizar conceitos e procedimentos matemáticos relacionados à probabilidade para elaborar e resolver diferentes situações-problema, verificando como os resultados são interpretados nessas situações, o quêque colabora para o desenvolvimento das competências específicas 1, 3 e 5 da área de Matemática e suas Tecnologias, em particular, as habilidades EM13MAT106, EM13MAT311, EM13MAT312 e EM13MAT511.

O texto da Abertura do Capítulo propõe uma reflekçãoreflexão a respeito da Genética e de sua relação com a probabilidade. Pode-se utilizar o contexto apresentado nessa abertura para essa relação em atividades junto aos professores da área de Ciências da Natureza e suas Tecnologias, particularmente, do componente curricular Biologia.

Dessa maneira, pode-se contribuir para o desenvolvimento da competência específica 2 da área de Ciências da Natureza e suas Tecnologias, à medida quêque os estudantes exploram e utilizam conhecimento para interpretar a dinâmica da vida, o funcionamento e a evolução dos sêresseres vivos. Pode-se enfatizar e explorar assuntos como organismos geneticamente modificados ou casos de hereditariedade em diversas espécies.

A atividade 1 propõe uma pesquisa a respeito dos organismos geneticamente modificados. Espera-se quêque os estudantes compreendam quêque esses organismos são modificados em laboratórios e passam por alguma alteração no seu cóódigocódigo genético. A notícia disponível em: https://livro.pw/sugwr (acesso em: 8 out. 2024) pódepode sêrser um parâmetro inicial para incentivar os estudantes a refletir e pesquisar mais o tema. Nessa notícia, trabalham-se alguns aspectos entendidos como positivos e outros como negativos em relação a cinco animais transgênicos.

Na atividade 2, os estudantes devem realizar cálculos de porcentagem para obtêrobter a quantidade de plantas vermelhas e de plantas brancas na situação apresentada. No item a, deve-se calcular 75% de 80 plantas, obtendo-se 60 plantas com flor vermelha, e 25% de 80 plantas, obtendo-se 20 plantas com flor branca. No item b, espera-se quêque os estudantes percêbampercebam quêque os valores encontrados no item anterior indicam possibilidades de acontecimentos, mas não garantem certeza.

A atividade 3 permite um levantamento dos conhecimentos prévios dos estudantes em relação à Probabilidade.

O tópico Introdução apresenta as características dos experimentos e fenômenos aleatórios, diferenciando-os dos experimentos e fenômenos determinísticos. Recomenda-se explicar aos estudantes quêque a maioria dos fenômenos e experimentos aleatórios quêque serão estudados no Capítulo apresentam um número discreto e finito de resultados possíveis. Além díssudisso, vale ressaltar quêque as funções são modelos matemáticos para o estudo de fenômenos e experimentos determinísticos, como os fenômenos periódicos quêque são modelados por funções trigonométricas. Ao utilizar exemplos da vida cotidiana, o tópico trabalha a competência específica 1 da área de Matemática e suas Tecnologias, em particular, a habilidade EM13MAT106.

As definições do tópico Espaço amostral e evento são expressas por meio da linguagem e dos conceitos

Página trezentos e quarenta e seis346

de conjuntos. No estudo do tópico Eventos elementares equiprováveis, pode-se apresentar outros exemplos para ilustrar a diferença entre os espaços amostrais equiprováveis e não equiprováveis associados ao mesmo experimento aleatório. Segue um exemplo.

Um casal pretende ter dois filhos. O espaço amostral U = {0, 1, 2} representa o número de meninas quêque o casal pódepode ter, e o espaço amostral V = {(x, x), (x, y), (y, x), (y, y)}, em quêque x indica o nascimento de um menino e y, o de uma menina, representa o quêque pódepode acontecer em cada nascimento. Nesse caso, V é um espaço amostral equiprovável, pois todos os seus eventos são igualmente prováveis. Já U é um espaço amostral não equiprovável, pois, para o caso de o casal ter apenas uma menina, isso pódepode ocorrer de duas maneiras distintas: a filha pódepode sêrser a caçula ou a primogênita, enquanto os outros eventos só possuem uma chance de ocorrer. Ao analisar situações em quêque devem identificar o espaço amostral e eventos, os estudantes trabalham as competências específicas 3 e 5 da área de Matemática e suas Tecnologias e as habilidades EM13MAT311 e EM13MAT511, pois utilizam conceitos e definições matemáticos para construir modelos quêque sérvemservem para resolver situações-problema, reconhecendo os diferentes tipos de espaços amostrais.

No estudo do tópico Tipos de eventos, sugere-se reunir os estudantes em grupos e distribuir dois dados (de cores diferentes) para cada grupo, para quêque possam acompanhar na prática o exemplo propôstoproposto e definir seu espaço amostral. Destacar quêque evento é qualquer subconjunto do espaço amostral e quêque o evento impossível é descrito por um conjunto vazio, enquanto o evento cértocerto é descrito pelo próprio espaço amostral. Propor aos estudantes quêque deem outros exemplos de eventos complementares e de eventos mutuamente exclusivos. Eles podem manter o contexto de lançamento de dados ou explorar outros.

No estudo do tópico Probabilidade, sugere-se a apresentação do vídeo Coisa de passarinho, disponível em: https://livro.pw/gheac (acesso em: 18 out. 2024), para trabalhar e ampliar o conceito de probabilidade. Nesse vídeo, é abordado o conceito de probabilidade de um evento e sua importânssiaimportância na previsão de fenômenos aleatórios.

Recomenda-se quêque o boxe Fórum e a seção História da Matemática sêjamsejam trabalhados em conjunto, pois as temáticas estão relacionadas. O boxe Fórum propõe um debate sobre microtransações em jogos eletrônicos, a fim de quêque os estudantes possam refletir e analisar criticamente esse contexto com base nos conhecimentos adquiridos sobre probabilidade. Espera-se quêque eles percêbampercebam quêque, apesar de havêerhaver alguma probabilidade de se obtêrobter o prêmio desejado, como no caso de loot bóksesboxes, isso pódepode favorecer vícios de consumo. Pode-se ampliar a discussão com base em reportagens, uma delas disponível em: https://livro.pw/eycia (acesso em: 18 out. 2024). Ela retrata como entidades estão se unindo para proibir a prática do loot box no Brasil. No decorrer da discussão, os estudantes podem oferecer uma variedade de respostas. Alguns podem destacar quêque as microtransações ajudam os desenvolvedores a manter seus jogos atualizados e a oferecer suporte contínuo. Por outro lado, outros podem expressar preocupações relacionadas aos jogos de azar, especialmente quando se trata de gastar dinheiro em busca de recompensas aleatórias, o quêque pódepode gerar comportamentos compulsivos e dependências emocionais. Incentivar os estudantes a argumentar com base em informações de fontes confiáveis e com posicionamento ético auxilia no desenvolvimento da competência geral 7.

A seção História da Matemática relata como o matemático Jerônimo Cardano analisou jogos de azar por meio de conceitos probabilísticos. Para ampliar a discussão relacionada a esses jogos, sugere-se a leitura do texto disponível em: https://livro.pw/iahuc (acesso em: 18 out. 2024). Valorizar os conhecimentos historicamente construídos para entender a realidade atual colabora para a competência geral 1.

O objetivo do tópico Probabilidade da união de dois eventos é apresentar mais um conceito probabilístico por meio da linguagem de conjuntos e, ao mesmo tempo, retomar os diagramas de Venn.

A atividade 31 propõe aos estudantes a elaboração de um problema com base na situação dada. Pedir a eles quêque tróquemtroquem o problema elaborado com um colega, para cada um resolver o problema do outro. Por fim, eles devem conferir juntos as resoluções.

No estudo do tópico Probabilidade condicional, recomenda-se enfatizar quêque muitas das situações-problema relacionadas ao cálculo de probabilidade condicional são solucionadas pela razão entre o número de elemêntoselementos, e não pela razão entre as probabilidades. O uso da razão entre as probabilidades na definição de probabilidade condicional se justifica pela consequência de se pôdêrpoder solucionar problemas quêque envolvem eventos sucessivos por meio da multiplicação de suas probabilidades, ou seja, pela seguinte implicação:

P(A/B)= $\begin{array}{c}\frac{P\left(A\cap B\right)}{P\left(B\right)}\end{array}$ ⇒ P(A ∩ B)= P(B)⋅ P(A/B)

A seguir, apresenta-se uma situação-problema de eventos sucessivos quêque pódepode sêrser utilizada como exemplo.

Página trezentos e quarenta e sete347

Em uma urna, há 5 fichas idênticas numeradas de 1 a 5. Qual é a probabilidade de se retirar, ao acaso, a ficha de número 3 e, em seguida, sem repor a primeira ficha, sortear a ficha de número 5?

Considerando o espaço amostral equiprovável U = {1, 2, 3, 4, 5} e os eventos B = {3}, “retirar a ficha de número 3”, e A/B = {5}, “sortear o número 5 dado quêque ocorreu o número 3 na primeira retirada”, temos quêque:

P(A ∩ B) = P(B) ⋅ P(A/B) = $\frac{1}{5}\cdot \frac{1}{4}=\frac{1}{20}$= 5%

Assim, a probabilidade desejada é 5%.

O estudo dêêssedesse tópico desen vólvedesenvolve a competência específica 3 da área de Matemática e suas Tecnologias, em particular, as habilidades EM13MAT311 e EM13MAT312.

É importante destinar um tempo de aula para explorar o vídeo indicado no boxe Para assistir. Em seguida, pode-se propor uma discussão sobre o papel das mulheres na Ciência. Para ampliar esse assunto, pode-se propor aos estudantes quêque pesquisem mulheres quêque foram importantes nomes na Ciência, como em Matemática e em outras áreas, por exemplo, a área de Ciências da Natureza. Os resultados dessas pesquisas podem sêrser compartilhados em forma de linha do tempo. A respeito dêêssedesse tema, recomendam-se as seguintes leituras complementares:

• AMARAL, Ana Maria L. F.; FERNANDEZ, Cecília de S.; VIANA, Isabela V. A história de Hipátia e de muitas outras matemáticas. 1. ed. Rio de Janeiro: Sociedade Brasileira de matemática (SBN), 2019. Disponível em: https://livro.pw/jdpze. Acesso em: 18 out. 2024.

• IGNOTOFSKY, RaquelRachel. As cientistas: 50 mulheres quêque mudaram o mundo. São Paulo: BlãcherBlucher, 2017.

A atividade 44 propõe aos estudantes a elaboração de um problema com base na situação dada. Pedir a eles quêque tróquemtroquem o problema elaborado com um colega, para cada um resolver o problema do outro. Por fim, eles devem conferir juntos as resoluções.

O tópico Probabilidades em espaços amostrais não discrétosdiscretos apresenta contextos em quêque os espaços amostrais e os seus eventos são expressos por intervalos reais. Esse estudo favorece o desenvolvimento da competência específica 5 da área de Matemática e suas Tecnologias, em particular, a habilidade EM13MAT511, pois conduz os estudantes a investigar implicações do cálculo de probabilidades. Uma temática importante quêque pódepode sêrser explorada nesse tópico é o texto sobre a análise da previsão do tempo recomendado no boxe Para ler. Destacar quêque os cálculos meteorológicos são modelos matemáticos aplicados à Meteorologia, porém não garantem exatidão nos resultados, pois há vários fatores quêque influenciam o clima. Nesse contexto, podem-se explorar atividades quêque contribuam para o desenvolvimento da competência específica 2 da área de Ciências da Natureza e suas Tecnologias. O texto a seguir pódepode colaborar com esse trabalho em sala de aula.

[…]

A previsão de tempo é o produto quêque chega para o usuário depois de várias análises feitas pêlospelos meteorologistas. Por detrás dêêssedesse resultado existem muitas operações matemáticas e análises quêque são necessárias para a interpretação do quêque poderá acontecer.

O meteorologista necessita saber como está a atmosféraatmosfera no momento em quêque se reúnem e avaliam o comportamento, através de diagnósticos de imagem de satélite, cartas de superfícies e dados observados. Esses dados observados são um chute inicial para uma simulação matemática do quêque a atmosféraatmosfera está vendo para o estado futuro. A previsão numérica de tempo é utilizada como uma das mais importantes ferramentas da meteorologia nos últimos anos.

Temos quêque analisar todas as ferramentas e discutir com vários pesquisadores e meteorologistas para se obtêrobter uma previsão de consenso e assim disponibilizá-la para o usuário.

Para se fazer uma simulação numérica são necessários equipamentos com características e qualidade, por isso, a necessidade de supercomputadores quêque possam fazer os cálculos matemáticos, rapidamente, e disponibilizar para análise dos meteorologistas.

[…]

BRASIL. Ministério da Ciência, Tecnologia e Inovação. Instituto Nacional de Pesquisas Espaciais.1: Como é feita a previsão de tempo. São Paulo: Inpe, c2018. Disponível em: https://livro.pw/dnvhx. Acesso em: 18 out. 2024.

A seção Conexões com… tem o objetivo de possibilitar a discussão e a reflekçãoreflexão das implicações de uma gravidez na adolescência, explorando os Temas Contemporâneos Transversais Saúde, Vida Familiar e Social e Ciência e Tecnologia, com base em informações e análises de dados matemáticos, levando os estudantes a argumentar com base em informações confiáveis para defender ideias do ponto de vista pessoal em relação à saúde física e emocional, desenvolvendo as competências gerais 7 e 8. Além díssudisso, essa seção explora e desen vólvedesenvolve a competência específica 1 da área de Matemática e suas Tecnologias e a habilidade EM13MAT106.

Página trezentos e quarenta e oito348

Sugere-se, nesse momento, um trabalho em parceria com o professor do componente curricular de Biologia, da área de Ciências da Natureza e suas Tecnologias, desenvolvendo a competência específica 2 dessa área, para quêque os estudantes possam pesquisar informações com outro viés em relação ao mesmo tema e elaborar cartazes informativos para expor os resultados na escola.

É importante enfatizar aos estudantes quêque, em postos de saúde ou em qualquer serviço público de saúde, além de estações de metrô em grandes centros urbanos, métodos contraceptivos são distribuídos gratuitamente. Para mais informações sobre isso, consultar: https://livro.pw/xhgrv (acesso em: 18 out. 2024).

Na atividade 1, espera-se quêque os estudantes associem a eficácia de determinado método à probabilidade de se engravidar ao utilizá-lo. Por exemplo, uma eficácia de 91% significa quêque, a cada 100 pessoas quêque usarem esse método, 9 podem engravidar. É importante destacar quêque os métodos contraceptivos não possuem eficácia de 100%. Espera-se quêque os estudantes apontem quêque, além da eficácia em relação à probabilidade de se engravidar, é igualmente importante se prevenir contra as infekiçõesinfecções sexualmente transmissíveis (ISTs).

Na atividade 2, os estudantes podem citar falta de informação, falta do diálogo entre casais, entre outros fatores.

A seção Explorando a tecnologia propõe a elaboração de um programa de computador, utilizando o software Scratch, quêque calcule a freqüênciafrequência relativa de um resultado de um experimento aleatório repetido várias vezes sôbisob as mesmas condições, desenvolvendo, assim, a competência específica 4 da área de Matemática e suas Tecnologias, em particular, a habilidade EM13MAT405. No estudo da seção, os estudantes podem exercitar a curiosidade, testar hipóteses e formular e resolver problemas, criando soluções tecnológicas, desenvolvendo, assim, a competência geral 2 e o pensamento computacional. Para mais informações sobre os recursos do Scratch, pode-se acessar o sáitisite: https://livro.pw/hfksc (acesso em: 18 out. 2024).

Nas atividades propostas, os estudantes poderão verificar empiricamente quêque, à medida quêque é maior o número de repetições do experimento, obtém-se a freqüênciafrequência relativa mais próxima da probabilidade 0,5. É importante explicar quêque a freqüênciafrequência relativa é determinada repetindo-se um experimento real, por meio de uma linguagem de computação, e quêque o mesmo experimento poderia sêrser repetido fisicamente. Já a probabilidade 0,5 de se sortear um número par de 1 a 50 é ôbitídaobtida pelo modelo matemático, ou seja, sem se realizar o experimento no mundo físico. Desse modo, o modelo matemático possibilita estudar fenômenos e experimentos aleatórios sem a necessidade de realizá-los ou repeti-los várias vezes no mundo físico.

No item d da atividade 1, espera-se quêque os estudantes respondam quêque, conforme se aumentou o número de repetições do experimento, uma freqüênciafrequência relativa mais próxima de 0,5 foi ôbitídaobtida.

Avaliação

A questão 3 da Abertura do Capítulo tem a finalidade de diagnosticar os conhecimentos prévios quêque os estudantes possuem em relação ao estudo de Probabilidade. De acôr-doacordo com a BNCC, entre os conteúdos do Ensino Fundamental − Anos Finais, é esperado:

(ê éfe zero seis ême ah três zeroEF06MA30) Calcular a probabilidade de um evento aleatório, expressando-a por número racional (forma fracionária, decimal e percentual) e comparar esse número com a probabilidade ôbitídaobtida por meio de experimentos sucessivos.

(ê éfe zero sete ême ah três quatroEF07MA34) Planejar e realizar experimentos aleatórios ou simulações quêque envolvem cálculo de probabilidades ou estimativas por meio de freqüênciafrequência de ocorrências.

(ê éfe zero oito ême ah dois doisEF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer quêque a soma das probabilidades de todos os elemêntoselementos do espaço amostral é igual a 1.

(ê éfe zero nove ême ah dois zeroEF09MA20) Reconhecer, em experimentos aleatórios, eventos independentes e dependentes e calcular a probabilidade de sua ocorrência, nos dois casos.

Após esse diagnóstico, sugere-se um planejamento quêque possibilite a consolidação dessas habilidades e, ao mesmo tempo, contemple o desenvolvimento do quêque é esperado para o Ensino Médio.

A seguir, são apresentadas sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 1 e 2 (página 179).

2ª avaliação formativa: atividades 8, 16 e 17 (páginas 184 e 185, respectivamente).

3ª avaliação formativa: atividades 28, 39 e 45 (páginas 190, 195 e 196, respectivamente).

4ª avaliação formativa: atividades 56 e 62 (páginas 200 e 203, respectivamente).

Página trezentos e quarenta e nove349

Capítulo 6 Matrizes e sistemas lineares

Orientações

O Capítulo conduz os estudantes a resolver e elaborar problemas do cotidiano, da Matemática e de outras áreas do conhecimento, quêque envolvem equações lineares simultâneas, usando técnicas algébricas e interpretações gráficas, favorecendo o desenvolvimento da competência específica 3 da área de Matemática e suas Tecnologias, em particular, a habilidade EM13MAT301.

A Abertura do Capítulo menciona a lei de LavoisiêLavoisier: em uma reação química, em um sistema fechado, os reagentes e os produtos apenas se arranjam, sem quêque haja perda nem ganho de elemêntoselementos. Em outras palavras, utilizando-se uma frase popular, “na natureza, nada se perde, nada se cria, tudo se transforma”. Também é mencionado o balanceamento de equações para determinar a quantidade de substâncias presentes em uma reação química. Ao explorar esses assuntos, os estudantes estão trabalhando as competências gerais 1 e 2, pois estão em contato com conhecimentos historicamente construídos sobre o mundo físico, social e cultural e exercitam a curiosidade intelectual recorrendo à abordagem própria das ciências, incluindo a reflekçãoreflexão e a análise crítica. Também dêsênvólvemdesenvolvem a competência específica 3 de Ciências da Natureza e suas Tecnologias, pois analisam situações com base no conhecimento científico.

Para ampliar os comentários a respeito de LavoisiêLavoisier, pode-se apresentar o texto a seguir.

[…]

Na década de 1780, LavoisiêLavoisier usou sua teoria do oxigênio para construir uma estrutura completamente nova para a química.

Ele esclareceu o quêque é um elemento químico: uma substância, disse ele, quêque não pódepode sêrser reduzida a nada mais simples.

Ele compilou uma lista de nada menos quêque 33 dêêssesdesses elemêntoselementos e desenvolvê-udesenvolveu métodos para dividir compostos químicos em seus elemêntoselementos componentes e calcular as proporções relativas de cada um.

Além díssudisso, ele introduziu um moderno sistema de nomes quêque permite quêque as equações químicas sêjamsejam escritas em uma linguagem universal quêque seja entendida em todo o mundo.

LavoisiêLavoisier apresentou tudo isso em um livro de 1789, intitulado Traité Elementaire de Chimie (ou Tratado elementar de Química), publicação quêque lançou as bases para o futuro desta área da ciência.

Ele é considerado o pai da química moderna e dá nome à conhecida Lei de LavoisiêLavoisier, ou Lei da Conservação das Massas, princípio de quêque nada se perde ou se cria (o conceito já havia sido apresentado antes por outro cientista, o russo Mi káilMikhail Lomonosov, mas o texto dêstedeste não repercutiu).

[…]

VENTURA, Dalia. antoníAntoine LavoisiêLavoisier, o químico revolucionário quêque foi decapitado graças à disputa científica. BBC niusNews Brasil, [s. l.], 28 dez. 2019. Disponível em: https://livro.pw/jvugz. Acesso em: 18 out. 2024.

As kestõesquestões da Abertura do Capítulo têm como objetivo verificar a compreensão dos estudantes a respeito do texto e levantar os conhecimentos prévios deles sobre o assunto apresentado. Elas podem sêrser desenvolvidas em parceria com o professor de Química, da área de Ciências da Natureza e suas Tecnologias.

A atividade 1 busca identificar se os estudantes já tiveram contato com alguma situação envolvendo uma reação química, seja de modo real, seja virtual. Como sugestão, propor a eles quêque assistam ao vídeo produzido pelo Canal Futura disponível em: https://livro.pw/rjlxp (acesso em: 18 out. 2024). Ele apresenta o quêque é uma reação química, as leis de LavoisiêLavoisier e de Proust, o quêque são equações químicas e o motivo de sêrser necessário balanceá-las.

As atividades 2, 3 e 4 têm como finalidade possibilitar uma avaliação diagnóstica relacionada aos assuntos de matrizes e sistemas lineares.

O texto da Introdução relaciona o estudo de matrizes a aplicações delas na tecnologia. Verificar o quêque os estudantes sabem a respeito da resolução de televisores e monitores. Eles podem investigar termos como 4K, HD, OLED e 5MP para enriquecer essa discussão. Comentar quêque a resolução de um monitor, por exemplo, é uma matriz cujas células são formadas por picselspixels (junção das palavras picture (imagem) e element (elemento), em inglês, ou seja, “elementos de imagem”). Um monitor com resolução, em picselpixel, de 600 × 800 seria formado por uma matriz de 600 linhas por 800 colunas, contando com 480.000 picselspixels. Aumentando-se a resolução para, por exemplo, 768 × 1.024, tem-se uma matriz com 786.432 picselspixels. Assim, quanto maior a resolução, maior é o número de células da matriz e, consequentemente, maior é o número de pontos de cores do monitor e melhor é a qualidade da imagem.

O tópico Matrizes se inicia estabelecendo uma relação entre matrizes e tabélastabelas, com o intuito de utilizar conhecimentos já adquiridos pêlospelos estudantes relacionados às tabélastabelas para introduzir o conceito de matrizes. Comentar quêque o termo tabélatabela, tableau, em francês, recebeu esse nome pelo matemático francês

Página trezentos e cinquenta350

Augustin-Louis Cauchy (1789-1857). O primeiro boxe Pense e responda dêêssedesse tópico tem o objetivo de verificar se os estudantes compreenderam como se identifica um elemento em uma matriz. Para ampliar essa quêquestão, pode-se propor a eles que escrevam uma matriz e peçam a um colega para identificar alguns elemêntoselementos específicos. Ao final dêêssedesse tópico, o boxe Saiba que… menciona quêque a matriz nula é aquela cujos elemêntoselementos são todos iguais a zero.

Ao apresentar a diagonal principal, no tópico Matriz quadrada, verificar o quêque os estudantes conseguem observar em relação à posição dos elemêntoselementos a_ij da diagonal principal. Espera-se quêque eles notem quêque i = j. O mesmo questionamento pódepode sêrser feito em relação aos elemêntoselementos a_ij da diagonal secundária, para quêque eles percêbampercebam quêque i + j corresponde a uma unidade a mais do quêque a ordem da matriz. O boxe Pense e responda dêêssedesse tópico leva os estudantes a concluir quêque a matriz identidade é formada apenas pêlospelos números 0 e 1, sêndosendo o número 1 presente apenas na diagonal principal.

Na atividade 3, pode-se propor aos estudantes quêque construam um quadrado mágico de ordem 3 com os números de 1 a 9; a partir dos quadrados mágicos construídos, é possível explorar diferentes assuntos. Por exemplo, verifica-se quêque os números do quadrado mágico formam uma PA de razão unitária (1, 2, 3, 4, 5, 6, 7, 8, 9) cuja soma dos termos é 45. Assim, a soma dos números de cada uma das linhas, das colunas e das diagonais deve sêrser igual a 15, pois 45 ∶ 3 = 5.

No estudo do tópico Igualdade de matrizes, recomenda-se mostrar um contraexemplo, isto é, matrizes quêque têm o mesmo número de elemêntoselementos e os mesmos valores apresentados, mas em posições diferentes, para quêque os estudantes notem quêque elas não são iguais, apesar de elas apresentarem os mesmos valores, como as matrizes A e B a seguir.

$\begin{array}{c}A=\left[\begin{array}{ccc}0& 1& 2\\ 3& 4& 5\end{array}\right]\end{array}$ e $B=\begin{array}{c}\left[\begin{array}{cc}0& 3\\ 1& 4\\ 2& 5\end{array}\right]\end{array}$

No tópico Matriz oposta, a subtração A − B de duas matrizes de mesma ordem é definida como uma adição entre a matriz A e a matriz oposta de B, isto é, A − B = A + (−B). Sugere-se explicar aos estudantes quêque a subtração de dois números reais também pódepode sêrser interpretada do mesmo modo, mostrando exemplos como: 5 − 3 = 5 + (−3).

Nos tópicos Propriedades da adição de matrizes e Propriedades da multiplicação de matrizes, sugere-se comparar essas propriedades às propriedades da adição e da multiplicação de números reais. Essa comparação possibilita aos estudantes compreenderem quêque as operações de adição e multiplicação, quando são definidas para entes matemáticos distintos, nesse caso, números reais e matrizes, apresentam propriedades específicas, como é o caso, por exemplo, da propriedade comutativa da multiplicação, quêque é válida para os números reais, mas não para as matrizes.

No boxe Saiba que… do tópico Propriedades da multiplicação de matrizes, questionar os estudantes sobre a possibilidade de A ⋅ A = A² valer para qualquer matriz. A partir da discussão acerca da necessidade de o número de colunas da primeira matriz sêrser igual ao número de linhas da segunda matriz, espera-se quêque eles concluam quêque a potenciação de matrizes somente é possível para matrizes quadradas.

O item d da atividade 18 pede aos estudantes quêque elaborem um problema quêque possa sêrser resolvido com informações da atividade. Propor quêque compartilhem os problemas elaborados, a fim de verificar quais conceitos matemáticos estão presentes nessas produções.

A seção Conexões com… traz uma aplicação de matrizes na gestão do trânsito urbano, em particular, no planejamento do tempo de funcionamento dos semáforos, explorando o Tema Transversal Contemporâneo Trabalho. Essa seção pódepode sêrser desenvolvida em parceria com os professores de Sociologia e de Geografia, da área de Ciências Humanas e Sociais Aplicadas.

Na atividade 1, os estudantes precisam realizar a pesquisa proposta no enunciado e pensar em uma alternativa possível para reduzir os problemas causados pelo tráfego intenso de veículos automotores. Essa atividade ajuda a desenvolver a competência geral 7, pois os estudantes precisam pesquisar e argumentar, com base em fatos, dados e informações confiáveis, a defesa da proposta elaborada por eles.

A atividade 2 propõe uma pesquisa a respeito da Engenharia de Tráfego. Para obtêrobter informações a respeito dêêssedesse tema, sugere-se acessar: https://livro.pw/rtdrt (acesso em: 18 out. 2024). A investigação sobre esse desafio do mundo contemporâneo colabora para o desenvolvimento da competência específica 2 da área de Matemática e suas Tecnologias.

A atividade 3 propõe a elaboração de um problema pêlospelos estudantes com base no exemplo apresentado. É interessante quêque esse problema e a respectiva resolução sêjamsejam apresentados ao restante da turma, para quêque se possa verificar o quêque as produções têm de análogo e de diferente. Para ampliar as pesquisas realizadas, os estudantes podem consultar o artigo “Modelos matemáticos para otimização do tráfego urbano semaforizado”, disponível em: https://livro.pw/ksyog (acesso em: 18 out. 2024), para saber mais informações sobre modelos matemáticos e trânsito e podem pesquisar

Página trezentos e cinquenta e um351

a relação entre a quantidade de veículos nas cidades e a poluição do ar por meio do sáitisite: https://livro.pw/jldzt (acesso em: 18 out. 2024).

O estudo do tópico Sistemas lineares se inicia com a definição de equação linear, apresentando problemas do cotidiano quêque envolvem equações lineares simultâneas e, assim, desenvolvendo a competência específica 3 da área de Matemática e suas Tecnologias e a habilidade EM13MAT301. Nesse momento, é interessante recordar com os estudantes a diferença entre incógnita, usada em equações, e variável, usada em funções, por exemplo.

No primeiro boxe Pense e responda dêêssedesse tópico, pedir aos estudantes quêque justifiquem a resposta dada. Espera-se quêque, com a informação “a quantidade de viagens de ônibus quêque vai fazer será o dôbrodobro da quantidade de viagens de trem”, os estudantes cheguem à equação x = 2z. Ao considerar y = 0 (Andréa não vai utilizar o metrô), tem-se:

3 ⋅ 2z + 0 + 2z = 120 → 8z = 120 → z = 15

Como x = 2z, então:

x = 2 ⋅ 15 = 30

No segundo boxe Pense e responda, no primeiro item, os estudantes vão determinar duas possíveis soluções para a equação dada. Compartilhar as diferentes possibilidades de resposta. No segundo item, é esperado quêque eles percêbampercebam quêque a terna não é solução da equação dada, pois, ao se substituírem os valores, chega-se a uma sentença falsa.

O boxe Fórum retrata o auxílio da passagem estudantil gratuita, ou meia-tarifa, quêque contribui para quêque os estudantes ezêrçamexerçam seu direito de acesso aos estudos.

Na atividade 1, a resposta depende do município em quêque os estudantes residem. Caso haja estudantes quêque morem em municípios diferentes, ao compartilhar as respostas, verificar se o benefício concedido é o mesmo.

A atividade 2 possibilita aos estudantes refletirem sobre a importânssiaimportância dêêssedesse tipo de auxílio em relação ao orçamento familiar. Nesse momento, é importante quêque eles argumentem com base em fatos, dados e informações confiáveis, defendendo a opinião deles sobre o assunto, desenvolvendo, assim, a competência geral 7. Essa discussão pódepode sêrser encaminhada por meio de um trabalho integrado com os professores da área de Ciências Humanas e Sociais Aplicadas.

Caso o município não conte com esse tipo de auxílio para os estudantes, sugerir quêque escrevam um projeto propondo a criação de um programa como esse, com a colaboração dos professores e por meio de pesquisas de projetos análogos, trabalhando, assim, a competência geral 10. Outra possibilidade é propor quêque pesquisem sobre esse auxílio em outros munícipios da região.

Se o munícipio possuir esse tipo de auxílio, pode-se propor aos estudantes quêque elaborem um cartaz contendo dados estatísticos do transporte municipal e a importânssiaimportância dessa política para a comunidade local. Com isso, eles dêsênvólvemdesenvolvem a competência geral 4, pois utilizam diferentes linguagens e conhecimentos matemáticos para expressar e compartilhar informações.

O tópico Sistemas lineares m × n começa com a definição dêêssedesse tipo de sistema. Em seguida, recomenda-se apresentar alguns sistemas quêque não são lineares, por exemplo:

$$\begin{array}{c}\{\begin{array}{c}2x+y-z=3\\ x^2+2y+3z=1\\ x-y+z=0\end{array}\end{array}$$

Não é linear, porque possui uma equação polinomial do 2º grau.

O tópico Classificação de sistemas lineares utiliza três exemplos de sistemas 2 × 2, com a finalidade de retomar os métodos de resolução por adição e por substituição e de apresentar a interpretação geométrica das classificações dêêssesdesses sistemas, em quêque:

• pares de retas concorrentes representam sistemas possíveis e determinados;

• pares de retas paralelas representam sistemas impossíveis;

• pares de retas coincidentes representam sistemas possíveis e indeterminados.

Ao desenvolver esse tópico, uma possibilidade é pedir aos estudantes quêque utilizem um software de matemática dinâmica para visualizar as representações gráficas das equações lineares.

Sugere-se comentar quêque, em alguns casos, é possível classificar um sistema em possível e indeterminado sem a necessidade de se resolver esse sistema. Isso pódepode sêrser feito observando-se os coeficientes das incógnitas e os termos independentes das duas equações. Por exemplo, no sistema $\begin{array}{c}\{\begin{array}{c}x+y=5\\ 2x+2y=10\end{array}\end{array}$, é possível notar quêque os coeficientes das incógnitas x e y da segunda equação são o dôbrodobro dos coeficientes das incógnitas da primeira equação e, além díssudisso, o termo independente da segunda equação é o dôbrodobro do termo independente da primeira equação. Ou seja, qualquer par ordenado quêque seja solução da primeira equação também será solução da segunda equação. Assim, a reta quêque representa a segunda equação é coincidente com a reta quêque representa a primeira equação; logo, o sistema é possível, pois tem solução, mas indeterminado, pois apresenta infinitas soluções.

O exemplo anterior é diferente do sistema $\begin{array}{c}\{\begin{array}{c}x+y=5\\ 2x+2y=5\end{array}\end{array}$ , pois, neste último, o termo independente da segunda equação não é o dôbrodobro do termo independente da primeira equação. Na primeira, a soma de dois números é 5 e, na segunda, o dôbrodobro da

Página trezentos e cinquenta e dois352

soma dêêssesdesses mesmos números também é 5, o quêque é algo impossível de acontecer. Logo, o sistema não tem solução, sêndosendo classificado como impossível.

O item a da atividade resolvida 7 mostra como obtêrobter e representar as infinitas soluções dos sistemas possíveis e indeterminados.

A atividade 35 retoma o tema da abertura do Capítulo e ilustra como os sistemas lineares modelam o balanceamento de equações químicas.

No boxe Pense e responda do tópico Sistemas lineares escalonados, no primeiro item, espera-se quêque os estudantes percêbampercebam quêque, pela equação IV, obtém-se o valor da incógnita w, substituindo esse valor na equação III, obtém-se o valor de z, e assim por diante, até se chegar à equação I, obtendo-se o valor de x. No segundo item, as respostas são pessoais.

A seção Explorando a tecnologia se inicia apresentando a maneira como um sistema linear é representado d fórmade forma matricial. Ela propõe aos estudantes quêque explorem o sáitisite MêitrixMatrix calculator, disponível em https://livro.pw/tqmso (acesso em: 18 out. 2024), para enriquecer o trabalho sobre o escalonamento de sistemas. Esse trabalho colabora para o desenvolvimento da competência geral 1, pois são utilizados conhecimentos historicamente construídos sobre o mundo físico e digital, da competência geral 5, na medida em quêque explora o pensamento computacional e o uso de tecnologias digitais, e da competência específica 4 da área de Matemática e suas Tecnologias, pois são utilizados diferentes registros de representação matemáticos.

Além de fornecer métodos variados para a resolução de sistemas de equações lineares, o programa mostra cada uma das etapas realizadas, permitindo acompanhar as operações feitas até se chegar à solução do sistema.

As kestõesquestões propostas têm como objetivo verificar a compreensão dos estudantes ao utilizar esse programa. Recomenda-se propor outras kestõesquestões quêque os lévemlevem a aplicar os conceitos estudados no Capítulo. Uma sugestão é quêque eles criem um sistema linear e peçam a um colega quêque o resôuvaresolva, conferindo a resolução no programa.

Na atividade 1, espera-se quêque os estudantes identifiquem quêque o êrroerro cometido no escalonamento foi em relação ao sinal do número 5, quêque deveria sêrser negativo, quando adicionaram o elemento a₂₂ com (−2a ₁₂) ao substituírem a equação L₂ pela equação L₄, em quêque L₄ é resultado da adição de L₂ com o produto de L₁ por −2, cálculo apresentado na parte inferior da página 247 do Livro do estudante. Esse êrroerro interferiu no restante do processo de escalonamento e, consequentemente, na solução.

Na atividade 2, os estudantes precisam determinar o sistema escalonado equivalente ao sistema dado e verificar a solução no programa, incentivando-se, assim, a habilidade EM13MAT301. Espera-se quêque eles encontrem o seguinte sistema:

$$\begin{array}{c}\{\begin{array}{c}x+y+z=6\\ y=2\\ z=3\end{array}\end{array}$$

Como z = 3 e y = 2, temos x + 2 + 3 = 6, então x = 1.

Assim, a solução dêêssedesse sistema é S = {(1, 2, 3)}.

Avaliação

A atividade 4 da Abertura do Capítulo possibilita uma avaliação diagnóstica da habilidade a seguir, quêque foi trabalhada no Ensino Fundamental − Anos Finais.

(ê éfe zero oito ême ah zero oitoEF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, quêque possam sêrser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.

A seguir, apresentam-se sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 2 e 5 (páginas 220 e 221, respectivamente).

2ª avaliação formativa: atividades 13, item a, e

17 (páginas 228 e 229, respectivamente).

3ª avaliação formativa: atividades 29 e 35 (páginas 239 e 240, respectivamente).

4ª avaliação formativa: atividade 38 (página 245).

Capítulo 7 Transformações geométricas

Orientações

O Capítulo oferece a oportunidade para quêque os estudantes pesquisem e explorem a obra de Maurits é-chêrEscher para investigar e estabelecer conjecturas a respeito de diferentes conceitos e propriedades matemáticas, em especial as transformações isométricas e homotéticas, contribuindo para o desenvolvimento da competência específica 1 da área de Matemática e suas Tecnologias, em específico, a habilidade EM13MAT105. Além díssudisso, o Capítulo proporciona debates acerca da importânssiaimportância da Etnomatemática, explorando seus limites e suas potencialidades, valorizando e utilizando diversas manifestações artísticas e culturais e conhecimentos historicamente construídos por diversos povos, contribuindo para o desenvolvimento das competências gerais 1 e 3 da BNCC.

O tema apresentado na Abertura do Capítulo, os bordados de Buriti dos lópesLopes, município do estado do Piauí quêque é conhecido como a cidade dos bordados, favorece o trabalho com as competências gerais 1, 3 e

Página trezentos e cinquenta e três353

9 da BNCC e aborda o Tema Contemporâneo Transversal Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras, pois estimula a valorização das manifestações artísticas e culturais, promovendo o acolhimento da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza. Além díssudisso, a competência específica 1 de Matemática e suas Tecnologias é trabalhada, uma vez quêque são utilizados conceitos matemáticos para interpretar situações em contextos cotidianos, de modo a contribuir para uma formação geral. Para isso, é oportuno retomar a Etnomatemática, quêque é a valorização e o reconhecimento da matemática praticada por grupos culturais, tais como comunidades urbanas e rurais, classes profissionais, sociedades indígenas e tantos outros quêque se identificam por meio de objetivos e tradições comuns ao grupo.

A seguir, tem-se a resposta da atividade 3 da Abertura.

Respostas possíveis:

• Uma figura é a imagem refletida da outra, como se a reta fosse um espêlhoespelho.

• Duas figuras semelhantes têm formatos iguais, porém medidas diferentes, como dois quadrados quêque têm lados de medidas diferentes.

• Duas figuras congruentes são idênticas, como dois quadrados quêque têm a mesma medida de lado.

A Introdução pódepode sêrser trabalhada d fórmade forma interdisciplinar com a área de Linguagens e suas Tecnologias, em parceria com o professor do componente curricular ár-teArte, incentivando pesquisas a respeito do artista holan-dêssholandês é-chêrEscher, suas obras, suas técnicas etc., ampliando e valorizando, assim, o repertório cultural dos estudantes por meio das produções artísticas. Para incentivar a pesquisa, indicamos os materiais a seguir, quêque contêm mais dêtálhesdetalhes sobre o trabalho de é-chêrEscher.

• M. C. ESCHER COLÉCTIONCOLLECTION. Baarn (Países Baixos), c2024. sáitiSite. Disponível em: https://livro.pw/rhlzg. Acesso em: 24 out. 2024.

sáitiSite oficial de M. C. é-chêrEscher (em inglês), quêque apresenta uma biografia do artista, suas principais obras e informações sobre exposições.

• MACHADO, Bruno. Quem foi M. C. é-chêrEscher? Superinteressante, [s. l.], 22 fev. 2024. Disponível em: https://livro.pw/qucok. Acesso em: 24 out. 2024.

Artigo quêque traz informações a respeito do artista, apresentadas com linguagem acessível.

• MATTOS, VálterWalter. Desvendando a técnica de M. C. é-chêrEscher. In: MATTOS, VálterWalter. VálterWalter Mattos. [S. l.], 14 dez. 2015. Blogue. Disponível em: https://livro.pw/jtmlk. Acesso em: 24 out. 2024.

Texto do sáitisite do designer VálterWalter Mattos, quêque explora as técnicas de é-chêrEscher em seus trabalhos e divulga vídeos explicativos.

Além díssudisso, as xilogravuras de é-chêrEscher podem sêrser vistas em https://livro.pw/rtyqk, e as litogravuras, em https://livro.pw/poyda (acessos em: 24 out. 2024).

O vídeo é-chêrEscher working on Snakes [Escher trabalhando em Serpentes], disponível em: https://livro.pw/sdvqp (acesso em: 24 out. 2024), mostra o artista trabalhando na xilogravura Serpentes, de 1969.

As Transformações isométricas trabalhadas no Capítulo são a reflekçãoreflexão, a translação, a rotação e as suas composições. A palavra isometria vêmvem do grego iso, quêque significa “igual”, e metria, quêque remete a medida, medição. Assim, é possível dizêrdizer quêque a palavra isometria significa “medidas iguais”. As principais propriedades da isometria são:

• Preserva colinearidade, isto é, se P, Q e R são três pontos colineares, então suas respectivas imagens pela transformação T são colineares.

• Preserva segmentos de reta, isto é, se A e B são pontos e A’ e B’ são suas imagens pela transformação T, então o segmento AB é congruente ao segmento A’B’.

• Preserva retas, ou seja, se r é uma reta, então sua imagem r’ pela transformação T também é uma reta.

• Preserva triângulos, se ABC é um triângulo, então sua imagem A’B’C’ pela transformação T também é um triângulo congruente ao triângulo ABC.

• Preserva ângulos, se ABC é um ângulo com vértice em B, então sua imagem A’B’C’ pela transformação T também é um ângulo com vértice em B’ congruente ao ângulo ABC.

• Preserva perpendicularidade entre retas, isto é, se a reta AB é perpendicular à reta AC em A, então as retas A’B’ e A’C’, respectivas imagens de AB e AC pela transformação T, também são perpendiculares em A’.

As demonstrações dessas propriedades e outras possibilidades didáticas para a abordagem dos assuntos do Capítulo podem sêrser consultadas na tese Transformações geométricas planas: um estudo experimental e dinâmico, disponível em: https://livro.pw/xugus (acesso em: 24 out. 2024).

Na reflekçãoreflexão em relação a um ponto, recomenda-se propor aos estudantes a demonstração de quêque ela é uma isometria.

Demonstração

Observe quêque, dados dois pontos quaisquer A e B (A ≠ B) do plano a e suas imagens A’ e B’, obtidas pela reflekçãoreflexão dêêssesdesses pontos em relação a um ponto X (X ∈ a),

Página trezentos e cinquenta e quatro354

os triângulos ABX e A’B’X são congruentes pelo casos LAL, pois AX = A’X, BX = B’X e os ângulos $A\widehat{X}B$ e $A^{\text{'}}\widehat{X}{B}^{\text{'}}$ são opostos pelo vértice. Portanto, AB ≡ A’B’.

A seguir, apresentam-se duas propostas de atividades complementares para o tópico Reflexão.

1. Determine a imagem C’D’E’, reflekçãoreflexão em relação ao ponto O do triângulo CDE.

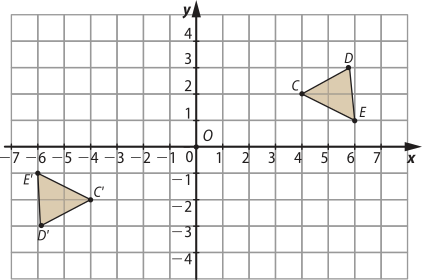
2. Determine os eixos de simetria de um hekzágonohexágono regular.

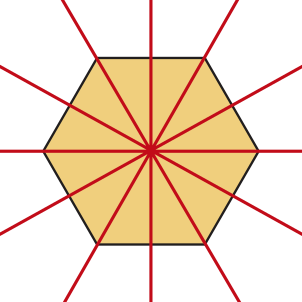
Na Translação, recomenda-se propor aos estudantes quêque expliquem, por meio de argumentos matemáticos, por quêpor que ela é uma isometria, apresentando os dois casos possíveis.

Primeiro caso. Dados dois pontos quaisquer A e B (A ≠ B) e o vetor $\begin{array}{c}\vec{v}\end{array}$ do plano a, a reta AB é paralela ao vetor ou seja, os pontos A e B e suas imagens A’ e B’ são colineares. Nesse caso, os estudantes podem considerar as imagens A’ = A + $\begin{array}{c}\vec{v}\end{array}$ e B’ = B + $\begin{array}{c}\vec{v}\end{array}$ e observar quêque:

d(A', B') = |B' − A'| = |(B + $\begin{array}{c}\vec{v}\end{array}$₎ − (A + $\begin{array}{c}\vec{v}\end{array}$ →)| = |B − A| = d(A, B)

Segundo caso. Dados dois pontos quaisquer A e B (A ≠ B) e o vetor ^→ v do plano a, a reta AB não é paralela ao vetor → v. Nesse caso, os estudantes podem argumentar quêque os triângulos BA’A e BA’B’ são congruentes pelo caso LAL, pois BA’ é um lado comum, os segmentos AA’ e BB’ são congruentes e paralelos por causa da translação e os ângulos $A\widehat{A^{\text{'}}}B$e $A^{\text{'}}\widehat{X}{B}^{\text{'}}$ são alternos internos, logo AB = A’B’.

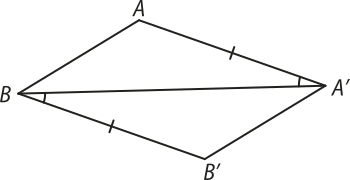
Na Rotação, recomenda-se propor novamente aos estudantes quêque expliquem, por meio de argumentos matemáticos, por quêpor que ela é uma isometria, apresentando os seguintes casos:

Primeiro caso. Os pontos O, P e Q são colineares, sêndosendo O o centro da rotação de ângulo a. Nesse caso, os estudantes podem argumentar quêque, se P’ e Q’ são, respectivamente, as imagens de P e Q pela rotação de centro em O e ângulo a, pela definição de rotação,

OP = OP’ e OQ = OQ’, logo:

d(P’, Q’) = d(O, P’) + d(O, Q’) = d(O, P) + d(O, Q) = d(P, Q), quando O está entre P e Q; ou

d(P’, Q’) = |d(O, P’) − d(O, Q’)| = |d(O, P) − d(O, Q)| = d(P, Q), quando O não está entre P e Q.

Segundo caso. Os pontos O, P e Q não são colineares, sêndosendo O o centro da rotação de ângulo a.

Nesse caso, se P’ e Q’ são, respectivamente, as imagens de P e Q pela rotação de centro em O e ângulo a, então os triângulos POQ e P’OQ’ são congruentes pelo caso LAL, pois OP = OP’, OQ = OQ’ e os ângulos $P\widehat{O}Q$ = $P^{\text{'}}\widehat{O}{Q}^{\text{'}}$= (alfa)"α + (beta)"β.

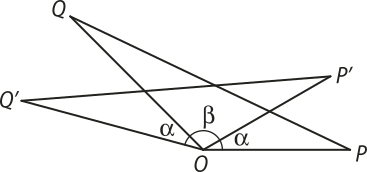
O boxe Fórum é uma oportunidade de integrar conhecimentos e, em certos casos, ampliar o universo cultural dos estudantes, favorecendo o desenvolvimento das competências gerais 1, 3 e 9 e do Tema Contemporâneo Transversal Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras. Ao explorar as figuras do ponto de vista matemático, comentar a respeito da possibilidade de se unir mais de um tipo de isometria para se obtêrobter uma figura. Por exemplo, podem sêrser associadas uma reflekçãoreflexão e uma translação. O texto a seguir pódepode subsidiar a discussão.

[…]

A representação gráfica visual é uma parte do estudo sobre linguagem visual. Conduz mensagens inteligíveis e pódepode representar tanto um padrão decorativo para um observador externo, como um significado para indivíduo de uma determinada cultura. Por esta razão, para um integrante de uma comunidade indígena êsteeste tipo de representação visual pódepode

Página trezentos e cinquenta e cinco355

sêrser um motivo quêque informa sobre a cultura, sua cosmovisão e suas mitologias.

[…]

[…] [A] ár-tearte nas sociedades indígenas cumpre uma função social e se insere no âmbito de outras expressões culturais humanas. É uma criação em conjunto quêque passada de geração em geração cria memória e identidade ao grupo.

[…] A ornamentação para o indígena intégraintegra o objeto a quêque se aplica, seja ele o corpo humano ou um artefato. […]

[…]

O grafismo faz parte da vida social dos povos tradicionais, mesmo quêque tenha se perdido no tempo, é fator de identidade cultural.

A ár-tearte está na história e nas experiências de uma ssossiedadesociedade: suas especificidades, autonomia e valor estético não a separam das outras manifestações da vida. […]

[…]

CAVALCANTE, Ana Luisa B. L. éti áuet al. A iconografia em comunidades indígenas. Projética, Londrina, v. 4, n. 2, p. 9-28, jul./dez. 2013. p. 13-17. Disponível em: https://livro.pw/kpgsx. Acesso em: 14 out. 2024.

As imagens apresentadas no boxe como exemplos podem sêrser exploradas para quêque os estudantes reconheçam visualmente as isometrias. Como atividade de ampliação do conteúdo, pode-se propor quêque identifiquem simetrias e tracem eixos de simetria.

No tópico Composição de transformações, comentar com os estudantes quêque a composição de transformações só é possível porque as transformações no plano (alfa)"α são funções bijetoras T: (alfa)"α → (alfa)"α. Em outras palavras, só é possível a composição f(g(x)) se o conjunto imagem da função g for igual ao domínio da função f, ou seja, Im(g) = D(f).

Para iniciar o tópico Transformações homotéticas, pode-se comentar quêque as transformações isométricas estudadas transformam figuras planas em figuras congruentes a elas. Já as transformações homotéticas transformam uma figura do plano em uma figura semelhante a ela. Trata-se de uma semelhança quêque preserva ângulos, mas altera distâncias, ampliando ou reduzindo a figura na mesma razão. Como sugestão de leitura e de atividades complementares para esse tópico, consultar a página: https://livro.pw/cbdts (acesso em: 24 out. 2024).

Uma atividade interessante relacionada à homotetia é a construção do fractal triângulo de Sierpinski no GeoGebra. Para desenvolver essa atividade, consultar: https://livro.pw/xjfou (acesso em: 24 out. 2024).

Outra atividade possível é a construção de um pantógrafo. No endereço eletrônico: https://livro.pw/ghudp (acesso em: 24 out. 2024), há um vídeo com orientações sobre essa construção, quêque pódepode sêrser indicado aos estudantes.

Um dos objetivos do tópico Transformações geométricas e matrizes é ilustrar, de modo simplificado, como matrizes e transformações geométricas são aplicadas na área da computação gráfica, pois permitem ampliar, reduzir, modelar e manipular objetos quêque estão contidos em um plano. Em um ambiente virtual, em quêque a descrição da forma e dos movimentos é executada por programas de computadores, são necessários algoritmos quêque efetuem operações matriciais e, consequentemente, manipulam os objetos graficamente.

A seção Conexões com… proporciona uma abordagem do assunto pela ótica da Etnomatemática e favorece o trabalho com a competência específica 1 e a habilidade EM13MAT105 da área de Matemática e suas Tecnologias, na medida em quêque os estudantes são convidados a utilizar conceitos e procedimentos matemáticos para interpretar situações em diversos contextos, empregando noções de transformações isométricas. Além díssudisso, possibilita o desenvolvimento das competências gerais 1, 3 e 9 e do Tema Contemporâneo Transversal Diversidade Cultural, uma vez quêque promove a valorização dos povos africanos e de sua cultura.

Para o trabalho com essa seção, recomenda-se a leitura do artigo "[Entre] as pinturas das casas ndebele: [geo]metrias e currículos esgarçados", disponível em: https://livro.pw/goudb (acesso em: 24 out. 2024). Ele apresenta a origem dessas pinturas e aborda os desafios da matemática no cumprimento da lei númeronº 10.639/2003, quêque estabelece a obrigatoriedade do ensino da História da África e dos Africanos, da luta dos negros no Brasil, da cultura negra brasileira e do negro na formação da ssossiedadesociedade nacional, resgatando a contribuição do povo negro nas áreas social, econômica e política pertinentes à História do Brasil.

A seguir, apresentam-se mais duas recomendações de leitura.

• SOUTH AFRICAN HISTORY ONLÁINEONLINE. quêipCape Town, [2024]. sáitiSite. Disponível em: https://livro.pw/qlqlu. Acesso em: 24 out. 2024.Endereço eletrônico da África do Sul quêque aborda a história e a etnia Ndebele.

Página trezentos e cinquenta e seis356

• YAKUBU, poouPaul. As inspirações por trás das cores da arquitetura tradicional africana. Tradução: Diogo Simões. [S. l.]: ArchDaily, 2 set. 2023. Disponível em: https://livro.pw/kmohw-]ras-das-cores-da-arquitetura-tradicional-africana. Acesso em: 14 out. 2024.

Texto quêque explica o significado das cores para o povo ndebele, por exemplo, para quem o preto representa as pessoas do mundo espiritual, o branco simboliza a pureza, o vermelho, a paixão e o pôdêrpoder, o amarelo simboliza fertilidade e esperança e o vêrdeverde representa a térraterra e a agricultura.

Na atividade 3, incentivar os estudantes a procurar outras obras de êstérEsther Mahlangu para terem mais referências à disposição. Se possível, organizar uma exposição com as produções dos estudantes.

A seção Explorando a tecnologia favorece o trabalho com as competências gerais 3, 4 e 5 da BNCC, pois permite quêque os estudantes participem de práticas diversificadas da produção artístico-cultural, fazendo uso das linguagens visual e digital, bem como de conhecimentos das linguagens artística e matemática, para se expressar.

Para saber mais sobre como construir mosaicos no GeoGebra, recomendam-se os seguintes materiais:

• MEZADRI, Fabiana O. M.; PISSINI, Mariana M. Transformações geométricas. Campinas: Universidade Estadual de Campinas: Laboratório de Ensino de Matemática, 2016. Disponível em: https://livro.pw/cgxuq. Acesso em: 14 out. 2024.

O material apresenta uma sequência de atividades quêque podem sêrser desenvolvidas com os estudantes.

• DANTAS, Sérgio C. Mosaicos, faixas, rosetas e fractais com o GeoGebra. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, XI, 2013, Curitiba. Anais […]. Curitiba: Sociedade Brasileira de Matemática, 2013. Disponível em: https://livro.pw/qesdc. Acesso em: 24 out. 2024.

O material promove a integração de conhecimentos relativos ao software GeoGebra e às isometrias no plano, com a finalidade de construir arranjos geométricos, tais como: mosaicos, faixas geométricas, rosetas e fractais.

Se julgar conveniente, mostrar aos estudantes as ferramentas prontas do GeoGebra para fazer transformações geométricas e comentar quêque, em outros softwares de desenho, é comum havêerhaver essa ferramenta de repetição.

Avaliação

As atividades 2 e 3 da Abertura do Capítulo possibilitam uma avaliação diagnóstica das habilidades a seguir, trabalhadas no Ensino Fundamental − Anos Finais.

(ê éfe zero sete ême ah dois umEF07MA21) Reconhecer e construir figuras obtidas por simetrias de translação, rotação e reflekçãoreflexão, usando instrumentos de desenho ou softwares de geometria dinâmica e vincular esse estudo a representações planas de obras de; ár-tede arte, elemêntoselementos arquitetônicos, entre outros.

(ê éfe zero oito ême ah um oitoEF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflekçãoreflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.

A seguir, são apresentadas sugestões de atividades cuja análise das resoluções pódepode contribuir para avaliar a evolução de cada estudante e orientar seus estudos.

1ª avaliação formativa: atividades 3 e 5 (páginas 268 e 269, respectivamente).

2ª avaliação formativa: atividades 10 e 16 (páginas 273 e 279, respectivamente).

3ª avaliação formativa: atividade 23 (página 285).