Resoluções das atividades
Capítulo 1 • Matemática financeira
Atividades
1. Relacionando as representações do qüadro, temos:
= 0,25 = 25%
= 0,065 = 6,5%
= 0,47 = 47%
= 0,08 = 8%
2. Como a porcentagem corresponde à representação de uma fração cujo denominador é 100, pode-se calcular:
a) ⋅ 3.000 = 420
b) ⋅ 250 = 22,5
c) ⋅ 300 = 1,8
d) ⋅ 1.000 = 240
3. a) Ao fim de um ano, a cidade terá um aumento de 2,5% no número de habitantes:
1,025 ⋅ 90.000 = 92.250
Logo, ao fim de 1 ano, a cidade terá 92.250 habitantes.
b) Ao fim do segundo ano, a cidade terá um aumento de 2,5% sobre o número de habitantes do ano anterior:
1,025 ⋅ 92.250 ≃ 94.556
Logo, ao fim de dois anos, a cidade terá aproximadamente 94.556 habitantes.
4. Sejam a e b as dimensões de um documento comum (uma fô-lha de tamãnho A4). Assim:
Área original = ab
Deseja-se obtêr um documento reduzido tal quê:
Área reduzido = Áreaoriginal
Área reduzido = ab
Sabendo quê:
=
conclui-se quê as dimensões do documento reduzido devem sêr e
Logo, deverá sêr digitado 50% no painel de comandos.
5. Segundo o enunciado, é solicitada a porcentagem quê representa 20% de 30%, ou seja:
= 0,06 = 6%
6. (1 + 0,05) ⋅ (1 + 0,05) ⋅ (1 + 0,05) ⋅ 200 = 1,157625 ⋅ 200 = 231,525
Logo, o preêço dessa mercadoria daqui a 3 anos será aproximadamente R$ 231,52.
7. a) O primeiro trecho da viagem corresponde a 40% de todo o trajeto, ou seja: ⋅ 800 = 320
Portanto, a distância percorrida no primeiro trecho é 320 km.
b) O segundo trecho da viagem corresponde a 55% do restante do trajeto, quê é de 480 km (pois 800 − 320 = 480). Assim: ⋅ 480 = 264
Portanto, a distância percorrida no segundo trecho é 264 km.
c) A distância percorrida no terceiro trecho é 216 km, pois:
800 − 320 − 264 = 216
Se o motorista mantiver uma velocidade média de 90 km/h, o tempo de percurso nesse trecho será de:
= 2,4 → ou 2h24min
8. Na creche, podem sêr atendidas 100 crianças anualmente, pois, nela, há 10 salas com capacidade para atender 10 crianças a cada ano. No ano passado, houve 400 nomes na lista de espera.
Neste ano, a creche continua podendo atender 100 crianças ao ano. Como o número de nomes na fila de espera cresceu 10%, tem-se: 400 ⋅ 1,10 = 440
No próximo ano, deseja-se ampliar a quantidade de crianças atendidas pela creche, com a meta de quê a lista de espera com 440 nomes dêste ano seja reduzida em 25%, quê corresponde a 330 nomes, pois: 440 ⋅ (1 − 0,25) = 330
Para quê isso ocorra, a creche precisa atender 110 novas crianças. Como cada sala de aula tem capacidade de atendimento para 10 crianças, devem sêr construídas, no mínimo, 11 novas salas.
Resposta: alternativa b.
9. De acôr-do com o enunciado, o aparelho custa R$ 8.000,00 e, no pagamento a prazo, ocorre acréscimo de 8%, então:
8.000 ⋅ (1 + 0,08) = 8.640
Logo, o valor de cada prestação será R$ 4.320,00, pois:
8.640 ∶ 2 = 4.320
10. Seja x o preêço da raquete na loja B. Assim, temos:
⋅ (x + 15) = x ⇒ 90x + 1.350 = 100x ⇒ x = 135
Logo, o preêço da raquete na loja B será R$ 135,00.
11. a) Se x = 15, o valor à vista, em reais, será:
8.000 ⋅ (1 − 0,15) = 6.800
Para pagamento a prazo, o comprador quitaria a primeira parcela de R$ 4.000,00 e aplicaria R$ 2.800,00, quê é a diferença entre o valor à vista com desconto e a primeira parcela (6.800 − 4.000 = 2.800), por um mês a uma taxa mensal de 25%. Essa aplicação resultaria em um valor total de R$ 3.500,00, pois:
2.800 ⋅ (1 + 0,25) = 3.500
Nessas condições, o comprador não teria o suficiente para quitar a segunda parcela de R$ 4.000,00. Portanto, não é vantajosa para ele a compra a prazo.
b) O valor de x quê torna indiferente a compra à vista ou a prazo é o valor cuja aplicação resulte nos R$ 4.000,00 a sêrem pagos na segunda parcela. O capital a ser aplicado é a diferença entre o valor à vista com desconto de x% e o valor de R$ 4.000,00 da primeira parcela:
8.000 ⋅ − 4.000
De acôr-do com o enunciado, a aplicação é feita a uma taxa de 25% ao mês, e o valor total resultante deve sêr R$ 4.000,00, então:
Logo, será indiferente a compra à vista ou a prazo se x = 10.
12. a) Se um vendedor conseguir obtêr R$ 120.000,00 em vendas, ele terá 1% de comissão sobre as vendas mais um bônus de R$ 600,00 pela meta atingida, ou seja:
120.000 ⋅ + 600 = 1.800
Logo, o vendedor receberá R$ 1.800,00 de comissão.
b) A comissão mínima, em reais, da terceira faixa de bonificação é:
200.000 ⋅ + 900 = 3.300.
Assim, para receber uma comissão de R$ 3.900,00, o vendedor precisará vender mais de R$ 200.000,00 em um mês. Seja x esse valor, tem-se:
x ⋅ + 900 = 3.900 ⇒ = 3.000 ⇒ x = 250.000
Logo, o vendedor precisará vender R$ 250.000,00.
Página trezentos e sessenta e um
c) A comissão mássima recebida pela primeira faixa de bonificação é: 80.000 ⋅ = 640
A comissão mínima recebida pela segunda faixa de bonificação é:
80.000 ⋅ + 600 = 1.400
Portanto, R$ 1.000,00 não é um valor válido para a comissão; pois, se ele vender até R$ 80.000,00, deverá receber R$ 640,00, e, se vender mais do quê R$ 80.000,00, deverá receber, no mínimo, R$ 1.400,00.
13. Sendo x o preêço inicial, em reais, da mercadoria, conclui-se:
[x ⋅ (1 + 0,18)] ⋅ (1 − 0,05) = x + 302,5
1,18x ⋅ 0,95 − x = 302,5
1,121x − x = 302,5 ⇒ x = = 2.500
Portanto, o preêço inicial da mercadoria era R$ 2.500,00.
14. Como o preêço de custo foi de R$ 250,00 e o lucro foi estipulado em 18%, então o lucro foi: 0,18 ⋅ 250,00 = 45
Desse modo, a mercadoria deverá sêr revendida por R$ 295,00, pois, ao se adicionar o preêço de custo ao lucro, tem-se:
250 + 45 = 295
15. O preêço de custo da mercadoria foi R$ 860,00.
Para quê o lucro de revenda dela seja de 20%, calcula-se:
860 ⋅ (1 + 0,2) = 860 ⋅ 1,2 = 1.032
Logo, a mercadoria deve sêr vendida por R$ 1.032,00.
16. O preêço de custo de dez sacas de batatas foi R$ 210,00. Então, cada saca custou R$ 21,00.
Seja x o preêço de venda, para saber por quanto cada saca deve sêr revendida calcula-se:
= 0,20 ⇒ 0,20x = x − 21 ⇒ 0,8x = 21 ⇒ x = 26,25
Logo, cada saca deverá sêr revendida por R$ 26,25.
17. Como o preêço com desconto de 17% era R$ 478,08, o preêço de etiqueta era:
x − x = 478,08 ⇒ 83x = 47.808 ⇒ x = 576
Como a enciclopédia é composta de 18 volumes, então cada volume, antes do desconto, custava:
= 32, ou seja, R$ 32,00
Resposta: alternativa e.
18. Descontando-se o imposto de 20% do preêço de venda, obtém-se o lucro do dono da loja, quê é de 30% sobre o preêço de custo. Sendo C o preêço de custo, tem-se:
39 ⋅ (1 − 0,2) = C ⋅ (1 + 0,3)
C = ⇒ C = 24
Logo, o preêço de custo é R$ 24,00.
19. Sejam C o preêço de custo, V o preêço de venda e L o lucro. Assim: C = V − L = 240 − (240 ⋅ 0,2) = 192
Portanto, o preêço de custo é R$ 192,00.
20. Sejam V o preêço de venda e C o preêço de custo, ambos em reais.
Assim, temos:
Resolvendo o sistema, têm-se: C = 6.000 e V = 8.000.
Portanto, o preêço de custo é R$ 6.000,00.
21. Ao final do primeiro mês, o valor da dívida se tornou R$ 1.100,00, pois: 1.000 ⋅ 1,1 = 1.100
Após um pagamento de R$ 300,00, o débito passou a sêr R$ 800,00.
Ao final do segundo mês, o valor da dívida se tornou R$ 880,00, pois: 800 ⋅ 1,1 = 880
Após um pagamento de R$ 500,00, o débito passou a sêr R$ 380,00.
Ao final do terceiro mês, o valor da dívida se tornou R$ 418,00, pois: 380 ⋅ 1,1 = 418
Portanto, para quitar a dívida, o último pagamento foi de R$ 418,00.
Resposta: alternativa a.
22. Calcula-se o valor da entrada: 0,2 ⋅ 3.000,00 = 600,00
Calcula-se, em seguida, o valor a sêr financiado:
3.000 − 600 = 2.400
Assim, considerando uma aplicação de R$ 2.400,00 a juros simples quê rendeu um montante de R$ 2.760,00 após 5 meses, temos:
2.760 = 2.400 ⋅ (1 + i ⋅ 5) ⇒ i = = 0,03 = 3%
Então, a taxa é de 3% a.m. (ao mês).
23. Em cada item, considera-se a expressão:
J = C ⋅ i ⋅ t
a) J = 7.000 ⋅ (0,025 ⋅ 4) ⇒ J = 7.000 ⋅ 0,1 = 700 ⇒ J = 700; R$ 700,00
b) Considerando quê t corresponde a 12 meses, tem-se:
J = 7.000 ⋅ (0,03 ⋅ 12) ⇒ J = 7.000 ⋅ 0,36 = 2.520 ⇒ J = 2.520; R$ 2.520,00
c) Como a taxa rende ao dia, o tempo também deve estar nessa unidade de medida. Três meses equivalem a 90 dias, portanto:
J = 7.000 ⋅ (0,0015 ⋅ 90) ⇒ J = 7.000 ⋅ 0,135 = 945 ⇒ J = 945; R$ 945,00
24. Como cada depósito de R$ 200,00 é uma aplicação a juros simples de 1,5% ao mês, então o juro mensal será, em reais:
200,00 ⋅ 0,015 = 3,00
Assim, o primeiro depósito, depois de um ano, terá um rendimento, em reais, de: 200 + 12 ⋅ 3 = 236
O segundo depósito, depois de 11 meses, terá um rendimento, em reais, de: 200 + 11 ⋅ 3 = 233
O terceiro depósito, depois de 10 meses, terá um rendimento, em reais, de: 200 + 10 ⋅ 3 = 230
E assim por diante para cada um dos 12 depósitos.
O último depósito terá um acréscimo de R$ 3,00, e o montante será R$ 203,00.
Então, o montante, após um ano, será, em reais:
M = 236 + 233 + 230 + … + 203 = 2.634
Portanto, o montante após um ano será R$ 2.634,00.
25. O período indicado no enunciado é de 2 meses. Logo:
J = 1.800,00 ⋅ 0,027 ⋅ 2 ⇒ J = 97,20; R$ 97,20
26. Considerando as informações contidas no enunciado, temos:
6.000 = C ⋅ 0,06 ⋅ 4 ⇒ 6.000 = C ⋅ 0,24 ⇒ C = = 25.000
Assim, o capital é R$ 25.000,00.
27. M = C ⋅ (1 + i ⋅ t)
M = R$ 12.000,00 ⋅ (1 + 0,015 ⋅ 9) ⇒ R$ 13.620,00
28. M = C ⋅ (1 + i ⋅ t)
9.200 = 8.000 ⋅ (1 + i ⋅ 6) ⇒ i = 0,025 → 2,5%
Então, a taxa é de 2,5% a.m. (ao mês).
29. M = C ⋅ (1 + i)t
M = R$ 200.000,00 ⋅ (1 + 0,007)6 ≃ R$ 208.548,38
30. M = C ⋅ (1 + i)t
M = R$ 20.000,00 ⋅ (1 + 0,006)8
M = R$ 20.000,00 ⋅ (1,006)8
M = R$ 20.000,00 ⋅ 1,0490 ≃ R$ 20.980,00
31. M = C ⋅ (1 + i)t
M = R$ 30.000,00 ⋅ (1 + 0,0095)24 ≃ R$ 37.642,03
32. M = C ⋅ (1 + i)t
R$ 8.000,00 = C ⋅ (1 + 0,02)6 ⇒ C ≃ R$ 7.103,77
33. Caso João espere dois meses, o montante, em reais, será:
M = 20.000 ⋅ (1,02)2 = 20.000 ⋅ 1,0404 = 20.808
Ou seja, ainda faltarão R$ 192,00.
Se ele esperar três meses, o montante, em reais, será:
M = 20.000 ⋅ (1,02)3 = 20.000 ⋅ 1,061208 = 21.224,16
Ou seja, sobrarão R$ 224,16, portanto, aproximadamente, R$ 225,00.
Resposta: alternativa c.
Página trezentos e sessenta e dois
34. M = C ⋅ (1 + i)t
R$ 25.000,00 = C ⋅ (1 + 0,05)6 ⇒ C ≃ R$ 18.655,38
Resposta: alternativa b.
35. Considerando as informações contidas no enunciado, temos:
M = 40.000 ⋅ (1,16)2 = 40.000 ⋅ 1,3456 = 53.824
J = M − C ⇒ J = 53.824 − 40.000 = 13.824
Assim, os juros obtidos foram R$ 13.824,00.
36. a) M = C ⋅ (1 + i)t
M = R$ 4.000,00 ⋅ (1,04)3 ≃ R$ 4.499,46
b) Como 10 anos correspondem a 120 meses, tem-se:
M = R$ 4.000,00 ⋅ (1,02) 120 ≃ R$ 43.060,65
c) Considerando o mês comercial (30 dias), 15 meses correspondem a 450 dias.
Desse modo: M = R$ 4.000,00 ⋅ (1,0002)450 ≃ R$ 4.376,66
37. M = C ⋅ (1 + i)t
M = R$ 5.000,00 ⋅ (1,03)5 ≃ R$ 5.796,37
Esse montante rendeu aproximadamente R$ 796,37 de juros, pois:
J = M − C ≃ R$ 5.796,37 − R$ 5.000,00 = R$ 796,37
38. Analisando a evolução mensal dos valores, em reais, das parcelas pagas ao amigo, temos:
1.000, 1.100, 1.200, 1.300
Esses valores formam uma progressão aritmética de razão 100. Analisando os valores das parcelas pagas ao banco, temos:
1.000, 1.100, 1.210, 1.331
Esses valores formam uma progressão geométrica de razão 1,1.
Resposta: alternativa d.
39. Seja C o capital aplicado por João no regime de juro simples, com i = 0,12 a.a. e t = 3 anos, tem-se o montante Ms:
Ms = C ⋅ (1 + i ⋅ t) ⇒ Ms = 1,36 ⋅ C
Seja C o capital aplicado por João no regime de juro compôzto, com i = 0,12 a.s. e t = 6 semestres, tem-se o montante Mc:
Mc = C ⋅ (1 + i)t ⇒ Mc = C ⋅ (1,12)6
Considerando Mc = Ms + 2.633,36 e utilizando 1,9738 como aproximação para (1,12)6, temos:
1,9738 ⋅ C ≃ 1,36 ⋅ C + 2.633,36 ⇒ C ≃ 4.290,26
Como Ms = 1,36 ⋅ C, segue quê: Ms ≃ R$ 5.834,75
Portanto, João recebeu aproximadamente R$ 1.544,49 de juro, pois:
J = Ms − C ≃ 5.834,75 − 4.290,26 = 1.544,49
40. M = C ⋅ (1 + i)t
M = R$ 15.000,00 ⋅ (1,02) 10
M = R$ 15.000,00 ⋅ (1,025)2
M = R$ 15.000,00 ⋅ (1,1)2
M = R$ 15.000,00 ⋅ 1,21 = R$ 18.150,00
Resposta: alternativa b.
41. César aplicou R$ 10.000,00 a uma taxa de juro compôzto igual a i.
Em reais, após um ano, o montante da aplicação será: 10.000 ⋅ (1 + i)
Depois de sacar R$ 7.000,00, o restante permanéce aplicado, ou seja: 10.000 ⋅ (1 + i) − 7.000 = 3.000 + 10.000i
No ano seguinte, o montante dessa aplicação será:
(3.000 + 10.000i) ⋅ (1 + i) = 6.000
Portanto: (3 + 10i) ⋅ (1 + i) = 6 ⇒ 10i2 + 13i − 3 = 0
Resolvendo a equação do 2º grau, obtém-se a raiz: i = 0,2
A raiz negativa deve sêr desconsiderada, pois i > 0.
Desse modo: (4i − 1)2 = (4 ⋅ 0,2 − 1)2 = 0,04
Resposta: alternativa d.
42. De acôr-do com o enunciado, sabe-se quê:
• depois de um investimento de 2 anos, o montante era R$ 2.012,85;
• depois de 3 anos, era R$ 2.314,77.
No entanto, não se sabe o capital investido nem a taxa anual da aplicação.
Com base nessas informações, é possível organizar o seguinte sistema:
Dividindo a primeira equação pela segunda, tem-se:
⇒ 1 + i = ⇒ i ≃ 0,15
Substituindo a taxa na segunda equação, tem-se:
2.012,85 = C ⋅ (1 + 0,15)2 ⇒ 2.012,85 = C ⋅ 1,3225 ⇒ C = ≃ 1.522
Resposta: alternativa c.
43. Considerando as informações contidas no enunciado, conclui-se quê o montante será:
M = 18.000 + 6.390 = 24.390
Logo, o tempo necessário será:
24.390 = 18.000 ⋅ (1,0281)t ⇒ 1,0281t = ⇒ 1,0281t = 1,355 ⇒ t ⋅ log 1,0281 = log 1,355 ⇒ t = ≃ 11
Portanto, o prazo é de aproximadamente 11 meses.
44. Considerando as informações contidas no enunciado, pode-se resolver o problema utilizando radiciação:
36.087 = 24.000 ⋅ (1 + i)7 ⇒ (1 + i)7 = ⇒ (1 + i)7 = 1,503625 ⇒ 1 + i = ⇒ i = 0,06 = 6%
Logo, a taxa mensal é de aproximadamente 6%.
45. I. Falsa, pois:
P(t) = P(0) ⋅ (1 + i)t ⇒ P(3) = 50.000 ⋅ (1 + 0,02)3 ⇒ P(3) ≃ 53.060 ⇒ P(3) ≃ 53.060 habitantes
II. Falsa, pois:
Px(2) = 19.600 ⋅ (1 + 0,02)2 ⇒ P x(2) ≃ 20.392 habitantes
Py(2) = 28.900 ⋅ (1 + 0,05)2 ⇒ Py(2) ≃ 31.862 habitantes
Logo:
III. Verdadeira, pois:
Px(2) = 129.600 ⋅ (1 + 0,05)2 ⇒ Px(2) = 142.884 habitantes
Py(2) = 122.500 ⋅ (1 + 0,08)2 ⇒ Py(2) = 142.884 habitantes
IV. Falsa, pois:
P(t) = P(0) ⋅ (1 + i)t ⇒ = (1 + i)t ⇒ t ⋅ log(1 + i) =log () ⇒ log(1 + i) = ⇒ i = 10 − 1
V. Verdadeira, pois, segundo o enunciado, atualmente o município tem 44.100 habitantes e deseja-se saber o número de habitantes quê havia dois anos antes. Para isso, pode-se considerar P(2) = 44.100 e P(0) a quantidade procurada.
Considerando quê a taxa anual de crescimento de 5% ocorre há cinco anos, tem-se i = 0,05. Logo:
44.000 = P(0) ⋅ (1 + 0,05)2 ⇒ P(0) = 4.000 habitantes
Resposta: F, F, V, F, V.
46. Considerando as informações contidas no enunciado, temos:
a) 85.400 = 80.000 ⋅ (1,022)t ⇒ (1,022)t = 1,0675 ⇒ t = ≃ 3
Portanto, aproximadamente 3 meses.
b) 134.868,80 = 80.000 ⋅ (1,022)t ⇒ (1,022)t = 1,68586 ⇒ t = ≃ 24
Portanto, aproximadamente 2 anos.
47. a) Considerando as proporções fornecidas no enunciado, tem-se:
Como P1 + P2 + P3 = 57.000, então:
P1 + = 57.000 ⇒ P1 = 12.000
Logo: P2 = = 15.000
Página trezentos e sessenta e três
P3 = = 30.000
Então, o valor de cada parcela é, respectivamente, R$ 12.000,00, R$ 15.000,00 e R$ 30.000,00.
b) Segundo a fórmula do montante no regime de juro compôzto, M = C ⋅ (1 + i)t, obtém-se: 12.738 = 12.000 ⋅ (1 + 0,01)t ⇒ = 1,01t ⇒ 1,06 ≃ 1,01t ⇒ log 1,06 ≃ t ⋅ log 1,01 ⇒ 0,0253 ≃ t ⋅ 0,0043 ⇒ t ≃ 6
Logo, aproximadamente 6 meses.
c) Utilizando a expressão do montante no regime de juro simples, M = C ⋅ (1 + i ⋅ t), e t = 24 meses, tem-se:
25.800 = 15.000 ⋅ (1 + i ⋅ 24) ⇒ = 1 + 24i ⇒ 1,72 = 1 + 24i ⇒ 0,72 = 24i ⇒ i = 0,03 = 3%
Então, a taxa é de 3% a.m. (ao mês).
48. Resposta pessoal. Sugestão de problema: Por motivos financeiros, Carla deixou de pagar uma fatura de seu cartão de crédito. Sabendo quê essa fatura fechou em R$ 2.000,00, quê não foi incluído nenhum tipo de multa e quê o total a pagar é corrigido a juro compôzto, qual será o valor da fatura após 1 ano?
De acôr-do com o qüadro, a taxa do cartão de crédito é 421,3% ao ano.
Logo: M = 2.000 ⋅ (5,213) 1 = 10.426
Assim, depois de 1 ano, o valor dessa fatura será R$ 10.426,00.
49. Para um capital inicial C, a uma taxa i = 1% a.m., tem-se M = 2C. Assim:
M = C ⋅ (1 + i)t
2C = C ⋅ (1 + 0,01)t
2 = (1,01)t ⇒ log 2 = t ⋅ log 1,01 ⇒ t = ≃ 70
Logo, para dobrar o capital inicial, é necessário quê o dinheiro fique aplicado por 70 meses.
Resposta: alternativa d.
50. O lucro L do banco foi:
L = 1.000 ⋅ 1,05 12 − 1.000 ⋅ 1,0112
L = 1.000 ⋅ (1,80 − 1,13)
L = 670
Resposta: alternativa c.
51. Ana Sofia pagou 153 reais (180 ⋅ 0,85) pela blusa e 104 reais (130 ⋅ 0,80) pela sandália. Como ela tinha R$ 300,00, recebeu de Trôco 43 reais (300 − 153 − 104), o quê corresponde a:
= 0,14333… = 14,333…%
Resposta: alternativa a.
52. Com base nas informações do enunciado, tem-se:
VP = ⇒ VP = ≃ 18.302,83
Logo, a pessoa deve pagar aproximadamente R$ 18.302,83 para quitar a dívida.
53. Com base nas informações do enunciado, tem-se:
4.000 = ⇒ VF ≃ 3.987,74
Logo, o valor do último pagamento de Lúcia foi aproximadamente R$ 3.987,74.
54. • Opção 1: 5.400 ⋅ (1 − 0,05) = 5.130
• Opção 2: ≃ 5.241,96
• Opção 3: 675 +
Logo, a opção 3 é a mais vantajosa.
55. Resposta pessoal. Espera-se quê os estudantes construam o qüadro em um software gratuito e comparem com os côlégas as possíveis soluções.
a) Um exemplo de preenchimento das despesas da 4ª coluna é: conta de á gua, R$ 78,00; conta de luz, R$ 145,60; telefone, R$ 289,90; conta de gás encanado, R$ 91,50; faculdade, R$ 1.098,00; transporte, R$ 480,00; supermercado, R$ 810,00; outros gastos, R$ 430,00. Nesse caso, o total dessa 4ª coluna é R$ 3.423,00, e o saldo é R$ 560,00.
b) Um exemplo de preenchimento das despesas da 5ª coluna é: conta de á gua, R$ 98,00; conta de luz, R$ 145,60; telefone, R$ 289,90; conta de gás encanado, R$ 101,50; faculdade, R$ 1.098,00; transporte, R$ 480,00; supermercado, R$ 810,00; outros gastos, R$ 450,00. Nesse caso, o total dessa 5ª coluna é R$ 3.473,00, e o saldo é R$ 510,00.
56. a) A primeira prestação é mais alta no SAC. Resposta pessoal. Espera-se, com o segundo quêstionamento, problematizar os fatores que estão envolvidos quando precisamos tomar uma dê-cisão como a de escolher o sistema de amortização em um empréstimo ou financiamento. Embora, na situação hipotética, estejamos considerando a mesma taxa de juro e o mesmo período, o quê normalmente não acontece na realidade, a ideia é quê os estudantes tênham uma situação mais simplificada para fazer comparações.
b) Resposta possível: Nas primeiras prestações, o valor amortizado no SAC é maior do quê no Sistema Price. Sim. Nas planilhas quê foram construídas pêlos estudantes, deve sêr possível observar com mais dêtálhes os pontos destacados, podendo-se, inclusive, adicionar todos os valores de juros quê estão dispostos nas colunas D e J da resolução da atividade resolvida 17: por exemplo, ao digitar, na célula D79, “=soma(D6:D78)” e pressionar Enter e, na célula J79, “=soma(J6:J78)” e pressionar Enter, é possível comparar os valores.
57. a) Para calcular o valor amortizado, basta dividir o valor financiado pelo número de prestações, nesse caso:
= 3.125
Logo, a amortização é R$ 3.125,00.
b) Para calcular o valor amortizado, primeiro deve-se subtrair a entrada do valor total:
40.000 − 12.000 = 28.000.
Depois, deve-se dividir o restante do valor financiado pelo número de prestações, nesse caso:
= 2.800
Logo, a amortização é R$ 2.800,00.
58. a) Como a entrada é 25% do valor, considera-se, então, quê o valor financiado será 75% do total:
75.000 ⋅ (0,75) = 56.250
Assim, o valor a sêr financiado é R$ 56.250,00.
b) Sugere-se quê todo o cálculo seja feito na calculadora, utilizando-se a seguinte fórmula:
P = V ⋅
Para o capital (V), considera-se o valor encontrado no item a, desconsiderando-se a entrada. Para a taxa (i), consideramos 2% a.m. ou 0,02. Por fim, para o tempo (n), 48 meses.
Substituindo os valores na fórmula, temos:
P = 56.250 ⋅ ⇒ P ≃ 1.833,85
Logo, a parcela será aproximadamente R$ 1.833,85.
c) Dividimos o valor financiado pelo número de prestações, nesse caso: = 1.171,875
Logo, a amortização será aproximadamente R$ 1.171,88.
Página trezentos e sessenta e quatro
d) Para essa atividade, devem-se utilizar as fórmulas de amortização Price e SAC e lançá-las na planilha, conforme orientação no Livro do estudante. Os estudantes devem atentar às posições na planilha, bem como à colocação dos parênteses no lugar correto. Sistema Price: R$ 31.774,96; SAC: R$ 27.562,50.
59. Do enunciado, pode-se concluir quê o valor do capital é R$ 1.700,00, (2.100 − 400), o valor da taxa é 4% e o prazo financiado é 10 meses.
Para calcular o valor de cada parcela, utiliza-se a fórmula:
P = V ⋅ ⇒ P = 1.700 ⋅ ≃ 209,59
Resposta: alternativa c.
Atividades complementares
1. Considerando as variações do PIB de 2015 a 2018, tem-se:
1,02 ⋅ 0,95 ⋅ 1,03 = 0,99807
Ou seja, houve decrescimento de aproximadamente 0,2%.
Resposta: alternativa a.
2. Como o lucro L é a diferença entre o preêço de venda V e o preêço de compra C e, nesse caso, V = (1 + 0,20) ⋅ C = 1,2C, segue quê: L = V − C ⇒ 150 = 1,2C − C ⇒ C = 750
Assim: V = 1,2C = 1,2 ⋅ 750 = 900
Logo, Ricardo recebeu R$ 900,00 pela venda da bicicleta.
Resposta: alternativa e.
3. Utilizando a expressão J = C ⋅ i ⋅ t, tem-se:
3.600 = 8.000 ⋅ 0,15 ⋅ t ⇒ t = = 3
Logo, o tempo é de 3 anos.
Resposta: alternativa b.
4. À vista, o produto custa 0,9C, sêndo C o preêço anunciado. A prazo, a primeira parcela (entrada) será 0,5C. Para obtêr a segunda parcela de 0,5C, considera-se quê a diferença de 0,4C em relação ao preêço à vista será aplicada por um mês. Assim:
M = C ⋅ (1 + i ⋅ t) ⇒ 0,5C = 0,4C ⋅ (1 + i ⋅ 1) ⇒ i = 0,25 = 25%
Logo, a taxa mensal no pagamento a prazo é 25%.
Resposta: alternativa a.
5. Primeira aplicação do sr. Paulo:
M1 = C + C ⋅ i ⋅ t ⇒ M1 = C + 0,12C = 1,12C
Segunda aplicação do sr. Paulo:
M2 = 1,12C + 1,12C ⋅ 0,03 ⋅ 9 ⇒ M2 = 1,12C + 1,12C ⋅ 0,27 = 1,4224C
Considerando o resultado anterior em uma única aplicação de 12 meses, tem-se:
1,4224C = C + C ⋅ i ⋅ 12 ⇒ 1,4224 = 1 + 12 ⋅ i ⇒ i = = 0,0352 = 3,52%
Logo, a taxa mensal deveria sêr de 3,52%.
Resposta: alternativa d.
6. Considerando as informações contidas no enunciado, conclui-se:
i = 6% a.m.; M = 1.960; t = 1 ano e 4 meses, ou 16 meses. Logo:
M = C ⋅ (1 + i ⋅ t) ⇒ 1.960 = C ⋅ (1 + 0,06 ⋅ 16) ⇒ 1,96 ⋅ C = 1.960 ⇒ C = 1.000
Logo, o capital aplicado foi R$ 1.000,00.
Resposta: alternativa a.
7. A entrada para a compra do veículo corresponde a 60% de 30.000, ou seja, 18.000 (0,6 ⋅ 30.000 = 18.000). Ao restante, R$ 12.000,00, serão acrescidos 2% de juros durante 5 meses: J = 0,02 ⋅ 5 ⇒ J = 10%
Logo: M = 12.000 + 0,10 ⋅ 12.000 = 13.200
Então, o valor, em reais, de cada prestação será: P = ⇒ P = 2.640
Resposta: alternativa c.
8. Para o cálculo utiliza-se a expressão M = C ⋅ (1 + i)t e considera-se, conforme as informações do enunciado, quê, a cada mês, a taxa de juros compostos é i = 0,01. Desse modo:
• No início do primeiro mês considerado, C1 = 10.000. Assim: M1 = 10.000 ⋅ (1 + 0,01) 1 = 10.100
Após a doação de R$ 100,00 no fim do mês, restaram R$ 10.000,00.
• No início do segundo mês, o capital aplicado era o montante restante do mês anterior, isto é, C2 = 10.000. Assim:
M2 = 10.000 ⋅ (1 + 0,01) 1 = 10.100
Nesse mês não houve doação.
• No início do terceiro mês, o capital aplicado era o montante restante do mês anterior, isto é, C3 = 10.100. Assim:
M3 = 10.100 ⋅ (1 + 0,01) 1 = 10.201
Após a doação de R$ 100,00 no fim do mês, restaram R$ 10.101,00. Logo, a quantia aplicada após 3 meses era R$ 10.101,00.
Resposta: alternativa b.
9. Após 3 anos de uso, o preêço do automóvel é dado por:
V(3) = V0 ⋅ (0,8)3 = 0,512 ⋅ V0 = 51,2% ⋅ V0
Assim, decorridos 3 anos, temos quê o valor do automóvel é 51,2% do valor inicial, o quê mostra uma desvalorização de 48,8% ou aproximadamente 49%.
Resposta: alternativa c.
10. Considerando um capital de R$ 10.000,00, temos:
• Aplicação básica
Rendimento bruto mensal: 0,00542 ⋅ 10.000 = 54,20
Rendimento líquido mensal: 54,20 − 0,30 = 53,90
• Aplicação pessoal
Rendimento bruto mensal: 0,00560 ⋅ 10.000 = 56,00
Taxa administrativa: 0,038 ⋅ 56,00 = 2,128
Rendimento líquido mensal: 56,00 − 2,128 ≃ 53,87
Portanto, a aplicação quê fornecerá maior rendimento líquido é a aplicação básica, com rendimento líquido de R$ 53,90.
Resposta: alternativa a.
11. O valor a sêr pago, em reais, na opção financiada é R$ 1.800,00, pois: 1.500 ⋅ 1,2 = 1.800.
Portanto, cada parcela será de R$ 600,00.
No ato da compra, será paga a primeira parcela, de modo quê, em relação ao preêço à vista, temos um saldo devedor no valor de R$ 900,00, pois: 1.500 − 600 = 900
Considerando i a taxa de juro, após um mês, o novo valor, em reais, a sêr pago é: 900 ⋅ (1 + i)
A segunda parcela também é de R$ 600,00.
Portanto, o novo saldo devedor será: 900 ⋅ (1 + i) − 600
Passado mais um mês, o saldo devedor, em reais, será:
[900 ⋅ (1 + i) − 600] ⋅ (1 + i) = 900 ⋅ (1 + i)2 − 600 ⋅ (1 + i)
Após o pagamento da terceira parcela de R$ 600,00, o saldo devedor será 0. Então:
900 ⋅ (1 + i)2 − 600 ⋅ (1 + i) − 600 = 0 ⇒ 3i2 + 4i − 1 = 0
Resolvendo essa equação de segundo grau, obtemos:
Logo: i = 21,5%
Resposta: alternativa d.
12. Analisando a situação mês a mês, tem-se a descrição a seguir.
No 1º mês, depósito de R$ 2.300,00.
No 2º mês, rendimento, em reais, de: M = 2.300 ⋅ (1 + 0,02) = 2.346
Adicionando-se esse rendimento ao segundo depósito no valor de R$ 2.300,00, o saldo no 2º mês é R$ 4.646,00.
No 3º mês, rendimento, em reais, de:
M = 4.646 ⋅ (1 + 0,02) = 4.738,92
Adicionando-se esse rendimento ao terceiro depósito no valor de R$ 2.300,00, o saldo acumulado é R$ 7.038,92.
Resposta: alternativa c.
13. Considerando as informações contidas no enunciado, conclui-se: A = 1.370; i = 25% a.a.; e M = 480.
Substituindo esses valores na expressão dada, podemos encontrar n, equivalente ao tempo, em anos. Assim:
M = A ⋅ (1 + i) n ⇒ 5.480 = 1.370 ⋅ (1 + 0,25) n ⇒ = 1,25n ⇒ 1,25 n = 4
Página trezentos e sessenta e cinco
Aplicando o logaritmo nos dois membros, temos:
log 1,25 n = log 4 ⇒ n ⋅ log 1,25 = log 4 ⇒ n ⋅ log = log 22 ⇒ n(log 125 − log 100) = 2 log 2 ⇒ n(3 log5 − 2) = 2 log 2 ⇒ n[3(log 10 − log 2) − 2] = 2 log 2 ⇒ n[3(1 − log 2) −2] = 2 log 2 ⇒ n = ⇒ n = 6
Resposta: alternativa a.
14. No Sistema Price, a expressão de cálculo da prestação P para o valor financiado V é:
P = V ⋅
Nas condições descritas, tem-se P = 6.720, i = 0,16 e n = 5.
Substituindo os valores na expressão, temos:
6.720 = V ⋅ ⇒ V = 22.000
Calculando os juros incidentes sobre a primeira prestação, obtemos:
J = 22.000 ⋅ 0,16 = 3.520
Segue-se, portanto, quê a amortização decorrente do pagamento da primeira prestação será R$ 3.200,00, pois:
6.720 − 3.520 = 3.200
Resposta: alternativa e.
15. Avaliando cada afirmação, conclui-se quê:
a) Correta, pois a inflação depende de vários índices de preços.
b) Incorreta, pois o aumento dos preços não é, necessariamente, incontrolável.
c) Incorreta, pois a inflação não é medida somente pêlos gastos, mas também depende de outros fatores.
d) Incorreta, pois o aumento da massa salarial causa deflação.
e) Incorreta, pois o aumento do crédito não é a definição da inflação, é a causa.
Resposta: alternativa a.
16. De acôr-do com o enunciado, temos f = 5% = 0,05 e i = 10% = 0,1. Substituindo os valores na equação dada temos:
1 + r = ⇒ 1 + r = ⇒ r ≃ 4,76% ≃ 4,7%
Logo, a classificação é regular, com ganho real próximo de 4,7%.
Resposta: alternativa c.
Capítulo 2 • Poliedros
Atividades
1. Pela relação de Óiler, válida para qualquer poliedro convexo, temos
V − A + F = 2 ⇒ V − 16 + 9 = 2 ⇒ V = 9
Sendo assim, o poliedro tem 9 vértices.
2. O poliedro possui 7 faces, das quais 5 são quadrangulares e 2 são pentagonais. Determinando o número de arestas, obtém-se:
5 faces quadrangulares: 5 ⋅ 4 = 20;
2 faces pentagonais: 2 ⋅ 5 = 10.
Como cada aresta foi contada duas vezes, temos:
2A = 20 + 10 ⇒ A = 15
Aplicando a relação de Óiler, temos:
V − A + F = 2 ⇒ V − 15 + 7 = 2 ⇒ V = 10
Logo, o poliedro tem 15 arestas e 10 vértices.
3. O poliedro possui 9 faces, das quais 3 são quadrangulares, 2, triangulares e 4, pentagonais. Determinando o número de arestas, obtém-se:
3 faces quadrangulares: 3 ⋅ 4 = 12;
2 faces triangulares: 2 ⋅ 3 = 6;
4 faces pentagonais: 4 ⋅ 5 = 20.
Como cada aresta foi contada duas vezes, temos:
2A = 12 + 6 + 20 ⇒ A = 19
Aplicando a relação de Óiler, temos:
V − A + F = 2 ⇒ V − 19 + 9 = 2 ⇒ V = 12
Portanto, o poliedro tem 12 vértices.
4. O poliedro possui 7 faces, das quais 3 são triangulares, 1 é quadrangular, 1, pentagonal e 2, hexagonais. Determinando o número de arestas, tem-se:
3 faces triangulares: 3 ⋅ 3 = 9;
1 face quadrangular: 1 ⋅ 4 = 4;
1 face pentagonal: 1 ⋅ 5 = 5;
2 faces hexagonais: 2 ⋅ 6 = 12.
Como cada aresta foi contada duas vezes, temos:
2A = 9 + 4 + 5 + 12 ⇒ A = 15
Aplicando a relação de Óiler, temos:
V − A + F = 2 ⇒ V − 15 + 7 = 2 ⇒ V = 10
Portanto, o poliedro tem 10 vértices.
5. Na figura apresentada no enunciado, nota-se quê a quantidade de faces triangulares é igual à quantidade de vértices do cubo. Como há 8 vértices em um cubo, o poliedro terá 8 faces triangulares. Além díssu, cada face do cubo determina uma face quadrada do poliedro. Como o cubo possui 6 faces, o poliedro terá 6 faces quadradas.
Resposta: alternativa b.
6. a) A afirmação é verdadeira, pois o octaedro possui 6 vértices, e o hexaedro possui 6 faces. Além díssu, ao jogar o dado esférico, o peso se alojará sobre um dos vértices do octaedro, quê será a região em contato com o plano horizontal. Assim, quatro vértices estarão localizados na superfícíe da esféra, pela qual passa um plano paralelo ao plano horizontal quê contém o centro da esféra, e um vértice estará no topo dela (cada um deles representando um número do dado). Assim, a disposição dos vértices do octaedro se assimila à disposição das faces do dado em formato de hexaedro regular.
b) A afirmação é falsa. O número de vértices do octaedro (6) é igual ao número de faces do hexaedro (6).
c) A afirmação é verdadeira, pois o octaedro e o hexaedro possuem 12 arestas cada. Porém, isso não justifica o fato de a cavidade no interior da esféra sêr octaédrica, pois não relaciona os vértices do octaedro com as faces do hexaedro.
d) A afirmação é verdadeira, pois o octaedro possui 8 faces e o hexaedro possui 8 vértices. Porém, isso não justifica o fato de a cavidade no interior da esféra sêr octaédrica, pois não relaciona os vértices do octaedro com as faces do hexaedro.
e) A afirmação é falsa. O número de faces do octaedro (8) é igual ao número de vértices do hexaedro (8).
Resposta: alternativa a.
7. a) Verdadeira. A relação de Óiler é válida para todos os poliedros convexos, incluindo todos os poliedros de Platão.
b) Falsa. Nos poliedros de Platão, as faces não precisam sêr polígonos regulares, portanto um poliedro póde sêr de Platão e não sêr regular.
c) Verdadeira. Para um poliedro sêr classificado como poliedro de Platão, por definição, é necessário quê todas as suas faces contenham o mesmo número de arestas.
d) Verdadeira. As faces de um poliedro convexo serem regulares e congruentes entre si é uma das características quê definem um poliedro regular.
Resposta: Alternativa b.
8. O poliedro é compôzto de 12 faces pentagonais e 20 hexagonais, isto é, possui 32 faces. Para determinar o número de ligações, deve-se calcular o número de arestas, obtendo-se:
12 faces pentagonais: 12 ⋅ 5 = 60;
20 faces hexagonais: 20 ⋅ 6 = 120.
Como cada aresta foi contada duas vezes, temos:
2A = 60 + 120 ⇒ A = 90
Aplicando a relação de Óiler, temos:
V − A + F = 2 ⇒ V − 90 + 32 = 2 ⇒ V = 60
Portanto, essa molécula possui 60 hátomus e 90 ligações.
Página trezentos e sessenta e seis
9. Um cubo de aresta 8 cm possui 6 faces quadradas de lado 8 cm.
Sendo assim, a área total dêêsse cubo, em cm2, é igual a 6 vezes a área de um quadrado de lado 8 cm:
St = 6 ⋅ 82 = 384
10. Sejam a, b e c as dimensões do paralelepípedo, D a diagonal do paralelepípedo e d a diagonal da face de dimensões a e b.
Sendo assim, temos:
D2 = d2 + c2 ⇒ c2 = 132 − 52 ⇒ c = ±12
Como c é uma dimensão do paralelepípedo, c = 12 dm. Também se deve considerar, segundo o enunciado, quê:
4 ⋅ (a + b + c) = 76 ⇒ a + b + 12 = 19 ⇒ a + b = 7
Sabendo quê D2 = a2 + b2 + c2 ⇒ a2 + b2 = 25, tem-se o seguinte sistema:
Resolvendo o sistema, obtêm-se a = 3 e b = 4.
Portanto, as dimensões do paralelepípedo são 3 dm, 4 dm e 12 dm.
11. Como o prisma é pentagonal e regular, sua superfícíe lateral é formada por cinco retângulos de dimensões 4 cm e 20 cm.
Logo, sua área lateral, em cm2, é dada por:
S(éli)" = 5 ⋅ 4 ⋅ 20 = 400
12. Como M é ponto médio de , então = , portanto o triângulo MHG é isósceles. Por sêr isósceles, a altura dêêsse triângulo em relação à base passa pelo ponto médio M(minutos)" dêêsse segmento. Projetando esse ponto d fórma perpendicular ao segmento, percebe-se quê corresponde à hipotenusa de um triângulo retângulo cujos catetos médem 4 u.c. Portanto, pelo teorema de Pitágoras, temos = 4.
Assim, a área do triângulo MHG, em u.a., é igual a:
S = = 8
Resposta: alternativa c.
13. Segundo as informações contidas no enunciado, pode-se considerar a seguinte figura:
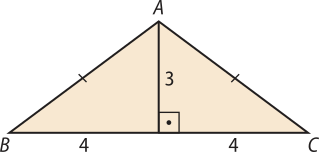
Pelo teorema de Pitágoras, a medida do segmento dado em dm, é igual a:
AC2 = 32 + 42 ⇒ AC = 5
Assim, o perímetro da base do prisma, em dm, é igual a:
AB + AC + BC = 5 + 5 + 8 = 18
Portanto, sêndo a altura h do prisma um terço dessa medida, tem-se h = 6 dm.
Calculando as áreas dêêsse prisma, em dm2, tem-se:
Sb = = 12
S(éli)" = 6 ⋅ (5 + 5 + 8) = 108
St = S(éli)" + 2Sb = 108 + 2 ⋅ 12 = 132
14. Segundo as informações do enunciado, pode-se considerar uma figura como a apresentada a seguir.
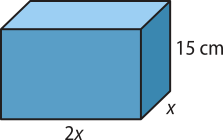
A área total da superfícíe dêêsse paralelepípedo, em cm2, é igual a:
St = S(éli)" + 2Sb ⇒ St = 2 ⋅ (2x ⋅ 15 + x ⋅ 15) + 2 ⋅ 2x ⋅ x ⇒ 424 = 2 ⋅ (2x2 + 45x)
A última equação póde sêr reescrita como 2x2 + 45x − 212 = 0, cujas raízes são x(minutos)" = 4 e x(segundos)" = . Como x é a medida de uma dimensão do paralelepípedo, desconsidera-se o valor negativo. Portanto, as dimensões desconhecidas do paralelepípedo são 8 cm e 4 cm.
15. Sejam x − 1, x e x + 1 as dimensões das arestas do paralelepípedo. Como um paralelepípedo tem quatro arestas de cada dimensão, pode-se determinar x, em cm, da seguinte maneira:
4 ⋅ (x − 1 + x + x + 1) = 84 ⇒ x = 7
Logo, as arestas médem 6 cm, 7 cm e 8 cm, portanto a área total do paralelepípedo, em cm2, é dada por:
St = 2 ⋅ (6 ⋅ 7 + 6 ⋅ 8 + 7 ⋅ 8) = 292
16. A estufa póde sêr representada por um prisma de base pentagonal. Essa base póde sêr decomposta em um triângulo isósceles e um retângulo. Portanto, a área da base do prisma, em m2, é dada por:
Sbase = Striângulo + Sretângulo = + 8 ⋅ 3 ⇒ Sbase = 36
A área da face retangular lateral da estufa, em m2, é igual a:
Sparede = 70 ⋅ 3 = 210
Para calcular a área do telhado, é necessário determinar a medida (éli)", em m, dos lados congruentes do triângulo isósceles quê compõem a fachada da estufa.
Pelo teorema de Pitágoras, tem-se:
(éli)"2 = 32 + 42 ⇒ (éli)" = 5
Assim, a área de cada face retangular, em m2, quê forma o telhado da estufa é igual a:
Stelhado = 70 ⋅ 5 = 350
Logo, a área da superfícíe total da estufa, em m2, é dada por:
Sestufa = 2 ⋅ (36 + 210 + 350) = 1.192
17. Seja (éli)" a medida da aresta da base triangular do prisma. Sabe-se quê essa base póde sêr inscrita em uma circunferência de raio 2 dm. Como o lado de um triângulo equilátero inscrito em uma circunferência de raio r corresponde a r, segue quê (éli)" = 2 dm. Portanto, a área da base dêêsse prisma, em dm2, é igual a:
Sb = = 3
Segundo o enunciado, a área da superfícíe lateral do prisma é igual ao quádruplo da área da base. Logo, a área lateral, em dm2, é:
S(éli)" = 4 ⋅ Sb ⇒ S(éli)" = 4 ⋅
Assim, a área total do prisma, em dm2, é igual a:
St = S(éli)" + 2Sb ⇒ St =
Multiplicando o valor obtído por , tem-se o seguinte resultado:
dm2 = 54 dm2
18. a) Pode-se representar a planificação do prisma, com medidas indicadas em cm, da seguinte maneira:

Página trezentos e sessenta e sete
Assim, as áreas dêêsse prisma, em cm2, são dadas por:
Sb = 8 ⋅ 5 = 40
S(éli)" = 2 ⋅ (5 ⋅ 15 + 8 ⋅ 15) = 390
St = S(éli)" + 2Sb = 390 + 2 ⋅ 40 = 470
b) Pode-se representar a planificação do prisma, com medidas indicadas em m, da seguinte maneira:
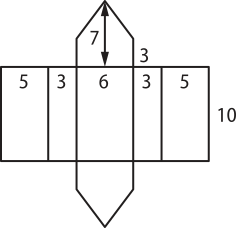
A base do prisma póde sêr decomposta em um retângulo de dimensões 3 m e 6 m e em um triângulo isósceles de altura 4 m e base 6 m.
Calculando as áreas dêêsse prisma, em m2, tem-se:
Sb = Striângulo + Sretângulo ⇒ Sb = + 6 ⋅ 3 = 30
S(éli)" = 2 ⋅ (5 ⋅ 10) + 2 ⋅ (3 ⋅ 10) + 6 ⋅ 10 = 220
St = S(éli)" + 2Sb = 220 + 2 ⋅ 30 = 280
19. Uma planificação do paralelepípedo do enunciado é dada pela figura a seguir.
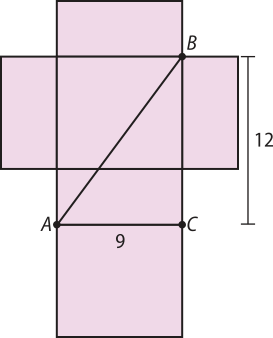
Na planificação da caixa, é possível notar quê a menor distância entre os pontos A e B é a hipotenusa do triângulo retângulo ACB, de catetos 9 e 12. Pelo teorema de Pitágoras, tem-se:
AB2 = 122 + 92 ⇒ AB = 15
20. Como o tijolo tem a forma de um paralelepípedo, então o volume de argila necessário para produzi-lo é igual ao volume de um paralelepípedo. Sendo assim, o volume de cada tijolo, em cm3, é dado por:
Vtijolo = a ⋅ b ⋅ c = 18 ⋅ 9 ⋅ 6 = 972
Para produzir 5.000 tijolos, será necessária uma quantia de argila equivalente a:
5.000 ⋅ 972 cm3 = 4.860.000 cm3 = 4,86 m3
21. Sendo a, b e c as medidas das arestas do paralelepípedo, é possível escrever:
a = ; ; , em quê q é a razão da progressão geométrica.
Como o volume do paralelepípedo é dado por V = a ⋅ b ⋅ c, então:
⇒ 64 = ⇒ q = 8
Determinando as arestas b e c, em cm, tem-se:
b = ⋅ 8 = 4
c = ⋅ 64 = 32
Logo, as outras duas arestas do paralelepípedo médem 4 cm e 32 cm.
22. A diagonal do cubo é definida por . Como a diagonal do cubo em questão méde m, então ⇒ a = 2.
Assim, o volume dêêsse cubo, em m3, é V = a3 = 23 = 8.
Como 1 m3 de á gua corresponde a 1.000 L, então 8 m3 correspondem a 8.000 L.
Resposta: alternativa c.
23. Resposta pessoal. Sugestão de problema: Determine o custo total quê a empresa terá para produzir 10 bôm-bôns do tipo 1 ao leite e 10 bôm-bôns do tipo 2 brancos.
O volume do bombom de cada tipo, em cm3, é:
V1= 4 ⋅ 4 ⋅ 4 = 64
V2= 6 ⋅ 5 ⋅ 2 = 60
Portanto, o custo em reais de cada bombom, de acôr-do com a encomenda será:
C1 = 0,03 ⋅ 64 = 1,92
C2 = 0,04 ⋅ 60 = 2,40
Assim, o custo total em reais, na produção de 10 unidades de cada tipo de bombom, é igual a:
10 ⋅ 1,92 + 10 ⋅ 2,40 = 43,20
24. Como o volume do paralelepípedo é dado por V = a ⋅ b ⋅ c e as dimensões internas da caixa-d’água são 1,2 m, 1 m e 0,7 m, então seu volume, em m3, é igual a:
V = 1,2 ⋅ 1 ⋅ 0,7 ⇒ V = 0,84
Como 1 m3 de á gua corresponde a 1.000 L, então 0,84 m3 corresponde a 840 L.
Resposta: alternativa c.
25. Primeiro, deve-se determinar a quantidade de chuva quê entrou pela abertura superior da caixa-d’água. A área da abertura quadrada, em cm2, é dada por:
Sabertura = 402 = 1.600
Assim, a área da abertura superior da caixa-d’água é de 1.600 cm² = 0,16 m².
Como a chuva foi de 70 mm, ou seja, o equivalente a 70 L de á gua por métro quadrado, então a caixa-d’água recebeu uma quantidade de á gua, em litro, igual a:
70 ⋅ 0,16 = 11,2
Como 1 L de á gua corresponde a 0,001 m3, então 11,2 L correspondem a 0,0112 m3.
Portanto, o aumento na altura do nível da á gua dentro da caixa, em m, foi de:
V = 0,0112 ⇒ 1,4 ⋅ 0,8 ⋅ h = 0,0112 ⇒ h = = 0,01
Logo, o nível da á gua dentro da caixa aumentou 0,01 m = 1 cm.
Resposta: alternativa b.
26. O volume do prisma é dado por V = S b ⋅ h. Como a base do prisma é um triângulo equilátero, então a área da base, em cm2, é:
Sb = = 4
Portanto, o volume do prisma, em cm3, é igual a:
V = 4 ⋅ 12 = 83,04
27. A área de um octógono regular de lado x é definida por:
Soctógono = 2x2 ⋅ (1 + )
Considerando quê o volume de um prisma é dado por V = Sb ⋅ h, então o volume ocupado pelas 400 caixas de pitssa corresponde a:
Vtotal = 400 ⋅ 2x2 ⋅ (1 + ) ⋅ y ⇒ V total = 800x2y (1 + )
28. a) Representando a base do prisma, tem-se:
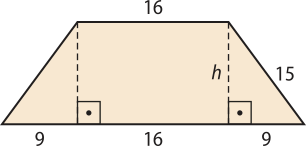
Ao determinar a altura a do trapézio, em cm, utilizando o teorema de Pitágoras, tem-se:
a2 = 152 − 92 ⇒ a = 12
Página trezentos e sessenta e oito
Logo, a área da base do prisma, em cm2, é dada por:
Sb = = 300
Assim, o volume do prisma, em cm3, é igual a:
V = Sb ⋅ h = 300 ⋅ 40 = 12.000
b) A densidade d de um corpo é definida por , em quê m é a massa e V, o volume do corpo. Portanto, para o prisma em questão, tem-se:
7,5 g/cm3 = ⇒ m = 90.000 g
Dessa maneira, a massa do prisma de ferro é 90.000 g, ou 90 kg.
29. a) A superfícíe lateral de um prisma hexagonal regular é constituída de seis retângulos congruentes. Logo, a área lateral da estrutura de madeira utilizada para a construção da coluna, em m2, é igual a:
S(éli)" = 6 ⋅ (2 ⋅ 8) = 96
b) A base da estrutura de madeira é um hekzágono regular. Assim, a área dessa base, em m2, é igual a:
Sb = 6 ⋅
Ao calcular o volume da coluna, em m3, obtém-se:
V = Sb⋅ h ⇒ V =
Portanto, o volume de concreto necessário para preencher a forma da coluna é m3.
30. Pode-se notar quê a cunha tem formato de prisma de base triangular. Em particular, esse triângulo é retângulo, e seus catetos médem 10 cm e 15 cm. Além díssu, a altura do prisma é de 10 cm. Logo, o volume da cunha, em cm3, é igual a:
V = S b ⋅ h ⇒ V = ⋅ 10 = 750
Resposta: alternativa c
31. Esse sólido é um prisma de base triangular cuja altura corresponde à medida da aresta do cubo ABCDEFGH. Assim, o triângulo GFQ tem base 8 u.c. e altura 8 u.c. Desse modo, sua área, em u.a., é igual a:
Sb = = 32
Portanto, o volume dêêsse sólido, em u.v., é V = 32 ⋅ 8 = 256.
Resposta: alternativa c.
32. a) Seja OM = m o apótema da base. No caso de uma pirâmide quadrangular regular, esse apótema é definido por m = ,
em quê (éli)" é a medida do lado da base da pirâmide. Assim, a medida do apótema da base, em cm, é igual a:
m = = 6
b) Considere VM = g o apótema da pirâmide, h = 4 cm e m = 6 cm. Aplicando o teorema de Pitágoras no triângulo
VOM, tem-se:
g2 = h2 + m2 ⇒ g2 = 42 + 62 ⇒ g = 2
Dessa maneira, a medida do apótema da pirâmide é 2 cm.
c) Seja VB = a a medida da aresta lateral da pirâmide. Aplicando o teorema de Pitágoras no triângulo VBM, tem-se:
a2 = g2 + ⇒ a2 = ⇒ a =
Sendo assim, a medida da aresta lateral da pirâmide é 2 cm.
d) Calculando as áreas dessa pirâmide, em cm2, obtém-se:
S b = 122 = 144;
S(éli)" = 4 ⋅;
St = S(éli)" + Sb = + 144 = 48(3 + ).
33. a) Sejam M o ponto médio de BC e OM = m o apótema da base.
No caso de uma pirâmide de base hexagonal, m é a altura do triângulo equilátero OBM, isto é, o apótema da base é definido por m = , em quê (éli)" é a medida do lado da base da pirâmide. Assim, a medida do apótema da base, em cm, é igual a:
m =
b) Considere VM = g o apótema da pirâmide, h = 6 cm e m = 4 cm. Aplicando o teorema de Pitágoras no triângulo
VOM, tem-se:
g2 = h2 + m2 ⇒ g2 = 62 + ⇒ g = 2
Sendo assim, a medida do apótema da pirâmide é 2cm.
c) Seja VB = a a medida da aresta lateral da pirâmide. Aplicando o teorema de Pitágoras no triângulo VBM, tem-se:
a2 = g2 + ⇒ a2 = ⇒ a = 10
Sendo assim, a medida da aresta lateral da pirâmide é 10 cm.
d) Calculando as áreas dessa pirâmide, em cm2, obtém-se:
Sb = 6 ⋅ ;
S(éli)" = 6 ⋅;
St = S(éli)" + S b =
Assim, a medida da área total é cm2.
34. Com as informações do enunciado, pode-se construir a imagem a seguir:

Do enunciado, tem-se quê VB = 13 cm e VM = 12 cm. Aplicando o teorema de Pitágoras no triângulo VBM, obtém-se a medida de BC em cm:
VB2 = VM2 + 2 ⇒ = 132 − 122 ⇒ BC = 10
Portanto, a área lateral da pirâmide, em cm2, é dada por:
S(éli)" = 3 ⋅ = 180
35. Como todas as arestas têm a mesma medida, pode-se afirmar quê a pirâmide é formada por quatro triângulos equiláteros de lado (éli)" = 15. Portanto, a área total dessa pirâmide, em cm2, é:
S t = 4 ⋅= 225
36. Como o perímetro da base é 40 cm, então a medida (éli)" da aresta da base, em cm, é:
(éli)" = = 10
Para determinar a medida da área lateral da pirâmide, é necessário calcular o apótema g da pirâmide. Como a base dela é quadrada, então o apótema da base m é dado por .
Assim, a medida g é dada por:
g2 = h2 + m2 ⇒ g2 = 122 + 2 ⇒ g = ±13
Como g é o apótema da pirâmide, tem-se g = 13 cm. Assim, a área lateral da pirâmide, em cm2, é igual a:
S(éli)" = 4 ⋅= 260
37. Da planificação da pirâmide, obtém-se:
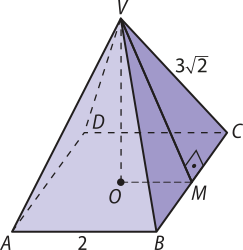
Página trezentos e sessenta e nove
Aplicando o teorema de Pitágoras no triângulo VMB, obtém-se:
VB2 = VM2 + MB2 ⇒ (3)2 = VM2 + 12 ⇒ VM2 = 17
Aplicando o teorema de Pitágoras no triângulo VOM, obtém-se:
VM2 = VO2 + OM2 ⇒ 17 = VO2 + 12 ⇒ VO = 4
Considerando quê VO = h, ao calcular o volume da pirâmide, em u.v., tem-se:
V = Sb ⋅ h = ⋅ 22 ⋅ 4 =
38. Segundo o enunciado, a pirâmide tem V = 9 cm3 e h = 4cm. Assim, pode-se determinar a área de sua base por meio da relação:
V = Sb ⋅ h ⇒ 9 cm3 = Sb ⋅ 4 cm ⇒ Sb = cm2
Como a base da pirâmide é um triângulo equilátero, conclui-se quê a medida a da aresta, em cm, é:
S b = ⇒ a = ±3
Sendo a a medida da aresta, desconsidera-se o valor negativo.
Logo, a = 3 cm.
Resposta: alternativa b.
39. Sejam (éli)" e g as medidas da aresta da base e do apótema da pirâmide, respectivamente. Ao considerar quê a área da base é igual à mêtáde da área lateral, obtém-se:
Sb = ⋅ S(éli)" ⇒ 6 ⋅ = g
Substituindo (éli)"= g na relação g2 = h2 + m2, tem-se:
((éli)")2 = 62 + = 36 ⇒ (éli)" = ±4
Sendo (éli)" a aresta da base, desconsidera-se o valor negativo. Portanto, o volume mais próximo da pirâmide, em cm3, é:
V = Sb ⋅ h ⇒ V = ⋅ 6 ⇒ V ≃ 83
40. a) O volume do bloco retangular, em u.v., é dado por:
V bloco = Sb ⋅ h = 4 ⋅ 4 ⋅ 8 = 128
Ao calcular a área da base da pirâmide triangular, em u.a., obtém-se:
Sb = = 16
b) Para quê o volume da pirâmide seja igual ao do bloco retangular, a altura h da pirâmide, em u.c., deve sêr igual a:
Vbloco = Vpirâmide ⇒ 128 = Sb⋅ h ⇒ 128 = ⋅ h ⇒ h =
41. Com as informações do enunciado, pode-se construir a imagem a seguir:
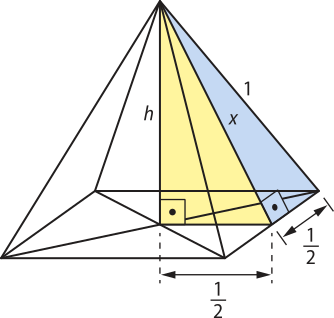
Aplicando o teorema de Pitágoras no triângulo de lados 1, x e , tem-se:
Ao aplicar o teorema de Pitágoras no triângulo de lados x, h e , obtém-se:
Conhecida a medida h, sabe-se quê a altura do paralelepípedo será o dôbro dêêsse valor. Assim, o volume do paralelepípedo será dado por:
V = 1 ⋅ 1 ⋅ 2 ⋅
Resposta: alternativa c.
42. De acôr-do com as informações contidas no enunciado, obtém-se a figura a seguir:
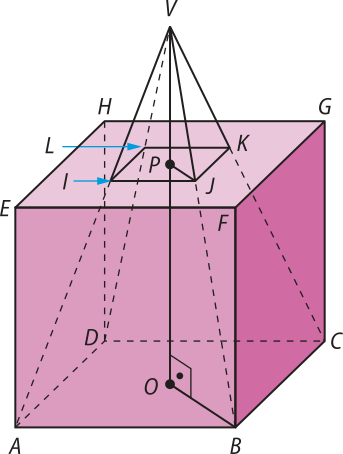
Ainda, segundo o enunciado, pode-se considerar quê VO = 20 cm e IJ = JK = 5 cm. Além díssu, OP corresponde à medida da aresta do cubo.
Como os triângulos VPJ e VOB são semelhantes, conclui-se quê:
⇒ OP2 − 20 ⋅ OP + 100 = 0
Resolvendo a equação anterior, tem-se quê OP = 10 cm.
Calculando o volume do cubo, em cm3, obtém-se:
V = OP3 = 103 = 1.000
43. A partir da ilustração e dos dados do enunciado, tem-se a figura:
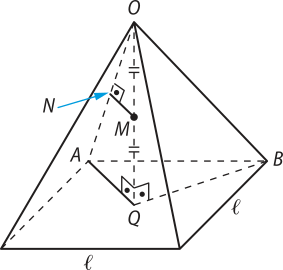
De acôr-do com o enunciado, pode-se afirmar quê OQ = (éli)" e MN = a. Também se póde estabelecer a relação (triângulo)"OQA ∼ (triângulo)"ONM. Logo:
Como o triângulo OQA é retângulo, ao aplicar o teorema de Pitágoras, obtém-se a medida de OA:
(OA)2 = (OQ)2 + (AQ)2 ⇒ (OA)2 = (éli)"2 + ⇒ OA =
Sabendo quê OM = , substituindo em I obtém-se:
⇒ (éli)" =
Dessa maneira, o volume da pirâmide, em função de a, é dado por:
Página trezentos e setenta
44. Resposta pessoal. Sugestão de problema: Considerando quê o custo por litro para todas as tintas é o mesmo, determine o custo mássimo para pintar as faces laterais da pirâmide usando duas côres (uma cor para cada duas faces) sabendo quê são necessárias duas demãos para realizar a pintura.
Inicialmente, deve-se determinar a área lateral da pirâmide. Para isso, é necessário encontrar o apótema da pirâmide, dado pela relação:
g2 = h2 + m2 ⇒ g2 = 42 + 32 ⇒ g = ±5
Como g é o apótema da pirâmide, tem-se g = 5 m. Assim, a área lateral da pirâmide, em m2, é igual a:
Como mêtáde da superfícíe lateral da pirâmide (equivalente aduas faces) será pintada com uma côr e a outra mêtáde, com uma côr distinta, segue quê cada côr deve cobrir uma área de 30 m2 por demão.
Para obtêr o custo mássimo da pintura, devem-se usar as tintas com menor rendimento, quê são as de côr roxa e vermelha. Como o rendimento de ambas é o mesmo e como cada face receberá duas demãos, a quantidade de litros de tinta de cada côr necessária para a pintura será de 60 ∶ 22 ≃ 2,73.
Considerando x o custo por litro de tinta, então o custo mássimo será de aproximadamente 5,46x.
Atividades complementares
1. Considerando o cubo presente na questão e nomeando cada um de seus vértices, chega-se à seguinte figura:
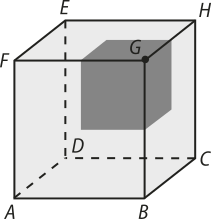
A partir dela, percebe-se quê o vértice G é comum às três faces do cubo parcialmente pintadas. Além díssu, analisando as possibilidades de planificação para esse cubo nas alternativas, percebe-se quê as duas faces superiores das planificações são comuns a todas.
Considere quê essas duas faces são faces adjacentes do cubo quê foram pintadas, conforme a figura a seguir:
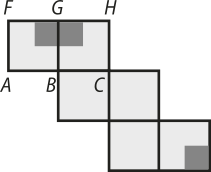
Nessa planificação, é possível determinar, pelo encontro das arestas, quê, abaixo da face planificada GHCB, estará a face BCDA. Seguindo esse raciocínio, determina-se a posição das demais faces e a posição na qual o vértice G estará na figura planificada:
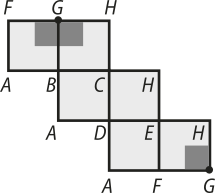
Resposta: alternativa d.
2. Como o poliedro tem 20 faces triangulares e cada face tem 3 arestas, o número total de arestas dêêsse poliedro é dado por:
Assim, ao aplicar a relação de Óiler, obtém-se:
Resposta: alternativa b.
3. O poliedro possui 13 vértices e 19 faces. Portanto, pela reação de Óiler, tem-se:
Como uma face é hexagonal, ou seja, possui 6 arestas, e 18 faces são poligonais do tipo P, com n arestas, pode-se assumir quê:
Portanto, o polígono P é um triângulo.
Resposta: alternativa e.
4. Segundo a planificação do poliedro, ele possui 8 faces, das quais 4 são hexagonais e 4, triangulares. Ao determinar o número de arestas, obtém-se:
4 faces hexagonais: 4 ⋅ 6 = 24;
4 faces triangulares: 4 ⋅ 3 = 12.
Como cada aresta foi contada duas vezes, tem-se:
Ao aplicar a relação de Óiler, obtém-se:
Resposta: alternativa a.
5. Sendo q o número de faces quadrangulares e t o número de faces triangulares do poliedro, quê possui 20 arestas, pode-se escrever:
I
Sabe-se quê a soma dos ângulos internos das faces do poliedro é 2.880°. Como a soma dos ângulos internos de cada face triangular é 180° e a soma dos ângulos internos de cada face quadrangular é 360°, conclui-se quê:
II
Considerando as equações I e II, obtém-se o seguinte sistema:
Ao resolver o sistema, obtêm-se as soluções t = 8 e q = 4, ou seja, o poliedro em questão possui 8 faces triangulares.
Resposta: alternativa a.
6. Pela relação de Óiler, temos quê:
I
Como o deltaedro é compôzto de faces triangulares, é possível estabelecer a seguinte relação:
II
Substituindo II em I, tem-se:
Logo, o deltaedro tem 12 faces.
Resposta: alternativa e.
7. Sejam c, l e h o comprimento, largura e a profundidade da piscina, respectivamente. Pode-se calcular a área total da superfícíe da piscina pela relação:
Calculando a área total de cada projeto, em m2, tem-se:
SI = 25 ⋅ 2 + 2 ⋅ 2 ⋅ 1,8 + 2 ⋅ 25 ⋅ 1,8 = 147,2;
S II = 9 ⋅ 5 + 2 ⋅ 5 ⋅ 2 + 2 ⋅ 9 ⋅ 2 = 101;
S III = 15 ⋅ 6 + 2 ⋅ 6 ⋅ 1 + 2 ⋅ 15 ⋅ 1 = 132;
SIV = 4 ⋅ 15 + 2 ⋅ 15 ⋅ 1,5 + 2 ⋅ 4 ⋅ 1,5 = 117;
S V = 12 ⋅ 3 + 2 ⋅ 3 ⋅ 2,5 + 2 ⋅ 12 ⋅ 2,5 = 111.
Portanto, o projeto quê o casal deverá escolher, por apresentar menor área de revestimento, será o projeto II.
Resposta: alternativa b.
Página trezentos e setenta e um
8. Conforme o enunciado, pode-se construir a figura a seguir:

Para calcular a área do triângulo PQR, devem-se determinar as medidas PR, RQ e PQ. Como é a diagonal de um quadrado de lado 1 dm, sua medida, em dm, é igual a:
O segmento RQ ‾ equivale à diagonal de um cubo de aresta 1 dm.
Logo, sua medida, em dm, é igual a:
Já a medida PQ equivale à medida da diagonal de um retângulo de lados 1 dm e 2 dm. Aplicando o teorema de Pitágoras, tem-se a medida de PQ:
PQ2 = 12 + 22 ⇒ PQ2 = 5
Note quê o triângulo PQR satisfaz o teorema de Pitágoras, pois
(PQ)2 = 5 = 2 + 3 = = (PR)2 + (RQ)2
Logo, o triângulo PQR é retângulo em R, portanto sua área, em dm2, é dada por:
Resposta: alternativa a.
9. Sejam c, l e h o comprimento, largura e altura, respectivamente, do contêiner original. Considere S1 a área das paredes internas e externas dêêsse contêiner e S2 a área de seu piso. Assim, a medida dessas áreas é de:
S1 = 2 ⋅ (2 ⋅ c ⋅ h + 2 ⋅ l ⋅ h) = 4ch + 4lh
S2 = c ⋅ l = cl
Após a mudança no projeto, o contêiner passou a ter o dôbro do comprimento e da largura. Seja S3 a nova área das paredes internas e externas do contêiner e S4 a nova área de seu piso. Assim, a medida dessas áreas é de:
S3 = 2 ⋅ (2 ⋅ 2c ⋅ h + 2 ⋅ 2l ⋅ h) = 8ch + 8lh = 2 ⋅ (4ch + 4lh) = 2 ⋅ S1
S4 = 2c ⋅ 2l = 4 ⋅ cl = 4 ⋅ S2
Portanto, a quantidade de tinta necessária para pintar as paredes dobrou, enquanto, para o piso, a quantidade necessária quadruplicou. Logo, o fornecedor II deve sêr o escolhido pelo construtor.
Resposta: alternativa b.
10. Pode-se notar quê o volume V da escada é dado pela soma dos volumes de 20 paralelepípedos reto-retângulos de mesma base, cujas dimensões são 20 cm por 50 cm. Além díssu, as alturas dos degraus formam uma progressão aritmética de razão 10. Portanto, se o primeiro degrau possui 10 cm de altura, o vigésimo degrau terá altura de 20 ⋅ 10 cm = 200 cm e, assim, a soma das alturas de todos os degraus, em cm, será dada por:
Logo, o volume da escada, em cm3, será igual a:
V = 20 ⋅ 50 ⋅ 2.100 = 2.100.000
Portanto, o volume da escada será de 2.100.000 cm3 = 2,1 m3.
Resposta: alternativa a.
11. Sejam a, b e c as medidas das arestas do paralelepípedo. Pelo enunciado, pode-se considerar quê ab = 2, bc = 3 e ac = 4.
Dessa forma:
Como abc representa o volume do paralelepípedo, desconsidera-se o valor negativo. Assim, o volume é cm3.
Resposta: alternativa b.
12. Sejam a e (éli)" as medidas das arestas do cubo e do tetraedro, respectivamente. A área da superfícíe de um cubo é dada por
. Já a área da superfícíe de um tetraedro regular é definida por .
Considerando quê o cubo e o tetraedro têm áreas de superfícíe iguais, então:
Resposta: alternativa c.
13. Considerando a altura da pirâmide igual a 10 cm e a base quadrada de lado (éli)" = 3 cm, segue quê o volume da pirâmide, em cm3, é:
V = Sb ⋅ h = ⋅ 32 ⋅ 10 = 30
Resposta: alternativa b.
14. A partir da figura do enunciado, acrescenta-se o apótema da base.
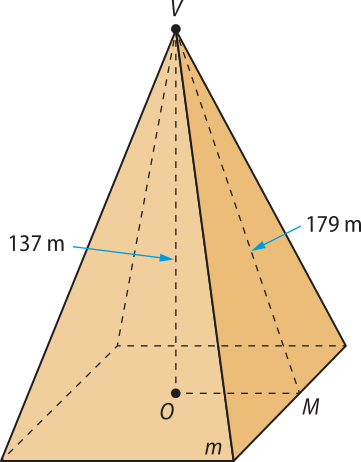
Ao aplicar o teorema de Pitágoras no triângulo VOM, obtém-se:
1792 = 1372 + (OM)2 ⇒ OM2 = 13.272
Como o lado (éli)" da base quadrada da pirâmide é igual ao dôbro do apótema da base, cuja medida é dada por OM, conclui-se quê:
(éli)" = 2 ⋅ OM ⇒ (éli)"2 = (2 ⋅ OM)2 ⇒ (éli)"2 = 4 ⋅ 13.272 = 53.088
Logo, a área da base dessa pirâmide é de 53.088 m2.
Resposta: alternativa d.
15. Segundo os dados do enunciado, os volumes de T1 e T2 podem sêr expressos por:
Após passar pelo aerador A1, o volume de líquido quê vêm do tanque T1 aumenta em 15%, passando a sêr igual a 1,15V T 1. Já ao passar pelo aerador A2, ele ganha um novo aumento de volume de 10%, passando a ter um volume de 1,1 ⋅ 1,15V T 1 = 1,265V T 1.
Portanto, o volume do tanque V T 2 deve sêr igual ao volume do tanque V T 1 após esses aumentos consecutivos, ou seja:
V T 2 = 1,265V T 1 ⇒ c ⋅ L ⋅ y = 1,265 ⋅ c ⋅ L ⋅ x ⇒ y = 1,265x
Assim, a relação das alturas y e x dos tanques é dada por y = 1,265x.
Resposta: alternativa a.
16. Para atingir uma altura de 15 cm, a altura da coluna de á gua no paralelepípedo deve ter um aumento de 15 cm − 8 cm = 7 cm. Assim, o volume de á gua no interior do paralelepípedo, em cm3, deve aumentar em:
V = Sb ⋅ h = 4 ⋅ 3 ⋅ 7 = 84
Como cada bó-linha quê será colocada dentro do recipiente possui volume de 6 cm3, então o número de bó-linhas necessárias para proporcionar esse aumento de volume é igual a 84 ∶ 6 = 14.
Resposta: alternativa a.
Página trezentos e setenta e dois
17. Sabe-se quê um cubo possui 8 vértices. Dessa forma, segundo o enunciado, serão retiradas do cubo 8 pirâmides, de modo quê o volume do sólido resultante será de: Vsólido = Vcubo − 8 ⋅ V pirâmide. Analisando a figura da atividade, nota-se quê a aresta AK da pirâmide AIJK é perpendicular à base AIJ e quê AK = IA = AJ = . Assim, o volume de AIJK é dado por:
Vpirâmide = Sb ⋅ h =
Dessa forma, o volume do sólido é dado por:
Vsólido = a3 − 8 ⋅
Resposta: alternativa e.
18. Sejam V1 o volume do cubo de aresta (alfa)" e V2 o volume do cubo de aresta (alfa)" + 1. Segundo o enunciado, a diferença entre V2 e V1 é de:
V2 − V1 = 271 ⇒ ((alfa)" + 1)3 − (alfa)"3 = 271 ⇒ 3(alfa)"2 + 3(alfa)" − 270 = 0
Calculando as raízes dessa última equação, obtém-se (alfa)"(minutos)" = 9 e (alfa)"(segundos)" = −10. Como (alfa)" é a medida da aresta de um cubo, desconsidera-se o valor negativo, de modo quê (alfa)" = 9 m.
Resposta: alternativa c.
19. Com as informações do enunciado, pode-se construir a imagem a seguir:
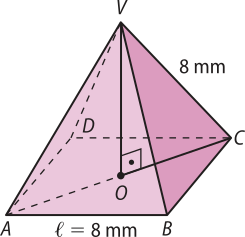
O volume do octaedro é o dôbro do volume da pirâmide regular de base quadrada, cuja aresta méde 8 mm.
Como OC equivale à mêtáde da diagonal do quadrado ABCD, segue quê:
Aplicando o teorema de Pitágoras no triângulo VOC, obtém-se a medida, em mm, do segmento :
VC2 = VO2 + OC2 ⇒ 64 = VO2 + ()2 ⇒ VO =
Como Sb = (8 mm)2 = 64 mm2, então o volume da pedra, em mm3, é dado por:
Capítulo 3 • Corpos redondos
Atividades
1. Pelo enunciado, tem-se quê h = 5 cm e r = 6 cm. Logo, as áreas, em cm², são:
a) Sb = (pi)"r2 = (pi)" ⋅ 62 = 36(pi)"
b) S(éli)" = 2(pi)"rh = 2(pi)" ⋅ 6 ⋅ 5 = 60(pi)"
c) St = S(éli)" + 2Sb = 60(pi)" + 2 ⋅ 36(pi)" = 132(pi)"
2. Sabendo quê o perímetro da base é de 62,8 cm, segue quê o raio da base e a altura do cilindro, em cm, médem:
C = 2(pi)"r ⇒ 62,8 = 2(pi)"r ⇒ r = = 10
h = = 5
Logo, a área lateral, em cm2, será:
S(éli)" = 2(pi)"rh = 62,8 ⋅ 5 = 314
3. Pelo enunciado tem-se quê S(éli)" = 20(pi)" cm2 e r = 5 cm. Assim, a altura h, em cm, é dada por:
S(éli)" = 2(pi)"rh ⇒ 20(pi)" = 2(pi)" ⋅ 5 ⋅ h ⇒ h = 2
4. Como a área da base é de 25(pi)" cm2 conclui-se quê r = 5 cm, portanto h = 9 cm. Logo, a área total do cilindro, em cm2, será:
St = S(éli)" + 2Sb = 2(pi)"rh + 2 ⋅ 25(pi)" = 2 ⋅ (pi)" ⋅ 5 ⋅ 9 + 50(pi)" = 140(pi)"
5. Como o diâmetro da base méde 8 cm, então seu raio méde 8 cm ∶ 2 = 4 cm. Já a altura do cilindro é de 18 cm. Logo, sua área total, em cm2, é igual a:
St = S(éli)" + 2Sb = 2(pi)"rh + 2 ⋅ (pi)"r2 = 2 ⋅ (pi)" ⋅ 4 ⋅ 18 + 2 ⋅ (pi)" ⋅ 42 = 176(pi)"
6. Considerando quê a área S da secção meridiana do cilindro equilátero é 400 cm2, pode-se concluir quê:
a) S = h2 ⇒ h2 = 400 ⇒ h = ±20
Como h é a altura do cilindro, segue quê h = 20 cm.
b) h = 2r ⇒ r = = 10St = S(éli)" + 2S b = 2(pi)"rh + 2 ⋅ (pi)"r2 = 2 ⋅ (pi)" ⋅ 10 ⋅ 20 + 2 ⋅ (pi)" ⋅ 102 = 600(pi)"
Logo, a área total da superfícíe do cilindro é de 600(pi)" cm2.
7. Durante sete dias, cada habitante consome, em média, 7 ⋅ 120 L = 840 L de á gua. Como o povoado tem 100 habitantes, seu consumo médio de á gua nesse período é 100 ⋅ 840 L = 84.000 L = 84 m3, sêndo esse o volume mínimo do reservatório.
Do volume do cilindro, obtemos a altura mínima h, em métro, procurada:
Resposta: alternativa d.
8. A embalagem cilíndrica tem área superficial total, em cm2, igual a:
St = S(éli)" + 2Sb = 2(pi)"rh + 2 ⋅ (pi)"r2 = 2 ⋅ 3 ⋅ 2 ⋅ 10 + 2 ⋅ 3 ⋅ 22 = 144
A embalagem quê é um paralelepípedo tem área superficial total S, em cm2, igual a:
S = 2 ⋅ (4 ⋅ 5 + 4 ⋅ 6 + 5 ⋅ 6) = 148
Portanto, a embalagem quê terá o menor custo de fabricação é a cilíndrica, pois possui menor área superficial. Como 144 cm2 = 0,0144 m2, o custo da embalagem cilíndrica, em reais, é de: 25 ⋅ 0,0144 = 0,36
Resposta: alternativa a.
9. Analisando as dimensões de cada modelo de caixa, é possível determinar seu armazenamento mássimo de latas de tinta:
• Modelo I: No comprimento cabem 8 ∶ 4 = 2, na largura cabem 8 ∶ 4 = 2 e na altura cabem 40 ∶ 6 ≃ 6,7 ≃ 6. Portanto, nessa caixa cabe uma quantidade de latas igual a 2 ⋅ 2 ⋅ 6 = 24;
• Modelo II: No comprimento cabem 8 ∶ 4 = 2, na largura cabem 20 ∶ 4 = 5 e na altura cabem 14 ∶ 6 ≃ 2,3 ≃ 2. Portanto, nessa caixa cabe uma quantidade de latas igual a 2 ⋅ 5 ⋅ 2 = 20;
• Modelo III: No comprimento cabem 18 ∶ 4 = 4,5 ≃ 4, na largura cabem 5 ∶ 4 = 1,25 ≃ 1 e na altura cabem 35 ∶ 6 ≃ 5,8 ≃ 5. Portanto, nessa caixa cabe uma quantidade de latas igual a 4 ⋅ 1 ⋅ 5 = 20;
• Modelo IV: No comprimento cabem 20 ∶ 4 = 5, na largura cabem 12 ∶ 4 = 3 e na altura cabem 12 ∶ 6 = 2. Portanto, nessa caixa cabe uma quantidade de latas igual a 5 ⋅ 3 ⋅ 2 = 30;
• Modelo V: No comprimento cabem 24 ∶ 4 = 6, na largura cabem 8 ∶ 4 = 2 e na altura cabem 14 ∶ 6 ≃ 2,3 ≃ 2. Portanto, nessa caixa cabe uma quantidade de latas igual a 6 ⋅ 2 ⋅ 2 = 24.
Portanto, o modelo IV possui maior armazenamento.
Resposta: alternativa d.
10. Sejam M e N as projeções ortogonais, respectivamente, dos segmentos e em r. Para calcular o volume do sólido solicitado, é necessário calcular o volume do cilindro gerado pela revolução do retângulo MNCB e, dele, subtrair o volume do cilindro gerado pela revolução do retângulo MNDA.
Para determinar a altura do retângulo ABCD, deve-se utilizar o teorema de Pitágoras no triângulo BCD:
52 = (BC)2 + (5 − 2)2 ⇒ BC = 4
Página trezentos e setenta e três
Sendo assim:
VMNCB = (pi)" ⋅ 52 ⋅ 4 = 100(pi)"
VMNDA = (pi)" ⋅ 22 ⋅ 4 = 16(pi)"
Portanto: V = 100(pi)" − 16(pi)" = 84(pi)"
Resposta: alternativa d.
11. Vamos indicar o cilindro de raio menor por C1 e o de raio maior por C2. Logo:
a) A área da superfícíe do sólido, em cm², será:
b) O volume do sólido, em cm, é igual a:
12. Considerando quê (pi)" ≃ 3, pode-se calcular o raio da nova cistérna, em m:
81 = (pi)" ⋅ r2 ⋅ 3 ⇒ r ≃ 3
Como o raio da cistérna antiga possuía 1 m e o da cistérna atual deve medir aproximadamente 3 m, será necessário aumentar o raio em aproximadamente 2 m.
Resposta: alternativa c.
13. Considerando as informações do enunciado, calcula-se o raio da base, em cm:
St = S(éli)" + 2Sb ⇒ 80(pi)" = 30(pi)" + 2 ⋅ (pi)" ⋅ r2 ⇒ r = 5
Dessa maneira, calcula-se h, em cm:
S(éli)" = 2(pi)"rh ⇒ 30(pi)" = 2 ⋅ (pi)" ⋅ 5 ⋅ h ⇒ h = 3
Assim, o volume do cilindro, em cm3, é dado por:
V = (pi)"r2h = (pi)" ⋅ 52 ⋅ 3 = 75(pi)"
14. O volume da jarra cilíndrica é equivalente a 8 ⋅ 300 ml = 2.400 ml = 2.400 cm3. Dessa maneira, a área de sua base, em cm2, é dada por:
V = (pi)"r2h ⇒ V = Sb ⋅ h ⇒ 2.400 = Sb ⋅ 30 ⇒ Sb = 80
Resposta: alternativa d.
15. a) Considerando as informações do enunciado e (pi)" = 3,14, calculam-se os volumes das latas, em cm3:
b) Calculando o preêço, em reais, por cm3 de cada lata, tem-se:
Como P1 possui menor custo por cm3, segue quê a lata (1) apresenta melhor preêço para o consumidor.
16. Considerando (pi)" = 3,14, calculam-se os volumes Vp do prisma e Vc do cilindro, em cm3:
Vp = 5 ⋅ 5 ⋅ 80 = 2.000
Vc = (pi)"r2h = 3,14 ⋅ (2,5)2 ⋅ 80 = 1.570
Dessa maneira, cada peça gera uma sóbra de madeira, em cm3, igual a 2.000 − 1.570 = 430. Logo, 1.000 peças geram uma sóbra de 1.000 ⋅ 430 cm3 = 4,3 ⋅ 105 cm3 de madeira.
Resposta: alternativa c.
17. Considerando quê o sólido é formado por dois cilindros cujos raios da base são 40 cm e cujas alturas são 5 cm e um cilindro cujo raio da base é 10 cm e a altura é 30 cm, pode-se afirmar quê o volume do sólido, em cm³, é igual a:
V = 2 ⋅ ((pi)" ⋅ 402 ⋅ 5) + (pi)" ⋅ 102 ⋅ 30 = 19.000(pi)"
18. Resposta pessoal. Sugestão de problema: Qual é o custo aproximado com chapas de aço para se construir uma caixa-d’água em formato cilíndrico com altura de 8 m e capacidade de 40 mil litros? Considere (pi)" = 3,14.
Para construir a caixa-d’água, precisa-se de duas chapas de aço quadradas, cuja medida do lado é o dôbro do raio da base do cilindro, e de duas chapas retangulares, quê serão soldadas na lateral, cujas dimensões são a altura do cilindro e mêtáde do comprimento da circunferência da base.
Como 40.000 L = 40 m3 de á gua, segue quê V = 40. Desse modo, o raio da base do cilindro, em m, é dado por:
V = (pi)"r2h ⇒ 40 = 3,14 ⋅ r2 ⋅ 8 ⇒ r ≃ 1,26
Já o comprimento da circunferência da base, em cm, é de:
c = 2 ⋅ (pi)" ⋅ r = 2 ⋅ 3,14 ⋅ 1,26 ≃ 7,91
Logo, a soma das áreas das chapas quadradas e retangulares, em m2, é igual a:
St = 2 ⋅ Sq + 2 ⋅ Sr = 2 ⋅ (2r)2 + 2 ⋅ h ⋅ = 2 ⋅ (2,52)2 + 8 ⋅ 7,91 ≃ 76
Logo, o custo total das chapas, em reais, é de, aproximadamente, 200 ⋅ 76 = 15.200.
19. Como o funil é representado por um cone reto, segue quê sua geratriz é a hipotenusa de um triângulo retângulo cujos catetos são o raio da base do cone e sua altura. Desse modo, a medida de sua geratriz, em cm, é dada por:
g2 = 32 + 42 ⇒ g = 5
Portanto, a área lateral do funil, em cm2, é:
S(éli)" = (pi)"rg = 3,14 ⋅ 3 ⋅ 5 = 47,1
20. a) A partir da rotação do triângulo em torno de , forma-se um cone reto cujo raio da base méde 6 cm e cuja altura méde 8 cm. Logo, a medida de sua geratriz, em cm, é dada por:
g2 = 62 + 82 ⇒ g = 10
Com esses dados, pode-se calcular a área total do cone, em cm2:
St = S(éli)" + Sb = (pi)"rg + (pi)"r2 = 6 ⋅ 10 ⋅ (pi)" + 62 ⋅ (pi)" = 96(pi)"
b) A partir da rotação do triângulo em torno de , forma-se um cone reto cujo raio da base méde 8 cm e cuja altura méde 6 cm. Logo, a medida de sua geratriz, em cm, é dada por:
g2 = 82 + 62 ⇒ g = 10
Com esses dados, pode-se calcular a área total do cone, em cm2:
St = S(éli)" + Sb = (pi)"rg + (pi)"r2 = 8 ⋅ 10 ⋅ (pi)" + 82 ⋅ (pi)" = 144(pi)"
21. a) A partir da revolução do triângulo, obtém-se:
Desse modo, a medida da geratriz dêêsse cone, em cm, é de:
g2 = h2 + R2 ⇒ g2 = 32 + 42 ⇒ g = 5
Já sua área total, em cm2, é igual a:
S = S(éli)" + Sb = (pi)"Rg + (pi)"R2 = 4 ⋅ 5 ⋅ (pi)" + 42 ⋅ (pi)" = 36(pi)"
b) Utilizando as definições dadas pela atividade, obtêm-se (éli)" e r, em cm:
(éli)" = R + h + g = 4 + 3 + 5 = 12
S = (éli)" ⋅ 2(pi)"r ⇒ 36(pi)" = 12 ⋅ 2(pi)" ⋅ r ⇒ r = 1,5
22. A geratriz de um cone equilátero é igual ao dôbro do raio de sua base. Então:
g = 2r ⇒ 20 cm = 2r ⇒ r = 10 cm
Assim, a área da base do cone, em cm2, é dada por:
Sb = (pi)"r2 = (pi)" ⋅ 102 = 100(pi)"
23. Considere g = 15 cm e (alfa)" = 120° = rad. O comprimento do setor circular será igual ao comprimento da circunferência da base do cone. Logo, o raio da base do cone, em cm, é dado por:
2(pi)"r = (alfa)" ⋅ g ⇒ 2 ⋅ (pi)" ⋅ r = ⋅ 15 ⇒ r = 5
Como o cone construído pelo setor circular é reto, segue quê a sua altura, em cm, é dada por:
g2 = h2 + r2 ⇒ 152 = h2 + 52 ⇒ h = 10
Página trezentos e setenta e quatro
24. O raio da peça circular corresponde à geratriz do cone a sêr construído. Considere, assim, g = 10 cm e (alfa)" = rad = rad. O comprimento do setor circular será igual ao comprimento da circunferência da base do cone. Logo, o raio da base do cone, em cm, é dado por:
2(pi)"r = (alfa)" ⋅ g ⇒ 2 ⋅ (pi)" ⋅ r = ⋅ 10 ⇒ r = 9
Como o cone construído pelo setor circular é reto, segue quê a sua altura, em cm, é dada por:
g2 = h2 + r2 ⇒ 102 = h2 + 92 ⇒ h =
25. Considerando o cilindro, conclui-se quê suas áreas, em m2, médem:
S(éli)" = 2(pi)"rh = 2(pi)" ⋅ 3 ⋅ 10 = 60(pi)"
Sb = (pi)"r2 = (pi)" ⋅ 32 = 9(pi)"
Considerando o cone, obtém-se a medida de sua geratriz, em m, e de sua área lateral, em m2:
g2 = h2 + r2 ⇒ g2 = 42 + 32 ⇒ g = 5
S(éli)" = (pi)"rg = (pi)" ⋅ 3 ⋅ 5 = 15(pi)"
Portanto, a área total, em m2, será:
St = 60(pi)" + 9(pi)" + 15(pi)" = 84(pi)" = 263,76
Se, com uma lata de tinta, podem-se pintar 10 m2, tem-se:
= 26,376
Portanto, o número mínimo de latas será 27.
26. Considerando quê 45° equivale a rad, obtém-se:
Portanto, tem-se:
H2 + R2 = g2 ⇒ H2 + R2 = 64R2 ⇒ H = 3R
27. De acôr-do com o enunciado, segue quê r = h − 2 e g = h + 2.
Logo, a medida h, em m, é:
g2 = h2 + r2 ⇒ (h + 2)2 = h2 + (h − 2)2 ⇒ h = 8
Desse modo, r = 6 m e g = 10 m. Assim, a área total do cone em m2, é de:
St = S(éli)" + Sb = (pi)"rg + (pi)"r2 = 6 ⋅ 10 ⋅ (pi)" + 62 ⋅ (pi)" = 96(pi)"
28. A partir das informações do enunciado, pode-se determinar a geratriz, a altura do cone, em cm, e seu volume, em cm3:
S(éli)" = (pi)"rg ⇒ 15(pi)" = (pi)" ⋅ 3 ⋅ g ⇒ g = 5
g2 = r2 + h2 ⇒ 52 = 32 + h2 ⇒ h = 4
V = ⋅ (pi)" ⋅ r2 ⋅ h ⇒ V = (pi)" ⋅ 32 ⋅ 4 = 12(pi)"
29. Seja (triângulo)"ABC a seguir, obtído a partir das informações do enunciado, em quê AB = AC.
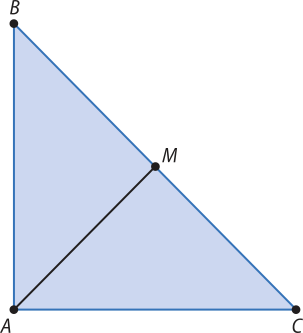
O sólido formado pela rotação completa dêêsse triângulo em torno de é compôzto de dois cones congruentes cujo raio da base méde AM e cuja altura é BM = 1 cm.
Pelo teorema de Pitágoras, sabendo quê BC = 2 cm, obtêm-se os valores, em cm, de AB = AC = (éli)":
(BC)2 = (AB)2 + (AC)2 ⇒ 4 = 2(éli)"2 ⇒ (éli)" =
Como o triângulo ABC é retângulo isósceles, segue quê , portanto pode-se determinar, pelo teorema de Pitágoras, a medida AM, em cm:
(AB)2 = (AM)2 + (BM)2 ⇒ (AM)2 = 1 ⇒ AM = 1
Logo, o volume do sólido, em cm3, será o dôbro do volume de um cone de raio da base r = 1 cm e altura h = 1 cm:
30. Sendo p o perímetro da secção meridiana do cone, a partir das informações do enunciado, pode-se determinar a geratriz, a altura do cone, em cm, e seu volume, em cm3:
p = 2 ⋅ (g + r) ⇒ 16 = 2 ⋅ (g + 3) ⇒ g = 5
g2 = h2 + r2 ⇒ 52 = h2 + 32 ⇒ h = 4
V = (pi)"r2 h ⇒ V = (pi)" ⋅ 32 ⋅ 4 = 12(pi)"
31. Pode-se considerar o seguinte triângulo quê, ao sêr rotacionado completamente em torno de , origina a figura da atividade.
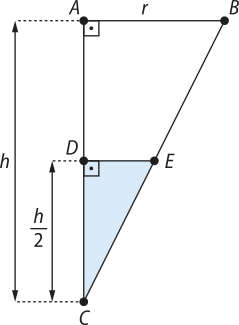
Como (triângulo)"ABC e (triângulo)"DEC são semelhantes, segue quê DE = .
Desse modo, considerando V(minutos)" o volume do líquido e V o volume do recipiente, tem-se:
32. Considere h a altura de um dos cones, 2h a altura do cilindro e r o raio da base comum a ambos. Dessa maneira, tem-se
Vcone = (pi)"r2h e Vcilindro = (pi)"r2 ⋅ (2h). Assim:
33. A partir do enunciado, pode-se construir a seguinte figura.
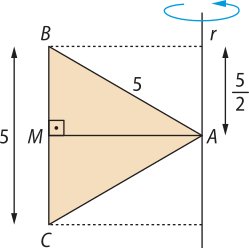
Sejam B(minutos)" e C(minutos)" as respectivas projeções de B e C sobre r. Dessa maneira, o volume do sólido formado será igual ao volume do cilindro formado pela rotação de CBB(minutos)"C(minutos)" em torno de r retirando-se o volume de dois cones congruentes formados pela rotação de ABB(minutos)" em torno de r.
Como é a altura do triângulo equilátero, pelo teorema de Pitágoras, tem-se sua medida em dm:
Assim, o volume do sólido, em dm3, é:
Página trezentos e setenta e cinco
34. Resposta pessoal. Sugestão de problema: Uma escola vai construir uma cistérna com 3 metros de altura interna. Sabe-se quê a altura do cilindro será o dôbro da altura do cone e quê a base possui um raio interno de 1,8 métro. Quantos litros de á gua essa cistérna póde armazenar? (Considere (pi)" = 3,14.)
O volume da cistérna corresponde à soma dos volumes do cilindro e do cone. Logo, deve-se calcular o volume de um cilindro de raio da base igual a 1,8 m e altura (h 1) 2 m e de um cone, de mesmo raio da base (1,8 m), cuja altura (h 2) é igual a 1 m.
V = (pi)" ⋅ r2 ⋅ h1 + ⋅ (pi)" ⋅ r2 ⋅ h 2 = (pi)" ⋅ (1,8)2 ⋅ 2 + ⋅ (pi)" ⋅ (1,8)2 ⋅ 1 = 23,7384
Assim, a cistérna póde armazenar até 23,7384 m3, ou 23.738,4 L.
35.
a) É necessário medir o raio interno da base do cone e a sua altura. Alternativamente à medida da altura, poderia sêr medida a geratriz do cone e a altura poderia sêr calculada com o teorema de Pitágoras a partir das duas medidas feitas no cone. Para realizar as medições, poderiam sêr usados instrumentos de medida, como régua, fita métrica e paquímetro.
b) Sejam r o raio interno da base do canudinho e R = 4r o raio do póte cilíndrico, ambos de altura h. A quantidade n de canudinhos de doce de leite quê é possível montar nesse caso é:
c) A capacidade V do canudinho, em cm3, é:
V = ⋅ (pi)" ⋅ r2 ⋅ h = ⋅ 3,14 ⋅ 12 ⋅ 6 = 6,28
Como 1 cm3 = 1 mL, a capacidade do canudinho é 6,28 mL.
Da densidade do recheio, obtemos a massa m, em grama, de doce de leite usada em cada canudinho:
d = ⇒ m = 6,28 ⋅ 1,32 ≃ 8,3
d) Resposta pessoal. Espera-se quê os estudantes identifiquem alguma demanda da comunidade e, a partir díssu, consigam organizar uma ação social quê auxilie no atendimento a essa demanda, seja por meio da arrecadação de recursos, seja de práticas de voluntariado.
36. A capacidade do recipiente equivale à soma dos volumes da esféra e do cilindro:
Portanto, a capacidade é de 3.334,68 cm3, ou 3.334,68 mL.
37. Do enunciado, conclui-se quê o volume do recipiente, em cm3, é igual a:
V = Vext − Vint
Logo:
V = (pi)"R3 − (pi)"r3 = (pi)" ⋅ (203 − 173) = 2.058(pi)"
d = ⇒ 0,7 = ⇒ m ≃ 4.523,48
A massa do recipiente é aproximadamente 4.523,48 g, ou 4,52 kg.
38. O raio r da semi-esféra méde 18 m ∶ 2 = 9 m. Dessa maneira, o volume do reservatório, em m3, é de:
V = (pi)"r3 = (pi)" ⋅ 93 = 486(pi)"
39. Como 1 L = 1.000 mL = 1.000 cm3, segue quê:
a) Vá gua = (pi)" ⋅ r2 ⋅ h − 1.000
V á gua = (pi)" ⋅ 152 ⋅ 50 − 1.000 = 34.325
Portanto, o volume de á gua é 34.325 mL, ou 34,325 L.
b) Para transbordarem 2 litros de á gua, o volume da esféra deve sêr de 3.000 cm3, então:
V = (pi)" ⋅ R3 ⇒ 3.000 = (pi)" ⋅ R3 ⇒ R ≃ 8,95
Logo, o raio da esféra deve sêr de aproximadamente 8,95 cm.
40. Sejam r 1 o raio da bola B1 e r 2 = 3r 1 o raio da bola B2. Assim, tem-se:
Resposta: alternativa d.
41. Da figura, temos H = 13 − 2R. A área total St do objeto é a soma da área lateral do cilindro e da superfícíe esférica. Logo:
St = 2(pi)"RH + 4(pi)"R2 ⇒ 78(pi)" = 2(pi)"R ⋅ (13 − 2R + 2R) ⇒ R = 3
Portanto, H = (13 − 2 ⋅ 3) cm = 7 cm.
Resposta: alternativa d.
42. Sabe-se quê o raio da base do cilindro méde a e quê, sêndo ele equilátero, sua altura méde 2a. Como a esféra está inscrita a ele, segue quê seu raio também méde a. Assim:
43. O volume Vr do recipiente de sorvete, em cm3, é dado por:
Vr = (pi)"R2H = (pi)" ⋅ 92 ⋅ 5 = 405(pi)"
O volume de sorvete em uma casquinha é igual ao volume Vc do cone da casquinha somado ao volume Vs da semi-esféra correspondente a meia bola de sorvete. Assim, o volume de cada casquinha, em cm3, é de:
Assim, um recipiente de sorvete sérve uma quantidade de casquinhas equivalente a:
44. O sólido gerado será compôzto de uma esféra A de raio 2 da qual foram retiradas duas esferas menóres B de raio 1. Logo, o volume V do sólido é dado por:
V = VA − 2 ⋅ VB = (pi)" ⋅ 2 3 − 2 ⋅ (pi)" ⋅ 1 3 = 8(pi)"
45. a) O volume do brigadeiro, em cm3, é igual a
b) A capacidade da forminha, em cm3, é igual a
c) Um papel-cartão de dimensões 68 cm × 48 cm póde sêr decomposto, no comprimento, em 68 ∶ 4 = 17 quadrados e, na largura, em 48 ∶ 4 = 12 quadrados. Portanto, o papel-cartão póde sêr decomposto ao todo em 17 ⋅ 12 = 204 quadrados. Como cada caixinha possui 6 faces quadradas, segue quê uma fô-lha de papel-cartão póde sêr utilizada para confeksionar 204 ∶ 6 = 34 caixinhas cúbicas.
46. O raio da esféra, em cm, é dado por:
47. Com base nas informações do enunciado, pode-se elaborar a figura a seguir:
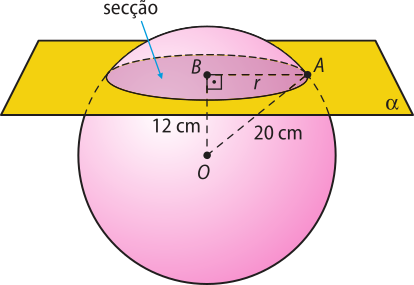
Página trezentos e setenta e seis
Pode-se determinar o quadrado do raio do círculo da secção por meio do teorema de Pitágoras:
202 = 122 + r2 ⇒ r2 = 256
Logo, a área da secção, em cm2, é igual a:
S = (pi)" ⋅ r2 = (pi)" ⋅ 256 = 256(pi)"
48. Considerando AO = r = 5, pode-se determinar a área superficial da esféra em cm2:
S = 4(pi)"r2 = 4(pi)" ⋅ 52 = 100(pi)"
49. a) A área total da superfícíe da Terra, em km2, é dada por:
S = 4(pi)"r2 ≃ 4 ⋅ 3 ⋅ 6.4002 = 491.520.000
b) ≃ 0,0859 = 8,59%
50. A altura h do cone, em dm, é dada por:
Vcone = (pi)"r2 ⋅ h ⇒ 12(pi)" = (pi)" ⋅ 32 ⋅ h ⇒ h = 4
Logo, a medida da geratriz, em dm, será:
g2 = h2 + r2 ⇒ g2 = 42 + 32 ⇒ g = 5
Logo, a área total do cone, em dm2, é:
STcone = (pi)"rg + (pi)"r2 = (pi)" ⋅ 3 ⋅ 5 + (pi)" ⋅ 32 = 24(pi)"
Portanto, o raio da esféra, em dm, é dado por:
Sesféra = STcone ⇒ 4(pi)"R2 = 24(pi)" ⇒ R =
51. O raio R da esféra é tal quê:
O raio r da secção plana circular é tal quê:
S = (pi)"r 2 ⇒ 24(pi)" = (pi)"r 2 ⇒ r =
Por meio do teorema de Pitágoras, obtemos o valor de d, em cm:
R 2 = r 2 + d 2 ⇒ 72 = ()2 + d2 ⇒ d = 5
Resposta: alternativa c.
52. A distância d do centro da esféra até o plano (alfa)", o raio R da esféra e o raio r do círculo da secção formam um triângulo retângulo cuja hipotenusa méde R. Dessa maneira, pelo teorema de Pitágoras, o valor de R, em cm, é dado por:
R 2 = r 2 + d 2 ⇒ R 2 = 92 + 122 ⇒ R = 15
Assim, o volume da esféra, em cm3, é igual a:
V = (pi)"R 3 = ⋅ (pi)" ⋅ 15 3 = 4.500(pi)"
53. A circunferência da bola corresponde ao comprimento de uma circunferência mássima. Logo, seu raio R é:
A área da superfícíe da bola é dada por:
Assim, uma área 10% maior quê essa medida corresponde a:
S(minutos)" = 1,1 ⋅ S = 1,1 ⋅
Resposta: alternativa b.
54. A área do fuso esférico, em m2, é dada por:
Sfuso = = 6(pi)"
55. O volume da cunha, em cm3, é dado por:
Vcunha = = 36(pi)"
56. Trata-se da projeção de Mercator, quê é uma projeção cilíndrica e conforme, ou seja, uma projeção quê preserva as formas (e distorce as áreas).
Resposta: alternativa a.
57. A projeção de Mercator, quê é uma projeção cilíndrica e conforme, tem a desvantagem de distorcer as áreas, principalmente nas altas latitudes (polos).
Resposta: alternativa c.
58. Trata-se de uma projeção cônica, utilizada quando se deseja representar latitudes médias.
Resposta: alternativa e.
59. a) A região representada é a região da Terra quê compreende a Antártida, a Oceania, boa parte da América do Sul e o sul da África.
b) Considerando quê a projeção completa (360°) equivale a 12 fusos, tem-se quê:
a = = 30°
60. Com base na figura do enunciado, é possível verificar quê a projeção para a primeira figura é do tipo azimutal, pois está tangente à superfícíe terrestre. A segunda é uma projeção do tipo cilíndrica, e a terceira é do tipo cônica.
Resposta: alternativa b.
61. A projeção cilíndrica mostrada na alternativa a apresenta tangência na linha do equador, portanto representará uma região próxima à linha do equador com a menor distorção da escala principal.
Resposta: alternativa a.
62. Afirmação I: incorréta. A projeção conforme preserva as formas e distorce as áreas.
Afirmação II: correta. A projeção equivalente preserva as áreas e distorce as formas. A projeção de píters é um exemplo de projeção equivalente.
Afirmação III: incorréta. Na projeção afilática, nem formas, nem áreas, nem comprimentos são preservados.
Afirmação IV: correta. A projeção equidistante preserva comprimentos e distorce áreas e formas.
Resposta: alternativa b.
Atividades complementares
1. Calculando o volume da embalagem antiga, obtém-se, em cm3:
Vantiga = (pi)"r2h = (pi)" ⋅ 22 ⋅ 13,5 = 54(pi)"
Já a área de seu rótulo, em cm2, é igual a:
Santiga = 2(pi)"RH = 2 ⋅ (pi)" ⋅ 2 ⋅ 13,5 = 54(pi)"
Sabe-se quê Vnova = 54(pi)" e quê seu raio R = . Desse modo, sua altura H, em cm, é de:
Vnova = (pi)"R 2H ⇒ 54(pi)" = (pi)" ⋅ 2⋅ H ⇒ H = 6
Assim, a área do rótulo da nova embalagem, em cm2, é:
Snova = 2(pi)"RH = 2 ⋅ (pi)" ⋅ 3 ⋅ 6 = 36(pi)"
Analisando a razão dos rótulos, obtém-se:
Portanto, houve redução de na área do rótulo, quê custará ⋅ R$ 0,60 = R$ 0,40.
Resposta: alternativa b.
2. Considerando o formato cilíndrico da piscina, obtém-se seu volume, em m3:
V = (pi)"r2h = 3,1 ⋅ (2,5)2 ⋅ 1,6 = 31
Como 1 m3 = 1.000 L, então 31 m3 = 31.000 L.
A massa x de produto a sêr misturada na piscina é:
x = ⋅ 25 g = 1.550 g = 1,55 kg
Resposta: alternativa b.
3. Como o cone é equilátero, conclui-se quê:
g = 2r; g2 = h2 + r2 ⇒ h =
Do enunciado, obtém-se quê St = V, então:
(pi)" ⋅ r ⋅ (g + r) = (pi)" ⋅ r2 ⋅ h ⇒ 3(pi)" ⋅ r2 = (pi)" ⋅ r3 ⋅ ⇒ = 9 ⇒ r =
Resposta: alternativa a.
Página trezentos e setenta e sete
4. A área da base de A méde 144 cm2. Portanto, o valor de x, em cm, é: 144 = x2 ⇒ x = 12
Além díssu, o volume de A, em cm3, é igual a 144 ⋅ 15 = 2.160.
Como V A = V B, o valor de h, em cm, é de:
2.160 = (pi)"r2h ⇒ 2.160 = 3 ⋅ 62 ⋅ h ⇒ h = 20
Resposta: alternativa b.
5. Com base nos dados do enunciado, é possível determinar o volume de á gua da chuva, em m³:
V = (pi)"r2 ⋅ h ≃ 3,14 ⋅ 22 ⋅ 0,25 = 3,14
Sabendo quê esse volume corresponde a 5% do volume total:
Logo, o volume total é de aproximadamente 63 m3.
Resposta: alternativa c.
6. Sabendo quê h = 3 m e r = 8 m ∶ 2 = 4 m, a medida da geratriz do cone, em m, e a área total do cone, em m2, são dadas por:
g2 = h2 + r2 ⇒ g2 = 32 + 42 ⇒ g = 5
St = S(éli)" + Sb = (pi)"rg + (pi)"r2 = 4 ⋅ 5 ⋅ (pi)" + 42 ⋅ (pi)" = 36(pi)"
Resposta: alternativa b.
7. O círculo quê circunscreve um hekzágono regular de lado 8 cm tem raio com a mesma medida, 8 cm. Assim, a altura h, em cm, do cone é: Vcone = (pi)"r 2h ⇒ 128(pi)" = (pi)" ⋅ 82⋅ h ⇒ h = 6
A altura h’, em cm, do cilindro é:
Vcilindro = (pi)"r 2h’ ⇒ 128(pi)" = (pi)" ⋅ 82⋅ h' ⇒ h' = 2
Logo, a razão entre a altura h do cone e a altura h’ do cilindro é = 3.
Resposta: alternativa d.
8. Seja r o raio da Terra e R o raio de Júpiter, tem-se:
VTerra = (pi)"r 3
VJúpiter = (pi)"R 3 = (pi)" ⋅ (11r) 3 = 1.331 ⋅ (pi)"r 3 = 1.331 ⋅ VTerra
Resposta: alternativa e.
9. O volume Vm de cada microesfera, em mm3, é de:
Vm = (pi)"r 3 = ⋅ (pi)" ⋅ (0,5)3 =
Cada cápsula é formada pela junção de um cilindro de altura H = (15 − 3 − 3) mm = 9 mm e raio R = 3 mm e duas semiesferas de mesmo raio R. Logo, o volume Vc de cada cápsula, em mm3, é de Vc = (pi)"R 2H + (pi)"R 3 = (pi)" ⋅ 32 ⋅ 9 + (pi)" ⋅ 33 = 117(pi)"
Portanto, em cada cápsula, cabe a seguinte quantidade de microesferas:
Resposta: alternativa 03.
10. O volume das três esferas antes da fundição, em cm³, é:
V = 3 ⋅ (pi)" ⋅ r3 = 3 ⋅ ⋅ (pi)" ⋅ (1)3 = 4(pi)"
Após a fundição, considerando quê nenhum material foi perdido, com R dado em cm, temos: V = (pi)"R3 ⇒ 4(pi)" = ⋅ (pi)" ⋅ R3 ⇒ R =
Resposta: alternativa a.
11. Utilizando como referência a vista frontal do esquema, pode-se construir a figura a seguir:
Pelo triângulo ABC, determina-se a medida AB, em m, a partir da relação:
tg 60° = = 5,19
Dessa maneira, pode-se calcular a medida h em m:
h + 2 = 5,19 ⇒ h = 3,19 ≃ 3,20
Resposta: alternativa c.
12. Como a esféra está inscrita no cubo, tem-se 2r = 4 cm, ou seja, r = 2 cm. Logo, a área da superfícíe da esféra, em cm2, é de:
S = 4(pi)"r2 = 4(pi)" ⋅ 22 = 16(pi)"
Resposta: alternativa c.
13. Analisando item por item, temos:
I. Correta.
II. Incorreta. As projeções equivalentes, como a de píters, preservam a proporcionalidade das áreas, porém distorcem as formas e não apresentam exatidão na geometria angular.
III. Incorreta. As projeções de Mercator preservam as formas, porém distorcem as áreas nas extremidades do mapa, como nas latitudes altas.
Resposta: alternativa a.
Capítulo 4 • Análise combinatória
Atividades
1. a) As possibilidades de caminho são: (x, 1); (x, 2); (y, 1); (y, 2); (z, 1) e (z, 2).
b) Com base no princípio multiplicativo, tem-se: 3 ⋅ 2 = 6.
c) 
2. a) 
b) Como cada lançamento tem 2 possibilidades (cara ou coroa), então, pelo princípio multiplicativo, a quantidade de resultados possíveis para esse experimento é dada por 2 ⋅ 2 ⋅ 2.
3. Pelo princípio multiplicativo, temos:
4 ⋅ 3 ⋅ 2 = 24
Portanto, o café da manhã póde sêr compôzto de 24 maneiras diferentes.
Página trezentos e setenta e oito
4. O gabarito póde sêr preenchido em 40 etapas, em quê cada etapa é a resolução de uma das 40 kestões. Como, para cada questão, há 5 possibilidades de resposta, temos, pelo princípio multiplicativo:
Logo, podem sêr construídos 540 gabaritos.
Resposta: alternativa a.
5. Resposta pessoal. Espera-se quê os estudantes usem a criatividade para elaborar um problema cuja resolução possa sêr expressa pelo diagrama apresentado na atividade. Sugestão de problema: Um corredor dispõe de duas camisetas nas cores rosa e laranja, quatro chórts nas cores cinza, vermelho, amarelo e roxo e dois pares de tênis, um azul e um vêrde. De quantas formas possíveis esse corredor póde se vestir com uma camiseta, um short e um par de tênis? Resposta: 16 maneiras, pois, pelo princípio multiplicativo, 2 ⋅ 4 ⋅ 2 = 16.
6. Para o primeiro lugar há 8 possibilidades. Definido o vencedor da corrida, há 7 possibilidades para o segundo lugar. Por fim, restam 6 possibilidades para o terceiro lugar. Logo, pelo princípio multiplicativo, o número de possibilidades de chegada para os três primeiros lugares é 8 ⋅ 7 ⋅ 6 = 336.
7. A primeira pessoa tem 6 opções de cadeira para escolher. A segunda tem 5 opções, e assim sucessivamente. Pelo princípio multiplicativo, temos: 6 ⋅ 5 ⋅ 4 ⋅ 3 = 360
Logo, as quatro pessoas podem se sentar de 360 modos nas seis cadeiras.
8. Há 8 opções de vaga para o primeiro carro. Para o segundo, há 7 opções, e assim sucessivamente. Pelo princípio multiplicativo: 8 ⋅ 7 ⋅ 6 ⋅ 5 = 1.680
Logo, os quatro carros podem ocupar quatro vagas de 1.680 maneiras.
9. Se o número é divisível por 5, seu último algarismo deve sêr o 5 (pois o zero não está disponível, segundo o enunciado). Assim, há apenas uma possibilidade para o último algarismo.
Para o primeiro algarismo, há 4 possibilidades (1, 3, 7 e 9). Já para o segundo algarismo, há 3 possibilidades. Por fim, para o terceiro algarismo, há 2 possibilidades. Logo, pelo princípio multiplicativo, temos: 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
Portanto, podem sêr escritos 24 números distintos.
10. a) Sugestão de resposta: {dó, ré, mi, fá}; {ré, mi, fá, sol}; {fá, sól, lá, si}; {mi, fá, sól, lá}; {dó, mi, fá, sol}
b) Para a primeira nota, há 7 possibilidades. Para as demais, há 6 (para se obterem notas consecutivas distintas). Assim, pelo princípio multiplicativo, temos: 7 ⋅ 6 ⋅ 6 ⋅ 6 = 1.512
Portanto, podem sêr compostas 1.512 melodias distintas.
11. a) Como o algarismo da unidade de milhar não póde sêr 0, então, pelo princípio multiplicativo: 9 ⋅ 10 ⋅ 10 ⋅ 10 = 9.000
Logo, há 9.000 números com quatro algarismos.
b) Como o algarismo da unidade de milhar não póde sêr 0 e não podemos ter algarismos repetidos, então, pelo princípio multiplicativo, temos: 9 ⋅ 9 ⋅ 8 ⋅ 7 = 4.536
Logo, há 4.536 números com quatro algarismos distintos.
c) Um número é divisível por 5 quando termina em 0 ou 5.
Quantificando os números quê terminam em 0, temos, pelo princípio multiplicativo: 9 ⋅ 8 ⋅ 7 ⋅ 1 = 504
Para os números quê terminam em 5, temos quê o algarismo da unidade de milhar não póde sêr 0 nem 5, e o algarismo da centena não póde sêr 5 nem o algarismo utilizado na unidade de milhar. Assim, pelo princípio multiplicativo, temos: 8 ⋅ 8 ⋅ 7 ⋅ 1 = 448
Pelo princípio aditivo, temos:
504 + 448 = 952
Logo, há 952 números com quatro algarismos distintos quê são divisíveis por 5.
12. Pelo princípio multiplicativo, o total de possibilidades é:
5 ⋅ 4 = 20
Como Maria não deseja as combinações sáia azul com blusa azul e sáia preta com blusa preta, a quantidade de formas diferentes como ela póde se vestir é:
20 − 2 = 18
Resposta: alternativa c.
13. a) 6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720
b) 10! = 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3.628.800
c)
d)
e)
f)
14. Considere os quadrados nomeados do seguinte modo:
Vamos dividir a resolução em dois casos:
1) os quadrados A e C têm cores iguais.
= 150
2) os quadrados A e C têm cores diferentes.
= 480
Pelo princípio aditivo, temos:
150 + 480 = 630
Logo, há 630 maneiras distintas de pintar a figura
15. Aplicando a definição de fatorial em cada item, temos:
a)
b)
16. Ao resolver as equações, obtém-se:
a) (n − 2)! = 720 ⇒ (n − 2)! = 6! ⇒ n − 2 = 6 ⇒ n = 8
Logo, o conjunto solução é S = {8}.
b) (n − 2)! = 2(n − 4)! ⇒ (n − 2) ⋅ (n −3) ⋅ (n − 4)! = 2(n − 4)! ⇒ (n − 2) ⋅ (n − 3) = 2 ⇒ n2 − 5n + 4 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes n’ = 1 e n” = 4.
A solução n = 1 não convém, pois, pela definição de fatorial, (n − 2) e (n − 4) devem sêr números naturais.
Logo, o conjunto solução é S = {4}.
17. Ao resolver a equação, obtém-se:
= 6n − 4 ⇒ = 6n − 4 ⇒ n ⋅ (n − 1) + (n + 1) ⋅ n = 6n − 4 ⇒ n2 − 3n + 2 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes n’ = 2 e n” = 1.
A solução n = 1 não convém, pois, pela definição de fatorial, (n − 2) deve sêr um número natural.
Logo, o conjunto solução é S = {2}.
18. Como os três primeiros caracteres devem sêr vogais minúsculas distintas e os três últimos caracteres devem sêr algarismos distintos, tem-se, pelo princípio multiplicativo:
5 ⋅ 4 ⋅ 3 ⋅ 10 ⋅ 9 ⋅ 8 = 43.200
Logo, podem sêr criadas 43.200 senhas distintas.
Página trezentos e setenta e nove
19. PAZ, PZA, APZ, AZP, ZPA e ZAP.
20. Como não há restrição para a forma com quê essas pessoas podem se sentar na vã, então o número de possibilidades é dado pela permutação dessas 9 pessoas nas poltronas:
P9 = 9! = 362.880
Resposta: alternativa d.
21. a) Como a primeira letra é fixa, o número de anagramas é determinado pela permutação das demais lêtras, ou seja:
P6 = 6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720
b) Como a primeira e a última letra são fixas, o número de anagramas é determinado pela permutação das demais lêtras, ou seja:
P5 = 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
22.
a) Como, na palavra FELINO, não há repetição de lêtras, então o número de anagramas é dado por: 6! = 720.
b) Fixando-se uma letra, sobram outras cinco para serem utilizadas no anagrama. Dessa forma, tem-se 120 anagramas, pois 5! = 120.
c) As vogais da palavra são E, I e O. Ao fixar cada uma, tem-se 5! anagramas terminados com uma vogal. Como são três vogais, têm-se 360 anagramas distintos, pois 3 ⋅ 5! = 360.
d) Há quatro posições para quê as lêtras E, L e I estejam juntas: E L I _ _ _, _ E L I _ _, _ _ E L I _ e _ _ _ E L I.
Portanto, sobram 3 lêtras para serem permutadas. Logo, a quantidade de anagramas distintos é 24, pois 4 ⋅ 3! = 24.
e) Do item anterior, têm-se 24 anagramas para as lêtras em uma ordem fixa. Como elas podem estar em qualquer ordem, tem-se 24 ⋅ 3! = 144.
23. a) Como há 6 algarismos distintos, então haverá 720 possibilidades, pois 6! = 720.
b) Considerando apenas números quê comecem com 1, 2 ou 3, haverá 3 ⋅ 5! = 360 combinações possíveis.
Portanto, a posição da primeira ocorrência do número quê começa com o algarismo 4 é a 361ª.
c) O primeiro número quê termina com o algarismo 2 é 134.562. Há 24 números cujos dois primeiros algarismos começam com 12, nessa ordem, pois 4! = 24. Além díssu, há 6 números cujos primeiros dígitos são 132 (pois 3! = 6), 2 números cujos primeiros dígitos são 1.342 (pois 2! = 2) e ainda há o número 134.526.
Portanto, como 24 + 6 + 2 + 1 = 33, há 33 números menóres quê 134.562, cuja posição é a 34ª.
24. São 4 livros de Matemática, 3 livros de Física e 2 livros de Química. Considerando as permutações dos livros da mesma disciplina, tem-se:
P4 ⋅ P3 ⋅ P2 = 4! ⋅ 3! ⋅ 2! = 288
Como as posições das coleções podem sêr trocadas, tem-se:
P3 ⋅ 288 = 3! ⋅ 288 = 1.728
Portanto, os livros podem sêr enfileirados de 1.728 modos distintos.
25. AAARR, AARAR, AARRA, ARARA, ARAAR, ARRAA, RRAAA, RARAA, RAARA e RAAAR.
26. Como as palavras têm repetições de uma ou mais lêtras, o total de anagramas é:
a)
b)
c)
27. Como os números têm repetições de um ou mais algarismos, a quantidade de números distintos é:
a)
b)
28. De acôr-do com o enunciado, obtêm-se as iniciais: A, A, R, R e E. Considerando a permutação dessas lêtras, tem-se:
Portanto, são possíveis 30 siglas distintas.
29. Considerando a permutação das 6 ma-ssãns e das 4 peras na retirada das frutas, tem-se:
Portanto, ela poderá retirar as frutas de 210 maneiras distintas.
30. Como a última letra é fixa, o número de anagramas é obtído pela permutação das demais lêtras. Considerando a repetição da letra A, tem-se:
Portanto, a palavra tem 840 anagramas distintos.
31. AR póde estar em 4 posições diferentes, e as demais lêtras (C, L e A) podem sêr permutadas. Assim:
4 ⋅ P3 = 4 ⋅ 3! = 24
Portanto, as lêtras AR aparécem juntas, e nessa ordem, em 24 anagramas distintos.
32. Para sair de A e chegar até B, é necessário se deslocar 4 unidades para cima e 5 unidades para a direita. A quantidade de caminhos possíveis é a permutação dêêsses 9 deslocamentos, descontando-se as repetições.
Então:
Portanto, podem sêr feitos 126 caminhos distintos.
33. O primeiro a se sentar tem 5 opções de lugares, o segundo, 4 opções, o terceiro, 3 opções, e o último tem 2 opções de lugares. Logo, pelo princípio multiplicativo, temos 5 ⋅ 4 ⋅ 3 ⋅ 2 = 120.
Resposta: alternativa e.
34. Julia e Guilherme, estando lado a lado, podem ocupar 7 posições diferentes nessa fila. Considerando a permutação dos demais dançarinos e a permutação de Julia e Guilherme, temos:
7 ⋅ P6 ⋅ P2 = 7 ⋅ 6! ⋅ 2! = 7! ⋅ 2!
Portanto, há 7! ⋅ 2! modos de compor essa fila.
Resposta: alternativa a.
35. Resposta pessoal. Exemplo de problema: Olívia vai colocar lado a lado em uma prateleira seus 4 livros de História e seus 3 livros de Matemática. Sabendo-se quê ela quêr que todos os livros de História fiquem à esquerda dos de Matemática, de quantas maneiras ela póde fazer isso?
36. a) Pelo princípio multiplicativo:
9 ⋅ 8 ⋅ 7 = 504
Pela fórmula de arranjo simples:
A9, 3= = 504
Logo, as pessoas podem se sentar de 504 maneiras diferentes.
b) Pelo princípio multiplicativo:
9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 = 15.120
Pela fórmula de arranjo simples:
A9, 5= = 15.120
Logo, podem sêr formados 15.120 números distintos.
37. Resposta pessoal. Exemplo de problema: De quantas maneiras as quatro primeiras posições em uma corrida podem sêr determinadas, se há 12 competidores?
38.
(A, B, C) (A, C, B) (B, A, C) (B, C, A) (C, A, B) (C, B, A)
(A, B, D) (A, D, B) (B, A, D) (B, D, A) (D, A, B) (D, B, A)
(A, C, D) (A, D, C) (C, A, D) (C, D, A) (D, A, C) (D, C, A)
(B, C, D) (B, D, C) (C, B, D) (C, D, B) (D, B, C) (D, C, B)
Página trezentos e oitenta
39. Há 40 assentos numerados para 25 turistas. Logo, a quantidade de modos distintos quê essas pessoas podem sêr acomodadas no ônibus é dada por:
A 40, 25 =
Resposta: alternativa a.
40. Há 9 assentos disponíveis para 7 pessoas. Logo, o número de formas distintas de acomodar a família nesse vôo é dado por:
A 9, 7 =
Resposta: alternativa a.
41. O 4 póde sêr o primeiro, o segundo ou o terceiro algarismo do número. Para compor os dois algarismos restantes, há 8 algarismos disponíveis. Assim:
3 ⋅ A 8, 2 = 3 ⋅ = 168
Logo, podemos formár 168 números.
42. a) Há 7 possibilidades de cores para 4 faixas. Logo, a quantidade de possibilidades distintas para pintar a bandeira é:
A7, 4= = 840
b) Se a côr amarela estiver sempre presente, deve-se considerar quê ela póde ocupar qualquer uma das faixas, ou seja, para cada combinação de cores, podem-se obtêr 4 variações, devido à posição da faixa amarela. Para as outras 3 faixas, restam 6 opções de cores. Assim:
4 ⋅ A 6, 3 = 4 ⋅ = 480
Portanto, podem sêr pintadas 480 bandeiras distintas.
43. O número total de resultados possíveis para as três primeiras colocações dessa competição é dado por A 12, 3.
O número de resultados em quê há somente meninas nos três primeiros lugares é dado por A 7, 3.
Logo, o número de resultados em quê há pelo menos um menino em uma das três primeiras colocações é:
A 12, 3 − A 7, 3 = = 1.110
44. O total de partidas do campeonato foi:
A 20, 2 = = 380
Subtraindo o número de empates dêêsse total, temos quê houve ganhador em 254 jogos, pois 380 − 126 = 254.
Resposta: alternativa c.
45. Elaborar um cóódigo da etiqueta póde ocorrer em duas etapas. A primeira etapa é selecionar 4 lêtras distintas entre as 26 para compor as iniciais da etiqueta. O número de possibilidades dessa etapa é A 26, 4.
A segunda etapa é selecionar 4 algarismos distintos entre os 10 para compor os quatro dígitos finais do cóódigo da etiqueta. O número de possibilidades dessa etapa é A 10, 4.
Então, pelo princípio multiplicativo, o número total de etiquetas é:
A 26, 4 ⋅ A 10, 4
Resposta: alternativa c.
46. {A, B, C}, {A, B, D}, {A, B, E}, {A, B, F}, {A, C, D}, {A, C, E}, {A, C, F}, {A, D, E}, {A, D, F}, {A, E, F}, {B, C, D}, {B, C, E}, {B, C, F}, {B, D, E}, {B, D, F}, {B, E, F}, {C, D, E}, {C, D, F}, {C, E, F}, {D, E, F}
47. Há 8 atletas disponíveis para a escolha dos 5 jogadores. Logo, o número de maneiras com quê se póde escalar o tíme é:
C 8, 5 = = 56
48. Deve-se organizar uma comissão formada por brasileiros (C 6, 3)
e japoneses (C 4, 2). Logo:
C 6, 3 ⋅ C 4, 2 = = 120
Portanto, a diretoria póde sêr composta de 120 modos distintos.
49. Deve-se organizar um grupo formado por rapazes (C5, 2) e moças (C6, 3). Logo:
C5, 2 ⋅ C 6, 3 = 200
Portanto, podem sêr formados 200 grupos distintos.
50. Deve-se organizar uma próva composta de duas kestões de Álgebra (C 5, 2) e três kestões de Trigonometria (C 6, 3). Logo:
C 5, 2 ⋅ C 6, 3 = = 200
Portanto, podem sêr elaboradas 200 provas distintas.
51. Resposta pessoal. Exemplo de problema: De quantas maneiras o professor de uma turma de 30 alunos póde selecionar 5 deles para formár um grupo de trabalho?
52. Deve-se escolher para a competição alunos do primeiro ano (C5, 3), do segundo ano (C5, 3) e do terceiro ano (C7, 5). Logo:
C 5, 3 ⋅ C 5, 3 ⋅ C 7, 5 = = 2.100
Portanto, o técnico póde fazer essa escolha de 2.100 maneiras diferentes.
Resposta: alternativa d.
53. a) P6 = 6! = 720
A fila póde ter sido formada de 720 maneiras.
b) A 6, 3 = 120
Os doces podem ter sido distribuídos de 120 modos.
c) C6, 3 = = 20
Os times podem ter sido formados de 20 maneiras.
54. a) Do enunciado, verificamos quê, juntos, João e Maria têm 5 amigos homens e 4 amigas mulheres. O número de maneiras de convidarem 3 homens e 3 mulheres é:
C 5, 3 ⋅ C 4, 3 = = 40
Portanto, João e Maria podem fazer o convite de 40 maneiras distintas.
b) Para convidarem 3 homens e 3 mulheres, com cada um deles convidando exatamente 3 pessoas, entre seus respectivos amigos, consideraremos duas situações:
• João escolhe 2 homens e 1 mulher e Maria escolhe 1 homem e 2 mulheres;
• João escolhe 1 homem e 2 mulheres e Maria escolhe 2 homens e 1 mulher.
O número de maneiras será:
C 3, 2 ⋅ C 2, 1 ⋅ C 2, 1 ⋅ C 2, 2 + C 3, 1 ⋅ C 2, 2 ⋅ C 2, 2 ⋅ C 2, 1 = 18
Assim, João e Maria podem convidar essas pessoas de 18 maneiras diferentes.
55. C 10, 6 = = 210
Portanto, podem sêr feitos 210 tipos de salada distintos.
56. Seja n o número de equipes participantes. Como ocorreram 272 partidas (de turno e returno), segue quê o campeonato teve, em cada turno, 136 partidas. Assim:
C n, 2 = 136 ⇒ = 136 ⇒ n2 − n − 272 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes n’ = 17 e n” = −16.
Como n é o número de equipes, deve-se considerar apenas a raiz positiva. Logo, houve 17 equipes participantes.
57. Há duas possibilidades para a escolha da comissão:
• 1 aluno do 1º ano e 2 alunos do 2º ano;
• 2 alunos do 1º ano e 1 aluno do 2º ano.
Como se inscreveram 5 alunos do 1º ano e 4 alunos do 2º ano, tem-se quê o número de maneiras de se escolher os alunos da comissão é:
C 5, 1 ⋅ C 4, 2 + C 5, 2 ⋅ C 4, 1 = 70
Resposta: alternativa d.
Página trezentos e oitenta e um
58. Sendo n o número de professores, tem-se:
C n, 2 = 210
= 210 ⇒ = 210 ⇒ n2 − n − 420 = 0
Resolvendo a equação do 2º grau, obtêm-se as raízes n’ = 21 e n” = −20.
Como n é o número de professores, deve-se considerar apenas a raiz positiva. Logo, havia 21 professores na reunião.
59. Devem sêr escolhidos 2 estudantes de Engenharia de Produção (C28, 2), 2 estudantes de Engenharia Elétrica (C18, 2) e 2 estudantes de Engenharia de Telecomunicações (C12, 2). Logo, o número de maneiras como a comissão póde sêr formada é dada por:
C 28, 2 × C 18, 2 × C 12, 2 = 14 × 27 × 9 × 17 × 6 × 11
Resposta: alternativa b.
60. Deve-se formár cada tíme com 1 goleira (C3, 1) e com 4 jogadoras nas demais posições (C17, 4). Logo, o número de times possíveis é dado por C3, 1 ⋅ C17, 4.
Resposta: alternativa e.
61. Na semicircunferência, é possível formár 8 triângulos retângulos ao escolher A e B como vértices.
Logo, podem sêr formados 112 triângulos não retângulos com três pontos distintos dessa semicircunferência, pois:
C 10, 3 − 8 = 112
Resposta: alternativa d.
Atividades complementares
1. A quantidade mássima de formas distintas de entrar e sair do campus é:
A 7, 2 = = 42
Resposta: alternativa a.
2. Considerando quê a empresa espera ter 1 milhão de clientes, as possibilidades de senha devem estar entre 1 milhão e 2 milhões.
Verificando o número de senhas possíveis em cada opção, tem-se:
I: 26 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 2.600.000
II: 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 1.000.000
III: 26 ⋅ 26 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 6.760.000
IV: 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 100.000
V: 26 ⋅ 26 ⋅ 26 ⋅ 10 ⋅ 10= 1.757.600
Logo, a opção V é a quê mais se adéqua às condições da empresa.
Resposta: alternativa e.
3. Cada contador póde assumir 10 algarismos. Logo:
10 ⋅ 10 ⋅ 10 ⋅ 10 = 10.000
Resposta: alternativa a.
4. Para cada uma das bolas, há duas possibilidades: ir para a pessoa A ou para a pessoa B. Como são cinco bolas, tem-se, pelo princípio multiplicativo, um total de 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32 possibilidades. Porém, devemos retirar o caso em quê todas as bolas vão para a pessoa A e o caso em quê todas as bolas vão para a pessoa B.
Haverá, portanto, 30 formas distintas.
Resposta: alternativa 02.
5. Considerando quê cada uma das 6 barras póde assumir a côr branca ou preta, tem-se, pelo princípio multiplicativo:
2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 64
Devemos retirar o caso em quê todas as barras são brancas e o caso em quê todas as barras são pretas.
Portanto, podem sêr formados 62 códigos distintos.
Resposta: alternativa c.
6. Para o pronto-socorro: C 8, 3 = = 56.
Para o setor cirúrgico: C 5, 3 = 10.
Para a ala pediátrica: C 2, 2 = 1.
Logo, a distribuição póde sêr feita de 560 maneiras distintas, pois: 56 ⋅ 10 ⋅ 1 = 560
Resposta: alternativa 04.
7. A quantidade de números menóres quê 61.573 é igual ao total de permutações utilizando os cinco algarismos (1, 3, 5, 6 e 7) menos a quantidade de permutações maiores quê 61.573 e o próprio 61.573.
Total de permutações: P5 = 5! = 120
Calculando quantas permutações resultam em números maiores quê 61.573, tem-se:
• Números quê iniciam com o algarismo 7:
1 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
• Números quê iniciam com 6, com a casa dos milhares diferente de 1:
1 ⋅ 3 ⋅ 3 ⋅ 2 ⋅ 1 = 18
• Números quê iniciam com 6, com a casa dos milhares diferente de 1 e a casa das centenas igual a 7:
1 ⋅ 1 ⋅ 1 ⋅ 2 ⋅ 1 = 2
Portanto, como 24 + 18 + 2 = 44, há 44 permutações maiores quê 61.573.
Logo, há 75 números menóres do quê 61.573, pois 120 − 44 − 1 = 75.
Resposta: alternativa c.
8. Como serão formados números de dois a seis algarismos utilizando-se apenas 1, 2, 4, 5, 7 e 8, deve-se considerar cada possibilidade em quê o primeiro dígito é par e o último é ímpar.
Calculando as quantidades de números possíveis em cada caso, tem-se:
• 2 algarismos:
• 3 algarismos: =36
• 4 algarismos:
• 5 algarismos:
• 6 algarismos:
Logo, há 585 números, pois 9 + 36 + 108 + 216 + 216 = 585.
Resposta: alternativa d.
9. Calculando as quantidades de possibilidades em cada caso, tem-se:
• Primeira fileira: = 8
• Segunda fileira: = 6
Logo, há 48 maneiras, pois 8 ⋅ 6 = 48.
Resposta: alternativa e.
10. Para sair de A e chegar a C, é necessário se deslocar 3 unidades para cima e 3 unidades para a direita.
O total de caminhos é:
Para sair de C e chegar a B, é necessário se deslocar 4 unidades para a direita e duas unidades para cima.
O total de caminhos é:
Logo, são 300 os caminhos possíveis, pois 20 ⋅ 15 = 300.
Resposta: alternativa d.
Página trezentos e oitenta e dois
11. A senha é formada pêlos dígitos 1, 3, 3 e x. Há 8 possibilidades para o dígito x e há dois casos possíveis para quê o dígito 1 não seja sucedido imediatamente por um dígito 3.
• Caso 1: o dígito 1 é o último.
• Caso 2: o dígito 1 é sucedido pelo dígito x.
Há 3 posições possíveis para os dígitos 1 e x. Assim:
Logo, pelo princípio aditivo, Ana escreverá 48 possibilidades de senha, pois 24 + 24 = 48.
Resposta: alternativa a.
12. Há 7 possibilidades de modelos de carros, 2 possibilidades de motor, 2 possibilidades de central multimídia (ter ou não ter), 2 possibilidades de rodas de liga leve (ter ou não ter), 2 possibilidades de bancos de couro (ter ou não ter) e x possibilidades de cores. Então, pelo princípio multiplicativo, temos:
7 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ x > 1.000 ⇒ x > 8,9
Portanto, a quantidade mínima de cores quê a montadora deverá disponibilizar a seus clientes é 9.
Resposta: alternativa b.
13. I) Correta, pois
II) Incorreta, pois
III) Correta, pois
Resposta: alternativa b.
14. Suponha quê os oitos lugares vagos estejam numerados consecutivamente de 1 a 8. Pelas condições impostas pelo problema, Pedro e Marineide podem ocupar, em qualquer ordem, os lugares (1 e 4), (2 e 5), (3 e 6), (4 e 7) e (5 e 8). Desse modo, há 10 possibilidades de Pedro e Marineide escolherem os seus lugares e P6 possibilidades para os outros 6 amigos se sentarem.
Logo, há 7.200 maneiras para os amigos se disporem nas cadeiras, pois 10 ⋅ P6 = 7.200.
Resposta: alternativa d.
15. A primeira pessoa a se sentar tem 6 possibilidades de escolha. A segunda tem 4 possibilidades, uma vez quê não póde se sentar no lugar já escolhido nem no lugar ôpôsto à primeira pessoa. Analogamente, a terceira pessoa tem 2 possibilidades.
Assim, eles podem escolher o lugar de 48 formas diferentes, pois, pelo princípio multiplicativo, 6 ⋅ 4 ⋅ 2 = 48.
Resposta: alternativa a.
16. João póde formár 24 trajes diferentes, pois, pelo princípio multiplicativo:
3 ⋅ 2 ⋅ 4 = 24
Resposta: alternativa b.
17. As duas pessoas quê vão se sentar juntas podem ocupar 5 posições diferentes nessa fileira. Considerando a permutação dessas pessoas e a permutação dos demais amigos, temos:
5 ⋅ P2 ⋅ P4 = 240
Logo, eles podem se organizar de 240 maneiras.
Resposta: alternativa b.
18. Calculando o número de possibilidades em cada caso, temos:
• Acomodar a família Sousa: 3 ⋅ 3!
• Acomodar o casal (após a família Sousa): 2 ⋅ 2 ⋅ 2!
• Acomodar as outras 4 pessoas: 4!
Logo, há 3.456 maneiras de dispor os passageiros, pois, pelo princípio multiplicativo:
3 ⋅ 3! ⋅ 2 ⋅ 2 ⋅ 2! ⋅ 4! = 3.456
Resposta: alternativa e.
19. Há 9 possibilidades para escolher o andar e C 6, 2 possibilidades para escolher os dois apartamentos (pois a pessoa não quer os apartamentos terminados em 7 ou 8). Logo:
9 × C 6, 2 = 9 ×
Resposta: alternativa b.
20. Como há 10 consoantes disponíveis para se escolherem 2 e 5
vogais para se escolher 1 e considerando quê a ordem dos elemêntos não altera o conjunto, tem-se quê o número de conjuntos possíveis é:
C 10, 2 ⋅ C 5, 1 = = 225
Resposta: alternativa e.
21.
01) Incorreta. Há 15 números pares no conjunto. Assim, a quantidade de maneiras de se escolherem 3 dêêsses números é:
C15,3 = = 455
02) Incorreta. O número de senhas possíveis é igual a: P5 = 5! = 120
04) Correta. O algarismo da unidade deve sêr 5. Assim, restam 6 algarismos para as outras três ordens. Portanto, a quantidade de números quê podem sêr formados é 6 ⋅ 5 ⋅ 4 = 120, quê é um número maior quê 60.
08) Incorreta. Desenvolvendo a equação dada, temos:
Resolvendo a equação do 2º grau, obtêm-se as raízes n’ = 4 e n” = −9. Pela definição de fatorial, (n + 3) e (n + 1) devem sêr números naturais. Assim, deve-se desconsiderar a raiz negativa. Portanto, a equação tem solução S = {4}.
16) Correta. Como 5 e 2 são fatores de todos os números fatoriais quê estão sêndo adicionados, sabemos quê todos eles são múltiplos de 10, portanto o algarismo da unidade da soma é 0. Por outro lado, temos:
12 + 14 + 16 + 18 + 20 = 80
Assim, os algarismos da unidade de ambas as somas são iguais (a zero).
Resposta: alternativas 04 e 16.
Capítulo 5 • Probabilidade
Atividades
1. Para descrever os elemêntos do espaço amostral dêêsse experimento, utilizando a notação de par ordenado (x, y), considere x e y como as observações das faces superiores dos dados branco e vêrde, respectivamente. Desse modo:
a) U = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
b) A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
c) B = {(1, 4), (2, 3), (3, 2), (4, 1)}
d) n(U) = 36; n(A) = 6; n(B) = 4
2. Seja U o espaço amostral dêêsse experimento. Desse modo:
a) Como A ∩ B = ∅ e A ∪ B = U, segue quê os eventos A e B são complementares.
b) Como C ∩ D = ∅ e C ∪ D ≠ U, segue quê os eventos C e D são mutuamente exclusivos.
c) Como E = U, segue quê o evento E é cérto.
d) Como F = ∅, segue quê F é um evento impossível.
3. O espaço amostral U possui eventos elementares não equiprováveis, pois, por exemplo:
• para quê a soma dos números das fichas seja 3, há duas maneiras possíveis, quê são (1, 2) e (2, 1);
• para quê a soma dos números das fichas seja 5, há quatro maneiras possíveis, quê são (1, 4), (4, 1), (2, 3) e (3, 2).
O espaço amostral V possui eventos elementares equiprováveis, pois só existe uma única maneira para cada evento elementar ocorrer. Além díssu, as fichas são idênticas e retiradas ao acaso, ou seja, não existe nada no experimento quê favoreça um resultado em relação aos demais.
Página trezentos e oitenta e três
4. Resposta pessoal. Sugestão de problema: Considere quê a mãe de um filhote de coelho quê nascerá tem genes c + c h e quê o pai tem c h como um de seus genes. Há algum tipo de pelagem impossível para esse filhote?
Se o outro gene do pai for:
• c +, então U = {(c + c h), (c h c h), (c + c +), (c h c +)};
• c ch, então U = {(c + c h), (c h c h), (c + c ch), (c h c ch)};
• c h, então U = {(c + c h), (c h c h), (c + c h), (c h c h)};
• c, então U = {(c + c h), (c h c h), (c + c), (c h c)}.
Segundo o qüadro com as combinações de genes e tipos de pelagem, só é impossível quê o filhote tenha o tipo de pelagem albino, pois cc não é um elemento do espaço amostral em nenhum dos casos.
5. Seja U o espaço amostral dêêsse experimento, em quê A representa o evento de retirar uma bola azul da caixa e B, o evento de retirar uma bola amarela. Assim, tem-se:
6. Considerando U o espaço amostral do lançamento do dado cúbico, tem-se:
U = {1, 2, 3, 4, 5, 6} ⇒ n(U) = 6
a) A = {1} ⇒ n(A) = 1 ⇒ P(A) =
b) B = {2, 3, 5} ⇒ n(B) = 3 ⇒ P(B) =
c) C = {2, 4, 6} ⇒ n(C) = 3 ⇒ P(C) =
d) D = {1, 2, 3, 4} ⇒ n(D) = 4 ⇒ P(D) =
e) E = ∅ ⇒ n(E) = 0 ⇒ P(E) = 0
7. Considerando todos os números de três algarismos distintos quê podem sêr formados pêlos algarismos 3, 5 e 7, obtém-se o seguinte espaço amostral:
U = {357, 375, 537, 573, 735, 753} ⇒ n(U) = 6
a) Considere o evento A: o número é múltiplo de 3. Como a soma dos algarismos é sempre igual a 15, todos os números são múltiplos de 3. Logo:
n(A) = 6 ⇒ P(A) = = 1 = 100%
b) Considere o evento B: o número é par. Como os algarismos 3, 5 e 7 são ímpares, todos os números de três algarismos distintos quê podem sêr formados com eles serão ímpares.
Logo:
n(B) = 0 ⇒ P(B) = = 0 = 0%
8. Considerando dois dados distintos, o espaço amostral será compôzto de um número de combinações dado por:
6 ⋅ 6 = 36
Logo:
n(U) = 36
a) A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)} ⇒ n(A) = 6
P(A) =
b) B = {(3, 6), (4, 5), (5, 4), (6, 3)} ⇒ n(B) = 4
P(B) =
c) C = {(1, 1), (1, 2), (2, 1)} ⇒ n(C) = 3
P(C) =
d) D = {(6, 2), (2, 6)} ⇒ n(D) = 2
P(D) =
9. Como o envelope possui 20 fichas, tem-se: n(U) = 20
a) A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19} ⇒ n(A) = 10
P(A) =
b) B = {8, 9, 10, …, 18, 19, 20} ⇒ n(B) = 13
P(B) =
c) C = {5, 10, 15, 20} ⇒ n(C) = 4
P(C) =
d) D = {3, 6, 9, 12, 15, 18} ⇒ n(D) = 6
P(D) =
10. Considerando um baralho com 52 cartas, tem-se: n(U) = 52
a) Há 4 damas no baralho, portanto:
b) Há 1 dama de paus no baralho, portanto:
c) Há 13 cartas de ouros no baralho, portanto:
d) As cartas com figuras são a dama, o valete e o rei de cada naipe. Considerando os 4 naipes, tem-se:
4 ⋅ 3 = 12
Assim, há 12 cartas com figura no baralho, portanto:
n(D) = 12 ⇒ P(D) =
11. Considerando o número de elemêntos do espaço amostral, tem-se:
n(U) = 3 + 2 + 4 + 3 = 12
a)
b)
c)
12. São considerados 20 números dentre 100. Desse modo, a probabilidade de sêr sorteada uma senha com um número de 1 a 20 é .
Resposta: alternativa c.
13. Seja U o espaço amostral das mulheres fumantes com idade acima de 40 anos. Sejam os eventos A, ter câncer, com probabilidade de aproximadamente 75,6%, e B, não ter câncer, relacionados a esse espaço amostral. Como eles são complementares, tem-se:
P(A) + P(B) = 1 ⇒ P(B) = 1 − 0,756 = 0,244 = 24,4%
Portanto, a probabilidade de uma mulher fumante com mais de 40 anos não ter câncer é de aproximadamente 24,4%.
14. a) Considerando dois lançamentos sucessivos de um dado não viciado de seis faces, as possibilidades para o produto dos números obtidos são: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 30 e 36. Portanto, esses são os números quê Pedro póde ter anotado.
b) O número de elemêntos do espaço amostral dêêsse experimento é: n(U) = 6 ⋅ 6 = 36
Seja o evento A: Pedro anotou o número 25. Como 25 é o produto obtído em apenas uma possibilidade de lançamento dos dois dados (ocorrendo quando o número obtído é 5 em ambos os dados), segue quê: n(A) = 1
Logo: P(A) =
c) Seja o evento B: Pedro anotou um número ímpar. Para quê o produto de dois números naturais seja ímpar, é necessário quê cada um dêêsses números também seja ímpar. Assim, segue quê: n(B) = 3 ⋅ 3 = 9
Logo: P(B) =
d) Seja o evento C: Pedro anotou um número par. Como um número natural só póde sêr par ou ímpar, segue quê P(B) e
P(C) são eventos complementares. Logo:
P(B) + P(C) = 1 ⇒ P(C) = 1 −
Página trezentos e oitenta e quatro
15. Considerando o lançamento de dois dados não viciados de seis faces, as possibilidades para a soma dos números obtidos são: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. O número de elemêntos do espaço amostral dêêsse experimento é: n(U) = 6 ⋅ 6 = 36
Seja o evento A: a soma dos números obtidos é 7 ou 11.
Para quê a soma seja 7, há seis possibilidades, quê são:
(1, 6), (2, 5), (3, 4), (4, 3), (5, 2) e (6, 1)
Para quê a soma seja 11, há duas possibilidades, quê são:
(5, 6) e (6, 5)
Desse modo: n(A) = 6 + 2 = 8
Logo: a probabilidade de o palpite de Jaqueline ocorrer é dada por:
16. Seja U o conjunto com todos os triângulos distintos quê podem sêr formados com os vértices de um hekzágono regular.
n(U) = C 6, 3 = 20
Seja A o subconjunto dos triângulos retângulos distintos quê podem sêr formados com os vértices de um hekzágono regular.
A partir de cada vértice, podem-se formár 2 triângulos retângulos distintos. Desse modo, tem-se:
n(A) = 6 ⋅ 2 = 12
A probabilidade é dada por: P(A) = = 0,6 = 60%
17. a) Considerando quê, na palavra INTEGRAL, há 8 lêtras e deseja-se formár conjuntos com 3 lêtras distintas, o número de possibilidades é dado por: C 8, 3 = = 56
b) Seja U o espaço amostral de todos os conjuntos de 3 lêtras distintas quê podem sêr formados usando as 8 lêtras da palavra
INTEGRAL. Seja A o evento quantidade de conjuntos em quê a letra L está inserida. Desse modo, tem-se:
n(U) = 56; n(A) = C7, 2= = 21
P(A) =
18. Sejam P(K1) e P(L1) as probabilidades de se sortearem os personagens K e L, respectivamente. Pelo enunciado, tem-se:
P(K1) = 3 ⋅ P(L1)
Os eventos K1 e L1 são complementares, logo:
P(K1) + P(L1) = 1 ⇒ 3 ⋅ P(L1) + P(L1) = 1 ⇒ P(L1) =
Logo, a probabilidade de adquirir o personagem K é:
P(K1) = 1 − P(L1) ⇒ P(K1) = 1 − ⇒ P(K1) = = 0,75 = 75%
19. Sejam P(X1), P(Y1) e P(Z1), respectivamente, as probabilidades de os cavalos X, Y e Z vencerem a disputa. Pelo enunciado, tem-se:
P(X1) = 2 ⋅ P(Y1)
P(Y1) = 2 ⋅ P(Z1)
a) Como os eventos X1, Y1 e Z1 são complementares, tem-se:
P(X1)+ P(Y1) + P(Z1)= 1 ⇒ P(X1) + = 1 ⇒ P(X1)=
b) P(Y1) =
c) P(Z1) =
20. Seja U o espaço amostral em quê a soma dos números das faces superiores dos dados é 9. Esse conjunto contém os elemêntos (1, 2, 6), (1, 3, 5), (1, 4, 4), (2, 2, 5), (2, 3, 4), (3, 3, 3) e suas permutações. Logo:
Seja A o evento: os números das faces superiores são ímpares. Ele é compôzto dos elemêntos (1, 3, 5), (3, 3, 3) e suas permutações. Logo:
Desse modo, conclui-se quê: P(A) =
21. O total de anagramas quê podem sêr formados com as lêtras da palavra COVEST é P6 = 6! = 720.
Desse total, o número de anagramas quê começam e terminam com consoantes, pelo princípio fundamental da contagem, é 4 ⋅ 3 ⋅ 4! = 288. A probabilidade de, escolhido ao acaso, um anagrama começar e terminar com consoante é:
Resposta: alternativa d.
22. Considera-se:
• o evento A "todas as bó-linhas sorteadas são azuis";
• o evento B"ao menos uma bó-linha sorteada é vermelha";
• o espaço amostral do experimento, em quê os eventos A e B são complementares.
Logo: P(A) + P(B) = 1 ⇒ P(B) = 1 −
23. Há 7 ex-estudantes com 1 filho, 6 com 2 filhos e 2 com 3 filhos. Portanto, há 25 crianças no total. Dessas, 7 são filhas únicas. Logo, a probabilidade de se sortear um filho único é igual a .
Resposta: alternativa e.
24. Sejam U o conjunto de todos os estudantes, V o conjunto dos estudantes quê jogam vôlei e F o conjunto dos estudantes quê jogam futeból. Desse modo, tem-se o seguinte diagrama:
Considere U1 o espaço amostral de todos os estudantes.
a) Evento A: estudante jogar vôlei.
P(A) =
b) Evento B: estudante jogar futeból.
P(B) =
c) Evento C: estudante jogar vôlei e futeból
P(C) = P(A ∩ B) =
d) Evento D: estudante jogar vôlei ou futeból.
P(D) = P(A ∪ B) = P(A) + P(B) − P(A ∩ B) =
e) Evento E: estudante jogar somente futeból
P(E) =
f) Evento F: estudante não praticar nenhum dêêsses esportes.
Os eventos D e F são complementares. Logo:
P(D) + P(F) = 1 ⇒ P(F) = 1 −
25. Seja U o espaço amostral relacionado às dez kestões. Sejam J o evento"Jorge rêzouvêo a questão", C o evento"César rêzouvêo a questão" e T o evento"Teresa rêzouvêo a questão". Desse modo:
a)
b)
c) São complementares o evento em quê Jorge ou César ou Tereza rêzouvêo a questão (J ∪ C ∪ T) e o evento N, nenhum dos três rêzouvêo a questão. Logo:
P(N) = 1 − P(J ∪ C ∪ T)
Página trezentos e oitenta e cinco
26. Sejam A e B os eventos em quê Roberto é aceito pelas empresas A e B, respectivamente. Pelo enunciado, tem-se:
a)
b) Seja C o evento em quê Roberto é aceito apenas pela empresa A ou apenas pela empresa B. Logo:
27. Sendo R o evento"sair uma carta rei" e E o evento"sair uma carta de espadas", tem-se:
28. Pelo enunciado, tem-se:
n(U) = 30
a) Evento A: número sêr par.
P(A) =
b) Evento B: número sêr ímpar.
P(B) =
c) Evento C: número sêr par e menor quê 15.
C = {2, 4, 6, 8, 10, 12, 14}
P(C) =
d) Evento D: número sêr múltiplo de 4.
D = {4, 8, 12, 16, 20, 24, 28}
Evento E: número sêr múltiplo de 5.
E = {5, 10, 15, 20, 25, 30}
D ⋃ E = {20}
P(D) =
P(E) =
P(D ∩ E) =
Portanto, conclui-se quê:
29. Com os dados do enunciado, constrói-se o seguinte diagrama:
a) Os sócios quê estão em dúvida entre votar em B ou em C, mas não em A, correspondem, na figura, a (B ∩ C) − A. São, portanto, 20 sócios.
O número de sócios quê não votariam em B é:
40 + 10 + 100 = 150
Na figura, correspondem a
b) O total de sócios quê participaram da pesquisa é:
40 + 70 + 10 + 10 + 20 + 100 + 150 = 400
A probabilidade de quê o sócio escolhido não tenha ainda se decidido por um candidato é:
30. Sejam o evento H"sortear um homem", o evento V"sortear um homem quê trabalha em vendas", o evento P"sortear uma mulher quê trabalha na produção" e o evento M"sortear uma mulher quê trabalha em vendas".
a) P(H) =
b) Como a interseção dos dois eventos é nula, segue quê:
c)
31. Resposta pessoal. Sugestões de problema:
1. Qual é a probabilidade de Fabiano pegar da pilha de camisetas, aleatoriamente, uma camiseta de côr vêrde ou azul?
Sejam a pilha de 15 camisetas o espaço amostral U, o evento A "pegar uma camiseta de côr verde" e o evento B"pegar uma camiseta de côr azul". Desse modo, como esses eventos são mutuamente exclusivos, tem-se:
2. Considerando as possíveis combinações de calças e camisetas de Fabiano, qual é a probabilidade de, escolhendo-se aleatoriamente, obter-se uma combinação de camiseta branca e calça azul?
Pelo enunciado, conclui-se quê:
n(camisetas) = 15; n(calças) = 10
P 1 (camiseta branca) =
P 2 (calça azul) =
32. Análise da redução de chance de cada jogador:
• A redução nas chances de Ana acertar é igual à diferença entre a probabilidade de a face superior sêr branca ou um número par e a probabilidade de a face superior sêr branca e um número par:
• A redução nas chances de Bruna acertar é igual à diferença entre a probabilidade de a face superior sêr branca ou o número 5 e a probabilidade de a face superior sêr branca e o número 5:
• A redução nas chances de Carlos acertar é igual à diferença entre a probabilidade de a face superior sêr preta ou um número menor do quê 2 e a probabilidade de a face superior sêr preta e um número menor do quê 2:
• A redução nas chances de Diego acertar é igual à diferença entre a probabilidade de a face superior sêr preta ou um número maior do quê 2 e a probabilidade de a face superior sêr preta e um número maior do quê 2:
• A redução nas chances de Érica acertar é igual à diferença entre a probabilidade de a face superior sêr branca ou um número menor do quê 4 e a probabilidade de a face superior sêr branca e um número menor do quê 4:
Portanto, o jogador quê terá maior redução nas suas chances de acertar é Diego.
Resposta: alternativa d.
33. Considere o evento A"face superior sêr par" e o evento B"face superior sêr maior do quê 4". Assim, tem-se:
34. Considere o evento A"uma das faces superiores é 5" e o evento B "a soma das faces superiores é 8". Assim, tem-se:
A = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}
B = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
Página trezentos e oitenta e seis
35. De acôr-do com o enunciado, a quantidade de elemêntos do espaço amostral é n(U) = 52. Logo:
a)
b)
P(A/B) =
P(B/A) =
36. Considere o evento A"primeira carta sêr de paus" e o evento B/A "segunda carta sêr de copas". Sendo esses eventos sucessivos, tem-se:
P(A ∩ B) = P(A) ⋅ P(B/A) =
37. Sejam U o conjunto de todos os estudantes, I o conjunto dos estudantes quê falam inglês e E o conjunto dos estudantes quê falam espanhol. Desse modo, tem-se o seguinte diagrama:
Considere o evento A “o estudante fala espanhol” e o evento B “o estudante não fala inglês”. Pelo diagrama, tem-se:
n(B) = 600
n(A ∩ B) = 300
Logo:
P(A/B) =
Resposta: alternativa a.
38. De acôr-do com o enunciado, pode-se elaborar o qüadro a seguir:
Tamanho P |
Tamanho M |
Total |
|
|---|---|---|---|
Camisetas Lisas |
33 |
26 |
59 |
Camisetas Estampadas |
67 |
24 |
91 |
Total |
100 |
50 |
150 |
Considere o evento E “a camiseta é estampada” e o evento M “o tamãnho da camiseta é M”. Pelo qüadro, tem-se:
n(M) = 50
n(E ∩ M) = 24
Logo:
Resposta: alternativa c.
39. Considere o evento C “votar em branco” e o evento D “não votar no candidato B”. Pelo qüadro, tem-se:
P(D) = 60%
P(C ∩ D) = 20%
Logo: P(C/D) =
Resposta: alternativa d.
40. Considere o evento I “declaração inconsistente”, o evento F “declaração fraudulenta” e o evento C “declaração consistente e fraudulenta”. Segundo o enunciado, tem-se:
Logo:
Resposta: alternativa e.
41. Considere o evento A “digitar corretamente o penúltimo dígito da senha” e o evento B “digitar corretamente o último dígito da senha”. Os dígitos são distintos, então a probabilidade desejada é:
Resposta: alternativa b.
42. Restaram na sacola 25 pedrinhas brancas e 15 pedrinhas pretas, totalizando 40 pedrinhas. Considere o evento A “a primeira pedrinha jogada após o lanche é branca” e o evento B “a segunda pedrinha jogada após o lanche é branca”. Logo, a probabilidade desejada é:
Resposta: alternativa b.
43. Considere o evento A “a primeira bola retirada é branca”, o evento B “a segunda bola retirada é branca” e o evento C “a terceira bola retirada é preta”. Como cada bola retirada não é devolvida à caixa, tem-se:
Resposta: alternativa b.
44. Resposta pessoal. Sugestão de problema: Em uma caixa, há cinco bolas idênticas, diferentes apenas pela côr, sêndo três amarelas e duas vermelhas. Qual é a probabilidade de, retirando uma bola ao acaso, sem reposição, a primeira sêr amarela e a segunda sêr vermelha?
Considere o evento A “a primeira bola retirada é amarela” e o evento B “a segunda bola retirada é vermelha”. Como não há reposição das bó-linhas, tem-se:
45. Evandro e Mariana podem receber, na máquina de pelúcias, dois cachorros (evento A), ou dois gatos (evento B), ou dois ursos (evento C). Como esses eventos são mutuamente exclusivos, temos:
Logo, a probabilidade de Evandro e Mariana receberem bichos de pelúcia do mesmo tipo é .
46. Uma pessoa contraiu febre amarela e, um tempo depois, contraiu dengue tipo 2. Quando uma pessoa adqüire um dêêsses vírus e sobrevive, ela desen vólve memória imunológica, evitando um novo contágio pelo mesmo microrganismo. Desse modo, ela póde contrair 5 doenças: dengue tipo 1; dengue tipo 3; dengue tipo 4; zika e chikungunya.
Considere o evento A “essa pessoa contrair dengue” e o evento B “essa pessoa contrair chikungunya”. Como essa pessoa adqüire memória imunológica, então a probabilidade desejada é:
Resposta: alternativa c.
47. Seja U o espaço amostral do lançamento de um dado de seis faces. Considere os eventos A e B como aqueles em quê o número na face superior do dado no primeiro e no segundo lançamentos, respectivamente, é menor do quê 3. Como esses eventos são independentes, tem-se:
Página trezentos e oitenta e sete
48. Considere o evento A “obter um número maior quê 3 na face superior de um dado de seis faces” e o evento B “obter cara no lançamento de uma moeda”. Como esses eventos são independentes, tem-se:
49. Considere F e M os eventos em quê o sexo da criança quê nascerá é feminino e masculino, respectivamente. Suponha quê esses eventos sêjam equiprováveis, ou seja:
P(F) = P(M) =
Como esses eventos são independentes, tem-se:
P(F ∩ F ∩ F ∩ F) = P(F) ⋅ P(F) ⋅ P(F) ⋅ P(F) =
50. Em um baralho convencional de 52 cartas, há 13 cartas de cada naipe. Considere A e B os eventos em quê se retira uma carta de ouros e uma de espadas, respectivamente. Como esses eventos são independentes (por havêer reposição), tem-se:
51. Seja A o evento em quê a pessoa pega uma chave A na primeira gaveta e o cadeado aberto por ela na segunda gaveta e seja B o evento em quê a pessoa pega a chave B na primeira gaveta e um cadeado aberto por ela na segunda gaveta. Desse modo:
Como esses eventos são mutuamente exclusivos, tem-se:
Assim, a probabilidade de o cadeado sêr aberto pela chave escolhida é .
52. Sejam K e C os eventos em quê a jogada de uma moeda resulta em cara (K) e coroa (C), respectivamente, ambos sêndo eventos elementares equiprováveis. Pedro póde finalizar o jôgo de cinco maneiras distintas: (K, K, K), (K, K, C), (K, C), (C, K) e (C, C). Entre elas, três terminam com o resultado sêndo coroa, cujas probabilidades de ocorrência são:
P(K ∩ K ∩ C) = P(K) ⋅ P(K) ⋅ P(C) =
P(K ∩ C) = P(K) ⋅ P(C) =
P(C ∩ C) = P(C) ⋅ P(C) =
Como esses resultados são mutuamente exclusivos, a probabilidade de Pedro tirar coroa na última jogada é:
Resposta: alternativa d.
53. a) Sejam K e C os eventos em quê a jogada de uma moeda resulta em cara (K) e coroa (C), respectivamente. Como ambos são eventos complementares, segundo os dados do enunciado, tem-se:
P(K) + P(C) = 1 ⇒ 3 ⋅ P(C) + P(C) = 1 ⇒ P(C) =
Desse modo:
P(K) =
b) A ocorrência de apenas uma cara no lançamento da moeda três vezes, é dada pelo elemento (K, C, C) e suas permutações com repetição. Logo, a probabilidade dessa ocorrência é dada por:
54. Considere os eventos B1: retirar um cubo branco da primeira caixa e B2: retirar um cubo branco da segunda caixa. Como são eventos independentes, tem-se:
P(B1 ∩ B2) = P(B1) ⋅ P(B2) =
55. Considere os eventos A: o piloto sobe ao pódio se chover, B: o piloto sobe ao pódio se não chover, C: chove no dia da próva e D: não chove no dia da próva. Como os eventos C e D são complementares, segundo os dados do enunciado, tem-se:
P(C) + P(D) = 1 ⇒ P(D) = 1 − 0,75 = 0,25
Como os eventos A e C e os eventos B e D são independentes, segue quê:
Como esses resultados são mutuamente exclusivos, a probabilidade de o piloto subir ao pódio é:
56. Considere o evento A “retirar uma bola preta (A)” e o evento B "retirar uma bola branca (B)".
a) A ocorrência de “retirar duas bolas pretas e uma branca”, é representada pelo elemento (A, A, B) e suas permutações com repetição. Logo, a probabilidade dessa ocorrência é dada por:
b) Considere o evento C “as três bolas retiradas são da mesma cor” e o evento D “as três bolas retiradas não são todas da mesma cor”. O evento C é representado pêlos elemêntos (A, A, A) e (B, B, B), e suas probabilidades de ocorrência são dadas por:
Como C e D são eventos complementares, segue quê:
Por fim, a probabilidade de serem retiradas duas bolas pretas e uma branca, sabendo quê não foram retiradas três bolas de mesma côr, é:
57. Considere o evento S “o atleta utilizou a substância (S)” e o evento N “o atleta não utilizou a substância (N)”.
No exame feito pelo modo I, a ocorrência de o atleta quê utilizou a substância sêr um dos três sorteados dentre os 200 atletas é representada pelo elemento (S, N, N) e suas permutações com repetição. Logo, a probabilidade dessa ocorrência é dada por:
No exame feito pelo modo II, mantém-se a representação dos elemêntos quê indicam a ocorrência do atleta sorteado ter utilizado a substância, contudo, ele será sorteado dentre uma das 20 equipes com 10 atletas cada, ou seja:
No exame feito pelo modo III, há três possibilidades distintas de a equipe da qual faz parte o atleta quê utilizou a substância sêr uma das três sorteadas (por causa de suas permutações com repetição). Considerando quê cada equipe possui 10 atletas, tem-se:
Logo:
P(I) = P(II) = P(III)
Resposta: alternativa e.
58. Seja o intervalo real U =]0, 360] o espaço amostral dêêsse experimento aleatório. Logo, seu comprimento é 360. Como a roleta foi dividida em 12 regiões congruentes, o comprimento do evento A"obter um desconto mássimo de 10%" é:
360 ∶ 12 = 30
Admitindo quê todos os pontos do intervalo do espaço amostral são equiprováveis, temos:
Resposta: alternativa a.
Página trezentos e oitenta e oito
59. Segundo o enunciado, a probabilidade de quê P pertença a uma região contida em S é dada pela razão entre a medida da área dessa região e a medida da área de S. Logo, a probabilidade de quê P pertença a ambas as regiões será:
Sendo X a região em destaque na figura, pode-se afirmar quê a área é de (A ∩ B) = 42 (pi)" − 4 ⋅ SX = 16(pi)" − 4S X.
Observando o triângulo retângulo OLN, verifica-se, pela lei dos senos, quê med = 60°. Assim, as áreas, em cm2, do setor circular OMN e do triângulo OLN são, respectivamente, iguais a SOMN = e SOLN =
Logo:
cm2
Com base nesses valores, tem-se:
Como a medida da área do retângulo S, em cm2, é 50 ⋅ 20 = 1.000, a probabilidade P desejada será:
60. Seja o intervalo real U =]0, 360] o espaço amostral do experimento. Logo, seu comprimento é 360. De modo análogo, o comprimento do:
• evento X “o ponteiro parar no setor roxo” é 45;
• evento S “o ponteiro parar no setor cor-de-rosa” é 30;
• evento O “o ponteiro parar no setor marrom” é 90;
• evento Z “o ponteiro parar no setor azul” é 75;
• evento A “o ponteiro parar no setor amarelo” é 120.
a) O setor amarelo é o único cujo ângulo central é obtuso. Assim, a probabilidade de quê o ângulo central do setor seja obtuso é:
Os setores quê possuem ângulos centrais agudos são o roxo, o cor-de-rosa e o azul. Então, a probabilidade de quê o ângulo central do setor seja agudo é:
b) Dos cinco ângulos, os únicos quê são internos de um polígono regular são o ângulo de 90° (ângulo interno do quadrado) e o ângulo de 120° (ângulo interno do hekzágono regular). Assim, ao girar a roleta, a probabilidade de o ponteiro não parar em nenhum dêêsses dois setores é:
Logo, a probabilidade de quê ao menos um dos dois giros pare em um setor cujo ângulo central é um ângulo interno de um polígono regular é:
61. Como os ônibus saem a cada 30 minutos, considere o intervalo real U =]0, 30] como espaço amostral dêêsse experimento aleatório. Pelos horários da tabéla, considere também o intervalo:
• B =]0, 10] como o evento “viajar com a empresa BOMPASSEIO”;
• A =]10, 30] como o evento “viajar com a empresa ANDABEM”.
Desse modo, o comprimento do espaço amostral U é 30, o comprimento do evento B é 10 e o comprimento do evento A é 20. Admitindo-se quê todos os pontos do intervalo do espaço amostral são equiprováveis, então:
;
Desse modo, a probabilidade de Carlos viajar em um ônibus da empresa ANDABEM é duas vezes maior do quê a probabilidade de ele viajar em um ônibus da BOMPASSEIO.
Resposta: alternativa d.
62. Considere o intervalo real U =]0, 4(pi)"r2] como o espaço amostral dêêsse experimento, compreendendo toda a região do alvo. Considere também o intervalo:
• A =]0, (pi)"r2] como o evento "acertar a região I do alvo”;
• B =](pi)"r2, 4(pi)"r2] como o evento “acertar a região II do alvo”.
Desse modo, o comprimento do espaço amostral U é 4(pi)"r2 e o comprimento do evento B é 4(pi)"r2 − (pi)"r2 = 3(pi)"r2. Admitindo-se quê todos os pontos do intervalo do espaço amostral são equiprováveis, então:
Resposta: alternativa c.
63. Seja o intervalo real U =]0, 360] o espaço amostral do experimento realizado individualmente em cada uma das três roletas. Logo, seu comprimento é 360. De modo análogo, o comprimento do evento A “a seta parar na região A”, o do evento B “a seta parar na região B” e o do evento C “a seta parar na região C” correspondem a:
• na roleta 1, A é 180, B é 90 e C é 90;
• na roleta 2, A é 120, B é 120 e C é 120;
• na roleta 3, A é 120, B é 30 e C é 210.
Desse modo, a probabilidade de as três roletas serem giradas e a seta parar simultaneamente em uma mesma região é:
Assim, conclui-se quê:
P(A) > P(C) > P(B)
Resposta: alternativa c.
64. Seja o intervalo real U = [0, 60] o espaço amostral do experimento em quê uma das pessoas chega ao local, em quê 0 indica 12 h e 60 indica 13 h. Assim, seu comprimento é 60. Seja X ∈ [0, 60] o horário em quê a primeira pessoa chegará ao local do encontro e Y ∈ [0, 60] o horário em quê a segunda pessoa chegará. Para quê as duas se encontrem, é necessário quê:
As duas pessoas encontram-se quando as regiões das inequações e se intersectam no plano cartesiano XY:
Página trezentos e oitenta e nove
A área em destaque no plano XY corresponde à área de um quadrado de comprimento 60 do qual foram retirados dois triângulos iguais, com altura e base de medida 40.
Logo, a probabilidade de as duas pessoas se encontrarem é igual à razão entre a área S destacada na côr alaranjada no plano e a área T quê compreende todas as possibilidades de chegada das duas pessoas no local de encontro, cujo comprimento é:
60 ⋅ 60 = 3.600
Então:
Resposta: alternativa c.
Atividades complementares
1. Representando o espaço amostral, temos:
1º lançamento |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|---|---|---|---|---|---|---|---|---|---|
2º lançamento |
1 |
(1, 1) |
(2, 1) |
(3, 1) |
(4, 1) |
(5, 1) |
(6, 1) |
(7, 1) |
(8, 1) |
2 |
(1, 2) |
(2, 2) |
(3, 2) |
(4, 2) |
(5, 2) |
(6, 2) |
(7, 2) |
(8, 2) |
|
3 |
(1, 3) |
(2, 3) |
(3, 3) |
(4, 3) |
(5, 3) |
(6, 3) |
(7, 3) |
(8, 3) |
|
4 |
(1, 4) |
(2, 4) |
(3, 4) |
(4, 4) |
(5, 4) |
(6, 4) |
(7, 4) |
(8, 4) |
|
5 |
(1, 5) |
(2, 5) |
(3, 5) |
(4, 5) |
(5, 5) |
(6, 5) |
(7, 5) |
(8, 5) |
|
6 |
(1, 6) |
(2, 6) |
(3, 6) |
(4, 6) |
(5, 6) |
(6, 6) |
(7, 6) |
(8, 6) |
|
7 |
(1, 7) |
(2, 7) |
(3, 7) |
(4, 7) |
(5, 7) |
(6, 7) |
(7, 7) |
(8, 7) |
|
8 |
(1, 8) |
(2, 8) |
(3, 8) |
(4, 8) |
(5, 8) |
(6, 8) |
(7, 8) |
(8, 8) |
|
P(soma 8) =
Resposta: alternativa e.
2. Considerando o evento A como a retirada de peça perfeita, tem-se:
Resposta: alternativa c.
3. Segundo o enunciado, n(U) = 200. Considere o evento A"não sêr solteiro". Desse modo, tem-se:
P(A) == 0,55
Resposta: alternativa c.
4. O número de diagonais de um hekzágono regular é:
A quantidade de combinações distintas para a escolha de dois vértices do hekzágono é dada por:
C 6, 2 = = 15
Desse modo, a probabilidade desejada é igual a:
P =
Resposta: alternativa c.
5. Seja U o espaço amostral do experimento. Pelo princípio fundamental da contagem, tem-se:
n(U) = 6 ⋅ 6 = 36
Considere o evento A"soma das faces sêr maior ou igual a 9" e o evento B"soma das faces sêr menor quê 9".
A = {(3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)} ⇒ n(A) = 10
Como os eventos A e B são complementares, segue quê:
Resposta: alternativa d.
6. Sejam x a quantidade de bolas amarelas na urna e n a quantidade total de bolas na urna. De acôr-do com a informação I, conclui-se quê a quantidade de bolas vermelhas é 2x. De acôr-do com a informação II, tem-se:
A quantidade de bolas brancas é dada por n − x − 2x, o quê equivale a:
De acôr-do com a informação III, tem-se quê:
Logo, a quantidade de bolas brancas é:
8 + 4 = 12
Resposta: alternativa c.
7. Pelo princípio fundamental da contagem, o número de elemêntos do espaço amostral é dado por:
6 ⋅ 6 = 36
Considere as possibilidades de sair um número menor do quê 3 nos lançamentos:
A = {(1, 1), (2, 1), (1, 2), (2, 2)} ⇒ n(A) = 4
Assim, a probabilidade é dada por:
P(A) =
Resposta: alternativa d.
8. Considere o evento A"o morador se atrasa para o serviço se chover", o evento B"o morador se atrasa para o serviço se não chover", o evento C"chove no dia" e o evento D"não chove no dia". Como os eventos C e D são complementares, segundo os dados do enunciado, tem-se:
Como os eventos A e C e os eventos B e D são independentes, segue quê:
Como esses resultados são mutuamente exclusivos, a probabilidade de o morador se atrasar para o serviço é:
P = 0,15 + 0,175 = 0,325
Resposta: alternativa c.
9. Sejam o evento M "paciente sêr mulher", o evento A "paciente ter mais de 18 anos" e o evento H "paciente sêr homem", tem-se:
Logo, a probabilidade de sêr escolhido um paciente aleatoriamente e ele sêr homem, sabendo-se quê tem mais de 18 anos, é:
Resposta: alternativa e.
10. Considere o evento A "um parafuso sêr produzido pela máquina A" e o evento D"o parafuso sêr defeituoso". Como na caixa há 100 parafusos produzidos pela máquina A e 100 produzidos pela máquina B, espera-se quê haja 15 parafusos defeituosos produzidos pela máquina A e 5 parafusos defeituosos produzidos pela máquina B:
n(D) = 15 + 5 = 20
n(A ∩ D) = 15
Desse modo, a probabilidade de um parafuso sêr produzido pela máquina A, sabendo-se quê ele é defeituoso é:
Resposta: alternativa e.
Página trezentos e noventa
11. A probabilidade de o casal ter no mássimo dois filhos de olhos azuis é a soma das probabilidades de não terem filho de olhos azuis com a de terem 1 filho de olhos azuis e com a de terem 2 filhos de olhos azuis.
P(filho não ter olhos azuis) =
P(nenhum filho de olhos azuis) =
P(1 filho de olhos azuis) =
P(2 filhos de olhos azuis) =
Portanto, a probabilidade desejada é dada por:
Resposta: alternativa c.
12. Das 15 kestões difíceis, 9 são sobre sistema respiratório. Logo, a probabilidade P do evento desejado é:
P = = 0,6 = 60%
Resposta: alternativa b.
13. Como, na palavra chatbot, a letra t se repete duas vezes, o número total de anagramas possíveis é dado por . O evento desejado ocorre quando os anagramas começam e terminam com t, podendo as demais lêtras estar em qualquer ordem. Logo, a probabilidade Q do evento desejado é dada por:
Então, aproximadamente, 4,8%.
Resposta: alternativa a.
14. Considere:
• P o evento"escolher aleatoriamente a caixa P e retirar ao acaso um medicamento vencido";
• Q o evento"escolher aleatoriamente a caixa Q e retirar ao acaso um medicamento vencido";
• R o evento"escolher aleatoriamente a caixa R e retirar ao acaso um medicamento vencido".
Desse modo, a probabilidade de se escolher aleatoriamente uma das caixas e retirar dela uma cartela com medicamento com prazo de validade ultrapassado é dada por:
Resposta: alternativa d.
15. Pelos dados da tabéla, a probabilidade P do evento desejado é:
P = ≃ 0,56
Resposta: alternativa b.
16. Para sortear o número 50, é necessário sortear 0 (zero), algarismo da ordem das unidades, entre os algarismos de 0 a 9, e, em seguida, sortear 5, algarismo da ordem das dezenas, entre os algarismos de 1 a 5. Logo, a probabilidade P de o número 50 sêr sorteado é:
Para sortear o número 02, é necessário sortear 2, algarismo da ordem das unidades, entre os algarismos de 0 a 9, e, em seguida, sortear 0 (zero), algarismo da ordem das dezenas, entre os algarismos de 0 a 5. Logo, a probabilidade Q de o número 02 sêr sorteado é:
Resposta: alternativa a.
17. De acôr-do com o enunciado, foram colocados na urna 200 cartões com nomes de estudantes do primeiro ano, 300 do segundo ano e 300 do terceiro ano. Então, a probabilidade P do evento desejado é:
P =
Resposta: alternativa e.
18. Na sequência das três figuras ordenadas pelo jogador, há duas ocorrências favoráveis a ele. O total de possibilidades distintas e como as quatro figuras podem sêr ordenadas pela banca, por havêer duas figuras repetidas, é de . Desse modo, a probabilidade P(J) de o jogador vencer é:
Resposta: alternativa c.
19. Identificando por A, B, C, D, E, F, G, H, I e J as dez cadeiras, da esquerda para a direita, as cinco garotas podem estar sentadas nas seguintes cadeiras adjacentes:
(A, B, C, D, E), (B, C, D, E, F), (C, D, E, F, G), (D, E, F, G, H), (E, F, G, H, I) e (F, G, H, I, J)
dêsses 6 modos possíveis, em apenas dois, (A, B, C, D, E) e (F, G, H, I, J), os cinco garotos também poderão se sentar em cadeiras adjacentes. Logo, a probabilidade P do evento desejado é:
P =
Resposta: alternativa c.
20. Considerando o evento A"os lançamentos da moeda formarem exatamente o nome ALINE" e o evento J"os lançamentos da moeda formarem exatamente o nome JORGE". Por serem eventos mutuamente exclusivos, tem-se:
Resposta: alternativa c.
Capítulo 6 • Matrizes e sistemas lineares
Atividades
1. Ao associar as lêtras do alfabeto aos números de acôr-do com o qüadro fornecido no enunciado, obtém-se:
U |
N |
I |
M |
O |
N |
T |
E |
S |
|---|---|---|---|---|---|---|---|---|
21 |
14 |
9 |
13 |
15 |
14 |
20 |
5 |
19 |
Desse modo, a matriz quê codifica essa palavra é:
Resposta: alternativa b.
2. A matriz A = 3x3, em quê = 3i − j2, é dada por:
3. Analisando a soma dos elemêntos de cada linha, coluna, diagonal principal e diagonal secundária da matriz A, conclui-se quê todas as somas são iguais a 12. Do mesmo modo, analisando a soma dos elemêntos de cada linha, coluna, diagonal principal e diagonal secundária da matriz B, conclui-se quê todas as somas são iguais a 34. Desse modo, as matrizes A e B são quadrados mágicos. Por outro lado, tomando-se, por exemplo, a soma dos elemêntos da diagonal principal da matriz C, quê é igual a 16, e a soma dos elemêntos da diagonal secundária, quê é 15, percebe-se quê elas são distintas. Logo, a matriz C não é um quadrado mágico.
Página trezentos e noventa e um
4. a) A matriz , em quê , é dada por:
b) A matriz , em quê , é dada por:
c) A matriz , em quê = , é dada por:
5. Segundo a matriz do enunciado, o tempo de treinamento do atleta B no terceiro dia corresponde ao elemento a23.
Como tem-se:
Logo, o tempo de treinamento do atleta B foi de 90 min ou 1 h e 30 min.
Resposta: alternativa a.
6. Considerando as possíveis distâncias entre os vértices do quadrado, pode-se obtêr:
• quando i = j, ;
• quando i e j forem números consecutivos ou quando |i − j| = 3, ;
• quando |i − j| = 2, , pois corresponderá à medida da diagonal do quadrado de lado 1.
Logo:
Resposta: alternativa b
7. Considere a matriz , em quê = i − j.
Os elemêntos de sua diagonal principal são nulos, uma vez quê esses elemêntos correspondem aos casos em quê i = j.
A soma dos elemêntos de sua diagonal secundária é:
Desse modo, conclui-se quê:
8. a) Com base nas informações do enunciado, é possível determinar as seguintes matrizes:
b) Considere a matriz C = A + B. Desse modo, tem-se:
9. a)
Desse modo, tem-se:
A + B = B + A
b)
Desse modo, tem-se:
A + (B + C) = (A + B) + C
c)
Desse modo, tem-se:
d)
Desse modo, tem-se:
C + (−C) =
10. Por definição, como, pode-se admitir quê:
11. a)
b)
c)
d)
12. a)
Desse modo, tem-se:
2 ⋅ (3X) = (2 ⋅ 3)X
b)
Desse modo, tem-se:
2 ⋅ (X + Y) = 2X + 2Y
c)
Desse modo, tem-se:
d)
Desse modo, tem-se:
1 ⋅ Y = Y
Página trezentos e noventa e dois
13. As matrizes A e B são de mesma ordem. Além díssu, ao se multiplicar uma matriz por um número real, sua ordem não se altera, de modo quê é possível efetuar os seguintes cálculos:
a)
b)
14. Pelo enunciado, tem-se:
e
a)
b)
15. a) Como a primeira matriz é de ordem 3 × 4 e a segunda é de ordem 4 × 2, é possível multiplicá-las, nessa ordem, e o resultado será uma matriz A cujos elemêntos são:
Logo:
b) Como a primeira matriz é de ordem 2 × 2, a segunda é de ordem 3 × 3 e 2 ≠ 3, conclui-se quê é não é possível determinar o produto entre elas.
c) Como a primeira matriz é de ordem 3 × 1 e a segunda é de ordem 1 × 3, é possível multiplicá-las, nessa ordem, e o resultado será uma matriz C dada por:
16. Considerando as matrizes A e B do enunciado, tem-se:
Como AB ≠ BA, segue quê A e B não comutam.
17. Segundo o enunciado:
e
Desse modo, por definição, o elemento é dado por:
18. a)
b)
c)
O elemento da segunda linha e da segunda coluna da matriz T ⋅ E representa a quantidade de zíperes médios encomendados para o mês de novembro, isto é, 650 zíperes.
d) Resposta pessoal. Sugestão de problema: Qual é a quantidade total necessária de zíperes pequenos para confeksionar as mochilas encomendadas para os meses de outubro a dezembro?
De acôr-do com a matriz T ⋅ E elaborada no item anterior, a quantidade total necessária de zíperes para confeksionar a demanda de mochilas dêêsse trimestre é igual à soma dos elemêntos da primeira linha da matriz, isto é:
300 + 700 + 1.000 = 2.000
19. Desenvolvendo a multiplicação das matrizes, obtém-se:
Isolando x em I e substituindo, em II, tem-se:
4 ⋅ (2 − y) − ay = 3
Isolando x em I e substituindo, em III, tem-se:
a ⋅ (2 − y) − 4y = −1
Assim, forma-se o sistema:
Resolvendo o último sistema, obtém-se:
a = 2
20. Associando números às lêtras do alfabeto, conforme o enunciado, tem-se:
F |
L |
O |
R |
|---|---|---|---|
6 |
12 |
15 |
18 |
Logo, a matriz C quê representa essa palavra é:
Seja . Desse modo, tem-se:
Assim, formam-se os seguintes sistemas:
e
Resolvendo os dois últimos sistemas, obtém-se a11 = −6, a12 = 6, a21 = −7 e a22 = 11. Portanto, conclui-se quê:
Resposta: alternativa b.
Página trezentos e noventa e três
21. Somente a equação do item a é linear, pois as demais apresentam uma multiplicação entre duas ou mais incógnitas ou, ainda, incógnitas com expoente diferente de 1.
Resposta: alternativa a.
22. Substituindo cada par ordenado no primeiro membro da equação 2x − 3y = 9, obtém-se:
• 2 ⋅ 0 − 3 ⋅ (−3) = 9
Portanto, (0, −3) é solução da equação.
• 2 ⋅ 1 − 3 ⋅ 2 = −4 ≠ 9
Portanto, (1, 2) não é solução da equação
•
Portanto, é solução da equação.
•
Portanto, não é solução da equação.
23. Não, pois, qualquer quê seja o par ordenado (a, b), tem-se quê:
24. Para quê (−1, 2, −3) seja solução da equação 2a − 4b + mc = 0, é necessário quê:
25. Uma equação linear é dita homogênea quando seu termo independente é igual a 0. Logo, a equação x − 4y + z = m2 − 4
será homogênea se m2 − 4 = 0, isto é, se m = 2 ou m = −2.
26. Substituindo o par ordenado (−1, 2) no primeiro membro de cada equação do sistema, obtém-se:
Como o par ordenado satisfaz a ambas as equações, então (−1, 2) é solução do sistema.
27. Considere o sistema:
Multiplicando a segunda equação por −2 e adicionando-a à primeira equação, obtém-se:
2x − y + (−2x − 6y) = 15 + (−50) ⇒ y = 5
Substituindo y = 5 na primeira equação, obtém-se x = 10.
Portanto, conclui-se quê S = {(10, 5)}.
28. Considere as variáveis a e m como a distância percorrida, em km, pelo trabalhador de automóvel e de motocicleta, respectivamente. Pelo enunciado, tem-se:
(I)
Isolando a em II e substituindo-o em I, obtém-se:
Substituindo m = 325 em II, obtém-se:
a = 225
Logo, o trabalhador deve percorrer 325 km de motocicleta e 225 km de automóvel para quê o custo total mensal seja R$ 70,00.
29. a) Considere as caixas do tipo A como x e as caixas do tipo B
como y. Pelo enunciado, forma-se o sistema:
b) Isolando x em I e substituindo-o em II, obtém-se:
Substituindo y = 37 em I, obtém-se x = 21.
Logo, o caminhão levará 21 caixas do tipo A e 37 do tipo B.
30. Resposta pessoal. Sugestão de problema: Sarah e mateus são irmãos. A diferença entre o dôbro da idade de Sarah e a idade de mateus é 5 anos. Além díssu, a soma das idades deles é 7 anos. Calcule a idade de cada irmão.
Considerando x a idade de Sarah e y a idade de mateus, obtém-se o sistema:
Resolvendo esse sistema, obtém-se x = 4 e y = 3.
Substituindo o par ordenado (4, 3) no primeiro membro de cada equação do segundo sistema da atividade, obtém-se:
Assim, ambos os sistemas têm o mesmo conjunto solução S = {(4, 3)}.
31. a) 
Como os gráficos se intersectam em um único ponto, o sistema é possível e determinado.
b) 
Como as retas dos gráficos são paralelas e distintas, o sistema é impossível.
c) 
Como as retas dos gráficos são paralelas e coincidentes, o sistema é possível e indeterminado.
32. a) Substituindo a terna ordenada (2, −1, 1) no primeiro membro de cada equação do sistema, obtém-se:
Como a terna ordenada satisfaz às equações, então (2, −1, 1) é solução do sistema.
Página trezentos e noventa e quatro
b) Substituindo a terna ordenada (0, 0, 0) no primeiro membro de cada equação do sistema, obtém-se:
Como a terna ordenada não satisfaz às equações, então (0, 0, 0) não é solução do sistema.
33. Do enunciado, obtém-se o sistema a seguir:
De III, temos quê q = 10. Substituindo q = 10 em I e II, forma-se o sistema:
Multiplicando IV por −2 e adicionando à equação V, obtém-se:
Substituindo p = 30 em IV, tem-se: m = 18
Logo, a diferença entre o número de quartos triplos e o número de quartos duplos é: p − m = 30 − 18 = 12
Resposta: alternativa c.
34. Considerando como p0, p1 e p2 os comprimentos, em passos, da ponte, da pista 1 e da pista 2, respectivamente, obtém-se o sistema:
Tomando I − II, conclui-se quê p1= 400. Substituindo p1= 400 em III, conclui-se quê p 2 = 350. Portanto, o comprimento da ponte, em passos, é dado por:
p0 = 757 − p1 − p2 = 757 − 400 − 350 = 7
Resposta: alternativa c.
35. a) Considerando (alfa)" = x, (beta)" = y e ω = z, tem-se:
Isolando x na primeira equação e y na segunda, obtém-se:
x = z e y =
Logo, o conjunto solução do sistema é , sêndo esse um sistema possível e indeterminado.
b) Como y = , a menor solução inteira positiva ocorre para z = 2. Logo: S = {(2, 1, 2)}
c) Para (alfa)" = 2, (beta)" = 1 e ω = 2, tem-se: 2H2 + O2 → 2H2O
36. a) Considerando o sistema dado:
Isolando y na equação II, obtém-se:
y = 20
Substituindo y = 20 em I, tem-se:
3x + 2 ⋅ 20 = 70 ⇒ x = 10
Portanto: S = {(10, 20)}
b) Considerando o sistema dado:
Isolando z na equação III, obtém-se:
Substituindo z = 3 em II, tem-se:
Substituindo y = 7 e z = 3 em I
Portanto:
c) Considerando o sistema dado, tem-se:
Isolando d na equação IV, obtém-se:
d = 1
Substituindo d = 1 em III, tem-se:
Substituindo c = 1 e d = 1 em II, tem-se:
Substituindo b = 1, c = 1 e d = 1 em I, tem-se:
Portanto:
d) Considerando o sistema dado, tem-se:
Analisando a equação III, verifica-se quê não há nenhum número real para z quê satisfaça essa equação. Portanto:
S = ∅
e) Considerando o sistema dado, tem-se:
Analisando a equação II, verifica-se quê a igualdade é válida para qualquer valor real atribuído a y, considerando-se y = λ, λ ∈ ℝ. Desse modo, isolando x em I, conclui-se quê o conjunto solução dêêsse sistema é:
f) Considerando o sistema dado, tem-se:
Analisando a equação IV, verifica-se quê não há nenhum número real para d quê satisfaça essa equação. Portanto:
S = ∅
37. Considerando o sistema dado, tem-se:
Isolando z na equação III, obtém-se: z =
Substituindo z = em II, tem-se:
Substituindo y = e z = em I, tem-se:
Seja t = (alfa)" um número real qualquer.
Desse modo, a solução do sistema é dada por:
38. a) Considerando o sistema dado, tem-se:
Primeiro, substituímos a equação L2 pela equação L5, em quê L5 é o resultado da adição de L2 com o produto de L1 por −1.
Página trezentos e noventa e cinco
Depois, substituímos a equação L3 pela equação L6, em quê L6 é a adição de L3 com L2. Por fim, substituímos a equação L4 pela equação L7, em quê L7 é a adição de L4 com L3.
Resolvendo o sistema escalonado, obtém-se:
• −2t = −8 ⇒ t = 4
• 2z − 2 ⋅ 4 = −2 ⇒ z = 3
• −2y + 2 ⋅ 3 − 2 ⋅ 4 = 2 ⇒ y = −2
• x + (−2) − 3 + 4 = 0 ⇒ x = 1
Logo, o conjunto solução do sistema é S = {(1, −2, 3, 4)}, sêndo esse um sistema possível e determinado.
b) Considerando o sistema dado, tem-se:
Primeiro, trocamos de lugar as equações L1 e L2.
Depois, substituímos a equação L1 pela equação L4, em quê L4 é o resultado da adição de L1 com o produto de L2 por −2. Por fim, substituímos a equação L3 pela equação L5, em quê L5 é o resultado da adição de L3 com o produto de L2 por −1.
Como as equações L4 e L5 são idênticas, temos um sistema escalonado com três incógnitas e duas equações. Admitindo quê a incógnita z = λ, λ ∈ ℝ, obtém-se:
• 5y = 5 ⇒ y = 1
• x − 1 + 2 ⋅ λ = 2 ⇒ x = 3 − 2λ
Logo, o conjunto solução do sistema é S = {(3 − 2λ, 1, λ) | λ ∈ ℝ}, sêndo esse um sistema possível e indeterminado.
39. a) Considerando o sistema dado, tem-se:
Primeiro, trocamos de lugar as equações L1 e L2:
Depois, substituímos a equação L1 pela equação L4, em quê L4 é o resultado da adição de L1 com L2. Posteriormente, substituímos a equação L3 pela equação L5, em quê L5 é o resultado da adição de L3 com o produto de L2 por −2.
Por fim, substituímos a equação L5 pela equação L6, em quê L6 é o resultado da adição de L5 com L4.
Resolvendo o sistema escalonado, obtém-se:
• −3z = 0 ⇒ z = 0
• 3y + 3 ⋅ 0 = 9 ⇒ y = 3
• x + 2 ⋅ 3 + 4 ⋅ 0 = 4 ⇒ x = −2
Logo: S = {(−2, 3, 0)
b) Considerando o sistema dado, tem-se:
Primeiro, trocamos de lugar as equações L1 e L2:
Depois, substituímos a equação L1 pela equação L4, em quê L4 é o resultado da adição de L1 com o produto de L2 por −2. Posteriormente, substituímos a equação L3 pela equação L5, em quê L5 é o resultado da adição de L3 com o produto de L2 por −3.
Por fim, substituímos a equação L5 pela equação L6, em quê L6 é o resultado da adição de L5 com o produto de L4 por .
Resolvendo o sistema escalonado, obtém-se:
•
• −5y − 6 ⋅ 2 = −2 ⇒ y = −2
• x + 2 ⋅ (−2) + 4 ⋅ 2 = 5 ⇒ x = 1
Logo: S = {(1, −2, 2)}
40. Sejam x, y e z, respectivamente, as quantidades, em grama, dos alimentos dos tipos A, B e C. Considerando as informações do enunciado, tem-se:
Simplificando as equações, tem-se:
Isolando x em I e substituindo-o em II e III, obtém-se:
Resolvendo o último sistema, obtém-se:
z = 20
Portanto, a mistura deve ter 20 gramas do tipo de alimento C.
41. Do enunciado, obtém-se o seguinte sistema:
Substituindo x por y + z em II e III, tem-se:
Resolvendo o último sistema, obtém-se: y = 800
Logo, o valor da gratificação foi R$ 800,00.
Página trezentos e noventa e seis
Atividades complementares
1. Analisando os elemêntos da matriz genérica A e seus valores correspondentes, pode-se determinar qual possibilidade apresenta uma despesa mínima, em milhares de reais:
• a11 + a22 + a33 = 53 + 87 + 36 = 176
• a11 + a23 + a32 = 53 + 41 + 92 = 186
• a12 + a23 + a31 = 96 + 41 + 60 = 197
• a13 + a22 + a31 = 37 + 87 + 60 = 184
Logo, a despesa mínima será R$ 176.000,00.
Resposta: alternativa a.
2.
Resposta: alternativa b
3. Analisando cada uma das alternativas, tem-se:
a) Falsa. A quantidade de produtos P2 vendidos pela loja L2 é 10.
b) Falsa. A quantidade de produtos P1 vendidos pela loja L3 é 20.
c) Falsa. A soma das quantidades de produtos P3 vendidos pelas três lojas é 39.
d) Falsa. A soma das quantidades de produtos P i vendidos pelas três lojas Li, i = 1, 2, 3, é igual a: 30 + 10 + 11 = 51
e) Verdadeira. A soma das quantidades dos produtos dos tipos P1 e P2 vendidos na loja L1 é: 30 + 15 = 45
Resposta: alternativa e.
4.
Resposta: alternativa a.
5.
Resposta: alternativa b.
6. Seja s a posição das bicicletas em cada instante de tempo t. Para obtêr o momento do encontro delas, forma-se o sistema:
Isolando s em I e II e igualando as expressões encontradas, obtém-se: 10 + 20t = 70 − 10t ⇒ t = 2
Logo, as bicicletas se encontram em t = 2 s.
Resposta: alternativa c.
7. Seja . Desse modo, tem-se:
Por meio da igualdade, é possível determinar quê:
m11 = 15; m13 = 13; m12 = 15 + 26 − 40 = 1
m21 = 19; m 23 = 13; m22 = 19 + 26 − 44 = 1
m31 = 1; m33 = 0; m32 = 1 + 0 + 10 = 11
Associando números às lêtras do alfabeto e ao sín-bolo de exclamação, conforme o enunciado, tem-se:
m11 |
m12 |
m13 |
m21 |
m22 |
m23 |
m31 |
m32 |
m33 |
|---|---|---|---|---|---|---|---|---|
15 |
1 |
13 |
19 |
1 |
13 |
1 |
11 |
0 |
P |
A |
N |
T |
A |
N |
A |
L |
! |
Resposta: alternativa c
8. De acôr-do com o enunciado, tem-se:
Desse modo, conclui-se quê:
Logo, as coordenadas de P(minutos)" são:
Resposta: alternativa e.
9. Com base na matriz M do enunciado, tem-se:
Página trezentos e noventa e sete
Analisando cada uma das alternativas, tem-se:
a) Falsa. Existem 4 pares de pessoas diferentes quê não possuem conexões de grau 2.
b) Verdadeira.
c) Falsa. Existem 2 pares de pessoas diferentes quê possuem conexões de grau 2 diferentes.
d) Falsa. Existem 2 pessoas quê possuem conexões de grau 2 com todas as outras pessoas da rê-de social.
e) Falsa. Segundo a matriz M, existem 2 pessoas Pi(i ≠ 3) tal quê Pi e P3 seguem-se mutuamente.
Resposta: alternativa b.
10. Como o sanduíche de 250g possui 500 calorias, então cada grama de sanduíche possui uma quantia de calorias igual a:
500 ∶ 250 = 2
A porção de batatas possui 200 g e 560 calorias, ou seja, cada grama de batata possui uma quantia de calorias igual a:
560 ∶ 200 = 2,8
Logo, a expressão algébrica quê relaciona corretamente x, y e a quantidade de calorias para a refeição é dada por:
2x + 2,8y = 462
Resposta: alternativa a.
11. Considerando o sistema dado, tem-se:
Isolando x em I e substituindo-o em II, tem-se:
3 ⋅ (4 − 2y) − y = 5 ⇒ y = 1
Substituindo y = 1 em I, obtém-se:
x = 2
Portanto, o gráfico dêêsse sistema é compôzto de duas retas quê se intersectam no ponto (2, 1). Além díssu, ao substituir x por 0 em I, obtém-se y = 2 e, ao substituir x por 0 em II, obtém-se y = −5. Assim, as retas quê representam as equações I e II interceptam o eixo y nos pontos (0, 2) e (0, −5), respectivamente.
Resposta: alternativa e.
12. Simplificando as equações do sistema dado, tem-se
Substituindo a equação L2 pela equação L3, em quê L3 é o resultado da adição de L2 com o produto de L1 por −1, tem-se:
Resolvendo o sistema escalonado, obtém-se:
z = −5 − 2y
x = 30 − 5y − 3 ⋅ (−5 − 2y) = y + 45
Desse modo, tem-se:
x + y + z = y + 45 + y −5 −2y = 40
Resposta: alternativa c.
13. Considere as variáveis x, y e z como representação para pão, fruta e iogurte, respectivamente. Desse modo, obtém-se o seguinte sistema e sua simplificação:
)
Isolando z em I, obtém-se: z = 4 − 2x
Substituindo z = 4 − 2x em III, tem-se:
4x + 3 ⋅ (4 − 2x) = 10 ⇒ x = 1
Substituindo x = 1 em I, tem-se: z = 2
Substituindo x = 1 e z = 2 em II, tem-se: y = 3
Portanto essa pessoa deve ingerir uma pôr-ção de pão, 3 pôr-ções de fruta e duas pôr-ções de iogurte para consumir as quantidades de nutrientes recomendadas para seu café da manhã.
Capítulo 7 • Transformações geométricas
Atividades
1. Construindo retas verticais pelo centro das imagens dos itens a e b, é possível observar simetria de reflekção das imagens em relação às respectivas retas. Já na figura do item c, não é possível construir nenhuma reta passando pela imagem de modo a determinar uma simetria de reflekção da imagem em relação à reta.
2. Em relação à figura F, tem-se:
• A figura I representa a reflekção da figura F em relação a uma reta vertical;
• A figura II representa a translação da figura F pelo vetor , ou seja, a translação quê tem sentido ôpôsto ao de ;
• A figura III representa a translação da figura F pelo vetor ;
• A figura IV representa a rotação da figura F em 180° em torno do ponto O ou, ainda, a reflekção de F em relação a esse ponto;
• A figura V representa a reflekção da figura F em relação a uma reta horizontal.
Desse modo, conclui-se quê:
a) A figura I.
b) A figura III.
c) A figura IV.
3.
4. Para quê haja simetria, O deve sêr o ponto médio do segmento formado por um ponto P qualquer da figura original e o seu ponto correspondente P(minutos)" da figura simétrica.
Destacando três pontos da figura original, relativos aos vértices do triângulo preto, pode-se determinar seus simétricos e, consequentemente, a forma da nova figura:
Resposta: alternativa e.
Página trezentos e noventa e oito
5. A partir da figura original, são construídas as seguintes figuras, obtidas por meio das transformações geométricas descritas em cada item:
• A figura ficaria igual à apresentada no item b, pois, ao fazer uma rotação de 180°, no sentido horário ou anti-horário, obtém-se a mesma figura.
6. Para recolocar a tela na posição original, pode-se fazer uma rotação de um ângulo de 135° em torno do ponto B no sentido horário ou uma rotação de um ângulo de 225° em torno do ponto B no sentido anti-horário. Entre essas duas opções, a quê apresenta menor ângulo é a primeira.
Resposta: alternativa b.
7. Analisando o espaço à direita do espaço indicado pela seta na figura A, percebe-se quê a peça escolhida deve ter um triângulo liso de côr cinza claro, ou seja, exclui-se a possibilidade de se utilizar a peça 1.
Ao rotacionar a peça 2 em 90° no sentido anti-horário (ou 270° no sentido horário), a peça ficará na posição correta quê preenche o espaço indicado na figura A.
Resposta: alternativa c.
8. Por causa das figuras no centro das cartas, as imagens das cartas 5 de espadas e 6 de cópas não apresentarão a mesma imagem após uma rotação de 180°. Dessa forma, das cinco cartas, apenas três exibirão exatamente a mesma imagem após essa rotação.
Resposta: alternativa c.
9. A partir do polígono P, são construídos os seguintes polígonos Pa e Pb, obtidos por meio das transformações geométricas descritas nos itens a e b, respectivamente:
10.
11. Resposta possível: considere o polígono P obtído pela translação pelo vetor do polígono P1, conforme a ilustração a seguir.
O polígono P2 é obtído pela reflekção do polígono P em relação à reta r.
12. Com as transformações indicadas pelo professor aplicadas ordenadamente, obtemos o polígono de vértices (−4, 2), (−2, 2), (−2, 1), (−1, 1), (−1, 3), (−3, 3), (−3, 4), (−4, 4).

Resposta: alternativa b.
13. Aplicando as transformações geométricas ordenadamente, obtém-se a seguinte figura:
Resposta: alternativa d.
14. a) Como a figura 2 está invertida em relação à figura 1, trata-se de uma homotetia invérsa.
b) A homotetia é uma redução invérsa, logo: −1 < k < 0. Além díssu, o módulo da razão da homotetia é igual à razão de semelhança das figuras.
Considerando o lado horizontal na parte de baixo da figura 1 (de medida 5 u.c.) e o lado correspondente na figura 2 (de medida 1 u.c.), determina-se quê a razão negativa da homotetia é dada por:
|k| = ⇒ k = = − 0,2
15. a) Como a reta determinada pêlos pontos homólogos B e B(minutos)" passa por A e a reta determinada pêlos pontos homólogos C e C(minutos)" também passa por A, concluímos quê o ponto A é o centro de homotetia.
Página trezentos e noventa e nove
b) A razão da homotetia é igual à razão de semelhança. A altura do triângulo AB(minutos)"C(minutos)" em relação à base é 4 u.c. e a altura do triângulo ABC em relação à base é 11 u.c. Logo, a razão da homotetia é:
k =
16.
17. Como a homotetia é diréta, segue quê sua razão k é igual à razão de semelhança dos dois triângulos. Dessa forma, a razão entre as áreas dos dois triângulos é igual a k2, portanto a razão positiva da homotetia é igual a:
18. Na figura 1, como o ponto central da homotetia não pertence aos segmentos quê unem os pontos dessa figura aos seus correspondentes da figura F, segue quê a homotetia é diréta. Para calcular sua razão, podemos comparar a altura da figura 1 (igual a 9 u.c.) com a altura da figura F (igual a 5 u.c.). Logo, a razão da homotetia é:
k = = 1,8
Logo, essa é uma homotetia de ampliação diréta.
Na figura 2, como o ponto central da homotetia pertence aos segmentos quê unem os pontos dessa figura aos seus correspondentes da figura F, segue quê a homotetia é invérsa. Para calcular sua razão, podemos comparar a altura da figura 2 (igual a 3 u.c.) com a altura da figura F (igual a 5 u.c.). Logo, a razão da homotetia é:
k = = − 0,6
Logo, essa é uma homotetia de redução invérsa.
• Como a homotetia é uma transformação geométrica quê preserva as formas, alterando apenas seu posicionamento e suas dimensões, então pode-se afirmar quê há homotetia entre as figuras 1 e 2. Nesse caso, a figura 2 póde sêr ôbitída por meio de uma homotetia de redução invérsa da figura 1, cuja razão é:
k =
19. Considerando os vértices A(2, 2), B(1, 4), C(−2, 4), D(−3, 0), E(−1, −3) e F(1, −2) do hekzágono, tem-se:
Portanto, determinam-se os seguintes vértices da imagem ôbitída pela reflekção do hekzágono em relação ao eixo y: A(minutos)"(−2, 2),
B(minutos)"(−1, 4), C(minutos)"(2, 4), D(minutos)"(3, 0), E(minutos)"(1, −3) e F(minutos)"(−1, −2).
20. Uma translação de 4 unidades para a esquerda é uma translação horizontal quê diminui 4 unidades da coordenada x e não altera a coordenada y. Portanto, a primeira coordenada do vetor é −4 e a segunda é 0, ou seja, o vetor é representado por .
Resposta: alternativa c.
21. Da figura, temos o vetor . A translação póde sêr representada do seguinte modo:
Dessa forma, tem-se:
Portanto,
Resposta: alternativa c.
22. a) Na notação matricial, a abscissa do ponto fica na primeira linha e a ordenada do ponto fica na segunda linha. Temos, portanto:
b) A1 = ; B1 = ; C1 =
Portanto, A1(3, −1), B1(−2, −4) e C1(−2, 2).
c)
Portanto, A2(4, 4), B2(−1, 7) e C2(−1, 1).
d) D1 = ; E1=F1 =
Portanto, D1(−2, 0), E1(0, 3) e F1(4, −1).
e)
Portanto, D2 (−1, ), E2 () e F2().
23. a) Como a matriz tem 4 colunas, o polígono tem 4 vértices. Logo, o polígono P é um quadrilátero.
b)
c)
d)
24. Como (alfa)" < 0, a rotação ocorre no sentido horário. Uma rotação de ângulo (alfa)" no sentido horário equivale a uma rotação de ângulo (360° − (alfa)") no sentido anti-horário. Desse modo, temos:
Como cos (360° − (alfa)") = cos (alfa)" e sen (360° − (alfa)") = −sen (alfa)", então:
Resposta: alternativa b.
25.
Portanto,
Página quatrocentos
Atividades complementares
1. A figura a seguir apresenta a letra R do enunciado e a figura simétrica a ela em relação à reta s.
Resposta: alternativa c.
2. Na figura completa, há dois pentágonos cortados pela reta r e dois quadrados cortados pela reta s. Além díssu, em cada quadrante, há 4 polígonos quê não são cortados pelas retas r e s. Como o polígono ABCDEFGH…A é compôzto de 1 lado de cada figura, ele tem um número de lados igual a 2 + 2 + 4 ⋅ 4 = 20.
Resposta: alternativa b.
3. Inicialmente, sabe-se quê a rotação é uma transformação geométrica quê preserva a forma da figura rotacionada. Além díssu, note quê ⋅ 360° = 270°. Assim, houve uma rotação da roleta em 270° no sentido horário ou, ainda, d fórma equivalente, uma rotação de 90° no sentido anti-horário em torno de seu centro, cuja figura é representada na alternativa e.
Resposta: alternativa e.
4. De acôr-do com as transformações isométricas apresentadas ordenadamente pelo enunciado, têm-se as seguintes figuras:
Resposta: alternativa c.
5. Analisando cada uma das possibilidades, tem-se:
a) Falsa. Caso fosse aplicada uma reflekção na figura 1 em relação a um de seus lados e uma rotação em relação ao seu centro, não haveria como deslocar essa figura até a posição em quê se encontra a figura 2.
b) Falsa. Caso fosse aplicada uma reflekção na figura 1 em relação a uma de suas diagonais, a figura ôbitída seria igual à própria figura 1, d fórma quê, com apenas uma rotação em relação a um de seus vértices, seria impossível deslocar essa imagem e obtêr a figura 2.
c) Falsa. Considerando-se uma reta paralela a um dos lados do quadrado da figura 1, apenas com as transformações de translação e reflekção por essa reta seria impossível obtêr a rotação necessária quê resultasse na figura 2.
d) Falsa. Considerando uma reta paralela a um dos lados do quadrado da figura 1, apenas com as transformações de rotação por um vértice do quadrado e reflekção por essa reta seria impossível obtêr o deslocamento necessário quê resultasse na figura 2.
e) Verdadeira. Pode-se considerar uma rotação (de um ângulo aparente de 45°) no sentido horário em torno do centro do quadrado, seguida de uma translação.
Resposta: alternativa e.
6.
Portanto, P(minutos)" = (0, 2).
Resposta: alternativa d.
7. O comprimento da curva ôbitída na segunda figura é cm. Nas figuras seguintes, o comprimento de cada curva será igual a do comprimento da curva da figura anterior. Logo, o comprimento da sexta curva será de cm.
Resposta: alternativa c.
8. A razão da homotetia é dada por:
k = = 4
Resposta: alternativa c.
9. A transformação T póde sêr reescrita do seguinte modo:
Trata-se, portanto, da rotação de 90° em torno da origem no sentido anti-horário. A figura quê melhor representa essa transformação aplicada ao triângulo ABC do enunciado é a figura da alternativa b.
Resposta: alternativa b.
10. O pentágono AB(minutos)"C(minutos)"D(minutos)"E(minutos)" é a imagem do pentágono ABCDE por uma homotetia de centro A e razão:
Sendo S a área do pentágono AB(minutos)"C(minutos)"D(minutos)"E(minutos)", temos, em m2:
Assim, a área da região sombreada é igual a 495 m2 − 220 m2 = 275 m2.
Resposta: alternativa d.
11. A multiplicação matricial póde sêr reescrita do seguinte modo:
Trata-se, portanto, da rotação de P em 90° no sentido anti-horário em torno da origem (0, 0).
Resposta: alternativa b.
1 BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MÉC, 2018. p. 462. Disponível em: https://livro.pw/asnqu. Acesso em: 11 set. 2024.