UNIDADE 1
CONJUNTOS
Banco de dados
Diversas atividades quê realizamos no dia a dia envolvem a tecnologia de banco de dados, quê consiste em um sistema de gerenciamento de informações quê possibilita a organização e a busca de conteúdos em diferentes categorias de maneira rápida e assertiva.
Imagine, por exemplo, um aplicativo de loja de calçados com milhares de itens disponíveis para venda. Para comprar um calçado, um cliente póde selecionar opções nas categorias organizadas no banco de dados da loja, de acôr-do com suas preferências, restringindo informações como tamãnho, preêço, côr e marca.
O nome do estabelecimento e as marcas dos produtos quê aparécem na figura são fictícios.
Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. dêz-creva uma situação do seu dia a dia em quê você acredita quê esteja envolvida a tecnologia de banco de dados.
2. Você já comprou algum produto ôn láini utilizando opções de filtro? dêz-creva como foi essa experiência.
3. Dois clientes da loja virtual representada na imagem selecionaram as mesmas opções de tamãnho, côr e marca de calçado. Porém apenas um deles selecionou uma opção de preêço. Para qual dêêsses clientes serão apresentados menos itens para compra? Explique.
Página doze
Noção de conjunto
O nome do estabelecimento e as marcas dos produtos quê aparécem na figura são fictícios.
Na abertura desta Unidade, foi apresentado quê um sistema de gerenciamento de banco de dados póde sêr utilizado para selecionar um ou mais objetos de uma coleção. Uma coleção de objetos quaisquer é chamada de conjunto. Cada objeto de um conjunto é chamado de elemento dêêsse conjunto. Por exemplo, no aplicativo de loja descrito na abertura, todos os pares de calçados cadastrados formam um conjunto em quê cada par de calçado é um elemento dêêsse conjunto.
Usualmente, um conjunto é indicado por uma letra maiúscula do alfabeto, e um elemento é indicado por uma letra minúscula. pôdêmos representar um conjunto de diferentes maneiras.
Exemplos:
a) Seja A o conjunto cujos elemêntos são todos os divisores positivos de 20. Acompanhe algumas maneiras de representar esse conjunto.
• Colocando seus elemêntos entre chaves e separados por vírgula.
A = {1, 2, 4, 5, 10, 20}
• Apresentando as características quê definem seus elemêntos.

• Utilizando um esquema conhecido como diagrama de Venn. Nele, cada elemento é representado por uma marcação ao lado da sua indicação.
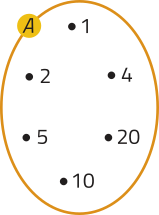
b) Para conjuntos com “muitos” elemêntos, podemos usar as reticências. Seja B o conjunto de todos os números naturais menóres quê 100.
B = {0, 1, 2, 3, 4, 5, ..., 97, 98, 99}
Quando um elemento faz parte de um conjunto, dizemos quê ele pertence a esse conjunto. E quando um elemento não faz parte de um conjunto, dizemos quê ele não pertence a esse conjunto. Por exemplo, em relação ao conjunto A = {1, 2, 4, 5, 10, 20}, temos:
• ![]()
•![]()
Agora, considere os conjuntos a seguir.
B = {x | x é capital da Bahia}
C = {x | x é um número ímpar múltiplo de 2}
Resposta esperada: Falsa, pois a expressão indica quê o número 10 não pertence ao conjunto A, mas 10 é divisor positivo de 20. Portanto, 10 pertence a A (10 ∈ A).
PARA PENSAR
A expressão 10 ∉ A é verdadeira ou falsa? Explique.
Página treze
Em relação a esses conjuntos, temos:
• B é um conjunto unitário, pois tem um único elemento: o município de Salvador.
• C é um conjunto vazio, pois não há número ímpar múltiplo de 2; portanto, o conjunto não tem nenhum elemento. Para denotar um conjunto vazio, utilizamos ∅ ou {}, ou seja, C = ∅ ou C = {}.
Outro conjunto quê podemos destacar é o conjunto universo, geralmente denotado por U. A esse conjunto pertencem todos os elemêntos de determinada situação em estudo. Por exemplo, considerando B como o conjunto das capitais brasileiras quê começam com a letra B, o conjunto universo U é formado por todas as capitais do Brasil.
Outro conceito importante no estudo de conjuntos é a ideia de conjuntos finitos e infinitos. Dizemos quê um conjunto é finito se ele for vazio ou tiver uma quantidade finita de elemêntos, de modo quê seja possível contá-los e chegar ao final. Quando não é finito, dizemos quê o conjunto é infinito.
Exemplos:
a) O conjunto A das capitais da Região Sul do Brasil é um conjunto finito.
A = {Curitiba, Florianópolis, Porto Alegre}
b) O conjunto B dos números possíveis de serem sorteados em um dado comum é um conjunto finito.
B = {1, 2, 3, 4, 5, 6}
c) O conjunto C dos números pares é um conjunto infinito.

d) O conjunto D dos múltiplos positivos de 5 é um conjunto infinito.
D = {5, 10, 15, 20, 25, ...}
Em um conjunto finito, podemos determinar a quantidade de elemêntos quê esse conjunto tem. Indicamos por n(A) a quantidade de elemêntos do conjunto finito A. Assim, nos exemplos a e b, temos n(A) = 3 e n(B) = 6.
Igualdade de conjuntos
Considere os conjuntos A = {x | x é um estado da Região Norte} e B = {Acre, Amapá, Amazonas, Pará, Rondônia, Roraima, Tocantins}. Note quê os conjuntos A e B têm os mesmos elemêntos. Nesse caso, dizemos quê A é igual a B e indicamos A = B.
PARA PENSAR
Os conjuntos A = {1, 2, 3} e B = {x | x é um divisor positivo de 6} são iguais? Justifique.
Não, pois 6 ∈ B e 6 ∉ A.
Dois conjuntos A e B são iguais quando todo elemento de A pertence a B e, de maneira recíproca, todo elemento de B pertence a A.

Se algum elemento de um conjunto C não pertence a um conjunto D, então dizemos quê esses conjuntos são diferentes e indicamos C ≠ D.
Página quatorze
Relação de inclusão de conjuntos
Considere os conjuntos:
A = {−2, −1, 0, 1, 2}
B = {−1, 0, 1}
C = {5, 6, 7, 8}
D = {7, 8, 9}
Agora, obissérve a representação da relação entre alguns dêêsses conjuntos por meio do diagrama de Venn.
• Conjuntos A e B.
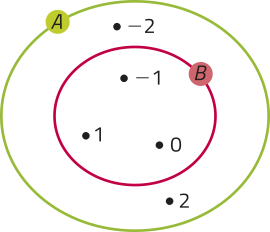
Note quê todos os elemêntos do conjunto B também são elemêntos do conjunto A. Assim, dizemos quê B é parte de A, ou B está contido em A, ou, ainda, quê B é um subconjunto de A.
Indicamos:

A relação B ⊂ A é chamada de relação de inclusão.
• Conjuntos C e D.
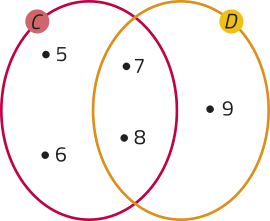
Note quê há elemento do conjunto D quê não é elemento do conjunto C (o elemento 9). Assim, dizemos quê D não é parte de C, ou D não está contido em C, ou, ainda, quê D não é um subconjunto de C.
Indicamos:

Propriedades da inclusão de conjuntos
Vamos destacar algumas propriedades da relação de inclusão de conjuntos. Para isso, considere os conjuntos A, B e C quaisquer.
• O conjunto vazio é subconjunto de qualquer conjunto: ∅ ⊂ A.
Para demonstrar essa propriedade, podemos realizar uma próva por absurdo, ou seja, supor por hipótese quê isso não acontece e concluir uma contradição. Nesse caso, supondo ∅ ⊄ A, existiria um elemento x ∈ ∅ de maneira quê x ∉ A. No entanto, isso é um absurdo, uma vez quê, por definição, elemento algum pertence a ∅. Portanto, ∅ ⊂ A.
• Propriedade reflexiva: A ⊂ A.
Um conjunto qualquer está contido em si mesmo.
• Propriedade antissimétrica: se A ⊂ B e B ⊂ A, então A = B.
Essa propriedade póde sêr utilizada quando é necessário demonstrar quê dois conjuntos são iguais. Nesse caso, basta mostrar quê A ⊂ B (todo elemento de A também é elemento de B) e quê B ⊂ A (todo elemento de B também é elemento de A).
• Propriedade transitiva: se A ⊂ B e B ⊂ C, então A ⊂ C.
Página quinze
MATEMATICA NA HISTÓRIA
Em Matemática, o conceito de conjunto foi tratado no decorrer da história por diversos estudiosos, com destaque para o russo Georg Cantor (1845-1918), quê, em 1874, começou a desenvolver seu trabalho inovador em Teoria dos Conjuntos. Outros contribuintes para o desenvolvimento dessa área da Matemática foram Julius uiu rélm ríchard Dedekind (1831-1916), Giuseppe Peano (1858-1932) e Kurt Gödel (1906-1978).
Fonte dos dados: BOYER, Cal Benjamin. História da matemática. Tradução: Elza Furtado Gomide. 1. ed. São Paulo: Edgard Blãcher, 1974. p. 414.
ATIVIDADES
1. Analise o diagrama a seguir e represente os conjuntos A, B e C, indicando seus elemêntos entre chaves.
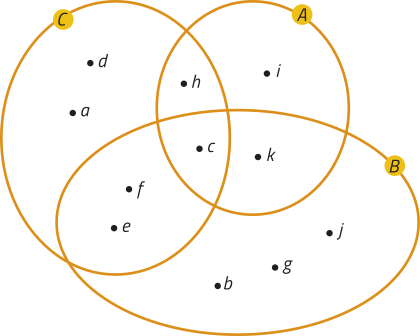
A = {c, h, i, k},
B = {b, c, e, f, g, j, k} e
C = {a, c, d, e, f, h}
2. Considere os seguintes conjuntos e resôuva as kestões.
• A = {x | x é número par positivo, menor quê 7}.
• B = {y | y é divisor positivo de 12}.
• C = {z | z é número quadrado perfeito menor quê 30}.
a) Represente cada conjunto, indicando seus elemêntos entre chaves.
2. a) A = {2, 4, 6}, B = {1, 2, 3, 4, 6, 12} e C = {1, 4, 9, 16, 25}
b) Entre esses conjuntos, algum é subconjunto de outro? Justifique.
2. b) Sim, A é subconjunto de B, pois todo elemento de A também é elemento de B.
3. escrêeva quatro subconjuntos do conjunto A = {3, 6, 9}.
Respostas possíveis: ∅, {3, 6, 9}, {3, 6}, {3, 9}, {6, 9}, {3}, {6}, {9}.
4. Represente, em um único diagrama, os conjuntos A = {1, 2, 3}, B = {1, 4, 5, 6}, C = {4, 6} e D = {3}. Depois, copie os itens a seguir e substitua cada pelo sín-bolo ⊂ ou ⊄.
a) D ___ A
⊂
b) B ___ C
⊄
c) A ___ B
⊄
d) C ___ B
⊂
e) ∅ ___ D
⊂
f) B ___ D
⊄
Resposta nas Orientações para o professor.
5. Agora é a sua vez! Com base nos conjuntos A, B, C e D da atividade anterior, escrêeva outros dois itens quê relacionem os conjuntos por meio dos símbolos ⊂ e ⊄.
Resposta possível: ∅ ⊂ A; B ⊄ A.
6. Leia o texto a seguir.
Reino animal
Os sêres vivos do reino animal podem sêr classificados em dois grandes grupos, conforme segue.
Invertebrados: animais quê não apresentam coluna vertebral. Os moluscos, como caramujos, lesmas e ôstras, são exemplos de animais invertebrados.
Vertebrados: animais dotados de espinha ou coluna vertebral. Os répteis, como lagartos, cobras e tartarugas, são exemplos de animais vertebrados.
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto: Artméd, 2015.
Agora, considere os conjuntos a seguir.
A = {a | a é animal}
V = {v | v é animal vertebrado}
I = {i | i é animal invertebrado}
R = {r | r é réptil}
M = {m | m é molusco}
a) Construa um diagrama para representar os conjuntos descritos anteriormente.
6. a) Resposta nas Orientações para o professor.
b) Qual destas sentenças é falsa? Justifique.
• V ⊂ A
• I ⊂ V
• M ⊂ A
• R ⊂ V
I ⊂ V. Resposta nas Orientações para o professor.
c) pôdêmos dizêr quê determinada tartaruga é elemento de quais dêêsses conjuntos?
A, V e R
Página dezesseis
7. Seis funcionários de uma empresa se inscreveram para participar de um treinamento visando à melhoria contínua de suas práticas. Algumas informações sobre esses funcionários foram organizadas em uma planilha eletrônica. Observe.
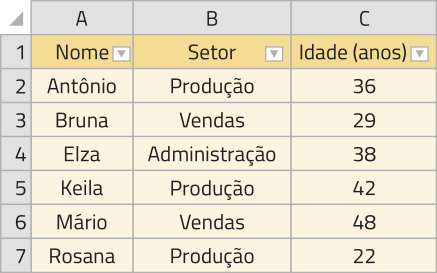
a) Quantos dêêsses funcionários são do setor de produção? Independentemente do setor, quantos têm idade inferior a 30 anos?
3 funcionários; 2 funcionários
b) pôdêmos afirmar quê todos os funcionários com idade entre 30 e 40 anos quê se inscreveram são exclusivamente do setor de administração? Explique.
7. b) Não, pois existe um funcionário nessa faixa etária quê é do setor de produção; no caso, Antônio, com 36 anos de idade.
c) Para a primeira etapa de treinamento, foram selecionados funcionários com mais de 40 anos de idade, dos setores de administração ou de produção. Quais funcionários participaram dessa etapa de treinamento?
Keila
![]() d) Pense e registre no caderno um critério para a seleção dos funcionários quê participarão da segunda etapa de treinamento. De acôr-do com esse critério, apenas Rosana e Bruna devem sêr selecionadas. Por fim, compare sua resposta com a de outros côlégas.
d) Pense e registre no caderno um critério para a seleção dos funcionários quê participarão da segunda etapa de treinamento. De acôr-do com esse critério, apenas Rosana e Bruna devem sêr selecionadas. Por fim, compare sua resposta com a de outros côlégas.
7. d) Resposta possível: Selecionar apenas funcionários com idade inferior a 30 anos.
![]() 8. Pesquise aspectos diferentes daqueles mencionados na atividade 6 relacionados aos sêres vivos do reino animal, como alimentação (carnívoro, herbívoro, onívoro), simetria (assimétrico, simétrico radial, simétrico bilateral), reprodução (sexuada, assexuada) e regulação térmica (endotérmicos e ectotérmicos). Com base nas características pesquisadas, elabore uma situação-problema envolvendo a ideia de conjunto. Depois, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve a quê ele elaborou. Ao final, confiram juntos as resoluções.
8. Pesquise aspectos diferentes daqueles mencionados na atividade 6 relacionados aos sêres vivos do reino animal, como alimentação (carnívoro, herbívoro, onívoro), simetria (assimétrico, simétrico radial, simétrico bilateral), reprodução (sexuada, assexuada) e regulação térmica (endotérmicos e ectotérmicos). Com base nas características pesquisadas, elabore uma situação-problema envolvendo a ideia de conjunto. Depois, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve a quê ele elaborou. Ao final, confiram juntos as resoluções.
Resposta pessoal.
NO MUNDO DO TRABALHO
Proatividade e melhoria contínua
O mercado de trabalho tem exigido dos profissionais, além dos conhecimentos técnicos de cada profissão, o desenvolvimento de competências comportamentais chamadas de soft skills. Entre essas competências estão a proatividade e a melhoria contínua. O profissional proativo é aquele quê busca antecipar-se a problemas e necessidades da empresa antes quê eles surjam, além de resolver tarefas e auxiliar os côlégas sem quê lhe seja ordenado. Já o profissional quê tem a competência da melhoria contínua desenvolvida está disposto a estudar, fazer cursos de capacitação, inovar suas práticas de trabalho, entre outras ações quê visam melhorar seus resultados constantemente.
Acesse o podcast indicado a seguir para obtêr mais informações sobre as soft skills.
• BBC LÊ: o quê são'soft skills': habilidades comportamentais cada vez mais buscadas por empregadores. Locução de: Rodrigo Durão. [S. l.]: BBC nius Brasil, 14 ago. 2022. Podcast. Disponível em: https://livro.pw/plgot. Acesso em: 25 jun. 2024.
Página dezessete
Operações com conjuntos
União e interseção de conjuntos
Observe os conjuntos A = {1, 3, 6, 7, 8} e B = {3, 4, 8} representados no diagrama ao lado direito da página.
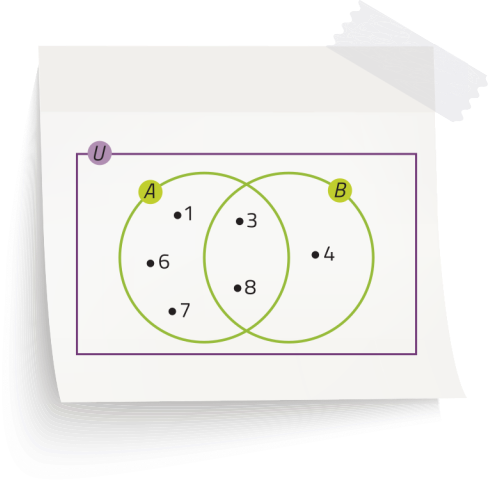
pôdêmos determinar um conjunto C, formado por todos os elemêntos quê pertencem a A ou a B, ou seja, tal conjunto terá elemêntos quê pertencem apenas a A, ou apenas a B, ou a ambos os conjuntos. Nesse caso, C = {1, 3, 4, 6, 7, 8}. Esse conjunto é denominado união dos conjuntos A e B, denotado por A ⋂ B (lê-se: A união B).
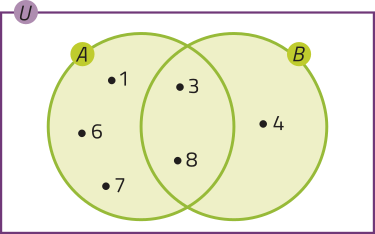
Sejam A e B dois conjuntos quaisquer. Denominamos união (ou reunião) de A e B, indicada por A ⋂ B, o conjunto C formado pêlos elemêntos quê pertencem a A ou a B.
C = A ⋂ B = {x | x ∈ A ou x ∈ B}
Também podemos determinar um conjunto D, formado por todos os elemêntos quê pertencem a A e a B, ou seja, tal conjunto terá elemêntos quê pertencem simultaneamente aos conjuntos A e B. Nesse caso, D = {3, 8}. Esse conjunto é denominado interseção dos conjuntos A e B, denotado por A ⋃ B (lê-se: A interseção B).
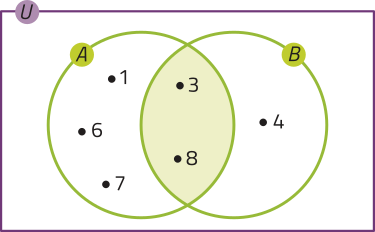
Sejam A e B dois conjuntos quaisquer. Denominamos interseção de A e B, indicada por A ⋃ B, o conjunto D formado pêlos elemêntos quê pertencem a A e a B.
D = A ⋃ B = {x | x ∈ A e x ∈ B}
DICA
A palavra ou, utilizada na definição de união de conjuntos, não tem apenas sentido de exclusão, como póde ocorrer na linguagem habitual, por exemplo, quando dizemos “vou à escola ou vou à livraria”.
Página dezoito
ATIVIDADES RESOLVIDAS
R1. Considere os conjuntos A = {5, 9}, B = {−1, 1, 2, 9} e C = {0, 1, 4} e determine:
a) A ⋃ B
b) A ⋂ B
c) A ⋂ C
Resolução
Para resolver cada item, podemos representar os conjuntos por meio de diagramas de Venn.
a) 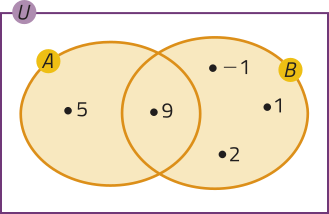
A ⋃ B = {−1, 1, 2, 5, 9}
b) 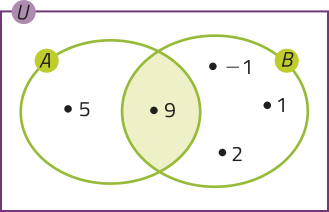
A ⋂ B = {9}
c) 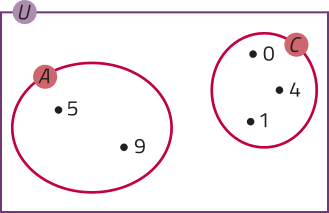
A ⋂ C = ∅
Note quê A ⋂ C é um conjunto vazio, pois não há elemento algum quê pertença simultaneamente a A e a C. Nesse caso, dizemos quê A e C são conjuntos disjuntos.
Sejam D e E dois conjuntos quaisquer. Dizemos quê D e E são conjuntos disjuntos quando D e E não têm elemento comum.
D e E são disjuntos ⇔ D ⋂ E = ∅
R2. Dados os conjuntos B = {−1, 2, 7, 8}, A ⋃ B = {−4, −1, 1, 2, 5, 7, 8} e A ⋂ B = {2, 7}, determine o conjunto A.
Resolução
Para resolver esta quêstão, podemos elaborar um algoritmo, que consiste em etapas com instruções descritas e ordenadas. Acompanhe.
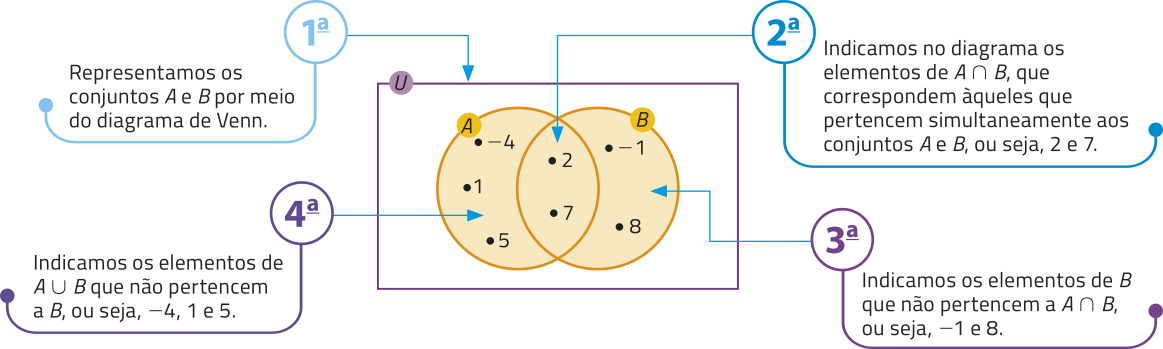
Portanto, A = {−4, 1, 2, 5, 7}.
PARA PENSAR
Esse algoritmo póde sêr adaptado para resolver outras kestões com estruturas parecidas.
No caderno, determine os elemêntos de um conjunto E, dados os conjuntos D = {−3, −1, 0, 7, 9},
D ⋃ E = {−3, −1, 0, 2, 5, 7, 9} e D ⋂ E = {−1, 7, 9}.
E = {−1, 2, 5, 7, 9}
Página dezenove
Quantidade de elemêntos da união de dois conjuntos
Dados os conjuntos C = {−5, 0, 4, 6, 7} e D = {−2, 0, 6}, temos:
• n(C) = 5
• n(D) = 3
• C ⋃ D = {−5, −2, 0, 4, 6, 7} e n(C ⋃ D) = 6
• C ⋂ D = {0, 6} e n (C ⋂ D) = 2
Note quê n(C ⋃ D) ≠ n(C) + n(D), pois os elemêntos quê pertencem a C ⋂ D (no caso, 0 e 6) estão sêndo considerados nesse cálculo duas vezes, tanto em n(C) quanto em n(D). Assim, podemos escrever a igualdade a seguir.
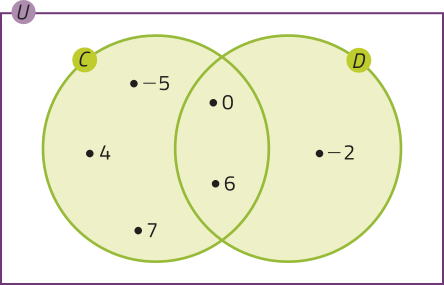
De modo geral, dados os conjuntos A e B finitos, a quantidade de elemêntos da união de A e B póde sêr expressa por:
n(A ⋃ B) = n(A) + n(B) − n(A ⋂ B)
Observe quê, se A ⋂ B = {}, então n(A ⋂ B) = 0. Com isso, n(A ⋃ B) = n(A) + n(B) − 0. Assim, quando os conjuntos A e B forem disjuntos, temos n(A ⋃ B) = n(A) + n(B).
ATIVIDADES RESOLVIDAS
R3. Considere o conjunto A com 7 elemêntos e o conjunto B com 5 elemêntos. Sabendo quê esses conjuntos têm 2 elemêntos em comum, determine quantos elemêntos há em A ⋃ B.
Resolução
De acôr-do com o enunciado, temos: n(A) = 7, n(B) = 5 e n(A ⋂ B) = 2. Dessa maneira:
n(A ⋃ B) = n(A) + n(B) − n(A ⋂ B) = 7 + 5 − 2 = 10
Logo, A ⋃ B tem 10 elemêntos.
Outra maneira de resolver essa atividade é representando os conjuntos A e B por meio de um diagrama de Venn e realizando as seguintes etapas.
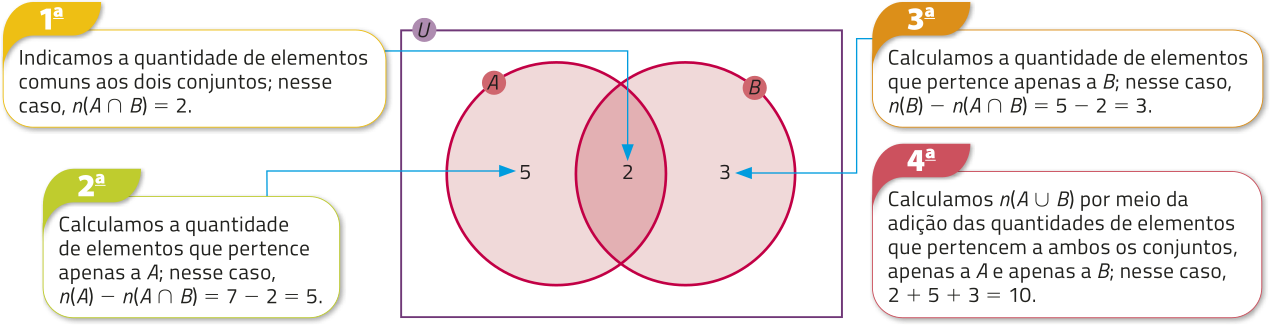
DICA
Note quê os números indicados nesse diagrama representam quantidades de elemêntos.
Por exemplo, o número 2 indica a quantidade de elemêntos de A ⋂ B.
Página vinte
R4. Em uma pesquisa realizada com 50 estudantes de uma escola, identificou-se quê todos eles têm acesso à internet por meio de banda larga fixa ou móvel. Observe os dados obtidos nessa pesquisa e determine quantos estudantes têm acesso à internet por ambos os tipos de conexão.
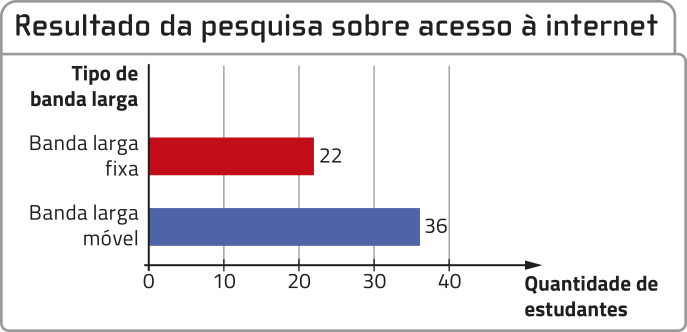
Fonte: Dados fictícios.
Resolução
Para resolver essa atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• 50 estudantes foram entrevistados e todos eles têm acesso à internet por meio de banda larga fixa ou móvel;
• 22 estudantes têm acesso à internet por banda larga fixa;
• 36 estudantes têm acesso à internet por banda larga móvel.
Temos de determinar quantos estudantes têm acesso à internet por meio de ambos os tipos de conexão.
2ª ELABORAR UM PLANO
Considerando F o conjunto dos estudantes quê têm acesso à internet por banda larga fixa e M o conjunto dos estudantes quê têm acesso por banda larga móvel, temos:
• n(F ⋃ M) = 50;
• n(F) = 22;
• n(M) = 36.
Então, temos de determinar n(F ⋂ M), quê póde sêr obtído por meio da expressão expressão a seguir.
n(F ⋃ M) = n(F) + n(M) − n(F ⋂ M)
3ª EXECUTAR O PLANO
Substituindo os valores na expressão n(F ⋃ M) = n(F) + n(M) − n(F ⋂ M), temos:
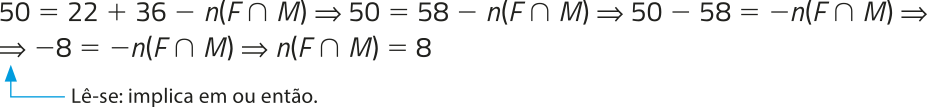
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado obtído, podemos utilizar um diagrama de Venn.
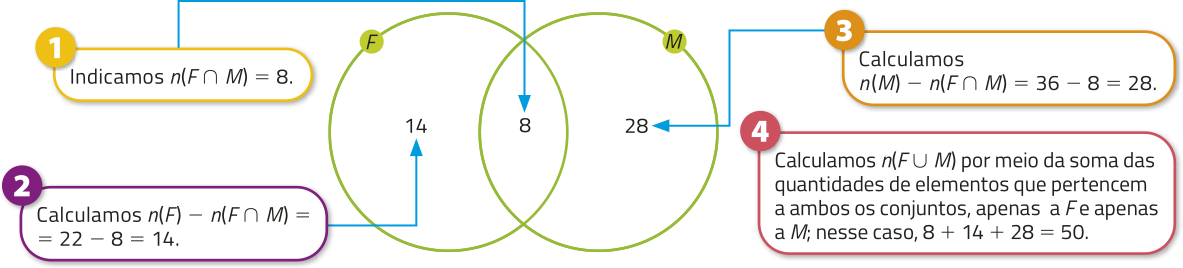
Portanto, 8 estudantes têm acesso à internet em ambos os tipos de conexão.
Página vinte e um
Diferença entre conjuntos
Considere os conjuntos C = {a, b, c, d} e D = {b, c, e, f, g}. pôdêmos determinar um conjunto E, formado por todos os elemêntos quê pertencem a C, mas quê não pertencem a D. Nesse caso, E = {a, d}. Esse conjunto é denominado diferença entre os conjuntos C e D, e o denotamos por C − D.
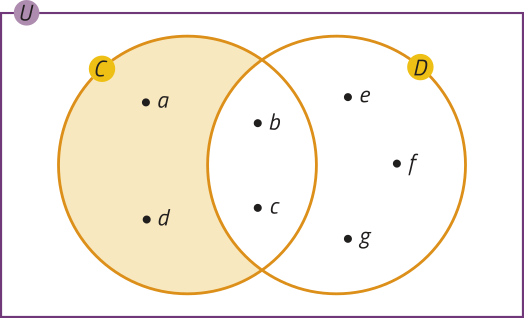
PARA PENSAR
Quando realizamos a operação de subtração de números reais, também costumamos utilizar o sín-bolo “−”, como em 10 − 3 = 7.
O sín-bolo “−” tem o mesmo significado na operação de subtração de números reais e na operação de diferença entre conjuntos? Explique a um colega.
Resposta pessoal.
Sejam A e B dois conjuntos quaisquer. Denominamos diferença entre A e B, indicada por A − B, o conjunto formado pêlos elemêntos quê pertencem a A e não pertencem a B.
A − B = {x | x ∈ A e x ∉ B}
ATIVIDADE RESOLVIDA
R5. Dados os conjuntos A = {0, 1, 2, 3, 4}, B = {1, 2, 4} e C = {0, 1, 4, 5}, determine:
a) A − B
b) A − C
Resolução
Para resolver cada item, podemos representar os conjuntos por meio de diagramas de Venn.
a) 
A − B = {0, 3}
b) 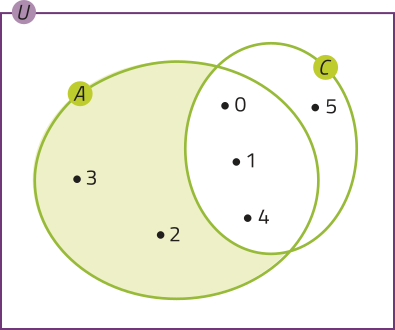
A − C = {2, 3}
Note quê, no item a, temos B ⊂ A. Nesse caso, A − B também é chamado de complementar de B em relação a A e denotamos por (lê-se: complementar de B em relação a A).
Sejam A e B dois conjuntos quaisquer, em quê B ⊂ A. Denominamos complementar de B em relação a A, indicado por o conjunto A − B.
Página vinte e dois
ATIVIDADES
9. Dados os conjuntos A = {−4, −2, 0, 2, 4}, B = {0, 1, 2, 3, 4} e C = {−2, 5, 7, 9}, determine:
a) A ⋃ C
{−4, −2, 0, 2, 4, 5, 7, 9}
b) C ⋂ A
{−2}
c) B ⋂ C
∅
d) C ⋃ (A ⋂ B)
{−2, 0, 2, 4, 5, 7, 9}
e) B − A
{1, 3}
f) A − (B ⋃ C)
{−4}
g) B ⋂ (A − C)
{0, 2, 4}
h) (A ⋃ B) − (A ⋂ B)
{−4, −2, 1, 3}
10. Em qual item a seguir a parte destacada em vêrde do diagrama representa o conjunto (A ⋃ B) − C? Justifique sua resposta. Depois, escrêeva uma expressão para representar a parte destacada em vêrde nos demais diagramas.
a) 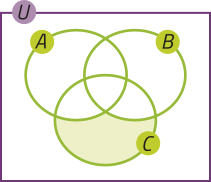
b) 
c) 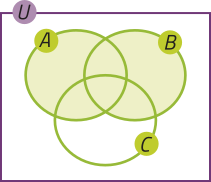
d) 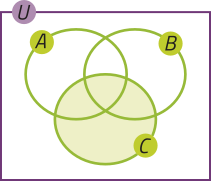
10. Alternativa b, pois a parte destacada em vêrde no diagrama corresponde aos elemêntos quê pertencem aos conjuntos A ou B e não pertencem ao conjunto C, expressa por (A ∪ B) − C. a: C − (A ∪ B); c: (A ∪ B); d: C.
11. Observe o diagrama de Venn a seguir e classifique cada sentença como V (verdadeira) ou F(falsa). Faça a justificativa.
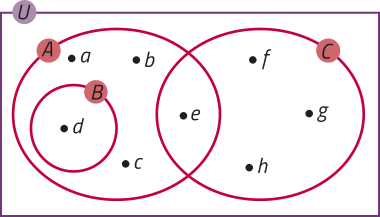
a) B ⋃ C = ∅
b) A ⋂ B = B
c) n(A) = 5
d) n(C ⋃ A) = 7
e) = {a, b, c, e}
f) B − A = {a, b, c}
Resposta nas Orientações para o professor.
12. Considere dois conjuntos A e B não vazios. A união dêêsses conjuntos apresenta 31 elemêntos, e a interseção, 12 elemêntos. Determine a quantidade de elemêntos em A.
a) Com os dados fornecidos, é possível resolver o problema? Justifique sua resposta.
b) Se não for possível resolver, indique o(s) dado(s) faltante(s) e a solução correspondente.
Respostas nas Orientações para o professor.
![]() 13. Reúna-se com um colega, pesquisem e respondam às seguintes kestões.
13. Reúna-se com um colega, pesquisem e respondam às seguintes kestões.
a) Em quantas regiões o Brasil é dividido? Em qual delas vocês moram?
5 regiões. Resposta pessoal.
b) Quantas unidades da Federação (UF) existem no Brasil? Em qual delas vocês moram?
27 unidades da Federação. Resposta pessoal.
Agora considere os conjuntos a seguir e, depois, respondam às kestões.
• F, formado por todas as unidades da Federação do Brasil.
• E, formado pelas unidades da Federação da região em quê vocês moram.
c) Liste todos os elemêntos de E e determine n(E).
As respostas dependem da região em quê os estudantes moram.
d) Explique o quê representa o conjunto e determine quantos são seus elemêntos.
13. d) Conjunto formado pelas unidades da Federação localizadas nas regiões do Brasil em quê os estudantes não moram. A quantidade de elemêntos dêêsse conjunto depende da região em quê os estudantes moram.
14. Considere os conjuntos A e B, em quê
A ∪ B = {−5, −1, 2, 3, 4, 6, 8}, A − B = {−1, 6} e B − A = {3, 4, 8}.
a) escrêeva um algoritmo para determinar os elemêntos dos conjuntos A e B e represente-os em um diagrama de Venn.
a) Resposta nas Orientações para o professor.
![]() b) No caderno, defina dois conjuntos finitos C e D. Em uma fô-lha avulsa, escrêeva os elemêntos de C ∪ D, C − D e D − C e troque-a com um colega para quê ele, utilizando o algoritmo elaborado no item a, determine os conjuntos C e D, enquanto você faz o mesmo na fô-lha quê receber. Ao final, confiram juntos as resoluções.
b) No caderno, defina dois conjuntos finitos C e D. Em uma fô-lha avulsa, escrêeva os elemêntos de C ∪ D, C − D e D − C e troque-a com um colega para quê ele, utilizando o algoritmo elaborado no item a, determine os conjuntos C e D, enquanto você faz o mesmo na fô-lha quê receber. Ao final, confiram juntos as resoluções.
Resposta pessoal.
15. A escola de música em quê Meire estuda oferece aulas de três instrumentos musicais: flauta, teclado e violão. Sabe-se quê:
• 27 pessoas estudam flauta;
• 17 pessoas estudam flauta e violão;
• 32 pessoas estudam teclado;
• 25 pessoas estudam teclado e violão;
• 45 pessoas estudam violão;
• 16 pessoas estudam flauta, teclado e violão;
• 19 pessoas estudam flauta e teclado.
Quantas pessoas, no total, estudam nessa escola de música?
59 pessoas
Página vinte e três
16. Um clube recreativo analisou os hábitos dos 1.450 sócios com relação ao uso de suas instalações em cérto mês. Foi constatado quê, nesse mês, 930 sócios usaram a piscina, 310 usaram a piscina e a academia e 140 usaram apenas outras instalações. Quantos sócios dêêsse clube usaram apenas a academia?
380 sócios
17. Doenças como poliomielite, sarampo e rubéula foram comuns no Brasil e no mundo. Atualmente, estão quase erradicadas no território nacional, graças à vacinação massiva da população brasileira. O Programa Nacional de Imunizações avança a cada ano, proporcionando melhor qualidade de vida à população com a prevenção de doenças.
Fonte dos dados: BRASIL. Ministério da Saúde. Vacinação. Brasília, DF: MS, [2024]. Disponível em: https://livro.pw/ibjts. Acesso em: 26 jun. 2024.
Ciente da importânssia da vacinação, uma escola realizou uma pesquisa com todos os estudantes a fim de identificar se eles tí-nhão recebido as vacinas Dupla Adulto (dT) e HPV. Observe uma tabéla construída para resumir os dados coletados.
Estudantes da escola quê receberam as vacinas
Vacina |
Quantidade de estudantes |
|---|---|
Apenas Dupla Adulto (dT) |
98 |
Apenas HPV |
67 |
Ambas as vacinas |
115 |
Nenhuma dessas vacinas |
33 |
Fonte: Dados fictícios.
PARA AMPLIAR
Acesse êste sáiti para mais informações sobre a importânssia da vacinação e sobre o Programa Nacional de Imunizações.
• BRASIL. Ministério da Saúde. Vacinação. Brasília, DF: MS, [2024]. Disponível em: https://livro.pw/ibjts. Acesso em: 26 jun. 2024.
De acôr-do com os dados apresentados, responda às kestões.
a) Represente os dados da tabéla em um diagrama de Venn. Para isso, nomeie como A o conjunto dos estudantes quê receberam a vacína Dupla Adulto (dT) e como B o conjunto dos estudantes quê receberam a vacína HPV.
Resposta nas Orientações para o professor.
b) Quantos estudantes foram entrevistados nessa pesquisa?
313 estudantes
c) Quantos entrevistados receberam:
• a vacína Dupla Adulto (dT)?
213 estudantes
• a vacína HPV?
182 estudantes
• ambas as vacinas?
115 estudantes
d) Quantos estudantes receberam ao menos uma das vacinas?
280 estudantes
e) Para regularizar todos os estudantes em relação a essas duas vacínas, a escola pretende realizar uma campanha de vacinação. Quantas doses de vacina de cada tipo devem sêr aplicadas nessa campanha?
100 vacinas Dupla Adulto (dT); 131 vacinas HPV
18. Para uma reportagem, certa revista ôn láini realizou uma pesquisa com 100 pessoas sobre as platafórmas de streaming quê elas utilizam. Foi constatado quê, dos entrevistados, 35 utilizam a platafórma A, 49 utilizam a platafórma B e 23 utilizam ambas as platafórmas. Das pessoas entrevistadas, quantas não utilizam nenhuma dessas platafórmas de streaming?
39 pessoas
![]() 19. Observe a tabéla a seguir e elabore um problema envolvendo operações com conjuntos. Em seguida, junte-se a um colega, e tróquem o problema para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
19. Observe a tabéla a seguir e elabore um problema envolvendo operações com conjuntos. Em seguida, junte-se a um colega, e tróquem o problema para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
Domicílios brasileiros quê tí-nhão automóvel ou motocicleta, 2022
Veículo |
Porcentual |
|---|---|
Automóvel |
49,8 |
Motocicleta |
25,0 |
Automóvel e motocicleta |
13,1 |
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Pesquisa Nacional por Amostra de Domicílios Contínua: características gerais dos domicílios e dos moradores 2022. Rio de Janeiro: hí bê gê hé, 2024. Disponível em: https://livro.pw/wkmam. Acesso em: 26 jun. 2024.
Página vinte e quatro
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Transfusão sanguínea
Você sabe o quê é transfusão sanguínea? Esse procedimento médico consiste em transferir o sangue, ou parte de seus componentes, de uma pessoa (doadora) para outra (receptora). É importante ressaltar quê, anualmente no Brasil, milhares de pessoas precisam dêêsse procedimento e, para isso, contam com a doação voluntária de sangue, quê é a única maneira de obtê-lo, pois somente o organismo do sêr humano é capaz de produzi-lo.
Em uma transfusão, um aspecto quê deve sêr considerado é a compatibilidade entre o sangue do receptor e o sangue do doador. Para isso, são analisados os tipos de antígeno presentes nos glóbulos vermelhos de cada um dos envolvidos. Esse teste determina em qual tipo sangüíneo – A, B, AB ou O –, pertencente ao sistema ABO, se enquadram o receptor e o doador.
Observe no diagrama a seguir a representação do sistema ABO em relação à presença de antígenos no sangue. Nesse esquema, o conjunto A e o conjunto B indicam os tipos sangüíneos quê têm presença do antígeno A e do antígeno B, respectivamente.
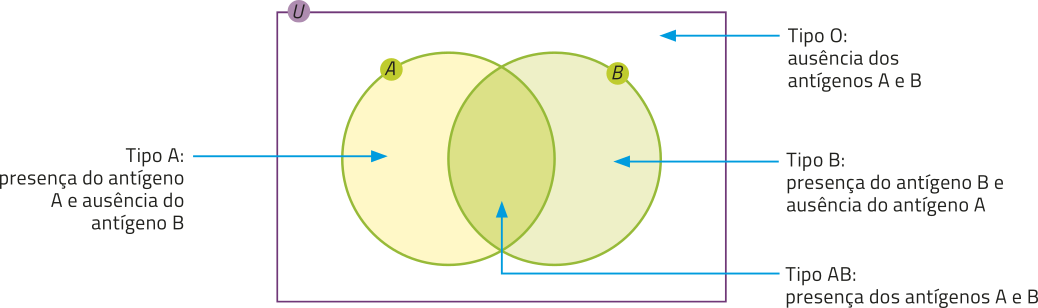
- Antígeno
- : é uma substância quê, ao sêr introduzida no receptor, provoca uma resposta imune.
Por exemplo, caso um indivíduo com sangue tipo A receba acidentalmente sangue tipo B, serão produzidos anticorpos contra o antígeno B, pois seu organismo não o reconhece. Isso póde obstruir vasos e artérias.
Simultaneamente à análise do sistema ABO, é necessário avaliar o fator Rh. Quando o sangue apresenta o antígeno Rh, dizemos quê o sangue do indivíduo é Rh positivo (Rh+). Quando há ausência dêêsse antígeno, dizemos quê o sangue do indivíduo é Rh negativo (Rh−). Por exemplo, no caso de uma transfusão, haveria incompatibilidade entre um receptor de sangue Rh− e um doador de sangue Rh+, porque o organismo do receptor, quê não tem o antígeno Rh, produziria anticorpos contra o antígeno Rh do doador.
Fonte dos dados: POTTER, Patricia A. éti áu. Fundamentos de enfermagem. Tradução: Mayza Ritomy Ide éti áu. 8. ed. Rio de Janeiro: Elsévier, 2013. p. 931.
Ao analisar as características do Sistema ABO e do fator RH, pódemos identificar quem póde receber e quem pode doar sangue a um indivíduo com determinado tipo sangüíneo. Observe o exemplo ao lado direito da página para um indivíduo cujo tipo sangüíneo é A−.
Doa para |
Recebe de |
|
|---|---|---|
A− |
A+, A−, AB+ e AB− |
A− e O− |
Página vinte e cinco
PENSANDO NO ASSUNTO
1. Responda às kestões a seguir.
Respostas pessoais.
a) Você sabe qual é seu tipo sangüíneo, de acôr-do com o sistema ABO? E o fator Rh?
b) Em seu entendimento, qual é a importânssia de conhecermos nosso tipo sangüíneo e o das pessoas de nosso convívio? Pense no assunto e, se necessário, realize uma pesquisa.
c) No município ou na região em quê você mora, é comum a realização de campanhas incentivando a doação de sangue? De quê modo você acredita quê essas campanhas impactam a ssossiedade? Qual é a importânssia delas?
2. Observe o diagrama quê representa o sistema ABO, apresentado na página 24. Em relação à presença ou à ausência dos antígenos A e B nas hemácias, interpréte os conjuntos a seguir.
A − B A ∩ B B − A U − (A ∪ B)
Resposta nas Orientações para o professor.
3. Justifique as afirmativas a seguir.
a) Em uma transfusão sanguínea, um receptor AB− é incompatível com um doador B+.
3. a) Resposta esperada: Apesar de o doador apresentar em suas hemácias o mesmo antígeno B do receptor, ele também apresenta em suas hemácias o antígeno Rh (Rh+), o quê o torna incompatível com o receptor, quê não tem o antígeno Rh (Rh−).
b) Em uma transfusão sanguínea, um doador A− é compatível com um receptor A+.
3. b) Resposta esperada: Como o doador apresenta o mesmo antígeno A do receptor e tem ausência de antígeno Rh (Rh−) em suas hemácias, ele é compatível com o receptor.
![]() 4. Em relação ao sistema ABO e ao fator Rh, costuma sêr chamado de doador universal o indivíduo quê póde doar sangue àqueles de qualquer tipo sangüíneo. Já o receptor universal é o indivíduo quê póde receber sangue de qualquer tipo sangüíneo.
4. Em relação ao sistema ABO e ao fator Rh, costuma sêr chamado de doador universal o indivíduo quê póde doar sangue àqueles de qualquer tipo sangüíneo. Já o receptor universal é o indivíduo quê póde receber sangue de qualquer tipo sangüíneo.
Em grupos, investiguem quais tipos sangüíneos correspondem aos doadores e receptores universais. Para isso, resolvam os itens a seguir.
a) ob-sérvim a página 24 e respondam: para quem o indivíduo A− é doador? E de quem ele é receptor?
É doador para: A+, A−, AB+ e AB−. É receptor de: A− e O−.
b) Identifiquem todos os possíveis tipos sangüíneos e, para cada um deles, construam um qüadro indicando de quem ele recebe e para quem doa.
Resposta nas Orientações para o professor.
c) Analisem os quadros quê vocês construíram e respondam: quais tipos sangüíneos correspondem ao doador e ao receptor universal? Explique como vocês pensaram.
4. c) Resposta esperada: O doador universal corresponde ao tipo O−, pois ele póde doar sangue a todos os tipos sangüíneos; e o receptor universal corresponde ao tipo AB+, pois ele póde receber sangue de todos os tipos sangüíneos.
![]() 5. Nesta questão, será explorada a seguinte situação-problema.
5. Nesta questão, será explorada a seguinte situação-problema.
Como orientar um habitante do município em quê você mora a respeito da doação de sangue?
Para isso, junte-se a dois côlégas, e façam o quê se pede em cada um dos itens.
Respostas pessoais.
a) Investiguem, no município e na região em quê moram, quais estabelecimentos de saúde recebem doação de sangue da comunidade.
b) Nesses estabelecimentos, há informações sobre os estoques de sangue obtidos por doações? Caso essas informações estejam disponíveis, registrem-nas.
c) Pesquisem quais tipos sangüíneos têm maior demanda nesses estabelecimentos.
d) Em livros ou sáites especializados, pesquisem informações sobre as etapas relacionadas à doação de sangue.
e) Com base no quê estudamos nesta seção e nas kestões anteriores, elaborem uma peça publicitária com o objetivo de estimular a doação de sangue no município em quê moram. Vocês podem optar por fôlder, cartaz, vídeo, podcast, entre outros meios. É importante quê essa peça publicitária contenha informações como:
• características e objetivo da doação de sangue;
• tipos sangüíneos de maior demanda para doação;
• etapas da doação e pré-requisitos para sêr um doador.
Lembrem-se de utilizar uma linguagem adequada, simples e objetiva, fazendo uso de recursos visuais para chamar a atenção e incentivar as pessoas. Para divulgar essa peça publicitária, póde sêr utilizado o mural da escola ou mídias sociais, por exemplo.
DICA
Na peça publicitária, ressaltem quê o ato de doar sangue é estritamente voluntário.
Página vinte e seis
Conjunto dos números naturais (ℕ) e conjunto dos números inteiros (ℤ)
Há indícios de quê a habilidade de contar seja uma atividade humana quê remonta a milhares de anos, como póde sêr sugerido em diversas pinturas rupestres encontradas em diferentes sítios arqueológicos.
Com o passar do tempo, o processo de contar foi desenvolvido para atender a situações de grandes contagens, como as de populações e de produção agrícola. Há registros, por exemplo, de um censo realizado na chiina, em 2238 a.C., para a contagem da população e das lavouras cultivadas.
Desde então, muitos anos se passaram, e o sêr humano continua trabalhando com a habilidade de contagem. Em várias situações do nosso dia a dia, realizamos contagens, por exemplo, para determinar: a quantidade de dias quê faltam para nosso aniversário, a quantidade de pratos e talheres quê devem sêr colocados à mesa para atender a todos quê vão participar de uma refeição, entre outras situações.
Os números quê costumamos utilizar para realizar contagens, incluindo o zero, formam o quê atualmente denominamos conjunto dos números naturais. Esse conjunto tem infinitos elemêntos e póde sêr indicado da seguinte maneira.
ℕ = {0, 1, 2, 3, 4, ...}
PARA AMPLIAR
Assista a êste vídeo para mais informações sobre o Museu do Homem Americano.
• CONHECENDO museus: ep. 44: Museu do Homem Americano. [S. l.: s. n.], 2015. 1 vídeo (26 min). Publicado pelo canal Conhecendo Museus. Disponível em: https://livro.pw/yhxbk. Acesso em: 26 jun. 2024.

Página vinte e sete
pôdêmos representar os números naturais na reta numérica. Observe.

Note quê todo número natural tem um sucessor e, com exceção do zero, também tem um antecessor natural. Além díssu, a diferença entre um número natural qualquer e seu antecessor é igual a 1. Assim, o sucessor de qualquer número natural n é dado por n + 1, e o antecessor dêêsse número, para n > 0, é dado por n − 1.
pôdêmos indicar o subconjunto de ℕ formado por todos os números naturais positivos da seguinte maneira.
ℕ* = {1, 2, 3, 4, 5, ...}
Dizemos quê ℕ é um conjunto fechado para as operações de adição e multiplicação, ou seja, ao adicionar ou multiplicar quaisquer dois números naturais, o resultado também será um número natural. No entanto, isso não ocorre com a subtração; por exemplo, embora 8 − 3 resulte no número natural 5, não obtemos em ℕ o resultado de 3 − 8.
PARA PENSAR
Existe um número natural quê seja menor quê todos os outros números naturais? E um número natural quê seja maior quê qualquer um dos demais? Justifique.
Respostas esperadas: Sim, o número zero é o menor dos naturais. Não, pois, na sequência dos números naturais, é sempre possível obtêr o próximo número, adicionando 1 ao número anterior.
No decorrer da história, algumas situações, como aquelas relacionadas a débitos e dívidas em transações comerciais, cuja ideia póde sêr associada ao fato de o conjunto dos números naturais não sêr fechado para a operação de subtração, contribuíram para o surgimento do conceito de número negativo.
Dessa maneira, foi necessário ampliar o conjunto dos números naturais, acrescentando os números inteiros negativos {..., −4, −3, −2, −1}, para formár o conjunto dos números inteiros. Esse conjunto tem infinitos elemêntos e póde sêr indicado da seguinte maneira.
ℤ = {..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...}
PARA PENSAR
Existe um número inteiro quê seja menor quê todos os outros números inteiros? E um número inteiro quê seja maior quê qualquer um dos demais? Justifique.
Respostas esperadas: Não, pois, na sequência dos números inteiros, é sempre possível obtêr o antecessor de um número, subtraindo 1 dêêsse número. Não, pois, na sequência dos números inteiros, é sempre possível obtêr o sucessor de um número adicionando 1 a ele.
Página vinte e oito
Acompanhe a representação dos números inteiros na reta numérica.
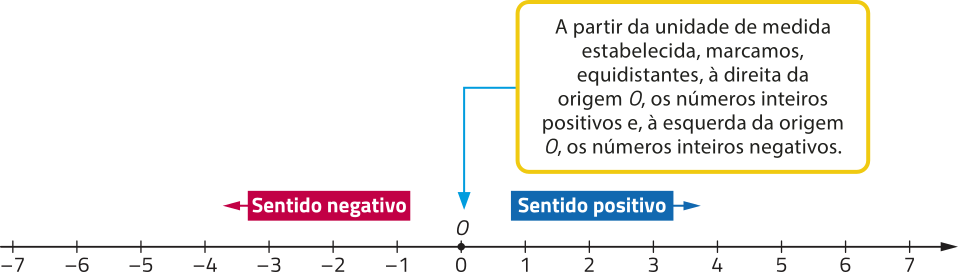
Note quê todo número inteiro m tem um antecessor, dado por m − 1, e um sucessor, dado por m + 1.
pôdêmos destacar alguns subconjuntos de ℤ.
• Conjunto dos números inteiros não nulos:
ℤ* = {..., −4, −3, −2, −1, 1, 2, 3, 4,...} = ℤ − {0}.
• Conjunto dos números inteiros não negativos:
ℤ+ = {0, 1, 2, 3, 4,...} = ℕ.
• Conjunto dos números inteiros positivos:
= {1, 2, 3, 4,...} = ℕ*.
• Conjunto dos números inteiros não positivos:
ℤ− = {..., −4, −3, −2, −1, 0}.
• Conjunto dos números inteiros negativos:
= {..., −4, −3, −2, −1}.
Como todo elemento de ℕ também é elemento de ℤ, temos quê ℕ ⊂ ℤ, ou seja, ℕ é subconjunto de ℤ.
Conjunto dos números racionais (ℚ)
Estudamos quê o conjunto ℕ é fechado exclusivamente para as operações de adição e de multiplicação. O conjunto ℤ, por sua vez, é fechado para as operações de adição, subtração e multiplicação, porém não é fechado para a divisão; por exemplo, não obtemos em ℤ o resultado de 5 ∶ 2.
Assim, foi necessário ampliar o conjunto dos números inteiros, de maneira a obtêr o conjunto dos números racionais, cujos elemêntos correspondem aos quocientes de dois números inteiros quaisquer, sêndo o divisor diferente de zero. Esse conjunto tem infinitos elemêntos e póde sêr indicado da seguinte maneira.
ℚ =
PARA PENSAR
Elabore uma situação-problema envolvendo o conjunto dos números naturais e o conjunto dos números inteiros. Dê preferência a algum contexto relacionado ao seu dia a dia. Depois, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve a quê ele elaborou.
Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página vinte e nove
Há indícios de quê a necessidade de números racionais positivos não inteiros foi identificada, inicialmente, em situações quê envolviam medições. Nas construções de moradias, de grandes obras e nas demarcações de terras, muitas vezes a unidade de medida escolhida para fazer uma medição poderia “não caber” uma quantidade inteira de vezes naquilo quê se queria medir.
Observe exemplos de números racionais.
a) = 3,5
b) = 4
c) = 0,444...
d) = −5
e) = 0,17
Note quê qualquer número inteiro póde sêr escrito na forma , com a ∈ ℤ, b ∈ ℤ e b ≠ 0, como é o caso de 9 = , 4 = e −5 = . Assim, todo número inteiro é também racional e ℤ ⊂ ℚ, ou seja, ℤ é subconjunto de ℚ. O diagrama de Venn representado mostra a relação de inclusão dêêsses conjuntos.

MATEMÁTICA NA HISTÓRIA
No Egito antigo, em algumas situações, como na medição de terras para o plantio, eram utilizadas kórdas demarcadas com nós indicando certa unidade de comprimento. No entanto, nem sempre as unidades cabiam uma quantidade inteira de vezes nessas medições. Nesses casos, era necessário utilizar frações dessa unidade.

A seguir, estão indicadas algumas frações da maneira como os egípcios escreviam.
Notação atual |
||||
|---|---|---|---|---|
Representação egípcia |
|
|
|
|
Fonte dos dados: IFRAH, diórges. História universal dos algarismos: a inteligência dos homens contada pêlos números e pelo cálculo. Tradução: Alberto Muñoz e Ana Beatriz Katinsky. Rio de Janeiro: Nova Fronteira, 1997. p. 348-349.
PARA PENSAR
No Egito antigo, de maneira geral, as frações não unitárias eram expressas por adições de frações unitárias. Mostre como a fração póde sêr expressa pela soma de duas frações unitárias. Lembre-se de quê frações unitárias são aquelas de numerador 1.
Uma resposta possível: .
Página trinta
Representação de número racional
Você provavelmente estudou, em anos anteriores, como podemos transformar um número racional na forma de fração para a forma de número decimal e como transformar um número racional na forma decimal para a forma de fração. Agora, vamos relembrar e ampliar esse estudo.
Transformação de um número racional na forma de fração para a forma de decimal
Uma maneira prática de obtêr a forma decimal de um número racional na forma de fração consiste em realizar a divisão indicada pela fração, ou seja, determinar o quociente entre o numerador e o denominador dela.
Exemplos:
a) = −9 ∶ 5 = − 1,8
Nessa divisão, em quê o résto é zero, o quociente está na forma de um número decimal exato.
b) = 11 ∶ 3 = 3,666... =

Nessa divisão, em quê não é possível obtêr résto igual a zero, o algarismo 6 se repete indefinidamente no quociente. Em casos como esse, dizemos quê o quociente está na forma de dízima periódica.
PARA PENSAR
Mostre, por meio do algoritmo da divisão, por quê o algarismo 6 se repete indefinidamente no quociente de 11 ∶ 3.
Resposta pessoal.
Outra maneira consiste em determinar uma fração decimal equivalente para, em seguida, realizar a divisão indicada.
Exemplos:
a)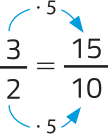 = 1,5
= 1,5
b)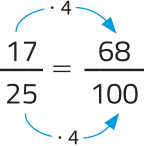 = 0,68
= 0,68
PARA PENSAR
Em seu entendimento, por quê foram escolhidas essas frações equivalentes nos exemplos?
Resposta esperada: As frações equivalentes são frações decimais (com denominadores 10, 100 etc.), o quê facilita o cálculo da divisão.
Transformação de um número racional na forma de decimal para a forma de fração
Acompanhe, inicialmente, os exemplos em quê números racionais na forma de decimal exato são transformados na forma de fração.
Exemplos:
a) 0,8 =
b) 2,48 =
Também podemos transformar uma dízima periódica em uma fração, ou seja, obtêr uma fração geratriz. Acompanhe, nos casos a seguir, um modo de determinar a fração geratriz de uma dízima periódica.
DICA
Observe quê há dois tipos possíveis de representação decimal para os números racionais: a finita ou a infinita periódica.
Página trinta e um
Exemplos:
a)
x = 0,222... ← Representamos 0,222... por x.
10x = 2,222... ← Multiplicamos cada membro da equação por 10.
10x = 2 + ← Decompomos 2,222... em 2 + 0,222...
10x = 2 + x ← Como 0,222... = x, realizamos a substituição.
9x = 2 ← Subtraímos x em cada membro da equação.
x = ← Dividimos por 9 cada membro da equação 9x = 2.
← A fração geratriz de é .
b) = 0,7575...
x = 0,7575...
100x = 75,7575...
100x = 75 +
100x = 75 + x
99x = 75
x =
c) = 1,3222...
x = 1,3222...
10x = 13,222...
10x = 13 +
10x = 13 +
10x =
x =
PARA PENSAR
Explique por quê em uma das etapas da obtenção da fração geratriz de e de os membros da igualdade são multiplicados por 10, enquanto na obtenção da fração geratriz de os membros da igualdade são multiplicados por 100.
Resposta esperada: Para se obtêr, no membro da direita, um número racional cuja parte decimal corresponda apenas a algarismos do período da dízima periódica.
Observe alguns números racionais representados na reta numérica.

ATIVIDADES
20. Copie os itens a seguir e substitua cada pelo sín-bolo ∈ ou ∉.
a) 2,5 ___ ℤ
∉
b) −3 ___ℕ
∉
c) 0 ___ ℤ
∈
d) ___ ℚ
∈
e) 54 ____ ℕ
∈
f) ____ ℤ
∉
g) 9 ___ ℚ
∈
h) −7,6 ___ ℚ
∈
21. Considere A = {x ∈ ℕ | x é divisor de 12} e B = {y ∈ ℤ | −1 ≤ y < 4} e determine os elemêntos de cada conjunto a seguir.
a) A
21. a) A = {1, 2, 3, 4, 6, 12}
b) B
21. b) B = {−1, 0, 1, 2, 3}
c) A ∪ B
21. c) A ∪ B = {−1, 0, 1, 2, 3, 4, 6, 12}
d) A ∩ B
21. d) A ∩ B = {1, 2, 3}
22. escrêeva cada número racional a seguir na forma de número decimal.
a)
b)
5,2
c)
d)
0,068
23. escrêeva cada número racional a seguir na forma de fração irredutível.
a) 0,65
b) 8,024
c)
d)
Página trinta e dois
24. Desenhe um diagrama para representar os conjuntos ℕ e ℤ. Depois, com a côr de sua preferência, destaque a parte correspondente a ℤ − ℕ. Quais números pertencem ao conjunto correspondente a essa parte destacada?
Resposta nas Orientações para o professor.
![]() 25. Reúna-se a um colega para resolver os itens a seguir.
25. Reúna-se a um colega para resolver os itens a seguir.
Respostas pessoais.
a) Escolham dois números racionais x e y, com x < y. Depois, determinem um número racional z quê esteja entre x e y, ou seja, x < z < y.
b) Agora, entre os números racionais z e y quê vocês indicaram no item anterior, determinem um número racional w, ou seja, z < w < y. Repita essa operação mais duas vezes com os números seguintes.
c) No entendimento de vocês, sempre será possível obtêr um número racional quê esteja entre dois números racionais quaisquer? Escrevam um breve texto argumentando suas escôlhas.
d) Para verificar a proposição do item anterior, considerem dois números racionais a e b quaisquer, com a < b, e pensem em uma estratégia para obtêr um número racional c quê esteja entre eles, ou seja, a < c < b. Para auxiliar, vocês podem representar esses números na reta numérica.
26. Na página 29, estudamos algumas frações na escrita do Egito antigo. Nos itens a seguir, estão indicadas, nessa escrita, frações não unitárias expressas pela soma de frações unitárias. Em cada item, determine, em notação atual, a adição e a fração não unitária representadas.
a) ![]()
26. a)
b) ![]()
26. b)
c) ![]()
26. c)
27. Marcelo precisa comprar um cano com 2,3 m de comprimento e cuja medida do diâmetro é indicada por ,ou seja, três quartos de polegada. Sabe-se quê 1(segundos)" corresponde a aproximadamente 2,54 cm. pôdêmos afirmar quê a medida do diâmetro dêêsse cano, em centímetro, está entre:
a) 0,75 e 1
b) 1 e 1,5
c) 1,5 e 2
d) 2 e 2,5
e) 2,5 e 3
alternativa c
![]() • Todos os dados informados no enunciado desta atividade foram necessários para resolvê-la? Comente com um colega.
• Todos os dados informados no enunciado desta atividade foram necessários para resolvê-la? Comente com um colega.
27. • Resposta esperada: Não, o comprimento do cano, por exemplo, é um dado desnecessário para a resolução desta atividade.
28. Flávia definiu o seguinte conjunto numérico: A = {x | x = 2n + 1, com n ∈ ℕ}.
a) escrêeva cinco elemêntos de A.
28. a) Algumas respostas possíveis: 1; 3; 5; 7; 9; 11.
b) A qual dos itens a seguir corresponde o conjunto A?
I) Conjunto dos números naturais quadrados perfeitos.
II) Conjunto dos números naturais ímpares.
III) Conjunto dos números naturais primos.
28. b) II
c) Da mesma maneira quê Flávia, utilize notação matemática para representar o conjunto B dos números naturais pares.
28. c) B = {x | x = 2n, com n ∈ ℕ}
d) Que elemento pertence simultaneamente aos conjuntos A e B? Justifique.
28. d) Resposta esperada: Nenhum elemento, pois A ⋃ B = ∅, uma vez quê não há número quê seja simultaneamente par e ímpar.
![]() 29. Você possivelmente já estudou a paridade dos números naturais; por exemplo, um número natural é necessariamente par ou ímpar. Vamos estudar propriedades relacionadas a esses números.
29. Você possivelmente já estudou a paridade dos números naturais; por exemplo, um número natural é necessariamente par ou ímpar. Vamos estudar propriedades relacionadas a esses números.
Para isso, junte-se a dois côlégas, e calculem as potências indicadas a seguir.
12 22 32 42 52 62
72 82 92 102 112 122
29. 12 = 1; 22 = 4; 32 = 9; 42 = 16; 52 = 25; 62 = 36; 72 = 49; 82 = 64; 92 = 81; 102 = 100; 112 = 121; 122 = 144
![]() a) Comparem a base de cada potência com o resultado correspondente. Que regularidades, em relação à paridade dêêsses números, vocês podem identificar?
a) Comparem a base de cada potência com o resultado correspondente. Que regularidades, em relação à paridade dêêsses números, vocês podem identificar?
Resposta pessoal.
b) De acôr-do com as regularidades quê vocês identificaram no item a e sem realizar cálculos, classifiquem os resultados das potências a seguir em número par ou ímpar.
3422 1.6552 2.7782 812
29. b) número par: 3422 e 2.7782; número ímpar: 1.6552 e 812
![]() • Agora, utilizando calculadora, verifiquem se a classificação feita por vocês está correta.
• Agora, utilizando calculadora, verifiquem se a classificação feita por vocês está correta.
Resposta pessoal.
c) Escrevam conjecturas para expressar as regularidades identificadas.
Resposta nas Orientações para o professor.
Professor, esta obra está atualizada conforme a grafia estabelecida pelo SI na publicação: INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA; INSTITUTO PORTUGUÊS DA QUALIDADE. Sistema Internacional de Unidades (SI). Tradução: Grupo de Trabalho luso-brasileiro do Inmetro e IPQ. Brasília, DF: Inmetro; Caparica: IPQ, 2021. p. iii. Tradução luso-brasileira da 9ª edição. Disponível em: https://livro.pw/vbxre. Acesso em: 27 jun. 2024.
- Conjecturas
- : afirmações quê se supõem verdadeiras, mas quê não foram provadas como válidas ou não.
Página trinta e três
Números racionais e algumas aplicações
Compreender as características e propriedades dos números racionais é fundamental para a interpretação e a análise crítica de situações envolvendo diferentes áreas do conhecimento. A seguir, estudaremos alguns temas em quê podemos perceber isso.
Densidade demográfica
Densidade demográfica é um indicador quê representa a distribuição de habitantes em certa região, auxiliando na avaliação de possíveis riscos humanos e ambientais e contribuindo para o planejamento urbano. Esse cálculo corresponde à razão entre a quantidade de habitantes e a extensão territorial de uma região e costuma sêr expresso em habitantes por quilômetro quadrado (hab./km2). Assim:
densidade demográfica = .
Observe, a seguir, como podemos calcular a densidade demográfica de Taboão da Serra (SP), o município com a maior densidade demográfica do Brasil.

Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Taboão da Serra. Rio de Janeiro: hí bê gê hé, [2022]. Localizável em: menú Panorama. Disponível em: https://livro.pw/mnqru. Acesso em: 26 jun. 2024.
PARA PENSAR
• É possível afirmar quê o país com a menor população do mundo também é o de menor densidade demográfica? Justifique.
Resposta esperada: Não, pois a densidade demográfica é uma medida quê também está relacionada com a extensão territorial do país.
• Considere um município quê, de um ano para outro, permaneceu com a mesma extensão territorial. Explique como a densidade demográfica dêêsse município póde ter aumentado nesse mesmo período.
Resposta esperada: A população dêêsse município aumentou nesse período.
Página trinta e quatro
Índice de Massa Corporal (hí eme cê)
O Índice de Massa Corporal (hí eme cê) tem como objetivo avaliar, de maneira simples e rápida, o estado corporal de uma pessoa com relação à massa e à altura dela. No entanto, essa avaliação não é muito precisa, o quê torna necessário consultar profissionais especializados, como um nutricionista ou um nutrólogo, para quê ela seja realizada de maneira mais adequada.
Esse índice é calculado por meio da fórmula a seguir, quê corresponde à razão entre a massa (m), em quilograma, e o quadrado da altura (a), em métro quadrado.
hí eme cê =
Para a avaliação de pessoas adultas, o resultado do cálculo do hí eme cê deve sêr comparado com a seguinte classificação, definida pela Organização Mundial da Saúde (hó ême ésse).
BAIXO PESO
Menor quê 18,5 kg/m2
PESO ADEQUADO
Maior ou igual a 18,5 e menor quê 25 kg/m2
SOBREPESO
Maior ou igual a 25 e menor quê 30 kg/m2
OBESIDADE
Maior ou igual a 30 kg/m2
Fonte dos dados: BIBLIOTECA VIRTUAL EM SAÚDE DA ATENÇÃO PRIMÁRIA À SAÚDE. Cálculo do índice de massa corporal. São Paulo: BVS APS, [2024]. Disponível em: https://livro.pw/zciua. Acesso em: 26 jun. 2024.
Considerando, por exemplo, uma pessoa adulta com 68,5 kg de massa e 1,70 m de altura, temos:
hí eme cê = ≃ 23,7
Portanto, o hí eme cê dessa pessoa é de aproximadamente 23,7 kg/m2, quê póde sêr classificado como “peso adequado”, pois 18,5 < 23,7 < 25.
DICA
É importante considerar quê o hí eme cê não apresenta uma avaliação nutricional da pessoa. Essa informação somente póde sêr ôbitída com auxílio de um profissional de saúde.
PARA PENSAR
O quê uma pessoa adulta, cujo hí eme cê é classificado como “sobrepeso”, tem de fazer para quê esse índice seja ajustado de maneira a sêr classificado como “peso adequado”? Justifique.
Resposta esperada: Por sêr adulta, consideramos quê a altura da pessoa permanecerá aproximadamente a mesma; então, para esse ajuste, ela deve reduzir a massa corporal.
NO MUNDO DO TRABALHO
Nutricionista e nutrólogo
O nutricionista e o nutrólogo lidam diretamente com cuidados, doenças e distúrbios relacionados à alimentação, mas têm atuações distintas e complementares. Entre as funções do nutricionista, está a avaliação nutricional do corpo do paciente, incluindo a indicação de mudanças na diéta alimentar. Já o médico nutrólogo atua na prevenção, no diagnóstico e no tratamento de doenças e distúrbios alimentares.
Acesse êste sáiti para ler um texto com mais informações sobre as atividades do nutricionista e do nutrólogo.
• O QUE faz um nutrólogo?: tire suas dúvidas sobre esse profissional. In: VIDA SAUDÁVEL. [S. l.], 21 jun. 2023. Disponível em: https://livro.pw/eneuk. Acesso em: 26 jun. 2024.
Página trinta e cinco
Taxa de mortalidade infantil
A taxa de mortalidade infantil é um importante indicador social, pois é a partir dela quê pódemos investigar e interpretar algumas das condições de nascimento e de vida de uma população em determinado ano, possibilitando, por exemplo, aprimorar e corrigir problemas relacionados à saúde pública. O cálculo da taxa de mortalidade infantil em determinado ano e região pode sêr realizado da seguinte maneira:
⋅ 1.000
A taxa de mortalidade infantil é classificada de acôr-do com o resultado dêste cálculo: baixa se menor quê 20, média se de 20 até 49 e alta se maior ou igual a 50.
Fonte dos dados: BRASIL. Ministério da Saúde. Rede Interagencial de Informações para a Saúde. Indicadores de mortalidade. Brasília, DF: MS: Ripsa, [2000]. Disponível em: https://livro.pw/psyuh. Acesso em: 26 jun. 2024.
Por exemplo, em 2020, o município de Uberaba (MG) registrou 3.861 nascidos vivos e 40 óbitos de menóres de 1 ano de idade. Nesse caso, a taxa de mortalidade infantil é dada por:
⋅ 1.000 ≃ 0,01036 ⋅ 1.000 = 10,36
Portanto, a taxa de mortalidade infantil nesse município, em 2020, foi de aproximadamente 10,36 óbitos de menóres de 1 ano de idade por 1.000 nascidos vivos, quê póde sêr classificada como baixa, pois 10,36 < 20.
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Uberaba: taxa de mortalidade infantil. Rio de Janeiro: hí bê gê hé, [2020]. Disponível em: https://livro.pw/tawlm. Acesso em: 26 jun. 2024.
PARA PENSAR
O quê póde representar uma baixa taxa de mortalidade infantil? E uma alta taxa de mortalidade infantil?
Respostas esperadas: Representa poucos óbitos de menóres de 1 ano de idade em relação à quantidade de nascidos vivos, o quê póde indicar boas condições na saúde pública de uma região em cérto ano. Representa muitos óbitos de menóres de 1 ano de idade em relação à quantidade de nascidos vivos, o quê póde indicar condições precárias na saúde pública de uma região em cérto ano.
ATIVIDADES
30. Para prevenir doenças e melhorar a qualidade de vida, Sueli procurou o auxílio de profissionais da saúde para fazer um acompanhamento nutricional e realizar atividades físicas supervisionadas. Observe a ficha de Sueli com as anotações do acompanhamento.
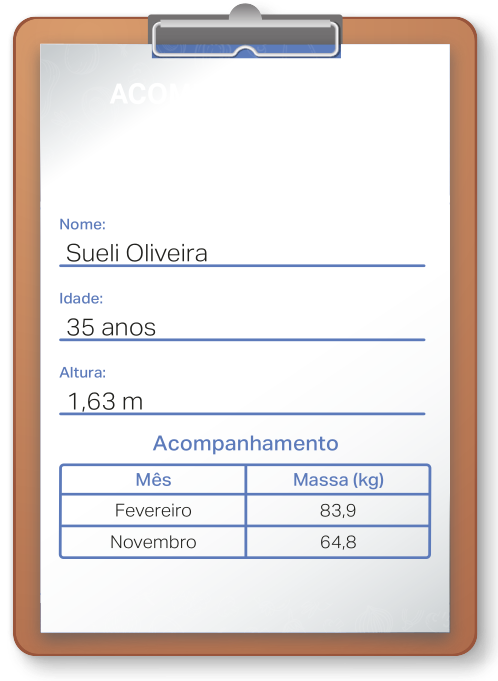
Com base nesse período de acompanhamento físico e nutricional, resôuva as kestões.
a) Como póde sêr classificado o hí eme cê de Sueli em fevereiro? Justifique.
obesidade, pois 31,6 > 30
b) Ao todo, de quantos quilogramas foi a redução de massa de Sueli?
19,1 kg
c) Um dos objetivos da reeducação alimentar e do treino propostos era ajustar o hí eme cê de Sueli para sêr classificado como “peso adequado”. É possível afirmar quê esse objetivo foi alcançado no período apresentado? Justifique.
Resposta esperada: Sim, pois, para sêr classificado como “peso adequado”, o hí eme cê deve estar entre 18,5 kg/m2 e 25 kg/m2, e o hí eme cê de Sueli, no mês de novembro, foi de aproximadamente 24,4 kg/m2.
Página trinta e seis
![]() d) Junte-se a um colega, e leiam o trecho de texto a seguir.
d) Junte-se a um colega, e leiam o trecho de texto a seguir.
Ana não gosta do próprio corpo. Ela é magra, inclusive está abaixo do peso ideal para a altura quê tem. Mas, quando chega perto do espêlho, a única imagem quê consegue vêr é de uma mulher obesa. Por isso, quando come, sente culpa. Ana também não se sente à vontade quando veste uma roupa. Acredita quê nenhuma peça lhe cai bem. Apesar de sentir tanta angústia, não consegue falar com os amigos ou com a família sobre o assunto.
DISMORFIAS corporais e transtôrnos alimentares são doenças graves quê precisam de atenção. In: BLÓGUI DA SAÚDE. [S. l.], 24 jun. 2016. Disponível em: https://livro.pw/uobfh. Acesso em: 26 jun. 2024.
Apesar de Ana sêr uma personagem fictícia, casos semelhantes ao dela são cada vez mais comuns. Realizem uma breve pesquisa sobre distúrbios nutricionais e transtôrnos alimentares. Depois, escôlham um dos temas pesquisados e elaborem um texto trazendo informações sobre as principais causas, sintomas e possíveis tratamentos de saúde.
Resposta pessoal.
31. Observe a tabéla a seguir.
Registros de nascidos vivos e óbitos de menóres de 1 ano de idade em alguns estados brasileiros, 2020
Estado |
Quantidade |
|
|---|---|---|
Nascidos vivos |
Óbitos |
|
Amazonas |
75.635 |
1.051 |
Ceará |
121.904 |
1.417 |
Goiás |
92.768 |
1.054 |
Santa Catarina |
97.916 |
913 |
Rio de Janeiro |
199.124 |
2.508 |
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Brasil: taxa de mortalidade infantil. Rio de Janeiro: hí bê gê hé, 2020. Localizável em: Selecionar local: Estados: Ano 2020. Disponível em: https://livro.pw/oemnv. Acesso em: 23 ago. 2024.
![]() a) Utilizando uma calculadora, calcule a taxa de mortalidade infantil aproximada dos estados apresentados.
a) Utilizando uma calculadora, calcule a taxa de mortalidade infantil aproximada dos estados apresentados.
Amazonas: 13,9; Ceará: 11,6; Goiás: 11,4; Santa Catarina: 9,3; Rio de Janeiro: 12,6
b) As diferenças entre os valores calculados no item a são significativas? Comente.
31. b) Respostas possíveis: Sim, ao compararmos, por exemplo, a maior taxa de mortalidade calculada com a menor taxa de mortalidade calculada há uma diferença de 4,6 óbitos de menóres de 1 ano de idade por 1.000 nascidos vivos, valor significativo quando expresso em números absolutos. Não, ao compararmos, por exemplo, a taxa de mortalidade do estado do Ceará com a de Goiás, a diferença é de apenas 0,2 óbito de menóres de 1 ano de idade por 1.000 nascidos vivos.
![]() c) Com um colega, investiguem quais fatores podem estar atrelados às diferenças nas taxas de mortalidade infantil apresentadas nos estados brasileiros. Depois, numa roda de conversa com toda a turma, discutam essa questão.
c) Com um colega, investiguem quais fatores podem estar atrelados às diferenças nas taxas de mortalidade infantil apresentadas nos estados brasileiros. Depois, numa roda de conversa com toda a turma, discutam essa questão.
Resposta pessoal.
![]() d) Formem grupos de três ou quatro integrantes e pesquisem qual é a taxa de mortalidade do município em quê moram. Em seguida, discutam sobre ações quê podem contribuir para a redução da taxa de mortalidade infantil, como: investir no atendimento pré-natal, ampliar a rê-de de saneamento básico etc. Por fim, compartilhem com a comunidade escolar e local as informações pesquisadas e discutidas.
d) Formem grupos de três ou quatro integrantes e pesquisem qual é a taxa de mortalidade do município em quê moram. Em seguida, discutam sobre ações quê podem contribuir para a redução da taxa de mortalidade infantil, como: investir no atendimento pré-natal, ampliar a rê-de de saneamento básico etc. Por fim, compartilhem com a comunidade escolar e local as informações pesquisadas e discutidas.
Resposta pessoal.
32. O Programa de Etiquetagem Veicular (PBE-V) é uma iniciativa do Inmetro quê, entre outras funções, classifica os veículos produzidos no Brasil de acôr-do com seu consumo de combustível.
Certa empresa compara a média de consumo semestral de cada veículo da frota com a média disponibilizada pelo PBE-V. Caso a média do veículo seja menor quê 85% da média apresentada pelo PBE-V, o veículo é encaminhado para revisão. Observe os dados referentes aos veículos de cérto modelo dessa frota, cuja média de consumo indicada no PBE-V foi de 8,5 km/L.
Dados semestrais de veículos do modelo A
Veículo |
Distância percorrida (km) |
Consumo de combustível (L) |
|---|---|---|
1 |
1.400 |
156 |
2 |
1.750 |
232 |
3 |
1.522 |
179 |
4 |
2.300 |
330 |
5 |
2.150 |
230 |
Fonte: Dados fictícios.
a) Calcule a média de consumo aproximada, em km/L, de cada um dos veículos indicados na tabéla.
32. a) veículo 1: 8,97 km/L; veículo 2: 7,5 km/L; veículo 3: 8,5 km/L; veículo 4: 6,97 km/L; veículo 5: 9,3 km/L
b) Qual dêêsses veículos a empresa deve encaminhar à revisão?
veículo 4
Página trinta e sete
33. O Índice de Desenvolvimento da Educação Básica (Ideb) foi criado em 2007 pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep) e formulado para medir a qualidade do aprendizado nacional e estabelecer metas para a melhoria do ensino. De maneira simplificada, para cada escola, o Ideb (I) póde sêr obtído por meio da fórmula indicada a seguir.
I = t
Nessa fórmula, t corresponde à taxa de aprovação dos alunos da unidade de ensino, e M e P correspondem, respectivamente, às notas médias de Matemática e de Língua Portuguesa nos exames oficiais do Ministério da Educação (MÉC).
Fontes dos dados: BRASIL. Ministério da Educação. Ideb: apresentação. Brasília, DF: MÉC, c2018. Disponível em: https://livro.pw/eyzkn.
BRASIL. Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Nota informativa do Ideb 2023. Brasília, DF: MÉC, Inep: 2023. p. 6. Disponível em: https://livro.pw/wzuqx. Acessos em: 23 ago. 2024.
Observe os dados de certa escola para três níveis de ensino no ano de 2023 e responda às kestões a seguir.
Índices educacionais por nível de ensino, 2023
Nível de Ensino |
Ensino Fundamental – Anos iniciais |
Ensino Fundamental – Anos finais |
Ensino Médio |
|---|---|---|---|
Taxa de aprovação |
0,98 |
0,96 |
0 ,90 |
Média em Matemática |
6,2 |
4,9 |
4,5 |
Média em Língua Portuguesa |
5,4 |
6 |
3,7 |
Fonte: Dados fictícios.
a) Que nível de ensino teve a maior taxa de aprovação nessa escola?
Ensino Fundamental – Anos iniciais
b) Calcule o Ideb dessa escola para cada um dos níveis de ensino apresentados.
33. b) Ensino Fundamental – Anos iniciais: 5,684; Ensino Fundamental – Anos finais: 5,232; Ensino Médio: 3,69
![]() • Converse com o professor e os côlégas sobre a importânssia do Ideb para o desenvolvimento de políticas públicas na área da educação.
• Converse com o professor e os côlégas sobre a importânssia do Ideb para o desenvolvimento de políticas públicas na área da educação.
Resposta pessoal.
34. Observe a tabéla.
População e extensão territorial das regiões do Brasil, 2022
Região |
População estimada (hab.) |
Extensão territorial (km2) |
|---|---|---|
Norte |
17.354.884 |
3.850.593,105 |
Nordeste |
54.658.515 |
1.552.175,42 |
sudéste |
84.840.113 |
924.558,341 |
Sul |
29.937.706 |
576.736,822 |
Centro-Oeste |
16.289.538 |
1.606.354,086 |
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. tabéla 9514: população residente, por sexo, idade e forma de declaração de idade. Rio de Janeiro: hí bê gê hé: Sidra, 2023. Disponível em: https://livro.pw/nhaft. Acesso em: 26 jun. 2024.
![]() a) Calcule a densidade demográfica de cada região do Brasil, em 2022.
a) Calcule a densidade demográfica de cada região do Brasil, em 2022.
34. a) valores aproximados: Norte: 4,51 hab./km2; Nordeste: 35,21 hab./km2; sudéste: 91,76 hab./km2; Sul: 51,91 hab./km2; Centro-Oeste: 10,14 hab./km2
b) Você concórda com a afirmativa a seguir? Justifique sua resposta, com base na tabéla e nos cálculos realizados no item a.
A distribuição da população brasileira, entre as cinco regiões do país, ocorre de maneira desigual.
34. b) Resposta esperada: Sim, pois a densidade demográfica varia consideravelmente de uma região para outra do Brasil.
![]() c) O conhecimento sobre a densidade demográfica de uma região permite entender a dinâmica populacional e realizar um planejamento mais eficaz para enfrentar diferentes desafios.
c) O conhecimento sobre a densidade demográfica de uma região permite entender a dinâmica populacional e realizar um planejamento mais eficaz para enfrentar diferentes desafios.
Junte-se a um colega, e pesquisem aspectos, positivos e negativos, quê podem decorrer da alta e da baixa densidade demográfica de uma região e os tipos de ação ou de planejamento quê podem sêr realizados para lidar com os pontos levantados. Em seguida, investiguem a densidade demográfica do município em quê moram e façam uma análise comparativa com base na pesquisa quê realizaram anteriormente. Ao final, elaborem um relatório com essas informações e compartilhem-no com a comunidade local.
Resposta pessoal.
Página trinta e oito
Conjunto dos números irracionais (𝕀)
Estudamos quê há indícios de quê o desenvolvimento da ideia de número racional teve início a partir de situações práticas envolvendo medições. Ao longo da história da humanidade, acreditou-se, em muitos períodos, quê os números racionais eram suficientes para expressar diferentes situações observadas na natureza ou desenvolvidas pelo sêr humano.
Apesar de essa crença ter prevalecido em alguns momentos, sabemos quê, por meio da história, há cerca de 2.500 anos um grupo de estudiosos na Grécia antiga descobriu a existência de outro tipo de número, o quê, na época, causou uma crise nos fundamentos da Matemática até então desenvolvidos.
Os responsáveis por essa descoberta foram os integrantes da chamada Escola Pitagórica. Eles estudaram uma situação quê não podia sêr expressa por um número racional, no caso, o valor da medida da diagonal de um quadrado de lado unitário. Para determinar essa medida, eles utilizaram o teorema de Pitágoras.
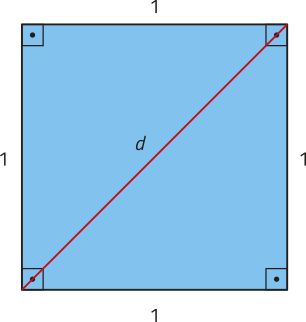
d2 = 12 + 12
d2 = 1 + 1
d2 = 2
DICA
Lembre-se: de acôr-do com o teorema de Pitágoras, em um triângulo retângulo qualquer, o quadrado da medida a da hipotenusa é igual à soma dos quadrados das medidas b e c dos catetos.
a2 = b2 + c2
MATEMÁTICA NA HISTÓRIA
Pitágoras (c. 585 a.C.-c. 500 a.C.) nasceu na ilha de Samos, na Grécia. Em Crotona, na Itália, ele fundou a Escola Pitagórica, um centro de estudos de Filosofia, Matemática e Ciências Naturais. Uma das descobertas mais famosas desenvolvidas nessa escola e creditadas a Pitágoras é o chamado teorema de Pitágoras, quê corresponde a uma relação entre os lados de um triângulo retângulo: o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 94-96.
Página trinta e nove
Assim, concluiu-se quê a medida d correspondia a um número positivo cujo quadrado era igual a 2. Foi um grande problema para os pitagóricos constatar quê esse número, quê expressa a medida da diagonal de um quadrado de lado 1, não era racional. Em notação atual, esse número é indicado por .
pôdêmos notar quê é um número entre 1 e 2, pois < 2 < . De modo análogo, utilizamos uma calculadora para verificar outras aproximações para .
• 1,4 < < 1,5, pois < 2 < < 2 < .
• 1,41 < < 1,42, pois < 2 < < .
• 1,414 < < 1,415, pois < 2 < .
Ao continuarmos esse processo, notamos quê, por mais quê aumentemos o número de casas decimais das aproximações para , o valor ao quadrado não será igual a 2. Observamos, também, quê parece não havêer periodicidade na representação decimal. Ou seja, é possível quê raiz de 2 não seja um número racional por não ter representação decimal finita ou infinita e periódica (não sêr uma dízima periódica). De fato, podemos demonstrar isso. Observe.
Suponhamos quê seja racional, então utilizaremos argumentações válidas para chegar a uma contradição, o quê demonstrará quê esse número não é racional. Acompanhe.
Supor quê seja racional implica quê esse número póde sêr expresso como uma fração irredutível , com a ∈ ℤ, b ∈ ℤ e b ≠ 0. Dessa maneira, temos:
2 =
2b2 = a2
Como 2b2 = a2, temos quê a2 é um número par e, por consequência, a também é par.
Assim, podemos escrever o número a da seguinte maneira: a = 2m, com m ∈ ℤ. Substituindo a = 2m na igualdade ôbitída anteriormente, temos:
2b2 = (2m)2
b2 =
b2 = 2m2
PARA PENSAR
Utilizando o processo apresentado, e com o auxílio de uma calculadora, determine o número racional, com quatro casas decimais, cujo valor mais se aproxima de .
1,4142
Página quarenta
Com base no resultado b2 = 2m2, temos quê b2 é par ou, ainda, quê b também é par.
Como a e b são números pares, 2 é um fator comum do numerador e do denominador da fração . Logo, não é uma fração irredutível, pois póde sêr simplificada por 2. Entretanto, esse resultado é uma contradição, pois supomos inicialmente quê essa fração era irredutível.
Portanto, podemos concluir quê não é um número racional, pois não póde sêr expressa como uma fração irredutível , com a ∈ ℤ, b ∈ ℤ e b ≠ 0 ou seja, é um número irracional.
DICA
Nessa demonstração, foram utilizadas as seguintes propriedades, quê também podem sêr demonstradas.
• Ao multiplicar qualquer número natural por 2, o produto é par.
• Se o quadrado de um número é par, então esse número também é par.
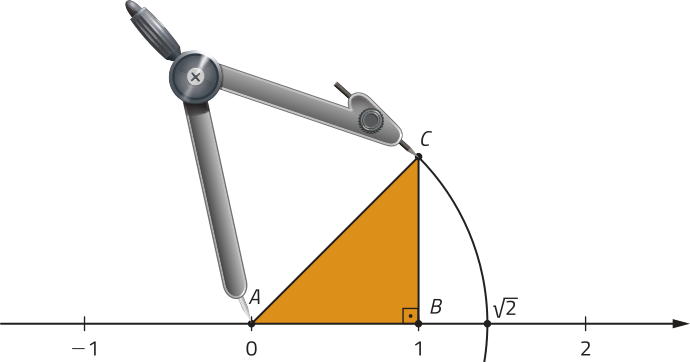
Agora, obissérve como podemos representar geometricamente na reta numérica.
1
Representamos um triângulo retângulo isósceles ABC, com catetos medindo 1 u, vértices A e B sobre a origem e abscissa 1 da reta numérica, respectivamente.
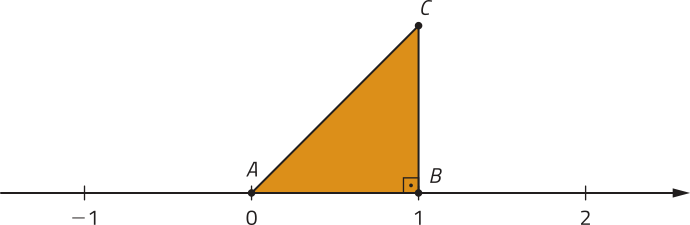
2
Temos quê a medida da hipotenusa é dada por:
(AC)2 = (AB)2 + (BC)2 ⇒ (AC)2 = 12 + 12 ⇒ AC =
Assim, com a abertura de um compasso igual a e ponta-seca na origem da reta numérica, traçamos um arco quê cruza essa reta em um ponto correspondente a .
Página quarenta e um
Os números quê não podem sêr expressos na forma , com a ∈ ℤ, b ∈ ℤ e b ≠ 0, formam o conjunto dos números irracionais, quê póde sêr indicado por 𝕀.
Ao serem representados na forma de número decimal, os números irracionais têm infinitas casas decimais sem, porém, um período. De maneira simplificada, podemos dizêr quê um número irracional é um número cuja representação decimal não é uma dízima periódica nem um decimal exato. Observe, por exemplo, as quinze primeiras casas decimais de obtidas em um programa de computador.
≃ 1, 414213562373095
Um número é irracional se, e somente se, tem representação decimal infinita e não periódica.
Observe outros exemplos de números irracionais.
a)
b)
c)
d)
e)
f)
É possível demonstrar quê a raiz quadrada de todo número natural quê não é um quadrado perfeito é um número irracional.
Acompanhe algumas propriedades relacionadas a números irracionais.
• Sejam a ∈ ℕ, n ∈ ℕ e n > 1; se não é um número inteiro, então é um número irracional.
Exemplo:
não é um número inteiro, pois 13 < 6 < 23, ou seja, 1 < < 2. Portanto, é um número irracional.
• A soma ou a diferença de um número racional com um número irracional é um número irracional.
Exemplos:
a) + 2 é um número irracional, pois é um número irracional e 2 é um número racional.
b) − 0,5 é um número irracional, pois é um número irracional e 0,5 é um número racional.
• O produto ou o quociente de um número racional não nulo por um número irracional também é um número irracional.
Exemplos:
a) é um número irracional, pois é um número irracional e 4 é um número racional.
b) −5 ∶ é um número irracional, pois −5 é um número racional e é um número irracional.
O conjunto 𝕀 não é fechado para nenhuma das quatro operações básicas, isto é, a soma, a diferença, o produto e o quociente de dois números irracionais podem não sêr irracionais.
PARA PENSAR
• Consulte as propriedades apresentadas e verifique se e são números irracionais. Justifique sua resposta.
Resposta esperada: Temos quê não é irracional, pois = 2 ⋅ 4 = 8. Já é irracional, pois 2 < < 3.
• Pense em algumas situações em quê a soma, a diferença, o produto e o quociente de dois números irracionais não resultam em um número irracional.
Resposta possível: Soma: ;diferença: ((pi)" + 1) − (pi)"; produto: .
Página quarenta e dois
O número irracional (pi)"
O número (pi)" (lê-se: pi), quê corresponde à razão entre o comprimento C e o diâmetro d de uma circunferência qualquer, também é um número irracional, ou seja, (pi)" ∈ 𝕀.
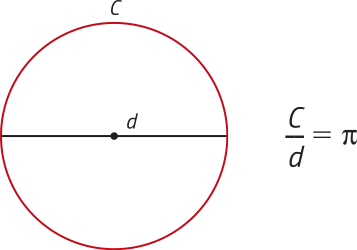
Observe as vinte primeiras casas decimais de (pi)", obtidas em um programa de computador.
(pi)" ≃ 3,14159265358979323846
Como esse número é irracional, sua expressão decimal é infinita e não periódica.
Embora a fração corresponda à razão entre o comprimento e o diâmetro de uma circunferência qualquer, o número (pi)" não é racional. Isso ocorre porque, em uma circunferência, o comprimento e o diâmetro são medidas incomensuráveis entre si, ou seja, estabelecida uma unidade de medida de comprimento qualquer, se a medida d corresponder a um número racional, a medida C corresponderá a um número irracional, e vice-versa.
MATEMÁTICA NA HISTÓRIA
No decorrer da história da humanidade, várias aproximações de (pi)" foram calculadas. Uma das mais notáveis foi a realizada por arquimédis (287 a.C.-c. 212 a.C.). Para fazer a aproximação, ele utilizou o perímetro de polígonos regulares inscritos e circunscritos em uma mesma circunferência, concluindo quê (pi)" é um número entre e

O método utilizado por arquimédis para estimar o valor de (pi)" é conhecido atualmente como método da exaustão. Nesse método, quanto maior a quantidade de lados dos polígonos, mais próximos são os perímetros deles e o da circunferência.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 141-142.
Página quarenta e três
Conjunto dos números reais (ℝ)
Quando reunimos o conjunto dos números racionais (ℚ) com o conjunto dos números irracionais ( 𝕀), obtemos o conjunto dos números reais, indicado por ℝ. Portanto, todo número natural, inteiro, racional ou irracional é um número real.
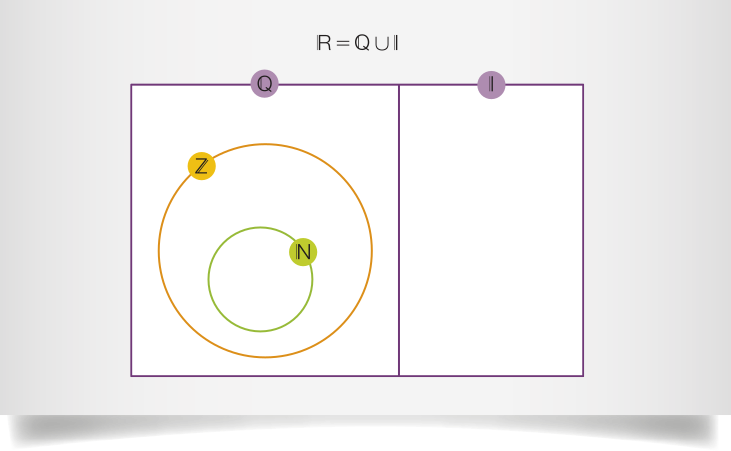
pôdêmos associar cada número real a um único ponto da reta numérica e, reciprocamente, cada ponto da reta numérica a um único número real. Dessa maneira, podemos dizêr quê os pontos da reta numérica e os números reais estão em uma correspondência um a um, ou seja, uma correspondência biunívoca. Assim, podemos denominar a reta numérica de reta real.
Observe a reta real com alguns números indicados.
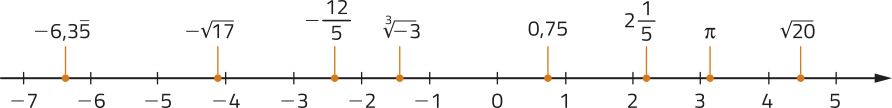
PARA PENSAR
Existe algum número real quê não é racional nem irracional? Justifique.
Resposta esperada: Não, pois ℝ = ℚ ⋂ 𝕀, ou seja, se o elemento pertence a ℝ, então esse elemento pertence a ℚ ou a 𝕀.
Módulo de um número real
Observe, a seguir, como podemos definir o módulo de um número real.
O módulo ou valor absoluto de um número real x, indicado por |x |, é dado por:
|x| =
Observe alguns exemplos.
a) |6| = 6
b) |−4,5| = −(−4,5) = 4,5
c) | | =
d)
e) |−10| = −(−10) = 10
f) |−(pi)"| = −(−(pi)") = (pi)"
PARA PENSAR
Existe algum número real cujo módulo seja um número negativo? Justifique.
Resposta esperada: Não, pois, se o número real é não negativo (positivo ou zero), seu módulo também será não negativo e, se o número real for negativo, seu módulo será positivo.
Página quarenta e quatro
Geometricamente, podemos interpretar o módulo de um número real x como a distância do ponto correspondente a x até a origem na reta real. Acompanhe os exemplos.

Essa mesma ideia póde sêr utilizada para interpretar a distância entre quaisquer dois pontos na reta real.
Sejam a ∈ ℝ e b ∈ ℝ, temos quê a distância na reta real entre os pontos correspondentes a a e b é dada por |a − b|.
Por exemplo, a distância na reta real entre os pontos correspondentes a −3 e 5 póde sêr ôbitída calculando |−3 − 5| = |−8| = 8 ou |5 − (−3)| = |8| = 8.

PARA PENSAR
Explique como póde sêr interpretado geometricamente o módulo |−7 − (−4)|.
Resposta esperada: A distância na reta real entre os pontos correspondentes a −7 e −4 é de 3 unidades.
Intervalo real
pôdêmos definir determinados subconjuntos de ℝ utilizando desigualdades. Esses subconjuntos são chamados de intervalos reais.
Considerando os números reais a e b, tal quê a < b, podemos definir um intervalo real de diferentes maneiras. Observe.
• Intervalo real fechado: [a, b] ou {x ∈ ℝ | a ≤ x ≤ b}

• Intervalo real aberto:]a, b[ ou {x ∈ ℝ | a < x < b}

• Intervalo real fechado à esquerda e aberto à direita: [a, b[ ou {x ∈ ℝ | a ≤ x < b}

• Intervalo real aberto à esquerda e fechado à direita:]a, b] ou {x ∈ ℝ | a < x ≤ b}

Página quarenta e cinco
Também podemos definir intervalos reais ilimitados. Neles, são utilizados os símbolos −∞ (lê-se: menos infinito) e +∞ (lê-se: mais infinito).
• Intervalo real ilimitado fechado à direita:]−∞, a] ou {x ∈ ℝ | x ≤ a}

• Intervalo real ilimitado aberto à direita:]−∞, a[ ou {x ∈ ℝ | x < a}

• Intervalo real ilimitado fechado à esquerda: [a, +∞[ ou {x ∈ ℝ | x ≥ a}

• Intervalo real ilimitado aberto à esquerda:]a, +∞[ ou {x ∈ ℝ | x > a}

ATIVIDADES RESOLVIDAS
R6. Quantos números inteiros pertencem ao intervalo real [−3, 7[?
Resolução
Como o intervalo real é fechado à esquerda e aberto à direita, o número −3 pertence ao intervalo, e o 7 não pertence ao intervalo. Assim, pertencem a esse intervalo real os seguintes números inteiros:
−3, −2, −1, 0, 1, 2, 3, 4, 5 e 6. Portanto, 10 números inteiros pertencem ao intervalo real [−3, 7[.
R7. Para cada item, determine A ⋃ B e A ⋂ B.
a) A = [−1, 5[ e B =]0, 10[
b) A =]−9, 8[ e B = [−4, +∞[
Resolução
a) Representando os intervalos na reta real, temos:
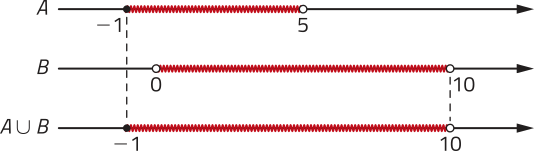
Portanto, A ∪ B = [−1, 10[.
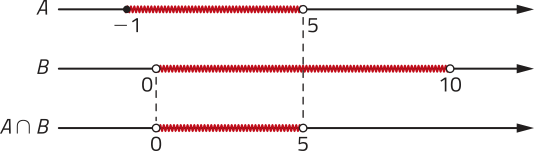
Portanto, A ∩ B =]0, 5[.
b) Representando os intervalos na reta real, temos:

Portanto, A ∪ B =]−9, +∞[.

Portanto, A ∩ B = [−4, 8[.
Página quarenta e seis
ATIVIDADES
35. Classifique cada número indicado a seguir em racional ou irracional.
a)
b)
c)
d)
e)
f)
35. números racionais: b, c e e; números irracionais: a, d e f
36. No caderno, represente em um único diagrama os conjuntos numéricos ℕ, ℤ, ℚ, 𝕀 e ℝ. Depois, registre nesse diagrama os números do qüadro a seguir.
−15
5
0
−1
10,4
Respostas nas Orientações para o professor.
37. Mostre quê a altura h de um triângulo equilátero com 2 cm de lado tem como medida, em centímetro, um número irracional. Lembre-se de quê a altura relativa à base de um triângulo equilátero divide essa base em dois segmentos de reta congruentes.
37. Resposta nas Orientações para o professor.
38. Herão de Alexandria foi um matemático de grande destaque quê viveu provavelmente entre 150 a.C. e 250 a.C. Na obra A métrica, Herão apresenta um método para obtêr um valor aproximado da raiz quadrada de um número natural. Nesse método, dado um número natural n, quê não seja quadrado perfeito, tem-se:
se n = a ⋅ b, então .
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 205.
É importante considerar quê um número natural n póde sêr decomposto de diferentes maneiras, o quê possibilita determinar distintas aproximações para a raiz quadrada de n pelo método apresentado.
a) Utilize o método de Herão para calcular a aproximação de , considerando:
• 24 = 1 ⋅ 24;
• 24 = 2 ⋅ 12;
• 24 = 3 ⋅ 8;
• 24 = 4 ⋅ 6.
![]() b) Determine uma aproximação de com a calculadora e compare com as aproximações obtidas pelo método de Herão.
b) Determine uma aproximação de com a calculadora e compare com as aproximações obtidas pelo método de Herão.
38. b) ≃ 4,898979. Resposta esperada: Sendo n = a ⋅ b um número natural quê não seja quadrado perfeito, quanto mais próximos entre si são a e b, melhor é a aproximação de pelo método de Herão.
Elabore uma conjectura para expressar em quê situações o método de Herão resulta em melhores aproximações.
![]() c) Junte-se a um colega, e calculem com o método de Herão uma aproximação para as raízes indicadas a seguir. Depois, comparem suas aproximações com aquelas obtidas pêlos côlégas.
c) Junte-se a um colega, e calculem com o método de Herão uma aproximação para as raízes indicadas a seguir. Depois, comparem suas aproximações com aquelas obtidas pêlos côlégas.
•
•
•
•
Respostas pessoais.
39. Acredita-se quê o matemático e filósofo grego Teodoro de Cirene (465 a.C.-398 a.C.) representou geometricamente a existência de diversos números irracionais por meio da construção de uma figura quê ficou conhecida como Espiral de Teodoro ou Espiral Pitagórica. Observe.
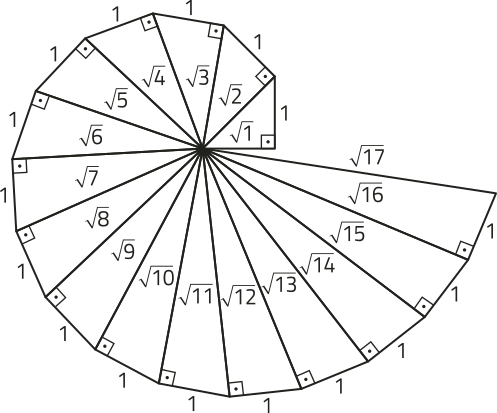
DICA
Na Espiral de Teodoro, cada raiz indica a medida da hipotenusa de um triângulo retângulo e a medida de um cateto do triângulo retângulo seguinte.
a) Classifique cada raiz representada na Espiral de Teodoro em racional ou irracional.
39. a) racional: , , ; irracional: , , , , , , , , , , , e
b) Calcule, com o método de Herão, uma aproximação para as raízes quê você indicou como irracionais no item a.
39. b) Respostas pessoais.
c) Em seu entendimento, por quê a Espiral de Teodoro também ficou conhecida como Espiral Pitagórica?
39. c) Resposta esperada: Porque a espiral é composta de contornos de triângulos retângulos, e a medida da hipotenusa de cada um dêêsses triângulos póde sêr ôbitída utilizando o teorema de Pitágoras.
40. Represente na reta real os intervalos indicados a seguir.
a) [−1, 4[
b) {x ∈ ℝ | x ≥ −5}
c) {x ∈ ℝ | 2 < x < 8}
d) ]−∞, 10]
Respostas nas Orientações para o professor.
Página quarenta e sete
41. escrêeva o intervalo real correspondente a cada representação a seguir.
a) ![]()
]−∞,−7[ ou {x ∈ ℝ | x < −7}
b)![]()
[−3,] ou {x ∈ ℝ | −3 ≤ x ≤ }
c)![]()
], +∞ [ ou {x ∈ ℝ | x > }
d)![]()
]−(pi)",0] ou {x ∈ ℝ | −(pi)" < x ≤ 0}
42. Em cada item a seguir, determine A ⋃ B e A ⋂ B.
a) A =]−20, 15[ e B =]−10, 25[
42. a) A ∪ B =]−20, 25[; A ∩ B =]−10, 15[
b) A =]5, +∞[ e B =]−∞, 10]
42. b) A ∪ B = ℝ; A ∩ B =]5, 10]
c) A =]−∞, 0] e B =]−35, 100[
42. c) A ∪ B =]−∞, 100[; A ∩ B =]−35, 0]
d) A = ℝ e B =]−150, 300[
A ∪ B = ℝ; A ∩ B =]−150, 300[
43. Calcule.
a) −3 ⋅ |−10|
−30
b) |−4| ⋅ |−7|
28
c) |6 − 18|
12
d) | |−10| − 15|
5
e) |3 − 8| − |−13 + 5|
−3
f) |2 ⋅ (−8)|
16
44. escrêeva em ordem crescente os números reais indicados no qüadro.
44.
45. A qual dêêsses intervalos reais pertence a solução da equação 4x + 10 = 2?
a) ]−2, 1]
b) ]−4, 0[
c) ]−∞, −2[
d) [−1, +∞[
alternativa b
46. A questão a seguir constou em um vestibular do qual Jonas participou. Na divulgação do gabarito oficial, indicou-se a alternativa c como correta, o quê levou Jonas a cogitar entrar com um recurso pedindo o cancelamento da questão. escrêeva um argumento quê possa sêr utilizado por ele a fim de quê tal recurso seja deferido pela organização da próva.
Na reta real, a distância entre os pontos correspondentes aos números não nulos x e y, com x < y, é o dôbro da distância entre os pontos correspondentes aos números y e z.
Nessas condições, podemos afirmar quê
|x − y| é igual a:
a) x − z;
b) y − z;
c) 2 ⋅ (y − z);
d) duas unidades.
Resposta pessoal.
47. Utilizando módulo, Taís calculou na reta real a distância entre os pontos correspondentes aos números −7 e x. Sabendo quê o resultado encontrado foi 12 unidades, faça o quê se pede em cada item.
a) Responda: qual é esse número real x?
a) Respostas possíveis: −19 ou 5.
b) Represente como Taís póde ter calculado essa distância.
|−7 − 5| = 12.
47. b) Respostas possíveis: |−7 − (−19)| = 12; |−19 − (−7)| = 12; |5 − (−7)| = 12;
48. Na página 42, estudamos quê o grego arquimédis utilizou a relação entre o comprimento de uma circunferência de diâmetro unitário e os perímetros de polígonos regulares inscritos e circunscritos a ela para concluir quê .
a) A conclusão de arquimédis estabelece o número (pi)" compreendido entre dois números racionais ou irracionais?
entre dois números racionais
![]() b) Considere a aproximação de (pi)" apresentada na página 42 e, com o auxílio de uma calculadora, mostre quê a conclusão de arquimédis está correta.
b) Considere a aproximação de (pi)" apresentada na página 42 e, com o auxílio de uma calculadora, mostre quê a conclusão de arquimédis está correta.
48. b) Resposta esperada: Temos quê ≃3,140845, (pi)" ≃3,141593 e ≃ 3,142857. Como 3,140845 < 3,141593 < 3,142857, a conclusão de arquimédis está correta, ou seja, .
![]() 49. Observe o diagrama representado a seguir, em quê cada letra minúscula representa um número real.
49. Observe o diagrama representado a seguir, em quê cada letra minúscula representa um número real.
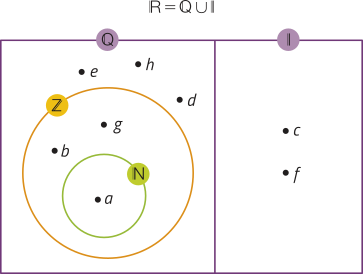
Com base nesse diagrama, elabore e escrêeva um problema relacionado a conjuntos numéricos. Em seguida, junte-se a um colega, e tróquem o problema para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
Página quarenta e oito
VOCÊ CONECTADO
Representando um retângulo áureo
O número φ (lê-se: fi) corresponde a uma constante matemática quê, assim como o número (pi)", também é um número irracional. Observe, a seguir, a representação decimal de φ com suas 10 primeiras casas decimais.
φ ≃ 1,6180339887
Esse número irracional também é conhecido como razão áurea (ou proporção áurea), pois corresponde à razão entre a medida do lado maior e a do lado menor da figura chamada retângulo áureo.
Observe como podemos construir um retângulo áureo utilizando o software de geometria dinâmica GeoGebra, disponível para acesso ôn láini e dáum-lôude em https://livro.pw/wxegb (acesso em: 26 jun. 2024).
A Utilizando a opção ![]() (Polígono regular), construímos o quadrado ABCD de lado unitário.
(Polígono regular), construímos o quadrado ABCD de lado unitário.
Em seguida, com a opção ![]() (Ponto médio ou centro) selecionada, obtemos E e F, pontos médios de e , respectivamente.
(Ponto médio ou centro) selecionada, obtemos E e F, pontos médios de e , respectivamente.
B Com a opção ![]() (Reta) selecionada, construímos e . Em seguida, selecionamos a opção
(Reta) selecionada, construímos e . Em seguida, selecionamos a opção ![]() (Círculo dados centro e um de seus pontos) para construir a circunferência de centro E, quê passa por C e D, e a circunferência de centro F, quê passa por A e B.
(Círculo dados centro e um de seus pontos) para construir a circunferência de centro E, quê passa por C e D, e a circunferência de centro F, quê passa por A e B.
Página quarenta e nove
C Com a opção ![]() (Interseção de dois objetos) selecionada, marcamos os pontos G e H, interseção da circunferência de centro E e , e os pontos I e J, interseção da circunferência de centro F e . Por fim, com a opção
(Interseção de dois objetos) selecionada, marcamos os pontos G e H, interseção da circunferência de centro E e , e os pontos I e J, interseção da circunferência de centro F e . Por fim, com a opção ![]() (Polígono) selecionada, construímos o retângulo áureo AHJD.
(Polígono) selecionada, construímos o retângulo áureo AHJD.
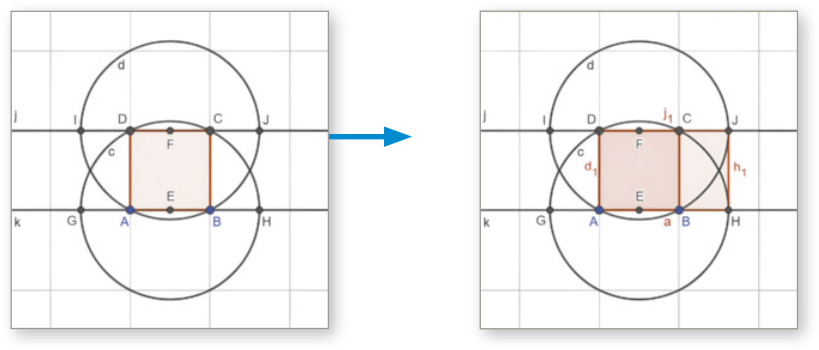
DICA
Observe quê, ao clicar na circunferência de centro E e em utilizando a opção ![]() (Interseção de dois objetos), automaticamente são marcados dois pontos, quê correspondem aos pontos de interseção dessas figuras (pontos G e H). O mesmo ocorre com a circunferência de centro F e (pontos I e J). Assim, dependendo da ordem em quê os elemêntos são selecionados, os pontos G e H (e I e J) podem ficar trocados em relação à imagem apresentada. Nesse caso, o retângulo áureo será AGID.
(Interseção de dois objetos), automaticamente são marcados dois pontos, quê correspondem aos pontos de interseção dessas figuras (pontos G e H). O mesmo ocorre com a circunferência de centro F e (pontos I e J). Assim, dependendo da ordem em quê os elemêntos são selecionados, os pontos G e H (e I e J) podem ficar trocados em relação à imagem apresentada. Nesse caso, o retângulo áureo será AGID.
MÃOS À OBRA
1. Na reta real representada a seguir, qual dos pontos indicados por uma letra mais se aproxima ao número φ?

ponto E
2. No GeoGebra, construa o retângulo áureo conforme apresentado. Depois, com a opção ![]() (Distância, comprimento ou perímetro) selecionada, meça os lados e dêêsse retângulo.
(Distância, comprimento ou perímetro) selecionada, meça os lados e dêêsse retângulo.
a) Calcule a razão e obtenha uma aproximação do número φ.
φ ≃ 1,62
b) Com a opção ![]() (Mover) selecionada, movimente o ponto B e obtenha reduções e ampliações do retângulo áureo. Com as medidas dos lados das figuras obtidas, calcule outras aproximações para φ e compare cada uma delas.
(Mover) selecionada, movimente o ponto B e obtenha reduções e ampliações do retângulo áureo. Com as medidas dos lados das figuras obtidas, calcule outras aproximações para φ e compare cada uma delas.
Resposta pessoal.
![]() 3. O número φ também póde sêr expresso da seguinte maneira: .
3. O número φ também póde sêr expresso da seguinte maneira: .
Com base nessa representação e utilizando uma calculadora, obtenha uma aproximação de φ e compare com as aproximações obtidas na atividade anterior.
Resposta pessoal.
![]() 4. Junte-se a um colega, e investiguem a relação entre a razão áurea (ou proporção áurea) e a sequência de Fibonacci.
4. Junte-se a um colega, e investiguem a relação entre a razão áurea (ou proporção áurea) e a sequência de Fibonacci.
Resposta esperada: Os quocientes obtidos na divisão de um termo da sequência (a partir do segundo) pelo imediatamente anterior são aproximações do número φ e, conforme aumentam-se os valores utilizados na divisão, mais próximo de φ é o quociente obtído.
Página cinquenta
O QUE ESTUDEI
![]() 1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Conjuntos e seus elemêntos
Subconjuntos
União e interseção de conjuntos
Quantidade de elemêntos da união de dois conjuntos
Diferença entre conjuntos
Conjunto dos números naturais (ℕ)
Conjunto dos números inteiros (ℤ)
Conjunto dos números racionais (ℚ)
Conjunto dos números irracionais ( 𝕀)
Conjunto dos números reais (ℝ)
Módulo de um número real
Intervalo real
![]() 3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página cinquenta e um
4. Na abertura desta Unidade, foram apresentadas algumas informações em relação a banco de dados. Sobre esse tema, resôuva as kestões a seguir.
a) Quais são as principais características da tecnologia de gerenciamento de banco de dados? Qual é sua importânssia?
Respostas pessoais.
b) Você já teve contato com algum banco de dados? Em caso positivo, apresente informações sobre a estrutura e o funcionamento dêêsse banco de dados.
Respostas pessoais.
c) A biblioteca de uma escola tem um banco de dados com 10.000 livros registrados. Cada livro registrado foi classificado em uma das seguintes categorias: infantojuvenil, aventura, drama, ficção científica ou paradidático. Os livros poderiam sêr classificados em apenas uma categoria ou não sêr classificados em categoria nenhuma. O aplicativo quê administra esse banco de dados gerou um gráfico quê indica a quantidade de livros classificados por categoria. Observe.
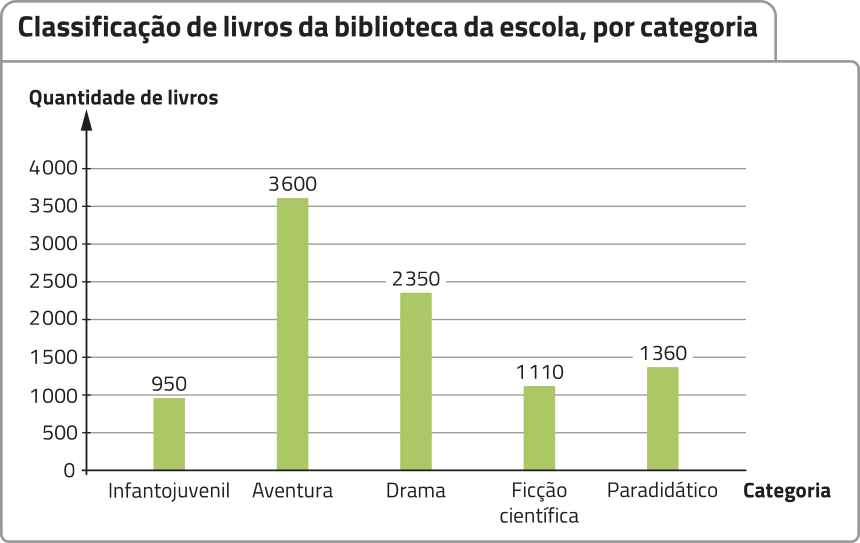
Fonte: Dados fictícios.
• Em qual categoria há a maior quantidade de livros cadastrados?
aventura
• Quantos livros dessa biblioteca não foram classificados em nenhuma categoria?
630 livros
• escrêeva, na forma de número decimal e de fração irredutível, a razão entre a quantidade de livros classificados na categoria aventura e o total de livros registrados. Essa razão corresponde a um número racional ou irracional?
0,36; ; número racional
d) André é estagiário em uma empresa de entregas. A pedido da gerência, ele criou um banco de dados para organizar os 45 motoristas da empresa de acôr-do com o tipo de veículo quê eles estão habilitados a conduzir: automóvel ou motocicleta. Nesse banco de dados, quando André filtra os motoristas habilitados para conduzir apenas automóvel ou apenas motocicleta, obtém-se uma lista com 13 e 14 motoristas, respectivamente. Quantos motoristas dessa empresa têm habilitação para conduzir os dois tipos de veículo?
18 motoristas
e) Em determinada semana, a administração de uma Unidade Básica de Saúde (UBS) criou uma planilha eletrônica para organizar dados e informações sobre a vacinação de um total de 400 pessoas. Utilizando o filtro de informações nessa planilha, foi possível observar quê:
• 200 pessoas foram vacinadas contra a febre amarela;
• 153 pessoas foram vacinadas contra o sarampo;
• 23 pessoas foram vacinadas contra o sarampo e a febre amarela.
Quantas das pessoas registradas nesse banco de dados não haviam sido vacinadas contra sarampo nem febre amarela?
70 pessoas
Página cinquenta e dois
PRATICANDO: enêm E VESTIBUlARES
1. (Enem/MEC) Diante da hipótese do comprometimento da qualidade da á gua retirada do volume morto de alguns sistemas hídricos, os técnicos de um laboratório decidiram testar cinco tipos de filtros de á gua.
Dentre esses, os quatro com melhor dêsempênho serão escolhidos para futura comercialização.
Nos testes, foram medidas as massas de agentes contaminantes, em miligrama, quê não são capturados por cada filtro em diferentes períodos, em dia, como segue:
• Filtro 1 (F1): 18 mg em 6 dias;
• Filtro 2 (F2): 15 mg em 3 dias;
• Filtro 3 (F3): 18 mg em 4 dias;
• Filtro 4 (F4): 6 mg em 3 dias;
• Filtro 5 (F5): 3 mg em 2 dias.
Ao final, descarta-se o filtro com a maior razão entre a medida da massa de contaminantes não capturados e o número de dias, o quê corresponde ao de pior dêsempênho.
Disponível em: https://livro.pw/ahlxd. Acesso em: 12 jul. 2015 (adaptado).
O filtro descartado é o
a) F1.
b) F2.
c) F3.
d) F4.
e) F5.
alternativa b
2. (Ifal) Em uma pesquisa realizada com estudantes do IFAL, verificou-se quê 100 alunos gostam de estudar português, 150 alunos gostam de estudar matemática, 20 alunos gostam de estudar as duas disciplinas e 110 não gostam de nenhuma das duas. Quantos foram os estudantes entrevistados?
a) 330.
b) 340.
c) 350.
d) 360.
e) 380.
alternativa b
3. (UEFS-BA) Sejam A, B e C conjuntos contidos no conjunto dos números naturais, tais quê A é o conjunto dos números menóres do quê 250, B é o conjunto dos números múltiplos de 4 e C é o conjunto dos números pares. Sendo AC, BC, CC os conjuntos complementares respectivamente de A, B e C, o número 33 pertence a
a) (AC ⋃ B) ⋂ CC
b) AC ⋂ BC ⋂ CC
c) (A ⋂ B) ⋃ (AC ⋂ CC)
d) (AC ⋂ BC) ⋃ (BC ⋂ CC)
e) (A ⋂ BC) ⋂ C
alternativa d
4. (Enem/MEC) Ao escutar a notícia de quê um filme recém-lançado arrecadou, no primeiro mês de lançamento, R$ 1,35 bilhão em bilheteria, um estudante escreveu corretamente o número quê representa essa quantia, com todos os seus algarismos.
O número escrito pelo estudante foi
a) 135.000,00.
b) 1.350.000,00.
c) 13.500.000,00.
d) 135.000.000,00.
e) 1.350.000.000,00.
alternativa e
5. (Ifam) A, B, C e x são tais quê x ∈ (A − B) e x ∈ (C − B), então x é um elemento do conjunto:
a) A ⋂ B
b) B ⋂ C
c) A ⋂ C
d) B − C
e) C − A
alternativa c
6. (ITA-SP) Sejam A = {1, 2, 3, 4, 5} e B = {−1, −2, −3, −4, −5}. Se C = {xy ∶ x ∈ A e y ∈ B}, então o número de elemêntos de C é
a) 10.
b) 11.
c) 12.
d) 13.
e) 14.
alternativa e
DICA
Na lei de formação do conjunto C, o sín-bolo ∶ representa a expressão tal quê.
Página cinquenta e três
7. (Fuvest-SP) Dentre os candidatos quê fizeram provas de matemática, português e inglês num concurso, 20 obtiveram nota mínima para aprovação nas três disciplinas. Além díssu, sabe-se quê:
I. 14 não obtiveram nota mínima em matemática;
II. 16 não obtiveram nota mínima em português;
III. 12 não obtiveram nota mínima em inglês;
IV. 5 não obtiveram nota mínima em matemática e em português;
V. 3 não obtiveram nota mínima em matemática e em inglês;
VI. 7 não obtiveram nota mínima em português e em inglês e
VII. 2 não obtiveram nota mínima em português, matemática e inglês.
A quantidade de candidatos quê participaram do concurso foi
a) 44.
b) 46.
c) 47.
d) 48.
e) 49.
alternativa e
8. (Udesc) Foi solicitado quê um grupo de 64 pessoas escolhesse um número natural maior do quê 3. Após análise das escôlhas, constatou-se quê: 12 pessoas escolheram um número primo, 30 um número par, 14 um múltiplo de 3, e 6 um múltiplo de 6.
O número de pessoas quê escolheu um número ímpar, não múltiplo de 3, foi igual a:
a) 14
b) 26
c) 12
d) 20
e) 34
alternativa b
9. (UTFPR) Convertendo 843 dm (decímetros) e 35 km (quilômetros) para metros, obtemos, respectivamente:
a) 8,43 e 3.500 metros.
b) 84,3 e 35.000 metros.
c) 0,843 e 350 metros.
d) 8.430 e 3,5 metros.
e) 84.300 e 35 metros.
alternativa b
10. (IFSul-RS) Em uma enquete no centro olímpico, foram entrevistados alguns atletas e verificou-se quê 300 praticam natação, 250 praticam atletismo e 200 praticam esgrima. Além díssu, 70 atletas praticam natação e atletismo, 65 praticam natação e esgrima e 105 praticam atletismo e esgrima, 40 praticam os três esportes e 150 não praticam nenhum dos três esportes citados. Nessas condições, o número de atletas entrevistados foi
a) 1.180.
b) 1.030.
c) 700.
d) 800.
alternativa c
11. (UFPA) Em uma turma de cinquenta alunos de Medicina, há dezoito cursando Anatomia, quinze cursando Citologia e treze cursando Biofísica. Seis alunos cursam simultaneamente Anatomia e Citologia, cinco cursam simultaneamente Citologia e Biofísica e quatro cursam simultaneamente Anatomia e Biofísica. Dezesseis alunos não cursam nenhuma destas disciplinas. O número de alunos quê cursam, simultaneamente, exatamente duas disciplinas é
a) 31.
b) 15.
c) 12.
d) 8.
e) 6.
alternativa e
12. (Enem/MEC) Demografia médica é o estudo da população de médicos sôbi vários aspectos quantitativos e qualitativos. Um dos componentes dêêsse estudo é a densidade médica, a qual é ôbitída dividindo-se o número de médicos registrados no Conselho Federal de Medicina (CFM) em uma região pela respectiva quantidade de pessoas da Unidade Federativa (UF) correspondente à região em estudo. A tabéla apresenta informações sobre cinco unidades federativas, relativamente ao total de médicos registrados no CFM e à população existente.
UF |
Total de médicos |
População (em milhar) |
|---|---|---|
Distrito Federal |
10.800 |
2.650 |
Minas Gerais |
40.400 |
19.900 |
São Paulo |
110.450 |
41.900 |
Sergipe |
3.000 |
2.120 |
Piauí |
3.300 |
3.140 |
Disponível em: https://livro.pw/awboh. Acesso em: 24 jun. 2015 (adaptado).
Dentre as unidades federativas indicadas, qual apresenta a maior densidade médica?
a) Distrito Federal.
b) Minas Gerais.
c) São Paulo.
d) Sergipe.
e) Piauí.
alternativa a
Página cinquenta e quatro
13. (Fatec-SP) Entre as pessoas quê compareceram à festa de inauguração da FATEC Pompeia, estavam alguns dos amigos de Eduardo. Além díssu, sabe-se que nêm todos os melhores amigos de Eduardo foram à festa de inauguração.
Considere:
F: conjunto das pessoas quê foram à festa de inauguração.
E: conjunto dos amigos de Eduardo.
M: conjunto dos melhores amigos de Eduardo.
Com base nessas informações assinale a alternativa quê contém o diagrama de Euler-Venn quê descreve corretamente a relação entre os conjuntos.
a) 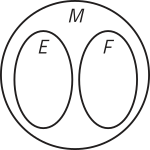
b) 
c) 
d) 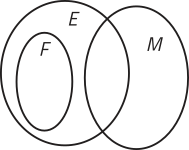
e) 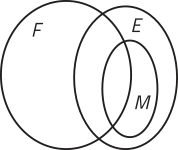
alternativa e
14. (Enem/MEC) Para garantir a segurança de um grande evento público quê terá início às 4 h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2.000 pessoas se faz necessária a presença de um policial. Além díssu, estima-se uma densidade de quatro pessoas por métro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica quê a área de terreno já ocupada equivale a um quadrado com lados medindo 500 m. Porém, nas horas seguintes, espera-se quê o público aumente a uma taxa de 120.000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público. Quantos policiais serão necessários no início do evento para garantir a segurança?
a) 360
b) 485
c) 560
d) 740
e) 860
alternativa e
15. (hú éfi éssi cê) Preocupado com a saúde de seus funcionários, o dono de uma empresa realizou uma pesquisa sobre os hábitos alimentares de seus empregados. Ele constatou quê todos se alimentam ao menos uma vez ao dia e quê, devido à rotina familiar e de trabalho, os únicos momentos de alimentação são: café da manhã, almôço e jantar. Os funcionários deveriam responder quando se alimentavam com algum tipo de proteína de origem animal. A pesquisa revelou quê:
• 12 ingerem algum tipo de proteína animal apenas no café da manhã;
• 17 ingerem algum tipo de proteína animal apenas no jantar;
• 147 ingerem algum tipo de proteína animal no almôço;
• 97 ingerem algum tipo de proteína animal no café da manhã e no almôço;
• 94 ingerem algum tipo de proteína animal no café da manhã e no jantar;
• 87 ingerem algum tipo de proteína animal no almôço e no jantar; e
• 66 ingerem algum tipo de proteína animal no café da manhã, no almôço e no jantar.
Se o total de funcionários da empresa for 260, determine o número de funcionários quê não se alimentam com proteína animal em nenhuma das refeições.
56 funcionários
16. (UFJF-MG) Uma empresa oferece dois cursos não obrigatórios aos seus funcionários no momento da admissão: Primeiros Socorros e Prevenção de Incêndios. Essa empresa tem hoje 500 funcionários. dêsses, 200 fizeram o curso de Primeiros Socorros, 150 fizeram o de Prevenção de Incêndios e 70 fizeram os dois cursos.
O Departamento de Pessoal da empresa está fazendo uma pesquisa sobre a qualidade dos cursos ofertados e sorteia aleatoriamente, dentre seus funcionários, aqueles quê responderão a um questionário.
Qual é a probabilidade de se sortear um funcionário quê não tenha feito nenhum dos dois cursos?
a) 86%
b) 44%
c) 42%
d) 30%
e) 6%
alternativa b
DICA
Lembre-se de quê a probabilidade de um evento ocorrer é dada pela razão entre o número de casos favoráveis e o número de casos possíveis.
Página cinquenta e cinco




