UNIDADE 2
RELAÇÕES ENTRE GRANDEZAS E NOÇÃO DE FUNÇÃO
O Sistema Internacional de Unidades (SI)
O Sistema Internacional de Unidades (SI) é utilizado em quase todo o mundo como um sistema universal de unidades, contribuindo para diversos aspectos da ssossiedade, como facilitar as relações comerciais. No SI, estão definidas não apenas as unidades de medida mas também seus nomes, símbolos, prefixos, múltiplos, submúltiplos etc.
Ao longo dos anos, mudanças são implementadas no SI para, por exemplo, sêrem adotadas definições de unidades de medida mais precisas e menos suscetíveis a alterações. A unidade de medida de massa quilograma (kg), por exemplo, desde sua inserção no SI, era definida por um protótipo cilíndrico de platina (Pt) e irídio (Ir) com 39 mm de diâmetro e 39 mm de altura (conforme a fotografia). No entanto, com o passar dos anos, esse objeto perdeu 50 microgramas de sua massa original. Por esse motivo, a partir de 2019, essa definição passou a ser baseada na relação massa-energia, de maneira quê a medida póde sêr ôbitída êsperimentalmente a partir de um procedimento quê relaciona um valor de corrente elétrica e o valor da constante de Planck (6,62607015 ⋅ 10−34 J ⋅ s), quê descreve as quantidades de energia emitidas em forma de radiação.


Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Em seu entendimento, qual é a importânssia das unidades de medida padronizadas?
2. Explique o motivo quê levou à redefinição do quilograma no SI.
3. Cite alguns exemplos de outras grandezas e as unidades de medida correspondentes. Se necessário, realize uma pesquisa.
Página cinquenta e seis
Grandezas
Na abertura desta Unidade, lemos informações relacionadas ao Sistema Internacional de Unidades (SI) e a alteração da definição da unidade de medida quilograma (kg), relacionada à grandeza massa. No dia a dia e em seus estudos, você provavelmente já trabalhou com diversas grandezas e unidades de medida. Agora, vamos retomar e aprofundar esse estudo.
Considere a situação a seguir.
Treinos de caminhada ou corrida, com orientações de um profissional capacitado, são considerados boas opções de atividade física. Alguns aplicativos para smartphone podem sêr usados para acompanhar treinos como esses. Observe o exemplo a seguir.
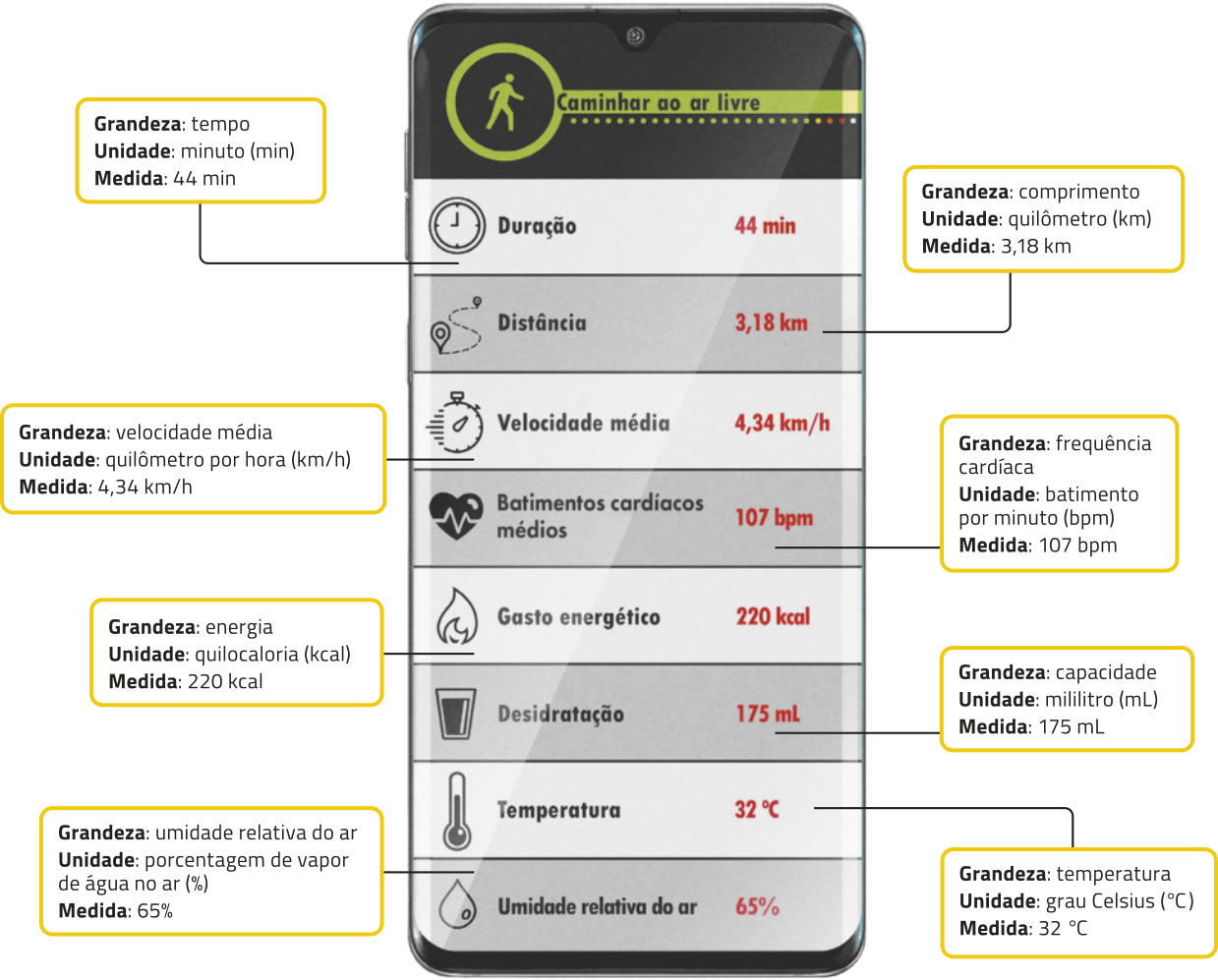
PARA AMPLIAR
Acesse esta cartilha sobre o novo Sistema Internacional de Unidades e obtenha mais informações sobre grandezas e unidades de medida.
• SOCIEDADE BRASILEIRA DE METROLOGIA; SOCIEDADE BRASILEIRA DE FÍSICA. O novo Sistema Internacional de Unidades (SI). Rio de Janeiro: SBM, 2019. Disponível em: https://livro.pw/omnfx. Acesso em: 27 jun. 2024.
Página cinquenta e sete
Utilizado na maioria dos países, o SI busca padronizar as medições e facilitar as relações entre o comércio local e o internacional. Observe.
Grandezas e unidades de base do SI
Grandeza |
Unidade (sín-bolo) |
|---|---|
Comprimento |
métro (m) |
Massa |
quilograma (kg) |
Tempo |
segundo (s) |
Corrente elétrica |
ampere (A) |
Temperatura termodinâmica |
kelvin (K) |
Quantidade de matéria |
mol (mol) |
Intensidade luminosa |
candela (cd) |
Fonte dos dados: INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA; INSTITUTO PORTUGUÊS DA QUALIDADE. Sistema Internacional de Unidades (SI). Tradução: Grupo de Trabalho luso-brasileiro do Inmetro e IPQ. Brasília, DF: Inmetro; Caparica: IPQ, 2021. p. 6. Tradução luso-brasileira da 9ª edição. Disponível em: https://livro.pw/vbxre. Acesso em: 27 jun. 2024.
Além das unidades estabelecidas para as grandezas de base do SI, consideramos seus múltiplos e submúltiplos. Em relação à unidade de comprimento métro, por exemplo, temos:
quilômetro (km) |
hectometro (hm) |
decâmetro (dam) |
métro (m) |
decimetro (dm) |
centímetro (cm) |
milímetro (mm) |
|---|---|---|---|---|---|---|
1 km = 1.000 m |
1 hm = 100 m |
1 dam = 10 m |
1 m |
1 dm = 0,1 m |
1 cm = 0,01 m |
1 mm = 0,001 m |
Observe como podemos converter 12 m para:
• quilômetro: 12 m = = 12 ⋅ 0,001 km = 0,012 km;
• decâmetro: 12 m = = 12 ⋅ 0,1 dam = 1,2 dam;
• centímetro: 12 m = =12 ⋅ 100 cm = 1.200 cm;
• milímetro: 12 m = =12 ⋅ 1.000 mm = 12.000 mm.
No SI, existem também as grandezas derivadas, cujas unidades de medida correspondem a produtos ou razões de unidades de base.
Exemplos de grandezas e unidades derivadas do SI
Grandeza |
Unidade (sín-bolo) |
|---|---|
Área |
métro quadrado (m2) |
Volume |
métro cúbico (m3) |
Velocidade |
métro por segundo (m/s) |
Aceleração |
métro por segundo ao quadrado (m/s2) |
Densidade |
quilograma por métro cúbico (kg/m3) |
Fonte dos dados: INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA; INSTITUTO PORTUGUÊS DA QUALIDADE. Sistema Internacional de Unidades (SI). Tradução: Grupo de Trabalho luso-brasileiro do Inmetro e IPQ. Brasília, DF: Inmetro; Caparica: IPQ, 2021. p. 14-15. Tradução luso-brasileira da 9ª edição. Disponível em: https://livro.pw/vbxre. Acesso em: 27 jun. 2024.
PARA PENSAR
Pense em uma situação do dia a dia em quê seja necessário realizar conversão de unidades entre os múltiplos e submúltiplos do métro e explique a um colega.
A resposta depende do tema escolhido pelo estudante.
Página cinquenta e oito
ATIVIDADES RESOLVIDAS
R1. A densidade d de um corpo é a razão entre sua massa m e seu volume v. Por exemplo, a prata tem densidade de 10,5 g/cm3, ou seja, cada 1 cm3 de prata tem 10,5 g. Observe os objetos representados a seguir e algumas de suas medidas. (As imagens apresentadas estão fora de proporção.)

Massa: 1.560 g.
Volume: 600 cm³.

Massa: 405 g.
Densidade do alumínio: 2,7 g/cm³.

Volume: 1.140 cm³.
Densidade do ferro: 7,9 g/cm³.
Com base nessas informações, determine:
a) a densidade do vidro, em grama por centímetro cúbico;
b) o volume do objeto decorativo em alumínio, em centímetro cúbico;
c) a massa do banco de ferro, em grama.
Resolução
Para resolver esses itens, podemos utilizar a expressão d = ,sendo d a densidade, m a massa e v o volume.
a) d = = 2,6; ou seja, 2,6 g/cm3.
b) 2,7 = = 150; ou seja, 150 cm3.
c) 7,9 = ⇒ m = 7,9 ⋅ 1.140 = 9.006; ou seja, 9.006 g.
R2. (Enem/MEC) Numa atividade de treinamento realizada no Exército de um determinado país, três equipes – Alpha, Beta e Gama – foram designadas a percorrer diferentes caminhos, todos com os mesmos pontos de partida e de chegada.
• A equipe Alpha realizou seu percurso em 90 minutos com uma velocidade média de 6,0 km/h.
• A equipe Beta também percorreu sua trajetória em 90 minutos, mas sua velocidade média foi de 5,0 km/h.
• Com uma velocidade média de 6,5 km/h, a equipe Gama concluiu seu caminho em 60 minutos.
Com base nesses dados, foram comparadas as distâncias dBeta; dAlpha e dGama percorridas pelas três equipes.
A ordem das distâncias percorridas pelas equipes Alpha, Beta e Gama é
a) dGama < dBeta < dAlpha
b) dAlpha = dBeta < dGama
c) dGama < dBeta = dAlpha
d) dBeta < dAlpha < dGama
e) dGama < dAlpha < dBeta
DICA
A velocidade média v é dada pela razão entre a distância d e o tempo t de percurso.
Página cinquenta e nove
Resolução
Para resolver esta atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Considerando v a velocidade média e t o tempo da realização do percurso das equipes, com base no enunciado, temos:
• vAlpha = 6 km/h e tAlpha = 90 min; • vBeta = 5 km/h e tBeta = 90 min; • vGama = 6,5 km/h e tGama = 60 min.
Precisamos determinar a ordem das distâncias percorridas pelas equipes.
2ª ELABORAR UM PLANO
Primeiro, é necessário converter o tempo de minuto (min) para hora (h), uma vez quê, nessa situação, as velocidades médias estão expressas em quilômetro por hora (km/h). Depois, basta substituir os valores de velocidade (indicados no enunciado) e de tempo (convertidos de minuto para hora) na expressão v =
3ª EXECUTAR O PLANO
Como 1 h = 60 min, realizamos as conversões:
• tAlpha = 90 min = h = 1,5 h; • tBeta = 90 min = h = 1,5 h; • tGama = 60 min = h = 1 h.
Assim, substituímos os tempos e as velocidades na expressão indicada anteriormente:
• vAlpha = ⇒ d Alpha= 9; ou seja, 9 km;
• vBeta = ⇒ d Beta= 7,5; ou seja, 7,5 km;
• vGama = ⇒ d Gama= 6, 5; ou seja, 6,5 km.
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado obtído, podemos calcular a velocidade média de cada equipe com base na distância calculada e no tempo indicado no enunciado.
• vAlpha = = 6; ou seja, 6 km/h;
• vBeta = = 5; ou seja, 5 km/h;
• vGama = = 6,5; ou seja, 6,5 km/h.
Como as velocidades médias calculadas correspondem às indicadas no enunciado, podemos concluir quê as distâncias obtidas estão corretas.
Portanto, a alternativa a é a correta, pois 6,5 < 7,5 < 9, ou seja, dGama < dBeta < dAlpha.
Página sessenta
Outras grandezas
Além das grandezas de base e das grandezas derivadas, adotadas no SI, há diversas outras quê são utilizadas em situações de diferentes áreas do conhecimento, como aquelas relacionadas à informática. Estudaremos, a seguir, algumas dessas grandezas.
Armazenamento de dados
Você conhece o sistema de armazenamento de dados em nuvem?
O armazenamento em nuvem permite quê dados sêjam “guardados” em um servidor ôn láini com grande capacidade de armazenamento. Nesse tipo de sistema, arquivos digitais podem sêr salvos, acessados e baixados a distância, em qualquer localidade com acesso a uma rê-de de internet. Acompanhe.
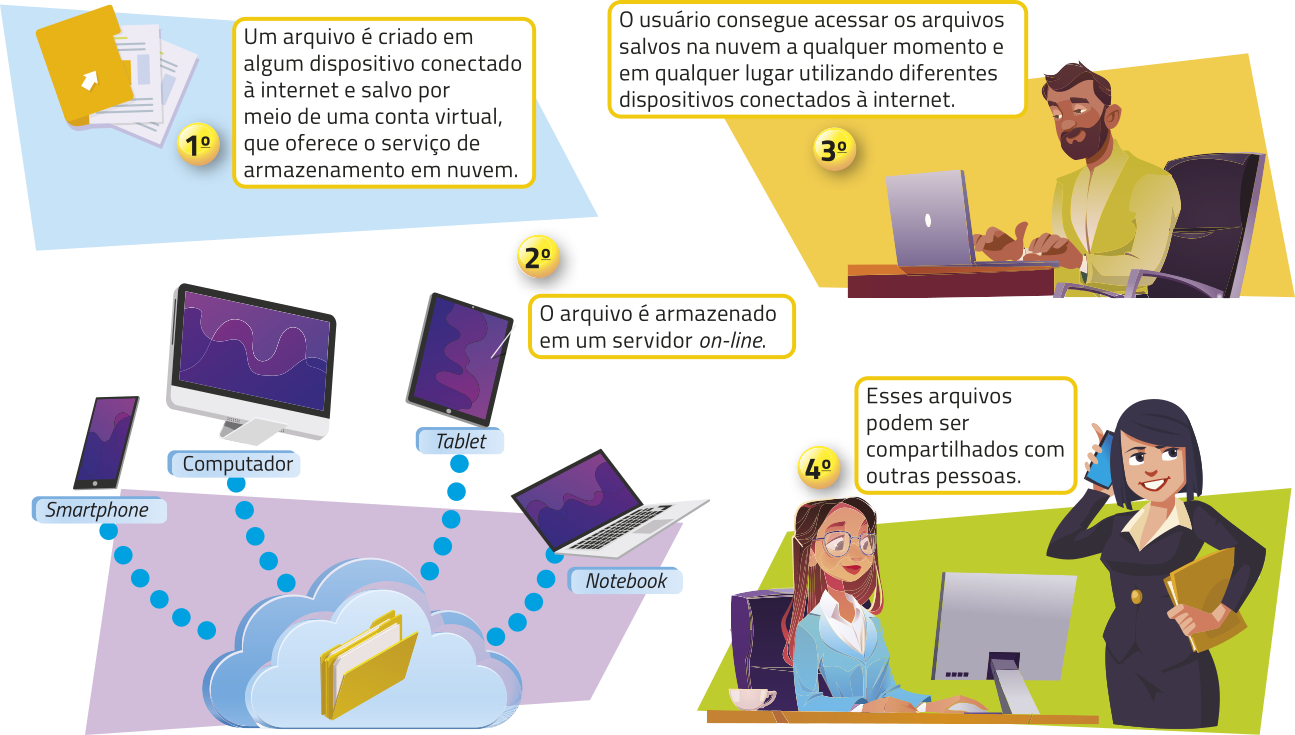
A capacidade de armazenamento de dados disponibilizada aos usuários de sêrviços de armazenamento em nuvem costuma ser expressa com a unidade de medida baite (B) ou um de seus múltiplos. Um baite (1 B) corresponde ao espaço ocupado por um caractere e equivale a 8 bites, sêndo o bite (b) a menor unidade de informação quê póde sêr armazenada por um computador.
Observe conversões entre o baite e alguns de seus múltiplos.
Unidade de medida de armazenamento (sín-bolo) |
Conversão |
|---|---|
baite (B) |
1 B = 8 b |
quilobaite (kB) |
1 kB = 1.024 B |
megabaite (MB) |
1 MB = 1.024 kB |
gigabaite (GB) |
1 GB = 1.024 MB |
terabaite (TB) |
1 TB = 1.024 GB |
Página sessenta e um
ATIVIDADES RESOLVIDAS
R3. Em cada item, realize as conversões indicadas.
a) 10 kB para baite.
b) 640 MB para gigabaite.
c) 2 TB para megabaite.
Resolução
a) 10 kB = 10 ⋅ = 10 ⋅ 1.024 B = 10.240 B
b) 640 MB = 640 = 0,625 GB
c) 2 TB = 2 ⋅ 1.024 ⋅ 1.024 MB = 2.097.152 MB
PARA PENSAR
Indique uma medida qualquer utilizando um dos múltiplos do baite como unidade. Depois, converta essa medida para outras duas unidades de medida de armazenamento.
Resposta pessoal.
R4. Uma agência de marketing digital produz vídeos para postagens em rêdes sociais. Por segurança, a agência pretende fazer um backup, em um HD externo, de 44.000 vídeos já produzidos. Cada vídeo dêêsses, em média, tem cerca de 1min30s de duração e 100 MB de tamãnho. Considerando as médias de duração e tamãnho de cada vídeo produzido, determine quais dos HDs externos representados a seguir podem sêr utilizados para esse backup.
a) 
b) 
c) 
d) 
e) 
Resolução
Considerando quê cada vídeo produzido pela agência tem 100 MB, calculamos quantos megabaites ao todo têm os 44.000 vídeos:
44.000 ⋅ 100 = 4.400.000, ou seja, 4.400.000 MB.
Como a capacidade dos HDs externos indicados nas alternativas é dada em gigabaite e terabaite, fazemos a conversão de 4.400.000 MB em gigabaite e terabaite:
4.400.000 MB = ≃ 4.297 GB
4.297 GB = ≃ 4,2 TB
Comparando os resultados obtidos com as capacidades dos HDs externos indicados nas alternativas, temos:
• 250 GB < 500 GB < 4.297 GB
• 4 TB < 4,2 TB < 8 TB < 16 TB
Portanto, os únicos HDs externos capazes de armazenar todos os 44.000 vídeos produzidos pela agência são aqueles indicados nas alternativas b e e.
PARA PENSAR
Todos os dados apresentados no enunciado da atividade foram utilizados na resolução? Comente.
Não. Por exemplo, o tempo médio de duração dos vídeos não foi utilizado na resolução.
Página sessenta e dois
Taxa de transferência de dados
Quando baixamos (dáum-lôude) ou enviamos (upload) um arquivo eletronicamente, podemos indicar a quantidade de dados quê é transferida em um intervalo de tempo pela chamada taxa de transferência.
Uma taxa de transferência de dados de 32 Mbps (lê-se: trinta e dois megabaites por segundo) indica quê a cada segundo, em média, são transferidos 32 megabaites (Mb) de dados. Por exemplo, considerando essa taxa de transferência, podemos estimar quanto tempo seria necessário para transferir um arquivo de 20 MB realizando as etapas a seguir.
1ª) Converter o tamãnho do arquivo de megabaites para megabaites.
Como 1 B equivale a 8 b, temos quê 1 MB equivale a 8 Mb. Assim:
20 MB = 20 ⋅ = 20 ⋅ 8 Mb = 160 Mb
2ª) Determinar o tempo para a transferência do arquivo.
Organizando as informações, obtemos:
Tamanho do arquivo (Mb) |
Tempo (s) |
|---|---|
32 |
1 |
160 |
x |
Como as grandezas tamãnho do arquivo e tempo são diretamente proporcionais, temos:
⇒ 32x = 160 ⇒ x = = 5
Portanto, com uma taxa de transferência de 32 Mbps, seriam necessários 5 s para transferir um arquivo de 20 MB.
ATIVIDADES
1. Em cada item, identifique a qual grandeza as medidas indicadas correspondem: comprimento, massa ou tempo. Depois, copie a igualdade e substitua ____ por um número quê a torne verdadeira.
a) 8,5 t = ____ kg
massa; 8.500
b) ____ m = 90 km
comprimento; 90.000
c) 10.800 s = ____ h
tempo; 3
d) ____ dm = 7 mm
comprimento; 0,07
e) ____ kg = 1.650 g
massa; 1,65
f) 4,2 min = ____ s
tempo; 252
2. Converta:
a) 4 TB para gigabaite.
4.096 GB
b) 512 B para quilobaite.
0,5 kB
c) 3.072 kB para megabaite.
3 MB
d) 0,5 GB para quilobaite.
524.288 kB
3. jã utiliza uma conta virtual para armazenar na nuvem os arquivos de fotografia do seu smartphone. Ele já utilizou 1.460 MB da capacidade total disponível dessa conta, quê é de 2 GB.
Sabendo quê cada arquivo de fotografia ôbitída por jã tem cerca de 4 MB, quantas fotografias ele ainda póde armazenar nessa conta?
147 arquivos de fotografia
4. Estudamos quê a densidade de um material é expressa pela razão entre sua massa e seu volume. Com base nessa ideia, determine os valores correspondentes às lêtras em destaque a seguir.
A: 2,4 g/cm³; B: aproximadamente 0,35 cm³; C: 42 g
Objeto |
Massa (g) |
Volume (cm3) |
Densidade (g/cm3) |
|---|---|---|---|
Caneca de porcelana |
384 g |
160 cm3 |
A |
Moeda de aço inoxidável |
2,8 g |
B |
7,9 g/cm3 |
Parafuso de latão |
C |
5 cm3 |
8,4 g/cm3 |
Página sessenta e três
5. Observe as informações sobre o planêta Marte e resôuva as kestões.
Dados marcianos
Diâmetro: 6.792 km
Distância média do Sol: 227,9 milhões de km
Período orbital: 687 dias terrestres
Período de rotação: 24,62 horas
Temperatura de superfícíe: −125 °C a 25 °C
Número de satélites: 2

Fonte dos dados: RIDPATH, Ian. Astronomia. Tradução: Maria Luiza X. de A. Borges. 4. ed. Rio de Janeiro: Zarrár, 2014. (Guia Ilustrado Zarrár, p. 103).
a) As medidas indicadas correspondem a quais grandezas?
5. a) comprimento: diâmetro e distância média do Sol; tempo: período orbital e período de rotação; tempera-túra: tempera-túra de superfícíe
b) Expresse a medida do diâmetro de Marte em:
• hectômetro;
67.920 hm
• centímetro;
679.200.000 cm
• métro.
6.792.000 m
c) Qual é a amplitude térmica da superfícíe de Marte?
150 °C
d) Determine o período de rotação de Marte em hora, minuto e segundo.
24h37min12s
e) ![]() Com dois côlégas, façam o quê se pede nos itens a seguir, recorrendo, quando necessário, a sáites e livros quê abordem assuntos de Física e de Astronomia.
Com dois côlégas, façam o quê se pede nos itens a seguir, recorrendo, quando necessário, a sáites e livros quê abordem assuntos de Física e de Astronomia.
Pesquisa e elaboração dos estudantes.
• Escolham um dos planêtas do Sistema Solar e pesquisem suas principais medidas, conforme o qüadro apresentado no início da atividade. Em seguida, elaborem um cartaz com as informações encontradas. Ao final, exponham aos côlégas da turma os cartazes elaborados.
• Investiguem como são determinadas atualmente as medidas: diâmetro de um planêta e distância média do Sol. Por fim, redijam um pequeno texto sistematizando as informações pesquisadas.
6. Leia o trecho de um artigo publicado em um sáiti de divulgação científica e responda às kestões.
[...] a grande dificuldade de aceitar os movimentos da Terra deve-se ao fato de quê não sentimos isso acontecer de uma maneira diréta. A velocidade de rotação da Terra é de aproximadamente 1.675 km/h e a de translação, 109 mil km/h – extremamente altas, considerando quê, em nosso cotidiano, nos deslocamos a velocidades na ordem de 100 km/h. Porém, é difícil sentir essa velocidade vertiginosa porque também estamos nos movendo junto com o planêta.
Uma imagem para ajudar a compreender: quando estamos dentro de um automóvel percorrendo uma estrada reta com velocidade constante, não percebemos quê estamos em movimento se olharmos apenas para dentro do carro. Se olhamos para a estrada, o quê vemos são os objetos se deslocando para trás. Parece estranho, mas, do nosso ponto de vista, estamos parados. O résto do mundo é quê se móve. Esse é o conceito de relatividade do movimento, percebido pelo físico e astrônomo italiano Galileu Galilei no komêsso do século 17.
OLIVEIRA, Adilson de. O Sol vai parar. Rio de Janeiro: Ciência Hoje, c2024. Disponível em: https://livro.pw/unpvp. Acesso em: 26 jun. 2024.
a) De quê movimentos da Terra esse trecho trata?
rotação e translação
b) Quais grandezas e unidades de medida são citadas nesse trecho?
6. b) grandeza: velocidade; unidade de medida: quilômetro por hora (km/h)
c) ![]() Com base em seu conhecimento sobre os movimentos da Terra e nas informações dêêsse trecho, estime a medida do comprimento da linha do equador. Depois, explique a um colega como você rêzouvêo essa questão.
Com base em seu conhecimento sobre os movimentos da Terra e nas informações dêêsse trecho, estime a medida do comprimento da linha do equador. Depois, explique a um colega como você rêzouvêo essa questão.
6. c) Resposta esperada: Como o movimento de rotação da Terra tem duração aproximada de 24 h, podemos multiplicar esse valor pela medida da velocidade de rotação da Terra, quê é de aproximadamente 1.675 km/h, para estimar a medida do comprimento da linha do equador em 40.200 km (1.675 ⋅ 24 = 40.200).
7. Um objeto sólido com 180 g de massa e 100 cm3 de volume encontra-se no fundo de um recipiente com 500 cm3 de um líquido A de densidade igual a 0,9 g/cm3. Ao adicionar 500 cm3 de um líquido B nesse recipiente, é formada uma mistura homogênea e o objeto passa a flutuar na mistura. Qual deve sêr a densidade mínima do líquido B?
2,7 g/cm3
DICA
A densidade dessa mistura póde sêr determinada por uma média ponderada, considerando a proporção da mistura e a densidade de cada líquido.
Página sessenta e quatro
8. Leia o trecho de um artigo publicado em um sáiti de divulgação científica e responda às kestões.
Algumas propriedades distinguem os vírus de outros microrganismos. A primeira está relacionada ao seu tamãnho, o qual póde variar de 10 a 300 nm. Dessa forma, são considerados os menóres microrganismos existentes, podendo sêr visualizados apenas através da microscopía eletrônica. Para fins de comparação, lembramos quê as bactérias e as hemácias possuem, em média, 10 a 15 vezes o tamãnho dos vírus, o quê possibilita a identificação dêstes por meio da microscopía óptica.
istífens, Paulo Roberto Soares éti áu. Virologia. In: MOLINARO, Etelcia Moraes; CAPUTO, Luzia Fátima Gonçalves; AMENDOEIRA, Maria Regina Reis (org.). Conceitos e métodos para formação de profissionais em laboratórios de saúde. Rio de Janeiro: Escola Politécnica de Saúde Joaquim Venâncio: Instituto ôsváldo Cruz, 2009. v. 4, p. 126. Disponível em: https://livro.pw/lmhpy. Acesso em: 27 jun. 2024.
a) Em uma régua escolar comum, a distância entre duas marcações consecutivas indica a medida de 1 mm, quê corresponde a 106 nanometros (nm). Determine, em milímetro, as dimensões mínima e mássima do tamãnho de um vírus.
8. a) de 0,00001 mm ou 10−5 mm até 0,0003 mm ou 3 ⋅ 10−4 mm
b) A imagem a seguir é uma ampliação do vírus SARS-CoV-2, quê causa a covid-19. méça o diâmetro dêêsse vírus, indicado na imagem, e expresse, em nanômetro, a medida ôbitída.
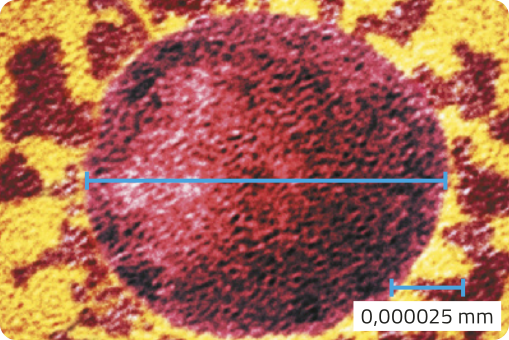
120 nm
c) Em média, qual é o intervalo de tamãnho de uma bactéria? Expresse as medidas em métro.
8. c) de 0,0000001 m (10−7 m) até 0,0000045 m (4,5 ⋅ 10−6 m)
9. Qual é o tempo estimado para realizar o dáum-lôude de um vídeo de 275 MB, com uma taxa de transferência média de 50 Mbps?
44 s
10. Elis organizou alguns arquivos em uma pasta armazenada em seu computador para fazer um backup, isto é, para fazer uma cópia de segurança dêêsses arquivos em outro dispositivo. Observe informações sobre esses arquivos.
Tipos de arquivo |
Espaço ocupado |
|---|---|
Imagem |
9 GB |
Áudio |
800 MB |
Documento |
210 MB |
Vídeo |
12 GB |
Elis vai utilizar apenas uma das opções de dispositivos indicados nas alternativas a seguir para fazer o backup dêêsses arquivos. Quais opções ela poderá escolher?
a) 1 pen dráivi de 16 GB.
b) 1 HD externo de 1 TB.
c) 5 dê vê dês de 4,7 GB cada.
d) 1 cartão de memória de 32 GB.
e) 10 cê dês de 700 MB cada.
Ela poderá escolher os dispositivos das alternativas b, c ou d.
![]() 11. Um problema comum após usar um smartphone por algum tempo é a falta de espaço de armazenamento. Em duplas, resolvam as kestões a seguir.
11. Um problema comum após usar um smartphone por algum tempo é a falta de espaço de armazenamento. Em duplas, resolvam as kestões a seguir.
a) Pesquisem informações sobre o quê é possível fazer para otimizar o espaço disponível de armazenamento nesses dispositivos.
Pesquisa dos estudantes.
b) Com os dados da pesquisa, elaborem uma questão envolvendo as medidas de capacidade de armazenamento de dados. Em seguida, tróquem os enunciados e resolvam um problema elaborado por outro grupo. Juntos, verifiquem se as respostas estão corretas.
Elaboração dos estudantes.
12. Observe algumas informações sobre o dáum-lôude de um programa de antivírus.

a) Quantos megabites tem o arquivo dêêsse dáum-lôude? E quantos megabaites?
1.176 Mb; 147 MB
b) Se o dáum-lôude dêêsse arquivo fosse realizado com uma taxa de transferência de 40 Mbps, qual seria o tempo estimado indicado?
29,4 s
Página sessenta e cinco
![]() 13. A preocupação com a sustentabilidade tem se tornado um assunto global e cada vez mais urgente. Em meio a esse cenário, a indústria da tecnologia desen vólve inúmeras pesquisas e recursos voltados para a preservação ambiental.
13. A preocupação com a sustentabilidade tem se tornado um assunto global e cada vez mais urgente. Em meio a esse cenário, a indústria da tecnologia desen vólve inúmeras pesquisas e recursos voltados para a preservação ambiental.
Entre esses recursos, o armazenamento de dados em nuvem vêm desempenhando um importante papel na redução do impacto ambiental. Alguns dos benefícios sustentáveis do armazenamento em nuvem são as reduções:
• de resíduos eletrônicos, pois as empresas diminuem a necessidade de atualizações de equipamentos eletrônicos e, consequentemente, o descarte dos equipamentos obsoletos;
• na emissão de CO2, uma vez quê, com menos servidores locais, a empresa reduz o consumo de energia elétrica e, consequentemente, a emissão de carbono associada à geração dessa energia;
• da utilização de papel, já quê, com a virtualização dos documentos, é dispensável ou pouco recomendado o uso de papel para a impressão dêêsses documentos.
a) Com base nas informações apresentadas no enunciado, responda aos itens a seguir.
• O enunciado ressalta de maneira positiva quê tipo de iniciativa?
13. a) • Resposta esperada: O desenvolvimento de tecnologias e recursos voltados à preservação do meio ambiente.
• O quê a tecnologia do armazenamento em nuvem permite? E quais são seus benefícios?
• Respostas esperadas: Permite quê arquivos digitais sêjam armazenados em sêrvidores especializados e possam ser acessados a qualquer momento. Possibilita reduzir a geração de resíduos eletrônicos, diminuir as emissões de CO2 e poupar o uso de papel para impressão de documentos.
b) Considere um sistema quê disponibilize um espaço de 10 GB de armazenamento de dados em nuvem e quê uma página de documento contendo texto e imagens tenha aproximadamente 80 kB. Quantas páginas de papel não precisarão sêr impréssas, caso seja utilizado todo o espaço de armazenamento dêêsse sistema?
131.072 páginas de papel
c) Utilizando um sistema de armazenamento em nuvem, o funcionário de uma empresa realizou o backup de 15 GB de arquivos criados em cérto dia, o quê demorou cerca de 4 minutos para a realização do upload. De quantos megabaites por segundo foi a taxa de transferência de dados, em média, na realização dêêsse backup?
512 Mbps
![]() d) Com um colega, pesquisem mais informações sobre o armazenamento em nuvem, como: as vantagens e desvantagens relatadas por usuários, alguns exemplos de platafórmas quê utilizam esse sistema e a influência no modo como pessoas e empresas salvam, acessam e compartilham informações. Depois, discutam os impactos sociais, econômicos e ambientais relacionados à utilização dessa tecnologia e elaborem um texto com base na pesquisa e na discussão realizadas.
d) Com um colega, pesquisem mais informações sobre o armazenamento em nuvem, como: as vantagens e desvantagens relatadas por usuários, alguns exemplos de platafórmas quê utilizam esse sistema e a influência no modo como pessoas e empresas salvam, acessam e compartilham informações. Depois, discutam os impactos sociais, econômicos e ambientais relacionados à utilização dessa tecnologia e elaborem um texto com base na pesquisa e na discussão realizadas.
Pesquisa dos estudantes.
NO MUNDO DO TRABALHO
Empregos verdes
Atualmente, há diversas iniciativas no mundo do trabalho quê visam à sustentabilidade, como é o caso dos chamados "empregos verdes", quê consistem em atividades profissionais quê se preocupam com a proteção dos éco-sistemas e da biodiversidade, utilizando estratégias e tecnologias com alto grau de eficiência para reduzir o consumo de energia, materiais e á gua, além de buscar a descarbonização da economia e a redução de todas as formas de poluição e produção de resíduos.
Os empregos verdes abrangem diferentes áreas e profissões, como o técnico instalador de painéis fotovoltaicos para a geração de energia limpa e renovável; o coletor de materiais recicláveis; o agricultor quê usa a á gua com racionalidade e prioriza insumos orgânicos; o engenheiro ambiental quê trabalha na proteção e na conservação do meio ambiente etc.
Acesse êste sáiti para assistir a um vídeo com mais informações sobre os empregos verdes.
• LEGNAIOLI, Stella. Empregos verdes: evitando o colapso com justiça ambiental. [São Paulo]: eCycle, c2010-2023. Disponível em: https://livro.pw/rdeso. Acesso em: 27 jun. 2024.
Página sessenta e seis
Relações entre grandezas
Em muitas situações do cotidiano, temos duas ou mais grandezas quê se relacionam de determinada maneira. Acompanhe, a seguir, alguns exemplos dessas situações.
Exemplo 1:
Considerando a alta demanda de consumo de plástico no mundo e quê, potencialmente, é necessário produzir uma grande quantidade de produtos quê utilizam esse material, temos no processo de reciclagem uma alternativa para diminuir a quantidade de insumos utilizados na produção de novos materiais e produtos plásticos. A á gua, por exemplo, é um dos insumos quê póde ter o consumo reduzido. Estima-se quê a cada 1 t de plástico reciclado sêjam economizados 450 L de á gua, quê seriam utilizados no processo de produção convencional dessa mesma quantidade de plástico.
Fonte dos dados: ASSOCIAÇÃO BRASILEIRA DA INDÚSTRIA DO PLÁSTICO. Perfil 2018. São Paulo: Abiplast, [2021]. Localizável em: p. 28 do pdf. Disponível em: https://livro.pw/pkhtg. Acesso em: 27 jun. 2024.

Com base nas informações apresentadas, podemos relacionar as grandezas massa de plástico reciclado e o volume de á gua economizada.
Massa de plástico reciclado (t) |
Volume de á gua economizada (L) |
|---|---|
1 |
450 |
2 |
900 |
3 |
1.350 |
4 |
1.800 |
5 |
2.250 |
Note quê, para cada quantidade de massa de plástico reciclado, está associada uma única quantidade de volume de á gua economizada. Nesse caso, podemos dizêr quê há uma relação entre a massa de plástico reciclado e o volume correspondente de á gua economizada.
Indicando por x a massa de plástico reciclado e por y o volume de á gua economizada correspondente, podemos escrever:
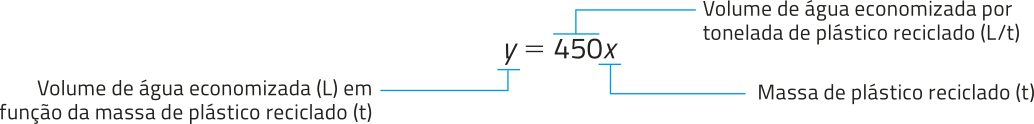
Nesse caso, o volume y de á gua economizada varia de acôr-do com a massa de plástico reciclado. Assim, dizemos quê y é a variável dependente e x é a variável independente da expressão y = 450x.
Página sessenta e sete
Com a expressão y = 450x, podemos calcular, por exemplo, quantos litros de á gua são economizados com a reciclagem de 8 t de plástico.
y = 450 ⋅ 8 = 3.600
Logo, são economizados 3.600 L de á gua com a reciclagem de 8 t de plástico.
Também podemos calcular, por exemplo, quantas toneladas de plástico reciclado correspondem a uma economia de 6.750 L de á gua no processo de produção.
6.750 = 450x
15 = x
Assim, ao reciclar 15 t de plástico, serão economizados 6.750 L de á gua na cadeia produtiva do plástico.
Exemplo 2:
Existem aplicativos de smartphone quê permitem ao usuário comprar produtos em lojas e recebê-los em casa, mediante o pagamento de uma taxa de entrega. Em cérto aplicativo, o cálculo da taxa de entrega considera um valor inicial fixo de R$ 5,50 mais R$ 0,25 a cada quilômetro percorrido entre a loja e o local da entrega. Essa relação entre a taxa de entrega e a distância percorrida póde sêr representada pela expressão a seguir.
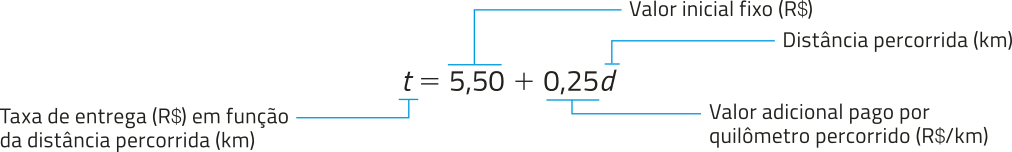
Nessa situação, a taxa de entrega t é a variável dependente, e a distância percorrida d, a variável independente.
PARA PENSAR
Com base na expressão ôbitída para essa relação, determine:
• o valor da taxa de entrega de uma compra cuja distância percorrida é de 6 km;
R$ 7,00
• a maior distância percorrida possível para quê o valor da taxa de entrega seja de até R$ 12,00.
26 km
DICA
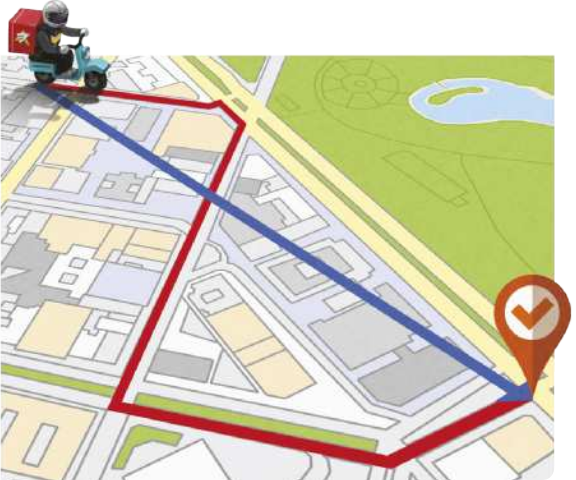
É importante destacar quê a “distância percorrida” é uma grandeza escalar, ou seja, póde sêr expressa pela medida do trajeto realizado.
Já o “deslocamento” é uma grandeza vetorial, ou seja, corresponde à medida, em linha reta, entre a posição inicial e a posição final do trajeto. Em relação à situação apresentada, na figura está indicado, em vermelho, um exemplo de trajeto realizado em uma entrega, correspondente à distância percorrida (em km). E, em azul, está indicado o vetor correspondente ao deslocamento realizado.
Página sessenta e oito
Exemplo 3:
Uma escola vai contratar o sêrviço de uma empresa de jardinagem para plantar grama em uma região a ser delimitada no pátio. Essa região deve ter formato de um retângulo cuja medida do comprimento seja o dôbro da medida da largura, como mostrado na figura, em quê x é a medida da largura, em métro.

O melhor preêço quê o colégio conseguiu foi o de uma empresa de jardinagem quê orçou em R$ 3,90 o plantio de cada métro quadrado de grama. Com base nessas informações, podemos relacionar o valor total v do serviço e a área 2x² da região retangular por meio da expressão a seguir.
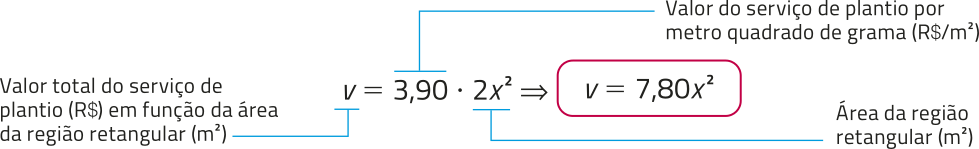
Nessa expressão, o valor total v do serviço de plantio é a variável dependente, e a medida x da largura da região retangular é a variável independente.
PARA PENSAR
Com base no exemplo 3, determine o valor total do serviço de plantio para diferentes medidas de largura da região retangular e registre em um qüadro.
Resposta pessoal.
ATIVIDADES
14. resôuva o item a seguir com base nas informações apresentadas no exemplo 1.
• Em 2021, no Brasil, foi reciclado cerca de 1 milhão de toneladas de plástico. Com isso, quantos litros de á gua foram economizados nessa cadeia produtiva?
450.000.000 L
15. Com base no exemplo 2, determine o valor da taxa de entrega para as seguintes distâncias percorridas: 3,8 km, 5 km, 6,5 km, 10 km e 12 km. Depois, registre os valores em um qüadro.
Resposta nas Orientações para o professor.
16. Com base nas informações apresentadas no exemplo 3, resôuva as kestões a seguir.
a) Qual será o valor do serviço de jardinagem para o plantio de grama caso a largura da região retangular seja de 12 m?
R$ 1.123,20
b) Sabendo quê o valor total do serviço foi de R$ 1.755,00, determine as medidas da região retangular em quê foi plantada grama.
15 m e 30 m
17. Considere um quadrado cuja medida do lado, em centímetro, é indicada por x.
a) escrêeva uma expressão quê relacione:
• o perímetro p dêêsse quadrado e a medida x;
p = 4x
• a área a dêêsse quadrado e a medida x.
a = x ²
b) Com base nas expressões quê você escreveu, calcule o perímetro e a área de um quadrado de lado x = 5.
perímetro: 20 cm; área: 25 cm²
c) Determine o valor de x para quê o quadrado tenha:
• 56 cm de perímetro;
x = 14
• 144 cm² de área.
x = 12
18. Em cérto restaurante sélf sérviss, é cobrado R$ 63,00 por quilograma de comida servida pelo cliente. escrêeva uma expressão quê relacione a massa m de comida, em grama, e a quantia p paga por uma refeição nesse restaurante, em reais.
p = 0,063m
Página sessenta e nove
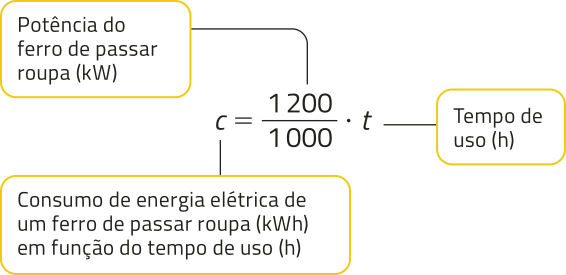
19. O consumo de energia elétrica de um equipamento póde sêr calculado por meio de uma expressão quê relaciona o consumo à potência do equipamento. Observe o exemplo.

DICA
A potência do ferro de passar roupa em watt (W) foi dividida por 1.000 para obtêr a potência em quilowatt (kW) e, consequentemente, o consumo de energia elétrica em quilowatt-hora (kWh).
a) A expressão quê representa o consumo de energia elétrica póde sêr simplificada e expressa de outras maneiras? Registre alguma delas.
19. a) Sim. Algumas respostas possíveis: c = ; c =; c = .
b) Determine o consumo de energia elétrica de um ferro de passar roupa dêêsse modelo, considerando quê tenha sido utilizado por 8 h em um mês.
9,6 kWh
c) Por quantas horas um ferro de passar roupa dêêsse modelo póde sêr usado para quê sêjam consumidos, no mássimo, 7,2 kWh?
19. c) 6 h no mássimo
d) Agora, escolha um dos equipamentos indicados a seguir e escrêeva uma expressão quê relacione o consumo c de energia elétrica (kWh) e o tempo t de uso do equipamento (h). Depois, estabêlêça o tempo de uso mensal dêêsse equipamento em uma residência e calcule o consumo de energia elétrica correspondente.
Equipamento |
Potência (W) |
|---|---|
Televisor |
90 |
Computador |
300 |
Aspirador de pó |
600 |
Condicionador de ar |
1.400 |
Micro-ondas |
2.000 |
19. d) televisor: c = ; computador: c = aspirador de pó: c = ; condicionador de ar: c = ; micro-ondas: c = ;
• Verifique a potência de alguns equipamentos elétricos de sua residência e determine, para cada um deles, o consumo de energia elétrica em função do tempo.
Resposta pessoal.
PARA AMPLIAR
Acesse êste sáiti para realizar uma simulação de tarifa de acôr-do com o consumo mensal de energia elétrica de alguns aparelhos. O consumo mensal será calculado ao indicar a potência dos aparelhos utilizados e o horário e a duração de uso.
• ENTIDADE NACIONAL DE ELETRICIDADE. Simulador de tarifas. [S. l.]: Enel, [2024]. Disponível em: https://livro.pw/ovmul. Acesso em: 24 jun. 2024.
20. (Enem/MEC) Os diretores de uma escola precisam construir um laboratório para uso dos alunos. Há duas possibilidades:
(i) um laboratório do tipo A, com capacidade para 100 usuários, a um custo de 180 mil reais e gastos de 60 mil reais por ano para manutenção;
(ii) um laboratório do tipo B, com capacidade para 80 usuários, a um custo de 120 mil reais e gastos com manutenção de 16 mil reais por ano.
Considera-se quê, em qualquer caso, o laboratório implantado será utilizado na totalidade de sua capacidade. A economia da escola, na utilização de um laboratório tipo B, em vez de um laboratório tipo A, num período de 4 anos, por usuário, será de:
a) 1,31 mil reais.
b) 1,90 mil reais.
c) 2,30 mil reais.
d) 2,36 mil reais.
e) 2,95 mil reais.
alternativa b
21. Com base na atividade 20, escrêeva para cada tipo de laboratório (A e B) uma expressão quê relacione o custo total c da utilização do laboratório por usuário, em reais, e o período t de uso dêêsse laboratório, em ano. Para isso, considere o uso da capacidade mássima do laboratório.
tipo A: c = 1.800 + 600t; tipo B: c = 1.500 + 200t
Página setenta
22. As espécies quê habitam um éco-sistema costumam sêr agrupadas em níveis tróficos, de acôr-do com sua principal fonte de nutrição e energia. A relação alimentar entre os indivíduos de cada nível dêêsses póde sêr representada por uma pirâmide ecológica, um esquema compôzto por figuras de retângulos ou de blocos de mesma altura correspondentes a cada nível trófico. Assim, a figura da base representa os produtores, seguidos, nessa ordem, pêlos consumidores primários, consumidores secundários e assim por diante.
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 1232-1241.
Um dos principais tipos de pirâmides ecológicas é a pirâmide de números, em quê é indicada a quantidade de indivíduos em cada nível trófico. Considere, por exemplo, a pirâmide de números representada a seguir, ôbitída a partir da amostragem de indivíduos de determinado éco-sistema.
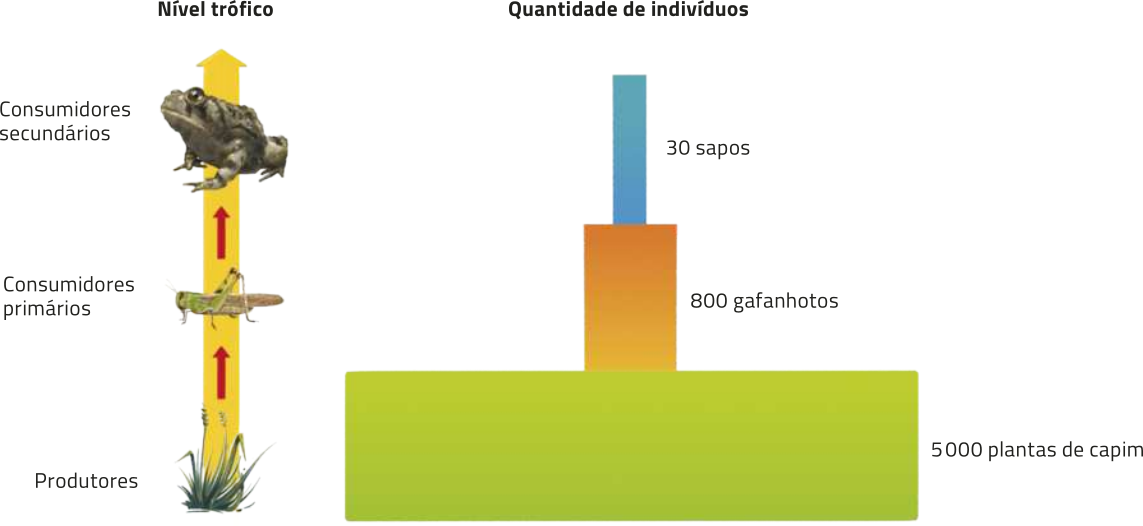
pôdêmos observar quê, no éco-sistema representado, são necessárias 5 000 plantas de capim para alimentar 800 gafanhotos e, por sua vez, são necessários 800 gafanhotos para alimentar 30 sapos. Considerando essas informações, resôuva os itens a seguir.
a) Em relação a esse éco-sistema, escrêeva uma expressão quê relacione a quantidade de:
• sapos e gafanhotos;
s = g, em quê s e g são as quantidades de sapos e de gafanhotos, respectivamente.
• gafanhotos e plantas de capim.
g = c, em quê g e c são as quantidades de gafanhotos e de plantas de capim, respectivamente.
b) Nesse éco-sistema, quantos sapos podem sêr alimentados com 560 gafanhotos?
21 sapos
c) Determine, nesse éco-sistema, quantas plantas de capim seriam necessárias para alimentar 1.000 gafanhotos.
6.250 plantas de capim
![]() d) Diversas ações do sêr humano impactam o meio ambiente e podem causar desequilíbrio da cadeia alimentar em alguns éco-sistemas. Por exemplo: a caça ilegal, a realização de queimadas, o desmatamento de vegetação nativa etc. Em grupo, pesquisem e coletem dados sobre algum dêêsses problemas e sobre alguma iniciativa existente quê vise minimizar o impacto de ações humanas em um éco-sistema específico. Depois, analisem as informações obtidas e elaborem uma proposta de intervenção ou conscientização para atenuar ou diminuir consideravelmente o problema pesquisado por vocês. Por fim, compartilhem com os côlégas os resultados da pesquisa e a proposta elaborada, dando exemplos e justificando os argumentos apresentados.
d) Diversas ações do sêr humano impactam o meio ambiente e podem causar desequilíbrio da cadeia alimentar em alguns éco-sistemas. Por exemplo: a caça ilegal, a realização de queimadas, o desmatamento de vegetação nativa etc. Em grupo, pesquisem e coletem dados sobre algum dêêsses problemas e sobre alguma iniciativa existente quê vise minimizar o impacto de ações humanas em um éco-sistema específico. Depois, analisem as informações obtidas e elaborem uma proposta de intervenção ou conscientização para atenuar ou diminuir consideravelmente o problema pesquisado por vocês. Por fim, compartilhem com os côlégas os resultados da pesquisa e a proposta elaborada, dando exemplos e justificando os argumentos apresentados.
Pesquisa e elaboração dos estudantes.
Página setenta e um
23. (Enem/MEC) O preêço médio cobrado por um pintor para executar um serviço consiste em uma taxa fixa de R$ 25,00 mais uma quantia proporcional à área pintada. O qüadro apresenta os valores cobrados por ele em trabalhos recentes.
Área pintada (m2) |
Total a pagar (R$) |
|---|---|
5 |
35,00 |
10 |
45,00 |
20 |
65,00 |
40 |
105,00 |
80 |
185,00 |
Qual o preêço cobrado para realizar um serviço de pintura de uma área de 150 m2?
a) R$ 300,00
b) R$ 325,00
c) R$ 400,00
d) R$ 1.050,00
e) R$ 3.750,00
alternativa b
24. Em relação à atividade 23, escrêeva uma expressão quê relacione o valor v cobrado pelo pintor, em reais, de acôr-do com a área a pintada, em métro quadrado.
v = 2a + 25
25. Sandra e Tiago vão utilizar um aplicativo de hospedagem para locar um apartamento durante uma viagem. Pelo apartamento escolhido, eles vão pagar R$ 150,00 por dia mais R$ 110,00 de taxas cobradas pelo aplicativo.
a) Que quantia será paga pela locação do apartamento se eles ficarem hospedados por 7 dias?
R$ 1.160,00
b) escrêeva uma expressão quê relacione o valor V pago pela locação dêêsse apartamento, em reais, e a quantidade de diárias d.
V = 150d + 110
c) Nessas mesmas condições, outro casal locou esse apartamento e pagou R$ 860,00 pela hospedagem. Por quantos dias esse casal locou o apartamento?
5 dias
26. Benício trabalha como técnico em uma companhia de abastecimento de á gua. Ao identificar um vazamento constante em certa tubulação, ele colocou por algum tempo um recipiente medidor com capacidade de 5 L para coletar a á gua quê gotejava e realizou anotações em diferentes momentos. Observe as anotações feitas por Benício e resôuva as kestões.
Tempo de gotejamento (min) |
Quantidade de á gua no recipiente (mL) |
5 |
90 |
12 |
216 |
20 |
360 |
28 |
504 |
35 |
630 |
45 |
810 |
a) Quantos mililitros de á gua havia no recipiente após 12 min de gotejamento?
216 mL
b) escrêeva uma expressão quê relacione a quantidade q de á gua no recipiente (mL) e o tempo t de gotejamento (min).
q = 18t
c) Calcule o valor de q para t = 60. O quê esse cálculo indica?
26. c) q = 1.080. Indica quê após 60 min de gotejamento havia 1.080 mL de á gua no recipiente.
d) Após quantas horas foi feito o reparo na tubulação, sabendo quê havia nesse momento 4.320 mL de á gua no recipiente medidor?
4 h
![]() 27. Quando vamos consumir um alimento industrializado, é importante ficarmos atentos às informações nutricionais indicadas nos rótulos das embalagens, como quantidades de proteína, fibra alimentar, sódio, gordura etc.
27. Quando vamos consumir um alimento industrializado, é importante ficarmos atentos às informações nutricionais indicadas nos rótulos das embalagens, como quantidades de proteína, fibra alimentar, sódio, gordura etc.
Em grupo, pesquisem informações nutricionais de um alimento em rótulos de embalagens e resolvam as seguintes kestões.
Pesquisa e elaboração dos estudantes.
a) Escolham um componente indicado nas informações nutricionais e escrevam uma expressão quê relacione a quantidade de pôr-ções do alimento e a quantidade correspondente do componente nutricional escolhido.
b) Elaborem uma questão envolvendo a expressão quê vocês escreveram. Depois, tróquem o enunciado com outro grupo e resolvam a quêstão que vocês receberam. Ao final, confiram juntos as resoluções.
Página setenta e dois
Conceito de função
Analisamos alguns exemplos de relações entre duas ou mais grandezas em quê uma grandeza varia de acôr-do com a variação de outra. Quando essa variação atende a determinados requisitos, é chamada de função. Todos os exemplos apresentados no tópico Relações entre grandezas são funções. Agora, ampliaremos e formalizaremos esse conceito, utilizando a associação entre elemêntos de dois conjuntos.
Dados dois conjuntos não vazios A e B, denominamos função de A em B a relação quê associa cada elemento x ∈ A a um único elemento y ∈ B. pôdêmos indicar uma função de A em B da maneira a seguir.
f: A → B ou AB (Lê-se: função f de A em B.)
Em uma função, dizemos quê y é a variável dependente e x é a variável independente da função.
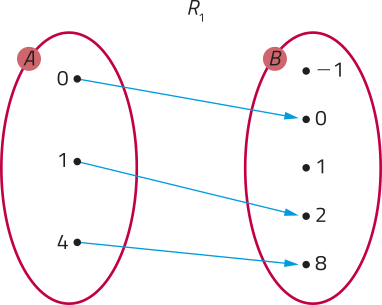
Considere, por exemplo, os conjuntos A = {0, 1, 4} e B = {−1, 0, 1, 2, 8} e as relações (R1, R2 e R3) de A em B.
• R1: dados x ∈ A e y ∈ B, temos y = 2x.
DICA
Associando os elemêntos de A em B, por meio de R1, temos:
x |
y = 2x |
|---|---|
0 |
y = 2 ⋅ 0 = 0 |
1 |
y = 2 ⋅ 1 = 2 |
4 |
y = 2 ⋅ 4 = 8 |
O esquema quê representa os conjuntos A e B, os seus elemêntos e as setas indicando a relação R1 é chamado de diagrama de flechas. Note quê cada elemento de A tem apenas um correspondente em B. Nesse caso, dizemos quê R1 é uma função de A em B, expressa por y = 2x.
• R2: dados x ∈ A e y ∈ B, temos y = x + 1.
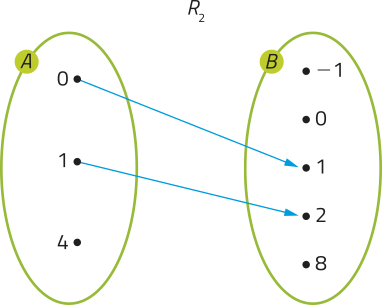
Note quê o elemento 4, em A, não está associado a qualquer elemento de B. Nesse caso, dizemos quê R2 não é uma função de A em B.
Página setenta e três
• R3: dados x ∈ A e y ∈ B, temos y ² = x.
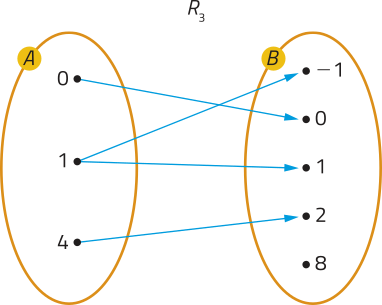
Note quê o elemento 1, em A, está associado a dois elemêntos de B: −1 e 1. Nesse caso, dizemos quê R3 não é uma função de A em B.
PARA PENSAR
Que alteração póde sêr feita no conjunto A ou no conjunto B para quê a relação:
• R2 seja uma função de A em B?
Resposta esperada: Excluir o elemento 4 do conjunto A ou incluir o elemento 5 no conjunto B.
• R3 seja uma função de A em B?
Resposta esperada: Excluir o elemento −1 ou o elemento 1 do conjunto B ou excluir o elemento 1 do conjunto A.
Uma vez definida uma função f de A em B, denominamos de:
• domínio da função, indicado por D(f), o conjunto A;
• contradomínio da função, indicado por CD(f), o conjunto B;
• imagem de x, indicada por f(x), o elemento y ∈ B associado a x ∈ A pela função f;
• conjunto imagem da função, indicado por Im(f), o conjunto formado por todas as imagens dos elemêntos de A. Matematicamente, podemos escrever:
Im(f) = {y ∈ B | y = f(x), para todo x ∈ A};
• lei de formação a expressão quê estabelece a correspondência entre os valores de x ∈ A e y ∈ B.
Observações:
• O conjunto imagem é um subconjunto do contradomínio da função.
• Nem toda função tem uma lei de formação quê póde sêr indicada por uma expressão matemática. Por exemplo, a função quê relaciona o número da matrícula a cada estudante de uma turma da escola.
MATEMÁTICA NA HISTÓRIA
Diversos matemáticos, no decorrer da história, contribuíram para o desenvolvimento do estudo das funções. Um deles foi o matemático e físico suíço Leonhard poou Óiler (1707-1783) quê, entre outras contribuições, propôs uma notação própria para funções, em quê a variável dependente y é substituída por f(x) na lei de formação.
Em relação à função cuja lei de formação é dada por y = 2x, temos:

Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 4. ed. Campinas: Editora da Unicamp, 2007. p. 519.

Página setenta e quatro
ATIVIDADES RESOLVIDAS
R5. Considerando os conjuntos A = {−3, −1, 0, 2, 4} e B = {−1, 0, 1, 3, 4, 6, 7} e a função f: A → B, representada pelo diagrama, resôuva os itens.
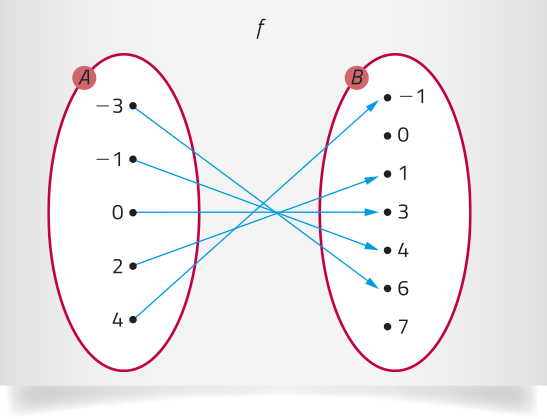
a) Determine o domínio e o contradomínio da função f.
b) Qual é a imagem de −3? E a imagem de 4?
c) Qual é o conjunto imagem de f?
PARA PENSAR
escrêeva uma possível lei de formação para a função f. Com suas palavras, explique a um colega como você obteve essa lei de formação.
Respostas possíveis: y = 3 − x; f(x) = 3 − x. Resposta pessoal.
Resolução
a) D(f) = A = {−3, −1, 0, 2, 4} e CD(f) = B = {−1, 0, 1, 3, 4, 6, 7}.
b) A imagem de −3 é 6, ou seja, f(−3) = 6. A imagem de 4 é −1, ou seja, f(4) = −1.
c) Im (f) = {−1, 1, 3, 4, 6}.
R6. Considere a função f: ℝ → ℝ definida pela lei de formação f(x) = x2.
a) Qual é a imagem de −7?
b) Determine os valores de x ∈ ℝ cuja imagem seja igual a 4.
c) Qual é o conjunto imagem de f?
Resolução
a) f(−7) = (−7)2 = 49
Portanto, a imagem de −7 é 49.
b) f(x) = 4 ⇒ x2 = 4 ⇒
Portanto, nessa função, 2 e −2 têm imagem igual a 4.
c) A função f associa cada número real x a um número real y quê é o quadrado de x. Uma vez quê o quadrado de todo número real é maior ou igual a zero e, também, quê todo número real maior ou igual a zero póde sêr expresso por um número real ao quadrado, por exemplo, x = _, para x ∈ ℝ+, temos quê Im(f) = {y ∈ ℝ | y ≥ 0}.
PARA PENSAR
pôdêmos calcular a raiz quadrada de quais números reais? Esses números formam qual conjunto numérico? Se necessário, utilize uma calculadora científica.
Respostas esperadas: Dos números reais não negativos. Esses números formam o conjunto ℝ+.
Página setenta e cinco
R7. cérto restaurante cobra pelas refeições de acôr-do com a massa de alimento servida no prato, conforme apresentado no cartaz.

a) escrêeva a lei de formação de uma função quê represente o preêço p cobrado nesse restaurante, em reais, por uma refeição com m quilograma.
b) Quanto esse restaurante cobrará por uma refeição com meio quilograma?
Resolução
a) Como no restaurante há duas maneiras de cobrar pelas refeições (até 600 g e mais de 600 g), escrevemos duas sentenças na lei de formação da função:
b) p(0,5) = 42,50 ⋅ 0,5 = 21,25 → R$ 21,25
DICA
Note quê, na função p, a sentença da lei de formação quê é utilizada para calcular uma imagem depende do valor de x. Assim, a sentença p(m) = 42,50m é utilizada para 0 < m ≤ 0,600, e a sentença 25,50, para m > 600. Funções como essa são chamadas de função definida por mais de uma sentença.
ATIVIDADES
28. Quais das relações representadas a seguir correspondem a uma função de A em B? Justifique sua resposta.
Alternativas a e d. Resposta pessoal.
a) 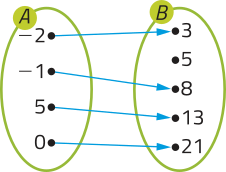
b) 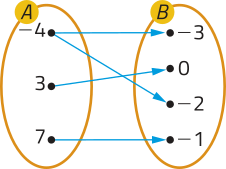
c) 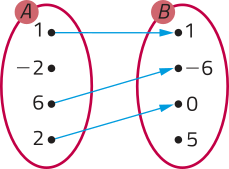
d) 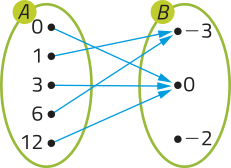
29. Utilizando diagrama, represente a função f: A → B, sêndo A = {−3, −2, 0, 1} e B = {−5, −3, 0, 1, 3, 5}, cuja lei de formação é dada por y = 2x + 1, com x ∈ A e y ∈ B. Em seguida, determine D (f), cê dê (f) e Im (f).
30. Dada a função g: ℕ → ℕ definida por g (x) = 3x + 5, calcule:
a) g (3).
14
b) g (0).
5
c) g (10).
35
d) g (5).
20
• Agora, defina uma função indicando o domínio, o contradomínio e a lei de formação. Em seguida, calcule a imagem de alguns valores do domínio dessa função.
Respostas pessoais.
31. Considerando os conjuntos A = {−15, −8, −2, 0, 4, 5} e B = {0, 1, 5, 7, 13, 14, 15, 19, 20}, determine quais das expressões a seguir correspondem à lei de formação de uma função de A em B.
a) h (x) = 22 + x
b) f(x) = 5 − x
c) m (x) = x + 15
d) g (x) = −1 − x
e) p (x) = −x
alternativas b e c
32. Dada a função AB, temos quê:
Resposta nas Orientações para o professor.
• D(f) = {−2, 0, 3, 5};
• CD(f) = {−5, −4, 0, 2, 3, 6, 8};
• Im(f) = {−4, 3, 6, 8}.
De acôr-do com essas informações, construa um diagrama para representar a função f.
29. Resposta nas Orientações para o professor. D(f) = {−3, −2, 0, 1}; CD(f) = {−5, −3, 0, 1, 3, 5}; Im(f) = {−5, −3, 1, 3}.
Página setenta e seis
33. Leia o texto e, em seguida, faça o quê se pede em cada item.
O Imposto de Renda da Pessoa Física (IRPF) é um imposto federal quê incide sobre a renda (salários, pensões, aluguéis etc.) de contribuintes quê residem no Brasil ou quê recebem renda de fontes no Brasil. Parte da arrecadação do IRPF é destinada a investimentos em saúde, educação, segurança, saneamento, programas de transferência de renda, entre outros. O valor do imposto cobrado de cada contribuinte varia de acôr-do com a renda, conforme segue.
tabéla de incidência mensal do IRPF, em vigor no ano-calendário de 2023*
Base de cálculo (R$)** |
Alíquota (%)*** |
Parcela a deduzir do IRPF(R$)**** |
|---|---|---|
Até 2.112,00 |
Isento |
0 |
De 2.112,01 até 2.826,65 |
7,5 |
158,40 |
De 2.826,66 até 3.751,05 |
15 |
370,40 |
De 3.751,06 até 4.664,68 |
22,5 |
651,73 |
Acima de 4.664,68 |
27,5 |
884,96 |
* Tributação a partir de maio de 2023. **Valor da renda mensal do contribuinte. ***Porcentual da renda do contribuinte referente ao valor do IRPF. ****Valor do desconto concedido sobre o valor do IRPF.
Fonte dos dados: BRASIL. Ministério da Fazenda. Receita Federal. Tributação de 2023. Brasília, DF: MF; RFB, 9 fev. 2024. Disponível em: https://livro.pw/sxmtf. Acesso em: 27 jun. 2024.
PARA AMPLIAR
Acesse êste vídeo para obtêr mais informações sobre o IRPF.
• HISTÓRIA do Imposto de Renda. [S. l.: s. n.], 2016. 1 vídeo (5 min). Publicado pelo canal Receita Federal. Disponível em: https://livro.pw/vwuci. Acesso em: 27 jun. 2024.
pôdêmos expressar uma função f por mais de uma sentença para relacionar o valor do IRPF(em reais) de acôr-do com a renda mensal r do contribuinte, ou seja, f(r) designa o valor do imposto a sêr pago.
Por exemplo:
• o contribuinte quê recebe até R$ 2.112,00 é isento, então:
f(r) = 0, se r ≤ 2.112,00;
• o contribuinte quê recebe de R$ 2.112,01 até R$ 2.826,65 tem alíquota de 7,5% e R$ 158,40 de dedução, então:
f(r) = 0,075r − 158,40, se 2.112,01 ≤ r ≤ 2.826,65.
a) Calcule o valor do IRPF para um contribuinte quê tem renda mensal de:
• R$ 2.000,00.
isento
• R$ 2.500,00.
R$ 29,10
• R$ 3.200,00.
R$ 109,60
b) Determine as sentenças quê expressem a função f para:
• 2.826,66 ≤ r ≤ 3.751,05.
f(r) = 0,15r − 370,40
• 3.751,06 ≤ r ≤ 4.664,68.
f(r) = 0,225r − 651,73
• r > 4.664,68.
f(r) = 0,275r − 884,96
c) Com base no enunciado e nas respostas ao item b, escrêeva a lei de formação da função f.
33. c) f(r) =
d) Calcule f(5.000) e interpréte o resultado obtído.
33. d) f(5.000) = 490,04. Esse cálculo indica quê um contribuinte, cuja renda mensal é R$ 5.000,00, paga R$ 490,04 de IRPF.
![]() e) Você e um colega devem escolher uma profissão e investigar o piso salarial correspondente dessa categoria profissional. Depois, calculem o IRPF a sêr pago pela categoria profissional escolhida, considerando o piso salarial.
e) Você e um colega devem escolher uma profissão e investigar o piso salarial correspondente dessa categoria profissional. Depois, calculem o IRPF a sêr pago pela categoria profissional escolhida, considerando o piso salarial.
Resposta pessoal.
Página setenta e sete
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Velocidade de conexão
No Brasil, a internet residencial começou a sêr comercializada em meados de 1995. O acesso era por meio da “internet discada”, quê ocupava a linha telefônica durante seu uso e, se comparada com a conexão disponível atualmente, póde sêr considerada lenta e limitada.
Com o passar do tempo, o desenvolvimento de novas tecnologias tornou possível navegar na internet usando a conexão de banda larga fixa, o quê possibilita maior velocidade e melhor qualidade, exigências dos usuários contemporâneos. Atualmente, há diversas operadoras de internet quê oferecem os mais variados planos de conexão e serviços de banda larga fixa para atender ao perfil do usuário.
Ao escolher um dêêsses planos, é importante ficar atento a alguns requisitos, como as velocidades de dáum-lôude e upload contratadas. A Agência Nacional de Telecomunicações (Anatel) é o órgão responsável pelas regulamentações e fiscalizações dos serviços prestados pelas operadoras de telefonia e internet no país. Dessa maneira, os consumidores quê se sentirem prejudicados pela operadora contratada e quê não tiveram a situação resolvida por ela, podem registrar uma reclamação na Anatel.
PARA AMPLIAR
Acesse êste sáiti para obtêr informações sobre como realizar uma reclamação acerca dos serviços prestados por operadoras de telefonia e internet.
• BRASIL. Ministério das Comunicações. Agência Nacional de Telecomunicações. Registrar reclamação. Brasília, DF: Mcom: Anatel, 28 dez. 2022. Disponível em: https://livro.pw/fjdaf. Acesso em: 28 mar. 2024.
São vários os tipos de serviço de internet disponibilizados hoje em dia, cada um deles com funcionalidade e eficiência específicas. Independentemente do tipo de conexão de internet, se discada, via rádio, banda larga, fibra óptica ou móvel (4G ou 5G), é importante escolher um plano quê atenda às necessidades específicas do usuário e verificar a velocidade de dáum-lôude e upload da conexão fornecida pelo plano de internet contratado.

Página setenta e oito
Teste de qualidade de conexão
Para atender às regulamentações da Anatel, foi criada a Entidade de Suporte à Aferição da Qualidade (Esaq), quê permite ao usuário medir a qualidade da conexão de internet. Essa medição póde sêr feita no sáiti https://livro.pw/unfxv (acesso em: 27 jun. 2024) ou no aplicativo Esaq, disponível nas lojas de aplicativos. Acompanhe, a seguir, as informações obtidas em um teste realizado com essa ferramenta.
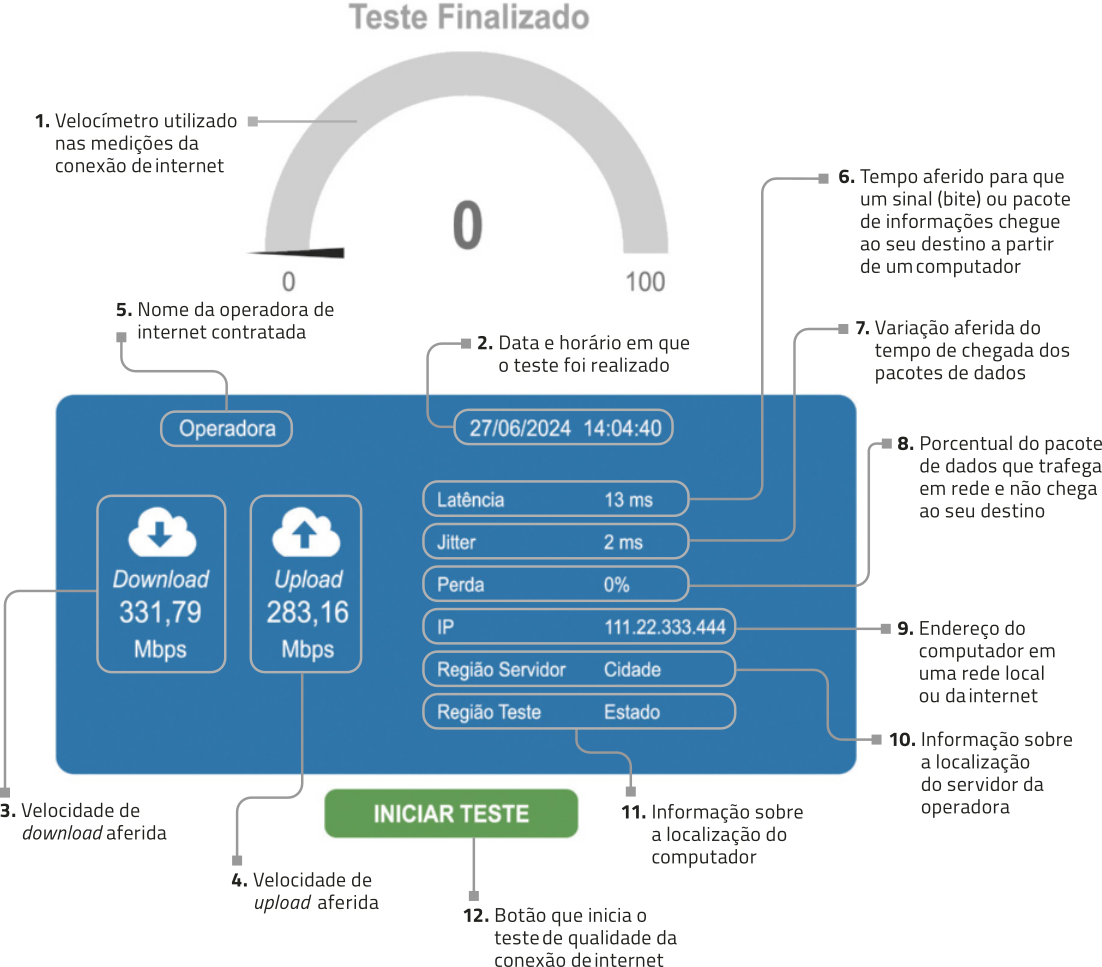
Fonte dos dados: ENTIDADE DE SUPORTE À AFERIÇÃO DA QUALIDADE. méça a qualidade da sua conexão. [S. l.]: Esaq, c2024. Disponível em: https://livro.pw/uvpqi. Acesso em: 19 ago. 2024.
DICA
Para aferir a velocidade de conexão de internet das operadoras de banda larga fixa, a Anatel distribuiu, a voluntários quê se inscreveram no sáiti da Esaq, aparelhos quê são conectados ao roteador e quê transmitem informações sobre a conexão.
Para aferir a velocidade de conexão de internet das operadoras de banda larga móvel, a Anatel busca as informações no aplicativo Esaq instalado por usuários de dispositivos móveis.
Os dados coletados pela Anatel são divulgados mensalmente no sáiti da Esaq (disponível em: https://livro.pw/swfmk; acesso em: 8 out. 2024).
Página setenta e nove
PENSANDO NO ASSUNTO
1. Upload e dáum-lôude são termos em inglês amplamente utilizados no contexto de tecnologia da informação e comunicação.
a) Qual é o significado de cada um dêêsses termos? Se necessário, realize uma pesquisa.
1. a) Upload (“subir”, em tradução simples) é a ação de transferir dados de um terminal local para um sistema remoto; dáum-lôude (“baixar” em tradução simples) corresponde ao ato de transferir dados de um sistema remoto para um terminal local.
b) Redija um pequeno texto, empregando os termos upload e dáum-lôude, quê dêz-creva uma situação cotidiana.
Resposta pessoal.
2. Quantos segundos seriam necessários para realizar, em cérto computador, o dáum-lôude de um arquivo de 4 MB, considerando o acesso de:
• internet discada com velocidade de dáum-lôude de 56 kbps?
aproximadamente 585 s
• banda larga com velocidade de dáum-lôude de 10 Mbps?
3,2 s
3. Bia contratou um plano de internet com velocidade de 500 Mbps para dáum-lôude e 35 Mbps para upload. Observe o histórico de medições da conexão de internet realizadas por ela.
Velocidade |
Medição |
||
|---|---|---|---|
1 |
2 |
3 |
|
Download (Mbps) |
509,48 |
185 |
410 |
Upload (Mbps) |
35,23 |
12,95 |
28,7 |
Faça uma análise comparando essas medições com o plano contratado por Bia. Para isso, considere como parâmetro de uma prestação de serviço adequada aquela em quê a velocidade de conexão de internet medida corresponda a, no mínimo, 80% da velocidade contratada.
3. Resposta esperada: A medição 1 está de acôr-do com o parâmetro estabelecido. A medição 2 não está de acôr-do com o parâmetro estabelecido. A medição 3 está de acôr-do com o parâmetro estabelecido.
![]() 4. Elabore uma situação-problema envolvendo o tema velocidade de conexão e o conceito de função estudado nesta Unidade. Em seguida, troque-a com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
4. Elabore uma situação-problema envolvendo o tema velocidade de conexão e o conceito de função estudado nesta Unidade. Em seguida, troque-a com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
![]() 5. Reúnam-se em grupos de três integrantes e investiguem um plano de internet de banda larga fixa disponível na região em quê moram. O plano póde sêr da residência de algum integrante do grupo, de uma pessoa fora do âmbito e do contexto escolares ou até mesmo da própria escola. Nessa investigação, explorem a questão a seguir.
5. Reúnam-se em grupos de três integrantes e investiguem um plano de internet de banda larga fixa disponível na região em quê moram. O plano póde sêr da residência de algum integrante do grupo, de uma pessoa fora do âmbito e do contexto escolares ou até mesmo da própria escola. Nessa investigação, explorem a questão a seguir.
A atividade póde sêr ampliada para quê os estudantes também possam verificar, de maneira aproximada, a velocidade média mensal de um plano de internet.
As velocidades de dáum-lôude e de upload do plano contratado com a operadora estão sêndo atendidas?
De acôr-do com o plano de internet escolhido, resolvam os itens propostos.
Respostas pessoais.
a) Identifiquem e registrem as velocidades de dáum-lôude e de upload do plano contratado.
b) Estabeleçam um parâmetro para quê seja considerada adequada a prestação de serviço da operadora. Por exemplo, quê seja atendida a velocidade de conexão de internet de, no mínimo, 80% da velocidade contratada.
c) Em um computador, naveguem na internet e façam dáum-lôude e upload. Registrem o quê vocês puderam perceber em relação à velocidade dessa internet.
d) Acessem o sáiti da Esaq e testem a qualidade da conexão de internet em alguns momentos de um mesmo dia. Registrem o horário de cada medição e as velocidades de dáum-lôude e upload aferidas. Por fim, escôlham algum recurso para representar esses dados, como: tabéla, esquema, gráfico, planilha eletrônica etc.
e) Com base nos itens resolvidos, elaborem um texto relacionando a questão proposta inicialmente na investigação com os dados obtidos sobre o plano de internet escolhido.
Página oitenta
Estudo do domínio de uma função real
Com base no conceito de função apresentado anteriormente, para definir formalmente uma função f de A em B, é necessário quê sêjam dados o domínio D(f) = A, o contradomínio CD(f) = B e a lei de formação de f, isto é, os conjuntos A e B e a relação de correspondência entre eles.
Agora, vamos analisar a situação a seguir.
Em cérto clube, há uma piscina com formato de bloco retangular cuja profundidade mássima é 160 cm. Para determinar a quantidade q de á gua nessa piscina, em métro cúbico, póde sêr utilizada uma função dada pela lei de formação q (p) = 0,5p, em quê p indica a altura do nível de á gua, em centímetro. Observe, a seguir, alguns valores de q (p) para determinados valores de p.

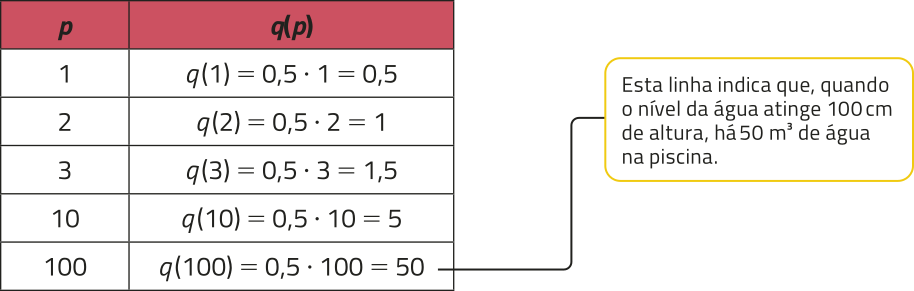
Note quê a piscina póde estar vazia, o quê indica zero centímetro no nível de á gua. O maior nível de á gua possível é 160 cm, quê corresponde à profundidade mássima da piscina. Com isso, podemos definir o domínio da função q como D(q) = {p ∈ ℝ | 0 ≤ p ≤ 160} e o contradomínio de q como CD(q) = ℝ.
DICA
O domínio da função q também póde sêr expresso pelo intervalo real D (q) = [0, 160].
Assim como na situação apresentada anteriormente, em alguns casos é possível indicar uma função de maneira diréta apenas por sua lei de formação, não explicitando seu domínio e seu contradomínio. Quando isso acontece, consideramos o domínio da função como o maior subconjunto de ℝ possível, restrito de acôr-do com o contexto em estudo ou pela lei de formação, e o contradomínio como o próprio ℝ.
Quando uma função tem, como domínio e contradomínio, subconjuntos de ℝ, dizemos quê ela é uma função real de variável real.
Página oitenta e um
ATIVIDADES RESOLVIDAS
R8. Determine o domínio da função definida por f(x) = .
Resolução
Para determinar o domínio da função, é preciso considerar o maior subconjunto possível de ℝ. Para isso, vamos analisar as restrições para os valores de x de acôr-do com a lei de formação. Como não há divisão por zero definida em ℝ, temos quê:
2x + 10 ≠ 0 ⇒ x ≠ −5
Portanto, D(f) = {x ∈ ℝ | x ≠ −5}.
R9. Obtenha o domínio da função definida por g (u) = .
Resolução
Como não está definida em ℝ a raiz quadrada de números negativos, temos quê:
4u − 7 ≥ 0 ⇒ u ≥
Portanto, D(g) = {u ∈ ℝ | u ≥ }.
R10. Explicite o domínio da função definida por f(x) = .
Resolução
Temos duas condições a sêr consideradas: 2x + 5 ≥ 0 e x − 2 ≠ 0. Segue quê:
• 2x + 5 ≥ 0 ⇒ x ≥ ;
• x − 2 ≠ 0 ⇒ x ≠ 2.
Como ambas as condições precisam sêr satisfeitas simultaneamente, o domínio da função será a interseção dos intervalos obtidos. Representando na reta real, temos:
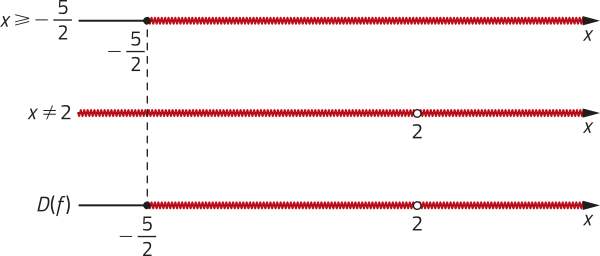
Portanto, D(f) = {x ∈ ℝ | x ≥ − e x ≠ 2}.
PARA PENSAR
Explique, com suas palavras, por quê foram consideradas as condições 2x + 5 ≥ 0 e x − 2 ≠ 0.
Resposta esperada: Porque não está definida em ℝ a raiz quadrada de números negativos e não há divisão por zero definida em ℝ.
ATIVIDADES
34. Obtenha o domínio da função definida em cada item.
a) f(x) =
34. a) D(f) = {x ∈ ℝ | x ≠ 3}
b) f(x) =
34. b) D(f) = {x ∈ ℝ | x > − }
c) f(x) =
34. c) D(f) = {x ∈ ℝ | x ≠ −9 e x ≠ 9}
d) f(x) =
34. d) D(f) = {x ∈ ℝ | x > − }
e) f(x) =
34. e) D(f) =
f) f(x) =
34. f) D(f) = {x ∈ ℝ | x ≠ 0}
g) f(x) = .
34. g) D(f) = {x ∈ ℝ | x < −4 ou x ≥ 3}
• Produza um texto explicando o procedimento geral utilizado para definir o domínio da função em cada item.
35. Qual destas funções tem como domínio o intervalo real representado a seguir? Justifique.

a) f(x) =
b) f(x) =
c) f(x) =
d) f(x) =
e) f(x) =
Alternativa d. Resposta pessoal.
DICA
Lembre-se de quê o quociente da divisão entre dois números é positivo se ambos os números são positivos ou se ambos são negativos.
Página oitenta e dois
36. Para uma atividade da aula de Matemática, Larissa construiu, no GeoGebra, um triângulo ABC inscrito em uma semicircunferência de raio 10 cm, como mostra a imagem a seguir.
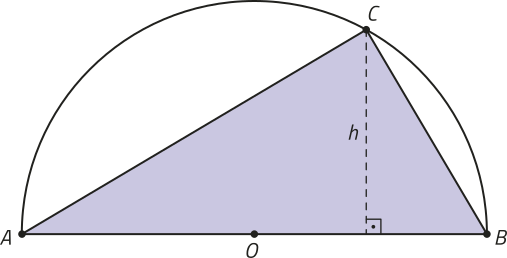
Na construção, é possível movimentar o ponto C sobre a semicircunferência, variando a medida da altura h.
a) Qual é a área do triângulo quando ajustamos o ponto C de maneira quê h = 4 cm?
40 cm2
b) escrêeva uma função A quê expresse a área do triângulo ABC em função do valor de h.
36. b) A(h) = ou A(h) = 10h
c) Obtenha o domínio da função A, descrita no item b.
D(A) = {h ∈ ℝ | 0 < h ≤ 10}
37. Um grupo de amigos foi jogar vôlei de praia. Eles tí-nhão rê-de, bola, trena e fita para fazer marcações. Quanto à quadra de jôgo, eles sabiam apenas quê tinha formato retangular com 48 m de perímetro.
DICA
Para resolver o item a, pense em como expressar a medida do outro par de lados da figura retangular a partir da medida x.
Com base nessas informações, resôuva os itens a seguir.
a) Represente a quadra de jôgo, considerando quê o perímetro é 48 m e quê um dos pares de lados méde x.
Resposta nas Orientações para o professor.
b) escrêeva a lei de formação de uma função f quê relacione a área da quadra de jôgo com a medida x.
f(x) = 24x − x ²
c) Qual é o domínio da função f cuja lei de formação você escreveu no item b? Justifique sua resposta.
37. c) D(f) = {x ∈ ℝ | 0 < x < 24}. O domínio corresponderá a todos os valores de x > 0 para os quais f(x) > 0, pois, de acôr-do com o contexto, x e f só podem assumir valores positivos.
d) Sabendo quê a quadra de jôgo de vôlei de praia tem medidas oficiais quando x = 8, determine as medidas de suas dimensões e de sua área.
dimensões: 8 m e 16 m; área: 128 m²
38. Marcos faz anúncios dos produtos de sua loja ôn láini em uma rê-de social. Ele percebeu quê, quanto mais anúncios são realizados nessa rê-de social, maior é a quantidade de vendas na loja. Para expressar essa relação, ele escreveu a função definida por V(x) = + 90, em quê V corresponde à quantidade de vendas semanais na loja e x, à quantidade de anúncios realizados em uma semana.
De acôr-do com o limite de anúncios permitido por essa rê-de social, Marcos utilizou a função quê escreveu e verificou quê, semanalmente, a loja póde atingir no mássimo 150 vendas. Qual é o domínio da função V escrita por Marcos?
D(V) = {x ∈ ℝ | 0 ≤ x ≤ 100}
![]() 39. Em trios, obissérvem a sequência de figuras formadas por quadrados vermelhos e verdes. Depois, resolvam as kestões.
39. Em trios, obissérvem a sequência de figuras formadas por quadrados vermelhos e verdes. Depois, resolvam as kestões.

a) Quantos quadrados vermelhos e verdes formam a próxima figura dessa sequência?
4 quadrados vermelhos e 12 verdes
b) Expliquem como as figuras dessa sequência podem sêr obtidas.
39. b) Resposta esperada: As figuras dessa sequência são formadas por quadrados vermelhos (fileira horizontal superior) e verdes (fileira horizontal inferior) cujas quantidades correspondem, respectivamente, à sequência dos números naturais positivos e à sequência dos múltiplos positivos de 3.
c) Quantos quadrados vermelhos e verdes formam a figura 133?
39. c) 133 quadrados vermelhos e 399 verdes.
d) Que figura dessa sequência é formada por 900 quadrados verdes? Essa figura é formada por quantos quadrados vermelhos?
39. d) Figura 300. Essa figura é formada por 300 quadrados vermelhos.
e) É possível quê uma figura dessa sequência seja formada por exatamente 31 quadrados verdes? Expliquem.
Não, pois 31 não é múltiplo positivo de 3.
f) Escrevam a lei de formação da função f quê descreve a quantidade de quadrados verdes a partir do número n da figura da sequência. Qual é o domínio dessa função?
f(n) = 3n. D (f) = {n ∈ ℕ | n > 0}.
g) Escrevam a lei de formação da função g quê descreve o número da figura a partir da quantidade x de quadrados verdes. Qual é o domínio dessa função?
39. g) g (x) = D(g) = {x ∈ ℕ | x é múltiplo positivo de 3 e x > 0}.
Página oitenta e três
Gráfico de uma função
Um dos modos de representar uma função é por meio do seu gráfico. Geralmente, o gráfico de uma função é construído em um plano cartesiano. Vamos retomar alguns elemêntos do plano cartesiano, assunto quê provavelmente você já estudou no Ensino Fundamental. Observe o plano cartesiano a seguir e um ponto P representado nele.
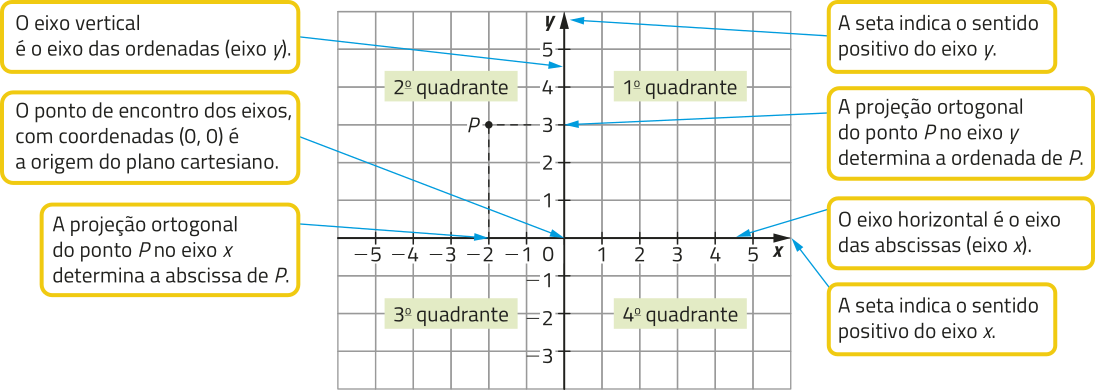
A localização de cada ponto do plano cartesiano é indicada por coordenadas cartesianas, quê são representadas por um par ordenado na forma (x, y), em quê x é a abscissa e y é a ordenada do ponto. No plano cartesiano apresentado, o ponto P tem coordenadas (−2, 3) e póde sêr indicado por P(−2, 3).
Para representar o gráfico de uma função em um plano cartesiano, indicamos a variável dependente no eixo das ordenadas e a variável independente no eixo das abscissas.
De modo geral, podemos dizêr quê:
O gráfico de uma função f é o conjunto dos pontos (x, f(x)) do plano cartesiano em quê x ∈ D(f).
Agora, acompanhe nos exemplos a seguir a construção do gráfico de algumas funções definidas pela mesma lei de formação, mas com domínios diferentes.
Exemplo 1:
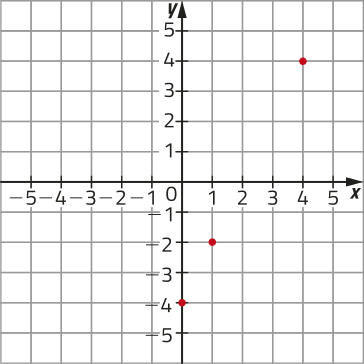
Seja uma função g: A → ℝ, com A = {0, 1, 4}, cuja lei de formação é dada por g(x) = 2x − 4.
Como o conjunto A é finito, o gráfico de g será compôzto dos pontos (x, g(x)) em quê x ∈ D(g). Assim, para construir o gráfico de g, calculamos a imagem y = g(x) para cada elemento x ∈ D(g), determinando os pares ordenados (x, g(x)). Por fim, representamos no plano cartesiano os pontos correspondentes a esses pares ordenados.
x |
g(x) = 2x − 4 |
(x, y) |
|---|---|---|
0 |
g(0) = 2 ⋅ 0 − 4 = −4 |
(0, −4) |
1 |
g(1) = 2 ⋅ 1 − 4 = −2 |
(1, −2) |
4 |
g(4) = 2 ⋅ 4 − 4 = 4 |
(4, 4) |
Página oitenta e quatro
Exemplo 2:
Agora, considere a função h: ℝ → ℝ cuja lei de formação é dada por h(x) = 2x − 4.
Note quê a lei de formação de h é a mesma da função g, apresentada no exemplo 1, mas os domínios delas são diferentes: D(g) = A = {0, 1, 4} e D(h) = ℝ, ou seja, D(g) ⊂ D(h). Assim, temos quê cada ponto do gráfico de g também é ponto do gráfico de h. Para esboçar o gráfico de h, podemos obtêr outros pares ordenados (x, y) para valores arbitrários de x ∈ ℝ.
x |
h(x) = 2x − 4 |
(x, y) |
|---|---|---|
−4 |
h(−4) = 2 ⋅ (−4) − 4 = −12 |
(−4, −12) |
−3 |
h(−3) = 2 ⋅ (−3) − 4 = −10 |
(−3, −10) |
−2 |
h(−2) = 2 ⋅ (−2) − 4 = −8 |
(−2, −8) |
−1 |
h(−1) = 2 ⋅ (−1) − 4 = −6 |
(−1, −6) |
0 |
h(0) = 2 ⋅ 0 − 4 = −4 |
(0, −4) |
1 |
h(1) = 2 ⋅ 1 − 4 = −2 |
(1, −2) |
2 |
h(2) = 2 ⋅ 2 − 4 = 0 |
(2, 0) |
3 |
h(3) = 2 ⋅ 3 − 4 = 2 |
(3, 2) |
4 |
h(4) = 2 ⋅ 4 − 4 = 4 |
(4, 4) |
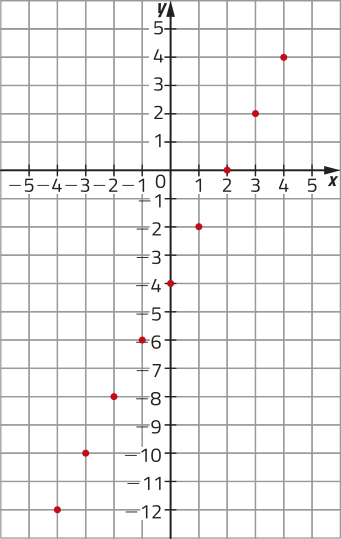
DICA
Note quê os pontos de coordenadas (0, −4), (1, −2) e (4, 4) também são pontos do gráfico da função g do exemplo 1.
Como D(h) = ℝ, existem infinitos pares ordenados (x, y) quê são pontos do gráfico de h. Nesse caso, é possível verificar quê o gráfico de h corresponde a uma reta.
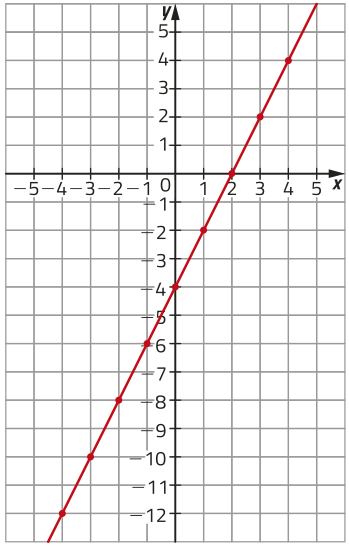
DICA
A função h é um exemplo de função afim cujo gráfico é uma reta. Esse tipo de função é apresentado com mais dêtálhes na Unidade 3 dêste Volume.
Página oitenta e cinco
ATIVIDADE RESOLVIDA
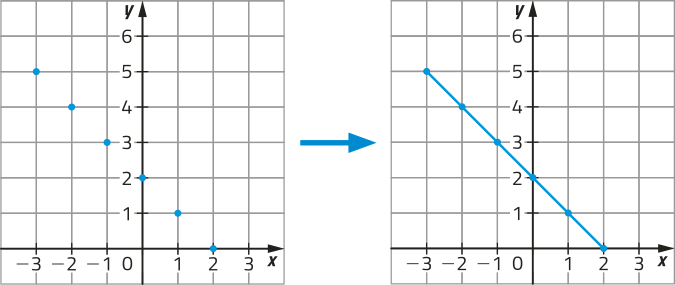
R11. Esboce o gráfico da função indicada em cada item.
a) g: [−3, 2] → ℝ, em quê g (x) = −x + 2
b) f: ℝ → ℝ, em quê f(x) =
Resolução
a) Note quê D(g) é o intervalo real [−3, 2]. Assim, atribuímos valores arbitrários para x ∈ [−3, 2] e determinamos os pares ordenados (x, y) correspondentes.
x |
g(x) = −x + 2 |
(x, y) |
|---|---|---|
−3 |
g(−3) = −(−3) + 2 = 5 |
(−3, 5) |
−2 |
g(−2) = −(−2) + 2 = 4 |
(−2, 4) |
−1 |
g(−1) = −(−1) + 2 = 3 |
(−1, 3) |
0 |
g(0) = −0 + 2 = 2 |
(0, 2) |
1 |
g(1) = −1 + 2 = 1 |
(1, 1) |
2 |
g(2) = −2 + 2 = 0 |
(2, 0) |
Como existem infinitos valores de x ∈ [−3, 2], é possível obtêr infinitos pares ordenados (x, y) por meio da lei de formação de g. Ao representar esses pares ordenados no plano cartesiano, obtemos um segmento de reta, quê corresponde ao gráfico de g.
b) Note quê a função f é definida por duas sentenças: uma para x < 0 e outra para x ≥ 0. Assim, inicialmente, atribuímos valores arbitrários para x < 0, determinamos os pares ordenados (x, y) correspondentes e, de acôr-do com os pares ordenados obtidos, esboçamos o gráfico de f para x < 0.
x |
f(x) = −2x − 2 |
(x, y) |
|---|---|---|
−4 |
f(−4) = −2 ⋅ (−4) − 2 = 6 |
(−4, 6) |
−3 |
f(−3) = −2 ⋅ (−3) − 2 = 4 |
(−3, 4) |
−2 |
f(−2) = −2 ⋅ (−2) − 2 = 2 |
(−2, 2) |
−1 |
f(−1) = −2 ⋅ (−1) − 2 = 0 |
(−1, 0) |
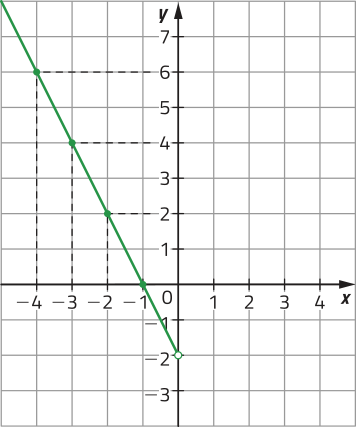
Página oitenta e seis
Depois, de maneira análoga à primeira parte, atribuímos valores quaisquer para x ≥ 0, determinamos os pares ordenados (x, y) correspondentes e esboçamos o gráfico de f para x ≥ 0.
x |
f(x) = x + 1 |
(x, y) |
|---|---|---|
0 |
f(0) = 0 + 1 = 1 |
(0, 1) |
1 |
f(1) = 1 + 1 = 2 |
(1, 2) |
2 |
f(2) = 2 + 1 = 3 |
(2, 3) |
3 |
f(3) = 3 + 1 = 4 |
(3, 4) |
4 |
f(4) = 4 + 1 = 5 |
(4, 5) |
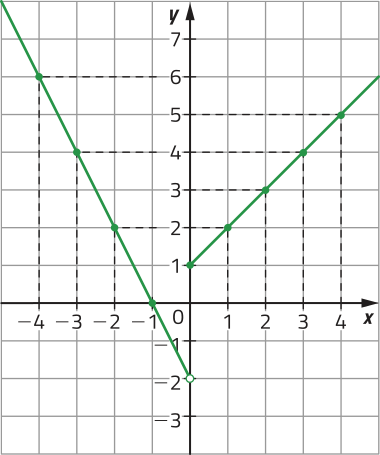
Análise do gráfico de uma função
Em alguns casos, podemos verificar se um gráfico corresponde a uma função, mesmo quê sua lei de formação, seu domínio e seu contradomínio não sêjam explícitos. Considere, por exemplo, os gráficos a seguir.
Note quê, para verificar intuitivamente a correspondência entre cada elemento de um intervalo real e um único ponto de um gráfico, podemos construir uma reta r (paralela ao eixo y) e deslocá-la horizontalmente para a direita e para a esquerda, observando se, em qualquer posição, ela sempre cruzará o gráfico em um único ponto.
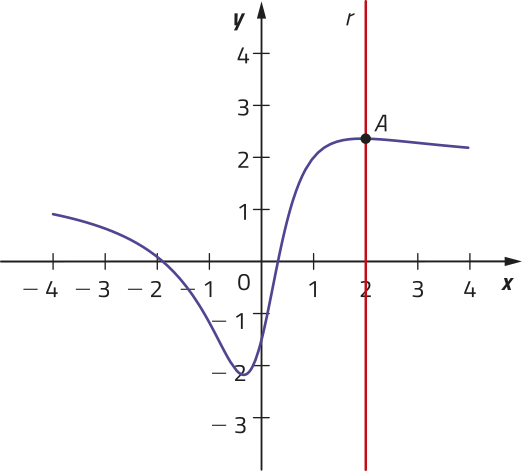
Dizemos quê êste gráfico representa uma função no intervalo [−4, 4], pois cada abscissa x ∈ [−4, 4] está associada a uma única ordenada y ∈ ℝ.
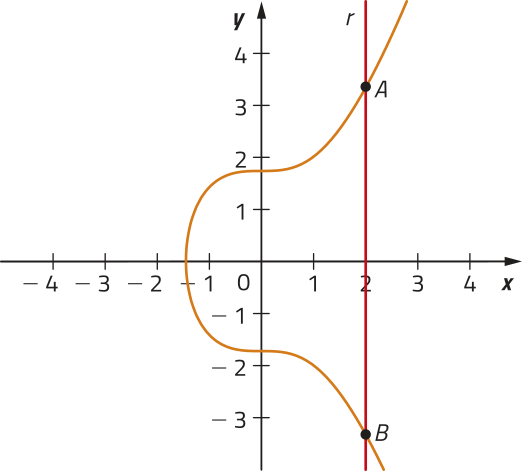
Neste caso, é possível deslocar a reta r (paralela ao eixo y) de maneira quê cruze o gráfico em mais de um ponto, por exemplo, nos pontos A e B. Assim, dizemos quê êste gráfico não representa uma função, pois existe pelo menos uma abscissa x associada a mais de uma ordenada y.
PARA PENSAR
Se uma reta paralela ao eixo x cruza cérto gráfico em dois pontos distintos, podemos afirmar quê esse gráfico não corresponde a uma função? Explique.
Resposta esperada: Não, pois, nesse caso, é possível afirmar quê duas abscissas distintas estão associadas a uma mesma ordenada, o quê póde ocorrer em uma função.
Página oitenta e sete
Domínio e imagem no gráfico de uma função
pôdêmos, em alguns casos, determinar o domínio e o conjunto imagem de uma função f analisando o gráfico de f. Por exemplo, para determinar graficamente o domínio de uma função, dado por um intervalo real, é necessário identificar as coordenadas no eixo das abscissas correspondentes ao ponto mais à direita do gráfico e ao ponto mais à esquerda do gráfico; para determinar graficamente o conjunto imagem de uma função, é necessário identificar as coordenadas no eixo das ordenadas correspondentes ao ponto mais “alto” do gráfico e ao ponto mais “baixo” do gráfico.
Observe o exemplo a seguir.
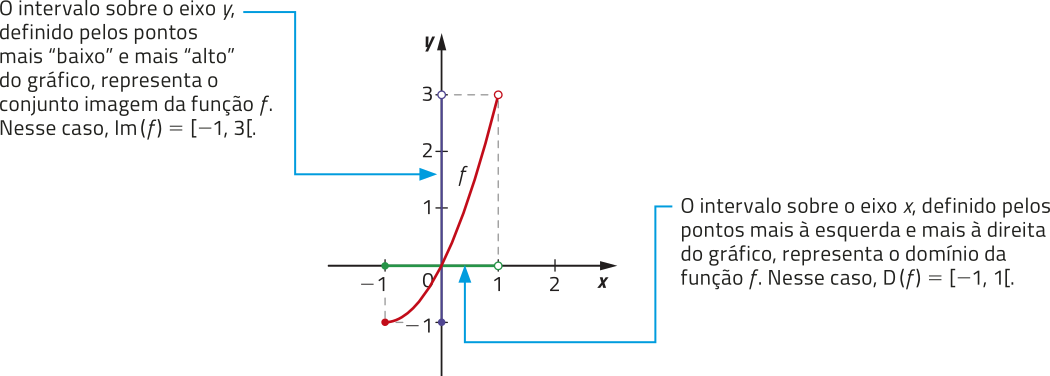
Crescimento e decrescimento de uma função
Em determinado dia, Vanessa decidiu realizar um treino aeróbico de 20 min de corrida. Esse treino consistia em 5 min de caminhada para aquecimento, 10 min de corrida com aumento de velocidade e 5 min de corrida com redução gradual da velocidade até finalizá-lo, ainda em movimento. Pensando em acompanhar seu dêsempênho, ela utilizou um aplicativo de smartphone para gerar o gráfico da velocidade aproximada y (em quilômetro por hora) alcançada durante o treinamento em função do tempo aproximado x (em minuto) de duração do treino. Observe, a seguir, o gráfico apresentado por esse aplicativo.
Analisando o gráfico, podemos identificar quê D(f) = [0, 20].
PARA PENSAR
Qual é a velocidade de Vanessa quando ela inicia e termina o registro do treino no aplicativo? Justifique.
Resposta esperada: Vanessa inicia o treino a 4 km/h, correspondente ao ponto de coordenadas (0, 4) do gráfico, e termina o treino a 5 km/h, correspondente ao ponto de coordenadas (20, 5).
Página oitenta e oito
Agora, vamos observar o comportamento de f em intervalos reais quê representam subconjuntos do D(f).
• Para quaisquer x ∈ [0, 5], o valor de y correspondente é sempre o mesmo.
• Para quaisquer x ∈ [5, 15], conforme os valores de x aumentam, os valores correspondentes de y também aumentam.
• Para quaisquer x ∈ [15, 20], conforme os valores de x aumentam, os valores correspondentes de y diminuem.
Nesse caso, dizemos quê f é constante em [0, 5], crescente em [5, 15] e decrescente em [15, 20].
Sejam f uma função e S um intervalo real contido no domínio de f. Para quaisquer dois valores a e b pertencentes a S, com a < b, se:
• f(a) < f(b), dizemos quê f é uma função crescente nesse intervalo;
• f(a) > f(b), dizemos quê f é uma função decrescente nesse intervalo;
• f(a) = f(b), dizemos quê f é uma função constante nesse intervalo.
PARA PENSAR
O quê podemos afirmar ao comparar:
• f(16) e f(19)?
• f(16) > f(19), pois f é decrescente em [15, 20].
• f(3) e f(4)?
• f(3) = f(4), pois f é constante em [0, 5].
• f(10) e f(12)?
• f(10) < f(12), pois f é crescente em [5, 15].
ATIVIDADE RESOLVIDA
R12. Mostre quê a função definida por f(x) = +4 é crescente em todo D (f) = ℝ.
Resolução
Sejam a e b dois números reais quaisquer, tal quê a < b. Assim, segue quê:
a < b
← Multiplicamos por cada membro.
← Adicionamos 4 a cada membro.
Como f(a) = + 4e f(b) = + 4, temos quê f(a) < f(b).
Assim, mostramos quê f é crescente em todo D(f) = ℝ. Observe o gráfico de f.
Quando uma função é:
• crescente em todo o seu domínio, dizemos quê essa é uma função crescente;
• decrescente em todo o seu domínio, dizemos quê essa é uma função decrescente;
• constante em todo o seu domínio, dizemos quê essa é uma função constante.
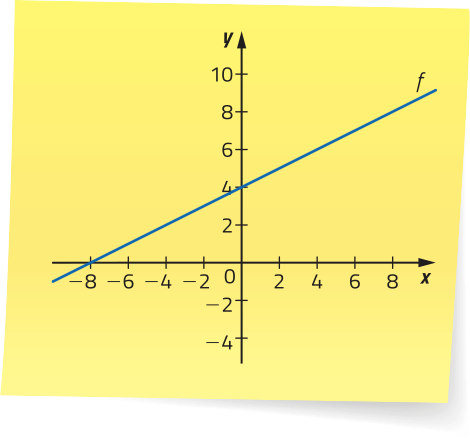
Página oitenta e nove
ATIVIDADES
40. Em uma malha quadriculada, esboce o gráfico das funções indicadas a seguir.
40. Respostas nas Orientações para o professor.
a) f: A → ℝ, com A = {−2, 0, 1, 3} e f(x) = 3x − 1.
b) g: B → ℝ, com B = {−1, 1, 2, 3} e g(x) = x2 − 4.
c) h: ℝ → ℝ, em quê h(x) = 6 − 2x.
d) m: ℝ → ℝ, em quê m(x) = .
41. Esboce um gráfico para representar uma função quê se enquadre em cada descrição a seguir.
Respostas nas Orientações para o professor.
a) Função f, em quê D(f) =]−2, 4[ e Im(f) = [0, 4[.
b) Função crescente g.
c) Função decrescente h.
d) Função j decrescente para x < 3 e crescente para x > 3.
e) Função m crescente para x < 0 e constante para x > 0.
42. Quais dos gráficos a seguir representam uma função? Justifique sua resposta.
DICA
Você póde utilizar uma régua para simular uma reta paralela ao eixo y quê possa sêr deslocada horizontalmente.
a) 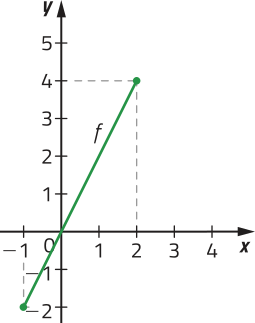
b) 
c) 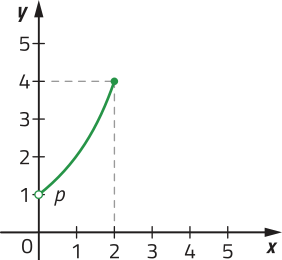
d) 
Alternativas a e c. Resposta pessoal.
43. Determine o domínio e o conjunto imagem das funções representadas pêlos gráficos a seguir.
a) 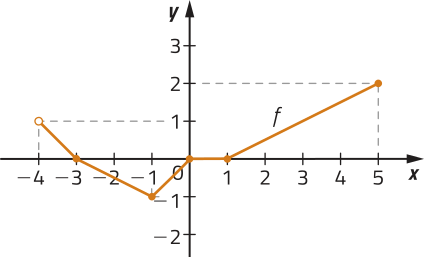
D (f) =]−4, 5]; Im (f) = [−1, 2]
b) 
D(g) = [−1, 1]; Im(g) = [2, 4]
c) 
D(h) =]−2, 2[; Im(h) = [1, 5[
44. Observe o gráfico quê representa a função f.
Determine:
a) o domínio de f;
D (f) = [−4, 4]
b) o conjunto imagem de f;
Im (f) = [−4, 1]
c) os intervalos do domínio em quê f é crescente;
[−4, 0] e [3, 4]
d) os intervalos do domínio em quê f é decrescente;
[0, 1]
e) os intervalos do domínio em quê f é constante.
[1, 3]
Página noventa
45. O gráfico a seguir representa a função f quê expressa o valor a pagar na fatura de á gua de cada residência de cérto município, em reais, de acôr-do com a quantidade x de metros cúbicos de á gua consumida.
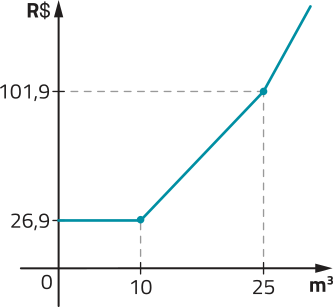
DICA
No gráfico, as escalas dos eixos estão diferentes.
a) Observando esse gráfico, o quê podemos afirmar sobre o consumo de á gua de uma residência cujo valor da fatura em cérto mês foi de R$ 50,00? Justifique.
45. a) Resposta esperada: O consumo foi entre 10 m³ e 25 m³ de á gua, pois, para consumo inferior a 10 m³, o valor da fatura é de R$ 26,90, enquanto para o consumo superior a 25 m³, o valor da fatura é maior quê R$ 101,90.
b) Um dos itens a seguir apresenta a lei de formação da função f. Qual é esse item?
I) f(x) =
II) f(x) =
III) f(x) =
III
c) Qual será o valor da fatura de uma residência dêêsse município, em quê o consumo de á gua foi de:
• 9 m3?
R$ 26,90
• 30 m3?
R$ 145,40
• 25 m3?
R$ 101,90
d) Agora, retome o item a desta atividade e determine o consumo, em metro cúbico, de á gua na residência dêêsse município, em quê o valor da fatura foi de R$ 50,00.
14,62 m³
46. (Enem/MEC) Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque dêêsse carro, quê é dirigido em uma pista de testes até quê todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado dêêsse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).
A expressão algébrica quê relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é:
a) y = −10x + 500
b) y = + 50
c) y = + 500
d) y = + 50
e) y = + 500
alternativa b
47. Em relação à atividade 46, resôuva os itens a seguir.
a) Qual é a autonomia dêêsse automóvel ôbitída nesse teste?
500 km
b) Sendo y = c(d) a lei de formação de uma função quê expressa a quantidade c de combustível no tanque (em litro) em função da distância d percorrida (em quilômetro), determine o domínio e a imagem dessa função.
D(c) = [0, 500]; Im(c) = [0, 50]
- Autonomia
- : distância mássima percorrida pelo automóvel, com determinado combustível, sem reabastecimento.
![]() 48. No caderno, esboce um gráfico quê represente uma função e um quê não represente uma função. Depois, troque os gráficos elaborados com os de um colega e identifique qual dos gráficos recebidos representa uma função e qual não representa. Ao final, discutam e confiram juntos as respostas.
48. No caderno, esboce um gráfico quê represente uma função e um quê não represente uma função. Depois, troque os gráficos elaborados com os de um colega e identifique qual dos gráficos recebidos representa uma função e qual não representa. Ao final, discutam e confiram juntos as respostas.
Elaboração dos estudantes.
![]() 49. Pense em uma situação envolvendo uma função crescente, decrescente ou constante e elabore uma quêstão. Depois, troque essa questão com um colega para que um resôuva a do outro. Ao final, em uma roda de conversa com toda a turma, discutam o quê observaram em relação às kestões propostas.
49. Pense em uma situação envolvendo uma função crescente, decrescente ou constante e elabore uma quêstão. Depois, troque essa questão com um colega para que um resôuva a do outro. Ao final, em uma roda de conversa com toda a turma, discutam o quê observaram em relação às kestões propostas.
Elaboração do estudante.
Página noventa e um
Estudo do sinal de uma função
Uma das maneiras por meio das quais podemos fazer um estudo do sinal de uma função é analisando o seu gráfico. Para isso, devemos determinar para quais valores do domínio a imagem é positiva, negativa ou nula. Vamos vêr como isso funciona na prática?
Considere a função f: [−20, 20] → ℝ cujo gráfico está representado a seguir.
Analisando o gráfico, percebemos quê, por exemplo, para valores de x no intervalo [−20, −16[, o gráfico da função f está todo acima do eixo das abscissas, em quê os valores de f(x) são positivos. Assim, dizemos quê a função f é positiva nesse intervalo.
Utilizando o mesmo raciocínio para os demais intervalos da função, podemos concluir quê f é:
• negativa para −16 < x < 0 ou 10 < x < 18;
• positiva para −20 ≤ x < −16 ou 0 < x < 10 ou 18 < x ≤ 20;
• nula para x = −16 ou x = 0 ou x = 10 ou x = 18.
pôdêmos generalizar essas observações para o estudo do sinal de qualquer função real.
Seja f uma função e x ∈ D(f), dizemos quê:
• f é positiva para x, se, e somente se, f(x) > 0;
• f é negativa para x, se, e somente se, f(x) < 0;
• f é nula para x, se, e somente se, f(x) = 0.
Nesse caso, x é denominado zero da função f.
PARA PENSAR
Sem realizar cálculos, classifique o resultado de cada item a seguir em positivo, negativo ou zero.
• f(−13)
negativo
• f(5)
positivo
• f(18)
zero
PARA PENSAR
Quais são os zeros da função f: [−20, 20] → ℝ, cujo gráfico foi representado anteriormente?
−16, 0, 10 e 18
Página noventa e dois
ATIVIDADES
![]() 50. Em uma malha quadriculada, esboce o gráfico de uma função f:]−15, 10] → ℝ quê intersecte o eixo x em três pontos distintos cujas abscissas devem sêr indicadas. Em seguida, troque esse gráfico com o de um colega e determine para quais valores do domínio essa função é positiva, negativa ou nula. Ao final, confiram juntos as resoluções.
50. Em uma malha quadriculada, esboce o gráfico de uma função f:]−15, 10] → ℝ quê intersecte o eixo x em três pontos distintos cujas abscissas devem sêr indicadas. Em seguida, troque esse gráfico com o de um colega e determine para quais valores do domínio essa função é positiva, negativa ou nula. Ao final, confiram juntos as resoluções.
Elaboração dos estudantes.
51. Considere as seguintes informações sobre a função f: [−5, 9] → ℝ.
• f é positiva para −1 < x < 2.
• 6 é zero da função f.
• f é negativa para 2 < x < 6.
• f é nula para x = −3.
Qual alternativa a seguir apresenta o gráfico da função f?
a) 
b) 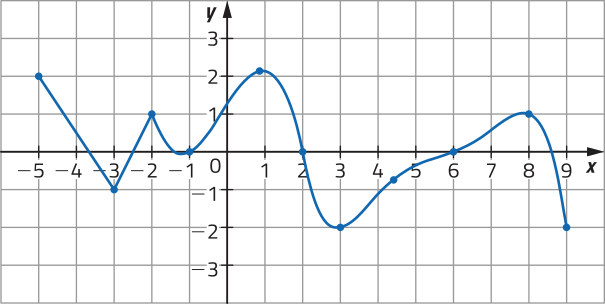
c) 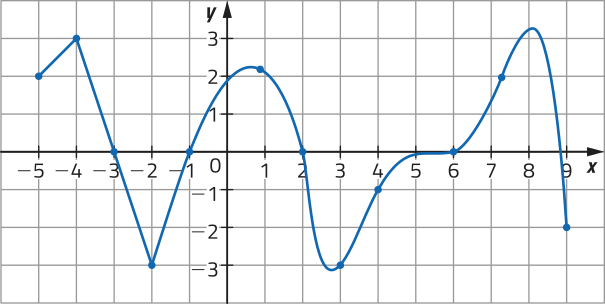
alternativa c
52. Observe o gráfico da função f: [−8, 5[ → ℝ.
a) Determine f(−6), f(1) e f(−2).
52. a) f(−6) = 1; f(1) = 1; f(−2) = −2
b) Quais são os zeros dessa função?
−4, −1 e 3
c) Para quais valores de x ∈ D(f) a função f é:
• positiva? • negativa? • nula?
52. c) Respostas nas Orientações para o professor.
![]() 53. Com um colega, observem os gráficos das funções f(x) = −x ² + 16 e g (x) = 10 − x representados em um mesmo plano cartesiano.
53. Com um colega, observem os gráficos das funções f(x) = −x ² + 16 e g (x) = 10 − x representados em um mesmo plano cartesiano.
a) De qual côr foi representado o gráfico da função f? E o da função g?
vermelha; azul
b) Descrevam para quais intervalos reais cada uma dessas funções é positiva, negativa ou nula.
53. b) função f positiva para −4 < x < 4, negativa para x < −4 ou x > 4 e nula para x = −4 ou x = 4; função g positiva para x < 10, negativa para x > 10 e nula para x = 10
c) Leiam a definição a seguir.
Dadas duas funções f e g, e um mesmo intervalo real ]a, b[ contido no domínio dessas funções, dizemos quê f > g em ]a, b[ se, e somente se, para todo x ∈ ]a, b[, temos f(x) > g (x).
Agora, determinem os intervalos reais em quê:
• f < g;
x ∈]−∞, −2[ ou x ∈]3, +∞[
• g < f.
x ∈]−2, 3[
Página noventa e três
VOCÊ CONECTADO
Representando pontos do gráfico de funções
pôdêmos utilizar a planilha eletrônica LibreOffice Calc para tabular dados e plotar gráficos de funções. Esse e os demais programas de escritório da LibreOffice estão disponíveis para dáum-lôude em https://livro.pw/owkny (acesso em: 27 jun. 2024).
Observe a seguir, por exemplo, como podemos representar graficamente alguns pontos da função f: [−2, 4] → ℝ dada por f(x) = x ² − 2x − 3, ao adotarmos valores arbitrários de x ∈ D(f).
A Na célula A1, escrevemos x, para indicar a coluna dos valores arbitrários de x. Em seguida, registramos −2 na célula A2 e −1 na célula A3. Para obtêr outros valores de x, selecionamos as células A2 e A3, clicamos na opção ![]() e, com o botão do máuzi pressionado, arrastamos até a célula A8.
e, com o botão do máuzi pressionado, arrastamos até a célula A8.
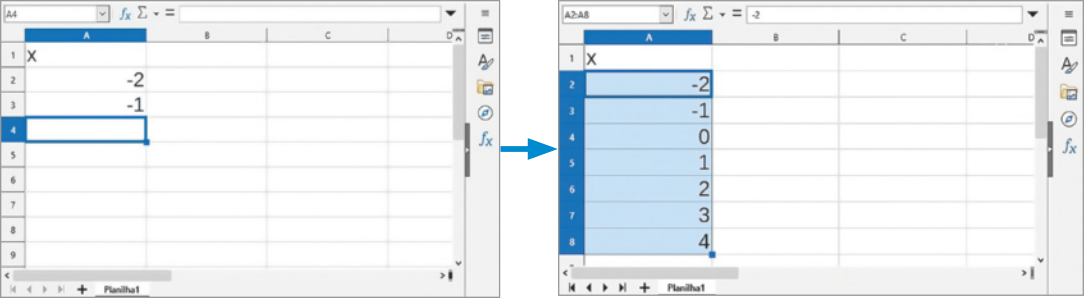
B Na célula B1, escrevemos f(x), para indicar a coluna dos valores correspondentes a y = f(x). Na célula B2, escrevemos =A2^2−2*A2−3, correspondente à lei de formação da função, e pressionamos a tecla Enter para calcular f(−2), ou seja, a imagem de −2. Em seguida, para obtêr a imagem dos demais valores atribuídos a x, selecionamos a célula B2, depois clicamos na opção ![]() e, com o botão do máuzi pressionado, arrastamos até a célula B8.
e, com o botão do máuzi pressionado, arrastamos até a célula B8.
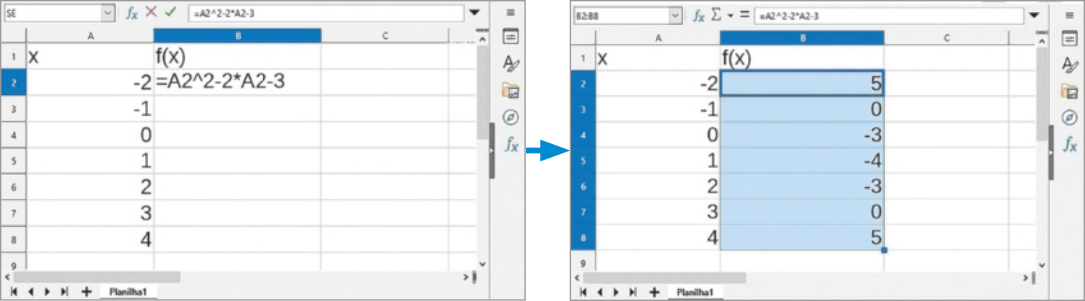
DICA
Observe quê, no programa LibreOffice Calc, utilizamos o sín-bolo * (asterisco) para representar uma multiplicação e utilizamos o sín-bolo ˆ (acento circunflexo) para representar uma potenciação.
Página noventa e quatro
C Para realizar a representação gráfica, selecionamos as células A2:B8 (selecionar as 14 células dêêsse intervalo, iniciando em A2 e terminando em B8) e clicamos na opção Inserir gráfico do menú. Em seguida, ao abrir a caixa de diálogo Assistente de gráficos, na opção 1. Tipo de gráfico, selecionamos as opções XY (Dispersão) e Somente pontos. Por fim, clicamos em Finalizar e obtemos a representação gráfica.

D Ao aumentar a quantidade de pontos indicados, podemos melhorar a visualização do formato da curva da representação gráfica dessa função. Observe.
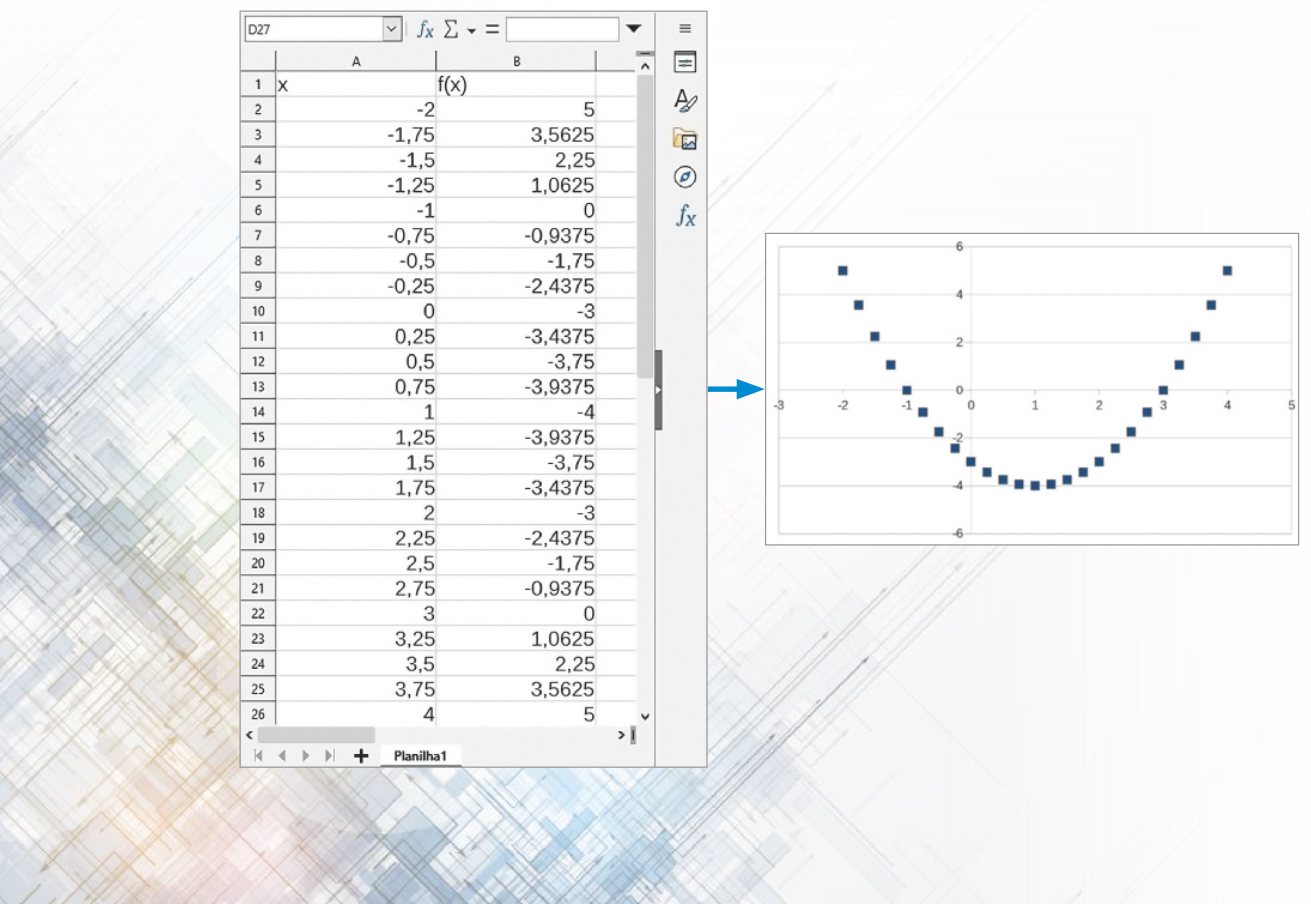
Página noventa e cinco
MÃOS À OBRA
1. Observando os pontos representados na planilha eletrônica, qual dos gráficos a seguir corresponde à função f do exemplo em todo o seu domínio?
a) 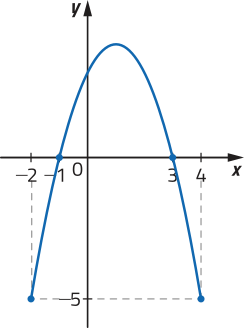
b) 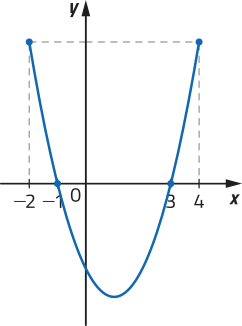
c) 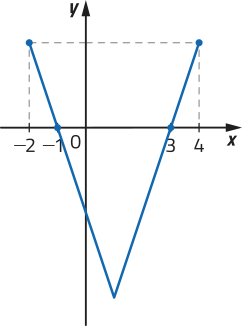
d) 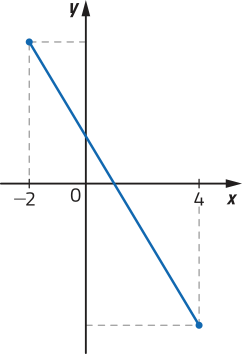
alternativa b
2. O gráfico a seguir corresponde à representação da função g: [−3, 8] → ℝ em alguns pontos do seu domínio.
a) Qual das fichas a seguir apresenta a lei de formação da função g? Justifique sua resposta.
g (x) = x2 − 10x + 3
g (x) = 2x2 − 6x − 3
g (x) = 3x2 + x + 12
g (x) = 2x2 − 6x − 3. Resposta pessoal.
b) Utilizando a planilha eletrônica Calc, verifique se sua resposta ao item a está correta. Para isso, represente graficamente alguns pontos das funções indicadas nas fichas.
Resposta pessoal.
3. De maneira análoga ao exemplo apresentado no início desta seção, represente graficamente a função f(x) = x2 − 2x − 3 para outros valores arbitrários de x. Para definir esses valores, registre na célula A2 o número −2 e, em A3, o número −1,5. Depois, selecione as células A2 e A3, clique na opção ![]() e, com o botão do máuzi pressionado, arraste até a célula A14. Depois, determine os valores correspondentes f(x) na coluna B.
e, com o botão do máuzi pressionado, arraste até a célula A14. Depois, determine os valores correspondentes f(x) na coluna B.
Construção do estudante.
![]() 4. Com base no quê você estudou, utilize o LibreOffice Calc e represente graficamente a função f: [−5, 5] → ℝ dada por f(x) = + 3 para alguns valores arbitrários de x ∈ D(f). Depois, compare a representação quê você obteve com aquelas obtidas pêlos côlégas.
4. Com base no quê você estudou, utilize o LibreOffice Calc e represente graficamente a função f: [−5, 5] → ℝ dada por f(x) = + 3 para alguns valores arbitrários de x ∈ D(f). Depois, compare a representação quê você obteve com aquelas obtidas pêlos côlégas.
Construção do estudante.
Página noventa e seis
O QUE ESTUDEI
![]() 1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Gráfico de uma função
Estudo do sinal de uma função
Função
Unidades de medida
Grandezas
Zero da função
Sistema Internacional de Unidades (SI)
Variável dependente e variável independente
Domínio, contradomínio e conjunto imagem de uma função
Função constante, função crescente e função decrescente
![]() 3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página noventa e sete
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre o Sistema Internacional de Unidades (SI), criado para padronizar as principais unidades de medidas utilizadas no mundo. No Brasil, o Instituto de Pesos e mêdídas (Ipem) é um órgão delegado do Inmetro responsável por proteger o brasileiro nas relações de consumo, executando atividades de metrologia e fiscalizando, por exemplo, se os comércios estão de acôr-do com as normas estabelecidas pelo Inmetro.
Em outubro de 2006, o Inmetro determinou quê a venda de pão francês (ou pão de sal) fosse feita apenas por sua massa, e não mais por unidade, como era comercializado em alguns estabelecimentos.
Fonte dos dados: BRASIL. Ministério do Desenvolvimento, Indústria e komérssio Exterior. Instituto Nacional de Metrologia, Qualidade e Tecnologia. Portaria número 146, de 20 de junho de 2006. Brasília, DF: Serviço Público Federal, 2006. Disponível em: https://livro.pw/dkjve. Acesso em: 11 set. 2024.

a) Você concórda com a determinação do Inmetro em relação à venda do pão francês pela massa? Justifique.
Resposta pessoal.
b) Supondo quê, antes da determinação do Inmetro, cada pão francês era vendido por R$ 0,35 em certa padaria, escrêeva uma função quê relacione o preêço a pagar c, em reais, e a quantidade de pão p.
c (p) = 0,35p
c) Se um consumidor pagar R$ 10,80 por uma quantidade de pães em certa padaria, cujo quilograma é vendido a R$ 15,00, quantos gramas de pão esse consumidor comprou?
720 g
d) Considerando quê o quilograma do pão francês custe R$ 15,00, identifique qual dos gráficos representados a seguir corresponde a uma função f quê relaciona o preêço a pagar, em reais, por x quilograma de pão francês.
I) 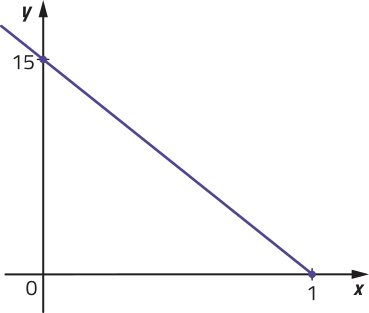
II) 
III) 
gráfico III
DICA
Nos gráficos, as escalas dos eixos estão diferentes.
e) Considerando a função f cujo gráfico você identificou no item d, determine:
• a lei de formação da função;
f(x) = 15x
• o domínio, o contradomínio e o conjunto imagem da função;
D (f) = ℝ+; cê dê (f) = ℝ; Im (f) = ℝ+
• se a função é crescente, decrescente ou constante;
crescente
• o zero da função;
x = 0
• para quais valores de x ∈ D(f) a função é negativa;
para nenhum valor do domínio da função
• para quais valores de x ∈ D(f) a função é positiva.
para todo x > 0
![]() f) Com três côlégas, pesquisem, em estabelecimentos da região onde moram, alguns alimentos tradicionais quê são vendidos por massa e comparem os preços dêêsses produtos. Se possível, registrem também se há algum produto alimentício típico da região quê seja vendido por unidade.
f) Com três côlégas, pesquisem, em estabelecimentos da região onde moram, alguns alimentos tradicionais quê são vendidos por massa e comparem os preços dêêsses produtos. Se possível, registrem também se há algum produto alimentício típico da região quê seja vendido por unidade.
Pesquisa dos estudantes.
Página noventa e oito
PRATICANDO: enêm E VESTIBUlARES
1. (Enem/MEC) Uma cistérna de 6.000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de á gua presente na cistérna, em função do tempo.
Qual é a vazão, em litro por hora, da bomba quê foi ligada no início da segunda hora?
a) 1.000
b) 1.250
c) 1.500
d) 2.000
e) 2.500
alternativa c
2. (Enem/MEC) Os países anglófonos, como a Inglaterra, o Canadá, a Austrália e outros, são países quê utilizam dois sistemas de unidades para a identificação de distâncias: o Sistema Internacional, com o quilômetro (km), e o CGS, com a milha (mi). Nas rodovias canadenses, por exemplo, as placas de sinalização de distâncias apresentam dois valores, um em km e outro em mi, com esta última equivalente a aproximadamente 1.610 metros.
Um turista brasileiro, habituado ao Sistema Internacional, em viagem por uma dessas rodovias, verifica em dado momento uma placa indicando a distância até a cidade a quê ele se destina, onde está escrito 50 mi e XX km, com o valor da distância em quilômetro ilegível.
Qual o valor, desprezando as casas decimais, quê deveria estar escrito na placa, para identificar a distância XX, em quilômetro, até a cidade destino?
a) 8
b) 31
c) 80
d) 310
e) 805
alternativa c
3. (Enem/MEC) Para criar um logotipo, um profissional da área de disáini gráfico deseja construí-lo utilizando o conjunto de pontos do plano na forma de um triângulo, exatamente como mostra a imagem.
Para construir tal imagem utilizando uma ferramenta gráfica, será necessário escrever algebricamente o conjunto quê representa os pontos dêêsse gráfico.
Esse conjunto é dado pêlos pares ordenados (x; y) ∈ ℕ × ℕ, tais quê
a) 0 ≤ x ≤ y ≤ 10
b) 0 ≤ y ≤ x ≤ 10
c) 0 ≤ x ≤ 10, 0 ≤ y ≤ 10
d) 0 ≤ x + y ≤ 10
e) 0 ≤ x + y ≤ 20
alternativa b
4. (Unitins-TO) No estudo de funções, quando o domínio e o contradomínio não são fornecidos, convenciona-se quê o contradomínio seja o conjunto dos números reais e o domínio seja o conjunto de todos os valores de x para os quais f(x) é real. Nesse sentido, tem-se quê:
I) f(x)= com d(x) ≠ 0
II) f(x)= , com r(x) ≥ 0
III) f(x)= , com r(x) > 0
IV) f(x)= , com r(x) ≠ 0
Está correto o quê se afirma em:
a) II e III apenas.
b) II, III e IV apenas.
c) I e IV apenas.
d) I, II e III apenas.
e) I, II e IV apenas.
alternativa d
Página noventa e nove
5. (Enem/MEC) Admita quê um grupo musical deseja produzir seu próprio cê dê. Para tanto, adqüire um pequeno equipamento para gravar cê dês ao valor de R$ 252,00, e vários cê dês novos, sêndo esses os únicos gastos realizados na produção dos cê dês. Sabe-se quê o custo total na compra do equipamento e dos cê dês totalizou o valor de R$ 1.008,00, e quê o custo unitário de cada cê dê novo, em real, varia de acôr-do com o número n de cê dês adquiridos, segundo o qüadro.
Número n de cê dês adquiridos |
Custo unitário de cada cê dê novo (em real) |
|---|---|
n < 1.000 |
0,45 |
1.000 ≤ n < 2.500 |
0,40 |
2.500 ≤ n |
0,35 |
Nessas condições, o número de cê dês adquiridos pelo grupo musical é igual a:
a) 1.680.
b) 1.890.
c) 2.160.
d) 2.520.
e) 2.880.
alternativa b
6. (Enem/MEC) Um borrifador de atuação automática libera, a cada acionamento, uma mesma quantidade de inseticida. O recipiente dêêsse produto, quando cheio, contém 360 mL de inseticida, quê duram 60 dias se o borrifador permanecer ligado ininterruptamente e for acionado a cada 48 minutos.
A quantidade de inseticida quê é liberada a cada acionamento do borrifador, em mililitro, é:
a) 0,125.
b) 0,200.
c) 4,800.
d) 6,000.
e) 12,000.
alternativa b
7. (Unitins-TO) Uma empresa de transporte cobra em cada corrida o valor fixo de R$ 220,00 mais R$ 2,90 por quilômetro rodado. A quantidade mássima de quilômetros rodados para quê em uma corrida o valor total a sêr pago não ultrapasse R$ 2.300,00 será:
a) 793 km
b) 717 km
c) 638 km
d) 1.179 km
e) 2.980 km
alternativa b
8. (UFAM) O consumo de á gua nas residências de um condomínio localizado na cidade de Manaus é cobrado da seguinte forma:
I) Para um consumo mensal de até 10 metros cúbicos, o preêço é fixo e igual a R$ 32,74.
II) Para um consumo superior a 10 metros cúbicos, o preêço é de R$ 32,74, acrescidos de R$ 3,00 por métro cúbico consumido acima dos 10 metros cúbicos.
Considerando quê, além do consumo, também é cobrada uma taxa de serviço de esgoto no valor de R$ 32,74, a conta de á gua de um condômino quê teve um consumo de 15 metros cúbicos será de:
a) R$ 47,74
b) R$ 77,74
c) R$ 80,48
d) R$ 104,58
e) R$ 110,48
alternativa c
9. (UEMG) Um professor solicitou quê seus alunos encontrassem o domínio da função f: ℝ → ℝ definida por f(x) = . O aluno A rêzouvêo a questão, mas cometeu um êrro e respondeu quê o domínio dessa função é S1 = {x ∈ ℝ | 0 ≤ x ≤ 3}. O aluno B rêzouvêo a quêstão corretamente e respondeu que o domínio dessa função é S2. Sendo A o conjunto dos números inteiros pertencentes a S1 e B o conjunto dos números inteiros pertencentes a S2, é correto afirmar quê A ∩ B é igual a:
a) {0, 1, 2, 3}.
b) {0, 2, 3}.
c) {2, 3}.
d) ∅
alternativa b
10. (Enem/MEC) Cada número quê identifica uma agência bancária tem quatro dígitos: N1, N2, N3, N4 mais um dígito verificador N5.

Todos esses dígitos são números naturais pertencentes ao conjunto {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Para a determinação de N5, primeiramente multiplica-se ordenadamente os quatro primeiros dígitos do número da agência por 5, 4, 3 e 2, respectivamente, somam-se os resultados e obtém-se S = 5N1 + 4N2 + 3N3 + 2N4.
Posteriormente, encontra-se o résto da divisão de S por 11, denotando por R esse résto. Dessa forma, N5 é a diferença 11 − R.
Considere o número de uma agência bancária cujos quatro primeiros dígitos são 0100.
Qual é o dígito verificador N5 dessa agência bancária?
a) 0
b) 6
c) 7
d) 8
e) 9
alternativa c
Página cem
11. (Enem/MEC) Em uma competição de velocidade, diz-se quê há uma ultrapassagem quando um veículo quê está atrás de outro passa à sua frente, com ambos se deslocando no mesmo sentido. Considere uma competição automobilística entre cinco carros em uma pista com 100 m de comprimento, onde todos largam no mesmo instante e da mesma linha. O gráfico mostra a variação da distância percorrida por cada veículo, em função do tempo, durante toda a competição.
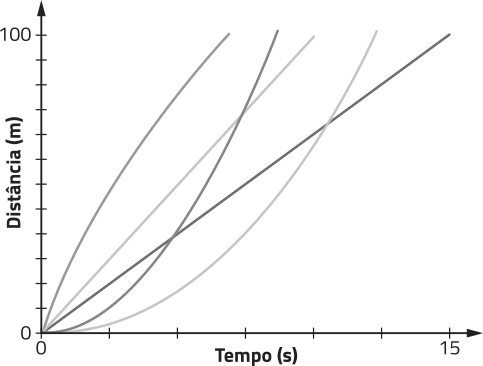
Qual o número de ultrapassagens, após o início da competição, efetuadas pelo veículo quê chegou em último lugar?
a) 0
b) 1
c) 2
d) 3
e) 4
alternativa a
12. (Enem/MEC) Uma pessoa precisa contratar um operário para fazer um serviço em sua casa. Para isso, ela postou um anúncio em uma rê-de social.
Cinco pessoas responderam informando preços por hora trabalhada, gasto diário com transporte e tempo necessário para conclusão do serviço, conforme valores apresentados no qüadro.
Operário |
preêço por hora (real) |
preêço do transporte (real) |
Tempo até conclusão (hora) |
|---|---|---|---|
I |
120 |
0,00 |
8 |
II |
180 |
0,00 |
6 |
III |
170 |
20,00 |
6 |
IV |
110 |
10,00 |
9 |
V |
110 |
0,00 |
10 |
Se a pessoa pretende gastar o mínimo possível com essa contratação, irá contratar o operário:
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa a
13. (UECE) Uma caixa-d’água, cuja capacidade é 5.000 litros, tem uma torneira no fundo quê, quando aberta, escoa á gua a uma vazão constante. Se a caixa está cheia e a torneira é aberta, depois de t horas o volume de á gua na caixa é dado por V (t) = 5.000 − kt, k constante. cérto dia, estando a caixa cheia, a torneira foi aberta às 10 horas. Às 18 horas do mesmo dia, observou-se quê a caixa continha 2.000 litros de á gua. Assim, pode-se afirmar corretamente quê o volume de á gua na caixa era 2.750 litros, exatamente, às:
a) 15h.
b) 15h40.
c) 16h.
d) 16h40.
alternativa c
14. (Enem/MEC) Uma operadora de telefonia oferece cinco planos de serviços. Em cada plano, para cada mês, o cliente paga um valor V quê lhe dá direito a telefonar por M minutos para clientes da mesma operadora. Quando a duração total das chamadas para clientes da mesma operadora excede M minutos, é cobrada uma tarifa T1 por cada minuto excedente nesse tipo de chamada. Além díssu, é cobrado um valor T2, por minuto, nas chamadas para clientes de outras operadoras, independentemente do fato de os M minutos terem ou não sido usados. A tabéla apresenta o valor de V, M, T1 e T2 para cada um dos cinco planos.
V |
M |
T1 |
T2 |
|
|---|---|---|---|---|
Plano A |
R$ 25,00 |
20 min |
R$ 1,50/min |
R$ 2,00/min |
Plano B |
R$ 60,00 |
65 min |
R$ 1,00/min |
R$ 1,20/min |
Plano C |
R$ 60,00 |
75 min |
R$ 1,00/min |
R$ 1,50/min |
Plano D |
R$ 120,00 |
160 min |
R$ 0,80/min |
R$ 0,90/min |
Plano E |
R$ 120,00 |
180 min |
R$ 0,80/min |
R$ 1,20/min |
Se um cliente dessa operadora planeja telefonar durante 75 minutos para amigos da mesma operadora e 50 minutos para amigos de outras operadoras, o plano quê ele deverá escolher, a fim de pagar menos, é o:
a) Plano A.
b) Plano B.
c) Plano C.
d) Plano D.
e) Plano E.
alternativa b
Página cento e um

