UNIDADE 4
FUNÇÃO QUADRÁTICA
Lançamento oblíquo
Quando um corpo qualquer é arremessado e forma determinado ângulo maior quê 0° e menor quê 90°, em relação à superfícíe horizontal, dizemos quê ocorreu um lançamento oblíquo ou de projétil.
Nesse lançamento, o corpo realiza um movimento compôzto de forças nas direções horizontal e vertical. Esse movimento é chamado de trajetória parabólica pelo seu formato, como estudaremos nesta Unidade. Na direção horizontal, o corpo realiza um movimento uniforme. Na direção vertical, o movimento é uniformemente variado, isto é, o corpo sobe em um lançamento vertical até atingir a altura mássima e, depois, realiza uma queda livre.
Os conceitos quê descrevem esse tipo de lançamento são aplicados no treinamento de atletas quê praticam modalidades esportivas, como salto em distância, lançamento de dardo e arremesso de peso. Observe, no esquema, algumas informações sobre a modalidade salto em distância.

Elaborado com base em: HEWITT, poou G. Física conceitual. 11. ed. Porto Alegre: búkmã, 2011. p. 174-179. CONFEDERAÇÃO BRASILEIRA DE ATLETISMO. Regras de competição: regras técnicas. [S. l.]: Cbat: WA: Abraat, 2024. p. 122-127. Edição 2024. Disponível em: https://livro.pw/qbklw. Acesso em: 18 jul. 2024.
Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Como póde sêr descrita a trajetória realizada por um objeto em um lançamento oblíquo? Você conhece outro exemplo de lançamento oblíquo?
2. De acôr-do com o texto, os conceitos quê descrevem o lançamento oblíquo são aplicados no treinamento de algumas modalidades do atletismo. por quê isso ocorre?
3. Represente, no caderno, a possível trajetória quê cérto corpo realiza em um lançamento oblíquo. Nessa representação, indique a posição da maior altura atingida e a distância horizontal percorrida.
Página cento e cinquenta e quatro
A parábola
Na abertura desta Unidade, foram apresentadas algumas informações sobre o lançamento oblíquo. Nesse tipo de lançamento, o objeto descreve uma trajetória parabólica. A parábola é uma curva com formato específico e quê, como estudaremos a seguir, está presente em diversos campos da Matemática. Também podemos identificar formatos quê lembram parábolas em construções ou objetos.

Acompanhe, a seguir, a definição de parábola e alguns de seus elemêntos.
Uma parábola é o conjunto de todos os pontos de um plano quê são equidistantes de um ponto F, denominado foco, e de uma reta r, denominada diretriz, com F ∉ r.
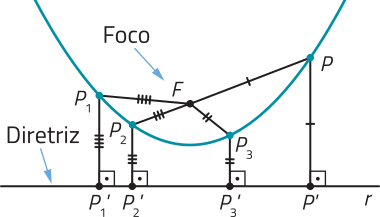
DICA
Nesta figura, os segmentos de reta com as mesmas marcações têm comprimentos iguais.
- Equidistantes
- : Sendo A e F dois pontos e r uma reta de um mesmo plano, dizemos quê A é equidistante de F e de r se a distância de A a F for igual à distância de A a r.
Além do foco F e da reta diretriz r, podemos identificar os seguintes elemêntos da parábola:
• a reta e, perpendicular à reta diretriz e quê passa pelo foco F, é o eixo de simetria da parábola;
• o ponto V, interseção da parábola com o eixo e, é o vértice da parábola e o ponto da parábola mais próximo da reta diretriz.
Com isso, da definição de parábola, podemos concluir quê a distância entre o foco e o vértice é igual à distância entre o vértice e a diretriz.
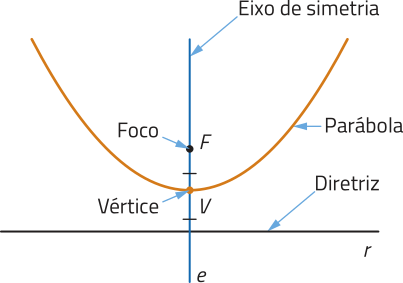
A seguir, estudaremos a função quadrática, cujo gráfico corresponde a uma parábola.
PARA PENSAR
Além de aplicações na arquitetura e na análise de um lançamento oblíquo, o estudo da parábola é aplicado em outras situações, como na ár-te, nos faróis de automóveis e holofotes, entre outros. Pesquise uma dessas aplicações e, em uma roda de conversa, compartilhe os resultados de sua pesquisa.
Pesquisa do estudante.
Página cento e cinquenta e cinco
Função quadrática: características e definição
Acompanhe a seguinte situação.
Pretende-se ampliar um campo de futeból quê tem 90 metros de comprimento e 60 metros de largura aumentando uma mesma medida x no comprimento e na largura, conforme o esquema a seguir.
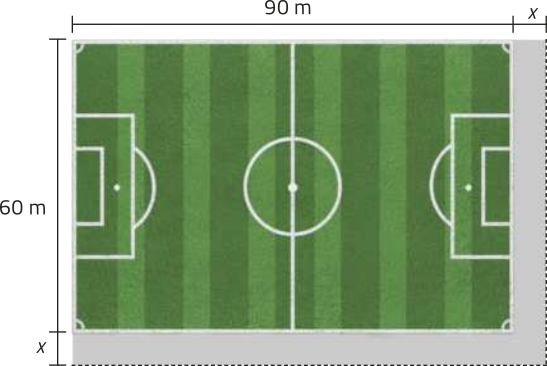
PARA PENSAR
Qual é a área dêêsse campo, em métro quadrado, antes da ampliação?
5.400 m2
A área dêêsse campo, após a ampliação das medidas de comprimento e largura em x métro, póde sêr expressa por meio de uma função f. Observe como a expressão quê representa f póde sêr ôbitída.
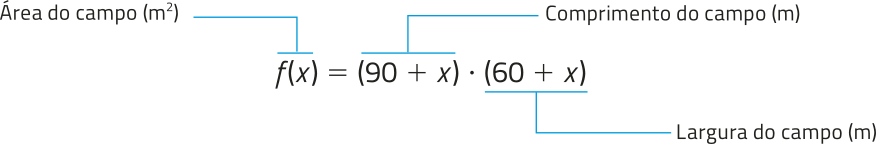
f(x) = 90 ⋅ 60 + 90x + 60x + x2 ⇒ f(x) = x2 + 150x + 5 400
Com essa lei de formação da função, podemos calcular f(12), por exemplo, para determinar a área do campo, caso a ampliação seja de 12 m no comprimento e 12 m na largura. Assim, temos:
f(12) = 122 + 150 ⋅ 12 + 5.400 = 144 + 1.800 + 5.400 = 7.344
Logo, a área do campo com 102 m de comprimento e 72 m de largura é igual a 7.344 m2.
Na situação inicial, é explorada a ideia de função quadrática, por meio da função f dada por f(x) = x2 + 150x + 5.400, quê expressa a área dêêsse campo após a ampliação.
Denominamos função quadrática toda função f: ℝ → ℝ, definida pela lei de formação f(x) = ax2 + bx + c, em quê a, b e c são números reais com a ≠ 0.
Dizemos quê a, b e c são os coeficientes da função quadrática.
PARA PENSAR
Considerando x = 30, qual é a área do campo, em métro quadrado, após a ampliação?
10.800 m2
Página cento e cinquenta e seis
Observe alguns exemplos de função quadrática.
f(x) = 2x2 − 4x + 19
a = 2
b = −4
c = 19
f(x) = x2 + 2x − 8
a = 1
b = 2
c = −8
f(x) = −0,2x2 − 7x
a = −0,2
b = −7
c = 0
f(x) = 3x2 −
a = 3
b = 0
c =
f(x) = −12x2
a = −12
b = 0
c = 0
ATIVIDADES RESOLVIDAS
R1. Dada a função quadrática f: ℝ → ℝ, definida por f(x) = −3x2 + 2x + 9, resôuva os itens a seguir.
a) Identifique os coeficientes a, b e c da função f.
b) Calcule f(3), f(−5), f, f(0,1) e f(0).
Resolução
a) a = −3, b = 2 e c = 9
b) • f(3) = −3 ⋅ 32 + 2 ⋅ 3 + 9 = −3 ⋅ 9 + 6 + 9 = −27 + 6 + 9 = −12
• f(−5) = −3 ⋅ (−5)2 + 2 ⋅ (−5) + 9 = −3 ⋅ 25 − 10 + 9 = −75 − 10 + 9 = −76
• f = −3 ⋅ + 2 ⋅ + 9 = −3 ⋅ + 1 + 9 = + 1 + 9 =
• f(0,1) = −3 · (0,1)2 + 2 ⋅ 0,1 + 9 = −3 ⋅ 0,01 + 0,2 + 9 = −0,03 + 0,2 + 9 = 9,17
• f(0) = −3 ⋅ 02 + 2 ⋅ 0 + 9 = 0 + 0 + 9 = 9
R2. Certa câmara fria tem capacidade para 8.000 L, e sua tempera-túra interior está programada para variar de −10 °C a −2 °C. Ao atingir a tempera-túra mássima, o motor dessa câmara liga automaticamente e permanéce assim até quê a tempera-túra interna káia para −10 °C, momento em quê o motor é desligado. Após o motor sêr ligado, a tempera-túra interna t dessa câmara fria varia de acôr-do com a função T dada por T(t)= − 2, com t em hora. Quantas horas após atingir a tempera-túra mássima o motor dessa câmara voltará a desligar?
Resolução
Note quê, no enunciado desta atividade, há dados quê não são essenciais para resolver a questão indicada. Então, vamos selecionar as informações necessárias para determinar depois de quanto tempo o motor da câmara fria voltará a desligar.
• A tempera-túra mínima dessa câmara é −10 °C.
• A lei de formação de T é dada por T (t)= − 2.
Com base nessas informações, vamos determinar o valor de t para T(t) = −10, quê é o momento em quê o motor vai desligar, pois a câmara atingiu a tempera-túra mínima (−10 °C). Assim:
T(t)= −10 ⇒ −2 = −10 ⇒ = 8 ⇒ t2 = 64 ⇒
Portanto, o motor dessa câmara voltará a desligar 8 h após atingir a tempera-túra mássima.
Página cento e cinquenta e sete
ATIVIDADES
1. Identifique em quais dos itens a seguir a lei de formação corresponde a uma função quadrática f: ℝ → ℝ. Justifique sua resposta.
a) f(x) = x2 + 9
b) f(x) = x (x − 1)
c) f(x) = x (x − 1) − x2
d) f(x) = 7 + 3x − 5x2
e) f(x) = (−x + 1)2
f) f(x) = 6x +
1. a, b, d e e. Todos os itens indicados podem sêr descritos pela lei de formação f(x) = ax² + bx + c, com a ≠ 0.
2. Nas funções quadráticas definidas a seguir, identifique os coeficientes a, b e c.
a) f(x) = −5x2 + 3x − 9
a = −5; b = 3; c = −9
b) f(x) = −0,4 + x2
a = 1; b = 0; c = −0,4
c) f(x) = x2 + 4 + x
a =; b = ; c =4
d) f(x) = 3,5x2
a = 3,5; b = 0; c = 0
e) f(x) = 4 + x2
a = ; b = 0; c = 4
f) f(x) = 4(x + 7)2
a = 4; b = 56; c = 196
3. Dadas as funções quadráticas definidas por f(x) = x2 + 5x − 7 e g(x) = −2x2 + 4x + 3, calcule:
a) f(2);
7
b) f(−3);
−13
c) g (5);
−27
d) g (−0,3);
1,62
e) f(−1) + g (9);
−134
f) 3 ⋅ f(3) − 2 ⋅ g (−1).
57
4. Observe a sequência de figuras compostas de quadrados.
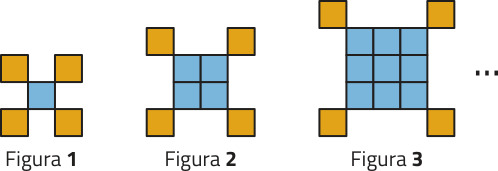
a) Quantos quadrados compõem cada uma dessas três primeiras figuras da sequência?
4. a) figura 1: 5 quadrados; figura 2: 8 quadrados; figura 3: 13 quadrados
b) Qual das fichas a seguir apresenta a lei de formação de uma função quê indica a quantidade de quadrados quê compõem a figura x, sabendo quê x é um número natural positivo?
f(x) = x2 + 3x + 5
f(x) = −3x2
f(x) = x2 + 4
f(x) = x2 + 3
f(x) = x2 + 4
c) Quantos quadrados compõem a figura 8 dessa sequência? Explique, com suas palavras, como você pensou.
68 quadrados.
Resposta pessoal.
5. Observe a figura de um quadrado.

a) escrêeva a lei de formação de uma função f quê relacione a área e a medida x do lado dêêsse quadrado.
f(x) = x2
b) Calcule f(5) e f(3). O quê esses cálculos indicam?
5. b) f(5) = 25; f(3) = 9. Resposta esperada: Esses cálculos indicam quê os quadrados cujos lados médem 5 u.c. e 3 u.c. têm área com medidas de 25 u.a. e 9 u.a., respectivamente.
c) Qual afirmativa a seguir é correta?
I) A área dessa figura é diretamente proporcional à medida do lado dela.
II) A área dessa figura é diretamente proporcional ao dôbro da medida do lado dela.
III) A área dessa figura é diretamente proporcional ao quadrado da medida do lado dela.
5. c) afirmativa III
6. pôdêmos calcular a quantidade d de diagonais de um polígono convexo de n lados por meio da função d (n) = . No caso de um hekzágono convexo, por exemplo, temos:
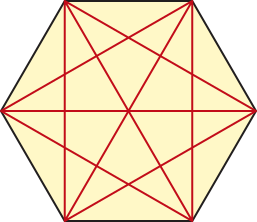
d (6) = = 9; 9 diagonais
a) Calcule a quantidade de diagonais de um polígono convexo com:
• 7 lados;
14 diagonais
• 14 lados;
77 diagonais
• 18 lados.
135 diagonais
b) Identifique os valores dos coeficientes da função quadrática d.
a =; b = ;c = 0
![]() c) Agora, com um colega, demonstrem a validade da expressão apresentada para calcular a quantidade de diagonais de um polígono convexo de n lados.
c) Agora, com um colega, demonstrem a validade da expressão apresentada para calcular a quantidade de diagonais de um polígono convexo de n lados.
Resposta nas Orientações para o professor.
Página cento e cinquenta e oito
![]() 7. Defina uma função quadrática indicando o domínio, o contradomínio e a lei de formação. Depois, destaque os coeficientes a, b e c e calcule o valor numérico dessa função para alguns elemêntos do domínio. Por fim, troque seus registros com os de um colega para quê um verifique se os procedimentos realizados pelo outro estão corretos.
7. Defina uma função quadrática indicando o domínio, o contradomínio e a lei de formação. Depois, destaque os coeficientes a, b e c e calcule o valor numérico dessa função para alguns elemêntos do domínio. Por fim, troque seus registros com os de um colega para quê um verifique se os procedimentos realizados pelo outro estão corretos.
Elaboração do estudante.
8. Uma cooperativa conta com 25 artesãos e produz bolsas utilizando retalhos de tecídos. Eles trabalham na produção durante cinco dias por semana e, por dois dias, vão à feira vender as bolsas produzidas. Para calcular o custo de produção diário, em reais, a cooperativa utiliza a função f(x) = 0,2x2 + 5x + 200. Nessa função, x é um número natural quê representa a quantidade de bolsas produzidas, tal quê 10 ≤ x ≤ 50.
a) Qual é o custo diário de produção dessa cooperativa quando são produzidas 15 bolsas? E quando são produzidas 40 bolsas?
8. a) R$ 320,00; R$ 720,00
b) cérto dia, nessa cooperativa, foram produzidas 35 bolsas, e todas foram vendidas por um total de R$ 1.400,00. Qual foi o lucro obtído nessa venda?
R$ 780,00
DICA
Para resolver esta atividade, você póde, inicialmente, selecionar apenas os dados necessários indicados no enunciado.
9. Observe o bloco retangular no qual as medidas das arestas, em métro, estão indicadas por expressões algébricas.
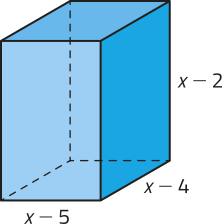
a) Determine a lei de formação de uma função f quê representa a área da base dêêsse bloco retangular, de acôr-do com a medida x.
9. a) f(x) = x2 − 9x + 20
b) escrêeva a lei de formação de uma função g quê representa a área total da superfícíe dêêsse bloco, de acôr-do com a medida x.
g(x) = 6x2 − 44x + 76
c) Qual é a área da base dêêsse bloco retangular para x = 10? E a área total de sua superfícíe?
30 m2; 236 m2
10. Leia o texto e, depois, faça o quê se pede.
MATEMÁTICA NA HISTÓRIA
O italiano Galileu Galilei (1564-1642) é considerado um dos mais importantes cientistas do século XVII. Dentre suas contribuições, está a relação conhecida como lei dos corpos em queda. Ao analisar o movimento de objetos em queda, Galileu concluiu quê, desprezando a resistência do ar, a distância percorrida por um objeto em queda livre, abandonado em repouso, é proporcional ao quadrado do tempo de sua queda.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 4. ed. Campinas: Editora da Unicamp, 2007. p. 354.

Observe, a seguir, o registro da distância percorrida por um objeto em queda livre, abandonado em repouso, no decorrer do tempo.
Tempo (s) |
0 |
1 |
2 |
3 |
4 |
… |
|---|---|---|---|---|---|---|
Distância (m) |
0 |
4,9 |
19,6 |
44,1 |
78,4 |
… |
a) Que relação é possível identificar entre os números da primeira linha e os números correspondentes da segunda linha dêêsse qüadro?
10. a) Resposta esperada: Cada número da segunda linha corresponde ao quadrado do respectivo número da primeira linha, multiplicado por 4,9.
DICA
Para identificar uma regularidade, divída cada número indicado na segunda linha por 4,9 e compare o resultado com o número correspondente da primeira linha.
b) De acôr-do com sua resposta ao item a, expresse a distância percorrida por um objeto em queda livre após t segundos de ele sêr abandonado em repouso.
4,9t2
c) escrêeva a lei de formação de uma função f quê determina a distância f(t) percorrida por esse objeto, em métro, de acôr-do com o tempo t de queda, em segundo. Essa função póde sêr classificada como função quadrática?
f(t) = 4,9t2; sim
d) Calcule a distância percorrida por esse objeto após 10 s em queda livre.
490 m
e) De acôr-do com a situação apresentada, na função f, o tempo t póde assumir qualquer valor real positivo? Justifique.
Não, após determinado tempo, o objeto deixa de estar em queda livre, pois atingirá uma superfícíe.
Página cento e cinquenta e nove
11. Leia uma das normas estabelecidas pela Associação Brasileira de Normas Técnicas (ABNT), para acessibilidade em rampas.
[...] A largura das rampas (L) deve sêr estabelecida de acôr-do com o fluxo de pessoas. A largura livre mínima recomendável para as rampas em rótas acessíveis é de 1,50 m, sêndo o mínimo admissível 1,20 m.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 9050: acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos. 4. ed. Rio de Janeiro: ABNT, 2020. p. 58. Disponível em: https://livro.pw/gxslr. Acesso em: 8 fev. 2024.

cérto escritório tem uma rampa de formato retangular, com 0,90 m de largura e 9 m de comprimento. Em uma reforma, pretende-se adequar essa rampa de acôr-do com a norma descrita, aumentando sua largura e comprimento em uma mesma medida x, em métro.
a) Determine a área atual dessa rampa.
8,1 m2
b) Caso a medida quê se aumentar na largura e no comprimento dessa rampa for de 50 cm, suas medidas estarão de acôr-do com a norma descrita?
11. b) Com esse aumento, a rampa passa a ter 1,40 m de largura, o quê a deixa “admissível” em relação à norma, mas abaixo do recomendado.
c) escrêeva a lei de formação de uma função g quê dêz-creva a área da rampa após a reforma, de acôr-do com a medida x.
11. c) g(x) = x2 + 9,9x + 8,1
d) De acôr-do com a lei de formação da função g quê você escreveu no item c, calcule g(0,6) e explique o quê o resultado obtído indica.
11. d) g(0,6) = 14,4. Esse resultado indica quê, aumentando 0,6 m no comprimento e na largura dessa rampa, sua área será de 14,4 m2.
![]() e) Com um colega, pesquisem uma rampa de acesso em algum prédio público do bairro ou do município onde vocês moram. Depois, meçam a largura dela e analisem se ela foi construída de acôr-do com a norma apresentada. Por fim, registrem essas informações.
e) Com um colega, pesquisem uma rampa de acesso em algum prédio público do bairro ou do município onde vocês moram. Depois, meçam a largura dela e analisem se ela foi construída de acôr-do com a norma apresentada. Por fim, registrem essas informações.
Pesquisa do estudante.
12. Leia o texto a seguir e, depois, faça o quê se pede.
MATEMÁTICA NA HISTÓRIA
O alemão Johann fridichi Cal Gauss (1777-1855) é considerado um dos principais matemáticos do século XIX. Conta-se quê, quando Gauss tinha por volta de 10 anos, seu professor propôs à turma quê adicionasse os números naturais de 1 até 100, ou seja, quê calculasse:
1 + 2 + 3 +... + 98 + 99 + 100
Pouco tempo depois, Gauss teria apresentado a resposta correta: 5.050. Acredita-se quê ele tenha observado quê:
• 1 + 100 = 101
• 2 + 99 = 101
• 3 + 98 = 101
⋮
• 98 + 3 = 101
• 99 + 2 = 101
• 100 + 1 = 101
ou seja, bastava adicionar o primeiro e o último número dessa sequência de números naturais, multiplicar o resultado pela quantidade de números e dividir esse produto por 2.
= 5.050
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 4. ed. Campinas: Editora da Unicamp, 2007. p. 519.
a) Com suas palavras, explique por quê, na suposta estratégia utilizada por Gauss para determinar a soma dos termos da sequência dos 100 primeiros números naturais positivos, dividiu-se por 2 o produto obtído da soma do primeiro e do último termos pela quantidade total de termos.
12. a) Resposta esperada: Porque, ao adicionar os termos extremos dessa sequência, obtêm-se 100 adições, e cada adição foi contada duas vezes. Assim, é preciso dividir por 2 para obtêr a soma correta.
![]() b) De maneira análoga a Gauss, determine a soma dos 20 primeiros números naturais positivos. Depois, confira o resultado obtído em uma calculadora.
b) De maneira análoga a Gauss, determine a soma dos 20 primeiros números naturais positivos. Depois, confira o resultado obtído em uma calculadora.
210
c) escrêeva a lei de formação de uma função s para expressar a soma dos n primeiros números naturais positivos.
12. c) s(n) = ou s(n) =
![]() d) Qual é a soma dos 130 primeiros números naturais positivos? E dos 801 primeiros números naturais positivos?
d) Qual é a soma dos 130 primeiros números naturais positivos? E dos 801 primeiros números naturais positivos?
8.515; 321.201
Página cento e sessenta
Zeros de uma função quadrática
Leia a situação descrita a seguir.
Para investigar a concentração de um medicamento na corrente sanguínea de determinada espécie animal, uma médica-veterinária realizou côlétas do sangue de um animal a cada uma hora e, com os dados obtidos, construiu um modelo matemático representado pela função quadrática c dada por c (t) = t2 + 6t, em quê y = c (t) indica, em miligrama por litro (mg/L), a concentração dêêsse medicamento na corrente sanguínea após t horas da aplicação.

De acôr-do com o estudo realizado, quanto tempo após a aplicação identificou-se nula a concentração do medicamento na corrente sanguínea dêêsse animal?
Para resolver a situação apresentada, temos de determinar os valores de t para os quais c (t) = 0, ou seja, temos de obtêr os zeros dessa função quadrática.
Dada uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, temos quê x ∈ ℝ é zero da função f se ax2 + bx + c = 0.
DICA
Considere quê o modelo matemático seja válido para o período da aplicação do medicamento até o momento em quê se identificou nula sua concentração na corrente sanguínea do animal.
Desse modo, para determinar os zeros da função f dada por f(x) = ax2 + bx + c, é preciso obtêr as raízes da equação ax2 + bx + c = 0.
Assim, em relação à situação apresentada, temos:
c (t) = 0 ⇒ t2 + 6t = 0 ⇒ t ⋅ ( t +6) = 0 ⇒
Portanto, de acôr-do com o modelo matemático obtído, a concentração do medicamento na corrente sanguínea dêêsse animal ficou novamente nula 30 horas após a primeira aplicação.
PARA PENSAR
Nesta situação, o quê representa t = 0?
Representa o momento em quê o medicamento foi aplicado no animal pela primeira vez.
NO MUNDO DO TRABALHO
Médico-veterinário
O trabalho de um médico-veterinário não se restringe apenas à área de saúde e bem-estar de animais em atendimentos em clínicas veterinárias. Esse profissional póde ezercêr, ainda, diferentes atividades ligadas, por exemplo, a consultoria; pesquisa; contrôle e diagnóstico de doenças transmissíveis ao sêr humano pelo animal; docência; perícia criminal, judicial ou administrativa; produção de alimentos saudáveis; e produção de vacinas e medicamentos de uso animal.
Acesse o vídeo indicado a seguir, quê contém informações sobre as áreas de atuação do médico-veterinário.
• DIA do médico-veterinário. [S. l.: s. n.], 2020. 1 vídeo (2 min). Publicado pelo canal Tevê CRMV-SP. Disponível em: https://livro.pw/ckuhi. Acesso em: 18 jul. 2024.
Página cento e sessenta e um
ATIVIDADES RESOLVIDAS
R3. Em cada item, calcule os zeros da função f: ℝ → ℝ, definida por:
a) f(x) = 5x2;
b) f(x) = 2x2 − 8;
c) f(x) = x2 + 4x;
d) f(x) = 4x2 − 20x + 25;
e) f(x) = x2 + 6x + 5.
Resolução
Para resolver esses itens, podemos utilizar técnicas de fatoração de polinômios, assunto quê você possivelmente estudou em anos anteriores.
a) f(x) = 0 ⇒ 5x2 = 0 ⇒ x2 = 0 ⇒ x = 0
Portanto, o zero da função f é 0.
b) f(x) = 0 ⇒ 2x2 − 8 = 0 ⇒ 2x2 = 8 ⇒ x2 = 4 ⇒
Portanto, os zeros da função f são 2 e −2.
c) f(x) = 0 ⇒ x2 + 4x = 0 ⇒ x ⋅ (x + 4) = 0 ⇒
Portanto, os zeros da função f são 0 e −4.
d) Fazendo f(x) = 0, temos 4x2 − 20x + 25 = 0. Como o 1º membro dessa equação corresponde a um trinômio quadrado perfeito, podemos escrevê-lo como um produto notável.
4x2 − 20x + 25 = 0 ⇒ (2x)2 − 2 ⋅ 2x ⋅ 5 + 52 = 0 ⇒ (2x − 5)2 = 0
Assim, segue quê:
(2x − 5)2 = 0 ⇒ 2x − 5 = 0 ⇒ x =
Portanto, o zero da função f é .
e) Fazendo f(x) = 0, temos x2 + 6x + 5 = 0. pôdêmos utilizar o método de completar quadrados para resolver a equação. Para isso, adicionamos 4 em cada membro da equação e obtemos um trinômio quadrado perfeito no 1º membro.
x2 + 6x + 5 + 4 = 0 + 4 ⇒ x2 + 2 ⋅ x ⋅ 3 + 32 = 4 ⇒ (x + 3)2 = 4
Assim, segue quê:
(x + 3)2 = 4 ⇒
Portanto, os zeros da função f são −1 e −5.
PARA PENSAR
Explique como podemos verificar se estão corretas as respostas dos itens apresentados nesta atividade resolvida.
Resposta esperada: Verificando, em cada item, se f(x) = 0 para cada valor de x obtído como zero da função f.
R4. Os zeros da função quadrática f(x) = x2 + bx + c, em quê b e c são números reais, são 3 e −5. Quais são os valores dos coeficientes b e c dessa função?
Resolução
Como 3 e −5 são os zeros da função quadrática f(x) = x2 + bx + c, temos f(3) = 0 e f(−5) = 0.
• f(3) = 0 ⇒ 32 + b ⋅ 3 + c = 0 ⇒ 3b + c = −9
• f(−5) = 0 ⇒ (−5)2 + b ⋅ (−5) + c = 0 ⇒ −5b + c = −25
Assim, podemos escrever e resolver, pelo método da adição, o seguinte sistema linear de duas equações do 1º grau com duas incógnitas:
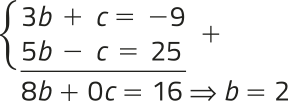
Substituindo b = 2 em 3b + c = −9, temos:
3 ⋅ 2 + c = −9 ⇒ c = −15
Portanto, b = 2 e c = −15.
Página cento e sessenta e dois
A fórmula resolutiva
Além das técnicas de fatoração para resolução de equações do 2º grau abordadas nas atividades resolvidas anteriores, é possível utilizar a fórmula resolutiva para resolver esse tipo de equação. Acompanhe a seguir.
MATEMÁTICA NA HISTÓRIA
As ideias gerais da fórmula resolutiva foram utilizadas há centenas de anos pêlos babilônios e gregos. No entanto, essas ideias foram difundidas com mais expressividade apenas alguns anos depois, sobretudo na obra Lilavati, de Bhaskara (c. 1114-1185).
Bhaskara nasceu em Vijayapura (Índia) e tem o seu nome, até os dias de hoje, associado à fórmula resolutiva de uma equação do 2º grau, a qual é comumente denominada fórmula de Bhaskara.
Fonte dos dados: BOYER, Cal Benjamin. História da matemática. Tradução: Elza Furtado Gomide. 3. ed. São Paulo: Edgard Blãcher, 2010. p. 152.

pôdêmos deduzir a fórmula resolutiva de uma equação do 2º grau na forma ax2 + bx + c = 0, em quê a, b, c são números reais e a ≠ 0. Acompanhe.
a x2 + bx + c = 0
x2 + = 0 ← Como a ≠ 0, podemos dividir ambos os membros da equação por a.
x2 + ← Subtraímos de ambos os membros da equação.
x2 + ← Utilizamos o método de completar quadrados. Para isso, adicionamos a ambos os membros da equação.
← Escrevemos o primeiro membro da equação como um produto notável.
x + ← Calculamos a raiz quadrada de ambos os membros da equação.
x = ← Subtraímos de ambos os membros da equação.
DICA
Nesta dedução, para expressar as raízes da equação utilizando o método de completar quadrados, busca-se determinar um trinômio quadrado perfeito no 1º membro da igualdade.
Na fórmula em destaque, denominamos b2 − 4ac de discriminante. A letra maiúscula grega delta é comumente utilizada para representar o discriminante. Assim, (delta)" = b2 − 4ac.
PARA AMPLIAR
Assista a êste vídeo para saber mais sobre as ideias históricas relacionadas à resolução de equações do 2º grau.
• ESSE tal de Bhaskara. [S. l.: s. n.], 2012. 1 vídeo (12 min). Publicado pelo canal M3 Matemática Multimídia. Disponível em: https://livro.pw/pfysh. Acesso em: 18 jul. 2024.
Página cento e sessenta e três
É possível estudar as raízes reais de uma equação do 2º grau com base no valor do discriminante (delta)" = b2 − 4ac. Acompanhe.
Se (delta)" > 0, então _ ∈ ℝ. Assim: x =
Nesse caso, a equação tem duas raízes reais distintas.
Se (delta)" = 0, então _ = 0. Assim: x =
Nesse caso, a equação tem duas raízes reais e iguais.
Se (delta)" < 0, então ∉ ℝ.
Nesse caso, a equação não tem raiz real.
Com isso, podemos concluir:
Seja uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, temos quê f:
• tem dois zeros reais distintos quando b2 − 4ac > 0;
• tem dois zeros reais e iguais quando b2 − 4ac = 0;
• não tem zero real quando b2 − 4ac < 0.
ATIVIDADES RESOLVIDAS
R5. Determine os zeros da função f: ℝ → ℝ, definida por f(x) = 4x2 + 16x − 20.
Resolução
Para resolver esta quêstão, podemos elaborar um algoritmo, que consiste em etapas com instruções descritas e ordenadas. Acompanhe.
1ª) Fazemos f(x) = 0, obtendo a equação 4x2 + 16x − 20 = 0.
2ª) Identificamos os valores dos coeficientes da equação: a = 4, b = 16 e c = −20.
3ª) Calculamos o valor do discriminante: (delta)" = 162 − 4 ⋅ 4 ⋅ (−20) = 256 + 320 = 576.
4ª) Utilizamos a fórmula resolutiva para obtêr os zeros da função f.
x =
Portanto, f tem dois zeros reais distintos: 1 e −5.
PARA PENSAR
Esse algoritmo póde sêr adaptado para resolver outras kestões com estruturas parecidas. No caderno, ajuste o algoritmo apresentado de maneira quê ele possa sêr utilizado para determinar os zeros de qualquer função quadrática. Depois, utilize-o para determinar os zeros das funções definidas por g(x) = 9x2 − 12x + 4 e h(x) = x2 − 4x + 10.
Dada uma função quadrática f, elaborar o seguinte algoritmo em etapas para determinar os zeros de f: 1ª) Escrever a equação do 2º grau f(x) = 0; 2ª) Identificar os coeficientes a, b e c da equação ôbitída; 3ª) Calcular o discriminante (delta)" = b2 − 4ac; 4ª) Se (delta)" < 0, a função f não tem zero real; se (delta)" ≥ 0, calcular os zeros da função por meio da fórmula resolutiva x = . A função g tem dois zeros reais e iguais a , e a função h não tem zero real.
Página cento e sessenta e quatro
R6. Dada a função quadrática f: ℝ → ℝ, definida por f(x) = 3x2 + 6x + k + 1, determine para quais valores reais de k é possível afirmar quê f:
a) tem dois zeros reais distintos;
b) tem dois zeros reais e iguais;
c) não tem zero real.
Resolução
Inicialmente, calculamos o discriminante (delta)":
(delta)" = 62 − 4 ⋅ 3 ⋅ (k + 1) = 36 − 12k − 12 = 24 − 12k
a) Para f ter dois zeros reais distintos, devemos ter (delta)" > 0:
24 − 12k > 0 ⇒ −12k > −24 ⇒ k < 2
Portanto, f terá dois zeros reais distintos se k < 2.
b) Para f ter dois zeros reais e iguais, devemos ter (delta)" = 0:
24 − 12k = 0 ⇒ −12k = −24 ⇒ k = 2
Portanto, f terá dois zeros reais e iguais se k = 2.
c) Para f não ter zero real, devemos ter (delta)" < 0:
24 − 12k < 0 ⇒ −12k < −24 ⇒ k > 2
Portanto, f não terá zero real se k > 2.
R7. Em uma indústria de cerâmica, o custo c de produção, em reais, de acôr-do com a quantidade q de vasos produzidos para uma encomenda, póde sêr determinado por c (q) = 0,01q2 − 2q + 110. É possível produzir uma encomenda de certa quantidade dêêsse vaso, de maneira quê o custo por unidade seja zero?
Resolução
Para quê o custo por vaso produzido seja zero, devemos ter:
c (q) = 0 ⇒ 0,01q2 − 2q + 110 = 0
Calculando o discriminante da equação ôbitída, temos:
(delta)" = (−2)2 − 4 ⋅ 0,01 ⋅ 110 = 4 − 4,4 = −0,4
Como (delta)" < 0, a equação 0,01q2 − 2q + 110 = 0 não tem raiz real.
Portanto, não é possível produzir nessa indústria uma encomenda com certa quantidade de vasos de maneira quê o custo por unidade seja zero.
R8. Determine os valores inteiros quê o número real m póde assumir, de maneira quê a função dada por f(x) = x2 − 2x + m não tenha zero real e a função dada por g (x) = −mx2 + 20x − 25 tenha dois zeros reais distintos.
Resolução
Para quê f não tenha zero real, é necessário quê:
• (delta)" < 0 ⇒ (−2)2 − 4 ⋅ 1 ⋅ m < 0 ⇒ 4 − 4m < 0 ⇒ −4m < −4 ⇒ m > 1
Para quê g tenha dois zeros reais distintos, é necessário quê:
• (delta)" > 0 ⇒ 202 − 4 ⋅ (−m) ⋅ (−25) > 0 ⇒ 400 − 100m > 0 ⇒ −100m > −400 ⇒ m < 4
Para satisfazer ambas as condições, temos 1 < m < 4.
Portanto, os valores inteiros quê o número real m póde assumir são 2 e 3.
Página cento e sessenta e cinco
ATIVIDADES
13. Determine os zeros da função f: ℝ → ℝ, definida por:
a) f(x) = 5x2 + 3
f não tem zero real.
b) f(x) = 8x − 2x2
0 e 4
c) f(x) = x2 − 10x + 25
5
d) f(x) = −2x2 + 3x − 5
f não tem zero real.
e) f(x) = 3x2 + 8x + 4
−2 e
f) f(x) = −2x2 + 2x + 24
−3 e 4
14. Retome a atividade 13 e confira as respostas usando uma estratégia diferente da quê você usou. Podem sêr empregadas técnicas de fatoração ou fórmula resolutiva.
Resposta pessoal.
15. Seja g: ℝ → ℝ uma função quadrática, definida por g(x) = (2m − 3)x2 + 2x + 2. Calcule para quais valores reais de m a função g:
a) tem dois zeros reais distintos;
m <
b) tem dois zeros reais e iguais;
m =
c) não tem zero real.
m >
16. O gestor de uma microempresa do ramo moveleiro, quê produz e vende móveis planejados, elaborou um modelo matemático para descrever o lucro y = s (x), em reais, obtído com a venda de cada unidade de cadeira produzida pela empresa, de acôr-do com a quantidade x de unidades vendidas na semana. Com base em dados registrados e utilizando um programa de computador, ele concluiu quê s (x) = −0,01x2 + 1,2x − 11.
a) Calcule s (20). O quê esse resultado representa?
16. a) s(20) = 9. Representa quê, se forem vendidas 20 cadeiras na semana, a microempresa terá um lucro de R$ 9,00 por cadeira.
b) Ao vender em certa semana 80 cadeiras, quantos reais, ao todo, essa microempresa terá de lucro com esse produto?
R$ 1.680,00
c) Para quê o lucro por unidade seja nulo, quantas cadeiras devem sêr vendidas em uma semana?
10 cadeiras ou 110 cadeiras
17. Em uma comunidade foi construída uma cistérna para armazenamento de á gua da chuva. Em uma visita técnica, foi constatado um vazamento por causa de uma rachadura na estrutura dessa cistérna. Com isso, identificou-se quê a cada hora o volume v de á gua na cistérna, em métro cúbico, diminuía de acôr-do com a função v dada por v (t) = t2 + 48, após t horas do início do vazamento e considerando-a inicialmente cheia.
a) Qual é a capacidade de armazenamento de á gua dessa cistérna?
48 metros cúbicos
b) Qual é o volume de á gua da cistérna 6 h após o início do vazamento?
45 metros cúbicos
c) Considerando quê a cistérna precisa estar completamente vazia para quê seja feito o reparo da rachadura, quantas horas após o início do vazamento poderá sêr realizado esse reparo?
24 h
18. O fluxograma a seguir representa um algoritmo quê descreve características das raízes de uma equação do 2º grau de acôr-do com o valor do discriminante (delta)". Nele, duas perguntas foram substituídas pelas lêtras A e B destacadas.
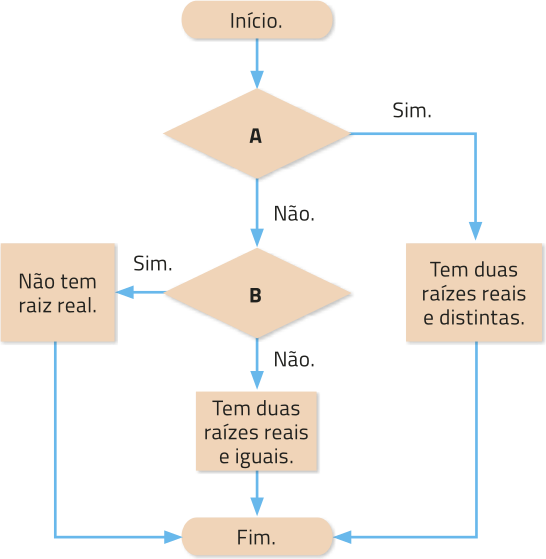
Associe cada uma das lêtras A e B destacadas no fluxograma a uma das kestões indicadas a seguir.
(delta)" = 0? (delta)" < 0? (delta)" > 0?
A: (delta)" > 0?; B: (delta)" < 0?
![]() 19. Junte-se a um colega e, utilizando a fórmula resolutiva, mostrem quê, sêndo x1 e x2 zeros da função quadrática f(x) = ax2 + bx + c, temos quê x1 + x2 = e x1 ⋅ x2 = .
19. Junte-se a um colega e, utilizando a fórmula resolutiva, mostrem quê, sêndo x1 e x2 zeros da função quadrática f(x) = ax2 + bx + c, temos quê x1 + x2 = e x1 ⋅ x2 = .
Resposta nas Orientações para o professor.
Página cento e sessenta e seis
Gráfico de uma função quadrática
Para esboçar o gráfico da função quadrática f: ℝ → ℝ, definida por f(x) = x2, podemos atribuir alguns valores arbitrários para x, obtêr pares ordenados (x, y) e representá-los no plano cartesiano. Acompanhe.
x |
f(x) = x2 |
(x, y) |
|---|---|---|
−3 |
f(−3) = (−3)2 = 9 |
(−3, 9) |
−2 |
f(−2) = (−2)2 = 4 |
(−2, 4) |
−1 |
f(−1) = (−1)2 = 1 |
(−1, 1) |
0 |
f(0) = 02 = 0 |
(0, 0) |
1 |
f(1) = 12 = 1 |
(1, 1) |
2 |
f(2) = 22 = 4 |
(2, 4) |
3 |
f(3) = 32 = 9 |
(3, 9) |
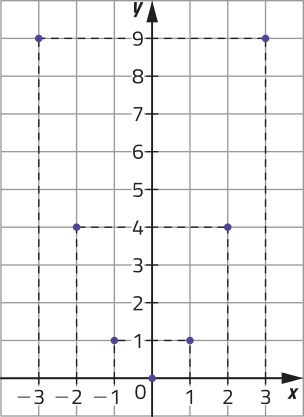
Como D(f) = ℝ, é possível obtêr, por meio da lei de formação, infinitos pares ordenados (x, y) correspondentes a pontos do gráfico de f.
Esse gráfico corresponde a uma parábola. Observe o gráfico de f, em quê foi destacado o eixo de simetria da parábola, quê a intersecta em um único ponto, denominado vértice da parábola.
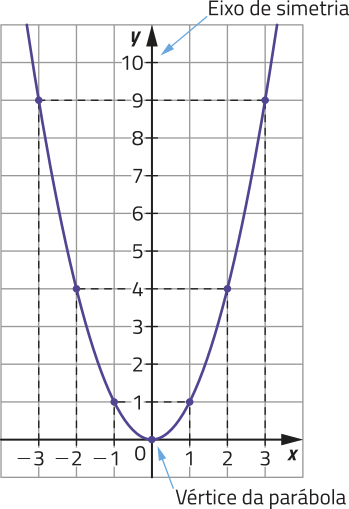
DICA
É possível demonstrar quê o gráfico de qualquer função quadrática f: ℝ → ℝ é uma parábola.
Para quaisquer dois pontos simétricos do gráfico de uma função quadrática f: ℝ → ℝ, têm-se quê esses pontos têm a mesma ordenada.
Agora, obissérve o esboço do gráfico da função g: ℝ → ℝ, definida por g (x) = x2 − 4x + 3.
x |
g(x) = x2 − 4x + 3 |
(x, y ) |
|---|---|---|
−1 |
g(−1) = (−1)2 − 4 ⋅ (−1) + 3 = 8 |
(−1, 8) |
0 |
g(0) = 02 − 4 ⋅ 0 + 3 = 3 |
(0, 3) |
1 |
g(1) = 12 − 4 ⋅ 1 + 3 = 0 |
(1, 0) |
2 |
g(2) = 22 − 4 ⋅ 2 + 3 = −1 |
(2, −1) |
3 |
g(3) = 32 − 4 ⋅ 3 + 3 = 0 |
(3, 0) |
4 |
g(4) = 42 − 4 ⋅ 4 + 3 = 3 |
(4, 3) |
5 |
g(5) = 52 − 4 ⋅ 5 + 3 = 8 |
(5, 8) |
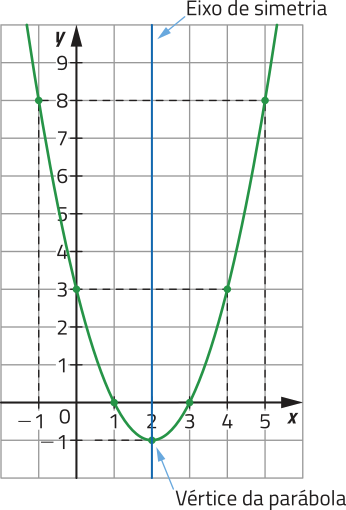
Página cento e sessenta e sete
Interseção do gráfico de uma função quadrática com os eixos cartesianos
Para esboçar o gráfico de uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, podemos determinar seus pontos de interseção com os eixos cartesianos.
Os pontos de interseção do gráfico de f com o eixo x, quando existem, são aqueles de coordenadas (x, 0). Assim, a abscissa x de cada um dêêsses pontos corresponde a um zero real da função, pois é ôbitída quando f(x) = 0.
O ponto de interseção do gráfico de f com o eixo y é aquele de coordenadas (0, y). Assim, a ordenada y dêêsse ponto corresponde a y = f(0).
Como f(0) = a ⋅ 02 + b ⋅ 0 + c ⇒ f(0) = c, então y = c.
Portanto, o gráfico de f intersecta o eixo y no ponto de coordenadas (0, c).
ATIVIDADES RESOLVIDAS
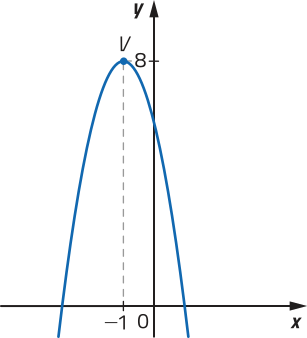
R9. Determine a lei de formação da função quadrática f: ℝ → ℝ cujo gráfico está representado na figura.
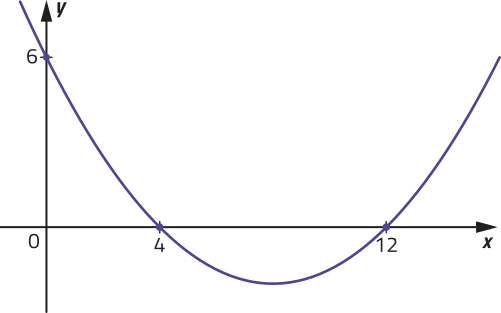
Resolução
Temos quê a função f é definida por f(x) = ax2 + bx + c.
Como o gráfico intersecta o eixo y no ponto de coordenadas (0, 6), segue quê c = 6.
Já o eixo x é intersectado pelo gráfico nos pontos de coordenadas (4, 0) e (12, 0), ou seja, 4 e 12 são os zeros de f. Assim:
• f(4) = 0 ⇒ a ⋅ 42 + b ⋅ 4 + 6 = 0 ⇒ 16a + 4b + 6 = 0
• f(12) = 0 ⇒ a ⋅ 122 + b ⋅ 12 + 6 = 0 ⇒ 144a + 12b + 6 = 0
Para obtêr os valores de a e b, resolvemos o seguinte sistema de equações:
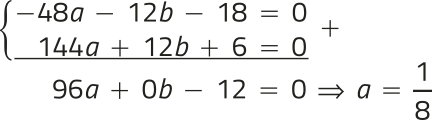
Substituindo a = na primeira equação dêêsse sistema, temos:
16 ⋅ +4b +6 = 0 ⇒ 2 + 4b + 6 = 0 ⇒ 4b = −8 ⇒ b = −2.
Logo, f(x) = − 2x + 6.
Página cento e sessenta e oito
R10. Determine as coordenadas dos pontos de interseção entre os eixos cartesianos e o gráfico da função f: ℝ → ℝ, definida por:
a) f(x) = − 1;
b) f(x) = −x2 + 4x − 4;
c) f(x) = −x2 − 2x + 3;
d) f(x) = 3x2 − 7x + 6.
Resolução
a) • Interseção com o eixo x:
f(x) = 0 ⇒ − 1 = 0 ⇒
⇒ x2 = 4 ⇒
• Interseção com o eixo y:
f(0) = − 1 = −1
Portanto, o gráfico de f intersecta o eixo x nos pontos de coordenadas (−2, 0) e (2, 0) e o eixo y no ponto de coordenadas (0, −1).
b) • Interseção com o eixo x:
f(x) = 0 ⇒ −x2 + 4x − 4 = 0
a = −1; b = 4; c = −4
(delta)" = 42 − 4 ⋅ (−1) ⋅ (−4) = 0
x = =2
• Interseção com o eixo y:
f(0) = −02 + 4 ⋅ 0 − 4 = −4
Portanto, o gráfico de f intersecta o eixo x
apenas no ponto de coordenadas (2, 0) e o eixo y no ponto de coordenadas (0, −4).
c) • Interseção com o eixo x:
f(x) = 0 ⇒ −x2 − 2x + 3 = 0
a = −1; b = −2; c = 3
(delta)" = (−2)2 − 4 ⋅ (−1) ⋅ 3 = 16
x = ⇒
⇒
• Interseção com o eixo y:
f(0) = −02 − 2 ⋅ 0 + 3 = 3
Portanto, o gráfico de f intersecta o eixo x nos pontos de coordenadas (−3, 0) e (1, 0) e o eixo y no ponto de coordenadas (0, 3).
d) • Interseção com o eixo x:
f(x) = 0 ⇒ 3x2 − 7x + 6 = 0
a = 3; b = −7; c = 6
(delta)" = (−7)2 − 4 ⋅ 3 ⋅ 6 = −23
Como (delta)" < 0, a equação f(x) = 0 não tem raiz real.
• Interseção com o eixo y:
f(0) = 3 ⋅ 02 − 7 ⋅ 0 + 6 = 6
Portanto, o gráfico de f intersecta o eixo y no ponto de coordenadas (0, 6) e não intersecta o eixo x.
R11. Analise a atividade resolvida R10 e explique em quais casos o gráfico de uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c:
a) intersecta o eixo x em dois pontos distintos;
b) intersecta o eixo x em um único ponto;
c) não intersecta o eixo x.
Resolução
Ao reconhecer padrões entre a quantidade de raízes reais distintas de uma função ou o valor do discriminante e a quantidade de vezes quê o gráfico dessa função intersecta o eixo x, é possível propor a seguinte generalização.
a) O gráfico de f intersecta o eixo x em dois pontos distintos quando ax2 + bx + c = 0 tem duas raízes reais distintas, ou seja, quando (delta)" > 0.
b) O gráfico de f intersecta o eixo x em um único ponto quando ax2 + bx + c = 0 tem duas raízes reais e iguais, ou seja, quando (delta)" = 0.
c) O gráfico de f não intersecta o eixo x quando ax2 + bx + c = 0 não tem raiz real, ou seja, quando (delta)" < 0. Nesse caso, o gráfico fica todo acima ou todo abaixo do eixo x.
Página cento e sessenta e nove
A parábola e os coeficientes de uma função quadrática
Estudaremos, agora, relações entre os coeficientes de uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, e a parábola correspondente ao seu gráfico.
Coeficiente a
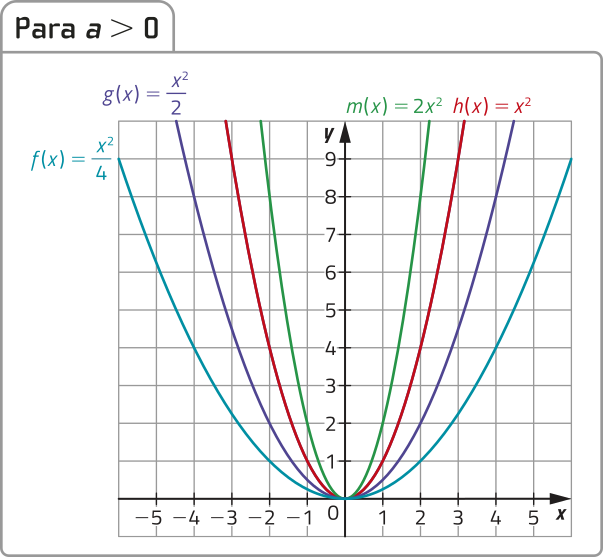
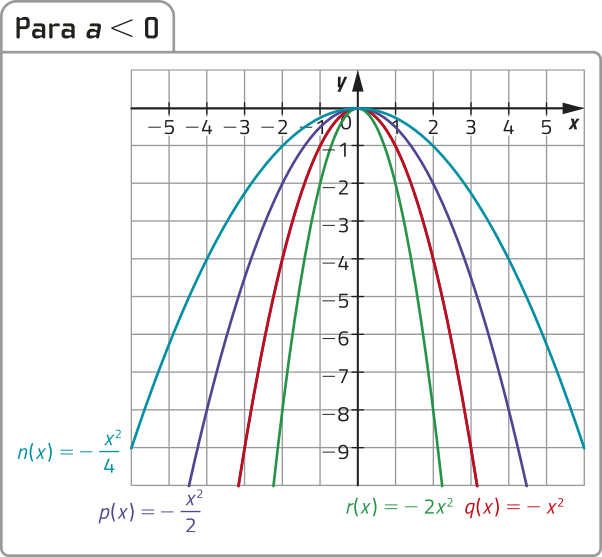
Observe a representação do gráfico de diversas funções quadráticas definidas por y = ax2 + bx + c alterando apenas o valor do coeficiente a.
PARA PENSAR
Note quê, no par de funções f(x) = e n(x) = , os valores absolutos do coeficiente a são iguais, ou seja, . Identifique, entre as funções apresentadas, outros pares de funções cujos valores absolutos do coeficiente a sêjam iguais. Depois, analise e responda: o quê você póde observar nos gráficos dêêsses pares de funções, com relação à abertura das parábolas?
Observando as parábolas de cada plano cartesiano, o quê elas têm em comum?
g e p, h e q, m e r. Resposta esperada: As parábolas têm a mesma abertura. Resposta esperada: Todas as parábolas do plano cartesiano da esquerda têm a concavidade voltada para cima, e todas as parábolas do plano cartesiano da direita têm a concavidade voltada para baixo.
Dada uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, temos quê:
• a concavidade da parábola correspondente ao gráfico de f é voltada para cima, se a > 0, e para baixo, se a < 0.
• quanto maior é o valor absoluto do coeficiente a, menor é a abertura da parábola correspondente.
Página cento e setenta
Coeficientes b e c
Observe, a seguir, os gráficos das funções quadráticas f, g e h.
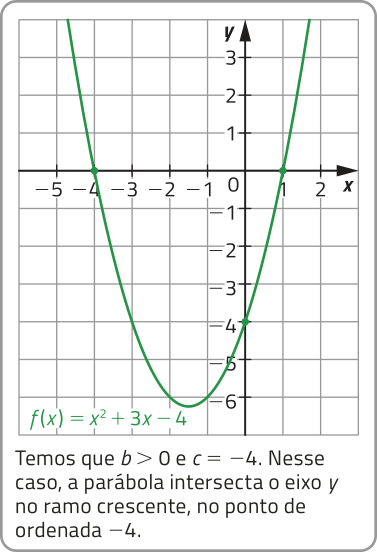
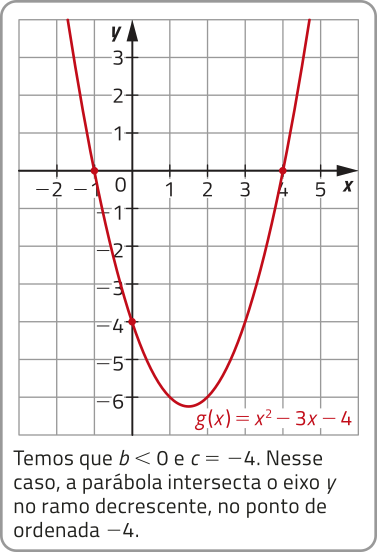
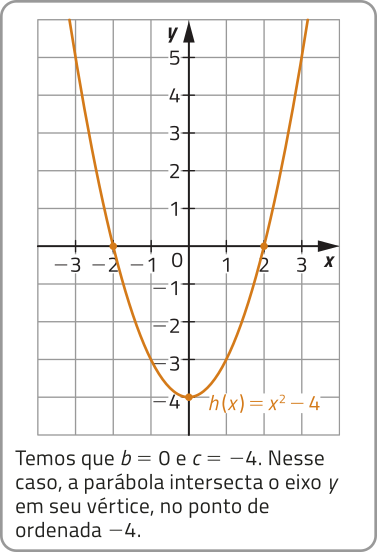
O ramo crescente e o ramo decrescente se reférem às partes do gráfico cujos pontos da função quadrática correspondem aos intervalos do domínio em quê essa função é crescente ou decrescente, respectivamente.
PARA PENSAR
No gráfico de uma função quadrática, em quê a > 0, o ramo crescente é localizado à esquerda ou à direita do vértice da parábola correspondente a esse gráfico? Explique como você pensou para responder a essa questão.
À direita. Resposta esperada: Analisando a concavidade da parábola no caso de a > 0.
A parábola correspondente ao gráfico de uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, intersecta o eixo y no ponto de ordenada c e:
• no ramo crescente, quando b > 0;
• no ramo decrescente, quando b < 0;
• em seu vértice, quando b = 0.
ATIVIDADES
20. Esboce o gráfico da função f: ℝ → ℝ, definida por:
Respostas nas Orientações para o professor.
a) f(x) = x2 − 5;
b) f(x) = −2x2 + 4x + 1;
c) f(x) = − 2x + 3;
d) f(x) = −x2 − 6x − 2.
21. Determine as coordenadas dos pontos do gráfico da função f: ℝ → ℝ, definida em cada item a seguir, quê intersectam os eixos cartesianos.
a) f(x) = 4x2 − 2x − 12
21. a) eixo x: e (2, 0); eixo y: (0, −12)
b) f(x) = −3x2 + 4x + 7
21. b) eixo x: (−1, 0) e ; eixo y: (0, 7)
c) f(x) = − 3x + 10
21. c) eixo x: (5, 0) e (10, 0); eixo y: (0, 10)
d) f(x) = −2x2 + 8x − 8
21. d) eixo x: (2, 0); eixo y: (0, −8)
Página cento e setenta e um
22. Os gráficos a seguir representam funções quadráticas f: ℝ → ℝ, definidas por f(x) = ax2 + bx + c. Em cada item, identifique se os coeficientes a, b e c são: maiores, menóres ou iguais a zero. Justifique as respostas.
Respostas nas Orientações para o professor.
a) 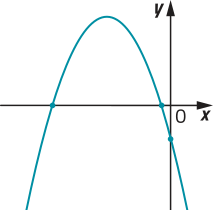
b) 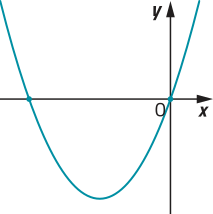
c) 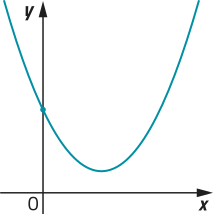
d) 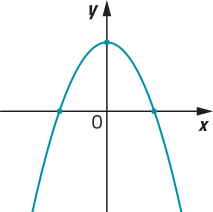
23. Determine a lei de formação da função quadrática f: ℝ → ℝ representada pelo gráfico a seguir e explique o procedimento quê você usou.
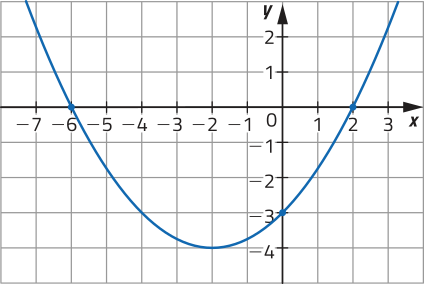
23. f(x) = + x − 3. Elaboração do estudante.
24. Observe, a seguir, o gráfico da função quadrática f(x)= + x + 4 com eixo de simetria e.
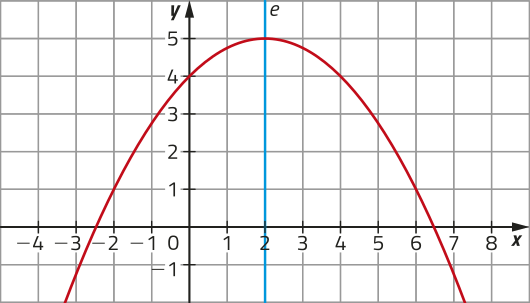
a) Com base nesse gráfico, escrêeva as coordenadas do vértice V e de dois pares de pontos simétricos em relação ao eixo de simetria e.
24. a) V(2, 5); Respostas possíveis: (0, 4) e (4, 4); (−2, 1) e (6, 1).
b) Que padrão você póde observar em relação às abscissas de quaisquer dois pontos simétricos quê você indicou no item a e a abscissa do vértice da parábola?
24. b) Resposta esperada: Quando dois pontos quaisquer do gráfico de uma função quadrática são simétricos em relação ao eixo de simetria, a média aritmética das abscissas dêêsses pontos corresponde à abscissa do vértice da parábola.
25. Para calcular a área de um polígono regular, podemos decompô-lo em triângulos congruentes e determinar a área de cada um deles.
Observe, por exemplo, o cálculo da área A de um hekzágono regular de lados medindo 2 cm.
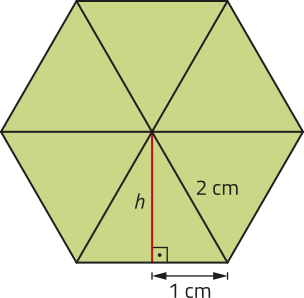
22 = 12 + h2 ⇒ h =
A = 6 ⋅ → cm2
Agora, considerando um hekzágono regular de lados medindo x centímetros, com x > 0, resôuva os itens a seguir.
a) Justifique os cálculos realizados no exemplo em quê foi determinada a área do hekzágono regular de lado medindo 2 cm.
25. a) Resposta nas Orientações para o professor.
b) escrêeva a lei de formação de uma função f para expressar o perímetro dêêsse hekzágono regular de acôr-do com a medida x.
f(x) = 6x
c) escrêeva a lei de formação de uma função g para expressar a área dêêsse hekzágono regular de acôr-do com a medida x.
g(x) = x2
d) Classifique f e g em: função afim, função linear, função modular ou função quadrática.
25. d) f: função afim e função linear; g: função quadrática
e) Quais são o perímetro e a área de um hekzágono com 4 cm de lado? E com 8 cm de lado?
25. e) Perímetro: 24 cm; área: cm2. Perímetro: 48 cm; área: cm2 .
f) Em um mesmo plano cartesiano, represente os gráficos de f e g. Você póde esboçar esses gráficos em uma malha quadriculada ou utilizando um programa de computador.
25. f) Resposta nas Orientações para o professor.
g) Leia as afirmativas verdadeiras a seguir e justifique a validade delas.
I) O perímetro de um hekzágono regular é diretamente proporcional à medida de seu lado.
II) A área de um hekzágono regular é diretamente proporcional ao quadrado da medida de seu lado.
25. g) Resposta nas Orientações para o professor.
Página cento e setenta e dois
![]() 26. A seguir, estão relacionadas as coordenadas de alguns pontos dos gráficos das funções quadráticas f, g e h.
26. A seguir, estão relacionadas as coordenadas de alguns pontos dos gráficos das funções quadráticas f, g e h.
x |
y = f(x) |
x |
y = g(x) |
x |
y = h(x) |
||
|---|---|---|---|---|---|---|---|
−2 |
A |
−2 |
−8 |
−2 |
2 |
||
−1 |
1 |
−1 |
−2 |
−1 |
C |
||
0 |
0 |
||||||
0 |
0 |
0 |
0 |
||||
1 |
|||||||
1 |
1 |
1 |
B |
||||
2 |
4 |
2 |
−8 |
2 |
2 |
Agora, com um colega, resolvam os itens a seguir.
a) Determinem os valores correspondentes às lêtras A, B e C.
A: 4; B: −2; C:
b) Utilizando um plano cartesiano para cada função, representem os gráficos de f, g e h.
26. b) Resposta nas Orientações para o professor.
c) Os coeficientes de cada função são maiores, menóres ou iguais a zero?
26. c) f: a > 0, b = 0 e c = 0; g: a < 0, b = 0 e c = 0; h: a > 0, b = 0 e c = 0
d) Escrevam a lei de formação das funções f, g e h. Em seguida, descrevam o quê elas têm em comum.
26. d) f(x) = x2; g (x) = −2x2; h(x) = . Resposta esperada: As três funções quadráticas são definidas por uma lei de formação do tipo y = ax2, com a ≠ 0, e o vértice da parábola correspondente ao gráfico de cada uma delas coincide com a origem O dos eixos cartesianos.
27. escrêeva a lei de formação de uma função quadrática f cujo gráfico corresponda a uma parábola com concavidade voltada para baixo e quê intersecta o eixo das ordenadas no seu ramo decrescente.
27. Resposta esperada: f(x) = ax2 + bx + c, com a < 0 e b < 0 e c um número real qualquer. Respostas possíveis: f(x) = −2x2 − 3x; f(x) = −x2 − x + 3.
28. Atualmente, existem diferentes robôs quê podem sêr utilizados em treinamentos de diversas modalidades esportivas. Por exemplo, robôs lançadores de bolas de tênis, quê possibilitam ao atleta treinar sózínho.

Em um experimento ao ar livre, utilizando um robô instalado em um piso plano, uma bola de tênis foi lançada do chão de maneira quê sua trajetória póde sêr descrita pela função f: [0, 8] → ℝ, definida por f(x) = −x2 + 8x, em quê y = f(x) corresponde à altura dessa bola, em métro, após x segundos do momento em quê ela foi lançada.
Acompanhe, a seguir, o gráfico dessa função, com alguns pontos destacados.
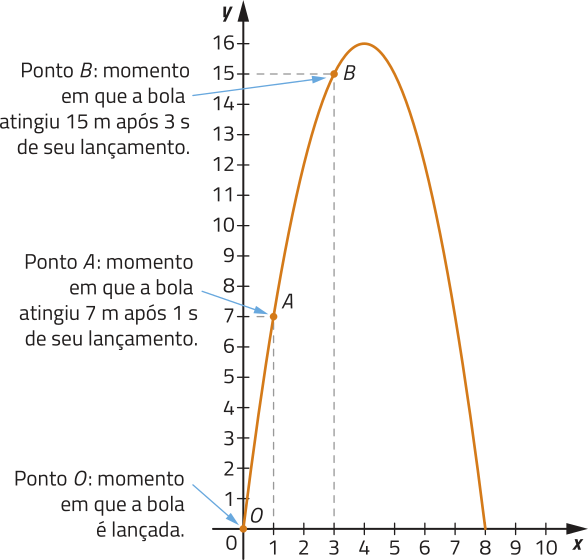
Para analisar quanto variou, em média, a altura da bola durante parte dessa trajetória, podemos calcular a taxa de variação média de f, para x variando de x1 até x2, com x1 ≠ x2, dada por .Por exemplo, a taxa de variação média de f no intervalo de tempo de 1 s até 3 s é dada por:
= 4
Portanto, podemos dizêr quê, no intervalo de tempo de 1 s até 3 s após o momento em quê a bola foi lançada, sua altura variou, em média, 4 m a cada segundo.
Agora, calcule a taxa de variação média dessa função para x variando de x1 = 0 até x2 = 3. Depois, interpréte esse resultado de acôr-do com o contexto apresentado.
28. 5; Resposta esperada: Esse resultado indica quê, no intervalo de tempo de 0 s até 3 s após o momento em quê a bola foi lançada, sua altura variou, em média, 5 m a cada segundo.
29. Determine a taxa de variação média da função f: ℝ → ℝ em cada caso a seguir.
a) f(x) = 3x2 + 2x, para x variando de −4 até 1.
−7
b) f(x) = −x2 − 8x + 5, para x variando de −3 até 4.
−9
c) f(x) = −5x2 + x − 4, para x variando de −6 até 0.
31
d) f(x) = + 3x + 1, para x variando de 2 até 10.
5
Página cento e setenta e três
30. Você sabe o quê é a distância de frenagem de um automóvel? É a distância quê ele percórre do momento em quê o motorista pisa no freio até o momento em quê o veículo para completamente. Considere quê a distância de frenagem d, em métro, de cérto automóvel em relação à velocidade v, em quilômetro por hora, póde sêr modelada de acôr-do com a função quadrática representada no gráfico a seguir.
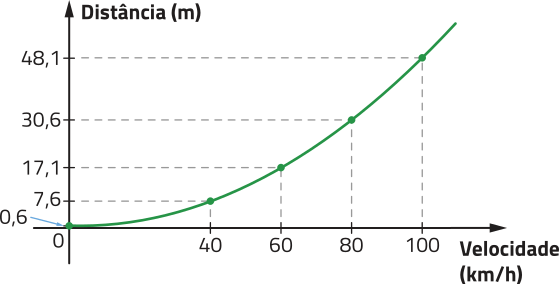
a) Com base em seus conhecimentos sobre o trânsito, responda aos itens a seguir.
• O motorista quê dirige utilizando o celular tem maior ou menor chance de se envolver em um acidente? Justifique.
• Quais são as consequências do uso do celular ao dirigir?
30. a) • Resposta esperada: Maior chance, pois o uso do celular é uma distração para o condutor. • Resposta esperada: Redução do tempo de reação (para realizar uma frenagem ou mesmo para perceber e respeitar os sinais de trânsito), dificuldade de manter corretamente o carro na pista e de manter uma distância segura do veículo da frente.
b) Explique o quê o ponto de coordenadas (40; 7,6) do gráfico indica em relação à situação apresentada.
30. b) Resposta esperada: Indica quê, ao pisar no freio dêêsse automóvel, quando ele está a uma velocidade de 40 km/h, o veículo percórre uma distância de 7,6 m antes de parar.
c) Qual é a distância de frenagem dêêsse automóvel a uma velocidade de 60 km/h?
17,1 m
d) Determine a velocidade dêêsse automóvel para quê a distância de frenagem seja igual a 48,1 m.
100 km/h
e) escrêeva a lei de formação da função quê relaciona a distância de frenagem d, em métro, percorrida por esse automóvel de acôr-do com a velocidade v, em quilômetro por hora, no momento da frenagem.
30. e) d(v) =
f) Considere quê esse automóvel esteja trafegando a uma velocidade de 50 km/h. O motorista, ao observar um obstáculo à sua frente, aciona o freio quando está a 8 m dêêsse obstáculo e se mantém em linha reta. O motorista vai conseguir evitar a colisão com o obstáculo? Justifique.
30. f) Não, pois, de acôr-do com o modelo matemático, a distância de frenagem será de 11,85 m, ou seja, maior quê a distância do automóvel até o obstáculo.
31. Observe, a seguir, as recomendações de cérto fabricante de aparelhos de ar-condicionado no quê se refere à relação entre a medida do lado de uma região quadrada e a quantidade mínima de BTUs (sigla em inglês cujo significado é “Unidade Térmica Britânica”) de um ar-condicionado. Nesse caso, está sêndo desconsiderada a existência de aparelhos elétricos e de pessoas na região.
Medida do lado (m) |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
Quantidade de BTUs |
600 |
2.400 |
5.400 |
9.600 |
15.000 |
a) Em um plano cartesiano, represente a relação indicada.
Resposta nas Orientações para o professor.
b) Divída cada número da segunda linha do qüadro por 600 e compare o resultado obtído com o número correspondente da primeira linha. Que relação é possível identificar entre os números da primeira linha e os números correspondentes da segunda linha dêêsse qüadro?
31. b) 600 ∶ 600 = 1 e 1 = 12; 2.400 ∶ 600 = 4 e 4 = 22; 5.400 ∶ 600 = 9 e 9 = 32; 9.600 ∶ 600 = 16 e 16 = 42; 15.000 ∶ 600 = 25 e 25 = 52. Resposta esperada: Cada número da segunda linha corresponde ao quadrado do respectivo número da primeira linha, multiplicado por 600.
c) Com base na sua resposta ao item b, expresse a quantidade de BTUs de acôr-do com a medida (éli)" do lado de uma região quadrada, em métro.
600(éli)"2
d) escrêeva a lei de formação de uma função quê relaciona a quantidade q de BTUs do ar-condicionado à medida do lado (éli)" de uma região quadrada, em métro, com (éli)" > 0. Essa função póde sêr classificada como função quadrática?
q((éli)") = 600(éli)"2; sim
e) Calcule quantos BTUs, no mínimo, esse fabricante recomendaria para uma região quadrada cuja medida do lado é igual a:
• 2,5 m;
3.750 BTUs
• 6 m;
21.600 BTUs
• 10 m.
60.000 BTUs
f) Para utilizar um ar-condicionado de 48.600 BTUs, é necessário quê a região quadrada tenha quantos metros de lado, no mássimo?
9 m
Página cento e setenta e quatro
Vértice da parábola
Estudamos quê o eixo de simetria de uma parábola a intersecta em um único ponto, denominado vértice da parábola. Agora, vamos estudar como obtêr as coordenadas dêêsse ponto.
Considere, por exemplo, a função quadrática f: ℝ → ℝ, definida por f(x) = x2 − 6x + 5, cujo gráfico está representado a seguir. Note quê os pontos A(0, 5) e A’(6, 5) são pontos da parábola quê têm ordenadas iguais e, portanto, são simétricos em relação ao eixo de simetria da parábola.
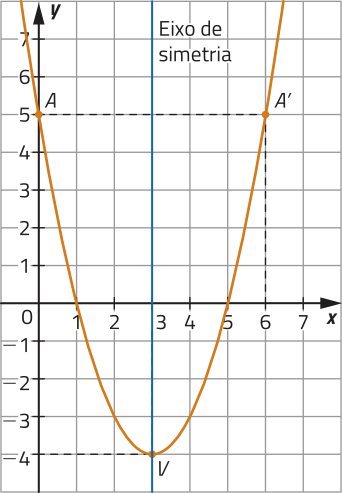
Ao calcularmos a média aritmética das abscissas dos pontos A e A’, obtemos a abscissa do vértice da parábola. Acompanhe.
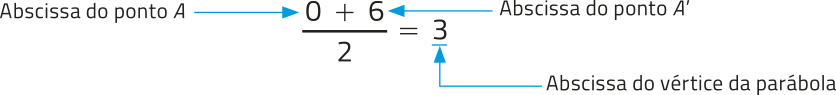
Para obtêr a ordenada do vértice da parábola, calculamos f(3).
f(3) = 32 − 6 ⋅ 3 + 5 = 9 − 18 + 5 = −4
Portanto, as coordenadas do vértice da parábola são V (3, −4).
pôdêmos obtêr as coordenadas do vértice V (xv, yv) de uma parábola a partir dos coeficientes da função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c. Para isso, consideramos dois pontos distintos da parábola, simétricos em relação ao eixo de simetria, de coordenadas (xv − p, yp) e (xv + p, yp), p > 0, conforme representado no gráfico a seguir.
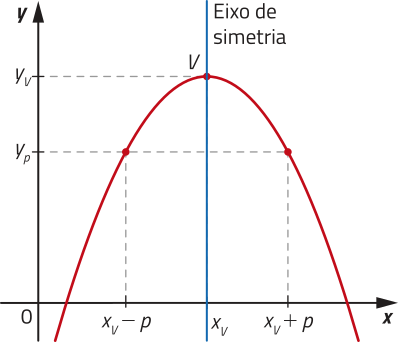
Página cento e setenta e cinco
Como f(xv − p) = yp e f(xv + p) = yp, temos:
f(xv − p) = f(xv + p) ⇒ a (xv − p)2 + b (xv − p) + c = a (xv + p)2 + b (xv + p) + c ⇒
⇒ a (x2v − 2xv p + p2) + b (xv − p) + c = a (x2v + 2xv p + p2) + b (xv + p) + c ⇒

⇒ −2axv p − bp = 2axv p + bp ⇒ −4axv p = 2bp ⇒ xv =
Para obtêr yv = f(xv):
yv = + c = a ⋅ + c =
=
Dada uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, e considerando o discriminante (delta)" = b2 − 4ac, as coordenadas do vértice da parábola correspondente ao gráfico de f são dadas por:
V
ATIVIDADE RESOLVIDA
R12. Calcule e represente graficamente as coordenadas do vértice V da parábola correspondente ao gráfico da função quadrática f: ℝ → ℝ, definida por:
a) f(x) = x2 − 3x − 10;
b) f(x) = −2x2 − 4x + 6.
Resolução
a) xv =
yv =
Portanto, V.
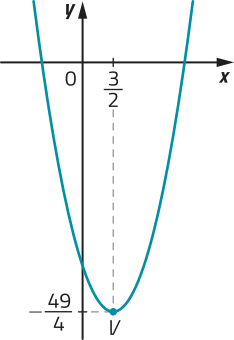
b) xv = = −1
yv = = 8
Portanto, V (−1, 8).
PARA PENSAR
Defina uma função quadrática cujo gráfico tenha vértice no ponto de coordenadas (1, 2). Depois, defina outra função quadrática cujo gráfico é uma parábola quê tem vértice nesse mesmo ponto. Agora, responda:
Respostas pessoais.
• No quê se diferem essas duas funções?
• Quantas funções quadráticas cujos gráficos tênham vértices todos no ponto de coordenadas (1, 2) você acredita quê existem?
Página cento e setenta e seis
Conjunto imagem de uma função quadrática
A fim de estudar o conjunto imagem de uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, podemos, inicialmente, analisar para quais valores de x ∈ D(f) essa função é crescente e para quais valores ela é decrescente. Assim, consideremos dois casos: a > 0 e a < 0.
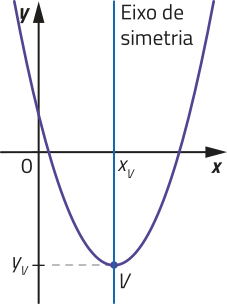
a > 0
Para a > 0, a concavidade da parábola é voltada para cima. Nesse caso, é possível verificar quê:
• f é decrescente para x < xv e crescente para x > xv;
• para qualquer x ∈ D(f), temos y = f(x) ≥ yv.
Portanto, o conjunto imagem de f é dado por: Im(f) = {y ∈ ℝ | y ≥ yv}.
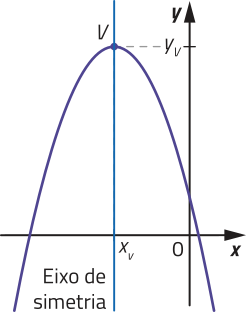
a < 0
Para a < 0, a concavidade da parábola é voltada para baixo. Nesse caso, é possível verificar quê:
• f é crescente para x < xv e decrescente para x > xv;
• para qualquer x ∈ D(f), temos y = f(x) ≤ yv.
Portanto, o conjunto imagem de f é dado por: Im(f) = {y ∈ ℝ | y ≤ yv}.
ATIVIDADES RESOLVIDAS
R13. Em cada item, determine para quais valores de x ∈ D(f) a função quadrática f: ℝ → ℝ é crescente e para quais é decrescente.
a) f(x) = 2x2 − 8x + 10
b) f(x) = − 3x − 4
Resolução
a) Calculando xv, temos:
xv = =2
Como a > 0, então f é decrescente para x < 2 e crescente para x > 2.
b) Calculando xv, temos:
xv = = −3
Como a < 0, então f é crescente para x < −3 e decrescente para x > −3.
R14. Determine o conjunto imagem da função quadrática f: ℝ → ℝ, definida por:
a) f(x) = − 2x + 2;
b) f(x) = −x2 + 6x − 5.
Resolução
a) Calculando yv, temos:
yv = = −1
Como a > 0, então Im(f) = {y ∈ ℝ | y ≥ −1}.
b) Calculando yv, temos:
yv = = 4
Como a < 0, então Im(f) = {y ∈ ℝ | y ≤ 4}.
Página cento e setenta e sete
ATIVIDADES
32. Calcule as coordenadas do vértice da parábola correspondente ao gráfico da função quadrática f: ℝ → ℝ, definida por:
a) f(x) = − 4x + 2;
V(20, −38)
b) f(x) = −3x2 + 6x + 8;
V(1, 11)
c) f(x) = −0,5x2 − 2x − 10;
V(−2, −8)
d) f(x) = 4x2 + 8x + 6.
V(−1, 2)
33. escrêeva o conjunto imagem correspondente a cada função f: ℝ → ℝ descrita a seguir.
a) f(x) = − 4x + 1
Im(f) = {y ∈ ℝ | y ≥ −5}
b) f(x) = −2x2 + 5x − 7
lm(f) =
c) f(x) = −x2 − 2x + 9
Im(f) = {y ∈ ℝ | y ≤ 10}
d) f(x) = + 3x + 7
lm(f) =
34. Determine os intervalos de crescimento e de decrescimento de cada função quadrática f: ℝ → ℝ representada a seguir.
a) 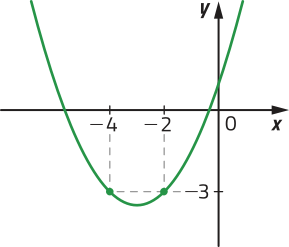
f é decrescente para x < −3 e crescente para x > −3.
b) 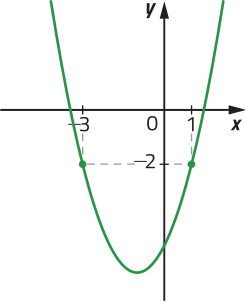
f é decrescente para x < −1 e crescente para x > −1.
c) 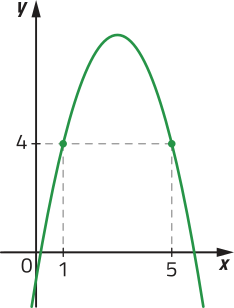
f é crescente para x < 3 e decrescente para x > 3.
35. Observe o gráfico a seguir de uma função quadrática f: ℝ → ℝ.
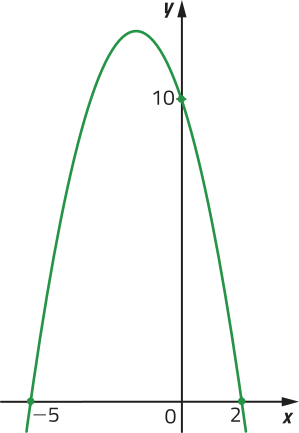
a) Determine para quais valores de x ∈ D(f) a função f é:
• crescente;
x < −1,5
• decrescente.
x > −1,5
b) escrêeva a lei de formação da função f e explique os procedimentos quê você realizou para encontrá-la.
f(x) = −x2 − 3x + 10. Resposta pessoal.
c) Quais são as coordenadas do vértice da parábola?
(−1,5; 12,25)
d) Qual é o conjunto imagem de f?
Im(f) = {y ∈ ℝ | y ≤ 12,25}
36. (Enem/MEC) A Igreja de São Francisco de Assis, obra arquitetônica modernista de Óscar Niemáiêr, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólicas. A seta na Figura 1 ilustra uma das abóbadas na entrada principal da capela. A Figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos.
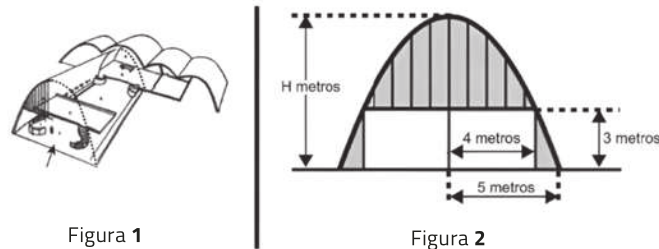
Qual a medida da altura H, em métro, indicada na Figura 2?
a)
b)
c)
d)
e)
alternativa d
Página cento e setenta e oito
Valor mássimo ou valor mínimo da função quadrática
Leia as situações descritas a seguir.




Situações como essas são exemplos em quê profissionais precisaram inovar para obtêr resultados mais efetivos, tendo de usar a criatividade e pensar em maneiras de otimizar determinado processo ou sêrviço. Algumas dessas situações podem ser descritas por funções. Nesses casos, é possível realizar o estudo do valor mássimo ou do valor mínimo da função, no domínio ou em um intervalo específico.
Dada uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, denominamos a ordenada do vértice yv:
• valor mássimo de f, quando a < 0;
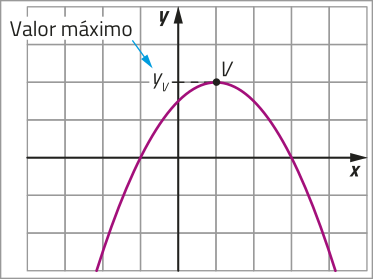
• valor mínimo de f, quando a > 0.
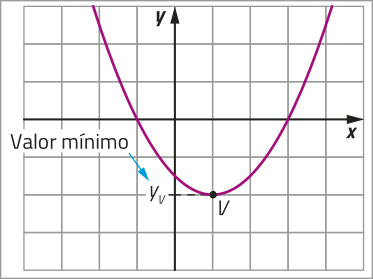
Agora, considere a situação descrita a seguir.
Para obtêr mais informações sobre o dêsempênho de um atleta de lançamento de disco, os treinos passaram a sêr acompanhados por alguns técnicos, quê estudaram a trajetória do disco em cada lançamento. Em cérto lançamento, por exemplo, a altura do disco y = h (x), em métro, de acôr-do com a distância horizontal x percorrida, em métro, foi modelada computacionalmente pela função quadrática h (x) = −0,02x2 + x + 1,5.

DICA
Note quê, na lei de formação da função h, temos a = −0,02 < 0, ou seja, h tem valor mássimo.
Página cento e setenta e nove
Para determinar a altura mássima atingida pelo disco nesse lançamento, podemos calcular o valor mássimo dessa função:
yv = = 14
Portanto, de acôr-do com esse modelo matemático, a altura mássima atingida pelo disco nesse lançamento foi de 14 m.
NO MUNDO DO TRABALHO
Inovação e criatividade
Em geral, sêr criativo e inovador são fatores essenciais para resolver problemas de maneira eficiente. Um profissional com essas capacidades analisa as próprias práticas, identifica oportunidades e propõe e desen vólve novas soluções. Atualmente, existem algumas estratégias e abordagens quê têm essas capacidades como um de seus pilares e quê buscam contribuir para a efetividade e a rentabilidade de certa ação, por exemplo, o disáini thinking, uma metodologia cujo objetivo é entender e atender às demandas de pessoas.
Acesse o vídeo indicado a seguir, quê contém informações sobre disáini thinking.
• PROCESSO criativo: disáini thinking. [S. l.: s. n.], 2015. 1 vídeo (7 min). Publicado pelo canal Sebrae Minas. Disponível em: https://livro.pw/diukv. Acesso em: 18 jul. 2024.
ATIVIDADES RESOLVIDAS
R15. (Enem/MEC) Viveiros de lagostas são construídos, por cooperativas locais de pescadores, em formato de prismas reto-retangulares, fixados ao solo e com telas flexíveis de mesma altura, capazes de suportar a corrosão marinha. Para cada viveiro a sêr construído, a cooperativa utiliza integralmente 100 metros lineares dessa tela, quê é usada apenas nas laterais.
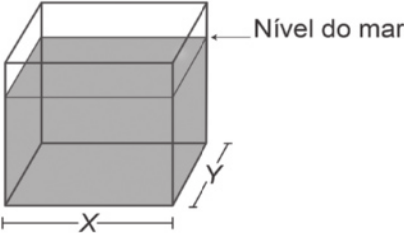
Quais devem sêr os valores de X e de Y, em métro, para quê a área da base do viveiro seja mássima?
a) 1 e 49
b) 1 e 99
c) 10 e 10
d) 25 e 25
e) 50 e 50
Resolução
Para resolver essa atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
De acôr-do com o enunciado, os viveiros têm formato de prisma cuja base corresponde a um retângulo de lados medindo X e Y e nas laterais de cada viveiro são utilizados 100 m lineares de tela. Temos de determinar os valores de X e Y para quê a área da base do viveiro seja a mássima possível.
2ª ELABORAR UM PLANO
Como nas laterais do viveiro são utilizados 100 m lineares de tela e o perímetro de sua base é dado por 2X + 2Y, temos quê 2X + 2Y = 100. Além díssu, podemos expressar a área da base dêêsse viveiro por X ⋅ Y. Com essas informações, podemos determinar uma função quadrática S quê descreve a área da base de acôr-do com a medida X. Em seguida, podemos analisar o valor mássimo dessa função e, assim, obtêr os valores de X e Y quê tornam mássima a área da base do viveiro.
Página cento e oitenta
3ª EXECUTAR O PLANO
Isolando Y na equação 2X + 2Y = 100, temos:
2X + 2Y = 100 ⇒ X + Y = 50 ⇒ Y = 50 − X
Escrevendo a lei de formação da função S, temos:
S(X) = X ⋅ ⇒ S(X) = −X2 + 50X
Como na lei de formação da função S o coeficiente a = −1 < 0, temos quê a abscissa do vértice corresponde ao valor de X com o qual a área da base do viveiro é mássima. Assim, segue quê:
X = = 25, ou seja, 25 m.
Substituindo X = 25 em Y = 50 − X, obtemos o valor de Y com o qual a área da base do viveiro é mássima.
Y = 50 − X ⇒ Y = 50 − 25 ⇒ Y = 25, ou seja, 25 m.
4ª VERIFICAR OS RESULTADOS
Temos quê a ordenada do vértice da função S corresponde à área mássima da base do viveiro, quê é dada por:
= 625, ou seja, 625 m2.
Calculando a área da base do viveiro de acôr-do com a expressão X ⋅ Y e considerando X = 25 e Y = 25, temos:
X ⋅ Y = 25 ⋅ 25 = 625, ou seja, 625 m2.
Portanto, a alternativa d é a correta, pois a área, em métro, da base do viveiro é mássima para X = 25 e Y = 25.
R16. Certa transportadora, para determinar o preêço do frete de um caminhão com 30 t de capacidade, na realização do trajeto entre um posto de abastecimento e um porto, calcula para cada tonelada de carga transportada R$ 120,00 mais R$ 8,00 por tonelada ociosa da capacidade do caminhão.
Qual é o maior valor quê a transportadora póde receber por um frete seguindo esses critérios?
Resolução
Para resolver esta atividade, podemos fazer a decomposição dela em kestões menóres, como estas a seguir, a fim de auxiliar a compreensão e a resolução.
1ª) Quantos reais essa transportadora cobra para transportar uma carga de 25 t?
2ª) Que lei de formação de uma função quadrática dada por p(x) = ax2 + bx + c determina o valor cobrado para sêr transportada uma carga de x toneladas?
3ª) Qual é o valor mássimo da função cuja lei de formação foi determinada na questão anterior?
Agora, podemos resolver cada questão e utilizar a resposta na resolução da questão seguinte. Acompanhe.
1ª) Quando são transportadas 25 t de carga, temos quê a capacidade ociosa do caminhão é de 5 t (30 − 25 = 5). Assim, segue quê:
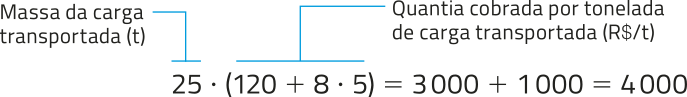
Página cento e oitenta e um
Assim, a transportadora cobra R$ 4.000,00 para transportar uma carga de 25 t.
2ª) Dos dados apresentados na atividade, temos quê:
p(x) = x ⋅ [120 + 8 ⋅ (30 − x)] ⇒ p(x) = −8x2 + 360x
3ª) Considerando a função ôbitída na 2ª questão, temos:
yV = = 4.050
Portanto, o valor mássimo da função p, ou seja, o maior valor quê a transportadora póde receber é R$ 4.050,00.
PARA PENSAR
Na situação apresentada, quantas toneladas da capacidade do caminhão devem estar ociosas para quê o valor do frete seja o maior possível?
22,5 t
ATIVIDADES
37. Dadas as funções f: ℝ → ℝ, definidas a seguir, identifique aquelas quê apresentam valor mássimo e as quê apresentam valor mínimo. Em seguida, determine o valor mássimo ou o valor mínimo de cada função.
a) f(x) = −2x2 + 3x − 8
valor mássimo; −6,875
b) f(x) = 7x2 − 2x
valor mínimo; aproximadamente −0,14
c) f(x) = 0,1x2
valor mínimo; 0
d) f(x) = −9x2 − 18x + 27
valor mássimo; 36
38. (IFBA) Jorge planta tomates em uma área de sua fazenda, e rêzouvêo diminuir a quantidade Q (em mil litros) de agrotóxicos em suas plantações, usando a lei Q (t) = 7 + t2 − 5t, onde t representa o tempo, em meses, contado a partir de t = 0. Deste modo, é correto afirmar quê a quantidade mínima de agrotóxicos usada foi atingida em:
a) 15 dias.
b) 1 mês e 15 dias.
c) 2 meses e 10 dias.
d) 2 meses e 15 dias.
e) 3 meses e 12 dias.
alternativa d
39. A comissão técnica de uma equipe de vôlei está analisando os toques realizados entre os jogadores de uma mesma equipe, em uma partida. A altura h, em métro, atingida pela bola em cérto toque, por exemplo, foi modelada pela função h(t) = −0,8t2 + 2t + 1,9, em quê 0 ≤ t ≤ 2 corresponde ao tempo, em segundo, entre o passe e a finalização da jogada.
a) De quê altura a bola parte nesse toque? E a quê altura ela termina sua trajetória?
39. a) 1,9 m; 2,7 m
b) Qual é a altura mássima, em métro, atingida pela bola nesse toque? Em quê instante isso ocorreu?
3,15 m; 1,25 s
c) Determine a taxa de variação média da função h para t variando de 0 até 2. O quê esse resultado indica?
39. c) 0,4. Resposta esperada: Indica quê, em média, a altura da bola variou 0,4 m a cada segundo nesse toque.
40. Em cérto município, a Secretaria de Educação realizou uma campanha incentivando as escolas a utilizar hortaliças plantadas na própria escola para o preparo da merenda dos estudantes. Para aderir a essa campanha, uma escola separou 112 m lineares de alambrado para cercar uma região retangular para sêr utilizada como horta. Quais devem sêr as medidas das dimensões dessa horta para quê ela tenha a maior área possível?
28 m de comprimento e 28 m de largura
41. A posição S de uma partícula, em métro, em função do tempo t, em segundo, póde sêr representada pela função cuja lei de formação é dada por S(t) = 1,2t2 − 6t + 8, com t ≥ 0.
Em quê posição o deslocamento dessa partícula muda de sentido? Qual é o tempo, em segundo, em quê isso ocorre?
0,5 m; 2,5 s
Página cento e oitenta e dois
42. Lucas tem 38 anos e pratíca corrida. Para isso, ele faz uso de diferentes produtos e serviços relacionados à prática dêêsse esporte, como academia, aplicativos de celular, acompanhamento com nutricionista e, também, com um treinador, quê elaborou um plano de treinamento para ele. Nesse plano, sua freqüência cardíaca mássima (FCM) foi calculada em 180 batimentos cardíacos por minuto (BPM), e foram estabelecidos quatro níveis de treinamento, cada um indicando um limite mássimo de BPM, conforme segue.
Nível |
Limite mássimo de BPM |
Descrição da corrida |
|---|---|---|
1 |
60% da FCM |
Ritmo fácil, respiração tranqüila. Início do treino aeróbico. |
2 |
70% da FCM |
Ritmo confortável com respiração mais profunda. Treino aeróbico básico. |
3 |
80% da FCM |
Ritmo moderado com maior esfôrço respiratório. Treino aeróbico ideal. |
4 |
90% da FCM |
Ritmo rápido com esfôrço respiratório intenso. Treino aeróbico intenso. |
Em um dos treinos, realizado em nível 2 e com duração de 38 min, o treinador modelou o número de batimentos cardíacos por minuto de Lucas pela função descrita a seguir, em quê t corresponde ao tempo de treino, em minuto.
f(t) = −0,32t2 + 12,8t + 70
Com base nas informações apresentadas, resôuva as kestões a seguir.
a) Quantos eram os batimentos cardíacos por minuto no início do treino? E com 5 min de treino?
70 BPM; 126 BPM
b) Qual foi o número mássimo de batimentos cardíacos por minuto nesse treino? Isso ocorreu quantos minutos após o início do treino?
198 BPM; 20 min
c) De acôr-do com o plano elaborado, em quê intervalo de tempo do treino o número de batimentos cardíacos por minuto esteve acima do limite mássimo para esse nível?
entre 5 min e 35 min do treino

43. (Enem/MEC) Um estudante está pesquisando o desenvolvimento de cérto tipo de bactéria. Para essa pesquisa, ele utiliza uma estufa para armazenar as bactérias. A tempera-túra no interior dessa estufa, em graus célcius, é dada pela expressão T (h) = −h2 + 22h − 85, em quê h representa as horas do dia. Sabe-se quê o número de bactérias é o maior possível quando a estufa atinge sua tempera-túra mássima e, nesse momento, ele deve retirá-las da estufa. A tabéla associa intervalos de tempera-túra em graus célcius, com as classificações: muito baixa, baixa, média, alta e muito alta.
Intervalos de tempera-túra (°C) |
Classificação |
|---|---|
T < 0 |
Muito baixa |
0 ≤ T ≤ 17 |
Baixa |
17 < T < 30 |
Média |
30 ≤ T ≤ 43 |
Alta |
T > 43 |
Muito alta |
Quando o estudante obtém o maior número possível de bactérias, a tempera-túra no interior da estufa está classificada como:
a) muito baixa.
b) baixa.
c) média.
d) alta.
e) muito alta.
alternativa d
Página cento e oitenta e três
44. A comissão de formatura dos estudantes do 3º ano do Ensino Médio está fazendo alguns orçamentos para a realização de uma festa para 480 convidados. Por exemplo, para a locação do salão de festas, eles receberam o seguinte orçamento:
Cada convidado presente na festa deve pagar R$ 8,00 acrescidos de R$ 0,10 por convidado ausente.
a) Quantos reais cada convidado presente na festa deve pagar, caso compareçam à festa apenas 200 convidados? Nesse caso, quanto custará ao todo a locação dêêsse salão de festas?
R$ 36,00; R$ 7.200,00
b) Para quê se gaste menos com a locação dêêsse salão, é mais vantajoso quê compareçam à festa 250 convidados ou 400 convidados? Justifique.
44. b) É mais vantajoso quê compareçam 400 convidados, pois o gasto com a locação será de R$ 6.400,00, uma vez quê, no caso de comparecerem 250 convidados, o gasto será de R$ 7.750,00.
c) Qual é o maior valor possível quê se póde pagar pela locação dêêsse salão? Nesse caso, quantos são os convidados quê comparecerão à festa?
R$ 7.840,00; 280 convidados
45. O gráfico a seguir corresponde a uma função quadrática g quê expressa a altura, em métro, de um projétil de acôr-do com o tempo x, em segundo, decorrido após o seu lançamento.
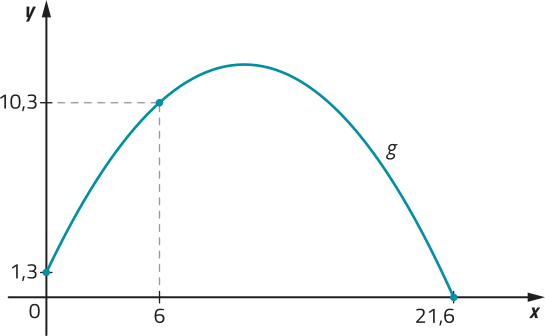
a) A quê altura esse projétil foi lançado?
1,3 m
b) O projétil tocou o solo quanto tempo após o seu lançamento?
21,6 s
![]() c) escrêeva a lei de formação da função g. Qual é o domínio dessa função? Se necessário, utilize uma calculadora.
c) escrêeva a lei de formação da função g. Qual é o domínio dessa função? Se necessário, utilize uma calculadora.
45. c) g(x) = −0,1x2 + 2,1x + 1,3; D(g) = {x ∈ ℝ | 0 ≤ x ≤ 21,6}
d) Qual é a altura mássima atingida pelo projétil nesse lançamento?
12,325 m
e) Determine o conjunto imagem da função g.
Im(g) = [0; 12,325]
![]() 46. escrêeva dois problemas quê envolvam o cálculo do valor mássimo ou do valor mínimo de uma função. Depois, troque os problemas com um colega para quê um resôuva os do outro. Ao final, confiram juntos as resoluções.
46. escrêeva dois problemas quê envolvam o cálculo do valor mássimo ou do valor mínimo de uma função. Depois, troque os problemas com um colega para quê um resôuva os do outro. Ao final, confiram juntos as resoluções.
46. Elaboração do estudante.
47. O gráfico a seguir representa uma função f definida por mais de uma sentença. Para os valores de x do domínio, tais quê x < 1, a função é quadrática; para x ≥ 1, a função é afim.
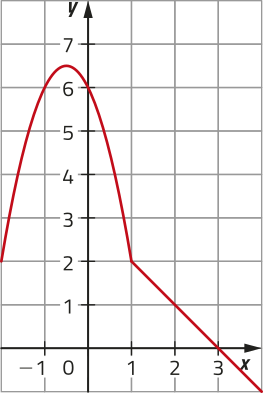
a) escrêeva a lei de formação da função f.
47. a) f(x) =
b) Qual é o valor mássimo dessa função?
6,5
![]() 48. Em uma marcenaria, uma peça de madeira tem o formato de triângulo retângulo, com lados medindo 1,5 m, 2 m e 2,5 m. O marceneiro quer utilizar essa peça para obtêr um painel retangular com o mínimo de desperdício de madeira, realizando apenas dois cortes paralelos às margens perpendiculares dessa peça.
48. Em uma marcenaria, uma peça de madeira tem o formato de triângulo retângulo, com lados medindo 1,5 m, 2 m e 2,5 m. O marceneiro quer utilizar essa peça para obtêr um painel retangular com o mínimo de desperdício de madeira, realizando apenas dois cortes paralelos às margens perpendiculares dessa peça.
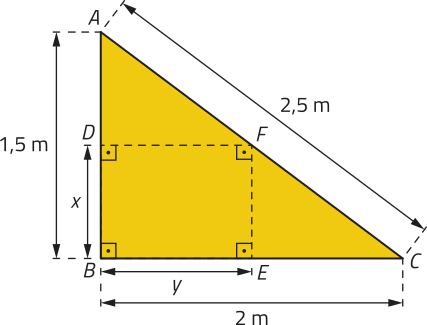
Em dupla, escrevam um texto explicando as posições em quê o marceneiro deve realizar os dois cortes nessa peça de madeira. Descrevam também como vocês pensaram para chegar a essa conclusão.
Resposta esperada: Um kórti deve sêr realizado paralelo e a 1 m da margem correspondente ao lado , e o outro, paralelo e a 0,75 m da margem correspondente ao lado . Resposta pessoal.
Página cento e oitenta e quatro
VOCÊ CONECTADO
Determinando as coordenadas do vértice de uma função quadrática
Leia o problema a seguir.
(Ifal) Em uma partida de futeból, um dos jogadores lança a bola e sua trajetória passa a obedecer à função h(t) = 8t − 2t2, onde h é a altura da bola em relação ao solo medida em metros e t é o intervalo de tempo, em segundos, decorrido desde o instante em quê o jogador chuta a bola. Nessas condições, podemos dizêr quê a altura mássima atingida pela bola é
a) 2 m.
b) 4 m.
c) 6 m.
d) 8 m.
e) 10 m.
PARA PENSAR
Com um colega, resolvam o problema anterior. Depois, elenquem os conteúdos estudados quê foram utilizados na resolução.
alternativa d. Resposta esperada: função quadrática, vértice da parábola, mássimo da função quadrática.
Note quê esse problema envolve uma função quadrática e as coordenadas de algum de seus pontos. Para resolvê-lo, é necessário obtêr o valor mássimo da função apresentada. Além da resolução manual, podemos utilizar o software de geometria dinâmica GeoGebra, disponível para acesso ôn láini e dáum-lôude em: https://livro.pw/qoubj (acesso em: 18 jul. 2024).
Observe como proceder.
A Para construir o gráfico da função h, clicamos em Entrada, digitamos h(t) = 8t − 2t^2 e pressionamos a tecla Enter. Em seguida, vamos obtêr dois pontos simétricos no gráfico de h, em relação ao eixo de simetria da parábola. Para isso, com a opção ![]() (Reta paralela) selecionada, clicamos no eixo x e em um ponto A qualquer da Janela de visualização, de maneira quê a reta f ôbitída, paralela ao eixo x, kórti o gráfico de h em dois pontos distintos. Por fim, com a opção
(Reta paralela) selecionada, clicamos no eixo x e em um ponto A qualquer da Janela de visualização, de maneira quê a reta f ôbitída, paralela ao eixo x, kórti o gráfico de h em dois pontos distintos. Por fim, com a opção ![]() (Interseção de dois objetos) selecionada, clicamos no gráfico de h e na reta f, obtendo os pontos simétricos B e C da parábola.
(Interseção de dois objetos) selecionada, clicamos no gráfico de h e na reta f, obtendo os pontos simétricos B e C da parábola.
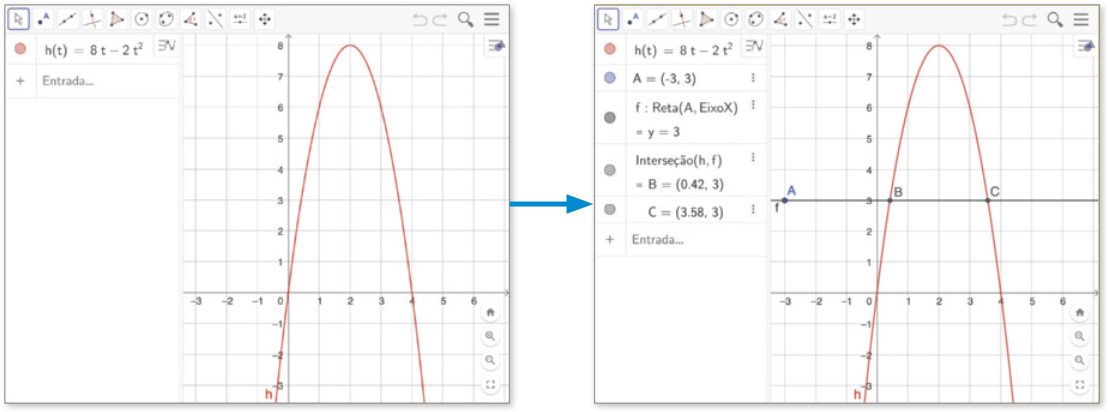
Página cento e oitenta e cinco
B Agora, vamos construir a reta g e o ponto E, correspondentes ao eixo de simetria e ao vértice da parábola, respectivamente. Para isso, com a opção ![]() (Ponto médio ou centro) selecionada, clicamos nos pontos B e C, obtendo D, ponto médio de . Em seguida, com a opção
(Ponto médio ou centro) selecionada, clicamos nos pontos B e C, obtendo D, ponto médio de . Em seguida, com a opção ![]() (Reta perpendicular) selecionada, clicamos na reta f e no ponto D, obtendo a reta g. Por fim, selecionamos a opção
(Reta perpendicular) selecionada, clicamos na reta f e no ponto D, obtendo a reta g. Por fim, selecionamos a opção ![]() (Interseção de dois objetos) e clicamos sobre a reta g e o gráfico de h, determinando o ponto E, cujas coordenadas podem sêr observadas na Janela de Álgebra.
(Interseção de dois objetos) e clicamos sobre a reta g e o gráfico de h, determinando o ponto E, cujas coordenadas podem sêr observadas na Janela de Álgebra.
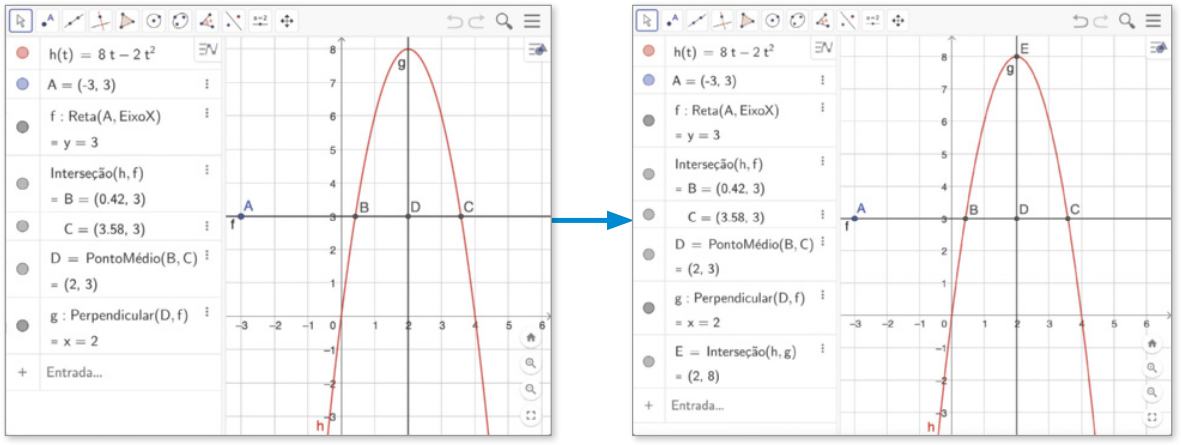
MÃOS À OBRA
1. Observando o exemplo apresentado e sem realizar cálculos, responda.
a) Quais são as coordenadas do vértice dessa parábola? Qual é a alternativa correta do problema apresentado?
E(2, 8); alternativa d
b) Utilizando as opções do GeoGebra, explique como é possível determinar geometricamente os zeros da função h.
1. b) Resposta esperada: Selecionamos a opção ![]() e clicamos sobre o eixo x e o gráfico de h, determinando os pontos em quê o gráfico intersecta o eixo x, cujas abscissas quê podem sêr observadas na Janela de Álgebra correspondem aos zeros da função h.
e clicamos sobre o eixo x e o gráfico de h, determinando os pontos em quê o gráfico intersecta o eixo x, cujas abscissas quê podem sêr observadas na Janela de Álgebra correspondem aos zeros da função h.
2. Uma empresa de materiais eletrônicos produz cérto produto com lucro quê póde sêr modelado por uma função L, definida por L(x) = −2x2 + 400x − 3.000, com o lucro L dado em reais e sêndo x a quantidade de unidades produzidas e vendidas. Utilizando o GeoGebra, determine a quantidade de unidades quê devem sêr produzidas e vendidas para quê o lucro seja mássimo e o valor dêêsse lucro mássimo, em reais.
2. 100 unidades; R$ 17.000,00
3. Utilizando o GeoGebra, resôuva geometricamente o problema apresentado a seguir.
(Cefet-MG) Meu avô quer construir, ao lado da mangueira de seu sítio, um lago para criar peixes. A figura a seguir mostra o projeto do engenheiro ambiental no qual a lagoa, vista por um kórti horizontal do terreno, é representada por uma parábola, com raízes P1 e P2 distantes 8 metros. O projeto inicial previa a parábola g (x) = x2 − 8x. Para conter gastos, essa parábola foi substituída pela parábola f(x) = − 2x.
Com essa mudança, a maior profundidade da lagoa, em metros, diminuiu
a) 4.
b) 8.
c) 12.
d) 16.
alternativa c
DICA
No enunciado desta questão, P1 e P2 correspondem aos zeros da função quadrática f.
Página cento e oitenta e seis
Estudando relações entre grandezas por meio de modelos correspondentes a funções quadráticas
pôdêmos utilizar a planilha eletrônica LibreOffice Calc, disponível para dáum-lôude em https://livro.pw/owkny (acesso em: 25 jun. 2024), para estudar o comportamento de duas grandezas quê se relacionam, construindo modelos correspondentes a funções quadráticas e representações de parábolas no plano cartesiano. Para isso, considere a situação a seguir.
Em um modelo de câmara fria, o refrigerador tem funcionamento automático e mantém a tempera-túra interna entre 0°C e 18°C. Esse refrigerador liga quando o interior da câmara fria atinge a tempera-túra mássima e desliga quando atinge a mínima. Durante um teste de funcionamento, a tempera-túra no interior dessa câmara fria foi aferida em alguns momentos, a partir do instante em quê o refrigerador ligou automaticamente.
No qüadro apresentado, estão indicados o tempo, após o refrigerador ligar, e a tempera-túra aferida nesse teste.
Tempo (h) |
Temperatura (°C) |
|---|---|
0 |
18 |
2 |
9 |
5 |
0,6 |
8 |
1,7 |
9 |
4,7 |
11 |
13 |
12 |
17,9 |
A fim de estimar a tempera-túra no interior dessa câmara fria em outros momentos durante esse teste, sabendo quê a situação póde sêr modelada por uma função quadrática, podemos obtêr na planilha eletrônica LibreOffice Calc a representação da parábola e a função quê melhor descrevem a relação entre o tempo, contado a partir do momento em quê o refrigerador liga, e a tempera-túra interna da câmara fria. Acompanhe as etapas.
A Organizamos os dados do qüadro na planilha eletrônica.
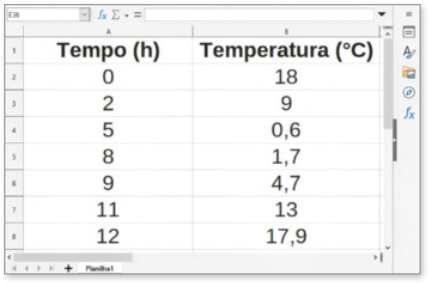
B Selecionamos as células A2:B8 e clicamos na opção Inserir gráfico do menú. Em seguida, ao abrir a caixa de diálogo Assistente de gráficos, na opção 1. Tipo de gráfico, selecionamos as opções XY (Dispersão) e Somente pontos. Por fim, clicamos em Finalizar e obtemos os pontos de coordenadas (x, y), quê indicam o tempo x, em hora, contado a partir do início do funcionamento do refrigerador, e a tempera-túra y, em grau célcius, correspondente ao interior da câmara fria.
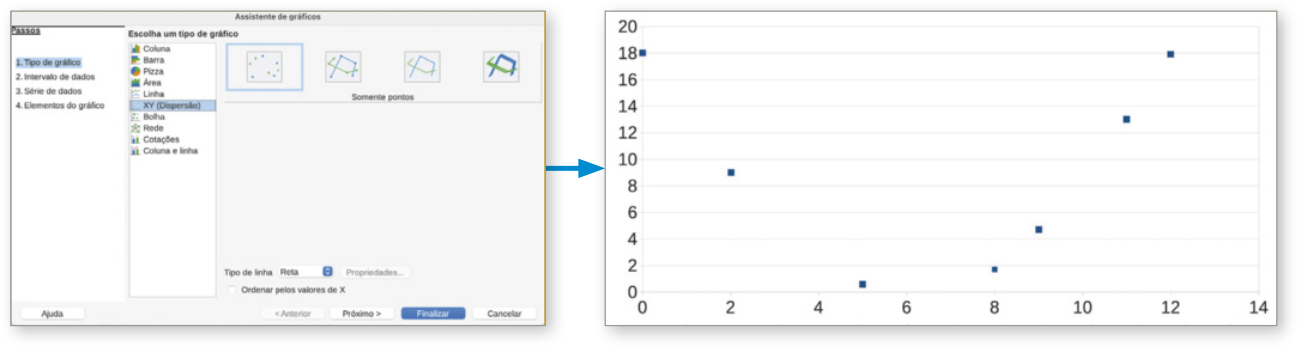
Página cento e oitenta e sete
C Para determinar a parábola e a função quadrática quê melhor descrevem a relação entre essas grandezas, clicamos sobre um dos pontos plotados para selecioná-lo. Depois, clicamos nas opções Inserir e Linha de tendência... do menú. Ao abrir a caixa de diálogo Linha de tendência para série de dados ‘Coluna B’, na opção Tipo de regressão, selecionamos a opção Polinomial e, em Grau, indicamos 2. Em seguida, em Opções, marcamos Mostrar equação. Por fim, clicamos em OK.
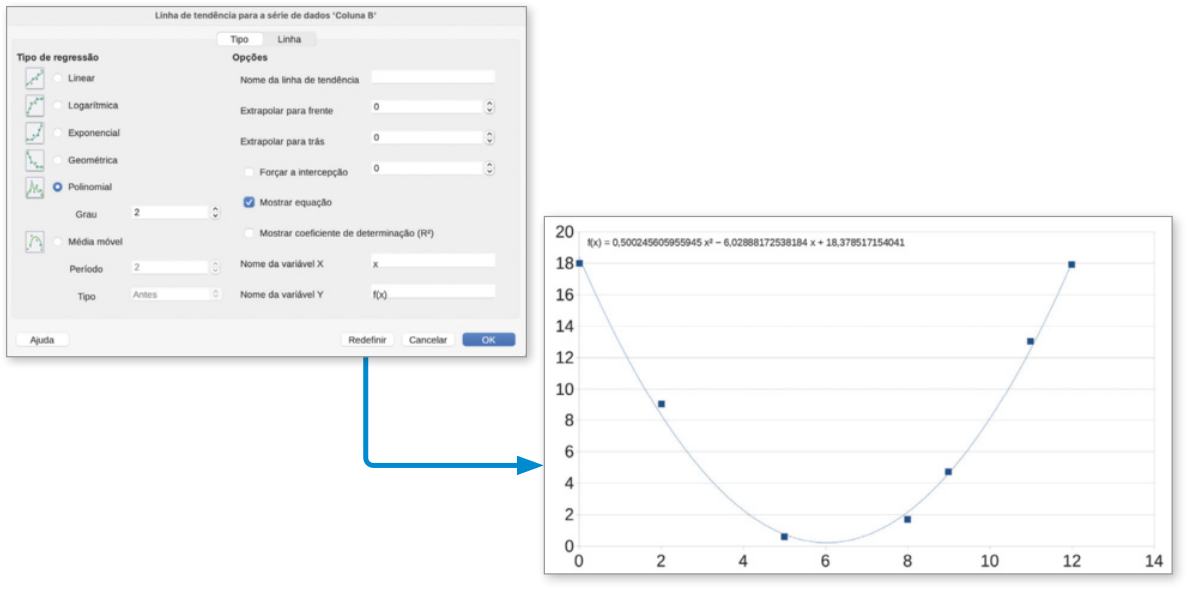
MÃOS À OBRA
1. De acôr-do com a situação apresentada no exemplo, resôuva os itens a seguir. Para isso, aproxime cada coeficiente da lei de formação da função f ao décimo mais próximo e faça os cálculos necessários na planilha eletrônica.
a) Calcule, em valor absoluto, a diferença entre cada tempera-túra da câmara fria indicada e a tempera-túra correspondente determinada pela função f.
tempo 0: 0,4°C; tempo 2: 0,6°C; tempo 5: 0,3°C; tempo 8: 0,7°C; tempo 9: 0,2°C; tempo 11: 0,1°C; tempo 12: 0,5°C
b) Utilizando a função f, estime a tempera-túra mínima aproximada dessa câmara fria.
0,4°C
2. Utilizando os mesmos procedimentos apresentados no exemplo anterior, represente os dados a seguir em uma planilha eletrônica e obtenha a representação da parábola e da função quadrática quê melhor descrevem a relação entre a altura do disco e o tempo após o seu lançamento.
Tempo (s) |
Altura do disco (m) |
|---|---|
1 |
5,6 |
2 |
8,9 |
3 |
10 |
4 |
9 |
5 |
5,5 |
6 |
0 |
Construção do estudante.
![]() • Com base nas informações do qüadro e da construção quê você realizou na planilha eletrônica, elabore um problema relacionado ao conteúdo de função quadrática. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
• Com base nas informações do qüadro e da construção quê você realizou na planilha eletrônica, elabore um problema relacionado ao conteúdo de função quadrática. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página cento e oitenta e oito
Estudo do sinal de uma função quadrática
Como estudamos anteriormente, o estudo do sinal de uma função f consiste em analisar os valores do domínio para os quais f é positiva, negativa ou se anula. Em particular, para estudar o sinal de uma função quadrática f: ℝ → ℝ, definida por f(x) = ax2 + bx + c, podemos analisar os valores do discriminante (delta)" da equação ax2 + bx + c = 0 e o coeficiente a da função f. Acompanhe.
(delta)" > 0
Nesse caso, o gráfico de f intersecta o eixo x em dois pontos distintos, ou seja, f tem dois zeros reais distintos: x1 e x2, com x1 < x2.
a > 0
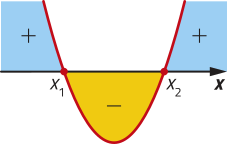
• f(x) > 0 para x < x1 ou para x > x2;
• f(x) = 0 para x = x1 ou para x = x2;
• f(x) < 0 para x1 < x < x2.
a < 0
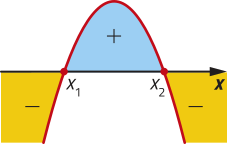
• f(x) > 0 para x1 < x < x2;
• f(x) = 0 para x = x1 ou para x = x2;
• f(x) < 0 para x < x1 ou para x > x2.
(delta)" = 0
Nesse caso, o gráfico de f intersecta o eixo x em um único ponto, ou seja, f tem dois zeros reais e iguais: x1 = x2.
a > 0
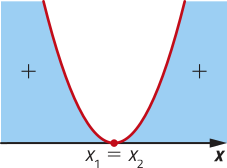
• f(x) > 0 para x ≠ x1;
• f(x) = 0 para x = x1;
• ∄ x ∈ D(f) | f(x) < 0
a < 0
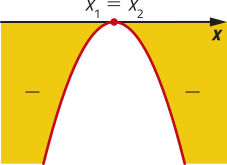
• ∄ x ∈ D( f) | f(x) > 0;
• f(x) = 0 para x = x1;
• f(x) < 0 para x ≠ x1.
DICA
∄ Lê-se: não existe.
(delta)" < 0
Nesse caso, o gráfico de f não intersecta o eixo x, ou seja, f não tem zero real.
a > 0
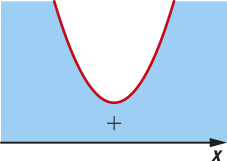
• f(x) > 0 ∀ x ∈ D(f);
• ∄ x ∈ D(f) | f(x) ≤ 0.
a < 0

• f(x) < 0 ∀ x ∈ D(f);
• ∄ x ∈ D(f) | f(x) ≥ 0.
DICA
∀ Lê-se: para todo.
Página cento e oitenta e nove
ATIVIDADES RESOLVIDAS
R17. Realize o estudo do sinal da função f: ℝ → ℝ, definida por:
a) f(x) = x2 + 2x − 3;
b) f(x) = −2x2 + 8x − 8;
c) f(x) = x2 − 4x + 5.
Resolução
a) Inicialmente, calculamos os zeros de f.
f(x) = 0 ⇒ x2 + 2x − 3 = 0
a = 1; b = 2; c = −3
(delta)" = 22 − 4 ⋅ 1 ⋅ (−3) = 16
Como a > 0 e (delta)" > 0, temos quê:
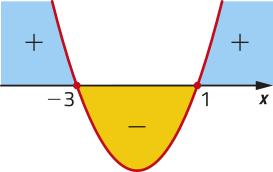
• f(x) > 0 para x < −3 ou para x > 1;
• f(x) = 0 para x = −3 ou para x = 1;
• f(x) < 0 para −3 < x < 1.
b) Inicialmente, calculamos os zeros de f.
f(x) = 0 ⇒ −2x2 + 8x − 8 = 0
a = −2; b = 8; c = −8
(delta)" = 82 − 4 ⋅ _ (−2) ⋅ (−8) = 0
Como a < 0 e (delta)" = 0, temos quê:
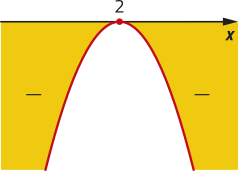
• ∄ x ∈ D(f) | f(x) > 0;
• f(x) = 0 para x = 2;
• f(x) < 0 para x ≠ 2.
c) Inicialmente, calculamos os zeros de f.
f(x) = 0 ⇒ x2 − 4x + 5 = 0
a = 1; b = −4; c = 5
(delta)" = (−4)2 − 4 ⋅ 1 ⋅ 5 = −4
A função não tem zeros reais, pois (delta)" < 0.
Como a > 0, temos quê:
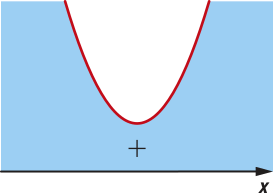
• f(x) > 0 para todo x ∈ D(f);
• ∄ x ∈ D(f) | f(x) ≤ 0.
R18. resôuva em ℝ a inequação x2 ≥ x + 2.
Resolução
x2 ≥ x + 2 ⇒ −x2 + x + 2 ≤ 0
pôdêmos resolver essa inequação fazendo o estudo do sinal da função f, definida por f(x) = −x2 + x + 2.
Para isso, inicialmente, calculamos os zeros de f.
f(x) = 0 ⇒ −x2 + x + 2 = 0
(delta)" = 12 − 4 ⋅ (−1) ⋅ 2 = 9
Como a < 0 e (delta)" > 0, temos quê:
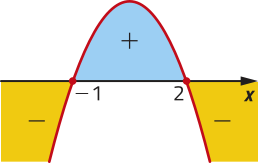
• f(x) > 0 para −1 < x < 2;
• f(x) = 0 para x = −1 ou para x = 2;
• f(x) < 0 para x < −1 ou para x > 2.
Portanto, o conjunto solução S da inequação x2 ≥ x + 2 corresponde a todos os valores reais de x para os quais f(x) ≤ 0, ou seja, S = {x ∈ ℝ | x ≤ −1 ou x ≥ 2}.
Página cento e noventa
R19. Certa empresa de turismo freta ônibus com 40 lugares para excursões a um parque aquático e oferece dois planos, conforme segue.
• 1º plano: Taxa fixa de R$ 250,00 mais R$ 40,00 por passageiro.
• 2º plano: Cada passageiro paga R$ 20,00 fixos mais uma taxa de R$ 2,00 por lugar vago.
Em quais circunstâncias o 1º plano é mais vantajoso quê o 2º plano para os clientes dessa empresa de turismo?
Resolução
pôdêmos expressar, por meio de funções, a quantia total a pagar, em reais, em cada um dos planos de uma excursão ofertados, de acôr-do com a quantidade x de passageiros.
• 1º plano: f(x) = 250 + 40x
• 2º plano: g (x) = x ⋅ [20 + 2 ⋅ (40 − x)] ⇒
⇒ g (x) = 100x − 2x2
Para saber a quantidade x de passageiros para a qual o 1º plano é mais vantajoso quê o 2º plano, fazemos:
f(x) < g (x) ⇒ 250 + 40x < 100x − 2x2 ⇒
⇒ −2x2 + 60x − 250 > 0
Para resolver a inequação ôbitída, podemos estudar o sinal da função h(x) = −2x2 + 60x − 250.
Para isso, inicialmente, calculamos os zeros de h.
h (x) = 0 ⇒ −2x2 + 60x − 250 = 0
a = −2; b = 60; c = −250
(delta)" = 602 − 4 ⋅ (−2) ⋅ (−250) = 1.600
Como a < 0 e (delta)" > 0, temos quê:
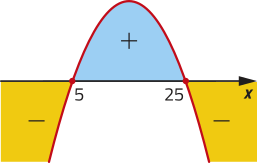
• h (x) > 0 para 5 < x < 25;
• h (x) = 0 para x = 5 ou para x = 25;
• h (x) < 0 para x < 5 ou para x > 25.
Assim, S = {x ∈ ℝ | 5 < x < 25} é o conjunto solução da inequação −2x2 + 60x − 250 > 0.
Portanto, para grupos entre 5 e 25 passageiros, o 1º plano é mais vantajoso para os clientes da excursão ao parque aquático quê o 2º plano.
PARA PENSAR
Considere a função definida por m(x) = f(x) − g(x).
• O quê essa função representa no contexto apresentado?
Resposta esperada: A função m representa a diferença, em reais, entre a quantia total a pagar no 1º e no 2º plano, respectivamente, de acôr-do com a quantidade x de passageiros.
• Realize o estudo do sinal da função m.
m(x) < 0 para 5 < x < 25; m(x) = 0 para x = 5 ou para x = 25; m(x) > 0 para x < 5 ou para x > 25
ATIVIDADES
49. Observe cada gráfico a seguir e faça o estudo do sinal da função quadrática f: ℝ → ℝ correspondente.
a) 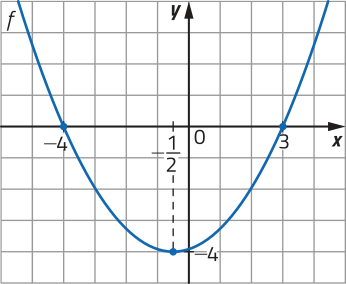
49. a) f(x) > 0 para x < −4 ou x > 3; f(x) = 0 para x = −4 ou x = 3; f(x) < 0 para −4 < x < 3
b) 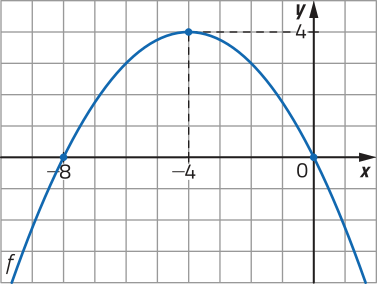
49. b) f(x) > 0 para −8 < x < 0; f(x) = 0 para x = −8 ou x = 0; f(x) < 0 para x < −8 ou x > 0
c) 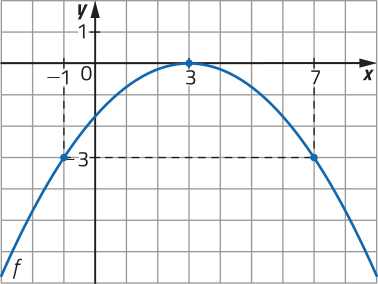
49. c) ∄ x ∈ D(f) tal quê f(x) > 0; f(x) = 0 para x = 3; f(x) < 0 para x ≠ 3
Página cento e noventa e um
50. Realize o estudo do sinal da função f: ℝ → ℝ, definida por:
a) f(x) = 4x2 + 5x + 2;
f(x) > 0 para todo x ∈ D(f); ∄ x ∈ D(f) | f(x) ≤ 0
b) f(x) = −2x2 + 7x − 3;
50. b) f(x) > 0 para 0,5 < x < 3; f(x) = 0 para x = 0,5 ou x = 3; f(x) < 0 para x < 0,5 ou x > 3
c) f(x) = −x2 − 6x − 9;
50. c) ∄ x ∈ D(f) | f(x) > 0; f(x) = 0 para x = −3; f(x) < 0 para x ≠ −3
d) f(x) = − x −4;
50. d) f(x) > 0 para x < −2 ou x > 4; f(x) = 0 para x = −2 ou x = 4; f(x) < 0 para −2 < x < 4
e) f(x ) = 0,4x2 − 2x + 2,5;
50. e) f(x) > 0 para x ≠ 2,5; f(x) = 0 para x = 2,5; ∄ x ∈ D(f) | f(x) < 0
f) f(x) = + 3x − 10.
∄ x ∈ D(f) | f(x) ≥ 0; f(x) < 0 para todo x ∈ D(f)
51. resôuva em ℝ as inequações a seguir.
a) 4x2 − 16x + 12 > 0
S = {x ∈ ℝ | x < 1 ou x > 3}
b) x2 + 15 ≤ 0,9x2 − 2x + 45
S = {x ∈ ℝ | −30 ≤ x ≤ 10}
c) x2 − 10x − < 3x2 + 10x + 13
S = {x ∈ ℝ | x < −8,5 ou x > −1,5}
d) x2 − 5x ≤ − 15
S = ∅
52. No GeoGebra, represente os gráficos das funções f(x) = 250 + 40x e g(x) = 100x − 2x2, apresentadas na resolução da atividade resolvida R19 da página anterior. Em seguida, com a ferramenta ![]() (Interseção de dois objetos) selecionada, determine os pontos de interseção entre os gráficos dessas funções. Por fim, verifique as coordenadas dêêsses pontos na Janela de Álgebra e determine qual é a relação dêstes com a resolução da atividade.
(Interseção de dois objetos) selecionada, determine os pontos de interseção entre os gráficos dessas funções. Por fim, verifique as coordenadas dêêsses pontos na Janela de Álgebra e determine qual é a relação dêstes com a resolução da atividade.
52. Resposta esperada: As abscissas dêêsses pontos determinam quê: para x < 5 e x > 25 ⇒ f(x) > g(x); para x = 5 e x = 25 ⇒ f(x) = g(x); para 5 < x < 25 ⇒ f(x) < g(x).
53. Dada a função quadrática f: ℝ → ℝ, definida por f(x) = (k − 2)x2 + 4x − 3, determine para quais valores reais de k temos f(x) < 0 para todo x real.
k <
54. Utilizando um programa de computador, Bruno construiu, em um mesmo plano cartesiano, os gráficos de uma função quadrática f: ℝ → ℝ e de uma função afim g: ℝ → ℝ. Observe.
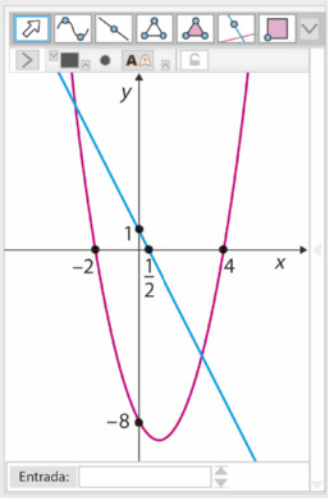
a) escrêeva a lei de formação da função f e da função g.
f(x) = x2 − 2x − 8; g (x) = −2x + 1
b) Para quais valores reais de x temos:
• f(x) < g (x)?
−3 < x < 3
• f(x) > g (x)?
x < −3 ou x > 3
• f(x) = g (x)?
x = −3 ou x = 3
55. Em cérto laboratório, uma câmara climática é utilizada para analisar o comportamento de bactérias de acôr-do com a variação da tempera-túra. Em um dos experimentos realizados, a tempera-túra T no interior dessa câmara climática, em grau célcius, varia em relação ao tempo x, em minuto, decorrido do início do experimento, de acôr-do com a função dada por T (x) = −0,02x2 + 5x − 48, para 0 ≤ x ≤ 250.
a) Entre quais intervalos de tempo a tempera-túra nessa câmara climática era:
• positiva?
entre 10 min e 240 min
• negativa?
entre 0 min e 10 min e entre 240 min e 250 min
b) Qual é a maior tempera-túra ôbitída nessa câmara climática durante esse experimento? Essa tempera-túra foi registrada quantos minutos após o início do experimento?
264,5°C; 125 min
Página cento e noventa e dois
Equação da parábola
Anteriormente, nesta Unidade, estudamos alguns elemêntos da parábola e, em seguida, constatamos quê os gráficos das funções quadráticas são parábolas. Agora, retomaremos a abordagem algébrica inicial para realizar o estudo da equação de uma parábola. Para isso, vamos considerar, inicialmente, o caso em quê a diretriz r é paralela ao eixo das ordenadas, o vértice V(0, 0) corresponde à origem do sistema de eixos cartesianos e está localizado à direita da diretriz e F(c, 0) corresponde ao foco. Nessa parábola, indicamos um ponto qualquer P(x, y). Observe a figura.
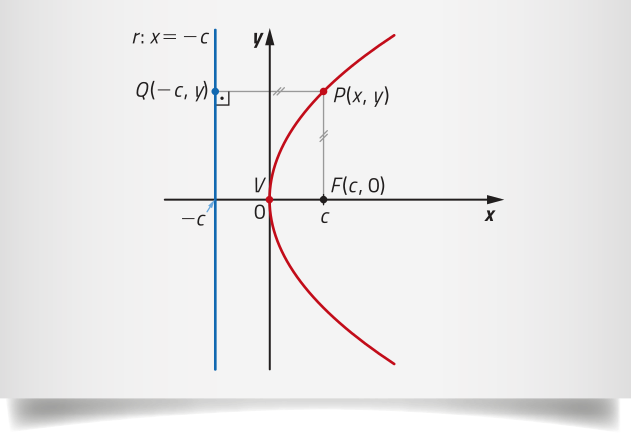
De acôr-do com a definição da parábola, a distância de P a F é igual à distância de P a r. Como a distância de P a r corresponde a PQ, temos:
PF = PQ ⇒ ⇒
⇒ (x − c)2 + (y − 0)2 = (x + c)2 + (y − y)2 ⇒
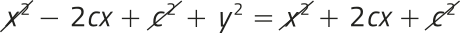
y2 = 4cx
DICA
A distância entre os pontos A(xA, yA) e B(xB, yB) no plano cartesiano póde sêr expressa por AB = .
Essa é a equação da parábola quando a diretriz é paralela ao eixo das ordenadas e o vértice corresponde à origem do plano cartesiano e está à direita da diretriz.
De maneira análoga, podemos representar a equação da parábola quando a reta diretriz e o vértice estão em outras posições. Acompanhe a seguir.

Página cento e noventa e três



DICA
O gráfico quê representa a função quadrática é uma parábola com diretriz paralela ou coincidente com o eixo das abscissas. Os demais casos de parábolas não correspondem a gráficos de funções.
Equação da parábola e função quadrática
Anteriormente nesta Unidade, estudamos quê o gráfico de uma função quadrática é uma parábola. Mas como relacionar a lei de formação de uma função quadrática à equação de uma parábola?
Para compreender essa relação, considere uma parábola cuja equação é (x − 1)2 = (y − 2). Com base na equação, podemos afirmar quê:
• a equação da parábola é do tipo (x − xv)2 = 4c (y − yv) → (x − 1)2 = 4c (y − 2);
• o vértice V (xv, yv) está localizado acima da diretriz e tem coordenadas V (1, 2);
• 4c = 1, ou seja, c = ;
• a diretriz é paralela ao eixo das abscissas e é dada por y = yv − c, ou seja, y = 2 − .
Página cento e noventa e quatro
Portanto, essa equação é de uma parábola com diretriz paralela aos eixos das abscissas e vértice qualquer acima da diretriz.
Desenvolvendo o produto notável da equação e isolando a variável y no primeiro membro, temos:
(x − 1)2 = (y − 2)
x2 − 2x + 1 = y − 2
x2 − 2x + 1 + 2 = y
y = x2 − 2x + 3
Note quê, tomando y = f(x), a equação ôbitída é a lei de formação de uma função quadrática f: ℝ → ℝ, definida por f(x) = x2 − 2x + 3, com a = 1, b = −2 e c = 3. Como nessa função a = 1 > 0, essa parábola tem concavidade voltada para cima.
Portanto, o gráfico da função quadrática f: ℝ → ℝ, definida por f(x) = x2 − 2x + 3, corresponde à parábola de equação (x − 1)2 = 4 ⋅ (y − 2), em quê:
• o vértice tem coordenadas V (1, 2);
• o foco tem coordenadas F(xv, yv + c) → F ();;
• a reta diretriz tem equação y = yv − c → y = .
Observe, a seguir, a representação dessa parábola no plano cartesiano.
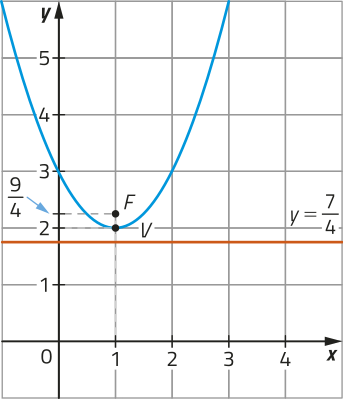
Uma parábola com diretriz paralela ao eixo das abscissas e vértice abaixo da diretriz também corresponde ao gráfico de uma função quadrática, mas com a concavidade para baixo. As parábolas com diretriz paralela ao eixo das ordenadas não representam gráficos de funções quadráticas.
PARA PENSAR
por quê uma parábola com diretriz paralela ao eixo das ordenadas não corresponde ao gráfico de uma função quadrática?
Resposta esperada: Uma parábola com diretriz paralela ao eixo das ordenadas não representa uma função, uma vez quê nela é possível identificar pares de pontos em que são associadas diferentes ordenadas a uma mesma abscissa.
Página cento e noventa e cinco
ATIVIDADES RESOLVIDAS
R20. Esboce no plano cartesiano a parábola indicada pela equação:
a) x2 + 8y = 0;
b) y2 − 8y + 12x = −4.
Resolução
a) Para esboçar uma parábola a partir de sua equação, é necessário determinar as coordenadas do vértice e o valor de c, quê indica a posição da reta diretriz.
x2 + 8y = 0 ⇒ x2 = −4 ⋅ 2 ⋅ y ⇒
⇒ (x − 0)2 = −4 ⋅ 2 ⋅ (y − 0)
Assim, comparando a equação ôbitída com as equações apresentadas anteriormente, conclui-se quê c = 2 e a parábola tem diretriz paralela ao eixo das abscissas, com vértice V(0, 0) abaixo da diretriz. Em relação a essa parábola, temos:
• foco: F(xV, yV − c) ⇒ F(0, −2);
• diretriz: y = yV + c ⇒ y = 2.
A partir da equação da parábola, também podemos obtêr pares ordenados correspondentes a alguns pontos dessa parábola, como (−4, −2),( −), e (4, −2).
Representando a parábola no plano cartesiano, temos:
b) Utilizando o método de completar quadrados, temos:
y2 − 8y + 12x = −4 ⇒ y2 − 8y + 16 =
= −12x − 4 + 16 ⇒ (y − 4)2 = −4 ⋅ 3(x − 1)
Assim, a parábola tem diretriz paralela ao eixo das ordenadas, com vértice V (1, 4) à esquerda da diretriz e c = 3. Em relação a essa parábola, temos:
• foco: F(xV − c, yV) ⇒ F(−2, 4);
• diretriz: x = xV + c ⇒ x = 4.
A partir da equação da parábola, também podemos obtêr pares ordenados correspondentes a alguns pontos dessa parábola, como (−11, −8), (−11, 16), (−2, −2) e (−2, 10).
Representando a parábola no plano cartesiano, temos:
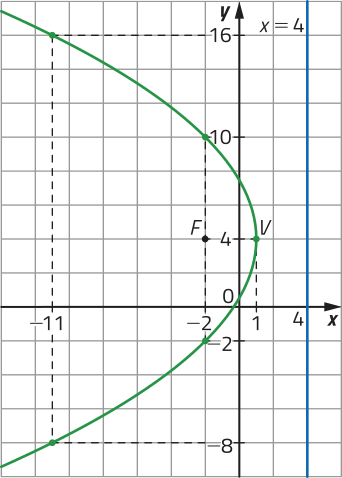
R21. escrêeva a lei de formação de uma função f cujo gráfico corresponda a uma parábola em que as coordenadas do vértice e do foco são dadas por V (3; −1,5) e F(3, 1), respectivamente.
Resolução
De acôr-do com as informações apresentadas, temos quê a parábola tem diretriz paralela ao eixo das abscissas, vértice V (3; −1,5) acima da diretriz e F(3, 1). Assim, a equação da parábola é da forma (x − xV)2 = 4c (y − yV).
Calculando o valor de c, temos: c = FV = = 2, 5
A equação da parábola é dada por:
(x − 3)2 = 4 ⋅ 2,5 ⋅ (y + 1,5) ⇒ x2 − 6x + 9 = 10y + 15 ⇒ y =
Portanto, f(x) = .
Página cento e noventa e seis
ATIVIDADES
56. Esboce no plano cartesiano a parábola indicada pela equação em cada item.
Respostas nas Orientações para o professor.
a) x2 − 8y = 0
b) x2 − 10x + 4y = −45
c) y2 − 4y + 16x = 28
d) y2 + 8y − 10x = 29
57. escrêeva a equação de cada parábola representada a seguir e explique, com suas palavras, o procedimento adotado em cada caso.
a) 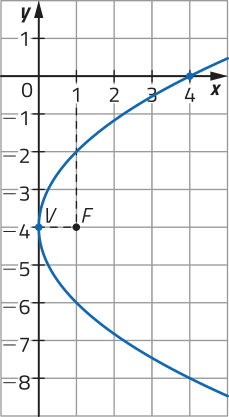
y2 − 4x + 8y = −16. Resposta pessoal.
b) 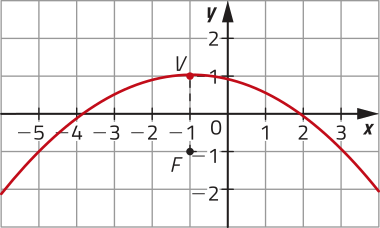
57. b) x2 + 2x + 8y = 7. Resposta pessoal.
58. (Unésp) Em um plano cartesiano ortogonal são dadas uma reta d, de equação x = −3, e um ponto F, de coordenadas (−1, 2). Nesse plano, o conjunto dos pontos quê estão à mesma distância do ponto F e da reta d forma uma parábola.
Na figura, estão nomeados dois pontos dessa parábola: o vértice V, de coordenadas (−2, 2), e o ponto P, de coordenadas (0, yp).
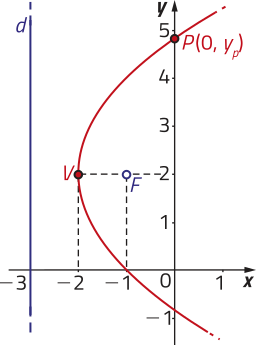
Determine as coordenadas de dois pontos quaisquer dessa parábola quê sêjam diferentes de V e de P. Em seguida, calcule yp.
58. algumas possíveis respostas: (−1, 0), (−1, 4), (2, −2), (2, 6), (7, −4), (7, 8); yp = 2( + 1) ≃ 4,83
59. Qual é a equação da parábola quê passa pêlos pontos A(0; −1,5), B (−2, 0) e C(2, −2) e tem eixo de simetria paralelo ao eixo das ordenadas?
59. x2 − 4x − 8y = 12
![]() 60. Observe as etapas quê podemos realizar para representar uma parábola usando papel, lápis, régua, um esquadro de 60°, fita adesiva e um pedaço de barbante.
60. Observe as etapas quê podemos realizar para representar uma parábola usando papel, lápis, régua, um esquadro de 60°, fita adesiva e um pedaço de barbante.
1ª
Em uma fô-lha de papel, marcamos o ponto F, foco da parábola. Em seguida, cortamos um pedaço de barbante cujo comprimento deve sêr igual ao do maior cateto do esquadro, fixamos uma extremidade do barbante em F e a outra no vértice do esquadro formado pela hipotenusa e pelo maior cateto.

2ª
Posicionamos a régua na fô-lha e apoiamos o cateto menor do esquadro sobre ela. Depois, esticamos o barbante apoiando a ponta do lápis no cateto maior do esquadro.

3ª
Deslizamos o esquadro sobre a régua fixa, mantendo o barbante esticado, traçando a parábola com o lápis.
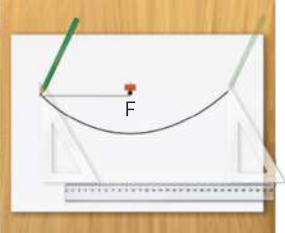
Agora, com um colega, resolvam os itens.
a) Em uma fô-lha de papel, representem uma parábola com as etapas apresentadas.
60. a) Resposta pessoal.
b) O quê é possível afirmar em relação à distância de F à ponta do lápis e à distância da ponta do lápis à régua? Justifique.
60. b) As distâncias são iguais, pois a ponta do lápis corresponde a um ponto da parábola, F corresponde ao foco da parábola, e a régua corresponde à reta diretriz.
Página cento e noventa e sete
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Antena parabólica
As antenas parabólicas começaram a sêr comercializadas, no Brasil, em meados da década de 1980 e, atualmente, fazem parte da paisagem urbana e rural de muitos municípios. Elas permitem captar com maior qualidade sinais de televisão, de rádio, telefonia móvel, internet etc. emitidos via satélite, mesmo em locais mais afastados dos centros urbanos, como zonas rurais e comunidades quilombolas e indígenas.
Programas governamentais de inclusão digital e social buscam promover ações voltadas às pessoas quê moram em áreas mais remotas e com menos infraestrutura de acesso às tecnologias da informação e da comunicação. O objetivo díssu é quê essas pessoas também sêjam inseridas digitalmente e tênham outras oportunidades de aprendizado, entretenimento e interação. Por meio de iniciativas dêêsse tipo, algumas comunidades e escolas indígenas, por exemplo, receberam antenas parabólicas, conexão à internet, computadores, entre outros.


Página cento e noventa e oito
A antena parabólica tem um formato quê lembra uma paraboloide de revolução, quê é a figura geométrica ôbitída ao rotacionarmos uma parábola em torno de seu eixo de simetria.
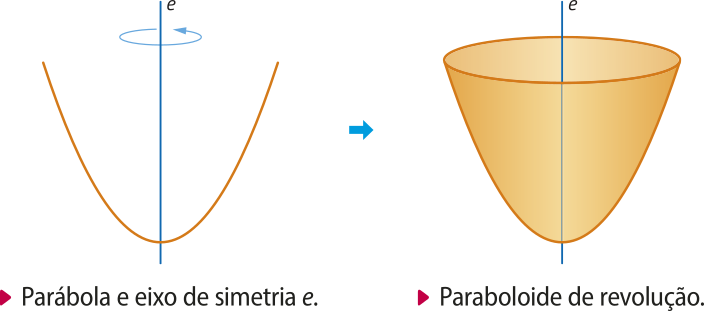
Você sabe por quê esse tipo de antena tem o formato parabólico?
Para essa compreensão, temos de estudar uma importante propriedade geométrica da parábola. Para isso, consideremos:
• um ponto P qualquer dessa parábola;
• uma reta r quê passa por P e é paralela ao eixo e de simetria;
• uma reta t tangente à parábola em P.
Com isso, é possível mostrar quê o ângulo (alfa)" formado entre r e t é congruente ao ângulo (beta)" formado entre e t.
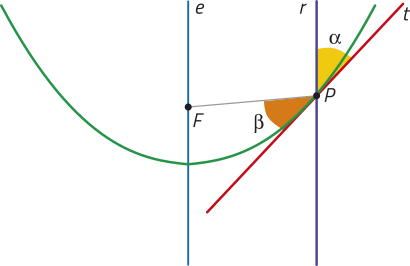
Essa propriedade é o quê fundamenta a escolha do formato parabólico da antena, pois permite quê esta seja posicionada de maneira quê os sinais emitidos pelo satélite sêjam recebidos no disco da antena, praticamente paralelos ao seu eixo de simetria. Com isso, esses sinais são irradiados e convérgem para um único ponto – o foco –, no qual é instalado o dispositivo “conversor de baixo ruído” (conhecido como LNB), equipamento quê converte os sinais recebidos em som e vídeo.
Fonte dos dados: LIMA, Elon Lages éti áu. A matemática do ensino médio. 6. ed. Rio de Janeiro: SBM, 2006. (Coleção do Professor de Matemática, v. 1, p. 135-141).
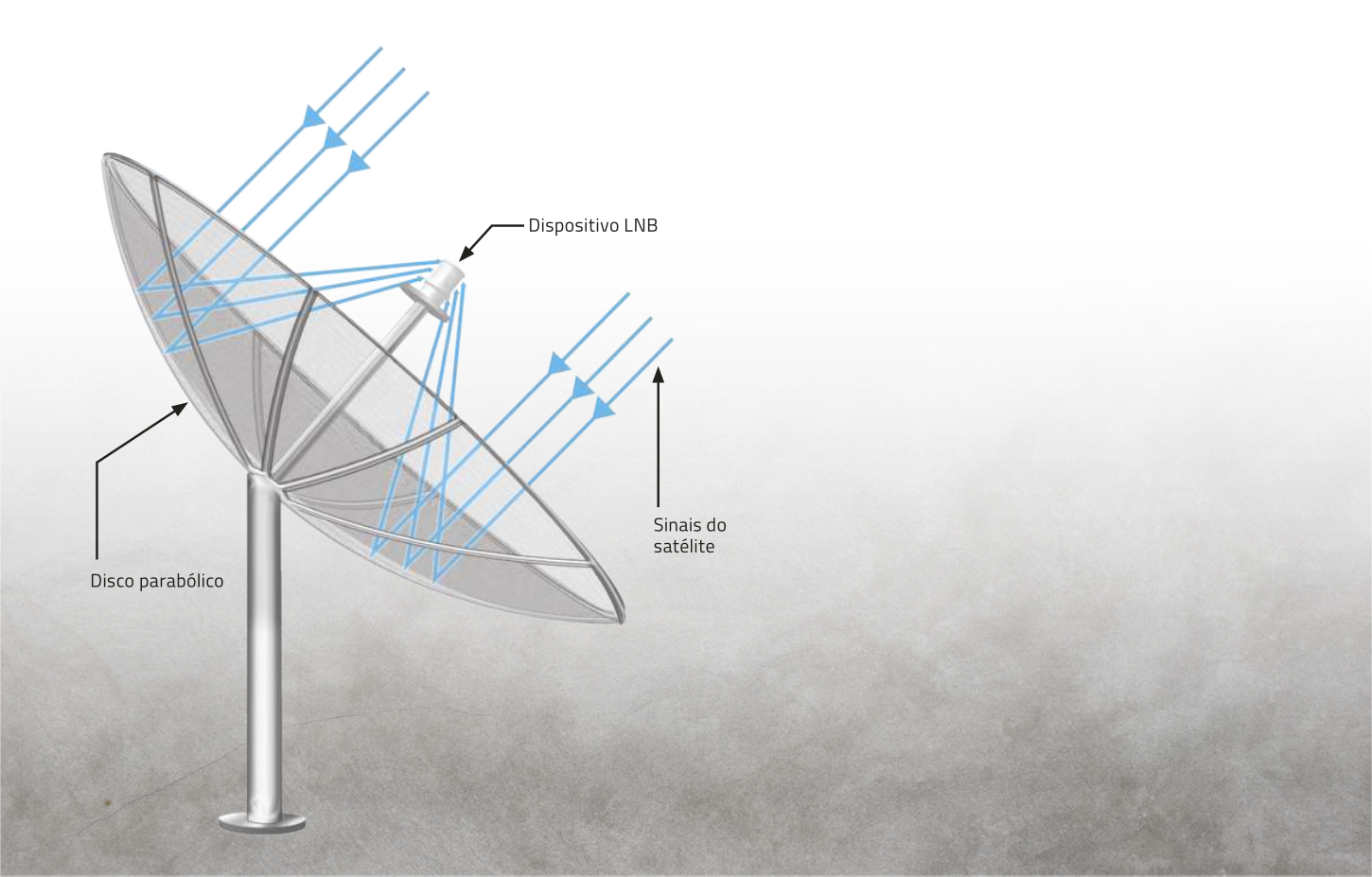
Página cento e noventa e nove
PENSANDO NO ASSUNTO
1. De acôr-do com o texto, qual é a importânssia de se oferecer acesso às tecnologias da informação e da comunicação para as pessoas quê vivem em áreas mais remotas?
1. Resposta esperada: Para quê essas pessoas também sêjam inseridas digitalmente e tênham outras oportunidades de aprendizado, entretenimento e interação.
2. Com base nas informações dadas no texto, apresente um argumento para justificar a escolha do formato da antena parabólica.
2. Resposta esperada: A propriedade geométrica do paraboloide garante sêr possível determinar um local para instalar um dispositivo de modo quê êste recepcione a maior quantidade possível do sinal enviado pelo satélite. Por isso, esse formato é escolhido para a transmissão de sinais de Tevê e internet (via satélite), por exemplo.
3. Observe, a seguir, a representação de uma antena parabólica.

Sabendo quê o disco parabólico dessa antena corresponde a um paraboloide, determine a equação de uma parábola quê gera esse paraboloide ao sêr rotacionada em torno de seu eixo de simetria, quê é paralelo ao eixo das ordenadas do plano cartesiano.
5x2 − 30x − 36y + 45 = 0
![]() 4. Junte-se a três côlégas para resolver esta questão.
4. Junte-se a três côlégas para resolver esta questão.
Leiam o trecho de uma reportagem sobre a inclusão digital de um povo indígena brasileiro.
A importânssia do acesso à internet para os povos do Alto Rio Negro, segundo eles, consiste em permitir o acesso à informação e a consulta a serviços disponíveis aos cidadãos. Serve também à divulgação de notícias e diversas informações regionais graças a sáites e blogues, como os quê eles mesmos mantêm, preenchendo a ausência de veículos de comunicação cobrindo a região. [...]
[...]
[...] os projetos de comunicação também incidem sobre a organização política dos grupos. Isto porque as posições de chefia ou liderança estão sêndo questionadas e reavaliadas neste processo. Não raro, as kestões colocadas pela chegada da internet na comunidade reconfiguram esses papéis.
KLEIN, Tatiane; RENESSE, Nicodème de. O quê dizem (e pensam) os indígenas sobre as políticas de inclusão digital? [S. l.]: Povos Indígenas no Brasil: ISA, 2023. Disponível em: https://livro.pw/laqok. Acesso em: 18 jul. 2024.
Discutam o trecho apresentado e elaborem um texto expressando suas opiniões e possíveis impactos da inserção da tecnologia em comunidades indígenas, avaliando, por exemplo, aspectos culturais, econômicos e sociais. Se necessário, façam pesquisas complementares, incluindo comunidades indígenas localizadas na região em quê vocês moram.
Resposta pessoal.
Página duzentos
O QUE ESTUDEI
![]() 1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Função quadrática
Gráfico de uma função quadrática
Valor mássimo ou valor mínimo da função quadrática
Zeros de uma função quadrática
Conjunto imagem de uma função quadrática
Estudo do sinal de uma função quadrática
Fórmula resolutiva de uma equação do 2º grau
Vértice da parábola
Equação da parábola
![]() 3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página duzentos e um
4. Na abertura desta Unidade, foram apresentadas informações sobre o lançamento oblíquo. Agora, considere quê, em uma partida de futeból feminino, uma jogadora realizou um chute de maneira quê a bola percorreu uma trajetória parabólica. Considere quê o gráfico a seguir corresponde a uma função quadrática g quê modela a trajetória dessa bola do momento do chute até tokár o solo novamente pela primeira vez, de maneira quê y indica a altura quê a bola atinge (em metro) e x, a distância horizontal (em metro).
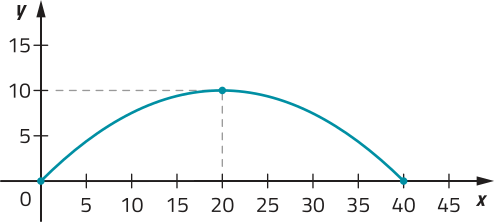
DICA
A distância horizontal corresponde à projeção ortogonal da bola na região plana do campo.
Considerando essas informações, resôuva os itens a seguir.
a) Qual é a altura mássima atingida pela bola?
10 m
b) A quantos metros do local do chute a bola tocou no campo pela primeira vez?
40 m
c) Defina a função g, indicando a lei de formação e o domínio.
g(x) = + x; D(g) = {x ∈ ℝ | 0 ≤ x ≤ 40}
d) Agora, considere as informações a seguir.
Em relação às dimensões do campo de futeból, apesar de a Federação Internacional de Futebol (Fifa) determinar quê os campos oficiais tênham comprimento entre 90 m e 120 m e largura entre 45 m e 90 m, eles recomendam quê, para os principais jogos nacionais e internacionais, o campo tenha dimensões iguais a 105 m e 68 m.
Para sediar jogos da cópa do Mundo em 2014, o Estádio Mané Garrincha, em Brasília (DF), por exemplo, precisou adequar as dimensões do campo quê eram um pouco maiores quê as recomendadas pela Fifa, conforme representado a seguir.
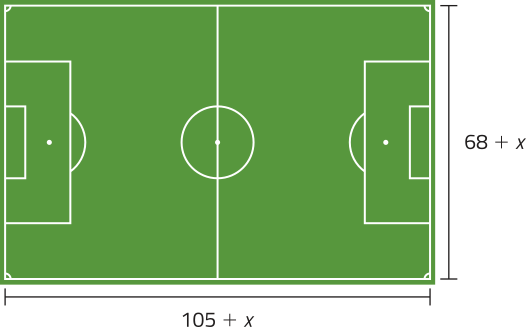
Fonte dos dados: BRASIL. Ministério do Esporte. Guia de recomendações de parâmetros e dimensionamentos para segurança e conforto em estádios de futeból. Brasília, DF: ME: FGV, [2014]. p. 78. Disponível em: https://livro.pw/mgbyt. Acesso em: 18 jul. 2024.
DICA
Na imagem, as medidas estão indicadas em métro, e x representa a medida do comprimento e da largura do campo do Estádio Mané Garrincha quê ultrapassavam as dimensões recomendadas pela Fifa.
Com base nessas informações, resôuva as kestões.
• escrêeva a lei de formação de uma função f para expressar a área A do campo do Estádio Mané Garrincha antes da adequação.
f(x) = x2 + 173x + 7.140
![]() • Supondo quê a área dêêsse campo era de 7.141,7301 m2, use a calculadora e determine quantos centímetros eram necessários reduzir do comprimento e da largura para quê ele ficasse de acôr-do com as dimensões recomendadas. Agora, responda: Você acredita quê esse campo teve realmente de sêr adequado em suas dimensões? Justifique.
• Supondo quê a área dêêsse campo era de 7.141,7301 m2, use a calculadora e determine quantos centímetros eram necessários reduzir do comprimento e da largura para quê ele ficasse de acôr-do com as dimensões recomendadas. Agora, responda: Você acredita quê esse campo teve realmente de sêr adequado em suas dimensões? Justifique.
1 cm. Resposta esperada: Não, uma vez quê, nesse contexto, a medida de 1 cm no comprimento e na largura póde sêr considerada uma imprecisão relacionada, entre outros motivos, aos instrumentos ou métodos de medição utilizados.
• Esboce o gráfico de uma função g: ℝ → ℝ cuja lei de formação seja a mesma da função f quê você indicou no primeiro item. Para isso, você póde utilizar um programa de computador.
Resposta nas Orientações para o professor.
Página duzentos e dois
PRATICANDO: enêm E VESTIBUlARES
1. (Enem/MEC) Um túnel deve sêr lacrado com uma tampa de concreto. A seção transversal do túnel e a tampa de concreto têm contornos de um arco de parábola e mesmas dimensões. Para determinar o custo da obra, um engenheiro deve calcular a área sôbi o arco parabólico em questão. Usando o eixo horizontal no nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a seguinte equação para a parábola:
y = 9 − x2, sêndo x e y medidos em metros.
Sabe-se quê a área sôbi uma parábola como esta é igual a da área do retângulo cujas dimensões são, respectivamente, iguais à base e à altura da entrada do túnel. Qual é a área da parte frontal da tampa de concreto, em métro quadrado?
a) 18
b) 20
c) 36
d) 45
e) 54
alternativa c
2. (Enem/MEC) A trajetória de uma pessoa quê pula de um andâime até o chão é descrita por uma função y = f(x), sêndo x e y medidos em métro, conforme mostra a figura.
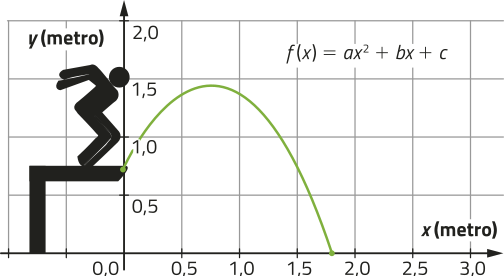
Seja D o domínio da função f(x), como definida na figura.
Para quê a situação representada na figura seja real, o domínio dessa função deve sêr igual a
a) {x2}, sêndo x2 a raiz positiva de f(x).
b) {x ∈ ℝ | 0 ≤ x ≤ x2}, sêndo x2 a raiz positiva de f(x).
c) {x ∈ ℝ | x1 ≤ x ≤ x2}, sêndo x1 e x2 raízes de f(x), com x1 < x2.
d) {x ∈ ℝ | x ≥ 0}.
e) x ∈ ℝ.
alternativa b
3. (Enem/MEC) Em jogos de voleibol, um saque é invalidado se a bola atingir o teto do ginásio onde ocorre o jôgo. Um jogador de uma equipe tem um saque quê atinge uma grande altura.
Seu récorde foi quando a batida do saque se iniciou a uma altura de 1,5 m do piso da quadra, e a trajetória da bola foi descrita pela parábola y = + 12, em quê y representa a altura da bola em relação ao eixo x (das abscissas) quê está localizado a 1,5 m do piso da quadra, como representado na figura. Suponha quê em todas as partidas algum saque dêêsse jogador atinja a mesma altura do seu récorde.
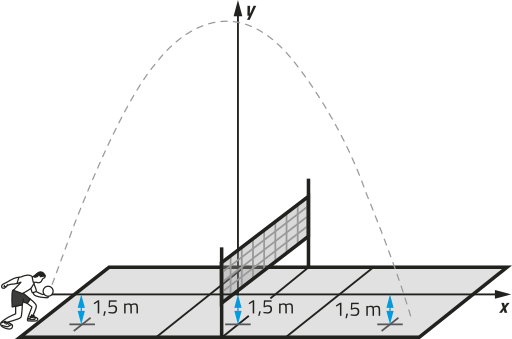
A equipe dêêsse jogador participou de um torneio de voleibol no qual jogou cinco partidas, cada uma delas em um ginásio diferente. As alturas dos tetos dêêsses ginásios, em relação aos pisos das quadras, são:
• ginásio I: 17 m;
• ginásio II: 18 m;
• ginásio III: 19 m;
• ginásio IV: 21 m;
• ginásio V: 40 m.
O saque dêêsse atleta foi invalidado:
a) apenas no ginásio I.
b) apenas nos ginásios I e II.
c) apenas nos ginásios I, II e III.
d) apenas nos ginásios I, II, III e IV.
e) em todos os ginásios.
alternativa d
4. (UFRGS-RS) Se p = 10 e q são as raízes reais da equação x2 − Sx + 20 = 0, então o valor de S é:
a) 0.
b) 2.
c) 6.
d) 10.
e) 12.
alternativa e
Página duzentos e três
5. (Enem/MEC) Ao analisar os dados de uma epidemia em uma cidade, peritos obtiveram um modelo quê avalia a quantidade de pessoas infectadas a cada mês, ao longo de um ano. O modelo é dado por p(t) = −t2 + 10t + 24, sêndo t um número natural, variando de 1 a 12, quê representa os meses do ano, e p(t) a quantidade de pessoas infectadas no mês t do ano. Para tentar diminuir o número de infectados no próximo ano, a Secretaria Municipal de Saúde decidiu intensificar a propaganda oficial sobre os cuidados com a epidemia. Foram apresentadas cinco propostas (I, II, III, IV e V), com diferentes períodos de intensificação das propagandas:
I) 1 ≤ t ≤ 2;
II) 3 ≤ t ≤ 4;
III) 5 ≤ t ≤ 6;
IV) 7 ≤ t ≤ 9;
V) 10 ≤ t ≤ 12.
A sugestão dos peritos é quê seja escolhida a proposta cujo período de intensificação da propaganda englobe o mês em quê, segundo o modelo, há a maior quantidade de infectados.
A sugestão foi aceita.
A proposta escolhida foi a:
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa c
6. (Enem/MEC) O chocolate é um dos alimentos mais apreciados e desejados do mundo. Uma loja especializada nesse produto oferece uma promoção para os bôm-bôns, quê custam R$ 2,00 cada. Cada cliente tem x% de desconto na compra de x bôm-bôns. A promoção é válida para a compra de até 40 bôm-bôns, ou seja, 40% é o desconto mássimo possível. Queremos escrever uma expressão para V em função de x, com x ≤ 40.
Qual é a expressão do valor V, em reais, na compra de x bôm-bôns da promoção, por cliente?
a) V = x2
b) V = 2 − x
c) V = 2x − x2
d) V = x − x2
e) V = 2x − x
alternativa c
7. (UEG-GO) A tempera-túra, em graus célcius, de um objeto armazenado em um determinado local é modelada pela função f(x) + 2x + 10 com x dado em horas. A tempera-túra mássima atingida por esse objeto nesse local de armazenamento é de
a) 0 °C
b) 10 °C
c) 12 °C
d) 22 °C
e) 24 °C
alternativa d
8. (UFG-GO) Uma companhia aérea oferece locação de aeronaves, para viagem de ida e volta de São Paulo a Fortaleza, com as seguintes condições: um avião, com lotação para 160 pessoas custa R$ 800,00 por pessoa e, se o número de desistentes for inferior a 80 pessoas, cada pessoa quê permanecer no grupo deverá pagar R$ 4,00 a mais por cada desistente do pacote de viagem. Se o número de desistentes for superior a 80 pessoas, a viagem será cancelada.
A viagem foi realizada, faturando-se R$ 125.504,00, então, o número de pessoas quê realizou a viagem foi igual a:
a) 84.
b) 96.
c) 148.
d) 158.
alternativa c
9. (UEG-GO) Dadas as funções f(x) = −x2 e g(x) = 2x, um dos pontos de intersecção entre as funções f e g é
a) (0, 2)
b) (−2, −4)
c) (2, 4)
d) (0, −2)
e) (−2, 4)
alternativa b
10. (Ifal) cérto fabricante, segundo levantamentos estatísticos, percebe quê seus clientes não têm comprado mais de 100 de seus produtos por compras. Para incentivar as compras em maior quantidade, ele estabelece um preêço unitário p por produto dado pela função p(x) = 400 − x, onde x é a quantidade de produtos comprados, considerando uma compra de, no mássimo, 300 produtos. Sabendo-se quê a receita de uma empresa é o valor arrecadado com a venda de uma certa quantidade de produtos, qual a receita mássima quê essa empresa póde ter quando fechar uma venda com um determinado cliente, na moeda corrente no Brasil?
a) R$ 200,00.
b) R$ 400,00.
c) R$ 20.000,00.
d) R$ 40.000,00.
e) R$ 80.000,00.
alternativa d
11. (UECE) No plano, com o sistema de coordenadas cartesianas usual, o gráfico da função f: ℝ → ℝ definida por f(x) = x2 + 2mx + 9 é uma parábola quê tangencia o eixo das abcissas, e um de seus pontos com ordenada igual a 9 tem abcissa negativa. Nessas condições, o valor do parâmetro m está entre
a) 1,5 e 2,5.
b) 2,5 e 3,5.
c) 3,5 e 4,5.
d) 4,5 e 5,5.
alternativa b
Página duzentos e quatro
12. (UEMG) Considere a parábola de equação y = ax2 + bx + c, com a, b e c reais e a ≠ 0. Sabe-se quê essa parábola intersecta o eixo das ordenadas no ponto P (0, 5), quê o ponto Q (−2, 8) pertence à parábola e quê a abscissa do vértice é xV = 2. Nessas condições, a ordenada do vértice dessa parábola é dada por
a) yV = 2,5.
b) yV = 3.
c) yV = 3,5.
d) yV = 4.
alternativa d
13. (hú- hê- érre jota) Uma ponte com a forma de um arco de parábola foi construída para servir de travessia sobre um rio. O esquema a seguir representa essa ponte em um sistema de coordenadas cartesianas xy. Nele, os pontos A, B e C correspondem, respectivamente, à margem esquerda, à margem direita e ao ponto mais alto da ponte.
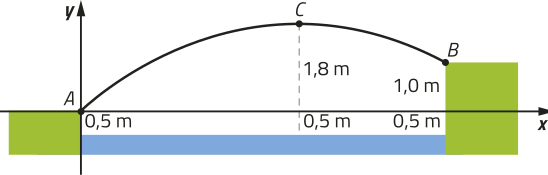
As distâncias dos pontos A, B, e C até a superfícíe do rio são iguais, respectivamente, a 0,5 m, 1,5 m e 2,3 m.
Sabendo quê o ponto C tem, nesse sistema, abscissa igual a 6 m, calcule, em metros, a largura do rio.
10 m
14. (Unicamp-SP) Sejam a e b números reais positivos. Considere a função quadrática f(x) = x(ax + b), definida para todo número real x. No plano cartesiano, qual figura corresponde ao gráfico de y = f(x)?
a) 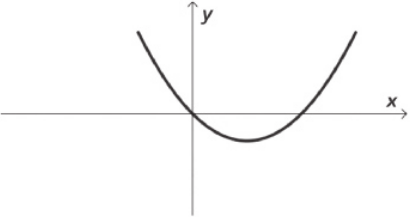
b) 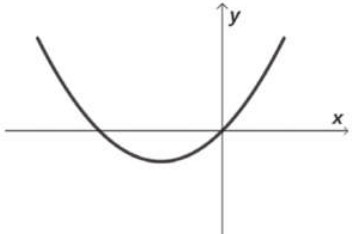
c) 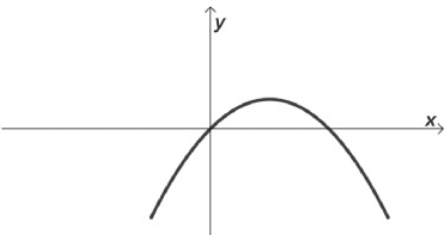
d) 
alternativa b
15. (Udesc) Uma circunferência tem o seu raio variando de acôr-do com a imagem da função f: [2, 6] → ℝ, onde f(x) = x2 + 3x + 4. A diferença entre o maior e o menor comprimento possível dessa circunferência é de:
a) (pi)"
b) 8(pi)"
c) 9(pi)"
d) 8,5(pi)"
e) 26(pi)"
alternativa c
16. (IFRS) Uma farmácia vende em média 1.050 remédios por mês. O preêço médio dos medicamentos dessa farmácia é de R$ 80,00. Para aumentar seu faturamento médio, o gerente pretende dar um desconto de R$ 1,00 no preêço médio dos medicamentos. Assim, 105 medicamentos serão vendidos a mais por mês. Nesse caso, qual é o preêço médio dos medicamentos, em reais, quê vai maximizar o faturamento da farmácia?
a) 80,00
b) 70,00
c) 45,00
d) 40,00
e) 35,00
alternativa c
17. (hú éfe pê érre) A distância quê um automóvel percórre a partir do momento em quê um condutor pisa no freio até a parada total do veículo é chamada de distância de frenagem. Suponha quê a distância de frenagem d, em metros, possa sêr calculada pela fórmula d (v) = (v2 + 8v), sêndo v a velocidade do automóvel, em quilômetros por hora, no momento em quê o condutor pisa no freio.
a) Qual é a distância de frenagem de um automóvel quê se desloca a uma velocidade de 40 km/h?
16 m
b) A quê velocidade um automóvel deve estar para quê sua distância de frenagem seja de 53,2 m?
76 km/h
Página duzentos e cinco

