UNIDADE 5
RELAÇÕES MÉTRICAS E TRIGONOMETRIA NO TRIÂNGULO
Métodos científicos
Em geral, para determinar a validade de cérto fato, pesquisadores utilizam algum método científico, por exemplo, o método científico indutivo e o método científico dedutivo.
O método indutivo parte de um caso particular para obtêr um resultado generalizado.
Por sua vez, o método dedutivo parte de uma ou mais premissas gerais, tidas como verdadeiras e amplamente aceitas, para obtêr conclusões a respeito de um resultado particular. Esse método é mais utilizado em áreas como Física e Matemática, para demonstrar leis e propriedades.


Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Qual é o objetivo dos métodos científicos apresentados?
2. Como é ôbitída uma conclusão no método indutivo? E no método dedutivo?
3. Pense em algum conceito matemático quê possa sêr estudado por meio do método dedutivo. Explique com suas palavras como seriam as etapas de desenvolvimento metodológico.
Página duzentos e seis
Teorema de Tales
Na abertura desta Unidade, foram apresentadas informações sobre dois métodos científicos, entre eles, o método dedutivo, normalmente utilizado na Matemática. Há indícios de quê a característica demonstrativa da Matemática tenha se iniciado com Tales de Mileto (c. 624-620 a.C.-c. 548-545 a.C.). Uma de suas principais contribuições à Matemática é o teorema de Tales, quê estudaremos a seguir.
Você lembra o quê é um feixe de retas paralelas? A partir dêêsse conceito, vamos enunciar o teorema de Tales, um resultado quê será bastante utilizado na resolução das atividades. Denominamos feixe de retas paralelas um conjunto de retas de um mesmo plano e paralelas entre si.
Teorema de Tales
Um feixe de retas paralelas determina, em duas retas transversais, segmentos de reta ordenadamente proporcionais.
De acôr-do com esse teorema, ao considerar um feixe de retas paralelas r, s e t e duas retas, u e v, transversais a esse feixe, podemos escrever as proporções a seguir.
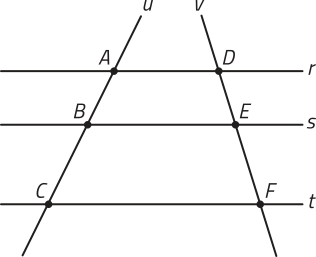
Observe, por exemplo, a representação de um feixe de retas paralelas r, s e t e de duas retas transversais a esse feixe, u e v.
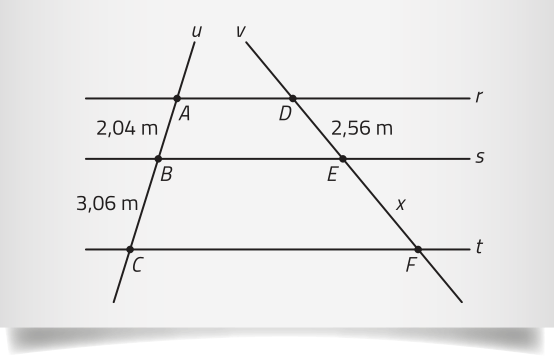
Utilizando o teorema de Tales, podemos determinar a medida x de EF.
⇒ 2, 04x = 7, 8336 ⇒ x = = 3, 84
Portanto, méde 3,84 m.
Página duzentos e sete
Vamos demonstrar a validade do teorema de Tales por meio do método dedutivo. Para isso, separamos em dois casos distintos: quando um feixe de retas paralelas determina, em uma reta transversal, segmentos de reta congruentes (caso 1); e quando esse feixe determina, nessa reta transversal, segmentos de reta com medidas racionais quaisquer (caso 2). Acompanhe.
Caso 1:
Seja um feixe de retas paralelas r, s e t, quê determina na reta transversal u os segmentos de reta congruentes e Uma reta transversal v cruza esse mesmo feixe de retas nos pontos D, E e F.
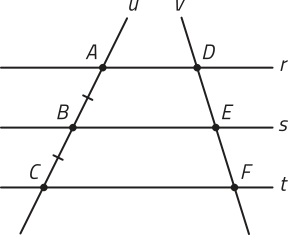
Traçando dois segmentos de reta DG e EH, paralelos à reta u, obtemos os paralelogramos ABGD e BCHE, nos quais e . Assim, .
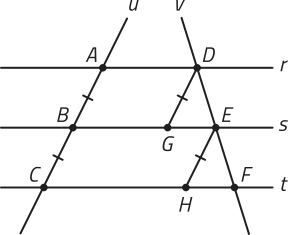
Como os segmentos de reta DG e EH são paralelos e intersectam as retas paralelas s e t, os ângulos e são congruentes. Note quê o par de ângulos e também são congruentes, pois são correspondentes.
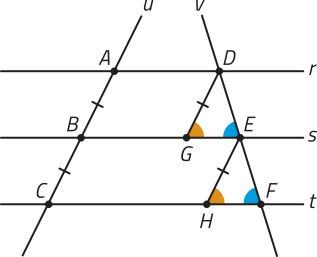
Assim, pelo caso de congruência de triângulos LAAo, os triângulos DGE e EHF são congruentes. Logo, . Além díssu, = 1, ou seja, os segmentos de reta e são proporcionais aos segmentos de reta e .
DICA
Em Matemática, dizemos quê existe congruência entre duas figuras se elas são idênticas no formato e no tamãnho. Em particular, dois segmentos de reta são congruentes quando têm medidas iguais. O mesmo ocorre com os ângulos. Analise os exemplos.
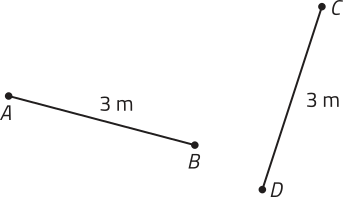
• e são segmentos de reta congruentes, o quê póde sêr indicado da seguinte maneira: ≡
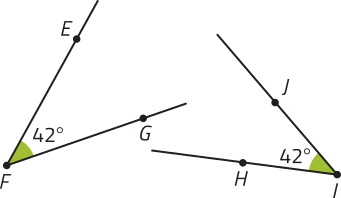
• e são ângulos congruentes, o quê póde sêr indicado da seguinte maneira: ≡
Página duzentos e oito
Caso 2:
Seja um feixe de retas paralelas r, s e t quê determina, em uma reta transversal u, os segmentos de reta e com medidas racionais quaisquer.
Dessa maneira, é possível dividir e em m e n segmentos de reta de medida x, respectivamente. Isso ocorre porque, nesse caso, pode-se estabelecer um número racional positivo x quê divída e em quantidades inteiras de partes.
DICA
No caso 2, consideramos m = 5 e n = 4, ou seja, os segmentos de reta e divididos em 5 partes e em 4 partes de medida x, respectivamente. Porém é possível utilizar esses mesmos procedimentos para quaisquer m e n naturais positivos, de modo quê x seja uma medida racional.
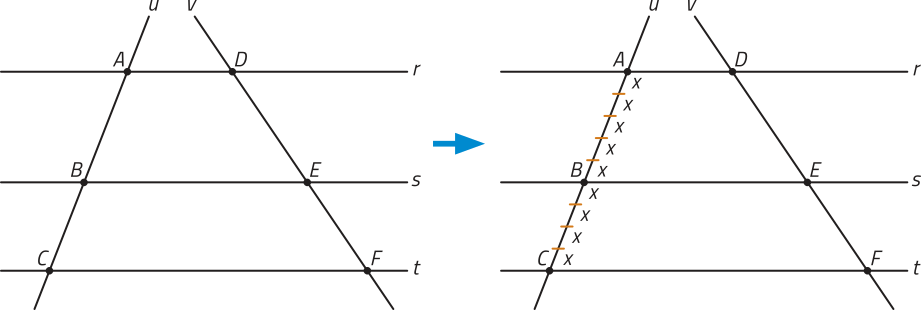
Ao traçar retas paralelas às do feixe, passando pelas extremidades dos segmentos de reta de medida x determinados em e obtemos m segmentos de reta dividindo e n segmentos de reta dividindo, respectivamente, na reta transversal v.
Pelo caso 1, como temos um feixe de retas paralelas quê determina na reta transversal u segmentos de reta congruentes de medida x, os segmentos de reta determinados em v também são congruentes entre si, de medida y, por exemplo.
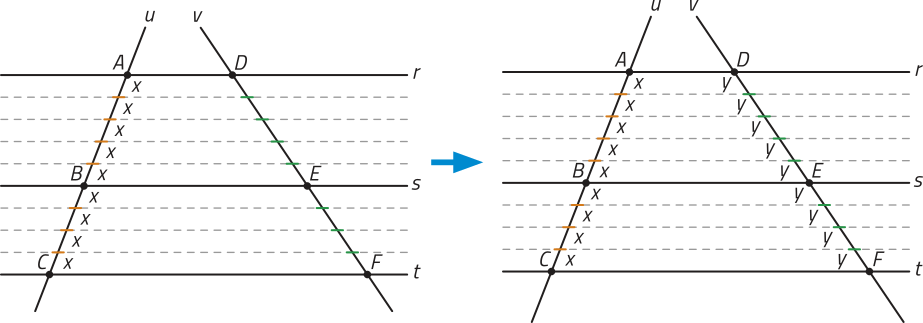
Assim, e ou seja, .
Demonstramos, pelo método dedutivo, quê o teorema de Tales é válido para os segmentos de reta e com medidas racionais. Porém esse teorema também é válido para esses segmentos de reta com medidas irracionais, o quê optamos por não explicitar nem demonstrar nesta coleção.
PARA PENSAR
Explique como dois segmentos de reta e medindo 5 cm e 3,4 cm, respectivamente, podem sêr divididos igualmente em partes inteiras.
Uma resposta possível: pôdêmos considerar um número racional positivo x qualquer e uma unidade de medida de comprimento e dividir os segmentos de reta e em partes iguais correspondentes a essa medida. Por exemplo, ao considerar x = 0,2 e a unidade centímetro, dividimos os segmentos de reta em 25 partes e 17 partes de medida 0,2 cm, respectivamente.
Página duzentos e nove
ATIVIDADES RESOLVIDAS
R1. Em cada item, determine o valor de x considerando quê as retas r, s e t são paralelas.
a) 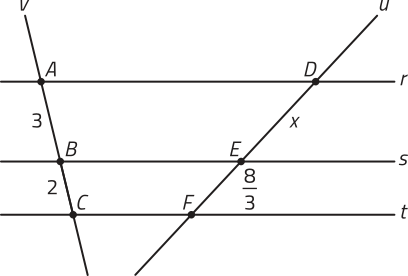
b) 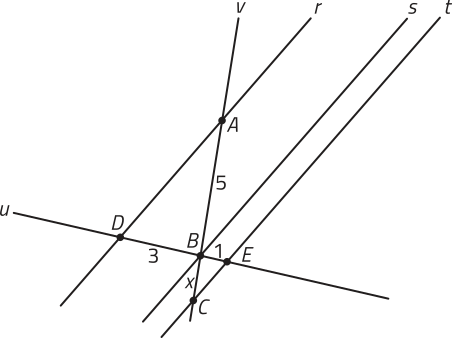
Resolução
a) Como as retas v e u são transversais quê intersectam o feixe de retas paralelas r, s e t, podemos utilizar o teorema de Tales para escrever a proporção a seguir.
⇒ 2x = 8 ⇒ x = 4
Portanto, x = 4.
b) De maneira análoga ao item anterior, temos:
⇒3x =5 ⇒ x =
Portanto, x = .
DICA
Note quê os segmentos de reta e estão contidos em u e os segmentos de reta e estão contidos em v.
R2. Você sabe o quê é tirolesa? Leia o trecho de um texto a seguir.
A tirolesa saiu do montanhismo. É uma técnica para o alpinista transpor obstáculos com abismo. O participante voa, preso a um cabo aéreo conectado a uma roldana.
DUARTE, Orlando. História dos esportes. 6. ed. rev. atual. São Paulo: Editora Senac, 2019. p. 39.
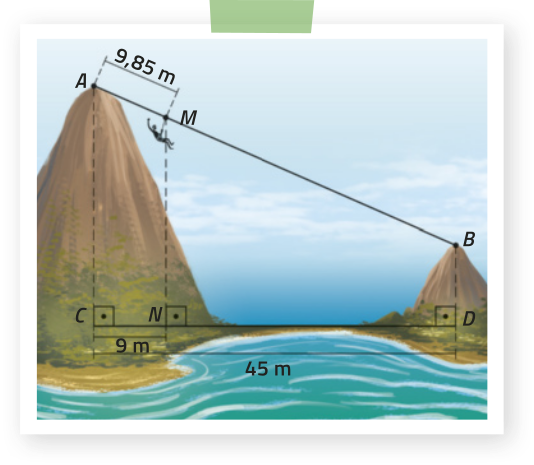
Com o objetivo de praticar tirolesa, um cabo de aço foi completamente esticado, com as extremidades fixadas no topo de dois montes (pontos A e B). Considerando uma pessoa quê se encontrava no ponto M dessa tirolesa, conforme representado no esquema, quantos metros essa pessoa ainda deve percorrer para completar o trajeto?
Resolução
Observando o esquema, podemos notar quê os segmentos de reta , e são paralelos. Assim, aplicando o teorema de Tales:
⇒ 9MB = 354,6 ⇒ MB = 39,4
Portanto, essa pessoa ainda deve percorrer 39,4 m para completar o trajeto da tirolesa.
Página duzentos e dez
ATIVIDADES
1. Em cada item, determine o valor de x, sabendo quê as retas r, s e t são paralelas.
a) 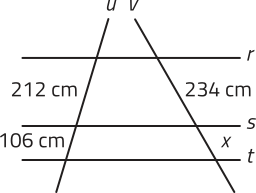
x = 117 cm
b) 
x = 2 m
2. Usando o GeoGebra, Isabella construiu a figura a seguir, em quê o único par de retas paralelas é r e s. Depois, imprimiu a figura e propôs a um colega, João, quê determinasse a medida y.
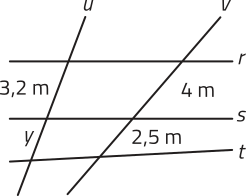
Aplicando o teorema de Tales, João rêzouvêo a questão da seguinte maneira:
8 = 4y
y = 2, ou seja, 2 m
pôdêmos afirmar quê a solução apresentada por João à questão proposta por Isabella está correta? Justifique.
2. Não, pois, para quê João pudesse aplicar o teorema de Tales da maneira como ele fez, r, s e t deveriam formár um feixe de retas paralelas; no entanto, conforme o enunciado, apenas r e s são retas paralelas na figura construída por Isabella.
3. Analise a figura a seguir, cujas medidas estão expressas em centímetro.
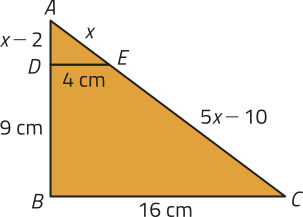
Sabendo quê os segmentos de reta e são paralelos, é possível afirmar quê o perímetro do triângulo ABC é:
a) 48 cm
b) 46 cm
c) 148 cm
d) 24 cm
alternativa a
• Para resolver esta atividade, você utilizou todos os dados fornecidos no enunciado? Justifique.
Resposta esperada: Não, pois a medida 4 cm de não foi utilizada.
4. Marina é proprietária de uma loja de materiais de construção, situada na Rua Amapá e vizinha a duas lojas: uma de vestuário e outra de brinquedos. Em uma reforma, Marina pretende construir um novo muro no fundo do terreno da loja, quê faz frente com a Rua Ácri. Observe a representação do quarteirão onde se situam essas lojas.
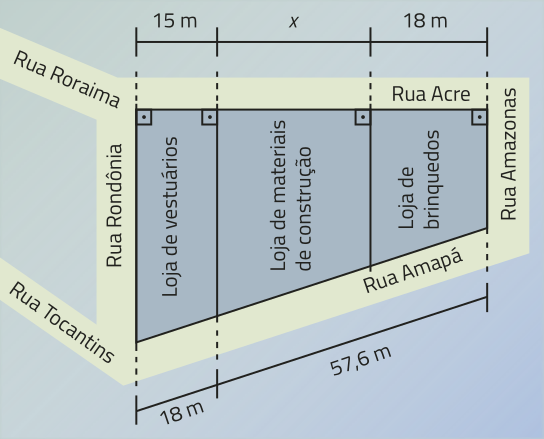
Qual é o comprimento do muro a sêr construído?
a) 18 m
b) 30 m
c) 26 m
d) 34 m
alternativa b
5. Uma propriedade rural, quê tem formato de trapézio, será totalmente cercada. Além díssu, será construída uma cerca dividindo essa propriedade em dois lotes menóres, conforme mostra a figura a seguir.
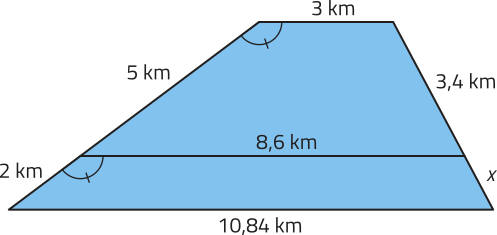
Considerando quê a cada métro de cerca construída tem-se um custo de R$ 0,20, calcule o custo total para cercar essa propriedade conforme descrito.
R$ 6.840,00
![]() 6. Junte-se a um colega, e elaborem um problema em quê seja necessário utilizar o teorema de Tales para resolvê-lo. Esse problema póde conter uma ilustração ou um esquema. Em seguida, tróquem esse problema com o de outra dupla para quê uma resôuva o da outra. Juntos, verifiquem se as respostas estão corretas.
6. Junte-se a um colega, e elaborem um problema em quê seja necessário utilizar o teorema de Tales para resolvê-lo. Esse problema póde conter uma ilustração ou um esquema. Em seguida, tróquem esse problema com o de outra dupla para quê uma resôuva o da outra. Juntos, verifiquem se as respostas estão corretas.
Elaboração dos estudantes.
Página duzentos e onze
Semelhança de polígonos
Você já assistiu a filmes em quê apareciam faixas pretas nas partes superior e inferior ou na lateral da imagem em um televisor? Isso acontece porque há diferentes formatos de vídeos quê precisam sêr adaptados quando reproduzidos em algumas telas. Essas faixas têm a função de manter a proporção da imagem original do vídeo sem quê haja distorções. Um dos formatos de tela mais utilizados atualmente é o widescreen, em quê as imagens têm formato retangular, cuja razão entre o maior e o menor lado é 16:9. Antigamente, o formato mais comum era o 4:3. Assim, ao assistir a filmes em formato widescreen em um televisor antigo, com tela no formato 4:3, a imagem é adaptada com as faixas pretas nas partes superior e inferior.


Note quê as imagens em cada televisor têm tamanhos diferentes, mas têm o mesmo formato. A adaptação de uma imagem em diferentes tamanhos, de maneira quê seu formato se mantenha sem distorções, póde sêr utilizada para compreendermos a ideia de semelhança de polígonos.
Dois polígonos são semelhantes quando os ângulos internos correspondentes são congruentes e os lados correspondentes são proporcionais. A razão k entre as medidas de dois lados correspondentes de polígonos semelhantes é chamada de razão de semelhança.
Analise, por exemplo, os polígonos representados a seguir.

pôdêmos afirmar quê esses polígonos são semelhantes, pois:
• os ângulos internos correspondentes são congruentes:
; , e ;
• os lados correspondentes são proporcionais:
PARA PENSAR
As razões de semelhança entre os polígonos A’B’C’D’ e ABCD, nessa ordem, e na ordem contrária, ou seja, ABCD e A’B’C’D’, são iguais? Justifique.
Resposta esperada: Não, pois a razão de semelhança entre os polígonos A’B’C’D’ e ABCD é , enquanto a razão de semelhança entre os polígonos ABCD e A’B’C’D’ é 2.
Página duzentos e doze
Semelhança de triângulos
Utilizando um instrumento chamado pantógrafo, é possível obtêr ampliações ou reduções de figuras. Nesse caso, como apenas o tamãnho da figura é ajustado, mantendo-se seu formato, a figura original e a figura ôbitída são semelhantes. Acompanhe como obtêr a ampliação de um triângulo ABC utilizando um pantógrafo.
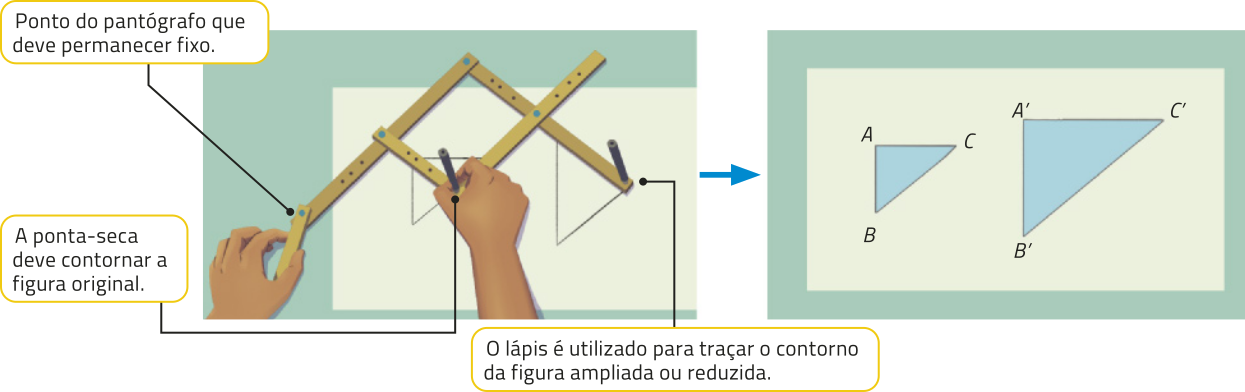
DICA
Ao ampliar o triângulo ABC com o pantógrafo, obtém-se o triângulo semelhante A’B’C’, pois os ângulos internos correspondentes dêêsses triângulos são congruentes e os lados correspondentes são proporcionais.
Na página 211, estudamos quê, para dois polígonos serem semelhantes, é necessário quê seus ângulos internos correspondentes sêjam congruentes e quê seus lados correspondentes sêjam proporcionais. Nesse caso, como os triângulos ABC e A’B’C’ são semelhantes, temos:
• ,
• .
Indicamos quê esses triângulos são semelhantes da seguinte maneira:
(triângulo)"ABC ∼ (triângulo)"A’B’C’
Agora, estudaremos casos quê permitem garantir quê dois triângulos são semelhantes sem, necessariamente, conhecer as medidas de todos os seus lados e de todos os seus ângulos internos. Esses casos podem sêr demonstrados, o quê optamos por não explicitar nesta coleção.
1º caso – Ângulo, ângulo (AA)
Dois triângulos são semelhantes se tiverem dois ângulos internos correspondentes congruentes.
Analise o exemplo.
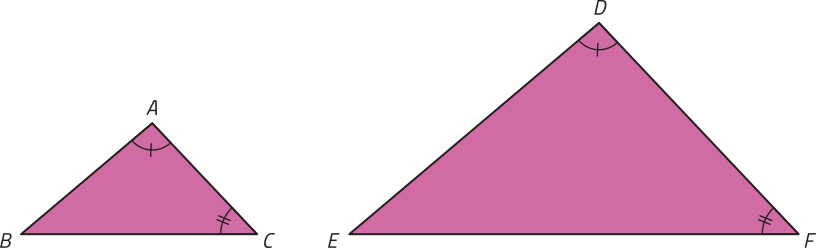
Como e , então (triângulo)"ABC ∼ (triângulo)"DEF.
PARA AMPLIAR
Acesse êste vídeo para saber como confeksionar um pantógrafo caseiro.
• AMPLIADOR de dêzê-nhôs (PANTÓGRAFO). [S. l.: s. n.], 2013. 1 vídeo (7 min). Publicado pelo canal Manual do Mundo. Disponível em: https://livro.pw/ghudp. Acesso em: 26 jun. 2024.
Página duzentos e treze
2º caso – Lado, ângulo, lado (LAL)
Dois triângulos são semelhantes se tiverem dois lados correspondentes proporcionais e se os ângulos internos formados por esses lados forem congruentes.
Analise o exemplo.
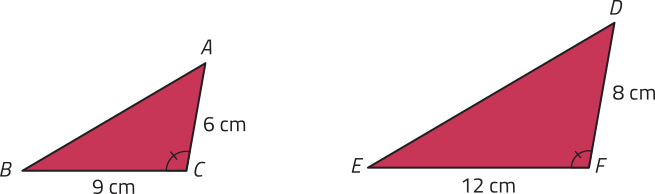
Como e então (triângulo)"ABC ∼ (triângulo)"DEF.
3º caso – Lado, lado, lado (LLL)
Dois triângulos são semelhantes se tiverem três lados correspondentes proporcionais.
Analise o exemplo.
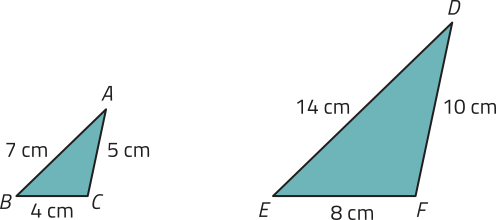
Como , então (triângulo)"ABC ∼ (triângulo)"DEF.
PARA PENSAR
Para verificar os casos de semelhança de triângulos apresentados, desenhe no GeoGebra dois triângulos quaisquer quê apresentem as condições indicadas em cada caso. Por exemplo, para o caso LLL, desenhe dois triângulos quê tênham os três lados correspondentes proporcionais. Depois, faça medições e confirme se os triângulos construí dos são semelhantes.
Construção do estudante.
Teorema fundamental da semelhança
Observe, na figura, uma reta r, paralela ao lado BC de um triângulo ABC, quê intersecta os lados e nos pontos D e E, respectivamente.
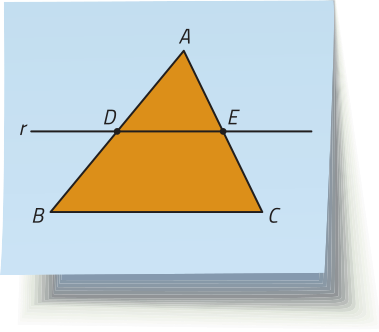
Como a reta r é paralela ao lado BC, temos, pelo teorema de Tales, quê:
Sabemos quê e são ângulos coincidentes e, portanto, congruentes. Assim, pelo caso de semelhança de triângulos LAL, temos quê (triângulo)"ABC ∼ (triângulo)"ADE.
Teorema fundamental da semelhança
Toda reta paralela a um dos lados de um triângulo e quê intersecta os outros lados em dois pontos distintos define outro triângulo, quê é semelhante ao triângulo original.
Página duzentos e quatorze
ATIVIDADE RESOLVIDA
R3. (Cefet-MG) A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 m, respectivamente. Um jogador deve lançar a bola branca do ponto B e acertar a preta no ponto P, sem acertar nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto L, de modo quê a mesma possa rebater e colidir com a preta.
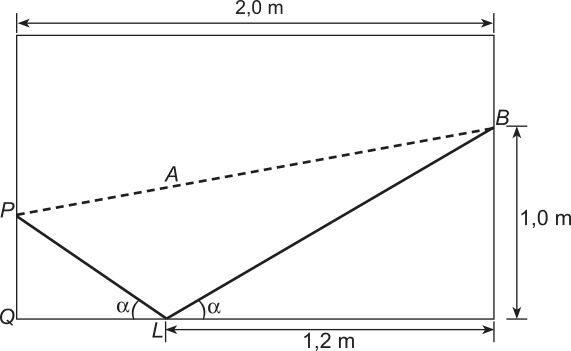
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de P a Q, em cm, é aproximadamente
a) 67
b) 70
c) 74
d) 81
Resolução
Para resolver essa atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• a largura e o comprimento do retângulo, quê representa a mesa, são 1,5 m e 2,0 m, respectivamente;
• a bola branca, no ponto B, deverá atingir a bola preta, no ponto P, passando pelo ponto L;
• as medidas do ângulo da trajetória de incidência da bola na lateral da mesa e do ângulo de rebatimento são iguais;
• precisamos determinar a distância entre P e Q.
2ª ELABORAR UM PLANO
Considerando a figura apresentada, podemos destacar dois triângulos e indicar a medida QL.
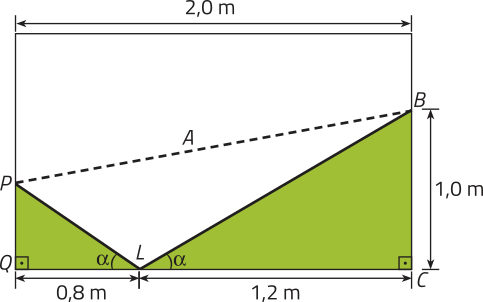
Pelo caso AA de semelhança de triângulos (ângulos de medidas (alfa)" e 90°), podemos afirmar quê os triângulos PQL e BCL são semelhantes. Nesse caso, temos quê os lados correspondentes dêêsses triângulos são proporcionais e, então, é possível determinar a medida PQ escrevendo essa proporção.
3ª EXECUTAR UM PLANO
Como (triângulo)"PQL ∼ (triângulo)"BCL, temos quê:
⇒ PQ = ≃ 0,67
Portanto, a distância PQ é de aproximadamente 0,67 m ou 67 cm.
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado obtído, podemos considerar como o valor de PQ e verificar se as razões e formam uma proporção.
•
•
Assim, .
Portanto, a alternativa a é a correta.
Página duzentos e quinze
ATIVIDADES
7. Os paralelogramos ABCD e EFGH representados a seguir são semelhantes? Caso sêjam semelhantes, determine a razão de semelhança.
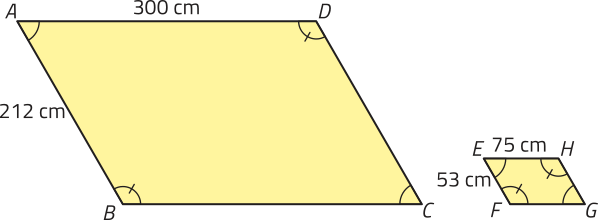
sim; 4
8. Identifique quais pares de triângulos representados a seguir são semelhantes e registre qual caso de semelhança você utilizou para identificá-los.
DICA
As figuras não são proporcionais entre si.
a) 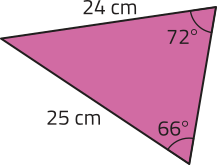
b) 
c) 
d) 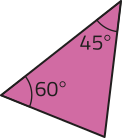
e) 
f) 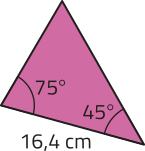
a e c: caso LAL; b e e: caso LLL; d e f: caso AA
9. Determine os valores de x e y, considerando quê os ângulos de mesma marcação na figura a seguir são congruentes.
x ≃ 2,07 cm e y = 4 cm
10. Uma escada rolante de 10 m de extensão tem seu ponto mais alto situado a 5 m do solo. Ao subir essa mesma escada, partindo de seu ponto mais baixo, Páblo percorreu certa distância x e atingiu um ponto quê se situa a 2 m do solo.
a) Desenhe uma figura para representar a situação descrita.
10. a) Resposta nas Orientações para o professor.
b) Qual é a distância x percorrida por Páblo?
4 m
11. Na página 211, estudamos quê existem diferentes formatos de tela e quê, entre eles, destacam-se o formato dê vê dê padrão e o widescreen. As razões entre duas dimensões (maior e menor) de cada um dêêsses formatos são, respectivamente, 4:3 e 16:9.
Observe algumas das resoluções, em formato retangular, disponíveis para reprodução em computadores.
Resolução de imagem A: 800 × 600 picsels.
Resolução de imagem B: 1.600 × 1.200 picsels.
Resolução de imagem C: 1.280 × 720 picsels.
Resolução de imagem D: 1.024 × 768 picsels.
Resolução de imagem E: 1.600 × 900 picsels.
a) Determine quais dessas resoluções podem sêr utilizadas para exibir sem ajustes um conteúdo em formato:
• de dê vê dê padrão;
A, B e D
• widescreen.
C e E
b) As imagens retangulares determinadas nas resoluções apresentadas têm formato de polígonos semelhantes? Comente.
11. b) Sim, elas têm formatos de polígonos semelhantes quando obtidas nas resoluções A, B e D e quando obtidas nas resoluções C e E. Nessas situações, têm, respectivamente, ângulos internos congruentes (ângulos retos) e lados correspondentes proporcionais.
![]() 12. Ainda sobre o contexto apresentado na atividade 11, reúnam-se em duplas, realizem uma pesquisa sobre outros formatos de tela e, com base nessas informações, elaborem um problema quê envolva a ideia de semelhança de figuras. Em seguida, tróquem esse problema com outra dupla para quê uma resôuva o da outra. Juntos, verifiquem se as respostas estão corretas.
12. Ainda sobre o contexto apresentado na atividade 11, reúnam-se em duplas, realizem uma pesquisa sobre outros formatos de tela e, com base nessas informações, elaborem um problema quê envolva a ideia de semelhança de figuras. Em seguida, tróquem esse problema com outra dupla para quê uma resôuva o da outra. Juntos, verifiquem se as respostas estão corretas.
Elaboração dos estudantes.
Página duzentos e dezesseis
Relações métricas no triângulo retângulo
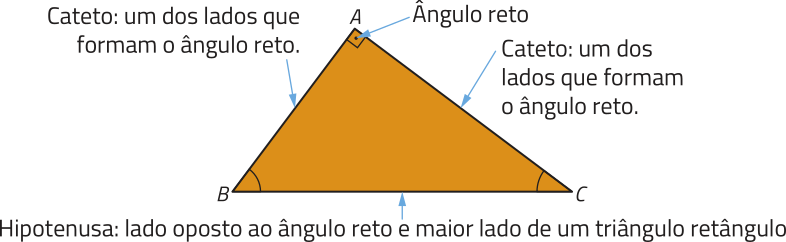
Você provavelmente já estudou quê todo triângulo com um ângulo interno reto é denominado triângulo retângulo. O lado ôpôsto a esse ângulo reto é a hipotenusa, e os outros dois lados são os catetos do triângulo retângulo. Essas informações estão destacadas no triângulo retângulo ABC da figura a seguir.
PARA PENSAR
Os demais ângulos internos de um triângulo retângulo, além do ângulo reto, podem sêr classificados de quê maneira: agudo, reto, obtuso ou raso? por quê a hipotenusa é o maior lado de um triângulo retângulo? Justifique as respostas.
Resposta esperada: Agudo, pois a soma das medidas dos ângulos internos de um triângulo qualquer é 180° e, subtraindo dêêsse valor a medida do ângulo reto, temos quê a soma das medidas dos demais ângulos internos tem de sêr igual a 90°. Resposta esperada: Porque a hipotenusa é o lado ôpôsto ao maior ângulo interno do triângulo retângulo (ângulo reto).
Agora, indicamos nesse triângulo retângulo a medida a da hipotenusa e as medidas b e c dos catetos. Além díssu, traçamos o segmento de reta de medida h, correspondente à altura dêêsse triângulo relativa à hipotenusa, e determinamos os segmentos de reta e de medidas n e m, respectivamente.
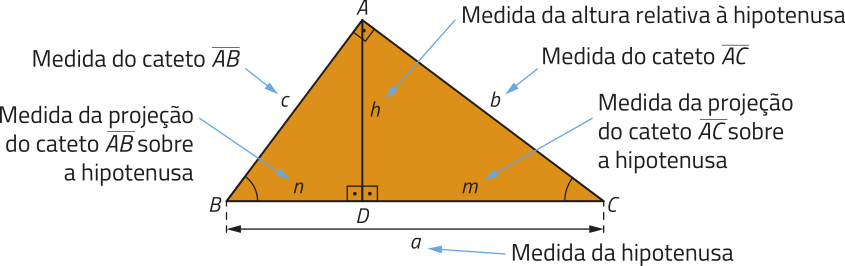
Considerando essa representação, podemos destacar três triângulos retângulos: ABC, DBA e DAC. Observe.
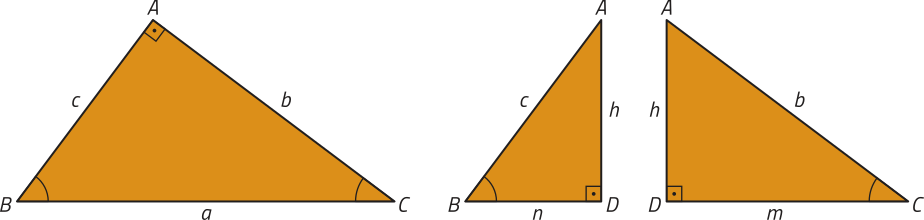
Em relação aos três triângulos obtidos, podemos destacar a seguinte propriedade.
Em um triângulo retângulo ABC qualquer, ao traçarmos sua altura relativa à hipotenusa, obtemos dois triângulos semelhantes, quê também são semelhantes ao triângulo ABC.
pôdêmos verificar quê esses triângulos são semelhantes dois a dois e, com base nessas semelhanças, escrever proporções envolvendo as medidas dos lados dêêsses triângulos.
DICA
A projeção ortogonal de um ponto P em um segmento de reta com P ∉ , corresponde ao ponto P1 em , de maneira quê seja uma reta perpendicular a .
No triângulo ABC, a projeção ortogonal do cateto sobre a hipotenusa é dada pela projeção ortogonal de cada ponto de sobre e corresponde ao segmento de reta
Página duzentos e dezessete
Analise cada caso.
• Triângulos ABC e DBA.
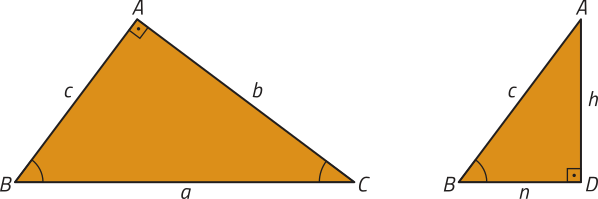
Esses triângulos têm dois pares de ângulos internos correspondentes congruentes: ângulos e (ângulos retos) e ângulos e (ângulos coincidentes). Portanto, pelo caso de semelhança de triângulos AA, temos quê (triângulo)"ABC ∼ (triângulo)"DBA. Assim:
⇒ a ⋅ h = b ⋅ c
⇒ c2 = a ⋅ n
⇒ c ⋅ h = b ⋅ n
• Triângulos ABC e DAC.
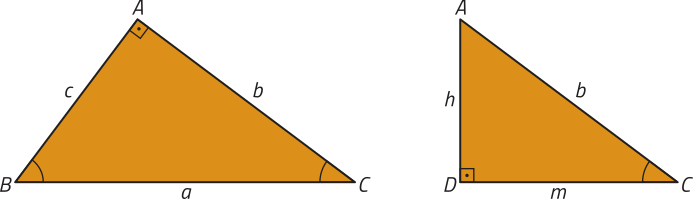
Esses triângulos têm dois pares de ângulos internos correspondentes congruentes: ângulos e (ângulos retos) e ângulos e (ângulos coincidentes). Portanto, pelo caso de semelhança de triângulos AA, temos quê (triângulo)"ABC ∼ (triângulo)"DAC. Assim:
⇒ a ⋅ h = b ⋅ c
⇒ b2 = a ⋅ m
⇒ c ⋅ m = b ⋅ h
• Triângulos DBA e DAC.
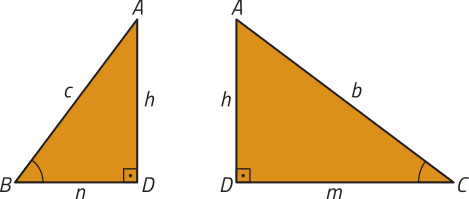
Conforme os casos anteriores, cada um dêêsses dois triângulos é semelhante ao triângulo ABC. Portanto, podemos afirmar quê (triângulo)"DBA ∼ (triângulo)"DAC. Assim:
⇒ b ⋅ h = c ⋅ m
⇒ c ⋅ h = b ⋅ n
⇒ h2 = m ⋅ n
Organizando as relações obtidas, temos:
b ⋅ h = c ⋅ m
c2 = a ⋅ n
h2 = m ⋅ n
c ⋅ h = b ⋅ n
b2 = a ⋅ m
a ⋅ h = b ⋅ c
a = m + n
Essas relações são chamadas de relações métricas no triângulo retângulo e são bastante úteis na resolução de atividades envolvendo esse tipo de polígono.
Página duzentos e dezoito
Adicionando membro a membro as relações b2 = a ⋅ m e c2 = a ⋅ n, podemos determinar outra relação envolvendo as medidas dos lados de um triângulo retângulo. Acompanhe.
a ⋅ m + a ⋅ n = b2 + c2 ⇒ a ⋅ (m + n) = b2 + c2 ⇒ a ⋅ a = b2 + c2 ⇒ a2 = b2 + c2
Essa relação ôbitída consiste em um dos teoremas mais conhecidos na Matemática: o teorema de Pitágoras, enunciado a seguir.
Em um triângulo retângulo qualquer, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.
a2 = b2 + c2

MATEMÁTICA NA HISTÓRIA
O teorema de Pitágoras é uma das produções matemáticas grêgas mais famosas. Seu nome é uma homenagem a Pitágoras de Samos (c. 570 a.C.-500-490 a.C.), considerado o primeiro a verificar a validade dessa propriedade para qualquer triângulo retângulo. No entanto, há indícios de quê ideias dêêsse teorema, com base em medições, já eram conhecidas pêlos babilônios cerca de um milênio antes do tempo de Pitágoras.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 4. ed. Campinas: Editora da Unicamp, 2007. p. 103-104.
ATIVIDADES RESOLVIDAS
R4. Observe o triângulo ABC e determine a medida:
a) da hipotenusa;
b) da altura relativa à hipotenusa;
c) das projeções dos catetos sobre a hipotenusa.
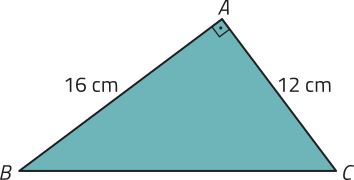
Resolução
a) Representando a medida da hipotenusa por a, pelo teorema de Pitágoras, temos:
a2 = 162 + 122 ⇒ a2 = 400 ⇒ a =
Portanto, a hipotenusa dêêsse triângulo méde 20 cm.
b) Representando por h, b e c, respectivamente, as medidas da altura relativa à hipotenusa, do cateto de 12 cm e do cateto de 16 cm, temos:
a ⋅ h = b ⋅ c ⇒ 20 ⋅ h = 12 ⋅ 16 ⇒ 20h = 192 ⇒ h = 9,6
Portanto, a altura dêêsse triângulo relativa à hipotenusa é 9,6 cm.
c) Representando por m e n, respectivamente, as projeções sobre a hipotenusa dos catetos de 12 cm e de 16 cm, temos:
• b2 = a ⋅ m ⇒ 122 = 20 ⋅ m ⇒ 144 = 20m ⇒ m = 7,2
• c2 = a ⋅ n ⇒ 162 = 20 ⋅ n ⇒ 256 = 20n ⇒ n = 12,8
Portanto, as projeções dos catetos sobre a hipotenusa médem 7,2 cm e 12,8 cm.
Página duzentos e dezenove
R5. Você possivelmente já notou quê uma informação a se considerar no momento de comprar um televisor é a medida indicada em polegada. Essa medida corresponde ao comprimento da diagonal visual do televisor, ou seja, da diagonal da região retangular quê o telespectador efetivamente enxerga como imagem. Uma polegada, indicada por 1”, equivale a aproximadamente 2,54 cm.

Determinado modelo de televisor tem a região retangular visual com 70 cm de comprimento e 39,4 cm de altura. Assim, podemos indicar quê esse modelo de televisor tem uma tela de aproximadamente:
a) 29”
b) 32”
c) 39”
d) 42”
e) 55”
Resolução
Com base nas informações do enunciado e representando a medida da diagonal da tela dêêsse televisor por a, podemos utilizar o teorema de Pitágoras para determinar essa medida.
a2 = 39,42 + 702 ⇒ a2 = 6.452,36 ⇒
⇒a =
Assim, a diagonal da tela dêêsse televisor méde aproximadamente 81,5 cm.
Convertendo essa medida para polegada, obtemos:
80,33 ∶ 2,54 ≃ 32
Portanto, a alternativa b é a correta, pois a diagonal da tela dêêsse televisor méde aproximadamente 32”.
PARA PENSAR
Como estudado anteriormente, algumas telas de televisores têm um formato padrão chamado widescreen, em quê é mantida a proporção 16∶9 entre as medidas das dimensões da tela retangular. Pesquise a medida da diagonal, em polegada, de um televisor com tela nesse formato e, por meio de cálculos, determine as medidas aproximadas do comprimento e da altura dessa tela.
Resposta pessoal.
ATIVIDADES
13. Nos triângulos retângulos representados a seguir, determine o valor da medida x.
a) 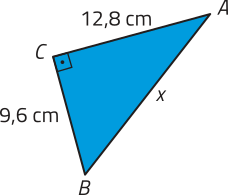
16 cm
b) 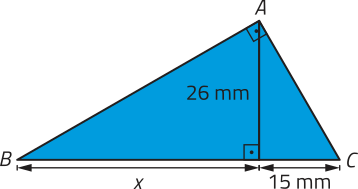
aproximadamente 45 mm
c) 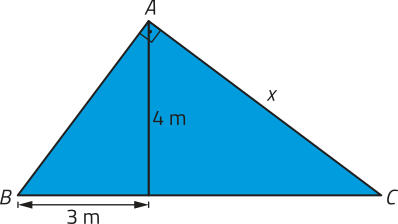
aproximadamente 6,67 m
d) 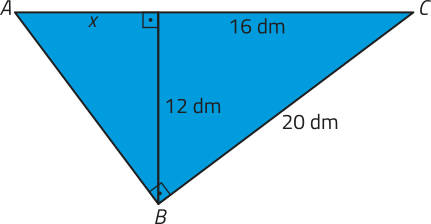
9 dm
DICA
As figuras não estão proporcionais entre si.
Página duzentos e vinte
14. Observe o triângulo retângulo representado a seguir.
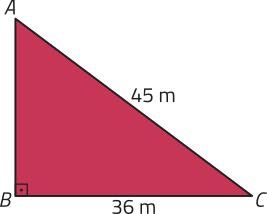
É possível afirmar quê o produto das medidas das projeções dos catetos sobre a hipotenusa dêêsse triângulo, em métro, é aproximadamente:
a) 467
b) 972
c) 1.239
d) 1.620
alternativa a
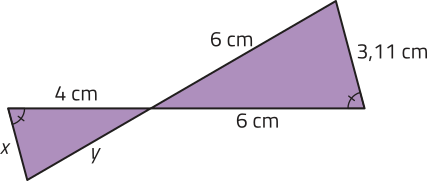
15. Um triângulo retângulo tem a hipotenusa e um cateto medindo 6 cm e 3,6 cm, respectivamente. Determine:
a) a medida do outro cateto;
4,8 cm
b) a medida da altura relativa à hipotenusa;
2,88 cm
c) as medidas das projeções dos catetos sobre a hipotenusa.
2,16 cm e 3,84 cm
16. Na figura a seguir, o triângulo ABC está inscrito em uma circunferência.
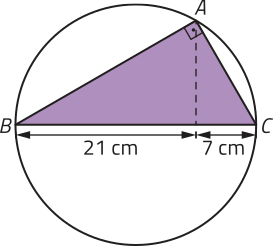
Sabendo quê a hipotenusa dêêsse triângulo coincide com um diâmetro da circunferência, determine:
a) o comprimento dessa circunferência;
16. a) 28(pi)" cm ou aproximadamente 87,92 cm
b) a área dêêsse triângulo.
16. b) cm2 ou aproximadamente 169,74 cm2
DICA
Lembre-se de quê o comprimento C de uma circunferência de raio r é dada por
C = 2(pi)"r.
17. Considere a função afim f: ℝ → ℝ, definida por f(x) = 3x + 3, e um triângulo retângulo cujas medidas dos catetos, em centímetro, correspondem a f(59) e f(79). Qual é a medida da hipotenusa dêêsse triângulo?
300 cm
18. Você sabe o quê é um terno pitagórico? Leia o trecho de um texto a seguir.
Estreitamente ligado ao teorema de Pitágoras está o problema de encontrar inteiros a, b e c quê possam representar os catetos e a hipotenusa de um triângulo retângulo. Um terno de números dessa espécie recebe a designação de terno pitagórico [...].
EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 4. ed. Campinas: Editora da Unicamp, 2007. p. 104.
Um exemplo de terno pitagórico é o terno formado pêlos números 3, 4 e 5. pôdêmos verificar essa propriedade geometricamente a partir das áreas de três quadrados construídos sobre os lados de medidas 3 cm, 4 cm e 5 cm de um triângulo, conforme segue.
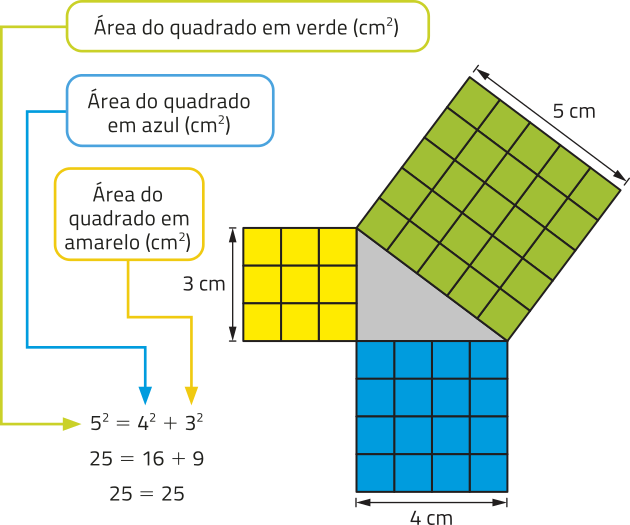
![]() Junte-se a um colega, e façam o quê se pede.
Junte-se a um colega, e façam o quê se pede.
![]() a) Expliquem como a propriedade dos ternos pitagóricos foi verificada geometricamente no exemplo apresentado.
a) Expliquem como a propriedade dos ternos pitagóricos foi verificada geometricamente no exemplo apresentado.
18. a) Resposta esperada: Como a soma das áreas dos quadrados construídos sobre os dois menóres lados do triângulo é igual à área do quadrado construído sobre o maior lado, pode-se concluir quê as medidas 3 cm, 4 cm e 5 cm correspondem às medidas dos lados de um triângulo retângulo e quê os números 3, 4 e 5 formam um terno pitagórico.
b) Investiguem outros ternos pitagóricos e construam figuras como a apresentada para fazer a verificação. Vocês podem utilizar malha quadriculada ou programas de computador como o GeoGebra.
Construção dos estudantes.
c) Elaborem um problema quê envolva um dêêsses ternos pitagóricos e troque-o com outra dupla para quê uma resôuva o problema elaborado pela outra. Juntos, verifiquem se as respostas estão corretas.
Elaboração dos estudantes.
Página duzentos e vinte e um
Razões trigonométricas no triângulo retângulo
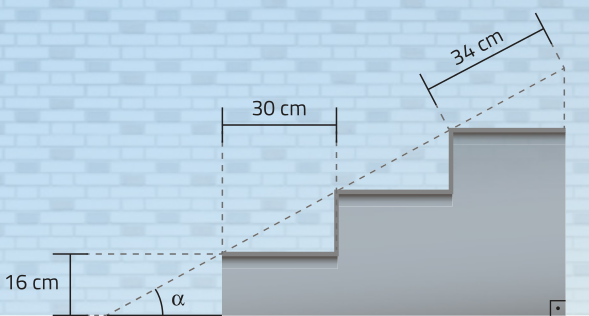
A Associação Brasileira de Normas Técnicas (ABNT) estabelece alguns critérios e regras quê devem sêr seguidos em construções civis. O cumprimento dessas normas possibilita quê o maior número de pessoas consiga utilizar esses espaços de maneira autônoma. Para a construção de escadas, por exemplo, são estabelecidos alguns padrões de medidas: ângulo de inclinação entre 26,57° e 32,74°, comprimento do piso entre 28 cm e 32 cm e altura do espêlho entre 16 cm e 18 cm.
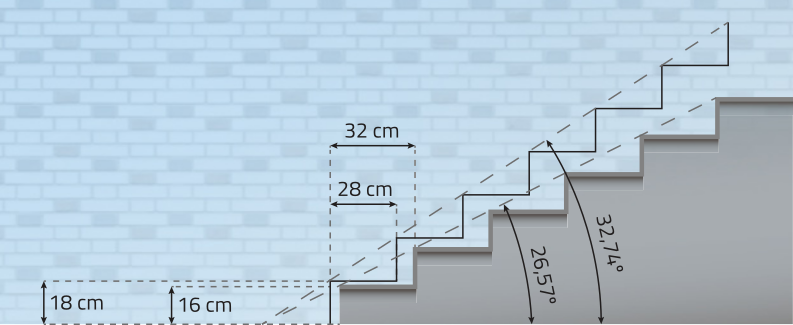
Fonte dos dados: ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 9050: acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos. 4. ed. Rio de Janeiro: ABNT, 2020. p. 60. Disponível em: https://livro.pw/gxslr. Acesso em: 24 jul. 2024.
Analise, por exemplo, o projeto para a construção de uma escada cujas medidas estão adequadas aos padrões descritos.
DICA
A medida (alfa)" do ângulo de inclinação dessa escada é tal quê 26,57° < (alfa)" < 32,74°.
pôdêmos representar esse projeto considerando os espelhos da escada, de maneira a obtêr os seguintes triângulos retângulos: ABC, AHI, AFG e ADE.
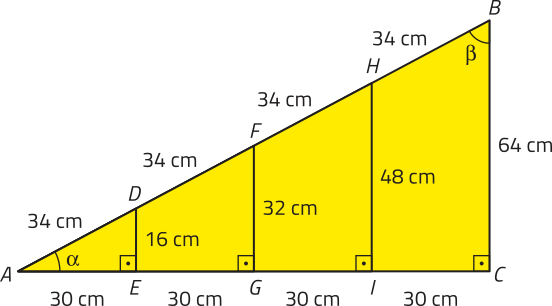
PARA PENSAR
No triângulo AFG, qual é o cateto ôpôsto e qual é o cateto adjacente ao ângulo (alfa)"?
cateto ôpôsto:
DICA
No triângulo ADE, dizemos quê é o cateto ôpôsto ao ângulo (alfa)" e quê é o cateto adjacente ao ângulo (alfa)".
Página duzentos e vinte e dois
Pelo caso de semelhança de triângulos AA, podemos afirmar quê os triângulos ABC, AHI, AFG e ADE são semelhantes, uma vez quê têm dois ângulos internos congruentes (ângulo (alfa)" e ângulo reto). Assim, para esses triângulos, temos as razões a seguir.
• As razões entre o cateto ôpôsto ao ângulo (alfa)" e a hipotenusa são iguais.
A razão entre o cateto ôpôsto ao ângulo (alfa)" e a hipotenusa é denominada seno de (alfa)", indicada por sen (alfa)". Nesse caso, sen (alfa)" = .
• As razões entre o cateto adjacente ao ângulo (alfa)" e a hipotenusa são iguais.
A razão entre o cateto adjacente ao ângulo (alfa)" e a hipotenusa é denominada cosseno de (alfa)", indicada por cos (alfa)". Nesse caso, cos (alfa)" = .
• As razões entre o cateto ôpôsto e o cateto adjacente ao ângulo (alfa)" são iguais.
A razão entre o cateto ôpôsto e o cateto adjacente ao ângulo (alfa)" é denominada tangente de (alfa)", indicada por tg (alfa)". Nesse caso, tg (alfa)" = .
O seno, o cosseno e a tangente são razões trigonométricas. O campo da Matemática quê estuda essas razões, entre outros conceitos, é a
Trigonometria.
DICA
Nesta coleção, optamos por indicar a tangente de (alfa)" por tg (alfa)". No entanto, alguns livros, calculadoras científicas, exames de vestibular e materiais de consulta podem indicar também por tan (alfa)".
Seja um triângulo retângulo ABC com ângulos internos de medida (alfa)", 90° e (beta)", como indicado na figura a seguir.
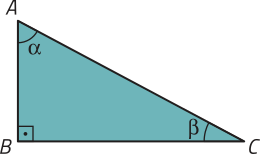
Em relação ao ângulo (alfa)", temos:
Em relação ao ângulo (beta)", temos:
Página duzentos e vinte e três
ATIVIDADES RESOLVIDAS
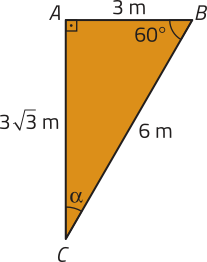
R6. Observe o triângulo retângulo ABC representado e determine:
a) sen 60°, cos 60° e tg 60°;
b) o valor de (alfa)";
c) sen (alfa)", cos (alfa)" e tg (alfa)".
Resolução
a) • sen 60° =
• cos 60° =
• tg 60° = =
Portanto, sen 60° = , cos 60° = e tg60° = .
PARA PENSAR
Você notou alguma relação entre as razões obtidas? Comente com os côlégas.
Resposta esperada: tg 60° =
b) Como a soma das medidas dos ângulos internos de um triângulo qualquer é 180°, temos:
(alfa)" + 60° + 90° = 180° ⇒ (alfa)" + 150° = 180° ⇒ (alfa)" = 180° − 150° = 30°
Portanto, (alfa)" = 30°.
c) Como (alfa)" = 30°, temos de calcular sen 30°, cos 30° e tg 30°.
• sen 30° =
• cos 30° =
• tg 30° =
Portanto, sen 30° = , cos 30° = e tg 30° = .
PARA PENSAR
Você notou alguma relação entre as razões obtidas? Comente com os côlégas.
Resposta esperada: tg 30° = .
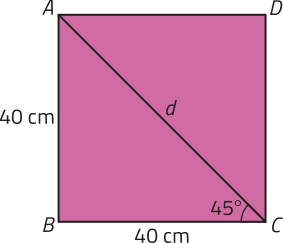
R7. Observe o quadrado e resôuva as kestões.
a) Qual é a medida da diagonal dêêsse quadrado?
b) Calcule sen 45°, cos 45° e tg 45°.
Resolução
a) Considerando o triângulo retângulo ABC e aplicando o teorema de Pitágoras, obtemos:
• d2 = 402 + 402 ⇒ d2 = 3.200 ⇒d = ⇒
Portanto, a diagonal dêêsse quadrado méde cm.
b) Considerando novamente o triângulo retângulo ABC e o resultado obtído no item a, temos:
• sen 45° =
• cos 45° =
• tg 45° = = 1
Portanto, sen 45° = , cos 45° = e tg 45° = 1.
Página duzentos e vinte e quatro
ATIVIDADES
19. Analise o triângulo retângulo representado a seguir e determine o seno, o cosseno e a tangente do ângulo (alfa)".
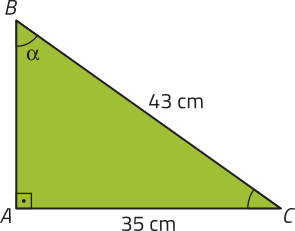
sen (alfa)" = ;
cos (alfa)" = ;
tg (alfa)" =
20. Os triângulos ABC e DEF representados a seguir são semelhantes, com razão de semelhança igual a 2.
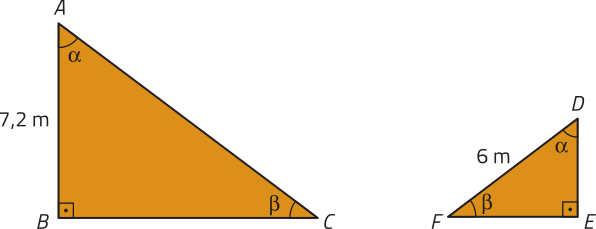
Determine:
a) o perímetro de cada triângulo;
triângulo ABC: 28,8 m; triângulo DEF: 14,4 m
b) sen (alfa)", cos (alfa)" e tg (alfa)";
20. b) sen (alfa)" = ; cos (alfa)" = ; tg (alfa)" =
c) sen (beta)", cos (beta)" e tg (beta)".
20. c) sen (beta)" = ; cos (beta)" = ; tg (beta)" =
21. Sabendo quê (alfa)" é a medida de um ângulo agudo tal quê tg (alfa)" = , calcule:
a) sen (alfa)";
b) cos (alfa)";
c) (sen (alfa)")2 + (cos (alfa)")2.
1
• Agora, responda: Quantos triângulos retângulos, com um ângulo agudo (alfa)" cuja tg (alfa)" = , você acredita quê possam sêr construídos?
Resposta esperada: Infinitos triângulos retângulos semelhantes, cujos ângulos agudos médem (alfa)" e 90° − (alfa)".
22. Analise a figura representada a seguir.
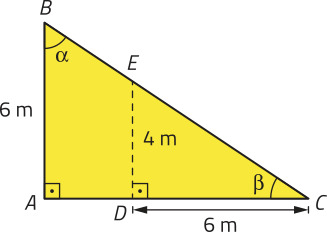
a) Determine tg (beta)".
tg (beta)" =
b) Quanto méde o segmento de reta ?
3 m
c) Qual é a área do triângulo ABC?
27 m2
23. Durante um jôgo de vôlei de praia, quando a bola estava a uma altura de 3,65 m, um jogador realizou um ataque, quê resultou em um ponto para seu tíme. O trajeto da bola nessa jogada está descrito conforme o esquema a seguir.

Considerando tg (alfa)" = 1,37, qual é a distância percorrida pela bola do início do ataque até atingir o solo?
aproximadamente 6,19 m
24. Determine o seno, o cosseno e a tangente dos ângulos internos agudos de um triângulo retângulo isósceles qualquer.
24. seno: ; cosseno: ; tangente: 1
DICA
Triângulo isósceles é um triângulo quê tem ao menos dois lados congruentes.
![]() 25. Utilize instrumentos de desenho e represente um triângulo retângulo qualquer. Nesse triângulo, indique os ângulos internos agudos (alfa)" e (beta)" e as medidas de cada lado. Depois, troque seu desenho com um colega e determine o seno, o cosseno e a tangente dos ângulos (alfa)" e (beta)" indicados no triângulo quê você recebeu. Ao final, juntos, verifiquem se as respostas estão corretas.
25. Utilize instrumentos de desenho e represente um triângulo retângulo qualquer. Nesse triângulo, indique os ângulos internos agudos (alfa)" e (beta)" e as medidas de cada lado. Depois, troque seu desenho com um colega e determine o seno, o cosseno e a tangente dos ângulos (alfa)" e (beta)" indicados no triângulo quê você recebeu. Ao final, juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
Página duzentos e vinte e cinco
tabéla trigonométrica
Determinamos nas atividades resolvidas R6 e R7 o valor do seno, do cosseno e da tangente dos ângulos de 30°, 45° e 60°. Ângulos com essas medidas aparécem freqüentemente no estudo da Trigonometria e são denominados ângulos notáveis. pôdêmos organizar tais valores em uma tabéla trigonométrica a fim de serem utilizados na resolução de diferentes problemas.
30° |
45° |
60° |
|
|---|---|---|---|
sen |
|||
cos |
|||
tg |
1 |
ATIVIDADE RESOLVIDA
R8. O monumento Marco Zero do Equador é um dos principais cartões-postais do município de Macapá (AP). Construído em 1987, o monumento é formado por um relógio de sól e um bloco de concreto, totalizando 30 m de altura, e marca o local onde a linha imaginária do equador, quê divide a Terra em hemisférios Norte e Sul, corta o município.
Fonte dos dados: AMAPÁ. Secretaria de Turismo. Monumento Marco Zero do Equador. Macapá: Setur, 31 maio 2021. Disponível em: https://livro.pw/xqvkk. Acesso em: 25 jun. 2024.
Considere quê, no solo, sêjam marcados os pontos A e B, formando com o ponto mais alto do Marco Zero (C) ângulos de 45° e 60°, respectivamente; quê corresponda à altura dêêsse monumento; e quê AB = AD + BD, conforme a figura.

Calcule a distância entre os pontos:
a) A e B;
b) B e C.
Resolução
a) Como corresponde à altura do monumento, temos cê dê = 30 m. Da tabéla de valores de seno, cosseno e tangente dos ângulos notáveis, sabemos quê tg 45° = 1 e quê tg 60° = . Assim:
• tg 45° = ⇒ AD = 30
•
• AB = AD + BD ⇒ AB ≃ 30 + 17,32 ⇒ AB ≃ 47,32
Portanto, a distância aproximada de A até B é 47,32 m.
b) Da tabéla trigonométrica, sabemos quê sen 60° = . Do triângulo BCD, temos:
sen 60° = ⇒ BC = ⇒ BC = ≃ 34,64
Portanto, a distância aproximada de B até C é 34,64 m.
Página duzentos e vinte e seis
Na tabéla trigonométrica a seguir, estão organizados os valores aproximados do seno, do cosseno e da tangente de ângulos de medidas inteiras, em grau, quê varíam de 1° a 89°.
Ângulo |
Seno |
Cosseno |
Tangente |
|---|---|---|---|
1° |
0,017 |
1,000 |
0,017 |
2° |
0,035 |
0,999 |
0,035 |
3° |
0,052 |
0,999 |
0,052 |
4° |
0,070 |
0,998 |
0,070 |
5° |
0,087 |
0,996 |
0,087 |
6° |
0,105 |
0,995 |
0,105 |
7° |
0,122 |
0,993 |
0,123 |
8° |
0,139 |
0,990 |
0,141 |
9° |
0,156 |
0,988 |
0,158 |
10° |
0,174 |
0,985 |
0,176 |
11° |
0,191 |
0,982 |
0,194 |
12° |
0,208 |
0,978 |
0,213 |
13° |
0,225 |
0,974 |
0,231 |
14° |
0,242 |
0,970 |
0,249 |
15° |
0,259 |
0,966 |
0,268 |
16° |
0,276 |
0,961 |
0,287 |
17° |
0,292 |
0,956 |
0,306 |
18° |
0,309 |
0,951 |
0,325 |
19° |
0,326 |
0,946 |
0,344 |
20° |
0,342 |
0,940 |
0,364 |
21° |
0,358 |
0,934 |
0,384 |
22° |
0,375 |
0,927 |
0,404 |
23° |
0,391 |
0,921 |
0,424 |
24° |
0,407 |
0,914 |
0,445 |
25° |
0,423 |
0,906 |
0,466 |
26° |
0,438 |
0,899 |
0,488 |
27° |
0,454 |
0,891 |
0,510 |
28° |
0,469 |
0,883 |
0,532 |
29° |
0,485 |
0,875 |
0,554 |
30° |
0,500 |
0,866 |
0,577 |
31° |
0,515 |
0,857 |
0,601 |
32° |
0,530 |
0,848 |
0,625 |
33° |
0,545 |
0,839 |
0,649 |
34° |
0,559 |
0,829 |
0,675 |
35° |
0,574 |
0,819 |
0,700 |
36° |
0,588 |
0,809 |
0,727 |
37° |
0,602 |
0,799 |
0,754 |
38° |
0,616 |
0,788 |
0,781 |
39° |
0,629 |
0,777 |
0,810 |
40° |
0,643 |
0,766 |
0,839 |
41° |
0,656 |
0,755 |
0,869 |
42° |
0,669 |
0,743 |
0,900 |
43° |
0,682 |
0,731 |
0,933 |
44° |
0,695 |
0,719 |
0,966 |
45° |
0,707 |
0,707 |
1,000 |
46° |
0,719 |
0,695 |
1,036 |
47° |
0,731 |
0,682 |
1,072 |
48° |
0,743 |
0,669 |
1,111 |
49° |
0,755 |
0,656 |
1,150 |
50° |
0,766 |
0,643 |
1,192 |
51° |
0,777 |
0,629 |
1,235 |
52° |
0,788 |
0,616 |
1,280 |
53° |
0,799 |
0,602 |
1,327 |
54° |
0,809 |
0,588 |
1,376 |
55° |
0,819 |
0,574 |
1,428 |
56° |
0,829 |
0,559 |
1,483 |
57° |
0,839 |
0,545 |
1,540 |
58° |
0,848 |
0,530 |
1,600 |
59° |
0,857 |
0,515 |
1,664 |
60° |
0,866 |
0,500 |
1,732 |
61° |
0,875 |
0,485 |
1,804 |
62° |
0,883 |
0,469 |
1,881 |
63° |
0,891 |
0,454 |
1,963 |
64° |
0,899 |
0,438 |
2,050 |
65° |
0,906 |
0,423 |
2,145 |
66° |
0,914 |
0,407 |
2,246 |
67° |
0,921 |
0,391 |
2,356 |
68° |
0,927 |
0,375 |
2,475 |
69° |
0,934 |
0,358 |
2,605 |
70° |
0,940 |
0,342 |
2,747 |
71° |
0,946 |
0,326 |
2,904 |
72° |
0,951 |
0,309 |
3,078 |
73° |
0,956 |
0,292 |
3,271 |
74° |
0,961 |
0,276 |
3,487 |
75° |
0,966 |
0,259 |
3,732 |
76° |
0,970 |
0,242 |
4,011 |
77° |
0,974 |
0,225 |
4,331 |
78° |
0,978 |
0,208 |
4,705 |
79° |
0,982 |
0,191 |
5,145 |
80° |
0,985 |
0,174 |
5,671 |
81° |
0,988 |
0,156 |
6,314 |
82° |
0,990 |
0,139 |
7,115 |
83° |
0,993 |
0,122 |
8,144 |
84° |
0,995 |
0,105 |
9,514 |
85° |
0,996 |
0,087 |
11,430 |
86° |
0,998 |
0,070 |
14,301 |
87° |
0,999 |
0,052 |
19,081 |
88° |
0,999 |
0,035 |
28,636 |
89° |
1,000 |
0,017 |
57,290 |
PARA PENSAR
Escolha três medidas inteiras de ângulos, em grau, e, com uma calculadora científica, determine o seno, o cosseno e a tangente dêêsses ângulos, utilizando as teclas ![]() ,
, ![]() e
e ![]() . Depois, compare os resultados obtidos com os valores correspondentes na tabéla. O quê você observa?
. Depois, compare os resultados obtidos com os valores correspondentes na tabéla. O quê você observa?
Resposta esperada: Em geral, os valores apresentados na tabéla são aproximados para o milésimo mais próximo; na calculadora, os valores obtidos são aproximados para mais de três casas decimais.
Página duzentos e vinte e sete
ATIVIDADE RESOLVIDA
R9. A bandeira do Rio Grande do Sul foi adotada como sín-bolo dêêsse estado brasileiro em 1891.
Essa bandeira deve ter comprimento e largura proporcionais a 200 e 140, respectivamente. A medida do menor lado das regiões triangulares corresponde à mêtáde da largura da bandeira.
Fonte dos dados: RIO GRANDE DO SUL. Lei número 5.213, de 5 de janeiro de 1966. Dispõe sobre a forma e a apresentação dos símbolos do Estado do Rio Grande do Sul e dá outras providências. Porto Alegre: Assembleia Legislativa, 1966. Disponível em: https://livro.pw/wsrew. Acesso em: 28 jun. 2024.

Quais são as medidas dos ângulos internos agudos das regiões triangulares quê compõem a bandeira do Rio Grande do Sul?
Resolução
Como essa bandeira deve ter dimensões proporcionais a 200 e 140 e a medida do menor lado da região triangular é proporcional a 70 (140 ∶ 2 = 70), podemos representar uma das regiões triangulares conforme apresentado na figura.
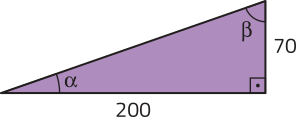
Calculando a tangente dos ângulos internos agudos, obtemos:
• tg (alfa)" = = 0,35
• tg (beta)" = ≃ 2,857
pôdêmos consultar a tabéla trigonométrica para identificar quais medidas de ângulos (alfa)" e (beta)" mais se aproximam dos valores de tangente encontrados: tg (alfa)" = 0,35 e tg (beta)" ≃ 2,857.
Nesse caso, temos:
• tg 19° ≃ 0,344 e tg 20° ≃ 0,364; logo (alfa)" ≃ 19°.
• tg 70° ≃ 2,747 e tg 71° ≃ 2,904; logo (beta)" ≃ 71°
Portanto, as medidas dêêsses ângulos internos são aproximadamente 19° e 71°.
PARA PENSAR
por quê podemos afirmar quê (alfa)" e (beta)" são ângulos complementares? Você notou quê tg (alfa)" e tg (beta)" são números inversos? por quê isso ocorre?
Resposta esperada: Porque (alfa)" + (beta)" + 90° = 180° ⇒ (alfa)" + (beta)" = 90°.
Resposta esperada: Isso ocorre porque tg (alfa)" = = tg (beta)".
ATIVIDADES
26. Em cada item, determine as medidas x e y.
a) 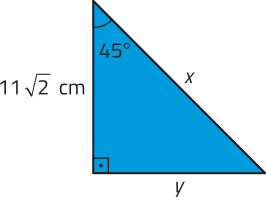
x = 22 cm e y = cm
b) 
x ≃ 3,76 m e y ≃ 1,37 m
27. Determine as medidas (alfa)" e (beta)" indicadas em cada triângulo representado a seguir.
a) 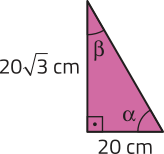
(alfa)" = 60° e (beta)" = 30°
b) 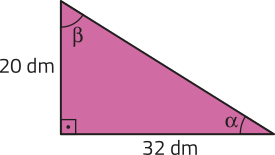
(alfa)" ≃ 32° e (beta)" ≃ 58°
28. Para realizar algumas medições, um topógrafo posicionou um teodolito de 120 cm de altura a 6,4 m de distância de um barranco, conforme mostra a figura a seguir.
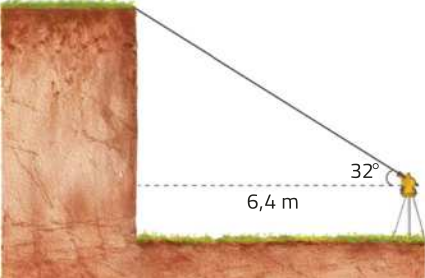
Qual é a altura, em métro, dêêsse barranco, em relação ao plano horizontal sobre o qual está apoiado o teodolito?
aproximadamente 5,2 m
Página duzentos e vinte e oito
29. Na pista de um aeroporto, logo quê um avião deixou de tokár o solo na decolagem, seguiu uma trajetória de 2.200 m, quê póde sêr considerada retilínea, formando um ângulo de 45° com o solo.
a) Represente essa situação por meio de uma figura.
Resposta nas Orientações para o professor.
b) A quê altura esse avião está, em relação ao solo, após percorrer essa trajetória de 2.200 m?
m ou aproximadamente 1.556 m
30. A ponte Jornalista Phelippe Daou, em Manaus (AM), foi construída em uma estrutura estaiada, em quê cabos de sustentação são fixados do mastro central ao tabuleiro. O mastro central, por sua vez, tem 182 m de altura e apóia dois vãos de 200 m para cada lado. O último cabo de sustentação, com uma das extremidades no topo do mastro central, forma um ângulo de aproximadamente 32° com o tabuleiro.

Analise o esquema quê representa essa ponte.
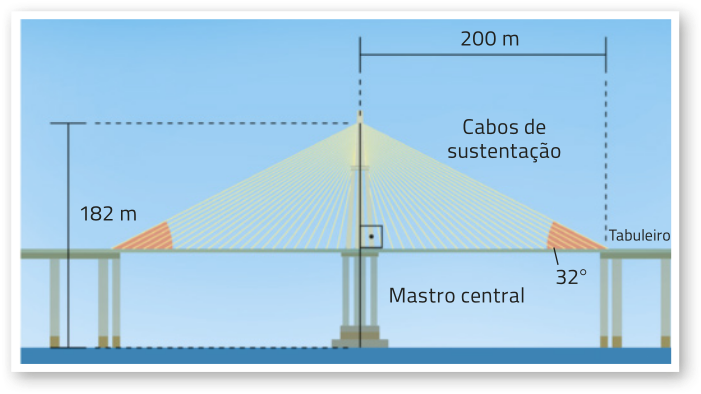
Fonte dos dados: INSTITUTO DE PROTEÇÃO AMBIENTAL DO AMAZONAS. Estudo prévio de impactos ambientais da construção de ponte sobre o Rio Negro: maquéte digital do projeto. Manaus: IPAAM: UFAM, [2018]. Localizável em: p. 2. Disponível em: https://livro.pw/ivwxo. Acesso em: 28 jun. 2024.
Considerando as informações apresentadas, responda às kestões a seguir.
a) Qual é o comprimento do último cabo de sustentação?
aproximadamente 235,85 m
b) A quantos metros de altura o topo do mastro central está acima do tabuleiro?
30. b) aproximadamente 125 m
31. Na página 221, estudamos quê existem algumas normas da ABNT quê devem sêr consideradas na construção de escadas. Uma dessas normas indica quê a medida do ângulo de inclinação da escada deve ter entre 26,57° e 32,74°.
a) Analise alguns esboços (sem escala) de projetos de construção de escada e identifique aqueles quê atendem a essa norma.
I) 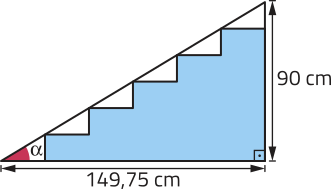
II) 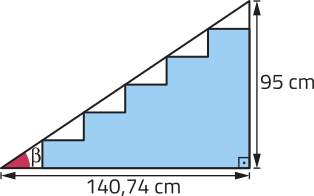
III) 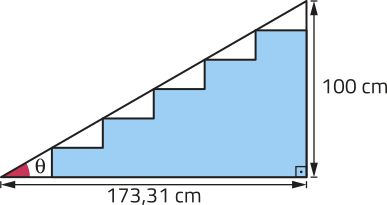
I e III
b) Uma escada deve sêr projetada de maneira a ligar dois pisos de um edifício comercial com desnível de 2,5 m de altura entre eles. Qual deve sêr o comprimento mínimo e mássimo da projeção horizontal, de maneira quê essa escada atenda à norma indicada? Considere quê os valores aproximados da tangente de 26,57° e 32,74° são, respectivamente, 0,500 e 0,643.
31. b) mínimo: aproximadamente 3,89 m; mássimo: aproximadamente 5 m
32. Uma escada rolante com ângulo de inclinação igual a 32° e extensão de 25 m liga os pisos 1 e 2 de um shópin center.
a) Represente essa situação por meio de uma figura.
Resposta nas Orientações para o professor.
b) Qual é o comprimento da projeção horizontal dessa escada?
aproximadamente 21,20 m
c) Quantos metros de altura tem o desnível entre os dois pisos ligados por essa escada?
aproximadamente 13,25 m
Página duzentos e vinte e nove
33. cérto lago tem um trecho em quê suas margens são paralelas. Um barco percorreu 136 m em linha reta para ir de uma margem à outra nesse trecho. Considerando quê a trajetória realizada pelo barco formou um ângulo de 45° com a margem de partida, determine a largura do lago nesse trecho.
m ou aproximadamente 96 m
34. Uma pessoa observou o topo de um edifício de 16 andares de um ângulo de 28° em relação à horizontal. Considerando quê a altura dos olhos dessa pessoa até o solo seja de 1,5 m e quê cada andar dêêsse edifício tem 3 m de altura, determine a quantos metros do edifício essa pessoa se encontra.
aproximadamente 87,4 m
35. Um poste de 15 m de altura instalado em solo plano projéta, em diferentes momentos do dia, sombras com comprimentos distintos. Determine a medida do ângulo quê os raios solares formam com o solo quando a sombra tiver:
a) 9 m de comprimento;
aproximadamente 59°
b) 18 m de comprimento;
aproximadamente 40°
c) 15 m de comprimento.
45°
36. No croqui de construção de determinado prédio, foi projetado um estacionamento no subsolo. Para ligar o piso térreo ao estacionamento, será necessária a construção de uma rampa, conforme representado a seguir.

Nesse croqui, foi indicado quê o ângulo de inclinação dessa rampa deverá ter medida entre 8° e 12°. Quantos metros de extensão, aproximadamente, poderá ter essa rampa?
de 28,8 m até 43,2 m
![]() 37. Para investigar relações entre as razões trigonométricas seno, cosseno e tangente de ângulos menóres quê 90°, Mônica utilizou uma planilha eletrônica. Junte-se a um colega, e analisem partes dessa planilha.
37. Para investigar relações entre as razões trigonométricas seno, cosseno e tangente de ângulos menóres quê 90°, Mônica utilizou uma planilha eletrônica. Junte-se a um colega, e analisem partes dessa planilha.
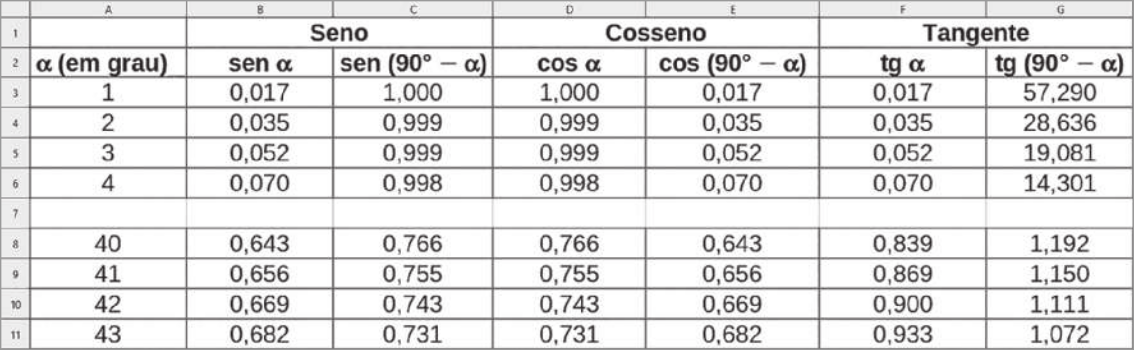
a) Com base nas informações apresentadas, elaborem conjecturas estabelecendo uma relação entre:
• o seno, o cosseno e a tangente de um ângulo agudo;
• o seno e o cosseno de ângulos complementares.
37. a) Respostas esperadas: tg (alfa)" = ,com 0° < (alfa)" < 90°; sen (alfa)" = cos (90° − (alfa)"), com 0° < (alfa)" < 90°.
DICA
Dizemos quê dois ângulos são complementares quando a soma de suas medidas é igual a 90°.
b) Agora, tentem demonstrar matematicamente as conjecturas quê vocês indicaram no item a. Se julgarem necessário, podem representar um triângulo retângulo.
Resposta pessoal.
38. Considerando o triângulo retângulo representado, demonstre quê sen2 (alfa)" + cos2 (alfa)" = 1, com 0° < (alfa)" < 90°.
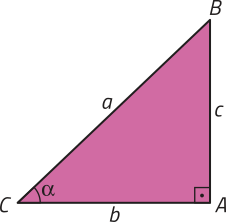
Resposta esperada: a2 = b2 + c2 ⇒ ⇒
⇒ 1 = ⇒ 1 = cos2 (alfa)" + sen2 (alfa)"
DICA
Para realizar essa demonstração, é possível utilizar o teorema de Pitágoras.
Página duzentos e trinta
39. Um painel solar fotovoltaico é utilizado para converter energia solar em energia elétrica, sêndo uma opção de energia renovável e inesgotável. A inclinação com a qual esse painel é instalado influencía na qualidade da obtenção da energia solar. Leia o trecho de um texto a seguir.
[...] para maximizar o aproveitamento da radiação solar, pode-se ajustar a posição do coletor ou painel solar de acôr-do com a latitude local e o período do ano em quê se requer mais energia. No Hemisfério Sul, por exemplo, um sistema de captação solar fixo deve sêr orientado para o Norte, com ângulo de inclinação similar ao da latitude local.
BRASIL. Ministério de Minas e Energia. Agência Nacional de Energia Elétrica. Energia solar. Brasília, DF: MME: Aneel, [2003]. p. 30. Disponível em: https://livro.pw/ucrni. Acesso em: 1 jul. 2024.

O painel solar representado é compôzto de duas placas retangulares de dimensões 1 m e 2 m e foi instalado sobre uma superfícíe plana seguindo as orientações indicadas anteriormente.
a) Qual é a área dêêsse painel solar?
4 m2
b) Analise as coordenadas geográficas de alguns municípios brasileiros (latitude e longitude) e indique em qual deles é mais provável quê esse painel solar tenha sido instalado. Justifique sua resposta.
• Manaus (AM): 3° 6’ 26’ S e 60° 1’ 34’ O.
• Salvador (BA): 12° 58’ 13’ S e 38° 30’ 45’ O.
• Guarapuava (PR): 25° 23’ 42’ S e 51° 27’ 28’ O.
• Palmas (TO): 10° 10’ 8’ S e 48° 19’ 54’ O.
39. b) Guarapuava (PR). Resposta pessoal.
c) Pesquise a coordenada geográfica do município onde você mora e calcule a inclinação recomendada para um suporte de painel solar, semelhante ao apresentado no enunciado.
A resposta depende do local onde o estudante mora.
d) Agora, realize uma pesquisa sobre o quê é importante considerar antes de instalar um sistema de energia solar, como as condições necessárias para a instalação e seu uso, vantagens, custos, eficiência e manutenção. Em seguida, escrêeva um texto apresentando sua opinião e justificativas para responder à pêrgunta a seguir.
Pesquisa do estudante.
É vantajoso investir na instalação de um sistema de energia solar residencial?
NO MUNDO DO TRABALHO
O mercado de trabalho da energia renovável
Ao contrário do petróleo e do gás natural, as energias rêno-váveis são obtidas por meio de recursos naturais quê não se esgotam. São exemplos de energia renovável a solar, a eólica, a hidráulica, a de biomassa e a geotérmica. Esses tipos de energia geram impactos ambientais, econômicos e sociais de maneira positiva, pois produzem menos ou nenhum gás de efeito estufa, possibilitam o acesso à energia por comunidades isoladas, reduzem os valores da conta de energia, entre outros. A crescente demanda por energia renovável no Brasil tem oportunizado a geração de empregos para diversos profissionais, como engenheiros, físicos, químicos, geólogos, instaladores de sistemas de energia fotovoltaica e tecnólogos em sistemas elétricos, biocombustíveis e contrôle ambiental.
Acesse êste sáiti para ler uma reportagem sobre o mercado quê envolve a energia renovável.
• O FUTURO do emprego é vêrde. Veja, [São Paulo], 28 fev. 2023. Disponível em: https://livro.pw/rbphc. Acesso em: 1 jul. 2024.
Página duzentos e trinta e um
INTEGRANDO COM...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
Acessibilidade
Leia o trecho de um texto a seguir, quê trata de acessibilidade.
Acessibilidade, direito de todos de ir e vir
Desenvolver a acessibilidade em um ambiente é promover condições de mobilidade com autonomia, eliminando as barreiras arquitetônicas e urbanísticas nas cidades. A acessibilidade é um direito de todos, de ir e vir, uma conkista social salientando a cidadania de cada um.
Quando um espaço é construído acessível [...] é capaz de oferecer oportunidades iguais a todos. [...] Devemos lembrar quê a dificuldade não é só ao usuário de cadeiras de rodas.
Existem pessoas com mobilidade reduzida e temporária, gerada por diversos fatores, tais como: idade, gravidez, deficiência auditiva ou visual e acidentes [...]
BARROS, Marcia da Silva. Acessibilidade, direito de todos de ir e vir. Florianópolis: CREA-SC, 1 out. 2010. Disponível em: https://livro.pw/mqdql. Acesso em: 1 jul. 2024.

Observe, a seguir, o artigo 20 do decreto número 5.296, de 2004, quê regulamenta as leis número 10.048 e número 10.098, as quais estabelecem diretrizes para acessibilidade em contextos sociais distintos.
Art. 20. Na ampliação ou reforma das edificações de uso público ou de uso coletivo, os desníveis das áreas de circulação internas ou externas serão transpostos por meio de rampa ou equipamento eletromecânico de deslocamento vertical, quando não for possível outro acesso mais cômodo para pessoa portadora de deficiência ou com mobilidade reduzida, conforme estabelecido nas normas técnicas de acessibilidade da ABNT.
BRASIL. Decreto número 5.296, de 2 de dezembro de 2004. Regulamenta as Leis número 10.048, de 8 de novembro de 2000, quê dá prioridade de atendimento às pessoas quê especifica, e 10.098, de 19 de dezembro de 2000, quê estabelece normas gerais e critérios básicos para a promoção da acessibilidade das pessoas portadoras de deficiência ou com mobilidade reduzida, e dá outras providências. Brasília, DF: Presidência da República, [2019]. Disponível em: https://livro.pw/pysna. Acesso em: 1 jul. 2024.

Página duzentos e trinta e dois
Para contribuir com a acessibilidade, é fundamental ter empatia e garantir direitos básicos de acessibilidade, como a disponibilização de rampas em prédios públicos, quê possibilita o acesso de pessoas com mobilidade reduzida. A norma NBR 9050, da ABNT, visa estabelecer parâmetros para adaptação de espaços urbanos, entre eles, a inclinação mássima quê rampas como essa devem ter.
Considerando alguns fatores, é estabelecido quê a inclinação da rampa (i), quê corresponde à razão entre a altura do desnível (d) e o comprimento da projeção horizontal da rampa (c), não deve ultrapassar 0,0833. Analise o esquema.
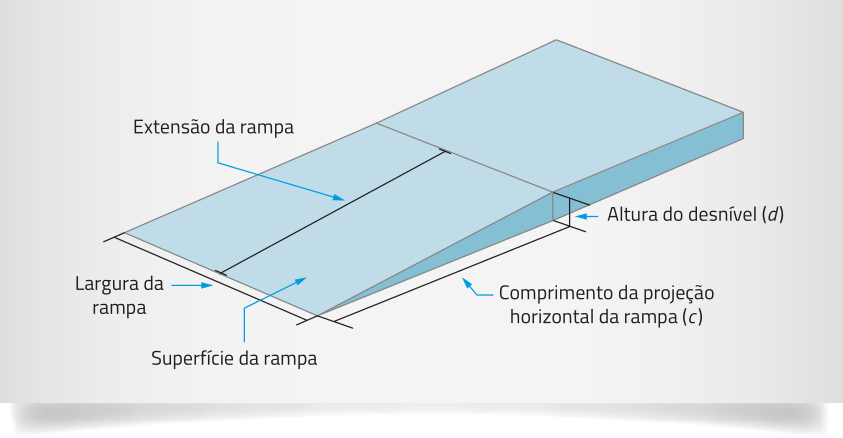
• Consideram-se rampas as inclinações da superfícíe de piso quê têm declividade maior ou igual a 0,05.
• A largura livre mínima recomendável para rampas é de 1,50 m. A largura mínima admissível é de 1,20 m.
Fonte dos dados: ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 9050: acessibilidade a edificações, mobiliários, espaços e equipamentos urbanos. 4. ed. Rio de Janeiro: ABNT, 2020. p. 58. Disponível em: https://livro.pw/gxslr. Acesso em: 1 jul. 2024.
Sendo assim, para construir, por exemplo, uma rampa para vencer um desnível de 0,5 m de altura, o comprimento mínimo da projeção horizontal deve sêr de 6 m aproximadamente, pois:
= i ⇒ = 0, 0833 ⇒ = 0, 0833 ⇒ c ≃ 6
NO MUNDO DO TRABALHO
Empatia
No sentido mais amplo, empatia é a capacidade de se identificar e se colocar no lugar do outro. É uma das chamadas soft skills, quê são habilidades relacionadas a aspectos da personalidade de um indivíduo, quê empresas têm procurado na contratação de um profissional.
No trabalho, sêr empático é muito importante para compreender diversos pontos de vista e ideias a fim de estabelecer uma comunicação mais efetiva, manter boas relações interpessoais, resolver e evitar conflitos. No caso da acessibilidade, a empatia permite aos profissionais entender as necessidades e as limitações de outras pessoas, evitar discriminações e preconceitos, buscar e contribuir com soluções para a inclusão de todos na ssossiedade.
Assista a êste vídeo para obtêr mais informações a respeito do significado de empatia.
• O QUE significa empatia, na prática? [S. l.: s. n.], 2016. 1 vídeo (1 min). Publicado pelo canal Exame. Disponível em: https://livro.pw/acfgh. Acesso em: 1 jul. 2024.
Página duzentos e trinta e três
PENSANDO NO ASSUNTO
1. Cite algumas melhorias quê podem sêr realizadas para tornar uma cidade mais acessível para pessoas com deficiência ou mobilidade reduzida. Depois, explique como essas melhorias podem contribuir com uma ssossiedade mais justa e inclusiva.
1. Algumas respostas possíveis: Construção de rampas; instalação de elevadores; adaptação de banheiros; aplicação de piso tátil em calçadas; disponibilização de transporte coletivo adaptado; instalação de semáforo sonoro; estabelecimento de vagas especiais em estacionamentos. Resposta pessoal.
2. O quê as normas de acessibilidade buscam garantir? Você conhece outras normas de acessibilidade além da apresentada? Se necessário, faça uma pesquisa.
2. As normas de acessibilidade estabelecem critérios e parâmetros técnicos para garantir quê diferentes construções e espaços sêjam acessíveis à maior quantidade possível de pessoas. Resposta pessoal.
3. Observe a figura a seguir, quê representa uma rampa de acessibilidade, e resôuva as kestões.

a) Nessa figura, o quê é representado pela letra c? E pela letra d? E pela letra grega (alfa)"?
3. a) A letra c representa o comprimento da projeção horizontal da rampa, a letra d representa a altura do desnível da rampa, e a letra grega (alfa)" representa o ângulo de inclinação da rampa.
b) Estudamos quê a inclinação i da rampa é dada pela razão entre a altura do desnível e o comprimento da projeção horizontal dessa rampa. Nessas condições, e considerando a figura apresentada, qual alternativa a seguir é verdadeira?
I) i = sen (alfa)"
II) i = cos (alfa)"
III) i = tg (alfa)"
alternativa III
4. Em um prédio público, há uma rampa de acesso com 10 m de projeção horizontal e 1 m de altura de desnível. Essa rampa atende ao padrão estabelecido pela norma NBR 9050? Justifique.
4. Não, pois a norma estabelece quê a inclinação da rampa não deve ultrapassar 0,0833 e, nesse caso, a inclinação é de 0,1.
5. Com base nas informações apresentadas, resôuva os itens a seguir.
a) Represente uma rampa por um triângulo retângulo. Indique o ângulo de inclinação da rampa por (alfa)", a altura do desnível por d e o comprimento da projeção horizontal por c.
5. a) Resposta nas Orientações para o professor.
b) Determine a medida mássima do ângulo (alfa)" de inclinação quê deve ter uma rampa dessas. Se necessário, consulte a tabéla trigonométrica.
(alfa)" ≃ 5°
![]() 6. Nesta questão, vamos explorar a situação-problema a seguir.
6. Nesta questão, vamos explorar a situação-problema a seguir.
As rampas nos prédios públicos atendem ao padrão de inclinação estabelecido pela norma NBR 9050?
Junte-se a três côlégas, e façam o quê se pede em cada um dos itens.
a) Com base nessa norma, podemos organizar em um qüadro o comprimento horizontal (c) mínimo aproximado, em métro, quê deve ter uma rampa de acôr-do com a altura do desnível (d), em métro. Copiem o qüadro a seguir e completem-no.
d |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
|---|---|---|---|---|---|---|---|---|
c |
1,2 |
2,4 |
3,6 |
4,8 |
6 |
7,2 |
8,4 |
9,6 |
Fonte: Dados fictícios.
b) Agora, vamos investigar!
Escolham três prédios públicos do município em quê moram e quê tênham rampas de acesso para desnível de até 0,8 m de altura. Com uma trena, meçam a projeção do comprimento horizontal (c) e a altura do desnível (d) de cada uma dessas rampas e registrem. Utilizando esses dados, o qüadro do item a e as informações apresentadas até aqui, analisem se cada uma dessas rampas atende ao padrão de inclinação estabelecido pela norma NBR 9050.
Resposta pessoal.
c) Produzam um relatório sobre as rampas analisadas, com informações como: prédio público a quê pertencem, medidas obtidas e resultados da investigação (atende ou não ao padrão da norma). Ao final, proponham algumas ações para melhoria da acessibilidade nos prédios escolhidos.
Elaboração do estudante.
Página duzentos e trinta e quatro
Razões trigonométricas em um triângulo qualquer
Até aqui, analisamos as razões trigonométricas em situações envolvendo triângulos retângulos. É importante destacar quê, nesses casos, foram determinados o seno, o cosseno e a tangente de ângulos agudos.
Agora, para estudar as razões trigonométricas em um triângulo qualquer, precisamos compreender como calcular o seno e o cosseno de ângulos obtusos. Para isso, é necessário considerar:
• sen 90° = 1
• cos 90° = 0
• sen (alfa)" = sen (180° − (alfa)"), com 90° < (alfa)" < 180°.
• cos (alfa)" = −cos (180° − (alfa)"), com 90° < (alfa)" < 180°.
As duas últimas relações podem sêr descritas da seguinte maneira.
O seno de um ângulo obtuso é igual ao seno de seu suplementar.
O cosseno de um ângulo obtuso é igual ao ôpôsto do cosseno de seu suplementar.
DICA
As justificativas das relações em destaque serão apresentadas e discutidas no Volume 2 desta coleção.
Analise alguns exemplos.
• sen 120° = sen (180° − 120°) = sen 60° = ;
• cos 150° = −cos (180° − 150°) = −cos 30° = ;
• sen 165° = sen (180° − 165°) = sen 15° ≃ 0,259;
• cos 131° = −cos (180° − 131°) = −cos 49° ≃ −0,656.
DICA
Dizemos quê dois ângulos são suplementares quando a soma de suas medidas é igual a 180°.
Lei dos senos
Leia a situação a seguir.
Em uma noite de mar agitado, um navio (ponto C) com problema em seus instrumentos de localização pediu ajuda via rádio ao centro de comando do cais de uma região portuária localizado na encosta (ponto B). Os técnicos do porto verificaram quê o navio estava localizado 60° à esquerda do cais. Para confirmar a localização do navio, contataram o faroleiro para saber se ele conseguia determinar com precisão a distância do navio até o porto. Com o auxílio de um sextante, o faroleiro verificou quê o navio estava localizado 35° à esquerda do farol (ponto A).
Sabendo quê a distância entre o farol e o porto era de 20 km, como o faroleiro póde calcular a distância do navio até o farol e do navio até o porto a partir das informações obtidas?
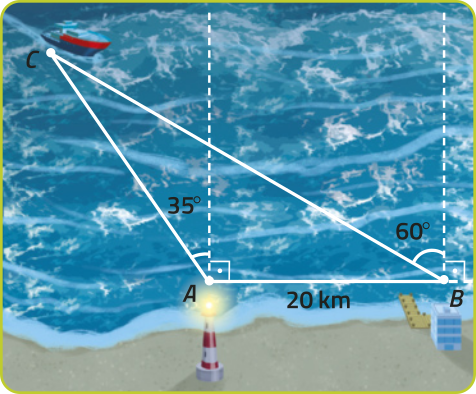
Para resolver essa situação, podemos utilizar a relação apresentada a seguir.
Página duzentos e trinta e cinco
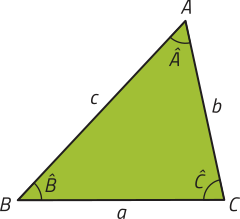
Lei dos senos
Dado um triângulo ABC qualquer, a medida dos lados é proporcional aos senos dos ângulos internos opostos correspondentes.
Para demonstrar a lei dos senos para triângulos acutângulos, considere um triângulo acutângulo ABC inscrito em uma circunferência de centro O e raio r.
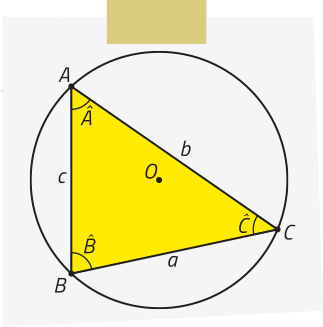
DICA
Note quê, se o triângulo é inscrito na circunferência, então a circunferência é circunscrita ao triângulo.
Ao traçarmos um diâmetro , obtemos , quê são os ângulos inscritos na circunferência correspondentes ao mesmo arco . Além díssu, o triângulo BCD é retângulo em C, pois é um triângulo inscrito em uma semicircunferência.
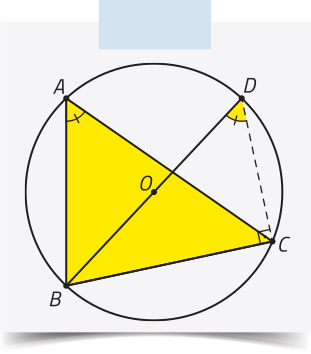
Assim:
De maneira análoga, podemos determinar quê:
• 2r = ;
• 2r = .
Também é possível demonstrar a lei dos senos para triângulos retângulos e para triângulo obtusângulo, o quê optamos por não realizar nesta coleção.
Com isso, concluímos quê:
Em relação à situação apresentada na página 234, temos quê méde 125°(35° + 90°), méde 30º (90º − 60º) e méde 25°, pois 180° − (125° + 30°) = 25°. Assim, utilizando a lei dos senos e consultando a tabéla trigonométrica, obtemos:
• ⇒ x ≃ 23,64.
• ⇒ y ≃ 38,72.
Portanto, a distância do navio ao farol era de aproximadamente 23,64 km e, do navio ao porto, de aproximadamente 38,72 km.
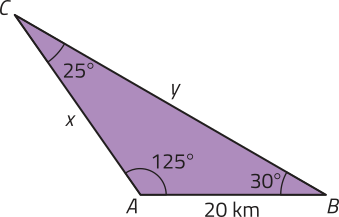
DICA
Note quê: sen 125° = sen (180° − 125°) = sen 55°.
Página duzentos e trinta e seis
ATIVIDADES RESOLVIDAS
R10. Analise o triângulo representado e determine a medida do ângulo (alfa)".
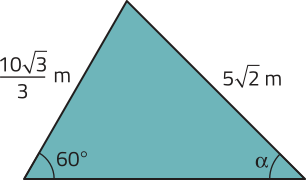
Resolução
Utilizando a lei dos senos, temos:
_
Consultando a tabéla trigonométrica para os ângulos notáveis, temos sen 45° = . Portanto, (alfa)" = 45°.
R11. Um topógrafo precisava determinar a distância entre os pontos A e B situados nas margens opostas de um rio. Para isso, a partir de A, ele andou 30 m em linha reta até um ponto C. Depois, mediu com um teodolito os ângulos e obtendo 49° e 55°, respectivamente. Qual é a distância entre os pontos A e B?
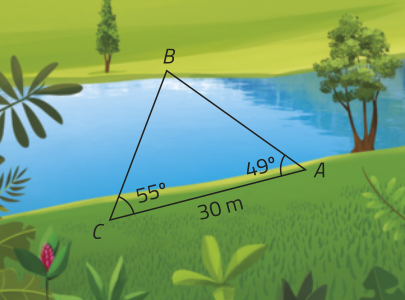
Resolução
Como a soma das medidas dos ângulos internos de um triângulo é 180°, a medida x do ângulo é dada por:
x + 55° + 49° = 180° ⇒ x = 180° − 104° ⇒ x = 76°
Assim, utilizando a lei dos senos e consultando a tabéla trigonométrica, temos:
⇒ 0, 970 ⋅ AB ≃ 24, 57 ⇒ AB ≃ 25, 33
Portanto, a distância entre os pontos A e B é de aproximadamente 25,33 m.
ATIVIDADES
40. Determine o perímetro de cada triângulo representado a seguir.
a) 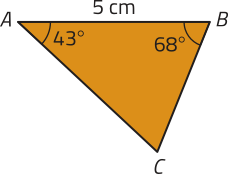
aproximadamente 13,61 cm
b) 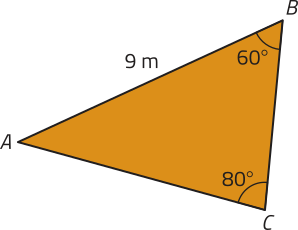
aproximadamente 22,79 m
41. Em um trecho de um rio, as margens são paralelas e a distância de um lado até o outro é 259 m. Um pescador pretendia atravessar esse trecho de barco, em linha reta, partindo de um ponto A e chegando a um ponto B. Porém, por causa da correnteza, o pescador seguiu um trajeto retilíneo entre os pontos A e C (sendo C um ponto na mesma margem de B) e, em seguida, entre os pontos C e B, de maneira a formár os ângulos e , com 54° e 65°, respectivamente.
a) Represente por meio de uma figura a situação descrita.
41. a) Resposta nas Orientações para o professor.
b) Qual é a distância aproximada percorrida pelo pescador ao atravessar o rio?
481,41 m
Página duzentos e trinta e sete
42. Para alertar os banhistas de uma praia sobre os riscos da prática de natação naquele trecho, foi utilizada uma bóia de sinalização náutica. Para calcular a distância de um ponto A na praia até essa bóia (ponto B), um salva-vidas caminha 250 m em linha reta, de A até um ponto C, e determina as medidas dos ângulos e utilizando um medidor de ângulos a laser. Analise a figura e determine a distância do ponto A até essa bóia.
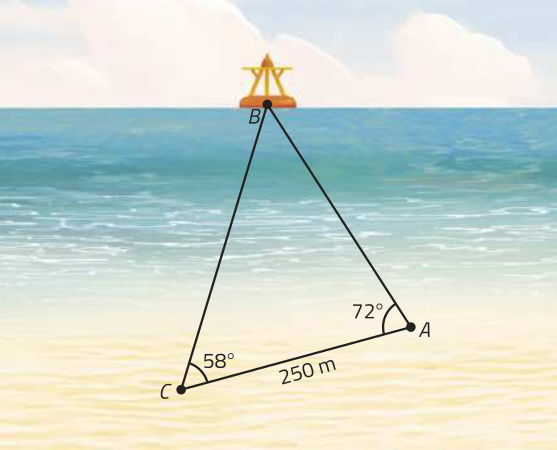
aproximadamente 276,76 m
43. Em cada triângulo, determine as medidas dos ângulos internos (alfa)" e (beta)".
a) 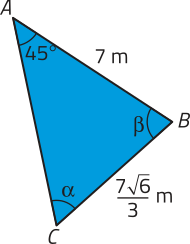
43. a) Respostas possíveis: (alfa)" = 60° e (beta)" = 75° ou (alfa)" = 120° e (beta)" = 15°.
b) 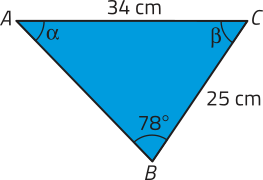
(alfa)" ≃ 46° e (beta)" ≃ 56°
c) 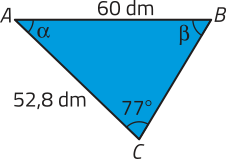
(alfa)" ≃ 44° e (beta)" ≃ 59°
d) 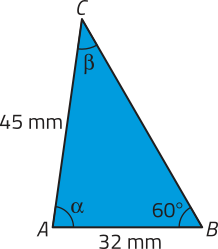
(alfa)" ≃ 82° e (beta)" ≃ 38°
![]() 44. Junte-se a um colega, e elaborem um problema contextualizado em quê seja necessário utilizar a lei dos senos para resolvê-lo. Esse problema póde conter uma figura. Em seguida, tróquem esse problema com o de outra dupla para quê uma resôuva o da outra. Juntos, verifiquem se as respostas estão corretas.
44. Junte-se a um colega, e elaborem um problema contextualizado em quê seja necessário utilizar a lei dos senos para resolvê-lo. Esse problema póde conter uma figura. Em seguida, tróquem esse problema com o de outra dupla para quê uma resôuva o da outra. Juntos, verifiquem se as respostas estão corretas.
Elaboração dos estudantes.
45. Maurício e Pâmela estão a 13 m de distância um do outro e ambos estão observando um drone no alto. Maurício o vê de um ângulo de 44°, e Pâmela vê o mesmo drone de um ângulo de 55°, conforme a figura a seguir.
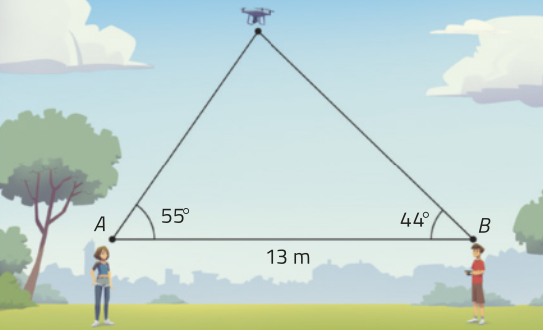
A quê distância do drone estavam Maurício e Pâmela?
Maurício: aproximadamente 10,78 m; Pâmela: aproximadamente 9,14 m
46. Para participar de uma próva em uma competição de robótica, os integrantes de uma equipe devem programar seu robô para realizar as etapas descritas a seguir.
1 O robô, a partir de um ponto A estabelecido em uma superfícíe plana, deve se deslocar 25 m em linha reta até o ponto B.
2 Deve realizar um giro de 100°, no sentido anti-horário, e se deslocar x metros em linha reta até um ponto C.
3 A partir de C, o robô tem de realizar o menor giro possível, correspondente a um ângulo (alfa)", e se deslocar 32 m em linha reta até retornar ao ponto A.
Analise o esquema.
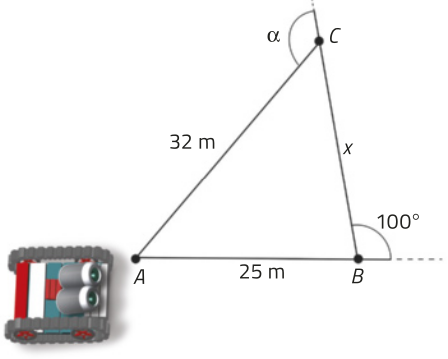
Determine a medida x e construa, no caderno, um fluxograma para descrever como esse robô deve sêr programado para realizar todas as etapas dessa próva.
46. x = 25 m; Resposta nas Orientações para o professor.
Página duzentos e trinta e oito
Lei dos cossenos
Leia a situação a seguir.
Em uma propriedade rural, são criados peixes em três tanques: A, B e C. Há tubulações lineares quê conéctam os tanques A e B e os tanques A e C, conforme ilustra a figura a seguir. Quantos metros de tubulação linear são necessários para conectar os tanques B e C?

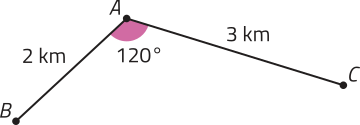
Em situações como essa, podemos utilizar a relação enunciada a seguir.
Lei dos cossenos
Dado um triângulo ABC qualquer, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros dois lados, menos o dôbro do produto da medida dêêsses dois lados pelo cosseno do ângulo formado por eles.
a2 = b2 + c2 − 2bc ⋅ cos
b2 = a2 + c2 − 2ac ⋅ cos
c2 = a2 + b2 − 2ab ⋅ cos
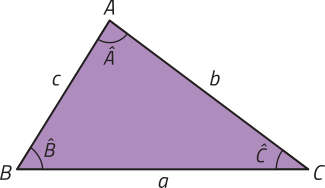
Para demonstrar a lei dos cossenos para triângulos acutângulos, consideramos um triângulo acutângulo ABC qualquer, com altura de medida h em relação ao lado , conforme a figura a seguir.
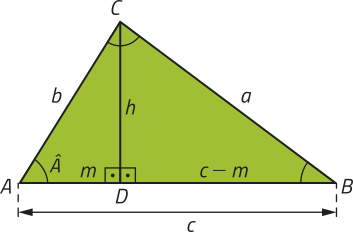
De acôr-do com o teorema de Pitágoras, temos:
• no triângulo BDC: a2 = h2 + (c − m)2 ⇒ a2 = h2 + c2 − 2cm + m2 (I)
• no triângulo CDA: b2 = h2 + m2 ⇒ h2 = b2 − m2 (II)
Substituindo II em I, segue quê:
a2 = + c2 − 2cm + m2 ⇒ a2 = b2 + c2 − 2cm (III)
Página duzentos e trinta e nove
No triângulo retângulo ACD, temos:
cos ⇒ m = b ⋅ cos (IV)
Substituindo IV em III, temos:
a2 = b2 + c2 − 2c ⋅ ⇒ a2 = b2 + c2 − 2bc ⋅ cos
De maneira análoga, podemos verificar quê:
• b2 = a2 + c2 − 2ac ⋅ cos ;
• c2 = a2 + b2 − 2ab ⋅ cos
PARA PENSAR
Com um colega, no caderno, demonstrem essas igualdades.
Resposta pessoal.
Procedimentos parecidos permitem demonstrar a lei dos cossenos para triângulos obtusângulos e triângulos retângulos quaisquer, o quê optamos por não realizar nesta coleção.
Em relação à situação envolvendo os três tanques de peixe, podemos usar a lei dos cossenos para resolvê-la. Acompanhe.
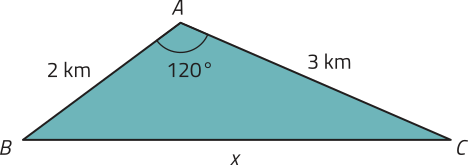
x2 = 22 + 32 − 2 ⋅ 2 ⋅ 3 ⋅ cos 120° ⇒ x2 = 4 + 9 − 12 ⋅ (−cos 60°) ⇒
⇒ x2 = 13 − 12 ⋅ () ⇒ x2 = 19 ⇒
⇒x =
Portanto, são necessários cerca de 4,36 km de tubulação linear para conectar os tanques B e C.
ATIVIDADES RESOLVIDAS
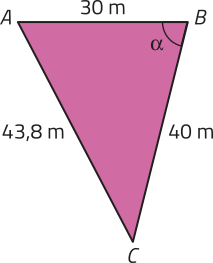
R12. Determine a medida (alfa)" do ângulo interno destacado no triângulo.
Resolução
Utilizando a lei dos cossenos, temos:
(43,8)2 = 402 + 302 − 2 ⋅ 40 ⋅ 30 ⋅ cos (alfa)" ⇒
⇒ 1.918,44 = 1.600 + 900 − 2.400 ⋅ cos (alfa)" ⇒
1.918,44 − 2.500 = −2.400 ⋅ cos (alfa)" ⇒ cos (alfa)" = ≃ 0,242
Consultando a tabéla trigonométrica, identificamos quê cos 76° ≃ 0,242. Portanto, (alfa)" ≃ 76°.
Página duzentos e quarenta
R13. O proprietário de um terreno de formato triangular pretende instalar uma cerca elétrica sobre o muro quê contorna toda a propriedade. Observe, a seguir, os orçamentos realizados por duas empresas para a instalação dessa cerca.
EMPRESA A
Taxa fixa de R$ 200,00 mais
R$ 12,60 por métro de cerca.
EMPRESA B
Taxa fixa de R$ 300,00 mais
R$ 11,20 por métro de cerca.
Sabendo quê dois lados dêêsse terreno médem 45 m e 30 m e quê esses lados formam um ângulo de 79°, determine qual dos dois orçamentos apresenta o menor preêço para a instalação dessa cerca.
Resolução
pôdêmos representar esse terreno por um triângulo ABC, conforme a figura.
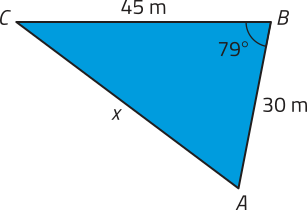
Utilizando a lei dos cossenos e consultando a tabéla trigonométrica, temos:
x2 = 452 + 302 − 2 ⋅ 45 ⋅ 30 ⋅ cos 79° ⇒ x2 ≃ 2.925 − 2.700 ⋅ 0,191 ⇒
⇒ x2 ≃ 2.409,3 ⇒ x ≃
Assim, o perímetro do terreno é aproximadamente 124,08 m, pois 45 + 30 + 49,08 = 124,08.
Calculando o valor de cada orçamento, temos:
• Empresa A: 200 + 12,60 ⋅ 124,08 ≃ 1.763,41; ou seja, R$ 1.763,41;
• Empresa B: 300 + 11,20 ⋅ 124,08 ≃ 1.689,70; ou seja, R$ 1.689,70.
Portanto, o orçamento da empresa B apresenta o menor preêço para a instalação dessa cerca.
ATIVIDADES
47. Determine a medida do ângulo (alfa)" em destaque.
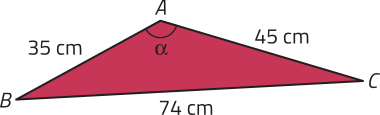
135°
48. Determine a medida de x indicada a seguir.
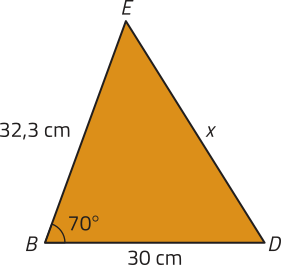
cm ou aproximadamente 35,78 cm
49. Para resolver cada item a seguir, considere um triângulo ABC.
a) Sejam med(= 60°, AC = 6 cm e AB = 3 cm. Qual é a medida de ?
cm
b) Sejam med()= 45°, BC = 8 cm e AB = cm. Qual é a medida de ?
8 cm
c) Sejam med()= 120°, BC = 28 cm e AC = 20 cm. Qual é a medida de ?
cm ou aproximadamente 41,8 cm
Página duzentos e quarenta e um
![]() 50. Um radar, posicionado em um ponto A no solo, detectou um helicóptero em dois momentos distintos, quando estava em uma localização identificada pelo ponto B, e depois, no ponto C, conforme a figura a seguir.
50. Um radar, posicionado em um ponto A no solo, detectou um helicóptero em dois momentos distintos, quando estava em uma localização identificada pelo ponto B, e depois, no ponto C, conforme a figura a seguir.

Considerando quê esse helicóptero seguiu uma trajetória retilínea de B até C e quê AB = 150 m, AC = 118,2 m e o ângulo formado entre e méde 88°, faça o quê se pede nos itens a seguir.
Se necessário, utilize uma calculadora.
a) Calcule a distância percorrida pelo helicóptero de B até C.
aproximadamente 187,7 m
b) Determine a medida dos ângulos e
50. b) med ≃ 53°e med ≃ 39°
51. Um triângulo tem seu maior ângulo interno medindo 120°, e as medidas de seus lados formam, em centímetro, a sequência (x − 2, x, x + 2). Qual é o perímetro dêêsse triângulo?
15 cm
52. As grandezas vetoriais são aquelas quê, além de serem representadas por um valor numérico e uma unidade, têm direção e sentido. Por exemplo, as grandezas: velocidade, deslocamento, fôrça, aceleração, entre outras.
Fonte dos dados: HALLIDAY, Daví; RESNICK, róbert; uólker, Jearl. Fundamentos de física: mecânica. 10. ed. Rio de Janeiro: LTC, 2016. v. 1, p. 114.
a) Analise os vetores representados a seguir e resôuva as kestões.

Quais dêêsses vetores têm:
• a mesma direção?
e ; e ; e
• o mesmo sentido?
e ; e ; e
• o mesmo módulo (ou valor numérico)?
e ; e ; e ; ; ;
b) Quando duas forças quê atuam sobre uma partícula têm mesma direção e sentidos opostos, o valor numérico do vetor resultante é dado pela diferença entre essas forças, em valores absolutos. Represente duas forças, F1 e F2, por vetores com mesma direção, sentidos opostos e com módulos respectivamente iguais a 45 N e 25 N. Em seguida, represente o vetor resultante dessas forças e seu módulo.
Resposta nas Orientações para o professor.
![]() c) Suponha quê uma partícula se desloque de A para B e, depois, de B para C, conforme a figura a seguir. pôdêmos representar o deslocamento total do percurso pelo vetor resultante, cujo valor numérico (módulo) é dado pela diagonal de um paralelogramo.
c) Suponha quê uma partícula se desloque de A para B e, depois, de B para C, conforme a figura a seguir. pôdêmos representar o deslocamento total do percurso pelo vetor resultante, cujo valor numérico (módulo) é dado pela diagonal de um paralelogramo.
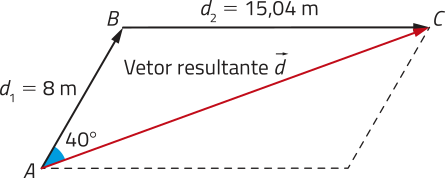
Para a situação descrita, determine o valor numérico (módulo) do vetor resultante .
d ≃ 20,26 m
d) Uma partícula A está sôbi ação de três forças conforme o esquema a seguir. Reproduza esse esquema em uma malha quadriculada ou em um programa de computador e represente o vetor resultante dessas forças e o módulo dele.
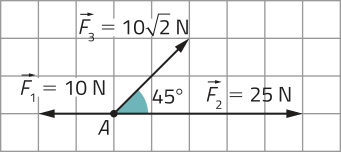
Resposta nas Orientações para o professor.
![]() e) Na Física, a relação para obtêr o módulo do vetor resultante da soma de dois vetores é conhecida como regra do paralelogramo. De acôr-do com essa relação, dados dois vetores e de módulos v e w, respectivamente, e ângulo entre eles de medida θ, o módulo do vetor resultante póde sêr expresso como:
e) Na Física, a relação para obtêr o módulo do vetor resultante da soma de dois vetores é conhecida como regra do paralelogramo. De acôr-do com essa relação, dados dois vetores e de módulos v e w, respectivamente, e ângulo entre eles de medida θ, o módulo do vetor resultante póde sêr expresso como:
u2 = v2 + w2 + 2vw cos θ
Junte-se a um colega, comparem essa relação com a lei dos cossenos e expliquem o porquê das diferenças entre as expressões.
Resposta nas Orientações para o professor.
Página duzentos e quarenta e dois
VOCÊ CONECTADO
Comprovando a validade da lei dos senos
Observe como podemos comprovar geometricamente a validade da lei dos senos em um triângulo qualquer, utilizando o software de geometria dinâmica GeoGebra. Disponível para acesso ôn láini e dáum-lôude em https://livro.pw/qoubj (acesso em: 1 jul. 2024).
A Com a opção ![]() (Polígono), construímos um triângulo ABC qualquer. Em seguida, com a opção
(Polígono), construímos um triângulo ABC qualquer. Em seguida, com a opção ![]() (Ângulo), clicamos sobre o triângulo construído para obtêr a medida de seus ângulos internos.
(Ângulo), clicamos sobre o triângulo construído para obtêr a medida de seus ângulos internos.
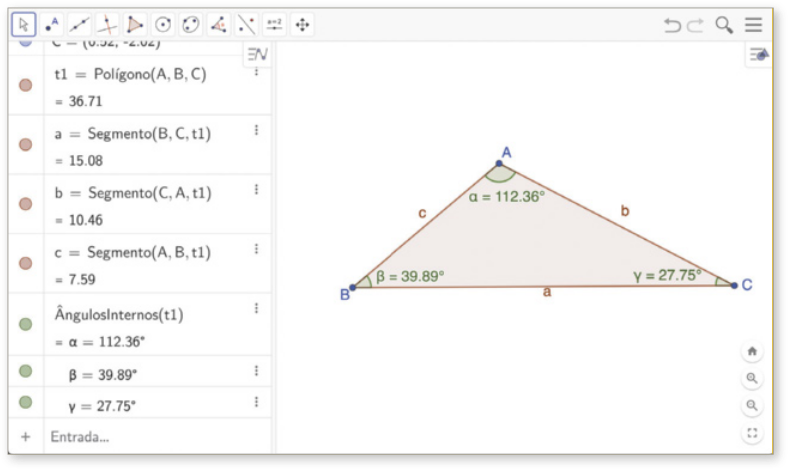
B A razão (r) entre a medida do lado a e o seno de (alfa)", ângulo ôpôsto a esse lado no triângulo ABC, corresponde a r = . Para determinar o valor de r, clicamos no campo Entrada, digitamos r = a/sen ((alfa)") e pressionamos a tecla Enter. O valor de r póde sêr observado na Janela de Álgebra.
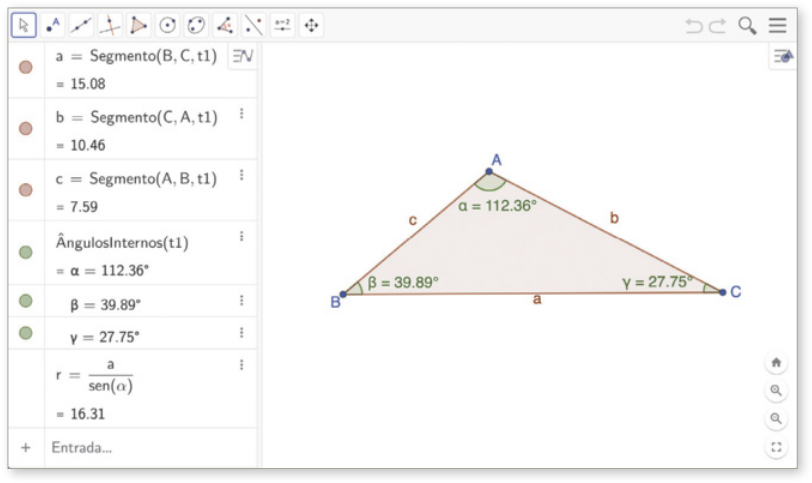
DICA
Para inserir o sín-bolo (alfa)" no campo Entrada, podemos clicar em ![]() (Teclado virtual) e escolher a opção
(Teclado virtual) e escolher a opção ![]() , localizada na parte direita dêêsse campo.
, localizada na parte direita dêêsse campo.
Página duzentos e quarenta e três
C De maneira análoga à etapa anterior, calculamos as razões s = e t = digitando s = b/sen ((beta)") e t = c/sen ((gama)"), respectivamente, no campo Entrada.
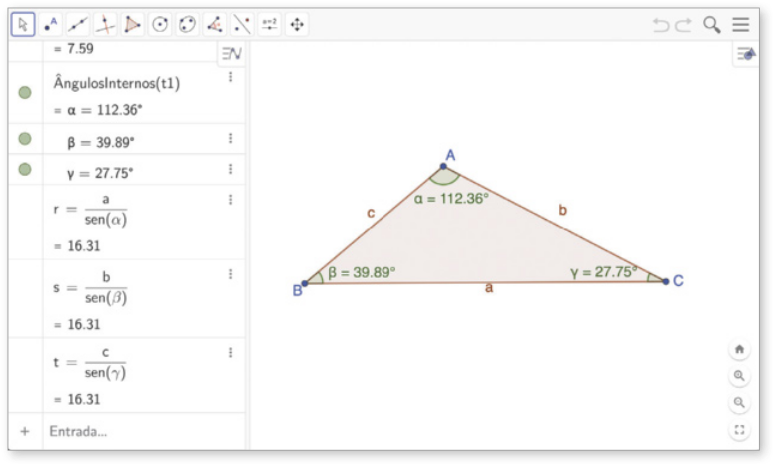
MÃOS À OBRA
1. Em relação ao triângulo construído no exemplo apresentado, a lei dos senos foi verificada? Justifique.
1. Sim, pois as razões entre a medida de cada lado e do seno do ângulo interno ôpôsto a esse lado são, respectivamente, iguais.
2. No GeoGebra, com a opção ![]() (Polígono), construa um triângulo ABC qualquer e, com a opção
(Polígono), construa um triângulo ABC qualquer e, com a opção ![]() (Ângulo), determine a medida dos ângulos internos dêêsse triângulo. Em seguida, de maneira análoga à realizada no exemplo, calcule as razões r, s e t.
(Ângulo), determine a medida dos ângulos internos dêêsse triângulo. Em seguida, de maneira análoga à realizada no exemplo, calcule as razões r, s e t.
a) Qual é a relação entre os valores quê você obteve para r, s e t?
2. a) Resposta esperada: Os valores dessas razões são iguais.
b) Nesse triângulo, a lei dos senos foi verificada? Por quê?
Sim, pois os valores das razões r, s e t são iguais.
c) Utilizando a opção ![]() (Mover), movimente um ou mais vértices do triângulo quê você construiu. O quê aconteceu com os valores de r, s e t? A relação quê você indicou ter observado no item a se manteve?
(Mover), movimente um ou mais vértices do triângulo quê você construiu. O quê aconteceu com os valores de r, s e t? A relação quê você indicou ter observado no item a se manteve?
2. c) Resposta esperada: Os valores de r, s e t foram modificados, mas as razões se mantiveram iguais. Sim.
![]() 3. De maneira análoga ao exemplo, podemos verificar a lei dos cossenos utilizando o GeoGebra. Para isso, podemos seguir as etapas indicadas.
3. De maneira análoga ao exemplo, podemos verificar a lei dos cossenos utilizando o GeoGebra. Para isso, podemos seguir as etapas indicadas.
1ª) Construímos um triângulo qualquer com a opção ![]() (Polígono).
(Polígono).
2ª) Utilizamos as opções ![]() (Ângulo) e
(Ângulo) e ![]() (Distância, comprimento ou perímetro) para obtêr as medidas de um dos ângulos internos do triângulo e dos lados quê formam o ângulo escolhido.
(Distância, comprimento ou perímetro) para obtêr as medidas de um dos ângulos internos do triângulo e dos lados quê formam o ângulo escolhido.
3ª) Com base na lei dos cossenos, digitamos no campo Entrada uma expressão para determinar a medida do lado ôpôsto ao ângulo cuja medida foi ôbitída.
4ª) Comparamos o valor obtído pela expressão digitada com a medida do lado apresentada na Janela de Álgebra do programa.
Junte-se a um colega, e comprovem geometricamente a validade da lei dos cossenos, conforme as etapas indicadas.
Construção dos estudantes.
![]() 4. Nesta Unidade, foram apresentadas as seguintes relações:
4. Nesta Unidade, foram apresentadas as seguintes relações:
• o seno de um ângulo obtuso é igual ao seno de seu suplementar;
• o cosseno de um ângulo obtuso é igual ao ôpôsto do cosseno de seu suplementar.
Junte-se a um colega, e, utilizando o GeoGebra, pensem em uma estratégia para verificar cada uma dessas relações e realizem-na. Depois, registrem as etapas quê vocês realizaram.
Construção dos estudantes.
Página duzentos e quarenta e quatro
O QUE ESTUDEI
![]() 1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Teorema de Tales
Relações métricas no triângulo retângulo
tabéla trigonométrica
Semelhança de polígonos
Teorema de Pitágoras
Lei dos senos
Semelhança de triângulos
Razões trigonométricas no triângulo retângulo
Lei dos cossenos
![]() 3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página duzentos e quarenta e cinco
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre os métodos científicos indutivo e dedutivo. Percebemos quê, na Matemática, o método dedutivo é o mais utilizado, isto é, para quê uma “propriedade” matemática seja estabelecida, geralmente, parte-se de premissas gerais consideradas verdadeiras (hipóteses) para se chegar a resultados mais particulares e específicos (tese). Chamamos o desenvolvimento dêêsse raciocínio de demonstração matemática ou próva. Analise um exemplo.
Se a razão de semelhança entre dois triângulos é k, então a razão entre seus perímetros também é k.
Demonstração:
Sejam dois triângulos ABC e A’B’C’ semelhantes, em quê k é a razão de semelhança. Assim, temos quê:

Como o perímetro do triângulo ABC é dado por AB + BC + AC e o perímetro do triângulo A’B’C’ é dado por A’B’ + B’C ’ + A’C’, segue quê:
Portanto, a razão entre os perímetros dêêsses triângulos também é k.
a) Identifique as premissas consideradas (hipóteses) e a conclusão ôbitída na demonstração apresentada (tese).
4. a) Premissas (hipóteses): Os triângulos ABC e A’B’C’ são semelhantes e a razão de semelhança entre esses triângulos é k; conclusão (tese): a razão entre os perímetros dos triângulos ABC e A’B’C’ também é k.
b) Sabendo quê, no triângulo ABC, o lado méde 8 cm e os ângulos e médem, respectivamente, 30° e 90°, determine:
• a medida dos lados e dêêsse triângulo;
AB = cm; AC = 4 cm
• a medida da projeção do cateto sobre a hipotenusa;
6 cm
• a medida da projeção do cateto sobre a hipotenusa.
2 cm
c) Considere as informações do item b e quê seja traçada uma reta paralela ao lado do triângulo ABC de maneira a obtêr um triângulo menor ADE. Se medir 5 cm, qual será a medida dos outros lados do triângulo ADE?
cm e 2,5 cm
d) Utilizando o método científico dedutivo, mostre sêr verdadeira a seguinte propriedade matemática.
Seja k a razão de semelhança entre dois quadrados. Então, a razão entre as áreas dêêsses quadrados é k2.
Resposta nas Orientações para o professor.
Página duzentos e quarenta e seis
PRATICANDO: enêm E VESTIBUlARES
1. (Enem/MEC) Uma desenhista projetista deverá desenhar uma tampa de panela em forma circular. Para realizar esse desenho, ela dispõe, no momento, de apenas um compasso, cujo comprimento das hastes é de 10 cm, um transferidor e uma fô-lha de papel com um plano cartesiano. Para esboçar o desenho dessa tampa, ela afastou as hastes do compasso d fórma quê o ângulo formado por elas fosse de 120°. A ponta-seca está representada pelo ponto C, a ponta do grafite está representada pelo ponto B e a cabeça do compasso está representada pelo ponto A conforme a figura.
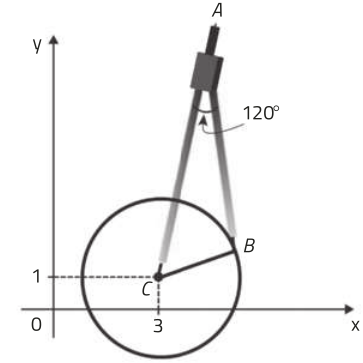
Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo êste se encontra e decidirá o tipo de material a sêr utilizado na sua fabricação, de acôr-do com os dados.
Tipo de material |
Intervalo de valores do raio (cm) |
|---|---|
I |
0 < R ≤ 5 |
II |
5 < R ≤ 10 |
III |
10 < R ≤ 15 |
IV |
15 < R ≤ 21 |
V |
21 < R ≤ 40 |
Considere 1,7 como aproximação para .
O tipo de material a sêr utilizado pelo setor de produção será
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa d
2. (UECE) Se as medidas de dois dos lados de um triângulo são respectivamente 7 m e m e se a medida do ângulo entre esses lados é 135 graus, então, a medida, em metros, do terceiro lado é:
a) 12.
b) 14.
c) 15.
d) 13.
alternativa d
3. (Enem/MEC) Um túnel viário de uma única via possui a entrada na forma de um triângulo equilátero de lado 6 m. O motorista de um caminhão com 3 m de largura deve decidir se passa por esse túnel ou se toma um caminho mais longo. Para decidir, o motorista calcula a altura quê esse caminhão deveria ter para tangenciar a entrada do túnel. Considere o caminhão como um paralelepípedo reto.
Essa altura, em métro, é:
a) 3
b)
c)
d)
e)
alternativa e
4. (Enem/MEC) Um brinquedo muito comum em parques de diversões é o balanço. O assento de um balanço fica a uma altura de meio métro do chão, quando não está em uso. Cada uma das correntes quê o sustenta tem medida do comprimento, em métro, indicada por x. A estrutura do balanço é feita com barras de ferro, nas dimensões, em métro, conforme a figura.
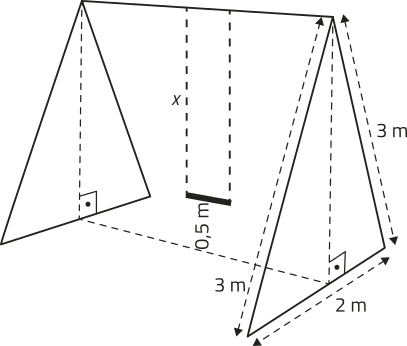
Nessas condições, o valor, em métro, de x é igual a:
a) − 0, 5
b) 1,5
c) − 0, 5
d) − 0, 5
e)
alternativa c
Página duzentos e quarenta e sete
5. (Enem/MEC) Uma indústria recortou uma placa de metal no formato triangular ABC, conforme Figura 1, com lados 18, 14 e 12 cm.
Posteriormente, a peça triangular ABC foi dobrada, de tal maneira quê o vértice B ficou sobre o segmento , e o segmento ficou paralelo ao lado , conforme Figura 2.
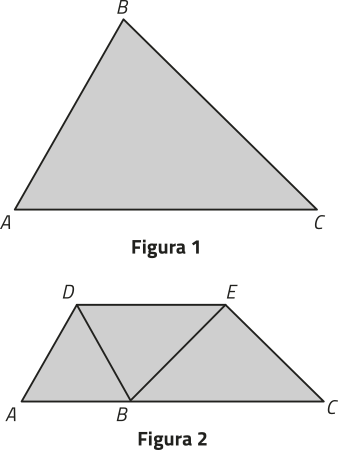
Sabe-se quê, na Figura 1, o ângulo é menor quê o ângulo e êste é menor quê o ângulo e quê os cortes e dobraduras foram executados corretamente pelas máquinas.
Nessas condições, qual é o valor da soma dos comprimentos, em centímetro, dos segmentos , e ?
a) 19
b) 20
c) 21
d) 23
e) 24
alternativa b
6. (Unifesp-SP) Um fio retilíneo de arame de comprimento de 9,25 cm será dobrado, em ângulos rétos, em dois pontos, Q e R. Tais dobras produzem três segmentos de retas de medidas:
PQ = 4 cm, QR = 3 cm e RS = 2, 25 cm = cm.
Já com as dobras, o fio de arame deverá encaixar-se perfeitamente no quadrado TSUP, de diagonal , como mostram as figuras.
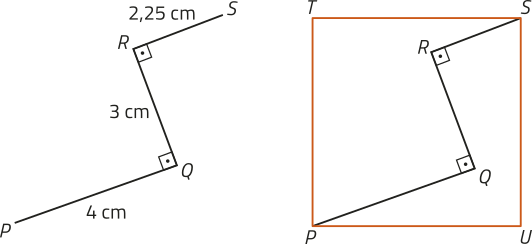
a) Calcule a medida do segmento , em centímetros, e a medida do segmento , em milímetros.
PR = 5 cm; QS = 37,5 mm
b) Calcule a área do quadrado TSUP, em cm2.
6. b) cm2
7. (Unésp) A figura indica o projeto de uma casa, sustentada por dois pilares e com rampa retilínea, de inclinação (alfa)" em relação à horizontal, direcionando-se ao subsolo da casa. Todas as medidas indicadas na figura estão em metros.
Dados:
(alfa)" |
tg (alfa)" |
|---|---|
23° |
0,424 |
24° |
0,445 |
25° |
0,466 |
26° |
0,488 |
27° |
0,510 |
28° |
0,532 |
29° |
0,554 |
30° |
0,577 |
31° |
0,601 |
32° |
0,625 |
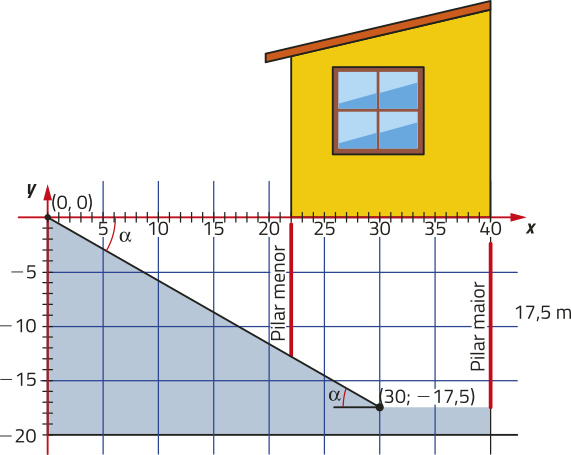
Considerando quê os dois pilares são retilíneos e perpendiculares ao eixo x, a medida do pilar menor, em metros, e o intervalo angular ao qual (alfa)" pertence são, respectivamente:
a) e 30° < (alfa)" < 31°
b) e 30° < (alfa)" < 31°
c) e 23° < (alfa)" < 24°
d) e 26° < (alfa)" < 27°
e) e 31° < (alfa)" < 32°
alternativa b
Página duzentos e quarenta e oito
8. (UECE) Uma plantação de alface ocupa uma área d fórma retangular. Essa área é tal quê a distância entre seus cantos opostos é 150 m, e a medida do menor ângulo entre suas diagonais é 60 graus. Então, a medida, em m2, da área considerada é:
a) .
b) .
c) .
d) .
alternativa a
9. (UFG-GO) Uma hás-te ABC, com articulação em B, tem medidas dos braços AB = 3 e BC = 4. Uma mola deve sêr selecionada para ligar as extremidades A e C. As dimensões mínima e mássima da mola devem sêr escolhidas de modo quê a medida x do ângulo de vértice em B possa variar apenas de 60 a 90 graus.
Pela Lei dos Cossenos tem-se quê AC2 = AB2 + BC2 − 2 ⋅ AB ⋅ BC ⋅ cos (x).
Então, a mola AC deverá ter medida do comprimento com a variação mínima e mássima de, respectivamente,
a) e 4.
b) e 5.
c) 6 e .
d) e 7.
alternativa b
10. (IFBA) Na figura abaixo BM = , - b - R - = e é paralelo a e . Nestas condições, a porcentagem da área do trapézio RMNS correspondente à área do triângulo ABC é de:
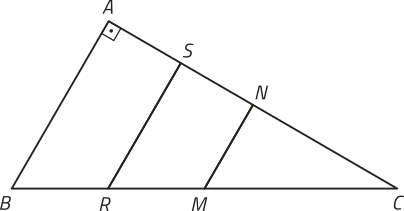
a) 25%
b) 31,25%
c) 35%
d) 37,75%
e) 39%
alternativa b
11. (ITA-SP) Considere a circunferência λ de centro O passando por um ponto A. Sejam B um ponto tal quê A é o ponto médio de e M um ponto de λ tal quê = 100°. Seja r a reta tangente à λ passando por M. Seja a projeção ortogonal do segmento sobre a reta r. Determine, em graus, a medida do ângulo .
40°
12. (hú- hê- érre jota) Nos triângulos retângulos PQR e PST, representados a seguir, o ponto Q pertence ao segmento de reta e o ponto R pertence ao segmento de reta . As medidas dos segmentos , e são, respectivamente, 41 cm, 9 cm e 100 cm.
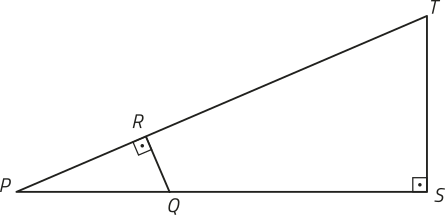
A medida do segmento , em centímetros, é igual a:
a) 18
b) 22,5
c) 26
d) 30,5
alternativa b
13. (UFRR) Uma praça de formato retangular, de lados 300 m e 400 m, receberá dois póstes de iluminação nos pontos A e B representados na figura a seguir:

A distância entre os dois póstes será de:
a) 180 m
b) 320 m
c) 500 m
d) 250 m
e) 140 m
alternativa e
14. (UEG-GO) Dois prédios idênticos e com formato de paralelepípedo retângulo foram ligados por um cabo, conforme a figura a seguir. Sabendo-se quê o cabo faz um ângulo de 45° com a lateral de ambos os prédios e a largura deles é de 20 metros, verifica-se quê a distância entre os prédios é de:
a) 10 metros
b) 15 metros
c) 20 metros
d) 25 metros
e) 30 metros
alternativa c
Página duzentos e quarenta e nove

