UNIDADE 1
FUNÇÃO EXPONENCIAL
Armazenamento de dados dos smartphones
Você já tentou instalar um aplicativo em um smartphone, mas não conseguiu porque o armazenamento interno dele estava sobrecarregado? Para evitar esses inconvenientes, os fabricantes investem cada vez mais no aumento da capacidade de armazenamento de smartphones. Hoje, há aparelhos disponíveis no Brasil com até 1 TB (terabaite) de capacidade interna; muito maior quê a dos primeiros smartphones criados, quê tí-nhão capacidade de armazenamento interno de cerca de 1 MB (megabaite).
Porém devemos ficar atentos ao fato de quê a capacidade de armazenamento de um smartphone não está totalmente disponível, já quê alguns de seus gigabaites são ocupados pelo sistema operacional do próprio aparelho.
Observe, no esquema, algumas atitudes para otimizar o uso do armazenamento interno de smartphones.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Toda a memória interna de um smartphone está disponível para o usuário? Justifique.
2. Você já passou por alguma situação em quê não conseguiu instalar um aplicativo por falta de memória do smartphone? Comente como foi essa situação.
3. Quais são as unidades de armazenamento de dados citadas nas informações do texto? Que outras unidades de armazenamento de dados você conhece?
Página doze
Potenciação
Na abertura desta Unidade, recebemos algumas informações sobre a capacidade de armazenamento interno de smartphones. Nesse sentido, assim como utilizamos o grama e o métro como unidades de medida de massa e de comprimento, respectivamente, utilizamos o baite (B) e seus múltiplos como unidade de medida de armazenamento de dados.

No Volume 1 desta coleção, você estudou a respeito do baite e seus múltiplos. Vamos retomar essas informações a seguir.
Observe como podemos relacionar o baite e dois de seus múltiplos: o quilobaite (kB) e o megabaite (MB).
• Como 1 kB equivale a 1.024 B, temos:
• Como 1 MB equivale a 1.024 kB, temos:
Note quê, para realizar conversões entre os múltiplos do baite, utilizamos o fator 1.024, quê póde sêr expresso por meio de uma potenciação:
Seja e , com n > 1. Na potenciação, o produto de n fatores a é indicado pela potência an, em quê a é a base e n é o expoente.

Também podemos definir quê, em uma potência:
• com expoente 1 e base igual a um número real a qualquer, o resultado é esse próprio número a:
• com expoente 0 e base igual a um número real a diferente de zero, o resultado é 1:
• com expoente igual a um número inteiro negativo e base diferente de zero, o resultado é o inverso da base elevado ao ôpôsto dêêsse expoente:
PARA PENSAR
Na legenda da fotografia do pen dráivi, é indicado quê nele é possível armazenar cerca de 2.048 fotografias digitais de 8 MB cada. Argumente de maneira a mostrar quê essa afirmação é verdadeira.
Resposta esperada: Temos quê a capacidade de armazenamento do pen dráivi é 16 GB = 16 ⋅ 1.024 MB = 16.384 MB. Assim, nele podem sêr armazenadas cerca de 2.048 fotografias de 8 MB cada, pois 16.384 ∶ 8 = 2.048.
Página treze
Exemplos:
a) 121 = 12
b) (pi)"0 = 1
c) 5−3 = =
d) (−2)5 = = −32
e)
f) (−0,4)5 =
Propriedades de potências com expoentes inteiros
Quando realizamos operações com potências, podemos utilizar algumas propriedades.
Propriedade I: Sendo a ∈ ℝ, m ∈ ℤ e n ∈ ℤ, com a ≠ 0, temos:
Observe como podemos justificar essa propriedade para m e n inteiros positivos.
Exemplos:
a)
b)
DICA
A propriedade I também póde sêr justificada para m e n inteiros negativos ou iguais a zero.
Propriedade II: Sendo a ∈ ℝ, m ∈ ℤ e n ∈ ℤ, com a ≠ 0, temos:
Observe como podemos justificar essa propriedade.
Exemplos:
a)
b)
Propriedade III: Sendo a ∈ ℝ, b ∈ ℝ e m ∈ ℤ, com a ≠ 0 e b ≠ 0, temos:
Observe como podemos justificar essa propriedade para m inteiro positivo.
Exemplos:
a)
b)
DICA
A propriedade III também póde sêr justificada para m inteiro negativo ou igual a zero.
Página quatorze
Propriedade IV: Sendo a ∈ ℝ, b ∈ ℝ e m ∈ ℤ, com a ≠ 0 e b ≠ 0, temos:
Observe como podemos justificar essa propriedade para m inteiro positivo.
Exemplos:
a)
b)
DICA
A propriedade IV também póde sêr justificada para m inteiro negativo ou igual a zero.
Propriedade V: Sendo a ∈ ℝ, m ∈ ℤ e n ∈ ℤ, com a ≠ 0, temos:
Observe como podemos justificar essa propriedade para m e n inteiros positivos.
Exemplos:
a)
b)
DICA
A propriedade V também póde sêr justificada para m e n inteiros negativos ou iguais a zero.
ATIVIDADE RESOLVIDA
R1. Utilizando as propriedades das potências apresentadas, resôuva a expressão
Resolução
PARA PENSAR
Identifique na resolução da expressão o uso das propriedades apresentadas.
propriedade I: 125 ⋅ 12 = 125+1; propriedade II: 128 ∶ 123 = 128−3;
propriedade III: 45 ⋅ 35 = (4 ⋅ 3)5; propriedade IV: propriedade V: (62 )3 = 62−3
Página quinze
ATIVIDADES
1. Calcule as potências.
a) 63
b) (−4)2
c)
d)
e)
f)
1
2. escrêeva as expressões a seguir na forma de uma única potência.
a)
b)
c)
d)
e)
f)
3. Calcule o valor numérico das expressões a seguir.
a)
b)
c)
d)
4. Leia o texto a seguir.
O jôgo de Xadrez
Segundo uma lenda antiga, o jôgo de xadrez foi inventado na Índia [...]. Encantado com o invento, o soberano, rei Shirham, quis recompensar seu súdito Sissa Bem Darrir, o inventor do xadrez. Shirham disse a Sissa quê lhe fizesse um pedido, quê ele, rei Shirham, o atenderia prontamente. Sissa disse, simplesmente:
— Bondoso rei, dê-me então um grão de trigo pela primeira casa do tabuleiro, dois pela segunda casa, quatro (= 22) pela terceira, oito (= 23) pela quarta, e assim por diante, até 2 63 grãos de trigo pela última casa do tabuleiro, isto é, a 64 ª casa.
[...]
ÁVILA, Geraldo. Números muito grandes: o jôgo de xadrez. Revista do Professor de Matemática, [São Paulo], n. 25, [1994]. Disponível em: https://livro.pw/xzstw. Acesso em: 24 jul. 2024.
Para termos uma noção de quão grande é a quantidade 2 63 grãos de trigo, a safra mundial de trigo 2022/2023 foi de 789,49 milhões de toneladas, o quê corresponde a aproximadamente 2 29 grãos. Quantas vezes seria necessário dobrar essa safra para obtêr a quantidade de grãos de trigo correspondentes à última casa do tabuleiro, de acôr-do com o pedido de Sissa?
Justifique sua resposta.
34 vezes. Resposta pessoal.

Fonte dos dados: IÚLNÁITED STATES DEPARTMENT OF AGRICULTURE. Foreign Agricultural sérvîss. Production: wheat. Uóchinton, DC: FAS, [2024]. Disponível em: https://livro.pw/czuld. Acesso em: 24 jul. 2024.
Página dezesseis
5. Mateus utiliza um serviço de armazenamento de dados em nuvem. Observe quanto do espaço contratado por ele encontra-se disponível.

Que porcentual da capacidade de armazenamento em nuvem contratada por Mateus ainda está disponível para uso?
aproximadamente 73,6%
6. Estudamos quê o baite (B) e seus múltiplos são unidades de medida de armazenamento de dados. Uma maneira de realizar conversões entre essas unidades de medida é usar o fato de quê 1.024 = 210 e estabelecer as seguintes relações.
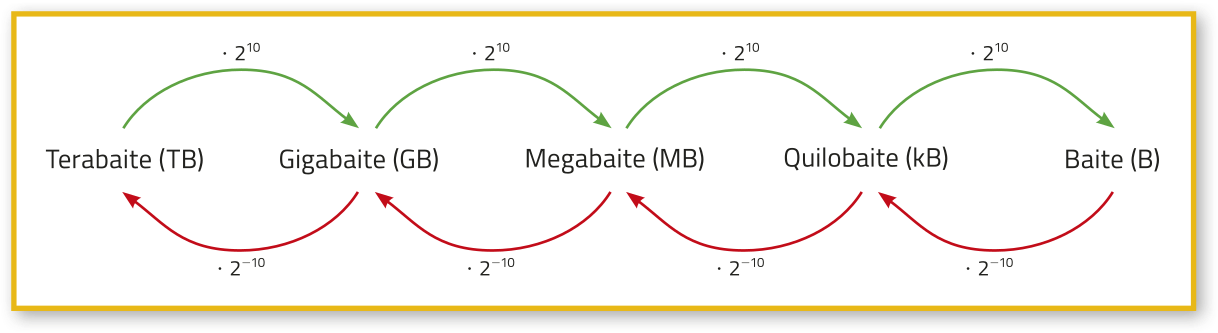
a) Converta, justificando seu procedimento:
Respostas nas Orientações para o professor.
• 3 kB para B;
• 5 MB para TB;
• 8 TB para kB;
• 7 B para GB.
b) Em quais itens a seguir o cartão de memória indicado tem capacidade para armazenar 2 13 MB de dados? Justifique.

I e III. Os cartões de memória apresentam, respectivamente, 214 MB, 212 MB, 215 MB de capacidade de armazenamento; logo, apenas os cartões I e III têm memória maior ou igual a 213 MB.
c) Você sabe o quê é um algoritmo? De modo geral, um algoritmo é um conjunto de regras ou procedimentos sequenciados quê póde ter como intuito a solução de um problema. Com base nas relações apresentadas, entre as unidades de medida baite e seus múltiplos, dêz-creva um algoritmo com o qual seja possível converter uma medida expressa em uma dessas unidades em outra.
Resposta pessoal.
7. Determine a soma dos algarismos do número obtído como resultado do cálculo .
7
8. ![]() Elabore cinco expressões envolvendo potências e troque-as com um colega para quê um simplifique as expressões do outro. Depois, cada um deve corrigir as simplificações das expressões quê elaborou, indicando quais propriedades foram utilizadas pelo colega. Por fim, conversem sobre as etapas realizadas.
Elabore cinco expressões envolvendo potências e troque-as com um colega para quê um simplifique as expressões do outro. Depois, cada um deve corrigir as simplificações das expressões quê elaborou, indicando quais propriedades foram utilizadas pelo colega. Por fim, conversem sobre as etapas realizadas.
Elaborações do estudante.
Página dezessete
Notação científica
Quando é necessário escrever números ou realizar cálculos com medidas “muito grandes”, como as quê envolvem distâncias entre planêtas, ou “muito pequenas”, como as relacionadas ao comprimento de microrganismos, podemos utilizar notação científica.
Dados a ∈ ℚ e n ∈ ℤ, com 1 ≤ a < 10, dizemos quê um número está representado em notação científica quando expresso da seguinte maneira:
DICA
De maneira geral, na notação científica, o número racional a é indicado na forma decimal.
Leia, por exemplo, êste trecho de uma reportagem.
Agências espaciais da Europa e Estados Unidos apresentaram [...] a primeira imagem de um buraco negro no Universo. Trata-se de uma descoberta do telescópio Event Horizon.
[...]
O buraco negro fotografado foi encontrado no centro da galáksia batizada de Messier 87, ou M87, região a 500 quintilhões de quilômetros de distância da Terra [...].
PADRÃO, Márcio. Primeira imagem real de um buraco negro é revelada. Tilt UOL, [s. l.], 16 abr. 2019. Disponível em: https://livro.pw/barhf. Acesso em: 24 jul. 2024.

PARA AMPLIAR
Acesse o sáiti a seguir e assista ao vídeo para obtêr informações sobre a primeira imagem de um buraco negro.
• COMO os cientistas conseguiram a proeza inédita de fotografar um buraco negro. BBC nius Brasil, [s. l.], 10 abr. 2019. Disponível em: https://livro.pw/fdexn. Acesso em: 24 jul. 2024.
No texto apresentado, foi mencionada uma distância de 500 quintilhões de quilômetros. Essa medida póde sêr expressa em notação científica conforme apresentado a seguir.
PARA PENSAR
Sabendo quê a distância média entre a Terra e a Lua é de 3,78 ⋅ 10 5 km, determine quantas vezes essa distância corresponde àquela entre a Terra e o buraco negro, mencionado anteriormente.
aproximadamente vezes
Professor, esta obra está atualizada conforme a grafia estabelecida pelo SI na publicação:
INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA; INSTITUTO PORTUGUÊS DA QUALIDADE. Sistema Internacional de Unidades (SI). Tradução: Grupo de Trabalho luso-brasileiro do Inmetro e IPQ. Brasília, DF: Inmetro; Caparica: IPQ, 2021. p. iii. Tradução luso-brasileira da 9ª edição. Disponível em: https://livro.pw/vbxre. Acesso em: 27 jun. 2024.
Página dezoito
Agora, considere a situação descrita a seguir.
O vírus dengue (DENV) é um arbovírus, grupo onde se encontram diversos patógenos humanos, quê foram assim chamados inicialmente por apresentarem parte do seu ciclo de vida em artrópodes. [...]
DENV é um vírus pequeno, envelopado e com 50 nm de diâmetro. [...]
AMARAL, Raquel Juliana Vionette do; DANSA-PETRETSKI, Marilvia. Interação patógeno-vetor: dengue. In: SILVA NETO, Mário Alberto Cardoso da éti áu. (ed.). Tópicos avançados em entomologia molecular. Rio de Janeiro: INCTEM, 2012. cap. 14, p. 1-35. p. 9. Disponível em: https://livro.pw/sgnxp. Acesso em: 24 jul. 2024.
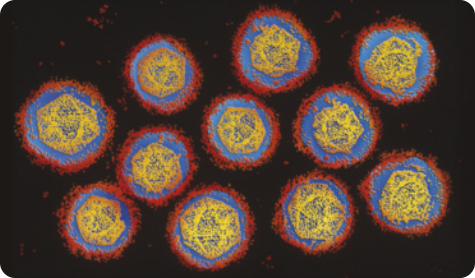
Onze vírus da dengue (imagem de microscopía eletrônica, aumento aproximado de 200.000 vezes; colorida artificialmente).
No texto, foi mencionada a medida do diâmetro de um vírus em nanômetro (nm). Como 1 nm equivale a 0,000001 mm, temos quê 50 nm equivalem a 0,00005 mm. Assim, podemos expressar essa medida em milímetro utilizando notação científica da maneira a seguir.
PARA AMPLIAR
Assista ao vídeo indicado a seguir para obtêr mais informações sobre as arboviroses e algumas dicas para combater os mosquitos transmissores de vírus como esses.
• ESPECIAL arboviroses. [S. l.: s. n.], 2017. 1 vídeo (9 min). Publicado pelo canal MultiRio. Disponível em: https://livro.pw/ofzvo. Acesso em: 24 jul. 2024.
Algarismos significativos
Em geral, ao realizarmos uma medição, temos a precisão do resultado limitada pelo instrumento utilizado. Observe um exemplo.

Com base nessa medição, podemos afirmar quê o comprimento do parafuso está entre 4,8 cm e 4,9 cm. Assim, um possível valor aproximado para essa medida é 4,85 cm, ou seja, submetemos à medida uma incerteza de 0,5 mm ou 0,05 cm. Essa incerteza corresponde à mêtáde da menor graduação do instrumento utilizado , o quê é admitido em consenso por pesquisadores e estudantes.
Página dezenove
Na aproximação 4,85 cm, não há dúvida quanto aos algarismos 4 e 8, de maneira quê podemos chamá-los de algarismos certos.
Já o algarismo 5 foi estimado e, assim, podemos chamá-lo de algarismo duvidoso.
O conjunto formado pêlos algarismos certos e duvidosos são os algarismos significativos quê compõem um número obtído em uma medição. No número 4,85, por exemplo, 4, 8 e 5 são os algarismos significativos da medida do comprimento do parafuso, em centímetro.
ATIVIDADES RESOLVIDAS
R2. (Enem/MEC) A volemia (V) de um indivíduo é a quantidade total de sangue em seu sistema circulatório (coração, artérias, veias e capilares). Ela é útil quando se pretende estimar o número total (N) de hemácias de uma pessoa, o qual é obtído multiplicando-se a volemia (V) pela concentração (C) de hemácias no sangue, isto é, Num adulto normal essa concentração é de 5.200.000 hemácias por mL de sangue, conduzindo a grandes valores de N. Uma maneira adequada de informar essas grandes quantidades é utilizar a notação científica, quê consiste em expressar N na forma , sêndo e n um número inteiro.
Considere um adulto normal, com volemia de 5.000 mL.
https://livro.pw/zwgrk. Acesso em: 23 fev. 2013 (adaptado).
Qual a quantidade total de hemácias dêêsse adulto, em notação científica?
a)
b)
c)
d)
e)
Resolução
Utilizando a expressão e considerando e , a quantidade total de hemácias dêêsse indivíduo é dada por:
Portanto, a alternativa d é a correta.
R3. Considere os números a seguir, expressos em notação científica.
•
•
•
•
Agora, faça os cálculos e expresse a resposta em notação científica.
a)
b)
c)
Resolução
a)
b)
c)
Página vinte
R4. Utilizando um paquímetro, Rafael mediu o diâmetro externo de um cano de metal. Observe a ilustração.

- Paquímetro
- : instrumento utilizado para medir comprimentos, principalmente diâmetros e espessuras de pequenos objetos com formato circular.
a) De acôr-do com a medição realizada por Rafael, determine a medida aproximada do diâmetro externo dêêsse cano, considerando três algarismos significativos.
b) Classifique cada algarismo da medida indicada no item a em algarismo cérto ou duvidoso.
Resolução
a) Com base na medição apresentada, podemos afirmar quê o diâmetro do cano está entre 4,6 cm e 4,7 cm. Assim, um possível valor aproximado para essa medida é:
, ou seja, 4,65 cm.
b) Na aproximação 4,65 cm, não há dúvida quanto aos algarismos 4 e 6, ou seja, esses são os algarismos certos. Já o algarismo 5 foi estimado, ou seja, é um algarismo duvidoso.
R5. Para determinar o volume de uma gota de á gua, um professor propôs quê, em grupo, os estudantes realizassem um experimento no qual enchessem uma burêta com 10 mL de á gua e retirassem 100 gotas dêêsse conteúdo. Por fim, cada grupo deveria determinar e indicar, considerando a incerteza da burêta apenas em relação às suas graduações, quantos mililitros de á gua foram retirados. Observe os registros realizados por dois grupos de estudantes.
Grupo A
• Bureta de 10 mL subdividida em 1 mL
• Volume de 100 gotas de á gua:
5,5 mL
Grupo B
• Bureta de 10 mL subdividida em 0,1 mL
• Volume de 100 gotas de á gua:
5,35 mL
- Bureta
- : instrumento compôzto de um tubo graduado e de uma torneira, quê possibilita medir o volume de substâncias líquidas.

Considerando quê as gotas tênham todas o mesmo volume, responda.
a) Qual dêêsses grupos obteve uma medida mais precisa?
b) Utilizando a medida ôbitída pelo grupo indicado no item anterior, calcule o volume aproximado de uma gota de á gua. Indique o resultado em notação científica.
Resolução
a) Quanto mais marcações referentes às subdivisões de uma unidade de medida um recipiente apresentar, maior será a precisão da medida ôbitída. Como o grupo B utilizou um recipiente subdividido em 0,1 mL, ele obteve uma medida mais precisa quê a do grupo A.
b) O volume de 100 gotas de á gua indicado pelo grupo B foi de 5,35 mL. Assim, o volume de cada gota de á gua é de:
PARA PENSAR
Com suas palavras, explique a um colega os argumentos indicados na resolução do item a, utilizando como exemplo outro instrumento graduado.
Resposta pessoal.
Página vinte e um
ATIVIDADES
9. Expresse os números em notação científica.
a) 568.000.000.000
b) 10.263.000.000.000.000
c) 907.000.000.000.000
d) 0,0000006
e) 0,00000000798
f) 0,000000000000604
10. Observe, a seguir, os números expressos em notação científica.
Agora, calcule as expressões e indique o resultado em notação científica.
a)
b)
c)
11. Para expressar medidas de comprimento “muito grandes” ou “muito pequenas”, além dos múltiplos do métro, podem sêr utilizadas outras unidades de medida. Leia as informações.
I) O ano-luz é uma unidade de medida utilizada principalmente em Astronomia, para expressar, por exemplo, distâncias entre corpos celéstes. Um ano-luz corresponde à distância quê a luz percórre no vácuo em 1 ano terrestre, o quê equivale a aproximadamente .
II) O angstrom (A °) é uma unidade de comprimento quê costuma sêr utilizada para expressar a medida de hátomus. Temos quê 1 A ° equivale a .
Fonte dos dados: HALLIDAY, Daví; RESNICK, róbert; uólker, Jearl. Fundamentos de física: mecânica. 10. ed. Rio de Janeiro: LTC, 2016. v. 1, p. 764.
Em cada item, realize conversões e escrêeva as medidas destacadas utilizando a unidade mais adequada: anos-luz ou angstrom.
a) A estrela mais brilhante da Via Láctea é a Eta Carinae e está localizada a cerca de 7,1 ⋅ 1016 m do Sistema Solar.
Fonte dos dados: por quê a estrela mais brilhante da galáksia é invisível a olho nu – e como se tornará aparente. G1, [s. l.], 10 jan. 2019. Disponível em: https://livro.pw/unhxh. Acesso em: 24 jul. 2024.
11. a) aproximadamente 7.505 anos-luz
b) ![]() Em 2020, o raio de carga médio do núcleo do hélio foi medido com a maior precisão até então: 1,67824 ⋅ 10−15 m.
Em 2020, o raio de carga médio do núcleo do hélio foi medido com a maior precisão até então: 1,67824 ⋅ 10−15 m.
Fonte dos dados: SERAFIM, Teresa Sofia. Raio do núcleo do hélio medido com uma precisão “sem precedentes”. Público, Lisboa, 27 jan. 2021. Disponível em: https://livro.pw/fkike. Acesso em: 24 jul. 2024.
• Agora, pesquise e registre informações ou dados científicos, diferentes dos apresentados nos itens anteriores, em quê sêjam citadas medidas de comprimento “muito grandes” ou “muito pequenas”, expressando-as em ano-luz ou angstrom. Depois, compartilhe suas descobertas com os côlégas.
Pesquisa do estudante.
12. Um instrumento bastante utilizado em laboratórios de química para obtêr medidas com maior precisão é a balança analítica, quê póde indicar a massa de objetos, em grama, com até quatro casas decimais. Considere quê um objeto com 2,83 mg de massa é colocado sobre uma balança dessas e responda.
a) Qual é a massa indicada no visor da balança?
b) escrêeva a medida quê você indicou no item a em notação científica.
13. De acôr-do com outro trecho da reportagem apresentada na página 17, o diâmetro do buraco negro méde 40 bilhões de quilômetros, cerca de 3 milhões de vezes o diâmetro da Terra.
pôdêmos afirmar quê o diâmetro da Terra, em quilômetro, corresponde a aproximadamente:
a)
b)
c)
d)
e)
alternativa d
Página vinte e dois
14. Determine a medida aproximada do diâmetro interno dos canos nas medições representadas a seguir. Para isso, considere a medida com três algarismos significativos.
a) 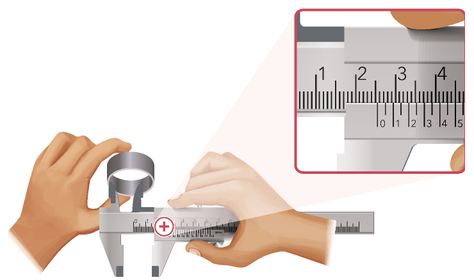
2,55 cm
b) 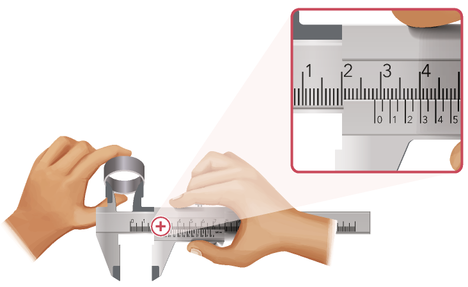
2,85 cm
c) 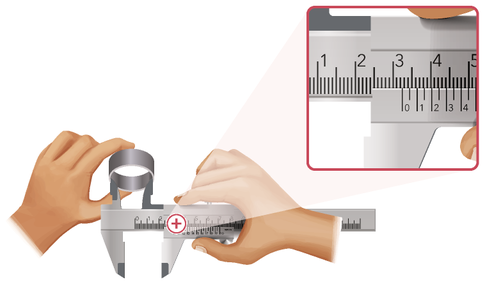
3,25 cm
15. Observe o recipiente graduado contendo cérto volume de líquido.

a) ![]() Que volume de líquido há nesse recipiente, em litro? Para escrever essa medida, considere dois algarismos significativos fazendo estimativas e arredondamentos. Depois, explique a um colega seus procedimentos.
Que volume de líquido há nesse recipiente, em litro? Para escrever essa medida, considere dois algarismos significativos fazendo estimativas e arredondamentos. Depois, explique a um colega seus procedimentos.
15. a) Resposta possível: Aproximadamente 1,6 L. Para estimar o volume de líquido, pode-se calcular a média aritmética de 1,5 L e 1,75 L, quê é 1,625 L, e arredondar essa medida ao décimo do litro mais próximo, obtendo 1,6 L.
b) Classifique cada algarismo da medida quê você escreveu no item a em algarismo cérto ou duvidoso.
Resposta possível: 1 é algarismo cérto; 6 é algarismo duvidoso.
16. Os objetos a seguir foram medidos com uma régua graduada em milímetro.
a) Em cada figura, identifique a ficha com a medida quê melhor expressa o comprimento aproximado do objeto. Depois, classifique cada algarismo dessa medida em algarismo cérto ou duvidoso.

3,86 cm; algarismos certos: 3 e 8; algarismo duvidoso: 6

7,43 cm; algarismos certos: 7 e 4; algarismo duvidoso: 3
b) Expresse em notação científica as medidas obtidas nos itens anteriores, utilizando o métro como unidade.
16. b) 3,86 cm = 3,86 ⋅ 10 −2 m; 7,43 cm = 7,43 ⋅ 10 −2 m
c) ![]() Com um colega, utilizem uma régua e meçam o comprimento de algum objeto como borracha, caderno, carteira escolar etc. Registrem o comprimento aproximado, em centímetro, do objeto escolhido e indiquem quais são os algarismos certos e o algarismo duvidoso dessa medida. Por fim, expressem, em métro, a medida do objeto em notação científica.
Com um colega, utilizem uma régua e meçam o comprimento de algum objeto como borracha, caderno, carteira escolar etc. Registrem o comprimento aproximado, em centímetro, do objeto escolhido e indiquem quais são os algarismos certos e o algarismo duvidoso dessa medida. Por fim, expressem, em métro, a medida do objeto em notação científica.
Respostas pessoais.
Página vinte e três
17. Os leucócitos, ou glóbulos brancos, são componentes celulares presentes no sangue humano, cujas principais funções são a defesa e a imunidade do organismo. Em exames laboratoriais, a contagem de leucócitos busca identificar a capacidade de resposta das células do corpo em diferentes situações. Em geral, as tabélas de referência indicam, por exemplo, quê um homem adulto deve ter entre de leucócitos por milímetro cúbico de sangue.
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 928-930.
Um homem, por indicação médica, realizou um exame de contagem de leucócitos e obteve como resultado um total de . Considerando quê o volume sangüíneo dêêsse homem é de cerca de 5,4 L, determine a concentração de leucócitos por milímetro cúbico de sangue e verifique se essa quantidade está entre os valores de referência.
17. Aproximadamente leucócitos por milímetro cúbico de sangue. Essa concentração de leucócitos está entre os valores de referência.
DICA
Lembre-se de quê 1 L equivale a 1.000.000 mm³.
18. Um texto científico é uma produção textual com a finalidade de divulgar as ideias ou resultados de um estudo ou pesquisa científica. Esses textos podem sêr divulgados em diferentes formatos, como artigos científicos publicados em revistas voltadas ou não a áreas específicas da Ciência. A Fundação ôsváldo Cruz (Fiocruz), por exemplo, é uma instituição vinculada ao Ministério da Saúde na qual são realizadas pesquisas e publicações científicas, entre outros serviços.
Observe um trecho de um dos artigos publicados por pesquisadores dessa instituição, cujo objetivo era compreender a distribuição e a função de células usadas em terapias avançadas.
[...] A quantidade de células injetadas em terapias celulares varia amplamente com o tipo celular, com a doença e com a via de injeção. Supondo uma terapia em quê se utilize 1 × 10 6 células-tronco mesenquimais por kg de peso corporal, em um paciente de 70 kg será administrado 0,7 mg de ferro incorporado às células. [...]
JASMIN; BOROJEVIC, Radovan. Uso de nanopartículas no rastreamento de células em terapias avançadas: possibilidades e desafios para a aplicação clínica. Revista Visa em Debate: Sociedade, Ciência & Tecnologia, Rio de Janeiro, v. 6, n. 1, p. 56-63, 2018. p. 59. Disponível em: https://livro.pw/hfrlw. Acesso em: 24 jul. 2024.
DICA
Você desconhece algum termo utilizado nesse texto da Fiocruz? Se necessário, realize uma pesquisa em livros ou sáites confiáveis.
Considerando a terapia mencionada nesse trecho, responda.
a) Quantas células-tronco são utilizadas em um paciente com 70 kg? Expresse o resultado em notação científica.
células-tronco
b) Considere quê a massa de ferro incorporada deva sêr proporcional ao peso corporal do paciente. Nessas condições, quantos gramas de ferro devem sêr incorporados às células injetadas em um paciente de 62 kg? Expresse o resultado em notação científica.
g
c) ![]() Com um colega, realizem uma pesquisa sobre as características de um texto científico, como a linguagem utilizada, o quê é considerado em sua produção/elaboração e qual é o público-alvo. Com base nas informações apresentadas nesta atividade e naquelas quê vocês pesquisaram, escrevam um texto argumentativo sobre a importânssia da divulgação científica para a ssossiedade atual.
Com um colega, realizem uma pesquisa sobre as características de um texto científico, como a linguagem utilizada, o quê é considerado em sua produção/elaboração e qual é o público-alvo. Com base nas informações apresentadas nesta atividade e naquelas quê vocês pesquisaram, escrevam um texto argumentativo sobre a importânssia da divulgação científica para a ssossiedade atual.
Pesquisa e elaboração dos estudantes
Página vinte e quatro
Radiciação
Em anos anteriores, você provavelmente estudou a operação de radiciação. Agora, retomaremos e ampliaremos esse estudo.
Na radiciação, sêndo a e b números reais não negativos e n um número natural maior quê 1, dizemos quê se, e somente se,
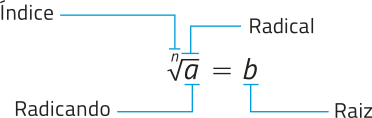
Exemplos:
a)
b) .
c)
d)
e)
f)
DICA
Para representar uma raiz quadrada, costumamos não indicar o índice. Assim, por exemplo, podemos representar por
PARA PENSAR
A afirmativa a seguir é verdadeira ou falsa? Argumente para defender sua resposta.
Pode-se calcular a raiz real de um número real negativo apenas no caso de o índice dessa raiz sêr um número natural ímpar maior quê 1.
Verdadeira. Resposta esperada: Ao multiplicar uma quantidade par de fatores com o mesmo sinal, o resultado é positivo e, ao multiplicar uma quantidade ímpar de fatores negativos, o resultado também é negativo. Assim, de acôr-do com a definição de radiciação, se a é um número real negativo, então se, e somente se, b n = a apenas no caso de n sêr um número natural ímpar maior quê 1.
Potência com expoente racional
É possível estabelecer uma relação entre uma potência com expoente racional escrito na forma de fração e uma raiz. Observe.
Sendo a um número real positivo, m e n números naturais com n > 1, definimos:
Exemplos:
a)
b)
c)
DICA
As propriedades de potências estudadas anteriormente também são válidas no caso de expoentes racionais.
Para justificar, por exemplo, a igualdade , podemos considerar .
Como , então segue quê: .
Assim, temos quê, .
Página vinte e cinco
Propriedades da radiciação
A partir da definição, podemos estabelecer algumas propriedades da radiciação. Utilizando as propriedades da potenciação, é possível justificar essas propriedades da radiciação. Acompanhe.
Propriedade I: Sendo e , com , temos:
= a
Observe como podemos justificar essa propriedade:
Exemplos:
a)
b)
Propriedade II: Sendo a ∈ ℝ e os números naturais m, n e p, com a e , temos:
Observe como podemos justificar essa propriedade:
•
•
Exemplos:
a)
b)
Propriedade III: Sendo a ∈ ℝ, b ∈ ℝ e n ∈ ℕ, com , temos:
e
Observe como podemos justificar essa propriedade.
•
•
Exemplos:
a)
b)
Propriedade IV: Sendo a ∈ ℝ, n ∈ ℕ e p ∈ ℕ, com , temos:
Observe como podemos justificar essa propriedade.
Exemplos:
a)
b)
Página vinte e seis
Propriedade V: Sendo a ∈ ℝ, m ∈ ℕ e n ∈ ℕ, com , temos:
Observe como podemos justificar essa propriedade.
Exemplos:
a)
b)
Potência com expoente real
Nesta Unidade, estudamos potências com expoente racional. Agora, vamos ampliar esse estudo abordando as potências com expoente irracional, e, dessa maneira, abordar potências em quê o expoente é qualquer número real.
Considere, por exemplo, a potência , em quê é um número irracional.
Inicialmente, note quê
Assim, temos:
pôdêmos concluir quê é um número real maior quê 8 e menor quê 16.
Para determinar aproximações racionais de , podemos utilizar uma calculadora para obtêr aproximações racionais de e, em seguida, calcular a potência ôbitída.
Exemplos:
a)
b)
c)
d)
Quanto mais próximo de é o número racional correspondente, mais próximo o resultado obtído é de . Por exemplo, dentre as aproximações obtidas, a mais próxima de é 8,951.
Dada uma potência , sêndo a um número real positivo qualquer e b um número irracional qualquer, podemos obtêr aproximações de calculando , sêndo r uma aproximação racional de b:
Quanto mais próximo b é de r, mais próximo é de .
DICA
As propriedades opêratórìas das potências com expoente racional quê estudamos anteriormente também são válidas para as potências com expoente irracional e, portanto, para as potências com expoente real.
Página vinte e sete
ATIVIDADES RESOLVIDAS
R6. Utilizando as propriedades apresentadas, simplifique a expressão .
Resolução
PARA PENSAR
Identifique na resolução da expressão o uso das propriedades apresentadas.
propriedade II:
propriedade III: ,
propriedade IV:
propriedade V:
R7. (Enem/MEC) Muitos processos fisiológicos e bioquímicos, tais como batimentos cardíacos e taxa de respiração, apresentam escalas construídas a partir da relação entre superfícíe e massa (ou volume) do animal. Uma dessas escalas, por exemplo, considera quê “o cubo da área S da superfícíe de um mamífero é proporcional ao quadrado de sua massa M ”.
HUGHES-HALLETT, D. éti áu. Cálculo e aplicações. São Paulo: Edgard Blãcher, 1999 (adaptado).
Isso é equivalente a dizêr quê, para uma constante , a área S póde sêr escrita em função de M por meio da expressão:
a)
b)
c)
d)
e)
Resolução
De acôr-do com as informações do enunciado, podemos escrever a expressão a seguir.
Como S corresponde a uma medida de superfícíe, temos . Assim, de acôr-do com a definição de radiciação e as propriedades de raízes e de potências apresentadas, temos:
Portanto, a alternativa d é a correta.
ATIVIDADES
19. escrêeva os radicais a seguir na forma de potência.
a)
b)
c)
35
d)
e)
f)
g)
h)
20. Em cada item, simplifique a expressão indicada, escrevendo-a como um único radical.
a)
b)
c)
d)
Página vinte e oito
21. Observe as etapas quê podem sêr realizadas para simplificar .
a) ![]() Reúna-se com um colega e, com base no exemplo apresentado, construam um fluxograma com as etapas quê podem sêr realizadas para simplificar uma raiz.
Reúna-se com um colega e, com base no exemplo apresentado, construam um fluxograma com as etapas quê podem sêr realizadas para simplificar uma raiz.
Resposta nas Orientações para o professor.
b) Agora, utilizem o fluxograma quê vocês elaboraram e simplifiquem as raízes a seguir.
•
•
•
•
22. Quando há um radical no denominador de uma fração, podemos racionalizá-lo, ou seja, obtêr uma fração equivalente sem radical no denominador. Observe os exemplos.
Racionalize os denominadores das frações a seguir.
a)
b)
c)
d)
23. Considere as seguintes expressões, em quê x representa um número real positivo.
I)
II)
Ao compará-las, podemos afirmar quê o valor da expressão I é maior, menor ou igual ao da expressão II? Justifique sua resposta.
23. Resposta esperada: Considerando as informações do enunciado, não é possível comparar os valores das duas expressões, pois, se , o valor da expressão I será maior quê o da expressão II; se , o valor da expressão I será menor quê o da expressão II; e se , as duas expressões terão valores iguais.
24. ![]() Elabore três expressões envolvendo radiciação e troque-as com um colega para quê um simplifique as expressões do outro. Depois, cada um deve corrigir as simplificações das expressões quê elaborou, indicando quais propriedades foram utilizadas pelo colega. Por fim, conversem sobre as etapas realizadas.
Elabore três expressões envolvendo radiciação e troque-as com um colega para quê um simplifique as expressões do outro. Depois, cada um deve corrigir as simplificações das expressões quê elaborou, indicando quais propriedades foram utilizadas pelo colega. Por fim, conversem sobre as etapas realizadas.
Elaborações do estudante.
25. ![]() Use uma calculadora e obtenha, para cada potência a seguir, uma aproximação racional, com uma casa decimal.
Use uma calculadora e obtenha, para cada potência a seguir, uma aproximação racional, com uma casa decimal.
a)
4,7
b)
22,2
c)
1,6
d)
8,8
26. Quais das potências a seguir são números reais maiores quê 50 e menóres quê 80?
a) 82
b) 28
c)
d)
d)
alternativa a
27. Considerando 1,4 como valor aproximado de , qual alternativa apresenta um número real mais próximo de ?
a)
b)
c)
d)
e)
alternativa a
Página vinte e nove
Função exponencial: características e definição
Você sabe o quê é mitose? A mitose é um processo quê faz parte da divisão celular e quê consiste na divisão do núcleo de uma célula em dois núcleos geneticamente idênticos. As “células-filha”, resultantes da mitose, têm o mesmo número de cromossomos quê a célula original.
Agora, obissérve o esquema a seguir com algumas etapas da mitose.
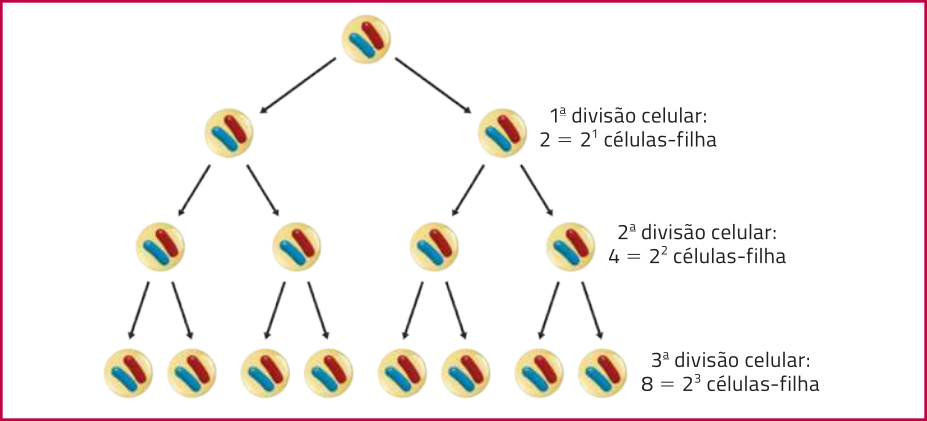
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 237.
PARA PENSAR
De acôr-do com o esquema, quantas células-filha haverá ao todo na 4ª divisão celular?
16 células-filha
Note quê, a cada divisão celular, a quantidade de células-filha obtidas está relacionada com a ordem da divisão celular. Desse modo, podemos estudar a quantidade total de células-filha obtidas a partir de uma única célula, por meio de uma função f, de acôr-do com a quantidade x de divisões celulares, com . A lei de formação da função póde sêr escrita como:
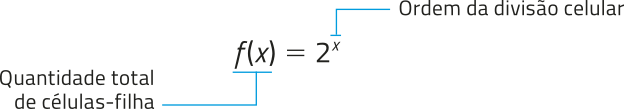
pôdêmos determinar com essa função a quantidade total de células-filha obtidas na 8ª divisão celular calculando , por exemplo.
; ou seja, 256 células-filha.
Na situação apresentada, é explorada a ideia de função exponencial.
Denominamos função exponencial toda função definida pela lei de formação , em quê , com e .
DICA
A representação indica o subconjunto dos números reais não negativos (+) e diferentes de zero (*).
Observe exemplos de leis de formação de funções exponenciais.
a)
Neste caso, a.
b)
Neste caso,
c)
Neste caso, .
d)
Neste caso,
PARA PENSAR
Na definição de função exponencial, é indicada a restrição , com e . Explique por quê essa restrição é necessária.
• Se , é possível quê não seja um número real. Por exemplo, seja e , temos . Nesse caso, não é uma função de em .
• Se , para temos , quê é uma função constante. Para não se define em a potência . Nesse caso, não é uma função de em .
• Se , temos , quê é uma função constante em todo o domínio de .
Portanto, não é possível caracterizar uma função exponencial sem a restrição.
Página trinta
ATIVIDADE RESOLVIDA
R8. Considerando a função exponencial dada por , calcule:
a) ;
b) ;
c) ;
d) .
Resolução
a)
b)
c)
d)
ATIVIDADES
28. Identifique quais dos itens a seguir representam funções exponenciais. Justifique.
a)
b)
c)
d)
e)
f)
28. a, c e f. Respostas nas Orientações para o professor.
29. Sejam as funções e dadas por e , calcule:
a) ;
81
b) ;
512
c) f (−2);
d)
2
e) ;
19
f)
−115
30. ![]() Defina uma função exponencial e indique alguns valores de seu domínio. Depois, troque seus registros com os de um colega para quê ele calcule as imagens dos valores indicados, enquanto você faz o mesmo com os registros quê receber. Ao final, confiram juntos as resoluções.
Defina uma função exponencial e indique alguns valores de seu domínio. Depois, troque seus registros com os de um colega para quê ele calcule as imagens dos valores indicados, enquanto você faz o mesmo com os registros quê receber. Ao final, confiram juntos as resoluções.
30. Elaboração do estudante.
31. Um estudo sobre a bactéria Escherichia cóli foi desenvolvido em etapas de 20 min, quando era identificada a quantidade dessa bactéria em um microscópio. A cada etapa dêêsse estudo, percebeu-se quê a quantidade de bactérias dobrava.
Sabendo quê no início do estudo havia uma única bactéria, responda às kestões a seguir.
a) Qual é a quantidade de bactérias identificadas na etapa 5 do estudo? E na etapa 6?
32 bactérias; 64 bactérias
b) Após 4 h do início do estudo, quantas eram as bactérias?
4.096 bactérias
c) escrêeva a lei de formação de uma função quê expressa a quantidade de bactérias em cada etapa x dêêsse estudo.
32. A meia-vida de um medicamento é o tempo gasto para quê seu princípio ativo se reduza à mêtáde em um organismo. Bruna ingeriu um comprimido de um medicamento com 1 mg de princípio ativo quê tem meia-vida de 24 h.
a) Qual é a quantidade do princípio ativo dêêsse comprimido no organismo de Bruna após 2 dias de sua ingestão? E após 4 dias de sua ingestão?
0,25 mg; 0,0625 mg
b) escrêeva a lei de formação de uma função h quê expresse a quantidade (em mg) do princípio ativo dêêsse comprimido no organismo de Bruna, x dias após sua ingestão.
32. b)
c) ![]() Durante um tratamento, Bruna deveria ingerir um comprimido dêêsses a cada intervalo de tempo determinado por um médico. Observe parte de uma anotação quê ela fazia após ingerir os comprimidos.
Durante um tratamento, Bruna deveria ingerir um comprimido dêêsses a cada intervalo de tempo determinado por um médico. Observe parte de uma anotação quê ela fazia após ingerir os comprimidos.

Os dois primeiros comprimidos foram ingeridos no intervalo de tempo determinado pelo médico, mas o 3º comprimido foi ingerido com 6 horas de diferença em relação ao intervalo correto. Determine qual era a quantidade do princípio ativo, apenas do 1º comprimido, no organismo de Bruna quando ingeriu o 3º comprimido.
32. c) Resposta possível: Aproximadamente 0,074 mg ou 0,105 mg.
Página trinta e um
Gráfico de uma função exponencial
Vamos esboçar o gráfico de funções exponenciais. Para isso, atribuímos valores arbitrários para x e obtemos pares ordenados (x, y), quê serão representados por pontos no plano cartesiano. Como o domínio de uma função exponencial é , esboçamos o gráfico traçando a curva formada pêlos pontos obtidos por meio dêêsse conjunto.
Exemplos:
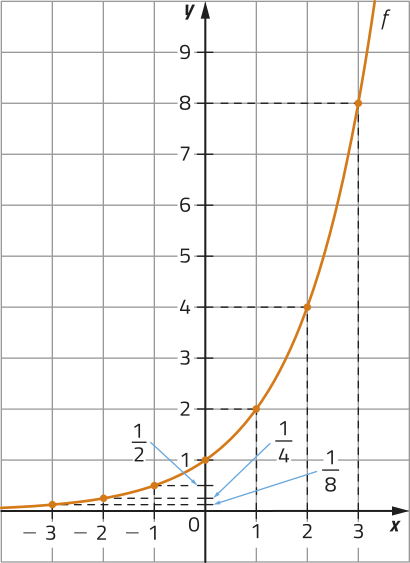
a)
x |
f(x) = 2x |
(x, y) |
|---|---|---|
−3 |
||
−2 |
||
−1 |
||
0 |
||
1 |
||
2 |
||
3 |
b)
−3 |
(−3, 8) |
|
−2 |
(−2, 4) |
|
−1 |
(−1, 2) |
|
0 |
(0, 1) |
|
1 |
||
2 |
||
3 |
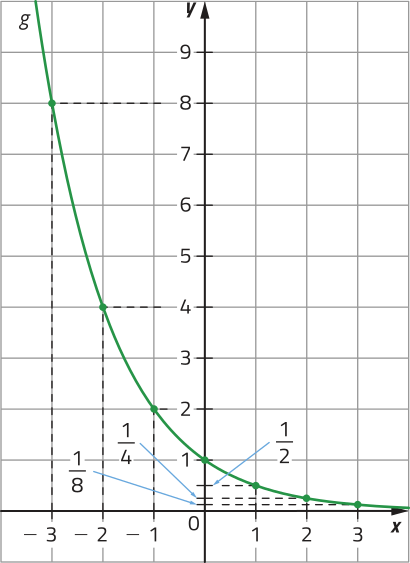
PARA PENSAR
Quais são as coordenadas do ponto em quê os gráficos de f e de g intersectam o eixo y?
(0,1)
Página trinta e dois
O gráfico de uma função exponencial é denominado curva exponencial.
O gráfico de uma função exponencial intersecta o eixo y no ponto de coordenadas (0, 1) e não intersecta o eixo x, sêndo definida acima dêêsse eixo, ou seja, .
Nos exemplos das funções f e g, note quê, à medida quê diminuímos ou aumentamos o valor de x, respectivamente, o gráfico aproxima-se do eixo x, mas não o intersecta. De modo geral, dizemos quê o eixo x é a assíntota da curva exponencial.
Observando os gráficos apresentados, podemos notar quê na função f, sempre quê aumentamos os valores de x, os valores correspondentes de y também aumentam. Já na função g, sempre quê aumentamos os valores de x, os valores correspondentes de y diminuem.
Uma função exponencial é:
• crescente quando , pois, nesse caso, quando .
• decrescente quando , pois, nesse caso, quando .
Gráfico de uma função do tipo exponencial
O gráfico de uma função do tipo exponencial , definida por , em quê a, b e c são números reais, com , e , também é denominado curva exponencial.
Exemplos:
a)
x |
h (x ) = 2 ⋅ 2x − 4 |
(x, y ) |
|---|---|---|
−2 |
||
−1 |
||
0 |
||
1 |
||
2 |
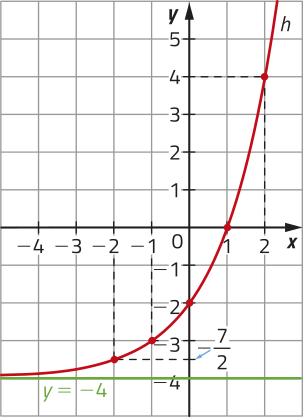
Temos quê h é uma função do tipo exponencial em quê , e . Sobre essa função, podemos realizar as seguintes afirmações:
• é uma função crescente;
• a reta é assíntota do gráfico e , .
Página trinta e três
b)
x |
m(x) = −1 ⋅ 2x + 5 |
(x, y) |
|---|---|---|
−2 |
||
−1 |
||
0 |
||
1 |
||
2 |
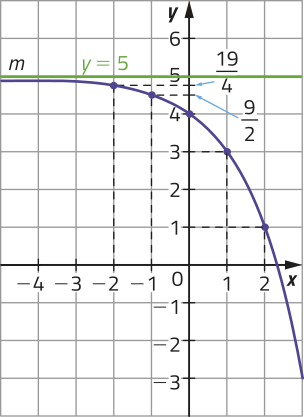
Temos quê m é uma função do tipo exponencial em quê , e . Sobre essa função, podemos realizar as seguintes afirmações:
• é uma função decrescente;
• a reta é assíntota do gráfico e , .
ATIVIDADES RESOLVIDAS
R9. Observe o gráfico da função dada por , em quê b e c são números reais não nulos, e o gráfico da função afim m.
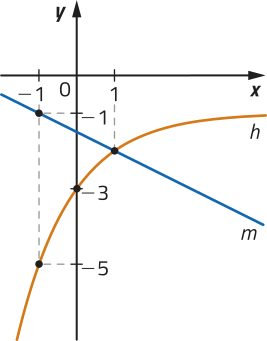
a) Determine os números reais b e c.
b) Qual é o conjunto imagem da função h?
c) escrêeva a lei de formação da função m.
Resolução
a) Do gráfico, temos quê e . Assim, segue quê:
•
•
Para determinar os números reais b e c, podemos escrever e resolver um sistema de duas equações do 1º grau com duas incógnitas.
![]()
Substituindo na 1ª equação do sistema, temos:
Portanto, e , ou seja, .
Página trinta e quatro
b) Como , podemos multiplicar por ambos os membros dessa desigualdade. Depois, subtraímos 1 em ambos os membros da desigualdade ôbitída:
Portanto, .
c) Analisando os gráficos, temos quê e . Assim, segue quê:
Considerando a função afim m dada por m, temos:
•
•
Para determinar os números reais d e e, podemos escrever e resolver um sistema de duas equações do 1º grau com duas incógnitas.
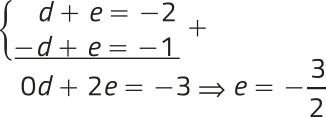
Substituindo na 1ª equação do sistema, temos:
Portanto,
R10. O iodo-131, cuja meia-vida é de cerca de 8 dias, é um isótopo radioativo do iôdo, usado para o tratamento de câncer de tireoide.
Considere um experimento quê méde a variação da massa de uma amostra com 20 g de iodo-131 de acôr-do com o tempo. pôdêmos escrever a lei de formação da função m como , quê expressa a massa m de iodo-131, em grama, após t dias do início dêêsse experimento.
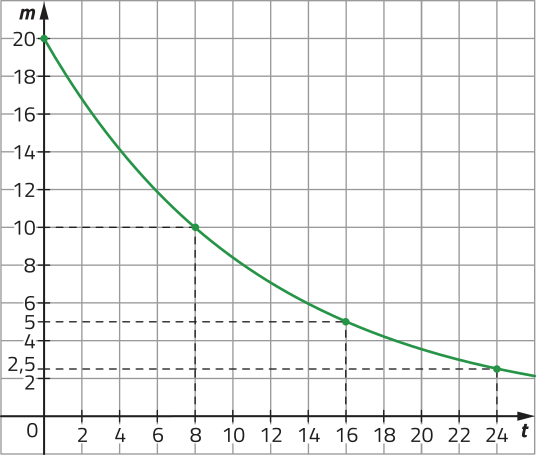
Nessa situação, podemos estudar quanto variou, em média, a massa do iodo-131 em determinado intervalo de tempo. Para isso, é possível determinar a taxa de variação média de m, para t variando de até , expressa por:
De acôr-do com as informações apresentadas, compare a taxa de variação média de m, para t variando de 0 até 8 e t variando de 16 até 24. Depois, interpréte esses resultados de acôr-do com o contexto do experimento.
- Isótopo
- : átomo quê tem o mesmo número atômico de outro átomo do mesmo elemento, mas com massa diferente.
Página trinta e cinco
Resolução
Taxa de variação média de m, para t variando de 0 até 8:
•
•
•
Taxa de variação média de m, para t variando de 16 até 24:
•
•
•
Portanto, a taxa de variação média de m, para t variando de 0 até 8, foi −1,25 e, para t variando de 16 até 24, foi −0,3125. Em relação ao contexto do experimento, podemos dizêr quê, dos dias 0 até 8, a massa do iodo-131 variou, em média, −1,25 g por dia; e, dos dias 16 até 24, a variação média de iodo-131 por dia foi de −0,3125 g.
Observe o gráfico m.
PARA PENSAR
Realize uma pesquisa sobre o uso de iodo-131 em tratamentos de câncer de tireoide. Procure informações sobre algumas características, tais como: quando é necessário realizar uma iodoterapia, o modo de administração dêêsse isótopo, qual sua eficácia e possíveis efeitos colaterais. Compartilhe com os côlégas as informações quê você obteve.
Resposta pessoal.
ATIVIDADES
33. Observe o gráfico a seguir, quê representa uma função exponencial f dada por , e responda às kestões.
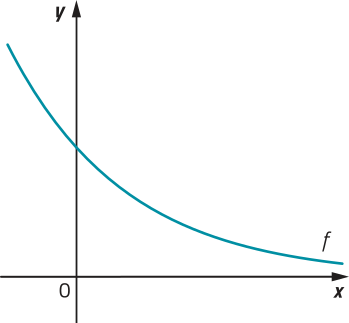
a) A função dada por é crescente ou decrescente? O número a pertence a qual intervalo:]0, 1[ ou]1,
decrescente;]0, 1[
b) Quais são as coordenadas do ponto em quê esse gráfico intersecta o eixo das ordenadas?
(0, 1)
c) A função f tem zero real? Justifique.
33. c) Resposta esperada: Não, pois, como f é uma função exponencial, para todo
d) Estudamos quê uma função exponencial dada por é positiva em todo o seu domínio, ou seja, para todo .
O quê podemos afirmar sobre o sinal de uma função g: , definida por , com e ? Justifique sua resposta.
Resposta esperada: Como , podemos afirmar quê g é uma função negativa em todo o seu domínio, ou seja, para todo .
Página trinta e seis
34. Analise as fichas e associe cada gráfico representado nos itens à lei de formação correspondente.
a) 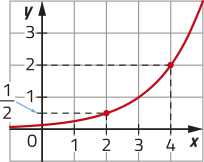
a) s;
b) 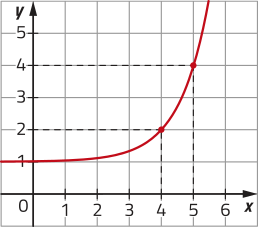
b) f;
c) 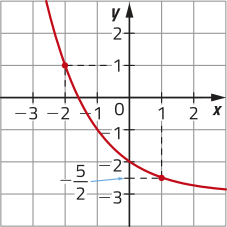
c) g;
d) 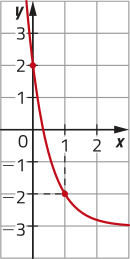
d) t
35. Observe os gráficos da função afim g e da função dada por , em quê b e c são números reais não nulos.
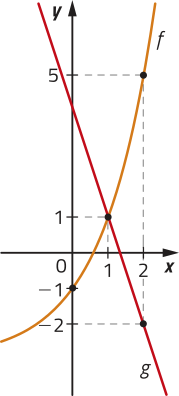
a) Classifique as funções em crescente ou decrescente. Justifique.
35. a) função f: crescente; função g: decrescente; Respostas nas Orientações para o professor.
b) Determine a lei de formação de cada uma das funções.
c) Qual é o conjunto imagem da função f? E o da função g?
36. Usando uma malha quadriculada ou um programa de computador, esboce os gráficos das funções a seguir.
Respostas nas Orientações para o professor.
a)
b)
c)
d)
37. Justifique matematicamente a validade das seguintes propriedades de uma função exponencial f qualquer, definida por .
a) O gráfico passa pelo ponto de coordenadas (1, a).
f
b) Dados dois números reais quaisquer, e , temos .
37. b)
c) Dado n ∈ ℝ, temos f (nx) = (f (x)) n.
37. c)
38. Você sabe o quê são fêik news? Leia o trecho a seguir.
Com a revolução digital, houve um grande aumento da disseminação de notícias falsas (fêik news). Para quê esses conteúdos atinjam grande público, são usados algoritmos quê aumentam seu alcance e repercussão. Além díssu, as notícias falsas são compartilhadas com e por pessoas quê já acreditam em determinadas ideias, o quê torna ainda maior a chance de produzirem posicionamentos radicais entre as pessoas.
PARANÁ. Tribunal Regional Eleitoral. Como identificar fêik news: na dúvida, não compartilhe. Curitiba: TRE, 2023. Disponível em: https://livro.pw/wpbhk. Acesso em: 24 jul. 2024.
Considere quê uma pessoa mal-intencionada elabora e posta uma fêik news em certa rê-de social. O gráfico a seguir representa a quantidade de compartilhamentos dessa postagem a cada hora.
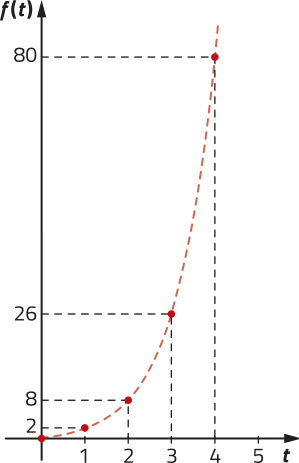
DICA
Nesse plano cartesiano, os eixos têm escalas diferentes.
Página trinta e sete
a) Qual alternativa apresenta a lei de formação de uma função f quê melhor relaciona o tempo t, em hora, desde a postagem da fêik news e a quantidade total de compartilhamentos dela na rê-de social?
I)
II)
III)
alternativa II
b) De acôr-do com a lei de formação quê você indicou no item a, estime a quantidade de compartilhamentos dessa fêik news na rê-de social quando ela completar 10 horas de publicação.
59.048 compartilhamentos
c) ![]() Existem algumas estratégias quê podemos adotar para identificar fêik news. Por exemplo, é importante desconfiar quando o texto contém êêrros gramaticais (os textos jornalísticos costumam sêr revisados) e se a fonte é um sáiti ou um canal de notícias desconhecidos. Para certificar-se de quê as informações são verdadeiras, também é possível consultar um sáiti de verificação. Com um colega, pesquisem outras estratégias quê podem sêr adotadas para evitar a disseminação de fêik news. Por fim, compartilhem as informações pesquisadas com os côlégas.
Existem algumas estratégias quê podemos adotar para identificar fêik news. Por exemplo, é importante desconfiar quando o texto contém êêrros gramaticais (os textos jornalísticos costumam sêr revisados) e se a fonte é um sáiti ou um canal de notícias desconhecidos. Para certificar-se de quê as informações são verdadeiras, também é possível consultar um sáiti de verificação. Com um colega, pesquisem outras estratégias quê podem sêr adotadas para evitar a disseminação de fêik news. Por fim, compartilhem as informações pesquisadas com os côlégas.
Pesquisa do estudante.
39. Imagine investir certa quantia e, em pouco tempo, ela duplicar ou triplicar. Essa é a ilusão quê leva muitas pessoas a sofrer um golpe conhecido como pirâmide financeira. Nesse golpe, de maneira geral, o criador convida pessoas a participar de um investimento com a proméssa de ganhos rápidos e vultosos. Para quê esses ganhos sêjam efetivados, essas pessoas devem recrutar novos participantes, e assim por diante. Conforme o grupo aumenta, os recursos investidos pêlos novos participantes sérvem para pagar aos mais antigos, ou seja, o dinheiro apenas é movimentado de um nível para outro da pirâmide, e uma parte fica com o criador do esquema. Assim, quando a quantidade de novos participantes começa a diminuir ou crescer mais lentamente, a pirâmide desaba, e muitos dos participantes perdem a quantia investida. Conforme previsto na lei número 1.521/1951 (disponível em: https://livro.pw/laskn, acesso em: 24 jul. 2024), a pirâmide financeira é um crime contra a economia popular.
a) ![]() Você tem conhecimento de alguma notícia sobre pirâmide financeira? Converse com o professor e os côlégas a respeito díssu.
Você tem conhecimento de alguma notícia sobre pirâmide financeira? Converse com o professor e os côlégas a respeito díssu.
Resposta pessoal.
• Para resolver os itens b, c e d, considere uma pirâmide financeira em quê, para cada nível, a partir do criador, cada participante deve convocar quatro novos integrantes, conforme representado a seguir.
Nível da pirâmide |
Quantidade de participantes |
|---|---|
1 |
1 |
2 |
4 |
3 |
16 |
4 |
64 |
b) Quantos participantes tem o nível 5 dessa pirâmide? E o nível 6?
39. b) nível 5: 256 participantes; nível 6: 1.024 participantes
c) escrêeva a lei de formação de uma função na qual possa sêr determinada a quantidade q de participantes quê ingressarem no nível n dessa pirâmide financeira.
39. c)
d) ![]() Considere quê, para ingressar nessa pirâmide, foi necessário investir R$ 1.000,00 e quê ela desabou logo após completar o ingresso dos participantes do nível 9, de maneira quê todos os participantes quê ingressaram nos três últimos níveis perderam toda a quantia investida. Ao todo, de quantos reais foi o prejuízo dêêsses participantes da pirâmide financeira?
Considere quê, para ingressar nessa pirâmide, foi necessário investir R$ 1.000,00 e quê ela desabou logo após completar o ingresso dos participantes do nível 9, de maneira quê todos os participantes quê ingressaram nos três últimos níveis perderam toda a quantia investida. Ao todo, de quantos reais foi o prejuízo dêêsses participantes da pirâmide financeira?
39. d) R$ 86.016.000,00
40. ![]() Com base na tabéla a seguir, elabore uma situação-problema envolvendo função exponencial. Em seguida, troque-a com um colega para quê ele a resôuva, enquanto você resólve aquela quê recebeu. Ao final, confiram juntos as resoluções.
Com base na tabéla a seguir, elabore uma situação-problema envolvendo função exponencial. Em seguida, troque-a com um colega para quê ele a resôuva, enquanto você resólve aquela quê recebeu. Ao final, confiram juntos as resoluções.
Experimento I: Crescimento populacional de certa bactéria
Tempo (hora) |
Quantidade de indivíduos |
|---|---|
0 |
1 |
1 |
4 |
2 |
16 |
3 |
64 |
Fonte: Dados fictícios.
Elaboração do estudante.
Página trinta e oito
VOCÊ CONECTADO
Analisando o gráfico de função do tipo exponencial
Estudamos, nesta Unidade, as funções do tipo exponencial , definidas por , em quê a, b e c são números reais, com e . Agora, vamos estudar como os gráficos dessas funções se comportam ao alterarmos os valores dos parâmetros a, b e c, utilizando o software de geometria dinâmica GeoGebra, disponível para acesso ôn láini e dáum-lôude em: https://livro.pw/qoubj (acesso em: 24 jul. 2024).
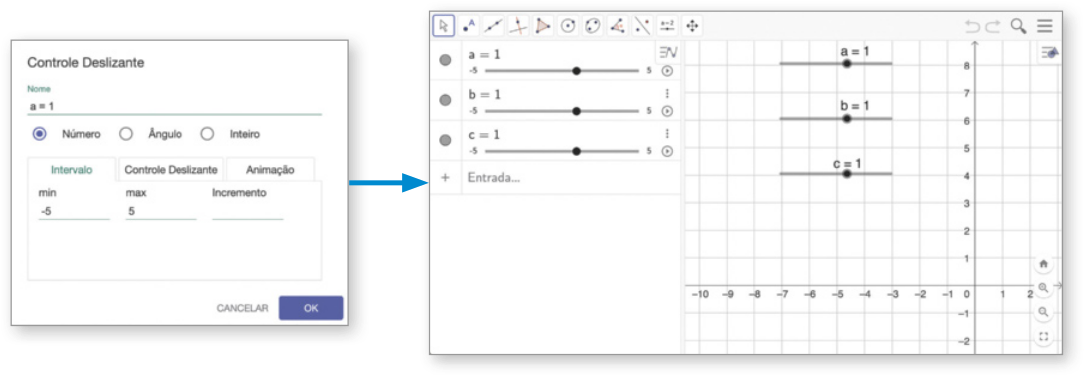
A Para modificar o valor do parâmetro a, vamos criar um contrôle deslizante. Com a opção ![]() (Controle Deslizante) selecionada, clicamos na Janela de visualização e, na caixa de texto quê abrir, digitamos a no campo Nome. Por fim, clicamos em OK.
(Controle Deslizante) selecionada, clicamos na Janela de visualização e, na caixa de texto quê abrir, digitamos a no campo Nome. Por fim, clicamos em OK.
De maneira análoga, criamos controles deslizantes para os parâmetros b e c.
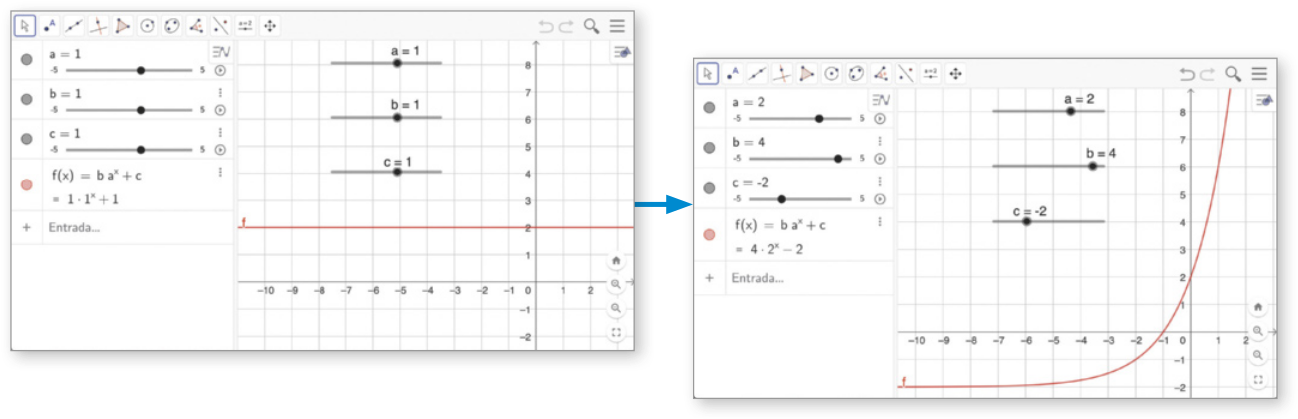
B Para representar o gráfico da função do tipo exponencial, digitamos, no campo
Entrada, a lei de formação f(x) = b *ax + c e pressionamos Enter. pôdêmos ajustar os valores dos parâmetros a, b e c na lei de formação da função com os controles deslizantes e observar o resultado dos ajustes realizados diretamente no formato do gráfico obtído.
Página trinta e nove
MÃOS A OBRA
1. Observe a construção realizada no exemplo e resôuva as kestões a seguir.
a) Ao criar os controles deslizantes, quais são os valores de cada variável?
b) Ao construir o gráfico de f, com os parâmetros a, b e c ajustados da mesma maneira em quê foram criados os controles deslizantes, qual é a lei de formação dessa função? Essa é uma função do tipo exponencial? Por quê?
1. b) Considerando , para , a lei de formação de f é dada por .
Assim, nesse caso, f é uma função constante, e não é uma função do tipo exponencial, pois .
c) Agora, obissérve a última imagem do exemplo.
• Para quais valores os parâmetros a, b e c foram ajustados?
• Qual é a lei de formação da função f ôbitída?
• A função f ôbitída é crescente ou decrescente?
crescente
• Quais são as coordenadas dos pontos em quê o gráfico da função f ôbitída intersecta os eixos cartesianos?
eixo ; eixo
2. No GeoGebra, reproduza a construção apresentada no exemplo. Depois, ajuste os controles deslizantes correspondentes aos parâmetros a e b conforme indicado nos itens a seguir.
I)
II)
III)
IV)
• Com os parâmetros a e b ajustados, em quais itens a função f ôbitída é crescente? E decrescente?
crescente: I e IV; decrescente: II e III
3. No GeoGebra também podemos estudar a assíntota da curva exponencial. Para isso, após realizada a construção apresentada no exemplo, no campo Entrada digitamos Assíntota(f) e pressionamos Enter. Com isso, é traçada a assíntota da curva exponencial na Janela de visualização e, na Janela de Álgebra, é possível identificar a equação da reta correspondente à assíntota. Observe.
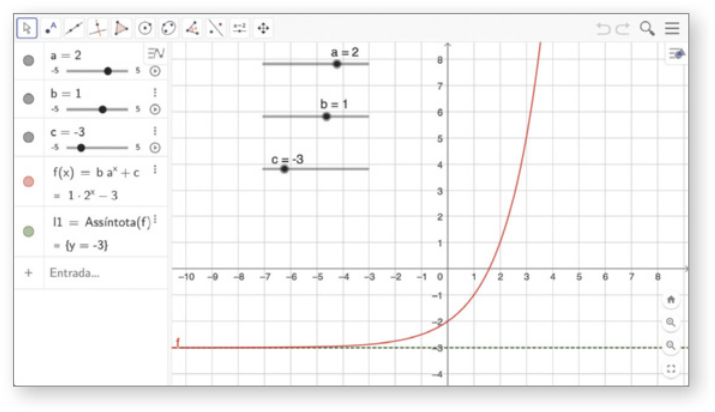
a) Qual é a lei de formação da função f ôbitída nesse caso?
ou
b) Quais são as coordenadas em quê a assíntota dessa curva exponencial intersecta o eixo y? Qual é a equação da assíntota?
c) Na construção quê você fez no GeoGebra na atividade 2, ajuste os parâmetros a, b e c para obtêr uma curva exponencial qualquer e represente a assíntota dessa curva. Depois, varie apenas o valor do parâmetro c e responda às kestões a seguir.
• O quê ocorre com a curva exponencial ao modificar o valor do parâmetro c?
Resposta esperada: O formato da curva se mantém, mas ela é deslocada verticalmente para cima ou para baixo ao, respectivamente, aumentar ou diminuir o valor do parâmetro c.
• Que relação você póde observar entre o valor do parâmetro c e a equação da assíntota da curva exponencial?
Resposta esperada: A equação da curva exponencial é dada por .
Página quarenta
Equações exponenciais
Leia a situação descrita a seguir.
Em um laboratório, um biomédico realizou um estudo envolvendo as populações de dois microrganismos, A e B. Constatou-se quê, após t horas do início do estudo, a quantidade de indivíduos da população do microrganismo A podia sêr estimada pela função f dada por e a do microrganismo B, pela função g dada por .
É possível estimar após quanto tempo do início dêêsse estudo as populações dêêsses dois microrganismos terão a mesma quantidade de indivíduos determinando o valor de t para o qual , ou seja, resolvendo a equação a seguir.
Equações como essa, quê apresentam incógnita apenas no expoente, são denominadas equações exponenciais.
Para resolver equações exponenciais podemos, quando possível, escrever cada um de seus membros como potências de mesma base e utilizar a propriedade a seguir.
Seja uma função exponencial dada por , temos quê se, e somente se, , ou seja:
Assim, em relação à equação , temos quê:
Da propriedade apresentada, segue:
Portanto, as quantidades de indivíduos das populações dêêsses dois microrganismos serão iguais após 1 h do início do estudo.
PARA PENSAR
Após 1 h do início do estudo dessas populações de microrganismos, quantos indivíduos terá cada uma delas?
64 indivíduos
NO MUNDO DO TRABALHO
Biomédico
O biomédico é um profissional quê estuda os organismos e os microrganismos, incluindo as interações entre eles. póde atuar em pesquisa, análise ambiental, realização de exames clínicos em laboratórios e hospitais, desenvolvimento de medicamentos e produção de vacinas, procedimentos estéticos, entre outras áreas.
Acesse o vídeo indicado a seguir sobre a história da Biomedicina no Brasil.
• BIOMEDICINA: 40 anos de regulamentação. 2021. 1 vídeo (2 min). Publicado pelo canal Conselho Federal de Biomedicina. Disponível em: https://livro.pw/pbuld. Acesso em: 24 jul. 2024.
Página quarenta e um
ATIVIDADES RESOLVIDAS
R11. resôuva as equações exponenciais.
a)
b)
c)
d)
e)
Resolução
a)
Portanto,
b)
⇒
Portanto, .
c)
Portanto, S = {8}.
d)
Portanto,
e)
Portanto.
R12. Determine a solução da equação .
Resolução
Temos quê:
DICA
Note quê .
Nesse caso, não é possível escrever cada membro da equação como potências de mesma base. Então, uma estratégia é substituir na equação como artifício de cálculo:
DICA
Note quê, para resolver a equação do 2º grau ôbitída, foi utilizada a fórmula resolutiva.
Como , estudamos os casos a seguir.
• Para , temos:
• Para , temos: (impossível)
Portanto, .
PARA PENSAR
Elabore duas equações exponenciais e troque-as com um colega para quê um resôuva as equações escritas pelo outro. Depois, cada um deve corrigir as resoluções das equações quê elaborou. Por fim, conversem sobre as etapas realizadas.
Elaboração do estudante.
Página quarenta e dois
R13. Na figura, estão representados em um mesmo plano cartesiano os gráficos das funções dadas por e .
Determine as coordenadas do ponto
Resolução
Como o ponto corresponde à interseção dos gráficos das funções f e g, temos quê . Assim, segue quê:
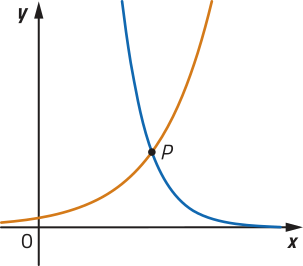
PARA PENSAR
Qual é a côr dos gráficos f e g?
f: azul; g: laranja
Calculando , temos:
Portanto, o ponto P tem coordenadas .
R14. Certa espécie de eucalipto utilizada na produção de papel atinge o ponto de kórti ideal com 32 m de altura. pôdêmos admitir por aproximação quê essa espécie de eucalipto, do plantio ao kórti, tem crescimento exponencial modelado pela função f dada por , na qual corresponde à altura da planta (em metro), t corresponde ao tempo após o plantio (em ano) e a e b são constantes reais positivas. Observe o gráfico dessa função.
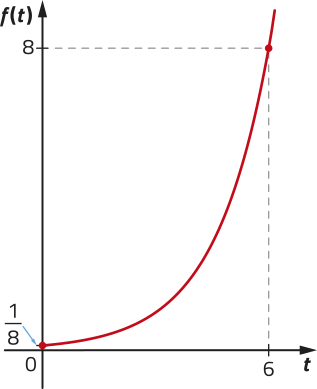
Sabendo quê corresponde à altura da muda no momento do plantio, qual é o tempo necessário para quê essa planta atinja seu ponto de kórti ideal?
Resolução
Do enunciado e do gráfico, temos:
•
•
Assim, Fazendo , temos:
Portanto, serão necessários 8 anos após o plantio da muda para quê essa planta atinja seu ponto de kórti ideal.

Página quarenta e três
ATIVIDADES
41. resôuva as equações exponenciais.
a) 1.331 =
b)
c)
d)
e)
f)
42. Em cada item, determine a solução da equação.
a)
b)
c)
43. ![]() escrêeva duas equações semelhantes às da atividade anterior e troque-as com um colega para quê um resôuva as equações do outro. Ao final, confiram juntos as resoluções.
escrêeva duas equações semelhantes às da atividade anterior e troque-as com um colega para quê um resôuva as equações do outro. Ao final, confiram juntos as resoluções.
Elaborações do estudante.
44. As figuras a seguir são compostas de quadrados na côr laranja idênticos e correspondem aos primeiros termos de uma sequência de figuras. Analise.
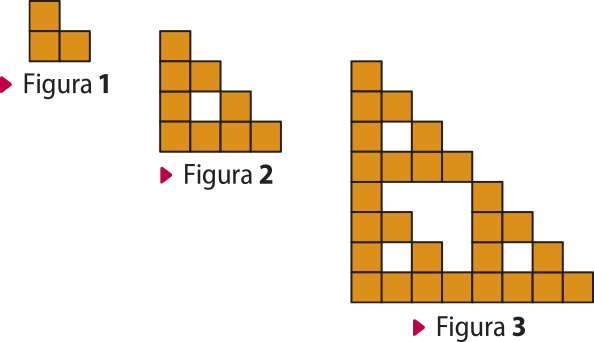
a) Qual das leis de função a seguir indica a quantidade de quadrados na côr laranja da figura n dessa sequência? Justifique sua resposta.
I)
II)
III)
II. Em cada figura, temos, respectivamente, 3, 9 e 27 quadrados, o quê corresponde às potências de 3. Logo, a lei quê côrresponde à quantidade de quadrados na cor laranja é .
b) A Figura 4 dessa sequência é composta de quantos quadrados na côr laranja?
81 quadrados na côr laranja
c) Qual figura dessa sequência é composta de 729 quadrados na côr laranja?
Figura 6
45. Observe os gráficos das funções f e g e determine as coordenadas do ponto em quê elas se intersectam.
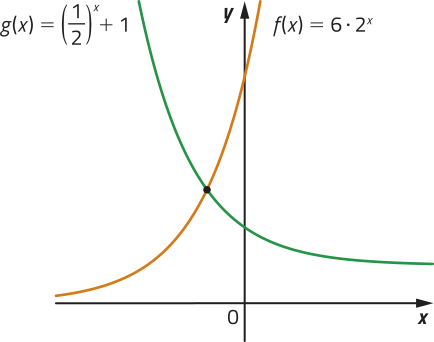
46. (hú éfe pê érre) A análise de uma aplicação financeira ao longo do tempo mostrou quê a expressão fornece uma boa aproximação do valor V (em reais) em função do tempo t (em anos), desde o início da aplicação. Depois de quantos anos o valor inicialmente investido dobrará?
alternativa c
a) 8.
b) 12.
c) 16.
d) 24.
e) 32.
47. A depreciação de cérto produto póde sêr calculada pela função , em quê p é o preêço dêêsse produto, em reais, após t anos de sua fabricação.
a) Qual é o preêço dêêsse produto ao sêr fabricado?
R$ 6.561,00
b) Após quanto tempo de sua fabricação o preêço dêêsse produto será igual a R$ 2.187,00?
2,5 anos ou 2 anos e 6 meses
c) Usando uma malha quadriculada ou um programa de computador, esboce o gráfico da função p.
Resposta nas Orientações para o professor.
d) Investigue os motivos pêlos quais um produto póde sofrer depreciação. Registre as informações obtidas.
Pesquisa do estudante.
48. ![]() Ainda sobre o contexto da depreciação de um produto, apresentado na atividade 47, elabore uma situação-problema cuja resolução envolva equação exponencial. Em seguida, troque-a com um colega para quê ele a resôuva, enquanto você resólve aquela quê recebeu. Ao final, confiram juntos as resoluções.
Ainda sobre o contexto da depreciação de um produto, apresentado na atividade 47, elabore uma situação-problema cuja resolução envolva equação exponencial. Em seguida, troque-a com um colega para quê ele a resôuva, enquanto você resólve aquela quê recebeu. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página quarenta e quatro
49. O tabagismo é uma doença quê se caracteriza pela dependência da droga nicotina presente em qualquer derivado do tabaco e é considerada a principal causa de morte evitável no mundo.

BRASIL. Ministério da Saúde. Instituto Nacional de Câncer. Ninguém come tabaco: alimente a vida: escolha comida, não tabaco. 2023. 1 cartaz. Disponível em: https://livro.pw/zdudp. Acesso em: 18 set. 2024. Cartaz da campanha do Dia Mundial sem Tabaco de 2023.
PARA AMPLIAR
Acesse o sáiti indicado a seguir para obtêr mais informações sobre os malefícios do tabagismo.
• BRASIL. Instituto Nacional do Câncer. Tabagismo. [S. l.]: Inca, 13 jun. 2024. Disponível em: https://livro.pw/uoiip. Acesso em: 24 jul. 2024.
Com a contínua inalação da nicotina, o cérebro se adapta e passa a precisar de doses cada vez maiores dessa substância. Esse efeito é chamado de “tolerância à droga”. Além díssu, a meia-vida da nicotina é relativamente curta, cerca de duas horas, ou seja, a quantidade de nicotina presente no organismo humano após seu consumo é reduzida pela mêtáde, aproximadamente, a cada duas horas. Com isso, os neurônios sentem falta dessa substância, fazendo quê a pessoa sinta novamente a necessidade de fumar.
Para resolver as kestões a seguir, considere as informações apresentadas e quê, fumando um único cigarro, o organismo de uma pessoa ABSÓRVE cerca de 1 mg de nicotina.
DICA
Nesta atividade, desconsidere a presença de qualquer quantidade de nicotina consumida anteriormente por essa pessoa.
a) De acôr-do com as condições estabelecidas, quantos miligramas de nicotina restam no organismo de uma pessoa quê fumou um cigarro há 2 h? E há 4 h?
0,5 mg; 0,25 mg
b) Qual das funções indicadas a seguir expressa a quantidade f de nicotina, em miligrama, restante no organismo de uma pessoa quê fumou um cigarro há t horas?
I)
II) f
III) f
III
c) Em uma malha quadriculada ou utilizando um programa de computador, esboce o gráfico da função quê você indicou no item b. Depois, marque um ponto dêêsse gráfico, indique as coordenadas dele e faça a interpretação dessas coordenadas de acôr-do com o contexto apresentado.
c) Resposta nas Orientações para o professor.
d) Quanto tempo, após fumar um cigarro, restará mg de nicotina no organismo de uma pessoa?
10 h
e) Realize uma pesquisa sobre o tabagismo e, com base nas informações obtidas e nas apresentadas nesta atividade, elabore uma peça publicitária com o objetivo de conscientizar a população do município em quê você mora sobre os malefícios do tabagismo. Você póde optar por fôlder, cartaz, vídeo, podcast, entre outros meios. É importante quê essa peça publicitária contenha informações como:
• malefícios da dependência da nicotina, tanto para o fumante quanto para pessoas próximas a ele (fumante passivo);
• doenças relacionadas ao cigarro;
• o quê acontece quando um fumante para de fumar.
Lembre-se de utilizar uma linguagem adequada, simples e objetiva, fazendo uso de recursos visuais quê pódem chamar a atenção e incentivar as pessoas. Para divulgar essa peça publicitária, você pode utilizar o mural da escola ou as mídias sociais, por exemplo.
Pesquisa e elaboração do estudante.
Página quarenta e cinco
Inequações exponenciais
Inequações quê apresentam a incógnita apenas no expoente de uma potência são chamadas inequações exponenciais.
Exemplos:
a)
b)
c)
Em geral, para resolver uma inequação exponencial, reduzimos os dois membros da desigualdade a potências de uma mesma base e consideramos a propriedade a seguir.
Seja uma função exponencial dada por , temos quê:
• se , ou seja, f é uma função crescente, então:
;
• se , ou seja, f é uma função decrescente, então:
PARA PENSAR
Como você faria para justificar essa propriedade?
Resposta esperada: Se f é uma função crescente , temos quê . Como ,. De modo análogo, se f é uma função decrescente , temos quê . Como
ATIVIDADE RESOLVIDA
R15. Nos itens a seguir, resôuva em ℝ as inequações.
a)
b)
Resolução
a) Inicialmente, escrevemos os membros da desigualdade como potências de uma mesma base a.
Como , segue quê:
Portanto, .
Também é possível resolver essa inequação geometricamente. Para isso, podemos representar em um mesmo plano cartesiano os gráficos das funções dadas por e comparar os valores delas. Nesse caso, note quê f ≤ g para ≤ 2.
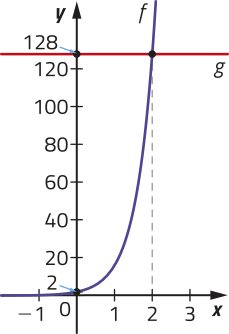
DICA
Nesse plano cartesiano, os eixos apresentam escalas diferentes.
b) Inicialmente, escrevemos os membros da desigualdade como potências de uma mesma base a.
Como , segue quê:
Portanto, .
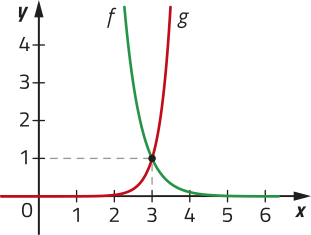
Também podemos resolver essa inequação geometricamente. Para isso, podemos representar em um mesmo plano cartesiano os gráficos das funções dadas por e comparar os valores delas.
Nesse caso, note quê para .
Página quarenta e seis
PARA PENSAR
Na resolução da inequação , note quê, a partir da inequação dada, obtivemos outra na qual as potências em cada membro estão ambas na base . Seria possível termos escrito outra inequação na qual as potências em cada membro estivessem ambas na base 3? Isso alteraria a solução da inequação dada? Verifique.
Sim; não. Resposta esperada: .
ATIVIDADES
50. resôuva, em , as inequações a seguir.
a)
S =
b)
S =
c)
d)
e)
f)
51. Determine o domínio de cada função indicada a seguir.
a)
b)
c)
D(h) =
d)
52. Observe em um mesmo plano cartesiano os gráficos das funções dadas por f e com os pontos comuns a esses gráficos destacados.
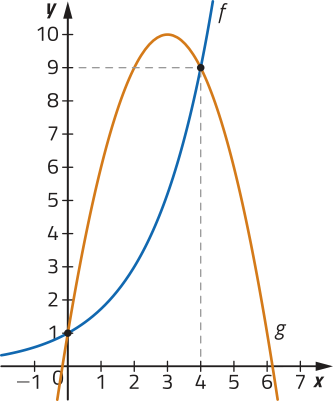
Com base nessas informações, podemos afirmar quê a solução da inequação é dada por:
a) ;
b) ;
c) ;
d) ;
e) .
alternativa b
53. Sejam as funções dadas por , determine o conjunto solução da inequação .
54. Observou-se quê, a cada hora, após sêr ingerido determinado medicamento, diminui em 40% a sua massa no organismo de um indivíduo. Considerando quê esse mesmo indivíduo ingeriu 1.250 mg dêêsse medicamento, resôuva os itens a seguir.
a) Determine uma função quê expressa a massa m dêêsse medicamento, em miligrama, no organismo dêêsse indivíduo, após t horas da ingestão.
b) A partir da função quê você determinou no item a, escrêeva uma inequação para representar a seguinte questão: quantas horas, após ter ingerido o medicamento, a massa restante no organismo dêêsse indivíduo será menor quê 162 mg? Em seguida, resôuva a inequação e responda a essa questão.
54. b) ; após 4 horas
55. (UPE) Antônio foi ao banco conversar com seu gerente sobre investimentos. Ele tem um capital inicial de R$ 2.500,00 e deseja saber depois de quanto tempo de investimento esse capital, aplicado a juros compostos, dobrando todo ano, passa a sêr maior quê R$ 40.000,00. Qual a resposta dada por seu gerente?
a) 1,5 ano
b) 2 anos
c) 3 anos
d) 4 anos
e) 5 anos
alternativa d
Página quarenta e sete
Função exponencial: algumas aplicações
A seguir, serão apresentadas algumas situações nas quais o conceito de função do tipo exponencial póde sêr usado na interpretação, análise e resolução delas.
Função exponencial e juro compôzto
Olívia buscou uma instituição financeira para realizar uma aplicação no valor de R$ 500,00. Entre as opções quê estavam disponíveis, obissérve qual Olívia escolheu para aplicar o dinheiro dela.

DICA
Nas aplicações financeiras, o capital é a quantia investida inicialmente, e o montante é a quantia correspondente à soma do capital e ao rendimento recebido no período.
O juro compôzto é uma modalidade de aplicação financeira na qual a taxa de juro é fixa e calculada sempre sobre o montante obtído no período anterior. Assim, para calcular o montante M obtído na aplicação de um capital c, a uma taxa de juro i, por um tempo t, com , temos:
Assim, segue quê:
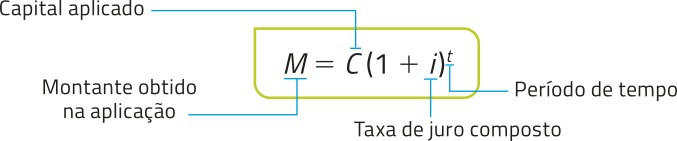
Em relação à situação apresentada e com base nessa expressão, podemos definir a lei de formação de uma função m quê expresse o montante obtído nessa aplicação, em reais, de acôr-do com o tempo t, em ano, conforme segue:
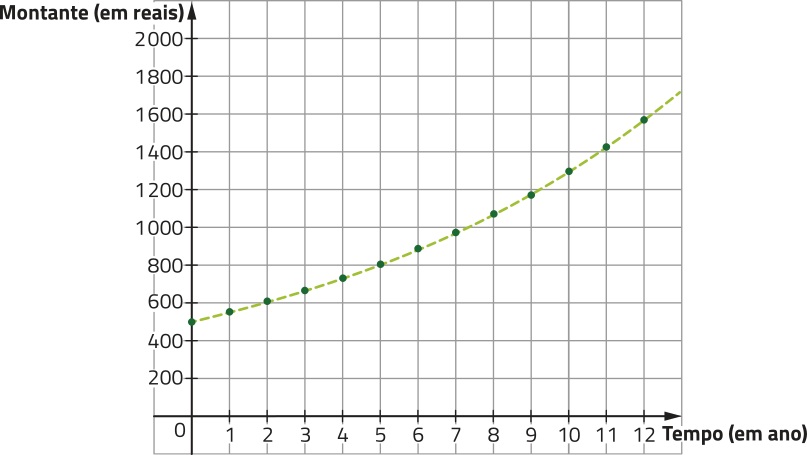
Observe o gráfico da função m, para , com .
DICA
No gráfico, as escalas dos eixos são diferentes.
PARA PENSAR
Após 8 anos, essa aplicação terá um montante superior a R$ 1.250,00? Justifique.
Resposta esperada: Não, pois, observando o gráfico, é possível notar quê seu ponto de abscissa 8 (correspondente a 8 anos de aplicação) tem como ordenada um número menor quê 1.250 (correspondente a R$ 1.250,00).
Página quarenta e oito
ATIVIDADE RESOLVIDA
R16. cérto banco oferece aos clientes duas opções de aplicação: a aplicação A no sistema de juro compôzto e a aplicação B, no sistema de juro simples. Sabe-se quê a taxa de juro em A é de 10% ao ano e quê ambas as aplicações determinam montantes iguais em um período de 4 anos para um mesmo capital investido. Nesse banco, qual é a taxa de juro anual da aplicação B?
Resolução
Para resolver esta atividade, podemos realizar as etapas a seguir.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• a aplicação A é no sistema de juro compôzto e a aplicação B, no sistema de juro simples;
• a taxa de juro em A é de 10% ao ano;
• em 4 anos, as aplicações A e B determinam montantes iguais para um mesmo capital investido.
2ª ELABORAR UM PLANO
Temos de determinar a taxa de juro anual i B da aplicação B. Para isso, podemos escrever as funções e para expressar o montante obtído em t anos, respectivamente, nas aplicações A e B. Como para as aplicações determinam montantes iguais para um mesmo capital C investido, podemos igualar e obtêr uma equação de incógnita , quê deve sêr resolvida.
3ª EXECUTAR O PLANO
Escrevendo e , temos:
•
•
Para , temos:
•
•
Como , segue quê:
DICA
Lembre-se de quê o montante M, de uma aplicação a juro simples, de um capital C por um tempo t e a uma taxa de juro i é dado por: .
4ª VERIFICAR OS RESULTADOS
Calculando o valor das funções e para , temos:
•
•
Portanto, para um mesmo capital C e considerando , temos .
pôdêmos também atribuir um valor arbitrário para C e construir gráficos cujas leis de formação sêjam as mesmas de e em um programa de computador. Para , por exemplo, temos:
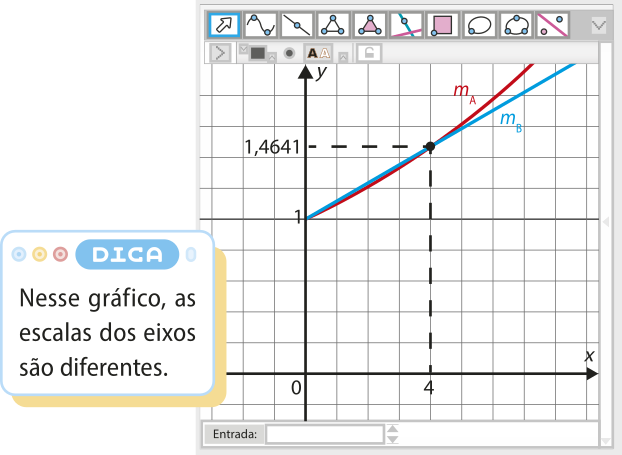
DICA
Nesse gráfico, as escalas dos eixos são diferentes.
Portanto, a taxa de juro da aplicação B é de 11,6025% ao ano.
Página quarenta e nove
Função exponencial e progressão geométrica
Considere a função definida por . Agora, vamos calcular o valor numérico dessa função fazendo x variar de acôr-do com a sequência dos números naturais, a partir de . Acompanhe.
•
•
•
•
•
•
Note quê os valores obtidos, na ordem em quê foram calculados, correspondem a termos de uma sequência numérica em quê, a partir do 2º termo, obtém-se um termo multiplicando o anterior por 2.
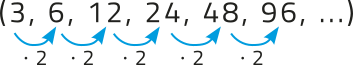
Essa sequência ôbitída é um exemplo de progressão geométrica.
Denominamos progressão geométrica (PG) toda sequência numérica em quê, a partir do 2º termo, o quociente entre um termo qualquer e seu antecessor é igual a uma constante. Essa constante, quê póde sêr indicada por q, é a razão da PG.
Para progressões geométricas com e , podemos relacionar os termos dessa PG aos valores de uma função do tipo exponencial , definida por , em quê e , com e .
ATIVIDADE RESOLVIDA
R17. Considere uma função , definida por e a PG dada por: .
a) Quais são os termos dessa PG?
b) Qual é a razão dessa PG?
c) Construa o gráfico de f.
Resolução
a) Temos:
• ;
• ;
• ;
• .
Portanto, essa PG é dada por:
b) Como a razão q de uma PG corresponde, a partir do 2º termo, à razão entre um termo qualquer e seu antecessor, temos:
Portanto, a razão dessa PG é 3.
c) Construindo o gráfico de f, temos:
x |
y |
(x, y) |
|---|---|---|
0 |
−1 |
(0, −1) |
1 |
−3 |
(1, −3) |
2 |
−9 |
(2, −9) |
3 |
−27 |
(3, −27) |
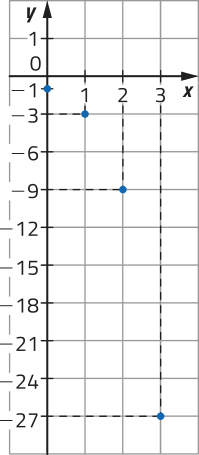
DICA
Neste plano cartesiano, os eixos apresentam escalas diferentes.
PARA PENSAR
Nesse gráfico, podemos ligar os pontos indicados? Justifique.
Resposta esperada: Não, pois .
Página cinquenta
ATIVIDADES
56. Renata investiu cérto capital em uma aplicação no sistema de juro simples por um período de 3 anos. Em seguida, todo o montante foi resgatado e reinvestido em uma aplicação no sistema de juro compôzto por 4 anos. Analise e identifique o gráfico quê melhor descreve a variação do montante nessas aplicações em todo o período de investimento. Justifique sua resposta.
a) 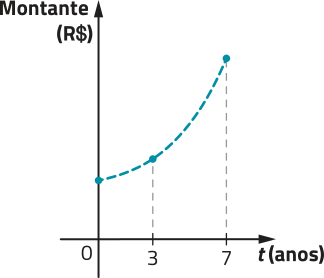
b) 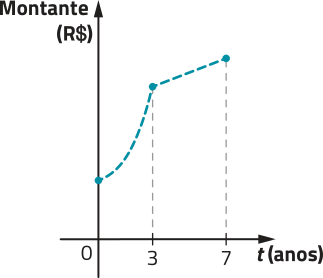
c) 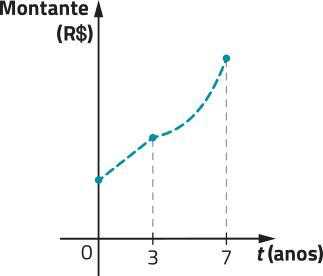
Alternativa c. Resposta nas Orientações para o professor.
57. Leia as informações sobre os investimentos quê Sérgio e Carla têm em um banco.
Investimento de Sérgio
Sistema de juro simples.
Início em janeiro de 2024.
Função quê expressa o montante em t meses: .
Investimento de Carla
Sistema de juro compôzto.
Início em janeiro de 2024.
Função quê expressa o montante em t meses: .
a) Qual é o capital aplicado por Sérgio? E por Carla?
R$ 3.150,00; R$ 600,00
b) Em quê mês o investimento de Sérgio determina um montante de R$ 3.780,00?
junho de 2024
c) Qual é a taxa de juro mensal em cada um dêêsses investimentos?
investimento de Sérgio: 4% ao mês; investimento de Carla: 3% ao mês
d) ![]() Utilizando uma calculadora, determine o montante obtído no investimento de Carla ao final do ano de 2024.
Utilizando uma calculadora, determine o montante obtído no investimento de Carla ao final do ano de 2024.
aproximadamente R$ 830,54
58. Para realizar um investimento, certa pessoa consultou uma instituição financeira e recebeu uma proposta a juro compôzto e outra a juro simples. Observe, na planilha a seguir, as simulações realizadas para cada um dêêsses investimentos, considerando o mesmo capital. Depois, resôuva as kestões.

a) Qual proposta corresponde ao investimento a juro compôzto? Por quê?
58. a) B. Resposta esperada: Porque, a partir do 2º mês nesse investimento, as razões entre os montantes de cérto mês e o mês anterior são aproximadamente iguais.
b) Qual é o valor do capital simulado nessas propostas de investimento?
R$ 500,00
c) Qual é a taxa de juro mensal oferecida em cada proposta de investimento?
A: 6%; B: 5%
d) Para cada proposta de investimento, escrêeva uma função M quê expressa o montante obtído em real, de acôr-do com o tempo t, em meses, de investimento. Em seguida, classifique as funções quê você escreveu em: função afim, função quadrática, função modular ou função do tipo exponencial.
58. d) , função afim;
B: t, função do tipo exponencial
e) Analise as propostas de investimento e indique em quê período cada uma delas é mais rentável em relação à outra.
58. e) A: de 1 a 8 meses; B: a partir de 9 meses
f) Em qual dos itens a seguir os gráficos nas cores lilás e laranja representam as propostas de investimento A e B, respectivamente?
II
Página cinquenta e um
I) 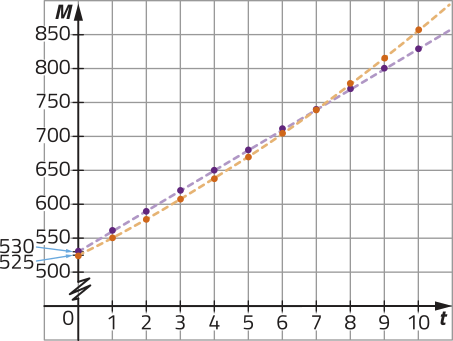
II) 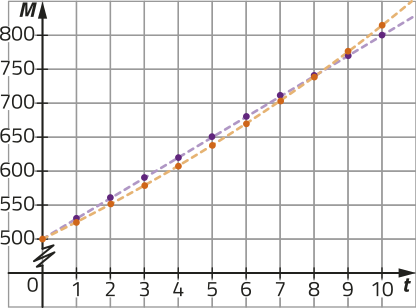
III) 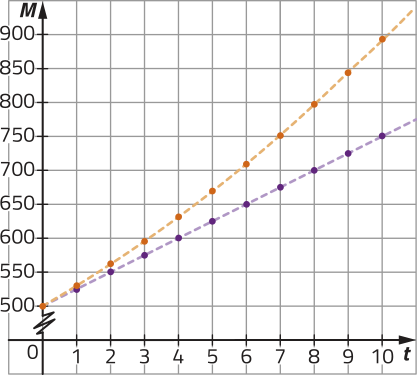
DICA
Nos itens, os eixos do plano cartesiano têm escalas diferentes, e as linhas tracejadas foram traçadas para facilitar a visualização do comportamento de cada gráfico.
59. (Enem/MEC) O acréscimo de tecnologias no sistema produtivo industrial tem por objetivo reduzir custos e aumentar a produtividade. No primeiro ano de funcionamento, uma indústria fabricou 8.000 unidades de um determinado produto. No ano seguinte, investiu em tecnologia adquirindo novas máquinas e aumentou a produção em 50%. Estima-se quê esse aumento percentual se repita nos próximos anos, garantindo um crescimento anual de 50%. Considere P a quantidade anual de produtos fabricados no ano t de funcionamento da indústria.
Se a estimativa for alcançada, qual é a expressão quê determina o número de unidades produzidas
P em função de t, para ?
a)
b)
c)
d)
e)
alternativa e
60. Utilizando a função indicada na atividade 59, calcule a quantidade de unidades do produto quê essa indústria estima fabricar no:
a) quinto ano de funcionamento;
40.500 unidades
b) sétimo ano de funcionamento.
91.125 unidades
61. Marcela estuda investir certa quantia em uma aplicação com 6 anos de duração. Nessa aplicação, nos três primeiros anos é considerada a modalidade de juro compôzto e, nos três anos finais, a modalidade de juro simples. Observe o gráfico quê Marcela construiu para estimar o montante a sêr obtído no decorrer dessa aplicação.
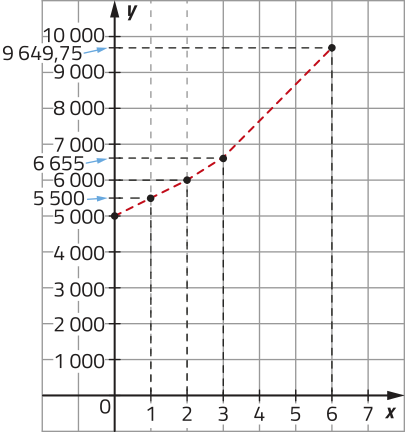
DICA
Neste plano cartesiano, os eixos têm escalas diferentes.
a) Quantos reais Marcela estuda investir nessa aplicação?
R$ 5.000,00
b) Ao final dos 6 anos de aplicação, qual será o montante obtído por Marcela?
R$ 9.649,75
c) escrêeva a lei de formação de uma função M quê expresse o montante obtído em t anos nessa aplicação.
61. c)
62. Considere uma função , definida por
.
a) Determine os 5 primeiros termos dessa PG.
62. a)
b) Qual é a razão dessa PG?
c) Construa o gráfico de f.
Resposta nas Orientações para o professor.
Página cinquenta e dois
63. Em um laboratório, foi realizado um estudo para analisar a influência das substâncias A e B em cérto tipo de bactéria. Para isso, foi separada uma bactéria para sêr submetida a cada substância, tendo suas populações obtidas no processo reprodutivo quantificadas em medições simultâneas, conforme indicado a seguir.
Populações de bactérias em cada medição
Medição |
|||||
|---|---|---|---|---|---|
1 |
2 |
3 |
4 |
5 |
|
Substância A |
2 |
5 |
8 |
11 |
14 |
Substância B |
4 |
32 |
256 |
2.048 |
16.384 |
Fonte: Dados fictícios.
Nesse estudo, verificou-se quê as quantidades de indivíduos das populações submetidas às substâncias A e B, na medição m, podem sêr modeladas, respectivamente, por funções cujas leis de formação são dadas por , sêndo a, b, c e d números naturais.
a) Em qual dessas populações de bactérias a quantidade de indivíduos, a cada medição, cresce de acôr-do com uma PG? Justifique sua resposta.
63. a) População submetida à substância B, pois a razão entre a quantidade de indivíduos dessa população de uma medição e da anterior, a partir da 2ª medição, é constante e igual a 8.
b) Determine os valores de a, b, c e d e escrêeva as leis de formação das funções f e g.
63. b) e e
c) De acôr-do com os modelos matemáticos obtidos no item b, calcule a quantidade de indivíduos determinada na 7ª medição para cada substância.
63. c) população submetida à substância A: 20 bactérias; população submetida à substância B: 1.048.576 bactérias
64. Uma bó-linha de borracha é lançada ao solo de uma altura h e quica sucessivas vezes, de maneira quê a altura atingida a cada vez quê retorna do solo é mêtáde da altura ôbitída anteriormente, conforme o esquema a seguir.

a) Qual progressão geométrica representa a altura dessa bó-linha, a partir do momento em quê foi lançada ao solo, considerando ? Qual é a razão q dessa progressão geométrica?
b) Defina uma função f de maneira quê corresponda à progressão geométrica quê você indicou no item a.
Resposta esperada: .
65. Observe nos gráficos a seguir a representação das progressões geométricas de razões q 1 e q 2, dadas, respectivamente, por definidas por e .
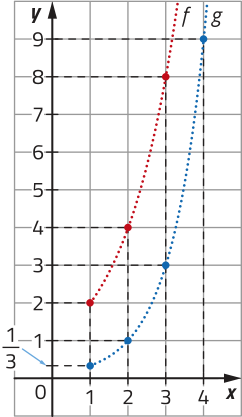
a) Qual é a razão de cada PG?
65. a) razão da PG determinada pela função f: 2; razão da PG determinada pela função g: 3
b) Calcule os valores de a e b e escrêeva a lei de formação das funções f e g.
65. b)
66. (UECE) Sejam e a função definida por , onde p e q são números reais. Se a imagem de f é a progressão geométrica com e razão igual , então, a soma é igual a
a)
b) .
c) .
d) .
alternativa c
67. ![]() Elabore um problema envolvendo uma progressão geométrica e uma função , definida por , em quê a e , com e . Em seguida, junte-se a um colega, e tróquem o problema para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Elabore um problema envolvendo uma progressão geométrica e uma função , definida por , em quê a e , com e . Em seguida, junte-se a um colega, e tróquem o problema para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página cinquenta e três
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Datação de fósseis
Leia, a seguir, o trecho de uma reportagem.
Uma reconstrução da face de Luzia, fóssil humano mais antigo das Américas, está guardada na Universidade de São Paulo (úspi). O crânio dela, descoberto nos anos 1970 na região de Lagoa Santa, Minas Gerais, estava no acervo do Museu Nacional, no Rio de Janeiro, atingido por um incêndio [...].
[...] O fóssil era um registro das primeiras populações humanas quê entraram no continente americano.
Arqueólogos acreditam quê Luzia, como o crânio foi batizado, tenha vivido há mais de 11 mil anos. O achado mudou a teoria da povoação dos continentes americanos.
O crânio de Luzia foi considerado mais largo do quê o da população quê vivia na Ásia e já tinha passado por transformações físicas. Esse grupo atravessou o estrêito de Bering – quê na época ainda se conectava à América do Norte – e desceu até chegar à América do Sul.
Pesquisadores quê estudaram Luzia acharam quê ela se parecia com humanos mais antigos ainda: os primeiros quê saíram da África, cruzaram a Ásia e vieram direto para as Américas até chegar ao Brasil.
MENEZES, César. Reconstrução da face de Luzia, fóssil humano mais antigo das Américas, está guardada na úspi. G1, [s. l.], 3 set. 2018. Disponível em: https://livro.pw/cyrmk. Acesso em: 24 jul. 2024.

Página cinquenta e quatro
A estimativa da idade de Luzia foi realizada por meio de um processo denominado datação de fósseis, quê se baseia no decaimento de isótopo radioativo de diversos elemêntos químicos. Nesse processo, o carbono-14, por sêr instável e se desintegrar em um período quê lhe é característico, costuma sêr um dos mais utilizados.
Decaimento radioativo do carbono-14
Na fotossíntese, as plantas captam dióxido de carbono (CO2), quê contém os isótopos carbono-12 (12C), carbono-13 (13C) e carbono-14 (14C). Por meio da cadeia alimentar, os animais e os sêres humanos também absorvem esses isótopos, quê se mantêm em cada organismo na mesma proporção em quê estão presentes na atmosfera e permanecem praticamente constantes em toda a sua vida.
Como o 14C é radioativo, seus hátomus estão sempre decaindo, mas, por meio de um processo natural, são substituídos por novos hátomus, mantendo sua proporção. Quando o sêr vivo morre, ele para de acumular carbono, com isso a quantidade já existente no organismo de 12C se mantém, e a quantidade de 14C decai a uma taxa constante, até quê esse isótopo se torna um elemento estável, o nitrogênio-14 (14N).
O processo de decaimento radioativo do 14C permite quê os cientistas, por exemplo, contabilizem a quantidade restante dêêsse isótopo em um fóssil e comparem-na com a razão de 14C e 12C presentes na atmosféra. Depois, sabendo quê a meia-vida do 14C é de 5.730 anos, ou seja, quê nesse tempo sua quantidade presente no fóssil se reduz à mêtáde, em relação à quantidade anterior, estima-se a idade desse fóssil. Esse método de datação com 14C é eficiente para fósseis de sêres quê viveram há até 75.000 anos. Em fósseis mais antigos é difícil detectar a presença dêêsse isótopo.
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 32-33, 524.
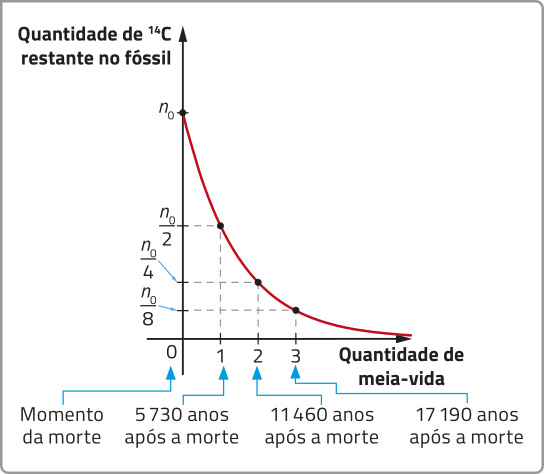
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 32-33, 524.
Relação entre quantidade de meia-vida, anos após a morte e 14 C restante no fóssil
Quantidade de meia-vida |
Quantidade de anos após a morte |
Quantidade de 14C restante no fóssil |
|---|---|---|
0 |
0 |
n0 |
1 |
5.730 |
n0 |
2 |
11.460 |
n0 |
3 |
17.190 |
n0 |
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 32-33, 524.
Página cinquenta e cinco
PENSANDO NO ASSUNTO
1. Explique por quê a descoberta e os estudos realizados com o crânio de Luzia são importantes para a história natural do Brasil e do continente americano. Se necessário, realize uma pesquisa.
Resposta nas Orientações para o professor.
2. É conveniente realizar com 14 C a datação de um fóssil quê viveu há mais de 120 mil anos? Justifique.
2. Resposta esperada: Não, pois esse método de datação com 14C é eficiente para fósseis quê viveram há até 75.000 anos; em fósseis mais antigos é difícil detectar a presença dêêsse isótopo.
3. ![]() Sobre a meia-vida do 14 C, com um colega, resolvam as kestões a seguir.
Sobre a meia-vida do 14 C, com um colega, resolvam as kestões a seguir.
a) A quantos anos corresponde a meia-vida do 14C? O quê essa meia-vida indica em um fóssil?
3. a) 5.730 anos. Indica quê a cada 5.730 anos a quantidade de 14C diminui pela mêtáde em um fóssil, em relação ao período anterior.
b) A quantos anos correspondem duas meias-vidas do 14C? E três meias-vidas?
11.460 anos; 17.190 anos
c) Considerando quê os pesquisadores utilizaram 14C na datação do fóssil Luzia, quantas meias-vidas, aproximadamente, passaram desde sua morte?
duas meias-vidas
d) Escrevam a lei de formação de uma função n para expressar a quantidade de 14C remanescente em um fóssil de acôr-do com a quantidade x de meias-vidas de 14C passadas desde a morte do indivíduo.
3. d)
e) Com base nos itens anteriores, resolvam a situação a seguir.
cérto fóssil foi datado com cerca de 40 mil anos de idade. Mostre quê a quantidade de 14 C remanescente nesse fóssil é menor quê 1% em relação à quantidade de quando o indivíduo era vivo.
3. e) Resposta esperada: Temos quê 40.000 anos correspondem a aproximadamente sete meias-vidas do 14C, pois . Assim, , ou seja, em um fóssil datado com cerca de 40 mil anos, a quantidade remanescente de 14C é aproximadamente 0,78% daquela quê havia no indivíduo quando ele estava vivo.
4. ![]() Junte-se a dois côlégas para investigar a questão a seguir.
Junte-se a dois côlégas para investigar a questão a seguir.
Como ocorreu a chegada da espécie humana ao continente americano?
Até os dias de hoje, não se sabe ao cérto como a espécie humana chegou ao continente americano, mas existem teorias quê indicam algumas possibilidades. Pesquisadores e historiadores elaboraram essas teorias com base em vestígios encontrados, como fósseis, utensílios e artes rupestres. Leiam o trecho a seguir, no qual são apresentadas duas dessas teorias.
A hipótese mais antiga, e quê permaneceu como a mais aceita por mais tempo, é a conhecida em inglês como Clovis-first (Clóvis-primeiro). Deve seu nome a um sítio descoberto em 1939, no Novo México, Estados Unidos, no qual foram encontradas pontas de flechas feitas de pedra datadas de 11,4 mil anos. Segundo essa hipótese, a chegada teria ocorrido há cerca de 12 mil anos.
[...]
Uma segunda teoria foi proposta pelo bioantropólogo Válter Alves Néves e pelo geógrafo Luís Beethoven Piló [...]. Eles a chamam de Dois Componentes Biológicos Principais, porque, segundo essa tese, houve duas levas migratórias iniciais: a primeira há 14 mil anos e a segunda, há 11 mil, também vindas da Ásia pelo estrêito de Bering.
A mais antiga seria composta por uma população com traços quê lembram os dos africanos e aborígenes australianos. É dêêsses pioneiros quê descenderia a famosa Luzia [...].
SILVEIRA, Evanildo da. dê ene há de fósseis do Brasil desafia teorias de ‘descoberta’ da América. BBC nius Brasil, [s. l.], 8 nov. 2018. Disponível em: https://livro.pw/chaju. Acesso em: 24 jul. 2024.
Realizem pesquisas sobre as teorias apresentadas no texto anterior, buscando mais informações sobre as hipóteses propostas em cada uma delas, destacando, por exemplo, fatos em quê se baseiam. Em seguida, discutam e escôlham com qual dessas teorias vocês concórdam mais e elaborem um texto ou uma apresentação na qual descrevam e justifiquem a teoria escolhida.
Pesquisa e elaboração dos estudantes.
Página cinquenta e seis
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Algarismos significativos
Potenciação
Notação científica
Potência com expoente racional
Função exponencial: características e definição
Equações exponenciais
Função exponencial: algumas aplicações
Propriedades da potenciação
Radiciação
Propriedades da radiciação
Gráfico de uma função exponencial
Inequações exponenciais
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página cinquenta e sete
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre a capacidade de armazenamento de dados dos smartphones. Agora, vamos retomar esse contexto por meio das kestões a seguir.

a) Considere as informações sobre o modelo de smartphone representado.
I) Utilizando potência, expresse a capacidade de armazenamento de dados dêêsse smartphone, em baite.
2 38 B
II) Considere quê, com certos ajustes, uma fotografia ôbitída com a câmera dêêsse smartphone gere um arquivo de 2 MB. Qual alternativa mais se aproxima da quantidade de fotografias necessárias para ocupar 50% da capacidade de armazenamento dêêsse smartphone?
• 650
• 6.500
• 65.000
• 6.500.000
65.000
b) O avanço tecnológico quê póde sêr observado nos modelos de smartphones, com cada vez mais recursos disponíveis, também implicou uma série de desafios aos fabricantes, como a necessidade de bateria com maior capacidade de carga e com menor tempo de recarga.
Considere, por exemplo, um smartphone hipotético cuja bateria está completamente descarregada. O modelo matemático descreve o porcentual aproximado C da capacidade total da bateria dêêsse smartphone de acôr-do com o tempo t, em minuto, após o início da recarga até o momento em quê a bateria ficou completamente carregada.
I) A função correspondente a esse modelo matemático póde sêr classificada como: afim, quadrática, modular ou tipo exponencial?
tipo exponencial
II) Calcule o valor numérico dêêsse modelo matemático para e interpréte o resultado obtído.
4. b) II. , quê indica quê após 100 min carregando a bateria do smartphone estava com aproximadamente 88,56% de sua capacidade carregada.
III) No GeoGebra ou em outro programa de computador similar, construa o gráfico correspondente a esse modelo matemático e responda: em quanto tempo após o início da recarga, a bateria do smartphone ficou completamente carregada?
4. b) III. Resposta nas Orientações para o professor. Aproximadamente 120 min ou 2 h.
c) Com freqüência, são lançados novos modelos de smartphones com diversas melhorias e mais recursos disponíveis. Aparelhos quê hoje são considerados de última geração provavelmente passarão a sêr considerados ultrapassados em pouco tempo, sofrendo assim depreciação em seu valor.
Considere, por exemplo, uma pesquisa realizada em um sáiti de vendas de smartphones usados em relação a um modelo cujo preêço no lançamento era de R$ 2.000,00. Nessa pesquisa, foi constatado quê o valor de venda do aparelho usado correspondia à mêtáde do valor pago 10 meses antes, no seu lançamento. Com base nos dados obtidos nessa pesquisa, foi modelada uma função do tipo , em quê f é o valor em real de venda dêêsse aparelho, x é o tempo de uso, em meses transcorridos desde a compra dêêsse aparelho no seu lançamento, e a e b são constantes reais não nulas.
De acôr-do com os dados apresentados, resôuva as kestões a seguir.
I) Determine os valores de a e b e escrêeva a lei de formação da função f.
a = 2 000 e b = −0,1; f(x) = 2 000 ⋅ 2−0,1x
II) Calcule o valor aproximado de venda dêêsse smartphone após 5 meses da compra no seu lançamento.
aproximadamente R$ 1.414,21
Página cinquenta e oito
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) O govêrno de uma cidade está preocupado com a possível epidemia de uma doença infectocontagiosa causada por bactéria. Para decidir quê medidas tomar, deve calcular a velocidade de reprodução da bactéria. Em experiências laboratoriais de uma cultura bacteriana, inicialmente com 40 mil unidades, obteve-se a fórmula para a população:
em quê t é o tempo, em hora, e é a população, em milhares de bactérias.
Em relação à quantidade inicial de bactérias, após 20 min, a população será
a) reduzida a um terço.
b) reduzida à mêtáde.
c) reduzida a dois terços.
d) duplicada.
e) triplicada.
alternativa d
2. (Enem/MEC) As hemácias são células sanguíneas responsáveis pelo transporte de uma substância chamada hemoglobina, a qual tem a função de levar oxigênio dos pulmões para os tecídos. Hemácias normais têm diâmetro médio de metros.
GUYTON, A. C.; HALL, J. E. Tratado de fisiologia médica. Rio de Janeiro: Elsévier, 2006 (adaptado).
O diâmetro médio dessas hemácias, em metros, é representado pela razão , em quê d é igual a:
a) 10.000.
b) 100.000.
c) 1.000.000.
d) 10.000.000.
e) 100.000.000.
alternativa d
3. (UFRGS-RS) O valor de para e é:
a) 2.017.
b) 2.071.
c) 2.107.
d) 2.170.
e) 2.710.
alternativa c
4. (UFGD-MS) Um grupo de estudantes verificou quê o crescimento de uma determinada população de bactérias é dado pela função , na qual P identifica a população e a variável t indica o tempo em anos. Considerando as condições apresentadas, qual o tempo mínimo para quê a população de bactérias seja o triplo da população inicial?
a) 3 meses.
b) 4 meses.
c) 6 meses.
d) 8 meses.
e) 12 meses.
alternativa d
5. (UFMS) A depreciação de um carro ocorre segundo a expressão , em quê y é o valor do bem e x é o tempo quê passou em anos, com V e a constantes. Se hoje o valor do carro é R$ 200.000,00, daqui a quatro anos o valor será a mêtáde. Logo, o seu valor daqui a oito anos será:
a) R$ 100.000,00.
b) R$ 75.000,00.
c) R$ 50.000,00.
d) R$ 25.000,00.
e) R$ 12.500,00.
alternativa c
6. (IFPE) No início do ano de 2017, Carlos fez uma análise do crescimento do número de vendas de refrigeradores da sua empresa, mês a mês, referente ao ano de 2016. Com essa análise, ele percebeu um padrão matemático e conseguiu descrever a relação , onde V representa a quantidade de refrigeradores vendidos no mês x. Considere: referente ao mês de janeiro; referente ao mês de dezembro. A empresa de Carlos vendeu, no 2º trimestre de 2016, um total de
a) 39 refrigeradores.
b) 13 refrigeradores.
c) 127 refrigeradores.
d) 69 refrigeradores.
e) 112 refrigeradores.
alternativa c
Página cinquenta e nove
7. (UEFS-BA) Considerando-se quê, sôbi cértas condições, o número de colônias de bactérias, t horas após sêr preparada a cultura, póde sêr dado pela função , pode-se estimar quê o tempo mínimo necessário para esse número ultrapassar 678 colônias é de
01) 2 horas.
02) 3 horas.
03) 4 horas.
04) 5 horas.
05) 6 horas.
alternativa 02
8. (Ifal) Sabendo quê , determine o valor de :
a) 4.
b) 2.
c) 0.
d) .
e) .
alternativa e
9. (UPE) Os técnicos de um laboratório observaram quê uma população de cérto tipo de bactérias cresce segundo a função com “t” sêndo medido em horas. Qual o tempo necessário para quê ocorra uma reprodução de bactérias?
a) 1h
b) 3h
c) 4h
d) 6h
e) 16h
alternativa a
10. (Enem/MEC) O gráfico informa a produção registrada por uma indústria nos meses de janeiro, março e abril.
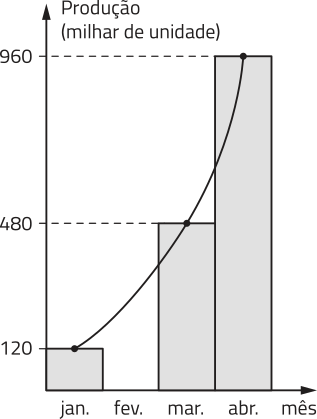
Por problemas logísticos, não foi feito o levantamento sobre a produção no mês de fevereiro. Entretanto, as informações dos outros três meses sugérem quê a produção nesse quadrimestre cresceu exponencialmente, conforme aponta a curva de tendência traçada no gráfico. Assumindo a premissa de quê o crescimento nesse período foi exponencial, pode-se inferir quê a produção dessa indústria no mês de fevereiro, em milhar de unidade, foi:
a) 0.
b) 120.
c) 240.
d) 300.
e) 400.
alternativa c
11. (UFPA) Uma substância ingerida pelo organismo é excluída pelo sistema excretor segundo uma função exponencial. A vida média é o tempo quê mêtáde de uma quantidade ingerida leva para decair à mêtáde, quê, para a substância em questão, é de 12 horas. A quantidade da substância, em miligramas, a sêr ingerida de modo quê, ao final de 36 horas, a quantidade restante seja de 10 mg é de
a) 30.
b) 60.
c) 80.
d) 90.
e) 100.
alternativa c
12. (ITA-SP) Sejam f e g funções reais definidas da seguinte forma:
e .
Considere as afirmações:
I) , para todo .
II) , para todo .
III) , para todo .
É (são) sempre verdadeira(s):
a) apenas I.
b) apenas II.
c) apenas III.
d) todas.
e) nenhuma.
alternativa b
13. (UEMG) Muitos vírus e bactérias têm crescimento exponencial, isso é uma das causas quê os torna tão perigosos.
Supondo o surgimento de um novo vírus com um crescimento exponencial de acôr-do com a seguinte lei de formação , na qual Q é a quantidade de vírus e t é o tempo em dias. Analisando uma cultura dêêsse vírus, quanto tempo demora para quê ele alcance a quantidade de 54.675?
a) 6 dias.
b) 7 dias.
c) 8 dias.
d) 9 dias.
alternativa b
Página sessenta
14. (UFJF-MG) Em um experimento, dois microrganismos A e B são colocados em um mesmo ambiente. As colônias dêstes microrganismos crescem até o momento em quê suas populações se igualam e inicia-se um processo de competição entre elas. O número de indivíduos das populações de A e de B, em milhares, do início do experimento (tempo ) até o momento em quê as populações se igualam, são descritos por e , respectivamente. Qual é a população (em milhares) do microrganismo A quando se inicia a competição?
a) 8
b) 12
c) 13
d) 16
e) 18
alternativa d
15. (UEL-PR) O processo de decomposição do corpo começa alguns minutos depois da morte. Quando o coração para, ocorre o algor mortis ou o frio da morte, quando a tempera-túra do corpo diminui até atingir a tempera-túra ambiente.
(Adaptado de: <https://livro.pw/dykho>. Acesso em: 29 maio 2017.)
Suponha quê um cadáver é analisado por um investigador de polícia às 5 horas da manhã do dia 28, quê detalha as seguintes informações em seu bloco de anotações:

Imediatamente após escrever, o investigador utiliza a Lei de Resfriamento
para revelar a todos os presentes quê faz t horas quê a morte ocorreu. Assinale a alternativa quê apresenta, corretamente, a hora e o dia da morte, segundo o investigador.
a) 11 horas (da noite) do dia 27
b) 8 horas (da noite) do dia 27
c) 2 horas da manhã do dia 28
d) 4 horas da manhã do dia 28
e) 10 horas da manhã do dia 27
alternativa a
16. (Unésp) Três insetos da mesma espécie foram introduzidos em um ambiente no instante zero. Sete meses depois, constatou-se quê havia uma população de 18.000 dêêsses insetos no ambiente. Considere quê o modelo de crescimento da população dêêsses insetos é exponencial, dado por , em quê t e u são constantes reais e é a população de insetos após x meses do início da cultura.
Observe o gráfico da função , em quê x é um número inteiro maior do quê 2, e quê apresenta os valores aproximados das ordenadas de alguns de seus pontos.
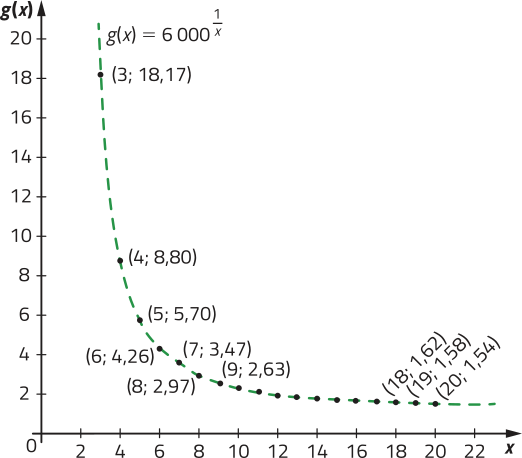
Com os dados fornecidos, segue quê é, aproximadamente,
a) 5,09.
b) 10,26.
c) 6,47.
d) 7,62.
e) 7,26.
alternativa c
Página sessenta e um
