UNIDADE 2
LOGARITMO E FUNÇÃO LOGARÍTMICA
Altitude e pressão atmosférica
A pressão atmosférica está relacionada à altitude, quê póde sêr compreendida como o “peso do ar”. À medida quê a altitude aumenta, a pressão atmosférica diminui.
Em um local ao nível do mar, a uma pressão atmosférica de 1 atm (1 atmosfera), tem-se uma pressão parcial de oxigênio correspondente a 0,21 atm. Já em uma localização a uma pressão atmosférica de 0,9 atm, a pressão parcial de oxigênio cai para 0,189 atm.
À medida quê a pressão parcial do oxigênio diminui, também cai sua disponibilidade, deixando o ar rarefeito, o quê reduz a quantidade de moléculas de oxigênio disponíveis em cada ciclo de respiração. Por isso, é bastante comum, quando uma pessoa está em um local com grande altitude, ou seja, muito acima do nível do mar, sentir alguns sintomas, como dor de cabeça, falta de ar e aceleração dos batimentos cardíacos.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. O quê ocorre com a pressão parcial de oxigênio quando há um deslocamento de menor altitude para maior altitude? De quê maneira isso implica a respiração?
2. Qual é a altitude e a pressão atmosférica do município em quê você mora? Se necessário, faça uma pesquisa.
3. Considere um modelo matemático quê determina a pressão atmosférica aproximada p (em atm) em função de uma altitude h (em km) de certa localidade. Calcule e explique o quê esse resultado indica.
Fonte dos dados: ASSOCIAÇÃO PAULISTA PARA O DESENVOLVIMENTO DA MEDICINA. Os efeitos da altitude no nosso organismo. São Paulo: SPDM, 20 fev. 2017. Disponível em: https://livro.pw/okgzx. Acesso em: 26 jul. 2024.
Página sessenta e dois
Logaritmo
Na abertura desta Unidade, são apresentadas algumas informações sobre a pressão atmosférica.
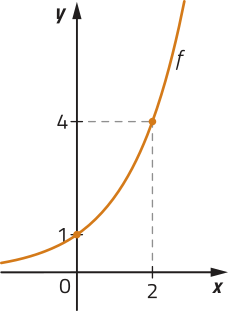
Considere quê, em certa localidade, a pressão atmosférica p (em atm) póde sêr expressa de maneira simplificada por uma função exponencial definida por , em quê h corresponde à altitude (em km). Ao realizar uma escalada, um alpinista consultou seu barôometro e verificou quê a pressão atmosférica indicada era de 0,53 atm. A quê altitude ele se encontrava?

Para responder a essa quêstão, devemos considerar a pressão atmosférica que o alpinista observou no barôometro. Assim, escrevemos a equação a seguir.
Uma estratégia para resolver essa equação exponencial é escrever cada membro como potência de mesma base, o quê, neste caso, não é possível fazer com os estudos quê realizamos até o momento. Assim, faz-se necessário utilizarmos outra estratégia, quê envolve o uso de logaritmos.
- Logaritmo
- : palavra quê dêríva da composição das palavras grêgas logos (razão) e arithmós (número).
Página sessenta e três
MATEMÁTICA NA HISTORIA
O surgimento dos logaritmos é atribuído ao matemático, astrônomo e físico escocês, Diôn Napier (1550-1617), quê publicou os resultados de seus estudos sobre logaritmo em sua obra Mirifici logarithmorum canonis descriptio (Uma descrição da maravilhosa regra dos logaritmos), em 1614. O uso dos logaritmos foi fundamental para auxiliar nos longos e trabalhosos cálculos realizados, principalmente, por astroônomos e navegadores da época.
Fonte dos dados: BOYER, Cal Benjamin. História da matemática. Tradução: Elza Furtado Gomide. 1. ed. São Paulo: Edgard Blãcher, 1974. p. 228.

Considere as situações a seguir.
• A qual expoente x se deve elevar a base 2 para obtêr 32 como resultado?
Nesse caso, temos:
Dizemos quê 5 é o logaritmo de 32 na base 2 e escrevemos log2 .
• Em uma potência de base 10, cujo resultado é , qual é o valor y do expoente?
Nesse caso, temos:
Dizemos quê −3 é o logaritmo de na base 10 e escrevemos log10 = −3.
Dados dois números reais a e b, com , e , denominamos logaritmo de b na base a o número real c tal quê , ou seja:
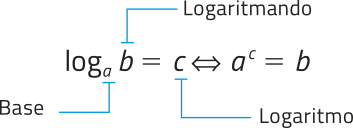
Observe alguns exemplos.
a) log5 625 = 4, pois 54 = 625.
b) log2 64 = 6, pois 26 = 64.
c) log7 1 = 0, pois 70 = 1.
d) log3 = −4, pois 3−4 = .
e) log0,1 (0,001) = 3, pois (0,1)3 = 0,001
f) log10 100 = 2, pois 102 = 100.
DICA
Por convenção, costuma-se omitir a indicação da base em logaritmos de base 10. Esses logaritmos são denominados logaritmos decimais. Por exemplo, log10 100 póde sêr indicado por: log 100
PARA PENSAR
Explique por quê os logaritmos a seguir não estão definidos.
• log1 10
Para qualquer , temos quê .
• log (−4)
Para qualquer , temos quê .
• log0 (1,5)
Para qualquer *, temos quê .
• log−2 8
Para qualquer c ∈ ℝ, temos quê .
• log5 0
Para qualquer c ∈ ℝ, temos quê .
Página sessenta e quatro
Consequências da definição de logaritmo
Analise, a seguir, algumas relações quê decorrem da definição de logaritmo.
•
Note quê, considerando , obtemos:
Exemplos:
a) log5
b)
c)
•
Note quê, considerando , obtemos:
Exemplos:
a) log6
b) log20
c)
•
Note quê, para todo n real e considerando log a , obtemos:
Exemplos:
a) log 4
b) log 5
c) log 0,12
•
Note quê, considerando log a , temos .
Substituindo log a em , obtemos:
Exemplos:
a)
b)
c)
•
Para justificar quê , consideramos . Assim, temos quê ax = b e ax = c.
Logo, segue quê .
Agora, para justificar quê , consideramos e quê , obtemos . Assim, segue quê . Portanto, temos:
Exemplos:
a) Se então .
b) Se então .
c) , então z = 0,4.
PARA PENSAR
Para cada consequência da definição de logaritmo descrita, escrêeva um exemplo diferente dos apresentados. Depois, troque seus exemplos com um colega para quê um analise os do outro, identificando a propriedade utilizada em cada caso.
Respostas pessoais.
Página sessenta e cinco
ATIVIDADES RESOLVIDAS
R1. Calcule.
a)
b) 64
c)
Resolução
a) Considerando , obtemos:
Portanto,
b) Considerando , obtemos:
Portanto,
c) Considerando , obtemos:
Portanto, log25 .
R2. Considere Qual é o valor de z?
a) 0
b)
c) 1
d) 4
Resolução
pôdêmos utilizar a relação , quê decorre da definição de logaritmo, para resolver . Assim, temos:
Para , da definição de logaritmos, temos:
Substituindo y = , segue quê:
Portanto, a alternativa d está correta.
PARA PENSAR
Explique a um colega outra maneira de mostrar quê é a solução dessa atividade.
Uma resposta possível: Inicialmente, podemos substituir em e obtêr, pela definição de logaritmo, . Em seguida, como , substituímos em o resultado obtído anteriormente e determinamos uma igualdade verdadeira:
R3. Na página 62, analisamos uma situação em quê um alpinista, ao realizar uma escalada, consultou o barôometro e verificou quê a pressão atmosférica era de 0,53 atm. Considerando log 0,9 , determine a quê altitude o alpinista se encontrava, aproximadamente.

Resolução
Da definição de logaritmo, temos quê:
Como, na situação apresentada, a pressão atmosférica póde sêr expressa por uma função definida por , em quê h corresponde à altitude (em km), temos quê:
Como log0,9 , segue quê .
Portanto, o alpinista se encontrava a aproximadamente 6 km de altitude.
Página sessenta e seis
R4. Determine para quais valores reais de x estão definidos os logaritmos indicados a seguir.
a)
b)
Resolução
De acôr-do com a definição de logaritmo, temos quê existe quando a e b são números reais, sêndo , e
a) Em log9 a base é 9. Neste caso, as condições de quê a base seja maior do quê zero e diferente de 1 são satisfeitas. Resta analisar a condição . Assim:
Portanto, log9 existe para qualquer tal quê .
b) Neste caso, vamos analisar para quais valores de x a base de é positiva e diferente de 1 e o logaritmando é positivo.
• Base:

• Logaritmando:
Fazendo o estudo de sinal da função quadrática dada por , temos:
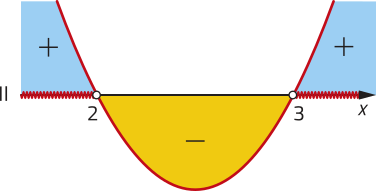
Portanto, para ou para .
Como essas condições precisam sêr satisfeitas simultaneamente, precisamos obtêr o conjunto I ⋃ II. Assim:
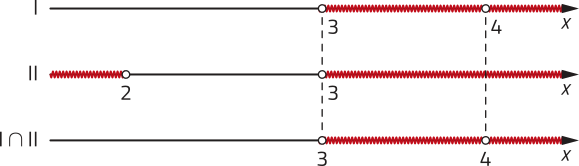
Portanto, está definido para qualquer , tal quê .
PARA PENSAR
Escolha um número real para o qual o logaritmo indicado no item b não esteja definido. Depois, argumente por quê isso ocorre.
Uma resposta possível: Para , por exemplo, temos quê a base do logaritmo seria dada por um número negativo o quê não póde ocorrer por definição de logaritmo.
Página sessenta e sete
ATIVIDADES
1. De acôr-do com a definição de logaritmo, calcule:
a) ;
b) ;
−2
c) ;
−3
d) .
5
2. Determine, em cada equação a seguir, o valor de x.
a)
b)
c)
d)
3. ![]() Você sabia quê a maioria dos smartphones tem calculadora científica instalada em seu sistema operacional? Para calcular logaritmos, podemos utilizar essas calculadoras ou programas de computador específicos. Observe, por exemplo, a sequência de teclas quê devem sêr pressionadas, em um modelo de calculadora científica, para obtêr o valor aproximado de log 62.
Você sabia quê a maioria dos smartphones tem calculadora científica instalada em seu sistema operacional? Para calcular logaritmos, podemos utilizar essas calculadoras ou programas de computador específicos. Observe, por exemplo, a sequência de teclas quê devem sêr pressionadas, em um modelo de calculadora científica, para obtêr o valor aproximado de log 62.

Portanto, .
Agora, utilize uma calculadora científica e determine os logaritmos a seguir. escrêeva o resultado aproximado com duas casas decimais.
a) log 110
2,04
b) log 24
1,38
c) log 51
1,71
d) log (0,6)
−0,22
4. Determine para quê valores reais de x os logaritmos a seguir podem sêr definidos.
a)
b)
e x ≠ −2
c)
e x ≠ −9
d)
5. Simplifique as expressões.
a)
2
b)
1
c)
−9
d)
6. Sabendo quê o logaritmo de um número na base 4 é igual a 4,5, determine o logaritmo do dôbro dêêsse número na mesma base.
5
7. Mariana rêzouvêo investir um capital de R$ 5.700,00 a uma taxa de 6% a.m. em uma aplicação no sistema de juro compôzto. Após quanto tempo, aproximadamente, Mariana obterá um montante de R$ 14.478,00? Considere .
16 meses
8. Leia as informações a seguir e resôuva as kestões.
MATEMÁTICA NA HISTORIA
Os logaritmos briggsianos ou comuns são os logaritmos de base 10, utilizados hoje em dia. Esses logaritmos foram desenvolvidos por Diôn Napier (1550-1617) e ênrri Briggs (1561-1630), com o objetivo de criar tábuas de logaritmos mais úteis na realização de cálculos. Essas tábuas consistem, basicamente, de um qüadro com duas colunas em quê, na primeira coluna, são indicados números naturais e, na segunda, as respectivas aproximações dos logaritmos de base 10 dêêsses números. Em 1624, Briggs publicou Arithmetica logarithmica, uma tábua quê continha logaritmos dos números de 1 a 20.000 e de 90.000 a 100.000.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 4. ed. Campinas: Editora da Unicamp, 2007. p. 345-346.
Observe a representação de parte da tábua de logaritmos briggsianos.

a) De maneira análoga à realizada para a linha 5, escrêeva o logaritmo indicado para cada linha da parte da tábua apresentada.
8. a)
b) ![]() Utilizando uma calculadora, construa uma tábua de logaritmos de base 10 para os números naturais de 6 até 10.
Utilizando uma calculadora, construa uma tábua de logaritmos de base 10 para os números naturais de 6 até 10.
8. b)
Logaritmando |
Logaritmo aproximado na base 10 |
6 |
0,77815125 |
7 |
0,84509804 |
8 |
0,903089987 |
9 |
0,954242509 |
10 |
1 |
Página sessenta e oito
Propriedades opêratórìas dos logaritmos
Analise, a seguir, algumas propriedades quê contribuem na realização de operações com logaritmos.
DICA
Para estudar as propriedades opêratórìas dos logaritmos, se necessário, retome o estudo das propriedades das potências.
Logaritmo do produto
Sendo a, b e c números reais, com , e , temos:
Observe como podemos justificar essa propriedade.
Considerando e , temos:
•
•
•
Assim, segue quê:
Exemplos:
a)
b)
DICA
Esta propriedade póde sêr descrita da seguinte maneira.
O logaritmo do produto de dois números reais positivos, de certa base, é igual à soma dos logaritmos dêêsses números, ambos nessa mesma base.
Logaritmo do quociente
Sendo a, b e c números reais, com e , temos:
Observe como podemos justificar essa propriedade.
Considerando loga b e , temos:
•
•
•
Assim, segue quê:
Exemplos:
a)
b)
PARA PENSAR
Com suas palavras, dêz-creva esta propriedade.
Resposta esperada: O logaritmo do quociente de dois números reais positivos, de certa base, é igual à diferença dos logaritmos dêêsses números, ambos nessa mesma base.
Logaritmo da potência
Sendo a, b e n números reais, com e , temos:
Página sessenta e nove
Observe como podemos justificar essa propriedade. Considerando logab = x e logabn = y temos:
•
•
Assim, segue quê:
Exemplos:
a)
b)
PARA PENSAR
Com suas palavras, dêz-creva essa propriedade.
Resposta esperada: O logaritmo de uma potência de um número real positivo de expoente real qualquer, de certa base, é igual ao produto dêêsse expoente pelo logaritmo dêêsse número real nessa mesma base.
Mudança de base
Sendo a, b e c números reais, com e , temos:
Observe como podemos justificar essa propriedade. Considerando e , temos:
•
•
•
Como e , segue quê:
Exemplos:
Resposta esperada: O logaritmo de um número real positivo de certa base é igual à razão entre o logaritmo dêêsse número real pelo logaritmo do número correspondente a essa base, ambos em uma mesma base.
PARA PENSAR
Mostre, de duas maneiras diferentes, quê, sêndo a e b números reais, com e , temos . Indique quais propriedades opêratórìas dos logaritmos você utilizou.
Resposta esperada: Propriedade do logaritmo do quociente:
Propriedade do logaritmo da potência:
Exemplos:
a)
b)
PARA PENSAR
Com suas palavras, dêz-creva essa propriedade.
Alguns modelos de calculadora científica não têm uma tecla específica para o cálculo de logaritmos em uma base definida qualquer. Nesse caso, podemos utilizar a propriedade da mudança de base de logaritmos. Acompanhe, a seguir, as etapas para calcular utilizando um modelo de calculadora em quê há tecla para logaritmos de base decimal.
1ª) Utilizamos a propriedade da mudança de base:
2ª) Pressionamos a seguinte sequência de teclas:


O resultado indicado na calculadora é uma aproximação de .
DICA
A ordem em quê as teclas devem sêr pressionadas póde sêr diferente da apresentada de acôr-do com o modelo da calculadora.
Página setenta
ATIVIDADES RESOLVIDAS
R5. Dados e , determine o valor de:
a) log 49
b) log 70
c) log 1,4
d) log2 35
Resolução
a)
b)
c)
d)
PARA PENSAR
escrêeva um logaritmo, diferente dos apresentados nesta atividade, cujo valor aproximado possa sêr determinado com base nos cálculos envolvendo os três logaritmos indicados no enunciado. Troque com um colega o logaritmo quê você escreveu para quê um resôuva o do outro. Depois, faça a correção dos itens quê você propôs. Ao final, todos devem compartilhar com a turma suas produções.
Resposta pessoal.
R6. Mostre quê , sêndo a e b números reais tais quê e.
Resolução
Aplicando em log a b a mudança de base para logaritmos de base b, temos:
Portanto, .
R7. Considere as informações nas fichas a seguir e resôuva as equações exponenciais.
a)
b)
c)
Resolução
a)
b)
c)
PARA PENSAR
Escolha um dos itens propostos e, com suas palavras, explique a um colega cada etapa da resolução da equação.
Resposta pessoal.
R8. (Enem/MEC) Com o avanço em ciência da computação, estamos próximos do momento em quê o número de transistores no processador de um computador pessoal será da mesma ordem de grandeza quê o número de neurônios em um cérebro humano, quê é da ordem de 100 bilhões.
Página setenta e um
Uma das grandezas determinantes para o dêsempênho de um processador é a densidade de transistores, quê é o número de transistores por centímetro quadrado. Em 1986, uma empresa fabricava um processador contendo 100.000 transistores distribuídos em 0,25 cm² de área. Desde então, o número de transistores por centímetro quadrado quê se póde colocar em um processador dobra a cada dois anos (Lei de Moore).
Disponível em: https://livro.pw/ncbqw. Acesso em: 1 dez. 2017. (adaptado).
Considere 0,30 como aproximação para log10 2.
Em quê ano a empresa atingiu ou atingirá a densidade de 100 bilhões de transistores?
a) 1999
b) 2002
c) 2022
d) 2026
e) 2146
Resolução
Para resolver esta atividade, podemos realizar as etapas a seguir.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• a densidade de transistores é o número de transistores por centímetro quadrado;
• em 1986, uma empresa fabricava um processador contendo 100.000 transistores distribuídos em 0,25 cm² de área;
• o número de transistores por centímetro quadrado quê se póde colocar em um processador dobra a cada dois anos (Lei de Moore);
• considerar log10 2 ≃ 0,30.
2ª ELABORAR UM PLANO
Temos de determinar em quê ano a empresa atingiu ou atingirá a densidade de 100 bilhões de transistores. Para isso, podemos calcular a densidade de transistores dos processadores em 1986 (Do) e escrever a função D (t) para expressar a densidade de transistores em t anos. Depois, igualamos D(t) a 100 bilhões e obtemos uma equação de incógnita t, quê deverá sêr resolvida. Por fim, adicionamos a quantidade de anos ôbitída ao ano inicial (1986).
3ª EXECUTAR O PLANO
Calculando D o, temos: .
Escrevendo D(t), segue quê: , em quê .
Como 100 bilhões correspondem a 1011, fazemos D(t) = 1011 e resolvemos a equação exponencial ôbitída:
Como consideramos 1986 o ano inicial, segue quê: 1.986 + 36 = 2.022. Portanto, a empresa atingiu a densidade de 100 bilhões de transistores em 2022.
PARA PENSAR
Com suas palavras, explique a expressão encontrada para D(t).
Resposta pessoal.
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado, podemos determinar, por meio da função D, a densidade de transistores em 2021 e em 2022, ou seja, 35 e 36 anos passados de 1986, respectivamente. Para isso, é possível usar uma calculadora científica.
•
•
DICA
Note quê 74 bilhões < 100 bilhões < 105 bilhões.
Portanto, a alternativa c é a correta, pois a empresa atingiu a densidade de 100 bilhões de transistores 36 anos após 1986, ou seja, em 2022.
Página setenta e dois
ATIVIDADES
9. Em cada item, escrêeva as expressões na forma de um único logaritmo.
a)
log
b)
c)
d) log9 4 + log3 2
10. Considerando log3 2 ≃ 0,63, log3 5 ≃ 1,46 e log3 7 ≃ 1,77, determine o valor aproximado de:
a)
3,86
b)
3,26
c)
0,82
d)
−0,32
11. ![]() Utilizando uma calculadora científica, determine o valor dos logaritmos a seguir.
Utilizando uma calculadora científica, determine o valor dos logaritmos a seguir.
a)
aproximadamente 1,44
b)
aproximadamente 6,64
c)
−0,3
d)
aproximadamente 0,93
12. ![]() Observe como podemos resolver a equação com uma calculadora científica.
Observe como podemos resolver a equação com uma calculadora científica.
Da definição de logaritmos, temos quê:
Para calcular o valor aproximado de 22,8, pressionamos a seguinte sequência de teclas em cérto modelo de calculadora científica.

Agora, com uma calculadora científica, determine o valor aproximado de x nos itens a seguir.
a) log3 x = 0,9
2,688
b) log5 x = 3,9
532,09
c) log7 x = −1,2
0,097
d) log x = 0,01
1,02
13. ![]() (Fuvest-SP) O Floco de Neve de Kóki (ou Estrela de Kóki) é uma construção geométrica recursiva cujos primeiros passos se dêsênvólvem da seguinte forma:
(Fuvest-SP) O Floco de Neve de Kóki (ou Estrela de Kóki) é uma construção geométrica recursiva cujos primeiros passos se dêsênvólvem da seguinte forma:
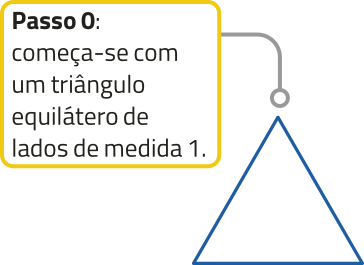


Os passos seguintes (Passo 3, Passo 4, Passo 5, …) seguem o mesmo procedimento descrito no Passo 1, em cada lado da figura ôbitída no passo anterior. Considerando os passos descritos e os próximos passos, responda:
a) Qual é o número de lados da figura no Passo 3?
192 lados
b) Qual é o perímetro da figura no Passo 5?
c) A partir de qual Passo o número de lados da figura supera 6.000.000.000.000 (seis trilhões)?
Passo 21
Note e adote:
14. A quantidade aproximada q de indivíduos de certa cultura de bactérias, de acôr-do com o tempo t (em minuto), é representada pela função dada por . Nessas condições, e considerando , em quantos minutos essa cultura terá 1084 bactérias?
175 min
Página setenta e três
15. ![]() O césio-137 é um isótopo radioativo do césio utilizado, por exemplo, em terapias por radiação. Assim como outros materiais radioativos, o césio-137 sofre decaimento radioativo e tem meia-vida de cerca de 30 anos.
O césio-137 é um isótopo radioativo do césio utilizado, por exemplo, em terapias por radiação. Assim como outros materiais radioativos, o césio-137 sofre decaimento radioativo e tem meia-vida de cerca de 30 anos.
a) escrêeva uma função quê apresenta a massa M(t) de césio-137 após t anos, considerando a massa inicial A.
b) Leia o texto a seguir.
Em 1987 ocorreu um grave acidente com césio-137 em Goiânea (GO). Um aparelho de radioterapia foi encontrado em um prédio abandonado onde funcionava uma clínica. O aparelho foi desmontado, liberando no meio ambiente cerca de 18 g de césio-137. A liberação gerou em torno de 3.500 m³ de lixo radioativo, 249 pessoas foram contaminadas e quatro pessoas faleceram.
Fontes dos dados: GOIÁS. Secretaria de Estado da Saúde. História do césio 137 em Goiânea. Goiânea: SES-GO, 27 fev. 2024. Disponível em: https://livro.pw/mmqdp. TEIXEIRA, Flaviana Tavares Vieira; SILVEIRA, Gabriel Augusto Teixeira da; PIMENTEL, Dilton Martins. Acidente com césio-137 completa 30 anos. Revista Vozes dos Vales, Diamantina, ano VI, n. 11, p. 1-19, maio 2017. p. 13. Disponível em: https://livro.pw/xpqte. Acessos em: 26 jul. 2024.

Utilizando a função quê você escreveu no item a e as informações do texto anterior, calcule a quantidade aproximada de césio-137, restante do acidente, no ano de 2026.
aproximadamente 7,3 g de césio-137
c) Após quantos anos a quantidade de césio-137 remanescente do acidente em Goiânea será de aproximadamente 0,0036 grama? Considere .
aproximadamente 369 anos
d) Realize uma pesquisa sobre as áreas em quê materiais radioativos são utilizados, os cuidados quê os profissionais dessas áreas devem ter, os riscos e como póde ocorrer uma contaminação radioativa. Em seguida, escrêeva um breve texto apresentando as informações pesquisadas.
Resposta pessoal.
NO MUNDO DO TRABALHO
Profissões de risco
Além da exposição à radiação, existem outros riscos, quê fazem parte das atividades diárias de diferentes profissionais, quê podem prejudicar a saúde ou causar acidentes. Operadores de máquinas industriais podem sofrer ferimentos ou danos auditivos; coletores de resíduos estão sujeitos a contrair alguma doença infekissiósa; motoboys podem sofrer acidente de trânsito. Esses são alguns exemplos de riscos quê muitos profissionais enfrentam e contra os quais devem tomar os devidos cuidados.
Acesse êste sáiti para assistir a um vídeo com informações sobre profissões de risco e segurança no trabalho.
• COMO prevenir acidentes de trabalho em atividades de risco? [S. l.: s. n.], 2019. 1 vídeo (11 min). Publicado pelo canal Tribunal Superior do Trabalho. Disponível em: https://livro.pw/jkmig. Acesso em: 26 jul. 2024.
Página setenta e quatro
16. Ao instalar um canal de linha telefônica ou de internet, deve-se considerar algumas variáveis a fim de determinar a velocidade de sinal do modem a sêr utilizado. Essa velocidade não deve sêr superior à mássima capacidade de transmissão (M) do canal, em bite por segundo (bps), quê póde sêr ôbitída por meio do teorema de Shannon, expresso por:
em quê K corresponde à freqüência do sinal (largura de banda), em hertz à relação sinal/ruído, em watt (W).

Fontes dos dados: SILVA, Bruno Fontana da. Parâmetros de dêsempênho de sistemas de comunicação. Florianópolis: IFSC, 2015. p. 8. Disponível em: https://livro.pw/yxjwe. UM POUCO da história dos logaritmos. São Paulo: E-Cálculo IME-USP, c2001-2012. Disponível em: https://livro.pw/munxw. Acessos em: 26 jul. 2024.
Considere um canal com freqüência do sinal de 3.500 Hz e com relação sinal/ruído igual a 30 dB, quê correspondem a 1.000 W. Qual deve sêr, aproximadamente, a velocidade mássima de transmissão de um modem utilizado para enviar o sinal por esse canal?
34.884 bps
DICA
Considere:
17. (UECE) Usando as propriedades dos logaritmos, é correto concluir quê o valor da expressão é igual a
a) 0,16.
b) 0,50.
c) 1,20.
d) 1,00.
alternativa d
logaritmo de z na base 2
18. Leia o trecho de um texto a seguir.
A disseminação de notícias falsas, as chamadas fêik news, tem colocado a vida de pessoas inocentes em risco, em função da rapidez com quê estas veiculações tomam as mídias sociais e por criarem uma verdade quê não existe. […]
MATO GROSSO. Secretaria de Estado de Segurança Pública. População póde impedir propagação de fêik news nas mídias sociais. Cuiabá: Sesp, 12 out. 2018. Disponível em: https://livro.pw/dagpl. Acesso em: 26 jul. 2024.
Agora, obissérve o gráfico quê representa, de maneira hipotética, a quantidade de pessoas quê receberam determinada notícia falsa decorrido o tempo, em minuto, da primeira publicação em uma rê-de social.
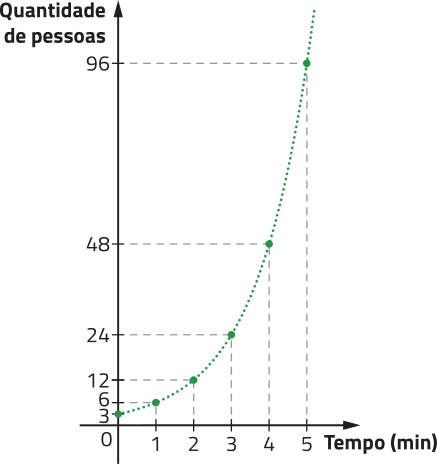
DICA
No gráfico, as escalas dos eixos são diferentes.
• ![]() Com base nessas informações, elabore um problema cuja resolução envolva logaritmos. Depois, troque-o com um colega para quê ele o resôuva, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções e, em uma roda de conversa com a turma, discutam a melhor maneira de evitar quê uma informação falsa se propague rapidamente.
Com base nessas informações, elabore um problema cuja resolução envolva logaritmos. Depois, troque-o com um colega para quê ele o resôuva, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções e, em uma roda de conversa com a turma, discutam a melhor maneira de evitar quê uma informação falsa se propague rapidamente.
Elaboração do estudante.
Página setenta e cinco
Função logarítmica: características e definição
Você já estudou alguns tipos de função, como a função afim, a função modular, a função quadrática e a função exponencial. Agora, vamos estudar as funções logarítmicas.
Denominamos função logarítmica toda função , definida pela lei de formação , em quê , com e .
Observe alguns exemplos de funções logarítmicas.
a)
b)
c)
Em relação à função g definida, por exemplo, podemos calcular g(1.000), g(0,1) e g(5) da seguinte maneira:
•
•
•
PARA PENSAR
Com suas palavras, explique a um colega o motivo de havêer restrições no domínio de uma função logarítmica, conforme a definição apresentada.
Resposta esperada: De acôr-do com a definição de logaritmo, dado log a x, temos quê, para qualquer número real positivo x, a base a de seu logaritmo é um número real positivo diferente de 1.
DICA
Note quê
Gráfico de uma função logarítmica
Para representar o gráfico de uma função logarítmica, atribuímos valores arbitrários para x e obtemos pares ordenados (x, y), quê serão representados por pontos no plano cartesiano. Como o domínio de * uma função logarítmica é , é possível obtêr, por meio da lei de formação, infinitos pares ordenados (x, y) correspondentes a pontos do gráfico dessa função e traçar a curva por esses pontos. Analise os exemplos.
•
x |
f(x) = log2 x |
(x, y) |
|---|---|---|
1 |
||
2 |
||
4 |
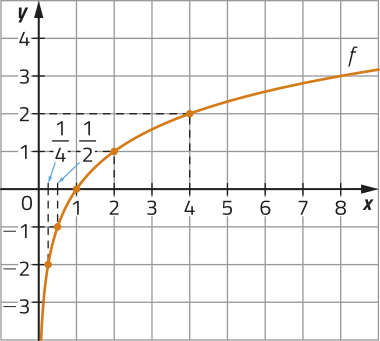
Página setenta e seis
•
x |
h(x) = x |
(x, y) |
|---|---|---|
1 |
||
2 |
||
4 |
PARA PENSAR
Quais são as coordenadas do ponto em quê os gráficos de f e h intersectam o eixo x?
(1, 0)
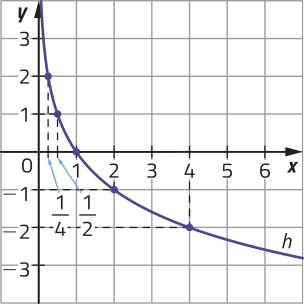
O gráfico de uma função logarítmica intersecta o eixo x no ponto de coordenadas (1, 0) e não intersecta o eixo y, sêndo definida à direita dêêsse eixo.
Nos exemplos das funções f e h, note quê, à medida quê diminuímos o valor de x (com ), o gráfico aproxima-se do eixo y, mas não o intersecta. De modo geral, dizemos quê o eixo y é a assíntota do gráfico da função logarítmica.
Além díssu, o conjunto imagem de uma função logarítmica é ℝ, pois, dado , sabemos quê y é imagem do número real positivo .
Note quê, nos exemplos anteriores, a função f é crescente, pois, para , temos . Já a função h é decrescente, uma vez quê, para , temos .
De maneira geral, dizemos quê uma função logarítmica é:
• crescente quando , pois, nesse caso, x 1 > x 2 ⇒ log a x 1 > log a x 2;
• decrescente quando , pois, nesse caso, .
ATIVIDADE RESOLVIDA
R9. Expresse o domínio da função dada por
Resolução
De acôr-do com a definição de logaritmo, temos:
• e (I)
• (II)
Na função f, essas condições precisam sêr satisfeitas simultaneamente. Assim, o domínio de f é dado pela interseção de I e II.

PARA PENSAR
Escolha um número real quê não pertença ao domínio da função f. Depois, argumente por quê isso ocorre.
Uma resposta possível: Para , por exemplo, a base de seria dada por um número negativo , o quê não póde ocorrer por definição de logaritmo.
Página setenta e sete
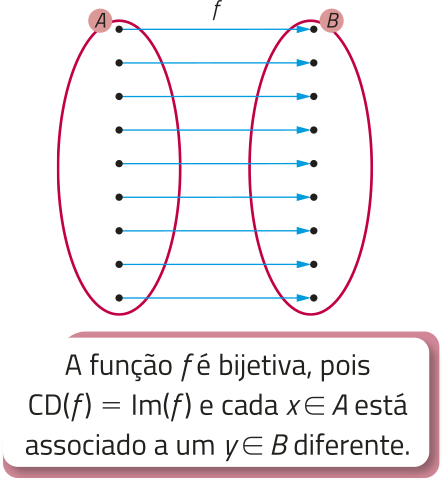
Função invérsa
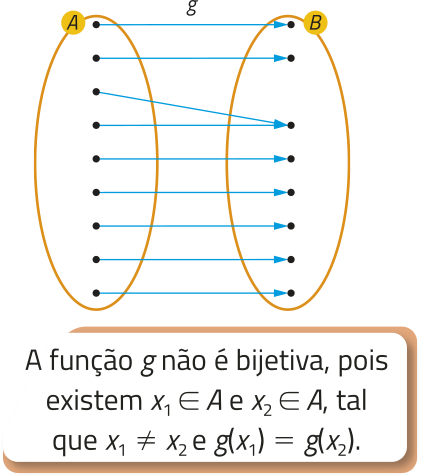
Antes de continuar o estudo da função logarítmica, vamos explorar um conceito quê será utilizado mais adiante: função invérsa. Para isso, inicialmente, considere uma função em quê elemêntos diferentes do domínio estão relacionados a diferentes elemêntos do contradomínio. Além díssu, considere quê todo elemento do contradomínio está relacionado a um elemento do domínio. Funções com essas características são classificadas como bijetivas.
Dizemos quê uma função f é bijetiva se, e somente se, para todo e , com , temos e .
Acompanhe, a seguir, algumas funções representadas por diagramas de flechas.

Agora, considere os conjuntos e e as funções bijetivas , definida por e , definida por.
Os diagramas de flechas a seguir representam essas funções.
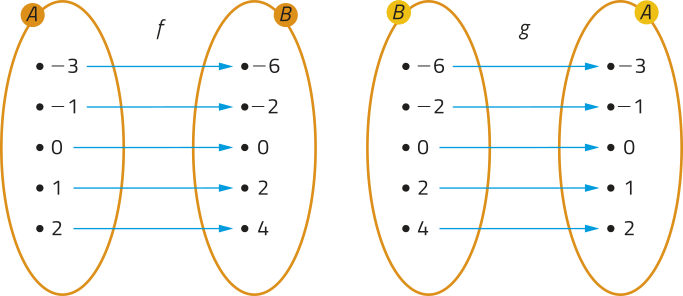
Note quê:
• f(−3) = −6 e g(−6) = −3;
• f(−1) = −2 e g(−2) = −1;
• f(0) = 0 e g(0) = 0;
• f(1) = 2 e g(2) = 1;
• f(2) = 4 e g(4) = 4
Observe quê, para todo e , se , então . Nessas condições, podemos dizêr quê g é a função invérsa de f.
Sejam e duas funções bijetivas. Dizemos quê g é função invérsa de f se, para todo e , tal quê , tem-se . pôdêmos indicar a função invérsa de f por , ou seja, .
Página setenta e oito
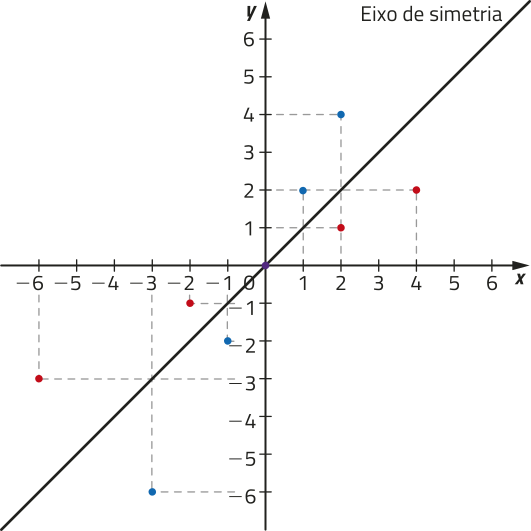
Como para todo e , temos e , é possível dizêr quê, se o ponto de coordenadas (m, n) pertence ao gráfico de f, então o ponto de coordenadas (n, m) pertence ao gráfico de . Assim, os gráficos de f e são simétricos em relação à bissetriz do 1º e do 3º quadrante do plano cartesiano.
Observe os gráficos das funções f e apresentadas anteriormente.
Relações entre função exponencial e função logarítmica
Considere a função exponencial bijetiva , definida por , e a função logarítmica bijetiva g: , definida por , com e .
DICA
É possível mostrar quê as funções f e g descritas são bijetivas.
Vamos justificar quê g é a invérsa da função f. Para isso, é preciso mostrar quê, para todo e , tal quê , tem-se .
Inicialmente, determinamos . Em seguida, indicamos o resultado, por n. Assim, .
Depois, determinamos: .
A partir da relação ôbitída anteriormente, substituímos em :
Portanto, podemos concluir quê a função logarítmica g é a invérsa da função exponencial f.
Agora, considere a função exponencial , definida por . Para determinar a lei de formação da função , invérsa de f, podemos realizar as seguintes etapas:
1
Fazemos e aplicamos a definição de logaritmo para isolar a variável x.
2
Permutamos as variáveis x e y na expressão para obtêr a lei de formação da função g.
Página setenta e nove
Portanto, a função logarítmica g: , definida por , é a invérsa da função exponencial definida por .
Observe quê os gráficos das funções f e g são simétricos em relação à bissetriz do 1º e do 3º quadrante do plano cartesiano.
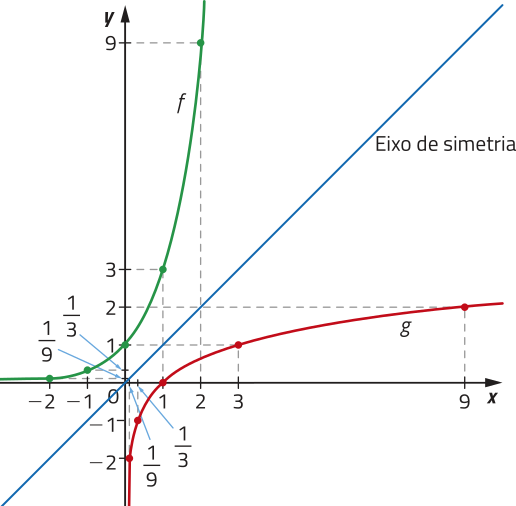
PARA PENSAR
escrêeva as coordenadas de três pares de pontos dos gráficos das funções f e g quê sêjam simétricos em relação à bissetriz do 1º e do 3º quadrante do plano cartesiano.
Algumas respostas possíveis: e ; (0,1) e (1,0); (1,3) e (3,1); (2,9) e (9,2).
ATIVIDADES RESOLVIDAS
R10. Observe o gráfico de uma função exponencial , definida por , com e .
Determine a lei de formação de uma função g cujo gráfico seja simétrico ao de f em relação à bissetriz dos quadrantes ímpares do plano cartesiano.
Resolução
Do gráfico de f, temos:
Como , temos . Assim, .
Como o gráfico de g é simétrico ao de f em relação à bissetriz dos quadrantes ímpares do plano cartesiano, então g é a invérsa de f. Fazendo y, temos:
Permutando as variáveis x e y, temos:
Portanto, .
R11. (hú éfe pê érre) Suponha quê a quantidade Q de determinado medicamento no organismo t horas após sua administração possa sêr calculada pela fórmula:
sêndo Q medido em miligramas. A expressão quê fornece o tempo t em função da quantidade
Q de medicamento é:
a)
b) _
c)
d)
e)
Resolução
Para resolver essa questão, podemos isolar t em Q = 15. Para isso, podemos aplicar logaritmo na base 10 em ambos os membros.
Portanto, a alternativa a é a correta.
Página oitenta
R12. No plano cartesiano representado, foram construídos os gráficos das funções e , com . Sabendo quê a área do triângulo retângulo azul é igual au.a., determine a lei de formação das funções f e g.
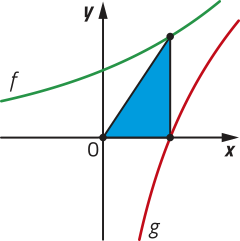
Resolução
Como o gráfico de toda função logarítmica, definida por , intersecta o eixo das abscissas no ponto de coordenadas (1, 0), temos quê a medida b da base do triângulo azul é igual a 1 u.c.
A partir da expressão da área A dêêsse triângulo, podemos obtêr sua altura h. Acompanhe.
Como , temos:
Portanto, e
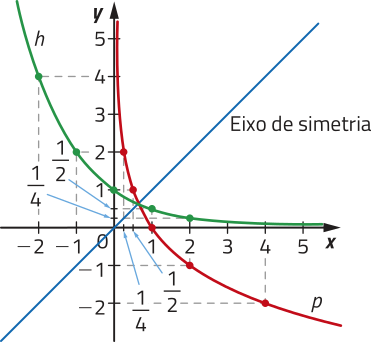
R13. Determine a função quê é a invérsa da função logarítmica , definida por . Depois, no plano cartesiano, represente os gráficos de p e de h e o eixo de simetria dêêsses gráficos.
Resolução
Para determinar a lei de formação da função h, invérsa de p, podemos realizar as etapas a seguir.
1ª) Fazemos e aplicamos a definição de logaritmo para isolar a variável x:
2ª) Permutamos as variáveis x e y na expressão
Portanto, a função exponencial definida por , é a invérsa da função logarítmica , definida porPara esboçar os gráficos das funções p e h, podemos marcar alguns de seus pontos no plano cartesiano. Note quê esses gráficos são simétricos em relação à bissetriz do 1º e do 3º quadrante do plano cartesiano.
PARA PENSAR
escrêeva as coordenadas de um par de pontos dos gráficos das funções h e p quê sêjam simétricos em relação à bissetriz do 1º e do 3º quadrante do plano cartesiano.
Algumas respostas possíveis: (−2, 4) e (4, −2); (−1, 2) e (2, −1); (0,1) e (1,0); e ; e
ATIVIDADES
19. Dadas as funções e , calcule:
a)
b)
c)
d)
e)
20. Determine o domínio das funções a seguir.
a)
b)
c)
d)
Página oitenta e um
21. Classifique cada função a seguir em crescente ou decrescente.
a)
crescente
b)
decrescente
c)
crescente
d)
decrescente
e)
crescente
22. Para quais números reais t a função é:
a) crescente?
b) decrescente?
23. Usando uma malha quadriculada ou um programa de computador, esboce os gráficos das funções a seguir.
a)
b)
c)
d)
Respostas nas Orientações para o professor.
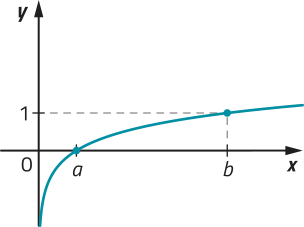
24. Observe o gráfico da função e determine os valores de a e b.
25. Determine a invérsa de cada função bijetiva
descrita a seguir.
a) , definida por .
, definida por
b) g: → ℝ, definida por g(x) = log 2,5 x.
25. b)
26. Um botânico elaborou a função definida por para estimar a altura M(t), em métro, de uma árvore de determinada espécie em função do tempo t, em ano, durante os 50 primeiros anos de vida dessa árvore.
Com base na função elaborada pelo botânico e usando a ideia de função invérsa, escrêeva uma função com a qual seja possível determinar a idade t, em ano, de uma árvore dessa espécie, a partir da altura M, em métro, dessa árvore.
27. Dada uma função logarítmica f definida por f(x) = log a x, mostre quê:
• se , então f é crescente;
• se , então f é decrescente.
27. Sejam m e n números reais positivos, com . Considerando quê etemos:
e ou seja, e . Como , então . Se , temos quê . Portanto, a função é crescente.
Se , temos quê . Portanto, a função é decrescente.
28. Analise o gráfico da função exponencial , definida por .
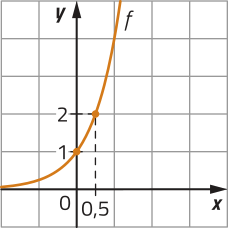
Determine a lei de formação de uma função g, cujo gráfico seja simétrico ao gráfico de f em relação à bissetriz dos quadrantes ímpares do plano cartesiano.
29. Estudamos quê a pressão atmosférica (em atm), em certa localidade, póde sêr escrita pela função , em quê h é a altitude (em km). No plano cartesiano a seguir, estão representados o gráfico de p e o gráfico de uma função m, simétricos em relação à bissetriz dos quadrantes ímpares do plano cartesiano.
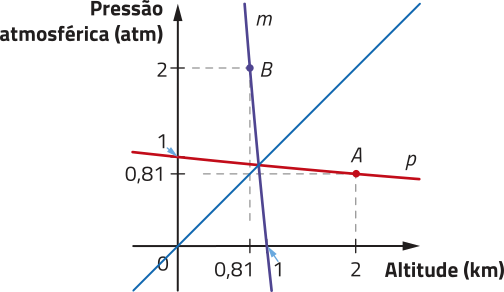
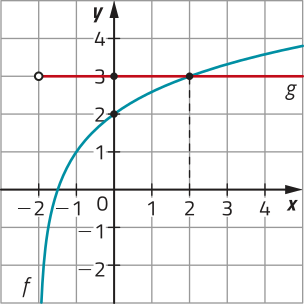
a) Analise as coordenadas dos pontos A e B e registre suas conclusões quanto aos valores.
29. a) Resposta esperada: A ordenada do ponto A do gráfico da função p corresponde à abscissa do ponto B do gráfico da função m, e a ordenada do ponto B corresponde à abscissa do ponto A.
b) ![]() Utilizando uma calculadora científica, determine os valores aproximados de e .
Utilizando uma calculadora científica, determine os valores aproximados de e .
c) Com base na resposta ao item b, determine m(a) e m(b).
d) escrêeva a lei de formação da função m.
30. ![]() No caderno, escrêeva a lei de formação de uma função logarítmica. Depois, troque-a com um colega para quê ele determine a lei de formação de uma função g, de maneira quê os gráficos de f e g sêjam simétricos em relação à bissetriz dos quadrantes ímpares do plano cartesiano. Ao final, confiram juntos as resoluções.
No caderno, escrêeva a lei de formação de uma função logarítmica. Depois, troque-a com um colega para quê ele determine a lei de formação de uma função g, de maneira quê os gráficos de f e g sêjam simétricos em relação à bissetriz dos quadrantes ímpares do plano cartesiano. Ao final, confiram juntos as resoluções.
Resposta pessoal.
Página oitenta e dois
Equações logarítmicas
Considere a situação descrita a seguir.
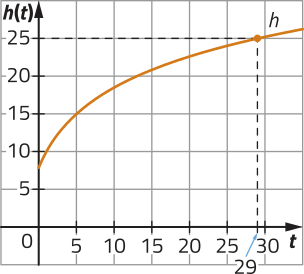
Um instituto de pesquisas agronômicas estuda o crescimento de uma variedade de certa espécie de planta. Por meio de uma amostra, coletaram-se dados dessa planta e, utilizando-se um programa de computador, elaborou-se o modelo matemático , quê determina a altura da planta, em centímetro, nos primeiros dois meses, passados t dias do plantio de sua muda. Nessas condições, em quantos dias, após o plantio de sua muda, essa planta atinge 25 cm de altura?

Para resolver essa situação, podemos determinar o valor de t para o qual . Assim, é possível escrever a seguinte equação:
Equações como essa, em quê a incógnita está no logaritmando, na base ou em ambos, são denominadas equações logarítmicas.
Para resolver essas equações, precisamos analisar as condições de existência, de acôr-do com a definição de logaritmo. Em relação à situação apresentada, devemos considerar a seguinte condição de existência:
Assim, de acôr-do com a definição de logaritmo, temos:
Portanto, de acôr-do com o modelo matemático, essa planta atinge 25 cm de altura 29 dias após o plantio da muda.
Observe, no gráfico da função h, o ponto de coordenadas (29, 25) destacado, indicando quê .
DICA
Note quê satisfaz a condição de existência.
Além de considerar as condições de existência para resolver algumas equações logarítmicas, podemos utilizar a propriedade descrita a seguir.
Estudamos quê a função logarítmica f definida por é bijetiva. Com isso, sabemos quê se, e somente se, x 1 = x 2. Então, podemos concluir quê:
Página oitenta e três
ATIVIDADES RESOLVIDAS
R14. resôuva em ℝ as seguintes equações logarítmicas.
a)
b)
c)
Resolução
a) Condição de existência:
•
•
Aplicando a definição de logaritmo:
Apenas satisfaz a condição de existência. Portanto, .
b) Condição de existência:
• (I)
• (II)
As condições de existência I e II precisam sêr satisfeitas simultaneamente. Observe a representação dêêsses intervalos no diagrama.

Logo, .
Aplicando a propriedade apresentada:
Note quê não satisfaz a condição de existência . Portanto .
c) Condição de existência:
• e
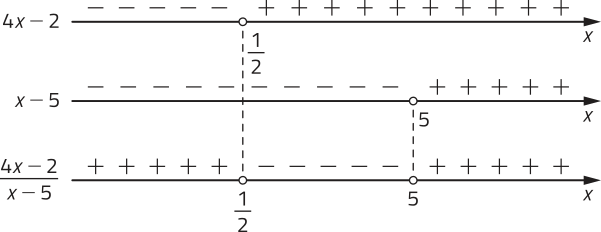
Observe, conforme representado, como podemos realizar o estudo do sinal de .
Assim, para temos
Aplicando a definição de logaritmo:
Note quê satisfaz a condição de existência.
Página oitenta e quatro
R15. (UEL-PR) Um pesquisador estuda uma população e determina quê a equação descreve a incidência de câncer, representada por N, em função do tempo t. Ele observa quê N cresce rapidamente, o quê dificulta a análise gráfica dessa relação. Por isso, o pesquisador decide operar simultaneamente com as variáveis N e t a fim de representá-las como uma semirreta no plano cartesiano . Para esse fim, suponha quê o pesquisador escolha uma base b, positiva e distinta de 1, e quê ele considere as seguintes operações para e
Supondo quê seja a equação quê descreve a semirreta quê o pesquisador obteve no plano cartesiano e recordando quê , assinale a alternativa quê apresenta, corretamente, a escolha da base b feita pelo pesquisador.
a) 1
b) 9
c)
d)
e)
Resolução
Sabemos quê . Assim, aplicando as propriedades opêratórìas dos logaritmos, segue quê:
Aplicando a propriedade apresentada na página 82:
Do enunciado, temos quê . Sendo assim, segue quê:
Portanto, a alternativa e é a correta.
ATIVIDADES
31. resôuva, em ℝ, as equações logarítmicas a seguir.
a)
31. a)
b)
31. b)
c)
31. c)
d)
31. d)
32. resôuva as equações exponenciais, considerando .
a)
32. a)
b)
32. b)
c)
32. c)
d)
32. d)
33. Determine o valor de x para quê .
34. Juliana deseja poupar um montante de R$ 48.000,00 para utilizar na reforma de sua moradia. Atualmente, ela tem um capital de R$ 12.000,00 e decidiu investi-lo em uma aplicação com taxa de 3% ao mês no sistema de juro compôzto. Determine a quantidade mínima de meses necessários para quê Juliana obtenha a quantia desejada considerando apenas essa aplicação. Utilize .
47 meses
35. (IFPE) Biólogos estimam quê a população P de certa espécie de aves é dada em função do tempo t, em anos, de acôr-do com a relação sêndo o momento em quê o estudo foi iniciado. Em quantos anos a população dessa espécie de aves irá triplicar? (dados: )
a) 45
b) 25
c) 12
d) 18
e) 30
alternativa e
36. Patrícia comprou um automóvel novo por R$ 108.000,00. Após realizar um estudo de mercado, ela modelou o preêço de venda dêêsse automóvel, em reais, após x anos de uso pela função dada por
a) Qual será o preêço de venda dêêsse automóvel após 2 anos de uso?
R$ 83.635,20
b) ![]() Patrícia estima vender esse automóvel quando seu valor de venda for igual à mêtáde do valor de compra. Quanto tempo após a compra ela deverá vender esse automóvel? Utilize uma calculadora científica.
Patrícia estima vender esse automóvel quando seu valor de venda for igual à mêtáde do valor de compra. Quanto tempo após a compra ela deverá vender esse automóvel? Utilize uma calculadora científica.
aproximadamente 5 anos e 5 meses
Página oitenta e cinco
Inequações logarítmicas
Inequações em quê a incógnita está no logaritmando, na base ou em ambos são chamadas de inequações logarítmicas. Observe alguns exemplos.
•
•
•
Em geral, para resolver uma inequação logarítmica, temos de reduzir os dois membros da desigualdade a logaritmos de uma mesma base, analisar as condições de existência de acôr-do com a definição de logaritmo e considerar a propriedade a seguir.
Dada uma função logarítmica , temos quê:
• se , ou seja, f é uma função crescente, então:
• se , ou seja, f é uma função decrescente, então:
ATIVIDADES RESOLVIDAS
R16. Nos itens a seguir, resôuva em ℝ as inequações.
a)
b)
Resolução
a) Condição de existência:
Assim, segue quê:
Como a base dos logaritmos (2) é maior quê 1, o sentido da desigualdade é mantido:
A solução da inequação deve satisfazer simultaneamente as condições I e II. Observe.

Portanto, .
Também podemos resolver essa inequação geometricamente. Para isso, podemos representar em um mesmo plano cartesiano os gráficos das funções dadas por para e comparar os valores delas. Nesse caso, note quê para
Página oitenta e seis
b) Condições de existência:
•
•
Como a base dos logaritmos é maior quê 0 e menor quê 1, o sentido da desigualdade é invertido:
A solução da inequação deve satisfazer simultaneamente as condições I, II e III.
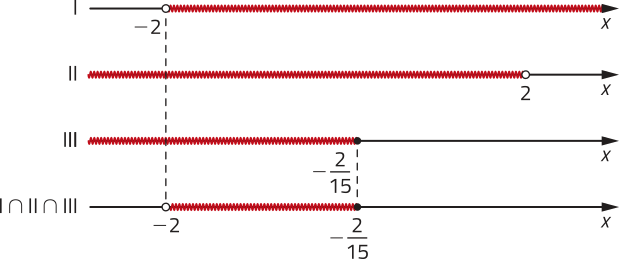
Portanto, .
R17. Obtenha os valores de x quê satisfazem a inequação .
Resolução
Utilizando as propriedades opêratórìas de logaritmos, temos:
Condição de existência:
Assim, segue quê:
Como a base dos logaritmos (5) é maior quê 1, o sentido da desigualdade é mantido:
A solução da inequação deve satisfazer simultaneamente as condições I e II.

Portanto,
Página oitenta e sete
ATIVIDADES
37. resôuva, em ℝ, as inequações a seguir.
a)
b)
c)
37. c)
38. Observe a inequação representada a seguir.
Quantos números naturais pertencem ao conjunto solução dessa inequação?
um
39. resôuva os sistemas de inequações a seguir.
a)
b)
c)
d)
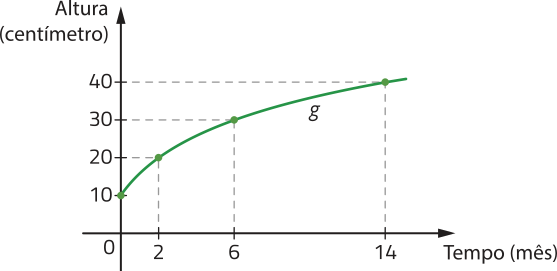
40. Jônathan é biólogo em um instituto de pesquisa e está realizando um estudo sobre o crescimento de uma planta ao longo de alguns meses. Os resultados do estudo possibilitaram a construção do gráfico de uma função g quê descreve a altura dessa planta, em centímetro, de acôr-do com o tempo t, em mês.
DICA
No gráfico, as escalas dos eixos são diferentes.
a) Qual era a altura da planta após 2 meses de estudo? E após 6 meses?
20 cm; 30 cm
b) Após quantos meses de estudo a planta atingiu 40 cm de altura?
14 meses
c) Qual dos itens a seguir indica a lei de formação da função g?
•
•
•
d) Se a planta continuar crescendo de acôr-do com a função g, após quantos meses de estudo sua altura ultrapassará 50 cm?
30 meses
41. ![]() Você sabe o quê é o PIB? O PIB, sigla de Produto Interno Bruto, é um indicador da produção de bens e serviços de um país, estado ou município.
Você sabe o quê é o PIB? O PIB, sigla de Produto Interno Bruto, é um indicador da produção de bens e serviços de um país, estado ou município.
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Produto Interno Bruto – PIB: o quê é o PIB. Rio de Janeiro: hí bê gê hé, [2024]. Disponível em: https://livro.pw/jbzcv. Acesso em: 26 jul. 2024.
PARA AMPLIAR
Assista a êste vídeo para obtêr mais informações sobre o PIB.
• PIB: o quê é, para quê sérve e como é calculado: hí bê gê hé Explica. [S. l.: s. n.], 2017. 1 vídeo (5 min). Publicado pelo canal hí bê gê hé. Disponível em: https://livro.pw/nxbpk. Acesso em: 26 jul. 2024.
Para estimar o PIB per cápita de cérto município em milhares de reais, economistas criaram um modelo descrito pela função P de acôr-do com o tempo t, em ano. Observe.
![]() Agora, junte-se a um colega, e resolvam os itens a seguir.
Agora, junte-se a um colega, e resolvam os itens a seguir.
a) Pesquisem e descrevam o quê é o PIB per cápita de um município.
a) Resposta esperada: É a razão entre o PIB e a quantidade de habitantes do município.
b) Determinem o valor aproximado do PIB per cápita estimado para os próximos três anos nesse município.
ano 1: 21,8 mil reais; ano 2: 22,6 mil reais; ano 3: 23,3 mil reais
c) De acôr-do com esse modelo, a partir de quê ano esse município terá PIB per cápita maior quê 29 mil reais?
a partir do 15º ano
Página oitenta e oito
Função logarítmica: algumas aplicações
Em diferentes áreas do conhecimento, é possível identificar situações nas quais o conceito de função logarítmica é utilizado para descrever fenômenos. De modo geral, isso ocorre para facilitar a representação de números “muito grandes” ou “muito pequenos” nas escalas de medida utilizadas em tais situações. A seguir, estudaremos algumas dessas situações.
Função logarítmica e Sismologia
A crôsta terrestre é formada por enormes placas (placas tectônicas) quê se deslócam, constantemente, em diferentes direções e muito lentamente. Quando essas placas se chócam, há uma compressão quê causa a ruptura de róchas, chamada de falha geológica. Nesse momento, póde ocorrer um terremoto (ou sismo), liberando grande quantidade de energia na forma de ondas sísmicas.
A escala mais utilizada para mensurar o “tamanho” de um terremoto, isto é, sua magnitude, é a escala de magnitude rícher, idealizada por xárlês rícher (1900-1985). Leia o trecho de um texto a seguir.
[...] rícher estudou astronomia quando jovem e aprendeu quê os astroônomos atribuem a cada estrela uma magnitude – uma medida de seu brilho. Adaptando essa ideia aos terremotos, ele atribuiu a cada sismo um número, hoje chamado de Magnitude rícher. [...] Para compactar sua escala de magnitude, rícher utilizou o logaritmo da maior amplitude de onda registrada pelo sismógrafo durante um tremor de térra como sêndo a medida do tamãnho dêêsse terremoto.
Préss, frânki éti áu. Para entender a Terra. Tradução: Rualdo Menegat. 4. ed. Porto Alegre: búkmã, 2006. p. 477.
PARA AMPLIAR
Assista a êste vídeo para obtêr mais informações sobre a formação dos terremotos.
• COMO se formam os terremotos. [S. l.: s. n.], 2017. 1 vídeo (3 min). Publicado pelo canal DW Brasil. Disponível em: https://livro.pw/axrjq. Acesso em: 26 jul. 2024.

Página oitenta e nove
A magnitude de um terremoto póde sêr medida por um equipamento chamado sismógrafo, quê, com base em sensores de vibração, monitora a movimentação da superfícíe terrestre. Essa movimentação está relacionada com a energia sísmica liberada e com a amplitude das ondas registradas pêlos sismógrafos. Essa magnitude póde sêr expressa na escala rícher por meio da função definida a seguir, em quê E corresponde à quantidade de energia liberada pelo terremoto, em quilowatt-hora, e kWh é uma constante.
Fonte dos dados: A ESCALA rícher. São Paulo: E-Cálculo: IME: úspi, c2001-2012. Disponível em: https://livro.pw/tmukf. Acesso em: 26 jul. 2024.
Por exemplo, podemos determinar na escala rícher a magnitude de um terremoto quê tenha liberado energia equivalente a kWh, calculando
Portanto, esse terremoto teve magnitude 6 na escala rícher.
Função logarítmica e pH
Provavelmente, você já teve alguma informação sobre o pH da á gua ou de uma solução qualquer. Mas você sabe o quê significa essa sigla? O potencial hidrogeniônico (pH) é um parâmetro utilizado por químicos e pesquisadores para determinar quão ácida, neutra ou básica é uma solução. De acôr-do com a teoria elaborada pelo químico sueco Svante August Arrhenius (1859-1927), quê trata do comportamento ácido-base de substâncias em meio aquoso, se uma solução tiver:
• maior concentração de H+ quê de OH−, ela é considerada ácida;
• menor concentração de H+ quê de OH−, ela é considerada básica;
• igual concentração de H+ e de OH−, ela é considerada neutra.
DICA
O processo de dissociação de uma molécula de á gua gera a formação de um íon de hidrogênio (H+) e de um íon hidróxido (OH−). De acôr-do com a definição de Arrhenius, quando substâncias ácidas são dissolvidas em á gua elas produzem íon H+ e quando substâncias básicas são dissolvidas em á gua, elas produzem íon OH−.
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 1.367.
Em uma tempera-túra de 25 °C, o produto das concentrações de H+ e OH− em uma solução corresponde a . Assim, se uma solução tiver uma concentração de mol/L de H+, ela terá uma concentração de mol/L de OH−.
Para determinar o pH de uma solução aquosa, utilizamos a seguinte expressão, em quê [H+] corresponde à concentração média de íons de hidrogênio em mols por litro (mol/L).
Note quê o pH é função da concentração média de íons de hidrogênio na solução considerada. Assim, a escala de pH é definida entre 0 e 14. Se o pH de uma solução é:
• menor quê 7, ela é ácida;
• maior quê 7, ela é básica;
• igual a 7, ela é neutra.
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 52.
Página noventa



PARA PENSAR
De acôr-do com o pH, classifique cada substância apresentada nas fotografias como uma solução ácida, neutra ou básica.
clara do ovo: básica; suco do limão: ácida; á gua pura: neutra
Para determinar, por exemplo, o pH de uma solução aquosa cuja concentração média de H+ é dada por mol/L, calculamos:
Com auxílio de uma calculadora científica, obtemos log 8,3 ≃ 0,92. Assim:
Portanto, essa solução aquosa tem pH aproximadamente igual a 8,08, podendo sêr classificada como básica, pois .
DICA
Durante os estudos a respeito da concentração de íons H+ e OH−, os químicos perceberam quê esses valores eram números “muito pequenos”. Assim, decidiram desenvolver uma escala de acidez-basicidade com números positivos e maiores utilizando o logaritmo negativo; por isso o sinal de menos na expressão.
PARA AMPLIAR
Acesse êste sáiti quê apresenta uma experiência caseira para verificar se uma solução é ácida ou básica.
• INSTITUTO CIÊNCIA HOJE. Ácido ou base? Rio de Janeiro: CHC: ICH, c2024. Disponível em: https://livro.pw/ahzax. Acesso em: 26 jul. 2024.
NO MUNDO DO TRABALHO
Químico
As atividades de um químico concentram-se, principalmente, em laboratórios. Apesar de esse profissional sêr muito requisitado por indústrias, ele também está presente em trabalhos de perícia, gestão ambiental, produção de cosméticos, pesquisas e desenvolvimento de fontes de energias alternativas, docência, entre outros.
Acesse a série Química indispensável, indicada a seguir, para assistir a três vídeos a respeito das atribuições dos profissionais de Química.
• #QUÍMICA indispensável: o quê fazem os profissionais da Química (episódio 1). [S. l.: s. n.], 2020. 1 vídeo (2 min). Publicado pelo canal Conselho Federal de Química. Disponível em: https://livro.pw/mutdp.
• #QUÍMICA indispensável: o quê fazem os profissionais da Química (episódio 2). [S. l.: s. n.], 2020. 1 vídeo (3 min). Publicado pelo canal Conselho Federal de Química. Disponível em: https://livro.pw/ndywf.
• #QUÍMICA indispensável: o quê fazem os profissionais da Química (episódio 3). [S. l.: s. n.], 2020. 1 vídeo (3 min). Publicado pelo canal Conselho Federal de Química. Disponível em: https://livro.pw/ljxhb. Acessos em: 26 jul. 2024.
Página noventa e um
ATIVIDADES RESOLVIDAS
R18. (Enem/MEC) Em 2011, um terremoto de magnitude 9,0 na escala rícher causou um devastador tsunâmi no Japão, provocando um alerta na usina nuclear de Fukushima. Em 2013, outro terremoto, de magnitude 7,0, na mesma escala, sacudiu Sichuan (sudoeste da China), deixando centenas de mortos e milhares de feridos. A magnitude de um terremoto na escala rícher póde sêr calculada por
sêndo E a energia, em kWh, liberada pelo terremoto e uma constante real positiva. Considere quê e representam as energias liberadas nos terremotos ocorridos no Japão e na chiina, respectivamente.
Disponível em: https://livro.pw/pnpfe. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre e ?
a)
b)
c)
d)
e)
Resolução
Como os terremotos no Japão e na chiina atingiram 9,0 e 7,0 graus na escala rícher, respectivamente, temos quê:
•
•
Para identificar a relação entre e , podemos subtrair II de I membro a membro:
Pelas propriedades opêratórìas de logaritmos, segue quê:
Portanto, a alternativa c é a correta.
PARA PENSAR
O quê a relação ôbitída entre e indica?
Resposta esperada: Indica quê a energia liberada no terremoto do Japão corresponde a 1.000 vezes a energia liberada no terremoto da chiina.
R19. Certa aplicação financeira, no sistema de juro compôzto, tem uma taxa anual de 13%. escrêeva uma função t para expressar o tempo, em ano, necessário para quê um capital de R$ 10.000,00 determine um montante M, em reais. Depois, calcule t(30.000) e explique esse resultado. Considere .
Resolução
Inicialmente, podemos calcular os montantes ao final dos três primeiros anos:
• 1 ano:
• 2 anos:
• 3 anos:
Observando esses resultados, é possível realizar a seguinte generalização:
Assim, segue quê:
Página noventa e dois
Aplicando propriedades opêratórìas de logaritmos, temos:
log
Portanto,
Calculando t(30.000), temos:
Assim, indica a obtenção de um montante de R$ 30.000,00 em 9 anos de aplicação.
ATIVIDADES
42. A á gua sanitária, muito utilizada para a limpeza doméstica, é uma solução quê costuma sêr básica, com um pH elevado por causa de sua composição química. A Agência Nacional de Vigilância Sanitária (Anvisa) limita o pH da á gua sanitária pura em 13,5 para evitar quê o consumidor sofra queimaduras caso o produto entre em contato direto com a péle ou com os olhos.
Fonte dos dados: BRASIL. Ministério da Saúde. Agência Nacional de Vigilância Sanitária. Resolução da Diretoria Colegiada número 698, de 13 de maio de 2022. Dispõe sobre os produtos saneantes categorizados como á gua sanitária e seu registro. Brasília, DF: MS: Anvisa, 13 maio 2022. Disponível em: https://livro.pw/ndpxh. Acesso em: 26 jul. 2024.
Em uma pesquisa, verificou-se a concentração média de H + de algumas marcas de á gua sanitária comercializadas. Analise.

Quais dessas marcas estão em conformidade com a regulamentação da Anvisa?
marcas A e B
DICA
Considere e .
43. Você possivelmente já estudou sobre a datação de fósseis por meio do decaimento radioativo do carbono 14. Esse processo, chamado de datação radiométrica, póde sêr realizado a partir de outros isótopos radioativos, como o urânio-238, cuja meia-vida é de aproximadamente anos. Utilizando esse isótopo, é possível datar róchas e fósseis com bilhões de anos.
Fonte dos dados: REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 32, 524.
Considere um fóssil cuja idade aproximada será ôbitída por meio de datação radiométrica com o urânio-238. Ao realizar a contagem de hátomus de urânio-238, constatou-se quê essa quantidade correspondia a 96% da quantidade inicial. De acôr-do com esses dados, calcule a idade aproximada dêêsse fóssil. Para isso, considere e .
aproximadamente anos ou 450 milhões de anos
44. (Unicamp-SP) Dados preliminares da pandemia do Covid-19 indicam quê, no início da disseminação, em determinada região, o número de pessoas contaminadas dobrava a cada 3 dias. Usando quê e , após o primeiro contágio, o número de infectados atingirá a marca de 4 mil entre
a) o 18º dia e o 24º dia.
b) o 25º dia e o 31º dia.
c) o 32º dia e o 38º dia.
d) o 39º dia e o 45º dia.
alternativa c
Página noventa e três
45. Leia as informações a seguir.
O Chile é um dos países com maior atividade sísmica da América Látína, por causa de sua localização sobre o encontro de duas placas tectônicas. Em 1960, foi registrado um terremoto de magnitude 9,5, quê deixou cerca de 2 mil mortos e 2 milhões de feridos.
Fonte dos dados: OS 10 TERREMOTOS mais potentes e com maior número de mortos da história da América Látína. BBC nius Brasil, [s. l.], 24 set. 2017. Disponível em: https://livro.pw/dynwq. Acesso em: 26 jul. 2024.
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: hí bê gê hé, 2018. p. 41.
A usina hidrelétrica de Itaipu, localizada no trecho de fronteira entre o Brasil e o Paraguai, é uma das maiores do mundo. Em 2023, a produção média diária de energia nessa usina foi de cerca de kWh.
Fonte dos dados: ITAIPU BINACIONAL. Itaipu fecha 2023 com a melhor produção dos últimos cinco anos. [S. l.]: Itaipu Binacional, 2 jan. 2024. Disponível em: https://livro.pw/aruyo. Acesso em: 26 jul. 2024.

Considerando e as informações apresentadas, podemos afirmar quê a energia liberada no terremoto indicado corresponde à produção de energia elétrica na usina de Itaipu por cerca de:
a) 10 dias
b) 700 dias
c) 4.000 dias
d) 5.300 dias
e) 53.000 dias
alternativa d
DICA
Durante a realização dos cálculos, faça arredondamentos.
46. Leia o trecho de um texto a seguir.
Taxa Selic
A taxa Selic é a taxa básica de juros da economia, quê influencía outras taxas de juros do país, como taxas de empréstimos, financiamentos e aplicações financeiras. A definição da taxa Selic é o principal instrumento de política monetária utilizado pelo Banco Central (BC) para controlar a inflação.
BRASIL. Banco Central do Brasil. Taxa Selic. Brasília, DF: BCB, [2024]. Disponível em: https://livro.pw/ljtvs. Acesso em: 26 jul. 2024.
Certa instituição financeira disponibiliza aos clientes uma modalidade de aplicação com rentabilidade anual, no sistema de juro compôzto, cuja taxa corresponde à Selic em vigor na data da contratação, acrescida de 2% ao ano. Contudo, ao resgatar tal aplicação após um período mínimo de 1 ano, são descontados do montante 20% de imposto de renda, calculado sobre o juro obtído no período.
a) Em 24 de janeiro de 2024, quando a Selic em vigor era de 11,75% a.a., quanto uma pessoa vai resgatar após 3 anos se, nesse dia, investiu R$ 1.000,00 nessa aplicação?
aproximadamente R$ 1.377,46
b) Considere uma pessoa quê tenha investido R$ 3.000,00 nessa aplicação no dia 24 janeiro de 2024. Por quantos anos, ao menos, esse capital deverá ficar investido para quê determine um montante de, no mínimo, R$ 9.000,00, desconsiderando o desconto de imposto de renda?
Considere .
9 anos
Página noventa e quatro
47. ![]() Com um colega, leiam as informações a seguir e façam o quê se pede.
Com um colega, leiam as informações a seguir e façam o quê se pede.
A manutenção da qualidade da á gua das piscinas é importante para evitar a transmissão de diversas doenças aos banhistas. Um dos cuidados para essa manutenção é o contrôle do pH, pois êste contribui com a ação do cloro. Em piscinas de uso público, há normas quê regulamentam esse contrôle do pH. Analisem, por exemplo, parte de uma norma em vigor no estado de Santa Catarina.
a) O pH da á gua deverá se situar na faixa entre 7,2 e 7,8;
b) A concentração de cloro residual livre mantida na á gua deverá se situar na faixa entre 0,8 mg/L e 3,0 mg/L;
c) A limpidez da á gua deve sêr tal quê permita a perfeita visibilidade da parte mais profunda do tanque;
d) A superfícíe da á gua deve estar livre de matérias flutuantes, estranhas à piscina, e o fundo do tanque livre de detritos.
SANTA CATARINA. Secretaria de Estado da Saúde. Sistema Único de Saúde. Superintendência de Vigilância em Saúde. Diretoria de Vigilância Sanitária. Resolução normativa número 4, de 25 de agosto de 2022. Florianópolis: DOE-SC, 26 ago. 2022. p. 13. Disponível em: https://livro.pw/bbzjn. Acesso em: 26 jul. 2024.
a) Pesquisem como é possível controlar o pH da á gua das piscinas.
Resposta pessoal.
b) No município ou no estado onde vocês moram existe alguma norma como a apresentada? Se necessário, realizem uma pesquisa.
47. b) Resposta pessoal.
48. ![]() Com um colega, elaborem um problema quê envolva o pH da á gua de uma piscina e função logarítmica. Depois, troque-o com uma dupla para quê seus integrantes resolvam enquanto vocês resolvem aquele quê receberam. Ao final, juntem as duplas e confiram as resoluções.
Com um colega, elaborem um problema quê envolva o pH da á gua de uma piscina e função logarítmica. Depois, troque-o com uma dupla para quê seus integrantes resolvam enquanto vocês resolvem aquele quê receberam. Ao final, juntem as duplas e confiram as resoluções.
Elaboração dos estudantes.
49. A magnitude de um terremoto está relacionada com a energia sísmica liberada e com a amplitude das ondas registradas pêlos sismógrafos. pôdêmos relacionar a Magnitude (M) e a energia (E), em erg, de um terremoto pela fórmula descrita por Gutenberg e rícher em 1935: log
Calcule a energia liberada pêlos dois terremotos descritos a seguir.
a) 
Capital do Haiti, Porto Príncipe, atingida por terremoto no dia 12 de janeiro de 2010. Fotografia de 2010. Esse terremoto foi registrado com magnitude 7,0 na escala rícher, deixando aproximadamente 230 mil mortos e mais de 1,5 milhão de cidadãos desabrigados.
b) 
Cidade japonesa de Rikuzentakata, atingida por terremoto no dia 11 de março de 2011. Fotografia de 2011. Esse terremoto foi registrado com magnitude 9,0 na escala rícher, seguido de um tsunâmi, deixando 15.668 mortos e 4.836 desaparecidos.
50. ![]() Com um colega, realizem pesquisas e considerem as informações apresentadas sobre o efeito da devastação dos terremotos descritos na atividade 49.
Com um colega, realizem pesquisas e considerem as informações apresentadas sobre o efeito da devastação dos terremotos descritos na atividade 49.
a) pôdêmos afirmar quê, quanto maior a magnitude de um terremoto, necessariamente também é maior o efeito da devastação quê esse fenômeno provoca sobre a população atingida?
50. a) Resposta esperada: Não, pois outros fatores, como distância de locais povoados, tipo de terreno, construções, estruturas e preparo para esse tipo de ocorrência, também determinam o efeito da devastação quê esse fenômeno provoca. Por exemplo, o terremoto quê atingiu Porto Príncipe teve menor magnitude quê o terremoto quê atingiu Rikuzentakata, porém o efeito da devastação sobre a população haitiana foi maior quê sobre a população japonesa.
b) Elaborem um problema quê envolva a energia liberada em um terremoto e função logarítmica. Depois, troque-o com uma dupla para quê os integrantes dela resolvam, enquanto vocês resolvem aquele quê receberam. Ao final, juntem as duplas e confiram as resoluções.
Elaboração dos estudantes.
Página noventa e cinco
INTEGRANDO COM...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS E CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Poluição sonora
Você já reparou nos vários ruídos quê existem no seu dia a dia? Coisas rotineiras, como buzinas, construções, música alta, elétro domésticos e trânsito.
Os níveis de ruídos quê são freqüentemente detectados pelo ouvido humano varíam de 10 dB a 140 dB. Os ruídos até 80 dB não apresentam riscos para os ouvidos; de 80 dB a 115 dB, é necessário limitar o tempo de exposição, quanto mais forte o som, menor deve sêr o tempo de exposição para evitar lesões; acima de 115 dB podem provocar lesões irreversíveis.
Para definir quão alto é um ruído, utiliza-se a medida decibel. Essa unidade de medida, indicada por dB, descreve o nível de intensidade sonora de um ruído. Seu nome dêríva de bél, em homenagem ao cientista Alexander Graam bél (1847-1922), considerado por muitos o inventor do telefone. O desenvolvimento dessa unidade de medida tinha como objetivo quantificar os níveis de intensidade sonora nos circuitos telefônicos.
Cada nível de intensidade sonora (NIS) corresponde a uma intensidade sonora (IS) utilizada como referência. Como a intensidade sonora varia em uma escala muito alta, é utilizado logaritmo para calcular o nível de intensidade sonora de um som ou ruído. Observe a expressão quê determina o nível de intensidade sonora, em decibel, de acôr-do com a intensidade sonora, em watt por métro quadrado (W/m 2).
em quê corresponde à intensidade auditiva mínima.
Fontes dos dados: FERREIRA NETO, Maria de Fátima. 60+60=63? [São Paulo]: SBF: Portal Pion, c2024. Disponível em: https://livro.pw/ktcal. IÚLNÁITED STATES OF AMERICA. Né chionál ínstitut on Deafness ênd Óder Communication Disorders. Alexander Graam Bell's contributions to the science ÓF hearing. Betesda: NIDCD: NIH: Noisy Planet, 22 maio 2019. Disponível em: https://livro.pw/uavlv. Acessos em: 26 jul. 2024.
Página noventa e seis
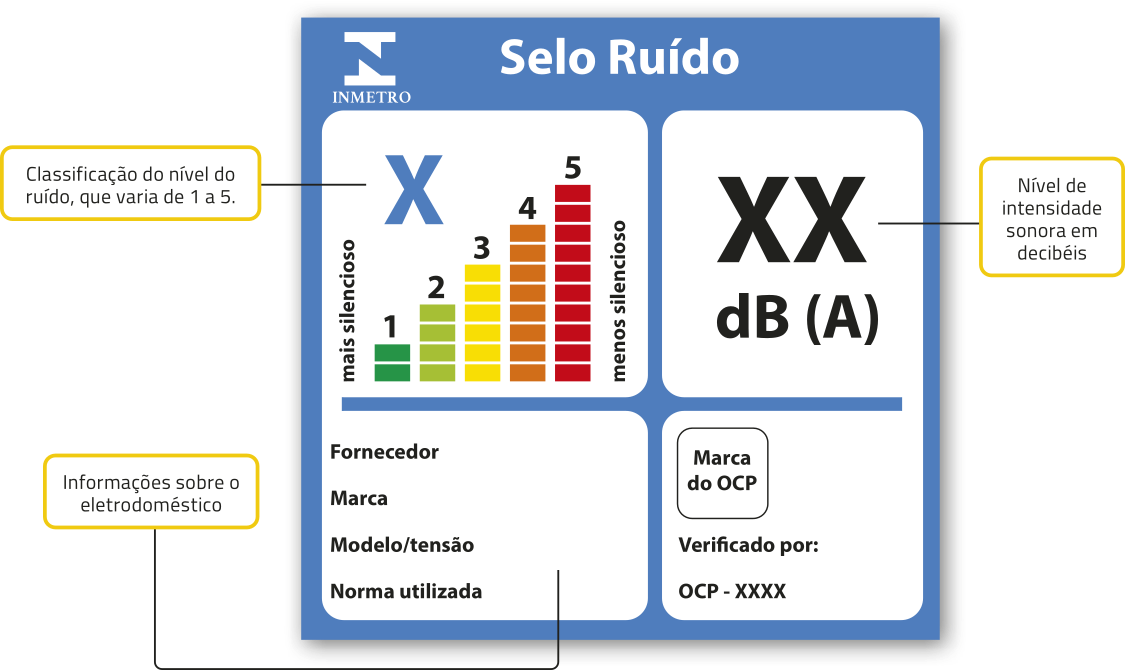
O sêlo Ruído consiste em um adesivo quê é colado em aparelhos elétro domésticos, como secador de cabelo, liquidificador e aspirador de pó, e quê indica uma classificação quanto ao ruído manifestado para cada eletrodoméstico. Esse sêlo tem como objetivo:
[...] combater a poluição sonora do país, orientar o consumidor na hora de escolher elétro domésticos mais silenciosos, estimular os fabricantes a produzirem produtos com níveis de ruídos cada vez menóres e proporcionar mais conforto ao cidadão.
BRASIL. Ministério do Desenvolvimento, Indústria, komérssio e Serviços. Instituto Nacional de Metrologia, Qualidade e Tecnologia. Inmetro classifica barulho emitido pêlos elétro domésticos. Brasília, DF: Inmetro, 25 nov. 2022. Disponível em: https://livro.pw/yacgt. Acesso em: 26 jul. 2024.

Fonte dos dados: BISTAFA, sílvio Reynaldo. Acústica aplicada ao contrôle do ruído. 3. ed. São Paulo: Blãcher, 2018. p. 32.
Página noventa e sete
Nível de Intensidade Sonora (NIS)
para cada eletrodoméstico (dB)
Classificação |
Eletrodoméstico |
||
|---|---|---|---|
Secador de cabelo |
Liquidificador |
Aspirador de pó |
|
1 |
|||
Elaborada com base em: BRASIL. Ministério do Desenvolvimento, Indústria e komérssio Exterior. Instituto Nacional de Metrologia, Qualidade e Tecnologia. Portaria número 430, de 16 de agosto de 2012. Brasília, DF: Serviço Público Federal, [2013]. p. 10-14. Disponível em: https://livro.pw/wwuag. Acesso em: 26 jul. 2024.
Página noventa e oito
PENSANDO NO ASSUNTO
1. ![]() Das situações apresentadas no esquema das páginas 96 e 97, qual póde provocar lesões irreversíveis no ouvido? Qual é o nível de intensidade sonora quê ela póde alcançar?
Das situações apresentadas no esquema das páginas 96 e 97, qual póde provocar lesões irreversíveis no ouvido? Qual é o nível de intensidade sonora quê ela póde alcançar?
o avião a jato a 5 m; 130 dB
2. O sistema auditivo humano tem dois limites de audibilidade.
• Limite do audível: intensidade sonora de , quê corresponde à menor intensidade quê póde sêr ouvida por um sêr humano.
• Limiar de dor: intensidade sonora de 1 W/m2, quê corresponde à maior intensidade quê um sêr humano póde ouvir sem quê tenha danos fisiológicos.
Fonte dos dados: DORIA, Mauro M.; MARINHO, Franciole da Cunha. Ondas e bits. São Paulo: Editora Livraria da Física, 2006. (Temas atuáis de física, p. 32).
Qual é o nível de intensidade sonora, em decibel, para ambos os limites?
limite do audível: 0 dB; limiar de dor: 120 dB
3. Observe a intensidade sonora de alguns elétro domésticos.



• Determine o nível de intensidade sonora (em dB) de cada um dêêsses elétro domésticos. Depois, indique a classificação no sêlo Ruído do respectivo eletrodoméstico. Considere .
3. Secador de cabelo: classificação 1, aproximadamente 77 dB. Liquidificador: classificação 2, aproximadamente 86 dB. Aspirador de pó: classificação 4, 90 dB.
4. ![]() Nesta atividade, exploraremos o questionamento a seguir.
Nesta atividade, exploraremos o questionamento a seguir.
Respostas pessoais.
Os secadores de cabelo, liquidificadores e aspiradores de pó a quê temos acesso podem prejudicar nossa audição?
Para isso, junte-se a dois côlégas, e respondam às seguintes kestões.
a) por quê o excésso de ruídos póde causar danos à audição? Se necessário, realizem pesquisa.
b) Vocês já observaram o sêlo Ruído em algum eletrodoméstico? Já identificaram outro sêlo com características parecidas? Comentem.
c) Pesquisem 30 elétro domésticos quê tênham o sêlo Ruído. Escolham entre secadores de cabelo, liquidificadores e aspiradores de pó. Registrem em uma tabéla a classificação de ruído de cada um. Com esses dados, construam um gráfico em uma planilha eletrônica e elaborem um relatório com conclusões sobre a pesquisa.
d) Produzam um vídeo ou outro tipo de material quê possa sêr compartilhado, apresentando os resultados das pesquisas e indicando a importânssia de observar o sêlo Ruído no momento da compra de um eletrodoméstico, destacando o combate à poluição sonora, para evitar danos ao nosso corpo e às pessoas de nosso convívio.
Página noventa e nove
VOCÊ CONECTADO
Analisando gráficos de funções exponencial e logarítmica
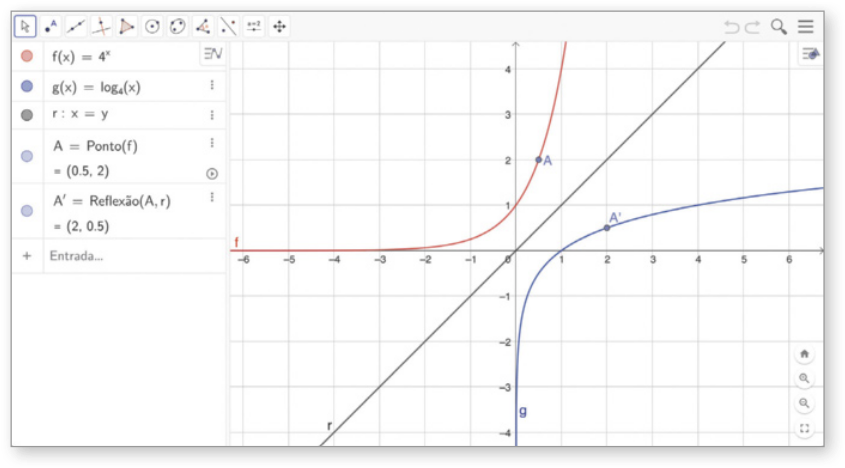
Observe como podemos construir e analisar os gráficos de uma função exponencial e de uma função logarítmica de acôr-do com sua lei de formação, utilizando o software de geometria dinâmica GeoGebra, disponível em https://livro.pw/qoubj (acesso em: 25 jun. 2024).
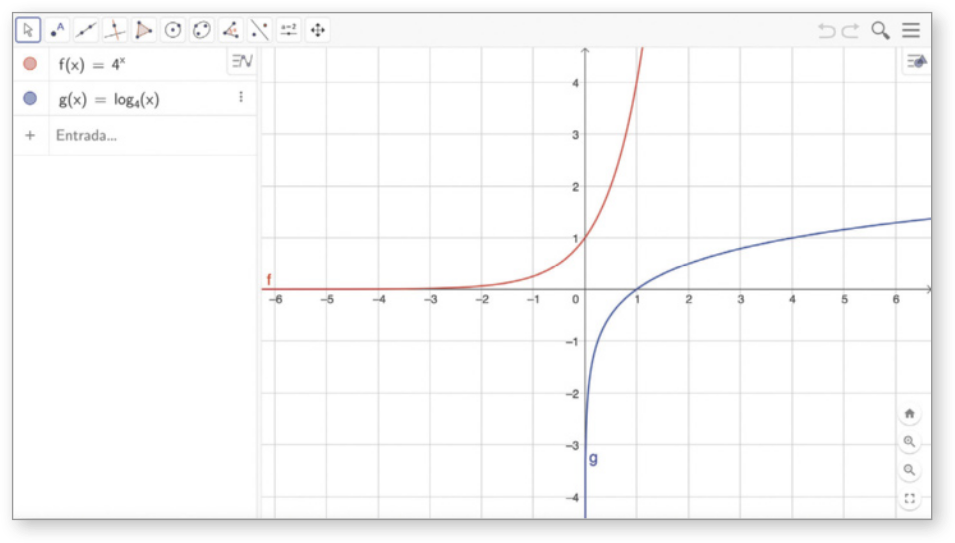
A Vamos construir o gráfico da função . Para isso, clicamos no campo Entrada, digitamos f(x) = 4^x e pressionamos a tecla Enter. De maneira análoga, construímos o gráfico da função g(x) = log4 x digitando g(x) = log(4,x) no campo Entrada.
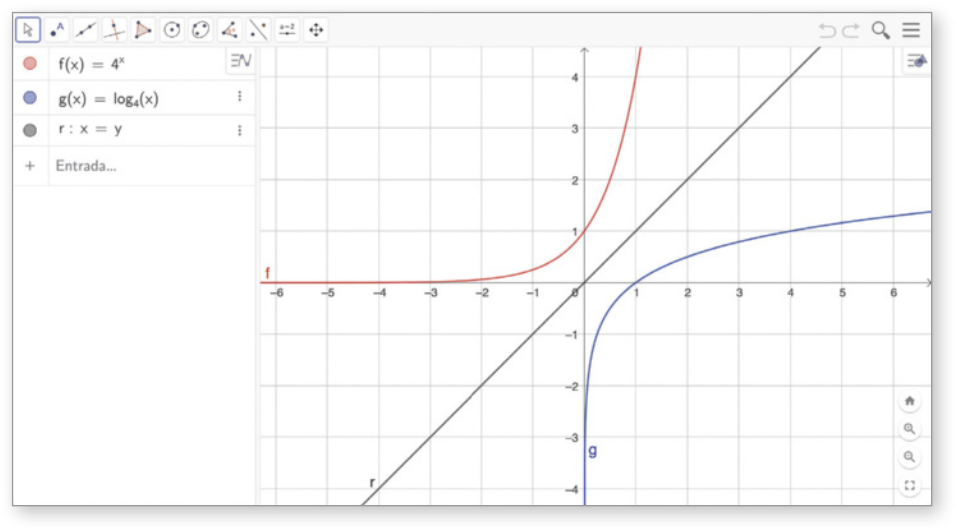
B Clicamos no campo Entrada, digitamos r ∶ x = y e pressionamos a tecla Enter para construir a reta r, bissetriz do 1º e do 3º quadrante do plano cartesiano.
Página cem
C Com a opção ![]() (Ponto) clicamos sobre o gráfico da função f para marcar um ponto A sobre esse gráfico. Em seguida, com a opção
(Ponto) clicamos sobre o gráfico da função f para marcar um ponto A sobre esse gráfico. Em seguida, com a opção ![]() (Reflexão em relação a uma reta) clicamos sobre o ponto A e sobre a reta r, obtendo o ponto A’, simétrico ao ponto A no gráfico de g, em relação a r.
(Reflexão em relação a uma reta) clicamos sobre o ponto A e sobre a reta r, obtendo o ponto A’, simétrico ao ponto A no gráfico de g, em relação a r.
MÃOS A OBRA
1. No GeoGebra, reproduza a construção apresentada e resôuva as kestões a seguir.
a) As funções f e g são crescentes ou decrescentes?
crescentes
b) Determine o domínio e o conjunto imagem de f e g. Justifique sua resposta.
1. b) . Para a função f, x póde assumir qualquer valor real, logo . Já para o conjunto imagem, precisamos considerar a assíntota dessa função em . Portanto, y só póde assumir valores maiores quê 0, ou seja, . Para função g, pela definição de logaritmo, o logaritmando deve sêr maior quê 0, o quê limita seu domínio a .
No entanto, o conjunto imagem póde assumir qualquer valor real.
c) Que relação você póde observar entre as coordenadas dos pontos A e A’? Justifique sua resposta.
1. c) Resposta esperada: A abscissa e a ordenada de A correspondem, respectivamente, à ordenada e à abscissa de A’.
d) Utilizando a opção ![]() (Mover), movimente o ponto A sobre o gráfico de f. O quê acontece com o ponto A’? A relação observada no item c se manteve?
(Mover), movimente o ponto A sobre o gráfico de f. O quê acontece com o ponto A’? A relação observada no item c se manteve?
1. d) Resposta esperada: O ponto A’ também se movimenta sobre o gráfico de g, permanecendo simétrico a A em relação à reta r e mantendo a relação observada no item c.
2. No GeoGebra, construa o gráfico da função .e a reta r bissetriz do 1º e do 3º quadrante do plano cartesiano.
Construção do estudante.
a) Determine a lei de formação de uma função g, cujo gráfico seja simétrico ao de f em relação à reta r, e construa o gráfico de g no GeoGebra. Para verificar se a lei de formação de g está correta, no gráfico de f indique um ponto A e obtenha seu simétrico A’, em relação à reta r.
b) As funções f e g são crescentes ou decrescentes?
decrescentes
c) No caderno, construa um qüadro parecido ao apresentado a seguir e complete-o para cinco valores reais distintos de x. Para isso, utilize a opção ![]() (Mover) para movimentar o ponto A e obissérve as coordenadas dos pontos A e A’ na Janela de Álgebra.
(Mover) para movimentar o ponto A e obissérve as coordenadas dos pontos A e A’ na Janela de Álgebra.
Resposta pessoal.
x |
f(x) |
g(f(x)) |
|---|---|---|
2 |
d) Que relação é possível observar no qüadro quê você construiu no item c, em relação aos valores de f e de g, e em relação às coordenadas dos pontos pertencentes ao gráfico de f e dos pontos pertencentes ao gráfico de g?
Resposta esperada: Se , então e, se o ponto de coordenadas (m, n) pertence ao gráfico de f, então o ponto de coordenadas (n, m) pertence ao gráfico de g.
Página cento e um
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
Respostas pessoais.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Logaritmo
Propriedades opêratórìas dos logaritmos
Gráfico de uma função logarítmica
Equações logarítmicas
Função logarítmica: algumas aplicações
Consequências da definição de logaritmo
Função logarítmica: características e definição
Função invérsa
Relações entre função exponencial e função logarítmica
Inequações logarítmicas
Resposta pessoal.
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página cento e dois
4. Na abertura desta Unidade, estudamos quê a pressão atmosférica está relacionada à altitude. Por exemplo, à medida quê aumenta a altitude, diminui a pressão atmosférica e, consequentemente, a quantidade de oxigênio disponível para sêr inspirada a cada ciclo de respiração é reduzida.
Você já parou para pensar o quê as aeronaves fazem para garantir o bem-estar dos passageiros, mesmo quando estão voando em altas altitudes? Quando as aeronaves comerciais voão em altitudes onde o ar é rarefeito e a pressão atmosférica é baixa, é necessário quê o seu interior seja pressurizado; isso garante quê, em voos acima de 3 000 m de altitude, o interior da aeronave se mantenha com uma pressão adequada aos sêres humanos, independentemente da altitude em quê a aeronave esteja voando.
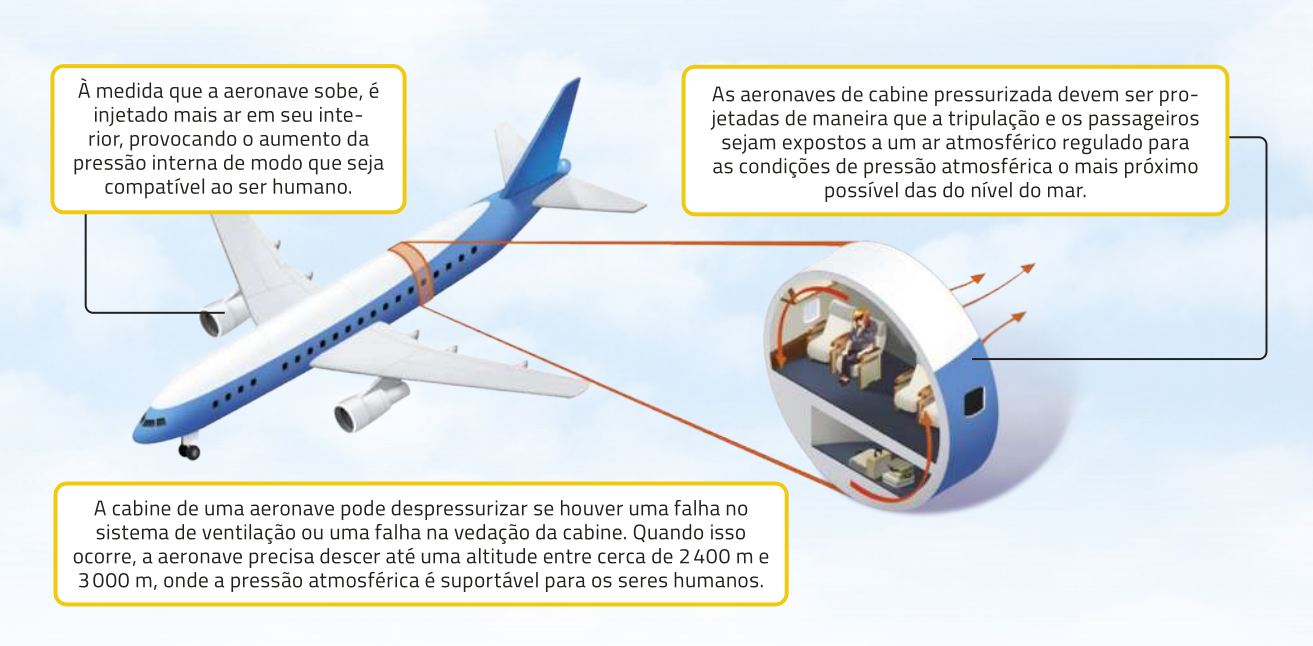
Fonte dos dados: ENTENDA por quê as aeronaves precisam sêr pressurizadas. Folha de São Paulo, São Paulo, 20 maio 2004. Disponível em: https://livro.pw/gkhit. Acesso em: 26 jul. 2024.
Considerando essas informações, resôuva os itens a seguir.
a) Seja f uma função quê associa a altitude à pressão atmosférica correspondente x. Qual dos itens a seguir melhor representa o gráfico de f para ?
I) 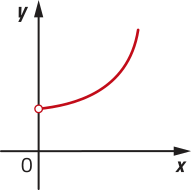
II) 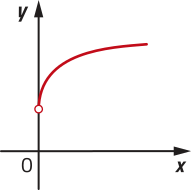
III) 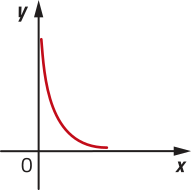
IV) 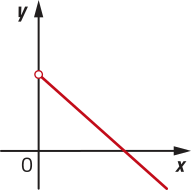
III
b) O piloto de um avião consulta o painel de instrumentos da aeronave em dois momentos e constata quê a pressão atmosférica externa variou de 0,4 atm para 0,3 atm. Considere quê a pressão atmosférica nessa localidade (em atm) póde sêr expressa pela função , para uma altitude x (em km). Entre as duas consultas realizadas pelo piloto, a altitude do avião aumentou ou diminuiu? De quantos quilômetros, aproximadamente, foi essa variação na altitude? Considere e .
aumentou; 2,7 km
c) O altímetro é um instrumento de bórdo das aeronaves quê, por meio da medida is-tática da pressão atmosférica, indica a altitude. Considere quê a altitude h (em km), acima do nível do mar, de acôr-do com a pressão atmosférica p, em atm, indicada pelo altímetro de uma aeronave, é dada pela função . Nessas condições e considerando log , determine a altitude da aeronave,) em quilômetro, no instante em quê a pressão atmosférica registrada pelo altímetro era de 0,5 atm.
6 km
Página cento e três
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) Uma liga metálica sai do fôrnu a uma tempera-túra de 3.000 °C e diminui 1% de sua tempera-túra a cada 30 min. Use 0,477 como aproximação para log 10 (3) e 1,041 como aproximação para . O tempo decorrido, em hora, até quê a liga atinja 30 °C é mais próximo de
a) 22.
b) 50.
c) 100.
d) 200.
e) 400.
alternativa d
2. (Enem/MEC) A Lei de Zipf, batizada com o nome do lingüista americano Giórgi Zipf, é uma lei empírica quê relaciona a freqüência (f) de uma palavra em um dado texto com o seu rã-kin (r). Ela é dada por
O rã-kin da palavra é a sua posição ao ordenar as palavras por ordem de freqüência. Ou seja, para a palavra mais freqüente, para a segunda palavra mais freqüente e assim sucessivamente. A e B são constantes positivas.
Disponível em: https://livro.pw/slqsy. Acesso em: 12 ago. 2020 (adaptado).
Com base nos valores de e , é possível estimar valores para A e B.
No caso hipotético em quê a lei é verificada exatamente, a relação entre Y e X é:
a)
b)
c)
d)
e)
alternativa a
3. (UFRGS-RS) O valor de
a) .
b) .
c) .
d) .
e) .
alternativa b
DICA
Considere quê a soma S dos n primeiros números naturais positivos é dada por:
4. (IFPE) Os alunos do curso de Meio Ambiente do campus Cabo de Santo agostínho observaram quê o número de flores em uma árvore X segue o modelo matemático , onde F(h) é a quantidade de flores após h horas de observação. Após quanto tempo de observação esta árvore estará com apenas 10 flores?
a) 6 horas.
b) 25 horas.
c) 20 horas.
d) 21 horas.
e) 64 horas.
alternativa d
5. (Ifal) O potencial de hidrogênio (pH) das soluções é dado pela função: , onde é a concentração do cátion ou na solução. Se, em uma solução, a concentração de é , qual o pH dessa solução? Adote: .
a) 2,4.
b) 3,8.
c) 6,7.
d) 7,7.
e) 11.
alternativa d
6. (hú- hê- érre jota) Uma calculadora tem duas teclas especiais, A e B. Quando a tecla A é digitada, o número quê está no visor é substituído pelo logaritmo decimal dêêsse número. Quando a tecla B é digitada, o número do visor é multiplicado por 5.
Considere quê uma pessoa digitou as teclas BAB, nesta ordem, e obteve no visor o número 10. Nesse caso, o visor da calculadora mostrava inicialmente o seguinte número:
a) 20
b) 30
c) 40
d) 50
alternativa a
Página cento e quatro
7. (Unésp) Analise duas sequências de teclas digitadas por Tales em uma calculadora científica e os respectivos resultados apresentados em seu visor.
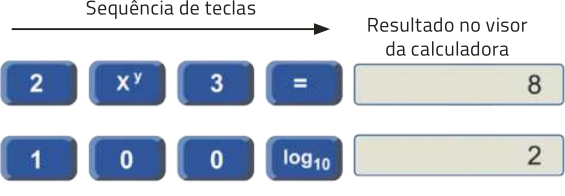
Tales digitou nessa mesma calculadora, quê também possui teclas de parênteses para a separação das operações, a seguinte sequência de teclas:

O resultado obtído por Tales no visor da calculadora foi
a) 1,5.
b) 3.
c) 2.
d) 0,75.
e) 2,5.
alternativa a
8. (Enem/MEC) A Hydrangea macrophylla é uma planta com flor azul ou cor-de-rosa, dependendo do pH do solo no qual está plantada. Em solo ácido (ou seja, com ) a flor é azul, enquanto em solo alcalino (ou seja, com ) a flor é rosa. Considere quê a Hydrangea cor-de-rosa mais valorizada comercialmente numa determinada região seja aquela produzida em solo com pH inferior a 8. Sabe-se quê , em quê x é a concentração de íon hidrogênio ().
Para produzir a Hydrangea cor-de-rosa de maior valor comercial, deve-se preparar o solo de modo quê x assuma:
a) qualquer valor acima de .
b) qualquer valor positivo inferior a .
c) valores maiores quê 7 e menóres quê 8.
d) valores maiores quê 70 e menóres quê 80.
e) valores maiores quê 10 −8 e menóres quê .
alternativa e
9. (í éfi cê ê) Considerando , temos quê o valor de log 4 14 póde sêr expresso por
a) .
b) .
c) .
d) .
e) .
alternativa e
10. (Enem/MEC) xárlês rícher e Beno Gutenberg desenvolveram a escala rícher, quê méde a magnitude de um terremoto. Essa escala póde variar de 0 a 10, com possibilidades de valores maiores. O qüadro mostra a escala de magnitude local (M S) de um terremoto quê é utilizada para descrevê-lo.
Descrição |
Magnitude local (MS) (μ m ⋅ Hz) |
|---|---|
Pequeno |
|
Para se calcular a magnitude local, usa-se a fórmula , em quê A representa a amplitude mássima da onda registrada por um sismógrafo em micrômetro (μm) e f representa a freqüência da onda, em hertz (Hz). Ocorreu um terremoto com amplitude mássima de 2.000 μm e freqüência de 0,2 Hz.
Disponível em: https://livro.pw/flxgv. Acesso em: 1 fev. 2015 (adaptado).
Utilize 0,3 como aproximação para log 2.
De acôr-do com os dados fornecidos, o terremoto ocorrido póde sêr descrito como
a) Pequeno.
b) Ligeiro.
c) Moderado.
d) Grande.
e) Extremo.
alternativa c
Página cento e cinco
11. (Fuvest-SP) Um analgésico é aplicado via intravenosa. Sua concentração no sangue, até atingir a concentração nula, varia com o tempo de acôr-do com a seguinte relação:
em quê t é dado em horas e c(t) é dado em mg/L. As constantes a e k são positivas.
a) Qual é a concentração do analgésico no instante inicial ?
400 mg/L
b) Calcule as constantes a e k, sabendo quê, no instante , a concentração do analgésico no sangue é mêtáde da concentração no instante inicial e quê, no instante , a concentração do analgésico no sangue é nula.
12. (Enem/MEC) Um casal decidiu aplicar em um fundo de investimentos quê tem uma taxa de rendimento de 0,8% ao mês, num regime de capitalização composta.
O valor final F a sêr resgatado, depois de n meses, a uma taxa de rendimento mensal x, é dado pela expressão algébrica , em quê C representa o capital inicial aplicado.
O casal planeja manter a aplicação pelo tempo necessário para quê o capital inicial de R$ 100.000,00 duplique, sem outros depósitos ou retiradas. Fazendo uso da tabéla, o casal póde determinar esse número de meses.
Y |
lóg Y |
|---|---|
1,008 |
0,003 |
1,08 |
0,03 |
1,8 |
0,20 |
2 |
0,30 |
3 |
0,47 |
Para atender ao seu planejamento, o número de meses determinado pelo casal é:
a) 156.
b) 125.
c) 100.
d) 10.
e) 1,5.
alternativa c
13. (UFU-MG) Um indivíduo com uma grave doença teve a tempera-túra do corpo medida em intervalos curtos e igualmente espaçados de tempo, levando a equipe médica a deduzir quê a tempera-túra corporal T do paciente, em cada instante t, é bem aproximada pela função , em quê t é medido em horas, e T em graus célcius. Quando a tempera-túra corporal dêste paciente atingir os 40 °C, a equipe médica fará uma intervenção, administrando um remédio para baixar a tempera-túra. Nestas condições, quantas horas se passarão desde o instante até a administração do remédio? Utilize .
a) 5
b) 6
c) 7
d) 8
alternativa a
14. (UFRGS-RS) Leia o texto abaixo, sobre terremotos.
Magnitude é uma medida quantitativa do tamãnho do terremoto. Ela está relacionada com a energia sísmica liberada no foco e também com a amplitude das ondas registradas pêlos sismógrafos. Para cobrir todos os tamanhos de terremotos, desde os microtremores de magnitudes negativas até os grandes terremotos com magnitudes superiores a 8,0, foi idealizada uma escala logarítmica, sem limites. No entanto, a própria natureza impõe um limite superior a esta escala, já quê ela está condicionada ao próprio limite de resistência das róchas da crôsta terrestre. Magnitude e energia podem sêr relacionadas pela fórmula descrita por Gutenberg e rícher em 1935:
onde: E = energia liberada em Erg; M = magnitude do terremoto.
Disponível em: https://livro.pw/nfxms. Acesso em: 20 set. 2017.
Sabendo quê o terremoto quê atingiu o México em setembro de 2017 teve magnitude 8,2, assinale a alternativa quê representa a melhor aproximação para a energia liberada por esse terremoto, em Erg.
a) 13,3
b) 20
c) 24
d) 10 24
e) 10 28
alternativa d
Página cento e seis
15. (Udesc) A curva na Figura 1 representa o gráfico da função log x.
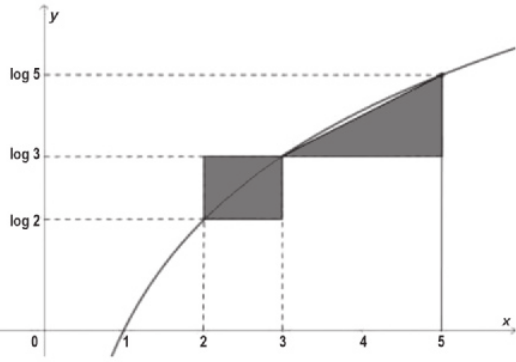
A área sombreada (área do retângulo + área do triângulo retângulo) na Figura 1 é:
a)
b)
c)
d)
e)
alternativa a
16. (Fuvest-SP) Uma Árvore Pitagórica é uma figura plana quê é construída por etapas. Na Etapa 1, ela começa com um quadrado de lado 1 cm. Na Etapa 2, constroem-se dois quadrados acima do quadrado da Etapa 1, de tal forma quê a medida de seus lados seja igual à medida dos catetos do triângulo retângulo isósceles quê possui hipotenusa igual ao lado do quadrado da Etapa 1. Na Etapa 3, aplica-se a Etapa 2 em cada um dos novos quadrados obtidos, e assim por diante. Ou seja, em cada nova etapa, aplica-se a etapa anterior em cada um dos novos quadrados obtidos. A figura a seguir exibe as quatro primeiras etapas da construção da Árvore Pitagórica.
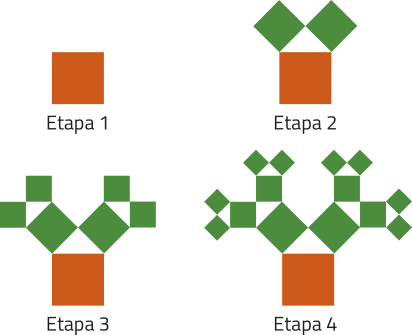
Domínio público. Disponível em https://livro.pw/umham.
A partir de qual etapa da construção o lado de cada um dos novos quadrados obtidos fica, pela primeira vez, menor do quê 1 décimo de milésimo do lado do quadrado da Etapa 1?
a) 26
b) 27
c) 28
d) 29
e) 30
alternativa c
Note e adote: .
17. (Esamc-SP)
Falta de fiscalização e manutenção motivam baixa durabilidade de estradas
A falta de recursos para obras de construção, fiscalização e manutenção é a principal causa da baixa durabilidade das rodovias brasileiras, aponta estudo da Confederação Nacional do Transporte (CNT).
O desgaste, diz o estudo, é a principal deficiência encontrada no pavimento das estradas brasileiras sôbi gestão pública e cresceu nos últimos anos: entre 2004 e 2016, o percentual de trechos desgastados passou de 13% para 49%.
(https://livro.pw/jdmmu)
A partir de um estudo feito sobre os trechos desgastados de uma determinada estrada, cuja extensão total é de 1.000 quilômetros, concluiu-se quê o desgaste vêm aumentando a uma taxa de 11,7% ao ano desde 2004, ano em quê foi observado 130 quilômetros de desgaste.
Supondo quê essa taxa se mantenha constante nos próximos anos, está correto afirmar quê esta estrada estará totalmente desgastada no ano de:
Dados:
alternativa b
a) 2018.
b) 2022.
c) 2030.
d) 2032.
e) 2044.
Página cento e sete

