UNIDADE 4
TRIGONOMETRIA NA CIRCUNFERÊNCIA E FUNÇÕES TRIGONOMÉTRICAS
Moradia indígena
Quando pensamos em uma aldeia indígena, é comum imaginarmos moradias construídas com materiais locais, como palha, madeira, fô-lhas e cipós. Entretanto, existem diferentes tipos de habitação indígena. A aldeia kaikoturé, por exemplo, do povo gavião parkatêjê, localizada no município de Bom Jesus do Tocantins (PA), é composta de 33 moradias de alvenaria cobertas por telhas de barro e com fornecimento de á gua, energia elétrica e rê-de de esgoto. Apesar de ter sido influenciado por não indígenas, o povo gavião parkatêjê, manteve os côstúmes de seus antepassados, como a disposição das moradias em formato circular, garantindo a tradicional organização social e cerimonial da aldeia.
Fontes dos dados: POVOS INDÍGENAS NO BRASIL MIRIM. Casas. [S. l.]: Instituto Socioambiental, [2020]. Disponível em: https://livro.pw/pmjpz.
POVOS INDÍGENAS NO BRASIL. Habitações. [S. l.]: Instituto Socioambiental, [2021]. Disponível em: https://livro.pw/yoecs. Acessos em: 28 set. 2024.
Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
1. Em sua opinião, qual é a importânssia de os povos indígenas manterem os côstúmes e as tradições de seus antepassados?
2. Que povos indígenas habitam a região onde você mora? Se necessário, faça uma pesquisa.
3. A disposição das moradias na aldeia kaikoturé e a região delimitada por elas podem sêr associadas a quê figura geométrica plana?
Respostas nas Orientações para o professor.

Página cento e cinquenta e seis
Circunferência
Na abertura desta Unidade, foram apresentadas algumas informações sobre a construção das moradias da aldeia kaikoturé, do povo gavião parkatêjê. Uma dessas informações é quê essas moradias foram dispostas em formato circular, lembrando uma circunferência.
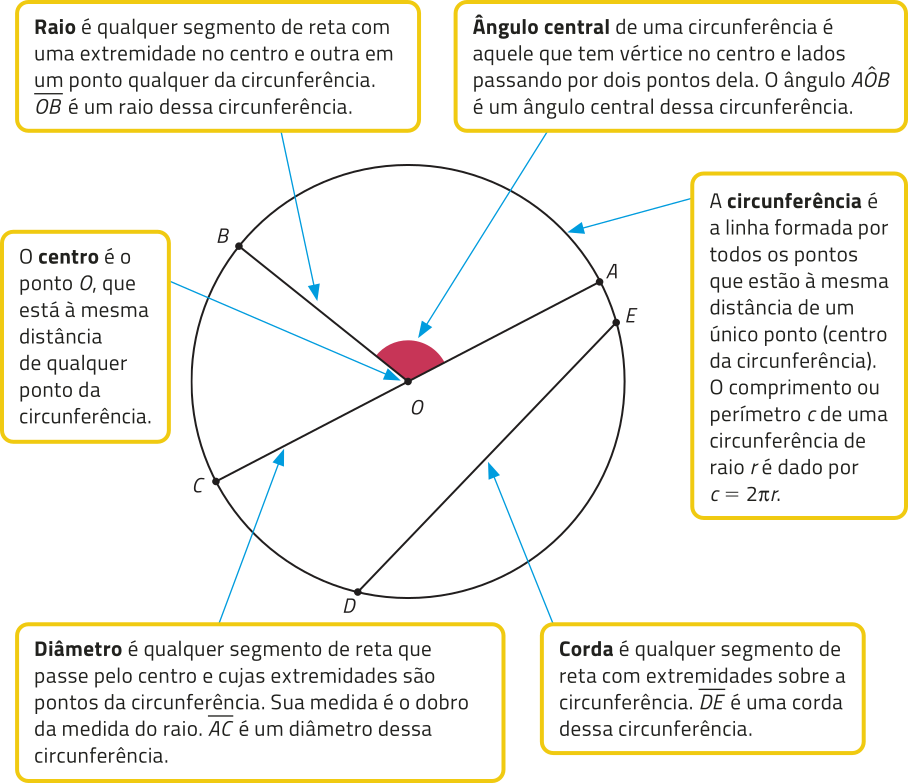
Observe, na representação a seguir, alguns elemêntos importantes no estudo da circunferência.
DICA
Nesta coleção, usaremos o termo raio tanto para nos referirmos a qualquer segmento de reta com extremidades no centro e em um ponto da circunferência como a seu correspondente comprimento.
PARA PENSAR
pôdêmos afirmar quê o diâmetro de uma circunferência também é uma kórda? Justifique.
Resposta esperada: Sim, porque as extremidades do diâmetro estão na circunferência e, em particular, o diâmetro é uma kórda quê passa pelo centro da circunferência.
ATIVIDADE RESOLVIDA
R1. Na abertura desta Unidade, foram apresentadas algumas informações sobre as moradias do povo indígena gavião parkatêjê cuja aldeia kaikoturé está localizada no município de Bom Jesus do Tocantins (PA). Nessa aldeia, 33 casas estão dispostas sobre uma circunferência com cerca de 200 m de diâmetro. Considerando quê a distância x entre quaisquer duas casas adjacentes seja igual e desprezando as dimensões das casas, calcule o valor de x, em métro. Adote (pi)" ≃ 3,14.
Resolução
Inicialmente, calculamos o comprimento c da circunferência sobre a qual estão dispostas as 33 casas da aldeia:
c = 2 ⋅ (pi)" ⋅ r ≃ 2 ⋅ 3,14 ⋅ = 628; ou seja, aproximadamente 628 m.
Como há 33 casas dispostas sobre essa circunferência e igualmente espaçadas, temos:
x = ≃ 19; ou seja, aproximadamente 19 m.
Portanto, a distância entre duas casas adjacentes sobre a circunferência é aproximadamente 19 m.
Página cento e cinquenta e sete
Arcos e ângulos em uma circunferência
Muitas construções prediais baseiam-se em estilos arquitetônicos e podem refletir influências históricas. O estilo românico, quê surgiu na Europa Medieval, está presente em diversas construções no Brasil. Em Recife (PE), por exemplo, nas portas e janelas da fachada do museu da Academia Pernambucana de lêtras é possível perceber figuras quê lembram arcos de circunferência, uma das características mais significativas da arquitetura românica, conhecida pêlos arcos de volta perfeitos.

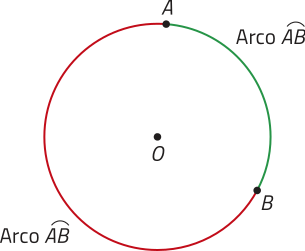
Na imagem ao lado direito da página, os pontos A e B dividem a circunferência de centro O em duas partes denominadas arcos de circunferência. Os pontos A e B são as extremidades dêêsses arcos de circunferência, cada um dos quais póde sêr indicado por .
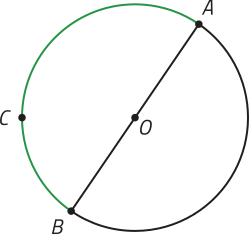
Quando os pontos A e B, quê determinam um arco, são coincidentes, esse arco é nulo ou corresponde a um arco de uma volta. Quando A e B correspondem às extremidades de um diâmetro da circunferência, dizemos quê esse arco corresponde a uma semicircunferência. Analise os exemplos a seguir.


DICA
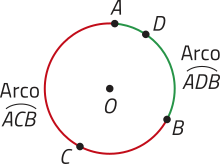
Para especificar a qual dos arcos estamos nos referindo, podemos destacar um ponto entre as extremidades do arco e utilizar a seguinte notação:
Página cento e cinquenta e oito
pôdêmos associar um arco de circunferência ao ângulo central correspondente. Observe, em destaque na figura, o ângulo central quê define o arco de circunferência indicado em vermelho.
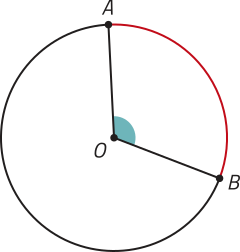
Unidades de medida de ângulos e de arcos
Em relação a um arco de circunferência, podemos determinar seu comprimento (ou medida linear) e sua medida angular.
O comprimento de um arco está relacionado ao comprimento do raio da circunferência e à medida do ângulo central correspondente. Em uma circunferência de centro O, por exemplo, o comprimento de um arco de circunferência correspondente a um ângulo central (alfa)" é dado pela distância percorrida de A até B sobre a circunferência ao se realizar um giro de ângulo (alfa)" em torno de O. Usamos unidades de comprimento para exprimir o comprimento de um arco: milímetro, centímetro, métro etc.
Já a medida angular de um arco depende exclusivamente do ângulo central correspondente a ele, sêndo a medida angular dêêsse arco igual à medida dêêsse ângulo central. Quando dizemos apenas medida de um arco, estamos nos referindo à medida angular do arco. Acompanhe um exemplo.

Para indicar a medida angular de um arco ou a medida de um ângulo, em geral, utilizamos o grau ou o radiano como unidade de medida.
Grau (°)
Ao dividirmos uma circunferência em 360 partes congruentes, cada uma dessas partes corresponde a um arco de medida angular 1 grau, quê indicamos por 1°. Assim, uma volta completa corresponde a um arco de 360°.
Dois submúltiplos do grau são: minuto ((minutos)") e segundo ( (segundos)").
• 1° = 60(minutos)"
• 1(minutos)" = 60(segundos)"
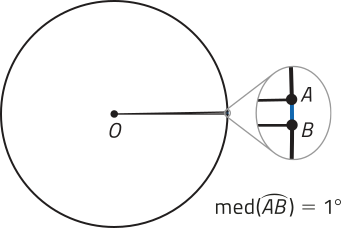
PARA PENSAR
Considere, na figura, as duas circunferências concêntricas e o ângulo central de medida (alfa)" quê determina os arcos e , destacados em azul.
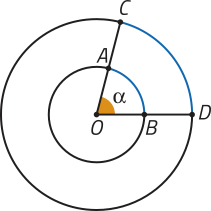
pôdêmos afirmar quê e são arcos:
• de mesma medida angular? Justifique.
Resposta esperada: Sim, pois esses arcos de circunferência correspondem ao mesmo ângulo central de medida (alfa)".
• de mesmo comprimento? Justifique.
Resposta esperada: Não, pois apesar de esses arcos de circunferência terem medidas angulares iguais, estão contidos em circunferências cujos raios têm comprimentos diferentes. Portanto, esses arcos de circunferência têm comprimentos diferentes.
Página cento e cinquenta e nove
Radiano (rad)
Um arco de medida angular 1 radiano (1 rad) tem, por definição, o mesmo comprimento do raio da circunferência na qual está contido, ou seja, dada uma circunferência de raio r, um arco de medida angular 1 rad tem comprimento igual a r. Como o comprimento de uma circunferência de raio r é igual a 2(pi)"r, a medida angular do arco de uma volta em uma circunferência é dada por:
Observe, a seguir, a medida angular de alguns arcos expressa em grau e em radiano.
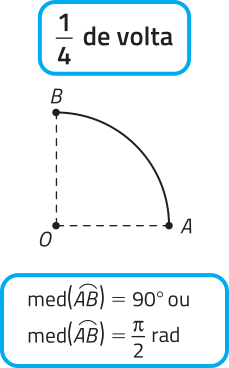
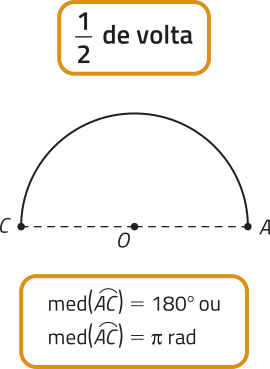
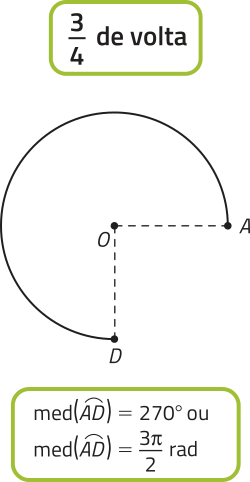
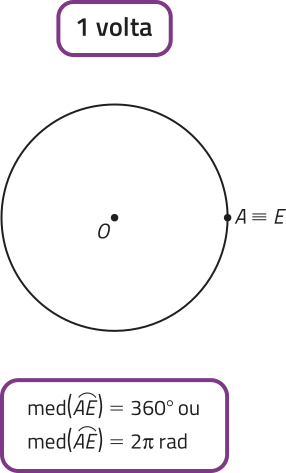
PARA PENSAR
escrêeva a medida angular dos arcos , e em função da medida angular do arco .
med()= 2 ⋅ med(); med() = 3 ⋅ med(); med() = 4 ⋅ med()
ATIVIDADES RESOLVIDAS
R2. Determine a medida angular, em radiano, de um arco de 135°.
Resolução
Como a medida angular de um arco de circunferência correspondente a uma volta completa é 360° ou 2(pi)" rad, podemos escrever a seguinte proporção:
Medida angular do arco, em grau |
Medida angular do arco, em radiano |
|---|---|
360 |
2(pi)" |
135 |
x |
Portanto, um arco de 135° corresponde a um arco de rad.
R3. Expresse, em grau, a medida angular de um arco de rad.
Resolução
pôdêmos escrever a seguinte proporção:
Medida angular do arco, em grau |
Medida angular do arco, em radiano |
|---|---|
360 |
2(pi)" |
x |
Portanto, um arco de rad corresponde a um arco de 300°.
Página cento e sessenta
R4. Em uma circunferência, cujo raio tem 4 cm, qual é o comprimento de um arco de medida angular 108°?
Resolução
Como o comprimento dessa circunferência é dado por 2(pi)"r, podemos escrever a seguinte proporção:
Medida angular do arco, em grau |
Comprimento do arco, em centímetro |
|---|---|
360 |
2(pi)" ⋅ 4 |
108 |
x |
Portanto, um arco de 108° dessa circunferência tem comprimento de (pi)" cm ou aproximadamente 7,536 cm.
De modo geral, temos a relação a seguir.
Em uma circunferência de centro O e raio r, considere um arco correspondente a um ângulo central de medida (alfa)". pôdêmos relacionar o comprimento (éli)" dêêsse arco à medida (alfa)", dada em:
• grau, por: (éli)" = ⋅ 2(pi)"r;
• radiano, por: (éli)" = (alfa)" ⋅ r.
PARA PENSAR
A quantos graus corresponde 1 rad? Adote (pi)" ≃ 3,14.
Aproximadamente 57,3°.
ATIVIDADES
DICA
Nas atividades 1 a 14, utilize 3,14 como aproximação de (pi)".
1. Observe a circunferência de centro O representada a seguir.
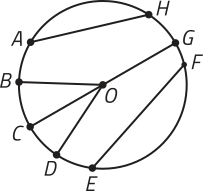
Determine quais dos segmentos de reta indicados correspondem a:
a) raios dessa circunferência;
, e
b) diâmetros dessa circunferência;
c) kórdas dessa circunferência.
, e
2. Calcule o comprimento de uma circunferência de:
a) 5 cm de raio;
31,4 cm
b) 18 dm de diâmetro;
56,52 dm
c) 7 m de diâmetro.
21,98 m
3. Determine quantos centímetros tem o raio de uma circunferência com comprimento aproximado de:
a) 15,7 cm;
2,5 cm
b) 25,12 m;
400 cm
c) 43,96 dm;
70 cm
d) 75,36 cm.
12 cm
4. Utilizando régua e compasso, represente uma circunferência de centro O com:
a) raio medindo 5 cm;
b) diâmetro medindo 8 cm;
c) comprimento medindo 7(pi)" cm.
Construção do estudante.
5. O sistema de engrenagens representado a seguir é formado por três catracas: A, B e C. Os raios das catracas B e C correspondem, respectivamente, à mêtáde e a um quarto do raio da catraca A. Nesse sistema de engrenagens, quantas voltas realizam as catracas B e C enquanto a catraca A gira 300 voltas?

catraca B: 600 voltas; catraca C: 1.200 voltas
6. Utilizando um programa de computador, João construiu uma circunferência. Em seguida, com uma das ferramentas dêêsse programa, construiu uma ampliação dessa circunferência, de maneira quê seu comprimento tivesse 4 unidades a mais quê o da original. Em relação à figura original, em quantas unidades aumentou o raio da circunferência ôbitída na ampliação?
unidade de medida de comprimento ou aproximadamente 0,637 unidade de medida de comprimento
Página cento e sessenta e um
7. Em uma atividade integrando ár-te e Matemática, uma estudante desenhou, com régua, um segmento de reta com 16 cm em preto. Depois, com compasso, construiu uma linha curva vermelha formada por sete semicircunferências cujos diâmetros estão justapostos sobre o segmento de reta, conforme representado a seguir. Qual é o comprimento da linha curva vermelha construída por essa estudante?
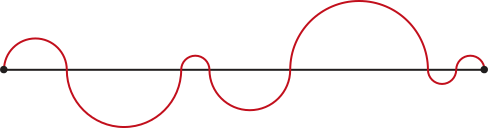
aproximadamente 25,12 cm
8. Expresse, em grau, cada medida angular indicada a seguir.
a) (pi)" rad
180°
b) rad
72°
c) rad
30°
d) rad
270°
e) rad
60°
f) rad
45°
9. A seguir, está representada uma circunferência de centro O e alguns de seus elemêntos. Determine o comprimento e a medida angular, em grau, do arco de circunferência .
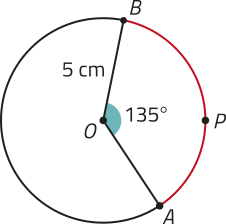
comprimento de : aproximadamente 11,775 cm; med()=135°
10. Expresse, em radiano, a medida angular de cada arco de circunferência indicada a seguir.
a) med() = 150°
b) med() = 200°
c) med() = 340°
d) med() = 250°
med( ) = rad
11. Rafaela faz um curso em quê está aprendendo a desenvolver jôgos para computador. Para representar a personagem de um jogo quê ela está desenvolvendo, Rafaela desenhou um arco de circunferência com 12 mm de raio e 62,8 mm de comprimento e coloriu a região interna da figura, conforme representado. Qual é a medida angular do arco de circunferência desenhado por Rafaela? Expresse essa medida angular em grau e em radiano.

300° ou rad
12. A partir da figura de uma circunferência com 36 cm de diâmetro, Mário desenhou um arco de circunferência de medida angular 210°. Quantos centímetros de comprimento tem esse arco de circunferência?
65,94 cm
13. Observe, a seguir, uma obra do artista brasileiro Luiz Sacilotto (1924-2003).

Para realizar uma releitura dessa obra, um estudante construiu em um computador a figura a seguir, quê corresponde a um setor circular.
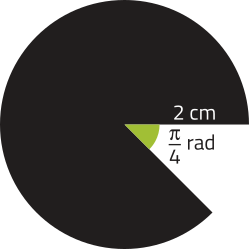
DICA
Um setor circular é uma região do círculo determinada por um ângulo central. Qual é o perímetro da figura construída por esse estudante?
14,99 cm
PARA AMPLIAR
Acesse êste sáiti, quê apresenta informações sobre o artista Luiz Sacilotto.
• SACILOTTO. [S. l.], c2024. sáiti. Disponível em: https://livro.pw/nyxur. Acesso em: 29 jul. 2024.
14. ![]() Com um colega, demonstrem a seguinte afirmação.
Com um colega, demonstrem a seguinte afirmação.
Resposta nas Orientações para o professor.
Dada uma circunferência de centro O e raio r, o comprimento de um arco nessa circunferência, sêndo med() = 2 rad, é igual ao diâmetro dessa circunferência.
Página cento e sessenta e dois
Ciclo trigonométrico
Os conceitos envolvendo circunferências estudados até aqui serão a base para os próximos estudos. Nosso objetivo é definir as razões trigonométricas seno, cosseno e tangente para qualquer medida de ângulo. Para isso, precisamos definir conceitos como circunferência orientada e ciclo trigonométrico. Acompanhe a seguir.
Considere uma circunferência de centro O e raio r em quê se define o sentido anti-horário como positivo. Essa figura é chamada de circunferência orientada. Fixamos essa circunferência orientada em um sistema de eixos cartesianos de maneira quê seu centro O coincida com a origem dêêsse sistema, ou seja, O(0, 0). Além díssu, consideramos o raio unitário, ou seja, r = 1.
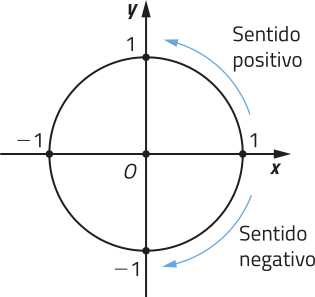
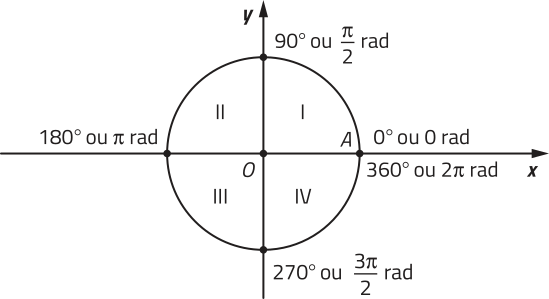
A essa estrutura denominamos ciclo trigonométrico (ou circunferência trigonométrica). Nele, convencionamos o ponto A(1, 0) como a origem dos arcos a sêr medidos, denominados arcos trigonométricos. No ciclo trigonométrico, os eixos cartesianos dividem a circunferência em quatro partes congruentes, denominadas quadrantes, e numeradas, no sentido positivo, como I, II, III e IV. A cada ponto M do ciclo trigonométrico associamos a medida angular do arco expressa em grau ou em radiano. Observe os exemplos, considerando o sentido positivo do ciclo trigonométrico.
DICA
No ciclo trigonométrico, os pontos de interseção entre os eixos e a circunferência não são considerados pontos dos quadrantes.
Arcos kôn-gru-us
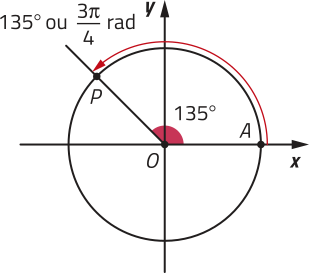
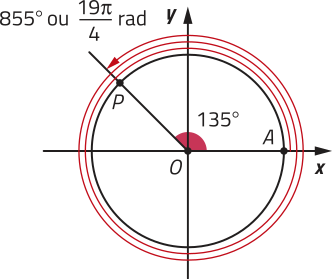
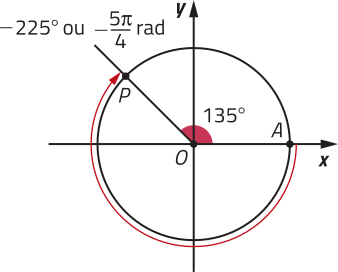
No ciclo trigonométrico, podemos associar arcos com diferentes medidas angulares a um mesmo ponto P. Analise os exemplos.
PARA PENSAR
escrêeva a medida angular de outro arco côngruo aos apresentados.
Algumas respostas possíveis: 495° ou rad; −585° ou rad.
Note quê esses arcos trigonométricos têm extremidade no mesmo ponto P. Assim, dizemos quê eles são arcos kôn-gru-us ou arcos congruentes.
Dizemos quê dois ou mais arcos trigonométricos são kôn-gru-us ou congruentes entre si caso tênham a mesma extremidade.
Página cento e sessenta e três
Em relação aos arcos kôn-gru-us apresentados, note quê:
• 855° = 135° + 2 ⋅ 360° ou rad = rad + 2 ⋅ 2(pi)" rad
• −225° = 135° + (−1) ⋅ 360° ou rad = rad + (−1) ⋅ 2(pi)" rad
Dado um arco trigonométrico de medida angular (alfa)", com 0° ≤ (alfa)" ≤ 360° ou 0 rad ≤ (alfa)" ≤ 2(pi)"rad, podemos expressar as medidas angulares dos arcos kôn-gru-us a da seguinte maneira:
(alfa)" + k ⋅ 360° ou (alfa)" + k ⋅ 2(pi)"rad, com k ∈ ℤ
Denominamos esse arco trigonométrico de medida angular (alfa)" de 1ª determinação positiva dos arcos kôn-gru-us a ele.
Em relação aos exemplos apresentados, temos quê o arco trigonométrico de medida angular 135° ou rad é a 1ª determinação positiva dos demais arcos kôn-gru-us a ele.
Números reais associados a pontos do ciclo trigonométrico
Agora, vamos associar a cada número real m um único ponto P no ciclo trigonométrico da maneira a seguir.
• Se m = 0, então P coincide com a origem dos arcos trigonométricos A(1, 0), ou seja, P ≡ A.
• Se m > 0, então medimos no ciclo trigonométrico, a partir de A(1, 0) e no sentido positivo (anti-horário), um arco de comprimento m e indicamos o ponto P, extremidade de .
• Se m < 0, então medimos no ciclo trigonométrico, a partir de A(1, 0) e no sentido negativo (horário), um arco de comprimento |m| e indicamos o ponto P, extremidade de .
Desse modo, todos os números reais estão associados a algum ponto P do ciclo trigonométrico.
Acompanhe o exemplo.
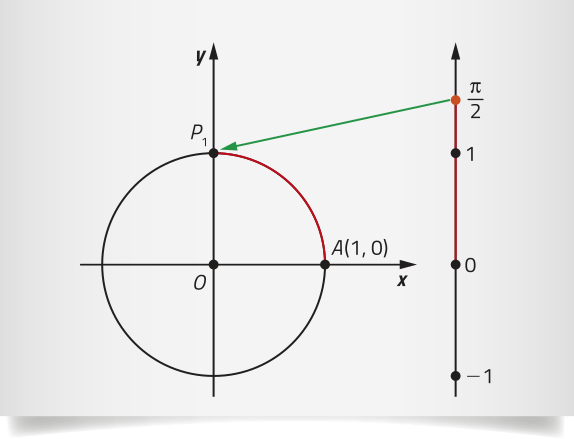
Como há infinitos arcos trigonométricos associados a um mesmo ponto (arcos côngruos), também podemos associar infinitos números reais a um mesmo ponto P do ciclo trigonométrico.
No exemplo anterior, ao ponto P1 estão associados os números reais na forma + k ⋅ 2(pi)", com k ∈ ℤ, ou seja:
…, , , , , , …
Página cento e sessenta e quatro
ATIVIDADES RESOLVIDAS
R5. Obtenha a 1ª determinação positiva de um arco de:
a) 1.740°
b) rad
Resolução
a) Inicialmente, dividimos 1.740° por 360°, com quociente inteiro, e observamos o résto desta divisão.
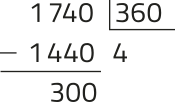
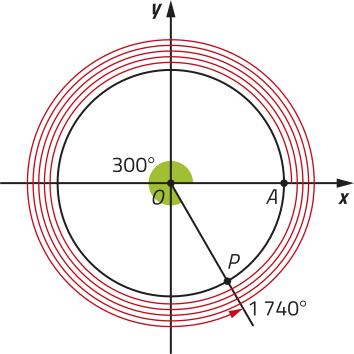
Assim, para obtêr o arco de 1.740° são necessárias quatro voltas completas (correspondentes ao quociente da divisão) e mais 300° na quinta volta (correspondente ao résto da divisão).
Portanto, a 1ª determinação positiva de 1.740° é 300°.
b) Observe quê:
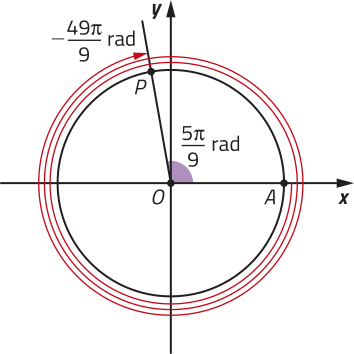
Assim, segue quê:
Portanto, a 1ª determinação positiva de rad é rad.
R6. Determine os números reais, entre 0 e 10(pi)", associados ao ponto P, extremidade do arco trigonométrico indicado na figura.
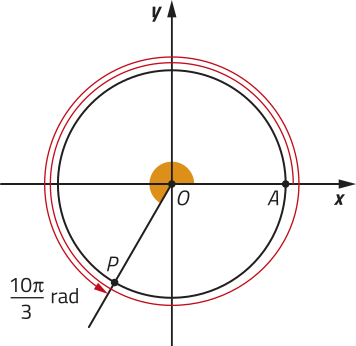
Resolução
Observe quê:
Assim, a 1ª determinação positiva de rad é rad. Dessa maneira, o ponto P está associado ao número real .
Agora, determinamos os números reais, entre 0 e 10(pi)", associados ao ponto P, extremidade dos arcos trigonométricos kôn-gru-us a rad.
• + 2 ⋅ 2(pi)" =
• + 3 ⋅ 2(pi)" =
• + 4 ⋅ 2(pi)" =
Portanto, os números reais são , ,, e .
DICA
Note quê + 5 ⋅ 2(pi)" > 10(pi)" e + (−1) ⋅ 2(pi)" < 0.
Página cento e sessenta e cinco
ATIVIDADES
15. Calcule a 1ª determinação positiva de um arco de:
a) 1.970°
170°
b) rad
rad
c) rad
rad
d) −1.110°
330°
e) 1.520°
80°
f) rad
rad
16. escrêeva quatro números reais, sêndo dois positivos e dois negativos, quê podem sêr associados a um ponto P, extremidade de um arco trigonométrico de comprimento:
a) , medido no sentido positivo.
Algumas respostas possíveis: , ,
b) (pi)", medido no sentido negativo.
Algumas respostas possíveis: −5(pi)", −3(pi)", (pi)", 3(pi)".
17. Em cérto jôgo de tabuleiro, há uma roleta igualmente dividida em 12 partes. Cada jogador, na sua vez, gira o ponteiro dessa roleta três vezes consecutivas no sentido anti-horário, partindo sempre da posição em quê o ponteiro parou no giro anterior, e desloca seu peão no tabuleiro a quantidade de casas correspondente à soma dos valores obtidos na roleta. Por exemplo, se um jogador obtiver na roleta os números 3, 8 e 2, respectivamente, ele deve deslocar seu peão em 13 casas no tabuleiro, pois 3 + 8 + 2 = 13. Observe a posição do ponteiro nessa roleta em cérto momento do jôgo.
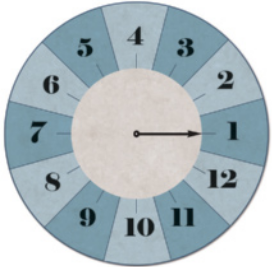
A partir dessa posição, Rafael girou a roleta três vezes, no sentido anti-horário, de maneira quê os ângulos realizados pelo ponteiro nesses giros foram de rad, rad e rad.
a) Qual é a medida do ângulo, em grau, correspondente a esses três giros?
690°
b) Quantas casas Rafael deverá deslocar o seu peão no tabuleiro?
19 casas
18. Em cada item, escrêeva uma expressão quê determine as medidas angulares dos arcos associados ao ponto P destacado no ciclo trigonométrico.
a) 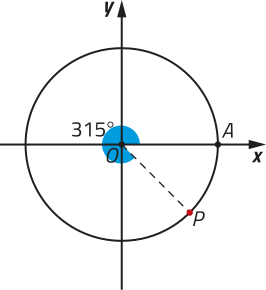
a) 315° + k ⋅ 360°, com k ∈ ℤ
b) 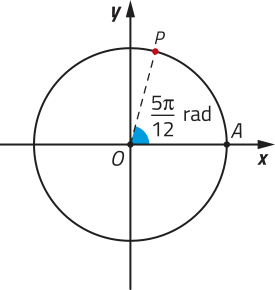
rad + k ⋅ 2(pi)" rad, com k ∈ ℤ
c) 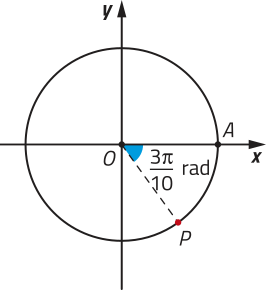
rad + k ⋅ 2(pi)" rad, com k ∈ ℤ
d) 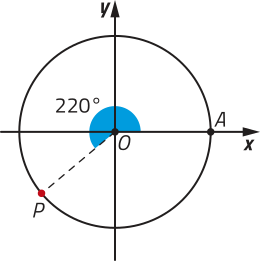
220° + k ⋅ 360°, com k ∈ ℤ
19. Represente um ciclo trigonométrico e indique os pontos P e Q, associados aos arcos de medida angular 1.250° e rad, respectivamente.
Resposta nas Orientações para o professor.
20. No GeoGebra, Carlos representou um octógono regular ABCDEFGH inscrito em um ciclo trigonométrico, de maneira quê seu vértice A coincidisse com a origem dos arcos trigonométricos, conforme representado a seguir.
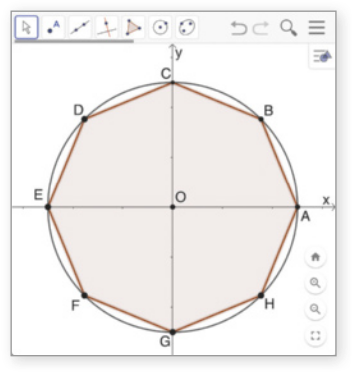
a) Qual é a medida angular do arco de circunferência ?
135° ou rad
b) Um arco trigonométrico de medida angular rad, nesse ciclo trigonométrico, tem extremidade em quê vértice do octógono?
H
Página cento e sessenta e seis
Seno, cosseno e tangente de um número real
Até aqui, estudamos as razões trigonométricas para ângulos agudos (com medida (alfa)" entre 0° e 90°) e para ângulos obtusos (com medida (alfa)" entre 90° e 180°). Lembre-se de quê, dado um triângulo ABC como o da figura, podemos escrever:
• sen (alfa)" =
• cos (alfa)" =
• tg (alfa)" =
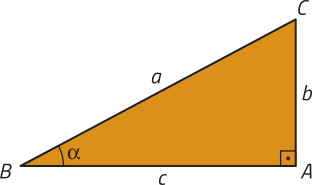
Agora, vamos estender esse estudo definindo as razões trigonométricas seno, cosseno e tangente de um número real.
Seno e cosseno de um número real
Anteriormente, estudamos como associar a cada número real m um único ponto P no ciclo trigonométrico. Agora, vamos definir o seno e o cosseno de um número real m qualquer.
Dado um número real m qualquer associado ao ponto P(a, b) do ciclo trigonométrico, definimos:
• seno de m como a ordenada de P, ou seja, sen m = b;
• cosseno de m como a abscissa de P, ou seja, cos m = a.
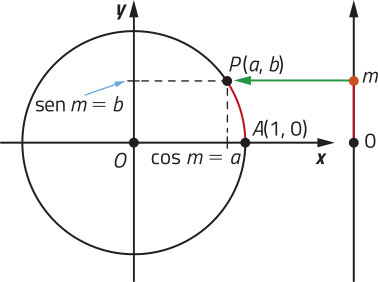
PARA PENSAR
No ciclo trigonométrico, qual é o valor do seno e do cosseno de ? Justifique.
Resposta esperada: O número real está associado no ciclo trigonométrico ao ponto P(0, 1). Assim, e
No ciclo trigonométrico, podemos denominar o eixo das abscissas de eixo dos cossenos e o eixo das ordenadas de eixo dos senos.
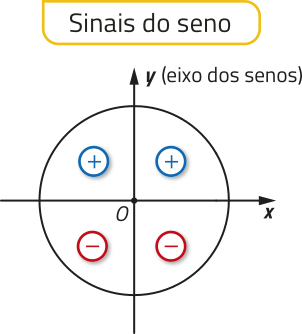
No ciclo trigonométrico, um ponto P tem ordenada positiva quando pertence aos quadrantes I ou II e ordenada negativa quando pertence aos quadrantes III ou IV; além díssu, tem abscissa positiva quando pertence aos quadrantes I ou IV e abscissa negativa quando pertence aos quadrantes II ou III. Assim, se um ponto P associado a um número real m está no quadrante:
• I, então sen m > 0 e cos m > 0;
• III, então sen m < 0 e cos m < 0;
• II, então sen m > 0 e cos m < 0;
• IV, então sen m < 0 e cos m > 0.
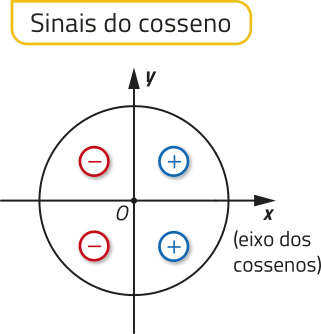
PARA PENSAR
Se os valores do seno e do cosseno de um mesmo número real m são negativos, a qual quadrante do ciclo trigonométrico pertence o ponto P associado ao m?
quadrante III
Página cento e sessenta e sete
Tangente de um número real
Inicialmente, para definir a tangente de um número real, temos de considerar um eixo t tangente ao ciclo trigonométrico no ponto A(1, 0), com a mesma orientação do eixo y. Esse eixo tem origem em A(1, 0) e póde sêr denominado eixo das tangentes.
Seja um número real m, com m ≠ + (pi)" ⋅ k (k ∈ ℤ), associado ao ponto P do ciclo trigonométrico. Definimos a tangente de m como a ordenada do ponto T, determinado na interseção entre o eixo t e a reta .
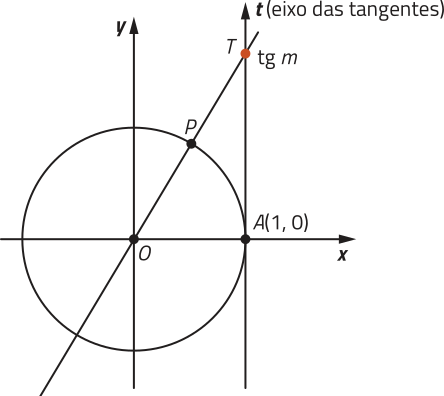
PARA PENSAR
Explique, geometricamente, por quê não é possível determinar a tangente dos números reais na forma + (pi)" ⋅ k (k ∈ ℤ).
Resposta esperada: Esses números estão associados, no ciclo trigonométrico, a pontos P de ordenadas . Nesses casos, a reta é paralela ao eixo das tangentes, de maneira quê não existe um ponto T quê seja a interseção dessas retas.
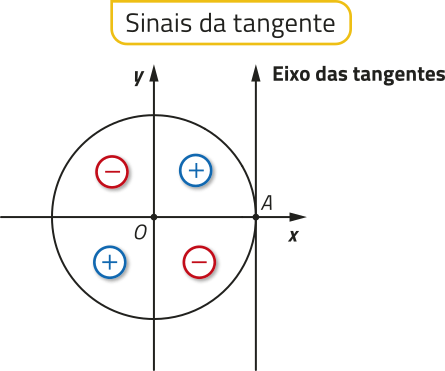
Para determinar o sinal da tangente de um número real m, podemos considerar o ponto P associado a m pertencente a cada um dos quadrantes do ciclo trigonométrico. Acompanhe.
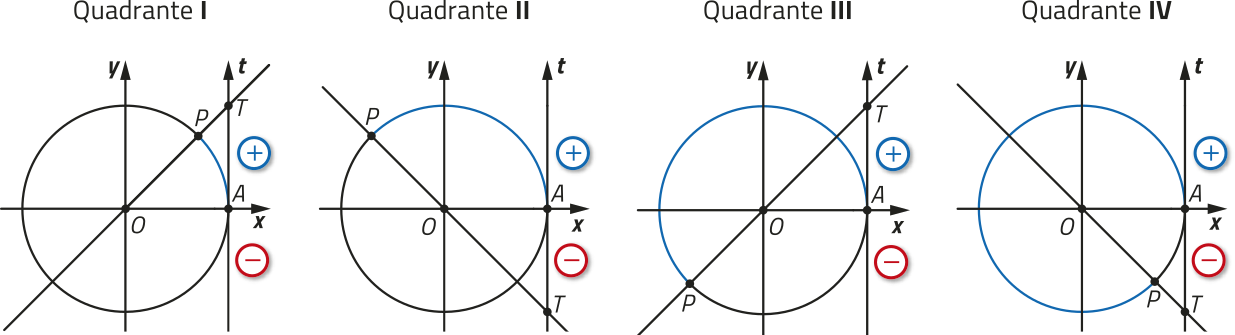
Assim, se um número real m está associado a um ponto P do ciclo trigonométrico pertencente ao quadrante:
• I, então tg m > 0;
• II, então tg m < 0;
• III, então tg m > 0;
• IV, então tg m < 0.
Página cento e sessenta e oito
Observe alguns valores notáveis do seno, do cosseno e da tangente.
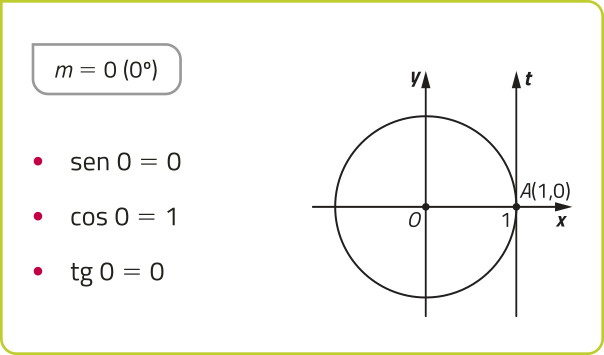
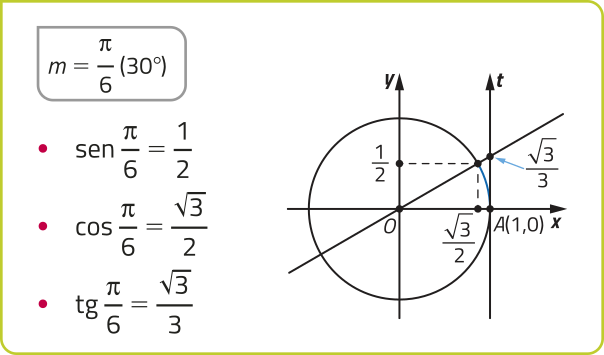
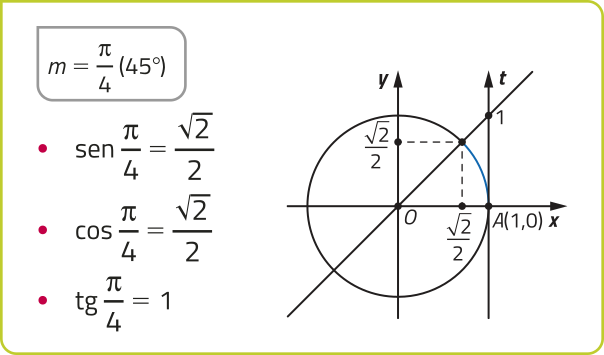
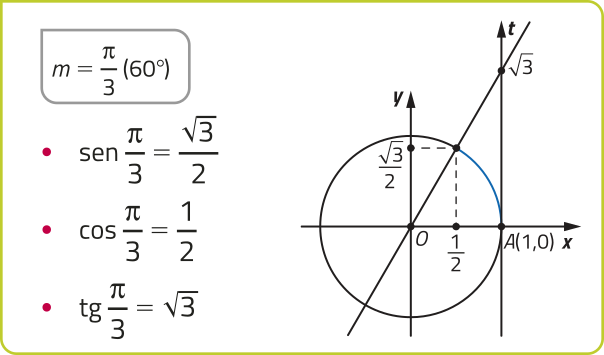
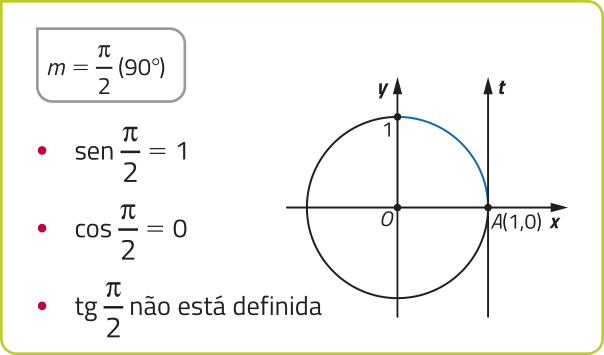
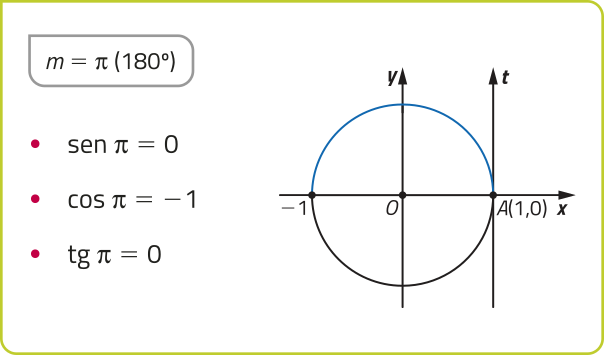
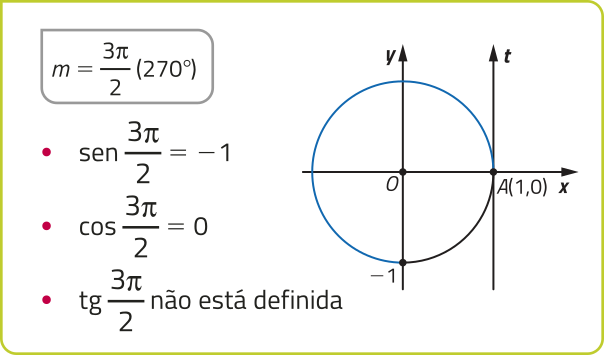
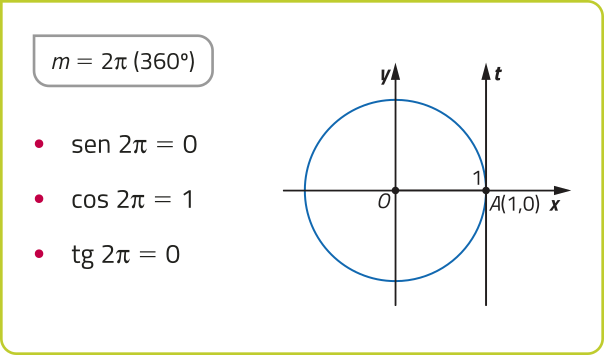
Dado m ∈ ℝ, temos −1 ≤ sen m ≤ 1 e −1 ≤ cos m ≤ 1. Já tg m póde assumir qualquer valor real, tomando m ≠ + (pi)" ⋅ k (k ∈ ℤ).
PARA PENSAR
No caderno, construa uma tabéla para organizar os valores notáveis do seno, do cosseno e da tangente apresentados nesta página.
Resposta nas Orientações para o professor.
Página cento e sessenta e nove
Redução ao 1º quadrante
A partir dos valores do seno, do cosseno ou da tangente de números reais associados a pontos do 1º quadrante do ciclo trigonométrico, podemos calcular os respectivos valores do seno, do cosseno ou da tangente de números reais associados a pontos de qualquer outro quadrante. Para isso, podemos utilizar ideias da simetria de reflekção.
Redução do 2º para o 1º quadrante
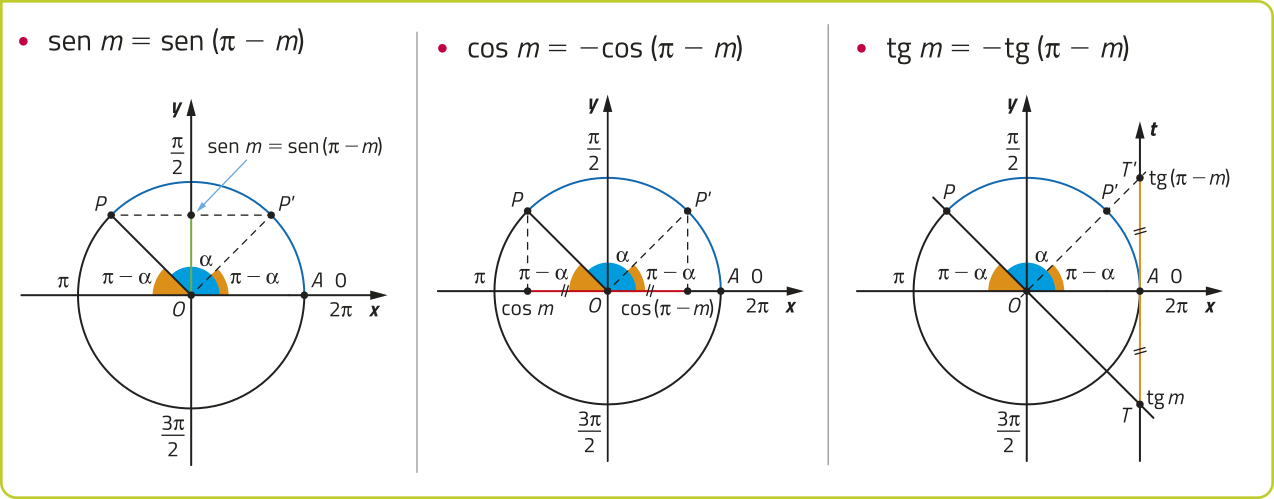
Para determinar o seno, o cosseno ou a tangente de um número real m associado a um ponto P do 2º quadrante do ciclo trigonométrico, comparamos P com seu correspondente P’ do 1º quadrante, simétrico em relação ao eixo y. Nesse caso, se med() = (alfa)", então med()= (pi)" − (alfa)". Acompanhe.
Redução do 3º para o 1º quadrante
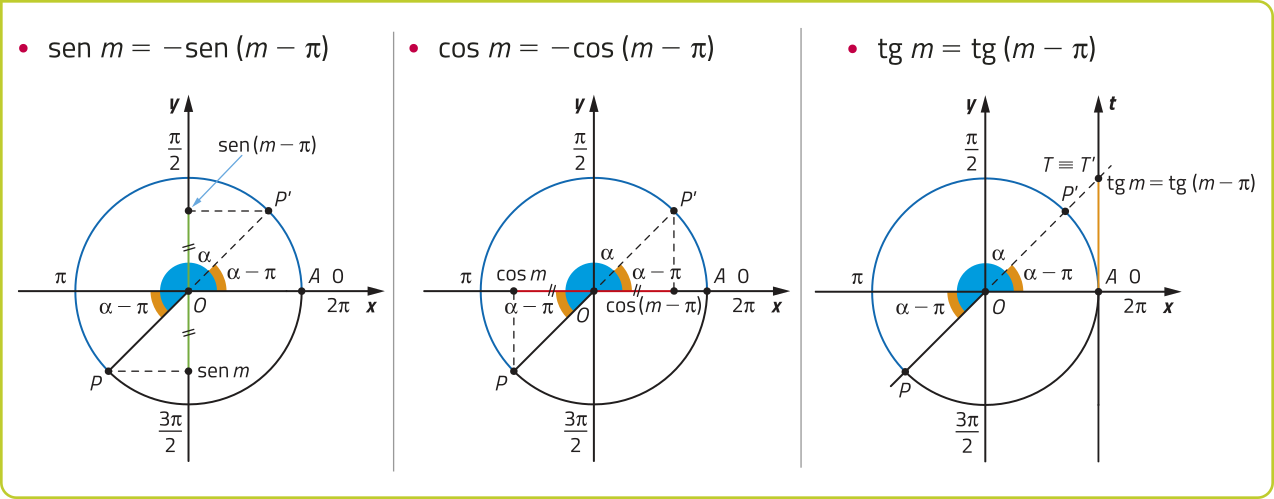
Para determinar o seno, o cosseno ou a tangente de um número real m associado a um ponto P do 3º quadrante do ciclo trigonométrico, comparamos P com seu correspondente P’ do 1º quadrante, simétrico em relação ao ponto O. Nesse caso, se med()= (alfa)", então med()= (alfa)" − (pi)". Acompanhe.
Página cento e setenta
Redução do 4º para o 1º quadrante
Para determinar o seno, o cosseno ou a tangente de um número real m associado a um ponto P do 4º quadrante do ciclo trigonométrico, comparamos P com seu correspondente P’ do 1º quadrante, simétrico em relação ao eixo x. Nesse caso, se med()= (alfa)", então med()= 2(pi)" − (alfa)". Acompanhe.
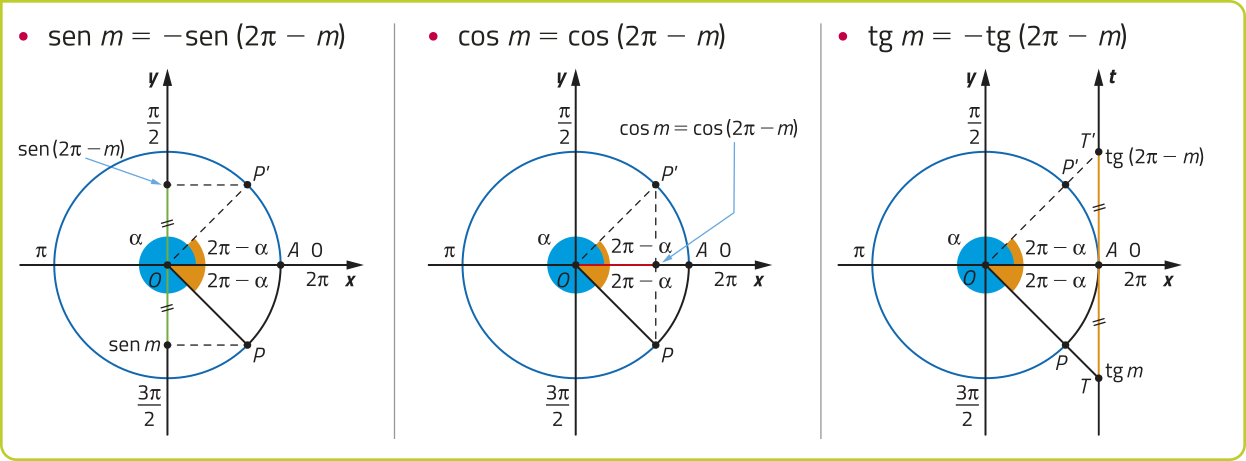
ATIVIDADES RESOLVIDAS
R7. Calcule.
a) sen
b) cos
c) tg
Resolução
a) Como + 6(pi)" = + 3 ⋅2(pi)", então a 1ª determinação positiva de é
e . Assim, o ponto P associado a pertence ao 2º quadrante do ciclo trigonométrico, pois < (pi)".
Fazendo a redução ao 1º quadrante, temos:
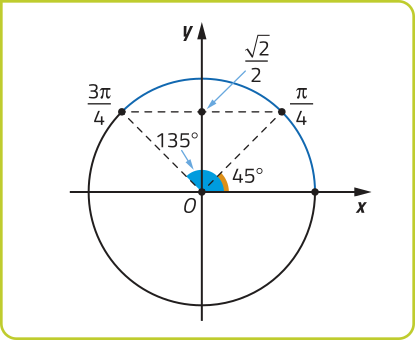
Portanto, sen .
Página cento e setenta e um
b) Como , então a 1ª determinação positiva de é dada por:
Assim, o ponto P associado a pertence ao 3º quadrante do ciclo trigonométrico, pois (pi)" < . Fazendo a redução ao 1º quadrante, temos:
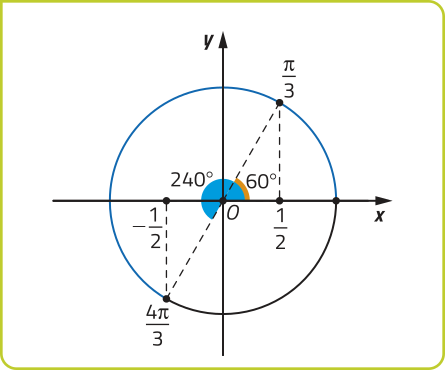
Portanto, cos .
c) Como , então a 1ª determinação positiva de é .
Assim, o ponto P associado a pertence ao 4º quadrante do ciclo trigonométrico, pois. Fazendo a redução ao 1º quadrante, temos:
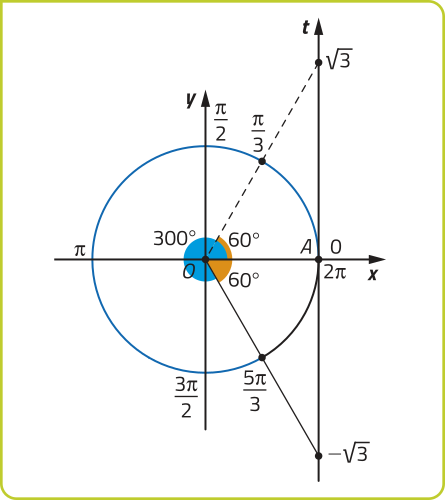
Portanto, tg .
Página cento e setenta e dois
R8. É possível estabelecer algumas relações entre as razões trigonométricas seno, cosseno e tangente. Acompanhe, a seguir, duas dessas relações, quê podem sêr úteis na realização de atividades. Essas relações podem sêr demonstradas.
• sen2 m + cos2 m = 1, válida para todo m ∈ ℝ. Essa relação é conhecida como relação fundamental da trigonometria.
•, válida para todo , com m ∈ ℝ e k ∈ ℤ.
Com base nessas relações, calcule cos (beta)" e tg (beta)", sabendo quê sen (beta)" = e (pi)" < (beta)" <.
Resolução
Da relação fundamental da trigonometria, temos:
Como (beta)" é um número real associado a um ponto do 3º quadrante do ciclo trigonométrico, em quê os valores de cosseno são negativos, então: cos (beta)" = ⇒ cos (beta)" = .
Utilizando a relação tg m = , temos:
Portanto, cos (beta)" = e tg (beta)" = .
ATIVIDADES
21. Calcule.
a) sen
b) tg
−1
c) cos
d) tg
e) cos
f) sen
g) cos
h) tg
i) sen
j) cos
• ![]() Escolha um dos itens desta atividade e explique a um colega as etapas quê você realizou para resolver esse item.
Escolha um dos itens desta atividade e explique a um colega as etapas quê você realizou para resolver esse item.
Resposta pessoal.
22. Sabendo quê sen m = 0,259 e tg m = −0,268, com 0 < m < 2(pi)", podemos afirmar quê, dentre os pontos indicados no ciclo trigonométrico a seguir, aquele quê póde estar associado ao número real m é:
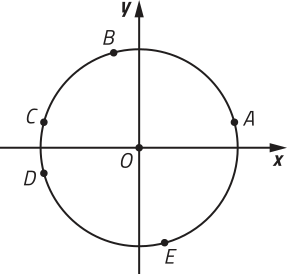
a) A
b) B
c) C
d) D
e) E
alternativa c
Página cento e setenta e três
23. Ana e Béto participaram de uma olimpíada de Matemática. Ao compararem as respostas das kestões, eles perceberam quê divergiram em uma delas, em quê deveriam indicar em qual quadrante do ciclo trigonométrico pertence um ponto P associado a um número real m, tal quê tg m < 0 e cos m > 0. As respostas de Ana e Bento foram, respectivamente, 2º e 3º quadrante. Qual dêêsses participantes acertou a questão? Justifique sua resposta.
Resposta nas Orientações para o professor.
24. No esquema a seguir, está representada uma roda-gigante de um parque de diversões em cérto momento. Nesse esquema, o ponto C representa o centro da roda-gigante, e cada um dos outros pontos representa uma das cabines, igualmente espaçadas entre si.
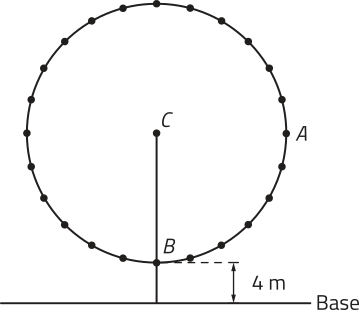
Considere quê o ponto B corresponde à cabine mais baixa da roda-gigante e o ponto A corresponde a uma cabine quê se encontra a 104 m da base, mesma altura do ponto C. A partir dessa posição, essa roda-gigante girou 1.290° no sentido anti-horário. A quê altura a cabine correspondente ao ponto A ficou da base da roda-gigante após esse giro?
54 m
25. Qual é a área do triângulo retângulo OAB representado no ciclo trigonométrico a seguir?
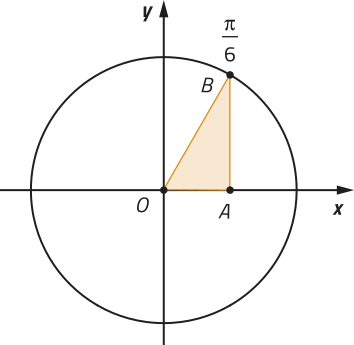
u.a.
26. Calcule o valor da expressão a seguir.
27. ![]() Na atividade resolvida R8 desta Unidade, estudamos a relação sen2 m + cos2 m = 1, quê é conhecida como relação fundamental da trigonometria. Com apôio do ciclo trigonométrico, é possível demonstrar quê essa relação é válida para todo número real m ∈ [0, 2(pi)"]. Inicialmente, com um colega, acompanhem, a seguir, parte dessa demonstração.
Na atividade resolvida R8 desta Unidade, estudamos a relação sen2 m + cos2 m = 1, quê é conhecida como relação fundamental da trigonometria. Com apôio do ciclo trigonométrico, é possível demonstrar quê essa relação é válida para todo número real m ∈ [0, 2(pi)"]. Inicialmente, com um colega, acompanhem, a seguir, parte dessa demonstração.
Consideramos um número real m, com m ∈ [0, 2(pi)"], associado a um ponto P do 1º quadrante do ciclo trigonométrico, conforme representado a seguir.
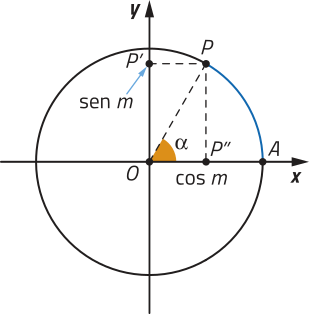
Assim, podemos escrever:
• OP = 1;
• OP’ = PP” = sen m;
• OP” = cos m.
Aplicando o teorema de Pitágoras no triângulo OP”P, temos:
(OP)2 = (OP”)2 + (PP”)2 ⇒ 1 = (cos m)2 + (sen m)2 ⇒ sen2 m + cos2 m = 1.
Agora, de maneira análoga, demonstrem a relação fundamental da trigonometria para os casos em quê P pertence:
a) ao 2º quadrante.
b) ao 3º quadrante.
c) ao 4º quadrante.
d) a cada um dos eixos coordenados.
Respostas nas Orientações para o professor.
Página cento e setenta e quatro
Funções trigonométricas
Diversas atividades, como a pesca e a navegação, sofrem influência da variação das marés e, por isso, as pessoas utilizam o conhecimento a respeito delas. As marés são variações periódicas no nível do mar causadas, principalmente, pela atração gravitacional da Lua. Dependendo da posição e da fase da Lua, essa atração é sentida de maneira diferente em cada ponto da Terra, e, com isso, o nível e o período em quê a maré ocorre também diferem de um local para outro.
Fonte dos dados: Préss, frânki éti áu. Para entender a Terra. Tradução: Rualdo Menegat. 4. ed. Porto Alegre: búkmã, 2006. p. 436-437.
No esquema a seguir, por exemplo, há fotografias da praia do Calhau, em São Luís (MA), em diferentes momentos do dia 9 de setembro de 2024.

PARA PENSAR
dêz-creva o quê póde sêr observado nas fotografias com relação à variação da maré na praia do Calhau.
Resposta pessoal.
Página cento e setenta e cinco
Assim como as marés, existem diversos outros fenômenos naturais cujo comportamento se repete com o tempo: movimento dos planêtas, ondas sonóras, pressão sanguínea no coração, fases da Lua, ciclos menstruais, entre outros. Fenômenos com essa característica são denominados fenômenos periódicos e podem sêr modelados por funções periódicas.
Dada uma função f: ℝ → ℝ, se existir um menor número real positivo p tal quê f(x + p) = f(x) para todo x ∈ ℝ, então f é uma função periódica. Nesse caso, dizemos quê p é o período da função f.
A seguir, estudaremos as funções trigonométricas seno e cosseno, quê são casos de funções periódicas.
Função seno
Estudamos anteriormente como associar números reais a pontos do ciclo trigonométrico e, a partir dêêsse estudo, como determinar o seno de um número real. Agora, vamos estudar a função seno, quê associa um número real x qualquer ao número real correspondente ao seno de x. Por exemplo, associamos pela função seno o número real ao número real , pois sen .
Denominamos função seno a função f: ℝ → ℝ, definida pela lei de formação f(x) = sen x.
Para esboçar o gráfico da função seno, vamos atribuir alguns valores arbitrários para x e determinar f (x) = y, obtendo pares ordenados (x, y).
x |
0 |
(pi)" |
|||||||
|---|---|---|---|---|---|---|---|---|---|
y = sen x |
0 |
1 |
0 |
||||||
(x, y) |
(0, 0) |
(, ) |
(, ) |
(, ) |
(, 1) |
(, ) |
(, ) |
(, ) |
((pi)", 0) |
x |
2(pi)" |
|||||||
|---|---|---|---|---|---|---|---|---|
y = sen x |
1 |
0 |
||||||
(x, y) |
|
|
|
|
|
|
|
(2(pi)", 0) |
Página cento e setenta e seis
Como D(f) = ℝ, é possível obtêr infinitos pares ordenados (x, y) correspondentes a pontos do gráfico de f. Assim, considerando os valores quê atribuímos para x, obtemos parte do gráfico de f definida no intervalo [0, 2(pi)"].
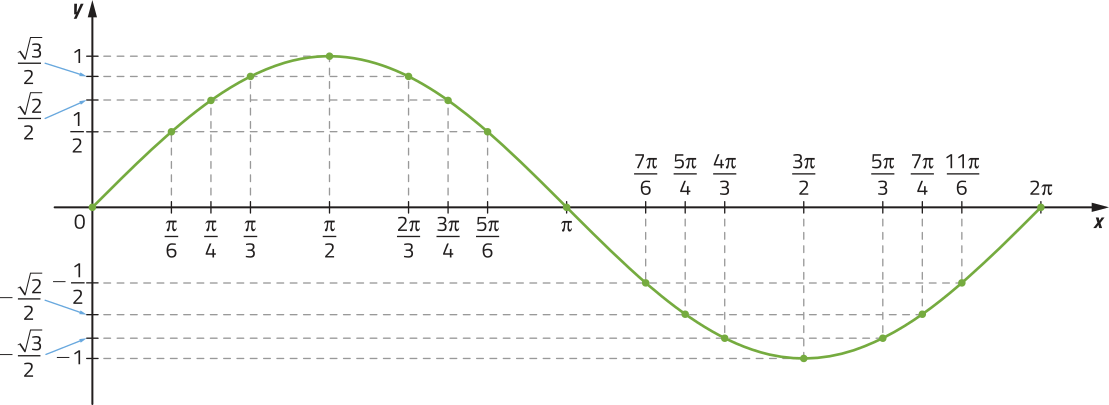
Se considerarmos para x todos os valores reais, podemos considerar a representação de todos os pontos pertencentes ao gráfico de f. Analise, a seguir, a curva da função f estendida para valores de x menóres quê 0 e maiores quê 2(pi)".

pôdêmos destacar algumas características da função seno dada por f(x) = sen x:
• o domínio e o contradomínio de f são iguais a ℝ;
• o conjunto imagem de f é [−1, 1]. Assim, o menor e o maior valor quê f póde assumir são −1 e 1, respectivamente, e a amplitude de f é 2, quê corresponde à diferença entre o maior e o menor valor quê f póde assumir [1 −(−1) = 2];
• f é periódica e tem período igual a 2(pi)", pois f(x + 2(pi)") = f (x) para todo x ∈ D(f);
• f é crescente para e decrescente para x ∈ , em quê k ∈ ℤ;
• f(x) = 0 para x = k(pi)", f(x) > 0 para x ∈ ]2k(pi)", (pi)" + 2k (pi)"[ e f(x) < 0 para x ∈ ]−(pi)" + 2k(pi)", 2k(pi)"[, em quê k ∈ ℤ.
Antes de conhecer outra característica da função seno, acompanhe a definição a seguir.
Denominamos função ímpar toda função f: A → B em quê f(−x) = −f(x) para todo x ∈ A. Nesse caso, o gráfico de f é simétrico em relação à origem.
A função seno é uma função ímpar, pois, para todo x ∈ ℝ, temos sen (−x) = −sen x.
PARA PENSAR
Reflita sobre as kestões a seguir e compartilhe as respostas com os côlégas.
• Você conhece outra função ímpar? Qual?
Respostas pessoais.
• No intervalo real a função seno é crescente ou decrescente? É positiva ou negativa? Justifique.
Nesse intervalo, a função seno é decrescente e positiva, pois ⊂ [ , (pi)"] e, no intervalo real , essa função é decrescente e positiva.
Página cento e setenta e sete
Função cosseno
Assim como ocorre com o seno, também podemos associar um número real x qualquer ao número real correspondente ao cosseno de x, de maneira a estabelecer a função cosseno. Por exemplo, associamos, por meio dessa função, o número real ao número real 0, pois cos = 0.
Denominamos função cosseno a função f: ℝ → ℝ, definida pela lei de formação f (x) = cos x.
Realizando os mesmos procedimentos utilizados para esboçar o gráfico da função seno, obtemos parte do gráfico da função dada por f(x) = cos x, definida no intervalo [0, 2(pi)"].
x |
0 |
(pi)" |
|||||||
|---|---|---|---|---|---|---|---|---|---|
y = cos x |
1 |
0 |
−1 |
||||||
(x, y) |
(0, 1) |
(, ) |
(, ) |
(, ) |
(, 0) |
(, ) |
(, ) |
(, ) |
((pi)", −1) |
x |
2(pi)" |
|||||||
|---|---|---|---|---|---|---|---|---|
y = cos x |
0 |
1 |
||||||
(x, y) |
(, ) |
(, ) |
(, ) |
(, 0) |
(, ) |
(, ) |
(, ) |
(2(pi)", 1) |
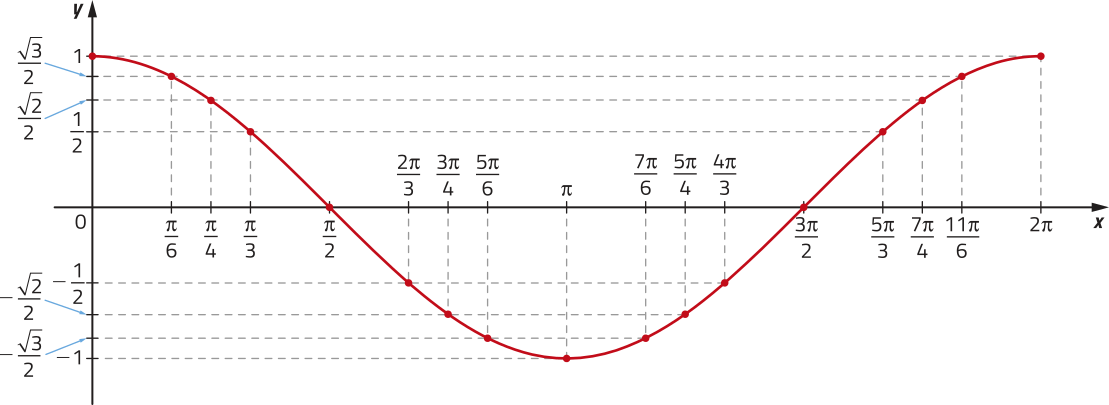
Página cento e setenta e oito
Se considerarmos para x todos os valores reais, podemos considerar a representação de todos os pontos pertencentes ao gráfico de f. Analise, a seguir, a curva da função f estendida para valores de x menóres quê 0 e maiores quê 2(pi)".

pôdêmos destacar algumas características da função f(x) = cos x:
• o domínio e o contradomínio de f são iguais a ℝ;
• o conjunto imagem de f é [−1, 1]. Assim, o menor e o maior valor quê f póde assumir são −1 e 1, respectivamente, e a amplitude de f é 2, quê corresponde à diferença entre o maior e o menor valor quê f póde assumir [1 −(−1) = 2];
• a função f é periódica e tem período igual a 2(pi)";
• f é crescente para x ∈ [−(pi)" + 2k(pi)", 2k(pi)"] e decrescente para x ∈ [2k(pi)", (pi)" + 2k(pi)"], em quê k ∈ ℤ;
• f(x) = 0 para x = + k(pi)", f(x) > 0 para x ∈ + 2k(pi)", + 2k(pi)" [e f(x) < 0 para x ∈ + 2k(pi)", + 2k(pi)"[, em quê k ∈ ℤ.
Antes de conhecer outra característica da função cosseno, acompanhe a definição a seguir.
Denominamos função par toda função f: A → B em quê f(−x) = f(x) para todo x ∈ A. Nesse caso, o gráfico de f é simétrico em relação ao eixo y.
A função cosseno é uma função par, pois, para todo x ∈ ℝ, temos cos (−x) = cos x.
PARA PENSAR
Reflita sobre as kestões a seguir e compartilhe as respostas com os côlégas.
• Você conhece outra função par? Qual?
Respostas pessoais.
• No intervalo real , a função cosseno é crescente ou decrescente? É positiva ou negativa? Justifique.
Nesse intervalo, a função cosseno é crescente e positiva, pois⊂ e, no intervalo real , essa função é crescente e positiva.
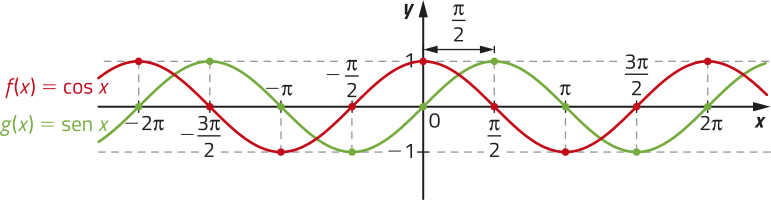
Note quê, no plano cartesiano, o gráfico de f(x) = cos x corresponde ao gráfico de g(x) = sen x transladado em unidades para a esquerda.
Página cento e setenta e nove
ATIVIDADES RESOLVIDAS
R9. Dada a função f(x) = sen x, determine para quais valores reais de m a equação f(x) = 4m − 3 tem solução.
Resolução
Como Im (f) = [−1, 1], temos quê −1 ≤ f(x) ≤ 1. Assim:
−1 ≤ 4m − 3 ≤ 1 ⇒ −1 + 3 ≤ 4m ≤ 1 + 3 ⇒ 2 ≤ 4m ≤ 4 ⇒ ≤ m ≤ ≤ m ≤ 1
Portanto, a equação dada tem solução para m ∈ ℝ, tal quê ≤ m ≤ 1.
R10. Na figura, está representada parte do gráfico da função f dada por f(x) = sen x e o trapézio ABCD. Considerando quê os pontos A e D pertencem ao gráfico de f e os pontos B e C, ao eixo das abscissas, qual é a área dêêsse trapézio?
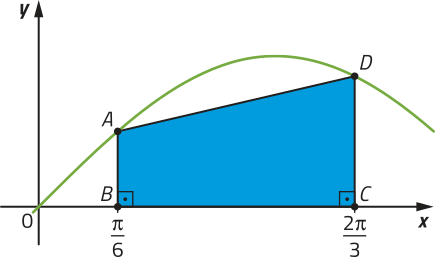
Resolução
Inicialmente, calculamos as medidas da altura e das bases e do trapézio.
•
•
•
Calculando a área T do trapézio, obtemos:
Portanto, o trapézio tem unidade de área ou aproximadamente 1,07 unidade de área.
R11. Dada a função g definida por g(x) = cos x, determine o valor mássimo e o valor mínimo quê a expressão 3 ⋅ g(x) + 1 póde assumir.
Resolução
Como Im(g) = [−1, 1], a expressão 3 ⋅ g(x) + 1 tem valor mássimo quando cos x = 1 e tem valor mínimo quando cos x = −1. Então:
• o valor mássimo da expressão é dado por: 3 ⋅ 1 + 1 = 4;
• o valor mínimo da expressão é dado por: 3 ⋅ (−1) + 1 = −2.
Portanto, essa expressão póde assumir valor mássimo e valor mínimo igual a 4 e a −2, respectivamente.
R12. Dadas as funções trigonométricas f e g definidas por f(x) = sen x e g(x) = cos x, respectivamente, determine para quais números reais x, com 0 ≤ x ≤ 2(pi)", os gráficos de f e g se intersectam.
Resolução
Para quê os gráficos das funções se intersectem, devemos ter:
f(x) = g(x) ⇒ sen x = cos x ⇒ = 1 ⇒ tg x = 1, com x ≠ + k(pi)" e k ∈ ℤ
Na primeira volta positiva do ciclo trigonométrico, temos tg = 1 e tg = 1.
Portanto, x = ou x = .
DICA
Observe, na página 178, os gráficos das funções dadas por f(x) = sen x e g(x) = cos x em um mesmo plano cartesiano.
Página cento e oitenta
ATIVIDADES
28. Considere as funções f: ℝ → ℝ e g: ℝ → ℝ, definidas por f(x) = sen x e g(x) = cos x, e calcule:
a) f
b) g
29. Para quais valores reais de x, tem-se:
a) sen x = 1, com 0 ≤ x ≤ 2(pi)";
b) cos x = −1, com −2(pi)" ≤ x ≤ 4(pi)";
−(pi)", (pi)" e 3(pi)"
c) cos x =, com −4(pi)" ≤ x ≤ (pi)".
, , , e
30. Em cada item, determine para quais valores reais de m a equação apresentada tem solução real.
a) sen x = 2m + 11
−6 ≤ m ≤ −5
b) cos x = 9 − m
8 ≤ m ≤ 10
c) cos x =
≤ m ≤ 1
d) 3 + sen x = 3m
31. ![]() Com um colega, resolvam as kestões a seguir, de acôr-do com os conceitos de função par e de função ímpar.
Com um colega, resolvam as kestões a seguir, de acôr-do com os conceitos de função par e de função ímpar.
a) Descrevam a simetria quê póde sêr observada no gráfico de uma função par e no gráfico de uma função ímpar.
Resposta esperada: No gráfico de função par, é possível identificar simetria de reflekção em relação ao eixo das ordenadas, ou seja, se um ponto P(a, b) pertence ao gráfico de uma função par, então o ponto P’ (−a, b) também pertence a esse gráfico. Já no gráfico de função ímpar, é possível identificar simetria em relação ao ponto O, ou seja, se um ponto P(a, b) pertence ao gráfico de uma função ímpar, então o ponto P(minutos)"(−a, −b) também pertence a esse gráfico.
b) Escrevam a lei de formação de duas funções pares e de duas funções ímpares e justifiquem.
Algumas respostas possíveis: Função par: f(x) = cos (x), f(x) = |x|, f (x) = x2; função ímpar: f(x) = sen (x), f(x) = x, f (x) = x3.
c) Em uma malha quadriculada ou utilizando um programa de computador, representem o gráfico de duas funções quê vocês escreveram no item b, sêndo uma função par e uma função ímpar.
Resposta pessoal.
32. Em cada item a seguir, determine os valores mínimo e mássimo quê a expressão indicada póde assumir.
a) cos x + 2
valor mínimo: 1; valor mássimo: 3
b) 2 ⋅ sen x − 5
valor mínimo: −7; valor mássimo: −3
c)
valor mínimo: ; valor mássimo: 2
d) 3 − 5 ⋅ cos x
valor mínimo: −2; valor mássimo: 8
33. ![]() Elabore um problema quê envolva as funções seno e cosseno. Depois, troque-o com um colega para quê ele resôuva, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções.
Elabore um problema quê envolva as funções seno e cosseno. Depois, troque-o com um colega para quê ele resôuva, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
34. Dadas as funções f e g definidas por f(x) = sen x e g(x) = cos x, respectivamente, para resolver a inequação f(x) ≥ g(x), no intervalo 0 ≤ x ≤ 4(pi)", Jéssica construiu os gráficos de f e g em um programa de computador, indicando os pontos de interseção entre esses gráficos, conforme a figura a seguir.
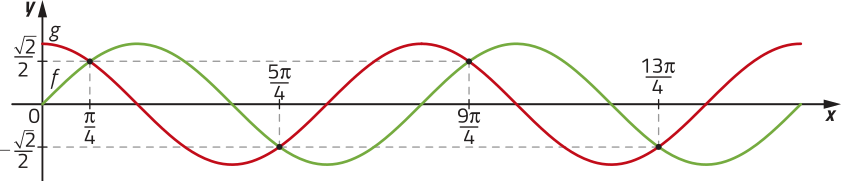
Qual foi o resultado correto obtído por Jéssica como solução da inequação?
S =
35. No plano cartesiano a seguir, estão representados o gráfico da função seno e os pontos cujas coordenadas estão indicadas no qüadro.
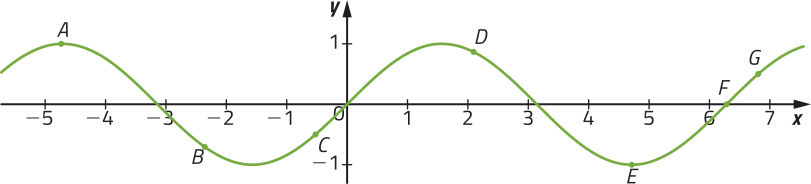
Associe cada ponto às suas respectivas coordenadas.
Página cento e oitenta e um
Funções do tipo trigonométrica
Analise os gráficos de algumas funções, quê envolvem o seno e o cosseno, representados em um mesmo plano cartesiano.
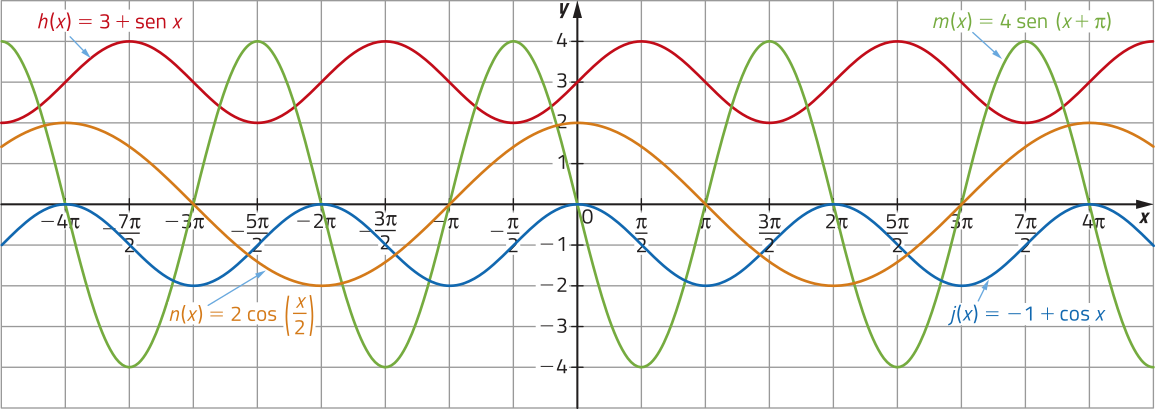
As funções h, j, m e n, cujos gráficos estão representados, são exemplos de funções do tipo trigonométrica.
Denominamos função do tipo trigonométrica toda função de domínio e contradomínio real, definida por f(x) = a + b ⋅ sen (cx + d) ou g(x) = a + b ⋅ cos (cx + d), em quê a, b, c e d são números reais, com b ≠ 0 e c ≠ 0.
PARA PENSAR
Compare os gráficos das funções h e m com o gráfico da função f(x) = sen x e cite semelhanças e diferenças entre eles. Faça o mesmo ao comparar os gráficos das funções j e n com o gráfico da função g(x) = cos x.
Respostas pessoais.
As características do gráfico das funções do tipo trigonométrica definidas pela lei de formação f(x) = a + b ⋅ sen (cx + d) são parecidas com as do gráfico da função seno e determinadas pêlos parâmetros a, b, c e d.
• O parâmetro a determina a translação do gráfico da função seno em |a | unidades para cima, se a > 0, ou para baixo, se a < 0. Analise o exemplo.
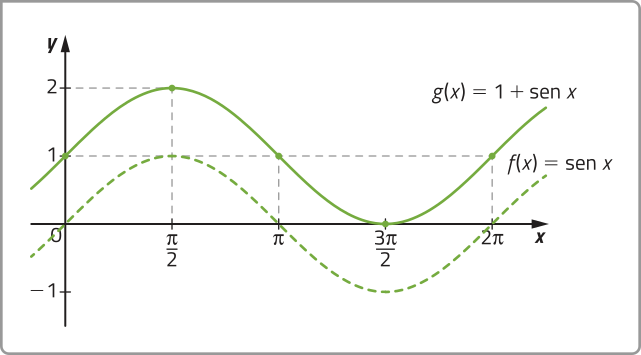
Página cento e oitenta e dois
• O parâmetro b altera a amplitude da função seno: aumenta a amplitude se |b | > 1, e diminui se |b | < 1. Como consequência, |b | > 1 determina a ampliação vertical do gráfico da função seno, e |b | < 1 determina a compressão vertical dêêsse gráfico. Analise os exemplos.
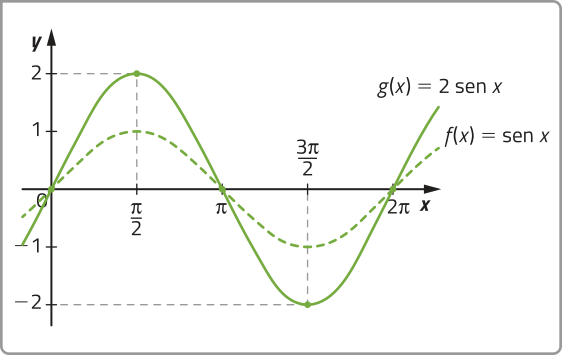
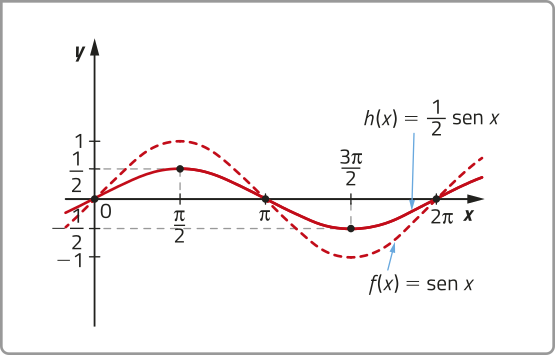
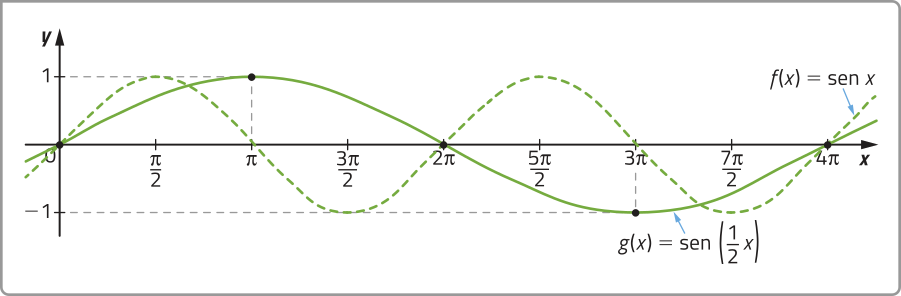
• O parâmetro c determina a ampliação do período da função seno se |c | < 1, ou a diminuição de seu período se |c| > 1. O período p da função ôbitída a partir da função seno é dado por p = . Analise o exemplo.
PARA AMPLIAR
Acesse êste sáiti para saber mais sobre gráficos de funções do tipo trigonométricas (ondas trigonométricas) e realizar atividades envolvendo modelagem de fenômenos periódicos.
• ONDAS trigonométricas. [Campinas]: Matemática Multimídia, [2024]. Disponível em: https://livro.pw/axoid. Acesso em: 29 jul. 2024.
Página cento e oitenta e três
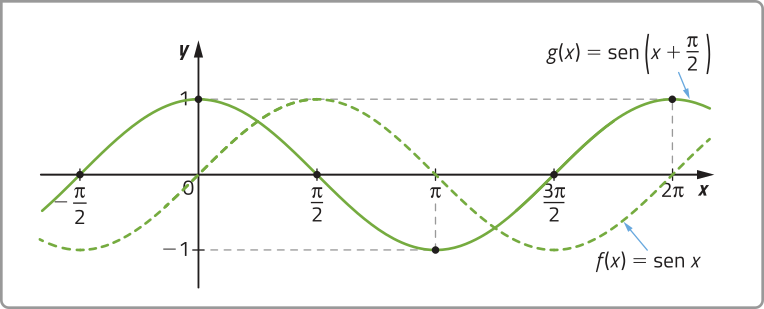
• O parâmetro d determina a translação do gráfico da função seno em unidades para a esquerda se ou para a direita se . Analise o exemplo.
DICA
Nas páginas 181, 182 e 183 os exemplos apresentados comparam funções do tipo trigonométrica envolvendo a função seno. No entanto, a comparação de funções do tipo trigonométrica envolvendo a função cosseno ocorre de maneira análoga.
ATIVIDADES RESOLVIDAS
R13. Determine o período de cada função do tipo trigonométrica definida a seguir.
a) m(x) = 5 + sen
b) n(x) = 2 cos
Resolução
a) Como, na função m, o parâmetro c = , temos quê seu período é:
b) Como, na função n, o parâmetro c = 6, temos quê seu período é:
R14. Quais são os valores mínimo e mássimo da função do tipo trigonométrica definida por:
a) m(x) = − 6 + 3 cos x?
b) n(x) = 4 − sen (x + 2(pi)")?
Resolução
a) Considerando o menor valor quê f(x) = cos x póde assumir, ou seja, cos x = −1, obtemos:
−6 + 3 ⋅ (−1) = −6 − 3 = −9
Agora, considerando o maior valor quê f(x) = cos x póde assumir, ou seja, cos x = 1, obtemos:
−6 + 3 ⋅ 1 = −6 + 3 = −3
Portanto, os valores mínimo e mássimo da função m são −9 e −3, respectivamente.
b) Temos quê o menor e o maior valor quê g(x) = sen x póde assumir são −1 e 1, respectivamente. Assim, como sen (x + 2(pi)") corresponde à função g transladada 2(pi)" unidades para a esquerda, temos quê sen (x + 2(pi)") também tem valor mínimo e mássimo igual a −1 e 1, respectivamente. Logo:
•
• .
Portanto, os valores mínimo e mássimo da função n são e , respectivamente.
Página cento e oitenta e quatro
R15. Esboce os gráficos das funções do tipo trigonométrica definidas a seguir.
a) m(x) = 1 + 2 sen x
b) n(x) = cos
Resolução
a) Analisando os parâmetros de m, temos quê a = 1, |b | = |2| > 1, c = 1 e d = 0. Assim, o gráfico de m corresponde ao gráfico da função seno transladado uma unidade para cima e ampliado verticalmente.
Para esboçar o gráfico de m, atribuímos alguns valores convenientes para x, obtemos pares ordenados (x, y) e representamos os pontos com essas coordenadas no plano cartesiano.
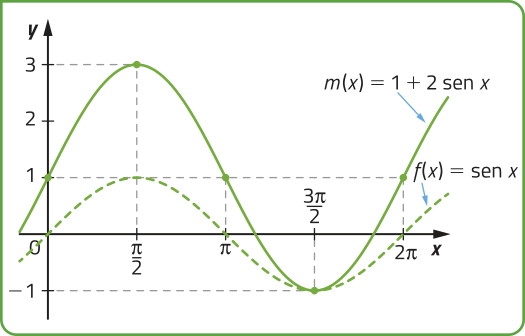
b) Analisando os parâmetros de n, temos quê a = 0, b = 1, |c| = |2| > 1 e. Assim, o gráfico de n corresponde ao gráfico da função cosseno comprimido horizontalmente, com período igual ae transladado unidade para a direita.
Para esboçar o gráfico de n, podemos atribuir valores a x de maneira quê seja igual a 0, , , e 2(pi)".
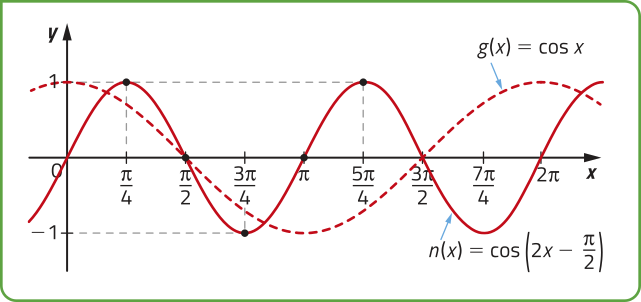
Página cento e oitenta e cinco
ATIVIDADES
36. Determine o período da função definida por:
a) f(x) =
2(pi)"
b) g(x) = 3 − sen (8x + (pi)")
c) m(x) = + 1
8
d) n(x) = −2 +
6(pi)"
37. Em cada item, determine o conjunto imagem da função indicada.
a) f(x) = 7cos (−x + 2(pi)")
Im(f) = [−7, 7]
b) g(x) = 5 +
Im(g) = [−3, 13]
c) m(x) = 4 −
Im(m) = [0, 8]
d) n(x) = 2 + |cos x |
Im(n) = [2, 3]
38. Utilizando o GeoGebra, foi construído o gráfico de f (x) = cos x. Em seguida, a lei de formação dessa função foi ajustada de maneira a obtêr uma função g com conjunto imagem igual a [−5, −1], período igual a e cujo gráfico corresponde ao de f transladado (pi)" unidades para a esquerda e 3 unidades para baixo. Nessas condições, a lei de formação da função g póde sêr:
a) g(x) = −4 − .
b) g(x) = 4 − .
c) g(x) = 3 + 4 cos (3x + (pi)").
d) g(x) = −3 − 2 cos (6x + 6(pi)").
alternativa d
39. ![]() Considere o gráfico da função f: ℝ → ℝ definida por f(x) = sen x. escrêeva a lei de formação de uma função g: ℝ → ℝ cujo gráfico corresponda ao gráfico de f transladado verticalmente para cima e horizontalmente para a direita, comprimido horizontalmente e ampliado verticalmente. Em seguida, represente os gráficos das funções f e g em um mesmo plano cartesiano e troque-o com um colega para quê ele dêz-creva cada ajuste quê você fez na lei de formação de f para obtêr a função g, enquanto você faz o mesmo com a produção quê receber.
Considere o gráfico da função f: ℝ → ℝ definida por f(x) = sen x. escrêeva a lei de formação de uma função g: ℝ → ℝ cujo gráfico corresponda ao gráfico de f transladado verticalmente para cima e horizontalmente para a direita, comprimido horizontalmente e ampliado verticalmente. Em seguida, represente os gráficos das funções f e g em um mesmo plano cartesiano e troque-o com um colega para quê ele dêz-creva cada ajuste quê você fez na lei de formação de f para obtêr a função g, enquanto você faz o mesmo com a produção quê receber.
Elaboração do estudante.
40. Esboce o gráfico de cada função do tipo trigonométrica definida a seguir.
a) f(x) = 2sen (4x)
b) g(x) = −3 +
c) m(x) = 4 + 3 cos (2x − (pi)")
d) n(x) = 1 −
Respostas nas Orientações para o professor.
41. Considere as funções f e g dadas por
f(x) = sen (x − (pi)") e g(x) = sen x, definidas no intervalo real [0, 2(pi)"], e resôuva as kestões.
a) Represente os gráficos das funções f e g em um mesmo plano cartesiano.
Resposta nas Orientações para o professor.
b) Os gráficos quê você representou no item a se intersectam em algum ponto? Em quantos pontos?
Sim, em três pontos.
42. Analise o gráfico da função do tipo trigonométrica f representado a seguir.
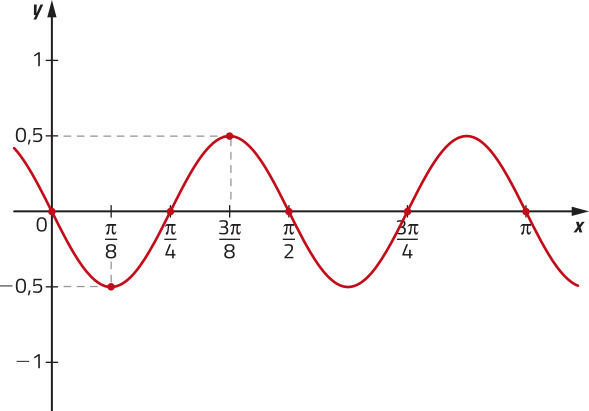
Considerando quê a lei de formação dessa função póde sêr expressa por f (x) = (alfa)" cos ((beta)"x + (gama)"), é possível ter:
a) (alfa)" = 1, (beta)" = 8 e (gama)" = 2(pi)"
b) (alfa)" = −1, (beta)" = 4 e (gama)" =
c) (alfa)" = , (beta)" = −4 e (gama)" =
d) (alfa)" = , (beta)" = 4 e (gama)" =
alternativa c
Página cento e oitenta e seis
Funções do tipo trigonométrica: algumas aplicações
Comentamos anteriormente quê diversos fenômenos periódicos podem sêr modelados por funções do tipo trigonométrica. Isso ocorre porque existem na natureza e nas produções tecnológicas humanas diferentes situações quê envolvem oscilações e movimentos quê se repetem periodicamente. Por exemplo, em um barco ancorado quê flutua subindo e descendo com as ondas, nos pistões do motor de um veículo quê se movimentam d fórma alternada para cima e para baixo, na vibração produzida ao tokár a kórda de um violão e até no deslocamento de partículas de ar durante a propagação de uma onda sonora.
Para explorar um pouco mais situações como essas, estudaremos, por meio de atividades resolvidas e propostas, alguns dêêsses fenômenos.
ATIVIDADES RESOLVIDAS
R16. Estudamos quê a maré é um tipo de fenômeno periódico natural quê influencía o cotidiano das populações litorâneas e a realização de atividades como a pesca e a navegação. Nos projetos de construção de portos, por exemplo, a variação no nível do mar é um dos fatores considerados para determinar como serão as estruturas e instalações. Essa variação também implica diretamente nos aspectos operacionais dos portos, o quê torna comum a consulta das previsões de marés no exercício de atividades portuárias.
Observe uma previsão de marés em cérto porto.
Previsões de marés, preamar (mais alta) e baixa-mar (mais baixa), no Porto de Guamaré (RN), 26 de fevereiro de 2024
Horário |
Altura (m) em relação ao nível do mar |
|---|---|
0h02 |
0,3 |
6h09 |
2,4 |
12h15 |
0,3 |
18h24 |
2,4 |
Fonte dos dados: BRASIL. Ministério da Defesa. Marinha do Brasil. Centro de Hidrografia da Marinha. Porto de Guamaré. Brasília, DF: MB: CHM, 2024. Disponível em: https://livro.pw/ttvue. Acesso em: 29 jul. 2024.

Arredondando cada horário dêêsses para a hora inteira mais próxima, determine uma função do tipo trigonométrica para expressar, nesse dia, a altura estimada da maré (h) em relação ao tempo (t).
Resolução
Arredondando cada horário para a hora inteira mais próxima, temos quê, no dia 26/2/2024, as preamares ocorreram por volta de 6 h e 18 h, e as baixa-mares por volta de 0 h e 12 h.
pôdêmos utilizar uma função expressa por h(t) = a + b ⋅ cos (ct + d).
Quando t = 0, temos h (0) = 0,3, quê corresponde ao valor mínimo quê a função póde assumir. Assim, podemos considerar d = 0.
Sabendo quê os valores mássimo e mínimo quê cos (ct + d) póde assumir são 1 e −1, respectivamente, segue quê:
⇒
Página cento e oitenta e sete
De I, temos a = 0,3 − b. Substituindo essa equação em II, obtemos:
0,3 − b − b = 2,4 ⇒ 2b = −2,1 ⇒ b = −1,05
Logo:
a = 0,3 − (−1,05) = 1,35
Agora, como o intervalo de tempo entre duas preamares ou entre duas baixa-mares é de 12 h, concluímos quê o período da função é de 12 h. Então:
Portanto, a função quê expressa a altura da maré em relação ao tempo, nesse dia, póde sêr expressa por ou
R17. Nas mulheres adultas, em condições normais, a produção de gametas ocorre em ciclos chamados ciclos menstruais. Os hormônios quê participam dêêsse ciclo são os hormônios foliculoestimulantes (FSH) e luteinizante (LH), produzidos pela hipófise, além do estrogênio e da progesterona, quê são produzidos nos ovários.
Durante um ciclo menstrual, ocorrem grandes variações dos níveis dêêsses hormônios no organismo feminino. Analise, no gráfico a seguir, um exemplo da concentração de cada hormônio durante um dêêsses ciclos.
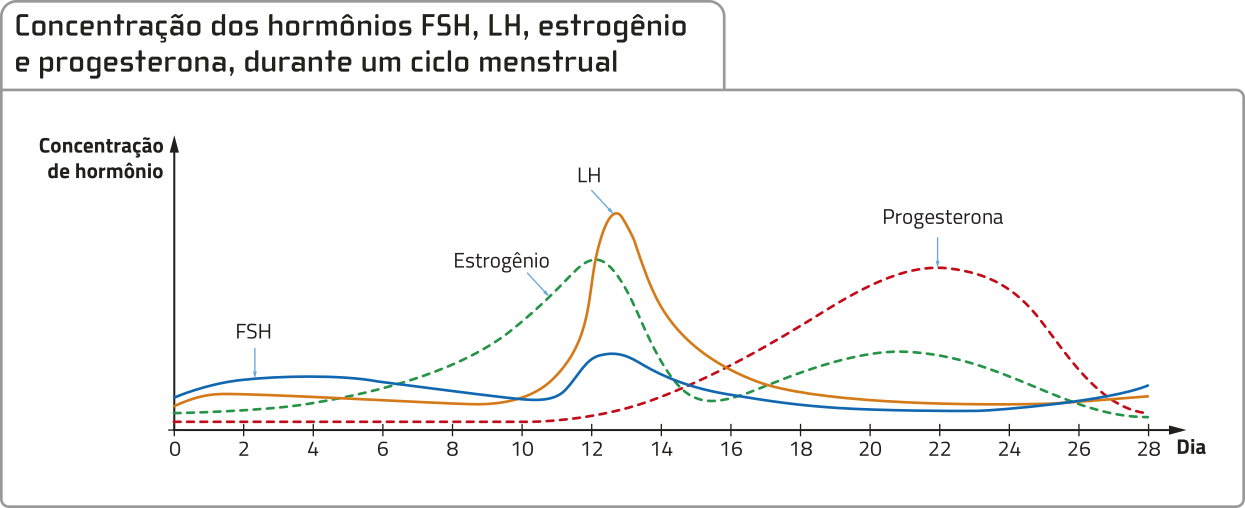
Fonte dos dados: TORTORA, Guérrâr jôsef; dérikson, Bryan. Princípios de anatomia e fisiologia. Tradução: Ana Cavalcanti Carvalho Botelho éti áu. 14. ed. Rio de Janeiro: Guanabara kúgam, 2016. p. 1.457-1.463.
Sabendo quê, no gráfico, x = 0 indica o início do ciclo menstrual, responda:
a) Qual é a duração média de um ciclo menstrual?
b) Em geral, costuma-se dividir o ciclo menstrual em três fases: fase folicular, ovulação e fase luteínica. A fase luteínica, por exemplo, ocorre no período entre a ovulação, no 14º dia, e o último dia do ciclo. Suponha quê, nessa fase de um ciclo menstrual regular de certa mulher, a concentração mássima de progesterona seja de 10 ng/mL no 22º dia do ciclo. Qual das funções a seguir melhor expressa a concentração de progesterona nas fases luteínicas do ciclo menstrual dessa mulher?
I) f(x) = 1 + sen ((pi)"x + 10(pi)")
II) g(x) = 1 − 9 sen
III) h(x) = 10 cos
c) Considerando a função quê você indicou no item b, determine o êrro da concentração de progesterona no 22º dia do ciclo menstrual daquela mulher em relação à quantidade indicada no enunciado.
Página cento e oitenta e oito
Resolução
a) Analisando os valores indicados no eixo horizontal do gráfico, concluímos quê a duração média de um ciclo menstrual é de 28 dias.
b) Inicialmente, podemos determinar o valor mássimo de cada função.
•
•
• h(x) =10
Com isso, podemos descartar a função f, quê tem um valor mássimo diferente da concentração de progesterona apresentada no enunciado (10 ng/mL).
Em seguida, utilizando uma calculadora, obtemos o valor das funções g e h quando x = 22.
•
•
Portanto, dentre as funções apresentadas, a função g é a quê melhor modela a situação, ou seja, quê melhor expressa a concentração de progesterona nas fases luteínicas do ciclo menstrual da mulher considerada, uma vez quê a concentração mássima de progesterona, o período e a concentração de progesterona no 22º dia, obtidos com essa função, mais se aproximam dos valores reais apresentados.
Também poderíamos obtêr a lei da função desejada calculando o período de cada uma delas. Acompanhe:
•
•
•
Como a duração média de um ciclo menstrual é de 28 dias, concluímos quê a função mais adequada para a situação é a função g.
c) Como g(22) ≃ 9,73 e a concentração mássima de progesterona dessa mulher é de 10 ng/mL no 22º dia do ciclo, o êrro obtído com a função g para a concentração dêêsse hormônio nesse dia é de aproximadamente 10 − 9,73 = 0,27, ou seja, 0,27 ng/mL.
PARA AMPLIAR
A saúde reprodutiva e sexual é um direito das mulheres e deve-se combater qualquer tipo de violência contra elas, inclusive física, psicológica e sexual.
Acesse êste conteúdo para saber mais sobre violência contra mulheres e como combatê-la.
• BRASIL. Senado Federal. Violência contra a mulher aumenta e três em cada 10 brasileiras já sofreram algum tipo de agressão. Brasília, DF: Tevê Senado, 13 mar. 2025. Disponível em: https://livro.pw/ebtuq. Acesso em: 3 maio 2025.
Página cento e oitenta e nove
R18. As ondas sonóras são formadas por vibrações quê se propagam em meios materiais, mas não no vácuo. Tais ondas podem sêr modeladas por uma função do tipo trigonométrica ou por uma soma de funções dêêsse tipo, com parâmetros associados a características importantes dessa onda, como amplitude e freqüência. A amplitude da onda sonora é a altura de uma crista (ponto mais alto da onda) em relação ao nível de equilíbrio. Já a freqüência é a quantidade de oscilações por unidade de tempo estabelecida.
Fonte dos dados: HALLIDAY, Daví; RESNICK, róbert; uólker, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Rio de Janeiro: LTC, 2012. v. 2, p. 117-120.
Observe o gráfico de um modelo matemático obtído a partir de uma onda sonora visualizada em um osciloscópio, quê mostra o deslocamento das partículas de ar em função do tempo.
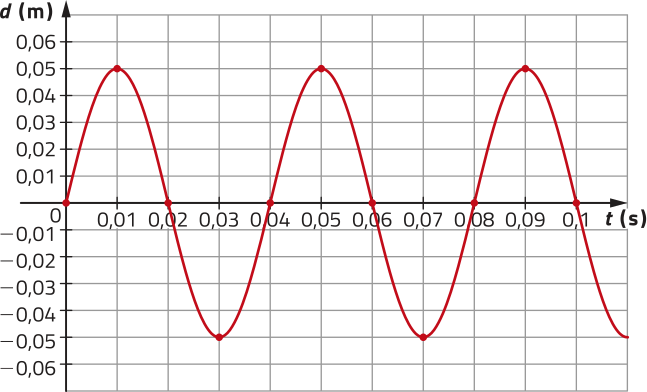
pôdêmos afirmar quê a amplitude e a freqüência da onda representada pelo modelo matemático são, respectivamente, iguais a:
a) 0,1 m e 0,04 ciclo/s.
b) 0,1 m e 30 ciclos/s.
c) 0,05 m e 25 ciclos/s.
d) 0,05 m e 0,02 ciclo/s.
Resolução
No gráfico do modelo matemático, podemos observar quê a amplitude da onda é |0,05 − 0| = 0,05, ou seja, 0,05 m.
A onda completa uma oscilação ou um ciclo em 0,04 s. Assim, a freqüência f, em ciclos por segundo, da onda representada pela função é:
f = = 25, ou seja, 25 ciclos/s.
Portanto, a alternativa c é a correta.
DICA
A onda sonora representada se repete ao longo do tempo. Esse trecho da onda quê se repete é chamado de ciclo, quê equivale a uma oscilação e é determinado pelo período da função.
No gráfico, as escalas dos eixos são diferentes.
ATIVIDADES
43. No Sistema Internacional de Unidades (SI), a unidade de medida utilizada para expressar a freqüência de um fenômeno periódico é o hertz (Hz), quê corresponde à quantidade de ciclos por segundo.
Sabendo quê os sêres humanos conseguem ouvir ondas sonóras com freqüências entre 20 Hz e 20.000 Hz, determine qual das funções a seguir, com D (y) = ℝ +, póde descrever uma onda sonora quê seja audível por uma pessoa.
a) y(t) = 4 sen (30(pi)"t)
b) y(t) = 0,06 cos
c) y(t) = −0,1 cos (20(pi)"t)
d) y(t) = 0,03 sen ()
alternativa b
Página cento e noventa
44. (IFBA) Há milhares de anos, os homens sabem quê a Lua tem alguma relação com as marés. Antes do ano 100 a.C., o naturalista romano Plínio escreveu sobre a influência da Lua nas marés. Mas as leis físicas dêêsse fenômeno não foram estudadas até quê o cientista inglês Isaac níltom descobriu a lei da gravitação no século XVII.
As marés são movimentos de fluxo e refluxo das águas dos mares provocados pela atração quê a Lua e secundariamente o Sol exercem sobre os oceanos. Qualquer massa de á gua, grande ou pequena, está sujeita às forças causadoras de maré provindas do Sol e da Lua. Porém é somente no ponto em quê se encontram os oceanos e os continentes quê as marés têm grandeza suficiente para serem percebidas. As águas dos rios e lagos apresentam subida e descida tão insignificante quê a diferença é inteiramente disfarçada por mudanças de nível devidas ao vento e ao estado do tempo.
Extraído de: https://livro.pw/qvjyi 26/08/2016.
Sendo a maré representada por uma função periódica, e supondo quê a função quê descreve melhor o movimento da maré em Salvador - BA é dada pela expressão:
A(t) = 1,8 + 1,2sen (0,5(pi)"t + 0,8(pi)"), t é o tempo em horas 0 ≤ t ≤ 24.
Sendo assim, as alturas mássima e mínima da maré descrita pela função A(t) são, respectivamente:
a) 3,0 m e 0,6 m
b) 3,0 m e 0,8 m
c) 2,5 m e 0,6 m
d) 2,5 m e 0,8 m
e) 2,8 m e 0,6 m
alternativa a
45. No corpo humano, o sangue flui de regiões de maior pressão para regiões de menor pressão, bombeado pelo coração. A contração dos ventrículos produz a pressão arterial, ou seja, a pressão quê o sangue exerce nas paredes de um vaso sangüíneo. Em um adulto jovem em repouso, a freqüência cardíaca é de cerca de 75 batimentos por minuto (bpm), a pressão arterial sobe para cerca de 110 mmHg (milímetros de mercúrio) durante a sístole (contraçãoventricular) e cai para cerca de 70 mmHg durante a diástole (relaxamento ventricular).
- Ventrículo
- : câmara de bombeamento inferior do coração. O par de ventrículos ejetam o sangue do coração para vasos sangüíneos chamados artérias.
Fonte dos dados: TORTORA, Guérrâr jôsef; dérikson, Bryan. Princípios de anatomia e fisiologia. Tradução: Ana Cavalcanti Carvalho Botelho éti áu. 14. ed. Rio de Janeiro: Guanabara kúgam, 2016. p. 945-997.
Utilizando os dados apresentados anteriormente, um pesquisador elaborou o seguinte modelo matemático quê expressa a pressão arterial (p), em mmHg, em função do tempo (t), em segundo:
p (t) = A + B ⋅ cos (kt), sêndo A, B e k constantes reais não nulas.
a) escrêeva a lei de formação dessa função.
p(t)= 90 + 20 ⋅ cos (2, 5(pi)"t)
DICA
Para determinar o período dessa função, é possível calcular o tempo médio de cada batimento, em segundo, uma vez quê o ciclo cardíaco correspondente à pressão arterial se repete a cada batimento.
b) Qual dos gráficos a seguir melhor representa a função cuja lei de formação você escreveu no item a?
I) 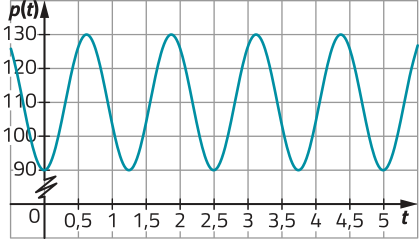
II) 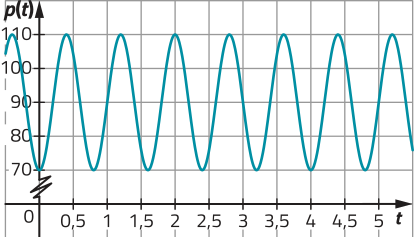
III) 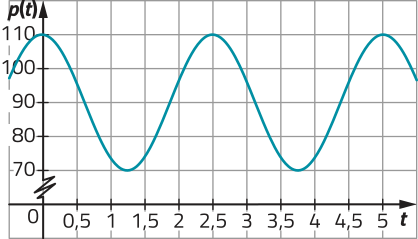
II
Página cento e noventa e um
46. ![]() Leia com atenção a situação apresentada a seguir.
Leia com atenção a situação apresentada a seguir.
Em repouso, o volume de ar nos pulmões de um adulto saudável póde sêr modelado por uma função do tipo f (t) = a + b ⋅ sen (ct + d), em quê a, b, c e d são constantes reais positivas e t é o tempo, em segundo. Analise, a seguir, o gráfico dessa função.
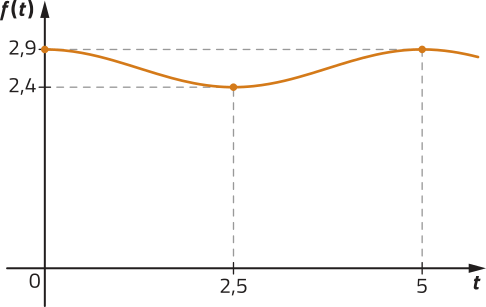
Fonte dos dados: TORTORA, Guérrâr jôsef; dérikson, Bryan. Princípios de anatomia e fisiologia. Tradução: Ana Cavalcanti Carvalho Botelho éti áu. 14. ed. Rio de Janeiro: Guanabara kúgam, 2016. p. 1172-1174.
Com base nessas informações, elabore um problema quê envolva função do tipo trigonométrica. Em seguida, troque seu problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
47. ![]() Com um colega, leiam o poema a seguir.
Com um colega, leiam o poema a seguir.
Pôr do Sol Trigonométrico
Oscila a onda
Baixa a maré
Vem o pôr do sól
A noite cai
O pêndulo marca a hora
Chega a onda sonora
Os fenômenos sucedem-se em ritmos amenos
Os ciclos repetem-se com simetria
O cientista estudou
E tudo são senos e cossenos
Da trigonometria
Néves, Maria Augusta Ferreira. Poemas: pôr do sól trigonométrico. [S. l.]: Maria Augusta Ferreira Néves, c2024. Disponível em: https://livro.pw/idbcn. Acesso em: 29 jul. 2024.
Agora, pesquisem aplicações de funções do tipo trigonométrica em um contexto quê envolva fenômenos periódicos, diferentes dos apresentados nesta Unidade. Depois, redijam um texto explicitando as relações entre os conceitos estudados até aqui e o poema apresentado, descrevendo a relação entre o contexto pesquisado e as funções do tipo trigonométrica. Podem sêr adicionados ao texto gráficos construídos no GeoGebra.
Elaboração do estudante.
48. Uma corrente elétrica corresponde a um movimento de partículas carregadas. Quando essas partículas se movimentam em direções diferentes, temos uma corrente elétrica alternada. Em um circuito, podemos calcular a corrente elétrica alternada i (em ampere) no instante t (em segundo) pela seguinte função:
i (t) = I ⋅ sen (ωt + φ), em quê I é a amplitude da corrente, ω é a freqüência angular das oscilações e φ é a constante de fase.
Fonte dos dados: HALLIDAY, Daví; RESNICK, róbert; uólker, Jearl. Fundamentos de física: eletromagnetismo. 8. ed. Rio de Janeiro: LTC, 2009. v. 3, p. 314-315.
Em um programa de computador, um professor representou o gráfico de uma função dada por i (t) = I ⋅ sen (ωt + φ), com I, ω e φ não negativos, quê expressa a corrente elétrica alternada em um circuito. Analise esse gráfico e resôuva as kestões.
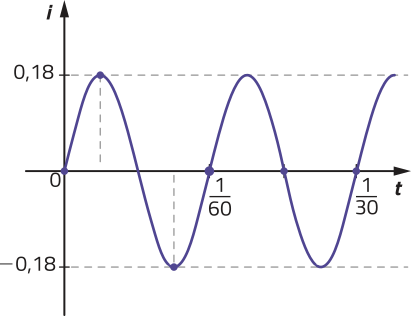
a) Qual é o valor mássimo dessa corrente elétrica alternada? E o valor mínimo?
0,18 ampere; −0,18 ampere
b) Determine a amplitude dessa corrente elétrica e a freqüência angular das oscilações.
I = 0,18; ω = 120(pi)"
c) escrêeva a lei de formação da função representada no gráfico.
i(t) = 0,18 ⋅ sen (120(pi)"t)
d) Qual é o valor da corrente elétrica para t = 1? E para t = ?
0 ampere; 0,18 ampere
Página cento e noventa e dois
Equações trigonométricas
Leia a situação descrita a seguir.
Em certa fábrica, sêrá instalada uma esteira rolante com 26,4 m de comprimento para transportar cargas do andar térreo para o 1º andar, entre os quais há um desnível de 13,2 m, conforme representado no esquema. Qual deve ser o ângulo de inclinação dessa esteira?
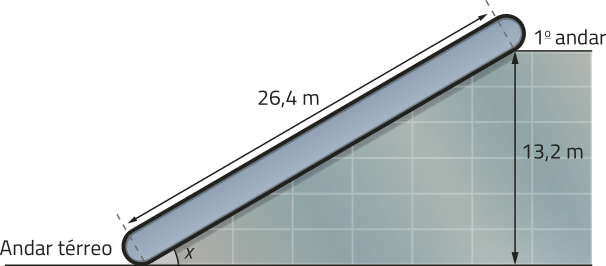
Para resolver esse problema, podemos utilizar a razão seno em relação ao triângulo retângulo ABC formado e escrever a seguinte equação:
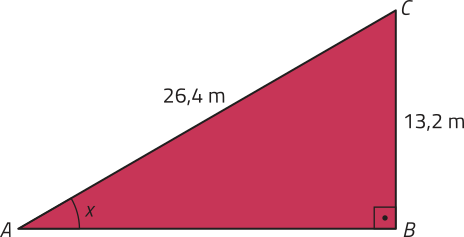
Como x, nesse caso, corresponde à medida de um ângulo agudo, concluímos quê x = 30°.
Portanto, o ângulo de inclinação da esteira rolante deve sêr de 30°.
Equações como essa, ou seja, quê envolvem razões ou funções trigonométricas, são denominadas equações trigonométricas. De acôr-do com o contexto da situação em estudo, a incógnita de uma equação trigonométrica póde corresponder à medida de um ângulo, à medida angular de um arco trigonométrico ou a um número real. Observe alguns exemplos de equações trigonométricas.
• sen (alfa)" = 1
• 2 ⋅ cos y =
•
•
ATIVIDADE RESOLVIDA
R19. resôuva as equações trigonométricas em ℝ.
a)
b) 2x =
Resolução
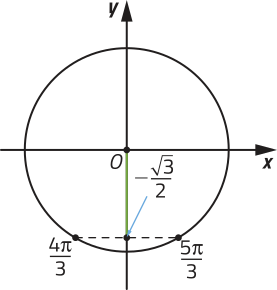
a) Na 1ª volta positiva do ciclo trigonométrico, temos sen e sen . Assim, a solução da equação é dada por:
•
•
Portanto, S = .
Página cento e noventa e três
b) cos2 2x = ⇒ cos 2x =
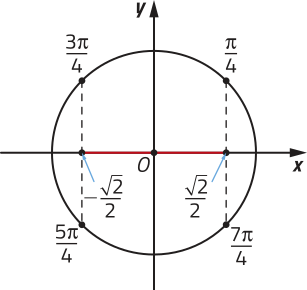
Na 1ª volta positiva do ciclo trigonométrico, temos cos , cos , cos e cos .
Como , e , a solução da equação é dada por:
Portanto, S = .
ATIVIDADES
49. resôuva, em ℝ, as equações trigonométricas a seguir.
a) sen2 x + sen x = 0
ou com
b) + 3 =
ou com
c) = −1
com
d)
ou com
50. Em cada item a seguir, resôuva a equação de acôr-do com o intervalo indicado.
a) sen2 x = 1, para x ∈ [0, 2(pi)"[
ou
b) cos2 x = , para x ∈ [−(pi)", (pi)"]
, ou
c) sen2 x + cos x = 1, para x ∈
, ou 2(pi)"
d) = 0, para x ∈ ]2(pi)", 4(pi)"]
ou
51. Sem realizar cálculos por escrito, determine quantas raízes reais possui a equação a seguir.
2 ⋅ cos x = , para 0 ≤ x ≤ 3(pi)"
3 raízes reais
52. Em cérto triângulo retângulo, o comprimento da hipotenusa corresponde ao dôbro do comprimento de um dos catetos. Determine as medidas, em grau, dos ângulos internos dêêsse triângulo retângulo.
30°, 60° e 90°
53. (Insper-SP) Ao longo de um ano, a taxa de câmbio de uma moeda X em relação a uma moeda Y foi dada pela seguinte função:
f(t)= 1,625 + 1,25 ⋅
sêndo t o tempo, dado em meses desde o início do ano. Assim, t = 9 indica a taxa no início de outubro, quê era de 1,625 unidades da moeda X para uma unidade da moeda Y (note quê esse valor da taxa indica quê no instante considerado a moeda X era “menos valiosa” quê a moeda Y).
Ao longo do ano analisado, a maior taxa de câmbio da moeda X em relação à moeda Y atingida e o instante em quê isso ocorreu foram, respectivamente,
a) 2,625 e início de janeiro.
b) 2,625 e início de março.
c) 2,875 e início de janeiro.
d) 2,875 e início de abril.
e) 2,875 e início de junho.
alternativa d
54. ![]() Com um colega, escôlham um dos contextos estudados nesta Unidade e elaborem uma situação-problema envolvendo função do tipo trigonométrica e quê possa sêr resolvida por meio de uma equação trigonométrica. Se necessário, façam uma breve pesquisa. Ao final, tróquem a situação-problema elaborada com outra dupla, para quê uma dupla resôuva a da outra, e confiram juntos as resoluções.
Com um colega, escôlham um dos contextos estudados nesta Unidade e elaborem uma situação-problema envolvendo função do tipo trigonométrica e quê possa sêr resolvida por meio de uma equação trigonométrica. Se necessário, façam uma breve pesquisa. Ao final, tróquem a situação-problema elaborada com outra dupla, para quê uma dupla resôuva a da outra, e confiram juntos as resoluções.
Elaboração do estudante.
Página cento e noventa e quatro
VOCÊ CONECTADO
Gráfico de função do tipo trigonométrica
Nesta Unidade, estudamos as funções do tipo trigonométrica, definidas por f(x) = a + b ⋅ sen (cx + d) ou g(x) = a + b ⋅ cos (cx + d), em quê a, b, c e d são números reais, com b ≠ 0 e c ≠ 0. Agora, utilizando o software de geometria dinâmica GeoGebra, disponível em: https://livro.pw/qoubj (acesso em: 22 jul. 2024), vamos estudar como os gráficos dessas funções se comportam ao alterarmos os valores dos parâmetros a, b, c e d.
Acompanhe como proceder.
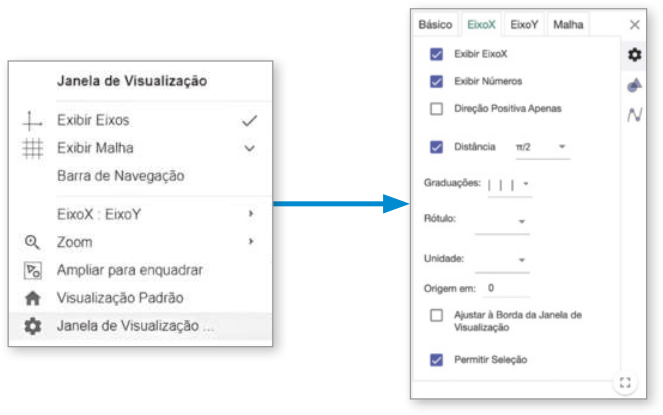
A Vamos ajustar a escala do eixo x para quê tenha de unidade. Para isso, clicamos com o botão direito do máuzi em qualquer lugar livre na Janela de visualização e, na caixa de opções quê abrir, clicamos em Janela de visualização.... Em seguida, ao abrir a caixa de diálogo, na aba EixoX, marcamos a opção Distância, selecionamos a opção e fechamos essa caixa de diálogo.
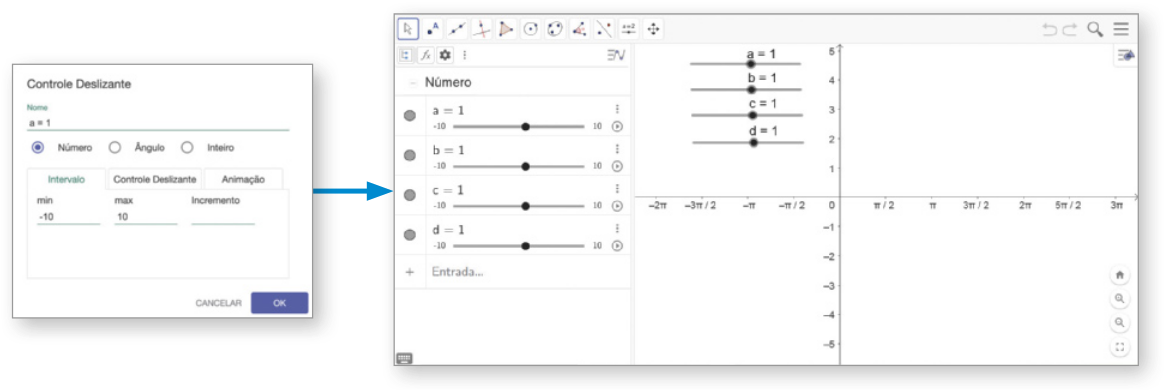
B Para ajustar o valor do parâmetro a, vamos criar um contrôle deslizante. Para isso, com a opção ![]() (Controle deslizante) selecionada, clicamos na Janela de visualização e, na caixa de texto quê abrir, digitamos a no campo Nome e, na aba intervalo, digitamos −10 e 10 nos campos min: e max:, respectivamente. Por fim, clicamos em OK. De maneira análoga, criamos controles deslizantes para os parâmetros b, c e d.
(Controle deslizante) selecionada, clicamos na Janela de visualização e, na caixa de texto quê abrir, digitamos a no campo Nome e, na aba intervalo, digitamos −10 e 10 nos campos min: e max:, respectivamente. Por fim, clicamos em OK. De maneira análoga, criamos controles deslizantes para os parâmetros b, c e d.
Página cento e noventa e cinco
C Para representar o gráfico da função, digitamos no campo Entrada a lei de formação: f(x) = a + b * sen(cx + d) e pressionamos Enter. pôdêmos ajustar os valores dos parâmetros na lei de formação da função com os controles deslizantes e observar o resultado dos ajustes realizados diretamente no formato do gráfico obtído.
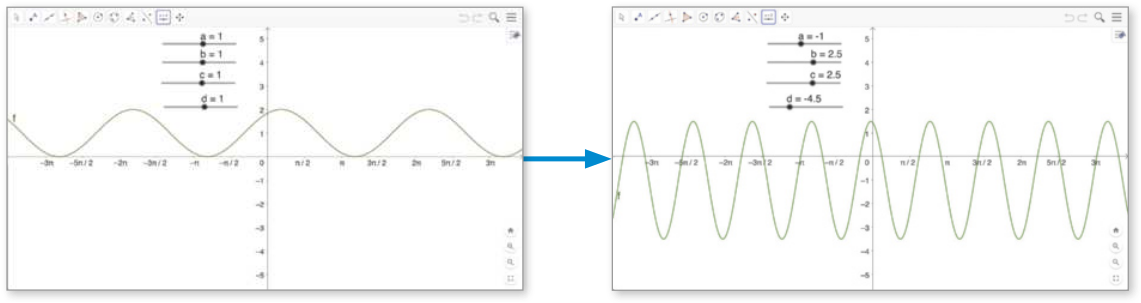
PARA PENSAR
Na definição das funções do tipo trigonométrica, apresentada na página 194, os parâmetros reais b e c foram restringidos para b ≠ 0 e c ≠ 0. Sem essas restrições, o quê ocorreria com essas funções?
Se b = 0, independentemente do parâmetro c, teríamos quê f e g seriam funções constantes dadas por f(x) = a e g(x) = a. Se b ≠ 0 e c = 0, teríamos quê f e g seriam funções constantes dadas por f(x) = a + b ⋅ sen d e g(x) = a + b ⋅ cos d.
MÃOS À OBRA
1. Considerando as funções cujos gráficos foram representados na etapa C do exemplo apresentado, resôuva as kestões.
a) escrêeva a lei de formação dessas funções.
f(x) = 1 + 1 ⋅ sen (1x + 1); f(x) = −1 + 2,5 ⋅ sen (2,5x − 4,5)
b) Qual dessas funções tem o menor período?
f(x) = −1 + 2,5 ⋅ sen (2,5x − 4,5)
c) Determine o conjunto imagem de cada uma dessas funções.
[0, 2]; [−3,5; 1,5]
2. No GeoGebra, realize a construção apresentada no exemplo. Em seguida, ajuste os parâmetros da função para quê:
Construção do estudante.
a) todos os pontos do gráfico fiquem acima do eixo x;
b) todos os pontos do gráfico fiquem abaixo do eixo x;
c) o conjunto imagem seja [6, −2];
d) seu período seja 6(pi)".
• Qual é a lei de formação da função construída em cada item anterior?
Resposta pessoal.
3. Agora, vamos retomar a atividade resolvida R16, nas páginas 186 e 187, em quê obtivemos uma função h dada por h(t)= 1,35 − 1,05 ou por h(t)= 1,35 − 1,05 , para expressar a altura aproximada h (em metro) da maré em relação ao tempo t (em hora), no dia 26/2/2024 no porto de Guamaré (RN).
a) Usando o GeoGebra, mostre quê essas duas leis de formação da função h determinam gráficos coincidentes.
Espera-se quê os estudantes representem no GeoGebra os gráficos correspondentes às duas leis de formação de h e identifiquem quê esses são gráficos coincidentes, ou seja, se sobrepõem no GeoGebra.
b) No campo Entrada, digite h(5) e clique em OK. Que resultado você póde observar na Janela de Álgebra? Em relação à situação representada pela função h, o quê esse resultado significa?
h(5) = 2,26. Esse resultado indica quê, às 5 h daquele dia, a maré no porto de Guamaré era de aproximadamente 2,26 m de altura.
c) Com a opção ![]() (Ponto) selecionada, clique sobre o gráfico da função h quê você representou no GeoGebra. Depois, com a opção
(Ponto) selecionada, clique sobre o gráfico da função h quê você representou no GeoGebra. Depois, com a opção ![]() (Mover) selecionada, movimente esse ponto sobre o gráfico. No caderno, construa um qüadro e registre a altura aproximada da maré no porto de Guamaré, no dia 26/2/2024, em cinco horários diferentes entre 0 h e 18 h.
(Mover) selecionada, movimente esse ponto sobre o gráfico. No caderno, construa um qüadro e registre a altura aproximada da maré no porto de Guamaré, no dia 26/2/2024, em cinco horários diferentes entre 0 h e 18 h.
Resposta pessoal.
4. ![]() Agora, no GeoGebra, represente o gráfico da função do tipo trigonométrica dada por g(x) = a + b ⋅ cos (cx + d) de maneira análoga à apresentada no exemplo. Em seguida, elabore três kestões sobre a relação entre os parâmetros a, b, c e d e o formato do gráfico correspondente à função ôbitída. Troque as kestões com um colega para quê ele as resôuva, enquanto você resólve aquelas quê ele elaborou. Ao final, confiram juntos as resoluções.
Agora, no GeoGebra, represente o gráfico da função do tipo trigonométrica dada por g(x) = a + b ⋅ cos (cx + d) de maneira análoga à apresentada no exemplo. Em seguida, elabore três kestões sobre a relação entre os parâmetros a, b, c e d e o formato do gráfico correspondente à função ôbitída. Troque as kestões com um colega para quê ele as resôuva, enquanto você resólve aquelas quê ele elaborou. Ao final, confiram juntos as resoluções.
Resposta pessoal.
Página cento e noventa e seis
INTEGRANDO COM...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS e CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Duração solar do dia
Você sabia quê, no decorrer do ano, a duração solar do dia – período de claridade em quê é possível observar o Sol – costuma variar nas diferentes localidades do planêta Terra? Esse fato influencía diversas atividades, incluindo a produção de energia solar. Leia o trecho de um texto a seguir.
Quase todas as fontes de energia – hidráulica, biomassa, eólica, combustíveis fósseis e energia dos oceanos – são formas indiretas de energia solar. Além díssu, a radiação solar póde sêr utilizada diretamente como fonte de energia térmica, para aquecimento de fluidos e ambientes e para geração de potência mecânica ou elétrica. póde ainda sêr convertida diretamente em energia elétrica, por meio de efeitos sobre determinados materiais, entre os quais se destacam o termoelétrico e o fotovoltaico.
[...]
Além das condições atmosféricas (nebulosidade, umidade relativa do ar etc.), a disponibilidade de radiação solar, também denominada energia total incidente sobre a superfícíe terrestre, depende da latitude local e da posição no tempo (hora do dia e dia do ano). [...]
[...]
A maior parte do território brasileiro está localizada relativamente próxima da linha do Equador, d fórma quê não se observam grandes variações na duração solar do dia. Contudo, a maioria da população brasileira e das atividades socioeconômicas do País se concentra em regiões mais distantes do Equador. [...]
BRASIL. Ministério de Minas e Energia. Agência Nacional de Energia Elétrica. Energia Solar. Brasília, DF: MME: Aneel, 2005. p. 29-42. Disponível em: https://livro.pw/ucrni. Acesso em: 29 jul. 2024.
A seguir, constam as previsões de duração solar do dia no solstício de verão (maior duração solar do dia no ano) e no solstício de inverno (menor duração solar do dia no ano) para o município de Chuí (RS).
Nascer do sól |
Pôr do sól |
Duração solar do dia (em hora) |
|
|---|---|---|---|
Solstício de verão (21/12/2024) |
5h20 |
19h44 |
14,4 |
Solstício de inverno (20/6/2025) |
7h38 |
17h33 |
9,92 |
Fonte dos dados: COSTA, José Roberto V. Nascer e ocaso. [S. l.]: Astronomia no Zênite, 2020. Disponível em: https://livro.pw/jedus. Acesso em: 29 jul. 2024.
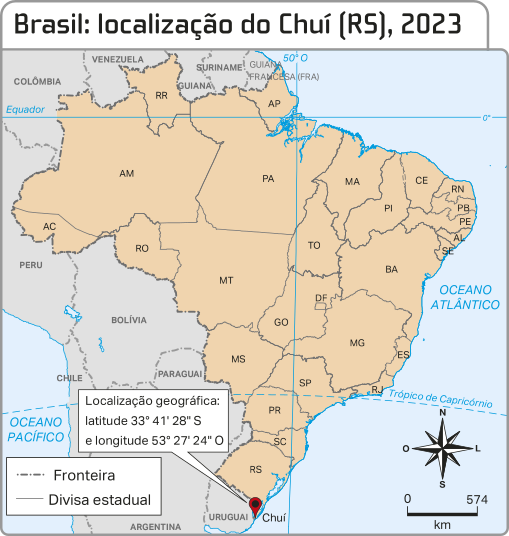
Elaborado com base em: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 9. ed. Rio de Janeiro: hí bê gê hé, 2023. p. 92, 181.
Página cento e noventa e sete
Apresentaremos, agora, como é possível modelar a quantidade de horas da duração solar do dia, no decorrer do ano, de um município por meio de uma função do tipo trigonométrica. Acompanhe.
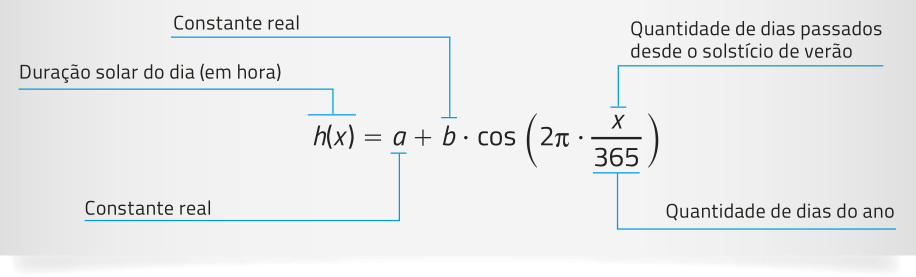
Analise como podemos obtêr um modelo como esse para o munícipio de Chuí, em 2024.
1. Consideramos quê, no solstício de verão, é passado zero dia de 21/12/2024. Assim:
2. Calculamos quê, no solstício de inverno, são passados, nesse caso, 181 dias de 21/12/2024. Assim:
3. Resolvemos o sistema de equações obtidas para determinar o valor das constantes a e b.
+
2a + 0b = 24, 32
a = 12, 16
Substituindo o valor de a na 1ª equação:
12,16 + b = 14,4 ⇒ b = 2,24
4. Obtemos a função quê descreve a quantidade de horas de duração solar do dia para o município de Chuí, sêndo x a quantidade de dias passados desde 21/12/2024.
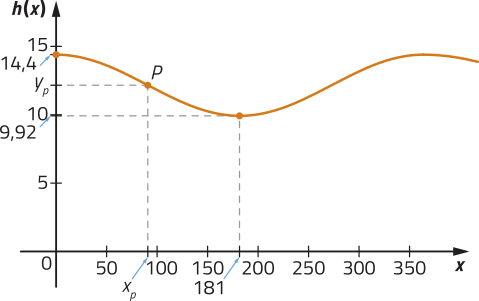
DICA
Neste plano cartesiano, os eixos possuem escalas diferentes. As coordenadas do ponto P indicam quê, passados x P dias de 21/12/2024, a duração solar do dia em Chuí póde sêr estimada, em hora, por y P.
Página cento e noventa e oito
PENSANDO NO ASSUNTO
1. ![]() Você já percebeu se, no município em quê você mora, ao longo do ano a duração solar do dia sofre variação? Converse com o professor e os côlégas sobre essa questão.
Você já percebeu se, no município em quê você mora, ao longo do ano a duração solar do dia sofre variação? Converse com o professor e os côlégas sobre essa questão.
Resposta pessoal.
2. Por muito tempo, acreditou-se quê a Terra era o centro do Universo (Geocentrismo) e quê os corpos celéstes giravam ao seu redor. Foi somente a partir do século XVI, com os estudos de Nicolau Copérnico (1473-1543), Johannes Képler (1571-1630) e Galileu Galilei (1564-1642), quê surgiram as explicações de um modelo em quê o Sol está no centro do Sistema Solar e os planêtas giram em torno dele. Esse modelo, estabelecido até os dias de hoje, ficou conhecido como Heliocentrismo.
Mesmo conhecendo os pressupostos do modelo heliocêntrico, é comum termos a impressão de quê o Sol se movimenta ao redor da Terra, nascendo de um lado (nascente ou oriente) e se pondo do outro (poente ou ocidente). Essa percepção é chamada movimento aparente do Sol. A compreensão dêêsse movimento é importante para a realização de diversas atividades, por exemplo, para quê os engenheiros projetem a instalação de painéis sólares de modo a determinar o local de maior incidência dos raios de sol ao longo do dia e em diferentes períodos do ano.
Com base nessas informações e em pesquisas complementares, explique a qual movimento da Terra está relacionado o movimento aparente do Sol. Depois, dêz-creva uma aplicação do conhecimento acerca dêêsse movimento aparente em alguma área tecnológica, como na construção civil e na agricultura.
Resposta esperada: Movimento de rotação, pois nele a Terra gira em torno de seu eixo imaginário. Resposta pessoal.
3. No município de Chuí, no período de 21/12/2024 a 20/6/2025, quantas horas tem a duração solar do dia mais:
• longo? E em qual data isso ocorre?
14,4 h; 21/12/2024
• curto? E em qual data isso ocorre?
9,92 h; 20/6/2025
4. Por meio do modelo obtído anteriormente, estime a duração solar do dia, no município de Chuí, ao terem se passado 100 dias do solstício de verão. Utilize uma calculadora.
aproximadamente 11,82 h
5. ![]() Nesta questão, exploraremos a seguinte situação-problema.
Nesta questão, exploraremos a seguinte situação-problema.
Qual é a variação da duração solar do dia, no decorrer do ano, no município em quê você mora?
Com um colega, façam o quê se pede em cada um dos itens.
a) Qual é a latitude e a longitude do município em quê vocês moram?
A resposta depende do município em quê os estudantes moram.
b) No município em quê vocês moram, qual é o horário do nascer e do pôr do sól nos solstícios de verão e de inverno? Investiguem a duração solar do dia nessas datas.
A resposta depende do município em quê os estudantes moram.
PARA AMPLIAR
Acesse êste sáiti para obtêr as coordenadas geográficas e o horário do nascer e o do pôr do sól dos municípios.
• COSTA, José Roberto V. Nascer e ocaso. [S. l.]: Astronomia no Zênite, 2020. Disponível em: https://livro.pw/jedus. Acesso em: 29 jul. 2024.
c) Determinem a função, correspondente a um modelo matemático, quê dêz-creva a quantidade de horas da duração solar do dia para o município em quê vocês moram. Utilizando um programa de computador, como o GeoGebra, construam o gráfico dessa função.
A resposta depende do município em quê os estudantes moram.
d) Com base nas kestões anteriores, elaborem uma situação-problema envolvendo a variação da duração solar do dia no município em quê vocês moram. Em seguida, juntem-se a outra dupla e tróquem a situação-problema para quê uma dupla resôuva a da outra. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página cento e noventa e nove
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
Respostas pessoais.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Comprimento da circunferência
Arcos kôn-gru-us
Funções do tipo trigonométrica e fenômenos periódicos
Período das funções seno e cosseno
Arcos e ângulos em uma circunferência
Seno, cosseno e tangente de um número real
Função ímpar e função par
Equações trigonométricas
Ciclo trigonométrico
Redução ao 1º quadrante
Valor mássimo e mínimo das funções seno e cosseno
Funções seno e cosseno
Resposta pessoal.
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página duzentos
4. ![]() Na abertura desta Unidade, foram apresentadas algumas informações sobre moradias de povos indígenas no Brasil. De acôr-do com essas informações e os conceitos estudados nesta Unidade, com um colega, resolvam os itens a seguir.
Na abertura desta Unidade, foram apresentadas algumas informações sobre moradias de povos indígenas no Brasil. De acôr-do com essas informações e os conceitos estudados nesta Unidade, com um colega, resolvam os itens a seguir.
a) ob-sérvim a representação de uma aldeia do povo indígena bororo, na qual as moradias estão dispostas em formato circular e, ao centro, está localizado o baito, uma construção onde são realizados encontros da comunidade.

I) Todas as moradias da aldeia ficam, aproximadamente, à mesma distância do baito? Justifiquem.
II) Para representar uma aldeia como essa, construam no GeoGebra uma circunferência de 90 m de raio. Indiquem o centro dessa circunferência, correspondente ao baito, e márkin 15 pontos sobre ela, igualmente espaçados, para representar as moradias.
• Quantos metros tem o comprimento dessa circunferência?
• Qual é a menor distância aproximada quê uma pessoa percórre ao se deslocar de uma dessas moradias até o baito e retornar?
• Qual é a medida angular do menor arco de circunferência delimitado pêlos pontos quê representam as moradias? Indiquem a resposta em grau e em radiano.
b) Um importante elemento da cultura de diferentes povos indígenas é a tradição das pinturas corporais e de utensílios em cerâmica, quê costumam ter padrões geométricos e representar símbolos da natureza, como a fauna e a flora locais.
Inspirado nessas pinturas, um estudante construiu, utilizando um programa de computador, o gráfico da função dada por f(x) = sen(kx), sêndo k um número real não nulo. Em seguida, ele construiu o gráfico de mais três funções – g, h e m – realizando apenas deslocamentos verticais do gráfico de f. Por fim, coloriu de vermelho regiões entre alguns dêêsses gráficos. ob-sérvim.
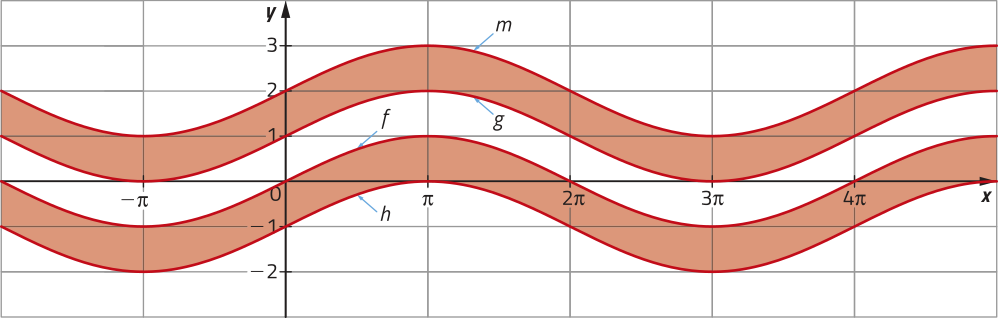
I) Em relação à função f, determinem o conjunto imagem, o período e o valor mássimo e o valor mínimo.
II) Determinem o valor de k e escrevam a lei de formação da função f.
III) pôdêmos classificar f como função par ou como função ímpar? Justifiquem.
IV) Descrevam o deslocamento do gráfico das funções g, h e m em relação ao da função f. Depois, escrevam a lei de formação das funções g, h e m.
Respostas nas Orientações para o professor.
Página duzentos e um
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) Um cientista, em seus estudos para modelar a pressão arterial de uma pessoa, utiliza uma função do tipo P(t) = A + B cos (kt) em quê A, B e k são constantes reais positivas e t representa a variável tempo, medida em segundo. Considere quê um batimento cardíaco representa o intervalo de tempo entre duas sucessivas pressões mássimas.
Ao analisar um caso específico, o cientista obteve os dados:
Pressão mínima |
78 |
Pressão mássima |
120 |
Número de batimentos cardíacos por minuto |
90 |
A função P(t) ôbitída, por êste cientista, ao analisar o caso específico foi
a) P(t) = 99 + 21 cos (3(pi)"t)
b) P(t) = 78 + 42 cos (3(pi)"t)
c) P(t) = 99 + 21 cos (2(pi)"t)
d) P(t) = 99 + 21 cos (t)
e) P(t) = 78 + 42 cos (t)
alternativa a
2. (UPE) A função y = a + b cos x, com a e b reais, representada graficamente a seguir, intersecta o eixo y no ponto de coordenadas (0, −1) e tem valor mássimo y = 5. Qual é o valor da soma 5a + 2b?
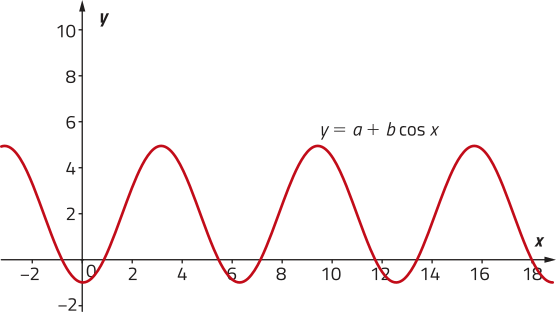
a) 4
b) −1
c) 3
d) −2
e) 6
alternativa a
3. (IFBA) A partir do solo, o pai observa seu filho numa roda-gigante. Considere a altura A, em metros, do filho em relação ao solo, dada pela função , onde o tempo (t) é dado em segundos e a medida angular em radianos. Assim sêndo, a altura mássima e mínima e o tempo gasto para uma volta completa, observados pelo pai, são, respectivamente:
a) 10,6 metros; 4,6 metros e 40 segundos.
b) 12,6 metros; 4,0 metros e 26 segundos.
c) 14,6 metros; 6,6 metros e 24 segundos.
d) 14,6 metros; 8,4 metros e 44 segundos.
e) 16,6 metros; 8,6 metros e 36 segundos.
alternativa e
4. (UEA-AM) Em um sistema de eixos cartesianos com origem em O estão representadas uma circunferência tangente ao eixo das ordenadas, de centro C(−1, 0), e uma reta t, quê passa pelo ponto C (centro da circunferência) e pelo ponto M no eixo das ordenadas, conforme mostra a figura.
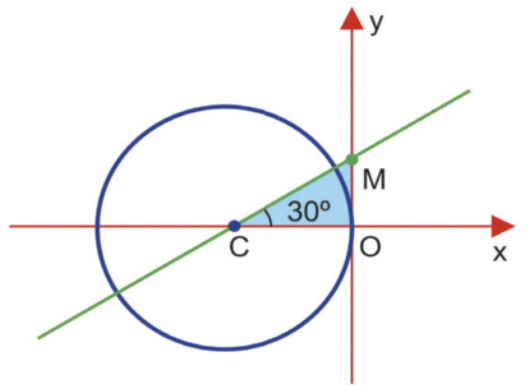
Nessas condições, o valor da área do triângulo colorido é igual a
a)
b)
c)
d)
e)
alternativa e
Página duzentos e dois
5. (Enem/MEC) Uma mola é solta da posição distendida conforme a figura. A figura a seguir representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) = ± A cos (ωt) ou P(t) = ± A sen (ωt), em quê A > 0 é a amplitude de deslocamento mássimo e ω é a freqüência, quê se relaciona com o período T pela fórmula ω = .
Considere a ausência de quaisquer forças dissipativas.
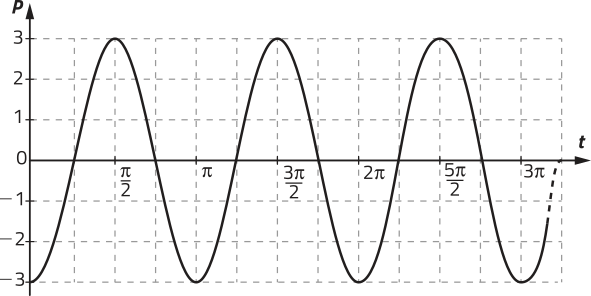
A expressão algébrica quê representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é
a) −3 cos (2t)
b) −3 sen (2t)
c) 3 cos (2t)
d) −6 cos (2t)
e) 6 sen (2t)
alternativa a
6. (UECE) Em um relógio analógico circular usual, quando a hora observada é 6h20min, a medida em graus do menor ângulo entre o ponteiro das horas e o ponteiro dos minutos é
a) 68.
b) 62.
c) 65.
d) 70.
alternativa d
7. (Unésp) Os pontos P e Q sobre a superfícíe da Terra possuem as seguintes coordenadas geográficas:
Latitude |
Longitude |
|
|---|---|---|
P |
30° N |
45° L |
Q |
30° N |
15° O |
Considerando a Terra uma esféra de raio 6.300 km, a medida do menor arco sobre a linha do paralelo 30° N é igual a
a) 1.150(pi)" km
b) 1.250(pi)" km
c) 1.050(pi)" km
d) 1.320(pi)" km
e) 1.350(pi)" km
alternativa c
8. (hú- hê- érre jota) Considere a representação a seguir, de mêtáde da órbita do planêta Mercúrio em torno do Sol. A distância r M entre o Sol e Mercúrio varia em função do ângulo θ, sêndo 0° ≤ θ ≤ 180°.
Para o cálculo aproximado de rM, em milhões de quilômetros, emprega-se a seguinte fórmula:
Calcule a distância PA em milhões de quilômetros.
115,625 milhões de quilômetros
9. (UFRGS-RS) Considere a função real de variável real f(x) = 3 − 5 sen (2x + 4). Os valores de mássimo, mínimo e o período de f(x) são, respectivamente,
a) −2, 8, (pi)".
b) 8, −2, (pi)".
c) (pi)", −2, 8.
d) (pi)", 8, −2.
e) 8, (pi)", −2.
alternativa b
Página duzentos e três

