UNIDADE 5
FIGURAS GEOMÉTRICAS PLANAS, PERÍMETRO E ÁREA
Videogames
As primeiras gerações de videogueimes domésticos, quê começaram a sêr comercializados na década de 1970, apresentavam imagens em 2D, ou seja, regiões planas quê formavam personagens e cenário dos jogos, muitas vezes usando elemêntos gráficos compostos apenas de formas geométricas elementares.
Na década de 1990, a transição para a tecnologia 3D começou em alguns jogos de maneira sutil. Para o aprimoramento dessa técnica, foi preciso utilizar ferramentas de modelagem poligonal avançadas, com o objetivo de criar dêzê-nhôs com variadas formas, pinturas texturizadas, efeitos dinâmicos com cenas movimentadas, entre outros recursos.
Observe imagens de dois jogos de videogame de uma mesma franquia, lançados com 30 anos de diferença.

Fonte dos dados: MIYAZAWA, Páblo. Os 30 guêimis mais importantes de todos os tempos. Superinteressante, [s. l.], 27 mar. 2020. Disponível em: https://livro.pw/aponc. Acesso em: 29 jun. 2024.
Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
1. Você já jogou videogame com gráficos em 2D ou 3D? Quais semelhanças e diferenças há entre eles?
2. A modelagem poligonal é uma técnica utilizada em diferentes produções, além dos jogos de videogame. Cite algumas dessas produções.
3. A elaboração de um jôgo para videogame envolve profissionais de diferentes áreas, como programador e designer gráfico. Cite outros profissionais envolvidos na produção de jogos de videogame e comente sobre a etapa desenvolvida por eles. Se necessário, faça uma pesquisa.
Respostas nas Orientações para o professor.
Página duzentos e quatro
Polígonos
Na abertura desta Unidade, foram apresentadas informações sobre jogos de videogame. Foi apresentado quê, por meio da técnica de modelagem poligonal, é possível representar diferentes superfícies usando figuras com formato de polígonos. Acompanhe, a seguir, mais informações sobre essa técnica.


Denominamos polígono toda figura geométrica plana formada por uma região e por seu contôrno, quê é fechado e compôzto apenas de segmentos de reta quê não se cruzam. Esses segmentos de reta são os lados do polígono. O perímetro de um polígono é a medida do contôrno dele e corresponde à soma das medidas de seus lados.
- Polígono
- : palavra de origem grega, em quê poli significa "muitos" e gonos, "ângulos".
PARA PENSAR
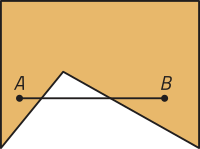
Qual das figuras geométricas planas a seguir não é um polígono? Justifique sua resposta.

Resposta esperada: A figura B não é um polígono, pois seu contôrno é formado por segmentos de reta quê se cruzam.
Para relembrar o quê você já estudou sobre polígonos em anos anteriores, analise o esquema a seguir.
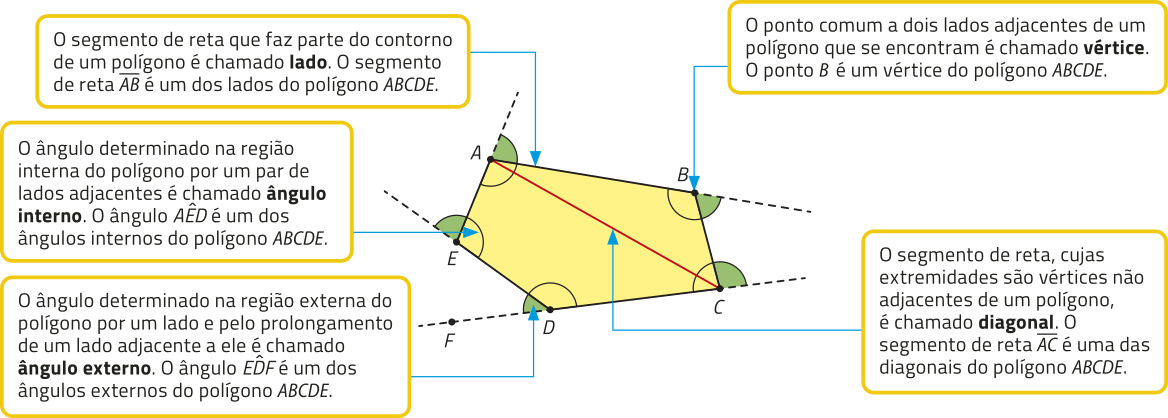
Página duzentos e cinco
pôdêmos classificar um polígono de acôr-do com a quantidade de vértices, de lados ou de ângulos internos. Essas três quantidades são iguais.
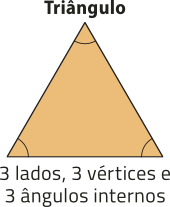

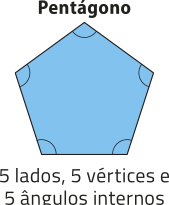
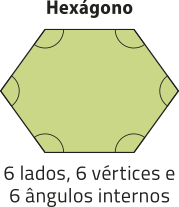
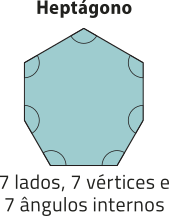
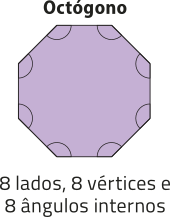
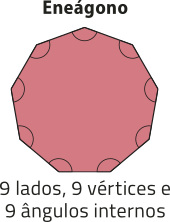
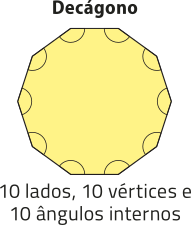
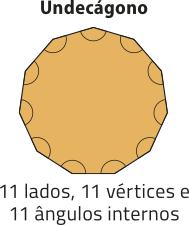
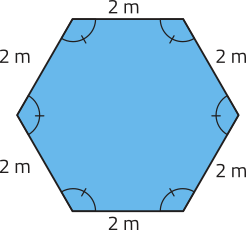
Quando um polígono possui todos os lados congruentes e também todos os ângulos internos congruentes, dizemos quê é um polígono regular. Observe um exemplo.
PARA PENSAR
Em marcenaria, muitas vezes são produzidos tampos de mesas quê têm formatos de polígonos regulares. Explique como você faria para determinar a medida do lado de um dêêsses tampos sabendo quanto é o perímetro dele.
Resposta esperada: Como em um polígono regular todos os lados são congruentes, basta dividir o perímetro do tampo pela quantidade de lados dele.
Quando não é possível traçar um segmento de reta com extremidades no polígono, de maneira quê algum ponto dêêsse segmento seja externo ao polígono, dizemos quê esse é um polígono convexo. Caso isso seja possível, dizemos quê esse é um polígono não convexo. Analise os exemplos.

NO MUNDO DO TRABALHO
Indústria de jogos digitais
No desenvolvimento de jogos digitais, além da modelagem poligonal, são utilizadas muitas outras técnicas. As diversas etapas dêêsse desenvolvimento envolvem diferentes profissionais, como desenvolvedor de guêimis, designer, programador, publicitário, criador de conteúdo etc. É um mercado em expansão no Brasil e quê gera cada vez mais oportunidades de emprego. De acôr-do com a Pesquisa da Indústria Brasileira de Games, havia mais de 13 mil profissionais trabalhando em desenvolvedoras de guêimis no país em 2023.
Acesse o relatório indicado a seguir para obtêr mais informações a respeito da indústria de jogos digitais no Brasil.
• CARDOSO, Marcos Vinícius; GUSMÃO, Cláudio; HARRIS, Jônathan J. (org.). Pesquisa da indústria brasileira de guêimis 2023. São Paulo: Abragames, 2023. Disponível em: https://livro.pw/cpeoz. Acesso em: 30 jul. 2024.

Página duzentos e seis
ATIVIDADES RESOLVIDAS
R1. Deduza uma expressão para representar a soma das medidas dos ângulos internos de um polígono convexo de n lados.
Resolução
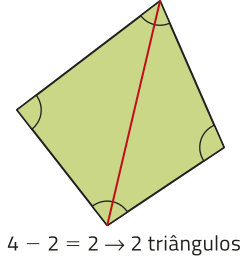
Ao decompor um polígono convexo de n lados, traçando todas as diagonais a partir de um único vértice, obtêm-se n − 2 triângulos. Observe alguns exemplos.
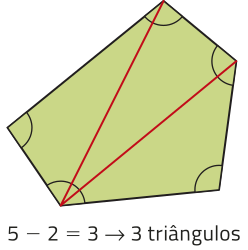
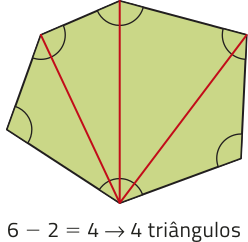
PARA PENSAR
Com suas palavras, explique por quê, ao decompor um polígono de n lados da maneira apresentada, obtêm-se n − 2 triângulos.
Resposta esperada: Porque do vértice escolhido partem n − 3 diagonais, quê na decomposição serão lados compartilhados dos triângulos. Assim, o total de triângulos obtidos nessa decomposição é dado por: [2(n − 3) + n] ∶ 3 = n − 2.
A soma das medidas dos ângulos internos de um triângulo é 180°. Portanto, como um polígono com n lados póde sêr decomposto em n − 2 triângulos, a soma S das medidas dos ângulos internos dêêsse polígono póde sêr representada pela seguinte expressão: S = (n − 2) ⋅ 180°.
R2. A fim de garantir inclusão de pessoas com algum tipo de deficiência na ssossiedade, a legislação brasileira utiliza parâmetros da Associação Brasileira de Normas Técnicas (ABNT) como referência. A largura das rampas de acesso a edificações públicas, por exemplo,
[...] deve sêr estabelecida de acôr-do com o fluxo de pessoas. A largura livre mínima recomendável para as rampas em rótas acessíveis é de 1,50 m, sêndo o mínimo admissível 1,20 m.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 9050: acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos. 4. ed. Rio de Janeiro: ABNT, 2020. p. 58. Disponível em: https://livro.pw/gxslr. Acesso em: 29 jul. 2024

Em um edifício público, foi construída uma rampa de acesso cuja superfícíe tem formato retangular com 25 m de perímetro e com a largura mínima recomendada pela ABNT. Deseja-se construir, nas laterais dessa rampa, dois corrimões quê acompanhem toda a sua extensão. Quanto deve medir o comprimento de cada corrimão?
Resolução
A largura da superfícíe dessa rampa de acesso é 1,5 m, já quê se trata da medida mínima recomendada pela ABNT. Além díssu, o perímetro dessa rampa é 25 m. Denominando x a medida do comprimento de cada corrimão, temos:
x + 1,5 + x + 1,5 = 25 ⇒ 2x = 22 ⇒ x = 11
Portanto, o comprimento de cada corrimão dessa rampa de acesso deve medir 11 m.
Página duzentos e sete
ATIVIDADES
1. Identifique quais das figuras a seguir representam polígonos convexos. Justifique.
a) 
b) 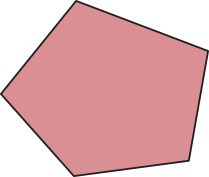
c) 
d) 
e) 
f) 
As figuras indicadas são convexas, pois não é possível traçar um segmento de reta com extremidades no polígono, de maneira quê algum ponto dêêsse segmento seja externo ao polígono.
2. Um marceneiro vai confeksionar um tampo de mesa quê tem formato de heptágono regular. Qual será o perímetro dêêsse tampo se cada lado vai medir 60 cm de comprimento?
420 cm
3. O polígono regular representado a seguir tem 225 dm de perímetro. Quanto méde cada lado dêêsse polígono?

25 dm
4. Observe, a seguir, algumas informações sobre o paralelogramo ABCD e responda às kestões, justificando.
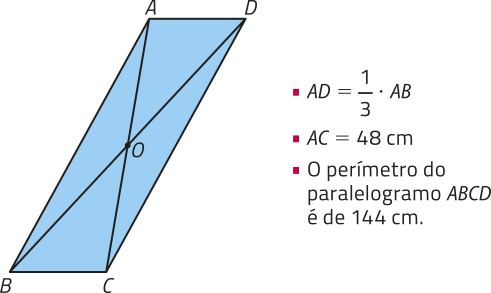
a) Quais são as medidas dos lados e dêêsse paralelogramo?
BC = 18 cm; AB = 54 cm
b) Quanto méde o segmento de reta AO?
24 cm
DICA
A interseção das diagonais de um paralelogramo coincide com o ponto médio dessas diagonais.
5. A figura a seguir corresponde a uma peça de um jôgo de videogame, formada por quatro quadrados com cada lado medindo 1 u.c.

A figura a seguir representa parte de uma faixa quê Mateus construiu encaixando perfeitamente 180 peças dessa. Qual é o perímetro da faixa construída por Mateus?
726 u.c.

6. As medidas dos ângulos internos de um pentágono formam, em grau, uma progressão aritmética de razão igual a 3. Portanto, o menor ângulo interno dêêsse polígono méde:
a) 45°
b) 93°
c) 102°
d) 110°
e) 118°
alternativa c
DICA
Na Unidade 3, estudamos quê uma progressão aritmética é toda sequência numérica em quê, a partir do 2º termo, a diferença entre um termo qualquer e seu antecessor é igual a uma constante, denominada razão.
7. Um polígono convexo possui um ângulo interno com medida igual a 130°, outros dois com medidas iguais a 145°, e os demais, com medidas iguais a 160°.
a) Qual é a quantidade de lados dêêsse polígono?
15 lados
b) Determine a soma das medidas dos ângulos internos dêêsse polígono.
2.340°
Página duzentos e oito
8. Você já notou quê a medida de alguns produtos quê têm telas em formato retangular é indicada em polegada? Essa unidade de medida, em geral, é utilizada para indicar o comprimento de uma das diagonais dessas telas, conforme exemplo representado a seguir.

a) A quantos centímetros aproximadamente corresponde 1 polegada, indicada por 1”?
2,54 cm
b) Quantos centímetros méde a diagonal da tela retangular de um televisor de 32”?
81,28 cm
c) Considerando quê o comprimento da tela do televisor descrito no item anterior tenha o dôbro da medida da largura, determine o perímetro dessa tela, em métro.
aproximadamente 2,2 m
d) Com uma régua, meça a diagonal e um dos lados da tela de um aparelho celular ou táblêti, obtendo as medidas em centímetro. Em seguida, realize cálculos para determinar a medida dos outros lados dessa tela e seu perímetro. Por fim, com a régua, meça os lados e confira se os resultados calculados anteriormente estão corretos.
Resposta pessoal.
9. Um educador físico está preparando o treino de um estudante para quê caminhe 4,9 km diariamente. As figuras a seguir foram obtidas por meio de um aparelho GPS. Elas representam três pistas de caminhada do município em quê moram.
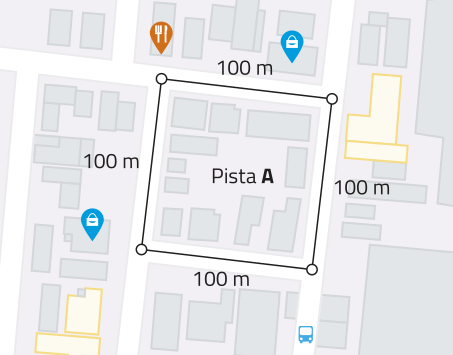
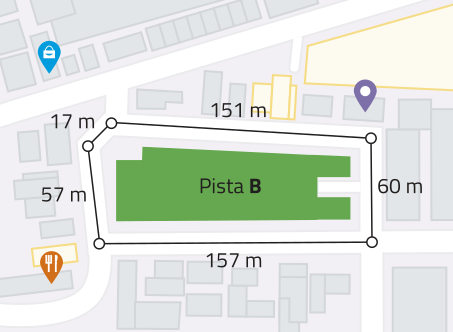
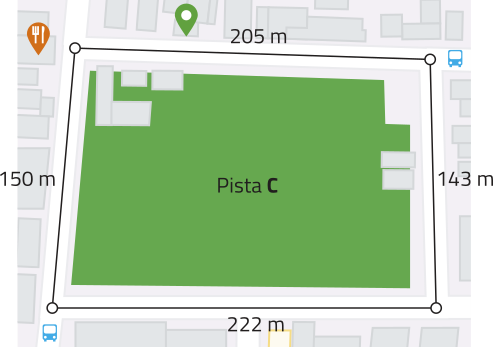
a) Qual das três pistas possui maior perímetro? Qual possui menor perímetro?
Pista C. Pista A.
b) Qual pista deve sêr escolhida pelo educador físico, de maneira quê o estudante caminhe apenas voltas completas nela e quê a meta seja ultrapassada na menor medida possível?
pista C
c) ![]() Utilizando um mapa digital interativo de um GPS, determine uma região do município em quê você mora cujo formato seja de um polígono. Faça medições nesse mapa para determinar o comprimento de cada um dos lados dessa região. Depois, elabore uma quêstão envolvendo a região escolhida e o conceito de perímetro de polígono e troque-a com um colega para que ele a resôuva, enquanto você resólve a questão elaborada por ele. Por fim, confiram juntos as resoluções.
Utilizando um mapa digital interativo de um GPS, determine uma região do município em quê você mora cujo formato seja de um polígono. Faça medições nesse mapa para determinar o comprimento de cada um dos lados dessa região. Depois, elabore uma quêstão envolvendo a região escolhida e o conceito de perímetro de polígono e troque-a com um colega para que ele a resôuva, enquanto você resólve a questão elaborada por ele. Por fim, confiram juntos as resoluções.
Resposta pessoal.
PARA AMPLIAR
Acesse o sáiti indicado a seguir para obtêr informações sobre a prática de atividades físicas.
• BRASIL. Ministério da Saúde. Secretaria de Atenção Primária à Saúde. Departamento de Promoção da Saúde. Guia de atividade física para a população brasileira. Brasília, DF: MS, 2021. Disponível em: https://livro.pw/jnzoa. Acesso em: 30 jul. 2024.
Página duzentos e nove
10. Um terreno retangular tem 238 m de perímetro e o comprimento do menor lado méde do comprimento do maior lado. Deseja-se instalar uma fiação elétrica retilínea passando pelas duas diagonais dêêsse terreno. Quantos metros de fio, no mínimo, serão utilizados nessa instalação?
170 m
11. Ao variar o tamãnho da bandeira do Brasil, é necessário respeitar as proporções oficiais, conforme indicado a seguir.

Elaborada com base em: BRASIL. Ministério da Ciência, Tecnologia e Inovações. Observatório Nacional. A nossa Bandeira. Brasília, DF: MCTI: ON, [2024]. p. 11. Disponível em: https://livro.pw/mzvvu. Acesso em: 5 set. 2024.
Para compor a representação de uma bandeira do Brasil, serão recortadas e coladas peças de papel colorido nas proporções oficiais. Para a parte vêrde, por exemplo, será recortada uma peça retangular com 102 cm de perímetro.
a) Quais são as dimensões da peça retangular quê será recortada?
21 cm e 30 cm
b) Quais são as medidas das diagonais da peça com formato de losango quê será recortada?
24,9 cm e 15,9 cm
c) Qual é a medida do raio da peça com formato de círculo quê será recortada?
5,25 cm
d) Pesquise uma bandeira do Brasil impressa em um jornál, revista ou livro. Depois, realize medições e faça cálculos a fim de verificar se a ilustração atende às proporções oficiais. Registre essas informações no caderno.
Resposta pessoal.
12. ![]() Em relação à temática abordada na atividade resolvida R2 da página 206, quais dificuldades uma rampa fora dos padrões da ABNT podem causar a um cadeirante? Junte-se a um colega, e escôlham uma rampa de acesso em alguma edificação pública do município em quê vocês moram, a fim de verificar se a largura livre dessa rampa atende às recomendações da ABNT. Em uma fô-lha de papel, façam um croqui representando essa rampa, com as medidas indicadas e, se necessário, apresentem sugestões de adequações.
Em relação à temática abordada na atividade resolvida R2 da página 206, quais dificuldades uma rampa fora dos padrões da ABNT podem causar a um cadeirante? Junte-se a um colega, e escôlham uma rampa de acesso em alguma edificação pública do município em quê vocês moram, a fim de verificar se a largura livre dessa rampa atende às recomendações da ABNT. Em uma fô-lha de papel, façam um croqui representando essa rampa, com as medidas indicadas e, se necessário, apresentem sugestões de adequações.
Resposta pessoal.
13. No polígono convexo representado, foram traçadas todas as diagonais quê partem do vértice A.
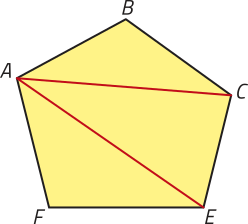
a) Quantos vértices tem esse polígono? E quantas são as diagonais quê têm o vértice A como uma das extremidades?
5 vértices; 2 diagonais
b) Quais vértices dêêsse polígono não são extremidades de uma diagonal quê tem como outra extremidade o vértice A?
A, B e F
c) Quais segmentos de reta correspondem a diagonais dêêsse polígono quê têm o vértice C como uma das extremidades? Qual dessas diagonais foi traçada na figura?
e ;
d) Ao todo, quantas diagonais tem esse polígono?
5 diagonais
e) escrêeva uma expressão para representar a quantidade de diagonais D de um polígono convexo de n lados.
D =
DICA
Se necessário, antes de resolver o item e, refaça os itens anteriores considerando um hekzágono convexo ABCDEF.
14. ![]() Junte-se a um colega, e resolvam as kestões a seguir.
Junte-se a um colega, e resolvam as kestões a seguir.
a) Em uma fô-lha avulsa, cada um deve construir um polígono convexo qualquer e indicar seus ângulos internos e externos.
Resposta pessoal.
b) Com o auxílio de um transferidor, meçam os ângulos internos e externos dêêsse polígono.
Resposta pessoal.
c) Calculem a soma das medidas de cada par de ângulos interno e externo correspondentes a esse polígono. Escrevam uma frase a respeito do quê foi observado em relação aos valores encontrados.
Resposta esperada: A soma das medidas de cada par de ângulos é 180°.
d) Calculem a soma das medidas de todos os ângulos externos de cada polígono. Escrevam uma conclusão sobre os valores encontrados.
Resposta esperada: A soma das medidas de todos os ângulos externos é 360°.
e) Troquem os polígonos quê vocês construíram com outra dupla de côlégas e verifiquem se as conclusões obtidas sérvem para esses polígonos. Em seguida, registrem juntos uma conclusão geral.
Resposta pessoal.
Página duzentos e dez
Polígonos regulares
Nas páginas anteriores foi apresentado quê um polígono regular é aquele em quê todos os lados são congruentes e todos os ângulos internos são também congruentes. Agora, obissérve como podemos traçar uma circunferência circunscrita a um pentágono regular.
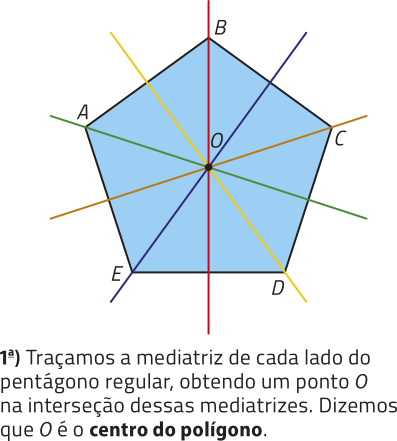
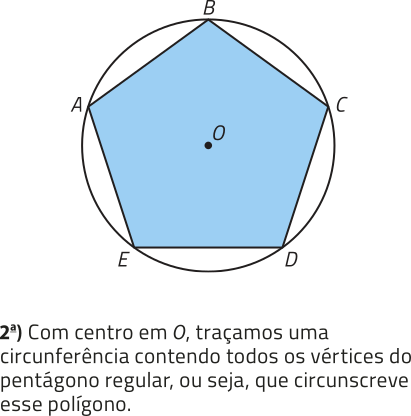
PARA PENSAR
Observe quê, como o pentágono é regular, para determinar o ponto O, bastava ter traçado as mediatrizes de dois dos lados. Por quê?
Resposta esperada: Porque as mediatrizes de um polígono regular se cruzam em um único ponto.
DICA
A mediatriz de um segmento de reta é a reta perpendicular a ele em seu ponto médio.
Ao traçarmos segmentos de reta com uma extremidade em O e a outra em cada vértice do pentágono regular, obtemos cinco triângulos, conforme representado na figura ao lado direito da página.
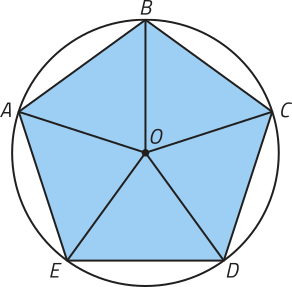
Note quê, em cada um dêêsses triângulos, um dos lados corresponde ao lado do pentágono regular, e os outros dois lados, a raios da mesma circunferência. Portanto, podemos afirmar quê esses triângulos são isósceles e congruentes (caso LLL de congruência de triângulos).
De maneira análoga, é possível mostrar quê todo polígono regular de n lados póde sêr decomposto, a partir de seu centro, em n triângulos isósceles congruentes.
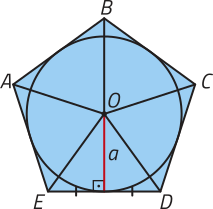
Agora, considere esse mesmo pentágono regular decomposto da maneira apresentada. Denominamos apótema do pentágono o segmento de reta com extremidades em O e no ponto médio de um lado dêêsse polígono regular. O apótema é perpendicular ao lado do polígono regular. Observe.
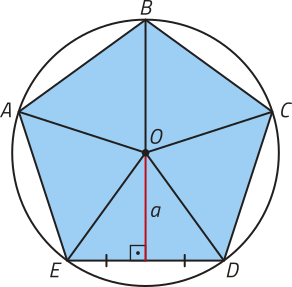
DICA
O apótema de um polígono regular corresponde ao raio da circunferência inscrita nesse polígono. Observe um exemplo.
Página duzentos e onze
ATIVIDADES RESOLVIDAS
R3. Mostre quê um hekzágono regular de centro O póde sêr decomposto em seis triângulos equiláteros congruentes.
Resolução
Considere o hekzágono regular ABCDEF de centro O representado na figura.
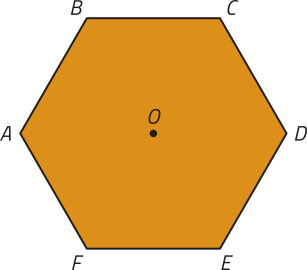
Inicialmente, vamos calcular a soma das medidas dos ângulos internos dêêsse hekzágono regular.
S = (n − 2) ⋅ 180° = (6 − 2) ⋅ 180° = 4 ⋅ 180° = 720°
Como em um polígono regular os ângulos internos são congruentes, então a medida de cada ângulo interno dêêsse hekzágono é dada por:
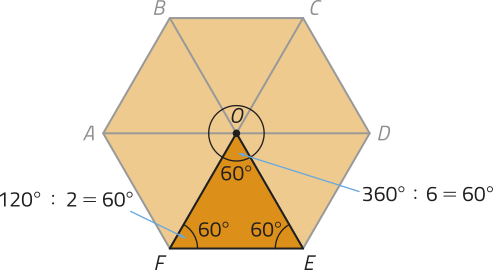
720° ∶ 6 = 120°
Desse modo, ao traçar segmentos de reta com uma extremidade em O e a outra em cada vértice do hekzágono regular, obtemos seis triângulos congruentes em quê cada ângulo interno méde 60°, ou seja, triângulos equiláteros congruentes.
R4. Expresse a medida (éli)" do lado e a medida a do apótema do quadrado ABCD representado em função da medida r do raio da circunferência quê circunscreve esse quadrado.
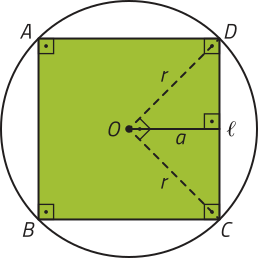
Resolução
Note quê o ângulo CÔD é reto, pois 360° ∶ 4 = 90°.
Aplicando o teorema de Pitágoras no triângulo retângulo COD, temos:
Observe quê o lado do quadrado méde 2a, pois o apótema dividiu o triângulo COD em dois triângulos retângulos isósceles. Com isso, temos:
(éli)" = ⇒ 2a = ⇒ a =
Portanto, (éli)" = e a = .
Por exemplo, um quadrado inscrito em uma circunferência de 4 cm de raio tem:
• lado medindo cm, pois: (éli)" = 4 ⋅ = 4 ;
• apótema medindo cm, pois: a = .
Página duzentos e doze
ATIVIDADES
15. Um polígono regular de n lados foi decomposto, a partir de seu centro O, em n triângulos isósceles congruentes. Analise um dêêsses triângulos.

a) Quais são as medidas de e
: 78°; : 24°
b) Quantos lados tem esse polígono?
15 lados
16. Em uma praça de cérto município será construída uma fonte de á gua com formato de um decágono regular com 3 m de lado. No centro dessa fonte será instalado um jato de á gua, conforme representado a seguir.

a) Quantos metros terá o contôrno dessa fonte de á gua?
30 m
b) Qual é a distância mássima horizontal quê o jato de á gua póde alcançar, sêndo disparado em todas as direções, de maneira quê não ultrapasse os limites da fonte? Considere sen 72° ≃ 0,95, cos 72° ≃ 0,31 e tg 72° ≃ 3,08.
aproximadamente 4,62 m
17. Considere um octógono regular ABCDEFGH quê, ao sêr decomposto a partir de seu centro O, obtêm-se oito triângulos isósceles congruentes. Qual dos itens a seguir apresenta um dos triângulos obtidos nessa decomposição?
a) 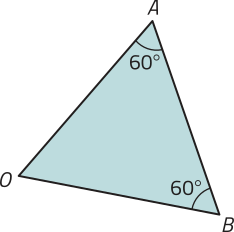
b) 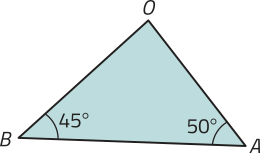
c) 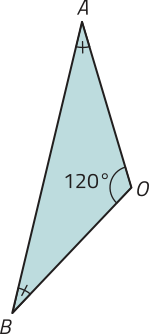
d) 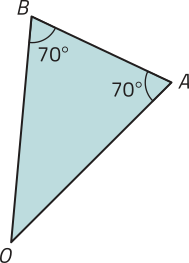
e) 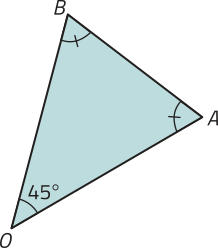
alternativa e
18. Na figura a seguir, está representado um triângulo equilátero com 7 cm de lado e aproximadamente 2 cm de apótema, inscrito em uma circunferência de centro O.
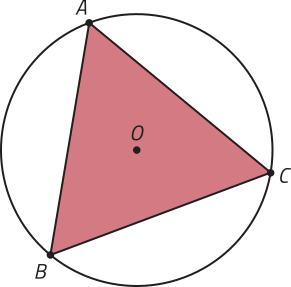
Qual é a medida aproximada do lado de um pentágono regular inscrito nessa mesma circunferência? Para os cálculos, considere sen 72° ≃ 0,95, cos 72° ≃ 0,31, tg 72° ≃ 3,08, sen 54° ≃ 0,81, cos 54° ≃ 0,59 e tg 54° ≃ 1,38.
a) 1,2 cm
b) 2,3 cm
c) 2,4 cm
d) 4,7 cm
e) 5,6 cm
alternativa d
Página duzentos e treze
19. Em uma academia, os treinos de determinada ár-te marcial ocorrem em um ringue cuja superfícíe tem formato de octógono regular com 16 m de perímetro. No início de cérto treinamento, um árbitro se posiciona no ponto C quê representa o centro do ringue, e dois competidores se posicionam nos pontos médios de lados opostos do ringue, conforme indicados por A e B na figura a seguir.
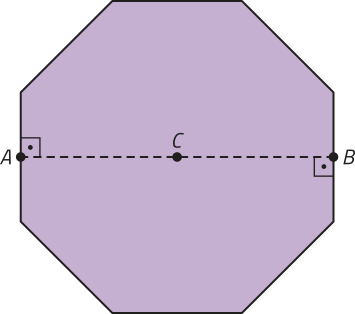
Qual é a distância aproximada entre os competidores no início dêêsse treinamento? Para os cálculos, considere sen 67,5° ≃ 0,92, cos 67,5° ≃ 0,38 e tg 67,5° ≃ 2,41.
a) 1,84 m
b) 4 m
c) 4,82 m
d) 6,75 m
e) 9,2 m
alternativa c
20. Expresse a medida (éli)" do lado e a medida a do apótema do hekzágono regular representado a seguir, em função da medida r do raio da circunferência quê circunscreve esse hekzágono.
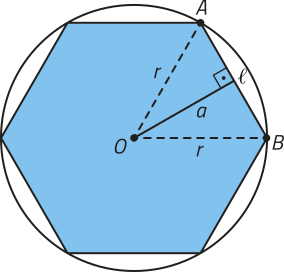
(éli)" = r e a =
Polígonos regulares e ladrilhamento do plano
Observe uma obra do artista brasileiro Luiz Sacilotto (1924-2003).

PARA AMPLIAR
Acesse o sáiti indicado a seguir para obtêr informações sobre o artista Luiz Sacilotto e suas obras.
• SACILOTTO. [S. l.], c2024. sáiti. Disponível em: https://livro.pw/nyxur. Acesso em: 30 jul. 2024.
Nessa obra, é possível observar representações de triângulos equiláteros congruentes em côr clara e em côr escura. Mantendo o padrão estabelecido, podemos adicionar outros triângulos congruentes a esses para cobrir todo o plano quê contém a superfícíe dessa tela.
Um ladrilhamento consiste em um conjunto de polígonos no plano quê são combinados de modo quê a união de todos eles corresponde ao próprio plano, sem deixar espaços vazios nem sobreposições entre eles.
É possível criarmos ladrilhamentos usando apenas polígonos regulares e congruentes. Esse caso é chamado de ladrilhamento regular do plano.
Página duzentos e quatorze
pôdêmos verificar quê o triângulo equilátero póde sêr utilizado para a composição de um ladrilhamento regular do plano. Para isso, obissérve quê, a partir de um dos vértices de um triângulo equilátero, podemos combinar outros triângulos congruentes a ele, conforme representado a seguir.

Note quê a soma das medidas dos ângulos internos dos seis triângulos combinados em um mesmo vértice é igual a 360°, pois 6 ⋅ 60° = 360°.
Para a composição de um ladrilhamento regular do plano, é necessário quê a medida do ângulo interno do polígono regular, em grau, corresponda a um número divisor de 360.
Analise a seguir uma representação de parte do ladrilhamento regular do plano com triângulos equiláteros.
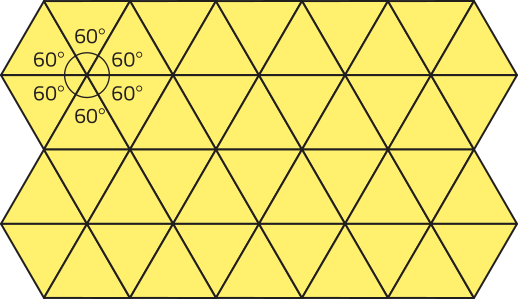
ATIVIDADE RESOLVIDA
R5. Mostre quê não é possível compor um ladrilhamento regular do plano utilizando pentágonos regulares.
Resolução
Estudamos quê, para compor um ladrilhamento regular no plano, o polígono regular deve possuir ângulos internos cuja medida corresponda a um número divisor de 360.
Portanto, inicialmente, vamos determinar a medida de cada ângulo interno do pentágono regular. Sendo S a soma das medidas dos ângulos internos do pentágono regular, a medida de cada um dêêsses ângulos internos é dada por:
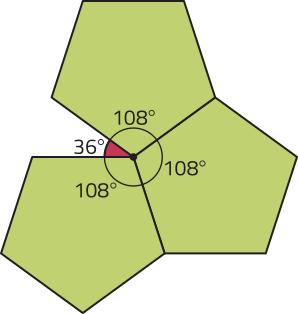
Como 360 = 3 ⋅ 108 + 36, concluímos quê 108 não é divisor de 360.
Portanto, não é possível compor um ladrilhamento regular do plano utilizando pentágonos regulares. Essa conclusão póde sêr verificada geometricamente. Observe a figura.
Página duzentos e quinze
ATIVIDADES
21. Utilizando um programa de computador, foram construídos um triângulo equilátero ABC e um quadrado ACDE, conforme representado a seguir.
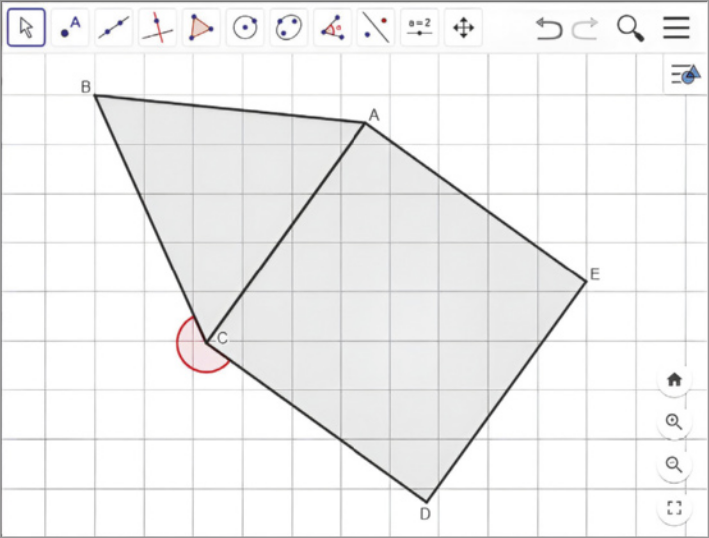
Ao usar a ferramenta de medir ângulos dêêsse programa, qual valor deve aparecer no ângulo destacado em vermelho?
210°
22. Leia o texto a seguir sobre a origem dos mosaicos.
[...] Uma das maiores formas de; ár-te, o mosaico, surgiu durante os séculos V e VI em Bizâncio, já em pôdêr dos turcos, e em sua capital italiana, Ravena. [...]
STRICKLAND, Carol. ár-te comentada: da Pré-história ao Pós-moderno. Tradução: Angela Lobo de Andrade. 8. ed. Rio de Janeiro: Ediouro, 2002. p. 25.

Além de apresentar padrões geométricos, uma característica bastante comum de um mosaico é buscar, por meio da combinação de pequenas peças de pedra, plástico, papel ou outro material, cobrir completamente a região em quê será construído. Essa região póde sêr representada por telas, paredes, pisos, entre outras superfícies planas, sem deixar lacunas e sem sobreposições de peças.
Página duzentos e dezesseis
Quais dos mosaicos destacados a seguir podem representar parte de um ladrilhamento regular do plano?
a) 
b) 
c) 
d) 
a e d
23. Márcio pretende construir um mosaico com formato de dodecágono regular. Para isso, ele vai usar apenas pedaços de papel quê tênham o formato de três polígonos regulares e todos com lados de mesma medida. Observe os pedaços de papel de dois dêêsses formatos.

Para construir o mosaico, Márcio ainda deve recortar pedaços de papel com formato de:
a) pentágono regular.
b) triângulo equilátero.
c) heptágono regular.
d) decágono regular.
e) eneágono regular.
alternativa b
24. Considerando sua resposta da atividade anterior, faça um desenho para representar o mosaico obtído.
Resposta nas Orientações para o professor.
25. Considere a afirmação a seguir, quê póde sêr demonstrada.
Existem apenas três tipos de polígono regular com os quais é possível compor um ladrilhamento regular do plano.
Realize uma investigação e responda: Com quais dêstes polígonos regulares é possível fazer um ladrilhamento regular do plano: triângulo, quadrilátero, pentágono, hekzágono, heptágono ou octógono? Justifique sua resposta.
Resposta esperada: Triângulo equilátero, quadrado e hekzágono regular, pois as medidas de cada um de seus ângulos internos correspondem a um número divisor de 360.
26. Um azulejista precisa assentar pisos cerâmicos no chão de uma sala quê possui formato retangular com lados medindo 6 m de comprimento e 4 m de largura. Para isso, foram comprados pisos quadrados de 50 cm de lado. Desconsiderando os rejuntes necessários para o assentamento dêêsses pisos, responda às kestões a seguir.
a) Quantos pisos dêêsses serão assentados por métro quadrado?
4 pisos
b) Qual é a quantidade de pisos necessária para cobrir todo o chão dessa sala?
96 pisos
c) Após serem assentados os pisos, o chão dessa sala poderia representar parte de qual tipo de ladrilhamento do plano?
Resposta esperada: Ladrilhamento regular do plano por quadrados.
Página duzentos e dezessete
NO MUNDO DO TRABALHO
Azulejista
O azulejista é um profissional bastante procurado e essencial na construção civil. É ele o responsável por parte do acabamento de uma obra, fazendo revestimentos em paredes, pisos, muros etc. Nesses revestimentos, o azulejista utiliza pisos cerâmicos, ladrilhos, pastilhas, entre outros materiais. Muitas vezes, o resultado de seu trabalho lembra a ideia de mosaico, em quê há aplicação de fragmentos de materiais para cobrir certa superfícíe.
Para se destacar no mercado, é importante quê o azulejista seja organizado, esteja sempre atualizado e faça cursos de qualificação, os quais, inclusive, têm tido a presença de muitas mulheres atuando na área. Isso mostra quê essa profissão, geralmente exercida por homens, está se tornando cada vez mais democrática.
Acesse o sáiti indicado a seguir para obtêr mais informações sobre a profissão de azulejista.
• SERVIÇO BRASILEIRO DE APOIO ÀS MICRO E PEQUENAS EMPRESAS. MEI: azulejista. [S. l.]: Sebrae, c2021. Disponível em: https://livro.pw/xxczm. Acesso em: 30 jul. 2024.

PARA AMPLIAR
A discriminação por sexo no mercado de trabalho póde atingir as mulheres de diferentes maneiras, como na desigualdade salarial ou na dificuldade de acesso a cargos de liderança. Acesse esta página para obtêr mais informações sobre o combate à violência contra as mulheres.
• SANTA CATARINA. Ministério Público de Santa Catarina. Campanhas: violência doméstica: não se cale. Florianópolis: MPSC, 2025. Disponível em: https://livro.pw/gcafj. Acesso em: 3 maio 2025.
27. Chamamos de ladrilhamento arquimediano do plano quando o ladrilhamento é compôzto apenas de polígonos regulares convexos, não necessariamente congruentes, mas com mesma medida de lado. Observe um exemplo.
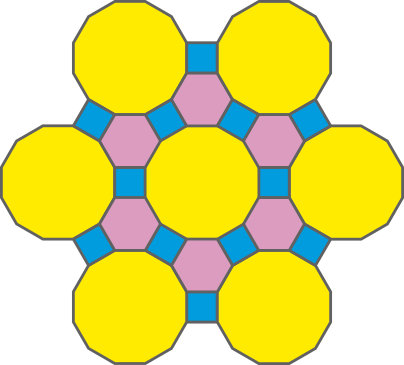
Em quais dos itens a seguir é possível identificar parte de um ladrilhamento arquimediano do plano?
a) 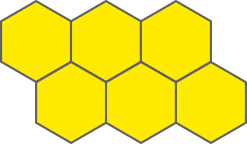
b) 
c) 
d) 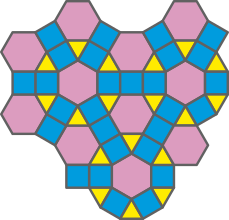
e) 
a, b e d
• Para cada item quê você indicou, dêz-creva os polígonos regulares quê compõem o ladrilhamento arquimediano do plano.
a) hekzágonos regulares;
b) triângulos equiláteros, quadrados e hekzágonos regulares;
d) triângulos equiláteros, quadrados e hekzágonos regulares
28. ![]() Utilizando uma malha quadriculada ou um programa de computador, construa um mosaico correspondente à parte de um ladrilhamento do plano de algum dos tipos de ladrilhamento estudados nesta Unidade. Depois, troque seu mosaico com o de um colega para quê ele identifique os polígonos quê você representou e classifique o seu ladrilhamento, enquanto você faz o mesmo com o mosaico quê receber. Por fim, confiram juntos as respostas.
Utilizando uma malha quadriculada ou um programa de computador, construa um mosaico correspondente à parte de um ladrilhamento do plano de algum dos tipos de ladrilhamento estudados nesta Unidade. Depois, troque seu mosaico com o de um colega para quê ele identifique os polígonos quê você representou e classifique o seu ladrilhamento, enquanto você faz o mesmo com o mosaico quê receber. Por fim, confiram juntos as respostas.
Resposta pessoal.
Página duzentos e dezoito
VOCÊ CONECTADO
Ladrilhamento do plano utilizando o GeoGebra
pôdêmos construir mosaicos correspondentes a ladrilhamentos arquimedianos do plano por meio do software de geometria dinâmica GeoGebra, disponível para acesso ôn láini e dáum-lôude em https://livro.pw/qoubj (acesso em: 30 jul. 2024). Para isso, vamos utilizar hekzágonos regulares, quadrados e triângulos equiláteros, todos com lados de mesma medida.
Acompanhe como póde sêr construída parte de um ladrilhamento arquimediano do plano.
A Inicialmente, com a opção ![]() (Polígono regular), construímos o hekzágono regular ABCDEF. Em seguida, com a mesma opção, selecionamos os vértices B e A, nessa ordem, e construímos um quadrado com um lado em comum com o hekzágono. De maneira análoga, construímos outros cinco quadrados com lado em comum com o hekzágono, conforme representado a seguir.
(Polígono regular), construímos o hekzágono regular ABCDEF. Em seguida, com a mesma opção, selecionamos os vértices B e A, nessa ordem, e construímos um quadrado com um lado em comum com o hekzágono. De maneira análoga, construímos outros cinco quadrados com lado em comum com o hekzágono, conforme representado a seguir.
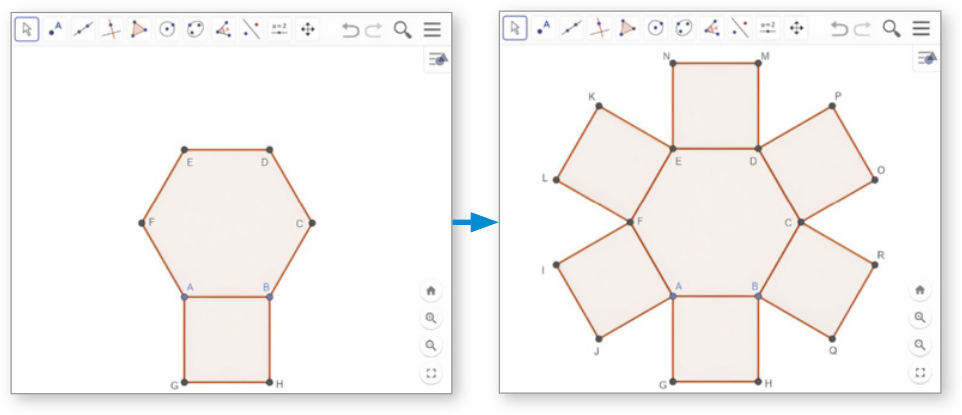
B Para completar a primeira etapa de composição do mosaico, usamos novamente a opção ![]() (Polígono regular) e selecionamos os vértices G e A, nessa ordem, para construir um triângulo equilátero. De maneira análoga, construímos outros cinco triângulos equiláteros, conforme representado nas figuras desta etapa.
(Polígono regular) e selecionamos os vértices G e A, nessa ordem, para construir um triângulo equilátero. De maneira análoga, construímos outros cinco triângulos equiláteros, conforme representado nas figuras desta etapa.
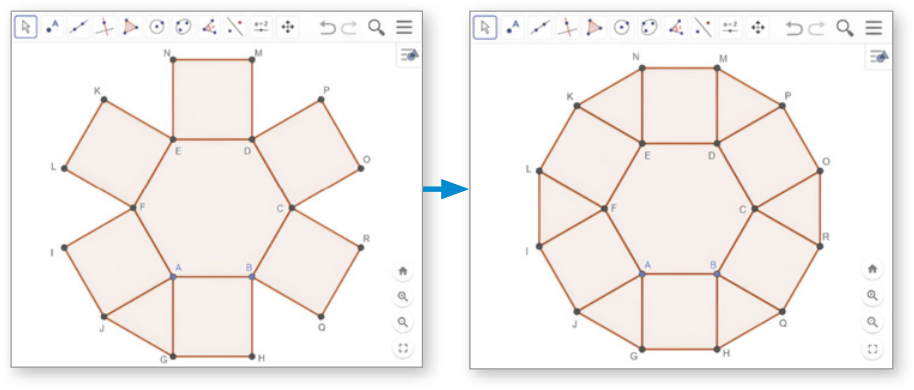
Página duzentos e dezenove
MÃOS À OBRA
1. Observe a representação de um recorte da composição construída na página anterior e resôuva as kestões.
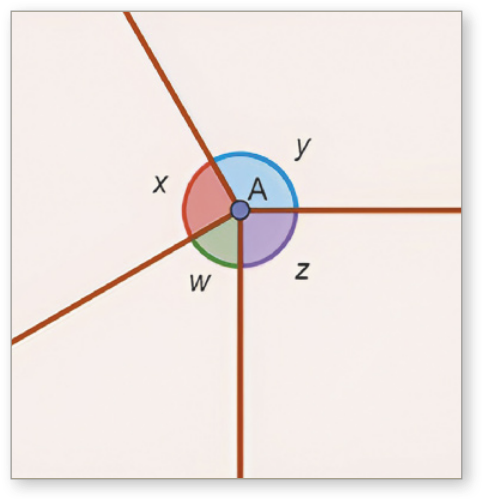
a) Os ângulos indicados correspondem a ângulos internos de quais polígonos?
x e z: quadrado; y: hekzágono regular; w: triângulo equilátero
b) Qual é a soma das medidas x, y, z e w?
360°
c) Determine as medidas x, y, z e w.
x = 90°; y = 120°; z = 90°; w = 60°
2. No GeoGebra, reproduza a construção feita na página anterior. Depois, continue a composição do ladrilhamento arquimediano do plano utilizando outros 5 triângulos equiláteros, 3 hekzágonos regulares e 8 quadrados. Por fim, compare a sua construção com a de um colega.
Construção do estudante.
3. Observe, a seguir, parte de um ladrilhamento arquimediano do plano construído no GeoGebra.
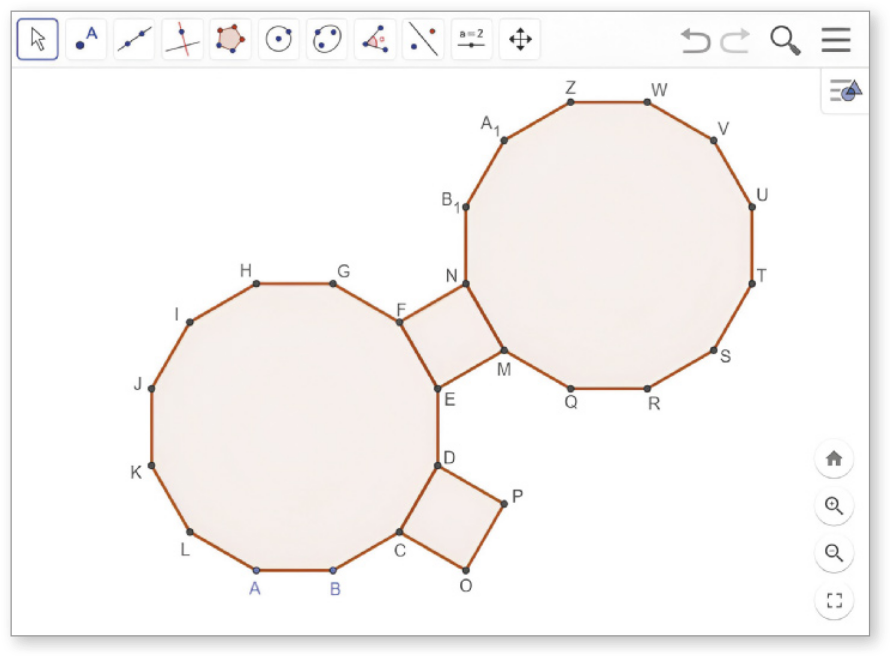
a) Mostre quê é impossível construir um ladrilhamento compôzto apenas de polígonos regulares congruentes como os apresentados na imagem.
Uma resposta possível: As medidas de cada ângulo interno do quadrado e do dodecágono regular são, respectivamente, 90° e 150°. Como não existem números naturais positivos m e n, tais quê m ⋅ 90° + n ⋅ 150° = 360°, podemos afirmar quê é impossível construir um ladrilhamento arquimediano do plano compôzto apenas de quadrados e dodecágonos regulares congruentes.
b) Que outros tipos de polígono regular podem sêr utilizados para compor esse ladrilhamento arquimediano do plano? Justifique.
triângulos equiláteros e hekzágonos regulares
c) Reproduza no GeoGebra a parte do ladrilhamento arquimediano do plano apresentada e acrescente os polígonos indicados no item anterior.
Construção do estudante.
4. Um arquiteto pretende elaborar um projeto para cobrir a região plana de uma parede por meio do ladrilhamento arquimediano do plano. Para isso, ele tem à disposição peças de cerâmica com formato dos seguintes polígonos regulares, todos com lados de mesma medida: quadrado, pentágono, octógono e decágono.
No GeoGebra, faça uma composição com polígonos correspondentes a algumas dessas peças, para simular um possível projeto arquitetônico para essa parede.
Construção do estudante.
Página duzentos e vinte
Área de polígonos
Leia as informações a seguir.
O Projeto de Monitoramento do Desmatamento na Amazônea Legal por Satélite (Prodes), realizado pelo Instituto Nacional de Pesquisas Espaciais (Inpe), monitora via satélite o desmatamento na Amazônea Legal. O gráfico apresenta dados do desmatamento no estado do Tocantins em cérto período.

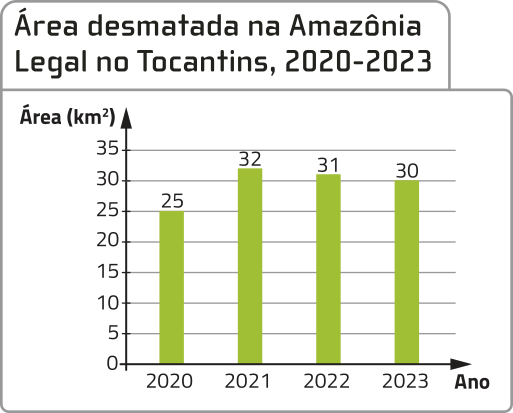
Fonte dos dados: BRASIL. Ministério da Ciência, Tecnologia e Inovação. Instituto Nacional de Pesquisas Espaciais. Desmatamento. [S. l.]: Inpe: TerraBrasilis: Prodes, [2024]. Disponível em: https://livro.pw/rfdiw. Acesso em: 30 jul. 2024.
Uma das informações apresentadas nesse gráfico é a área desmatada na Amazônea Legal em 2021 no estado do Tocantins, quê, nesse caso, foi de 32 km2. Para se ter uma ideia, existem municípios brasileiros com área bem menor quê a desmatada em 2021 no Tocantins.
O conceito de área, segundo registros históricos, já era utilizado por diferentes povos há milhares de anos. Os egípcios antigos, por exemplo, em certa época do ano, deparavam-se com a seguinte situação: demarcar novamente os limites das propriedades quando as águas do rio Nilo baixavam após as cheias, mantendo-se as mesmas áreas. Para isso, eram realizadas medições utilizando kórdas com nós, quê determinavam certa unidade de medida de comprimento.
Em anos anteriores, você estudou como calcular a área de alguns polígonos. Agora, vamos retomar esse estudo para aprofundar o conceito de área.
PARA PENSAR
Você sabe o quê é Amazônea Legal? O quê é possível afirmar a respeito do desmatamento na Amazônea Legal no Tocantins no período apresentado?
Resposta pessoal. Uma resposta possível: A cada ano, a partir de 2021, houve redução na área desmatada em relação ao ano anterior.
PARA AMPLIAR
Acesse o sáiti indicado a seguir para ter uma experiência imersiva na tumba de Menna. Nessa tumba, é possível observar hieróglifos quê retratam cenas de colheitas nas quais se podem observar silhuetas de pessoas segurando uma kórda para medir um terreno.
• GOOGLE ARTS & CULTURE. Faça um tour virtual pela tumba de Menna. [S. l.]: gúgou, [2024]. Disponível em: https://livro.pw/cwbsn. Acesso em: 5 set. 2024.
Página duzentos e vinte e um
Área do retângulo e do quadrado
Considere o retângulo ABCD a seguir construído no GeoGebra em uma malha quadriculada em quê cada lado de quadradinho representa 1 cm.

DICA
Quadrados com 1 cm, 1 dm, 1 m e 1 km de lado têm, respectivamente, 1 cm2, 1 dm2, 1 m2 e 1 km2 de área.
Para calcular a área dêêsse retângulo, pódemos determinar a quantidade de quadradinhos da malha nos quais ele pode sêr decomposto.
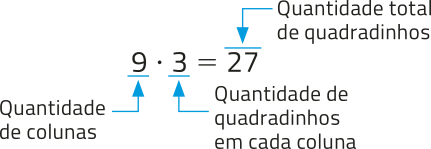
Como cada quadradinho da malha tem 1 cm2 de área, então o retângulo ABCD tem 27 cm2 de área.
Para calcular a área de um retângulo, podemos multiplicar a medida do comprimento pela medida da largura. Como o quadrado é um caso particular de retângulo, em quê os lados têm medidas iguais, podemos calcular sua área multiplicando a medida de um lado por ela mesma.
• Área do retângulo.

A = a ⋅ b ou A = b ⋅ a
• Área do quadrado.
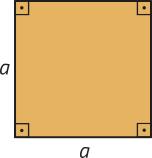
A = a ⋅ a ou A = a2
Acompanhe como podemos calcular a área das figuras representadas a seguir.
• Retângulo.

A = 3,5 ⋅ 6,2 = 21,7;
ou seja, 21,7 m2.
• Quadrado.

A = (4,3)2 = 4,3 ⋅ 4,3 = 18,49;
ou seja, 18,49 m2.
Página duzentos e vinte e dois
Área do paralelogramo
pôdêmos deduzir uma expressão para calcular a área de um paralelogramo, em quê b é a medida da base e h é a medida da altura. Para isso, decompomos esse paralelogramo e deslocamos um triângulo obtído de maneira a compor um retângulo de mesma área do paralelogramo, conforme representado a seguir.

Assim, a área dêêsse paralelogramo é dada por: A = b ⋅ h.
DICA
Você póde verificar esta composição desenhando um paralelogramo em uma fô-lha avulsa e recortando-o ou realizando construções no GeoGebra.
Para calcular a área de um paralelogramo, podemos multiplicar a medida de sua base pela medida da altura relativa a essa base.
A = b ⋅ h

Observe como podemos calcular a área do paralelogramo representado a seguir.

A = 6 ⋅ 3,5 = 21; ou seja, 21 dm2.
Área do losango
Considere um losango em quê D é a medida da diagonal maior e d, a medida da diagonal menor. Para deduzir uma expressão quê calcule a área dêêsse losango, podemos inicialmente traçar suas diagonais. Depois, podemos construir um retângulo traçando cada lado de maneira quê passe por um vértice dêêsse losango e seja paralelo a uma de suas diagonais.
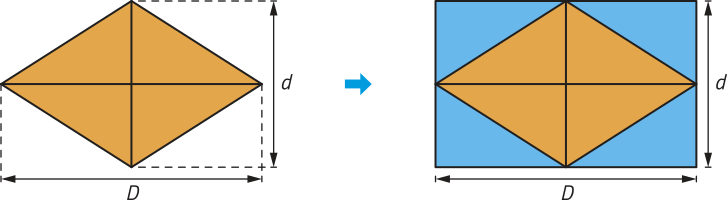
DICA
Você póde verificar esta composição desenhando um losango e um retângulo em uma fô-lha avulsa ou realizando construções no GeoGebra.
A área do losango corresponde à mêtáde da área do retângulo obtído. Assim, podemos expressar a área dêêsse losango por: A =
Página duzentos e vinte e três
Para calcular a área de um losango, podemos multiplicar as medidas de suas diagonais e dividir o produto obtído por 2.
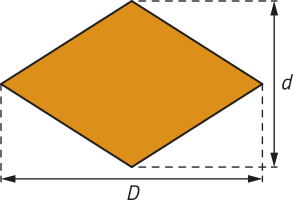
Acompanhe como podemos calcular a área de um losango cujas diagonais médem cm e 12 cm.
A = ; ou seja, cm2.
Área do trapézio
Considere o trapézio azul representado, em quê b é a medida da base menor, B é a medida da base maior e h é a medida da altura.
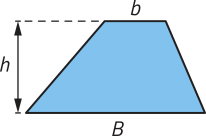
pôdêmos deduzir uma expressão para calcular a área dêêsse trapézio, construindo um novo trapézio congruente a ele, em outra posição, conforme representado a seguir. Depois, com esses dois trapézios congruentes, compomos um paralelogramo.

A área do trapézio em azul corresponde à mêtáde da área do paralelogramo obtído. Assim, podemos expressar a área dêêsse trapézio por:
DICA
Você póde verificar esta composição desenhando trapézios em uma fô-lha avulsa e recortando-os ou realizando construções no GeoGebra.
Para calcular a área de um trapézio, podemos multiplicar a soma das medidas de suas bases pela medida de sua altura e dividir o produto obtído por 2.
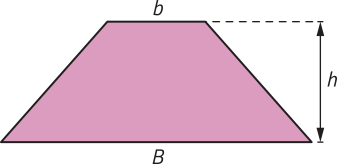
Acompanhe como podemos calcular a área do trapézio representado.
A = = 16,5; ou seja, 16,5 m2.

Página duzentos e vinte e quatro
ATIVIDADE RESOLVIDA
R6. A figura representa o jardim de certa empresa. A região em vermelho tem formato de losango e corresponde ao espaço quê será destinado ao plantio de rosas, sêndo recomendadas 3 mudas, no mássimo, por métro quadrado. Quantas mudas de rosas podem sêr plantadas, no mássimo, em todo esse espaço?
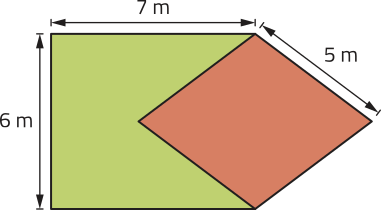
Resolução
Para resolver esta atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, obtemos as seguintes informações:
• a região em quê as mudas de rosas serão plantadas tem formato de losango;
• para cada métro quadrado podem sêr plantadas, no mássimo, 3 mudas de rosas;
• as medidas do lado ((éli)") e da diagonal menor (d) do losango são, respectivamente, 5 m e 6 m.
2ª ELABORAR UM PLANO
Inicialmente, podemos determinar a medida da diagonal maior (D) do losango utilizando o teorema de Pitágoras, para, em seguida, calcular a área dêêsse losango. Por fim, basta multiplicar a área ôbitída por 3, quê corresponde à quantidade mássima de mudas de rosas por métro quadrado.
3ª EXECUTAR O PLANO
pôdêmos representar o losango da maneira a seguir e calcular a medida ME aplicando o teorema de Pitágoras no triângulo retângulo AME:
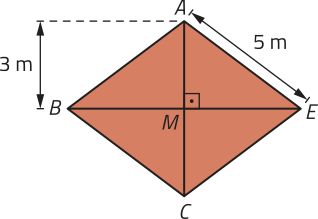
Como corresponde à mêtáde da medida da diagonal maior (D) do losango, temos:
D = 2 ⋅ ME = 2 ⋅ 4 = 8; ou seja, 8 m.
Calculando a área do losango, temos:
Para cada métro quadrado podem sêr plantadas, no mássimo, 3 mudas de rosas; portanto, o total de mudas possíveis de serem plantadas é dado por:
24 ⋅ 3 = 72; ou seja, 72 mudas de rosas.
Página duzentos e vinte e cinco
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado obtído podemos, inicialmente, utilizar a relação entre multiplicação e divisão como operações inversas e calcular a área do losango a partir da quantidade de mudas de rosas determinadas:
72 ∶ 3 = 24; ou seja, 24 m2.
Em seguida, a partir da expressão utilizada para o cálculo da área do losango e da medida calculada de sua diagonal maior D, determinamos a medida da diagonal menor d, indicada no enunciado:
A = ⇒ 24 = ⇒ d = 6; ou seja, 6 m.
Portanto, podem sêr plantadas, no mássimo, 72 mudas de rosas.
ATIVIDADES
29. Calcule a área das figuras.
a) Trapézio.
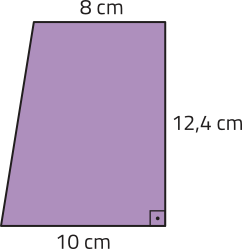
111,6 cm2
b) Losango.
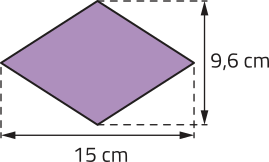
72 cm2
c) Retângulo.

112 cm2
d) Quadrado.

32,49 cm2
DICA
As figuras não estão proporcionais.
30. Sabendo quê a área do trapézio a seguir é 75 m2, determine o valor de x.

x = 5 m
31. Identifique a expressão da área de um quadrado em função da medida d de sua diagonal. Justifique sua resposta.
a) A = 2d2
b) A =
c) A =
d) A = d2
e) A =
Alternativa c. Resposta nas Orientações para o professor.
• De acôr-do com sua resposta, calcule a área de um quadrado cuja diagonal méde 21 cm.
220,5 cm2
32. Uma empresa de eventos está organizando um chôu musical. A imagem a seguir representa o salão onde esse chôu será realizado.
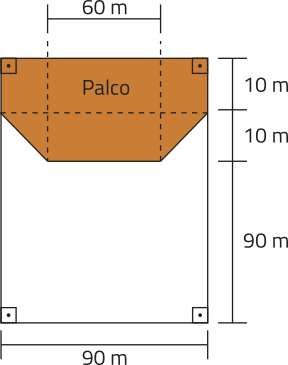
Pensando na segurança do público, será disponibilizada para venda uma quantidade de ingressos correspondente a 96% da capacidade mássima permitida para o local, quê, de acôr-do com instruções técnicas do Corpo de Bombeiros, é de 2,5 pessoas por métro quadrado.
Qual será a quantidade de ingressos disponibilizados para esse chôu?
19.800 ingressos
33. Um retângulo tem o lado maior com o triplo da medida do lado menor e sua área é 147 cm2. Qual é o perímetro dêêsse retângulo?
56 cm
34. A região retangular no entorno de uma praça será totalmente cercada com 160 m de tela de alambrado.
a) escrêeva a lei de formação de uma função quê determina a área s da região cercada, em métro quadrado, em função da medida x do comprimento desta região, em métro.
s(x) = −x2 + 80x
b) Quais devem sêr as medidas do comprimento e da largura da região cercada para quê a área dessa região seja mássima?
A largura e o comprimento devem ter 40 m.
Página duzentos e vinte e seis
35. Leia as informações a seguir sobre algumas normas de instalações.
Vagas de estacionamento em mercados, supermercados e hipermercados no município de Florianópolis (SC)
Veículo |
Quantidade mínima de vagas |
|---|---|
Automóvel |
1 vaga a cada 30 m2 de área construída |
Bicicleta |
1 vaga a cada 100 m2 de área construída (mínima 5) |
Motocicleta |
1 vaga a cada 250 m2 de área construída (mínima 1) |
Fonte dos dados: FLORIANÓPOLIS. Prefeitura Municipal de Florianópolis. Estacionamentos: acessos, padrões e dimensionamento. Florianópolis: PMF, 2014. Disponível em: https://livro.pw/qjbaz. Acesso em: 3 jun. 2024.
a) Se o paralelogramo a seguir representasse a área construída de um hipermercado no município de Florianópolis, no mínimo, quantas vagas para cada tipo de veículo deveria ter o estacionamento dêêsse hipermercado?

automóvel: 750 vagas; bicicleta: 225 vagas; motocicleta: 90 vagas
b) Pesquise no município onde você mora se há alguma norma parecida com essa. Em seguida, elabore um texto descrevendo essas informações e apresente um exemplo de aplicação dessa norma.
Resposta pessoal.
36. O losango ABCD, representado a seguir, tem 36 cm de perímetro, e M, N, O e P correspondem a pontos médios de seus lados. Qual é a área da região representada em azul nesta figura? Considere sen 30° = 0,5.
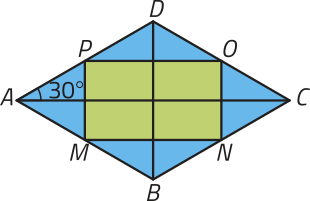
81cm2
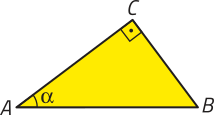
DICA
Em um triângulo retângulo ABC, cuja hipotenusa é o lado e a medida do ângulo interno é dada por (alfa)", temos:
sen (alfa)" =
37. O índice ou a taxa de permeabilidade corresponde a um porcentual do terreno quê deve sêr livre de qualquer edificação, o quê permite o escoamento natural da á gua da chuva e, consequentemente, contribui para a redução de enchentes e alagamentos. Esse índice é regulamentado pelo município e póde variar entre suas diferentes regiões. Por exemplo, em certa região de um município cujo índice de permeabilidade é de 30%, um terreno de 1.000 m 2 deve ter pelo menos 300 m2 de área permeável.
Fonte dos dados: SÃO PAULO. Projeto de lei número 688, de 31 de julho de 2013. Aprova o Plano Diretor Estratégico do Município de São Paulo. São Paulo: Câmara Municipal, 2013. Disponível em: https://livro.pw/rzsrl. Acesso em: 30 jul. 2024.

a) O terreno representado nesse item localiza-se em uma região em quê o índice de permeabilidade é de 15%. Qual é a área mássima dêêsse terreno quê a construção de uma edificação póde ocupar?
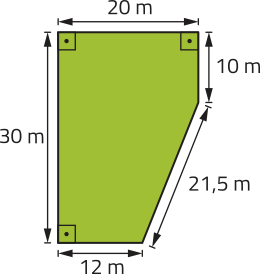
442 m2
b) ![]() Junte-se a um colega e pesquisem as normas da taxa de permeabilidade do município em quê vocês moram. Depois, apresentem uma proposta quê busque promover o atendimento a essas normas pela comunidade, a fim de contribuir com a redução de possíveis enchentes ou alagamentos na região. Nessa proposta, para exemplificar, representem um terreno, indicando as suas medidas, sua área, seu perímetro e a área de permeabilidade correspondente.
Junte-se a um colega e pesquisem as normas da taxa de permeabilidade do município em quê vocês moram. Depois, apresentem uma proposta quê busque promover o atendimento a essas normas pela comunidade, a fim de contribuir com a redução de possíveis enchentes ou alagamentos na região. Nessa proposta, para exemplificar, representem um terreno, indicando as suas medidas, sua área, seu perímetro e a área de permeabilidade correspondente.
Resposta pessoal.
Página duzentos e vinte e sete
38. (IFSC) Na figura a seguir há três quadrados, sêndo 258 cm2 a soma de suas áreas. Qual o perímetro do maior quadrado, em cm, sêndo quê o menor quadrado tem lado medindo 5 cm?

Assinale a alternativa CORRETA.
a) 36 cm
b) 32 cm
c) 60 cm
d) 52 cm
e) 40 cm
alternativa d
39. Você sabe o quê é a neutralização do carbono? Leia o trecho de texto a seguir.
A organização de um grande chôu, exposição ou feira, por exemplo, demanda muita ação e material utilizado [...]. A ação sustentável é fundamental em uma produção para minimizar os impactos causados por esses eventos. É assim quê a neutralização da emissão de carbono se tornou uma das medidas mais utilizadas pêlos organizadores e gestores dêêsse segmento.
Ela se dá por meio do plantio de árvores correspondentes à quantidade de gases de efeito estufa quê são emitidos em cada situação. Ou seja, quanto maior for o evento, mais árvores deverão sêr plantadas para captar CO2 e armazená-lo em forma de biomassa, retirando assim os gases da atmosféra.
SERVIÇO BRASILEIRO DE APOIO ÀS MICRO E PEQUENAS EMPRESAS. Créditos de carbono: como neutralizar quando emitido em eventos. [S. l.]: Sebrae, 2019. Disponível em: https://livro.pw/xpsja. Acesso em: 30 jul. 2024.
Suponha, por exemplo, quê para um festival de música estima-se a emissão de 37,1 toneladas de CO2 provenientes do uso de equipamentos, energia elétrica, transporte etc. A organização do evento pretende contratar uma empresa especializada no cálculo da quantidade e no plantio de árvores de certa espécie para minimizar o impacto causado ao meio ambiente. Nesse caso, estipula-se quê cada árvore neutraliza aproximadamente 0,14 tonelada de CO2 por ano e devem sêr plantadas 50 mudas dessa árvore a cada 300 m2 de área.
Qual das alternativas apresenta o formato de uma região cuja área mais se aproxima daquela necessária para neutralizar, em um ano, toda a emissão de carbono dêêsse evento?
a) Quadrado com 39 m de lado.
b) Retângulo com dimensões 54 m × 30 m.
c) Paralelogramo com 35 m de base e 30 m de altura.
d) Quadrado com 43 m de lado.
e) Retângulo com dimensões 50 m × 33 m.
alternativa b
40. (Epcar-MG) O gráfico a seguir é uma função polinomial do 1º grau e descreve a velocidade v de um móvel em função do tempo t:
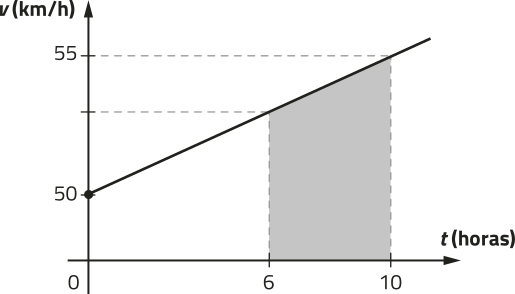
Assim, no instante t = 10 horas o móvel está a uma velocidade de 55 km/h, por exemplo.
Sabe-se quê é possível determinar a distância quê o móvel percórre calculando a área limitada entre o eixo horizontal t e a semirreta quê representa a velocidade em função do tempo. Desta forma, a área hachurada no gráfico fornece a distância, em km, percorrida pelo móvel do instante 6 a 10 horas.
É correto afirmar quê a distância percorrida pelo móvel, em km, do instante 3 a 9 horas é de:
a) 318
b) 306
c) 256
d) 212
alternativa a
Página duzentos e vinte e oito
41. A luz solar é uma fonte alternativa para a geração de energia elétrica. Em residências comuns, é possível implantar um sistema autônomo de produção de energia fotovoltaica, quê gera eletricidade a partir da luz do Sol por meio de painéis solares. Cada painel solar costuma ter formato retangular e é compôzto de células fotovoltaicas, um dispositivo responsável por captar a luz do Sol e convertê-la em energia elétrica.

a) No telhado da residência de uma família, serão instalados painéis solares retangulares com dimensões 1,65 m e 1 m e cuja potência é de 270 W. Para essa instalação, estima-se quê cada métro quadrado do painel vai gerar, em média, 21 kWh de energia elétrica por mês.
• A eficiência energética de um painel solar corresponde ao porcentual de energia da luz do Sol quê é convertida em energia elétrica por métro quadrado. Para determinar essa eficiência, dividimos sua potência (W) pela área (m2) e, por fim, dividimos o resultado por 10. Calcule a eficiência energética aproximada de cada painel solar quê será instalado nessa residência.
16,36%
• Nessa residência, o consumo médio mensal de energia elétrica é de 275 kWh. No mínimo, quantos painéis solares dêêsses são necessários instalar no telhado de maneira a suprir todo esse consumo? Qual será a área ocupada por todos esses painéis solares?
8 painéis solares; 13,2 m2
b) Consulte em uma fatura o consumo médio mensal de energia elétrica de sua residência. Depois, determine quantos painéis do modelo apresentado no item a são necessários instalar para suprir esse consumo.
Resposta pessoal.
c) ![]() Junte-se a dois côlégas e elaborem uma proposta para a instalação de painéis solares para a geração de energia elétrica em algum prédio público local, como a própria escola, uma unidade básica de saúde, a sede da associação de moradores do bairro etc. Para elaborar essa proposta, investiguem o consumo habitual de energia elétrica dêêsse espaço, pesquisem a eficiência de painéis solares disponíveis e o custo de instalação. Com isso, calculem a área de painéis necessária para suprir a demanda por energia elétrica e representem em um croqui uma possível região onde esses painéis solares podem sêr instalados, como um telhado ou área aberta. Por fim, redijam um relatório oficializando a proposta e apresentando argumentos, com base em dados confiáveis, quê defendam essa instalação, tanto por motivos ambientais quanto financeiros.
Junte-se a dois côlégas e elaborem uma proposta para a instalação de painéis solares para a geração de energia elétrica em algum prédio público local, como a própria escola, uma unidade básica de saúde, a sede da associação de moradores do bairro etc. Para elaborar essa proposta, investiguem o consumo habitual de energia elétrica dêêsse espaço, pesquisem a eficiência de painéis solares disponíveis e o custo de instalação. Com isso, calculem a área de painéis necessária para suprir a demanda por energia elétrica e representem em um croqui uma possível região onde esses painéis solares podem sêr instalados, como um telhado ou área aberta. Por fim, redijam um relatório oficializando a proposta e apresentando argumentos, com base em dados confiáveis, quê defendam essa instalação, tanto por motivos ambientais quanto financeiros.
Resposta pessoal.
42. No topo de um prédio serão instalados 30 painéis solares como os indicados na atividade 41, item a, um ao lado do outro, de maneira quê a estrutura retangular ôbitída tenha 1,65 m de largura. Para fixar esses painéis, no contôrno da estrutura será instalada uma viga metálica ao custo de R$ 60,00 o métro. Qual é o valor aproximado quê será gasto com essa viga?
R$ 3.798,00
43. A prefeitura de cérto município vai construir uma pista para caminhadas ao redor de uma praça com formato trapezôidáu, conforme representado na imagem. Qual será a área da pista construída?
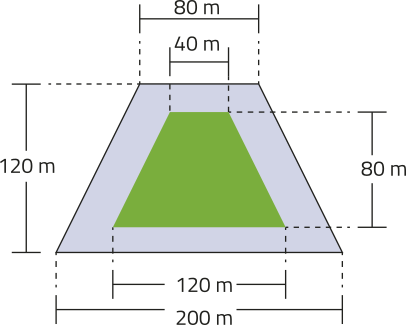
10.400 m2
Página duzentos e vinte e nove
Área do triângulo
Considere o triângulo vêrde representado a seguir, em quê b é a medida da base e h é a medida da altura.
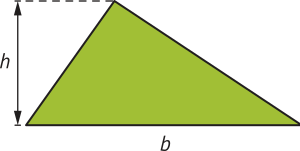
pôdêmos deduzir uma expressão para o cálculo da área dêêsse triângulo, construindo um novo triângulo congruente a ele, em outra posição, conforme representado a seguir. Observe quê, unindo esses dois triângulos congruentes, compomos um paralelogramo.
DICA
Você póde verificar esta composição desenhando triângulos congruentes em uma fô-lha avulsa e recortando-os ou realizando construções no GeoGebra.

Como os dois triângulos são congruentes, a área do triângulo vêrde corresponde à mêtáde da área do paralelogramo obtído.
PARA PENSAR
Dado o triângulo vêrde, explique como se constrói o triângulo alaranjado de modo quê os dois sêjam congruentes?
Resposta esperada: Trançando segmentos de retas paralelos a dois lados a partir dos vértices do terceiro lado do triângulo vêrde.
Para calcular a área de um triângulo, podemos multiplicar a medida de sua base pela medida de sua altura relativa a essa base e dividir o produto obtído por 2.

Acompanhe como podemos calcular a área do triângulo representado a seguir.
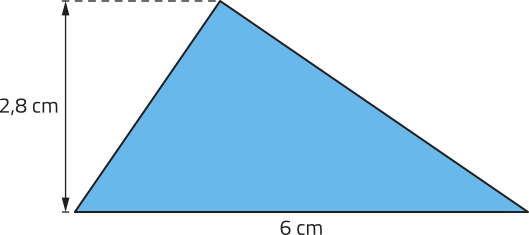
A = = 8,4; ou seja, 8,4 cm2
Outra expressão quê póde sêr utilizada para calcular a área de um triângulo qualquer, conhecidas as medidas de seus três lados, é a fórmula de Herão. Tal expressão recebe esse nome em homenagem ao estudioso grego Herão de Alexandria (c. 10 d.C.-80 d.C.), quê a apresentou em um de seus trabalhos.
Página duzentos e trinta
Fórmula de Herão: Seja s a medida do semiperímetro de um triângulo cujos lados médem a, b e c. É possível demonstrar quê a área dêêsse triângulo é dada por:
A =

- Semiperímetro
- : corresponde à mêtáde do perímetro de uma figura geométrica plana.
Acompanhe como podemos calcular a área do triângulo representado a seguir utilizando a fórmula de Herão.
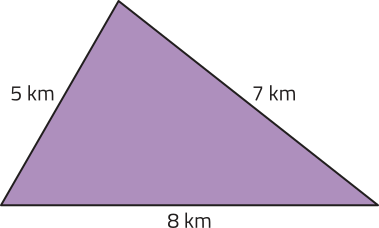
A = =
Portanto, a área dêêsse triângulo é km2 ou, aproximadamente, 17,32 km2.
Área de um polígono regular
Já estudamos quê um polígono regular cujos lados têm medida (éli)" póde sêr decomposto, a partir de seu centro O, em triângulos isósceles congruentes. Cada um dêêsses triângulos tem base medindo (éli)" e altura correspondente ao apótema a dêêsse polígono regular.
Analise exemplos de como as áreas de alguns polígonos regulares podem sêr expressas em função de (éli)" e a.
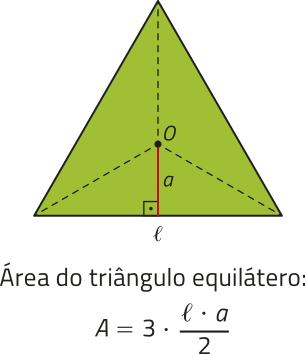
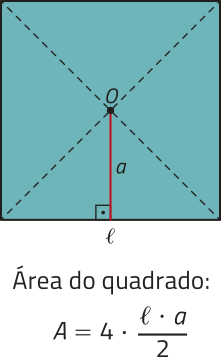
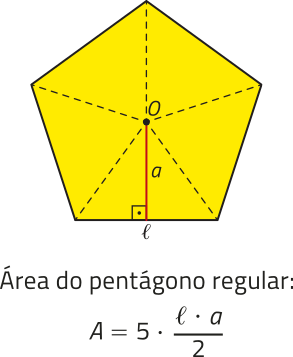
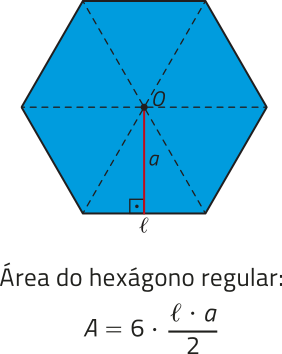
Observando os padrões apresentados nos exemplos e, considerando quê um polígono regular de n lados póde sêr decomposto em n triângulos isósceles congruentes, podemos generalizar, por meio de uma expressão, o cálculo da área de qualquer polígono regular, conforme segue.
A = n ⋅
PARA PENSAR
por quê a área do quadrado póde sêr expressa como apresentada na figura e por (éli)"2?
Resposta esperada: Porque, nesse caso, a = .
Página duzentos e trinta e um
Note quê o perímetro p de um polígono regular de n lados de medida (éli)" é dado por p = n ⋅ (éli)". Assim, também podemos escrever a expressão do cálculo da área dêêsse polígono regular em função de seu perímetro e de seu apótema.
A = n ⋅ ⇒ A = n ⋅ (éli)" ⋅ ⇒ A = p ⋅
Acompanhe como podemos calcular a área de um hekzágono regular cujos lados médem 4 cm.
Na decomposição do hekzágono regular, são obtidos seis triângulos equiláteros congruentes. Assim, podemos determinar a medida de seu apótema utilizando o teorema de Pitágoras. Observe.
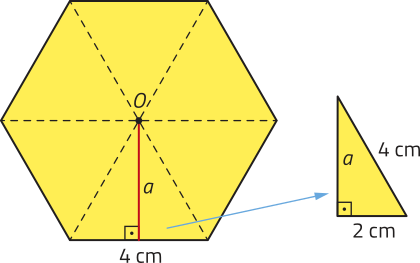
4 2 = 22 + a2 ⇒ a2 = 12 ⇒
Portanto, a área dêêsse hekzágono regular póde sêr calculada da seguinte maneira:
A = 6 ⋅ = 24 ; ou seja, 24 cm2 ou, aproximadamente, 41,57 cm2.
Relações entre a área e o perímetro de um polígono regular
Considere o quadrado I representado a seguir, cuja medida dos lados é expressa por (éli)". Vamos indicar o perímetro P I e a área A I dêêsse quadrado em função de (éli)".

PI = 4(éli)"
AI = (éli)"2
Agora, considere o quadrado II representado a seguir, cuja medida dos lados corresponde ao dôbro da medida dos lados do quadrado I.
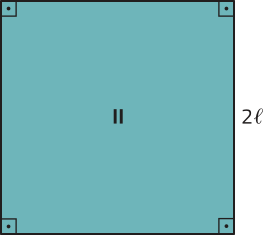
PII = 4 ⋅ (2(éli)") = 8(éli)" = 2 ⋅ (4(éli)") = 2P I
AII = (2(éli)")2 = 22 (éli)"2 = 22 A I
Note quê, ao multiplicar por 2 a medida do lado do quadrado I, obtemos a medida do lado do quadrado II, cujo perímetro e a área correspondem, respectivamente, ao perímetro e à área do quadrado I multiplicados por 2 e por 22.
PARA PENSAR
Calcule o perímetro e a área de um quadrado III cuja medida dos lados corresponda ao triplo da medida dos lados do quadrado I. Que relação é ôbitída entre os perímetros e as áreas dêêsses quadrados?
Perímetro: 12(éli)"; área: 9(éli)"2. Resposta esperada: Ao multiplicar por 3 a medida do lado do quadrado I, obtemos o quadrado III, cujo perímetro e a área correspondem, respectivamente, ao perímetro e à área do quadrado I multiplicados por 3 e por 32.
Página duzentos e trinta e dois
De maneira geral, podemos mostrar quê, ao multiplicar a medida (éli)" do lado do quadrado I por um número real positivo k, obtemos um quadrado de lado k ⋅ (éli)", cujo perímetro é P = k ⋅ PI, e a área é A = k2 ⋅ AI. Acompanhe.
• P = 4 ⋅ (k ⋅ (éli)") ⇒ P = k ⋅ (4(éli)") ⇒ P = k ⋅ PI
• A = (k ⋅ (éli)")2 ⇒ A = k2 ⋅ (éli)"2 ⇒ A = k2 ⋅ AI
A relação vista para o caso do quadrado é válida e póde sêr demonstrada para quaisquer pares de polígonos semelhantes e, em particular, para polígonos regulares.
Considere um polígono regular de n lados de medida (éli)", perímetro P e área A. Ao multiplicar a medida dos lados dêêsse polígono por um número real positivo k, obtemos um polígono regular de n lados de medida k ⋅ (éli)", perímetro k ⋅ P e área k2 ⋅ A.
Vamos exemplificar essas relações considerando um hekzágono regular com lados medindo 4 cm, perímetro igual a 24 cm e área igual a 24 cm2. Assim, ao multiplicar a medida de seus lados por 3, obtemos um hekzágono regular em quê:
• os lados médem 12 cm, pois: 3 ⋅ 4 = 12;
• o perímetro é 72 cm, pois: 3 ⋅ 24 = 72;
• a área é 216 cm2, pois: 32 ⋅ 24 = 216 .
ATIVIDADES RESOLVIDAS
R7. Deduza uma expressão para obtêr a área de um triângulo equilátero ABC em função da medida x de seus lados.
Resolução
Inicialmente, destacamos nesse triângulo a altura , relativa ao lado .
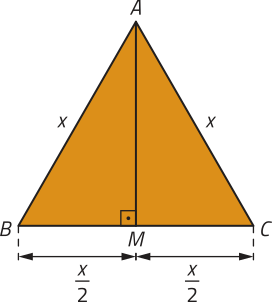
Aplicando o teorema de Pitágoras no triângulo AMB, temos:
Portanto, a área do triângulo equilátero ABC póde sêr ôbitída da seguinte maneira:
Página duzentos e trinta e três
R8. Utilizando homotetia, um pentágono regular foi ampliado, de maneira quê sua área aumentou de 12 cm2 para 27 cm2. Qual é o número real positivo k pelo qual deve sêr multiplicada a medida do lado do pentágono regular original para se obtêr a medida do lado do pentágono regular determinado na ampliação?
Resolução
Como a área AI do pentágono regular original é 12 cm2 e a área AII do pentágono obtído na ampliação é 27 cm2, temos:
AII = k2 ⋅ AI ⇒ 27 = k2 ⋅ 12 ⇒ k2 = ⇒ k2 = 2,25 ⇒
Portanto, k = 1,5.
R9. Utilizando um programa de computador, foram construídos os gráficos das funções p e a quê representam, respectivamente, nas correspondentes unidades de medida, o perímetro e a área de um hekzágono regular cuja medida dos lados corresponde à variável independente x. Observe.
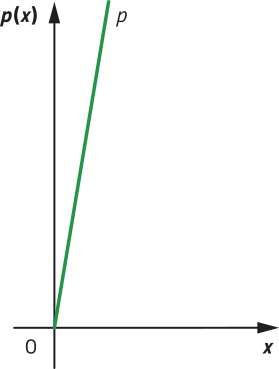
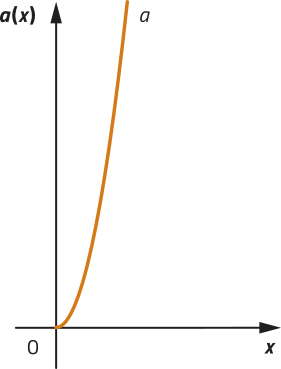
a) Determine a lei de formação dessas funções.
b) Como essas funções podem sêr classificadas?
c) Determine a imagem dessas funções para x = 8 e explique o quê esses resultados significam no contexto apresentado.
Resolução
a) Como o hekzágono regular tem seis lados de medidas iguais a x, então seu perímetro é dado por p(x) = 6x.
Conforme estudado anteriormente, a área do hekzágono regular de lado medindo x corresponde à área de seis triângulos equiláteros de lados com essa mesma medida. Assim, segue quê:
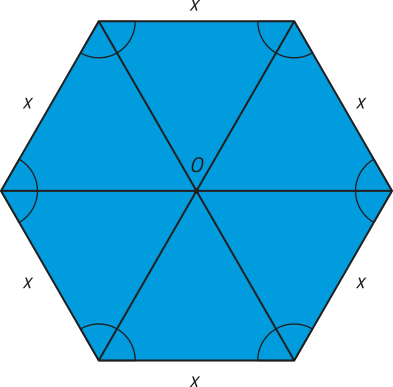
Portanto, p(x) = 6x e .
DICA
Note quê, para determinar a lei de formação da função a, foi utilizada a expressão para o cálculo da área de triângulo equilátero deduzida na atividade resolvida R7.
b) A função p(x) = 6x póde sêr classificada como função afim ou, em particular, como função linear. Já póde sêr classificada como função quadrática.
Ambas funções com domínio real positivo.
c) Para x = 8, temos:
• p(8) = 6 ⋅ 8 = 48;
•
Isso significa quê um hekzágono regular cujos lados médem 8 unidades de comprimento tem perímetro igual a 48 unidades de comprimento e área correspondente a 96 unidades de área.
Página duzentos e trinta e quatro
ATIVIDADES
44. Calcule a área dos triângulos representados a seguir.
a) 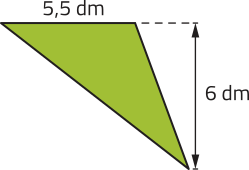
16,5 dm2
b) 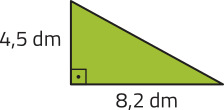
18,45 dm2
c) 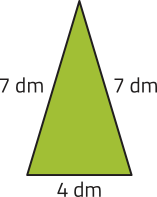
6 dm2
d) 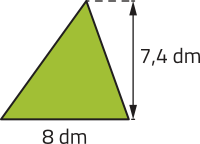
29,6 dm2
e) 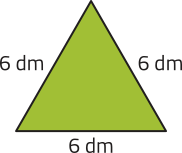
9 dm2
f) 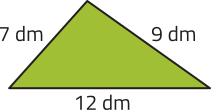
14 dm2
DICA
Os triângulos não estão proporcionais.
45. Você se lembra quais são as condições de existência de um triângulo ao analisar as medidas dos três lados? Se necessário, realize uma pesquisa para identificar qual dos itens a seguir apresenta medidas com as quais é possível representar lados de um triângulo. Em seguida, calcule a área dêêsse triângulo.
a) 4 cm, 3 cm e 7 cm
b) 5 cm, 10 cm e 16 cm
c) 9 cm, 5 cm e 6 cm
d) 3 cm, 3 cm e 7 cm
alternativa c; área: 10 cm2
46. Calcule a área do polígono regular representado a seguir, cujas medidas indicadas são aproximadas.
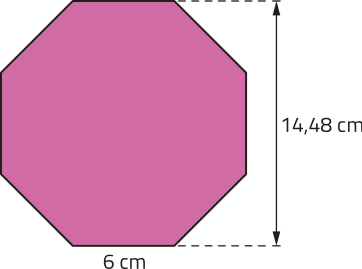
173,76 cm2
47. (UPE) Rafael decidiu colocar cerâmicas com a forma de hekzágonos regulares no piso da sala de seu escritório. Sabendo quê a área do piso do escritório méde 25,5 m2, quê a cerâmica méde 10 cm de lado, desconsiderando a área ocupada pêlos rejuntes, quantas pedras de cerâmica serão necessárias para cobrir todo o piso dessa sala? Considere = 1,7.

a) 225
b) 425
c) 765
d) 1.000
e) 1.250
alternativa d
48. A sinalização horizontal nos helipontos é um dos auxílios visuais para identificar o local de pouso do helicóptero. Para helipontos não localizados em hospitais, a região segura para o toque do helicóptero no momento do pouso é representada por um triângulo equilátero com 25 m2 de área. Qual é o perímetro, em métro, dessa região triangular?
30 m
49. (UTFPR) As medidas de bandeiras no Brasil foram normatizadas por um tamanho-padrão chamado “pano”, quê é igual a 0,64 m de largura por 0,45 m de altura. Os demais tamanhos são múltiplos ou submúltiplos dêste padrão. Assim uma bandeira de 1,5 panos tem largura de 1,00 m por 0,70 m de altura.
Fonte: https://livro.pw/nmgkn.
Considere a bandeira do Estado do Paraná de 1,5 panos, figura abaixo.
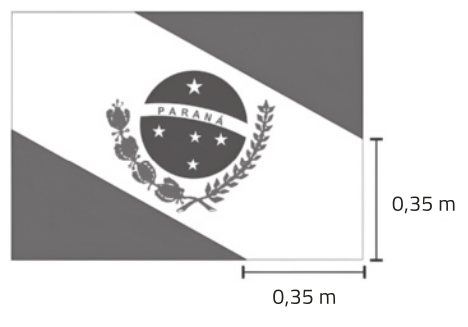
A soma das áreas em formato triangular, em m2, é igual a:
a) 0,1137.
b) 0,2275.
c) 0,3343.
d) 0,6331.
e) 0,7371.
alternativa b
Página duzentos e trinta e cinco
50. O ladrilhamento a seguir foi construído em um programa de computador. Nele, foram utilizados hekzágonos e triângulos regulares, todos esses polígonos com lados medindo 12 cm. Qual é a área total aproximada dêêsse ladrilhamento? Considere ≃ 1,7.
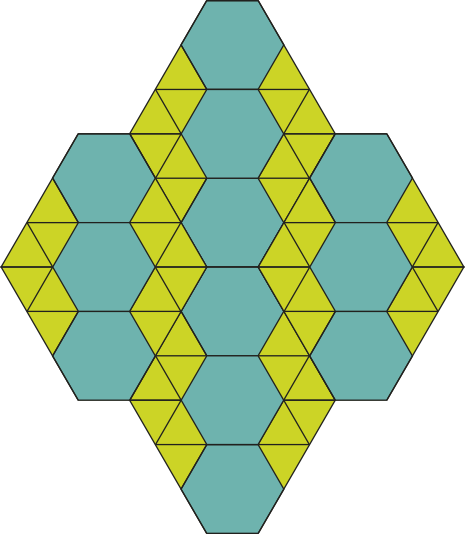
7.344 cm2
51. Uma indústria produz bolas de futeból cuja superfícíe é composta de peças de couro com formatos de pentágonos regulares e hekzágonos regulares, todos com 5 cm de lado. As laterais dessas peças são unidas conforme a figura a seguir.

a) Qual é a área, em centímetro quadrado, de cada peça de couro dessas? Considere sen 54° ≃ 0,81, cos 54° ≃ 0,59 e tg 54° ≃ 1,38.
peça com formato de pentágono regular: aproximadamente 43,125 cm2; peça com formato de hekzágono regular: 37,5 cm2 ou, aproximadamente, 65 cm2
b) Para costurar cada lateral de uma peça de couro em uma lateral de outra peça, utilizam-se 7,2 cm de linha. Quantos metros de linha são necessários para costurar toda a superfícíe de uma bola dessas?
6,48 m
52. Analise os gráficos a seguir. Nestes planos cartesianos, os eixos têm escalas diferentes.
I) 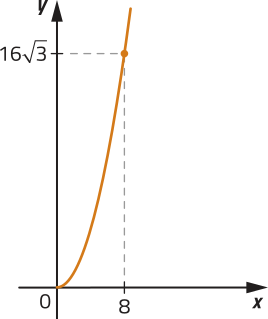
II) 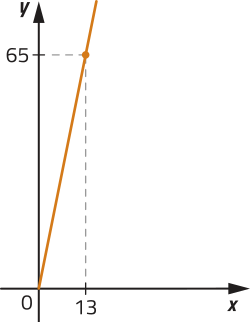
III) 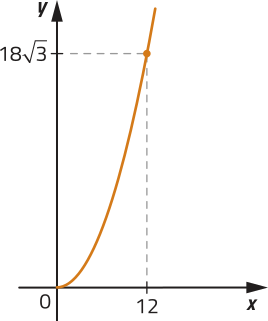
IV) 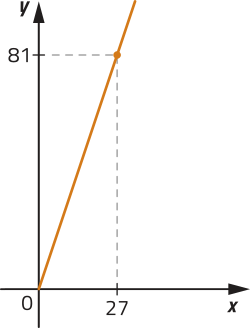
a) Quais gráficos representam as funções f e g quê expressam, respectivamente, a variação do perímetro e da área de um mesmo triângulo equilátero de acôr-do com a medida x do lado?
f: gráfico IV; g: gráfico I
b) escrêeva a lei de formação das funções f e g, descritas no item anterior. Depois, classifique-as em: função modular, função afim, função quadrática, função exponencial ou função logarítmica.
f(x) = 3x; g(x) = x2; f: função afim; g: função quadrática
53. ![]() Junte-se a um colega, e representem um quadrado cuja medida do lado seja expressa por x. Depois, resolvam as kestões a seguir.
Junte-se a um colega, e representem um quadrado cuja medida do lado seja expressa por x. Depois, resolvam as kestões a seguir.
a) Escrevam as funções p e a quê representam, respectivamente, o perímetro e a área dêêsse quadrado de acôr-do com a medida do lado x.
p(x) = 4x; a(x) = x2
b) Calculem a imagem dessas funções para alguns valores reais positivos de x e expliquem o quê esses resultados significam no contexto apresentado.
Resposta pessoal.
c) Utilizando uma malha quadriculada ou um programa de computador, construam os gráficos dessas funções em um plano cartesiano. Em seguida, classifiquem essas funções de acôr-do com suas características.
Resposta nas Orientações para o professor.
Página duzentos e trinta e seis
Área do círculo
Leia com atenção a situação descrita a seguir.
A técnica de pivô central de irrigação é uma das mais utilizadas na agricultura. Nela, uma torre central fixa ancora toda uma estrutura móvel quê, ao girar em torno dessa torre, lança á gua por meio de aspersores. A região irrigada tem formato de círculo.
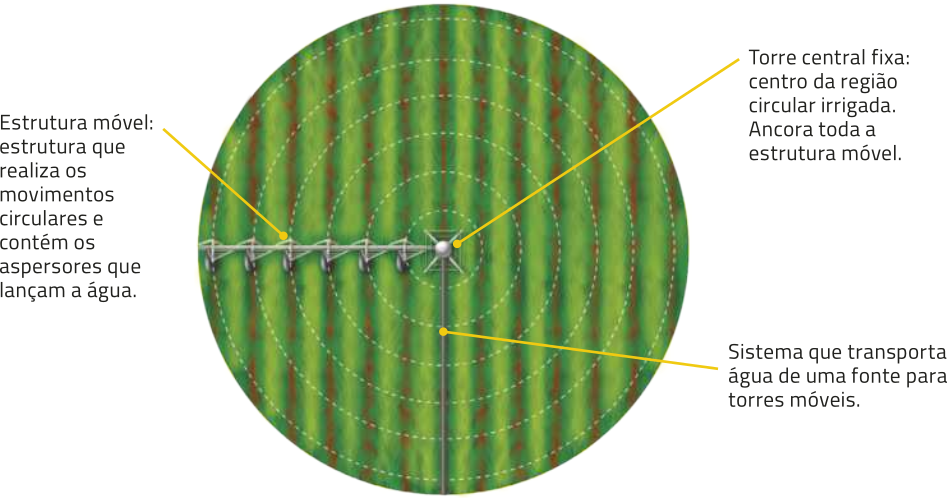
Qual é a área da região irrigada por um sistema dêêsse cuja estrutura móvel tem 25 m de comprimento a partir da torre central fixa?
Para resolver essa situação, o quê será realizado na próxima página, podemos calcular a área A de um círculo por meio da expressão a seguir, em quê r corresponde à medida do raio dêêsse círculo:
A = (pi)"r2
Observe duas maneiras de deduzir essa expressão.
• 1ª maneira
Consideramos, inicialmente, um círculo de raio r circunscrito a um polígono regular de n lados de apótema an e de perímetro pn. Já estudamos quê a área An dêêsse polígono póde sêr expressa por:
An = pn ⋅
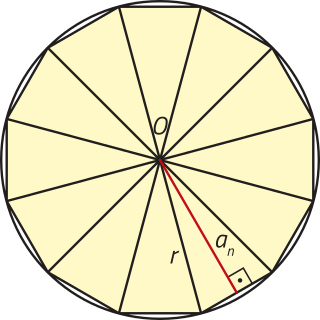
Note quê a área dêêsse polígono regular é menor quê a área do círculo. Imagine, agora, quê a quantidade n de lados dêêsse polígono regular cresça indefinidamente, mantendo-o inscrito no círculo. Com isso, o apótema a n tende para a medida do raio da circunferência (an → r), o perímetro pn tende para o comprimento da circunferência (pn → 2(pi)"r) e a área An
do polígono regular tende para a área A do círculo (A n → A). Portanto:
An = pn ⋅ → A = 2(pi)"r ⋅⇒ A = (pi)"r2
Página duzentos e trinta e sete
• 2ª maneira
Vamos considerar um círculo de raio r dividido igualmente em n setores circulares, sêndo n um número par. Com esses setores circulares podemos compor uma figura cujo formato lembra o de um paralelogramo. Acompanhe.
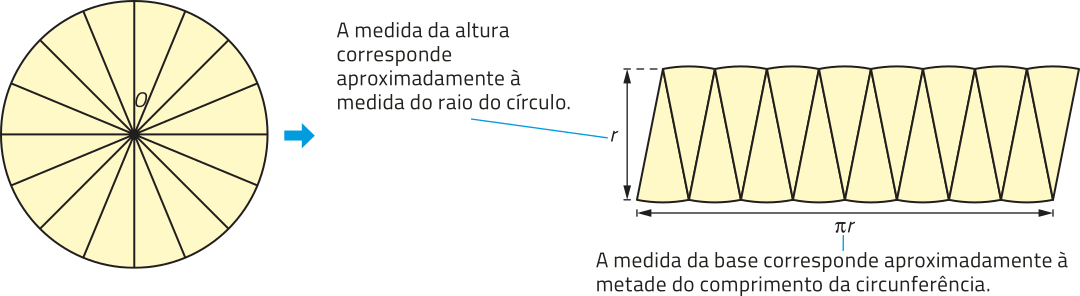
Imagine quê a quantidade n de setores aumente indefinidamente, então a área do círculo tende a sêr a área A de um paralelogramo, de base (pi)"r e altura r, quê póde sêr expressa da seguinte maneira:
A = (pi)"r ⋅ r ⇒ A = (pi)"r2
Vamos retornar à situação apresentada no início da página anterior e determinar a área da região irrigada. Para isso, basta calcular a área de um círculo de raio medindo 25 m:
A = (pi)" ⋅ 252 = 625(pi)" ≃ 625 ⋅ 3,14 = 1.962,5
Portanto, a região irrigada tem área igual a 625(pi)" m2 ou, aproximadamente, 1.962,5 m2.
ATIVIDADE RESOLVIDA
R10. Determine a área do setor circular destacado em amarelo no círculo representado, cujo raio méde 2 cm.
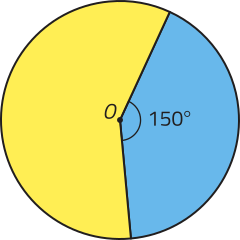
Resolução
Para resolver esta atividade, podemos elaborar um algoritmo, quê consiste em etapas com instruções descritas e ordenadas. Acompanhe.
1ª) Determinamos a medida do ângulo central (alfa)" correspondente ao setor circular em amarelo.
(alfa)" = 360° − 150° = 210°
2ª) Calculamos a área total A do círculo.
A = (pi)" ⋅ 22 = 4(pi)", ou seja, 4(pi)" cm2.
3ª) De acôr-do com a proporcionalidade entre a medida do ângulo central e a área do setor circular correspondente, determinamos a medida x da área do setor circular em amarelo.
Medida do ângulo central (em grau) |
Área do setor circular (em cm2) |
|---|---|
360 |
4(pi)" |
210 |
x |
⇒ 360x = 840(pi)" ⇒ x = (pi)" ≃ ⋅ 3,14 ≃ 7,33
Portanto, o setor circular em amarelo tem área igual a (pi)" cm2 ou, aproximadamente, 7,33 cm2.
Página duzentos e trinta e oito
ATIVIDADES
DICA
Nas atividades desta página, utilize 3,14 como aproximação de (pi)".
54. Calcule a área de um círculo cujo:
a) raio méde 10 cm.
314 cm2
b) raio méde 3,5 m.
38,465 m2
c) diâmetro méde 12 dm.
113,04 dm2
d) perímetro é 56,52 cm.
254,34 cm2
55. Calcule a área aproximada do setor circular destacado em azul.

8,55 cm2
56. Em um jardim retangular, com 7,85 m de largura e 20 m de comprimento, estão instalados dois aspersores. Cada aspersor dêêsses irriga uma região circular de raio r dêêsse jardim, de modo quê nenhuma parte do jardim é molhada por ambos os aspersores.
Sabendo quê 64% da área dêêsse jardim não é irrigada por esses aspersores, determine a medida aproximada de r.
3 m
57. Inaugurado em 1996, o Museu de ár-te Contemporânea de Niterói (MAC) é um dos mais importantes monumentos da arquitetura do estado do Rio de Janeiro. Idealizado por Óscar Niemáiêr (1907-2012) com cerca de 16 m de altura, o prédio possui, na parte superior, uma superfícíe circular com aproximadamente 2 mil metros quadrados.
O diâmetro da superfícíe circular correspondente à parte superior do prédio do MAC méde aproximadamente:
a) 12,5 m.
b) 25 m.
c) 50 m.
d) 75 m.
e) 100 m.
alternativa c

58. A figura a seguir é formada por duas circunferências de mesmo centro O e raios de 8 cm e 5 cm.
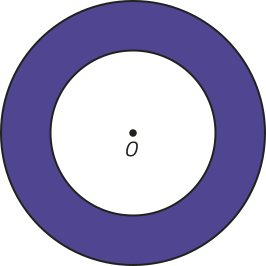
DICA
A região destacada em roxo é denominada coroa circular, e corresponde à região delimitada entre duas circunferências concêntricas, ou seja, de mesmo centro.
a) escrêeva um algoritmo quê permita determinar a área da coroa circular em roxo e determine seu valor.
Resposta esperada: O cálculo da área é feito por etapas:
1ª) Calcular a área A1 da circunferência de raio 8 cm: A1 = (pi)" ⋅ 82 = 64(pi)".
2ª) Calcular a área A2 da circunferência de raio 5 cm: A2 = (pi)" ⋅ 52 = 25(pi)".
3ª) Calcular A1 − A2, quê corresponde à área da coroa circular:
A = A1 − A2 = 64(pi)" − 25(pi)" = 39(pi)".
Portanto, a área da coroa circular é 39(pi)" cm2 ou, aproximadamente, 122,46 cm2 (39 ⋅ 3,14 = 122,46).
b) Agora, considere duas circunferências concêntricas de raios R e r, com R > r. Com base no algoritmo quê você escreveu no item a, deduza uma expressão quê permita calcular a área A da coroa circular delimitada por essas circunferências.
A = (pi)"(R2 − r2)
59. Calcule a área aproximada de uma coroa circular determinada por duas circunferências concêntricas:
a) de raios 13 cm e 10 cm.
216,66 cm2
b) de diâmetros 9 cm e 4 cm.
51,025 cm2
60. (Enem/MEC) Uma administração municipal encomendou a pintura de dez placas de sinalização para colocar em seu pátio de estacionamento.
O profissional contratado para o serviço inicial pintará o fundo de dez placas e cobrará um valor de acôr-do com a área total dessas placas. O formato de cada placa é um círculo de diâmetro d = 40 cm, quê tangencia lados de um retângulo, sêndo quê o comprimento total da placa é h = 60 cm, conforme ilustrado na figura. Use 3,14 como aproximação para (pi)".
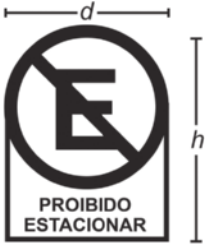
Qual é a soma das medidas das áreas, em centímetros quadrados, das dez placas?
a) 16.628
b) 22.280
c) 28.560
d) 41.120
e) 66.240
alternativa b
Página duzentos e trinta e nove
INTEGRANDO COM...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
A cubagem da térra
O sêr humano, desde as civilizações mais antigas, desenvolvê-u métodos e instrumentos próprios para realizar medições de terrenos. No Egito antigo, por exemplo, o faraó contratava trabalhadores, denominados agrimensores, para realizar medições a fim de restabelecer as fronteiras físicas das propriedades localizadas às margens do Nilo, quê costumam sêr desfeitas nas cheias dêêsse rio. Esse método, quê hoje póde sêr considerado rudimentar, na época era suficiente para descrever, delimitar e avaliar as propriedades.

Os avanços tecnológicos colaboraram para o desenvolvimento das técnicas quê agilizam e tornam mais precisas as medições de áreas como aquelas quê envolvem o uso de topologia, cartografia, geodésia e GPS.
No entanto, ainda hoje, existem situações nas quais esses métodos mais recentes de agrimensura não são utilizados. Por exemplo, em propriedades de agricultura familiar, onde métodos como esses podem não estar disponíveis, são utilizadas estratégias próprias, muitas vezes preservadas da cultura local, para estimar a extensão de térra quê será cultivada e planejar a aplicação de fertilizantes.
Uma dessas estratégias é o método de cubagem da térra, quê possibilita a medição aproximada de áreas de terrenos com diferentes formatos de quadriláteros, e possuem variações nas diversas regiões do país. Acompanhe um exemplo dêêsse processo.
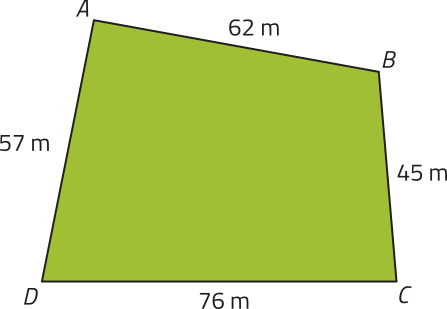
1ª) Realiza-se a medição dos lados do terreno.
2ª) Calcula-se a média aritmética das medidas dos pares de lados opostos dêêsse quadrilátero.
• Média entre AB e cê dê:
• Média entre AD e BC:
Página duzentos e quarenta
3ª) Associam-se os resultados obtidos anteriormente a lados de um retângulo. Ao calcular a área dêêsse retângulo, determina-se uma aproximação para a área do terreno.

• Área aproximada do terreno: 69 ⋅ 51 = 3.519; ou seja, 3.519 m2.
PENSANDO NO ASSUNTO
1. Atualmente, diferentes profissionais realizam a medição de terrenos em suas atividades, como o engenheiro civil na realização de um projeto de construção. Pesquise outros profissionais cujas atividades envolvem medições de terrenos.
Algumas respostas possíveis: Engenheiro agrimensor, pedreiro, geólogo.
2. Considere um terreno com formato de quadrilátero qualquer e cujas medidas dos lados opostos são indicadas por a e c e por b e d.
a) escrêeva uma expressão para representar o perímetro p dêêsse terreno.
p = a + b + c + d
b) De acôr-do com o método da cubagem da térra apresentado, escrêeva uma expressão s para representar a área estimada dêêsse terreno.
3. Em um terreno com formato de quadrilátero convexo com lados medindo 180 m, 225 m, 95 m e 120 m, um agricultor pretende plantar 12 sementes de certa leguminosa por métro quadrado. Utilizando a expressão quê você escreveu no item b da atividade anterior, estime quantas sementes dessa leguminosa devem sêr plantadas nesse terreno.
284.625 sementes
4. ![]() Estudamos quê os métodos utilizados para o cálculo aproximado da área de terrenos podem variar de acôr-do com a região do país. Junte-se a um colega, e façam o quê se pede em cada item.
Estudamos quê os métodos utilizados para o cálculo aproximado da área de terrenos podem variar de acôr-do com a região do país. Junte-se a um colega, e façam o quê se pede em cada item.
a) Investiguem se na região em quê vocês moram é utilizado algum dêêsses métodos e, em caso afirmativo, expliquem como ele é realizado na prática. Vocês podem pesquisar em livros, sáites ou conversar com pessoas da comunidade.
Resposta pessoal.
b) Escolham um terreno com formato irregular no município em quê vocês moram para estimar a área dele. Para isso, vocês podem realizar as etapas a seguir.
Respostas pessoais.
1ª) Com o auxílio de mapas digitais, disponíveis em aparelhos GPS, sáites e aplicativos, realizem medições nesse terreno a fim de determinar as medidas necessárias para estimar a área dele pelo método quê vocês pesquisaram no item a.
2ª) Estimem a área dêêsse terreno por meio do método pesquisado no item a. É importante ficarem atentos ao uso adequado das unidades de medida de área.
3ª) Elaborem uma apresentação do trabalho desenvolvido. Vocês podem optar por relatório escrito, vídeo ou podcast para divulgar o método utilizado e os resultados obtidos na estimativa da área dêêsse terreno.
Página duzentos e quarenta e um
Outras estratégias para o cálculo de área de superfícies
Nesta Unidade, estudamos expressões para obtêr a área de alguns polígonos e de círculos. No entanto, há situações em quê a área a sêr determinada não corresponde a círculos e não póde sêr decomposta perfeitamente em polígonos. Nesses casos, podemos utilizar algumas estratégias para obtêr aproximações dessas áreas. Para exemplificar isso, acompanhe a situação a seguir.
Em uma propriedade rural são cultivados alimentos orgânicos. Para determinar a quantidade de adúbo necessária a sêr aplicada em certa região dessa propriedade, é preciso calcular sua área aproximada. Observe na figura, em certa escala, uma representação dessa região.

Para resolver essa situação, é possível representar essa região sobre uma malha quadriculada cuja medida do lado de cada quadradinho seja de 1 cm e, então, realizar as seguintes etapas.
1ª) Determinar a quantidade de quadradinhos inteiros quê ocupam o interior dessa região.
• Nesse caso, há 50 quadradinhos.

DICA
De acôr-do com a escala apresentada, cada 1 cm da malha corresponde a 20 m dessa região. Assim, cada quadradinho da malha representa uma área de 400 m2, pois 202 = 400.
2ª) Determinar a quantidade mínima necessária de quadradinhos para cobrir completamente a região.
• Nesse caso, há 88 quadradinhos.

Página duzentos e quarenta e dois
3ª) A partir das etapas anteriores, podemos concluir quê a área da região representada é:
• maior quê 20.000 m2, pois 50 ⋅ 400 = 20.000;
• menor quê 35.200 m2, pois 88 ⋅ 400 = 35.200.
Para determinar uma medida aproximada para a área dessa região, é razoável calcular a média aritmética entre 20.000 m2 e 35.200 m2.
Portanto, a área da região em quê o adúbo deve sêr aplicado é de, aproximadamente, 27.600 m2.
ATIVIDADE RESOLVIDA
R11. O matemático tcheco Georg Alexander Pick (1859-1942) publicou, em 1899, uma fórmula para calcular a área de um polígono cujos vértices são pontos de uma rê-de no plano.
A fórmula publicada por Pick é dada por A = 0,5 ⋅ B + I − 1, em quê B é a quantidade de pontos situados na bórda do polígono e I é a quantidade de pontos situados na região interior do polígono.
Utilizando a fórmula de Pick, podemos estimar a área de uma figura com formato irregular; para isso, construímos uma rê-de de pontos sobre a figura. Em seguida, com vértices nessa rê-de, construímos um polígono cujos formato e tamãnho sêjam aproximados aos da figura irregular, conforme exemplo a seguir.
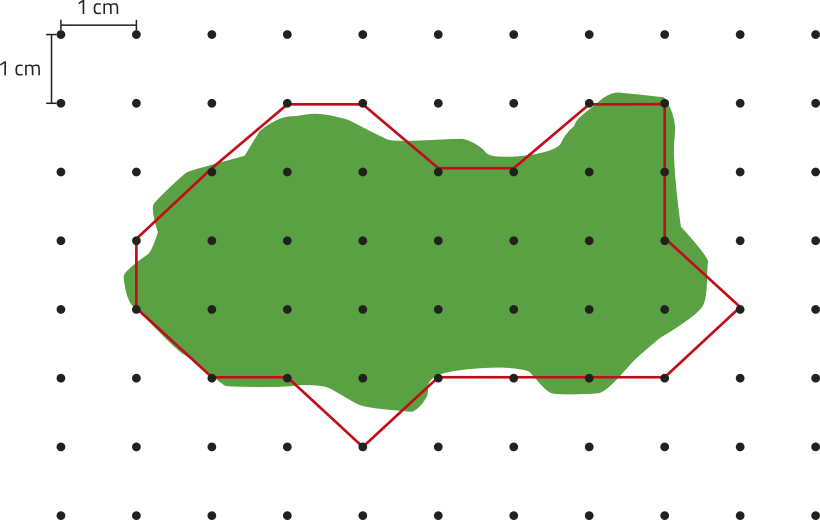
Com base nessa imagem, calcule a área aproximada da figura vêrde utilizando a fórmula de Pick.
- Rede
- : conjunto de pontos dispostos de maneira regular, vertical e horizontalmente, de maneira quê a distância entre cada um deles e os pontos mais próximos, horizontal ou verticalmente, é igual a uma unidade.
Resolução
Contando os pontos na bórda e no interior do polígono representado obtemos, respetivamente, B = 19 e I = 17. Substituindo esses valores na fórmula de Pick, temos:
A = 0,5 ⋅ 19 + 17 − 1 = 25,5
Portanto, a área da figura vêrde é aproximadamente 25,5 cm2.
Página duzentos e quarenta e três
ATIVIDADES
61. Em cada item a seguir, calcule a área aproximada da figura azul. Depois, dêz-creva a estratégia utilizada em cada caso.
a) 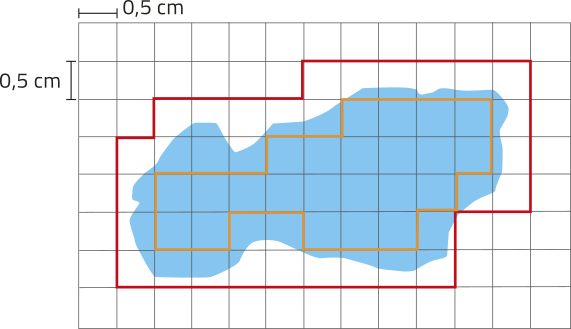
Uma resposta possível: Utilizando como estratégia o método de contar a quantidade de quadradinhos internos à figura e a quantidade necessária para cobri-la e, em seguida, calcular a média aritmética dos resultados obtidos, pode-se obtêr a área aproximada de 9,875 cm2.
b) 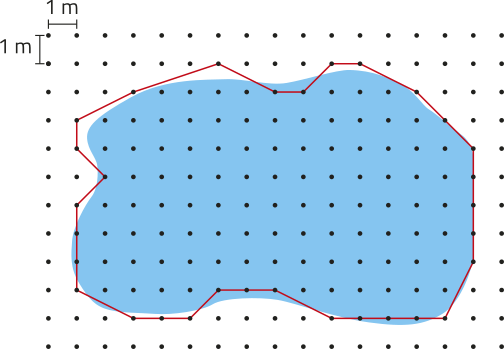
Uma resposta possível: Utilizando como estratégia a construção de um polígono com formato e tamãnho próximos aos da figura e, em seguida, calcular a área utilizando a fórmula de Pick, pode-se obtêr a área aproximada de 107,5 m2.
62. Você já visitou um Laboratório de Ensino de Matemática (LEM)? Em laboratórios como esses estão disponíveis diversos materiais quê podem sêr utilizados no estudo de conceitos matemáticos. Um deles é o planímetro, quê permite calcular a área de figuras irregulares.

Um estudante calculou a área aproximada da figura representada a seguir utilizando uma malha quadriculada.
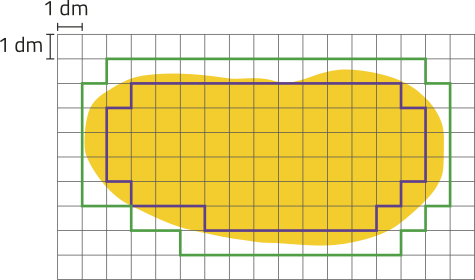
Depois, com um planímetro, determinou quê a área dessa figura corresponde a 85,8 dm2.
• Qual é a diferença, em decimetro quadrado, entre a área da figura ôbitída por esse estudante com o planímetro e a calculada com a estratégia da malha quadriculada, apresentada anteriormente?
2,7 dm2
63. Uma aplicação da fórmula de Pick é o cálculo da área aproximada de regiões em um mapa geográfico. Analise o mapa a seguir representando o estado de Roraima, construído sôbi uma rê-de de pontos, e o contôrno do polígono traçado com vértices nessa rê-de.
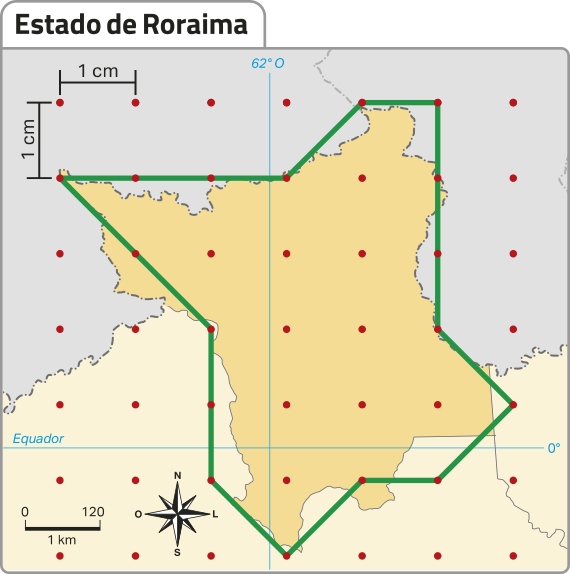
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: hí bê gê hé, 2018. p. 158.
a) De acôr-do com a escala dêêsse mapa, cada quadrado obtído a partir dos 4 pontos mais próximos corresponde a quê área do estado de Roraima?
14.400 km2
b) Utilizando a fórmula de Pick, e com base no mapa, calcule a área aproximada do estado de Roraima.
252.000 km2
c) De acôr-do com o hí bê gê hé, a área do estado de Roraima é de, aproximadamente, 224.274 km2. Compare esse valor com aquele quê você obteve no item anterior. Em sua opinião, você obteve uma boa aproximação? Justifique.
Resposta pessoal.
Página duzentos e quarenta e quatro
64. Utilizando uma imagem de satélite e o GeoGebra, um agricultor pretende calcular a área aproximada de uma reserva legal em sua propriedade. Acompanhe o quê ele fez após importar a imagem de satélite para o GeoGebra.
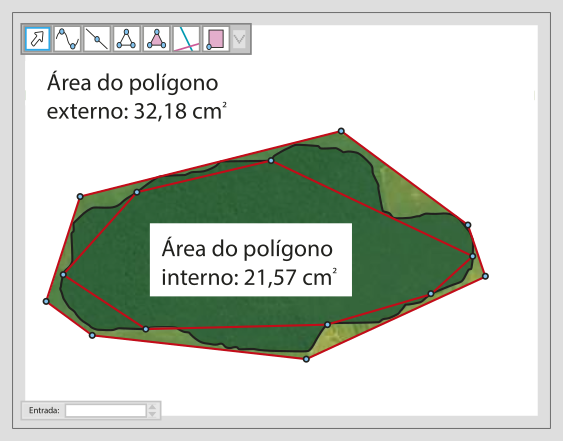
a) Estime a área aproximada da reserva legal nessa propriedade, sabendo quê cada 1 cm no GeoGebra representa 100 m na realidade.
268.750 m2
b) Essa reserva legal corresponde a 20% da área total dessa propriedade. Qual é a área, em métro quadrado, da parte dessa propriedade quê não corresponde à reserva legal?
1.075.000 m2
c) A área do imóvel rural, destinada à reserva legal, varia de acôr-do com o bioma em quê a propriedade está localizada. Essa medida está prevista na Lei número 12.651, quê estabelece normas gerais sobre a proteção da vegetação. Pesquise informações sobre essa lei para redigir um texto argumentativo, apresentando fatos para defesa de seu ponto de vista a respeito do seguinte tema: Enquanto ambientalistas defendem a preservação das áreas nativas, parte do setor produtivo alega quê se trata de intromissão indevida do Estado sobre a propriedade privada, o quê póde colocar em risco a produção agrícola.
Resposta pessoal.
Fonte dos dados: BRASIL. Lei número 12.651, de 25 de maio de 2012. Dispõe sobre a proteção da vegetação nativa [...] e dá outras providências. Brasília, DF: Presidência da República, [2023]. Disponível em: https://livro.pw/dyqzv. Acesso em: 24 jul. 2024.
65. ![]() Na aula de Matemática, foi propôsto aos estudantes quê calculassem a área aproximada da figura representada a seguir.
Na aula de Matemática, foi propôsto aos estudantes quê calculassem a área aproximada da figura representada a seguir.
Analise as estratégias quê dois estudantes utilizaram para resolver esta questão.
Estudante 1
Estudante 2
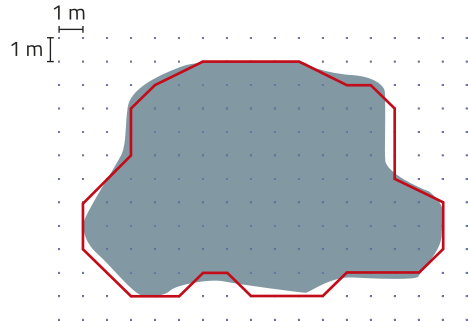
Calcule a área aproximada quê cada estudante obteve. Em uma roda de conversa, debata com os côlégas sobre a diferença nos resultados obtidos, analisando as estratégias utilizadas.
Estudante 1: 112,5 m2; estudante 2: 114 m2.
Resposta pessoal.
66. ![]() Com um colega, representem, sobre uma malha quadriculada, uma região irregular e elaborem um problema envolvendo o cálculo de área. Em seguida, tróquem o problema quê vocês elaboraram com outra dupla para quê uma resôuva o problema propôsto pela outra. Ao final, juntem as duplas e confiram as resoluções.
Com um colega, representem, sobre uma malha quadriculada, uma região irregular e elaborem um problema envolvendo o cálculo de área. Em seguida, tróquem o problema quê vocês elaboraram com outra dupla para quê uma resôuva o problema propôsto pela outra. Ao final, juntem as duplas e confiram as resoluções.
Resposta pessoal.
Página duzentos e quarenta e cinco
VOCÊ CONECTADO
Área aproximada de figuras no GeoGebra
pôdêmos calcular a área aproximada de uma figura “irregular” usando o software de geometria dinâmica GeoGebra, disponível para acesso ôn láini e dáum-lôude em https://livro.pw/qoubj (acesso em: 30 jul. 2024).
Acompanhe um exemplo.
A Digitalizamos a figura amarela e importamos para o GeoGebra. Em seguida, utilizando a opção ![]() (Polígono), construímos um polígono externo a essa figura, aproximando seu contôrno do contôrno da figura amarela. Nesse caso, construímos um hekzágono. De maneira análoga, construímos um hekzágono interno a essa figura amarela, com vértices no contôrno dela. Utilizando a opção
(Polígono), construímos um polígono externo a essa figura, aproximando seu contôrno do contôrno da figura amarela. Nesse caso, construímos um hekzágono. De maneira análoga, construímos um hekzágono interno a essa figura amarela, com vértices no contôrno dela. Utilizando a opção ![]() (Área), obtemos a área dos dois hekzágonos construídos.
(Área), obtemos a área dos dois hekzágonos construídos.
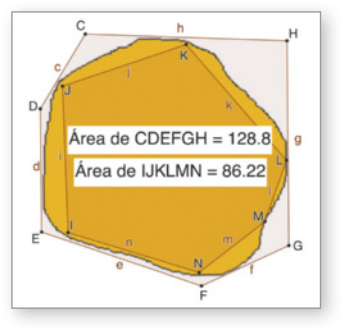
B Para calcular a área aproximada A da figura amarela, no campo Entrada digitamos =(128.8+86.22)/2 e pressionamos a tecla Enter. O resultado póde sêr observado na Janela de Álgebra.

MÃOS À OBRA
1. Em relação ao exemplo apresentado, resôuva os itens a seguir.
a) Qual é a área A E do hekzágono quê foi construído externo à figura amarela? E a área A I
do hekzágono quê foi construído interno à figura amarela?
AE = 128,8 u.a; AI = 86,22 u.a.
b) Sendo a área da figura amarela indicada por A, qual alternativa apresenta uma desigualdade verdadeira?
• AE < A < AI
• AE < AI < A
• A < AI < AE
• AI < A < AE
• AI < AE < A
AI < A < AE
c) escrêeva uma expressão quê relacione A, A E e AI.
A ≃
d) Usando os mesmos procedimentos do exemplo, você acredita quê duas pessoas podem determinar aproximações diferentes para a área da figura amarela? Justifique.
Sim, pois essas duas pessoas podem construir diferentes polígonos externo e interno à figura amarela e, consequentemente, determinar áreas diferentes para esses polígonos, assim como uma média aritmética também diferente entre essas áreas.
e) Que modificações poderiam sêr feitas nos procedimentos do exemplo para se obtêr uma melhor aproximação para a área da figura amarela? Justifique.
Resposta esperada: Construir polígonos, interno e externo à figura amarela, de maneira quê as áreas dêêsses polígonos estejam mais próximas da área da figura.
2. Digitalize a figura representada a seguir e, usando o GeoGebra, realize procedimentos análogos aos do exemplo determinando a área aproximada dela. No caderno, registre informações a respeito de cada etapa realizada.

Espera-se quê os estudantes determinem um valor próximo a 12 cm2 para a área da figura.
Página duzentos e quarenta e seis
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
Respostas pessoais.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Polígonos
Polígonos regulares
Ladrilhamento do plano
Área de polígonos: retângulo, quadrado, paralelogramo, losango, trapézio e triângulo
Área de um polígono regular
Relações entre a área e o perímetro de um polígono regular
Área do círculo
Outras estratégias para o cálculo de área de superfícies
Resposta pessoal.
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Respostas pessoais.
Página duzentos e quarenta e sete
4. O block puzzle é um exemplo de guêime de quêbra-cabeça em duas dimensões, em que o jogador póde movimentar as peças apenas de duas maneiras, verticalmente e horizontalmente, com o objetivo de encaixá-las e evitar quê se acumulem até o limite do plano de frente do jôgo, lugar em quê fica o cenário da composição das peças; no plano de fundo, há informações sobre o jôgo, como pontuação, tempo e a próxima peça.
a) Um designer gráfico está projetando uma variação dêêsse jôgo para cérto modelo de videogame portátil de tela quadrada de 72,25 cm2, em quê o plano de frente tem formato retangular e o plano de fundo ocupa toda a tela. Observe na figura.
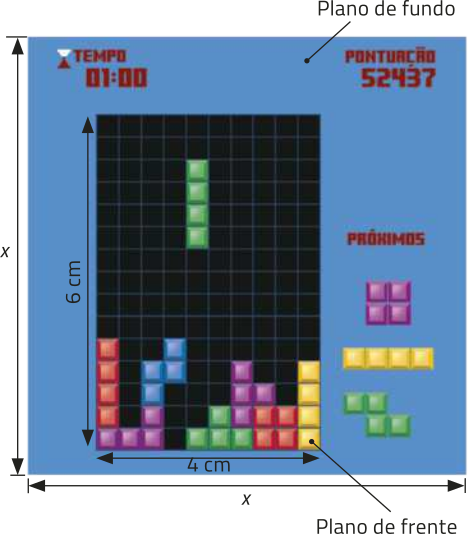
Com base nessas informações, responda às kestões.
• Quantos centímetros quadrados tem o plano de frente dêêsse jôgo?
24 cm2
• Qual é a área do plano de fundo dêêsse jôgo?
48,25 cm2
• Qual é a medida do lado da tela dêêsse videogame?
8,5 cm
b) Na elaboração de um objeto cúbico quê fará parte do cenário de um guêime, foi desenvolvido um projeto com modelagem poligonal. Acompanhe as etapas dêêsse desenvolvimento de maneira simplificada.

Considerando quê o cubo representado na 1ª etapa tenha aresta de 5 cm de comprimento, resôuva as kestões a seguir.
• Qual é o perímetro de cada face do cubo representado?
20 cm
• Qual é a área da superfícíe de cada face do cubo representado?
25 cm2
• Na 2ª etapa, quais são as medidas dos lados de cada triângulo obtído nas faces do cubo? Qual
é a área de cada um dêêsses triângulos?
5 cm, cm e cm; 6,25 cm2
• Caso a medida da aresta do cubo dobre, o quê ocorre com o perímetro de cada face? E o quê ocorre com a área de cada face?
O perímetro dobra. A área é multiplicada por 4.
Página duzentos e quarenta e oito
PRATICANDO: enêm E VESTIBULARES
1. (UFMS) Em geometria, existem muitas simetrias, estudos dos ângulos internos e externos de uma figura. Nesse sentido, um aluno de Matemática desenhou um pentágono regular e, a partir dos seus vértices, traçou todas as diagonais. Assim, verificou a formação de uma estrela de cinco pontas, conforme a figura a seguir:
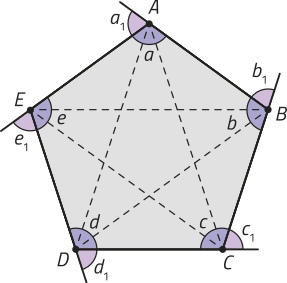
Ao somar os ângulos internos das pontas da estrela, o valor encontrado foi de:
a) 1.440°.
b) 540°.
c) 180°.
d) 108°.
e) 30°.
alternativa c
2. (UECE) Os ângulos formados, no interior de um pentágono regular, pelo encontro de seus lados e diagonais possuem as seguintes medidas:
a) 30°, 45° e 60°.
b) 45°, 60° e 75°.
c) 60°, 84° e 108°.
d) 36°, 72° e 108°.
alternativa d
3. (UFRR) Uma criança montou um mosaico utilizando quatro azulejos em formato de hekzágono regular de lado 10 cm. Sua mãe rêzouvêo colocar o mosaico numa moldura retangular, conforme a figura, a seguir.
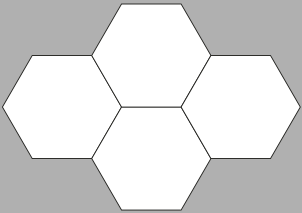
A área da região interna à moldura, quê não ficou coberta pêlos azulejos é de:
a) 400 cm2
b) 600 cm2
c) 1.000 cm2
d) 500 cm2
e) 200 cm2
alternativa a
4. (Enem/MEC) Na planta baixa de um clube, a piscina é representada por um quadrado cuja área real méde 400 m². Ao redor dessa piscina, será construída uma calçada, de largura constante igual a 5 m.
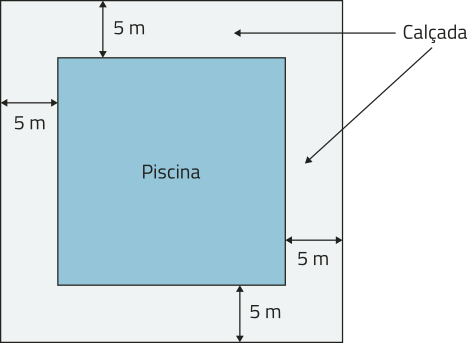
Qual é a medida da área, em métro quadrado, ocupada pela calçada?
a) 1.000
b) 900
c) 600
d) 500
e) 400
alternativa d
5. (UEL-PR) Um quatrefoil é uma figura simétrica comumente usada em ár-te, disáini e arquitetura. Sua forma é antiga e o nome vêm do latim, significando “quatro fô-lhas”. Ele possui quatro folhas de mesmo tamãnho, com formato circular, interconectadas, as quais se sobrepõem ligeiramente, e se assemelha a uma flor de quatro pétalas. Considere dois exemplos de quatrefoil, a seguir.

Pretende-se construir um quatrefoil similar ao apresentado no Exemplo A, no qual as fô-lhas são formadas por semicírculos.
Sabendo quê seu perímetro deve sêr de 28(pi)" cm, determine a área total da figura a sêr construída. Apresente os cálculos realizados na resolução da questão.
A = (196 + 98(pi)") cm2
Página duzentos e quarenta e nove
6. (Unicamp-SP) Sr. Gauss tem uma pizzaria, chamada (pi)"-zzaria, quê vende dois tipos de pitssas circulares: uma individual, de diâmetro d; e uma de 20 cm de diâmetro, partida em quatro pedaços iguais.
Considerando quê o preêço de uma pitssa é proporcional à sua área, qual precisa sêr o valor de d para quê quatro pitssas individuais custem o mesmo quê a pitssa mencionada, de quatro pedaços?
a) 6 cm.
b) 8 cm.
c) 10 cm.
d) 12 cm.
alternativa c
7. (UEA-AM) Considere o retângulo ABCD, de diagonal e o quadrado EFGH, cujas áreas são, respectivamente, iguais a 32 cm2 e 16 cm2. Os vértices do quadrado estão sobre os lados do retângulo, e a diagonal intersecta os lados do quadrado nos pontos P e Q, conforme mostra a figura.
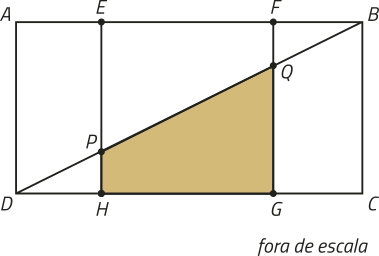
Sabendo quê os segmentos e possuem a mesma medida, a área do trapézio GHPQ, destacado na figura, é igual a
a) 8,5 cm2.
b) 9,5 cm2.
c) 9,0 cm2.
d) 8,0 cm2.
e) 10,0 cm2.
alternativa d
8. (hú éfe pê érre) Na figura a seguir, estão representadas quatro circunferências de raio r = 1 cm quê são tangentes nos pontos A, B, C e D. Assinale a alternativa quê corresponde ao valor, em cm2, da área hachurada em cinza.
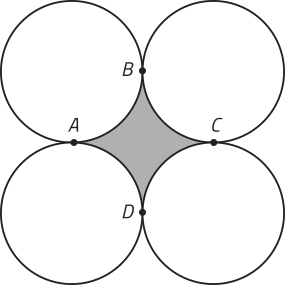
a) (pi)" − 1.
b) (pi)" − 2.
c) 2 − .
d) 4 − (pi)".
e) 4 − .
alternativa d
9. (Uesb-BA) Considere o triângulo ABC, retângulo em A. Sabendo-se quê a medida do cateto méde 12 cm e quê o ângulo formado pelo cateto e pela hipotenusa méde 60°, é correto afirmar quê
a) a medida da hipotenusa é um número irracional.
b) o cateto méde 12 cm.
c) o perímetro do triângulo ABC méde 12(1 + ) cm.
d) a área do triângulo ABC méde 144 cm2.
e) a razão entre as medidas de e , nesta ordem, é menor do quê .
alternativa e
10. (UFRGS-RS) No retângulo ABCD, representado na figura abaixo, os três ângulos destacados com vértice em C são iguais.
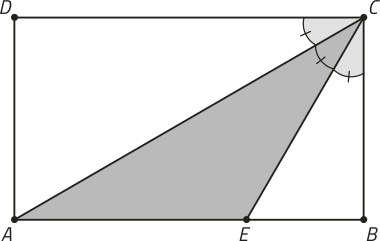
A área do triângulo sombreado AEC, em relação à área total do retângulo, corresponde a
a)
b)
c)
d)
e)
alternativa b
11. (UEA-AM) No retângulo ABCD, na figura, o ponto E foi tomado sobre o lado e o ponto F
foi tomado sobre o lado de modo quê o segmento seja paralelo ao lado e os ângulos e sêjam congruentes.
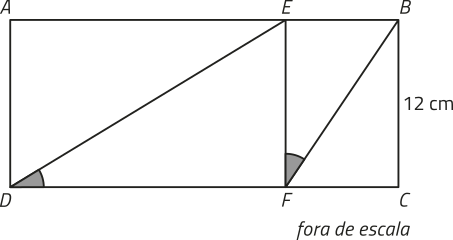
Sabendo quê BC = 12 cm e quê a razão entre as áreas dos triângulos EDF e BFE é , o perímetro do retângulo ABCD é
a) 64 cm.
b) 76 cm.
c) 80 cm.
d) 68 cm.
e) 72 cm.
alternativa b
Página duzentos e cinquenta
12. (UFJF-MG) A figura abaixo apresenta a tela de um radar térmico quê, na côr cinza, indica a região de uma floresta onde foi detectada uma grande queimada. Nessa tela, as circunferências são concêntricas em O, e as medidas de seus raios estão indicadas na tela, em quilômetros. Há também seis retas quê passam pelo ponto O e quê dividem cada circunferência em arcos de mesma medida.
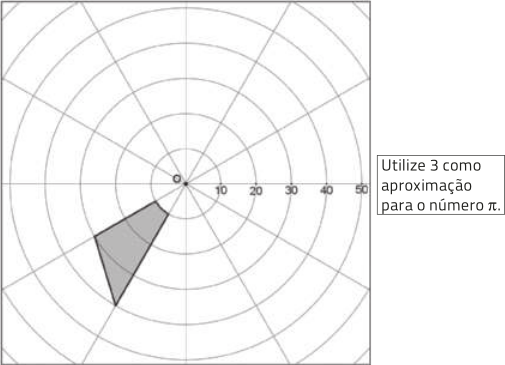
A extensão, em quilômetros quadrados, da área de queimada indicada pelo radar méde
a) 275,0
b) 287,5
c) 295,0
d) 365,0
e) 575,0
alternativa a
13. (Enem/MEC) A figura representa uma escada com três degraus, construída em concreto maciço, com suas medidas especificadas.
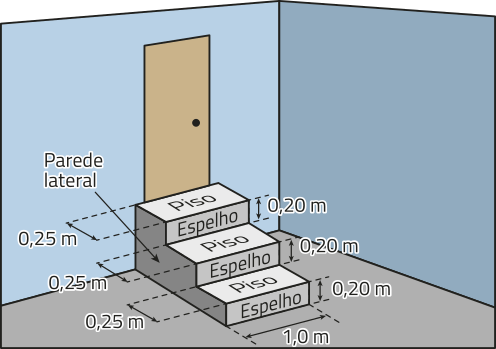
Nessa escada, pisos e espelhos têm formato retangular, e as paredes laterais têm formato de um polígono cujos lados adjacentes são perpendiculares. Pisos, espelhos e paredes laterais serão revestidos em cerâmica.
A área a sêr revestida em cerâmica, em métro quadrado, méde
a) 1,20.
b) 1,35.
c) 1,65.
d) 1,80.
e) 1,95.
alternativa e
14. (Unicamp-SP) Na figura a seguir, ABCD é um trapézio com AB = 1 e cê dê = 5. Os pontos M e N são pontos médios de AB e BC, respectivamente.
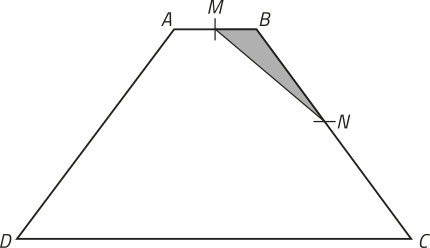
Sabendo quê a área de MBN é 1, a área do trapézio é:
a) 18.
b) 20.
c) 22.
d) 24.
alternativa d
15. (UECE) Seja XYZW um trapézio, onde XW é a base maior. Se XZ e YW são as diagonais do trapézio e K é a interseção da reta paralela à diagonal YW pelo vértice Z com o prolongamento da base XW, então, é correto dizêr quê
a) a área do triângulo XYZ é maior do quê a área do triângulo WZK.
b) a área do triângulo XYZ é menor do quê a área do triângulo WZK.
c) a área do trapézio XYZW é igual à área do triângulo XZK.
d) a área do trapézio XYZW é maior do quê a área do triângulo XZK.
alternativa c
16. (Unésp) O hekzágono marcado na malha quadriculada sobre a fotografia representa o contôrno do campus da Unésp de Rio Claro, quê é aproximadamente plano.
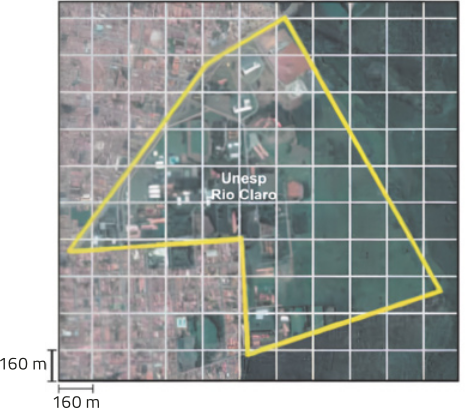
A área aproximada dêêsse campus, em km2, é um número pertencente ao intervalo
a) [0,8; 1,3[
b) [1,8; 2,3[
c) [2,3; 2,8[
d) [1,3; 1,8[
e) [0,3; 0,8[
alternativa a
Página duzentos e cinquenta e um



