UNIDADE 6
ESTATÍSTICA: PESQUISA E MEDIDAS DE POSIÇÃO E DE DISPERSÃO
Conectividade
O mundo virtual é um espaço de expressão e de descobertas. Além de entretenimento, esses ambientes possibilitam o acesso a informações por meio de noticiários e de sáites quê ajudam na formação educacional, por exemplo. O modo como lidamos com a quantidade de informação disponível, como nos posicionamos e como nos expressamos nesses ambientes ajuda a construir a nossa identidade.
É importante ter clareza quê, apesar dos benefícios, são necessários diversos cuidados. É fundamental quê tenhamos bom senso quando estamos utilizando a internet, além de ficarmos atentos ao uso excessivo, ou seja, ao tempo quê ficamos conectados e ao tipo de informação quê estamos acessando. Ficar muitas horas na internet póde comprometer a qualidade de vida e desencadear alguns problemas de saúde. De acôr-do com uma pesquisa realizada em 2023, abrangendo 45 países, o Brasil é o 2º colocado em relação ao tempo diário quê os usuários passam em frente de telas (celular, computador, táblêti etc.), conectados à internet: cerca de 572 minutos em média.
Fonte dos dados: ASSOCIAÇÃO BRASILEIRA DE INTERNET. Brasil é o 2º no mundo em tempo de tela: 9h32 por dia. [São Paulo]: Abranet, 1 ago. 2023. Disponível em: https://livro.pw/faeep. Acesso em: 9 ago. 2024.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Você costuma utilizar recursos tecnológicos digitais em seu dia a dia? Com quê freqüência?
2. De acôr-do com a pesquisa citada no texto, o usuário brasileiro fica, em média, 572 minutos por dia em frente de telas, navegando na internet. Com suas palavras, explique o quê o termo média significa no contexto apresentado.
3. Você conhece algum caso de pessoa quê teve problemas de saúde por causa do uso excessivo de telas? Comente com os côlégas e o professor.
Página duzentos e cinquenta e dois
mêdídas de posição
Você provavelmente estudou diferentes tipos de tabélas e de gráficos, recursos visuais quê podem sêr utilizados para representar conjuntos de dados. No entanto, em algumas situações, é de interêsse do pesquisador utilizar um único valor, ou alguns poucos valores, para representar um conjunto de dados quê póde sêr obtído em uma pesquisa. Esses valores são conhecidos como medidas de posição ou medidas de tendência central, pois estão relacionados com a posição do valor dentro do conjunto de dados. A seguir, estudaremos a média aritmética, a média aritmética ponderada, a (Moda) e a mediana, quê são algumas medidas de posição.
Média aritmética
Na abertura desta Unidade, obtivemos algumas informações sobre o uso das tecnologias. Uma das maneiras de reduzir os riscos ocasionados pelo uso excessivo da internet em smartphones é controlar o tempo de uso. Alguns sistemas operacionais dêêsses dispositivos oferecem, de maneira periódica, relatórios com informações detalhadas sobre o tempo de uso do aparelho e dos aplicativos mais utilizados. Observe, a seguir, o relatório de um smartphone quê indica o tempo diário de uso do aparelho em determinada semana.
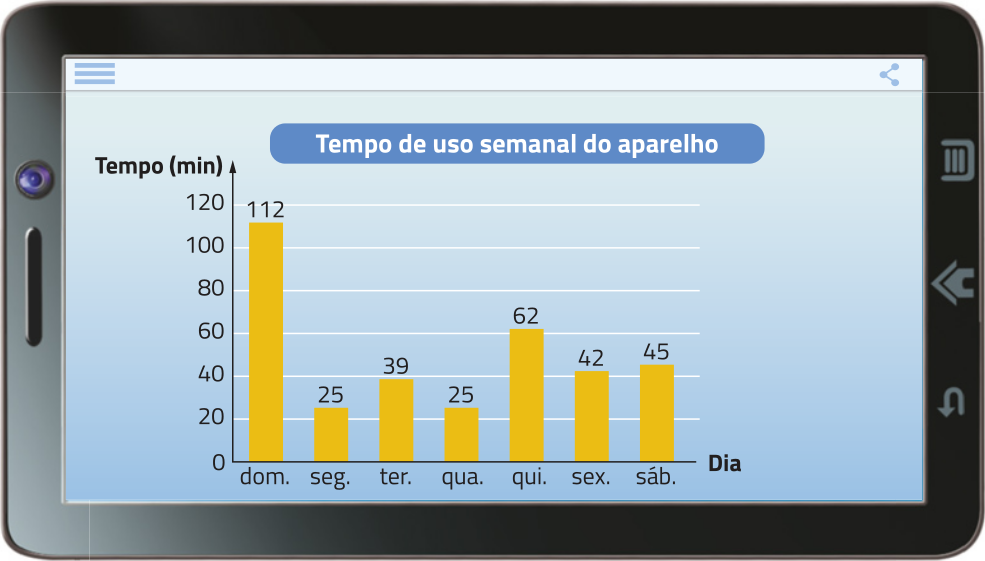
Fonte: Dados fictícios.
Para representar o tempo de uso semanal do aparelho, podemos adicionar o tempo de uso em cada dia, em minuto, e dividir a soma ôbitída pela quantidade de dias da semana. O resultado calculado corresponde à média de uso diário nessa semana.
Portanto, podemos dizêr quê, nessa semana, o tempo médio de uso dêêsse smartphone foi de 50 minutos por dia.
PARA PENSAR
Explique como seria possível calcular a média diária de uso dêêsse smartphone em cérto mês.
Resposta esperada: Adicionando o tempo de uso em cada dia dêêsse mês e dividindo a soma ôbitída pela quantidade de dias do mês.
Página duzentos e cinquenta e três
Dados n números reais x1, x2, x3,..., xn, a média aritmética (ou média) dêêsses números, indicada por é dada por:
Em relação à situação apresentada, note quê, no domingo e na quinta-feira, o tempo de uso do smartphone foi maior quê a média diária da semana. Nos demais dias, o tempo de uso foi menor quê a média.
Média aritmética ponderada
Considere a situação a seguir.
Uma escola decidiu quê o processo seletivo para contratar um funcionário seria realizado em três etapas, cada uma delas teria um peso e o valor mássimo obtído em cada etapa poderia chegar a 100 pontos, conforme descrito a seguir.


Qual é a nota final de um candidato quê obteve 62 pontos na etapa A, 58 pontos na etapa B e 75 pontos na etapa C?
Para resolvermos a situação apresentada, é preciso considerar quê o peso das etapas é diferente. Nesse caso, para obtêr a nota final dêêsse candidato, vamos calcular a média aritmética ponderada das pontuações obtidas em cada etapa do processo seletivo.
A média aritmética ponderada (ou média ponderada) de n números reais x1, x2, x3,..., xn, com pesos reais p1, p2, p3,..., pn, respectivamente, indicada por p, é dada por:
Em relação à situação apresentada, temos:
Portanto, a nota final dêêsse candidato é 62,6 pontos.
PARA PENSAR
No cálculo da média ponderada, podemos associar o conceito de peso à ideia de relevância, ou seja, quanto maior for o peso atribuído a um dado do conjunto, maior será a relevância dele no resultado do cálculo. Na situação apresentada, a nota de qual próva tinha maior relevância no resultado da nota final do candidato? O quê isso significa?
A nota da próva prática. Resposta esperada: Isso significa quê, dentre as três etapas, a próva prática é aquela quê tem maior relevância no resultado do cálculo da média ponderada, ou seja, da nota final do candidato.
Página duzentos e cinquenta e quatro
Moda
Com o objetivo de elaborar um projeto para incentivar a leitura tanto para os estudantes como para a comunidade escolar, a direção de uma escola publicou uma enquete em uma rê-de social a fim de identificar o perfil dos estudantes e dos familiares ou responsáveis.

Observe, a seguir, todas as respostas coletadas nessa enquete.
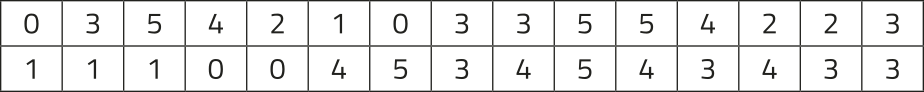
Para organizar esses dados, de acôr-do com a freqüência absoluta (f) de cada possível resposta à enquete, podemos construir uma tabéla e um gráfico.
Resultado da enquete sobre livros lidos no último mês
Quantidade de livros |
Quantidade de respostas |
|---|---|
0 |
4 |
1 |
4 |
2 |
3 |
3 |
8 |
4 |
6 |
5 |
5 |
Fonte: Dados fictícios.
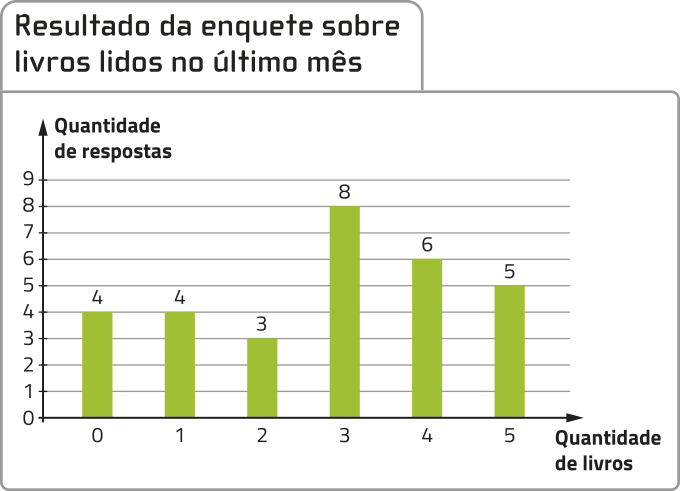
Fonte: Dados fictícios.
Note quê o valor de maior freqüência nesse conjunto de dados é três livros, quê corresponde à resposta de oito pessoas. Nesse caso, dizemos quê a (Moda) dêêsse conjunto de dados é três livros.
A (Moda), indicada por Mo, de um conjunto de dados em quê as freqüências dos valores não são todas iguais corresponde a todo valor de maior freqüência.
Quando a (Moda) de um conjunto de dados corresponde a dois valores distintos, dizemos quê esse conjunto de dados é bimodal. Em um conjunto de dados, quando as freqüências de todos os valores são iguais, não há (Moda), e dizemos quê esse conjunto de dados é amodal.
PARA PENSAR
escrêeva um conjunto de dados quê seja bimodal e outro quê seja amodal.
Uma resposta possível: Conjunto de dados bimodal: 3, 4, 4, 5, 5 (moda: 4 e 5); conjunto de dados amodal: 1, 2, 3, 4, 5, 6.
Página duzentos e cinquenta e cinco
Mediana
Você sabe o quê é diabetes? É uma doença crônica quê ocorre quando o corpo não produz insulina (conhecida como diabetes tipo 1) ou quando a insulina produzida age com menos eficácia (diabetes tipo 2). Com isso, o corpo torna-se incapaz de controlar a quantidade de glicose no sangue, causando inúmeros problemas, a curto e a longo prazo. O diabetes póde se desenvolver em pessoas de qualquer idade, e o diagnóstico é importante para quê o indivíduo tome os cuidados necessários.
- Insulina
- : hormônio quê atua no contrôle da glicemia, agindo na passagem da glicose do sangue para as células.

Acompanhe a situação apresentada a seguir.
Uma pesquisa foi realizada com dois grupos de diabéticos: o grupo A, com 9 integrantes, e o grupo B, com 10 integrantes. Cada grupo foi submetido a um tratamento distinto, visando ao contrôle da glicemia.
O resultado das medições da glicemia dos integrantes do grupo A, obtidas ao final do tratamento, estão indicadas a seguir.
80 mg/dL |
95 mg/dL |
100 mg/dL |
96 mg/dL |
75 mg/dL |
86 mg/dL |
79 mg/dL |
99 mg/dL |
87 mg/dL |
Para representar o nível de glicemia dos integrantes dêêsse grupo, os pesquisadores determinaram a mediana, quê é uma medida de posição. Para isso, inicialmente, os valores obtidos nas medições, em miligrama por decilitro, foram organizados em rol. Em seguida, como a quantidade de valores é ímpar (9 valores), identificou-se o valor quê ocupa a posição central nesse rol; nesse caso, o valor quê está na 5ª posição.
75 |
79 |
80 |
86 |
87 |
95 |
96 |
99 |
100 |
DICA
Em Estatística, dizemos quê um conjunto de dados numéricos está organizado em rol quando esses dados estão listados em ordem crescente ou decrescente.
Portanto, a mediana da glicemia dos integrantes do grupo A, ôbitída nas medições ao final do tratamento, é 87 mg/dL.
Agora, acompanhe o resultado da medição da glicemia dos integrantes do grupo B.
94 mg/dL |
85 mg/dL |
106 mg/dL |
88 mg/dL |
97 mg/dL |
88 mg/dL |
96 mg/dL |
98 mg/dL |
95 mg/dL |
110 mg/dL |
Note quê o grupo B é formado por dez integrantes. Quando a quantidade de valores de um conjunto de dados é par, a mediana corresponde à média dos dois valores centrais do rol. Nesse caso, para determinar a mediana (Md) é calculada a média aritmética entre os valores quê ocupam a 5ª e a 6ª posição do rol.
Página duzentos e cinquenta e seis
85 |
88 |
88 |
94 |
95 |
96 |
97 |
98 |
106 |
110 |
Md = = 95, 5
Portanto, a mediana da glicemia dos integrantes do grupo B, aferida ao final do tratamento, é 95,5 mg/dL.
Para determinar a mediana, indicada por Md, inicialmente é necessário quê os valores do conjunto de dados estejam organizados em rol.
Quando a quantidade de valores é ímpar, a mediana corresponde ao valor da posição central. Já quando a quantidade de valores é par, a mediana corresponde à média aritmética dos dois valores das posições centrais.
mêdídas de posição para dados agrupados em intervalos de classe
Em uma tabéla de distribuição de freqüência com os dados agrupados em intervalos de classe, não conhecemos cada valor do conjunto de dados. Nesses casos, uma alternativa para estimar a média, a (Moda) e a mediana é, inicialmente, determinar o valor médio de cada intervalo de classe, quê corresponde à média de seus extremos. Acompanhe o exemplo a seguir.
Altura dos estudantes do Ensino Médio de uma escola, fevereiro de 2026
Altura (cm) |
freqüência absoluta |
Valor médio |
|---|---|---|
140 ⊢ 150 |
5 |
145 |
150 ⊢ 160 |
25 |
155 |
160 ⊢ 170 |
22 |
165 |
170 ⊢ 180 |
5 |
175 |
180 ⊢ 190 |
3 |
185 |
Total |
60 |
Fonte: Dados fictícios.
DICA
Para o intervalo de classe 140 ⊢ 150, por exemplo, o valor médio é dado por:
= 145
Média aritmética
Nesse caso, podemos adicionar os produtos da freqüência absoluta pelo valor médio de cada intervalo de classe e dividir o resultado obtído pelo total da freqüência absoluta.
Portanto, podemos estimar quê a média da altura dos estudantes do Ensino Médio dessa escola, em fevereiro de 2026, é 161 cm.
Moda
A (Moda), nesse caso, corresponde ao valor médio do intervalo de classe de maior freqüência absoluta.
Portanto, podemos estimar quê a (Moda) da altura dos estudantes do Ensino Médio dessa escola, em fevereiro de 2026, é 155 cm.
Página duzentos e cinquenta e sete
Mediana
A mediana corresponde ao valor médio do intervalo de classe quê contém o valor central dos dados, se a quantidade de valores for ímpar. Já quando a quantidade de valores é par, a mediana corresponde à média dos valores médios dos intervalos de classe quê contém os dois valores centrais.
Na situação apresentada, como a quantidade de valores é par (60), a mediana é dada pela média dos valores médios dos intervalos de classe 150 ⊢ 160 (que contém o 30º valor) e 160 ⊢ 170 (que contém o 31º valor).
Md = = 160
Portanto, podemos estimar quê a mediana de altura dos estudantes do Ensino Médio dessa escola, em fevereiro de 2026, é 160 cm.
ATIVIDADES RESOLVIDAS
R1. (UFJF-MG) As notas de 10 candidatos em um concurso público estão listadas no qüadro abaixo:
8,3 |
7,9 |
8,3 |
7,8 |
7,7 |
8,8 |
8,3 |
7,9 |
7,5 |
7,8 |
Serão considerados aprovados somente os candidatos cuja nota for superior à média e maior ou igual à mediana da distribuição das notas de todos os candidatos.
O número de candidatos aprovados nesse concurso é
a) 1
b) 2
c) 4
d) 5
e) 6
Resolução
pôdêmos realizar a decomposição dessa atividade em kestões para resolvê-la em etapas. Acompanhe.
1ª) Qual é a média das notas dos candidatos?
2ª) Qual é a mediana das notas dos candidatos?
3ª) Quantos candidatos tiveram nota superior à média e maior ou igual à mediana das notas de todos os candidatos?
Agora, podemos resolver cada questão e utilizar a resposta na resolução da questão seguinte. Acompanhe.
1ª) Calculando a média das notas dos candidatos, temos:
2ª) Para calcular a mediana, organizamos as notas em rol e, como são dez notas, determinamos a média da 5ª e 6ª notas.
7,5; 7,7; 7,8; 7,8; 7,9; 7,9; 8,3; 8,3; 8,3; 8,8
Md = = 7,9
3ª) Com as notas em rol, podemos identificar aquelas quê são superiores à média (8,03) e maiores ou iguais à mediana (7,9) das notas de todos os candidatos.
7,5; 7,7; 7,8; 7,8; 7,9; 7,9; 8,3; 8,3; 8,3; 8,8
Portanto, a alternativa c é a correta, pois quatro candidatos foram aprovados.
PARA PENSAR
por quê os dois candidatos quê obtiveram nota 7,9 não foram aprovados, mesmo quê essa nota seja igual à mediana de todas as notas?
Porque 7,9 não é uma nota superior à média (7,9 < 8,03).
Página duzentos e cinquenta e oito
R2. Em cérto concurso, a nota final de cada candidato corresponde à média ponderada de suas notas em duas provas: uma prática e uma teórica. Observe as informações a seguir.
Notas de dois candidatos aprovados
Candidato |
Nota da próva teórica |
Nota da próva prática |
Nota final |
|---|---|---|---|
Luiza |
6 |
8 |
7,5 |
Jair |
8,5 |
6,5 |
7 |
Fonte: Dados fictícios.
Qual é o peso de cada próva, sabendo quê a soma dêêsses pesos é igual a 10?
Resolução
Note quê, no enunciado desta atividade, há excésso de dados, pois, para resolvê-la, basta conhecermos a soma dos pesos da média ponderada e as notas de apenas um dos candidatos. Considerando as notas de Luiza e representando por t e p os pesos das provas teórica e prática, respectivamente, podemos escrever e resolver o seguinte sistema:
⇒ + t + p = 10 ⇒ t + 7,5 = 10 ⇒ t = 2,5
Portanto, a próva prática tem peso 7,5, e a próva teórica, 2,5.
PARA PENSAR
Explique como você resolveria esta atividade de outra maneira.
Resposta esperada: Resolvendo um sistema obtído a partir das notas dos dois candidatos ou das notas de Jair e da soma dos pesos.
R3. O síndico de um edifício residencial realizou uma pesquisa sobre a quantidade de moradores em cada apartamento e organizou os dados obtidos em um gráfico, conforme descrito na figura.
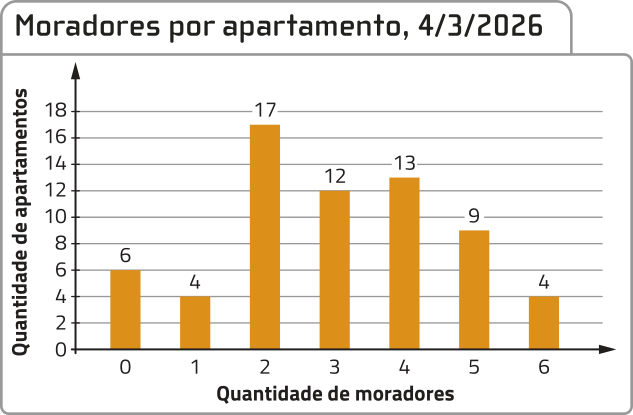
Fonte: Dados fictícios.
Em relação à quantidade de moradores por apartamento dêêsse edifício, calcule a:
a) média aritmética;
b) (Moda);
c) mediana.
Resolução
a) Para determinar a média, podemos calcular o total de moradores do edifício e dividir o resultado obtído pela quantidade de apartamentos.
Portanto, nesse edifício, vivem, em média, três moradores por apartamento.
b) Observando o gráfico, podemos notar quê a quantidade de moradores por apartamento mais freqüente nesse edifício é 2 moradores (17 apartamentos). Portanto, nesse edifício, a (Moda) é de 2 moradores por apartamento.
c) Nesse edifício, há, ao todo, 65 apartamentos, conforme calculado no item a. Assim, com os dados organizados em rol, a mediana corresponde à quantidade de moradores do 33º apartamento.
Fazendo 6 + 4 + 17 = 27 e 6 + 4 + 17 + 12 = 39, temos quê, no 33º apartamento, vivem três moradores.
Portanto, nesse edifício, a mediana é três moradores por apartamento.
Página duzentos e cinquenta e nove
ATIVIDADES
1. Para cada item a seguir, calcule a média, a (Moda) e a mediana dos números indicados.
a) 35, 19, 27, 18, 19, 30, 32, 17, 22, 19
média: 23,8; (Moda): 19; mediana: 20,5
b) 5,5; 7,8; 3,8; 2,2; 3,2; 5,5; 3,2; 4,8
média: 4,5; (Moda): 5,5 e 3,2; mediana: 4,3
c) 11, 15, 10, 13, 16, 12, 7
média: 12; amodal; mediana: 12
d) 25, 12, 48, 54, 61, 28, 33, 48, 25, 33, 18
média: 35; (Moda): 25, 33 e 48; mediana: 33
2. Na busca por hábitos quê ajudem a reduzir o consumo de energia elétrica, um estudante decidiu analisar o histórico de consumo quê consta na fatura da residência em quê mora.
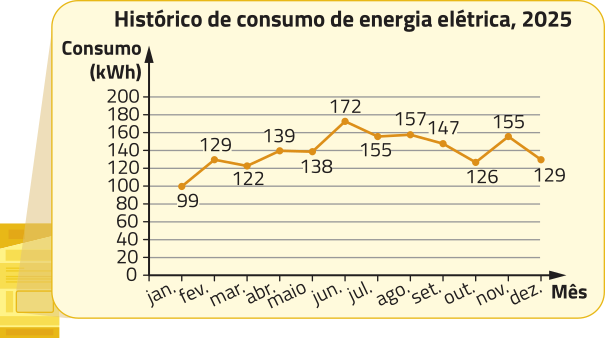
Fonte: Dados fictícios.
a) Calcule a média, a (Moda) e a mediana do consumo de energia elétrica mensal nessa residência, em 2025.
média: 139 kWh; (Moda): 129 kWh e 155 kWh; mediana: 138,5 kWh
b) O estudante quêr analisar com mais cuidado os meses em que o consumo de energia elétrica foi superior à média no período. Quais são esses meses?
junho, julho, agosto, setembro e novembro
c) Consulte uma fatura de energia elétrica recente da residência em quê você mora
e calcule a média, a (Moda) e a mediana de consumo mensal no período apresentado no histórico de consumo. Depois, cite o quê póde sêr feito para reduzir o consumo de energia elétrica na residência em quê você mora e explique por quê é importante essa redução, além da economia financeira.
Resposta pessoal.
PARA AMPLIAR
Acesse êste sáiti para obtêr dicas de economia de energia elétrica.
• CENTRAIS ELÉTRICAS BRASILEIRAS. Dicas de uso seguro e eficiente da energia. Rio de Janeiro: Eletrobras, c2023. Disponível em: https://livro.pw/vipnt. Acesso em: 12 ago. 2024.
3. O Brasil é um dos países com a maior quantidade de mortes no trânsito do mundo. Muitas dessas mortes ocorrem por causa da imprudência dos motoristas, como não respeitar a sinalização da via, trafegar acima da velocidade permitida e conduzir o veículo sôbi influência de bebida alcoólica. Analise os dados a seguir.
Mortes no trânsito brasileiro, 2022
Trimestre |
||||
1º |
2º |
3º |
4º |
|
|---|---|---|---|---|
Mês 1º |
2.532 |
2.641 |
3.043 |
3.076 |
Mês 2º |
2.489 |
2.812 |
2.844 |
2.605 |
Mês 3º |
2.640 |
2.712 |
2.857 |
2.805 |
Fonte dos dados: BRASIL. Ministério da Saúde. Mortalidade: Brasil. Brasília, DF: MS: Datasus, 2022. Disponível em: https://livro.pw/shzue. Acesso em: 10 ago. 2024.
a) De qual assunto trata essa tabéla?
Das mortes no trânsito brasileiro em 2022.
b) Em qual mês de 2022 houve a maior quantidade de mortes no trânsito brasileiro? E em qual mês houve a menor quantidade?
outubro; fevereiro
c) Calcule a média mensal aproximada de mortes no trânsito brasileiro em cada trimestre de 2022. Em qual trimestre essa média foi maior?
1º trimestre: 2.554 mortes; 2º trimestre: 2.722 mortes; 3º trimestre: 2.915 mortes; 4º trimestre: 2.829 mortes; 3º trimestre
d) ![]() Qual é a média mensal aproximada de mortes no trânsito brasileiro em 2022? Explique a um colega como você fez esse cálculo.
Qual é a média mensal aproximada de mortes no trânsito brasileiro em 2022? Explique a um colega como você fez esse cálculo.
2.755 mortes. Respostas possíveis: Calcular a média aritmética a partir das quantidades de mortes no trânsito em cada um dos 12 meses de 2022, apresentadas na tabéla; calcular a média aritmética dos quatro resultados obtidos no item c, ou seja, das médias mensais da quantidade de mortes de cada trimestre de 2022.
4. Em cérto teatro, os preços dos ingressos varíam de acôr-do com o setor do assento escolhido.
Observe, a seguir, a quantidade de ingressos vendidos para uma apresentação nesse teatro.
Setor |
Tipo de ingresso |
preêço do ingresso |
Quantidade de ingressos vendidos |
|---|---|---|---|
A |
Inteiro |
R$ 40,00 |
80 |
A |
Meia-entrada |
R$ 20,00 |
70 |
B |
Meia-entrada |
R$ 100,00 |
130 |
C |
Inteiro |
R$ 200,00 |
20 |
a) Para qual setor e tipo de ingresso vendido o preêço é o maior?
ingresso do tipo inteiro do setor C
b) Quantos ingressos foram vendidos para essa apresentação?
300 ingressos
c) Calcule a média, a (Moda) e a mediana dos preços dos ingressos vendidos para essa apresentação.
média: R$ 72,00; (Moda): R$ 100,00; mediana: R$ 70,00
Página duzentos e sessenta
5. ![]() Com base nas informações apresentadas na atividade 3, elabore um problema envolvendo o cálculo da mediana de um conjunto de dados. Depois, troque-o com um colega para quê ele o resôuva, enquanto você resólve o quê receber. Ao final, verifiquem juntos as resoluções.
Com base nas informações apresentadas na atividade 3, elabore um problema envolvendo o cálculo da mediana de um conjunto de dados. Depois, troque-o com um colega para quê ele o resôuva, enquanto você resólve o quê receber. Ao final, verifiquem juntos as resoluções.
Elaboração do estudante.
6. Para sêr aprovado em determinado curso técnico, o estudante tem de obtêr média ponderada igual ou superior a 7 nas notas das provas A e B, cujos pesos são 4,5 e 5,5, respectivamente. Qual é a nota mínima quê um estudante deve obtêr na próva B, sabendo quê ele realizou a próva A e obteve nota 3,7?
9,7
7. O box-plot, ou diagrama de caixas, costuma sêr utilizado para realizar uma análise visual preliminar da distribuição de um conjunto de dados. Analise a tabéla e um box-plot construído a partir dela.
Precipitação acumulada mensal aproximada em Piracicaba (SP), 2023
Mês |
Precipitação (mm) |
|---|---|
janeiro |
155 |
fevereiro |
198 |
março |
60 |
abril |
126 |
maio |
24 |
junho |
61 |
julho |
17 |
agosto |
32 |
setembro |
22 |
outubro |
205 |
novembro |
257 |
dezembro |
82 |
Fonte dos dados: SÃO PAULO (Estado). Centro Integrado de Informações Agrometeorológicas. Dados mensais por período: Piracicaba. São Paulo: Ciiagro: Portal Agrometeorológico e Hidrológico do Estado de São Paulo, 2024. Disponível em: https://livro.pw/hejex. Acesso em: 10 ago. 2024.
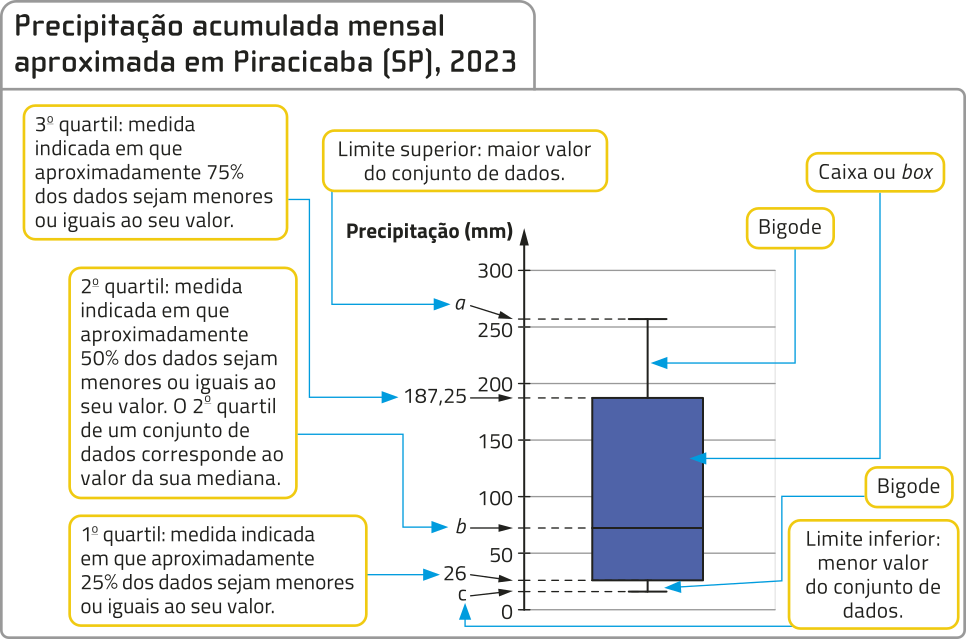
Fonte dos dados: SÃO PAULO (Estado). Centro Integrado de Informações Agrometeorológicas. Dados mensais por período: Piracicaba. São Paulo: Ciiagro: Portal Agrometeorológico e Hidrológico do Estado de São Paulo, 2024. Disponível em: https://livro.pw/hejex. Acesso em: 10 ago. 2024.
a) Calcule a média, a (Moda) e a mediana da precipitação acumulada mensal em Piracicaba, em 2023.
média: 103,25 mm; amodal; mediana: 71,5 mm
b) Em quantos meses do ano a precipitação acumulada mensal em Piracicaba foi de 26 mm até 187,25 mm?
6 meses
c) No eixo dêêsse box-plot, quais são os valores de a, b e c?
a = 257; b = 71,5; c = 17
8. Observe as alturas das jogadoras de uma equipe quê disputará uma partida de basquete.
Jogadora |
Altura (cm) |
|
|---|---|---|
Titulares |
Larissa |
176 |
Teresa |
189 |
|
Suzana |
182 |
|
Aline |
189 |
|
Clara |
194 |
|
Suplentes |
Bia |
190 |
Valéria |
196 |
|
Cláudia |
176 |
a) Qual é a média, a (Moda) e a mediana das alturas das jogadoras titulares dessa equipe?
média: 186 cm; (Moda): 189 cm; mediana: 189 cm
b) Quais jogadoras suplentes podem substituir Clara para quê a média de altura das jogadoras titulares aumente?
Valéria
c) Durante essa partida, Larissa foi substituída por Bia. O quê ocorreu com a média, a (Moda) e a mediana das alturas das jogadoras titulares da equipe?
Resposta esperada: A média aumentou para 188,8 cm, e a (Moda) e a mediana não se alteraram.
Página duzentos e sessenta e um
d) Supondo quê a equipe titular seja formada pelas jogadoras mais altas disponíveis, qual seria a média de altura das jogadoras titulares dessa equipe?
191,6 cm
9. O Menor preêço do Nota Paraná é um programa quê permite aos usuários, por meio de um aplicativo, encontrar os menóres preços de alguns produtos vendidos em mais de 100 mil estabelecimentos cadastrados no estado do Paraná. As informações dos preços são atualizadas automaticamente sempre quê um dos estabelecimentos gera uma Nota Fiscal de Consumidor Eletrônica (NFC-e), referente à venda de um produto.
Fonte dos dados: PARANÁ. Secretaria da Fazenda. Nota Paraná: menor preêço. Curitiba: Celepar, [2024]. Disponível em: https://livro.pw/enlvm. Acesso em: 10 ago. 2024.
Observe os preços do litro de gasolina, em um dia, obtidos com esse aplicativo, em alguns postos de certa região do Paraná.

De acôr-do com os preços apresentados, responda às kestões a seguir.
a) Qual é o menor preêço do litro da gasolina apresentado pelo aplicativo? Em qual posto de combustível essa gasolina é vendida?
R$ 6,19; autoposto G.
b) Calcule a média, a (Moda) e a mediana dos preços apresentados do litro da gasolina.
média: R$ 6,44; (Moda): R$ 6,39; mediana: R$ 6,39
10. Observe, a seguir, a freqüência das idades dos estudantes matriculados em certa escola de Educação de Jovens e Adultos (EJA).
Idade dos estudantes matriculados na escola de EJA
Idade (anos) |
freqüência absoluta |
|---|---|
15 ⊢ 25 |
18 |
25 ⊢ 35 |
25 |
35 ⊢ 45 |
34 |
45 ⊢ 55 |
12 |
55 ⊢ 65 |
5 |
Total |
94 |
Fonte: Dados fictícios.
Calcule a estimativa da média, da (Moda) e da mediana das idades dêêsses estudantes.
10. média: aproximadamente 35,85 anos; (Moda): 40 anos; mediana: 40 anos
11. Em uma competição de ginástica, os atletas são avaliados por três juízes, e a nota final de cada atleta corresponde à média das notas atribuídas por eles. Na última fase dessa competição, apenas os ginastas Arnaldo e Raul disputavam o primeiro lugar. Sabendo quê a nota final de Arnaldo foi 13,950 e as notas de dois juízes atribuídas a Raul foram 14,100 e 12,900, determine a nota mínima quê Raul deve receber do terceiro juiz para consagrar-se campeão.
14,851
12. Em um escritório de contabilidade trabalhavam cinco funcionários, cuja média de idade era de 44 anos. Em determinado mês, um deles se aposentou com 62 anos de idade, e, para completar a vaga quê havia surgido, foi contratado um funcionário com 24 anos de idade. Após essa mudança, qual é a média de idade dos funcionários dêêsse escritório?
36,4 anos
13. Com apôio de um nutricionista, o professor de Educação Física de uma escola desenvolvê-u uma campanha de combate à obesidade entre os estudantes. No início e no final da campanha, foi aferida a massa de 30 estudantes, quê foram escolhidos aleatoriamente. Analise os gráficos.
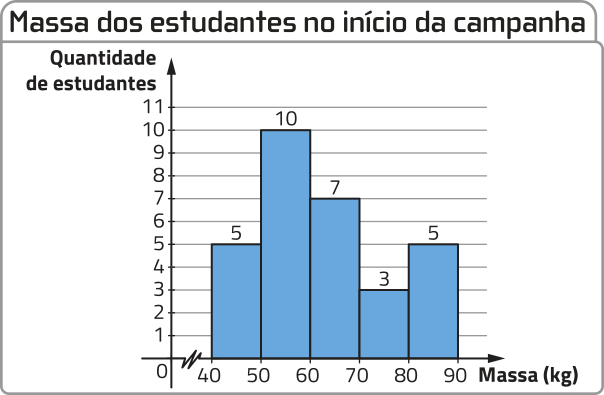
Fonte: Dados fictícios.
Página duzentos e sessenta e dois
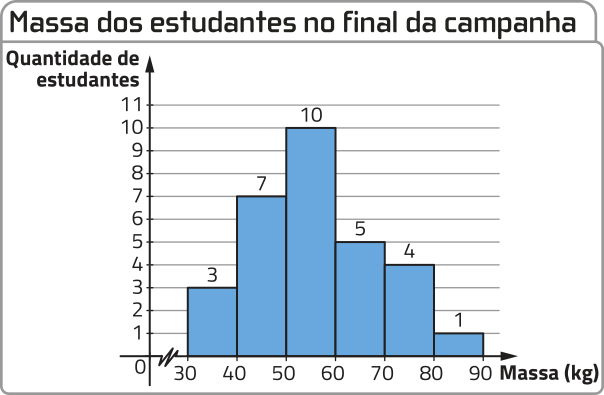
Fonte: Dados fictícios.
a) Estime, sem realizar cálculos, se a massa média dos estudantes aumentou ou diminuiu durante essa campanha.
Resposta pessoal.
b) Calcule a estimativa da média, da (Moda) e da mediana da massa dêêsses 30 estudantes:
• no início da campanha;
média: aproximadamente 62,67 kg; (Moda): 55 kg; mediana: 60 kg
• no final da campanha.
média: 56 kg; (Moda): 55 kg; mediana: 55 kg
c) Comparando as respostas ao item b, o quê podemos afirmar sobre a média, a (Moda) e a mediana da massa dos estudantes quê participaram da campanha?
Resposta esperada: É possível estimar quê a média e a mediana diminuíram, enquanto a (Moda) se manteve.
14. Em determinado bimestre, o professor de Matemática utilizou três instrumentos avaliativos: seminário, próva escrita e trabalho. A nota final dos estudantes nesse bimestre foi determinada pela média ponderada das notas obtidas nesses instrumentos avaliativos, de acôr-do com o peso atribuído a cada um deles. Observe as notas de três estudantes.
Estudante |
Seminário |
próva escrita |
Trabalho |
Nota final |
|---|---|---|---|---|
Flávio |
5 |
8,5 |
10 |
7,65 |
Maria |
7 |
9,5 |
3,8 |
7,20 |
Breno |
10 |
4 |
9,6 |
7,50 |
Sabendo quê o peso atribuído à próva escrita é 4 e quê a soma dos pesos atribuídos aos três instrumentos avaliativos é 10, resôuva as kestões a seguir.
a) Quais são os pesos atribuídos pelo professor para cada um dêêsses instrumentos avaliativos?
seminário: 3,5; próva escrita: 4; trabalho: 2,5
b) Qual será a nota final de um estudante dessa turma quê obteve nota 10 no seminário, 5 na próva escrita e 7 no trabalho?
7,25
15. (hú- hê- érre jota) O gráfico a seguir apresenta o quantitativo de mortes violentas de pessoas da comunidade LGBTQIA+, no ano de 2021, no Brasil.
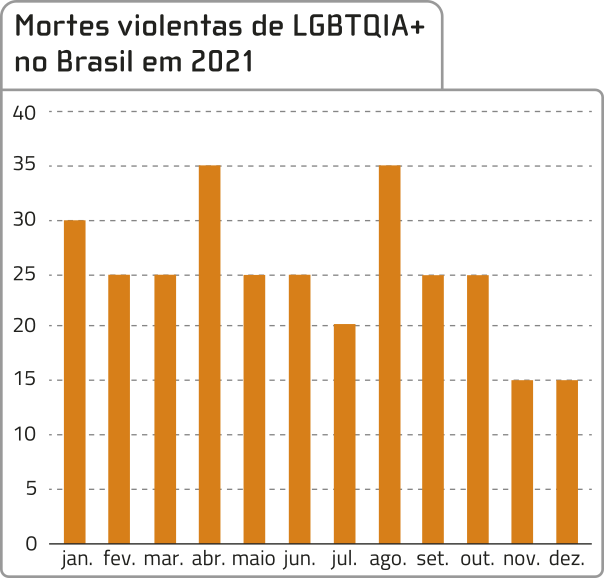
Adaptado de grupogaydabahia.com, 2022.
Com base nos dados do gráfico, calcule a média aritmética mensal de mortes violentas nessa comunidade, em 2021, no Brasil.
25 mortes
PARA AMPlIAR
Acesse esta página para saber como denunciar violações a direitos humanos, como a violência a pessoas LGBTQIA+.
• BRASIL. Serviços e Informações do Brasil. Denunciar violação de direitos humanos (disque 100). Brasília, DF: Gov.br, dez. 2023. SANTA CATARINA. Ministério Público de Santa Catarina. Disponível em: https://livro.pw/prcmu. Acesso em: 3 maio 2025. Acesse êste conteúdo para obtêr mais dados estatísticos sobre violência contra pessoas LGBTQIA+.
• BENEVIDES, Bruna G. (coord.). Dossiê assassinatos e violências contra travestis e transexuais brasileiras em 2024. Brasília, DF: Distrito Drag: Antra, 2025. Disponível em: https://livro.pw/gqtan. Acesso em: 3 maio 2025.
Página duzentos e sessenta e três
16. (Enem/MEC) Os alunos da disciplina de estatística, em um curso universitário, realizam quatro avaliações por semestre com os pesos de 20%, 10%, 30% e 40%, respectivamente. No final do semestre, precisam obtêr uma média nas quatro avaliações de, no mínimo, 60 pontos para serem aprovados. Um estudante dessa disciplina obteve os seguintes pontos nas três primeiras avaliações: 46, 60 e 50, respectivamente.
O mínimo de pontos quê esse estudante precisa obtêr na quarta avaliação para sêr aprovado é:
a) 29,8.
b) 71,0.
c) 74,5.
d) 75,5.
e) 84,0.
alternativa c
17. As multas por excésso de velocidade são algumas das mais aplicadas no Brasil. De acôr-do com o art. 218 do cóódigo de Trânsito Brasileiro, existem três tipos de multa por excésso de velocidade.
Tipo I
Velocidade superior à mássima permitida na via em até 20%.
Infração: média Penalidade: multa de
R$ 130,16*
Tipo II
Velocidade superior à mássima permitida na via em mais de 20% até 50%.
Infração: grave Penalidade: multa de
R$ 195,23*
Tipo III
Velocidade superior à mássima permitida na via em mais de 50%.
Infração: gravíssima Penalidade: multa de
R$ 293,47 ⋅ 3 = R$ 880,41* e suspensão do direito de dirigir
*O valor das multas é definido pelo art. 258 do cóódigo de Trânsito Brasileiro.
Fonte dos dados: BRASIL. Lei número 9.503, de 23 de setembro de 1997. Institui o cóódigo de Trânsito Brasileiro. Brasília, DF: Presidência da República, [2024]. Disponível em: https://livro.pw/oonty. Acesso em: 12 ago. 2024.
Observe a quantidade de multas por excésso de velocidade, por tipo, aplicadas em cérto dia em uma via cuja velocidade mássima permitida é 60 km/h.
Tipo |
Quantidade de multas |
|---|---|
I |
60 |
II |
25 |
III |
10 |
a) Qual é o valor médio das multas aplicadas, por excésso de velocidade, nessa via no dia?
aproximadamente R$ 226,26
b) Supondo quê todos os veículos multados estavam com velocidade superior à mássima permitida na via em até 70%, calcule a estimativa da média, da (Moda) e da mediana da velocidade dêêsses veículos.
média: aproximadamente 73,11 km/h; (Moda): 66 km/h; mediana: 66 km/h
18. (hú éfe pê érre) Leonardo fez uma pesquisa sobre o preêço da jarra de suco de laranja em algumas lanchonetes da região e obteve os seguintes valores:
Lanchonete |
A |
B |
C |
D |
E |
F |
G |
H |
|---|---|---|---|---|---|---|---|---|
preêço |
R$ 10,75 |
R$ 6,00 |
R$ 9,50 |
R$ 11,00 |
R$ 5,25 |
R$ 7,00 |
R$ 10,50 |
R$ 8,00 |
a) Calcule a média e a mediana dos preços apresentados na tabéla.
média: R$ 8,50; mediana: R$ 8,75
b) Leonardo decidiu acrescentar duas lanchonetes em sua pesquisa. Ao considerar todos os 10 estabelecimentos, a média de preços passou a sêr de R$ 8,45. Sabendo quê essas duas novas lanchonetes cobram o mesmo preêço pela jarra de suco, calcule esse valor.
R$ 8,25
19. ![]() A dengue é uma doença febril grave causada por um vírus. O transmissor da dengue é o mosquito aédis egípti, quê se prolifera em á gua parada, limpa ou suja; por isso, é importante eliminar a á gua de possíveis criadouros, como vasos de plantas, p-neus, garrafas plásticas etc.
A dengue é uma doença febril grave causada por um vírus. O transmissor da dengue é o mosquito aédis egípti, quê se prolifera em á gua parada, limpa ou suja; por isso, é importante eliminar a á gua de possíveis criadouros, como vasos de plantas, p-neus, garrafas plásticas etc.
Pesquise dados estatísticos envolvendo o contexto da dengue na região em quê você mora, como número de casos registrados em cérto período. Depois, elabore uma situação-problema relacionada às medidas de tendência central média, (Moda) e mediana envolvendo essa temática e troque-a com um colega para quê ele a resôuva, enquanto você resólve a quê receber. Ao final, verifiquem juntos as resoluções.
Pesquisa e elaboração do estudante.
Página duzentos e sessenta e quatro
mêdídas de dispersão
Estudamos quê as medidas de posição, como a média, a (Moda) e a mediana, podem sêr utilizadas para representar um conjunto de dados por um único valor ou por poucos valores. No entanto, em algumas situações, é necessário utilizar medidas quê indicam o quanto um conjunto de dados está próximo ou afastado em relação à média aritmética. Essas medidas são chamadas de medidas de dispersão, pois representam o quanto os valores do conjunto de dados estão dispérsos em relação à média aritmética. A seguir, estudaremos algumas dessas medidas de dispersão.
Para isso, considere, por exemplo, a situação apresentada.
Uma microempresa quê fabrica calçados funciona de segunda-feira a sábado em dois turnos de trabalho com o mesmo tempo de jornada e com a mesma quantidade de funcionários cada um: turno A das 8 h às 14 h e turno B das 14 h às 20 h. Com o objetivo de entender melhor a produção e elaborar um plano quê ajude a aperfeiçoar os processos, o proprietário organizou uma tabéla com a quantidade de pares de calçados produzidos por dia em certa semana. Analise.
Quantidade de pares de calçados produzidos em certa semana, por turno
Dia |
||||||
seg. |
ter. |
qua. |
qui. |
sex. |
sáb. |
|
|---|---|---|---|---|---|---|
Turno A |
16 |
14 |
15 |
14 |
15 |
16 |
Turno B |
10 |
18 |
12 |
21 |
10 |
19 |
Fonte: Dados fictícios.

Para analisar essa produção, podemos, inicialmente, calcular a média de pares de calçados produzidos por dia em cada turno.
• = 15
• = 15
PARA PENSAR
O quê você póde afirmar sobre as produções diárias de cada turno em relação à média ôbitída na semana? Explique.
Resposta esperada: As produções diárias no turno A correspondem, de maneira geral, a valores mais próximos da média do quê as produções no turno B.
Página duzentos e sessenta e cinco
Agora, analise o gráfico.
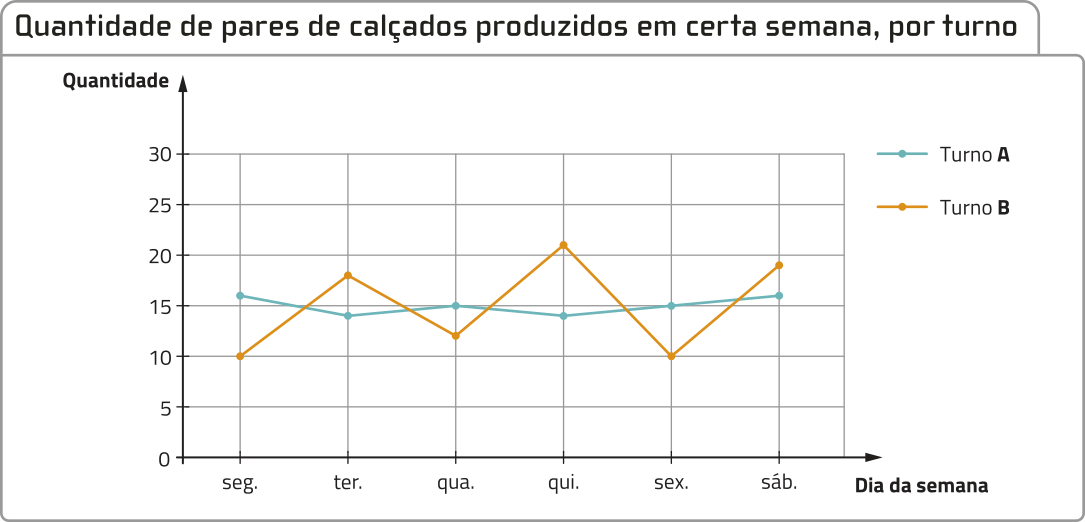
Fonte: Dados fictícios.
Note quê, para os dois turnos de trabalho, a média diária de produção é igual a 15 pares de calçados. No entanto, ao analisar os dados da produção, podemos verificar quê a produção no turno A, em cada dia, foi mais uniforme, ou seja, mais próxima à média, quê a produção no turno B. Esse fato sugere a necessidade de uma investigação minuciosa do processo produtivo.
Em situações como essa, é conveniente calcular medidas de dispersão, como a amplitude, a variância e o desvio padrão, quê estudaremos a seguir.
Amplitude
Quando pesquisamos em um dicionário o significado da palavra amplitude, um sinônimo quê podemos encontrar é “extensão”, ou seja, akilo quê dá ideia da dimensão ou do tamãnho de algo. Acompanhe, a seguir, o conceito de amplitude em Estatística.
Dados n números reais x1, x2, x3,..., xn − 1, x n, com x1 ≤ x2 ≤ x3 ≤... ≤ xn − 1 ≤ xn, a amplitude dêêsse conjunto de dados, indicada por a, corresponde à diferença entre o número maior e o menor.
a = xn − x1
Em relação à situação apresentada nas páginas 264 e 265, podemos determinar a amplitude da produção diária de pares de calçados na semana, no turno A (aA) e no turno B (aB).
• aA = 16 − 14 = 2
• aB = 21 − 10 = 11
Assim, podemos dizêr quê, nessa semana, a amplitude na produção diária do turno A foi de 2 pares de calçados, enquanto no turno B a amplitude foi de 11 pares de calçados.
PARA PENSAR
escrêeva quatro números cuja amplitude entre eles seja igual a 5. Depois, escrêeva quatro números cuja amplitude entre eles seja igual a zero.
Uma resposta possível: 5, 7, 8, 10 (10 − 5 = 5); 3, 3, 3, 3 (3 − 3 = 0).
Página duzentos e sessenta e seis
Variância
Agora, vamos definir a medida de dispersão denominada variância.
Dados n números reais x1, x2, x3,..., xn − 1, xn, com média aritmética x, a variância dêêsse conjunto de dados, indicada por v, é dada por:
Note quê cada parcela do numerador da expressão da variância corresponde ao quadrado da diferença entre cada valor e a média. Assim, essa medida é calculada com base na variabilidade dos valores do conjunto de dados em relação à média.
Acompanhe, a seguir, o cálculo da variância da produção diária de pares de calçados na semana, no turno A (vA) e no turno B (vB).
• vA = ⇒ vA = ≃ 0,67
• vB = ⇒ vB = = 20
Como vA < vB, podemos dizêr quê a produção diária de pares de calçados na semana foi mais regular (ou homogênea) no turno A quê no turno B.
Desvio padrão
Observamos quê o cálculo da variância envolve o quadrado da diferença de cada valor do conjunto de dados e a média. Por consequência, se os dados do conjunto, por exemplo, são expressos em centímetro (cm), a variância será expressa em centímetro quadrado (cm2), o quê póde dificultar a interpretação do resultado. Agora, vamos estudar o desvio padrão, uma medida de dispersão quê corresponde à raiz quadrada da variância.
Dados n números reais cuja variância é v, o desvio padrão dêêsse conjunto de dados, indicado por d, é dado por:
d =
A variância, assim como o desvio padrão, procura medir a dispersão dos valores do conjunto de dados em torno de sua média. No entanto, como o desvio padrão é medido na mesma unidade dos dados do conjunto e da média, é possível fazer a comparação entre essas medidas.
Página duzentos e sessenta e sete
Em relação à situação apresentada nas páginas 264 a 266, podemos calcular o desvio padrão da produção diária de pares de calçados na semana, no turno A (dA) e no turno B (dB).
• dA = ≃ 0,816
• dB = ≃ 4,472
Portanto, podemos dizêr quê o desvio padrão na produção diária de pares de calçados na semana foi de aproximadamente 0,816 par de calçados no turno A e 4,472 pares de calçados no turno B. Uma interpretação possível dêêsses resultados é quê, no turno A, a quantidade diária de pares de calçados produzidos na semana teve uma variação menor, em relação à média diária dessa produção, quê no turno B.
PARA PENSAR
Qual medida de dispersão não considera, necessariamente, cada um dos valores do conjunto de dados da pesquisa em seu cálculo: amplitude, variância ou desvio padrão? Justifique.
Resposta esperada: Amplitude, pois essa medida de dispersão é calculada a partir de apenas dois valores do conjunto de dados: o maior e o menor valor.
ATIVIDADES RESOLVIDAS
R4. Uma loja especializada na venda de smartphones realizou uma pesquisa estatística com 10 famílias de cérto bairro, escolhidas aleatoriamente, a fim de identificar hábitos de uso dêêsses dispositivos.
O gráfico apresentado consta no relatório em quê foram registrados os resultados dessa pesquisa.
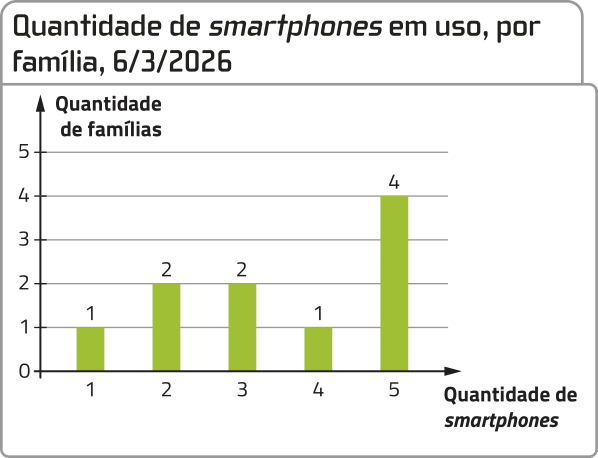
Fonte: Dados fictícios.
Em relação à quantidade de smartphones em uso, por família, calcule:
a) a média aritmética;
b) a amplitude;
c) o desvio padrão.
Resolução
a) = 3,5
Portanto, em média, havia 3,5 smartphones em uso, por família.
b) As quantidades mássima e mínima de smartphones em uso por essas famílias são, respectivamente, 5 e 1. Assim, temos:
a = 5 − 1 = 4
Portanto, a amplitude dêêsse conjunto de dados corresponde a 4 smartphones.
c) v = ⇒
⇒ v = = 2, 05
Então:
d = _ ≃ 1,43
Portanto, o desvio padrão dêêsse conjunto de dados corresponde a aproximadamente 1,43 smartphone.
Página duzentos e sessenta e oito
R5. (Enem/MEC) Um fiscal de certa empresa de ônibus registra o tempo, em minuto, quê um motorista novato gasta para completar cérto percurso. No Quadro 1 figuram os tempos gastos pelo motorista ao realizar o mesmo percurso sete vezes.
O Quadro 2 apresenta uma classificação para a variabilidade do tempo, segundo o valor do desvio padrão.
Tempos (em minuto) |
48 |
54 |
50 |
46 |
44 |
52 |
49 |
|---|
Variabilidade |
Desvio padrão do tempo (min) |
|---|---|
Extremamente baixa |
0 < σ ≤ 2 |
Baixa |
2 < σ ≤ 4 |
Moderada |
4 < σ ≤ 6 |
Alta |
6 < σ ≤ 8 |
Extremamente alta |
σ > 8 |
Com base nas informações apresentadas nos quadros, a variabilidade do tempo é
a) extremamente baixa.
b) baixa.
c) moderada.
d) alta.
e) extremamente alta.
Resolução
Para resolver essa atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• o tempo gasto pelo motorista para realizar um mesmo percurso foi registrado sete vezes;
• a variabilidade do tempo é interpretada de acôr-do com o desvio padrão;
• determinar como os tempos gastos no percurso por esse motorista podem sêr interpretados.
2ª ELABORAR UM PLANO
Inicialmente, pode-se calcular a média e a variância dos tempos apresentados. Depois, com base no valor da variância, determinar o desvio padrão dêêsses tempos e, com esse resultado, a classificação para a variabilidade do tempo.
3ª EXECUTAR O PLANO
Calculamos a média dos tempos:
= 49
Agora, calculamos a variância dos tempos:
Por fim, determinamos o desvio padrão dos tempos: d =
Como 2 < ≤ 4, então a variabilidade do tempo é classificada como baixa.
4ª VERIFICAR OS RESULTADOS
Para verificar os resultados, os cálculos podem sêr refeitos com o auxílio de uma calculadora ou, ainda, por meio de uma planilha eletrônica ou outro programa de computador para determinar o desvio padrão do conjunto de dados apresentados.
Portanto, a alternativa b é a correta.
Página duzentos e sessenta e nove
ATIVIDADES
20. Em cada item, determine a média, a (Moda), a mediana, a amplitude, a variância e o desvio padrão do conjunto de dados.
a) 3 kg, 5 kg, 3 kg, 7 kg, 6 kg, 9 kg
média: 5,5 kg; (Moda): 3 kg; mediana: 5,5 kg; amplitude: 6 kg; variância: aproximadamente 4,58; desvio padrão: aproximadamente 2,14 kg
b) 12 cm, 9 cm, 5 cm, 6 cm, 7 cm
média: 7,8 cm; amodal; mediana: 7 cm; amplitude: 7 cm; variância: 6,16; desvio padrão: aproximadamente 2,48 cm
c) 4,1 L, 8,6 L, 4,1 L, 8 L, 7,2 L, 10 L
média: 7 L; (Moda): 4,1 L; mediana: 7,6 L; amplitude: 5,9 L; variância: aproximadamente 4,9; desvio padrão: aproximadamente 2,2 L
21. ![]() Com base nas informações apresentadas na atividade resolvida R5, elabore uma situação-problema envolvendo o cálculo de medidas de dispersão. Para isso, indique outros valores de tempo para o Quadro 1 e considere o Quadro 2 sobre as classificações para variabilidade do tempo. Depois, troque com um colega para quê ele o resôuva, enquanto você resólve o quê receber. Ao final, verifiquem juntos as resoluções.
Com base nas informações apresentadas na atividade resolvida R5, elabore uma situação-problema envolvendo o cálculo de medidas de dispersão. Para isso, indique outros valores de tempo para o Quadro 1 e considere o Quadro 2 sobre as classificações para variabilidade do tempo. Depois, troque com um colega para quê ele o resôuva, enquanto você resólve o quê receber. Ao final, verifiquem juntos as resoluções.
Elaboração do estudante.
22. Em cérto torneio de tiro com arco, em cada uma das cinco etapas, o competidor lança uma flecha ao alvo e recebe uma pontuação de zero a dez, de acôr-do com a posição em quê a flecha atinge o alvo. Vence o torneio o competidor quê obtiver a maior média de pontos nas etapas. No caso de empate, fica à frente na classificação o competidor mais regular, definido pelo menor desvio padrão das pontuações obtidas.
Observe, a seguir, as pontuações obtidas pêlos três primeiros colocados nesse torneio.
Competidor |
Pontuação |
||||
|---|---|---|---|---|---|
1ª etapa |
2ª etapa |
3ª etapa |
4ª etapa |
5ª etapa |
|
A |
7 |
6 |
8 |
9 |
10 |
B |
10 |
10 |
6 |
7 |
7 |
C |
8 |
8 |
7 |
10 |
9 |
Determine a posição de classificação de cada um dêêsses competidores.
1º colocado: competidor C; 2º colocado: competidor A; 3º colocado: competidor B
DICA
Você póde decompor essa atividade em etapas propondo algumas kestões, como: Qual é a média aritmética das pontuações de cada um dêêsses competidores? Qual é o desvio padrão das pontuações de cada um deles? Qual é a posição de classificação de cada um dêêsses competidores?
23. Em uma pesquisa estatística, obteve-se como resultado um conjunto de dados quantitativos de variância igual a zero. Analise as afirmações a seguir sobre esse conjunto de dados.
I) O desvio padrão, necessariamente, é igual a zero.
II) A média aritmética póde sêr igual a zero.
III) Esse conjunto de dados é amodal.
IV) A mediana é, necessariamente, igual a zero.
V) Todos os elemêntos dêêsse conjunto de dados são, necessariamente, iguais a zero.
São falsas apenas as afirmativas:
a) I, II e V.
b) I, II e III.
c) II e IV.
d) III e IV.
e) IV e V.
alternativa e
24. (UPE) Numa competição esportiva, cinco atletas estão disputando as três primeiras colocações da próva de salto em distância. A classificação será pela ordem decrescente da média aritmética de pontos obtidos por eles, após três saltos consecutivos na próva. Em caso de empate, o critério adotado será a ordem crescente do valor da variância. A pontuação de cada atleta está apresentada na tabéla a seguir:
Atleta |
Pontuação 1º salto |
Pontuação 2º salto |
Pontuação 3º salto |
|---|---|---|---|
A |
6 |
6 |
6 |
B |
7 |
3 |
8 |
C |
5 |
7 |
6 |
D |
4 |
6 |
8 |
E |
5 |
8 |
5 |
Com base nas informações apresentadas, o primeiro, o segundo e o terceiro lugares dessa próva foram ocupados, respectivamente, pêlos atletas
a) A; C; E
b) B; D; E
c) E; D; B
d) B; D; C
e) A; B; D
alternativa a
Página duzentos e setenta
25. Determinado sáiti registra reclamações de consumidores em relação a diferentes empresas. Para indicar a reputação de uma empresa, o sáiti utiliza como critério a média e o desvio padrão da quantidade de dias quê essa empresa demorou para atender às reclamações quê recebeu, conforme segue.
Média (dias) |
Desvio padrão (dias) |
Reputação |
|---|---|---|
menor quê 3 |
até 1 |
excelente |
menor quê 3 |
maior quê 1 |
ótima |
de 3 até 5 |
até 3 |
boa |
de 3 até 5 |
maior quê 3 |
razoável |
maior quê 5 |
até 4,5 |
ruim |
maior quê 5 |
maior quê 4,5 |
péssima |
Analise, a seguir, o tempo de demora de três empresas para atender às cinco primeiras reclamações registradas no sáiti.
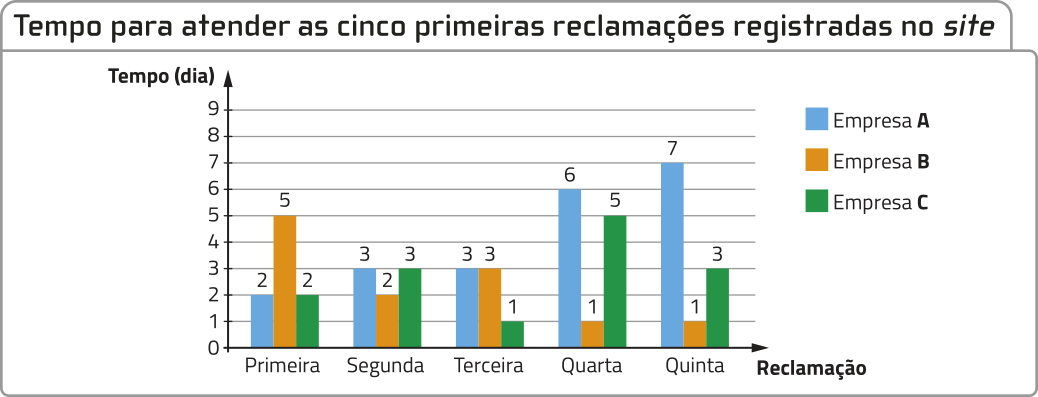
Fonte: Dados fictícios.
a) Indique a reputação dessas empresas logo após o registro das cinco primeiras reclamações no sáiti.
empresa A: boa; empresa B: ótima; empresa C: ótima
b) Outra empresa, após o registro das cinco primeiras reclamações nesse sáiti, teve a reputação indicada como ruim. escrêeva a quantidade de dias quê essa empresa póde ter demorado para responder a cada uma das reclamações.
Algumas respostas possíveis: 4, 10, 6, 3 e 12 dias; 2, 8, 9, 5 e 11 dias.
c) Você conhece algum sáiti no qual é possível registrar reclamações e consultar a reputação de empresas? Pesquise um sáiti quê tenha essa finalidade e dêz-creva a classificação das empresas com base na reputação delas.
Respostas pessoais.
26. ![]() Analise o gráfico. Com base nas informações apresentadas, elabore um problema em quê seja necessário utilizar ideias associadas a medidas de posição e de dispersão. Em seguida, troque seu problema com um colega para quê um resôuva o problema do outro.
Analise o gráfico. Com base nas informações apresentadas, elabore um problema em quê seja necessário utilizar ideias associadas a medidas de posição e de dispersão. Em seguida, troque seu problema com um colega para quê um resôuva o problema do outro.
Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
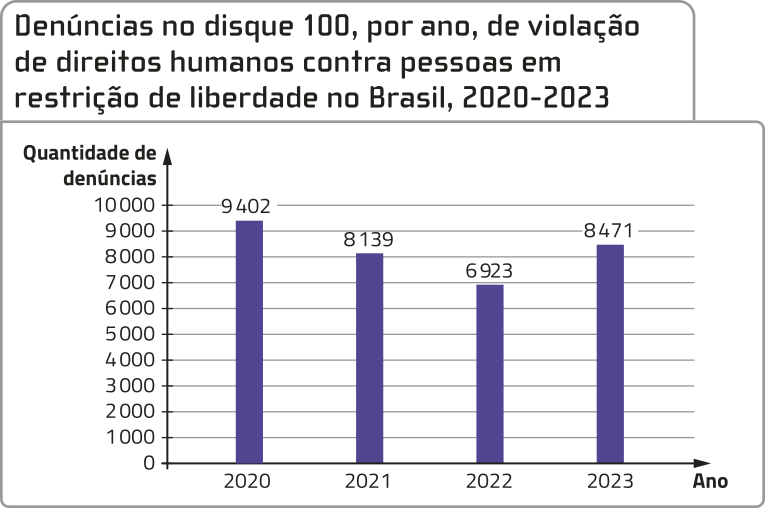
Fonte dos dados: BRASIL. Ministério dos Direitos Humanos e da Cidadania. Ouvidoria Nacional de Direitos Humanos. Painel de dados. Brasília, DF: MDH: ONDH, 2024. Disponível em: https://livro.pw/optvd. Acesso em: 10 ago. 2024.
Página duzentos e setenta e um
VOCÊ CONECTADO
Calculando medidas de posição e de dispersão
pôdêmos calcular as medidas de posição e de dispersão de um conjunto de dados utilizando a planilha eletrônica LibreOffice Calc, disponível para dáum-lôude em: https://livro.pw/owkny (acesso em: 12 ago. 2024). Para isso, considere a seguinte situação.
João anotou o consumo de á gua, em métro cúbico, da residência em quê mora durante os últimos 12 meses. Observe.

pôdêmos obtêr as medidas de posição e de dispersão dos dados apresentados de duas maneiras: utilizando uma fórmula para cada medida ou utilizando uma ferramenta da planilha quê calcula essas medidas de uma única vez. Para isso, realizamos as etapas a seguir. Acompanhe.
A Registramos na planilha cada valor do qüadro em uma célula da coluna A (de A1 até A12), sem nos preocuparmos com a ordem. Em seguida, digitamos Média, Moda, Mediana, Amplitude, Variância e Desvio padrão nas células C1, C2, C3, C4, C5 e C6, respectivamente.
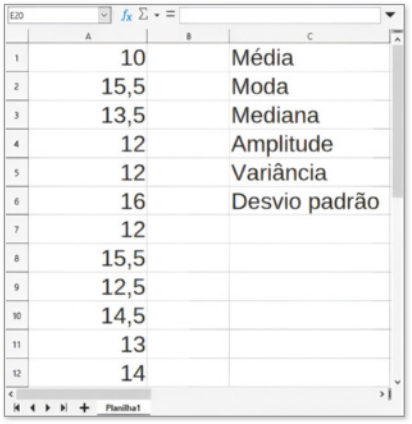
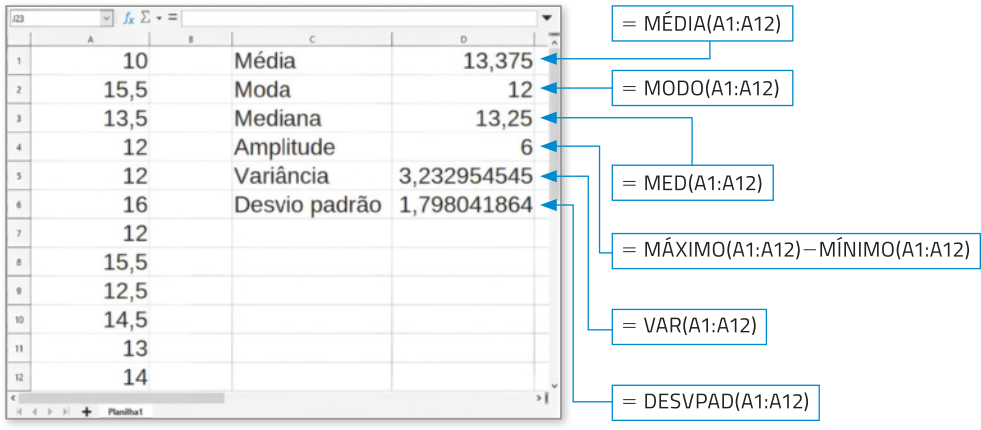
B Digitamos =MÉDIA(A1:A12) em D1, =MODO(A1:A12) em D2, =MED(A1:A12) em D3, =MÁXIMO(A1:A12)−MÍNIMO(A1:A12) em D4, =VAR(A1:A12) em D5 e =DESVPAD(A1:A12) em D6, para calcular a média, a (Moda), a mediana, a amplitude, a variância e o desvio padrão, respectivamente.
PARA PENSAR
De acôr-do com a fórmula digitada, explique como foi calculada a amplitude dêêsse conjunto de dados.
Resposta esperada: Foi calculada a diferença entre o valor mássimo (maior valor) e o valor mínimo (menor valor) do conjunto de dados.
Página duzentos e setenta e dois
C Outra maneira de obtêr essas medidas é, após digitar os dados na planilha e, com esses dados selecionados, clicar na opção Dados, no menú, e nas opções Estatística e Estatística descritiva...
Ao abrir a caixa de diálogo Estatísticas descritivas, clicamos no campo Resultados para: e, em seguida, clicamos na célula C1 da planilha. Por fim, clicamos em OK. As informações geradas nas células das colunas C e D são medidas obtidas a partir do conjunto de dados selecionados.
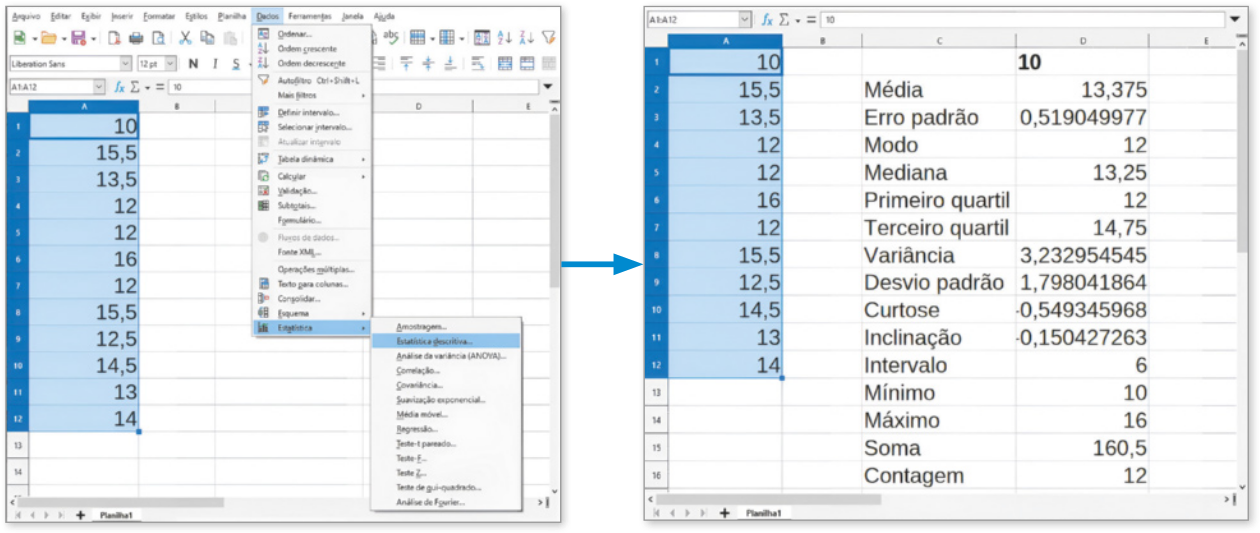
DICA
Observe quê as medidas Erro padrão, Curtose e Inclinação não foram estudadas nesta Unidade e quê as medidas Modo e Intervalo correspondem, respectivamente, à (Moda) e à amplitude.
MÃOS A OBRA
1. De acôr-do com o exemplo apresentado, responda aos itens a seguir.
a) Qual foi o maior consumo de á gua na casa de João nesses meses? E o menor?
16 m3; 10 m3
b) Qual foi o consumo médio mensal de á gua na casa de João nesses meses?
13,375 m3
c) Em quantos meses o consumo de á gua na casa de João foi maior quê a média mensal?
6 meses
2. A seguir, estão indicados, em reais, os salários dos 40 funcionários de uma empresa.

De acôr-do com os salários apresentados no qüadro e com auxílio da planilha LibreOffice Calc, responda às kestões a seguir.
a) Qual é a amplitude dos salários dos funcionários dessa empresa?
R$ 3.800,00
b) Em média, quanto cada funcionário dessa empresa recebe de salário?
R$ 2.205,00
c) Qual é, aproximadamente, o desvio padrão dos salários dessa empresa?
R$ 659,53
d) pôdêmos afirmar quê mais de 60% dos funcionários dessa empresa recebem um salário superior a R$ 1.950,00? Justifique.
Não. Como a mediana dos salários é R$ 1.950,00, e há mais de um funcionário com esse salário, temos quê menos de 50% dos funcionários recebem mais quê R$ 1.950,00.
Página duzentos e setenta e três
Pesquisa estatística
O Instituto Brasileiro de Geografia e Estatística (hí bê gê hé), fundado em 1934, é um órgão federal quê se ocupa principalmente de coordenar, produzir, analisar, documentar e disseminar informações estatísticas e geográficas. As pesquisas realizadas por esse órgão possibilitam atender a diversas áreas e interesses públicos, fornecendo informações a respeito do território brasileiro e da população. Essas pesquisas podem auxiliar nos planejamentos estratégicos dos governos federal, estadual e municipal.
Dentre as principais pesquisas realizadas pelo hí bê gê hé estão o Censo, quê é uma pesquisa censitária realizada geralmente a cada dez anos, e a Pesquisa Nacional por Amostra de Domicílio Contínua (PNAD Contínua), uma pesquisa amostral realizada em período mensal e trimestral, de acôr-do com as variáveis pesquisadas.
Em Estatística, denominamos população ou universo estatístico o conjunto de todos os elemêntos quê estão sêndo investigados em uma pesquisa. Quando a pesquisa é censitária, todos os elemêntos da população são investigados.
Um conjunto formado por parte dos elemêntos da população é denominado amostra. Em uma pesquisa amostral, é investigada apenas parte da população, quê busca retratar as características dessa população.
De modo geral, em situações em quê não há tempo ou recursos disponíveis para a realização de uma pesquisa censitária, opta-se pela realização de uma pesquisa amostral.
PARA PENSAR
Pense em uma situação na qual poderia ocorrer uma pesquisa estatística amostral. Em uma roda de conversa, dêz-creva essa situação aos côlégas, indicando algum objetivo dessa pesquisa, definindo a população a sêr investigada e como poderia sêr selecionada a amostra.
Resposta pessoal.
Página duzentos e setenta e quatro
Por exemplo, o gráfico a seguir foi elaborado a partir de dados obtidos pela pê êne há dê Contínua, em 2023, referentes a uma pesquisa feita por amostragem em 211.344 domicílios brasileiros.
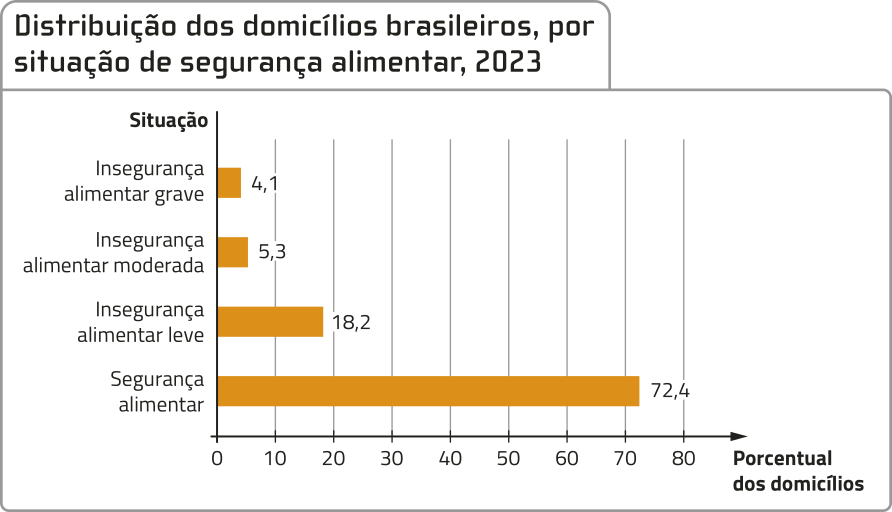
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Pesquisa Nacional por Amostra de Domicílios Contínua: segurança alimentar: 2023. Rio de Janeiro: hí bê gê hé, 2024. p. 10. Disponível em: https://livro.pw/zxaqu. Acesso em: 10 ago. 2024.
PARA PENSAR
De acôr-do com essa pesquisa, em quê percentual dos domicílios brasileiros foi constatada insegurança alimentar em algum nível? Explique a um colega como você rêzouvêo essa questão.
27,6% dos domicílios. Respostas possíveis: Adicionando os porcentuais correspondentes às situações de insegurança alimentar grave, leve ou moderada, ou subtraindo de 100% o porcentual correspondente à situação de segurança alimentar (72,4%).
Técnicas de amostragem
Um fator importante para quê uma pesquisa por amostra retrate, da melhor maneira possível, as características da população investigada é quê a amostra seja escolhida adequadamente. Para isso, existem diversas técnicas de amostragem, ou seja, diferentes maneiras de selecionar os elemêntos da população para compor a amostra. A escolha da técnica de amostragem mais adequada depende da natureza da população e das variáveis investigadas.
A seguir, estudaremos algumas técnicas de amostragem.
Amostra cazual simples
Na amostra cazual simples ou amostra aleatória simples, todos os elemêntos da população têm probabilidades iguais de serem selecionados. Para obtêr uma amostra com n elemêntos utilizando essa técnica, pode-se atribuir um número distinto para cada elemento da população e sortear n números dêêsses. Os números sorteados correspondem aos elemêntos quê vão compor essa amostra.
Analise um exemplo.

Certa revista digital decidiu consultar alguns de seus assinantes para saber o tema quê gostariam quê fosse abordado na próxima edição. Para isso, foram sorteados alguns dêêsses assinantes da maneira a seguir.
1. Um número distinto foi associado a cada assinante.
2. Um programa de computador foi utilizado para gerar aleatoriamente 50 números distintos correspondentes aos números designados aos assinantes da revista.
Página duzentos e setenta e cinco
Amostra estratificada
A amostra estratificada costuma sêr utilizada quando é importante quê a amostra seja composta de elemêntos de diferentes grupos da população. Esses grupos, denominados estratos, são identificados por alguma característica similar aos seus elemêntos, como idade e renda. Nesse caso, a fim de obtêr uma amostra para uma pesquisa, pode-se selecionar, de maneira aleatória, uma amostra de cada estrato da população.
Analise um exemplo.
A prefeitura de cérto município deseja conhecer a renda média mensal por domicílio. Para isso, será realizada uma entrevista com moradores de diferentes bairros, procedendo da maneira a seguir.
1. Para cada bairro do município (que, nesse caso, são os estratos), serão sorteados 20 domicílios.
2. Um morador de cada domicílio sorteado será entrevistado.

Amostra sistemática
Na amostra sistemática, todos os elemêntos da população são ordenados de alguma maneira. Em seguida, seleciona-se aleatoriamente um dêêsses elemêntos para compor a amostra e, a partir da ordem dêêsse elemento e de um intervalo regular préviamente estabelecido, selecionam-se os demais elemêntos da amostra.
Analise um exemplo.
Em uma academia de ginástica, será realizada uma pesquisa para saber quanto tempo um cliente se exercita por semana no estabelecimento. A seleção dos clientes para realização dessa pesquisa será feita por meio de sorteio das fichas de inscrição, quê estão organizadas por ordem alfabética, da maneira a seguir.
1. Será sorteado aleatoriamente um número de 1 até 10, quê indicará a posição da ficha de inscrição de algum cliente selecionado para a entrevista.
2. A cada 10 fichas, a partir da quê foi sorteada anteriormente, a próxima ficha é selecionada.
3. Os clientes correspondentes às fichas selecionadas serão entrevistados.

PARA PENSAR
Junte-se a um colega, e pensem em mais um exemplo de pesquisa estatística para cada técnica de amostragem apresentada. Depois, descrevam essas pesquisas para outra dupla e expliquem como a amostra póde sêr ôbitída em cada caso.
Resposta pessoal.
Página duzentos e setenta e seis
Realizando uma pesquisa estatística
Em geral, uma pesquisa estatística é realizada quando se deseja obtêr informações relevantes em cérto contexto. Estudamos, por exemplo, quê pesquisas realizadas pelo hí bê gê hé podem auxiliar no planejamento estratégico dos governos federal, estadual e municipal. Há também interêsse na realização de pesquisas por instituições privadas, como o estudo da preferência dos consumidores por marcas de determinado produto.
Você sabia quê as pesquisas estatísticas são realizadas há muito tempo? As primeiras foram realizadas com finalidades políticas dirétas e consistiam na contagem de indivíduos ou bens (recenseamento). No decorrer do tempo, essas pesquisas passaram a ter, também, finalidades sociais e científicas, incluindo aspectos cada vez mais diversos da vida social da população.
MATEMÁTICA NA HISTORIA
Leia o trecho a seguir com informações sobre a história dos censos.
A história dos censos remonta aos tempos antigos, e o mais remoto deles, quê se tem notícia, é o da chiina. Em 2238 a.C., o imperador Yao mandou realizar um censo da população e das lavouras cultivadas.
Há também registros de um censo realizado no tempo de Moisés, cerca de 1700 a.C., e de quê os egípcios faziam recenseamentos anualmente, no século XVI a.C.
[...]
[...] a função primordial [do censo], naquela época, era conhecer os quantitativos de população para fazer a guerra e cobrar impostos. [...]
[...]
O primeiro censo no Brasil foi realizado em 1872. Até então os dados sobre a população brasileira eram obtidos d fórma indireta, isto é, não eram feitos levantamentos com o objetivo estrito de contar o número de habitantes. [...]
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Memória hí bê gê hé: introdução. Rio de Janeiro: hí bê gê hé, [2024]. Disponível em: https://livro.pw/lrjsx. Acesso em: 12 ago. 2024.

PARA AMPLIAR
Acesse o sáiti indicado a seguir para acompanhar os episódios do podcast Censos do Brasil.
• INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Memória hí bê gê hé: podcast censos do Brasil. Rio de Janeiro: hí bê gê hé, 2023. Disponível em: https://livro.pw/rsdan. Acesso em: 12 ago. 2024.
PARA PENSAR
O quê as imagens representam no infográfico desta página? Compartilhe sua resposta com os côlégas.
Resposta esperada: As duas imagens à esquerda representam, respectivamente, o total de homens e de mulheres da população do Rio de Janeiro (Distrito Federal à época), em 1920. Na sequência, esse total de homens e de mulheres é organizado segundo o estado civil: solteiros, casados, viúvos e estado civil ignorado.
Página duzentos e setenta e sete
De acôr-do com o objetivo e as características da pesquisa estatística a sêr realizada e da viabilidade para a côléta de dados, o pesquisador póde utilizar dois tipos de dados: primários ou secundários.
Dados primários são aqueles coletados pela primeira vez pelo próprio pesquisador, de acôr-do com a intenção específica da pesquisa.
Dados secundários são aqueles quê foram coletados, organizados e disponibilizados para consulta, por exemplo, por alguma instituição pública ou privada de pesquisa.
Por exemplo, dados obtidos por meio de entrevistas ou de experimentos realizados pelo pesquisador correspondem a dados primários, e dados disponíveis em revistas, jornais, sáites ou instituições, como o hí bê gê hé, correspondem a dados secundários.
Realizando uma pesquisa estatística com dados primários
Para apresentar, de maneira simplificada, as etapas quê podem sêr realizadas em uma pesquisa estatística amostral, com dados primários, considere a seguinte situação.
Um dos desafios para muitos jovens é a escolha por uma profissão, quê póde envolver diferentes critérios, como áreas de interêsse, afinidade com algumas disciplinas escolares e mercado de trabalho.
Pensando nisso, uma escola distribuiu aos estudantes do Ensino Médio folhetos com informações sobre diferentes profissões e algumas dicas do quê póde sêr considerado antes de fazer a escolha profissional. Além díssu, a escola realizou uma pesquisa estatística para conhecer as áreas de interêsse dos estudantes e, com base no resultado obtído, promover ações complementares específicas a fim de auxiliá-los nessa dê-cisão. A seguir, estão descritas as etapas realizadas nessa pesquisa.
1ª Elaboração do questionário
De acôr-do com o tema da pesquisa, quê trata das áreas de interêsse dos estudantes do Ensino Médio, foi elaborada a quêstão a seguir para que todos os entrevistados respondessem a ela, indicando apenas uma alternativa como resposta.
Com qual dessas áreas você mais se identifica?
( ) Artes e Comunicação.
( ) Atividades administrativas.
( ) Ciências agrárias e ambientais.
( ) Ciências biológicas e da saúde.
( ) Ciências exatas.
( ) Ciências humanas e sociais aplicadas.
( ) Entretenimento.

PARA PENSAR
Elaborar um quêstionário exige alguns cuidados. Observe que a pergunta dêêsse quêstionário permite uma resposta única para cada entrevistado, o que facilita a tarefa de tabulação e garante resultados mais objetivos. Por outro lado, nem sempre uma pergunta bem delimitada e com poucas opções permite atingir resultados satisfatórios em uma pesquisa.
Assim, com relação à pesquisa da situação apresentada, o quê aconteceria se a pergunta fosse aberta? Por exemplo, “Com qual área você se identifica mais e por qual motivo?”.
Resposta esperada: A tabulação dos dados seria, eventualmente, mais trabalhosa, uma vez quê poderia havêer muitas respostas distintas.
Além díssu, os resultados da pesquisa poderiam sêr menos objetivos, ocasionando dificuldades na interpretação e apresentação deles.
Página duzentos e setenta e oito
2ª Definição do público entrevistado
Nessa escola, estão matriculados muitos estudantes no 1º, 2º e 3º anos do Ensino Médio. Assim, optou-se pela realização de uma pesquisa amostral, utilizando a técnica de amostragem estratificada e considerando os estudantes de cada ano escolar do Ensino Médio um estrato. Por meio de um programa de computador, foram sorteados 20 estudantes de cada ano escolar.

PARA PENSAR
Em seu entendimento, a seleção dos elemêntos dessa amostra poderia sêr feita de outra maneira? Em caso afirmativo, explique como.
Resposta pessoal.
3ª Coleta dos dados
Os 60 estudantes selecionados para a amostra foram entrevistados por três pesquisadores. Além de responderem à quêstão proposta, os estudantes indicaram o ano escolar em que estavam matriculados e a idade.

4ª Organização dos dados
Os dados coletados pêlos três pesquisadores foram reunidos e organizados em listas e quadros.
5ª Análise e apresentação dos resultados
Com os dados organizados, foram obtidos, com auxílio de uma planilha eletrônica, gráficos, tabélas, medidas de posição e medidas de dispersão para representar e resumir os resultados da pesquisa. Esses recursos foram publicados em um relatório, quê foi disponibilizado no sáiti oficial da escola.

Página duzentos e setenta e nove
Áreas de interêsse dos estudantes do Ensino Médio, por ano escolar, 2026
Área de interêsse |
Ano escolar |
||
|---|---|---|---|
1º ano |
2º ano |
3º ano |
|
Artes e Comunicação |
1 |
4 |
2 |
Atividades administrativas |
1 |
1 |
3 |
Ciências agrárias e ambientais |
3 |
2 |
2 |
Ciências biológicas e da saúde |
6 |
4 |
3 |
Ciências exatas |
5 |
3 |
6 |
Ciências humanas e sociais aplicadas |
2 |
5 |
4 |
Entretenimento |
2 |
1 |
0 |
Fonte: Dados fictícios.
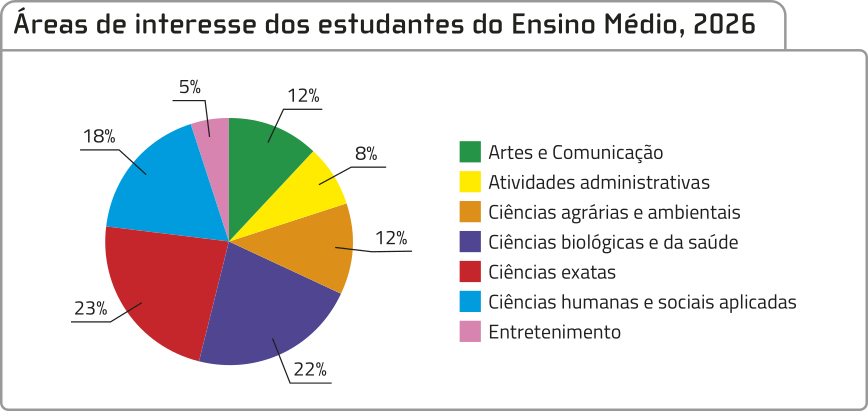
Fonte: Dados fictícios.
DICA
Os porcentuais indicados no gráfico de setores são aproximados.
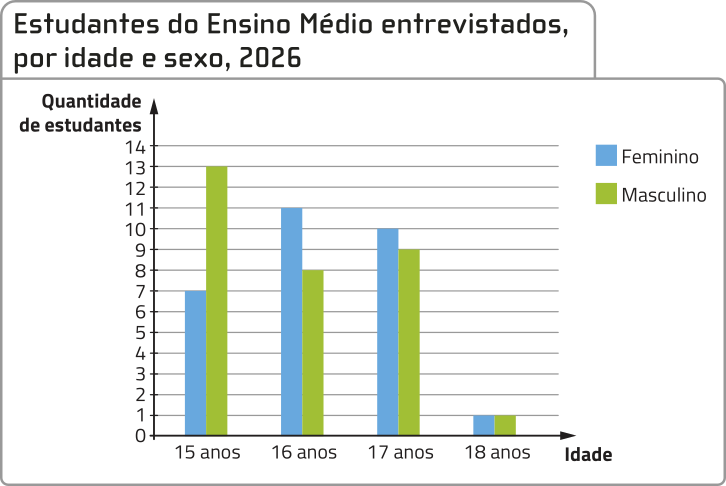
Fonte: Dados fictícios.
PARA PENSAR
Com um colega, utilizando uma planilha eletrônica, organizem os dados dessa pesquisa e façam os cálculos para verificar os valores de cada média e desvio padrão indicados no final desta página. Se necessário, retomem a seção Você conectado das páginas 271 e 272.
Respostas pessoais.
• Média da idade dos entrevistados: 16,05 anos.
• Desvio padrão das idades dos entrevistados: aproximadamente 0,88 ano.
• Média das indicações de uma área de interêsse dos entrevistados: aproximadamente 8,57 indicações.
• Desvio padrão das indicações de uma área de interêsse dos entrevistados: aproximadamente 3,85 indicações.
Página duzentos e oitenta
Realizando uma pesquisa estatística com dados secundários
Para realizar uma pesquisa estatística com dados secundários, pode-se, inicialmente, estabelecer um objetivo e pesquisar dados quê já foram coletados, organizados e disponibilizados para consulta. Em seguida, pode-se reorganizar os dados obtidos em tabélas ou gráficos, analisá-los e apresentar resultados de acôr-do com o objetivo estabelecido.
Considere, por exemplo, a situação a seguir.
Suponha quê um estudante tenha recebido informações sobre vários casos de crianças menóres de 5 anos de idade quê morreram por diarreia e gastroenterite. Após investigar algumas hipóteses sobre o quê poderia ter causado essas doenças, ele rêzouvêo realizar uma pesquisa para verificar uma possível relação entre as mortes por essas doenças e a falta de acesso da população à rê-de de á gua tratada. Com base nos resultados obtidos, esse estudante encaminharia uma proposta a governantes com o objetivo de serem desenvolvidas ações quê minimizem as incidências de tais doenças.
Para realizar a pesquisa, o estudante consultou alguns sáites governamentais para obtêr dados relacionados ao tema. Observe os dados quê ele obteve.
Proporção de óbitos por diarreia e gastroenterite em menóres de 5 anos de idade, por região do Brasil, 2022
Região |
Proporção de óbitos (%) |
|---|---|
Centro-Oeste |
2,43 |
Nordeste |
1,80 |
Norte |
4,15 |
sudéste |
1,10 |
Sul |
0,73 |
Fonte dos dados: BRASIL. Ministério da Saúde. Painel de monitoramento da mortalidade CID-10. Brasília, DF: MS: Plataforma Ivis, 2024. Disponível em: https://livro.pw/seego. Acesso em: 10 ago. 2024.
Índice de atendimento com rê-de de á gua tratada, do total da população, por região do Brasil, 2022
Região |
Índice de atendimento (%) |
|---|---|
Centro-Oeste |
89,8 |
Nordeste |
76,9 |
Norte |
64,2 |
sudéste |
90,9 |
Sul |
91,6 |
Fonte dos dados: BRASIL. Ministério das Cidades. Secretaria Nacional de Saneamento Ambiental. Diagnóstico temático: serviços de á gua e esgoto: visão geral: ano de referência 2022. Brasília, DF: MCID: SNSA: SNIS, 2023. p. 33. Disponível em: https://livro.pw/jqegr. Acesso em: 10 ago. 2024.
PARA PENSAR
Em seu entendimento, quais são as vantagens e as desvantagens da pesquisa estatística com dados secundários em relação àquela realizada com dados primários?
Resposta esperada: Algumas vantagens são o menor custo e a maior rapidez na realização da pesquisa. Algumas desvantagens podem sêr a indisponibilidade dos dados de interêsse e a confiabilidade dos dados disponíveis.
Página duzentos e oitenta e um
Depois de analisar os dados obtidos, com o auxílio de uma planilha eletrônica, foi possível construir os seguintes gráficos para representar os resultados da pesquisa.
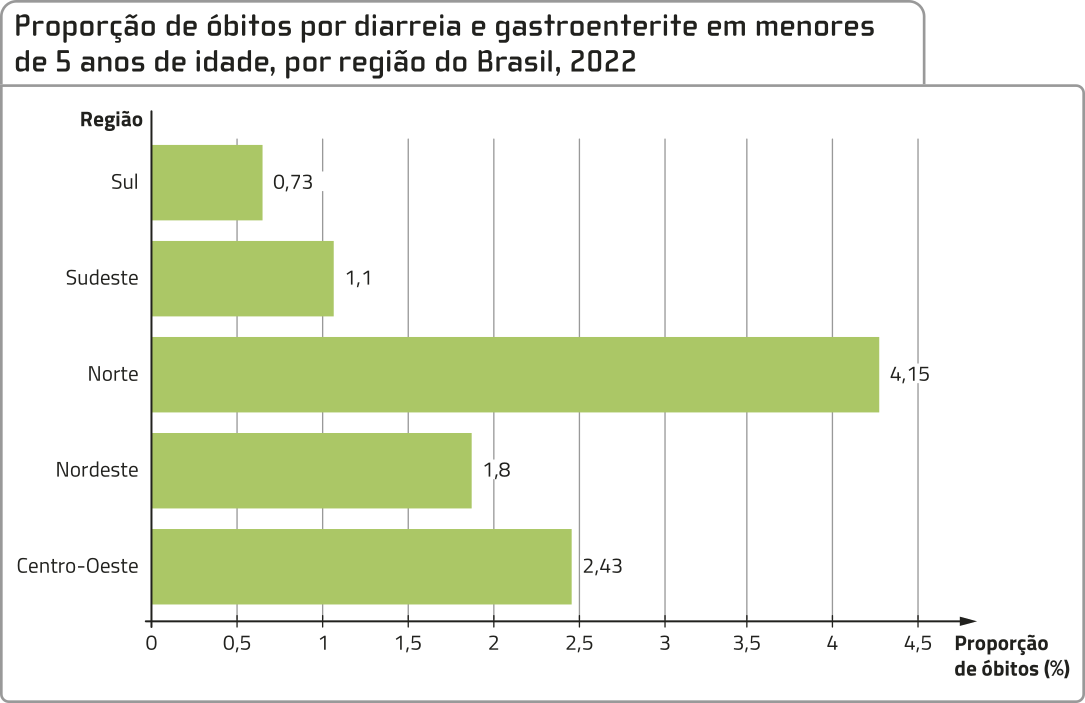
Fonte dos dados: BRASIL. Ministério da Saúde. Painel de monitoramento da mortalidade CID-10. Brasília, DF: MS: Plataforma Ivis, 2024. Disponível em: https://livro.pw/seego. Acesso em: 10 abr. 2024.
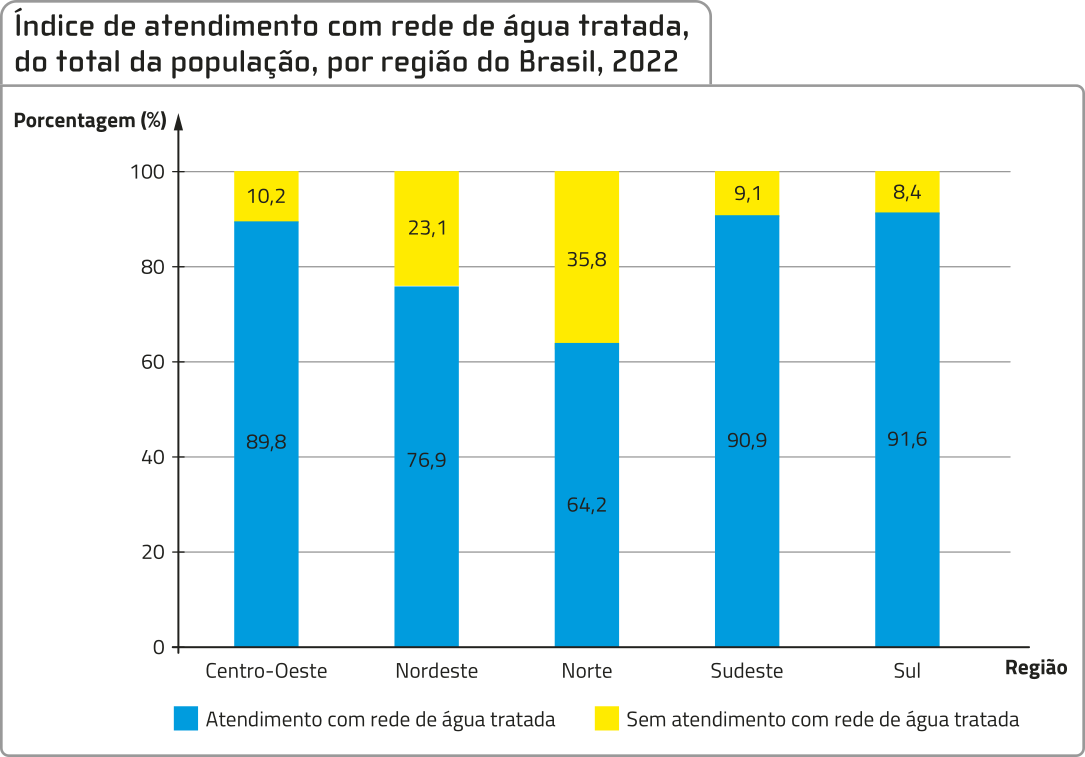
Fonte dos dados: BRASIL. Ministério das Cidades. Secretaria Nacional de Saneamento Ambiental. Diagnóstico temático: serviços de á gua e esgoto: visão geral: ano de referência 2022. Brasília, DF: MCID: SNSA: SNIS, 2023. p. 33.Disponível em: https://livro.pw/jqegr. Acesso em: 10 ago. 2024.
Página duzentos e oitenta e dois
ATIVIDADES
27. Leia as seguintes situações.
I) Em um terreno, é plantada a mesma quantidade de semente de trigo por métro quadrado. Esse terreno é dividido em regiões com 1 m2, das quais é coletada uma amostra da semente germinada para a realização de uma análise.
II) Uma clínica odontológica analisou a ficha de todos os pacientes e identificou quê 45% deles precisariam utilizar aparelho ortodôntico.
III) Em um hospital com 180 pacientes internados, foram selecionados 20 aleatoriamente para realizar uma entrevista sobre seus hábitos alimentares.
IV) Para realizar um teste de resistência, a cada 50 peças de aço fabricadas por certa empresa, uma é selecionada, de acôr-do com a ordem de fabricação.
a) Qual(is) dessas situações menciona(m) uma pesquisa censitária? E uma pesquisa amostral?
pesquisa censitária: II; pesquisa amostral: I, III e IV
b) Indique qual técnica de amostragem póde ter sido utilizada nas pesquisas amostrais indicadas
no item anterior.
I: estratificada; III: cazual simples; IV: sistemática
28. Em relação à pesquisa com dados primários descrita nas páginas 277 a 279, resôuva os itens a seguir.
a) Qual foi o objetivo dessa pesquisa?
Resposta esperada: Conhecer as áreas de interêsse dos estudantes do Ensino Médio e, com base nos resultados obtidos, promover ações complementares específicas a fim de auxiliá-los na escolha profissional.
b) Nessa pesquisa, foram entrevistados mais estudantes do sexo feminino ou do sexo masculino?
masculino
c) Quais áreas de interêsse tiveram mais indicações quê a média?
ciências exatas, ciências biológicas e da saúde, ciências humanas e sociais aplicadas
d) Essa pesquisa foi censitária ou amostral? Justifique a escolha pela realização dêêsse tipo de pesquisa pela escola.
Resposta esperada: Amostral, pois na escola estavam matriculados estudantes em grande quantidade no Ensino Médio.
e) Explique como a seleção dos estudantes poderia sêr realizada nessa pesquisa utilizando outra técnica de amostragem.
Resposta pessoal.
f) Observe as ações quê a escola estabeleceu para serem promovidas de acôr-do com o resultado da pesquisa e determine quais delas deverão sêr realizadas.
ação I
I) Se o desvio padrão das idades dos entrevistados for menor ou igual a 1, será realizada uma palestra para apresentar mais informações sobre algumas profissões de cada área, como atividade profissional, mercado de trabalho e pré-requisitos para se atuar na profissão.
II) Se cada área de interêsse for indicada por mais de 10% dos estudantes, será organizada uma visita em uma instituição de Ensino Superior para conhecer a rotina de alguns cursos da área indicada.
III) Se cada área de interêsse for indicada entre 5% e 20% dos estudantes, serão organizadas rodas de conversa com alguns profissionais de cada área para quê os estudantes possam esclarecer possíveis dúvidas ou curiosidades.
Página duzentos e oitenta e três
29. Em relação à pesquisa com dados secundários descrita nas páginas 280 e 281, resôuva os itens a seguir.
a) Qual era o objetivo da pesquisa realizada?
Resposta esperada: Verificar uma possível relação entre as mortes por diarreia e gastroenterite em pessoas menóres de 5 anos de idade e a falta de acesso da população à rê-de de á gua tratada no Brasil, em 2022.
b) Como os dados analisados foram obtidos para a realização dessa pesquisa?
Os dados foram obtidos em sáites governamentais, vinculados ao Ministério da Saúde e ao Ministério das Cidades.
c) No Brasil, a proporção total de óbitos por diarreia e gastroenterite em menóres de 5 anos de idade foi de 1,86%. Em qual(is) região(ões) essa proporção foi maior quê a observada em todo o território nacional?
Região Norte e Região Centro-Oeste
d) Em 2022, o índice de atendimento com rê-de de á gua tratada, do total da população do Brasil, foi de 84,9%. Em qual(is) região(ões) esse índice foi menor quê o observado em todo o território nacional?
Região Norte e Região Nordeste
e) De acôr-do com os resultados apresentados na pesquisa, responda: Você acredita sêr possível estabelecer alguma inferência relacionando o índice de atendimento à rê-de de á gua tratada à população com a proporção de óbitos por diarreia e gastroenterite em menóres de 5 anos de idade? Justifique sua resposta.
Uma resposta possível: Possivelmente sim, pois, nas regiões em quê há maior falta de atendimento à rê-de de á gua tratada à população, ocorrem uma proporção maior de óbitos de crianças com menos de 5 anos de idade por diarreia e gastroenterite.
No entanto, para embasar melhor essa pesquisa, uma sugestão é investigar outras possíveis causas para a incidência dessas doenças, como a falta de acesso à rê-de de tratamento de esgoto e de acesso ao atendimento médico para a população.
f) Além da diarreia, a falta de saneamento básico póde causar outras doenças, como a leptospirose, infekição potencialmente grave causada por bactérias transmitidas pela urína de animais infectados, principalmente a de ratos. Analise o gráfico de setor.
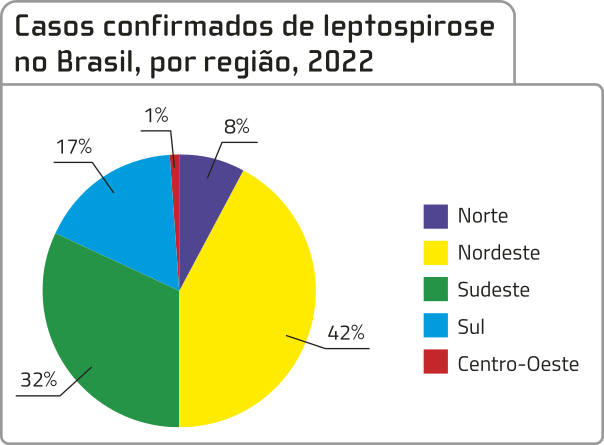
Fonte dos dados: BRASIL. Ministério da Saúde. Painel de monitoramento da mortalidade CID-10. Brasília, DF: MS: Plataforma Ivis, 2024. Disponível em: https://livro.pw/seego. Acesso em: 10 ago. 2024.
Realize uma pesquisa sobre outras doenças quê podem estar relacionadas com a falta de saneamento básico à população (falta de acesso às rêdes de á gua tratada e de esgoto sanitário). Depois, registre no caderno os dados obtidos nessa pesquisa e sugira iniciativas quê possam melhorar esse panorama nas diferentes regiões do país.
Pesquisa do estudante.
30. Leia as situações a seguir em quê estão descritas pesquisas amostrais realizadas e como essas amostras foram definidas.
I) Em uma sala de aula, o professor realizou uma pesquisa com os estudantes para verificar se eles conseguiam enxergar claramente informações escritas na lousa. Para a amostra dessa pesquisa, foram escolhidos os cinco estudantes quê se sentavam na primeira carteira das respectivas fileiras.
II) Certa fábrica opera em três turnos de produção: T1 das 8 h às 16 h; T2 das 16 h à 0 h e, T3, da 0 h às 8 h. O departamento de recursos humanos dessa empresa realizou uma pesquisa com os funcionários sobre a qualidade da iluminação do ambiente de trabalho. Para a amostra dessa pesquisa, foram selecionados ao acaso 30 funcionários do turno T1.
a) Para cada situação, explique por quê a maneira como a amostra da pesquisa foi definida póde apresentar inadequações.
Resposta nas Orientações para o professor.
b) Explique como cada situação apresentada póde sêr ajustada de maneira quê a amostra evite a ocorrência de inadequações. Para isso, sugira o uso de uma das técnicas de amostragem estudada.
Uma resposta possível: I) Para a elaboração da amostra dessa pesquisa, poderia sêr utilizada a técnica de amostra cazual simples, de maneira quê, por sorteio, fossem selecionados alguns estudantes da turma ao acaso. II) Para a elaboração da amostra dessa pesquisa, poderia sêr utilizada a técnica de amostra estratificada, de maneira quê, de cada turno, fosse sorteada a mesma quantidade de funcionários.
Página duzentos e oitenta e quatro
31. ![]() Junte-se a quatro côlégas, e realizem uma pesquisa estatística amostral. A seguir, estão apresentadas algumas dicas para cada etapa a sêr considerada nessa pesquisa. Não se esqueçam de quê cada uma dessas etapas é fundamental.
Junte-se a quatro côlégas, e realizem uma pesquisa estatística amostral. A seguir, estão apresentadas algumas dicas para cada etapa a sêr considerada nessa pesquisa. Não se esqueçam de quê cada uma dessas etapas é fundamental.
Pesquisa dos estudantes.
Elaborar o questionário
Realizem um debate e escôlham um tema para a pesquisa. É importante quê o tema escolhido seja de interêsse social e os resultados da pesquisa possam sêr de interêsse da escola, da comunidade ou do município em quê moram. Algumas sugestões de temas são: alimentação saudável, direitos da criança e do adolescente, consumo consciente, educação ambiental, respeito e valorização dos idosos etc. Após a escolha do tema, elaborem uma ou mais kestões para a entrevista.
Definir o público entrevistado
Definam a população da pesquisa: estudantes da escola, moradores do bairro ou do município, entre outras opções. Em seguida, decidam quantas pessoas devem compor a amostra e qual será a técnica de amostragem mais apropriada para representar a população escolhida.
Coletar os dados
Realizem a entrevista com as pessoas quê compõem a amostra selecionada por vocês. Para isso, organizem com antecedência os materiais necessários para a entrevista, definam como sêrão anotadas as respostas e dividam as tarefas a ser realizadas pêlos integrantes do grupo.
Organizar os dados
Após a realização da entrevista, organizem as respostas obtidas em listas ou quadros, o quê póde sêr feito com auxílio de uma planilha eletrônica.
Analisar e apresentar os resultados
Utilizando os dados organizados, escôlham recursos quê representem esses resultados, como tabélas e gráficos, de acôr-do com as características dos dados quê desê-jam comunicar, destacar ou resumir. Caso contribua para a compreensão de algum resultado, calculem medidas de posição e de dispersão dos dados coletados. Para isso, podem sêr utilizadas diferentes ferramentas, como planilha eletrônica ou outro programa de computador específico. Por fim, escrevam um relatório quê dêz-creva a pesquisa realizada, apresentando uma interpretação dos resultados obtidos e, com base neles, propostas de soluções ou ações de acôr-do com o tema escolhido. Esse relatório póde sêr impresso ou publicado em algum meio digital.
DICA
Caso, por algum motivo, seja inviável a realização de uma pesquisa amostral com dados primários, ou seja, fazendo entrevistas na côléta de dados, pode-se optar por uma pesquisa com dados secundários. Nesse caso, será necessário consultar os dados em diferentes fontes confiáveis, como sáites governamentais.
Página duzentos e oitenta e cinco
INTEGRANDO COM...
CIÊNCIAS HUMANAS E SOCIAIS APLICADAS
O jovem e o mercado de trabalho
Elaborar um bom currículo e conquistar uma colocação no mercado de trabalho é um desafio para a maioria das pessoas. E esse desafio é ainda maior para os jovens quê procuram o primeiro emprego, uma vez quê precisam lidar com a falta de experiência e de qualificação em um mercado de trabalho cada vez mais competitivo.
Nesse sentido, uma opção para incentivar o primeiro emprego e a profissionalização é a inscrição no programa brasileiro Jovem Aprendiz, regulamentado pela lei número 10.097/2000. Nesse programa, jovens entre 14 anos e 24 anos imcomplétos, quê estão cursando, ou já concluíram, o Ensino Fundamental e o Ensino Médio, são contratados em regime especial da Consolidação das Leis do Trabalho (CLT) com tempo predeterminado.
Atualmente, há diversas instituições e sáites quê anunciam vagas para aprendizes e fazem a integração entre as empresas e os jovens. Os jovens selecionados podem ocupar vagas relacionadas ao varejo, à indústria, à administração, à gastronomia etc. Uma oportunidade como essa propicía, além do conhecimento do ofício, a oportunidade de aprender outras relações no mundo corporativo, como autonomia, responsabilidade, atitudes comportamentais e de cidadania, por exemplo.
Fonte dos dados: BRASIL. Lei número 10.097, de 19 de dezembro de 2000. Altera dispositivos da Consolidação das Leis do Trabalho – CLT, aprovada pelo Decreto-Lei número 5.452, de 1º de maio de 1943. Brasília, DF: Presidência da República, [2022]. Disponível em: https://livro.pw/cowyx. Acesso em: 12 ago. 2024.

Página duzentos e oitenta e seis
Acompanhe, a seguir, informações obtidas na pesquisa Empregabilidade Jovem Brasil, realizada em 2022 pelo Ministério do Trabalho e Emprego, a respeito da empregabilidade de jovens no Brasil.

Fonte dos dados: ALBUQUERQUE, Flávia. Pesquisa mostra 5,2 milhões de jovens entre 14 e 24 anos sem emprego. Agência Brasil, Brasília, DF, 26 maio 2023. Disponível em: https://livro.pw/boiyv. Acesso em: 10 ago. 2024.
NO MUNDO DO TRABALHO
Currículo
Em geral, um documento essencial para ingressar no mercado de trabalho é o currículo. Nesse documento, quê permite a uma pessoa se candidatar a uma vaga de emprego, são apresentadas informações quê possam interessar ao recrutador ou chamar a atenção dêste. Um currículo deve sêr completo, objetivo, contendo essencialmente dados pessoais, objetivo profissional, qualidades, experiências e formação. No caso do programa Jovem Aprendiz, é esperado pelo recrutador quê o candidato tenha pouca ou nenhuma experiência. Assim, é importante quê as demais informações no currículo estejam bem organizadas e escritas. A formação póde sêr indicada pela escolaridade e pêlos cursos quê o candidato tenha feito.
Assista ao vídeo indicado a seguir para obtêr dicas do quê não póde faltar em um currículo de Jovem Aprendiz.
• MELHORE seu currículo de jovem aprendiz com essas 5 dicas. [S. l.: s. n.], 2023. 1 vídeo (4 min). Publicado pelo canal Senai Play. Disponível em: https://livro.pw/usgbo. Acesso em: 10 ago. 2024.
Página duzentos e oitenta e sete
PENSANDO NO ASSUNTO
1. Em seu entendimento, o quê é necessário considerar no momento de escolher uma profissão?
Resposta pessoal.
2. Você já pensou na profissão quê pretende ezercêr? O quê é necessário fazer para alcançar esse objetivo?
Respostas pessoais.
3. De acôr-do com o texto, o quê é necessário para sêr um Jovem Aprendiz?
É necessário ter entre 14 anos e 24 anos de idade imcomplétos e estar cursando, ou ter concluído, o Ensino Fundamental ou o Ensino Médio e procurar instituições ou sáites quê realizam a integração entre a empresa e o jovem.
4. Em relação à pesquisa descrita na página 286, resôuva os itens a seguir.
a) Em quê ano essa pesquisa foi realizada? Que órgão realizou essa pesquisa?
2022. Ministério do Trabalho e Emprego.
b) Se uma pesquisa como essa fosse realizada atualmente, você acredita quê os resultados seriam parecidos? Por quê?
Respostas pessoais.
c) Havia no Brasil mais aprendizes ou estagiários? Quantos jovens de diferença?
Havia cerca de 142 mil jovens estagiários a mais que aprendizes.
d) Escolha uma informação sobre os resultados dessa pesquisa e indique um tipo de gráfico, tabéla ou medida de posição ou dispersão quê possa sêr utilizada para representá-la.
Resposta pessoal.
e) Uma pesquisa realizada pela Rede de Observatórios do Trabalho aponta quê o jovem negro tem maior dificuldade de acesso ao mercado de trabalho e remuneração menor do quê outros grupos de cor/raça. Pesquise o tema e escrêeva um texto sobre a importânssia do combate ao racismo estrutural, inclusive no mercado de trabalho.
Fonte dos dados: BRASIL. Ministério do Trabalho e Emprego. Desigualdade racial persiste no mercado de trabalho brasileiro. Brasília, DF: MTE, 19 nov. 2024. Disponível em: https://livro.pw/qhnyi. Acesso em: 3 maio 2025.
Resposta pessoal. Sugestões de sáites para pesquisa:
• TOKARNIA, Mariana. Jovens negros têm menos acesso ao mercado de trabalho, diz pesquisa. Agência Brasil, Brasília, DF, 16 nov. 2022. Disponível em: https://livro.pw/opzhi.
• BANCO MUNDIAL. Jovens negros e o mercado de trabalho. [S. I.]: Banco Mundial, [202-]. Disponível em: https://livro.pw/tfwnz. Acessos em: 5 maio 2025.
5. Nesta questão, exploraremos a seguinte situação-problema.
Que experiências no mercado de trabalho têm os jovens quê estudam na mesma escola quê você?
a) Você está inserido ou já teve alguma experiência no mercado de trabalho como: Jovem Aprendiz, estagiário, freelancer etc.?
Resposta pessoal.
b) ![]() No município em quê mora, há alguma instituição quê realiza a integração entre o jovem e a empresa pelo programa Jovem Aprendiz?
No município em quê mora, há alguma instituição quê realiza a integração entre o jovem e a empresa pelo programa Jovem Aprendiz?
Resposta pessoal.
c) Agora, forme um grupo com quatro côlégas para a realização de uma pesquisa, quê póde seguir as etapas apresentadas anteriormente nesta Unidade. O tema deve estar relacionado à inserção do jovem no mercado de trabalho. É importante quê os grupos formados na turma tênham propostas distintas a fim de identificar diferentes características sobre esse tema. Na etapa de organização dos dados, póde sêr utilizada planilha eletrônica para a construção de gráficos e tabélas ou para o cálculo das medidas de posição ou dispersão. Os resultados da pesquisa devem sêr interpretados para quê sêjam realizadas propostas de acôr-do com o tema escolhido. Ao final, os resultados das pesquisas dos grupos da turma podem sêr reunidos em um único relatório e divulgados em formato impresso ou publicado em algum meio digital.
Pesquisa e elaboração dos estudantes.
PARA AMPlIAR
Assista a um vídeo sobre as origens e consequências do racismo estrutural no Brasil, com foco no mercado de trabalho.
• RACISMO estrutural: jornada. [S. l.: s. n.], 2023. 1 vídeo (18 min). Publicado pelo canal Tribunal Superior do Trabalho. Disponível em: https://livro.pw/hwmdv. Acesso em: 3 maio 2025.
Página duzentos e oitenta e oito
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
Respostas pessoais.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Média aritmética
Moda
mêdídas de posição para dados agrupados em intervalos de classe
Variância
Média aritmética ponderada
Amplitude
Mediana
Pesquisa estatística
Desvio padrão
Técnicas de amostragem: cazual simples, estratificada e sistemática
Resposta pessoal.
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas.
Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações.
Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página duzentos e oitenta e nove
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre o uso da internet e de outras tecnologias digitais. Sobre esse tema, obissérve a tabéla a seguir e resôuva as kestões.
Crianças e adolescentes no Brasil, por freqüência de uso da internet e por faixa etária, 2023
freqüência de uso |
Faixa etária |
|||
|---|---|---|---|---|
De 9 a 10 anos |
De 11 a 12 anos |
De 13 a 14 anos |
De 15 a 17 anos |
|
Mais de uma vez por dia |
972.048 |
816.316 |
1.349.506 |
1.589.624 |
Pelo menos uma vez por dia |
261.001 |
957.089 |
261.252 |
273.238 |
Pelo menos uma vez por semana |
147.872 |
133.800 |
78.719 |
73.087 |
Pelo menos uma vez por mês |
71.609 |
72.136 |
17.287 |
36.460 |
Menos de uma vez por mês |
43.985 |
38.260 |
39.400 |
14.503 |
Fonte dos dados: CENTRO REGIONAL DE ESTUDOS PARA O DESENVOLVIMENTO DA SOCIEDADE DA INFORMAÇÃO. [Microdados] TIC Kids on láine Brasil: 2023: pais e responsáveis. São Paulo: Cetic.br, 2023. Disponível em: https://livro.pw/ebeau. Acesso em: 12 ago. 2024.
a) Caso você fosse entrevistado nessa pesquisa, qual seria sua resposta em relação à freqüência com quê usa a internet?
Resposta pessoal.
b) Nessa pesquisa, a população-alvo era composta de crianças e adolescentes com idades entre 9 e 17 anos, residentes no Brasil. Para sua realização, foi selecionada apenas uma parte dessa população-alvo para sêr entrevistada. Essa foi uma pesquisa censitária ou amostral? Em seu entendimento, por quê isso ocorreu?
A pesquisa foi amostral. Resposta esperada: Porque a população-alvo era muito grande, de maneira quê entrevistar todas as crianças e adolescentes de 9 a 17 anos residentes no Brasil poderia implicar diversas dificuldades, como tempo e custo.
c) Qual foi a freqüência de uso de internet pela maioria das crianças e dos adolescentes em 2023? E pela minoria deles?
mais de uma vez por dia; menos de uma vez por mês
d) Determine a média, a (Moda) e a mediana das idades das crianças e dos adolescentes considerados na tabéla, em anos.
média: aproximadamente 12,80 anos; (Moda): 11,5 anos; mediana: 13,5 anos
e) Que porcentual dos jovens de 15 a 17 anos de idade usam a internet mais de uma vez por dia?
aproximadamente 80%
f) Em certa turma de Ensino Médio, há apenas estudantes com 16 e 17 anos de idade. Para estimar quantas horas por dia da semana os estudantes dessa turma usam a internet, a professora de Matemática sorteou um estudante com 16 anos de idade e outro com 17. Em seguida, solicitou a eles quê registrassem na lousa a quantidade de horas aproximada de uso diário, obtendo os dados a seguir. Acompanhe.
Idade |
Dia |
||||||
|---|---|---|---|---|---|---|---|
seg. |
ter. |
qua. |
qui. |
sex. |
sáb. |
dom. |
|
16 anos |
3,5 |
3 |
3,5 |
4,5 |
4,5 |
6 |
6,5 |
17 anos |
2,5 |
3,5 |
3,5 |
2,5 |
3 |
5 |
4,5 |
Em relação ao tempo, em hora, de uso de internet por dia quê cada estudante indicou, determine:
• a amplitude;
estudante com 16 anos: 3,5 h; estudante com 17 anos: 2,5 h
• a média aritmética;
estudante com 16 anos: 4,5 h; estudante com 17 anos: 3,5 h
• a variância;
estudante com 16 anos: 1,5; estudante com 17 anos: aproximadamente 0,79
• o desvio padrão.
estudante com 16 anos: aproximadamente 1,22 h; estudante com 17 anos: aproximadamente 0,89 h
g) Na situação descrita no item f, quê técnica de amostragem a professora utilizou para definir os estudantes entrevistados?
Resposta esperada: Amostra estratificada.
Página duzentos e noventa
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) Um gerente decidiu fazer um estudo financeiro da empresa onde trabalha analisando as receitas anuais dos três últimos anos. Tais receitas são apresentadas no qüadro.
Ano |
Receita (bilhão de reais) |
|---|---|
I |
2,2 |
II |
4,2 |
III |
7,4 |
Estes dados serão utilizados para projetar a receita mínima esperada para o ano atual (ano IV), pois a receita esperada para o ano IV é ôbitída em função das variações das receitas anuais anteriores, utilizando a seguinte regra: a variação do ano IV para o ano III será igual à variação do ano III para o II adicionada à média aritmética entre essa variação e a variação do ano II para o I.
O valor da receita mínima esperada, em bilhão de reais, será de
a) 10,0.
b) 12,0.
c) 13,2.
d) 16,8.
e) 20,6.
alternativa c
2. (UPE) Ao realizar o levantamento das famílias de uma pequena cidade do interior, cujos filhos são beneficiários de algum programa social, um pesquisador obteve os seguintes dados:
Beneficiados em Programa Social
Número de filhos |
Quantidade de famílias |
|---|---|
5 |
03 |
4 |
07 |
3 |
21 |
2 |
28 |
1 |
23 |
0 |
18 |
Total |
100 |
Com base nessas informações, é CORRETO
afirmar quê o desvio padrão do número de filhos dessa amostra é de, aproximadamente:
a) 1,4
b) 1,8
c) 2,0
d) 2,5
e) 6,7
alternativa a
3. (Enem/MEC) Um produtor de café irrigado em Minas Gerais recebeu um relatório de consultoria estatística, constando, entre outras informações, o desvio padrão das produções de uma safra dos talhões de sua propriedade. Os talhões têm a mesma área de 30.000 m2 e o valor obtído para o desvio padrão foi de 90 kg/talhão.
O produtor deve apresentar as informações sobre a produção e a variância dessas produções em sacas de 60 kg por hectare (10.000 m2).
A variância das produções dos talhões expressa em (sacas/hectare)2 é
a) 20,25.
b) 4,50.
c) 0,71.
d) 0,50.
e) 0,25.
alternativa e
4. (UFMS) A despesa mensal de uma família foi de R$ 6.240,00 durante os primeiros 3 meses, R$ 6.780,00 durante os próximos 4 meses e R$ 7.236,00 durante os últimos 5 meses de um ano. Se a economia total durante o ano foi de R$ 7.080,00, qual foi a renda média mensal da família?
a) R$ 6.245,00.
b) R$ 6.752,00.
c) R$ 6.834,00.
d) R$ 6.957,50.
e) R$ 7.425,00.
alternativa e
5. (IFPE) Embora pouco conhecida, a “média harmônica” é utilizada em várias situações do dia a dia. Por exemplo, para calcular a velocidade média em um percurso quê é feito mêtáde da distância com velocidade v 1 e a outra mêtáde com velocidade v 2. pôdêmos definir a média harmônica entre dois valores não nulos x e y, como sêndo o número H, tal quê:
Utilizando a definição anterior, encontre uma expressão algébrica destacando H em função de x e y.
a) H = .
b) H =
c) H =
d) H =
e) H =
alternativa c
Página duzentos e noventa e um
6. (Enem/MEC) A tabéla apresenta uma estimativa da evolução da população brasileira por faixa etária, em milhões de pessoas, para 2020, 2030 e 2045.
Faixa etária |
Ano |
||
|---|---|---|---|
2020 |
2030 |
2045 |
|
Até 14 anos |
49 |
48 |
48 |
De 15 a 49 anos |
111 |
112 |
110 |
De 50 anos ou mais |
50 |
63 |
78 |
Total |
210 |
223 |
236 |
STEFANO, F. Mais velho e mais rico: os ganhos da maturidade. Exame, ed. 1003, ano 45, n. 21, 2 nov. 2011 (adaptado).
Com base na tabéla, o valor quê mais se aproxima da média dos percentuais da população brasileira na faixa etária até 14 anos, nos anos de 2020, 2030 e 2045, é
a) 21,5.
b) 21,7.
c) 48,0.
d) 48,3.
e) 48,5.
alternativa b
7. (Unitins-TO) Ana, João, José e Maria são alunos do 3º ano do Ensino Médio e estão comparando as médias anuais obtidas nas disciplinas de Matemática, Física, Química e Biologia.
O qüadro a seguir demonstra os resultados obtidos ao longo de um ano de estudos.
Aluno |
Disciplina |
|||
|---|---|---|---|---|
Matemática |
Física |
Química |
Biologia |
|
Ana |
8,9 |
9,6 |
8,5 |
9,3 |
João |
9,3 |
8,9 |
8,7 |
9,8 |
José |
9,7 |
8,9 |
9,0 |
9,5 |
Maria |
9,2 |
9,1 |
8,6 |
9,5 |
De acôr-do com as notas obtidas por cada aluno, é possível afirmar quê:
a) Ana e João apresentam a mesma mediana das disciplinas pesquisadas.
b) a média e a mediana apresentadas por José, nas quatro disciplinas, são iguais.
c) a mediana das disciplinas apresentada por José é 0,25 unidade maior do quê a apresentada por Maria.
d) a média das disciplinas de Maria é 0,175 unidade maior do quê a apresentada por José.
e) a média de João nas quatros disciplinas é 9,075.
alternativa a
8. (Enem/MEC) Uma empresa de transporte faz regularmente um levantamento do número de viagens realizadas durante o dia por todos os 160 motoristas cadastrados em seu aplicativo. m um cérto dia, foi gerado um relatório, por meio de um gráfico de barras, no qual se relacionaram a quantidade de motoristas com a quantidade de viagens realizadas até aquele instante do dia.
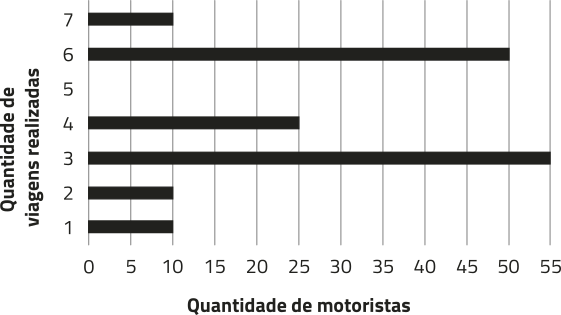
Comparando os valores da média, da mediana e da (Moda) da distribuição das quantidades de viagens realizadas pêlos motoristas cadastrados nessa empresa, obtém-se
a) mediana = média < (Moda).
b) mediana = (Moda) < média.
c) mediana < média < (Moda).
d) (Moda) < média < mediana.
e) (Moda) < mediana < média.
alternativa e
9. (PSC/UFAM) Em uma próva de seleção, o critério de aprovação leva em conta a média e o desvio padrão de três provas. Logo, a média e o desvio padrão de um candidato quê obteve nas três provas 64, 57 e 62 pontos são, respectivamente:
a) 49 e .
b) 52 e .
c) 61 e .
d) 74 e .
e) 81 e .
alternativa c
10. (UEA-AM) Em um grupo de 30 pessoas, 8 têm 14 anos, 7 têm 15 anos, 6 têm 16 anos e as demais têm 17 anos. Usando as abreviações Me para a média aritmética, Md para a mediana e Mo para a (Moda), para esse grupo de pessoas tem-se quê:
a) Mo < Md < Me
b) Me < Mo < Md
c) Me < Md < Mo
d) Md < Mo < Me
e) Md < Me < Mo
alternativa e
Página duzentos e noventa e dois
11. (Unifesp-SP) Um estudo médico recrutou 160 pacientes homens com histórico de alterações no antígeno prostático específico (PSA). Os pacientes foram submetidos aos exames laboratoriais de PSA total e de PSA livre e, em seguida, a uma biópsia da próstata. A biópsia apontou, em cada caso, se a patologia era maligna ou benigna. A tabéla apresenta os resultados das médias dos exames laboratoriais do grupo de pacientes com patologia maligna e do grupo de pacientes com patologia benigna.
PSA (média) |
Biópsia com indicação de patologia maligna |
Biópsia com indicação de patologia benigna |
|---|---|---|
PSA total (ng/mL) |
10 |
8 |
PSA livre (ng/mL) |
1,9 |
2 |
PSA livre ÷ PSA total |
0,19 |
0,25 |
Pedro foi um dos pacientes quê participou do estudo e seus exames indicaram PSA total =
= 9,5 ng/mL e PSA livre = 2,28 ng/mL.
a) Calcule o quociente entre o PSA livre e o PSA
total de Pedro. Usando esse indicador como referência na comparação com os dados da tabéla, indique se o resultado do exame de Pedro está numericamente mais próximo ao resultado médio do exame de quem tem a patologia maligna ou de quem tem a patologia benigna.
0,24; patologia benigna
b) Sabendo quê 40% dos pacientes foram diagnosticados com patologia maligna, calcule a média do PSA total dos 160 pacientes quê participaram do estudo.
8,8 ng/mL
12. (UEFS-BA) Conhecidos os percentuais de aprovação, por parte da população, de 10 projetos viáveis para desenvolvimento sustentável em dez cidades de certa região, como 15%, 12%, 15%, 8%, 86%, 13%, 13%, 83%, 11% e 13%, quanto aos valores percentuais da mediana (Me) e da (Moda) (Mo), é correto afirmar quê
a) Me < Mo.
b) Me ≤ Mo.
c) elas são equivalentes.
d) Me > Mo.
e) Me ≥ Mo.
alternativa c
13. (Enem/MEC) Uma grande rê-de de supermercados adota um sistema de avaliação dos faturamentos de suas filiais, considerando a média de faturamento mensal em milhão. A matriz da rê-de paga uma comissão para os representantes dos supermercados quê atingirem uma média de faturamento mensal (M), conforme apresentado no qüadro.
Comissão |
Média de faturamento mensal (M) |
|---|---|
I |
1 ≤ M < 2 |
II |
2 ≤ M < 4 |
III |
4 ≤ M < 5 |
IV |
5 ≤ M < 6 |
V |
M ≥ 6 |
Um supermercado da rê-de obteve os faturamentos num dado ano, conforme apresentado no qüadro.
Faturamento mensal (em milhão de real) |
Quantidade de meses |
|---|---|
3,5 |
3 |
2,5 |
2 |
5 |
2 |
3 |
4 |
7,5 |
1 |
Nas condições apresentadas, os representantes dêêsse supermercado avaliam quê receberão, no ano seguinte, a comissão de tipo
a) I.
b) II.
c) III.
d) IV.
e) V.
alternativa b
14. (UEG-GO) Os números de casos registrados de acidentes domésticos em uma determinada cidade nos últimos cinco anos foram: 100, 88, 112, 94 e 106. O desvio padrão dêêsses valores é aproximadamente
a) 3,6
b) 7,2
c) 8,5
d) 9,0
e) 10,0
alternativa c
Página duzentos e noventa e três

