UNIDADE 2
MATRIZES, SISTEMAS LINEARES E TRANSFORMAÇÕES DE FIGURAS
Grafos
A origem da teoria dos grafos está fundamentada em um problema conhecido como pontes de Königsberg, quê consiste em discutir a possibilidade de atravessar as sete pontes existentes nessa antiga cidade prussiana, sem passar mais de uma vez por alguma delas. Em 1736, o matemático suíço Leonhard Óiler (1707-1783) representou esse problema por meio de um esquema, em quê os caminhos das pontes eram indicados por linhas e as interseções, por pontos, criando, possivelmente, o primeiro grafo da história.
Atualmente, a teoria dos grafos é uma ferramenta eficiente para modelar e resolver problemas de diferentes áreas, como da própria Matemática, da Biologia, das engenharias, da indústria e do comércio.
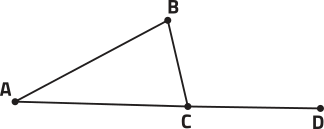
Por exemplo, considere um grupo de pessoas quê se comunicam por meio de uma rê-de social: Ana (A) é amiga de Béto (B) e Carla (C), quê também são amigos entre si; já Davi (D) é amigo apenas de Carla. Essa situação póde sêr representada por meio de um grafo, conforme mostrado no esquema.
Fonte dos dados: OSTROSKI, Alvaro; MENONCINI, Lúcia. Teoria dos grafos e aplicações. Synergismus scyentifica UTFPR, Pato Branco, v. 4, n. 2, p. 1-6, 2009. trabalho apresentado no XIII Encontro Regional de Matemática Aplicada e Computacional, 2009, Pato Branco. Disponível em: https://livro.pw/tbjdw. Acesso em: 6 ago. 2024.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
1. Que estudioso construiu um esquema considerado o primeiro grafo da história? Com quê objetivo ele fez essa construção?
2. Em um grafo, os pontos são chamados de vértices e as linhas, de arestas. Quantos vértices e quantas arestas tem o grafo representado nesta página?
3. Além do grafo apresentado, de quê outra maneira você representaria as relações de amizade entre Ana, Béto, Carla e Davi na rê-de social do exemplo descrito?
Respostas nas Orientações para o professor.
Página cinquenta
Matrizes
Na abertura desta Unidade, a relação do grupo de pessoas em uma rê-de social foi representada por meio de um grafo. Outra maneira de representar essa situação é por meio de uma tabéla: usamos o número 1 para indicar quando há relação entre duas pessoas e o número 0 para indicar quando não há relação (considerando quê uma pessoa não se relaciona com ela mesma). Como os dados numéricos da tabéla estão organizados em linhas (fileiras horizontais) e colunas (fileiras verticais), podemos denominá-la matriz e representá-la da maneira a seguir.

PARA PENSAR
Nesta matriz, qual elemento está localizado na segunda linha e na terceira coluna? O quê ele indica nesse contexto?
Elemento 1. Indica quê Béto e Carla se relacionam por meio da rê-de social.
Essa matriz tem quatro linhas e quatro colunas, portanto dizemos quê ela é uma matriz de ordem 4 × 4 (lê-se: quatro por quatro). Há uma convenção: primeiro, indicamos o número de linhas da matriz, depois, o número de colunas. O elemento da matriz localizado, por exemplo, na quarta linha e na segunda coluna indica quê Davi e Béto não se relacionam por meio da rê-de social.
Agora, analise os dados a seguir.
Brasileiros de 10 ou mais anos quê utilizaram a internet no período de referência (em mil pessoas)
Ano |
Usuário |
|
|---|---|---|
Homem |
Mulher |
|
2019 |
68.907 |
74.929 |
2021 |
74.640 |
81.067 |
2022 |
77.613 |
84.013 |
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Pesquisa Nacional por Amostra de Domicílio Contínua Anual: tabéla 6447. Rio de Janeiro: hí bê gê hé: Sidra, [2024]. Disponível em: https://livro.pw/cvxev. Acesso em: 6 ago. 2024.
pôdêmos representar esses dados pela matriz a seguir.
Nessa matriz, as linhas indicam a quantidade de brasileiros com 10 anos ou mais quê utilizaram a internet em 2019, 2021 e 2022; as colunas indicam a categoria dos usuários: homens e mulheres. A primeira linha, por exemplo, indica a quantidade de usuários homens e mulheres em 2019 e a segunda coluna, a quantidade de usuárias mulheres em cada ano apresentado. O elemento da matriz localizado na segunda linha e na primeira coluna, por exemplo, corresponde à quantidade de brasileiros homens quê utilizaram a internet em 2021.
PARA PENSAR
Essa matriz é de ordem 3 × 2 (lê-se: três por dois). O quê isso significa?
Resposta esperada: Significa quê essa matriz tem 3 linhas e 2 colunas.
Página cinquenta e um
Denominamos matriz de ordem m × n, com m e n números naturais não nulos, toda tabéla formada por m ⋅ n elemêntos organizados em m linhas e n colunas.
Uma matriz A de ordem m × n póde sêr representada genericamente por A = (aij)m × n e expressa da maneira apresentada.
Nessa matriz, aij indica o elemento quê está na linha i e coluna j. O elemento a13 (lê-se: a um três), por exemplo, tem i = 1 e j = 3, ou seja, ele está localizado na primeira linha e na terceira coluna.
A =
MATEMÁTICA NA HISTÓRIA
Há indícios de quê os chineses, por volta do século II a.C., já resolviam problemas utilizando procedimentos com a ideia de matrizes. Porém, em 1857, o mérito do desenvolvimento do conceito de matrizes foi dado ao matemático inglês artúr Cayley (1821-1895) a partir de estudos relacionados a transformações.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 243-244, 552.

Exemplos:
a) Matriz de ordem 2 × 6.
A =
b) Matriz de ordem 3 × 3.
B =
c) Matriz de ordem 4 × 3.
C =
d) Matriz de ordem 1 × 5.
D =
PARA PENSAR
Qual é o elemento c41na matriz C = (cij)4 × 3?
−1
Denominamos matriz quadrada toda matriz de ordem m × n, em quê m = n, ou seja, as quantidades de linhas e de colunas são iguais. Nesse caso, podemos dizêr quê a matriz é de ordem n.
Em uma matriz quadrada A = (aij)n, os elemêntos aij, em quê i = j, formam a diagonal principal da matriz.
Nos exemplos apresentados, B é uma matriz quadrada e póde sêr indicada por B3. Os elemêntos b11 = 20, b22 = 50 e b33 = −1 compõem a diagonal principal da matriz B.
Página cinquenta e dois
Igualdade de matrizes
Duas matrizes A e B, de mesma ordem, são iguais quando cada elemento de A é igual ao elemento correspondente (de mesma posição) em B (aij = bij). Indicamos, então, A = B. Para indicar quê duas matrizes A e B são diferentes, ou seja, não têm a mesma ordem ou não têm todos os elemêntos correspondentes iguais, escrevemos: A ≠ B.
Exemplos:
a) A = e B =
As matrizes A e B têm a mesma ordem e os elemêntos correspondentes são iguais. Portanto, A = B.
b) C = e D =
As matrizes C e D não têm a mesma ordem. Portanto, C ≠ D.
c) E = e F =
As matrizes E e F têm a mesma ordem, mas e21 ≠ f21. Portanto, E ≠ F.
PARA PENSAR
Qual é a ordem das matrizes A, B, C, D, E e F?
A: 3 × 2; B: 3 × 2; C: 1 × 4; D: 4 × 1; E: 2 × 2; F: 2 × 2
ATIVIDADES RESOLVIDAS
R1. Seis amigos decidiram compor uma chapa para participar da eleição do Grêmio Estudantil. Para escolher qual deles seria o presidente da chapa, realizaram uma votação: cada amigo recebeu um número de 1 a 6 e póde votar em até dois deles. Os votos foram organizados na matriz V = (vij)6 representada a seguir, em quê cada elemento vij foi indicado conforme apresentado.
- Chapa
- : grupo de candidatos a uma eleição.
• número 1, quando i votou em j;
• número 0, quando i não votou em j.
V =
Com base nessas informações, qual dos amigos foi escolhido para presidente da chapa?
Resolução
A quantidade total de votos quê cada amigo recebeu corresponde à soma dos votos em cada coluna:
• amigo 1: 1 + 1 = 2, ou seja, dois votos;
• amigo 2: 1 voto;
• amigo 3: 1 + 1 + 1 + 1 = 4, ou seja, quatro votos;
• amigo 4: 0 voto;
• amigo 5: 0 voto;
• amigo 6: 1 + 1 + 1 = 3, ou seja, três votos.
Portanto, o amigo 3 foi o escolhido para presidente da chapa.
PARA PENSAR
Quais amigos votaram em si mesmos nessa eleição? Explique como você rêzouvêo essa questão.
Resposta esperada: Amigo 2 e amigo 3, pois é apenas na segunda e na terceira linhas quê os elemêntos em quê i = j dessa matriz são iguais a 1.
Página cinquenta e três
R2. Em cada item, escrêeva a matriz conforme a lei de formação de seus elemêntos.
a) A = (aij)2 × 4, tal quê aij = 2i + j
b) B = (bij)3 × 3, tal quê bij =
Resolução
a) A ordem da matriz A é 2 × 4, então podemos representá-la da seguinte maneira:
A =
Vamos determinar os elemêntos da matriz A de acôr-do com a lei de formação:
• a11 = 2 ⋅ 1 + 1 = 2 + 1 = 3
• a12 = 2 ⋅ 1 + 2 = 2 + 2 = 4
• a13 = 2 ⋅ 1 + 3 = 2 + 3 = 5
• a14 = 2 ⋅ 1 + 4 = 2 + 4 = 6
• a21 = 2 ⋅ 2 + 1 = 4 + 1 = 5
• a22 = 2 ⋅ 2 + 2 = 4 + 2 = 6
• a23 = 2 ⋅ 2 + 3 = 4 + 3 = 7
• a24 = 2 ⋅ 2 + 4 = 4 + 4 = 8
Portanto, A = .
b) A ordem da matriz B é 3 × 3, então podemos representá-la da seguinte maneira:
B =
Utilizando as duas expressões quê definem os elemêntos da matriz B, temos:
I) se i ≥ j:
• b11 = 1 + 12 = 1 + 1 = 2
• b21 = 2 + 12 = 2 + 1 = 3
• b22 = 2 + 22 = 2 + 4 = 6
• b31 = 3 + 12 = 3 + 1 = 4
• b32 = 3 + 22 = 3 + 4 = 7
• b33 = 3 + 32 = 3 + 9 = 12
II) se i < j:
• b12 = 2 − 3 ⋅ 1 = 2 − 3 = −1
• b13 = 3 − 3 ⋅ 1 = 3 − 3 = 0
• b23 = 3 − 3 ⋅ 2 = 3 − 6 = −3
Portanto, B = .
ATIVIDADES
1. pôdêmos definir um grafo dos estados da Região Norte do Brasil de maneira quê cada vértice representa um estado e dois estados são adjacentes (têm ligação por aresta) quando têm uma fronteira comum entre si. Observe.
Respostas nas Orientações para o professor.
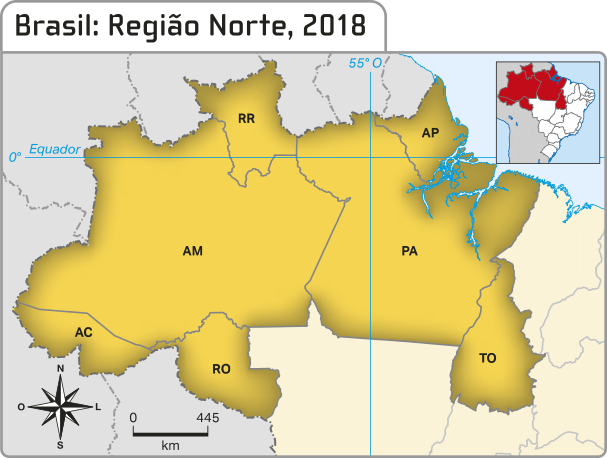
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: hí bê gê hé, 2018. p. 94.
a) Faça um desenho quê represente esse grafo.
b) Com base no item anterior, construa uma tabéla, indicando 1 para os estados quê fizerem divisa, e 0 para os quê não fizerem. Depois, escrêeva uma matriz F correspondente a essa tabéla.
2. Em cada item a seguir, escrêeva a matriz conforme a lei de formação de seus elemêntos.
Respostas nas Orientações para o professor.
a) A = (aij)1 × 5, tal quê aij = (i − 2)j
b) B = (bij)2 × 2, tal quê bij =
c) C = (cij)4 × 3, tal quê cij = 3i − j
d) D = (dij)5 × 5, tal quê dij =
Página cinquenta e quatro
3. Analise a tabéla a seguir e resôuva as kestões.
Casos prováveis de dengue na Região Centro-Oeste do Brasil até a Semana Epidemiológica 52, 2022-2023
UF |
Ano |
|
|---|---|---|
2022 |
2023 |
|
Mato Grosso do Sul |
26.603 |
46.524 |
Mato Grosso |
35.453 |
28.424 |
Goiás |
210.460 |
69.719 |
Distrito Federal |
70.116 |
38.587 |
Fonte dos dados: BRASIL. Ministério da Saúde. Série histórica de casos prováveis de dengue: 2000-2023. Brasília, DF: MS, 2024. Disponível em: https://livro.pw/wyelu. Acesso em: 6 ago. 2024.
a) Represente essa tabéla por uma matriz. Qual é a ordem dessa matriz?
; matriz 4 × 2
b) O quê indicam os elemêntos da primeira coluna dessa matriz? E da segunda linha?
c) O quê representa o elemento da quarta linha e segunda coluna dessa matriz?
d) Observando essa matriz, como é possível identificar se determinada Unidade da Federação da Região Centro-Oeste teve redução na quantidade provável de casos de dengue em 2023 em relação ao mesmo período de 2022?
Respostas dos itens b, c e d nas Orientações para o professor.
4. Em uma pequena indústria são fabricados quatro modelos de embalagens de papelão: 1, 2, 3 e 4. Na matriz X = (xij)4 × 3 a seguir, o elemento xij representa a quantidade, em quilograma, de embalagens vendidas do modelo i para o cliente j no mês de abril.
X =
a) O quê indicam as linhas dessa matriz? E as colunas?
Resposta esperada: As linhas indicam a quantidade, em quilograma, de embalagens vendidas de cada modelo no mês de abril. As colunas indicam a quantidade, em quilograma, de embalagens compradas por cliente no mês de abril.
b) Qual elemento dessa matriz indica quantos quilogramas de embalagens do modelo 3 foram vendidos para o cliente 2 em abril?
x32 = 336
c) Em abril, qual cliente comprou menos quilogramas de embalagens do modelo 2?
cliente 1
d) Qual dêêsses clientes comprou mais quilogramas de embalagens no mês de abril? Quantos quilogramas?
cliente 2; 1.836 kg
5. ![]() Algumas matrizes recebem nomenclaturas especiais de acôr-do com suas características. Observe, a seguir, informações sobre algumas delas.
Algumas matrizes recebem nomenclaturas especiais de acôr-do com suas características. Observe, a seguir, informações sobre algumas delas.
Matriz linha
Toda matriz de ordem 1 × n.
Matriz coluna
Toda matriz de ordem m × 1.
Matriz diagonal
Toda matriz quadrada em quê aij = 0 para i ≠ j.
Matriz nula
Toda matriz de ordem m × n em quê aij = 0 para quaisquer quê sêjam i e j. Indicamos a matriz nula de ordem m × n por 0m × n.
Matriz identidade
Toda matriz quadrada em quê aij = 1 para i = j e aij = 0 para i ≠ j. Indicamos a matriz identidade de ordem n por In.
Elabore um exemplo para cada tipo de matriz apresentada. Depois, troque essas matrizes com um colega para quê ele as classifique de acôr-do com as características apresentadas, enquanto você faz o mesmo com as matrizes quê receber. Por fim, confiram juntos as respostas.
Elaboração do estudante.
6. Para toda matriz A = (aij)m × n, existe uma matriz transposta de A, indicada por At, correspondente à matriz At = (aji)n × m. Considerando
_A = , resôuva as kestões.
a) ![]() Com suas palavras, explique o quê é a transposta de uma matriz A.
Com suas palavras, explique o quê é a transposta de uma matriz A.
Resposta esperada: A transposta de uma matriz A é outra matriz, com os mesmos elemêntos de A, porém, em localizações diferentes: ordenadamente, os elemêntos das linhas da matriz A estão localizados nas colunas da sua transposta.
b) Qual é a ordem da matriz A? E a ordem da matriz At?
matriz 3 × 4; matriz 4 × 3
c) escrêeva At indicando seus elemêntos.
d) Mostre quê, dada uma matriz B = (bij)m × n qualquer, temos (Bt)t = B.
Respostas dos itens c e d nas Orientações para o professor.
Página cinquenta e cinco
Operações com matrizes
Adição de matrizes
Você sabe o quê é transplante de órgãos? É um procedimento cirúrgico quê substitui um órgão (coração, fígado, pâncreas, pulmão, rim etc.) de uma pessoa doente por outro órgão, mais saudável, de um doador vivo ou morto.
PARA AMPLIAR
Acesse êste sáiti para mais informações sobre a doação de órgãos.
• BRASIL. Ministério da Saúde. Sistema nacional de transplantes. Brasília, DF: SNT, [2024]. Disponível em: https://livro.pw/lkzwr. Acesso em: 6 ago. 2024.
Analise a seguir algumas informações sobre transplante de órgãos no Brasil.
tabéla 1
Quantidade de transplantes de coração realizados no Brasil, 2021-202
Ano |
Região |
||||
|---|---|---|---|---|---|
Centro-Oeste |
Norte |
Nordeste |
Sul |
sudéste |
|
2021 |
26 |
0 |
53 |
26 |
229 |
2022 |
32 |
0 |
55 |
44 |
232 |
Fonte dos dados: BRASIL. Ministério da Saúde. Sistema Nacional de Transplantes. Relatório de transplantes realizados: série histórica. Brasília, DF: MS: SNT, 2023. Disponível em: https://livro.pw/rbvpf. Acesso em: 6 ago. 2024.
tabéla 2
Quantidade de transplantes de fígado realizados no Brasil, 2021-2022
Ano |
Região |
||||
|---|---|---|---|---|---|
Centro-Oeste |
Norte |
Nordeste |
Sul |
sudéste |
|
2021 |
112 |
0 |
351 |
501 |
1.094 |
2022 |
115 |
4 |
358 |
578 |
1.107 |
Fonte dos dados: BRASIL. Ministério da Saúde. Sistema Nacional de Transplantes. Relatório de transplantes realizados: série histórica. Brasília, DF: MS: SNT, 2023. Disponível em: https://livro.pw/rbvpf. Acesso em: 6 ago. 2024.
Para calcular o total de transplantes de coração ou de fígado realizados em cada região do Brasil, nos anos de 2021 e 2022, podemos usar matrizes. Inicialmente, vamos representar cada tabéla por meio de uma matriz e, depois, adicionar essas matrizes, ou seja, adicionar os dados das tabélas.
Matriz ôbitída da tabéla 1:
A =
Matriz ôbitída da tabéla 2:
B =
A soma de duas matrizes de mesma ordem A = (aij)m × n e B = (bij)m × n é igual à matriz C = (cij)m × n, também de mesma ordem, tal quê cij = aij + bij, para todo 1 ≤ i ≤ m e 1 ≤ j ≤ n.
Página cinquenta e seis
Para calcular A + B, adicionamos os elemêntos correspondentes das matrizes A e B:
A + B = =
PARA PENSAR
Em relação à matriz A + B, qual é o elemento da segunda linha e terceira coluna? O quê ele indica?
413. Ele indica o total de transplantes de coração e de fígado realizados na Região Nordeste em 2022.
Matriz oposta
Denominamos matriz oposta de uma matriz A, indicada por −A, a matriz cuja adição com A resulta em uma matriz nula de mesma ordem, ou seja, Am × n + (−Am × n) = 0m × n.
Para A = , temos −A = , pois:

PARA PENSAR
Nas matrizes A e −A, quê relação há entre os elemêntos correspondentes?
Resposta esperada: Os elemêntos correspondentes são opostos.
Subtração de matrizes
A diferença de duas matrizes de mesma ordem A = (aij)m × n e B = (bij)m × n é igual à matriz C = (cij)m × n, também de mesma ordem, ôbitída a partir da soma da matriz A com a matriz oposta de B, ou seja, A − B = A + (−B) = C.
PARA PENSAR
Com suas palavras, explique a um colega como se calcula a adição e a subtração de matrizes.
Resposta pessoal.
Considerando, por exemplo, as matrizes A = e B = , temos:
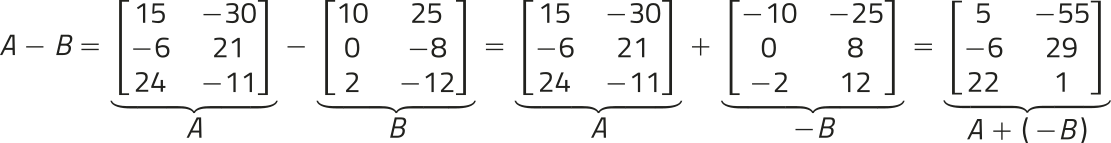
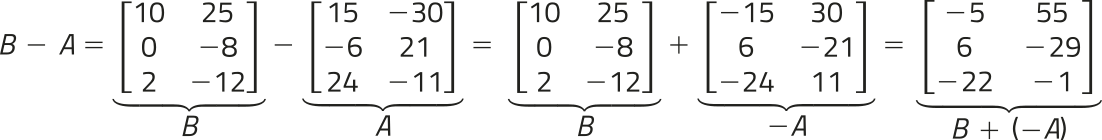
Página cinquenta e sete
Multiplicação de uma matriz por um número real
O produto de um número real k por uma matriz A = (aij)m × n é igual a uma matriz B = (bij)m × n, de mesma ordem, tal quê bij = k ⋅ aij, para todo 1 ≤ i ≤ m e 1 ≤ j ≤ n.
Se A = , então o dôbro da matriz A póde sêr obtído por:
2A = 2 ⋅ = =
DICA
Note quê determinar o dôbro de uma matriz A é o mesmo quê obtêr o resultado de A + A.
ATIVIDADE RESOLVIDA
R3. Dadas as matrizes A = , B = e C = , calcule:
a) A + B − C
b) 3(−A) + C
Resolução
a) Considerando A + B − C = A + B + (−C), temos:
+ + = =
b) 3 + = =
ATIVIDADES
7. Dada as matrizes A = , B = e C = , calcule:
a) A − C + B
b) A + 3B
c) B + C − (−A)
d) At − 2Ct
8. Considerando a matriz identidade I4 e a matriz A = (aij)4 × 4, tal quê aij = 2i − j, determine:
a) I4 + A
b) 3At − I4
9. Determine o valor das incógnitas para quê a igualdade seja válida.
+ =
x = 1; y = 2
Página cinquenta e oito
10. Considere a matriz M = (aij)3 × 3, tal quê aij = i + j se i = j e aij = 0 se i ≠ j. Determine a matriz A = M + M.
11. Em certa escola, foi realizada uma pesquisa com os estudantes do 1º, 2º e 3º anos do Ensino Médio sobre a área de atuação profissional de maior interêsse entre eles. Cada estudante poderia indicar apenas uma das áreas descritas a seguir.
I: Administração, negócios e serviços.
II: Ciências sociais, humanas, ár-te e disáini.
III: Ciências exatas, informática e engenharia.
IV: Ciências biológicas, da natureza e saúde.
As seguintes matrizes A e B representam, respectivamente, a quantidade de estudantes das turmas A e B, de cada ano escolar, quê responderam à pesquisa sobre a área de atuação profissional. Nessas matrizes, as linhas indicam, respectivamente, os anos escolares – 1º, 2º e 3º –, e as colunas, as áreas de atuação profissional I, II, III e IV. Note quê 6 turmas responderam à pesquisa.
A =
B =
a) Quantos estudantes do 2º ano, da turma B, indicaram interêsse na área de atuação profissional III?
12 estudantes
b) Quantos estudantes das turmas A indicaram interêsse na área de atuação profissional IV?
19 estudantes
c) Determine a matriz A + B. O quê representam os elemêntos dessa matriz?
A + B = . A quantidade total de estudantes das turmas A e B, do 1º, 2º e 3º anos do Ensino Médio, interessados em cada área de atuação profissional.
12. ![]() Reúnam-se em duplas e analisem as seguintes propriedades da adição de matrizes, considerando A, B e C matrizes de mesma ordem m × n e 0 a matriz nula, também de ordem m × n. Em seguida, mostrem a validade de cada propriedade.
Reúnam-se em duplas e analisem as seguintes propriedades da adição de matrizes, considerando A, B e C matrizes de mesma ordem m × n e 0 a matriz nula, também de ordem m × n. Em seguida, mostrem a validade de cada propriedade.
Respostas nas Orientações para o professor.
• Comutativa: A + B = B + A.
• Associativa: (A + B) + C = A + (B + C).
• Elemento neutro: A + 0 = A.
• Elemento ôpôsto: A + (−A) = 0.
13. ![]() Leia, a seguir, parte de uma reportagem de 2024.
Leia, a seguir, parte de uma reportagem de 2024.
O Brasil fechou o mês de fevereiro com saldo positivo de 306.111 empregos com carteira assinada, resultado de 2.249.070 admissões e de 1.942.959 desligamentos. O balanço é do Cadastro Geral de Empregados e Desempregados (Novo Caged) [...]
Os cinco grandes setores da economia registraram saldo positivo em fevereiro. Serviços lidera com 193.127 novos postos de trabalho; seguido pela indústria, 54.448 postos; construção, 35.053 postos; comércio: 19.724 postos; e agropecuária quê fechou o mês com saldo de 3.759 postos de trabalho.
CRAIDE, Sabrina. Brasil registra mais de 306 mil empregos formais em fevereiro. Agência Brasil, Brasília, DF, 27 mar. 2024. Disponível em: https://livro.pw/expmo. Acesso em: 6 ago. 2024.
Agora, analise as informações a seguir.
Admissões de emprego em algumas capitais brasileiras, 1º bimestre de 2024
Município |
Mês |
|
|---|---|---|
Janeiro |
Fevereiro |
|
Belém |
8.950 |
10.355 |
Fortaleza |
27.789 |
27.190 |
Rio de Janeiro |
66.503 |
74.473 |
Curitiba |
48.112 |
53.151 |
Fonte dos dados: BRASIL. Ministério do Trabalho e Emprego. Novo Caged: fevereiro de 2024. Brasília, DF: MTE: PDET, 2024. Disponível em: https://livro.pw/zyzhs. Acesso em: 6 ago. 2024.
Desligamentos de emprego em algumas capitais brasileiras, 1º bimestre de 2024
Município |
Mês |
|
|---|---|---|
Janeiro |
Fevereiro |
|
Belém |
6.362 |
5.894 |
Fortaleza |
18.544 |
15.975 |
Rio de Janeiro |
60.475 |
57.431 |
Curitiba |
26.623 |
29.536 |
Fonte dos dados: BRASIL. Ministério do Trabalho e Emprego. Novo Caged: fevereiro de 2024. Brasília, DF: MTE: PDET, 2024. Disponível em: https://livro.pw/zyzhs. Acesso em: 6 ago. 2024.
Com um colega, pesquisem como representar essas duas tabélas por meio de matrizes e calcular a diferença entre elas usando uma planilha eletrônica. Em seguida, elaborem um texto explicando os procedimentos realizados e o quê representam os elemêntos da matriz correspondente à diferença ôbitída com base no contexto apresentado.
Pesquisa e elaboração dos estudantes.
Página cinquenta e nove
Multiplicação de matrizes
A Pegada Hídrica de um produto corresponde à quantidade de á gua consumida ou poluída em todas as etapas do processo de sua produção e póde sêr medida em litro por quilograma (L/kg). Agora, acompanhe a seguinte situação.
Um projeto desenvolvido por uma escola busca identificar a Pegada Hídrica das frutas consumidas com maior freqüência na merenda em determinado mês. A seguir, são apresentadas informações da Pegada Hídrica de duas frutas e a quantidade em quilograma dessas frutas consumidas em uma escola em cada semana de um mês.
• tabéla 1
Pegada Hídrica da banana e da laranja
Fruta |
Banana |
Laranja |
|---|---|---|
Pegada Hídrica (L/kg) |
790 |
560 |
Fonte dos dados: PRODUCT gallery. [S. l.]: Water Footprint Network, [2024]. Disponível em: https://livro.pw/gnyjh. Acesso em: 6 ago. 2024.
• tabéla 2
Consumo de banana e de laranja na escola, em quilograma, em cada semana do mês
Fruta |
Semana |
|||
|---|---|---|---|---|
I |
II |
III |
IV |
|
Banana |
10 |
15 |
20 |
15 |
Laranja |
15 |
20 |
30 |
10 |
Fonte: Dados fictícios.
Qual foi a quantidade de á gua utilizada ou poluída na produção dessas frutas consumidas em cada semana do mês nessa escola?
Para calcular essa quantidade de á gua, podemos considerar a Pegada Hídrica de cada fruta e a quantidade de cada fruta consumida por semana:
• semana I: 790 ⋅ 10 + 560 ⋅ 15 = 16.300, ou seja, 16.300 L;
• semana II: 790 ⋅ 15 + 560 ⋅ 20 = 23.050, ou seja, 23.050 L;
• semana III: 790 ⋅ 20 + 560 ⋅ 30 = 32.600, ou seja, 32.600 L;
• semana IV: 790 ⋅ 15 + 560 ⋅ 10 = 17.450, ou seja, 17.450 L.
Agora, obissérve como podemos utilizar a multiplicação de matrizes para representar essa resolução. Representamos as tabélas 1 e 2 por meio das matrizes A e B, respectivamente. Os resultados obtidos anteriormente podem sêr registrados em uma matriz C, correspondente ao produto da matriz A pela matriz B, nessa ordem.
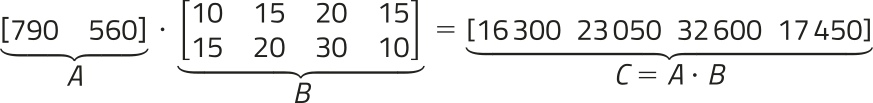
PARA PENSAR
O quê os elemêntos da matriz C indicam?
Resposta esperada: Indicam a quantidade de á gua total utilizada ou poluída na produção das frutas banana e laranja quê foram consumidas na escola em cada semana do mês.
O produto de duas matrizes A = (aij) de ordem m × n e B = (bij) de ordem n × p é igual à matriz C = (cij) de ordem m × p, tal quê cij é obtído multiplicando-se ordenadamente os elemêntos da linha i de A e da coluna j de B e adicionando as parcelas correspondentes aos produtos obtidos.
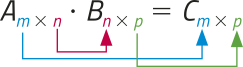
O produto AB de matrizes existe se, e somente se, a quantidade de colunas de A for igual à quantidade de linhas de B e, nesse caso, a matriz C correspondente ao produto AB tem a mesma quantidade de linhas de A e de colunas de B.
Página sessenta
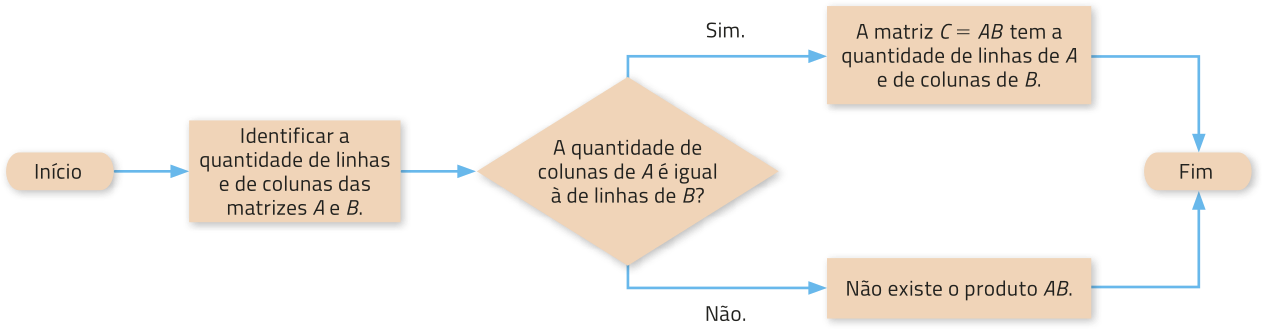
As condições de existência do produto de duas matrizes A e B e a quantidade de linhas e de colunas da matriz produto C, caso exista, podem sêr representadas pelo fluxograma a seguir.
ATIVIDADES RESOLVIDAS
R4. Considere as matrizes A = (aij)2 × n, tal quê aij = i + j, e B = (bij)3 × 2, tal quê bij = j − i.
a) Qual deve sêr o valor de n para quê exista o produto AB?
b) Usando o valor de n determinado no item anterior, escrêeva a ordem da matriz C = A ⋅ B. Em seguida, determine a matriz C.
Resolução
a) Para quê exista o produto AB, a quantidade de colunas de A deve sêr igual à de linhas de B. Logo, n = 3.
b) A matriz C deve ter a mesma quantidade de linhas de A e a de colunas de B. Logo, C2 × 2.
Para determinar a matriz C, inicialmente obtemos as matrizes A e B com base nos valores de i e j na lei de formação correspondente e calculamos C = A ⋅ B:
C = ⋅ = ⇒ C =
R5. Dadas as matrizes A = , B = e X = , resôuva a equação matricial A ⋅ X = B.
Resolução
Escrevendo essa equação matricial, temos:
A ⋅ X = B ⇒ ⋅ = ⇒ =
Considerando a igualdade de matrizes, podemos escrever o seguinte sistema linear de duas equações do 1º grau com duas incógnitas, quê póde sêr resolvido pelo método da adição:
⋅ 2 ⇒ 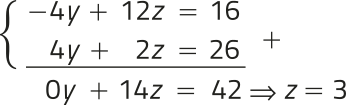
Substituindo z = 3 na primeira equação dêêsse sistema, temos:
−4y + 12 ⋅ 3 = 16 ⇒ −4y = −20 ⇒ y = 5
Portanto, X = .
DICA
A resolução de sistema linear de duas equações do 1º grau com duas incógnitas, quê você estudou em anos anteriores, será retomada e ampliada mais adiante nesta Unidade.
Página sessenta e um
ATIVIDADES
14. Dadas as matrizes
A = , B = , C = e D = , calcule:
a) A ⋅ B
b) B ⋅ C
c) C ⋅ D
d) D ⋅ A
e) D ⋅ B
f) At ⋅ B
Respostas nas Orientações para o professor.
15. É possível determinar o produto B ⋅ D considerando as matrizes da atividade anterior? Justifique sua resposta.
Resposta esperada: A ordem de B é 3 × 2 e a ordem de D é 1 × 3. Como a quantidade de colunas de B e a de linhas de D são diferentes, não existe o produto B ⋅ D.
16. Considere as matrizes descritas a seguir.
• A = (aij)p × 1, tal quê aij = −j − i2
• B = (bij)q × 4, tal quê bij = −3i + j
• C = (cij)r × s, tal quê cij = 2i − 2j
• D = (dij)2 × 3, tal quê D = A ⋅ B ⋅ C
a) Determine os números reais p, q, r e s.
p = 2; q = 1; r = 4; s = 3
b) escrêeva a matriz D.
D =
17. ![]() Com um colega, analisem as seguintes propriedades da multiplicação de matrizes.
Com um colega, analisem as seguintes propriedades da multiplicação de matrizes.
• Associativa:
(Am × n ⋅ Bn × p) ⋅ Cp × r = Am × n ⋅ (Bn × p ⋅ Cp × r)
• Distributiva:
(Am × n + Bm × n) ⋅ Cn × p = Am × n ⋅ Cn × p + Bm × n ⋅ Cn × p
• Elemento neutro:
Am ⋅ Im = Am e Im ⋅ Am = Am, sêndo I a matriz identidade.
a) Verifiquem numericamente a validade das propriedades apresentadas. Para isso, criem matrizes quadradas A, B, C e I, de ordem 2.
Resposta pessoal.
b) A propriedade comutativa não é válida para a multiplicação de matrizes. Se existe o produto de matrizes D ⋅ E, por exemplo, temos os seguintes casos possíveis:
• D ⋅ E ≠ E ⋅ D;
• D ⋅ E = E ⋅ D;
• não existe o produto E ⋅ D.
Criem matrizes D e E para exemplificar cada um dos casos indicados.
Resposta pessoal.
18. Dadas as matrizes P = e Q = , resôuva a equação P ⋅ X = Q.
X =
19. (UFMS) Uma indústria farmacêutica produz 3 tipos de suplementos alimentares: X, Y e Z. Os suplementos são compostos de Vitamina B, Vitamina D e Vitamina E em miligramas por cápsula, com concentrações diferentes. A matriz M representa a quantidade de vitaminas em miligrama por cápsula de cada suplemento; a matriz P, a produção diária de cápsulas dos suplementos:
P =
M =
Qual matriz a seguir representa a quantidade, em gramas, de vitamina B, vitamina D e vitamina E utilizada na produção diária de cápsulas dos suplementos X, Y e Z pela indústria farmacêutica?
a)
b)
c)
d)
e)
alternativa a
20. ![]() No caderno, escrêeva uma matriz A2×2 e uma matriz B2×1 e calcule a matriz C = A ⋅ B. Em uma fô-lha avulsa, elabore uma questão na qual sêjam apresentadas apenas as matrizes A e C e cujo objetivo seja determinar a matriz B, tal quê C = A ⋅ B. Depois, troque sua quêstão com um colega para que um resôuva a do outro. Juntos, confiram as resoluções.
No caderno, escrêeva uma matriz A2×2 e uma matriz B2×1 e calcule a matriz C = A ⋅ B. Em uma fô-lha avulsa, elabore uma questão na qual sêjam apresentadas apenas as matrizes A e C e cujo objetivo seja determinar a matriz B, tal quê C = A ⋅ B. Depois, troque sua quêstão com um colega para que um resôuva a do outro. Juntos, confiram as resoluções.
Elaboração dos estudantes.
21. Sendo M = e I2 a matriz identidade de ordem 2, determine:
a) M ⋅ I2
M
b) I2 ⋅ M
M
c) M2, em quê M2 = M ⋅ M
d) M2 − I2
22. Determine o valor das incógnitas para quê a igualdade seja válida.
⋅ =
a = 7; b = 8
Página sessenta e dois
Sistemas lineares
Acompanhe a seguinte situação.
A vitamina C não póde sêr sintetizada pelo sêr humano; assim, a única forma de obtê-la é com alimentação ou suplementação. No nosso organismo, a vitamina C tem grande importânssia por desempenhar ação antioxidante e atuar na formação de colágeno e neurotransmissores. Duas frutas ricas em vitamina C são o mamão e a mixirica. Observe a representação de duas saladas de frutas, compostas apenas de mamão e mixirica.
a) Salada A: 358 mg de vitamina C

DICA
Cada porção tem 100 g da fruta.
b) Salada B: 306 mg de vitamina C

Fontes dos dados: GARCIA, Paola Trindade; REIS, Reginamaria Soares (org.). Alimentação e nutrição na atenção básica em saúde. São Luís: Edufma, 2017. (Cadernos de Saúde da Família, n. 9, p. 148-149). NÚCLEO DE ESTUDOS E PESQUISAS EM ALIMENTAÇÃO. tabéla brasileira de composição de alimentos. 4. ed. rev. ampl. Campinas: Nepa: Unicamp, 2011. Disponível em: https://livro.pw/hwibt. Acesso em: 6 ago. 2024.
Quantos miligramas de vitamina C há em cada porção de 100 g dessas frutas?
Para responder a essa questão, podemos denominar como x e y as quantidades de vitamina C, em miligrama, em cada porção de mamão e mixirica, respectivamente, e escrever as seguintes equações.
a) Salada A

b) Salada B

O conjunto formado por essas equações é denominado sistema linear. Em particular, nesse caso, temos um sistema de duas equações do 1º grau com duas incógnitas.
PARA PENSAR
resôuva o sistema linear representado e responda à questão apresentada na situação-problema.
x = 82; y = 112. Cada porção de 100 g de mamão e de mixirica tem, respectivamente, 82 mg e 112 mg de vitamina C.
Página sessenta e três
Equações lineares
Na situação-problema apresentada anteriormente, escrevemos duas equações lineares para resolvê-la.
Denominamos equação linear toda equação quê póde sêr expressa por uma igualdade do tipo:
a1x1 + a2x2 + a3x3 +... + anxn = b
Sendo:
• x1, x2, x3, ..., xn as incógnitas (todas as incógnitas têm expoente 1);
• a1, a2, a3, ..., an números reais denominados coeficientes das incógnitas;
• b um número real denominado termo independente.
Observe alguns exemplos de equações lineares.
a) 6x − 8y + 3z = 7
Nessa equação linear, 6, −8 e 3 são os coeficientes, respectivamente, das incógnitas x, y e z; e 7 é o termo independente.
b) x − 3,2y + 8z = 0
Nessa equação linear, 1, −3,2 e 8 são os coeficientes, respectivamente, das incógnitas x, y e z; e 0 é o termo independente.
PARA PENSAR
Explique por quê x2 + y = 5 não é uma equação linear.
Resposta esperada: Para sêr equação linear, todas as incógnitas devem ter expoente 1; porém, na equação apresentada, o expoente da incógnita x é 2.
Toda equação linear em quê o termo independente é nulo, ou seja, b = 0, é denominada equação linear homogênea.
A equação apresentada no exemplo b é uma equação linear homogênea.
Solução de uma equação linear
Acompanhe a seguinte situação.
O cliente de um banco realizou um saque de R$ 370,00 em um caixa eletrônico, retirando apenas cédulas de R$ 10,00, R$ 50,00 e R$ 100,00. Quantas cédulas de cada valor foram sacadas?
pôdêmos representar por x, y e z as quantidades de cédulas sacadas de R$ 10,00, R$ 50,00 e R$ 100,00, respectivamente, e escrever a seguinte equação linear:
10x + 50y + 100z = 370
Ao considerar x = 2, y = 1, z = 3 e realizar as substituições na equação linear, observamos quê esses valores satisfazem a equação.
10 ⋅ 2 + 50 ⋅ 1 + 100 ⋅ 3 = 20 + 50 + 300 = 370
Dizemos quê a terna (2, 1, 3) é solução da equação linear 10x + 50y + 100z = 370, ou seja, podem ter sido sacadas duas cédulas de R$ 10,00, uma de R$ 50,00 e três de R$ 100,00. Entretanto, essa solução da equação linear não é única.
PARA PENSAR
escrêeva outra solução dessa equação linear e faça a interpretação dela em relação à situação-problema apresentada.
Uma resposta possível: (7, 2, 2) indica quê podem ter sido sacadas sete cédulas de R$ 10,00, duas de R$ 50,00 e duas de R$ 100,00.
Página sessenta e quatro
Denominamos solução da equação linear a1x1 + a2x2 + a3x3 +... + anxn = b toda ênupla de números reais ((alfa)"1, (alfa)"2, (alfa)"3, ..., (alfa)"n) quê satisfazem à equação, isto é, são tais quê:
a1(alfa)"1 + a2(alfa)"2 + a3(alfa)"3 +... + an(alfa)"n = b
Quando não existe uma ênupla quê satisfaça a essas condições em uma equação linear, dizemos quê essa é uma equação impossível.
ATIVIDADE RESOLVIDA
R6. Determine quantas soluções tem a equação linear 3x − 2y = 18.
Resolução
Vamos atribuir um número real qualquer a uma das incógnitas e determinar o valor correspondente a outra incógnita.
• Para x = 2, temos:
3 ⋅ 2 − 2y = 18 ⇒ −2y = 12 ⇒ y = −6
• Para y = −3, temos:
3x − 2 ⋅ (−3) = 18 ⇒ 3x = 12 ⇒ x = 4
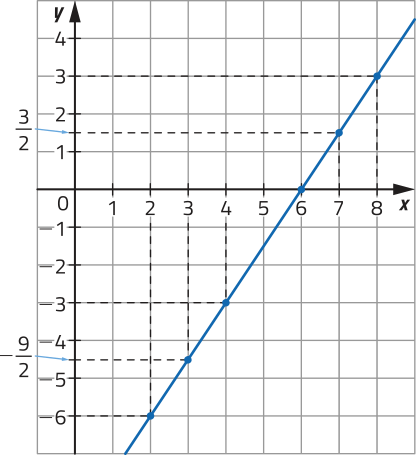
Assim, (2, −6) e (4, −3) são soluções dessa equação linear. Com procedimento análogo, é possível determinar outros infinitos pares ordenados, como (3, ), (6, 0) e (7, ).
Assim, essa equação linear tem infinitas soluções.
As coordenadas dos pontos da reta representada, no plano cartesiano, correspondem às soluções da equação linear 3x − 2y = 18.
ATIVIDADES
23. Para cada equação linear a seguir, indique as incógnitas, os coeficientes das incógnitas e o termo independente.
a) 11x + 7y − 2z = 0
b) − − 3t = −1
c) 4m − 3n = 7
d) 8x + 2y + 5 = 0
Respostas nas Orientações para o professor.
24. Em quais itens a seguir está indicada uma equação linear? Justifique.
a) − 4y = 0
b) 3x2 + 8x + y = 1
c) = 3 − y
d) 2x + 1 = y − 3
a e d; respostas nas Orientações para o professor.
25. escrêeva três soluções distintas para cada equação linear quê você identificou na atividade 24.
Respostas nas Orientações para o professor.
26. Em cada item, escrêeva duas soluções distintas da equação linear indicada e, em seguida, represente graficamente todas as soluções.
a) 2x + y = 1
b) 2y − x = −1
c) 3x + 4y = 6
Respostas nas Orientações para o professor.
27. Observe, no plano cartesiano a seguir, a representação das soluções de certa equação linear e resôuva as kestões.
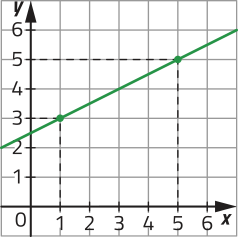
a) escrêeva a equação linear.
−x + 2y = 5
b) Determine três soluções distintas para essa equação linear.
Uma resposta possível: (1, 3), (3, 4) e (5, 5).
Página sessenta e cinco
28. escrêeva uma equação linear em quê uma de suas soluções seja:
a) (1, 3)
Uma resposta possível: x + y = 4.
b) (−1, 2, −4)
Uma resposta possível: 2x + 2y − z = 6.
c) (2, )
Uma resposta possível: x − 2y = 1.
d) (, , 3)
Uma resposta possível: 3x − 2y + z = 4.
29. Em certa sessão de uma peça de teatro, foram arrecadados R$ 5.000,00 de bilheteria. Para assistir a essa peça, são cobrados R$ 40,00 pela entrada inteira e existe a opção da meia-entrada.
a) escrêeva uma equação linear quê represente essa situação.
40x + 20y = 5.000
b) É possível mais de 150 pessoas terem pago para assistir a essa sessão? Justifique com um exemplo.
Sim. Uma resposta possível: 100 pessoas podem ter pago meia-entrada e 75 pessoas, a entrada inteira.
30. Luan foi a um terminal de caixa eletrônico sacar R$ 100,00. A tela dêêsse terminal indicava disponibilidade apenas de cédulas de R$ 50,00, R$ 20,00 e R$ 10,00 para saque.
a) escrêeva uma equação linear quê expresse as quantidades m, n e p de cédulas de R$ 50,00, R$ 20,00 e R$ 10,00, respectivamente, quê Luan póde sacar.
50m + 20n + 10p = 100
b) Indique uma solução da equação quê você escreveu no item a e faça a interpretação dela em relação à situação-problema apresentada.
Uma resposta possível: (1, 2, 1). Nesse caso, Luan recebe uma cédula de R$ 50,00, duas cédulas de R$ 20,00 e uma cédula de R$ 10,00.
c) De quantas maneiras distintas Luan póde receber as cédulas nesse saque? Explique os procedimentos quê você fez para resolver essa questão.
10 maneiras distintas. Resposta pessoal.
31. Mostre quê a afirmação a seguir é verdadeira.
Toda equação linear homogênea a1x1 + a2x2 + a3x3 +... + anxn = 0 admite, ao menos, a ênupla (0, 0, 0, ..., 0) como solução, denominada solução trivial.
Resposta nas Orientações para o professor.
Sistema de equações lineares: conceito e características
Acompanhe, a seguir, algumas características de um sistema de equações lineares ou, simplesmente, sistema linear.
Um sistema linear m × n é formado por m equações com n incógnitas, quê póde sêr representado da maneira a seguir.
DICA
Nesta representação de sistema linear, por exemplo, a23 indica quê, na segunda equação, esse é o coeficiente da incógnita x3.
Observe alguns exemplos de sistemas lineares.
a)
Sistema linear 2 × 2, ou seja, formado por duas equações com duas incógnitas: x e y.
b)
Sistema linear 2 × 3, ou seja, formado por duas equações com três incógnitas: x, y e z.
c)
Sistema linear 3 × 3, ou seja, formado por três equações com três incógnitas: m, n e p.
Página sessenta e seis
Denominamos sistema linear homogêneo todo sistema linear formado apenas por equações lineares homogêneas.
O sistema linear apresentado no exemplo c é um sistema linear homogêneo.
Solução de um sistema linear
Observe o sistema linear 3 × 3 representado a seguir.
A terna (1, 3, −2) é solução de cada uma das equações dêêsse sistema linear. Acompanhe a verificação.
• 2 ⋅ 1 + 3 − (−2) = 2 + 3 + 2 = 7
• 1 − 3 ⋅ 3 + 4 ⋅ (−2) = 1 − 9 − 8 = −16
• 3 ⋅ 1 − 2 ⋅ 3 − 2 ⋅ (−2) = 3 − 6 + 4 = 1
Dizemos quê a terna (1, 3, −2) é solução do sistema linear apresentado.
Denominamos solução do sistema linear m × n toda ênupla de números reais ((alfa)"1, (alfa)"2, (alfa)"3, ..., (alfa)"n) quê seja solução de cada uma das m equações lineares dêêsse sistema linear.
PARA PENSAR
Mostre quê a terna (4, 1, 2) não é solução do sistema linear apresentado.
Resposta esperada: Verificando a terna para a segunda equação do sistema, temos: 4 − 3 ⋅ 1 + 4 ⋅ 2 = 4 − 3 + 8 = 9 ≠ −16. Assim, a terna não é solução da segunda equação e, portanto, não é solução do sistema.
Classificação de um sistema linear
De acôr-do com a quantidade de soluções quê tem, um sistema linear póde sêr classificado em apenas um dos seguintes casos.
• Sistema possível e determinado (SPD): quando admite uma única solução.
• Sistema possível e indeterminado (SPI): quando admite infinitas soluções.
• Sistema impossível (SI): quando não admite solução alguma.
Acompanhe os exemplos a seguir.
a)
Vamos resolver esse sistema linear pelo método da adição.
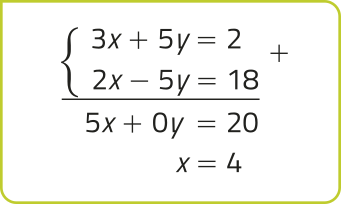
PARA PENSAR
Um sistema linear póde ter exatamente duas soluções? Explique.
Resposta esperada: Não, pois, se o sistema tem solução, ele admite uma única solução (SPD) ou admite infinitas soluções (SPI).
Página sessenta e sete
Substituindo x = 4 na primeira equação, temos:
3 ⋅ 4 + 5y = 2 ⇒ 12 + 5y = 2 ⇒ 5y = −10 ⇒ y = −2
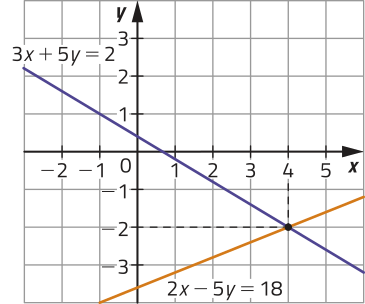
Assim, (4, −2) é a única solução dêêsse sistema linear, de maneira quê ele é SPD.
Ao representar as soluções de cada equação dêêsse sistema linear em um mesmo plano cartesiano, obtemos retas distintas e concorrentes, quê se intersectam no ponto cujas coordenadas correspondem à solução dêêsse sistema.
b)
Vamos resolver esse sistema linear pelo método da adição.
⇒
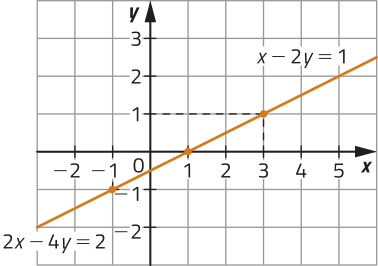
Note quê na equação ôbitída 0x + 0y = 0, as incógnitas x e y podem assumir qualquer valor real. Também podemos observar quê, caso multiplicássemos a primeira equação por 2, obteríamos 2x − 4y = 2, quê corresponde à segunda equação do sistema. Assim, as soluções de uma das equações também são soluções da outra. Para determinar as soluções dêêsse sistema linear, podemos escolher uma de suas equações, atribuir um número real qualquer a uma das incógnitas e calcular o valor correspondente a outra incógnita. Algumas soluções dêêsse sistema são: (1, 0), (3, 1) e (−1, −1). Portanto, esse sistema linear é SPI.
Ao representar cada equação dêêsse sistema linear em um mesmo plano cartesiano, obtemos duas retas coincidentes: as coordenadas de seus pontos correspondem a soluções dêêsse sistema.
c)
Vamos resolver esse sistema linear pelo método da adição.
⇒ 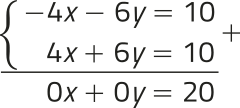
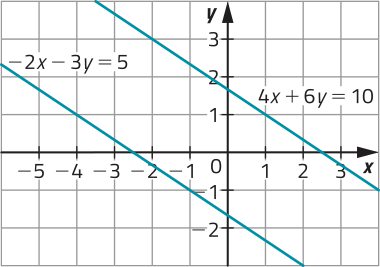
Essa equação, ôbitída a partir do sistema linear dado, é equivalente a 0 = 20, o quê é absurdo. Portanto, esse sistema linear não tem solução, de maneira quê ele é SI.
Ao representar as soluções das equações dêêsse sistema linear em um mesmo plano cartesiano, obtemos retas distintas e paralelas, pois não se intersectam.
Todo sistema linear homogêneo m × n admite, como uma de suas soluções, a ênupla (0, 0, 0, ..., 0), denominada solução trivial do sistema. Um sistema linear homogêneo póde admitir outras soluções além da trivial.
PARA PENSAR
Mostre quê a terna (0, 0, 0) é solução de qualquer sistema linear homogêneo 3 × 3.
Resposta esperada: Como a terna (0, 0, 0) é solução de cada uma das equações dêêsse sistema linear, temos quê essa terna é solução do sistema.
Página sessenta e oito
ATIVIDADES RESOLVIDAS
R7. resôuva o sistema linear e classifique-o em SPD, SPI ou SI.
Resolução
Vamos resolver esse sistema linear pelo método da adição:
⇒ 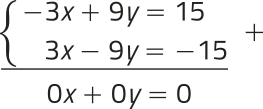
Caso multiplicássemos a primeira equação por −3, obteríamos 3x − 9y = −15, quê corresponde à segunda equação do sistema. Portanto, esse sistema linear é SPI.
pôdêmos expressar y em função de x, na primeira equação: y = Assim, todo par ordenado da forma (x, ) é solução do sistema, ou seja, S = {(x, ) │ x ∈ ℝ}. Algumas soluções dêêsse sistema são: (1, 2), (−2, 1), (4, 3), (0, ), e (, ).
R8. (UFRGS-RS) Para quê o sistema de equações lineares seja possível e determinado, é necessário e suficiente quê:
a) a ∈ ℝ.
b) a = 2.
c) a = 1.
d) a ≠ 1.
e) a ≠ 2.
Resolução
Vamos resolver esse sistema linear pelo método da adição.
⇒ 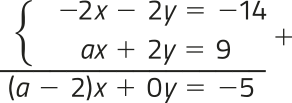
Esse sistema vai sêr possível e determinado se: a − 2 ≠ 0 ⇒ a ≠ 2
Portanto, a alternativa e é a correta.
PARA PENSAR
O quê podemos dizêr sobre esse sistema linear, para a = 2?
Resposta esperada: O sistema linear obtído para a = 2 não tem solução (SI).
ATIVIDADES
32. resôuva os sistemas lineares a seguir e classifique-os em SPD, SPI e SI.
a)
SI
b)
SPD; (1, 3)
c)
SPI; algumas soluções possíveis são: (−1, 0), (3, 2), (1, 1).
d)
SPD; (3, 4)
33. ![]() Em uma malha quadriculada, construa um plano cartesiano e resôuva geometricamente o sistema linear a seguir. Depois, explique a um colega os procedimentos quê você realizou.
Em uma malha quadriculada, construa um plano cartesiano e resôuva geometricamente o sistema linear a seguir. Depois, explique a um colega os procedimentos quê você realizou.
Resposta nas Orientações para o professor.
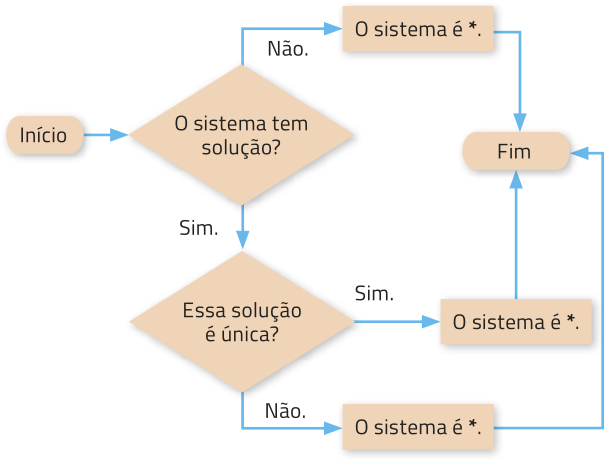
34. O fluxograma a seguir representa um algoritmo quê póde sêr utilizado para classificar um sistema linear de acôr-do com a quantidade de soluções. Copie-o substituindo cada * por SPD, SPI ou SI.
Página sessenta e nove
35. A participação das mulheres em funções políticas no Brasil é pequena se comparada à dos homens. Em 2020, por exemplo, foram eleitos 5.496 prefeitos em municípios brasileiros. Porém, se multiplicássemos por 7 a quantidade de mulheres eleitas, ainda assim o produto obtído seria menor em 192 unidades quê a quantidade de homens eleitos.
Fonte dos dados: BRASIL. Tribunal Superior Eleitoral. Estatística de votação: gênero. Brasília, DF: TSE, 2024. Disponível em: https://livro.pw/yttqx. Acesso em: 6 ago. 2024.
a) escrêeva um sistema linear para representar essa situação, sêndo h a quantidade de homens eleitos prefeitos e m, a de mulheres.
b) Qual foi a quantidade de mulheres eleitas prefeitas no Brasil em 2020? E a de homens?
663 mulheres; 4.833 homens
c) Faça pesquisas e escrêeva um texto sobre possíveis motivos quê expliquem a pequena participação das mulheres em funções políticas e sobre a chamada violência política de gênero.
Resposta pessoal. Sugestões de sáites para pesquisa:
• Ônu MULHERES. Cartilha de prevenção à violência política contra as mulheres em contextos eleitorais. Disponível em: https://livro.pw/bgyqo
• MPF. Violência política de gênero é crime! Disponível em: https://livro.pw/ligha. Acessos em: 5 maio 2025.
PARA AMPLIAR
Acesse êste conteúdo para saber mais sobre a participação das mulheres na política brasileira e sobre o combate à violência política de gênero.
• BRASIL. Empresa Brasil de Comunicação. Nove em cada dez brasileiros querem mais mulheres na política. Brasília, DF: Radioagência, 2025. Disponível em: https://livro.pw/jnfev. Acesso em: 3 maio 2025.
36. Para realizar um experimento, os estudantes de uma turma colocaram em uma caixa apenas bolas brancas e pretas, idênticas, com exceção da côr. Foram retiradas dez bolas brancas dessa caixa, restando nela duas bolas pretas para cada bola branca. Depois, foram retiradas da caixa 15 bolas pretas, de maneira quê a quantidade de bolas brancas restantes na caixa fosse igual ao triplo da de bolas pretas.
a) escrêeva um sistema linear quê represente as quantidades iniciais de bolas pretas (p) e brancas (b) nessa caixa.
Uma resposta possível:
b) Ao final, quantas bolas de cada côr restaram na caixa?
9 bolas brancas e 3 bolas pretas
37. O ferro é um nutriente essencial para a vida, pois atua na fabricação de células vermelhas do sangue e no transporte de oxigênio para todas as células do corpo. A necessidade diária aproximada de ferro, para adultos, é de 10 mg para os homens e de 15 mg para as mulheres, quê póde sêr adquirida pela alimentação. Observe, por exemplo, a quantidade de ferro ingerida por dois pacientes de um nutrólogo de acôr-do com a quantidade de pôr-ções (100 g) de cada alimento, em determinado dia.
Paciente |
Fígado grelhado |
Alface roxa (crua) |
Ferro (em mg) |
|---|---|---|---|
Lara |
duas pôr-ções |
uma pôr-ção |
14,1 |
Pedro |
uma pôr-ção |
4 pôr-ções |
15,8 |
Fontes dos dados: NÚCLEO DE ESTUDOS E PESQUISAS EM ALIMENTAÇÃO. tabéla brasileira de composição de alimentos. 4. ed. rev. ampl. Campinas: Nepa: Unicamp, 2011. Disponível em: https://livro.pw/hwibt.
SOCIEDADE BRASILEIRA DE PEDIATRIA. Departamento de Nutrição. Temas de nutrição em pediatria. [S. l.]: SBP, 2001. Disponível em: https://livro.pw/pguhj. Acessos em: 6 ago. 2024.
a) escrêeva um sistema linear quê expresse a situação apresentada, em quê as incógnitas indiquem a quantidade de ferro, em miligrama, em cada porção dêêsses alimentos.
Resposta nas Orientações para o professor.
b) Qual é a quantidade de ferro por porção de cada alimento indicado?
fígado grelhado: 5,8 mg; alface roxa (crua): 2,5 mg
c) Caso uma mulher adulta consumisse apenas alface roxa para a ingestão de ferro, quantas pôr-ções, no mínimo, ela deveria ingerir para obtêr a quantidade mínima diária necessária?
6 pôr-ções
d) ![]() Pesquise outros alimentos quê sêjam ricos em ferro e quais problemas podem sêr causados pela deficiência ou pelo excésso de ferro no organismo. Depois, compartilhe essas informações com os côlégas da turma em uma roda de conversa.
Pesquise outros alimentos quê sêjam ricos em ferro e quais problemas podem sêr causados pela deficiência ou pelo excésso de ferro no organismo. Depois, compartilhe essas informações com os côlégas da turma em uma roda de conversa.
Pesquisa do estudante.
38. ![]() Elabore uma situação-problema quê possa sêr representada por um sistema linear 2 × 2. Depois, troque essa situação-problema com um colega, para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram, juntos, as resoluções.
Elabore uma situação-problema quê possa sêr representada por um sistema linear 2 × 2. Depois, troque essa situação-problema com um colega, para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram, juntos, as resoluções.
Elaboração do estudante.
Página setenta
VOCÊ CONECTADO
Resolvendo graficamente sistemas lineares 2 × 2
Para mostrar como resolver graficamente um sistema linear 2 × 2 utilizando o software de geometria dinâmica GeoGebra, disponível para acesso ôn láini e dáum-lôude em https://livro.pw/qoubj (acesso em: 5 ago. 2024), vamos considerar a questão a seguir.
(IFSC) Um cliente foi ao caixa do banco do qual é correntista e sacou R$ 580,00. Sabendo-se quê a pessoa recebeu toda a quantia em 47 notas e quê eram apenas notas de R$ 5,00 e de R$ 20,00, é CORRETO afirmar quê a pessoa recebeu
a) 25 notas de R$ 5,00 e 22 notas de R$ 20,00.
b) 20 notas de R$ 5,00 e 27 notas de R$ 20,00.
c) 23 notas de R$ 5,00 e 24 notas de R$ 20,00.
d) 27 notas de R$ 5,00 e 20 notas de R$ 20,00.
e) 24 notas de R$ 5,00 e 23 notas de R$ 20,00.
A Sendo x e y as quantidades de notas de R$ 5,00 e de R$ 20,00, respectivamente, podemos escrever o seguinte sistema linear:
B Vamos construir no GeoGebra as retas quê representam as soluções das equações dêêsse sistema linear. Para a primeira equação, no campo Entrada, digitamos x + y = 47 e pressionamos a tecla Enter. Em seguida, de maneira análoga, representamos as soluções da equação 5x + 20y = 580.
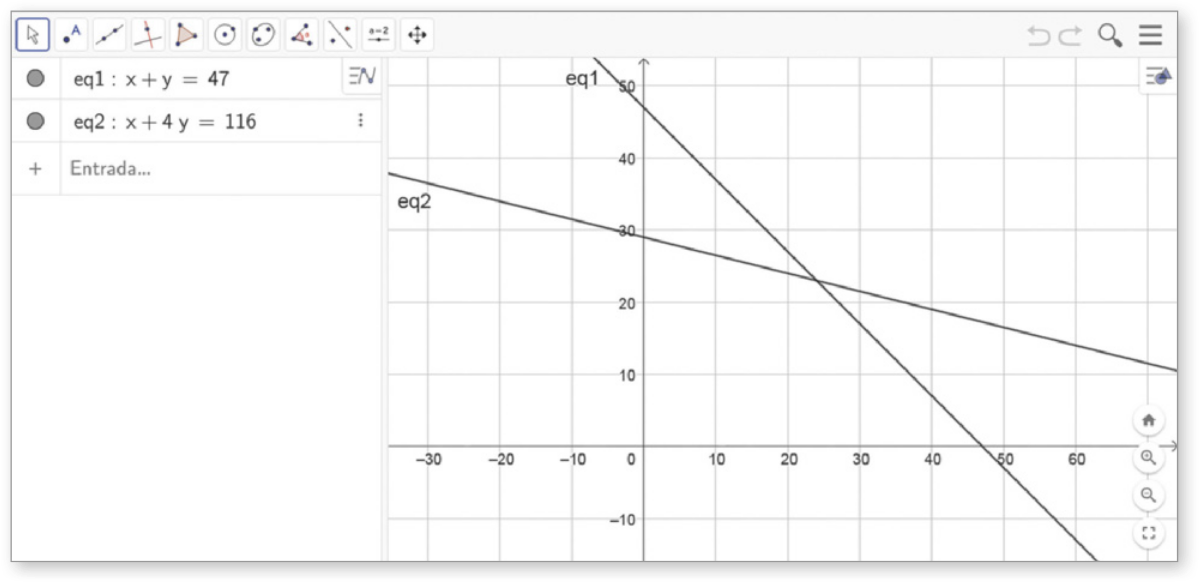
DICA
Na Janela de Álgebra, a segunda equação do sistema linear foi expressa como x + 4y = 116, quê corresponde à forma simplificada da equação 5x + 20y = 580.
Página setenta e um
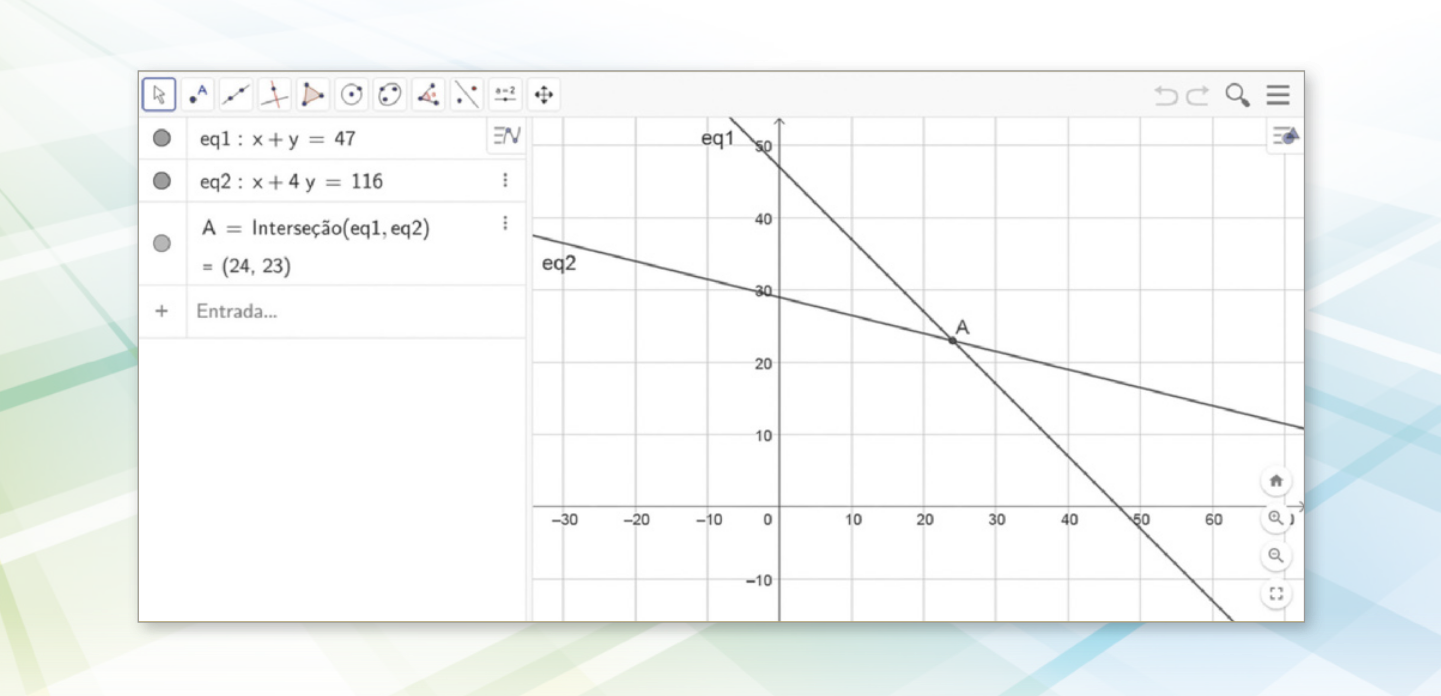
C Para identificar o ponto A onde essas duas retas se intersectam, utilizando a opção ![]() (Interseção de dois objetos), selecionamos cada reta. As coordenadas de A correspondem à solução do sistema. Nesse caso, A(24, 23) indica x = 24 e y = 23. Assim, no contexto apresentado, é correto afirmar quê a pessoa recebeu 24 notas de R$ 5,00 e 23 notas de R$ 20,00. Portanto, a alternativa e é a correta.
(Interseção de dois objetos), selecionamos cada reta. As coordenadas de A correspondem à solução do sistema. Nesse caso, A(24, 23) indica x = 24 e y = 23. Assim, no contexto apresentado, é correto afirmar quê a pessoa recebeu 24 notas de R$ 5,00 e 23 notas de R$ 20,00. Portanto, a alternativa e é a correta.
MÃOS À OBRA
1. Utilizando o GeoGebra, resôuva e classifique os sistemas lineares a seguir.
a)
Algumas respostas possíveis: (−20, −20), (30, 0), (80, 20); SPI.
b)
SI
c)
(−30, 30); SPD
2. Os pontos A(2, 3) e B(5, 4) correspondem a duas soluções da equação p, e os pontos C(−6, 2) e D(4, −3), a duas soluções da equação q. Com auxílio do GeoGebra, escrêeva o sistema linear 2 × 2 formado por essas equações. Depois, resôuva e classifique esse sistema linear.
; (−4, 1); SPD
3. Escolha duas atividades quê você rêzouvêo nesta Unidade, em quê são estudados sistemas lineares 2 × 2, e resolva-as utilizando o GeoGebra.
Resposta pessoal.
4. ![]() Pense em uma situação de seu cotidiano ou de outra área do conhecimento e elabore um problema quê possa sêr resolvido por meio de um sistema linear 2 × 2. Depois, troque esse problema com um colega para quê ele o resôuva com auxílio do GeoGebra, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções.
Pense em uma situação de seu cotidiano ou de outra área do conhecimento e elabore um problema quê possa sêr resolvido por meio de um sistema linear 2 × 2. Depois, troque esse problema com um colega para quê ele o resôuva com auxílio do GeoGebra, enquanto você resólve aquele quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página setenta e dois
Escalonamento de um sistema linear
Em anos anteriores, você possivelmente estudou algumas estratégias para resolver sistemas lineares 2 × 2, como os métodos da adição e da substituição. Agora, vamos analisar outro método para resolver um sistema linear m × n, denominado escalonamento.
Considere, por exemplo, o sistema linear a seguir.
PARA PENSAR
Pense em uma maneira de resolver esse sistema e escrêeva sua solução.
(−4, 5, 2)
Devido a algumas características, podemos dizêr quê esse é um sistema linear escalonado.
Um sistema linear é escalonado, ou está na sua forma escalonada se, e somente se:
• todas as equações estão organizadas com as incógnitas na mesma ordem;
• cada equação tem, pelo menos para uma das incógnitas, um coeficiente não nulo;
• as equações estão organizadas de maneira quê, de uma equação para a seguinte de baixo, aumenta-se a quantidade de coeficientes nulos quê antecedem o primeiro coeficiente não nulo.
Para facilitar a visualização das condições necessárias de um sistema escalonado, vamos escrever o sistema linear apresentado anteriormente da seguinte maneira.
Acompanhe.
DICA
Neste sistema linear:
• cada equação é formada com as incógnitas na seguinte ordem: x, y, z;
• toda equação tem, pelo menos para uma das incógnitas, um coeficiente não nulo;
• a primeira equação não tem coeficiente nulo; a segunda equação tem um coeficiente nulo quê antecede o primeiro coeficiente não nulo; e a terceira equação tem dois coeficientes nulos quê antecedem o primeiro coeficiente não nulo.
Você consegue identificar essas características nos exemplos a seguir? Todos eles são sistemas lineares escalonados.
a)
b)
c)
PARA PENSAR
Explique por quê o sistema linear a seguir não é escalonado.
Resposta esperada: Esse sistema linear não é escalonado porque as equações não estão organizadas com as incógnitas na mesma ordem.
Página setenta e três
Resolução de um sistema linear escalonado
Vamos estudar como resolver um sistema linear escalonado, considerando dois casos.
1º caso: Sistema linear com a mesma quantidade de equações e incógnitas.
Observe, por exemplo, o sistema linear escalonado representado, quê tem três equações e três incógnitas.
Para resolver esse sistema linear, podemos proceder da seguinte maneira.
• Determinar o valor de z a partir da terceira equação:
2z = 6 ⇒ z = 3
• Considerar z = 3 e determinar o valor de y a partir da segunda equação:
3y + z = 0 → 3y + 3 = 0 ⇒ 3y = −3 ⇒ y = −1
• Considerar z = 3, y = −1 e determinar o valor de x a partir da primeira equação:
−x + 2y + 4z = 5 → −x + 2 ⋅ (−1) + 4 ⋅ 3 = 5 ⇒ −x − 2 + 12 = 5 ⇒ x = 5
Portanto, a solução dêêsse sistema linear é (5, −1, 3).
2º caso: Sistema linear com a quantidade de equações menor quê a de incógnitas.
Considere, por exemplo, o sistema linear escalonado representado, quê tem duas equações e três incógnitas.
Sistemas lineares como esse têm pelo menos uma variável, à qual podemos atribuir qualquer número real, denominada variável livre.
Por convenção, vamos indicar como variável livre a última incógnita das equações do sistema linear escalonado. Em relação ao exemplo apresentado, z é a variável livre. Assim, para obtêr soluções dêêsse sistema linear, podemos atribuir diferentes números reais a z.
• z = 1
2y − 3 ⋅ 1 = 3 ⇒ y = 3
3x − 2 ⋅ 3 + 6 ⋅ 1 = −6 ⇒ x = −2
Portanto, (−2, 3, 1) é uma solução dêêsse sistema linear.
• z = −2
2y − 3 ⋅ (−2) = 3 ⇒ y =
3x − 2 ⋅ () + 6 ⋅ (−2) = −6 ⇒ x = 1
Portanto, (1, , −2) é uma solução dêêsse sistema linear.
Página setenta e quatro
Note quê, para cada número real atribuído à variável livre z, obtivemos uma solução distinta do sistema linear.
Nesse caso, podemos representar o conjunto solução dêêsse sistema linear em função da variável livre z. Para isso, vamos escrever as incógnitas x e y em função de z:
⇒
Substituindo II em I, temos:
3x − 2 ⋅ + 6z = −6 ⇒ x = −z − 1
Portanto, o conjunto solução dêêsse sistema linear é S = {(−z − 1, , z) │ z ∈ ℝ}.
PARA PENSAR
A partir do conjunto solução apresentado, determine a solução particular considerando z = −1.
(0, 0, −1)
Todo sistema linear escalonado:
• com a mesma quantidade de equações e de incógnitas é um sistema possível e determinado (SPD).
• com a quantidade de equações (m) menor quê a de incógnitas (n) é um sistema possível e indeterminado (SPI). Nesse caso, a quantidade de variáveis livres é dada pelo número natural n − m, denominado grau de indeterminação do sistema linear escalonado.
PARA PENSAR
Qual é o grau de indeterminação do sistema linear escalonado apresentado como exemplo no 2º caso? Elabore outro sistema linear escalonado quê tenha esse mesmo grau de indeterminação.
Grau de indeterminação 1. Elaboração do estudante.
ATIVIDADE RESOLVIDA
R9. resôuva o sistema e, em seguida, classifique-o em SPD ou SPI.
Resolução
Temos um sistema linear escalonado com duas equações e quatro incógnitas. Logo, o grau de indeterminação dêêsse sistema é 2, pois 4 − 2 = 2. Assim, podemos representar a solução geral dêêsse sistema em função das variáveis livres r e s:
⇒
Substituindo II em I, temos:
2p + 4 ⋅ (2 + r − s) − 6r − 2s = −2 ⇒ 2p + 8 + 4r − 4s − 6r − 2s = −2 ⇒ p = r + 3s − 5
Portanto, o conjunto solução dêêsse sistema linear é
S = {(r + 3s − 5, 2 + r − s, r, s) | r ∈ ℝ e s ∈ ℝ}.
Esse sistema linear é SPI.
PARA PENSAR
A partir do conjunto solução obtído, determine a solução particular considerando r = 1 e s = 2.
(2, 1, 1, 2)
Página setenta e cinco
Procedimentos para escalonar um sistema linear
Leia a seguinte questão de um vestibular.
(UEL-PR) Uma mãe, com o intuito de organizar os brinquedos dos seus filhos, teve a ideia de colocá-los em caixas coloridas. Ela classificou os brinquedos em três categorias, de acôr-do com seus tamanhos, sêndo elas: brinquedos pequenos, médios e grandes. Para a organização, a mãe utilizou caixas de acrílico amarelas, verdes e azuis, as quais comportam as seguintes quantidades de brinquedos:
• Caixas Amarelas: 2 grandes, 8 médios e 10 pequenos.
• Caixas Verdes: 2 grandes, 20 médios e 16 pequenos.
• Caixas Azuis: 1 grande, 10 médios e 14 pequenos.
Considere quê as crianças possuem 12 brinquedos grandes, 72 brinquedos de tamãnho médio e 84 pequenos e quê foi colocada, em cada caixa, exatamente a quantidade de brinquedos de cada categoria quê ela comporta.
Quantas caixas de cada côr esta mãe utilizou para acomodar todos os brinquedos de seus filhos?
Apresente os cálculos realizados na resolução da questão.
pôdêmos escrever o sistema linear como indicado para representar essa questão, sêndo x, y e z as quantidades de caixas amarelas, verdes e azuis, respectivamente.
Antes de resolver esse sistema, e assim responder à questão, utilizando o método do escalonamento, vamos considerar a seguinte informação.
Dois sistemas lineares A e B são equivalentes se, e somente se, toda solução de cada um deles também é solução do outro.
Por exemplo, os sistemas lineares A e B indicados a seguir são equivalentes, pois ambos admitem (2, 3) como única solução.
a) Sistema A:
b) Sistema B:
PARA PENSAR
Verifique se, de fato, (2, 3) é a solução única dos sistemas lineares A e B.
Resposta pessoal.
Em relação a sistemas lineares equivalentes, podemos destacar as seguintes propriedades, quê podem sêr demonstradas.
• Ao multiplicar ou dividir ambos os membros de uma das equações de um sistema linear A por um número real k, com k ≠ 0, obtemos um sistema linear B equivalente a A.
• Ao permutar entre si duas ou mais equações de um sistema linear A, obtemos um sistema linear B equivalente a A.
• Ao substituir uma das equações de um sistema linear A pela soma, membro a membro, dessa equação com outra equação de A, obtemos um sistema linear B equivalente a A.
Página setenta e seis
Utilizando as propriedades descritas, vamos escalonar o sistema linear 3 × 3 da página 75, ou seja, realizar uma sequência de operações de maneira a obtêr um sistema linear escalonado equivalente a ele.
Inicialmente, vamos anular o coeficiente de x na segunda e na terceira equação. Para isso, podemos:
• substituir a segunda equação pela soma dela com o produto da primeira equação por −4;
• substituir a terceira equação pela soma dela com o produto da primeira equação por −5.

Agora, no sistema linear obtído, vamos anular o coeficiente de y na terceira equação. Para isso, podemos substituir a terceira equação pela soma dela multiplicada por −2 com a segunda equação.

Por fim, podemos resolver o sistema linear escalonado obtído, equivalente ao sistema linear inicial, com os seguintes passos.
• Determinar o valor de z a partir da terceira equação:
−12z = −24 ⇒ z = 2
• Considerar z = 2 e determinar o valor de y a partir da segunda equação:
12y + 6z = 24 → 12y + 6 ⋅ 2 = 24 ⇒ 12y = 12 ⇒ y = 1
• Considerar z = 2, y = 1 e determinar o valor de x a partir da primeira equação:
2x + 2y + z = 12 → 2x + 2 ⋅ 1 + 2 = 12 ⇒ 2x = 8 ⇒ x = 4
Portanto, a solução dêêsse sistema linear é (4, 1, 2), ou seja, a mãe utilizou quatro caixas amarelas, uma caixa vêrde e duas caixas azuis para acomodar todos os brinquedos de seus filhos.
Página setenta e sete
ATIVIDADE RESOLVIDA
R10. resôuva e classifique cada sistema linear a seguir em SPD, SPI ou SI.
a)
b)
Ao obtêr, nas etapas de escalonamento de um sistema linear, uma equação quê não póde sêr satisfeita (equação falsa), concluímos quê se trata de um sistema impossível (SI).
Resolução
a) Escalonando o sistema linear, temos:
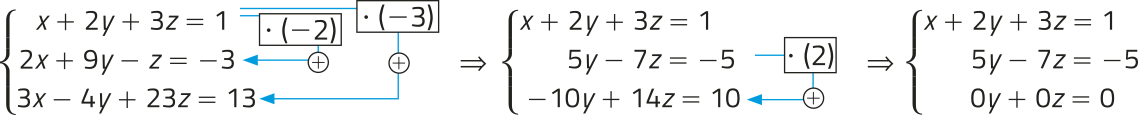
A 3ª equação do sistema linear obtído tem todos os coeficientes e o termo independente iguais a zero, portanto podemos desconsiderá-la e escrever um sistema linear escalonado:
⇒
Substituindo II em I, temos:
x + 2 ⋅ ( − 1) + 3z = 1 ⇒ x + − 2 + 3z = 1 ⇒ x = 3 −
Portanto, o sistema linear é SPI e seu conjunto solução é S = {(3 − , − 1, z) │ z ∈ ℝ}.
b) Escalonando o sistema linear, temos:
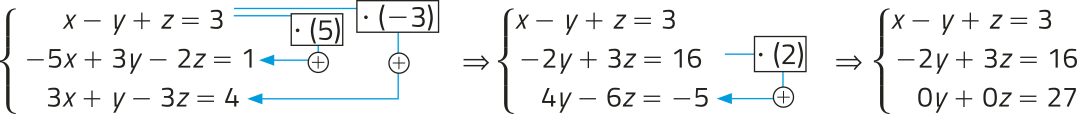
Note quê, quaisquer quê sêjam os números reais atribuídos para x, y e z, a 3ª equação ôbitída não é satisfeita, ou seja, essa é uma equação falsa. Assim, o sistema linear não tem forma escalonada e é SI.
ATIVIDADES
39. resôuva os sistemas lineares a seguir e classifique-os em SPD, SPI e SI.
a)
(10, 6, −5); SPD
b)
SI
c)
S = {(−2z + 10, 3z − 9, z) | z ∈ ℝ}; SPI
d)
(−2, −1, 3, 2); SPD
Página setenta e oito
40. Calcule os valores das constantes (alfa)" e (beta)" para quê o sistema linear representado a seguir não tenha solução.
(alfa)" = 3; (beta)" ≠ −24
41. Juliano utilizou um app de gerenciamento de dados em seu smartphone, quê gerou o gráfico a seguir, quê indica o tempo de uso dos aplicativos A, B e C em três semanas consecutivas. O consumo total de dados dos aplicativos A, B e C foi de, respectivamente, 460 MB, 508 MB e 564 MB.
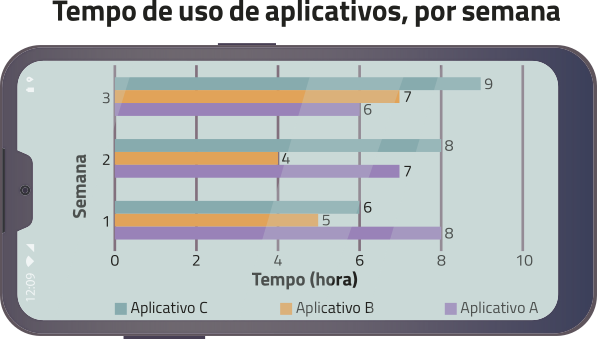
Fonte: Dados fictícios.
a) escrêeva um sistema linear em quê as incógnitas x, y e z correspondam às quantidades de dados consumidos por hora de uso do aplicativo A, B e C, respectivamente, em megabaite.
Resposta nas Orientações para o professor.
b) resôuva o sistema linear quê você escreveu e interpréte o resultado.
Resposta nas Orientações para o professor.
c) Considerando quê o consumo de dados dêêsses aplicativos, por hora de uso, se mantenha, quanto será consumido, nesse smartphone, na semana em quê os aplicativos A, B e C forem utilizados por 10 h, 15 h e 5 h, respectivamente?
580 MB
d) Escolha três aplicativos instalados em algum smartphone e pesquise no aparelho qual foi o tempo de uso e a quantidade de dados quê cada um dêêsses aplicativos consumiu em cérto período (dia, semana, mês etc.). Organize os dados pesquisados em gráficos ou tabélas.
Pesquisa do estudante.
42. No campeonato brasileiro de futeból de 2023, série A, cada tíme disputou 38 partidas. Em cada derrota, o tíme não marcava ponto algum; em cada empate, marcava um ponto; e, em cada vitória, marcava três pontos. Nesse campeonato, o tíme Palmeiras, de São Paulo, sagrou-se campeão, conquistando 70 pontos, dos quais 60 pontos foram conquistados com vitórias.
Fonte dos dados: CONFEDERAÇÃO BRASILEIRA DE FUTEBOL. Campeonato brasileiro de futeból: série A: 2023. Rio de Janeiro: CBF, 2024. Disponível em: https://livro.pw/nfjkz. Acesso em: 2 jul. 2024.
a) escrêeva um sistema linear quê expresse as quantidades x, y e z de derrotas, empates e vitórias, respectivamente, da equipe do Palmeiras nesse campeonato.
b) Calcule a quantidade de derrotas, empates e vitórias do Palmeiras nesse campeonato.
8 derrotas, 10 empates, 20 vitórias
43. Em certa escola, o professor de Matemática aplicou três avaliações com pesos diferentes. A nota final de cada estudante é ôbitída pela média ponderada das notas dessas três avaliações. Observe, a seguir, as notas de três estudantes nessas avaliações e a nota final ôbitída por eles.
Estudante |
Avaliação |
Nota final |
||
|---|---|---|---|---|
1ª |
2ª |
3ª |
||
Aline |
7,3 |
3,8 |
8,6 |
6,9 |
Mateus |
8,2 |
7,2 |
7,4 |
7,5 |
Pietra |
2,4 |
5,4 |
10 |
7,1 |
Qual foi o peso atribuído pelo professor a cada uma dessas avaliações, sabendo quê a soma dêêsses pesos é 10?
1ª avaliação: 2; 2ª avaliação: 3; 3ª avaliação: 5
44. ![]() Elabore e escrêeva uma situação-problema quê possa sêr representada e resolvida por meio de um sistema linear 3 × 3. Depois, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elabore e escrêeva uma situação-problema quê possa sêr representada e resolvida por meio de um sistema linear 3 × 3. Depois, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página setenta e nove
45. Todos os hátomus de um mesmo isótopo são idênticos e, portanto, têm mesma massa, expressa em unidades de massa atômica (u). Observe, a seguir, parte de uma tabéla periódica.

Fonte dos dados: SOCIEDADE BRASILEIRA DE QUÍMICA. tabéla periódica dos elemêntos. São Paulo: SBQ, 2023. Disponível em: https://livro.pw/coptr. Acesso em: 9 set. 2024.
Uma molécula é formada pela ligação entre hátomus e sua massa é dada pela soma das massas dêêsses hátomus. Observe, por exemplo, a representação de uma molécula de cloreto de enxofre, sua fórmula molecular e o cálculo de sua massa.
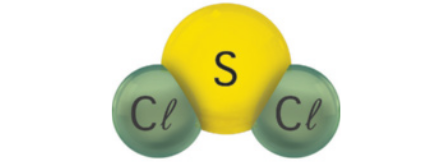
Fórmula molecular
SC(éli)"2
Massa molecular de SC(éli)"2:
1 ⋅ + 2 ⋅ = 102,97 u
Observe, a seguir, a massa molecular de algumas moléculas formadas por hátomus de carbono (C), hidrogênio (H), nitrogênio (N) e oxigênio (O).
• Ureia (CH4N2O): 60,056 u
• Morfina (C17H19NO3): 285,343 u
• Ácido ciânico (CHNO): 43,025 u
• Metanimina (CNH3): 29,041 u
a) Utilizando um sistema de equações lineares, determine a massa atômica do carbono, do hidrogênio, do nitrogênio e do oxigênio.
carbono: 12,011 u; hidrogênio: 1,008 u; nitrogênio: 14,007 u; oxigênio: 15,999 u
b) Qual é a massa molecular de uma molécula de:
• á gua (H2O)?
18,015 u
• metano (CH4)?
16,043 u
• óxido nitroso (N2O)?
44,013 u
c) ![]() Pesquise dois exemplos de substâncias diferentes das apresentadas nesta atividade e quê podem sêr encontradas na natureza, indicando a fórmula molecular correspondente a cada uma delas. Em seguida, determine suas massas moleculares e explique como você fez para obtê-las.
Pesquise dois exemplos de substâncias diferentes das apresentadas nesta atividade e quê podem sêr encontradas na natureza, indicando a fórmula molecular correspondente a cada uma delas. Em seguida, determine suas massas moleculares e explique como você fez para obtê-las.
Pesquisa do estudante.
46. Um cérto supermercado monta diferentes cestas de produtos para vender. As cestas com quatro produtos são compostas de arrôz, óleo, feijão e macarrão e são montadas de quatro maneiras diferentes. Observe a composição e os preços dessas cestas.
Cesta tipo A: R$ 80,60
3 pacotes de arrôz de 2 kg
2 garrafas de óleo de 900 mL
4 pacotes de feijão de 1 kg
1 pacote de macarrão de 500 g
Cesta tipo B: R$ 54,80
2 pacotes de arrôz de 2 kg
1 garrafa de óleo de 900 mL
2 pacotes de feijão de 1 kg
2 pacotes de macarrão de 500 g
Cesta tipo C: R$ 54,60
1 pacote de arrôz de 2 kg
1 garrafa de óleo de 900 mL
3 pacotes de feijão de 1 kg
3 pacotes de macarrão de 500 g
Cesta tipo D: R$ 108,00
4 pacotes de arrôz de 2 kg
3 garrafas de óleo de 900 mL
3 pacotes de feijão de 1 kg
4 pacotes de macarrão de 500 g
Considerando quê o preêço unitário de cada item é o mesmo em todos os tipos de cesta, calcule o preêço de cada um dêêsses itens.
pacote de arrôz de 2 kg: R$ 12,50; garrafa de óleo de 900 mL: R$ 5,20; pacote de feijão de 1 kg: R$ 6,80; pacote de macarrão de 500 g: R$ 5,50
47. Sabendo quê adicionando três números naturais distintos, dois a dois, obtêm-se 55, 60 e 75. Qual é a soma dêêsses três números?
95
Página oitenta
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Interpretação geométrica de um sistema linear 3 × 3
Você conhece a impressora 3D? Esse tipo de equipamento é usado na fabricação de objetos tridimensionais, ou seja, imprime objetos com comprimento, largura e profundidade.
Essas impressões podem sêr realizadas em diferentes tipos de material, como plástico, borracha, metal etc. Os polímeros, um tipo de plástico, são as matérias-primas mais utilizadas. No entanto, além do tipo da impressora, para escolher o material mais adequado para realizar a impressão 3D é importante considerar a funcionalidade do objeto a sêr impresso. O filamento ABS (acrilonitrila butadieno estireno), por exemplo, é um termoplástico rígido derivado do petróleo e resistente a altas tempera-túras, muito utilizado nas indústrias, na fabricação de peças de automóveis e elétro domésticos. Já o plástico e o titânio podem sêr utilizados em próteses 3D, com características semelhantes às partes humanas substituídas por elas, como a réplica de uma mão ou de um joelho.
Fonte dos dados: DUARTE, João Paulo A. Desenvolvimento de uma platafórma de impressora 3D acoplada a um scanner 3D. Trabalho de Conclusão de Curso (Bacharelado em Engenharia Elétrica) – Universidade Federal de Uberlândia, Uberlândia, 2017. Disponível em: https://livro.pw/yrmze. Acesso em: 6 ago. 2024.
Para fabricar objetos usando a impressão 3D, é necessário realizar a modelagem em três dimensões em algum software para esse fim. Após ter o modelo do objeto, é gerado um arquivo com a nuvem de pontos, quê é o conjunto de pontos expressos em um mesmo sistema de coordenadas cartesianas em um espaço euclidiano tridimensional, indicado por OXYZ. É possível associar uma terna ordenada (x, y, z) de números reais a cada ponto P do espaço, correspondente às coordenadas dêêsse ponto. A união de todos esses pontos representa a superfícíe externa do objeto. Após converter o arquivo para um formato padrão das impressoras 3D, é possível realizar a impressão do objeto.

Página oitenta e um
Observe, a seguir, como podemos relacionar o estudo de sistemas lineares 3 × 3 com representações de figuras em um espaço euclidiano tridimensional OXYZ, importante para compreender o trabalho com a impressão 3D de objetos.
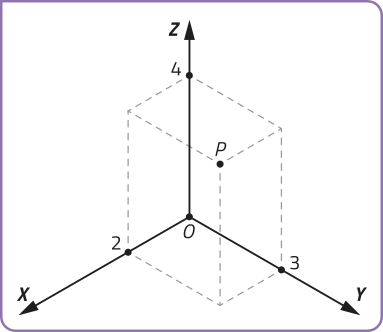
Um sistema OXYZ consiste em três eixos com a mesma origem OX, OY e OZ, perpendiculares entre si dois a dois. Observe o ponto P (2, 3, 4) representado no sistema OXYZ.
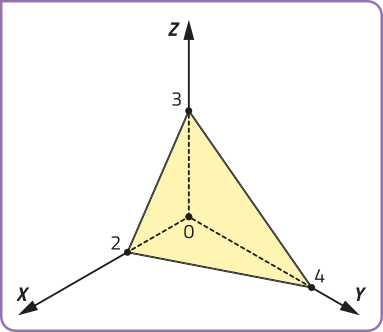
No sistema OXYZ, o conjunto das soluções de qualquer equação da forma ax + bai + cz = d, com a, b, c e d números reais, corresponde geometricamente a um plano.
pôdêmos estudar geometricamente a solução de um sistema linear 3 × 3 a partir da relação entre os planos correspondentes a cada equação dêêsse sistema. Analise as possibilidades:
A) Os planos são paralelos dois a dois.
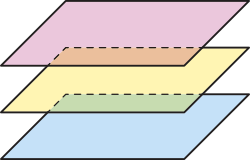
B) Dois planos são coincidentes e paralelos a outro plano.
C) Os três planos são coincidentes.

D) Dois planos são coincidentes e têm uma reta em comum com outro plano.
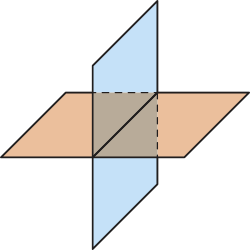
E) Os três planos são distintos e têm uma reta comum a eles.
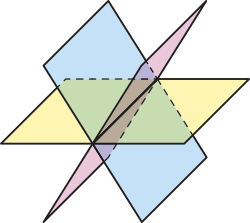
F) Dois planos são paralelos e cada um deles tem uma reta em comum com o terceiro plano, e essas retas são distintas.
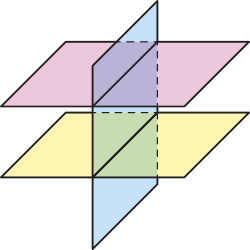
G) Os planos se intersectam dois a dois e não há um único ponto em comum aos três planos.
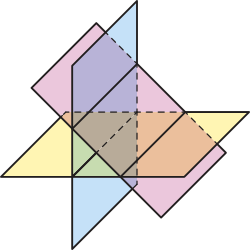
H) Os planos se intersectam dois a dois determinando três retas quê se intersectam em um único ponto comum aos três planos.
Fontes dos dados: LIMA, Elon Lages. Geometria analítica e álgebra linear. 1. ed. Rio de Janeiro: Impa, 2014. (Coleção matemática universitária, p. 164-167). FERREIRA, Maria Cristina C.; GOMES, Maria Laura M. Sobre o ensino de sistemas lineares. Revista do Professor de Matemática, [São Paulo], n. 32, [set./dez. 1996]. Disponível em: https://livro.pw/kndwa. Acesso em: 6 ago. 2024.
Página oitenta e dois
PENSANDO NO ASSUNTO
1. ![]() Você já observou um objeto sêndo produzido em uma impressora 3D? Comente.
Você já observou um objeto sêndo produzido em uma impressora 3D? Comente.
Resposta pessoal.
2. ![]() Junte-se a três côlégas para pesquisar mais informações sobre impressoras 3D. Cada grupo póde escolher um dos temas sugeridos a seguir.
Junte-se a três côlégas para pesquisar mais informações sobre impressoras 3D. Cada grupo póde escolher um dos temas sugeridos a seguir.
• Tipos de impressão.
• Matérias-primas para realizar uma impressão.
• Como funciona o processo de impressão.
• Custo de aquisição e manutenção de uma impressora.
• Impactos sócio-ambientais.
• Aplicações.
Após realizar a pesquisa, discutam e elaborem uma proposta de uso de impressoras 3D para benefício da ssossiedade, considerando a região em quê vocês moram, apresentando em quê área póde sêr utilizada (saúde, engenharia etc.), possíveis benefícios para a população e de quê maneira isso póde ocorrer, entre outros aspectos. Por fim, organizem as informações pesquisadas e a proposta elaborada pelo grupo e as apresentem para o restante da turma em um vídeo, podcast ou slides.
Pesquisa e elaboração dos estudantes.
3. Com suas palavras, explique como um ponto P póde sêr representado no sistema OXYZ a partir de suas coordenadas.
Resposta esperada: Com a primeira coordenada, identificamos a posição de P em relação ao eixo X; com a segunda coordenada, a posição de P em relação ao eixo Y; e, com a terceira coordenada, a posição de P em relação ao eixo Z.
4. Considere, no sistema OXYZ, o plano correspondente às soluções da equação 2x − 3y + z = 15. Quais pontos, cujas coordenadas estão indicadas a seguir, pertencem a esse plano?
A (5, 1, 8)
B (2, 2, 5)
C (−3, −2, 3)
D (2, −3, 2)
E (−1, −6, −1)
F (0, 4, 3)
A, D e E
5. ![]() Junte-se a um colega, leiam a situação a seguir e façam o quê se pede em cada um dos itens.
Junte-se a um colega, leiam a situação a seguir e façam o quê se pede em cada um dos itens.
Como é possível classificar um sistema linear 3 × 3 em SPD, SPI ou SI observando as representações geométricas de cada uma de suas equações no sistema OXYZ?
a) ob-sérvim o esquema da página 81 com todas as possibilidades de relações entre três planos no sistema OXYZ e indiquem em quais delas existe ao menos um ponto em comum aos três planos.
C, D, E e H
b) O quê podemos afirmar sobre as soluções dos sistemas lineares 3 × 3 correspondentes às possibilidades indicadas no item a?
Resposta esperada: Esses sistemas admitem, ao menos, uma solução.
c) Um sistema linear 3 × 3, classificado como SPD, tem quantos pontos em comum nos planos correspondentes às soluções de suas equações representadas no sistema OXYZ? Em qual das possibilidades indicadas no item a isso ocorre? Justifique.
Apenas um ponto em comum; possibilidade H.
d) Realizem o escalonamento do sistema linear a seguir. Depois, classifique esse sistema em SPD, SPI ou SI. Por fim, indiquem qual das possibilidades apresentadas representa a relação entre os planos correspondentes às soluções das equações dêêsse sistema.
; SPI; possibilidade C
e) Indiquem quais possibilidades apresentadas de relações entre três planos no sistema OXYZ representam soluções de um sistema 3 × 3 classificado como:
• SPD;
H
• SPI;
C, D e E
• SI.
A, B, F e G
Agora, escôlham uma das possibilidades apresentadas e elaborem um sistema linear 3 × 3 correspondente a ela. Em seguida, tróquem esse sistema com outra dupla para quê ela faça o escalonamento do sistema e identifiquem a relação entre os planos correspondentes, enquanto vocês fazem o mesmo com o sistema linear quê receberem. Ao final, confiram juntos as resoluções.
Elaboração dos estudantes.
Página oitenta e três
Transformações isométricas de figuras
Você sabe algo a respeito da isometria? Essa palavra dêríva do grego, em quê isos significa igual e metron significa medida. Em Matemática, as transformações isométricas consistem em estudar figuras geométricas congruentes, ou seja, de mesmo formato e medidas, distintas apenas por suas posições. Vamos estudar três tipos de transformação isométrica: simetria de translação, simetria de reflekção e simetria de rotação.
Simetria de translação
O uso de padrões geométricos póde sêr percebido em diferentes situações, como na ár-te e na arquitetura. Como exemplo, podemos observar o padrão geométrico presente no calçadão da praia de Copacabana, no município do Rio de Janeiro (RJ).
Para simular a composição dêêsse padrão geométrico, vamos destacar uma de suas partes, fazer reproduções e deslocá-las no plano.
Observe quê, nessa representação, o tamãnho e o formato da figura foram mantidos e os deslocamentos ocorreram de acôr-do com cérto comprimento, direção e sentido, indicados pelas setas. Assim, podemos dizêr quê essa transformação apresenta ideias de simetria de translação.
PARA PENSAR
No município em quê você mora, existe algum calçadão em área pública, no qual seja possível perceber padrões geométricos? Você sabe a origem histórica dêêsse calçadão? Explique como é estabelecido esse padrão geométrico e, se possível, faça o registro com fotografias.
Respostas pessoais.

Página oitenta e quatro
Na imagem anterior, cada seta representa um vetor. Dizemos quê um vetor consiste em um conjunto de segmentos de reta orientados quê têm mesmo comprimento, direção e sentido. Observe várias representações, no plano cartesiano, de um mesmo vetor .
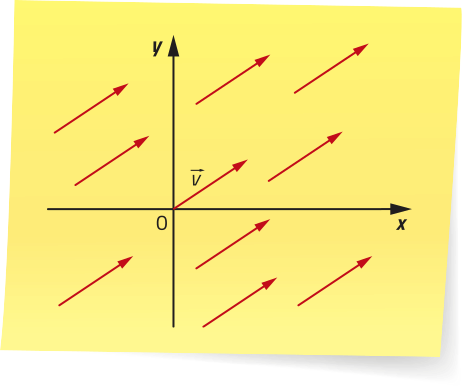
- Vetor
- : palavra quê dêríva do termo em latim vehere, quê significa “transportar”.
Um vetor quê tem origem em um ponto A e extremidade em um ponto B póde sêr indicado por .

Um vetor, cuja origem coincide com a origem do sistema de eixos cartesianos O (0, 0), também póde sêr indicado apenas pelas coordenadas do ponto correspondente à sua extremidade. Observe na figura, por exemplo, a representação do vetor = (2, 3).
Agora, com base nas ideias de vetor, podemos definir o quê é simetria de translação.
Sejam A um ponto e um vetor no plano. Uma transformação quê associa o ponto A a um ponto B, no mesmo plano, por meio de com determinado comprimento, direção e sentido, é denominada simetria de translação.
Para realizar a translação de uma figura por meio de , cada ponto dessa figura é transladado de maneira a obtêr outra figura, congruente à primeira.
Considere, por exemplo, o pentágono ABCDE e o vetor representados na malha quadriculada a seguir.
Página oitenta e cinco
Vamos construir a figura simétrica por translação do pentágono ABCDE em relação a com as seguintes etapas.
1ª
Para cada vértice do pentágono ABCDE, realizamos a translação de acôr-do com o comprimento (6 unidades), a direção (horizontal) e o sentido (da esquerda para direita), definidos por , e marcamos os cinco pontos obtidos.
2ª
Traçamos , , , e e colorimos a região interna da figura ôbitída. Assim, o pentágono A(minutos)"B(minutos)"C(minutos)"D(minutos)"E(minutos)" corresponde à figura simétrica por translação do pentágono ABCDE em relação ao vetor .
Também podemos transladar uma figura por meio de um vetor quê tem direção diferente da horizontal e da vertical. Observe, por exemplo, as etapas quê podem sêr realizadas para construir a figura simétrica por translação do quadrilátero ABCD em relação a .
Nesse caso, podemos associar aos vetores e , correspondentes aos deslocamentos representados por nas direções horizontal e vertical, respectivamente. Depois, realizamos a translação dos vértices do quadrilátero ABCD por meio de e, em seguida, realizamos a translação dos pontos obtidos por meio de . Por fim, representamos o quadrilátero A(segundos)"B(segundos)"C(segundos)"D(segundos)", quê corresponde à figura simétrica por translação do quadrilátero ABCD em relação a .
Página oitenta e seis
ATIVIDADES RESOLVIDAS
R11. Na figura a seguir, o quadrilátero EFGH foi obtído pela translação do quadrilátero ABCD em relação a . Quanto méde o comprimento dêêsse vetor?
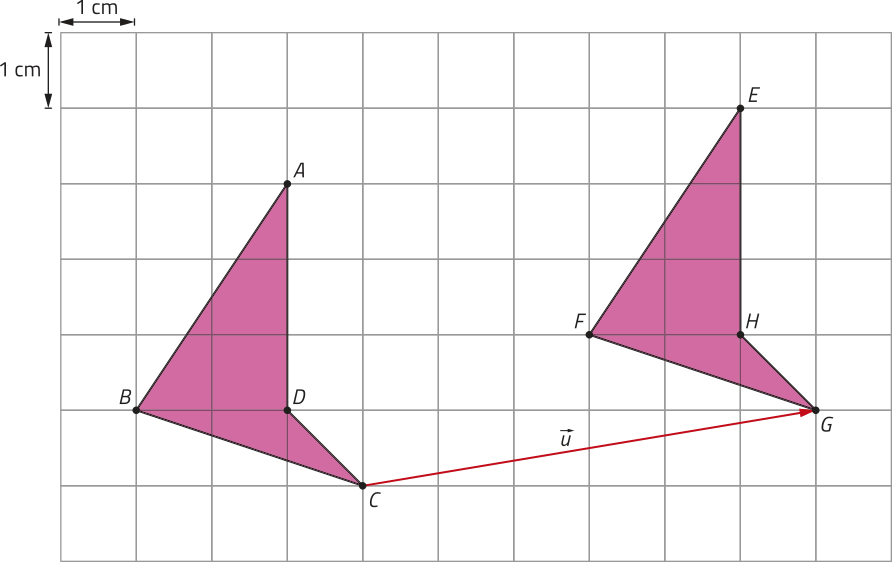
Resolução
O comprimento CG, correspondente a u, é dado pela medida da hipotenusa de um triângulo retângulo cujos catetos médem 1 cm e 6 cm. Aplicando o teorema de Pitágoras, temos:
(CG)2 = 12 + 62 = 1 + 36 = 37 ⇒
Portanto, tem comprimento igual a cm ou, aproximadamente, 6,08 cm.
R12. Determine as coordenadas dos vértices da figura simétrica ôbitída na translação do quadrilátero de vértices A(−1, 4), B(−1, 1), C(2, 2) e D(1, 5) em relação a = (4, 2).
Resolução
pôdêmos representar o quadrilátero ABCD e = (4, 2) em um plano cartesiano. Observe a figura.
O vetor indica quê cada ponto do quadrilátero ABCD deve sêr transladado em 4 unidades para a direita e em duas unidades para cima. Assim, ao transladar, por exemplo, o vértice A(−1, 4) por meio de , obtemos:
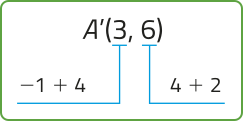
Ao transladar os vértices B, C e D por meio de , obtemos B(minutos)"(3, 3), C(minutos)"(6, 4) e D(minutos)"(5, 7), respectivamente.
Página oitenta e sete
Observe a representação do quadrilátero A(minutos)"B(minutos)"C(minutos)"D(minutos)" correspondente à figura simétrica por translação do quadrilátero ABCD em relação a = (4, 2).
R13. Represente, no plano cartesiano, a figura simétrica ôbitída na translação do triângulo de vértices E(4, −2), F(6, 1) e G(6, −3) em relação ao vetor com H(5, 3) e I(2, 5).
Resolução
Nesse caso, a origem do vetor não coincide com a origem do sistema de eixos cartesianos. Então, vamos obtêr um vetor de origem H(minutos)"(0, 0), com mesmo comprimento, direção e sentido do vetor .
Para determinar as coordenadas da extremidade do vetor , podemos subtrair de cada coordenada de I (extremidade do vetor ) a coordenada correspondente de H (origem do vetor ).
Por fim, vamos transladar cada ponto do triângulo EFG em 3 unidades para a esquerda e duas unidades para cima e representar o triângulo E(minutos)"F(minutos)"G(minutos)".
Portanto, as coordenadas dos vértices do triângulo E(minutos)"F(minutos)"G(minutos)", obtído da translação do triângulo EFG em relação ao vetor são E(minutos)"(1, 0), F(minutos)"(3, 3) e G(minutos)"(3, −1).
ATIVIDADES
48. Utilize uma malha quadriculada e reproduza o polígono e o vetor indicados em cada item. Depois, construa a figura simétrica por translação dêêsse polígono em relação a esse vetor.
Respostas nas Orientações para o professor.
a) 
b) 
Página oitenta e oito
49. Na figura a seguir, o hekzágono A(minutos)"B(minutos)"C(minutos)"D(minutos)"E(minutos)"F(minutos)" foi obtído pela translação do hekzágono ABCDEF em relação a Quanto méde o comprimento dêêsse vetor? Explique como você pensou.
2,5 cm. Resposta pessoal.
50. Nos itens a seguir, determine as coordenadas dos vértices da figura simétrica ôbitída na transformação isométrica indicada.
a) Translação do triângulo de vértices A(2, 5), B(4, 4) e C(2, 2) em relação a = (3, 1).
50. a) A(minutos)"(5, 6), B(minutos)"(7, 5) e C(minutos)"(5, 3)
b) Translação do retângulo de vértices E(6, 10), F(16, 10), G(16, 14) e H(6, 14) em relação ao vetor com J(12, 8) e K(0, 6).
E(minutos)"(−6, 8), F(minutos)"(4, 8), G(minutos)"(4, 12) e H(minutos)"(−6, 12)
51. No plano cartesiano, um pentágono A(minutos)"B(minutos)"C(minutos)"D(minutos)"E(minutos)" foi obtído, por simetria de translação, a partir de um pentágono ABCDE em relação a um vetor conforme representado a seguir.
a) Quais são as coordenadas da extremidade de , considerando sua origem em O (0, 0).
(−3, −1)
b) Quanto méde o comprimento de ?
u.c. ou aproximadamente 3,16 u.c.
52. Os grafismos produzidos por indígenas podem sêr encontrados em pinturas corporais, cerâmicas e artesanatos. Muitos deles se inspiram em elemêntos da natureza. Analise alguns exemplos.
I) 
AMOPAPAM significa escama do peixe tamatá.
II) 
KA’IAHOSA OU TATUPÉ significa denti de macaco ou casta de tatu.
III) 
MO’YRA significa semente.
Fonte dos dados: VIDAL, Lux (org.). Grafismo indígena: estudos de antropologia estética. 2. ed. São Paulo: Studio Nobél: Fapesp: Edusp, 2000. p. 123.
Em alguns dêêsses grafismos, é possível perceber a ideia de simetria de translação. No grafismo II, por exemplo, podemos considerar deslocamentos de linhas verticais compondo a figura.
a) Realize uma pesquisa sobre povos indígenas quê vivem na região mais perto de onde você mora, buscando informações sobre os grafismos realizados por eles, como seus significados, características e transformações isométricas quê podem sêr percebidas neles. Em seguida, reproduza um dêêsses grafismos e escrêeva um texto descrevendo suas características.
Pesquisa e elaboração do estudante.
b) Inspirado em algum elemento presente em seu dia a dia, elabore um grafismo e o represente em uma fô-lha avulsa. Nele, deve sêr possível identificar simetria de translação de figuras.
Elaboração do estudante.
Página oitenta e nove
53. A op art foi um movimento artístico quê teve seu auge na década de 1960 e quê privilegiou o trabalho com efeitos ópticos em superfícies planas. Geralmente, os artistas dêêsse movimento priorizavam representações abstratas e linhas retas. O lituano Kazys Varnelis (1917-2010) é um dos representantes da op art. Observe uma de suas obras.

Fonte dos dados: OP ART. In: ENCICLOPÉDIA Itaú Cultural de ár-te e Cultura Brasileira. São Paulo: Itaú Cultural, 23 fev. 2017. Disponível em: https://livro.pw/kzhtu. Acesso em: 6 ago. 2024.
Para reproduzir essa tela utilizando um programa de computador, um estudante construiu uma figura quadrada e obteve, por simetria de translação, outras 15 figuras congruentes a ela.
a) Desenhe, no caderno, a possível figura quadrada quê o estudante construiu.
Resposta nas Orientações para o professor.
b) Sabendo quê a figura quadrada construída pelo estudante tinha 5 cm de lado, qual foi a área total da reprodução da tela produzida por ele?
400 cm2
c) ![]() Junte-se a um colega e, em um software de geometria dinâmica como o GeoGebra, façam uma reprodução da tela apresentada utilizando simetria de translação.
Junte-se a um colega e, em um software de geometria dinâmica como o GeoGebra, façam uma reprodução da tela apresentada utilizando simetria de translação.
Elaboração dos estudantes.
54. Um padrão geométrico presente em algumas calçadas de São Paulo (SP) tornou-se um sín-bolo turístico do município. Esse padrão, também conhecido como piso paulista, foi criado em 1966 por Mirthes dos Santos Pinto. Na época, o desenho foi escolhido por meio de um concurso realizado pela prefeitura de São Paulo.
Fonte dos dados: MUSEU DE ár-te DA UNIVERSIDADE FEDERAL DO CEARÁ. Mirthes Bernardes. Fortaleza: Mauc, [201-]. Disponível em: https://livro.pw/zzxmn. Acesso em: 6 ago. 2024.

Para reproduzir o padrão do piso paulista, desenhou-se a figura I no plano cartesiano e, a partir dela, por simetria de translação, obteve-se a figura II representada a seguir. Quanto méde o comprimento do vetor utilizado para obtêr a figura II a partir da figura I por simetria de translação?
m ou aproximadamente 3,6 m
Página noventa
Simetria de reflekção
Observe, a seguir, uma das obras do artista plástico brasileiro Rubem Valentim (1922-1991).

PARA PENSAR
dêz-creva características sobre os elemêntos quê compõem essa obra, como os formatos e a distribuição das figuras.
Resposta pessoal.
Nessa obra, é possível notar características relacionadas à ideia de simetria de reflekção. Por exemplo, ao imaginar uma reta vertical dividindo a obra ao meio, vamos obtêr duas partes com figuras idênticas por sobreposição. Observe duas dessas figuras representadas, quê são simétricas por reflekção em relação à reta e.
Sejam e uma reta e A um ponto em um mesmo plano. Uma transformação isométrica quê associa o ponto A a um ponto B, no mesmo plano, é denominada simetria de reflekção em relação à reta e, quando esta reta é mediatriz do segmento de reta . A reta e é denominada eixo de simetria.
Para realizar a reflekção de uma figura em relação a uma reta e, cada ponto dessa figura é refletido, em relação a e, de maneira a obtêr outra figura, congruente à primeira.

PARA PENSAR
Sendo A e B pontos simétricos por reflekção em relação a uma reta e, todos em um mesmo plano, o quê podemos afirmar sobre as distâncias de A a e e de B a e? Justifique sua resposta.
Resposta esperada: As distâncias são iguais, pois e é a mediatriz do segmento de reta .
Página noventa e um
Na imagem apresentada anteriormente, podemos indicar os pontos A e A(minutos)" simétricos em relação ao eixo e. Ao traçar o segmento de reta , obissérve quê o eixo e corresponde à mediatriz dêêsse segmento de reta.
Agora, vamos construir, utilizando régua e compasso, o triângulo A(minutos)"B(minutos)"C(minutos)" simétrico ao triângulo ABC por reflekção em relação ao eixo e, conforme representado nas etapas a seguir.

1ª Posicionamos a ponta-seca do compasso em A e traçamos um arco de circunferência de maneira a intersectar o eixo e nos pontos P e Q.
2ª Posicionamos a ponta-seca do compasso em P e, com abertura PC, traçamos um arco de circunferência. Em seguida, posicionamos a ponta-seca do compasso em Q e, com abertura QC, traçamos outro arco de circunferência de maneira a obtêr o ponto C(minutos)" na interseção dos dois arcos.
3ª Procedemos de maneira análoga à etapa anterior para obtêr os pontos A(minutos)" e B(minutos)".
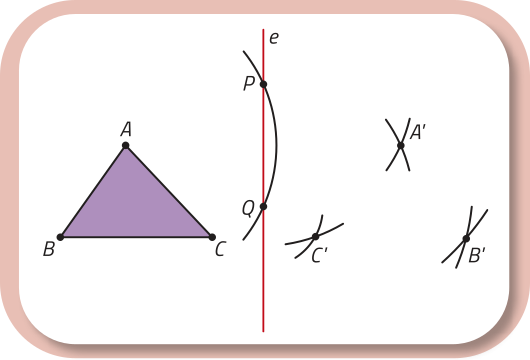
Página noventa e dois
4ª Por fim, traçamos , e e colorimos a região interna da figura, obtendo o triângulo A(minutos)"B(minutos)"C(minutos)" simétrico ao triângulo ABC por reflekção em relação ao eixo e.
PARA PENSAR
Com um colega, justifiquem todas as etapas da construção do triângulo A’B’C’, simétrico ao triângulo ABC por reflekção em relação ao eixo e.
Resposta pessoal.
ATIVIDADE RESOLVIDA
R14. Dado o quadrilátero ABCD, de vértices A(3, 2), B(4, 3), C(3, 5) e D(2, 3), represente, em um plano cartesiano, um polígono obtído a partir dêêsse quadrilátero após sêr realizada a seguinte sequência de transformações:
1ª) Reflexão em relação ao eixo x;
2ª) Reflexão em relação ao eixo y;
3ª) Translação determinada por = (0, 5).
Resolução
Vamos realizar as transformações indicadas para o vértice A. Na 1ª transformação, obtemos o ponto A'(3, −2); na 2ª transformação, obtemos o ponto A''(−3, −2); na 3ª transformação, o ponto A'''(−3, 3).
Analogamente, obtemos os vértices B(minutos)"(minutos)"(minutos)"(−4, 2), C(minutos)"(minutos)"(minutos)"(−3, 0) e D(minutos)"(minutos)"(minutos)"(−2, 2). Traçamos , , e e colorimos a região interna da figura para obtêr o polígono A(minutos)"(minutos)"(minutos)"B(minutos)"(minutos)"(minutos)"C(minutos)"(minutos)"(minutos)"D(minutos)"(minutos)"(minutos)", congruente ao quadrilátero ABCD.
ATIVIDADES
55. Reproduza o polígono ABCDEF e o eixo de simetria representados.
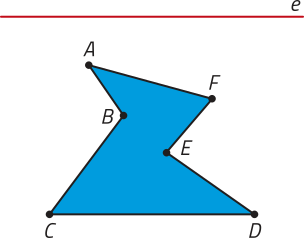
Utilizando régua e compasso, construa o polígono A(minutos)"B(minutos)"C(minutos)"D(minutos)"E(minutos)"F(minutos)", simétrico ao polígono ABCDEF por reflekção em relação ao eixo e.
Resposta nas Orientações para o professor.
Página noventa e três
56. Observe as fotografias de elemêntos da natureza. As imagens não estão em proporção.
I) 
Borboleta azul.
II) 
Flor da espécie Datura stramonium.
III) 
Pato em lago.
IV) 
Árvore seca.
V) 
Estrela-do-mar.
a) Em quais das fotografias o elemento em destaque apresenta a ideia de simetria de reflekção?
Resposta esperada: Fotografias I, III e V.
b) Explique como póde sêr traçado um eixo de simetria nos elemêntos em destaque nas fotografias quê você indicou no item a.
Resposta esperada: Fotografia I: póde sêr traçado um eixo vertical entre as asas da borboleta; fotografia III: póde sêr traçado um eixo horizontal sobre a linha de contato do pato com á gua; fotografia V: podem sêr traçados 5 eixos de simetria, cada eixo passando por um braço e pelo centro da estrela-do-mar.
c) Observe elemêntos da natureza quê estão presentes no seu cotidiano e fotografe alguns deles em quê seja possível perceber a ideia de simetria de reflekção. Com as orientações do professor, apresente suas fotografias para a turma.
Resposta pessoal.
57. Considere um trapézio de vértices A(1, 1), B(3, 3), C(5, 2) e D(2, −1). Quais devem sêr as coordenadas dos vértices do trapézio A(minutos)"B(minutos)"C(minutos)"D(minutos)" para quê ele seja simétrico ao trapézio ABCD por reflekção em relação a um eixo de simetria paralelo ao eixo das ordenadas, e quê tenha um dos vértices com coordenadas (−5, 3).
A(minutos)"(−3, 1), B(minutos)"(−5, 3), C(minutos)"(−7, 2) e D(minutos)"(−4, −1)
58. Na busca por uma harmonía estética ou expressão de um padrão rítmico, alguns escritores utilizam diferentes recursos em suas obras, como a ideia de simetria. Analise um poema do curitibano Paulo Leminski (1944-1989) com essa característica.

a) Explique como a simetria de reflekção se relaciona a esse poema.
Resposta esperada: Nesse poema, é possível observar algumas lêtras refletidas, remetendo a um dos sentidos do poema, o reflexo da Lua na á gua.
b) Quais lêtras dêêsse poema são refletidas em relação a eixos horizontais imaginários?
as lêtras L, U, A, N e G
c) Considerando as lêtras dêêsse poema, em quais delas é possível traçar um eixo de simetria?
nas lêtras A, M e U
d) escrêeva um pequeno texto no qual seja possível identificar a ideia de simetria de reflekção.
Resposta pessoal.
Página noventa e quatro
59. Geraldo de Barros (1923-1998) costumava utilizar diversas técnicas experimentais em suas obras de; ár-te. Ele é um dos pioneiros da fotografia abstrata e do Modernismo no Brasil, além de sêr considerado um dos mais importantes artistas do movimento concretista no país. Analise uma de suas obras.
Fonte dos dados: GERALDO de Barros. In: ENCICLOPÉDIA Itaú Cultural de ár-te e Cultura Brasileira. São Paulo: Itaú Cultural, 3 maio 2024. Disponível em: https://livro.pw/isncy. Acesso em: 10 set. 2024.

a) Utilizando um programa de computador, como o GeoGebra, faça uma reprodução dêêsse qüadro em escala menor. Explique a um colega os procedimentos quê você realizou.
Resposta pessoal.
b) ![]() Explique como você faria para traçar um eixo de simetria sobre uma reprodução dêêsse qüadro.
Explique como você faria para traçar um eixo de simetria sobre uma reprodução dêêsse qüadro.
Resposta esperada: Traçar o eixo de simetria de maneira quê passe pêlos pontos médios dos lados paralelos verticais da tela.
c) Considere as dimensões originais dessa obra e imagine quê será traçado um eixo de simetria sobre ela. Qual seria a medida do comprimento do segmento de reta obtído na interseção dêêsse eixo com a superfícíe da obra?
90 cm ou 0,9 m
d) Pesquise outra tela com características do movimento concretista no Brasil e quê seja possível identificar simetria de reflekção. Depois, componha um texto sobre essa tela, indicando algumas informações, como autor, título, técnica, dimensões etc. Não se esqueça de indicar as fontes de pesquisa.
Resposta pessoal.
60. Leia as informações a seguir.
O gráfico de uma função f: ℝ → ℝ é simétrico em relação ao eixo das ordenadas quando essa função é par, ou seja, quando f (x) = f (−x) para todo x ∈ ℝ.
Utilizando o GeoGebra, construa o gráfico das funções indicadas a seguir e identifique quais delas são funções pares. Justifique sua resposta.
Respostas nas Orientações para o professor.
a) f(x) = x2
b) g(x) = 2x
c) m(x) = |x | + 1
d) n(x) = x2 − x
• Agora, mostre por quê o gráfico das funções quê você não indicou não é simétrico em relação ao eixo das ordenadas. Sugestão: utilize contraexemplos.
61. Determine as coordenadas do vértice C do triângulo equilátero ABC, sabendo quê A (−6, 4) e B (6, 4) são dois vértices dele.
C(0, 4 + ) ou C (0, 4 − )
62. ![]() Uma maneira de determinar as coordenadas do ponto simétrico P(minutos)"(x(minutos)", y(minutos)") a um ponto P(x, y), em relação ao eixo das ordenadas, é resolvendo a equação matricial: ⋅ = .
Uma maneira de determinar as coordenadas do ponto simétrico P(minutos)"(x(minutos)", y(minutos)") a um ponto P(x, y), em relação ao eixo das ordenadas, é resolvendo a equação matricial: ⋅ = .
Com base nessa informação, junte-se a um colega, e resolvam os itens.
a) Determinem as coordenadas dos pontos simétricos, em relação ao eixo das ordenadas, aos pontos A(−10, 3), B(7, 0), C(−2, −5) e D(4, ).
A(minutos)"(10, 3), B(minutos)"(−7, 0), C(minutos)"(2, −5) e D(minutos)" (−4, )
b) Deduzam uma equação matricial com a qual seja possível determinar as coordenadas do ponto simétrico Q(minutos)"(x(minutos)", y(minutos)"), a um ponto Q(x, y), em relação ao eixo das abscissas.
⋅ =
c) Agora, escrevam as coordenadas de quatro pontos quaisquer. Depois, utilizem a equação matricial quê vocês deduziram no item b e determinem as coordenadas dos pontos simétricos a eles em relação ao eixo das abscissas.
Resposta pessoal.
Página noventa e cinco
Simetria de rotação
O holan-dêss Maurits Cornelis é-chêr (1898-1972) foi um artista quê utilizou diferentes ideias matemáticas em suas obras, criando padrões e efeitos visuais, conforme pode-se notar nesta obra.


Essa obra apresenta características relacionadas à ideia de simetria de rotação. Observe, por exemplo, duas figuras presentes nela quê são simétricas por rotação em torno do ponto O.
PARA PENSAR
pôdêmos dizêr quê essas duas figuras também são simétricas por reflekção? Explique.
Resposta esperada: Sim, pois é possível traçar um eixo de simetria, passando por O, de maneira quê essas duas figuras sêjam simétricas por reflekção em relação a esse eixo.
Sejam O e A pontos em um mesmo plano e um ângulo de medida (alfa)". Uma transformação isométrica quê associa o ponto A a um ponto B, no mesmo plano, é denominada simetria de rotação de medida de ângulo (alfa)", em relação ao ponto O, quando AO = BO e med (AB) = (alfa)". O ponto O é denominado centro de rotação e o ângulo (alfa)", ângulo de rotação. De modo geral, é também estabelecido o sentido da rotação: horário ou anti-horário.
Para realizar a rotação de uma figura em torno de um ponto O, de acôr-do com cérto ângulo de rotação e sentido estabelecidos, cada ponto dessa figura é rotacionado de maneira a obtêr outra figura, congruente à primeira.
Página noventa e seis
pôdêmos indicar, na imagem apresentada na página 95, os pontos A e A(minutos)", simétricos por rotação em 120°, no sentido anti-horário, em torno do ponto O.
Agora, utilizando régua, transferidor e compasso, vamos construir o triângulo A(minutos)"B(minutos)"C(minutos)", por meio de rotação do triângulo ABC em torno do ponto O, representados na figura, em 70° no sentido horário.
1. Com a régua, traçamos o segmento de reta Em seguida, com o transferidor, medimos um ângulo de 70° no sentido horário, de maneira quê O seja o vértice dêêsse ângulo e a semirreta seja um de seus lados. Em seguida, fazemos uma marcação.
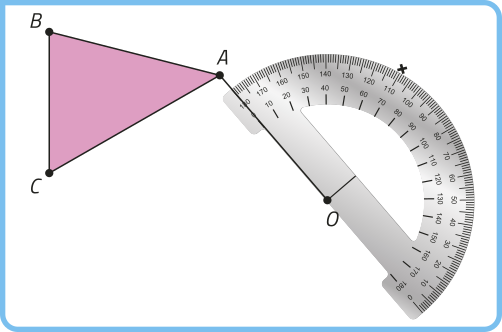
2. Com a régua, traçamos uma semirreta com origem em O quê intersecta a marcação indicada anteriormente. Posicionamos a ponta-seca do compasso em O e, com abertura OA, marcamos o ponto A‘ nessa semirreta traçada.
3. Analogamente, obtemos os pontos B(minutos)" e C(minutos)". Por fim, traçamos e colorimos a região interna da figura, obtendo o triângulo
PARA PENSAR
Com um colega, justifiquem todas as etapas da construção do triângulo A’B’C’, simétrico ao triângulo ABC por rotação em torno do ponto O, em 70° no sentido horário.
Resposta pessoal.
Página noventa e sete
ATIVIDADE RESOLVIDA
R15. Um ponto P (x, y) do plano cartesiano póde sêr representado pela matriz coluna . A rotação do ponto P em torno da origem do plano cartesiano corresponde a um ponto P’(x’, y’) quê póde sêr obtído pela equação matricial a seguir, em quê (alfa)" corresponde ao ângulo de rotação, no sentido anti-horário.
= ⋅
Determine as coordenadas de um ponto P’ obtído pela rotação de 30°, no sentido anti-horário, do ponto P(1, ), em torno da origem.
Resolução
Para resolver esta atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Pelo enunciado, sabemos quê:
• P’ é obtído a partir de P por simetria de rotação de 30°, em torno da origem de um sistema de eixos cartesianos, no sentido anti-horário;
• as coordenadas de P’ podem sêr obtidas por meio da equação matricial apresentada, com (alfa)" = 30°, x = 1 e y = .
2ª ELABORAR UM PLANO
Vamos determinar as coordenadas do ponto P’, substituindo (alfa)" = 30°, x = 1 e y = na equação matricial apresentada e resolvê-la.
3ª EXECUTAR O PLANO
Para (alfa)" = 30°, x = 1 e y = , temos:
Portanto, x’ = 0 e y’ = 2, ou seja, P’(0, 2).
4ª VERIFICAR OS RESULTADOS
Para verificar o resultado obtído, vamos representar, no plano cartesiano, os pontos O(0, 0), P(1, ), P(minutos)"(0, 2) e o ângulo PP' cuja medida pretendemos mostrar quê é 30°. Também vamos indicar os pontos auxiliares Q(1, 0) e R (0, ) correspondentes às projeções de P sobre o eixos x e y, respectivamente, e o ângulo PQ de medida (beta)".
No triângulo retângulo OPQ, temos:
tg (beta)" = = =
Como 0° < (beta)" < 90° e tg (beta)" = , então (beta)" = 60°. Assim:
(alfa)" + (beta)" = 90° → (alfa)" + 60° = 90° ⇒ (alfa)" = 30°
Portanto, P(minutos)"(0, 2).
Página noventa e oito
ATIVIDADES
63. Desenhe a representação de um trapézio ABCD qualquer e um ponto O externo a ele. Em seguida, construa o trapézio A(minutos)"B(minutos)"C(minutos)"D (minutos)", simétrico ao trapézio ABCD por rotação, em torno do ponto O, em:
a) 90° no sentido anti-horário;
Resposta pessoal.
b) 135° no sentido horário.
Resposta pessoal.
64. Uma simetria de rotação, em quê o ângulo de rotação é de 180°, é denominada simetria central. Determine em qual das alternativas a seguir a figura II póde sêr ôbitída por simetria central da figura I em torno do ponto O.
a) 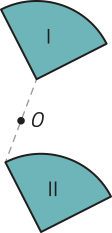
b) ![]()
c) 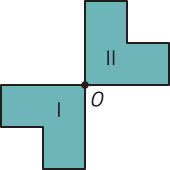
alternativa c
65. Na natureza, podemos observar simetria em diferentes situações. Os favos construídos por abelhas de certa espécie, por exemplo, são compostos de alvéolos quê correspondem a cavidades cujo formato lembra hekzágonos regulares.
Cada hekzágono do modelo matemático apresentado póde sêr obtído a partir de outro, utilizando simetria de translação, de reflekção ou de rotação. dêz-creva como é possível realizar cada uma dessas transformações isométricas para obtêr a representação de um hekzágono a partir de outro. Para isso, indique alguns elemêntos, como o segmento de reta considerado, o sentido e a medida do ângulo de rotação e o vetor utilizado.
Resposta pessoal.
66. Considere um triângulo de vértices A(−6, 2), B(−4, 0) e C(0, 4) e um triângulo A(minutos)"B(minutos)"C(minutos)", simétrico ao triângulo ABC por rotação em torno do ponto O(0, 0), de acôr-do com um ângulo de medida (alfa)", no sentido anti-horário.
a) escrêeva uma equação matricial para determinar as coordenadas de cada vértice do triângulo A(minutos)"B(minutos)"C(minutos)".
Resposta nas Orientações para o professor.
b) Utilizando a equação quê você escreveu no item a, determine quais são as coordenadas dos vértices do triângulo A(minutos)"B(minutos)"C(minutos)" quando (alfa)" = 120°.
A(minutos)"(3 − , − 1), B(minutos)"(2, ), C(minutos)"(, −2)
67. Considere o recorte do fractal árvore pitagórica representado no plano cartesiano a seguir e resôuva as kestões.
a) Quais pares de polígonos quê compõem esse recorte são simétricos por reflekção em relação ao eixo y?
quadrados DEFG e CEIH; quadrados FNOJ e IQPK; quadrados LMGJ e SRHK; triângulos FJG e IKH
b) A partir de quais polígonos é possível obtêr o quadrado FNOJ por translação de acôr-do com um vetor ? Determine o comprimento de em cada caso.
quadrado KPQI: com 3 u.c.; quadrado RSKH: com u.c.; quadrado GJLM: com u.c.
c) Um dos triângulos representados póde sêr obtído ao rotacionar outro triângulo. Quais devem sêr a medida do ângulo e as coordenadas do ponto correspondente ao centro de rotação para realizar essa transformação isométrica no sentido horário?
Respostas nas Orientações para o professor.
Página noventa e nove
d) Como é possível identificar a ideia de ampliação ou redução de figuras geométricas planas nesse recorte de fractal? Como esse tipo de transformação geométrica é chamado?
Respostas esperadas: A cada etapa (iteração) realizada, os triângulos ou os quadrados obtídos correspondem a uma redução do último triângulo ou quadrado obtido em uma etapa anterior. Transformação homotética.
e) ![]() Com dois côlégas, pesquisem informações sobre a árvore pitagórica, como a sua origem, quais são as etapas para sua construção, entre outras. Em seguida, em uma fô-lha avulsa ou com auxílio de um software de geometria dinâmica, realizem as etapas iniciais e representem parte dêêsse fractal. Por fim, investiguem outros fractais, escôlham um deles e descrevam possíveis relações com transformações isométricas.
Com dois côlégas, pesquisem informações sobre a árvore pitagórica, como a sua origem, quais são as etapas para sua construção, entre outras. Em seguida, em uma fô-lha avulsa ou com auxílio de um software de geometria dinâmica, realizem as etapas iniciais e representem parte dêêsse fractal. Por fim, investiguem outros fractais, escôlham um deles e descrevam possíveis relações com transformações isométricas.
Pesquisa dos estudantes.
68. ![]() Com um colega, utilizem uma malha quadriculada ou um programa de computador para elaborar um mosaico, inspirados na composição de figuras da atividade anterior, no qual possam sêr identificadas diferentes transformações isométricas. Depois, troque-o com outra dupla para quê ela dêz-creva as simetrias quê podem sêr observadas no mosaico de vocês, enquanto vocês fazem o mesmo com o mosaico quê receberem. Por fim, confiram juntos as resoluções.
Com um colega, utilizem uma malha quadriculada ou um programa de computador para elaborar um mosaico, inspirados na composição de figuras da atividade anterior, no qual possam sêr identificadas diferentes transformações isométricas. Depois, troque-o com outra dupla para quê ela dêz-creva as simetrias quê podem sêr observadas no mosaico de vocês, enquanto vocês fazem o mesmo com o mosaico quê receberem. Por fim, confiram juntos as resoluções.
Elaboração dos estudantes.
69. Você já observou alguma edificação cuja fachada é revestida de azulejos? Os azulejos dêsempênham um papel relevante na arquitetura brasileira, refletindo a herança cultural do país. Sua introdução remonta ao período colonial, quando os portugueses trousserão essa tradição artística de revestir pisos e paredes com peças de cerâmicas. No Brasil, os azulejos passaram a adornar igrejas, palácios e casas, muitas vezes retratando cenas religiosas, paisagens, elemêntos da vida cotidiana ou composições geométricas.

Observe alguns azulejos representados no plano cartesiano a seguir e dêz-creva uma sequência de transformações quê podem sêr realizadas para obtêr uma das figuras amareladas a partir da outra de mesma côr.
Uma resposta possível: Rotacionar a figura amarelada com um dos lados sobre o eixo x em 90° em torno do ponto de coordenadas (4, 2) no sentido anti-horário; transladar a figura ôbitída em relação a = (−4, 0) e, em seguida, em relação a = (0, 2).
NO MUNDO DO TRABALHO
Arquiteto
Além de ideias envolvendo transformações isométricas, o trabalho de um arquiteto aborda conhecimentos relacionados a; ár-te, história, tecnologias, sistemas estruturais etc.
Um arquiteto póde atuar em projetos de grandes áreas urbanas, residenciais ou no disáini de objetos. Esse profissional tem como objetivo planejar e projetar espaços considerando aspectos funcionais, estéticos, estruturais, de segurança e de conforto, de acôr-do com a necessidade do cliente.
Assista ao vídeo indicado a seguir para obtêr mais informações sobre a profissão do arquiteto.
• SE LIGA na profissão: arquiteto 18-02-2021. [S. l.: s. n.], 2021. 1 vídeo (10 min). Publicado pelo canal Tevê Câmara Campinas. Disponível em: https://livro.pw/rsvzu. Acesso em: 6. ago. 2024.
Página cem
Transformações homotéticas de figuras
Como você imagina quê eram feitas as alterações na escala de um mapa antes do desenvolvimento da computação gráfica? Um instrumento muito utilizado nesse processo era o pantógrafo, quê permitia contornar o mapa original e obtêr outro mapa em escala diferente, determinando uma ampliação ou redução.
Ampliar ou reduzir uma figura envolve a ideia de transformação homotética ou homotetia, quê consiste na transformação de qualquer figura em outra semelhante a ela.
- Homotetia
- : a palavra dêríva do termo grego homós, quê significa “semelhante”, e thet, quê significa “posto” ou “colocado”.
Sejam O e P pontos em um mesmo plano e k uma constante real positiva. Uma transformação quê associa P a um ponto P (minutos)", nesse mesmo plano, de modo quê P(minutos)" pertença à semirreta e quê OP(minutos)" = k ⋅ OP é denominada homotetia de centro O e razão k do ponto P.

OP(minutos)" = k ⋅ OP
Para realizar a homotetia de centro O e razão k de uma figura, cada um de seus pontos devem sêr transformados de maneira a obtêr outra figura, semelhante à primeira. Nesse caso, k é a razão de semelhança entre a figura ôbitída e a figura original.
O triângulo A(minutos)"B(minutos)"C (minutos)" é uma transformação do triângulo ABC por homotetia com centro em O e razão = = = k.
Acompanhe as etapas quê podemos realizar para obtêr um triângulo A(minutos)"B(minutos)"C(minutos)" correspondente a uma ampliação do triângulo ABC, representado na figura por homotetia de centro O e razão k = 2, utilizando régua e compasso.

1ª Com a régua, traçamos as semirretas , e Como k = 2, então OA(minutos)" = 2OA. Assim, com a ponta-seca do compasso em A e abertura OA, marcamos o ponto A(minutos)" sobre a semirreta De maneira análoga, marcamos os pontos B(minutos)" e C(minutos)".
Página cento e um
2ª Por fim, traçamos , e e colorimos a região interna da figura, obtendo o triângulo A(minutos)"B(minutos)"C(minutos)". Os triângulos A(minutos)"B(minutos)"C (minutos)" e ABC são semelhantes com razão de semelhança igual a 2.

PARA PENSAR
Com a régua, meça cada lado dêêsses triângulos. Que regularidade você observa ao comparar as medidas dos pares de lados correspondentes?
Resposta esperada: Cada lado do triângulo A(minutos)"B(minutos)"C(minutos)" tem o dôbro da medida do lado correspondente no triângulo ABC, pois a razão de semelhança entre os triângulos A(minutos)"B(minutos)"C(minutos)" e ABC é 2.
Agora, acompanhe como podemos obtêr um quadrilátero A(minutos)"B(minutos)"C(minutos)"D(minutos)" correspondente a uma redução do quadrilátero ABCD, representado a seguir, por homotetia na razão de 2 para 1, utilizando régua e compasso.
Inicialmente, marcamos um ponto O, externo ao quadrilátero, correspondente ao centro da homotetia a sêr realizada. Depois, traçamos as semirretas , , e . Como o quadrilátero ABCD deve sêr reduzido na razão de 2 para 1, então OA(minutos)" = . Assim, utilizando o compasso, marcamos A(minutos)", correspondente ao ponto médio do segmento de reta De maneira análoga, marcamos os pontos B(minutos)", C(minutos)" e D(minutos)". Por fim, traçamos , , e e colorimos a região interna da figura ôbitída. Nesse caso, os quadriláteros A(minutos)"B(minutos)"C(minutos)"D(minutos)" e ABCD são semelhantes com razão de semelhança igual a .
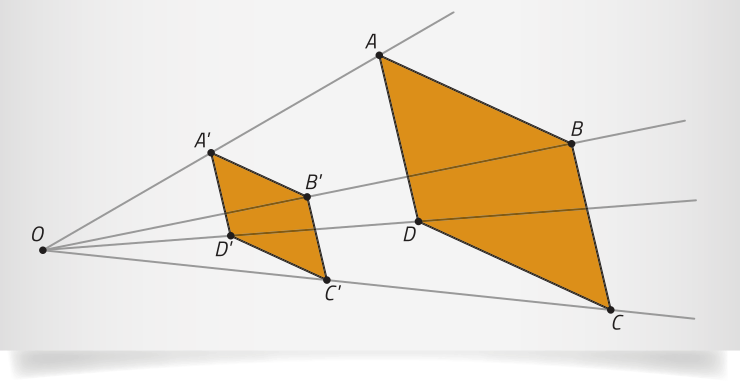
Página cento e dois
ATIVIDADE RESOLVIDA
R16. Em certa praça pública há um jardim com formato trapezôidáu, conforme representado. Deseja-se ampliar esse jardim, mantendo seu formato, de maneira quê a nova área corresponda ao quádruplo da área original. Explique como essa ampliação póde sêr realizada.
Resolução
Área do jardim original: AI = = = 54; ou seja, 54 m2.
O jardim ampliado deve ter o mesmo formato do jardim original; portanto, as figuras quê representam esses jardins devem sêr trapézios semelhantes com razão de semelhança k. Assim, a área do jardim ampliado é dada por:
AII = = 4 ⋅ 54 ⇒ = 216 ⇒ 108 k2 = 432 ⇒ k2 = ⇒ k2 = 4 ⇒
Logo, k = 2, ou seja, a razão de semelhança entre a figura quê representa o jardim ampliado e a quê representa o jardim original é 2. Assim, o trapézio A(minutos)"B(minutos)"C(minutos)"D quê representa o jardim após a ampliação póde sêr obtído por homotetia do trapézio ABCD com centro no ponto D e razão 2, conforme representado na figura.
ATIVIDADES
70. Na imagem a seguir, os pentágonos regulares II e III foram construídos por meio de transformações homotéticas de centro O a partir do pentágono regular I, quê tem 5 cm de lado.
a) Qual é a razão de semelhança entre os pentágonos II e I? E entre os pentágonos III e I? E entre os pentágonos III e II?
2; ;
b) Determine o perímetro de cada pentágono.
pentágono I: 25 cm; pentágono II: 50 cm; pentágono III: 12,5 cm
71. ![]() Junte-se a um colega e, com o auxílio de régua e compasso, façam o quê se pede a seguir.
Junte-se a um colega e, com o auxílio de régua e compasso, façam o quê se pede a seguir.
1º) Em uma malha quadriculada, construam um sistema de eixos cartesianos e indiquem a origem O (0, 0).
2º) Márkin um ponto P qualquer nesse plano cartesiano.
3º) Representem, no plano cartesiano, um quadrilátero ABCD qualquer.
4º) Por meio de uma transformação homotética em relação ao quadrilátero ABCD e com centro em P, definam uma razão k e construam um quadrilátero A(minutos)"B(minutos)"C(minutos)"D(minutos)".
Agora, tróquem a construção de vocês com outra dupla, para quê ela faça as medições necessárias e determine a razão k da homotetia realizada, enquanto vocês fazem o mesmo com a construção recebida. Por fim, confiram juntos as resoluções.
Construção do estudante.
Página cento e três
72. O cóódigo Florestal (lei número 12.651, de 25 de maio de 2012), disponível em: https://livro.pw/dyqzv; acesso em: 5 ago. 2024) define a porcentagem de área quê deve sêr destinada à reserva florestal nas propriedades rurais de cada região brasileira. Em determinado sítio, de 6 alqueires paulistas de área, há uma reserva florestal com formato de círculo, conforme representado na figura.
O proprietário do sítio deseja ampliar essa reserva florestal, mantendo seu formato, de maneira quê sua área corresponda ao quíntuplo da área original.
a) Qual será a medida do raio da nova região correspondente à reserva florestal? Utilize (pi)" = 3.
aproximadamente 109,6 m
b) Considerando quê 1 alqueire paulista equivale a 24.200 m2, qual é a porcentagem da área total do sítio destinada para a reserva florestal antes da ampliação? E após a ampliação?
aproximadamente 4,96%; aproximadamente 24,8%
73. A perspectiva cônica com um ponto de fuga é uma das técnicas utilizadas para a representação em perspectiva. Observe algumas etapas quê podem sêr realizadas para representar um bloco retangular usando a perspectiva cônica com um ponto de fuga.
1ª) Traçar uma reta r, marcar um ponto de fuga P nessa reta e construir um retângulo ABCD, com os lados e paralelos à r. Depois, traçar , , e e uma reta s paralela ao segmento de reta , determinando os pontos E e F sobre e , respectivamente.
2ª) Traçar uma reta t, paralela ao segmento de reta e passando por E, e marcar o ponto H, interseção de t com o segmento de reta . Depois, traçar uma reta u, paralela ao segmento de reta e passando por F, e marcar o ponto G, interseção de u com o segmento de reta .
3ª) Traçar os segmentos de reta correspondentes às arestas do bloco retangular e colorir as faces obtidas.
a) Nessa construção, o retângulo EFGH foi obtído por uma transformação homotética do retângulo ABCD, com centro no ponto P. Como é possível determinar a razão dessa homotetia? Essa transformação corresponde a uma ampliação ou a uma redução do retângulo ABCD?
Resposta esperada: Pode-se determinar, por exemplo, as medidas AP e EP e calcular a razão de homotetia k = .Redução.
b) Considerando AP = 5 cm e EP = 2 cm, qual é a razão de semelhança entre os retângulos EFGH e ABCD?
0,4 ou
c) Utilizando a ideia de perspectiva cônica com um ponto de fuga, construa, em uma fô-lha avulsa, a representação de um prisma qualquer.
Resposta pessoal.
74. ![]() Elabore uma situação-problema quê envolva transformações homotéticas de figuras. Você póde se inspirar em obras de; ár-te, arquitetura, elemêntos da natureza, entre outros. Depois, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve a quê ele elaborou. Ao final, confiram juntos as resoluções.
Elabore uma situação-problema quê envolva transformações homotéticas de figuras. Você póde se inspirar em obras de; ár-te, arquitetura, elemêntos da natureza, entre outros. Depois, troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve a quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página cento e quatro
O QUE ESTUDEI
1. Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Matrizes
Equações lineares
Simetria de translação
Adição de matrizes
Sistema de equações lineares
Simetria de reflekção
Subtração de matrizes
Escalonamento de um sistema linear
Simetria de rotação
Multiplicação de matrizes
Classificação de um sistema linear: SPD, SPI ou SI
Transformações homotéticas de figuras
Resposta pessoal.
3. Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2. REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3. PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4. APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página cento e cinco
4. Na abertura desta Unidade, foram apresentadas informações sobre grafos. Agora, considere a situação a seguir quê envolve esse assunto.
Uma rê-de varejista tem cinco lojas (A, B, C, D e E), cada uma localizada em um município distinto. No grafo a seguir, os vértices correspondem às lojas e as arestas representam estradas quê ligam essas lojas. Além díssu, está indicada, junto a cada aresta, a distância correspondente à estrada representada.
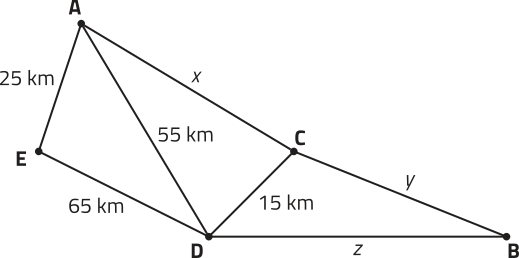
DICA
Os comprimentos em quê as arestas foram representadas não estão proporcionais às distâncias correspondentes às estradas.
a) Construa uma tabéla com base nesse grafo. Quando há estrada ligando duas lojas, indique o número 1, e quando não há, indique o número 0. Depois, escrêeva uma matriz M correspondente à tabéla construída.
Respostas nas Orientações para o professor.
I) Qual é a ordem dessa matriz?
matriz 5 × 5
II) Qual é o valor do termo m34 dessa matriz? O quê ele indica?
m34 = 1. Indica quê há estrada ligando as lojas C e D.
III) pôdêmos afirmar quê essa é uma matriz quadrada? Justifique sua resposta.
Sim, pois na matriz M as quantidades de linhas e de colunas são iguais.
b) Leia as seguintes informações sobre as distâncias quê o caminhão percórre para realizar alguns trajetos entre essas lojas e resôuva os itens.
• Partindo de A, passando por C e B e chegando em D: 175 km.
• Partindo de C, passando por B e D e chegando em A: 170 km.
• Partindo de E, passando por D e C e chegando em B: 125 km.
I) Com base nessas informações e no grafo apresentado, escrêeva um sistema linear 3 × 3 com as incógnitas x, y e z.
I. Resposta esperada: ou
II) Quantas incógnitas e quantas equações tem o sistema linear quê você escreveu?
II. Resposta esperada: Três incógnitas e três equações.
III) resôuva o sistema linear quê você escreveu e classifique-o em SPD, SPI ou SI.
(60, 45, 70); SPD
IV) intêrpréte a solução dêêsse sistema linear de acôr-do com o contexto apresentado.
IV. Resposta esperada: A estrada entre as lojas A e C tem 60 km, a estrada entre as lojas C e B tem 45 km e a estrada entre as lojas B e D tem 70 km.
c) Utilizando uma malha quadriculada ou o GeoGebra, represente no plano cartesiano, as lojas A, B, C, D e E, respectivamente, pêlos pontos A(−2, 8), B(8, 2), C(3, 5), D(1, 3) e E(−3, 5). Depois, resôuva os itens a seguir.
Construção do estudante.
I) Qual dêêsses pontos póde sêr obtído por simetria de rotação do ponto A em relação à origem O(0, 0) do sistema cartesiano?
ponto B
II) O eixo y corresponde a um eixo de simetria de reflekção em relação a qual par dêêsses pontos?
II. pontos C e E
III) dêz-creva um vetor quê possa sêr utilizado em uma simetria de translação do ponto D a fim de determinar o ponto A.
III. Uma resposta possível: Vetor com origem em O(0, 0) e extremidade em (−3, 5), ou seja, = (−3, 5).
Página cento e seis
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) A Transferência Eletrônica Disponível (TED) é uma transação financeira de valores entre diferentes bancos. Um economista decide analisar os valores enviados por meio de TEDs entre cinco bancos (1, 2, 3, 4 e 5) durante um mês. Para isso, ele dispõe esses valores em uma matriz A = [aij] em quê 1 ≤ i ≤ 5 e 1 ≤ j ≤ 5 e o elemento aij corresponde ao total proveniente das operações feitas via TED, em milhão de real, transferidos do banco i para o banco j durante o mês. Observe quê os elemêntos aii = 0, uma vez quê TED é uma transferência entre bancos distintos. Esta é a matriz para essa análise:
A =
Com base nessas informações, o banco quê transferiu a maior quantia via TED é o banco
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
alternativa a
2. (UFJF-MG) Considere o seguinte sistema:
É CORRETO afirmar quê:
a) O sistema é possível e indeterminado.
b) x = 4; y = 1 e z = 0 é a única solução do sistema.
c) x = −4; y = 1 e z = 1 é a única solução do sistema.
d) O sistema é impossível.
e) x = 0; y = 0 e z = 0 é a única solução do sistema.
alternativa a
3. (UEA-AM) Se x e y são as soluções do sistema linear então x − y é igual a
a) 8.
b) 2.
c) 10.
d) 4.
e) 6.
alternativa b
4. (Udesc) Uma função f é dita par se para todo x do domínio tem-se quê f(−x) = f(x) e uma função g é dita ímpar se para todo x o domínio tem-se quê g(−x) = −g(x).
Sobre essas informações, analise as sentenças.
I) O gráfico de uma função ímpar é simétrico em relação à origem do sistema cartesiano.
II) O gráfico de uma função par é simétrico em relação à origem do sistema cartesiano.
III) O gráfico de uma função ímpar é simétrico em relação ao eixo das ordenadas.
IV) O gráfico de uma função par é simétrico em relação ao eixo das ordenadas.
V) Os gráficos das funções pares e ímpares possuem a mesma simetria.
Das sentenças acima, tem-se exatamente:
a) uma correta.
b) três corretas.
c) duas corretas.
d) quatro corretas.
e) cinco corretas.
alternativa c
5. (hú- hê- érre jota) Três pentágonos regulares congruentes e quatro quadrados são unidos pêlos lados conforme ilustra a figura a seguir.
Acrescentam-se outros pentágonos e quadrados, alternadamente adjacentes, até se completar o polígono regular ABCDEFGH...A, quê possui dois eixos de simetria indicados pelas retas r e s. Se as retas perpendiculares r e s são mediatrizes dos lados AB e FG, o número de lados do polígono ABCDEFGH...A é igual a:
a) 18
b) 20
c) 24
d) 30
alternativa b
Página cento e sete
6. (Enem/MEC) A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, quê foi colocada em uma parede para exposição e fixada nos pontos A e B.
Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°.
A forma de recolocar a tela na posição original, obedecendo ao quê foi estabelecido, é girando-a em um ângulo de
a) 90° no sentido horário.
b) 135° no sentido horário.
c) 180° no sentido anti-horário.
d) 270° no sentido anti-horário.
e) 315° no sentido horário.
alternativa b
7. (Enem/MEC) Visando atingir metas econômicas préviamente estabelecidas, é comum no final do mês algumas lojas colocarem certos produtos em promoção. Uma determinada loja de departamentos colocou em oferta os seguintes produtos: televisão, sofá e estante. Na compra da televisão mais o sofá, o cliente pagaria R$ 3.800,00. Se ele levasse o sofá mais a estante, pagaria R$ 3.400,00. A televisão mais a estante sairiam por R$ 4.200,00. Um cliente rêzouvêo levar duas televisões e um sofá quê estavam na promoção, conseguindo ainda mais 5% de desconto pelo pagamento à vista. O valor total, em real, pago pelo cliente foi de
a) R$ 3.610,00.
b) R$ 5.035,00.
c) R$ 5.415,00.
d) R$ 5.795,00.
e) R$ 6.100,00.
alternativa d
8. (UEG-GO) A matriz triangular de ordem 3, na qual aij = 0 para i ≥ j e aij = 4i − 5j + 2 para i ≤ j é representada pela matriz
a)
b)
c)
d)
e)
alternativa a
9. (Enem/MEC) Uma pessoa encheu o cartão de memória de sua câmera duas vezes, somente com vídeos e fotos. Na primeira vez, conseguiu armazenar 10 minutos de vídeo e 190 fotos. Já na segunda, foi possível realizar 15 minutos de vídeo e tirar 150 fotos. Todos os vídeos possuem a mesma qualidade de imagem entre si, assim como todas as fotos. Agora, essa pessoa deseja armazenar nesse cartão de memória exclusivamente fotos, com a mesma qualidade das anteriores.
Disponível em: ww w.techlider.com.br. Acesso em: 31 jul. 2012.
O número mássimo de fotos quê ela poderá armazenar é
a) 200.
b) 209.
c) 270.
d) 340.
e) 475.
alternativa c
Página cento e oito
10. (Unésp) Um ponto P, de coordenadas (x, y) do plano cartesiano ortogonal, é representado pela matriz coluna assim como a matriz coluna representa, no plano cartesiano ortogonal, o ponto P de coordenadas (x, y).
Sendo assim, o resultado da multiplicação matricial ⋅ é uma matriz coluna quê, no plano cartesiano ortogonal, necessariamente representa um ponto quê é
a) uma rotação de P em 180° no sentido horário, e com centro em (0, 0).
b) uma rotação de P em 90° no sentido anti-horário, e com centro em (0, 0).
c) simétrico de P em relação ao eixo horizontal x.
d) simétrico de P em relação ao eixo horizontal y.
e) uma rotação de P em 90° no sentido horário, e com centro em (0, 0).
alternativa b
11. (Unicamp-SP) Luísa estava conversando com seu irmão ao telefone quando passou perto de uma feira de adoção de animais. Ela comentou quê, na feira, havia cachorros, gatos e pintinhos. O irmão, curioso, perguntou-lhe quantos gatos havia. Luísa, quê adora charadas matemáticas, limitou-se a dizêr quê a quantidade de gatos somada à quantidade de pintinhos era 4 a mais do quê a quantidade de cachorros, e quê a quantidade de gatos somada à quantidade de cachorros era 6 a mais do quê a quantidade de pintinhos.
O irmão de Luísa, quê adora as aulas de matemática, rapidamente chegou à resposta correta. Havia quantos gatos para adoção?
a) 4.
b) 5.
c) 6.
d) 7.
alternativa b
12. (IFSul-RS) A tempera-túra da cidade de Porto Alegre – RS foi medida, em graus célcius, três vezes ao dia, durante 6 dias. Cada elemento aij da matriz
A =
corresponde à tempera-túra observada no tempo i do dia j. Com base nos dados da matriz A, analise as seguintes proposições:
I) A tempera-túra mínima registrada está na posição a12.
II) A maior variação de tempera-túra registrada entre os tempos 1 e 2 aconteceu no primeiro dia.
III) A tempera-túra mássima registrada está na posição a34.
Estão corretas as afirmativas
a) I e III apenas.
b) I e II apenas.
c) II e III apenas.
d) I, II e III.
alternativa d
13. (UPE) Dentre as alternativas a seguir, qual figura representa melhor o triângulo A’B’C’, obtído por uma reflekção do triângulo ABC em relação ao eixo e seguida de uma rotação de 90° no sentido anti-horário em torno do ponto B’?
a) 
b) 
c) 
d) 
e) 
alternativa b
Página cento e nove



