UNIDADE 3
GEOMETRIA ESPACIAL DE POSIÇÃO
Geometria Euclidiana e Geometria não Euclidiana
Ao longo da história da Geometria, destacaram-se diversos estudiosos, dentre eles, Euclides de Alexandria (c. 325 a.C.-c. 265 a.C.).
Na sua obra mais conhecida, o conjunto de livros chamado de Elementos, são apresentados postulados e teoremas quê sintetizam conhecimentos matemáticos daquela época, os quais serviram de subsídio para o desenvolvimento da Geometria Euclidiana. A partir de meados do século XIX, questionamentos a respeito da Geometria Euclidiana, como o questionamento ao postulado das retas paralelas, conduziu estudiosos a desenvolver outras teorias geométricas, quê, posteriormente, seriam denominadas Geometrias não Euclidianas. Por exemplo, a Geometria Esférica, quê se desen vólve sobre a superfícíe de uma esféra, o quê permite relacioná-la ao estudo do glôbo terrestre e aplicá-la em diversas áreas, como Astronomia, Aviação e Navegação.
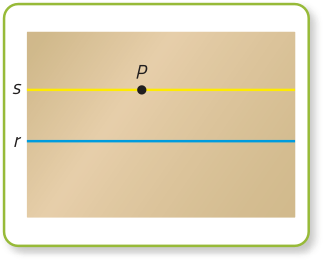
O postulado das retas paralelas, na Geometria Euclidiana, em um enunciado equivalente, expressa quê: em um plano, para qualquer reta r e qualquer ponto P quê não está em r, existe uma única reta s passando por P tal quê s seja paralela a r. Observe uma representação dêêsse postulado na Geometria Euclidiana e um contraexemplo de sua validade na Geometria Esférica.
Geometria Euclidiana
Em um plano, dada uma reta r e um ponto P quê não está em r, existe uma única reta s passando por P tal quê s seja paralela a r.
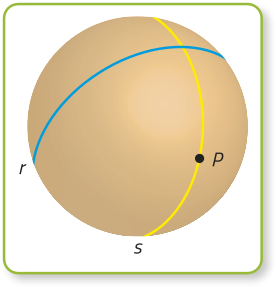
Geometria Esférica
Não existem linhas retas da mesma maneira quê na Geometria Euclidiana. O quê consideramos reta nesse tipo de Geometria são círculos, de mesmo raio quê o da esféra, quê passam por cérto ponto. Assim, na Geometria Esférica, não existem retas paralelas entre si, ou seja, quaisquer duas retas se intersectam.
Fontes dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 5. ed. Campinas: Editora da Unicamp, 2011. p. 539-544. ANTUNES, Marcelo Carvalho. Uma possível inserção das geometrias não euclidianas no ensino médio. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Universidade Federal do Rio Grande do Sul, Porto Alegre, 2009. Disponível em: https://livro.pw/orsge. Acessos em: 29 jul. 2024.
Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
1. Que elemêntos da Geometria Euclidiana você conhece?
2. De acôr-do com o texto, como começaram a sêr desenvolvidas as teorias da Geometria não Euclidiana?
3. Na Geometria Euclidiana, a menor distância entre dois pontos póde sêr representada por um segmento de reta quê os une. Como você imagina quê póde sêr representada a menor distância entre dois pontos em uma superfícíe esférica?
Respostas nas Orientações para o professor.
Página cento e dez
Geometria de posição no plano
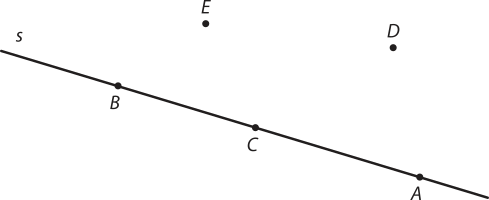
No estudo da Geometria Euclidiana, alguns conceitos e noções são aceitos como verdadeiros, sem a necessidade de demonstrações. Por exemplo, as noções de ponto, reta e plano, chamadas de noções primitivas, não são definidas formalmente, sêndo distinguidas intuitivamente.


DICA
Nesta coleção, de maneira geral, optamos por indicar os pontos por lêtras maiúsculas (A, B, C, ...), as retas por lêtras minúsculas (a, b, c, ...) e os planos por lêtras grêgas minúsculas ((alfa)", (beta)", (gama)", ...).
Essas noções primitivas sérvem de base para o estabelecimento dos postulados – quê são afirmações consideradas verdadeiras, sem a necessidade de demonstrações – e dos teoremas, quê correspondem a afirmações quê só são consideradas verdadeiras depois de demonstradas, usando postulados ou outros teoremas. Você se lembra de algum teorema de Geometria quê estudou em anos anteriores?
MATEMATICA NA HISTÓRIA
Elementos é considerada a obra-prima do matemático Euclides de Alexandria. Essa obra é composta de 465 proposições distribuídas em 13 livros, dos quais os livros I, III, IV, VI, XI e XII correspondem basicamente a textos referentes à Geometria Plana e à Geometria Espacial, sêndo muitos deles uma compilação de produções mais antigas, escritas por outros estudiosos. Desde sua primeira edição, impressa em 1482, mais de 1.000 edições já foram realizadas, tornando Elementos o trabalho científico mais consultado na história.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 5. ed. Campinas: Editora da Unicamp, 2011. p. 167-169.
No Ensino Fundamental, possivelmente, você estudou as posições relativas entre pontos e retas em um mesmo plano. Agora, vamos estender esse estudo para as posições relativas entre pontos e planos.
• Posições relativas entre ponto e reta

• Posições relativas entre pontos
Página cento e onze
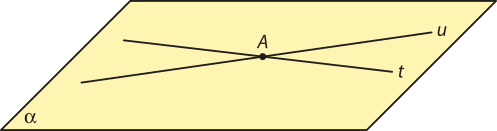
• Posições relativas entre retas contidas em um mesmo plano
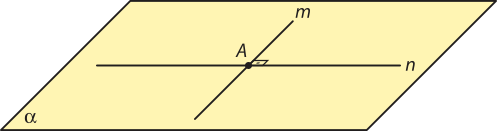

• Posições relativas entre ponto e plano

PARA PENSAR
Duas retas concorrentes são sempre perpendiculares.
Você concórda com essa afirmação? Justifique sua resposta.
Resposta esperada: A afirmação é falsa, pois duas retas concorrentes são perpendiculares apenas quando formam ângulos rétos no ponto em quê se intersectam.
Aprendemos quê postulados são afirmações quê não necessitam de demonstrações. Para estudar as posições relativas entre retas e planos no espaço, vamos considerar os seguintes postulados.
Postulado I
Retas e planos são conjuntos de pontos.
Postulado II
Existem infinitos pontos quê pertencem a uma reta, assim como infinitos pontos quê não pertencem a ela.
Postulado III
Existem infinitos pontos quê pertencem a um plano, assim como infinitos pontos quê não pertencem a ele.
Postulado IV
Dois pontos distintos A e B determinam uma única reta s.

Página cento e doze
Postulado V
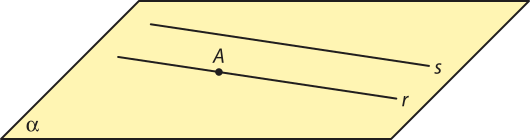
Sejam A um ponto e s uma reta em um plano (alfa)". Se A não pertence a s, existe apenas uma reta r quê passa por A e é paralela a s em (alfa)". Esse é conhecido como o quinto postulado de Euclides.
Postulado VI
Se dois pontos distintos A e B de uma reta s pertencem a um plano (alfa)", então s está contida em (alfa)" (s ⊂ (alfa)").

Postulado VII
Três pontos não colineares A, B e C determinam um único plano (alfa)".
DICA
Note quê um ponto é elemento de uma reta; assim, dizemos quê o ponto pertence à reta. Já uma reta é um conjunto de pontos; assim, dizemos quê uma reta está contida em um plano.
Determinação de um plano
Vamos usar alguns postulados apresentados para demonstrar os três teoremas a seguir, quê fazem referência à determinação de um plano.
• Teorema 1:
Uma reta s e um ponto A, não pertencente a s, determinam um único plano (alfa)".
Demonstração:
Pelos postulados I e II, podemos considerar dois pontos distintos B e C pertencentes a uma reta s e um ponto A fora dessa reta. Assim, A, B e C são pontos não colineares. Pelo postulado VII, concluímos quê A, B e C determinam um único plano (alfa)". O postulado IV garante quê s é a única reta determinada pêlos pontos B e C, e o postulado VI garante quê s está contida em (alfa)", pois B e C pertencem a s e pertencem a (alfa)". Portanto, existe um único plano (alfa)" quê contém a reta s e o ponto A.

Página cento e treze
• Teorema 2:
Duas retas paralelas r e s determinam um único plano (alfa)".
Demonstração:
De acôr-do com os postulados I, II e III, podemos considerar em um plano (alfa)" uma reta s e um ponto A não pertencente a s. Pelo postulado V, existe uma única reta r quê passa por A e é paralela a s em (alfa)".
Pelo teorema 1, apresentado anteriormente, existe um único plano quê contém o ponto A e a reta s. Portanto, existe um único plano quê contém as retas paralelas r e s.

• Teorema 3:
Duas retas concorrentes r e s determinam um único plano (alfa)".
Demonstração:
Vamos considerar o ponto A comum às retas r e s, e outros dois pontos distintos B e C, com B pertencendo a r e C pertencendo a s. Assim, A, B e C são não colineares.
Pelo postulado VII, os pontos A, B e C determinam um único plano (alfa)". O postulado IV garante quê r é a única reta determinada por A e B e quê s é a única reta determinada por A e C. Já o postulado VI garante quê r e s estão contidas em (alfa)", pois A e B pertencem a r e a (alfa)", e A e C pertencem a s e a (alfa)". Portanto, existe um único plano (alfa)" quê contém as retas r e s.

ATIVIDADE RESOLVIDA
R1. Demonstre o teorema a seguir.
Sejam um plano (alfa)" e uma reta r não contida nele. Se r intersecta (alfa)", então a interseção de r e (alfa)" é um único ponto.
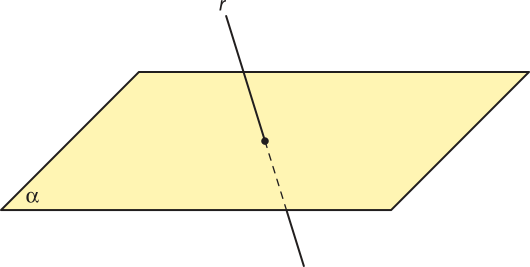
Resolução
Vamos supor quê existam pelo menos dois pontos distintos A e B quê estejam na interseção da reta r com o plano (alfa)". Assim, pelo postulado VI, concluímos quê r está contida em (alfa)". Porém isso é um absurdo, já quê, por hipótese, r não está contida em (alfa)". Portanto, a interseção de r e (alfa)" é um único ponto.
Página cento e quatorze
ATIVIDADES
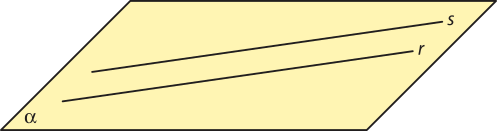
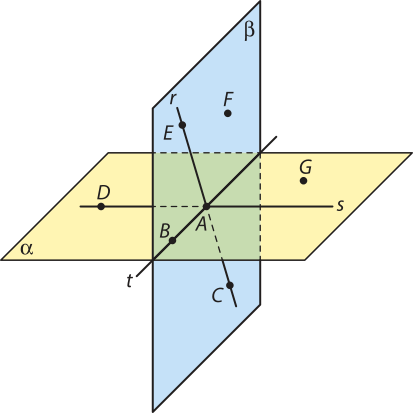
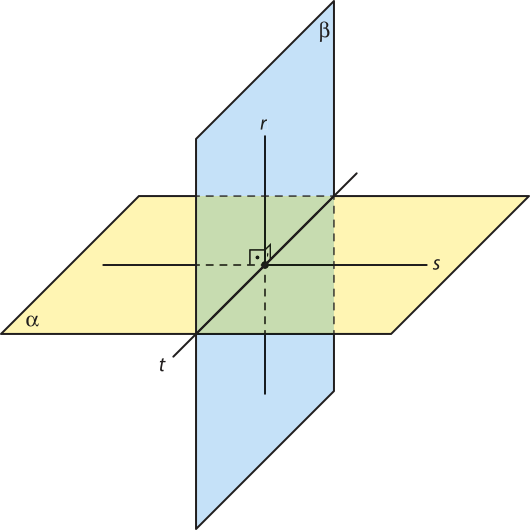
1. Observe os planos, as retas e os pontos representados a seguir e determine a relação de pertinência ou continência entre:
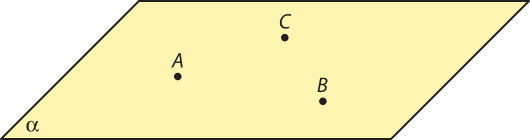
a) cada um dêêsses pontos e o plano (alfa)";
A ∈ (alfa)", B ∈ (alfa)", C ∉ (alfa)", D ∈ (alfa)", E ∉ (alfa)", F ∉ (alfa)" e G ∈ (alfa)"
b) cada uma dessas retas e o plano (beta)";
r ⊂ (beta)", s ⊄ (beta)" e t ⊂ (beta)"
c) cada um dêêsses pontos e as retas r, s e t.
A ∈ r, B ∉ r, C ∈ r, D ∉ r, E ∈ r, F ∉ r e G ∉ r; A ∈ s, B ∉ s, C ∉ s, D ∈ s, E ∉ s, F ∉ s e G ∉ s; A ∈ t, B ∈ t, C ∉ t, D ∉ t, E ∉ t, F ∉ t e G ∉ t
2. Classifique cada afirmação a seguir como verdadeira ou falsa.
a) Três pontos quaisquer determinam um único plano.
falsa
b) Ponto, reta e plano são conceitos primitivos.
verdadeira
c) Os postulados correspondem a afirmações quê são consideradas verdadeiras apenas depois quê são demonstradas.
falsa
d) Duas retas concorrentes têm dois ou mais pontos em comum.
falsa
e) Existem infinitas retas contidas em um plano (alfa)" qualquer, assim como existem infinitas retas não contidas nesse plano.
verdadeira
f) Os teoremas correspondem a afirmações quê só são consideradas verdadeiras após terem sido demonstradas.
verdadeira
g) Dois pontos quaisquer são sempre colineares.
verdadeira
3. reescrêva as sentenças falsas da atividade anterior, tornando-as verdadeiras.
Respostas esperadas: a) Três pontos não colineares determinam um único plano; c) Os postulados correspondem a afirmações tomadas como verdadeiras sem a necessidade de serem demonstradas; d) Duas retas concorrentes têm apenas um ponto em comum.
4. Considerando quatro pontos A, B, C e D, não coplanares e não colineares três a três, responda às kestões, explicando como você pensou.
a) Quantas retas distintas contendo dois dêêsses pontos é possível traçar?
6 retas distintas
b) Quantos planos distintos contendo três dêêsses pontos é possível traçar?
4 planos distintos
5. Tripés, bancos e cavaletes de pintura quê têm três pernas proporcionam maior estabilidade de apôio a objetos do quê aqueles com quatro pernas, já quê eles não balançam quando apoiados em qualquer tipo de piso. Utilizando os conceitos geométricos estudados, explique por quê objetos com três pernas não balançam, independentemente do tipo de piso em quê forem apoiados.

Resposta esperada: Pelo postulado VII, três pontos não colineares determinam um único plano. Considerando os três pontos correspondentes aos pontos de apôio dos pés dêêsses objetos no piso, podemos afirmar quê esses pontos de apôio determinam um único plano. Assim, mesmo quando apoiados em um piso irregular, esses três pontos de apôio determinam um único plano imaginário quê intersecta esse piso nesses pontos e, portanto, esses objetos não balançam.
6. Mostre a validade do teorema a seguir.
Se três retas r, s e t distintas são concorrentes duas a duas, de maneira quê não exista ponto comum às três retas, então essas retas estão contidas em um mesmo plano (alfa)".
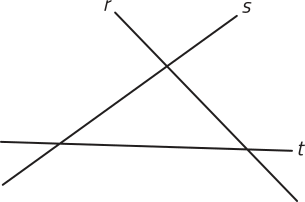
Resposta nas Orientações para o professor.
7. Dadas duas retas r e s, perpendiculares entre si, julgue a afirmação a seguir como verdadeira ou falsa e justifique.
Existe uma reta t, contida em um mesmo plano quê as retas r e s, quê é perpendicular a r e concorrente a s.
Falsa. Resposta esperada: Vamos supor, por hipótese, quê exista uma reta t perpendicular à reta r e concorrente à reta s, sêndo r e s perpendiculares entre si. Assim, temos os pontos A, B e C correspondentes às interseções de r e s, r e t e s e t, respectivamente. Considerando o triângulo ABC, temos, por hipótese, quê med() = 90°, med() = 90° e med() > 0°. Isso, no entanto, é um absurdo, pois a soma das medidas dos ângulos internos de qualquer triângulo é 180° e med() + med() + med() > 180°.
Página cento e quinze
Posições relativas no espaço
Estudamos as posições relativas entre retas e pontos em um mesmo plano. Agora, vamos ampliar esse estudo para posições relativas entre retas e planos no espaço.
Posições relativas entre retas no espaço
• Retas coplanares
Duas retas r e s são coplanares quando estão contidas em um mesmo plano.
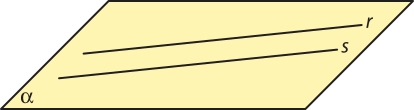
• Retas reversas
Duas retas r e s são reversas (ou não coplanares) quando não estão contidas em um mesmo plano. Duas retas reversas podem sêr reversas ortogonais ou reversas oblíquas.
a) Reversas ortogonais
Duas retas r e s são reversas ortogonais quando existe uma reta t perpendicular a uma delas e paralela à outra.
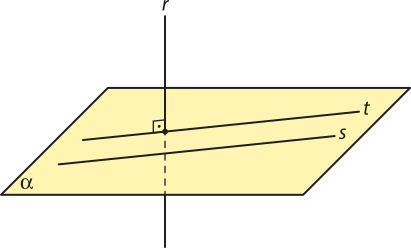
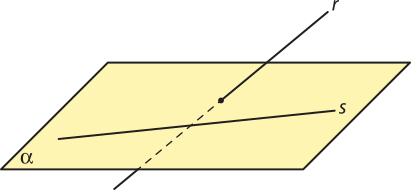
b) Reversas oblíquas
Duas retas reversas r e s são reversas oblíquas quando não são reversas ortogonais.
PARA PENSAR
É possível quê duas retas reversas também sêjam concorrentes? Justifique sua resposta.
Resposta esperada: Não, pois, para sêrem concorrentes, duas retas devem ser coplanares e, portanto, não reversas.
Posições relativas entre reta e plano
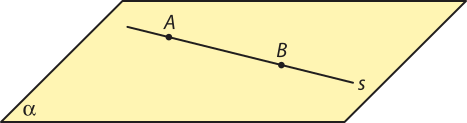
• Reta contida no plano
Uma reta s está contida em um plano (alfa)" quando pontos distintos A e B pertencentes a s também pertencem a (alfa)".
• Reta paralela ao plano
Uma reta s é paralela a um plano (alfa)" quando não há ponto em comum entre a reta s e o plano (alfa)". Nesse caso, podemos indicar s ⫽ (alfa)".

Página cento e dezesseis
• Reta secante ao plano
Uma reta s é secante (ou concorrente) a um plano (alfa)" quando há apenas um ponto A quê pertença tanto à reta s quanto ao plano (alfa)".
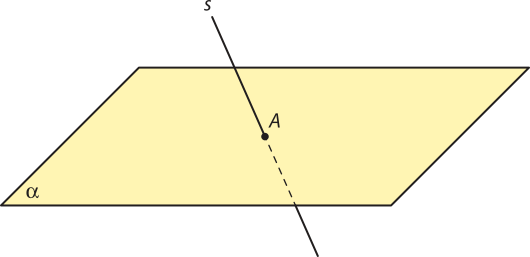
• Reta perpendicular ao plano
Uma reta s é perpendicular a um plano (alfa)" se, e somente se, é secante a esse plano e perpendicular a todas as retas concorrentes a ela e contidas em (alfa)". Nesse caso, podemos indicar s ⊥ (alfa)".
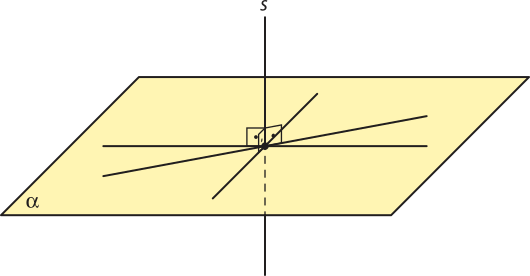
Posições relativas entre planos
• Planos coincidentes
Dois planos (alfa)" e (beta)" são coincidentes quando todos os pontos pertencentes a um dos planos também pertencem ao outro plano.

• Planos paralelos
Dois planos (alfa)" e (beta)" são paralelos se, e somente se, não têm pontos em comum, ou seja, nenhum ponto pertencente a (alfa)" pertence a (beta)".
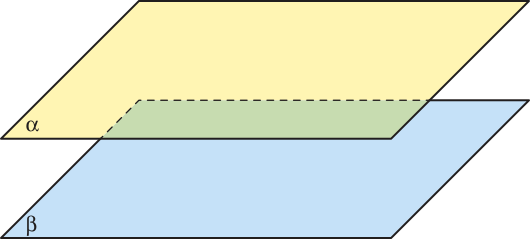
• Planos secantes
Dois planos (alfa)" e (beta)" são secantes (ou concorrentes) quando há apenas uma reta s contida tanto em (alfa)" quanto em (beta)".
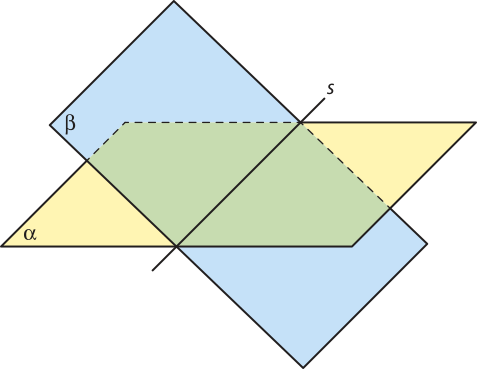
• Planos perpendiculares
Dois planos secantes (alfa)" e (beta)" são perpendiculares se, e somente se, um deles contém uma reta perpendicular ao outro plano.
Página cento e dezessete
ATIVIDADE RESOLVIDA
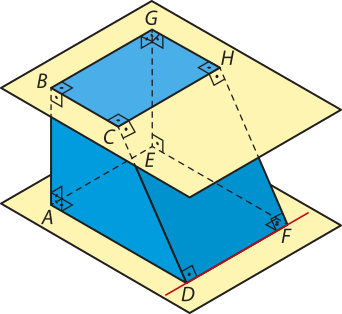
R2. Considerando as retas e os planos quê contêm, respectivamente, as arestas e as faces do poliedro representado na figura, resôuva os itens a seguir.
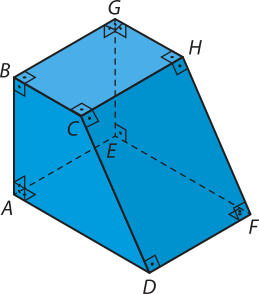
a) Quais são as retas reversas a ? Alguma delas é reversa oblíqua?
b) Decida se a afirmação a seguir é verdadeira ou falsa.
O plano quê contém a face correspondente ao quadrilátero CDFH é secante a todos os planos quê contêm as outras faces dêêsse poliedro.
c) Determine as retas perpendiculares ao plano quê contém a face correspondente ao quadrilátero ABCD.
d) Qual é a posição relativa entre os planos quê contêm as faces côrrespondentes aos quadriláteros BCHG e ADFE? E entre a reta quê contém a aresta e cada um dêêsses planos?
Resolução
a) As retas reversas a são aquelas quê não estão contidas em um mesmo plano quê ela. Nesse caso são: , , e . Dessas, é reversa oblíqua em relação a .
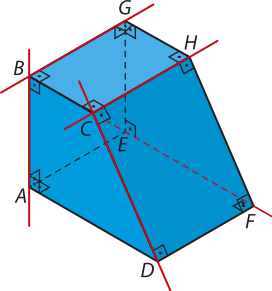
b) As faces correspondentes aos quadriláteros ABCD, ADFE, BCHG e EFHG têm uma aresta comum com a face correspondente ao quadrilátero CDFH e, portanto, os planos quê contêm essas faces são secantes ao plano quê contém a face correspondente ao quadrilátero CDFH. Prolongando as faces correspondentes aos quadriláteros CDFH e ABGE, podemos observar quê os planos quê contêm essas faces também são secantes. Portanto, a afirmação é verdadeira.
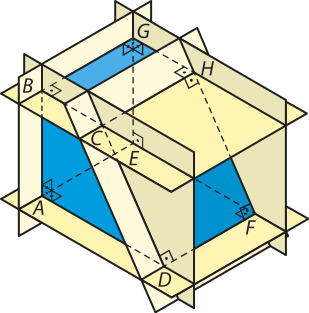
c) pôdêmos notar quê , , e são as retas perpendiculares ao plano quê contém a face correspondente ao quadrilátero ABCD, pois elas são perpendiculares a todas as retas dêêsse plano quê passam, respectivamente, pêlos pontos B, C, A e D.
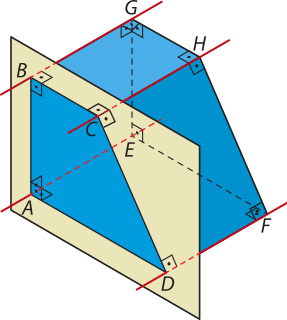
d) Os planos quê contêm as faces correspondentes aos quadriláteros BCHG e ADFE são paralelos. Como a aresta está contida na face correspondente ao quadrilátero ADFE, então é uma reta contida no plano quê contém a face correspondente ao quadrilátero ADFE e é paralela ao plano quê contém a face correspondente ao quadrilátero BCHG.
Página cento e dezoito
ATIVIDADES
8. Classifique cada afirmação a seguir como verdadeira ou falsa. Depois, reescrêva as falsas, tornando-as verdadeiras.
a) Duas retas quaisquer quê não têm ponto em comum são reversas.
Falsa. Resposta esperada: Duas retas quaisquer quê não têm ponto em comum são reversas ou paralelas.
b) Dois planos quaisquer secantes têm infinitos pontos comuns.
verdadeira
c) Se uma reta é perpendicular a um plano, então essa reta é perpendicular a todas as retas contidas nesse plano.
Falsa. Resposta esperada: Se uma reta é perpendicular a um plano, então essa reta é perpendicular a todas as retas contidas nesse plano e concorrentes a ela.
d) Se dois planos são paralelos, então eles correspondem ao mesmo conjunto de pontos.
Falsa. Resposta esperada: Se dois planos são coincidentes, então eles correspondem ao mesmo conjunto de pontos.
e) Duas retas reversas quaisquer são retas não coplanares.
verdadeira
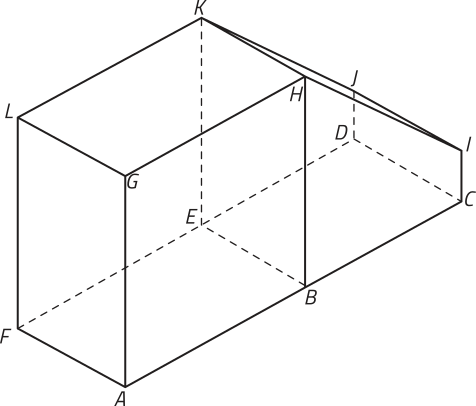
9. (EsPCex-SP) O sólido geométrico a seguir é formado pela justaposição de um bloco retangular e um prisma reto, com uma face em comum. Na figura estão indicados os vértices, tanto do bloco quanto do prisma.
Considere os seguintes pares de retas definidas por pontos dessa figura: as retas e ; as retas e e as retas e . As posições relativas dêêsses pares de retas são, respectivamente,
a) concorrentes; reversas; reversas.
b) reversas; reversas; paralelas.
c) concorrentes; reversas; paralelas.
d) reversas; concorrentes; reversas.
e) concorrentes; concorrentes; reversas.
alternativa e
10. É possível quê dois planos distintos tênham um único ponto em comum? Justifique sua resposta.
Resposta esperada: Não, pois, se dois planos distintos têm ponto em comum, então eles são secantes e, portanto, têm uma reta em comum, ou seja, infinitos pontos.
11. Em cada item, determine a posição relativa entre duas retas distintas r e s, de acôr-do com as informações indicadas.
a) Um plano (alfa)" quê contém r é perpendicular a s.
retas perpendiculares ou reversas ortogonais
b) Não existe ponto comum a r e s.
retas paralelas ou reversas
c) Um plano (alfa)" é paralelo a r e paralelo a s.
retas paralelas, concorrentes ou reversas
12. Considere um cubo ABCDEFGH e , e retas suporte de três arestas dêêsse cubo.
a) Determine a posição relativa entre essas retas, duas a duas.
retas perpendiculares
b) Que figura geométrica plana corresponde à interseção dêêsse cubo com o plano determinado pêlos vértices B, D e F?
triângulo
13. Um engenheiro pretende imprimir uma peça com formato de bloco retangular em uma impressora 3D. Observe, a seguir, essa peça feita em um programa de computador.
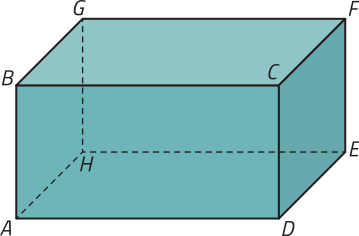
Considerando as retas quê contêm as arestas e os planos quê contêm as faces do bloco retangular representado, determine:
a) um par de faces cujos respectivos planos quê as contêm são paralelos;
Respostas possíveis: faces correspondentes aos quadriláteros: ABCD e EFGH; CDEF e ABGH; BCFG e ADEH
b) as faces cujos planos quê as contêm são paralelos a ;
faces correspondentes aos quadriláteros BCFG e CDEF
c) as posições relativas entre e os planos quê contêm as faces côrrespondentes aos quadriláteros ADEH e ABGH;
é uma reta contida no plano quê contém a face correspondente ao quadrilátero ADEH e é perpendicular ao plano quê contém a face correspondente ao quadrilátero ABGH.
d) os planos secantes aos planos quê contêm as faces côrrespondentes aos quadriláteros BCFG e AHED.
Planos quê contêm as faces correspondentes aos quadriláteros ABCD, CDEF, EFGH e ABGH.
14. Mostre quê o teorema a seguir é verdadeiro.
Sejam dois planos distintos (alfa)" e (beta)" e os pontos A, B e C, também distintos. Se A, B e C pertencem tanto a (alfa)" quanto a (beta)", então esses são pontos colineares.
Resposta esperada: Suponha quê os pontos A, B e C sêjam não colineares e pertencentes aos planos distintos (alfa)" e (beta)". Pelo postulado VII, esses pontos determinam um único plano e, assim, (alfa)" e (beta)" devem sêr coincidentes, o quê é um absurdo, pois temos por hipóteses quê (alfa)" e (beta)" são planos distintos. Portanto, os pontos A, B e C são pontos colineares. Nesse caso, (alfa)" e (beta)" são planos secantes.
Página cento e dezenove
15. Considere (alfa)" e (beta)" dois planos perpendiculares e uma reta r correspondente à interseção de (alfa)" e (beta)". Imagine dois pontos quaisquer A e B, de maneira quê A ∈ (alfa)", A ∉ (beta)", B ∈ (beta)" e B ∉ (alfa)". Qual é a posição de em relação:
a) ao plano (alfa)"?
secante
b) ao plano (beta)"?
secante
c) à reta r?
reversa
16. (USCS-SP) Um ponto H está sobre a base BCD de um prisma reto BCDGFE, mas não está sobre as arestas dessa base, conforme mostra a figura.
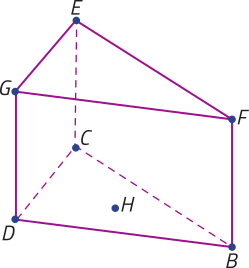
Considerando as retas quê passam por dois vértices dêêsse prisma ou por um vértice e por H, é possível afirmar quê
a) e são reversas.
b) e são concorrentes.
c) e são reversas.
d) e são paralelas.
e) e são perpendiculares.
alternativa c
17. Um designer produziu, em um programa de computador, o projeto de uma peça de metal, formada pela justaposição de duas outras peças, uma com formato de cubo e outra com formato de pirâmide reta, conforme a figura a seguir.
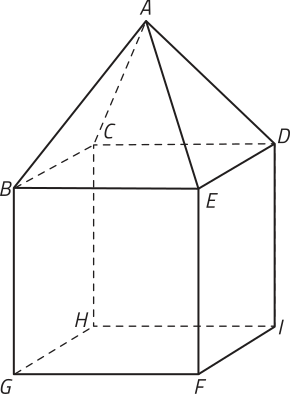
Em relação ao sólido obtído nesse projeto, indique a posição relativa entre os planos quê contêm as faces:
a) ABC e ADE.
secantes
b) ABC e DEFI.
secantes
c) BCHG e DEFI.
paralelos
d) BCHG e BEFG.
secantes e perpendiculares
18. ![]() Junte-se a um colega para resolver esta atividade. Além dos teoremas apresentados nesta Unidade, existem outros relacionados ao paralelismo no espaço. Acompanhem, a seguir, a demonstração de um dêêsses teoremas.
Junte-se a um colega para resolver esta atividade. Além dos teoremas apresentados nesta Unidade, existem outros relacionados ao paralelismo no espaço. Acompanhem, a seguir, a demonstração de um dêêsses teoremas.
Teorema: Se um plano (gama)" é secante a dois planos distintos e paralelos (alfa)" e (beta)", então a reta s, comum a (gama)" e a (alfa)", é paralela à reta r, comum a (gama)" e a (beta)".
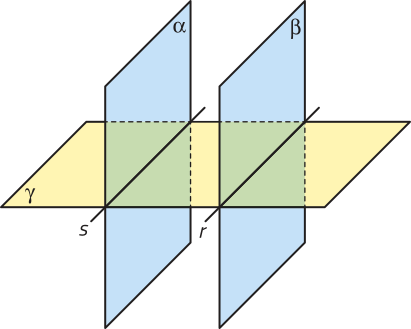
Demonstração: Como as retas s e r correspondem a interseções entre os planos (gama)" e (alfa)" e entre (gama)" e (beta)", respectivamente, então s e r são coplanares, pois ambas estão contidas no plano (gama)".
Já quê (alfa)" ⫽ (beta)", ou seja, não existe ponto comum a (alfa)" e a (beta)", e como s ⊂ (alfa)" e r ⊂ (beta)", podemos afirmar quê não existe ponto comum a s e a r, pois se existisse ponto comum a s e a r, então existiria ponto comum aos planos (alfa)" e (beta)".
Como s e r são coplanares e a interseção entre elas é vazia, concluímos quê essas retas são paralelas.
Agora, escôlham um dos teoremas a seguir, representem-no por uma figura e mostrem a validade dele.
• Teorema I: Uma reta r não contida em um plano (alfa)" é paralela a esse plano se for paralela a uma reta s contida em (alfa)".
• Teorema II: Dados dois planos paralelos (alfa)" e (beta)", toda reta r contida em um deles é paralela ao outro plano.
• Teorema III: Dados um plano (alfa)" e um ponto P, com P ∉ (alfa)", existe pelo menos uma reta r quê passa por P e é paralela a (alfa)".
Resposta nas Orientações para o professor.
Página cento e vinte
INTEGRANDO COM...
LINGUAGENS E SUAS TECNOLOGIAS
A linguagem matemática e o Sistema Braille
A linguagem póde sêr considerada uma construção humana quê utiliza sistemas compléksos de comunicação para quê seja possível se expressar, partilhar informações, ideias, sentimentos e produzir sentidos.
Algumas linguagens, por causa de seu caráter padronizado, são consideradas universais, ou seja, sua compreensão ultrapassa os limites regionais. Por exemplo, na Matemática, foi desenvolvida, ao longo do tempo, uma linguagem com simbologia própria e quê é uniforme no mundo todo, o quê permite representar e expor conceitos de maneira concreta e efetiva, quê todos possam compreender. Também no Sistema Braille é possível reconhecer uma tendência de universalização de linguagem, o quê possibilita e favorece a comunicação entre pessoas com ou sem deficiência visual. Sobre o Braille, leia o trecho de um texto a seguir.
O braille é um sistema de escrita e leitura tátil para as pessoas cegas inventado pelo francês Louis Braille, ele mesmo cego aos três anos de idade devido a um acidente quê causou a infekição dos dois olhos.
O sistema consta do arranjo de seis pontos em relevo, dispostos na vertical em duas colunas de três pontos cada, no quê se convencionou chamar de “cela braille”. A diferente disposição dêêsses seis pontos permite a formação de 63 combinações ou símbolos para escrever textos em geral [...]
BRASIL. Ministério da Educação. Instituto Benjamin Constant. O Sistema Braille. Rio de Janeiro: IBC, 24 fev. 2022. Disponível em: https://livro.pw/qvkjz. Acesso em: 29 jul. 2024.
PARA AMPLIAR
Acesse êste sáiti para obtêr mais informações sobre o Sistema Braille.
• BRASIL. Ministério da Educação. Instituto Benjamin Constant. O Sistema Braille. Rio de Janeiro: IBC, 24 fev. 2022. Disponível em: https://livro.pw/qvkjz. Acesso em: 29 jul. 2024.
A Agência Nacional de Vigilância Sanitária (Anvisa) estabelece quê as embalagens de medicamentos destinadas a pacientes precisam conter o nome comercial do medicamento ou a denominação genérica de cada princípio ativo em Sistema Braille, sem quê isso afete a legibilidade das informações.
Fonte dos dados: BRASIL. Ministério da Saúde. Agência Nacional de Vigilância Sanitária. Resolução-RDC número 71, de 22 de dezembro de 2009. Estabelece regras para a rotulagem de medicamentos. Brasília, DF: MS: Anvisa, 22 dez. 2009. Disponível em: https://livro.pw/lbifo. Acesso em: 7 out. 2024.

Página cento e vinte e um
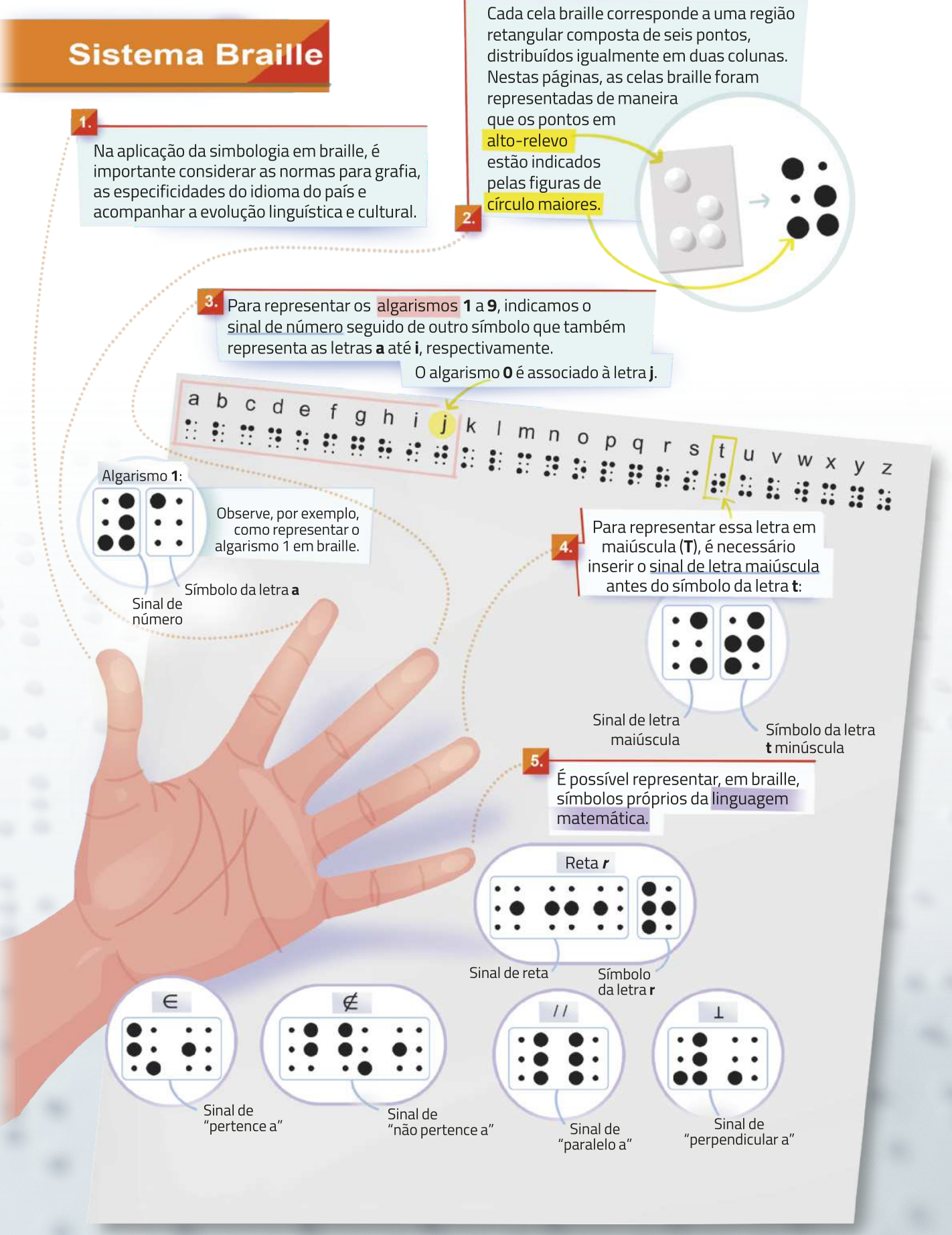
Fonte dos dados: BRASIL. Ministério da Educação. Secretaria de Educação Especial. cóódigo matemático unificado para a língua portuguesa. Brasília, DF: MÉC: Seesp, 2006. p. 31, 56, 79, 83. Disponível em: https://livro.pw/hctbw. Acesso em: 29 jul. 2024.
Página cento e vinte e dois
PENSANDO NO ASSUNTO
1. ![]() Cite situações do cotidiano em quê você faz uso da linguagem verbal para se comunicar.
Cite situações do cotidiano em quê você faz uso da linguagem verbal para se comunicar.
Resposta pessoal.
2. ![]() Em seu entendimento, ao se comunicar de maneira diréta e objetiva, é possível evitar conflitos? Converse com os côlégas e o professor a respeito díssu.
Em seu entendimento, ao se comunicar de maneira diréta e objetiva, é possível evitar conflitos? Converse com os côlégas e o professor a respeito díssu.
Resposta pessoal.
3. Realize uma pesquisa sobre acessibilidade atitudinal, quê consiste em um conjunto de atitudes adequadas e respeitosas diante de pessoas com deficiência. Com base nas informações obtidas, produza uma peça publicitária (fôlder, cartaz, vídeo ou podcast) com o objetivo de estimular a acessibilidade atitudinal na comunidade em quê vive. É importante quê essa peça publicitária explique o quê é acessibilidade atitudinal, dê exemplos de atitudes inclusivas e mostre situações quê limitem ou impeçam a inclusão de pessoas com deficiência. Sua peça publicitária póde sêr divulgada em um mural da escola ou em mídias sociais.
Pesquisa e produção do estudante.
4. ![]() Converse com os côlégas e o professor sobre os itens a seguir.
Converse com os côlégas e o professor sobre os itens a seguir.
a) Você já manipulou algum objeto com escritas em braille, como embalagens de produtos, placas indicativas ou livros? Comente como foi essa experiência.
Resposta pessoal.
b) por quê é fundamental a alfabetização para estudantes com deficiência visual na escola?
Resposta pessoal.
c) por quê é importante conhecer a linguagem braille, mesmo não tendo deficiência visual? Como essa linguagem sérve para a independência e a autonomia de pessoas cegas ou com baixa visão?
Respostas pessoais.
5. ![]() Junte-se a um colega para explorar a transcrição da linguagem matemática para a linguagem braille. Para isso, façam o quê se pede em cada um dos itens.
Junte-se a um colega para explorar a transcrição da linguagem matemática para a linguagem braille. Para isso, façam o quê se pede em cada um dos itens.
a) Quais são os termos representados em braille em cada caso a seguir?

livro

Euclides

300
b) Utilizando representações de celas braille, escrevam o nome e a idade de vocês.
Respostas pessoais.
c) As retas r e s, representadas a seguir, são paralelas. ob-sérvim como podemos indicar isso no Sistema Braille.
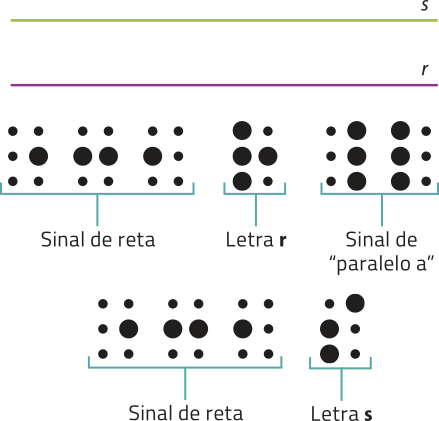
Agora, no caderno, façam um desenho para ilustrar a relação matemática representada em braille em cada ficha.
Resposta nas Orientações para o professor.


d) Pesquisem normas técnicas da escrita em braille para obtêr informações sobre altura do relevo e distância entre os pontos, as linhas e as celas.
Pesquisa dos estudantes.
e) Pesquisem tecnologias quê facilitam a impressão de textos em braille e os aplicativos disponíveis para pessoas cegas ou com baixa visão. Em seguida, escôlham um conceito estudado nesta Unidade, como postulados ou teoremas. Depois, façam a transcrição dêêsse conceito utilizando a representação das celas braille e troquem-na com outra dupla para conferir a transcrição dela. As tecnologias quê vocês pesquisaram podem sêr utilizadas na transcrição do conceito escolhido.
Pesquisa dos estudantes.
Página cento e vinte e três
Projeções ortogonais
Você já observou um drone em movimento? Ele é um aparelho controlado remotamente quê póde alcançar grandes alturas. Entre as várias funções dêêsse aparelho, é possível obtêr vistas superiores de alguns locais. Agora, imagine a seguinte situação: com o Sol a pino, os raios solares, quê são paralelos, projetam no solo a sombra de um drone durante um vôo.
- Sol a pino
- : expressão quê indica o momento em quê o Sol está posicionado no ponto mais alto do céu.

Nessa situação, a sombra do drone no solo nos remete à ideia de projeção ortogonal em um plano, conceito quê estudaremos a seguir.
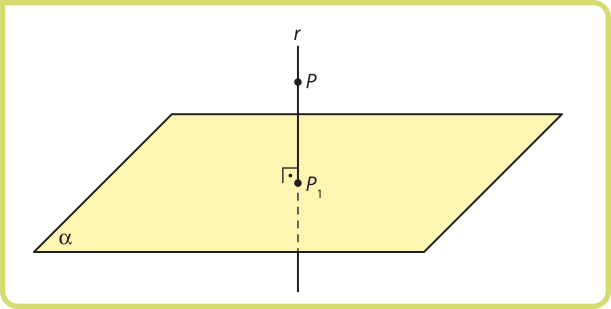
Denominamos projeção ortogonal de um ponto P, sobre um plano (alfa)", o ponto P1, correspondente à interseção do plano (alfa)" e da reta r, quê passa por P, sêndo r ⊥ (alfa)".
PARA PENSAR
O quê podemos afirmar a respeito do ponto P1, correspondente à projeção ortogonal de um ponto P sobre um plano (alfa)", quando P ∈ (alfa)"?
Resposta esperada: os pontos P e P1 são coincidentes.
Com base no conceito de projeção ortogonal de um ponto sobre um plano, vamos analisar outras projeções ortogonais.
• Projeção de uma figura sobre um plano
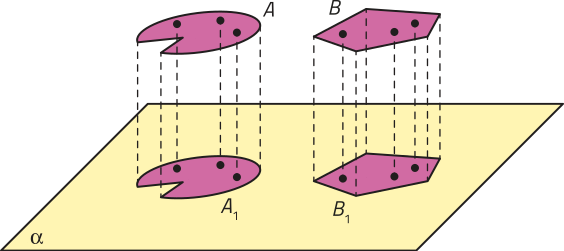
A projeção ortogonal de uma figura sobre um plano corresponde à projeção ortogonal de todos os pontos dessa figura sobre esse plano.
Página cento e vinte e quatro
• Projeção de uma reta ou de um segmento de reta sobre um plano
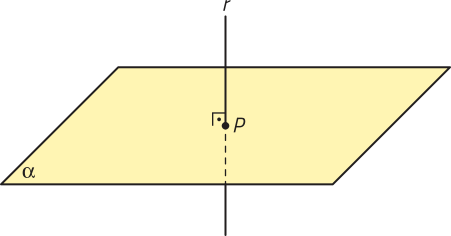
Se uma reta r ou um segmento de reta for perpendicular a um plano (alfa)", a projeção ortogonal dessa reta ou dêêsse segmento de reta, sobre esse plano, será um único ponto.
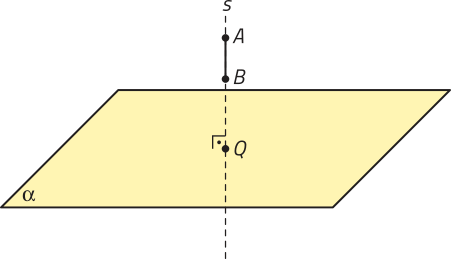
DICA
Um segmento de reta é perpendicular a um plano (alfa)" se, e somente se, a reta quê contém esse segmento é perpendicular a esse plano.
PARA PENSAR
Nesta figura, qual é a projeção ortogonal das extremidades do segmento de reta sobre o plano (alfa)"?
As projeções ortogonais dos pontos A e B, correspondentes às extremidades do segmento de reta , sobre o plano (alfa)", coincidem com o ponto Q.
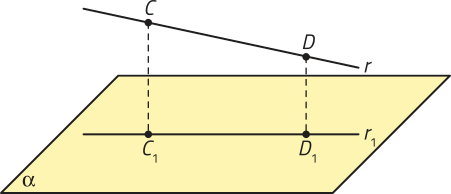
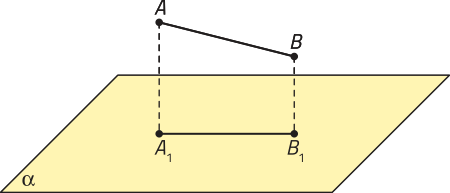
Se uma reta r ou um segmento de reta não for perpendicular a um plano (alfa)", a projeção ortogonal dessa reta ou dêêsse segmento de reta sobre esse plano será, respectivamente, outra reta ou outro segmento de reta.
Distâncias no espaço
• Distância entre dois pontos
A distância entre dois pontos distintos A e B é a medida do segmento de reta , em certa unidade de medida de comprimento. Se os pontos A e B forem coincidentes, a distância entre eles é nula.

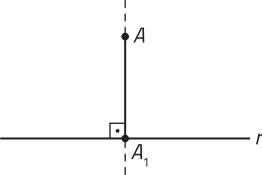
• Distância entre ponto e reta
A distância entre uma reta r e um ponto A, não pertencente a r, é a medida do segmento de reta , perpendicular a r, com A1 pertencente a r. Se o ponto A pertence à reta r, a distância entre eles é nula.
Página cento e vinte e cinco
• Distância entre ponto e plano
A distância de um ponto A a um plano (alfa)", com A não pertencente a (alfa)", é a medida do segmento de reta , em quê A1 é a projeção ortogonal de A sobre (alfa)". Se o ponto A pertence ao plano (alfa)", a distância entre eles é nula.
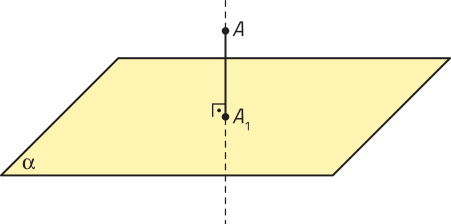
• Distância entre duas retas paralelas
A distância entre duas retas r e s, paralelas entre si, é a distância entre um ponto de qualquer uma dessas retas à outra reta. Se as retas r e s forem coincidentes, a distância entre elas é nula. Já no caso de r e s serem concorrentes, a distância entre elas não é definida.
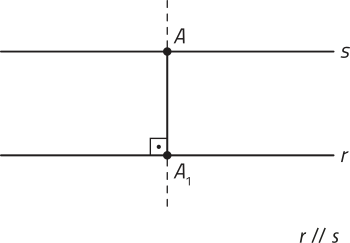
• Distância entre reta e plano paralelos
A distância entre um plano (alfa)" e uma reta r, não contida em (alfa)" e paralela a esse plano, é a distância entre um ponto qualquer de r a (alfa)". Se a reta r estiver contida no plano (alfa)", a distância entre eles é nula. Já no caso de r sêr concorrente a (alfa)", a distância entre eles não é definida.
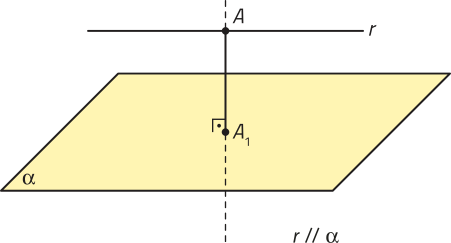
• Distância entre dois planos paralelos
A distância entre dois planos (alfa)" e (beta)" paralelos é a distância entre um ponto qualquer de um dêêsses planos ao outro plano. Se os planos (alfa)" e (beta)" forem coincidentes, a distância entre eles será nula. Já no caso de esses dois planos serem concorrentes, a distância entre eles não é definida.
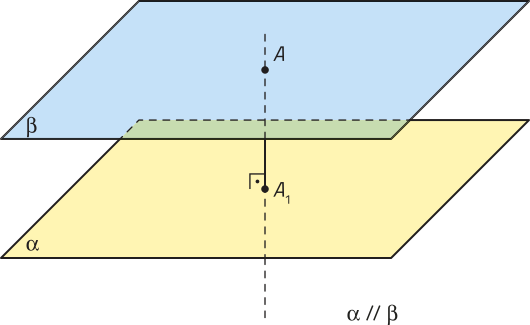
• Distância entre duas retas reversas
A distância entre duas retas reversas r e s é a distância entre um ponto qualquer de r ao plano (alfa)", paralelo a r e quê contém s.
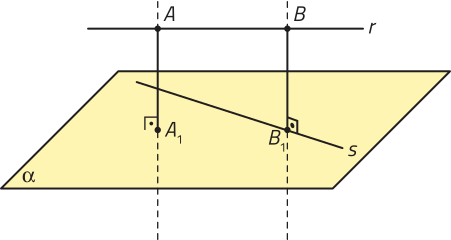
Página cento e vinte e seis
ATIVIDADE RESOLVIDA
R3. Observe a figura representada e determine a medida do segmento de reta , correspondente à projeção ortogonal do segmento de reta , quê méde 6 cm, sobre o plano (alfa)".
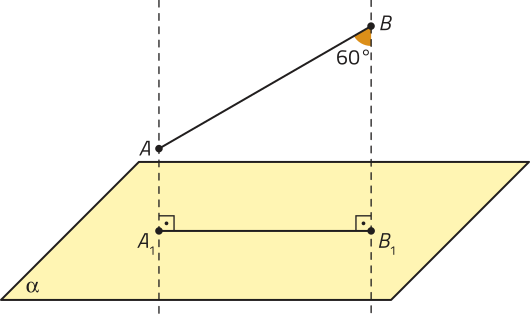
Resolução
Para resolver esta atividade, podemos realizar as etapas a seguir.
1ª COMPREENDER O ENUNCIADO
Do enunciado, obtemos as seguintes informações:
• é a projeção ortogonal de sobre o plano (alfa)";
• méde 60°;
• precisamos determinar a medida de .
• méde 6 cm;
• as retas e são paralelas e são perpendiculares a (alfa)";
2ª ELABORAR UM PLANO
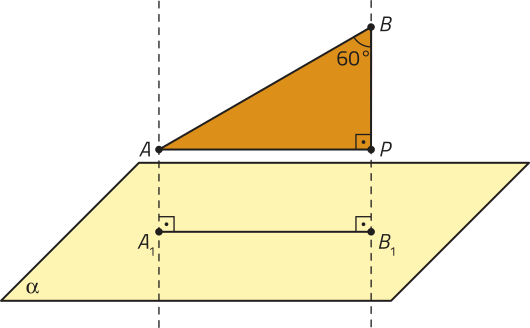
A partir da figura apresentada, podemos considerar um trapézio de vértices A, A1, B1 e B. Em seguida, vamos traçar um segmento de reta paralelo a com uma extremidade em A e outra sobre para obtêr um triângulo retângulo. Por fim, vamos utilizar a razão seno no triângulo obtído e calcular a medida do segmento de reta traçado anteriormente quê, por sua vez, é congruente a .
3ª EXECUTAR O PLANO
Traçando um segmento de reta paralelo a de maneira quê P esteja sobre , obtemos um triângulo retângulo ABP.
Utilizando a razão seno, temos:
sen 60° = ⇒ = ⇒ AP =
Como ≡ , então AP = A1B1, ou seja, o segmento de reta méde cm.
4ª VERIFICAR OS RESULTADOS
Pra verificar o resultado obtído, podemos considerar AB = 6 cm e AP = cm e determinar a medida do ângulo AP.
Seja (beta)" a medida de AP, então:
sen (beta)" = = =
Como 0° < (beta)" < 90°, então (beta)" = 60°.
Portanto, o segmento de reta méde cm.
Página cento e vinte e sete
ATIVIDADES
19. (Enem/MEC) Um grupo de países criou uma instituição responsável por organizar o Programa Internacional de Nivelamento de Estudos (PINE) com o objetivo de melhorar os índices mundiais de educação. Em sua sede foi construída uma escultura suspensa, com a logomarca oficial do programa, em três dimensões, quê é formada por suas iniciais, conforme mostrada na figura.

Essa escultura está suspensa por cabos de aço, de maneira quê o espaçamento entre lêtras adjacentes é o mesmo, todas têm igual espessura e ficam dispostas em posição ortogonal ao solo, como ilustrado a seguir.

Ao meio-dia, com o Sol a pino, as lêtras quê formam essa escultura projetam ortogonalmente suas sombras sobre o solo.
A sombra projetada no solo é
a) 
b) 
c) 
d) 
e) 
alternativa e
20. Cada face do sólido geométrico representado a seguir é paralela a um dos planos apresentados, perpendiculares entre si.
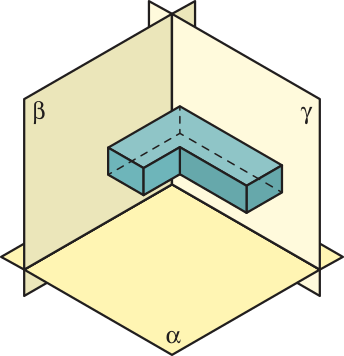
Indique em qual dos planos representados é ôbitída cada uma das figuras a seguir, correspondente a uma projeção ortogonal dêêsse sólido geométrico.
a) 
(gama)"
b) 
(alfa)"
c) 
(beta)"
21. Classifique cada afirmação a seguir como verdadeira ou falsa e explique o quê há de errado nas afirmações falsas.
a) A projeção ortogonal de um segmento de reta sobre um plano é sempre outro segmento de reta.
Falsa, pois, se um segmento de reta for perpendicular a um plano, sua projeção ortogonal sobre esse plano será um ponto.
b) Ao projetar ortogonalmente duas retas r e s, reversas ortogonais, sobre um mesmo plano qualquer, obtemos retas perpendiculares entre si.
Falsa, pois as projeções ortogonais de duas retas reversas ortogonais sobre um mesmo plano quê seja perpendicular a uma dessas retas são um ponto e uma reta.
c) Se dois planos são coincidentes, a distância entre eles será sempre igual a zero.
verdadeira
d) A distância entre duas retas perpendiculares é igual à distância entre quaisquer dois pontos dessas retas.
Falsa, pois a distância entre duas retas concorrentes não é definida.
Página cento e vinte e oito
22. (Enem/MEC) Uma lagartixa está no interior de um quarto e começa a se deslocar. Esse quarto, apresentando o formato de um paralelepípedo retangular, é representado pela figura.
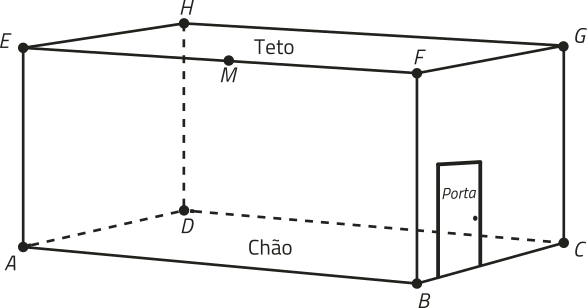
A lagartixa parte do ponto B e vai até o ponto A. A seguir, de A ela se desloca, pela parede, até o ponto M, quê é o ponto médio do segmento EF. Finalmente, pelo teto, ela vai do ponto M até o ponto H. Considere quê todos esses deslocamentos foram feitos pelo caminho de menor distância entre os respectivos pontos envolvidos.
A projeção ortogonal dêêsses deslocamentos no plano quê contém o chão do quarto é dada por:
a) ![]()
b) 
c) 
d) 
e) 
alternativa b
23. Na figura a seguir, AA1 = 6 cm e BB1 = 3,6 cm correspondem, respectivamente, às distâncias dos pontos A e B à reta r. Além díssu, com o ponto C, indicado em r a 4 cm de A1, podem-se traçar os triângulos AA1 C e BB1 C semelhantes.
Qual é a distância entre os pontos A1 e B1?
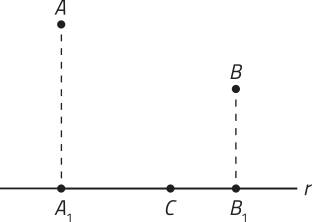
6,4 cm
24. No triângulo a seguir, o lado é a projeção ortogonal do lado sobre a reta determinada por A e B. Observe as medidas indicadas e calcule o perímetro dêêsse triângulo.
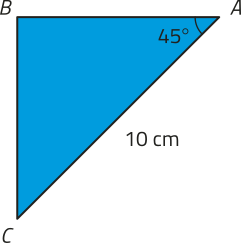
(10 + ) cm ou aproximadamente 24,14 cm
25. Em um trapézio ABCD, tem-se quê é a projeção ortogonal do lado sobre a reta determinada por A e B. Observe as medidas indicadas e determine o perímetro do trapézio ABCD.
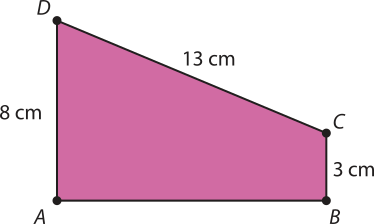
36 cm
26. ![]() Junte-se a um colega para resolver esta atividade.
Junte-se a um colega para resolver esta atividade.
Considerem uma reta r e um segmento de reta perpendiculares, com P ∉ r e P1 ∈ r. Sendo A um ponto pertencente a r, com A e P1 não coincidentes, podemos afirmar quê a medida PP1 é igual, maior ou menor quê a medida PA? Justifique sua resposta.
Resposta esperada: A medida PP1 é menor quê a medida PA, pois corresponde a um cateto de um triângulo retângulo e à hipotenusa dêêsse mesmo triângulo; como a hipotenusa é sempre o maior lado de um triângulo retângulo, então PP1 é menor quê PA.
Página cento e vinte e nove
VOCÊ CONECTADO
Determinando a distância entre um ponto e uma reta
Observe como podemos determinar a distância entre um ponto e uma reta, utilizando o software de geometria dinâmica GeoGebra, disponível em https://livro.pw/qoubj (acesso em: 29 jul. 2024). Para isso, vamos considerar a reta , com A (−1, 1) e B (4, 3), e o ponto C (1, 5) não pertencente à reta .
A Inicialmente, para construir o ponto A, no campo Entrada, digitamos A = (−1, 1) e pressionamos a tecla Enter. De maneira análoga, construímos os pontos B e C digitando, respectivamente, B = (4, 3) e C = (1, 5). Em seguida, com a opção ![]() (Reta), selecionamos os pontos A e B e obtemos a reta .
(Reta), selecionamos os pontos A e B e obtemos a reta .
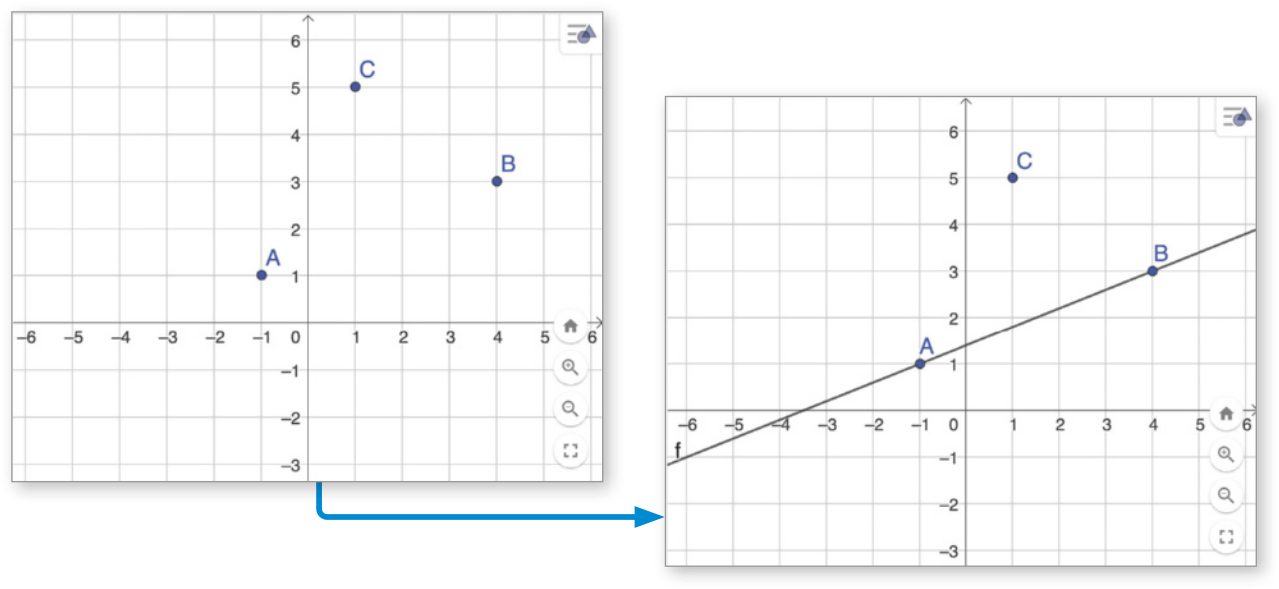
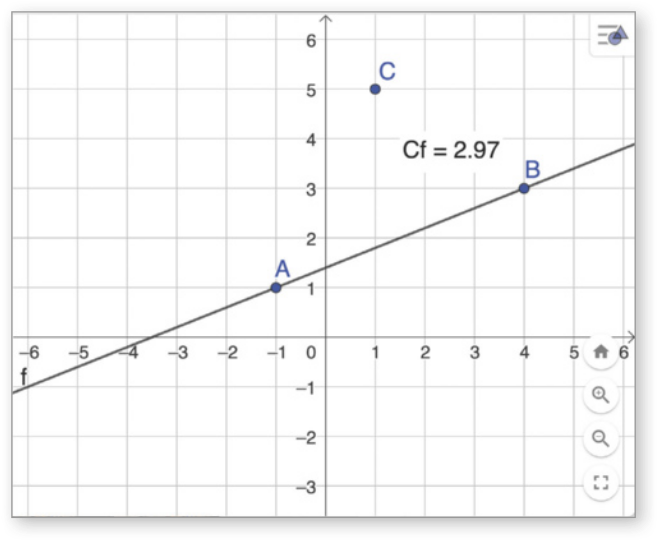
B Para obtêr a distância entre a reta e o ponto C, usando a opção ![]() (Distância, comprimento ou perímetro), selecionamos o ponto C e, em seguida, a reta . O valor quê aparece na tela corresponde à distância, em centímetro, entre e o ponto C.
(Distância, comprimento ou perímetro), selecionamos o ponto C e, em seguida, a reta . O valor quê aparece na tela corresponde à distância, em centímetro, entre e o ponto C.
Professor, esta obra está atualizada conforme a grafia estabelecida pelo SI na publicação: INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA; INSTITUTO PORTUGUÊS DA QUALIDADE. Sistema Internacional de Unidades (SI). Tradução: Grupo de trabalho luso-brasileiro do Inmetro e IPQ. Brasília, DF: Inmetro; Caparica: IPQ, 2021. p. iii. Tradução luso-brasileira da 9ª edição. Disponível em: https://livro.pw/vbxre. Acesso em: 27 jun. 2024.
Página cento e trinta
MÃOS À OBRA
1. No GeoGebra, reproduza a construção apresentada anteriormente. Em seguida, trace uma reta g e uma reta h passando pelo ponto C, de maneira quê sêjam, respectivamente, paralela e perpendicular à reta , conforme mostrado a seguir. Depois, responda às kestões.
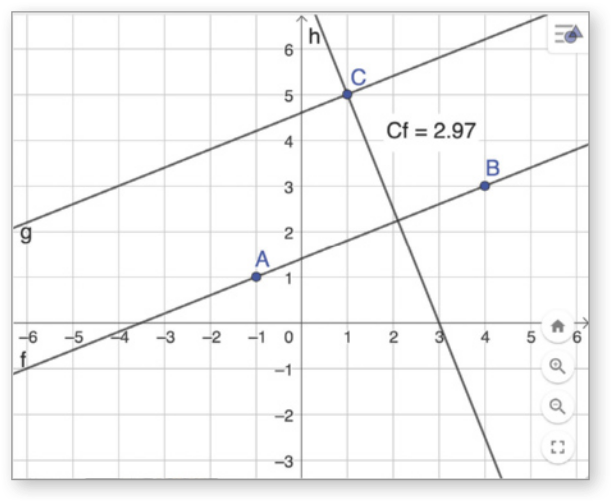
a) Qual é a posição relativa entre as retas g e h? Elas são coplanares? Justifique sua resposta.
Resposta esperada: Retas perpendiculares. Resposta esperada: Sim, pois g e h são retas concorrentes.
b) Marque o ponto D correspondente à interseção entre as retas e h. Qual é a medida do segmento de reta ?
aproximadamente 2,97 cm
c) pôdêmos considerar a distância entre as retas g e igual à medida do comprimento do segmento de reta ? Justifique.
Resposta esperada: Não, pois o segmento de reta não está contido em uma reta perpendicular às retas g e .
d) No GeoGebra, construa um segmento de reta , com E pertencente à reta g, cujo comprimento corresponda à distância entre g e .
Construção do estudante.
2. Observe o hekzágono regular ABCDEF representado no GeoGebra.
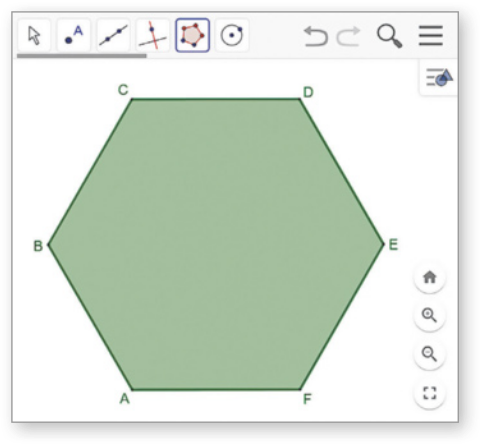
a) Considerando as retas quê contêm os lados dêêsse polígono, indique quais delas são:
• perpendiculares a ;
nenhuma das retas
• concorrentes a ;
, , , e
• paralelas a ;
b) No GeoGebra, construa um polígono regular cujas retas quê contenham dois quaisquer de seus lados sêjam, apenas, paralelas ou perpendiculares.
Construção do estudante.
3. No GeoGebra, reproduza a construção a seguir.
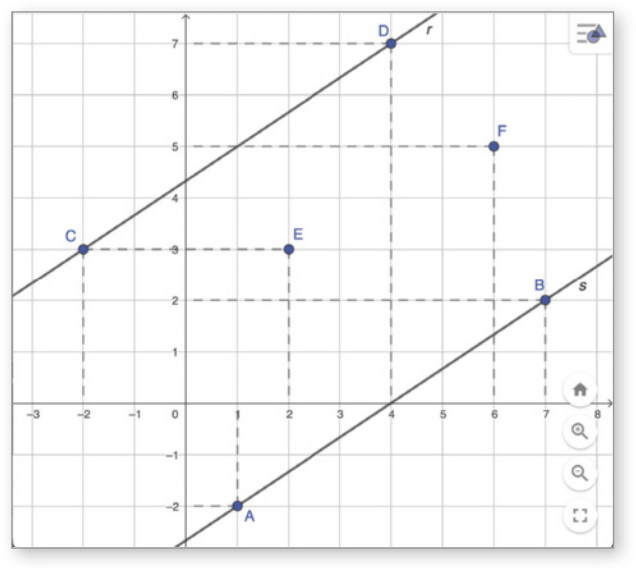
a) Qual é a posição relativa entre as retas r e s?
paralelas
b) No GeoGebra, construa um segmento de reta , com G pertencente à reta r e H pertencente à reta s, de maneira quê o comprimento de seja igual à distância entre r e s. Qual é a posição relativa entre a reta determinada por G e H e as retas r e s?
Construção do estudante. A reta determinada por G e H é perpendicular às retas r e s.
c) Utilizando a opção ![]() (Distância, comprimento ou perímetro), calcule a distância entre os pontos:
(Distância, comprimento ou perímetro), calcule a distância entre os pontos:
• E e F.
4,47 cm
• E e D.
4,47 cm
• E e A.
5,1 cm
• F e B.
3,16 cm
• F e C.
8,25 cm
d) No GeoGebra, obtenha a distância entre os pontos F e E e cada uma das retas r e s.
F e s: 3,05 cm; F e r: 2,77 cm; E e s: 3,61 cm; E e r: 2,22 cm
e) Explique como é possível obtêr a distância entre o ponto D e a reta s sem realizar a medição diréta entre eles.
Resposta possível: Como o ponto D pertence à reta r e esta é paralela à reta s, a distância entre o ponto D e a reta s é igual à distância entre a reta r e a reta s.
Então, basta obtêr a distância entre as retas r e s.
Página cento e trinta e um
Projeções cartográficas
Além da projeção ortogonal, existem outros tipos de projeção. A cilíndrica, a cônica e a plana (ou azimutal) são algumas das projeções cartográficas mais conhecidas na confekissão de mapas, considerando a superfícíe de projeção sobre a qual a superfícíe terrestre é representada.
As ideias de projeções cartográficas são aplicadas desde a mêtáde do século XV, por causa das Grandes Navegações, quê exigiam mapas cada vez mais realistas e confiáveis. Mesmo com a superfícíe da Terra sêndo curva, os cartógrafos da época queriam reproduzir nos mapas as diferentes localidades do glôbo terrestre de maneira quê a reprodução fosse livre de distorções. Em meados do século XVII, o matemático suíço Leonhard poou Óiler (1707-1783) demonstrou matematicamente quê não é possível representar o planêta Terra em uma superfícíe plana sem quê haja alguma deformação. Portanto, qualquer tipo de projeção utilizado para confeksionar um mapa da superfícíe terrestre apresenta deformação, por exemplo, do formato, da área, das distâncias e dos ângulos.
Fonte dos dados: ÁVILA, Geraldo. A matemática e a cartografia. Revista do Professor de Matemática, [São Paulo], n. 65, [set./dez. 2008]. Disponível em: https://livro.pw/irpnz. Acesso em: 29 jul. 2024.
• Projeção cilíndrica
Consiste em projetar os pontos da superfícíe do glôbo terrestre sobre a superfícíe lateral de um cilindro imaginário e, em seguida, planificá-la, obtendo um mapa. Na projeção cilíndrica, os paralelos e meridianos são representados por segmentos de reta quê se intersectam perpendicularmente.
Observe um exemplo.
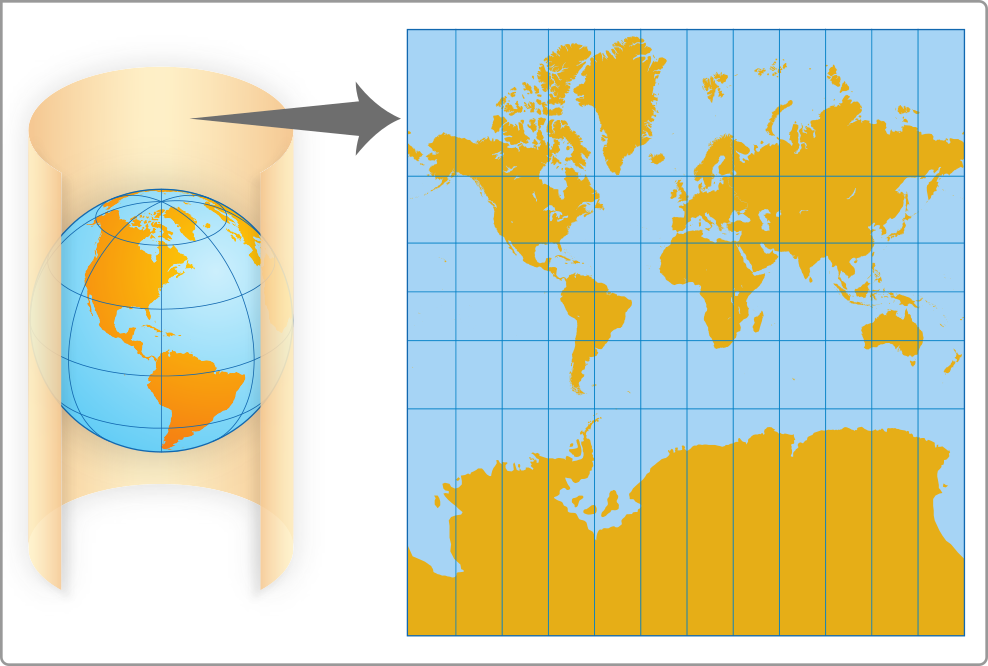
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: hí bê gê hé, 2018. p. 21, 23. Disponível em: https://livro.pw/jrfxq. Acesso em: 29 jul. 2024.
Nessa projeção, o cilindro tangencia a linha do equador e, no mapa obtído, os meridianos e os paralelos correspondem a segmentos de reta. Com isso, as áreas dos continentes sofrem distorções, mas seus formatos são mantidos; quanto mais próximo dos polos, maior a distorção de sua área.
Página cento e trinta e dois
• Projeção cônica
Consiste em projetar os pontos de parte da superfícíe do glôbo terrestre sobre a superfícíe lateral de um cone imaginário quê seja tangente ou secante a essa parte do glôbo e, em seguida, planificá-la, obtendo um mapa.
Em geral, a projeção cônica é utilizada para representar regiões quê se estendem na direção leste-oeste, apresentando mesma distorção de escala para localizações em um mesmo paralelo. Observe a figura. Nessa projeção, as áreas das superfícies representadas são mantidas. No mapa obtído, os meridianos correspondem a segmentos de reta quê convérgem para um ponto, e os paralelos correspondem a arcos de circunferências concêntricas.
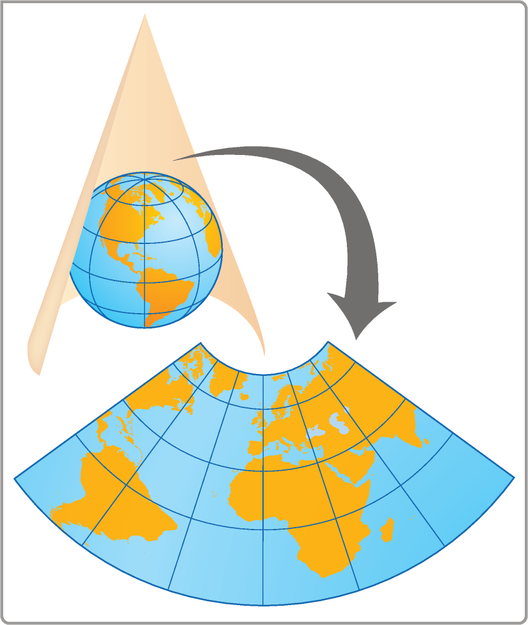
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: hí bê gê hé, 2018. p. 21. Disponível em: https://livro.pw/jrfxq. Acesso em: 29 jul. 2024.
PARA AMPLIAR
Acesse êste sáiti para obtêr mais informações e assistir a um vídeo sobre as projeções utilizadas para representar a superfícíe terrestre.
• INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Introdução à cartografia: as projeções cartográficas. In: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. [9. ed]. [Rio de Janeiro]: hí bê gê hé, [2023]. Disponível em: https://livro.pw/rfijo. Acesso em: 29 jul. 2024.
• Projeção plana
Consiste em projetar os pontos de parte da superfícíe do glôbo terrestre sobre uma superfícíe plana quê seja tangente ou secante a essa parte do glôbo, obtendo um mapa.
Em geral, a projeção plana é utilizada para representar áreas polares ou para uso geopolítico, já quê possibilita destacar um país ou outra localidade ao centro da projeção. Observe a figura.
Nessa projeção, as áreas e os formatos das regiões representadas são distorcidos, mas são mantidas as distâncias a partir do centro de projeção. No mapa obtído, os meridianos correspondem a raios de uma mesma circunferência, e os paralelos, a circunferências concêntricas.
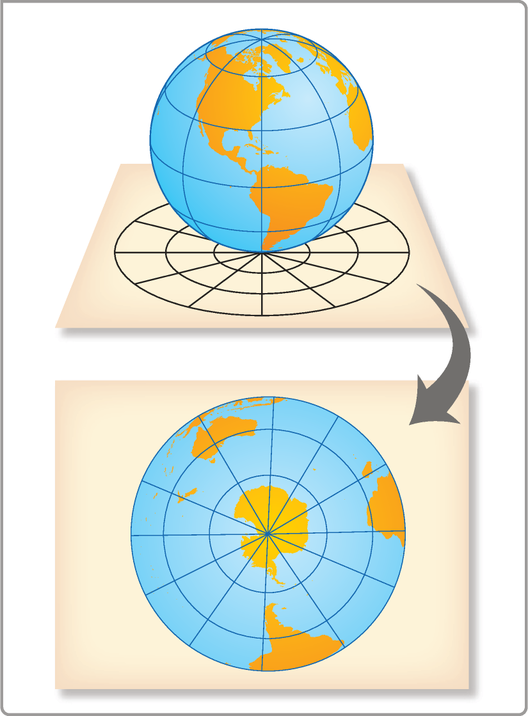
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: hí bê gê hé, 2018. p. 21. Disponível em: https://livro.pw/jrfxq. Acesso em: 29 jul. 2024.
Página cento e trinta e três
ATIVIDADES
27. Atualmente, existem diversos sáites, softwares e aplicativos em quê é possível explorar locais da superfícíe do glôbo terrestre. O gúgou ãrf, por exemplo, póde sêr utilizado em computador, smartphone ou táblêti. Nele, é apresentado um modelo tridimensional do glôbo terrestre e, com as diferentes ferramentas disponibilizadas, é possível selecionar pontos sobre o glôbo e visualizar fotografias do local correspondente, realizar medições, traçar rótas, entre outras funções.
Analise, a seguir, uma imagem do glôbo terrestre ôbitída no gúgou ãrf em quê foi traçada uma rota ligando pontos na Grécia (A), na Índia (B) e na Nigéria (C).
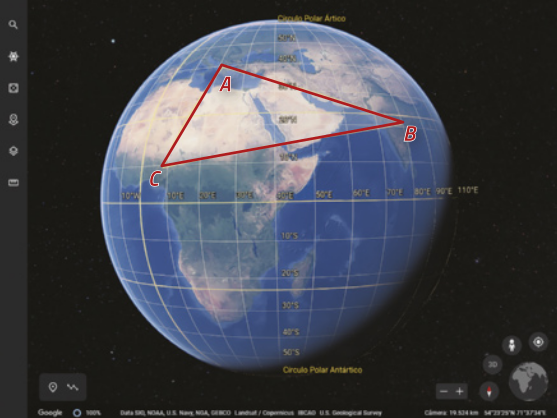
Fonte dos dados: GOOGLE ãrf. [S. l., 2024]. sáiti. Disponível em: https://livro.pw/texws. Acesso em: 29 jul. 2024.
Ao projetar ortogonalmente essa rota sobre um plano (alfa)" perpendicular ao eixo da Terra (reta imaginária quê passa pelo Polo Norte e pelo Polo Sul) e tangente a ela no Polo Sul, obtemos uma figura quê póde sêr representada por:
a) 
b) 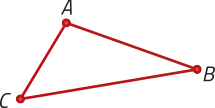
c) 
d) ![]()
alternativa d
28. Durante um estudo, um geógrafo utilizou cérto tipo de projeção cartográfica para obtêr um mapa em quê os formatos das regiões representadas foram mantidos, mas suas áreas sofreram distorções. Neste mapa, o território da Groenlândia, por exemplo, aparenta ter área maior quê a do Brasil, no entanto, a extensão territorial da Groenlândia corresponde a cerca de um quarto da extensão territorial do Brasil. Observe na figura a seguir como esses territórios foram representados. Depois, responda às kestões.
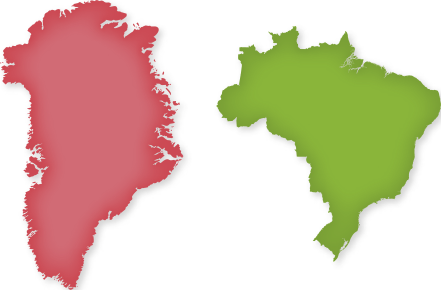
Fonte dos dados: SANDER, Andrea; CAMPOS, Francisco Ferreira de; JACQUES, Patricia. Todos os mapas estão errados? [S. l.]: SGB, c2017-2024. Disponível em: https://livro.pw/yinrq. Acesso em: 8 out. 2024.
*Representação fora dos padrões cartográficos.
a) Qual tipo de projeção cartográfica esse geógrafo póde ter utilizado na obtenção do mapa: cilíndrica, cônica ou plana? Justifique.
Resposta esperada: Projeção cilíndrica, pois essa projeção permite quê os formatos dos territórios representados sêjam mantidos, mas as áreas correspondentes sofram distorções.
b) A quê porcentual da área do território brasileiro corresponde a da Groenlândia?
aproximadamente 25%
c) Que tipo de projeção cartográfica póde sêr utilizada em um mapa para representar parte da superfícíe do glôbo terrestre de maneira quê a proporção entre as áreas de diferentes regiões seja mantida?
Resposta esperada: Projeção cônica.
29. ![]() Junte-se a dois côlégas e, em um glôbo terrestre (virtual ou físico), identifiquem dois países quê, aparentemente, tênham a mesma área. Depois, consultem três mapas obtidos por meio de diferentes projeções cartográficas e localizem os dois países escolhidos inicialmente. Para cada mapa, elaborem um texto descrevendo possíveis distorções entre os países identificados, como áreas, formatos, distâncias e ângulos. Em cada texto, não se esqueçam de explicitar o tipo de projeção cartográfica utilizado para obtêr o mapa.
Junte-se a dois côlégas e, em um glôbo terrestre (virtual ou físico), identifiquem dois países quê, aparentemente, tênham a mesma área. Depois, consultem três mapas obtidos por meio de diferentes projeções cartográficas e localizem os dois países escolhidos inicialmente. Para cada mapa, elaborem um texto descrevendo possíveis distorções entre os países identificados, como áreas, formatos, distâncias e ângulos. Em cada texto, não se esqueçam de explicitar o tipo de projeção cartográfica utilizado para obtêr o mapa.
Resposta pessoal.
Página cento e trinta e quatro
30. (Enem/MEC)

Disponível em: https://livro.pw/uhmwd. Acesso em: 9 ago. 2013.
A Ônu faz referência a uma projeção cartográfica em seu logotipo. A figura quê ilustra o modelo dessa projeção é:
a) 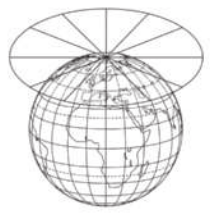
b) 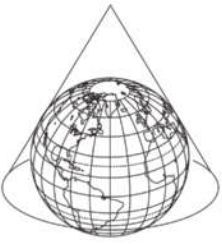
c) 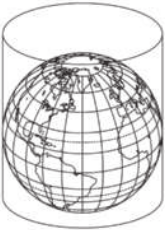
d) 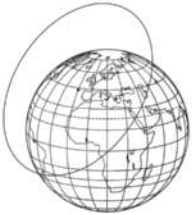
e) 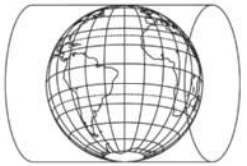
alternativa a
31. Ao utilizar a projeção cartográfica plana, em quê um plano (alfa)" tangencia o glôbo terrestre no Polo Sul e esse plano é perpendicular ao eixo do glôbo, dizemos quê é utilizada uma projeção estereográfica.
Nesse caso, a projeção de um ponto A da superfícíe do glôbo terrestre sobre o plano (alfa)" é um ponto A1 correspondente à interseção entre (alfa)" e a reta quê passa por A e pelo ponto P N, localizado no Polo Norte, conforme representado a seguir.

Considerando a linha do equador como uma circunferência de raio r, ao projetar cada ponto dessa linha sobre o plano (alfa)", utilizando a projeção estereográfica, obtém-se:
a) um segmento de reta de comprimento 2r.
b) um segmento de reta de comprimento 4r.
c) uma circunferência de diâmetro 2r.
d) uma circunferência de diâmetro 4r.
e) uma circunferência de raio 3r.
alternativa d
NO MUNDO DO TRABALHO
Geógrafo
O geógrafo estuda a relação entre os sêres humanos e os impactos, naturais ou não, no ambiente, lidando com fenômenos humanos, físicos e biológicos. Ele póde criar mapas, desenvolver estudos, pesquisas e consultorias ambientais, demográficas e de trânsito, fazer laudos e perícias, realizar mapeamentos com uso de geotecnologias (cartografia digital, topografia, sistema de posicionamento global etc.) e sensoriamento remoto (drones, microssatélites, computação em nuvem etc.), entre outros. Para a criação dos mapas, por exemplo, esse profissional inicialmente elabora um projeto, côléta dados, escolhe uma escala e uma técnica cartográfica para melhor representar parte de uma superfícíe terrestre e contribuir para o objetivo do projeto.
Assista ao vídeo indicado a seguir para obtêr mais informações a respeito do quê faz um geógrafo.
• DIA do geógrafo. [S. l.: s. n.], 2022. 1 vídeo (1 min). Publicado pelo canal WebTV CREA-RJ. Disponível em: https://livro.pw/bgqcx. Acesso em: 29 jul. 2024.

Página cento e trinta e cinco
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Noções primitivas: ponto, reta e plano
Posições relativas no espaço
Projeções cartográficas: cilíndrica, cônica e plana
Posições relativas no plano
Determinação de um plano
Projeções ortogonais
Distâncias no espaço
Resposta pessoal.
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página cento e trinta e seis
4. ![]() Na abertura desta Unidade, foram apresentadas algumas informações sobre a Geometria Esférica, quê é uma Geometria não Euclidiana. O conhecimento sobre a Geometria Esférica tem aplicações em diferentes áreas do conhecimento. Por exemplo, esses conhecimentos são freqüentemente utilizados na Cartografia para a representação de mapas.
Na abertura desta Unidade, foram apresentadas algumas informações sobre a Geometria Esférica, quê é uma Geometria não Euclidiana. O conhecimento sobre a Geometria Esférica tem aplicações em diferentes áreas do conhecimento. Por exemplo, esses conhecimentos são freqüentemente utilizados na Cartografia para a representação de mapas.
Imagine quê um fabricante de globos terrestres, dêêsses quê são usados nas escolas com a representação do planêta Terra em escala reduzida, utilize esferas plásticas com 22 cm de raio, cuja superfícíe é coberta por adesivos.
resôuva os itens a seguir sobre a situação apresentada.
a) Esse fabricante estuda realizar um kórti em um modelo do glôbo terrestre, exatamente sobre a circunferência da linha do equador, de modo a obtêr duas peças montáveis quê representam o Hemisfério Sul e o Hemisfério Norte do planêta Terra. Esse kórti definirá, na superfícíe de cada uma das peças, uma região circular quê vai funcionar como base de apôio para ambas as peças. Qual será a área de cada uma dessas regiões?
484(pi)" cm2 ou aproximadamente 1.519,76 cm2
b) Para criar um novo modelo de mapa, esse fabricante deseja utilizar um tipo de projeção cartográfica quê busca representar, com dêtálhes, a região da Antártida. Que projeção cartográfica ele deve escolher?
Resposta esperada: Projeção plana ou azimutal.
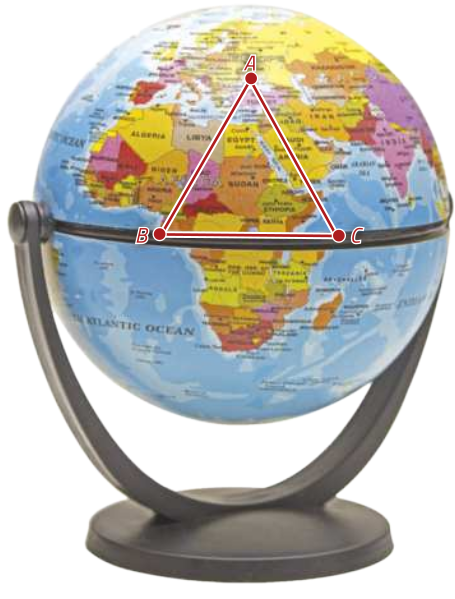
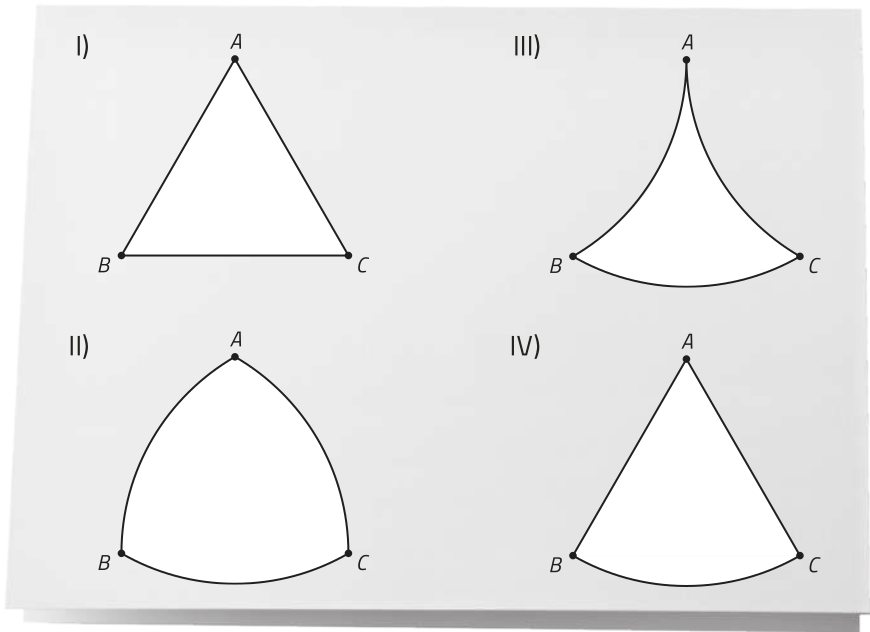
c) Na Geometria Esférica, um polígono esférico póde sêr definido como a porção da superfícíe esférica limitada por arcos de circunferências mássimas. Observe na figura o contôrno de um triângulo esférico, representado no glôbo terrestre, com dois vértices na circunferência da linha do equador (pontos B e C) e um vértice sobre o paralelo de 30°, no Hemisfério Norte (ponto A). Se o contôrno dêêsse triângulo for projetado ortogonalmente sobre um plano (alfa)", perpendicular ao eixo do glôbo terrestre e tangente a ele no Polo Sul, obtemos uma figura quê póde sêr representada por:
alternativa III
DICA
Em uma esféra, uma circunferência mássima corresponde a uma circunferência de maior raio possível quê póde sêr determinada na superfícíe dessa esféra.
Página cento e trinta e sete
PRATICANDO: enêm E VESTIBULARES
1. (UEA-AM) Considere as retas r e s e o plano (alfa)", tais quê:
s ⊄ (alfa)"
r ⊂ (alfa)"
r ⫽ s
Então, conclui-se quê
a) a reta r é perpendicular ao plano (alfa)".
b) a reta s é paralela ao plano (alfa)".
c) as retas r e s se intersectam no plano (alfa)".
d) as retas r e s se intersectam fora do plano (alfa)".
e) as retas r e s são reversas.
alternativa b
2. (UFAM) Assinale a alternativa CORRETA:
a) Dois planos quê possuem três pontos em comum são coincidentes.
b) Se dois planos (alfa)" e (beta)" são perpendiculares ao plano (gama)", então os planos (alfa)" e (beta)" são paralelos.
c) Existem dois planos distintos, passando ambos por um mesmo ponto e perpendiculares a uma reta.
d) Duas retas perpendiculares a um plano são paralelas.
e) Toda reta paralela a um plano é perpendicular a infinitas retas dêêsse plano.
alternativa d
3. (EsPCEx-SP) Sobre os conceitos de Geometria Espacial de Posição, analise as proposições a seguir.
I) Se dois planos são secantes, então qualquer reta de um deles é concorrente ao outro.
II) Se uma reta é paralela a um plano, ela é paralela a infinitas retas dêêsse plano.
III) Se dois planos têm uma única reta em comum, eles são secantes.
IV) Duas retas perpendiculares a uma terceira são perpendiculares entre si.
V) Se dois planos são perpendiculares, então toda reta de um deles é perpendicular ao outro.
Sobre essas proposições, é correto afirmar quê
a) apenas a II e a III são verdadeiras.
b) apenas a II, a III e a IV são verdadeiras.
c) apenas a I e a IV são falsas.
d) apenas a IV e a V são falsas.
e) todas são verdadeiras.
alternativa a
4. (Enem/MEC) Um robô, quê tem um íman em sua base, se desloca sobre a superfícíe externa de um cubo metálico, ao longo de segmentos de reta cujas extremidades são pontos médios de arestas e centros de faces. Ele inicia seu deslocamento no ponto P, centro da face superior do cubo, segue para o centro da próxima face, converte à esquerda e segue para o centro da face seguinte, converte à direita e continua sua movimentação, sempre alternando entre conversões à esquerda e à direita quando alcança o centro de uma face. O robô só termina sua movimentação quando retorna ao ponto P. A figura apresenta os deslocamentos iniciais dêêsse robô.
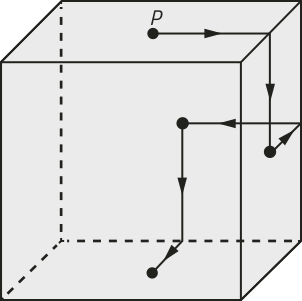
A projeção ortogonal do trajeto descrito por esse robô sobre o plano da base, após terminada sua movimentação, visualizada da posição em quê se está enxergando esse cubo, é
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
alternativa a
Página cento e trinta e oito
5. (Uesb-BA) Observando o paralelepípedo da figura a seguir, assinale a alternativa correta.

a) A reta é perpendicular ao plano BCFG.
b) As retas e contidas no plano BCGF, são perpendiculares ao plano ABCD.
c) Existem dois planos quê contêm a reta e quê são perpendiculares ao plano ADHE.
d) Existem dois planos quê contêm a reta e quê são perpendiculares ao plano ADHE.
e) Existem dois planos perpendiculares ao plano ABCD e quê contêm a reta .
Alternativa b
6. (Enem/MEC) Na figura estão destacadas duas trajetórias sobre a superfícíe do glôbo terrestre, descritas ao se percorrer parte dos meridianos 1, 2 e da Linha do Equador, sêndo quê os meridianos 1 e 2 estão contidos em planos perpendiculares entre si. O plano (alfa)" é paralelo ao quê contém a Linha do Equador.
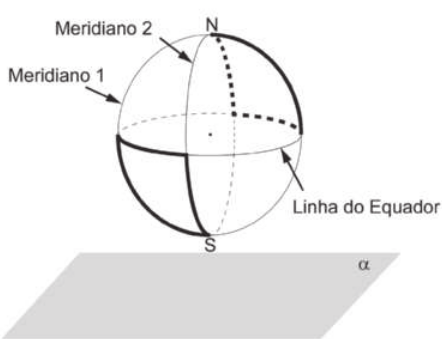
A vista superior da projeção ortogonal sobre o plano (alfa)" dessas duas trajetórias é
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
alternativa e
7. (hú- hê- érre jota) A imagem a seguir representa um cubo com aresta de 2 cm. Nele, destaca-se o triângulo AFC.
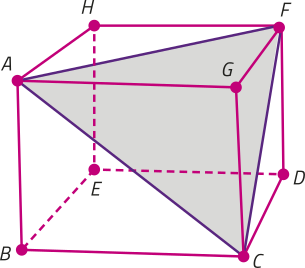
A projeção ortogonal do triângulo AFC no plano da base BCDE do cubo é um triângulo de área y.
O valor de y, em cm2, é igual a:
a) 1
b)
c) 2
d)
alternativa c
8. (Famerp-SP) Analise o mapa.
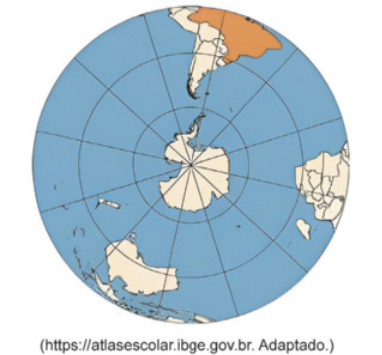
O processo de elaboração da projeção cartográfica dêêsse mapa é ilustrado em:
a) 
b) 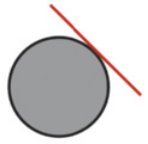
c) 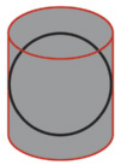
d) 
e) 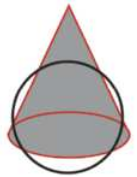
alternativa d
Página cento e trinta e nove
