UNIDADE 4
FIGURAS GEOMÉTRICAS ESPACIAIS, ÁREA DE SUPERFÍCIE E VOLUME
Concreto armado na construção civil
Na história da arquitetura, a partir do século XVII, com a Revolução Industrial, materiais como ferro, aço e concreto passaram a sêr produzidos em maior escala, influenciando uma nova maneira de criar, planejar e arquitetar obras urbanas.
A combinação do concreto com armações de aço em seu interior deu origem ao concreto armado. Ao se desenvolver esse material, foi possível construir elemêntos resistentes, das mais variadas formas e tamanhos, pois o concreto, depois de endurecido, tem resistência similar à das róchas naturais e, quando está fresco, sua plasticidade possibilita modelá-lo.
Observe, a seguir, de maneira resumida, as etapas para a execução de um projeto de construção de pilar estrutural em concreto armado.
Fonte dos dados: BASTOS, Paulo Sérgio. Fundamentos do concreto armado. Bauru: Unésp, 2023. p. 1-7. Disponível em: wwwp.feb.unesp.br/pbastos/concreto1/Fundamentos%20CA.pdf. Acesso em: 9 ago. 2024.

Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Você já observou alguma estrutura de concreto armado no município em quê mora?
2. Na construção de uma edificação em alvenaria, quê estruturas costumam sêr construídas em concreto armado? Se necessário, faça uma pesquisa.
3. O quê deve sêr considerado para determinar o volume de concreto necessário para a construção de uma viga?
Página cento e quarenta
Poliedros
Na abertura desta Unidade, aprendemos quê o concreto armado permite obtêr construções das mais variadas formas e tamanhos. Os formatos de muitas construções, cuja superfícíe é composta apenas de partes planas, lembram figuras geométricas espaciais chamadas poliedros.
Observe, a seguir, um poliedro quê associamos a uma construção.

→
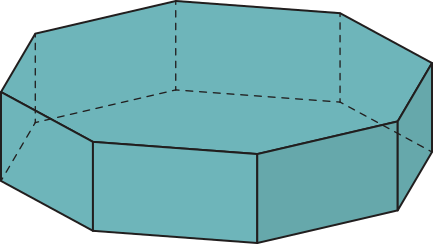
Você conhece alguma construção no bairro ou na cidade em quê você mora quê póde sêr associada a um poliedro? Agora, obissérve outros poliedros a seguir.
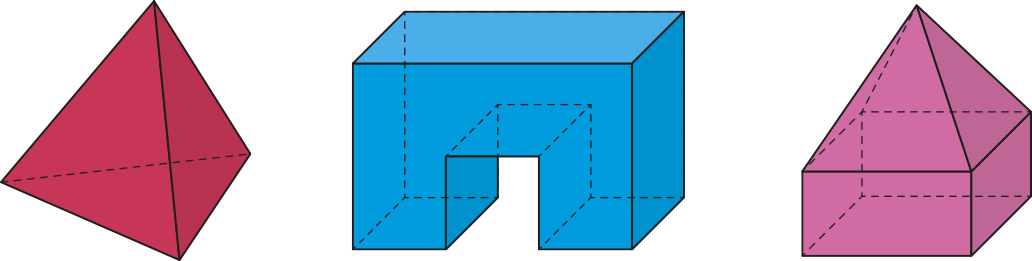
Denominamos poliedro toda figura geométrica espacial cuja superfícíe é formada por uma quantidade finita de polígonos de maneira quê:
• cada lado de um dêêsses polígonos é também lado de apenas um dos outros polígonos;
• dois polígonos adjacentes, ou seja, quê têm pontos em comum, não estão contidos em um mesmo plano;
• a intersecção de dois polígonos distintos do poliedro é um lado comum, um vértice ou o conjunto vazio.
PARA PENSAR
A figura geométrica espacial a seguir apresenta as características de um poliedro? Justifique sua resposta.
Resposta esperada: Não, pois um lado de um dos polígonos quê compõem sua superfícíe é também lado de outros três polígonos.
Página cento e quarenta e um
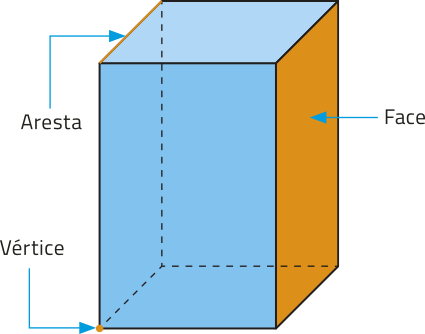
Em todo poliedro, podemos identificar os seguintes elemêntos:
• face é cada um dos polígonos quê compõem sua superfícíe;
• aresta é cada lado comum a duas faces quaisquer;
• vértice é cada ponto em quê se intersectam os lados das faces.
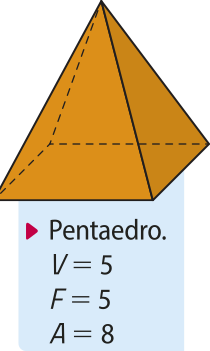
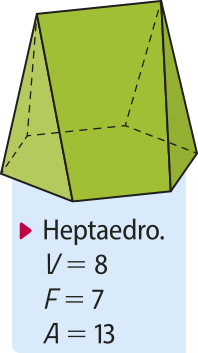
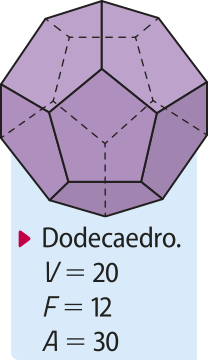
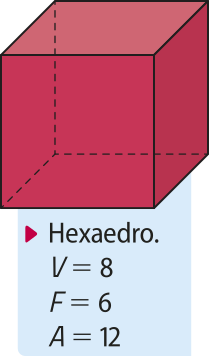
pôdêmos classificar um poliedro de acôr-do com a quantidade de faces. Observe, a seguir, algumas dessas classificações.
Quantidade de faces |
Classificação |
|---|---|
4 |
tetraedro |
5 |
pentaedro |
6 |
hexaedro |
7 |
heptaedro |
8 |
octaedro |
9 |
eneaedro |
10 |
decaedro |
11 |
undecaedro |
12 |
dodecaedro |
13 |
tridecaedro |
14 |
tetradecaedro |
15 |
pentadecaedro |
16 |
hexadecaedro |
17 |
heptadecaedro |
18 |
octadecaedro |
19 |
eneadecaedro |
20 |
icosaedro |
DICA
Dois poliedros podem ter a mesma quantidade de faces, mas ter diferentes quantidades de vértices e de arestas. Observe dois exemplos.
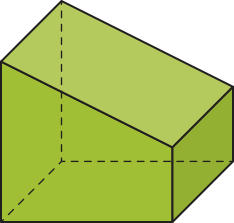
Para nos referirmos aos poliedros com mais de 20 faces, podemos dizêr apenas sua quantidade de faces, sem usar nome especial. Por exemplo, um poliedro de 25 faces.
Acompanhe outra maneira como os poliedros podem sêr classificados.
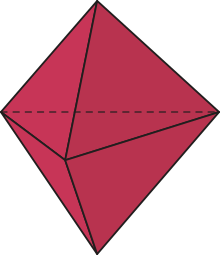
Um poliedro é convexo se qualquer segmento de reta, cujas extremidades são quaisquer dois pontos dêêsse poliedro, está inteiramente contido nele. Caso contrário, o poliedro é não convexo.
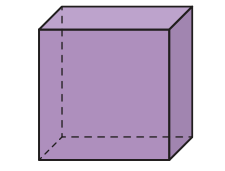
PARA PENSAR
Você lembra a definição de polígono convexo? E de polígono não convexo?
Respostas pessoais.
Página cento e quarenta e dois
Relação de Óiler
Reflita a respeito da seguinte situação.
Um poliedro convexo tem 15 vértices e 27 arestas. Quantas faces tem esse poliedro?
Antes de responder a essa questão, vamos estudar uma relação entre a quantidade de vértices (V), de arestas (A) e de faces (F) de poliedros convexos. Para isso, considere os poliedros a seguir.
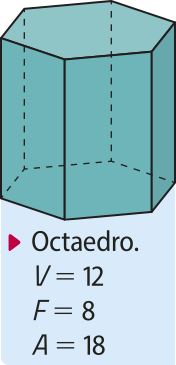
Para cada poliedro apresentado, adicione a quantidade de vértices à quantidade de faces. Você vai perceber quê o resultado é igual à quantidade de arestas mais duas unidades. Essa relação foi apresentada pelo matemático suíço Leonhard poou Óiler (1707-1783), sêndo mais uma dentre suas várias contribuições à Matemática.
Para todo poliedro convexo com A arestas, V vértices e F faces, é válida a seguinte igualdade, conhecida por relação de Óiler:
V + F = A + 2
PARA PENSAR
Escolha um dos poliedros convexos apresentados anteriormente nesta Unidade e verifique a validade da relação de Óiler para esse poliedro.
Resposta pessoal.
É importante considerar quê:
• existem alguns poliedros não convexos para os quais essa relação também é válida;
• não são todas as soluções da equação V + F = A + 2 quê têm um poliedro convexo correspondente. Por exemplo, V = 3, F = 0 e A = 1 é solução dessa equação, porém não existe um poliedro com 3 vértices, 0 face e 1 aresta.
Agora, utilizando a relação de Óiler, vamos retomar a questão proposta no início desta página, ou seja, determinar quantas faces tem o poliedro convexo com 15 vértices e 27 arestas.
V + F = A + 2 → 15 + F = 27 + 2 ⇒ F = 29 − 15 = 14
Portanto, esse poliedro convexo tem 14 faces.
PARA PENSAR
Por meio de um desenho, dê exemplo de um poliedro não convexo e verifique se, para ele, vale a relação de Óiler.
Resposta pessoal.
Página cento e quarenta e três
ATIVIDADES RESOLVIDAS
R1. Quantos vértices e quantas arestas tem um poliedro convexo com 8 faces triangulares e 2 faces quadrangulares?
Resolução
Nesse poliedro convexo, a quantidade total de lados das faces:
• triangulares é 24, pois 8 ⋅ 3 = 24;
• quadrangulares é 8, pois 2 ⋅ 4 = 8.
Cada aresta corresponde ao lado comum a duas faces de um poliedro.
Então, a quantidade total de arestas dêêsse poliedro é dada por:
A = = 16
Como o poliedro é convexo, podemos utilizar a relação de Óiler:
V + F = A + 2 ⇒ V + (8 + 2) = 16 + 2 ⇒ V = 18 − 10 = 8
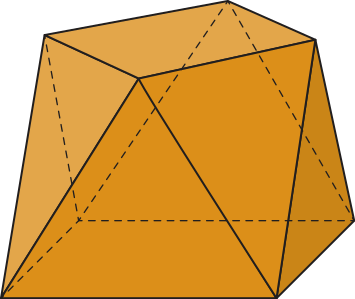
Portanto, esse poliedro tem 8 vértices, 16 arestas e 10 faces.
Observe, ao lado direito da página, um poliedro convexo com essas características.
R2. Alguns poliedros têm características particulares, como os poliedros de Platão, quê recebem esse nome em homenagem ao filósofo grego Platão (c. 427 a.C.-347 a.C.).
Um poliedro de Platão satisfaz às condições a seguir.
I) Todas as faces têm a mesma quantidade de lados.
II) De cada vértice parte a mesma quantidade de arestas.
III) É válida a relação de Óiler.
Em cada item, verifique se o hexaedro convexo apresentado é um poliedro de Platão.
a) 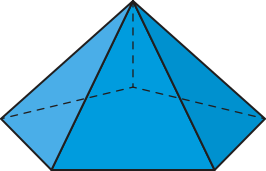
b) 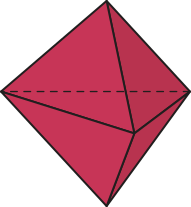
c) 
Resolução
a) Esse hexaedro tem cinco faces com três lados e uma face com cinco lados. Assim, a condição I não é satisfeita. Portanto, esse hexaedro não é um poliedro de Platão.
b) Nesse poliedro, é satisfeita a condição I, pois todas as faces são triangulares. No entanto, a condição II não é satisfeita, pois, de alguns vértices, partem três arestas e, de outros vértices, partem quatro arestas. Portanto, esse hexaedro não é um poliedro de Platão.
c) Esse hexaedro tem as seis faces quadrangulares, satisfazendo a condição I, e, ainda, de cada vértice, partem três arestas, satisfazendo a condição II. Por fim, é válida a relação de Óiler para esse poliedro, pois ele é um poliedro convexo, o quê satisfaz a condição III. Portanto, esse hexaedro é um poliedro de Platão.
Página cento e quarenta e quatro
ATIVIDADES
1. resôuva as kestões com base no poliedro a seguir.
a) Determine a quantidade de vértices, faces e arestas.
7 vértices; 7 faces; 12 arestas
b) Qual é o formato das faces?
4 faces triangulares e 3 faces quadrangulares
c) O vértice A é comum a quantas arestas? E o vértice B?
3 arestas; 4 arestas
2. Desenhe um poliedro convexo e um poliedro não convexo. Depois, para cada um, identifique o formato das faces.
Construção do estudante.
3. Você já montou um cubo mágico convencional? Ele é um quêbra-cabeça com formato de cubo em quê cada face é composta de 9 peças que lembram quadrados congruentes. Atualmente, existem diversas variações dêêsse quebra-cabeça. Uma delas tem o formato de um dodecaedro regular em quê cada face é composta de peças quê lembram 5 losangos congruentes, 5 trapézios congruentes e 1 pentágono regular.

Determine quantas peças de cada formato, ao todo, tem esse quebra-cabeça.
losango: 60 peças; trapézio: 60 peças; pentágono regular: 12 peças
4. Você sabe o quê é um poliedro regular?
Denominamos poliedro regular todo poliedro convexo em quê:
• todas as faces são polígonos regulares congruentes;
• de cada vértice parte a mesma quantidade de arestas.
Analise os cinco únicos poliedros regulares quê existem e suas respectivas planificações.



Agora, resôuva as kestões.
a) A relação de Óiler é válida para os poliedros regulares? Justifique sua resposta.
Resposta esperada: Sim, pois os poliedros regulares são poliedros convexos.
b) Determine a quantidade de faces, de arestas e de vértices e o polígono correspondente a cada face dos poliedros regulares. Indique também a quantidade de arestas quê parte de cada vértice. Organize essas informações em um qüadro.
Resposta nas Orientações para o professor.
c) Todo poliedro regular também é um poliedro de Platão? Justifique sua resposta.
Resposta esperada: Sim, pois, em um poliedro regular qualquer, todas as faces têm a mesma quantidade de lados, de cada vértice parte a mesma quantidade de arestas e é válida a relação de Óiler.
Página cento e quarenta e cinco
5. Qual é a quantidade de vértices de um hexadecaedro convexo formado apenas por faces triangulares?
10 vértices
6. cérto poliedro convexo tem cinco faces quadrangulares, cinco faces triangulares e uma face pentagonal. A quantidade de vértices e de arestas dêêsse poliedro é, respectivamente:
a) 20 e 11;
b) 11 e 40;
c) 11 e 20;
d) 22 e 20;
e) 22 e 40.
alternativa c
7. Considere um poliedro convexo com 30 arestas e 14 vértices cuja superfícíe é formada apenas por faces triangulares e quadrangulares.
pôdêmos afirmar quê esse poliedro tem exatamente faces com os seguintes formatos:
a) 6 triangulares e 12 quadrangulares;
b) 9 triangulares e 9 quadrangulares;
c) 8 triangulares e 10 quadrangulares;
d) 12 triangulares e 6 quadrangulares;
e) 12 triangulares e 12 quadrangulares.
alternativa d
8. Considere um poliedro de Platão em quê uma das faces é um pentágono.
a) Qual das expressões a seguir relaciona as quantidades de vértices V e de faces F dêêsse poliedro?
I) V + F = 10
II) V − 4F = 2
III) 2V − 3F = 4
III
b) Qual é o nome dêêsse poliedro?
dodecaedro
9. Um grupo de estudantes precisa confeksionar um dado quê será usado em um jôgo. O dado terá formato de octaedro regular e eles utilizarão pedaços de tecido para representar cada uma de suas faces. Ao costurar uma lateral de dois pedaços de tecido, unindo duas faces dêêsse dado, são utilizados 9,5 cm de linha. Nessas condições, para realizar toda a costura necessária na superfícíe dêêsse dado, serão utilizados, no mínimo, quantos centímetros de linha?
114 cm de linha
10. (Enem/MEC) No ano de 1751, o matemático Óiler conseguiu demonstrar a famosa relação para poliedros convexos quê relaciona o número de suas faces (F), arestas (A) e vértices (V): V + F = A + 2. No entanto, na busca dessa demonstração, essa relação foi sêndo testada em poliedros convexos e não convexos. Observou-se quê alguns poliedros não convexos satisfaziam a relação e outros não. Um exemplo de poliedro não convexo é dado na figura. Todas as faces quê não podem sêr vistas diretamente são retangulares.
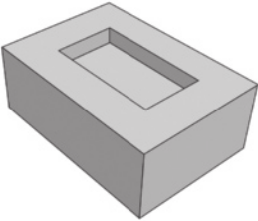
Qual a relação entre os vértices, as faces e as arestas do poliedro apresentado na figura?
a) V + F = A
b) V + F = A − 1
c) V + F = A + 1
d) V + F = A + 2
e) V + F = A + 3
alternativa e
11. (hú- hê- érre jota) Dois dados, com doze faces pentagonais cada um, têm a forma de dodecaedros regulares. Se os dodecaedros estão justapostos por uma de suas faces, quê coincidem perfeitamente, formam um poliedro kon kavu, conforme ilustra a figura.

Considere o número de vértices V, de faces F e de arestas A dêêsse poliedro kon kavu. A soma V + F + A é igual a:
a) 102
b) 106
c) 110
d) 112
alternativa d
DICA
Um poliedro não convexo também póde sêr denominado poliedro kon kavu.
12. Sejam A e B dois poliedros de Platão, em quê A é formado por faces pentagonais e B, por faces triangulares. Sabendo quê A e B têm a mesma quantidade de arestas e quê A tem 8 vértices a mais do quê B, determine a quantidade de faces, vértices e arestas de A e B. Depois, classifique esses poliedros quanto à quantidade de faces.
poliedro A: dodecaedro; 12 faces, 20 vértices e 30 arestas; poliedro B: icosaedro; 20 faces, 12 vértices e 30 arestas
Página cento e quarenta e seis
Prismas
Você sabe o quê são pisos intertravados de concreto? São revestimentos compostos de blocos de concreto assentados diretamente sobre uma camada de areia e travados entre si por contenção lateral. Esses blocos são dispostos com espaços entre eles quê, por sua vez, são preenchidos com areia fina ou pedriscos. Esse tipo de piso apresenta algumas vantagens sustentáveis, como o reaproveitamento de blocos já utilizados e a drenagem da á gua da chuva.
Observe dois modelos de blocos quê compõem um piso intertravado e cujos formatos lembram poliedros.
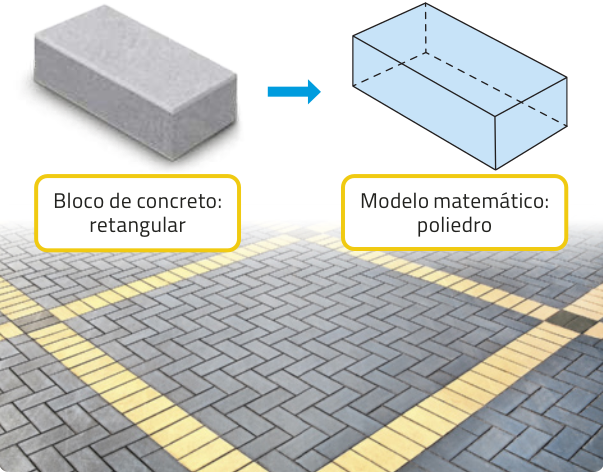
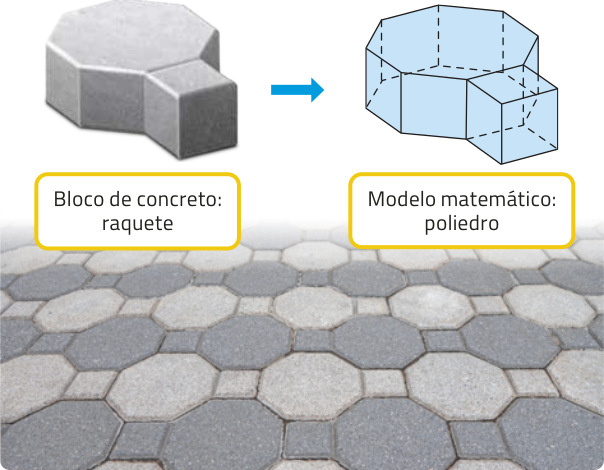
Os poliedros apresentados têm características quê nos permitem classificá-los em prismas.
Agora, vamos estudar prismas de maneira quê seja possível, por exemplo, determinar a área da superfícíe e o volume de pisos de concreto como os apresentados anteriormente.
Dados dois planos distintos e paralelos (alfa)" e (beta)", um polígono convexo contido em (alfa)" e uma reta r concorrente a esses planos, a reunião de todos os segmentos de reta paralelos a r com uma extremidade no polígono e a outra em (beta)" é denominada prisma. Analise o exemplo.
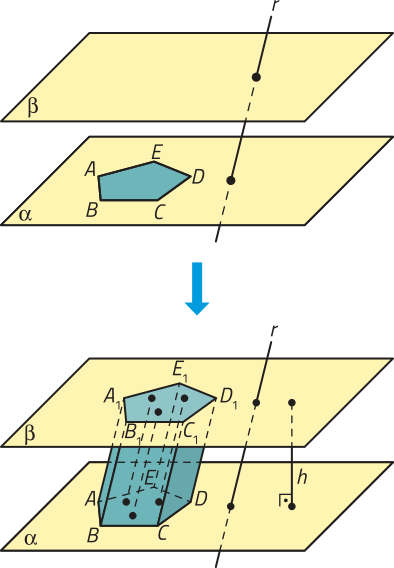
No prisma ABCDEA1B1C1D1E1, podemos destacar os seguintes elemêntos:
• os polígonos ABCDE e A1B1C1D1E1, congruentes, são as bases;
• , , , e são arestas da base ABCDE, e , , , e da base A1B1C1D1E1;
• , , , e são arestas laterais;
• os quadriláteros ABB1A1, BCC1B1, cê dê dê1C1, DEE1D1 e AEE1A1 são faces laterais e correspondem a paralelogramos;
• a distância h, entre o plano (alfa)" e o plano (beta)", é a altura do prisma.
Página cento e quarenta e sete
Os prismas podem sêr denominados de acôr-do com o polígono das bases. Analise alguns exemplos.

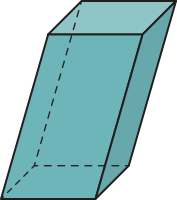

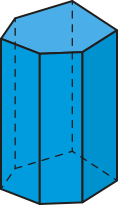
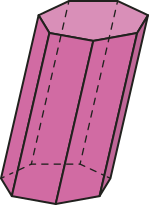
Além díssu, um prisma também póde sêr classificado de acôr-do com a inclinação das arestas laterais em relação aos planos das bases. Acompanhe.
• Os prismas cujas arestas laterais são perpendiculares aos planos quê contêm suas bases, ou seja, aqueles cujas faces laterais são retângulos, são denominados prismas rétos. Quando as bases de um prisma reto são polígonos regulares, dizemos quê ele é um prisma regular.
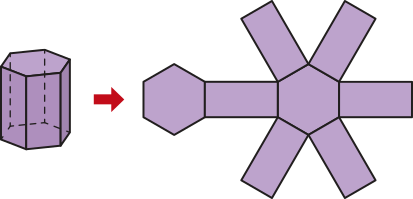
Planificação de um prisma hexagonal regular.
• Os prismas cujas arestas laterais são oblíquas aos planos quê contêm suas bases, ou seja, aqueles cujas faces laterais são paralelogramos quê não são retângulos, são denominados prismas oblíqüos.
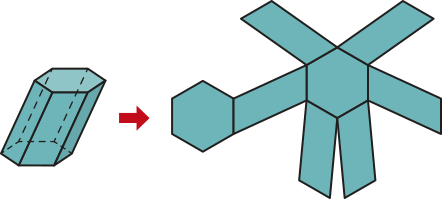
Planificação de um prisma hexagonal oblíquo.
Quando as bases de um prisma são paralelogramos, esse prisma também póde sêr chamado de paralelepípedo; no prisma reto, quando as bases são retângulos, ele também póde sêr chamado de paralelepípedo reto-retângulo ou bloco retangular.
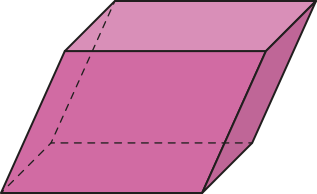
PARA PENSAR
por quê podemos dizêr quê o cubo é um caso particular de paralelepípedo reto-retângulo? Justifique sua resposta e desenhe em seu caderno a planificação do cubo.
Resposta nas Orientações para o professor.
Página cento e quarenta e oito
Área da superfícíe de um prisma
Em qualquer prisma, podemos destacar as seguintes áreas.
• A superfícíe lateral corresponde à reunião das faces laterais do prisma, portanto a área dessa superfícíe é a área lateral (A(éli)").
• A área da base (Ab) corresponde à área do polígono quê compõe cada base do prisma.
• A superfícíe total corresponde à reunião da superfícíe lateral e das bases do prisma, portanto a área dessa superfícíe é a área total (At).
Assim, a área total de um prisma póde sêr expressa por:
At = A(éli)" + 2Ab
ATIVIDADES RESOLVIDAS
R3. Determine a medida da diagonal do paralelepípedo reto-retângulo ABCDEFGH a seguir.
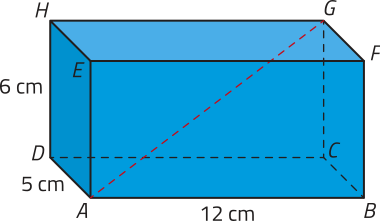
Denominamos diagonal de um prisma todo segmento de reta cujas extremidades estão em vértices quê não pertencem a uma mesma face dêêsse prisma.
Resolução
Como ABCDEFGH é um paralelepípedo reto-retângulo, ao traçarmos o segmento de reta obtemos dois triângulos retângulos: ACG e ABC.
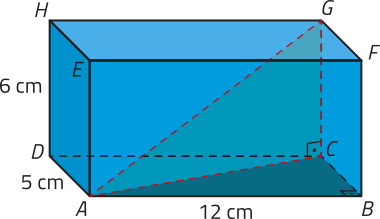
Aplicando o teorema de Pitágoras no triângulo ABC, temos:
(AC)2 = (AB)2 + (BC)2 ⇒ (AC)2 = 122 + 52 ⇒ (AC)2 = 169 ⇒
Agora, aplicando o teorema de Pitágoras no triângulo ACG, temos:
(AG)2 = (AC)2 + (CG)2 ⇒ (AG)2 = 132 + 62 ⇒ (AG)2 = 205 ⇒
Portanto, a medida da diagonal dêêsse paralelepípedo reto-retângulo é cm ou aproximadamente 14,32 cm.
Página cento e quarenta e nove
R4. (UEMG) Um designer projetou um chaveiro no formato de um prisma triangular reto com 12 cm de altura. Sabe-se quê as arestas da base formam um triângulo retângulo com catetos de medidas 6 cm e 8 cm. Para cobrir todas as faces dêêsse prisma, adquirindo a quantidade suficiente de papel adesivo, e, com isso, evitar o desperdício, será preciso saber a área total da superfícíe dêêsse prisma. Fazendo os cálculos corretos, obtém-se quê a área total dêêsse prisma méde
a) 336 cm2.
b) 324 cm2.
c) 316 cm2.
d) 312 cm2.
Resolução
Inicialmente, vamos calcular a área da base dêêsse prisma triangular reto, quê corresponde a um triângulo retângulo de catetos medindo 6 cm e 8 cm:
Ab = = 24; ou seja, 24 cm2.
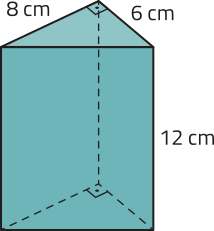
Aplicando o teorema de Pitágoras no triângulo retângulo presente nas bases dêêsse prisma, vamos determinar a medida x de sua hipotenusa, em centímetro:
x2 = 62 + 82 ⇒ x2 = 100 ⇒
Como esse prisma é reto, suas faces laterais são retângulos de dimensões 12 cm e 6 cm, 12 cm e 8 cm, e 12 cm e 10 cm. Assim, a área lateral dêêsse prisma é dada por:
A(éli)" = (12 ⋅ 6) + (12 ⋅ 8) + (12 ⋅ 10) = 72 + 96 + 120 = 288; ou seja, 288 cm2.
Agora, vamos calcular a área total dêêsse prisma:
At = A(éli)" + 2Ab = 288 + 2 ⋅ 24 = 336; ou seja, 336 cm2.
Portanto, a alternativa a é a correta.
ATIVIDADES
13. Mostre quê a medida d da diagonal do paralelepípedo reto-retângulo a seguir é dada por d = .
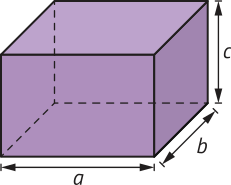
Resposta nas Orientações para o professor.
14. Em certa residência será construída uma piscina, cujo formato interno é o de um paralelepípedo reto-retângulo, com 1,5 m de profundidade, 5 m de comprimento e 4 m de largura. Para revestir toda a superfícíe interna dessa piscina, um azulejista cobra R$ 35,00 por métro quadrado. Qual será o valor, em reais, cobrado pelo azulejista para realizar esse serviço?
R$ 1.645,00
15. Um nicho decorativo foi compôzto de quatro partes idênticas, cada uma com formato de prisma hexagonal regular de 15 cm de altura, quê foram ajustadas de maneira quê algumas de suas faces laterais ficaram fixadas umas nas outras, sobrepondo-as, conforme representado a seguir.

Quantos centímetros quadrados de adesivo serão utilizados para revestir totalmente a parte lateral externa dêêsse nicho? Considere ≃ 1,7.
6.300 cm2
Página cento e cinquenta
16. O reaproveitamento de contêineres tem se tornado uma alternativa sustentável e econômica para a construção de residências, lojas, escritórios, restaurantes, entre outros estabelecimentos. Uma empresa especializada nesse ramo projetou o modelo representado a seguir, com formato de paralelepípedo reto-retângulo, em quê serão instaladas uma janela com formato quadrangular com 1,2 m de lado e uma porta com formato retangular de dimensões 2,1 m e 2 m.

Após a instalação da janela e da porta, será utilizada uma tinta impermeabilizante cujo rendimento é de 14 m2/L para pintar a superfícíe externa dêêsse contêiner, incluindo sua parte inferior. Quantos litros dessa tinta são necessários, no mínimo, para pintar 35 contêineres como esse?
169,6 L
17. Uma fábrica personaliza toda a superfícíe externa das tampas de caixas quê acondicionam alimentos. Observe as medidas aproximadas de dois modelos de tampa, um com formato de prisma quadrangular regular e outro com formato de prisma octogonal regular, ambos com altura de 4 cm.
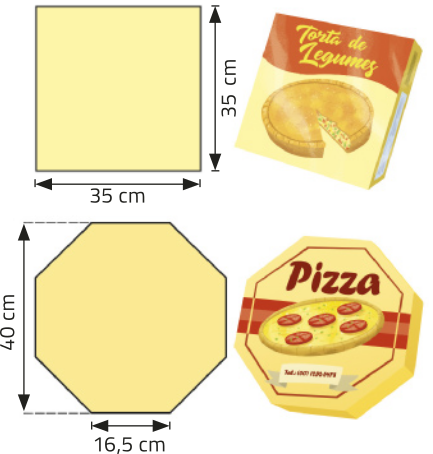
Quantos centímetros quadrados, aproximadamente, há de diferença entre a área da região de personalização dêêsses dois modelos da tampa?
63 cm2
18. Ao adicionar as medidas de todas as arestas do prisma oblíquo a seguir, cujas bases são hekzágonos regulares, obtém-se aproximadamente:
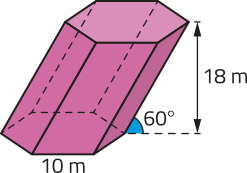
a) 140,7 m.
b) 184,7 m.
c) 211,7 m.
d) 228 m.
e) 244,7 m.
alternativa e
19. Um serralheiro, para confeksionar uma peça de aço, soldou duas partes cúbicas, de maneira quê os vértices de uma das bases da parte menor coincidissem com os pontos médios das arestas de uma das bases da parte maior, conforme representado na figura.
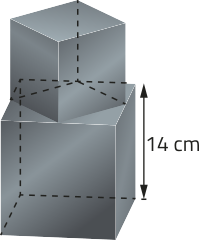
Após a soldagem, o serralheiro realizou um processo de galvanização na parte externa da peça. A área aproximada da região galvanizada dessa peça é:
a) 490 cm2.
b) 980 cm2.
c) 1.470 cm2.
d) 1.568 cm2.
e) 1.665 cm2.
alternativa d
- Galvanização
- : procedimento para revestir objetos metálicos com uma camada de zinco para protegê-los da corrosão.
20. ![]() Observe, a seguir, as medidas externas de caixas de papelão, com formato de paralelepípedo reto-retângulo, disponíveis para pronta-entrega de certa empresa.
Observe, a seguir, as medidas externas de caixas de papelão, com formato de paralelepípedo reto-retângulo, disponíveis para pronta-entrega de certa empresa.
Modelo |
Dimensões (mm) |
|---|---|
I |
100 × 100 × 100 |
II |
200 × 150 × 100 |
III |
300 × 200 × 300 |
IV |
400 × 300 × 300 |
V |
400 × 400 × 400 |
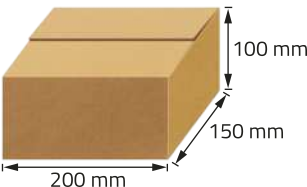
Com base nessas informações, elabore e escrêeva um problema envolvendo a área de prismas. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página cento e cinquenta e um
Volume de um prisma
Você sabia quê as piscinas olímpicas têm medidas padronizadas? De acôr-do com a Federação Internacional de Natação, uma piscina olímpica deve ter formato de paralelepípedo reto-retângulo com 50 m de comprimento e 25 m de largura, e a á gua deve atingir, no mínimo, 2 m de altura. Nessas condições, para determinar a quantidade mínima de á gua necessária em uma piscina olímpica, podemos determinar o volume dessa á gua, ou seja, o espaço quê ela ocupa na piscina.
Fonte dos dados: GURI, Paulo Guilherme. Olimpíadas 2024: quantos litros de á gua tem uma piscina olímpica? São Paulo: Anapp, 25 jun. 2024. Disponível em: https://livro.pw/stmgl. Acesso em: 13 set. 2024.

Para ilustrar essa situação, considere um paralelepípedo reto-retângulo cujas dimensões correspondem ao bloco de á gua da piscina, conforme apresentado a seguir.
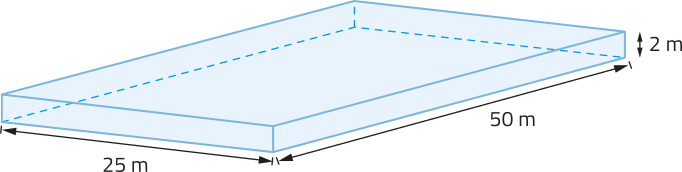
pôdêmos calcular o volume dêêsse paralelepípedo reto-retângulo imaginando sua decomposição em cubos com 1 m de aresta, ou seja, 1 m3 de volume. Nesse caso, são obtidas duas camadas com 25 fileiras de 50 cubos cada. Assim, a quantidade de cubos dêêsses em quê o paralelepípedo reto-retângulo foi decomposto é dada por:
2 ⋅ 25 ⋅ 50 = 2.500; ou seja, 2.500 cubos.
Como o volume de cada cubo dêêsses é 1 m3, então o volume dêêsse paralelepípedo reto-retângulo é 2.500 m3, quê corresponde ao volume mínimo de á gua quê uma piscina olímpica deve ter.
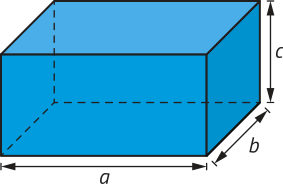
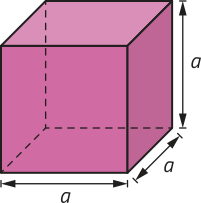
Para calcular o volume de um paralelepípedo reto-retângulo, podemos multiplicar as medidas de suas três dimensões, ou multiplicar a área da base Ab pela medida da altura. Como o cubo é um caso particular de paralelepípedo reto-retângulo, em quê as arestas têm medidas iguais, podemos calcular seu volume de maneira análoga.
• Volume do paralelepípedo reto-retângulo
• Volume do cubo
Página cento e cinquenta e dois
Agora, vamos estudar como calcular o volume de um prisma qualquer. Para isso, considere dois empilhamentos compostos de peças de blocos lógicos quê lembram prismas idênticos e, por consequência, de mesmo volume, conforme representado a seguir.

DICA
Os blocos lógicos foram criados pelo matemático húngaro Zoltan poou Dienes (1916-2014), em meados da década de 1950, com o objetivo de auxiliar no desenvolvimento de atividades pedagógicas e do raciocínio lógico.
PARA PENSAR
Como você calcularia o volume de cada empilhamento dêêsses?
Resposta esperada: Determinar o volume de cada peça e multiplicar o resultado obtído pela quantidade de peças de cada empilhamento.
Cada empilhamento tem a mesma quantidade de peças e cada peça tem o mesmo volume, portanto esses empilhamentos também têm volumes iguais. Isso ocorre independentemente de como empilharmos essa quantidade de peças.
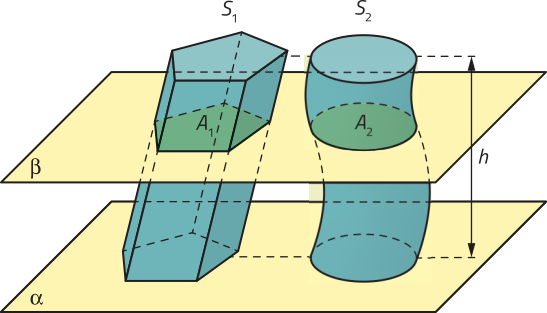
Essa comparação entre os volumes dêêsses dois empilhamentos envolve ideias do princípio de Cavalieri, conforme enunciado a seguir.
Sejam dois sólidos geométricos espaciais S1 e S2 de mesma altura h apoiados em um mesmo plano (alfa)". Se qualquer plano (beta)", paralelo ou coincidente a (alfa)", quê secciona esses sólidos determina neles duas regiões planas de mesma área A1 e A2, então o volume de S1 é igual ao volume de S2.
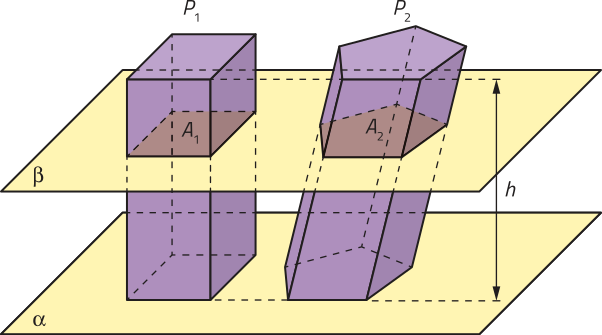
Utilizando o princípio de Cavalieri, é possível determinar o volume de um prisma qualquer. Para exemplificar, considere um paralelepípedo reto-retângulo P1 e um prisma qualquer P2, ambos com altura h e bases com áreas iguais, apoiados em um mesmo plano (alfa)". Qualquer plano (beta)", paralelo a (alfa)", secciona esses prismas determinando neles duas regiões planas A1 e A2, respectivamente, de mesma área. Assim, pelo princípio de Cavalieri, o volume de P2 é igual ao volume de P1.
Sabemos quê o volume do paralelepípedo reto-retângulo P1 é dado por VP1 = Ab ⋅ h; então, o volume de um prisma qualquer P2 também é dado por VP2 = Ab ⋅ h.
Página cento e cinquenta e três
O volume V de um prisma qualquer póde sêr calculado multiplicando-se a área de sua base Ab pela medida da sua altura h.
V = Ab ⋅ h
ATIVIDADES RESOLVIDAS
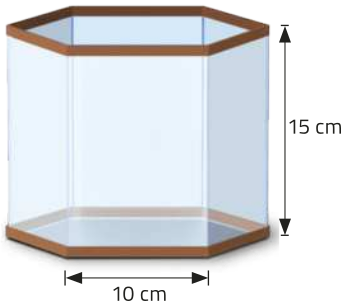
R5. Na figura, estão indicadas as medidas das dimensões internas de um aquário com formato de prisma hexagonal regular. Quantos mililitros de á gua podem sêr colocados nesse aquário para quê seja ocupado de sua capacidade?
Resolução
Para resolver esta atividade, podemos considerar o prisma hexagonal regular correspondente à região interna dêêsse aquário e realizar a decomposição da atividade em kestões para resolvê-la em etapas.
Acompanhe.
1ª) Qual é a medida do apótema da base dêêsse prisma?
2ª) Qual é a área da base dêêsse prisma?
3ª) Qual é o volume dêêsse prisma?
4ª) Quanto é do volume dêêsse prisma?
Agora, podemos resolver cada questão e utilizar a resposta na resolução da questão seguinte.
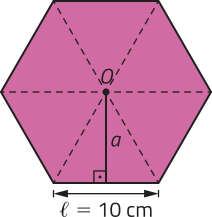
1ª) pôdêmos decompor o polígono da base dêêsse prisma em triângulos equiláteros congruentes, conforme indicado na figura. Depois, utilizando o teorema de Pitágoras, calculamos a medida do apótema a, em centímetro.
102 = a2 + ()2 ⇒ a2 = 100 − 25 ⇒
2ª) pôdêmos calcular a área Ab da base dêêsse prisma, em centímetro quadrado, multiplicando por 6 a área de cada triângulo equilátero em quê essa base foi decomposta.
Ab = 6 ⋅ → Ab = 6 ⋅ =
3ª) Assim, temos quê o volume V dêêsse prisma, em centímetro cúbico, é dado por:
V = Ab ⋅ h → V = ⋅ 15 =
4ª) Calculando do volume dêêsse prisma, em centímetro cúbico, temos:
⋅ =
Portanto, como 1 cm3 = 1 mL, podem sêr colocados mL ou aproximadamente 2.922,8 mL de á gua nesse aquário para quê seja ocupada da capacidade dele.
Página cento e cinquenta e quatro
R6. (Enem/MEC) Um petroleiro possui reservatório em formato de um paralelepípedo retangular com as dimensões dadas por 60 m × 10 m de base e 10 m de altura. Com o objetivo de minimizar o impacto ambiental de um eventual vazamento, esse reservatório é subdividido em três compartimentos, A, B e C, de mesmo volume, por duas placas de aço retangulares com dimensões de 7 m de altura e 10 m de base, de modo quê os compartimentos são interligados, conforme a figura. Assim, caso haja rompimento no casco do reservatório, apenas uma parte de sua carga vazará.
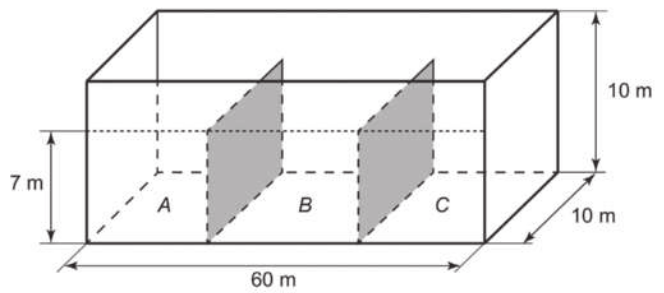
Suponha quê ocorra um desastre quando o petroleiro se encontra com sua carga mássima: ele sofre um acidente quê ocasiona um furo no fundo do compartimento C.
Para fins de cálculo, considere desprezíveis as espessuras das placas divisórias.
Após o fim do vazamento, o volume de petróleo derramado terá sido de
a) 1,4 × 103 m3
b) 1,8 × 103 m3
c) 2,0 × 103 m3
d) 3,2 × 103 m3
e) 6,0 × 103 m3
Resolução
Para resolver esta atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, obtemos as seguintes informações:
• o reservatório tem formato de paralelepípedo reto-retângulo com dimensões de 10 m, 60 m e 10 m e é subdividido em três compartimentos de mesmo volume, separados por placas retangulares de 7 m de altura e 10 m de base;
• após um suposto acidente, tem-se um furo no fundo do compartimento C, quê resulta em vazamento;
• precisamos determinar o volume de petróleo derramado nesse suposto vazamento.
2ª ELABORAR UM PLANO
• Inicialmente, podemos calcular o volume total de petróleo no reservatório. Em seguida, calcular o volume em cada compartimento. Por fim, subtrair do volume total de petróleo do reservatório o volume correspondente a dois compartimentos (A e B), resultando no volume de petróleo derramado.
3ª EXECUTAR O PLANO
O volume total de petróleo no reservatório é dado por:
VR = 60 ⋅ 10 ⋅ 10 = 6.000; ou seja, 6.000 m3.
O volume de cada compartimento é dado por:
VC = 20 ⋅ 10 ⋅ 7 = 1.400; ou seja, 1.400 m3.
Subtraindo o volume de petróleo de dois compartimentos do volume total do reservatório, obtemos:
VR − 2 ⋅ VC = 6.000 − 2 ⋅ 1.400 = 3.200 = 3,2 ⋅ 103; ou seja, 3,2 ⋅ 103 m3.
Página cento e cinquenta e cinco
4ª VERIFICAR OS RESULTADOS
Vamos adicionar o volume de petróleo quê estava contido no compartimento C ao volume quê estava contido apenas na parte superior do reservatório (acima das placas divisórias). Para isso, podemos calcular o volume V1 de um paralelepípedo reto-retângulo com dimensões de 60 m, 10 m e 3 m (10 − 7) e o volume V2 de outro paralelepípedo reto-retângulo com dimensões de 20 m, 10 m e 7 m para obtêr o volume total V de petróleo derramado:
V1 = 60 ⋅ 10 ⋅ 3 = 1.800; ou seja, 1.800 m3.
V2 = 20 ⋅ 10 ⋅ 7 = 1.400; ou seja, 1.400 m3.
V = V1 + V2 = 1.800 + 1.400 = 3.200 = 3,2 ⋅ 103; ou seja, 3,2 ⋅ 103 m3.
Portanto, a alternativa d é a correta.
ATIVIDADES
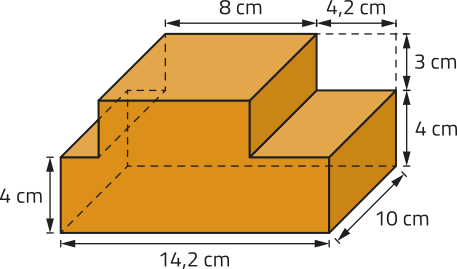
21. Calcule o volume do sólido geométrico a seguir, quê póde sêr decomposto em paralelepípedos reto-retângulos.
808 cm3
22. O armazenamento de á gua da chuva em reservatórios póde sêr uma alternativa consciente para reaproveitar a á gua em tarefas domésticas, como lavar calçadas e regar plantas. Para quê essa á gua não se torne criadouro do mosquito aédis egípti, transmissor de diversas doenças, são necessários alguns cuidados, por exemplo, misturar 2 mL de á gua sanitária para cada litro de á gua e manter o reservatório fechado.
Um dêêsses reservatórios tem formato de paralelepípedo reto-retângulo cujas medidas das dimensões internas são 3 m, 2 m e 1,2 m. Quantos litros de á gua sanitária são necessários misturar quando esse reservatório estiver com á gua até 80% da sua capacidade total?
11,52 L
DICA
Você póde decompor esta atividade em etapas propondo algumas kestões, como: qual é a capacidade total dêêsse reservatório? A quantos litros correspondem 80% da capacidade dêêsse reservatório? Quantos mililitros de á gua sanitária serão necessários misturar quando esse reservatório estiver com á gua ocupando 80% da capacidade total dele?
23. Um fresador mecânico confeccionou a peça de metal representada, cujo formato é de um prisma hexagonal regular, com um furo com formato de paralelepípedo reto-retângulo.

a) Qual é o volume dessa peça? Considere ≃ 1,7.
aproximadamente 135,6 cm3
b) Qual é a massa dessa peça, sabendo quê o metal utilizado tem densidade de 2,7 g/cm3?
366,12 g
DICA
A densidade de um material é dada pela razão entre sua massa e seu volume.
24. Para enviar uma mercadoria quê está acondicionada em uma embalagem moldável, de 25 L de volume, uma transportadora disponibilizou alguns modelos de caixa, com formato de paralelepípedo reto-retângulo, conforme apresentado a seguir.
Modelo |
Dimensões internas (cm) |
Custo do envio (R$) |
|---|---|---|
A |
36 × 27 × 18 |
16,05 |
B |
54 × 36 × 27 |
21,15 |
C |
27 × 27 × 36 |
22,50 |
D |
27 × 22,5 × 13,5 |
8,15 |
a) Calcule, em litro, a capacidade de armazenamento de cada modelo de caixa apresentado.
A: 17,496 L; B: 52,488 L; C: 26,244 L; D: aproximadamente 8,201 L
b) Qual modelo de caixa póde sêr escolhido para acomodar a mercadoria descrita, de maneira quê o custo de envio seja o menor possível?
modelo B
Página cento e cinquenta e seis
25. As bases dêste prisma oblíquo correspondem a triângulos equiláteros. Determine a medida da aresta da base dêêsse prisma, sabendo quê seu volume é igual a dm3.
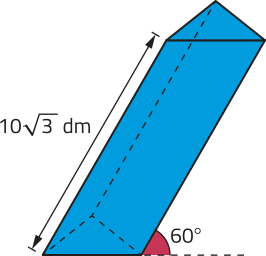
dm
26. Estudamos, anteriormente, quê os pisos intertravados são revestimentos compostos de blocos de concreto. Considere um modelo dêêsses blocos cujo formato é o de um paralelepípedo reto-retângulo e cujas dimensões são 20 cm, 10 cm e 6 cm.
DICA
Considere quê o bloco seja instalado de maneira quê a dimensão de 6 cm fique posicionada na vertical.
Desconsiderando a área correspondente aos vãos entre os blocos, calcule quantos metros cúbicos de concreto são necessários para produzir blocos dêêsse modelo quê sêjam suficientes para pavimentar uma região retangular de 8 m de comprimento e 5 m de largura.
2,4 m3
27. Na figura a seguir, está representada a planificação de um prisma reto cujo formato da base é um triângulo retângulo. Determine o volume dêêsse prisma.
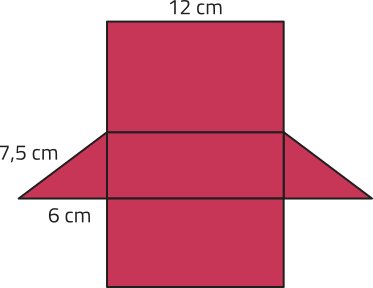
162 cm3
28. ![]() Pesquise em uma fonte de informação confiável, como sáiti, jornál ou revista, uma notícia quê envolva alguma unidade de medida de capacidade. Dê preferência a alguma notícia quê seja de interêsse da comunidade em quê você vive.
Pesquise em uma fonte de informação confiável, como sáiti, jornál ou revista, uma notícia quê envolva alguma unidade de medida de capacidade. Dê preferência a alguma notícia quê seja de interêsse da comunidade em quê você vive.
Com base nessa pesquisa, elabore um problema quê contenha um trecho da notícia pesquisada – não se esqueça de indicar a fonte dessa notícia – e cuja resolução envolva o cálculo do volume de um prisma. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Pesquisa e elaboração do estudante.
29. Uma empresa de côléta de resíduos de construção civil utiliza caçambas com formato quê lembra um prisma reto. Observe as dimensões internas de uma dessas caçambas.
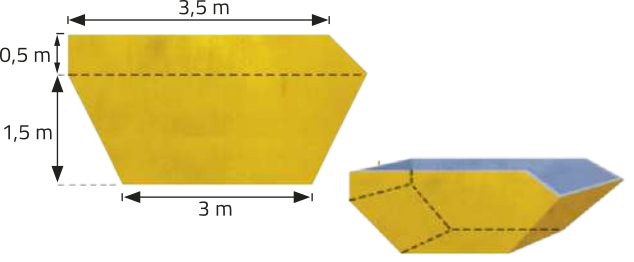

Qual é o volume mássimo aproximado de resíduos quê póde sêr coletado nessa caçamba, sabendo quê não póde havêer resíduos ultrapassando suas bordas?
a) 5,3 m3
b) 7,1 m3
c) 17,8 m3
d) 20 m3
e) 21,4 m3
alternativa c
30. No Brasil, em 2022, o consumo médio diário de á gua por habitante foi cerca de 148 L de á gua, 38 L a mais do quê o recomendado pela Organização das Nações Unidas (Ônu).
Fonte dos dados: TRATA BRASIL. Água. [S. l., 2024]. Disponível em: https://livro.pw/adwin. Acesso em: 9 ago. 2024.
• Desenhe um paralelepípedo reto-retângulo, indicando as medidas de suas arestas, de maneira quê seu volume corresponda à quantidade de á gua para consumo recomendada pela Ônu.
Algumas respostas possíveis: Paralelepípedo reto-retângulo com dimensões de 4 dm, 5,5 dm e 5 dm; paralelepípedo reto-retângulo com dimensões de 5 dm, 11 dm e 2 dm.
31. (UFRGS-RS) Um prisma reto de base hexagonal regular tem a mesma altura de um prisma cuja base é um triângulo equilátero. Considere h a medida da aresta da base do prisma hexagonal e t a medida da aresta da base do prisma triangular. Se ambos os prismas têm o mesmo volume, então a razão vale
a) .
b) .
c) 1.
d) .
e) 6.
alternativa a
Página cento e cinquenta e sete
32. As leis brasileiras quê buscam garantir a inclusão de pessoas com deficiência na ssossiedade, em geral, são validadas pela Associação Brasileira de Normas Técnicas (ABNT). Uma dessas leis diz respeito às normas para acessibilidade, como aquelas relacionadas às rampas de acesso. Analise algumas normas referentes a isso.
• Consideram-se rampas as inclinações da superfícíe de piso quê têm declividade maior ou igual a 5%. Para garantir a acessibilidade de pessoas com deficiência, a inclinação de rampas não deve ultrapassar 8,33%.
• A inclinação de rampas (ou declividade) deve sêr calculada de acôr-do com a expressão i = , em quê i representa a inclinação em porcentagem, h é a altura do desnível e c é o comprimento da projeção horizontal, conforme a figura.

• A largura livre recomendada para rampas é de 1,50 m.
Fonte dos dados: ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 9050: acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos. 4. ed. Rio de Janeiro: ABNT, 2020. p. 56-57. Disponível em: https://livro.pw/gxslr. Acesso em: 9 ago. 2024.
Para atender às condições de acessibilidade de certa escola, um arquiteto está projetando uma rampa de acesso quê será construída com concreto maciço e terá o formato de um prisma triangular reto. Para esse projeto, será considerada uma rampa com altura de desnível de 0,60 m, inclinação de 8% e cuja largura livre é igual à recomendada pela ABNT.
DICA
A inclinação da rampa, dada em porcentual, corresponde à razão entre a altura do desnível e o comprimento da projeção horizontal da rampa.
a) Determine o comprimento da projeção horizontal dessa rampa.
7,5 m
b) Quantos metros cúbicos de concreto serão necessários para a construção dessa rampa? Desconsidere as ferragens quê possam sêr utilizadas.
3,375 m3
c) ![]() Junte-se a dois côlégas, e elaborem uma proposta para a construção de uma rampa de acesso. Nessa proposta, é importante justificar a escolha do local para a construção da rampa e indicar algumas referências a sêr consideradas, como a inclinação, a altura do desnível, o comprimento da projeção horizontal, a largura livre e a quantidade de metros cúbicos de concreto necessária.
Junte-se a dois côlégas, e elaborem uma proposta para a construção de uma rampa de acesso. Nessa proposta, é importante justificar a escolha do local para a construção da rampa e indicar algumas referências a sêr consideradas, como a inclinação, a altura do desnível, o comprimento da projeção horizontal, a largura livre e a quantidade de metros cúbicos de concreto necessária.
Elaboração dos estudantes.
33. Para realizar um experimento, foram utilizados dois recipientes: um com formato de prisma hexagonal regular e outro com formato de prisma quadrangular regular. Observe algumas medidas internas dêêsses recipientes.
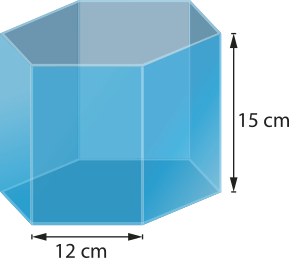

Durante o experimento, foi colocada á gua no recipiente I de maneira quê êste ficou completamente cheio. Em seguida, despejou-se todo esse conteúdo no recipiente II. pôdêmos afirmar quê o recipiente II:
a) não ficou completamente cheio.
b) ficou completamente cheio e a á gua não transbordou.
c) ficou completamente cheio e transbordaram menos de 200 mL de á gua.
d) ficou completamente cheio e transbordaram mais de 300 mL de á gua.
alternativa d
Página cento e cinquenta e oito
Pirâmides
No Egito antigo, os faraós construíam grandes monumentos quê eram utilizados como tumbas. Muitos turistas viajam para o Egito com o objetivo de visitar essas construções, principalmente o conjunto arquitetônico de Gizé, na cidade do Cairo, onde se encontram as pirâmides construídas pêlos faraós Quéops, Quéfren e Miquerinos.
Construída por volta de 2600 a.C., a pirâmide de Quéops, mais conhecida como a Grande Pirâmide de Gizé, é considerada uma das maiores obras de engenharia e arquitetura da Antigüidade, sêndo a única das Sete Maravilhas do Mundo Antigo quê sobreviveu ao tempo. Essa pirâmide deteve o posto de construção mais alta do mundo, até a inauguração da Torre Eiffel, no século XIX.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 67-68.

O formato da construção apresentada na fotografia lembra um tipo de poliedro denominado pirâmide.
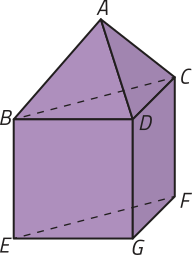
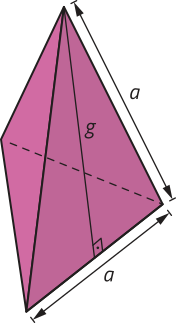
Dados um plano (alfa)", um polígono convexo contido em (alfa)" e um ponto V não pertencente a (alfa)", a reunião de todos os segmentos de reta com uma extremidade em V e a outra extremidade em um ponto dêêsse polígono é denominada pirâmide. Analise um exemplo de pirâmide.
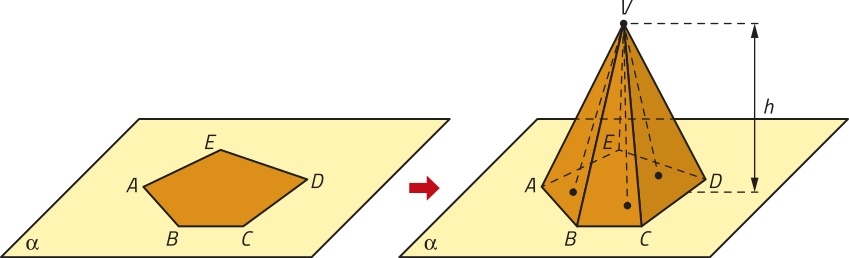
Na pirâmide VABCDE, podemos destacar os seguintes elemêntos:
• o ponto V é o vértice da pirâmide;
• o polígono ABCDE é a base;
• , , , e são as arestas da base;
• , , , e são as arestas laterais;
• os triângulos VAB, VBC, VCD, VDE e VAE são as faces laterais;
• a distância h, entre o ponto V e o plano (alfa)", é a altura da pirâmide.
PARA PENSAR
Prismas e pirâmides têm as faces laterais correspondentes a um mesmo polígono? Explique.
Resposta esperada: Não, pois as faces laterais dos prismas são sempre paralelogramos, e as faces laterais das pirâmides, triângulos.
PARA PENSAR
Assim como ocorre com os prismas, podemos nomear uma pirâmide de acôr-do com o polígono da base. No caderno, desenhe quatro pirâmides cujas bases são polígonos com diferentes quantidades de lados e nomeie-as.
Resposta pessoal.
Página cento e cinquenta e nove
Algumas características da pirâmide permitem classificá-la em pirâmide regular. Você sabe quais são elas?
Denominamos pirâmide regular aquela cuja base é um polígono regular e a projeção do vértice dessa pirâmide sobre o plano quê contém sua base coincide com o centro dessa base. Em uma pirâmide regular, as arestas laterais são congruentes, e as faces laterais são triângulos isósceles congruentes.
Nas pirâmides regulares, o apótema do polígono regular da base é o apótema da base da pirâmide (m), e a altura de uma face lateral é o apótema da pirâmide (g).
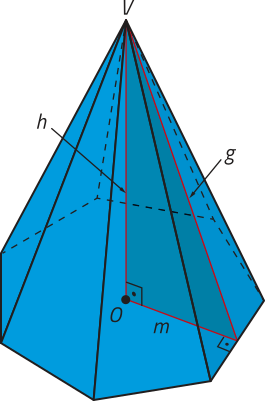
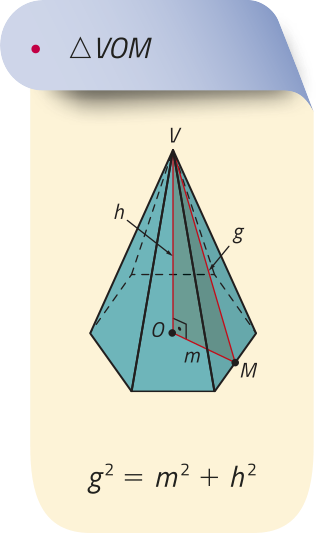
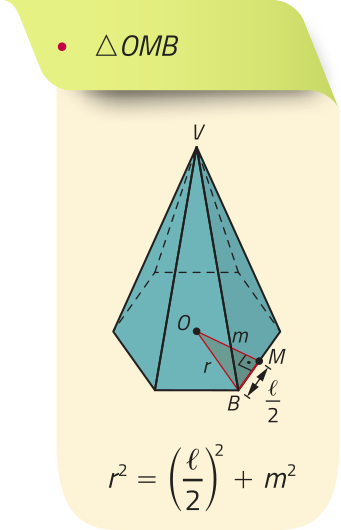
Nas pirâmides regulares, podemos destacar quatro triângulos retângulos por meio dos quais, utilizando o teorema de Pitágoras, é possível relacionar as medidas dos seguintes elemêntos: aresta lateral (L), aresta da base ((éli)"), raio da circunferência quê circunscreve a base (r), apótema da pirâmide (g), apótema da base (m) e altura (h). Analise, na pirâmide hexagonal regular a seguir, os triângulos destacados e as relações obtidas.
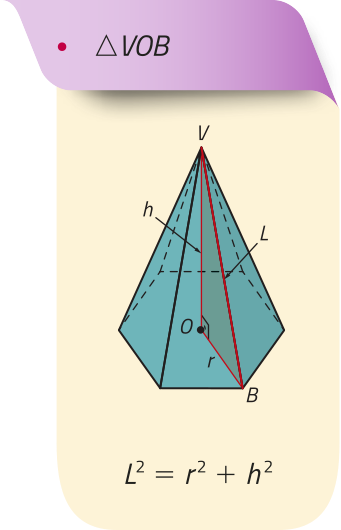
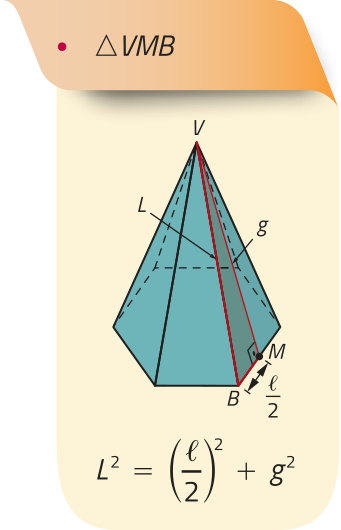
Área da superfícíe de uma pirâmide
De maneira análoga ao quê estudamos em relação aos prismas, em uma pirâmide temos as seguintes áreas.
• A superfícíe lateral corresponde à reunião das faces laterais da pirâmide, portanto a área dessa superfícíe é a área lateral (A(éli)").
• A área da base (Ab) corresponde à área do polígono da base da pirâmide.
• A superfícíe total corresponde à reunião da superfícíe lateral e da base da pirâmide, portanto a área dessa superfícíe é a área total (At).
PARA PENSAR
escrêeva uma expressão para representar a área total de uma pirâmide (At) em função da área lateral (A(éli)") e da área da base (Ab).
Resposta esperada: At = A(éli)" + Ab.
Página cento e sessenta
ATIVIDADES RESOLVIDAS
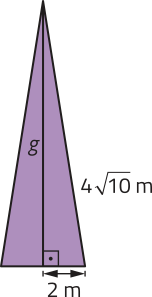
R7. Calcule a área total do seguinte tetraedro regular.
Resolução
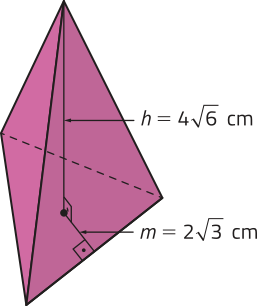
O tetraedro regular corresponde a uma pirâmide triangular regular em quê todas as faces são triângulos equiláteros congruentes. Vamos determinar a medida a de cada uma de suas arestas. Para isso, inicialmente, utilizamos o teorema de Pitágoras no triângulo retângulo determinado por g (medida do apótema da pirâmide), h e m.
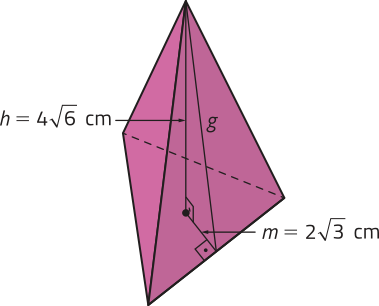
g2 = h2 + m2 → g2 = ()2 + ()2 ⇒ g2 = 108
Agora, aplicamos o teorema de Pitágoras no triângulo retângulo de lados a, g e :
a2 = ()2 + g2 → a2 = + 108 ⇒ = 108 ⇒ a2 = 144
Agora, determinamos a área total do tetraedro regular:
At = 4 ⋅ = 4 ⋅ =
Portanto, a área total dêêsse tetraedro regular é cm2 ou aproximadamente 249,42 cm2.
R8. Em relação à pirâmide hexagonal regular de 12 m de altura e aresta da base medindo 4 m, calcule a:
a) medida do apótema da base;
b) medida da aresta lateral;
c) medida do apótema da pirâmide;
d) área da base;
e) área lateral;
f) área total.
Resolução
a) A base dessa pirâmide corresponde a um hekzágono regular quê póde sêr decomposto em seis triângulos equiláteros congruentes, com 4 m de lado. A medida p do apótema da base corresponde à altura de um dêêsses triângulos.
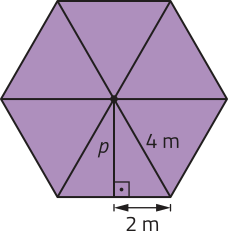
Assim, temos:
42 = p2 + 22 ⇒ p2 = 12 ⇒
Portanto, o apótema da base da pirâmide méde m ou aproximadamente 3,46 m.
b) Sendo L a medida da aresta lateral dessa pirâmide, temos:

L2 = 122 + 42 ⇒ L2 = 160 ⇒
Portanto, a aresta lateral da pirâmide méde m ou aproximadamente 12,65 m.
Página cento e sessenta e um
c) Sendo g a medida do apótema dessa pirâmide, temos:
()2 = g2 + 22 ⇒ g2 = 156 ⇒
Portanto, o apótema da pirâmide méde m ou aproximadamente 12,49 m.
d) Como a base dessa pirâmide hexagonal regular póde sêr decomposta em seis triângulos equiláteros congruentes, com 4 m de lado, temos:
Ab = 6 ⋅ =
Portanto, a área da base da pirâmide é m2 ou aproximadamente 41,57 m2.
e) Como a superfícíe lateral dessa pirâmide corresponde à reunião de seis triângulos isósceles de 4 m de base e m de altura, temos:
A(éli)" = 6 ⋅ =
Portanto, a área lateral da pirâmide é m2 ou aproximadamente 149,88 m2.
f) Para determinar a área total dessa pirâmide, adicionamos a área da base e a área lateral:
At = + = 24( + )
Portanto, a área total dessa pirâmide é 24( + ) m2 ou aproximadamente 191,45 m2.
PARA PENSAR
No caderno, faça um resumo de todas as etapas realizadas na resolução desta atividade.
Resposta pessoal.
ATIVIDADES
34. Uma pirâmide quadrangular regular, de 7 cm de altura, tem as arestas da base medindo 2 cm.
Com relação a essa pirâmide, determine a:
a) medida do apótema da base;
1 cm
b) medida do apótema da pirâmide;
cm ou aproximadamente 7,07 cm
c) medida da aresta lateral;
cm ou aproximadamente 7,14 cm
d) área da base;
4 cm2
e) área lateral;
cm2 ou aproximadamente 28,28 cm2
f) área total.
4( + 1) cm2 ou aproximadamente 32,28 cm2
35. Para estudar algumas relações envolvendo as quantidades de vértices, arestas e faces de uma pirâmide, resôuva os itens a seguir.
a) No caderno, reproduza e complete o qüadro a seguir, em quê n indica a quantidade de lados do polígono da base e V, A e F, as quantidades de vértices, arestas e faces da pirâmide, respectivamente.
Polígono da base da pirâmide |
Quantidade n |
Quantidade V |
Quantidade A |
Quantidade F |
|---|---|---|---|---|
Triângulo |
3 |
4 |
6 |
4 |
Quadrilátero |
4 |
5 |
8 |
5 |
Pentágono |
5 |
6 |
10 |
6 |
hekzágono |
6 |
7 |
12 |
7 |
b) Analisando esse qüadro, faça o reconhecimento de padrões e expresse V, A e F em função de n.
V = n + 1; A = 2n; F = n + 1
36. Uma pirâmide hexagonal regular tem área total igual a 6(15 + ) cm2. Sabe-se quê o raio da circunferência quê circunscreve a base dessa pirâmide méde 2 cm. Qual é a medida do apótema dessa pirâmide?
15 cm
Página cento e sessenta e dois
37. Uma estrutura decorativa é composta de duas peças: uma com formato de pirâmide quadrangular regular, de 40 cm de altura; e uma cúbica, de modo quê dois vértices da base da pirâmide coincidem com os pontos médios de duas arestas dessa peça, conforme representado na figura.

Considerando quê a peça cúbica tem área total igual a 13.824 cm2, qual é a área total da superfícíe da estrutura ôbitída?
(13.248 + ) cm2 ou aproximadamente 15.252,54 cm2
38. Um designer está projetando uma embalagem em papel, com formato de pirâmide quadrangular regular. Observe o mólde de uma dessas embalagens representado a seguir.
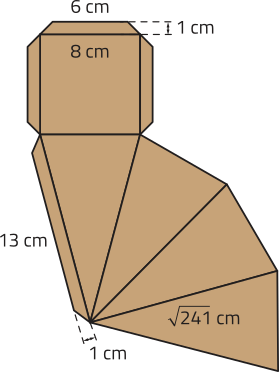
DICA
As abas quê compõem o mólde têm formato de trapézio isósceles, sêndo três delas idênticas.
a) Qual é a área aproximada de papel a sêr utilizado nessa embalagem?
339,26 cm2
b) Quantos centímetros de altura, aproximadamente, tem a pirâmide correspondente a essa embalagem?
14,46 cm
39. ![]() Estudamos quê a Grande Pirâmide de Gizé é a única das Sete Maravilhas do Mundo Antigo quê continua de pé. Originalmente, a pirâmide tinha cerca de 146,5 m de altura, o quê fez dela a mais alta estrutura erguida pelo sêr humano até o século XIV. Considerando quê a base dessa pirâmide corresponde a um quadrado com lados medindo 214 m, use a calculadora para determinar a medida aproximada do seu apótema.
Estudamos quê a Grande Pirâmide de Gizé é a única das Sete Maravilhas do Mundo Antigo quê continua de pé. Originalmente, a pirâmide tinha cerca de 146,5 m de altura, o quê fez dela a mais alta estrutura erguida pelo sêr humano até o século XIV. Considerando quê a base dessa pirâmide corresponde a um quadrado com lados medindo 214 m, use a calculadora para determinar a medida aproximada do seu apótema.
Fonte dos dados: BECK, Vinícius Carvalho. A matemática no Egito Antigo. In: ENCONTRO REGIONAL DE ESTUDANTES DE MATEMÁTICA, 16., [2010], Porto Alegre. Anais [...]. Porto Alegre: PUCRS, [2010]. p. 54. Disponível em: https://livro.pw/nuxsy. Acesso em: 9 ago. 2024.
aproximadamente 181,41 m
40. Um engenheiro civil projetou a construção do telhado de uma casa de maneira quê seu formato correspondesse à superfícíe lateral de uma pirâmide de base retangular em quê as arestas laterais são congruentes e médem m.
Observe, a seguir, a vista frontal e a vista lateral dêêsse telhado.

Nesse projeto, estima-se utilizar 12 telhas por métro quadrado do telhado e considera-se um desperdício de 10% de telhas sobre essa estimativa. Nessas condições, quantas telhas dessas, aproximadamente, devem sêr compradas para a execução dêêsse projeto?
a) 5.500 telhas
b) 6.100 telhas
c) 6.800 telhas
d) 7.200 telhas
e) 7.500 telhas
alternativa b
41. Uma empresa produz barracas com cobertura em lona, quê costumam sêr utilizadas em eventos. O custo de produção dessas barracas é R$ 4,00 por métro quadrado de lona utilizada. Observe, a seguir, a representação de uma barraca com cobertura em lona cujo formato corresponde ao de uma composição de um paralelepípedo reto-retângulo e uma pirâmide, de mesma base, em quê as faces laterais são dois pares de triângulos congruentes.
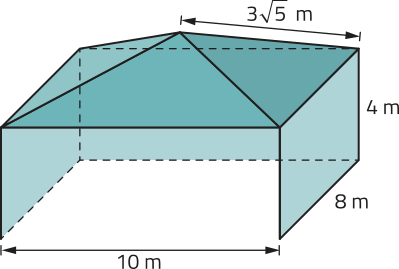
Considerando quê, nesse modelo de barraca, não é colocada lona no chão nem na parte frontal, quê corresponde a um retângulo de dimensões de 10 m e 4 m, qual é o custo de produção dessa barraca?
aproximadamente R$ 767,20
Página cento e sessenta e três
Volume de uma pirâmide
Observe uma pirâmide cuja base é um polígono P apoiado em um plano (alfa)" e a representação de um plano (beta)", paralelo a (alfa)", quê determina nessa pirâmide uma região poligonal p, semelhante ao polígono P. A seção da pirâmide pelo plano (beta)" determina uma pirâmide menor, de altura h, semelhante à pirâmide original, de altura H.
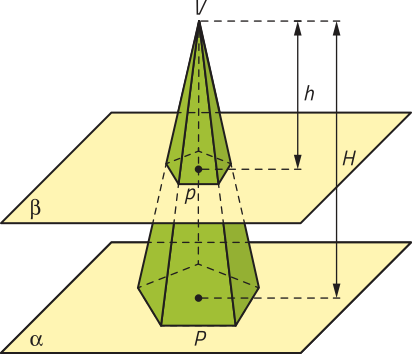
Você se lembra de razões entre figuras semelhantes? Se duas figuras geométricas são semelhantes com razão k, então a razão entre as áreas dessas figuras é dada por k2. Na figura apresentada, tomando k como a razão entre as medidas das alturas H e h das pirâmides semelhantes, temos k = e, portanto, k2 = ()2. Como os polígonos das bases dessas pirâmides são semelhantes, então a razão entre suas áreas é igual a k2. Portanto, = ()2. Isso está relacionado com o teorema a seguir.
Duas pirâmides quê têm a mesma altura e bases com áreas iguais têm volumes iguais.
Para demonstrar esse teorema, vamos considerar duas pirâmides de mesma altura (H), apoiadas sobre um mesmo plano (alfa)", ambas com bases P1 e P2, de mesma área, e um plano (beta)", paralelo a (alfa)", quê determina duas regiões planas (p1 e p2) nessas pirâmides e duas pirâmides menóres, de altura h, semelhantes às respectivas pirâmides de altura H.
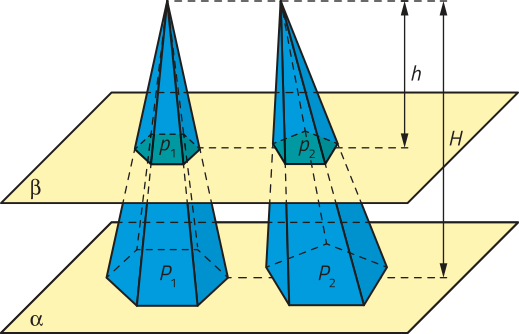
De acôr-do com o quê observamos anteriormente, temos:
• = ()2
• = ()2.
Assim, podemos concluir quê:
= .
Como a área de P1 e de P2 são iguais, então a área de p1 é igual à área de p2 para qualquer plano (beta)" paralelo a (alfa)". Portanto, pelo princípio de Cavalieri, os volumes dessas pirâmides são iguais.
PARA PENSAR
Na verificação do teorema apresentado anteriormente, utilizamos a igualdade = ()2. O quê garante quê essa igualdade é verdadeira?
Resposta esperada: Essa igualdade é verdadeira pelo fato de as pirâmides de base P1 e p1 serem semelhantes e, portanto, a razão entre as áreas de suas bases é igual ao quadrado da razão entre quaisquer duas medidas de suas dimensões correspondentes, nesse caso, o quadrado da razão entre as alturas dessas pirâmides.
Página cento e sessenta e quatro
Usando o resultado anterior, vamos mostrar quê o volume de uma pirâmide de base triangular corresponde à terça parte do volume de um prisma de mesma base e mesma altura. Para isso, decompomos um prisma de base triangular conforme a figura.
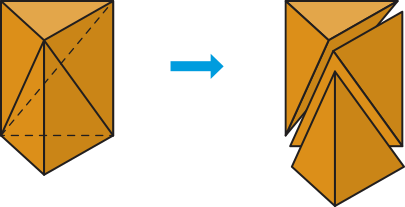
Nomeando os vértices do prisma e, consequentemente, os vértices das pirâmides obtidas na decomposição, temos:
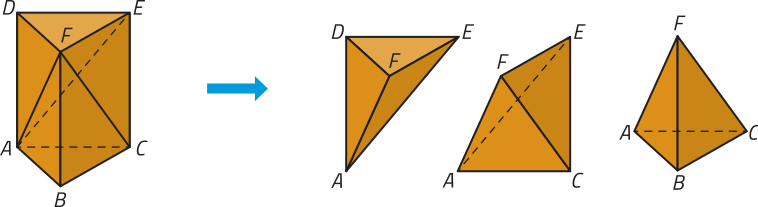
Vamos comparar as pirâmides obtidas, duas a duas, para deduzir uma relação entre os volumes.
I) As pirâmides ADEF e FABC têm o mesmo volume, pois:
• os triângulos DEF e ABC têm áreas iguais, pois são triângulos congruentes uma vez quê ambos são bases do prisma;
• as alturas e dessas pirâmides em relação às respectivas bases DEF e ABC são iguais à altura do prisma.
II) As pirâmides ADEF e FACE têm o mesmo volume, pois:
• os triângulos ADE e ACE são congruentes;
• as alturas relativas às faces ADE e ACE são iguais, uma vez quê correspondem à distância do ponto F à face ACED do prisma.
DICA
Os triângulos ADE e ACE são congruentes pelo caso de congruência LLL, uma vez quê têm o lado em comum, e os lados e e os lados e são pares de lados opostos de um retângulo.
Assim, os volumes das três pirâmides são iguais. Portanto, o volume de uma pirâmide de base triangular corresponde à terça parte do volume de um prisma de mesma base e mesma altura.
Vprisma = 3 ⋅ Vpirâmide ⇒ Vpirâmide =
Estudamos quê o volume de um prisma é dado por V = Ab ⋅ h, em quê Ab é a área da base. Assim, o volume de uma pirâmide de base triangular é dado por:
Vpirâmide = ⇒ Vpirâmide =
Essa relação póde sêr ampliada para qualquer pirâmide. Para isso, vamos considerar uma pirâmide qualquer de altura h e área da base Ab e uma pirâmide de base triangular com a mesma altura e a mesma área da base.
Utilizando o princípio de Cavalieri, essas duas pirâmides com a mesma altura e bases com áreas iguais têm volumes iguais. Portanto, o volume (V) de uma pirâmide qualquer é dado por:
V =
Página cento e sessenta e cinco
ATIVIDADES RESOLVIDAS
R9. Calcule o volume da pirâmide triangular apresentada.
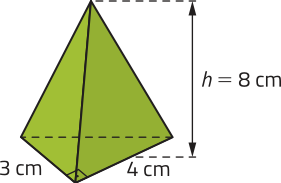
Resolução
A base da pirâmide é um triângulo retângulo, de catetos medindo 3 cm e 4 cm; então, sua área é dada por:
Ab = = 6; ou seja, 6 cm2.
Assim, podemos calcular o volume dessa pirâmide:
V = = = 16
Portanto, o volume dessa pirâmide é 16 cm3.
R10. Ao seccionar uma pirâmide de vértice V e altura H, por um plano (alfa)" paralelo à sua base, determinamos dois poliedros: uma pirâmide menor de altura h, semelhante à pirâmide original, e um tronco de pirâmide. Quando a pirâmide original é uma pirâmide regular, as bases do tronco de pirâmide são polígonos regulares semelhantes, suas faces laterais são trapézios isósceles, e a altura dêêsses trapézios é chamada de apótema do tronco. Observe o exemplo a seguir.
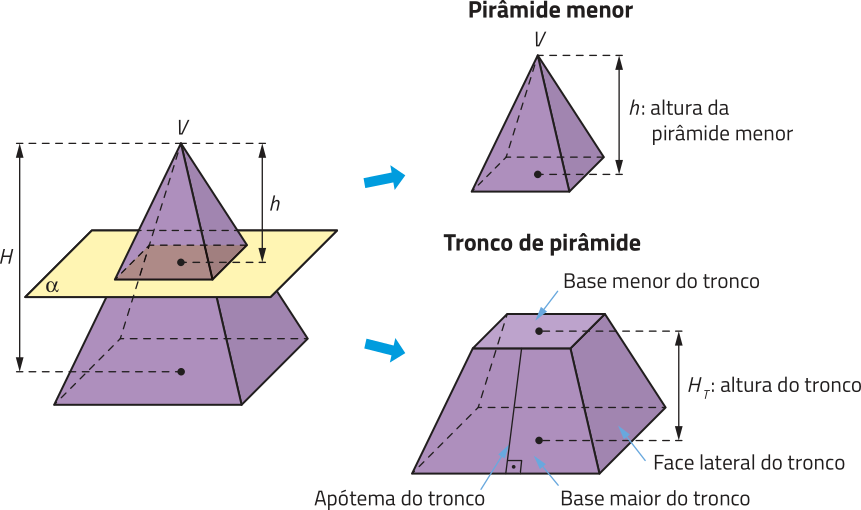
O volume VT de um tronco de pirâmide póde sêr obtído calculando a diferença entre o volume VP da pirâmide original e o volume Vm da pirâmide menor:
VT = VP − Vm
Agora, considere o tronco de uma pirâmide quadrangular regular a seguir e resôuva as kestões.
a) Qual é a área total dêêsse tronco de pirâmide?
b) Qual é o volume dêêsse tronco de pirâmide?
Página cento e sessenta e seis
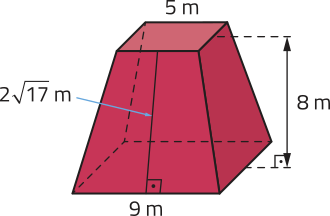
Resolução
a) As bases menor e maior dêêsse tronco de pirâmide correspondem a quadrados de 5 m e 9 m de lado, respectivamente. Assim:
• Ab = 52 = 25; ou seja, 25 m2;
• AB = 92 = 81; ou seja, 81 m2.
A área lateral do tronco corresponde à soma das áreas de quatro trapézios congruentes de bases 5 m e 9 m e altura m. Assim:
A(éli)" = 4 ⋅ = = ; ou seja, m2.
Assim, a área total do tronco de pirâmide é dada por:
AT = Ab + AB + A(éli)" = 25 + 81 + = 106 +
Portanto, a área total dêêsse tronco de pirâmide é (106 + ) m2 ou aproximadamente 336,89 m2.
b) Considerando HT a altura do tronco, h a altura da pirâmide menor e H a altura da pirâmide original, temos:
• = ⇒ = ⇒ 5h + 40 = 9h ⇒ h = 10; ou seja, 10 m.
• H = h + HT ⇒ H = 10 + 8 = 18; ou seja, 18 m.
Assim, o volume do tronco de pirâmide é:
VT = VP − Vm = − = − =
Portanto, o volume do tronco de pirâmide é m3 ou aproximadamente 402,67 m3.
ATIVIDADES
42. Uma artesã confeccionou duas peças decorativas de madeira maciça, uma com formato de pirâmide pentagonal (A) e outra, de pirâmide heptagonal (B). Com base nas informações de cada peça, calcule o volume de madeira usada em cada uma.
Peça A
Altura da pirâmide: 12 cm.
Área da base: 144 cm2.
Peça B
Altura da pirâmide: 6 cm.
Área da base: 72 cm2.
peça A: 576 cm3; peça B: 144 cm3
43. Um objeto maciço com formato de octaedro regular foi colocado em uma caixa cúbica com capacidade para 64 L, de maneira quê os vértices dêêsse objeto coincidiram com os centros das faces da caixa. Nessas condições, é possível afirmar quê o volume dêêsse objeto é:
a) L.
b) 32 L.
c) L.
d) 256 L.
e) L.
alternativa a
44. Uma pirâmide hexagonal regular tem apótema medindo cm e aresta da base 6 cm. De acôr-do com essas informações, responda às kestões.
a) Qual é a área da superfícíe dessa pirâmide?
54( + ) cm2 ou aproximadamente 430,76 cm2
b) Qual é o volume dessa pirâmide?
cm3 ou aproximadamente 561,18 cm3
45. O quilate indica quantas partes de ouro correspondem ao total de 24 partes de uma liga. Em uma peça de ouro 18 quilates, por exemplo, a cada 24 g dessa peça, 18 g correspondem a ouro. Observe.
Quantidade de quilates |
24 |
22 |
20 |
18 |
16 |
|---|---|---|---|---|---|
Fração de ouro na composição de uma peça |
Página cento e sessenta e sete
Utilizando ouro 18 quilates, um ourives confeccionou um pingente de 12 g, com formato de pirâmide quadrangular regular com 1 cm de aresta da base e 1,5 cm de altura.
a) Quantos gramas dêêsse pingente correspondem a ouro?
9 g
b) Qual é o volume dêêsse pingente?
0,5 cm3
c) Calcule a densidade dêêsse pingente, em grama por centímetro cúbico.
24 g/cm3
46. Uma pirâmide de base retangular tem 1,5 dm de altura e 6 dm3 de volume. Sabe-se quê as arestas da base dessa pirâmide têm medidas inteiras em decímetro. Quais são as possíveis medidas das arestas da base dessa pirâmide?
1 dm e 12 dm; 2 dm e 6 dm; 3 dm e 4 dm
47. Jorge produz velas artesanais de parafina com formatos de prismas e pirâmides regulares. Observe três modelos dessas velas.
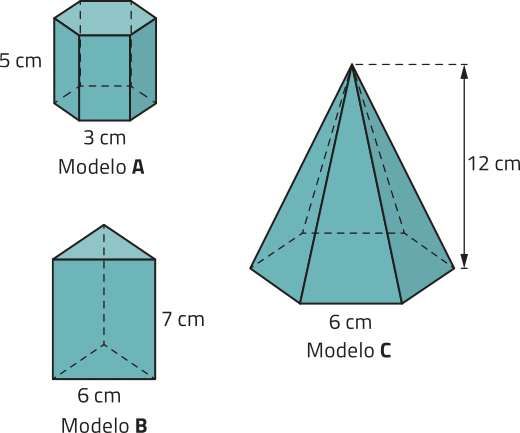
O custo de produção de cada vela é R$ 0,03 por centímetro cúbico de parafina utilizada.
Para determinar o preêço de venda de cada vela, Jorge multiplica o valor do custo por 2,5.
a) Qual é o custo de produção aproximado de cada um dêêsses modelos?
modelo A: R$ 3,51; modelo B: R$ 3,27; modelo C: R$ 11,22
b) Por quantos reais Jorge venderá cada modelo de vela?
modelo A: R$ 8,78; modelo B: R$ 8,18; modelo C: R$ 28,05
c) Em certa semana, Jorge arrecadou R$ 800,00 com venda de velas. Quantos reais ele lucrou com essas vendas? Considere quê o lucro, nesse caso, corresponda à diferença entre o valor arrecadado com as vendas e o custo de produção das velas vendidas.
R$ 480,00
48. O tronco de pirâmide a seguir foi obtído a partir de uma pirâmide hexagonal regular.
a) Qual é a área total dêêsse tronco de pirâmide?
() cm2 ou aproximadamente 190,83 cm2
b) Qual é o volume dêêsse tronco de pirâmide?
cm3 ou aproximadamente 158,48 cm3
49. Observe, a seguir, a planificação de um tronco de pirâmide, determinado a partir de uma pirâmide quadrangular regular.
a) Qual é a área total dêêsse tronco de pirâmide?
(320 + dm2 ou aproximadamente 652,55 dm2
b) Qual é o volume dêêsse tronco de pirâmide?
dm3 ou aproximadamente 844,76 dm3
50. ![]() A parte inferior de um troféu tem o formato de um tronco de pirâmide hexagonal regular.
A parte inferior de um troféu tem o formato de um tronco de pirâmide hexagonal regular.

Elabore um problema quê envolva as informações descritas de maneira quê seja necessário utilizar ideias associadas à área da superfícíe ou ao volume de tronco de pirâmide para resolvê-lo. Em seguida, troque seu problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
51. (Unimontes-MG) Uma pirâmide tem 4 m de altura e 160 m3 de volume. Paralelamente a sua base e a 2 m de seu vértice, traça-se um plano quê a divide em uma pirâmide menor e um tronco de pirâmide. O volume, em m3, do tronco dessa pirâmide é igual a
a) 140.
b) 100.
c) 80.
d) 20.
alternativa a
Página cento e sessenta e oito
Cilindro circular
O Brasil é um dos principais produtores de grãos do mundo, como soja e milho. Na safra 2023/2024, por exemplo, foi estimada uma produção de cerca de 294 milhões de toneladas de grãos no país. Para acondicionar toda essa produção, costumam sêr utilizados silos de armazenamento. Um dos modelos mais comuns dêêsses silos tem parte de sua estrutura com formato de cilindro, como o mostrado a seguir.

Fonte dos dados: BRASIL. Ministério do Desenvolvimento Agrário e Agricultura Familiar. Companhia Nacional de Abastecimento. Safra de grãos 2023/2024 está estimada em 294,1 milhões de toneladas. Brasília, DF: MDA: Conab, 11 abr. 2024. Disponível em: https://livro.pw/nrjdl. Acesso em: 9 ago. 2024.
DICA
O formato da parte superior da estrutura dêêsses silos lembra um cone, figura geométrica espacial quê será estudada posteriormente nesta Unidade.
Para calcular a quantidade aproximada de material necessário para fabricar um silo dêêsses ou sua capacidade de armazenamento, é necessário ter conhecimentos sobre cilindros. Você se lembra de alguns conceitos estudados no Ensino Fundamental a respeito dessa figura geométrica espacial?
MATEMATICA NA HISTÓRIA
Diversos estudos sobre Geometria surgem a partir de problemas práticos. Por exemplo, 26 dos 110 problemas apresentados nos papiros egípcios de Moscou e de Rhind tratam de elemêntos geométricos. Um dêêsses problemas propõe um procedimento para o cálculo aproximado do volume de um cilindro, provavelmente motivado pela necessidade de se calcular a capacidade de estocagem de grãos em silos cilíndricos. Em escavações realizadas em Tell Edfu, no Egito, arqueólogos encontraram estruturas cilíndricas quê possivelmente eram utilizadas como silos para estocagem de cevada e trigo.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 5. ed. Campinas: Editora da Unicamp, 2011. p. 75.

Página cento e sessenta e nove
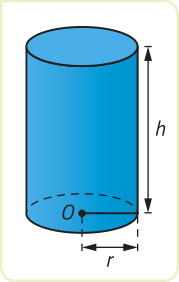
Dados dois planos distintos e paralelos (alfa)" e (beta)", um círculo de centro O e raio r contido em (alfa)" e uma reta t concorrente a esses planos, a reunião de todos os segmentos de reta paralelos a t com uma extremidade no círculo e outra em (beta)" é denominado cilindro circular. Analise um exemplo de cilindro circular.
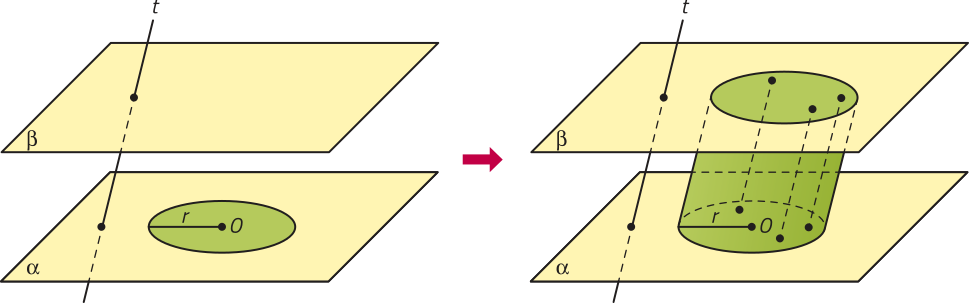
Em um cilindro circular, podemos destacar os seguintes elemêntos:
• os círculos de raio r e centros O e O’, paralelos, são as bases;
• a reta é o eixo;
• os segmentos de reta paralelos a com extremidades nas circunferências das bases são as geratrizes;
• a distância entre os planos quê contêm as bases é a altura;
• a reunião de todas as geratrizes é a superfícíe lateral.
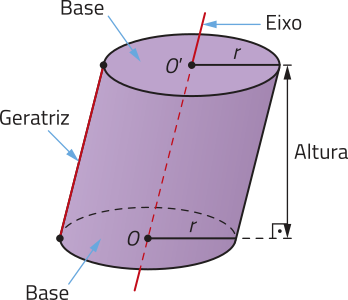
De acôr-do com a inclinação das geratrizes em relação aos planos quê contêm as bases, um cilindro póde sêr classificado em cilindro oblíquo ou cilindro reto.
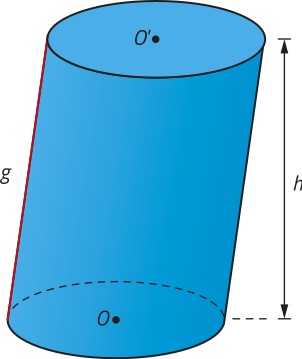
• Cilindro oblíquo é aquele cujas geratrizes são oblíquas aos planos quê contêm suas bases.
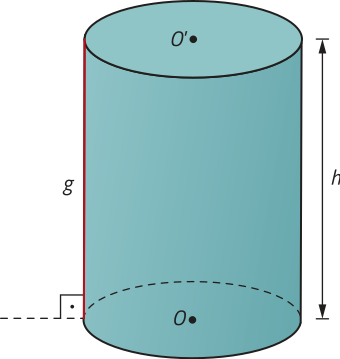
• Cilindro reto é aquele cujas geratrizes são perpendiculares aos planos quê contêm suas bases.
DICA
Nesta coleção, será abordado apenas o cilindro circular, quê será tratado simplesmente como cilindro.
Página cento e setenta
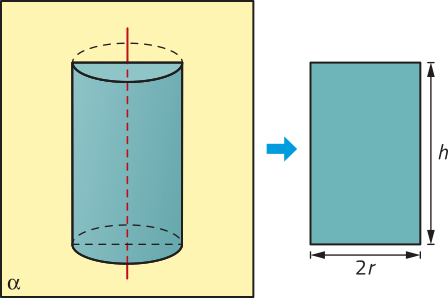
O cilindro reto também é denominado cilindro de revolução, uma vez quê póde sêr obtído por meio da rotação em 360° de um retângulo em torno de um eixo quê contém um de seus lados.
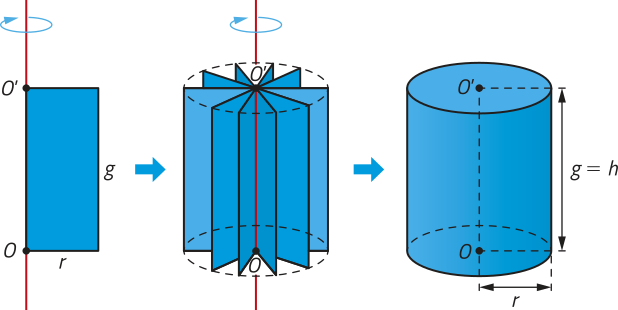
A região ôbitída na interseção de um cilindro por um plano quê contém o seu eixo é denominada seção meridiana.
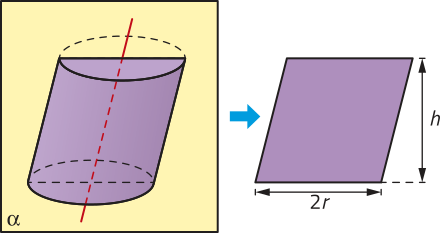
PARA PENSAR
Todo cilindro cuja seção meridiana corresponde a um quadrado, é denominado cilindro equilátero. Nesse tipo de cilindro, quê relação há entre as medidas da altura, do raio da base e da geratriz?
Resposta esperada: As medidas da altura e da geratriz são iguais ao dôbro da medida do raio da base.
Área da superfícíe de um cilindro reto
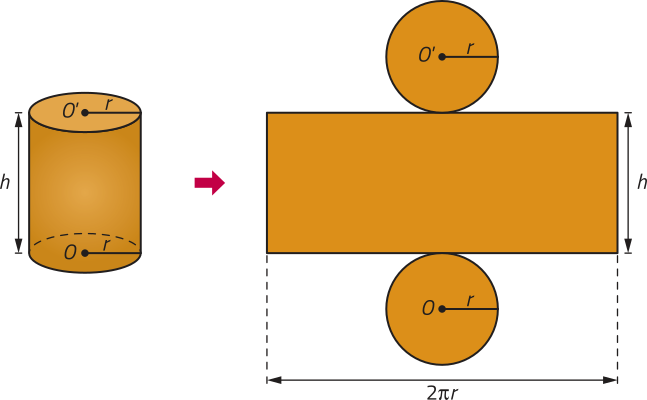
Vamos analisar a planificação de um cilindro reto para compreender como se calcula a área da superfícíe dele.
A planificação de um cilindro reto de altura h e raio da base r corresponde à reunião de dois círculos de raio r e um retângulo de largura h e comprimento 2(pi)"r, conforme representado na imagem.
DICA
O comprimento dêêsse retângulo é igual ao comprimento da circunferência da base do cilindro.
De acôr-do com essa planificação, podemos destacar as seguintes áreas.
• A área da base é dada por: Ab = (pi)"r2
• A área lateral é dada por: A(éli)" = 2(pi)"rh
• A área total é dada por: At = 2Ab + A(éli)" ou At = 2(pi)"r(r + h).
Página cento e setenta e um
ATIVIDADE RESOLVIDA
R11. Observe informações a respeito de uma coifa de exaustão quê tem, na parte superior, um tubo com formato de cilindro reto.
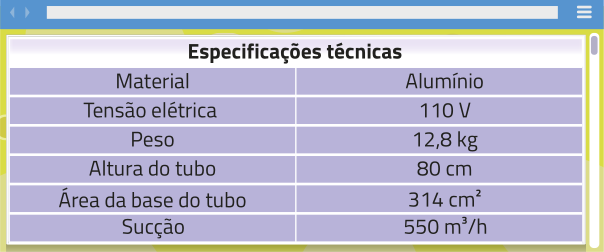
Fonte: Dados fictícios.
Quantos centímetros quadrados de uma placa de alumínio são necessários para fabricar a superfícíe lateral dêêsse tubo?
Resolução
Note quê no enunciado há dados quê não são essenciais para resolvermos a atividade, como a tensão elétrica da coifa. Nesse caso, podemos selecionar apenas as informações necessárias, conforme segue.
• Altura do tubo: 80 cm.
• Área da base do tubo: 314 cm2.
De acôr-do com esses dados, vamos calcular a medida r do raio das bases do tubo cilíndrico, em centímetro, considerando a planificação de sua superfícíe lateral um retângulo com dimensões de 2(pi)"r cm e 80 cm e a área da base igual a 314 cm2.
Ab = (pi)"r2 → 314 ≃ 3,14 ⋅ r2 ⇒ r2 ≃ ⇒
Assim, como o raio da base é aproximadamente 10 cm, calculamos a área da placa, em centímetro quadrado:
A(éli)" = 2(pi)"rh → A(éli)" ≃ 2 ⋅ (pi)" ⋅ 10 ⋅ 80 ≃ 5.024
Portanto, são necessários aproximadamente 5.024 cm2 de uma placa de alumínio para fabricar a superfícíe lateral do tubo cilíndrico dessa coifa.
ATIVIDADES
DICA
Nestas atividades, utilize 3,14 como aproximação de (pi)".
52. Nos itens a seguir, calcule a área total, em centímetro quadrado, de cada cilindro.
a) 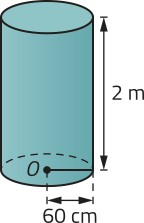
31.200(pi)" cm2 ou aproximadamente 97.968 cm2
b) 
4.600(pi)" cm2 ou aproximadamente 14.444 cm2
DICA
As figuras não estão proporcionais entre si.
53. Para encapar totalmente uma pequena caixa, com formato de cilindro reto de 30 cm de altura, foram utilizados 350(pi)" cm2 de papel. Qual é a medida mássima do raio das bases dessa caixa?
5 cm
54. Quanto méde a altura de um cilindro equilátero cuja área total é 48(pi)" cm2?
cm ou aproximadamente 5,66 cm
55. Observe, a seguir, o projeto de uma manta térmica para cobertura de uma edificação, quê será instalada na superfícíe externa.
preêço da instalação da manta térmica, por métro quadrado: R$ 9,60.
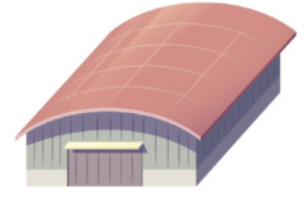
Que quantia, em reais, no mínimo, será necessária para a instalação dessa manta térmica?
R$ 7.536,00
Página cento e setenta e dois
Volume de um cilindro
Anteriormente, obtivemos informações sobre um silo de armazenamento de grãos em quê parte da estrutura tem formato quê lembra um cilindro. Para determinar, por exemplo, a capacidade de armazenamento de silos como esse, podemos utilizar ideias relacionadas ao volume de um cilindro.
Vamos obtêr uma expressão para o cálculo do volume de um cilindro usando o princípio de Cavalieri. Para isso, vamos considerar um prisma e um cilindro de mesma altura h, cujas bases têm áreas iguais a Ab e estão apoiadas em um mesmo plano (alfa)". Qualquer plano (beta)", paralelo a (alfa)", quê secciona esses sólidos, determina neles duas regiões planas com áreas iguais a Ab.
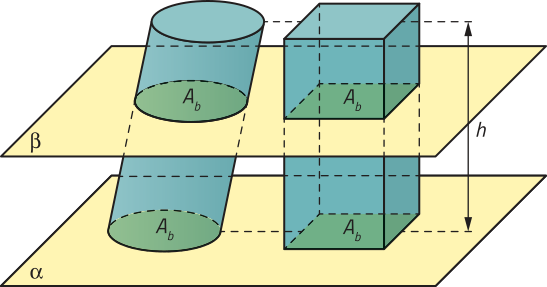
Pelo princípio de Cavalieri, podemos afirmar quê os volumes do prisma e do cilindro são iguais. Como estudado anteriormente, o volume de um prisma é dado por Vp = Ab ⋅ h, portanto o volume do cilindro é dado por:
V = Ab ⋅ h
O volume de um cilindro de raio r e altura h é dado por:
V = Ab ⋅ h ou V = (pi)"r2h
ATIVIDADE RESOLVIDA
R12. Leia, a seguir, o trecho de uma reportagem sobre silos cilíndricos usados pêlos egípcios há mais de 3 mil anos.
Essas caixas de armazenamento, presumivelmente para cevada e trigo usados para alimentação e como meio de troca, foram construídas com tijolos de barro, com diâmetros de 18 a 22 pés. Se sua altura fosse maior quê o diâmetro, o quê era comum, os silos provavelmente teriam pelo menos 25 pés de altura.
WILFORD, Diôn Noble. Escavações revelam modo de vida de cidadãos comuns no antigo Egito. G1, [s. l.], 4 jul. 2008. Disponível em: https://livro.pw/uxmdk. Acesso em: 12 ago. 2024.
Imagine quê um dêêsses silos tivesse 20 pés de diâmetro da base e 25 pés de altura, com 770 kg de trigo armazenados em cerca de 1 m3. Considerando 1 pé equivalendo a aproximadamente 0,3 m, quantos quilogramas de trigo seria possível armazenar nesse silo?
Resolução
Vamos determinar, em métro, as medidas do raio da base r e da altura h do cilindro reto correspondente a esse silo.
• r = ⋅ 0, 3 = 3; ou seja, 3 m.
• h = 25 ⋅ 0,3 = 7,5; ou seja, 7,5 m.
Considerando (pi)" aproximadamente igual a 3,14, vamos calcular o volume aproximado dêêsse cilindro:
V = (pi)"r2h → V ≃ 3,14 ⋅ 32 ⋅ 7,5 = 211,95; ou seja, 211,95 m3.
Como cada 770 kg de trigo ocupam cerca de 1 m3, temos: 770 ⋅ 211,95 = 163.201,5.
Portanto, um silo dêêsse tipo teria capacidade para armazenar cerca de 163.201,5 kg de trigo.
Página cento e setenta e três
ATIVIDADES
DICA
Nas atividades das páginas 173 e 174, utilize 3,14 como aproximação de (pi)".
56. Determine o volume dos cilindros a seguir, em quê O corresponde ao centro de uma base.
a) 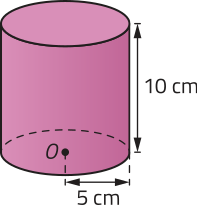
56. a) 250(pi)" cm3 ou aproximadamente 785 cm3
b) 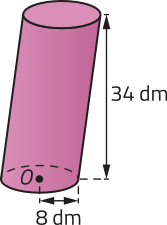
2.176(pi)" dm3 ou aproximadamente 6.832,64 dm3
DICA
As figuras não são proporcionais entre si.
57. Qual é o volume de um cilindro equilátero com área total de 216(pi)" cm2?
432(pi)" cm3 ou aproximadamente 1.356,48 cm3
58. Uma empresa organizou equipes para elaborar propostas de novas embalagens para armazenar entre 230 mL e 250 mL de cérto produto. Observe informações sobre os formatos e as medidas internas de alguns modelos apresentados pelas equipes.
I) Formato de cilindro reto com 6 cm de diâmetro da base e 7,5 cm de altura.
II) Formato de cilindro reto com 3,5 cm de raio da base e 7 cm de altura.
III) Formato de prisma hexagonal regular, com 3 cm de aresta da base e 5,4 cm de aresta lateral.
IV) Formato de paralelepípedo reto-retângulo com dimensões de 9 cm, 6 cm e 4,5 cm.
Qual dêêsses modelos de embalagem póde sêr utilizado pela empresa? A superfícíe dessa embalagem tem quantos centímetros quadrados de área?
modelo IV; 243 cm2
NO MUNDO DO TRABALHO
Trabalho em equipe e criatividade
Para um bom trabalho em equipe, é importante quê cada integrante dela desempenhe seu papel e quê escute e respeite os demais, considerando as diferenças e o compartilhamento de conhecimentos e ideias. É primordial, ainda, quê dividam responsabilidades, sempre pensando na melhor maneira de executarem uma tarefa.
Em uma empresa, o trabalho em equipe é essencial para um bom dêsempênho, além da criatividade na busca por soluções de um problema ou de uma demanda. Essas são duas importantes soft skills, competências comportamentais relacionadas à personalidade do profissional, quê empresas têm considerado na contratação de pessoas para escolher aquela quê lida melhor com os desafios do dia a dia.
Ouça o podcast indicado a seguir para obtêr mais informações a respeito de soft skills.
• BBC LÊ: o quê são ‘soft skills’: habilidades comportamentais cada vez mais buscadas por empregadores. Locução de: Rodrigo Durão. [S. l.]: BBC nius Brasil, 14 ago. 2022. Podcast. Disponível em: https://livro.pw/plgot. Acesso em: 9 ago. 2024.
59. Em uma fazenda, há um silo para armazenamento de grãos cujo formato corresponde à composição de um cilindro reto e de um cone reto, ambos de mesma base, conforme representado. Quantos metros cúbicos de grãos podem sêr armazenados na parte cilíndrica?

108(pi)" m3 ou aproximadamente 339,12 m3
Página cento e setenta e quatro
60. As canetas esferográficas recebem esse nome porque têm em sua ponta uma pequena esféra quê, ao sêr girada em contato com a superfícíe, transporta a tinta para o papel.

Em cérto modelo de caneta esferográfica sem uso, o reservatório de tinta tem formato de cilindro reto, com 3 mm de diâmetro interno e 130 mm de altura. A tinta ocupa cerca de 90% da capacidade dêêsse reservatório.
a) Qual é a capacidade do reservatório de tinta dessa caneta?
292,5(pi)" mm3 ou aproximadamente 918,45 mm3
b) Qual é o volume de tinta, em milímetro cúbico, contido no reservatório de uma caneta dessas? Esse volume corresponde a mais ou a menos do quê 1 mL?
aproximadamente 827 mm3; menos do quê 1 mL
61. Em uma obra de drenagem, foram utilizadas 100 manilhas de concreto, com formato de cilindro reto de 1,2 m de altura, para o escoamento de águas pluviais.
Os diâmetros externo e interno de cada manilha médem, respectivamente, 40 cm e 24 cm. Qual é o volume total de concreto, em métro cúbico, utilizado para a fabricação dessas manilhas? Desconsidere as ferragens quê possam sêr utilizadas.

aproximadamente 9,65 m3
62. Observe o retângulo a seguir.

Considere os cilindros rétos I e II, obtidos ao realizar a rotação dêêsse retângulo em 360°, em torno de e , respectivamente.
a) Qual é o volume dos cilindros I e II?
cilindro I: 1.350(pi)" cm3 ou aproximadamente 4.239 cm3; cilindro II: 540(pi)" cm3 ou aproximadamente 1.695,6 cm3
b) Qual é a diferença entre as áreas totais dos cilindros I e II?
378(pi)" cm2 ou aproximadamente 1.186,92 cm2
63. A área lateral de um cilindro reto é aproximadamente 87,92 cm2. Sabendo quê o perímetro de sua seção meridiana é 22 cm, determine:
a) a medida do raio de sua base;
Respostas possíveis: 2 cm ou 3,5 cm.
b) a medida de sua altura;
Respostas possíveis: 7 cm ou 4 cm.
c) sua área total;
Respostas possíveis: 36(pi)" cm2 (aproximadamente 113,04 cm2) ou 52,5(pi)" cm2 (aproximadamente 164,85 cm2).
d) seu volume.
Respostas possíveis: 28(pi)" cm3 (aproximadamente 87,92 cm3) ou 49(pi)" cm3 (aproximadamente 153,86 cm3).
64. Observe um retângulo ABCD, no plano cartesiano, em quê a unidade de medida de comprimento utilizada é o centímetro.
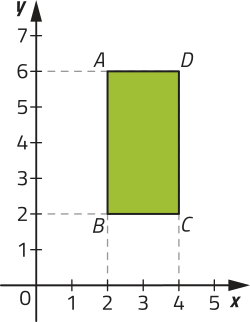
Qual é o volume do sólido geométrico obtído ao rotacionar esse retângulo em 360°, em torno do eixo x?
64(pi)" cm3 ou aproximadamente 200,96 cm3
65. Um cubo de cm de aresta tem o mesmo volume de um cilindro equilátero. Em relação a esse cilindro equilátero, calcule:
a) o seu volume;
54(pi)" cm ou aproximadamente 169,56 cm3
b) a medida do raio de sua base;
3 cm
c) sua área lateral.
36(pi)" cm2 ou aproximadamente 113,04 cm2
66. ![]() Para armazenar o gel fixador de cabelo, contido na embalagem representada a seguir, uma empresa planeja criar uma embalagem com outro formato.
Para armazenar o gel fixador de cabelo, contido na embalagem representada a seguir, uma empresa planeja criar uma embalagem com outro formato.

Elabore o projeto de uma nova embalagem para o armazenamento do gel fixador, de maneira quê esta tenha formato diferente do apresentado, mas com capacidade aproximadamente igual. Para isso, represente essa nova embalagem com desenho, indicando suas medidas, e apresente os respectivos cálculos.
Com base nas informações do enunciado e no seu projeto de embalagem, elabore um problema em quê seja necessário utilizar ideias associadas a volume e área de figuras geométricas espaciais. Em seguida, troque seu problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
Página cento e setenta e cinco
Cone circular
Quando descartado de maneira incorréta, o óleo de cuzinha é um dos produtos domésticos quê mais causam danos ao meio ambiente, poluindo os rios e o solo. Além díssu, esse descarte também póde causar o entupimento dos encanamentos.
Para evitar esses tipos de problema, é importante realizar o descarte do óleo corretamente. Observe as etapas de descarte a seguir.

Em geral, são utilizados coadores de metal resistentes a altas tempera-túras cujo formato lembra o de um cone, o quê permite maior área de contato do óleo com o coador.
Fonte dos dados: SÃO PAULO (Estado). Casa Civil. Reciclagem: aprenda a descartar corretamente o óleo de cuzinha. São Paulo: Casa Civil, [2024]. Disponível em: https://livro.pw/jtbfj. Acesso em: 13 ago. 2024.
PARA AMPLIAR
Assista a êste vídeo para obtêr mais informações sobre a reciclagem do óleo de cuzinha.
• MEIO ambiente por inteiro: reciclagem do óleo de cuzinha. [S. l.: s. n.], 2018. 1 vídeo (24 min). Publicado pelo canal Rádio e Tevê Justiça. Disponível em: ww.youtube.com/watch?v=lIpirOW3DVQ. Acesso em: 12 ago. 2024.
Dados um plano (alfa)", um círculo de centro O e raio r contido em (alfa)" e um ponto V não pertencente a (alfa)", a reunião de todos os segmentos de reta com uma extremidade em V e outra em um ponto dêêsse círculo é denominada cone circular. Analise um exemplo de cone circular.
Em um cone, como o anterior, podemos destacar os seguintes elemêntos:
• o ponto V é o vértice;
• o círculo de raio r e centro O é a base;
• os segmentos de reta com uma extremidade na circunferência da base e a outra no vértice V são as geratrizes;
• a reta é o eixo;
• a distância h, entre o ponto V e o plano (alfa)", é a altura do cone;
• a reunião de todas as geratrizes é a superfícíe lateral.
DICA
Nesta coleção, será abordado apenas o cone circular, quê será tratado simplesmente como cone.
Página cento e setenta e seis
De acôr-do com a inclinação do eixo em relação ao plano quê contém a base, um cone póde sêr classificado em cone oblíquo ou cone reto.
• Cone oblíquo é aquele cujo eixo é oblíquo ao plano quê contém sua base.
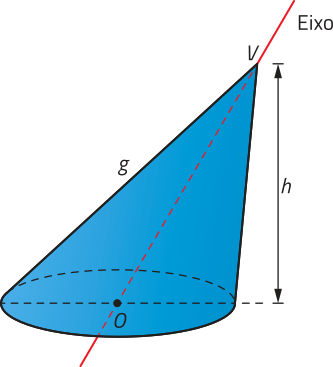
• Cone reto é aquele cujo eixo é perpendicular ao plano quê contém sua base.
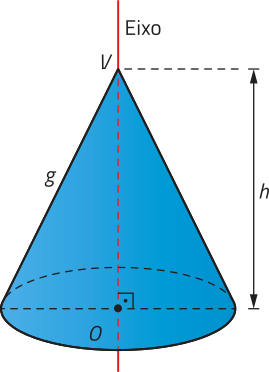
PARA PENSAR
escrêeva uma expressão quê relacione a medida do raio da base (r), da geratriz (g) e da altura (h) de um cone circular reto.
Resposta esperada: g2 = h2 + r2.
O cone reto também é denominado cone de revolução, uma vez quê póde sêr obtído por meio da rotação em 360° de um triângulo retângulo em torno de um eixo quê contém um de seus catetos.
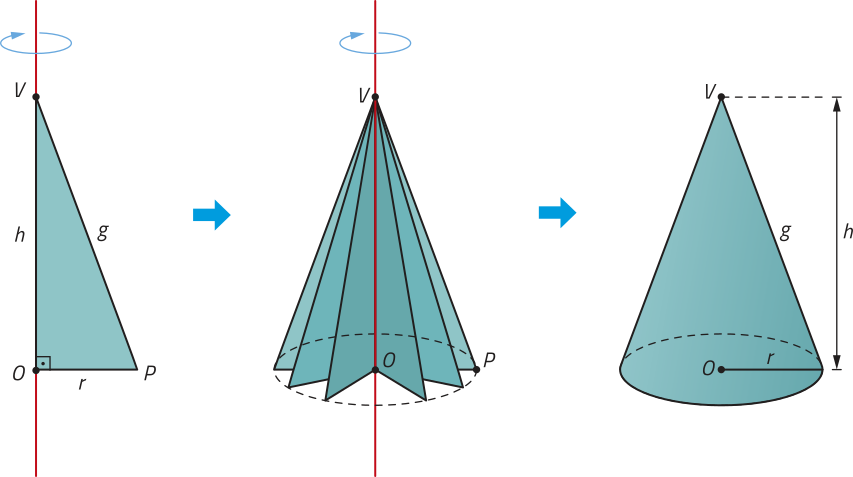
A seção transversal de um cone corresponde à interseção do cone por um plano (beta)" paralelo à sua base. Note quê a região ôbitída nessa interseção é um círculo.
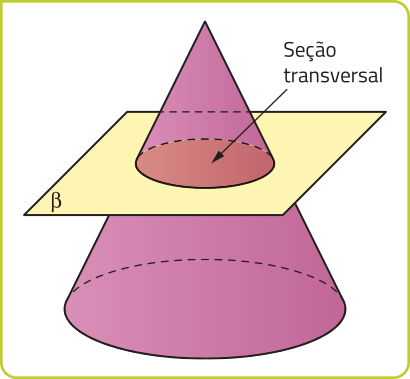
Página cento e setenta e sete
A região ôbitída na interseção de um cone por um plano (beta)" quê contém o seu eixo é denominada seção meridiana.
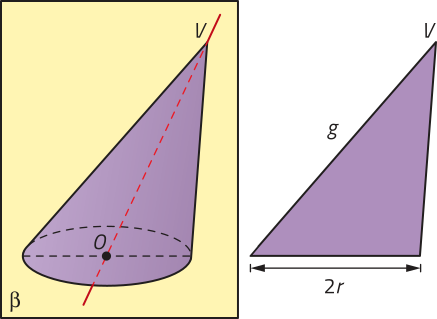
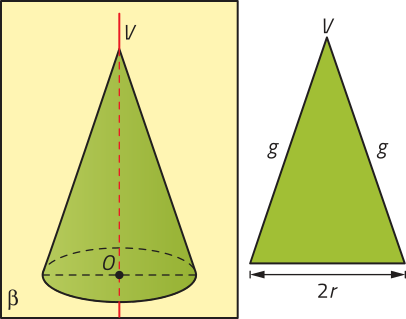
PARA PENSAR
Todo cone cuja seção meridiana corresponde a um triângulo equilátero é denominado cone equilátero. escrêeva expressões quê relacionem a medida da geratriz (g) e a medida da altura (h) de um cone equilátero em função da medida do raio de sua base (r).
Resposta esperada: g = 2r; h = .
Área da superfícíe de um cone reto
Para calcular a área da superfícíe de um cone reto, vamos, primeiramente, analisar sua planificação.
A planificação de um cone reto de geratriz de medida g e raio da base r corresponde à reunião de um círculo de raio r e um setor circular de raio g e arco de circunferência de 2(pi)"r de comprimento, conforme representado a seguir.

DICA
O comprimento do arco de circunferência correspondente ao setor circular é igual ao comprimento da circunferência da base do cone.
Você se lembra de quê a área de um setor circular é diretamente proporcional ao comprimento do arco de circunferência correspondente? Usando essa ideia, podemos determinar a área lateral (A(éli)") de um cone reto:
= ⇒ A(éli)" = (pi)"rg
Nesse cone reto, podemos destacar as seguintes áreas:
• a área lateral é dada por: A(éli)" = (pi)"rg;
• a área da base é dada por: Ab = (pi)"r2
• a área total é dada por: At = Ab + A(éli)" ou At = (pi)"r (r + g)
Página cento e setenta e oito
ATIVIDADE RESOLVIDA
R13. Um cone reto tem 10 cm de diâmetro da base e 12 cm de altura. Em relação a esse cone, calcule a:
a) área da base;
b) medida da geratriz;
c) área lateral;
d) área total;
e) medida do ângulo central, em grau, do setor circular quê compõe a planificação de sua superfícíe lateral;
f) área da seção meridiana.
Resolução
a) Sendo Ab a área da base dêêsse cone, temos:
Ab = (pi)" ⋅ r2 = (pi)" ⋅ ()2 = 25(pi)"
Portanto, a área da base do cone é 25(pi)" cm2 ou aproximadamente 78,5 cm2.
b) Sendo g a medida da geratriz dêêsse cone, temos:
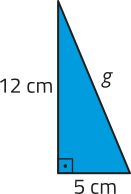
g2 = 52 + 122 ⇒ g2 = 169 ⇒
Portanto, a geratriz do cone méde 13 cm.
c) Sendo A(éli)" a área lateral dêêsse cone, temos:
A(éli)" = (pi)"rg = (pi)" ⋅ 5 ⋅ 13 = 65(pi)"
Portanto, a área lateral do cone é 65(pi)" cm2 ou aproximadamente 204,1 cm2.
d) Sendo At a área total dêêsse cone, temos:
At = Ab + A(éli)" = 25(pi)" + 65(pi)" = 90(pi)"
Portanto, a área total do cone é 90(pi)" cm2 ou aproximadamente 282,6 cm2.
e) Vamos calcular a medida do comprimento do arco de circunferência de raio 13 cm determinado pelo ângulo central de medida (alfa)".
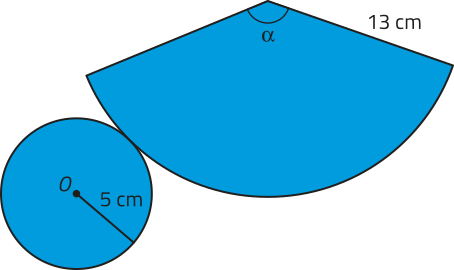
Para isso, primeiramente, vamos obtêr a medida do comprimento de uma circunferência de raio 13 cm:
2 ⋅ (pi)" ⋅ 13 = 26(pi)"; ou seja, 26(pi)" cm.
Agora, calculamos o comprimento da circunferência da base do cone:
2 ⋅ (pi)" ⋅ 5 = 10(pi)"; ou seja, 10(pi)" cm.
Com isso, podemos compor a seguinte proporção:
Medida do ângulo central (em grau) |
Comprimento (em cm) |
|---|---|
360 |
26(pi)" |
(alfa)" |
10(pi)" |
= ⇒ 26(pi)" ⋅ (alfa)" = 360 ⋅ 10(pi)" ⇒ (alfa)" = ≃ 138,46
Portanto, (alfa)" ≃ 138,46°.
f) Sendo A m a área do triângulo isósceles correspondente à seção meridiana do cone, temos:
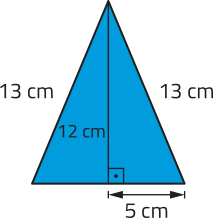
A m = = = 60
Portanto, a área da seção meridiana do cone é 60 cm2.
Página cento e setenta e nove
ATIVIDADES
DICA
Nestas atividades, utilize 3,14 como aproximação de (pi)".
67. Em cada item a seguir, calcule a área da base, a área lateral e a área total do cone reto.
a) 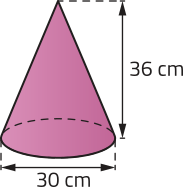
área da base: 225(pi)" cm2 ou aproximadamente 706,5 cm2; área lateral: 585(pi)" cm2 ou aproximadamente 1.836,9 cm2; área total: 810(pi)" cm2 ou aproximadamente 2.543,4 cm2
b) 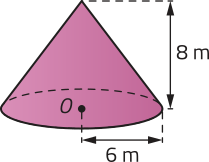
área da base: 36(pi)" m2 ou aproximadamente 113,04 m2; área lateral: 60(pi)" m2 ou aproximadamente 188,4 m2; área total: 96(pi)" m2 ou aproximadamente 301,44 m2
DICA
As figuras não são proporcionais entre si.
68. Um cone reto tem 15 cm de raio da base e geratriz medindo cm. Em relação a esse cone, calcule a:
a) medida da altura;
30 cm
b) área da base;
225(pi)" cm2 ou _ aproximadamente 706,5 cm2
c) área lateral;
cm2 ou aproximadamente 1.579,78 cm2
d) área total.
225(pi)" (1 + )cm2 ou aproximadamente 2.286,28 cm2
69. Uma peça com formato de cone reto, com 18 cm de raio da base, foi cortada de maneira quê fossem obtidas duas peças idênticas, como a representada a seguir.
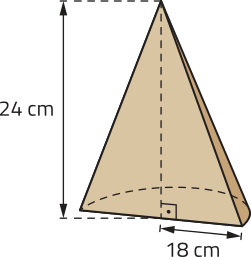
Qual é a área total de cada parte ôbitída?
432((pi)" + 1) cm2 ou aproximadamente 1.788,48 cm2
70. Um cone equilátero tem base de 14 cm de diâmetro. Em relação a esse cone, calcule a:
a) medida da geratriz;
14 cm
b) área lateral;
98(pi)" cm2 ou aproximadamente 307,72 cm2
c) área total;
147(pi)" cm2 ou aproximadamente 461,58 cm2
d) área da seção meridiana;
cm2 ou aproximadamente 84,77 cm2
e) medida (alfa)" do ângulo central do setor circular quê compõe a planificação da superfícíe lateral.
180°
71. Um triângulo retângulo tem catetos medindo 6 cm e 8 cm. Qual é a área total do sólido geométrico obtído ao rotacionar em 360° esse triângulo em torno de um eixo quê contém seu maior cateto? E em torno de um eixo quê contém seu menor cateto?
96(pi)" cm2 ou aproximadamente 301,44 cm2; 144(pi)" cm2 ou aproximadamente 452,16 cm2
72. Certa fábrica produz três modelos de coadores de metal, próprios para coar óleo de cuzinha usado, todos com formato de cone reto, cujas medidas do diâmetro da base e da altura estão indicadas a seguir.


DICA
Para resolver esta atividade, desconsidere possíveis desperdícios de metal na produção, além da espessura e dos furos dêêsses modelos de coador.
a) Desconsiderando o metal utilizado no cabo dêêsses coadores, ao utilizar de 900 cm2 até 1.000 cm2 dêêsse metal, é possível produzir cerca de:
I) dois coadores do modelo A e três do modelo B;
II) dois coadores do modelo A e um do modelo C;
III) um coador do modelo B e um do modelo C;
IV) um coador de cada modelo.
alternativa II
b) ![]() Como o óleo de cuzinha é descartado na residência onde você mora? Comente.
Como o óleo de cuzinha é descartado na residência onde você mora? Comente.
Resposta pessoal.
c) ![]() Em grupos de três integrantes, pesquisem, no município ou na região em quê vocês moram, pontos de côléta de óleo de cuzinha usado (ecopontos). Com alguma ferramenta digital, elaborem um mapa virtual com esses ecopontos, a fim de divulgá-los na mídia digital, com informações sobre os horários de funcionamento e a importânssia do descarte correto do óleo de cuzinha usado.
Em grupos de três integrantes, pesquisem, no município ou na região em quê vocês moram, pontos de côléta de óleo de cuzinha usado (ecopontos). Com alguma ferramenta digital, elaborem um mapa virtual com esses ecopontos, a fim de divulgá-los na mídia digital, com informações sobre os horários de funcionamento e a importânssia do descarte correto do óleo de cuzinha usado.
Pesquisa e elaboração dos estudantes.
PARA AMPLIAR
Acesse o sáiti indicado a seguir para obtêr mais informações sobre pontos de côléta de óleo de cuzinha usado.
• ÓLEO SUSTENTÁVEL. Pontos de entrega. [S. l.]: Abiove: Óleo Sustentável, c2024. Disponível em: https://livro.pw/vowuu. Acesso em: 12 ago. 2024.
Página cento e oitenta
Volume de um cone circular
Para determinar uma expressão para o cálculo do volume de um cone, vamos considerar um cone e uma pirâmide, ambos com altura h e bases com áreas iguais a Ab, apoiados em um mesmo plano (alfa)". Consideremos também um plano (beta)" qualquer, paralelo a (alfa)", quê secciona esses sólidos a uma distância d de seus vértices, determinando neles duas regiões planas de área A1 e A2, respectivamente.
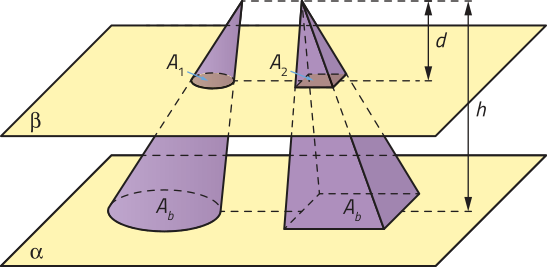
De acôr-do com o quê estudamos anteriormente, há semelhança entre o cone original e o cone menor obtído na seção do plano (beta)", portanto = . De maneira análoga, para a pirâmide original e a pirâmide menor ôbitída na seção do plano (beta)", temos = . Com isso, chegamos à seguinte proporção:
= ⇒ A1 = A2
Pelo princípio de Cavalieri, podemos afirmar quê os volumes do cone e da pirâmide são iguais. Você estudou quê o volume da pirâmide é dado por VP = , logo o volume do cone é dado por:
V =
Dado um cone circular de raio da base r e altura h, seu volume é dado por:
V = ou V =

Agora, vamos observar o quê ocorre com um cone e um cilindro, ambos com altura h e bases de raio r.
• Vcone =
• Vcilindro = (pi)"r2 h
A partir dessas igualdades, temos: Vcone = ⇒ Vcilindro = 3 ⋅ Vcone
Portanto, para um cilindro e um cone de mesmo raio da base e mesma altura, o volume dêêsse cilindro é o triplo do volume do cone ou, de maneira equivalente, o volume dêêsse cone corresponde à terça parte do volume do cilindro.
Página cento e oitenta e um
ATIVIDADES RESOLVIDAS
R14. Uma confeitaria produz doces compostos de uma casquinha de biju recheada. O recheio ocupa completamente o espaço interno da casquinha, cujo formato corresponde ao de um cone circular reto de 10 cm de altura e 6 cm de diâmetro interno da base. Quantos mililitros de recheio vão em cada doce dêêsses? Considere (pi)" ≃ 3,1.
Resolução
O raio da base e a altura do cone circular reto, correspondentes à região interna da casquinha, médem 3 cm (6 ∶ 2 = 3) e 10 cm, respectivamente. Assim, o volume aproximado dêêsse cone é dado por:
V = → V ≃ = 93; ou seja, 93 cm3.
Como 1 cm3 equivale a 1 mL, então cada doce terá aproximadamente 93 mL de recheio.
R15. Ao seccionar um cone reto de vértice V, altura H e raio da base R, por um plano (alfa)" paralelo à sua base, determinamos duas figuras geométricas espaciais: um cone reto menor de altura h e raio da base r, semelhante ao cone original, e um tronco de cone reto.
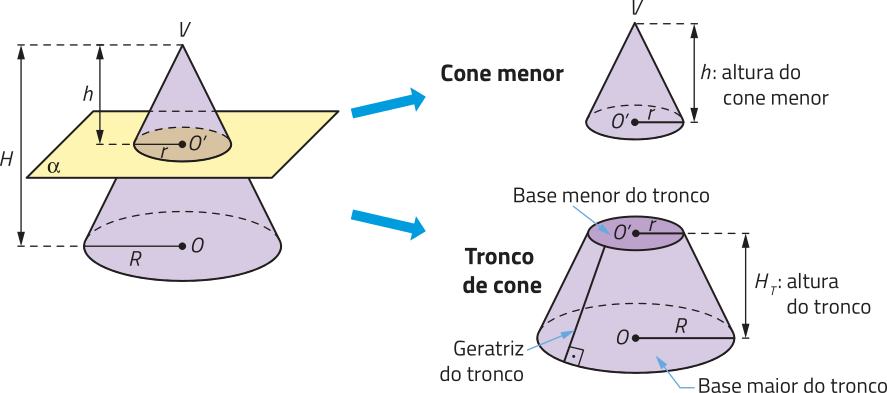
Considere o tronco de cone circular reto a seguir e resôuva o quê se pede em cada item.
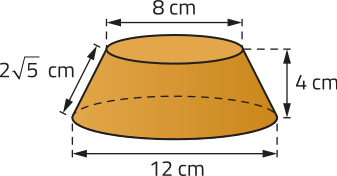
a) Qual é a área total dêêsse tronco de cone?
b) Determine o volume dêêsse tronco de cone.
Resolução
Esse tronco de cone póde sêr obtído a partir de um cone reto de vértice V, raio da base medindo 6 cm e geratriz G, conforme a figura a seguir.
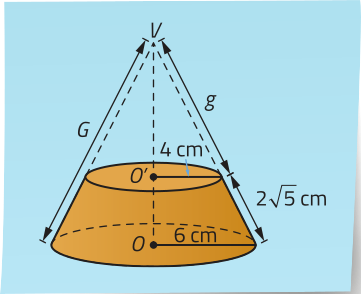
Página cento e oitenta e dois
a) Vamos calcular as áreas das bases menor (Ab) e maior (AB) dêêsse tronco de cone:
• Ab = (pi)" ⋅ 42 = 16(pi)"; ou seja, 16(pi)" cm2;
• AB = (pi)" ⋅ 62 = 36(pi)"; ou seja, 36(pi)" cm2.
A área lateral (A(éli)") dêêsse tronco de cone corresponde à diferença entre as áreas laterais do cone original e do cone menor. Como esses cones são semelhantes entre si, temos:
= ⇒ 6g = 4g + ⇒ g = = ; ou seja, cm.
Com isso, calculamos a área lateral:
A(éli)" = (pi)"RG − (pi)"rg → A(éli)" = (pi)" ⋅ 6 ⋅ ( + ) − (pi)" ⋅ 4 ⋅ = (pi)";
ou seja, (pi)" cm2.
Agora, vamos calcular a área total (AT) dêêsse tronco:
AT = Ab + AB + A(éli)" = 16(pi)" + 36(pi)" + (pi)" = 52(pi)" + (pi)"
Portanto, a área total dêêsse tronco de cone é (52 + )(pi)" cm2 ou aproximadamente 303,7 cm2.
b) Para determinar o volume dêêsse tronco de cone (VT), podemos calcular a diferença entre os volumes do cone original (VC) e do cone menor (Vc).
Considerando HT a altura do tronco, h a altura do cone menor e H = HT + h a altura do cone original, temos:
= ⇒ 6h = 4h + 4 ⋅ 4 ⇒ 2h = 16 ⇒ h = 8; ou seja, 8 cm.
Assim, temos:
VT = VC − Vc = − = − =
Portanto, o volume dêêsse tronco de cone é cm3 ou aproximadamente 318,19 cm3.
ATIVIDADES
DICA
Nas atividades das páginas 182 a 184, utilize 3,14 como aproximação de (pi)".
73. Determine o volume de cada cone a seguir.
a) 
324(pi)" cm3 ou aproximadamente 1.017,36 cm3
b) 
51.200(pi)" m3 ou aproximadamente 160.768 m3
DICA
As figuras não são proporcionais entre si.
74. Qual é o volume de um cone reto com diâmetro da base e altura medindo, respectivamente, 6 cm e 11 cm?
33(pi)" cm3 ou aproximadamente 103,62 cm3
75. Um cone reto tem raio da base de 12 m e geratriz de 20 m. Em relação a esse cone, calcule:
a) a medida de sua altura;
16 m
b) seu volume.
768(pi)" m3 ou aproximadamente 2.411,52 m3
76. Calcule o volume de um cone equilátero com raio da base medindo 13 dm.
dm3 ou aproximadamente 3.982,9 dm3
77. Um cone reto tem cm3 de volume e 6 cm de altura. Qual é a medida do raio da base dêêsse cone?
4,5 cm
78. O proprietário de um buffet precisa comprar taças de aproximadamente 300 mL de capacidade e com formato interno de cone reto. Desenhe um modelo de taça quê atenda a esses requisitos, indicando suas medidas em centímetro.
Resposta possível: Taça com 12 cm de diâmetro da base e 8 cm de altura na região interna de formato de cone.
Página cento e oitenta e três
79. Para produzir uma escultura, um artesão separou uma peça maciça de argila, com formato de cilindro reto de 9 cm de altura. Em seguida, com um torno, ele fez um furo com formato de cone reto, centralizado nessa peça, de mesma altura quê a do cilindro, conforme representado a seguir.
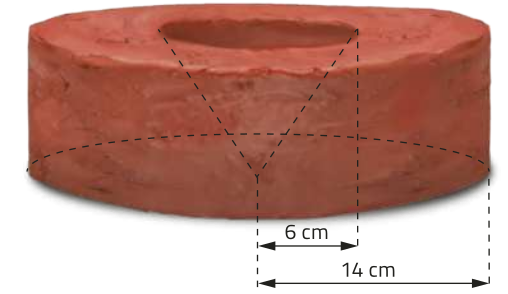
Após finalizada, qual será o volume de argila dessa escultura?
1.656(pi)" cm3 ou aproximadamente 5.199,84 cm3
80. Um tanque é utilizado em uma indústria para armazenar óleo dízel, quê mantém geradores elétricos em funcionamento quando falta energia na rê-de. Observe a representação dêêsse tanque com as medidas internas indicadas.

Nessa indústria, há cinco geradores elétricos quê, quando acionados, consomem cerca de 31 L de óleo dízel por hora, cada um. Quantas horas, no mássimo, todos esses geradores podem sêr mantidos simultaneamente em funcionamento com o óleo dízel disponível nesse tanque, quando cheio?
8 h
81. Observe um cone oblíquo cujo eixo corresponde a e a base está contida em um plano (alfa)".
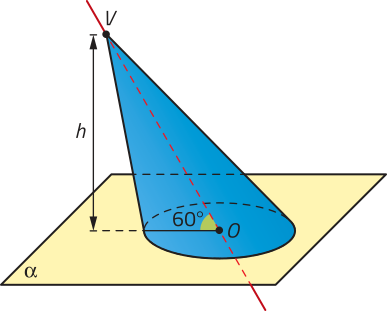
Sabendo quê OV = 9 cm e quê o raio da base dêêsse cone méde 3 cm, determine:
a) a medida de sua altura h;
cm ou aproximadamente 7,79 cm
b) o seu volume.
cm3 ou aproximadamente 73,42 cm3
82. ![]() Na figura a seguir, é a reta suporte da hipotenusa do triângulo retângulo ABC. Qual é o volume do sólido de revolução obtído ao rotacionar esse triângulo em 360° em torno de ? Explique a um colega seus procedimentos.
Na figura a seguir, é a reta suporte da hipotenusa do triângulo retângulo ABC. Qual é o volume do sólido de revolução obtído ao rotacionar esse triângulo em 360° em torno de ? Explique a um colega seus procedimentos.
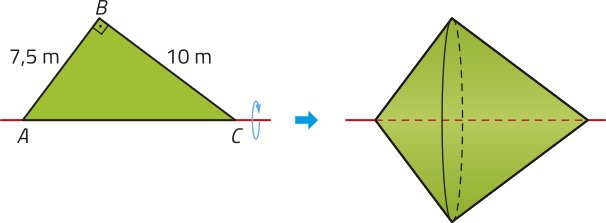
150(pi)" m3 ou aproximadamente 471 m3
83. Buscando inovar nas embalagens de seus produtos, uma indústria de cosméticos planeja lançar uma nova linha de batons, em embalagens acrílicas com formato de cone reto. Essa embalagem será completamente coberta por um adesivo cujo mólde está representado na figura.
a) Qual será a área aproximada da superfícíe de cada embalagem acrílica dessas?
23,04(pi)" cm2 ou 72,35 cm2
b) Qual será a capacidade aproximada, em mililitro, de cada embalagem dessas? Para os cálculos, desconsidere o volume de acrílico da embalagem.
13,03(pi)" mL ou 40,91 mL
Página cento e oitenta e quatro
84. Um recipiente, completamente cheio de á gua, tem formato de cone reto com medidas internas do raio da base igual a 5 cm e altura, 15 cm. Toda á gua dêêsse recipiente será despejada em um póte com formato de cilindro reto, com raio da base e altura com medidas internas de 6 cm e 8 cm, respectivamente.
a) Qual será a altura alcançada pelo nível da á gua nesse póte?
cm ou aproximadamente 3,47 cm
b) Qual é a capacidade dêêsse póte, em mililitro?
288(pi)" mL ou aproximadamente 904,32 mL
c) Que porcentual da capacidade dêêsse póte ficará com á gua?
aproximadamente 43,4%
85. Qual deve sêr a medida do raio da base de um cone equilátero para quê seu volume seja igual ao volume de um paralelepípedo reto-retângulo com dimensões de cm, 8 cm e 12(pi)" cm?
12 cm
86. Analise, a seguir, o modelo de lustre pendente, com cúpula em um formato quê lembra o de um tronco de cone reto e quê terá a superfícíe lateral externa pintada.
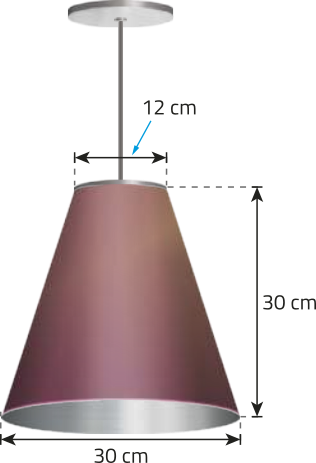
Qual é a área dêêsse lustre quê será pintada?
aproximadamente 2.065 cm2
87. De acôr-do com a Associação Brasileira de Normas Técnicas (ABNT), os copos plásticos não podem ter furos, rachaduras ou pontas afiadas, e devem sêr protegidos com embalagens plásticas para comercialização. Por quêstão de segurança, os diferentes modelos de copos plásticos descartáveis devem ter massas mínimas estabelecidas pela ABNT, que varíam de acôr-do com a capacidade total dos copos, conforme indicado a seguir.
Relação entre capacidade e massa de copos plásticos
Capacidade (mL) |
Massa mínima (g) |
|---|---|
50 |
0,75 |
200 |
2,2 |
500 |
6,3 |
770 |
12 |
Fonte dos dados: ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 14865: copos plásticos descartáveis. Rio de Janeiro: ABNT, 2002. p. 3. Disponível em: https://livro.pw/vvgzu. Acesso em: 10 out. 2024.
O setor de contrôle de qualidade de uma indústria selecionou uma amostra de dois modelos de copos, com formato semelhante a um tronco de cone reto, produzidos em cérto lote, para verificar se estão adequados às normas da ABNT. Analise as informações a seguir.
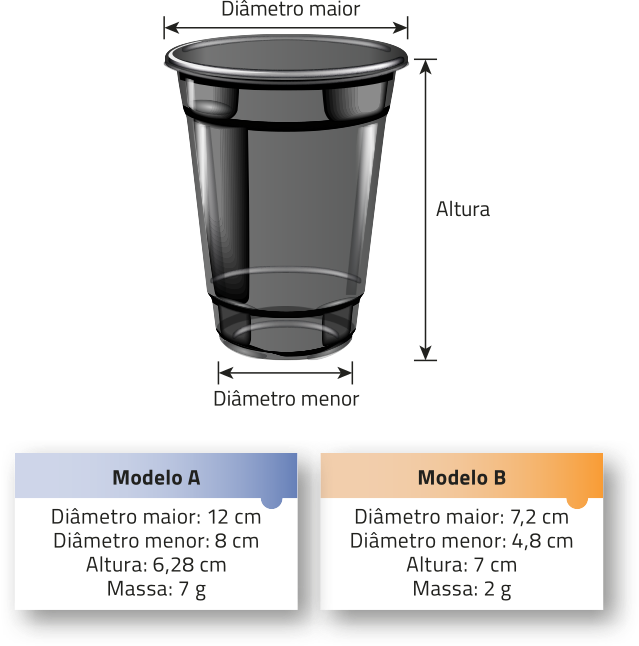
a) Qual dêêsses modelos não atende às especificações da ABNT? Justifique.
modelo B
b) ![]() Junte-se a três côlégas, e escôlham um modelo de copo plástico descartável quê tenha o formato semelhante a um tronco de cone reto. Em seguida, investiguem se o modelo de copo escolhido está adequado às normas apresentadas. Por fim, elaborem um relatório de pesquisa para descrever a investigação realizada, apresentando todos os cálculos e argumentos necessários.
Junte-se a três côlégas, e escôlham um modelo de copo plástico descartável quê tenha o formato semelhante a um tronco de cone reto. Em seguida, investiguem se o modelo de copo escolhido está adequado às normas apresentadas. Por fim, elaborem um relatório de pesquisa para descrever a investigação realizada, apresentando todos os cálculos e argumentos necessários.
Resposta pessoal.
Página cento e oitenta e cinco
esféra
Você provavelmente já observou representações do Sistema Solar em livros, revistas ou sáites. De modo geral, essas representações não mantêm a proporção entre todos os astros. Isso ocorre, principalmente, por causa da grande diferença de tamãnho entre alguns deles, como o Sol e os planêtas. Observe, por exemplo, a representação, em proporção, da Terra e de Júpiter, maior planêta do Sistema Solar.
Fonte dos dados: NÉCHIONAL AERONAUTICS ênd SPÊICE ADMINISTRATION. Jupiter bai the numbers. [Washington, D.C.]: Nasa, [2024]. Disponível em: https://livro.pw/dyafl. Acesso em: 29 out. 2024.
PARA AMPLIAR
Assista ao vídeo indicado a seguir para obtêr mais informações sobre o Sistema Solar.
• ASTROLAB: Sistema Solar. [S. l.: s. n.], 2018. 1 vídeo (4 min). Publicado pelo canal Tevê Unésp. Disponível em: https://livro.pw/ydvvf. Acesso em: 12 ago. 2024.
Os formatos dos planêtas do Sistema Solar lembram esferas. A seguir, vamos estudar essa figura geométrica espacial e os cálculos da área de sua superfícíe e de seu volume.
Dado um ponto C e uma medida real positiva r, a reunião de todos os pontos do espaço cujas distâncias ao ponto C são menóres ou iguais a r é denominada esféra. Observe alguns elemêntos quê podemos destacar em uma esféra:
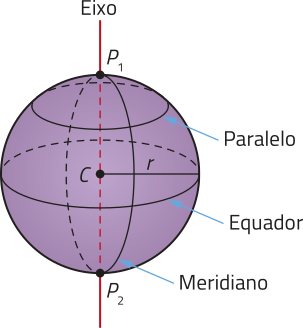
• o ponto C é o centro;
• a reta quê contém o centro da esféra é o eixo;
• a circunferência determinada ao seccionar a esféra por um plano perpendicular ao eixo e quê contém o centro C é o equador;
• as circunferências determinadas ao seccionar a esféra por planos paralelos ao equador são os paralelos;
• as circunferências determinadas ao seccionar a esféra por planos quê contêm o eixo são os meridianos;
• os pontos P1 e P2 determinados na interseção entre o eixo e a superfícíe da esféra são os polos.
Página cento e oitenta e seis
Volume de uma esféra
Vamos determinar uma expressão para o cálculo do volume de uma esféra. Para isso, consideramos uma esféra de centro C e raio r, conforme a figura, e o plano (alfa)" seccionando essa esféra de maneira a determinar um círculo de raio R e centro O, com OC = d.
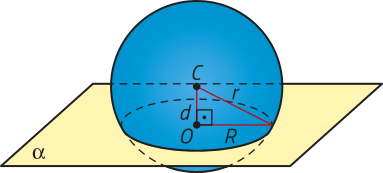
Aplicando o teorema de Pitágoras no triângulo destacado na figura, temos:
r2 = d2 + R2 ⇒ R2 = r2 − d2
Assim, podemos expressar a área do círculo de centro O da seguinte maneira:
(pi)"R2 = (pi)"(r2 − d2)
Agora, vamos considerar um sólido geométrico M determinado ao “retirar” de um cilindro equilátero de raio r dois cones de raio r, altura r e vértice B, conforme a figura a seguir. O volume dêêsse sólido é dado por:
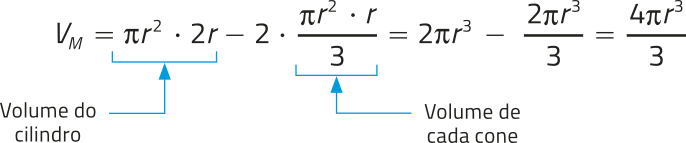
Analise, no esquema a seguir, a esféra de centro C e o sólido geométrico M, seccionados pelo plano (alfa)" e apoiados em um plano (beta)", paralelo ao plano (alfa)".
DICA
É possível mostrar quê o triângulo BO’P é isósceles e concluir quê O’B = O’P = d.
A área do círculo de centro O determinado na seção da esféra pelo plano (alfa)" é dada por (pi)"(r2 − d2). A seção do plano (alfa)" no sólido M determina uma coroa circular cuja área é dada por:
(pi)"r2 − (pi)"d2 = (pi)"(r2 − d2)
Como a seção do plano (alfa)" determina regiões de mesma área na esféra e no sólido M, pelo princípio de Cavalieri, concluímos quê o volume dessa esféra e dêêsse sólido são iguais.
Portanto, o volume da esféra de raio r é dado por: V = .
Dada uma esféra de raio r, conforme a figura, seu volume é dado por:
V =
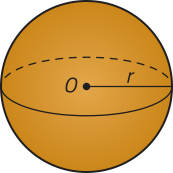
Página cento e oitenta e sete
Área da superfícíe de uma esféra
Para calcular a área A da superfícíe de uma esféra de centro C e raio r, vamos considerá-la decomposta em n sólidos geométricos congruentes, conforme a imagem.
Os sólidos obtidos nessa decomposição têm formato parecido ao de uma pirâmide de vértice C, altura r e área da base Ab, cujo volume é dado por VP = .
Sendo Vn o volume das n pirâmides correspondentes aos sólidos obtidos nessa decomposição, temos:
Vn = n ⋅ Vp ⇒ Vn = n ⇒ Vn = n ⋅ Ab ⋅
Quando n cresce indefinidamente, Vn tende ao volume V da esféra e n ⋅ Ab tende à área A da superfícíe da esféra. Dessa forma, temos:
Vn = n ⋅ Ab ⋅ → V = A ⋅ ⇒ = A ⋅ ⇒ A = ⋅ ⇒ A = 4(pi)"r2
Dada uma esféra de raio r, a área de sua superfícíe é dada por:
A = 4(pi)"r2
ATIVIDADE RESOLVIDA
R16. A esféra também é um sólido de revolução, pois póde sêr ôbitída por meio da rotação em 360° de um semicírculo em torno de um eixo quê contém seu diâmetro.
Agora, determine a área da superfícíe e o volume da esféra ôbitída ao rotacionar em 360°, em torno do eixo das abscissas, o semicírculo representado no plano cartesiano a seguir.

Resolução
O diâmetro dêêsse semicírculo tem extremidades nos pontos de coordenadas (1, 0) e (5, 0), logo a medida do seu comprimento d é dada por: d = 5 − 1 = 4; ou seja, 4 unidades de comprimento.
Assim, a esféra ôbitída ao rotacionar esse semicírculo tem raio medindo duas unidades de comprimento (4 ∶ 2 = 2). Com isso, podemos calcular a área da superfícíe A e o volume V dessa esféra:
• A = 4(pi)" ⋅ 22 = 16(pi)"; ou seja, 16(pi)" unidades de área;
• V = = ; ou seja, unidades de volume.
Página cento e oitenta e oito
ATIVIDADES
DICA
Nas atividades das páginas 188 e 189, utilize 3,14 como aproximação de (pi)".
88. Calcule o volume e a área da superfícíe aproximados de uma esféra cujo:
a) raio méde 6 dm;
volume: 904,32 dm3; área da superfícíe: 452,16 dm2
b) diâmetro méde 30 mm;
volume: 14.130 mm3; área da superfícíe: 2.826 mm2
c) equador méde 28,26 cm.
volume: 381,51 cm3; área da superfícíe: 254,34 cm2
89.
Um hemisfério corresponde a cada uma das metades de uma esféra. Qual é o volume e a área da superfícíe de um hemisfério cujo raio méde 9 cm?
volume: 1.526,04 cm3; área da superfícíe: 763,02 cm2
90. Qual é a medida do raio da base de um cone reto de 25 cm de altura cujo volume é igual ao de uma esféra de 10 cm de diâmetro?
cm ou aproximadamente 4,47 cm
91. Determine a medida aproximada do raio de uma esféra cujo volume é 2.304(pi)" dm3.
12 dm
92. Considere uma esféra cuja área da superfícíe é 192(pi)" m2. Em relação a essa esféra, calcule:
a) o comprimento do equador;
(pi)"m ou aproximadamente 43,51 m.
b) o volume.
(pi)" m3 ou aproximadamente 1.392,29 m3
93. O tênis de mesa é um esporte olímpico quê surgiu na Inglaterra. Ao longo de sua história, houve algumas modificações tanto nas regras quanto nos equipamentos do jôgo. Por exemplo, a bola quê antes tinha 2,5 g e 38 mm de diâmetro, atualmente deve ter 2,7 g e 40 mm de diâmetro.
Fonte dos dados: CATALDO, Diego. Tênis de mesa: regras, equipamentos, história e como funciona. GE, [s. l.], 25 jul. 2024. Disponível em: https://livro.pw/hjtnq. Acesso em: 14 set. 2024.

Com base nessas informações, o volume da bola de tênis de mesa, após as modificações, teve um aumento aproximado de:
a) 17%
b) 25%
c) 28%
d) 36%
e) 40%
alternativa a
94. As esferas para rolamentos são peças geralmente utilizadas em diversos setores industriais para auxiliar a movimentação de equipamentos. Observe, a seguir, informações refentes a um tipo de esféra em aço para rolamentos.

a) Qual é a diferença, em centímetro cúbico, entre os volumes mínimo e mássimo de uma esféra dêêsse tipo?
aproximadamente 14.082,31 cm3
b) Determine a massa de uma esféra cujo diâmetro seja mínimo.
aproximadamente 374,36 g
95. Em cérto sítio, será construída uma cistérna com capacidade para 30.000 L. A parte destinada ao armazenamento da á gua da chuva terá formato cilíndrico, e a tampa, formato de hemisfério, conforme a figura.

Para construir a tampa dessa cistérna, um pedreiro cobra R$ 32,00 por métro quadrado. Qual será o custo, em reais, cobrado pelo pedreiro para construir essa tampa?
R$ 803,84
DICA
Para resolver esta atividade, você póde, inicialmente, selecionar apenas os dados necessários indicados no enunciado.
96. Observe, na imagem, uma esféra inscrita em um cubo e calcule o volume dessa esféra, considerando quê a diagonal _ dêêsse cubo méde cm.
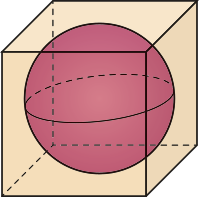
4.846,59 cm3
Página cento e oitenta e nove
97. Leia as informações a seguir.
O fuso esférico é uma parte da superfícíe da esféra ôbitída pela rotação de (alfa)" graus (0° < (alfa)" < 360°) de uma semicircunferência em torno do eixo quê contém seu diâmetro.
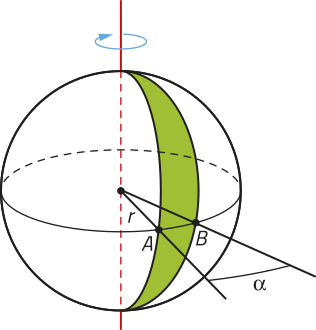
A área do fuso esférico é diretamente proporcional ao ângulo (alfa)", ou seja, para uma superfícíe esférica cuja área é 4(pi)"r2, temos 360° como ângulo correspondente.
a) escrêeva uma expressão para calcular a área A f de um fuso esférico em função do raio r e do ângulo (alfa)", em grau.
Resposta esperada: Af =
b) Calcule a área de um fuso esférico de 135° e cujo raio méde 10 m.
471 m2
98. Leia o trecho de um texto a seguir sobre o sistema de fuso horário do planêta Terra.
O sól não póde iluminar a Terra toda ao mesmo tempo, existindo por isso a diversidade de horário.
[...]
Teoricamente, dividindo-se os 360° de longitude pelas 24 horas do dia, a cada deslocamento de 15° de longitude tem-se uma variação de 1 hora.
O fuso horário (ou simplesmente fuso) é a faixa norte-sul entre dois meridianos quê distam entre si 15° de longitude, dentro da qual a hora é a mesma [...].
INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Noções cartográficas para base operacional geográfica: módulo III. Rio de Janeiro: hí bê gê hé, 1985. v. 3, p. 139, 141. Disponível em: https://livro.pw/irfkh. Acesso em: 13 ago. 2024.
Considere quê o planêta Terra tenha o formato de uma esféra com 12.756 km de diâmetro. Qual é a área aproximada correspondente a cada fuso horário da Terra?
21.288.616 km2
99. Determine o volume e a área da superfícíe da esféra ôbitída por revolução ao rotacionar em 360° êste semicírculo em torno de um eixo quê contém seu diâmetro.
volume: 1.766,25 cm3; área da superfícíe: 706,5 cm2
100. Em uma metalúrgica, quatro peças de metal esféricas e maciças, com 32 mm de diâmetro cada, foram fundidas de maneira a obtêr uma única peça esférica maciça maior, cujo raio méde:
a) mm;
b) mm;
c) 14 mm;
d) mm;
e) mm.
alternativa e
101. (EsPCEx-SP) A angioplastia é um procedimento médico caracterizado pela inserção de um cateter em uma veia ou artéria com o enchimento de um pequeno balão esférico localizado na ponta dêêsse cateter. Considerando quê, num procedimento de angioplastia, o raio inicial do balão seja desprezível e aumente a uma taxa constante de 0,5 mm/s até quê o volume seja igual a 500 mm3, então o tempo, em segundos, quê o balão leva para atingir esse volume é
a) 10.
b) .
c) .
d) .
e) .
alternativa e
102. ![]() Leia as informações a seguir sobre os planêtas Mercúrio e Vênus.
Leia as informações a seguir sobre os planêtas Mercúrio e Vênus.
Planeta Mercúrio
Diâmetro: 4.879 km
Distância média do Sol: 57,9 milhões km
Planeta Vênus
Diâmetro: 12.104 km
Distância média do Sol: 108,2 milhões km
Fonte dos dados: RIDPATH, Ian. Astronomia. Tradução: Maria Luiza X. de A. Borges. 4. ed. Rio de Janeiro: Zarrár, 2014. (Guia Ilustrado Zarrár, p. 91, 93).
Com base nessas informações, elabore e escrêeva um problema envolvendo o cálculo do volume e da área da superfícíe de uma esféra. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página cento e noventa
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Madeira de reflorestamento
Você já imaginou como nóssos hábitos de consumo impactam o meio ambiente? Alimentação, vestuário e deslocamento pela cidade podem trazer implicações significativas para o éco-sistema e, consequentemente, para a atual e as futuras gerações. Por exemplo, você já reparou quê o lápis, o caderno e as fô-lhas de papel sulfite quê compõem o seu material escolar foram fabricados a partir de madeira reflorestada? Geralmente, as embalagens dêêsses produtos apresentam selos indicando a procedência da matéria-prima.
Essas madeiras são obtidas de árvores quê foram plantadas para serem extraídas e, assim, dar espaço para quê novas árvores sêjam plantadas no mesmo local, d fórma quê continue o ciclo produtivo. Uma vantagem de usar esse tipo de madeira é quê não ocorre, nesse caso, o desmatamento de mata nativa.
É importante destacar quê a realização de um projeto de silvicultura, para fins comerciais, depende de alguns fatores, como a qualidade do solo, a determinação da espécie quê melhor se adapta ao clima da região, a produção de mudas, o contrôle de insetos, entre outros. A silvicultura, quando praticada de maneira responsável e sustentável, gera impactos positivos quê contribuem com o equilíbrio e a conservação ambiental.
- Silvicultura
- : cultivo de florestas com a finalidade de produzir madeiras e outros derivados para satisfazer às necessidades do mercado e, ao mesmo tempo, promover o uso racional das florestas.

Página cento e noventa e um
No Brasil, é comum a prática de cultivo e extração de madeira reflorestada de árvores, como a do eucalipto, quê apresenta rápido crescimento por causa das condições climáticas do país. Analise os infográficos a seguir.

Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Produção da extração vegetal e da silvicultura 2022. PEVS, Rio de Janeiro, v. 37, 2023. p. 1. Disponível em: https://livro.pw/vsqya. Acesso em: 13 ago. 2024.

Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Produção da extração vegetal e da silvicultura 2022. PEVS, Rio de Janeiro, v. 37, 2023. p. 5. Disponível em: https://livro.pw/vsqya. Acesso em: 13 ago. 2024.
*Representação fora dos padrões cartográficos.
PENSANDO NO ASSUNTO
1. Cite hábitos quê podemos desenvolver em nosso dia a dia pensando no consumo consciente.
Respostas possíveis: Optar pelo uso do transporte público, comprar produtos quê utilizam a madeira de reflorestamento como matéria-prima, diminuir o tempo de uso do chuveiro e de equipamentos elétricos.
2. Além dos materiais escolares citados no texto, quê outros produtos podem ter a madeira de reflorestamento como matéria-prima? Se necessário, faça uma pesquisa.
Respostas possíveis: Lápis de côr, móveis, palítos de denti, palítos de fósforo.
3. De acôr-do com as informações apresentadas sobre a silvicultura no Brasil, em 2022, resôuva os itens a seguir.
a) Que fração da área de floresta plantada melhor representa a parte correspondente ao cultivo de eucalipto
•
•
•
•
b) pôdêmos afirmar quê em todas as regiões do país a área ocupada com o plantio de eucalipto era maior quê a ocupada com o plantio de pínus? Justifique sua resposta.
Não, pois, na região Sul, a área ocupada com o plantio de pínus era maior quê a ocupada com o plantio de eucalipto.
c) Em 2022, a área total aproximada de florestas plantadas no Brasil era de 9,5 milhões de hectares. Determine, em quilômetro quadrado, a área aproximada de floresta plantada com:
• eucalipto;
73.435 km2
• pínus;
17.765 km2
• outras espécies.
3.800 km2
DICA
Lembre-se de quê 1 hectare equivale à área de um quadrado com 100 m de lado.
d) Qual era a área ocupada com o plantio de eucalipto na região onde você mora?
Resposta pessoal.
Página cento e noventa e dois
4. ![]() Em grupos de dois ou três integrantes, pesquisem se há áreas de reflorestamento, para fins comerciais ou ecológicos, no município ou em alguma região próxima de onde vocês moram. Anotem informações como o tipo e o objetivo do reflorestamento, as espécies de árvores plantadas, o tamãnho da área de plantio e as técnicas utilizadas. Por fim, elaborem um texto apresentando essas informações e descrevendo os impactos dessa área de reflorestamento no contexto local.
Em grupos de dois ou três integrantes, pesquisem se há áreas de reflorestamento, para fins comerciais ou ecológicos, no município ou em alguma região próxima de onde vocês moram. Anotem informações como o tipo e o objetivo do reflorestamento, as espécies de árvores plantadas, o tamãnho da área de plantio e as técnicas utilizadas. Por fim, elaborem um texto apresentando essas informações e descrevendo os impactos dessa área de reflorestamento no contexto local.
Pesquisa e elaboração dos estudantes.
5. ![]() Um dos desafios no cultivo de árvores para a extração de madeira é medir o volume de madeira produzido. Dois métodos muito utilizados nessa medição estão descritos a seguir.
Um dos desafios no cultivo de árvores para a extração de madeira é medir o volume de madeira produzido. Dois métodos muito utilizados nessa medição estão descritos a seguir.
1 Para estimar o volume de uma tora, inicialmente determina-se a medida do contôrno e cada base. Em seguida, calcula-se a área do círculo quê representa cada base. Por fim, determina-se a média aritmética das duas áreas obtidas e multiplica-se o resultado pelo comprimento da tora.

2 Quando as tóras de madeira estão empilhadas, conforme representado na imagem, o
volume de madeira é estimado por meio da multiplicação das medidas das dimensões do empilhamento.
Fonte dos dados: OLIVEIRA, Edilson Batista éti áu. Determinação da quantidade de madeira, carbono e renda da plantação florestal. Colombo: Embrapa Florestas, 2011. (Documentos, n. 220, p. 11-12). Disponível em: https://livro.pw/frtpk. Acesso em: 12 ago. 2020.
Com um colega, façam o quê se pede em cada um dos itens.
a) Indiquem quê figura geométrica espacial é usada para fazer os cálculos do método 1 e justifiquem a estratégia de cálculo apresentada nesse método. Depois, escrevam uma expressão matemática para representar o volume V estimado de uma tora cujas áreas aproximadas da base são representadas por g1 e g 2 e o comprimento da tora por h.
Resposta esperada: No método 1, para realizar os cálculos, usa-se um cilindro circular reto. As medições e os cálculos a sêr realizados em relação aos contornos das bases da tora possibilitam determinar a área de um círculo quê corresponde a uma aproximação das áreas das bases dêêsse cilindro.
Como o volume de um cilindro é dado pelo produto da área de sua base e da medida da altura, então, pelo método 1, multiplica-se a média das áreas estimadas para as bases pela medida do comprimento dessa tora: V = () ⋅ h.
b) Indiquem quê figura geométrica espacial é usada para fazer os cálculos do método 2 e justifiquem a estratégia de cálculo apresentada nesse método. Depois, escrevam uma expressão matemática para representar o volume V estimado de um empilhamento de tóras cujas dimensões são representadas por a, b e c.
Resposta esperada: No método 2, para realizar os cálculos, usa-se um paralelepípedo reto-retângulo. Como o cálculo do volume de um paralelepípedo reto-retângulo é dado pelo produto das medidas das suas três dimensões, então, pelo método 2, multiplicam-se as medidas do comprimento, da largura e da altura dêêsse empilhamento de tóras: V = a ⋅ b ⋅ c.
c) Com base nos itens a e b, elaborem um problema envolvendo o cálculo do volume estimado de uma tora ou de um empilhamento de tóras. Depois, troquem-no com outra dupla para quê ela o resôuva, enquanto vocês fazem o mesmo com o problema quê receberem. Por fim, confiram juntos as resoluções.
Elaboração dos estudantes.

Página cento e noventa e três
VOCÊ CONECTADO
Construindo figuras geométricas espaciais no GeoGebra
pôdêmos construir diferentes figuras geométricas espaciais, obtêr suas planificações, calcular seu volume e a área da sua superfícíe por meio do software de geometria dinâmica GeoGebra, disponível em: https://livro.pw/qoubj (acesso em: 13 ago. 2024).
Como exemplo, vamos construir um prisma pentagonal regular e obtêr sua planificação. Para isso, utilizamos as janelas de visualizações 2D e 3D, simultaneamente, e realizamos as etapas a seguir.
A Inicialmente, abrimos a Janela de visualização 3D. Para isso, selecionamos a opção Exibir na barra de ferramentas e, em seguida, a opção Janela de visualização 3D. Na Janela de visualização, com a opção ![]() (Polígono regular) selecionada, construímos um pentágono regular com 2 cm de lado, correspondente a uma base do prisma.
(Polígono regular) selecionada, construímos um pentágono regular com 2 cm de lado, correspondente a uma base do prisma.
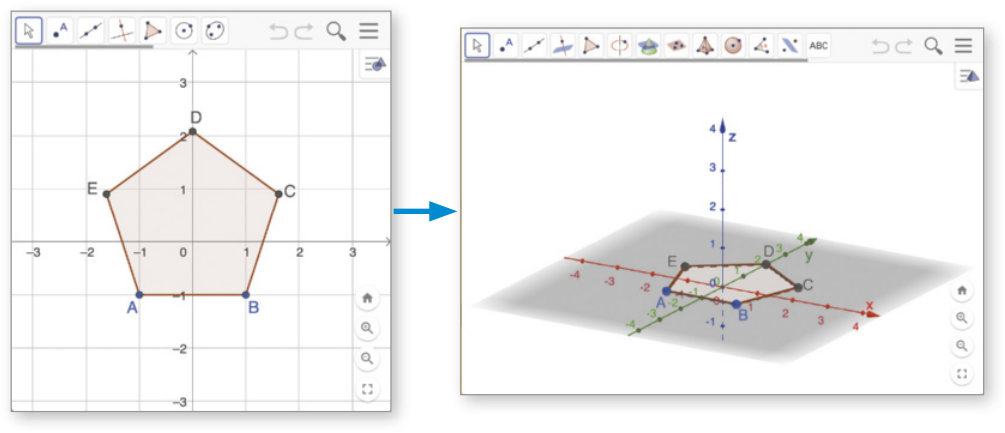
B Na região da Janela de visualização 3D, com a opção ![]() (Extrusão para prisma), selecionamos o pentágono. Na caixa de texto quê abrir, digitamos 3, quê corresponde à altura do prisma, e confirmamos com OK. Na Janela de visualização 3D, obtemos um prisma pentagonal regular. Para calcular o volume dêêsse prisma, na região da Janela de visualização 3D, com a opção
(Extrusão para prisma), selecionamos o pentágono. Na caixa de texto quê abrir, digitamos 3, quê corresponde à altura do prisma, e confirmamos com OK. Na Janela de visualização 3D, obtemos um prisma pentagonal regular. Para calcular o volume dêêsse prisma, na região da Janela de visualização 3D, com a opção ![]() (Volume), selecionamos o prisma construído. O valor quê aparece junto ao prisma corresponde ao seu volume.
(Volume), selecionamos o prisma construído. O valor quê aparece junto ao prisma corresponde ao seu volume.
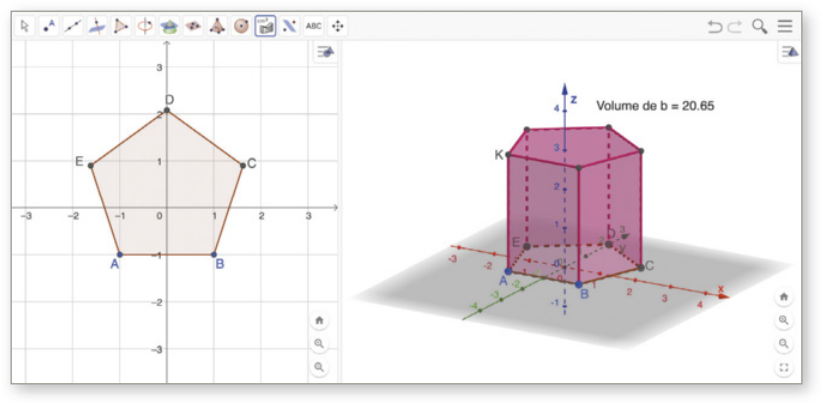
Página cento e noventa e quatro
C Para obtêr a planificação dêêsse prisma, na região da Janela de visualização 3D, com a opção ![]() (Planificação) selecionamos o prisma construído. A planificação do prisma regular pentagonal é ôbitída tanto na Janela de visualização quanto na Janela de visualização 3D.
(Planificação) selecionamos o prisma construído. A planificação do prisma regular pentagonal é ôbitída tanto na Janela de visualização quanto na Janela de visualização 3D.
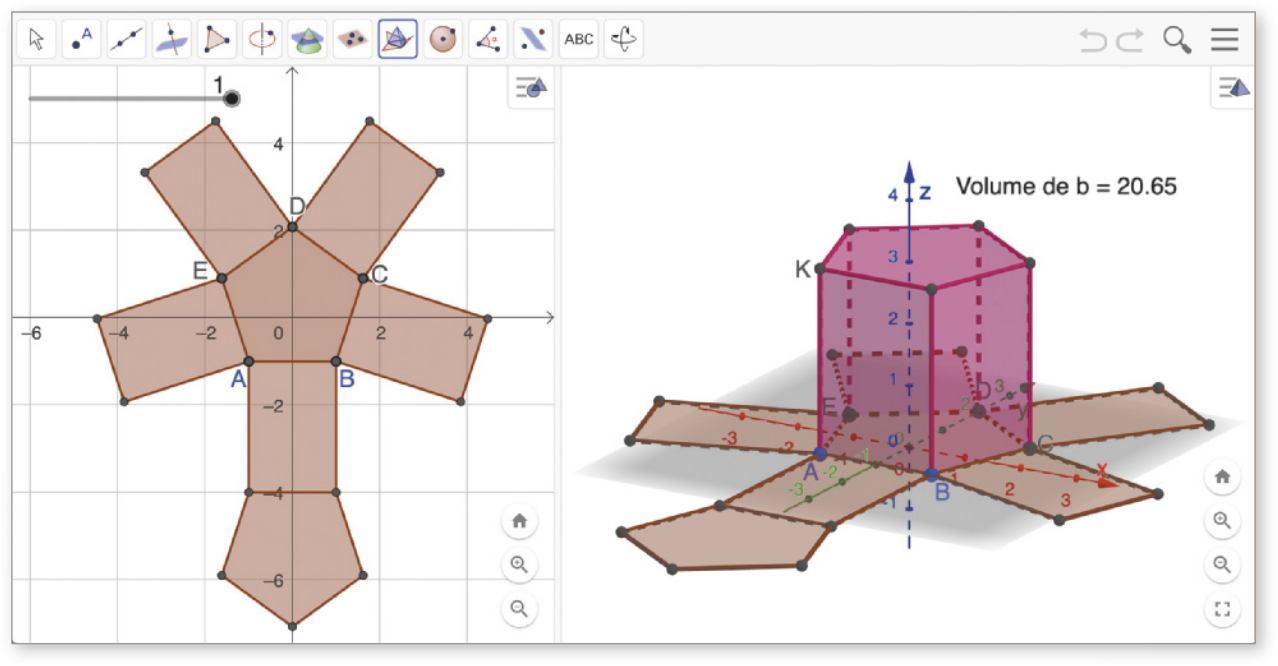
DICA
Na Janela de visualização, é gerado um contrôle deslizante quê, ao sêr movimentado, altera a posição das partes quê compõem a planificação na Janela de visualização 3D.
MÃOS À OBRA
1. No GeoGebra, reproduza a construção apresentada anteriormente e resôuva os itens a seguir.
a) Qual é o volume aproximado do prisma construído?
20,65 cm3
b) Selecione a região da Janela de visualização e, com a opção ![]() (Área), obtenha a área de cada face do prisma; em seguida, calcule a área total dele.
(Área), obtenha a área de cada face do prisma; em seguida, calcule a área total dele.
área de cada face lateral: 6 cm2; área de cada base: 6,88 cm2; área total: 43,76 cm2
c) Utilizando a opção ![]() (Mover) na Janela de visualização 3D:
(Mover) na Janela de visualização 3D:
• selecione uma base do prisma e realize movimentos verticais com a figura. O quê aconteceu com o prisma construído?
Resposta esperada: A altura do prisma se ajustou de acôr-do com o movimento realizado.
• selecione um ponto qualquer fora do prisma construído e faça movimentos em diferentes direções com esse ponto. O quê aconteceu?
de acôr-do com o movimento realizado. Resposta esperada: A vista do prisma se ajustou
2. De maneira análoga à apresentada no exemplo e utilizando as opções ![]() (Círculo: Centro & Raio) e
(Círculo: Centro & Raio) e ![]() (Extrusão para prisma) do GeoGebra, construa um cilindro reto de raio 3 cm e altura 5 cm.
(Extrusão para prisma) do GeoGebra, construa um cilindro reto de raio 3 cm e altura 5 cm.
Construção do estudante.
a) dêz-creva os procedimentos quê você realizou nessa construção.
Resposta pessoal.
b) Utilizando a opção ![]() (Volume), calcule o volume do cilindro quê você construiu.
(Volume), calcule o volume do cilindro quê você construiu.
141,37 cm3
3. ![]() Elabore um problema quê envolva o cálculo do volume ou da área total de um prisma reto ou de um cilindro circular reto e cuja resolução deva sêr realizada com auxílio do GeoGebra. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elabore um problema quê envolva o cálculo do volume ou da área total de um prisma reto ou de um cilindro circular reto e cuja resolução deva sêr realizada com auxílio do GeoGebra. Em seguida, troque o problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
Página cento e noventa e cinco
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você: concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as atividades escolares propostas para casa.
g) Respeitei os côlégas nas atividades em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conceitos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum conceito para melhor compreen-dê-lo.
Resposta pessoal.
Princípio de Cavalieri
Cone circular
Área da superfícíe e volume de um cilindro circular
Área da superfícíe e volume de uma pirâmide
Área da superfícíe e volume de uma esféra
Cilindro circular
Área da superfícíe e volume de um prisma
Relação de Óiler
Área da superfícíe e volume de um cone circular
Poliedros
Prisma
esféra
Pirâmide
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades resolvidas. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página cento e noventa e seis
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre construções em concreto armado. Leia a seguinte situação e, depois, resôuva os itens.
A estrutura da fachada de uma residência será construída em concreto armado. Essa estrutura consiste em três colunas, com formato de cilindro reto, e uma viga com formato de paralelepípedo reto-retângulo. Observe.

a) Desconsiderando o volume de ferragens utilizado, quantos metros cúbicos de concreto serão necessários para construir essa estrutura?
(1,8 + 0,54(pi)") m3 ou aproximadamente 3,5 m3
b) Após construída, a superfícíe dessa estrutura será pintada com uma tinta cujo rendimento é de 10 m2/L por demão. No mínimo, quantos litros dessa tinta serão necessários para essa pintura, sabendo quê serão realizadas três demãos?
aproximadamente 7 L
c) Para produzir o concreto necessário utilizado nessa estrutura, será usada uma betoneira cujo tambor tem formato quê lembra o de uma composição de um tronco de cone reto e um cilindro reto, conforme a imagem.
Considerando quê nessa betoneira podem sêr utilizados no mássimo 75% da capacidade de seu tambor, calcule:
• o volume mássimo de concreto produzido em uma única vez nessa betoneira;
aproximadamente 0,39 m³
• a quantidade mínima de vezes quê essa betoneira será usada para produzir todo o concreto utilizado nessa estrutura.
9 vezes
d) Em qual das fichas a seguir está descrito um sólido geométrico cujo volume mais se aproxima do volume de concreto utilizado nessa estrutura?
II

I Prisma regular triangular com altura medindo 3 m e aresta da base, 1 m.
II esféra com raio medindo 94 cm.
III Cone com raio da base medindo 12 dm e altura, 35 dm.
IV Pirâmide quadrangular regular com arestas da base medindo 1,8 m e altura, 2,5 m.
Página cento e noventa e sete
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) Uma fábrica comercializa chocolates em uma caixa de madeira, como na figura.
A caixa de madeira tem a forma de um paralelepípedo reto-retângulo cujas dimensões externas, em centímetro, estão indicadas na figura. Sabe-se também quê a espessura da madeira, em todas as suas faces, é de 0,5 cm.
Qual é o volume de madeira utilizado, em centímetro cúbico, na construção de uma caixa de madeira como a descrita para embalar os chocolates?
a) 654
b) 666
c) 673
d) 681
e) 693
alternativa c
2. (Enem/MEC) Um lapidador recebeu de um joalheiro a encomenda para trabalhar em uma pedra preciosa cujo formato é o de uma pirâmide, conforme ilustra a Figura 1. Para tanto, o lapidador fará quatro cortes de formatos iguais nos cantos da base. Os cantos retirados correspondem a pequenas pirâmides, nos vértices P, Q, R e S, ao longo dos segmentos tracejados, ilustrados na Figura 2.
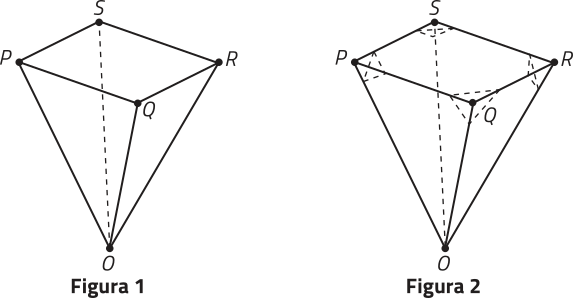
Depois de efetuados os cortes, o lapidador obteve, a partir da pedra maior, uma jóia poliédrica cujos números de faces, arestas e vértices são, respectivamente, iguais a
a) 9, 20 e 13.
b) 9, 24 e 13.
c) 7, 15 e 12.
d) 10, 16 e 5.
e) 11, 16 e 5.
alternativa a
3. (Enem/MEC) Um artista plástico esculpe uma escultura a partir de um bloco de madeira de lei, em etapas. Inicialmente, esculpe um cone reto com 36 cm de altura e diâmetro da base medindo 18 cm. Em seguida, remove dêêsse cone um cone menor, cujo diâmetro da base méde 6 cm, obtendo, assim, um tronco de cone, conforme ilustrado na figura.
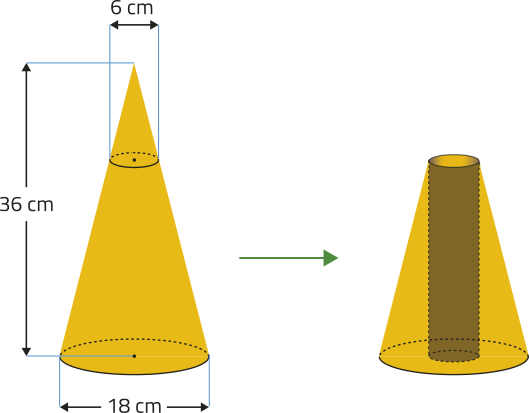
Em seguida, perfura esse tronco de cone, removendo um cilindro reto, de diâmetro 6 cm, cujo eixo de simetria é o mesmo do cone original. Dessa forma, ao final, a escultura tem a forma de um tronco de cone com uma perfuração cilíndrica de base a base.
O tipo de madeira utilizada para produzir essa escultura tem massa igual a 0,6 g por centímetro cúbico de volume. Utilize 3 como aproximação para (pi)".
Qual é a massa, em grama, dessa escultura?
a) 1.198,8
b) 1.296,0
c) 1.360,8
d) 4.665,6
e) 4.860,0
alternativa b
Página cento e noventa e oito
4. (UFRGS-RS) Considere o paralelepípedo de vértices A, B, C, D, E, F, G, H e a pirâmide de vértices B, F, G, H, inscrita no paralelepípedo, representados na figura a seguir.
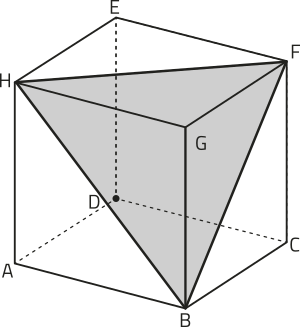
A razão entre o volume da pirâmide e o volume do paralelepípedo é
a)
b)
c)
d)
e)
alternativa a
5. (Uesb-BA) Um paralelepípedo retângulo tem as seguintes dimensões: 5 cm, a cm e b cm. Sabe-se quê a razão entre a e b é 3 ∶ 4 e quê o volume dêêsse paralelepípedo méde 540 cm3. Nessas condições, a área total dêêsse paralelepípedo méde
a) 486 cm2.
b) 446 cm2.
c) 432 cm2.
d) 426 cm2.
e) 416 cm2.
alternativa d
6. (UFAM) Um cilindro reto possui área total igual a 32(pi)" cm2. Sabendo quê o raio da base é da medida da altura dêêsse cilindro, então a área lateral dêêsse cilindro méde:
a) 12(pi)" cm2.
b) 18(pi)" cm2.
c) 20(pi)" cm2.
d) 24(pi)" cm2.
e) 28(pi)" cm2.
alternativa d
7. (UEG-GO) Uma bola inflável foi cheia até quê o seu diâmetro fosse duas vezes maior quê seu diâmetro inicial. Assim, verifica-se quê o volume final da bola, em relação ao volume inicial, é
a) duas vezes maior
b) 4 vezes maior
c) 6 vezes maior
d) 8 vezes maior
e) 10 vezes maior
alternativa d
8. (hú- hê- érre jota) Um depósito de óleo tem a forma de um cone circular reto cujo eixo vertical forma com suas geratrizes o ângulo de 45°. Foram retirados dêêsse depósito 19 m3 de óleo. Com isso, a altura do nível de óleo foi reduzida em 1 m e passou a ter X metros de altura.
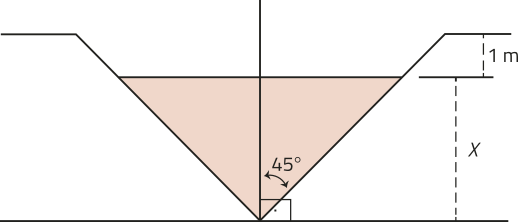
Considerando (pi)" = 3, calcule a altura X do nível de óleo.
2 m
9. (Unicamp-SP) Se um tetraedro regular e um cubo têm áreas de superfícies iguais, a razão entre o comprimento das arestas do tetraedro e o comprimento das arestas do cubo é igual a
a)
b)
c)
d)
alternativa c
10. (UEMG) Observe as figuras.
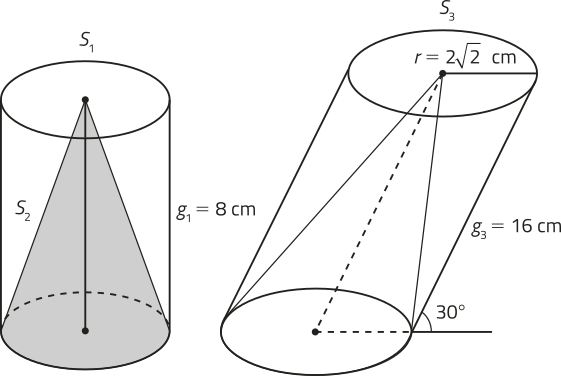
Nas figuras, tem-se um cilindro circular equilátero (S1), circunscrevendo um cone (S2), e um cilindro circular oblíquo (S3). A razão determinada pelo volume de S3 com a superfícíe total de S2 é
a) cm.
b) − 1 cm.
c) cm.
d) ( + 16) cm.
alternativa b
Página cento e noventa e nove


