UNIDADE 6
PROBABILIDADE
Meteorologia
Ao sair de casa amanhã logo cedo, devo levar o guarda-chuva? Deve chover nos próximos meses para quê o agricultor faça o plantio? Há risco de chuva forte nas próximas horas; será quê póde ocasionar enchente ou alagamento em alguma região?
Esses questionamentos são freqüentes em nosso cotidiano, o quê nos leva a fazer uma breve busca para consultar a previsão do tempo e a probabilidade de chover em certa região, por exemplo. As previsões meteorológicas envolvem diversas etapas, como a côléta de dados (umidade, pressão atmosférica, tempera-túra de superfícíe, precipitação etc.), quê ocorre em estações meteorológicas ou por meio de outros recursos, como aviões, navios, BÓIAS e satélites. Com esses dados, os meteorologistas elaboram modelos matemáticos com o objetivo de prever, com certa confiabilidade, as condições climáticas futuras. Essa etapa envolve cálculos probabilísticos e, em geral, é realizada com apôio de supercomputadores.

PARA AMPLIAR
Acesse êste vídeo para obtêr mais informações sobre como é realizada a previsão do tempo.
• SAIBA como é feita a previsão do tempo. [S. l.: s. n.], 2024. 1 vídeo (4 min). Publicado pelo canal Tevê Unicamp. Disponível em: https://livro.pw/zaxrc. Acesso em: 30 ago. 2024.
Após ler as informações, converse com os côlégas e o professor sobre os itens a seguir.
Respostas nas Orientações para o professor.
1. Você tem o hábito de pesquisar a previsão do tempo? Por quê? Quais dispositivos você utiliza?
2. Em seu entendimento, a meteorologia colabora para melhorar a qualidade de vida da ssossiedade? Justifique.
3. Pesquise a probabilidade de chuva para o dia de amanhã na região em quê você mora. De acôr-do com essa informação, responda: é mais provável quê chova ou quê não chova? Justifique.
Página duzentos e quarenta e oito
O estudo da probabilidade
Na abertura desta Unidade, obtivemos algumas informações sobre os estudos meteorológicos. Atualmente, podemos acessar previsões meteorológicas atualizadas por meio de diversos aplicativos ou sáites, como o do Centro de Previsão de Tempo e Estudos Climáticos (Cptec), nos quais é possível consultar informações relacionadas a previsões do tempo e do clima. Observe.
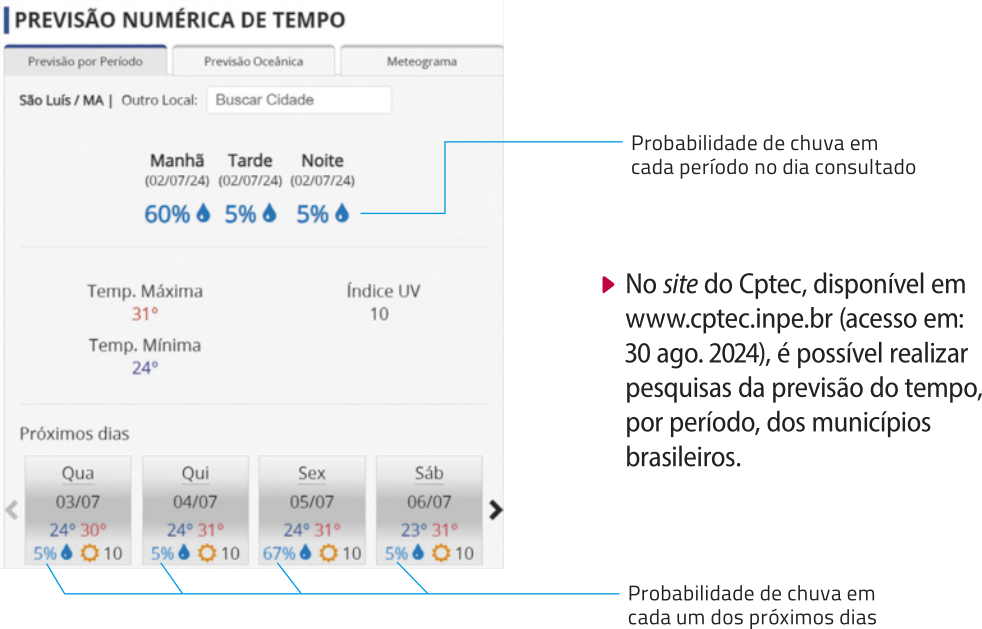
Note quê algumas informações meteorológicas envolvem a ideia de probabilidade. Além da meteorologia, a probabilidade é aplicada em outras áreas. Por exemplo, no contrôle de qualidade de uma produção industrial (engenharia), na análise genética (medicina), na avaliação de variedades de plantas (agricultura) e na previsão de riscos em investimentos financeiros (economia).
Você sabia quê alguns registros evidenciam quê o início do estudo sistematizado de probabilidade está relacionado à discussão em torno de jogos de azar?
MATEMATICA NA HISTÓRIA
Apesar de as ideias relacionadas à probabilidade remeterem à Antigüidade, há evidências de quê não tenha ocorrido tratamento matemático sistematizado da probabilidade até por volta do século XV. O desenvolvimento das bases da teoria das probabilidades é creditado aos matemáticos Blaise Pascal (1623-1662) e Piérre de Fermat (1601-1665), a partir de correspondências quê trocaram a respeito de um problema envolvendo jogos de azar, conhecido como “problema dos pontos”. Porém Girolamo Cardano (1501-1576), antecessor de Pascal e Fermat, também abordou algumas kestões relacionadas à probabilidade, incluindo as dêêsse mesmo problema, apresentadas em um manual de jogos, quê foi publicado apenas em 1663.
Fonte dos dados: EVES, ráuard. Introdução à história da matemática. Tradução: Hygino Hugueros Domingues. 3. ed. Campinas: Editora da Unicamp, 2004. p. 365-366.
Nesta Unidade, retomaremos e ampliaremos o estudo sobre probabilidade realizado no Ensino Fundamental.
Página duzentos e quarenta e nove
Experimento aleatório, espaço amostral e evento
Há experimentos ou fenômenos cujo resultado é impossível prever com certeza, apesar de repetidos sôbi as mesmas condições. Por exemplo, o lançamento de um dado comum ou o sorteio de uma loteria. Situações como essas são denominadas experimentos aleatórios.
Agora, considere a seguinte situação.
PARA PENSAR
Você conhece o significado da palavra aleatório? Se necessário, pesquise em um dicionário.
Resposta esperada: Akilo quê depende do acaso.
No jôgo de palítos para dois participantes, cada um deles recebe três palítos e, sem quê o outro veja, esconde parte dessa quantidade de palítos em uma das mãos, quê é colocada fechada sobre uma mesa. Cada participante, na sua vez, tem de tentar adivinhar a quantidade total de palítos nas duas mãos sobre a mesa. O vencedor da rodada é aquele quê acertar esse total. A seguir, estão apresentadas todas as possíveis maneiras com as quais esses participantes podem esconder os palítos.
Participante II |
|||||
|---|---|---|---|---|---|
0 |
1 |
2 |
3 |
||
Participante I |
0 |
(0, 0) |
(0, 1) |
(0, 2) |
(0, 3) |
1 |
(1, 0) |
(1, 1) |
(1, 2) |
(1, 3) |
|
2 |
(2, 0) |
(2, 1) |
(2, 2) |
(2, 3) |
|
3 |
(3, 0) |
(3, 1) |
(3, 2) |
(3, 3) |
|

Assim, temos 16 maneiras possíveis por meio das quais os participantes podem esconder os palítos.
Experimento aleatório é todo experimento (ou fenômeno) quê, mesmo repetido sôbi as mesmas condições, apresenta resultado imprevisível.
Apesar de não sêr possível prever o resultado de experimentos aleatórios, muitas vezes conseguimos determinar todas as possibilidades de resultado para esse experimento, quê formam o chamado espaço amostral.
Em um experimento aleatório, o espaço amostral é indicado por (ômega)" (lê-se: ômega). Cada subconjunto do espaço amostral é denominado evento.
Em relação à situação apresentada, do jôgo de palítos, o espaço amostral é dado por (ômega)" = {(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3), (3, 0), (3, 1), (3, 2), (3, 3)}. pôdêmos indicar como A, por exemplo, o evento em quê os participantes têm a mesma quantidade de palítos escondidos, ou seja, A = {(0, 0), (1, 1), (2, 2), (3, 3)}.
Página duzentos e cinquenta
Analise outros exemplos.
a) Em um sorteio, ao acaso, de uma letra do nosso alfabeto, o espaço amostral é dado por:
(ômega)" = {a, b, c, d, e, ..., v, w, x, y, z}
Considerando A o evento “sortear uma vogal”, temos:
A = {a, e, i, o, u}
b) No lançamento de uma moeda, o espaço amostral é dado por:
(ômega)" = {cara, coroa}
Considerando B o evento “obter cara” em um lançamento da moeda, temos:
B = {cara}
Nesse caso, como um único elemento pertence ao evento B, dizemos quê esse é um evento simples ou evento unitário.

c) Na anotação do número obtído na face superior de um dado comum após lançá-lo, o espaço amostral é dado por:
(ômega)" = {1, 2, 3, 4, 5, 6}
Considerando C o evento “obter um número natural menor quê 7”, temos:
C = {1, 2, 3, 4, 5, 6}
Nesse caso, como todos os elemêntos do espaço amostral pertencem ao evento C (C = (ômega)"), dizemos quê esse é um evento cérto, ou seja, um evento quê vai ocorrer com certeza.
d) No sorteio, ao acaso, de um estado da Região Norte do Brasil, o espaço amostral é dado por:
(ômega)" = {Acre, Amapá, Amazonas, Pará, Rondônia, Roraima, Tocantins}
Considerando D o evento correspondente a sortear um estado da Região Norte do Brasil cuja letra inicial do nome seja B, temos:
D = ∅
Nesse caso, como nenhum elemento pertence ao evento D, dizemos quê esse é um evento impossível, ou seja, quê com certeza não vai ocorrer.
Denominamos evento simples (ou unitário) o evento quê é formado por apenas um elemento do espaço amostral. Quando o evento corresponde ao próprio espaço amostral, denominamos evento cérto; quando o evento é representado pelo conjunto vazio, ou seja, nenhum elemento do espaço amostral pertence a ele, êste é denominado evento impossível.
PARA PENSAR
Com um colega, criem contextos descrevendo experimentos aleatórios. Depois, estabeleçam exemplos de eventos. Por fim, compartilhem o quê vocês criaram em uma roda de conversa.
Elaboração do estudante.

Página duzentos e cinquenta e um
Agora, considere a situação descrita a seguir.
Para a realização de um experimento, foram escritos em fichas idênticas todos os números de dois algarismos distintos quê podem sêr formados pêlos algarismos 2, 5, 7 ou 9, com cada número em uma única ficha. Em seguida, essas fichas foram colocadas em uma sacola de tecido não transparente e, sem quê se olhe dentro dela, uma ficha será sorteada.

Em relação à situação apresentada, o espaço amostral póde sêr indicado por (ômega)" = {25, 27, 29, 52, 57, 59, 72, 75, 79, 92, 95, 97}. Além díssu, podemos destacar o evento A correspondente a sortear uma ficha quê contém um número múltiplo de 3, e o evento B, de sortear uma ficha quê contém um número maior quê 80. Assim, temos:
• A = {27, 57, 72, 75};
• B = {92, 95, 97}.
Note quê os eventos A e B não têm elemento em comum. Nesse caso, dizemos quê A e B são eventos mutuamente exclusivos.
Dados dois eventos A e B, eles são denominados eventos mutuamente exclusivos quando não têm elemento em comum, ou seja, A ⋂ B = ∅.
ATIVIDADES RESOLVIDAS
R1. Em uma brincadeira, são lançados dois dados: um dado branco cúbico numerado de 1 a 6, e um dado azul com formato quê lembra um tetraedro regular, no qual, próximo a cada um de seus vértices, em cada uma das faces, é indicado um número natural de 1 até 4. Esses dois dados são lançados simultaneamente, e um número é formado com os resultados verificados. O algarismo obtído no dado branco indica a dezena, e o algarismo obtído no dado azul indica a unidade dêêsse número. Por exemplo, os lançamentos representados a seguir indicam o número 24.

Com base nessas informações, determine:
a) o espaço amostral dessa brincadeira;
b) o evento A quê corresponde à formação de um número par;
c) o evento B quê corresponde à formação de um número maior quê 50;
d) o evento C quê corresponde à formação de um número com dois algarismos iguais.
Página duzentos e cinquenta e dois
Resolução
pôdêmos construir uma tabéla de dupla entrada para representar todos os números possíveis de serem formados nessa brincadeira.
|
1 |
2 |
3 |
4 |
|---|---|---|---|---|
1 |
11 |
12 |
13 |
14 |
2 |
21 |
22 |
23 |
24 |
3 |
31 |
32 |
33 |
34 |
4 |
41 |
42 |
43 |
44 |
5 |
51 |
52 |
53 |
54 |
6 |
61 |
62 |
63 |
64 |
a) (ômega)" = {11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44, 51, 52, 53, 54, 61, 62, 63, 64}
b) A = {12, 14, 22, 24, 32, 34, 42, 44, 52, 54, 62, 64}
c) B = {51, 52, 53, 54, 61, 62, 63, 64}
d) C = {11, 22, 33, 44}
R2. A cantina de certa escola oferece um combo de lanche com um copo de suco de uva ou de laranja e um pão de queijo no valor de R$ 12,00. Porém os estudantes podem:
• trocar o copo de suco de uva ou de laranja por um copo de suco de abacaxi por mais R$ 1,50;
• trocar o pão de queijo por um sanduíche natural por mais R$ 5,00.
Determine o espaço amostral dos preços do combo correspondentes a todas as opções oferecidas aos estudantes.
PARA PENSAR
Nessa cantina, quanto custa um combo formado por um copo de suco de abacaxi e um sanduíche natural?
R$ 18,50
Resolução
pôdêmos construir uma árvore de possibilidades para representar todas as opções oferecidas aos estudantes para compor um combo.

Assim, o espaço amostral é dado por (ômega)" = {R$ 12,00, R$ 13,50, R$ 17,00, R$ 18,50}.
Página duzentos e cinquenta e três
ATIVIDADES
1. Identifique quais dos itens a seguir apresentam experimentos (ou fenômenos) aleatórios.
a) Duzentos bilhetes idênticos, diferenciando-se apenas pela numeração, foram colocados em uma urna para quê um deles fosse sorteado.
b) Aquecer a á gua pura ao nível do mar e verificar a quê tempera-túra ela entrará em ebulição.
c) Contagem da quantidade de artefatos defeituosos em um intervalo de duas horas na linha de produção de uma fábrica.
d) Registrar o tempo em quê um relógio em bom funcionamento demora para quê o ponteiro maior complete uma volta.
a; c
2. Considere quê duas moedas idênticas e perfeitas são lançadas simultaneamente, e verifica-se qual face de cada uma delas ficou voltada para cima: cara ou coroa.
a) escrêeva o espaço amostral dêêsse experimento.
Considerando C a obtenção de cara e K, de coroa, temos (ômega)" = {CC, CK, KC, KK}.
b) Determine o evento A correspondente a obtêr exatamente duas coroas nesse experimento e o evento B côrrespondente a obtêr apenas uma cara.
A = {KK}; B = {CK, KC}
3. Para a realização de uma pesquisa e de um seminário, sêrá sorteado, para cada atividade, um dos seguintes temas: Educação (E), Saúde (S) ou Cultura (C). Nesse sorteio, cada tema deve ser escrito em pedaços de papel idênticos, colocados em uma caixa e, sem quê se olhe, o primeiro papel sorteado indicará o tema da pesquisa e o segundo, o tema do seminário. Para esse sorteio foram propostas duas maneiras diferentes, conforme segue.
• Proposta I: o papel do primeiro tema sorteado é devolvido à caixa para o segundo sorteio.
• Proposta II: o primeiro papel sorteado não é recolocado na caixa.
a) Qual é o espaço amostral quê representa todos os resultados possíveis dos sorteios em relação à proposta I? E em relação à proposta II?
proposta I: (ômega)" = {EE, ES, EC, SS, SE, SC, CC, CE, CS}; proposta II: (ômega)" = {ES, EC, SE, SC, CE, CS}
b) Para cada proposta, determine o evento A
quê corresponde ao sorteio do tema Educação para ao menos uma das atividades e o evento B quê corresponde ao sorteio do mesmo tema para ambas as atividades.
proposta I: A = {EE, ES, EC, SE, CE}, B = {EE, SS, CC}; proposta II: A = {ES, EC, SE, CE}, B = ∅
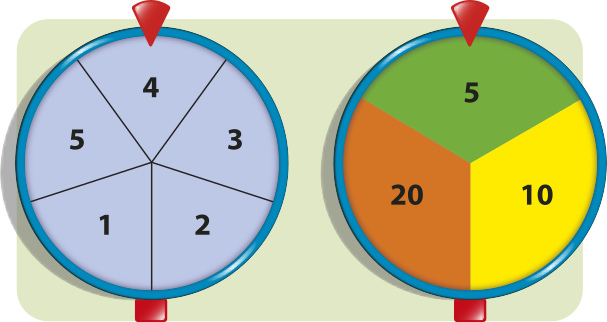
4. Na promoção de certa loja, quando um cliente realiza uma compra acima de R$ 200,00, ele gira duas roletas e ganha um cupom de desconto. O valor dêêsse cupom corresponde ao produto dos números indicados nas roletas, em reais. Observe.
DICA
Cada roleta foi dividida em partes iguais.
No exemplo apresentado, o valor do cupom corresponde a R$ 20,00, pois 4 ⋅ 5 = 20.
a) Quantas são as composições de multiplicação possíveis de serem obtidas nesse sorteio?
15 composições
b) Determine o espaço amostral com todas as opções de valores do cupom de desconto. Se necessário, construa uma árvore de possibilidades.
Resposta nas Orientações para o professor.
c) escrêeva o conjunto quê representa o evento:
Respostas nas Orientações para o professor.
• A de sortear um cupom de desconto cujo valor seja maior ou igual a R$ 40,00;
• B de sortear um cupom de desconto cujo valor seja maior quê R$ 60,00 e menor quê R$ 80,00;
• C de sortear um cupom de desconto cujo valor, em reais, seja múltiplo de 5;
• D de sortear um cupom de desconto cujo valor seja menor quê R$ 10,00;
• E de sortear um cupom de desconto cujo valor esteja entre R$ 10,00 e R$ 30,00.
Página duzentos e cinquenta e quatro
5. Com base no item c da atividade 4, responda aos itens a seguir.
a) Quais pares dêêsses eventos, não vazios, são mutuamente exclusivos?
A e D; A e E; D e E
b) Classifique os eventos B, C e D em simples, cérto ou impossível.
B: impossível; C: cérto; D: simples
6. Considere um experimento em quê ocorre o lançamento simultâneo de uma moeda comum e um dado com formato quê lembra um dodecaedro regular, com as faces numeradas de 1 a 12. Em relação ao espaço amostral dêêsse experimento, podemos afirmar quê é um evento impossível de ocorrer:
a) cara na moeda e um número ímpar no dado.
b) coroa na moeda e um número maior quê 12 no dado.
c) cara na moeda e um número primo no dado.
d) coroa na moeda e um número par menor quê 5 no dado.
e) cara na moeda e um número par no dado.
alternativa b
7. ![]() Obsérve, a seguir, informações sobre dois tipos de espaço amostral.
Obsérve, a seguir, informações sobre dois tipos de espaço amostral.
Espaço amostral discreto: todo espaço amostral formado por um conjunto finito ou infinito de resultados contáveis. Exemplos:
a) lançar uma moeda comum e registrar qual face fica voltada para cima;
b) lançar um dado comum e registrar a pontuação indicada na face voltada para cima.
Espaço amostral contínuo: todo espaço amostral não contável. Exemplos:
a) sortear um número real maior quê 1 e menor quê 2;
b) sortear um número irracional positivo.
Com base nessas informações, dêz-creva um experimento para cada tipo de espaço amostral apresentado. Depois, troque essas descrições com um colega para quê ele classifique o espaço amostral de cada experimento em discreto ou contínuo, enquanto você faz o mesmo com as descrições quê receber. Por fim, confiram juntos as respostas.
Elaboração do estudante.
Cálculo de probabilidade
O dado representado costuma sêr utilizado em alguns jogos de RPG (Role-Playing Game) – jogos em quê os participantes interprétam personagens e, interagindo entre si, criam uma história. Ele tem formato quê lembra um tetraedro regular; próximo a cada um de seus vértices, em cada uma das faces, é indicado um número natural de 1 até 4.

Considere cérto experimento aleatório em quê esse dado tenha sido lançado 500 vezes e o número obtído no vértice superior foi anotado. Analise a tabéla com a freqüência absoluta e a freqüência relativa dos resultados dêêsses lançamentos.
Resultado do experimento aleatório
Número obtído |
freqüência absoluta (f) |
freqüência relativa (fr) |
|---|---|---|
1 |
124 |
0,248 ou 24,8% |
2 |
132 |
0,264 ou 26,4% |
3 |
128 |
0,256 ou 25,6% |
4 |
116 |
0,232 ou 23,2% |
Total |
500 |
1 ou 100% |
Fonte: Dados fictícios.
Página duzentos e cinquenta e cinco
Note quê as freqüências relativas correspondentes aos números indicados nos dados são próximas umas das outras. Se aumentarmos a quantidade de lançamentos do dado nesse experimento, a tendência é quê as freqüências relativas dos números obtidos sêjam ainda mais próximas entre si. Nesse caso, dizemos quê o espaço amostral nesse experimento aleatório é um espaço amostral equiprovável.
Seja A um evento de um espaço amostral equiprovável (ômega)", finito e não vazio. Dizemos quê a probabilidade de ocorrer algum elemento de A, indicada por P(A), é dada pela razão entre a quantidade de elemêntos de A e de (ômega)", ou seja:
P(A) =
DICA
pôdêmos interpretar a expressão do cálculo de probabilidade como a razão entre o número de casos favoráveis (quantidade de elemêntos do evento considerado) e o número total de casos possíveis (quantidade de elemêntos do espaço amostral).
Retomando o experimento aleatório do lançamento do dado, apresentado anteriormente, o espaço amostral é dado por (ômega)" = {1, 2, 3, 4}. Assim, sêndo o evento A = {3}, quê corresponde à obtenção do número 3 em um lançamento do dado, temos:
P(A) = = 0,25
Portanto, a probabilidade de obtêr o número 3 no lançamento dêêsse dado é de 1 em 4, ou seja, , 0,25 ou 25%.
Em um espaço amostral equiprovável (ômega)", finito e não vazio, as probabilidades dos eventos simples são todas iguais. Além díssu, P((ômega)") = 1, pois, de acôr-do com o conceito de probabilidade apresentado anteriormente, temos:
P((ômega)") = = 1.
Agora, considere um evento E de um espaço amostral equiprovável (ômega)", finito e não vazio. Nesse caso, temos:
∅ ⊂ E ⊂ (ômega)" ⇒ n (∅) ≤ n (E) ≤ n ((ômega)")
Como (ômega)" é finito e não vazio, temos n ((ômega)") > 0. Assim, segue quê:
≤ ≤ ⇒ ≤ ≤ ⇒ 0 ≤ P(E)≤ 1
Dado um evento E de um espaço amostral equiprovável qualquer, finito e não vazio, temos quê:
0 ≤ P(E) ≤ 1
Página duzentos e cinquenta e seis
Eventos complementares
Considere a situação descrita a seguir.
Para a realização de um experimento, foram numeradas dez bolas idênticas de 1 a 10, colocadas de maneira aleatória em uma caixa para quê uma delas seja sorteada, sem quê se veja as outras.

Inicialmente, vamos denominar (ômega)" o espaço amostral do experimento apresentado, A o evento sortear uma bola quê contém um número primo e B o evento sortear uma bola quê não contém um número primo. Assim, temos:
• (ômega)" = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
• A = {2, 3, 5, 7};
• B = {1, 4, 6, 8, 9, 10}.
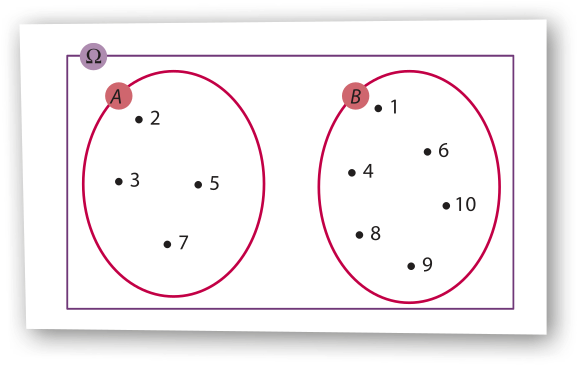
Note quê os eventos A e B são mutuamente exclusivos, ou seja, A ⋃ B = ∅. Além díssu, todo elemento de (ômega)" pertence a B ou pertence a A, ou seja, A ⋂ B = (ômega)". Nesse caso, podemos dizêr quê B é complementar de A em relação a (ômega)" e, reciprocamente, quê A é complementar de B em relação a (ômega)". Dizemos também quê A e B são eventos complementares. O diagrama de Venn, a seguir, representa essa situação.
PARA PENSAR
Calcule P((ômega)"), P(A) e P(B). Que relação você póde perceber entre os resultados obtidos?
P((ômega)") = 1, P(A) = e P(B) = ; P((ômega)") = P(A) + P(B)
Dado um evento A de um espaço amostral equiprovável (ômega)", finito e não vazio, denominamos evento complementar de A em relação a (ômega)", indicado por , o evento formado apenas pêlos elemêntos quê pertencem a (ômega)" e quê não pertencem a A, ou seja, = (ômega)" − A.
Nesse caso, a probabilidade de ocorrência do evento complementar de A em relação a (ômega)", indicada por P(), é dada por:
P() = P((ômega)") − P(A) ⇒ P() = 1 − P(A)
Página duzentos e cinquenta e sete
ATIVIDADES RESOLVIDAS
R3. Mostre quê, dado um espaço amostral equiprovável (ômega)" qualquer, finito e não vazio, temos:
a) se A é um evento impossível qualquer, então P(A) = 0;
b) se B é um evento cérto qualquer, então P(B) = 1.
Resolução
a) Como A é um evento impossível, A não tem elemêntos, ou seja, n (A) = 0. Assim:
P(A) = = = 0
Portanto, P(A) = 0.
b) Como B é um evento cérto, temos quê B = (ômega)". Assim:
P(B) = = = 1
Portanto, P(B) = 1.
R4. No lançamento de um dado honesto de seis faces, qual é a probabilidade de:
a) obtêr o número 5?
b) obtêr um número divisível por 3?
c) não obtêr um número quadrado perfeito?

- Dado honesto
- : dado quê não tem alteração em suas faces com a finalidade de influenciar os resultados obtidos. Também podemos chamar de dado não viciado ou dado perfeito. Nesse tipo de dado, a probabilidade de se obtêr qualquer uma das faces é a mesma.
Resolução
Inicialmente, determinamos o espaço amostral, quê é dado por (ômega)" = {1, 2, 3, 4, 5, 6}.
a) Considerando A o evento obtêr o número 5 no lançamento do dado, temos A = {5} e n (A) = 1. Logo:
P(A) = = ≃ 0, 167 = 16,7%
Portanto, a probabilidade de obtêr o número 5 é de ou aproximadamente 0,167 ou 16,7%.
b) Considerando B o evento obtêr um número divisível por 3 no lançamento do dado, temos B = {3, 6} e n (B) = 2. Logo:
P(B) = = = ≃ 0,333 = 33,3%
Portanto, a probabilidade de obtêr um número divisível por 3 é de ou aproximadamente 0,333 ou 33,3%.
c) Considerando C o evento obtêr um número quadrado perfeito no lançamento do dado, temos C = {1, 4} e n (C) = 2. Para determinar a probabilidade de não obtêr um número quadrado perfeito, podemos calcular a probabilidade de ocorrência do evento complementar de C em relação a (ômega)".
P() = 1 − P(C) ⇒ P() = 1 − = = ≃ 0,667 = 66,7%
Portanto, a probabilidade de não obtêr um número quadrado perfeito é de ou aproximadamente 0,667 ou 66,7%.
Página duzentos e cinquenta e oito
R5. Em um experimento, três moedas perfeitas são lançadas simultaneamente, e verifica-se qual face de cada uma delas fica voltada para cima: cara ou coroa. Qual é a probabilidade de obtêr ao menos duas caras nesse experimento?
Resolução
pôdêmos construir uma árvore de possibilidades para representar todas as possibilidades nos lançamentos das moedas. Para isso, indicamos por C a obtenção de cara e por K, de coroa.
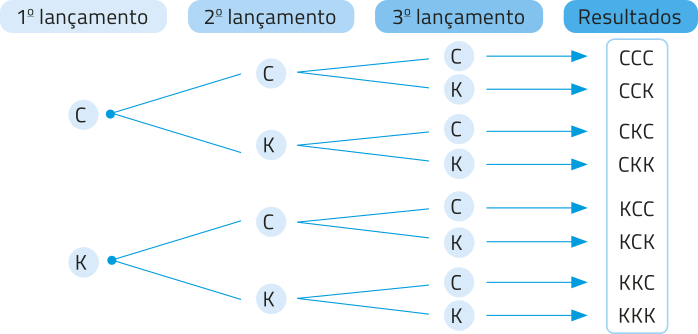
Para obtêr ao menos duas caras, é necessário quê ocorra cara exatamente em dois ou em três lançamentos.
Observando a árvore de possibilidades, temos quê são três as possibilidades de obtêr exatamente duas caras (CCK, CKC e KCC) e há uma possibilidade de obtêr três caras (CCC).
Assim, a probabilidade P de obtêr ao menos duas caras póde sêr calculada por:
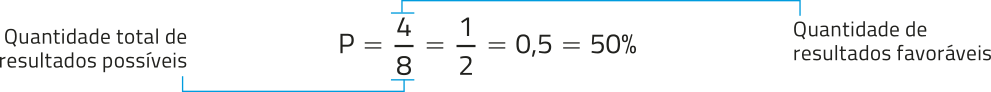
R6. (Enem/MEC) A figura ilustra uma partida de Campo Minado, o jôgo presente em praticamente todo computador pessoal. Quatro quadrados em um tabuleiro 16 × 16 foram abertos, e os números em suas faces indicam quantos dos seus 8 vizinhos contêm minas (a serem evitadas). O número 40 no canto inferior direito é o número total de minas no tabuleiro, cujas posições foram escolhidas ao acaso, d fórma uniforme, antes de se abrir qualquer quadrado.

Em sua próxima jogada, o jogador deve escolher, dentre os quadrados marcados com as lêtras P, Q, R, S e T, um para abrir, sêndo quê deve escolher aquele com a menor probabilidade de conter uma mina.
O jogador deverá abrir o quadrado marcado com a letra
a) P.
b) Q.
c) R.
d) S.
e) T.
Resolução
Para resolver essa atividade, podemos realizar as seguintes etapas.
1ª COMPREENDER O ENUNCIADO
Do enunciado, temos quê:
• o tabuleiro do jôgo tem, ao todo, 256 quadrados (16 ⋅ 16 = 256);
• 4 quadrados do tabuleiro já foram abertos;
• cada quadrado do tabuleiro tem 8 vizinhos;
• os quadrados já abertos têm 2, 1, 4 e 3 minas nos quadrados vizinhos, sêndo os quadrados com as lêtras P, Q, S e T, respectivamente, um dêêsses vizinhos;
• há ao todo 40 minas no tabuleiro;
• determinar qual quadrado tem a menor probabilidade de conter uma mina, entre aqueles marcados com as lêtras P, Q, R, S ou T.
2ª ELABORAR UM PLANO
Inicialmente, podemos calcular as probabilidades de os quadrados marcados com as lêtras P, Q, S e T conterem uma mina e, em seguida, fazer o mesmo para o quadrado marcado com a letra R. Por fim, podemos comparar as probabilidades calculadas.
Página duzentos e cinquenta e nove
3ª EXECUTAR O PLANO
Calculando a probabilidade de os quadrados marcados com as lêtras P, Q, S e T conterem uma mina, temos:
• P: = = 0,25 = 25%
• S: = = 0,50 = 50%
• Q: = 0,125 = 12,5%
• T: = 0,375 = 37,5%
Antes de calcular a probabilidade de o quadrado marcado com a letra R conter uma mina, precisamos considerar quê, das 40 minas do tabuleiro, 10 minas são vizinhas dos quadrados já abertos (2 + 1 + 4 + 3). Além díssu, nenhum dêêsses quadrados vizinhos daqueles já abertos são vizinhos do quadrado marcado com a letra R.
Excluindo os quadrados quê já foram abertos (4) e seus respectivos vizinhos do total de quadrados do tabuleiro (8 + 8 + 8 + 8 = 32), temos:
256 − 4 − 32 = 220; ou seja, 220 quadrados.
A quantidade de minas restantes nesses 220 quadrados é dada por:
40 − 10 = 30; ou seja, 30 minas.
Logo, a probabilidade de o quadrado marcado com a letra R conter uma mina é:
R: ≃ 0,136 = 13,6%
Comparando as probabilidades calculadas, o jogador deverá abrir o quadrado marcado com a letra Q, pois nele há menor probabilidade de conter uma mina.
4ª VERIFICAR OS RESULTADOS
Observando o tabuleiro, podemos afirmar quê, entre os quadrados marcados com as lêtras P, Q, S e T, aquele com menor probabilidade de conter uma mina é o marcado com Q, uma vez quê ele é vizinho do quadrado aberto com o menor número indicado. Assim, uma maneira de verificar o resultado é comparar as probabilidades de conter uma mina nos quadrados marcados com as lêtras Q e R.
Portanto, a alternativa b é a correta.
ATIVIDADES
8. Em uma gincana, os participantes foram numerados de 1 até 25, conforme a ordem de inscrição. Um participante será sorteado para iniciar as provas da gincana. Para fazer esse sorteio, o número de cada participante foi escrito em pedaços de papel idênticos, quê foram colocados em uma caixa para quê um deles fosse retirado aleatoriamente. Qual é a probabilidade de sêr sorteado um participante de número:
a) par?
12 em 25, ,0,48 ou 48%
b) ímpar?
13 em 25, , 0,52 ou 52%
c) múltiplo de 8?
3 em 25, , 0,12 ou 12%
d) maior quê 17?
8 em 25, , 0,32 ou 32%
e) compôzto?
15 em 25, , 0,6 ou 60%
9. Considere todos os números de três algarismos distintos formados pêlos algarismos 4, 1 e 5. Qual é a probabilidade de, ao escolher ao acaso um dêêsses números, o algarismo 5 ter valor posicional 50?
2 em 6, , aproximadamente 0,333 ou 33,3%
Página duzentos e sessenta
10. Observe, a seguir, a quantidade de estudantes matriculados no Ensino Médio de uma escola, por ano escolar.
Ano |
Quantidade de estudantes |
|---|---|
1º |
72 |
2º |
60 |
3º |
68 |
Para representar a escola em uma Feira de Ciências, a direção vai realizar um sorteio de maneira quê cada um dêêsses estudantes tenha a mesma probabilidade de sêr sorteado.
a) Quantos estudantes do Ensino Médio estão matriculados nessa escola?
200 estudantes
b) Qual é a probabilidade de um estudante do 1º ano sêr sorteado?
72 em 200,, 0,36 ou 36%
c) Qual é a probabilidade de o estudante sorteado não estar matriculado no 3º ano?
132 em 200, , 0,66 ou 66%
d) É mais provável quê seja sorteado um estudante do 2º ano ou um estudante do 3º ano? Justifique.
Resposta esperada: Um estudante do 3º ano, pois há mais estudantes matriculados no 3º ano do quê no 2º ano.
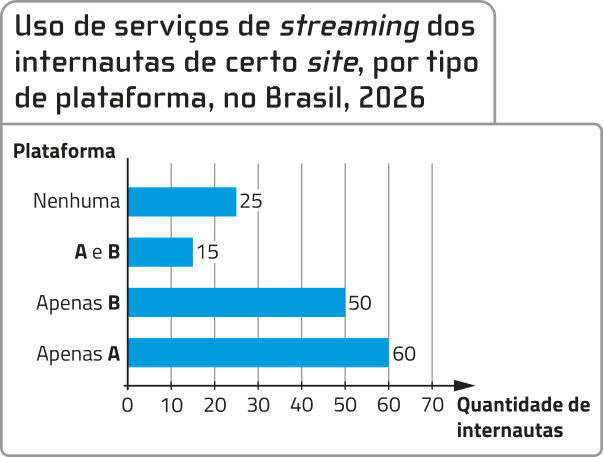
11. O gerente de uma empresa decidiu realizar uma enquete com os internautas quê acessaram o sáiti da companhia com o objetivo de identificar quantos deles utilizam serviços de streaming por meio das platafórmas A ou B. Para incentivar a participação na enquete, ao final, um dos internautas participantes será sorteado e receberá um prêmio oferecido pelo sáiti. Analise o resultado dessa enquete.
Fonte: Dados fictícios.
Qual é a probabilidade de quê o internauta sorteado utilize serviços de streaming:
a) apenas da platafórma A?
60 em 150, , 0,4 ou 40%
b) de ambas as platafórmas (A e B)?
15 em 150, , 0,1 ou 10%
c) da platafórma B?
65 em 150, , aproximadamente 0,433 ou 43,3%
12. Um colecionador separou seis moedas de valores distintos da segunda família do real. Observe informações sobre essas moedas.
Massa (g) |
Diâmetro (mm) |
Espessura (mm) |
|
|---|---|---|---|
|
2,43 |
17 |
1,65 |
|
4,1 |
22 |
1,65 |
|
4,8 |
20 |
2,23 |
|
7,55 |
25 |
2,25 |
|
7,81 |
23 |
2,85 |
|
7 |
27 |
1,95 |
Fonte dos dados: BRASIL. Banco Central do Brasil. Segunda família das moedas brasileiras: conheça todas as características técnicas. Brasília, DF: BCB, [2024]. Disponível em: https://livro.pw/pgpos. Acesso em: 31 ago. 2024.
Em um experimento, esse colecionador vai colocar essas seis moedas em um pacote de fêeutro e, sem olhar, vai sortear apenas uma e observar seu valor. Qual é o espaço amostral dêêsse experimento? pôdêmos dizêr quê esse é um espaço amostral equiprovável? Justifique.
Resposta nas Orientações para o professor.
Página duzentos e sessenta e um
13. Leia a tirinha a seguir.

HUMOR COM CIÊNCIA. [Aleatória Mente]. Humor com Ciência. [S. l.], 1 jan. 2019. Disponível em: https://livro.pw/qncxj. Acesso em: 2 jul. 2024.
Considere quê esse dado mencionado na tirinha seja honesto, tenha formato de icosaedro regular e, em cada uma de suas faces, é indicado um número natural de 1 até 20.
Com base nessas informações, resôuva os itens a seguir.
a) Qual foi o número quê Caco escolheu? E qual foi o número obtído no lançamento do dado?
13; 12
b) Em seu entendimento, por quê Caco utilizou a expressão “Por pouco” após o lançamento do dado?
Resposta esperada: Porque, considerando a sequência dos números naturais, o número obtído no lançamento do dado (12) é antecessor do número quê Caco escolheu (13).
c) Em um lançamento dêêsse dado, o espaço amostral é equiprovável ou não equiprovável? Justifique sua resposta de acôr-do com o texto da tirinha.
Resposta esperada: Equiprovável, pois o tucano está supondo quê o dado é honesto ao dizêr: “A chance de sair 13 é igual pra qualquer outro número do dado”.
d) Qual era a probabilidade de Caco acertar o número obtído no lançamento do dado?
1 em 20, , 0,05 ou 5%
14. Considere um dado não honesto, cujo formato lembra um octaedro regular, sêndo indicado em suas faces um número natural de 1 até 8. A probabilidade de obtêr uma face voltada para cima em um lançamento é diretamente proporcional ao número indicado na face correspondente.

a) Qual é o espaço amostral correspondente a um lançamento dêêsse dado? É correto afirmar quê esse espaço amostral é equiprovável? Justifique.
(ômega)" = {1, 2, 3, 4, 5, 6, 7, 8}. Resposta esperada: Não, pois as probabilidades de ocorrerem os números indicados nas faces não são iguais entre si no lançamento do dado.
b) Qual número é mais provável de se obtêr no lançamento dêêsse dado? Justifique.
Resposta esperada: O número 8, pois esse é o maior número indicado nas faces do dado, e a probabilidade de se obtêr cada face é proporcional ao número indicado correspondente.
c) Ao lançar esse dado, qual é a probabilidade de se obtêr o número 6?
6 em 36, , aproximadamente 0,167 ou 16,7%
d) O quê é mais provável de se obtêr no lançamento dêêsse dado: um número ímpar ou um número par? Justifique.
Número par, pois a soma dos números pares indicados nas faces é 20, enquanto a soma dos números ímpares é 16, sêndo 20 > 16.
15. ![]() Elabore e escrêeva um problema envolvendo o cálculo de probabilidade e a construção de uma árvore de possibilidades. Em seguida, troque esse problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elabore e escrêeva um problema envolvendo o cálculo de probabilidade e a construção de uma árvore de possibilidades. Em seguida, troque esse problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
16. (IME-RJ) Em um jôgo de RPG “Role-Playing Game” em quê os jogadores lançam um par de dados para determinar a vitória ou a derrota quando se confrontam em duelos, os dados são icosaedros regulares com faces numeradas de 1 a 20. Vence quem soma mais pontos na rolagem dos dados e, em caso de empate, os dois perdem. Em um confronto, seu adversário somou 35 pontos na rolagem de dados. É sua vez de rolar os dados. Qual sua chance de vencer êste duelo?
a)
b)
c)
d)
e)
alternativa e
Página duzentos e sessenta e dois
17. Os dados do gráfico e da tabéla representados a seguir foram coletados pelo hí bê gê hé no Censo 2022.

Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Ribeirão Preto. Rio de Janeiro: hí bê gê hé, [2022]. Localizável em: menú Pesquisas: Censo 2022: População residente: Sexo. Disponível em: https://livro.pw/fwelq. Acesso em: 30 ago. 2024.
Faixa etária |
freqüência absoluta |
|---|---|
0 ⊢ 15 |
117.707 |
15 ⊢ 30 |
150.827 |
30 ⊢ 45 |
178.547 |
45 ⊢ 60 |
130.105 |
60 ⊢ |
121.456 |
Fonte dos dados: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Ribeirão Preto. Rio de Janeiro: hí bê gê hé, [2022]. Localizável em: menú Panorama. Disponível em: https://livro.pw/hrvza. Acesso em: 29 ago. 2024
DICA
No gráfico, parte do eixo vertical foi suprimido.
Em comemoração ao aniversário de Ribeirão Preto, suponha quê a prefeitura vá sortear, ao acaso, um habitante do município para ganhar um prêmio. Com base nessas informações, podemos afirmar quê:
a) é mais provável quê um habitante com 60 anos ou mais seja sorteado em relação a um habitante com idade menor quê 30 anos;
b) a probabilidade de um habitante do sexo feminino sêr sorteado é de 48%;
c) é mais provável quê um habitante do sexo masculino seja sorteado do quê um do sexo feminino;
d) a probabilidade de um habitante com idade maior ou igual a 30 e menor quê 45 anos sêr sorteado é maior quê 25%.
alternativa d
18. ![]() Com base nas informações apresentadas na atividade 17, elabore uma situação-problema envolvendo o cálculo de probabilidade. Em seguida, troque essa situação-problema com um colega para quê um resôuva a do outro. Juntos, verifiquem se as respostas estão corretas.
Com base nas informações apresentadas na atividade 17, elabore uma situação-problema envolvendo o cálculo de probabilidade. Em seguida, troque essa situação-problema com um colega para quê um resôuva a do outro. Juntos, verifiquem se as respostas estão corretas.
Elaboração do estudante.
19. Observe a situação a seguir, proposta por um professor de Matemática.
De um jôgo de dominó completo, é retirada ao acaso uma de suas peças, e os pontos indicados nas duas partes são somados. Qual é a probabilidade de o resultado obtído sêr 6?
Agora, analise a resposta dada a essa questão por dois estudantes.
• élam: A probabilidade é de , pois 6 é um dos 12 resultados possíveis (soma de 0 até 12).
• Bruna: A probabilidade é de , pois em 4 das 28 peças do jôgo de dominó a soma dos pontos é igual a 6.
Qual dêêsses estudantes acertou a questão? Argumente.
Resposta esperada: Bruna acertou a questão, pois, das 28 peças, em 4 delas a soma das partes é igual a 6, sêndo elas 0 + 6 = 6, 1 + 5 = 6, 2 + 4 = 6 e 3 + 3 = 6. Já élam errou por considerar quê o espaço amostral dêêsse experimento, correspondente à soma dos pontos da peça de dominó sorteada, fosse equiprovável, o quê não ocorre.
Página duzentos e sessenta e três
Probabilidade da união de dois eventos
Considere a situação a seguir.
Nove fichas idênticas, numeradas de 1 a 9, foram viradas e embaralhadas sobre uma mesa. Um experimento consiste em escolher ao acaso uma dessas fichas, virá-la e observar o número indicado. Agora, considere os dois eventos descritos a seguir.
• A: o número obtído é divisor de 8.
• B: o número obtído é divisor de 12.
Qual é a probabilidade de quê, nesse experimento, ocorra ao menos um dêêsses eventos?
Note quê determinar a probabilidade de ocorrência de ao menos um dos eventos indicados é o mesmo quê dizêr quê um evento ou outro devem ocorrer. Assim, para resolver a situação apresentada, temos de calcular P(A ⋂ B).
Para isso, vamos indicar os elemêntos do espaço amostral (ômega)" e dos eventos A e B e interpretar uma representação em um diagrama de Venn. Acompanhe.
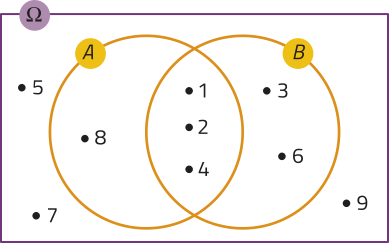
• (ômega)" = {1, 2, 3, 4, 5, 6, 7, 8, 9} → n((ômega)") = 9
• A = {1, 2, 4, 8} → n(A) = 4
• B = {1, 2, 3, 4, 6} → n(B) = 5
Observando o diagrama, temos:
• A ⋃ B = {1, 2, 3, 4, 6, 8} → n(A ⋃ B) = 6
Aplicando a definição de probabilidade:
P(A ⋃ B) = = =
Portanto, a probabilidade de quê ocorra ao menos um dos eventos A ou B é de .
DICA
Note quê os eventos A e B não são mutuamente exclusivos, pois A ⋃ B ≠ ∅.
Em situações como essa, podemos utilizar a propriedade n (A ⋃ B) = n (A) + n (B) − n (A ⋂ B), quê estudamos na Unidade 1 do Volume 1 desta coleção. Nesse caso, considere a divisão de ambos os membros dessa igualdade por n ((ômega)"):
= + − ⇒ P(A ⋃ B) = P(A) + P(B) − P(A ⋂ B)
Sejam A e B eventos de um espaço amostral equiprovável (ômega)", finito e não vazio. A probabilidade de quê ocorra ao menos um dêêsses eventos, indicada por P(A ⋃ B), é dada por:
P(A ⋃ B) = P(A) + P(B) − P(A ⋂ B)
Em relação à situação apresentada, como A ⋂ B = {1, 2, 4} → n(A ⋃ B) = 3, n(A) = 4 e n(B) = 5, temos:
P(A ⋃ B) = P(A) + P(B) − P(A ⋂ B) = + − = =
Página duzentos e sessenta e quatro
ATIVIDADES RESOLVIDAS
R7. Em uma academia aquática, são disponibilizados aos estudantes treinos de diversas modalidades. Em uma pesquisa, realizada com todos os 600 estudantes, verificou-se quê 365 treinam natação, 243 treinam hidroginástica e 100 não treinam nenhuma dessas modalidades. Um estudante dessa academia será sorteado para receber um prêmio. Qual é a probabilidade de esse estudante sorteado treinar as duas modalidades: natação e hidroginástica?
Resolução
Sejam A e B os conjuntos formados pêlos estudantes quê treinam natação e pêlos estudantes quê treinam hidroginástica, respectivamente. Assim, temos:
• n (A ⋃ B) = 600 − 100 = 500;
• n (A) = 365;
• n (B) = 243.
Para resolver essa questão, temos de calcular P(A ⋂ B). Assim, temos:
P(A ⋃ B) = P(A) + P(B) − P(A ⋂ B) ⇒ = + − P(A ⋂ B) ⇒
⇒ P(A ⋂ B) = = = 0,18 = 18%
Portanto, a probabilidade de esse estudante sorteado treinar ambas as modalidades, natação e hidroginástica, é de , 0,18 ou 18%.
R8. Ivone recortou cinco pedaços de papel idênticos e escreveu neles cada letra de seu nome. Em seguida, colocou todos eles dentro de uma caixa e sorteou cada pedaço de papel, sem reposição, registrando o anagrama formado. Qual é a probabilidade de o anagrama formado terminar em vogal ou começar em consoante?
Resolução
Inicialmente, indicamos por:
• (ômega)" o espaço amostral compôzto de todos os anagramas possíveis de serem formados;
• A o evento no qual o anagrama formado termine em vogal;
• B o evento no qual o anagrama formado comece em consoante.
Agora, calculamos n((ômega)"), n(A), n(B). Em seguida, determinamos n(A ⋃ B), quê corresponde à quantidade de anagramas formados quê terminam em vogal e começam em consoante.
• n((ômega)") = 5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
• n(A) = 72, pois:
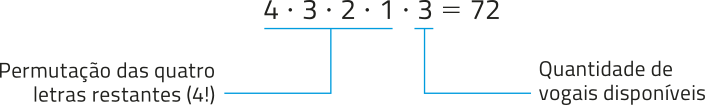
• n(B) = 48, pois:

Página duzentos e sessenta e cinco
• n(A ⋃ B) = 36, pois:

Como a probabilidade de o anagrama formado terminar em vogal ou começar em consoante corresponde a P (A ⋂ B), temos:
P(A ⋂ B) = P(A) + P(B) − P(A ⋃ B) = + − = = = 0,7 = 70%
Portanto, a probabilidade de o anagrama formado terminar em vogal ou começar em consoante é de 7 em 10, , 0,7 ou 70%.
ATIVIDADES
20. Em cérto jôgo de bingo infantil, as bó-linhas, diferenciadas apenas pela numeração indicada, são colocadas em um glôbo, de onde são sorteadas. Em certa rodada dêêsse jôgo, a probabilidade de sortear uma bó-linha com um número maior ou igual a 60 era de 20% e de sortear uma bó-linha com um número menor ou igual a 60 era de 85%. Um jogador, para vencer nessa rodada, precisaria quê a bó-linha com o número 60 fosse sorteada. Qual é a probabilidade de esse jogador vencer nessa rodada?
5%
21. Em uma urna, foram colocadas 100 fichas idênticas numeradas de 1 a 100.
a) escrêeva um algoritmo para determinar a probabilidade de, sorteando ao acaso uma ficha dessa urna, obter-se um número natural ímpar ou menor ou igual a 25.
Resposta possível: 1ª) Representamos por (ômega)", A e B o espaço amostral compôzto de todos os números naturais de 1 a 100, o evento no qual obtém-se um número ímpar e o evento no qual obtém-se um número menor ou igual a 25, respectivamente. 2ª) Determinamos n((ômega)"), n(A), n(B) e n(A ⋃ B), ou seja, n((ômega)") = 100, n(A) = 50, n(B) = 25 e n(A ⋃ B) = 13. 3ª) Calculamos P(A ⋂ B), correspondente à probabilidade de se obtêr um número natural ímpar ou menor ou igual a 25: P(A ⋂ B) = P(A) + P(B) − P(A ⋃ B) = + − = = = 0,62 = 62%.
b) Com base no algoritmo quê você escreveu no item a, calcule a probabilidade de, sorteando ao acaso uma ficha dessa urna, obter-se um número natural:
• par ou múltiplo de 5.
, 0,6 ou 60%
• menor ou igual a 15 ou maior quê 80.
, 0,35 ou 35%
• múltiplo de 4 ou divisor de 100.
, 0,31 ou 31%
22. Tanto a probabilidade da união quanto a da interseção dos eventos A e B é de 45%. Sabendo quê a probabilidade de ocorrer o evento A é de 32%, determine a probabilidade de ocorrer o evento B.
58%
23. O Senado brasileiro é compôzto de 81 senadores quê representam os 26 estados e o Distrito Federal. Observe a tabéla a seguir com informações sobre os senadores em exercício em 2024.
Senadores em exercício no Brasil, por faixa de idade e gênero, 3/7/2024
Idade (ano) |
Gênero Masculino |
Gênero Feminino |
|---|---|---|
35 ⊢ 45 |
5 |
1 |
45 ⊢ 55 |
14 |
5 |
55 ⊢ 65 |
21 |
6 |
65 ⊢ 75 |
19 |
3 |
75 ⊢ 85 |
6 |
1 |
Fonte dos dados: BRASIL. Senado Federal. Senadores em exercício. Brasília, DF: Senado Federal, 3 jul. 2024. Disponível em: https://livro.pw/gdash. Acesso em: 3 jul. 2024.
Escolhendo-se ao acaso um dos senadores em exercício em 3/7/2024, qual é a probabilidade de sêr:
a) mulher?
, aproximadamente 0,198 ou 19,8%
b) homem e ter 65 anos de idade ou mais?
, aproximadamente 0,309 ou 30,9%
c) mulher ou ter menos de 55 anos?
, aproximadamente 0,432 ou 43,2%
24. Sejam A e B eventos mutuamente exclusivos de um espaço amostral (ômega)", finito e não vazio, com P(A) = 0,38 e P(B) = 0,24. Nessas condições, podemos afirmar quê P(A ⋃ B), P(A ⋂ B) e P(A) correspondem, respectivamente, a:
a) 0; 0,62 e 0,14;
b) 0; 0,38 e 0,76;
c) 0; 0,62 e 0,62;
d) 0,14; 0,24 e 0,38.
alternativa c
Página duzentos e sessenta e seis
25. Em determinado modelo de baralho, as 52 cartas são divididas igualmente em 4 naipes: cópas, ouros, espadas e paus. Das 13 cartas quê compõem cada naipe, 9 são numeradas de 2 a 10, uma contém a letra A e as outras três contêm as figuras Valete, Dama e Rei, indicadas pelas lêtras J, Q e K, respectivamente.

Ao se retirar aleatoriamente uma carta de um baralho dêêsses, qual é a probabilidade de ela sêr:
a) uma dama de cópas?
, aproximadamente 0,02 ou 2%
b) uma carta com a letra A ou uma carta de ouros?
, aproximadamente 0,31 ou 31%
c) uma carta de espadas ou uma carta numerada de 2 a 10?
, aproximadamente 0,77 ou 77%
d) uma carta quê contém uma figura ou uma carta de paus?
aproximadamente 0,42 ou 42%
26. Em cérto jôgo, a cada rodada os participantes devem lançar um dado com formato quê lembra um icosaedro regular e com faces coloridas e numeradas de 1 a 20, conforme a planificação a seguir.
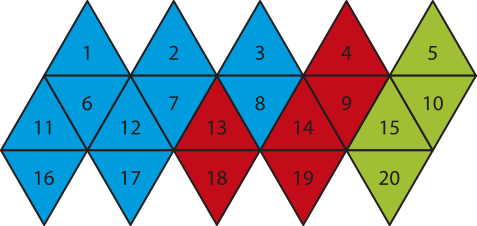
Em determinada rodada dêêsse jôgo, para avançar de nível, cada jogador, ao lançar o dado, deve satisfazer a condição descrita a seguir.
• João: face azul e número múltiplo de 3.
• Paulo: face vermelha ou número primo.
• Mariana: face vêrde ou número maior quê 15.
a) Qual dos participantes tem a maior probabilidade de avançar de nível nessa rodada do jôgo? E qual tem a menor probabilidade?
Paulo; João
b) Suponha quê, na condição para João avançar de nível, a conjunção “e” seja trocada por “ou”. As suas respostas para o item b se manteriam? Justifique.
Não, pois, nesse caso, João teria a maior probabilidade de avançar de nível e Mariana, a menor.
27. (UEPG-PR) Em um grupo de 500 estudantes, 90 estudam Química, 160 estudam Biologia e 20 estudam Química e Biologia. Se um aluno é escolhido ao acaso, indique o quê for correto.
01) A probabilidade de quê ele estude Química ou Biologia é de 0,46.
02) A probabilidade de quê ele não estude Química nem Biologia é de 0,54.
04) A probabilidade de quê ele estude Química e Biologia é de 0,04.
08) A probabilidade de quê ele estude somente Química é de 0,16.
07 (01 + 02 + 04)
28. Em uma pesquisa estatística amostral, 80 pessoas foram entrevistadas sobre a marca de iogurte quê já consumiram, entre as marcas A e B. Ao organizar os dados coletados, constatou-se quê 35 pessoas indicaram ter consumido iogurte da marca A; 43 pessoas, da marca B; e 12 pessoas indicaram não consumir iogurte de nenhuma dessas marcas. Escolhendo-se ao acaso uma dessas pessoas entrevistadas, qual é a probabilidade de ela ter indicado consumir o iogurte da marca A ou da marca B?
, 0,85 ou 85%
29. A afirmação a seguir é verdadeira ou falsa? Justifique sua afirmativa.
Dados A e B eventos mutuamente exclusivos de um espaço amostral equiprovável (ômega)", finito e não vazio, então:
P(A ⋂ B) = P(A) + P(B)
Resposta esperada: É verdadeira, pois, como A e B são eventos mutuamente exclusivos, temos quê A ⋃ B = ∅ e, por consequência, P(A ⋃ B) = 0.
Página duzentos e sessenta e sete
30. Uma escola realizou uma pesquisa com os 120 estudantes do Ensino Médio sobre as áreas de preferência deles para os cursos em universidades. Analise os resultados.
Área de preferência dos estudantes do Ensino Médio de certa escola para os cursos em universidades, 2026
Área |
Quantidade de estudantes |
|---|---|
Biológicas |
46 |
Exatas |
57 |
Humanas |
43 |
Exatas e humanas |
10 |
Biológicas e exatas |
21 |
Humanas e biológicas |
18 |
Sem preferência |
12 |
Fonte: Dados fictícios.
Escolhendo-se ao acaso um dêêsses estudantes, qual é a probabilidade de ele preferir cursos na área de:
a) exatas ou humanas?
, 0,75 ou 75%
b) humanas ou biológicas?
, aproximadamente 0,592 ou 59,2%
c) biológicas ou exatas?
, aproximadamente 0,683 ou 68,3%
d) exatas ou não ter preferência por área?
, 0,575 ou 57,5%
31. ![]() A seguir, estão representados dois dados honestos, um dado comum e um dado com formato quê lembra um octaedro regular.
A seguir, estão representados dois dados honestos, um dado comum e um dado com formato quê lembra um octaedro regular.

Com base nos dados apresentados, elabore uma situação-problema relacionada ao cálculo da probabilidade da união de dois eventos. Troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Probabilidade condicional
Leia a situação descrita a seguir.
Observando as fichas clínicas em um consultório oftalmológico, verificou-se quê foram atendidos em cérto dia 40 pacientes, dos quais 14 têm hipermetropia, 21 têm miopia e 8 têm ambos os problemas de visão.
Em um experimento aleatório equiprovável, a ficha de um dos pacientes será sorteada para quê ele responda, por telefone, a um questionário sobre satisfação do atendimento. Qual é a probabilidade de o paciente sorteado ter ambos os problemas de visão?
Denominando H o evento no qual o paciente sorteado tem hipermetropia e M o evento em quê o paciente tem miopia, podemos representar essa situação pelo diagrama a seguir.
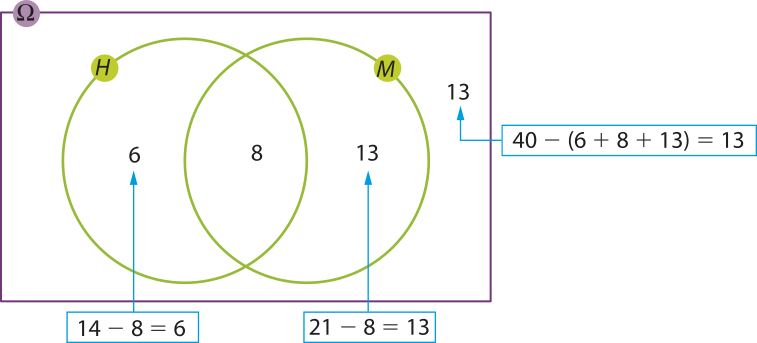
Página duzentos e sessenta e oito
Para determinar a probabilidade de o paciente sorteado ter os dois problemas de visão, precisamos calcular P(H ⋃ M). Assim:
P(H ⋃ M) = = = = 0,20 = 20%
Portanto, a probabilidade de sortear um paciente com ambos os problemas de visão é de , 0,20 ou 20%.
PARA AMPLIAR
Acesse o sáiti a seguir para obtêr informações sobre problemas de visão e êêrros de refração quê podem sêr apresentados pelo olho.
• ENTENDA os êêrros de refração e quais são as opções de tratamento! Veja Bem. São Paulo: CBO, n. 18, ano 6, 2018. Disponível em: https://livro.pw/xvgfh. Acesso em: 30 ago. 2024.
Agora, vamos considerar quê, ao realizar esse sorteio, observou-se quê esse paciente tem, ao menos, hipermetropia. Nesse caso, note quê o espaço amostral quê devemos considerar no cálculo da probabilidade é H, uma vez quê sabemos quê o paciente tem hipermetropia. Assim, temos:
= = ≃ 0,571 = 57,1%
Portanto, a probabilidade de sortear um paciente com ambos os problemas de visão, sabendo quê esse paciente tem hipermetropia, é de ou aproximadamente 0,571 ou 57,1%.
Sejam A e B eventos de um espaço amostral equiprovável (ômega)", finito e não vazio. Denominamos probabilidade condicional de B em relação a A a probabilidade de quê ocorra o evento B dado quê o evento A tenha ocorrido. Essa probabilidade, indicada por P(B | A), é dada por:
P(B | A) =
Em relação à expressão P(B | A) = , ao dividirmos o numerador e o denominador do membro da direita por n ((ômega)"), temos:
P(B | A) = = =
No cálculo da probabilidade condicional de B em relação a A, as expressões a seguir são equivalentes.
P(B | A) = ou P(B | A) =
Página duzentos e sessenta e nove
ATIVIDADES RESOLVIDAS
R9. Em uma cerimônia de colação de grau de certa universidade, 30 mulheres e 20 homens receberam seus diplomas de concluintes em curso de nível superior. Entre as mulheres, formaram-se 10 arquitetas, 14 médicas e 6 engenheiras. Entre os homens, formaram-se 2 arquitetos, 10 médicos e 8 engenheiros. Durante essa cerimônia, um dos formandos foi escolhido ao acaso para fazer o juramento em nome de todos. Sabendo quê o formando sorteado foi uma mulher, qual é a probabilidade de quê ela seja uma médica formanda?
Resolução
Em relação ao sorteio apresentado, o espaço amostral (ômega)" corresponde a todos os formandos, ou seja, n((ômega)") = 30 + 20 = 50. Assim, podemos definir o evento:
• A, em quê o formando é mulher, com n(A) = 30;
• B, em quê o formando é médico, com n(B) = 14 + 10 = 24.
Dessa maneira, temos quê A ⋃ B corresponde aos formandos quê são mulheres e médicas, em quê n(A ⋃ B) = 14.
Assim, temos quê a probabilidade de sortear uma médica formanda, sabendo quê o formando sorteado é uma mulher, é dada por:
P(B | A) = = = ≃ 0, 467= 46,7%
Portanto, a probabilidade de sortear uma médica formanda, dado quê o formando sorteado seja uma mulher, é , aproximadamente 0,467 ou 46,7%.
R10. Considere quê, de um baralho comum, tênham sido separadas as 9 cartas numéricas de naipe ouros, conforme indicado a seguir. Essas cartas foram colocadas sobre uma mesa com a face numérica voltada para baixo e, em seguida, embaralhadas.

Uma dessas cartas foi retirada ao acaso, e verificou-se quê o número sorteado era par. Qual é a probabilidade de esse número sêr menor quê 7?
Resolução
pôdêmos resolver essa questão de duas maneiras.
1ª maneira:
Em relação ao experimento de retirar uma dessas cartas ao acaso, e observar o número indicado, o espaço amostral é dado por (ômega)" = {2, 3, 4, 5, 6, 7, 8, 9, 10}. Assim, podemos definir o evento:
• A, em quê a carta sorteada tem número par, ou seja, A = {2, 4, 6, 8, 10};
• B, em quê a carta sorteada tem número menor quê 7, ou seja, B = {2, 3, 4, 5, 6}.
Dessa maneira, temos A ⋃ B = {2, 4, 6}.
Assim, como n (A ⋃ B) = 3 e n(A) = 5, a probabilidade de sortear uma carta com um número menor quê 7, dado quê a carta sorteada tem um número par, é dada por:
P(B | A) = = = 0,6
Página duzentos e setenta
2ª maneira:
Também podemos, nesse caso, restringir o espaço amostral ao conjunto A, uma vez quê sabemos quê a carta sorteada tem número par. Assim, entre os cinco números pares possíveis, há três deles menóres quê 7, quê são os números 2, 4 e 6. Logo:
P(B | A) = = 0,6
Portanto, a probabilidade de sortear uma carta com um número menor quê 7, dado quê a carta sorteada tem um número par, é de , 0,6 ou 60%.
ATIVIDADES
32. Sejam A e B eventos de um espaço amostral equiprovável (ômega)", finito e não vazio, tais quê P(A | B) = 0,5 e P(A ⋃ B) = 0,4. Qual é o valor de P(B)?
, 0,8 ou 80%
33. Antes de lançar um produto no mercado, uma empresa realiza pesquisas amostrais sobre a aceitação dêêsse produto de acôr-do com o público consumidor: mulheres, homens e crianças. Analise o resultado de uma dessas pesquisas realizadas com 80 homens adultos, 120 mulheres adultas e 50 crianças.
Pesquisa de aceitação dos produtos X e Y, por tipo de consumidor
Tipo de consumidor |
Consumiria o produto X |
Consumiria o produto Y |
|---|---|---|
Homem |
53 |
36 |
Mulher |
72 |
78 |
Criança |
28 |
44 |
Fonte: Dados fictícios.
Considere um experimento aleatório, em quê uma das pessoas entrevistadas é sorteada para receber um prêmio. Além díssu, considere os eventos A e B em quê a pessoa sorteada consumiria os produtos X e Y, respectivamente, e os eventos H, M e C em quê a pessoa sorteada é homem, mulher e criança, respectivamente.
Nessas condições, dêz-creva o significado de cada probabilidade indicada a seguir.
a) P(A | H)
b) P(C | B)
c) P(M | A)
d) P(H | B)
e) P(A | C)
f) P(B | M)
Respostas nas Orientações para o professor.
34. De acôr-do com as informações da atividade 33, resôuva as kestões a seguir.
a) Calcule a probabilidade indicada em cada item e apresente o resultado em porcentagem.
a: 66,25%; b: aproximadamente 27,8%; c: aproximadamente 47,1%; d: aproximadamente 22,8%; e: 56%; f: 65%
b) De acôr-do com os resultados dessa pesquisa, a empresa vai lançar o produto voltado ao consumidor quê teve maior porcentual de aceitação. Qual produto e para qual tipo de consumidor ele será lançado?
Será lançado o produto Y para crianças.
35. Visando o bem-estar dos idosos, a prefeitura de cérto município estuda a instalação de academias ao ar livre em alguns bairros. Para isso, foi realizada uma pesquisa com 100 idosos quê residem nesse município e constatou-se quê 45 deles praticam esportes coletivos, 58 praticam esportes individuais e 26 não praticam esporte algum. Sorteando-se ao acaso um dêêsses idosos entrevistados, qual é a probabilidade de ele praticar:
a) esporte coletivo e individual?
, 0,29 ou 29%
b) esporte individual, dado quê ele pratíca esporte coletivo?
, aproximadamente 0,644 ou 64,4%
c) esporte coletivo, dado quê ele pratíca esporte individual?
, 0,5 ou 50%
36. Ao lançar um dado comum e honesto duas vezes consecutivas, observa-se o número obtído em cada lançamento e verifica-se quê a soma deles é maior quê 7. Qual é a probabilidade de quê, em ao menos um dos lançamentos, se tenha obtído o número 4?
, aproximadamente 0,333 ou 33,3%
Página duzentos e setenta e um
37. Considere quê uma peça seja retirada aleatoriamente de um jôgo de dominó comum e completo. Qual é a probabilidade de, ao adicionar os pontos das duas partes dessa peça, a soma sêr:
a) igual a 6?
, aproximadamente 0,143 ou 14,3%
b) maior quê 8, sabendo quê a peça tem 5 pontos em uma das partes?
, aproximadamente 0,429 ou 42,9%
c) igual a 6, sabendo quê a peça tem uma quantidade ímpar de pontos em uma das partes?
, aproximadamente 0,111 ou 11,1%
38. Uma professora dos Anos Iniciais do Ensino Fundamental produziu fichas de EVA, todas de mesmo tamãnho, e indicou nelas cada letra do alfabeto uma única vez, colocando-as em uma urna para propor uma brincadeira aos estudantes. Em cada rodada dessa brincadeira, a professora sorteia uma ficha e dá alguma dica aos estudantes para quê tentem acertar a letra indicada. Em seguida, a ficha sorteada é devolvida à urna para o sorteio da próxima rodada. Observe as dicas dadas nas rodadas 1, 2 e 3.

a) Em cada rodada, qual é a probabilidade de os estudantes acertarem a letra da ficha sorteada, considerando a dica da professora?
rodada 1: , 0,2 ou 20%; rodada 2: , 0,25 ou 25%; rodada 3: , 0,1 ou 10%
b) Em uma rodada, a professora sorteia a ficha e, ao observá-la, pensa em duas opções de dica, conforme apresentado a seguir.
Opção I: É uma vogal.
Opção II: Tem no nome da Vilma.
Qual dessas dicas a professora póde dar aos estudantes para quê a probabilidade de eles acertarem seja maior? Justifique sua resposta e considere quê os estudantes tênham acesso a apenas uma das dicas.
Respostas nas Orientações para o professor.
39. (Enem/MEC) Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes 20% das declarações de imposto de renda quê lhe foram encaminhadas. Uma declaração é classificada como inconsistente quando apresenta algum tipo de êrro ou conflito nas informações prestadas. Essas declarações consideradas inconsistentes foram analisadas pêlos auditores, quê constataram quê 25% delas eram fraudulentas. Constatou-se ainda quê, dentre as declarações quê não apresentaram inconsistências, 6,25% eram fraudulentas.
Qual é a probabilidade de, nesse ano, a declaração de um contribuinte sêr considerada inconsistente, dado quê ela era fraudulenta?
a) 0,0500
b) 0,1000
c) 0,1125
d) 0,3125
e) 0,5000
alternativa e
40. ![]() Leia as informações apresentadas a seguir. Para pesquisar a eficácia de alguns medicamentos no tratamento de certa doença, foi realizado um teste em alguns voluntários acometidos por ela, conforme indicado na tabéla.
Leia as informações apresentadas a seguir. Para pesquisar a eficácia de alguns medicamentos no tratamento de certa doença, foi realizado um teste em alguns voluntários acometidos por ela, conforme indicado na tabéla.
Quantidade de pessoas quê se submeteram ao tratamento de certa doença, por tipo de medicamento e sexo
Medicamento |
Sexo Masculino |
Sexo Feminino |
|---|---|---|
A |
59 |
43 |
B |
36 |
55 |
C |
49 |
38 |
D |
36 |
84 |
Fonte: Dados fictícios.
Com base nas informações apresentadas, elabore uma situação-problema relacionada ao cálculo de probabilidade condicional. Troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve a quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e setenta e dois
Probabilidade de eventos independentes e de eventos dependentes
Na realização de um experimento aleatório, a ocorrência de dois ou mais eventos sucessivos ou simultâneos podem ou não estar relacionados entre si.
Para compreender melhor esse assunto, considere a situação descrita a seguir.
Um professor de Geografia de uma turma de Ensino Médio propôs a realização de duas atividades avaliativas: um seminário e uma redação. Essas atividades deviam tratar de um dos seguintes temas: Cultura, Sociedade ou Território.
Para determinar o tema de cada atividade, o professor escreveu em três pedaços de papel idênticos o nome dos temas e colocou-os em uma caixa. O 1º papel sorteado indicará o tema do seminário e o 2º papel, o tema da redação.
Qual é a probabilidade de quê o tema do seminário seja Cultura e o da redação, Sociedade?
Para resolver a quêstão apresentada, temos de analisar duas maneiras diferentes em que os sorteios sucessivos dos temas podem sêr realizados, ou seja, com ou sem a reposição do 1º papel sorteado na caixa antes do sorteio do 2º papel.
• Sorteio com reposição
Nesse caso, o 1º papel sorteado é reposto na caixa antes do sorteio do 2º papel.
Inicialmente, podemos construir uma tabéla de dupla entrada.
Possibilidades de composição de temas para o seminário e para a redação, em sorteio com reposição
Seminário |
RedaçãoCultura (C) |
Redação Sociedade (S) |
Redação Território (T) |
|---|---|---|---|
Cultura (C) |
(C; C) |
(C; S) |
(C; T) |
Sociedade (S) |
(S; C) |
(S; S) |
(S; T) |
Território (T) |
(T; C) |
(T; S) |
(T; T) |
Fonte: Dados fictícios.
PARA PENSAR
No sorteio com reposição, é possível quê o seminário e a redação sêjam sobre um mesmo tema? Justifique.
Resposta esperada: Sim, pois, ao repor na caixa o 1º papel sorteado, ele poderá sêr sorteado novamente.
Note quê, no sorteio com reposição, o espaço amostral tem 9 elemêntos. Assim, a probabilidade (PA) de quê os temas do seminário e da redação sêjam, respectivamente, Cultura e Sociedade (C; S), é dada por:
PA =
• Sorteio sem reposição
Nesse caso, o 1º papel retirado é reservado e não é reposto na caixa antes do sorteio do 2º papel.
Página duzentos e setenta e três
Construindo uma tabéla de dupla entrada, obtemos:
Possibilidades de composição de temas para o seminário e para a redação, em sorteio sem reposição
Seminário |
Redação Cultura (C) |
Redação Sociedade (S) |
Redação Território (T) |
|---|---|---|---|
Cultura (C) |
(C; S) |
(C; T) |
|
Sociedade (S) |
(S; C) |
(S; T) |
|
Território (T) |
(T; C) |
(T; S) |
Fonte: Dados fictícios.
Note quê, no sorteio sem reposição, o espaço amostral tem apenas 6 elemêntos, uma vez quê não é possível quê seja sorteado o mesmo tema para o seminário e para a redação. Assim, a probabilidade (PB) de quê os temas do seminário e da redação sêjam, respectivamente, Cultura e Sociedade (C; S), é dada por:
PB =
Em relação à situação apresentada, temos quê o evento “sortear o tema Cultura para o seminário” e o evento “sortear o tema Sociedade para a redação” são independentes quando os sorteios são realizados com reposição, ou seja, o resultado de um deles não influencía no resultado do outro. Já quando os sorteios são realizados sem reposição, temos quê esses eventos são dependentes, ou seja, o resultado de um deles influencía no resultado do outro.
Estudamos quê a probabilidade de quê ocorra um evento B, dado quê o evento A já tenha ocorrido, é expressa por P(B | A) = . Assim, a probabilidade de quê ocorram ambos os eventos, indicada por P(A ⋃ B), é dada por:
P(B | A) = ⇒ P(A ⋃ B) = P(A) ⋅ P(B | A)
Quando os eventos A e B são independentes, temos P(B | A) = P(B). Nesse caso, temos:
P(A ⋃ B) = P(A) ⋅ ⇒ P(A ⋃ B) = P(A) ⋅ P(B)
Sejam A e B eventos de um mesmo espaço amostral equiprovável (ômega)", finito e não vazio, com P(A) ≠ 0 e P(B) ≠ 0.
Dizemos quê A e B são eventos independentes se, e somente se, P(B | A) = P(B). Nesse caso, temos:
P(A ⋃ B) = P(A) ⋅ P(B)
Do mesmo modo, dizemos quê A e B são eventos dependentes se, e somente se, P(B | A) ≠ P(B). Nesse caso, temos:
P(A ⋃ B) = P(A) ⋅ P(B | A)
PARA PENSAR
De acôr-do com os conceitos de eventos independentes e dependentes introduzidos, faça uma análise da situação-problema apresentada na página 272.
Resposta nas Orientações para o professor.
Página duzentos e setenta e quatro
ATIVIDADES RESOLVIDAS
R11. Uma moeda honesta é lançada duas vezes consecutivas. Considere os eventos:
• A, obtêr coroa no primeiro lançamento.
• B, obtêr coroa no segundo lançamento.
Mostre quê os eventos A e B são independentes.
Resolução
Em relação a esses lançamentos e representando por C e K o lançamento em quê é obtído cara e o quê é obtído coroa, respectivamente, o espaço amostral dos lançamentos e os eventos A e B são dados por:
• (ômega)" = {CC, CK, KC, KK}
• A = {KK, KC}
• B = {KK, CK}
Dessa maneira, temos A ⋃ B = {KK}.
pôdêmos resolver essa questão de duas maneiras.
1ª maneira:
Calculando as probabilidades de ocorrência de A, B e A ⋃ B, temos:
• P(A) = = 0,5
• P(B) = = 0,5
• P(A ⋃ B) = = 0,25
Portanto, como P(A ⋃ B) = 0,25 = 0,5 ⋅ 0,5 = P(A) ⋅ P(B), concluímos quê os eventos A e B são independentes.
2ª maneira:
Também podemos, nesse caso, calcular a probabilidade de ocorrer o evento B, dado quê já tenha ocorrido o evento A:
P(B | A) = = = = 0,5
Como P(B) = 0,5, temos quê P(B | A) = P(B) e, portanto, os eventos A e B são independentes.
R12. (EsPCEx-SP) Numa sala existem duas caixas com bolas amarelas e verdes. Na caixa 1, há 3 bolas amarelas e 7 bolas verdes. Na caixa 2, há 5 bolas amarelas e 5 bolas verdes. De forma aleatória, uma bola é extraída da caixa 1, sem quê se saiba a sua côr, e é colocada na caixa 2. Após esse procedimento, a probabilidade de extrair uma bola amarela da caixa 2 é igual a
a) .
b) .
c) .
d) .
e) .
Resolução
Inicialmente, vamos considerar quê as bolas se diferenciem apenas pela côr. Como a bola extraída da caixa 1 é inserida na caixa 2, esse resultado influencía no resultado da extração da bola da caixa 2 e, portanto, esses são eventos dependentes.
Vamos analisar as probabilidades de ocorrerem os seguintes eventos:
• A: extrair uma bola amarela na caixa 1 e uma bola amarela na caixa 2;
• B: extrair uma bola vêrde na caixa 1 e uma amarela na caixa 2.
Assim:
P(A) = ⋅ =
P(B) = ⋅ =
A probabilidade de extrair uma bola amarela na caixa 2 é dada pela soma da probabilidade de ocorrência de A e da probabilidade de ocorrência de B:
P(A) + P(B) = + =
Portanto, a alternativa c é a correta.
Página duzentos e setenta e cinco
ATIVIDADES
41. Em cada item, classifique os eventos em dependentes ou independentes.
a) Lançar uma moeda honesta duas vezes consecutivas.
b) Retirar ao acaso uma ficha numerada de uma urna e, em seguida, sem reposição, retirar outra ficha.
c) Sortear uma carta com determinada figura de um baralho com 52 cartas e, em seguida, com reposição, sortear outra carta com mesma figura.
d) Sortear um rapaz de uma turma com rapazes e moças e, em seguida, sortear outro rapaz nessa turma.
eventos dependentes: b, d; eventos independentes: a, c
42. Sejam A e B eventos independentes de um mesmo espaço amostral equiprovável (ômega)", finito e não vazio, tais quê P(A) = 0,2 e P(B) = 0,8. Calcule:
a) P(A ⋃ B)
0,16
b) P(A | B)
0,2
c) P(B | A)
0,8
43. Durante uma gincana, para ganhar pontos extras em cada próva realizada, a equipe vencedora deve girar duas vezes uma roleta, dividida igualmente em cinco partes, conforme indicado a seguir, e somar os pontos obtidos.
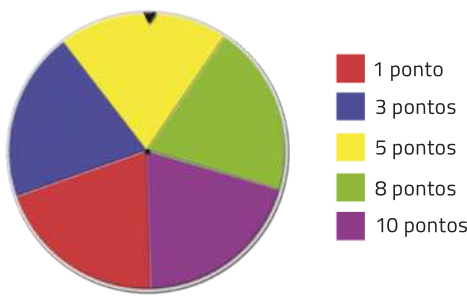
a) Os eventos A e B correspondentes aos valores obtidos ao girar a roleta a primeira e a segunda vez, respectivamente, são dependentes ou independentes?
eventos independentes
b) Qual é a pontuação mínima possível quê uma equipe póde obtêr ao girar a roleta as duas vezes? Qual é a probabilidade de se obtêr essa pontuação?
2 pontos; , 0,04 ou 4%
c) Qual é a probabilidade de uma equipe conseguir mais do quê 15 pontos extras realizando dois giros nessa roleta?
, 0,16 ou 16%
44. Em uma urna, existem 12 bolas quê diferem entre si apenas pela côr. Quatro dessas bolas são amarelas e as demais, vermelhas. Retirando-se aleatoriamente duas bolas dessa urna, uma de cada vez, calcule a probabilidade de:
a) a segunda bola retirada sêr vermelha, sabendo quê houve reposição entre os sorteios;
, aproximadamente 0,667 ou 66,7%
b) serem retiradas duas bolas amarelas, sabendo quê não houve reposição entre os sorteios;
, aproximadamente 0,091 ou 9,1%
c) sêr retirada uma bola amarela, após ter sido retirada uma bola vermelha, sem reposição entre os sorteios.
, aproximadamente 0,364 ou 36,4%
45. Considere quê uma carta foi retirada aleatoriamente de um baralho tradicional de 52 cartas. Em seguida, sem reposição da primeira carta, retirou-se outra carta dêêsse baralho. Calcule a probabilidade de:
a) a primeira carta conter algum número e a segunda conter alguma letra;
, aproximadamente 0,217 ou 21,7%
b) as duas cartas conterem figuras;
, aproximadamente 0,05 ou 5%
c) a primeira carta conter o sín-bolo de cópas e a segunda, o de espadas;
, aproximadamente 0,064 ou 6,4%
d) a primeira carta conter o sín-bolo de ouros.
, 0,25 ou 25%
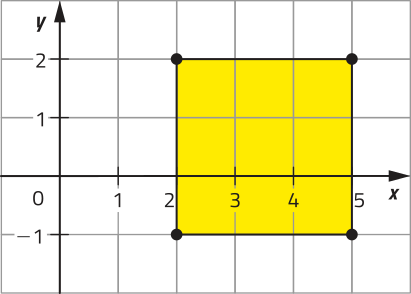
46. Um dado honesto é lançado duas vezes consecutivas, e os valores a e b, obtidos, respectivamente, nesses lançamentos, são considerados para indicar um par ordenado (a + b, a − b). Qual é a probabilidade de, ao lançar esse dado, o par ordenado formado corresponder a um ponto do contôrno do quadrado representado no plano cartesiano?
, aproximadamente 0,139 ou 13,9%
Página duzentos e setenta e seis
47. ![]() dêz-creva uma situação em quê dois eventos:
dêz-creva uma situação em quê dois eventos:
a) A e B são dependentes entre si;
Elaboração do estudante.
b) C e D são independentes entre si.
Elaboração do estudante.
• Agora, para cada situação quê você descreveu, elabore uma situação-problema relacionada ao cálculo da probabilidade de ocorrência de eventos dependentes e de eventos independentes. Troque essas situações-problema com um colega para quê ele as resôuva, enquanto você resólve aquelas quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
48. Ao efetuar um diagnóstico da presença ou não de uma doença em um paciente, um médico póde utilizar testes diagnósticos e obtêr, de acôr-do com a capacidade dêêsse teste em detectar tal doença, conclusões com determinada precisão.
Os possíveis resultados de um teste diagnóstico para detectar certa doença em alguns pacientes podem sêr organizados da maneira apresentada a seguir.
Resultados de um teste diagnóstico em pacientes enfermos e saudáveis
Resultado do teste |
Paciente Enfermo |
Paciente Saudável |
|---|---|---|
Positivo |
VP |
FP |
Negativo |
FN |
VN |
Fontes dos dados: LIBERAL, Tarciana. Modelos de probabilidade e inferência estatística. João Pessoa: UFPB: Departamento de Estatística, 2014. Localizável em: p. 4 do pdf. Disponível em: https://livro.pw/xxbaw.
KAWAMURA, Takao. Interpretação de um teste sôbi a visão epidemiológica: eficiência de um teste. Arquivos Brasileiros de Cardiologia, Rio de Janeiro, v. 79, n. 4, p. 437-441, out. 2002. p. 437. Disponível em: https://livro.pw/wfqiq.
SHIMAKURA, Silvia Emiko. Valor de predição de um teste. Curitiba: hú éfe pê érre: Laboratório de Estatística e Geoinformação, set. 2012. Disponível em: https://livro.pw/mndyd. Acessos em: 30 ago. 2024.

Legenda:
• Verdadeiro positivo (VP): quando o resultado é positivo e o paciente é enfermo (portador da doença).
• Verdadeiro negativo (VN): quando o resultado é negativo e o paciente é saudável (não portador da doença).
• Falso positivo (FP): quando o resultado é positivo, mas o paciente é saudável.
• Falso negativo (FN): quando o resultado é negativo, mas o paciente é enfermo.
Os índices de acêrrrto de um teste diagnóstico em pessoas enfermas ou saudáveis são denominados sensibilidade e especificidade, respectivamente. A sensibilidade corresponde à probabilidade de o teste apresentar resultado positivo para um paciente enfermo. Já a especificidade corresponde à probabilidade de o teste apresentar resultado negativo para paciente saudável.
Ao receber o resultado do teste de um paciente para uma doença, costumam sêr avaliadas as duas kestões a seguir.
I) Qual é a probabilidade de o paciente sêr enfermo dado um resultado positivo?
Essa probabilidade é chamada de valor de predição positiva do teste (VPP) e póde sêr calculada por:
P(paciente enfermo | resultado positivo) =
Página duzentos e setenta e sete
II) Qual é a probabilidade de o paciente sêr saudável dado um resultado negativo?
Essa probabilidade é chamada de valor de predição negativa do teste (VPN) e póde sêr calculada por:
P(paciente saudável | resultado negativo) =
De acôr-do com as informações apresentadas, resôuva as kestões.
a) É possível quê um teste diagnóstico apresente resultado positivo para certa doença, mesmo para um paciente saudável? Justifique.
Resposta esperada: Sim, isso é o quê ocorre no chamado resultado falso positivo (FP).
b) Alguns pacientes de cérto laboratório serão submetidos a um teste cujo objetivo é detectar a presença de determinada doença. Para isso, esse laboratório póde optar por um dos testes indicados a seguir.
• Teste A: sensibilidade de 97% e especificidade de 89%
• Teste B: sensibilidade de 95% e especificidade de 98%
Por qual dos testes esse laboratório deve optar? Justifique.
Pelo teste A, pois êste apresenta a maior probabilidade de resultado positivo para um paciente enfermo.
c) Considere um estudo sobre um teste diagnóstico cujos resultados estão apresentados a seguir.
Resultados do teste diagnóstico realizado com pacientes saudáveis e enfermos
Resultado do teste |
Paciente Enfermo |
Paciente Saudável |
Paciente Total |
|---|---|---|---|
Positivo |
33% |
6% |
39% |
Negativo |
2% |
59% |
61% |
Total |
35% |
65% |
100% |
Fonte: Dados fictícios.
De acôr-do com esse estudo, resôuva as kestões a seguir.
• Qual é a probabilidade de esse teste apresentar um resultado falso positivo? E de apresentar um resultado falso negativo?
6%; 2%
• Qual é a probabilidade de o paciente sêr saudável caso o resultado do teste seja negativo?
aproximadamente 96,7%
• Qual é a probabilidade de o paciente sêr enfermo caso o resultado do teste seja positivo?
aproximadamente 84,6%
• Determine a sensibilidade e a especificidade aproximadas dêêsse teste.
sensibilidade: aproximadamente 94,3%; especificidade: aproximadamente 90,8%
NO MUNDO DO TRABALHO
Médico
O médico é um profissional a serviço da saúde, cujo trabalho envolve prevenir, diagnosticar e tratar doenças. Ele póde atuar em consultórios, pronto atendimentos, serviços de resgate, procedimentos cirúrgicos, realização de pesquisas, entre outros.
No Brasil, o curso de Medicina tem duração mínima de 6 anos. Depois de se formár, esse profissional póde se especializar em uma área, entre muitas opções, como cardiologia, geriatria, neurologia, cirurgia geral, ginecologia, ortopedia, pediatria, psiquiatria e urologia.
Assista ao vídeo indicado a seguir para obtêr mais informações sobre o curso de Medicina, o mercado de trabalho e as áreas de atuação de um médico no Brasil.
• GUIA de profissões: medicina. [S. l.: s. n.], 2016. 1 vídeo (12 min). Publicado pelo canal Tevê Unésp. Disponível em: https://livro.pw/gwfqd. Acesso em: 30 ago. 2024.
Página duzentos e setenta e oito
Probabilidade em experimentos binomiais
Considere o jôgo descrito a seguir.
Em um jôgo, um dado comum e honesto é lançado cinco vezes consecutivas. Antes do lançamento, o participante deve indicar a quantidade de vezes em quê serão obtidos mais de 4 pontos na face superior do dado. Para vencer esse jôgo, será necessário acertar a indicação feita.

De acôr-do com as regras dêêsse jôgo, para cada lançamento, temos o espaço amostral (ômega)" = {1, 2, 3, 4, 5, 6}. O evento correspondente a obtêr mais de 4 pontos nesse lançamento é dado por A = {5, 6}. Além díssu, o evento complementar de A, quê corresponde a obtêr 4 ou menos pontos nesse lançamento, é dado por = {1, 2, 3, 4}. Assim, temos:
• P(A) = = =
• P(A) = = =
DICA
Também podemos determinar P(A) da seguinte maneira:
P() = 1 − P(A) = 1 − =
Agora, vamos analisar a probabilidade quê um participante tem de vencer o jôgo, indicando quê em 2 dos 5 lançamentos serão obtidos mais de 4 pontos na face superior do dado.
Nesse caso, estamos interessados em determinar a probabilidade de quê o evento A ocorra em 2 lançamentos e o evento , em 3 lançamentos. Por exemplo, como A e são eventos independentes, a probabilidade de quê A ocorra nos 2 primeiros lançamentos e , nos 3 lançamentos seguintes, é dada por:
P(A ⋃ A ⋃ ⋃ ⋃ ) = P(A) ⋅ P(A) ⋅ P() ⋅ P() ⋅ P() =
= [P(A)]2 ⋅ [P()]3 = ()2 ⋅ ()3 = ⋅ =
Como essa é apenas uma das possíveis maneiras de se obtêr os eventos A e em 2 e 3 lançamentos, respectivamente, podemos multiplicar esse resultado pela quantidade de combinações de 5 lançamentos, tomados 2 a 2.
P = C5, 2 ⋅ = ⋅ = 10 ⋅ =
Portanto, a probabilidade de esse participante vencer o jôgo é de , aproximadamente 0,329 ou 32,9%.
Essa situação ilustra um caso especial de probabilidade, conhecido como probabilidade binomial. Nele, ao considerarmos cérto evento A, avaliamos duas possibilidades de resultado: A ocorrer (sucesso) e A não ocorrer (fracasso). Acompanhe, a seguir, a definição de probabilidade binomial.
PARA PENSAR
Calcule a probabilidade de quê, no jôgo descrito, um participante vença tendo indicado quê em 3 dos 5 lançamentos serão obtidos mais de 4 pontos na face superior do dado.
ou aproximadamente 16,5%
Página duzentos e setenta e nove
Seja A um evento de um espaço amostral equiprovável (ômega)", finito e não vazio, de um experimento aleatório. A probabilidade de quê A ocorra em p de n realizações dêêsse experimento, sêndo p e n números naturais com p ≤ n, é dada por:
ATIVIDADES RESOLVIDAS
R13. (Unicamp-SP) Um atleta participa de um torneio compôzto por três provas. Em cada próva, a probabilidade de ele ganhar é de , independentemente do resultado das outras provas. Para vencer o torneio, é preciso ganhar pelo menos duas provas. A probabilidade de o atleta vencer o torneio é igual a
a) .
b) .
c) .
d) .
Resolução
Uma vez quê para vencer o torneio o atleta precisa ganhar pelo menos duas provas, temos de calcular a probabilidade de ele ganhar duas ou três provas. Além díssu, se a probabilidade de o atleta ganhar cada próva é , então a probabilidade de não ganhar é . Assim, de acôr-do com o princípio aditivo da contagem, temos:
 = 3 ⋅ ⋅ + 1 ⋅ ⋅ 1 = + =
= 3 ⋅ ⋅ + 1 ⋅ ⋅ 1 = + =
Portanto, a alternativa c é a correta.
R14. A Olimpíada Brasileira de Física das Escolas Públicas (OBFEP) é uma competição para estudantes do Ensino Médio e do último ano do Ensino Fundamental de escolas públicas. A OBFEP ocorre em duas fases e, em cada uma delas, os estudantes são organizados em três níveis. Por exemplo, na 1ª fase, a próva do Nível C destina-se exclusivamente aos estudantes da 3ª série do Ensino Médio. Essa próva é composta de 15 kestões objetivas, e cada questão contém quatro alternativas, das quais apenas uma é correta.
Fonte dos dados: SOCIEDADE BRASILEIRA DE FÍSICA. Olimpíada Brasileira de Física das Escolas Públicas: sobre. [São Paulo]: SBF: Obfep, c2024. Disponível em: https://livro.pw/utyum. Acesso em: 30 ago. 2024.
Calcule a probabilidade de um estudante da 3ª série do Ensino Médio, ao escolher aleatoriamente todas as respostas da próva do Nível C da OBFEP, acertar exatamente 9 kestões.
Resolução
Considerando o evento A escolher a alternativa correta em uma quêstão, temos que corresponde ao evento escolher a alternativa incorréta em uma questão. Assim, temos:
• P(A) =
• P() = 1 − P(A) = 1 − =
Assim, com auxílio de uma calculadora, determinamos a probabilidade de o evento A ocorrer exatamente 9 vezes (p) em 15 tentativas (n).
P = Cn, p ⋅ [P(A)]p ⋅ [P()]n − p =
= C15, 9 ⋅ ()9 ⋅ ()15 − 9 =
= 5.005 ⋅ ()9 ⋅ ()6 ≃ 0,0034 = 0,34%
Portanto, essa probabilidade é de aproximadamente 0,0034 ou 0,34%.
Página duzentos e oitenta
ATIVIDADES
DICA
Nas atividades desta e da próxima página, utilize a calculadora quando necessário.
49. A partir de uma pesquisa realizada por certa loja virtual, observou-se quê a probabilidade de um cliente optar por um tipo de frete mais barato na realização de uma compra, mesmo com prazo de entrega maior, é de . Considerando um dia em quê 15 clientes realizam compras nessa loja, calcule a probabilidade de quê:
a) exatamente 8 deles prefiram pagar mais barato pelo frete;
aproximadamente 0,177 ou 17,7%
b) ao menos 12 deles prefiram pagar mais barato pelo frete;
aproximadamente 0,09 ou 9%
c) todos eles prefiram pagar mais barato pelo frete.
aproximadamente 0,00047 ou 0,047%
50. Em uma linha de produção de certa fábrica, a probabilidade de se obtêr uma peça com defeito é de 30%. Ao vistoriar uma amostra de 50 peças, qual é a probabilidade de se obtêr mêtáde delas com defeito?
aproximadamente 0,00144 ou 0,144%
51. Em cérto bairro, 80% dos moradores são favoráveis a um projeto propôsto pela associação de moradores. Ao sortear aleatoriamente 10 moradores dêêsse bairro, a probabilidade de quê mais de 7 deles sêjam favoráveis a esse projeto é:
a) menor quê 60%.
b) igual a 57%.
c) maior quê 65%.
d) igual a 37,5%.
alternativa c
52. Considere uma moeda não honesta cuja probabilidade de obtêr coroa na face voltada para cima em um lançamento é igual a . Se essa moeda for lançada 7 vezes consecutivas, qual é a probabilidade de se obtêr nesses lançamentos:
a) exatamente 5 coroas?
aproximadamente 0,22 ou 22%
b) 2 coroas, no mássimo?
aproximadamente 0,146 ou 14,6%
53. Uma pesquisa realizada, em 2021, pelo Banco Central do Brasil entrevistou parte da população brasileira sobre o uso do dinheiro e outros meios de pagamento. Observe algumas informações obtidas nessa pesquisa:
• 31% dos entrevistados utilizam cartão de crédito em compras acima de R$ 500,00;
• 47% dos entrevistados utilizam moedas em pequenas compras e para facilitar o Trôco.
Fonte dos dados: BRASIL. Banco Central do Brasil. O brasileiro e sua relação com o dinheiro: pesquisa 2021. Brasília, DF: BCB, 2021. Localizável em: p. 13, 19 do pdf. Disponível em: https://livro.pw/yrleh. Acesso em: 31 ago. 2024.
Suponha quê sêjam selecionados aleatoriamente 8 entrevistados quê participaram dessa pesquisa. Nessas condições, determine a probabilidade de quê:
a) 3 dêêsses entrevistados não utilizem cartão de crédito em compras acima de R$ 500,00;
aproximadamente 0,053 ou 5,3%
b) todos esses entrevistados utilizem moedas em pequenas compras e para facilitar o Trôco.
aproximadamente 0,0024 ou 0,24%
• ![]() Leia o trecho de texto a seguir.
Leia o trecho de texto a seguir.
Todos os dias, uma enorme quantidade de moedas sai de circulação porque as pessoas acham quê elas não têm valor e acabam guardando ou esquecendo em bolsos e gavetas. Isso causa muitos problemas. Um deles você conhece de perto: a falta de Trôco.
[...] Cada moeda quê você deixa de usar vira um prejuízo para a economia do Brasil e para você, quê acaba desperdiçando seu dinheiro.
BRASIL. Banco Central do Brasil. Cuide bem do seu dinheiro: ele vale ouro! Brasília, DF: BCB, [2024]. Localizável em: p. 2 do pdf. Disponível em: https://livro.pw/uxzep. Acesso em: 31 ago. 2024.
Junte-se a quatro côlégas para realizar uma pesquisa. Inicialmente, definam uma amostra a sêr pesquisada, como uma turma da escola ou moradores de uma rua do bairro onde moram. Nessa pesquisa, determinem o porcentual dos entrevistados quê utilizam moedas em suas compras no dia a dia, evitando deixá-las esquecidas em gavetas, bolsos, cofrinhos etc. Por fim, elaborem um cartaz de incentivo à circulação das moedas no comércio, indicando os dados coletados na pesquisa e informações sobre esse assunto disponíveis no sáiti do Banco Central do Brasil.
Pesquisa e elaboração dos estudantes.
Página duzentos e oitenta e um
54. (Fuvest-SP) Uma seta aponta para a posição zero no instante inicial. A cada rodada, ela poderá ficar no mesmo lugar ou mover-se uma unidade para a direita ou mover-se uma unidade para a esquerda, cada uma dessas três possibilidades com igual probabilidade.
Qual é a probabilidade de quê, após 5 rodadas, a seta volte à posição inicial?
a)
b)
c)
d)
e)
alternativa b
55. Leia o trecho de texto a seguir.
O diabetes mellitus (DM) compreende um grupo de distúrbios metabólicos quê se caracteriza por hiperglicemia causada por defeito na ação e/ou secreção da insulina, quê leva a alterações no metabolismo de carboidratos, lipídios e proteínas, determinando, ao longo do tempo, o comprometimento da função e estrutura vascular de diferentes órgãos.
[...]
O diagnóstico de diabetes mellitus geralmente ocorre após os 40 anos de idade, sêndo comum sua associação com excésso de peso e história familiar de DM. Estima-se quê a população mundial com diabetes totalize 382 milhões de pessoas e quê no ano de 2035 serão 471 milhões, o quê póde sêr considerado uma epidemia […].
[...]
A maioria das pessoas com diabetes permanéce assintomática durante anos. Apenas 30% dessas apresentam sintomas clássicos da doença.
PARANÁ. Secretaria de Estado da Saúde do Paraná. Superintendência de Atenção à Saúde. Linha guia de diabetes mellitus. 2. ed. Curitiba: Sesa, 2018. p. 12, 16. Disponível em: https://livro.pw/tuaic. Acesso em: 30 ago. 2024.
PARA AMPLIAR
Acesse o sáiti a seguir para obtêr mais informações sobre o diabetes melito.
• BRASIL. Ministério da Saúde. Diabetes (diabetes mellitus). Brasília, DF: MS, [2024]. Disponível em: https://livro.pw/jthlc. Acesso em: 30 ago. 2024.

a) ![]() Você conhece alguma pessoa quê tenha sido diagnosticada com diabetes melito? Comente.
Você conhece alguma pessoa quê tenha sido diagnosticada com diabetes melito? Comente.
Resposta pessoal.
b) De acôr-do com o texto, considere quê seja de 30% a probabilidade de uma pessoa com diabetes melito apresentar sintomas clássicos da doença.
• Qual é a probabilidade de uma pessoa com diabetes melito não apresentar sintomas clássicos dessa doença?
0,7, ou 70%
• Considere quê, em uma pesquisa, foram identificadas cinco pessoas com diabetes melito. Qual é a probabilidade de ao menos três dessas pessoas não apresentarem sintomas clássicos dessa doença?
aproximadamente 0,837 ou 83,7%
c) Realize uma pesquisa sobre como é possível diminuir os riscos de desenvolver diabetes melito, com cuidados com a alimentação e a prática de atividades físicas. Pesquise também a importânssia de diagnosticar o diabetes melito logo no início de seu desenvolvimento.
Registre as informações obtidas.
Pesquisa do estudante.
56. ![]() Com base nas informações apresentadas na atividade 55, elabore uma situação-problema relacionada ao cálculo de probabilidade em experimentos binomiais. Troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Com base nas informações apresentadas na atividade 55, elabore uma situação-problema relacionada ao cálculo de probabilidade em experimentos binomiais. Troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e oitenta e dois
Probabilidade e estatística
Estudamos quê a probabilidade de ocorrência de um evento A de um espaço amostral equiprovável (ômega)", finito e não vazio, póde sêr calculada pela razão entre a quantidade de elemêntos de A e de (ômega)". No entanto, nem sempre é possível determinar a probabilidade de ocorrência de um evento dessa maneira. Nesses casos, a probabilidade de ocorrer um evento póde sêr estimada com base na freqüência relativa de sua ocorrência em várias repetições de um experimento ou em registros históricos.
Por exemplo, em um planejamento familiar, ao escolher um método contraceptivo, é importante analisar alguns fatores como a taxa de eficácia dos métodos existentes, quê implica a probabilidade de evitar uma gravidez. Um dos métodos contraceptivos mais utilizados atualmente são os Anticoncepcionais Orais Combinados (AOCs).
[...]
• São pílulas quê contêm baixas doses de dois hormônios – um progestógeno e um estrógeno – similares aos hormônios naturais progesterona e estrógeno existentes no corpo da mulher. Os anticoncepcionais orais combinados (AOCs) também são chamados simplesmente de “a Pílula”[...].
• Funcionam basicamente impedindo a liberação de óvulos pêlos ovários (ovulação).
[...]
ORGANIZAÇÃO MUNDIAL DA SAÚDE; UNIVERSIDADE JOHNS HOPKINS. Planejamento familiar: um manual global para profissionais e serviços de saúde. Tradução: Lula Ramires. Baltimór: CPC; Genebra: hó ême ésse, 2007. p. 1. Disponível em: https://livro.pw/axiap. Acesso em: 31 ago. 2024.

De acôr-do com a Organização Mundial da Saúde, os AOCs correspondem a um método contraceptivo de alta eficácia, uma vez quê, se ingeridos corretamente e de modo consistente, em média 997 de 1.000 mulheres não engravidam no primeiro ano de uso. Nessas condições, podemos estimar quê a probabilidade de uma mulher quê usa esse método contraceptivo não engravidar é de , 0,997 ou 99,7%.
Página duzentos e oitenta e três
ATIVIDADE RESOLVIDA
R15. Entre outros fatores controláveis, o sucesso de uma safra depende do uso de sementes de alta qualidade quê apresentam, por exemplo, alto nível de germinação.
Para realizar um teste de germinação de cérto tipo de semente, foi selecionada uma amostra com 260 sementes, de maneira quê representassem todas as sementes do mesmo tipo. As sementes selecionadas foram plantadas sôbi determinadas condições adequadas e apenas 4 delas não germinaram. Observe, na tabéla, o tempo de germinação das outras sementes.
Sementes de cérto tipo germinadas de acôr-do com o tempo
Tempo (dia) |
Quantidade de sementes germinadas |
|---|---|
4 |
20 |
5 |
85 |
6 |
97 |
7 |
42 |
8 |
12 |
Total |
256 |
Fonte: Dados fictícios.
Considerando as sementes quê efetivamente germinaram, resôuva as kestões.
a) Construa um gráfico de colunas para representar a probabilidade estimada de germinação dessas sementes em relação ao tempo.
b) Na embalagem utilizada para comercializar essas sementes, é indicado um tempo médio de germinação de 6 dias. Determine a probabilidade de se plantar uma semente dêêsse tipo e ela germinar após 6 dias.
Resolução
a) Inicialmente, considerando as 256 sementes quê germinaram, calculamos a probabilidade estimada de cada uma delas germinar em relação ao tempo, conforme a tabéla a seguir.
Probabilidade estimada de germinação das sementes de cérto tipo em relação ao tempo
Tempo (dia) |
Quantidade de sementes germinadas |
Probabilidade |
|---|---|---|
4 |
20 |
≃ 8% |
5 |
85 |
≃ 33% |
6 |
97 |
≃ 38% |
7 |
42 |
≃ 16% |
8 |
12 |
≃ 5% |
Fonte: Dados fictícios.
Em seguida, utilizando os valores obtidos, construímos o gráfico de colunas.
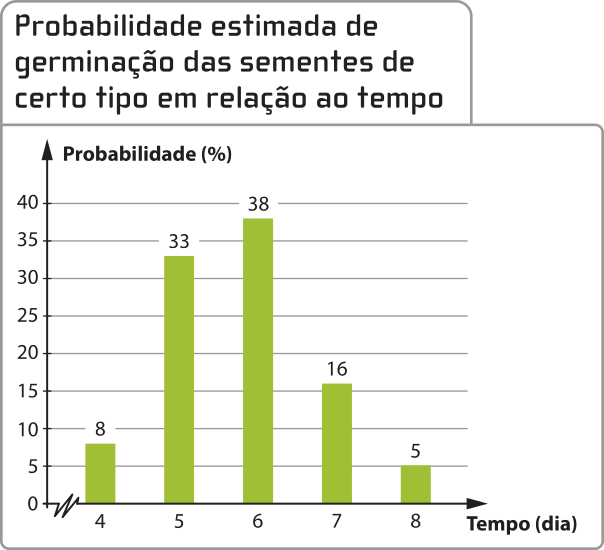
Fonte: Dados fictícios.
b) Considerando os cálculos do item a, a probabilidade do evento A de a semente germinar após 6 dias é dada pela soma das probabilidades de ela germinar em 7 e em 8 dias:
P(A) ≃ 16% + 5% = 21%
Portanto, a probabilidade estimada de se plantar uma semente dessas e ela germinar após 6 dias é de aproximadamente 21%.
Página duzentos e oitenta e quatro
ATIVIDADES
57. (Fuvest-SP) Carros quê saem da cidade A rumo a alguma das cidades turísticas E, F e G fazem caminhos diversos, passando por pelo menos uma das cidades B, C e D, apenas no sentido indicado pelas setas, como mostra a figura. Os números indicados nas setas são as probabilidades, dentre esses carros, de se ir de uma cidade a outra.
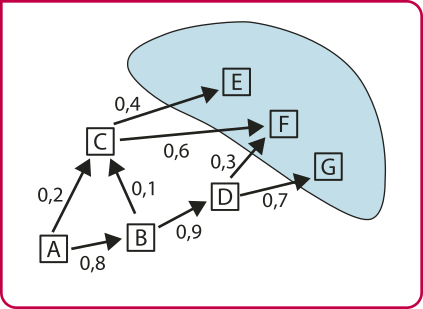
Nesse cenário, a probabilidade de um carro ir de A a F é
a) 0,120.
b) 0,216.
c) 0,264.
d) 0,336.
e) 0,384.
alternativa e
58. Após disputar algumas partidas, cérto tíme de basquete constatou quê os índices de aproveitamento em arremessos de seus jogadores A, B e C foram de 85%, 78% e 94%, respectivamente. Além díssu, os jogadores A e C realizaram, cada um, 21% do total de arremessos a favor do tíme, e o jogador B realizou 36% dos arremessos.
Considerando apenas as informações apresentadas, resôuva as kestões a seguir.
a) Qual dêêsses três jogadores tem maior probabilidade de acertar o primeiro arremesso do tíme na próxima partida?
jogador B
b) Na próxima partida, qual é a probabilidade de o primeiro arremesso sêr realizado pelo jogador C e ele errar esse arremesso?
1,26%
59. Para definir o medicamento a sêr ingerido por um paciente durante um tratamento, um médico apresentou a ele duas opções, conforme seguem.
• Medicamento A: ingerir 2 comprimidos por semana.
• Medicamento B: ingerir 1 comprimido a cada 48 horas.
Além díssu, explicou ao paciente quê ambos os medicamentos podem causar náuseas ou dores de cabeça, sêndo a probabilidade de quê isso ocorra de 7% para o medicamento A e de 4% para o medicamento B. Após analisar as duas opções disponíveis, por qual medicamento você acredita quê esse paciente deve optar caso prefira aquele com menor probabilidade de ocorrência de náuseas ou dores de cabeça na primeira semana do tratamento?
medicamento A
60. (Vunesp-SP) A tabéla indica o chaveamento de 8 times quê chegaram às quartas de final de um torneio de futeból. Nos jogos de quartas de final, as porcentagens ao lado de cada tíme indicam sua probabilidade de seguir adiante no torneio. Nos jogos da semifinal, as probabilidades de cada tíme dos grupos E e F são iguais a 50%.
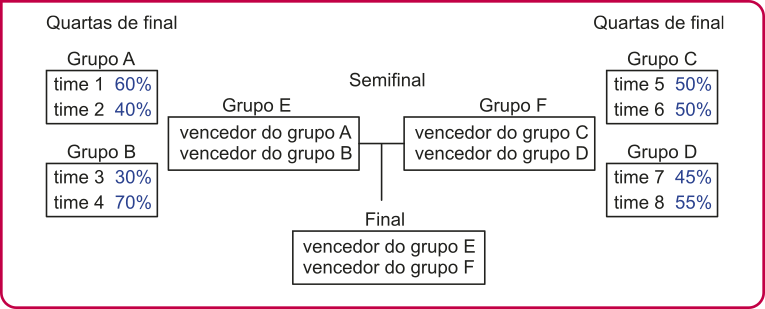
Qual é a probabilidade de o tíme 1 disputar a final dêêsse torneio contra os times 5 ou 7?
a) 16,25%
b) 14,25%
c) 15,75%
d) 15,50%
e) 12,50%
alternativa b
Página duzentos e oitenta e cinco
61. Estudamos anteriormente quê um dos fatores a sêr analisado na escolha de um método contraceptivo é a taxa de eficácia dos métodos existentes. A seguir, são apresentadas informações sobre a eficácia de alguns métodos contraceptivos, considerando seu uso correto e de modo consistente.
Eficácia de alguns métodos contraceptivos
Método |
Descrição resumida |
Quantidade de gravidezes no primeiro ano de uso |
|---|---|---|
Anticoncepcionais orais combinados |
Pílulas com baixas doses de progestógeno e estrógeno. |
3 por 1.000 mulheres |
Pílulas só de progestógeno* |
Pílulas com doses muito baixas de progestógeno. |
3 por 1.000 mulheres (que estejam amamentando) 9 por 1.000 mulheres (que não estejam amamentando) |
Injetáveis só de progestógeno |
Injetáveis com doses de progestógeno. |
3 por 1.000 mulheres |
Injetáveis mensais |
Injetáveis mensais com doses de progestógeno e estrógeno. |
5 por 10.000 mulheres |
Implantes |
Cápsulas ou hastes plásticas quê libéram progestógeno. |
5 por 10.000 mulheres |
Dispositivo Intrauterino (DIU) com cobre |
Dispositivo intrauterino com cobre quê provoca danos ao êspérma e ao óvulo antes de se encontrarem. |
6 a 8 por 1.000 mulheres |
Esterilização feminina |
Contracepção permanente para mulheres. |
5 por 1.000 mulheres |
Fonte dos dados: ORGANIZAÇÃO MUNDIAL DA SAÚDE; UNIVERSIDADE JOHNS HOPKINS. Planejamento familiar: um manual global para profissionais e serviços de saúde. Tradução: Lula Ramires. Baltimór: CPC; Genebra: hó ême ésse, 2007. p. 1-2, 25-26, 59-60, 81-82, 109-110, 131, 165. Disponível em: https://livro.pw/axiap. Acesso em: 31 ago. 2024.
* Por não conter estrógeno e apresentar baixa dosagem de progestógeno, podem sêr usadas por mulheres em período de amamentação.
a) Para cada método contraceptivo apresentado, calcule a probabilidade estimada de quê uma mulher engravide no primeiro ano de uso. Expresse as respostas em porcentual.
anticoncepcionais orais combinados: 0,3%; pílulas só de progestógeno: 0,3% (caso esteja amamentando) e 0,9% (caso não esteja amamentando); injetáveis só de progestógeno: 0,3%; injetáveis mensais: 0,05%; implantes: 0,05%; DIU com cobre: 0,6% a 0,8%; esterilização feminina: 0,5%
b) Qual dos métodos contraceptivos apresentados é o mais eficaz para se evitar uma gravidez no primeiro ano de uso, considerando uma mulher quê não esteja amamentando? Justifique.
Injetáveis mensais e implantes, pois são os métodos com os quais a mulher tem a menor probabilidade de engravidar.
c) Por quais dêêsses métodos pode-se optar para quê a probabilidade de gravidez de uma mulher, durante o primeiro ano de uso e sem estar amamentando, seja menor ou igual a 0,4%?
anticoncepcionais orais combinados, injetáveis só de progestógeno, injetáveis mensais ou implantes
D) A saúde reprodutiva é um direito das mulheres e envolve o bem-estar físico, mental e social relacionado ao sistema reprodutivo. Faça uma pesquisa e elabore um texto sobre esse tema, enfatizando a importânssia do combate à violência contra a mulher.
Resposta pessoal. Os estudantes podem acessar os sáites indicados no boxe Para ampliar para realizar essa pesquisa.
PARA AMPLIAR
Acesse estes conteúdos para saber mais sobre o combate à violência contra as mulheres e sobre seus direitos sexuais e reprodutivos.
• BRASIL. Serviços e Informações do Brasil. Saúde reprodutiva da mulher. Brasília, DF: Gov.br, c2025. Disponível em: https://livro.pw/cjujb. Acesso em: 3 maio 2025.
• BRASIL. Defensoria Pública do Distrito Federal. Escola de Assistência Jurídica. Direitos sexuais e direitos reprodutivos das mulheres. Brasília, DF: TJDFT, 2021. Disponível em: https://livro.pw/bkraw. Acesso em: 3 maio 2025.
Página duzentos e oitenta e seis
d) ![]() Observe no esquema, de maneira simplificada, como os AOCs agem no organismo da mulher. Observação: Os órgãos representados não estão na mesma escala.
Observe no esquema, de maneira simplificada, como os AOCs agem no organismo da mulher. Observação: Os órgãos representados não estão na mesma escala.
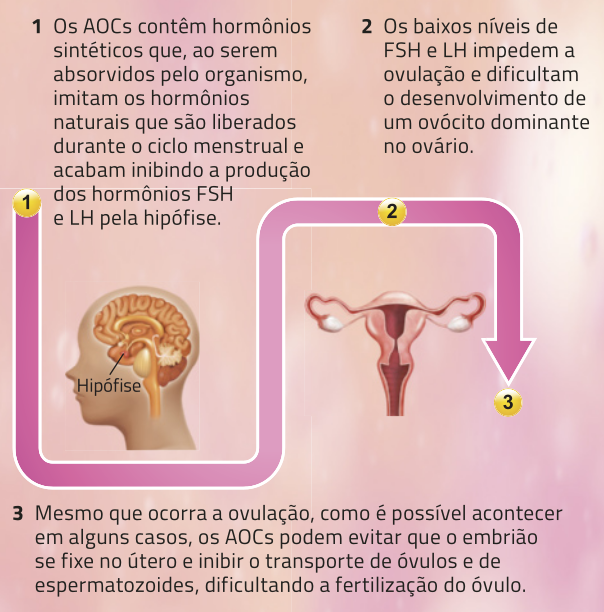
Agora, junte-se a dois côlégas e, em grupo, escôlham um dos métodos contraceptivos apresentados e realizem uma pesquisa sobre ele, detalhando funcionamento, eficácia, efeitos colaterais, benefícios e riscos à saúde. Com as informações pesquisadas, elaborem um relatório.
Pesquisa e elaboração dos estudantes.
62. Para auxiliar nas análises de riscos, uma seguradora coletou informações sobre os motociclistas de um município e verificou em quantos acidentes de trânsito se envolveram em cérto ano. Acompanhe.
Motociclistas do município quê se envolveram ou não em algum acidente de trânsito em cérto ano
Faixa etária |
Quantidade de acidentes: Nenhum |
Quantidade de acidentes: Apenas 1 |
Quantidade de acidentes: 2 ou mais |
|---|---|---|---|
Até 20 anos |
411 |
412 |
16 |
21 a 25 anos |
200 |
336 |
10 |
26 a 30 anos |
366 |
375 |
5 |
31 a 35 anos |
271 |
97 |
3 |
36 a 40 anos |
300 |
83 |
3 |
41 a 45 anos |
139 |
34 |
0 |
Mais de 45 anos |
113 |
24 |
2 |
Fonte: Dados fictícios.
Considerando quê esses motociclistas representam o comportamento ou o perfil dos motociclistas nesse município, resôuva os itens a seguir.
a) Qual é a probabilidade de um motociclista não se envolver em nenhum acidente de trânsito nesse município?
56,25%
b) Construa um gráfico para representar a probabilidade estimada de um motociclista dêêsse município se envolver em algum acidente, no ano, de acôr-do com cada faixa etária.
Resposta nas Orientações para o professor.
c) Qual é a probabilidade de um motociclista dêêsse município, na faixa etária de 21 a 30 anos, envolver-se em algum acidente?
aproximadamente 56%
63. ![]() Um instituto de pesquisas agrícolas desenvolvê-u um estudo acerca da eficiência de germinação de variedades de sementes de cérto vegetal. Analise o resultado dessa pesquisa apresentado no gráfico a seguir.
Um instituto de pesquisas agrícolas desenvolvê-u um estudo acerca da eficiência de germinação de variedades de sementes de cérto vegetal. Analise o resultado dessa pesquisa apresentado no gráfico a seguir.
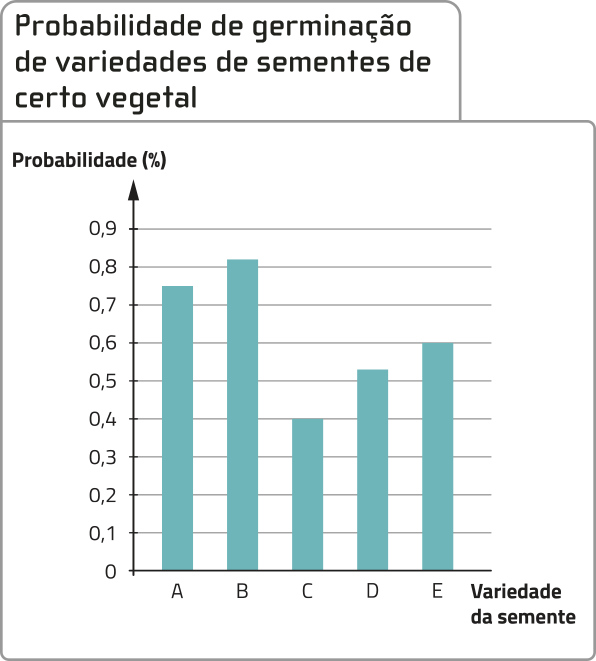
Fonte: Dados fictícios.
Com a temática apresentada, elabore uma situação-problema envolvendo o cálculo da probabilidade estimada. Troque essa situação-problema com um colega para quê ele a resôuva, enquanto você resólve aquela quê ele elaborou. Ao final, confiram juntos as resoluções.
Elaboração do estudante.
Página duzentos e oitenta e sete
INTEGRANDO COM...
CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
Genética
Você sabe o quê é herança genética? Leia o trecho de texto a seguir.
Dentro das células, as estruturas denominadas cromossomos contêm material genético na forma de dê ene há (ácido desoxirribonucleico). [...]
Cada vez quê uma célula se divide, o dê ene há é primeiramente replicado, ou copiado, e cada uma das duas células-filhas herda um conjunto completo de cromossomos idênticos ao originalmente presente na célula-mãe. Cada cromossomo contém uma longa molécula de dê ene há com centenas ou milhares de genes, cada um representando um setor do dê ene há do cromossomo. Os genes são a unidade de herança transferida dos pais para os filhos. Eles codificam a informação necessária para formár todas as moléculas sintetizadas dentro de uma célula e, assim, estabelecem a identidade e função celular. Cada um de nós se originou a partir de uma única célula portando dê ene há herdado dos nóssos pais. A replicação dêêsse dê ene há durante cada rodada da divisão celular transmitiu cópias do dê ene há até o quê, por fim, se tornou os trilhões de células quê compõem o nosso corpo. Juntamente com o crescimento e divisão celular, a informação genética codificada pelo dê ene há direcionou o nosso desenvolvimento [...].
REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 5.

Página duzentos e oitenta e oito
Há muito tempo o sêr humano estuda a existência de características quê apresentam variações entre sêres de uma mesma espécie, chegando à conclusão de quê algumas dessas características passam de geração para geração. O monge Gregor Mendel (1822-1884) foi um dos precursores em pesquisas na área de hereditariedade. Por meio de experimentos, ele formulou leis quê, atualmente, levam seu nome e fundamentaram o ramo da Biologia chamado de Genética.
Acompanhe, no esquema a seguir, a representação de um dos experimentos desenvolvidos por Mendel envolvendo o estudo de variações presentes entre plantas de uma espécie de ervilha.

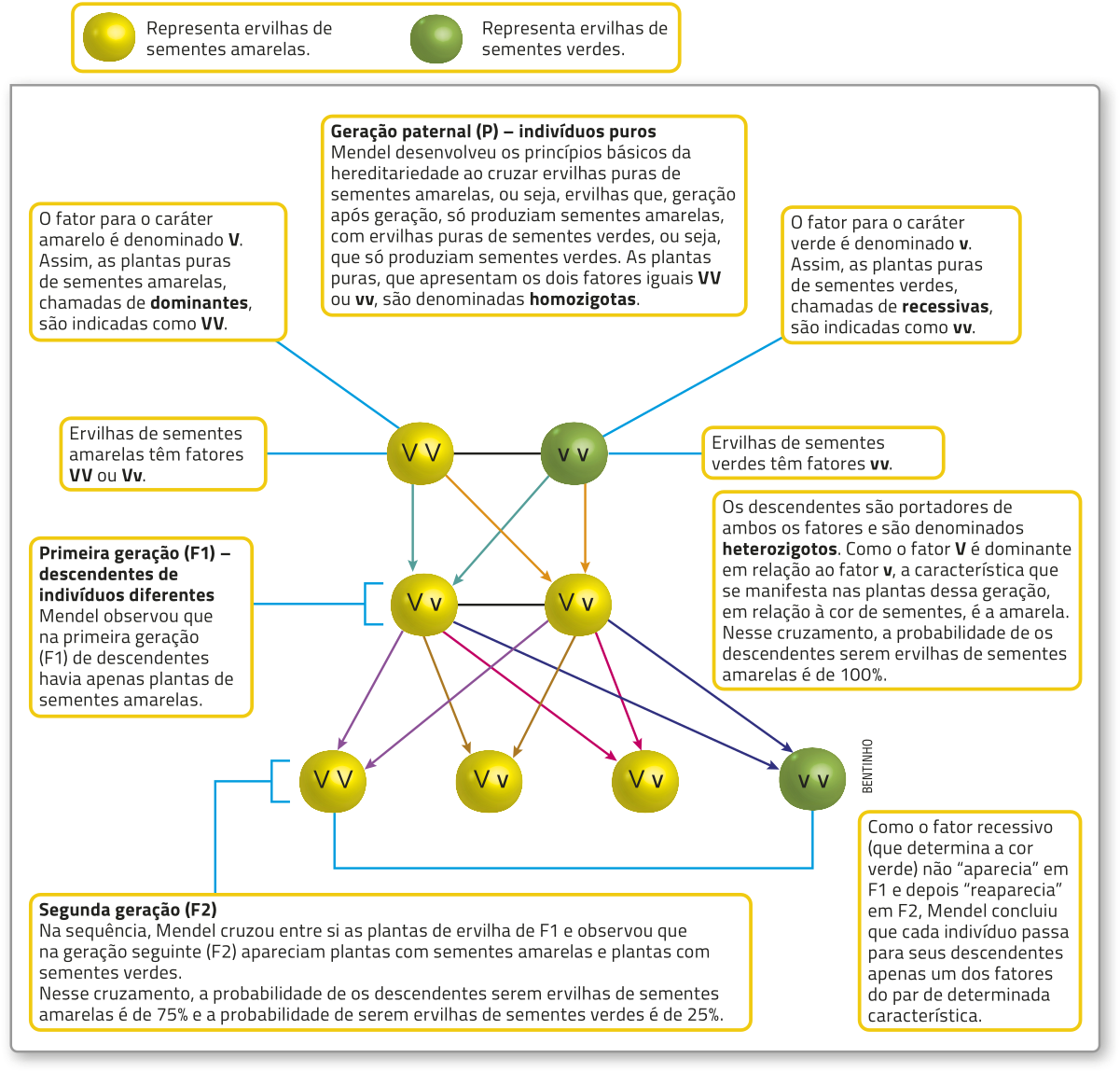
Fontes dos dados: FRIDMAN, Cíntia. Evolução das Ciências II: tópico 1: as 1 ª e 2ª leis de Mendel e conceitos básicos de citogenética. São Paulo: Cepa: Ifusp, [202-]. p. 3, 14. Disponível em: https://livro.pw/bspyc. Acesso em: 4 jul. 2024. REECE, diêine B. éti áu. Biologia de Campbell. 10. ed. Porto Alegre: Artméd, 2015. p. 267-274.
Página duzentos e oitenta e nove
A ética e a genética
Desde o surgimento das teorias da genética desenvolvidas por Mendel até a descoberta da estrutura da molécula de dê ene há e o sequenciamento de genomas, a Genética motivou sucessivos questionamentos. Ainda mais se considerar quê, nos últimos anos, a possibilidade de manipulação genética de sêres vivos se tornou tecnicamente real, o quê gerou reflekções sobre os valores importantes para a ssossiedade.
Leia o trecho de texto a seguir sobre o caso dos primeiros bebês chineses geneticamente modificados do mundo, quê gerou uma série de críticas e debates sobre ética profissional na comunidade científica.
Anunciado em novembro de 2018, durante o Congresso Mundial de Edição Genética, em rôn kôn, o experimento do cientista chinês He Jiankui, quê revelou ter editado embriões saudáveis com a técnica de CRISPR-cas9, uma ferramenta genética quê corta a sequência do dê ene há e o reconfigura para obtêr uma modificação – no caso, tornando-o imune ao vírus agá hí vê – causou apreensão e gerou uma série de debates entre seus pares e nas sociedades científicas mundiais.
[...]
Ainda quê a experiência narrada por Jiankui seja questionada, o cerne da discussão gira em torno dos limites entre as possíveis aplicações da técnica para o contrôle e prevenção de doenças, o quê de fato se busca, e a possibilidade de edições genéticas futuras em quê embriões humanos possam sêr editados geneticamente apenas para alterar características físicas.
O temor justifica-se não apenas pêlos problemas decorrentes de mudanças no genoma de futuras gerações, mas também pelo quê poderia sêr caracterizado como eugenia, prática considerada eticamente inaceitável por cientistas e instituições de pesquisa.
BRASIL. Instituto de Pesquisa Econômica Aplicada. Centro de Pesquisa em Ciência, Tecnologia e Sociedade. Experimento chinês confronta limites entre ética e ciência. [Rio de Janeiro]: Ipea: CTS, 2 set. 2021. Disponível em: https://livro.pw/xqdec. Acesso em: 31 ago. 2024.
PENSANDO NO ASSUNTO
1. Cite exemplos de aplicações da pesquisa genética. Se necessário, realize uma pesquisa.
Algumas respostas possíveis: Na pesquisa genética, pode-se investigar se uma pessoa é mais ou é menos propensa a desenvolver uma doença e, se for o caso, pôdêr preveni-la; avaliar as reações do organismo de uma pessoa a um tratamento ou a um medicamento; entre outras aplicações.
2. ![]() Em seu entendimento, é correto realizar edições genéticas em humanos? Para justificar sua resposta, realize argumentações consistentes.
Em seu entendimento, é correto realizar edições genéticas em humanos? Para justificar sua resposta, realize argumentações consistentes.
Resposta pessoal.
3. De acôr-do com as informações apresentadas, o quê são organismos heterozigotos?
São organismos quê apresentam ambos os fatores, dominante e recessivo.
4. Represente por meio de lêtras as possibilidades de um organismo homozigoto.
Resposta esperada: VV ou vv.
5. Na página 288, há um esquema representando um experimento realizado por Mendel a partir do cruzamento de duas ervilhas. Considerando esse cruzamento, resôuva as kestões a seguir.
a) Qual é a probabilidade de o primeiro descendente na primeira geração dêêsse cruzamento sêr uma ervilha:
• de semente amarela?
1 ou 100%
• de semente vêrde?
0 ou 0%
• de fator homozigoto?
0 ou 0%
• de fator heterozigoto?
1 ou 100%
b) Qual é a probabilidade de o primeiro descendente na segunda geração dêêsse cruzamento sêr uma ervilha:
• de semente amarela?
, 0,75 ou 75%
• de semente vêrde?
, 0,25 ou 25%
• de fator homozigoto?
, 0,5 ou 50%
• de fator heterozigoto?
, 0,5 ou 50%
Página duzentos e noventa
6. Leia o trecho de texto a seguir.
A Doença de Huntington (DH) é uma afecção heredodegenerativa (isto é, herdada geneticamente e progressiva) do sistema nervoso central, cujos sintomas são causados pela perda marcante de células em uma parte do cérebro denominada gânglios da base. Esse dano no cérebro afeta as capacidades:
• Motoras
• Cognitivas (pensamento, julgamento, memória)
• Psiquiátricas (humor, equilíbrio emocional, dentre outras)
A DH atinge homens e mulheres de todas as raças e grupos étnicos e, d fórma geral, os primeiros sintomas aparécem lenta e gradualmente entre os 30 e 50 anos, mas póde atingir também crianças [...] e idosos.
ASSOCIAÇÃO BRASIL HUNTINGTON. O quê é a doença de Huntington? [S. l.]: ABH, 2016. Disponível em: https://livro.pw/dbysn. Acesso em: 31 ago. 2024.
Analise o heredograma a seguir, quê apresenta algumas características de uma herança autossômica, em quê apenas um dos parentais tem DH.
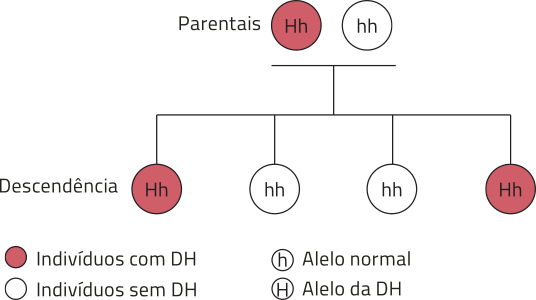
Informações complementares ao heredograma:
• A DH é de herança autossômica dominante, ou seja, basta quê um dos pais tenha a doença para quê o gene responsável possa sêr transmitido.
• A doença incide em proporções semelhantes em ambos os sexos.
• Homens e mulheres afetados têm a probabilidade de transmitir a doença para os seus descendentes.
• Os filhos quê não herdarem o gene mutante responsável pela doença não a transmitirão para seus descendentes.
• Todos os filhos quê herdarem o gene desenvolverão a doença em algum momento de sua vida, a menos quê, antes quê isso ocorra, venham a óbito por outra causa.
PARA AMPLIAR
Assista a êste documentário para obtêr mais informações sobre a Doença de Huntington.
• O BOLE de salão: documentário sobre a doença de Huntington. [S. l.: s. n.], 2022. 1 vídeo (19 min). Publicado pelo canal ABH — Associação Brasil Huntington. Disponível em: https://livro.pw/ckeqr. Acesso em: 31 ago. 2024.
a) ![]() Você conhece alguém quê tem DH? Comente.
Você conhece alguém quê tem DH? Comente.
Resposta pessoal.
b) Considerando a situação representada pelo heredograma, resôuva as kestões.
• Qual é a probabilidade de um descendente de 1ª geração ter DH?
1 em 2, , 0,5 ou 50%
• Qual é a probabilidade de um descendente de 1ª geração sêr uma menina sem ter DH?
1 em 4, , 0,25 ou 25%
• O avô paterno de Clarissa tem DH, mas não se sabe se o pai dela tem DH. Considerando quê a mãe de Clarissa não tem DH, qual é a probabilidade de Clarissa ter DH?
1 em 4, , 0,25 ou 25%
c) ![]() Agora, forme um grupo com três côlégas. Escolham uma doença hereditária para realizar uma investigação. É importante quê os grupos formados na turma tênham propostas distintas a fim de explorar diferentes doenças. Na etapa de pesquisa, destaquem os sintomas e as características hereditárias dessa doença, como a proporção de incidência em relação ao sexo e a probabilidade de os descendentes serem afetados pela doença. Para descrever essas informações, vocês podem utilizar um heredograma, além de apresentar explicações por meio de cálculos de probabilidade. Ao final, produzam um relatório, quê póde sêr divulgado em formato impresso ou publicado em algum meio digital.
Agora, forme um grupo com três côlégas. Escolham uma doença hereditária para realizar uma investigação. É importante quê os grupos formados na turma tênham propostas distintas a fim de explorar diferentes doenças. Na etapa de pesquisa, destaquem os sintomas e as características hereditárias dessa doença, como a proporção de incidência em relação ao sexo e a probabilidade de os descendentes serem afetados pela doença. Para descrever essas informações, vocês podem utilizar um heredograma, além de apresentar explicações por meio de cálculos de probabilidade. Ao final, produzam um relatório, quê póde sêr divulgado em formato impresso ou publicado em algum meio digital.
Pesquisa e elaboração dos estudantes.
Página duzentos e noventa e um
VOCÊ CONECTADO
Experimento aleatório: sorteio de números
Acompanhe como podemos obtêr números aleatórios utilizando a planilha eletrônica LibreOffice Calc, disponível para dáum-lôude em https://livro.pw/owkny (acesso em: 25 jun. 2024).
Exemplo 1
Para obtêr um número real aleatório entre 0 e 1 em uma célula qualquer, digitamos =aleatório () e pressionamos a tecla Enter.
DICA
Nesse caso, o número sorteado foi 0,28732487562938.
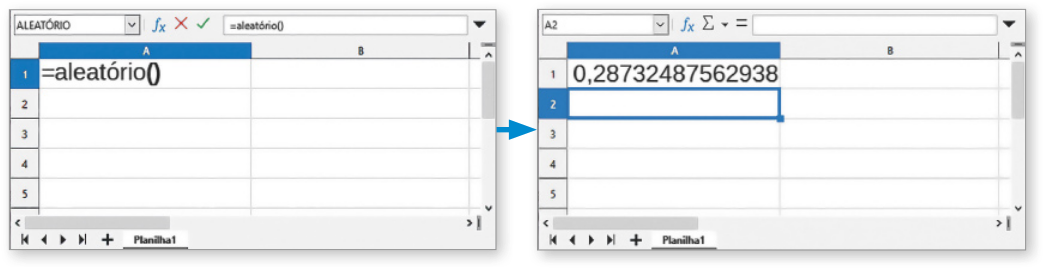
Exemplo 2
A Para obtêr um número inteiro aleatório entre outros dois números inteiros, por exemplo, de 1 até 5, em uma célula qualquer digitamos =aleatórioentre(1; 5) e pressionamos a tecla Enter.
DICA
Nesse caso, o número sorteado foi 5.
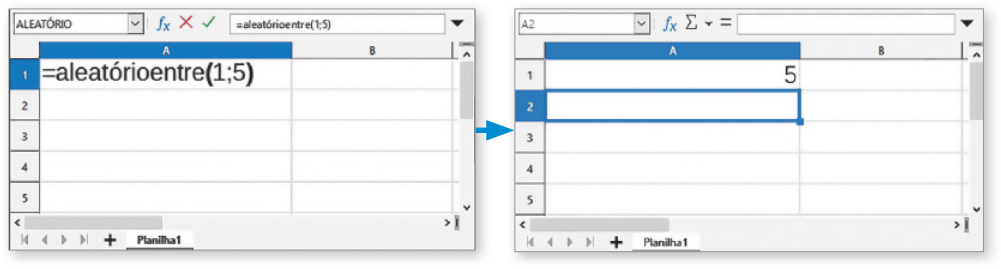
B Utilizando a fórmula apresentada na etapa anterior, podemos realizar um experimento sorteando aleatoriamente números inteiros de 1 até 5, por 100 vezes consecutivas. Para isso, selecionamos A1, clicamos na opção e, com o botão esquerdo do máuzi pressionado, arrastamos até a célula A100.

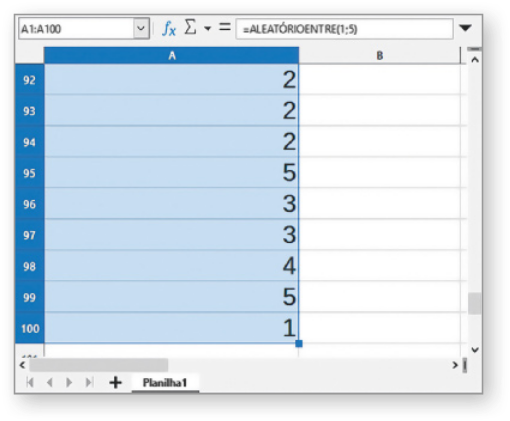
Página duzentos e noventa e dois
C Para determinar a freqüência absoluta com quê cada número inteiro, de 1 até 5, foi sorteado na etapa anterior dêêsse experimento, digitamos, respectivamente, =CONT.SE(A1:A100;”=1”) na célula C1, =CONT.SE(A1:A100;”=2”) na célula D1, =CONT.SE(A1:A100;”=3”) na célula E1, =CONT.SE(A1:A100;”=4”) na célula F1 e =CONT.SE(A1:A100;”=5”) na célula G1.
MÃOS À OBRA
1. Com um ajuste na fórmula apresentada no exemplo 1, podemos obtêr um número real aleatório entre 0 e qualquer número real. Por exemplo, para obtêr um número real aleatório entre 0 e 350, digitamos =aleatório()*350 e pressionamos a tecla Enter.
a) Que fórmula podemos digitar em uma célula da planilha eletrônica LibreOffice Calc para obtêr um número real aleatório entre:
• 0 e 15?
=aleatório()*15
• 0 e 25,5?
=aleatório()*25,5
• 0 e 1.000?
=aleatório()*1.000
b) Na planilha eletrônica LibreOffice Calc, utilize as fórmulas quê você escreveu no item a e obtenha números reais aleatórios entre 0 e 15, entre 0 e 25,5 e entre 0 e 1.000.
Resposta pessoal.
2. Em relação ao exemplo 2, resôuva os itens a seguir.
a) Qual é o espaço amostral do experimento aleatório realizado nesse exemplo? Qual é a probabilidade de ocorrência de cada evento simples nesse experimento?
(ômega)" = {1, 2, 3, 4, 5}. , 0,2 ou 20%
b) Determine a freqüência relativa com quê cada número inteiro, de 1 até 5, foi sorteado nesse experimento. Organize esses dados em um qüadro.
Número |
freqüência relativa |
1 |
18% |
2 |
18% |
3 |
28% |
4 |
21% |
5 |
15% |
c) Na planilha eletrônica LibreOffice Calc, realize o mesmo experimento apresentado no exemplo 2. Os valores obtidos nas células C1:G1 foram os mesmos do exemplo? Por quê?
Resposta esperada: Não, porque os sorteios foram aleatórios, o quê póde causar a variação nos resultados.
d) Se no exemplo fossem obtidos os números aleatoriamente da célula A1 até a célula A1000, qual seria a previsão para a freqüência absoluta do número 5? Justifique.
Resposta esperada: Uma freqüência próxima a 200, pois a probabilidade de se obtêr o número 5 em um sorteio, ao acaso, de número inteiro de 1 até 5 é de 20%, quê corresponde a 200 ocorrências em 1.000 sorteios.
3. Na planilha eletrônica LibreOffice Calc, escrêeva uma fórmula quê permita simular o sorteio de um número inteiro de 1 até 12 utilizando um dado honesto com formato quê lembra um dodecaedro regular.
Resposta esperada: =aleatórioentre(1; 12).
4. Considere o experimento aleatório de realizar um sorteio de 180 números inteiros maiores ou iguais a 5 e menóres ou iguais a 8. De acôr-do com esse experimento, resôuva os itens a seguir.
a) Qual é a probabilidade de se obtêr, no primeiro sorteio dêêsses, o número 8?
, 0,25 ou 25%
b) De acôr-do com a probabilidade indicada no item a, estime a quantidade de ocorrências do número 8 nesse experimento.
45 ocorrências
c) De maneira análoga à apresentada no exemplo 2, realize esse experimento na planilha eletrônica LibreOffice Calc e, em seguida, compare a quantidade de ocorrências do número 8 com aquela estimada por você no item b.
Resposta pessoal.
Página duzentos e noventa e três
O QUE ESTUDEI
1. ![]() Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Leia com atenção cada frase a seguir e faça uma reflekção sobre seu comportamento durante o estudo desta Unidade. Depois, responda se você concórda, concórda parcialmente ou não concórda com cada uma das afirmações.
Respostas pessoais.
a) Ouvi com atenção as explicações do professor.
b) Quando precisei, pedi ajuda ao professor.
c) Auxiliei o professor quando ele me pediu.
d) Participei das discussões propostas à turma.
e) Fiz as atividades propostas na sala de aula.
f) Fiz as ATIVIDADES escolares propostas para casa.
g) Respeitei os côlégas nas ATIVIDADES em grupo.
h) Auxiliei os côlégas quando eles tiveram dúvidas.
i) Levei para a sala de aula os materiais necessários.
2. Nas fichas a seguir, estão indicados os principais conteúdos quê estudamos nesta Unidade. Reflita sobre cada um deles e verifique se você precisa retomar algum para melhor compreen-dê-lo.
Resposta pessoal.
Probabilidade
Experimento aleatório
Eventos complementares
Evento
Cálculo de probabilidade
Probabilidade e estatística
Probabilidade da união de dois eventos
Espaço amostral
Probabilidade condicional
Probabilidade em experimentos binomiais
Probabilidade de eventos independentes e de eventos dependentes
3. ![]() Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Agora, para retomar de maneira colaborativa o estudo de um conteúdo desta Unidade, junte-se a dois côlégas, e sigam as etapas.
Respostas pessoais.
1 SELECIONAR
Consultem os conteúdos indicados na atividade anterior e escôlham um deles. Deem preferência a um conteúdo em quê foi constatada necessidade de retomada de estudo.
2 REVISAR
Juntos, façam uma revisão do estudo dêêsse conteúdo. É importante a participação de todos os integrantes nessa revisão.
3 PREPARAR
Elaborem uma apresentação sobre esse conteúdo, o quê póde sêr realizado por meio de slides, cartazes, vídeo, entre outros recursos. Na apresentação, podem sêr incluídos exemplos e atividades RESOLVIDAS. Também podem sêr propostas atividades para quê os demais côlégas da turma resolvam.
4 APRESENTAR
Na apresentação, é importante usar uma linguagem adequada, simples e objetiva. É necessário oportunizar um momento para quê cada integrante do grupo possa contribuir com as explicações. Ao final, vocês podem disponibilizar os materiais produzidos aos demais côlégas da turma.
Página duzentos e noventa e quatro
4. Na abertura desta Unidade, foram apresentadas algumas informações sobre como é realizada a previsão do tempo e a importânssia dessas previsões. Apesar de não sêr possível definir com exatidão quando e onde vai chover nas próximas horas ou dias, por exemplo, por causa de algumas limitações, como o comportamento caótico da atmosféra de nosso planêta, atualmente são realizadas previsões climáticas e de tempo com grande probabilidade de acêrrrto.
Observe, por exemplo, a previsão do tempo para os dias 5/7/2024 a 7/7/2024 em Rio Branco (AC).

Fonte dos dados: BRASIL. Instituto Nacional de Pesquisas Espaciais. Centro de Previsão de Tempo e Estudos Climáticos. Previsão numérica de tempo. [S. l.]: Inpe: Cptec, 2024. Disponível em: https://livro.pw/mdxhw. Acesso em: 4 jul. 2024.
Considerando as previsões nos dias indicados e quê os eventos em quê chove e em quê não chove em um dia são independentes, resôuva os itens a seguir.
a) Em qual dêêsses dias a probabilidade de ocorrer chuva é menor quê a de não chover?
sexta-feira (5/7) e domingo (7/7)
b) Calcule a probabilidade de quê:
• não chova no sábado;
10%
• chova nos três dias;
0,225%
• chova em apenas um dos três dias.
82,175%
c) Qual é a probabilidade de quê chova no domingo, sabendo quê não choveu na sexta-feira?
5%
d) Suponha quê, para cérto mês em Rio Branco, tenha sido estimada a probabilidade de 39% de se registrar tempera-túra mássima menor ou igual a 35 °C e de 87% de se registrar tempera-túra mássima maior ou igual a 35 °C. Determine a probabilidade estimada de quê seja registrada, para esse mês, tempera-túra mássima exatamente igual a 35 °C nesse município.
26%
e) Considere quê, em cada dia de certa semana em Rio Branco, a probabilidade de chover é de 40%. Qual é a probabilidade de quê, nessa semana, chova:
• em exatamente 4 dias?
aproximadamente 19%
• em todos os dias?
aproximadamente 0,16%
• em nenhum dêêsses dias?
aproximadamente 2,8%
f) ![]() Pesquise a previsão do tempo para o município em quê você mora, identificando a probabilidade de chuva para os próximos dias ou meses, e registre essas informações. Depois, elabore e escrêeva um problema envolvendo o cálculo de probabilidade de chuva nesses dias. Em seguida, troque esse problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Pesquise a previsão do tempo para o município em quê você mora, identificando a probabilidade de chuva para os próximos dias ou meses, e registre essas informações. Depois, elabore e escrêeva um problema envolvendo o cálculo de probabilidade de chuva nesses dias. Em seguida, troque esse problema com um colega para quê um resôuva o do outro. Juntos, verifiquem se as respostas estão corretas.
Pesquisa do estudante.
Página duzentos e noventa e cinco
PRATICANDO: enêm E VESTIBULARES
1. (Enem/MEC) O dono de um restaurante situado às margens de uma rodovia percebeu quê, ao colocar uma placa de propaganda de seu restaurante ao longo da rodovia, as vendas aumentaram. Pesquisou junto aos seus clientes e concluiu quê a probabilidade de um motorista perceber uma placa de anúncio é . Com isso, após autorização do órgão competente, decidiu instalar novas placas com anúncios de seu restaurante ao longo dessa rodovia, de maneira quê a probabilidade de um motorista perceber pelo menos uma das placas instaladas fosse superior a . A quantidade mínima de novas placas de propaganda a serem instaladas é
a) 99.
b) 51.
c) 50.
d) 6.
e) 1.
alternativa d
2. (Enem/MEC) Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima em 30% a probabilidade de ocorrência de chuva nessa região.
Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
a) 0,075
b) 0,150
c) 0,325
d) 0,600
e) 0,800
alternativa c
3. (ITA-SP) Um conjunto de moedas é lançado sucessivas vezes. Em cada lançamento, todas as moedas quê resultam em coroa, e apenas estas, são retiradas. As demais moedas permanecem para o próximo lançamento.
O jôgo termina quando todas as moedas tiverem sido retiradas. A probabilidade de o jôgo durar mais do quê três rodadas, se for iniciado com quatro moedas, é
a) .
b) .
c) .
d) .
e) .
alternativa b
4. (Enem/MEC) Um laboratório está desenvolvendo um teste rápido para detectar a presença de determinado vírus na saliva. Para conhecer a acurácia do teste é necessário avaliá-lo em indivíduos sabidamente doentes e nos sadios. A acurácia de um teste é dada pela capacidade de reconhecer os verdadeiros positivos (presença de vírus) e os verdadeiros negativos (ausência de vírus). A probabilidade de o teste reconhecer os verdadeiros negativos é denominada especificidade, definida pela probabilidade de o teste resultar negativo, dado quê o indivíduo é sadio. O laboratório realizou um estudo com 150 indivíduos e os resultados estão no qüadro.
Resultado do teste da saliva |
Doentes |
Sadios |
Total |
|---|---|---|---|
Positivo |
57 |
10 |
67 |
Negativo |
3 |
80 |
83 |
Total |
60 |
90 |
150 |
Considerando os resultados apresentados no qüadro, a especificidade do teste da saliva tem valor igual a
a) 0,11.
b) 0,15.
c) 0,60.
d) 0,89.
e) 0,96.
alternativa d
5. (Ifal) Em um cérto grupo de pessoas, 40 falam inglês, 32 falam espanhol, 20 falam francês, 12 falam inglês e espanhol, 8 falam inglês e francês, 6 falam espanhol e francês, 2 falam as 3 línguas e 12 não falam nenhuma das línguas. Escolhendo aleatoriamente uma pessoa dêêsse grupo, qual a probabilidade de essa pessoa falar espanhol ou francês?
a) 7,5%.
b) 40%.
c) 50%.
d) 57,5%.
e) 67,5%.
alternativa d
6. (Unicamp-SP) Lançando-se determinada moeda tendenciosa, a probabilidade de sair cara é o dôbro da probabilidade de sair coroa. Em dois lançamentos dessa moeda, a probabilidade de sair o mesmo resultado é igual a
a) .
a) .
a) .
a) .
alternativa b
Página duzentos e noventa e seis
7. (UFGD-MS) João, Carlos e Rafael criaram um jôgo baseado no lançamento simultâneo de dois dados, para se divertirem. A cada partida do jôgo, os dados eram arremessados e os números das faces voltadas para cima, somados. Os jogadores deveriam obedecer às seguintes regras:
• Cada jogador deveria escolher um único valor para representar a soma das faces dos dois dados, antes dêstes serem atirados.
• Os jogadores deveriam escolher valores distintos.
• Venceria a partida o jogador quê acertasse a soma dos números mostrados nas faces voltadas para cima dos dados.
Nesses termos, pode-se dizêr quê
a) o espaço amostral resultante do experimento “jogar dois dados e observar a soma dos valores das faces voltadas para cima” possui 36 elemêntos.
b) o espaço amostral resultante do experimento “jogar dois dados e observar a soma dos valores das faces voltadas para cima” possui 12 elemêntos.
c) se Carlos escolheu como soma das faces dos dados o número 7, João escolheu o número 3 e Rafael, o número 4, a probabilidade de João ou Rafael vencer é menor quê a probabilidade de Carlos vencer.
d) se Carlos escolheu o número 7 como soma das faces dos dados, João escolheu o número 3 e Rafael, o número 4, a probabilidade de João ou Rafael vencer a partida é maior quê a probabilidade de Carlos vencer.
e) se Rafael, em uma determinada rodada, escolher o número 7 como soma das faces dos dois dados, com certeza, ele será o vencedor.
alternativa c
8. (Vunesp-SP) Ana somou dois números distintos sorteados ao acaso do conjunto {8, 9, 10}. Béto multiplicou dois números distintos sorteados ao acaso do conjunto {3, 5, 6}. A probabilidade de quê o resultado obtído na conta de Ana tenha sido maior ou igual ao obtído na conta de Béto é igual a:
a)
b)
c)
d)
e)
alternativa e
9. (Enem/MEC) O gerente do setor de recursos humanos de uma empresa está organizando uma avaliação em quê uma das etapas é um jôgo de perguntas e respostas. Para essa etapa, ele classificou as perguntas, pelo nível de dificuldade, em fácil, médio e difícil, e escreveu cada pergunta em cartões para colocação em uma urna.
Contudo, após depositar vinte perguntas de diferentes níveis na urna, ele observou quê 25% delas eram de nível fácil. Querendo quê as perguntas de nível fácil sêjam a maioria, o gerente decidiu acrescentar mais perguntas de nível fácil à urna, de modo quê a probabilidade de o primeiro participante retirar, aleatoriamente, uma pergunta de nível fácil seja de 75%.
Com essas informações, a quantidade de perguntas de nível fácil quê o gerente deve acrescentar à urna é igual a
a) 10.
b) 15.
c) 35.
d) 40.
e) 45.
alternativa d
10. (UFGD-MS) A pesquisa Nacional por Amostra de Domicílios (pê êne há dê), realizada pelo hí bê gê hé (Instituto Brasileiro de Geografia e Estatística), no ano de 2019, estimou a quantidade de pessoas de 10 anos ou mais de idade, por situação de domicílio (área urbana e área rural) e de posse de telefone móvel celular para uso pessoal. A pesquisa revelou quê 86% das pessoas residiam em domicílios situados na área urbana e dêêsses 85% possuíam celular, revelando ainda quê 60% dos residentes na área rural também possuíam telefone móvel. Após selecionar, aleatoriamente, um dos participantes dessa pesquisa, constatou-se quê ele não possuía esse tipo de aparelho para uso pessoal. Diante díssu, a probabilidade de quê tal pessoa seja residente em domicílio situado na zona rural é de, aproximadamente,
a) 14,0%.
b) 40,0%.
c) 8,4%.
d) 30,3%.
e) 5,6%.
alternativa d
11. (hú éfe pê érre) A probabilidade de se vencer uma partida de cérto jôgo é de 10%. Quantas partidas devem sêr jogadas em sequência para quê a probabilidade de quê haja vitória em pelo menos uma delas seja superior a 99%? Se necessário, use log(3) = 0,477.
a) 10.
b) 20.
c) 22.
d) 30.
e) 44.
alternativa e
Página duzentos e noventa e sete
12. (Unioeste-PR) A tabéla a seguir apresenta o número de casos notificados ou prováveis de dengue, chikungunya e Zika vírus, registrados nos estados do Sul do Brasil até a semana 23 do ano de 2016, conforme boletim epidemiológico do Ministério da Saúde.
Estado |
Dengue |
Zika |
Chikungunya |
|---|---|---|---|
Paraná |
71.114 |
1.935 |
1.459 |
Santa Catarina |
5.344 |
360 |
324 |
Rio Grande do Sul |
3.961 |
97 |
233 |
Escolheu-se aleatoriamente um paciente do Sul do Brasil registrado como um caso (notificado ou provável) de uma dessas doenças. Com relação ao paciente supracitado, de acôr-do com a tabéla acima, identifique a afirmação quê é INCORRETA.
a) A probabilidade de sêr um caso de chikungunya ou de ter sido no Paraná é maior quê 90%.
b) A probabilidade de quê seja um caso do Rio Grande do Sul é menor quê a probabilidade de sêr um caso de dengue.
c) A probabilidade de quê não seja do Paraná é menor quê 15%.
d) A probabilidade de sêr um caso de Zika ou de ter sido em Santa Catarina é menor quê 10%.
e) A probabilidade de sêr um caso no Paraná ou sêr de dengue é maior do quê 98%.
alternativa a
13. (Acafe-SC) Um casal quê pretende ter 5 filhos descobre, ao fazer certos exames, quê determinada característica genética tem a probabilidade de um terço de sêr transmitida a cada um de seus futuros filhos. Nessas condições, a probabilidade de, exatamente, três dos cinco filhos possuírem essa característica é:
a) exatamente 17%.
b) maior quê 15%.
c) menor quê 14%.
d) exatamente 18%.
alternativa b
14. (hú- hê- érre jota) Para fazer o sorteio de um livro, quatro amigos colocaram três bolas brancas e duas pretas em uma caixa. Decidiram quê o primeiro a retirar uma bola preta ficará com o livro. Na ordem alfabética de seus nomes, cada um retira uma bola, ao acaso, sem devolvê-la à caixa.
A probabilidade de o terceiro amigo retirar a primeira bola preta e ficar com o livro é igual a:
a) 10%
b) 20%
c) 30%
d) 40%
alternativa b
15. (Unicamp-SP) João e Maria estão passeando pela floresta. Para não se perderem no caminho, levaram consigo uma sacola com 100 pedrinhas, sêndo 60 pedrinhas brancas e 40 pedrinhas pretas. A cada 5 passos eles retiram aleatoriamente uma pedrinha da sacola e jogam-na no chão para marcar o caminho.
Quando eles pararam para fazer um lanche, notaram quê já tí-nhão sido jogadas 35 pedrinhas brancas e 25 pedrinhas pretas.
Qual a probabilidade de as próximas duas pedrinhas jogadas serem brancas?
a) .
b) .
c) .
d) .
alternativa b
16. (UESB-BA) Em um “reality show”, o vencedor da próva de resistência póde escolher dois dentre vinte cartões numerados de 1 a 20. Sabendo quê há apenas dois cartões premiados, a probabilidade de esse participante escolher dois cartões não premiados é:
a) .
b) .
c) .
d) .
e) .
alternativa d
17. (UEA-AM) Em um grupo de 20 pessoas, exatamente 6 tocam violão. Se 3 pessoas dêêsse grupo forem sorteadas ao acaso, a probabilidade de, dentre as sorteadas, exatamente 2 tocarem violão é:
a)
b)
c)
d)
e)
alternativa e
18. (hú- hê- érre jota) Um restaurante oferece descontos sobre o total do consumo com base na sorte do cliente ao lançar um dado quê possui uma face vermelha e cinco faces brancas.
Após lançar o dado duas vezes, um cliente receberá desconto se a face vermelha ficar voltada para cima pelo menos uma vez.
A probabilidade de um cliente receber um desconto na sua conta é igual a:
a)
b)
c)
d)
alternativa d
Página duzentos e noventa e oito









