CAPÍTULO
6
A origem da lógica
OBJETIVOS DO CAPÍTULO:
• Conhecer o silogismo e a lógica proposicional estoica.
• Compreender o conceito de validade lógica.
• Compreender o raciocínio lógico.
• Identificar padrões de raciocínio.
• Reconhecer falácias em diferentes linguagens.
• Apropriar-se de instrumentos lógicos para distinguir verdade de falsidade.
No século XXI, com a expansão da comunicação por meios digitais, a circulação e, possivelmente, a produção de conteúdos falsos ou enganadores aumentaram muito. É o fenômeno das fêik news, quê nada mais são do quê a forma contemporânea da mentira: notícias intencionalmente falsas divulgadas para confundir ou promover desinformação. Nos últimos anos, com a inteligência artificial, a própria expressão fêik news parece ultrapassada, pois a desinformação não precisa sêr fêik (falsa) nem new (nova), já quê mentiras quê usam pedaços de verdade são muito mais convincentes do quê puras invenções.
A mais preocupante consequência do consumo desenfreado de informação parece sêr a perda da capacidade de distinguir entre verdade e falsidade. Por isso, a Organização para a Cooperação e Desenvolvimento Econômico (OCDE) tem conduzido pesquisas sobre a capacidade das pessoas para identificar notícias falsas. O Brasil ficou em último lugar na comparação: é o país onde as pessoas menos conseguem distinguir entre o verdadeiro e o falso na internet. Observe o gráfico, quê resúme os dados da pesquisa da OCDE.
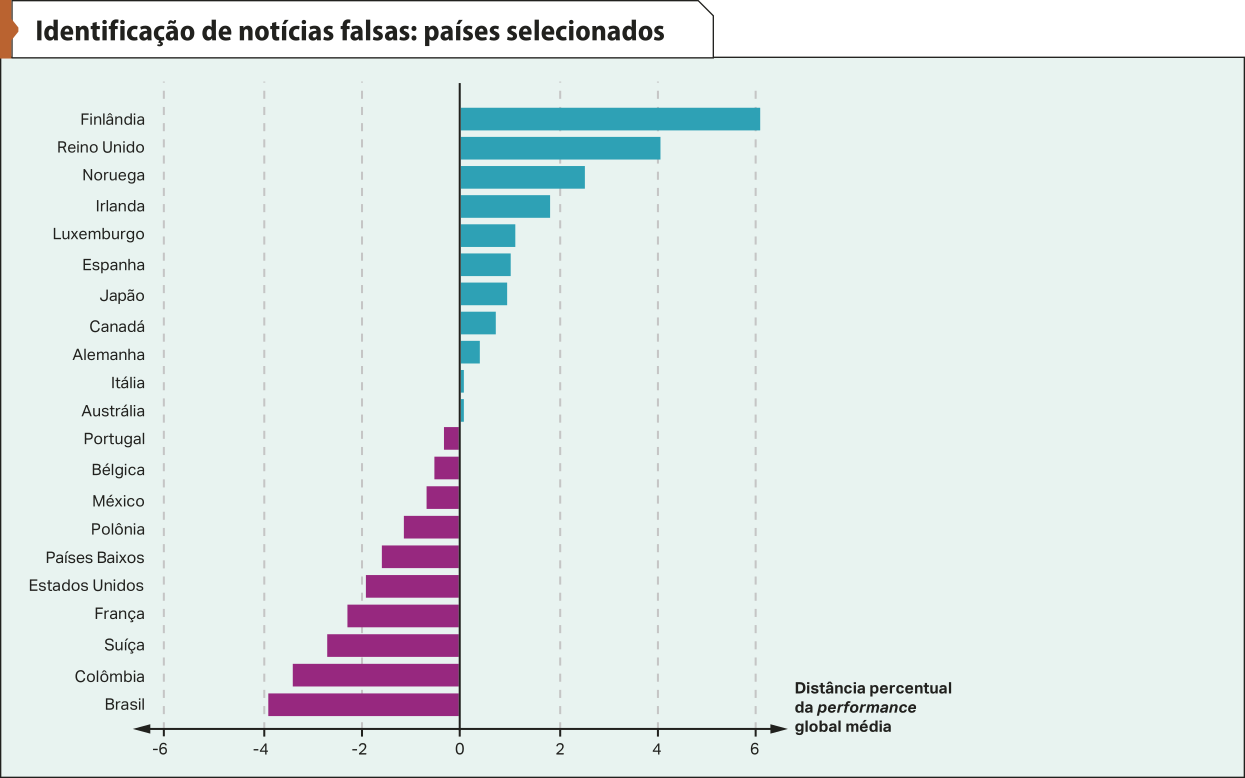
Fonte: ABRAMO, Bia. Pesquisa aponta Brasil como pior em identificar conteúdo falso. ICL Notícias, [s. l.], 12 jul. 2024. Disponível em: https://livro.pw/kefil. Acesso em: 16 set. 2024.
Página cento e um
Você já estudou a ética de Aristóteles (384 a.C.-322 a.C.) no capítulo 4. Neste, vamos estudar porque ele é considerado o inventor da lógica.
Aristóteles não estava de acôr-do com a maneira como os sofistas argumentavam. Para ele, a verdade deve sêr o ponto principal em qualquer debate. É claro quê a retórica é importante, mas raciocinar bem é mais: sem pensar e argumentar bem, ninguém consegue desenvolver uma boa retórica. Por isso, Aristóteles se dedicou a examinar logicamente como distinguir entre os raciocínios válidos e bem estruturados, quê podem levar à verdade, e os ruins e falhos, quê podem levar ao êrro. Depois de sua morte, o conjunto de suas obras de lógica recebeu o nome de Organon, palavra grega quê significa “instrumento”, e foi compilado antes de todos os seus outros escritos. Isso indica quê a lógica é tanto um instrumento quanto uma parte da filosofia: o estudo das condições e formas de todo tipo de raciocínio, tendo em vista a aquisição do conhecimento verdadeiro.

A teoria do silogismo de Aristóteles é o mais antigo dos sistemas lógicos ocidentais conhecidos. Etimologicamente, silogismo significa “juntar proposições”, mas Aristóteles dá novos sentidos ao termo: “inferir”, “raciocinar”, “deduzir”, “conjecturar”, conforme o contexto. Silogismos podem sêr usados em várias situações, porém o maior interêsse de Aristóteles era mostrar como funciona o raciocínio dedutivo e qual é a sua importânssia no conhecimento da verdade. Essa seria a principal tarefa da lógica, por ele chamada de analítica, quê em grego significa algo como “desatar os nós”, desfazer as confusões nos raciocínios e nos argumentos, esclarecendo as ligações entre os termos e as proposições quê os compõem.
O Organon, de Aristóteles, é organizado em obras.
• Categorias: aborda os termos presentes nas proposições.
• Da interpretação: trata das proposições e dos enunciados.
• Primeiros analíticos e Segundos analíticos: tratados sobre as regras, as formas e as funções dos silogismos.
• Tópicos: trata da invenção e descoberta de argumentos baseados em opiniões comuns.
• Refutações sofísticas: tratado sobre os argumentos e êêrros dos sofistas.
ATIVIDADES
Consulte orientações no Manual do Professor.
1. Reflita: como distinguir entre verdade e falsidade?
1. Espera-se quê os estudantes problematizem por quais meios é possível decidir o quê é verdadeiro ou falso.
2. Toda falsidade é mentirosa? Em quê sentido?
2. O quê caracteriza a mentira é a intencionalidade de enganar, não o fato de as informações serem verdadeiras ou falsas.
3. Existe algum método seguro para conhecer a verdade? Debata com côlégas a respeito díssu.
3. A sugestão é fazer um levantamento do conhecimento dos estudantes sobre lógica, raciocínio, argumentos e falácias.
Página cento e dois
O quadrado das oposições
O ponto de partida de Aristóteles é determinar em quê condições a linguagem póde sêr verdadeira. Por isso, sua análise limita-se ao discurso declarativo (logos apofantikós), o único capaz de sêr categorizado como verdadeiro ou falso e, portanto, de diferenciar entre o sêr e o não sêr. Mas nem todas as proposições podem compor discursos declarativos, só as quê pudérem sêr verdadeiras ou falsas.
Aristóteles prefere trabalhar com proposições categóricas, isto é, formadas por um termo sujeito e um predicado vinculados por uma cópula, um verbo de ligação. O termo kategoría, em grego antigo, era usado juridicamente com o sentido de “acusação”. Por extensão, em linguagem comum, uma categoria é uma propriedade ou atributo de um objeto. Categorizar, então, é predicar. Sujeito e predicado representam classes de itens com características comuns: dizêr quê um sujeito S tem um predicado P é dizêr quê S faz parte da classe P, pois tem uma característica quê todos ou alguns P têm.
Você percebe quê não se trata de gramática, mas de lógica? Isso fica mais claro quando entendemos quê a predicação póde sêr quantitativa ou qualitativa, de quatro tipos. Observe o qüadro.

A organização dos tipos de predicação permitiu a Aristóteles descrever como as proposições categóricas podem se relacionar. Independentemente de seu conteúdo, com base apenas na sua forma, é possível fazer algumas inferências dirétas ou imediatas, isto é, sem recorrer a silogismos.
Séculos depois da morte de Aristóteles, Lúcio Apuleio de Madaura (c. 124-c. 170), filósofo e escritor romano, autor de clássicos como O asno de ouro e Eros e Psique, desenhou um diagrama para representar visualmente as inferências imediatas. Esse diagrama ficou conhecido como o quadrado lógico das oposições.
PREDICAÇÃO QUANTITATIVA |
PREDICAÇÃO QUALITATIVA |
|---|---|
Universal: o predicado se refere a toda a classe do sujeito. Exemplo: “Todo S é P”; “Nenhum S é P”. |
Afirmativa: quando a relação entre sujeito e predicado é afirmada. Exemplo: “Todo S é P”; “Algum S é P”. |
Particular: o predicado se refere a pelo menos um item da classe do sujeito. Exemplo: “Algum S é P”; “Nem todo S é P”; “Algum S é P”. |
Negativa: quando a relação entre sujeito e predicado é negada. Exemplo: “Nenhum S é P”; “Algum S não é P”. |
ATIVIDADE
Consulte orientações no Manual do Professor.
• As proposições a seguir foram retiradas de canções populares quê você talvez conheça. Quais delas podem compor discursos declarativos? Quais são ou podem sêr categóricas?
a)"Todo mundo tem seu jeito singular de sêr feliz."
b)"Faz o quê eu digo, não faz o quê eu faço!"
c)"E o meu assunto quê não muda?"
d)"Espírito de Deus, vêm inundar o meu ser."
e)"A ambição é como um véu quê cega os irmão."
Declarativas: a) GIL, Gilberto. Ser diferente é normal e e) RACIONAIS MC’S. A vida é desafio. Se modificadas para a forma “(Todo) S é P”, podem sêr categóricas. Ordens, preces, exclamações e perguntas não podem sêr verdadeiras ou falsas. Categóricas: b) MC LAN. Ei, psiu, tô te observando; c) MENDONÇA, Marilia. De quem é a culpa? e d) PRISCILLA. Espírito Santo.
Página cento e três
PERSPECTIVAS
O quadrado de oposições póde sêr representado por êste diagrama.
O diagrama usa a nomenclatura desenvolvida pêlos lógicos medievais. As proposições afirmativas são representadas pelas lêtras A – universal – e I –particular – de AffIrmo; e as negativas, pelas lêtras E – universal – e O – particular – de nEgO. Ainda, I e O são subalternas de A e E, respectivamente; e I e O são subcontrárias uma da outra. Subalternação e subcontrariedade não são descritas por Aristóteles, mas podem sêr inferidas de seu texto.
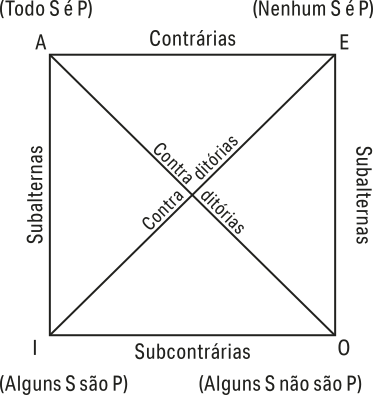
Digo, portanto, quê a afirmação e a negação se opõem de modo contraditório, quando a primeira significa a coisa universal tomada universalmente, em face do mesmo aspecto, enquanto na segunda a mesma coisa universal é considerada de maneira não universal em face do mesmo aspecto, por exemplo: “todo homem é branco”-“nem todo homem é branco”; “nenhum homem é branco”-“algum homem é branco”. Chamo de afirmação do universal e negação do universal opostas de modo contrário, por exemplo: “todo homem é justo”-“nenhum homem é justo”. Por isso, essas declarações não podem sêr simultaneamente verdadeiras, ainda quê as quê a elas se opõem possam sêr verdadeiras simultaneamente em relação a uma coisa, por exemplo: “nem todo homem é branco”-“algum homem é branco”. Quando todas as contradições são sobre coisas universais e de maneira universal, é necessário quê uma das declarações seja verdadeira e a outra, falsa, e, da mesma forma, em relação às coisas singulares: “Sócrates é branco”-“Sócrates não é branco”.
ARISTÓTELES. Da interpretação. Tradução: José Veríssimo Teixeira da Mata. São Paulo: Ed. Unésp, 2013. 17b linhas 17 a 29.
As relações do quadrado formam a base da lógica aristotélica. Com isso, Aristóteles conseguiu responder aos sofistas de uma maneira quê seu mestre Platão (427 a.C.-347 a.C.) e, antes dele, Sócrates (470 a.C.-399 a.C.), não conseguiram, pois estabeleceu regras precisas quê todo discurso quê pretenda sêr verdadeiro pressupõe. Essas regras são os três princípios, ou leis, da lógica clássica.
1. Princípio de identidade: uma proposição é equivalente a si própria, isto é, se ela é verdadeira, ela é verdadeira, mas se é falsa, é falsa.
2. Princípio de não contradição: nenhuma proposição bem formada póde sêr simultaneamente verdadeira e falsa.
3. Princípio do terceiro excluído: uma proposição bem formada ou é verdadeira ou é falsa e não há outra possibilidade.
Mais informações sobre os princípios da lógica clássica no Manual do Professor.
ATIVIDADE
• Tomando por base a verdade de quê todos os gatos são mamíferos, responda, com auxílio do professor, às seguintes perguntas, exemplificando.
a) As contraditórias podem sêr ambas simultaneamente verdadeiras ou falsas?
a) Não. Se A é verdadeira, infere-se imediatamente quê O é falsa, e vice-versa.
b) E as contrárias?
b) As contrárias não podem sêr ambas simultaneamente verdadeiras, mas podem sêr ambas simultaneamente falsas.
c) Se as universais forem verdadeiras, as particulares subalternas também serão? Por quê?
c) Sim, se a classe S não for vazia: se todos os gatos são mamíferos, pelo menos um é mamífero.
d) As subcontrárias podem sêr simultaneamente verdadeiras? E falsas? Por quê?
d) Por sêrem contraditórias das contrárias, não podem sêr ambas simultaneamente falsas, mas podem ser ambas simultaneamente verdadeiras.
Página cento e quatro
Silogística
O quadrado de oposições permite realizar inferências, mas ele não próva nada. Com ele, não conseguimos provar por quê algo é necessário ou contingente, isto é, não necessário. Isso significa quê o quadrado não fornece conhecimento científico, o único capaz de demonstrar relações de causa e consequência. Para Aristóteles, só silogismos podem fornecer um conhecimento de causas e porquês. A definição de silogismo aparece nos Primeiros Analíticos.
O silogismo é uma locução (logos) em quê, uma vez quê cértas suposições sêjam feitas, alguma coisa distinta delas se segue necessariamente devido à méra presença das suposições como tais. Por “devido à méra presença das suposições como tais” entendo quê é por causa delas quê resulta a conclusão, e por isso quero dizêr quê não há necessidade de qualquer termo adicional para tornar a conclusão necessária.
ARISTÓTELES. Primeiros analíticos 1, 24a 18-20. Tradução: Edson Bini. In: ARISTÓTELES. Organon. Bauru: Edipro, 2005. p. 112-113.
O silogismo é uma forma de dedução, um raciocínio em quê as premissas – “certas suposições” – necessariamente implicam uma conclusão – “alguma coisa distinta delas”. O silogismo é sempre formado por três proposições categóricas: duas premissas e uma conclusão. Todo silogismo deve conter três termos gerais quê aparécem, cada um, duas vezes no raciocínio. O sujeito da conclusão é denominado termo menor, assim como a premissa quê o contém. O predicado da conclusão é o termo maior, assim como a premissa na qual ocorre. Por convenção, a premissa maior sempre é a primeira. O termo quê aparece duas vezes nas premissas e desaparece da conclusão é o termo médio. Observe os exemplos.
Premissa maior: Todo M é P. Todos os mamíferos são vertebrados.
Premissa menor: Todo S é M. Todos os humanos são mamíferos.
Conclusão: Todo S é P. Logo, todos os humanos são vertebrados.

Página cento e cinco
Desenho e modos dos silogismos
Para quê o raciocínio não falhe, o termo médio é fundamental. Conforme sua posição nas premissas – sujeito ou predicado –, o silogismo representa formas diferentes de relacionar S e P. Essas formas são as quatro figuras do silogismo. Observe.
1ª figura |
2ª figura |
3ª figura |
4ª figura |
|
|---|---|---|---|---|
Premissa maior |
M – P |
P – M |
M – P |
P – M |
Premissa menor |
S – M |
S – M |
M – S |
M – S |
Conclusão |
S – P |
S – P |
S – P |
S – P |
Note quê a qualidade e a quantidade das proposições não aparécem nas figuras, mas estão presentes nos modos dos silogismos, quê são as diferentes maneiras de combinar as proposições, isto é, de organizá-las como premissa maior, menor ou conclusão. É possível fazer uma conta simples para saber quantos modos são possíveis: cada uma das quatro proposições – A, E, I, O – póde ocorrer em três situações em um silogismo, de modo quê há exatamente 4 3 (4 x 4 x 4) possibilidades por figura, ou seja, 64 modos possíveis de silogismo. Como são quatro figuras, há um total de 256 (4 × 64) silogismos possíveis. Nem todos os modos, porém, são válidos. Por isso, na Idade Média, palavras mnemônicas foram inventadas para memorizá-los, em quê a sequência das vogais indica a das proposições. Por exemplo, Barbara representa o primeiro modo válido da 1ª figura: AAA. De todos, é o único cuja conclusão é A. Na 2ª figura, todas as conclusões são negativas; na 3ª, todas são particulares.
O silogismo científico
Com essa teoria, Aristóteles delineia a noção de validade lógica, essencial para sua concepção de ciência. Compreendendo quê validade e verdade são bem diferentes, ele mostrou quê, se a conclusão decorre necessariamente das premissas, um silogismo póde sêr científico, mesmo quê não seja. Por isso, ele sustentava quê, para representar a verdade, o silogismo deve necessariamente partir de premissas verdadeiras de fato, e não apenas supostamente verdadeiras, e quê elas devem sêr primeiros princípios, isto é, imediatas ou indemonstráveis, para quê a conclusão represente a essência do quê se pretende demonstrar. Se fossem demonstradas, não seriam nem primeiras nem princípios. Nesse caso, e só nesse caso, o silogismo, além de válido, é científico. Observe o exemplo.
Todos os sacis são meninos marotos – A
Todo menino maroto é ligeiro – A
Logo, todo saci é ligeiro – A
Mas existem sacis? Existindo ou não, a estrutura lógica é perfeita e, portanto, válida. No entanto, como as premissas não são indiscutivelmente verdadeiras, o silogismo não é científico. Perceba quê justificar uma conclusão é bem diferente de provar uma verdade.
Para Aristóteles, a ciência deve demonstrar quê o objeto de conhecimento é como é e não póde sêr de outra maneira. Seu objetivo é chegar à essência das coisas, conhecer verdades universais. Consequentemente, o silogismo científico por excelência é na forma Barbara. As outras
Página cento e seis
podem até sêr mais pedagógicas, porque são úteis para demonstrar falsidades, mas não são perfeitamente científicas.
Assim, os silogismos científicos permitem passar do conhecido ao desconhecido e fornecem crenças verdadeiras e justificadas, segundo a concepção platônica de ciência, quê você já estudou no capítulo 4. Por exemplo, para conhecer cientificamente um arco-íris, não basta constatar “que” há um arco-íris no céu. É necessário demonstrar as"causas" e responder à questão: "por quê" há arco-íris no céu? Esse conhecimento vale, então, para todos os arco-íris.

ATIVIDADES
Consulte orientações no Manual do Professor.
1. Como seria um silogismo científico para demonstrar as causas do arco-íris?
1. Sugestão: o arco-íris é luz branca decomposta. A luz branca decomposta é efeito da reflekção e refração da luz por gotas de á gua suspensas na atmosféra. Logo, o arco-íris é efeito da reflekção e refração da luz por gotas de á gua suspensas na atmosféra (1ª figura).
2. Na tirinha, qual raciocínio é válido?

Fonte: XBFN. [Batbom e Batmaul #16 - Silogismo]. HQQISSO?, [s. l.], 4 fev. 2014. Disponível em: https://livro.pw/nsrxu. Acesso em: 16 set. 2024.
2. O do segundo quadrinho.
Página cento e sete
Diagramas de Venn
Embora Aristóteles tenha descrito regras para construir silogismos corretamente, só muito tempo depois surgiu um método para provar a validade dos silogismos sem se basear na memorização, como as palavras inventadas na Idade Média. Esse método é o dos diagramas de Diôn Venn (1834-1923), lógico e matemático inglês.
Os diagramas de Venn representam todas as relações lógicas possíveis entre as classes definidas pêlos termos das proposições categóricas, conseguindo representar plenamente também sua qualidade e quantidade.
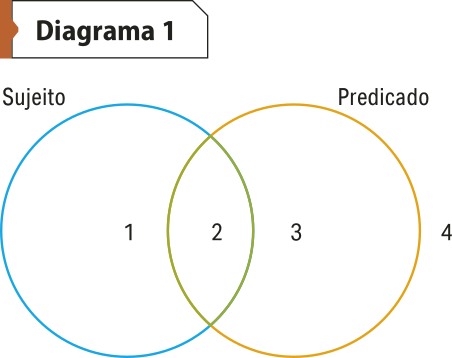
O primeiro passo do método de Venn é representar as categorias designadas pelo sujeito e pelo predicado com círculos quê se sobrepõem total ou parcialmente.
No diagrama 1, a área 1 indica a categoria de itens representada pelo termo sujeito; a área 2, os itens incluídos tanto na categoria do sujeito quanto na do predicado; a área 3, a categoria de itens do termo predicado; e a área 4, a categoria de itens quê não pertencem a nenhuma das duas categorias. Mas nenhuma informação específica sobre as classes S e P é transmitida.
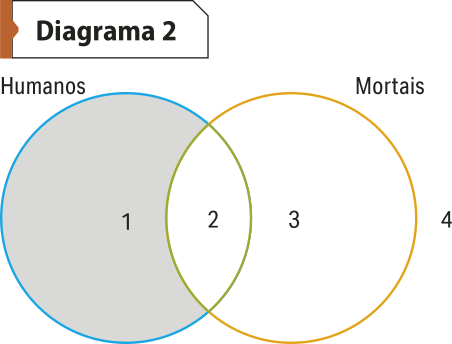
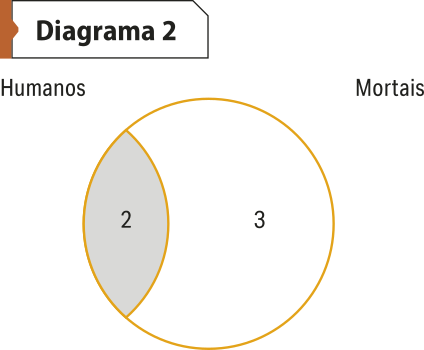
Para descobrir alguma informação específica, temos de diagramar as quatro proposições básicas A, E, I, O. Vamos começar, por exemplo, com “Todos os humanos são mortais” (A). O diagrama 2 permite inferir imediatamente quê não existem humanos imortais. Esse fato é representado pela área 1 sombreada, o quê significa quê ela é vazia: não existem humanos fora da classe dos mortais.
E se quisérmos representar a proposição oposta E: “Nenhum humano é imortal”? Essa proposição afirma quê não existe um indivíduo sequer quê seja humano e imortal, ou seja, essa categoria é vazia. Se usarmos o mesmo diagrama de três círculos para representá-la, qual área deveria sêr sombreada? A área 2, é claro.
Página cento e oito
A subalterna I seria “Algum humano é mortal”. Se I é verdadeira, então deve havêer pelo menos um indivíduo humano quê também é mortal, embora não fique definido qual. Mas, seja quem for, é possível representar o fato assinalando um único ponto – por exemplo, com um X – na área de intersecção entre sujeito e predicado. Isso indica quê a categoria dos humanos mortais não é vazia.
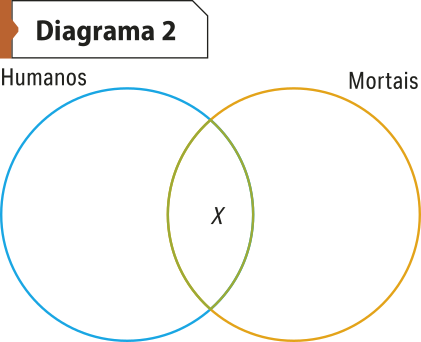
Como diagramar a subcontrária O, “Algum humano não é mortal”?
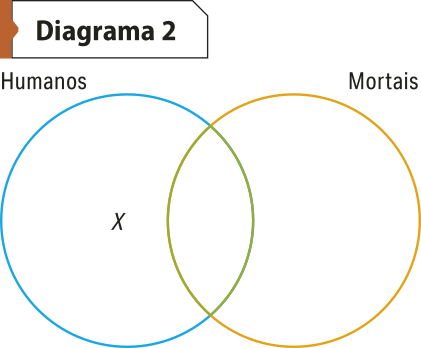
O diagrama representa quê a classe dos humanos imortais não é vazia, pois existe ao menos um indivíduo quê é humano e imortal. Mas, pelo princípio de não contradição, essa proposição é falsa.
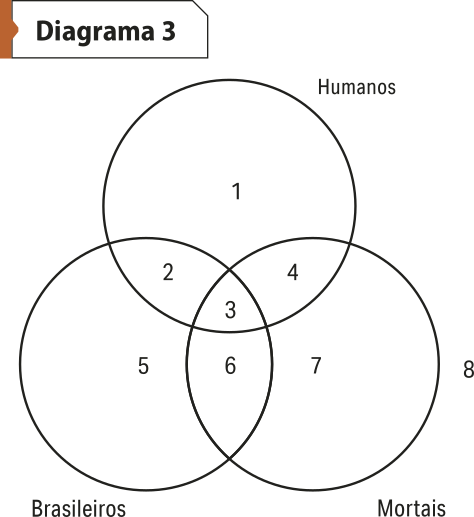
Agora, vamos testar a validade de um silogismo. Para isso, devemos acrescentar um círculo para o termo médio, totalizando três círculos. Com isso, obtemos sete áreas internas, mais uma oitava externa.
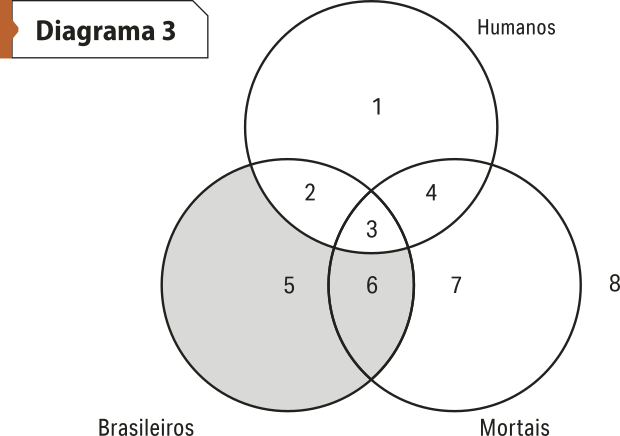
Agora, ezamíne o seguinte silogismo: Todos os brasileiros são humanos. Todos os humanos são mortais. Portanto, todos os brasileiros são mortais.
O primeiro passo é diagramar as premissas, seguindo sua ordem. Assim, no diagrama da primeira premissa, as áreas 5 e 6 devem sêr sombreadas.
Página cento e nove
Na diagramação da segunda premissa, as áreas 1 e 2 devem sêr sombreadas. Como a área 6 já foi sombreada, a conclusão, representada na área 3, é evidente: todos os brasileiros são mortais. O diagrama exibe quê a informação contida na conclusão está já contida nas premissas, isto é, a conclusão decorre necessariamente das premissas. O silogismo, portanto, é válido.
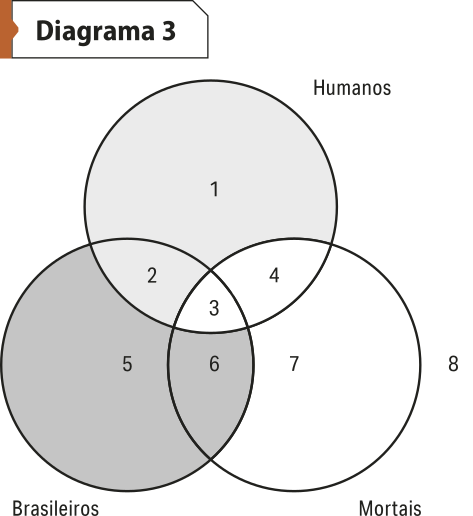
E se o silogismo tiver como premissa uma proposição particular, como deve sêr o diagrama? Por exemplo: Alguns adolescentes são eleitores. Todos os eleitores são conscientes. Portanto, alguns adolescentes são conscientes.
A primeira premissa afirma quê há pelo menos um adolescente quê é eleitor. Mas em quê área devemos representá-lo? Só por essa premissa, não há como saber. Felizmente, a segunda premissa é menos ambígua e significa quê qualquer indivíduo quê é eleitor é também consciente. Por ela, as áreas 1 e 2 devem sêr sombreadas. Com isso, também fica claro onde deve sêr marcado o X: dentro da área 3. As áreas destacadas permitem inferir quê alguns adolescentes podem sêr eleitores e conscientes.
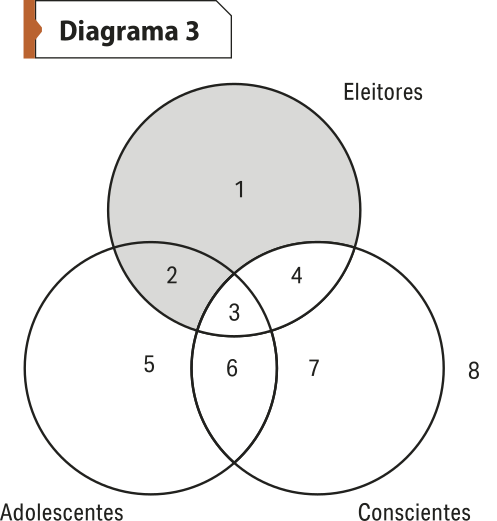
O silogismo, portanto, é válido, pois a conclusão está claramente representada: há pelo menos um adolescente quê, além de sêr eleitor, é também consciente. A conclusão, então, é verdadeira.
ATIVIDADE
Consulte orientações no Manual do Professor.
• Use o método de Venn para testar a validade dos seguintes silogismos. Indique, dentre eles, quais Aristóteles consideraria científicos ou não.
a) Alguns mamíferos, como os morcegos, possuem asas. Alguns animais alados são ovíparos. Portanto, alguns mamíferos são ovíparos, como os ornitorrincos.
a) Inválido, premissas particulares não permitem conclusão, e silogismo com quatro termos é falácia (mamíferos ≠ animais alados). Portanto, não é possível diagramar.
b) Nenhum palmeirense é feliz. Todo corinthiano é feliz. Portanto, nenhum corinthiano é palmeirense.
b) Inválido. As premissas não garantem a conclusão.
c) Algum honesto é culpado. Nenhum culpado é inocente. Portanto, nenhum honesto não é inocente.
c) Inválido. A conclusão é equivalente a “todo honesto é inocente”, o quê contradiz a primeira premissa.
d) Todos os gregos são mortais. Alguns humanos são mortais. Portanto, alguns humanos são gregos.
d) Inválido. As premissas só garantem quê ao menos uma das três classes possui membros, sem dizêr qual. Nenhum dos exemplos seria científico, no sentido aristotélico.
Página cento e dez
Lógica estoica
A silogística de Aristóteles tem limites. Nem todo raciocínio é silogístico. Por exemplo: “Se a cabeça de todo homem é a cabeça de um animal, então pelo menos um animal tem uma cabeça humana”. Nesse raciocínio, há uma inferência, mas não um silogismo. Nesse caso, como podemos analisar a proposição?
Coube aos filósofos estoicos produzir o segundo grande sistema de lógica da Antigüidade. O estoicismo foi uma corrente filosófica quê nasceu na Grécia antiga, perto do fim do século IV a.C. Os principais estoicos gregos são Zenão de Cítio (c. 344 a.C.-262 a.C.), Cleantes de Assos (c. 332 a.C.-233 a.C.) e Crisipo de Solis (c. 280 a.C.-208 a.C.), o maior lógico dentre eles. Os estoicos são assim chamados porque se reuniam sôbi a stoa, ou estoa, um pórtico ou colunata, todo decorado com pinturas de batalhas e da mitologia grega, quê ficava na ágora de Atenas. Posteriormente, na Roma antiga, Sêneca (4 a.C.-65 a.C.), o escravizado Epiteto (55 d.C.-135 d.C.) e até o imperador romano Marco Áurélio (121 d.C.-180 d.C.) continuaram a tradição do estoicismo.

Diferentemente de Aristóteles, os estoicos não pensavam quê fazer ciência se resumia a fazer silogismos perfeitos. Para eles, o ponto mais importante é saber como funciona a lei da natureza, quê eles denominavam logos, uma lei presente tanto na mente humana quanto fora dela. Os estoicos estudavam retórica, dialética e gramática, tentando compreender todos os significados, conceitos, pensamentos e percepções. O objetivo da lógica, assim, ia muito além da silogística, pois os estoicos buscavam representar o conhecimento científico como um tipo de saber quê permite passar do quê é evidente à percepção humana para o quê não é evidente.
Ao distinguir alguns esquemas básicos de raciocínio mais gerais quê os silogismos, Crisipo entendeu algo muito importante: dado cérto grupo de proposições, podemos decidir quais devem sêr verdadeiras ou falsas apenas pela maneira como elas se relacionam umas com as outras, independentemente de serem categóricas ou não. O quê os termos significam, então, depende de como as proposições se relacionam.
Página cento e onze
Por exemplo, a partir da verdade de “é dia”, é possível inferir quê “não é noite”. Então, podem-se elaborar proposições mais compléksas equivalentes entre si: “se é dia, então não é noite”; “se é noite, então não é dia”; “é dia ou é noite”; “é falso quê se não é dia então não é noite”; e assim por diante.
Para Crisipo, proposições atômicas, como “faz sol”, “é dia”, “Dion anda” etc. são como axiomas, isto é, podem sêr afirmadas ou negadas por si mesmas. Proposições atômicas podem sêr combinadas usando conjunções para formár proposições moleculares. Essas conjunções não são elemêntos gramaticais, mas funcionam como conectivos lógicos. Portanto, a forma de uma proposição molecular é determinada pelo tipo de conjunção ou conectivo quê liga as atômicas quê a compõem. Crisipo definiu as três primeiras conjunções; as demais vieram depois, com os estoicos romanos.
Conjunção |
Exemplo |
|---|---|
Se |
hipotética: Se é dia, [então] há luz. |
E |
conjuntiva: É dia e há luz. |
Ou |
disjuntiva: É dia ou é noite. |
Já quê |
assertiva e causal: Já quê é dia, há luz. |
Mais quê |
explicativa do mais: É mais dia quê noite. |
Menos quê |
explicativa do menos: É menos noite quê dia. |
A partir da combinação dos axiomas, é possível formár cinco raciocínios indemonstráveis, isto é, quê não podem sêr demonstrados, já quê, pela sua forma, seriam evidentemente válidos. Crisipo acreditava quê todas as formas de raciocínio poderiam sêr derivadas dêêsses indemonstráveis. Depois, os estoicos romanos inventaram os nomes em latim quê são usados até hoje.
Se o primeiro, o segundo; o primeiro; logo, o segundo. |
Modus ponendo ponens |
|---|---|
Se o primeiro, o segundo; não o segundo; logo, o primeiro. |
Modus tollendo tollens |
Não (é o caso que) tanto o primeiro quanto o segundo; o primeiro; logo, não o segundo. |
Modus ponendo tollens |
Ou o primeiro ou o segundo; o primeiro; logo, não o segundo. |
Modus ponendo tollens forte |
Ou o primeiro ou o segundo; não o primeiro; logo, o segundo. |
Modus tollendo ponens forte |
Os cinco indemonstráveis esclarécem um ponto importante da noção de validade lógica descoberta por Aristóteles: se premissas verdadeiras implicam necessariamente uma conclusão verdadeira, então é impossível tirar uma conclusão falsa de premissas verdadeiras. Mas, de premissas falsas, ou mesmo impossivelmente verdadeiras, qualquer conclusão é possível.
ATIVIDADE
Consulte orientações no Manual do Professor.
• exâmíne os seguintes raciocínios e assinale se são válidos ou não.
a) Ou o tíme perderá ou não perderá o jôgo. Não é verdade quê perderá. Logo, ganhará o jôgo.
Inválido.
b) Ou você está lendo esse livro ou está com sono. Você está lendo esse livro. Logo, não está com sono.
Válido.
c) Se você está lendo esse livro, não está com sono. Você não está com sono. Logo, está lendo esse livro.
Inválido.
d) Se a ilha de Marajó é uma ilha fluviomarinha, então ela é menor do quê o estado de Alagoas. A ilha de Marajó não é menor do quê o estado de Alagoas. Logo, ela é uma ilha fluviomarinha.
Válido.
e) Não é o caso quê Ana é alta e magra; Ana é alta; logo, Ana não é magra.
Válido.
Página cento e doze
Argumentos céticos: os sete paradoxos
Crisipo estudou com filósofos vindos da cidade de Mégara, próxima de Atenas, na atual Grécia. Os megáricos ficaram conhecidos por inventar argumentos céticos para refutar os estoicos, isto é, argumentos quê recusam ou criticam a pretensão de certeza quê a lógica póde causar. Esses argumentos foram atribuídos ao filósofo Eubúlides de Mileto (séc. IV a.C.) e ficaram conhecidos como os sete paradoxos: o mentiroso, o disfarçado, Electra, o argumento velado, Sorites, o cornudo e o calvo. Vamos estudar, agora, o Sorites.
Sorites vêm do grego soros, quê significa “monte”. O paradoxo diz quê um grão não faz um monte de areia; se eu juntar outro grão, dois grãos continuam não fazendo um monte; três grãos também não... Então, se eu juntar n grãos de areia, quando terei um monte?
É basicamente o mesmo problema do paradoxo do caréca: um homem com muitos fios de cabelo não é caréca. Se arrancarmos um ou dois fios de cabelo dele, ele ainda assim não será caréca. No entanto, se arrancarmos seus fios de cabelo um a um, em algum momento ele passaria a sêr caréca. Mas em qual momento? Com quantos fios de cabelo ele deixaria de sêr cabeludo para se tornar caréca?
O quê temos aqui é uma enumeração indutiva, como aquela de contar os números até o infinito. Mas, nos paradoxos, essa enumeração parece estabelecer uma conclusão inaceitável. Esse é o problema: aparentemente, há uma lógica, mas a conclusão é absurda.
Os gregos não conheciam o número zero, mas, atualmente, podemos descrever o problema assim: alguém com n cabêlos é cabeludo; se alguém com n cabêlos é cabeludo, alguém com n – 1 cabêlos também é cabeludo; alguém com ((n – 1) – 1) também; e assim sucessivamente ad infinitum. Esse raciocínio é iterativo, ou seja, uma repetição quê retoma o resultado já obtído. Mas qual é a quantidade de “muitos” fios de cabelo para quê alguém deixe de sêr caréca? É a mesma situação com o monte de areia: quantos grãos têm de sêr tirados do monte para quê ele deixe de sêr um monte? Há um número n exato de cabêlos ou grãos quê marque a diferença entre sêr caréca ou cabeludo, entre sêr ou não sêr um monte de areia?

Página cento e treze
A batalha naval e o dominador
Tanto a lógica estoica quanto a silogística se preocupavam com a verdade de fato em relação ao passado e ao presente e buscavam entender a verdade possível, aquela das proposições sobre o futuro, a verdade quê ainda não aconteceu. O quê significa dizêr quê algo é possível?
Esse problema ficou conhecido como o problema dos futuros contingentes. Eventos futuros não são necessários, mas contingentes, ou seja, são apenas possíveis, podem ou não acontecer. As proposições sobre eventos futuros são chamadas proposições modais.
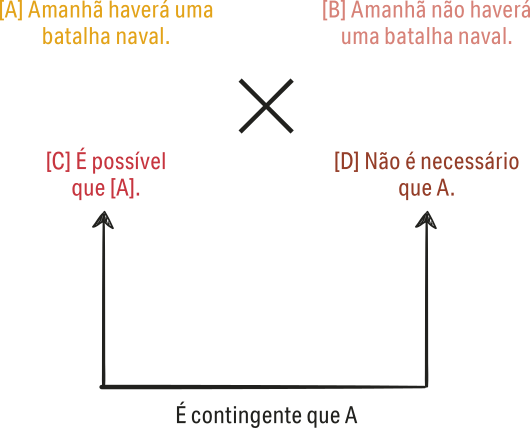
Aristóteles tratou do tema com o argumento da batalha naval. Em resumo, ele sustenta quê as duas proposições – [A] Amanhã haverá uma batalha naval e [B] Amanhã não haverá uma batalha naval – são contingentes, quer dizêr, não é necessário quê sêjam nem verdadeiras, nem falsas, mas podem sêr ambas verdadeiras ou falsas. Só a alternativa é necessária: ou haverá ou não haverá batalha naval amanhã. O argumento póde sêr representado no diagrama a seguir.
Se A é verdadeira agora, no presente, então amanhã necessariamente haverá uma batalha naval e é impossível quê não haja. Então, B só póde sêr falsa. Assim, a necessidade contradiz a contingência e contraria a possibilidade. Afirmar quê algo é necessário é o mesmo quê afirmar quê é impossível quê não aconteça. O possível contradiz o impossível e contraria o contingente, embora possa coexistir com êste. Então, afirmar quê algo é impossível é afirmar quê não póde sêr necessário, mas só contingente.

Página cento e quatorze
Os estoicos também trataram dêêsse problema, mas com um argumento chamado dominador, ou argumento mestre ou vitorioso. O argumento é atribuído a Diodoro Crono, filósofo do século IV a.C., mas seu único registro conhecido é por Epiteto, já no século I d.C.
Segundo o “dominador”, se os acontecimentos futuros são necessariamente implicados pêlos acontecimentos do presente, então nada de diferente do quê já existe póde acontecer e tudo já está determinado. Se não, tudo póde acontecer e nada está determinado, nem a verdade nem a falsidade.
O ponto de partida é uma aparente incoerência lógica entre as seguintes proposições:
(A) A verdade sobre o passado é necessária: o quê é passado não póde sêr mudado.
(B) O quê é possível tem consequências limitadas: uma proposição possível não implica quaisquer proposições impossíveis, mas somente algumas possíveis.
(C) A existência de possibilidades quê não se realizaram é possível: muitas possibilidades podem coexistir no tempo.
Por exemplo: em qualquer dia, é possível tanto quê você venha à aula quanto quê não venha. Então, antes de você vir ou não à aula, as possibilidades são iguais, mas apenas uma delas se realizará. Agora, será quê conseguimos organizar essas três proposições juntas em um argumento? Isso não é fácil.
A perplexidade surge quando tentamos determinar qual das três proposições deve sêr a conclusão: parece quê somos obrigados a concluir quê tudo o quê é possível ou já é de fato ou necessariamente de fato será. Mas, se for isso mesmo, se tudo o quê podemos fazer é o quê de fato fazemos ou faremos, onde está o livre-arbítrio?
O “argumento dominador” e o “argumento da batalha naval” são os mais controversos argumentos filosóficos acerca da possibilidade e da necessidade do futuro.

Você viria à escola ou não viria. As duas possibilidades eram contingentes: poderiam ou não se realizar. Nesse caso, apenas o “ou” é necessário, pois somente uma das possibilidades se realizaria.
ATIVIDADE
Consulte orientações no Manual do Professor.
• Alguém, dentre nós, humanos, conseguiria negar o quê é possível? Em outras palavras: se é necessário agir, hoje, de certa maneira, isso significa quê amanhã será impossível agir de outra maneira? Redija seus argumentos e debata com côlégas.
Produção pessoal. O tema antecipa a discussão sobre o livre-arbítrio.
Página cento e quinze
CONEXÕES com...
ár-te
Representações do real
Na imagem, a inscrição em francês diz: “Isto não é um cachimbo”. Ela é verdadeira ou falsa?
A pintura do belga Renê Magritte (1898-1967) representa bem o paradoxo do mentiroso, mencionado no estudo do estoicismo. Na sua formulação tradicional, o paradoxo apresenta a seguinte situação. Epimênides, o cretense, declara quê todos os cretenses são mentirosos. Epimênides mente ou diz a verdade? Uma maneira de formulá-lo é a seguinte. escrêeva numa fô-lha de papel em branco a seguinte proposição: “ESTA PROPOSIÇÃO É FALSA”. A afirmação, aparentemente simples, é autocontraditória: se for verdadeira, então é falsa; e se for falsa, então é verdadeira.

Magritte foi um dos principais representantes do Surrealismo, um importante movimento de vanguarda do início do século XX, como você estudará no capítulo 12.
Os surrealistas quêstionavam as fronteiras entre realidade e sonho, pois julgavam que o racionalismo exagerado teria levado a Europa à Primeira Guerra Mundial. Para o filósofo alemão Válter Benjamin (1892-1940), o Surrealismo era um movimento radicalmente libertário, capaz de enxergar o inusitado no cotidiano e mostrar aspectos despercebidos da realidade. Já o crítico de; ár-te estadunidense Clement Greenberg (1909-1994) escreveu quê surrealistas como o espanhol Salvador Dalí (1904-1989) estariam mais preocupados em retratar a própria consciência do quê a realidade.
De todos os surrealistas, Magritte era o mais filosófico. Suas obras são intencionalmente paradoxais e freqüentemente representam situações ou objetos comuns, mas descontextualizados ou mostrados de maneira pouco usual. A traição das imagens é um bom exemplo. O paradoxo não deixa de apresentar uma verdade: o quê se vê realmente não é um cachimbo, mas a imagem de um.
Se a filosofia almeja a verdade, a; ár-te sempre nos desafia. O encontro da filosofia com a; ár-te póde sêr desconcertante!
- vanguarda
- : do francês avant-garde, literalmente, guarda da frente, a primeira tropa de um exército, a quê vai na frente e dá o primeiro combate ao inimigo. No século XX, o termo passou a sêr usado para nomear movimentos políticos ou artísticos de natureza progressista, quê questionam radicalmente leis ou normas vigentes.
ATIVIDADES
Consulte orientações no Manual do Professor.
1. A aparência é um êrro ou uma forma de se aprossimár da realidade?
1. Resposta pessoal.
2. É melhor suspeitar do engano ou aceitá-lo?
2. Indicações para trabalho com o paradoxo do mentiroso no Manual do Professor.
Página cento e dezesseis
Falácias, ou como identificar os maus argumentos
Os paradoxos são argumentos com premissas aparentemente verdadeiras, mas as contradições a quê levam parecem impossíveis de serem resolvidas. Paradoxos, porém, não são falácias.
A falácia é um êrro de raciocínio ou de argumento, por vezes difícil de identificar.
O primeiro estudo sistemático das falácias foi feito por Aristóteles. Nas Refutações sofísticas, ele analisou como os sofistas defendiam ou criticavam alguma tese e concluiu quê utilizavam “argumentos quê parecem sêr refutações (contestações), porém são realmente falácias”. Ele também distinguiu duas categorias de falácias. As falácias quê dependem da linguagem, atualmente denominadas formais, têm problemas na forma do raciocínio. Estudaremos algumas dessas no próximo capítulo. Já as falácias quê não dependem da linguagem são atualmente denominadas informais. Nestas, o problema está no teor das proposições, ou no efeito pretendido sobre os outros, e não na estrutura lógica. Vamos estudá-las agora.
Desde Aristóteles, é comum o entendimento de quê um argumento falacioso tem a intenção de enganar. Por isso, falácias também são denominadas sofismas. O filósofo alemão artúr Schopenhauer (1788-1860) considerava quê o uso de sofismas era próprio da dialética erística, isto é, a técnica argumentativa quê visa vencer um debate por quaisquer meios, lícitos ou não. As falácias seriam, então, estratagemas ilícitos quê permitiriam a quem argumenta “ficar com a razão”.

Página cento e dezessete
Por isso, para estudar falácias, a distinção entre verdade e falsidade deve sêr combinada com muitos outros fatores contextuais, como a quêm o argumento é dirigido, com qual intencionalidade, por quem é formulado, de qual perspectiva, em qual contexto, com que linguagem etc. Talvez o equívoco não seja intencional e não haja sofisma, mas apenas um paralogismo, isto é, um argumento quê tenta provar uma conclusão, mas é ineficaz para isso.
Portanto, nem todos os êêrros de raciocínio são ruins a ponto de invalidar o argumento. Os lógicos e matemáticos Válter Carnielli (1952-) e ríchard Epstein (1943-) defendem quê, às vezes, é possível consertar o argumento, seja eliminando alguma premissa falsa ou duvidosa, seja complementando as premissas com alguma informação, seja adicionando uma nova premissa. Isso só funciona se o argumento resultante for válido ou mais forte do quê o original; se a premissa acrescentada for plausível ou aceitável, inclusive para quêm originalmente elaborou o argumento; ou se essa premissa for mais plausível do que a conclusão.
Se nada díssu for possível, provavelmente há falácia. Segundo os autores, há falácia:
• quando não houver realmente um argumento;
• quando a falta de lógica e coerência for tão grande quê se torna impossível acrescentar qualquer coisa à discussão;
• quando as premissas do argumento forem falsas ou muito duvidosas e for impossível eliminá-las sem destruir o argumento;
• quando a premissa quê deveria sêr obviamente acrescentada, em vez de melhorar, enfraquece ou invalída o argumento;
• quando a premissa quê deveria sêr obviamente acrescentada para melhorar o argumento é falsa;
• quando a conclusão é evidentemente falsa.
São muitos os tipos de falácias e não há consenso quanto à sua classificação. No entanto, há algumas categorias comumente aceitas, quê às vezes se sobrepõem.
Falácias de ambigüidade não esclarécem o ponto exato do argumento. Por exemplo, anfibologias e equívocos falham porque não especificam o significado dos termos.
Falácias de relevância apresentam premissas irrelevantes para a conclusão pretendida. Por exemplo, a falácia ad verecundiam consiste em citar uma autoridade em vez de dar razões ou evidências, para disfarçar a falta de argumento com falsa modéstia (“verecúndia” significa"vergonha","humildade","despretensão"). Uma falácia dessa categoria, muito comum em propagandas, discursos demagógicos e rêdes sociais, para conseguir mais consumidores, seguidores e cliques, é a ad misericordiam, quê é apelar às emoções e aos sentimentos em vez de dar razões.
Saiba mais
•![]() ALMOSSAWI, Ali. Um livro ilustrado de maus argumentos. Tradução: Diogo Lindner. Nova iórk: JasperCollins Publishers, 2014. Disponível em: https://livro.pw/aqoua. Acesso em: 16 set. 2024. O livro traz, d fórma divertida, definições e ilustrações de algumas falácias.
ALMOSSAWI, Ali. Um livro ilustrado de maus argumentos. Tradução: Diogo Lindner. Nova iórk: JasperCollins Publishers, 2014. Disponível em: https://livro.pw/aqoua. Acesso em: 16 set. 2024. O livro traz, d fórma divertida, definições e ilustrações de algumas falácias.
•![]() RODRIGUES, Abílio éti áu. Lógica viva: ação coletiva. Brasil, c2020-2022. YouTube: [Canal] @logicaviva. Disponível em: https://livro.pw/xqybo. Acesso em: 16 set. 2024. O canal, formado por professores e pesquisadores brasileiros, tem vários vídeos sobre diversas falácias.
RODRIGUES, Abílio éti áu. Lógica viva: ação coletiva. Brasil, c2020-2022. YouTube: [Canal] @logicaviva. Disponível em: https://livro.pw/xqybo. Acesso em: 16 set. 2024. O canal, formado por professores e pesquisadores brasileiros, tem vários vídeos sobre diversas falácias.
Página cento e dezoito
Falácias de pressuposição inadequada dependem de suposições ocultas ou tácitas, ou premissas falsas, implausíveis ou inaceitáveis. Por exemplo, a falácia da evidência anedótica acontece quando alguém se baseia em observações duvidosas, experiências ou histoórias pessoais, sem qualquer comprovação ou estudo, para justificar uma conclusão.
Falácias de indução defeituosa são parecidas, mas dependem de premissas insuficientes ou tendenciosas. Por exemplo, uma generalização apressada se baseia em amostragem insuficiente ou enviesada. Você estudará a indução no próximo capítulo.
ATIVIDADE
Consulte orientações no Manual do Professor.
• Os textos a seguir apresentam exemplos ou críticas a três tipos de falácias: pressuposto inadequado, ad verecundiam e ad misericordiam. Identifique qual exemplifica ou critíca cada um deles.
a)

SALLES, Diogo [Sabe, minha filha, eu falo com os pobres]. Jornal da Tarde, São Paulo, 27 set. 2010.
b)

THYAGÃO. [Resultados da vacína Coronavac]. Diário do Nordeste, Fortaleza, 23 out. 2020.
c)

a) ad misericordiam; b) pressuposto inadequado (evidência anedótica); e c) ad verecundiam.
Página cento e dezenove
RECAPITULE
Na abertura dêste capítulo, citamos o problema das fêik news. Sobretudo em época de eleições, no Brasil e em muitos países, as rêdes sociais são tomadas por fêik news, a ponto de algumas instituições tomarem medidas para combatê-las. Recentemente, a Organização das Nações Unidas para a Educação, a Ciência e a Cultura (Unesco) divulgou um diagrama para representar o entrecruzamento de três conceitos: informação incorréta (misinformation), desinformação (disinformation) e informação enganosa ou má informação (malinformation).
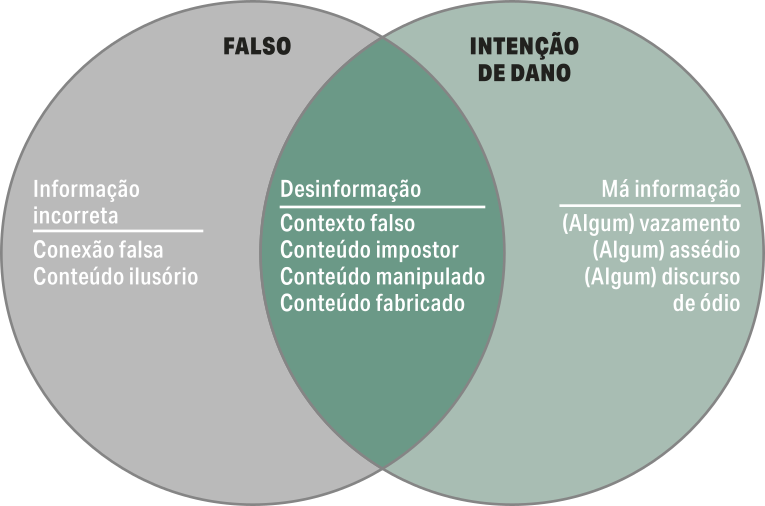
Fonte: IRETON, Cherilyn; POSETTI, Julie. Jornalismo, fêik news e desinformação: manual para educação e treinamento em jornalismo. Tradução: Sarah Rebouças Reedman. Paris: Unesco; Brasília, DF: Representação da Unesco, 2019. (Série Unesco sobre Educação em Jornalismo, p. 48). Disponível em: https://livro.pw/ncxae. Acesso em: 16 set. 2024.
Ao estudar a origem da lógica, ganhamos alguns instrumentos para distinguir entre verdade e falsidade, o quê é fundamental para distinguir entre informação, desinformação e má informação.
Com Aristóteles, você aprendeu a diferença entre validade lógica e verdade científica. Outro ponto importante são os três princípios fundamentais da lógica: identidade, não contradição e terceiro excluído. Esses princípios nos mostram quê há pressupostos para a verdade. Você também aprendeu o método de Venn para representar silogismos com diagramas e compreender mais facilmente inclusão e exclusão em classes.
Com a lógica dos estoicos, consolidamos o conceito fundamental quê liga todos os outros dêste capítulo: validade lógica. Um raciocínio, silogístico ou não, é logicamente válido quando é impossível tirar uma conclusão falsa de premissas verdadeiras. Com isso, entendemos por quê paradoxos e argumentos sobre o futuro desafiam a lógica.
Validade lógica e verdade científica também ajudam a avaliar quando estamos diante de uma falácia ou não, isto é, raciocínios falhos em quê uma conclusão não é suportada por razões ou evidências, e se é possível repará-los.
Agora, uma informação para você refletir: a pesquisa citada na abertura também descobriu quê, no Brasil, as pessoas identificam muito bem informações verdadeiras, ficando atrás apenas de Itália e Estados Unidos. Será quê, no Brasil, o raciocínio lógico tem alguma relação com isso?
Página cento e vinte
ATIVIDADES FINAIS
Consulte orientações no Manual do Professor.
1. O diagrama apresenta algumas falácias comuns, segundo a classificação quê você estudou. Em grupo, pesquisem sobre cada uma delas, identifiquem exemplos e contextos práticos em quê podem ocorrer. Anotem e discutam as diferentes classificações quê encontrarem.
Produção pessoal dos grupos.
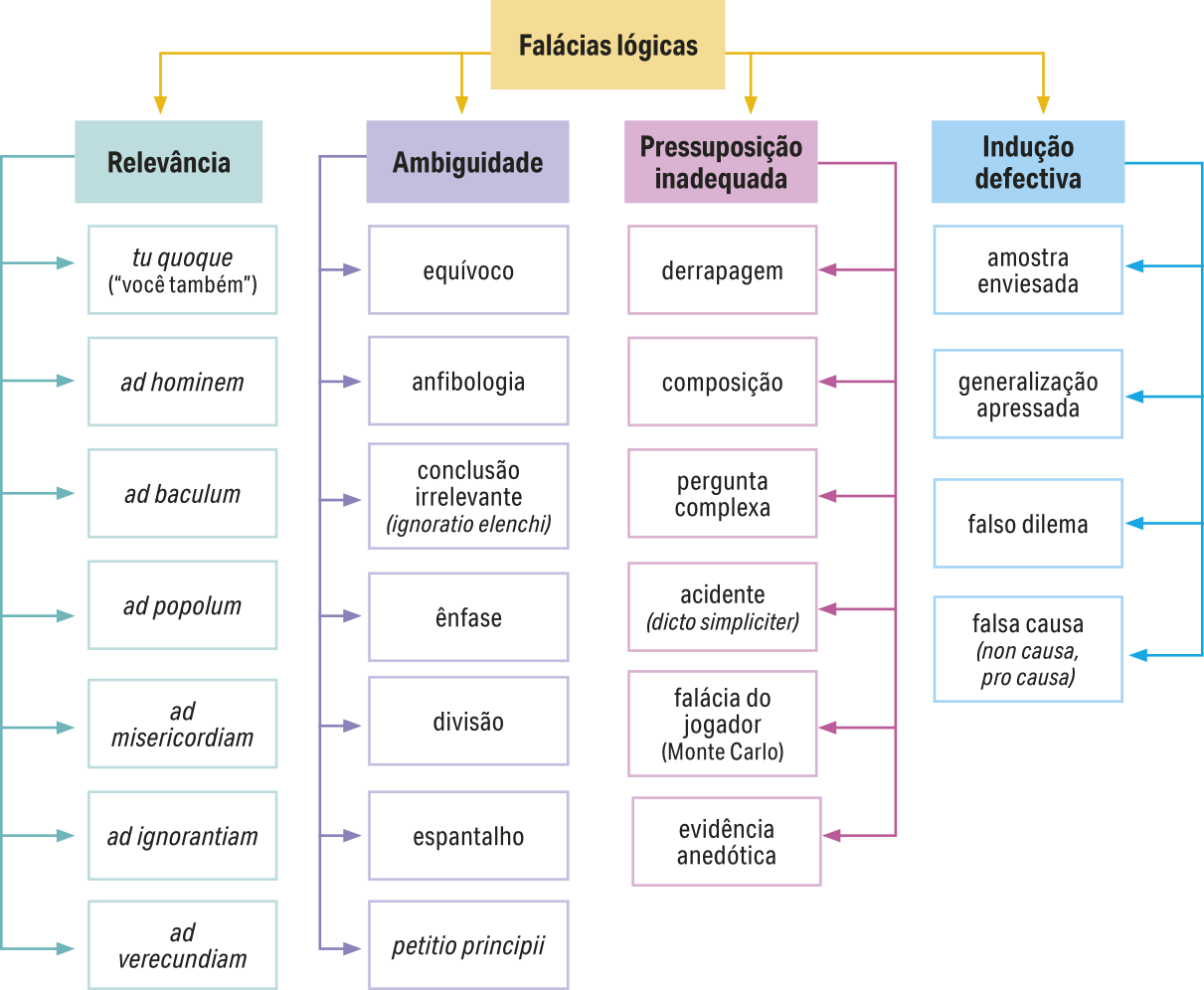
Fonte: SOURATI, Zhivar éti áu. Robust ênd explainable identification ÓF logical fallacies in natural language arguments. Knowledge-Based Systems, [s. l.], v. 266, 22 apr. 2023. p. 4. Tradução nossa. Disponível em: https://livro.pw/sarcr. Acesso em: 17 set. 2024.
2. (Fatec-SP – 2019) Silogismo é uma estrutura lógica quê designa uma forma de raciocínio dedutivo, quê é exemplificado no cartum.

< https://livro.pw/qeoez > Acesso em: 17.06.2019.
Assinale a alternativa quê apresenta a estrutura tradicional pela qual o silogismo é formado.
a) Uma premissa e uma conclusão quê se segue da premissa.
b) Uma premissa e duas conclusões quê decorrem da premissa.
c) Duas premissas e uma conclusão quê se segue delas.
d) Duas premissas e nenhuma conclusão.
e) Três premissas e nenhuma conclusão.
Resposta: c.
Página cento e vinte e um
INVESTIGAÇÃO
Consulte orientações no Manual do Professor.
Por uma ssossiedade menos preconceituosa
O mundo contemporâneo é marcado por grande pluralidade cultural. Os diálogos e as trocas entre grupos com culturas próprias contribuíram para a ampliação da diversidade das práticas e tradições humanas. Ainda assim, o preconceito é um grande problema social na atualidade.
O preconceito manifesta-se de diferentes formas, como nas práticas racistas presentes em muitas sociedades, no desrespeito às culturas de povos tradicionais, na discriminação contra grupos minoritários, no machismo, entre outros exemplos. As práticas e posturas preconceituosas são violentas e geram opressão e limitação dos direitos de indivíduos e grupos ao redor do planêta.
Isso também ocorre na ssossiedade brasileira. O país é marcado por diversas posturas preconceituosas, sêndo o racismo uma das expressões mais recorrentes díssu. De acôr-do com a pesquisa Percepções sobre o racismo no Brasil, realizada pelo instituto Inteligência em Pesquisa e Consultoria Estratégica (Ipec) em 2023, 96% das pessoas negras consideram quê são o grupo quê mais sofre com racismo no país. Além díssu, 57% dos indígenas e 38% dos imigrantes africanos afirmam quê são os quê mais sofrem com práticas racistas. Outro dado da pesquisa é quê mais da mêtáde dos brasileiros afirma já ter presenciado atos racistas e 60% da população considera quê o Brasil é um país racista.
Nesse cenário, é fundamental refletir sobre o racismo e outras formas de preconceito, valorizando as iniciativas e ações de grupos e indivíduos quê lutam pela construção de uma ssossiedade quê valorize e respeite a pluralidade cultural.

Objetivo
Por meio da atividade, vocês vão produzir uma apresentação digital destacando exemplos de iniciativas quê podem contribuir para a construção de uma ssossiedade mais tolerante à pluralidade.
Página cento e vinte e dois
ETAPA
1
Pesquisa
Em grupo, pesquisem informações a respeito do preconceito no Brasil. Identifiquem:
• elemêntos quê contribuem para a compreensão da origem e da permanência das práticas preconceituosas no país;
• dados a respeito dos grupos mais afetados;
• impactos do preconceito na vida cotidiana de diferentes grupos e indivíduos.
ETAPA
2
Produção de texto
Pesquisem informações a respeito do problema na comunidade onde você vive, compreendendo d fórma mais adequada como essa questão se dá no seu cotidiano.
Em seguida, escrevam um texto de aproximadamente duas páginas registrando e organizando akilo quê aprenderam sobre o tema.
ETAPA
3
Exemplos de ações
Nesta etapa, vocês vão pesquisar exemplos de ações criadas por indivíduos, grupos ou instituições governamentais para enfrentar o problema do preconceito e valorizar a pluralidade cultural do país. É possível selecionar ações quê valorizem tradições e côstúmes quê sofrem historicamente com práticas de preconceito, bem como iniciativas visando à conscientização da população e ao enfrentamento do problema. Outra possibilidade é identificar leis e programas sociais quê possam contribuir para reduzir as práticas de preconceito e valorizar a diversidade.
A pesquisa póde sêr feita por meio de buscas na internet, selecionando sáites de organizações não governamentais quê atuem na luta contra o preconceito, bem como órgãos públicos, centros de pesquisa, jornais ou revistas, entre outras fontes com informações qualificadas sobre o tema. Dê maior destaque a exemplos de ações quê foram organizadas em sua comunidade, aproximando a quêstão da realidade que vocês vivenciam cotidianamente.

Página cento e vinte e três
ETAPA
4
Aprofundamento
Com base na pesquisa, escôlham duas iniciativas quê o grupo considere mais impactante ou importante. Ampliem a pesquisa a respeito dos exemplos, obtendo um detalhamento mais abrangente dessas iniciativas. Registrem e organizem as informações de modo quê possam socializar o material com côlégas em sala de aula.
ETAPA
5
Socialização
Durante a socialização, utilizem as kestões a seguir para discutir as informações apresentadas por todos.
• O quê há em comum entre os diversos exemplos de iniciativas selecionados?
• De quê modo as iniciativas quê lutam contra o preconceito impactaram positivamente na ssossiedade?
• O quê ainda póde sêr feito para ampliar os impactos de iniciativas semelhantes às selecionadas?
• De quê modo é possível mobilizar as ideias pesquisadas a fim de transformar positivamente a comunidade onde você vive?
• De quê maneira é possível mobilizar conceitos filosóficos estudados para refletir e pensar em iniciativas visando à luta contra o preconceito na comunidade?
ETAPA
6
Montagem
De posse das informações e discussões, cada grupo deverá montar uma parte da apresentação digital a respeito dos exemplos selecionados. A apresentação deve conter:
• informações das iniciativas pesquisadas;
• ideias quê possam sêr mobilizadas pela comunidade para lutar contra o preconceito e contribuir para a criação de uma ssossiedade mais tolerante.
A apresentação digital póde utilizar recursos multimídias variados, como textos, áudios, imagens e vídeos. É possível combinar esses recursos com ferramentas práticas disponíveis na internet ou outros recursos utilizados pêlos membros do grupo.

Página cento e vinte e quatro
ETAPA
7
Apresentação
Após a preparação da apresentação, os grupos devem reunir todo o material em um único espaço, no qual o trabalho possa sêr divulgado. É possível criar uma página em rêdes sociais ou registrar todo o material em um sáiti. Existem platafórmas gratuitas quê podem sêr utilizadas com essa finalidade.
ETAPA
8
Divulgação
Divulguem o material produzido à comunidade, compartilhando os línkis de acesso da apresentação. Além díssu, com a supervisão do professor, organizem um momento de discussão coletiva da apresentação com a comunidade escolar. Nesse momento, expliquem como o projeto foi organizado e destaquem as principais descobertas. Além díssu, abram espaço para escutar sugestões da comunidade, ampliando o escôpo do trabalho.
ETAPA
9
Autoavaliação
A etapa de autoavaliação é importante para promover a discussão a respeito do papel desempenhado por cada estudante. O roteiro a seguir póde contribuir para essa discussão.
• Como você avalia os resultados do projeto como um todo?
• O quê poderia ter sido feito de outra forma?
• Como os membros do grupo trabalharam e se comunicaram entre si?
• Como foi a receptividade da apresentação na comunidade?
• Como você avalia sua participação no grupo?
• O quê você mais gostou de fazer?
• De quê forma você ajudou o grupo?
• Você acredita quê poderia ter ajudado mais?


Página cento e vinte e cinco