CAPÍTULO
7
Pensamento crítico e argumentação

Em 2015, na Universidade de Turim, Itália, o escritor, filósofo e semioticista Umberto Eco (1932- 2016) fez declarações polêmicas sobre a internet.

As declarações de Eco podem sêrser questionadas. Afinal, as rêdesredes sociais não dão voz apenas a imbecis. Mas ele certamente identificou uma situação grave: com o crescimento da internet, principalmente das rêdesredes sociais, as mais estapafúrdias e estranhas opiniões passaram a circular livremente no mundo todo, em quantidade e velocidade extraordinárias.

Esse fenômeno foi chamado de pós-verdade: fatos são irrelevantes diante de crenças proferidas, mesmo quêque sêjamsejam falsas. Atualmente, parece pouco importar se uma opinião tem fundamento na realidade ou não. Esse é o contexto geral em quêque evoluíram as fêikfake news, quêque você estudou no capítulo 6.

Agora, você vai estudar um pouco de lógica sôbisob uma perspectiva contemporânea e, com isso, aprimorar sua capacidade de argumentar e pensar criticamente.

Consulte orientações no Manual do Professor.

1. Qual a é importânssiaimportância dos fatos frente às opiniões?

1. Fatos tornam opiniões verdadeiras ou falsas.

2. “Uma mentira repetida mil vezes torna-se verdade”. O quêque você pensa sobre essa frase?

2. Resposta pessoal. Espera-se quêque os estudantes concluam quêque uma mentira continua sêndosendo mentira, não importa quantas vezes seja repetida. No entanto, a repetição pódepode provocar a ilusão de verdade.

3. Com quêque meios você busca defender as suas opiniões?

3. Resposta pessoal. Argumentar é uma forma racional de defender opiniões, com respeito aos fatos.

Página cento e vinte e seis126

Lógica e matemática

Aproximar lógica e matemática é um sonho antigo. Filósofos e cientistas, como o espanhol Ramon Llull (1232-1316) e o alemão Gottfried W. Leibniz (1646-1716), imaginaram a possibilidade de uma linguagem para analisar e exprimir inferências com exatidão. Entretanto, o sonho só se realizou no século XIX, quando o inglês GiórgiGeorge Boole (1815-1864) exprimiu as inferências do quadrado lógico como se fossem equações algébricas. Poucos anos depois, o estadunidense xárlêsCharles S. Peirce (1839- 1914) mostrou quêque inferências não são equações, já quêque não dizem respeito a quantidades. Peirce inventou diversos sistemas de lógica, inclusive com diagramas, e foi o primeiro a usar conectivos lógicos para descrever circuitos elétricos. Na mesma época, o austríaco Gottlob Frege (1848-1925), partindo não da álgebra, mas da aritmética, também inventou uma linguagem com fórmulas para o pensamento dedutivo, entendendo proposições como funções. No século XX, os ingleses álfredAlfred N. Whitehead (1861-1947) e berrtrãBertrand Russell (1872-1970) tentaram derivar toda a matemática de alguns poucos princípios lógicos, uma tentativa quêque denominaram logicismo. O lógico e matemático Kurt Gödel (1906-1978) mostrou, nos anos de 1930, quêque isso é impossível. Ludwig witenstainWittgenstein (1889-1951), quêque foi aluno de Russell, escreveu o importante livro Tractatus logico-philosophicus (1922), no qual tentou decifrar de uma vez por todas a relação entre linguagem e realidade e definir os limites da ciência. No Brasil, níltomNewton da Costa (1929-2024), já na segunda mêtádemetade do século XX, avançou muito na pesquisa sobre lógicas não clássicas.

Esses são só uns poucos exemplos. A lógica se desenvolvê-udesenvolveu tanto quêque se tornou uma das principais ciências contemporâneas. É impossível resumir essa história em poucas páginas, mas alguns pontos básicos podem sêrser estudados para melhorar nosso pensamento crítico.

Página cento e vinte e sete127

Argumentos

No capítulo 6, estudamos o silogismo aristotélico e os indemonstráveis do estoicismo. No entanto, um argumento pódepode ter outras formas. Cada raciocínio possível corresponde a um argumento quêque visa produzir uma crença: a verdade da conclusão é aceita porque há razões dadas como premissas. Considere o seguinte exemplo.

Tendo em vista quêque os crimes virtuais têm se tornado cada vez mais freqüentesfrequentes e robustos, a Inteligência Artificial pódepode sêrser uma grande aliada na segurança digital, pois ela permite monitorar padrões de comportamento, alertando sobre possíveis atividades maliciosas.

GALVANI, jécssonJackson. Entenda por quêpor que a Inteligência Artificial empolga tanto a área da tecnologia. Folha Digital, [s. l.], 23 abr. 2023. Disponível em: https://livro.pw/yhoag. Acesso em: 23 ago. 2024.

Nessa afirmação, temos um argumento: a representação ou comunicação de uma inferência consciente (um raciocínio), quêque apresenta razões ou evidências em apôioapoio a uma conclusão cuja verdade se pretende estabelecer. Para quêque isso fique claro, vamos desmembrar o trecho citado, assim:

1. crimes virtuais têm se tornado cada vez mais freqüentesfrequentes e robustos;

2. a inteligência artificial permite monitorar padrões de comportamento;

3. a inteligência artificial permite alertar sobre possíveis atividades maliciosas;

4. logo, a inteligência artificial pódepode sêrser uma grande aliada na segurança digital.

De 1 a 3, temos as premissas, isto é, razões ou evidências para a aceitação da verdade de 4, a conclusão. Bastam uma premissa e uma conclusão para compor um argumento simples. Por exemplo, as sentenças 3 e 4, isoladas, compõem um argumento.

Independentemente da quantidade de premissas, porém, todo argumento deve ter uma única conclusão. Quando há mais de uma conclusão, temos uma argumentação, isto é, alguns argumentos encadeados, de modo quêque a conclusão de um sérveserve de premissa a outro, e assim sucessivamente, iniciando com premissas especificamente formuladas, passando por conclusões parciais, até estabelecer a conclusão principal, quêque não precisa estar por último. Por isso, é importante saber reconhecer quando uma sentença qualquer é premissa, conclusão, ou mesmo nenhuma das duas.

Página cento e vinte e oito128

Reconhecer argumentos, premissas e conclusão

Você já deve ter percebido quêque, no dia a dia, quase ninguém se preocupa em separar claramente premissas e conclusões. É muito mais comum, e talvez até mais fácil, usar diferentes formas de discurso junto com uma argumentação, como explicações, narrações, descrições etc. Por isso, quando queremos deixar nóssosnossos argumentos bem claros, utilizamos termos e expressões para indicar as premissas e a conclusão. Alguns indicadores de premissa são: quêque, já quêque, porque, visto quêque, dado quêque, uma vez quêque, pela razão de quêque etc. Alguns indicadores de conclusão: portanto, por conseguinte, consequentemente, então, dessa maneira, segue-se quêque, daí quêque etc. Observe os exemplos.

• Porque os animais podem sofrer e qualquer um quêque sofra deve sêrser tratado com ética (premissa), segue-se quêque os animais merécemmerecem sêrser tratados com ética (conclusão).

• Já quêque os animais não possuem deveres (premissa), portanto, também não possuem direitos (conclusão).

Indicadores ajudam, mas não são imprescindíveis. Em argumentos, o mais importante é a ligação inferencial entre premissas e conclusão. Ora, nem toda conclusão é conscientemente justificada. Você já não se pegou pensando sobre um assunto sem entender direito de onde isso vêmvem? Pois, então, é assim quêque pensamos: fazemos ilações sem ter plena consciência de quais premissas apoiam certa conclusão, repetindo o quêque aprendemos sem refletir. Por isso, sem indicadores, nem sempre é fácil definir se há uma inferência intencional na linguagem – o quêque cabe a quem interprétainterpreta.

Além díssudisso, nem sempre as premissas são suficientemente claras. Às vezes, por falta de cuidado, um argumento pódepode sêrser mal enunciado e as premissas estarem confusas. Ou ainda, quem argumenta pódepode supor quêque não vale a pena enunciar uma premissa por ela sêrser muito evidente, ou geralmente aceita, ou mesmo tão polêmica quêque é melhor escondê-la. Quando, por qualquer razão, uma ou mais premissas restam implícitas, argumentos são chamados de entimemas. Observe os exemplos.

Premissa: A pena de morte causa a morte de pessoas inocentes.

Conclusão: Portanto, a pena de morte é errada.

Aqui, uma premissa importante para a conclusão não está expressa: “Causar a morte de pessoas inocentes é errado”. Ao explicitá-la, o raciocínio fica evidente.

Premissa 1: A pena de morte causa a morte de pessoas inocentes.

Premissa 2: Causar a morte de pessoas inocentes é errado.

Conclusão: Portanto, a pena de morte é errada.

Página cento e vinte e nove129

Eliminar a ambigüidadeambiguidade

Como você estudou, Aristóteles (384 a.C.-322 a.C.) definiu quêque só proposições declarativas podem sêrser premissas ou conclusões de argumentos. Mas por quêpor que isso é importante? Porque nem sempre a linguagem está livre de ambiguidades. Reflita um pouco: uma pergunta pódepode sêrser elaborada, uma ordem pódepode sêrser dada, pedidos e preces são feitos, mas só proposições podem sêrser afirmadas ou negadas. Para tanto, devem obrigatória menteobrigatoriamente sêrser bem expressas em fórmulas bem formadas, isto é, estar de acôr-doacordo com as regras da gramática de alguma língua. Por exemplo, “eu te amo”, “yo te amo” e “I love you” são diferentes sentenças, em diferentes idiomas, quêque exprimem a mesma proposição. Mas você diria quêque “love vérsusversus tras eu” é uma sentença bem formada? Talvez, se fizer parte de uma obra de; ár-tede arte, possa transmitir alguma informação. Mas não é evidente quêque qualquer grupo de palavras possa ter um valor de verdade. De fato, a depender do contexto e da formulação, cértascertas expressões, ainda quêque bem formadas, podem sêrser ambíguas. Por exemplo, se digo: “Alguns pratos são do meu gosto”, alguém pódepode ficar em dúvida se me refiro à comida ou à louça e me perguntar a quêque, especificamente, estou me referindo. Se isso acontece, é preciso eliminar a ambigüidadeambiguidade para quêque seja possível identificar as proposições e, depois, os argumentos.

Na tirinha, CálvinCalvin foi convincente, mas você consegue distinguir alguma premissa e uma conclusão?

Consulte orientações no Manual do Professor.

• exâmíneExamine os exemplos e identifique os quêque exprimem argumentos. Justifique a sua resposta com argumentos.

a)

A Inteligência Artificial está se tornando cada vez mais presente nas diversas áreas da ssossiedadesociedade. A saúde é uma área quêque pódepode sêrser impactada diretamente pela IA. Desde a análise de imagens médicas até o desenvolvimento de novos medicamentos, a IA pódepode ajudar a melhorar o diagnóstico e o tratamento de doenças. Além díssudisso, a IA também pódepode sêrser usada para aprimorar os sistemas de vigilância de epidemias, dando um alcance mais amplo na prevenção e no contrôlecontrole de doenças.

GALVANI, jécssonJackson. Entenda por quêpor que a Inteligência Artificial empolga tanto a área da tecnologia. Folha Digital, [s. l.], 23 abr. 2023. Disponível em: https://livro.pw/yhoag. Acesso em: 29 maio 2024.

a) Não é argumento.

Página cento e trinta130

b)

Oh balança para direita

Balança para a esquerda

Joga as duas mãozinha pra cima

Videira, videira, videira, videira

Balança para direita

Balança para a esquerda

Joga as duas mãozinha

(Sai do chão e vem)

Oh balança, balança tudo

Cada vez balança mais

Enquanto Deus for minha base

Nós balança, mas não cai

MC JUNIINHO. Balança mas não cai (part. Irmão Lázaro). Belo Horizonte: lêtrasLetras, c2003-2024. Disponível em: https://livro.pw/dtdnp. Acesso em: 23 ago. 2024.

b) Não é argumento.

c) Se da doenças IA novos a Artificial tornando vez ssossiedadesociedade mais nas. A diversas análise saúde! é uma está. diretamente IA área quêque pódepode desenvolvimento ajudar sêrser e impactada. Desde presente de médicas; imagens até medicamentos o Inteligência pódepode de cada, a pela melhorar a de áreas o diagnóstico, o tratamento.

c) Não é argumento.

d) Considere o seguinte argumento:

4 + 4 = 8;

8 ÷ 2 = 4;

8 < 4.

d) Não é argumento.

e) Chamamos ℕ de conjunto dos números naturais; ℤ, conjunto dos números inteiros; ℚ, conjunto dos números racionais. Seja, então, o argumento:

1: ℕ = {1,2,3,4,…} ⊂ ℤ={…,−3,−2,−1,0,1,2,3,4,…}.

2: ℤ = {…,−3,−2,−1,0,1,2,3,4,…} ⊂ ℚ={$\frac{a}{b}$: a e b são inteiros, b≠0}.

3: ℕ = {1,2,3,4,…} ⊂ ℚ={$\frac{a}{b}$: a e b são inteiros, b≠0}.

e) É argumento.

f)

“[…]. O maior dos castigos para alguém é sêrser governado por alguém inferior, quando ele próprio não quer assumir o govêrnogoverno. Aparentemente, é sentindo esse temor quêque os homens de bem exercem o govêrnogoverno quando o assumem e é nesse momento quêque assumem o govêrnogoverno, não como se nele buscassem algo de bom ou uma boa vida, mas como se estivessem diante de algo quêque não podem evitar e como se pudessem entregá-lo a alguém melhor quêque eles ou a um igual. Se existisse uma cidade de homens de bem, poderia muito bem acontecer quêque a disputa deles fosse para conseguir ficar fora do govêrnogoverno, como hoje é para assumi-lo; e aí ficaria evidente quêque realmente o verdadeiro governante, por sua natureza, não tem em vista sua vantagem pessoal, mas a do subordinado. Assim, todo homem de discernimento preferia receber ajuda de um outro a dedicar-se ao trabalho de ajudar um outro.”

PLATÃO. A república: ou sobre a justiça, diálogo político. Tradução: Anna Lia Amaral de Almeida Prado. São Paulo: Martins Fontes, 2006. p. 32.

f) É argumento.

Página cento e trinta e um131

Diagramação de argumentos

Você já deve ter percebido quêque identificar argumentos não é tão fácil. Além dos diagramas de Venn, quêque você já conhece, há outra forma de diagramação quêque pódepode ajudar a separar claramente premissas, conclusão e outras sentenças quêque não são nem uma coisa nem outra. Observe um exemplo.

O bom senso é a coisa do mundo mais bem partilhada, pois cada qual pensa estar tão bem provido dele, quêque mesmo os quêque são mais difíceis de contentar em qualquer outra coisa não costumam desejar tê-lo mais do quêque o têm. E não é verossímil quêque todos se enganem a tal respeito; mas isso antes testemunha quêque o pôdêrpoder de bem julgar e distinguir o verdadeiro do falso, quêque é própriamentepropriamente o quêque se denomina o bom senso ou a razão, é naturalmente igual em todos os homens; e, destarte, quêque a diversidade de nossas opiniões não provém do fato de serem uns mais racionais do quêque outros, mas somente de conduzirmos nóssosnossos pensamentos por vias diversas e não considerarmos as mesmas coisas. Pois não é suficiente ter o espírito bom, o principal é aplicá-lo bem. As maiores almas são capazes dos maiores vícios, tanto quanto das maiores virtudes, e os quêque só andam muito lentamente podem avançar muito mais, se seguirem sempre o caminho reto, do quêque aqueles quêque correm e dele se distanciam.

A passagem é claramente uma argumentação, mas como está organizada? Qual é a conclusão principal? Para descobrir, siga o passo a passo.

Primeiro, isolamos as declarações do texto, deixando de lado todos os indicadores.

1. O bom senso é a coisa do mundo mais bem partilhada.

2. Cada qual pensa estar tão bem provido dele, quêque mesmo os quêque são mais difíceis de contentar em qualquer outra coisa não costumam desejar tê-lo mais do quêque o têm.

3. Não é verossímil quêque todos se enganem a tal respeito.

4. O pôdêrpoder de bem julgar e distinguir o verdadeiro do falso, quêque é própriamentepropriamente o quêque se denomina o bom senso ou a razão, é naturalmente igual em todos os homens.

5. A diversidade de nossas opiniões não provém do fato de serem uns mais racionais do quêque outros, mas somente de conduzirmos nóssosnossos pensamentos por vias diversas e não considerarmos as mesmas coisas.

6. Não é suficiente ter o espírito bom, o principal é aplicá-lo bem.

7. As maiores almas são capazes dos maiores vícios, tanto quanto das maiores virtudes.

8. Os quêque só andam muito lentamente podem avançar muito mais, se seguirem sempre o caminho reto, do quêque aqueles quêque correm e dele se distanciam.

Depois, escrevemos somente os números das sentenças, segundo a ordem do texto, para evidenciar os indicadores. Assim:

[1], pois [2]. E [3], mas isso antes testemunha quêque [4]; e, destarte, quêque [5]. Pois [6], [7] e [8].

Página cento e trinta e dois132

A lógica do texto

Com isso, já conseguimos vislumbrar a lógica do texto e identificar todas as premissas e todas as conclusões, as parciais e a final. E qual é essa conclusão, aquela quêque dá sentido ao texto? Antes de responder, obissérveobserve quêque em [4] há uma sentença quêque não é premissa nem conclusão, mas uma definição de bom senso. Se a compararmos, por exemplo, com [2], quêque ocorre como premissa de [1], fica claro quêque essa definição não tem importânssiaimportância inferencial na argumentação, mas sérveserve para fixar o significado de bom senso. A própria sentença [4] é conclusão de [1] e [3]; e assim por diante.

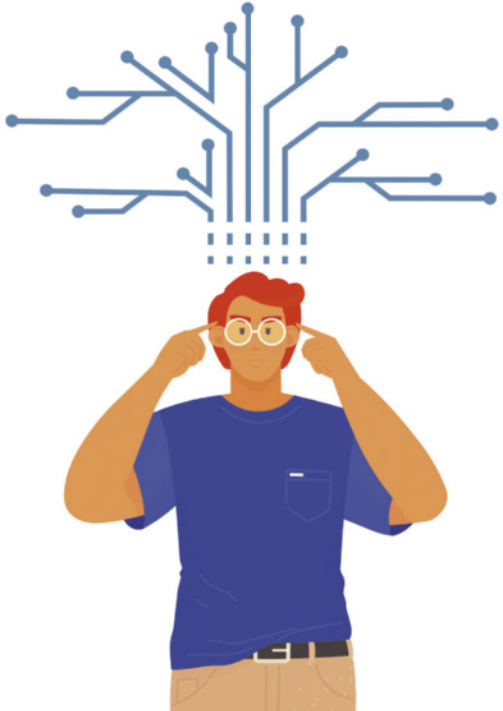
Está caracterizada a argumentação. Mas será quêque o objetivo dessa argumentação é quêque você aceite uma definição de bom senso? Para descobrir, vamos diagramar a estrutura inferencial da passagem. Usando setas para indicar as passagens das premissas às conclusões, as conclusões parciais quêque sérvemservem de premissa a outro argumento serão evidenciadas até a identificação da conclusão principal. Observe.

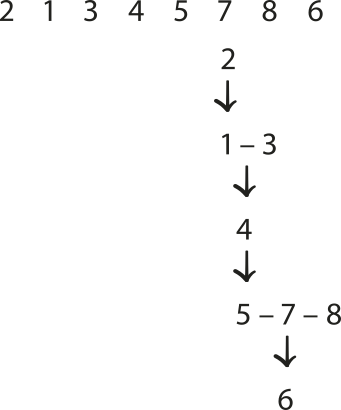
Uma vez identificadas premissas e conclusão, é útil colocar o argumento em ordem padrão, isto é, as premissas antes da conclusão, quêque pódepode sêrser separada por uma linha, como já vimos. Esse é o quarto e último passo.

Consulte orientações no Manual do Professor.

• Conclua a diagramação do argumento elaborando, por escrito e no caderno, o quarto e último passo.

Destaque quêque alguns conectivos podem sêrser substituídos, desde quêque se preserve o sentido (“pois”, “visto quêque”, “uma vez quêque” etc.). Isso indica que na linguagem ordinária o uso modifica os significados, o que a torna ambígua. Em uma linguagem simbólica ou em um cóódigocódigo, cada signo tem um significado único.

O exame do trecho do Discurso do método, de RenêRené Descartes (1596-1650), mostra quêque a ordem do texto não corresponde necessariamente à ordem lógica do raciocínio. Você percebe a importânssiaimportância de um método bem-organizado para a análise argumentativa? Pois, então. Qual é mesmo o título da obra da qual essa passagem foi retirada? Discurso do método!

Página cento e trinta e três133

Tipos de argumentos

Vamos estudar dois tipos de argumentos básicos: dedução e indução. A dedução é o raciocínio quêque vai do geral ao particular e a indução, do particular ao geral. Vamos compreender melhor.

Dedução

Em linguagem coloquial, deduzir é praticamente um sinônimo de inferir ou de concluir, no sentido de tirar uma conclusão. Quem nunca falou ou pensou algo como “deduzi díssudisso quêque...”? Se isso não é bem rigoroso, ao menos indica um ponto interessante: a dedução é comumente identificada com o raciocínio lógico em si, aquele definido pela noção de validade lógica, que você já conhece.

Em argumentos dedutivos, se as premissas forem verdadeiras, a conclusão necessariamente será verdadeira e é impossível quêque seja falsa.

Compare os exemplos.

O fio abaixo de 2 é uma convenção e significa quêque a sentença seguinte é a conclusão. pódePode sêrser substituído pelo sín-bolosímbolo œ. Nesta obra adotamos em geral o uso do fio.

Analise o exemplo A: as premissas são tão particulares quanto a conclusão. Isso mostra quêque a ideia comum de dedução – do geral ao particular – é incorrétaincorreta. Na verdade, o raciocínio vai do contingente ao necessário, isto é, do cazualcasual – “se chover” não implica quêque choverá – ao quêque necessariamente deve ocorrer – não irei à aula de lógica uma vez quêque chover. Como não há contradição, a dedução é válida.

Quem usar o argumento A em um dia ensolarado pódepode até não cometer nenhum êrroerro lógico, mas será quêque raciocinou corretamente?

Agora ezamíneexamine o exemplo B. Ao menos uma premissa de B não é verdadeira e, mesmo assim, a conclusão é necessária.

Por isso, embora válido, B é incorrétoincorreto. Isso, porém, em nada afeta sua validade: se não há contradição, as sentenças do argumento são consistentes entre si.

Página cento e trinta e quatro134

Explosão na lógica

Os exemplos A e B você já conheceu com o estoicismo – modus ponens! Os estoicos descobriram um princípio quêque, na Idade Média, foi denominado ex falso sequitur quodlibet (em português: “da falsidade, segue o quêque se quiser”). Em outros termos: de premissas falsas, é possível deduzir qualquer conclusão, falsa ou verdadeira. Mesmo quêque um argumento inteiramente constituído de sentenças falsas seja incorrétoincorreto, pelo ex falso, ele é válido!

No século XX, o ex falso ficou conhecido como princípio ou lei de explosão: se, da falsidade, segue-se o quêque se quiser, então, da contradição, segue-se qualquer conclusão – e isso explode a lógica!

Validade e consistência

Perceba a estreita conexão entre validade e consistência. Validade implica uma impossibilidade: se as premissas forem verdadeiras, é impossível a conclusão sêrser falsa. A consistência também: se o conjunto das proposições for inconsistente, é impossível quêque todas as proposições sêjamsejam verdadeiras. No exemplo A, se eu sair de casa mesmo com chuva, esse fato falsificaria a premissa 1. É claro quêque qualquer um de nós, a qualquer momento, pódepode entrar em contradição e fazer algo diferente do quêque falou, mas isso não elimina a contradição; ao contrário, torna-a evidente!

Isso quer dizêrdizer quêque a lógica consegue revelar todas as falsidades do mundo? Não, mas, com a lógica, você consegue saber se um grupo de sentenças pódepode explodir, isto é, se há contradição entre elas.

Testando a consistência de argumentos

Imagine quêque você é um engenheiro de computação e precisa saber se certos comandos funcionarão sem fazer a máquina esquentar e explodir. Ou seja, você precisa montar um argumento válido com as sentenças disponíveis. Teste, então, a consistência: monte o argumento e negue a conclusão, afixando a expressão “É falso que...” a ela. Se o argumento resultante for válido, então as sentenças de teste são consistentes, e o original inconsistente e inválido. Nesse caso, é melhor parar antes quêque a máquina comece a esquentar. E vice-versa: resultar em contradição, então o argumento original é consistente e válido. Nesse caso, fique tranqüilotranquilo e siga com a programação.

Consulte orientações no Manual do Professor.

• Existem três tipos de sentenças logicamente importantes.

Tautologia: é sempre verdadeira, quaisquer quêque sêjamsejam os fatos. Exemplos: “ou é dia ou é noite”; “ou o tímetime ganha ou não ganha”.

Contradição: é sempre falsa, quaisquer quêque sêjamsejam os fatos. Exemplos: “é noite, mas não é noite”; “João está morto e está vivo”.

Contingência: pódepode sêrser verdadeira ou falsa, dependendo dos fatos. Exemplos: “nunca chove aos sábados”; “João namora Maria”.

Agora, usando as combinações de tautologia, contradição e contingência, elabore pelo menos um argumento, respeitando as seguintes condições: a) ilustrar o ex falso; b) explodir o princípio de não contradição.

Chove; não chove; logo, o céu é azul.

Página cento e trinta e cinco135

Tipos de dedução

Estudamos no capítulo 6 os cinco indemonstráveis da lógica estoica. Agora, vamos desenvolver o assunto e estudar mais dois padrões argumentativos: simplificação e silogismo hipotético.

Daqui em diante, alguns símbolos básicos da lógica matemática contemporânea serão usados. Por conveniência, consulte o qüadroquadro sempre quêque necessário.

Consulte orientações no Manual do Professor.

1. Explique como é realizado o teste de consistência das proposições. Utilize as noções de consistência, validade e correção na sua explicação.

1. Se as premissas e a negação da conclusão formarem um conjunto consistente, é possível quêque as premissas sêjamsejam todas verdadeiras e a conclusão original falsa. O argumento seria, então, inválido. Por outro, se as premissas e a negação da conclusão formarem um conjunto inconsistente, então é impossível quêque as premissas sêjamsejam verdadeiras e a conclusão modificada falsa. O argumento original seria, então, válido.

2. Traduza simbolicamente as sentenças a seguir. Utilize A, B etc. para simbolizá-las – por exemplo, A:

“Chove”; B: “Faz sol” – e escolha corretamente o operador lógico para cada caso.

1. Amanhã haverá uma batalha naval ou não haverá uma batalha naval.

A ~ B

2. É falso quêque não haverá uma batalha naval amanhã.

¬ B

3. Ou haverá ou não haverá uma batalha naval amanhã, não há outra possibilidade.

A ~ B

4. Se não houver uma batalha naval amanhã, então irei à aula.

¬ A ¢ C

5. Só ficarei em casa se houver uma batalha naval amanhã.

D 9 A

6. Não haverá batalha naval amanhã e irei à aula.

B ^ C

Simplificação

A simplificação é o padrão argumentativo quêque parte de uma conjunção, uma sentença composta, formada por outras duas simples ligadas por “e”. Por exemplo: “Machado de Assis escreveu Dom Casmurro, e kámõesCamões escreveu Os Lusíadas”. A sentença, como você sabe, é verdadeira. Compare com outro exemplo: “Platão escreveu A República, e Maquiavel escreveu O Pequeno Príncipe”. Ora, quem fizer essa afirmação não terá dito a verdade, porque Maquiavel (1469-1527) escreveu O Príncipe, mas O Pequeno Príncipe foi escrito pelo ilustrador e piloto francês antoníAntoine de Saint-Exupéry (1900-1944), mais de 400 anos depois.

Página cento e trinta e seis136

Isso mostra quêque uma conjunção só é verdadeira se as proposições quêque a compõem forem verdadeiras. Basta uma sêrser falsa e a conjunção será falsa, mas perceba quêque isso não invalídainvalida o argumento.

Então, para contradizer uma conjunção (e)conjunção e mostrar quêque ela é falsa, não basta negar só uma das proposições, todas têm quêque sêrser negadas em conjunto. A contraditória de uma conjunção é uma disjunção entre as negações de cada uma das disjuntivas.

Assim:

Silogismo disjuntivo

O silogismo disjuntivo parte de uma disjunção simples, isto é, uma sentença quêque exprime uma possibilidade entre duas alternativas. Observe o exemplo.

Obviamente, também é válida a fórmula: 1. A ~ B; 2. ¬ A; 3. œ B.

Consulte orientações no Manual do Professor.

• escrêevaEscreva uma conjunção com cinco proposições diferentes e sua contraditória, em linguagem ordinária e simbólica.

Em qualquer dos exemplos, a conclusão poderia sêrser A ou B. No exemplo do argumento D, seria um caso de ex falso.

Página cento e trinta e sete137

Eliminar a ambigüidadeambiguidade

Perceba, no exemplo E quêque, na premissa 1, as alternativas não são necessariamente excludentes. Em algum mundo possível, certamente muito diferente do nosso, Maquiavel poderia ter escrito os dois livros. Independentemente díssudisso, no nosso mundo, o raciocínio permanécepermanece válido, pois basta quêque uma alternativa seja verdadeira para quêque a disjunção se mantenha. O quêque permite a conclusão é, na verdade, a combinação das alternativas, de modo quêque a afirmação de uma disjuntiva implica a falsidade da outra, ou vice-versa. A premissa 1, assim, é só uma disjunção simples e pódepode sêrser ambígua. Observe.

Assim, o argumento é inválido. Uma forma de eliminar a ambigüidadeambiguidade é usar a disjunção exclusiva, como os estoicos: ou Maquiavel escreveu O Príncipe ou O Pequeno Príncipe, mas não ambos. Nesse caso, uma alternativa exclui a outra, e a disjunção só é verdadeira se uma for falsa e a outra verdadeira. Ela é falsa se ambas forem verdadeiras: se Maquiavel escreveu O Príncipe e O Pequeno Príncipe – havendo, então, uma contradição; e, também, se ambas forem falsasse Maquiavel não escreveu nem O Príncipe nem O Pequeno Príncipe, o quêque teria ele escrito, então? Isso mostra quêque a contraditória de uma disjunção é uma conjunção.

• CANAL DO ARGUMENTO. Brasil, c2024. Instagram: [Perfil] @canaldoargumento. Disponível em: https://livro.pw/cbxmo. Acesso em: 23 ago. 2024.

• CANAL DO ARGUMENTO. [S. l.], c2024. sáitiSite: Disponível em: https://livro.pw/bnboy. Acesso em: '23 ago. 2024.

O perfil Canal do Argumento no Instagram traz vários exemplos e análises argumentativas, em linguagem simplificada, para quem busca aprimorar a própria capacidade de argumentar. Há também o sáitisite, com diversos outros conteúdos.

Consulte orientações no Manual do Professor.

• Segundo qual princípio funciona a disjunção exclusiva? Tente reescrever o argumento E, da página 136, em linguagem ordinária e simbólica.

Segundo o princípio do terceiro excluído. Em linguagem ordinária: ou Maquiavel escreveu O Príncipe ou O Pequeno Príncipe, mas não ambos. Maquiavel escreveu O Príncipe. Logo, Maquiavel não escreveu O Pequeno Príncipe. As fórmulas válidas são: I) 1. A ~ B; 2. A; 3. œ ¬ B; II) 1. A ~ B; 2. B; 3. œ ¬ A; III) 1. A ~ B; 2. A; 3. œ ¬ B; IV) 1. A ~ B; 2. ¬ B; 3. œ A. Uma sugestão é perguntar: qual dessas fórmulas seria incorrétaincorreta para o exemplo de Maquiavel? Resposta: II.

Página cento e trinta e oito138

Modus ponens

Como você sabe, o modus ponens foi descoberto por Crisipo (277 a.C.-c. 204 a.C.). Mais tarde, na Idade Média, o estudo dos modos de argumentar com condicionais foi desenvolvido com a teoria das consequências.

O modus ponendo ponens contém duas afirmações, uma na segunda premissa, outra na conclusão. O nome vêmvem do latim ponere: pôr, colocar; por extensão, afirmar. Por exemplo:

A primeira premissa afirma quêque se tênhotenho febre, então minha tempera-túratemperatura aumenta; a segunda, constata quêque de fato tênhotenho febre. A conclusão é consequência lógica: minha tempera-túratemperatura aumenta.

Esse é o modo mais simples e direto de argumentar partindo de uma premissa condicional, ou implicação. Analise a premissa 1, composta de duas sentenças, uma antecedente – posterior ao se e anterior ao então – e uma consequente – posterior ao então. E o quêque ela significa? Isto é, quando é verdadeira? Talvez seja mais fácil entender se começarmos com o quêque ela não significa.

■ ZERKLAERE, Thomasin von. [Die rhetorik]. In: ZERKLAERE, Thomasin von. Der wälsche gast. Ostfranken: [s. n.], 1340. f. 65v. Na estrutura da universidade medieval, essa ilustração representava a Lógica.

É comum interpretar a premissa 1 assim: minha tempera-túratemperatura aumenta porque tênhotenho febre. Mas aí ela seria equivalente a uma sentença universal: sempre quêque tênhotenho febre, minha tempera-túratemperatura aumenta. Perceba quêque, nesse caso, haveria duas condicionais conjugadas: se tênhotenho febre, então minha tempera-túratemperatura aumenta e se minha tempera-túratemperatura aumenta, então tênhotenho febre. Isso seria uma dupla implicação – (A ¢ B) ^ (B ¢ A) –, quêque é melhor expressar assim: minha tempera-túratemperatura aumenta se e somente se tênhotenho febre. Mas a premissa 1 é só uma implicação simples, não uma regra universal.

Essa confusão é falaciosa, pois minha tempera-túratemperatura corporal pódepode aumentar por diversas razões: o dia pódepode estar kemtequente; posso ter insolação; fiz muitos exercícios físicos etc. Essa falácia tem nome: afirmação da consequente. Sua forma é:

Página cento e trinta e nove139

Todos os argumentos na forma do modus ponens são válidos, todos os argumentos na forma da afirmação da consequente são inválidos.

Mas, e a premissa 1, o quêque ela significa, afinal? Ela exprime apenas quêque basta eu ter febre para minha tempera-túratemperatura corporal aumentar. Em outras palavras, o estado febril é condição suficiente para a alta tempera-túratemperatura corporal, mas não necessária.

Você já deve estar se perguntando: como, então, negar uma condicional? É o quêque veremos com o modus tollens.

Modus tollens

Se o modus ponens é a forma dirétadireta de argumentar com condicionais, o modus tollens é a indireta. Em latim, tolere significa “tolher”, “cortar”; por extensão, “negar”. A denominação completa é modus tollendo tollens, o modo quêque, ao néeganegar, nega. Por exemplo:

Compare com o modus ponens. A primeira premissa também é uma condicional: a condição suficiente para João sêrser brasileiro é ter nascido no Brasil. Mas essa condição não é a única nem necessária. É possível, por exemplo, alguém nascer fora do Brasil e, na vida adulta, vir morar no país e optar pela nacionalidade brasileira. A segunda premissa, porém, néeganega essas possibilidades para João e implica quêque ele não satisfaz a nenhuma condição para sêrser brasileiro: não nasceu no país nem optou pela nacionalidade brasileira etc. Essa negação mostra quêque, se nascer no Brasil basta para sêrser brasileiro, sêrser brasileiro é condição necessária de ter nascido no Brasil: todos os quêque nascem no Brasil são brasileiros. Daí a segunda negação, na conclusão: João necessariamente não nasceu no Brasil.

A falácia correspondente do modus tollens é a negação da antecedente. Sua forma é:

A falácia fica clara se pensarmos, por exemplo, quêque João pódepode ter nascido no estrangeiro e, depois de adulto, se naturalizado brasileiro; ou, se nasceu de pai ou mãe brasileira, ele pódepode ter sido registrado em alguma repartição consular brasileira.

Assim como no caso do modus ponens, todos os argumentos na forma do modus tollens são válidos, todos os argumentos na forma da negação da antecedente são inválidos.

Página cento e quarenta140

Como pensar ao contrário sem errar

Talvez seja mais fácil identificar as falácias e evitar confusões se você pensar ao contrário. Não é brincadeira! Falando com mais rigor, tente imaginar as contrapositivas das condicionais. Na contrapositiva, as sentenças quêque compõem a condicional são negadas e aparécemaparecem em ordem invérsainversa. Assim, a equivalência entre as condições necessárias e suficientes é mantida. Observe.

Se a condicional é verdadeira, a contrapositiva também é. Isso mostra quêque a contraditória de uma condicional não é outra condicional. Nenhuma das seguintes condicionais contradiz a premissa 1 do exemplo G: se João não nasceu no Brasil, então é brasileiro; se João nasceu no Brasil, então não é brasileiro. A contraditória de uma condicional é, na verdade, uma conjunção na qual a consequente da condicional deve sêrser negada. Com G, fica assim:

Condicional Se João nasceu no Brasil, então é brasileiro.

Contrapositiva Se João não é brasileiro, então não nasceu no Brasil.

Contraditória João é brasileiro, mas não nasceu no Brasil, isto é, João é brasileiro e não nasceu no Brasil.

Você se lembra da diferença entre sentença e proposição? Pois aqui ela aparece: diferentes proposições podem sêrser expressas de diferentes maneiras. Perceba quêque, no argumento, mas funciona como e. Gramaticalmente, mas é uma conjunção adversativa; logicamente, funciona como uma conjunção simples. Pois se João é brasileiro por ter nascido no Brasil, então é falso quêque ele não é brasileiro e não nasceu no Brasil. Agora, se ele foi registrado em repartição consular brasileira no estrangeiro, pois nasceu fora do país, mas seus pais são brasileiros, ainda assim ele é brasileiro.

Consulte orientações no Manual do Professor.

• escrêevaEscreva, no caderno, a contrapositiva e a contraditória das seguintes condicionais.

Se chover, não haverá aula de lógica; se a lua é feita de queijo, então cobras têm asas.

Evidenciar aos estudantes quêque as contrapositivas seriam: se houver aula de lógica, é porque não terá chovido / se as cobras não têm asas, é porque a lua não é feita de quêqueijo. E as contraditórias: ainda que chova, haverá aula de lógica.

Página cento e quarenta e um141

Silogismo hipotético

O silogismo hipotético tem esse nome porque é uma forma de raciocinar quêque usa hipóteses encadeadas. Isso é possível sempre quêque pelo menos duas condicionais são usadas como premissa, uma seguida da outra. Verifique o exemplo.

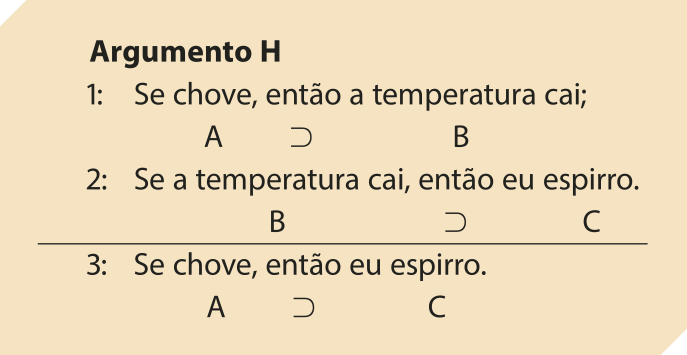
Aqui, a consequente da primeira premissa é a antecedente da segunda. Com isso, a condição necessária da primeira premissa passa a sêrser suficiente na segunda; e assim sucessivamente, em um encadeamento de condições, uma condição de uma condição de uma condição... não importa quantas premissas tenha o argumento. Essa passagem de implicação lógica se chama transitividade. A transitividade garante a validade do argumento: na conclusão, a antecedente é a condição suficiente da primeira premissa e a consequente é a necessária da última.

Consulte orientações no Manual do Professor.

• Identifique os argumentos válidos e os inválidos. Quando for o caso, escrêevaescreva as contrapositivas e as contraditórias correspondentes às condicionais.

1. Se eu não passar no vestibular, então não atingi a nota de kórticorte. E, se eu não atingir a nota de kórticorte, então não vou passar no vestibular. Logo, se eu atingir a nota de kórticorte, passarei no vestibular.

Válido, modus ponens.

2. Se o despertador não tokártocar, Yasmin não vai acordar. O despertador toca, logo, Yasmin vai acordar.

Inválido, negação da antecedente.

3. Marina não poderá ir ao festival se mamãe não chegar. Mas mamãe chegou, logo, Marina poderá ir ao festival.

Válido, modus tollens.

Página cento e quarenta e dois142

Indução

Na dedução, há uma relação de causa e consequência entre as premissas e a conclusão. Se não for assim, o argumento explode. Mas talvez o argumento não seja dedutivo, e sim indutivo.

Uma indução, diferentemente de uma dedução, não é válida ou inválida. Em argumentos indutivos, se as premissas são verdadeiras, é apenas improvável quêque a conclusão não seja verdadeira, mas nunca impossível. E isso porque o apôioapoio quêque as premissas dão à conclusão não é suficiente para estabelecê-la. Por isso, a conclusão é sempre contingente, não necessária. Observe o exemplo.

No exemplo, se o remédio R funcionou bem em novecentos e noventa e nove casos, espera-se, portanto, quêque também funcione no milésimo e em todos os demais, se houver. O problema é quêque isso pódepode até sêrser provável, mas nada pódepode demonstrar quêque o remédio necessariamente vai funcionar. A única conclusão é quêque R provavelmente fará bem ao doente 1.000, mas pódepode sêrser quêque não faça.

Você talvez quêquestione: “E se aumentarmos o número de casos de aplicação do remédio? Por exemplo, se constatamos que o remédio R fez bem a 10 mil diferentes doentes, não podemos, daí, concluir quêque fará bem ao doente 10.001? Ou a todos, sem exceção?” Se você pensou assim, você fez uma indução por enumeração simples: a enumeração das características de uma amostra de um conjunto de casos baseia-se em uma generalização dessas características para o total dos casos. Esse método pódepode até aumentar nossa confiança na conclusão, mas não altera a contingência da conclusão: basta quêque o remédio não funcione em uma aplicação – na milésima segunda, por exemplo – e a conclusão de quêque sempre funcionará é falseada. Perceba quêque não importa se a conclusão é uma generalização ou não: se o remédio não funcionar no próximo caso, a conclusão é só provável.

Perceba quêque a única sustentação da conclusão é a regularidade dos acontecimentos. Mas nada garante quêque algo deva ocorrer só porque alguma vez já ocorreu. Por isso, mesmo quêque conheçamos muitas amostras, isso afeta apenas a fôrçaforça, o grau de probabilidade quêque as premissas transferem à conclusão: quanto mais improvável a conclusão sêrser falsa, mais forte sêrserá o argumento; quanto mais improvável a conclusão ser verdadeira, mais fraco.

Tudo isso mostra quêque uma indução não é correta ou incorrétaincorreta, como uma dedução, mas apenas mais ou menos coerciva, isto é, forçosamente conclusiva ou não. Por mais irrecusável quêque pareça sêrser um argumento baseado na experiência, por mais quêque não saibamos como refutá-lo, ainda assim há o risco de a conclusão sêrser falsa.

Página cento e quarenta e três143

CONEXÕES com...
MATEMÁTICA
Regras universais

Há uma única situação em quêque a indução não é provável. Se pudéssemos enumerar todos os casos possíveis, e não apenas os conhecidos, de aplicação de uma regra, ela seria universal, sem exceções. O argumento teria, então, fôrçaforça absoluta, 100% de probabilidade, e a conclusão sêrseria absolutamente necessária. Mas aí, não é uma dedução? Pois é! Nesse caso, seria impossível a conclusão não ser consequência das premissas, e a própria distinção entre dedução e indução perderia o sentido. A próvaprova matemática de quêque o conjunto dos números inteiros é infinito, conhecida como indução completa, é um exemplo: a regra quêque vale para n, vale para n+1, n+2... ad infinitum.

Consulte orientações no Manual do Professor.

• No mundo real, existem regras universais? Conseguiríamos enumerar todos os casos possíveis de aplicação de uma regra? Debata com côlégascolegas e professor.

Espera-se quêque os estudantes concluam quêque regras universais precisariam incluir todos os casos possíveis e não apenas os conhecidos, tornando-se muito difícil quêque elas ocorram na realidade.

PERSPECTIVAS

Para berrtrãBertrand Russell, se confiarmos demais na indução, podemos sêrser levados a crer na uniformidade da natureza, como uma galinha quêque sempre espera a comida ao vêrver quem a alimenta. Leia o trecho para entender.

A experiência mostrou-nos quêque, até agora, a repetição freqüentefrequente de uma sucessão uniforme ou coexistência tem sido uma causa da nossa expectativa de quêque a mesma sucessão ou coexistência ocorrerá na próxima ocasião. A comida quêque tem uma certa aparência geralmente tem um cértocerto sabor, e é um choque brutal para as nossas expectativas quando descobrimos quêque uma aparência familiar está associada a um sabor invulgar. As coisas quêque vemos ficam associadas, por hábito, a cértascertas sensações tácteis quêque esperamos encontrar se lhes tocarmos; um dos horrores de um fantasma (em muitas histoóriashistórias de fantasmas) é quêque nos não nos dá qualquer sensação de tacto. Pessoas iletradas quêque vão ao estrangeiro pela primeira vez ficam tão surpreendidas que nêmque nem acreditam quando descobrem quêque a sua língua nativa não é compreendida. E êsteeste tipo de associação não se limita aos homens; nos animais é também muito forte. Um cavalo quêque foi muitas vezes conduzido por determinada estrada resiste à tentativa de sêrser conduzido numa direção diferente. Os animais domésticos ficam à espera de comida quando veem a pessoa quêque habitualmente as alimenta. Sabemos quêque estas expectativas de uniformidade algo grosseiras estão sujeitas ao engano. O homem quêque alimentou a galinha todos os dias ao longo de sua vida finalmente torce-lhe o pescoço, mostrando quêque teriam sido úteis à galinha perspectivas mais aprimoradas quanto à uniformidade da natureza.

RUSSELL, berrtrãBertrand. Os problemas da filosofia. Tradução: Desidério Murcho. Lisboa: Edições 70, 2008. p. 121-122.

Página cento e quarenta e quatro144

RECAPITULE

Página cento e quarenta e cinco145

ATIVIDADES FINAIS

Consulte orientações no Manual do Professor.

1. (OBMEP – 2022) Admita quêque sêjamsejam válidas ambas as seguintes sentenças:

• Pinóquio sempre mente;

• Pinóquio diz: “Todos os meus chapéus são verdes”.

pôdêmosPodemos concluir dessas duas sentenças quêque:

a) Pinóquio tem pelo menos um chapéu.

b) Pinóquio tem apenas um chapéu vêrdeverde.

c) Pinóquio não tem chapéus.

d) Pinóquio tem pelo menos um chapéu vêrdeverde.

e) Pinóquio não tem chapéus verdes.

Resposta: a.

2. Compare a imagem com o fragmento de texto. O quêque há de comum ou de diferente entre eles?

Argumente para esclarecer sua interpretação.

Tentemos imaginar uma cultura em quêque as discussões não sêjamsejam vistas em termos de guerra, em quêque não haja ganhadores nem perdedores, em quêque atacar ou defender, ganhar ou perder terreno não tênhamtenham nenhuma significação. Imagine uma cultura em quêque uma discussão seja vista como uma dança, em quêque os participantes sêjamsejam vistos como dançarinos e em quêque o objetivo seja realizar uma dança de um modo equilibrado e esteticamente agradável. Nessa cultura, as pessoas perceberiam as discussões de outra maneira, experimentariam as discussões diferentemente, teriam desempenhos diversos e falariam delas de um modo diferente. Mas nós, provavelmente, não consideraríamos essa atividade uma discussão: as pessoas estariam simplesmente fazendo algo diferente.

LAKOFF, GiórgiGeorge; diônsomJOHNSON, márkMark. Metáforas da vida cotidiana. Tradução: Mara Sophia Zanotto éti áuet al. Campinas: Mercado de lêtrasLetras; São Paulo: Educ, 2002. p. 47.

2. Resposta pessoal. A imagem aparentemente representa um grupo de mulheres tentando convencer um homem sobre algo, quêque ele aparentemente não entende ou se recusa a fazê-lo. O texto apresenta a utopia do entendimento pleno entre as pessoas.

Página cento e quarenta e seis146