Página 372
UNIDADE 6
A FÍSICA NA RELAÇÃO ENTRE O SER HUMANO E O AMBIENTE
As primeiras máquinas a vapor foram desenvolvidas para bombeamento de água. No entanto, a partir do desenvolvimento tecnológico e dos estudos teóricos sobre o funcionamento dessas máquinas, novos tipos de máquinas a vapor foram criados, processo que resultou na Revolução Industrial no século XVIII.
Para funcionar, as máquinas a vapor, como as locomotivas, necessitam da queima de um combustível, que pode ser carvão mineral, lenha ou óleo diesel. Dessa maneira, elas transformam o calor em movimento, realizando sua função. Porém, esse processo gera a emissão de resíduos poluentes na atmosfera.
O aperfeiçoamento dessas máquinas levou ao surgimento dos motores a combustão interna, utilizados atualmente nos veículos, ampliando o uso de combustíveis fósseis derivados do petróleo, o que, por sua vez, ocasionou o aumento de poluentes na atmosfera terrestre e as alterações climáticas vistas atualmente.
a ) Cite algumas vantagens e desvantagens do surgimento das máquinas térmicas.
b ) O que é necessário para que o motor a combustão interna de um veículo funcione?
c ) Qual é a principal diferença entre o funcionamento de uma locomotiva a vapor e do motor a combustão interna de um veículo?
Respostas nas Orientações para o professor.
Nesta unidade, vamos estudar...
- máquinas a vapor e motores a combustão interna;
- transformações gasosas;
- lei geral dos gases;
- trabalho em transformações gasosas;
- energia interna de um gás;
- primeira e segunda leis da termodinâmica;
- ciclos termodinâmicos;
- ondas sonoras;
- características e propriedades do som;
- fenômenos e instrumentos sonoros;
- luz e saúde dos olhos;
- alterações da visão e suas correções.
Página 373

Página 374
CAPÍTULO24
Queima de combustíveis fósseis
Máquinas a vapor e motores de combustão interna
Leia a seguir um trecho de reportagem sobre a extração e a utilização de combustíveis fósseis atualmente.
[...]
Os gases do efeito estufa lançados na atmosfera vêm aumentando a temperatura do planeta desde a Revolução Industrial (séculos 18 e 19), principalmente por meio da queima de combustíveis fósseis, o que impulsiona a atual crise climática, marcada por eventos extremos, como o calor excessivo, as secas prolongadas e as chuvas intensas.
[...]
LEÓN, Lucas Pordeus. Entenda estudo da Nasa sobre 'Brasil inabitável' em 50 anos. Agência Brasil, 24 jul. 2024. Disponível em: https://s.livro.pro/eddh55. Acesso em: 4 set. 2024.
1. Como são formados os combustíveis fósseis?
Resposta: O objetivo desta questão é analisar o conhecimento dos estudantes acerca dos combustíveis fósseis e de sua escassez. Sua formação é dada por meio de processos naturais relacionados à decomposição de organismos (matéria orgânica).
2. Qual é a importância dos combustíveis fósseis para a sociedade atual?
Resposta pessoal. Espera-se que os estudantes mencionem seu alto valor calorífico, o que o torna uma grande fonte de energia térmica, além de resultar em um alto crescimento econômico.
3. Cite uma vantagem e uma desvantagem relacionadas ao uso de máquinas industriais em substituição aos processos manufaturados. Qual das duas formas polui mais o ambiente e de que maneira isso ocorre?
Resposta pessoal. Espera-se que os estudantes citem como vantagens da utilização de máquinas: a velocidade de produção, a redução de custos nos processos de produção e o maior acesso da sociedade aos produtos produzidos. Enquanto algumas das desvantagens são: a poluição ambiental, o maior consumo de energia e a possibilidade de perdas de postos de trabalho (substituição de mão de obra humana). A utilização de máquinas resulta no aumento da poluição do ambiente, com a emissão de gases e a produção de lixo industrial, além de outros efeitos danosos.
Mesmo com as inúmeras desvantagens, como a quantidade limitada e a causa de diversos problemas ambientais e de saúde, o uso de combustíveis fósseis segue aumentando. A vantagem de sua utilização está na grande quantidade de energia produzida e no melhor custo-benefício, comparando a outros tipos de energia.
Como abordado na reportagem, a queima dos combustíveis fósseis é responsável por emitir grandes quantidades de gases, como o dióxido de carbono abre parênteses C O subscrito 2 fecha parênteses, que colabora para a intensificação do efeito estufa natural. Alguns tipos de combustíveis fósseis são o petróleo, o carvão mineral e o gás natural. Eles são utilizados como fontes de energia para o funcionamento de diversos dispositivos e máquinas, por exemplo, a gasolina e o diesel são derivados do petróleo e são utilizados, principalmente, em motores de máquinas e de veículos.



Página 375
Com o crescimento do setor industrial, ocorrido em meados do século XVIII na Grã-Bretanha e posteriormente em vários outros países, houve a necessidade de novas fontes de energia para o funcionamento das máquinas.
A partir da Revolução Industrial, as máquinas movidas a vapor desempenharam papel fundamental, uma vez que foram as responsáveis pela transformação do calor em movimento, isto é, por meio do motor a vapor era realizada a conversão da energia térmica em energia mecânica na forma de realização de trabalho.
Ainda que os princípios básicos para a construção do motor a vapor tenham sido descritos pelo matemático grego Heron de Alexandria (10 d.C.-70 d.C.), por volta do século I, e que grandes contribuições posteriores tenham sido apresentadas por outros estudiosos – como o inventor francês Denis Papin (1647-1712) em 1679, o engenheiro inglês Thomas Savery (1650-1715) em 1698 e o engenheiro inglês Thomas Newcomen (1664-1729) em 1712 –, o motor a vapor rotatório só foi efetivamente desenvolvido em 1765, pelo cientista escocês James Watt (1736-1819).
Watt desenvolveu um tipo de motor que era capaz de girar em um eixo, em vez de realizar apenas o movimento de subir e descer, por meio de engrenagens que convertiam esse deslocamento em movimento circular. O motor a vapor rotativo de Watt pôde então ser utilizado com variadas aplicações, por exemplo, movimentar máquinas nas fábricas e usinas de algodão.
Nas máquinas a vapor, a fonte de energia utilizada para aquecer a água e transformá-la em vapor é o carvão mineral, um tipo de combustível fóssil.

Compartilhe ideias
As máquinas a vapor tiveram grande importância para o desenvolvimento da sociedade e das tecnologias utilizadas atualmente. Com base nisso, faça o que se pede.
a ) Forme dupla com um colega e discutam quais impactos positivos e negativos as máquinas a vapor impuseram à sociedade. Quais mudanças ocorreram na organização social, no trabalho e no modo de vida, por exemplo?
Resposta pessoal. Os estudantes podem argumentar que os modos de fabricação dos produtos deixaram de ser um processo artesanal para se tornarem produção industrial em larga escala. Entre os impactos positivos dessa mudança, podem destacar o aumento do rendimento do trabalho, a redução dos custos de produção, o progresso científico e tecnológico, a melhoria dos sistemas de transporte, entre outros. Em relação os impactos negativos, podem citar as condições precárias de trabalho, com alta jornada e baixos salários, a exploração do trabalho infantil e a remuneração desigual entre homens e mulheres, o crescimento desordenado das cidades em virtude do surgimento e a concentração de empresas e indústrias nesses locais, o aumento da desigualdade social pela concentração de renda na mão dos donos das indústrias e grandes comerciantes etc.
b ) Quais impactos ambientais foram impostos pela utilização em massa das máquinas a vapor?
Resposta pessoal. Os estudantes podem refletir sobre o fato de as máquinas a vapor utilizarem o carvão mineral (combustível fóssil) como fonte de energia para aquecer a água nas caldeiras e gerar o vapor. Assim, a utilização dessas máquinas implicou em um aumento significativo da poluição do meio ambiente. Além disso, a elevação na produção exigiu um aumento na necessidade por matéria-prima para fabricação dos produtos, o que gerou um aumento no desmatamento das florestas; o crescimento desordenado das cidades provocou a contaminação de rios com esgotos de residências e resíduos das indústrias, entre outros.
A partir do desenvolvimento das máquinas movidas a vapor, foram surgindo outras tecnologias mais avançadas, capazes de alcançar maiores rendimentos. O motor a vapor desenvolvido por Watt era capaz de converter apenas cerca de 2% da energia térmica em movimento. Em 1900, após algumas melhorias, a eficiência do motor a vapor aumentou para aproximadamente 17%.
O motor de combustão interna é produto desse avanço de tecnologia. Já no início dos anos 1900, esse tipo de motor havia substituído o motor a vapor como o principal sistema para a geração de energia. Entre os fatores que levaram a essa substituição, está o fato de ele ter maior eficiência térmica (entre 20% e 35%).
Para o estudo do funcionamento desses motores, é necessário compreender primeiro o comportamento dos gases, que são sujeitos a várias transformações, as quais serão definidas a seguir.
Página 376
CONEXÕES com ... HISTÓRIA e SOCIOLOGIA
Revoluções industriais
No final do século XVIII, a indústria têxtil da Inglaterra estava com problemas para produzir em larga escala, de forma mais rápida e com menos custos para mercados consumidores em crescimento, pois o processo de produção dependia da força humana, animal ou de fontes naturais de energia, como a água ou o vento, para movimentar as máquinas de fiar.
A invenção da máquina a vapor, nessa mesma época, foi um dos catalisadores para a Primeira Revolução Industrial, trazendo mudanças significativas nas práticas tradicionais de agricultura, manufatura e transporte.
O antigo modelo de produção caseira foi substituído por um sistema de fábricas com máquinas movidas por motores a vapor. Essas máquinas podiam realizar a função de muitos operários, aumentando a capacidade produtiva das indústrias. O desenvolvimento das máquinas a vapor também permitiu o surgimento de novas formas de transporte, como trens e barcos a vapor. Houve ainda o aparecimento das mineradoras e das siderúrgicas para prover combustíveis e materiais para a produção das máquinas a vapor, respectivamente.

Quase um século depois, entre 1860 e 1914, ocorreu a Segunda Revolução Industrial, com a invenção de novas tecnologias, como motor de combustão interna e tecnologias de geração e transmissão de energia elétrica, além de aparelhos de comunicação como telégrafo, telefone e rádio.
Essas tecnologias geraram um aumento significativo na produção em massa e uma redução nos custos de produção. A segunda revolução também mudou a maneira como as pessoas viviam e trabalhavam. Os avanços nos transportes, com a expansão das ferrovias e o surgimento dos automóveis, mudaram a dinâmica das cidades e facilitaram a mobilidade das pessoas. No entanto, esses avanços não trouxeram benefícios a todos, pois em diversos bairros operários, próximos às fábricas, não havia rede de esgoto nem abastecimento de água e a poluição industrial prejudicava a saúde dos moradores desses bairros.
Já a Terceira Revolução Industrial tem início na década de 1970, um período caracterizado pela integração de tecnologias avançadas, como a eletrônica, a computação, a criação da internet e a invenção da robótica. O uso de computadores e as melhorias em telecomunicações aumentaram a produtividade industrial. Os avanços da biotecnologia na indústria alimentícia transformaram a estrutura da agricultura em vários países.
Além disso, inovações em sistemas de transporte e comunicação tornaram possível que empresas multinacionais instalassem fábricas em diferentes países, expandindo o comércio e padronizando certos bens e hábitos de consumo.

Página 377
Esse cenário de transformação contínua e de inovação tecnológica estabelecido pela Terceira Revolução Industrial provocou a Quarta Revolução Industrial, a partir de meados de 2010. À medida que o uso de computadores e a automação foram intensificados, houve uma evolução das tecnologias digitais, combinada com avanços na inteligência artificial (IA), internet das coisas (IoT), big data e robótica, moldando uma nova era industrial, chamada de Indústria 4.0.
O desenvolvimento de biomateriais e a biorrobótica abriu novas fronteiras na Medicina e na produção industrial. A fabricação de próteses avançadas usando biomateriais compatíveis com o corpo humano e a biorrobótica, que busca integrar sistemas robóticos e biológicos, com dispositivos que interagem de forma natural com o corpo humano, promoveram maior qualidade de vida de pessoas com deficiência.
Na indústria, o controle numérico computadorizado (CNC) aumentou a precisão e a produtividade na fabricação de produtos. Diferente dos métodos manuais, as máquinas e robôs CNC são programados para executar tarefas específicas com exatidão e repetibilidade consistentes. Isso resulta em produtos de alta qualidade com menos defeitos. Outra técnica atual é a impressão 3D (três dimensões), que permite a produção de objetos complexos e personalizados, diretamente com base em modelos digitais, utilizando softwares baseados em algoritmos avançados para garantir a precisão e a qualidade das peças produzidas.

Apesar de a Quarta Revolução Industrial acontecer no século XXI, as bases para ela foram desenvolvidas em séculos anteriores por diversos cientistas, entre os quais podemos destacar a matemática inglesa Ada Lovelace (1815-1852) e a matemática estadunidense Grace Murray Hopper (1906-1992).
Ada Lovelace é considerada a primeira programadora da história. Ela foi responsável por descrever um algoritmo para ser processado por uma máquina analítica, gerando uma sequência numérica por meio de alguns cálculos. Sua visão sobre como uma máquina poderia ser programada para realizar operações complexas contribuiu para a computação moderna. Esses princípios são essenciais para o funcionamento de máquinas CNC, robôs industriais e impressoras 3D. Já Grace Hopper foi pioneira no desenvolvimento de linguagens de programação, na qual o computador interpretava comandos em inglês no lugar de números ou símbolos. Essa abordagem tornou a programação mais acessível, abrindo caminho para linguagens de programação utilizadas atualmente e teve um papel importante na integração dos computadores na indústria.
a ) Como a produção em massa e a mecanização do trabalho contribuíram para a concentração de riqueza e o aumento das desigualdades sociais ao longo das revoluções industriais?
Resposta: A produção em larga escala e a redução dos custos de produção geraram grandes lucros para os proprietários das fábricas, enquanto os trabalhadores recebiam apenas baixos salários, por longas horas de trabalho. Além disso, a mecanização e a automação de tarefas causaram o desemprego de muitos trabalhadores, especialmente daqueles em setores tradicionais que foram substituídos por máquinas, gerando mais pobreza e aumento da desigualdade.
b ) Qual é o papel da Ciência e da pesquisa no desenvolvimento das tecnologias que impulsionaram cada Revolução Industrial?
Resposta: Desde a Primeira Revolução Industrial, a Ciência foi a propulsora de novas mudanças, com a inclusão de novas descobertas a serviço da sociedade. A relação entre Ciência, pesquisa e indústria tem se intensificado ao longo do tempo, tornando o intervalo entre as novas revoluções cada vez menor.
c ) Como os sistemas cada vez mais automatizados e a inteligência artificial podem impactar o mercado de trabalho? E quais são as novas habilidades e competências que serão demandadas dos profissionais do futuro?
Resposta: A automação e a IA podem substituir empregos em tarefas repetitivas e previsíveis; por outro lado, podem gerar novos empregos em áreas como programação, análise de dados, assim como o surgimento de novas profissões. Para se preparar para esse novo mercado de trabalho, é necessário adquirir habilidades como pensamento crítico, criatividade e manter um aprendizado contínuo.
d ) Com as revoluções industriais acontecendo de maneira cada vez mais rápida e diante de novas formas de trabalho, quais são as habilidades humanas que não podem ser replicadas pelas máquinas?
Resposta: A capacidade de "pensar fora da caixa" e encontrar soluções originais para problemas complexos, assim como a empatia, a colaboração e a comunicação eficaz, são habilidades que as máquinas ainda não conseguem replicar com a mesma profundidade e complexidade que os seres humanos.
Página 378
Transformações gasosas
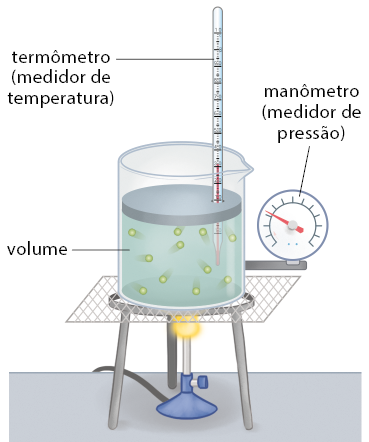
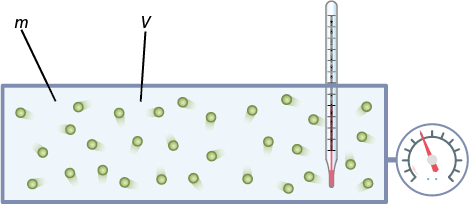
Uma substância que assume a fase física gasosa é constituída por minúsculas partículas (átomos, moléculas, íons etc.), que são dotadas de movimentos aleatórios. Por causa disso, o gás ocupa todo o espaço no interior do recipiente que o contém. Dessa maneira, o volume do gás é o volume do próprio recipiente, isto é, o gás tem a forma e o volume definidos pelo recipiente no qual está contido.
Considerando um gás confinado em um recipiente, seu comportamento pode ser analisado em função de grandezas macroscópicas, como a temperatura abre parênteses T fecha parênteses, o volume abre parênteses V fecha parênteses e a pressão abre parênteses p fecha parênteses, denominadas variáveis de estado. Essas três variáveis definem o estado termodinâmico do gás. Assim, conhecendo-as, podemos definir as propriedades físicas do gás.
Imagens desta página sem proporção e em cores fantasia.
4. O enchimento dos balões de ar quente se dá pelo aquecimento do ar contido em seu interior. Explique como isso ocorre.
Resposta: Durante o preparo de um balão de ar quente, o ar de seu interior é aquecido, elevando sua temperatura e expandindo seu volume, que corresponde a uma expansão do volume do balão. Esse comportamento é relacionado a uma transformação isobárica, no qual a pressão permanece constante.
5. Verificamos que as bolhas de ar em um líquido aumentam de tamanho durante sua ascendência até a superfície. Explique por que isso acontece.
Resposta: Durante um mergulho, por exemplo, as bolhas liberadas pela respiração sobem. Durante a subida, a pressão da água sobre a bolha diminui à medida que ela se aproxima da superfície; assim, a bolha se expande, aumentando seu volume. Esse fato é relacionado a uma transformação isotérmica, cuja temperatura é praticamente constante.
6. Explique o que ocorre com uma panela de pressão ao receber do fogão grande quantidade de calor.
Resposta: Espera-se que os estudantes mencionem o aumento da temperatura e, consequentemente, o aumento da pressão do vapor no interior da panela. Essa ocorrência se deve ao fato de não haver variação de volume, tratando-se, portanto, de uma transformação isovolumétrica.
A grandeza temperatura está relacionada com o grau de agitação das partículas que constituem o gás, de modo que, quanto maior o grau de agitação, maior é a medida da temperatura. Por causa dessa agitação, as partículas colidem com as paredes do recipiente, imprimindo força sobre elas, resultando na pressão exercida pelo gás.
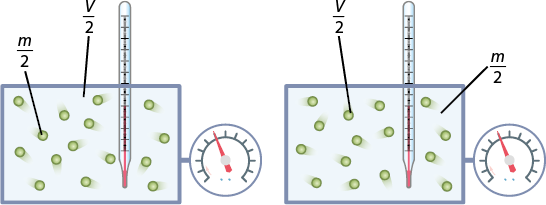
As variáveis de estado podem ser divididas em intensivas e extensivas. As classificadas como intensivas são independentes da massa do gás, enquanto as extensivas variam em função da massa.
Por exemplo, se uma quantidade de gás é dividida em duas partes iguais, cada uma delas apresentará os mesmos valores das variáveis intensivas, como pressão e temperatura. No entanto, as variáveis extensivas terão metade de seu valor inicial, como a massa de gás e o volume.
Página 379
O estudo do comportamento dos gases é realizado por meio de modelos idealizados, que simplificam as relações matemáticas entre as variáveis de estado. Nesses modelos, os gases considerados são chamados de gases ideais ou gases perfeitos.
Os gases ideais têm as seguintes características:
- são compostos de partículas de mesma massa;
- o volume das moléculas é desprezível;
- suas partículas se distribuem uniformemente por todo o volume determinado pelo recipiente que os contém;
- o movimento de suas partículas é aleatório e obedece às leis de Newton;
- uma vez que suas moléculas estão muito distantes entre si, as forças gravitacional e elétrica entre elas são desprezíveis;
- as colisões das moléculas entre si e com as paredes do recipiente são perfeitamente elásticas, conservando o momento linear e a energia mecânica do sistema.
As transformações de um gás ocorrem em relação às variáveis de estado pressão, volume e temperatura. A variação de uma delas provoca a variação das outras. No entanto, alguma delas pode permanecer constante enquanto as outras variam. Essas transformações serão trabalhadas a seguir.
Dica
Os gases reais presentes na atmosfera, como o oxigênio abre parênteses O subscrito 2 fecha parênteses, o nitrogênio abre parênteses N subscrito 2 fecha parênteses e o gás carbônico abre parênteses C subscrito 2 fecha parênteses, comportam-se, em determinadas condições, como gases ideais.
Dica
A transformação gasosa não está diretamente relacionada à transformação de fase. No entanto, em algumas situações, a transformação gasosa pode estar acompanhada de uma transformação de fase física.
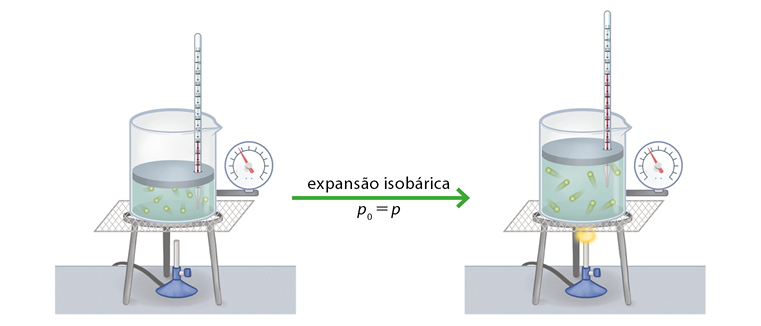
A transformação gasosa na qual a pressão do gás permanece inalterada enquanto o volume e a temperatura variam é chamada de isobárica.
Considere um recipiente cilíndrico com um êmbolo móvel, que seja livre para descer ou subir, sem atrito com as paredes do cilindro. Aquecendo o gás por meio de uma fonte de calor, verifica-se o aumento das medidas de temperatura e volume. No entanto, a quantidade de choques das moléculas do gás com as paredes do recipiente não se altera, mantendo, assim, a pressão constante, como mostrado a seguir.
Imagem sem proporção e em cores fantasia.
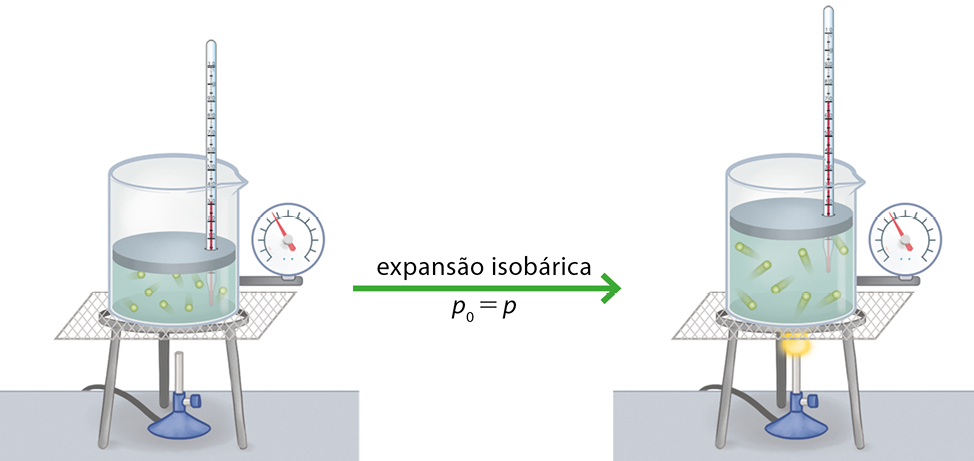
Professor, professora: Explique que, com o aquecimento do gás, as partículas aumentam sua energia cinética, logo, provocam o aumento de temperatura. Como a transformação ocorre com pressão constante, o volume aumenta.
Página 380
A relação entre as variáveis volume e temperatura para uma transformação isobárica foi verificada e comprovada em épocas distintas pelo físico Jacques Charles (1746-1823) e pelo químico Joseph Louis Gay-Lussac (1778-1850), ambos franceses. Essa relação está descrita e expressa a seguir.
Durante um processo em que a pressão de um gás é mantida constante, o volume e a temperatura absoluta do gás são diretamente proporcionais.
Matematicamente, essa relação pode ser escrita como:
início de fração, numerador: V subscrito 0, denominador: T subscrito 0, fim de fração é igual a V sobre T é igual a constante
em que:
- V subscrito 0 é o volume inicial do sistema;
- T subscrito 0 é a temperatura absoluta inicial do sistema;
- V é o volume do sistema após a transformação isobárica;
- T é a temperatura absoluta do sistema após a transformação isobárica.
Dica
A temperatura absoluta representa a temperatura graduada na escala kelvin. Portanto, qualquer outra medida deve ser convertida para essa escala. A conversão das escalas Celsius e Fahrenheit é dada, respectivamente, por:
T subscrito K é igual a T subscrito C mais 273 e início de fração, numerador: T subscrito K menos 273, denominador: 5, fim de fração é igual a início de fração, numerador: T subscrito F menos 32, denominador: 9, fim de fração
A razão obtida entre volume e temperatura é sempre constante em uma transformação isobárica, ou seja, a razão entre o volume inicial e a temperatura inicial é igual à razão entre o volume final e a temperatura final. Considerando que a substância continue em sua fase gasosa com valores abaixo de 0 grau Celsius, ao atingir o valor de menos 273 graus Celsius, zero absoluto, obteríamos um valor nulo de volume. Isso não é possível, pois em valores próximos a menos 273 graus Celsius todo gás se liquefaz.
Para esse tipo de transformação, o diagrama da pressão em função do volume abre parênteses p vezes V fecha parênteses corresponde a uma reta horizontal, isto é, uma função constante. No entanto, como a relação entre o volume e a temperatura é linear, o diagrama abre parênteses V vezes T fecha parênteses é representado por uma reta crescente.
Diagrama abre parênteses p vezes V fecha parênteses para uma transformação isobárica

Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 240.
Diagrama abre parênteses V vezes T fecha parênteses para uma transformação isobárica
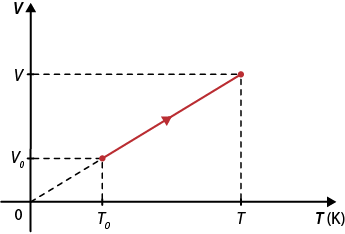
Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 232.
Professor, professora: Peça aos estudantes que atentem às unidades de medida das respectivas variáveis e à obrigatoriedade do uso da escala kelvin (escala absoluta).
Durante o preparo de um balão de ar quente, o aquecimento do ar em seu interior provoca o aumento de seu volume até que obtenha o formato definido. Durante a expansão, a pressão é mantida constante, isto é, o ar atmosférico passa por uma transformação isobárica.

Página 381
A transformação gasosa na qual o gás sofre variação de volume e pressão, enquanto sua temperatura permanece constante, é chamada de isotérmica.
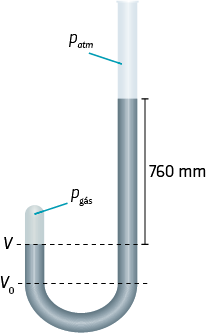
Os primeiros estudos analíticos das propriedades dos gases foram conduzidos pelo físico e químico irlandês Robert Boyle (1627–1691). No seu experimento, publicado em 1660, Boyle utilizou um tubo em formato de letra J com a extremidade inferior fechada e a superior aberta. Na calibragem do experimento, colocamos mercúrio no tubo enquanto o ar flui entre as extremidades e nivelamos a altura da coluna de mercúrio em ambas as pontas, o que garante que a pressão na extremidade fechada seja igual à pressão atmosférica.
Ao adicionar lentamente mercúrio à extremidade aberta, verificamos que a pressão excedente exercida pelo desnível da coluna de mercúrio aumenta a pressão sobre a extremidade fechada, que, por sua vez, comprime o gás aprisionado.
Com isso, Boyle atestou que, diferentemente de um sólido ou um líquido, um gás pode sofrer compressão ou expansão à medida que a pressão exercida sobre ele aumenta ou diminui.
Imagens desta página sem proporção e em cores fantasia.
Considerando o mesmo esquema da página anterior, o gás passa por uma contração de seu volume, provocada pela ação da força peso de dois objetos de massa posicionados sobre o êmbolo. Com o espaço reduzido, a quantidade de colisões das moléculas do gás com as paredes do recipiente aumenta, de modo a aumentar a pressão, mas mantendo a temperatura constante, como na imagem a seguir.
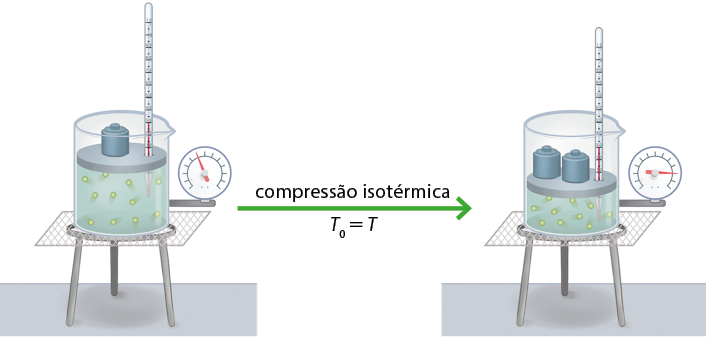
Professor, professora: Explique que a compressão, isto é, a diminuição do volume, é causada pela ação da força peso dos objetos sobre o êmbolo. A diminuição do espaço ocupado pelas moléculas causa o aumento no número de suas colisões com as paredes do recipiente, logo provoca o aumento da pressão.
As observações da relação inversamente proporcional entre as variáveis pressão e volume para uma transformação isotérmica são conhecidas como lei de Boyle-Mariotte. Veja a descrição e a expressão dessa relação a seguir.
Durante um processo em que a temperatura absoluta de um gás é mantida constante, sua pressão e seu volume são inversamente proporcionais.
Matematicamente, essa relação pode ser escrita como:
p subscrito 0 vezes V subscrito 0 é igual a p vezes V é igual a constante
em que:
- p é a pressão final do sistema após a transformação isotérmica;
- V é o volume final do sistema após a transformação isotérmica.
Página 382
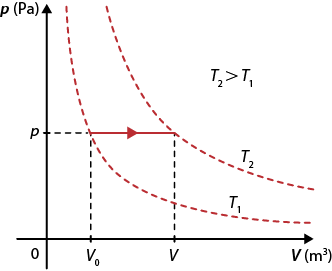
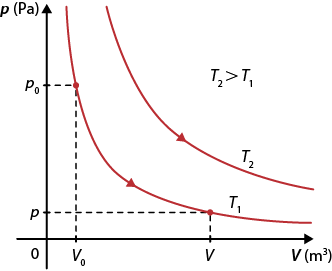
O diagrama de pressão em função do volume abre parênteses p vezes V fecha parênteses de uma transformação isotérmica é representado por uma função hiperbólica, chamada de isoterma. Nesse tipo de representação, para cada valor de temperatura, cria-se uma isoterma diferente, como mostra o diagrama.
Diagrama abre parênteses p vezes V fecha parênteses para uma transformação isotérmica

Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 240.
Uma transformação isotérmica pode ser observada em um experimento simples, utilizando uma seringa e um pequeno balão de festa com um pouco de ar em seu interior. Ao vedarmos a saída de ar da seringa e pressionarmos o êmbolo, ocorre o aumento da pressão em seu interior, como consequência, o volume do balão de festa diminui (A). Quando puxamos o êmbolo, a pressão no interior da seringa diminui, como consequência, o volume do balão de festa aumenta (B).
A.
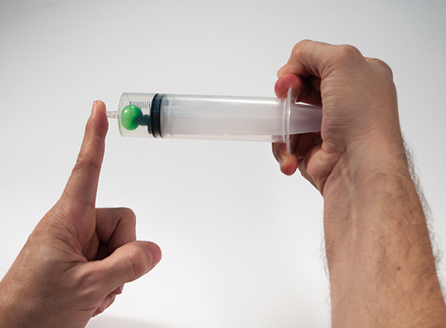
B.
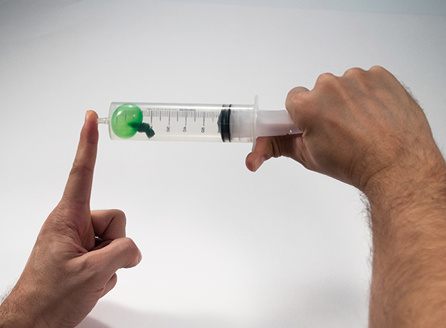
A transformação isovolumétrica ocorre quando o volume do gás permanece constante, variando tanto a pressão quanto a temperatura do sistema. Essa transformação também é chamada de isométrica ou isocórica.
Com base nos esquemas anteriores, considera-se que o gás no interior do cilindro é aquecido, de modo que o êmbolo não se mova, mantendo, assim, o volume constante. O aumento da temperatura faz aumentar o grau de agitação das moléculas, elevando a quantidade de choques com as paredes do recipiente, isto é, elevando a pressão no interior do recipiente, conforme mostra a imagem a seguir.
Imagem sem proporção e em cores fantasia.
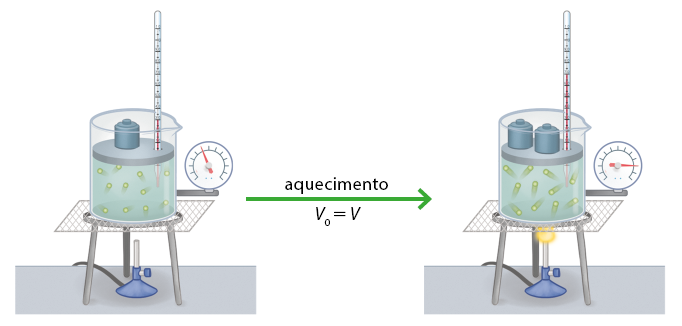
Professor, professora: Explique que, com o aquecimento das moléculas que constituem o gás, ocorre o aumento da temperatura, consequentemente, aumenta a quantidade de choques das partículas com as paredes do recipiente, isto é, aumenta a pressão do gás.
Página 383
A relação diretamente proporcional entre as grandezas pressão e temperatura foi definida por Jacques Charles e pode ser descrita como apresentado a seguir.
Durante um processo em que o volume de um gás é mantido constante, a pressão e a temperatura absoluta desse gás são diretamente proporcionais.
Matematicamente, essa relação pode ser expressa por:
início de fração, numerador: p subscrito 0, denominador: T subscrito 0, fim de fração é igual a p sobre T é igual a constante
em que:
- p é a pressão final do sistema após a transformação isovolumétrica;
- T é a temperatura absoluta final do sistema após a transformação isovolumétrica.
O diagrama da pressão em função do volume abre parênteses p vezes V fecha parênteses para uma transformação isovolumétrica é dado por uma reta vertical, enquanto o diagrama da pressão em função da temperatura abre parênteses p vezes T fecha parênteses é dado por uma reta crescente, tratando-se de uma função linear, como são representados a seguir.
Diagrama abre parênteses p vezes V fecha parênteses para uma transformação isovolumétrica
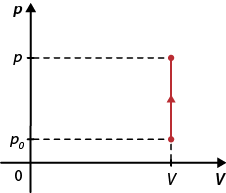
Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 240.
Diagrama abre parênteses p vezes T fecha parênteses para uma transformação isovolumétrica

Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 230.
Essa transformação é percebida nos pneus de um automóvel, por exemplo, pois, conforme eles se deslocam, o atrito dos pneus com o solo provoca o aumento da temperatura do gás em seu interior. Como o volume dos pneus permanece praticamente constante, a pressão em seu interior aumenta. Por esse motivo, a calibragem dos pneus com frequência é fundamental para garantir seu melhor desempenho e a máxima segurança do usuário.
Outra situação na qual podemos observar uma transformação isométrica é quando tentamos abrir a porta de uma geladeira, ou freezer, imediatamente após fechá-la. Isso exige um esforço físico maior do que quando abrimos após um longo período em que ela ficou fechada. Como o volume do interior da geladeira é constante, o ar que foi aprisionado nela enquanto a porta ficou aberta sofre uma redução de temperatura. Logo, a velocidade de translação das suas partículas diminui, causando a redução das colisões com as partes internas da geladeira, ou seja, a pressão no interior do aparelho diminui, ficando menor do que a pressão externa. Dessa diferença de pressão surge uma força resultante, contrária à abertura da porta. Após certo intervalo de tempo, o valor da pressão interna se iguala ao da pressão externa, em razão de um mecanismo de entrada de ar na geladeira.
Imagem sem proporção e em cores fantasia.

Página 384
A transformação gasosa chamada de adiabática ocorre em situações nas quais o gás não efetua trocas de energia com o meio externo na forma de calor. Nesse tipo de transformação, as três variáveis de estado (volume, pressão e temperatura) sofrem alterações durante o processo. Para que essa troca de calor não ocorra durante a transformação, uma alternativa é confinar o gás em um recipiente termicamente isolado. No entanto, a transformação adiabática também ocorre caso o processo seja rápido o bastante para que as trocas de calor possam ser desprezíveis, pelo fato de o processo de transmissão de calor por condução ou convecção ser relativamente lento.
A formação das nuvens e a formação de neblina em dias frios, por exemplo, são resultados da transformação adiabática. Quando uma quantidade de ar sobe para regiões em que a pressão atmosférica é cada vez menor, seu volume sofre uma expansão rápida o suficiente para que não haja trocas de calor e sua temperatura diminui até a condensação da água, como mostra o esquema a seguir.
Imagem sem proporção e em cores fantasia.
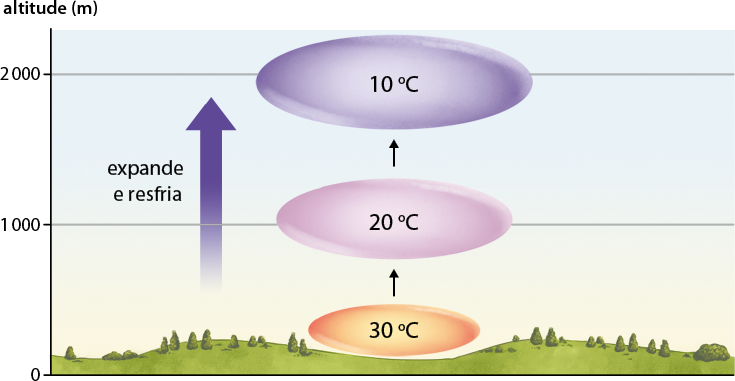
Imagem elaborada com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 341.
O diagrama da pressão em função do volume abre parênteses p vezes V fecha parênteses para uma transformação adiabática é representado por uma curva. Essa curva adiabática decai mais rapidamente do que a isotérmica, como mostra o diagrama.
Diagrama abre parênteses p vezes V fecha parênteses para uma transformação adiabática
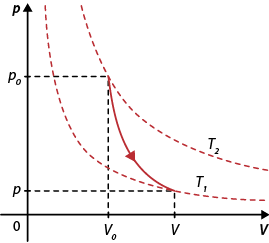
Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 240.
No cotidiano, esse tipo de transformação é bastante utilizado nos aerossóis, por exemplo.
Um aerossol é composto da mistura de dois líquidos confinados em um recipiente sujeito a uma grande pressão interna. Um dos líquidos é o próprio produto. O outro é um gás chamado de propelente, o qual se encontra na fase líquida por causa da grande pressão no interior do recipiente. Ao acionarmos a válvula de escape, a pressão interna do recipiente diminui e o propelente assume novamente a fase gasosa, aumentando seu volume. Com isso, ele escapa com grande violência, levando parte do produto junto.
A expansão do gás propelente ocorre sem haver trocas de calor com o meio externo, resultando na diminuição da temperatura interna, sentida pelo resfriamento do recipiente quando os gases são expelidos.

Página 385
Lei geral dos gases
Quando estudamos transformações nas quais todas as variáveis de estado sofrem alteração, é necessário considerar as relações de proporcionalidade que existem entre elas em cada processo individualmente. Por exemplo, vimos que, em um processo isobárico, o volume e a temperatura são diretamente proporcionais. Já em um processo isotérmico, a pressão e o volume são inversamente proporcionais. E, na transformação isovolumétrica, a pressão e a temperatura também são diretamente proporcionais.
Com base nessas relações, o físico francês Benoit Paul Émile Clapeyron (1799-1864) estabeleceu uma única equação que sintetiza todas as transformações de um gás ideal, chamada de lei geral dos gases ideais:
início de fração, numerador: p subscrito 0 vezes V subscrito 0, denominador: T subscrito 0, fim de fração é igual a início de fração, numerador: p vezes V, denominador: T, fim de fração é igual a constante
Essa equação relaciona as três variáveis de estado de um gás ideal para qualquer tipo de transformação, desde que não ocorra variação da quantidade de gás, isto é, para o número de mol abre parênteses n fecha parênteses constante:
- início de fração, numerador: V subscrito 0, denominador: T subscrito 0, fim de fração é igual a V sobre T, para uma transformação isobárica abre parênteses p subscrito 0 é igual a p fecha parênteses;
- p subscrito 0 vezes V subscrito 0 é igual a p vezes V, para uma transformação isotérmica abre parênteses T subscrito 0 é igual a T fecha parênteses;
- início de fração, numerador: p subscrito 0, denominador: T subscrito 0, fim de fração é igual a p sobre T, para uma transformação isovolumétrica abre parênteses V subscrito 0 é igual a V fecha parênteses;
- início de fração, numerador: p subscrito 0 vezes V subscrito 0, denominador: T subscrito 0, fim de fração é igual a início de fração, numerador: p vezes V, denominador: T, fim de fração, para uma transformação adiabática abre parênteses Q é igual a 0 fecha parênteses.
Dica
O mol corresponde à quantidade de partículas, definido pelo número de Avogadro abre parênteses N subscrito A fecha parênteses, em que:
N subscrito A é igual a 1 mol é igual a 6 vírgula 0 23 vezes 10 elevado a 23 partículas
O número de mol de uma substância pode ser determinado em função de sua massa abre parênteses 'm' fecha parênteses e de sua massa molar abre parênteses M fecha parênteses, de modo que:
n é igual a 'm' sobre M
Logo, a constante determinada por Clapeyron, chamada de constante universal dos gases ideais e representada pela letra R, é válida para qualquer tipo de gás. Assim, podemos escrever:
início de fração, numerador: p vezes V, denominador: T, fim de fração é igual a n vezes R portanto p vezes V é igual a n vezes R vezes T
Para as variáveis de estado expressas nas unidades do SI, isto é, pressão em pascal abre parênteses P a fecha parênteses, volume em metro cúbico abre parênteses metro elevado ao cubo fecha parênteses e temperatura em kelvin K, a constante universal R tem valor igual a:
R é igual a 8 vírgula 31 pascals vezes m elevado ao cubo barra mol vezes K
Como 1 pascal é igual a 1 N barra m elevado ao quadrado e 1 joule é igual a 1 N vezes m, a constante universal, ainda no SI, também pode ser escrita da seguinte maneira:
R é igual a 8 vírgula 31 joules barra mol vezes K
No entanto, caso as variáveis sejam expressas em a t m (pressão), L (volume) e K (temperatura), sendo 1 a t m é igual a 1 vírgula 0 1 vezes 10 elevado a 5 pascal e 1 L é igual a 10 elevado a menos 3 metros cúbicos, temos:
R é igual a 0 vírgula 0 82 a t m vezes L barra mol vezes K
Página 386
PRÁTICA CIENTÍFICA
Transformações gasosas
Por dentro do contexto
Atualmente, muitas máquinas fazem parte de nosso dia a dia e seria difícil imaginar a vida sem elas. Do motor dos automóveis à panela de pressão, a termodinâmica está presente em muitos fenômenos do cotidiano.
Desde o surgimento das máquinas a vapor, que foram fundamentais para a Revolução Industrial, ocorrida na Inglaterra em meados do século XVIII, os estudos da termodinâmica possibilitaram a análise de propriedades da matéria em determinadas situações de temperatura e pressão, o que permitiu sua aplicação em diversos processos que envolvem as transformações gasosas e as mudanças de estado da matéria.

Tais processos são encontrados na meteorologia, como em instrumentos de medição de pressão, temperatura e umidade relativa do ar, nas usinas termelétricas, em turbinas de aviões, não deixando de citar sua aplicação em larga escala nos automóveis, em que o processo de combustão envolve a liberação de energia.
a ) Como é possível produzir movimento alterando o estado de um gás?
Resposta pessoal. Espera-se que os estudantes respondam que podemos variar a pressão, a temperatura e o volume de um gás, fazendo-o mover o pistão de um motor, por exemplo, convertendo energia térmica em movimento.
Materiais
- 3 seringas descartáveis de 20 mililitros com tampa
- 2 recipientes de plástico (tipo embalagem de sorvete)
- recipiente para aquecer a água
- água
- cubos de gelo
- fogão ou bico de Bunsen
- cola instantânea
Como proceder
A. Prepare as 3 seringas. Para isso, deixe o êmbolo de uma delas na posição de 20 mililitros, coloque um pouco de cola instantânea na tampa e vede a ponta da seringa.
B. Repita o procedimento A, vedando a segunda seringa com o êmbolo na posição de 10 mililitros e a terceira seringa com o êmbolo na posição de 0 mililitro (totalmente fechada).
Imagem sem proporção e em cores fantasia.

C. Encha um dos recipientes com água à temperatura ambiente e adicione os cubos de gelo.
D. No outro recipiente, coloque água aquecida.
Página 387
E. Coloque a seringa que está com o êmbolo na posição de 10 mililitros no pote com água e gelo até uma altura que possa cobrir a seringa até a marca dos 15 mililitros, pelo menos. Observe por alguns minutos e anote suas conclusões.
Imagens desta página sem proporção e em cores fantasia.

F. Em seguida, coloque a seringa que está com o êmbolo na posição de 10 mililitros no pote com água quente até uma altura que possa cobrir a seringa até a marca dos 15 mililitros, pelo menos. Observe por alguns minutos e anote suas conclusões.
Cuidado
Tenha cuidado ao colocar a seringa dentro do recipiente com água quente. Se possível, utilize uma pinça.

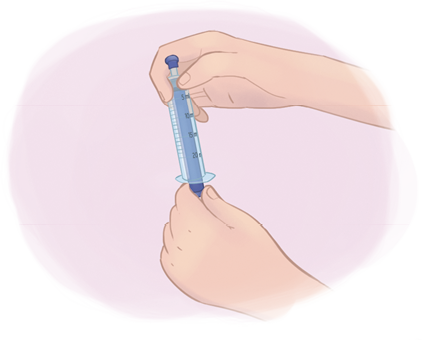
G. Pegue a seringa que foi vedada com o êmbolo na posição de 0 mililitro e puxe a haste do êmbolo, soltando-a na sequência. Depois, observe o que acontece.
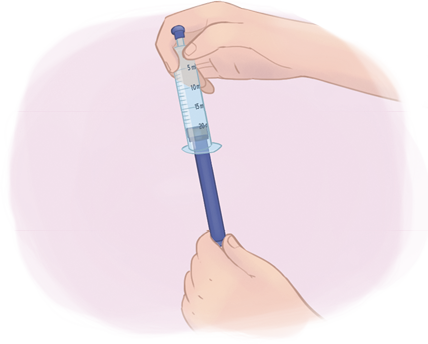
H. Na seringa que foi vedada com o êmbolo na posição de 20 mililitros, empurre a haste do êmbolo até onde conseguir, depois solte-a e verifique o que aconteceu.
Análise e divulgação
1. O que aconteceu quando a seringa foi colocada na água com gelo? Explique por que isso ocorreu.
Resposta: Espera-se que os estudantes respondam que o êmbolo da seringa desceu ao ser colocado na água gelada, pois a massa do gás aprisionado teve sua temperatura diminuída, reduzindo o volume do gás, mantendo sua pressão aproximadamente constante.
2. O que aconteceu quando a seringa foi colocada na água aquecida? Explique por que isso ocorreu.
Resposta: O êmbolo da seringa subiu ao ser colocado na água quente, porque a massa do gás aprisionado teve sua temperatura elevada, aumentando o volume do gás, mantendo sua pressão aproximadamente constante.
3. Quais tipos de transformações gasosas foram observados nas etapas E e F? E nos procedimentos G e H?
Resposta: Espera-se que os estudantes respondam que as variáveis de estado que caracterizam o gás (temperatura, pressão e volume) sofreram alterações. Porém, nas etapas E e F, a pressão do gás pode ser considerada praticamente constante, caracterizando uma transformação chamada isobárica. Já nas etapas G e H, a temperatura do gás pode ser considerada constante, dessa maneira o gás sofreu transformações isotérmicas.
4. Qual é a transformação de energia que pôde ser observada durante a realização da investigação?
Resposta: Foi possível notar a energia térmica de uma massa gasosa sendo transformada em energia mecânica ao perceber o deslocamento do êmbolo da seringa.
5. Com a ajuda de um colega, filme o experimento, explicando cada parte da execução e suas conclusões. Em seguida, compartilhe o vídeo com a turma. Cite casos semelhantes das transformações gasosas visualizadas que ocorrem também em eventos do cotidiano.
Resposta: O objetivo desta questão é levar os estudantes a compartilhar suas observações e conclusões com os colegas. Eles podem citar que o aquecimento ou resfriamento do gás no interior de pneus, a expansão do gás gerado na queima de combustíveis nos motores ou o resfriamento do ar no interior das geladeiras e freezers são exemplos de transformações gasosas.
Página 388
ATIVIDADES
1. Analise as afirmações a seguir e julgue-as como verdadeiras ou falsas, justificando as falsas.
I ) Em uma transformação isobárica, o volume de determinado gás ideal não sofre alteração.
Resposta: Falsa. Nas transformações isobáricas, a grandeza que permanece constante é a pressão. Uma transformação na qual o volume do gás não sofre alteração é denominada isométrica, isovolumétrica ou isocórica.
II ) A transformação isocórica ocorre quando o volume permanece constante e as grandezas pressão e temperatura sofrem variações.
Resposta: Verdadeira.
III ) Em um processo adiabático, o sistema não troca calor com o meio externo.
Resposta: Verdadeira.
IV ) Na transformação isotérmica, as grandezas pressão e volume se relacionam de maneira proporcional e direta.
Resposta: Falsa. Em uma transformação isotérmica, pressão e volume são grandezas inversamente proporcionais.
2. Em um experimento com gases ideais, um estudante obteve o gráfico do volume em função da temperatura de uma transformação isobárica, representado a seguir. Determine a temperatura T em kelvin.
Diagrama abre parênteses V vezes T fecha parênteses para uma transformação isobárica
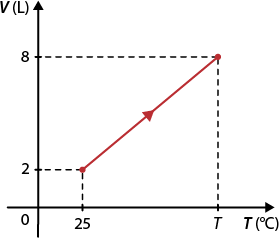
Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 240.
Resposta: T é igual a 1.192 Kelvin
3. Em determinada transformação gasosa, um gás perfeito inicialmente ocupa um volume de 10 litros e é submetido a uma pressão de 2 a t m. Ao sofrer uma expansão isotérmica, seu volume passa para 30 litros. Calcule, em pascal, a nova pressão.
Resposta: p é igual a 6 vírgula 7 vezes 10 elevado a 4 pascal
4. Em uma viagem, os pneus de um carro foram calibrados igualmente quando a temperatura era 14 graus Celsius. Chegando ao município de destino, a temperatura dos pneus aumentou para 57 graus Celsius. Supondo que não houve variação do volume, calcule a pressão interna dos pneus ao chegar ao destino em função da pressão inicial p subscrito 0.
Resoluções das questões 2, 3 e 4 nas Orientações para o professor.
Resposta: p é igual a 1 vírgula 15 vezes p subscrito 0
5. O comportamento térmico dos gases nos ajuda a entender como as propriedades dos gases mudam com a variação de temperatura. Um exemplo é o aquecimento de um balão. Quando um balão cheio de ar é colocado em um ambiente mais quente, a temperatura do gás dentro do balão aumenta, o que leva as partículas de ar a se moverem mais rapidamente. De acordo com a Lei de Charles, a uma lacuna constante, o volume de um gás aumenta com o aumento da temperatura. Por outro lado, se a temperatura de um gás lacuna a um volume constante, a pressão do gás lacuna, de acordo com a Lei de Gay-Lussac. Por exemplo, se um balão com pressão constante for inflado com um volume de 3 litros a 300 Kelvin e depois a temperatura for aumentada para 450 Kelvin, o volume final será igual a lacuna.
A alternativa que preenche corretamente as lacunas é:
a ) pressão – aumenta – aumenta – 4 vírgula 5 litros.
b ) massa – aumenta – diminui – 3 vírgula 5 litros.
c ) pressão – diminui – diminui – 3 vírgula 5 litros.
d ) quantidade de mols – diminui – aumenta – 2 litros.
e ) velocidade – diminui – aumenta – 4 vírgula 5 litros.
Resposta: Alternativa a.
6. É possível provocar o aquecimento de determinada quantidade de gás sem que seja fornecido calor ao sistema? Justifique sua resposta.
Resposta: Sim, comprimindo rapidamente o gás, de modo a evitar que ele consiga trocar calor com o ambiente. Isso ocorre quando se bombeia ar rapidamente para dentro do pneu de uma bicicleta. Esse processo é realizado por meio de uma transformação gasosa adiabática (sem troca de calor com o meio).
7. Um gás ideal é um modelo teórico que simplifica o comportamento dos gases reais e é descrito por um conjunto de leis que relacionam suas propriedades de pressão abre parênteses p fecha parênteses, volume abre parênteses V fecha parênteses e temperatura abre parênteses T fecha parênteses. Sobre o comportamento dos gases, leia as afirmativas a seguir, julgando se são verdadeiras ou falsas. Na sequência, corrija as falsas.
I ) Um gás ideal tem volume V subscrito 0 à tempera- tura T subscrito 0. Se o volume for dobrado à pressão constante, a temperatura será dividida pela metade.
II ) Um gás ideal é selado em um recipiente a volume constante. Se a temperatura T subscrito 0 for aumentada para 4 vezes T subscrito 0, a pressão será aumentada para 4 vezes p subscrito 0.
III ) Ao inspirar, expandimos o volume dos pulmões, reduzindo a pressão interna e permitindo a entrada do ar.
IV ) Quando você fecha a tampa de uma garrafa de água quente, a pressão interna da garrafa aumenta conforme a água esfria.
Resposta: I) Falsa. Se o volume for dobrado à pressão constante, a temperatura também dobra. II) Verdadeira. III) Verdadeira. IV) Falsa. Após fechar a tampa da garrafa, a pressão interna diminui conforme a água esfria.
Página 389
8. De acordo com o gráfico de uma transformação isotérmica, representado a seguir, calcule o valor de V.
Diagrama abre parênteses p vezes V fecha parênteses de uma transformação isotérmica
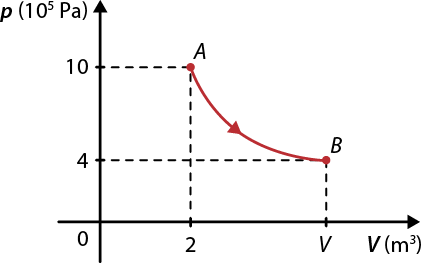
Fonte de pesquisa: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo Sérgio de Biasi. 9. ed. Rio de Janeiro: LTC, 2013. v. 2. p. 240.
Resposta: V é igual a 5 metros cúbicos
9. Um recipiente com êmbolo fixo contendo 15 litros de gás ideal em uma temperatura de 23 graus Celsius sofre uma transformação e tem sua pressão reduzida a 1 terço de p subscrito 0. Qual é a temperatura T do gás?
Resposta: T é aproximadamente igual a 98 vírgula 7 Kelvin
10. Um gás ideal confinado em um recipiente com volume inicial de 15 centímetros cúbicos e temperatura de 10 graus Celsius sofre uma expansão isobárica quando recebe calor e tem sua temperatura elevada a 65 graus Celsius. Qual é o volume final ocupado pelo gás?
Resposta: V é aproximadamente igual a 17 vírgula 9 centímetros cúbicos
11. A atmosfera terrestre é composta de cinco camadas, separadas de acordo com a altitude em relação ao nível do mar. A camada mais próxima da superfície da Terra, denominada troposfera, vai do nível do mar até a altitude de 12 quilômetros. Nessa camada, formam-se os fenômenos climáticos, como chuvas, nuvens e relâmpagos, e sua temperatura pode variar de 40 graus Celsius até menos 60 graus Celsius. Supondo que um balão, cujo volume de 10 litros está completamente preenchido com gás hélio abre parênteses H e fecha parênteses, a 1 a t m e 27 graus Celsius, suportasse alcançar o topo da troposfera, onde a temperatura é cerca de menos 50 graus Celsius e a pressão é 0 vírgula 25 a t m, qual seria o volume do balão?
Resposta: V é aproximadamente igual a 29 vírgula 7 litros
12. Determinada quantidade de gás ideal ocupava um volume de 2 centímetros cúbicos quando submetida a uma pressão de 2 a t m e temperatura de 30 graus Celsius. Em seguida, a temperatura desse gás foi elevada a 180 graus Celsius e o volume do recipiente foi elevado a 6 centímetros cúbicos. Calcule, em pascal, a nova pressão do gás.
Resposta: p é aproximadamente igual a 10 elevado a 5 pascal
13. Um balão meteorológico, carregado com 8 vírgula 8 mols de hélio, está prestes a ser lançado para coletar dados atmosféricos a diferentes altitudes. A pressão atmosférica no local do lançamento é 1 a t m e a temperatura ambiente é 25 graus Celsius. Sob essas condições, determine o volume do balão.
Dados: R é igual a 0 vírgula 0 82 a t m vezes L barra mol vezes K.
Resposta: V é igual a 215 vírgula 0 4 litros
14. Em condições em que um gás é considerado perfeito, as variáveis de estado assumem os valores p subscrito 0 é igual a 2 a t m, V subscrito 0 é igual a 2 litros e T subscrito 0 é igual a 293 Kelvin. Ao sofrer determinada transformação, as variáveis passam a assumir os valores p é igual a 1 vírgula 5 a t m, V é igual a 4 litros e T. Calcule, em grau Celsius, o valor de T.
Resposta: T é igual a 166 vírgula 5 graus Celsius
15. Um experimento comum para ilustrar a pressão atmosférica é aquecer uma lata de alumínio com um pouco de água em seu interior até que ela se transforme totalmente em vapor. Na sequência, se a lata de alumínio for colocada em um recipiente contendo água fria, com a abertura voltada para a água, ela sofre uma deformação e fica amassada, como mostrado na fotografia a seguir.

Utilizando os conceitos de transformações gasosas, explique o que ocorre com o gás no interior da lata e o que provoca sua implosão.
Resposta nas Orientações para o professor.
16. Uma amostra gasosa que está à temperatura de 300 Kelvin exerce uma pressão de 3 a t m nas paredes de um recipiente com volume de 6 litros. Se o gás for comprimido para um volume de 4 litros e a temperatura elevada até 400 Kelvin, qual será o valor da nova pressão exercida pelo gás?
Resoluções das questões 8, 9, 10, 11, 12, 13, 14 e 16 nas Orientações para o professor.
Resposta: p é igual a 6 a t m
Página 390
CAPÍTULO25
Termodinâmica
Trabalho em uma transformação gasosa
Durante o funcionamento de um motor a combustão interna, ocorrem vários tipos de transformações gasosas.
1. Como é possível obter energia mecânica em um automóvel movido a gasolina?
Resposta: O objetivo desta questão é levantar os conhecimentos prévios dos estudantes em relação ao trabalho realizado por um gás. Eles podem citar que a queima da gasolina produz gases que se expandem e movimentam os pistões do motor, transformando energia química em cinética. Essa energia sofre outras transformações até ser transmitida para as rodas, resultando na energia cinética do automóvel.
Vamos retomar o funcionamento dos motores a combustão interna para entender melhor como ele funciona.
A combustão é uma reação química entre uma substância combustível e o gás oxigênio abre parênteses O subscrito 2 fecha parênteses que libera energia térmica, ou seja, calor. A quantidade de energia liberada na combustão varia de acordo com o combustível utilizado. Por exemplo, a gasolina libera 47 vírgula 87 quilojoules por grama; já o etanol, cerca de 29 vírgula 67 quilojoules por grama.
Nos motores a gasolina, a combustão da mistura de ar e combustível normalmente é iniciada por uma centelha (faísca elétrica) no interior da câmara de combustão. Os gases produzidos nessa reação se expandem e empurram os pistões. Em razão da inércia do movimento causado por queimas anteriores, os pistões se deslocam continuamente em um movimento oscilatório para cima e para baixo, alterando o volume da câmara.
Esse movimento é mantido por sucessivas queimas e, então, transferido às rodas pelas engrenagens do sistema de transmissão do veículo. Como consequência, a energia liberada na combustão é transformada em energia cinética, que faz o veículo se locomover.

Nem toda energia liberada pela combustão é utilizada para a produção de movimento. Parte dela provoca aquecimento do motor e outra parte é dissipada na forma de energia sonora.
Para entender como os gases gerados na combustão interagem com os pistões, vamos considerar que eles se comportam como gases ideais contidos em um recipiente cilíndrico, fechado com um êmbolo móvel, conforme mostrado a seguir. O gás encontra-se em um estado termodinâmico inicial com pressão inicial abre parênteses p subscrito 0 fecha parênteses, volume inicial abre parênteses V subscrito 0 fecha parênteses e temperatura inicial abre parênteses T subscrito 0 fecha parênteses.
Imagem sem proporção e em cores fantasia.
Página 391
Ao receber calor, a temperatura do gás aumenta e a quantidade de choques entre as partículas do gás e as paredes do recipiente também.
Isso provoca um deslocamento do êmbolo, aumentando o volume e mantendo a pressão, ou seja, o gás sofre uma transformação isobárica até atingir o estado de pressão final p é igual a p subscrito 0, volume final V é maior do que V subscrito 0 e temperatura final T é maior do que T subscrito 0.
Nesse caso, dizemos que o gás realizou trabalho termodinâmico sobre o êmbolo, pois o deslocamento do êmbolo ocorre por causa da força aplicada pelo gás sobre ele. Podemos definir o trabalho termodinâmico por meio de uma analogia ao trabalho mecânico levando em consideração a intensidade da força aplicada abre parênteses 'F' fecha parênteses e o respectivo deslocamento:
tau é igual a 'F' vezes delta 's' vezes cosseno teta
em que
- delta 's' é o deslocamento do êmbolo;
- teta é o ângulo entre a direção da força e do deslocamento.
Professor, professora: Apresente a expressão matemática para o cálculo do trabalho termodinâmico, fazendo uma analogia ao cálculo do trabalho mecânico, no caso da transformação ilustrada, e deduzindo a fórmula. Peça que os estudantes observem o gráfico e explique como é feita a representação da transformação isobárica em um diagrama da pressão versus volume.
No exemplo, o deslocamento do êmbolo ocorre na mesma direção da aplicação da força, assim teta é igual a 0 grau e cosseno 0 grau é igual a 1. A pressão é dada pela razão entre a intensidade da força aplicada e a área. Desse modo, a força pode ser descrita como:
p é igual a 'F' sobre A implica em 'F' é igual a p vezes A
Como o recipiente é cilíndrico, a variação no volume abre parênteses delta V fecha parênteses será dada pelo produto entre a área abre parênteses A fecha parênteses e o deslocamento do êmbolo abre parênteses delta 's' fecha parênteses:
delta V é igual a A vezes delta 's' implica em delta 's' é igual a início de fração, numerador: delta V, denominador: A, fim de fração
Assim, o trabalho termodinâmico em uma transformação isobárica pode ser descrito da seguinte maneira:
tau é igual a 'F' vezes delta 's' vezes cosseno teta implica em tau é igual a p vezes A vezes início de fração, numerador: delta V, denominador: A, fim de fração vezes 1 portanto tau é igual a p vezes delta V
Para calcular o trabalho em joule abre parênteses J fecha parênteses, a pressão deve ser expressa em pascal abre parênteses P a fecha parênteses; o volume, em metros cúbicos abre parênteses metro elevado ao cubo fecha parênteses.
O trabalho termodinâmico também pode ser obtido por meio da representação da transformação gasosa no diagrama da pressão em função do volume (diagrama p vezes V).
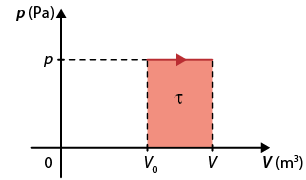
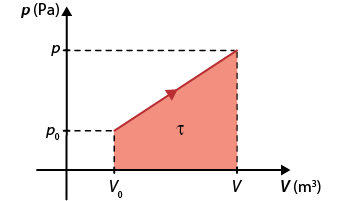
No diagrama p vezes V, é representada uma transformação isobárica de um gás com volume inicial V subscrito 0 e volume final V.
Observe que, na representação gráfica de uma transformação gasosa, é indicado o sentido da transformação por meio de uma seta sobre o gráfico.
Transformação isobárica em um diagrama p vezes V
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 232.
A região compreendida entre o gráfico e o eixo do volume corresponde a um retângulo, cuja área é dada pela multiplicação da altura (que equivale a valores de pressão) pela largura (que equivale a valores de volume). Dessa maneira:
tau expressão com detalhe acima, início da expressão, é igual a, fim da expressão, início do detalhe acima, N, fim do detalhe acima área
Página 392
Nota-se que o trabalho realizado por um gás depende da variação do volume. Desse modo, em uma expansão, o gás realiza trabalho abre parênteses tau é maior do que 0 fecha parênteses; em uma compressão, o gás recebe trabalho do meio externo abre parênteses tau é menor do que 0 fecha parênteses; já em uma transformação isovolumétrica, não é realizado trabalho abre parênteses tau é igual a 0 fecha parênteses.
A representação de uma transformação gasosa em um diagrama do tipo p vezes V pode ser utilizada para qualquer tipo de transformação. Confira a seguir alguns exemplos de transformações gasosas representadas em diagramas p vezes V.
Expansão isobárica em um diagrama p vezes V
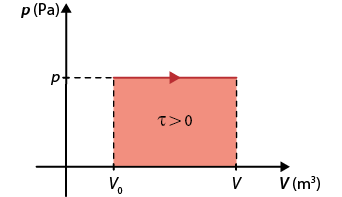
Expansão isobárica: o gás realiza trabalho abre parênteses tau é maior do que 0 fecha parênteses, pois delta V é maior do que 0.
Transformação isovolumétrica em um diagrama p vezes V

Transformação isovolumétrica: o gás não realiza nem recebe trabalho abre parênteses tau é igual a 0 fecha parênteses, pois delta V é igual a 0.
Compressão isobárica em um diagrama p vezes V
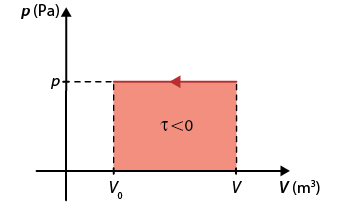
Compressão isobárica: o gás recebe trabalho abre parênteses tau é menor do que 0 fecha parênteses, pois delta V é menor do que 0.
Expansão gasosa em um diagrama p vezes V
Expansão gasosa qualquer: o trabalho realizado pode ser calculado pela análise da área do gráfico, pois há variação de volume e pressão.
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 231-233.
ATIVIDADES RESOLVIDAS
R1. O gráfico p vezes V mostra a expansão de um gás ideal. Determine o trabalho realizado por ele nessa transformação.
Gráfico p vezes V de uma transformação gasosa
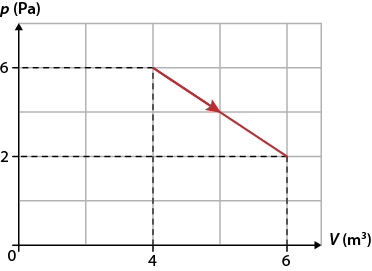
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 231-233.
Resolução:
Podemos notar que o volume aumenta, indicando que o trabalho é positivo. Além disso, verifica-se que as unidades de pressão e volume mostradas no gráfico estão no SI, não sendo necessária qualquer transformação. Da propriedade que a área sob a curva do gráfico é numericamente igual ao trabalho, temos:
tau expressão com detalhe acima, início da expressão, é igual a, fim da expressão, início do detalhe acima, N, fim do detalhe acima área do trapézio
tau expressão com detalhe acima, início da expressão, é igual a, fim da expressão, início do detalhe acima, N, fim do detalhe acima início de fração, numerador: abre parênteses base maior mais base menor fecha parênteses vezes altura, denominador: 2, fim de fração
tau é igual a início de fração, numerador: abre parênteses 2 mais 6 fecha parênteses vezes abre parênteses 6 menos 4 fecha parênteses, denominador: 2, fim de fração implica em tau é igual a início de fração, numerador: 8 vezes 2, denominador: 2, fim de fração implica em portanto é igual a 8 joules
Página 393
Energia interna de um gás
Uma amostra de uma substância qualquer armazena energia de variadas formas.
A temperatura de um corpo está relacionada ao movimento das partículas que o compõem, ou seja, está relacionada à energia cinética de translação das partículas.
Além dessa energia, temos a energia química armazenada nas ligações químicas, a energia associada a outros tipos de movimento, como a rotação e a vibração, mostradas a seguir, e a energia potencial advinda das interações químicas.
Imagens desta página sem proporção e em cores fantasia.


Representação dos movimentos realizados pelas partículas de um gás. Todos fazem parte da energia interna do gás.
Todas as formas de energia citadas constituem a energia interna abre parênteses U fecha parênteses da substância.
A energia interna pode ser modificada em uma transformação gasosa. Quando um gás absorve calor, sua energia interna aumenta. Por outro lado, quando ele cede calor, sua energia interna diminui.
Considerando um gás ideal e monoatômico, ou seja, constituído de um único átomo, seu movimento será composto apenas da translação. Assim, a energia interna do gás (determinada pela energia cinética média das partículas) está relacionada apenas com a temperatura. Matematicamente, essa relação entre a energia interna de um gás e a temperatura do gás pode ser descrita como:
U é igual a 3 meios vezes n vezes R vezes T
em que
- U é a energia interna do gás em joule abre parênteses J fecha parênteses;
- n é a quantidade de matéria (em mols) da amostra;
- R é a constante universal dos gases ideais, que vale 8 vírgula 31 joules barra mol vezes K, em unidades do Sistema Internacional de Unidades (SI);
- T é a temperatura do gás na escala absoluta abre parênteses K fecha parênteses.
Professor, professora: Comente que a energia interna é intrínseca ao sistema, sendo a soma de todas as energias de todas as moléculas em uma média. Apesar de a energia interna ser diretamente ligada à grandeza temperatura, o calor é apenas uma consequência de sua diferença entre sistemas.
Essa equação é válida apenas para gases monoatômicos. Como os átomos dos gases são livres para se moverem livremente, eles têm três graus de liberdade de translação, isto é, movimentam-se nas três dimensões do espaço. Nos casos em que o gás não é monoatômico, é preciso levar em consideração os graus de liberdade associados aos movimentos de rotação e vibração.
Nesses casos, ainda é possível encontrar uma relação que depende apenas da temperatura. A unidade de medida da energia interna no SI, assim como o calor e outras formas de energia, é o joule abre parênteses J fecha parênteses.
Dica
Para gases diatômicos, aqueles que têm dois átomos formando uma substância, a equação da energia interna é:
U é igual a 5 meios vezes n vezes R vezes T
Página 394
ATIVIDADES
1. Um gás ideal sofre uma transformação isovolumétrica variando sua pressão de 1 a t m para 3 a t m. Determine o trabalho termodinâmico realizado pelo gás e explique o resultado obtido.
Resposta: O trabalho realizado nessa transformação gasosa é nulo abre parênteses tau é igual a 0 fecha parênteses, pois, como a transformação é isovolumétrica, não há variação de volume. Portanto, não é realizado trabalho.
2. Calcule o trabalho realizado por um gás que sofre uma transformação, de acordo com o diagrama a seguir.
Gráfico p vezes V de uma transformação gasosa

Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 233.
Resposta: tau subscrito total é igual a 12 vezes 10 elevado a 5 Joules. Resolução nas Orientações para o professor.
3. O diagrama a seguir mostra diferentes caminhos para a transformação gasosa de um gás ideal.
Gráfico p vezes V de transformações gasosas
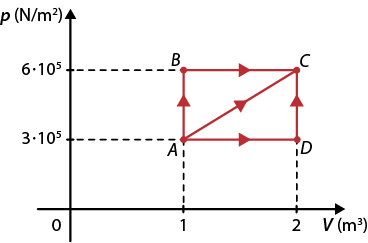
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 233.
a ) Calcule o trabalho da transformação realizada pelo caminho A B C.
Resposta: tau início subscrito, A B 'C', fim subscrito é igual a 6 vezes 10 elevado a 5 Joules.
b ) Calcule o trabalho da transformação realizada pelo caminho A D C.
Resposta: tau início subscrito, A D 'C', fim subscrito é igual a 3 vezes 10 elevado a 5 Joule.
c ) Calcule o trabalho da transformação realizada pelo caminho A C.
Resposta: tau início subscrito, A 'C', fim subscrito é igual a 4 vírgula 5 vezes 10 elevado a 5 Joules. Resoluções nas Orientações para o professor.
4. Um mol de um gás ideal sofre uma transformação a volume constante e outra a pressão constante, conforme indicado no diagrama da pressão em função do volume mostrado a seguir.
Gráfico p vezes V de transformações gasosas
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 233.
Sabendo que no ponto B sua temperatura é de 500 Kelvin, qual é o trabalho realizado pelo gás na transformação A seta para a direita B seta para a direita 'C'? Utilize para a constante universal dos gases ideais R é igual a 0 vírgula 0 82 L vezes a t m vezes K elevado a menos 1 vezes mo l elevado a menos 1 e 1 a t m vezes L é igual a 101 vírgula 3 joules.
Resposta: tau é igual a 4.153 vírgula 3 joules. Resolução nas Orientações para o professor.
5. Se a energia em forma de calor flui de maneira espontânea do corpo de maior temperatura para outro com menor temperatura, é correto dizer que isso ocorre do corpo de maior energia interna para outro de menor energia interna? Explique sua resposta.
Resposta: Não. A equação que descreve a energia interna depende não somente da temperatura, mas também da quantidade de matéria presente no sistema por meio do número de mols. Assim, um corpo de menor temperatura pode ter energia interna maior do que a de um corpo com uma temperatura mais elevada em razão do número de mols.
6. Uma quantidade de 4 mols de um gás monoatômico, inicialmente a uma temperatura de 20 graus Celsius, está confinada em um recipiente cilíndrico fechado sobre uma fonte calorífica. Sabendo que o gás será aquecido até 60 graus Celsius, determine a variação causada na energia interna do gás (utilize R é igual a 8 vírgula 3 joules barra mol vezes K).
Resposta: delta U é igual a 1.992 joules. Resolução nas Orientações para o professor.
7. De acordo com o conceito de energia interna, julgue as afirmações a seguir como verdadeiras ou falsas, corrigindo as falsas.
a ) A energia interna de um gás diminui em uma expansão livre.
b ) A energia interna de uma massa gasosa aumenta em uma expansão isobárica.
c ) A energia interna diminui em uma transformação isotérmica.
d ) A energia interna de um gás não varia em uma transformação isovolumétrica.
e ) Em um gás ideal não ocorre interações intermoleculares associados à uma energia potencial.
Resposta: a) Verdadeira. b) Verdadeira. c) Falsa. Como em uma transformação isotérmica a temperatura não varia, não há variação da energia interna. d) Falsa. A energia interna de um gás pode aumentar ou diminuir em uma transformação isovolumétrica, pois a temperatura do gás pode aumentar ou diminuir. e) Verdadeira.
Página 395
Primeira lei da Termodinâmica
Como vimos anteriormente, a combustão de gasolina ou etanol faz os gases realizarem trabalho nos pistões de um motor.
2. Além das partes para produzir a queima dos combustíveis, no motor dos automóveis há um dispositivo denominado radiador, que compõe um sistema de resfriamento. Você sabe para que serve o radiador de um automóvel?
Resposta pessoal. O objetivo desta questão é resgatar os conhecimentos prévios dos estudantes em relação ao funcionamento dos radiadores e da necessidade desse dispositivo nos automóveis. Eles podem citar que os radiadores servem para resfriar o motor, retirando parte do calor que é gerado na queima dos combustíveis e que aquece o motor.
Outro resultado da explosão dos combustíveis é a liberação de calor, que faz a temperatura do motor aumentar. Sendo assim, em muitos motores, é necessária a presença de um radiador, que faz parte do sistema de resfriamento da máquina.
Esse sistema é composto de tubos preenchidos com líquidos refrigerantes e tem como objetivo fazer trocas de calor com o ambiente.
O líquido passa por uma tubulação em torno do motor e deste retira calor. Depois, passa pelo radiador, transferindo calor para o ambiente e evitando que a temperatura do motor passe do limite seguro para seu funcionamento.
Imagem sem proporção e em cores fantasia.

Imagem elaborada com base em: YADAV, J. P.; SINGH, B. R. Study evaluation of automotive radiator. SAMRIDDHI-A Journal of Physical Sciences, Engineering and Technology. v. 2. 2011. p. 48.
Assim como outras máquinas térmicas, o motor de um automóvel não utiliza toda a energia do combustível para realizar trabalho. Parte dessa energia é convertida em energia interna do sistema em razão do aumento da temperatura do motor e de suas peças.
Essa propriedade das máquinas térmicas é descrita pela primeira lei da Termodinâmica, que é baseada no princípio da conservação de energia. A quantidade de calor abre parênteses Q fecha parênteses adicionada a um sistema pode aumentar sua energia interna abre parênteses delta U fecha parênteses e possibilitar que o sistema realize trabalho abre parênteses tau fecha parênteses. Matematicamente, a primeira lei da Termodinâmica pode ser descrita como:
Q é igual a tau mais delta U
Nessa relação, todas as grandezas são expressas em joule abre parênteses J fecha parênteses, no SI.
Vamos analisar como cada variável da primeira lei da Termodinâmica se comporta nas transformações gasosas que vimos anteriormente.
Transformação isobárica em um diagrama p vezes V
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 231.
Uma transformação isobárica ocorre entre duas temperaturas e dois volumes diferentes. Ao analisar essa situação por meio da primeira lei da Termodinâmica abre parênteses Q é igual a tau mais delta U fecha parênteses, temos que:
- se o gás recebe calor abre parênteses Q é maior do que 0 fecha parênteses, sua temperatura abre parênteses delta T é maior do que 0 fecha parênteses e sua energia interna aumentam abre parênteses delta U é maior do que 0 fecha parênteses, e ele se expande, realizando trabalho abre parênteses tau é maior do que 0 fecha parênteses;
- se o gás cede calor abre parênteses Q é menor do que 0 fecha parênteses, sua temperatura abre parênteses delta T é menor do que 0 fecha parênteses e sua energia interna diminuem abre parênteses delta U é menor do que 0 fecha parênteses, e o meio externo realiza trabalho sobre o gás, que se contrai abre parênteses tau é menor do que 0 fecha parênteses.
Página 396
Considere agora uma transformação isotérmica. Como a variação de temperatura é nula abre parênteses delta T é igual a 0 fecha parênteses, a variação de energia interna também é nula abre parênteses delta U é igual a 0 fecha parênteses.
Uma transformação isotérmica, analisada segundo a primeira lei da Termodinâmica, pode ser descrita como:
Q é igual a tau mais delta U é igual a tau mais 0 portanto Q é igual a tau
Portanto:
- se o gás recebe calor abre parênteses Q é maior do que 0 fecha parênteses, ele se expande e realiza trabalho abre parênteses tau é maior do que 0 fecha parênteses;
- se o gás cede calor abre parênteses Q é menor do que 0 fecha parênteses, é realizado trabalho sobre o gás abre parênteses tau é menor do que 0 fecha parênteses e ocorre uma compressão.
Transformações isotérmicas em um diagrama p vezes V
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 231.
Para uma transformação isovolumétrica, a variação de volume é nula abre parênteses delta V é igual a 0 fecha parênteses. Isso demonstra que o gás não realiza nem recebe trabalho abre parênteses tau é igual a 0 fecha parênteses.
A análise de uma transformação isovolumétrica, segundo a primeira lei da Termodinâmica, pode ser descrita como:
Q é igual a tau mais delta U é igual a 0 mais delta U portanto Q é igual a delta U
Assim:
- se o gás recebe calor abre parênteses Q é maior do que 0 fecha parênteses, ele se aquece abre parênteses delta T é maior do que 0 fecha parênteses e sua energia interna aumenta abre parênteses delta U é maior do que 0 fecha parênteses;
- se o gás cede calor abre parênteses Q é menor do que 0 fecha parênteses, ele diminui de temperatura abre parênteses delta T é menor do que 0 fecha parênteses, diminuindo também sua energia interna abre parênteses delta U é menor do que 0 fecha parênteses.
Transformação isovolumétrica em um diagrama p vezes V
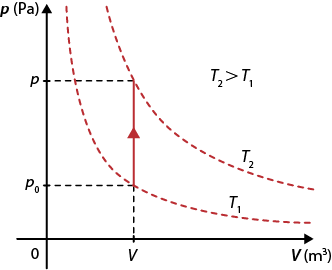
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 231.
Considerando agora uma transformação adiabática, precisamos lembrar que, nesse tipo de transformação gasosa, não há trocas de calor com o meio externo abre parênteses Q é igual a 0 fecha parênteses.
Se o sistema tem paredes que impedem trocas de calor com o ambiente (garrafa térmica, caixa de isopor etc.) ou caso o processo ocorra de forma rápida, não havendo tempo suficiente para que sejam realizadas trocas de calor, a transformação é caracterizada como adiabática.
Analisando uma transformação adiabática por meio da primeira lei da Termodinâmica, temos:
Q é igual a tau mais delta U implica em 0 é igual a tau mais delta U portanto tau é igual a menos delta U
Portanto:
- se o gás sofre uma expansão adiabática, ele realiza trabalho abre parênteses tau é maior do que 0 fecha parênteses e sua temperatura diminui abre parênteses delta T é menor do que 0 fecha parênteses. Assim, a energia interna também diminui abre parênteses delta U é menor do que 0 fecha parênteses;
- se o gás sofre uma compressão adiabática, o trabalho é realizado sobre ele abre parênteses tau é menor do que 0 fecha parênteses e sua temperatura aumenta abre parênteses delta T é maior do que 0 fecha parênteses. Dessa maneira, a energia interna também aumenta abre parênteses delta U é maior do que 0 fecha parênteses.
Transformação adiabática em um diagrama p vezes V
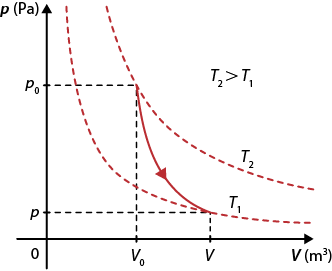
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 231.
Página 397
Primeira lei da Termodinâmica e fenômenos meteorológicos
A primeira lei da Termodinâmica é utilizada pelos meteorologistas para explicar diferentes fenômenos atmosféricos, analisar o clima e realizar previsões do tempo. Isso porque a temperatura do ar atmosférico se altera quando há adição ou retirada de calor, quando a pressão do ar é modificada por meio da realização de trabalho ou quando ambas as situações ocorrem.
A atmosfera é um sistema bastante dinâmico. Ela está sujeita a diferentes fenômenos, como condensação de vapor de água, evaporação da chuva, absorção tanto da radiação solar quanto da radiação infravermelha emitida pela Terra e perda de calor para o espaço, que alteram o volume e a temperatura do ar atmosférico.
Há ainda processos atmosféricos em que a quantidade de calor absorvido ou cedido por uma massa de ar é muito pequena. Assim, esses fenômenos podem ser considerados praticamente adiabáticos. Nesses casos, a temperatura do ar varia de acordo com a pressão, diminuindo à medida que a pressão diminui e aumentando quando a pressão aumenta.
Lembrando que o ar se torna cada vez mais rarefeito com o aumento da altitude e que a pressão atmosférica diminui continuamente para acréscimos na altitude em virtude dessa expansão do ar. Isso explica o fato de a temperatura do ar diminuir conforme a altitude cresce. Para uma massa de ar seco, a temperatura diminui aproximadamente 10 graus Celsius para uma elevação de 1 quilômetro de altitude até uma altitude de cerca de 10 quilômetros.
Imagem sem proporção e em cores fantasia.

Imagem elaborada com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 341.
As transformações adiabáticas que ocorrem na atmosfera são típicas de massas de ar cujas dimensões são grandes o suficiente para que o ar externo não se misture com o ar dela própria (desde dezenas de metros até muitos quilômetros).
As nuvens cumulonimbus, por exemplo, são resultado da expansão adiabática de uma massa de ar úmido que se eleva e do vapor de água presente no ar, que se condensa e forma a chuva.

Por outro lado, se uma massa de ar a certa altitude desce, ocorre uma compressão adiabática e sua temperatura sobe.
Geralmente, na movimentação de massas de ar na atmosfera, aquelas mais quentes (menos densas) que o ar em sua volta se elevam e as mais frias (mais densas) descem. Em alguns casos, ocorre um fenômeno no qual massas de ar frio que estão em baixa altitude sofrem um aquecimento, mas não conseguem subir porque há uma massa de ar mais quente sobre elas, impedindo seu movimento. Esse fenômeno é denominado inversão térmica.
A inversão térmica é responsável por aprisionar a fumaça e outros poluentes atmosféricos próximos à superfície terrestre em grandes municípios.
a ) Como a variação na temperatura do ar em função da altitude pode ser explicada com base na primeira lei da Termodinâmica?
Resposta: Considera-se que, conforme a altitude aumenta, o ar se expande de maneira adiabática abre parênteses Q é igual a 0 fecha parênteses. Assim, pela primeira lei da Termodinâmica, teremos: Q é igual a tau mais delta U implica em 0 é igual a tau mais delta U portanto delta U é igual a menos tau. Dessa forma, a variação de energia interna tem comportamento oposto ao trabalho. Quando o ar se expande de forma adiabática, realizando trabalho, a energia interna diminui. Como a energia interna está ligada à temperatura do ar, se a energia diminui, isso implica uma diminuição de temperatura também.
b ) Uma massa de ar com temperatura de menos 40 graus Celsius está inicialmente localizada a uma altitude de 7 quilômetros. Caso ela desça até o nível do mar, qual será sua temperatura, supondo que ela varie em 10 graus Celsius a cada quilômetro?
Resposta: Como o ar é comprimido adiabaticamente, conforme desce, sua temperatura aumenta. Considerando um acréscimo de 10 graus Celsius para cada quilômetro de redução na altitude, sua temperatura no nível do mar será de: T subscrito final é igual a T subscrito inicial mais 10 vezes 7 implica em T subscrito final é igual a menos 40 mais 70 é igual a 30 portanto T subscrito final é igual a 30 graus Celsius.
Página 398
Segunda lei da Termodinâmica
Anteriormente, vimos ser possível construir uma máquina térmica que, ao receber calor de uma fonte externa, sofra uma variação de energia interna e possa realizar trabalho.
3. De acordo com o que vimos até agora, seria possível construir uma máquina que convertesse todo o calor recebido em trabalho?
Resposta: Os estudantes podem citar que, de acordo com a primeira lei da Termodinâmica, que trata da conservação de energia, seria possível a construção de uma máquina com essas características. O objetivo desta questão é introduzir a discussão sobre máquinas ideais ou de rendimento 100%, que fazem parte das discussões da segunda lei da Termodinâmica.
Analise a ilustração a seguir. Ela representa dois corpos, inicialmente com temperaturas diferentes, que são colocados em contato no interior de uma região termicamente isolada. Assim, eles trocam calor entre si, mas não com o ambiente. O corpo A tem temperatura inicial maior do que a do corpo B.
Imagens desta página sem proporção e em cores fantasia.

Imagem elaborada com base em: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 10. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2016. v. 2. p. 208.
Naturalmente, o calor flui do corpo de maior temperatura para o de menor temperatura. No exemplo dado, à medida que o corpo A cede calor, ele se resfria, e o corpo B, que recebe calor, se aquece, até que ambos atinjam equilíbrio térmico (temperaturas iguais). Nesse processo, a energia é conservada e, assim, é respeitada a primeira lei da Termodinâmica.
Imagine agora que o corpo de maior temperatura, por acaso, retirasse calor do corpo frio, de modo que sua temperatura aumentasse ainda mais. Esse processo não viola a primeira lei da Termodinâmica, pois o corpo frio se tornaria mais frio na mesma intensidade que o corpo quente se tornaria ainda mais quente. Assim, a energia se conservaria da mesma forma.
Se a segunda situação descrita não viola a conservação de energia, então por que ela não é observada? A resposta é a segunda lei da Termodinâmica, que está relacionada com o sentido da transformação de energia dos fenômenos naturais. Ela pode ser enunciada de diversas maneiras, sendo a mais simples descrita da seguinte maneira.
O calor nunca flui espontaneamente de um corpo com menor temperatura para um corpo com maior temperatura.
O sentido do fluxo de calor pode ser invertido em algumas situações, porém, para que isso ocorra, é necessário realizar trabalho sobre o sistema. Nesse caso, é adicionada energia de uma fonte externa, como ocorre nos refrigeradores ou nos aparelhos de ar-condicionado.
Para compreender melhor a segunda lei da Termodinâmica, vamos considerar um recipiente fechado que contenha certa quantidade de gás ideal conectado a outro recipiente, inicialmente evacuado. Entre eles, há uma válvula fechada, impedindo o fluxo do gás entre os dois frascos, como mostra a figura.
Imagem elaborada com base em: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 10. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2016. v. 2. p. 259.
Página 399
Caso a válvula seja aberta e a temperatura mantida constante, o gás se expandirá espontaneamente e ocupará o volume dos dois recipientes até que as pressões se igualem.
Caso quiséssemos realizar o processo inverso, no qual o gás distribuído nos dois recipientes ocupasse espontaneamente o interior de apenas um deles, isso não seria possível.
O fato de as partículas terem um movimento aleatório torna muito maior a probabilidade de haver um aumento na desordem de sua distribuição do que o contrário.
Esse tipo de fenômeno pode ser exemplificado com uma piscina de bolinhas. Mesmo que as bolinhas de plástico sejam colocadas na piscina, uma cor por vez, após algumas crianças brincarem nessa piscina, a maior probabilidade é de que as bolinhas coloridas fiquem todas misturadas. Ou seja, o grau de desordem do sistema aumentou.
Imagens desta página sem proporção e em cores fantasia.


Apesar de haver uma pequena probabilidade de as bolinhas de uma cor se concentrarem em uma região da piscina, ou de um gás se concentrar em um único recipiente, para que o sistema retorne para uma situação de mais ordenamento, é preciso que algum agente externo atue no sistema. No exemplo da piscina de bolinhas, uma pessoa deve pegar as bolinhas de plástico e organizá-las novamente. No caso dos gases, é possível utilizar uma bomba de vácuo e colocar o gás de volta em apenas um dos recipientes. Esses exemplos mostram que, espontaneamente, os fenômenos tendem a ocorrer de modo a aumentar a desordem de um sistema.
O nível de ordem de um sistema está associado ao conceito de energia útil, ou seja, que pode ser aproveitada para realizar trabalho. Conforme a energia é utilizada, ela se transforma em energia desorganizada (ou degradada), isto é, em formas de energia não úteis para a realização de trabalho. A grandeza que mede o grau de desordem da energia de um sistema é a entropia abre parênteses S fecha parênteses. Dessa maneira, quanto maior o grau de desordem, maior será sua entropia.
Como a energia útil tende a se degradar, a entropia total do Universo sempre aumenta. Para entender essa ideia, pense nas relações entre os seres vivos na Terra. As plantas retiram do ar, do solo e da água elementos para se desenvolver. Nesse processo, a entropia diminui, pois os seres vivos são estruturas mais complexas e ordenadas que os nutrientes utilizados. Contudo, a vida é possível por causa da energia emitida pelo Sol, que aquece o planeta e que é utilizada pelas plantas para realizar fotossíntese.

Imagem elaborada com base em: KLEIDON, A. Thermodynamics Foundations of the Earth system. Cambridge: Cambridge University Press, 2016. p. 7.
Página 400
Dessa forma, o desenvolvimento da vida diminui localmente a entropia. No entanto, isso só acontece porque no Sol está ocorrendo um nível de desordem muito maior nas reações termonucleares que transformam energia nuclear em outros tipos de energia.
Concluímos, então, que a entropia local na Terra está diminuindo (no intervalo de tempo no qual os seres vivos estão se desenvolvendo), mas a entropia total está, na realidade, aumentando.
Com base no conceito de entropia, é possível definir a segunda lei da Termodinâmica em termos dessa grandeza como: nos processos espontâneos, a ordem de um sistema tende para a desordem, ou seja, a entropia sempre aumenta.
A entropia e a segunda lei da Termodinâmica permitem explicar por que alguns processos são espontâneos, isto é, ocorrem naturalmente, enquanto outros não. Isso está ligado ao sentido natural da ocorrência dos fenômenos. Analisando as fotografias a seguir, sabemos que a ordem das etapas é do copo inteiro para o copo quebrado, pois o copo cair e quebrar é um processo irreversível, o que implica que o copo quebrado jamais voltará, por conta própria, a ficar inteiro novamente.


Rendimento de uma máquina térmica e o ciclo de Carnot
Os dispositivos capazes de converter calor em trabalho são denominados máquinas térmicas.
Compartilhe ideias
As primeiras máquinas térmicas foram idealizadas na Antiguidade, mas não tinham uma aplicação prática.
a ) Junte-se a três colegas para pesquisar as primeiras máquinas térmicas a vapor e o aperfeiçoamento delas. Em seguida, juntos, produzam uma linha do tempo para ser exposta em sala de aula, destacando as principais características das máquinas, suas funções e seus desenvolvedores.
Resposta pessoal. Os estudantes podem citar que uma das primeiras máquinas térmicas idealizadas foi a eolípila de Heron de Alexandria, que consistia em uma esfera metálica preenchida com água, com dois canos, e que girava quando a água era aquecida e o vapor era expelido pelos canos. Na sequência, eles podem citar as máquinas a vapor, como bombas-d'água, trens a vapor, barcos a vapor e motores a combustão interna.
No desenvolvimento das máquinas térmicas, percebeu-se que, para obter resultados melhores, as máquinas deveriam ter uma fonte quente (com temperatura mais alta) e uma fonte fria (com temperatura mais baixa), para que ocorresse um fluxo espontâneo de calor.
Em seu funcionamento, a máquina térmica recebe calor da fonte quente e converte uma fração dessa energia em trabalho. A fração de energia que não é aproveitada aumenta a energia interna da máquina. Na sequência, essa energia, que não foi convertida em trabalho, é direcionada para a fonte fria na forma de calor.
Considerando um motor de combustão interna, como o de um automóvel, o calor da queima do combustível corresponde à fonte quente, os gases a alta temperatura realizam trabalho sobre o pistão, enquanto parte da energia em forma de calor é rejeitada para o meio ambiente ou para a fonte fria.
Página 401
Suponha que a fonte quente de uma máquina térmica esteja à temperatura T subscrito 1 e fornece a quantidade de calor Q subscrito 1. A fonte fria está a uma temperatura menor T subscrito 2 e recebe calor Q subscrito 2, que foi rejeitado pela máquina. Nesse caso, o trabalho realizado pela máquina térmica é determinado pela diferença entre as duas quantidades de calor.
tau é igual a Q subscrito 1 menos Q subscrito 2
Note que uma máquina térmica sempre dependerá do fluxo natural de calor, respeitando a segunda lei da Termodinâmica – ela sempre rejeitará uma parcela do calor recebido para a fonte fria. Dessa forma, concluímos que ela tem um rendimento que é dado por:
etá é igual a início de fração, numerador: tau, denominador: Q subscrito 1, fim de fração
em que o símbolo etá (lê-se ni) é o rendimento da máquina térmica, o qual indica a parcela da energia recebida pela fonte quente que é efetivamente convertida em trabalho. Quanto menor for a quantidade de calor rejeitada abre parênteses Q subscrito 2 fecha parênteses, maior será o rendimento da máquina.
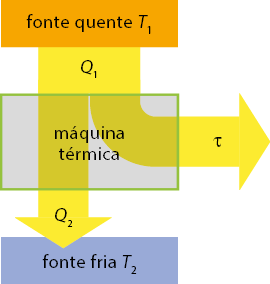
Imagem elaborada com base em: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 10. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2016. v. 2. p. 265.
Uma vez que o trabalho realizado pela máquina térmica pode ser escrito em termos das quantidades de calor recebido abre parênteses Q subscrito 1 fecha parênteses e rejeitado abre parênteses Q subscrito 2 fecha parênteses, o rendimento pode ser expresso apenas em função das respectivas quantidades de calor:
etá é igual a início de fração, numerador: tau, denominador: Q subscrito 1, fim de fração implica em etá é igual a início de fração, numerador: Q subscrito 1 menos Q subscrito 2, denominador: Q subscrito 1, fim de fração portanto etá é igual a 1 menos início de fração, numerador: Q subscrito 2, denominador: Q subscrito 1, fim de fração
Portanto, caso conheçamos as quantidades de calor recebido e rejeitado pela máquina térmica, seremos capazes de calcular seu rendimento sem a necessidade de calcular o trabalho realizado por ela. Essa equação representa o rendimento real de uma máquina térmica.
O fato de as máquinas térmicas sempre rejeitarem uma parcela importante do calor recebido motivou a busca por melhorar seu rendimento. Nesse contexto, o físico francês Nicolas Léonard Sadi Carnot (1796-1832) analisou o funcionamento de uma máquina térmica e descobriu que a parcela da energia fornecida que pode ser convertida em trabalho sempre depende da diferença de temperatura entre a fonte quente e a fonte fria, mesmo em condições ideais.
O rendimento máximo de uma máquina térmica pode ser obtido considerando que ela opere em um ciclo reversível, composto de duas transformações adiabáticas (B seta para a direita 'C' e D seta para a direita A) e duas transformações isotérmicas (A seta para a direita B e 'C' seta para a direita D), como mostra o diagrama. Nesse ciclo, ocorrem trocas de calor somente entre o gás e as fontes quente e fria, ou seja, não existe dissipação.
O diagrama p vezes V representado é denominado ciclo de Carnot. Ele ilustra o rendimento ideal de uma máquina térmica, ou seja, o rendimento máximo que ela pode obter.
Ciclo de Carnot para uma máquina térmica ideal
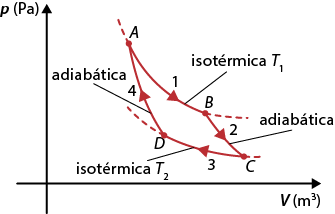
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 256.
Página 402
O rendimento de uma máquina térmica que opera segundo o ciclo de Carnot (rendimento ideal) é calculado em relação às temperaturas das fontes quente e fria, podendo ser descrito como:
etá é igual a início de fração, numerador: T subscrito 1 menos T subscrito 2, denominador: T subscrito 1, fim de fração portanto etá é igual a 1 menos início de fração, numerador: T subscrito 2, denominador: T subscrito 1, fim de fração
Muitos acreditavam que seria possível construir uma máquina térmica que convertesse toda a energia térmica recebida em trabalho. Mas, de acordo com a segunda lei da Termodinâmica, uma máquina terá seu rendimento máximo se operar o ciclo de Carnot. Em razão das descobertas de Carnot, percebeu-se que nenhuma máquina que opera em ciclos pode atingir um rendimento de 100%. Em outras palavras, nenhuma máquina térmica é capaz de transformar todo o calor recebido da fonte quente em trabalho.
Outros ciclos termodinâmicos
Além do ciclo de Carnot, há outros ciclos que têm aplicações no cotidiano, como é o caso dos ciclos de motores a combustão. O ciclo de Otto foi desenvolvido pelo engenheiro alemão Nikolaus August Otto (1832-1891) em 1876. Esse ciclo é aplicado nos motores de automóveis movidos a gasolina ou etanol. Ele é composto de quatro etapas (ou quatro tempos): admissão, compressão, combustão e exaustão.
Na etapa de admissão, trecho A seta para a direita B no diagrama apresentado, o pistão do motor é deslocado para baixo, a válvula de admissão é aberta, e uma mistura de ar e combustível é inserida no interior da câmara de combustão.
Gráfico p vezes V do ciclo Otto teórico
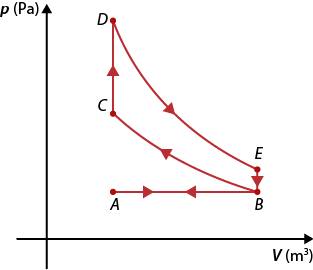
Fonte de pesquisa: ÇENGEL, Y. A.; BOLES, M. A. Termodinâmica. 7. ed. Tradução: Paulo Maurício Costa Gomes. Porto Alegre: AMGH, 2013. p. 498.

Na etapa de compressão, trecho B seta para a direita 'C', as válvulas permanecem fechadas, o pistão desloca-se no sentido contrário e comprime a mistura, fazendo a temperatura aumentar.
Já na terceira etapa, trecho 'C' seta para a direita D, com o sistema no estado de compressão máxima do conjunto, é ligada a vela, que produz uma faísca elétrica, provocando a explosão e a combustão do combustível. A energia térmica liberada pela combustão impulsiona o pistão, que se desloca, aumentando o volume, trecho D seta para a direita E, ao passo que tanto a temperatura quanto a pressão diminuem.
Na etapa quatro do ciclo de Otto, é aberta a válvula de escape, fazendo que a pressão e a temperatura diminuam, enquanto o volume permanece constante, trecho E seta para a direita B. Os resíduos da queima são retirados da câmara de combustão, trecho B seta para a direita A, para que, então, o ciclo possa recomeçar.
Outro ciclo utilizado em motores de automóveis é o de Diesel, que, como o próprio nome sugere, é aplicado aos motores movidos a óleo diesel. Esse ciclo foi desenvolvido pelo engenheiro francês Rudolf Diesel (1858-1913) em 1893.
No ciclo Diesel, o cilindro do motor é semelhante àquele do motor a gasolina, mas no lugar da vela é colocado um bico injetor de combustível. No ciclo Diesel, não há necessidade da centelha para realizar a queima do combustível, pois a temperatura atingida na compressão do ar e do combustível é suficiente para iniciar sua queima.
Página 403
Na primeira etapa desse ciclo, é adicionado apenas ar no cilindro, trecho A seta para a direita B no "Gráfico p vezes V do ciclo Diesel teórico". Na segunda etapa, trecho B seta para a direita 'C', o cilindro comprime o ar de maneira adiabática até atingir o estado mínimo de volume do sistema.
Na terceira etapa, trecho 'C' seta para a direita D, o combustível é colocado na câmara de combustão. Nesse momento, ele encontra uma temperatura alta o suficiente para que haja a combustão sem a necessidade das faíscas. Após essa etapa, trecho D seta para a direita E, a energia impulsiona o pistão, que realiza uma expansão adiabática. Na sequência, trecho E seta para a direita B, a válvula de escape é aberta e os gases são expulsos da câmara, para então o ciclo ser reiniciado, trecho B seta para a direita A.
Gráfico p vezes V do ciclo Diesel teórico
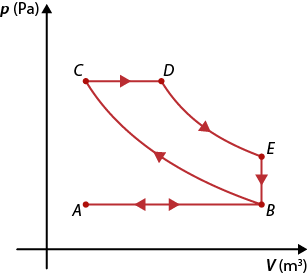
Fonte de pesquisa: ÇENGEL, Y. A.; BOLES, M. A. Termodinâmica. 7. ed. Tradução: Paulo Maurício Costa Gomes. Porto Alegre: AMGH, 2013. p. 502.
Os motores que se baseiam no ciclo Diesel têm rendimento maior que os que utilizam o ciclo de Otto. No caso dos motores a diesel, o rendimento está entre 30% e 38%, enquanto os motores do tipo Otto têm tipicamente rendimento entre 22% e 30%.
Outros exemplos de máquinas térmicas utilizadas no cotidiano e que funcionam em ciclos termodinâmicos são os refrigeradores. Eles funcionam de modo inverso ao dos motores a combustão, que recebem calor da fonte quente, transformam parte da energia em trabalho e rejeitam o restante do calor recebido.
O refrigerador retira calor da fonte fria e transfere o calor para a fonte quente. Apesar de esse fato aparentemente contrariar a segunda lei da Termodinâmica, isso não ocorre, pois essa transferência não é espontânea, ou seja, é realizado trabalho externo sobre a máquina, como mostrado na figura apresentada.
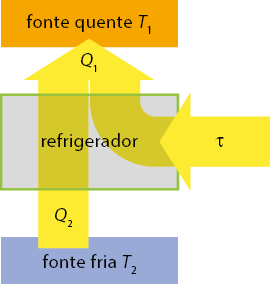
Imagem elaborada com base em: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 10. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2016. v. 2. p. 270.
Dessa forma, um refrigerador utiliza energia externa, como a energia elétrica, para tornar possível esse fluxo de calor não espontâneo. Se o refrigerador for desligado, ocorrerá um fluxo espontâneo de calor da fonte quente (ambiente externo) para a fonte fria (interior do refrigerador).
O refrigerador é composto de um sistema de tubulações que conectam o compressor, a válvula descompressora, o radiador e o congelador. A função da tubulação é permitir o fluxo do fluido refrigerante que realiza as trocas de calor.
O "Gráfico p vezes V do ciclo de um refrigerador" representa o ciclo de funcionamento de um refrigerador.
Gráfico p vezes V do ciclo de um refrigerador
Fonte de pesquisa: ÇENGEL, Y. A.; BOLES, M. A. Termodinâmica. 7. ed. Tradução: Paulo Maurício Costa Gomes. Porto Alegre: AMGH, 2013. p. 307.
Nas tubulações do congelador, o fluido aquece e se vaporiza, enquanto o interior da geladeira é resfriado, trecho A seta para a direita B. Em seguida, o fluido vai para o compressor, que realiza trabalho sobre o fluido, aumentando sua pressão e temperatura, trecho B seta para a direita 'C'.
Na sequência, trecho 'C' seta para a direita D, o fluido dirige-se ao radiador, onde troca calor com o ambiente, diminuindo sua temperatura e condensando.
Para finalizar, o fluido passa pela válvula descompressora, sofre uma expansão e sua temperatura diminui. Assim, ele vai até o congelador, para então recomeçar o ciclo, trecho D seta para a direita A.
Página 404
ATIVIDADES
1. De acordo com a primeira lei da Termodinâmica, julgue as afirmações a seguir como verdadeiras ou falsas, corrigindo as incorretas.
I ) Se um gás não realiza trabalho e cede calor ao ambiente, sua energia interna diminui.
Resposta: I) Verdadeira.
II ) Em uma transformação isobárica, se o gás recebe calor, ele realiza trabalho e sua energia interna aumenta.
Resposta: II) Verdadeira.
III ) Em uma transformação adiabática, a energia interna do gás aumenta à medida que ele realiza trabalho.
Resposta: III) Falsa. Em uma transformação adiabática, a energia interna diminui quando o gás realiza trabalho abre parênteses delta U é igual a menos tau fecha parênteses.
IV ) O calor recebido por um gás em uma transformação isotérmica é convertido em energia interna.
Resposta: IV) Falsa. O calor recebido pelo gás em uma transformação isotérmica é convertido em trabalho abre parênteses Q é igual a tau fecha parênteses.
2. O diagrama a seguir mostra a pressão P em função do volume V de um ciclo termodinâmico de um mol de um gás ideal. As transformações A seta para a direita B e 'C' seta para a direita D são isobáricas, enquanto as transformações B seta para a direita 'C' e D seta para a direita A são isovolumétricas. Sobre esse ciclo, julgue os itens a seguir como verdadeiros ou falsos, corrigindo os falsos.
Gráfico p vezes V para o ciclo de uma máquina térmica
Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2013. v. 2. p. 233.
I ) O trabalho total realizado pelo gás em um ciclo é dado por P subscrito 2 vezes V subscrito 2.
II ) Na transformação D seta para a direita A, o aumento da energia interna do gás é igual ao calor fornecido a ele.
III ) Na transformação A seta para a direita B, é fornecido calor ao gás; na transformação 'C' seta para a direita D, o gás cede calor.
IV ) Em um ciclo completo, o calor fornecido menos o calor cedido é igual ao trabalho líquido realizado pelo gás.
Resposta: I) Falsa. O trabalho total em um ciclo é dado por tau é igual a P subscrito 2 vezes abre parênteses V subscrito 2 menos V subscrito 1 fecha parênteses menos P subscrito 1 vezes abre parênteses V subscrito 2 menos V subscrito 1 fecha parênteses. II) Verdadeira. III) Verdadeira. IV) Verdadeira.
3. Um gás monoatômico, inicialmente a uma temperatura de 20 graus Celsius está confinado em um recipiente cilíndrico fechado, de êmbolo móvel e base com área de 200 centímetros quadrados. O recipiente é colocado sobre uma fonte calorífica e o gás recebe 400 joules de energia na forma de calor. Considerando que dentro do recipiente estão contidos 4 mol do gás e R é igual a 8 vírgula 3 joules barra mol vezes K, determine o que se pede nos itens a seguir.
Resoluções nas Orientações para o professor.
a ) A variação da energia interna do gás quando sobre ele é realizado um trabalho de 80 joules, além do calor recebido pela fonte.
Resposta: delta U é igual a 480 joules
b ) A temperatura final do gás se ele realizar 120 joules de trabalho ao receber o calor da fonte.
Resposta: T é aproximadamente igual a 298 vírgula 6 Kelvin ou T é aproximadamente igual a 25 vírgula 6 graus Celsius
c ) O trabalho realizado pelo gás ao elevar o êmbolo do recipiente em 5 centímetros em uma transformação isobárica a 3 a t m de pressão.
Resposta: tau é igual a 300 joules
d ) A temperatura final do gás se o êmbolo for impedido de se mover enquanto o gás receber calor da fonte.
Resposta: T é aproximadamente igual a 301 Kelvin ou T é aproximadamente igual a 28 graus Celsius.
4. Qual é a relação entre a entropia, compreendida como uma medida da desordem de um sistema, e a impossibilidade da existência de uma máquina térmica que apresente 100% de rendimento? Exemplifique essa lei com situações do cotidiano.
Resposta nas Orientações para o professor.
5. Qual é a relação entre o rendimento de um automóvel, a temperatura do motor e a temperatura do ambiente no qual está inserido? Explique sua resposta.
Resposta: Tratando-se do motor de um automóvel, que pode ser considerado uma máquina de Carnot, o ambiente é a fonte fria; quanto maior a diferença entre as temperaturas da fonte quente e da fonte fria, maior é o rendimento de uma máquina de Carnot.
6. Considere que uma máquina térmica, operando segundo o ciclo de Carnot, cuja fonte quente esteja à temperatura de 373 Kelvin ceda 1.200 joules à sua fonte fria, que está a 273 Kelvin. Calcule o rendimento e o trabalho realizado por essa máquina.
Resposta: etá é aproximadamente igual a 0 vírgula 27 ou etá é aproximadamente igual a 27 por cento; tau é igual a 324 joules. Resolução nas Orientações para o professor.
7. Duas máquinas termodinâmicas que trabalham por ciclos estão sendo projetadas para funcionar com um gás ideal. As características das máquinas estudadas estão listadas a seguir.
- Máquina 1: Q subscrito 1 é igual a 700 joules; T início subscrito, Q subscrito 1, fim subscrito é igual a 600 Kelvin; T início subscrito, F subscrito 1, fim subscrito é igual a 300 Kelvin; tau subscrito 1 é igual a 600 joules.
- Máquina 2: Q subscrito 2 é igual a 800 joules; T início subscrito, Q subscrito 2, fim subscrito é igual a 600 Kelvin; T início subscrito, F subscrito 2, fim subscrito é igual a 300 Kelvin; tau subscrito 2 é igual a 300 joules.
Sobre as duas máquinas, responda:
a ) Qual máquina obedece à primeira lei da Termodinâmica? Justifique.
Resposta: As duas máquinas obedecem, pois o trabalho realizado pelo gás é menor que a energia transmitida da fonte quente para o gás.
b ) Qual máquina obedece à segunda lei da Termodinâmica? Justifique.
Resposta: Apenas a máquina 2. Resolução nas Orientações para o professor.
Página 405
8. Uma máquina térmica opera entre duas fontes com as seguintes temperaturas: 480 graus Celsius e 30 graus Celsius, respectivamente. A cada ciclo termodinâmico, a máquina retira da fonte quente 2.000 joules de energia em forma de calor e realiza 800 joules de trabalho.
Resoluções nas Orientações para o professor.
a ) Calcule o rendimento real da máquina térmica.
Resposta: etá é igual a 0 vírgula 4 ou etá é igual a 40 por cento.
b ) Qual é a quantidade de calor rejeitado pela máquina a cada ciclo?
Resposta: Q subscrito 2 é igual a 1.200 joules.
c ) Calcule o rendimento máximo dessa máquina térmica.
Resposta: etá é aproximadamente igual a 0 vírgula 6 ou etá é aproximadamente igual a 60 por cento.
9. Uma máquina térmica cíclica recebe 1.200 joules da fonte quente a cada ciclo e produz um trabalho equivalente a 480 joules. Sabendo que seu rendimento é equivalente ao de uma máquina de Carnot, dois possíveis valores, respectivamente, para as temperaturas da fonte fria e da fonte quente são:
a ) 400 Kelvin e 800 Kelvin.
b ) 300 Kelvin e 500 Kelvin.
c ) 200 Kelvin e 900 Kelvin.
d ) 240 Kelvin e 750 Kelvin.
Resposta: Alternativa b. Resolução nas Orientações para o professor.
10. Em razão da segunda lei da Termodinâmica, o calor flui espontaneamente do corpo mais quente para o corpo mais frio. Refrigeradores, entretanto, parecem violar esse princípio. Explique sucintamente como os refrigeradores não violam esse princípio.
Resposta nas Orientações para o professor.
11. Uma máquina térmica em uma indústria está sendo projetada para funcionar por meio de um ciclo termodinâmico cuja temperatura da fonte quente é de 800 Kelvin e a temperatura da fonte fria é de 300 Kelvin. Essa máquina deverá absorver a cada ciclo o equivalente a 2.500 joules e produzir um trabalho útil de 125 joules. Sobre ela, julgue as afirmativas a seguir como verdadeiras ou falsas, justificando as incorretas.
I ) O rendimento dessa máquina é de 37,5%.
II ) A energia não utilizada pela máquina a cada ciclo é de 2.375 joules.
III ) Se essa máquina tivesse o mesmo rendimento da de Carnot e estivesse operando nas mesmas temperaturas, o trabalho útil dela seria de 937 vírgula 5 joules.
IV ) Essa máquina funciona de acordo com a segunda lei da Termodinâmica.
V ) Como o calor rejeitado pela máquina é maior que o trabalho útil realizado, ela está violando a primeira lei da Termodinâmica.
Resposta: I) Falsa. O rendimento da máquina é de 5%. II) Verdadeira. III) Falsa. Se essa máquina operasse em um ciclo de Carnot, o trabalho útil seria de 1.562 vírgula 5 joules. IV) Verdadeira. V) Falsa. A primeira lei da Termodinâmica seria violada se a soma do calor rejeitado com o trabalho útil fosse maior que o calor fornecido pela fonte quente. Resoluções nas Orientações para o professor.
12. Um mol de gás monoatômico ideal é utilizado em uma máquina térmica cíclica, sofrendo as transformações térmicas mostradas a seguir, compostas de duas isobáricas e duas isovolumétricas.
Gráfico p vezes V para o ciclo de uma máquina térmica

Fonte de pesquisa: HALLIDAY, David et al. Fundamentos de física: gravitação, ondas e termodinâmica. 9. ed. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2016. v. 2. p. 279.
Qual é o rendimento dessa máquina térmica?
a ) 10%
b ) 30%
c ) 50%
d ) 65%
Resposta: Alternativa c.
13. Atualmente, a busca por fontes de energia mais eficientes e sustentáveis tem sido uma prioridade global. As usinas termelétricas, que utilizam combustíveis fósseis, como carvão, petróleo ou gás natural, ainda são muito utilizadas em várias partes do mundo. Nesses sistemas, as máquinas térmicas são fundamentais para a geração de eletricidade ao converter energia térmica em energia mecânica, que por sua vez é transformada em eletricidade. No entanto, o uso desses combustíveis gera grandes quantidades de gases de efeito estufa, contribuindo para as mudanças climáticas. Além disso, a segunda Lei da Termodinâmica impõe limitações à eficiência dessas usinas, fazendo com que parte do calor seja desperdiçada, diminuindo o aproveitamento da energia. Imagine uma pessoa que trabalha em uma usina termelétrica e está encarregada de otimizar o processo de geração de energia. Ela sabe que a eficiência da usina está diretamente relacionada às temperaturas da fonte quente e da fonte fria. Ela também considera o impacto ambiental da usina e busca maneiras de reduzir a emissão de poluentes enquanto potencializa a eficiência energética. Com base na situação descrita, explique o funcionamento de uma usina termelétrica, a aplicação da segunda lei da Termodinâmica nesses tipos de usinas e os impactos ambientais com relação ao uso de combustíveis fósseis. Por fim, cite exemplos de possibilidades de aumentar o rendimento e reduzir o impacto ambiental.
Resposta: Espera-se que os estudantes mencionem que esse tipo de usina converte a energia térmica em energia elétrica por meio da queima de combustíveis fósseis. Além disso, devido à segunda Lei da Termodinâmica, parte do calor gerado é sempre desperdiçada para uma fonte fria. Por fim, espera-se que os estudantes citem a utilização de fontes renováveis para a diminuição dos impactos ambientais.
Página 406
CAPÍTULO26
Sons e audição humana
Ondas sonoras
A audição é um dos cinco sentidos que permite ao ser humano obter estímulos e interpretar o ambiente ao redor. Além de perceberem sons do ambiente, as orelhas têm estruturas que auxiliam no equilíbrio e no senso de localização.
1. Qual é o tipo de estímulo do ambiente que percebemos por meio do sentido da audição?
Resposta: Espera-se que os estudantes respondam que percebemos as ondas sonoras por conta da audição.
2. Qual é o órgão do corpo responsável por captar esses estímulos?
Resposta: As orelhas.
3. Ao usar seu smartphone ou outros aparelhos de áudio, você toma os cuidados recomendados para preservar sua saúde auditiva?
Resposta pessoal. O objetivo desta questão é levar os estudantes a refletir sobre a relação deles com a tecnologia e os cuidados que devem ser tomados com a saúde auditiva, que estão relacionados à intensidade do som e ao tempo que usam os fones de ouvido. A falta desses cuidados pode levar ao desenvolvimento de problemas auditivos.
Nos últimos anos, a Organização Mundial da Saúde (OMS) vem alertando sobre a grande incidência de problemas auditivos na população global, muitas vezes causados por hábitos que poderiam ser evitados. Leia a manchete e a linha fina a seguir.
Você tem o costume de usar fone de ouvido? Saiba como o mau uso pode causar perda auditiva
Alguns hábitos modernos estão ligados a problemas auditivos em pacientes cada vez mais jovens; veja como prevenir
PERES, Edis Henrique. Você tem o costume de usar fone de ouvido? Saiba como o mau uso pode causar perda auditiva. Gov.br, 3 mar. 2023. Disponível em: https://s.livro.pro/iky03h. Acesso em: 13 ago. 2024.
Atualmente, o uso de fones de ouvido faz parte do cotidiano de muitas pessoas. No entanto, o uso inadequado dessa tecnologia pode prejudicar a saúde. Escutar música usando fones de ouvido, com volume acima do recomendado e por longos períodos, pode causar danos irreversíveis ao aparelho auditivo, isso porque a fonte sonora está muito perto da orelha interna.
Mas não é somente o uso de fones de ouvido que pode prejudicar a saúde. No cotidiano, geralmente estamos expostos a vários tipos de ruídos, com diferentes intensidades. A exposição prolongada ao ruído pode gerar dores de cabeça, cansaço, elevação da pressão arterial, perda de concentração e irritabilidade. Além disso, pode prejudicar o funcionamento dos sistemas circulatório, respiratório e digestório.
Os níveis sonoros aos quais as orelhas são submetidas e a duração da exposição são os dois principais fatores a serem considerados com relação à saúde auditiva. Pequenos ruídos, inofensivos em um primeiro momento, podem levar a graves consequências com o passar do tempo, como a perda total da audição.

Página 407
A tabela apresenta alguns limites de tolerância para ruídos contínuos e intermitentes. Para termos uma referência, o nível sonoro de 100 decibeis corresponde ao som de um fone de ouvido com volume alto.
| Nível sonoro do ruído (decibel) | Máxima exposição diária indicada |
|---|---|
|
85 |
8 horas |
|
90 |
4 horas |
|
94 |
2 horas |
|
100 |
1 hora |
|
104 |
35 minutos |
|
112 |
10 minutos |
|
115 |
7 minutos |
Fonte de pesquisa: BRASIL. Ministério da Saúde. Perda auditiva induzida por ruído (Pair). Brasília: MEC, 2006. (Série A. Normas e Manuais Técnicos). p. 11. Disponível em: https://s.livro.pro/qfok7c. Acesso em: 6 set. 2024.
Para compreender melhor como ouvimos e como os ruídos intensos podem prejudicar nossa audição, vamos analisar as características das ondas sonoras.
Uma onda sonora é qualquer onda de natureza mecânica longitudinal e tridimensional que pode ser produzida pela vibração de materiais, como as cordas e/ou as membranas de instrumentos musicais.
As ondas e os fenômenos ondulatórios relacionados a elas estão muito presentes no dia a dia das pessoas e são fundamentais, especialmente para os seres humanos que têm órgãos dos sentidos especializados para recebê-las – as orelhas e os olhos, por exemplo.

4. As ondas que estimulam o sistema auditivo são as mesmas que estimulam o sistema visual? Justifique sua resposta.
Resposta: Espera-se que os estudantes respondam que são ondas de natureza diferentes. As ondas que estimulam o sistema auditivo são as mecânicas (sons); já as ondas que estimulam o sistema visual são as eletromagnéticas (luz).
Ondas são perturbações que se propagam transportando energia, sem que ocorra o transporte de matéria. Essa é uma definição geral que abrange todas as ondas, como as que ocorrem na água, as sonoras, as luminosas, as de rádio, entre outras.
Uma perturbação na água, por exemplo, permite verificar a formação e propagação de uma onda. Quando a superfície da água em equilíbrio sofre uma perturbação, a energia fornecida é transportada pela superfície. De acordo com a perturbação, a onda pode se propagar na água em duas dimensões, como mostrado na fotografia apresentada.

Compartilhe ideias
As ondas são perturbações que transportam energia pelo espaço sem o transporte de matéria.
a ) Junte-se a um colega e encontrem uma maneira de mostrar que, ao provocar uma oscilação em um meio material, ela transfere energia ao longo de todo o meio. Em seguida, gravem e editem um vídeo para mostrar aos colegas como vocês fizeram.
Resposta: Espera-se que os estudantes percebam que a oscilação transfere energia ao longo de toda a mola ao notar que o pulso percorre toda a sua extensão e, ao chegar à outra extremidade, sofre reflexão e retorna até perder energia. Também é esperado que verifiquem que não há transporte de matéria, pois, quando a onda se desloca pela extensão da mola, a fita de tecido permanece no mesmo local onde foi colocada.
Página 408
Quanto à luz e ao som, ambos são perturbações que se propagam como ondas, mas têm naturezas completamente diferentes. Enquanto o som é uma onda mecânica, a luz é uma onda eletromagnética.
As ondas mecânicas necessitam de um meio material para se propagar, ou seja, a perturbação causada em um meio material gera uma onda que se propaga pelo próprio meio. As ondas em uma corda, as ondas na água, o som e as ondas sísmicas✚ são exemplos de ondas mecânicas.
Como essas ondas se propagam em meios materiais, sua velocidade depende das características desse meio, sendo constante em meios homogêneos.
5. As ondas mecânicas se propagam no vácuo? Justifique sua resposta.
Resposta: Espera-se que os estudantes respondam que não, pois, no vácuo, por definição, não há matéria para que as ondas mecânicas se propaguem.
As ondas eletromagnéticas têm propriedades elétricas e magnéticas e não necessitam de um meio material para se propagar. Ondas luminosas, de rádio e de televisão, raios X, radiação ultravioleta e infravermelha são exemplos de ondas eletromagnéticas.
No vácuo, as ondas eletromagnéticas se propagam com a velocidade da luz, representada pelo símbolo cabre parênteses c é igual a 3 vezes 10 elevado a 8 metro por segundo fecha parênteses, e diferem entre si nos valores de suas frequências e de seus comprimentos de onda.
Características de uma onda
A maior parte das informações que recebemos do ambiente ao redor chega até nós por meio de ondas. Algumas delas podem ser visualizadas em um osciloscópio✚, como na fotografia apresentada, que apresenta a forma da onda sonora gerada por um instrumento musical.
O osciloscópio mostra a amplitude, o comprimento de onda, o período e a frequência do som emitido pelo instrumento.

Considere a imagem a seguir, que representa uma onda se propagando por uma corda, com uma de suas extremidades fixas, mas sem que ocorra sua reflexão. Nessa configuração, destacamos duas de suas características: a amplitude e o comprimento de onda.
Imagem sem proporção e em cores fantasia.
Imagem elaborada com base em: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo S. de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 2. p. 119.
Página 409
A amplitude abre parênteses A fecha parênteses é a distância máxima de afastamento de cada ponto da corda em relação ao ponto de equilíbrio, e é expressa em metro metro no SI. A parte mais elevada da onda é chamada crista e a parte mais baixa, vale. Perceba que a amplitude está relacionada com a energia fornecida à corda, pois, quanto mais alto a mão da pessoa se elevar, mais energia ela fornecerá e maior será a amplitude da onda.
O comprimento de onda abre parênteses lambda fecha parênteses é a distância entre duas cristas consecutivas, ou entre dois vales consecutivos, e é expresso em metro metro no SI. Para que a energia percorra um comprimento de onda, cada parte da corda deve executar uma oscilação completa, ou seja, executar um movimento para cima, para baixo, e retornar à posição de equilíbrio.
O período e a frequência são duas outras características que definem uma onda. Para qualquer movimento periódico, período abre parênteses T fecha parênteses é o tempo necessário para que ocorra uma oscilação completa, expresso em segundo segundo no SI, e frequência abre parênteses f fecha parênteses corresponde ao número de repetições por unidade de tempo, expressa em hertz no SI.
T é igual a 1 sobre f ou f é igual a 1 sobre T
Professor, professora: Explique aos estudantes que a frequência e, consequentemente, o período de uma onda dependem da fonte que os gerou.
Dica
Acesse o simulador do Phet Interactive Simulations e gere diferentes tipos de ondas. Ajuste seus elementos e observe os efeitos provocados. Disponível em: https://s.livro.pro/6jk5f7. Acesso em: 12 set. 2024.
Velocidade de propagação de uma onda
A velocidade de propagação de uma onda está relacionada à sua natureza e ao meio físico no qual ela se propaga. Em meios homogêneos e isotrópicos, como não há mudança em suas propriedades físicas, a onda se propaga com velocidade constante.
Para verificar uma forma de calcular a velocidade das ondas, considere novamente uma onda se propagando por uma corda. Cada perturbação na corda leva um intervalo de tempo abre parênteses T fecha parênteses para percorrer a distância de um comprimento de onda abre parênteses lambda fecha parênteses. Assim, considerando o cálculo da velocidade constante com base na velocidade média, temos que:
v é igual a início de fração, numerador: delta 's', denominador: delta 't', fim de fração é igual a lambda sobre T portanto v é igual a lambda sobre T
Como o período é o inverso da frequência, a velocidade de propagação de uma onda pode ser escrita como:
v é igual a lambda vezes f
Essa relação é conhecida como equação fundamental das ondas e vale para qualquer tipo de onda.
Professor, professora: Pergunte aos estudantes por que, durante uma tempestade, vemos a luz emitida por um relâmpago segundos antes de ouvirmos o ruído do trovão gerado pelo mesmo raio. Espera-se que relacionem esse fato à natureza das duas ondas e à interferência do meio na velocidade de sua propagação.
Dica
Se as características do meio não forem alteradas, para ondas que se propagam com a mesma velocidade, o comprimento de onda será inversamente proporcional à frequência. Da mesma forma, se a frequência das ondas é a mesma, quanto maior for seu comprimento de onda, maior será sua velocidade, proporcionalmente à distância percorrida pela energia a cada oscilação.
Página 410
Além das características citadas anteriormente, as ondas podem ser classificadas como transversais e longitudinais de acordo com sua forma.
Quando geramos uma oscilação em uma corda tensionada, cada parte da corda realiza um movimento para cima e para baixo em torno da posição de equilíbrio enquanto a onda se propaga. Nesse caso, o movimento de cada elemento da corda é perpendicular à sua direção de propagação, o que caracteriza uma onda transversal.
Imagens desta página sem proporção e em cores fantasia.
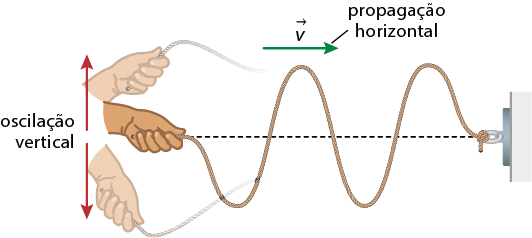
Imagem elaborada com base em: HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física: gravitação, ondas e termodinâmica. Tradução: Ronaldo S. de Biasi. 10. ed. Rio de Janeiro: LTC, 2016. v. 2. p. 119.
Dica
As ondas na água e as ondas eletromagnéticas são exemplos de ondas transversais.
Outro modo de oscilação das ondas acontece quando as partes que constituem o meio se movem para a frente e para trás enquanto a onda se propaga. Considere uma mola posicionada na horizontal, tendo uma de suas extremidades livre, puxada e empurrada rapidamente. Essa perturbação fornece à mola energia que se propaga na forma de um pulso.
Se a perturbação causada na mola se repetir periodicamente, as partes da mola vão oscilar na mesma direção de propagação da onda, caracterizando uma onda longitudinal. Essa propagação ocorre por compressão e rarefação do meio físico.
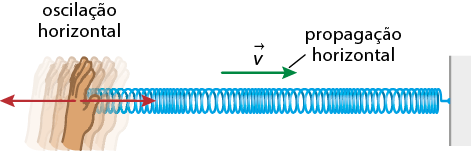
As ondas sonoras também são exemplos de ondas longitudinais, pois o movimento oscilatório de partes do meio tem a mesma direção da propagação da onda. No ar, o som é constituído por compressões e rarefações das partículas do ar, como representado na imagem.

Imagens elaboradas com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 378.
Características do som
Durante a fala de uma pessoa, as ondas sonoras emitidas por ela são captadas pelas orelhas, que as convertem em estímulos nervosos. A orelha humana é constituída de três regiões principais: orelha externa, orelha média e orelha interna.
6. De olhos vendados, você consegue reconhecer uma pessoa somente pelo som de sua voz? De que forma?
Resposta: O objetivo desta questão é levar os estudantes a perceber que podemos identificar uma pessoa analisando algumas características de sua voz, como timbre.
Página 411
As ondas sonoras são captadas pela orelha externa e direcionadas pelo canal auditivo para a membrana timpânica, que vibra com a mesma frequência da onda incidente. Essa vibração é transmitida ao martelo, à bigorna e ao estribo, pequenos ossos da orelha média.
Imagens desta página sem proporção e em cores fantasia.
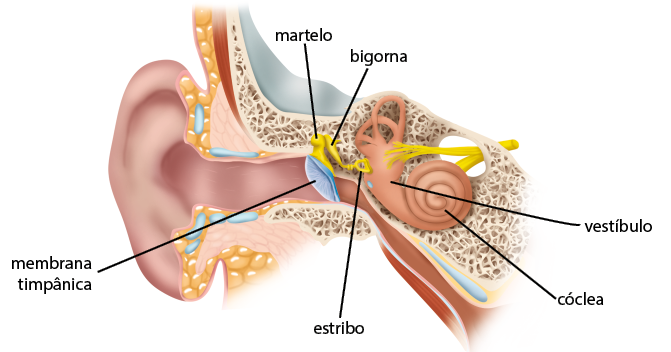
Imagem elaborada com base em: TORTORA, Gerard J.; DERRICKSON, Bryan. Corpo humano: fundamentos de anatomia e fisiologia. Tradução: Alexandre Lins Verneck et al. 10. ed. Porto Alegre: Artmed, 2017. p. 311.
Dica
A orelha de uma pessoa sem problemas de audição é capaz de detectar sons na faixa de 20 hertz a 20.000 hertz abre parênteses 20 quilo-hertz fecha parênteses, que são as frequências audíveis. Ondas sonoras com frequência abaixo de 20 hertz são chamadas infrassons e ondas com frequência acima de 20.000 hertz, ultrassons.
O estribo movimenta-se para a frente e para trás, transmitindo esse movimento à janela do vestíbulo e à cóclea. Dentro dela há pequenos cílios, cujos movimentos emitem sinais elétricos, transmitidos pelo sistema nervoso até o cérebro, onde o som é interpretado.
A forma como o corpo humano recebe e interpreta o som também depende das características das ondas sonoras, como você já deve ter percebido. A frequência das fontes emissoras faz com que o sistema auditivo seja estimulado por diferentes vibrações, que estão relacionadas à altura, ao timbre e à intensidade das ondas.
A altura qualifica os sons em graves ou agudos. Apesar do costume de relacionarmos erroneamente a altura de um som ao seu volume, o som baixo tem frequência baixa, o que caracteriza um som mais grave, como o emitido por um contrabaixo.
Já o som alto tem frequência alta, o que caracteriza um som mais agudo, como o emitido por uma guitarra elétrica. Confira a comparação de duas ondas sonoras emitidas por um contrabaixo e uma guitarra para um intervalo de 0 vírgula 1 segundo.
Professor, professora: Explique aos estudantes que uma onda sonora tem direção de perturbação longitudinal. No entanto, a onda representada na ilustração consiste em uma onda transversal. Diga que essa escolha de representação é meramente ilustrativa para fins didáticos.
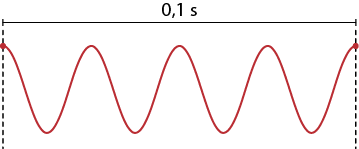
Imagens elaboradas com base em: TREFIL, James; HAZEN, Robert M. Física viva: uma introdução à física conceitual. Tradução: Ronaldo S. de Biasi. Rio de Janeiro: LTC, 2006. v. 2. p. 9.
Sons de mesma altura, ou seja, mesma frequência, podem ser emitidos por fontes sonoras distintas, como uma flauta ou um violino.
Porém, é possível diferenciar o som emitido por esses instrumentos por causa do timbre, característica que o torna diferente dos demais.
Página 412
Quando instrumentos musicais diferentes emitem a mesma nota musical, os sons escutados têm a mesma altura, pois é a frequência que define a nota. Por exemplo, uma nota Lá com frequência de 440 hertz pode ser emitida por diversos instrumentos.
O diapasão é um dispositivo de metal em forma de forquilha, utilizado para afinar instrumentos por meio de fenômenos ondulatórios que estudaremos a seguir. Ele pode estar fixado a uma caixa de ressonância, que amplifica o som gerado, e um martelo de percussão, utilizado para perturbá-lo, como na fotografia. Ao ser perturbado, o diapasão emite um som com uma única frequência constante.

Diferentemente do diapasão, que emite uma frequência única, na maioria dos sons musicais, a frequência resulta de uma composição de sons com frequências diferentes, chamados componentes. A variedade desses componentes e suas intensidades relativas definem o timbre do instrumento, ou seja, seu som característico.
Assim, uma mesma nota musical emitida por instrumentos diferentes terá seus timbres característicos, pois, como cada onda terá a própria composição, o formato da onda resultante será distinto, como mostrado nas imagens a seguir.
Imagens desta página sem proporção e em cores fantasia.


Imagens elaboradas com base em: TREFIL, James; HAZEN, Robert M. Física viva: uma introdução à física conceitual. Tradução: Ronaldo S. de Biasi. Rio de Janeiro: LTC, 2006. v. 2. p. 37.
O resultado é que, ao escutarmos as mesmas notas musicais emitidas pela flauta e pelo violino, é possível distinguir de qual instrumento o som foi emitido pelas características próprias das ondas, isto é, em razão do timbre de cada instrumento.
O mesmo ocorre com a voz: conseguimos diferenciar e identificar as pessoas por ela, porque cada indivíduo tem um timbre distinto.
A intensidade é a qualidade que permite diferenciar um som forte de um som fraco. Ela representa a energia transportada pela onda sonora desde sua fonte e pode ser intensificada ao aumentar a amplitude de vibração da fonte sonora.
Quando estamos próximo de uma fonte emissora e escutamos um som, a quantidade de energia recebida pelas orelhas é maior do que quando ouvimos o mesmo som estando distante da fonte, tornando-o mais forte ou mais fraco.
Professor, professora: Relacione o que foi mencionado no parágrafo anterior ao uso de fones de ouvido. Quando eles estão em nossa orelha, ouvimos os sons em volume alto. Quando os tiramos, ouvimos os sons em um volume fraco.
Dica
O mesmo som pode ser considerado mais forte ou mais fraco se suas oscilações tiverem amplitudes maiores ou menores, respectivamente.
Página 413
Propriedades do som
Quando falamos em intensidade, é importante considerar que, embora o som dependa da amplitude de vibração da fonte, as ondas sonoras transportam energia de uma região à outra.
Portanto, a intensidade abre parênteses I fecha parênteses de uma onda sonora está relacionada com a energia abre parênteses E fecha parênteses transportada pela onda por uma superfície a cada intervalo de tempo abre parênteses delta 't' fecha parênteses, ou seja, está relacionada com a potência abre parênteses P fecha parênteses de transferência da energia por área abre parênteses A fecha parênteses onde o som se propaga.
I é igual a início de fração, numerador: E, denominador: delta 't' vezes A, fim de fração portanto I é igual a P sobre A
Dica
Lembre-se de que a potência é dada por: P é igual a início de fração, numerador: E, denominador: delta 't', fim de fração.
Imagem sem proporção e em cores fantasia.

No SI, potência é expressa em watt abre parênteses W fecha parênteses, área é expressa em metro quadrado abre parênteses m elevado ao quadrado fecha parênteses e intensidade é expressa em watt por metro quadrado abre parênteses watts barra metro quadrado fecha parênteses. Assim, quanto mais distante da fonte emissora, menor a intensidade da onda sonora, pois maior é sua área de propagação.
A intensidade do som corresponde a um atributo físico de uma onda sonora, mas o volume do som, por outro lado, é uma sensação fisiológica, pois cada pessoa pode caracterizar um mesmo som de diferentes formas.
O limiar da audição humana corresponde a uma intensidade abre parênteses I subscrito 0 fecha parênteses de 10 elevado a menos 12 Watt por metro quadrado, valor tomado como referência, mesmo correspondendo a um som dificilmente escutado. Já uma onda com intensidade de 1 watt por metro quadrado, como o som ouvido em uma apresentação musical quando estamos próximo ao palco, tem energia que pode danificar estruturas internas da orelha. Em razão do desconforto causado, essa intensidade é conhecida como limiar da dor.

Como o intervalo de intensidades sonoras que o ser humano é capaz de escutar é amplo, utilizamos uma escala para representar essas potências de base 10, denominada nível sonoro abre parênteses beta fecha parênteses, cuja grandeza é medida em bel abre parênteses B fecha parênteses.
Essa unidade de medida foi chamada dessa forma em homenagem ao cientista escocês, naturalizado estadunidense, Alexander Graham Bell (1847-1922), que desenvolveu trabalhos relacionados à fisiologia e à transmissão do som, dos quais resultou uma de suas mais famosas contribuições: a invenção do telefone.
O nível sonoro é baseado na intensidade mínima I subscrito 0, correspondendo a zero bel abre parênteses beta é igual a 0 B fecha parênteses, e expresso utilizando o submúltiplo do decibel decibel, sendo que 1 baite equivale a 10 decibeis (dez decibéis).
Podemos determinar o nível sonoro, tendo I subscrito 0 como referência, com a relação a seguir.
beta é igual a 10 vezes log início de fração, numerador: I, denominador: I subscrito 0, fim de fração
Dica
A multiplicação por 10 expressa o valor do nível sonoro obtido em decibel.
Os danos fisiológicos ao sistema auditivo começam a acontecer quando as orelhas são expostas a níveis sonoros a partir de 85 decibeis, dependendo do tempo de exposição e das características de sua frequência. Tais danos podem ser temporários ou permanentes, dependendo dos danos causados nas células que compõem o órgão de Corti, localizado na orelha interna, responsável por converter o som em sinais elétricos.
Página 414
Fenômenos sonoros
Diversos fenômenos sonoros do cotidiano estão relacionados a efeitos que ocorrem quando as ondas sonoras atingem obstáculos. Um exemplo disso é o eco. Para compreender como esses fenômenos ocorrem, vamos estudar a seguir alguns fenômenos ondulatórios.
7. Você já presenciou uma situação em que ocorreu o eco? Por que ele acontece em alguns lugares e em outros não?
Resposta pessoal. O objetivo desta questão é levantar os conhecimentos prévios dos estudantes sobre alguns fenômenos sonoros relacionados ao eco. Espera-se que eles relacionem o eco à reflexão do som e notem que podemos perceber esse fenômeno de acordo com alguns fatores, como a distância da fonte sonora, o obstáculo e nossas orelhas.
Reflexão do som
As ondas sonoras refletem em superfícies, assim como as ondas luminosas, seguindo as leis da reflexão, em que o ângulo de incidência abre parênteses ângulo i fecha parênteses tem a mesma medida que o ângulo de reflexão abre parênteses ângulo r fecha parênteses.
Quando uma fonte emite som, podemos ouvi-lo pelas ondas que chegam diretamente às orelhas e pelas ondas refletidas em obstáculos, como representado na imagem.
De acordo com a situação, a reflexão do som pode ser percebida de diferentes formas. A orelha humana tem uma persistência auditiva de aproximadamente 0 vírgula 1 segundo, que corresponde ao intervalo de tempo da sensação auditiva de um som. Logo, dois sons podem ser distinguidos quando escutados em intervalos de tempo maiores do que a persistência auditiva.
Imagem sem proporção e em cores fantasia.
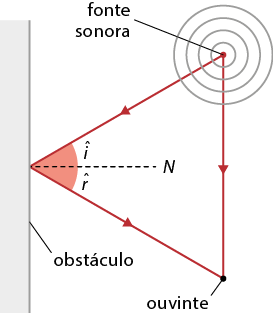
Quando o intervalo de tempo em que a orelha recebe o som diretamente e o som refletido é muito menor do que 0 vírgula 1 segundo, a sensação auditiva é reforçada e o som fica mais intenso. É o que ocorre quando cantamos no boxe do banheiro.
Se o intervalo de percepção entre os sons for aproximadamente 0 vírgula 1 segundo, ocorre o fenômeno da reverberação, quando sons refletidos em obstáculos chegam à orelha antes da extinção total da sensação auditiva do som que chegou diretamente. Nesse caso, apenas um som é escutado, com duração prolongada. A reverberação pode ser percebida em quadras esportivas fechadas, auditórios e locais de eventos. A arquitetura, como a de conchas acústicas, melhora a acústica e o som gerado em um ambiente.
Quando o intervalo de tempo em que a orelha recebe o som direto e o som refletido é maior do que 0 vírgula 1 segundo, pode ocorrer o fenômeno do eco. Nesse caso, a pessoa ouve os dois sons distintamente.
Dica
Considerando a velocidade do som no ar como 340 metros por segundo, uma pessoa consegue ouvir o eco da própria voz quando o intervalo de tempo entre o som gerado e a percepção do som escutado é maior do que 0 vírgula 1 segundo, ou seja, a 17 metros de um obstáculo.
O eco é usado em sonares de navios, que enviam ondas sonoras e medem o intervalo de tempo em que recebem as ondas refletidas, determinando assim obstáculos e profundidades, além de certos animais, como o golfinho, que realizam a ecolocalização. Os golfinhos enviam ondas sonoras geralmente em uma frequência inaudível para o ser humano. Elas se chocam com as presas e os obstáculos, retornam na forma de eco e são decodificadas pelos animais.
Página 415
Refração do som
Assim como a luz varia sua velocidade ao passar de um meio físico para outro, podendo desviar sua trajetória, as ondas sonoras também sofrem refração, variando sua velocidade e seu comprimento de onda. No entanto, não ocorre a variação da sua frequência, que depende apenas da fonte emissora, independentemente do seu meio de propagação.
A velocidade de uma onda mecânica depende do meio onde ela é produzida e como ela é propagada, podendo ter valores diferentes quando se propaga em um mesmo meio. A presença de vento e a temperatura do ambiente são fatores que alteram as características do ar, como sua densidade, e, consequentemente, alteram a velocidade de propagação das ondas sonoras. Confira a seguir.
Em dias quentes, a camada de ar mais próximo ao solo tem maior temperatura do que as camadas superiores. Com isso, a velocidade do som nessa camada é maior por causa da maior vibração das partículas que compõem o ar. As ondas sonoras, então, sofrem uma redução de velocidade quando passam entre as camadas, curvando-se para cima de modo a se afastar do solo (imagem A). Quando a camada de ar próximo ao solo está mais fria, ocorre o desvio contrário (imagem B).
Imagens desta página sem proporção e em cores fantasia.
A.
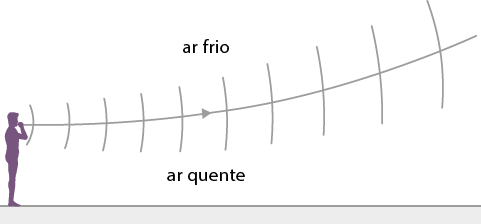
B.

Imagens elaboradas com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 381.
Difração do som
8. Por que conseguimos ouvir uma pessoa que esteja do outro lado de uma porta, mesmo sem poder vê-la?
Resposta pessoal. Espera-se que os estudantes respondam, com base em sua vivência, que as ondas sonoras são capazes de contornar obstáculos.
A situação da questão anterior está relacionada a um fenômeno chamado difração, no qual as ondas contornam a barreira de um obstáculo ou atravessam orifícios com dimensões próximo a seu comprimento de onda, espalhando-se para o ambiente.
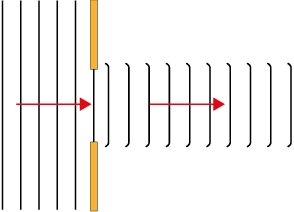
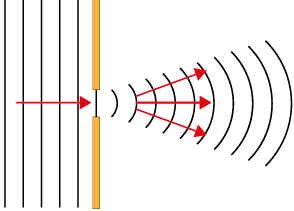
Imagens elaboradas com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 546.
9. Cite outra situação em que podemos perceber a difração do som.
Resposta. Os estudantes podem citar duas pessoas, uma em cada lado de um muro, conversando. Embora não possam se ver, elas podem conversar, pois o som emitido por uma consegue contornar o muro e chegar à outra.
Dica
Quando uma onda sofre difração, permanecem constantes a frequência, o comprimento de onda e a velocidade de propagação da onda.
Página 416
Interferência das ondas sonoras
As ondas sonoras, como qualquer outro tipo de onda, podem ter interferências. Elas ocorrem quando duas ou mais ondas, propagando-se no mesmo meio, cruzam-se gerando efeitos ondulatórios que podem ser somados, reduzidos ou neutralizados, dando origem a uma interferência construtiva ou destrutiva.
A interferência pode ocorrer com base na superposição de ondas sonoras emitidas por duas ou mais fontes, ou por ondas que são refletidas. Em certos pontos do meio onde ocorre a interferência, o som gerado terá intensidade maior, pois os efeitos das fontes se somam. É o caso da figura a seguir, na qual uma pessoa está à mesma distância de dois alto-falantes. Considerando que as fontes emitem sons idênticos e com frequência fixa, o som que chega até o ouvinte será de intensidade maior. As ondas se encontram em fase, pois percorrem a mesma distância, e terão suas amplitudes somadas.
Se esse ouvinte andar para o lado, a meio comprimento de onda em relação às fontes, o som produzido será fraco ou ocorrerá um silêncio. Tal efeito é considerado uma interferência destrutiva e é aplicado em tecnologias antirruído, como em cabines de aviões.
Imagem sem proporção e em cores fantasia.
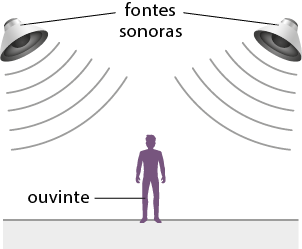
Imagem elaborada com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 384.
Ressonância das ondas sonoras
No dia 7 de novembro de 1940, a Ponte de Tacoma Narrows, localizada sobre o Estreito de Tacoma, em Washington, Estados Unidos, desabou. Esse fato histórico está relacionado a um fenômeno ondulatório conhecido como ressonância. Na ocasião, a frequência dos ventos no local era igual a uma das frequências naturais✚ da ponte, fazendo a ponte oscilar em máxima amplitude, destruindo-a.

A ressonância é basicamente um fenômeno em que ocorre a transferência de energia de um sistema para outro. Assim, se um sistema físico passa a receber energia de forma periódica, com uma frequência igual à sua frequência natural, passa a vibrar com amplitudes crescentes, com tendência para o maior valor possível. Quando isso ocorre, dizemos que o sistema entrou em ressonância.
Em acústica, esse fenômeno corresponde a uma sobreposição de ondas sonoras, aumentando a intensidade do som e provocando a sensação de que o som ficou mais alto. Se o corpo que interage com a onda sonora tem frequência igual à da fonte de emissão, ele absorverá energia e passará a vibrar.
Professor, professora: Explique aos estudantes que as caixas de ressonância funcionam como amplificadores de som. O ar que está contido em seu interior entra em vibração com a mesma frequência da fonte sonora, aumentando a intensidade do som produzido.
- Frequências naturais:
- é a frequência com que um sistema vibra livremente, de acordo com as características dos materiais e a maneira como ele foi construído, sem considerar as interferências externas.↰
Página 417
Efeito Doppler
Sabemos que a frequência de uma onda não se altera, pois está diretamente associada à fonte emissora, não importa por qual fenômeno ondulatório a onda passe.
Esse efeito pode ser percebido em situações que apresentam fontes que emitem ondas sonoras em todas as direções. Se dois observadores em repouso, um no ponto P e o outro no ponto P linha, recebem o som emitido pela buzina de um veículo, também em repouso, ambos percebem o som com a mesma frequência.
Se a fonte sonora se deslocar com certa velocidade na direção do ponto P linha, o observador colocado nesse ponto receberá as frentes de onda com maior frequência, percebendo um som mais alto, ou seja, mais agudo, e o comprimento de onda parecerá menor. Já o observador no ponto P receberá frentes de onda com uma frequência menor, percebendo um som mais baixo, ou seja, mais grave, e o comprimento de onda parecerá maior.
Essa mudança na frequência percebida por causa do movimento relativo entre a fonte sonora e o observador é conhecida como efeito Doppler, em homenagem ao matemático e físico austríaco Christian Johann Doppler (1803-1853). Ele verificou, em 1842, que o efeito era válido tanto para as ondas sonoras quanto para as luminosas.
Existem várias aplicações do efeito Doppler no cotidiano. Alguns aparelhos de ultrassonografia utilizam o efeito Doppler para analisar o fluxo sanguíneo nas veias. O aparelho emite um ultrassom que é refletido pelas células do sangue, principalmente as hemácias, e analisa a onda refletida.
Imagens desta página sem proporção e em cores fantasia.
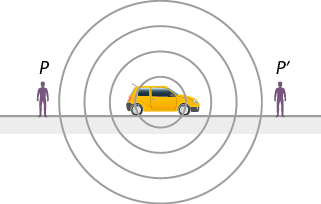
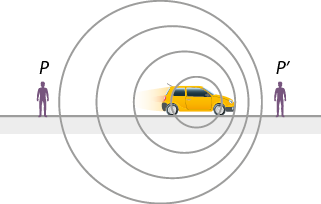
Imagens elaboradas com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 365-366.
Se as células se movem na direção do detector, a frequência da onda refletida é maior do que a da onda emitida; quando se movem na direção oposta, a onda refletida tem frequência menor. Por convenção, o fluxo na direção do detector é identificado pela cor vermelha, e na direção oposta ao detector, pela cor azul.
Professor, professora: Peça aos estudantes que citem uma situação do cotidiano em que podemos notar o efeito Doppler. Eles podem citar como exemplo uma ambulância ou viatura de polícia passando com a sirene ligada, situação em que percebemos sons diferentes na aproximação e no afastamento.
Dica
O físico francês Hyppolyte Fizeau (1819-1896) realizou experimentos sobre o mesmo fenômeno para determinar os deslocamentos das estrelas em relação à Terra, por isso o fenômeno também é conhecido por efeito Doppler-Fizeau.
Página 418
ATIVIDADES
1. Os antigos indígenas norte-americanos encostavam a orelha no chão a fim de averiguar se havia cavalaria vindo em sua direção. Explique o motivo dessa atitude.
Resposta: A velocidade do som nos sólidos é maior do que nos gases. Assim, o som emitido pelo galope dos cavalos é transmitido mais rapidamente pelo chão do que pelo ar, contribuindo para que os indígenas percebam com antecedência a sua chegada.
2. Escreva a alternativa correta com relação à altura do som, propriedade que o caracteriza como grave ou agudo.
a ) Um som grave é aquele com frequência alta.
b ) Um som agudo se propaga mais rapidamente do que um som grave.
c ) A velocidade de propagação é a mesma tanto para o som agudo como para o grave.
d ) A altura do som está relacionada com a amplitude da onda sonora.
Resposta: Alternativa c. As ondas sonoras têm a mesma velocidade no ar, aproximadamente, independentemente de o som ser agudo ou grave.
3. Durante um ensaio, o vocalista de uma banda percebe algumas diferenças nos sons emitidos pelos instrumentos e comenta com o engenheiro de som: "A guitarra parece mais aguda em algumas partes, enquanto o baixo soa mais grave. Além disso, mesmo que o volume da bateria esteja parecido com o das cordas, consigo distinguir facilmente cada instrumento".
Com base nas características fisiológicas do som, analise as afirmações a seguir e escolha a opção correta:
a ) A diferença entre os sons agudos e graves percebidos pelo vocalista está relacionada à intensidade do som emitido pelos instrumentos.
b ) A capacidade do vocalista de distinguir entre os sons da bateria e dos outros instrumentos está associada à diferença de altura entre os sons emitidos.
c ) A guitarra ser percebida como "aguda" e o baixo como "grave" corresponde à diferença de frequência das ondas sonoras produzidas por esses instrumentos.
d ) O fato de o vocalista identificar todos os instrumentos, mesmo com volumes semelhan- tes, deve-se à maior intensidade sonora da bateria em relação às cordas.
e ) A percepção de sons agudos e graves está relacionada diretamente ao timbre dos instrumentos musicais.
Resposta: Alternativa c.
4. Determine a intensidade de uma onda sonora que transporta 0 vírgula 3 joule de energia por uma área de 4 centímetros quadrados, a cada 2 segundos.
Resposta: I é igual a 375 watts barra m elevado ao quadrado
5. Um pescador, parado no oceano, observa o movimento das ondas ao seu redor. Ele nota que, a cada 2 segundos, uma nova onda passa pelo seu barco. Ao medir a distância entre duas cristas consecutivas, ele observa uma distância de 4 metros. Qual é a frequência e o comprimento de onda das ondas que o pescador está observando?
Resoluções das questões 4 e 5 nas Orientações para o professor.
Resposta: f é igual a 0 vírgula 5 hertz e lambda é igual a 4 metros.
6. Em um imóvel, as paredes delimitam cada cômodo, assim como suas portas e janelas. Uma pessoa localizada na cozinha consegue conversar com uma pessoa localizada no quarto se a porta estiver totalmente aberta. Escreva a alternativa que apresenta o(s) fenômeno(s) que ocorre(m) com as ondas sonoras e que torna(m) possível a situação descrita.
a ) Reflexão.
b ) Difração.
c ) Reflexão e refração.
d ) Reflexão e difração.
e ) Reflexão, refração e difração.
Resposta: Alternativa d.
7. Um navio da marinha utiliza um sonar para detectar um obstáculo submerso. O intervalo de tempo que o pulso leva para chegar ao obstáculo e retornar ao navio é de 4 segundos. Sabendo que a velocidade do som na água é de 1.500 metros por segundo, determine a distância do obstáculo em relação ao navio.
Resposta:
delta 's' é igual a 3.000 metros
Como o tempo registrado é para ida e volta do pulso, o tempo
somente de ida é igual a
2 segundos. Logo, a distância é dada por:
v é igual a início de fração, numerador: delta 's', denominador: delta 't', fim de fração implica em 1.500 é igual a início de fração, numerador: delta 's', denominador: 2, fim de fração implica em delta 's' é igual a 3.000 metros.
8. Em um concerto de rock, o alto-falante de um dos amplificadores emite ondas sonoras de 2 quilo-hertz uniformemente em todas as direções. A 20 metros de distância do amplificador, a intensidade do som é de 10 elevado a menos 2 Watt por metro quadrado. Analise as afirmativas a seguir, considerando o limiar da audição como 10 elevado a menos 12 Watt por metro quadrado.
I ) O nível sonoro do alto-falante a 20 metros de distância é de 100 decibeis.
II ) A potência sonora do alto-falante é de aproximadamente 50 vírgula 3 watts.
III ) Uma pessoa a 4 metros de distância do alto-falante sentirá desconforto, pois o nível sonoro nessa distância é de 120 decibeis.
IV ) A frequência de 2 quilo-hertz representa a altura do som emitido.
Resolução nas Orientações para o professor.
Está(ão) correta(s):
a ) I.
b ) II e III.
c ) I e II.
d ) III e IV.
e ) I, II e IV.
Resposta: Alternativa e.
Página 419
9. O efeito Doppler é caracterizado pela alteração na frequência percebida de um som em razão do movimento relativo entre o emissor e o receptor. Considere que uma viatura de polícia com a sirene ligada está se movendo em direção a um observador em uma calçada e avalie as afirmativas a seguir.
I ) A frequência percebida será maior que a real se o observador estiver em repouso.
II ) A frequência percebida será menor que a real se o observador estiver em movimento em direção à fonte.
III ) A frequência percebida será igual se o observador estiver em movimento em direção à fonte.
IV ) A frequência percebida será menor que a real após a viatura passar pelo observador e começar a se afastar dele.
V ) A frequência percebida será maior que a real se o observador estiver em movimento em direção à fonte.
Estão corretas as afirmativas:
a ) I e III.
b ) I e IV.
c ) II, IV e V.
d ) I, II e IV.
e ) I, IV e V.
Resposta: Alternativa e.
10. Durante uma apresentação musical, um cantor de ópera começa a cantar uma nota alta e constante. Em um momento, um copo de cristal é colocado sobre a mesa próximo ao palco. À medida que o cantor mantém a nota, o copo começa a vibrar até quebrar. Escreva a alternativa que apresenta o fenômeno que ocorre com as ondas sonoras e que torna possível a situação descrita anteriormente.
a ) Difração.
b ) Ressonância.
c ) Reflexão.
d ) Refração.
e ) Efeito Doppler.
Resposta: Alternativa b.
11. Durante uma palestra em um auditório, um dos estudantes percebe que, mesmo sentado atrás de uma parede que bloqueia a visão do palco, ele ainda consegue ouvir claramente o que o palestrante está dizendo. Ele se pergunta como isso é possível, já que a parede deveria bloquear o som, assim como bloqueia a luz.
Sobre essa situação, assinale a alternativa que melhor explica o fenômeno.
a ) O som consegue contornar a parede porque a velocidade do som é maior que a da luz.
b ) A capacidade do estudante de ouvir o palestrante se deve ao fenômeno de refração do som, que permite que as ondas atravessem a parede.
c ) O estudante consegue ouvir o palestrante devido à difração do som, que permite que as ondas sonoras contornem obstáculos e se espalhem.
d ) A presença da parede reduz o volume do som, mas não impede que ele passe, devido à dispersão das ondas sonoras.
e ) O som atravessa a parede porque as ondas sonoras têm menor frequência do que as ondas luminosas, permitindo que cheguem até o estudante.
Resposta: Alternativa c.
12. Um veículo emite som por meio de uma buzina numa frequência de 300 hertz. Sabendo que ele se movimenta com uma velocidade de 15 metros por segundo e que a velocidade do som no ar é 340 metros por segundo, calcule a frequência percebida por uma pessoa em repouso quando o veículo se afasta e quando o veículo se aproxima dela.
Resolução nas Orientações para o professor.
Dica
Utilize a equação geral do efeito Doppler, em que f linha é a frequência percebida, f é a frequência da fonte, v subscrito s é a velocidade do som no meio, v subscrito o é a do observador e v subscrito f é a da fonte.
f ' é igual a f vezes início de fração, numerador: v subscrito s mais ou menos v subscrito o, denominador: v subscrito s mais ou menos v subscrito f, fim de fração
Para a velocidade da fonte, atribuímos sinal positivo quando ela se afasta do observador e sinal negativo quando ela se aproxima do observador.
Resposta: f linha é aproximadamente igual a 287 vírgula 3 hertz para o veículo se afastando e f ' é aproximadamente igual a 313 vírgula 8 hertz para o veículo se aproximando.
13. João está correndo a uma velocidade de 2 metros por segundo quando ouve o som de uma sirene vindo de uma ambulância. Se a frequência da fonte é igual a 80 hertz e a ambulância se move a uma velocidade de 30 metros por segundo em direção a João, qual é a frequência percebida por ele? A velocidade do som é igual a 340 metros por segundo.
Resolução nas Orientações para o professor.
Resposta: f ' é igual a 88 vírgula 2 hertz.
14. Em uma excursão em uma floresta, um grupo de estudantes percebe que o som de suas vozes retorna após bater em uma parede rochosa (I). Também perceberam que o som de uma queda-d'água parece se espalhar quando passa através de duas árvores próximas (II). Mais à frente, percebem que o som do rio se mistura com o canto dos pássaros (III). O professor de Física que acompanha o grupo explica que esses fenômenos estão relacionados, respectivamente, a:
a ) (I) Reflexão, (II) Difração, (III) Interferência.
b ) (I) Refração, (II) Reflexão, (III) Interferência.
c ) (I) Difração, (II) Reflexão, (III) Refração.
d ) (I) Reflexão, (II) Refração, (III) Difração.
e ) (I) Interferência, (II) Difração, (III) Reflexão.
Resposta: Alternativa a.
Página 420
Instrumentos sonoros
Entre os instrumentos musicais tradicionais, temos aqueles que emitem ondas sonoras pela oscilação de cordas, os que emitem ondas sonoras pela vibração do ar em tubos e instrumentos que emitem ondas sonoras pela oscilação de uma membrana quando percutida: os instrumentos de percussão.

Imagens desta página sem proporção e em cores fantasia.



Ao reproduzir a mesma nota musical em cada instrumento musical, a onda gerada terá sempre a mesma frequência, contudo sempre formará um som percebido de forma diferente pelo ouvinte em razão do seu timbre próprio. A seguir, faremos um estudo mais detalhado dos instrumentos de corda e de tubo.
Cordas sonoras
Instrumentos de corda são aqueles que produzem ondas sonoras no ar por conta da oscilação de suas cordas, como o violão, o violino, o piano, a harpa e o cavaquinho.



Como as cordas são fixas em suas extremidades, as ondas geradas por uma perturbação se refletem, mantendo sua amplitude, seu comprimento de onda e sua frequência de propagação, mas com a fase invertida.
Em alguns comprimentos de onda específicos, que correspondem à frequência de ressonância da corda, a interferência das ondas em cada ponto resulta em uma onda estacionária, quando em alguns pontos da corda formam-se nós e, em outros, ventres. Cada modo de oscilação estacionário, com certo número de nós e ventres, é chamado harmônico. O modo mais simples é denominado fundamental, ou primeiro harmônico, quando ocorre a formação de uma onda estacionária com dois nós e um ventre, como mostrado a seguir.
O som que ouvimos é gerado pela oscilação da corda nesse modo, causando uma perturbação no ar ao redor da corda de mesma frequência, que se propaga de forma longitudinal até as orelhas. Assim, se o desejo é emitir uma nota musical de frequência 440 hertz, é preciso estabelecer uma onda estacionária da corda de mesma frequência.

Imagem elaborada com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 395.
Página 421
No caso do primeiro harmônico mostrado anteriormente, o comprimento 'L' da corda corresponde a meio comprimento de onda abre parênteses início de fração, numerador: lambda subscrito 1, denominador: 2, fim de fração fecha parênteses, de modo que a frequência f subscrito 1 emitida é determinada da seguinte forma.
'L' é igual a início de fração, numerador: lambda subscrito 1, denominador: 2, fim de fração implica em lambda subscrito 1 é igual a 2 vezes 'L'
v é igual a lambda vezes f é igual a 2 vezes 'L' vezes f subscrito 1 implica em f subscrito 1 é igual a início de fração, numerador: v, denominador: 2 vezes 'L', fim de fração
O segundo modo de oscilação é o segundo harmônico, quando são formados três nós e dois ventres. O comprimento da corda 'L' corresponde a um comprimento de onda abre parênteses lambda subscrito 2 fecha parênteses, de modo que a frequência f subscrito 2 emitida é determinada a seguir.
'L' é igual a início de fração, numerador: 2 vezes lambda subscrito 2, denominador: 2, fim de fração implica em lambda subscrito 2 é igual a início de fração, numerador: 2 vezes 'L', denominador: 2, fim de fração é igual a 'L'
v é igual a lambda vezes f é igual a início de fração, numerador: 2 vezes 'L', denominador: 2, fim de fração vezes f subscrito 2 implica em f subscrito 2 é igual a início de fração, numerador: 2 vezes v, denominador: 2 vezes 'L', fim de fração
Imagens desta página sem proporção e em cores fantasia.
Note que f subscrito 2 é igual a 2 vezes f subscrito 1, ou seja, a frequência do segundo harmônico é o dobro da frequência do primeiro harmônico. Isso pode ser verificado nas notas musicais, pois a cada intervalo de oitavas as notas se repetem, mas com frequências que valem o dobro. Por exemplo, se uma nota Dó tem frequência 261 vírgula 6 hertz, uma nota Dó oitava acima tem frequência 523 vírgula 2 hertz, correspondendo a uma oitava mais aguda.
O terceiro modo de oscilação é o terceiro harmônico, quando são formados quatro nós e três ventres. O comprimento da corda 'L' corresponde a um comprimento de onda e meio abre parênteses início de fração, numerador: 3 vezes lambda subscrito 3, denominador: 2, fim de fração fecha parênteses, de modo que a frequência f subscrito 3 emitida é determinada da seguinte forma:
'L' é igual a início de fração, numerador: 3 vezes lambda subscrito 3, denominador: 2, fim de fração implica em lambda subscrito 3 é igual a início de fração, numerador: 2 vezes 'L', denominador: 3, fim de fração
v é igual a lambda vezes f é igual a início de fração, numerador: 2 vezes 'L', denominador: 3, fim de fração vezes f subscrito 3 implica em f subscrito 3 é igual a início de fração, numerador: 3 vezes v, denominador: 2 vezes 'L', fim de fração
Imagens elaboradas com base em: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 395.
A frequência do terceiro harmônico vale 3 vezes f subscrito 1. Com esses três exemplos, é possível notar que, sendo v a velocidade da onda na corda, 'L' o comprimento da corda e n o número do harmônico, que corresponde ao número de ventres, a frequência de qualquer harmônico pode ser obtida da seguinte forma:
f subscrito n é igual a início de fração, numerador: n vezes v, denominador: 2 vezes 'L', fim de fração implica em f subscrito n é igual a n vezes f subscrito 1 abre parênteses n é igual a 1 vírgula 2 vírgula 3 vírgula 4 vírgula reticências fecha parênteses
O cálculo mostra como podemos obter as frequências da mesma nota musical em diversas oitavas, que é a mesma para qualquer instrumento. Nas imagens apresentadas para demonstrar as ondas estacionárias, usamos a forma tradicional de uma onda transversal.
Em instrumentos de corda, além de cada corda corresponder a uma nota, é possível pressioná-las em locais específicos do braço do instrumento, mudando assim o comprimento 'L' das cordas e alterando a frequência do som emitido por cada uma. Dessa forma, o som emitido ao perturbar todas as cordas juntas corresponde a um acorde específico.
Em instrumentos de corda, como o violão, a vibração da corda é captada pelo cavalete, que a transmite para a caixa de ressonância, que amplifica o som produzido. Alguns modelos vêm equipados com um microfone que capta as ondas sonoras e as converte em sinais elétricos, que, por sua vez, são encaminhados a um amplificador que emite o som pelo alto-falante. Em instrumentos elétricos, como nas guitarras, a vibração das cordas causa efeitos eletromagnéticos que geram sinais elétricos, encaminhados a amplificadores.
Página 422
Tubos sonoros
Os instrumentos de sopro e de percussão são os mais utilizados pelos indígenas em festas ou rituais.

Instrumentos de sopro, como apitos, trombetas e flautas, são feitos com materiais que emitem sons de timbres agradáveis quando se sopra por uma cavidade. São exemplos desses materiais: troncos, bambu, cerâmica, ossos e carapaças de animais.
Nos instrumentos sonoros de tubo, ondas estacionárias são geradas no ar em seu interior, em razão de uma perturbação provocada por um sopro na embocadura. Em uma flauta, as diferentes posições dos dedos servem para fechar ou abrir orifícios, alterando assim o comprimento da coluna de ar onde será gerada a onda estacionária, resultando na nota musical com a frequência desejada.
Imagens desta página sem proporção e em cores fantasia.
Os tubos geralmente utilizados como instrumentos musicais são classificados como tubo aberto, com as duas extremidades abertas, e tubo fechado, cuja extremidade oposta à entrada de ar é fechada.


A formação de ondas estacionárias em tubos de ar, sejam abertos, sejam fechados, é semelhante à formação de ondas estacionárias em cordas. A extremidade fechada do tubo corresponde a uma extremidade fixa da corda, onde ocorre a formação de nós, e a extremidade aberta, aos trechos da corda onde ocorre a formação de ventre.
Tubo aberto
Para tubos com as duas extremidades abertas, a perturbação causada pelo sopro em uma extremidade se propaga em direção à outra, onde encontra o meio externo com características diferentes de temperatura, pressão e densidade. As ondas então sofrem refração, mas também refletem, retornando ao tubo e encontrando outras ondas geradas. Para certos comprimentos de onda correspondentes às frequências de ressonância do tubo, a interferência causa ondas estacionárias. A onda estacionária terá ventres nas duas extremidades.
O modo fundamental de oscilação, ou primeiro harmônico, tem um nó no ponto médio entre as duas extremidades, como representado a seguir. O comprimento 'L' do tubo corresponde a meio comprimento de onda abre parênteses início de fração, numerador: lambda subscrito 1, denominador: 2, fim de fração fecha parênteses, de modo que a frequência f subscrito 1 emitida é determinada da seguinte forma:
'L' é igual a início de fração, numerador: lambda subscrito 1, denominador: 2, fim de fração implica em lambda subscrito 1 é igual a 2 vezes 'L'
v é igual a lambda vezes f é igual a 2 vezes 'L' vezes f subscrito 1 implica em f subscrito 1 é igual a início de fração, numerador: v, denominador: 2 vezes 'L', fim de fração
Imagem elaborada com base em: TREFIL, James; HAZEN, Robert M. Física viva: uma introdução à física conceitual. Tradução: Ronaldo S. de Biasi. Rio de Janeiro: LTC, 2006. v. 2. p. 36.
Página 423
O segundo modo de vibração é o segundo harmônico, quando são formados dois nós no interior do tubo. O comprimento do tubo 'L' corresponde a um comprimento de onda abre parênteses lambda subscrito 2 fecha parênteses, de modo que a frequência f subscrito 2 emitida é determinada a seguir.
'L' é igual a início de fração, numerador: 2 vezes lambda subscrito 2, denominador: 2, fim de fração implica em lambda subscrito 2 é igual a início de fração, numerador: 2 vezes 'L', denominador: 2, fim de fração é igual a 'L'
v é igual a lambda vezes f é igual a início de fração, numerador: 2 vezes 'L', denominador: 2, fim de fração vezes f subscrito 2 implica em f subscrito 2 é igual a início de fração, numerador: 2 vezes v, denominador: 2 vezes 'L', fim de fração

Imagens desta página sem proporção e em cores fantasia.
Note que f subscrito 2 é igual a 2 vezes f subscrito 1, ou seja, a frequência do segundo harmônico é o dobro da frequência do primeiro harmônico.
O terceiro modo de vibração é o terceiro harmônico, quando são formados três nós. O comprimento do tubo 'L' corresponde a um comprimento de onda e meio abre parênteses início de fração, numerador: 3 vezes lambda subscrito 3, denominador: 2, fim de fração fecha parênteses, de modo que a frequência f subscrito 3 emitida é determinada da seguinte forma:
'L' é igual a início de fração, numerador: 3 vezes lambda subscrito 3, denominador: 2, fim de fração implica em lambda subscrito 3 é igual a início de fração, numerador: 2 vezes 'L', denominador: 3, fim de fração
v é igual a lambda vezes f é igual a início de fração, numerador: 2 vezes 'L', denominador: 3, fim de fração vezes f subscrito 3 implica em f subscrito 3 é igual a início de fração, numerador: 3 vezes v, denominador: 2 vezes 'L', fim de fração
Imagens elaboradas com base em: TREFIL, James; HAZEN, Robert M. Física viva: uma introdução à física conceitual. Tradução: Ronaldo S. de Biasi. Rio de Janeiro: LTC, 2006. v. 2. p. 36.
Note que f subscrito 3 é igual a 3 vezes f subscrito 1. Assim, para uma onda de velocidade v, um tubo aberto de comprimento 'L', a frequência de qualquer harmônico n pode ser obtida da seguinte forma:
f subscrito n é igual a início de fração, numerador: n vezes v, denominador: 2 vezes 'L', fim de fração implica em f subscrito n é igual a n vezes f subscrito 1 abre parênteses n é igual a 1 vírgula 2 vírgula 3 vírgula 4 vírgula reticências fecha parênteses
Tubo fechado
Para tubos com uma extremidade fechada, a perturbação causada pelo sopro na extremidade aberta se propaga em direção à fechada, que corresponde à extremidade fixa de uma corda. Para certos comprimentos de onda correspondentes às frequências de ressonância do tubo, a interferência das ondas refletidas com outras ondas geradas causa ondas estacionárias, com ventre na extremidade aberta e nó na extremidade fechada.
O modo fundamental de oscilação, ou primeiro harmônico, possui um nó na extremidade fechada, como representado a seguir. O comprimento 'L' do tubo corresponde a um quarto de comprimento de onda abre parênteses início de fração, numerador: lambda subscrito 1, denominador: 4, fim de fração fecha parênteses, de modo que a frequência f subscrito 1 emitida é determinada da seguinte forma:
'L' é igual a início de fração, numerador: lambda subscrito 1, denominador: 4, fim de fração implica em lambda subscrito 1 é igual a 4 vezes 'L'
v é igual a lambda vezes f é igual a 4 vezes 'L' vezes f subscrito 1 implica em f subscrito 1 é igual a início de fração, numerador: v, denominador: 4 vezes 'L', fim de fração

Por conta da forma como as ondas são formadas, o próximo modo de vibração corresponde ao terceiro harmônico, pois o comprimento do tubo 'L' corresponde a três quartos do comprimento de onda abre parênteses início de fração, numerador: 3 vezes lambda subscrito 3, denominador: 4, fim de fração fecha parênteses. A frequência f subscrito 3 emitida é determinada da seguinte forma:
'L' é igual a início de fração, numerador: 3 vezes lambda subscrito 3, denominador: 4, fim de fração implica em lambda subscrito 3 é igual a início de fração, numerador: 4 vezes 'L', denominador: 3, fim de fração
v é igual a lambda vezes f é igual a início de fração, numerador: 4 vezes 'L', denominador: 3, fim de fração vezes f subscrito 3 implica em f subscrito 3 é igual a início de fração, numerador: 3 vezes v, denominador: 4 vezes 'L', fim de fração

Imagens elaboradas com base em: TREFIL, James; HAZEN, Robert M. Física viva: uma introdução à física conceitual. Tradução: Ronaldo S. de Biasi. Rio de Janeiro: LTC, 2006. v. 2. p. 36.
A frequência do terceiro harmônico vale 3 vezes f subscrito 1.
Assim, para uma onda de velocidade v, em um tubo fechado de comprimento 'L', formam-se apenas harmônicos ímpares, sendo as frequências obtidas a seguir.
f subscrito n é igual a início de fração, numerador: n vezes v, denominador: 4 vezes 'L', fim de fração implica em f subscrito n é igual a n vezes f subscrito 1 abre parênteses n é igual a 1 vírgula 3 vírgula 5 vírgula reticências fecha parênteses
Página 424
CONEXÕES com ... BIOLOGIA
Pair
A audição humana é um sentido que está em constante funcionamento, pois dificilmente estamos em uma situação em que não escutamos nenhum tipo de som ou ruído. Até mesmo no "silêncio" da noite, quando nos deitamos para dormir, a audição capta pequenos ruídos distantes, como o barulho do vento na janela e sons emitidos por pássaros e insetos. Esses ruídos continuam ativando as estruturas da orelha, ou seja, elas não atingem um estado de equilíbrio estático. Tal movimentação contínua, somada à exposição diária a ruídos intensos, pode causar desgastes e sérios danos à orelha.
Dependendo dos níveis sonoros aos quais a orelha é submetida, sons e ruídos podem causar desconforto, estresse, enjoo, perda do sono, falta de concentração, irritabilidade, redução temporária da capacidade auditiva ou perda total da audição. Da mesma forma, ruídos aparentemente baixos, mas aos quais as orelhas são submetidas por uma longa duração, podem levar a graves consequências com o passar do tempo. Esses são os dois fatores principais a serem considerados em relação à saúde da orelha e do sentido da audição.
A perda de audição induzida por ruído (Pair) é o mais frequente problema relacionado à saúde auditiva. Ele leva à redução temporária da capacidade auditiva em razão da fadiga das estruturas, podendo alterar permanentemente o limiar da audição. A exposição a ruídos intensos pode causar danos às células ciliadas, que ficam dentro da cóclea. Essas células sensoriais podem ser danificadas pela exposição à música ou a barulhos intensos por muito tempo ou por um estrondo de curta duração, como o barulho de uma explosão, e, uma vez destruídas, não são substituídas, o que pode levar à perda auditiva permanente.
Esse problema é comum em indivíduos que se expõem continuamente a ruídos de cerca de 85 decibeis por várias horas diariamente.
Há uma grande variedade de profissões que são mais propícias ao desenvolvimento de problemas auditivos devido à exposição a ruídos altos, como músicos, trabalhadores da construção civil e operadores de máquinas. Esses profissionais devem usar protetores auriculares para proteger sua audição.
Além disso, ouvir áudio por meio de fones de ouvido em altas intensidades pode causar perda auditiva temporária ou permanente e zumbido. Ajustar nossos fones de ouvido ou auriculares para não ultrapassar mais que 50 a 60% do nível máximo ajuda a proteger nossa audição por toda a vida.

Além dos cuidados diários com a própria audição, para contribuir com a saúde auditiva, todos devemos evitar a propagação de sons e ruídos excessivos ou desnecessários nos ambientes.
a ) Você faz uso contínuo de fones de ouvido com volume alto? Se sim, considerando o parâmetro de 100 decibeis, o tempo diário que você passa utilizando o fone está dentro das recomendações?
Resposta: O nível sonoro do som emitido por fones de ouvido depende do volume selecionado no botão do aparelho. Oriente os estudantes a consultar a página 407 para checar o tempo recomendado ao parâmetro indicado. Embora o tempo indicado seja 1 hora por dia, comente com eles que, de modo geral, os limites máximos devem ser evitados, pois, com o passar do tempo, podem ocasionar danos.
b ) Cite algumas atitudes que podem ser tomadas por pessoas, fábricas, indústrias e governos para auxiliar na redução da emissão de ruídos sonoros.
Resposta pessoal. Os estudantes podem citar o incentivo ao uso de protetores auriculares em casos de exposição a ruídos intensos, procurar escutar música em volume adequado, evitar buzinar no trânsito, entre outras medidas. Além disso, os governantes devem realizar campanhas de conscientização da população para reduzir a emissão de ruídos desnecessários e aumentar a fiscalização de estabelecimentos e veículos que emitem ruídos com intensidade inadequada em locais públicos.
c ) Quando os ruídos frequentes em um local podem provocar danos à saúde do ser humano e de outros animais, dizemos que esse local apresenta poluição sonora. Os locais que você frequenta diariamente apresentam poluição sonora? Converse com os colegas sobre os motivos para esse fenômeno ser chamado de poluição.
Resposta pessoal. Espera-se que os estudantes reflitam sobre a poluição como um fenômeno de degradação de aspectos físicos e químicos dos ecossistemas. Portanto, tal como a poluição do ar ou das águas, os excessos de ruídos propagados no som que ouvimos são considerados poluição sonora.
Página 425
PRÁTICA CIENTÍFICA
Produção e propagação do som
Por dentro do contexto
As ondas sonoras se propagam nos mais diversos meios materiais, e o meio mais comum para sua propagação é o ar, que conduz as vibrações até nossas orelhas.
Quando uma fonte sonora causa uma perturbação no ar, a propagação da onda sonora ocorre por compressões e rarefações do meio, que só causam impacto quando são percebidas pela orelha e interpretadas pelo cérebro.
Mas será que existe a possibilidade de perceber o som de outra maneira? E ver o som, seria possível?
a ) Como você explicaria o funcionamento de um alto-falante?
Resposta pessoal. O objetivo desta questão é levar os estudantes a refletir sobre as formas de produção de ondas sonoras. Sinais elétricos fazem o cone do alto-falante vibrar, provocando compressões e rarefações no ar próximo a ele, produzindo ondas sonoras.
b ) Como podemos perceber as ondas sonoras sem utilizar a audição?
Resposta pessoal. O objetivo desta questão é levar os estudantes a relacionar as formas de propagação do som em meios sólidos com a possibilidade de observar alguns dos fenômenos sonoros, como a ressonância da membrana em relação às frequências das ondas emitidas pela fonte e a percepção da vibração por meio do tato.
Materiais
- filme de PVC
- elásticos de borracha
- 1 recipiente redondo de vidro ou plástico de 5 centímetros de diâmetro (xícara, tigela ou vidraria de laboratório)
- 1 smartphone
- caixa de som
- areia fina seca (pode ser sal, açúcar ou confeitos coloridos de uso culinário)
- tesoura com pontas arredondadas
Como proceder
A. Cubra o recipiente com o filme de PVC bem esticado, de modo que fique vedado; caso necessário, utilize os elásticos de borracha para ajustar o filme de PVC no recipiente.
B. Espalhe uma pequena quantidade de areia sobre o filme de PVC para verificar a vibração da membrana por meio do movimento do material, quando estiver exposto às fontes sonoras.

C. Verifique a vibração do material usando diferentes fontes sonoras, como batucar algum recipiente metálico. Pode-se usar o smartphone conectado à caixa de som para amplificar a onda sonora emitida. Ainda é possível verificar a vibração com diferentes tons musicais, usando aplicativos de smartphone ou site de geradores de tons.
Dica
Peça a ajuda de um adulto para manipular objetos cortantes, caso necessário.
Análise
1. Quais evidências comprovaram a possibilidade de observar a onda sonora em um meio sólido, como uma membrana?
2. As ondas sonoras geradas pelas diferentes fontes criaram um mesmo padrão de vibração no material usado sobre a membrana durante as observações?
3. Os modos de vibração do material usado para observar a onda sonora têm relação com as características do som emitido pela fonte? Cite um exemplo.
4. De que forma essa investigação pode ser relacionada com o sentido da audição humana?
Respostas nas Orientações para o professor.
Página 426
ATIVIDADES
1. Se uma corda de um instrumento musical fosse cortada pela metade, ou então fosse dobrado o seu tamanho, o que aconteceria com sua frequên- cia? E com o comprimento de onda? Justifique sua resposta.
Resposta: Se diminuída pela metade, a frequência dobraria e o comprimento de onda diminuiria pela metade. Se dobrada de tamanho, a frequência diminuiria pela metade e dobraria o comprimento de onda. Isso ocorre pelo fato de a frequência ser inversamente proporcional ao comprimento da corda, se mantida a velocidade constante.
2. Ao dedilhar seu violão, um estudante de música percebe que, ao tocar uma das cordas, formam-se quatro nós e três ventres. Suponha que o comprimento da corda é 50 centímetros e a velocidade das ondas na corda é 300 metros por segundo. Qual é a frequência do harmônico produzido?
Resposta: f subscrito 3 é igual a início de fração, numerador: 3 vezes v, denominador: 2 vezes 'L', fim de fração é igual a início de fração, numerador: 3 vezes 300, denominador: 2 vezes 0 vírgula 5, fim de fração é igual a 900 hertz
3. Um músico sabe que as ondas produzidas pelas cordas de seu violão também produzirão as ondas sonoras que se propagarão por meio do ar. Pode-se afirmar que tanto as ondas produzidas pelas cordas quanto as ondas sonoras têm a(o) mesma(o):
a ) amplitude.
b ) comprimento de onda.
c ) velocidade de propagação.
d ) frequência.
e ) não apresentam relação.
Resposta: Alternativa d.
4. As cordas vibrantes produzem ondas sonoras em diversos instrumentos musicais, como violões, violinos e pianos. Faça a soma das afirmações corretas.
01 ) Quando uma corda vibrante forma dois ventres, ela está vibrando em seu segundo harmônico.
02 ) A velocidade de propagação da onda em uma corda é sempre igual à velocidade de propagação da onda no ar.
04 ) Em uma corda vibrante, os nós são os pontos onde a amplitude da onda é máxima.
08 ) A frequência fundamental de uma corda vibrante é diretamente proporcional ao seu comprimento.
16 ) Pressionar a corda de um violão em diferentes pontos altera o comprimento efetivo da corda e, consequentemente, a frequência do som.
Resposta: 01 mais 16 é igual a 17
5. O tubo mais longo de um órgão, com as duas extremidades abertas, é de 4 metros. Qual é a frequência fundamental produzida por esse tubo, considerando a velocidade do som igual a 340 metros por segundo?
Resposta: f subscrito 1 é igual a 42 vírgula 5 hertz
6. Durante uma aula de música, um estudante está experimentando um tubo sonoro. O tubo é fechado em uma extremidade e aberto na outra, e tem um comprimento de 1 vírgula 2 metro. Sabendo que a velocidade do som no ar é 340 metros por segundo, qual é a frequência fundamental produzida pelo tubo?
Resposta: f subscrito 1 é igual a 70 vírgula 8 hertz
7. A frequência fundamental de um tubo de órgão fechado é igual à primeira frequência harmônica de um tubo de órgão aberto. Se o comprimento do tubo aberto for de 120 centímetros, qual será o comprimento do tubo fechado?
Resposta: 'L' subscrito fechado é igual a 0 vírgula 6 metro
8. A produção dos sons nos pianos acústicos envolve a atuação de um mecanismo complexo, acionado pelas teclas e que faz uma peça chamada martelo bater nas cordas que produzem o som. Para as teclas de sons mais graves, são utilizadas cordas espessas e únicas, mas à medida que os sons vão ficando mais agudos, são utilizados conjuntos de cordas mais finas para que a intensidade do som emitido por todas as teclas seja mantida.

Sabendo que a frequência da primeira nota Dó emitida por um piano é de 32 vírgula 7 hertz, responda às questões a seguir.
a ) Qual é a frequência da nota Dó 5 oitavas acima da primeira nota Dó do piano?
Resposta: f é igual a 1.046 vírgula 4 hertz
b ) As cordas referentes à nota Dó 5 oitavas acima devem ter comprimento maior ou menor que as referentes ao primeiro Dó?
Resposta: Espera-se que os estudantes respondam que as cordas da nota Dó mais aguda devem ser menores do que as cordas referentes ao primeiro Dó.
9. Um estudante está construindo um xilofone de PVC para um projeto de música. Ele cortou um tubo de PVC para que seu comprimento seja de 1 vírgula 5 metro. Suponha que a velocidade do som no ar seja 340 metros por segundo. Qual é a frequência fundamental do tubo de PVC?
Resoluções das questões 5, 6, 7, 8 e 9 nas Orientações para o professor.
Resposta: f subscrito 1 é igual a 113 vírgula 3 hertz
Página 427
10. Na acústica, há dois tipos de tubos sonoros: os abertos e os fechados. Os tubos abertos têm ambas as extremidades livres enquanto os tubos fechados têm uma extremidade fechada e outra aberta. Sobre os tubos sonoros, analise as afirmativas a seguir.
I ) A frequência fundamental de um tubo aberto é determinada pelo comprimento do tubo e pela velocidade do som no ar.
II ) A velocidade do som em um tubo fechado é maior do que em um tubo aberto de comprimento igual.
III ) Em um tubo fechado em uma extremidade, a extremidade fechada é sempre um nó e a extremidade aberta é um ventre.
IV ) Um tubo fechado em uma extremidade não pode produzir o segundo harmônico.
Está(ão) correta(s):
a ) II.
b ) III.
c ) I e II.
d ) I, III e IV.
e ) I, II, III e IV.
Resposta: Alternativa d.
11. Um tubo fechado em uma extremidade e aberto na outra pode produzir diferentes frequências. Qual das alternativas está correta sobre os tubos fechados? Escreva a alternativa correta, justificando-a.
a ) Apenas os harmônicos pares são produzidos.
b ) A frequência fundamental é produzida quando há dois ventres no tubo.
c ) Apenas os harmônicos ímpares podem ser produzidos.
d ) A frequência fundamental é o dobro da de um tubo aberto de mesmo comprimento.
e ) O comprimento da onda produzida é sempre igual ao comprimento do tubo.
Resposta: Alternativa c.
12. Complete as lacunas com a alternativa correta, escrevendo a frase completa: Um tubo aberto em ambas as extremidades pode produzir uma série de frequências chamadas de harmônicos. A frequência fundamental nesse tubo é produzida quando o tubo tem ■ e o comprimento de onda é igual a ■ comprimento de onda.
a ) um ventre em cada extremidade, meio.
b ) um nó em cada extremidade, um quarto de.
c ) dois ventres e um nó no meio do tubo, um.
d ) três ventres e dois nós, um terço de.
e ) um ventre em uma extremidade, um.
Resposta: Alternativa a.
13. Ao fabricar uma corda de instrumento musical, para testá-la e poder enviá-la ao comerciante, ela é presa e tensionada por determinada força. A corda é colocada em um aparelho que imprime sobre ela uma frequência de vibração de 150 hertz, produzindo uma onda estacionária equivalente ao terceiro modo de vibração. Sabendo que a corda tem comprimento de 1 vírgula 0 metro, calcule a velocidade de propagação da onda na corda.
Resposta: v é igual a 100 metros por segundo
14. O espetáculo do Blue Man Group é famoso por suas apresentações musicais que envolvem instrumentos de percussão alternativos, alguns deles são feitos por tubos de PVC encaixados entre si. Na execução das músicas, os integrantes do grupo alteram o comprimento dos tubos de PVC para modificar a frequência do som emitido.

Considere dois tubos de mesmo comprimento 'L', sendo um fechado e outro aberto. Sendo f subscrito A e f subscrito B as frequências fundamentais, respectivamente, qual é a relação entre as frequências?
Resoluções das questões 13 e 14 nas Orientações para o professor.
Resposta: f subscrito A é igual a início de fração, numerador: f subscrito B, denominador: 2, fim de fração
15. Em uma aula de música, o professor demonstra como uma flauta produz som. Ele explica que o tubo da flauta é aberto em ambas as extremidades e que, ao soprar, cria-se uma onda estacionária dentro do tubo, gerando as notas musicais.
Com base nesse contexto, assinale a alternativa correta sobre ondas estacionárias em tubos sonoros abertos:
a ) A frequência fundamental em um tubo sonoro aberto é gerada quando há um nó em cada extremidade do tubo.
b ) Nos tubos sonoros abertos, a frequência fundamental ocorre quando há um ventre em uma extremidade e um nó na outra.
c ) Em um tubo sonoro aberto, a frequência fundamental ocorre quando há um nó no centro do tubo e ventres nas extremidades.
d ) Em tubos sonoros abertos, a frequência fundamental ocorre quando há ventres em ambas as extremidades do tubo.
e ) As ondas estacionárias em tubos sonoros abertos sempre têm frequências mais baixas que as de tubos fechados de mesmo comprimento.
Resposta: Alternativa d.
Página 428
CAPÍTULO27
Luz e visão humana
Uso da tecnologia e olhos humanos
Leia a seguir a manchete de uma reportagem sobre os problemas de visão humana causados pelo uso excessivo de aparelhos eletrônicos.
O futuro dos olhos pode estar condicionado à chamada Síndrome Visual do Computador, um fenômeno novo na oftalmologia causado pelo uso constante da visão de perto. Esse problema, alavancado na pandemia com a diminuição de circulação ao ar livre e recebimento da luz natural, tem causado algumas mudanças no comportamento visual, principalmente em crianças.
São três aspectos principais que envolvem essa síndrome: o cansaço dos olhos, causado pela sobrecarga muscular no ato de "olhar de perto", ressecamento do olho, principalmente pela falta do piscar constante e, também, a própria radiação luminosa emitida pelos aparelhos eletrônicos, como smartphones e computadores.
[...]
LÍDICE, Sarah. Cansaço e ressecamento dos olhos podem indicar uso excessivo de computador. Jornal da USP, 31 maio 2021. Disponível em: https://s.livro.pro/0oax8o. Acesso em: 9 set. 2024.
No texto anterior, é destacado que o uso de aparelhos eletrônicos, como computadores, televisores, videogames, tablets e celulares, entre outros, caso ocorra por longos períodos, pode prejudicar a visão. Pesquisadores descobriram uma relação entre as horas de uso diário de dispositivos eletrônicos e o índice de doenças da superfície ocular. Eles estabeleceram que problemas relacionados à visão aumentam proporcionalmente conforme também aumenta o tempo de uso desses equipamentos.
A tecnologia evoluiu de tal forma que o uso de dispositivos eletrônicos se tornou rotineiro. Por vezes, utilizamos esses equipamentos por longos intervalos de tempo, tanto para diversão quanto para estudos e trabalho.

Esses aparelhos têm emissores de luz no fundo para produzir a imagem, dando brilho e clareza para a tela. O tipo de iluminação das telas emite luz azul, que pode ser prejudicial para nossa visão.
O tempo de uso diário considerado seguro para evitar danos à visão ainda não está bem estabelecido, contudo há algumas práticas para uma relação mais saudável com essas tecnologias.
Entre essas práticas, podemos citar as seguintes.
Faça pequenas pausas de 20 segundos, olhando para objetos distantes, a cada 20 minutos de uso de alguma tela de aparelho eletrônico. Como geralmente as telas ficam próximas dos nossos olhos, a musculatura do olho fica contraída. Olhar para objetos distantes ajuda a relaxar essa musculatura e prevenir a fadiga e o cansaço.
Página 429
- Procure piscar os olhos com frequência, para evitar seu ressecamento. Quando utilizamos aparelhos eletrônicos, a taxa com que piscamos é reduzida em cerca de 50%.
- Estabeleça limites para o tempo de uso de telas.
- Evite usar aparelhos eletrônicos em ambientes com pouca luz e perto do horário em que você costuma dormir. A luz azul emitida pelas telas pode afetar nosso relógio biológico, mantendo-nos acordados, pois diminui os níveis de melatonina, hormônio responsável por nos ajudar a adormecer. Por isso, é importante desligar todos os dispositivos eletrônicos cerca de duas horas antes de dormir.
Compartilhe ideias
Uso consciente dos aparelhos eletrônicos.
a ) Pense a respeito do uso de aparelhos eletrônicos com telas, como computadores, televisores, videogames, tablets, celulares etc. Cite quais deles você utiliza com frequência e anote quanto tempo você usa cada um diariamente. Em seguida, discuta com seus colegas se o tempo de uso é excessivo ou se consideram que a atual relação com a tecnologia é saudável.
Resposta pessoal. Os estudantes podem argumentar que o uso excessivo de aparelhos eletrônicos potencialmente causa problemas na visão e interfere na produção de melatonina, afetando o sono. Além disso, leve-os a refletir sobre como o tempo gasto com telas pode reduzir as oportunidades para atividades sociais importantes, como a interação com a família e amigos.
Alguns estudos sugerem ainda que o excesso de luz azul (de energia mais alta na faixa do espectro visível) emitida pelas telas dos equipamentos eletrônicos pode prejudicar diretamente a visão. Essa luz pode danificar as células da retina, representando um fator de risco para o surgimento do processo de degeneração macular relacionada à idade, que leva à perda progressiva da visão central.
O sentido da visão engloba os olhos, o nervo óptico e o cérebro.
O olho tem a função de receber a luz emitida pelos objetos e direcioná-la até a retina para formar as imagens. Ele é um órgão que funciona de forma similar a uma máquina fotográfica. No processo da formação das imagens, a córnea e o cristalino agem como lentes, refratando e desviando a trajetória da luz. As imagens são projetadas de forma invertida na retina. No entanto, o cérebro é capaz de fazer a interpretação dessas informações, invertendo as imagens para a orientação normal que coincide com a posição real dos objetos.
A retina é constituída de células fotorreceptoras chamadas de cones e bastonetes.
Os bastonetes são capazes de reconhecer diferentes níveis de luminosidade, permitindo a gradação entre claro e escuro e a visão de formas e movimento. Já os cones são responsáveis pela visão das cores.
Imagem sem proporção e em cores fantasia.
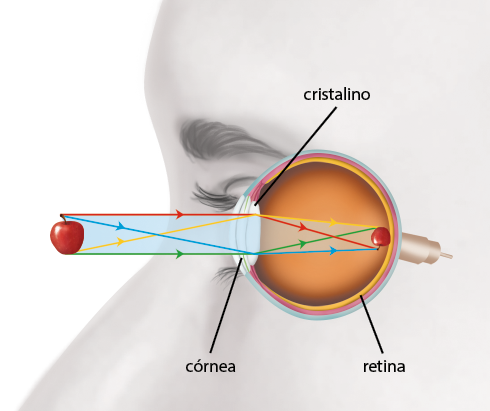
Imagem elaborada com base em: PARKER, Steve. O livro do corpo humano: um guia ilustrado de sua estrutura, funções e disfunções. Barueri: Ciranda Cultural, 2007. p. 92.
Há três tipos de cones, um que responde melhor à luz vermelha, outro, à luz verde e um terceiro, à luz azul. São as células sensíveis à luz azul que podem ser danificadas pela luz emitida por telas de aparelhos eletrônicos. Por isso a importância dos cuidados em relação ao uso prolongado desses equipamentos.
As células fotorreceptoras sensibilizadas pela luz que chega à retina transformam essa informação em um impulso nervoso, que é transmitido ao cérebro pelo nervo óptico.
O cérebro tem a função de fazer a interpretação dessas informações, gerando os resultados para cor, tamanho, forma, distância dos objetos etc.
Além da exposição excessiva da visão à luz emitida pelas telas dos equipamentos eletrônicos, há muitas outras situações que prejudicam a visão humana. Vamos estudar algumas delas.
Página 430
Luz solar
A luz solar, apesar de iluminar os ambientes possibilitando nossa visão, pode ser prejudicial para nossos olhos.
1. Você costuma usar óculos de sol? Que tipo de proteção você considera importante para seus olhos ao escolher um par de óculos?
Resposta pessoal. O objetivo desta questão é levar os estudantes a refletir sobre suas ações e verificar a importância de usar óculos que oferecem proteção contra radiação UV. Espera-se que eles reconheçam que usar sem o filtro UV pode ser mais prejudicial do que não utilizá-los, pois a lente escura deixa as pupilas mais abertas e podem focalizar a radiação ultravioleta em um ponto no interior do olho, causando lesões graves.
A radiação ultravioleta (UV) presente na luz solar pode ser dividida em três faixas: UV-A, UV-B e UV-C.
O UV-C tem mais energia, porém é absorvido pela atmosfera. Parte do UV-B é absorvida pela atmosfera e parte chega à superfície terrestre, sendo capaz de provocar queimaduras na pele e induzir o surgimento de câncer de pele.
Praticamente todo o UV-A penetra na atmosfera. Essa faixa do UV pode ser bastante prejudicial para os olhos, pois é absorvida pelo cristalino ao penetrá-los, danificando os olhos humanos e, consequentemente, a visão.
Imagens desta página sem proporção e em cores fantasia.
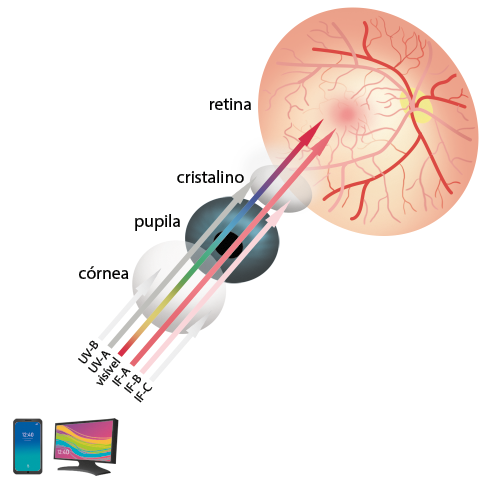
Imagem elaborada com base em: CLARK, Andrew J. et al. Ocular Tolerance of Contemporary Electronic Display Devices. Ophthalmic Surgery, Lasers & Imaging Retina, v. 49, n. 5, 2018. p. 346-354.
A exposição excessiva à radiação ultravioleta pode causar danos imediatos ou tardios à visão. Confira a seguir.
A ceratoconjuntivite é uma inflamação que afeta a córnea. É normalmente causada por infecções por bactérias ou vírus, mas também pode acontecer por exposição à radiação UV-B.
A fotoceratite, mostrada na fotografia A, é uma inflamação da córnea causada pelos raios UV-B.
A.
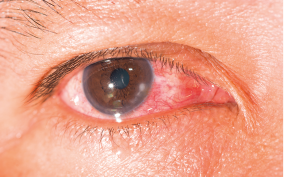
Por sua vez, a fotoconjuntivite é uma inflamação da conjuntiva do olho, membrana que reveste a superfície interna das pálpebras e a parte branca dos olhos, quando esta é submetida a altas doses de radiação UV-B.
A catarata, fotografia B, é um dano que se manifesta em longo prazo. Ela é caracterizada pela opacidade parcial ou total do cristalino. O tratamento desse problema é cirúrgico.
B.
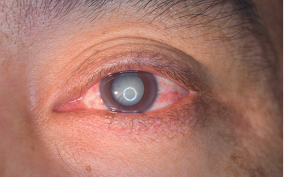
Já o pterígio, fotografia C, é o crescimento de uma membrana fibrovascular sobre a córnea, que acaba invadindo a superfície do olho. A radiação UV é um dos fatores que desencadeiam seu desenvolvimento.
C.
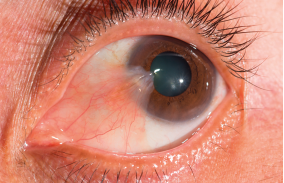
Para se proteger da radiação UV, é necessário utilizar óculos de sol com proteção (filtro) contra esse tipo de radiação quando estamos expostos à luz solar. Alguns óculos de sol de baixa qualidade não têm filtro UV, e utilizá-los pode ser prejudicial para os olhos. Dependendo da curvatura da lente, ela pode focalizar a radiação UV em uma pequena área, causando queimaduras no olho. É importante lembrar que olhar diretamente para qualquer fonte de luz de grande intensidade também pode causar danos à visão. Assim, jamais olhe diretamente para o Sol ou incida um feixe de laser diretamente nos olhos.
Página 431
Alterações da visão
Imagens desta página sem proporção e em cores fantasia.
Existem vários problemas relacionados aos olhos e à visão além dos estudados anteriormente. Eles têm diferentes características, causas e correções.
Problemas de visão podem produzir dores de cabeça, em virtude do esforço para enxergar corretamente, ou problemas de aprendizagem, em razão de o estudante não conseguir enxergar com nitidez as palavras ou os números.
Dica
Os problemas ou alterações da visão devem ser diagnosticados e tratados pelo médico especialista em olhos, o oftalmologista. Se possível, consulte regularmente esse especialista.
Compartilhe ideias
Observando as coisas ao seu redor.
a ) Observe objetos que estão longe de você, como os do outro lado da sala de aula. Em seguida, observe objetos próximos, como caneta, lápis, caderno, as marcações em uma régua etc. Depois, junte-se a um colega e conversem sobre se vocês são capazes de visualizar bem os objetos próximos e distantes. Discutam quais são as atitudes corretas a se tomar caso tenham alguma dificuldade nesse sentido.
Resposta pessoal. O objetivo desta atividade é fazer um levantamento em sala de aula a respeito dos problemas de visão entre os estudantes, como dificuldade de enxergar objetos posicionados distantes do observador ou próximos a ele. Além disso, deve-se incentivar a consulta ao oftalmologista sempre que considerar necessário.
Por causa das alterações no formato do globo ocular, na curvatura do cristalino e da córnea e nas células da retina, há diferentes problemas de visão. Na sequência, estudaremos alguns.
A miopia é um problema que causa dificuldade em ver com nitidez objetos distantes.
No olho míope, a imagem é formada antes da retina, como mostrado em A. Essa alteração acontece quando o bulbo do olho é alongado, bem como quando o olho tem um cristalino de maior espessura.
A.
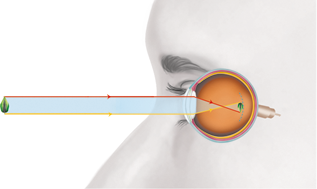
A miopia pode ser corrigida por meio da utilização de lentes esféricas divergentes (B). Esse tipo de lente faz que os raios de luz cheguem mais afastados ao olho. Assim, a córnea e o cristalino conseguem focalizar a luz na retina.
B.
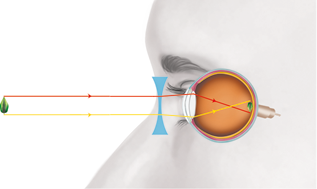
A hipermetropia é um problema que causa dificuldade em ver com nitidez os objetos próximos.
No olho hipermetrope, a imagem é formada atrás da retina, como mostrado em C. Essa alteração da visão ocorre quando o bulbo do olho é curto, assim como quando o cristalino é muito fino.
C.
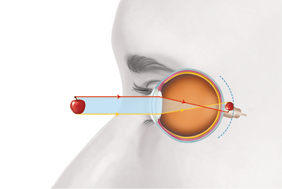
A correção para esse problema é realizada com a utilização de lentes esféricas convergentes (D), que fazem os raios de luz chegarem ao olho mais próximo uns dos outros, permitindo que a córnea e o cristalino focalizem a imagem corretamente na retina.
D.
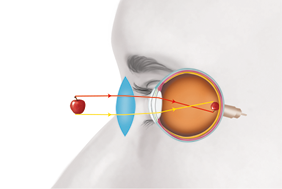
Imagens elaboradas com base em: TORTORA, Gerard J. Corpo humano: fundamentos de anatomia e fisiologia. 10. ed. Porto Alegre: Artmed, 2017. p. 309.
Página 432
A presbiopia é uma alteração na visão em que, assim como na hipermetropia, a imagem é projetada atrás da retina. Por isso, pessoas que apresentam presbiopia normalmente afastam os objetos a serem observados para enxergá-los com maior nitidez.
Em razão do envelhecimento, a lente do olho perde sua elasticidade, o que prejudica a capacidade de focalizar objetos próximos.
Essa alteração na visão é corrigida por meio do uso de lentes bifocais ou multifocais. No primeiro caso, os objetos distantes são observados através da parte superior da lente, enquanto os objetos próximos são vistos através da parte inferior. No caso das lentes multifocais, elas têm uma transição gradual, possibilitando a visão de objetos a curtas, médias ou longas distâncias.

A alteração na visão conhecida como astigmatismo é causada por irregularidades na córnea ou na lente do olho. Nesse caso, há uma alteração no formato da córnea ou na curvatura da lente, impedindo que os raios de luz sejam focalizados adequadamente na retina, causando a impressão de a imagem estar distorcida ou embaçada, como quando tentamos enxergar através de um vidro irregular, como o dos vitrôs de janelas.
A correção do astigmatismo é feita pelo uso de lentes cilíndricas, que têm superfície com maior curvatura em determinadas direções, como mostram as imagens.
Imagens desta página sem proporção e em cores fantasia.
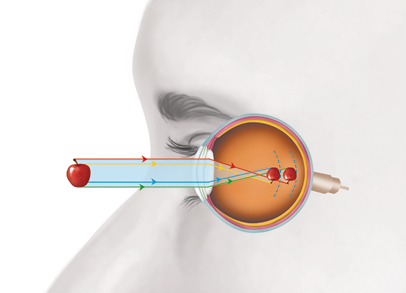
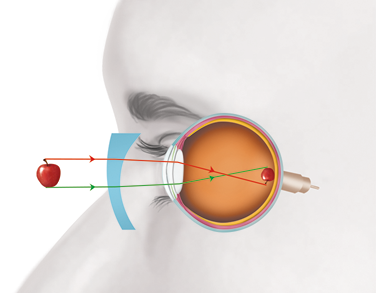
Imagens elaboradas com base em: TORTORA, Gerard J. Corpo humano: fundamentos de anatomia e fisiologia. 4. ed. Porto Alegre: Artmed, 2000. p. 272.
GREF (Grupo de Reelaboração do Ensino de Física). Física 2: física térmica/óptica. 5. ed. São Paulo: Edusp, 2007. p. 271-272.
O daltonismo, por sua vez, é uma alteração associada ao funcionamento das células do tipo cone, que são as especializadas na identificação das cores.
Existem ao todo três tipos de cones, cada um deles sendo mais sensível a uma cor: luz vermelha, luz verde e luz azul. As outras cores podem ser obtidas pela estimulação de mais de um tipo de cone simultaneamente.
Confira as figuras a seguir.

Você consegue identificar os números no interior de cada círculo? Pessoas com daltonismo não são capazes de enxergar essas informações, pois elas têm ausência de um dos três tipos de cone, isto é, são incapazes de diferenciar algumas cores.
Página 433
Há diversas formas de daltonismo. Cada tipo está relacionado ao problema de um respectivo cone. A protanopia, por exemplo, é a ausência dos cones sensíveis ao vermelho. Nesse caso, a pessoa enxerga os tons de vermelho de uma imagem em tons de bege. A deuteranopia, relacionada à ausência dos cones sensíveis ao verde, faz que a pessoa enxergue os tons de verde em tons de marrom. A tritanopia, relacionada à ausência dos cones sensíveis ao azul, faz a pessoa enxergar os diferentes tons de azul em tons rosados. Por fim, há ainda alguns casos raros, em que não se é capaz de distinguir cor alguma, enxergando apenas imagens em escalas de cinza.
O estrabismo é um problema de visão que ocorre quando os olhos não estão perfeitamente alinhados, isto é, apontam em diferentes direções.
O cérebro é responsável por controlar os músculos dos olhos, que devem estar equilibrados e trabalhando juntos. A pessoa com estrabismo tem alguma disfunção nesses músculos, que pode ser causada por dificuldade motora, grau elevado de hipermetropia, doenças neurológicas (causadas por traumas, AVC, paralisia cerebral etc.), problemas genéticos e infecções.
As imagens a seguir mostram os tipos de estrabismo (A, B, C e D) e uma pessoa com visão considerada normal (E).
Imagens desta página sem proporção e em cores fantasia.
A.
B.
C.
D.
E.
Imagens elaboradas com base em: AAPOS. Strabismus. Disponível em: https://s.livro.pro/npv0x7. Acesso em: 28 out. 2024.
Para a visão normal, o cérebro combina as imagens dos dois olhos, formando uma única imagem tridimensional. Desse modo, temos a percepção de altura, largura e profundidade (distância dos objetos). No entanto, quando um dos olhos não está alinhado ao outro, formam-se duas imagens diferentes.
No caso de uma criança estrábica, por exemplo, o cérebro ignora a imagem do olho não alinhado e, com isso, ela perde a percepção de profundidade. No entanto, no caso de estrabismo em adultos, eles têm uma visão dupla, como mostra a imagem. A posição da segunda imagem depende da direção em que o olho desalinhado está direcionado. Nesse caso, o cérebro considera a imagem formada em cada olho e já tem a percepção de profundidade dos objetos.
O tratamento do estrabismo é realizado por meio de diagnóstico e posterior correção do mecanismo que causa o problema no funcionamento dos respectivos músculos. Entre as medidas de tratamento, destacam-se o uso de óculos, exercícios para o fortalecimento dos músculos etc. Apenas em alguns casos é recomendada a realização de cirurgia, quando os outros métodos de tratamento não surtem o efeito desejado.
Página 434
ATIVIDADES
1. Explique por que as pessoas com idade mais avançada, quando leem livros ou revistas, seguram-nos em uma posição mais afastada dos olhos do que as pessoas mais jovens.
Resposta: As pessoas que colocam objetos em posição mais afastada dos olhos têm o problema de visão chamado presbiopia, causado pelo enrijecimento do músculo ocular, fazendo que o ponto próximo esteja mais afastado do olho do que normalmente deveria estar. Assim, ao afastar os objetos, instintivamente, estamos adequando-os em uma posição correta.
2. O olho humano tem o cristalino, que atua como lente convergente. As imagens produzidas por uma lente convergente são sempre de cabeça para baixo. Isso significa que as imagens que vemos estão de cabeça para baixo na retina? Justifique sua resposta.
Resposta: Sim, estão de cabeça para baixo, porém o cérebro é capaz de invertê-las e interpretar corretamente a posição real dos objetos.
3. Um experimento para demonstrar como a mistura de cores de luz pode produzir novas cores foi realizado em sala de aula, conforme as imagens a seguir.
Imagens desta página sem proporção e em cores fantasia.


Dois estudantes observam o experimento. Um tem visão considerada normal; o outro, daltonismo do tipo protanopia, caracterizado pela ausência de cones sensíveis ao vermelho. Em quais partes da imagem os dois estudantes observarão as mesmas cores?
a ) Nas partes magenta e azul.
b ) Nas partes amarela e verde.
c ) Nas partes azul e verde.
d ) Nas partes azul e amarela.
e ) Nas partes magenta e verde.
Resposta: Alternativa c.
4. Com relação ao uso de aparelhos eletrônicos com telas emissoras de luz, como televisores, computadores e aparelhos celulares, julgue as afirmações a seguir como verdadeiras ou falsas, justificando as falsas.
I ) A utilização de aparelhos eletrônicos com telas emissoras de luz por longos intervalos de tempo pode prejudicar a visão, pois eles fazem uso de luz azul potente, que por sua vez é a que tem a maior energia, considerando apenas a faixa do espectro eletromagnético que corresponde à luz visível.
II ) A utilização dos equipamentos eletrônicos é segura para a visão, desde que o tempo diário de uso não ultrapasse seis horas.
III ) Não se sabe ao certo quanto tempo de uso diário de equipamentos eletrônicos é seguro para a visão, contudo há práticas que ajudam a manter uma relação saudável com esse tipo de tecnologia, como habituar-se a piscar os olhos em uma frequência normal (em torno de 15 vezes por minuto), fazer pausas regulares etc.
IV ) Apesar de a utilização por longos períodos causar desconforto para a visão, a luz artificial emitida pelas telas dos aparelhos eletrônicos não apresenta riscos de danos à visão em longo prazo.
V ) Utilizar os eletrônicos à noite, pouco antes de dormir, não representa nenhum efeito sobre a qualidade do sono.
Respostas: I) Verdadeira; II) Falsa. Não existe um tempo de uso diário definido que seja considerado seguro para a visão; III) Verdadeira; IV) Falsa. Estudos sugerem que o excesso de luz azul emitida pelas telas dos equipamentos eletrônicos pode causar danos às células da retina. Isso pode tornar-se um fator de risco para a degeneração macular relacionada à idade, processo que causa a perda progressiva da visão; V) Falsa. A luz azul emitida por esses aparelhos interfere na produção de melatonina e, consequentemente, no sono.
5. Muitas pessoas têm problemas com a visão, que afetam a capacidade de enxergar, como miopia, hipermetropia e presbiopia, que podem ser corrigidos com lentes de óculos, de contato ou cirurgias. Em relação a essas alterações na visão, analise as afirmações a seguir.
I ) Pessoas com presbiopia costumam aproximar os objetos dos olhos para enxergá-los melhor.
II ) A miopia pode ser corrigida por meio de lentes convergentes.
III ) A hipermetropia é a dificuldade de ver com nitidez objetos próximos.
IV ) Na presbiopia e na hipermetropia, a imagem é projetada atrás da retina.
Estão corretas as afirmativas:
a ) Apenas I.
b ) Apenas I e II.
c ) Apenas III e IV.
d ) Apenas I, II e III.
e ) Apenas II, III e IV.
Resposta: Alternativa c.
Página 435
6. O cristalino é uma lente biconvexa, transparente e flexível, situada atrás da íris do olho humano. Sua função principal é:
a ) proteger o olho contra infecções e danos externos, funcionando como uma barreira.
b ) ajustar seu formato para focalizar a luz na retina, permitindo que os objetos a diferentes distâncias sejam vistos com nitidez.
c ) detectar a intensidade da luz e enviar sinais ao cérebro para ajustar a pupila.
d ) produzir o fluido aquoso que lubrifica e nutrir a parte frontal do olho, garantindo sua saúde.
e ) regular a quantidade de luz que entra no olho, atuando como um filtro de luz.
Resposta: Alternativa b.
7. Astrônomos amadores devem tomar certos cuidados ao realizarem observações solares, pois a grande maioria dos telescópios não tem filtros internos e necessita do encaixe de filtros solares na objetiva do telescópio, a fim de garantir a segurança do observador. Discuta o que aconteceria se um observador descuidado utilizasse um telescópio sem filtro solar, apontado diretamente para o Sol.
Resposta: Os estudantes devem comentar que utilizar o telescópio sem o filtro solar pode causar danos à retina, que podem ser temporários ou permanentes, podendo levar à cegueira. Isso porque o telescópio é formado por lentes e espelhos que focalizam a luz em uma pequena região.
8. Em relação aos danos causados à visão pela radiação ultravioleta, julgue as afirmações a seguir como verdadeiras ou falsas, justificando as falsas.
I ) Apesar de não ser capaz de atravessar toda a estrutura do olho e chegar à retina, a radiação ultravioleta pode danificar seriamente a visão, gerando uma série de danos em várias estruturas, como córnea, cristalino, conjuntiva etc.
II ) A radiação ultravioleta é basicamente absorvida pela atmosfera terrestre, não representando riscos à visão.
III ) O ultravioleta de mais baixa energia (UV-A) não apresenta riscos para a saúde dos olhos.
IV ) O UV-A, apesar de menos energia do que os outros tipos de radiação UV, penetra em parte do olho, depositando sua energia principalmente no cristalino, sendo capaz de produzir uma catarata. Já o UV-B pode produzir tanto a catarata quanto a opacidade da córnea.
Resposta: I) Verdadeira; II) Falsa. Apenas a radiação UV-C é absorvida totalmente na atmosfera. Tanto a radiação UV-B (pelo menos parte dela) quanto a UV-A chegam à superfície terrestre e requerem óculos com filtros de proteção para esse tipo de radiação; III) Falsa. Apesar de ter mais baixa energia, a radiação UV-A consegue penetrar em algumas estruturas dos olhos e pode causar danos à visão; IV) Verdadeira.
9. Julgue as afirmações a seguir como verdadeiras ou falsas, justificando as falsas.
I ) A miopia é um problema de visão em que a pessoa não consegue enxergar com nitidez objetos localizados distantes do observador. Sua correção é feita com a utilização de lentes divergentes.
II ) Daltonismo é uma alteração causada por problemas nas células do tipo bastonete presentes na retina. Esse tipo de célula é muito sensível à luz, sendo capaz de diferenciar as cores.
III ) O estrabismo se caracteriza pelo desalinhamento dos olhos. Quando ocorre na infância, a criança não desenvolve a capacidade de perceber a noção de profundidade. Quando em adultos, por causa de uma infecção, trauma etc., a pessoa observa duas imagens simultaneamente do mesmo objeto, cuja direção varia de acordo com a respectiva direção de desalinhamento do olho.
IV ) No astigmatismo, a pessoa não é capaz de focalizar bem as imagens na retina por conta de uma alteração em seu formato.
V ) A presbiopia é uma alteração causada pela perda de elasticidade da lente do olho, tornando-o incapaz de focalizar objetos próximos ao observador. Como a pessoa não perde a capacidade de enxergar nitidamente objetos distantes, são utilizados óculos com lentes bifocais ou multifocais, que permitem enxergar com clareza objetos em diferentes distâncias.
Resposta: I) Verdadeira; II) Falsa. As células sensíveis às cores e cuja deficiência causa o daltonismo são as do tipo cone; III) Verdadeira; IV) Falsa. O astigmatismo é causado por alteração no formato da córnea ou na curvatura do cristalino, provocando visão embaçada ou distorcida; V) Verdadeira.
RETOME O QUE ESTUDOU
Refletindo sobre o que estudou nesta unidade, responda às questões a seguir.
1. Escreva, em pedaços de papel, as transformações gasosas, diferenciando as expansões das compressões. Em seguida, entregue os papéis ao professor e, com os colegas, montem um quadro, identificando como a quantidade de calor, o trabalho e a energia interna do gás comportam-se em cada uma das transformações.
Atividade(s) adaptada(s) acessível(is)
1. Faça uma síntese explicando as transformações gasosas, diferenciando as expansões das compressões e identificando como a quantidade de calor, o trabalho e a energia interna do gás se comportam em cada uma das transformações.
Resposta: Espera-se que os estudantes comentem que nas expansões o gás realiza trabalho e nas compressões o meio externo realiza trabalho sobre o gás. Além disso, eles devem citar que, nas transformações em que a temperatura aumenta, a energia interna também aumenta; se a temperatura diminui, a energia interna também diminui. Caso eles tenham dificuldade em realizar a atividade, retome os conteúdos trabalhados nos capítulos 24 e 25.
2. Converse com um colega sobre quais são as condições necessárias para que uma máquina térmica tenha rendimento de 100%. Em seguida, compartilhem suas conclusões com a turma e digam se, com a tecnologia atual, seria viável manter o funcionamento dessa máquina.
3. Em um intervalo de dois minutos, escreva em um pedaço de papel características, propriedades e fenômenos das ondas sonoras. Na sequência, entregue o papel ao professor e, com os colegas, montem uma tabela descrevendo cada ponto que vocês citaram no papel e diferenciando as características do som e da luz.
Atividade(s) adaptada(s) acessível(is)
3. Faça uma lista contendo as características, as propriedades e os fenômenos relacionados às ondas sonoras, diferenciando-as da luz.
Resposta: Nesta atividade, os estudantes devem descrever as propriedades e os fenômenos referentes às ondas sonoras. Aproveite a oportunidade para avaliar o conhecimento deles, retomando partes do conteúdo, se necessário. Eles podem citar que as ondas sonoras são: mecânicas, longitudinais; caracterizadas por sua altura (frequência), seu timbre e sua intensidade (amplitude); e que podem sofrer refração, reflexão, difração, interferência e efeito Doppler. Verifique o que eles compreenderam de cada uma dessas características, incentivando-os a retomar o capítulo 26, quando necessário, a fim de confrontar suas argumentações com os conteúdos estudados.
4. Junte-se a um colega e escrevam um panfleto sobre os problemas causados pela luz das telas de equipamentos eletrônicos e pela luz solar, destacando os cuidados necessários para manter a saúde dos olhos. Em seguida, distribuam os panfletos para os colegas da escola.
Respostas nas Orientações para o professor.
Página 436
MAIS QUESTÕES
1. (UFAM) Certa quantidade de gás ideal passa do estado A para o estado D, através dos processos indicados no diagrama p menos V, a seguir:
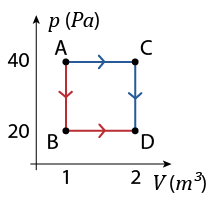
Considere as seguintes afirmativas:
I ) A isoterma que passa pelo estado A também passa pelo estado D.
II ) A quantidade de calor trocada pelo gás é menor no percurso A C D que no percurso A B D.
III ) O trabalho realizado pelo gás no percurso A C D é maior que o trabalho realizado no percurso A B D.
IV ) A temperatura do gás no estado C é quatro vezes maior que sua temperatura no estado B.
Assinale a alternativa CORRETA:
a ) Somente as afirmativas I, II e III são verdadeiras.
b ) Somente as afirmativas I e III são verdadeiras.
c ) Somente as afirmativas I, III e IV são verdadeiras.
d ) Somente as afirmativas II e IV são verdadeiras.
e ) Somente as afirmativas III e IV são verdadeiras.
Resposta: Alternativa c.
2. (Unesp) Em uma brincadeira, uma pessoa coloca um copo com a boca para baixo, encostada na superfície parada da água de uma piscina e, cuidadosamente, o afunda 2 vírgula 5 metros abaixo da superfície da água, onde mantém o copo em repouso, ainda de boca para baixo, com um pouco de ar aprisionado em seu interior e com um pouco de água que entrou no copo. A figura mostra o copo nessas duas posições.
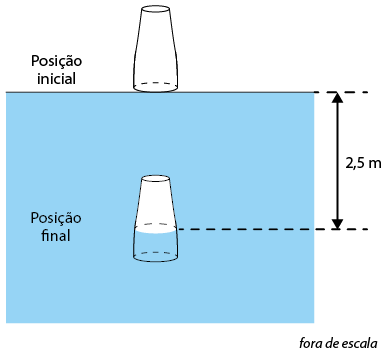
Considere o ar um gás ideal e os valores 10 elevado ao cubo início de fração, numerador: quilograma, denominador: metro cúbico, fim de fração para a densidade da água da piscina, 10 elevado a 5 pascal para a pressão atmosférica local e 10 início de fração, numerador: m, denominador: s elevado ao quadrado, fim de fração para a aceleração da gravidade. Sendo V subscrito 1 o volume ocupado pelo ar no copo na posição inicial, V subscrito 2 o volume ocupado pelo ar no copo na posição final, e considerando a temperatura do ar dentro do copo constante nesse processo, o valor da razão início de fração, numerador: V subscrito 2, denominador: V subscrito 1, fim de fração é
a ) 0,50.
b ) 0,80.
c ) 0,75.
d ) 0,25.
e ) 0,40.
Resposta: Alternativa b.
3. (UFPR) Uma certa massa de gás ideal está num estado termodinâmico em que a pressão vale P subscrito 0, o volume vale V subscrito 0, e a temperatura vale T subscrito 0. Essa massa de gás sofre um processo termodinâmico, e o volume passa a ser V, a pressão passa a ser P, e a temperatura passa a ser T. Sabe-se que P é igual a 4 P subscrito 0 e T é igual a 2 T subscrito 0. Considerando as informações apresentadas, assinale a alternativa que apresenta corretamente o valor do volume V em função do volume V subscrito 0.
a ) V é igual a V subscrito 0
b ) V é igual a início de fração, numerador: V subscrito 0, denominador: 4, fim de fração
c ) V é igual a 4 V subscrito 0
e ) V é igual a 2 V subscrito 0
e ) V é igual a início de fração, numerador: V subscrito 0, denominador: 2, fim de fração
Resposta: Alternativa e.
4. (UECE) A termodinâmica é um importante ramo da física que estuda, dentre outros assuntos, as trocas de calor. Como exemplo desses processos, é possível citar uma roupa secando no varal ou, mesmo, o aquecimento de água para fazer um café. Sobre os conceitos relacionados à termodinâmica, é correto afirmar que
a ) os processos reversíveis são necessariamente quase estáticos.
b ) em uma transformação isotérmica, a variação da energia interna é diferente de zero.
c ) quando um gás se expande, pode-se dizer que o trabalho foi realizado pelo meio.
d ) em uma mesma transformação adiabática, é possível um gás se expandir e aumentar sua temperatura.
Resposta: Alternativa a.
5. (UPF-RS) Um gás ideal inicialmente à temperatura de 27 graus Celsius e volume de 0 vírgula 0 2 metro cúbico é submetido a uma transformação isobárica, elevando seu volume para 0 vírgula 0 6 metro cúbico. Nessas condições, é possível afirmar que sua temperatura final é, em grau Celsius, de:
a ) 627
b ) 81
c ) 900
d ) 1173
e ) 300
Resposta: Alternativa a.
Página 437
6. (UFSC) O ciclo de Carnot é um modelo teórico idealizado que serve como referência para processos termodinâmicos reversíveis, ou seja, processos que podem ser revertidos sem qualquer aumento na entropia do sistema ou do ambiente. Esse ciclo foi formulado em 1824 por Sadi Carnot e é composto por quatro etapas – duas isotérmicas e duas adiabáticas –, conforme ilustrado abaixo.
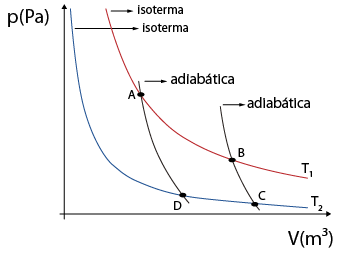
De acordo com o exposto, é correto afirmar que:
01 . na primeira etapa isotérmica A implica em B, o sistema realiza trabalho enquanto absorve uma quantidade Q subscrito 1 de calor de uma fonte térmica à temperatura T subscrito 1. Nesse estágio, a expansão ocorre de forma tão lenta que o gás permanece em equilíbrio térmico com a fonte de calor.
02 . na etapa B implica em C, o sistema passa por uma expansão adiabática. Aqui, ele continua a se expandir e realizar o trabalho, mas sem trocar calor com o ambiente. O gás se contrai até que sua temperatura atinja T subscrito 2, que é menor que T subscrito 1.
04 . na etapa D implica em A, o sistema passa por uma compressão adiabática até retornar ao seu estado inicial. Durante esse processo, o sistema realiza trabalho sobre o ambiente, mas há troca de calor.
08 . o rendimento é expresso em termos de temperaturas absolutas T subscrito 1 e T subscrito 2 das fontes quentes e frias, respectivamente.
16 . independentemente do sentido do ciclo de Carnot, A implica em B implica em C implica em D implica em A ou A implica em D implica em C implica em B implica em A sempre representará uma máquina térmica quente.
32 . a etapa C implica em D é uma compressão isotérmica durante a qual o sistema cede calor Q subscrito 2 para uma fonte fria à temperatura T subscrito 2. O gás é comprimido lentamente, em equilíbrio térmico com a fonte fria.
Resposta: Soma: 01 mais 0 8 mais 32 é igual a 41
7. (UECE) É comum se ouvir o comentário de que um carro com motor turbo é mais potente. Em termos simplificados, um motor de carro tem uma câmara que recebe ar e combustível, passando essa mistura por um processo de combustão (queima) muito rápido. No motor turbo, se comparado a um motor regular, consegue-se injetar mais ar, o que permite a injeção de mais combustível e assim uma maior potência. O ar injetado passa por um processo de compressão em um dispositivo chamado turbina. Caso essa compressão ocorra sem transferência de calor, o ar, após passar pela turbina, tem sua temperatura
a ) elevada e sua pressão aumentada.
b ) elevada e sua pressão reduzida.
c ) reduzida e sua pressão aumentada.
d ) reduzida e sua pressão diminuída.
Resposta: Alternativa a.
8. (Epcar-MG) Um cilindro, contendo certa massa de gás perfeito, tem um pistão que está ligado a uma mola ideal. Ao fornecer certa quantidade de calor Q, para esse sistema termodinâmico, observa- -se uma expansão do gás com a consequente deformação da mola delta x, conforme indica figura a seguir.
Em outro momento, para as mesmas condições iniciais anteriores, ao se fornecer o dobro da quantidade de calor 2 Q, a esse sistema, observa-se que a mola sofre uma deformação duas vezes maior, 2 delta x. Considerando que nas duas expansões o sistema tenha sofrido a mesma variação de energia interna e que não houve atrito entre o pistão e o cilindro, pode-se afirmar que a constante elástica da mola vale
a ) início de fração, numerador: 2 Q, denominador: delta x, fim de fração
b ) início de fração, numerador: 3 Q, denominador: delta x elevado ao quadrado, fim de fração
c ) início de fração, numerador: 2 Q, denominador: 3 delta x elevado ao quadrado, fim de fração
d ) início de fração, numerador: 4 Q, denominador: delta x, fim de fração
Resposta: Alternativa c.
Página 438
9. (Epcar-MG) A figura a seguir representa trocas de calor e realização de trabalho em uma máquina térmica. Nela estão indicados os valores da temperatura T subscrito 1 e da quantidade de calor cedido Q subscrito 1, relativos à fonte quente, e do trabalho τ realizado por essa máquina. Além disso, tem-se que T subscrito 2 e Q subscrito 2 correspondem, respectivamente, à temperatura e à quantidade de calor rejeitada para a fonte fria
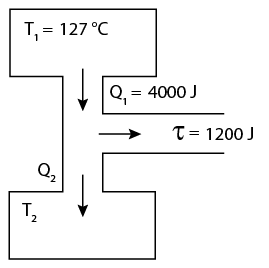
Seu rendimento corresponde a 75% do rendimento da máquina de Carnot, em regime de funcionamento entre as temperaturas T subscrito 1 e T subscrito 2. Nessas condições, a temperatura T subscrito 2, da fonte fria, é, em kelvin,
a ) 100
b ) 240
c ) 513
d ) 613
Resposta: Alternativa b.
10. (UEA-AM) Um guarda salva-vidas faz o seguinte trajeto com um jet-ski: primeiramente, ele sai da beira da praia em direção ao mar e depois volta pelo mesmo caminho que fez anteriormente. Tanto na ida quanto na volta, o jet-ski manteve a mesma velocidade constante em relação à areia da praia e a direção de seu movimento foi sempre perpendicular às ondas. O guarda salva-vidas nota que, durante o caminho de ida, a frequência com que o jet-ski atravessa as ondas é maior do que na volta, porém, em relação à praia, as ondas continuam com a mesma periodicidade. O efeito ondulatório que melhor explica essa constatação do salva-vidas é o efeito
a ) de difração.
b ) de absorção.
c ) Doppler.
d ) de dispersão.
e ) de reflexão.
Resposta: Alternativa c.
11. (UEA-AM) O som é uma onda ■ e por isso, só pode se propagar em meios materiais, como ■.
As lacunas do texto são preenchidas, respectivamente, por:
a ) eletromagnética — a água.
b ) mecânica — o vácuo.
c ) eletromagnética — o ar.
d ) eletromagnética — o vácuo.
e ) mecânica — o ar.
Resposta: Alternativa e.
12. (FCMSCSP) Nas transmissões de corridas automobilísticas, é perceptível que a frequência do som emitido pelo motor de um automóvel, captado por um microfone estático quando o automóvel dele se aproxima, é diferente da frequência quando ele se afasta. A frequência do som captado quando o automóvel se aproxima e a frequência do som captado quando se afasta, em relação à frequência do som emitido pelo motor, são, respectivamente,
a ) igual e maior.
b ) igual e menor.
c ) maior e menor.
d ) menor e igual.
e ) menor e maior.
Resposta: Alternativa c.
13. (UFSC) Os excertos abaixo foram retirados dos livros Torto arado e A alma encantadora das ruas. Neles, podemos observar menções a ondas sonoras.
Ela gritava para meu pai, que colhia com as mãos trêmulas ervas nos canteiros próximos à casa, impaciente, transmitindo seu desespero na voz, que se tornou mais aguda, além do olhar espantado. (Torto arado)
A voz estava tão fraca que só eu pude escutar o que dizia. (Torto arado)
[...] encheram-se de canções, de vozes de violão e de guitarra e, de novo, pelas ruas os realejos, os violinos, as gaitas, recomeçaram o seu triunfo. (A alma encantadora das ruas)
Ao lado da máquina, na aglomeração, uma voz de mulher fez de repente: [...]. (A alma encantadora das ruas)
Considerando o exposto, é correto afirmar que:
01 . as características da voz "aguda" e "fraca" correspondem, fisicamente, à mesma propriedade do som.
02 . o violão, a guitarra, o violino e a gaita são instrumentos de cordas.
04 . a frequência do som de uma das cordas de um violão depende do comprimento da corda.
08 . o som agudo refere-se à altura do som e diz respeito à amplitude sonora.
16 . em uma mesma sala, um som fraco e um forte têm a mesma velocidade.
32 . os instrumentos de cordas produzem ondas estacionárias, que são criadas por causa dos fenômenos de reflexão e interferência.
Resposta: Soma: 04 mais 16 mais 32 é igual a 52